79 trang 13 lượt tải

Đề cương đại số tuyến tính

25

Đề cương đại số tuyến tính 

Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 1.6 K tài liệu

Tác giả:

Profile

Mơ Nguyễn

1 năm trước
Tải xuống Chia sẻ Báo cáo
Danh sách Quiz
Tải xuống
/79
lOMoARcPSD|27790909

 !"#$%"&!'())*+,#)"$
+-)./,)0)%12345).67)897)'"')%":67;)
<)=>=)?).7) <@A)B
<#$%#?3;C2DC"&,5E
F <@A)GH%,I='"J).
F ,)1K+$+%72*+).67G2/02
F ,)1K+$+%7/LMG2*+)"$/,)0)%1
N4)N).67)O)"4P))&).67+Q+)#4)N)1!R)%R)41).
)%S,R)41).R),TU#UE/%+B%+VC+W)37)XCDHY
C+%O,+Z))4!#$%;R):)N+,))@8)[14)1<) !\
$)4!+8!%)67))5]1,#N<)%))94())"&
, # ) "$B ^. 4 47 # 4 )N _ )% )4! O1 , P1 )` U!1E
1U)+%7a!1B%!
^bCDc0d2C2eCfgChi2DC
j kU#UE)l7Emm1U)B%!m
j n1U#%%RE)l7EmmTTTBo1U#%%RB%!m1U)
j p%+=E)l7Emm=%+=B%!m"Um0R)kqpr7O
j CUU+1!E)l7EmmB!Umstu<g7vUTwTxCxy
j x%#UE)l7EmmTTTB<%#UB%!m)1Um<zMC<vn{wy)RMr|H=T
C)1K!>7)(TU#UC1U)B%! u
Downloaded by M? M? (nguyenmo081102@gmail.com)
  ^yyzyj )4!)y
lOMoARcPSD|27790909
 ^yyzyj)4!)y
C )1K!>7)(TU#U C1U)B% ! q
lOMoARcPSD|27790909
^}}
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB u
^}}BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB q
~•€•‚DcCxƒC„22^h2yBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBz
2€•BC…|2†|GLG‡2ˆ‚jDc|2‰BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBz
2€•B^gCM…GŠ2C2‰G2i|2€•CM‹2BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBByt
2€•B02egHŒCLMBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBqq
2€•HB‡2ˆ‚CxƒC„2BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB z•
2€•HBp‚DLCxƒC„29p‚CLh|2€•902egŒpŒ9€^ŽC
/…2gBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB •u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
~•€•‚DcCxƒC„22^h2y
2€•BC…|2†|GLG‡2ˆ‚jDc|2‰
/yE67#,+P)••]1,#N)I!)1
1Y ‘gFV/FY’F
#Y ‘gFV/FY’F/
-
1B C14#,+P)••
g / 
V/FY gFV/FY ‘gFV/FY’F
“ “ “ “ “ y
“ “ y y “ y
“ y “ y “ y
“ y y y “ y
y “ “ “ “ y
y “ y y y y
y y “ y y “
y y y y y y
#B C14#,+P)••
g / 
g
/F
gFV/FY
‘gFV/FY’F/
“ “ “ y “ “ “
“ “ y y y y “
“ y “ y y y y
“ y y y y y y
y “ “ “ “ “ “
y “ y “ y “ “
y y “ “ y “ “
y y y “ y “ “
/uBV0u“y”uY)%79O,!)B21!)V7FOYFO"7OF4%R):•
HZ1%•
-
C14#,+P)••
7 O
7 O
V7FOYFO
7O
“ “ y “ “
“ y y y y
y “ “ y y
y y y y y
F F
C)1K!>7)(TU#UC1U)B%! z
 ^yyzyj)4!)y
lOMoARcPSD|27790909
C–#,+P)••14)NR@6)1!)+$%B
/qB)I!)+—E
1Y gF/"VgFFF/Y Vg/Y%B
#Y VgF/YF"gFV/FYR):%B
Y gF/"gF/%B
-
1BC14#,+P)••
g /
g / VgF/Y gF/
gF/
VgFFF/Y Vg/Y
“ “ y y “ y y y
“ y y “ “ “ “ “
y “ “ y “ “ “ “
y y “ “ y “ y y
H6<)1!)+$%#B
_g˜/˜˜“B0)4
gF/˜y™VgF/YF˜“
/F˜y™gFV/FY˜y
H6<$)1!)+$R):%BBC1
4#,+P)••
g /
g
gF/
gF/
g F/
“ “ y y “ “
“ y y “ y y
y “ “ “ y y
y y “ y “ “
H6<)1!)+$%B
/zV0u“ytyYB)%,!)g9/")š1!›VgFYFV/FY"VgFYFV/FY
,!)œB)I!)+—gF/!)œB
-
C14EVgFYFV/FY"VgFYFV/FY,!)œBVyY
_gF/!)1)ZR):!8A)•O,14EgFy"/F“
F“FgFFy"/FF“FVgFYFV/FY1VuY
FyFgFFy"/FF“FVgFYFV/FY1VqY
C–VyY9VuY"VqY1)8<+—_+$1$gF/!)œB
 ^yyzyj)4!)y
lOMoARcPSD|27790909
/”B)%!)%ž@u“u“K)Z4)1)@)%qžB2š!)œ)1<1•
)()•
-
p%u“u“)Ÿ$u“u“K!)1V,+P)••#—“Y
u“u“)1)@)%q!)1V,+P)••#—“Y
^!)%@u“u“K)Z4)1)@)%q!3!)R %)U%$•<!3!)
œB
/•B)%)!o¡,P)+$FB2!o,)4)N¡,P)#?!)EžH&!.¡
y
9
¡
u
)367M9@
o¡
F
y
FF
o¡
F
u
F)Z¡
y
F¡
u
žB2›<=¢,R()N=>!)+$"!)
7)]P)]14BC–41+1,))I!)!3)!R):7),)B
-
^)#1 EžF¡¡
yu
9 FF9
o¡
FF
y
F
o¡
F
u
FF¡
y
F¡
u
ž
^)7)]P)EžF¡¡
yu
9 FF9
o¡
FF
y
F
o¡
F
u
FF¡
y
F¡
u
ž
)"6<N)I!)y)!R):,)1)` )`+1F¡¡
yu
9!¡
y
F¡
u
"o¡FF
y
Fo¡F
u
FB
/tB_oV¡Y9V¡Y,)!¡,P)+$FB0(),67)71E
gF£¡FF∣oV¡YF“¤9/F£¡FF∣V¡YF“¤B/N=>67) !7)+Z)1O1)167)7ę g9/E
1Y o¡¡VYBVYF“
#Y ‘VY’o¡
u
F‘VY’¡
u
F“
-
Fo¡VYF“
1B o¡¡VYBVYF“FF¡VYF“
F
FC67)!FgF/
#B ‘VY’o¡
u
F‘VY’¡
u
FF“ o¡VYF¡VYF“
FC67)!pFFg /
/¥V0u“yzyYB)%,67)7gF‘q™•Y9/FVy™”Y9F‘u™z’Bˆ,P)67)7VgF/Y¦B
-
gF‘q™•Y™/FVy™”Y™F‘u™z’
C)1K!>7)(TU#UC1U)B%! •
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FgF/F‘q™”YFVgF/Y¦FVz™”Y
/rB)%g9/99p,67)7#8RZ9)I!)E
1Y gFV/¦ YFVgF/Y¦VgFYB
#Y gFV/¦gYFgF/B
Y Vg/¦YFV¦pYFVgFY¦V/FpYV0u“y”yY
-
1B gFV/¦YFFFgV/YFFFg/
FVgF/Y¦VgFYFgF/FgF
FgF/FVgFYFVgF/FgYFVgF/FY
FgF/F V=%gFgFFY
H6<gFV/¦ YFVgF/Y¦VgFYB
#B gFV/g¦YFFFgV/ gYFVg/FFFYVggYFFg /B
H6<gFV/¦gYFgF/B
B Vg/¦YFVp¦ YFFFFg/ p
VgFY¦V/FFFFFpY g / pFFFgV/FpYF
g
F
/
F

F
pB
H6<Vg/¦ YFV¦pYFVgFY¦V/FpYB
/y“B)%)1,)¡
oEF¦£“¤FF EFFF
¡F y ™ ¡F u¡u¡ yF¡
1B ‡)¡%,)9%,)9CZ!VFY
#B ˆ,P),)¡)˜Fo
-
1Yso¡FF
y
Fo¡F
u
FF
y
F
y
F¡
y
F¡
u
FF¡¡
yu
9 FF¦£“¤F ¡y
¡u
Fo,)B
 ^yyzyj)4!)y
lOMoARcPSD|27790909
p%F¡FF¦£“¤No¡VYF
y
F“FFFoR):%,)B¡
F¡FFyF¡FuFFyuF¡¡
y
uF
y
u
F
¡
¡
u
uu
y
^ VqYFu¡Fq¡
u
FFq q¡
u
Fu¡FFq“V":)!Y$
¡VY
R):
%,)B
F
F
Fy
u
F
F
F
FVuYF
”
z
$¡VYR):,)B
sCZ!MV Y
C14E¡
u
uF¡yF¡
§u§
u
F
¡
yFu
§u§
§
¡
¡§FyV1)<Y
HF1FF‘y™y’E7)+Z)u¡F1¡F
u
FyF
4)!)W
FFFzFz1
u
F“F$MV YFF‘y™y’B
#BFoFo¡V VYYFuFy
¡
F uu¡
yFyu ¡
Fy¡
/yyB)I!),A))8]1)")P))]1,)¡oEˆFx
1Y ogV F/YFogV YFo/V Y™g/9 FˆB
#Y oVgF/YFoVgYFoV/Y™g9/FˆB$"(=')IšR):œB
Y o
Fy
Vg/FYFo
Fy
VYgFo
Fy
VY/g/x™9F
=Y oVg
Fy
F/YFoVgY
Fy
FoV/Y™g9/
Fy
Fx
UY o
Fy
Vg/¦YFo
Fy
VYg¦o
Fy
VY/g/™9Fx
-
1Y F<FogV F/Y9o¡VYF<)Z¡FgF/
F¡Fg F<FogV Y VyY
C)1K!>7)(TU#UC1U)B%! ¥
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FF¡F/FFF<Fo/V YF<FogV YFo/V YFogV F/YFogV YFo/V Y
F
FogV YFogV F/Y9o/V YFogV F/Y
FogV YFo/V YFogV F/YVuY
C–VyY"VuYFogV YFo/V YFogV F/YFg/9 FˆB
#Y sC14gF/FgFogVF/YFogV Y
CWogV F/YFo/V Y
p%4ogV F/YFogV YFo/V Y
sH(='R):œˆ o
¡VYF¡g
u
9F£u¤9/FF£u¤
0)4ogV F/YFF™ogV YFo/V YF£z¤B
Y ¡Fo
Fy
VgF/YFo¡VYFgF/FFFFFo¡o¡VYVYFF/gFFFF¡¡FF¨F
Fy
y
VV/gYY
FF¡ o
Fy
VYgFo
Fy
VY/9Fg/9FxB
=Y ¡Fo
Fy
VgF/YFo¡VYFgF/FFFFFFo¡o¡VYVYFF/gFFFF¡¡FF¨FFyyVV/gYYFF¡ oFyVYgFo
FyVYB/
UY ¡Fo
Fy
Vg/¦ YFo¡VYFg/¦ FFFFFFo¡o¡VYVYFgFFF¡FoFFyyVV/gYYFF¡ oFyVYgo¦FyVY/
F/ F¡Fo
/yuB)%,)¡oEFFF ¡,P)#?o¡VYF¡
u
Fz¡FFF”9¡F9"gF£¡FF∣FqF¡Fq¤B
ˆ,P),67)7oVgY"oVgY
Fy
B
-
 ^yyzyj)4!)y
lOMoARcPSD|27790909
/yqV0u“y•yYB)%,)¡oEF
u
FF
u
¡,P)#&o¡<V9 YFV¡F<¡9 F<Y"67gFFV¡
<9YFF
u
∣¡
u
F<
u
FrFBˆ,P),67)7ogV Y"o
Fy
VYgB
-
C1¡ V¡<™ YFgFo¡<V™ YFV¡F<¡™ F<Y
H1V¡F<Y
u
FV¡F<Y
u
FuF¡
u
F<
u
FFy¥
^SR),9@uF"uFy¥)ZFFFFu"FFFuFFFFFu"FFFuFr
FogVYFFV¡<™YFF
u
§§¡
u
F<
u
Fy¥F
ˆ o"V™YFVF"™ F"YFg
FFV"Y
u
FFV"Y
u
FFFFr
u
"
u
z9”
H
u
F"
u
Fz9”)Zo"V™YFg
p%"6<$o
Fy
VYgFFV¡<™YFF
u
∣¡
u
F<
u
Fz9”FB
/yzV0u“ytyYB)%,)¡oEF
u
FF
u
9¡,P)#?o¡<V™YFF¡
u
F<¡™ F<FB‡)¡o4,)9
%,)R):•HZ1%•
-
C)1K!>7)(TU#UC1U)B%! y“
u
VY “uVY” uz VY9z¡o¡ ¡¡¡ o¡ o¡
F F
FFFFFFFF FF
j
u
q z “ uuq¥VY ¡o¡ ¡ ¡
FFFFFFFFF
j
u
q “ u •z uVY ¡¡o¡ ¡
FFFFFFFFFF
B
)Z"%##@)$
y
‘u‘uuq™uVY •’ •™uuq’o g
F
FFF FFFFFFFF B
 ^yyzyj)4!)y
lOMoARcPSD|27790909
ˆ o¡<Fyy™FFo¡<Fu™uFFFFFFF¡¡yuFF<<yFF¡¡uuFF<<uFFFF¡¡yuFF<¡yyFF¡¡uuuFF<¡uu
y y u u y
C14)N)8<oV“™FyYFoVyF™“YFVy™FyYFoR):,)B
/y”B)%67F
z
F£“™y™u™q¤+1#P6)7)))1E"&1#9FF
z
141©#F
V1F#Y!%=zB
1Y )I!)+—©!37) 7%,4+$F
z
B
#Y 2šFF
z
©
F47)!3)4!R):•
-
1Y C14F1#9Fª
z
)ZV1#FY!%=z£y™u™q™F “¤Fª
z
F©!37) 7%,4+$ª
z
B
#Y FF
z
9©
F!3)4!"ZE
sC()R@)7EV©Y1#FF‘V1F#Y!%=zF’!%=zFV1F#FY!%=zF1©V©Y#
sC()E47) _+)X1“E©“1 F“©11F FF1ª
z
sFF1ª
z
47) _¡IEy©qFu©zF“B
/y•B)%FFo9o9o9o9o9o
yuqz”•
F67,,)¡–F¦£“™y¤FF¦£“™y¤¡,P))1E
o¡
y
VYF¡o™
u
V¡YF
y
™o
q
V¡YFyF
y
™o
z
VY¡F
y
™o
”
V¡YFyF¡o™
•
V¡YF
¡
B
yF¡ ¡ ¡ ¡Fy1BC()o
y
Fo
u
#B67#N#N=>,+Po
y
Fo
u
"&!.«9FyBB•B
Y)I!)¢"&7) 7%,7) 7A),)¡67))!3)4!R):g#UB
-
1Yo
y
Fo
u
Fo
y
Fo
u
VY¡FF
y
yF
¡
#Y
F
o
y
o
u
o
q
o
z
o
”
o
•
 ^yyzyj)4!)y
lOMoARcPSD|27790909
o
y
o
y
o
u
o
q
o
z
o
”
o
•
o
u
o
u
o
q
o
y
o
•
o
z
o
”
o
q
o
q
o
y
o
u
o
”
o
•
o
z
o
z
o
z
o
”
o
•
o
y
o
u
o
q
o
”
o
”
o
•
o
z
o
q
o
y
o
u
o
•
o
•
o
z
o
”
o
u
o
q
o
y
Yp%V9YF7) 7%,4
s|) 7)74A))8R@)7
s|) _+)X1Eo
y
s|) _¡IEo
y
Fo
y
Fo
u
Fo
q
Fo
z
Fo
z
Fo
”
Fo
”
Fo
•
Fo
y
Fo
y
^o
z
Fo
u
Fo
”
Fo
•
Fo
u
Fo
z
FV9YF!3)4!R):g#UB
/ytB$+Q,671"&,7) 7%,3")•):)-467))!3")9+-
R):•
1Y C67,<$KB
#Y C67,<$)ŸB
Y C67,)[`B
=Y ˆFF£1 #u∣1#9FF¤B
UY xFF£1#q∣1#9FF¤
-
1Y 0):")9+-V"Z7) 7%1sR):4R(Y
yuFªFFF
#Y ")9R):+-VV9YFYR):)4!9)¬)
Y +-
=Y ")9R):+-VV9YFYR):)4!9)¬)
y
F
q
F
u
Fˆ
qF u ” ”
F y 1#F q 1 # F
Y+-FFF1#F qF1uFq#uF1uFq#uF1uFq#u qFx9FV1#™YFV“™“YFFFB
C)1K!>7)(TU#UC1U)B%! yu
 ^yyzyj)4!)y
lOMoARcPSD|27790909
/y¥B/N=>,7)I1=&)()-E1Y
VyFqY
r
VyFY
uy
#Y
yq
VyFY
Y VuyuYVqyYF
”
F
yy
B
-
1Y VyFqY
r
F
F
FuF
F
FF%
F
qF
F
q
F
FFF
F
F
r
FFu
r
F
F F
%
F
F
F
F
F
F
uy
Fy F
#Y VyFYyquyF FF uFF z zFFFyqFuzF uFF u
y
F
uzB
VyFY FFFuFF%FFFFFFFFF FyuFF yu
F z zFF
Y VuFyuYVq
”
FY
yy
F
F
Fz
F
FF%
F
qF
F
q
F
FF
F
FF
”
F
F
F
F
u
F
FF%
F
•
F
F
F
•
F
F
FF
F
F
F
yy
F
Fu
uy
FFFFF
y
uFF
F
u
qFF
FFFFFFF u
q
FF
y
u
F
FFFFuVuq
yr
FuY
/yrBCZ!,®#6¥]17)IE{yqFFB
-
{FFyqFu
F
F
F%
F
q
F
F
F
q
F
F
F
FF,®#6¥]1
{
E
 ^yyzyj)4!)y
lOMoARcPSD|27790909
q
uB%FF FFFuRFFFFuRFFF
F q Fq F9RF“9tB
F ¥ ¥ F
F F
/u“BCZ!)!7)I]17)+Z)1E
1Y{
u
F{FyF“ #Y{
u
Fu{F”F“ Y{
z
Fq{
u
FzF“
=Y{
•
Ft{
q
F¥F“ UY{
t
F
y“uz
q
 oY{
¥
VqF
FFYy{
Y{
u
FFVy¥Y{FFtytF“V0u“ytyY
-
1Y {
u
F{FyF“F
F
F
{
q
Fy
F{F%
uR
F
F
uR
F
™RFy™u
F{Fy q q
#Y {
u
Fu{FFFF”“ V{Y
u
FFFFFz { u
Y {
z
Fq{
u
FzF“BS{
u
FF
u
FqFzF“
F F F
FF
F
FF
q
u
F
F
FuFF
F
F
”
u
F
F
FuFFFF

FFFz

FFFFF{
{
uuFFz
FFFFF
{
{FFFFVuFFFy
u
FF
9
uYy
u
FFF
F F
• q q u FF¥ F{Fu
=Y {Ft{F¥F“BS{FFFtF¥F“FFFyFFF{FFy
F
UY {
t
F
y“uz
q
F{
t
F{
q
Fy“uzF§{§
y“
Fy“uzF§{§Fu
{
F{F§{{§uFz{FzttFy“uzq F{zFuzF{FuFF%uRzFFuRzFFFF9RF“
9q{ { F
oY {
¥
VqFFFYy
C)1K!>7)(TU#UC1U)B%! yz
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F F
F
F
F
F{¥Fy
F
F
q
F uuFF
F
FF%%qzFFqzFFF
F
FFyF%Ft
F
F
Ft
F
FF
FF
F uFF yu yuF
y
F
F
F
yu
tFFuRFFF
yu
tFFuRFFFF9RF“9t
FF{ F%
F
¥
F
F F
Y {
u
FFVy¥Y{FFtytF“
FFF{
u
V¥Y{FVyttYFF“
FFFF{FFu¥FFFuFtFytF •qzFzFqF ”zFFFFyF quFFFuFFFF{{FFq”FFu
/uyBV0u“yzyYB)%FF
yu
99F9F
u“yz
,®#6u“yz7)•#7)I]1"PyBC()
u“yz
gFFF
u
B
Fy
-
u“yz
FF
yu
9 9FB9F
u“yz
u“yz®#6]1u“yz]1yBg
F
FF
R
u
B
RFy
C14F
R
F%
uR
F
F
uR
F
9RF“9u“yq
Vw<&F
u“yz
FF
“
Y
u“yz u“yz
FgFu“yzFRFyFFF%y““tuRFFy““tuRFFFF
FuFy““tFR
Fy
FFF%uRFFuRFFFFFFF=%uVRy““tFy““tYFFuFFy““tuRFFFF
y““t y““t
y““t
y•
¥
u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FFuFF
R
RFy y““t
H&F
R
9RFy9y““t,®#6y““t]1yB^F
R
y““t
Fy$)U%HUUEFF
R
F“FgF“B
RFy
V¡FFyY
r
y
/uuB)%7)+Z) F“B¡
1Y CZ!,)!]17)+Z)+$B
#Y C()!:]1,) !Bę
¥ RF
Y C()A)]1,)!–4A)F B
RF
y
r
-
1Y ¡
R
FFFy %
uR
F
F
uR
F
9RFy9¥VS¡FzFY
r r
#Y ¡RF FFFyF%uRrFFFFuFFFFuRrFFFFuFuRrF
Y FF¥RFFR ¡RFy¥F¥¡R
RFy r RFyu u RFy
^¡RR9 Fy 9¥)!]1V¡FyYrFyF“FFrrF¡FyF“$)U%HUUFF¥¡RFr
¡ Fy RFy
¥
RFr
FFrF u
¥
RFy
/uqV0u“y•yYB)%,)¡oEFFF9VYo{F{
u
FFVz{YFr"&"P%Bˆ,P)o
Fy
V£t¤Y
-
C14E{
u
FFVz{YFFrt
F{
u
FFVyzY{FVtFFrY “
C)1K!>7)(TU#UC1U)B%! y•
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FFFF{FyFuzFFFuFrFtFuFy”zFuyzF”FFFFF ”uFFFu
F{FFFuq
Fy
F£t¤YFF£uFq™qF¤
FF{FqF Fo
F
/uzV0u“ytyYB)%{{
yu
9 )1)!7)I]17)+Z){
u
F{F1F“9"&1!3)W
""P%BCZ!1#@{
y
u
F{
u
u
FyB
-
{
u
FFFFFF{1 “ {
y
u
{
y
1{™
u
u
FF{
u
1
F{yuF{uuF{yF{uFy{
y
u
F{
u
u
FF{
y
F{
u
FF{
y
F{
u
FF{
y
F{
u
F{
y
F
{
u
F{
y
F{
u
Fy
C14EFF{{{yyuF{FuyBFyB
F
S{
y
FFFFFF"B{
u
y"B
FFFFFFV{"yFF{BYVyuFFyFF"VuBYFFyY1uFz"uFyFFFFVuVyFFyYYuFF"z
u
"Fu
“FyFFFFFFy“99""FF““
F1F"VyFYF"F“B
2€•B^gCM…GŠ2C2‰G2i|2€•CM‹2
Fy Fq uF Fu y yF
/yB)%,!1+6gFF
F
FF“uyqFFuyF
F
FF9/FFF
F
FFyu uqz“F
F
FF9FF
F
F
F
u
y y
z
F
u
u
F
F
FB
 ^yyzyj)4!)y
lOMoARcPSD|27790909
C+%,7) 7%,1E/
C
9g/g/g/F9
F
F9VY9VgFqYB/
C
97) 7%,%)W)
B@)W))%#@R@OB
-
,7) 7%,4)N)W)E/B
C
™
VgFqYB/
C
Fu y yFFFy uF Fy •F
/B
C
FF
F
Fu q“
FF
FFF y z
F
FF
F
F” ¥
F
F
FFy u zFFFFu FuFF FFr uFF
Fy Fq uF Fu y yF Ft “ ”F
gFq/F
F
Fu y Fy
F
FFq
F
FFu q “
F
FFF
F
Fz y“ Fy
F
F
FF“ q FuFF FFy u zFF FFq r y“FF
Ft “ ”FFFy uF Fq zF
FVgFqYB/
C
FF
F
Fz y“Fy
FF
FFF y z
F
FF
F
Fyu qz
F
F
FFq r y“FFFFu FuFF FFu• uuFF
Fy qF FFy “F
/uV0u“y”uYB)%gFFF
yu
FF9/FFF
y y
FF"Œ!1+6"P87uF
1Y C()nFg
u
Fqg
#Y CZ!!1+6ˆ)š1!›Fg
u
F”ŒˆF F/
C
FqgFg
u
F
-
1Y g
u
F
F
FFF
yq
yu
F
FF
u
FFF
FF
F
ur
qy
F
FFFg
u
FqgF
F
FF
F
“
”“
F”FF
F
FF”Œ
#Y C)U%•1?+$14Eg
u
FqgF”ŒFF“ g
u
F”ŒFqg9qggF
u
F”Œ
F ¯!ˆ)š1!›EqgˆF/
C
B”ŒFˆF g
Fy
9/
C
V=%=UgF“Y
FFu FyF
F F
FˆF ”qFFFFyyuqFFFyFFFFF“y y“FFFFFFFqy quFFF
FFq qFF
C)1K!>7)(TU#UC1U)B%! y¥
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Fy Fu qF
/qB)%!1+6g
FF
F
u Fz y
F
F
"1)Io¡VYqF¡
u
Fu¡F”BC()ogV YB
FFq F” qFF
-
Fy Fu qF F• Fr y“F Fuy Fuq uzF
gF
F
Fu Fz y
F
FFg
u
FF
F
Fq Ft ”
F
FFogVYFqg
u
FugF”ŒFF
F
Fyq qz yqF
F
FFq F” qFF FFu Fy yqFF FF“ t q¥FF
/zBC()g
"&
F1 y “F
F%1F%11F
F
FFF“ 1 yFFB
1YgFFF1 FB #Yg FF“ “ 1FF
-
F%R1 FR1F
F%1 F1F
1Y gFFFR1 %R1
F
FBw<7gF
F
F1 %1
F
F
FFyBœB
s_!)œ"&FRFF
©
RFyFFFF%R1R1F%R1R1FFFFFFF%11F%11FFFFFFF%VVRRFFyYyY11
F%VVRRFFyYyY11FFF
g
F^)œ"&RFyB
F%1 F1F
H6<gFFF1 %1FFB
F1y “F F“ y “F
#Y g
FF
F“ 1
yF
FF1B
q
F/9
q
!1+6"P87q9/
F
F
F
“ “
yF
F
FF“ “ 1FF FF“ “ “FF
F“ “ yF
 ^yyzyj)4!)y
lOMoARcPSD|27790909
)6¡ /
u
F
F
F“ “ “
F
F™/
FR
FFF“R q
FF“ “ “FF
FgFF/F1BqFFF/BFyB1F1B“BF/1yBBFyF/1uBuBFu
F“
FVFyY1 1BFy 1uBFuF
F11BFBFyB/1FuBFuB/uFFF “ VFyY1 1BFyFF
FF “ “ VFyY1
FF
/”BCZ!8,!1+6":87u)%!›E
F“ “F
1Yˆ
u
FF
F“ “
F
F
F1
u
F#F“
1YgFFFF#1=FFF9guF“F
F
FFF1#1
FF=#=FF““
FF#F=
u
F“
F#F“F1F=F“
F#F“F1F=F“
-
Fy
#YˆuFF“
F
“F
yFF
F“ #FF“
H6<,!1+6)š1!›EFF“ “FFFF™
“FF1 #FFu F
“
FFFF™
F
1
FF1F#F“
#YgFFF#1 =FFF9guFFFFF#11VuFF#=YFF=
1uVF#F=FYyF“F
sV1=FYFF“ 1
u
F#Fy
F1F=Fy°#FF“
sV1F=YF“FFF1F=FFy°#FF“
Fy “F FFy “F F1 #FFu F
H6<,!1+6)š1!›EFF“ yFF™FF“ FyFF™FF F1FF1F#Fy
C)1K!>7)(TU#UC1U)B%! u“
 ^yyzyj)4!)y
lOMoARcPSD|27790909
/•B
F1 #F ¡
u
FFFFFV1=¡1=#Y
1Y )I!)+—!1+6gFF
=
F
F
)%!›7)+Z)1E
F
#Y )I!)"&g!1+6":87u)Zg
R
F“VRFFuY g
u
F“
-
F1uF#1##=F F
1Y guFFF1==F uF#FFFguFFV1=gYFV1=#FY
F1
u
F#FFV1=11=#YF
1##=F FFV1=#Y F
F
F
F FFV1=Y =
u
F#FFV1==1=#YFF
F
FF
“
F 1=
Fg)š1!›7)+Z)¡
u
FFV1=¡1=#YF F F“B
#Y MQ+g
u
F“)Zg
u
FFF“R uB
_g
R
F“"&RFuBC1)I!)g
u
F“
g
u
FF“ =UgFF“1=#F FF“ g
u
FFV1=gYF“V)U%•1Y
FFV1=YFF“ g
u
F“
FV1F=YF“Fg
RFu
FFg
u
FV1F=gY FFF“Fg
RFy
F“B
CW,)!?+$
Fg
u
F“
/tB0):R)1+NP))I!=¢,A))8]1P))IN)I!)E
1
y
F#¡
y
1
y
F#¡
y
y
1
y
#
y
y
y 1 #y 1 1
u
1Y1
u
F#¡
u
1
u
F#¡
u
u
FFu¡1
u
#
u
u
#Yy#1Fy# #
u
B1
q
F#¡
q
1
q
F#¡
q
q
1
q
#
q
q
y 1#y
u
-
1F#¡
y
y 1yF#¡y u1y y
y y
u u u
q q
#¡1
1 #¡
1 #¡
F
F
F
yy
u u
q q
u
#
¡#
#
F
 ^yyzyj)4!)y
y
u
q
y
u
q
y
y
y
1
#
lOMoARcPSD|27790909
1Y 1F#¡
u
F1
u
F#¡
u
u1
u
u
F
u
F
y
F
u
F1F#¡
q
q1qF#¡qu1qq
1F#¡
y
1 y 1y y
Fu1F#¡
u
1u1uuFyFuFyF1F#¡
q
1q1qq
1y #y
FFu¡1
u
#
u
1q
#q
y1 #1#VFF#Y
#Y y#1Fy##1VF#F1YF
u
FV1F#FYF
q
F
q
F1#1VF#F
1#Y
1u
Fy #
u
FF
y
FV1#F#F1YF
q
F
q
F
u
/¥BC(),P))I1E
y q ” Fy
1F#
u Fy Fy z
1Yg F #Y/F#F
Fy tF1
t t r y
1#
#
1
1uF
#u#u
Fu
1u
Fu
y
y
YpF
u
u
y
uF¡
u
q
q
u
u
y
y
q
q
”
rF
¡
u
-
y q ” Fyy q ” Fy
Ft Fyy •Ft Fyy •
u Fy Fy z“ Ft Fyy •
1Y gFFFyz Fu• yuFFyz Fu• yu
” y Fy t“ Fyz Fu• yu
FyzFu•¥““Fzttry“FyzFu•¥
Ft Fyy
FFzFFyyu
Fyz Fu•
C)1K!>7)(TU#UC1U)B%! uu
u
q
B
y
y
1
F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
1F# 1# 1
u
F#
u
1F #1VFY V1F1YVFY
#Y /F#F # #
u
F
u
F#F1 #VF1YV#F1#Y VF1YF
y
F
u
F
y
™
u
F
q
F
u
FF11
u
F1
u
F1 1
u
F1
u
y # 1Fy # 1F
FV1F#Y VF1Yy #F1FV1F#YVF1Y“ #F #FF
u
F
y
F
u
F
F1 1
u
F1
u
F1 1
u
F1
u
y 1F#F 1F
FV1F#Y VF1Y““#FFV1F#Y VF1YVF#YFF1
u
F
u
F1FV1F1YVF#FYFFF11
u
F
u
F1
u
F1
u
FV1F##YV FYVF1YV1#F#F1YB
yy u
uF¡
u
uF¡
u
u
Y p FF
z
F
q
F
z
F
qq y
q“ “
y yy y u
FFzF¡Fy uF¡ F“ yF¡
u
“FF
y
F
u
F
u qu q y
FFzF¡
u
FFFyF¡
u
FFFF¡
u
FzF
/rB
1Y )I!)@g!1+67)¡I87K)Z=UVgYF“B
#Y )%g!1+6":87u“yrB)I!)=UgF Fg
C
FF“B
-
1Y =UgF=Ug
C
F=UVFgYF=%g
C
FFgF_g87KF=UVFF
FgYVyY
=UgFF=Ug
p%"6<=UgFF=UgF=UgF“B
#Y C14EVggF
CC
YFg
C
FFFFg Vgg
C
Y
y
y
u
u
F
u
u
qu y
u q y
y ” u
y “r ¡
F
F
F F
uu
u
u z
y
¡
F F
F
u
uy
q y
u y
¡
FFF
u
q
q
”
z ¡
F
u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FgFg
C
!1+67)¡I87KV87u“yrYF=UVggF
C
YF“/y“BCZ!
)]1,!1+61E
Fy q ” FyF
1Y gFFFu Fy Fy zFF
F” y Fy tF
F F
Ft t r yF
Fz qF” u qF
F
F¥ •Ft z u
F
F
#Y /FFz qF¥ u tF
FFz q y uF”FF
FF¥ •Fy zF•FF
-1Y
Fy q ” FyF Fy q ” FyF Fy q ” FyF
F
gFFF
F
t”u Ftyy FFryytyzFF
F
FFFF
F
F“““ FFyzt FFu•yyyu•F
F
FFF
F
F
qz
u
FF
F
”t
u
yy
y
FF
F
qz
u
FF
F
FFFF
F
FF“““ F““t FFFyyzzF“•zFF
F
FFFFF
q
z
FFuu
u
uFF
q
zFFF
F F F Fyz Fu• ¥FFF F
Fy q ” FyF
F
FF
“ Ft Fyy •
FFBH•<VY+gFzB
F“ “ Fz “F
FF“ “ “ FzFF
,)uE=UgFFyyuF“9g!1+6":87zF+1RgFzB
Fz qF” u qF Fz qF” u qF
z qF¥ u t “ “Fq “ z
C)1K!>7)(TU#UC1U)B%! uz
 ^yyzyj)4!)y
lOMoARcPSD|27790909
#Y/FFFF
F
FF
F
¥¥z ••qFFytyzzuFFu•”FFF
F
FF
F
FFFF
F
FF
F
“““ “““ r•q “““
FFFyuz¥FFF
F
FF
F
F
F
FFF
F

q”z
u
FFFF
F
u
u
yz

y
zF
F
Fqz
u
”FFFFF
F
Fz qF” u qF
FFFFF
“
“ ““ q“““F“zFFFFF
F

q
zFFu
u
uFF
q
z
F
F
F
BH6<+/V YFu
F“ “ • “ “
F
F
F
F

”
Fq
u
F
”
FF
FF“ “ r “ “FF
Fy Fy y uF
/yyV0u“yzyYBCZ!!N)]1!1+6g
FFF
F
y u u
yF
F
#—uB
FFy “ z !FF
-
Fy Fy y uF Fy Fy y u F
gFF
F
FFFyy “u zu!y
F
FFFF
F
FFF““ yy qq !qFuF
F
FFF
F
F
q
u
F
F
y
y
F
F
q
u
F
FF
Fy Fy y u F
FFF“ y q q FFFqFuFqFB
FF“ “ “ !F”FF
H6<+gV YFuF!F”
/yuBCZ!!1+6)P)%]1,!1+61E
 ^yyzyj)4!)y
lOMoARcPSD|27790909
1YgFFF”qtzF
F
F#Y/F
F
F
F
F
Fuq
q
F
F
Fz
”
q”y
y
F
FF
FF
YFFFFFF
F
y“
“
“Fy“
“
1Fy
“
“1
F
y
““1
F
FFFF
F
B
F
-
1Y gFFFF”q tzFFFFg
Fy
F =U
y
gFgF
C
Fy
y
FFF
F
F
t
”
F
q
z
FF
F
F
F
FFF
t
”
F
q
zF
FF
Fq Fz ”F Fu Fuy yyF FFumq t FyymqF
#Y /F
F
Fu Fq y
F
FF/
Fy
F =U
y
/9/F
C
F F
y
q
F
Fy Fyu tF
F
FF
F
F
ymq z
Ftmq
F
FB
FFq F” yFF FFFy q FyFF FFymq Fy ymqFF
Fy F1 “ “F
Y ,)yEF
F
F
“ y F1 “FF
BC14E=UFyBCZ!F
+
F

Fy
FF
+
F“ “ y F1F
F F
F“ “ “ yF
,)uE|)7),71
F1Fy Fy 1F
/yqV0u“y”yYBCZ!1N!1+6g
FF
F
q 1Fy
qF
F
R))P)B
FF1Fy “ 1FyFF
C)1K!>7)(TU#UC1U)B%! u•
 ^yyzyj)4!)y
lOMoARcPSD|27790909
-
1Fy Fy 1
Fy 11Fy Fy
§ g§Fq1Fy qFV1FyYFV1FyY
1Fy qq 1Fy
1Fy “ 1Fy
FV1FyYFFFFq 1
u
F1F1
u
Fu1FzFFFV1FyYV1FyY
gR))P)F=UgF“FV1FyYV1FyYF“F1FFyB
/yzB)I!)+—!1+6g":87)%!›1g
R
R
F1
RFy
g
RFy
FFFF1g1Œ
y “
F“
"&1
“
F“)Zg!1+6R))P)B
-
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F
FgR))P)"g
Fy
FF/
FFy u yF FFy uF
/y”B)%gFFFu q zFF™/FFFqzFF™FFFFu•
yuy•
FFq y FyFF FF“ qFF
gˆF/F
C
B
-
Fu •F FFy uF Fq zF
gˆF
C
F/F
F
Fyu y•
F
FF
F
Fqz
F
FFF
F
r yu
F
FFp
FFy“ tFF FF“ qFF FFy“ zFF
y“F
t
FBCZ!!1+6ˆ)š1!›
F
FFy
Fz
F
^=UgFu¥F“FˆFg
Fy
FpF
y
FgpF
C
FF
F
F
y
u
=Ug
FFy
F
FFz/y•B)7)+Z)1E
Fy
yz
”F
u¥F
FFq zF Fu
yzqFFFFr
yuFFFFFq
F
F
y
FFFFy“zFF
FFFy
zFF
yF
uFFB
yFF
Fq¡
y
F”¡
u
Fu¡
q
Fz¡
z
Fu
F
Fz¡
u
F¡
q
Fq¡
z
F” 
1YFt¡
y
F
”¡
y
Ft¡
u
Fz¡
q
F•¡
z
Fq
F
F q¡
y
F¡
u
Fq¡
q
Fy
F

#Y
FFFFuz¡¡y
y
FFu¡u¡
u
FFz¡¡q
q
FFzq
F
Fy“¡F”¡F•¡FFy“
F
y u q
Fu¡
y
Fq¡
u
Fz¡
q
Fy
F
Fq¡
y
F¡
u
F¡
q
FuB
YFF”¡yFu¡uF”¡qFq
FF¡
y
Fz¡
u
Fq¡
q
Fy
C)1K!>7)(TU#UC1U)B%! u¥
 ^yyzyj)4!)y
lOMoARcPSD|27790909
)!B
#Y
Fq¡
y
F¡
u
Fq¡
q
Fy
24=<)8y)!)š1!›E
F
Fu¡Fy”¡
q
Fyq
u
tt
S¡qFF¡uFFy“FyF¡yFFq¡
u
Fz¡
q
F qFyz
yy u uu
H6<
F¡¡¡yuq™ ™ FFFFF qyzFuu™FFyy“yy™FFFB
/ytB)7)+Z)1#—7)7),71E
F¡Fu<F{FqFyu F¡Fu<Fq{FzFFz
-
1Y
VY VY+g +g
F
p% $)":
q
uy y”¡
F
F
F
FF
qyu
¥”
9 9 “™ ™¡¡¡
F F
F F
F F
F F
Y
VY uVY q+g+g
F FFF
F
24":)!)š1!›
qy u
qu
u zq y
yy y“ y
¡¡ ¡
¡¡
F F F
F
F
F FF
F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
1Y
F
FFqu¡¡FF•”<<FFz{{FFyqyylFFzrzrV0u“ytyY
#Y
F
FFFq¡¡FFut<<FFzy“{F{uFyyFFFFqyy
V0u“y”yY
F
FF¡Fu<Fu{FrFqq FF¡Fu<Fu{FtFF•
-1Y
F 24)!=<)8)š1
F¡
y
Fu¡
u
F¡
q
Fq¡
z
Fyu
F¡uF¡qF”¡zFu”!›FFFF¡q
Fz¡zFyq
FF u¡
z
F¥
FF¡¡¡¡
yuqz
™ ™ ™ FFFVy™u™q™zY
#Y
F¡
y
Fu¡
u
Fq¡
q
Fz¡
z
FFz
F
¡
u
F¡
q
F¡
z
Fy
+gVYF+
gVY
F
FFz24)!=<)8)š1!›
F
FF¡q
Fu¡
z
Fy
FF ¡
z
FFy
FF¡¡¡¡
yuqz
™ ™ ™ FFVy™y™y™FFyY
FV1F”Y¡F q<FVu1FyY{F“
/y¥V0u“ytyYBCZ!1N)
F
F 1¡FV1FyY<F z{F“4)!R): !)-B
F
FV1F”Y¡FV1FuY<F ”{F“
-
C)1K!>7)(TU#UC1U)B%! q“
 ^yyzyj)4!)y
lOMoARcPSD|27790909
24)!R): !)-F=UgF“V=%)) )8Y
F1F” q u1FyF1F” q u1Fy1F” q u1Fy
H&gF
F
F1 1Fy z
F
FF=Ug F1 1Fy z1 1Fy z
FF1F” 1Fu ” FF1F” 1Fu ”“ 1Fy zFu1
FV1F”Y‘V1FyYVzFuY1FzV1FyY’F1B‘qBVzFuY1FVu1FyYV1FyY’
FV1F”YFFu1
u
Fu1FF1FFu1
u
F”1FyqF
FFu1
q
F¥1
u
Fy“1Fu1
q
F”1
u
Fyq1
FFq1
u
Fq1FFqV11FyY
F1F“
=UgF“FF1FFyB
F
F!¡
y
Fu¡
u
F¡
q
Fq
/yrV0u“ytuYBCZ!!)7)+Z)
F
F¡
y
F!¡
u
Fu¡
q
Fz4)!=<)8B
F
Fu¡
y
Fq¡
u
F¡
q
FF!
-
F! u Fy qF! u Fy
g
FF
Fy ! u
zF
F24)!=<)8Fy ! uF“
FFu q y F!FFu q y
u u u
F!Fy
F!F¥FqFVu!F•!FuYF“F!F”Fz!FuF“F!Fz!FqF“FF!Fq
F
F ¡
y
Fu¡
u
F¡
q
F!¡
z
Fz
F
F F¡
y
F¡
u
Fq¡
q
Fu¡
z
FR B
/u“B)%)7)+Z)FFu¡yF¡uFq¡qFV!FyY¡zFq
FF ¡
y
F¡
u
F¡
q
Fu!¡
z
F”
1Y )7)+Z)R)!Fu9RF”B
#Y CZ!RN)4)!=<)8B
Y CZ!RN)7)+Z)4":)!B
F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
-
1Y !Fu9RF”)4)!<)8F¡¡¡¡yuqz™ ™ ™ FFFVr™y™”™FF”YB
#Y 24)!=<)8Fu!Fy¥F“F!FrB
F
u!Fy¥F“ F
F!Fr B
Y 24":)!F
F
FFFyyRF
y”
F
“
FFFF
R
FF
yy
y”
C)1K!>7)(TU#UC1U)B%! qu
 ^yyzyj)4!)y
lOMoARcPSD|27790909
2€•B02egHŒCLM
/yBC67H"&,7) 7%,47)R):1" R):•
1YHF£V¡9<9{Y¡9<9{∣ FF¤"&,7) 7%,¡,P))1E
V¡<{99YFF¡<{
F
9
F
9
F
FFF¡F¡<
F
9F<{
F
9F{
F
F

R¡<{V99YFVR¡R<R{§9§ § 9§ ∣ Y
#YHFF¡FF¡9¡
y u
F∣¡
y
F“9¡
u
F
“
FFF
u
"&,7) 7%,¡,P))1E
F¡9¡
yu
FFF<9<
yu
FFF¡<9¡<
y y u u
F°R¡9¡F
y
u
FFF¡9¡
y
R
u
R
F+%4R)W#8R±B
-
1Y)6¡ FR
y
FR
u
FFV¡<{™™YFFR
y
FR¡R
u
™
y
FR
u
<R™
y
FR{
u
F
FFR¡
y
FR¡R<
u
™
y
FR
u
<R{™
y
FR{
u
FFR¡<{
y
V™™YFR
u
V¡<¡™™Y
FHR):R):1"U%+B
#Y
FVH9FY!3)4!1%)%,
FFR¡¡FF
y
9
u
FFF<<
y
9
u
FFFFF¡<¡<
y
R
y
R
9
u
R
u
R
FFR¡¡F
y
9
u
FFR<<F
y
9
u
F
FFRRyFuFF¡¡y9uFFF¡yRyFRu9¡uRyFRuFFR¡¡yFy9uFFR¡¡uFy9uF
FRR¡¡
y
F
u
F
y
9
u
FFFFRR
yu
FFB¡¡
y
9
u
F
FyBF¡¡
y
9
u
FFF¡¡
y
9
u
F
FH!3R):1"U%+B
/uB)I!),67)7%]1,R):1" OU)31,R):1" %
]1)œE
1Y C67ŒF£F¡9¡9¡
y u q
FFF
q
∣u¡
y
F”¡
u
Fq¡
q
F“¤
#Y C67,1)I4)#6)8#—“V)]1¡Y]10HC|¡
‘’
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Y C•7,!1+61!,+$]1,!1+6":87
=Y C67,!1+6¡I]167,!1+6":87
UY C67,!1+67)¡I]167,!1+6":87F1«FF1«F
-
1Yˆ 
y
FF¡¡¡
yuq
9 9 FFŒ9
u
FF<<<
yu
9 9
q
FFŒ
F
y
F
u
FF¡
y
F<¡
yu
9 F<¡
uq
9 F<
q
FFŒ
p%uF¡
y
F<
y
FF”F¡
u
F<
u
FFqF¡
q
F<
q
FFFu¡
y
F”¡
u
Fq¡
q
FFFu<
y
F”<
u
Fq<
q
FF“RFM
)ZR
y
FŒ=%
R
Fu¡
y
F”¡
u
Fq¡
q
FF“
FŒ0HC%]1M
q
B
#Y
||yu9 4)#6)8#—“FFFFR||yyF4)#˜“|u4)#˜“FFRM
FC67,1)I4)#6)8#—“]1|¡
‘’0HC%]1|¡
‘’B
F7FOFk™F7O9Fk
9=9UY^CC19#B
F
FR7
Fk™FFRM97Fk
)Zk0HC%)#?H
/qB)%H
y
9H
u
)1R):1" %]10HCHB)I!)E
1Y H
y
FH
u
0HC%]1HB
#Y H
y
FHE
u
FF
y
F
u
∣
y
FH9
y u
FH
u
F0HC%]1HB
-
1Y"H9FyFHuFFFF"H99FFyuFFFF"H"HFFFFyuF"HFFyFHu
FF"H
C)1K!>7)(TU#UC1U)B%! qz
 ^yyzyj)4!)y
lOMoARcPSD|27790909
HRF
y
9FFFMRH
y
9WRHFFFF
u
RH
y
H
u
p%4H
y
FH
u
0HC%]1HB
#Y"9FHyFHuFFF"FF"yyFF"uuFyF"uFHy9uF"uFHuF
F
F"F FF
y
F"
y
FFF
u
F"
u
FFH
y
FH
u
jRRF
y
FR
u
FFHH
y u
=%R
y
FHR
y
9
u
FH
u
FFH
y
H
u
0HC%]1H
/zB)%H9H
yu
)1R):1" %]10HCHBC14H9H
yu
#¢)1@
H
y
FH
u
FH9H
y
FH
u
F£¤FB)I!)+—H9H
yu
#¢)1R)")`R)!." ]1H4#N=>
=<)8=&=F
y
F9
u
F
y
FH9
y u
FH
u
FB
-
HH
yu
9#¢)1FFFHH
yu
HH™
y
FFH
u
£“¤
FFF"H)Z"F"
y
F""
u
F
y
FH"
yu
9 FH
u
F
_#N=><R):=<)8F"F"
y
F"
u
F"
y
F
F"
u
F
F"
y
F
F"
y
FFFFF"
y
"
y
F
"
u
F
"
u
^"
y
FF"
y
F
H"
yu
9
F
FFFFF"
u
H
u
H
u
£“¤V!•)\YF#N=>=<)8B
p%!*"U%+FH#N=>=&=F
y
F
u
F
y
FH
yu
9 FH
u
FFFFHHH
yu
_¡HFFFFFFF
y
H
u
¡“¡¡“V!\)\A)=<)8YFFFH
y
H
u
£“¤
H6<147!B
/”BC+%0HCH9)%)" F99y uF99 yFF7)')3<@A)"
F99y uF9F)367<@A)B)I!)
yF
•)7<@A)]1," 
99
yu
F9
B-
F
y
9
u
9F9
9
Fy
F7)')3<@A)
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Fy
FFR
9Fy9FyR):5)-#—“)š1!›FR

F“
Fy
Fy
@R
Fy
F“FFR

F“FF
yu
9 9F9
F7)')3<@A)V!•)\Y
Fy

FR
FRFyF“FF FFy²
Fy
R
Fy
CI
Fy
•)7<@A)]1
yu
9 9F9
B
/•B
)%
F"9"9
yu
F9"
!
F))]1k999
y
F
yu
F9
F))]1k
u
"&k9k
yu
",
R):1%]1HB)I!)F"9
y
F9"999
!yu
F9
F))]1k
y
Fk
u
B
-
ˆ Fk
y
Fk
u
FF
y
F
F
u
F
F
y
F
Fk
y
9
u
F
Fk
u
F
!
^
F""
yu
9 9F9"
!
F))]1k
y
FFR

E
y
F
FFR"

FFR
u
F“F
Fy
CWF
«
E
u
F
FF
« «
FF
u
«
F“F
«Fy
!
FFFR"

FF
« «
FFR
u
FF
u
«
F“F
Fy «Fy
FF""
yu
9 9F9"
!
9
yu
99F9
F))]1kk
y
F
u
B
/tBC+%F
q
¡ ¡U!,)" 1367<@A))1<7)')3<@A)E
1Y "
y
FVz™u™•Y9"F
u
FFV•™q™FrYB
#Y "
y
FVu™q™yY9"F
u
FVq™y™”Y9"F
q
FFVy™q™FzYB
Y "
y
FVy™u™qY9"
u
FVq™•™tY9"
q
FFVq™y™qY9"
z
FV“™z™uYB
C)1K!>7)(TU#UC1U)B%! q•
 ^yyzyj)4!)y
lOMoARcPSD|27790909
-
1Y "
u
F
Fq
"
y
FF""
y
9
u
F7)')3<@A)B
u
u q Fy
#Y q Fy qFFFr “F
)
F"""
yuq
9
9
F367<@A)B
Fy ” z
Y p%""""
yuqz
999)3R):1"U%+M
q
B
^=!M
q
Fq$)z"U%+#8R±:7)')3<@A)FF""""
yuqz
9 9
9
F7)'
)3<@A)B
/¥BC+%R):1|‘¡’
u
9¡ ¡U!)" /FF
y
FFyu¡9
u
Fq¡F¡9
u
q
FuF¡F¡
u
F367
<@A))1<7)')3<@A)B
-
Fy “ uF
.g!1+6]1/"&?)())IFy™™¡¡
u
F]1|¡
¡
‘’Fg
FF
F
u q F
yF
F
9
FF“ Fy yFF
=UgFFFu “F/367<@A)B
/rBC+%F
q
9)I!)"
y
FVy™y™yY9"
u
FVy™y™uY9"
q
FVy™u™qY67))!3?Bˆ,P)!1+6
)<N–?)()-1?+$"¯!%3]1¡FV•™r™yzY"&?+$)U%)1,)
+WJ@7"=¢:)I•.13B
-
yy y
C1 4y y uFFFy “F
)"U%+
F"""
yuq
9
9
F367<@A)
y u q
^=!F
q
FF
q
F"""
yuq
9
9
F?]1M
q
B
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Fyy yF
^1+6)<N?–)()-1F"""yuq9 9FEF
FFyy
uFF
FFy u
qFF
©YCZ!.13]1¡FV•™r™yzY"&?F"""yuq9 9FF/
F1F#FF•
,)yE¡F1"
y
F#"
u
F"
q
F
F
F1F#FuFr FV1#99YFVy9u9qY

F
F1Fu#FqFyz
Fy y yF
Fy
F•F FFy
,)uE‘’¡
Œ
F
Fy
F‘’¡
Œ
F
F
Fy y u
F
FF
F
Fr
F
FF
FF
FFuB
FFy
u qFF
FFyzFF FFFFq
FFy
F‘’¡
/
F
FF
FFu
FFFFq
/y“BC+%,+-)719)I!)/FF"""
yuq
9
9
F!3?]1F
q
"¯!‘’"
/
#@
+—E
1Y "
y
FVu™y™yY9"
u
FV•™u™“Y9"
q
FVt™“™tY9"Vy”™q™F yYB
#Y "
y
FV“™y™yY9"
u
FVu™q™“Y9"
q
FVy™“™yY9"FVu™q™“YB
-
u • t
1Y y u “FFu¥F“F/367<@A)F/?]1M
q
y “ t
‘’"
/
F‘’/
F
Œ
y
F‘’"
Œ
FŒ?)()-9‘’/
Œ
!1+6)<N?–Œ1/Y
Fu • tF
Fy
Fy”F FF”muF
F
F
Fy u “
F
FF
F
Fq
F
FF
F
Fyymz
F
F
FFy “ tFF FFyFFFFymuFF
“ u y
#Y y q “FFF” “F/?]1M
q
B
C)1K!>7)(TU#UC1U)B%! q¥
 ^yyzyj)4!)y
lOMoARcPSD|27790909
y “ y
F“ u yF
Fy
FFu FF“
‘’"
/
F‘’/
F
Œ
y
F‘’"
Œ
F
F
Fyq “F
F
F
FF
FFqF
FF
FFy
FFy “ yFF FFFF“FFFF“
/yyBC+%|‘¡’
q
)%," "
y
Fy9"
u
FFy¡9"
q
FF¡ ¡9"
u
z
FF¡
u
¡
q
B
1Y )I!)/FF"9"9"9"
y u q z
F!3?]1|‘¡’
q
B
#Y CZ!%3]1" "FuFq¡F¡
u
Fu¡
q
"&?+$B
Y CZ!.13]1" "FFF1
“
1¡
y
1¡
u
u
F1¡
q
q
"&?+$B
-
Fy y “ “F
1Y ^1+6.13]1/•"&%?)()-Œ/“F
F
F“ y y “
F
F
F“ “ y yF
F F
F“ “ “ yF
=%=U/
“
FFy /367<@A)F/?]1|¡
q
‘’
Fy y “ “F
Fy
FuF FFzF
F
#Y ‘’"
Œ
F/“FyF‘’"ŒFF“y y “FF FFFqFFFFF•FF
F“ “y yF FFyF FFqF
F F F F F F
F“ “ “yF FuF FuF
Fy y “ “F
Fy
F1
“
F Fy Fy y FyFF1
“
F F1
“
F1
y
F1
u
F1
q
F
F
“ y y “
F F
Y ‘’"ŒF/“
Fy
F‘’"ŒFFF“ “ y yF FF1
y
u
F
FF
F
F“ y Fy y
F
F
FFFF
F
1
y
uF
F
FFF
F
1
y
Fu1
u
Fq1
q
FF
F
F F1F F“ “ y Fy 1F 1F1
F F F F F FF F F F
F“ “ “ yF F1
q
F F“ “ “ yFF1
q
F F 1
q
F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
/yuV0u“y”yYBC+%F
z
9)%," 1E
y
FVy™q™
u™yY9F
u
FFVu™q™y™yY9
q
FVu™y™“™yY9FFFVy™y™
q™YB!
CZ!!NFD71F
yuq
9 9FB
-
F
71
F
yuq
9
9
FFF¡¡¡
yu
99
q
)š1!›F¡
yy
F¡
uu
F¡
qq

F¡
y
Fu¡
u
Fu¡
q
Fy
FF
q¡
y
Fq¡
u
F¡
q
FFy 4)!R): !)-BF
FFF
u¡
yF
¡
uF
“¡
qFF
q
FF¡
y
F¡
u
F¡
q
F!
24)!R): !)-FuyVr!FrYF“F!FFyB
/yqB)%0HC|¡
q
‘’")" 1E
"
y
FFFy¡
u
¡"
q
9
u
FFF¡¡
u
u¡"
q
9
q
FFFu¡q¡"
q
9
z
FFFFFy¡¡
u
uB¡
q
1YCZ!)]1)"  #YCZ!!3?]1R):1
71
F""""
yuqz
9
9
F
-
1Y^1+6g
]1)
F""""
yuqz
9 9
9
F"&?)()-
C)1K!>7)(TU#UC1U)B%! z“
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Fy “ u FyF Fy “ u FyF Fy “ u FyF Fy “ u FyF
gF
F
“ y y y
F
FF
F
F“ y y y
F
FF
F
F“ y y yF
F
FF
F
“ y y y
F
F
F
Fy Fy “ FyF F“ Fy Fu “F F“ “ Fy yF F“ “ Fy yF
FFy u q uFF FF“ u y qFF FF“ “ Fy yFF FF“ “ “ “FF
H6<+gV YFq)1<)]1)"UF""""yuqz9 9 9FqB
#Yˆ !1+6.13)E
Fy “ y yF Fy “ y yF Fy “ y yF Fy “ y yF
F
F
“ y Fy uF
F
F
F
F“ y Fy u
F
FF
F
F“ y Fy uF
F
FF
F
“ y Fy u
F
F
Fu y “ qF F“ y Fu yF F“ “ Fy FyF F“ “ Fy FyF
F
FFy y Fy u
F
F
F
F“ y “ qF
F F
F“ “ y y
F
F
F
F“ “ “ “
F
F
F^3?]1
71
F""""
yuqz
9 9
9
F

FFyFF¡
u
¡
q
FF™¡¡FF
u
u¡
q
FF™FF¡
u
¡
q
FFB
/yzBCZ!?")]1R):1%)#?)" 1E
1Y
FFu™y™q™z9F"
u
FFy™u™“™y9F"
q
FFFy™y™q™F“F+%F
z
B
#Y"
y
FVu™“™y™q™yY9"F
u
FVy™y™“™y™yY9"F
q
FV“™u™y™”™qY9"F F
z
FFVy™q™u™r™F”Y
+%F
”
B
-
1Y ^1+6.13)
Fu y q zF Fy u “ yF Fy u “ yF
F
y u “ y
F
FF
F
Fu y q z
F
FF
y
F
u
FF
F
F“ Fq qu
F
F
F
FF
q
u
F
Fu
y
y
F
F
q
u
F
FF
F
FFFy y Fq “FF FFFy y Fq “FF FF“ q Fq yFF
Fy u “ yF
FFF“ Fq q uFFFqFuFqF
FF“ “ “ qFF
F=!HFq94£Vy™u™“™yY™V“9Fq™q™uY™V“™“™“™qY¤
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Fu “ y q FyF Fu “ y q FyF
#Y FFy“ Fyu y“ F”y FyqFF
F
F
F
FF““ Fuu Fyy F””
Fqq
F
FFFFFuu
u
zFF
y
yFFz
u
FFF
F
F
Fy Fq u r F”
F
F
F
F“ F• q y” Fr
F
F
Fu “ y q FyF
FF
F
F“““uF“y F“”“qF
F
FFF
q
zFFq
u
uFF
q
zFFF
F
F F
F“ “ “ “ “F
F=!HFu94£Vu™“™y™q™FyY™V“™u™Fy™F”™qY¤B
/y”BC+%F
z
)%," E
y
FVy™“™y™“Y9
u
FV“™y™y™FyY9
q
FVy™y™y™uY9
z
FV“™“™y™yYB
SH
y
F
719
F
y u
F9H
u
F
719
F
q z
FBCZ!?")]1,0HCH
y
FH9
H
uy
FH
u
B
-
1Y 71F
yuqz
9 9 9FFH
y
FH
u
Fy “ y “F Fy “ y “F Fy “ y “F Fy “ y “F
F
F“ y Fy y
F
FF
F
F“ y Fy yF
F
F
F
F“ y Fy yF
F
F
F
F“ y Fy y
F
F
Fy y y uF F“ y “ uF F“ “ y yF F“ “ y yF
F F F F F F F F
F“ “ y yF F“ “ y yF F“ “ y yF F“ “ “ “F
F=!71F
y
9
u
9
q
9
z
FF=!H
y
FH
u
Fq9£Vy™“™y™“Y™V“™y™y™yY™V“™“™F y™yY¤B
#Y ˆ HFFFF
y
H
u
¡¡¡¡
yuqz
™ ™™ EF¡
yy
F¡
uu
F¡
qq
F¡
zz
F¡
yy
F¡
uu
F¡
qq
F¡
zz
F“²
F¡
y
F¡
q
F“
FF¡uF¡qF“ F¡yF¡uF¡qFF¡z
FFF¡yF¡uF¡qF¡zF“
FF¡
y
Fu¡
q
F¡
z
F“
C)1K!>7)(TU#UC1U)B%! zu
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FF¡
y
F
y
F
u
FF¡
y
BVy™y™“™FyYF=!H
y
FH
u
Fy9£Vy™y™“™yY¤B
/y•V0u“y”yYB)%R):1|
u“y”
‘’¡j,1)I#6R):O,u“y”"67k
y
F£7F
|
u“y”
‘’¡∣7VF¡YF7¡VY9FF¡
M
FB)I!)+—k
y
R):1%]1|
u“y”
‘’¡B)`+1
)"!3?]1k
y
VR): )I!)YB
-
k
y
FF7F|
u“y”
‘’VY¡7¡F7VF¡YF
Fˆ 977
yu
FkO
y
9F7
y
F7
u
BC14VO¡FFY7
y
VFF¡Y7
u
VFF¡Y7¡
y
VYF7¡
u
VYFO¡VY
FFF7
y
7
u
k
y
FF7
y
kR
y
9FFMR7
y
VFF¡YR7¡
y
VYFR7
y
Fk
y
H6<k
y
0HC%]1|
u“y”
‘’¡
p%7VF¡YF7¡VYF1)I7¡VY)`5!,)_#6)Ÿ]1¡
y““t
21<7¡VYFF1¡

F
u
F=!k
y
Fy““¥9!3?/FFy™¡
u
™¡
z
™F™¡
u“yz
FB
F“
/ytBCZ!?")]1R):1)!]1)7)+Z)) )81E
F #YFz¡y
1YFFFFFF¡qu¡yy¡¡F
y
FyFuF¡¡u¡¡u
u
uFFFFuqu¡¡¡qq¡q
q
FFFFu¡¡¡z¡z
z
zFFFFq”¡¡¡¡
”
”””FFFF““““
FFF
F
uu¡¡yyFFFu¡¡u¡uuFFFq¡”¡qq¡FqF¥Fu¡¡¡zzzFFFutz¡¡¡
-
Fy Fy u u FyF Fy Fy u u FyF
1YgF
F
FFyqu Fyu yq Fyy”qFF
F
F
F
FF““Fqy Fyq
FFqq•”
F
FFFFF
F
q
u
zFF
F
uq
y
yy
F
FF

u
zqFF
F
FF
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FF Fy Fu Fy yFF FF“ u F¥ Ft zFFF
Fy Fy u u FyF Fy Fy u u FyF
F
FF“ Fy y FFq•
F
FF
F

q
z
FFqu
u
u
FF
q
z
F
F
F
F
FFF
“
“ F“y Fy•
F
Fyqq y••
F
FFF
q
F
z
F
F“ “ “ yu uqF
F
F
F“ “ F• Fyq y•
F
F
F
F“ “ “ Fyu uq
F
F
F¡
y
F¡
u
Fu¡
q
Fu¡
z
F¡
”
F“
F
F
FFFFF•¡
u
¡qFF¡yq
q
F¡qz¡F
z
y•F•¡”¡
”
FF““S¡”FF¡zF yuuq¡™qF Ftuy“t
¡™uFFyu¥r¡™yFFtutrFFFyu¡
z
Fuq¡
”
F“B
FˆFF¡¡¡¡¡yuqz”™ ™ ™ ™ FFFFFFtutr™Ftu¥r™Ftuy“t
uq™yu™yFFF
F0):1)!4=!yF9?
F
FF
F
FF
F
tu
tr
™
F
tu
¥r
™
F
tu
y“tuq
™
yu
™y
F
FF
F
FFB
Fu Fy q Fu zF Fu Fy q Fu zF
#YgF
F
FFFzu FFuy y” ¥ytu
F
FFFF
F
FFF““ ““ FFuy y“” FFuyF
F
FFFF
F
q
u
F
F
u
y
y
F
F
q
u
F
F
F
Fu Fy q Fu zF
FF
F
“ “ Fy ” Fy
F
FF
q
Fu
u
F
q
F
FF“ “ “ “ “FF
Fu¡yF¡uFqq¡qFzu¡z”Fz¡”F“SFF¡yzFF1¡9”F#F¡qF”1F#¡9uFuF¥1F#
FF F¡F”¡F¡F“ F¡
F
C)1K!>7)(TU#UC1U)B%! zz
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FˆFF¡¡¡¡¡
yuqz”
™ ™ ™ ™ FF1V“™¥™”™y™“YF#V“™y™
y™“™F yYFVy™u™“™“™“Y
F0):1)!4=!q9?£V“™¥™”™y™“Y™V“™y™y™“™yY™Vy™u™“™F “™“Y¤
/y¥B)%9H,R):1%)[))]1R):1" kBB
)I!)=!VFHYF=!VYF=!VHYF=!VFHY
-
?9H Fyu99F9!FF™""yu99F9"F
s@FHF£“¤FF
yu
™ ™F9""
!
™™
yu
™F™"
F367<@A)"?]1VFHY
F=!VFHYF!FF=!F=!HF=!VFHY
s@=!VFHYF7
9?
F++
y
9
u
9F9+
7
FFg
/•!7F"U%++
7Fy
9F9+
!
"%gN?]1B
/•F7"U%++
!Fy
™F9+
7!FF
"%gN?]1HB
C1)I!)DFF++
y
9
u
9F9++
7
9
7Fy
9F9+
!
9+
!Fy
9F9+
7!F F
F?]1HF
TF FH)ZTTFyFTuFF!R+FFFFFFF7!R+««F7+««FFFF7FRFO+FFFFFF7!R+F!R+
Fy
F
FFFFFFFFF«!FFy
F «Fy !FFy+FFy
T
FF++
y
9
u
9F9++
7
9
7Fy
9F9++
!
9
!Fy
9F9+
7!F F
F))]1HF
7!F F ! 7!FF !
FF+F“)ZFF+FFF+FFHFFF+FHFFF“ FF 7Fy9!
!F Fy Fy !FFy FFy
7 7!FF
F
FF

+FFF

+F“FF

FFF“ y997F!Fy9F7F!F2DCCFD?BFy !F F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
2€•HB‡2ˆ‚CxƒC„2
/yB)%,)¡oEF
q
FF
u
¡,P)#?:)I
o¡¡¡
F
yuq
9
9
FFFq¡
y
F¡
u
F¡
q
9u¡
y
F¡
q
FB
1Y )I!)o,)¡<@A)B
#Y CZ!!1+6]1o"&S7?)()-B
Y CZ!!3?]1RU+oB
-
1Y ˆ 
y
9
u
FF
q
FoF
y
F
u
FFFqF¡
y
F<
y
FFFF¡
u
F<
u
FFF¡
q
F<
q
F9uF¡
y
F<
y
FFF¡
q
F<
q
F
FFq¡
y
F¡
u
F¡
q
9u¡
y
F¡
q
FFFq<
y
F<
u
F<
q
9u<
y
F<
q
F
FoFF
y
FoF
u
F
ˆ 
y
FF
q
9RFFFoRF
y
FFFqR¡
y
FR¡
u
FR¡
q
9uR¡
y
FR¡
q
FFRFq¡
y
F¡
u
F¡
q
9u¡
y
F¡
q
FFRoFF
y
H6<o,)¡<@A)B
#Y C14EoVy9“9“YFVq9uY™oV“™y™“YFVy™“Y™oV“™“™yYFFVy™yY
F^1+6]1o"&S7?)(),gF
F
F
F
q
u
y
“
F
y
yF
FF
Y ¡F0U+oFo¡VYF“F
F
F
q
u
¡
¡
y
y
F
F
¡
¡
u
q
F
F
¡
“
q
F“
F
S¡
q
FF¡
y
FFu

9¡
u
F
”
u

F¡FF
F
F
F
u
y”
™ u™y
F
FF
F=!0U+oFy9?FFF
F
FF
F
u
y”
™
u
™y
FF
F
FF
F
B
/uB)%,)¡o|¡E
u
‘’F|¡
z
‘’¡,P))1Eo7VYFF7¡7
u
9FF7|¡
u
‘’
1Y )I!)o,)¡<@A)B
C)1K!>7)(TU#UC1U)B%! z•
 ^yyzyj)4!)y
lOMoARcPSD|27790909
#Y CZ!!1+6]1o"&S7?)()-Œ
y
FFy9¡9¡
u
F]1|‘¡’
u
"Œ
u
FFy9¡9¡9¡9¡
uqz
F
]1|‘¡’B
z
Y CZ!!1+6]1o"&S7?Œ
y
F
FFyF¡9u¡9yF¡
u
F]1|‘¡’
u
"Œ
u
FFy9¡9¡9¡9¡
uqz
F]1
|‘¡’B
z
-
1Y p>)8<FF7y97uF|¡u‘’)ZoF7yF7uFFoF7yFFoF7uF™oR7FyFFRoF7yF
FRFF
Fo,)¡<@A)B
#Y C14oVyYFFy ¡
u
9o¡VYFF¡ ¡
q
9o¡F
u
FFF¡
u
¡
z
Fy “ “F
F
F“ y “
F
F
F^1+6]1o"&S7?ŒŒ
yu
9 gFFy “ yF
F F
F“ y “F
FF“ “ yFF”qF
Y oVyFFFFF¡Y y ¡ ¡
u
¡
q
9oVuY¡FFu¡ u¡
q
9oFyF¡
u
FFFy u¡
u
F¡
z
Fy“yF
F
Fyu“
F
F
F^1+6]1o"&S7?ŒŒ
yu
F
9 /FFy“uFB
F F
Fyu“F
FF““yFF
/qV0u“y”yYB)%,)¡<@A)oE|‘¡’
u
F|‘¡’
u
)š1!›EoFyF¡
u
FFFFFqq¡
•¡
u
9oFq¡Fu¡
u
FFFFyt¡y•¡
u
9oFuFF•¡q¡
u
FFFFqut¡u”¡
u
B
1Y CZ!!1+6]1o"&?)()-]1|¡
u
‘’BC()oFyF¡
u
FB
 ^yyzyj)4!)y
lOMoARcPSD|27790909
#Y F
F
oFyF¡
u
FF
F
ŒFgF
FF
“FF
F
y q Fz
FFF
F“F
F
F”
F
FoFyF¡
u
FFFFFyq ”¡
¥¡
u
FFFFy FFFt • FyFFFFFFy FFF¥FFY
"FFFy¡ !¡
u
F!oFF¡¡
y
9
u
9¡
q
E"F¡
y
FFFF¥ ¡ t¡
u
FF¡
u
FrFFq¡ •¡
u
FF¡
q
FFFF”
¡
u
FFF¡
u
F“F
FF¥¡
y
Fr¡
u
F”¡
q
Fy
Fˆ )
F
FF¡
y
Fq¡
u
Fz¡
q
Fy4)!R): !)-
F
FFt¡
y
F•¡
u
F¡
q
F!
F24)!F!F“B
H6<!F“)Z"F!oB
/zB)%,)¡oEFF
q
F
q
¡,P)#-
o¡9¡9¡
F
yuq
FFFFF¡
y
¡
u
¡9¡
qy
FFFFF¡
u
¡
9¡
qy
¡
u
¡
q
FCZ!!1+•]1o"&?/FFF"
y
Vy™“™“Y9"
u
FVy™y™“Y9"
u
FVy™y™yYFB
-
Fy y FyF
C)1K!>7)(TU#UC1U)B%! z¥
#Yˆ,P)
!
N" "FFFy ¡ !¡
u
)3!o
-
F Fy “ uF FFq
1YF
F
F
F
F
oVyY’‘VY’
Œ
o¡
Œ
F
Fo¡F
u
F
F
FŒF
F
F
F
F
“ q
•
F
F
F
F
Fq
FF FFFy u qFF FFF•
yt
y
y•
quF
t
F
F
VŒ?)()-]1|¡
u
‘’
F
u”FF
FFq yt quFFy
F^1+6]1o"&ŒgF
F
F
q y t
FF
FF
F
FFF•y•u”FFFFFy
FFyFF¥rF”FFFyFFyqF
“
q
u
uF
Fy
FF¥ r F”F
•
F
F FF
F
Fy q Fz
F
F
qFF FFFt • FyFF
FF F FFF F F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
^1+6]1o"&?)()-g
FF
F
y Fy
yF
F
FFFy y yFF
Fy y yF
^1+6)<N?–Œ1/D
FF
F
“ y
yF
F
FF“ “ yFF
Fy y yF
Fy
Fy y FyFFy y yF F“ u “F
F^1+6]1o"&/D
Fy
FgDF F
F
F
“ y y
F
F
F
F
F
y Fy y
FF
FF
F“y y
F
F
FF
F
u “
“F
F
FF“ “ yFF FFFy y yFFFF“ “ yFF FFFy “ yFF
/”V0u“y”yYB)%,)¡<@A)oE|‘¡’
u
F|‘¡’
u
)š1!›EoFyF¡
u
FFFFFqq¡
•¡
u
9oFq¡Fu¡
u
FFFFyt¡y•¡
u
9oFuFF•¡q¡
u
FFFFqut¡u”¡
u
B
1Y CZ!!1+6]1o"&?)()-]1|¡
u
‘’BC()oFyF¡
u
FB
#Y ˆ,P)
!
N" "FFFy ¡ !¡
u
)3!o
-
,)!W#qB
Fy q FyF
/•B)%g
FF
F
u “
”F
F
!1+6]11¡loE|‘¡’
u
F|‘¡’
u
"&?/FF"9"9"
yuq
F
FF• Fu zFF
+%4E"
y
FFq¡¡"q
u
9
u
FFFFyq¡¡"u
u
9
q
FFFqt¡¡u
u
1Y CZ!o"FFy9o"FuF9o"FqFB
#Y CZ!oFyF¡
u
FB
-
1Y o"FF
y
FF"
y
u"
u
F•"
q
FFq¡q¡
u
FFFFuFyq¡u¡
u
FF•qFFFt¡u¡
u
FFyr¡
u
F”y¡Fy•o"FF
u
Fq"
y
Fu"
q
FqqF¡Fq¡
u
FFuqFFFt¡u¡
u
FF”¡
u
FF”¡•o"FF
q
FF
F"
y
”"
u
Fz"
q
FFFq¡q¡
u
FFFF”Fyq¡u¡
u
FFzqFFFt¡u¡
u
FFy”¡
u
Fz“¡Ft
 ^yyzyj)4!)y
lOMoARcPSD|27790909
#Y./
“
!1+6]1o"&?)()-Œ
D!1+6)<N?–/1ŒFD
Fy
!1+6)<N–Œ1/Y
F“ Fy qFFy q FyFF“ Fy qF
Fy
Fuqrmuz Fy•ymuz
BF/“FDFyFgDF FFFq q tFFFFFu “ ”FFFFFq q tFF FFFu“ym¥ Fyyym¥
FFq u uFFFF• Fu zFFFFq u uFF FF•ymyu Fqymyu
u¥rmuzF
uztm¥
F
F
y“tmyuFF
FFy FuuF
FFFo¡F
u
FyFFFŒF/
“
F
FF
FF“F
F
F”•B
F
F
FFFFyFFyzFF
Fq Fu y “F
/tB)%!1+6g
FF
F
y • u y
F
F
!1+6]1,)¡<@A)oEFF
z
F
q
"&
FFFq “ t yFF
S7?/FF"9"9"9"
yu qz
F]1F
z
"/
F
FF99
y u q
F]1F
q
+%4E
"
y
FV“™y™y™yY9"
u
FVu™y™y™yY9"FF
q
FVy™z™y™uY9"F
z
FV•™r™z™uY"
y
FV“™¥™¥Y9
u
FFVt™¥™yY9
q
FFV•™r™yY
1Y CZ!FFo"FF
y
FFFF/F o"FF
u
FFFF/F9o"FF
q
FFFF/©9o"FF
z
FF/FB
#Y C!o"FFy9o"FuF9o"FqF9o"FzFB
Y CZ!oVu™u™“™“YB
-
FqF FFuF FFy FF“
1Y FFo"FFyFFŒ³FFFyFF™FFo"FFuFF/³FFF•FF™FFo"FFqFF/³FFFFFu™FFo"FFzFF/³FF
FFFy
FFFqFF FF“FF FFFFt FFFFy
#Y o"FF
y
FFFFq
y
u
q
q
Vyy™”™uuY
o"F
u
FFFFFFu
y
•
u
Vzu™qu™y“YF
o"F
q
FFFFFF
y
u
u
t
q
V”•™¥t™ytYo"F
z
FFFFF
u
q
Vyq™yt™uYB
C)1K!>7)(TU#UC1U)B%! ”“
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Y _Vu™u™“™“Y
F¡"
yy
F¡"
uu
F¡"
qq
F¡"
zz
FF¡¡¡¡
yuqz
™ ™
™
FFVy™y™“™“Y
FoVu™u™“™“YFyBo"FF
y
FyBo"FF
u
F“Bo"FF
q
F“Bo"FF
z
FFVqy™qt™yuYB
/¥B)%%,_<@A)+$|¡
u
‘’¡,P)#?E
oVyFuY¡FFFyr yu¡Fu¡
u
™oVuFFFFF¡Y
r¡ ¡
u
™o¡F
u
FFFFz
u¡
u
CZ!!1+6]1o"&?)()-]1|¡
u
‘’"¯!+1RVoYB
-
F uF¡
u
Fr¡FyzFFFu¡
u
Fyu¡FyrF
C–#FF
F
FFuVyYooVyYFFuVYo¡o¡VYFFFFFFFyzyryur¡¡u¡Fuu¡uFFFFF¨¡VYVyYFF¡uFr¡FyzFuVuq¡
FqYF¡uF”¡FF¥u¡F
FF
F
o¡F
u
FFFFz
u¡
u
F
F
o¡F
u
FFFu¡
u
Fu¡Fz
FF
FFq F¥ zF
F^1+6]1o"&?)()-g
FF
F
u ” Fu
F
F
FF“ y FuFF
FFq F¥ zF FFq F¥ zF FFq F¥ zF
F
F
Fu ” Fu
F
FF
F
F“ y FuF
F
FF
F
“ y Fu
F
F
FF“ y FuFF FF“ y FuFF FF“ “ “FF
F+1RVoYF+1RgFuB
/rB)%H9H
F
u0HC)"oEHFH
F
,)¡<@A)B)I!),R)¬P)1
+%E
1Y o,)B #Yo%,)B Yo%,)B
-
 ^yyzyj)4!)y
lOMoARcPSD|27790909
s_o,)FRU+oF£¤FB^=!0U+oF=!!oFF=!H
F
F=!!oF=!H
F
^!o0HC%]1H
F
F!oFH
F
Fo%,)B
_o%,)F!oFH
F
F=!!oF=!H
F
F=!0U+oF=!H
F
F=!!oFF“ 0U+oF£¤FFo,)
Fo%,))1<,!)1E1Yo
,)
#Y o%,)
Y o%,)B
/y“V0u“yzyYB)%%,_<@A)+$F
q
¡,P)#?
o¡¡¡
F
yuq
™
™
FFFFF¡
y
u¡
u
¡¡
qy
™FF¡
u
¡!¡
q
™
y
FF¡
u
¡
q
F9"&
!
)1!Bˆ,P)!1+6]1o"&
?)()-]1F
q
"¯!
!
No!3%,)B-
Fy Fu yF
^1+6]1o"&?)()-]1F
q
ggE
FF
F
y y F
yF
F
FF! Fy yFF
o%,)F=!!oF=!F
q
FFq +1RgFq
Fy Fu yF Fy Fu yF
gFFF
F
F!y Fyy FyyFF
F
FFFF
F
F““
u!qFyyFFu!FF
F
FF
F
F
q
u
F
F
!
y
F
yF
u
qF
F
F
Fy Fu y F
F
F
F“ q Fu
F
FFq
q
FVu!FyY
u
F
q
F
FF“ “ qVyF!YFuVu!FyYFF
H6<+gV YFFq qVyF!YFuVu!FFyY “FFy!F“F!FFyB
/yyBCZ!,,+P+$"?R):1+$]1,!1+6E
Fu Fy “F
C)1K!>7)(TU#UC1U)B%! ”u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F
1YgFFFF¥qF“yFFF #Y/FFFFy“zFFurFF YF
F
FFFF
”
yF“
q
F
q
u
F
FFF
F“ y “F Fz F” uF
=Yp
FFF
Fz z “
F
F UYŒ
FF
F” Ft q
F
F
FFFu y uFF FF• Fr zFF
-
qFF“FFFq
1Y =UVgFFY F¥ FFyFFVFFFqYV FyYF=UVgFFYF“FF
F
FF
y

F
FFFFq"
g
VqY0+$]1g90)!]1VgFqY¡F“
F“¡
y
F“¡
u
F“
F
F
¥¡y
Fz¡
u
F“
F¡
u
Fu¡
y
F"
g
VqYF71V£y™u¤YB
F
Fz¡
y
F“¡
u
F“
FFFFy9"
g
VyYF 0VgF¡Y F“FF¥¡y
F“¡
u
F“
FF¡¡
y
™
u
FF
V“™“YF"
g
VyYF F£¤F
F
#Y ,)!W•1EFFz9"
/
VzYF71FFF
F
FF
q
u
™y
F
FF
F
FF
uFFFy “
Y=UVFFY F” FFqFqFFVFFFFyYFF
u
FzF”FF=UVFFYFFF“Fy
Fy “ FFuF
F¡
y
F¡
u
F“
H&+P+$FFy9"VyY0)!]1)FF”¡yFz¡uFq¡qF“
F
FF¡
y
Fq¡
q
F“
FF¡¡¡
yuq
™ ™ FFFFFVq™q™yY"
VyYF71£Vq™q™yY¤FF
FFy “
 ^yyzyj)4!)y
lOMoARcPSD|27790909
=Y =UVpFFYFFz zFF“FFVFFuY
q
F=UVFFYFFF“Fu
Fu y uFF
FFu¡
y
F¡
u
F“
H&FFu9"
p
VuY)!)
F
FFFFFzu¡¡
y
yFFu¡u¡
u
FF““F"
p
VuYF71
F
FF
F
FF
y
u
™y™“™V“™“™“YB
F
FF
F
FF
zFFF” u
UY =UVŒFFY F” FFtFqFFFF
u
VFyYF,+P+$FFF“9FyB
• Fr zFF
Fz¡
y
F”¡
u
Fu¡
q
F“
FFF“9"
Œ
V“Y0
F
F”¡
y
Ft¡
u
Fq¡
q
F“
F
F•¡
y
Fr¡
u
Fz¡
q
F“
FF¡¡¡
y
™
u
™
q
FFB
F
FF
yu
qq™™y
F
FFF"
Œ
V“YF71
F
FF
F
FF
yu
qq™ ™y
F
FF
F
FF
Fq¡
y
F”¡
u
Fu¡
q
F“
FFFy9"
Œ
VyY0
F
F”¡
y
F¥¡
u
Fq¡
q
F“FF¡¡¡
yuq
™
™
FFVy™y™yYF"
Œ
VyYF71VVy™y™yY¤
F
F•¡
y
Fr¡
u
Fq¡
q
F“
/yuB)%#@•<@A)oE|‘¡’
u
F|‘¡’
u
¡,P))1Eo
1F“F1¡
y
F1¡
u
u
FFF”1
“
F•1
y
Fu1
u
FFF1
y
F¥1
u
F¡FF1
“
Fu1
u
F¡
u
B
1Y CZ!,+P+$]1oB
#Y CZ!,"U%++$I]1,+P+$¯!B
-
F” • uF
^1+6]1o"&?)()-g
FF
F
“ Fy F
¥F
F
FFy “ FuFF
”FF• u
C)1K!>7)(TU#UC1U)B%! ”z
 ^yyzyj)4!)y
lOMoARcPSD|27790909
²F§gFF§F“ FFyFF¥FFVFFFFqYVFzYV FqYFFVFFFqYV
u
FzY²
y “ FFuF
F,+P+$FFFq9FFz
Fu¡
y
F•¡
u
Fu¡
q
F“
FFFq9"
g
VqY0
F
F Fz¡
u
Fr¡
q
F“FF¡¡¡
yu
™™
q
FFBV”™uF™yY
F
F¡
y
F”¡
q
F“
F"
g
VqYF71£V”™u™yY¤BF
Fr¡
y
F•¡
u
Fu¡
q
F“
FFFFz9"
g
VzYF 0
F
FFFq¡¡y
u
FFu¥¡¡q
q
FF““FF¡¡¡
y
™
u
™
q
FFBFF
F
Fu™
¥
q™y
F
FF
F"
g
VzYFF71£Vu™F¥q™yY¤B
/yqBCZ!!1+6|!) %)41g"¡,P)|g|
Fy
R)4"&
FFyz yuF
1YgFF
F
F
u“ yt
FF
H6='A)g
Fy
#Y/FF
•
F
“F
FyFF
Fy “
Y F
F
F“ y
FF“y
“F
y
F
F
yFF
Fu
=Yp
FF
F“
FF“
y
q
“
FuF
y
FF
q
FF
-
FyzFFyu
1Y
FVFFFyYV FuYF+P+$FFFy9Fu
Fu“ ytFF
o
FFy”¡y
u
Fyu¡u
u
F“
y u
Fz
™y
F
FF"
o
VyYF71F
F
F
F
”
z
™yFF
FF
FFB
FFFyF"VyY0FFu“¡Fy•¡F“FF¡¡™ FFFF” F FF
F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FFFuF"
o
VuYF71FFFF
F q
z™yFF
F
FF
F
FpFFF
F”
y
mz q
y
mz
FF
F
)Z
p
Fy
FgpF FFF
Fy
“ u
“
FF
F
BF
#Y pFFFFyyyq“FFFF)ZpFyF/pF FFF
F
y“ F“yFFFB
F
Fy “ “F FyFF“ “F
Y F
F
F“ y y
F
FF§FF§F
F
F“ yFFyF
F
FFFFFV FyYV FuY
FF“ y yFF FF“ y yFFFF
F,+P+$FFFF“9Fy9Fu
FFFy9"
VyYF71£Vy™“™“Y¤
FFF“9"
V“YF71£V“™y™yY¤F
FFFu9"
VuYF71£V“™y™yY¤
F“ y “F F“ “ “F
FpFF
F
Fy “ y
F
F)Zp
Fy
FpFF
F
F“ y “
F
F
FFy “ yFF FF“ “ uFF
uFFy FF
=Y §pFF§F“
qFFyFFVFFFqYV
u
FuY
“ “ qFF
FFFq9"
p
VqYF71£Vy™y™“Y¤
FFFu9"
p
VuYF71£Vy™“™“Y¤
p%p)`41u"U%++$CC$pR):) %)41B
V
p
Fy
gp
F
D
4=) %)41FgpDpFBB
Fy
Fg

FpDpDB
B
Fy
9
=1) %YB
/yzB^1+6g45="&!1+6) %R):•@49¯!!1+6) %4E
FFy z FuF F” “ “F F“ “ “F
C)1K!>7)(TU#UC1U)B%! ”•
 ^yyzyj)4!)y
lOMoARcPSD|27790909
1Yg
FFF
Fq z “
F
F #Y/
FF
Fy ” “F
F
Y
FF
F“ “ “
F
F
FFFq y qFF FF“ y ”FF FFq “ yFF
-
1Y §gFF§FFVFFyYVFFuYVFFqY
FFFFy"
g
VyYF71£Vy™y™yY¤
FFFFu"
g
VuYF71FF
F
F
u
q™y™y
F
FF
F
FF
FF
FFFFq"
g
VqYF71FFFFF
Fyq
zz™ ™yFF
F
FF
F
Fy “ “F
Fg) %)419!1+6) %p
FF
F
“ u
“F
F
B
FF“ “
qFF
#Y §/FF§FFFVF”Y
q
FFF”9"
/
V”YF71£V“™“™yY¤
F/R):) %)419IR):5!1+6) %5="&/BY§
FF§FFFF
u
VFyY
FFF“9"

V“YF71FFFV“™y™“Y™FF
FF
q
y
™“™yFF
F
FF
F
FFFy9"

VyYF71£V“™“™yY¤
F“ “ “F
F) %)419!1+6) %)41
p
FF
F
“ “
“F
F
FF“ “ yFF
/y”BCZ!??]1F
q
N!1+6]1oEF
q
FF
q
4=) %+%4
1Y o¡¡¡F
yuq
99 FFFu¡
y
F¡
u
F¡¡
qy
9 Fu¡
u
F¡¡
qy
9 F¡
u
Fu¡
q
FB
 ^yyzyj)4!)y
lOMoARcPSD|27790909
#Y o¡¡¡F
yuq
99 FFFu¡
y
F¡
u
F¡¡
qy
9 F¡
u
9F¡
y
F¡
u
Fu¡
q
F
-
Fu y yF
1Y ^1+6]1o"&?)()-]1F
q
g
FF
F
y u
yF
F
FFy y uFF
Fy “ “F FFy Fy yF
) %)41gpE
Fy
FgpF
FF
F“ y “
F
F"&p
FF
Fy “ y
F
F
FF“ “ zFF FF“ y yFF
F? ¯!£Vy™yF ™“Y™Vy™“™yY™Vy™F y™yY¤B
Fu Fy FyF
#Y ^1+6]1o"&?)`)-]1F
q
/
FF
F
y Fy
“F
F
FFFy y uFF
Fy “ “ F Fu Fy Fy F
) %)41/pE
Fy
F/pFF
F
F“ yF q “
F
F9pFF
F
y FFu q FFu q
F
F
FF“ “ yF qFF FFy y y FF
F? ¯!£Vu™y™yYEVu™FFFu q™yY™Vy™FFFuq™yY¤B
/y•V0u“ytuYB)%%,_<@A)+$F
q
¡,P)#?Eo
Vy™u™FyYFVz™Fu™F•Y9oVy™y™uYFV”™”™“Y9oVy™“™“YFVy™u™yY
1Y CZ!!NFV•™Fq™!YF!VoYB
#Y CZ!,,+P+$"" +$]1oB
-
1Y F!oFF71£Vz™Fu™F•Y™V”™”™“Y™Vy™u™yY¤
Fz¡
y
F”¡
u
F¡
q
F•
F2
F
FFu¡
y
F”¡
u
Fu¡
q
FFq4)!
F
FF•¡
y
F¡
q
F!
C)1K!>7)(TU#UC1U)B%! ”¥
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F24)!Fz!Fq•F“F!FFr)1<F!oF!FFrB
Fy y yF Fz ” yF
#Y C14F
F
FF
oU
FF
y
FF
Œ
FF
oU
FF
u
FF
Œ
F
F
oU
FF
qŒ
F
F
FF
F
FF
u y
“
F
F
FF
F
F
u ”
u
F
F
+%4Œ?
FFFy u “FF FFF• “ yFF
)()-]1F
q
9ŒFFUUU
yuq
™
™
FB
Fz ” yFFy y yF
Fy
Fy u yF
F^1+6]1o"&ŒgFF
F
Fu ” u
FF
FFF
y “F
F
FF
F
uFy u
F
F
FFF• “ yFFFFFy u “FF FFy Fq yFF
yFFu y
C14§gFF§ Fu FFyFuFFFF
u
V FyYFC+P+$FF“9FFy
y Fq yFF
FFF“9"
g
V“YF71£Vy™“™yY¤F
FFFy9"
g
VyYF71FFF
F
FF
F
u
q
™
F
u
y
™y
F
FF
F
FF
/ytB)%oEHFH%,_<@A)B_o
u
FooEHF FH4,+P+$F
u
B
)I!)+—!3+%u,+PF)%SFF,+P+$]1oB
-
1#%,"E^1+6g#@g
u
4+P+$F
u
B
 )I!)g4+P+$F)%-FFB
C14E=UFg
u
FF
u
FF“ F§gFF§B§gFF§F“
F§gFF§“F
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FF
§gF
F
§“F
Fg4+P+$F)%-FFBV7!Y
F
FFq y uF
/y¥V0u“y•yYB)%,)¡<@A)o|¡E
u
‘’F|¡
u
‘’4!1+6g
FF
F
• “ Fq
F
F
"&
FFFy“ u
•FF?)()-Fy99¡¡
u
F]1|¡
u
‘’B
1Y C()oFyF¡F¡
u
FBCZ!
!
N"FyF¡F!¡
u
)30U+oB
#Y CZ!!3?]1|¡
u
‘’N!1+6]1o"&?44=) %B
-
FFy FFq y uFFFy F“F
1YF
F
oFyF¡F¡
u
FF
F
ŒFgF
FF
FF
yF
F
F
• “ Fq
FFF
FFF
FyF
F
F
q
F
F
FoFyF¡F
¡
u
FFq¡Fu¡
u
FFFFyFFFy“ u•FFFFFFyFFFuFF
FyF Fu!FzF“
"FFy ¡F!¡
u
F0U+oFoFyF¡F!¡
u
FFFFg
FF
F
F
y
F
F
FFFFF
F
q!F•F“F!FFuB
FF!FF
F
F•!FyuF“
F“ “ “F Fymu ymu ymzF
#Y) %)41gEp
Fy
FgpF
FF
F“ y “
F
F"&p
FF
F
F
ymu “ Fqmz
F
F
FF“ “ uFF FF y y y FF
F? ¯!F
FF
F
y
u
™
F
u
y
™y™
FF
FFFF
y
u
™“™y™FF
FF
FF
y
z
™
F
z
q
™y
F
FFFF
F
B
FF
/yrB)%g!1+6R())&!F9/!1+6R())&F7B)I!)+—+1RVg/YF
!£+1RVgY9+1RV/Y¤9"%++1R VgYF)]1!1+6gB
-

g9/!1+6]1o9²"&S7?I
C)1K!>7)(TU#UC1U)B%! •“
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F!VoFYF!oF+g/V YF=!!Vo´YF=!!oF+gV Y
F0U+F0U+VoFYF=!!VoFYF=!!
V=%=!F=!!F=!0U+F=!!VoFYF=!0U+VoFYY
F+g/V YF+/VY
 ^yyzyj)4!)y
lOMoARcPSD|27790909
2€•HBp‚DLCxƒC„29p‚CLh|2€•902egŒpŒ9
€^ŽC/…2g
/yB)%o=%<@A)+$R):1" q)H4!1+6"&?
Fy Fy “F
/FF
yu
99
q
Fg
FFF
F
u “ F
uF
F
B)%)EHFH,)¡<@A)4!1+6"&?
FFq z ”FF
FFy y yF
//
FFF
FqFzu
F
FB
FFyFu
FqFF
1Y ˆ,P)oF
yq
™ F™oF
y
F
u
F
q
9u
y
Fq
u
F
q
F
#Y )I!),)¡"V9YFo)"V9VYY=%<@A)+$HBCZ!!1+6]14
"&?/9
-
1YoF
yq
9FF“
oF
y
F
u
F
q
9u
y
Fq
u
F
q
FFuoF
yy
9FFqoF
yu
9FFoF
yq
9FFuoF
uy
9FFqoF
u
q
9 F
FoF
uq
9FFuoF
qy
9FFqoF
qu
9 FFoF
qq
9 FFyz

#Y0N!)IFFF
y
F1"
u
9
y
F#"
u
FFF1"F
yy
9FFFF"F
yu
9FFF1"F
uy
9
FFF#"F
uu
9F"V9YFo)"V9VYYF)‘’
F
C
Fg)"F‘VY’
F
F‘’
F
C
Fg/"FF§§
F
g/FF^1+6]1"&?Fg/B
/uB)%=%<@A)+$|¡
u
‘’¡,P)#?oV7¡VY9O¡VYYF7VyYVuYO BCZ!!1+6"#N
)I]1o"&?)()-B
-
C)1K!>7)(TU#UC1U)B%! •u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
oVy9yYFy™oVy9¡YFu™oFy9¡
u
FFz
o¡V9yYFy™o¡¡V9YFu™oF¡¡9
u
FF
zo¡F
u
9yFFy™o¡F
u
9¡FFu™o
¡F
u
9¡
u
FFz
Fy u zF
^1+6]1o"&?)()-
F
Fy u
zF
F
FFy u zFF
o1¡Fy
u
F#¡
y
F1¡
y
9
u
u
F#¡
u
F
u
FFz11
yu
Fu1#
yu
F1
yu
Fz#1
yu
Fu##
yu
F#
yu
Fz1
yu
Fu#
yu
F
yu
B
/qBC+$F
q
)%,=%7)F4#N)I.13E
FyF¡¡¡yuq9 9 FF¡yuF”¡uuFz¡quFu¡¡yuFz¡¡yqBFuF¡¡¡yuq9
9 FF¡¡yuFz¡¡yqF¡¡uqB1Y/—7)7),71+1U91
=%7)"=)()-B
#Yˆ ¡U!,=%7)¡,P)=9¡,P)•!R):•-

sTyFFF¡yu”¡uuz¡qu“Fu¡¡yuFz¡¡yq
FFF¡yuFu¡¡yFuFu¡qFFF¡uFu¡qFuFFFFF”¡uuFz¡quFF¡uFu¡qFuFF
FF¡yFF¡uu¡qFuFFz¡uuFF¥zqu ¡¡uqFFF¡yF¡uFu¡qFuFFu¡uF¡qFuFr¡quF<yuF<uuF<qu
<
y
FFF¡
y
¡
u
u¡<
qu
9 Fu¡
u
F¡<
qq
9 Fq¡
q
FT
y
R):¡,P)=9R):¡,P)•!
sTuF¡¡yuFz¡¡yqF¡¡uq
 ^yyzyj)4!)y
lOMoARcPSD|27790909
S¡
y
FF<
y
<¡
uu
9FF<
y
<¡
uq
9F<
q
FT
u
F<
y
u
F<
u
u
F
z
F<
y
F<
u
F<
q
FF<
y
F<
u
FF<
q
F<yuF<yFz<qF<qFF<uuFz<<uqF<<uqF<yuF”<<yqF<uuFq<<uq
FFFF<yF ”u<qFFFuFFFF<uF uq<qFFFuFz<qu
FyuFuuFquFFFyF<yF ”q<q™uF<uF qu<q™qFz<qFFF
FT
u
R):4=8¡,P)B
/zBˆ,P)1,=%7)¡,P)=E
1Y ”¡
y
u
FF¡
u
u
1¡
q
u
Fz¡¡
yu
Fu¡¡
yq
Fu¡¡
uq
B
#Y u¡
y
u
FF¡
u
u
q¡
q
u
Fu1¡¡
yu
Fu¡¡
yq
B
Y Y¡
y
u
FF¡
u
u
”¡
q
u
Fu1¡¡
yu
Fu¡¡
yq
Fz¡¡
uq
B
-
F” u FyF
1Y ^1+6]1o"&?)()-g
FF
Fu y F
yF
F
FFFy Fy 1FF
” u
FF
y
”9FF
u
Fy9FF
q
§g§F1Fu
u y
FT¡,P)=F1Fu
Fu 1 yF
#Y ^1+6]1o"&?)`)-/
FF
F
1 y
“F
F
FFy “ qFF
FF
y
u™FF
u
uF1
u
™FF
q
qFFuF1
u
FFFy ”Fq1
u
F
FT¡,P)=
FF
F
u
F
F1
u
u
F
F
“
“F1
u
F”
qFFq
y”
F1F q
y”
B
C)1K!>7)(TU#UC1U)B%! •z
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FF” q1
Fy 1 FyF
Y ^1+6]1o"&?)()-
FF
F
1y
uF
F
FFFy u ”FF
FFFFFFFFF
y
y™
u
y1
u
™
q
”1
u
z1
F
u
FT¡,P)=
F
FFFFyFF”11
u
F
F
z
“
1
F
“
F
F
F
FFFFFFFFyz
q
1
1
y
“
FFFF
”
z
1“B
F
/”B)%=%<@A)+$F
q
¡,P)#?E
FF¡¡¡
yuq
9 9 FF9<<<
yu
9
9
q
FFFu¡<
yy
F¡<
yu
F¡<
uy
F1¡<
uu
Fu¡<
uq
Fu¡<
qu
Fq¡<
qq
V1)1!YBCZ!!1+6]1=%<@A)+$"&?)()-]1F
q
"¯!
R]11N=%<@A)!3A)":)&+$F
q
B
-
Fu y “F
^1+6]1=%<@A)›)%"&?)()-F
q
g
FF
F
y 1 F
uF
F
FF“ Fu qFF
p%<@A)+$A)":)&@4¡,P)=
FFF
y
u™FF
u
u1FFFy™
q
•1FyyF
Fu1FFy “
yy
FFF•1FyyF“F1F •
/•BC+%F
q
+1#P!3=%<@A))1E
Fz u FyF
 ^yyzyj)4!)y
lOMoARcPSD|27790909
o¡<V9YFF¡¡
y
9
u
9¡
q
FFg<<
y
9
u
9<
q
F
"&Eg
FF
F
u q
zF
F
"¡FF¡¡¡
yuq
9
F9<FF<<<
y
9
u
9
q
FBˆ,
FFFy1
u
u1FF
P)1NoV¡9<Y!3A)":)&+$F
q
B
-
o¡<V™YyA)":)&+$F
q
Fo¡,P)=VyY
^FFFFFFF
y
z™
u
¥™
q
y¥1
u
FFy•1yy
F
$VyYFF1uFzu F1FF
FFy¥1Fy•1FyyF“
H6<R):51)š1!›B
/tB_H0HC)"&?/FFU9U9
yu
F9U
FBH&9"," ]1H141UF
y
y
F1U
uu
FFF1U"#U

™F
yy
F#U
uu
FFF#U

BS
"F9FF1#
yy
F1#
uu
FFF1#

1Y )I!)FF"9 !3A)":)&+$HB
#Y ‡7=')%+-)7HFF
q
9"&U
y
FVy™“™yY9U
u
FVy™y™yY9UF
q
FV“™y™yY9FVu™y™uY9"F
F FVu™“™”YBC()FF9"B
Y ‡7=')%+-)7HF|‘¡’
u
9"&/FFy™¡™¡
u
F9FuFq¡9"
u
F•Fq¡Fq¡
u
BC()F"9FB
=Y ‡7=')%+-)7HF|‘¡’
u
9"&/FFyF¡™u¡™¡F¡
u
F9FuFq¡9"
u
F•Fq¡Fq¡
u
BC()
F"9FB
-
1Y0N!)IEFF"9FFF"9F
j FFFF
y
F"
u
9 F "
y
9 F "
u
9
j F9FF“F"F9 FF“FFFB
#Y /
“
F£Vy™“™yY™Vy™y™yY™V“™Fy™yY¤y?]1F
q
‘’
M
“
F/
“
y
F‘’
Œ
F/
“
y
!1+6)<N?–Œ1/
“
F
C)1K!>7)(TU#UC1U)B%! ••
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Fy y “FFuF FyF
F
F
F“ yy
FF
FFFFy
F
FFF
F
Fq
F
FFF111
y
™
u
™
q
FFVy™q™FyY
FFy FyyFFFFFuFFFFyFF
CW
F###
yuq
™ ™
FFVu™”™tYFF"9FFF•
FFu F•F
Y ‘’
/
F
FF
FF“™‘’"
/
FF
F
Fq
F
FFF"9FFu•FF“BVqYF FFFqVqYFq
FFFFq FFFqFF
Fy “ “FFFu FuF F•F
=Y ‘’

F
F
Fy u y
FFF
FFFF“F
F
F”
F
F9‘’"

FFF
F
qF
F
FF"9FFuB•FFF”VqYFFVqY
u
F•
BFF“ “ FyFFFFFFq FFFqFFFFFqFF
/¥Bˆ R):1|‘¡’
q
B0N!+1,=FF79O147)A)":)&)1<R):•
1Y F79OFF7V“YOV“YF7VyYOVyYF7VuYOVuY
#Y F79OFF7V“YV“YO F7VyYOVyYF7VuYOVuYF7VqYOVqY
Y F7O9FFF
y
7¡O¡=¡VYVY
Fy
C+%+-)7A)":)&A)FF79O"&7FFuq¡”¡F
u
F¡BO
q
FFFz¡q¡
u
Fu¡
q
-
1Y F779FF7
u
V“YF7
u
VyYF7
u
VuYF“
F779 FF“F7V“YF7VyYF7VuYF“
).7¡¡FVFyYV¡FFuY|¡
q
‘’)Z7F“"F779FF“
FF7O9FR):A)":)&
#Y 4A)":)&F7O9 FFFO79F
FF7
y
F 7
u
9OFF7O
y
9 FF7
u
9O
F779 FF“™FR)F7˜“Y
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F y
u
VY FF“ 7¡VYF“Y
Y 4A)":)&V7¡=¡
Fy
H&7FFuq¡F”¡
u
F¡O
q
™FFFz¡q¡
u
Fu¡
q
F7O9FF¥FyuF¥“FqtzFztz
F7O9FFFF
y
yFuFq¡F”¡
u
F¡
q
FFzF¡Fq¡
u
Fu¡
q
F=¡F
yz••
y“”
B
/rB)%HR):1Œ=UB)I!)E
1Y µF"µµ
u
FF"µ
u
FuFµµµµ
u
F"
u
FB
#Y F"FµF"µµµµµ
u
F
u
F "
u
99"F FHB
-
1Y
µF"µ
u
FFF "9FFFF" 9FFF""9FFFu"9F
Fµµµµ
u
F"
u
FFu"9Fµ"Fµ
u
FFF""9FFFF9FFF""9FFFu"9FFµµµµ
u
F"
u
F
Fu"9F
FFµ"µµ
u
F"Fµ
u
FFuVµµµµ
u
F"
u
F
#Y
µ"FµµµµµF
u
F"
u
FFu"9F
F"FF"9FF“Fµ"FµµµµµF
u
F"
u
E7!
/y“B)%?/F£Vy™y™FuY9Vu™“™yY9Vy™u™qY¤+%R):1F
q
"&A)":)&)()-B
C+W)¶)41+1!jD)!=?/N)?+W)¶/
F
"¯!.13]1" F
V”™¥™•Y"&?/
F
B
-
C)1K!>7)(TU#UC1U)B%! •¥
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F
FymF
F
y u q
F
C
F
y y• ty
C
F
FF
‘’
{
FF 9 9 9 FF FFFy•m ”F
F • ” •uF FF
FFtymFF
/yyB)%F
z
"&A)":)&)()-B)%
y
FV•™q™q™•Y9F
u
FV”™y™q™FyYBCZ!?+W
)¶]1R):1)#?F
y
9
u
FB
-
y
FV•™q™q™•Y™F
u
FV”™y™q™FyY
"yFyFFFu™y™Fy™uFFyFy“
y“y“y“F
"uF"uF""uy9 yFV”9y9q9FyYFy•9FF u9 y 9Fy9 u FF
y“F y“ y“ y“ y“F
FF
F
r”
9
F”q
9
F”t
9
F”yyF
F
F
F
"
u
F""
u
u
FFF
F
u•”u•”u•”u
•”r
9
Fq
9
Ft
9
FyyF
F
F
F
F/FFFFF u 9 y 9Fy9 uFFFF™ r 9 Fq 9 Ft 9FyyFFFF
FF y“ y“ y“ y“FFu•”u•”u•”u•”FF
•
•u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
F71/F71F
y
9
u
FB
/yuBC+%|‘¡’
u
P))·1A)":)&F79O
FF
FF
y
y7V¡YOV¡Y=¡"&79OF|‘¡’
u
B
1Y C+W)¶)%,+1!jD)!=?/FFy™¡™¡
u
FN)6?+W)¶gB
#Y CZ!‘+’
g
#@+FuFq¡Fq¡
u
-
1Y S"
y
Fy9"
u
F¡"9
q
F¡
u
F¡F“B
y
F
¡F
u
F
#Y ‘’+
g
F
F
FF
+9
y
+9
u
+9
q
F
F
C
FgFF
y
9
/yqBCZ!)Z))@+W1%]1" $R):1)#?" "E
1Y FVy™q™Fu™zY9"FVu™Fu™z™”Y
#Y FVz™y™u™q™qY9"F FFVy™u™”™y™F zY
-
1Y TyFF"9FF"F ¥Vu9u9z9F ”YFFF y•zr9Fzry•quz“9zrzr9 FFF
F""9F zr F
#Y TuFF"F""99FFF"FFzt”VyF9u9”9y9F zYFFFFztzt”9y“9Fztu”9ztF”9Fztu“FFFB
C)1K!>7)(TU#UC1U)B%! t“
 ^yyzyj)4!)y
lOMoARcPSD|27790909
/yzB)%R):1F
q
"&A)":)&)()-"," FVq™u™yY9F "
y
FVu™u™yY9"
u
F
Vu™”™zYBSkF
71
F""
yu
9
FBˆ,P))Z))@+W1%]1" $R):1kB
-
sC+W)¶)41F""
yu
9
F
yF""yyFFFFuuyqqq9 9 FFF
u
F"
u
F"
u
9
yy
FVu9”9zYF•F
F
FF
uuy
qqq9 9FF
F
FFVu9y9uYF
u
F
F
FF
F
q
uyu
9qq9
F
FF
s.T)Z))@]1$kF71F""
yu
9F
FTF9
yy
F9
u
u
F
F
FF
uuy
qqq9 9
F
FFFFVuYFF
F
F
F
q
uyu
9qq9
F
FF
FVu9“9FyY
/y”V0u“y•yYBC+%R):1F
q
"&A)":)&)()-9)%," FVy™u™FyY9"F
Vq™•™qY"S2FFTFF
q
∣TFF
1Y CZ!!3?+W)¶]1R):12B
#Y CZ!)Z))@+W1%]1"$R):12
-
1Y TF2FT
y
FuT
u
FT
q
F“VFT9FF“Y
FFT 1Vy9“9yYFF#Vu9y9“YFF2 71£Vy9“9yY™Vu9y9“Y¤F
"yFVy9“9uyYFFFFyu9“9yuFFF
²
"
u
FFVu9y9“YF uVyYFF
F
FF
y
u9“9
y
uFF
F
FFVu9y9“YFVy9“9yYFFVy9y9yY
u
FF
y y yF
F""
y
9
u
Fy?+W)¶]12
F"F
F
9 9
F
F/F
F F
q q q
 ^yyzyj)4!)y
lOMoARcPSD|27790909
#Y )Z))@+W1%]1"$2"VFVq9•9qYYF"""9
yy
F""9
u
"
u
Fqu
F
F
FF
y
u9“9
y
uFF
F
FuqF
F
F
F
q
y
9
y
q9
y
q
F
FF
FVy9u9”YB
/y•BC+%F
”
"&A)":)&)()-)%," "
y
FVy™y™“™“™“Y9"
u
FV“™y™y™u™yY9"F
q
FVu™q™y™u™F yYB.HFF¡FF
”
∣¡F"9
Fy™u™qF
1Y )I!)HR):1" %]1F
”
B
#Y CZ!=!HB
-
F¡
y
F¡
u
F“
C14E¡FHF¡"9

F“9Fy9qF
F
F¡
u
F¡
q
Fu¡
z
F¡
”
F“
F
Fu¡
y
Fq¡
u
F¡
q
Fu¡
z
F¡
”
F“
F¡FFF¡¡¡¡
u
9
u
9
q
9
z
9F¡
u
F¡
q
Fu¡
z
F
F¡
u
VyF9y9“9“9FyYF¡
q
V“9“9y9“9yYF¡
z
V“9“9“9y9FuY
F=!HFqB
.H0HC%]1F
”
EFFFFF""R"yuF9yF
F
FF
HR
H
9
F
FF
""
B
yF9F""uF9F“F "yFF""uF9 F“F"yFF"uF
FH
/ytB)%HR):1Œ=U
)9H
y
R):1%
!
)]1HB.H
u
FF¡FH
¡ ∣ F"9FF"HB
y
F
1Y )I!)H
u
R):1" %]1HB
#Y )I!)H
y
"H
u
#¢)1B
Y CZ!=!H
u
B
-
1Y )I!)E1#9FH
u
FF1H9FFF#H9FFFF“"H
y
FFF1#"9FF“F1F#FH
u
1FHR
u
9FF
FFR1H9FFR1HF9FFFF“"H
y
FR1FH
u
C)1K!>7)(TU#UC1U)B%! tu
 ^yyzyj)4!)y
u
lOMoARcPSD|27790909
FH
u
0HC%]1H
#Y ˆ /
y
FF¡¡
y
9
u
9F9¡
!
F?+W)¶]1H
y
/•!F"U%+N%?+W)¶]1HF¡¡
y
9
u
9F9¡¡
!
9
!Fy
9F9¡
F
SkF71F¡
!Fy
9F9¡
F
jTkF FTFFF

¡

FT¡9

FFF“ y9!FTHF
u
FkFH
u

!
FF
"FH
u
F"FFF

¡
B^"¡9

FFF“ y9!FFFFF
y9!
Fy
F"FFF

F¡

F"FkFH
u
Fk
!FFy
p%"6<kFH
u
9$HH
y
9
u
#])1
0)4=>)8<=!H
u
FF!B
/y¥B) %)%,+W1%,!1+61
Fy “ “F Fy Fy “F Ft Fu “F
1YgFFFF““ yy yyFFFF #Y/FFFFFuzt uztFFF YFFFFFF
“y “y y“FFFF=YpFFFFFF“u •u ”uFFFFF
-
Fy “ “F
1YgF
F
F“ y y
F
FF§ gFF §F FFFV
FyYVFFuYFF“ y yFF
j FF“F"gV“YF71£V“™y™yY¤F F"U%++$EFFF“9Fuy9yFFF
 ^yyzyj)4!)y
lOMoARcPSD|27790909
j FFFy"
g
VyYF71£Vy™“™“Y¤F"U%++$EVy™“™“Y
j FFuF"gVuYF71£V“9y9yY¤F"U%++$EFFF“9yu9yuFFF
F Fy yF F y yF
C14q"U%++$+W)¶FF“9 u9 uFF™Vy™“™“Y™“9FF u9 uFFœ"&,+P+$“9y9u
F“ “ “F F “ y “ F
F|g|
C
F
F
F“ y “
F
F"4|FFF
F
ym“ym u
F
F
FF“ “ uFF
F
F
ym“ ym u
F
F
FFt uzF
#Y/FF
uz t
FFF‘/FFFF’FV
Fu”Y
F
j FFu”14"U%++$+W)¶EFFF””qz9 FFFB
j FFFu”14"U%++$+W)¶
F
FF
F
”
zq
9
”
FF
F
C Fu” “F Fqm” Fym”F
F|/|FFF“ Fu”FF"&|FFFzm” qm”FF
F“ “ “F FFym u “ Fym FF
Y ||C FF
F
FF““ y“ “uFFFF"?|FFF
F
F
ym“u y“ ym“uFFFF
Fq “ “F FFymq umq FumqF
=Y |p|
C
F
F
F“ • “
F
F"&|FF
F
Fumq ymq umq
F
F
FF“ “ rFF FFumq umq ymqFF
C)1K!>7)(TU#UC1U)B%! tz
u
u
u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
/yrB1=%7)"=)()-#—7)7),7+W1%
1Y ¡yuFFF¡uu ¡quu¡¡yu
#Y t¡
y
u
F•¡
u
u
F”¡
q
u
Fz¡¡
yu
Fz¡¡
uq
-
1YSo¡VYF¡
y
u
F¡
u
u
F¡
q
u
Fu¡¡
yu
Fy y “F
^1+6]1o"&?)()-F
q
gF
F
F
y y “
F
F
FF“ “ yFF
C14§gFFFFFFF§VFyYVFuY
FFF“F"
g
V“YF71£Vy9y9“Y¤F 9+W)¶)41
F
F
Fy
9
y
9“
F
F
F F
FFFFy "
g
VyYF71£“9“9y¤9+W)¶)41V“9“9yY
FFFuF"
g
VuYF71£y9y9“¤9+')¶)41
Fy
9
y
9“
F
F
F
F“ “ “F FFym“ ym F
p%"6<|g|+FFFFF““y““uFFFF"4|FFF
F
F
F
ym“ y“ ym“ FFFF
21<o¡VYF<uuFu<¡qu‘’/FF<y <u <qFC9/FFFFFFy9y9“™V“9“9yY™FFFFy9y9“FFFF
u u
F
F
u
u
F
u
u
u u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
FF F F
FF#YCW•1o¡VYFq<
y
u
F•<
u
u
Fr<¡
q
u
‘’
/
FF<<
y
9
u
9<
q
F
C
9/FFFF
F
FF
F
q
y
9
F
q
uu
9q
FF
FFFF™
uyu
qqq9 9
FF
FFFF™
F
q
uuy
9qq9
F
FF
F
FFB
/u“B)6=-%7)¬1E
1Yu¡
u
Fz¡<<F
u
FF¥ “B #Y¡
u
Fu¡<<F
u
F¥¡<FF“B
Yyy¡
u
Fuz¡<Fz<
u
Fy”“FB =Yu¡
u
Fz¡<F”<
u
FuzB
-
u u
Fu FuF
1Y p%7)TFu¡Fz¡<F<4!1+6gFFFF
u
F
y
FF
C
FFu “F Fym ” Fum ”F
) %)41+W1%gE|g|FF
“ q
FF9|FFFF
um ” ym ”
FFF
F
FF¡ Fym ” Fum ”FF¡
F
F
SFFFF<FFFFum ” ym ”FFFFFF<FFF
F|)+Z)-%EFu¡
Fu
Fq<
Fu
F¥F)<7U+#%
u u
Fy yF
#Y p%7)TF¡Fu¡<F<4!1+6gF
F
F
y y
F
F
C
Fu “F Fym u Fym uF
) %)41+W1%gE|g|FFF
“ “
FF9|FFFF
ym u ym u
FFF
FF¡ Fym u Fym uFF¡
F
F FuFr¡FFt<FF“F71+1#%
SFF<FFFFym u ym uFFFFF<FFFF|)+Z)-%E¡ u
u
FF
Fyy yuF
C)1K!>7)(TU#UC1U)B%! t•
u u u u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Y gFF
yu z
F
F
4u'+$u“9F”
F
F4)N1%7)yy¡
u
Fuz¡<Fz<
u
"u“¡
Fu
F”<
Fu
F
|)+Z)-%Eu“¡
Fu
F”<
Fu
Fy”F“F)<7U+#%
=Y Vqy¥Y¡
Fu
FVqF ¥Y<
Fu
FuzFU7UB
/uyB)6=,!S#6u1E
1Y ¡
y
u
FFF¡
u
u
¡
q
u
u¡¡
yu
FzB
#Y ”¡
u
F<
u
FF{
u
•¡<Fu¡{Fu¡<FyB
Y u¡
y
u
Fu¡
u
u
Fq¡
q
u
Fu¡¡
yu
Fu¡¡
uq
Fy•B
-
Fy y “F
1Y ^1+6]1=%7)"&?)()-gF
F
Fy y “
F
F
FF“ “ yFF
) %)41+W1%gE|g|FF
C
FFF
F
“““
““u
F
FFFF9|FFFFFFFFyymm“ y““yymm“uuFFFFFF
F¡yuF¡uuF¡quFu¡¡yuF¡uFuFu¡qFu
F|)+Z)!S%E¡
u
Fu
Fu¡
q
Fu
FzFU7%=B
F” Fq yF
#Y ^1+6]1=%7)TF”¡
u
F<
u
F{
u
F•¡<Fu¡{Fu<{Fyg
FFF
F
q y Fy
F
F
B
FFy Fy yFF
4u+P+$FFF
y
9
u
9
q
)!]1FFFF
q
t
u
FFz “
) %)41+W1%g1=%7)"=TFFFF
y
¡
Fu
F
u
<
Fu
F
q
{
Fu
F|)+Z)!S%FFF
y
¡
Fu
F
u
<
Fu
F
q
{
Fu
FyF2<7U+#%%=y FFF
y
9
u
F“9F
q
F“FB
u
u
 ^yyzyj)4!)y
lOMoARcPSD|27790909
Fu Fy “F
Y g
FFF
F
y u Fy
F
F
4q+P+$FFF
y
9
u
9
q
F“)!FFFFF
q
t
u
FyzFFt “
FF“ Fy qFF
F|)+Z)!S%FFF
y
¡
Fu
F
u
<
Fu
F
q
{
Fu
Fy•FU7%=B
/uuB)%w¡9¡9¡F
y u q
FFr¡
y
u
Ft¡
u
u
Fyy¡
q
u
F¥¡¡
yu
F¥¡¡
yq
BCZ!
y
uFFF^1¡
u
u
q
uy•w¡9¡9¡FyuqF9¡^¡
y
uF^u
u
FF¡
q
uy•F¡9¡9¡yuqFBH&,+P%)Zw
¡9¡9¡FyuqF!1¡9!B¡¡¡
-
Fr Fz zF
gFF
F
Fz t “
F
F!1+6]1w"&?)()-
FFz “ yyFF
Fq “ “F Fumq ymq umqF
) %)41+W1%g|g|E
+
F
F
F“ r “
F
F9|F
F
FumqFumq FymqF
F
FF“ “ y”FF FFFymq Fumq umqFF
F<
y
F F¡
y
F
FwFq<yuFr<uuFy”<qu"FF<uFFF|FyFFF¡uFF
FF<
q
FF FF¡
q
FF
^|+W1%F¡¡9FFF|<|<9FFV|<|<<||<<<YB
C
F
C
B
C
BBF
C
BFF<<9FFF¡
u
FF<
u
Fy•F
qBy•FFwy”By•
FFz FF“
!wFqBy•F¡F|B“
FF
FF9!1¡wFy”By•F¡F|B“
FF
FF
FFFF“ FFFFz
/uqB)%g9/,!1+6":¡I8748,,+P+$=B)I
!)g/F;48,,+P+$=B-
ˆ o™u=%7)I"&!1+6g/9 V"&?)()-Y
C)1K!>7)(TU#UC1U)B%! t¥
 ^yyzyj)4!)y
lOMoARcPSD|27790909
p%g9/":9¡I8748+P+$=Fp%7)o9 I
¡,P)=B
FFo ¡,P)B^gF/!1+6]1oF"&?)()-FgF/
48+P+$=V7!YB

Preview text:

LỜI NÓI ĐẦU

Cuốn tài liệu “Giải đề cương Đại số” được sưu tầm và biên soạn lại với mục đích hỗ trợ các bạn sinh viên trường Đại học Bách Khoa Hà Nội có nguồn tài liệu học tập chất lượng, phục vụ cho việc ôn tập cũng như luyện thi dễ dàng hơn ở học phần Đại số tuyến tính.

Cuốn tài liệu này được biên soạn lại bởi đội ngũ Tài Liệu HUST với các nguồn tài liệu:

  • Đề cương Đại số tuyến tính – Viện toán ứng dụng và tin học
  • Các tài liệu được chia sẻ trên group Hỗ trợ học tập đại cương – ĐHBKHN
  • Các tài liệu được chia sẻ trên group BCORN – Hỗ trợ sinh viên Bách Khoa

Để có thể học tập hiệu quả hơn và có định hướng học tập rõ ràng hơn bạn có thể tham khảo khóa học Đại số hoặc các khóa học khác tại website: Bcorn.org (Trực thuộc phòng CTSV)

Gi

ả

i đ

ề

cương Đ

ạ

i s

ố

MI1141

-

nhóm ngành 1

lOMoARcPSD|27790909

Trong quá trình nhóm biên soạn tài liệu cũng không thể tránh được hết tất cả những sai sót hay nhầm lẫn nên nhóm rất mong nhận được phản hồi của các bạn để tài liệu này càng hoàn thiện hơn, có ích hơn với các bạn sinh viên. Mọi đóng góp bạn có thể gửi cho nhóm qua các địa chỉ email: tailieuhustgroup@gmail.com

MỘT SỐ KÊNH THÔNG TIN CỦA TÀI LIỆU HUST

  • Website: https://tailieuhust.com/
  • Facebook: https://www.facebook.com/tailieuhust
  • Discord: https://discord.com/invite/GKkhW3D9pq
  • Telegram: https://t.me/+72guyAp_ewQwYTY1
  • Youtube: https://www.youtube.com/channel/UCy4RUTy_FzQ1UhiklR9PVdw

MỤC LỤC

LỜI NÓI ĐẦU 2

MỤC LỤC 3

GIẢI ĐỀ CƯƠNG ĐẠI SỐ TUYẾN TÍNH NHÓM NGÀNH 1 4

CHƯƠNG I. TẬP HỢP – LOGIC – ÁNH XẠ - SỐ PHỨC 4

CHƯƠNG II. MA TRẬN – ĐỊNH THỨC – HỆ PHƯƠNG TRÌNH 16

CHƯƠNG III. KHÔNG GIAN VECTOR 28

CHƯƠNG IV. ÁNH XẠ TUYẾN TÍNH 38

CHƯƠNG V. DẠNG SONG TUYẾN TÍNH, DẠNG TOÀN PHƯƠNG, KHÔNG GIAN EUCLIDE, ĐƯỜNG MẶT BẬC HAI 51

GIẢI ĐỀ CƯƠNG ĐẠI SỐ TUYẾN TÍNH NHÓM NGÀNH 1

CHƯƠNG I. TẬP HỢP – LOGIC – ÁNH XẠ - SỐ PHỨC

Bài 1: Lập bảng giá trị chân lý của các biểu thức mệnh đề sau

  1. [A  (B  C)]  C
  2. [A(B C )]B

Lời giải

  1. Ta có bảng giá trị chân lý

A

B

C

(B C)

A  (B  C)

[A  (B  C)]  C

0

0

0

0

0

1

0

0

1

1

0

1

0

1

0

1

0

1

0

1

1

1

0

1

1

0

0

0

0

1

1

0

1

1

1

1

1

1

0

1

1

0

1

1

1

1

1

1

  1. Ta có bảng giá trị chân lý

A

B

C

A

B C

A(B C )

[A(B C )]B

0

0

0

1

0

0

0

0

0

1

1

1

1

0

0

1

0

1

1

1

1

0

1

1

1

1

1

1

1

0

0

0

0

0

0

1

0

1

0

1

0

0

1

1

0

0

1

0

0

1

1

1

0

1

0

0

Bài 2. (CK 20152) Cho p, q là các mệnh đề. Hai mệnh đề ( p  q)  q và p q có tương đương logic không? Vì sao?

Lời giải

Ta có bảng giá trị chân lý

p

q

p q

( p  q)  q

p q

0

0

1

0

0

0

1

1

1

1

1

0

0

1

1

1

1

1

1

1

 

Từ bảng giá trị chân lý ta có thể kết luận hai mệnh đề trên là tương đương logic.

Bài 3. Chứng minh rằng:

  1. AB và (A  B) (A B) là tương đương logic.
  2. (A  B)  C và A  (B  C) không tương đương logic.
  3. A  B và A  B là tương đương logic.

Lời giải

a. Ta có bảng giá trị chân lý

A

B

A

B

(A  B)

A  B

AB

(A  B) (A B)

0

0

1

1

0

1

1

1

0

1

1

0

0

0

0

0

1

0

0

1

0

0

0

0

1

1

0

0

1

0

1

1

Vậy hai mệnh đề trên là tương đương logic b. Giả sử A = B = C = 0. Khi đó

AB = 1; (A  B)  C = 0

BC = 1; A  (B  C) = 1

Vậy nên hai mệnh đề trên không tương đương logic. c. Ta có bảng giá trị chân lý

A

B

A

AB

A  B

A  B

0

0

1

1

0

0

0

1

1

0

1

1

1

0

0

0

1

1

1

1

0

1

0

0

Vậy hai mệnh đề trên tương đương logic.

Bài 4 (GK 20171). Cho các mệnh đề A, B và C thỏa mãn (A  C)  (B  C) và (A  C)  (B  C) là các mệnh đề đúng. Chứng minh rằng AB là mệnh đề đúng.

Lời giải

Ta có: (A  C)  (B  C) và (A  C)  (B  C) là các mệnh đề đúng. (1)

Giả sử AB là mệnh đề sai thì không mất tính tổng quát ta có: A1 và B 0

C  0  A  C  1 và B  C  0  (A  C)  (B  C) sai (2)

C  1 A  C  1 và B  C  0  (A  C)  (B  C) sai (3)

Từ (1), (2) và (3) ta thấy rằng giả sử trên là sai nên AB là mệnh đề đúng.

Bài 5. Cho mệnh đề logic "Nếu 2020 là số lẻ thì nó chia hết cho 3". Hỏi mệnh đề là đúng hay sai? Giải thích?

Lời giải

Do 2020 chẵn nên 2020 là số lẻ là mệnh đề sai (giá trị chân lý bằng 0)

2020 chia hết cho 3 là mệnh đề sai (giá trị chân lý bằng 0)

Mà mệnh đề logic “Nếu 2020 là số lẻ thì nó chia hết cho 3” là một mệnh đề kéo theo nên đây là một mệnh đề đúng.

Bài 6. Cho hàm số f xác định trên  . Hàm số f là đơn ánh có thể được xác định bởi mệnh đề: "Với mọi x1, x2 thuộc tập R , nếu f x1  f x2 thì x1x2". Hãy dùng các kí hiệu để diễn tả mệnh đề trên và mệnh đề phủ định của nó. Từ đó đưa ra cách chứng minh một hàm số không phải là đơn ánh.

Lời giải

Mệnh đề ban đầu: "x x1 2, , f x 1 f x2  x1  x2 "

Mệnh đề phủ định: "x x1 2, , f x 1 f x2 x1  x2 "

Như vậy để chứng minh 1 hàm số không là đơn ánh ta chỉ cần chỉ ra x x1 2, mà x1 x2 và f x 1  f x 2.

Bài 7. Giả sử f (x),g(x) là các hàm số xác định trên  . Kí hiệu các tập hợp sau:

A  {x  ∣f (x)  0} , B  {x  ∣g(x)  0}.Biểu diễn tập nghię̂ m phương trình sau qua hai tập hợp A,B :

  1. f x g x( ). ( )  0
  2. [ ( )]f x 2[ ( )]g x 2 0

Lời giải

 f x( )  0

  1. f x g x( ). ( )  0 g x( )  0

 Tập nghiệm C  AB

  1. [ ( )]f x 2[ ( )]g x 2  0 f x( )g x( )0

 Tập nghiệm D  A B

Bài 8 (GK20141). Cho các tập hợp A  [3;6), B  (1;5),C  [2;4] . Xác định tập hợp (A  B) \ C .

Lời giải

A  [3;6); B  (1;5);C  [2;4]

 A  B  [3;5)  (A  B) \ C  (4;5)

Bài 9. Cho A,B,C , D là các tập hợp bất kì, chứng minh:

  1. A  (B C\ )  (A  B) \ (A  C) .
  2. A  (B \ A)  A  B .
  3. (A B\ )  (C \ D)  (A  C) \ (B  D) (GK20151)

Lời giải

  1. A(B C\ )  A (B C)  A B C

 (A B) \ (AC)  A B  AC

 A B (A C)  (A B  A)(A B C)

 A B C (do A A  )

Vậy A  (B C\ )  (A  B) \ (A  C) .

  1. A(B A\ )  A (B A)(A B  ) (A A)  A B.

Vậy A  (B \ A)  A  B .

  1. (A B\ )(C D\ )   A B C D

(AC)\(B    D) A C B D   A C (BD)  A B C D.

Vậy (A B\ )  (C \ D)  (A  C) \ (B  D).

Bài 10. Cho hai ánh xạ

f :\{0} g: 

x 1 ; x 2x2 x 1x

  1. Ánh xạ nào là đơn ánh, toàn ánh, Tìm g()
  2. Xác định ánh xạ h = g  f

Lời giải

a) + f x 1  f x 2  1 1  x1  x2x x1 2, \{0} x1 x2

 f là đơn ánh.

Do x\{0} để f x( )  1  0  f không là toàn ánh. x

g x 1  g x 2 12xx12  12xx222

1

Mà g(3)2x3x2 3 3x22x 3 0 (vô nghiệm) nên g x( ) không là toàn ánh.

g 12 g(2)  54 nên g x( ) không là đơn ánh.

+ Tìm g R( )

Ta có: x22x1  x|2 |2 x1  2| 2 ||xx| 1 (Cauchy)

Và a  [ 1;1] : phương trình 2x  a x 2 1 có nghiệm thực   4  4a2  0 nên g R( )  [ 1;1].

b. g  f  g f x( ( ))  2 1x  22x

1 12 x 1 x

Bài 11. Chứng minh các tính chất của ảnh và nghịch ảnh của ánh xạ f :X Y

  1. f A(  B)  f A( )  f B( ); A B,  X .
  2. f (A  B)  f (A)  f (B);A,B  X. Nêu ví dụ chứng tỏ điều ngược lại không đúng.
  3. f 1(A B ) f 1( )A f 1( )B A B Y; , 
  4. f ( A1 B)f ( A)1 f ( B);A,B1 Y
  5. f 1(A B\ ) f 1( )A \ f 1( )B A B; , Y

Lời giải

  1.  y  f A(  B), f x( )  y thì x AB

x A  y  f A( ) (1)

 x B   y  f B( )  y  f A( )  f B( )  f A(  B)  f A( ) f B( )

 f A( )  f A(  B), f B( )  f A(  B)

 f A( )  f B( )  f A(  B) (2)

Từ (1) và (2)  f A( )  f B( )  f A(  B)A B,  X .

  1. + Ta có A  B  A  f A(  B)  f A( )

Tương tự f A(  B)  f B( )

Do đó f A(  B)  f A( )  f B( )

+ Ví dụ điều ngược lại là không đúng Xét f x( )x A2, {2},B { 2}

Khi đó f A(  B)  ; f A( )  f B( )  {4} .

  1. x f

1(AB)  f x( )AB   f xf x( )( )BA xx ff 11((BA))

 x f 1( )A f 1( )B ,A B, Y.

  1. x f 1(AB)  f x( )AB  f xf x( )( )BAxx ff 11((BA))  x f 1( )A f 1( ).B
  2. x f 1(A B\ )  f x( )A B\ f xf x( )( )Ax f 11((BA))  x f 1( )A f\ 1( )B

B x f

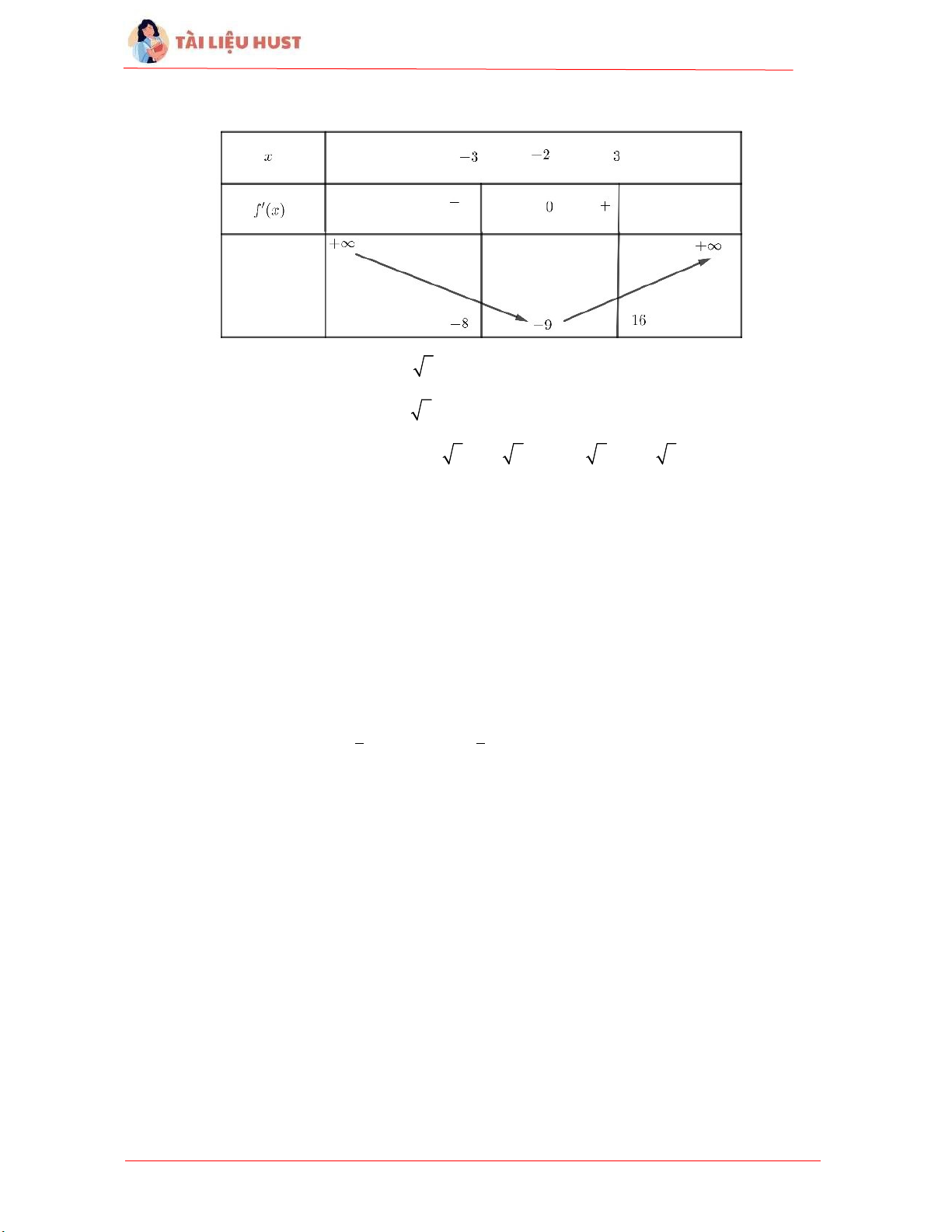
Bài 12. Cho ánh xạ f :  xác định bởi f x( )x24x  5, x , và A  {x  ∣3  x  3}.

Xác định các tập hợp f (A) và f ( A)1 .

Lời giải

2

()

0

2

()

5

2

4

()

,

4

x

fx

x

x

x

fx

fx

  



-

2

3

4

0

2 2 3

8

()

x

fx

x

x

       

-

2

3

0

2

6

4

2

()

x

x

fx

x

       

.

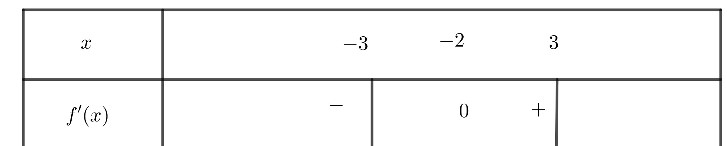
Nhìn vào bảng biến thiên

1

[2

[ 2 2 3; 2

()

6]

6; 2 2 3]

f

A

 

     

.

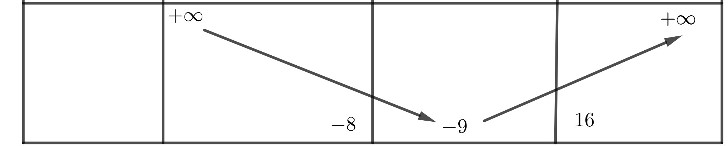
Bài 13 (CK 20161). Cho ánh xạ f :2 2 xác định bới f x y( , )  (x  y x,  y) và tập A (x y, )2∣x2  y2  9. Xác định các tập hợp f A( ) và f 1( )A .

Lời giải

Ta xét (x y; ) A  f x y( ; )  (x  y x;  y)

Va (x  y)2  (x  y)2  2x2  y2  18

Mặt khác, nếu u2  v2 18 thì  u 2 v 2   u 2 v 2  9

 f A( ) (x y; )2 || x2  y2 18

Xét f u v( ; )  (u  v u;  v) A

 (u v)2 (u v)2    9 u2 v2 4,5

Và u2v2 4,5 thì f u v( ; )  A

Do vậy nên f 1( )A  (x y; )2∣x2  y2  4,5.

Bài 14 (GK 20171). Cho ánh xạ f :2 2, xác định bởi f x y( ; )  x2  y x;  y. Ánh xạ f có là đơn ánh, toàn ánh không? Vì sao?

Lời giải

Xét f x y 1 1;   f x y 2; 2  xx12yy1xx22yy2  xx12yx11xx222yx22

1 1 2 2 1

Ta có thể thấy f (0;1)  f ( 1 ;0)  (1;1)  f không là đơn ánh.

Bài 15. Cho tập 4 {0;1;2;3} được trang bị luật hợp thành như sau: với a b, 4 ta có a *b  (a  b) mod 4.

  1. Chứng minh rằng * là một phép toán đóng trên 4.
  2. Hỏi 4*  có phải là một nhóm không?

Lời giải

  1. Ta có a b, Z4 thì (a b )mod4 {1;2;3; 0}Z4

 * là một phép toán đóng trên Z4.

  1. 4,* là một nhóm vì:

+ Tính kết hợp: ( * )a b  c  [(a  b) mod 4  c]mod 4  (a  b  c) mod 4  a *( * )b c

+ Tính: có phần tử trung hòa là 0: *0a 0*a a  a Z4

+  a Z4 đều có phần tử đối xứng: 1*3 2*4  0.

Bài 16. Cho G f ,f ,f ,f ,f ,f1 2 3 4 5 6 là tập các ánh xạ từ  \{0;1}   \{0;1} xác định như sau:

f x1( )  x f; 2(x)  1 ; f3(x)  1 1 ; f4 ( )x  1 ; f5(x)  1 x f; 6 (x)  x .

1 x x x x 1 a. Tính f1f2

b. Lập bảng để biểu diễn giá trị f1f2 với mọi i j, 1..6.

c) Chứng minh G cùng với phép toán là phép tích ánh xạ lập thành một nhóm không Abel.

Lời giải

a) f1  f2  f1 f2( )x   1 1 x

b)

f1

f2

f3

f4

f5

f6

f1

f1

f2

f3

f4

f5

f6

f2

f2

f3

f1

f6

f4

f5

f3

f3

f1

f2

f5

f6

f4

f4

f4

f5

f6

f1

f2

f3

f5

f5

f6

f4

f3

f1

f2

f6

f6

f4

f5

f2

f3

f1

c) Do (G, ) là phép toán đóng

+ Phép hơp có tính chất kết hợp

+ Phần tử trung hòa: f1

+ Phần tử đối xứng: f1 f1 f2 f3 f4 f4  f5 f5  f6 f1 f1

Mà f4 f2  f5  f6  f2 f4  (G, ) là một nhóm không Abel.

Bài 17. Nêu rõ các tập sau với các phép toán cộng và nhân thông thường có lập thành một vành, trường không?

  1. Tập các số nguyên lẻ.
  2. Tập các số nguyên chẵn.
  3. Tập các số hữu tỉ.
  4. X  {a b 2∣a b, }.
  5. Y  {a b 3∣a b, }

Lời giải

  1. Không là vành, trường (vì phép toan + không đóng kín)

12Z

  1. Là vành, không trường ((G, ) ) không là nhóm, chẳng hạn
  2. Là trường
  3. là vành, không là trường ((G, ) ) không là nhóm, chẳng hạn 1 3 2 X

3 2 5 5

 1 a b 3 a b 

c) Là trường  a b 3  a2 3b2  a2 3b2  a2 3b2 3Y,(a b; )  (0;0).

Bài 18. Biểu diễn các số phức sau dưới đạng chính tắc: a) (1i 3)9

(1 i)21

  1. 13

(1i)

  1. (2 i 12) ( 3 1) 5 11.

Lời giải

  1. (1 i 3)9 2cos3  isin3 9  29

 cosisin21 1 

  1. (1i)1321   2  4 4  13  24  2  i 21  24.i

(1i)  2 cos isin   12  i 12

 4 4 

  1. (2  i 12) ( 35 i)11 4cos3  isin3 5 2cos 6 isin 611

 221 12  i 23      23  i 12  2 (2 3192 )i

Bài 19. Tìm các căn bậc 8 của số phức: z 1 i 3 .

Lời giải

z  1 i 3  2cos 3isin 3  Các căn bậc 8 của z là:

3 2. cos 2k 2k

 3 isin 3 ,k0,7.

 8 8 

 

Bài 20. Tìm nghiệm phức của phương trình sau:

a) z2  z 1  0 b) z2  2iz  5  0 c) z4  3iz2  4  0

d) z6  7z3 8  0 e) z7 10243 f) z8( 3  i) 1 i z

g) iz2 (1 8)i z 7 17i0 (GK20171)

Lời giải

  1. z2  z 1 0  z3 1 z  cos 2k isin 2k;k 1;2

z  1 3 3

  1. z22iz   5 0 (z i)2    4 z i 2
  2. z4  3iz2  4  0 . Đặt z2  u  u2  3iu  4  0

  

u 32i2 52i2 uu  4ii  zz22 4iizz ( 2 12ii,2)12 

 

6 3 3 2 u  8 z  2

  1. z  7z 8  0 . Đặt z  u  u  7u 8  0  u 1  z  1

  1. z7 10243  z7  z3  1024 | z |10 1024 | z | 2

z

z  | zz|2  4z  477  10243  z4  24  z  2cos 2k4isin 2k4,k  0,3 z z 

  1. z8( 3  i) 1 i

  

 z8  1i3  22coscos 34 iisinsin34   1 cos 7isin 7 i   2  12 12 

1 1272kisin 1272k,k 0,7

 z cos

8

16

8

2

 

  1. iz2 (1 8)i z 7 17i0

  z2 (i 8)z(17 7 ) i 0

  z  i 28 2  7i 17  634  4i  3i  54  1 32 i2  zz  352i i

Bài 21. (GK 20141). Cho  1 2, ,,2014 là các căn bậc 2014 phân biệt phức của đơn vị 1. Tính

2014

A  i2 .

i1

Lời giải

2014

1 2, ,.,2014 là 2014 căn bậc của 2014 của 1. Ak2 .

k1

Ta có k  cos 2k  i sin 2k , k  0, 2013 (Quy ước 20140 )

2014 2014

 A 2014k1 cos10072kisin10072k

 21007k1cos 2kisin 2k   do 2(k 10071007) 210072k

1007 1007

1007

 2 k

k1 1007

Với k ,k 1,1007 là các căn bậc 1007 của 1 . Mà k1007 1 nên theo Viete: k  0 A 0.

k1

(x 1)9 1

Bài 22. Cho phương trình 0. x

  1. Tìm các nghiệm của phương trình trên.
  2. Tính môđun của các nghię̂ m.

8 k

  1. Tính tích của các nghiệm từ đó tính sin .

k1 9

Lời giải

  1. xk   1 cos 2k i sin 2k, k  1,8 (Đặt x4  t )

9 9

  1. xk  1cos 2k92 sin 2k92  2sin k9
  2.  8 sin k k xk  18 8 xk

k1 9 k1 2 2 k1

Mà x kk, 1,8 là nghiệm của (x1)9 1  0  9 C9i  xi1  0 nên theo Viete  8 xk  9

x i1 k1

8 k 9

 sin 9  28

k1

Bài 23 (CK 20161). Cho ánh xạ f :  , ( )f z iz2 (4 i z) 9i với i là đơn vị ảo. Xác định f 1({7})

Lời giải

Ta có: iz2 (4 i z)  9i 7

z2 (1 4 )i z(7i 9) 0

  z 124i 2  97i  2i 154  214 5i  i  52 2

z   2 3i 1{7})  { 23i;3i}

 z  3i  f

Bài 24 (GK 20171). Cho z z1 2, là hai nghiệm phức của phương trình z2  z  ai  0 , với a là một số thực và i là đơn vị ảo. Tìm a biết z12  z22 1.

Lời giải

z2      z ai 0 z12 z1 ai z; 22  z2 ai

 z12  z22  z1  z2 1 z12  z22  z1  z2 z1  z2   z1  z2 z1  z2  z1z2 1

Ta có: zz z11 2 z21.i1.

Đặt z1     u iv. z2 1 u iv.

(zu iv1z. )(12 1 i iv(2. )u1)ai2 4v2 1u(2(1uu1))2v42v2 01uu 10,,vv00

 a  v(1 u)  vu  0.

CHƯƠNG II. MA TRẬN – ĐỊNH THỨC – HỆ PHƯƠNG TRÌNH

1 3 2   2 1 1

Bài 1. Cho các ma trận A  02 13 21,B   12 23 40,C  21 14 22.

Trong các phép toán sau: BCT, A BC A B C A BC ,  , ( ), (A3 ).B CT,phép toán nào thực hiện được. Nếu thực hiện được cho biết kết quả.

Lời giải

Các phép toán có thể thực hiện được là: B C. T ; (A3 ).B CT

 2 1 1 1 2  1 6

BC. T   2 3 0   1 4   5 8

 1 2 4   2 2 9 2

1 3 2   2 1 1  7 0 5 

A3B  2 1 132 3 0   4 10 1

0 3 2  1 2 4  3 9 10

 7 0 5  1 2   3 4 

 (A3 ).B CT   4 10 1   1 4   12 34

 3 9 10   2 2 26 22

 1 3 1 0

Bài 2 (CK 20152). Cho A  1 2,B   1 1 và E là ma trận đơn vị cấp 2 

  1. Tính F  A2  3A
  2. Tìm ma trận X thỏa mãn A2 5E X  BT 3A A2

Lời giải

  1. A2 1 31 22  2 93 1  A2 3A  05 05 5E
  2. Theo câu a ở trên ta có: A23A5E 0 A25E3A, 3A A 2 5E

 Cần tìm X thỏa mãn: 3AX  BT .5E  X 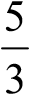 A1, BT (do det A 0 )

2 1

 

X  53 11 23 1 01 10   31 32 

 3 3 

1 2 3

Bài 3. Cho ma trận A 2 4 1 và đa thức f x( ) 3 x22x5. Tính f A( ) .

3 5 3

Lời giải

1 2 3  6 9 10  21 23 24

A  2 4 1  A2   3 7 5   f A( )  3A2 2A5E   13 34 13

3 5 3  2 1 13  0 7 38

Bài 4. Tính An với

a 1 0

cosa cossinaa 0 a 1 .

a) A  sin a  . b) A 0 0 a

Lời giải

coska sinka n cosna sinna

  1. A  sinka coska  . Quy nạp A  sinna cosna

 n  1. Đúng.

+ Giả sử mệnh đề đúng với n  k  *

k1  cossin kaka cossinkaka    cossinaa cossinaa  cos(sin(kk1)1)aa cos(sin(kk1)1)aa

A

 Mệnh đề đúng với k1.

n cosna sinna

Vậy A  sinna cosna .

a 1 0 0 1 0

  1. A  0 a 1  a I. 3  B I, 3 là ma trận đơn vị cấp 3, B 0 0 1

0 0 a 0 0 0

0 0 1

Nhận xét B2 0 0 0;Bk   0 k 3

0 0 0

n

 An  B  a I. 3n  C Bni . n1.ai  I C a. n0. n  C B an1. . n1  C B an2. 2. n2

i0

(n1)an na. n1 C an2. n2 

a I nan.  . n1.B C a n2. n2.B2  0 (n1)an na. n1 

 0 0 (n1)an

Bài 5. Tìm tất cả các ma trận vuông cấp 2 thoả mãn:

0 0

a) X2  0 0

a2 bc  0

a) A  ba cd, A2  0  abac cdbd 00

bc  d2  0

bc  0 a  d  0

bc  0  a d  0

Lời giải

1

b) X2  0

0

1

0 b 0

Vậy các ma trận thỏa mãn là: 0 0  ; c

0 a b  2 

0  ; c a a bc  0

b) A  ba cd , A2  I  b aa(2 bcd)dc a2( bc d) 1 0 

+ (a d ) 0 a2bc1

a  d 1 & b  c  0

+ (a  d)  0  a  d  1 & b  c  0

1 0 1 0  a b   2 

Vậy các ma trận thỏa mãn là: 0 1 ; 0 1 ; c a a  bc 1

Bài 6.

a b x2    (a dx ad bc) 0.

  1. Chứng minh rằng ma trận A  c d thoả mãn phương trình sau:
  2. Chứng minh với A là ma trận vuông cấp 2 thì Ak 0(k 2) A2 0

Lời giải

a2 bc ab bd 

  1. A2 ac cd d 2 bc A2  (a d A) (ad bc I )

a2 bc (a d a ad bc)   ab bd  (a d b) 

  (a d c) d2 bc (a d d ad bc)   0

 ac cd

 A thỏa mãn phương trình x2 (a d x ad bc)   0.

  1. Rõ ràng A2  0 thì A2   0 k 2.

Giả sử Ak  0 với k  2. Ta chứng minh A2  0

A2  0 det A 0 ad bc  0 A2 (a d A) 0 (theo câu a)

 (a d) 0 A2 0

(a  d)  0  Ak2 A2 (a  d A)   0  Ak1  0.

Tương tự cách làm ở trên

 A2  0

Bài 7. Không khai triển định thức mà dùng các tính chất của định thức để chứng minh:

a1 b x1 a1 b x1 c1a1 b1 c11 a bc1 a a2

a) a2 b x2 a2 b x2 c2 2x a2 b2 c2 b) 1 b ac  1 b b2. a3 b x3 a3 b x3 c3a3 b3 c31 c ab1 c c2

Lời giải

a b x1 1 a1 b x1 2a1 c1

1

1

2

2

2

3

3

bx

a

c

a

bx

a

bx

c

1

1

2

2

3

3

2

b

c

xb

c

c

b

1

2

3

.

c

c

c

1

1

a

c

  1. a b x2 c  a2 b x2 2a2 c2C2 C1 C2 a b x3 3 a3 b x3 2a3 c3

1

2

3

1

2

3

1

c

1

1

a

b

c

a b x1 a 1 a1 c1

 2 a b x2 a 2 a2 c2C1 C2 C1 a b x3 a 3 a3 c3

a1 b1

 2x a2 b2 a3 b3

1 a bca b( cc bc)

  1. 1 b ac 1 b b a( bc ac C) 2 (abc)C3 C3 abc a( bc ab)

a2

 1 b2C1(ab bc  ca)C3  C3

c2

Bài 8. Tính các định thức sau:

  1. 3 5 1

a  b

  1. 1 1 4

a) A  b) B  bc

5 1 1 7 ca

7 7 9 1

ab bc ca

a2  b2 b2 c2 a2 c2

1

1

c) D 

2

2

1

2 x2

3

3

2

2

1

1

3

3

5

9 x2

Lời giải

    1. 3 5 11 3 5 1

7 11 67 11 6

    1. 1 1 40 7 11 6
  1. A  14 26 12  14 26 12

5 1 1 70 14 26 12

14 26 80 0 4 7 7 9 10 14 26 8

7 11

 4 112

14 26

a b ab a2 b2 a c b a( c) (a c a)(  c)

  1. B b  c bc b2  c2  b  a c b(  a) (b  a b)(  a)L1  L2  L L1; 2  L3  L2 c  a ca c2  a2 c  a ca c2  a2

1 b ac1 b ac

 (ac b)( a)1 c ba  (a c b)( a)0 c b bcL2  L1  L2

ca ca c2 a2ca ca c2 a2

1 abc ac

 (ac b)( a)0 0 b c (ac b)( a c)( b)a2 c2 ac(ac a)( bc) ca a2 c2 ac c2 a2

 (a  b b)(  c)(c  a)(ab  bc  ca).

11 2

1

1

2

2

2

2

3

2

1

2

3

1

1

5

2

1

0

9

x

2

2

2

2

4

1

x

2

2

1

3

1

2

1

x



2

3

3

5

4

x

2

2 x2 2 x2 2

  1. D L4  L3  L4

33 1

30 0

    1. 11 1 2

 4 x 1 2 x  0 1 x2 0 L  L1  L2

    1. 32 3 1

 4 x2  1 x2x2 4

Bài 9.

  1. Chứng minh nếu A là ma trận phản xứng cấp n lẻ thì det(A)  0.
  2. Cho A là ma trận vuông cấp 2019. Chứng minh det A AT   0 .

Lời giải

  1. det A  det AT  det(A)do AT  A Giả sử A cấp n lẻ det(  A) ( 1)ndet Adet A

Do vậy det A det Adet A 0.

  1. Ta có: (A A T T) AT   A (A AT)

 A  AT là ma trận phản xứng cấp lẻ (cấp 2019) det(A A T)0 Bài 10. Tìm hạng của các ma trận sau:

1 3 5 1

  1. A  2 1 1 4 

5 1 1 7 

 

7 7 9 1 

4 3 5 2 3 

8 6 7 4 2

  1. B4 3 8 2 7 

4 3 1 2 5

8 6 1 4 6

Lời giải a)

1 3 5 1 1 3 5 1 1 3 5 1

A  752 711 911 714   000 147 2611 126 LLL342 572LLL111LLL342   000 007 1144 064LL34 22LL22  LL34 

   14 26 8  

1 3 5 1

 0 7 11 6 . Vây ( )r A  4.

0 0 4 0 

0 0 0 4

Cách 2: det A  112  0, A là ma trận vuông cấp 4  rank A  4.

4 3 5 2 3  4 3 5 2 3 

4 3 8 2 7 0 0 3 0 4

b) B884 663 171 442 265000 000 963 000 1248 L L LLL LL3542  221L4L L14L3L425

4 3 5 2 3 

00 00 30 00 04L LL L3422 2L3L4. Vậy r B( )  2

0 0 6 0 0 L L5 3 2 L5 

0 0 9 0 0 

 1 1 1 2

Bài 11 (GK20141). Tìm m để hạng của ma trận A  1 2 2 1 bằng 2.

 1 0 4 m

Lời giải

 1 1 1 2 1 1 1 2 

A   11 02 42 m1  00 11 33 m32LL32 LL11 LL32 

1 1 1 2 

 0 1 3 3 L3  L2  L3.

0 0 0 m5

Vậy r A( )  2  m  5

Bài 12. Tìm ma trận nghịch đảo của các ma trận sau:

a) A  53 74 b) B 233 453 511 c) C  1000 100a 100a 100a.

Lời giải

  1. A  53 74  A1  det1 A  AT  1175 3475 34

3 4 5  2 21 11 2/3 7 11/3

  1. B  2 3 1  B1  det1B ,BT  13 1 12 7    1/3 4 7/3  .

3 5 1 1 3 1  1/3 1 1/3 

1 a 0 0 

  1. Cách 1: C  0 1 a 0 . Ta có: det C  1.T ì m C r C 1  C r

0 0 1 a

 

0 0 0 1 

Cách 2: Phương pháp Gauss

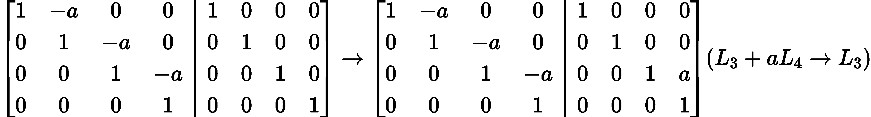
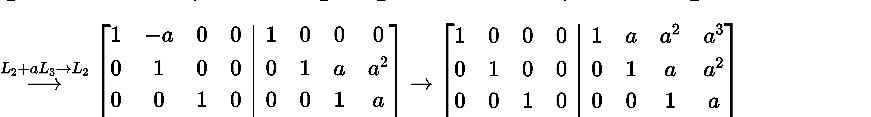
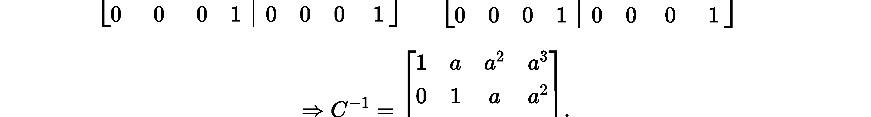
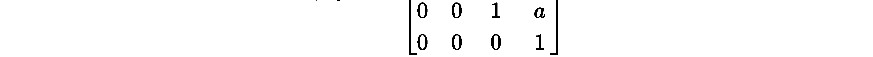
a 1 1 a 

Bài 13(GK 20151). Tìm a để ma trận A  3 a 1 3  khả nghịch.

a 1 0 a 1

Lời giải

a1 1 a

1 aa1 1

| A|3 a1 3 (a1)(a1)

a1 33 a1

a1 0 a1

 (a 1) 3 a2  a  a2  2a  4  (a 1)(a 1)

A khả nghịch  det A  0  (a 1)(a 1)  0  a  1.

Bài 14. Chứng minh rằng ma trận A vuông cấp n thoả mãn a Ak k ak1Ak1   a A a E1 0 0

với a00 thì A là ma trận khả nghịch.

Lời giải

A khả nghịch và A1 B

1 2 1  1 2

Bài 15. Cho A   2 3 4 ;B  3 4;C  26 1216

 3 1 1  0 3

AX  B  CT .

Lời giải

 2 6  1 2  3 4 

AX  CT  B  12 16   3 4   9 12  D

10 7   0 3 10 4 

10

7  . Tìm ma trận X thỏa mãn

1

 4

Mà det A  28  0  X  A1 D  1  A DT    12

det A

1

  4 Bài 16. Giải hệ phương trình sau:

1

14

5 

28  3 4   2

143  9 12   3

1 10 4  1

4 

1

2 .

1

3x1 5x2  2x3 4x4  2

4x2  x3 3x4  5

a)  7x1

5x1 7x2 4x3 6x4  3

 3x1  x2 3x3 1

b)  24xx11  2x2x24xx33  43

10x 5x 6x  10

1 2 3

2x1 3x2  4x3 1

 3x1  x2  x3  2 .

c) 5x1  2x2 5x3  3

 x1 4x2 3x3 1

Lời giải

a)

()

()

rA

rA

Do

nên hệ vô

nghiệm.

b)

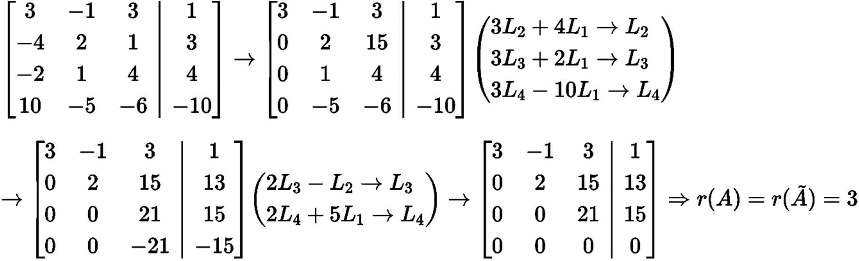
3x1  x2 3x3 1

Hệ có duy nhất 1 nghiệm thỏa mãn:  2x 15x3 13

2

7 7

3

21

15

x

3

12

85

,

,

0

;

;

x x x

c)

()

2

()

3

rA

rA

  

Hệ có vô số nghiệm thỏa mãn

3

1

2

3

2

2

4

3

1

11

10

1

x

x

x

x

x

Đặt x3  t  x2  10t 1  x1  3x2  4x3  3 14t

11 2 22

Vậy x x x1 2 3; ;  3 1422 t ; 1 1011 t ;t.

Bài 17. Giải hệ phương trình sau bằng phương pháp Gauss:

 x 2y  z  3t 12 x  2y 3z  4t  4

a) 32xx65yy4zz1311tt  4949 (GK 20171) b)3xx27yy410z z2t11 t  3 11 (GK20151)

 x2y 2z  9t  33 x  2y  2z  7t  6

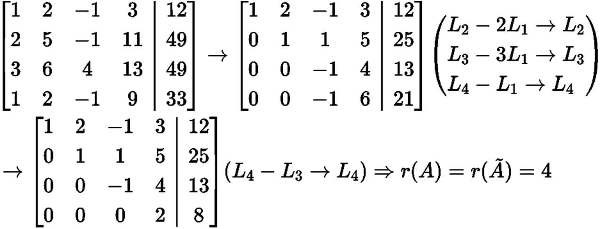Lời giải a)

 Hệ có nghiệm duy nhất thỏa

x1  2x2  x3  3x4 12

 x2  x3  5x4  25 mãn  x3  4x4 13

 2x4  8

x x x x1 2 3 4; ; ;   ( 1;2;3;4)

b)

x1  2x2 3x3  4x4  4

x2  x3  x4 1 r A( ) r A( ) 4 Hệ có nghiệm duy nhất thỏa mãn  x3 2x4 1

 x4  1

x x x x1 2 3 4; ; ;  (1;1; 1; 1)

(a5)x 3y (2a1)z  0

Bài 18(GK 20171). Tìm a để hệ ax(a1)y  4z  0 có nghiệm không tầm thường.

(a5)x(a 2)y  5z  0

Lời giải

Hệ có nghiệm không tầm thường  det A  0 (do hệ thuần nhất)

a5 3 2a1a 5 3 2a 1a 5 3 2a 1

Với A   a a1 4   det A a a1 4a a 1 4

a5 a2 5 a 5 a 2 50 a 1 42a

 (a5)[(a1)(42 )a 4(a1)]a.[3.(42 )a (2a1)(a 1)]

 (a5)2a2  2aa2a2 5a 13

 2a3 8a2 10a 2a3 5a2 13a

 3a2 3a  3 (a a 1)

a  0 det A  0  a  1.

 mx1 2x2  x3  3

Bài 19(CK 20172). Tìm m đề hệ phương trình  x1 mx2 2x3  4 có nghiệm duy nhất.

2x1 3x2  x3  m

Lời giải

m 2 1 3 m 2 1

A  1 m 2 4  Hệ có nghiệm duy nhất 1 m 2 0

2 3 1 m2 3 1

2 2 2 m 1

 m 83(2m  6m 2)  0  m 5 4m 2  0  m  4m 3  0  m  3

 x1  2x2  x3  mx4  4

 x1  x2  3x3  2x4  k .

Bài 20. Cho hệ phương trình 2x1  x2 3x3  (m 1)x4  3

 x1  x2  x3  2mx4  5

  1. Giải hệ phương trình khi m  2,k  5 .
  2. Tìm điều kiện để hệ có nghiệm duy nhất.
  3. Tìm điều kiện để hệ phương trình có vô số nghiệm.

Lời giải

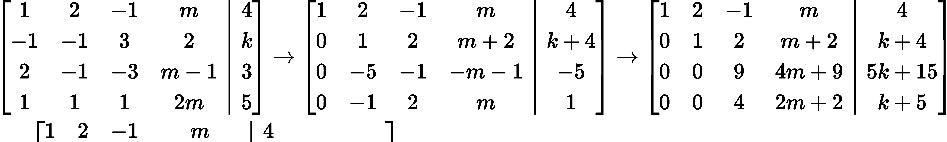
  1. m  2,k  5 hệ có nghiệm đuy nhất x x x x1 2 3 4; ; ;   ( 9; 1; 5;  5).
  2. Hệ có nghiệm duy nhất  2m18 0 m9.

2m18  0 m  9 .

  1. Hệ có vô số nghiệm  11k 15 0  k  1115

CHƯƠNG III. KHÔNG GIAN VECTOR

Bài 1. Tập V với các phép toán có phải là không gian véc tơ không?

a) V  {(x, y,z) x, y,z∣  } với các phép toán xác định như sau:

(x y z, , )x y z, ,   xx y,  y z, z

k x y z( , , )  (k x k y k z| ,| | ,| ∣ )

b) V x x ,x1 2∣x1 0,x2 0 2 với các phép toán xác định như sau:

x ,x1 2   y ,y1 2   x y ,x y1 1 2 2  & k x ,x 1 2   x ,x1k 2k  trong đó k là số thực bất kỳ.

Lời giải

a) Nhận xét k1  k2 (x y z; ; )   k1  k x k2 ; 1  k2 y k; 1  k z2

  k x1  k x k y2 ; 1  k2 y k z; 1  k z2   k x y z1( ; ; )  k2 (x y x; ; )

 V không là không gian vector.

b)

(V,) là một nhóm giao hoán

 k x x 1, 2   y y1, 2  x y x y1k 1k , 2k 2k  k x x 1, 2 k y y 1, 2

k k1  2 x x1, 2 x1k1k2 , x2k1k2  k x x1  1, 2 k x x n2  1, 2 

k k x x1 2 1, 2 kk1 2  . x x1, 2

1.x x1, 2 x x1, 2

 V là một không gian vector.

Bài 2. Chứng minh các tập hợp con của các không gian véc tơ quen thuộc sau là các không gian véc tơ con của chúng:

  1. Tập E {x ,x ,x1 2 33∣2x1 5x2 3x3 0}
  2. Tập các đa thức có hệ số bậc nhất bằng 0 (hệ số của x) của KGVT P xn[ ]
  3. Tâp các ma trận tam giác trên của các ma trận vuông cấp n
  4. Tập các ma trận đối xứng của tập các ma trận vuông cấp n
  5. Tập các ma trận phản xứng của tập các ma trận vuông cấp n aij  a ji 

Lời giải

a) Xét u1 x x x1 2 3, , E u, 2 y y y1 2, , 3E

u1 u2 x1  y x1 2,  y x2 3,  y3E

Do 2x1  y15x2  y23x3  y3 2x1 5x2 3x3  2y1 5y2 3y30 kR thì ku1E do k2x1 5x2 3x3  0

 E là KGVT con của R3.

b)

P P1 2, có hệ số bậc nhất bằng 0  kPP11 có hsbn = 0P2 có hsbn = 0 k R

 Tập các đa thức có hệ số bậc nhất bằng 0 của P xn[ ] là KGVT con của P xn[ ].

p qW;p q, W

c, d, e) CMTT giống a, b. kpW; k R, pW thì W là KGVT con sinh bởi V

Bài 3. Cho V1, V2 là hai không gian véc tơ con của KGVT V. Chứng minh:

  1. V1V2 là KGVT con của V .
  2. V1 V :2 u1 u2∣u1V,u1 2 V2 là KGVT con của V .

Lời giải

a) u v V,  1V2 u v V,,  12 u v Vu v V   12 u v V  1V2

u v V

u V k 1,   R ku V1, tương tự ku V   2 ku V1 V2 Do đó V1V2 là KGVT con của V .

b) u v, V1 V2  uv  vu11vu22 u1  v2 V u1, 2  v2 V2 

u v u1 v1  u2 v2V1 V2

- ku ku 1ku2 V V1 2do ku1V ku1, 2V2  V1 V2 là KGVT con của V

Bài 4. Cho V, V1 2 là hai không gian véc tơ con của KGVTV. Ta nói V, V1 2 là bù nhau nếu

V1V2 V,V1V2 { } . Chứng minh rằng V, V1 2 bù nhau khi và chỉ khi mọi véc tơ u của V có biểu diễn duy nhất dưới dạng u  u1 u , u2 1V,u1 2 V2 .

Lời giải

V V1 2, bù nhau   V V1 2 V V; 1 V2 {0}

 v V thì v  v1 v v21V v1 2, V2

Giả sử biểu diễn này không duy nhất  v  v1  v2  v1v2v1 v1     v1 v1v2v2

Mà v1 v1V v1 2,     v2 V2 V1 V2 {0} (mâu thuẫn)  biểu diễn duy nhất.

Do mỗi vector uV đều biểu diễn được dưới dạng u u1 u u21V u1 2, V2   V V V1 2

Giả sử x V      1 V2 x 0 x x 0 (mẫu thuẫn tính duy nhất)   V1 V2 {0}

Vậy ta có đpcm.

Bài 5. Trong KGVTV , cho hệ véctơ u ,u ,1 2 ,u ,un n 1  là phụ thuộc tuyến tính và u ,u ,1 2 , un là hệ độc lập tuyến tính. Chứng minh un 1 là tổ hợp tuyến tính của các véc tơ u,u ,1 2 ,un. Lời giải

u u1, 2,,u un, n1 phụ thuộc tuyến tính

n1

k ii, 1,n1 không đồng thời bằng 0 thỏa mãn kui i 0

i1

n1

Nếu kn1  0k ut i 0u u1 2, ,,un phụ thuộc tuyến tính (mâu thuẫn)

i1

n ki

 kn1  0   ui  un1 $

i1 kn1

Tức là un1 là tổ hợp tuyến tính của u u1 2, ,,un.

Bài 6. Cho v ,v ,1 2 ,vm là hệ sinh của W , u ,u ,1 1 2 ,un là hệ sinh của W2 với W, W1 2 và là các không gian con của V . Chứng minh v ,1 ,v ,u ,u ,m 1 2 ,un là hệ sinh của W1W2.

Lời giải

Xét u W1 W2  u  u1 u2u1W u1, 2W2

m

Mà v v1 2, ,,vm là hệ sinh của W1 k ui : 1 kvi i ki2  0

i1

n

Tương tự g j :u2 g uj j g 2j  0

j1

m n

u  k vi i g uj j ki2 g 2j  0

i1 j1

v v1 2, ,,v u um, 1 2, ,,un là hệ sinh của W W12.

Bài 7. Trong 3 xét xem các hệ véc tơ sau độc lập tuyến tính hay phụ thuộc tuyến tính:

  1. v1(4; 2;6),v 2  ( 6;3;9).
  2. v1(2;3; 1),v 2 (3; 1;5),v 3  ( 1;3;4).
  3. v1(1;2;3),v2 (3;6;7),v3 ( 3;1;3),v4 (0;4;2).

Lời giải

  1. v2 3 v1  v v1, 2 phụ thuộc tuyến tính.

2

2 3 1

  1. 3 1 3  9 0  hệ v v v1 2 3, ,  độc lập tuyến tính.

1 5 4

  1. Do v v v v1 2 3 4, , , đều thuộc không gian vector R3.

Mà dim R3  3 nên hệ 4 vector bất kỳ luôn phụ thuộc tuyến tính v v v v1 2 3 4, , ,  phụ thuộc tuyến tính.

Bài 8. Trong không gian P[x]2 , xét xem hệ véc tơ Bu1  1 2x, u2  3x  x ,u2 3  2 x  x2 độc lập tuyến tính hay phụ thuộc tuyến tính.

Lời giải

1 0 2 

Gọi A là ma trận của B đối với cơ sở chính thức 1; ;x x2 của P xx[ ]  A  2 3 1,

0 1 1 

det A  2 0 B độc lập tuyến tính.

Bài 9. Trong 3, chứng minh v1(1;1;1),v2 (1;1;2),v3 (1;2;3) lập thành một cơ sở. Xác định ma trận chuyển từ cơ sở chính tắc sang cơ sở trên và tìm toạ độ của x  (6;9;14) đối với cơ sở trên theo hai cách trực tiếp và dùng công thức đổi tọa độ.

Lời giải

1 1 1

Ta có 1 1 2  1 0 hệ vector v v v1 2 3, ,  độc lập tuyến tính

1 2 3

Mà dim3  3 v v v1 2 3, ,  là cơ sở của R3.

1 1 1

Ma trận chuyển cơ sở từ chính tắc sang v v v1 2 3, ,  là: C  1 1 2 1 2 3

*) Tìm tọa độ của x  (6;9;14) đối với cơ sở v v v1 2 3, ,  B

abc  6

Cách 1: x  av1 bv2 cv3 ab2c  9  (a b c, , )  (1,2,3)

a2b3c 14

1 1 11  6   1

Cách 2: [ ]x E  C1 [ ]x E 1 1 2  9     2 .

1 2 3 14   3

 1

[ ]x B   2

  3

Bài 10. Trong các trường hợp sau, chứng minh B v v v1 2 3, ,  là một cơ sở của 3 và tìm [ ]v B biết rằng:

  1. v1(2;1;1),v2 (6;2;0),v3 (7;0;7),v (15;3; 1).
  2. v1(0;1;1),v2 (2;3;0),v3 (1;0;1),v(2;3;0).

Lời giải

2 6 7

  1. 1 2 0 28  0  B độc lập tuyến tính  B là cơ sở của R3
    1. 0 7

[ ]v B [ ]B E1[ ]v E E là cơ sở chính tắc, [ ]BE là ma trận chuyển cơ sở từ E sang B )

2 6 71 15 5/ 2

1 2 0  3   11/ 4

1 0 7  1   1/ 2 

0 2 1

  1. 1 3 0  5 0  Blà cơ sở của R3.
    1. 0 1

0 2 11  2  0

[ ]v B [ ]B E1 [ ]v E 1 3 0  3    1

1 0 1   0   0

Bài 11. Trong P[x]3 cho các véc tơ v1 1,v2  1 x,v3  x x ,v2 4  x2 x3.

  1. Chứng minh B v ,v ,v ,v1 2 3 4 là một cơ sở của P[x]3 .
  2. Tìm toạ độ của véc tơ v  2  3x  x2  2x3 đối với cơ sở trên.
  3. Tìm tọa độ của véc tơ v  a0 a x1 a x2 2 a x3 3 đối với cơ sở trên.

Lời giải

1 1 0 0

  1. Ma trận tọa độ của B đổi với co sở chính tắc E là B0  0 1 1 0

0 0 1 1

 

0 0 0 1

do det B0  1 B độc lập tuyến tính  B là cơ sở của P x3[ ]

1 1 0 01  2  4

  1. [ ]v E  B01 [ ]v E  0 1 1 0  3    6 

0 0 1 1 1 3

     

0 0 0 1  2   2 

1 1 0 01 a0  1 1 1 1 a0  a0 a1 a2 a3

0 1 1 0 

  1. [ ]v E  B01 [ ]v E  0 0 1 1 a12   0 1 1 1 a12   a1 2a2 3a3 

 a  0 0 1 1 a  a a

         

0 0 0 1 a3  0 0 0 1  a3   a3

Bài 12(CK 20151). Trong 4 , cho các véc tơ sau: u1(1;3; 2;1), u2  ( 2;3;1;1),u3(2;1;0;1),u  (1; 1; 3; ). m

Tìm m để uSpanu u u1 2 3, , .

Lời giải

uspanu u u1 2 3, ,   x x x1 2, , 3 thỏa mãn uxu1 1xu2 2xu3 3

x1  2x2  2x3 1

3x1  3x2  x3  1 có nghiệm không tầm thường.  2x1  x2  0x3  3

x1  x2  x3  m

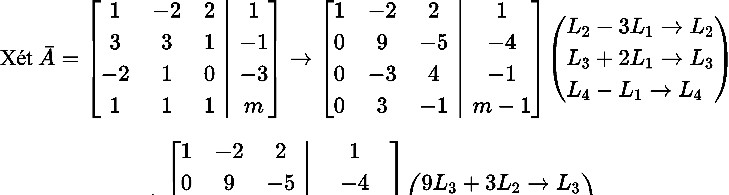
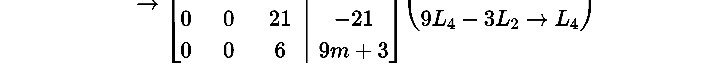
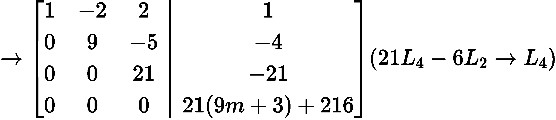
Hệ có nghiệm không tầm thường  21(9m  9)  0  m  1.

Bài 13. Cho KGVTP x3[ ] và hệ véc tơ sau:

v1   1 x2 x v3, 2   x x2 2x v3, 3   2 x 3x v3, 4    1 x x2 2 .x3

a) Tìm hạng của hệ véc tơ b) Tìm một cơ sở của không gian spanv v v v1 2 3 4, , ,

Lời giải

a) Ma trận A của hệ v v v v1 2 3 4, , ,  đối với cơ sở chính tắc là

1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1

A  0 1 1 1   0 1 1 1   0 1 1 1   0 1 1 1

1 1 0 1 0 1 2 0  0 0 1 1  0 0 1 1 

1 2 3 2  0 2 1 3  0 0 1 1  0 0 0 0 

Vậy r A( )  3 hay hạng của hệ vectơ v v v v1 2 3 4, , ,  là 3.

b) Xét ma trận tọa độ hàng:

 1 0 1 1 1 0 1 1 1 0 1 1  1 0 1 1 

0 1 1 20 1 1 2  0 1 1 2   0 1 1 2

 2 1 0 3 0 1 2 1 0 0 1 1 0 0 1 1

1 1 1 20 1 0 3 0 0 1 1 0 0 0 0

 Một cơ sở của spanv v v v1 2 3 4, , , là 1 x2 x3 ; x x 2 2x3 ;  x2 x3 .

Bài 14. Tìm cơ sở và số chiều của không gian con sinh bởi hệ véc tơ sau: a) 2 ; 1 ; 3 ; 4 ,  v2 1 ; 2 ; 0 ; 1 ,  v3   1 ; 1 ; 3 ;  0trong 4 .

b) v1(2;0;1;3; 1),v 2 (1;1;0; 1;1),v 3 (0; 2;1;5; 3),v  4  (1; 3;2;9;5) trong 5.

Lời giải

  1. Ma trận tọa độ hàng

 2 1 3 4  1 2 0 1 1 2 0 1

1 2 0 1   2 1 3 4L1  L2  0 3 3 2LL32 2L1L1L3L2 

1 1 3 0 1 1 3 0 0 3 3 1

1 2 0 1

 0 3 3 2L3  L2  L3

0 0 0 3

 dimV  3, có cs {(1;2;0;1);(0,3;3;2);(0;0;0;3)}

2 0 1 3 1 2 0 1 3 1

  1. 10 12 10 51 1300 22 11 55 3322LL24  LL11  LL42 

1 3 2 9 50 6 3 15 9

2 0 1 3 1

 00 02 01 05 03 LL34 3LL22LL3 4 

 

0 0 0 0 0 

 dimV  2, có cs {(2;0;1;3;1);(0;2;1;5;3)}.

Bài 15. Trong 4 cho các véc tơ: u1(1;0;1;0),u2 (0;1; 1; 1), u3(1;1;1;2),u4 (0;0;1;1). Đặt V1 span u ,u1 2,V2 span u ,u3 4. Tìm cơ sở và số chiều của các KGVT V1V, V2 1V2.

Lời giải

  1. spanu u u u1 2 3 4, , ,  V1 V2

1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0

0 1 1 1  0 1 1 10 1 1 10 1 1 1

1 1 1 2 0 1 0 2 0 0 1 1 0 0 1 1

       

0 0 1 1 0 0 1 1 0 0 1 1 0 0 0 0

 dimspanu u u u1, 2, 3, 4  dimV1 V2  3,cs{(1;0;1;0);(0;1; 1;1);(0;0; 1;1)}.

  1. Xét u V  1 V2 x x x x u1 2 3 4; ; ; : xu1 1xu2 2 xu3 3xu4 4

xu1 1xu2 2xu3 3xu4 4 0$

x1  x3  0

x2  x3  0  x1  x2  x3  x4

 x1  x2  x3  x4  0

x1  2x3  x4  0

u  x u11 u2  x1.(1;1;0;1)dimV1 V2 1,cs{(1;1;0;1)}.

Bài 16 (CK 20151). Cho không gian P2015[ ]x - các đa thức bậc không quá 2015 và tập W1 {p

P2015[ ]x ∣p(x)  p x( ), x R. Chứng minh rằng W1 là không gian con của P2015[ ]x . Chỉ ra số chiều và một cơ sở của W1 (không cần chứng minh).

Lời giải

W1 pP2015[ ] ( )x p x  p(x)

 Xét ,p p1 2W q1,  p1p2. Ta có (q x ) p1( x) p2( x) p x1( )p x2( )q x( )

  p1 p2 W1  p1 W k1,  R kp1( x) kp x1( )kp1W1

Vậy W1 là KCVT con của P2015[ ]x

Do p(x)  p x( )  Đa thức p x( ) chỉ gồm các hạng tử bậc chẵn của x

1007

Hay p x( )  a xi 2i dimW1 1008, một cơ sở là B 1;x2;x4;;x2014.

i0

Bài 17. Tìm cơ sở và số chiều của không gian nghiệm của hệ phương trình thuần nhất sau:

 b) 4x1

a) x32x11xx11 2xx2xx222232xxx33x332xxx4x44435xxxx55550000 22xx112xx2x223x5x33x382xxx444274xxx555000

Lời giải

1 1 2 2 1 1 1 2 2 1

a) A  132 12 13 11 53 00 31 13 33 65 LLL324 23L1LL11LLL243 

 1 2 1 1  0 2 8 7 4 

1 1 2 2 1 1 1 2 2 1

 0 1 1 3 6 LL34 32LL22 LL34 00 01 16 133 166 L3  L4

0 0 0 12 23

0 0 6 13 160 0 0 12 23

x1  x2  2x3  2x4  x5  0

6x2x3x133 x34x4166x5x500 Đặt x5  t  x4  1223 t x; 3  72107 t x; 2  1289 t x; 1  7279 t 12x4  23x5  0.

 X x x x x x1 2 3 4 5; ; ; ;   7279;7289;72107 23;12;1t

 Không gian nghiệm có dim 1 , cơ sở  7279; 7289; 72107 23;12 ;1.

2 1 3 2 4 2 1 3 2 4 

b) A  42 21 15 81 72  00 00 21 105 21LL32 L21L1L3L2

2 1 3 2 4 

 0 0 1 5 1L3 2L2  L3

0 0 0 0 0 

2x1  x2 3 3x3 4 2x45  4x5  0 Đặt x14 ca x, 5  b  x3  5a  b x, 2  2c  8a  b

  x  5x  x  0 x

 X x x x x x1 2 3 4 5; ; ; ;   a(0;8;5;1;0)b(0;1; 1;0; 1)c(1;2;0;0;0)

 Không gian nghiệm có dim 3, cơ sở {(0;8;5;1;0);(0;1; 1;0;1);(1;2;0; 0;0)}

Bài 18. Cho U, V là các không gian con hữu hạn chiều của không gian véc tơ W..

Chứng minh dim(U V )  dim(U )  dim(V )  dim(U V )

Lời giải

Cơ sở U, V lần lượt là u u1 2, ,,um ; v v1 2, ,,vn

+ Nếu U V {0}u u1 2; ;,u v vm; ;1 2;;vn độc lập tuyến tính và là cơ sở của (U  V )

 dim(U V )  m  n  dimU  dimV  dim(U V )

+ Nếu dim(U V )  p , cơ sở r r1, 2,,rp  A

Bổ sung m p vector rp1,,rm vào A để được cơ sở của U .

Bổ sung n p vector rm1;,rn p m  vào A để được cơ sở của V .

Ta chứng minh S  r r1, 2,,r rp , p1,,rm,rm1,,rn p m   là cơ sở của U V

w U V thì w w 1 w2 m kri i  n  p m k rj j  p g rj j p ki q ri  i  n  p m kri i  m kri i

i1 j m 1 j1  j1 i m 1 i r 1

wi

 r r1, 2,,r rp , p1,,r rm, m1,,rn p m   là hệ sinh của U V

n p m  m n p m  m

 i ir  0 thì i ir   i ir U V  i ir V i  0  i p1,m

i m 1 i1 i m 1 i n 1

p n p m 

i ir   i ir  0i   0 i 1, ,p i  m1,n pm Hệ S ĐLTT S là cơ sở. i1 i m n 

CHƯƠNG IV. ÁNH XẠ TUYẾN TÍNH

Bài 1. Cho ánh xạ f : 3  2 xác định bởi công thức f x x x1 2 3, ,  3x1  x2 x3,2x1  x3.

  1. Chứng minh f là ánh xạ tuyến tính.
  2. Tìm ma trận của f đối với cặp cơ sở chính tắc.
  3. Tìm một cơ sở của kerf.

Lời giải

  1. Xét u u1, 2 3  f u 1  u2   3x1  y1 x2  y2   x3  y3 ,2x1  y1   x3  y3

3x1 x2 x3,2x1 x3  3y1  y2  y3,2y1 y3

 f u 1  f u 2

Xét u13,k f ku 1 3kx1 kx2 kx3,2kx1 kx3  k3x1  x2  x3,2x1  x3  kf u 1

Vậy f là ánh xạ tuyến tính.

  1. Ta có: f (1,0,0)  (3,2); f (0;1;0)  (1;0); f (0;0;1)  ( 1;1)

 Ma trận của f đối với cặp cơ sở chính tác là A  32 10 11

  1. x Ker f  f x( )  0  32xx11 xx23 x03  0

Đặt x3  t x1  2t ,x2 52t  x t21 5; 2;1

 dim Ker f 1, cơ sở  21 5; 2;1.

Bài 2. Cho ánh xạ f P x: 2[ ]P x4[ ] xác định như sau: f p( ) p x p2 , p P x2[ ]

  1. Chứng minh f là ánh xạ tuyến tính.
  2. Tìm ma trận của f đối với cặp cơ sở chính tắc E1 1,x,x2 của P[x]2 và E2  1,x,x ,x ,x2 3 4 của P[x].4
  3. Tìm ma trận của f đối với cặp cơ sở E11 x,2x,1 x2 của P[x]2 và E2 1,x,x ,x ,x2 3 4 của P[x].4

Lời giải

  1. Dễ thấy  p1, p2  P x2[ ] thì f  p1  p2  f  p1 f  p2; f kp 1  kf  p1

k  

 f là ánh xạ tuyến tính.

  1. Ta có f (1)  1 x2, f x( )  x x3, f x 2  x2 x4

1 0 0

0 1 0

 Ma trận của f đối với cặp cơ sở E E1 2, là A  1 0 1

 

0 1 0

0 0 15 3

  1. f (1    x) 1 x x2 x3, f (2 )x  2x 2x3, f 1 x2 1 2x2  x4

1 0 1

1 2 0

 Ma trận của f đối với cặp cơ sở E E1 2, là B1 0 2.

 

1 2 0

0 0 1

Bài 3 (CK 20151). Cho ánh xạ tuyến tính f :P[x]2 P[x]2 thỏa mãn: f 1 x2  3 3x 6x2, f 3x  2x2  17 x 16x2, f 2  6x 3x2  32 7x 25x2.

  1. Tìm ma trận của f đối với cơ sở chính tắc của P x2[ ]. Tính f 1 x2 .

b) Xác định m để véc tơ v   1 x mx2 thuộc Imf

Lời giải

  1 0 2 3

a) Đề  f (1)] [ ( )]E f x E  f x 2E 0 3 6 3

 1 2 3 6

17

1

16

32

7 (E là cơ sở chính tắc của P x2[ ]

25

3 17 32  1

 Ma trận của f đối với E là A  3 1 7    0

6 16 25  1  1 8 9 5  1 13

0

3

2

21 8 9 5

6   1 3 4

3 7 6 1

       

  1. f 1 x2 E  A 0  1 3 4   0  5  f 1 x2  13 5x 8x2   1 7 6 1    1  8  c)

v   1 x mx2 Im f x x1, 2, x3 :v  x1  8 x 7x2 x2 9  3x 6x2 x3   5 4x x2 xi2  0

8x1 9x2 5x3 1

 Xét hệ x1 3x2 4x3 1 có nghiệm không tầm thường

7x1 6x2  x3  m

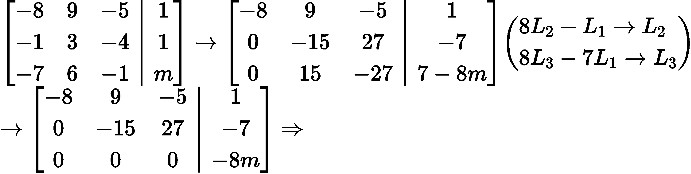
Hệ có nghiệm  m  0.

Vậy m0 thì v  Im f .

Bài 4. Cho ánh xạ f : 3 3 xác định bời f x ,x ,x1 2 3   x1 x2 x ,x3 1    x2 x , x3 1 x2 x3 Tìm ma trân của f đối với cơ sở B v1 (1;0;0),v2 (1;1;0),v2 (1;1;1).

Lời giải

 1 1 1

Ma trận của f đối với cơ sở chính tắc là A  1 1 1 

1 1 1 

1 1 1

Ma trận chuyển cơ sở từ E sang B là S  0 1 1

0 0 1

1 1 11  1 1 1 1 1 1  0 2 0

 Ma trận của f đối với B là S 1  A S  0 1 1 1 1 1    0 1 1  2 0 0

0 0 1 1 1 1   0 0 1 1 0 1

Bài 5 (CK 20151). Cho ánh xạ tuyến tính f :P[x]2 P[x]2 thỏa mãn: f 1 x2  3 3x 6x2, f 3x  2x2  17 x 16x2, f 2  6x 3x2  32 7x 25x2.

  1. Tìm ma trận của f đối với cơ sở chính tắc của P x2[ ]. Tính f 1 x2 .
  2. Xác định m để véc tơ v   1 x mx2 thuộc Imf

Lời giải Cách làm tương tự bài số 3.

1 3 1

Bài 6. Cho A  2 0 5  là ma trận của axtt f :P[x]2 P[x]2 đối với cơ sở Bv ,v ,v1 2 3

6 2 4 

trong đó: v1  3x x v3 2, 2   1 3x x v2 2, 3   3 7x x2 2

  1. Tìm f v 1 , f v 2, f v 3.
  2. Tìm f 1 x2 .

Lời giải

a) f v 1  v1 2v2  6v3  3x 3x2    2 1 3x 2x2 6 3  7x 2x219x2 51x16 f v 2  3v1  2v3  3 3 x 3x2 2 3  7x 2x2 5x2  5x 6 f v 3  v1 5v2  4v3  3x 3x2    5 1 3x 2x2 4 3  7x 2x215x2  40x 7

b) Gọi B0 là ma trận của f đối với cơ sở chính tắc E

S là ma trận chuyển cơ sở từ B sang E  S 1 là ma trận chuyển từ E sang B )

0 1 3 1 3 1 0 1 31 239/ 24 161/ 24

. B0  S 1  A S  3 3 7   2 0 5    3 3 7   201/8 111/8

3 2 2  6 2 4   3 2 2  61/12 31/12

289/ 24

247/8

107/12

 1 22

  f x 2 1E  B0   0  56 .

  1 14

 3 2 1 0

Bài 7. Cho ma trận A  1 6 2 1 là ma trận của ánh xạ tuyến tính f : 4 3 đối với

3 0 7 1

cặp cơ sở B v ,v ,v ,v1 2 3 4 của 4 và Bu ,u ,u1 2 3 của 3 trong đó:

v1 (0;1;1;1),v2 (2;1; 1; 1),v  3 (1;4; 1;2),v 4 (6;9;4;2) và u1 (0;8;8),u2  ( 7;8;1),u3  ( 6;9;1)

  1. Tìm f v 1   B f v 2   B , f v 3   B* , f v 4 B .
  2. Tim f v 1 , f v 2, f v 3, f v 4.
  3. Tìm f (2;2;0;0) .

Lời giải

 3  2  1  0

  1.  f v 1 E '   1 ; f v 2 B'   6 ; f v 3 B'    2 ; f v 4 B'    1

3  0    7   1

  1. f v 1    3u1 u2 3u3 (11;5;22) f v 2    2u1 6u2 ( 42;32; 10) f v 3     u1 2u2 7u3 ( 56;87;17) f v 4    u2 u3 ( 13;17;2).
  2. Giả sử (2 ; 2 ; 0 ; 0)  xv1 1x v2 2 x v3 3 x v4 4 x x x x1 2 3 4; ; ; (1;1;0;0)

 f (2;2;0;0) 1.f v 1 1.f v 2 0.f v 3 0.f v 4  ( 31;37;12).

Bài 8. Cho toán tử tuyến tính trên P x2[ ] xác định bởi:

f (1 2 )x  19 12x 2x2; f (2   x) 14 9x x2; f x 2  4 2x 2x2

Tìm ma trận của f đối với cơ sở chính tắc của P x2[ ] và tìm rank ( f ) .

Lời giải

 2x2 9x 14  2x2 12x19

Từ đề bài2 (1)f f(1)2 ( )f xf x( )    1419 129xx2 x22x2  ff x( )(1)  x2 9x142(23x 3)  x2 5x82x 

f x 2  4 2x 2x2 f x 22x2 2x 4



3 8 4 

 Ma trận của f đối với cơ sở chính tắc là A  2 5 2

 0 1 2

3 8 4  3 8 4  3 8 4 

 2 5 2   0 1 2   0 1 2

 0 1 2  0 1 2  0 0 0 

 rank( f )  rank A  2 .

Bài 9. Cho V,V là 2KGVTn chiều và f : V  V là ánh xạ tuyến tính. Chứng minh các khẳng định sau tương đurong:

  1. f là đơn ánh. b) f là toàn ánh. c) f là song ánh.

Lời giải

+ Giả sử f đơn ánhker f { }. Mà dimKer f dimImf dimVdimImf dimV

Mà Im f là KGVT con của VImf Vf toàn ánh.

Giả sử f toàn ánhImf VdimImf dimV

dimKer f dimVdimImf  0 Ker f { } f đơn ánh

 f toàn ánh hay các mệnh đề sau tương đương: a) f đơn ánh

  1. f toàn ánh
  2. f song ánh.

Bài 10 (CK 20141). Cho toán tử tuyến tính trên 3 xác định bởi f x x x1 2 3; ;    x1 2x2 x x3 1;  x2 x mx3; 1 x2 x3, với m là tham số. Xác định ma trận của f đối với cơ sở chính tắc của 3 và tìm m để f là một toàn ánh. Lời giải

1 2 1 

Ma trận của f đối với cơ sở chính tắc của 3 là A A:  1 1 1

m 1 1 

f là toàn ánh dimImf dim3  3 rankA3

1 2 1  1 2 1 

A  m1 11 11  00 2m31 12mLL32 mLL1 1 L2L3 

1 2 1 

0 3 2 3L3 (2m1)L2  L3

0 0 3(1m)2(2m1)

Vậy r A( )  3 3(1 m)  2(2m  1) 0  1 m  0  m  1.

Bài 11. Tìm các giá trị riêng và cơ sở không gian riêng của các ma trận:

 2 1 0 

a) A  83 01 b) B  104 29 c) C  51 03 32

 0 1 0 4 5 2

d) D   4 4 0 e) E  5 7 3

2 1 2 6 9 4

Lời giải

3 0 3

  1. det(AI) 8  1  ( 3)( 1)  det(AI)  0   1

   3 vA(3) là KG riêng của A , là KG nghiệm của (A  3 )I x  0

0x1  0x2  0

8x1  4x2  0  x2  2x1  vA(3)  span({1;2}).

4x1  0x2  0

 1,vA( 1) là KGN (A  I x)  0  8x1  0x2  0  x x1; 2  (0;0)  vA( 1) { }

  1. Cách làm tương tự câu a:  4,vB (4)  span32;1

2 1 0

c)det(C I) 5  3  3 (  1) 2 4 5  det(C I)   0  1

1 0  2 

x1 x2  0

Với trị riêng 1,vC(1) là KG nghiệm của hệ 5x1 4x2 3x3  0

x1 3x3  0

x x x1 2 3; ;     t( 3; 3;1) vC(1) span{( 3; 3;1)} 

 1 0

  1. det(D I)  4 4 0 (2)3  det(C I)   0  2

2 1 2

2x1  x2  0

Với 2,vD(2) là nghiệm hệ 42xx11  2x2x200  vD(2)  span 12;1;0 ;(0;0;0) . 

4 5 2

  1. det(E I) 5  7  3 2 ( 1)  Giá trị riêng   0,  1.

6 9 4

4x1 5x2 2x3  0

 0,vE(0) là KGN 5x1 7x2 3x3  0

6x1 9x2 4x3  0

 x x x1; 2; 3  t.1 23 3; ;1  vE (0)  span1 23 3; ;1

3x1 5x2 2x3  0

1,vE(1) là KGN 5x1 8x2 3x3  0 x x x1 2 3; ; t(1;1;1)vE(1) span((1;1;1)}

6x1 9x2 3x3  0

Bài 12. Cho biến đổi tuyến tính f:P[x]2 P[x]2 xác định như sau: f a 0 a x1 a x2 25a0  6a1  2a2  a1 8a2xa0  2a2x2.

  1. Tìm các trị riêng của f.
  2. Tìm các vector riêng tương ứng của các trị riêng tìm được.

Lời giải

5 6 2 

Ma trận của f đối với cơ sở chính tắc là A  0 1 8

1 0 2

5 6 2

$| AI |0  1  8 (  3)( 4)( 3)  ( 3) (2 4) $

1 0  2 

 Các trị riêng   3, 4

2x1 6x2 2x3  0

3,vA(3) là KGN  4x2 9x3  0 x x x1 2; ; 3 t.(5; 2 ;1)

 x1 5x3  0

vA(3)span{(5; 2;1)}.

9x1 6x2 2x3  0

  4,vA( 4) là KGN  3xx1228xx33  00x x x1; 2; 3  t.2;83;1

 vA( 4)  span{( 2; 83 ;1)}.

Bài 13. Tìm ma trận P làm chéo hóa A và xác định P AP1 khi đó với

14 12

a) A 20 17

Vận dụng tính An

1 b) B  6

0 

1

1 0

c) C 0 1 0 1

0

1

1

2 d) D  0

0

1

3

0

2

1 

3 

Lời giải

14  12

  1.  ( 1)(  2)  trị riêng   1,  2

20 17 

f 15x12 12x22  0 1 2  4 ;1  v f (1)  span 54 ;1.

1 v (1) là KGN 20x 16x  0  x x;   t  5  

 2  vf (2)  span  34;1n  D  51/ 4 31/ 4 thì D1  A D  10 20. 

  1. D1 113 0 thì D1 B D  10 01 .

1 0 0 1 0 0 

  1. C  0 1 1 |C I |  0 1 1    ( 1)( 2)

0 1 1  0 1 1

 Các trị riêng    0,  1,  2

  1,vC(1)span{(1;0;0)}

  0,vC(0)span{(0; 1;1)}

  2,vC(2)span{(0;1;1)}

 0 1 0 0 0 0

 D   1 0 1 thì D1 C D  0 1 0

 1 0 1 0 0 2

2 1 

  1. | DI |0 3 1 ( 3) (2 2)

0 0 3

 3,vD (3)  span{(1;1;0)}

 2,vD (2)  span{(1;0;0)}

Do D chỉ có tối đa 2 vector riêng ĐLTT nên D không chéo hóa được.

( D 1AD S có dạng chéo hóaA DSD . . 1An DS D S. n. 1, n dang chéo).

Bài 14. Ma trận A có đồng dạng với ma trận chéo không? Nếu có, tìm ma trận chéo đó:

1 4 2 5 0 0 0 0 0

a) A  3 4 0  b) B 1 5 0 c) C 0 0 0

3 1 3  0 1 5 3 0 1

Lời giải

  1. | A I | (1)( 2)( 3)

   1 vA(1) span{(1;1;1)}

   2 vA(2) span23;1;1



   3 vA(3) span1 34 4; ;1

1 0 0

 A chéo hóa được, ma trận chéo D  0 2 0. 0 0 3

  1. |BI| ( 5)3  5,vB(5)span{(0;0;1)}

 B không chéo hóa được, tức không tồn tại ma trận chéo đồng dạng với B . c) |CI|2( 1)

  0,vC (0)  span (0;1;0);31;0;1

  1,vC (1)  span{(0;0;1)}

0 0 0

 C chéo hóa được, ma trận chéo hóa D  0 0 0

0 0 1

Bài 15. Tìm cở sở của 3 để ma trận của f : 3  3 có dạng chéo trong đó

  1. f x x x 1 2 3, ,  2x1  x2  x x3 1, 2x2  x x3 1,  x2 2x3.
  2. f x x x 1 2 3, ,  2x1  x2 x x3 1, x2,x1  x2 2x3

Lời giải

2 1 1

  1. Ma trận của f đối với cơ sở chính tắc của 3 là A 1 2 1

1 1 2

1 0 0 1 1 1

Chéo hóa A D: 1 A D  0 1 0 với D   1 0 1

0 0 4  0 1 1

 Cơ sở cần tìm {( 1;1 ;0);( 1;0;1);(1; 1;1)} .

 2 1 1

  1. Ma trận của f đối với cơ sở chỉnh tắc của 3 là B  1 1 0 

1 1 2 

1 0 0  2 1 1 

Chéo hóa B D: 1 B D  0 1 3 0 , D  1  2 3  2 3

0 0 1 3 1 1 1 

Cơ sở cần tìm {(2;1;1):( 2;  2 3;1);( 1;  2 3;1)}.

Bài 16 (CK 20172). Cho toán tử tuyến tính trên 3 xác định bởi: f (1;2;1)  (4;2;6), f (1;1;2)  (5;5;0), f (1;0;0)  (1;2;1)

  1. Tìm m để u  (6;3;m) Im(f ) .
  2. Tìm các giá trị riêng và véc tơ riêng của f .

Lời giải

  1. u  Im f  u  span{(4;2;6);(5;5;0);(1;2;1)}

4x1 5x2  x3  6

 Hệ 2x1 5x2  2x3  3 có nghiệm

6x1  x3  m

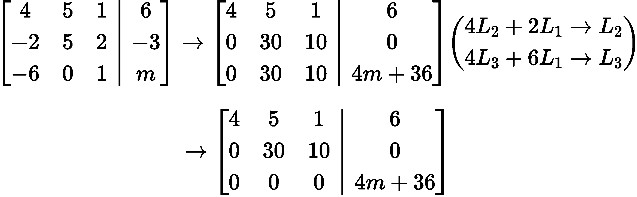
 Hệ có nghiệm  4m36  0  m  9 hay u  Im f  m  9 .

 1 1 1  4 5 1

  1. Ta có  f e 1 E  f e 2 E f e 3 E   2 1 0 2 5 2 trong đó E là cơ sở

1 2 0 6 0 1

chính tắc của 3,E e e e1 2 3; ; .

 4 5 1  1 1 11 1 2 1

 Ma trận của f đối với E là A   2 5 2   2 1 0  2 1 2

6 0 1  1 2 0 1 3 1

1 2 1

Ta có | AI |2  1  2 2( 1) Trị riêng 0, 1

1 3 1

  0,vA(0) span{( 1;0;1)}

  1,vA(1) span23;21;1

Bài 17. Cho f :V V là toán tử tuyến tính. Giả sử f 2  f f : V  V có giá trị riêng 2 .

Chứng minh rằng một trong 2 giá trị  hoặc  là giá trị riêng của f.

Lời giải Đưa bải toán về: Ma trận A biết A2 có trị riêng là 2 .

Cần chứng minh A có trị riêng  hoắc .

Ta có: detA2 2I   0 | AI |.| A I | 0

| AI | 0

 | AI | 0  A có trị riêng  hoắc .(đpcm)

 3 1 2 

Bài 18 (CK 20161). Cho ánh xạ tuyến tính f P x: 2[ ]P x2[ ] có ma trận A  6 0 3 đối với

10 2 6  cơ sở chính tắc 1, ,x x2 của P x2[ ].

  1. Tính f 1 x  x2 . Tìm m để v  1 x  mx2 thuộc Ker f .
  2. Tìm một cơ sở của P x2[ ] để ma trận của f đối với cơ sở đó có dạng chéo.

Lời giải

 1  3 1 2   1  0 

a) f 1 x x2E  A  1  6 0 3     1  3  f 1 x  x2   3x  2x2

  1 10 2 6     1 2

 1  2m4  0

v  1 x  mx2 Ker f  f 1 x  mx2   A  1  3m6  0  m  2.

m 6m12  0

0 0 0  1/ 2 1/ 2 1/ 4 

b) Chéo hóa A: D1 A D  0 1 0 với D   1/ 2 0 3/ 4

0 0 2  1 1 1 

 Cơ sở cần tìm là 12; 21;1 ;    12;0;1 ;    14 ; 43;1.



Bài 19. Cho A là ma trận kích thước m  n, B là ma trận kích thước np . Chứng minh rằng rank(AB)  min{rank(A),rank(B)}, vor ranki (A)  hạng của ma trận A .

Lời giải

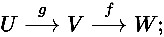
A, B là ma trận của f, $ đối với cặp cơ sở tương ứng

 Im( f  g)  Im f  r AB( )  dim Im( f • g)  dim Im f  r A( )

 Ker g  Ker( f  g)  dim Im( f  g)  dim Im g

(do dimU  dimImg dimKer g  dimIm( f g)dimKer( f g))

r AB( )  r B( )

CHƯƠNG V. DẠNG SONG TUYẾN TÍNH, DẠNG TOÀN PHƯƠNG, KHÔNG GIAN EUCLIDE, ĐƯỜNG MẶT BẬC HAI

Bài 1. Cho f là dạng song tuyến tính trên không gian véc tơ 3 chiều V có ma trận đối với cơ sở

 1 1 0 

Bu u1 2, , u3là A  2 0 2. Cho h:VV là ánh xạ tuyến tính có ma trận đối với cơ sở

 3 4 5 

1 1 1 

B là B  3 4 2  .  1 2 3

  1. Xác định f u u 1 3; ; f u 1 u2 u3,2u1 3u2 u3
  2. Chứng minh ánh xạ g u v( , )  f u h v( , ( )) là dạng song tuyến tính trên V . Tìm ma trận của nó đối với cơ sở B ,

Lời giải

a) f u u 1 3,   0

f u 1 u2 u3,2u1 3u2 u3  2 f u u 1 1, 3f u u 1 2,  f u u 1 3, 2 f u u 2 1, 3f u u 2 3, 

 f u u 2 3, 2 f u u 3 1, 3f u u 3 2,  f u u 3 3,  14

b)Kiểm chứng g u1  u av2, 1 bv2 ag u v 1 1, g u v 1 2, ag u v 2 1, bg u v 2 2,  g u v( , )  f u h v( , ( ))  h u[ ]T A h v[ ( )][ ]u T  A B v | |g AB  Ma trận của g đối với cơ sở  là AB.

Bài 2. Cho dạng song tuyến tính trên P x2[ ] xác định bởi f ( p x( ),q x( ))  p(1) (2)q . Tìm ma trận và biểu thức của f đối với cơ sở chính tắc.

Lời giải

f (1,1) 1; f (1, x)  2; f 1, x2   4 f x( ,1) 1; f x x( , )  2; f x x, 2   4 f x 2,1 1; f x 2, x  2; f x 2, x2   4

1 2 4

Ma trận của f đối với cơ sở chính tắc là 1 2 4

1 2 4

f a x 1 2  b x1  c a x1, 2 2  b x2  c2   4a a1 2  2a b1 2  a c1 2  4ba1 2  2bb1 2  bc1 2  4c a1 2  2c b1 2  c c1 2.

Bài 3. Trên 3 cho các dạng toàn phương  có biểu thức tọa độ:

1x x x1 2 3, ,   x12 5x22 4x32 2x x1 2 4x x1 3. 2x x x1 2 3, ,   x x1 2 4x x1 3 x x2 3. a) Bằng phương pháp Lagrange, đưa dạng toàn phương về dạng chính tắc.

b) Xét xem các dạng toàn phương xác định dương, xác định âm không? Lời giải

+ w1   x12 5x22 4x3202x x1 2 4x x1 3

x12 2x x1 2 2x3  x2 2x32   5x22 4x32 x2 2x32

 x1  x2 2x32 4x22  8 432 x x2 3  x1  x2  2x3 2  2x2  x3 2 9x32  y12  y22  y32 y1  x1 x2 2x y3 2, 2x2x y3 3, 3x3

w1không xác định dương, không xác định âm

+ w2 xx1 24xx1 3x x2 3

Đặt x1 y1 y x2 2,  y1 y x2 3, y3 w2  y12  y22 4y1  y2 y3 y1  y2 y3

 y12  y14y3  y3 y22 4y y2 3  y y2 3  y12 5y y1 3  y22 3y y2 3

  y1  52 y3 2  y2  23 y3 2  4y32

 u12 u22 u32 u1  y1  53 y u3; 2  y2  32 y u3; 3  4y3 

w2 không có dấu xác định.

Bài 4. Xác định a đề các dạng toàn phương xác định dương:

  1. 5x12 x22 ax324x x1 22x x1 32x x2 3.
  2. 2x12  x22 3x32 2ax x1 2 2x x1 3.
  3. c) x12  x22 5x32 2ax x1 2 2xx1 34x x2 3.

Lời giải

 5 2 1

  1. Ma trận của f đối với cơ sở chính tắc là A   2 1 1

1 1 a 

5 2

 1 5, 21, 3 | A| a  2

2 1

w xác định dương  a  2

2 a 1

  1. Ma trận của f đối với cơ sở chỉnh tắc là B  a 1 0

1 0 3

 1 2; 2 2 a2; 3 32a2  1 53a2

w xác định dương 2a2200 a2  53  315  a 315 .

5 3a

 1 a 1

  1. Ma trận của f đối với cơ sở chính tắc là C  a 1 2 

1 2 5 

       1 1; 2 1 a2; 3 5a2 4a

2

w xác định dương 15aa2 40a0    143 aa 10  54 a 0.

Bài 5. Cho dạng song tuyến tính trên 3 xác định bởi:

x x x1 2 3, ,  , y y y1 2, , 3  2x y1 1 x y1 2 x y2 1 ax y2 2 2x y2 3 2x y3 2 3x y3 3

(a là tham số). Tìm ma trận của dạng song tuyến tính trên đối với cơ sở chính tắc của 3 và tìm điều kiện của a để dạng song tuyến tính là một tích vô hướng trên 3 .

Lời giải

2 1 0 

Ma trận của dạng song tuyến tính đã cho đối với cơ sở chính tắc 3 là A 1 a 2

0 2 3 

Dạng song tuyến tính trên là tích vô hướng nếu nó xác định dương

 1 2; 2 2a  1; 3 6a11

2a  1 0 11

 6a 11 0  a  6

Bài 6. Trong 3 trang bị một dạng song tuyến tính như sau:

 4 2 1

f x y( , )  x x1, 2 , x3  A y y1, 2, y3 t với: A  2 3 4  và x x x x1 2 3, , , y y y y1, 2, 3. Xác

1 a2 2a

định a để f (x, y) là một tích vô hướng trên 3 .

Lời giải

f x y( ; ) là 1 tích vô hướng trên 3f xác định dương (1)

Mà      1 4; 2 8; 3 18a2 16a 11

Nên (1)  a2  42  a

18a 16a 11 0

Vậy không tồn tại a thỏa mãn.

Bài 7. Giả sử V là KGVT n chiều với cơ sở Be ,e ,1 2 ,en. Với u,v là các véc tơ của V ta có u ae 1 1ae2 2  ae v ben n;  1 1be2 2  ben n.Đặt t u v , ab1 1ab2 2  abn n

  1. Chứng minh  u v, là một tích vô hướng trên V .
  2. Áp dụng cho trường hợp V  3, với e1(1;0;1),e2 (1;1; 1),e 3 (0;1;1),u(2; 1; 2),v  (2;0;5). Tính  u,v .
  3. Áp dụng cho trường hợp VP[x]2 , với B  1;x;x2,u  2  3x ,v2  6 3x 3x2 . Tính u v,  .
  4. Áp dụng cho trường hợp VP[x]2 , với B 1 x;2x;x  x2,u  23x ,v2  63x 3x2 . Tính

u v, .

Lời giải

a) Kiểm chứng: u v,   v u, 

  •    u1  u v2,  u v1,  u v2,
  • u u,   0u và u u,   0  u .
  1. B0 {(1;0;1);(1;1; 1);(0; 1;1)} là 1 cơ sở của 3

[ ]u R0  B01 [ ]u E B01 là ma trận chuyển cơ sở từ E sang B0

1 1 0  2   1 

0 1 1   1   3 a a a1; 2; 3  (1; 3; 1)

1 1 1  2  1 

Tương tự b b b1 2 3; ;   (2;5;7) u v,   6

 2  6 

  1. [ ]u B   0 ;[ ]v B   3  u v,   2 6 0.( 3)   3 ( 3)  3

  3 3

1 0 0   2  2   6 

  1. [ ]u n 1 2 1      0   5 ,[ ]v n   3  u v,   2.6  5 ( 3) ( 3)2  6 . 0 0 1    3 3 3

Bài 8. Xét không gian P[x]3 . Kiểm tra các dạng  p,q sau có phải là tích vô hướng hay không?

  1.  p,q  p(0)q(0)  p(1)q(1)  p(2)q(2)
  2.  p,q  p(0) (0)q  p(1)q(1)  p(2)q(2)  p(3)q(3)
  3. p q, 1 p x q x dx( ) ( )

1

Trong trường hợp là tích vô hướng tính  p,q với p 2 3x 5x 2x .q3   4 x 3x22x3

Lời giải

  1. p p,  p2(0)p2(1)p2(2)0

 p p,   0  p(0)  p(1)  p(2)  0

Chọn p x x ( 1)(x 2) P x3[ ] thì p  0 và  p p,   0

  p q,  không là tích vô hướng

  1. Có là tích vô hướng  p q,   q p, 

 p1  p2,q  p q1,   p2,q

 p p,   0; khi  p=0)

1 2( )  0 p x( )0)

  1. Có là tích vô hướng (p xdx

1

Với p 2 3x5x2x q3;   4 x 3x22x3

 p q,   8 12  80  374  474

 p q,   112  3x  5x2  x34  x  3x2  2x3dx  1466105 .

Bài 9. Cho V là không gian Euclide. Chứng minh:

  1. ‖ u  v ‖ ‖2  u  v ‖2 2‖ ‖ ‖ ‖u 2  v 2  .
  2. u  v‖uv‖ ‖ ‖ ‖ ‖2 u 2  v 2, u,v V.

Lời giải

  1. ‖uv‖2  u v u,    v u u, v v,   2 u v, 

‖ ‖ ‖ ‖u 2  v 2  2 u v, ‖u v ‖2 u v u v,   u u, v v,  2 u v,  ‖ ‖ ‖ ‖u 2  v 2  2 u v, 

 ‖u v‖ ‖2  u v ‖2 2( ‖ ‖ ‖ ‖u 2  v 2

  1. ‖u v ‖‖ ‖ ‖ ‖ u 2  v 2  2 u v, 

u v u v,  0 ‖u v ‖‖ ‖ ‖ ‖ u 2  v 2: đpcm

Bài 10. Cho cơ sở B  {(1;1;2),(2;0;1),(1;2;3)} trong không gian 3 với tích vô hướng chính tắc.

Trực chuẩn hóa Gram-Schmidt cơ sở B để thu được cơ sở trực chuẩn B và tìm tọa độ của véc tơ u  (5;8;6) đối với cơ sở B.

Lời giải

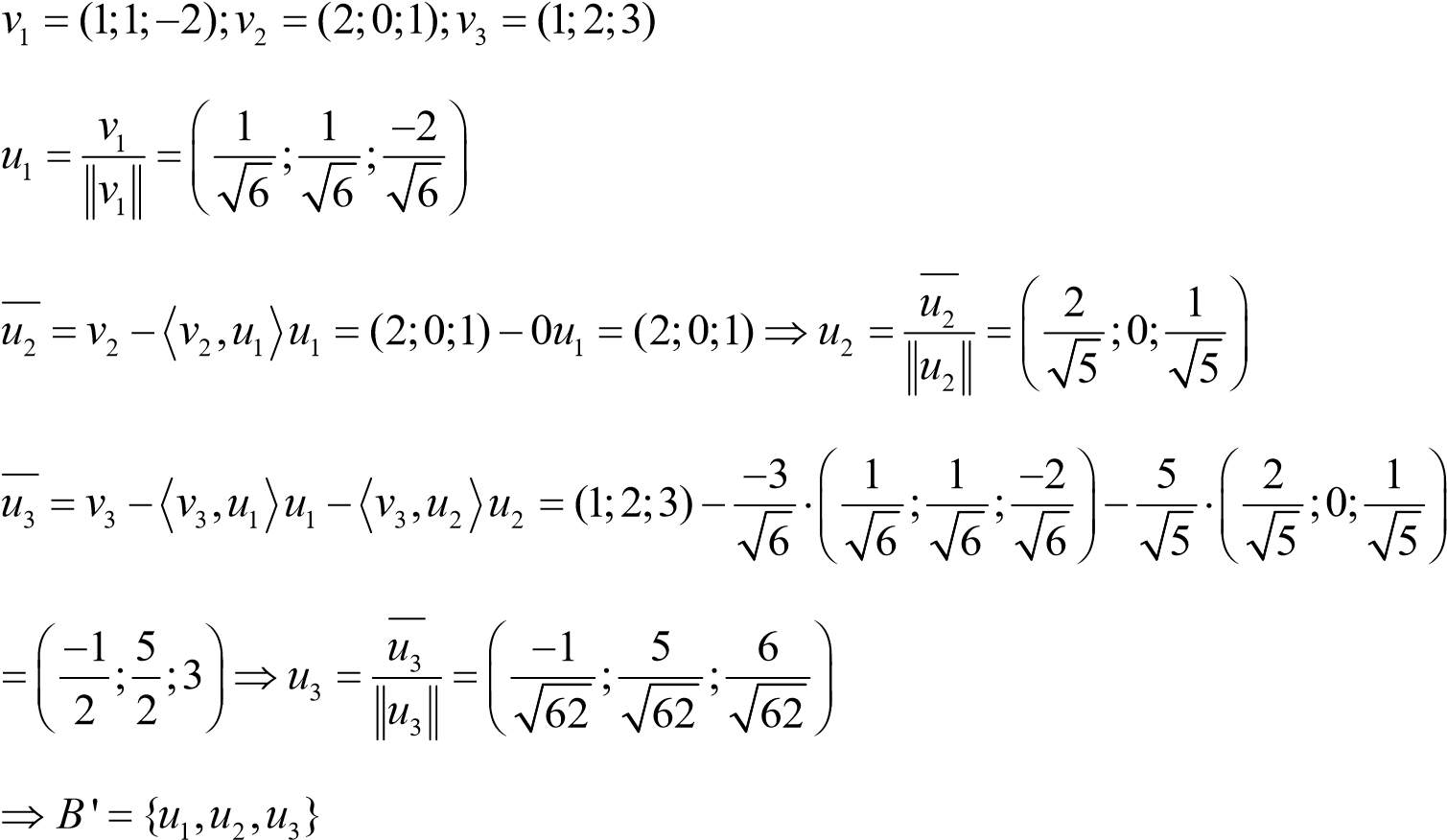
 1/

1 2 3 T 1 16 71T  

[ ]u z  u u, u u, u u,      16/ 5 

6

62

 6 5 62  

71/

Bài 11. Cho 4 với tích vô hướng chính tắc. Cho u1(6;3; 3;6),u 2 (5;1; 3; 1). Tìm cơ sở trực chuẩn của không gian sinh bởi u u1, 2 .

Lời giải

u1  (6;3; 3;6); u2  (5;1; 3; 1)

v1  u1  2 ; 1 ; 1 ; 2  u1  10 10 10 10 

v2  v2  u v v2 1, 1  (5,1, 3, 1) 16 , 2 , 1 , 1 , 2 

10  10 10 10 10 

 95 , 53, 57 , 511v2  vv22   2 65 2 65 2 65 2 659 , 3 , 7 , 11 

 B   2 , 1 , 1 , 2   ; 9 , 3 , 7 , 11 

 10 10 10 10   2 65 2 65 2 65 2 65 

 span B  spanu u1, 2.

Bài 12. Trong P[x]2 định nghĩa tích vô hướng p,q11p(x)q(x)dx với p,qP[x]2 .

  1. Trực chuẩn hoá Gram-Schmidt cơ sở B  1;x;x2 để nhận được cơ sở trực chuẩn A .
  2. Tìm [r]A biết r  2  3x  3x2

Lời giải

  1. Đặt v1 1,v2  x v, 3  x2

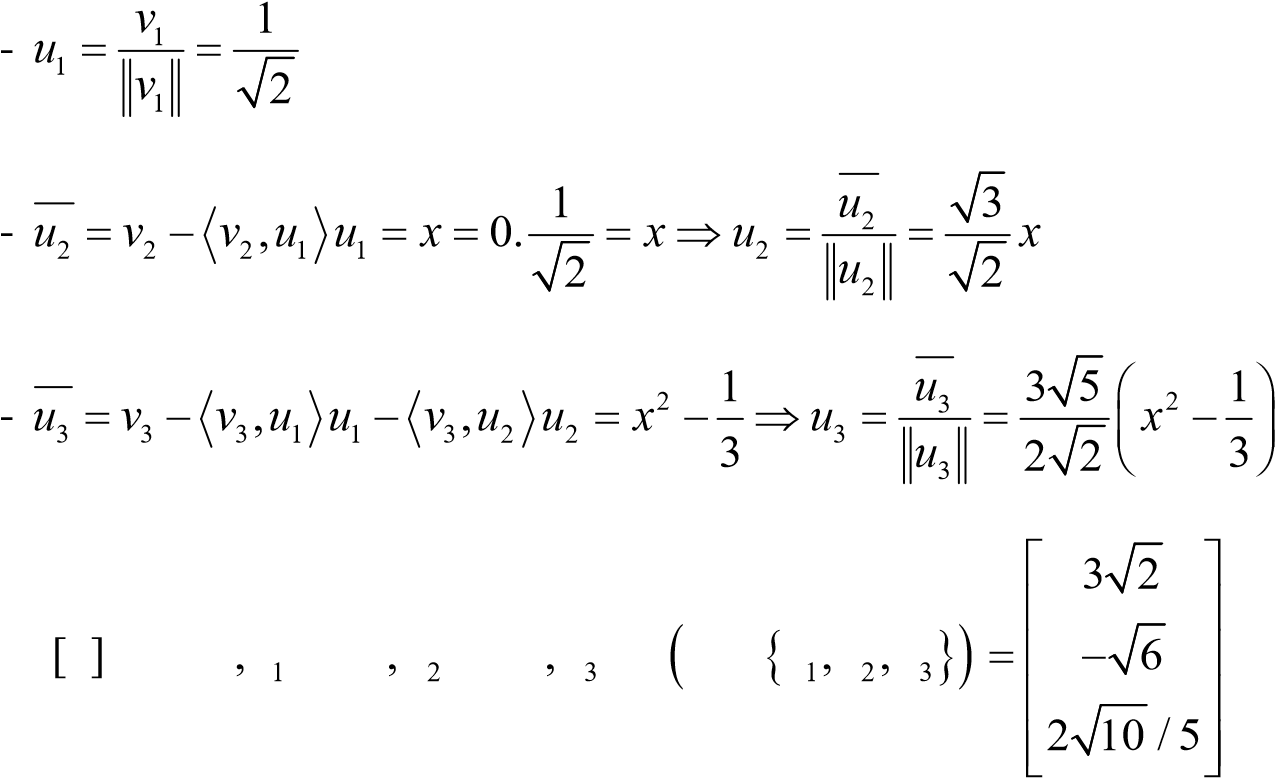 x  0. 1  x  u2

  1. [ ]r A  r u, 1 r u, 2 r u, 3 T A u u u1,

Bài 13. Tìm hình chiếu trực giao của véc tơ u lên không gian sinh bởi véc tơ v:

  1. u  (1;3;2;4), v  (2;2;4;5)
  2. u  (4;1;2;3; 3),v  ( 1; 2;5;1; 4)

Lời giải

  1. w1  u v, v  8 (2, 2,4, 5)  1649, 4916 32 40, 49 49, 

v v,  49 

  1. w2  u vv v, ,v  475 ( 1 , 2,5,1, 4)   47 475 ,10 , 4725, 475, 4720  .

Bài 14. Cho không gian 3 với tích vô hướng chính tắc và các véc tơ u(3; 2;1), v1 (2;2;1),v2  (2;5;4) . Đặt W spanv v1 2, . Xác định hình chiếu trực giao của véc tơ u lên không gian W .

Lời giải

+ Trực chuẩn hóa v v1 2,

u

1  vv11   2 2 13 3 3, , 

u2  v2  v u u2, 1 1  (2,5,4)6 2 2 13 3 3, ,   ( 2,1,2)  u2  32 1 2, 3 3, 

+ Gọi w là hình chiếu của u lên W  spanv v1 2, 

 w  u u u, 1 1  u u, 2 u2  2 2 13 3 3, ,  ( 2)32 1 2, 3 3,   (2,0,1)

Bài 15 (CK20161). Trong không gian 3 với tích vô hướng chính tắc, cho các véc tơ u  (1;2;1) , v  (3;6;3) và đặt H  w  3∣w  u

  1. Tìm một cơ sở trực chuẩn của không gian H .
  2. Tìm hình chiếu trực giao của v lên không gian H

Lời giải

  1. wH  w1  2w2  w3  0(w u,   0)

 w a(1,0,1)  b( 2,1,0)  H span{(1,0,1);( 2,1,0)}

v1  (1,0,21)   12 ,0, 12  $

v2  ( 2,1,0) 2( 1)  12 ,0, 12  ( 2,1,0)(1,0,1)  ( 1,1,1)

2  1 1 1  v v1, 2 là 1 cơ sở trực chuẩn của H

 v  , ,  B 



3

3

3

  1. u là hình chiếu trực giao của v lên H v(  (3,6,3)) u  v v v, 1 1  v v, 2 v2  3 2  12 ,0, 12  2 331 , 13 , 13   (1,2,5).

Bài 16. Trong 5 với tích vô hướng chính tắc cho các véc tơ v1(1;1;0;0;0),v2 (0;1; 1;2;1),v 3 (2;3; 1;2; 1). Gọi V x5∣x  v ,ii 1;2;3

  1. Chứng minh V là không gian véc tơ con của 5 .
  2. Tìm dimV.

Lời giải

x1  x2  0

Ta có: xV  x v, i  0,i 1,3  x2  x3  2x4  x5  0

2x1 3x2  x3  2x4  x5  0

 x   x x x x2, 2, 3, 4,x2  x3  2x4

 x2( 1 ,1,0,0,1) x3(0,0,1,0,1) x4(0,0,0,1,2)

 dimV  3 .

Gọi V là KGVT con của5 : v vkv1 2 ,1  V kV, v v.1 , i  v v2 , i  0  v1  v v2 , i  0  v1  v2 V

Bài 17. Cho V là không gian Euclide n chiều, V1 là không gian con m chiều của V . Gọi V2 xV x∣ v,  v V .1

  1. Chứng minh V2 là không gian véc tơ con của V .
  2. Chứng minh V1 và V2 bù nhau.
  3. Tìm dimV2 .

Lời giải

  1. Chứng minh: a b, V2  a V,   b V,    0 v V1   a b v,   0  a bV2 aV k2,   ka V,   k a V ,    0 v V1  kaV2

V2 là KGVT con của V

  1. Xét B1 x x1, 2,,xm là cơ sở trực chuẩn của V1

Bổ sung n m vector để được co sở trực chuẩn của V là x x1, 2,, x xm , m1,, xn

Đặt W  spanxm1,,xn

n

- w W  w  i xi  w x, i   0 i 1,m  w V 2 W V2

i m n  n

vV2  v  i xi. Mà v x, i   0 i 1,m   i 0 i 1,m

i1

n

 v  i xi  vW V2 W

i m 1

Do vậy W V2 , nên V V1, 2 bủ nhau

Khi đó dễ thấy dimV2  nm.

Bài 18. Chéo hoá trực giao các ma trận sau

1 0 0  1 1 0  7 2 0

a) A 00 11 11 b) B  247 247  c) C   01 01 10 d) D   02 62 52 

Lời giải

1 0 0

a) A  0 1 1 | AI | ( 1)(2) 0 1 1

  •  0  vA(0)  span{(0; 1;1)}  vector riêng: 0, 21 , 1 

2

  •  1 vA(1)  span{(1;0;0)} vector riêng: (1;0;0)
  •  2  vA(2)  span{(0,1,1)} vector riêng: 0, 12 , 12 

 1 1   1 1 

Ta có 3 vector riêng trực chuẩn 0, 2 , 2 ;(1;0;0); 0, 2 , 2  úng với các trị riêng 0,1,2

0 0 0  0 1 0 

 P APT 0 1 0 vói P  1/0 1/ 2

2

2

0 0 2 1/0 1/ 2

7 24

b) B  24 7  [B   I]  ( 25)(  25)

  •  25 ta có vector riêng trực chuẩn:  5 53 4,  .
  •  25 ta có vector riêng trực chuẩn  54 3,5

T 25 0  3/ 5 1/5

 P BP   0 25 với P  4/ 5 3/5 

0 0 0 1/ 2 0 1/

2

  1. P CPT  00 10 02 vởi P  1/0 2 10 1/0 2 

3 0 0 1/3 2/3 2/3

  1. P DPT 0 6 0 với P   2 / 3 1/ 3 2 / 3

0 0 9  2 /3 2/3 1/ 3 

Bài 19. Đưa dạng toàn phương về dạng chính tắc bằng phương pháp trực giao

  1. x12  x22 x32 2xx1 2
  2. 7x12 6x225x32 4x x1 2 4x x2 3

Lời giải

a) Đặt f x( )  x12  x22  x32  2x x1 2

1 1 0

Ma trận của f đối với cơ sở chính tắc 3 là A  1 1 0

0 0 1

Ta có | A   I | ( 1)(  2)

 0  vA(0)  span{( 1,1,0)} , trực chuẩn hóa được 1 , 1 ,0

 

2

2

 1 vA(1)  span{0,0,1}, trực chuẩn hóa được (0,0,1)

 2  vA(2)  span{1,1,0}, trụuc chuẩn hóa được  1 , 1 ,0

2

2

2

2

2

2

0 0 0 1/0 1/ 

Do vậy P APr  00 10 02 vói P   1/0 10 1/0 

Hay f x( )  y22  2y x32[ ]B  y1 y2 y3T ,B   1 , 1 ,0 ;(0,0,1);  1 , 1 ,0

    b) Tương tự câu a f x( )  3y12 6y22 9y x32[ ]B y y1, 2, y3T ,B   31, 32 2, 3    ; 2 1 23 3 3, ,    ; 32 2 1, 3 3, .

2

2

2

2

Bài 20. Nhận dạng đường cong phẳng sau:

a) 2x24xy y 2 8 0. b) x22xy y 28x y 0.

c) 11x224xy4y215 0 . d) 2x24xy5y2 24.

Lời giải

2 2  2 2

  1. Dạng toàn phương w  2x 4xy  y có ma trận A  2 1

T 2 0 1/ 5 2/ 5

Chéo hóa trực giao A được: P AP   0 3,P  2/ 5 1/ 5 

 x 1/ 5 2/ 5 x

Đặt  y  2/ 5 1/ 5 y 

 Phương trình đường cong là: 2x2 3y2  8  hyperbol

2 2 1 1

  1. Dạng toàn phương w  x  2xy  y có ma trận A  1 1

T 2 0 1/ 2 1/ 2

Chéo hóa trực giao A được: P AP  0 0,P  1/ 2 1/ 2 

 x 1/ 2 1/ 2 x 2  9 x  7 y  0  parabol

Đặt  y  1/ 2 1/ 2  y   Phương trình đường cong là: x 2 2

 

11 12

  1. A  12 4 có 2 tụ riêng 20,5

 có thể đưa đạng toàn phương 11x2  24xy  4y2 về 20x2 5y2  Phương trình đường cong là: 20x2 5y2 15  0  hyperbol

  1. (31 8)x2 (3 8)y2  24  elipse.

Bài 21. Nhận dạng các mặt bậc 2 sau:

  1. x12   x22 x32 2x x1 2 4.
  2. 5x2y2 z2 6xy2xz2xy1.
  3. 2x12 2x22 3x32 2xx1 2 2x x2 3 16.

Lời giải

1 1 0

  1. Ma trận của dạng toàn phương đối với cơ sở chính tắc là A  1 1 0

0 0 1

Chéo hóa trực giao A được: P AP  

2

2

T 000 100 002,P  11//0 100 11//0 22

 x12  x22  x32  2x x1 2  x22  2x32

 Phương trình mặt cong: x22  2x32  4  ellipsoid.

 5 3 1 

  1. Ma trận của dạng toàn phương w  5x2  y2  z2 6xy  2xz 2yz 1 là A  3 1 1.

 1 1 1 

Có 2 trị riêng 1, 2, 3 là nghiệm của   3 7 2  4 0

Chéo hóa trực giao A đưa dạng toàn phương về dạng w   1x2 2y2 3z2

 Phương trình mặt cong   1x2 2y2 3z2 1 Hyperboloid 1 tầng 1, 2  0,3  0.

 2 1 0 

  1. A  1 2 1 có 3 trị riêng 1, 2, 3  0 là nghiệm    3 7 2 14  7 0

 0 1 3 

 Phương trình mặt cong   1x2 2y2 3z2 16  ellipsoid.

Bài 22. Cho Q x ,x ,x 1 2 3 9x12 7x22 11x32 8x x1 2 8x x1 3. Tìm

12  Max22 32 16Q x ,x ,x 1 2 3,x Mx12Min22 x32 16x ,x ,x1 2 3 . Với giá trị nào thì Q x ,x ,x 1 2 3 đạt max, min. x x x

Lời giải

 9 4 4 

A   4 7 0  là ma trận của Q đối với cơ sở chính tắc

 4 0 11

3 0 0   2 / 3 1/3 2 / 3 

Chéo hóa trực giao A P AP: r 0 9 0 ,P   2/ 3 2 / 3 1/ 3

0 0 15 1/ 3 2/ 3 2 / 3 

y1  x1

 Q  3y12 9y22 15y32 vs y2  P1 x2

y3  x3

Mà P trực giao x x,   Py Py,   (Py Py y P Py y y) .T T . T . .  T .  y y,   xi2   yi2 16  3.16  Q 15.16

 4  0

minQ  3.16  x  P. 0  ,maxQ 15.16  x  P. 0  

  0   4

Bài 23. Cho A,B là các ma trận vuông đối xứng cấp n có tất cả các giá trị riêng đều dương. Chứng minh A B cũng có tất cả các giá trị riêng đều dương. Lời giải

Xét f; g là 2 dạng toàn phương ứng với ma trận A B, (đối với cơ sở chính tắc)

Do A, B vuông, đối xứng cấp n có tất cả trị riêng đều dương  Dạng toàn phương f g, tương ứng xác định dương.

 f g xác định đương. Mà A B là ma trận của f  g đối với cơ sở chính tắc  A B có tất cả trị riêng dương (đpcm).

Tài liệu liên quan: