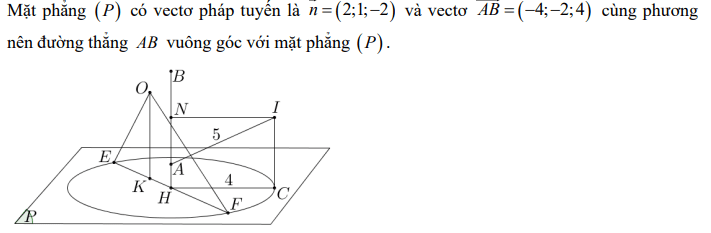
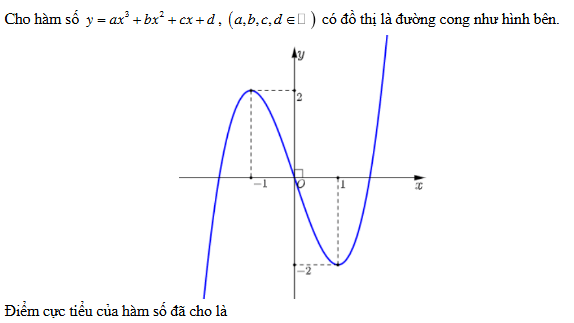
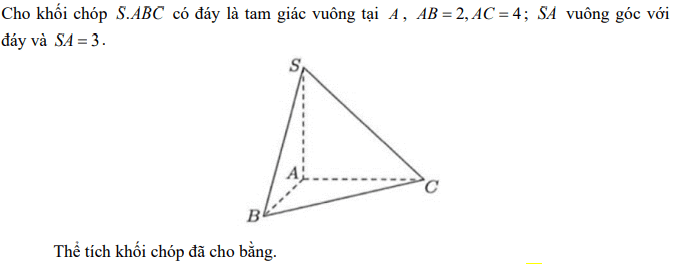
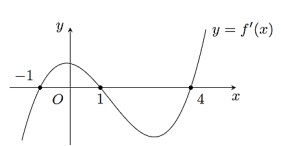
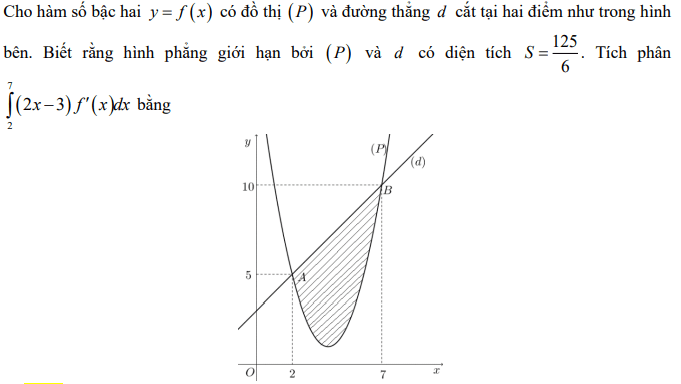
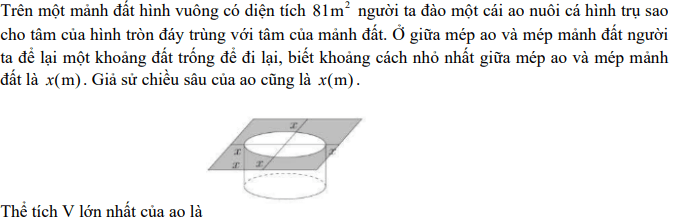
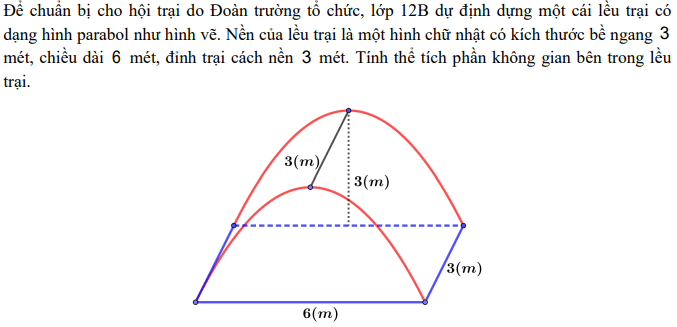
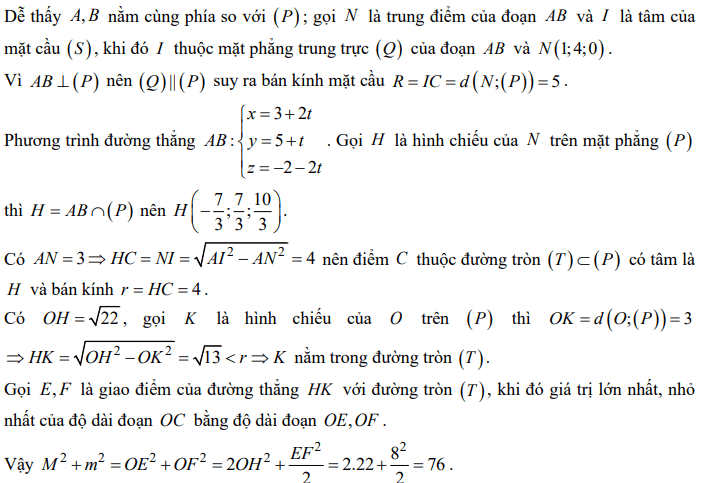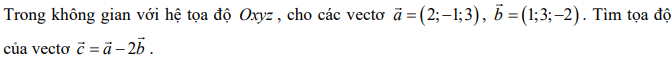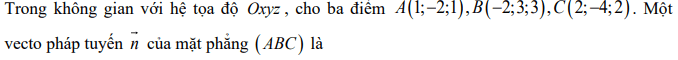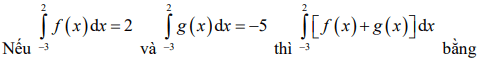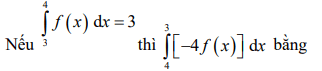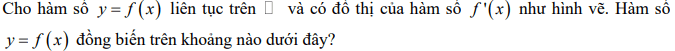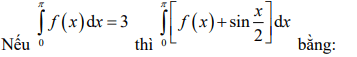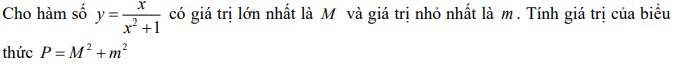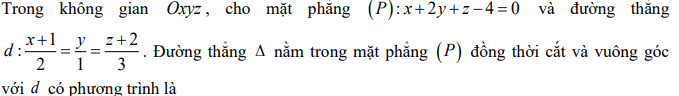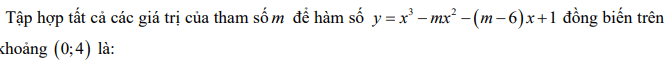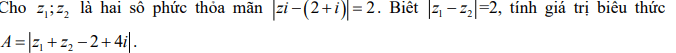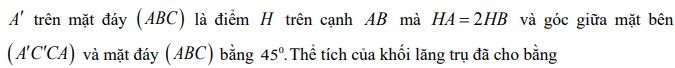Quiz: TOP 50 câu trắc nghiệm Đề toán luyện thi THPT 2025 Đề 11 (có đáp án) | Đề thi THPT Quốc Gia
Câu hỏi trắc nghiệm
Giải thích
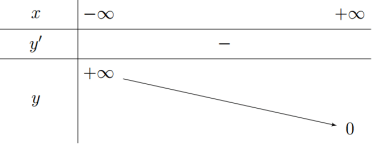
Từ đồ thị ta thấy điểm cực tiểu của hàm số đã cho là x =1
Giải thích
![]()
Giải thích
![]()
Giải thích
![]()
Giải thích
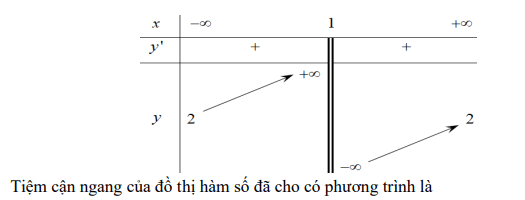
Từ đồ thị hàm số ta có tiệm cận ngang có phương trình y = 2 và tiệm cận đứng có phương trình x =1
Giải thích
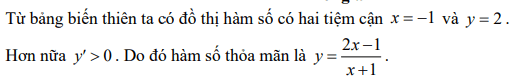
Giải thích
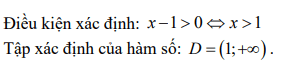
Giải thích
Thay tọa độ điểm P(1;2; -1 ) vào phương trình đường thẳng
d thấy thỏa mãn nên đường thẳng d đi qua điểm P(1;2; -1. )
Giải thích
![]()
Giải thích
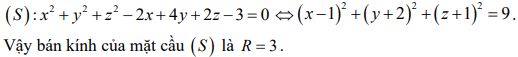
Giải thích
![]()
Giải thích
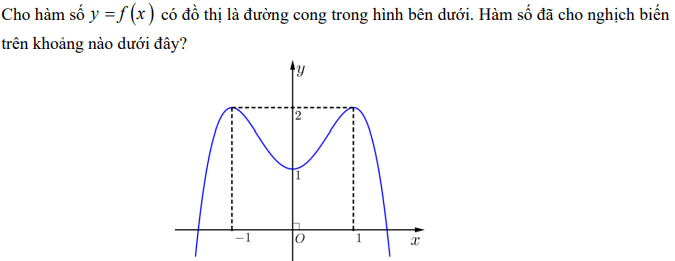
Dựa vào đồ thị, ta có: Hàm số nghịch biến trên khoảng (−1;0) và (1;+)
Giải thích
![]()
Giải thích
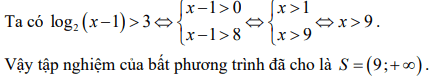
Giải thích
![]()
Giải thích
![]()
Giải thích

Giải thích
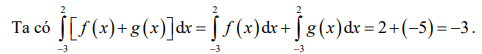
Giải thích
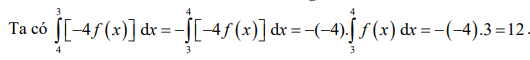
Giải thích
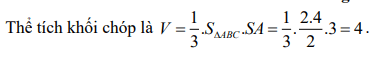
Giải thích
![]()
Câu hỏi 22 / 50
Giải thích
Mỗi số tự nhiên có 5 chữ số khác nhau lập từ 5 chữ số đã cho là một hoán vị của 5 phần tử. Nên số số tự nhiên cần tìm là 5! = 120 số.
Giải thích
![]()
Giải thích
![]()
Giải thích
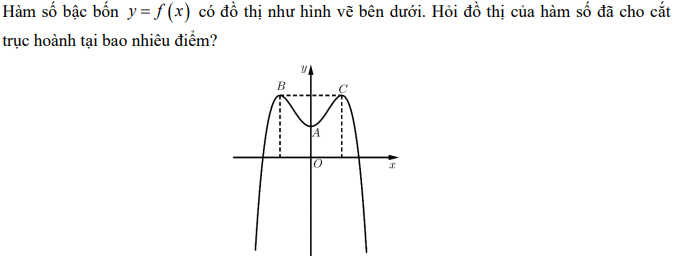
Đồ thị của hàm số cắt trục hoành tại 2 điểm.
Câu hỏi 26 / 50
Giải thích

Giải thích
![]()
Giải thích
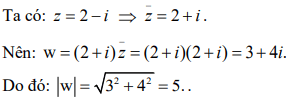
Giải thích
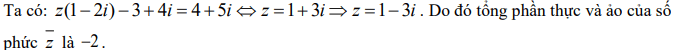
Giải thích
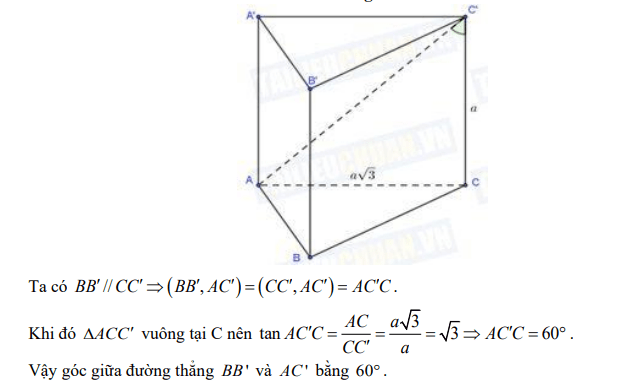
Giải thích
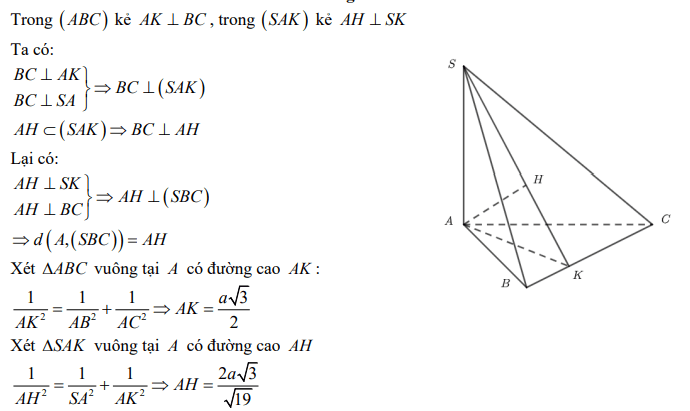
Giải thích
![]()
Giải thích
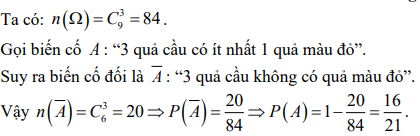
Giải thích
![]()
Giải thích
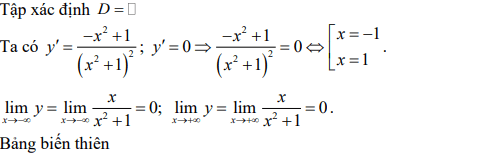
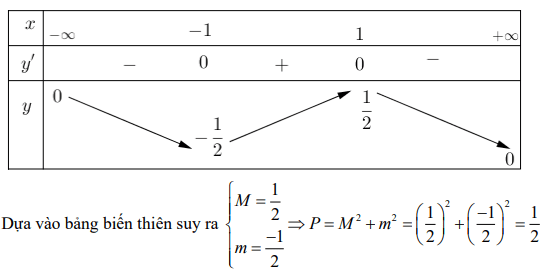
Giải thích
![]()
Giải thích
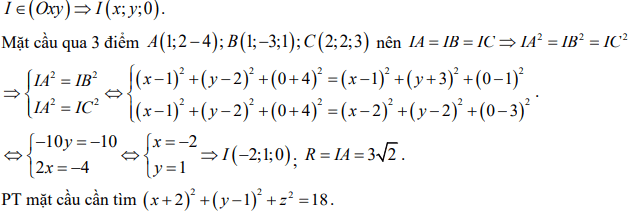
Giải thích
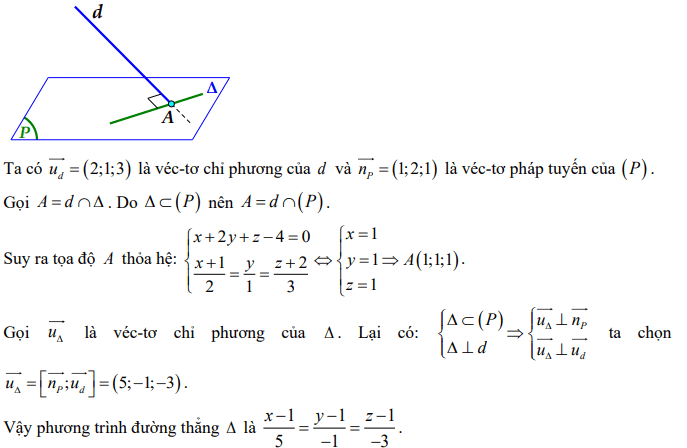
Giải thích
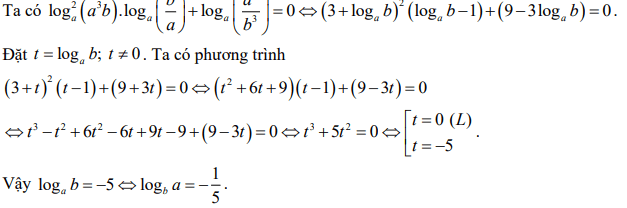
Giải thích
![]()

Giải thích
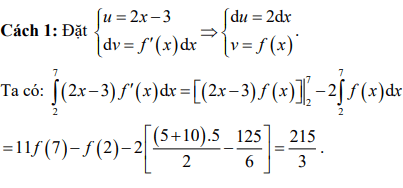
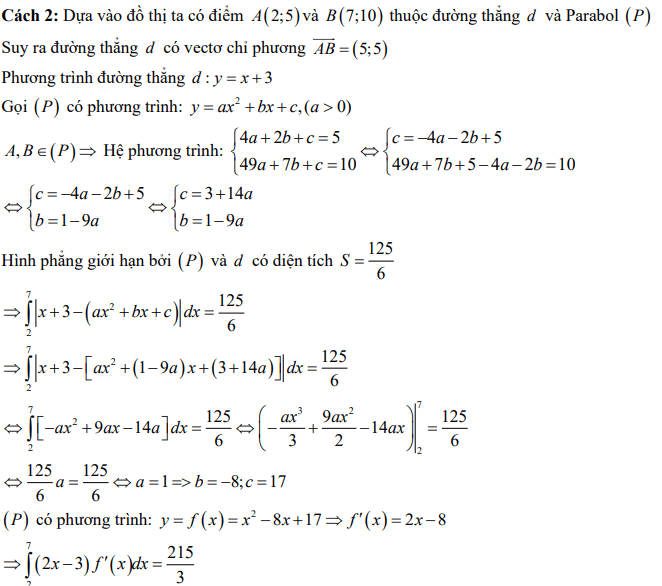
Giải thích
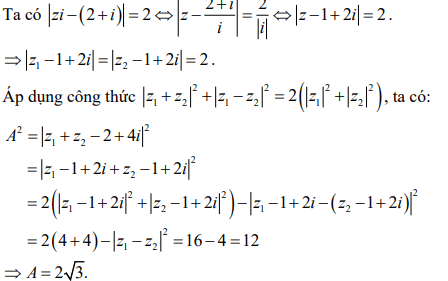
Giải thích

Giải thích
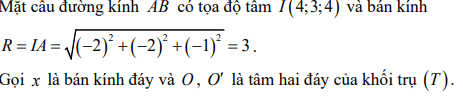

Giải thích
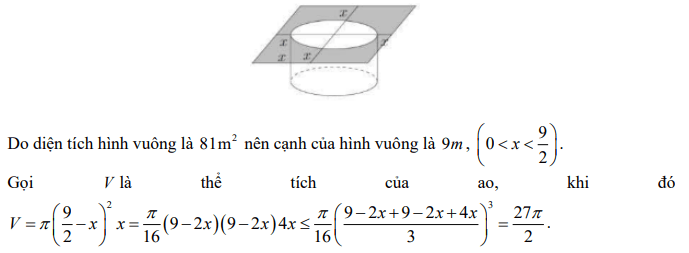
Giải thích
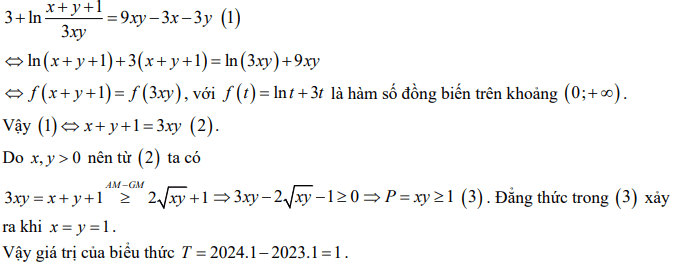
Giải thích
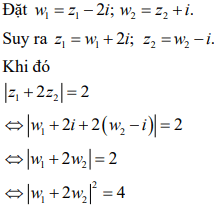
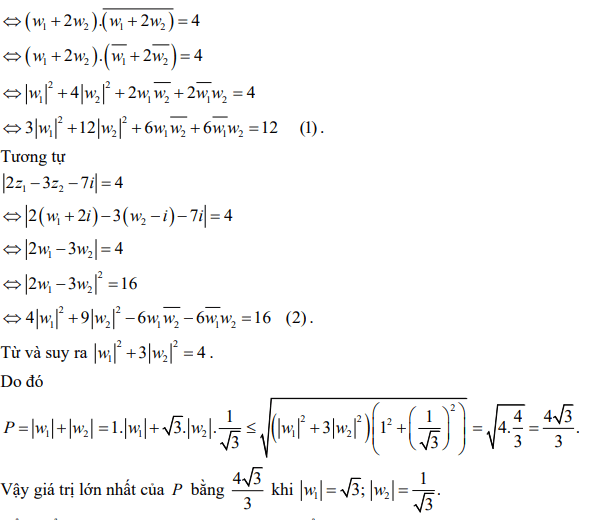
Giải thích
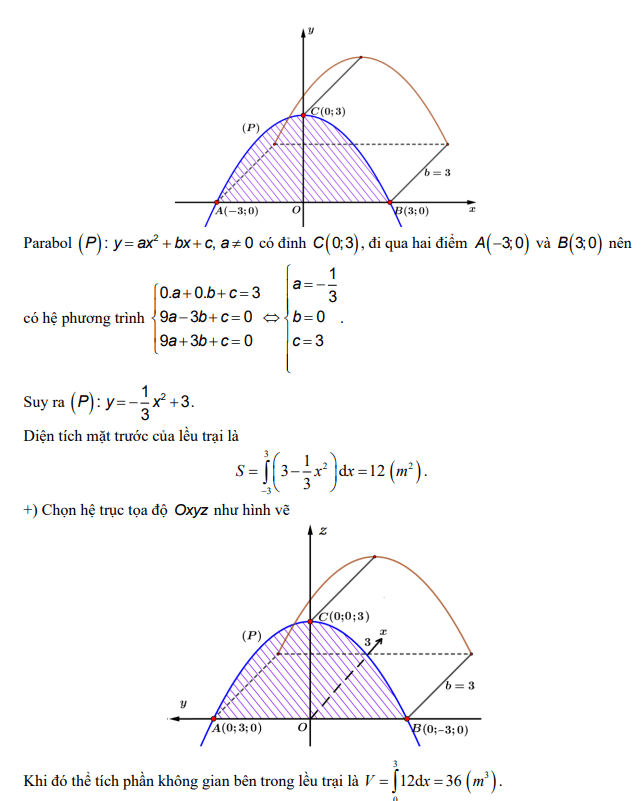

Giải thích
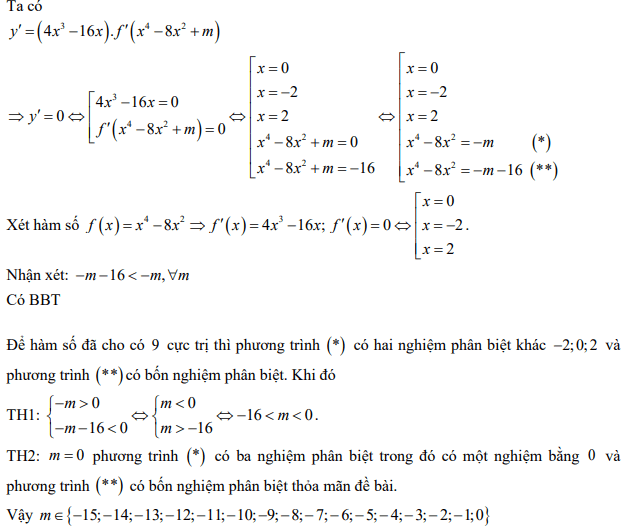
Giải thích