100 câu trắc nghiệm thể tích khối đa diện và tròn xoay vận dụng cao có đáp án và lời giải chi tiết

Trắc nghiệm vận dụng, vận dụng cao thể tích khối đa diện và tròn xoay có đáp án và lời giải chi tiết gồm 100 câu được soạn dưới dạng file word và PDF gồm 85 trang. Bài lập liên quan đến thể tích khối chóp, khối lăng trụ, khối nón, khối trụ. Các bạn xem và tải về ở dưới.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

84 trang 7 tháng trước

Tác giả:

Profile ha phan
Trang1
TRẮC NGHIỆM VẬN DỤNG VÀ VẬN DỤNG CAO
THỂ TÍCH KHỐI ĐA DIỆN
Câu 1. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt
đáy
ABCD
và góc giữa
SC
với mặt phẳng
SAB
bằng
30
. Gọi
là điểm di động
trên cạnh
CD
và
H
là hình chiếu vuông góc của
S
lên đường thẳng
BM
. Khi điểm
M
di động trên cạnh
CD
thì thể tích chóp
.S ABH
lớn nhất là
A.
3
2
6
a
V
. B.
3
2
12
a
V
. C.
3
2
15
a
V
. D.
3
2
8
a
V
.
Lời giải
Chọn B
Lấy điểm
N BC
sao cho
,0BN CM x x a
. Gọi
H AN BM
Xét
ABN
và
BCM
ta có:
BN CM
,
90ABN BCM
và
AB BC
ABN BCM
(c.g.c)
BAN CBM
Mà
90BAN BNA
nên
90CBM BNA
90BHN
hay
AH BM
Ta có:
BM AH
BM SAH SH BM
BM SA
Hình chiếu vuông góc của
S
lên
BM
là
H
.
Do
BHN
đồng dạng với
BCM
nên
BH BN
BC BM
22
BH x
a
xa

22
ax
BH
xa

Trang2
Tam giác
ABH
vuông tại
H
nên
2 2 4 2
2 2 2
2 2 2 2
22
a x a a
AH AB BH a
x a x a
xa

23
22
2 2 2 2
11
. . . .
2 2 2
ABH
a ax a x
S AH BH
xa
x a x a

3 4 3
.
22
1 1 2 2
. . 2. . .
3 3 2 12 12
S ABH ABH
a x a a
V SA S a
x a a
Câu 2.Cho hình chóp tam giác
.S ABC
có các góc
60ASB BSC CSA
và độ dài các cạnh
1SA
,
2SB
,
3SC
. thể tích của khối chóp
.S ABC
là
A.
32
2
V
. B.
3
2
V
. C.
2
2
V
. D.
6
2
V
.
Lời giải
Chọn C.
Gọi
B
,
C
lần lượt là điểm trên
SB
,
SC
sao cho
1SA SB SC
.
Suy ra
.S ABC

là tứ diện đều có
.
2
12
S AB C
V

.
Lại có
,
.
. 2.3
S ABC
S AB C
V
SB SC
V SB SC



..
2
6
2
S ABC S AB C
VV

.
Câu 3. Cho hình chữ nhật
ABCD
có cạnh
1AB
,
2BC
. Gọi
I
,
J
lần lượt là trung điểm của
hai cạnh
BC
và
AD
. Khi quay hình chữ nhật đó xung quanh
IJ
ta được một hình trụ
tròn xoay. thể tích của khối trụ tròn xoay được giới hạn bởi hình trụ tròn xoay đó là.
A
B
C
S
B'
C'
Trang3
A.
V
. B.
4V
. C.
2V
. D.
3
V
.
Lời giải
Chọn A.
2
.
. .1
4
Td
BC
V s h
.
Câu 4: Cho hình chóp đều
.S ABC
có đáy là tam giác đều cạnh
a
. Gọi
E
,
F
lần lượt là trung
điểm của các cạnh
,SB SC
. Biết mặt phẳng
()AEF
vuông góc với mặt phẳng
()SBC
.
Tính thể tích khối chóp
.S ABC
.
A.
3
5
.
24
a
B.
3
5
.
8
a
C.
3
3
.
24
a
D.
3
6
.
12
a
Lời giải
Chọn A
Gọi
O
là tâm đường tròn ngoại tiếp tam giác
ABC
, do
.S ABC
là hình chóp đều nên
SO ABC
.
Gọi
M
,
N
lần lượt là trung điểm của
BC
và
EF
.
Ta có
S
,
,
N
thẳng hàng và
SM BC
tại
,
SM EF
tại
N
.
Ta có
AEF SBC EF
SM SBC SM AEF MN AN
SM EF

ANM
vuông tại
N
.
Từ đó suy ra
ANM SOM∽
AN AM NM
SO SM OM
..NM SM AM OM
.
N
F
E
O
M
A
C
B
S
Trang4
Mà ta có
N
là trung điểm của
SM
(vì
E
,
F
lần lượt là trung điểm của
SB
,
SC
)
1
2
NM SM
;
ABC
đều cạnh
a
và
O
là tâm đường tròn ngoại tiếp tam giác
ABC
3
2
a
AM
;
3
6
a
OM
.
Vậy
2
2
1 3 3
.
2 2 6 4
a a a
SM 
2
a
SM
.
Ta có
22
22
15
2 12 6
a a a
SO SM OM
;
2
3
4
ABC
a
S
.
23
.
1 1 15 3 5
. . . .
3 3 6 4 24
S ABC ABC
a a a
V SO S
.
Câu 5.Cho hình chóp đều
.S ABC
có đáy là tam giác đều cạnh
a
. Gọi
E
,
F
lần lượt là các điểm
nằm trên các cạnh
SB
,
SC
sao cho
SE SF
k
SB SC

01k
. Biết mặt phẳng
()AEF
vuông góc với mặt phẳng
()SBC
. Tính thể tích khối chóp
.S ABC
.
A.
3
32
24 3 3
ak
k
. B.
3
32
8 3 3
ak
k
. C.
3
32
24 5 5
ak
k
. D.
3
32
12 3 3
ak
k
.
Lời giải
Chọn A
Câu 6. Cho hình chóp đều
.S ABCD
có đáy là tam giác đều cạnh
a
. Gọi
E
,
F
lần lượt là trung
điểm của các cạnh
,SB SC
. Biết mặt phẳng
()ADFE
vuông góc với mặt phẳng
()SBC
.
Tính thể tích khối chóp
.S ABCD
.
A.
3
2
6
a
. B.
3
2
2
a
. C.
3
2
12
a
. D.
3
2
18
a
.
Lời giải
Chọn A
Trang5
Ta có
INM SOM∽
..MN SM OM IM
2
2
1
22
a
SM
SM a
.
2
2 2 2
2
22
aa
SO SM OM a
.
3
2
.
1 1 2 2
. . . .
3 3 2 6
S ABCD ABCD
aa
V SO S a
.
Câu 7: Cho hình chóp đều
.S ABCD
có đáy là tam giác đều cạnh
a
. Gọi
E
,
F
lần lượt là các
điểm nằm trên các cạnh
SB
,
SC
sao cho
SE SF
k
SB SC

01k
. Biết mặt phẳng
()ADFE
vuông góc với mặt phẳng
()SBC
. Tính thể tích khối chóp
.S ABCD
.
A.
3
2
.
61
ak
k
. B.
3
21
.
6
ak
k
. C.
3
2
.
18 1
ak
k
. D.
3
21
.
18
ak
k
.
Câu 8:Cho khối chóp
.S ABCD
có đáy là hình bình hành
ABCD
. Gọi
M
,
N
,
P
,
Q
lần lượt là
trọng tâm các tam giác
SAB
,
SBC
,
SCD
,
SDA
. Biết thể tích khối chóp
.S MNPQ
là
V
,
khi đó thể tích của khối chóp
.S ABCD
là:
A.
27
4
V
. B.
2
9
2
V



. C.
9
4
V
. D.
81
8
V
.
Lời giải
Chọn A.
I
N
M
F
E
O
B
D
C
A
S
Trang6
Ta có
,
2
3
,
d S MNPQ
SM
SI
d S ABCD

.
Mặt khác gọi
ABCD
SS
ta có
1 1 1
.
4 2 8
DEJ
BDA
S
S

1
16
DEJ
SS

.
Tương tự ta có
1
4
JAI
DAB
S
S
1
8
JAI
S

.
Suy ra
1 1 1
1 4. 2.
16 8 2
HKIJ
S S S






.
Mà
2
24
39
MNPQ
HKIJ
S
S




2
9
MNPQ ABCD
SS
.
Suy ra
.
1
,.
3
S ABCD
V d S ABCD S
1 3 9 27
. , .
3 2 2 4
d S MNPQ S V
.
Câu 9:Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy
ABCD
, góc giữa hai mặt phẳng
SBD
và
ABCD
bằng
60
. Gọi
,
N
lần lượt là
trung điểm của
SB
,
SC
. Tính thể tích khối chóp
.S ADMN
.
A.
3
6
16
a
V
. B.
3
6
24
a
V 
C.
3
36
16
a
V 
D.
3
6
8
a
V 
Lời giải
Chọn A.
F
E
J
Q
P
H
N
K
M
I
O
D
S
A
B
C
Trang7
Gọi
O
là tâm của hình vuông
ABCD
. Khi đó ta có
SOA
là góc giữa hai mặt phẳng
SBD
và
ABCD
nên
60SOA 
. Khi đó
tan60
SA
AO

2
.tan60 . 3
2
SA AO a
6
2
a
.
Ta có
.
.
1
..
4
S AMN
S ABC
V
SA SM SN
V SA SB SC

và
.
.
1
..
2
S AND
S ACD
V
SA SN SD
V SA SC SD

.
Do đó
..
1 1 1
.
2 4 2
S ADMN S ABCD
VV




.
3
.
8
S ABCD
V
3
2
3 1 6 6
. . .
8 3 2 16
aa
a
.
Câu 10:Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy,
2SA a
. Gọi
B
,
là hình chiếu của
A
lần lượt lên
SB
,
SD
. Mặt phẳng
AB D

cắt
SC
tại
C
. thể tích khối chóp
SAB C D
là:
A.
3
23
9
a
V
. B.
3
22
3
a
V
. C.
3
2
9
a
V
. D.
3
23
3
a
V
.
Lời giải
ChọnC.
Ta có:
2
.
1
. . 2
3
S ABCD
V a a
3
2
3
a
.
O
N
M
A
D
B
C
S
C'
D'
O
D
A
B
C
S
B'
Trang8
Vì
B
,
là hình chiếu của
A
lần lượt lên
SB
,
SD
nên ta có
SC AB D

.
Gọi
C
là hình chiếu của
A
lên
SC
suy ra
SC AC
mà
AC AB D A

nên
AC AB D
hay
C SC AB D

.
Tam giác
SAC
vuông cân tại
A
nên
là trung điểm của
SC
.
Trong tam giác vuông
SAB
ta có
2
2
SB SA
SB SB
2
2
2
3
a
a
2
3
.
..
SAB C D SAB C SAC D
S ABCD S ABCD
V V V
VV
1
2
SB SC SD SC
SB SC SD SC




SB SC
SB SC

21
.
32
1
3
.
Vậy
3
2
9
SAB C D
a
V
.
Câu 11:Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Một mặt phẳng thay đổi nhưng
luôn song song với đáy và cắt các cạnh bên
SA
,
SB
,
SC
,
SD
lần lượt tại
M
,
N
,
P
,
Q
. Gọi
M
,
,
P
,
Q
lần lượt là hình chiếu vuông góc của
,
N
,
P
,
Q
lên mặt
phẳng
ABCD
. Tính tỉ số
SM
SA
để thể tích khối đa diện
.MNPQ M N P Q
đạt giá trị lớn
nhất.
A.
2
3
. B.
1
2
. C.
1
3
. D.
3
4
.
Lời giải
Chọn A.
Đặt
SM
k
SA
với
0;1k
.
Xét tam giác
SAB
có
//MN AB
nên
MN SM
k
AB SA

.MN k AB
N'
M'
Q'
Q
P
N
A
B
C
D
S
H
M
P'
Trang9
Xét tam giác
SAD
có
//MQ AD
nên
MQ SM
k
AD SA

.MQ k AD
Kẻ đường cao
SH
của hình chóp. Xét tam giác
SAH
có:
//MM SH
nên
MM AM
SH SA
11
SA SM SM
k
SA SA
1.MM k SH
.
Ta có
.
..
MNPQ M N P Q
V MN MQ MM
2
. . . . 1AB AD SH k k
.
Mà
.
1
..
3
S ABCD
V SH AB AD
2
..
3. . . 1
MNPQ M N P Q S ABCD
V V k k
.
thể tích khối chóp không đổi nên
.MNPQ M N P Q
V
đạt giá trị lớn nhất khi
2
.1kk
lớn nhất.
Ta có
3
2
2 1 . .
1 2 2
.1
2 2 3
k k k
kkk
kk



2
4
.1
27
kk
.
Đẳng thức xảy ra khi và chỉ khi:
21 kk
2
3
k
.
Vậy
2
3
SM
SA
.
Câu 12:Cho hình chóp
.S ABC
có đáy là tam giác đều. Đường cao
SH
với chân đường cao nằm
trong
ABC
và
2;SH BC
SBC
tạo với
ABC
một góc
0
60
. Biết có một điểm
O
thuộc
SH
sao cho
0, 0, , 1d AB d AC d O SBC
. Tính thể tích khối cầu ngoại
tiếp chóp đã cho.
A.
256
81
. B.
125
162
. C.
500
81
. D.
343
48
.
Lời giải
Chọn D.
Trang10
Gọi lần lượt là chân đường cao hạ từ xuống .
Tương tự
;
là tia phân giác của góc
là trung điểm của .
Kẻ , Đặt
, nên đều nên là chóp tam giác
đều.
Xét tam giác có .
Do đều và nên
vuông tại D
.
Câu 13:Xét khối tứ diện
ABCD
có cạnh
22
18AB CD
và các cạnh khác bằng 5. Biết thể tích tứ
diện
ABCD
đạt giá trị lớn nhất có dạng
ax
; , ;( , ) 1
4
m
xy
V x y N x y
. Khi đó x, y
thỏa mãn bất đẳng thức nào dưới đây
A.
2
4550x y xy
. B.
2 2550xy x y
.
C.
22
5240x xy y
. D.
2
19602xy
.
Lời giải
Chọn A
,EF
O
;AB AC
OE AB
AB SEO AB HE
SH AB
HF AC
HOE HOF HE HF
AH
BAC
AH BC D
BC
,1OK SD OK d O SBC
2AB BC CA a SH a
0
.cot60
3
a
HD a
33AD a HD
ABC
.S ABC
SOK
0
2
sin30
OK
SO 
DEF
OH DEF
1EO FO DO OK K D
DSO
2
2
3
.2
32
a
DH HS HO a a a
2 2 2
3 21
3 3;
24
AB AH SH SA SH AH
2
7 343
2 4 48
mc mc
SA
RV
SH
Trang11
Gọi M là trung điểm CD, và K là trung điểm AB
Ta có:
BM CD
và
SM CD
. Kẻ
SH BM
, tại
H BM
. Khi đó
()SH BCD
Đặt
0AB b
và
0CD a
2 2 2
1
100
2
BM BC MC a
;
2
1
100
2
SM BM a
2
11
. 100
24
BCD
S BM CD a a
2 2 2 2
1 1 82
100 ( ) 100 18
2 2 2
MK BM BK a b
1 1 82 82
..
2 2 2 4
ABM
S MK AB b b
Mặt khác:
2
2
82
2. .
2.
1 82.
4
.
1
2
100
100
2
BCD
BCD
b
S
b
S SH BM SH
BM
a
a
Ta có:
2
.
2
1 1 1 82. 82
. . . 100 .
3 3 4 12
100
A BCD BCD
b
V S SH a a ab
a
Theo Cô-si ta có:
22
9
2
ab
ab

Suy ra :
.
3 82
4
A BCD
V
. Dấu bằng xảy ra khi
3ab
Vậy
ax
3 82
4
m
V
. Suy ra
3; 82xy
Câu 14:Cho lăng trụ đứng
.ABC A B C
có cạnh
2,BC a
góc giữa hai mặt phẳng
ABC
và
A BC
bằng
60
. Biết diện tích của tam giác
ABC
bằng
2
2a
. Tính thể tích
V
của khối
lăng trụ
.ABC A B C
A.
3
3Va
. B.
3
3Va
. C.
3
2
3
a
V
. D.
3
3
3
a
V
.
Lời giải
Trang12
Chọn B.
Kẻ
AI BC
(
I BC
)
A I BC

.
Ta có
1
.
2
A BC
S A I BC
2
2a
2A I a

.
Do đó
.sin60AA A I


3a
,
.cos60AI AI

a
.
Vậy
3
.
1
.2 . . 3 3
2
ABC A B C
V a a a a

.
Câu 15: Cho lăngtrụđều
.ABC ABC
cócạnhđáy
4,a
biết diện tích của tam giác
ABC
bằng
8
. Tính
thể tích
V
của khối lăng trụ
.ABC A B C
.
A.
43V
. B.
83V
. C.
23V
. D.
10 3V
.
Lời giải
Trang13
Chọn B.
Gọi
I
làtrungđiểm
BC
. Tam giác
ABC
cân nên
1
.4
2
ABC
S A I BC

4AI

.
Khiđó
22
2AA AI A I

. Vậy
.
.
ABC A B C ABC
V AA S
83
.
Câu 16:Cho lăngtrụ
.ABC A B C
cóđáy
ABC
là tam giácđều cạnh
2a
, hình chiếu của
A
lên
ABC
trùng với trọng tâm tam giác
ABC
. Biết góc giữa cạnh bên và mặt đáy bằng
60
. thể tích
khối lăng trụ bằng
A.
3
3
4
a
V
. B.
3
3
8
a
V
. C.
3
23Va
. D.
3
43Va
.
Lời giải
ChọnC.
Gọi
I
là trung điểm
,BC
nên
22
3
3
a
AG AM
.tan60 2AG AG a
.
Vậy
3
.
. 2 3
ABC A B C ABC
V A G S a

Câu 17: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy
()ABCD
và
SA a
. Điểm
thuộc cạnh
SA
sao cho
,0 1.
SM
kk
SA
Khi đó giá trị
của
k
để mặt phẳng
()BMC
chia khối chóp
.S ABCD
thành hai phần có thể tích bằng
nhau là:
A.
15
2
k

. B.
15
2
k
. C.
15
4
k

. D.
12
2
k

.
Trang14
Lời giải
Chọn A.
Phân tích: Bài toán trên chính là bài toán về tỉ số thể tích, vì vậy trước hết phải xác định
thiết diện của hình chóp khi cắt bởi
()BMC
.
Do
()BMC
chứa
BC
song song với
AD
nên
()BMC
cắt
()SAD
theo giao tuyến song
song
AD
.
Để tính
.S BCNM
V
nếu xác định đường cao thì phức tạp vì vậy sẽ chia thành hai khối và sử
dụng bài toán tỉ số thể tích.
Kẻ
/ / ;MN AD N SD
khi đó thiết diện của hình chóp
.S ABCD
với
()BMC
là hình
thang
BCNM
. Suy ra
()BMC
chia khối chóp thành hai khối đa diện
SBCNM
và
DABCNM
.
Đặt
1.S BCNM
VV
;
2 DABCNM
VV
;
.S ABCD
VV
.
Để
12
VV
thì
1
1
2
VV
.
Ta có
2
.
SNMC
SADC
V
SN SM
k
V SD SA

2
1
.
2
SNMC
V k V
.
Ta có
SMCB
SABC
V
SM
k
V SA

1
.
2
SMCB
V k V
.
Vậy
2
1
1
( ).
2
V k k V
.
Khi đó
1
1
2
VV
2
1kk
15
2
15
2
k
k


.
Do
01k
nên
15
2
k

. Vậy chọn đáp án A.
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với đáy và
2SA a
. Gọi
B
,
lần lượt là hình chiếu vuông góc của
A
trên các cạnh
SB
,
SD
.
Mặt phẳng
AB D

cắt
SC
tại
C
. Tính thể tích của khối chóp
.S AB C D
.
A.
3
3
a
. B.
3
16
45
a
. C.
3
2
a
. D.
3
2
4
a
.
Lời giải.
Trang15
Chọn B.
Cách 1:
2
2
.
.
SD SD SA
SD SD SA
SD SD
22
2 2 2
4
5
SD SA SA
SD SD SA AD
.
Tương tự:
22
2 2 2
2
3
SC SA SA
SC SC SA AC
.
. . .
2 2. .
S AB C D S AD C S ADC
SD SC
V V V
SD SC


.
.
S ABDC
SD SC
V
SD SC

.
3
2
.
4 2 1 16
. . .2 .
5 3 3 45
S AB C D
a
V a a
.
Cách 2: Hoặc có thể áp dụng cách tính nhanh:
.
.
4
S A B C D
S ABCD
V
x y z t
V xyzt
2
xy
xyzt
2
zt
xyzt
với
SA
x
SA
,
SB
y
SB
,
SC
z
SC
,
SD
t
SD
.
Câu 19:Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai khối lập phương có diện tích toàn phần bằng nhau thì thể tích bằng nhau.
B.Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì thể tích bằng nhau.
C. thể tích của hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau là bằng
nhau.
D. thể tích của khối lăng trụ bằng diện tích đáy nhân chiều cao.
Câu 20:Cho hình chóp tứ giác đều có cạnh đáy bằng
1
chiều cao bằng
2
. Xét hình đa diện lồi
H
có các đỉnh là trung điểm của tất cả các cạnh hình chóp đó. Tính thể tích của
H
.
A.
9
2
. B.
4
. C.
23
. D.
.
Lời giải.
Chọn D.
Gọi
, , ,M N P Q
lần lượt là trung điểm của
, , ,SA SB SC SD
. Gọi
, , ,E F I J
lần lượt là
trung điểm của
, , ,AB BC CD AD
.Gọi
V
là thể tích của
H
.
Khi đó:
. , .
4.
S ABCD S MNPQ N EBF
V V V V
22
2
1 1 1 1 1 1
.2.1 .1. 4. .1. .
3 3 2 3 2 2
5
12
Trang16
Câu 21:Một hình chóp có đáy là tam giác đều cạnh bằng 2 và chiều cao bằng 4. Tính thể tích của
hình chóp đó.
A. 4 B.
43
3
C.
23
D. 2
Lời giải.
Chọn B.
Câu 22:Cho khối đa diện
H
được tạo thành bằng cách từ khối lập phương có cạnh bằng 3, ta bỏ đi
khối lập phương cạnh bằng 1 như hình vẽ. Gọi
S
là khối cầu có thể tích lớn nhất chứa
trong
H
và tiếp xúc với các mặt phẳng
( ' ' ' '),( ' ')A B C D BCC B
và
( ' ')DCC D
. Tính bán
kính của
S
.
A.
23
3
. B.
33
. C.
23
3
. D.
2
Lơ
i gia
i
Chọn B
Giải theo tự luận
Ta có
23CH
Gỉa sử khối cầu
S
có tâm I là tâm, bán kính
R
.
I’,M, P lần lượt là hình chiếu của I lên
( ' ' ' '),( ' ')A B C D BCC B
và
( ' ')DCC D
.
Vì
S
là khối cầu chứa trong
H
và tiếp xúc với các mặt phẳng
( ' ' ' '),( ' ')A B C D BCC B
và
( ' ')DCC D
nên
. ' ' ' 'MNPI M C P I
là hình lập phương cạnh
R
(
R
là bán kính khối
cầu
S
) và
'I C H
Ta có
' 2 3CH
,
'3C I R
Vậy khối cầu có thể tích lớn nhất khi khối cầu đi qua H tức
IH R
Vậy
''
2 3 3
33
C H IH C I
RR
R

Vậy chọn B
Câu 23:Cho tứ diện
ABCD
và các điểm
,
N
,
P
lần lượt thuộc các cạnh
BC
,
BD
,
AC
sao
cho
4BC BM
,
3AC AP
,
2BD BN
. Tính tỉ số thể tích hai phần của khối tứ diện
ABCD
được phân chia bởi
mp MNP
.
Trang17
A.
. B.
. C.
. D.
.
Lời giải
Chọn A.
(Địnhlý Menelaus Cho tam giác
ABC
đườngthảng
d
cắtcáccạnh
,,AB BC CA
lầnlượtại
,,M N P
ta có
. . 1
MA PB NC
MB PC NA
)
Gọi
, .I MN DC K AD PI
Áp dụng định lý Menelaus cho tam giác
BCD
và
3
điểm
,,M N I
ta có
1
. . 1 .1. 1 3
3
IC ND MB IC IC
ID NB MC ID ID
Áp dụng định lý Menelaus cho tam giác
ACD
và
3
điểm
,,P K I
ta có
12
. . 1 . .3 1
23
KD PA IC KD KD
KA PC ID KA KA
2 3 2 1
. . . .1
3 4 4 2
11
(3)
24
V
CP CM CN
CPMN
V CA CB CN
CABN
V V V
CPMN CABN ABCD
1 3 1
. . . .1
3 5 5
4 4 4 1 2
(4)
5 5 5 2 5
APKN
ACDN
NCPKD
NCPKD ACDN ABCD ABCD
ACDN
V
AP AK AN
V AC AD AN
V
V V V V
V
13
3 , 4
20
CMPKDN CPMN NCPKD ABCD
V V V V
7
13
ABMNKP
CMNDK
V
V

Câu 24:Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng
()
qua tâm đáy và tạo với mặt đáy một góc
0
60
tính tỷ số thể tích của hai phần khối
nón chia bởi mặt phẳng
()
?
Trang18
A.
2
. B.
1
21
. C.
2
3
. D.
34
6
.
Lời giải
Chọn D.
Không mất tính tổng quát ta giả sử
1R
.
Khi cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt
phẳng
()
qua tâm đáy và tạo với mặt đáy một góc
0
60
thì ta được thiết diện là một
đường parabol có đỉnh là gốc
0;0O
và đỉnh còn lại là
1;1A
, do đó thiết diện sẽ có
diện tích là
4
3
S
. Xét mặt phẳng đi qua cạnh đáy của thiết diện vuông góc với hình tròn
đáy của hình nón cắt hình nón làm đôi.
Gọi đa diện chứa mặt thiết diện đó là
H
. Gọi
K
là đa diện chứa đỉnh
O
của hình
nón được sinh bởi khi cắt thiết diện Parabol với đa diện
H
.
Khi đó khoảng cách từ
O
đến mặt thiết diện là
3
2
h
.
Suy ra thể tích của đa diện
K
là
1 3 4 2 3
..
3 2 3 9
K
V 
.
Mặt khác thể tích của nửa khối nón là
1 1 3
.3
2 3 6
.
Do đó thể tích của đa diện nhỏ tạo bởi thiết diện và khối nón là
3 4 3
3 2 3
6 9 18
V
.
Vậy tỉ số thể tích của hai phần khối nón chia
bởi mặt phẳng
là
3 4 3
34
18
6
3
3
.
Câu 25: Khối chóp
.S ABCD
có đáy là hình thoi cạnh
a
,
SA SB SC a
, cạnh
SD
thay đổi. thể
tích lớn nhất của khối chóp
.S ABCD
là:
A.
3
.
8
a
B.
3
.
4
a
C.
3
3
.
8
a
D.
3
.
2
a
Lời giải.
Trang19
Chọn. B.
Đặt
.SD x
Do đáy
ABCD
là hình thoi nên
. . .
22
S ABCD S BCD C SBD
V V V
.
Ta có
SAC BAC
SO BO
SBD
vuông tại S.
22
BD a x
22
2
4
ax
OA OC a
.
Và do
CO BD
CO SBD
CO SO

..
1
2 2. . .
3
S ABCD C SBD SBD
V V CO S
22
.
2 3 1
..
322
S ABCD
ax
V ax

2 2 2 3
2 2 2
3
3.
6 6 2 4
a a x a x a
x a x

dầu bằng xảy ra khi
6
2
a
x
.
Câu 26:Một cái phễu có dạng hình nón, chiều cao của phễu là
20cm
. Người ta đổ một lượng nước
vào phễu sao cho chiều cao của cột nước trong phễu bằng
10cm
(hình H1). Nếu bịt kín
miệng phễu rồi lật ngược phễu lên (hình H2) thì chiều cao của cột nước trong phễu gần
bằng với giá trị nào sau đây?
O
A
B
C
D
S
Trang20
A.
0,87cm
. B.
10cm
. C.
1,07cm
. D.
1,35cm
.
Lời giải
Chọn A.
+ Gọi
R
là bán kính đáy của phễu.
+ thể tích của lượng nước đổ vào phễu là
2
1
.10. .
32
R
V



(1).
+ Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì lượng nước tạo thành khối nón cụt có
chiều cao là
h
và bán kính đáy nhỏ trên là
r
. Ta có
20
1
20 20
r h h
rR
R



.
+ thể tích khối nón cụt cũng là thể tích lượng nước được tính theo công thức sau:
2
2
22
1 1 1
3 3 20 20
h hR h h
V R r Rr





(2).
+ Từ (1) và (2) ta có
2
5
21
6 3 20 20
h h h







0,0435
20
h

0,87h
.
Câu 27:Cho khối hộp có đáy là hình chữ nhật với ; . Hai mặt
bên và cùng tạo với đáy góc , cạnh bên của hình hộp bằng
(hình vẽ). thể tích của khối hôp là:
A. . B. . C. 5. D. .
Lời giải
Chọn A
.ABCD A B CD
3AB
7AD
ABB A

ADD A

45
1
7
33
77
B'
A'
C'
D'
B
A
H
D
I
C
K
Trang21
Hạ ;
(Do )
Chứng minh tương tự
Từ giả thiết suy ra:
Có là hình chữ nhật, ;
Nên là hình vuông suy ra
+
.
Câu 28:Cho hình chóp có chân đường cao nằm trong tam giác , các mặt bên ,
, cùng tạo với đáy góc . Biết , , , tính thể tích
khối chóp .
A. . B. . C. . D. .
Lời giải
ChọnA
,;A H ABCD H ABCD

,HI AD I AD
,HK AB K AB
''
'
A H ABCD A H AD
A I AD
IH AD

,
,
DD
A I AD IH AD
ABCD ADD A HIA
A A ABCD AD



90HIA
,ABCD ABB A HKA
45HIA HKA

HA HI HK
ABCD
,HI AD I AD
,HK AB K AB
AIHK
22AH HK A H

,A H ABCD H ABCD

AH A H

2 2 2 2
3AA A H HA A H
1
3
HA

.
. . 7
ABCD A B C D
V A H AB AD
.S ABC
ABC
SAB
SBC
SCA
60
3AB
4BC
5CD
.S ABC
23
63
53
10 3
Trang22
Hạ
; ,
Có (Do )
Chứng minh tương tự
Từ giả thiết suy ra:
Mà nằm trong tam giác nên và lần lượt là tâm và bán kính đường tròn nội
tiếp của tam giác
Có nên tam giác là tam giác vuông tại .
.
A
C
B
S
H
K
I
G
,SH ABC H ABC
,HI AB I AB
,HK BC K BC
,HG CA G CA
SH ABC SH AB
SI AB
IH AB

,SI AB IH AB
SAB ABC AB


,ABC SAB HIS
90HIS
,ABC SBC HKS
,ABC SAC SGH
60HIS SKH SGH
3 3 3SH HI HK HG
H
ABC
H
HI
ABC
2 2 2
AB BC AC
ABC
B
2
4.3
1
345
ABC
S
HI
AB BC CA
3SH
Trang23
.
Câu 29:Cho hình chóp có đáy là hình vuông, các mặt bên , cùng tạo
với đáy góc , mặt bên vuông góc với đáy. Biết khoảng cách từ đến mặt
phẳng bằng , tính thể tích khối chóp .
A. . B. . C. . D. .
Lời giải.
ChọnA
Hạ , do nên
Có là hình vuông
Có
(Do )
Chứng minh tương tự
.
1 1 3.4
. . 3. 2 3
3 3 2
S ABC
ABC
V SH S
.S ABCD
ABCD
SBC
SAD
60
SAB
A
SCD
21
7
.S ABC
3
12
3
6
3
8
3
8
B
A
D
C
S
H
M
I
,SH AB H AB
SAB ABCD
SH ABCD
SH BC
ABCD
AB BC
BC SAB
BC SB
,SB BC BC AB
SBC ABCD BC


,ABCD SBC SBH
90SAH
,ABCD SAD SAH
Trang24
Từ giả thiết suy ra: mà suy ra tam giác đều và là
trung điểm của .
Gọi là trung điểm của
Có
. Hạ thì
Có (Do
)
.
Câu 30: Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích
bằng
3
200m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí xây bể là
300
nghìn đồng/
2
m
(chi phí được tính theo diện tích xây dựng, bao gồm diện tích đáy và
diện tích xung quanh, không tính chiều dày của đáy và thành bể). Hãy xác định chi phí
thấp nhất để xây bể (làm tròn đến đơn vị triệu đồng).
A.
75
triệu đồng. B.
51
triệu đồng. C.
36
triệu đồng. D.
triệu đồng.
Lời giải
Chọn B
+) Gọi chiều rộng của đáy bể là
a
()m
thì chiều dài của đáy là
2a
()m
.
+) Do thể tích bể chứa nước là
3
200m
nên chiều cao của bể là
22
200 100
2
h
aa

.
+) Do đó diện tích xây dựng bể là
2
2 2. 2.2S a ah ah
2
600
2a
a

.
+ Ta có
2
600
2Sa
a

2
300 300
2a
aa
2
3
300 300
3 2 . .a
aa
3
30 180
, dấu bằng xảy ra
khi
3
15a
, suy ra chi phí thấp nhất để xây bể là
3
300.000x30 180
51
triệu đồng.
Chọn đáp án B
Nhận xét: Ta cũng có thể đánh giá
S
bằng cách đưa về tìm giá trị nhỏ nhất của hàm số
2
600
2f a a
a

trên khoảng
;a 
.
60SAH SBH
H AB
SAB
H
AB
M
CD
HM CD
SH ABCD SH CD
SHM SCD
HI SM
HI SCD
3
12
HI
2 2 2
1 1 1
HI SH HM

22
2
1 1 1
21 3
72
BC
AB
1AB
AB BC HM
.
1 1 3 1 3
. . .
3 3 2 2 12
S ABC
ABC
V SH S
Trang25
Câu 31: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam
giác vuông
BA BC a
, cạnh
bên
2AA a
,
là trung
điểm của
BC
(hình vẽ). Khoảng
cách giữa hai đường thẳng
AM
và
BC
là:
A.
2
2
a
.
B.
3
3
a
.
C.
5
5
a
.
D.
7
7
a
.
Lời giải
Chọn D
Cách 1
+) Gọi
N
là trung điểm
BB
, suy ra
B C AMN
. Do đó
,,d B C AM d B C AMN

,d C AMN
,d B AMN
+) Kẻ
, BH AM BK NK
. Chứng
minh được
BK AMN
. Vậy nên
,d B C AM
,d B AMN
BK
+) Tính
BH
22
22
BA BM
BA BM
5
5
a
BK
22
22
BH BN
BH BN
7
7
a
.
a
2
a
M
A'
B'
C'
C
A
B
B'
C'
A'
A
C
M
K
H
N
B
Trang26
Cách 2:
+) Tính được thể tích khối tứ diện
.B AMN
:
1
6
V BA BM BN
.
+) Tính diện tích tam giác
AMN
là
S
.
+)
,d B C AM
,d B AMN
3
V
S
.
Nhận xét: Học sinh dễ nhầm lẫn trong việc dựng
BK
nên điều chỉnh lại phương án nhiễu
như sau:
+) Nhầm lẫn 1:
BK MN
, khi đó phương án nhiễu là
2
3
a
, khoanh B
+) Nhầm lẫn 2:
BK AN
, khi đó phương án nhiễu là
6
3
a
, khoanh. C.
Câu 32: Cho hình trụ có và là hai đường tròn đáy nội tiếp hai mặt đối diện của một
hình lập phương.Biết rằng trong tam giác cong tạo bởi đường tròn và hình vuông
ngoại tiếp của có một hình chữ nhật kích thước (như hình vẽ dưới đây).Tính
thể tích V của khối trụ theo a.
A. . B. . C. . D. .
Lời giải:
ChọnB.
T
C
(C )
C
C
2aa
T
3
100
3
a
3
250 a
3
250
3
a
3
100 a
Trang27
Gọi M và N lần lượt là trung điểm CD và AB
Dễ thấy và là hình vuông cạnh bằng .
Do đó .Tương tự nên ba điểm thẳng hàng.
Kéo dài cắt tại
Đặt
Do mà ,
→ .Giải phương trình được (loại nghiệm )
Vậy .
Câu 33: Cho hình chóp có đáy là hình chữ nhật, , , tam giác
là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo diện tích
của mặt cầu ngoại tiếp hình chóp .
A. . B. . C. . D. .
Lời giải:
Chọn A.
M
O
A
C
D
B
N
H
K
ACMN
BDMN
a
45
o
MAC
45
o
OAC
,,A M O
CD
OH
K
AH OH OD x
2 2 2
OD OK DK
2DK BH x a
HK AC a
2 2 2
( 2 ) ( )x x a x a
5xa
xa
22
. . .5 .(2.5) 250
tru
V r h
.S ABCD
ABCD
3AB a
AD a
SAB
a
S
.S ABCD
2
5Sa
2
10Sa
2
4Sa
2
2Sa
A
B
C
D
S
G
I
O
M
Trang28
Theo bài ra ta có , ,
.
Vậy bán kính mặt cầu ngoại tiếp là: .
Vậy diện tích mặt cầu ngoại tiếp hình chóp là: .
Bài toán tổng quát:
Cách xác định bán kính mặt cầu ngoại tiếp hình chóp có mặt bên vuông góc với mặt đáy:
Gọi là chiều cao hình chóp và , là bán kính đường tròn ngoại tiếp mặt đáy và
mặt bên vuông góc với đáy; là độ dài giao tuyến của mặt đáy và mặt bên vuông góc
với đáy. Khi đó bán kính mặt cầu ngoại tiếp là: .
Trong đó mặt bên vuông góc với đáy thường là tam giác vuông, cân hoặc đều.
Lời giải
Để xác định tâm mặt cầu ngoại tiếp thì ta dựng trục của mặt đáy và mặt bên vuông góc
với đáy, giao của hai trục chính là tâm mặt cầu ngoại tiếp.
Giả sử hình chóp có đỉnh , giao tuyến của mặt đáy và mặt bên vuông góc với đáy là
với là trung điểm ; , là tâm đường tròn ngoại tiếp mặt bên vuông góc
với đáy và mặt đáy; là tâm mặt cầu. Khi đó, bán kính mặt cầu ngoại tiếp hình chóp là:
.
3GT AB a
2
d
AC
R
22
2
AB AD
a
3
3
b
AB
R
3. 3
3
a
a
2
22
3
4
a
R a a
5
2
a
.S ABCD
2
2
5
4. . 5
2
a
Sa






h
d
R
b
R
GT
2
22
4
db
GT
R R R
A
B
C
D
S
G
I
O
M
S
AB
M
AB
G
O
I
R SI
22
SG GI
22
b
R MJ
2 2 2
b
R JA MA
2
22
4
bd
AB
RR
Trang29
Câu 34: Cho hình chóp có đáy là hình vuông cạnh , tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp.
Lời giải
Giao tuyến của mặt bên và đáy là , bán kính đáy , bán
kính mặt bên .
Vậy bán kính mặt cầu ngoại tiếp hình chóp là:
.
Vậy diện tích mặt cầu ngoại tiếp hình chóp là: .
Câu 35: Cho hình chóp có đáy là tam giác là tam giác đều cạnh , tam giác
cân tại và có cạnh . Tính thể tích mặt cầu ngoại tiếp hình chóp.
Lời giải
.S ABCD
ABCD
a
SAB
A
B
C
D
S
O
GT AB a
2
d
AC
R
2
2
a
3
3
b
AB
R
3
3
a
2
22
4
db
GT
R R R
22
2
32
3 2 4
a a a
21
6
a
2
22
21 7
4 4. .
63
a
S R a




.S ABC
ABC
a
SAB
S
2SA a
Trang30
Giao tuyến của mặt đáy và mặt bên là: , bán kính đáy ,
bán kính đường tròn ngoại tiếp tam giác là: .
Khi đó bán kính mặt cầu ngoại tiếp hình chóp là:
.
Vậy thể tích mặt cầu ngoại tiếp hình chóp là:
.
Câu 36: Cho là các số thực dương. Xét các hình chóp có , các cạnh còn
lại đều bằng .Khi thay đổi , thể tích khối chóp có giá trị lớn nhất là
A. . B. . C. . D.
Lời giải:
A
C
B
S
GT AB a
3
3
d
AB
R
3
3
a
SAB
. . 4 15
4 15
b
SAB
SASB AB
Ra
S

2
22
4
db
GT
R R R
22
2
4 15 3
15 3 4
aa
a
115
10
a
3
4
3
VR
3
4 115
3 10
a




3
23 15
150
a
,xy
SABC
,SA x BC y
1
,xy
SABC
23
27
1
8
3
8
2
12
Trang31
Gọi M và N lần lượt là trung điểm của BC.
Do , → .
Chứng minh tương tự: .
Do đó là đoạn vuông góc chung của và và .
→ .
→ .
Do đó: =
Hay
Do →
Đặt →
Xét hàm số:
S
A
B
C
M
N
AM BC
SM BC
BC SAM
SA BCN
MN
SA
BC
SA BC
2
2 2 2
1
4
x
AM AB BM
22
2 2 2
1
44
xy
MN AM AN
22
1
4
xy
MN

1
. . ( ; ).sin( , )
6
V SA BC d SA BC SA BC
22
1
. . . 1 .sin90
64
o
xy
xy
22
1
. . . 1
64
xy
V x y

22
2x y xy
22
11
. . . 1 . . 1
6 4 6 2
x y xy
V x y x y
1
2
xy
t
2
2(1 )xy t
23
1 1 1
( ) .2.(1 ).
6 3 3
f t t t t t
Trang32
→ →
Vậy .Dấu bằng xảy ra khi: .
Câu 37: Cho tứ diện đều cạnh . Tính thể tích của khối bát diện đều có các đỉnh là trung
điểm các cạnh của tứ diện .
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi lần lượt là trung điểm của các cạnh
Gọi là thể tích của khối bát diện đều
Ta có:
Lại có là hình chóp tứ giác đều có tất cả các cạnh bằng
Vậy .
Câu 38: Người ta sản xuất một chiếc cốc thủy tinh có dạng hình trụ không có nắp với đáy cốc và
thành cốc làm bằng thủy tinh đặc, phần đáy cốc dày đều và thành xung quanh cốc
dày đều (hình vẽ). Biết rằng chiều cao của chiếc cốc là và khi ta đổ
nước vào thì đầy cốc. Nếu giá thủy tính thành phẩm được tính là đ/cm
3
thì giá tiền
thủy tính để sản xuất chiếc cốc đó gần nhất với số nào sau đây?
2
1
( ) 0
3
f t t
3
3
t
3 2 3
3 27
f




min
23
27
V
4
3
xy
ABCD
2a
ABCD
3
22
9
a
3
2
3
a
3
2a
3
2
6
a
, , , , ,M N P Q H K
, , , , ,AB AC CD BD BC AD
V
HMNPQK
.
2
K MNPQ
VV
.K MNPQ
a
3
.
2
2
3
K MNPQ
a
VV
1,5cm
0,2cm
15cm
180ml
500
Trang33
A. nghìn đồng. B. nghìn đồng. C. nghìn đồng. D. nghìn
đồng.
Lời giải
Chọn A.
Gọi , và theo thứ tự là bán kính, đường cao và thể tích của hình trụ phần vỏ cốc
và , , là bán kính, chiều cao và thể tích của hình trụ phần lòng cốc.
Ta có ; ; nên
.
thể tích của phần thủy tinh là
.
Vậy giá thành để sản xuất một chiếc cốc là nghìn đồng.
Câu 39: Một khúc gỗ có dạng khối nón có bán kính đáy , chiều cao . Anh thợ
mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi là thể
tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính .
31
40
25
20
1
R
1
h
1
V
2
R
2
h
2
V
12
0,2RR
12
1,5 15hh
2
13,5h
2
180V
2
2
2
40
3
V
R
h

1
40
0,2
3
R

2
1 2 1 1
180V V R h
2
40
0,2 .15 180 60,71
3




3
cm
60,71.500 30355
30 cmr
120 cmh
V
V
Trang34
A. . B. . C. . D.
.
Lời giải
Chọn D.
Gọi là chiều cao của khúc gỗ hình khối trụ, khúc gỗ hình khối trụ cần tìm. là
đỉnh của hình nón, là tâm của đáy hình nón, là tâm của đáy hình trụ và khác .
là một đường sinh của hình nón, là điểm chung của với khối trụ. Ta có
.
thể tích khối trụ là
Xét hàm số , .
Ta có hay .
Bảng biến thiên
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là
;
.
Câu 40: Cho khối chóp có đáy là hình chữ nhật, , , vuông
góc với mặt phẳng đáy và mặt phẳng tạo với mặt đáy một góc . Tính thể tích
của khối cầu ngoại tiếp khối chóp .
3
0,16 mV
3
0,024 mV
3
0,36 mV
3
0,016 mV
r
h
R
x
O
I
J
B
A
x
R
O
I
J
I
OA
B
OA
r h x
R h x
R
r h h
2
2
2
2
..
r
V x R x h x
h

2
2
2
.
r
V x x h x
h

0 xh
2
2
30
3
rh
V x h x h x x
h
xh
40 cm
3
h
x 
2
max
4
27
rh
V
2
4. .30 .120
27
3
16000 cm
3
0,016 m
.S ABCD
ABCD
3AB a
AD a
SA
SBC
60
V
.S ABCD
x
0
3
h
h
Vx
0
0
Vx
0
2
4
27
rh
0
Trang35
A. . B. . C. . D.
.
Lời giải
Chọn B
Ta có
thuộc mặt cầu đường kính (1).
Tương tự ta cũng chứng minh được
thuộc mặt cầu đường kính (2).
(vì ) thuộc mặt cầu đường kính (3).
Từ (1), (2) và (3) suy ra Mặt cầu đường kính là mặt cầu ngoại tiếp hình chóp
.
Ta có
.
.
là hình vuông cạnh .
Bán kính mặt cầu ngoại tiếp hình chóp
là .
Ta có .
Câu 41: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là điểm trên cạnh
SC
sao cho
52SM SC
, mặt phẳng
()
qua
,AM
và song song với đường thẳng
BD
cắt
hai cạnh
,SB SD
lần lượt tại hai điểm
,HK
. Tính tỉ số theo thể tích
.
.
B AMHK
S ABCD
V
V
.
3
13 13
6
a
V
3
55
6
a
V
3
13 13
24
a
V
3
5 10
3
a
V
I
O
C
A
D
B
S
90
SA ABCD SA BC
BC SAB BC SB SBC
BC AB gt
B
SC
90CD SAD CD SD SDC
D
SC
SA AC
SA ABCD
90SAC
A
SC
SC
.S ABCD
, 60
SBC ABCD BC
BC SAB cmt
SBC ABCD SBA
SAB ABCD AB
SAB SBC SB



.tan .tan60 3SA AB SBA a a
ABCD
a
2AC a
2 2 2 2
3 2 5SC SA AC a a a
.S ABCD
5
2
a
R
3
3
4 5 5
36
a
VR

Trang36
A.
1
5
. B.
8
35
. C.
1
7
. D.
6
35
.
Lời giải
Chọn D.
Ta gọi:
E SO AM
Dựng
Ex BD
cắt
,SB SD
lần lượt tại
,HK
AHMK

Gọi
F
là trung điểm của
MC
4
7
SM
SF

.
4
7
SE SM
SO SF
(vì
OFEM
).
4
7
SH SK SE
SB SD SO
( vì
HK BD
).
Ta có:
. . .
. . .
1 1 1 4 2 4 2 8
2 2 2 7 5 7 5 35
S AHMK S AHM S AMK
S ABCD S ABC S ADC
V V V
SH SM SM SK
V V V SB SC SC SD



.
Mà
..
..
3 3 8 6
4 4 35 35
B AHMK B AHMK
S AHMK S ABCD
VV
BH
V SH V
.
Câu 42: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
là trung điểm trên cạnh
SC
, mặt phẳng
qua
,AM
và song song với đường thẳng
BD
cắt hai cạnh
,SB SD
lần
lượt tại hai điểm
,HK
. Tính tỉ số theo thể tích
.
.
B AMHK
S ABCD
V
V
.
A.
1
5
. B.
1
4
. C.
1
7
. D.
1
6
.
Lời giải
Trang37
Chọn D.
Ta có:
E SO AM
Dựng
Ex BD
cắt
,SB SD
lần lượt tại
,HK
AHMK

. Khi đó ta có:
2
3
SH SK SE
SB SD SO
(vì
E
là trọng tâm của
SAC
)
Ta có:
. . .
. . .
1 1 1 2 1 1 2 1
2 2 2 3 2 2 3 3
S AHMK S AHM S AMK
S ABCD S ABC S ADC
V V V
SH SM SM SK
V V V SB SC SC SD



Mà
.
.
1
2
B AHMK
S AHMK
V
BH
V SH

.
.
1
6
B AHMK
S ABCD
V
V

Câu 43: Cho hình chóp có đáy là hình bình hành. Gọi là điểm trên cạnh
sao cho , mặt phẳng qua và song song với đường thẳng
cắt hai cạnh lần lượt tại hai điểm . Tính tỉ số theo thể tích .
A. . B. . C. . D. .
Lời giải
.S ABCD
ABCD
M
SC
( 1)SC xSM x
,AM
BD
,SB SD
,HK
.
.
B AMHK
S ABCD
V
V
2
1xx
1
x
xx
2
1xx
1
1
x
xx
Trang38
ChọnD.
Gọi: . Dựng cắt lần lượt tại .
Gọi là trung điểm của .
( vì ).
(vì ).
Ta có: .
Mặt khác: .
Chú ý: Bài toán trên có thể sử dụng kết quả sau đây để tính được tỉ số đơn giản hơn:
E SO AM
Ex BD
,SB SD
,HK
AHMK

F
MC
22
11
SM SE SM
SF x SO SF x

2
1
SE SM
SO SF x
EM OF
2
1
SH SK SE
SB SD SO x
HK BD






. . .
. . .
1 1 2
22
1
S AHMK S AHM S AMK
S ABCD S ABC S ADC
V V V
SH SM SM SK
V V V SB SC SC SD
xx
.
.
1
2
B AHMK
S AHMK
V
BH x
V SH

.
.
1
1
B AHMK
S ABCD
V
x
V
xx
SH
SB
Trang39
Cho hình chóp có đáy là hình bình
hành tâm . Mặt phẳng cắt các cạnh
và lần lượt tại .
Khi đó:
Áp dụng vào bài toán trên ta được (do , định lý
Ta-let).
Câu 44: Cho lăng trụ đứng có đáy là tam giác vuông cân tại , cạnh
. Góc giữa mặt phẳng và mặt phẳng bằng . Tính thể
tích của khối lăng trụ ?
A. B. C. D.
Lời giải
Chọn D
Cách 1.
+ Gọi là trung điểm của
+ Gọi lần lượt là hình chiếu vuông góc của trên
+ Khi đó .
+ Ta có .
+ Mặt khác .
+ Vậy thể tích của khối lăng trụ là
Cách 2.
.S ABCD
O
()P
,,SA SB SC
SD
', ', ',D'A B C
' ' ' '
SA SC SB SD
SA SC SB SD
2
SA SC SB SD SB
SA SM SH SK SH
HK BD
.ABC A BC
ABC
A
6BC a
'AB C
BCC B

0
60
V
.ABC A BC
3
23
.
3
a
V
3
3
.
2
a
V
3
33
.
4
a
V
3
33
.
2
a
V
M
BC AM BCC B


,HK
,MB
BC
o
, , 60B C AMH B C AH AB C BB C AH MH AHM
o
6
2
2
tan60 2
3
a
AM a
MH
22HK MH a
2 2 2
1 1 1
3B B a
BK BC B B
.ABC A BC
3
1 3 3
. . .
22
a
V B B AB AC

Trang40
+ Gọi chiều cao của hình lăng trụ là .
+ Đặt hệ trục tọa độ như hình vẽ. Khi đó , , ,
là trung điểm của .
+ Vì và nên là VTPT của
.
+ Ta có là VTPT của .
+ Theo giả thiết góc giữa và mặt phẳng bằng
+ Vậy thể tích của khối lăng trụ là
Câu 45: Khi xây nhà, anh Tiến cần xây một bể đựng nước mưa có thể tích dạng hình
hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung
quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là đ/m
2
và ở nắp
để hở một khoảng hình vuông có diện tích bằng diện tích nắp bể. Tính chi phí thấp
nhất mà anh Tiến phải trả (làm tròn đến hàng trăm nghìn)?
A. đ. B. đ. C. đ. D. đ.
Lời giải
ChọnB
Gọi chiều rộng của bể là: (với ĐK: ).
Chiều dài của bể là: Từ đó suy ra chiều cao của bể là:
Tổng diện tích của bể là: .
Vì nên ADBĐT Cô si cho 3 số dương :
.
h
Axyz
0;0;0A
3;0;0Ba
0; 3;0Ca
3;0;B a h
33
; ;0
22
aa
M




BC
AM BCC B

33
; ;0
22
aa
AM




1;1;0n
''BCC B
2
1
, 3;0; 3 ;0; 3AC AB ah a n h a


'AB C
AB C
BCC B

60
1
22
1
cos60 cos , 3
2
2. 3
h
n n h a
ha

.ABC A BC
3
33
.
2
a
V
3
6Vm
1.000.000
2
9
22000000
20970000
20965000
21000000
( ).xm
0x
3 ( ).xm
2
6
( ).
3
m
x
2
2
22
2 6 6 16 16
2 .3 2. .3 2. .
9 3 3 3
x
S x x x
x x x



0x
2
16 8 8
;;
3
x
xx
22
3
3
16 8 8 16 8 8 2
3 . . 6.
3 3 3
xx
x x x x
Trang41
Suy ra: .
Vậy chi phí thấp nhất để xây bể là: đ.
Câu 46: Cho hình nón có bán kính đáy , chiều cao và một hình trụ
nội tiếp hình nón (hình trụ có một đáy thuộc đáy hình nón và một đáy nằm trên
mặt xung quanh của hình nón). Tính thể tích của hình trụ có diện tích xung quanh
lớn nhất?
A. B. C. D.
Lời giải
ChọnA
(Đề xuất vẽ lại hình)
Gọi chiều cao hình trụ bằng
Ta có:
Dấu “=” xảy ra khi và chỉ khi
Câu 47: Cho hình nón có bán kính đáy , chiều cao và một hình trụ
nội tiếp hình nón (hình trụ có một đáy thuộc đáy hình nón và một đáy nằm trên
mặt xung quanh của hình nón). Tính thể tích của hình trụ có diện tích xung quanh
lớn nhất?
3
3
min
23
6
32
Sx
min
1.000.000. 20970000S
N
20( )r cm
60( )h cm
T
N
T
V
T
3
3000 cm .V
3
32000
cm .
9
V
3
3600 cm .V
3
4000 cm .V
.x
60 60
60 20 3
x R x
R

2
2
22
2 60 900 30 600
33
xq
S Rx x x x
30x cm
23
3000 cm .V R x

N
20( )r cm
60( )h cm
T
N
T
V
T
Trang42
A. B. C. D.
Lời giải
ChọnA
Gọi chiều cao hình trụ bằng
Ta có:
Dấu “=” xảy ra khi và chỉ khi
Câu 48: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy
2SA a
. Gọi
', 'BD
là hình chiếu của
A
lần lượt lên
,SB SD
. Mặt phẳng
''AB D
cắt
SC
tại
'C
. Tính thể tích khối chóp
. ' ' 'S AB C D
là:
A.
3
23
9
a
V
. B.
3
22
9
a
V
. C.
3
2
9
a
V
. D.
3
23
3
a
V
.
Lời giải
Chọn C
Ta có
2
2
' ' 2 2
33
SB SD a
SB SD a
nên suy ra
' '/ /B D BD
mà
BD SAC BD SC
.
Do đó
''B D SC
(1)
Ta có
'BC SAB BC AB
và
'AB SB
suy ra
'AB SC
(2)
3
3000 cm .V
3
32000
cm .
9
V
3
3600 cm .V
3
4000 cm .V
.x
60 60
60 20 3
x R x
R

2
2
22
2 60 900 30 600
33
xq
S Rx x x x
30x cm
23
3000 cm .V R x

S
A
D
C
B
D'
C'
B'
Trang43
Từ (1) và (2) suy ra
' ' 'AB C D SC
nên ta có
'AC SC
2
2
' 2 1
42
SC a
SC a

.
Ta có
' ' ' ' ' '
2
' ' 2 1 1
..
2 3 2 3
SA B C D SAB C
SABCD SABC
VV
SB SC
V V SB SC
.
Mà
3
2
12
.2
33
SABCD
a
V a a
.
Vậy
33
' ' '
1 2 2
.
3 3 9
SAB C D
aa
V 
.
Tổng quát: Cho hình chóp
.S ABCD
là hình bình hành. Một mặt phẳng
cắt
, , ,SA SB SC SD
tại
', ', ', 'A B C D
. Ta có
' ' ' '
1 ' ' ' '
. . .
4 ' ' ' '
SA B C D
SABCD
V
SA SB SC SD SA SB SC SD
V SA SB SC SD SA SB SC SD



Câu 49: Với một đĩa phẳng hình tròn bằng thép bán kính
R
, phải làm một cái phễu bằng cách cắt
đi một hình quạt của đĩa này và gấp phần còn lại thành một hình nón. Gọi độ dài cung
tròn của hình quạt còn lại là
x
. Tìm
x
để thể tích khối nón tạo thành nhận giá trị lớn
nhất.
A.
26
3
R
x
. B.
22
3
R
x
. C.
23
3
R
x
. D.
6
3
R
x
.
Lời giải
Chọn A.
Độ dài cung tròn của hình quạt còn lại là
x
nên chu vi đường tròn đáy của hình nón là
x
.
Do đó bán kính đường tròn đáy của hình nón là
2
x
r
.
Hình nón luôn có đường sinh là
R
.
Nên đường cao của hình nón là:
2
22
2 2 2 2
22
2 4 4
x x x
h R R h R



.
Suy ra thể tích khối nón là:
2 2 2
2 2 2
2 2 2
1 1 1
. . . . .
3 3 4 4 12 4
x x x
V h S R x R
Tính
2
2
22
2
2
2
2
1
2
'2
12 4
2
4
x
x
V x R x
x
R







22
2
22
2
2
2
48
6
4
xx
R
x
x
R








Trang44
26
'0
3
R
Vx
(vì
0x
)
Câu 50: Cho lăng trụ tam giác
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
22AB a
. Biết
8AC a
và tạo với mặt đáy một góc
0
45
. thể tích khối đa diện
ABCC B

bằng
A.
3
16 6
3
a
. B.
3
86
3
a
. C.
3
16 3
3
a
. D.
3
83
3
a
.
Lời giải
Chọn C.
- Gọi H là hình chiếu của
C
trên mặt đáy. Ta có
o
( ,( )) 45AC ABC C AH


- Chiều cao của lăng trụ là:
0
2
.sin45 8 . 4 2.
2
h AC a a
- Diện tích đáy
ABC
là:
22
2
3 (2 2) 3
23
44
ABC
AB a
Sa
- thể tích của khối lăng trụ
.ABC A B C
là:
23
.
. 2 3 .4 2 8 6
ABC A B C
V B h a a a
- thể tích khối đa diện
ABCC B

là:
3
3
'
2 2 16 6
.8 6 .
3 3 3
ABCC B ABCA B C
a
V V a
Câu 51: Cho tam giác
ABC
vuông tại
A
có
3AB a
,
AC a
. Gọi
Q
là mặt phẳng chứa
BC
và vuông góc với mặt phẳng
ABC
. Điểm
D
di động trên
Q
sao cho tam giác
DBC
nhọn và hai mặt phẳng
DAB
và
DAC
lần lượt hợp với mặt phẳng
ABC
hai góc
phụ nhau. Tính thể tích lớn nhất của khối chóp
.D ABC
.
A.
3
3
4
a
. B.
3
3
13
a
. C.
3
32
10
a
. D.
3
3
8
a
.
Lời giải
ChọnA
Theo giả thiết ta có,
tan tanDNH MDH
DH MH
NH DH

2
.DH NH MH
.
Đặt
03NH x x a
. Ta có
1
33
MH MH
MB a x

(do
ABC MBH
)
1
3
3
MH a x
. Do đó
2
1
3
3
DH a x x
2
13
32
a x x



2
3
4
a
3
2
DH
Dấu
""
xảy ra khi
3a x x
3
2
a
x
.
Trang45
Vậy
3
.
Max
1 1 3 3
. 3 . .
3 2 2 4
D ABC
aa
V a a
khi
3
2
a
DH
.
Câu 52: Cho hình hộp
.ABCD A B CD
có độ dài tất cả các cạnh bằng a và các góc
,BAD DAA
,
A AB
đều bằng 60°. Tính thể tích tứ diện
ACB D

theo a.
A.
3
2
24
a
. B.
3
2
36
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Lời giải
Chọn C.
Theo giả thiết ta có các tam giác
,,ABD BB C D DC

đều cạnh
a
BD BD B C DC a
Mặt khác
2 2 o
2 . .cos120 3AC AB AD AB BC AB BC a

Xét hình chóp đều
.AB D C

cạnh bên bằng
3a
, cạnh đáy bằng
a
ta có
2
3
4
d B D C
a
SS


Gọi
O
là trọng tâm tam giác đều
B D C

ta có
2 2 3 3
.
3 3 2 3
aa
CO CM
2
2 2 2
3 2 6
3
33
aa
h AO AC CO a




Trang46
Vậy
23
''
1 1 3 2 6 2
. . .
3 3 4 3 6
AB D C d
a a a
V S h
.
Câu 53: Cho hình hộp
.MNPQ M N P Q
có các cạnh đều bằng
, với
0;aaR
. Biết
60QMN 
,
120M MQ M MN

. Tính thể tích
V
của khối hộp
.MNPQ M N P Q
theo
a
.
A.
3
2.Va
. B.
3
4 2.Va
. C.
3
8.Va
. D.
3
2 2.Va
.
Lời giải
Chọn B.
.
Do hình chóp
.M NQM
có 3 cạnh bên cùng bằng
2a
nên chân đường cao của hình chóp
.M NQM
là tâm
O
của đường tròn ngoại tiếp mặt đáy
NQM
.
Như thế
..
6. 2 .
MNPQ M N P Q M NQM NQM
V V S OM

.
Từ giả thiết ta có
MNQ
đều, suy ra
2NQ a
.
Dùng định lý côsin cho
MMN
và
M MQ
ta tính được.
23MN M Q a


.
Dùng Hêrông cho
NQM
ta tính được
2
11.
NPM
Sa
.
Từ đó bán kính đường tròn ngoại tiếp
NQM
là
. . 6
4
11
NQM
NQQM NM a
ON
S


.
Xét tam giác
,OMN
ta có
22
2 22
11
a
OM MN ON
.
Vậy
23
.
2 22
2. 11. 4 2
11
MNPQ M N P Q
a
V a a

.
Câu 54: Cho hình hộp
.ABCD A B CD
có sáu mặt đều là hình thoi cạnh
a
và góc nhọn của hình
thoi bằng
60 .
Tính thể tích
V
của khối chóp
..A BB DD
P
P'
N'
Q
M
M'
Q'
N
N
M'
Q
M
O
Trang47
A.
3
2
.
18
a
V
B.
3
3
.
3
a
V
C.
3
.
9
a
V
D.
3
2
.
6
a
V
Lời giải
Chọn D
Ta có:
; A B A D aAB AD BD a AA
.A ABD
là tứ diện đều
Chân đường cao
AH
trùng với tâm của
ABD
2 2 3 3
.
3 3 2 3
aa
HA HB HD AO
22
2 2 2 2
36
99
aa
A H A A AH a

6
3
a
AH
.
33
..
22
;
12 4
A ABD A B C ABC
aa
VV
3
..
2
6
A BB D D ABC A B C A ABD
a
V V V
Câu 55: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,2A AB a
.
Đường chéo
AB
của mặt bên
ABB A

tạo với mặt phẳng đáy một góc
và
tan 2
.
Tính thể tích của khối trụ ngoại tiếp lăng trụ đã cho theo a.
A.
3
4 a
. B.
3
22a
. C.
3
8 a
. D.
3
2 a
.
Lời giải
Chọn D
Khối trụ ngoại tiếp lăng trụ có bán kính đường tròn đáy là
2
.
22
BC a
AH a
Ta có:
', 'AB ABC B AB

α
a
2
H
B
C
A'
B'
C'
A
Trang48
2 2 3
. 2. 2 2 .V Bh R h a a a
Câu 56: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy. Gọi
là trung điểm của
CD
. Biết khoảng cách giữa hai
đường thẳng
BC
và
SM
bằng
3
4
a
. Tính thể tích của khối chóp đã cho theo a.
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
3
6
a
. D.
3
3
12
a
.
Lời giải.
Chọn C
Ta gọi
N
là trung điểm của
AB
, suy ra
MN
song song với
BC
Ta có
( , ) ( ,( )) ( ,( ) ( ,( ))d SM BC d BC SMN d B SMN d A SMN
Gọi
H
là hình chiếu của
A
lên đường thẳng SN
Dễ dàng chứng minh được AH vuông góc với mặt phẳng
SMN
Ta có
2 2 2
1 1 1
AH SA AN

,
3
,
42
aa
AH AN
Nên
3
2
a
SA
và
23
1 1 3 3
..
3 3 2 6
ABCD ABCD
a
V SAS a a
Đáp án C đúng
Câu 57: Hình lăng trụ đứng
. ' ' 'ABC A B C
có diện tích đáy bằng
4
, diện tích ba mặt bên lần lượt là
9,18
và
10
. thể tích khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
4
11951
. B.
4
11951
2
. C.
11951
. D.
11951
2
.
S
A
D
B
C
N
M
H
Trang49
Lời giải
Chọn A
Gọi
, , 0a b c
là ba cạnh của tam giác đáy;
h
là chiều cao của lăng trụ
. ' ' 'ABC A B C
;
1 2 3
, , S S S
là diện tích ba mặt bên.
Ta có:
3
12
, ,
S
SS
a b c
h h h
( )( )( )S p p a p b p c
với
1 2 3
22
S S S
abc
p
h



1 2 3 1 2 3 1 2 3 1 2 3 3
12
2 2 2 2
S S S S S S S S S S S S S
SS
S
h h h h h h h
1 2 3 3 2 1 1 2 3 1 2 3
2 2 2 2
S S S S S S S S S S S S
S
h h h h
1 2 3 3 2 1 1 2 3 1 2 3
2
1
4
S S S S S S S S S S S S S
h
1 2 3 3 2 1 1 2 3 1 2 3
1
4
h S S S S S S S S S S S S
S
Vậy thể tích khối lăng trụ
. ' ' 'ABC A B C
là
4
1 2 3 3 2 1 1 2 3 1 2 3
1
. . 11951
4
V h S S S S S S S S S S S S S S
S
.
Câu 58: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy và khoảng
cách từ
A
đến mặt phẳng
SBC
bằng
2
2
a
. Tính thể tích
V
của khối chóp đã cho.
A.
3
2
a
V
. B.
3
Va
. C.
3
3
9
a
V
. D.
3
3
a
V
.
Hướng dẫn giải
Chọn D.
Gọi
H SAH B
. (1)
Trang50
Mà
,,BC SAB doBC AB BC SA SA ABCD
,
AH SAB
.
Nên
BC AH
. (2)
(1), (2) suy ra
AH SBC H
nên
2
2
a
AH
.
Tam giác vuông
SAB
có
2 2 2
1 1 1
AH AB SA

nên
2 2 2 2
1 1 1 1
SA AH AB a
hay
SA a
.
3
11
.
33
ABCD
V S SA a
.
Câu 59: Xét khối chóp
.S ABC
có đáy là tam giác vuông cân tại
A
,
SA
vuông góc với đáy,
khoảng cách từ
A
đến mặt phẳng
SBC
bằng
3.
Gọi
là góc giữa hai mặt phẳng
SBC
và
ABC
. Tính
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất.
A.
1
cos
3
. B.
3
cos
3
. C.
2
cos
2
. D.
2
cos
3
.
Lờigiải
ChọnB
Đặt
0 , 0 .AB AC x x SA y y
Gọi
I
là trung điểm của cạnh
BC
và
H
là
hình chiếu vuông góc của
A
lên
1.SI
Ta có:
, , 2 .BC AI BC SA BC SAI BC AH BC SI
Từ (1) và (2) suy ra
, 3.d A SBC AH
Góc giữa
SBC
và
ABC
bằng góc giữa
SI
và
.AI SIA

Ta có:
3
2 2 2 2 2 2 2 2 2 4 2
1 1 1 1 1 1 1 1 1 1 1
3.
9 AH AI SA AB AC SA x x y x y
2
3
42
11
81 3.
27
xy
xy
Mặt khác
2
1 1 27 3
..
6 6 2
V SA AB AC x y
min
27 3
2
V
dấu “=” xẩy ra khi và chỉ khi
3 3.xy
Suy ra:
2 3 3. 2 3 6
2 2 2 2
BC AB
AI
.
Trang51
Mà
. 9 2
. . .
2
SA AI
SI AH SA AI SI
AH
Vậy
3
cos
3
AI
SI

.
Câu 60: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
. Mặt bên
SAB
và
SAD
cùng vuông góc với đáy, góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
30
.
Tính tỉ số
3
3V
a
biết
V
là thể tích khối chóp
.S ABCD
.
A.
3
12
. B.
3
2
. C.
3
. D.
83
3
.
Lời giải
Chọn D.
Dễ thấy
SA ABCD
và góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
30
và là
góc
SBA
. Nên
23
.tan30
3
a
SA AB
, suy ra
3
2
1 2 3 8 3
. .4
3 3 9
aa
Va
3
3 8 3
3
V
a

.
Câu 61: Một hộp bóng bàn hình trụ có bán kính
R
, chứa được 5 quả bóng sao cho các quả bóng
tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Quả trên cùng và dưới
cùng tiếp xúc với hai nắp hộp. Tính phần thể tích của khối trụ mà thể tích của các quả
bóng bàn không chiếm chổ.
A.
3
10
2
R
B.
3
3
4
R
C.
0.
D.
3
10
3
R
Lời giải
Chọn D
+) Chiểu cao của hộp bóng bàn là
10hR
.
Suy ra thể tích của hộp bóng bàn là
23
()
10
H
V R h R


.
+) thể tích của 5 quả bóng bàn là
33
()
4 20
5.
33
B
V R R


.
Suy ra thể tích cần tính là
3 3 3
( ) ( )
20 10
10
33
HB
V V V R R R
.
Câu 47: [2H1-3] Cho hình đa diện
SABCD
như hình vẽ:
Trang52
Biết
4, 2, 3, 1SA SB SC SD
và
0
AS 60 .B BSC CSD DSA
thể tích
khối đa diện
SABCD
là
A.
3 2.
B.
32
2
C.
4 2.
D.
2.
Lời giải
Chọn A
Trên
,SA
,SB
SC
lần lượt lấy các điểm
', ', 'A B C
sao cho
' ' ' 1SA SB SC SD
. Khi
đó
. ' ' ' 'S A B C D
là một chóp tứ giác đều có tất cả các cạnh bằng
1
, có thể tích
0
1
32
V
.
. 0 0
1
4.3.2 12 2 2
2
S ABC
V V V



. 0 0
1
4.3 6 2
2
S ACD
V V V



Vậy
..
32
SABCD S ABC S ACD
V V V
Câu 62: Cho hình trụ và hình vuông
ABCD
có cạnh
a
. Hai đỉnh liên tiếp
,AB
nằm trên đường
tròn đáy thứ nhất và hai đỉnh còn lại nằm trên đường tròn đáy thứ hai, mặt phẳng
()ABCD
tạo với đáy một góc
45
. Khi đó thể tích khối trụ là
A.
3
2
8
a
. B.
3
32
8
a
. C.
3
2
16
a
. D.
3
32
16
a
.
D
C
B
S
A
C
B
A
O
B'
A'
D
C'
S
Trang53
Lời giải
Chọn D
Gọi
,OO
lần lượt là tâm của đường tròn hai đáy.
Gọi
,MN
lần lượt là hình chiếu của
O
và
O
lên các đoạn
AB
,
CD
; dễ dàng thấy
,MN
lần lượt là trung điểm của
,AB
CD
. Gọi
I
là giao của
OO
và
MN
.
Có
OM AB
AB IOM
nên góc giữa
ABCD
và đáy là góc
OMI
.
Vậy tam giác
IMO
vuông cân đỉnh
O
nên
OI OM
2
IM
2
4
a
.
Suy ra
2
2
a
OO
và
2 2 2
OA AM OM
22
2
4 16
aa

2
3
8
a
.
thể tích khối trụ bằng
2
..V O O OA
2
23
..
28
aa
3
32
16
a
.
Câu 63: Cho khối cầu tâm
O
bán kính là
6cm
. Mặt phẳng
P
cách
O
một khoảng là
x
cắt khối
cầu theo một hình tròn
C
. Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn
C
.
Biết khối nón có thể tích lớn nhất, giá trị của
x
bằng
A.
2cm
. B.
3cm
. C.
4cm
. D.
0cm
.
Lời giải
Chọn A.
Điều kiện
06x
.
-Bán kính của hình nón là:
2 2 2
6 36r x x
-thể tích khối nón lớn nhất với trường hợp chiều
6hx
-Khi đó thể tích khối nón là:
22
1
36 6 . ( )
3 3 3
V r h x x f x

+Ta có
2
'( ) 3 12 36f x x x
và
6 (L)
'( ) 0
2 ( )
x
fx
xN


2x
.
Vậy
2cmx
thì khối nón có thể tích lớn nhất.
Câu 64: Cho hình chóp đều
.S ABC
có đáy là tam giác đều cạnh
a
. Gọi
E
,
F
lần lượt là trung
điểm của các cạnh
SB
,
SC
. Biết mặt phẳng
AEF
vuông góc với mặt phẳng
SBC
.
thể tích khối chóp
.S ABC
bằng
A.
3
5
24
a
. B.
3
5
8
a
. C.
3
3
24
a
. D.
3
6
12
a
.
Trang54
Hướng dẫn giải
Chọn A.
Gọi
H
là trọng tâm của
ABC
, điểm
là trung điểm của
BC
và
I SM EF
.
Suy ra
I
là trung điểm của
SM
và
AI EF
(do
AEF
cân tại
A
).
Ta có
AEF SBC
EF AEF SBC
AI EF

AI SBC
AI SM
.
Do đó
SAM
cân tại
A
. Từ đó
3
2
a
SA AM
.
Ta có
23
33
a
AH AM
;
22
15
6
a
SH SA AH
.
Diện tích
22
33
44
ABC
AB a
S

.
thể tích
3
.
15
.
3 24
S ABC ABC
a
V S SH

.
Câu 65: Cho khối cầu
S
có tâm
I
, bán kính
R
không đổi. Một khối trụ thay đổi có chiều cao
h
và bán kính đáy
r
nội tiếp khối cầu. Tính chiều cao
h
theo
R
sao cho thể tích của khối
trụ lớn nhất.
A.
2
2
R
h
. B.
2hR
. C.
3
3
R
. D.
23
3
R
.
Hướng dẫn giải
Chọn D.
Bán kính đáy của hình trụ là
2
2
4
h
rR
.
O
O
Trang55
Do đó thể tích của khối trụ là
23
2 2 2
44
hh
V r h R h R h
.
Xét hàm số
3
2
4
h
f h R h
với
0;2hR
.
Ta có
2
2
3
4
h
f h R
,
23
0
3
R
f h h
.
Bảng biến thiên
Từ bảng biến thiên suy ra thể tích của khối trụ lớn nhất khi
23
3
R
h
.
Câu 66: Một khúc gỗ dạng nón có bán kính đáy bằng
30r cm
, chiều cao
120h cm
. Bác thợ
mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi
V
là thể
tích lớn nhất của khúc gỗ sau khi chế tác. Tính
V
.
A.
3
0,16 m
. B.
3
0,36 m
. C.
3
0,024 m
. D.
3
0,016 m
.
Lời giải.
Chọn D.
h
V
V
0
23
3
R

0
max
V
Trang56
Giả sử khối trụ có bán kính đáy và chiều cao lần lượt là
x
,
'h
0 30;0 ' 120xh
.
Ta có
' 30
120 30
hx
' 120 4hx
.
thể tích khối trụ
2
'V x h
2
120 4xx

23
120 4xx


,
0 30x
.
2
240 12V x x x


.
0Vx
0
20
x
x
.
Lập bảng biến thiên ta thấy hàm số đạt giá trị lớn nhất tại
20x
.
Vậy thể tích lớn nhất của khối trụ là
33
16000 0,016V cm m


.
Câu 67: Cho tứ diện đều cạnh
a
và điểm
I
nằm trong tứ diện. Tính tổng khoảng cách từ
I
đến
các mặt của tứ diện.
A.
6a
. B.
6
9
a
. C.
3
2
a
. D.
6
3
a
.
Lời giải
Chọn D
x
h
h'
B
O
A
Trang57
Gọi
V
là thể tích tứ diện đều
ABCD
và gọi
1
h
,
2
h
,
3
h
,
4
h
lần lượt là khoảng cách từ
I
đến các mặt
BCD
,
ACD
,
ABD
,
ABC
.
Đặt
1 IBCD
VV
,
2 IACD
VV
3 IABD
VV
,
4 IABC
VV
.
Ta có
1 2 3 4
V V V V V
.
11
1
.
3
BCD
V h S
1
1
3
BCD
V
h
S

Tương tự
2
2
3
ACD
V
h
S
,
3
3
3
ABD
V
h
S
,
4
4
3
ABC
V
h
S
.
Vậy
3
1 2 4
1 2 3 4
3
3 3 3
BCD ACD ABD ABC
V
V V V
h h h h
S S S S
.
Lại có tứ diện
ABCD
là tứ diện đều nên
2
3
4
BCD ACD ABD ABC
a
S S S S
Suy ra
1 2 3 4
1 2 3 4
2
3
3
4
V V V V
h h h h
a
2
3
3
4
V
a
3
2
2
3.
12
3
4
a
a
2
3
a
6
3
a
.
Cách trắc nghiệm: Chọn đặc biệt
IA
. Khi đó tổng khoảng cách từ
I
đến các mặt của
tứ diện bằng khoảng cách từ
A
đến mp
BCD
và bằng
6
3
a
.
Trang58
Câu 68: Cho hình hộp chữ nhật
.ABCD A B CD
có tổng diện tích của tất cả các mặt là
36
, độ dài
đường chéo
AC
bằng
6
. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu?
A.
8
. B.
82
. C.
16 2
. D.
24 3
.
Lời giải
Chọn B.
Gọi
a
,
b
,
c
là kích thước các mặt của hình hộp chữ nhật.
Không mất tính tổng quát giả sử
0 abc
.
Theo đề ta có:
2 2 2
18
36
ab ac bc
abc
62abc
Từ đó suy ra
62b c a
và
0 2 2a
.
18ab ac bc
2
18 6 2 18bc a b c a a
.
thể tích khối hộp là
2
6 2 18V abc a a a
.
Xét hàm
32
6 2 18f a a a a
với
0 2 2a
.
2
3 12 2 18f a a a
;
2
0 3 12 2 18 0f a a a
2
32
a
a
.
Bảng biến thiên:
Vậy thể tích lớn nhất của khối hộp là
82
.
Câu 69: Một cốc nước có dạng hình trụ đựng nước có chiều cao
12cm
, đường kính đáy
4cm
,
lượng nước trong cốc cao
8cm
. Thả vào cốc nước
4
viên bi có cùng đường kính
2cm
.
Hỏi nước dâng cao cách mép cốc bao nhiêu xăng - ti – mét? ( làm tròn sau dấu phẩy hai
chữ số thập phân, bỏ qua độ dày của cốc).
A.
2,67cm
. B.
2,75cm
. C.
2,25cm
. D.
2,33cm
.
Lời giải
Chọn A.
Trang59
thể tích của
4
viên bi là:
33
4 16
4.
33
r cm
.
Gọi
h
là chiều cao nước dâng lên. Khi đó thể tích của
4
viên bi đúng bằng thể tích nước
dâng lên. Do đó ta có
2
16 4
.2 .
33
h h cm
.
Vậy nước dâng cao cách mép cốc là:
48
12 8 2,67
33
cm
.
Câu 70: Cho hình trụ có đáy là hai đường tròn tâm
O
và
, bán kính đáy bằng
a
, chiều cao bằng
2a
. Trên đường tròn tâm
O
lấy điểm
A
, trên đường tròn tâm
lấy điểm
B
sao cho
7AB a
. thể tích của khối tứ diện
'OO AB
bằng:
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
2
a
.
Lời giải
Chọn B
Kẻ đường sinh
'AA
, gọi
D
là điểm đối xứng với
'A
qua tâm
'O
và
H
là hình chiếu
vuông góc của
B
trên
'AD
.
D
B
A'
A
O'
O
H
Trang60
Ta có
'
''
'
BH A D
BH AOO A
BH OO

nên
''
1
.
3
OO AB OO A
V S BH
Trong tam giác vuông
'A AB
có
22
' ' 3A B AB AA a
.
Trong tam giác vuông
'A BD
có
22
''BD A D A B a
.
Do đó suy ra tam giác
'BO D
đều nên
3
2
a
BH
.
Vậy
3
''
1 1 1 3
. . . '.
3 3 2 6
OO AB OO A
a
V S BH OAOO BH
.
Câu 71: Cho hình thoi
ABCD
có cạnh bằng
5
,
3
4
AC BD
. Gọi
, , ,E F G H
lần lượt là trung
điểm các cạnh
, , , .AB BC CD DA
Gọi
, , ,M N I K
lần lượt là trung điểm các cạnh
, , , .EF FG GH HE
Tính thể tích
V
của vật thể tròn xoay khi quay tứ giác
MNIK
quanh trục
HG
.
A.
9.
B.
18 .
C.
24 .
D.
30 .
Lời giải
Chọn B.
Gọi
O
là tâm hình thoi
ABCD
ta tính được
3OA
,
4OD cm
.
Gọi
1
V
là thể tích của khối nón cụt tạo bởi
IMNG
quay quanh
HG
.
1
V
có chiều cao là
2
, bán kính đáy là
3
2
r
và
3.R
2
2
1
1 3 3 21
.2 .3 3
3 2 2 2
V








.
Gọi
2
V
là thể tích của khối nón tạo bởi
NGI
quay quanh
HG
.
2
V
có chiều cao là
2
và
bán kính đáy là
3
.
2
2
3
.
2
V

thể tích cần tìm
12
2.( )V V V
18 .
Câu 72: Cho hình thang
ABCD
có
90AB
,
AB BC a
,
2AD a
. Tính thể tích khối tròn
xoay sinh ra khi hình thang
ABCD
quay quanh
CD
.
A.
3
7
12
a
. B.
3
72
6
a
. C.
3
72
12
a
. D.
3
7
6
a
.
Trang61
Lời giải
Chọn B.
Khối nón đỉnh
D
, trục
CD
có
2CD a
, bán kính đáy
2CA a
Nên khối nón có thể tích
3
2
1
1 2 2
..
33
a
V CD CA

.
Khối nón cụt có trục
2
2
a
CH
, hai đáy có bán kính
2CA a
và
2
2
a
HB
nên thể
tích khối nón cụt là
3
22
2
1 7 2
. . .
3 12
a
V CH CA HB CAHB
Khối nón đỉnh
C
, trục
CH
có thể tích
3
2
3
12
..
3 12
a
V CH HB

Vậy thể tích khối tròn xoay cần tính là:
3
1 2 3
72
6
a
V V V V
.
Câu 73: Cho hình thang
ABCD
vuông tại
A
và
B
có
AB a
,
3AD a
và
BC x
với
03xa
. Gọi
1
V
,
2
V
lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình
thang
ABCD
(kể cả các điểm trong) quanh đường thẳng
BC
và
AD
. Tìm
x
để
1
2
7
5
V
V
.
A.
3
4
a
x
. B.
7
5
a
x
. C. . D. .
Lời giải
Chọn B.
,
.Theo đề ta có .
2xa
xa
2
1
1
2
3
V a a x




2
2
2
3
V a a x




1
2
7
5
V
V
12
5 2 7
33
a x a x x a
A
D
B
C
H
B
A
Trang62
Câu 74: Cho tứ diện có . Khi thể tích khối tứ diện lớn
nhất thì khoảng cách giữa hai đường thẳng bằng
A. . B. . C. . D. .
Lời giải
Chọn C.
Gọi là trung điểm của , Vì cân , Kẻ
là đoạn vuông góc chung của , đặt
.
.
Áp dụng BĐT côsi: , dấu bằng xảy ra khi
.
Vậy .
Câu 75: Cho tứ diện có thay đổi, tất cả các cạnh còn lại bằng .Tính khoảng cách
giữa hai đường thẳng và trong trường hợp thể tích tứ diện lớn nhất.
A. B. C. . D.
Lời giải
Chọn B
ABCD
1AB AC BD CD
ABCD
, AD BC
1
2
2
3
1
3
1
3
M
BC
,DBC ABC
()BC ADM
MN AD MN
,AD BC
,AD x BC y
22
1
44
xy
MN
22
11
. . 1
6 6 4 4
ABCD
xy
V AD BC MN xy
22
2
( )( ) 1
3 2 2 4 4
x y x y
23
27
V
22
23
1
2 2 4 4 3
x y x y
xy
3
3
MN
ABCD
AB x
a
AB
CD
ABCD
3
.
3
a
6
.
4
a
3
.
4
a
6
.
3
a
Trang63
Gọi là trung điểm của , Vì đều , Kẻ
là đoạn vuông góc chung của ,
Dựng , ta có .
lớn nhất khi lớn nhất .
Khi đó vuông tại .
Câu 76: Cho hình chóp S.ABC có SA =SB = SC = 2, đáy ABC là tam giác vuông tại A, AB = 1.
Tìm thể tích lớn nhất của khối chóp S.ABC.
A. B. C. . D.
Lời giải
Chọn A
Gọi H là trung điểm của BC ta có và AC = x thì .
.
.
Dấu bằng xảy ra khi .
Câu 77: Cho hình chữ nhật S.ABCD có ABCD là hình chữ nhật với AD = 4a, các cạnh bên bằng
nhau bằng 6a. Tìm thể tích lớn nhất của khối chóp S.ABCD ?
A. B. C. . D.
Lời giải
Chọn C
Gọi O là tâm của đáy ta có .
Đặt AB = x ta được .
M
BC
,DBC ADC
()DC ABM
MN AB MN
,AD BC
()AH BM AH BDC
3
2
a
AH AM
ABCD
V
AH
3
2
a
AH AM
AMB
( , )M d AB CD MN
22
.6
4
AM MB a
AM MB

5
.
8
5
.
4
2
3
4
3
SH ABC
2
1
22
BC x
AH

2
22
15
2
x
SH SA AH
2
11
15
3 12
SABC ABC
V S SH x x
22
15 5
2.12 8
xx

22
30
15
2
x x x
3
130
.
3
a
3
125
3
a
3
128
3
a
3
250
3
a
SO ABCD
2
2
2
4
6
4
xa
SO a

2
2
32
4
x
a
Trang64
Suy ra :
.
Dấu bằng xảy ra khi : .
Câu 78: Cho hình chóp có thể tích bằng , đáy là hình vuông. Cạnh bên
và hợp với đáy góc . Mặt phẳng qua vuông góc với cắt
lần lượt tại . Tính thể tích khối chóp theo .
A. . B. . C. . D. .
Lời giải
Chọn A.
Có ; ;
.
Câu 79: Xét tứ diện có các cạnh và , thay đổi. Giá trị lớn
nhất của thể tích tứ diện bằng.
A. . B. . C. . D.
Lời giải
Chọn A.
Đặt .
1
.
3
SABCD ABCD
V SO S
2
2 2 2
12
4 32 128
3 4 3
x
ax a ax a x
2 2 2 3
2 128 128
3 2 3
x a x a
a


2
128 8x x x a
.S ABCD
V
ABCD
SA ABCD
SC
0
30
P
A
SC
,,SB SC SD
,,E F K
.S AEFK
V
10
V
2
5
V
3
10
V
5
V
1
4
SF
SC
2
5
SE
SB
2
5
SK
SD
1
10 10
SAEFK
SAEFK
SABCD
V
V
V
V
ABCD
1 AB BC CD DA
AC
BD
ABCD
23
27
43
27
23
9
43
9
BD y
AC x
1
. . , sin ,
6
V AC BD d AC BD AC BD
Trang65
là trung điểm của .
Từ kẻ , là trung điểm của .
.
.
Đặt .
.
Dấu “=” xảy ra .
Câu 80: Cho hình chóp có đáy là hình chữ nhật, và các cạnh bên
của hình chóp tạo với mặt đáy một góc . Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.
A. . B. . C. . D. .
Lời giải
Chọn C.
Gọi là hình chiếu của lên
Ta có cạnh bên của hình chóp tạo với mặt đáy một góc , nghĩa là:
H
BC
BD AH
BD CH
BD AC
sin ; 1AC BD
H
HK AC
;d AC BD HK
K
AC
22
1
4
xy
HK

22
11
11
6 4 6 2
x y xy
V xy xy M
2
1 0 2 2
2
xy
t xy t
2 3 3
1 1 1 1 1 2 1 2 2 3
1
3 3 3 3 27
27 27 27 27
M t t t t t t






23
3
xy
.S ABCD
ABCD
3, 4AB AD
60
250 3
3
V
125 3
6
V
500 3
27
V
50 3
27
V
M
H
C
B
A
D
S
I
H
S
ABCD
60
Trang66
Từ đó suy ra: hay là tâm của hình chữ nhật hay
Có .
Suy ra: và .
Gọi là trung điểm của . Trong mặt phẳng , dựng đường thẳng đi qua và
vuông góc với và cắt tại .
Khi đó điểm là tâm mặt cầu ngoại tiếp hình chóp .
Có: .
Vậy .
Câu 81: Cho hình chóp có đáy là tam giác vuông cân tại , . Gọi là trung
điểm . Hình chiếu vuông góc của lên mặt phẳng là điểm thỏa
. Góc giữa hai mặt phẳng và bằng . thể tích của khối chóp
là
A. . B. . C. . D. .
Lời giải
Chọn A
60SAH SBH SCH SDH
HA HB HC HD
H
ABCD
H AC BD
22
3 4 5AC BD
5 5 3
tan60 .
22
SH
5
.2 5
cos60 2
AH
SA
M
SA
SAH
M
SA
SH
I
I
.S ABCD
5
5.
. 5 3
2
3
53
2
SM SI SM SA
SMI SHA R SI
SH SA SH
3
3
4 4 5 3 500 3
3 3 3 27
VR




.S ABC
ABC
B
AB a
I
AC
S
ABC
H
3.BI IH
SAB
SBC
0
60
.S ABC
3
9
a
3
6
a
3
18
a
3
3
a
Trang67
Cách 1
- Gọi là hình chiếu của trên . Ta có
,
.
- Trường hợp 1:
Tam giác là tam giác đều cạnh nên , vô lý.
- Trường hợp 2:
có , ,
suy ra .
Vậy .
Cách 2
Chọn hệ trục tọa độ như hình vẽ, đặt . Ta có
.
.
K
I
SB
, ( )AC BH SB AC SBH
, ( )SB IK AC SB AKC
(( ),( )) ( , )SAD SBD KA KC
0
60AKC
AKC
2a
62
22
aa
KI BI
0
120AKC
AKI
0
6
tan60
6
AK a
KI
KI
4 2 2
33
a
BH BI
22
3
3
a
BK BI IK
SH BH
BKI BHS
KI BK
2
3
a
SH
3
1
.
39
ABC
a
V S SH
Bxyz
SH h
2 2 2 2 2 2
; ;0 , ; ;0 , 0;0;0 , 0; ;
2 2 2 2 3
a a a a a
A C B S h
2 2 2
, ; ;
2 2 3
ah ah a
BA BS







C
B
AS
H
K
I
x
y
z
Trang68
Ta chọn vectơ pháp tuyến của là .
.
Ta chọn vectơ pháp tuyến của là .
Suy ra . Vậy .
Câu 82: Cho hình trụ có hai đáy là hai hình tròn tâm , , bán kính đáy bằng chiều cao và bằng
, trên đường tròn đáy tâm lấy điểm , trên đường tròn đáy tâm lấy điểm sao
cho . thể tích tứ diện là
A. . B. . C. . D. .
Lời giải
ChọnC.
Hạ vuông góc với mặt phẳng đáy , .
Xét tam giác vuông ta có .
Gọi đối xứng với qua . Hạ đường cao xuống .
Dễ dàng nhận thấy .
Ta có .
Câu 83: Cho lăng trụ đứng có đáy là tam giác vuông tại , .
Mặt phẳng hợp với mặt phẳng một góc . Tính thể tích khối lăng trụ
đã cho.
A. . B. . C. . D. .
Lời giải
Chọn C
SAB
1
2 2 2
;;
2 2 3
hh
n





2 2 2
, ; ;
2 2 3
ah ah a
BC BS







SBC
2
2 2 2
;;
2 2 3
hh
n





12
12
| . |
12
| |.| | 2 3
nn
a
h
nn


3
1
.
39
ABC
a
V S SH
O
O
a
O
A
O
B
2AB a
OO AB
3
3
24
a
3
3
6
a
3
3
12
a
3
3
3
a
AA
O
AO

AA B
22
3A B AB AA a

M
A
O
BH
OM
2 2 2
1 1 1 3
2
a
BH
BH BA BM
..
1
2
OO AB B OO A B OO AA
V V V

1
..
6
OAA O
BH S

3
2
1 3 3
..
6 2 12
aa
a
.ABC A BC
ABC
A
2 , 3AB a AC a
A BC
ABC
60
3
3 39
26
a
3
9 39
26
a
3
18 39
13
a
3
6 39
13
a
Trang69
Ta có
Dựng
Dựng
Góc mặt phẳng với mặt phẳng là
Ta có
Ta có
Vậy
Câu 84: Cho tứ diện có khoảng cách giữa và bằng
góc giữa hai đường thẳng và bằng Tính thể tích khối tứ diện
A. . B. . C. . D. .
Lời giải
Chọn A
Lấy sao cho là hình bình hành
Ta có
Với
Do đó:
Câu 85: Cho khối lăng trụ tam giác mà mặt bên có diện tích bằng 4. Khoảng
cách giữa cạnh CC’ và bằng 7. thể tích khối lăng trụ là
A. 10. B. 12. C.14. D. 16.
Lời giải
// // //
;
A A BC A B C
B C BC A BC A B C A d BC B C
B C A B C BC A BC


dA H B C A H A
A K BC A K A d
A BC
ABC
60KA H KA H

22
22
. 6 13
13
A B A C
A H a
A B A C

0
6 39
tan60 .
13
BB HK A H a

3
.
1 1 6 39 18 39
.S .A . 2 .3
2 2 13 13
ABC A B C ABC
V BB AB C BB a a a a

ABCD
6,AB CD cm
AB
CD
12 ,cm
AB
CD
0
30 .
3
36 cm
3
25 cm
3
60cm
3
32 cm
'D
'DCBD
, , ' , ' 12d CD AB d CD AD B d D AD B
. . ' . ' '
1
, ' .
3
ABCD A BCD A DBD D AD B AD B
V V V V d D AD B S
''
1 1 1
. '. .6.6. 9
2 2 2
AD B AD B
S AB BD S
3
1
.12.9 36
3
ABCD
V cm
. ’ ’ ’ABC A B C
’’ABB A
’’ABB A
Trang70
Chọn C
Dựng khối hộp ta có:
Xem khối hộp là khối lăng trụ có hai đáy là và
Vậy
Trong đó:
và .
Câu 86: Cho hình lăng trụ đứng có đáy là tam giác vuông, . Biết
rằng góc giữa hai mặt phẳng và bằng (tham khảo hình vẽ bên). thể
tích của khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn A.
Ta có . Gọi G là trung điểm của , H là hình chiếu của
lên .
Ta có ,
Ta có suy ra .
Vậy góc giữa và là góc .
Ta có , , .
.
Câu 87: Một hộp bóng bàn hình trụ có bán kính , chứa được 5 quả bóng sao cho các quả bóng
tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Quả trên cùng và dưới
. ’ ’ ’ ’ABCD A B C D
..
1
2
ABC A B C ABCD A B C D
VV
. ’ ’ ’ ’ABCD A B C D
’’ABB A
’ ’.DCC D
.
.
ABCD A B C D ABB A
V S h
D , , 7h d C D C ABB A d CC ABB A
4
ABB A
S

.
1
.4.7 14
2
ABC A B C
V
.ABC A BC
ABC
AB BC a
()ACC
()AB C

60
.B ACCA
3
3
a
3
6
a
3
2
a
3
3
3
a
ACC AB C AC

AC

G
AC
()GH ACC A

GH AC
B G ACC A
B G AC


BH AC
AB C

ACC A

60GHB

.
1
.
3
B ACC A ACC A
V S B G
2
2
a
BG
6
.cot60
6
a
GH B G
GH AA
GC AC

22
6
6
2
2
2
a
x
a
xa

22
3
3
2
x
xa

xa
.B ACC A
V
12
. 2.
32
a
aa
3
3
a
R
Trang71
cùng tiếp xúc với hai nắp hộp. Tính phần thể tích của khối trụ mà thể tích của các quả
bóng bàn không chiếm chổ.
A. B. C. D.
Lời giải
Chọn D
+) Chiểu cao của hộp bóng bàn là .
Suy ra thể tích của hộp bóng bàn là .
+) thể tích của 5 quả bóng bàn là .
Suy ra thể tích cần tính là .
Câu 88: Cho hình đa diện như hình vẽ:
Biết và thể tích
khối đa diện là
A. B. C. D.
Lời giải
Chọn A
3
10
2
R
3
3
4
R
0.
3
10
3
R
10hR
23
()
10
H
V R h R


33
()
4 20
5.
33
B
V R R


3 3 3
( ) ( )
20 10
10
33
HB
V V V R R R
SABCD
D
C
B
S
A
4, 2, 3, 1SA SB SC SD
0
AS 60 .B BSC CSD DSA
SABCD
3 2.
32
2
4 2.
2.
Trang72
Trên lần lượt lấy các điểm sao cho . Khi
đó là một chóp tứ giác đều có tất cả các cạnh bằng , có thể tích .
Vậy
Câu 89: Cho hình chóp có , , . Hình chiếu của lên mặt
phẳng là điểm thỏa mãn . Biết rằng tổng diện tích
của các mặt cầu ngoại tiếp hình chóp , , bằng . thể tích
của khối chóp là
A. . B. . C. . D. .
Lời giải
Chọn D.
Vì nên tam giác vuông tại .
Gọi , , lần lượt là bán kính đường tròn ngoại tiếp tam giác , , và
, , lần lượt là bán kính mặt cầu ngoại tiếp các hình chóp , ,
.
Ta có .
Tương tự ; .
Gọi là trung điểm của . Đặt .
C
B
A
O
B'
A'
D
C'
S
,SA
,SB
SC
', ', 'A B C
' ' ' 1SA SB SC SD
. ' ' ' 'S A B C D
1
0
1
32
V
. 0 0
1
4.3.2 12 2 2
2
S ABC
V V V



. 0 0
1
4.3 6 2
2
S ACD
V V V



..
32
SABCD S ABC S ACD
V V V
.S ABC
3AB a
33AC a
6BC a
S
ABC
H
120AHB BHC CHA
.S AHB
.S BHC
.S CHA
2
288 a
.S ABC
3
93a
3
63a
3
33a
3
12 3a
2 2 2
BC AB AC
ABC
A
1
r
2
r
3
r
AHB
BHC
CHA
1
R
2
R
3
R
.S AHB
.S BHC
.S CHA
11
3
23
2sin120
sin 2sin
AB AB a
r r a
AHB AHB
2
6
23
2sin120
2sin
BC a
ra
BHC
3
33
3
2sin120
2sin
AC a
ra
CHA
J
SH
2SH x
Trang73
Khi đó ; ; .
Theo giả thiết
.
thể tích của khối chóp là
.
Câu 90: Cho hình chóp có đáy là tam giác đều cạnh . Hình chiếu của lên mặt
phẳng là điểm thỏa mãn , , . Biết rằng
tổng diện tích của các mặt cầu ngoại tiếp hình chóp , , bằng
. thể tích của khối chóp là
A. . B. . C. . D. .
Lời giải
Chọn D.
Gọi , , lần lượt là bán kính đường tròn ngoại tiếp tam giác , , và
, , lần lượt là bán kính mặt cầu ngoại tiếp các hình chóp , ,
.
Ta có .
Tương tự ; .
Gọi là trung điểm của . Đặt .
Khi đó ; ; .
Theo giả thiết
.
thể tích của khối chóp là .
2 2 2 2 2
11
3R SJ r x a
2 2 2 2 2
22
12R SJ r x a
2 2 2 2 2
33
9R SJ r x a
2 2 2 2
1 2 3
4 288S R R R a

2 2 2 2 2
3 24 72 16 4x a a x a x a
.S ABC
3
1 1 1 1
. . . . . .3 .3 3 .8 12 3
3 3 2 6
ABC
V S SH AB AC SH a a a a
.S ABC
ABC
a
S
ABC
H
150AHB 
120BHC 
90CHA 
.S AHB
.S BHC
.S CHA
2
31
3
a
.S ABC
3
12
a
3
2
a
3
3
a
3
6
a
1
r
2
r
3
r
AHB
BHC
CHA
1
R
2
R
3
R
.S AHB
.S BHC
.S CHA
11
2
2sin150
sin 2sin
AB AB a
r r a
AHB AHB
2
3
2sin120 3
2sin
BC a a
r
BHC
3
2sin90 2
2sin
AC a a
r
CHA
J
SH
2SH x
2 2 2 2 2
11
R SJ r x a
2
2 2 2 2
22
3
a
R SJ r x
2
2 2 2 2
33
4
a
R SJ r x
2 2 2 2
1 2 3
31
4
3
S R R R a

2 2 2
19 31
3
12 12
x a a
2
2
3
33
aa
xx
.S ABC
23
1 1 3 2 3
. . .
3 3 4 3 6
ABC
a a a
V S SH
Trang74
Câu 91: Cho hình chóp , đáy là hình vuông có độ dài cạnh bằng , là tam
giác cân tại và nằm trong mặt phẳng vuông góc với mặt phẳng Gọi lần
lượt là trung điểm của và là trọng tâm . Biết khoảng cách từ điểm đến
mặt phẳng bằng . Tính thể tích của khối chóp theo .
Lời giải
Gọi là giao điểm của và , dựng .
Vì là hình vuông
Mặt khác ta có vì ( là tam giác cân tại và nằm trong
mặt phẳng vuông góc với mặt phẳng ).
Vậy mà vậy .
là khoảng cách từ tới .
Xét tam giác vuông
Theo pitago ta có :
Xét và
Có : chung
.S ABCD
ABCD
2a
SAB
S
.ABCD
,HE
,AB BC
G
SCD
H
SED
32
4
a
.G AHED
a
F
HC
ED
HK SF
ABCD
HC ED
SH ED
SH ABCD
SAB
S
ABCD
ED SHC
ED HK
HK SF
HK SED
HK
H
SED
32
4
a
HK
HBC
2 2 2 2 2
5HC BC BH HC BC BH a
CFE
CBH
C
90CFE CBH
Trang75
.
Gọi là trung điểm
Trong mặt phẳng dựng vì ( )
Xét tam giác vuông theo hệ thức tam giác vuông ta có :
.
Vì là trọng tâm tam giác .
Xét chóp có : ,
.
Câu 92: Cho hình chóp , đáy là hình vuông có độ dài cạnh bằng , là tam
giác cân tại và nằm trong mặt phẳng vuông góc với mặt phẳng Gọi lần
lượt là trung điểm của và là trọng tâm . Biết thể tích của khối chóp
là . Tính khoảng cách từ điểm đến mặt phẳng theo .
Lời giải
Gọi là giao điểm của và , dựng .
Vì là hình vuông
CFE CBH
2
2
55
CF CE CF a a
CF
CB CH a
a
3
5
a
HF
I
CD
SHI
//GP SH GP AHED
SH ABCD
SHF
2 2 2
1 1 1
3HS a
HK HS HF
G
SCD
13
33
IG GP a
GP
IS SH
.G AHED
22
22
5
4
22
AHED ABCD HBE ECD
aa
S S S S a a
3
3
a
GP
23
.
1 1 3 5 5 3
. . . .
3 3 3 2 18
G AHED AHED
a a a
V GP S
.S ABCD
ABCD
a
SAB
S
.ABCD
,HE
,AB BC
G
SCD
.G AHED
3
53
144
a
H
SED
a
F
HC
ED
HK SF
ABCD
HC ED
Trang76
Mặt khác ta có vì ( là tam giác cân tại và nằm trong
mặt phẳng vuông góc với mặt phẳng ).
Vậy mà vậy .
là khoảng cách từ tới đặt .
Xét tam giác vuông
Theo pitago ta có :
Xét và
Có : chung ,
.
Xét chóp có :
.
Gọi là trung điểm
Trong mặt phẳng dựng vì ( )
Vì là trọng tâm tam giác .
Xét tam giác vuông theo hệ thức tam giác vuông ta có :
.
Câu 93: Cho hình chóp , đáy là hình vuông có độ dài cạnh bằng , là tam
giác cân tại và nằm trong mặt phẳng vuông góc với mặt phẳng Gọi lần
lượt là trung điểm của và là trọng tâm . Biết góc của và mặt phẳng
bằng . Tính thể tích của khối chóp theo .
Lời giải
SH ED
SH ABCD
SAB
S
ABCD
ED SHC
ED HK
HK SF
HK SED
HK
H
SED
HK x
HBC
2 2 2 2 2
5
2
a
HC BC BH HC BC BH
CFE
CBH
C
90CFE CBH
CFE CBH
2
5
5
2
a
CF CE CF a
CF
CB CH a
a






3
25
a
HF
.G AHED
2 2 2
2
5
8 4 8
AHED ABCD HBE ECD
a a a
S S S S a
23
.
1 1 5 5 3 3
. . . .
3 3 8 144 6
G AHED AHED
a a a
V GP S GP GP
I
CD
SHI
//GP SH GP AHED
SH ABCD
G
SCD
13
32
IG GP a
SH
IS SH
SHF
22
2 2 2 2
1 1 1 1 1 1 3 2
8
3 3 2
25
a
HK
HK HS HF x
aa
.S ABCD
ABCD
a
SAB
S
.ABCD
,HE
,AB BC
G
SCD
HC
SED
45
.G AHED
a
Trang77
Gọi là giao điểm của và , dựng .
Vì là hình vuông
Mặt khác ta có vì ( là tam giác cân tại và nằm trong
mặt phẳng vuông góc với mặt phẳng ).
Vậy mà vậy .
là góc của với vuông cân tại
Xét tam giác vuông
Theo pitago ta có :
Xét và
Có : chung ;
.
( vì vuông cân tại )
Vì là trọng tâm tam giác .
F
HC
ED
HK SF
ABCD
HC ED
SH ED
SH ABCD
SAB
S
ABCD
ED SHC
ED HK
HK SF
HK SED
HFK
HC
SED
45HFK
SHF
H
HBC
2 2 2 2 2
5
2
a
HC BC BH HC BC BH
CFE
CBH
C
90CFE CBH
CFE CBH
2
5
5
2
a
CF CE CF a
CF
CB CH a
a






3
25
a
HF
3
25
a
SH HF
SHF
H
G
SCD
1
3
25
IG GP a
GP
IS SH
Trang78
Xét chóp có :
;
.
Câu 94: Cho Cho hình chóp có đáy là hình vuông cạnh cạnh bên vuông
góc với mặt phẳng đáy, Gọi lần lượt là hình chiếu vuông góc của điểm
trên các cạnh (tham khảo hình vẽ bên). Góc giữa mặt phẳng và
đường thẳng bằng
A. . B. . C. . D. .
Lời giải
Chọn D.
Ta có (1)
Mặt khác theo giả thiết: (2)
Từ (1),(2) .Chứng minh tương tự:
Góc giữa đường thẳng và mặt phẳng là
Xét tam giác có , , vuông tại
Câu 95: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hai mặt phẳng và
cùng vuông góc với mặt đáy. Biết thể tích khối chóp là . Tính góc
giữa đường thẳng và mặt phẳng .
A. . B. . C. . D. .
Lời giải
Chọn C.
Hai mặt phẳng và cắt nhau theo giao tuyến và cùng vuông góc với
mặt phẳng nên .Do đó .
Tam giác vuông tại nên
.G AHED
2 2 2
2
5
8 2 8
AHED ABCD HBE ECD
a a a
S S S S a
25
a
GP
23
.
1 1 5 5 5
. . . .
3 3 8 240
25
G AHED AHED
a a a
V GP S
.S ABCD
ABCD
,a
SA
2.SA a
,MN
A
,SB SD
()AMN
SB
0
45
0
90
0
120
0
60
BC AB
BC SAB BC AM
BC SA
AM SB
AM SC
AN SC
()SC AMN
SB
()AMN
0
90 ( , )SB SC

SBC
3SB a
2SC a
BC a
SBC
B
1
tan
3
BC
BSC
SB

0
30BSC
00
90 ( , ) 60SB SC
SAB
SAD
.S ABCD
3
3
a
SB
SCD
0
45
0
60
0
30
0
90
SAB
SAD
SA
ABCD
SA ABCD
.
3
S ABCD
ABCD
V
SA a
S

SAD
A
22
2SD SA AD a
Trang79
Ta có
Vậy diện tích tam giác là : .Gọi là hình chiếu của lên
mặt phẳng khi đó . Mặt khác
Tam giác vuông tại nên .
Tam giác vuông tại nên
Vậy .
Câu 96: Cho tứ diện có đôi một vuông góc. Góc giữa đường thẳng
và bằng , , . Gọi là trung điểm của cạnh .
Góc giữa đường thẳng với mặt phẳng bằng:
A. . B. . C. . D. .
Lời giải
Chọn D.
Ta có Góc giữa và mp bằng .
Suy ra , ,
.
. Suy ra . .
Suy ra . Gọi là góc giữa với
suy ra .
,CD AD CD SA
CD SAD
CD SD
SCD
2
12
.
22
SCD
a
S SDCD
I
B
SCD
,,SB SCD SB SI BSI
BI
.
3
B SCD
SCD
V
S
.
3
2
S ABCD
SCD
V
S
2
2
a
SAB
A
22
2SB SA AB a
SIB
I
sin BSI
BI
SB
1
2
0
30BSI
0
, 30SB SCD
OABC
,,OA OB OC
AC
()OBC
0
60
OB a=
2OC a=
M
OB
OA
()ACM
3
arcsin
47
1
arcsi n
7
3
arcsin
27
1
arcsin
27
AC
OBC
0
60
0
.tan 60 6OA OC a==
22
5
2
a
AM OA OM= + =
22
3
2
a
CM OC OM= + =
22
22AC OC OA a= + =
2
14
2
ACM
a
S
D
=
3
.
13
..
66
A OCM
a
V OA OC OM==
.
3
3
( ,( ))
14
O ACM
ACM
V
d O ACM a
S
D
==
j
OA
()ACM
( ,( )) 1
sin
27
d O ACM
OA
j ==
Trang80
Câu 97: Cho hình chóp có đáy là hình vuông cạnh , tam giác là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy . Gọi là
trung điểm của . Tính côsin của góc giữa và .
A. . B. . C. . D.
Lời giải
Chọn A.
Gọi là trung điểm , . Ta có: tại
là hình chiếu của lên và tam giác vuông tại
; ;
Vậy .
Câu 98: Cho hình chóp có đáy ABC là tam giác vuông tại , . vuông
góc với , vuông góc với và góc giữa đường thẳng và mặt phẳng đáy
bằng . Tính thể tích khối cầu ngoại tiếp hình chóp .
A. . B. . C. . D. .
Lời giải
Chọn A.
Cách 1. Gọi là điểm đối xứng của qua trung điểm của , suy ra là hình
chữ nhật.
Ta có
Từ (1) và (2) suy ra .
Suy ra góc giữa đường thẳng và mặt phẳng đáy là góc .
.S ABCD
ABCD
a
SAB
ABCD
H
AB
SC
SHD
15
5
3
5
5
3a
.
5
2
K
AD
I CK HD
CI HD
CI SH
CI SHD
I
SI
SC
SHD
SIC
I
cos , cos , cosSC SHD SC SI CSI
DI
22
.DK DC
DK DC
5
a
IC
22
DC ID
2
5
a
SI
22
SC CI
6
5
a
cos ,SC SHD
cosCSI
SI
SC
15
5
.S ABC
B
;2AB a BC a
SA
AB
SC
BC
SC
0
60
.S ABC
3
82
3
a
3
2
3
a
3
22a
2
8 a
D
B
AC
ABCD
1
AB SA
AB SD
AB AD

2
BC SC
BC SD
BC CD

SD ABC
SC
SCD
Trang81
Từ đó . Xét tam giác vuông tại ta có .
Do tam giác vuông cân tại nên .
Gọi là trung điểm . Suy ra (do vuông tại ) và
(do vuông tại ). Suy ra . Hay là tâm mặt cầu ngoại
tiếp hình chóp .
Suy ra . Chọn đáp án A.
Cách 2. (Tọa độ hóa)
Gắn hệ trục tọa độ như hình vẽ. Khi đó
, , , , với .
Ta có .
Ta có
Suy ra .
Đường thẳng có véc-tơ chỉ phương là .
Mặt phẳng có véc-tơ pháp tuyến là .
Theo đề bài, góc giữa và mp là nên
.
Gọi là trung điểm . Suy ra là tâm mặt cầu ngoại tiếp hình chóp .
Ta có .
0
60SCD
SCD
D
2
cos60
DC
SC a
SBC
C
22SB a
I
SB
IA IB IS
SAB
A
IB IC IS
SBC
C
1
2
IA IB IC IS SB
I
.S ABC
3
2 2 2 3
1 1 4 8 2
4 3 2
3 322
a
R SB a a a a V R
Oxyz
(0;0;0)B
( ;0;0)Aa
(0;2 ;0)Ca
( ; ; )S x y z
, , 0x y z
( ) ( ): 0ABC Oxy z
; ; , ;0;0SA a x y z AB a
. 0 0 .SA AB SA AB a a x x a
;2 ; , 0;2 ;0SC x a y z BC a
. 0 2 2 0 2 .SC BC SC BC a a y y a
( ;2 ; )S a a z
SC
;0;CS a z
()ABC
0;0;1k
SC
()ABC
0
60
22
22
.
3
sin60 3 3 ;2 ; 3
2
.
SC k
z
z a z a S a a a
SC k
az
I
SB
I
.S ABC
2 2 2
11
4 3 2
22
R SB a a a a
Trang82
Vậy thể tích khối cầu là .
Câu 99: Cho là các số thực dương thay đổi. Xét hình chóp có , các
cạnh còn lại đều bằng . Khi thể tích khối chóp đạt giá trị lớn nhất thì tích
bằng
A. . B. . C. . D. .
Lời giải
Chọn. A.
Gọi lần lượt là trung điểm của . Ta có và
.
Lại có .
Và .
Diện tích tam giác là .
Suy ra .
Khi đó thể tích khối chóp là .
Ta có .
Đặt , . Khi đó .
Ta có và .
Bảng biến thiên:
3
3
4 8 2
3 3
a
VR

,xy
.S ABC
,SA x BC y
1
.S ABC
.xy
4
3
43
3
23
1
3
,IH
,SA BC
BI SA
SA BIC
CI SA

..S IBC A IBC
VV
22
BI SB SI
22
4
1
42
xx
22
22
4
2
xy
IH IB BH

IBC
22
1
.4
24
IBC
y
S IH BC x y
..S IBC A IBC
VV
22
1
. . 4
3 2 4
xy
xy
22
4
24
xy
xy
.S ABC
22
..
24
12
S ABC S IBC
xy
V V x y
22
2
xy
xy
22
22
4
24
xy
V x y
22
4t x y
0;2t
2
4
24
tt
V f t

2
34
24
t
ft

2
0
3
f t t
Trang83
Do đó đạt được khi .
Khi đó tích .
Cách 2:
Ta có
Hướng 1: Khảo sát hàm số như cách 1
Hướng 2 : Sử dụng MTCT thay các phương án vào ta được đáp ánA.
Câu 100: Cho khối chóp
.S ABC
có đáy ABC là tam giác vuông cân tại A,
, 90AB a SBA SCA
, góc giữa hai mặt phẳng
SAB
và
SAC
bằng
60
. Thể tích của khối
chóp đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Lời giải
Câu 49:Đáp án D
Gọi Hlà hình chiếu của S lên
ABC
.
Theo bài ra, ta có
,HC CA HB BA ABHC
là hình vuông cạnh a.
Gọi
O HA BC
, E là hình chiếu của O lên SA.
Ta dễ dàng chứng minh được
,EC SA EB SA
.
Từ đó, ta được: góc giữa
SAC
và
SAB
là góc giữa
EB
và
EC
.
max
23
27
V
22
33
t x y
4
.
3
xy
22
..
2 4 4 2
12 12
S ABC S IBC
xy xy
V V x y xy
Trang84
Vì
0
90CAB
nên
00
90 120 .BEC BEC
Ta dễ dàng chỉ ra được
0
60OEB OEC
.
Đặt
22
22
.2
2
22
AO SH xa
SH x SA x a OE
SA
xa
.
0
22
22
tan60 : 3
2
22
OC a xa
xa
OE
xa
.
Vậy
3
2
..
1 1 1
. . .
2 2 3 6
S ABC S HBAC
a
V V a a
.
| 1/84
| | Tải xuống

Có thể bạn quan tâm:

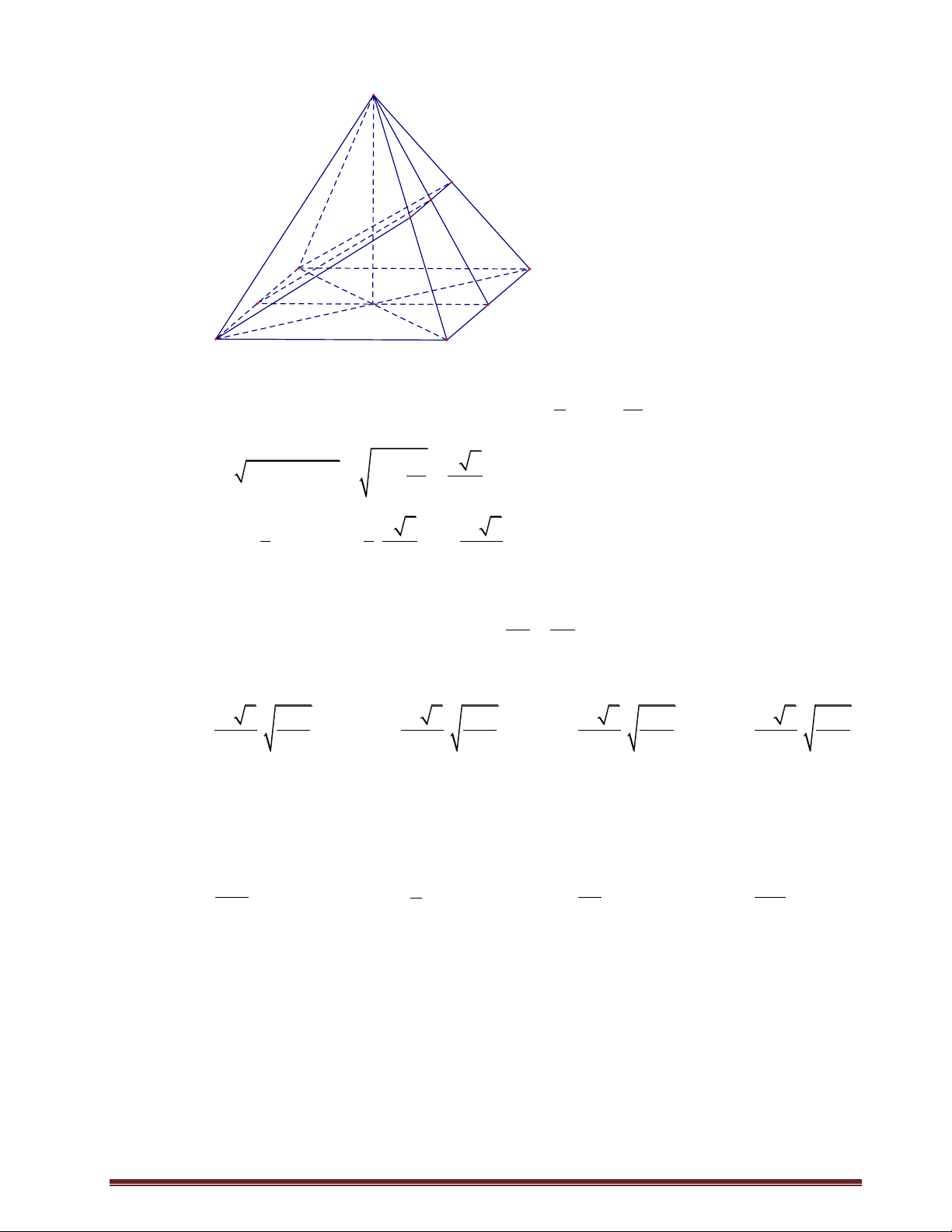
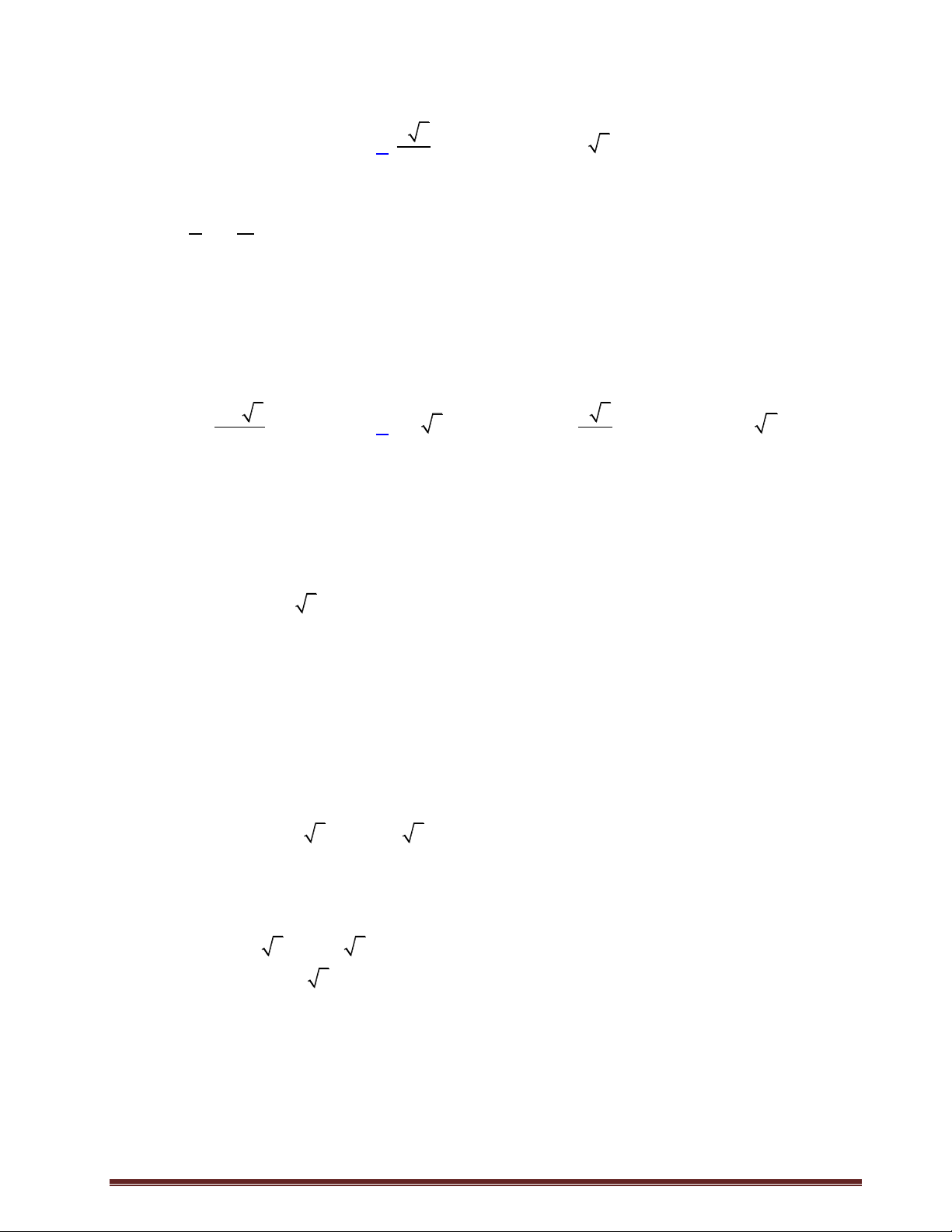
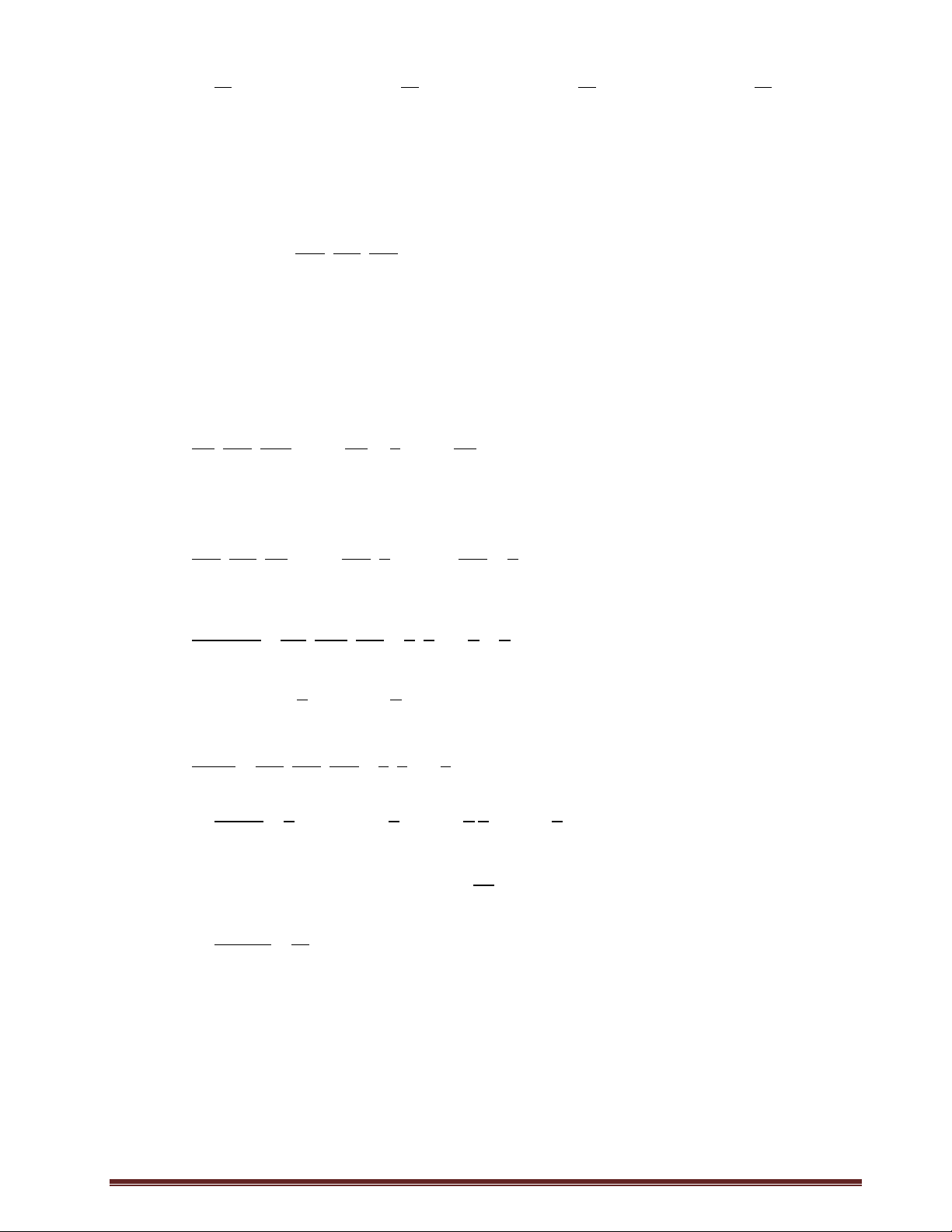
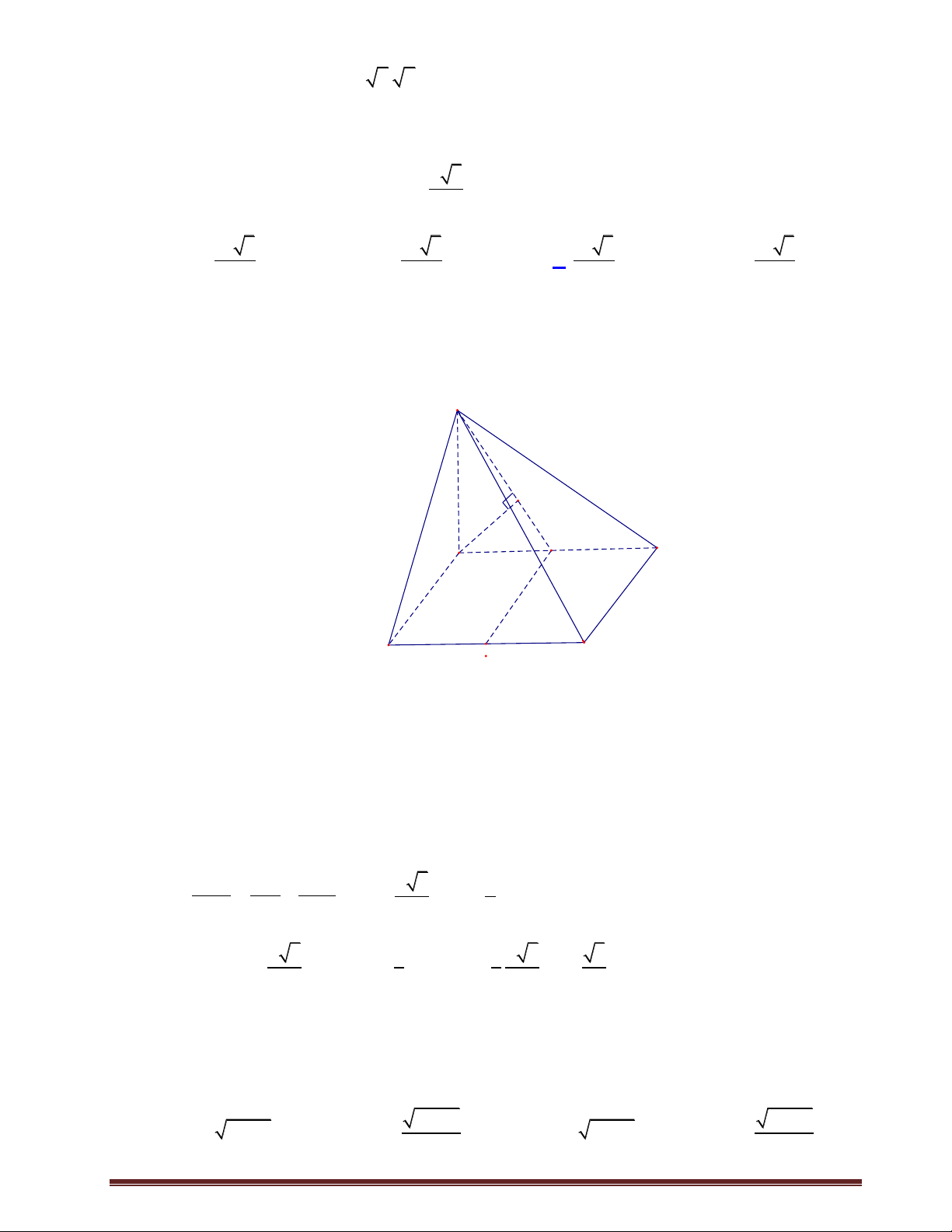
Preview text:

TRẮC NGHIỆM VẬN DỤNG VÀ VẬN DỤNG CAO
THỂ TÍCH KHỐI ĐA DIỆN Câu 1.
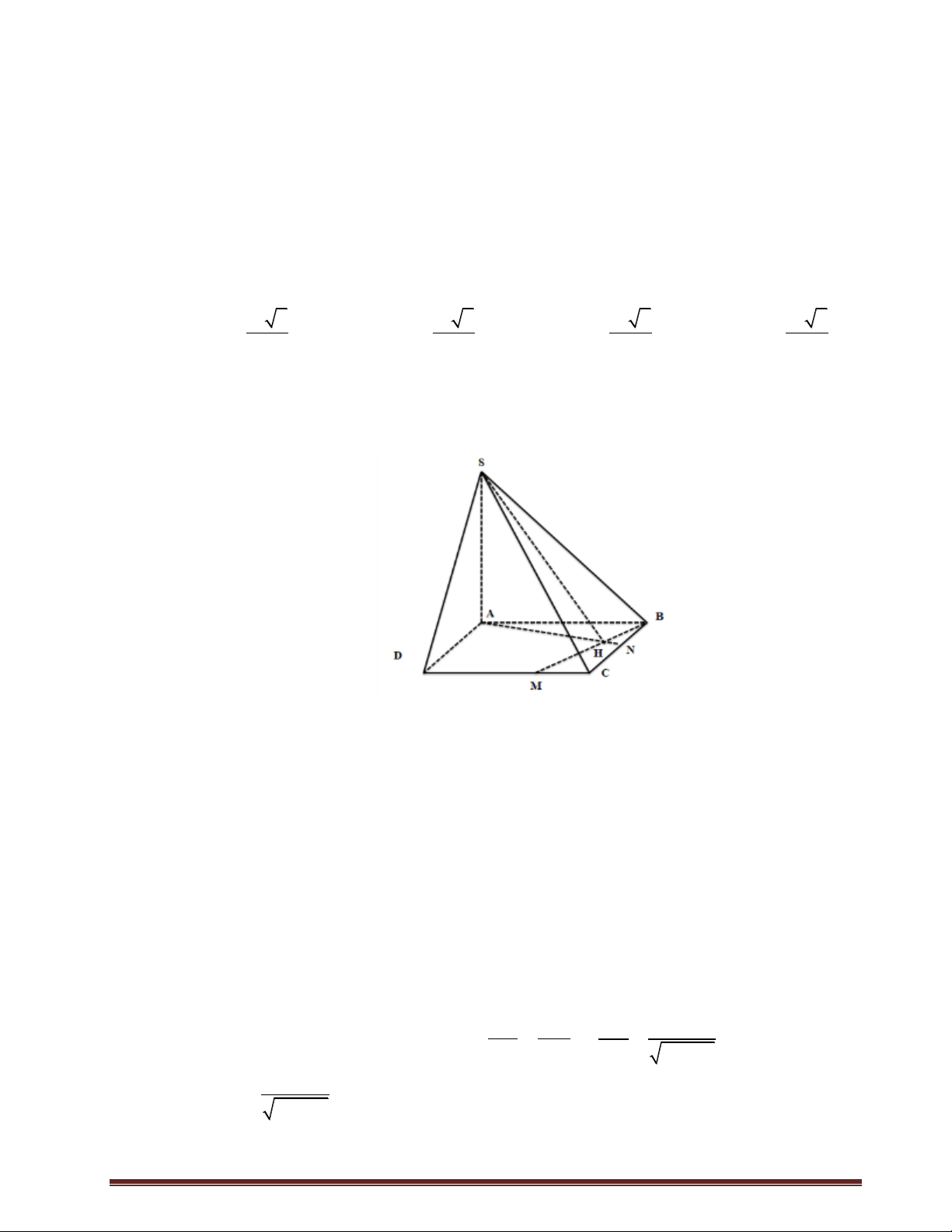
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt
đáy  ABCD và góc giữa SC với mặt phẳng SAB bằng 30 . Gọi M là điểm di động
trên cạnh CD và H là hình chiếu vuông góc của S lên đường thẳng BM . Khi điểm M
di động trên cạnh CDthì thể tích chóp S.ABH lớn nhất là 3 a 2 3 a 2 3 a 2 3 a 2 A. V  . B. V  . C. V  . D. V  . 6 12 15 8 Lời giải Chọn B
Lấy điểm N BC sao cho BN CM x, 0  x a . Gọi H AN BM Xét ABN  và B
CM ta có: BN CM ,  
ABN BCM  90 và AB BC ABN BCM (c.g.c)  
BAN CBM Mà  
BAN BNA  90 nên  
CBM BNA  90 
BHN  90 hay AH BM BM AH Ta có: 
BM  SAH   SH BM BM SA
Hình chiếu vuông góc của S lên BM là H . BH BN BH x Do B
HN đồng dạng với BCM nên    BC BM 2 2 a x a axBH  2 2 x a Trang1
Tam giác ABH vuông tại H nên 2 2 4 2 a x a a 2 2 2 AH
AB BH a    2 2 2 2 2 2 x a x a x a 2 3 1 1 a ax a x SAH.BH  . .  . ABH  2 2 2 2 2 2 2 2   2 x a x a x a 3 4 3 1 1 a x a 2 a 2 VS . A S  .a 2. .   . S. ABH ABH 2 2 3 3 2 x a 12a 12
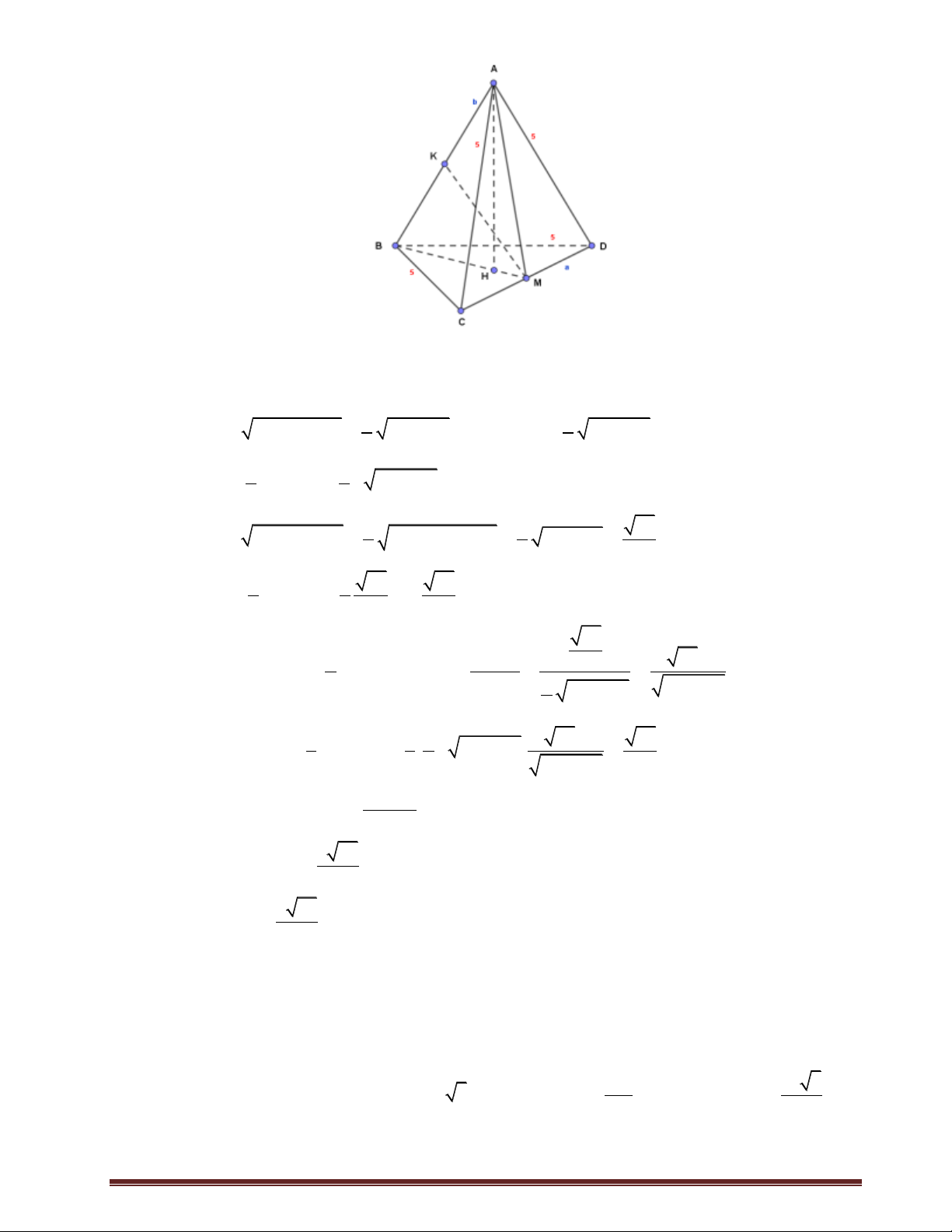
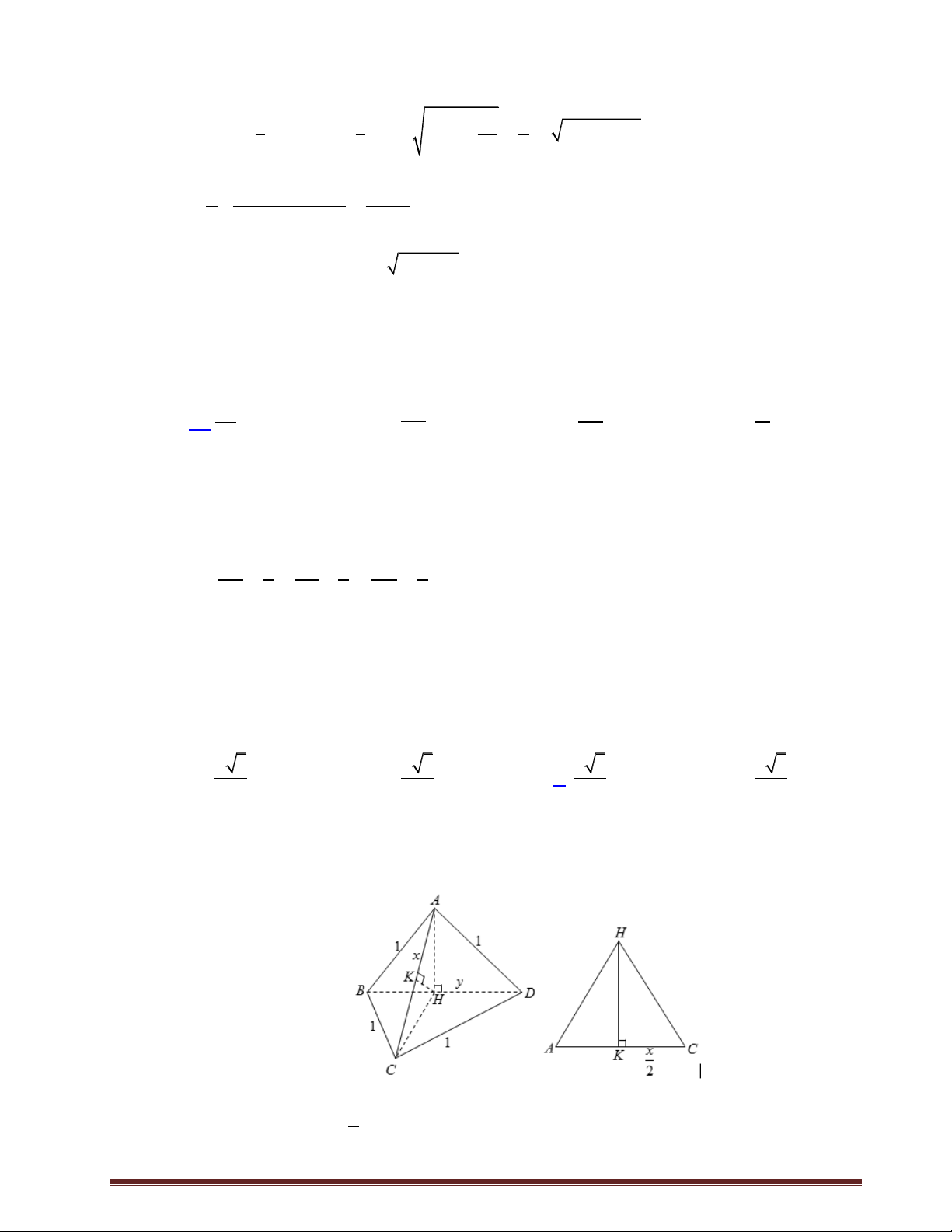
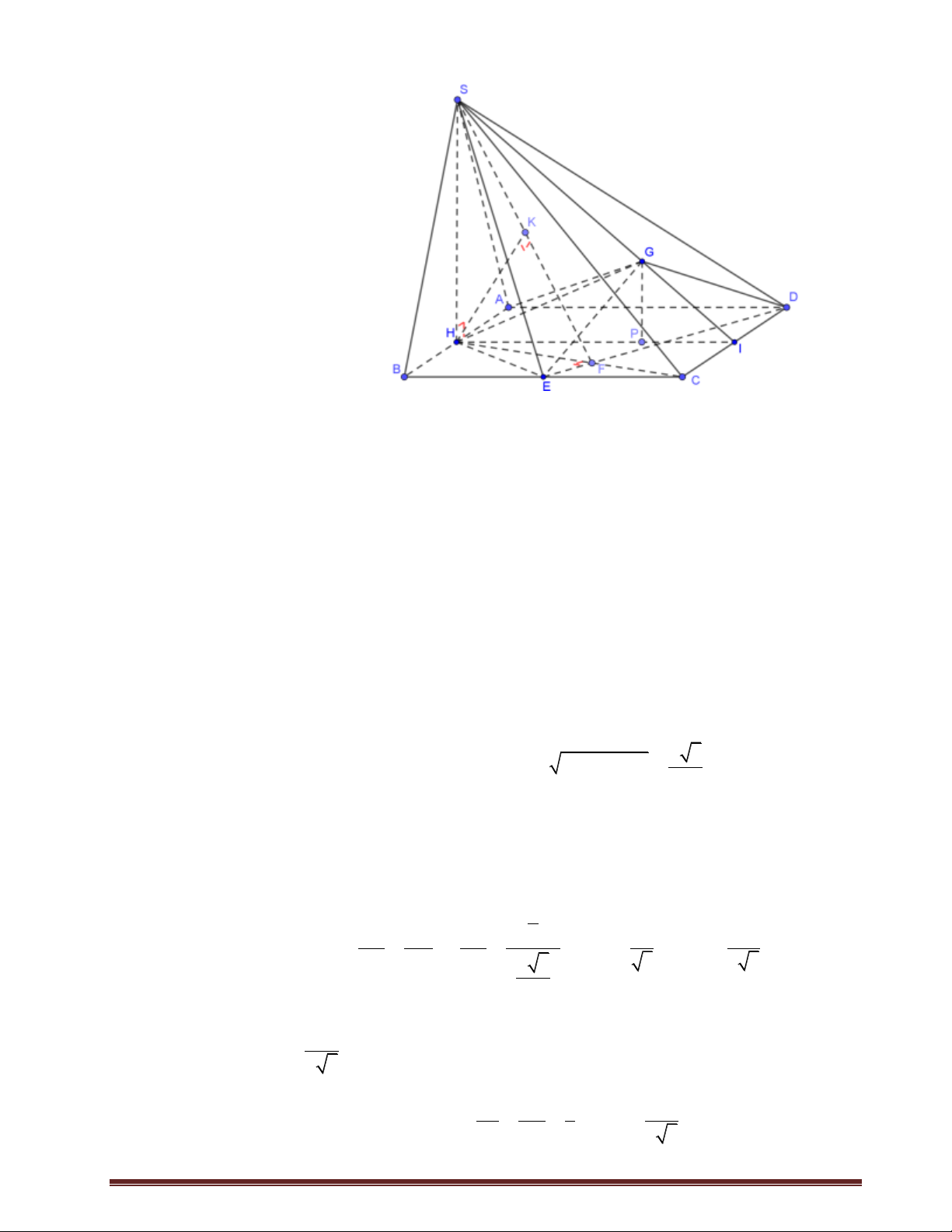
Câu 2.Cho hình chóp tam giác S.ABC có các góc   
ASB BSC CSA  60 và độ dài các cạnh
SA 1, SB  2 , SC  3 . thể tích của khối chóp S.ABC là 3 2 3 2 6 A. V  . B. V  . C. V  . D. V  . 2 2 2 2 Lời giải Chọn C. S C' B' A B C
Gọi B, C lần lượt là điểm trên SB , SC sao cho SA SB SC 1. 2 Suy ra S.AB C
  là tứ diện đều có V  . S. AB C   12 V Lại có S,ABC SB SC  2 .  2.3 V  6V    . V   S.ABC S.AB C   SB SC 2 S . AB C
Câu 3. Cho hình chữ nhật ABCD có cạnh AB  1, BC  2 . Gọi I , J lần lượt là trung điểm của
hai cạnh BC và AD . Khi quay hình chữ nhật đó xung quanh IJ ta được một hình trụ
tròn xoay. thể tích của khối trụ tròn xoay được giới hạn bởi hình trụ tròn xoay đó là. Trang2  A. V   . B. V  4 . C. V  2 . D. V  . 3 Lời giải Chọn A. 2 .BC
V s .h  .1   . T d 4 Câu 4:
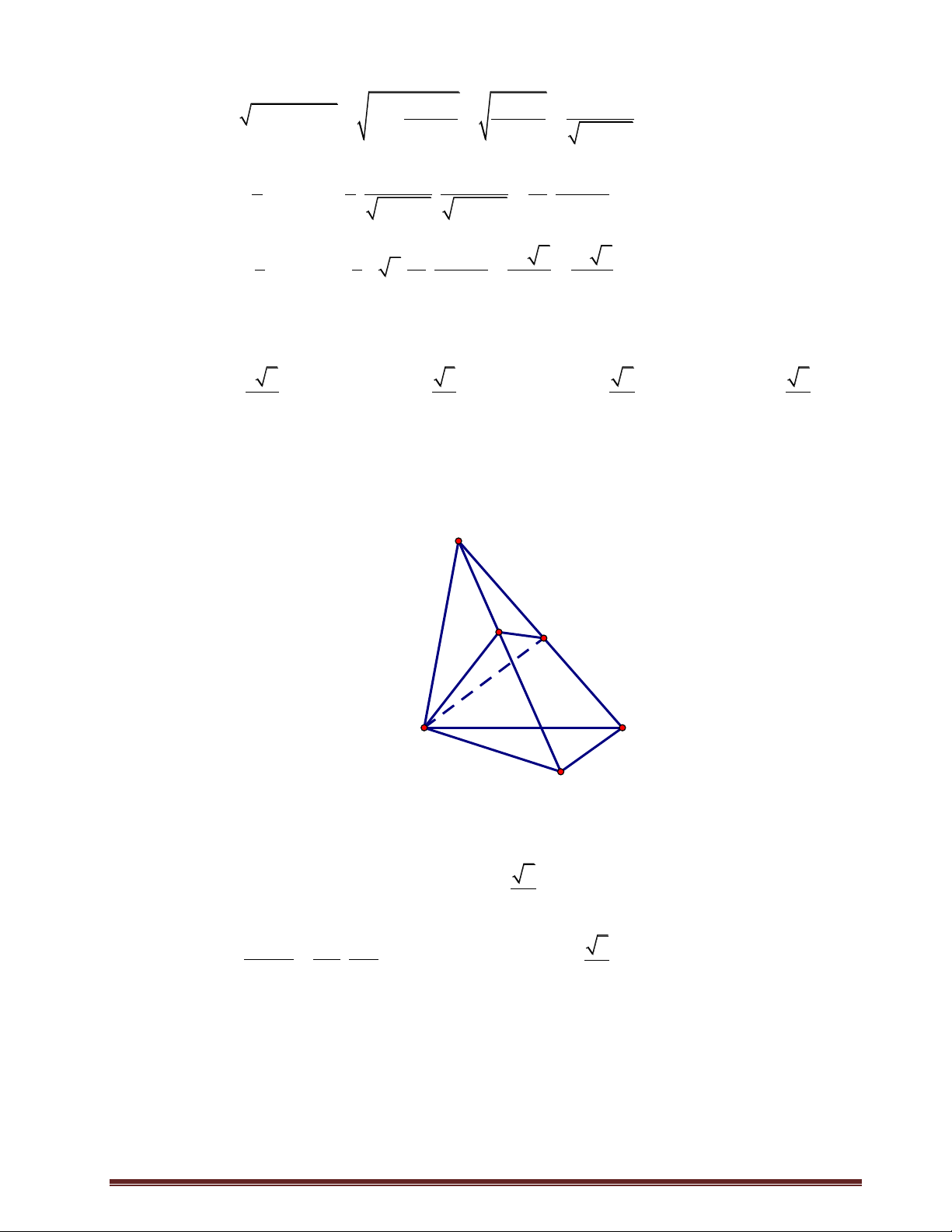
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a . Gọi E , F lần lượt là trung
điểm của các cạnh SB, SC . Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC) .
Tính thể tích khối chóp S.ABC . 3 a 5 3 a 5 3 a 3 3 a 6 A. . B. . C. . D. . 24 8 24 12 Lời giải Chọn A S F N E A C O M B
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC , do S.ABC là hình chóp đều nên
SO   ABC .
Gọi M , N lần lượt là trung điểm của BC và EF .
Ta có S , M , N thẳng hàng và SM BC tại M , SM EF tại N . Ta có
AEFSBC  EF
SM  SBC
  SM   AEF   MN AN A
NM vuông tại N .  SM EF  Từ đó suy ra ANM ∽ AN AM NM SOM   
NM.SM AM.OM . SO SM OM Trang3
Mà ta có N là trung điểm của SM (vì E , F lần lượt là trung điểm của SB , SC ) 1  NM SM ; 2 a 3 ABC
đều cạnh a và O là tâm đường tròn ngoại tiếp tam giác ABC AM  ; 2 a 3 OM  . 6 2 Vậy 1 a 3 a 3 a a 2 SM  .   SM  . 2 2 6 4 2 2 2 a a a 15 2 a 3 Ta có 2 2
SO SM OM    ; S  . 2 12 6 ABC 4 2 3 1 1 a 15 a 3 a 5 V  .S . O S  . .  . S. ABC 3 ABC 3 6 4 24
Câu 5.Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a . Gọi E , F lần lượt là các điểm nằm trên các cạnh SE SF
SB , SC sao cho 
k 0  k  
1 . Biết mặt phẳng ( AEF ) SB SC
vuông góc với mặt phẳng (SBC) . Tính thể tích khối chóp S.ABC . 3 a 3 2  k 3 a 3 2  k 3 a 3 2  k A. 24 3 . B. 3k 8 3  . C. 3k 24 5  . D. 5k 3 a 3 2  k 12 3  . 3k Lời giải Chọn A Câu 6.
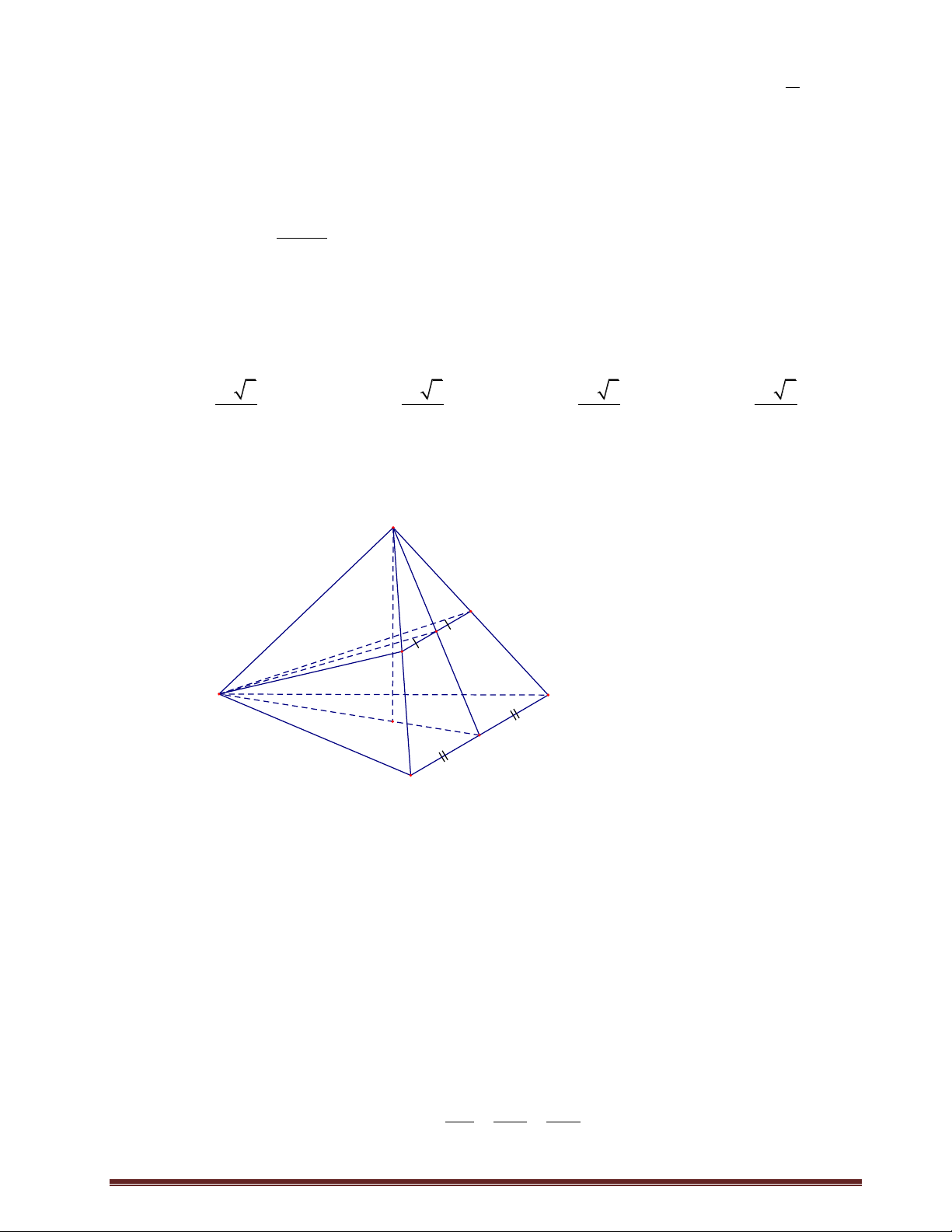
Cho hình chóp đều S.ABCD có đáy là tam giác đều cạnh a . Gọi E , F lần lượt là trung
điểm của các cạnh SB, SC . Biết mặt phẳng ( ADFE) vuông góc với mặt phẳng (SBC) .
Tính thể tích khối chóp S.ABCD . 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 6 2 12 18 Lời giải Chọn A Trang4 S F N E D C I M O A B 2 1 a Ta có I
NM ∽ S
OM MN.SM OM.IM 2  SM   SM a . 2 2 2 a a 2 2 2 2
SO SM OM a   . 2 2 3 1 1 a 2 a 2 2 V  .S . O S  . .a  . S.ABCD 3 ABCD 3 2 6 Câu 7:
Cho hình chóp đều S.ABCD có đáy là tam giác đều cạnh a . Gọi E , F lần lượt là các
điểm nằm trên các cạnh SE SF
SB , SC sao cho 
k 0  k   1 . Biết mặt phẳng SB SC
( ADFE) vuông góc với mặt phẳng (SBC ) . Tính thể tích khối chóp S.ABCD . 3 a 2 k 3 a 2 1 k 3 a 2 k 3 a 2 1 k A. . . . C. . . 6 1 . B. k 6 k 18 1 . D. k 18 k .
Câu 8:Cho khối chóp S.ABCD có đáy là hình bình hành ABCD . Gọi M , N , P , Q lần lượt là
trọng tâm các tam giác SAB , SBC , SCD , SDA . Biết thể tích khối chóp S.MNPQ là V ,
khi đó thể tích của khối chóp S.ABCD là: 2 27V  9  9V 81V A. . B. V   . C. . D. . 4  2  4 8 Lời giải Chọn A. Trang5 S N M P Q C K B H F O I E D J A
d S,MNPQ SM 2 Ta có   .
d S, ABCD SI 3 Mặt khác gọi S 1 1 1 S S ta có DEJ  .  1  SS . ABCDDEJ S 4 2 8 16 BDA Tương tự ta có S 1 JAI   1  S   . JAI S 4 8 DAB   1 1  1 Suy ra S  1 4.  2. S S . HKIJ      16 8  2 2 S   MNPQ 2 4 2 Mà      SS . S  3  9 MNPQ 9 ABCD HKIJ 1 1 3 9 27 Suy ra V
d S, ABCD .S  . d S,MNPQ. S V . S . ABCD    3 3 2 2 4
Câu 9:Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy
ABCD , góc giữa hai mặt phẳng SBDvà ABCD bằng 60. Gọi M , N lần lượt là
trung điểm của SB , SC . Tính thể tích khối chóp S.ADMN . 3 a 6 3 a 6 3 3a 6 3 a 6 A. V  . B. V   C. V   D. V   16 24 16 8 Lời giải Chọn A. Trang6 S N M A D O B C
Gọi O là tâm của hình vuông ABCD . Khi đó ta có 
SOA là góc giữa hai mặt phẳng  SA
SBD và  ABCD nên 
SOA  60 . Khi đó tan 60  AO 2  a SA A . O tan 60  6 . a 3  . 2 2 V SA SM SN 1 V SA SN SD 1 Ta có S.AMN  . .
 và S.AND  . .  . V SA SB SC 4 V SA SC SD 2 S .ABC S .ACD   3 Do đó 1 1 1 3 3 1 a 6 a 6 VV .   .V 2  . . .a  . S.ADMN S .   2 ABCD  4 2  . 8 S ABCD 8 3 2 16
Câu 10:Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy,
SA a 2 . Gọi B , D là hình chiếu của A lần lượt lên SB , SD . Mặt phẳng  AB D  
cắt SC tại C . thể tích khối chóp SAB CD   là: 3 2a 3 3 2a 2 3 a 2 3 2a 3 A. V  . B. V  . C. V  . D. V  . 9 3 9 3 Lời giải ChọnC. S C' D' B' D A O B C 1 3 a 2 Ta có: 2 V  .a .a 2  . S . ABCD 3 3 Trang7
Vì B , D là hình chiếu của A lần lượt lên SB , SD nên ta có SC   AB D   .
Gọi C là hình chiếu của A lên SC suy ra SC AC mà AC  AB D    A nên
AC   AB D
  hay C  SC  AB D   .
Tam giác S AC vuông cân tại A nên C là trung điểm của SC . 2 SBSA 2 2a
Trong tam giác vuông S AB ta có   2  . 2 SB SB 2 3a 3 V     V   V         SAB C D SAB C SAC D    1 SB SC SD SC   SB SC    2 1  1 .  . V V 2  SB SC SD SC SB SC 3 2 3 S.ABCD S .ABCD 3 Vậy a 2 V  . SAB CD   9
Câu 11:Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng thay đổi nhưng
luôn song song với đáy và cắt các cạnh bên SA, SB , SC , SD lần lượt tại M , N , P ,
Q . Gọi M  , N , P , Q lần lượt là hình chiếu vuông góc của M , N , P , Q lên mặt
phẳng  ABCD . Tính tỉ số SM để thể tích khối đa diện MN . PQ M NPQ
  đạt giá trị lớn SA nhất. 2 1 1 3 A. . B. . C. . D. . 3 2 3 4 Lời giải Chọn A. S M Q N P A D M' Q' H N' P' B C
Đặt SM k với k 0;  1 . SA MN SM
Xét tam giác SAB có MN //AB nên 
k MN k.AB AB SA Trang8 MQ SM
Xét tam giác SAD có MQ//AD nên 
k MQ k.AD AD SA
Kẻ đường cao SH của hình chóp. Xét tam giác SAH có: MM AM SA SM SM MM//SH nên    1
 1 k MM   1 k.SH . SH SA SA SA Ta có V   2  A . B A .
D SH.k .1 k      MN.M . Q MM . MNP . Q M N P Q 1 Mà VSH. . AB AD 2 V       3.V .k . 1 k . MNPQ.M N P Q S .ABCD   S . ABCD 3
thể tích khối chóp không đổi nên V 2
k . 1 k lớn nhất. MNP . Q M NPQ
  đạt giá trị lớn nhất khi  
2 1 k .k.k
1  2  2k k k  4
Ta có k .k     3 2 1     2
k .k   1  . 2 2  3  27
Đẳng thức xảy ra khi và chỉ khi: 21 k   2 k k  . 3 Vậy SM 2  . SA 3
Câu 12:Cho hình chóp S.ABC có đáy là tam giác đều. Đường cao SH với chân đường cao nằm trong ABC
và 2SH BC ; SBC  tạo với  ABC  một góc 0
60 . Biết có một điểm O
thuộc SH sao cho d 0, AB  d 0, AC  d  ,
O SBC  1. Tính thể tích khối cầu ngoại tiếp chóp đã cho. 256 125 500 343 A. . B. . C. . D. . 81 162 81 48 Lời giải Chọn D. Trang9
Gọi E, F lần lượt là chân đường cao hạ từ O xuống ; AB AC . OE AB
AB  SEO  AB HE SH AB
Tương tự HF AC  ; HOE H
OF HE HF AH là tia phân giác của góc BAC
AH BC D là trung điểm của BC .
Kẻ OK SD OK d  ,
O SBC   1 , Đặt AB BC CA  2a SH a a 0 HD  . a cot 60 
, AD a 3  3HD nên ABC
đều nên S.ABC là chóp tam giác 3 đều. OK
Xét tam giác SOK có SO   2 . 0 sin 30 Do D
EF đều và OH  DEF  nên EO FO DO 1 OK K D 2  a 3 DSO vuông tại D 2
DH HS.HO
a 2  a  a  3 2 3 21 2 2 2
AB  3 AH  3 ; SH   SA SH AH  2 4 2 SA 7 343  R    V   . mc 2SH 4 mc 48
Câu 13:Xét khối tứ diện ABCD có cạnh 2 2
AB CD  18 và các cạnh khác bằng 5. Biết thể tích tứ diện x y
ABCD đạt giá trị lớn nhất có dạng V ; , x y N    ;( ,
x y)  1. Khi đó x, y ax m 4
thỏa mãn bất đẳng thức nào dưới đây A. 2
x y xy  4550 .
B. xy  2x y  2550 . C. 2 2
x xy y  5240 . D. 2
x y  19602 . Lời giải Chọn A Trang10
Gọi M là trung điểm CD, và K là trung điểm AB
Ta có: BM CD và SM CD . Kẻ SH BM , tại H BM . Khi đó SH  (BCD)
Đặt AB b  0 và CD a  0 1 1 2 2 2 BM BC MC  100  a ; 2 SM BM  100  a 2 2 1 1 2 S
BM .CD a 100  a BCD 2 4 1 1 82 2 2 2 2 MK BM BK
100  (a b )  100 18  2 2 2 1 1 82 82 SMK.AB  .b b ABM 2 2 2 4 82 2. .b Mặt khác: 1 2.S 82.b BCD 4 S
SH.BM SH    BCD 2 2 BM 1 2 100 100  aa 2 1 1 1 82.b 82 Ta có: 2 V  .S
.SH  . a 100  a .  ab . A BCD BCD 2 3 3 4  12 100 a 2 2 a b
Theo Cô-si ta có: ab   9 2 3 82 Suy ra : V
. Dấu bằng xảy ra khi a b  3 . A BCD 4 Vậy 3 82 V
. Suy ra x  3; y  82 ax m 4
Câu 14:Cho lăng trụ đứng AB . C A BC
 có cạnh BC  2a, góc giữa hai mặt phẳng  ABCvà A B
C bằng60. Biết diện tích của tam giác A BC bằng 2
2a . Tính thể tíchV của khối lăng trụ AB . C A BC   3 2a 3 a 3 A. 3 V  3a . B. 3 V a 3 . C.V  . D.V . 3 3 Lời giải Trang11 Chọn B.
Kẻ AI BC ( I BC )  A I   BC . 1 Ta có S   2
 2a A I  2a .   A I.BC A BC 2
Do đó AA  A I
 .sin60  a 3 , AI A I.cos60  a . 1 Vậy 3 V      .2 . a . a a 3 a 3 . ABC. A B C 2
Câu 15: Cho lăngtrụđều AB . C A BC
 cócạnhđáy a  4, biết diện tích của tam giác A BC bằng8 . Tính
thể tíchV của khối lăng trụ AB . C A BC  . A. V  4 3 . B. V  8 3 . C. V  2 3 .
D. V  10 3 . Lời giải Trang12 Chọn B. Gọi 1
I làtrungđiểm BC . Tam giác ABC cân nên S
AI.BC  4  A I  4 . ABC 2 Khiđó 2 2 AA  AI A I   2 . VậyV       AA .S 8 3 . ABC. A B C ABC
Câu 16:Cho lăngtrụ AB . C A BC
 cóđáy ABC là tam giácđều cạnh 2a , hình chiếu của Alên ABC
trùng với trọng tâm tam giác ABC . Biết góc giữa cạnh bên và mặt đáy bằng 60. thể tích
khối lăng trụ bằng 3 a 3 3 a 3 A. V  . B. V  . C. 3 V  2a 3 . D. 3 V  4a 3 . 4 8 Lời giải ChọnC. 2 2a
Gọi I là trung điểm BC, nên AG AM   A G   A .
G tan 60  2a . 3 3 Vậy 3 V       A . G S 2a 3 ABC.A B C ABC
Câu 17: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy SM
( ABCD) và SA a . Điểm M thuộc cạnh SA sao cho
k,0  k  1.Khi đó giá trị SA
của k để mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau là: 1   5 1 5 1   5 1   2 A. k . B. k . C. k . D. k . 2 2 4 2 Trang13 Lời giải Chọn A.
Phân tích: Bài toán trên chính là bài toán về tỉ số thể tích, vì vậy trước hết phải xác định
thiết diện của hình chóp khi cắt bởi (BMC) .
Do (BMC) chứa BC song song với AD nên (BMC) cắt (SAD) theo giao tuyến song song AD . Để tính V
nếu xác định đường cao thì phức tạp vì vậy sẽ chia thành hai khối và sử S .BCNM
dụng bài toán tỉ số thể tích.
Kẻ MN / / AD; N SD khi đó thiết diện của hình chóp S.ABCD với (BMC) là hình
thang BCNM . Suy ra (BMC) chia khối chóp thành hai khối đa diện SBCNM và DABCNM . Đặt V V ; V V ; V V . 1 S .BCNM 2 DABCNM S . ABCD Để 1
V V thì V V . 1 2 1 2 V SN SM 1 Ta có SNMC 2  .  k 2  Vk .V . SNMC V SD SA 2 SADC V SM Ta có SMCB   1 k Vk.V . SMCB V SA 2 SABC Vậy 1 2 V
(k k ).V . 1 2  1 5 k  Khi đó 1 2 V V 2
k k  1   . 1 2  1 5 k   2 1   5
Do 0  k 1 nên k  . Vậy chọn đáp án A. 2
Câu 18: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , cạnh bên SA vuông góc với đáy và
SA  2a . Gọi B , D lần lượt là hình chiếu vuông góc của A trên các cạnh SB , SD . Mặt phẳng  AB D
  cắt SC tại C . Tính thể tích của khối chóp S.AB CD   . 3 a 3 16a 3 a 3 a 2 A. . B. . C. . D. . 3 45 2 4 Lời giải. Trang14 Chọn B. Cách 1: 2 SD .SD SA 2 2 SDSA SA 4 2
SD .SD SA       SD SD 2 2 2 SD SD SA  . AD 5 2 2  Tương tự: SC SA SA 2    2 2 2 SC SC SA  . AC 3 SDSCSDSCV       2V   2. . V . V . S . AB C D S . AD C S . ADC SD SC S . ABDC SD SC 3 4 2 1 16a 2  V      . . .2 . a a . S . AB C D 5 3 3 45
Cách 2: Hoặc có thể áp dụng cách tính nhanh: V          x y z t x y z t SB SC SD S. A B C D    với SA xyzt V 4xyzt 2xyzt 2xyzt SA , SB , SC , SD . S.ABCD
Câu 19:Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai khối lập phương có diện tích toàn phần bằng nhau thì thể tích bằng nhau.
B.Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì thể tích bằng nhau.
C. thể tích của hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau là bằng nhau.
D. thể tích của khối lăng trụ bằng diện tích đáy nhân chiều cao.
Câu 20:Cho hình chóp tứ giác đều có cạnh đáy bằng 1 chiều cao bằng 2 . Xét hình đa diện lồi H
có các đỉnh là trung điểm của tất cả các cạnh hình chóp đó. Tính thể tích của H . 9 5 A. . B. 4 . C. 2 3 . D. . 2 12 Lời giải. Chọn D.
Gọi M , N, P,Q lần lượt là trung điểm của S ,
A SB, SC, SD . Gọi E, F , I , J lần lượt là
trung điểm của AB, BC,CD, AD .Gọi V là thể tích của H . Khi đó: 2 2 1 1  1  1 1  1  5 V VV  4.V 2  .2.1  .1.  4. .1. .  S.ABCD S ,MNPQ N .EBF     3 3  2  3 2  2  12 Trang15
Câu 21:Một hình chóp có đáy là tam giác đều cạnh bằng 2 và chiều cao bằng 4. Tính thể tích của hình chóp đó. 4 3 A. 4 B. C. 2 3 D. 2 3 Lời giải. Chọn B.
Câu 22:Cho khối đa diện H được tạo thành bằng cách từ khối lập phương có cạnh bằng 3, ta bỏ đi
khối lập phương cạnh bằng 1 như hình vẽ. Gọi S là khối cầu có thể tích lớn nhất chứa
trong H và tiếp xúc với các mặt phẳng ( A' B 'C ' D '), (BCC ' B ') và (DCC ' D ') . Tính bán kính của S . 2  3 2 3 A. . B. 3  3 . C. . D. 2 3 3 Lời giải Chọn B Giải theo tự luận Ta có CH  2 3
Gỉa sử khối cầu S có tâm I là tâm, bán kính R .
I’,M, P lần lượt là hình chiếu của I lên (A' B 'C ' D '),(BCC ' B ') và (DCC ' D ') .
Vì S là khối cầu chứa trong H và tiếp xúc với các mặt phẳng ( A' B 'C ' D '), (BCC ' B ')
và (DCC ' D ') nên MNPI.M 'C ' P' I ' là hình lập phương cạnh R ( R là bán kính khối
cầu S ) và I C ' H
Ta có C ' H  2 3 , C ' I R 3
Vậy khối cầu có thể tích lớn nhất khi khối cầu đi qua H tức IH R
C ' H IH C ' I
Vậy  2 3  R R 3  R  3 3 Vậy chọn B
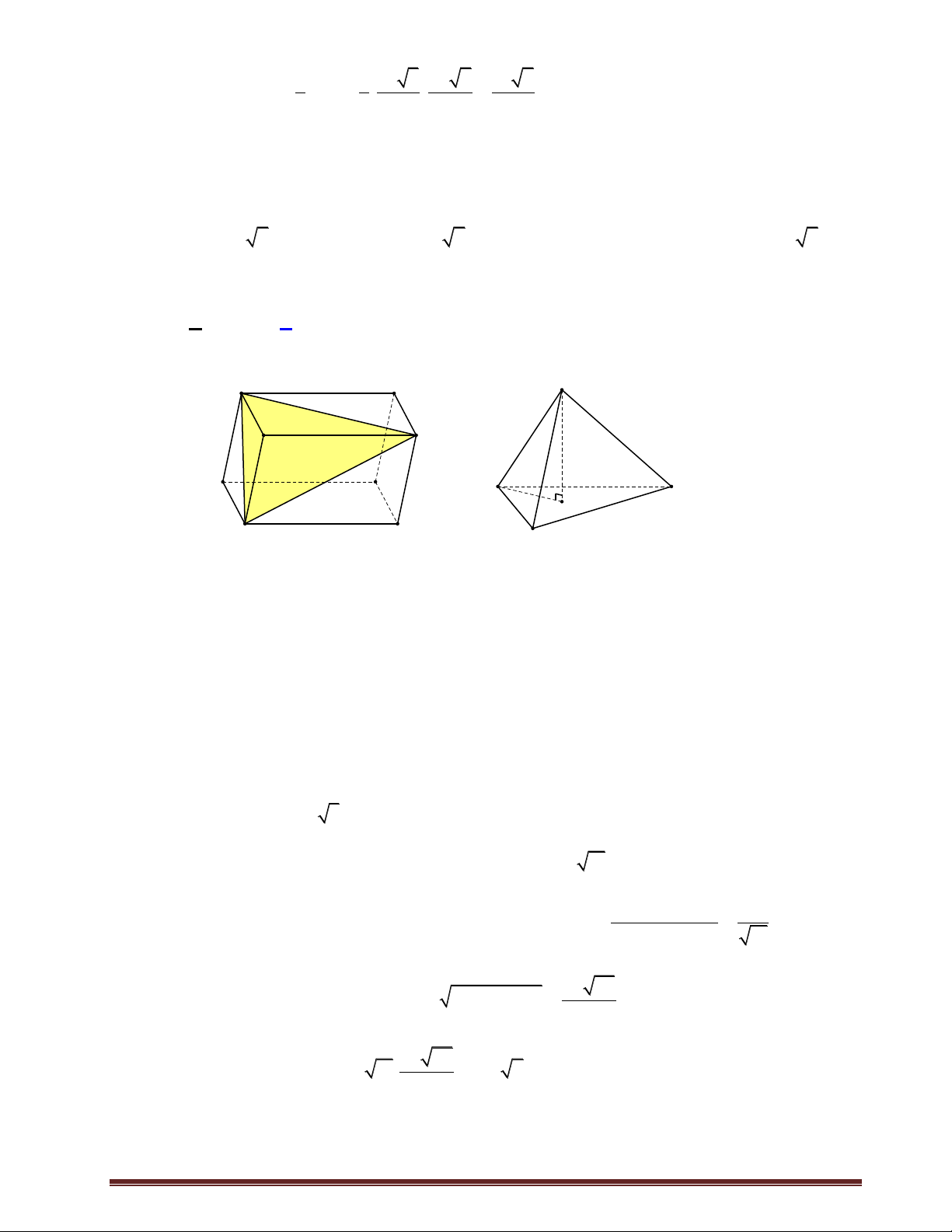
Câu 23:Cho tứ diện ABCD và các điểm M , N , P lần lượt thuộc các cạnh BC , BD , AC sao
cho BC  4BM , AC  3AP , BD  2BN . Tính tỉ số thể tích hai phần của khối tứ diện
ABCD được phân chia bởi mpMNP . Trang16 7 7 8 8 A. . B. . C. . D. . 13 15 15 13 Lời giải Chọn A.
(Địnhlý Menelaus Cho tam giác ABC đườngthảng d cắtcáccạnh AB, BC,CA lầnlượtại MA PB NC
M , N , P ta có . .  1) MB PC NA
Gọi I MN DC, K AD PI.
Áp dụng định lý Menelaus cho tam giác BCDvà 3 điểm M , N, I ta có IC ND MB IC 1 IC . .  1  .1. 1   3 ID NB MC ID 3 ID
Áp dụng định lý Menelaus cho tam giác ACD và 3 điểm P, K, I ta có KD PA IC KD 1 KD 2 . .  1  . .3  1   KA PC ID KA 2 KA 3 V CP CM CN 2 3 2 1 CPMN  . .  . .1   V CA CB CN 3 4 4 2 CABN 1 1  VVV (3) CPMN 2 CABN 4 ABCD V AP AK AN 1 3 1 APKN  . .  . .1  V AC AD AN 3 5 5 ACDN V 4 4 4 1 2 NCPKD    VVVV (4) V 5 NCPKD 5 ACDN 5 2 ABCD 5 ABCD ACDN     13 3 , 4  VVVV CMPKDN CPMN NCPKD 20 ABCD V 7 ABMNKP   V 13 CMNDK
Câu 24:Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng
( ) qua tâm đáy và tạo với mặt đáy một góc 0
60 tính tỷ số thể tích của hai phần khối
nón chia bởi mặt phẳng ( ) ? Trang17 2 1 2 3  4 A.  . B. . C. . 2    1 3 . D. 6 Lời giải Chọn D.
Không mất tính tổng quát ta giả sử R  1 .
Khi cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt
phẳng ( ) qua tâm đáy và tạo với mặt đáy một góc 0
60 thì ta được thiết diện là một
đường parabol có đỉnh là gốc O 0;0 và đỉnh còn lại là A1; 
1 , do đó thiết diện sẽ có diện tích là 4 S
. Xét mặt phẳng đi qua cạnh đáy của thiết diện vuông góc với hình tròn 3
đáy của hình nón cắt hình nón làm đôi.
Gọi đa diện chứa mặt thiết diện đó là  H  . Gọi K  là đa diện chứa đỉnh O của hình
nón được sinh bởi khi cắt thiết diện Parabol với đa diện  H  .
Khi đó khoảng cách từ O đến mặt thiết diện là 3 h  . 2
Suy ra thể tích của đa diện  1 3 4 2 3
K  là V  . .  . K 3 2 3 9 
Mặt khác thể tích của nửa khối nón là 1 1 3 . 3  . 2 3 6
Do đó thể tích của đa diện nhỏ tạo bởi thiết diện và khối nón là  3 2 3 3  4 3 V    . 6 9 18 3  4 3  3  4 18
Vậy tỉ số thể tích của hai phần khối nón chia bởi mặt phẳng   là  .  3 6 3
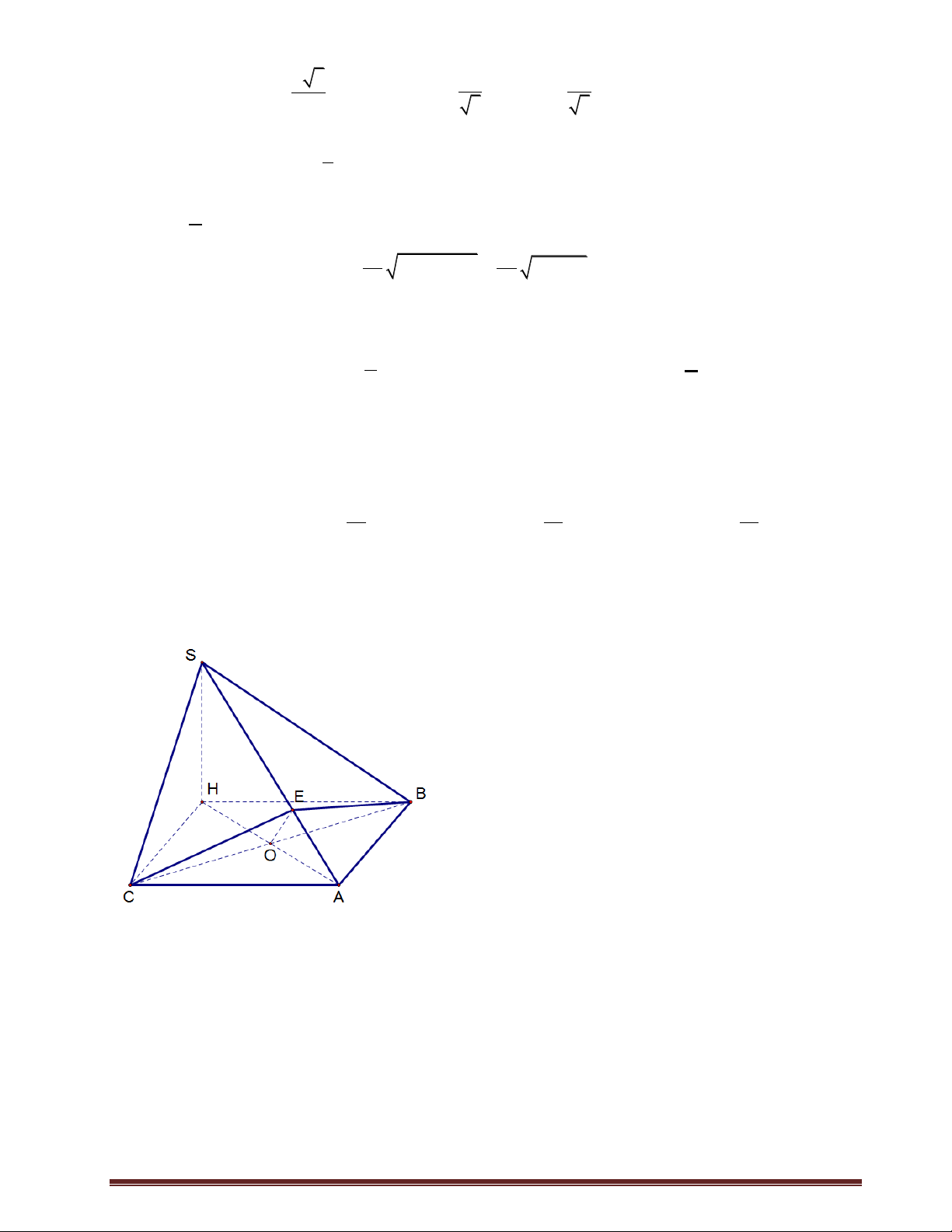
Câu 25: Khối chóp S.ABCD có đáy là hình thoi cạnh a , SA SB SC a , cạnh SD thay đổi. thể
tích lớn nhất của khối chóp S.ABCD là: 3 a 3 a 3 3a 3 a A. . B. . . D. . 8 4 C. 8 2 Lời giải. Trang18 Chọn. B. S A D O B C Đặt SD  . x
Do đáy ABCD là hình thoi nên V  2V  2V . S . ABCD S .BCD C.SBD Ta có SAC B
AC SO BO S
BD vuông tại S. 2 2  2 2  a x
BD a x 2
OA OC a  . 4 CO BD 1 Và do 
CO  SBD  V  2V  2. .C . O S CO SO S . ABCD C.SBD 3 SBD 2 2 2 3a x 1    a a x 3a x a V  . . ax
x 3a x  2 2 2 3 2 2 2  .  S . ABCD 3 2 2 6 6 2 4 dầu bằng xảy ra khi a 6 x  . 2
Câu 26:Một cái phễu có dạng hình nón, chiều cao của phễu là 20 cm . Người ta đổ một lượng nước
vào phễu sao cho chiều cao của cột nước trong phễu bằng 10cm (hình H1). Nếu bịt kín
miệng phễu rồi lật ngược phễu lên (hình H2) thì chiều cao của cột nước trong phễu gần
bằng với giá trị nào sau đây? Trang19 A. 0,87 cm . B. 10 cm . C. 1, 07 cm . D. 1, 35 cm . Lời giải Chọn A.
+ Gọi R là bán kính đáy của phễu. 2
+ thể tích của lượng nước đổ vào phễu là 1 R V .10.    .  (1). 3  2 
+ Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì lượng nước tạo thành khối nón cụt có    chiều cao là r 20 h h
h và bán kính đáy nhỏ trên là r . Ta có   r  1 R   . R 20  20 
+ thể tích khối nón cụt cũng là thể tích lượng nước được tính theo công thức sau:  h        V
R r Rr 2 2 hR h h 2 2  1   1  1     (2). 3 3   20   20    2     + Từ (1) và (2) ta có 5 h h h   h 2   1    
 0,0435  h  0,87 . 6 3  20  20    20
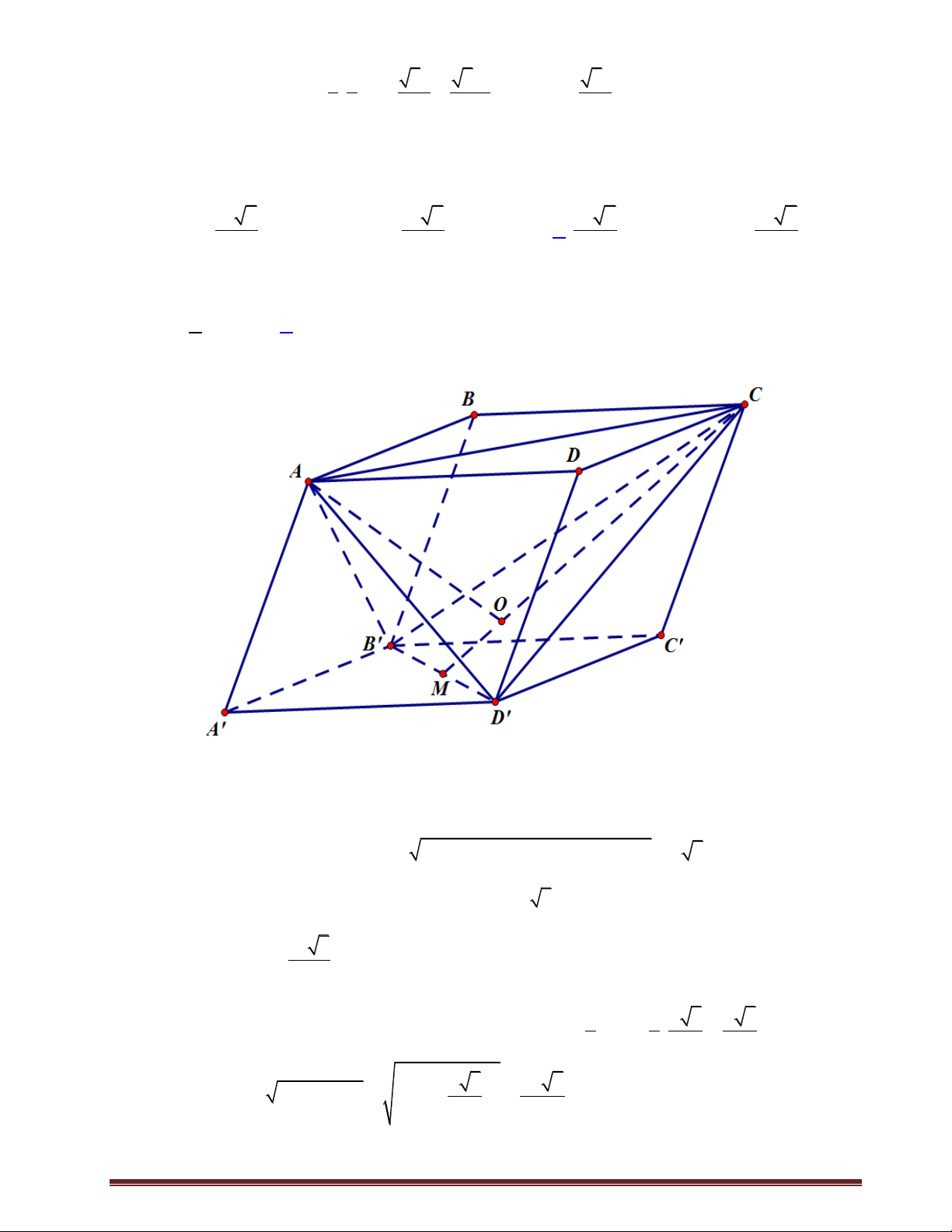
Câu 27:Cho khối hộp ABC . D A BCD
  có đáy là hình chữ nhật với AB  3 ; AD  7 . Hai mặt bên  ABB A
  và  ADD A
  cùng tạo với đáy góc 45, cạnh bên của hình hộp bằng 1
(hình vẽ). thể tích của khối hôp là: A. 7 . B. 3 3 . C. 5. D. 7 7 . Lời giải Chọn A B' C' A' D' B K C H A I D Trang20 Hạ A H
   ABCD, H  ABCD; HI AD, I AD ; HK AB, K AB
A' H   ABCD  A' H AD A'I AD IH AD  A I
  AD, IH AD 
   ABCD , ADD A     HIA (Do HIA  90 )  DD A A
  ABCD      AD
Chứng minh tương tự  ABCD, ABB A    HKA
Từ giả thiết suy ra: HIA  H
KA  45  HA  HI HK
Có ABCD là hình chữ nhật, HI AD, I AD ; HK AB, K AB
Nên AIHK là hình vuông suy ra AH HK 2  A H  2 2 2 2 2        + A H
   ABCD, H  ABCD  AH A HAA A H HA 3A H 1  HA  3 V        A H.A . B AD 7 . ABCD. A B C D
Câu 28:Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC , các mặt bên SAB ,
SBC,SCA cùng tạo với đáy góc 60. Biết AB  3, BC  4,CD  5, tính thể tích
khối chóp S.ABC . A. 2 3 . B. 6 3 . C. 5 3 . D. 10 3 . Lời giải ChọnA Trang21 S A C G H I K B
Hạ SH   ABC, H  ABC
HI AB, I AB ; HK BC, K BC , HG C , A G CA
SH   ABC   SH AB SI AB IH AB 
SI AB, IH AB  Có
   ABC,SAB  HIS (Do HIS  90 )
SAB ABC  AB
Chứng minh tương tự  ABC,SBC  HKS
 ABC,SAC  SGH
Từ giả thiết suy ra: HIS SKH SGH  60
SH HI 3  HK 3  HG 3
Mà H nằm trong tam giác ABC nên H và HI lần lượt là tâm và bán kính đường tròn nội
tiếp của tam giác ABC Có 2 2 2
AB BC AC nên tam giác ABC là tam giác vuông tại B . 2  S ABC 4.3 HI   1  SH  3 .
AB BC CA 3  4  5 Trang22 1 1 3.4  VSH.S  . 3.  2 3 . S . ABCABC 3 3 2
Câu 29:Cho hình chóp S.ABCD có đáy ABCD là hình vuông, các mặt bên SBC  , SAD cùng tạo
với đáy góc 60, mặt bên SAB vuông góc với đáy. Biết khoảng cách từ A đến mặt phẳng  21 SCD bằng
, tính thể tích khối chóp S.ABC . 7 3 3 3 3 A. . B. . C. . D. . 12 6 8 8 Lời giải. ChọnA S I C B H M A D
Hạ SH AB, H AB , do SAB   ABCD nên SH   ABCD  SH BC
Có ABCD là hình vuông  AB BC
BC  SAB  BC SB
SB BC, BC AB  Có
   ABCD,SBC  SBH
SBC ABCD  BC (Do SAH  90 )
Chứng minh tương tự  ABCD,SAD  SAH Trang23
Từ giả thiết suy ra: SAH S
BH  60mà H AB suy ra tam giác SAB đều và H là
trung điểm của AB .
Gọi M là trung điểm của CD HM CD
Có SH   ABCD  SH CD   3
SHM   SCD . Hạ HI SM thì HI  SCD  HI  12 1 1 1 1 1 1 Có     
AB 1 (Do AB BC HM 2 2 2 HI SH HM 2 2 2  21   3  BC AB     7 2     ) 1 1 3 1 3 VSH.S  . .  . S.ABCABC 3 3 2 2 12
Câu 30: Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 3
200m . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí xây bể là 300 nghìn đồng/ 2
m (chi phí được tính theo diện tích xây dựng, bao gồm diện tích đáy và
diện tích xung quanh, không tính chiều dày của đáy và thành bể). Hãy xác định chi phí
thấp nhất để xây bể (làm tròn đến đơn vị triệu đồng). A. 75triệu đồng. B. 51triệu đồng. C. 36 triệu đồng. D. 46 triệu đồng. Lời giải Chọn B
+) Gọi chiều rộng của đáy bể là a (m) thì chiều dài của đáy là 2a (m) .
+) Do thể tích bể chứa nước là 200 100 3
200m nên chiều cao của bể là h   . 2 2 2a a 600
+) Do đó diện tích xây dựng bể là 2
S  2a  2.ah  2.2ah 2  2a  . a 600 300 300 300 300 + Ta có 2 S  2a  2  2a   2 3  3 2a . . 3
 30 180 , dấu bằng xảy ra a a a a a khi 3
a  15 , suy ra chi phí thấp nhất để xây bể là 3
300.000x30 180  51triệu đồng. Chọn đáp án B
Nhận xét: Ta cũng có thể đánh giá S bằng cách đưa về tìm giá trị nhỏ nhất của hàm số f a 600 2  2a
trên khoảng a;  . a Trang24
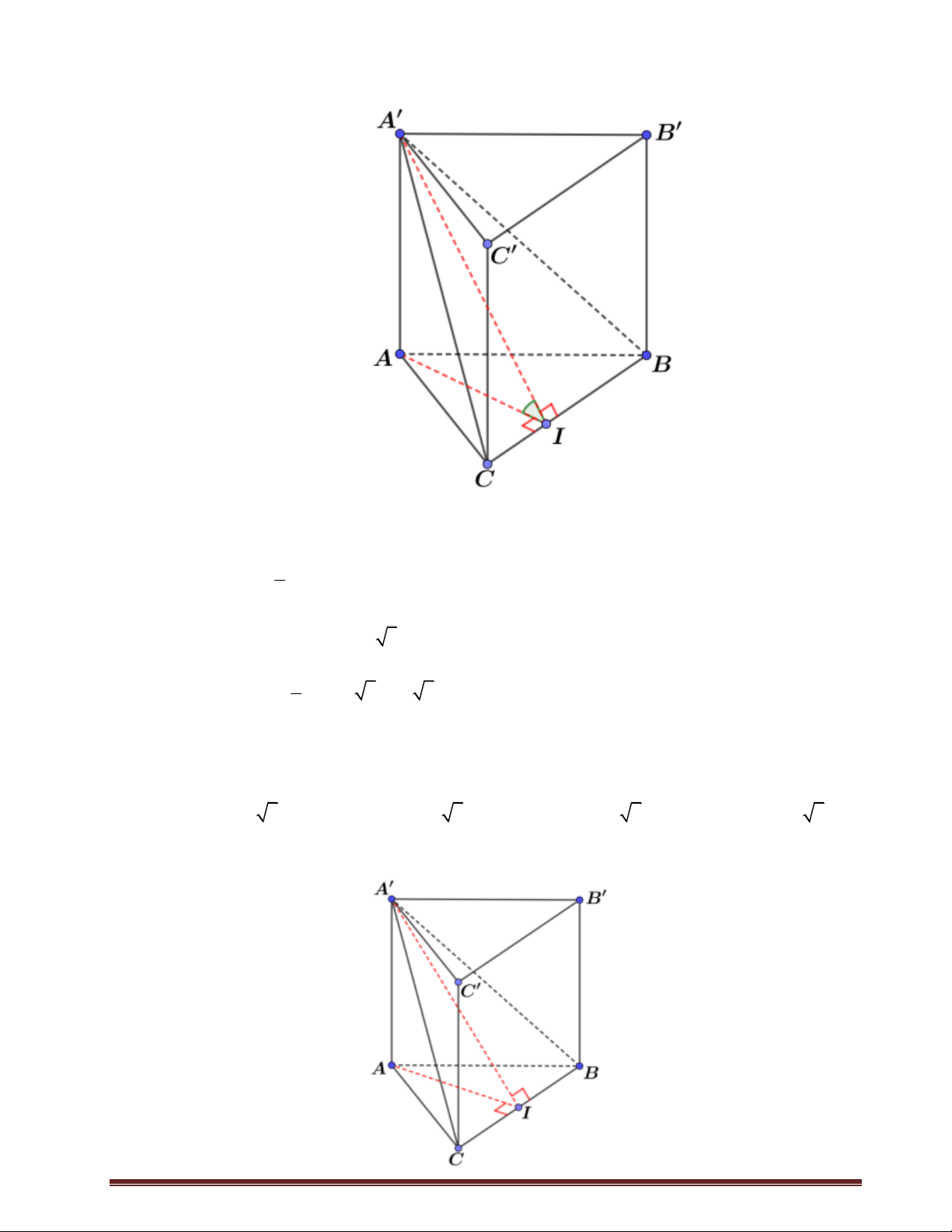
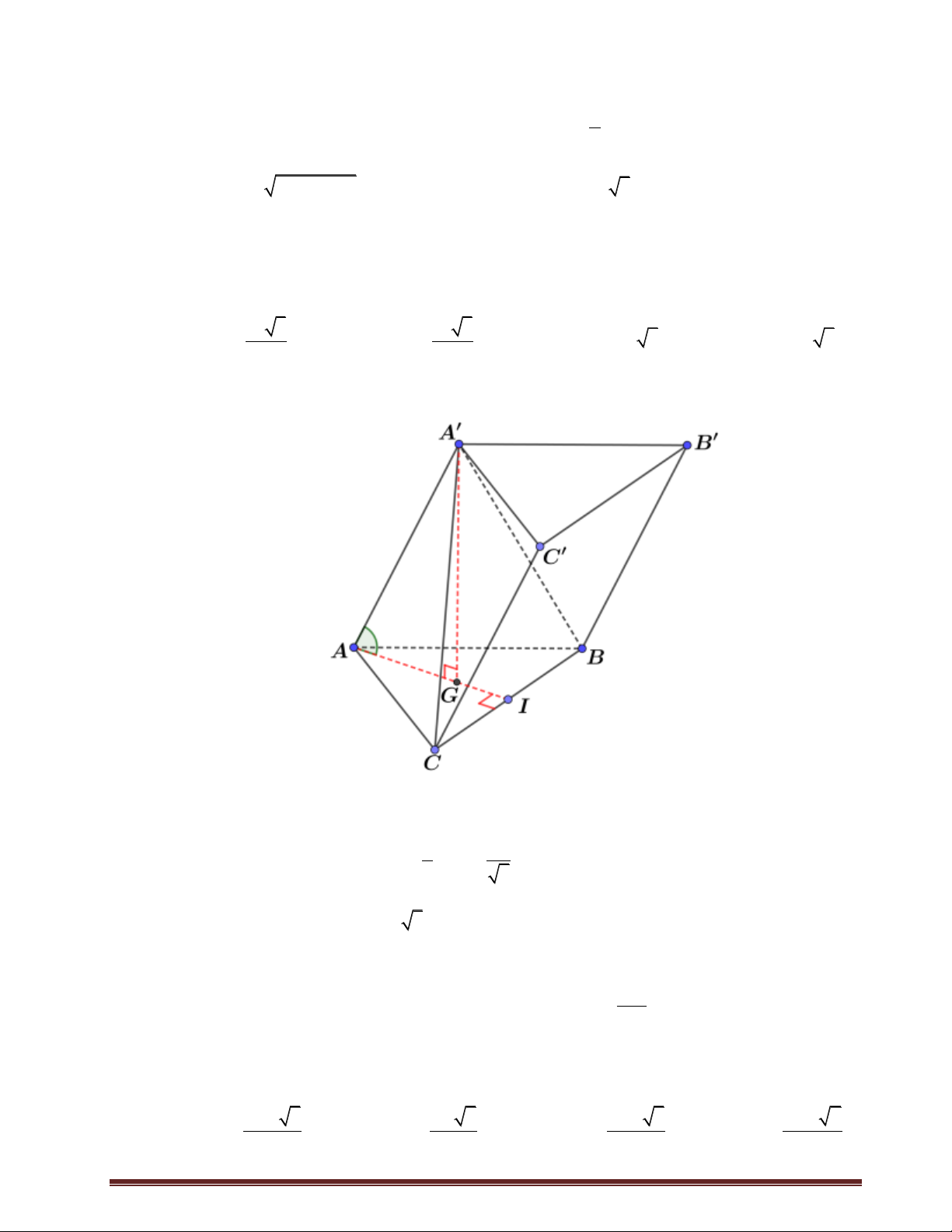
Câu 31: Cho hình lăng trụ đứng B' AB . C A BC
  có đáy ABC là tam C'
giác vuông BA BC a , cạnh
bên AA  a 2 , M là trung điểm của A'
BC (hình vẽ). Khoảng
cách giữa hai đường thẳng AM và B C  là: a 2 a 2 A. . M 2 C B a 3 B. . a 3 A a 5 C. . 5 a 7 D. . 7 Lời giải Chọn D Cách 1
+) Gọi N là trung điểm BB , suy ra B' C' B C
  AMN . Do đó d B C
 , AM   d B C  , AMN  A' N
d C, AMN   K
d B, AMN  M +) Kẻ B C
BH AM , BK NK . Chứng
minh được BK   AMN  . Vậy nên H d B C
 , AM   d B, AMN   BK A +) Tính 2 2 BA BM a 5 BH   2 2 BA BM 5 2 2 BH BN a 7 BK   . 2 2 BH BN 7 Trang25 Cách 2:
+) Tính được thể tích khối tứ diện 1 . B AMN : V
BABM BN . 6
+) Tính diện tích tam giác AMN là S . V +) d B C  , AM   3
d B, AMN   . S
Nhận xét: Học sinh dễ nhầm lẫn trong việc dựng BK nên điều chỉnh lại phương án nhiễu như sau: +) Nhầm lẫn 1: a
BK MN , khi đó phương án nhiễu là 2 , khoanh B 3 +) Nhầm lẫn 2: a
BK AN , khi đó phương án nhiễu là 6 , khoanh. C. 3
Câu 32: Cho hình trụ T  có C và (C )
 là hai đường tròn đáy nội tiếp hai mặt đối diện của một
hình lập phương.Biết rằng trong tam giác cong tạo bởi đường tròn C và hình vuông
ngoại tiếp của C có một hình chữ nhật kích thước a2a (như hình vẽ dưới đây).Tính
thể tích V của khối trụ T theo a. 3 100 a 3 250 a A. . B. 3 250 a . C. . D. 3 100 a . 3 3 Lời giải: ChọnB. Trang26 A N B H C K M D O
Gọi M và N lần lượt là trung điểm CD và AB
Dễ thấy ACMN và BDMN là hình vuông cạnh bằng a . Do đó  45o MAC  .Tương tự  45o OAC  nên ba điểm ,
A M , O thẳng hàng.
Kéo dài CD cắt OH tại K
Đặt AH OH OD x Do 2 2 2
OD OK DK mà DK BH x  2a , HK AC a → 2 2 2
x  (x  2a)  (x a) .Giải phương trình được x  5a (loại nghiệm x a ) Vậy 2 2 V
 .r .h  .5 .(2.5)  250 . tru
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  3a , AD a , tam giác
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a diện tích
S của mặt cầu ngoại tiếp hình chóp S.ABCD . A. 2 S  5 a . B. 2 S  10 a . C. 2 S  4 a . D. 2 S  2 a . Lời giải: Chọn A. S I G B C M O A D Trang27 AC 2 2 AB AD AB
Theo bài ra ta có GT AB a 3 , R    3 a , R d 2 2 b 3 a 3. 3   a . 3 a 3 a 2 2  2
Vậy bán kính mặt cầu ngoại tiếp là: R a a  5  . 4 2 2  
Vậy diện tích mặt cầu ngoại tiếp hình chóp a 5 S.ABCD là: 2 S  4. .   5 a .   2  
Bài toán tổng quát:
Cách xác định bán kính mặt cầu ngoại tiếp hình chóp có mặt bên vuông góc với mặt đáy:
Gọi h là chiều cao hình chóp và R , R là bán kính đường tròn ngoại tiếp mặt đáy và d b
mặt bên vuông góc với đáy; GT là độ dài giao tuyến của mặt đáy và mặt bên vuông góc 2
với đáy. Khi đó bán kính mặt cầu ngoại tiếp là: GT 2 2 R R R  . d b 4
Trong đó mặt bên vuông góc với đáy thường là tam giác vuông, cân hoặc đều. Lời giải S I G B C O M A D
Để xác định tâm mặt cầu ngoại tiếp thì ta dựng trục của mặt đáy và mặt bên vuông góc
với đáy, giao của hai trục chính là tâm mặt cầu ngoại tiếp.
Giả sử hình chóp có đỉnh S , giao tuyến của mặt đáy và mặt bên vuông góc với đáy là
AB với M là trung điểm AB ; G , O là tâm đường tròn ngoại tiếp mặt bên vuông góc
với đáy và mặt đáy; I là tâm mặt cầu. Khi đó, bán kính mặt cầu ngoại tiếp hình chóp là: 2 AB R SI 2 2  SG GI 2 2  R MJ 2 2 2
R JA MA 2 2  R R  . b b b d 4 Trang28
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB đều và nằm
trong mặt phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp. Lời giải S B C O A D
Giao tuyến của mặt bên và đáy là AC a
GT AB a , bán kính đáy R  2  , bán d 2 2 kính mặt bên AB 3 a R  3  . b 3 3 2
Vậy bán kính mặt cầu ngoại tiếp hình chóp là: GT 2 2 R R R d b 4 2 2 2
a 3   a 2  aa 21        .  3   2  4     6 2  
Vậy diện tích mặt cầu ngoại tiếp hình chóp là: a 21 7 2 2
S  4 R  4. .    a .   6 3  
Câu 35: Cho hình chóp S.ABC có đáy là tam giác ABC là tam giác đều cạnh a , tam giác SAB
cân tại S và có cạnh SA  2a . Tính thể tích mặt cầu ngoại tiếp hình chóp. Lời giải Trang29 S A C B
Giao tuyến của mặt đáy và mặt bên là: AB a GT AB  3
a , bán kính đáy R  3  , d 3 3
bán kính đường tròn ngoại tiếp tam giác S . A S . B AB 4 15 SAB là: R   a . b 4S 15 SAB 2
Khi đó bán kính mặt cầu ngoại tiếp hình chóp là: GT 2 2 R R R d b 4 2 2 2
 4 15   a 3  aa 115  a       .  15   3  4     10
Vậy thể tích mặt cầu ngoại tiếp hình chóp là: 3 4 4  a 115  23 15 3 V   R     3  a . 3   3 10   150 Câu 36: Cho ,
x y là các số thực dương. Xét các hình chóp SABC có SA x, BC y , các cạnh còn lại đều bằng 1 .Khi ,
x y thay đổi , thể tích khối chóp SABC có giá trị lớn nhất là 2 3 1 3 2 A. . B. . C. . D. 27 8 8 12 Lời giải: Trang30 S N A B M C
Gọi M và N lần lượt là trung điểm của BC.
Do AM BC , SM BC → BC  SAM  .
Chứng minh tương tự: SA   BCN  .
Do đó MN là đoạn vuông góc chung của SA và BC và SA BC . 2 x 2 2 x y 2 2 2
AM AB BM  1 → 2 2 2
MN AM AN  1  . 4 4 4 2 2 x y → MN  1 . 4 1 2 2 1 x y Do đó:V  . SA BC.d ( ; SA BC).sin( , SA BC) = . . x . y 1 .sin 90o 6 6 4 2 2 1 x y Hay V  . . x . y 1 6 4 2 2 1 x y 1 xy Do 2 2
x y  2xy →V  . . x . y 1  . x . y 1 6 4 6 2 xy Đặt 1  t → 2
xy  2(1 t ) 2 1 1 1 Xét hàm số: 2 3 f (t) 
.2.(1 t ).t t t 6 3 3 Trang31 1  3  2 3 2 f (
t)   t  3 0 → t  → f    3   3 3 27   2 3 4 Vậy V
.Dấu bằng xảy ra khi: x y  . min 27 3
Câu 37: Cho tứ diện đều ABCD cạnh 2a . Tính thể tích của khối bát diện đều có các đỉnh là trung
điểm các cạnh của tứ diện ABCD . 3 2a 2 3 a 2 3 a 2 A. . B. . C. 3 a 2 . D. . 9 3 6 Lời giải Chọn B
Gọi M , N, P,Q, H , K lần lượt là trung điểm của các cạnh AB, AC,CD, BD, BC, AD
Gọi V là thể tích của khối bát diện đều HMNPQK Ta có: V  2V K .MNPQ
Lại có K.MNPQ là hình chóp tứ giác đều có tất cả các cạnh bằng a 3 Vậy a 2 V  2V  . K .MNPQ 3
Câu 38: Người ta sản xuất một chiếc cốc thủy tinh có dạng hình trụ không có nắp với đáy cốc và
thành cốc làm bằng thủy tinh đặc, phần đáy cốc dày đều 1,5cm và thành xung quanh cốc
dày đều 0, 2cm (hình vẽ). Biết rằng chiều cao của chiếc cốc là 15cm và khi ta đổ 180ml
nước vào thì đầy cốc. Nếu giá thủy tính thành phẩm được tính là 500 đ/cm3 thì giá tiền
thủy tính để sản xuất chiếc cốc đó gần nhất với số nào sau đây? Trang32 A. 31nghìn đồng. B. 40 nghìn đồng. C. 25 nghìn đồng. D. 20 nghìn đồng. Lời giải Chọn A.
Gọi R , h và V theo thứ tự là bán kính, đường cao và thể tích của hình trụ phần vỏ cốc 1 1 1
và R , h , V là bán kính, chiều cao và thể tích của hình trụ phần lòng cốc. 2 2 2 V 40
Ta có R R  0, 2 ; h h 1,5  15  h  13, 5 ; V  180 2  R   nên 1 2 1 2 2 2 2 h 3 2 40 R   0,2 . 1 3 2  
thể tích của phần thủy tinh là 40 2
V V   R h 180   
 0,2 .15 180  60,71 1 2 1 1   3   3 cm .
Vậy giá thành để sản xuất một chiếc cốc là 60,71.500  30355 nghìn đồng.
Câu 39: Một khúc gỗ có dạng khối nón có bán kính đáy r  30 cm , chiều cao h  120 cm . Anh thợ
mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể
tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V . Trang33 A.V    3 0,16 m  . B.V    3 0, 024 m . C.V    3 0,36 m  . D. V    3 0, 016 m . Lời giải Chọn D. O B h J x I R r A
Gọi x là chiều cao của khúc gỗ hình khối trụ, R khúc gỗ hình khối trụ cần tìm. O là
đỉnh của hình nón, I là tâm của đáy hình nón, J là tâm của đáy hình trụ và khác I . OA
là một đường sinh của hình nón, B là điểm chung của OA với khối trụ. Ta có R h x
r h x   R  . r h h 2 thể tích khối trụ là r V   . x R   . x h x 2  2 2 h 2 r 2
Xét hàm số V x   . x h x 0  x h 2   , . h 2 r h
Ta cóV  x   h x
h  3x  0  x x h 2    hay . h 3 Bảng biến thiên h x 0 h 3 V  x  0  0 2 4 r h V x 27 0 0
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là h x   40 cm ; 3 2 4 r h 2 4. .30 .120 V      3 16000 cm     3 0, 016 m  . max 27 27
Câu 40: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a 3 , AD a , SA vuông
góc với mặt phẳng đáy và mặt phẳng SBC tạo với mặt đáy một góc 60. Tính thể tích
V của khối cầu ngoại tiếp khối chóp S.ABCD . Trang34 3 13 13 a 3 5 5 a 3 13 13 a 3 5 10 a A. V  . B. V  . C. V  . D. V  6 6 24 3 . Lời giải Chọn B S I A D O B C Ta có
SA   ABCD  SA BC BC SAB 
BC SB SBC  90
BC AB gt  
B thuộc mặt cầu đường kính SC (1).
Tương tự ta cũng chứng minh được CD  SAD 
CD SD SDC  90
D thuộc mặt cầu đường kính SC (2).
SA AC (vì SA   ABCD ) 
SAC  90  A thuộc mặt cầu đường kính SC (3).
Từ (1), (2) và (3) suy ra Mặt cầu đường kính SC là mặt cầu ngoại tiếp hình chóp S.ABCD . Ta có
SBC ABCD  BC
BC  SAB cmt      
SBC   ABCD  ,  SBA  60 .
SAB ABCD  AB   
SAB  SBC   SB   SA A . B tan SBA  .
a tan 60  a 3 .
ABCD là hình vuông cạnh a AC a 2 . 2 2 2 2 SC
SA AC  3a  2a a 5  Bán kính mặt cầu ngoại tiếp hình chóp a 5
S.ABCD là R  . 2 3 4 5 5 a Ta có 3 V   R  . 3 6
Câu 41: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC
sao cho 5SM  2SC , mặt phẳng ( ) qua ,
A M và song song với đường thẳng BD cắt hai cạnh V
SB, SD lần lượt tại hai điểm H , K . Tính tỉ số theo thể tích B.AMHK . VS.ABCD Trang35 1 8 1 6 A. . B. . C. . D. . 5 35 7 35 Lời giải Chọn D.
Ta gọi: E SO AM Dựng Ex BD cắt SB, SD lần lượt tại H , K      AHMK  Gọi SM 4
F là trung điểm của MC   . SF 7 SE SM 4    (vì EM OF ). SO SF 7 SH SK SE 4   
 ( vì HK BD ). SB SD SO 7 V 1  V V
 1  SH SM SM SK  1  4 2 4 2  8 Ta có: S.AHMK S . AHM S .AMK                  . V 2 V V 2    SB SC SC SD  2  7 5 7 5  35 S . ABCD S .ABC S .ADC V BH 3 V 3 8 6 Mà B.AHMK B.AHMK       . V SH 4 V 4 35 35 S.AHMK S .ABCD
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm trên cạnh
SC , mặt phẳng   qua ,
A M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại hai điểm V
H , K . Tính tỉ số theo thể tích B.AMHK . VS.ABCD 1 1 1 1 A. . B. . C. . D. . 5 4 7 6 Lời giải Trang36 Chọn D.
Ta có: E SO AM
Dựng Ex BD cắt SB, SD lần lượt tại H , K      AHMK  . Khi đó ta có: SH SK SE 2  
 (vì E là trọng tâm của SAC ) SB SD SO 3 V 1  V V
 1  SH SM SM SK  1  2 1 1 2  1 Ta có: S.AHMK S .AHM S .AMK                  V 2 V V 2    SB SC SC SD  2  3 2 2 3  3 S . ABCD S . ABC S . ADC V BH 1 V 1 Mà B.AHMK   B. AHMK   V SH 2 V 6 S . AHMK S . ABCD
Câu 43: Cho hình chóp .
S ABCDcó đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC
sao cho SC xSM(x  1) , mặt phẳng   qua A, M và song song với đường thẳng BD V
cắt hai cạnh SB,SD lần lượt tại hai điểm H,K . Tính tỉ số theo thể tích B.AMHK . VS.ABCD 2 x 2 x  1 A. . B. . C. . D. . x 1 xx x  1 x x  1 x x  1 Lời giải Trang37 ChọnD.
Gọi: E SOAM . Dựng Ex BD cắt SB,SD lần lượt tại H,K     AHMK . Gọi SM 2 SE SM 2
F là trung điểm của MC      . SF x  1 SO SF x  1 SE SM 2    ( vì  ). SO SF x EM OF 1 SH SK SE 2     (vì  ). SB SD SO x HK BD 1 V 1  V V
 1  SH SM SM SK  2
Ta có: S.AHMK
S.AHM S.AMK       .   V 2 V V 2 SB SC SC SD x x 1 S.ABCDS.ABC S.ADC       V BH x V x  Mặt khác: 1 1 B.AHMK    B.AHMK  . V SH 2 V x x 1 S.ABCD    S.AHMK SH
Chú ý: Bài toán trên có thể sử dụng kết quả sau đây để tính được tỉ số đơn giản hơn: SB Trang38 Cho hình chóp .
S ABCDcó đáy là hình bình
hành tâm O . Mặt phẳng (P) cắt các cạnh
SA,SB,SC và SD lần lượt tại A', B',C ', D' . Khi đó: SA SC SB SD    SA' SC ' SB' SD'
Áp dụng vào bài toán trên ta được SA SC SB SD SB     2
(do HK BD , định lý SA SM SH SK SH Ta-let).
Câu 44: Cho lăng trụ đứng AB . C A BC
  có đáy là tam giác ABC vuông cân tại A , cạnh
BC a 6 . Góc giữa mặt phẳng  AB 'C  và mặt phẳng  BCC B   bằng 0 60 . Tính thể
tích V của khối lăng trụ AB . C A BC  ? 3 2a 3 3 a 3 3 3a 3 3 3a 3 A. V  . B. V  . C. V  . D.V  . 3 2 4 2 Lời giải Chọn D Cách 1.
+ Gọi M là trung điểm của BC AM  BCC B  
+ Gọi H , K lần lượt là hình chiếu vuông góc của M , B trên B C  + Khi đó B C
   AMH   B C   AH  
ABC BBCAH MH  o , ,  AHM  60 . a 6 AM a 2 + Ta có 2 MH   
HK  2MH a 2 . o tan 60 3 2 + Mặt khác 1 1 1    B B   a 3 . 2 2 2 BK BC B B  3
+ Vậy thể tích của khối lăng trụ 1 3a 3 AB . C A BC
  là V B . B A . B AC  . 2 2 Cách 2. Trang39
+ Gọi chiều cao của hình lăng trụ là h .
+ Đặt hệ trục tọa độ Axyz như hình vẽ. Khi đó A0;0;0 , Ba 3;0;0 , C0;a 3;0,  a a
Ba 3;0;h  3 3 M  ;
; 0  là trung điểm của BC .   2 2     a 3 a 3  
+ Vì AM   BCC B
  và AM   ;
; 0  nên n  1;1;0 là VTPT của   BCC 'B' 2 2   .   
+ Ta có  AC, AB     2 ah 3;0; 3  a      AB'C 1 n
 ;h0; 3a là VTPT của .
+ Theo giả thiết góc giữa  AB C
  và mặt phẳng BCC B   bằng 60       1 h cos 60 cos , n     1 n h 3a 2 2 2 2. h  3a 3
+ Vậy thể tích của khối lăng trụ 3a 3 AB . C A BC   là V  . 2
Câu 45: Khi xây nhà, anh Tiến cần xây một bể đựng nước mưa có thể tích V   3 6 m  dạng hình
hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung
quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 1.000.000đ/m2 và ở nắp 2
để hở một khoảng hình vuông có diện tích bằng
diện tích nắp bể. Tính chi phí thấp 9
nhất mà anh Tiến phải trả (làm tròn đến hàng trăm nghìn)? A. 22000000 đ. B. 20970000 đ. C. 20965000 đ. D. 21000000 đ. Lời giải ChọnB
Gọi chiều rộng của bể là: x(m). (với ĐK: x  0 ). Chiều dài của bể là: 6
3x(m). Từ đó suy ra chiều cao của bể là: (m). 2 3x 2  2  6 6 16x 16
Tổng diện tích của bể là: 2 S  2  .3x  2. .3x  2. .x     . 2 2  9  3x 3x 3 x 2 16x 8 8 Vì x  0 nên ADBĐT Cô si cho 3 số dương ; ; : 3 x x 2 2 16x 8 8 16x 8 8 2 3 3    3 . .  6. . 3 x x 3 x x 3 Trang40 2 3 Suy ra: 3 3 S  6  x  . min 3 2
Vậy chi phí thấp nhất để xây bể là: 1.000.000.S  20970000 đ. min
Câu 46: Cho hình nón  N  có bán kính đáy r  20(c )
m , chiều cao h  60(cm) và một hình trụ T
nội tiếp hình nón N  (hình trụ T  có một đáy thuộc đáy hình nón và một đáy nằm trên
mặt xung quanh của hình nón). Tính thể tích V của hình trụ T  có diện tích xung quanh lớn nhất? 32000 A. V    3 3000 cm . B. V    3 cm . C. V    3 3600 cm . D. 9 V    3 4000 cm . Lời giải ChọnA
(Đề xuất vẽ lại hình)
Gọi chiều cao hình trụ bằng x. 60  x R 60  x Ta có:   R  60 20 3 2
S   Rx   x x     x   xq   2 2 60 900 30 2 2  600 3 3
Dấu “=” xảy ra khi và chỉ khi x  30cm 2
V   R x    3 3000 cm .
Câu 47: Cho hình nón  N  có bán kính đáy r  20(c )
m , chiều cao h  60(cm) và một hình trụ T
nội tiếp hình nón  N  (hình trụ T  có một đáy thuộc đáy hình nón và một đáy nằm trên
mặt xung quanh của hình nón). Tính thể tích V của hình trụ T  có diện tích xung quanh lớn nhất? Trang41 32000 A. V    3 3000 cm . B. V    3 cm . C. V    3 3600 cm . D. 9 V    3 4000 cm . Lời giải ChọnA
Gọi chiều cao hình trụ bằng x. 60  x R 60  x Ta có:   R  60 20 3 2
S   Rx   x x     x   xq   2 2 60 900 30 2 2  600 3 3
Dấu “=” xảy ra khi và chỉ khi x  30cm 2
V   R x    3 3000 cm .
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy
SA a 2 . Gọi B ', D ' là hình chiếu của A lần lượt lên SB, SD . Mặt phẳng  AB ' D ' cắt
SC tại C '. Tính thể tích khối chóp S.AB 'C ' D' là: 3 2a 3 3 2a 2 3 a 2 3 2a 3 A. V . B. V . C.V . D. V  . 9 9 9 3 Lời giải Chọn C S C' D' B' C D A B 2 SB ' SD ' 2a 2 Ta có  
 nên suy ra B'D'/ /BD mà BD  SAC  BD SC . 2 SB SD 3a 3
Do đó B' D'  SC (1)
Ta có BC  SAB  BC AB ' và AB'  SB suy ra AB'  SC (2) Trang42
Từ (1) và (2) suy ra  AB'C ' D'  SC nên ta có AC '  SC 2 SC ' 2a 1   . 2 SC 4a 2 V 2V SB ' SC ' 2 1 1
Ta có SA'B'C'D' SAB 'C '   .  .  . V 2V SB SC 3 2 3 SABCD SABC 3 1 a 2 Mà 2 Va .a 2  . SABCD 3 3 3 3 Vậy 1 a 2 a 2 V  .  .
SAB 'C ' D ' 3 3 9
Tổng quát: Cho hình chóp S.ABCD là hình bình hành. Một mặt phẳng   cắt S ,
A SB, SC, SD tại A ', B ', C ', D ' . Ta có V
1 SA' SB ' SC ' SD '  SA SB SC SD
SA' B 'C ' D '  . . .      V
4 SA SB SC SD SA' SB ' SC ' SD '  SABCD
Câu 49: Với một đĩa phẳng hình tròn bằng thép bán kính R , phải làm một cái phễu bằng cách cắt
đi một hình quạt của đĩa này và gấp phần còn lại thành một hình nón. Gọi độ dài cung
tròn của hình quạt còn lại là x . Tìm x để thể tích khối nón tạo thành nhận giá trị lớn nhất. 2 R 6 2 R 2 2 R 3  R 6 A. x . B. x . C. x . D. x  . 3 3 3 3 Lời giải Chọn A.
Độ dài cung tròn của hình quạt còn lại là x nên chu vi đường tròn đáy của hình nón là x .
Do đó bán kính đường tròn đáy của hình nón là x r  . 2
Hình nón luôn có đường sinh là R . 2 2 2  
Nên đường cao của hình nón là: x x x 2 2 2 2 h R   R   h R    . 2 2  2  4 4 2 2 2
Suy ra thể tích khối nón là: 1 1 x x 1 x 2 2 2 V  . . h S  . R  ..  x R  2 2 2 3 3 4 4 12 4     x 2 2    x x 2     2 R 2 1 x    2 2 x     Tính 2 2 2 V ' 2x R   x  4 8  2 2 12  4 x  2 6  x  2  2 R   2  R   2  4  2  4  Trang43 2 R 6
V '  0  x  (vì x  0 ) 3
Câu 50: Cho lăng trụ tam giác AB . C A BC
  có đáy ABC là tam giác đều cạnh AB  2a 2 . Biết
AC  8a và tạo với mặt đáy một góc 0
45 . thể tích khối đa diện ABCC B   bằng 3 16a 6 3 8a 6 3 16a 3 3 8a 3 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C.
- Gọi H là hình chiếu của C trên mặt đáy. Ta có  o ( AC ,
 (ABC))  C AH  45 2
- Chiều cao của lăng trụ là: 0
h AC .sin 45  8 . a  4a 2. 2 2 2 AB 3 (2a 2) 3
- Diện tích đáy ABC là: 2 S    2 3a ABC 4 4
- thể tích của khối lăng trụ AB . C A BC   là: 2 3 V       . B h 2 3a .4a 2 8 6a ABC.A B C 3 2 2 16a 6
- thể tích khối đa diện ABCC B  là: 3 V     V    .8 6a . ABCC ' B 3 ABCA B C 3 3
Câu 51: Cho tam giác ABC vuông tại A có AB  3a , AC a . Gọi Q là mặt phẳng chứa BC
và vuông góc với mặt phẳng  ABC. Điểm D di động trên Q sao cho tam giác DBC
nhọn và hai mặt phẳng DAB và DAC lần lượt hợp với mặt phẳng  ABC hai góc
phụ nhau. Tính thể tích lớn nhất của khối chóp . D ABC . 3 a 3 3 3a 3 3a 2 3 3a A. . B. . C. . D. . 4 13 10 8 Lời giải ChọnA Theo giả thiết ta có,   tan DNH DH MH tan MDH   2
DH NH.MH . NH DH Đặt MH MH 1
NH x 0  x  3a . Ta có   (do ABC MBH ) MB 3a x 3 2 1    2  1 1 3a x x  3a MH
3a x . Do đó 2 DH
3a xx     3  DH  3 3 3  2  4 2 Dấu a
"  " xảy ra khi 3a x  3 x x  . 2 Trang44 Vậy  a a 3a Va a  khi DH  . D ABC  3 1 1 3 3 . 3 . . . Max 3 2 2 4 2
Câu 52: Cho hình hộp ABC . D A BCD
  có độ dài tất cả các cạnh bằng a và các góc   BA , D DAA , 
AAB đều bằng 60°. Tính thể tích tứ diện ACB D   theo a. 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 24 36 6 12 Lời giải Chọn C.
Theo giả thiết ta có các tam giác ABD, BBC  , DD
C đều cạnh aBD B D    B C   D C   a Mặt khác 2 2 o
AC AB  AD 
AB BC  2A .
B BC.c os120  a 3 Xét hình chóp đều . A B DC
 cạnh bên bằng a 3 , cạnh đáy bằng a ta có 2 a 3 S Sd B DC  4 Gọi 2 2 a 3 a 3
O là trọng tâm tam giác đều B DC
 ta có CO CM  .  3 3 2 3 2  a 3  2a 6 2 2 2 h AO
AC CO  3a       3 3   Trang45 2 3 Vậy 1 1 a 3 2a 6 a 2 VS .h  . .  . AB ' D 'C 3 d 3 4 3 6
Câu 53: Cho hình hộp MN . PQ M NPQ
  có các cạnh đều bằng 2a , với a  0;a  R . Biết  QMN  60 ,   M MQ M M
N 120 . Tính thể tích V của khối hộp MN . PQ M NPQ   theo a . A. 3 V  2.a . B. 3 V  4 2.a . C. 3 V  8.a . D. 3 V  2 2.a . Lời giải Chọn B. N P M M Q P' N' N M' O M' Q' Q .
Do hình chóp M .NQM  có 3 cạnh bên cùng bằng 2a nên chân đường cao của hình chóp
M .NQM  là tâm O của đường tròn ngoại tiếp mặt đáy NQM  . Như thế V       6.V  2S .OM . MNP . Q M N P Q M .NQM NQM
Từ giả thiết ta có MNQ đều, suy ra NQ  2a .
Dùng định lý côsin cho MMN và MMQ  ta tính được. M N   M Q   2a 3 .
Dùng Hêrông cho NQM  ta tính được 2 S    a 11. . NPM  
Từ đó bán kính đường tròn ngoại tiếp  N . Q QM .NM 6a
NQM  là ON   . 4S NQM  11 2a 22
Xét tam giác OMN , ta có 2 2
OM MN ON  . 11 Vậy 2a 22 2 3 V       2.a 11. 4a 2 . MNPQ.M N P Q 11
Câu 54: Cho hình hộp ABC . D A BCD
  có sáu mặt đều là hình thoi cạnh a và góc nhọn của hình thoi bằng 60 .
 Tính thể tích V của khối chóp A.BB D   . D Trang46 3 2a 3 3a 3 a 3 2a A. V  . B. V  . C. V  . D.V  . 18 3 9 6 Lời giải Chọn D
Ta có: AB AD BD a; AA  A B   A D   a
A.ABD là tứ diện đều  Chân đường cao AH trùng với tâm của ABD  2 2 a 3 a 3 2 2  3a 6a
HA HB HD AO  .   2 2 2 2
AH A A  AH a   3 3 2 3 9 9  a 6 A H   . 3 3 3 2a 2aV    ;V A . ABD A BC  . 12 ABC 4 3 2a V       V    V A .BB D D ABC.A B C A ABD 6
Câu 55: Cho hình lăng trụ đứng AB . C A BC
 có đáy ABC là tam giác vuông cân tại , A AB a 2 .
Đường chéo AB của mặt bên ABB A
  tạo với mặt phẳng đáy một góc  và tan  2 .
Tính thể tích của khối trụ ngoại tiếp lăng trụ đã cho theo a. A. 3 4 a . B. 3 2 2 a . C. 3 8 a . D. 3 2 a . Lời giải A' C' Chọn D B'
Khối trụ ngoại tiếp lăng trụ có bán kính đường tròn đáy là BC 2a AH    . a 2 2 α
Ta có:  AB ABC  ',
B' AB   A C a 2 H B Trang47 2 2 3
V Bh   R h   a .a 2. 2  2 a .
Câu 56: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh bên SA
vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD . Biết khoảng cách giữa hai đường thẳng a
BC và SM bằng
3 . Tính thể tích của khối chóp đã cho theo a. 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 2 6 12 Lời giải. Chọn C S H A B M D C N
Ta gọi N là trung điểm của AB , suy ra MN song song với BC
Ta có d (SM , BC)  d (BC, (SMN ))  d (B, (SMN )  d ( , A (SMN ))
Gọi H là hình chiếu của A lên đường thẳng SN
Dễ dàng chứng minh được AH vuông góc với mặt phẳng SMN  Ta có 1 1 1   a 3 a , AH  , AN  2 2 2 AH SA AN 4 2 a 3 1 1 a 3 3 Nên SA  và 2 3 VS . A S  .a a 2 ABCD 3 ABCD 3 2 6 Đáp án C đúng
Câu 57: Hình lăng trụ đứng AB .
C A' B 'C ' có diện tích đáy bằng 4 , diện tích ba mặt bên lần lượt là
9,18 và 10 . thể tích khối lăng trụ AB .
C A' B 'C ' bằng 4 11951 11951 A. 4 11951 . B. . C. 11951 . D. . 2 2 Trang48 Lời giải Chọn A
Gọi a, b, c  0 là ba cạnh của tam giác đáy; h là chiều cao của lăng trụ AB .
C A' B 'C ';
S , S , S là diện tích ba mặt bên. 1 2 3 S S S Ta có: 1 2 3 a  , b  , c h h h
a b c
S S S S
p( p a)( p b)( p c) với 1 2 3 p   2 2h
S S S S S S
S   S S S
S   S S S S  1 2 3 1 2 3 1 1 2 3 2 1 2 3 3 S         2h  2h h  2h h  2h h
S S S S S S  S S S  S S S  1 2 3 3 2 1 1 2 3 1 2 3 S      2h  2h  2h  2h  1 S
S S S
S S S
S S S
S S S 2
 1 2 3 3 2 1 1 2 3 1 2 3 4h 1 h
S S S S S S S S S S S S 1 2 3   3 2 1   1 2 3   1 2 3  4S
Vậy thể tích khối lăng trụ AB .
C A' B 'C ' là 1 V  . h S S.
S S S S S S S S S S S S  4  11951 . 1 2 3 3 2 1 1 2 3 1 2 3 4S
Câu 58: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và khoảng cách từ a
A đến mặt phẳng SBC  bằng
2 . Tính thể tích V của khối chóp đã cho. 2 3 a 3 3a 3 a A. V  . B. 3 V a . C. V  . D. V  . 2 9 3 Hướng dẫn giải Chọn D.
Gọi H AH SB . (1) Trang49
Mà BC  SAB, do BC A ,
B BC SASA   ABCD , AH  SAB .
Nên BC AH . (2) a 2
(1), (2) suy ra AH  SBC   H nên AH  . 2 1 1 1 1 1 1 1
Tam giác vuông SAB có   nên    hay SA a . 2 2 2 AH AB SA 2 2 2 2 SA AH AB a 1 1 3 V S .SA a . 3 ABCD 3
Câu 59: Xét khối chóp S.ABC có đáy là tam giác vuông cân tại A , SA vuông góc với đáy,
khoảng cách từ A đến mặt phẳng SBC bằng 3. Gọi  là góc giữa hai mặt phẳng
SBC và ABC. Tính cos khi thể tích khối chóp S.ABC nhỏ nhất. 1 3 2 2 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 2 3 Lờigiải ChọnB
Đặt AB AC xx  0, SA y y  0. Gọi I là trung điểm của cạnh BC và H là
hình chiếu vuông góc của A lên SI   1 .
Ta có: BC AI , BC SA BC  SAI   BC AH , BC SI 2.
Từ (1) và (2) suy ra d  ,
A SBC  AH  3.
Góc giữa SBC và  ABC bằng góc giữa SI và 
AI SIA  . 1 1 1 1 1 1 1 1 1 1 1 Ta có:           3.3 2 2 2 2 2 2 2 2 2 4 2 9 AH AI SA AB AC SA x x y x y 1 1 2   3  x y  81 3. 4 2 27 x y Mặt khác 1 1 27 3 2 V S . A A . B AC x y  6 6 2 27 3 V
dấu “=” xẩy ra khi và chỉ khi x y  3 3. min 2 BC AB 2 3 3. 2 3 6 Suy ra: AI     . 2 2 2 2 Trang50 S . A AI 9 2
Mà SI.AH S . A AI SI   . AH 2 Vậy AI 3 cos   . SI 3
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a . Mặt bên SAB và
SAD cùng vuông góc với đáy, góc giữa hai mặt phẳng SBC và ABCD bằng 30.
Tính tỉ số 3V biết V là thể tích khối chóp S.ABCD . 3 a 3 3 8 3 A. . B. . C. 3 . D. . 12 2 3 Lời giải Chọn D.
Dễ thấy SA   ABCD và góc giữa hai mặt phẳng SBC và  ABCD bằng 30 và là 2a 3 3 1 2a 3 8a 3 góc 
SBA . Nên SA A . B tan 30  , suy ra 2 V  . .4a  3 3 3 9 3V 8 3   . 3 a 3
Câu 61: Một hộp bóng bàn hình trụ có bán kính R , chứa được 5 quả bóng sao cho các quả bóng
tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Quả trên cùng và dưới
cùng tiếp xúc với hai nắp hộp. Tính phần thể tích của khối trụ mà thể tích của các quả
bóng bàn không chiếm chổ. 3 10 R 3 3 R 3 10 R A. B. C. 0. D.  2 4 3 Lời giải Chọn D
+) Chiểu cao của hộp bóng bàn là h 10R .
Suy ra thể tích của hộp bóng bàn là 2 3 V
  R h 10 R . ( H )
+) thể tích của 5 quả bóng bàn là 4 20 3 3 V  5.  R   R . ( B ) 3 3
Suy ra thể tích cần tính là 20 10 3 3 3 V V
V  10 R   R   R . ( H ) ( B) 3 3
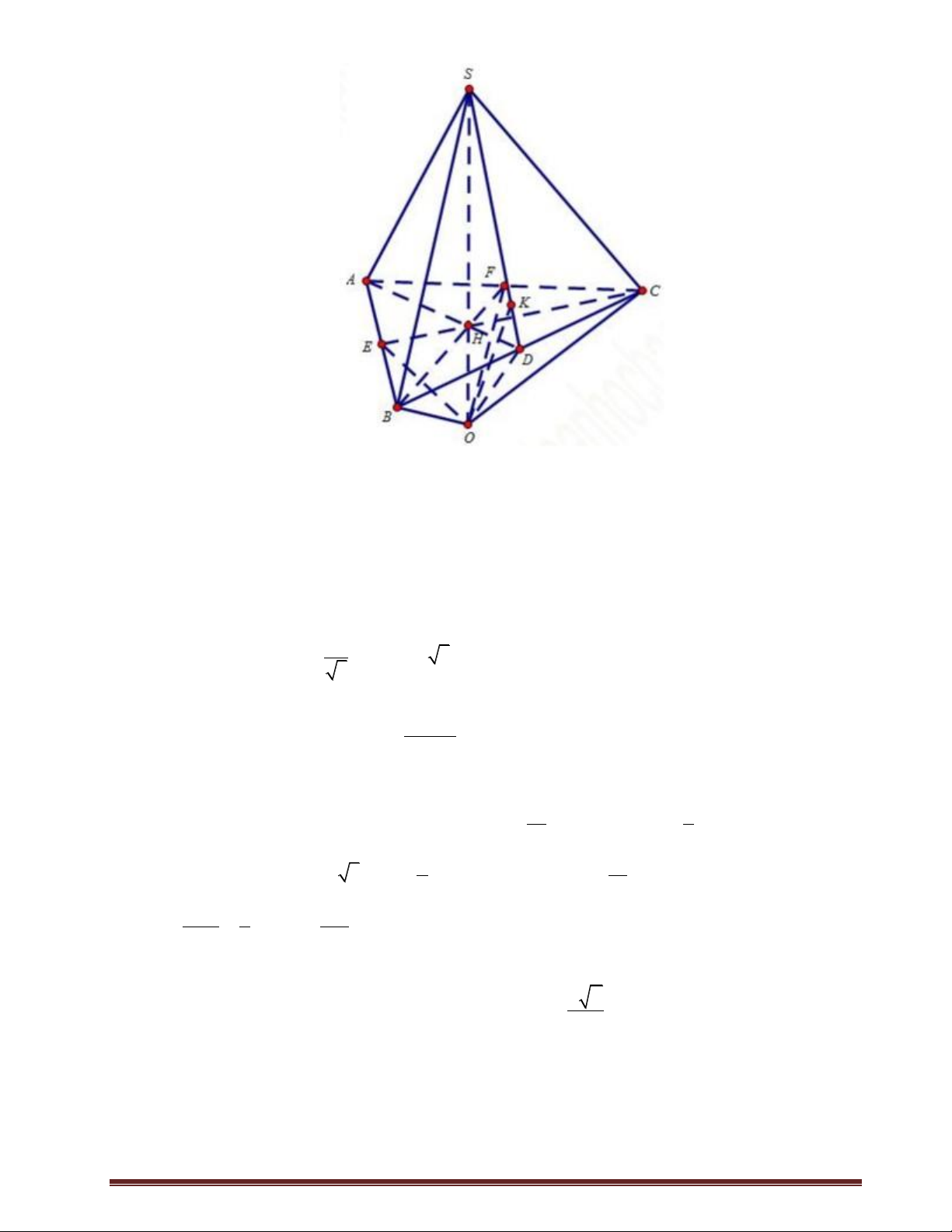
Câu 47: [2H1-3] Cho hình đa diện SABCD như hình vẽ: Trang51 S D C B A
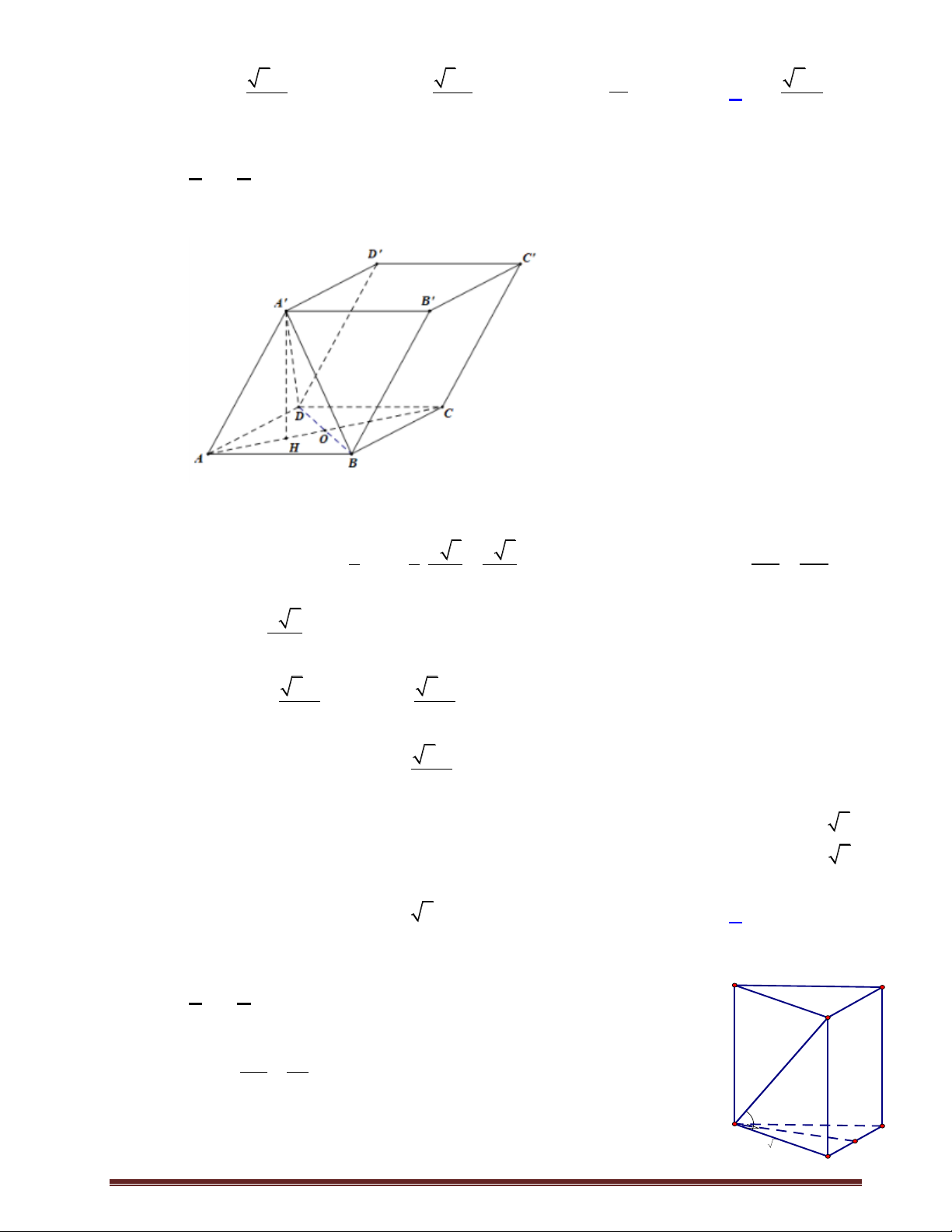
Biết SA  4, SB  2, SC  3, SD  1 và 0 A  SB BSC CSD   D
SA  60 . thể tích
khối đa diện SABCD là 3 2 A. 3 2. B.C. 4 2. D. 2. 2 Lời giải Chọn A S D C' O A' B' B C A Trên ,
SA SB, SC lần lượt lấy các điểm A ', B ', C ' sao cho SA'  SB'  SC '  SD 1. Khi đó 1
S.A' B 'C ' D' là một chóp tứ giác đều có tất cả các cạnh bằng 1, có thể tích V  . 0 3 2  1  V  4.3.2 V 12V  2 2 S.ABC  0  0  2   1  V  4.3 V  6V  2 S.ACD  0  0  2  Vậy VVV  3 2 SABCD S.ABC S .ACD
Câu 62: Cho hình trụ và hình vuông ABCD có cạnh a . Hai đỉnh liên tiếp ,
A B nằm trên đường
tròn đáy thứ nhất và hai đỉnh còn lại nằm trên đường tròn đáy thứ hai, mặt phẳng
( ABCD) tạo với đáy một góc 45. Khi đó thể tích khối trụ là 3  a 2 3 3 a 2 3  a 2 3 3 a 2 A. . B. . C. . D. . 8 8 16 16 Trang52 Lời giải Chọn D
Gọi O,O lần lượt là tâm của đường tròn hai đáy.
Gọi M , N lần lượt là hình chiếu của O và O lên các đoạn AB , CD; dễ dàng thấy
M , N lần lượt là trung điểm của AB, CD . Gọi I là giao của O O  và MN .
Có OM AB AB   IOM  nên góc giữa  ABCD và đáy là góc  OMI . Vậy tam giác IM a
IMO vuông cân đỉnh O nên OI OM  2  . 2 4 a 2 2 2 a 2a 2 3a Suy ra O O   và 2 2 2
OA AM OM    . 2 4 16 8 2 3
thể tích khối trụ bằng a 2 3a 3 2a 2 V O . O  .OA  . .  . 2 8 16
Câu 63: Cho khối cầu tâm O bán kính là 6cm . Mặt phẳng  P cách O một khoảng là x cắt khối
cầu theo một hình tròn C . Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn C .
Biết khối nón có thể tích lớn nhất, giá trị của x bằng A. 2cm . B. 3cm . C. 4cm . D. 0cm . Lời giải Chọn A.
Điều kiện 0  x  6.
-Bán kính của hình nón là: 2 2 2
r  6  x  36  x
-thể tích khối nón lớn nhất với trường hợp chiều h  6  x 1  
-Khi đó thể tích khối nón là: 2 V   r h   2
36  x  x  6  . f (x) 3 3 3 x  6  (L) +Ta có 2 f '(x)  3
x 12x  36 và f '(x)  0    x  2. x  2 (N)
Vậy x  2cm thì khối nón có thể tích lớn nhất.
Câu 64: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a . Gọi E , F lần lượt là trung
điểm của các cạnh SB , SC . Biết mặt phẳng  AEF  vuông góc với mặt phẳng SBC .
thể tích khối chóp S.ABC bằng 3 a 5 3 a 5 3 a 3 3 a 6 A. . B. . C. . D. . 24 8 24 12 Trang53 Hướng dẫn giải Chọn A.
Gọi H là trọng tâm của ABC
, điểm M là trung điểm của BC và I SM EF .
Suy ra I là trung điểm của SM và AI EF (do AEF cân tại A ). 
AEF   SBC 
Ta có EF   AEF   SBC   AI  SBC  AI SM . AI EF  Do đó a S
AM cân tại A . Từ đó 3 SA AM  . 2 2 a 3 a 15 Ta có AH AM  ; 2 2 SH SA AH  . 3 3 6 2 2 Diện tích AB 3 a 3 S   . ABC  4 4 3 thể tích 1 a 5 VS .SH  . S.ABC  3 ABC 24
Câu 65: Cho khối cầu  S  có tâm I , bán kính R không đổi. Một khối trụ thay đổi có chiều cao h
và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất. OO R 2 R 3 2R 3 A. h .
B. h R 2 . C. . D. . 2 3 3 Hướng dẫn giải Chọn D. 2
Bán kính đáy của hình trụ là h 2 r R  . 4 Trang54 2 3    
Do đó thể tích của khối trụ là h h 2 2 2
V   r h    R
 h    
R h .  4   4 
Xét hàm số f h 3 h 2  
R h với h0;2R . 4 3h R
Ta có f h 2 2  
R , f h 2 3  0  h  . 4 3 Bảng biến thiên 2R 3 h 0  3 V   0  V V max
Từ bảng biến thiên suy ra thể tích của khối trụ lớn nhất khi 2R 3 h  . 3
Câu 66: Một khúc gỗ dạng nón có bán kính đáy bằng r  30cm , chiều cao h 120cm . Bác thợ
mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể
tích lớn nhất của khúc gỗ sau khi chế tác. Tính V . A.   3 0,16 m  . B.   3 0,36 m . C.   3 0, 024 m  . D.   3 0, 016 m  . Lời giải. Chọn D. Trang55 h h' x O B A
Giả sử khối trụ có bán kính đáy và chiều cao lần lượt là x , h' 0  x  30;0  h' 120 . h ' 30  x Ta có 
h' 1204x . 120 30 thể tích khối trụ 2 V   x h ' 2
  x 120  4x 2 3
 120 x  4 x , 0  x  30 . V  x 2
 240 x 12 x . x
V  x  0 0   . x  20
Lập bảng biến thiên ta thấy hàm số đạt giá trị lớn nhất tại x  20 .
Vậy thể tích lớn nhất của khối trụ là V    3 cm     3 16000 0, 016 m .
Câu 67: Cho tứ diện đều cạnh a và điểm I nằm trong tứ diện. Tính tổng khoảng cách từ I đến các mặt của tứ diện. 6a 3a 6a A. a 6 . B. . C. . D. . 9 2 3 Lời giải Chọn D Trang56
Gọi V là thể tích tứ diện đều ABCD và gọi h , h , h , h lần lượt là khoảng cách từ I 1 2 3 4
đến các mặt BCD ,  ACD , ABD , ABC . Đặt V V , V V V V , V V . 1 IBCD 2 IACD 3 IABD 4 IABC
Ta có V V V V V . 1 2 3 4 1 3V V h .S 1  h  1 1 3 BCD 1 SBCD Tương tự 3V 3V 3V 2 h  , 3 h  , 4 h  . 2 S 3 S 4 S ACD ABD ABC Vậy 3V 3V 3V 3V 1 2 3 4
h h h h     . 1 2 3 4 S S S S BCD ACD ABD ABC 2 Lại có tứ diện a 3
ABCD là tứ diện đều nên SSSSBCD ACD ABD ABC 4 3 a 2
3V V V V 3. 1 2 3 4  3V a a
Suy ra h h h h   12  2  6  . 1 2 3 4 2 a 3 2 a 3 2 a 3 3 3 4 4 4
Cách trắc nghiệm: Chọn đặc biệt I A . Khi đó tổng khoảng cách từ I đến các mặt của
tứ diện bằng khoảng cách từ a
A đến mp  BCD và bằng 6 . 3 Trang57
Câu 68: Cho hình hộp chữ nhật ABC . D A BCD
  có tổng diện tích của tất cả các mặt là 36, độ dài
đường chéo ACbằng 6 . Hỏi thể tích của khối hộp lớn nhất là bao nhiêu? A. 8 . B. 8 2 . C. 16 2 . D. 24 3 . Lời giải Chọn B.
Gọi a , b , c là kích thước các mặt của hình hộp chữ nhật.
Không mất tính tổng quát giả sử 0  a b c .
ab ac bc 18 Theo đề ta có: 
a b c  6 2 2 2 2
a b c  36
Từ đó suy ra b c  6 2  a và 0  a  2 2 .
ab ac bc 18  bc
a b c 2 18
a  6 2a 18 .
thể tích khối hộp là V abc a 2
a  6 2a 18.
Xét hàm f a 3 2
a  6 2a 18a với 0  a  2 2 .  a f a 2
 3a 12 2a 18 ; f a 2
 0  3a 12 2a 18  2 0   . a  3 2 Bảng biến thiên:
Vậy thể tích lớn nhất của khối hộp là 8 2 .
Câu 69: Một cốc nước có dạng hình trụ đựng nước có chiều cao 12cm, đường kính đáy 4cm ,
lượng nước trong cốc cao 8cm . Thả vào cốc nước 4 viên bi có cùng đường kính 2cm .
Hỏi nước dâng cao cách mép cốc bao nhiêu xăng - ti – mét? ( làm tròn sau dấu phẩy hai
chữ số thập phân, bỏ qua độ dày của cốc). A. 2, 67cm . B. 2, 75cm . C. 2, 25cm . D. 2, 33cm . Lời giải Chọn A. Trang58  thể tích của 4 16 4 viên bi là: 3 4.  r   3 cm  . 3 3
Gọi h là chiều cao nước dâng lên. Khi đó thể tích của 4 viên bi đúng bằng thể tích nước  dâng lên. Do đó ta có 16 4 2
 .2 .h h  cm . 3 3
Vậy nước dâng cao cách mép cốc là: 4 8 12  8    2,67cm . 3 3
Câu 70: Cho hình trụ có đáy là hai đường tròn tâm O và O' , bán kính đáy bằng a , chiều cao bằng
2a . Trên đường tròn tâm O lấy điểm A , trên đường tròn tâm O' lấy điểm B sao cho
AB  7a . thể tích của khối tứ diện OO' AB bằng: 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 12 6 3 2 Lời giải Chọn B A' O' H D B A O
Kẻ đường sinh AA', gọi D là điểm đối xứng với A' qua tâm O' và H là hình chiếu
vuông góc của B trên A' D . Trang59
BH A'D 1 Ta có 
BH   AOO' A' nên VS .BH BH OO' OO ' AB OO ' 3 A
Trong tam giác vuông A ' AB có 2 2 A' B
AB AA'  3a .
Trong tam giác vuông A' BD có 2 2 BD
A' D A' B a . Do đó suy ra a
tam giác BO ' D đều nên 3 BH  . 2 3 Vậy 1 1 1 3a VS .BH  . O . A OO '.BH  . OO ' AB OO ' 3 A 3 2 6 3
Câu 71: Cho hình thoi ABCD có cạnh bằng 5 , AC
BD . Gọi E, F , G, H lần lượt là trung 4
điểm các cạnh AB, BC,CD, .
DA Gọi M , N , I , K lần lượt là trung điểm các cạnh EF , FG, GH , HE.
Tính thể tích V của vật thể tròn xoay khi quay tứ giác MNIK quanh trục HG . A. 9 . B. 18. C. 24. D. 30. Lời giải Chọn B.
Gọi O là tâm hình thoi ABCD ta tính được OA  3, OD  4cm .
Gọi V là thể tích của khối nón cụt tạo bởi IMNG quay quanh HG . V có chiều cao là 1 1 2 , bán kính đáy là 3 r  và R  3. 2 2 1  3 3    21 2  V  .2   .3 3      . 1 3  2  2   2 
Gọi V là thể tích của khối nón tạo bởi NGI quay quanh HG .V có chiều cao là 2 và 2 2 bán kính đáy là 3 . 2 3  V  . 2 2
thể tích cần tìm V  2.(V V ) 18. 1 2
Câu 72: Cho hình thang ABCD có  
A B  90 , AB BC a , AD  2a . Tính thể tích khối tròn
xoay sinh ra khi hình thang ABCD quay quanh CD . 3 7 a 3 7 2 a 3 7 2 a 3 7 a A. . B. . C. . D. . 12 6 12 6 Trang60 Lời giải Chọn B. BAH C B A D
Khối nón đỉnh D , trục CD có CD a 2 , bán kính đáy CA a 2 3 
Nên khối nón có thể tích 1 2 2 a 2 V C . D .CA  . 1 3 3 Khối nón cụt có trục a 2 a 2 CH
, hai đáy có bán kính CA a 2 và HB  nên thể 2 2  tích khối nón cụt là 1 a V
CH..CA HB C . A HB 3 7 2 2 2  2 3 12 3  Khối nón đỉnh 1 2 a
C , trục CH có thể tích 2
V CH..HB  3 3 12 3 
Vậy thể tích khối tròn xoay cần tính là: 7 2 a
V V V V  . 1 2 3 6
Câu 73: Cho hình thang ABCD vuông tại A và B có AB a , AD  3a và BC x với
0  x  3a . Gọi V , V lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình 1 2 V 7
thang ABCD (kể cả các điểm trong) quanh đường thẳng BC và AD . Tìm x để 1  . V 5 2 3a 7a A. x  . B. x  .
C. x  2a .
D. x a . 4 5 Lời giải Chọn B. 1 2 V   
a 2a x , 1    3  2 V 7     2 V   
a a x .Theo đề ta có 1  1 2
 5 2a x  7 a x x a . 2        3  V 5  3   3  2 Trang61
Câu 74: Cho tứ diện ABCD có AB AC BD CD  1. Khi thể tích khối tứ diện ABCD lớn
nhất thì khoảng cách giữa hai đường thẳng AD, BC bằng 1 2 1 1 A. . B. . C. . D. . 2 3 3 3 Lời giải Chọn C.
Gọi M là trung điểm của BC , Vì DBC, A
BC cân  BC  (ADM ) , Kẻ
MN AD MN là đoạn vuông góc chung của AD, BC , đặt AD x, BC y 2 2 x yMN  1  . 4 4 2 2 1 1 x y 2 2 2 x y x y VA . D B . C MN xy 1   ( )( ) 1  . ABCD 6 6 4 4 3 2 2 4 4 2 2 Áp dụng BĐT côsi: 2 3 x y x y 2 3 V  , dấu bằng xảy ra khi   1   x y  27 2 2 4 4 3 . Vậy 3 MN  . 3
Câu 75: Cho tứ diện ABCD có AB x thay đổi, tất cả các cạnh còn lại bằng a .Tính khoảng cách
giữa hai đường thẳng AB và CD trong trường hợp thể tích tứ diện ABCD lớn nhất. a 3 a 6 a 3 a 6 A. . B. . C. . . D. . 3 4 4 3 Lời giải Chọn B Trang62
Gọi M là trung điểm của BC , Vì DBC, ADC đều  DC  (ABM ) , Kẻ
MN AB MN là đoạn vuông góc chung của AD, BC , Dựng a
AH BM AH  3
(BDC) , ta có AH AM  . 2 a 3 V
lớn nhất khi AH lớn nhất  AH AM  . ABCD 2 Khi đó AM .MB a 6 A
MB vuông tại M d(AB,CD)  MN   . 2 2  4 AM MB
Câu 76: Cho hình chóp S.ABC có SA =SB = SC = 2, đáy ABC là tam giác vuông tại A, AB = 1.
Tìm thể tích lớn nhất của khối chóp S.ABC. 5 5 2 4 A. . B. . C. . D. 8 4 3 3 Lời giải Chọn A 2 
Gọi H là trung điểm của BC ta có BC x 1
SH   ABC  và AC = x thì AH   . 2 2 2 15  x 2 2 SH SA AH  . 2 1 1 2 2 x 15  x 5 2 VS SH x 15  x   . SABC 3 ABC 12 2.12 8 Dấu bằng xảy ra khi 30 2 2
x  15  x x . 2
Câu 77: Cho hình chữ nhật S.ABCD có ABCD là hình chữ nhật với AD = 4a, các cạnh bên bằng
nhau bằng 6a. Tìm thể tích lớn nhất của khối chóp S.ABCD ? 3 130a 3 125a 3 128a 3 250a A. . B. C. . D. 3 3 3 3 Lời giải Chọn C
Gọi O là tâm của đáy ta có SO   ABCD . x a 2 Đặt AB = x ta được x SO   a  2 2 2 4 6  2  32a  . 4 4 Trang63 Suy ra : 1 1 x 2 VS . O S  4ax 2 2 2 2 32a
ax 128a x SABCD 3 ABCD 3 4 3 2 2 2 3 2
x 128a x 128aa. 3 2 3
Dấu bằng xảy ra khi : 2
x  128  x x  8a .
Câu 78: Cho hình chóp S.ABCD có thể tích bằng V , đáy ABCD là hình vuông. Cạnh bên
SA   ABCD và SC 0
hợp với đáy góc 30 . Mặt phẳng P qua A vuông góc với SC cắt
SB, SC, SD lần lượt tại E, F, K . Tính thể tích khối chóp S.AEFK theo V . V 2V 3V V A. . B. . C. . D. . 10 5 10 5 Lời giải Chọn A. SF 1 SE SK Có  2 ;  2 ;  SC 4 SB 5 SD 5 V 1 V SAEFK   V  . V 10 SAEFK 10 SABCD
Câu 79: Xét tứ diện ABCD có các cạnh AB BC CD DA 1 và AC , BD thay đổi. Giá trị lớn
nhất của thể tích tứ diện ABCD bằng. 2 3 4 3 2 3 4 3 A. . B. . C. . D. 27 27 9 9 Lời giải Chọn A. BD y 1 Đặt   V AC. .
BD d AC, BDsin  AC, BD . AC x 6 Trang64 BD AH
H là trung điểm của BC  
BD AC  sin  AC;BD 1. BD CH 2 2  Từ x y
H kẻ HK AC d AC; BD  HK , K là trung điểm của AC . HK  1 4 . 2 2 1 x y 1 xy V xy 1  xy 1  M . 6 4 6 2 Đặt xy 2 t  1
 0  xy  2  2t . 2 1     M   1 1 1 1 2 1 2 2 3 2
1 t t   3 t t  3  t t          . 3 3 3   27 27  27 3  27 27 Dấu “=” xảy ra 2 3  x y  . 3
Câu 80: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  3, AD  4 và các cạnh bên
của hình chóp tạo với mặt đáy một góc 60. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho. 250 3 A. V   125 3 . B. V   500 3 . C. V   50 3 . D. V   . 3 6 27 27 Lời giải Chọn C. S M I B A H C D
Gọi H là hình chiếu của S lên  ABCD
Ta có cạnh bên của hình chóp tạo với mặt đáy một góc 60, nghĩa là: Trang65    
SAH SBH SCH SDH  60
Từ đó suy ra: HA HB HC HD hay H là tâm của hình chữ nhật ABCD hay
H AC BD Có 2 2
AC BD  3  4  5 . 5 5 3 AH Suy ra: SH  tan 60 .   5 và SA   .2  5 . 2 2 cos 60 2
Gọi M là trung điểm của SA. Trong mặt phẳng SAH  , dựng đường thẳng đi qua M và
vuông góc với SA và cắt SH tại I .
Khi đó điểm I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD . 5 5. SM SI SM .SA 5 3 Có: 2 SMI SHA    R SI    . SH SA SH 5 3 3 2 3   Vậy 4 4 5 3 500 3 3 V   R       .   3 3 3 27  
Câu 81: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB a . Gọi I là trung
điểm AC . Hình chiếu vuông góc của S lên mặt phẳng  ABC là điểm H thỏa  
BI  3.IH . Góc giữa hai mặt phẳng SAB và SBC  bằng 0
60 . thể tích của khối chóp S.ABC là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 9 6 18 3 Lời giải Chọn A Trang66 z y K H AS I C B x Cách 1
- Gọi K là hình chiếu của I trên SB . Ta có
AC BH , SB AC  (SBH ) ,
SB IK , AC SB  ( AKC)   
((SAD), (SBD))  (K , A KC) . - Trường hợp 1:  0 AKC  60 a 6 a 2
Tam giác AKC là tam giác đều cạnh a 2 nên KI   BI  , vô lý. 2 2 - Trường hợp 2:  0 AKC  120 AK a 6 a a 3 AKI có 0 tan 60   KI  4 2 2 , BH BI  , 2 2 BK BI IK KI 6 3 3 3 SH BH  2a BKI BHS    suy ra SH  . KI BK 3 3 Vậy 1 a V S .SH  . 3 ABC 9 Cách 2
Chọn hệ trục tọa độ Bxyz như hình vẽ, đặt SH h. Ta có  a 2 a 2   a 2 a 2    A   C   B  2a 2 ; ; 0 , ; ; 0 , 0; 0; 0 , S  0; ; h  .       2 2 2 2 3          ah 2 ah 2 2a  B , A BS    ; ;   .     2 2 3   Trang67   
Ta chọn vectơ pháp tuyến của  h 2 h 2 2
SAB là n   ; ;   . 1   2 2 3      ah 2 ah 2 2a
BC, BS   ;  ; .     2 2 3     
Ta chọn vectơ pháp tuyến của  h 2 h 2 2
SBC  là n   ;  ;  . 2   2 2 3     | n .n | 1 2a 3 1 a Suy ra 1 2     h  . Vậy V S .SH  . ABC | n | . | n | 2 3 3 9 1 2
Câu 82: Cho hình trụ có hai đáy là hai hình tròn tâm O , O , bán kính đáy bằng chiều cao và bằng
a , trên đường tròn đáy tâm O lấy điểm A , trên đường tròn đáy tâm O lấy điểm B sao
cho AB  2a . thể tích tứ diện OO AB là 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 24 6 12 3 Lời giải ChọnC.
Hạ AA vuông góc với mặt phẳng đáy O , AO .
Xét tam giác vuông AAB ta có 2 2 A B
  AB AA  a 3 .
Gọi M đối xứng với A qua O . Hạ đường cao BH xuống O M  . Dễ dàng nhận thấy 1 1 1 a 3    BH  . 2 2 2 BH BABM 2 1 3 1 a 3 a 3 Ta có V   1  2    VV   .BH .S   . .a . OO AB B.OO A B. 2 OO AA 6 OAA O 6 2 12
Câu 83: Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại A , AB  2a, AC  3a . Mặt phẳng  A B
C hợp với mặt phẳng  A BC
  một góc 60. Tính thể tích khối lăng trụ đã cho. 3 3a 39 3 9a 39 3 18a 39 3 6a 39 A. . B. . C. . D. . 26 26 13 13 Lời giải Chọn C Trang68
A ABC  AB C    Ta có B C  //BC
  ABC  AB C
   Ad //BC//B C   B C
    AB C  ; BC    A BC
Dựng AH B C
   AH Ad
Dựng AK BC A K   A d
Góc mặt phẳng  A B
C với mặt phẳng  A BC  là   KA H
  KAH  60 2 2 A B   .A C   6 13 Ta có A H    a 2 2 A B    A C   13 6 39 Ta có 0
BB  HK  tan 60 .A H   a 13 Vậy 1 1 6 39 18 39 3 V          BB .S A . B A . C BB 2 . a 3a a a ABC.A B C ABC 2 2 13 13
Câu 84: Cho tứ diện ABCD có AB CD  6cm, khoảng cách giữa AB và CD bằng 12cm,
góc giữa hai đường thẳng AB và CD bằng 0
30 . Tính thể tích khối tứ diện A.  3 36 cm  . B.  3 25 cm  . C. 3 60cm . D.  3 32 cm  . Lời giải Chọn A
Lấy D ' sao cho DCBD' là hình bình hành Ta có d C ,
D AB  d C ,
D AD ' B  d  ,
D AD ' B 12 1 VVVV
d D, AD ' B .S ABCD . A BCD . A DBD ' D. AD ' B    AD ' 3 B Với 1 1 1 S  . AB BD '.S  .6.6.  9 AD ' B AD ' 2 B 2 2 Do đó: 1 V  .12.9  36 cm ABCD  3 3
Câu 85: Cho khối lăng trụ tam giác AB . C ’ A ’ B ’
C mà mặt bên AB ’ B ’
A có diện tích bằng 4. Khoảng
cách giữa cạnh CC’ và  AB ’ B ’
A  bằng 7. thể tích khối lăng trụ là A. 10. B. 12. C.14. D. 16. Lời giải Trang69 Chọn C Dựng khối hộp 1 ABC . D ’ A ’ B ’ C ’ D ta có: V     V     ABC. A B C ABCD. 2 A B C D Xem khối hộp ABC . D ’ A ’ B ’ C ’
D là khối lăng trụ có hai đáy là AB ’ B ’ A và DC ’ C ’ D . Vậy V      S  .h ABCD. A B C D ABB A Trong đó: h d  D C D C  , ABB A
   d CC ,ABB A    7 1 và S       4 V    .4.7 14 . ABB A ABC. A B C 2
Câu 86: Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông, AB BC a . Biết
rằng góc giữa hai mặt phẳng (ACC )  và (AB C
 ) bằng 60 (tham khảo hình vẽ bên). thể
tích của khối chóp B .ACC A   bằng 3 a 3 a 3 a 3 3a A. . B. . C. . D. . 3 6 2 3 Lời giải Chọn A.
Ta có  ACC  AB C
   AC. Gọi G là trung điểm của A C
  , H là hình chiếu của G lên AC .
Ta có GH  ( ACC A
 ) ,GH AC Ta có B G    ACC A    B G
  AC suy ra BH AC.
Vậy góc giữa  AB C
  và  ACC A   là góc  GHB  60. 1 a 2 a Ta có V         S
 .B G , B G   6 , GH B . G  cot 60 . B . ACC A 3 ACC A 2 6 a 6 GH AA  6 x   x 3    x a GCAC 2 2 a 2 x  2a 2 2  3 x 2a 2 3  1 a 2 a V      . a a 2. . B . ACC A 3 2 3
Câu 87: Một hộp bóng bàn hình trụ có bán kính R , chứa được 5 quả bóng sao cho các quả bóng
tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Quả trên cùng và dưới Trang70
cùng tiếp xúc với hai nắp hộp. Tính phần thể tích của khối trụ mà thể tích của các quả
bóng bàn không chiếm chổ. 3 10 R 3 3 R 3 10 R A. B. C. 0. D.  2 4 3 Lời giải Chọn D
+) Chiểu cao của hộp bóng bàn là h 10R .
Suy ra thể tích của hộp bóng bàn là 2 3 V
  R h 10 R . ( H )
+) thể tích của 5 quả bóng bàn là 4 20 3 3 V  5.  R   R . ( B ) 3 3
Suy ra thể tích cần tính là 20 10 3 3 3 V V
V  10 R   R   R . ( H ) ( B) 3 3
Câu 88: Cho hình đa diện SABCD như hình vẽ: S D C B A
Biết SA  4, SB  2, SC  3, SD  1 và 0 A  SB BSC CSD   D
SA  60 . thể tích
khối đa diện SABCD là 3 2 A. 3 2. B.C. 4 2. D. 2. 2 Lời giải Chọn A Trang71 S D C' O A' B' B C A Trên ,
SA SB, SC lần lượt lấy các điểm A ', B ', C ' sao cho SA'  SB'  SC '  SD  . Khi 1 đó 1
S.A' B 'C ' D' là một chóp tứ giác đều có tất cả các cạnh bằng 1, có thể tích V  . 0 3 2  1  V  4.3.2 V 12V  2 2 S.ABC  0  0  2   1  V  4.3 V  6V  2 S.ACD  0  0  2  Vậy VVV  3 2 SABCD S.ABC S .ACD
Câu 89: Cho hình chóp S.ABC có AB  3a , AC  3 3a , BC  6a . Hình chiếu của S lên mặt
phẳng  ABC là điểm H thỏa mãn   
AHB BHC CHA  120 . Biết rằng tổng diện tích
của các mặt cầu ngoại tiếp hình chóp S.AHB , S.BHC , S.CHA bằng 2 288 a . thể tích
của khối chóp S.ABC là A. 3 9 3a . B. 3 6 3a . C. 3 3 3a . D. 3 12 3a . Lời giải Chọn D. Vì 2 2 2
BC AB AC nên tam giác ABC vuông tại A .
Gọi r , r , r lần lượt là bán kính đường tròn ngoại tiếp tam giác AHB , BHC , CHA và 1 2 3
R , R , R lần lượt là bán kính mặt cầu ngoại tiếp các hình chóp S.AHB , S.BHC , 1 2 3 S.CHA . AB AB 3a Ta có  2r r    a 3 .  1 1  sin AHB 2sin AHB 2sin120 Tương tự BC 6a AC 3a 3 r    2a 3 ; r    3a . 2  3 2sin BHC 2sin120  2sin CHA 2sin120
Gọi J là trung điểm của SH . Đặt SH  2x . Trang72 Khi đó 2 2 2 2 2
R SJ r x  3a ; 2 2 2 2 2
R SJ r x 12a ; 2 2 2 2 2
R SJ r x  9a . 1 1 2 2 3 3 Theo giả thiết S  4  2 2 2
R R R  2  288a 1 2 3 2 2 2 2 2
 3x  24a  72a x  16a x  4a . thể tích của khối chóp S.ABC là 1 1 1 1 3 V S .SH  . . . AB AC.SH  .3 .3 a 3 .8 a a  12a 3 . 3 ABC 3 2 6
Câu 90: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu của S lên mặt
phẳng  ABC là điểm H thỏa mãn  AHB  150 ,  BHC  120 , 
CHA  90. Biết rằng
tổng diện tích của các mặt cầu ngoại tiếp hình chóp S.AHB , S.BHC , S.CHA bằng 31 2
a . thể tích của khối chóp S.ABC là 3 3 a 3 a 3 a 3 a A. . B. . C. . D. . 12 2 3 6 Lời giải Chọn D.
Gọi r , r , r lần lượt là bán kính đường tròn ngoại tiếp tam giác AHB , BHC , CHA và 1 2 3
R , R , R lần lượt là bán kính mặt cầu ngoại tiếp các hình chóp S.AHB , S.BHC , 1 2 3 S.CHA . AB AB a Ta có  2r r    a .  1 1  sin AHB 2 sin AHB 2 sin150 Tương tự BC a a 3 AC a a r    ; r    . 2  3 2sin BHC 2sin120 3  2 sin CHA 2 sin 90 2
Gọi J là trung điểm của SH . Đặt SH  2x . 2 2 Khi đó a a 2 2 2 2 2
R SJ r x a ; 2 2 2 2
R SJ r x  ; 2 2 2 2
R SJ r x  . 1 1 2 2 3 3 3 4 Theo giả thiết 19 31 S  4  31 2 2 2
R R R  2   a 2 2 2  3x a a 1 2 3 3 12 12 2 a a 3 2  x   x  . 3 3 2 3
thể tích của khối chóp 1 1 a 3 2a 3 a
S.ABC là V S .SH  . .  . 3 ABC 3 4 3 6 Trang73
Câu 91: Cho hình chóp S.ABCD , đáy ABCD là hình vuông có độ dài cạnh bằng 2a , SAB là tam
giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD. Gọi H , E lần
lượt là trung điểm của AB, BC và G là trọng tâm S
CD. Biết khoảng cách từ điểm H đến mặt phẳng  3a 2 SED bằng
. Tính thể tích của khối chóp .
G AHED theo a . 4 Lời giải
Gọi F là giao điểm của HC và ED , dựng HK SF .
Vì ABCD là hình vuông  HC ED
Mặt khác ta có SH ED vì SH   ABCD ( S
AB là tam giác cân tại S và nằm trong
mặt phẳng vuông góc với mặt phẳng  ABCD).
Vậy ED  SHC  ED HK mà HK SF vậy HK  SED .  3a 2
HK là khoảng cách từ H tới SED  HK  . 4
Xét tam giác vuông HBC Theo pitago ta có : 2 2 2 2 2
HC BC BH HC
BC BH a 5 Xét CFE và CBH Có :  C chung  
CFE CBH  90 Trang74  CF CE CF a 2a a CFE CBH      CF  3  HF  . CB CH 2a a 5 5 5
Gọi I là trung điểm CD
Trong mặt phẳng SHI  dựng GP / /SH GP   AHED vì ( SH   ABCD )
Xét tam giác vuông SHF theo hệ thức tam giác vuông ta có : 1 1 1  
HS a 3 . 2 2 2 HK HS HF IG GP a
Vì G là trọng tâm tam giác SCD  1 3    GP  . IS SH 3 3 2 2 a 5a a Xét chóp . G AHED có : 2 2 SSSS  4a   a  3 , GP AHED ABCD HBE ECD 2 2 3 2 3 1 1 a 3 5a 5 3aV  .G . P S  . .  . G.AHED 3 AHED 3 3 2 18
Câu 92: Cho hình chóp S.ABCD , đáy ABCD là hình vuông có độ dài cạnh bằng a , SAB là tam
giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD. Gọi H , E lần
lượt là trung điểm của AB, BC và G là trọng tâm S
CD. Biết thể tích của khối chóp 3 5 3a . G AHED là
. Tính khoảng cách từ điểm H đến mặt phẳng SEDtheo a . 144 Lời giải
Gọi F là giao điểm của HC và ED , dựng HK SF .
Vì ABCD là hình vuông  HC ED Trang75
Mặt khác ta có SH ED vì SH   ABCD( S
AB là tam giác cân tại S và nằm trong
mặt phẳng vuông góc với mặt phẳng  ABCD).
Vậy ED  SHC  ED HK mà HK SF vậy HK  SED .
HK là khoảng cách từ H tới SED đặt HK x.
Xét tam giác vuông HBC a 5 Theo pitago ta có : 2 2 2 2 2
HC BC BH HC BC BH  2 Xét CFE và CBH Có :  C chung ,  
CFE CBH  90  a     CF CE CF   a 3a CFE  2 CBH      CF   HF  . CB CH aa 5  5 2 5   2   2 2 2 a a 5a Xét chóp . G AHED có : 2 SSSSa    AHED ABCD HBE ECD 8 4 8 2 3 1 1 5a 5 3a a 3 V  .G . P S  .G . P   GP  . G.AHED 3 AHED 3 8 144 6
Gọi I là trung điểm CD
Trong mặt phẳng SHI  dựng GP / /SH GP   AHED vì ( SH   ABCD ) IG GP a
Vì G là trọng tâm tam giác S  1 3 CD     SH  . IS SH 3 2
Xét tam giác vuông SHF theo hệ thức tam giác vuông ta có : 1 1 1 1 1 1 3a 2       HK  . 2 2 2 2 2 2 HK HS HF x     8 a 3 3a 2     2 5    
Câu 93: Cho hình chóp S.ABCD , đáy ABCD là hình vuông có độ dài cạnh bằng a , SAB là tam
giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD. Gọi H , E lần
lượt là trung điểm của AB, BC và G là trọng tâm S
CD. Biết góc của HC và mặt phẳng
SEDbằng 45. Tính thể tích của khối chóp .
G AHED theo a . Lời giải Trang76
Gọi F là giao điểm của HC và ED , dựng HK SF .
Vì ABCD là hình vuông  HC ED
Mặt khác ta có SH ED vì SH   ABCD( S
AB là tam giác cân tại S và nằm trong
mặt phẳng vuông góc với mặt phẳng  ABCD).
Vậy ED  SHC  ED HK mà HK SF vậy HK  SED . 
HFK là góc của HC với SED 
HFK  45  S
HF vuông cân tại H
Xét tam giác vuông HBC a 5 Theo pitago ta có : 2 2 2 2 2
HC BC BH HC BC BH  2 Xét CFE và CBH Có :  C chung ;  
CFE CBH  90  a     CF CE CF   a 3a CFE  2 CBH      CF   HF  . CB CH aa 5  5 2 5   2   3a
SH HF  ( vì S
HF vuông cân tại H ) 2 5 IG GP a
Vì G là trọng tâm tam giác S  1 CD     GP  . IS SH 3 2 5 Trang77 2 2 2 a a 5a a Xét chóp . G AHED có : 2 SSSSa    ; GP AHED ABCD HBE ECD 8 2 8 2 5 2 3 1 1 a 5a 5 5aV  .G . P S  . .  . G.AHED 3 AHED 3 2 5 8 240
Câu 94: Cho Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông
góc với mặt phẳng đáy, SA a 2. Gọi M , N lần lượt là hình chiếu vuông góc của điểm
A trên các cạnh SB, SD (tham khảo hình vẽ bên). Góc giữa mặt phẳng ( AMN ) và
đường thẳng SB bằng A. 0 45 . B. 0 90 . C. 0 120 . D. 0 60 . Lời giải Chọn D. BC AB Ta có 
BC  SAB  BC AM (1) BC SA
Mặt khác theo giả thiết: AM SB (2)
Từ (1),(2)  AM SC .Chứng minh tương tự: AN SC SC  (AMN )
 Góc giữa đường thẳng SB và mặt phẳng (AMN) là 0    90  (S , B SC)
Xét tam giác SBC có SB a 3 , SC  2a , BC a S
BC vuông tại B BC 1 tan BSC     0 BSC  30  0  0   90  (S , B SC)  60 SB 3
Câu 95: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hai mặt phẳng SAB và  3 a
SAD cùng vuông góc với mặt đáy. Biết thể tích khối chóp S.ABCD là . Tính góc  3
giữa đường thẳng SB và mặt phẳng SCD . A. 0   45 . B. 0   60 . C. 0   30 . D. 0   90 . Lời giải Chọn C.
Hai mặt phẳng SAB và SAD cắt nhau theo giao tuyến SA và cùng vuông góc với mặt phẳng  3V
ABCD nên SA   ABCD .Do đó S .ABCD SA   a . SABCD
Tam giác SAD vuông tại A nên 2 2
SD SA AD a 2 Trang78
Ta có CD AD, CD SA CD  SAD  CD SD 2 Vậy diện tích tam giác 1 a 2 SCD là : SS . D CD
.Gọi I là hình chiếu của B lên SCD 2 2 mặt phẳng    3V
SCD khi đó SB SCD  SB SI   , ,
BSI . Mặt khác BI B.SCD SSCD 3V a S .ABCD  2  2S 2 SCD
Tam giác SAB vuông tại A nên 2 2
SB SA AB a 2 . 1
Tam giác SIB vuông tại I nên 
sin BSI BI   0  BSI  30 SB 2 Vậy  SB SCD 0 ,  30 .
Câu 96: Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc. Góc giữa đường thẳng
AC và (OBC) bằng 0
60 , OB = a , OC = a 2 . Gọi M là trung điểm của cạnh OB .
Góc giữa đường thẳng OA với mặt phẳng (ACM ) bằng: 3 1 3 1 A. arcsin . B. arcsin . C. arcsin . D. arcsin . 4 7 7 2 7 2 7 Lời giải Chọn D.
Ta có Góc giữa AC và mp  0 OBC  bằng 60 . 5a 3a Suy ra 0
OA = OC. tan 60 = a 6 , 2 2 AM = OA + OM = , 2 2 CM = OC + OM = 2 2 . 2 a 14 3 1 a 3 2 2 AC =
OC + OA = 2 2a . Suy ra S = . V =
OA.OC.OM = . DACM 2 A.OCM 6 6 3V 3 Suy ra O. d( , O (ACM )) ACM = = a
. Gọi j là góc giữa OA với (ACM ) S 14 DACM d ( , O (ACM )) 1 suy ra sin j = = . OA 2 7 Trang79
Câu 97: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy  ABCD . Gọi H là
trung điểm của AB . Tính côsin của góc giữa SC và SHD . 15 3 a 3 2 A. . B. . C. . D. . 5 5 5 5 Lời giải Chọn A.  
Gọi K là trung điểm AD , I CK CI HD HD . Ta có: 
CI  SHDtại I CI SH
SI là hình chiếu của SC lên SHD và tam giác SIC vuông tại I
SC SHD  SC SI  cos , cos ,  cosCSI DK.DC a a a DI   ; IC  2 2 DC  2 ID  ; SI  2 2 SC CI  6 2 2 DK DC 5 5 5 Vậy SI
cos SC,SHD   cos CSI   15 . SC 5
Câu 98: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB a; BC  2a . SA vuông
góc với AB , SC vuông góc với BC và góc giữa đường thẳng SC và mặt phẳng đáy bằng 0
60 . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC . 3 8 2 a 3 2 a A. . B. . C. 3 2 2 a . D. 2 8 a . 3 3 Lời giải Chọn A.
Cách 1. Gọi D là điểm đối xứng của B qua trung điểm của AC , suy ra ABCD là hình chữ nhật. AB SA Ta có 
AB SD  1 AB ADBC SC
BC SD 2 BC CD
Từ (1) và (2) suy ra SD   ABC .
Suy ra góc giữa đường thẳng SC và mặt phẳng đáy là góc  SCD . Trang80 Từ đó  DC 0
SCD  60 . Xét tam giác SCD vuông tại D ta có SC   2a . cos 60
Do tam giác SBC vuông cân tại C nên SB  2 2a .
Gọi I là trung điểm SB . Suy ra IA IB IS (do S
AB vuông tại A ) và IB IC IS 1 (do S
BC vuông tại C ). Suy ra IA IB IC IS SB . Hay I là tâm mặt cầu ngoại 2
tiếp hình chóp S.ABC . 3 1 1 4 8 2 a Suy ra 2 2 2 3 R SB
a  4a  3a  2a V   R  . Chọn đáp án A. 2 2 3 3
Cách 2. (Tọa độ hóa)
Gắn hệ trục tọa độ Oxyz như hình vẽ. Khi đó B(0; 0; 0) , (
A a; 0; 0) , C(0; 2 ; a 0) , S ( ;
x y; z) , với x, y, z  0 .
( ABC)  (Oxy) : z  0  
Ta có SA  a  ;
x y; z , AB  a;0;0 .     SA AB  .
SA AB  0  a a x  0  x  . a   Ta có SC   ;
x 2a y; z , BC  0; 2a;0    
SC BC SC.BC  0  2a 2a y  0  y  2 . a Suy ra S ( ;
a 2a; z) . 
Đường thẳng SC có véc-tơ chỉ phương là CS   ; a 0; z  . 
Mặt phẳng (ABC) có véc-tơ pháp tuyến là k  0;0;  1 .
Theo đề bài, góc giữa SC và mp (ABC) là 0 60 nên   SC.k 3 z 2 2
sin 60     
z  3a z  3a S ; a 2 ; a 3a 2 2  . SC . k 2 a z
Gọi I là trung điểm SB . Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC . 1 1 Ta có 2 2 2 R SB
a  4a  3a  2a . 2 2 Trang81 3 
Vậy thể tích khối cầu là 4 8 2 a 3 V   R  . 3 3 Câu 99: Cho ,
x y là các số thực dương thay đổi. Xét hình chóp S.ABC có SA x, BC y , các
cạnh còn lại đều bằng 1. Khi thể tích khối chóp S.ABC đạt giá trị lớn nhất thì tích . x y bằng 4 4 3 1 A. . B. . C. 2 3 . D. . 3 3 3 Lời giải Chọn. A. BI SA
Gọi I , H lần lượt là trung điểm của , SA BC . Ta có 
SA  BIC và CI SA VV . S .IBC . A IBC 2 2  Lại có x 4 x 2 2 BI SB SI  1  . 4 2 2 2 4  x y Và 2 2
IH IB BH  . 2 Diện tích tam giác 1 y IBC là 2 2 SIH.BC  4  x y . IBC 2 4 1 x y xy Suy ra VV 2 2  . . 4  x y 2 2  4  x y . S .IBC . A IBC 3 2 4 24
Khi đó thể tích khối chóp xy S.ABC là 2 2 V  2V  4  x y . S . ABC S .IBC 12 2 2 x y 2 2 x y Ta có xy  2 2  V  4  x y . 2 24 t  2 4  t  Đặt 2 2
t  4  x y , t 0; 2. Khi đó V f t  . 24  t
Ta có f t  2 3 4 
và f t  2  0  t  . 24 3 Bảng biến thiên: Trang82 Do đó 2 3 V  2 2
đạt được khi t   x y  . max 27 3 3 Khi đó tích 4 . x y  . 3 Cách 2: xy xy Ta có 2 2 V  2V
4  x y  4  2xy S . ABC S .IBC 12 12
Hướng 1: Khảo sát hàm số như cách 1
Hướng 2 : Sử dụng MTCT thay các phương án vào ta được đáp ánA.
Câu 100: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A,  
AB a, SBA SCA  90 , góc giữa hai mặt phẳng SAB và SAC  bằng 60 . Thể tích của khối chóp đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6 Lời giải Câu 49:Đáp án D
Gọi Hlà hình chiếu của S lên  ABC .
Theo bài ra, ta có HC  ,
CA HB BA ABHC là hình vuông cạnh a.
Gọi O HABC , E là hình chiếu của O lên SA.
Ta dễ dàng chứng minh được EC  , SA EB SA .
Từ đó, ta được: góc giữa SAC và SAB là góc giữa EB và EC . Trang83 Vì  0 CAB  90 nên  0  0
BEC  90  BEC  120 .
Ta dễ dàng chỉ ra được   0
OEB OEC  60 . Đặt A . O SH xa 2 2 2
SH x SA
x  2a OE   . 2 2 SA 2 x  2a OC a 2 xa 2 0 tan 60   :
 3  x a . 2 2 OE 2 2 x  2a 3 Vậy 1 1 1 a 2 VV  . . . a a  . S . ABC S . 2 HBAC 2 3 6 Trang84