100 Câu Trắc Nghiệm Thể Tích Khối Lăng Trụ Theo Từng Mức Độ Có Lời Giải Chi Tiết

100 câu trắc nghiệm thể tích khối lăng trụ theo từng mức độ có lời giải chi tiết, được biên soạn dưới dạng file PDF gồm 54 trang. Tài liệu bao gồm tổng hợp toàn bộ kiến thức theo từng chủ đề khác nhau. Từ đó, giúp các em củng cố lại tri thức của mình, tự tin bước vào kỳ thi tốt hơn. Mời các em cùng tham khảo nhé!

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

54 trang 7 tháng trước

Tác giả:

Profile ha phan
Trang1


I. 
Chú ý:
1. 


:
..V a bc=
Þ




:
3
Va=
 




 tam giác
Bi ton 1: 
V

4
V


4
1
3
V
V
.

. ' ' 'ABC A B C
. 
. ' ' '
. ' ' '
1
3
C A B C
ABC A B C
V
V
.
a





.V Bh
+ B l diện tích đy
+ h l đường cao lăng trụ
S
xq
= Tổng diện tích cc mặt bên
S
tp
= S
xq
+ Diện tích 2 mặt đy
Trang2
Bi ton 2: 
V

5
V


5
2
3
V
V
.

. ' ' 'ABC A B C
. 
''
. ' ' '
2
3
A B ABC
ABC A B C
V
V
.
Bi ton 3: 
. ' ' 'ABC A B C
.  
', ', 'AA BB CC

,,M N P
sao cho
,,
' ' '
AM BN CP
a b c
AA BB CC
thì
.
. ' ' '
3
ABC MNP
ABC A B C
V
abc
V


Bi ton 1:
V

4
V

 
4
1
3
V
V
.
Bi ton 2:
V

4
V

 
4
1
6
V
V
.
Bi ton 3:
V

5
V


5
1
3
V
V
.
Trang3
Bi ton 4: 
. ' ' ' 'ABCD A B C D
.  
', ', ', 'AA BB CC DD


, , ,M Q P N
sao cho
, , ,
' ' ' '
AM BQ CP DN
a b c d
AA BB CC DD
và
a c b d
thì:
.
. ' ' ' '
4 2 2
ABCD MQPN
ABCD A B C D
V
a b c d a c b d
V
Chú ý: 
k

3
k
hay
3
1
2
V
k
V
Trang4



Câu 1.  thi THPT Quc Gia , 102)
Cho kh có di
2
3a
và chiu cao
2a
. Th tích kh ng:
A.
3
a
. B.
3
6a
. C.
3
3a
. D.
3
2a
.

Chn B.

23
. 3 .2 6V B h a a a
.
Câu 2.  thi THPT Quc Gia  3, 104)

12
,VV

1
2
V
V

A.
2
3
. B.
3
. C.
3
2
. D.
1
3
.

Chn D.

B
và
h
.
Ta có
1
1
2
2
1
1
3
3
V Bh
V
V
V Bh

.
Câu 3. 
B

h
là
A.
.V Bh
. B.
4
3
V Bh
. C.
1
3
V Bh
. D.
3V Bh
.



B

h
là:
.V Bh
.
Câu 4. 
B

V
là
A.
3V
h
B
. B.
3
V
h
B
. C.
B
h
V
. D.
V
h
B
.



B

V
là:
V
h
B
.
Trang5
Câu 5. 
V

h
là
A.
3V
B
h
. B.
3h
B
V
. C.
V
B
h
. D.
h
B
V
.



V

h
là:
V
B
h
.
Câu 6. 
B

2h
là
A.
2.V Bh
. B.
.V Bh
. C.
6V Bh
. D.
3V Bh
.



B

2h
là:
.2 2 .V B h Bh
.
Câu 7. 
A.  B.  C.  D. 



B

h
là:
.V Bh
.

2 . .
2
h
V B B h
.
Câu 8. 
B

3V
là
A.
6V
h
B
. B.
3
V
h
B
. C.
V
h
B
. D.
3V
h
B
.

 D

B

3V
là:
3V
h
B
.
Câu 9. 
V

3h
là
A.
3V
B
h
. B.
3h
B
V
. C.
3
V
B
h
. D.
V
B
h
.



V

3h
là:
3
V
B
h
.
Câu 10. 
6

A.
216
. B.
18
. C.
36
. D.
72
.

Trang6


6
là
3
6 216V 
.
Câu 11. 
3;4;5

A.
10
. B.
20
. C.
12
. D.
60
.

 D.
T
3.4.5 60V 
Câu 12. 
A.  B.  C.  D. 



B

h
là:
.V Bh
.

4 .4 16 .V B h Bh
.
Câu 13.  
A. . B. . C. . D. .



Câu 14. 
a

4a


A.
3
16a
B.
3
4a
C.
3
16
3
a
D.
3
4
3
a


23
. .4 4
day
V S h a a a
.
Câu 15. 
2
3a

6a

V

A.
3
32Va
B.
3
2Va
C.
3
2
3
a
V
D.
3
32
4
a
V



23
. 3. 6 3 2V B h a a a
Câu 16. 
6

A.
22
. B.
54 2
. C.
24 3
. D.
8
.
2; 4; 6
16
12
48
8
2.4.6 48.
Trang7



( )
0aa>
.
Þ

3a
.
Theo bài ra ta có:
3 6 2 3aa= Þ =
.

( )
3
2 3 24 3V ==
.
Câu 17. 
V

.ABCD A B C D

3AC a
.
A.
3
Va
B.
3
36
4
a
V
C.
3
33Va
D.
3
1
3
Va



;0xx

' ' 'A B C


'B
ta có:
2 2 2
' ' ' ' ' 'A C A B B C
2 2 2
2x x x
' ' 2A C x

''A AC


'A

2 2 2
' ' ' 'AC A A A C
2 2 2
32a x x
xa





.ABCD A B CD

3
Va
.
Câu 18. 
A.
27 3
.
4
B.
93
.
2
C.
93
.
4
D.
27 3
.
2
.



3
nên
2
3 3 9 3
.
44
S 

3h

9 3 27 3
. .3
44
V S h
.
Trang8
Câu 19. 
5

16


A.
21
. B.
64
. C.
80
. D.
80
3
.



5

5h =
.
Th tích kh là:
. 16.5 80
ABCD
V S h= = =
.
Câu 20. 
a

4a


A.
3
16a
B.
3
4a
C.
3
16
3
a
D.
3
4
3
a


23
. .4 4
day
V S h a a a
.
Câu 21. 
2
3a

6a

V

A.
3
32Va
B.
3
2Va
C.
3
2
3
a
V
D.
3
32
4
a
V



23
. 3. 6 3 2V B h a a a
Trang9



Câu 22. 
6

A.
22
. B.
54 2
. C.
24 3
. D.
8
.



( )
0aa>
.
Þ

3a
.
Theo bài ra ta có:
3 6 2 3aa= Þ =
.

( )
3
2 3 24 3V ==
.
Câu 23. 
V

.ABCD A B C D

3AC a
.
A.
3
Va
B.
3
36
4
a
V
C.
3
33Va
D.
3
1
3
Va



;0xx

' ' 'A B C


'B
ta có:
2 2 2
' ' ' ' ' 'A C A B B C
2 2 2
2x x x
' ' 2A C x

''A AC


'A

2 2 2
' ' ' 'AC A A A C
2 2 2
32a x x
xa
Trang10





.ABCD A B C D

3
Va
.
Câu 24. Th tích ca kh u có tt c các cnh bng
a
.
A.
3
3
12
a
V
B.
3
3
2
a
V
C.
3
3
4
a
V
D.
3
3
6
a
V

Chn C
3
2
3
.
3
4
4
ha
a
V h S
a
S
.
Câu 25. 
A.
27 3
.
4
B.
93
.
2
C.
93
.
4
D.
27 3
.
2
.



3
nên
2
3 3 9 3
.
44
S 

3h

9 3 27 3
. .3
44
V S h
.
Câu 26. ABC. A’B’C’ có
2 , ' 3AB a AA a

ABC. A’B’C’.
A.
3
3a
. B.
3
a
. C.
3
3
4
a
. D.
3
4
a
.


ABC. A’B’C’ 
ABC

'AA ABC
.

'AA ABC

'3h AA a
.

ABC

2AB a
ABC

Trang11
22
2
3 2 3
3
44
ABC
AB a
Sa
.

23
.
. 3. 3 3
S ABC ABC
V h S a a a
.
Câu 27. 
.ABCD A B C D

ACC A


2
22a


.ABCD A B C D
là:
A.
3
3
3
a
. B.
3
a
. C.
3
22a
. D.
3
23a
.

Chn C

x
0x
.
Xét
ABC

B
có:
2 2 2 2
2AC AB BC x x x
Ta có
2
. . 2 2 2 2
ACC A
S AA AC x x a x a

.

3
3
.
2 2 2
ABCD A B C D
V a a

.
Câu 28.    V

A.
3
33Va
. B.
3
22Va
. C.
3
Va
. D.
3
8Va
.


.ABCD A BC D
ACD
2
3a
Trang12

x
.
Ta có
2AC x
,
22
6
2
x
OD OD A A


ACD
là
2
1 1 6 3
. 2.
2 2 2 2
ACD
xx
S OD AC x
.

22
22
3
32
22
xx
a a x a
.

33
22V x a
.
Câu 29.    
V 
A.
3
33Va
. B.
3
22Va
. C.
3
Va
. D.
3
8Va
.



x
.
Ta có
2AC x
,
22
6
2
x
OD OD A A


ACD
là
2
1 1 6 3
. 2.
2 2 2 2
ACD
xx
S OD AC x
.

22
22
3
32
22
xx
a a x a
.

33
22V x a
.
O
D
C
A
A'
B'
C'
D'
B
.ABCD A B C D
ACD
2
3a
O
D
C
A
A'
B'
C'
D'
B
Trang13
Câu 30. 
.ABCD A B C D
có
3AB
,
4AD
,
5AA


A.
20
. B.
60
. C.
30
. D.
16
.

B
Ta có
. 3.4 12
ABCD
S AB AD
.

.
. 5.12 60
ABCD A B C D ABCD
V A A S
.
Câu 31. 
.ABCD A B C D
có
3AB
,
4AD
,
13AC

:
A.
156
. B.
144
. C.
120
. D.
116
.

B
Ta có
. 3.4 12
ABCD
S AB AD
;
2 2 2 2 2 2 2 2
13 3 4 12AA A C AC A C AB BC
.

.
. 12.12 144
ABCD A B C D ABCD
V A A S
.
Câu 32. Cho  
.ABCD A B C D

3,AD
4AB

AB
¢

bên
( )
ABB A
¢¢

5

A.
36V =
. B.
45V =
. C.
18V =
. D.
48V =
.


D'
A'
C
B'
C'
B
A
D
D'
A'
C
B'
C'
B
A
D
Trang14
.
Xét tam giác vuông
AA B
¢¢
có
22
3AA AB A B
¢ ¢ ¢ ¢
= - =

3.4 12
ABCD
S ==

.
12.3 36
ABCD A B C D
V
¢ ¢ ¢ ¢
==
.
Câu 33.  
.ABCD A B C D
¢ ¢ ¢ ¢
có
AB a=
,
2AC a=
 
A AC
¢
là tam

A
:
A.
3
23
3
a
. B.
3
23a
. C.
3
3a
. D.
3
33
2
a
.


Ta có:
2 2 2 2
43AD AC AB a a a= - = - =
Þ
2
. . 3 3
ABCD
S AB AD a a a= = =
.
Tam giác
A AC
¢
vuông cân 
A
nên
2A A AC a
¢
==
.

23
.
. 2 . 3 2 3
ABCD
ABCD A B C D
V A AS a a a
¢ ¢ ¢ ¢
¢
= = =
.
Câu 34. 
.ABCD A B C D
¢ ¢ ¢ ¢
có
3AB a=
,
4AD a=

BB D D
¢¢
là hình
:
A.
3
20a
. B.
3
60a
. C.
3
12a
. D.
3
30a
.


3
5
B'
A'
C'
C
D
A
B
D'
D'
A'
C
B'
C'
B
A
D
Trang15

2
. 3 .4 12
ABCD
S AB AD a a a
.
Ta có
( ) ( )
22
22
3 4 5BD AB AD a a a= + = + =
Do 
BB D D
¢¢
là hình vuông nên có
5BB BD a
¢
==
.

23
.
. 5 .12 60
ABCD
ABCD A B C D
V BB S a a a
¢ ¢ ¢ ¢
¢
= = =
.
Câu 35.   
.ABCD A B C D
¢ ¢ ¢ ¢
có
3AB a=
,
4BC a=
tam giác
A BC
¢
là tam

B
:
A.
3
20a
. B.
3
12 7a
. C.
3
47a
. D.
3
60a
.



2
. 3 .4 12
ABCD
S AB AD a a a
.
Do tam giác
A BC
¢

B
nên có
4A B BC a
¢
==
.
Ta có
( ) ( )
22
22
4 3 7AA A B AB a a a
¢¢
= - = - =

23
.
. 7.12 12 7
ABCD
ABCD A B C D
V AA S a a a
¢ ¢ ¢ ¢
¢
= = =
.
Câu 36. Cho  ch nht
.ABCD A B C D

3,AB
4AD

AC


ABCD
góc
45
:
A.
60
. B.
48
. C.
30
. D.
20
.

A
D'
A'
C
B'
C'
B
A
D
B'
A
B
D'
D
C'
C
A'
Trang16

. 3.4 12
ABCD
S AB AD
.
Ta có
,AA ABCD AC ABCD AC A
45
;
22
5 .tan45 5A C A B B C A A A C
.

.
12.5 60.
AABCD A B C D BCD
V S AA

.
Câu 37. Cho  ch nht
.ABCD A B C D

3,AB
4AD

AB


ABCD
góc
45
:
A.
36
. B.
48
. C.
30
. D.
20
.

A

. 3.4 12
ABCD
S AB AD
.
Ta có
,AA ABCD AB ABCD AB A
45
nên
.tan45 3A A A B
.

.
12.3 36.
AABCD A B C D BCD
V S AA
.
Câu 38. 
.ABCD A B C D
có
3 , 4AB a AD a
. 
AC


()A B BA

0
30

A.
3
6 39a
. B.
3
39a
. C.
3
18 39a
. D.
3
2 39a
.


D'
A'
C
B'
C'
B
A
D
Trang17

2
. 3 .4 12
ABCD
S AB AD a a a
.
Ta có
BC AB
BC B B
()BC ABB A
0
; 30A C ABB A CA B



.tan30 4A B BC a
43A B a
.

22
39A A A B AB a

.

.ABCD A B C D
là
3
.
. 6 39
ABCD A B C D ABCD
V A AS a

.
Câu 39. 
2 2 2
6 ;8 ;12a a a


A.
3
8a
. B.
3
12a
. C.
3
24a
. D.
3
18a



;;x y z

; ; 0x y z
.
  
;;xy yz zx
.
a có:
2 2 2 2 6 3
. . 6 .8 .12 ( ) 576 24xy yz zx a a a xyz a xyz a
.

3
24V xyz a
.
Câu 40. 
V

.ABCD A B C D

AB a
,
2AD a
,
14AC a
.
A.
3
5Va
. B.
3
14
3
a
V
. C.
3
2Va
. D.
3
6Va
.

Chn D
B'
A
B
D'
D
C'
C
A'
Trang18
Ta có:
2 2 2 2
AC AB AD AA

2 2 2
AA AC AB AD

2 2 2
14 4 3AA a a a a
.

.ABCD A B C D
là
3
. . 6V AB AD AA a

.
Câu 41. 
.ABC A B C
¢ ¢ ¢

a
và
2AA a


A.
3
3
2
a
. B.
3
3
6
a
. C.
3
3.a
D.
3
3
3
a
.


Tam giác
ABC

a
nên
2
3
4
ABC
a
S
D
=

.ABC A B C
¢ ¢ ¢

2AA a

23
33
. 2 . .
42
ABC
aa
V AA S a
D
¢
= = =
Câu 42.     
.ABC A B C
có
3BC a
 
ABC
     
B
và
2AC a

V

.ABC A B C
.
A.
3
2Va
. B.
3
2Va
. C.
3
2
3
a
V
. D.
3
62
a
V
.


a
14
2a
a
D'
C'
B'
D
B
C
A
A'
Trang19

ABC

B
và
2
2
22
AC a
AC a BC AC a
.
BB C

2
2 2 2
9 2 2B BB B C BC a a a

.
3
2
1 1 1 2
22
3 3 2 3
ABC
a
V BB S a a
.

.ABC A B C
là
3
2
3
a
V
.
Câu 43.   
.ABC A B C
¢ ¢ ¢

ABC
  
A

AB a=
,
2AC a=
và
3A B a
¢
=

.ABC A B C
¢ ¢ ¢
.
A.
3
22
3
a
. B.
3
5
3
a
. C.
3
5a
. D.
3
22a
.



1
.
2
ABC
S AB AC=
1
. .2
2
aa=
2
a=
.
+ Tam giác
ABA
¢

A
nên có
22
AA A B AB
¢¢
=-
( )
2
2
3aa=-
22a=
.

.
ABC
V S AA
¢
=
2
.2 2aa=
3
22a=
.
a
3a
2a
C'
B'
A
C
B
A'
Trang20
Câu 44. 
.ABCD A B C D
¢ ¢ ¢ ¢

ABCD

AB a=
,
2AD a=
,
5AB a
¢
=
. Tính theo
a

V

A.
3
2Va=
. B.
3
22Va=
. C.
3
10Va=
. D.
3
22
3
a
V =
.


2
. . 2 2
ABCD
S AB AD a a a= = =
.
Trong tam giác
ABB
¢
,
( )
2
2 2 2
52BB AB AB a a a
¢¢
= - = - =
.

23
. 2 . 2 2 2
ABCD
V BB S a a a
¢
= = =
.
Câu 45. 
.ABC A B C

a
và
'2AA a



A.
3
6
2
a
. B.
3
6
4
a
. C.
3
6
6
a
. D.
3
6
12
a
.


Ta có:
2
3
4
ABC
a
S
.
Trang21

23
.
36
. . 2
44
ABC A B C ABC
aa
V S AA a
.
Câu 46. 
.ABC AB C
có
BB a

ABC

B
và
2AC a

V

A.
3
3
a
V
B.
3
2
a
V
C.
3
Va
D.
3
6
a
V


Tam giác
ABC

B
2
AC
AB BC a
. Suy ra:
2
1
2
ABC
Sa
.

3
2
.
1
..
22
ABC A B C ABC
a
V S BB a a
Câu 47. 
. ' ' 'ABC A B C

2a
và
'3AA a



A.
3
63a
. B.
3
33a
. C.
3
2 3 .a
D.
3
3a
.


A'
C'
B'
B
C
A
Trang22

2
(2 ) 3
4
a

'3AA a


2
3
(2 ) 3
.3 3 3
4
a
aa
Câu 48. 
. ' ' 'ABC A B C

a
và
'3AA a


A.
3
4
a
. B.
3
2
a
. C.
3
3
4
a
. D.
3
3
2
a
.


Ta có
2
3
4
ABC
a
S
;
'3AA a
.

3
2
33
3.
44
a
V a a
.
Câu 49.     
.ABC A B C
¢ ¢ ¢
       
B
,
AB a=
và
3A B a
¢
=

.ABC A B C
¢ ¢ ¢
là
A.
3
3
2
a
B.
3
6
a
C.
3
2
a
D.
3
2
2
a


Ta có
22
2AA A B AB a
¢¢
= - =
,
2
2
1
22
ABC
a
S AB==
.
A'
C'
B'
B
C
A
a
3
a
C'
B'
A
B
C
A'
Trang23

3
2
.
2
ABC
a
V AA S
¢
==
.
Câu 50. 
. ' ' 'ABC A B C

a
,
'AB


o
60

. ' ' 'ABC A B C

A.
3
3
2
a
. B.
3
4
a
. C.
3
3
4
a
. D.
3
3
8
a
.



a

2
3
4
ABC
a
S
D
=
.
Vì
( )
( )
( )
o
' ' ' , 60AA ABC A BA A B ABC^ Þ = =
, suy ra:
o
' tan60 3AA AB a==

23
. ' ' '
33
. ' . 3 .
44
ABC A B C ABC
aa
V S AA a
D
= = =
Câu 51.     
. ' ' ' 'ABCD A B C D
      
A
và
D
, có
2 , 2, ' 2AB CD AD CD a AA a
.

A.
3
12a
. B.
3
6a
. C.
3
2a
. D.
3
4a
.

2a
a
2
a
2
C'
B'
D'
C
A
B
D
A'
Trang24


ABCD
là:
ABCD
S
.
2
AB CD AD
2.
2
CD CD AD
3.
2
CD AD
3. 2. 2
2
aa
2
3a
.

.
ABCD
V S AA
2
3 .2aa
3
6a
.
Câu 52. 
.ABCD A B C D

4 , 2 ,AA a AC a BD a
.

V

A.
3
8Va
. B.
3
2Va
. C.
3
8
3
Va
. D.
3
4Va
.


2a
a
2
a
2
C'
B'
D'
C
A
B
D
A'
Trang25

V

3
11
. . . . .2 . .4 4
22
ABCD
V S AA AC BD AA a a a a

.
Câu 53. 
.ABC AB C

2 ; 3 ; 4AA a AB a AC a
và
AB AC
.
A.
3
12a
. B.
3
4a
. C.
3
24a
. D.
3
8a
.


Ta có:
2
11
. 3 .4 6
22
ABC
S AB AC a a a
.

3
.
. 12
ABC A B C ABC
V AA S a

.
Câu 54. 
a

2
3a


A.
3
a
. B.
3
3a
. C.
3
2a
. D.
3
4a
.

Chn B
Trang26

ABB' A'

a
, mt
ABCD

2
3a
.
u cao
h AA' a
, di
2
3
ABCD
B S a
.
Suy ra th tích ca khi h
23
33V a a a
.
Câu 55. 
.ABCD A B C D

; 2 ; 21AB a BC a AC a
.

V

A.
3
4a
. B.
3
16a
. C.
3
8
3
a
. D.
3
8a
.


Xét tam giác vuông
ABC
, ta có:
22
5AC AB BC a
.
Trang27
Xét tam giác vuông
ACC
, ta có:
22
4CC AC AC a

.

.ABCD A B C D
là:
3
.2 .4 8V a a a a
.
Câu 56. 
3a

a

60


A.
3
33
4
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
33
2
a
.



3ha
.

60

22
33
2.
42
aa
S 

3
33
.
2
a
V S h
.
Câu 57. 
.ABCD A B C D
có
, 3 , 5AA a AB a AC a


A.
3
5a
. B.
3
4a
. C.
3
12a
. D.
3
15a
.


Xét
ABC

B
, ta có:
22
22
5 3 4BC AC AB a a a
.
2
. 3 .4 12
ABCD
S AB BC a a a
23
.
. 12 . 12
ABCD A B C D ABCD
V S AA a a a
.
Câu 58.     
.ABC A B C
có
BB a
 
ABC
     
, 2B AC a

Trang28
A.
3
3
a
. B.
3
6
a
. C.
3
a
. D.
3
2
a
.


Trong
2
2 2 2 2
: 2 2 .ABC AC AB BC AB a AB BC a

.ABC A B C
là:
3
.
1
. . . .
22
ABC A B C ABC
a
V S BB AB BC BB

Câu 59.     
.ABCD A B C D
¢ ¢ ¢ ¢
, có
ABCD
   
2a
 
23AC a
¢
=

.ABC A B C
¢ ¢ ¢

A.
3
4a
. B.
3
3a
. C.
3
2a
. D.
3
a
.


Ta có:
2 2 2 2 2 2
42AC AB AD AA AA a AA a
¢ ¢ ¢ ¢
= + + Þ = Þ =
.

.ABC A B C
¢ ¢ ¢
là
3
.
11
. . . .2 .2 .2 4
22
ABC A B C
V AB AD AA a a a a
¢ ¢ ¢
¢
= = =
.
Câu 60. 
. ' ' 'ABC A B C

ABC

A

BC a
và

''AA B B

. ' ' 'ABC A B C

A.
3
2
8
a
. B.
3
2
4
a
. C.
3
1
4
.a
D.
3
1
12
a
.

Trang29

Tam giác
ABC

22
22
BC a
A AB
2
2
1
24
.
ABC
a
S AB

''AA B B
là hình vuông
2
2
'.
a
AA AB

23
22
2 4 8
. ' ' "
'. . .
ABC A B C ABC
a a a
V AA S
Câu 61. 


A.
3
48cm
. B.
3
192cm
. C.
3
32cm
. D.
3
96cm
.





3
1
.6.4.8 96
2
V cm
.
Câu 62. 
a

A.
3
6
.
4
a
B.
3
2
.
4
a
C.
3
3
.
4
a
D.
3
3
.
12
a

a
C
B
A'
B'
C'
A
Trang30


2
3
4
a
S

ha

23
33
44
aa
Va
.
Câu 63. 
.ABC AB C
có
2 , 3AB a AA a

.

.ABC AB C
.
A.
3
3a
. B.
3
4
a
. C.
3
3
4
a
. D.
3
a
.



.ABC AB C
:
2
3
23
. 3. 3
4
ABC
a
V AA S a a
.
Câu 64. 
.ABCD A B C D

a
,
3BD a
và
4AA a

A.
3
23a
. B.
3
43a
. C.
3
23
3
a
. D.
3
43
3
a
.


Trang31

I AC BD
. Ta có:
3
,
22
BD a
AC BD BI
. Xét tam giác vuông
BAI

I
:
2
22
2 2 2 2 2
33
.
2 4 4 2
a a a a
AI BA BI a a AI AC a





ABCD
:
2
1 1 3 3
2S 2. . 2. .
2 2 2 2
ABCD ABC
aa
S BI AC a
.

2
3
.
3
. .4 2 3 .
2
ABCD A B C D ABCD
a
V S AA a a

Câu 65.  thi THPT Quc Gia )
 
.ABC AB C

ABC
 
A
,
2AB a


BC

ACC A


0
30

A.
3
3a
. B.
3
a
. C.
3
12 2a
. D.
3
42a
.

Chn D.
Trang32
Ta có:
BA BC
và
BA AA
BA ACC A


.
Suy ra góc
0
, , 30BC ACC A BC C A BC A
.
Ta giác
ABC
vuông ti
A
, có
.cot 2 3AC AB AC B a


.
Tam giác
CAC
vuông ti
C
, có
22
22CC AC AC a

.
Th tích kh là
3
1
. . . 4 2
2
V B h AB AC CC a
.
Câu 66.  thi THPT Quc Gia )
Cho kh   ng
.ABC A B C
 
ABC
là tam giác vuông cân ti
A
,
AB a
. Góc gia
ng thng
BC
và mt phng
ACC A

bng
30
. Th tích ca kh ng
A.
3
1
8
a
. B.
3
3
8
a
. C.
3
32
2
a
. D.
3
2
2
a
.

Chn D.
Di
2
1
.
22
ABC
a
S AB AC
.
B'
B
A'
A
C'
C
Trang33
Ta có:
·
·
, 30
AB AC
AB ACC A BC ACC A BC A
AB AA
.

2
2 2 2
.cot30 3 3 2AC AB a AA AC A C a a a
.
Vy, th tích kh 
2
3
2
. . 2 .
22
ABC
a
V S AA a a
.
Câu 67.  thi THPT Quc Gia )
Cho kh ng
. ' ' 'ABC A B C

ABC
là tam giác vuông cân ti
A
, cnh bên
2AA a
,
góc gia hai mt phng
A BC
và
ABC
bng
30
. Th tích ca kh ng
A.
3
24a
. B.
3
8
3
a
. C.
3
8a
. D.
3
8
9
a
.

Chn A.

AH BC
, ta có
AA ABC
nên
'AA BC
.
AH BC
và
'AA BC
suy ra
BC AA H A H BC

.

A BC
và
ABC
là
30A HA A HA

.
Δ'A AH

A
có
22
tan tan30 2 3.
tan30
AA a a
A HA AH a
AH AH
ΔABC

A
nên
2 4 3BC AH a
.
2
11
2 3 4 3 12 .
22
ABC
S AH BC a a a

. ' ' 'ABC A B C
là
Câu 68.  thi THPT Quc Gia )
H
B'
C'
A'
A
C
B
Trang34

.ABC AB C

ABC

A

2AA a
, góc

A BC
và
ABC

60

A.
3
8
9
a
. B.
3
8a
. C.
3
8
3
a
. D.
3
24a
.

Chn C.

I

BC
.
Ta có: +
ABC

A
nên
AI BC
+
.ABC AB C

AA BC
suy ra
BC AA I BC A I

.

A BC
và
ABC

AI
và
AI
, mà tam giác
AA I
vuông

A
nên ta có
AIA
.Suy ra 
A BC
và
ABC

60AIA

.
Trong tam giác vuông
AA I
, ta có
2
tan60
3
AA a
AI

.
ABC

A
nên
4
2
3
a
BC AI
,
26
3
2
BC a
AB AC
.

2
3
1 1 2 6 8
. . . .2 .
2 2 3 3
ABC
aa
V AA S AA AB AC a





.
Câu 69.  thi THPT Quc Gia t 1 - )
    
ABCD A B C D
    
2BD a
     
A BD
và
()ABCD

30

I
C'
B'
A
C
B
A'
Trang35
A.
3
63a
. B.
3
23
9
a
C.
3
23a
D.
3
23
3
a
.

Chn D.

O AC BD
.

ABCD
là
22
22
2
2
22
ABCD
BD a
S AB a
.
Ta có:
,( ) ; 30A BD ABCD AO AO
Xét tam giác
AOA

A
, ta có:
3
tan30
3
A A AO a

23
3 2 3
2
33
ABCD
V A A S a a a
.
Câu 70.  thi THPT Quc Gia t 1 - )
    
. ' ' ' 'ABCD A B C D
    
4BD a
     
'A BD
và
ABCD
=
30
o

A.
3
16 3
9
a
B.
3
48 3a
C.
3
16 3
3
a
D.
3
16 3a

Chn C.

O

BD
. Ta có:
''A AB A AD
suy ra
''A B A D
suy ra
'A BD
cân.
Trang36
Mà
'
'
A BD ABCD BD
A O BD
AO BD


, 30 .A BD ABCD A OA

=
30
o
.
Xét
A OA

A
có:
tan30
2
22
o
A A A A A A A A
AC BD
AO a
23
' 2 tan30
3
a
A A a
.
Xét hình vuông
ABCD
có:
2 2 2.BD AB AB a

2
'.V A A AB
=
2
23
. 2 2
3
a
a
=
3
16 3
3
a
.
Câu 71.  thi THPT Quc Gia t 1 - )
    
ABCD A B C D
    
2BD a
     
A BD
và
()ABCD

60

A.
3
23
9
a
B.
3
63a
C.
3
23
3
a
D.
3
23a

Chn D.

O AC BD
.
Ta có:
0
()
60
A BD ABCD BD
AO BD AOA
AC BD


Tam giác
AA O
có:
tan60 . 3AA OA a


và
2
2
ABCD
Sa

3
.
23
ABCD
ABCD A B C D
V AA S a
.
Câu 72.  thi THPT Quc Gia t 1 - )
Trang37

.ABCD A B C D

4BD a

A BD
và
ABCD

0
60

A.
3
48 3a
. B.
3
16 3
9
a
. C.
3
16 3
3
a
. D.
3
16 3a
.

Chn D.

ABCD
là hình vuông có
4 2 2BD a AB a
.

I

.BD
Vì
42BD a BI AI a
.
Tam giác
A AI

A
có:
0
tan60 2 3
AA
A A a
AI
.

2
3
. 2 2 .2 3 16 3
ABCD
V S A A a a a
.
Câu 73.      
. ' ' 'ABC A B C
có
,AB a
  
'AC
 

ABC

45 .

. ' ' 'ABC A B C

A.
3
3
4
a
. B.
3
3
2
a
. C.
3
3
12
a
. D.
3
3
6
a
.

Chn A.
Có:
( )
( )
·
·
= = °' , ' 45A C ABC A CA
.
Trang38
Xét tam giác
'A A C

,A
ta có:
·
= Þ =
'
tan ' ' .
AA
A CA AA a
AC

. ' ' 'ABC A B C
là:
23
33
'. . .
44
ABC
aa
V AA S a
Câu 74. 
.ABC AB C
có
4AB a

AC


ABC

o
45

.ABC AB C

A.
3
3
4
a
. B.
3
3
2
a
. C.
3
16 3a
. D.
3
3
6
a
.


.ABC AB C

.ABC AB C

Ta có:
o
, 45A A ABC A C ABC A CA
AAC


4A AA AC a
.
22
2
3 4 3
43
44
ABC
AB a
Sa
23
. ' ' '
. 4 .4 3 16 3
ABC A B C ABC
V AA S a a a
.
Câu 75. 
.ABC A B C
 
A BC
và
ABC
là
30
, tam giác
A BC

8

.ABC A B C
.
A.
83
. B.
8
. C.
33
. D.
82
.



,0AB x x

M

BC
.
Ta có
, 30
A BC ABC BC
AM BC A BC ABC A MA
A M BC

.
4a
4a
4a
45
0
B
A
C'
A'
B'
C
Trang39
Xét
AAM
, có
32
.
cos30 2
3
AM x
A M x
.
2
1
8 . 8 16 4
2
A BC
S A M BC x x
Suy ra
4. 3 1
.tan30 . 2
2
3
A A AM
;
16. 3
43
4
ABC
S 
.

.
. 2.4 3 8 3
ABC A B C ABC
V A A S
.
Câu 76. 
. ' ' 'ABC A B C

2
3
4
a

'A BC


0
60

. ' ' 'ABC A B C
.
A.
3
33
8
a
B.
3
3
8
a
C.
3
53
12
a
D.
3
32
8
a



ABC

2
3
4
a

a
.

M

BC
, ta có
'
'
BC AM
BC A M
BC AA


0
' , ' , ' 60A BC ABC A M AM A MA
.
Xét
'A AM
ta có
0
3
' .tan60
2
a
AA AM
x
30
°
M
C
B
A'
B'
C'
A
Trang40

. ' ' 'ABC A B C
là
3
. ' ' '
33
'.
8
ABC A B C ABC
a
V AA S
Câu 77. 
.ABC A B C

a
và
AB

BC
. Tính

V

A.
3
6
4
a
V
. B.
3
6
8
a
V
. C.
3
6Va
. D.
3
7
8
a
V
.



, , , x BA y BC z BB

AB BC

nên
22
2
2
. 0 0 . . . 0 .
2
os60
22
o
AB BC z x y z z y z x y x z z x y
aa
z x y c z


3
. ' ' '
16
. .sin60 .
28
o
ABC A B C
a
V AB AC BB

Câu 78.      
. ' ' 'ABC A B C
 
ABC
     
B

BA BC a

'AB

ABC

0
60

A.
3
2a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
2
a
.


Trang41

'AB

ABC
là
00
' 60 ' .tan60 3A BA A A AB a
.
Có
23
. ' ' '
13
. . '
2 2 2
ABC ABC A B C ABC
aa
S BABC V S A A
.
Câu 79. 
. ' ' 'ABC A B C

ABC

A
,
2,BC a=
'AB

0
60

A.
3
3
2
a
. B.
3
3
4
a
. C.
3
3
2
a
. D.
3
2
a
.


ABC

A
,
2
11
2.
22
ABC
BC a AB AC a S a a a
D
= Þ = = Þ = =
.
'AB

00
60 ' ' 60BA BÞ=
.
'
' ': tan ' ' 3 ' 3 ' ' 3.
''
v
BB
BA B BA B BB A B a
AB
D = = Þ = =

. ' ' 'ABC A B C
là:
3
2
. ' ' '
13
'. 3. .
22
ABC A B C ABC
a
V BB S a a
D
= = =
Câu 80.       
.ABC AB C
       
A
. Cho
2AC AB a

AC

ABC

30

.ABC AB C
.
A.
3
23
3
a
. B.
3
3
3
a
. C.
3
53
3
a
. D.
3
43
3
a
.

ChnD
Trang42

ABC
:
2
1
.2
2
ABC
S AB AC a
.

AC
lên
ABC
là
AC
.

AC

ABC

AC
và
AC
hay
C AC
Theo bài ra có
30C AC

.
Xét tam giác
C CA

C
có
23
.tan30
3
a
CC AC
.

.ABC AB C
là
3
2
.
2 3 4 3
. .2
33
ABC A B C ABC
aa
V CC S a
.
Câu 81. 
. ' ' 'ABC A B C

ABC

A
,
30ACB

 
'BC
  
''ACC A

 
1
sin
25
     

'AB
và
'CC

3a

V

. ' ' 'ABC A B C
.
A.
3
6Va
. B.
3
36
2
a
V
. C.
3
3Va
. D.
3
23Va
.


* Ta có:
// //CC AA CC AA B B
Trang43
Mà
' ' ' ,A B AA B B
nên
'; ' '; ' ' ' ' 3d CC A B d CC AA B B C A a
* Ta có:
' ' 3; ' ' ;AC A C a AB A B a

2
3
2
a
B dt ABC

''AB
''ACC A

'BC

''ACC A
là
''B CA
' ' 1
sin ' 2 5
'
25
AB
B C a
BC
2 2 2 2
' ' ' ' 20 4 4CC B C B C a a a

.V B h

'h CC
2
3
3
.4 2 3.
2
a
V a a
Câu 82.     
.ABC AB C
 
ABC
    
AB AC a
,
120BAC 

()AB C


60

V

A.
3
3
8
a
V
B.
3
9
8
a
V
C.
3
8
a
V
D.
3
3
4
a
V



H

BC


AB C


60AHA

.
Ta có
2
13
. .sin120
24
ABC
a
S AC AB
.
Trang44
2 2 2 2
1
2 . .cos120 2. . . 3
2
B C BC AB AC AB AC a a a a a

2
2
ABC
S
a
AH
BC

.tan6
3
2
0AA
a
AH

.

3
3
.
8
ACB
a
V S AA

.
Câu 83. 
. ' ' 'ABC A B C

ABC

a
và
'A BC

ABC

30

V

. ' ' 'ABC A B C
.
A.
a
V
3
3
8
. B.
a
V
3
3
12
. C.
a
V
3
3
24
. D.
a
V
3
3
8
.



H

A
trên
BC
. Suy ra
AH BC
.
'A H BC
.
Mà
'ABC A BC BC

'A BC
và
ABC

; ' 'AH A H AHA 30
.
Ta có:
ABC

a
nên
a
AH
3
2
,
' .tan
a
A A AH 30
2
.

. ' ' 'ABC A B C
là
'.
ABC
a a a
V A A S
23
33
2 4 8
.
Câu 84. 
.ABC ABC

ABC

A
và
AB a
,
3AC a
,

A BC

30

.ABC A B C

A.
3
3
12
a
. B.
3
3
3
a
. C.
3
33
4
a
. D.
3
3
4
a
.

Trang45


A BC


ABC

AH BC

H

BC

góc, ta có:
A H BC

; 30A BC ABC A HA

* Xét tam giác
ABC
có:
2 2 2 2 2
1 1 1 1 1 3
32
a
AH
AH AB AC a a
.

B

ABC
là:
2
.3
22
AB AC a
B
.
* Xét tam giác
A HA

A
, ta có:
.tan30
2
a
A A AH

.ABC A B C

23
33
..
2 2 4
a a a
V B h
.
Câu 85. 
ABC

A
,
2AB a=
, góc 
( )
' ' AB C
và mp
( )
ABC

0

A.
3
3a
. B.
3
33a
. C.
3
a
. D.
3
3a
.


Trang46

I

''BC
.

( )
' ' AB C
và mp
( )
ABC

( )
' ' AB C
và mp
( )
' ' 'A B C
Ta có
( ) ( )
' ' ' ' ' ''BC AB C A B CÇ=
Vì
ABC

A

''ABB A
và
''ACC A


' ' ' 'AC AB AB C= Þ D

A
''AI B CÞ^
Vì
' ' 'A B CD

'A
nên
' ' 'A I B C^

( )
' ' AB C
và mp
( )
ABC

0
' 60AIA =
Ta có
0
1
' ' ' .tan 60 3
2
A I BC a AA A I a= = Þ = =
( )
2
3
. ' ' '
1
'. 3. 2 3
2
ABC A B C ABC
V AA S a a aÞ = = =
Câu 86. 
.ABC A B C
¢ ¢ ¢

C

( )
ABC
¢

a

( )
ABC
¢
và
( )
BCC B
¢¢


1
cos
23
=

.ABC A B C
¢ ¢ ¢
.
A.
3
32
4
a
V =
. B.
3
32
2
a
V =
. C.
3
2
2
a
V =
. D.
3
32
8
a
V =
.



,MN

AB
và
BC
Do
( ) ( ) ( )
AB CC
AB MCC ABC MCC
AB CM
ì
¢
^
ï
ï
¢ ¢ ¢
Þ ^ Þ ^
í
ï
^
ï
î
.

CK

CM

K

( )
CK ABC
¢
^

( )
( )
;CK d C ABC a
¢
==
.
y
x
a
M
B'
C'
A
B
C
A'
K
E
Trang47

( )
, , 0, 0BC x CC y x y
¢
= = > >

3
2
x
CM =
( )
2 2 2 2 2 2
1 1 1 4 1 1
1
3CM CC CK x y a
+ = Û + =
¢
.

CE BC
¢
^

E

KEC
=
,
12
sin 11
1
1
12
KC a
EC a
= = =
-
.

( )
2 2 2 2
1 1 1 11
2
12x y CE a
+ = =
.

( ) ( )
1 , 2

6
2,
2
a
x a y==
.

.ABC A B C
¢ ¢ ¢
là:
2 2 3
3 6 4 3 3 2
..
4 2 4 2
x a a a
Vy= = =
Câu 87. 
.ABC AB C
có
6A B a

'AB


BC

a
.
A.
3
6
3
a
. B.
3
6a
. C.
3
3
4
a
. D.
3
9
4
a
.



.ABCD ABCD

ABCD
là hình thoi.

AB x
AD x
Tam giác
ABD
có góc
120BAD 

222
2 . . oscBD AB AD AB AD BAD
22
2 . .cos120x x x x
2
3x
Ta có:
' 6 6A B a A D a
Ta có:
//A D B C

A B AD


A BD


A
2 2 2
'BD A B A D
22
3 12xa
22
42x a x a

2 2 2
AA A B AB


2 2 2
6 4 2a a a
2AA a

Trang48
3
.
1 1 1 3 6
. 2. .2 .2 .
3 3 2 2 3
ABC A B C ABC
a
V AA S a a a
.
Câu 88. 
. ' ' 'ABC A B C

a

'A


''AB C

23
19
a

A.
3
3
4
a
B.
3
3
6
a
C.
3
3
2
a
D.
3
3
2
a



M

''BC
.
Ta có
' ' '
' ' '
AA B C
A M B C
' ' 'B C AA M
' ' 'AB C AA M

AM
.

'A H AM

'AA M
, suy ra
' ' 'A H AB C
.

'A

''AB C
là
23
'
19
a
AH
.
Ta có
2 2 2 2 2 2 2
1 1 1 1 1 1 1
' ' ' ' ' ' 4A H A A A M A A A H A M a
'2A A a
.

23
' ' '
33
'. 2 .
42
A B C
aa
V AA S a
.
Câu 89.   
.
ABC A B C
   
B
,
2AC a
 
A BC

60

V

A.
3
3
2
a
V
. B.
3
3
3
a
V
. C.
3
3
6
a
V
.
D.
3
6
6
a
V
.


Trang49
Tam giác
ABC

B
,
2AC a
AB BC a
.
2
2
ABC
a
S
.

A BC

60
A BA
.
.tan60 3

A A AB a
.
23
.
3
. . 3
22
ABC A B C ABC
aa
V S A A a
.
Câu 90. 
.ABC A B C

A BC
và
ABC

60

AB a

V

.ABC ABC
.
A.
3
3
4
Va
. B.
3
3
4
Va
. C.
3
33
8
Va
. D.
3
3Va
.


Trang50

M

BC
suy ra
AM BC
1
Ta có
BC AM
BC A M
BC AA

2

ABC A BC BC

3

1
,
2
,
3
suy ra
; 60ABC A BC A MA

.
Vì tam giác
ABC

2
3
4
ABC
a
S
và
3
2
a
AM
.
Ta có
3
.tan60
2
a
AA AM
.

23
.
3 3 3 3
..
2 4 8
ABC A B C ABC
a a a
V AA S
.
Câu 91. Cho 
.ABC A B C
là
a

A


A BC

2
a

A.
3
32
12
a
. B.
3
2
16
a
. C.
3
32
16
a
. D.
3
32
48
a
.



I

BC
và
H

A
trên
AI
. 
,
2
a
d A A BC AH

.
Trong tam giác vuông
AA I
ta có:
2 2 2
1 1 1
AH AA AI

22
2 2 2 2 2 2
1 1 1 1 1 4 4 8
33
3
2
2
AA AH AI a a a
a
a




Suy ra:
6
4
a
AA
.
Trang51

23
3 6 3 2
.
4 4 16
ABC
a a a
V S AA
.
Câu 92.     
.ABC A B C
 
ABC
    
,AB AC a
120BAC

()A BC


60

A.
3
3
8
a
V
. B.
3
9
8
a
V
. C.
3
3
8
a
. D.
3
33
8
a
V
.



B I A C

, 60A BC ABC B IB

Vì
120BAC

60BAI


sin 60
BI
BA

3
2
a
BI

.
Suy ra
tan
BB
B IB
BI
tan60
BB
BI
33
.3
22
aa
BB

11
. . . . 3
2 2 2
ABC
a
S AI BC a

2
3
4
a
.

23
3 3 3 3
..
4 2 8
a a a
V B h
.
Câu 93. 
.ABC ABC

a

AB

BCC B


30

.ABC A B C
theo
a
.
A.
3
3
4
a
. B.
3
4
a
. C.
3
6
12
a
. D.
3
6
4
a
.


Trang52

M

BC
. Do
.ABC A B C

AM BCC B

,AB BCC B AB M
30
.
Xét tam giác vuông
AB M
ta có
tan30
AM
AB

tan30
AM
AB

3
2
a
AB

.
Xét tam giác vuông
B BM
ta có
22
BB B M BM


22
9
44
aa

2a
.

.ABC A B C
là
.
1
. .sin 60 .
2
ABC A B C
V AB AC BB

3
6
4
a
.
Câu 94. 
.ABC A B C

ABC

a

tâm
O

ABC

A BC

6
a

.ABC A B C
.
A.
3
32
8
a
. B.
3
32
28
a
. C.
3
32
4
a
. D.
3
32
16
a
.



2
3
4
ABC
a
BS

.

;h d ABC A B C AA

.
Do tam giác
ABC

O

ABC

I

BC
,
H

A
lên
AI
ta có
;AH A BC d A A BC AH

Trang53
;
1
3
;
d O A BC
IO
IA
d A A BC

;
;
3 3 6
d A A BC
AH a
d O A BC
2
a
AH
Xét tam giác
A AI

A
ta có:
2 2 2
1 1 1
AH AA AI

2 2 2
1 1 1
AA AH AI
3
22
a
AA

3
22
a
h
3
.
32
16
ABC A B C
a
V

.
Câu 95. 
.ABC ABC

a

AC


60

xp
S

ABC

ABC
.
A.
2
333
36
xq
a
S
. B.
2
333
6
xq
a
S
. C.
2
111
6
xq
a
S
. D.
2
111
36
xq
a
S
.


B'
C'
A
B
C
A'
Trang54
Ta có
; 60A C ABC A CA

suy ra
.tan60 3AA AC a
.
Có
1 1 3 3
.
3 3 2 6
a
r GM AM a
và
22
l G M G G GM

2
2
3 111
3
36 6
aa
a
.

2
3 111 333
..
6 6 36
xp
a
S rl a a

.
G'
G
M
B'
C'
A
B
C
A'
| 1/54
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHỦ ĐỀ 5
THỂ TÍCH KHỐI LĂNG TRỤ
I. THỂ TÍCH KHỐI LĂNG TRỤ Thể tích
Diện tích xung quanh
Diện tích toàn phần
KHỐI LĂNG V  . B h
+ B là diện tích đáy
Sxq = Tổng diện tích các mặt bên
Stp = Sxq + Diện tích 2 mặt đáy TRỤ
+ h là đường cao lăng trụ Chú ý:
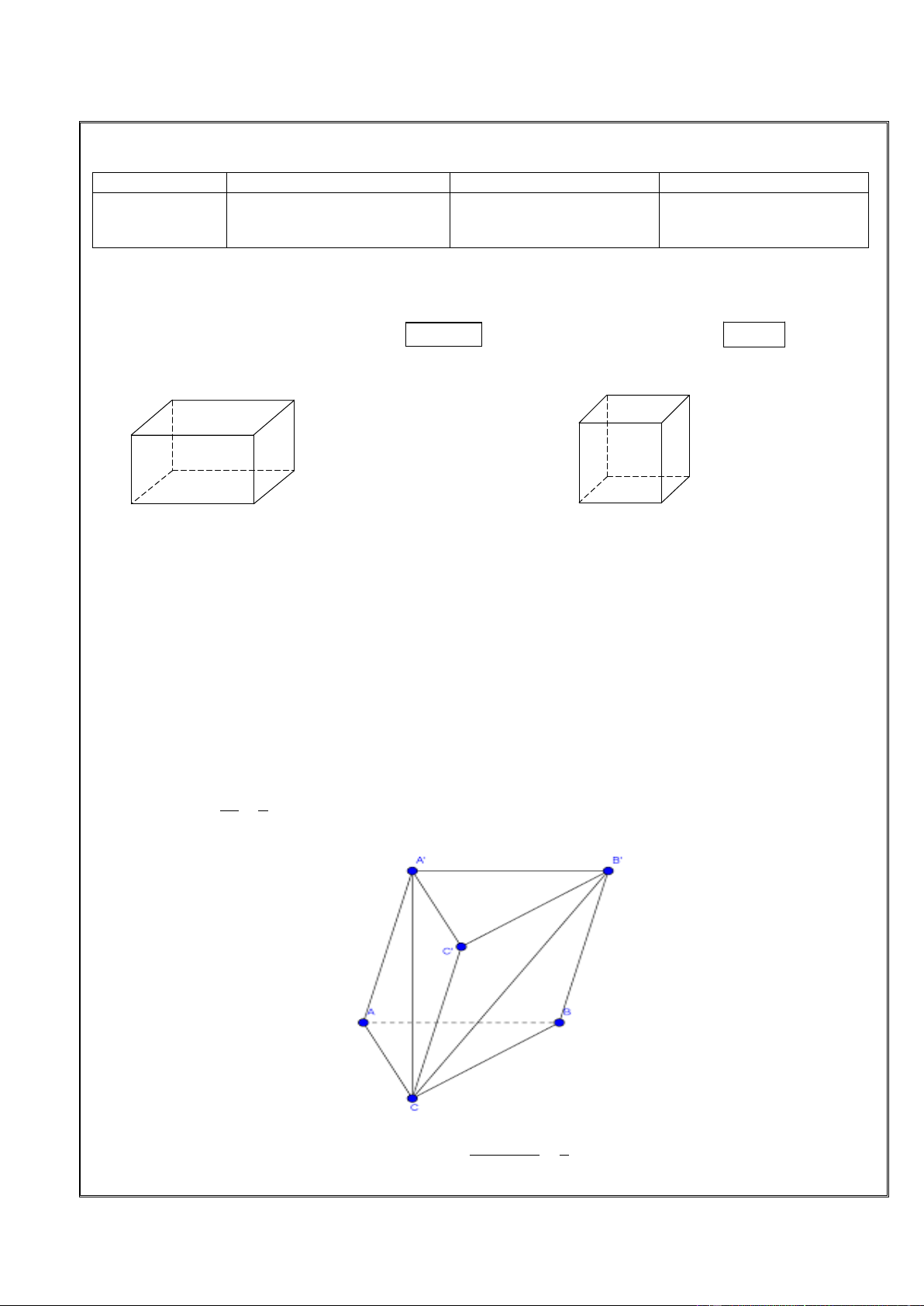
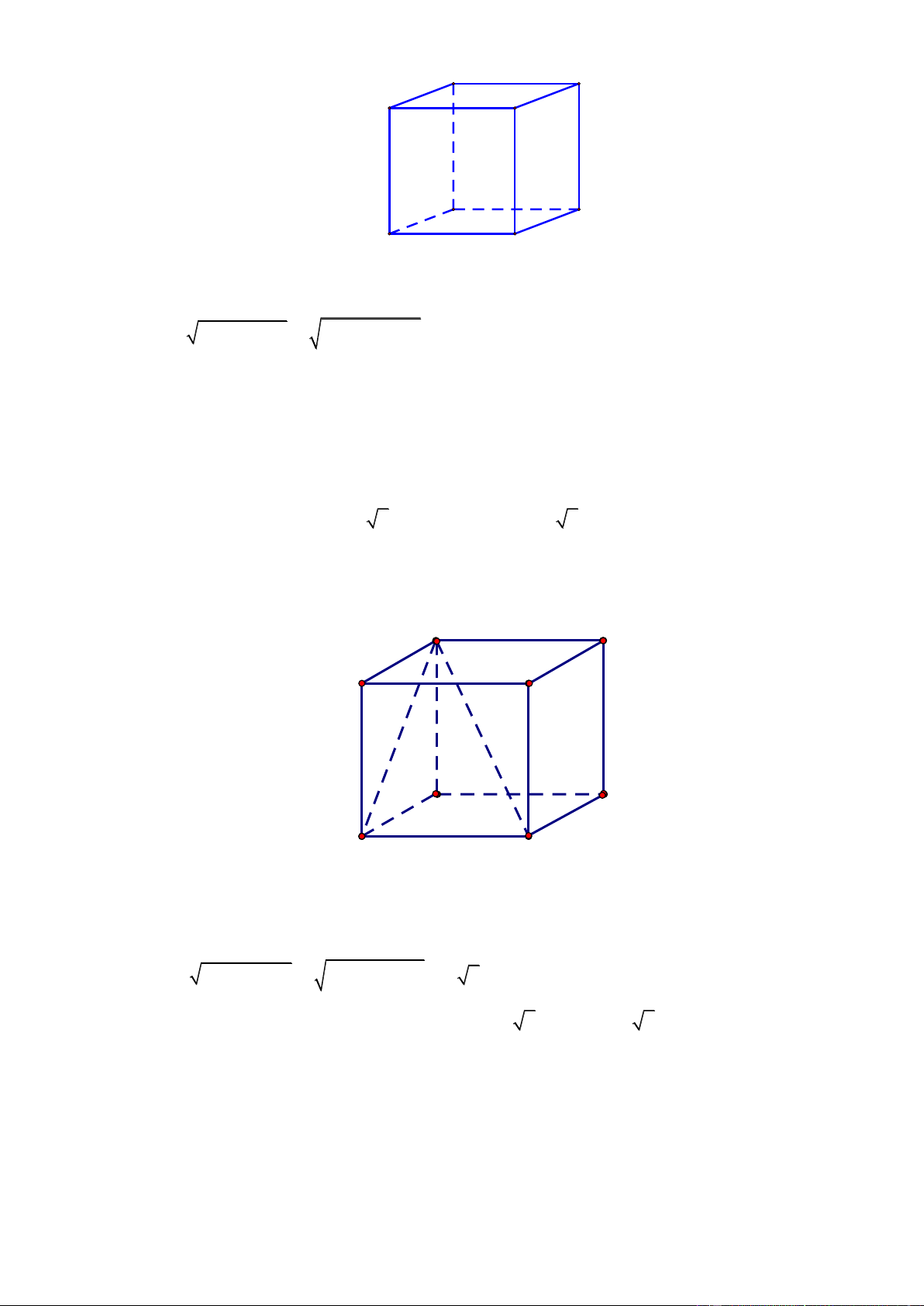
1. Thể tích khối hình hộp chữ nhật: V = a. .
b c Þ Thể tích khối lâ ̣p phương: 3 V = a a a a b a c Hình hộp chữ nhật Hình lập phương
2. Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều
+ Hình lăng trụ tam giác đều là hình lăng trụ đứng có đáy là tam giác đều.
+ Hình lăng trụ tứ giác đều là hình lăng trụ đứng có đáy là hình vuông.
II. CÁC CÔNG THỨC TÍNH NHANH TỈ LỆ THỂ TÍCH CỦA KHỐI LĂNG TRỤ
1. Khối trụ tam giác
Bài toán 1: Gọi V là thể tích khối lăng trụ, V là thể tích khối chóp tạo thành từ 4 trong 6 đỉnh của 4
lăng trụ. Khi đó: V 1 4  . V 3
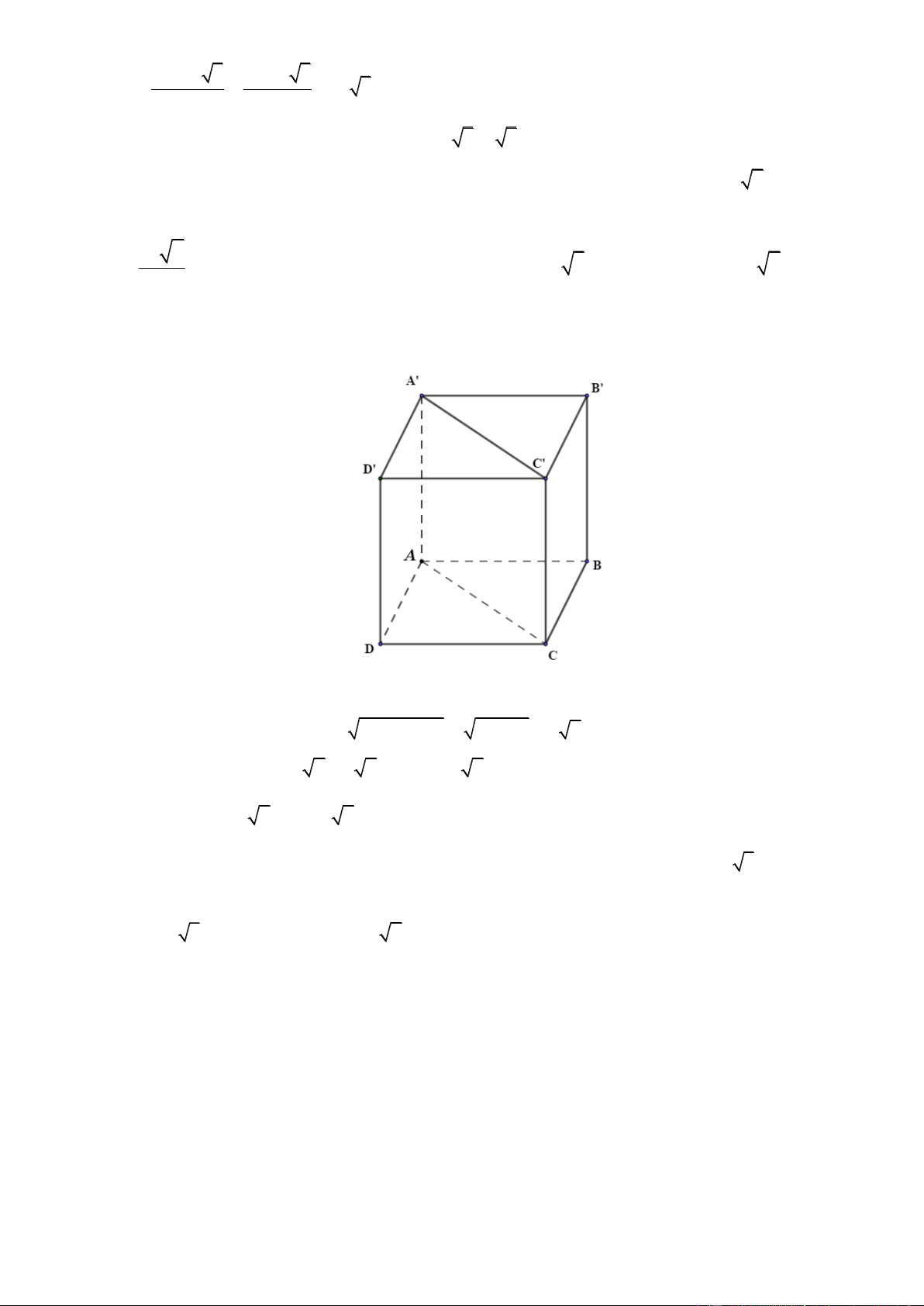
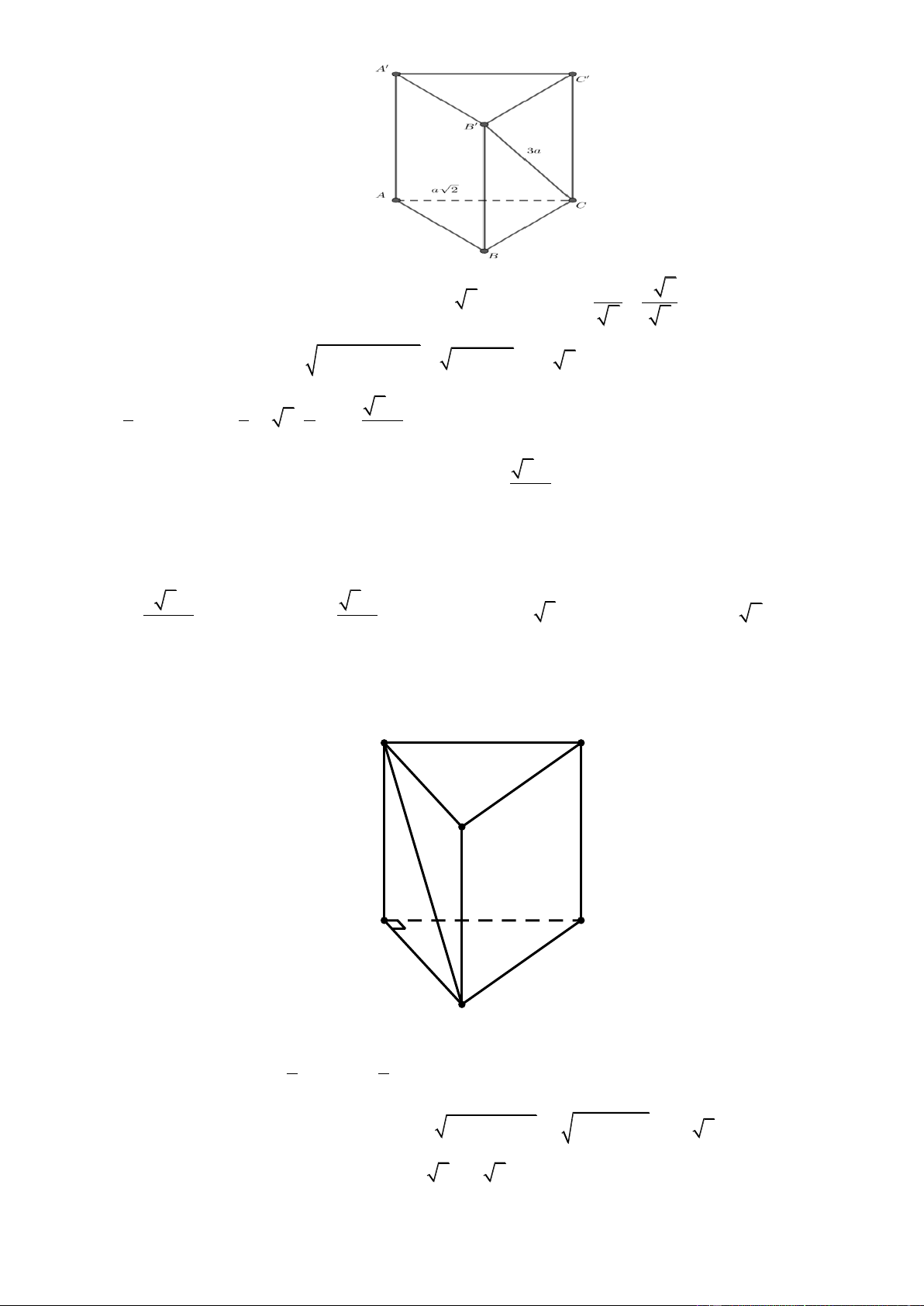
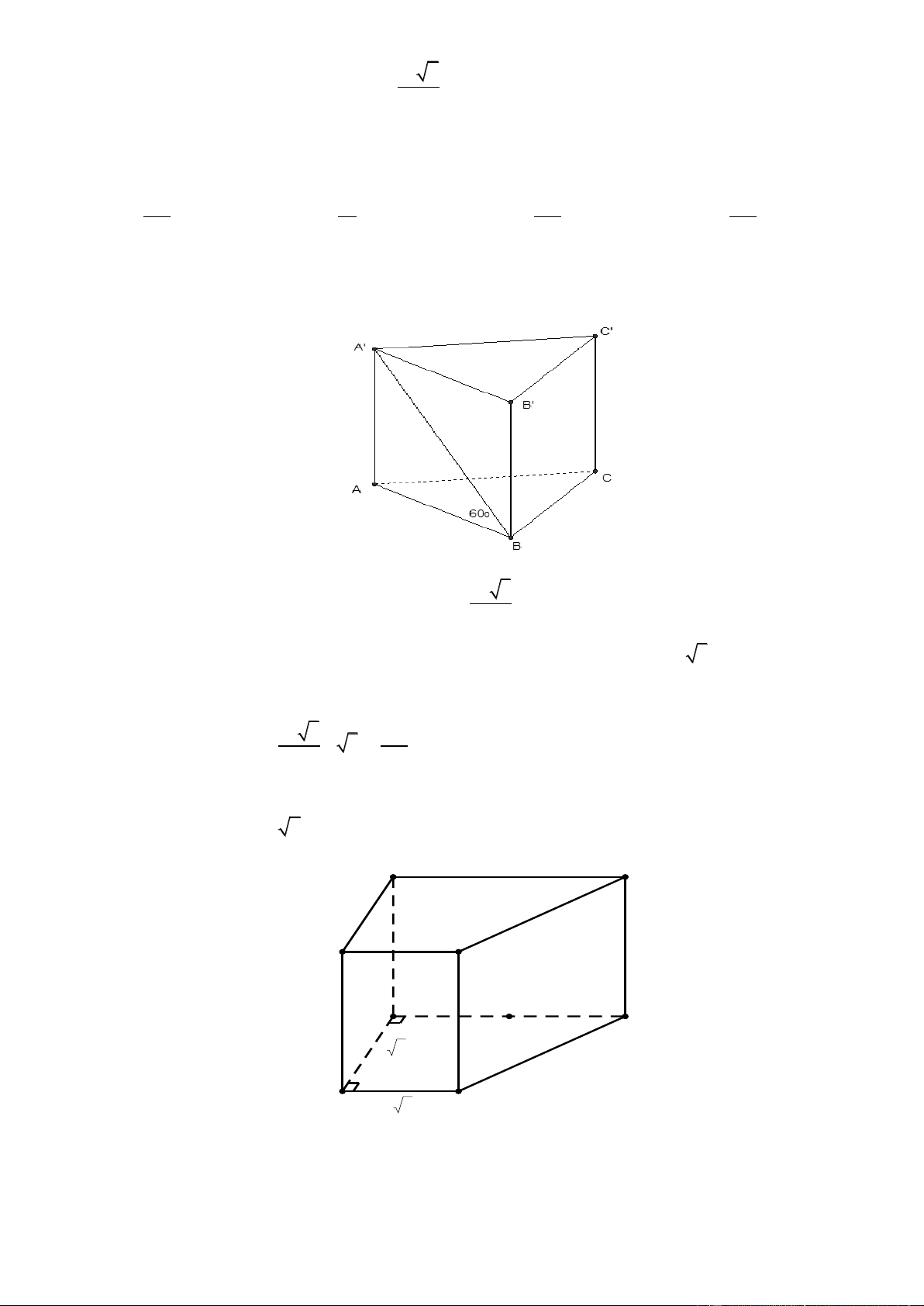
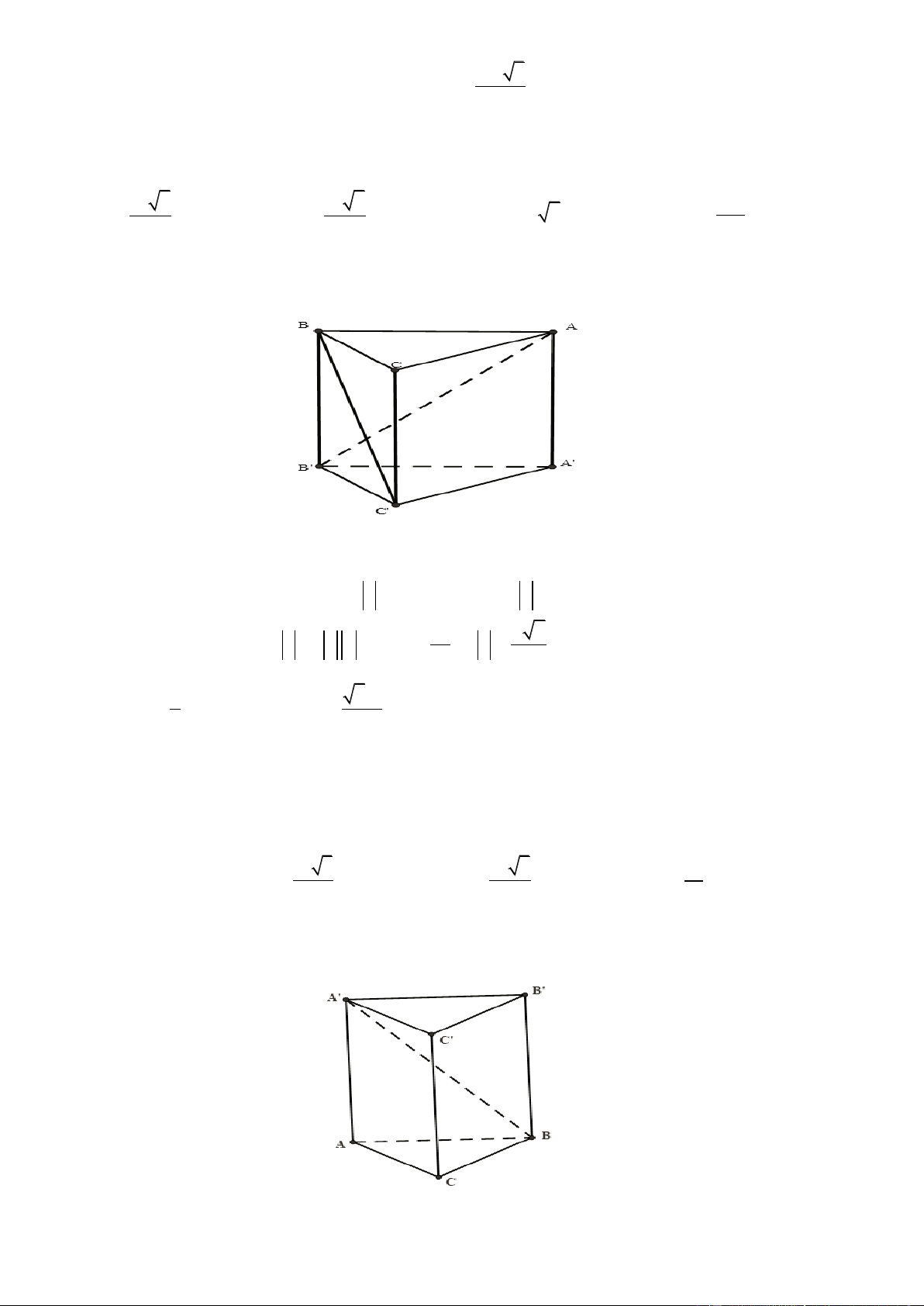
Cho hình lăng trụ tam giác V 1 AB .
C A' B 'C '. Khi đó:
C.A' B 'C '  . V 3
ABC.A' B 'C ' Trang1
Bài toán 2: Gọi V là thể tích khối lăng trụ, V là thể tích khối chóp tạo thành từ 5 trong 6 đỉnh của 5
lăng trụ. Khi đó: V 2 5  . V 3
Cho hình lăng trụ tam giác V 2 AB .
C A' B 'C '. Khi đó:
A' B ' ABC  . V 3
ABC. A' B 'C '
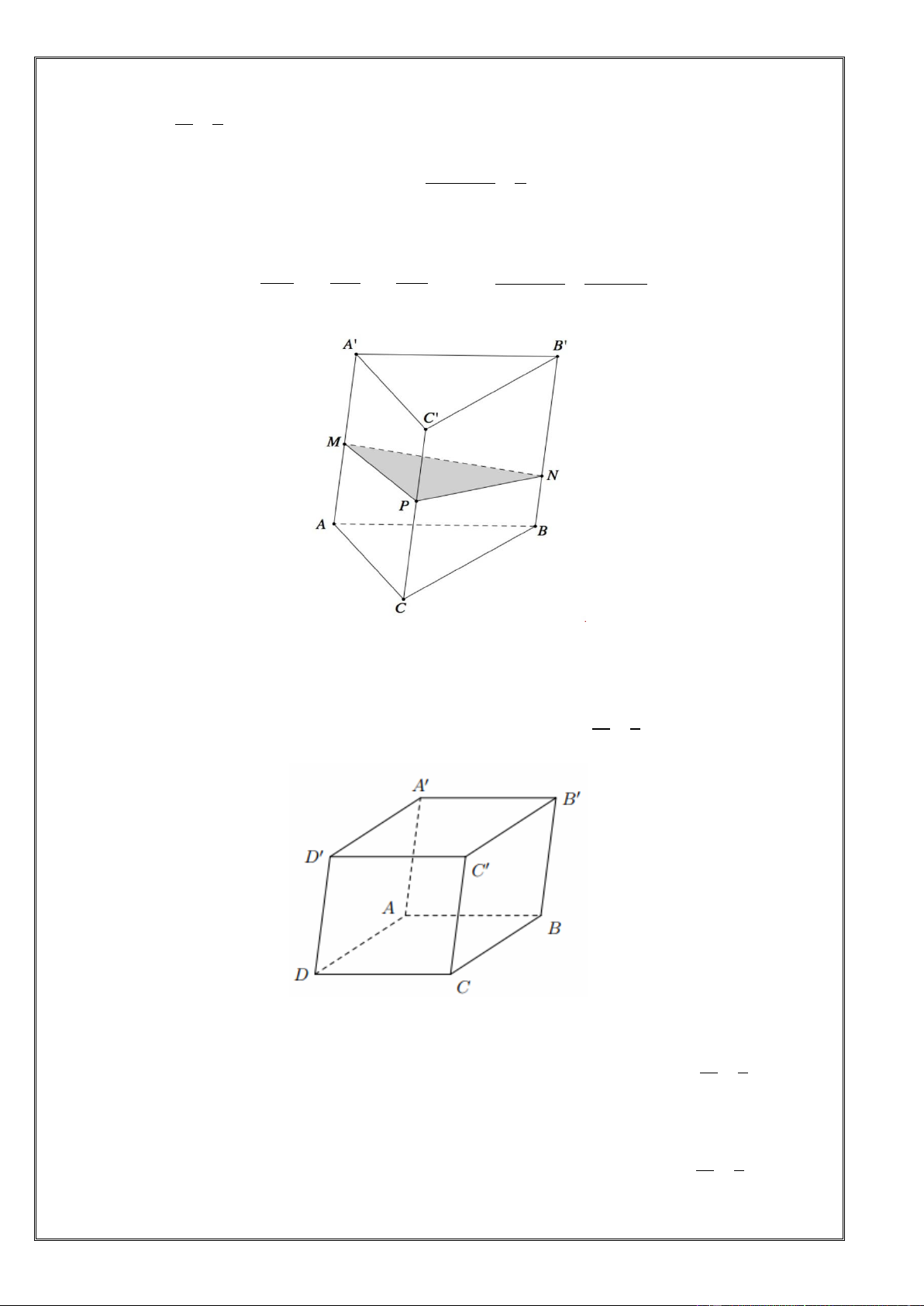
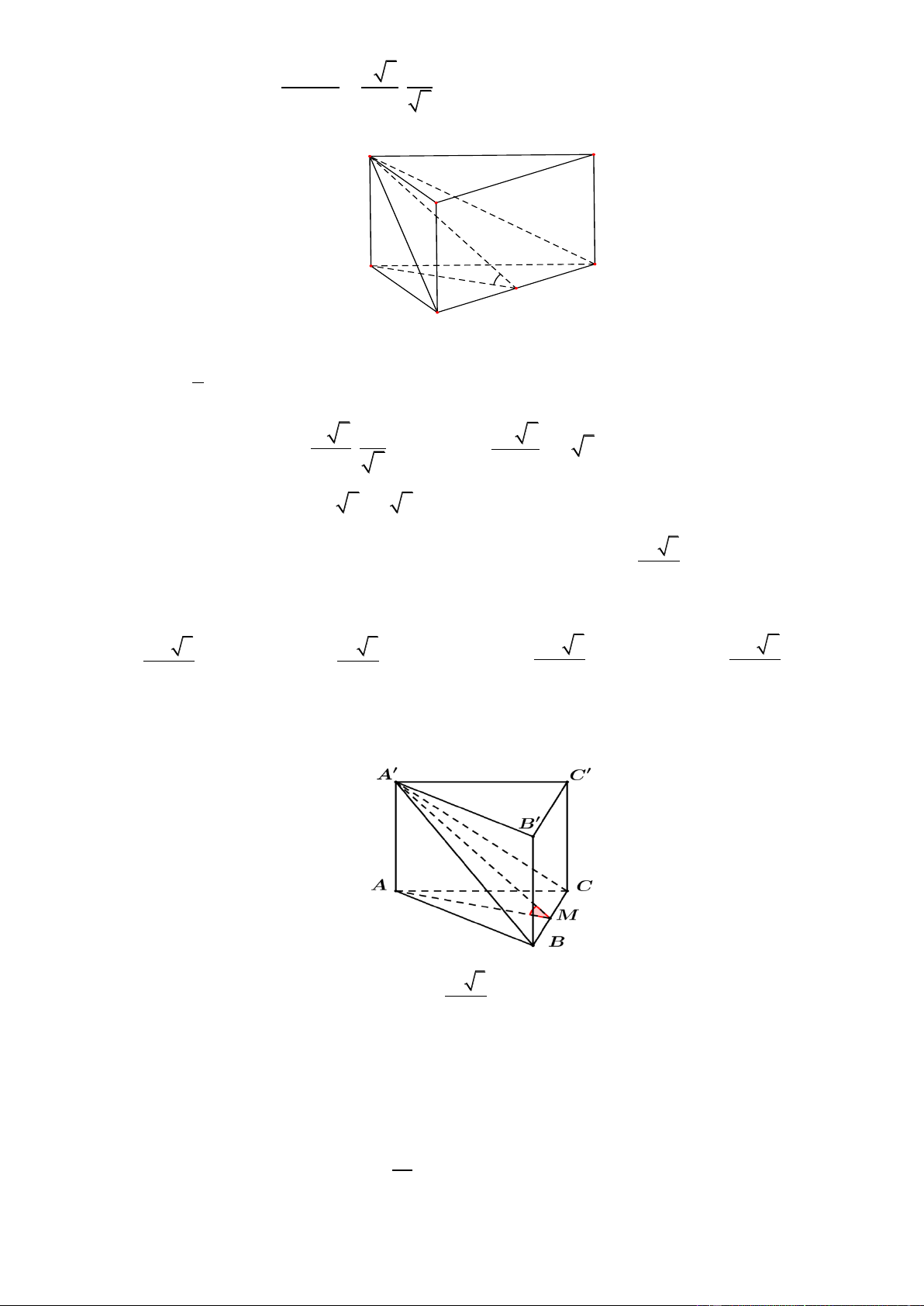
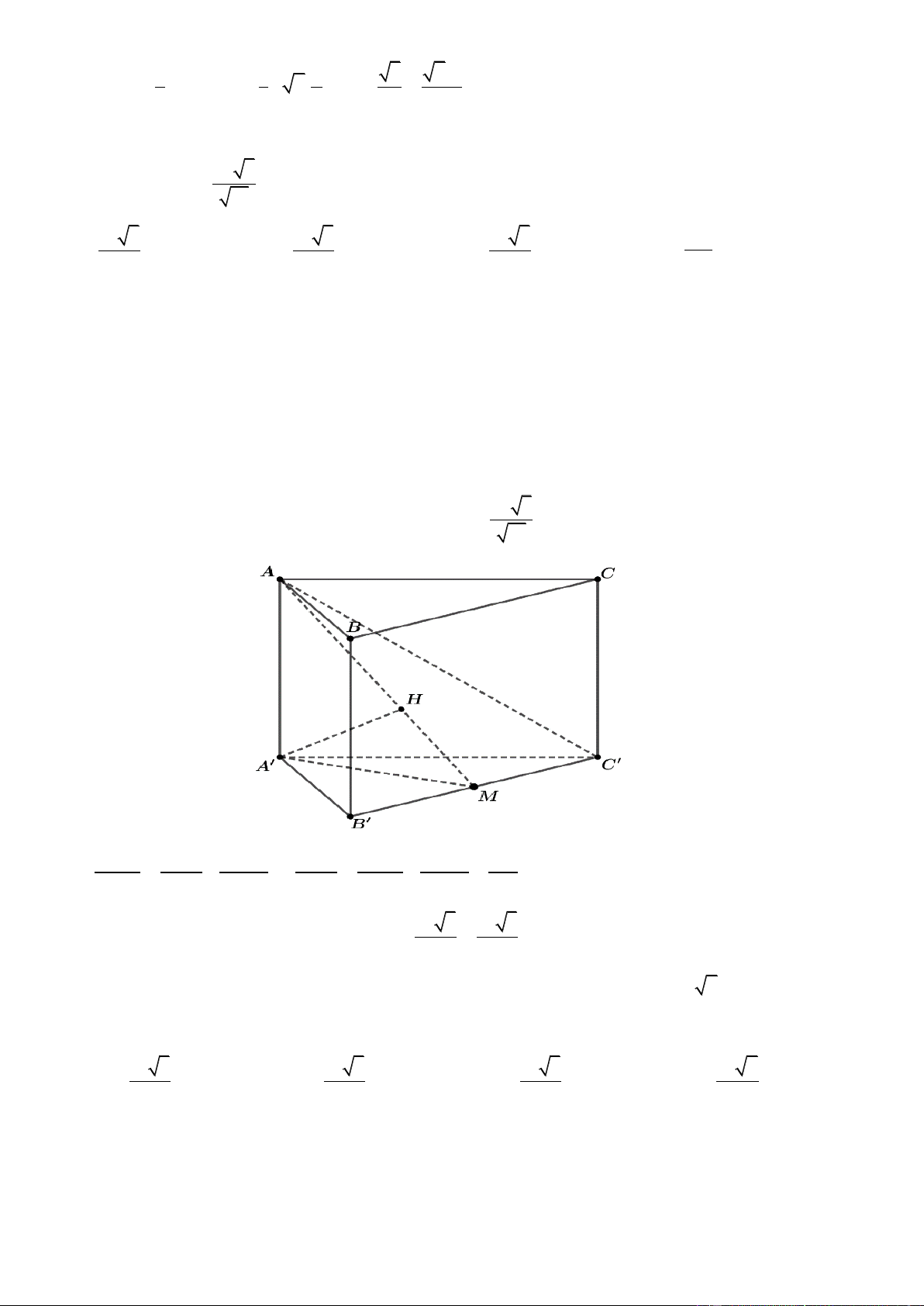
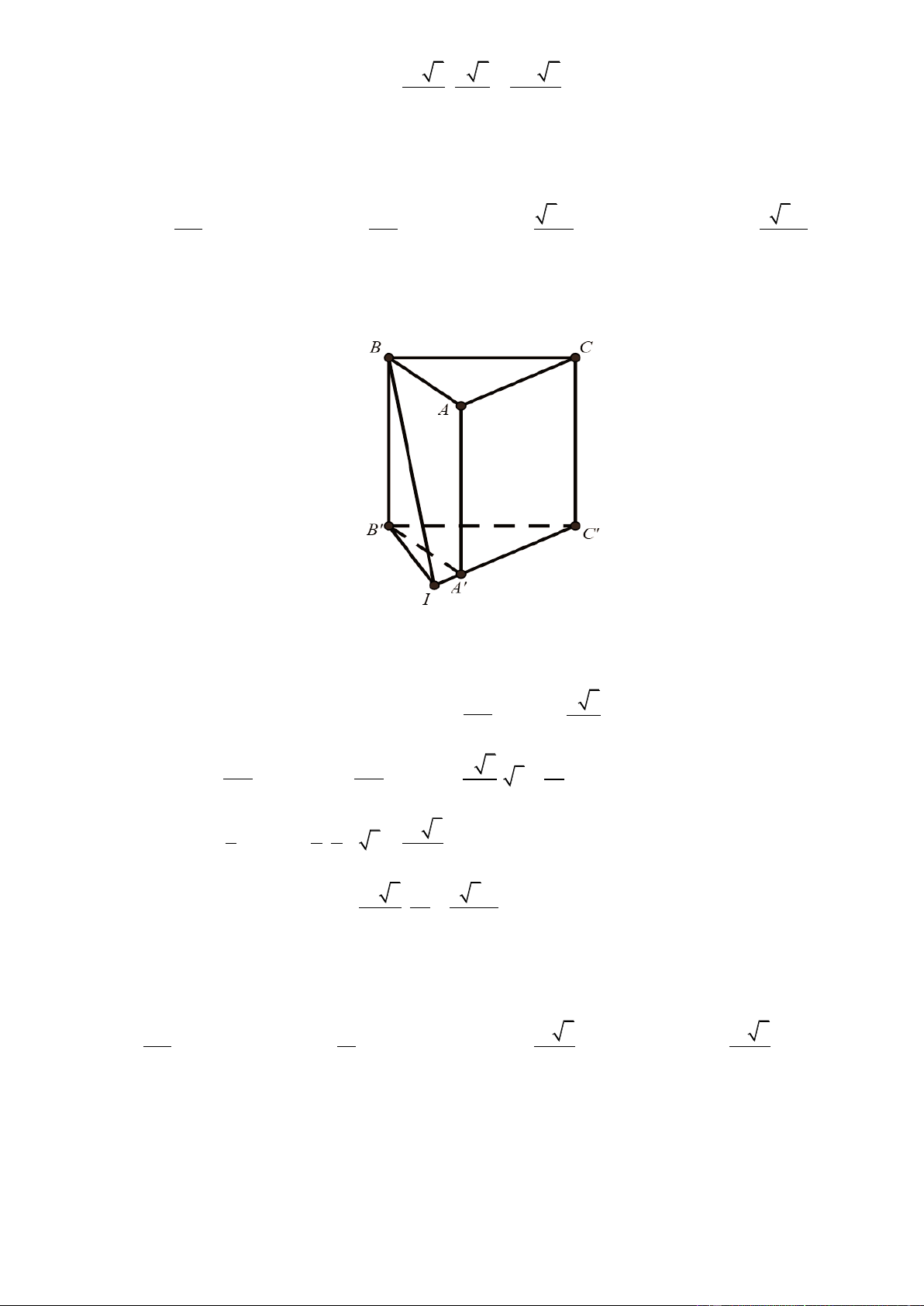
Bài toán 3: Cho hình lăng trụ tam giác AB .
C A' B 'C '. Mặt phẳng cắt các đường thẳng AA ', BB ',CC '   lần lượt tại AM BN CP V a b c
M , N , P sao cho  a,  b,
c thì ABC.MNP AA ' BB ' CC ' V 3
ABC.A' B 'C ' 2. Khối hộp
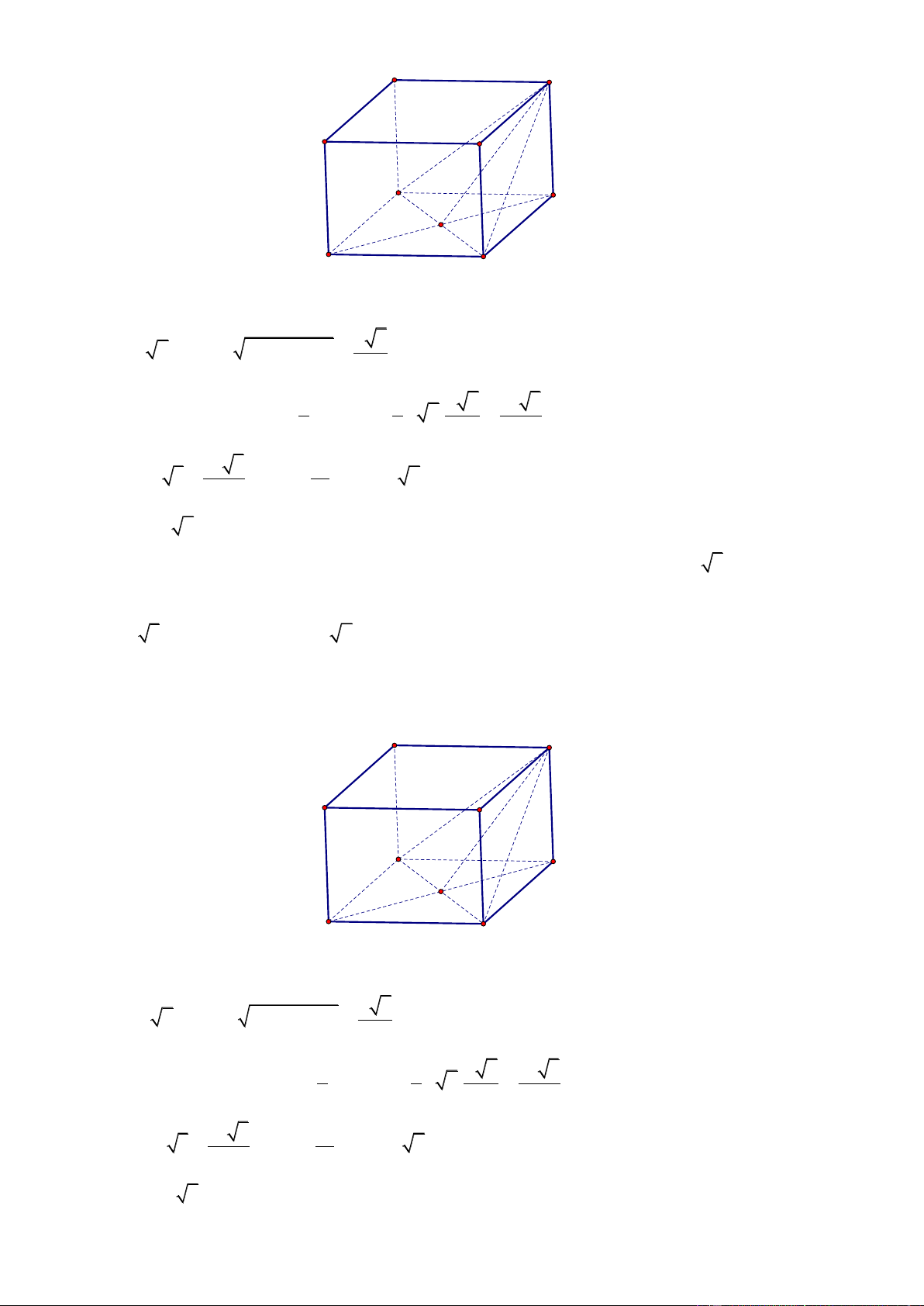
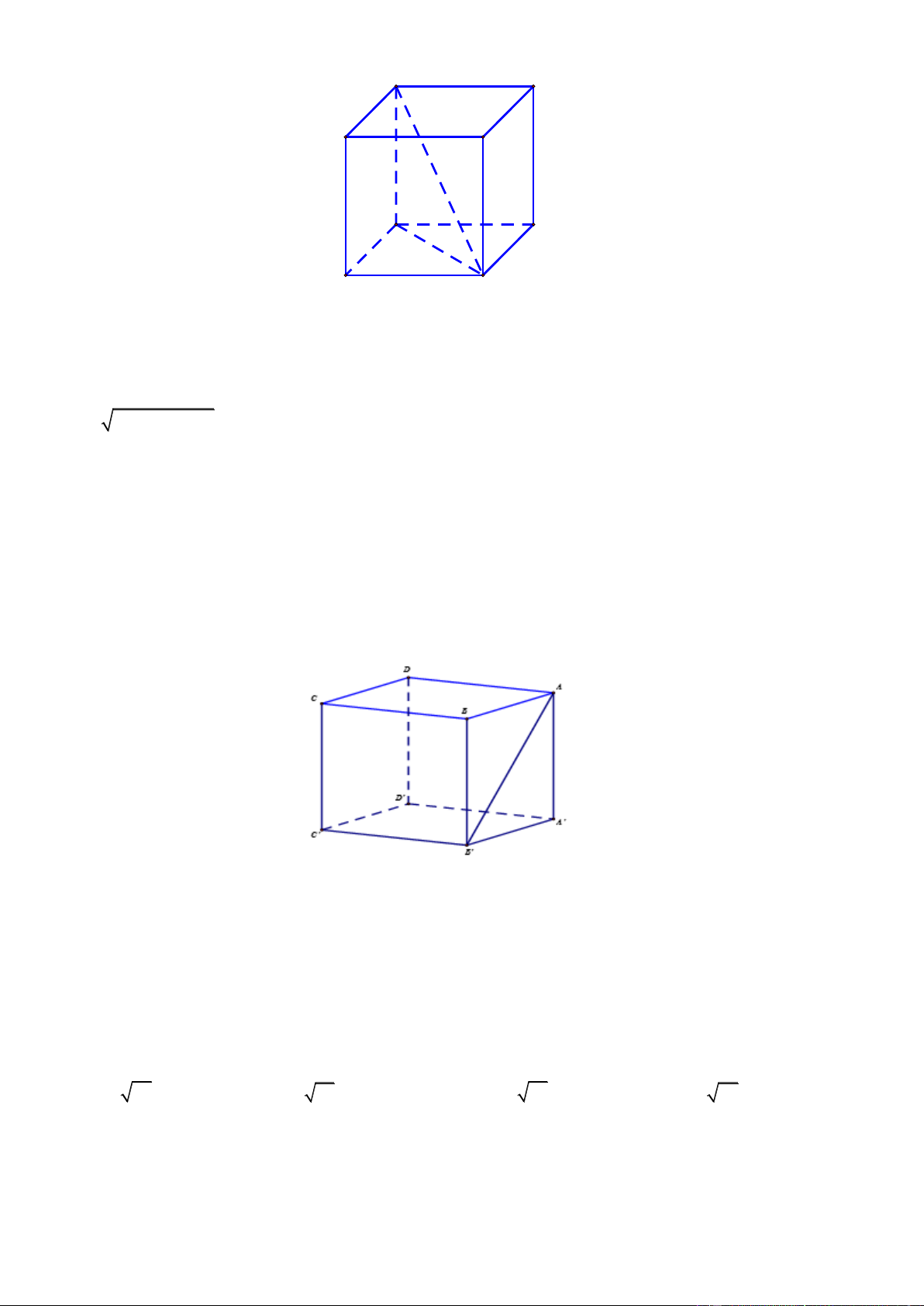
Bài toán 1:Gọi V là thể tích khối hộp, V là thể tích khối chóp tạo thành từ 4 trong 8 đỉnh của khối 4
hộp và 4 đỉnh này thuộc hai đường chéo của hai mặt song song V 1 . Khi đó: 4  . V 3
Bài toán 2:Gọi V là thể tích khối hộp, V là thể tích khối chóp tạo thành từ 4 trong 8 đỉnh của khối 4
hộp ( trừ trường hợp 4 đỉnh này thuộc hai đường chéo của hai mặt song song) V 1 . Khi đó: 4  . V 6
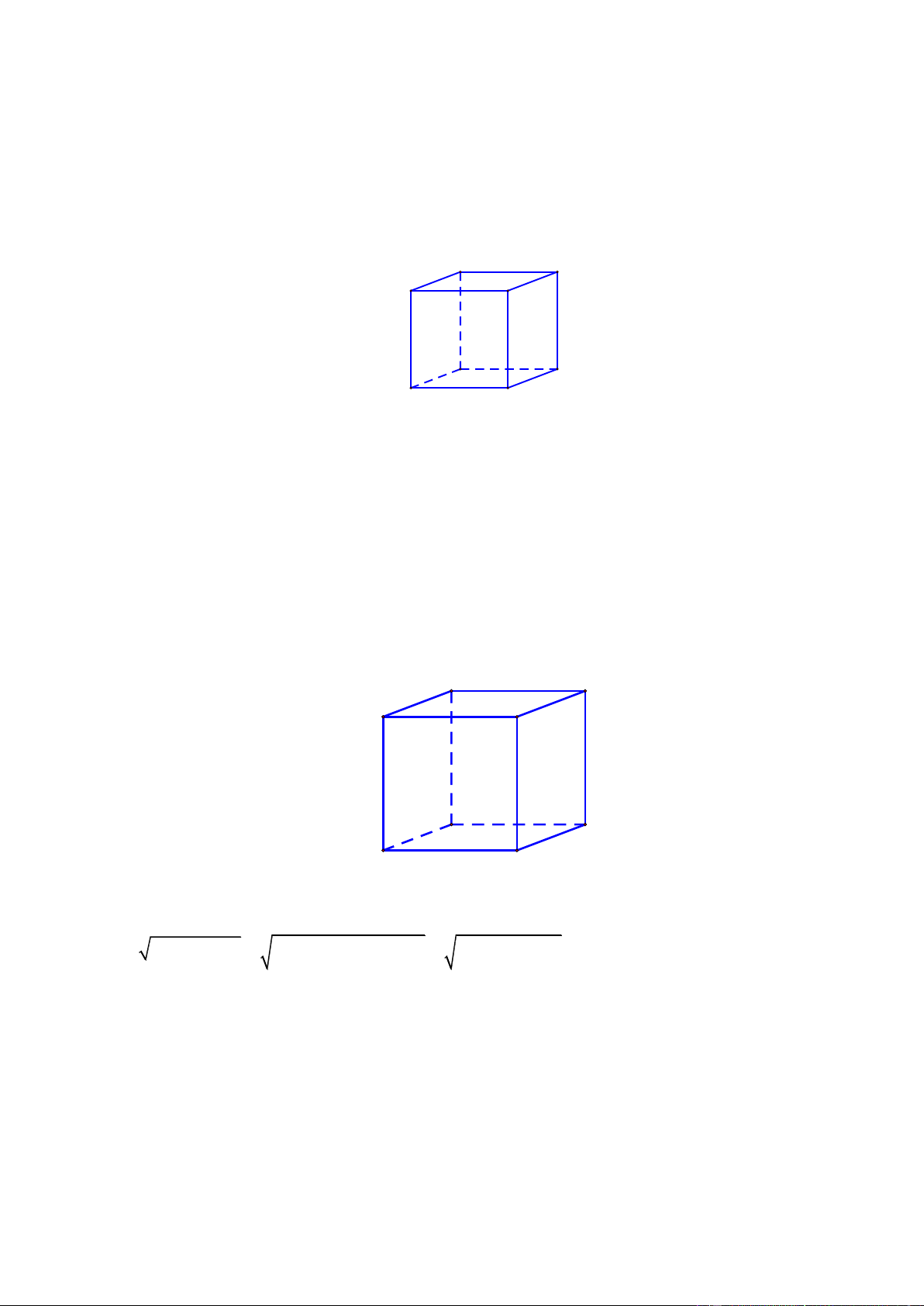
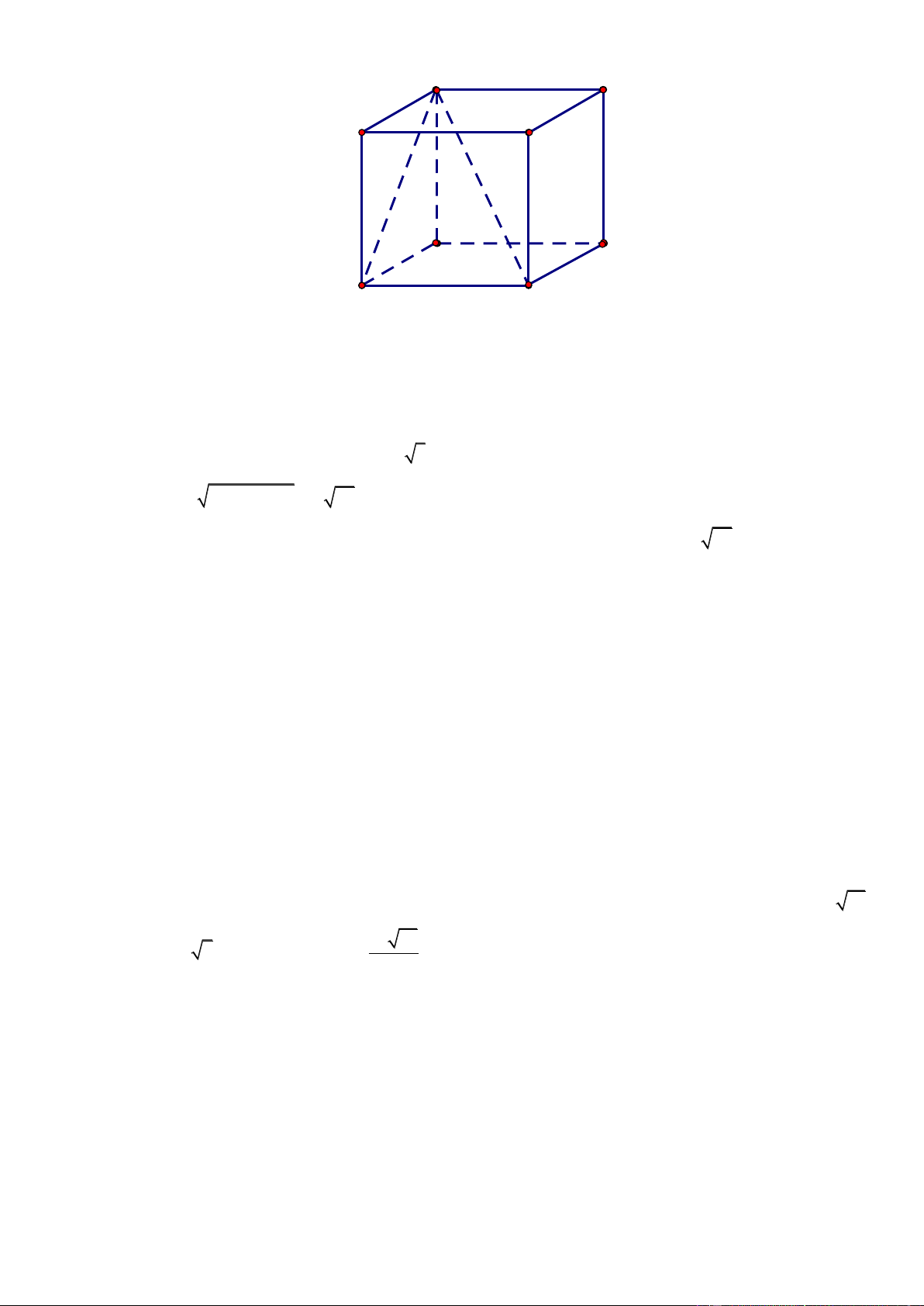
Bài toán 3:Gọi V là thể tích khối hộp, V là thể tích khối chóp tạo thành từ 5 trong 8 đỉnh của khối 5
hộp (1 đỉnh thuộc mặt phẳng đáy, 4 đỉnh còn lại thuộc mặt phẳng đáy còn lại). Khi đó: V 1 5  . V 3 Trang2
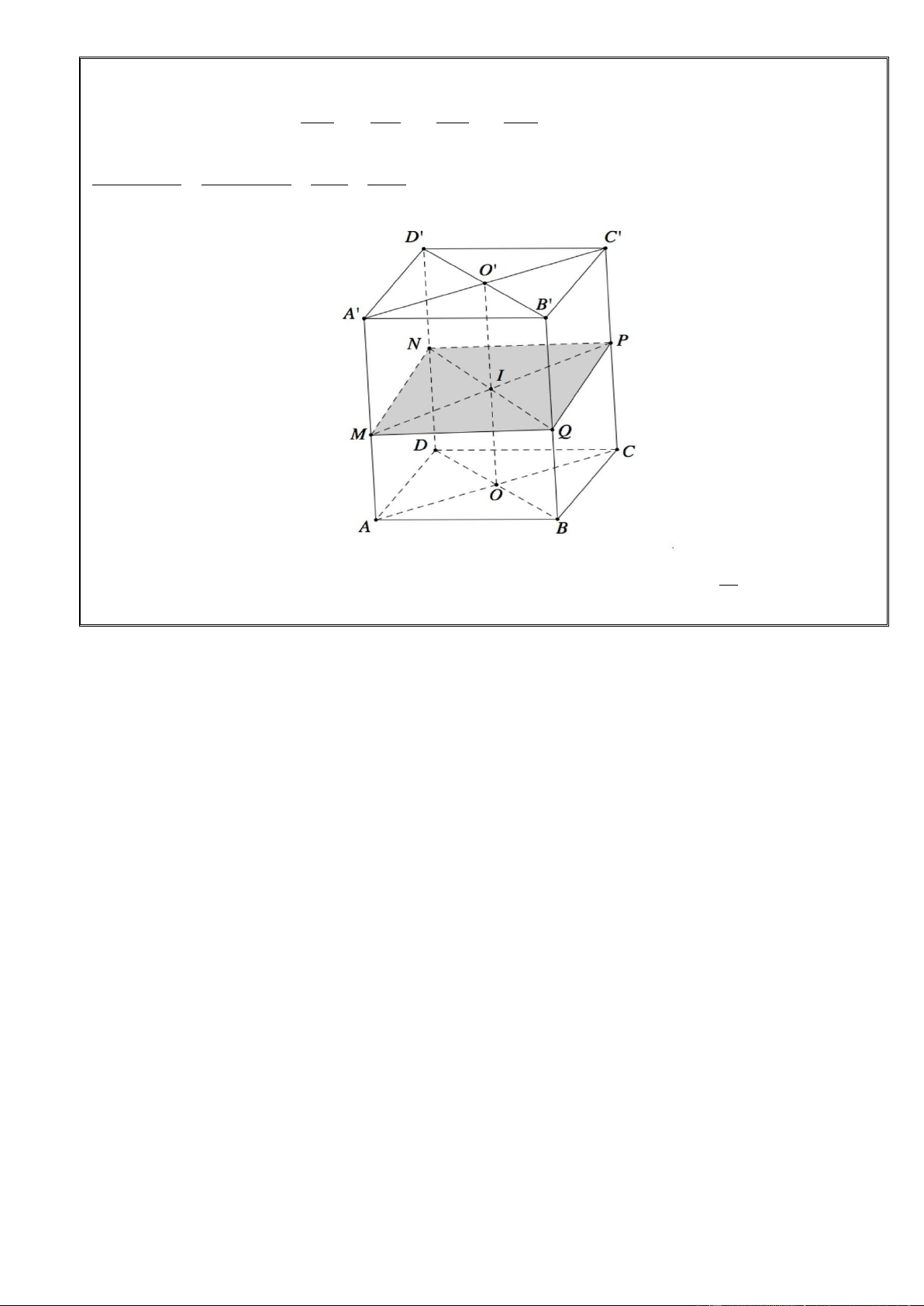
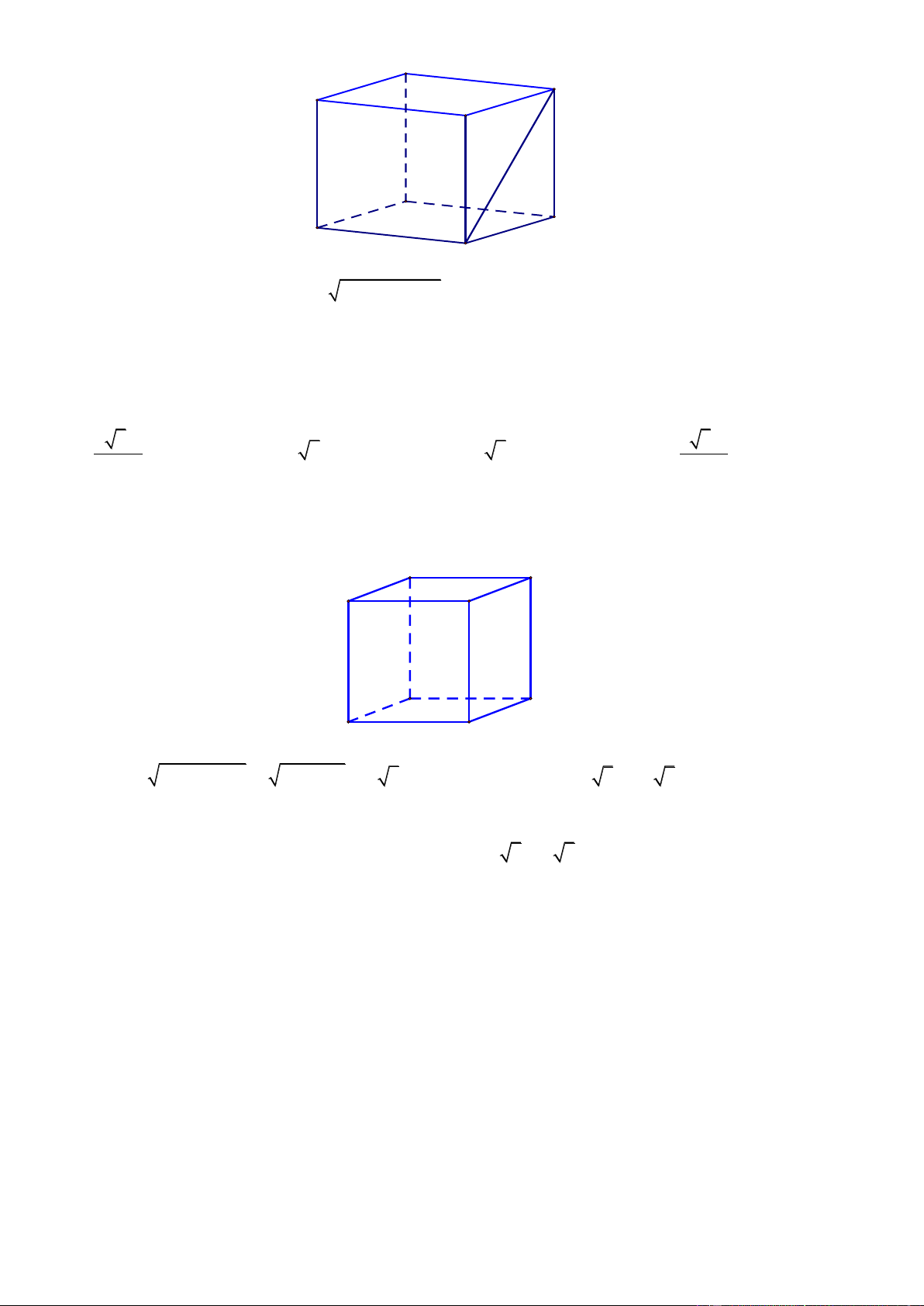
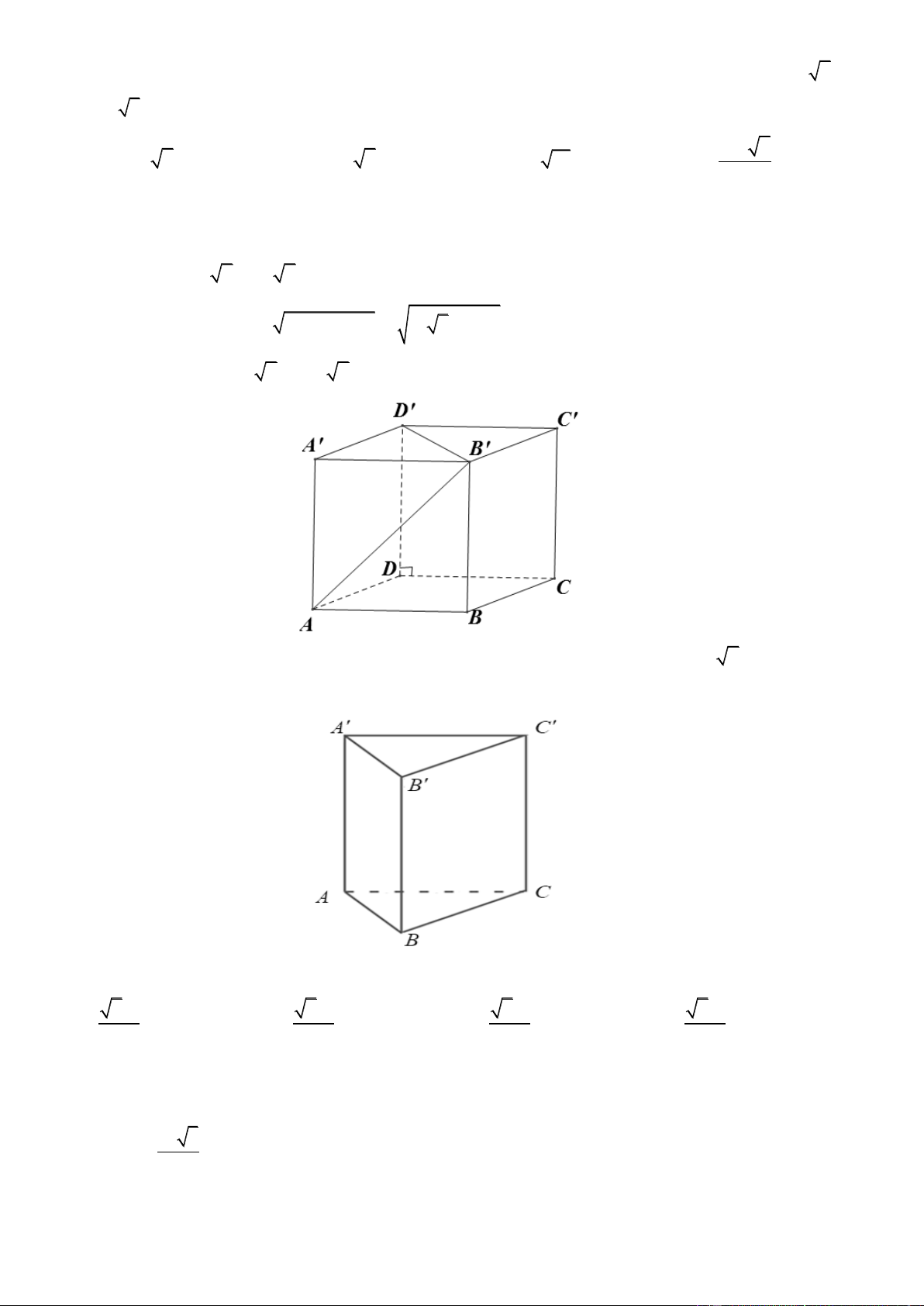
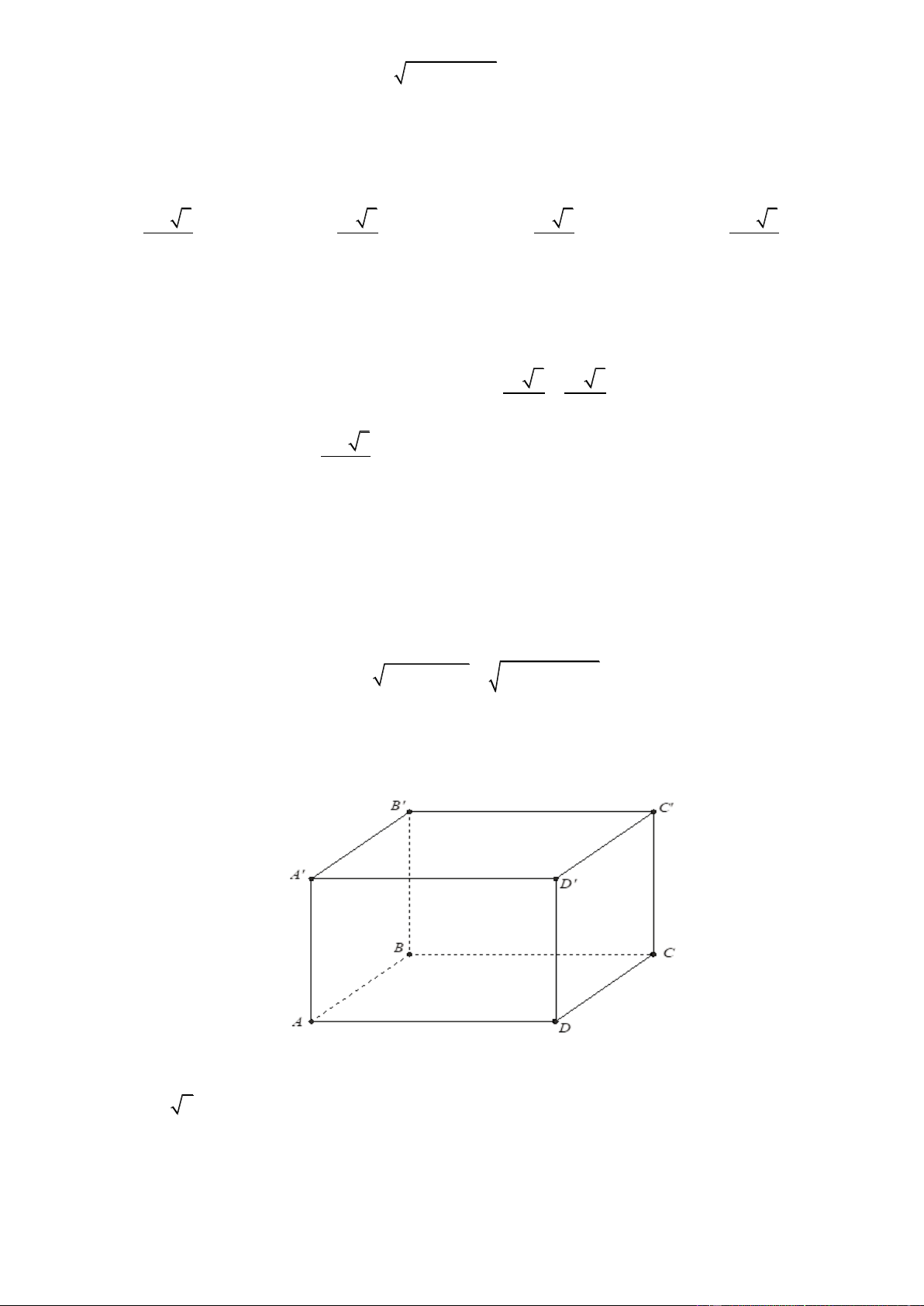
Bài toán 4: Cho hình hộp ABC .
D A' B'C ' D' . Mặt phẳng cắt các đường thẳng AA', BB ', CC ', DD ' lần lượt tại AM BQ CP DN
M , Q, P, N sao cho  a,  b,  c,
d và a c b d thì: AA ' BB ' CC ' DD ' V      ABCD.MQPN a b c d a c b d    V 4 2 2
ABCD.A' B 'C ' D' V
Chú ý: Hai khối đa diện đồng dạng với tỉ số k thì tỉ lệ thể tích của chúng là 3 k hay 1 3  k V2 Trang3 DẠNG 1
LÝ THUYẾT VÀ VẬN DỤNG
MỨC ĐỘ TRUNG BÌNH
Câu 1. (Đề thi THPT Quốc Gia – Năm 2022 –Mã đề 101, 102)
Cho khối lăng trụ có diện tích đáy 2
3a và chiều cao 2a . Thể tích khối lăng trụ đã cho bằng: A. 3 a . B. 3 6a . C. 3 3a . D. 3 2a . Lời giải Chọn B.
Thể tích khối lăng trụ: 2 3 V  .
B h  3a .2a  6a .
Câu 2. (Đề thi THPT Quốc Gia – Năm 2022 –Mã đề 103, 104)
Cho khốichóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần lượt là V
V ,V . Tỉ số 1 bằng 1 2 V2 2 3 1 A. . B. 3 . C. . D. . 3 2 3 Lời giải Chọn D.
Gọi diện tích đáy và chiều cao tương ứng của khối chóp và khối lăng trụ là B và h .  1 V   Bh V 1 1 Ta có 1  3   . V 3  2 V Bh  2
Câu 3. Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là 4 1 A. V  . B h . B. V Bh . C. V Bh .
D. V  3Bh . 3 3 Lờigiải Chọn A
Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là: V  . B h .
Câu 4. Chiều cao của khối lăng trụ có diện tích đáy B và thể tích V là 3V V B V A. h  . B. h  . C. h  . D. h  . B 3B V B Lờigiải Chọn D V
Chiều cao của khối lăng trụ có diện tích đáy B và thể tích V là: h  . B Trang4
Câu 5. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là 3V 3h V h A. B  . B. B  . C. B  . D. B  . h V h V Lờigiải Chọn C V
Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là: B  . h
Câu 6. Thể tích khối lăng trụ có diện tích đáy B và có chiều cao 2h là A. V  2 . B h . B. V  . B h .
C. V  6Bh .
D. V  3Bh . Lờigiải Chọn A
Thể tích khối lăng trụ có diện tích đáy B và có chiều cao 2h là: V  . B 2h  2 . B h .
Câu 7. Thể tích khối lăng trụ như thế nào khi tăng diện tích đáy lên 2 lần và giảm chiều cao 2 lần?
A. tăng lên 2 lần.
B. giảm 4 lần.
C. tăng lên 4 lần. D. giữ nguyên. Lờigiải Chọn D
Thể tích khối lăng trụ ban đầu có diện tích đáy B và có chiều cao h là: V  . B h . h
Thể tích khối lăng trụ sau tăng diện tích đáy lên 2 lần và giảm chiều cao 2 lần: V  2 . B  . B h . 2
Câu 8. Chiều cao của khối lăng trụ có diện tích đáy B và thể tích 3V là 6V V V 3V A. h  . B. h  . C. h  . D. h  . B 3B B B Lờigiải Chọn D 3V
Chiều cao của khối lăng trụ có diện tích đáy B và thể tích 3V là: h  . B
Câu 9. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao 3h là 3V 3h V V A. B  . B. B  . C. B  . D. B  . h V 3h h Lờigiải Chọn C V
Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao 3h là: B  . 3h
Câu 10. Cho khối lập phương có cạnh bằng 6 . Thể tích của khối lập phương đã cho bằng A. 216 . B. 18 . C. 36 . D. 72 . Lờigiải Trang5 Chọn A
Thể tích khối lập phương có cạnh bằng 6 là 3 V  6  216 .
Câu 11. Cho khối hộp chữ nhật có 3 kích thước 3; 4; 5 . Thể tích của khối hộp đã cho bằng? A. 10 . B. 20 . C. 12 . D. 60 . Lờigiải Chọn D.
Thể tích của khối hộp đã cho bằng V  3.4.5  60
Câu 12. Thể tích khối lăng trụ như thế nào khi tăng diện tích đáy lên 4 lần và tăng chiều cao 4 lần?
A. tăng lên 16 lần.
B. giảm 8 lần.
C. tăng lên 4 lần. D. giữ nguyên. Lời giải Chọn A
Thể tích khối lăng trụ ban đầu có diện tích đáy B và có chiều cao h là: V  . B h .
Thể tích khối lăng trụ sau khi tăng diện tích đáy lên 4 lần và tăng chiều cao 4 lần: V  4 . B 4h 16 . B h .
Câu 13. Cho khối hộp hình chữ nhật có ba kích thước 2; 4; 6 . Thể tích của khối hộp đã cho bằng A. 16 . B. 12 . C. 48 . D. 8 . Lờigiải Chọn C
Thể tích của khối hộp đã cho bằng 2.4.6  48.
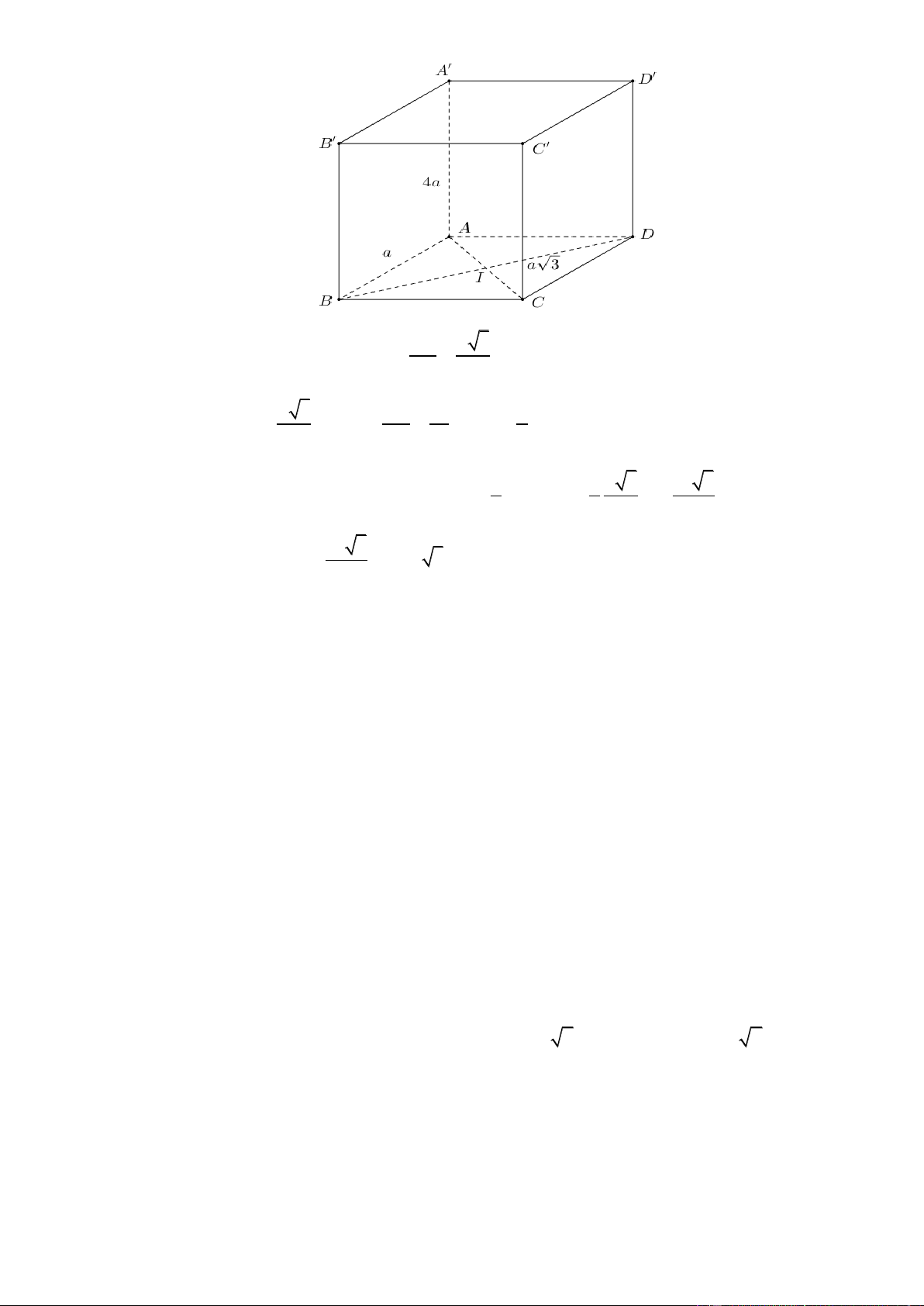
Câu 14. Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích của khối lăng trụ đã cho bằng 16 4 A. 3 16a B. 3 4a C. 3 a D. 3 a 3 3 Lờigiải Chọn B 2 3 V S
.h a .4a  4a . day
Câu 15. Cho khối lăng trụ có diện tích đáy bằng 2 a
3 , khoảng cách giữa hai đáy của lăng trụ bằng
a 6 . Tính thể tích V của khối lăng trụ 3 a 2 3 3a 2 A. 3 V  3a 2 B. 3 V a 2 C. V D. V  3 4 Lờigiải Chọn A
Thể tích khối lăng trụ là 2 3 V  . B h a 3.a 6  3a 2
Câu 16. Hình lập phương có độ dài đường chéo bằng 6 thì có thể tích là A. 2 2 . B. 54 2 . C. 24 3 . D. 8 . Trang6 Lờigiải Chọn C
Gọi cạnh của hình lập phương là a(a > ) 0 .
Þ đường chéo của hình lập phương là a 3 .
Theo bài ra ta có: a 3 = 6 Þ a = 2 3 .
Vậy thể tích của khối lập phương là: V = ( )3 2 3 = 24 3 .
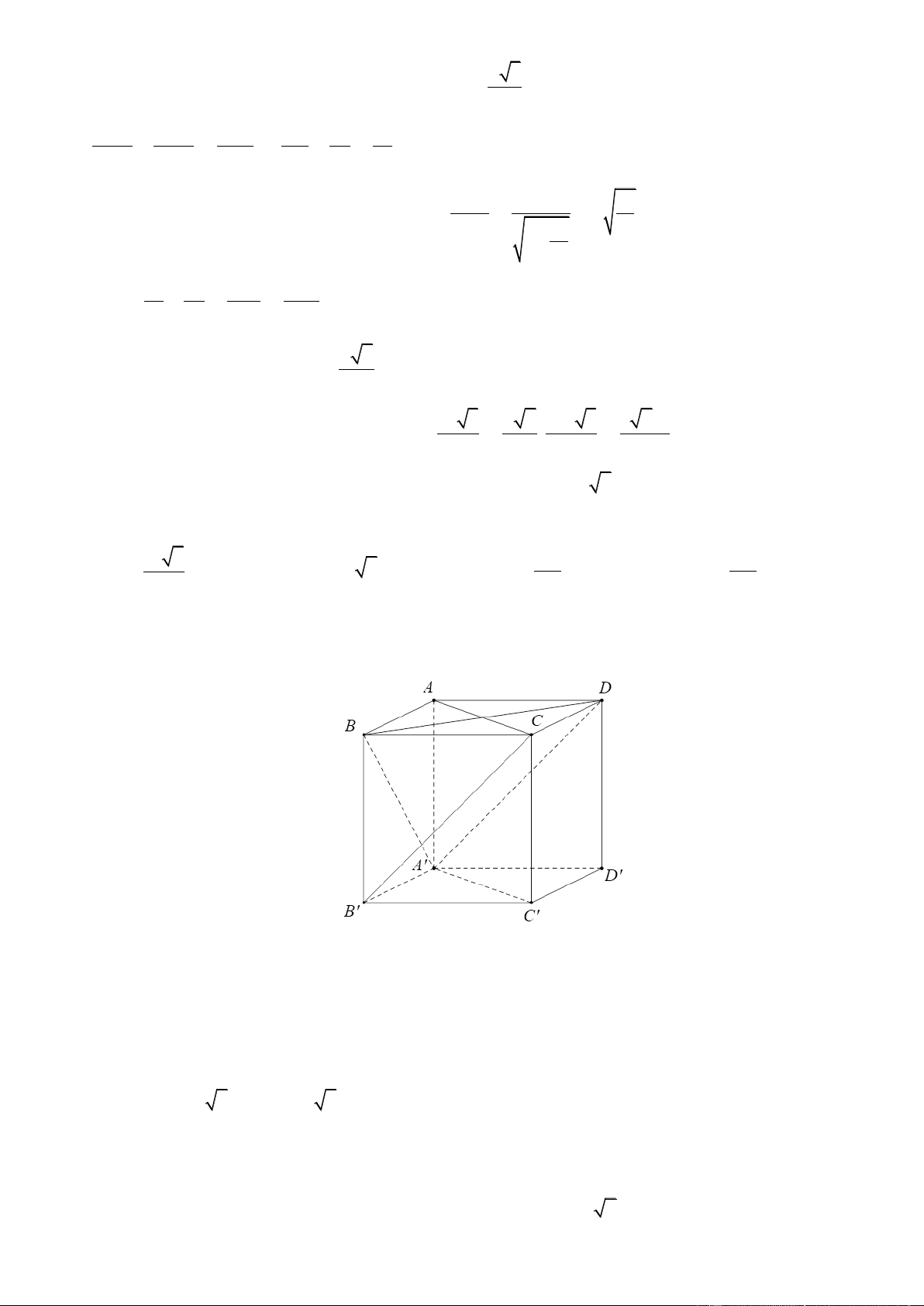
Câu 17. Tính thể tích V của khối lập phương ABC . D A BCD
  , biết AC  a 3 . 3 3 6a 1 A. 3 V a B. V C. 3
V  3 3a D. 3 V a 4 3 Lờigiải Chọn A
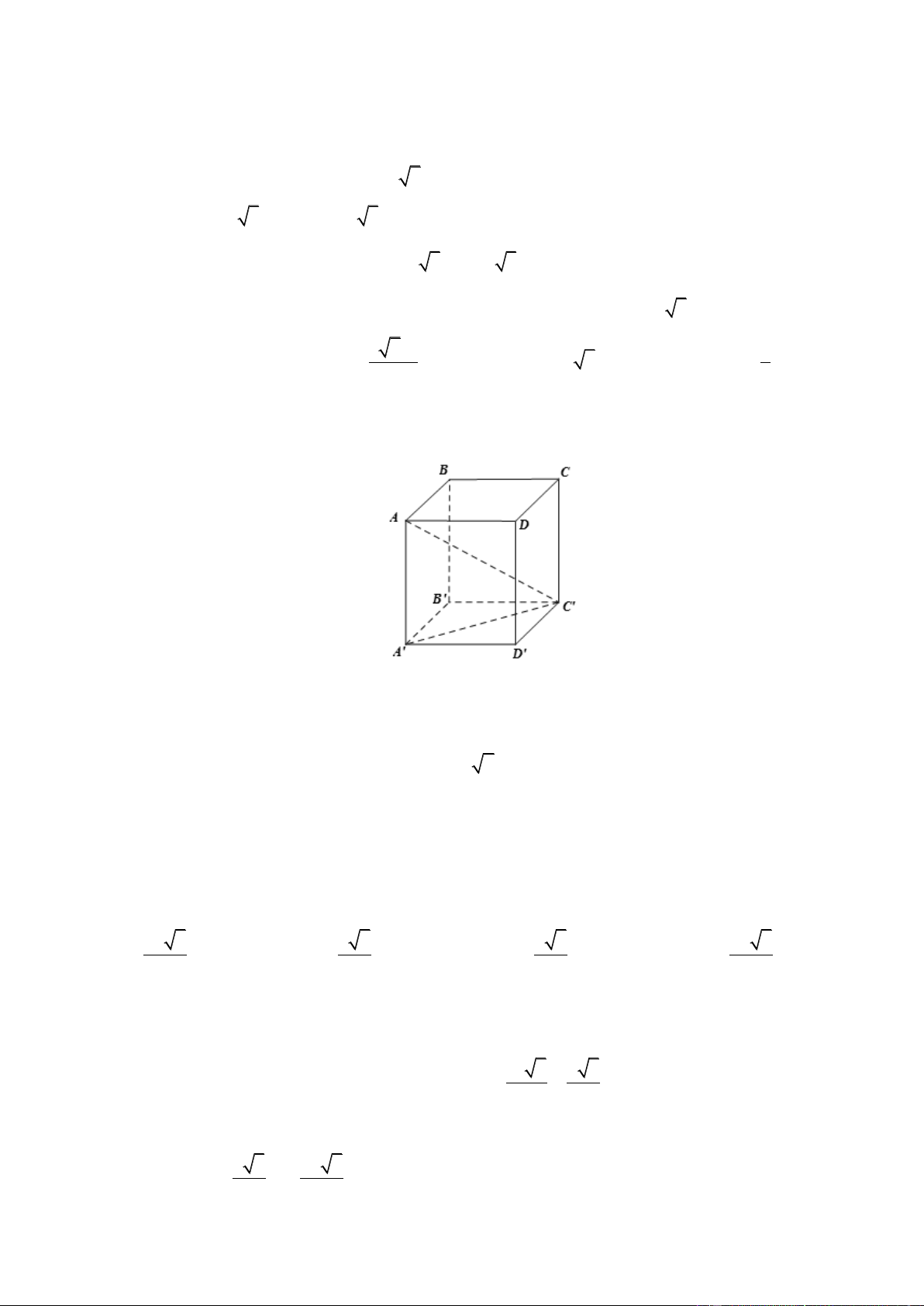
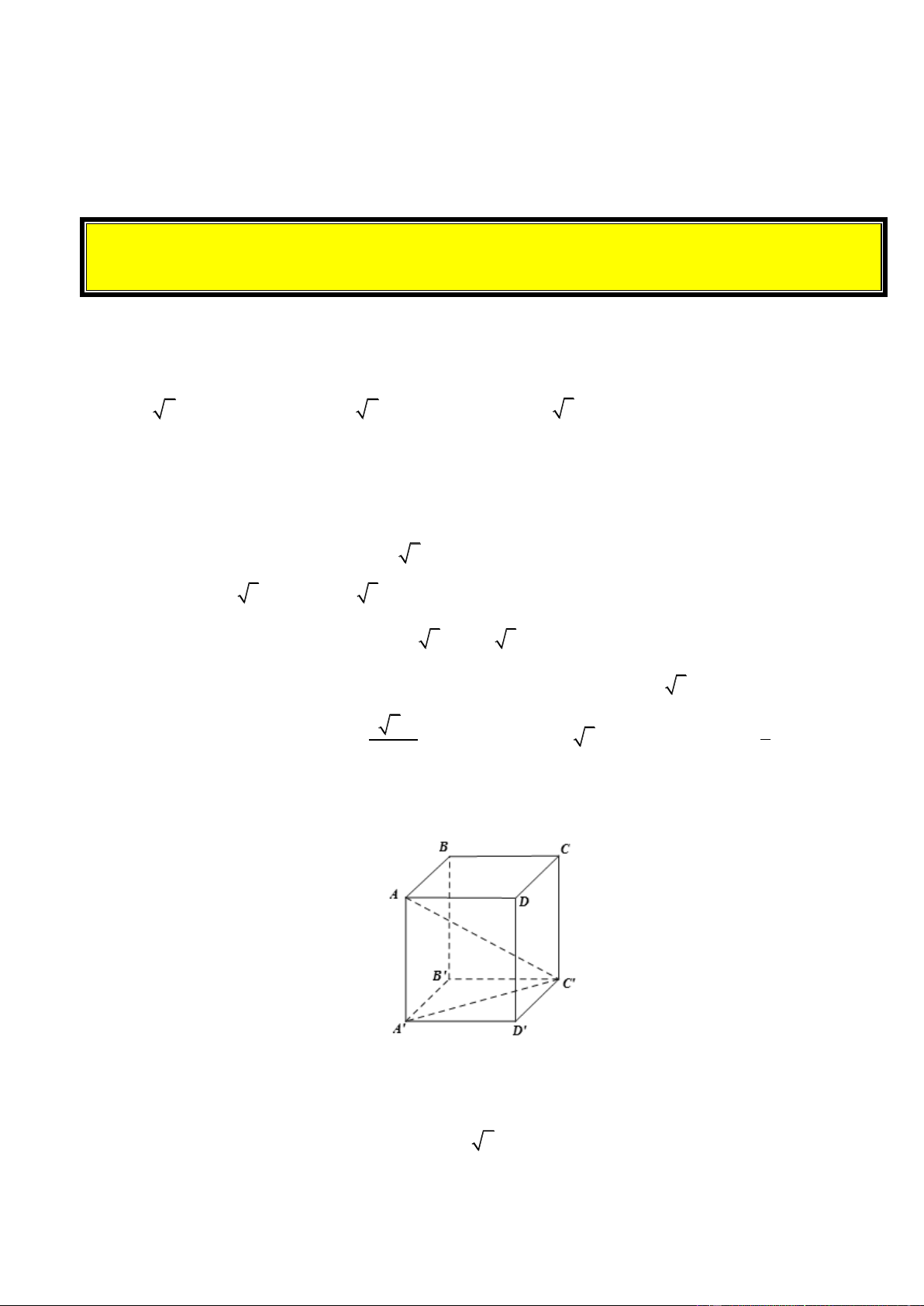
Giả sử khối lập phương có cạnh bằng ;
x x  0
Xét tam giác A' B'C ' vuông cân ta ̣i B ' ta có: 2 2 2
A 'C '  A ' B '  B 'C ' 2 2 2
x x  2x A'C '  x 2
Xét tam giác A' AC ' vuông ta ̣i A' ta có 2 2 2
AC '  A' A A'C ' 2 2 2
 3a x  2x x a
Thể tích của khối lâ ̣p phương ABC . D A BCD   là 3 V a .
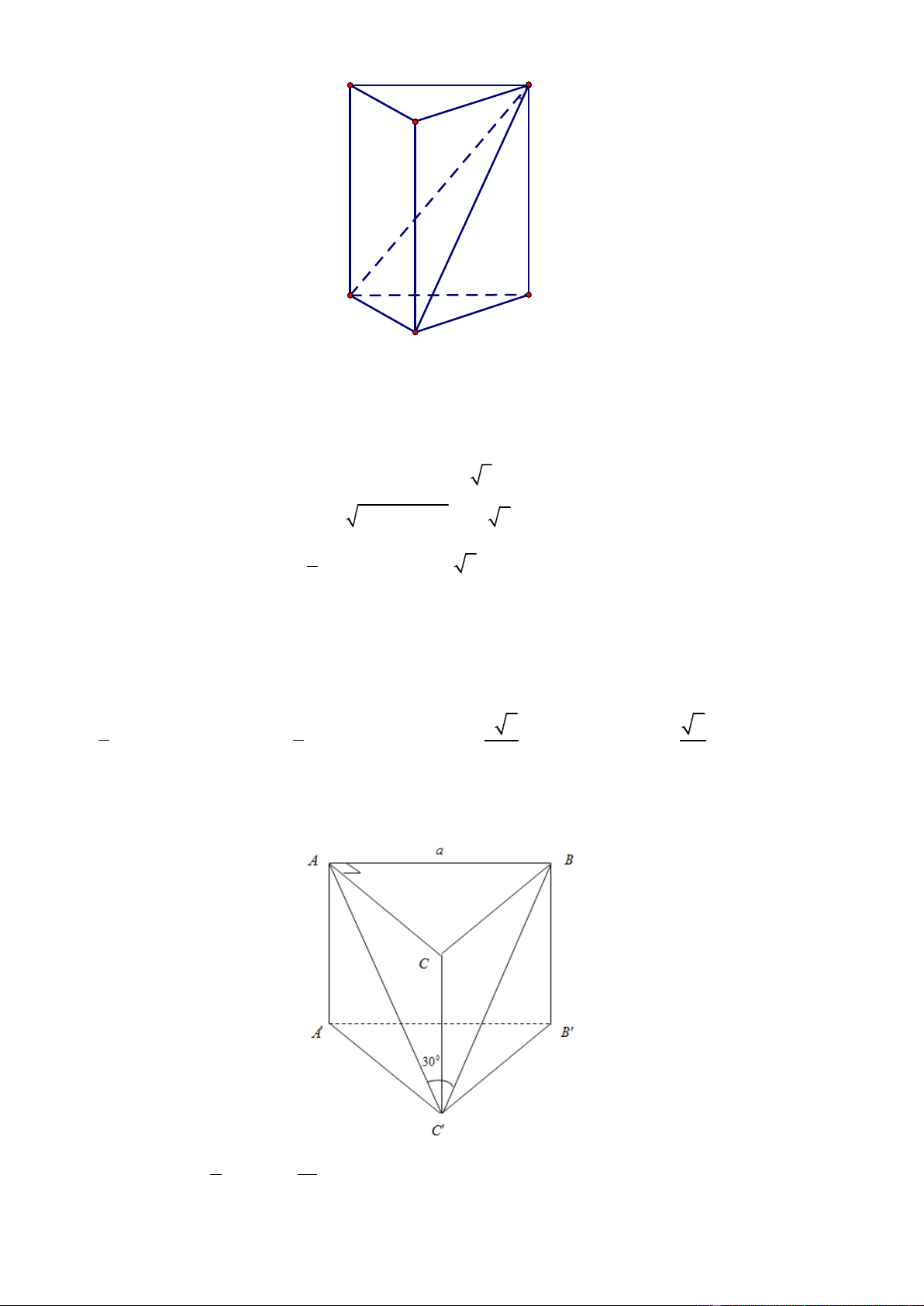
Câu 18. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng: 27 3 9 3 9 3 27 3 A. . B. . C. . D. .. 4 2 4 2 Lờigiải Chọn A 2
Đáy hình lăng trụ là tam giác đều cạnh bằng 3 3 9 3 3 nên S   . 4 4
Chiều cao của hình lăng trụ bằng h  3 Thể tích 9 3 27 3
V S.h  .3  . 4 4 Trang7
Câu 19. Cho khối hộp chữ nhật có cạnh bên bằng 5 , đáy là hình chữ nhật có diện tích bằng 16 . Hỏi thể
tích khối hộp chữ nhật bằng: 80 A. 21 . B. 64 . C. 80 . D. . 3 Lờigiải Chọn C
Khối hộp chữ nhật có cạnh bên bằng 5 nên có chiều cao h = 5.
Thể tích khối lăng trụ là: V = S .h = 16.5 = 80 . ABCD
Câu 20. Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích của khối lăng trụ đã cho bằng 16 4 A. 3 16a B. 3 4a C. 3 a D. 3 a 3 3 Lờigiải Chọn B 2 3 V S
.h a .4a  4a . day
Câu 21. Cho khối lăng trụ có diện tích đáy bằng 2 a
3 , khoảng cách giữa hai đáy của lăng trụ bằng
a 6 . Tính thể tích V của khối lăng trụ 3 a 2 3 3a 2 A. 3 V  3a 2 B. 3 V a 2 C. V D. V  3 4 Lờigiải Chọn A
Thể tích khối lăng trụ là 2 3 V  . B h a 3.a 6  3a 2 Trang8 DẠNG 2
THỂ TÍCH KHỐI LĂNG TRỤ ĐỨNG
MỨC ĐỘ TRUNG BÌNH
Câu 22. Hình lập phương có độ dài đường chéo bằng 6 thì có thể tích là A. 2 2 . B. 54 2 . C. 24 3 . D. 8 . Lờigiải Chọn C
Gọi cạnh của hình lập phương là a(a > ) 0 .
Þ đường chéo của hình lập phương là a 3 .
Theo bài ra ta có: a 3 = 6 Þ a = 2 3 .
Vậy thể tích của khối lập phương là: V = ( )3 2 3 = 24 3 .
Câu 23. Tính thể tích V của khối lập phương ABC . D A BCD
  , biết AC  a 3 . 3 3 6a 1 A. 3 V a B. V C. 3
V  3 3a D. 3 V a 4 3 Lờigiải Chọn A
Giả sử khối lập phương có cạnh bằng ;
x x  0
Xét tam giác A' B'C ' vuông cân ta ̣i B ' ta có: 2 2 2
A 'C '  A ' B '  B 'C ' 2 2 2
x x  2x A'C '  x 2
Xét tam giác A' AC ' vuông ta ̣i A' ta có 2 2 2
AC '  A' A A'C ' 2 2 2
 3a x  2x x a Trang9
Thể tích của khối lâ ̣p phương ABC . D A BCD   là 3 V a .
Câu 24. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V B. V C. V D. V  12 2 4 6 Lờigiải Chọn C h a 3  a 3 2   V  . 3 h S a  . S  4  4
Câu 25. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng: 27 3 9 3 9 3 27 3 A. . B. . C. . D. .. 4 2 4 2 Lờigiải Chọn A 2
Đáy hình lăng trụ là tam giác đều cạnh bằng 3 3 9 3 3 nên S   . 4 4
Chiều cao của hình lăng trụ bằng h  3 Thể tích 9 3 27 3
V S.h  .3  . 4 4
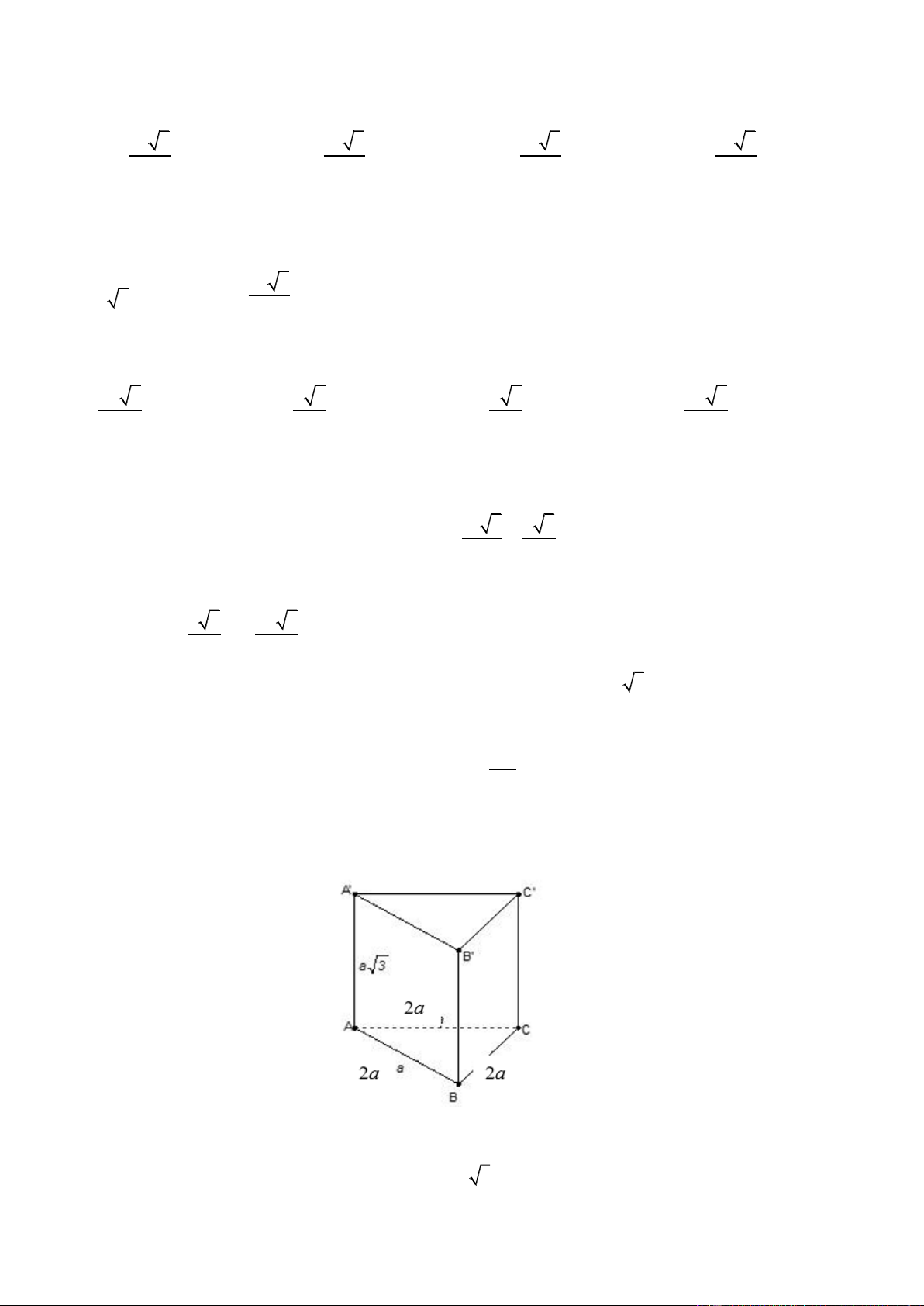
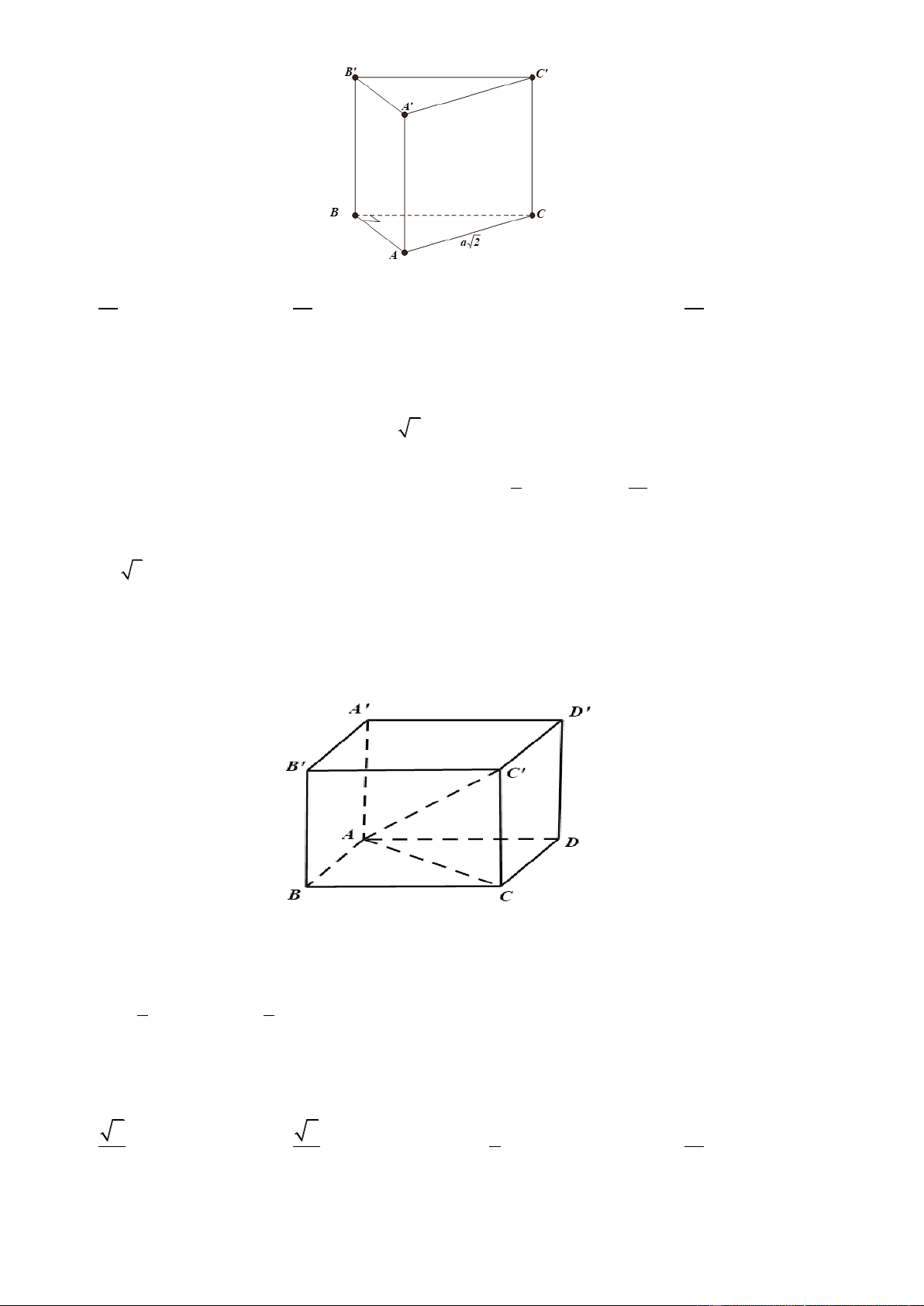
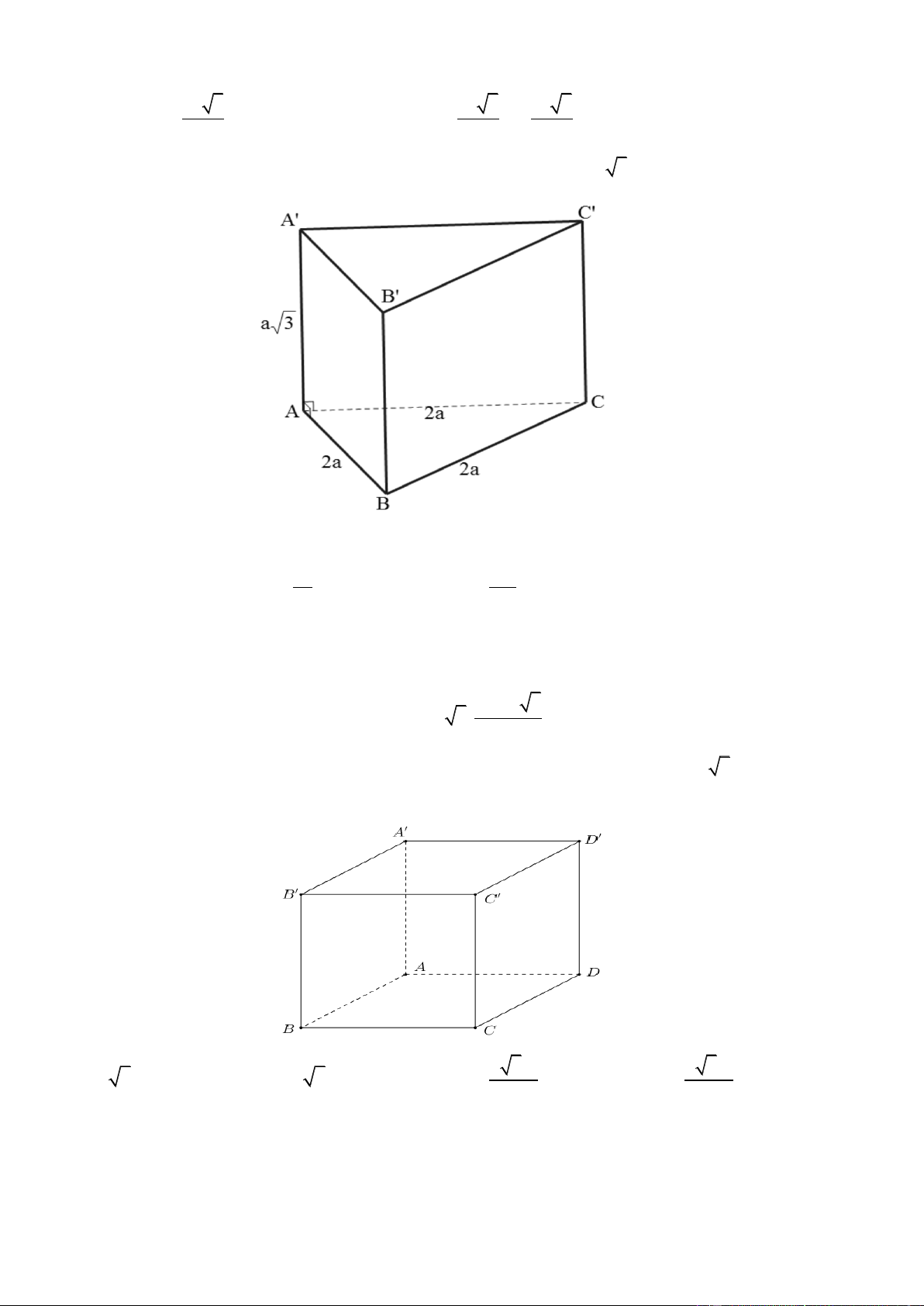
Câu 26. Cho hình lăng trụ tam giác đều ABC. A’B’C’ có AB  2 ,
a AA'  a 3 . Tính thể tích khối lăng
trụ ABC. A’B’C’. 3 3a 3 a A. 3 3a . B. 3 a . C. . D. . 4 4 Lờigiải Chọn A
Lăng trụ ABC. A’B’C’ là lăng trụ đều nên ABC
là tam giác đều và AA'   ABC  .
• AA'   ABC  chiều cao của lăng trụ là: h AA'  a 3 . • ABC
là tam giác đều có AB  2a ABC  diện tích là: Trang10
AB2 3 2a2 3 2 S    a 3 . ABC  4 4
 Thể tích khối lăng trụ là: 2 3 V  . h S
a 3.a 3  3a . S. ABC ABC
Câu 27. Cho hình lập phương ABC . D A BCD
  có diện tích mặt chéo ACC A   bằng 2 2 2a . Thể tích
của khối lập phương ABC . D A BCD   là: 3 a 3 A. . B. 3 a . C. 3 2a 2 . D. 3 2a 3 . 3 Lờigiải Chọn C
Giả sử hình lập phương có cạnh bằng x x  0 . Xét ABC  vuông tại B có: 2 2 2 2 AC AB BC
x x x 2 Ta có 2 S         AA .AC . x x 2 2 2a x a 2 . ACC A Vậy V       a a . A B C D  23 3 2 2 ABCD.
Câu 28. Cho hình lập phương 2 ABC . D A BCD
  có diện tích tam giác ACD bằng a 3 . Tính thể tích V
của hình lập phương. A. 3
V  3 3a . B. 3
V  2 2a . C. 3
V a . D. 3
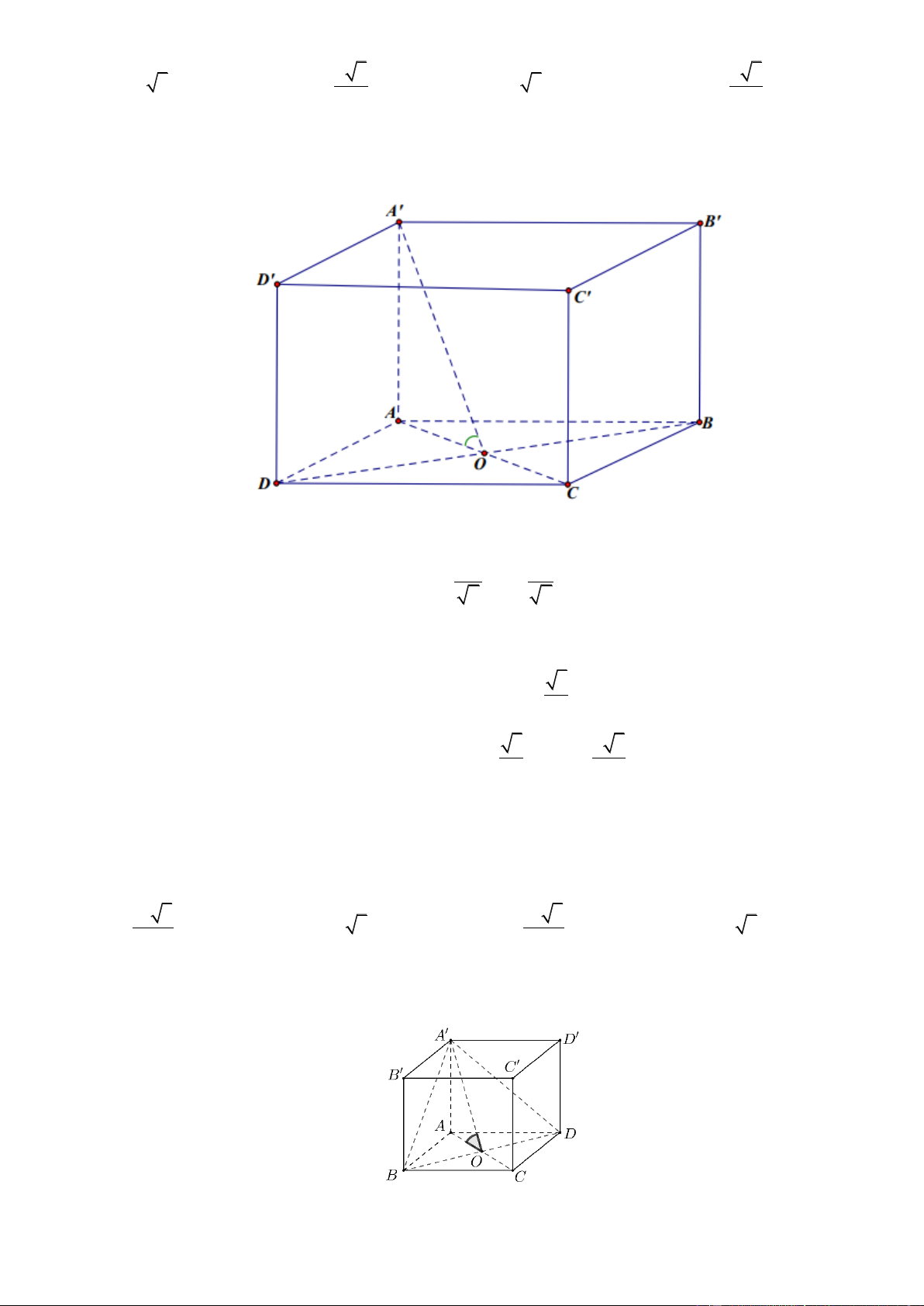
V  8a . Lờigiải Chọn B Trang11 A' D' B' C' D A O B C
Giả sử cạnh của hình lập phương có độ dài là x . x 6
Ta có AC x 2 , 2 2
OD  OD A A   2 2 Diệntíchtamgiác 1 1 x 6 x 3 ACD là S      OD .AC x 2. . ACD 2 2 2 2 2 2 Khi đó, ta có x 3 x 2 2 a 3   a   x a 2 . 2 2 Vậy 3 3
V x  2a 2 .
Câu 29. Cho hình lập phương ABC . D A BCD
  có diện tích tam giác ACD bằng 2 a 3 . Tính thể tích
V của hình lập phương. A. 3
V  3 3a . B. 3
V  2 2a . C. 3
V a . D. 3
V  8a . Lờigiải Chọn B A' D' B' C' D A O B C
Giả sử cạnh của hình lập phương có độ dài là x . x 6
Ta có AC x 2 , 2 2
OD  OD A A   2 2 Diện tích tam giác 1 1 x 6 x 3 ACD là S      OD .AC x 2. . ACD 2 2 2 2 2 2 Khi đó, ta có x 3 x 2 2 a 3   a   x a 2 . 2 2 Vậy 3 3
V x  2a 2 . Trang12
Câu 30. Cho khối hộp chữ nhật ABC . D A BCD
  có AB  3, AD  4 , A A
  5. Thể tích khối hộp đã cho bằng: A. 20 . B. 60 . C. 30 . D. 16 . Lờigiải Chọn B A D B C A' D' B' C' Ta có SA . B AD  3.4  12 . ABCD
Thể tích khối hộp đã cho bằng V         A . A S 5.12 60 . ABCD. A B C D ABCD
Câu 31. Cho khối hộp chữ nhật ABC . D A BCD
  có AB  3, AD  4 , A C
 13. Thể tích khối hộp đã cho bằng: A. 156. B. 144 . C. 120. D. 116 . Lờigiải Chọn B A D B C A' D' B' C' Ta có SA . B AD  3.4  12 ; ABCD 2 2 2 AA 
AC AC A C    2 2 AB BC  2    2 2 13 3  4   12 .
Thể tích khối hộp đã cho bằng V         A . A S 12.12 144 . ABCD. A B C D ABCD
Câu 32. Cho khối hộp chữ nhật ABC . D A BCD
  có đáy AD  3, AB  4 , đường chéo AB¢ của mặt bên (ABB A ¢ )
¢ có độ dài bằng 5 . Tính thể tích của khối hộp đã cho.
A.V = 36.
B.V = 45.
C.V = 18 .
D.V = 48. Lờigiải Chọn A Trang13 D A C B 5 D' A' C' 3 B' .
Xét tam giác vuông AA B ¢ ¢ có 2 2 AA¢= AB¢ - A B
¢ ¢ = 3 và có diện tích đáy S = 3.4 = 12 ABCD
Thể tích của khối hộp đã cho là V 12.3 36 ABCD. A B ¢ C ¢ D ¢ ¢ = = .
Câu 33. Cho khối hộp chữ nhật ABC . D A B ¢ C ¢ D
¢ ¢có AB = a , AC = 2a , biết tam giác A A ¢ C là tam
giác vuông cân tại A . Thể tích khối hộp đã cho bằng: 3 2 3a 3 3 3a A. . B. 3 2 3a . C. 3 3a . D. . 3 2 Lờigiải Chọn B A D B C A' D' B' C' Ta có: 2 2 2 2 AD = AC - AB =
4a - a = a 3 Þ 2 S = A . B AD = . a a 3 = a 3 . ABCD Tam giác A A
¢ C vuông cân tại A nên A A ¢ = AC = 2a .
Thể tích khối hộp đã cho là 2 3 V = A¢ . A S = 2 . a a 3 = 2 3a . ABCD. A B ¢ C ¢ D ¢ ¢ ABCD
Câu 34. Cho khối hộp chữ nhật ABC . D A B ¢ C ¢ D
¢ ¢có AB = 3a , AD = 4a, biết tứ giác BB D ¢ D ¢ là hình
vuông. Thể tích khối hộp đã cho bằng: A. 3 20a . B. 3 60a . C. 3 12a . D. 3 30a . Lờigiải Chọn B Trang14 A D B C A' D' B' C' Diện tích đáy 2 SA . B AD  3 .
a 4a 12a . ABCD 2 2 Ta có 2 2 BD = AB + AD =
(3a) + (4a) = 5a Do tứ giác BB D ¢ D
¢ là hình vuông nên có BB¢= BD = 5a .
Thể tích khối hộp đã cho là 2 3 V = BB .S ¢ = 5 .
a 12a = 60a . ABC . D A B ¢ C ¢ D ¢ ¢ ABCD
Câu 35. Cho khối hộp chữ nhật ABC . D A B ¢ C ¢ D
¢ ¢có AB = 3a , BC = 4a , biết tam giác A B ¢ C là tam
giác vuông cân tại B . Thể tích khối hộp đã cho bằng: A. 3 20a . B. 3 12a 7 . C. 3 4a 7 . D. 3 60a . Lờigiải Chọn B A' D' B' C' A D B C Diện tích đáy 2 SA . B AD  3 .
a 4a 12a . ABCD Do tam giác A B
¢ C là tam giác vuông cân tại B nên có A B ¢ = BC = 4a . 2 2 Ta có 2 2 AA¢= A B
¢ - AB = (4a) - (3a) = a 7
Thể tích khối hộp đã cho là 2 3 V = AA .S ¢
= a 7.12a = 12a 7 . ABCD. A B ¢ C ¢ D ¢ ¢ ABCD
Câu 36. Cho khối hộp chữ nhật ABC . D A BCD
  có đáy AB  3, AD  4 . Biết đường thẳng AC tạo
với mặt phẳng  ABCD góc 45. Thể tích khối hộp đã cho bằng: A. 60 . B. 48 . C. 30 . D. 20 . Lờigiải Chọn A Trang15 A D B C A' D' B' C' Diện tích đáy SA . B AD  3.4  12 . ABCD
Ta có AA   ABCD   AC  ABCD  ,  AC A    45; 2 2 A C    A B    B C    5  A A   A C  .tan 45  5 .
Thể tích khối hộp đã cho là V         S .AA 12.5 60 . ABCD. A B C D ABCD
Câu 37. Cho khối hộp chữ nhật ABC . D A BCD
  có đáy AB  3, AD  4 . Biết đường thẳng AB tạo
với mặt phẳng  ABCD góc 45. Thể tích khối hộp đã cho bằng: A. 36 . B. 48 . C. 30 . D. 20 . Lờigiải Chọn A Diện tích đáy SA . B AD  3.4  12 . ABCD
Ta có AA   ABCD   AB  ABCD  ,  AB A
   45 nên A A   A B  .tan 45  3.
Thể tích khối hộp đã cho là V         S .AA 12.3 36 . ABCD. A B C D ABCD
Câu 38. Cho hình hộp chữ nhật ABC . D A BCD
  có AB  3a, AD  4a . Đường thẳng AC  tạo với mặt
phẳng (AB ) BA một góc 0
30 . Thể tích khối hộp chữ nhật đã cho bằng: A. 3 6a 39 . B. 3 a 39 . C. 3 18a 39 . D. 3 2a 39 . Lờigiải Chọn A Trang16 A' D' B' C' A D B C Diện tích đáy 2 SA . B AD  3 .
a 4a 12a . ABCDBC AB  Ta có 
BC ABBA  A C   ABB A    0 ;  CA B   30 BC  ( ) BB Khi đó A .
B tan 30  BC  4a A B   4a 3 . Do vậy 2 2 A A   A B
  AB a 39 .
Vậy thể tích khối hộp chữ nhật ABC . D A BCD   là 3 V        A . A S 6a 39 . ABCD.A B C D ABCD
Câu 39. Cho hình hộp chữ nhật có diện tích ba mặt lần lượt là 2 2 2
6a ;8a ;12a . Tính thể tích khối hộp chữ nhật đó. A. 3 8a . B. 3 12a . C. 3 24a . D. 3 18a Lờigiải Chọn C
Gọi ba kích thước của hình hộp chữ nhật là ; x ;
y z , điều kiện: x; y; z  0 .
Diện tích ba mặt của hình hộp chữ nhật lần lượt là x ; y yz; zx . Theo giả thiết ta có: 2 2 2 2 6 3 x . y y .
z zx  6a .8a .12a  (xyz)  576a xyz  24a .
Vậy thể tích khối hộp chữ nhật là: 3
V xyz  24a .
Câu 40. Tính thể tích V của khối chữ nhật ABC . D A BCD
  biết rằng AB a , AD  2a , AC  a 14 . 3 a 14 A. 3 V a 5 . B. V  . C. 3
V  2a . D. 3 V  6a . 3 Lờigiải Chọn D Trang17 A ' D ' C ' B' a 14 2a A a D B C Ta có: 2 2 2 2
AC  AB AD AA 2 2 2
AA  AC  AB AD 2 2 2
AA  14a  4a a  3a .
Thể tích khối hộp chữ nhật ABC . D A BCD   là 3 V  . AB .
AD AA  6a .
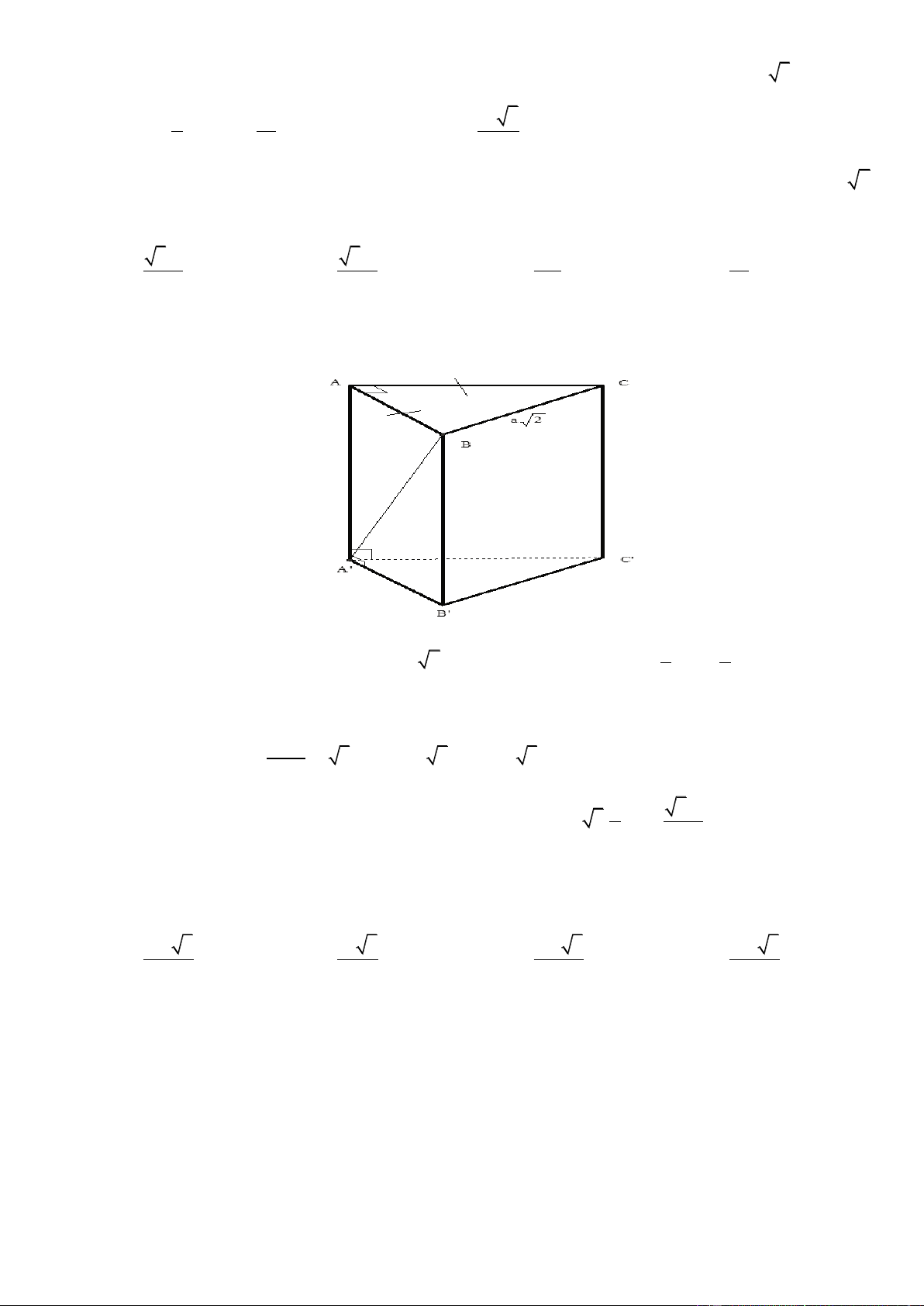
Câu 41. Cho khối lăng trụ đứng AB . C A B ¢ C
¢ ¢ có đáy là tam giác đều cạnh a và AA  2a . Thể tích của
khối lăng trụ đã cho bằng 3 3a 3 3a 3 3a A. . B. . C. 3 3a . D. . 2 6 3 Lờigiải Chọn A 2 a 3
Tam giác ABC đều cạnh a nên S = DABC 4
Do khối lăng trụ AB . C A B ¢ C
¢ ¢ là lăng trụ đứng nên đường cao của lăng trụ là AA  2a 2 3
Thể tích khối lăng trụ là a 3 3a V = AA .S ¢ = 2 . a = . DABC 4 2
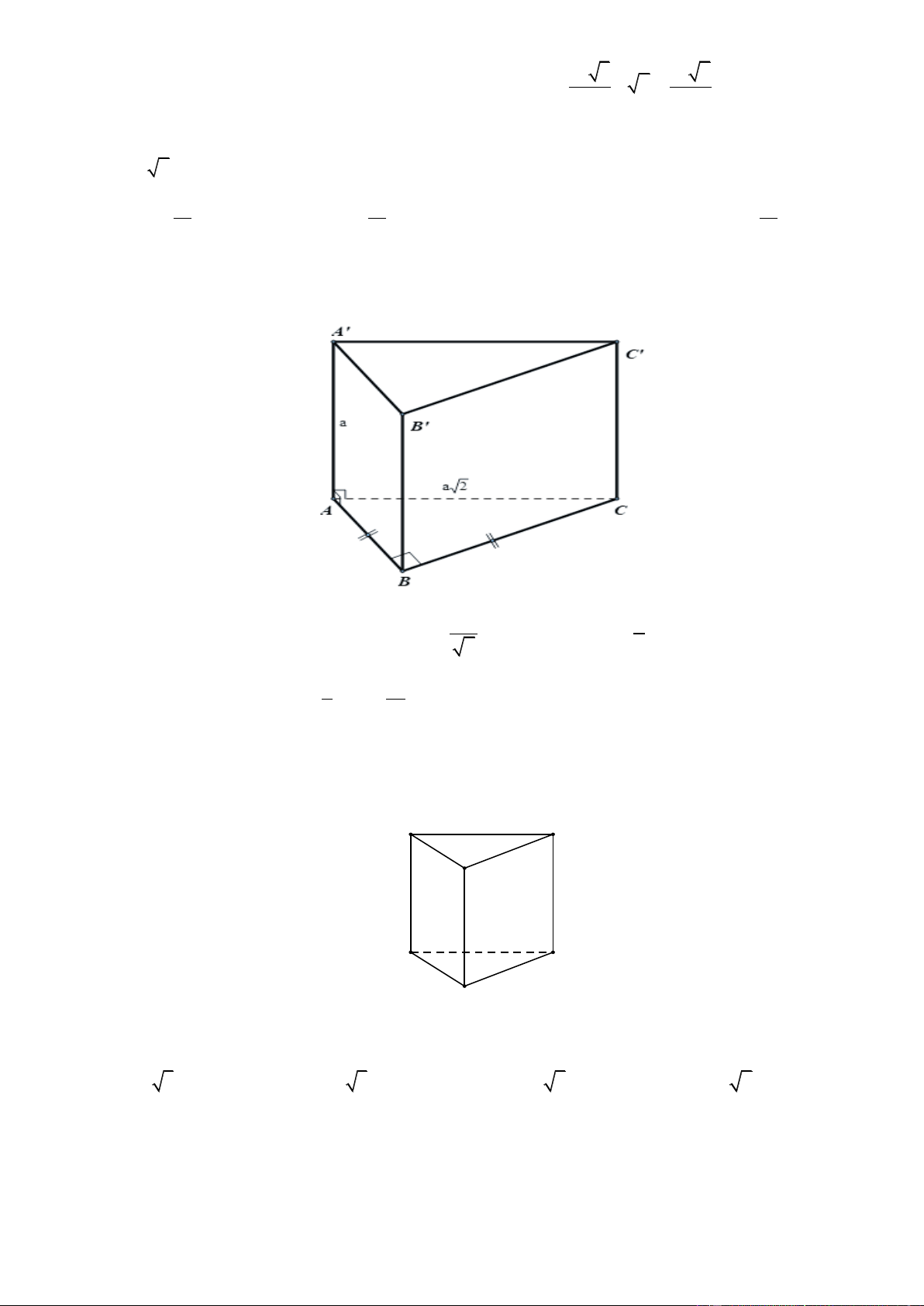
Câu 42. Cho khối lăng trụ đứng AB . C A BC  có B C
  3a , đáy ABC là tam giác vuông cân tại B và
AC a 2 . Tính thể tích V của khối lăng trụ đứng AB . C A BC  . 3 2a 3 a A. 3 V  2a . B. 3 V  2a . C. V  . D. V  . 3 6 2 Lờigiải Chọn C Trang18 Đáy AC a 2
ABC là tam giác vuông cân tại B và AC a 2  BC AC    a . 2 2 BB C
 vuông tại B BB  B C  2 2 2 2
BC  9a a  2a 2 . 3 1 1 1 2a 2 V   BB S
 2a 2  a   . 3 ABC 3 2 3 3
Vậy thể tích của khối lăng trụ đứng 2a AB . C A BC   là V  . 3
Câu 43. Cho hình lăng trụ đứng AB . C A B ¢ C
¢ ¢ có đáy ABC là tam giác vuông tại A , biết AB = a ,
AC = 2a và A B
¢ = 3a . Tính thể tích của khối lăng trụ AB . C A B ¢ C ¢ ¢. 3 2 2a 3 5a A. . B. . C. 3 5a . D. 3 2 2a . 3 3 Lờigiải Chọn D A' C' 3a B' 2a A C a B + Diện tích đáy là 1 1 S = A . B AC = . .2 a a 2 = a . ABC 2 2
+ Tam giác ABA¢ vuông tại A nên có 2 2 AA¢= A B ¢ - AB = ( )2 2
3a - a = 2a 2 .
+ Thể tích cần tính là: V = S .AA¢ 2 = a .2a 2 3 = 2 2a . ABC Trang19
Câu 44. Cho hình lăng trụ đứng ABC . D A B ¢ C ¢ D
¢ ¢ có đáy ABCD là hình chữ nhật, AB = a , AD = a 2
, AB¢= a 5 . Tính theo a thể tích V của khối lăng trụ đã cho. 3 2a 2 A. 3 V = a 2 . B. 3 V = 2a 2 . C. 3 V = a 10 . D. V = . 3 Lờigiải Chọn B 2 S = A . B AD = . a a 2 = a 2 . ABCD
Trong tam giác ABB¢, BB¢= AB¢ - AB = (a )2 2 2 2 5 - a = 2a . Vậy 2 3 V = BB .S ¢ = 2 . a a 2 = 2a 2 . ABCD
Câu 45. Cho khối lăng trụ đứng AB . C A BC
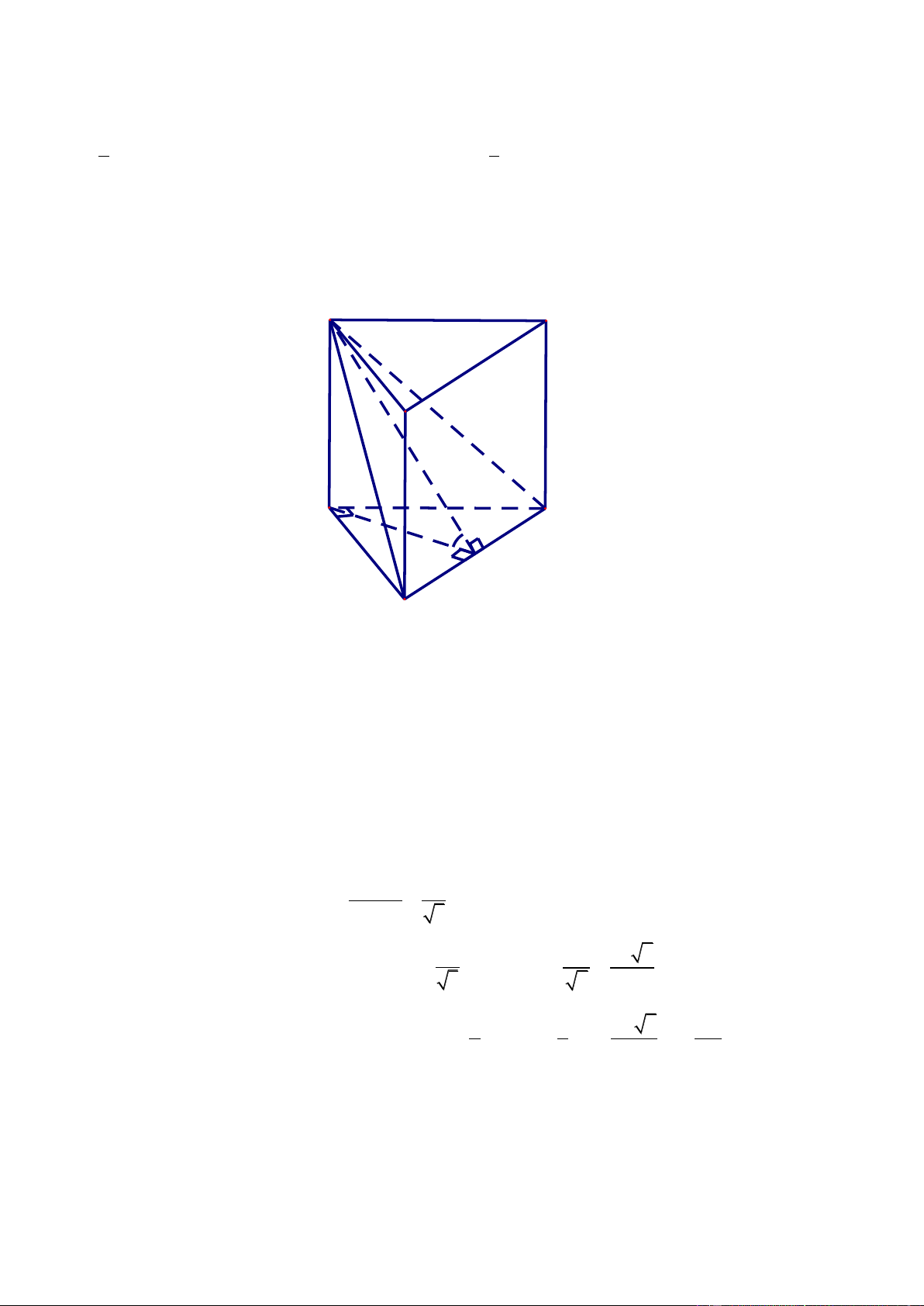
  có đáy là tam giác đều cạnh a và AA'  2a (minh họa
như hình vẽ bên dưới).
Thể tích của khối lăng trụ đã cho bằng 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 2 4 6 12 Lờigiải Chọn B 2 a 3 Ta có: S  . ABC  4 Trang20 2 3
Vậy thể tích của khối lăng trụ đã cho là: a 3 a 6 V        S .AA .a 2 . ABC.A B C ABC 4 4
Câu 46. Cho khối lăng trụ đứng AB . C A BC
  có BB  a , đáy ABC là tam giác vuông cân tại B và
AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. V B. V C. 3 V a D. V 3 2 6 Lờigiải Chọn B AC 1
Tam giác ABC vuông cân tại B AB BC   a . Suy ra: 2 Sa . ABC 2 2 3 Khi đó: 1 a 2 V        S .BB a .a ABC. A B C ABC 2 2
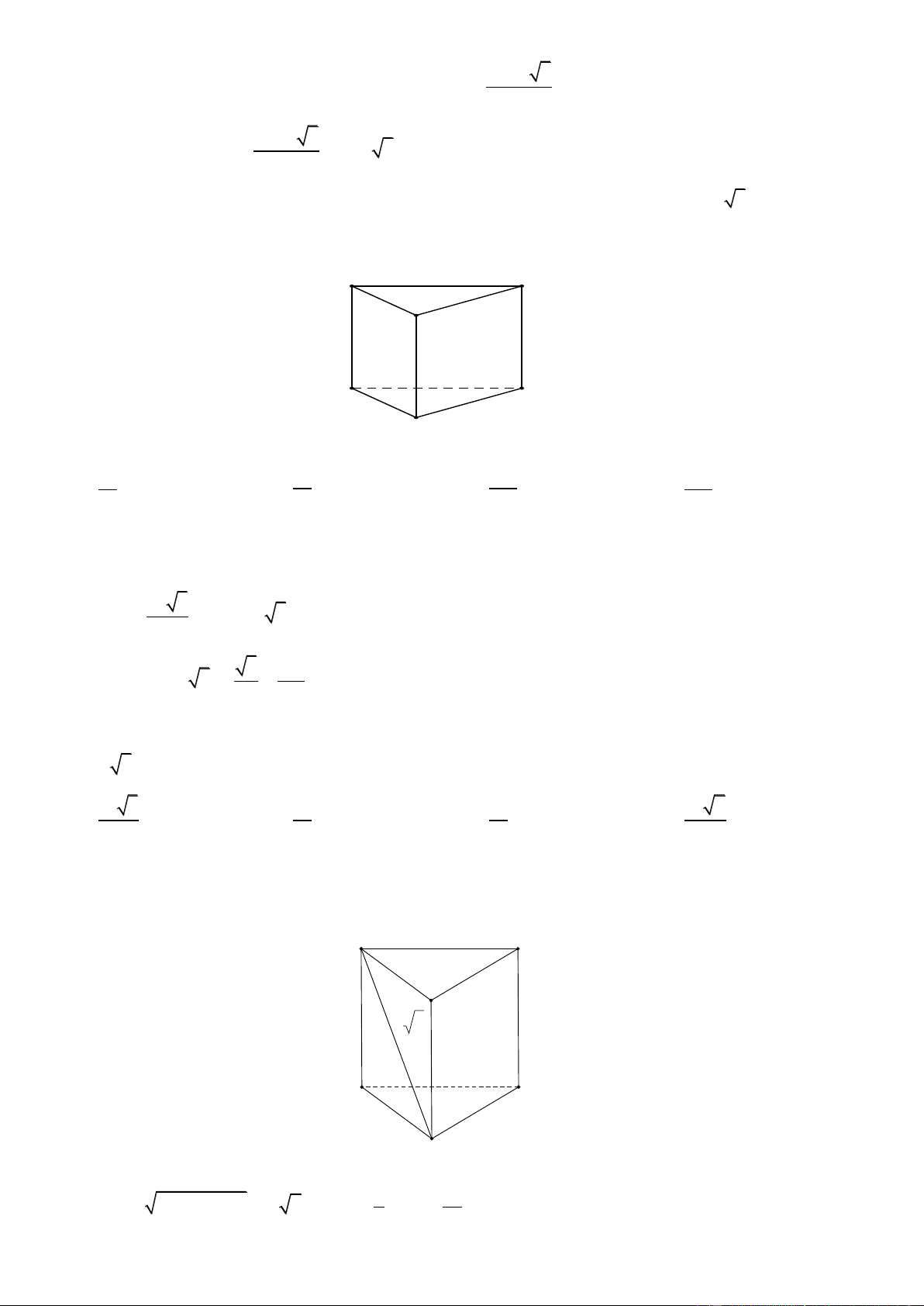
Câu 47. Cho khối lăng trụ đứng AB .
C A' B'C ' có đáy là tam giác đều cạnh 2a và AA'  3a (minh họa như hình vẽ bên). A' C' B' C A B
Thể tích của khối lăng trụ đã cho bằng A. 3 6 3a . B. 3 3 3a . C. 3 2 3a . D. 3 3a . Lờigiải Chọn B Trang21 2
Khối lăng trụ đã cho có đáy là tam giác đều có diện tích là (2a)
3 và chiều cao là AA'  3a (do là lăng 4 2
trụ đứng) nên có thể tích là (2a) 3 3
.3a  3 3a 4
Câu 48. Cho khối lăng trụ đứng AB .
C A' B 'C ' có đáy là tam giác đều cạnh a và AA '  3a (minh họa
hình vẽ bên). Thể tích khối lăng trụ đã cho bằng. A' C' B' C A B 3 3 3 a a 3a 3 3a A. . B. . C. . D. . 4 2 4 2 Lờigiải Chọn C 2 a 3 Ta có S  ; AA'  a 3 . ABC 4 3 Từ đó suy ra 3 3a 2
V a 3.a  . 4 4
Câu 49. Cho hình lăng trụ đứng AB . C A B ¢ C
¢ ¢ có đáy là tam giác vuông cân tại B , AB = a và A B
¢ = a 3 . Thể tích khối lăng trụ AB . C A B ¢ C ¢ ¢ là 3 a 3 3 a 3 a 3 a 2 A. B. C. D. 2 6 2 2 Lờigiải Chọn D C' A' B' a 3 A C a B 2 1 a Ta có 2 2 AA¢= A B ¢ - AB = a 2 , 2 S = AB = . ABC 2 2 Trang22 3
Thể tích khối lăng trụ là a 2 V = AA .S ¢ = . ABC 2
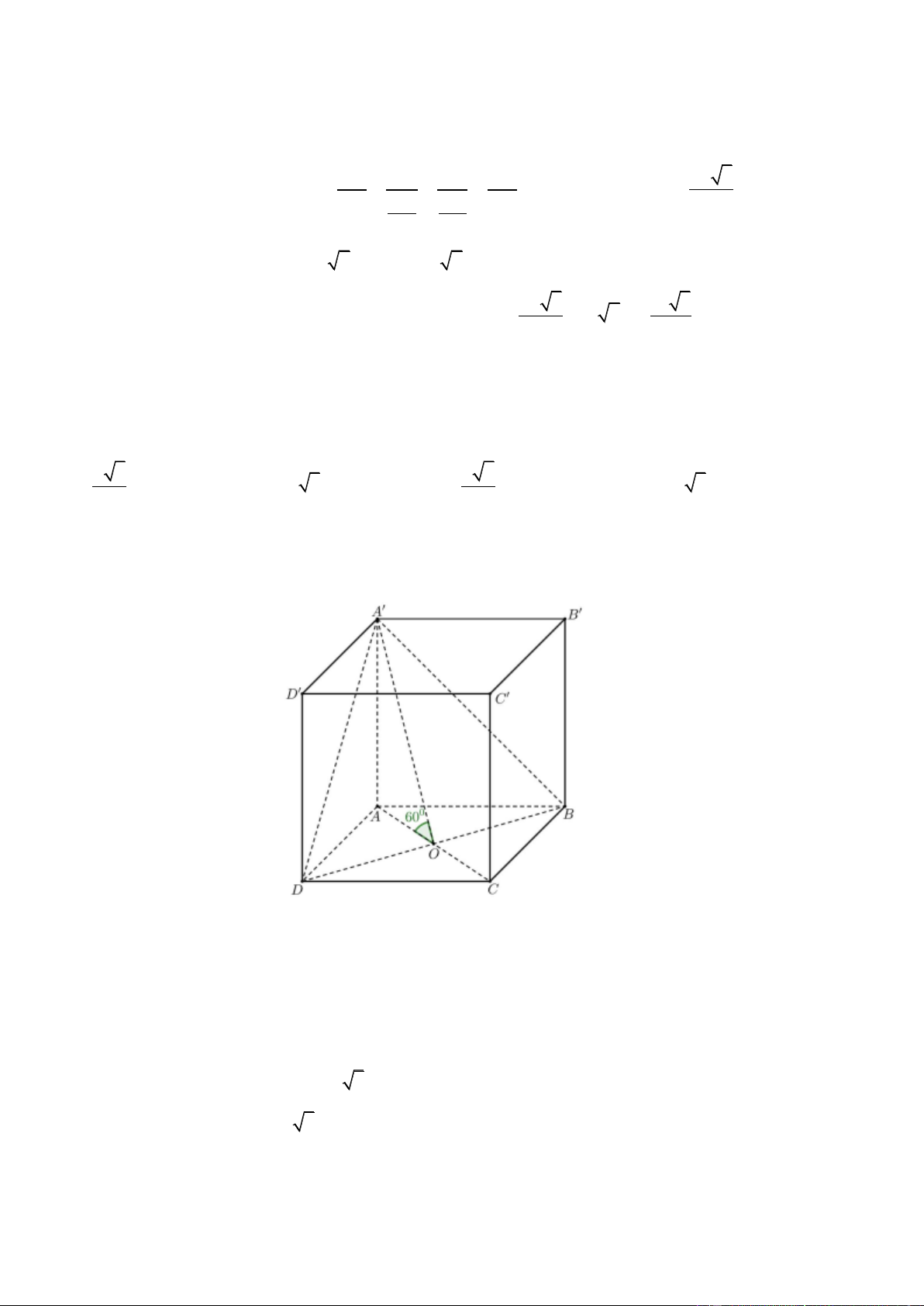
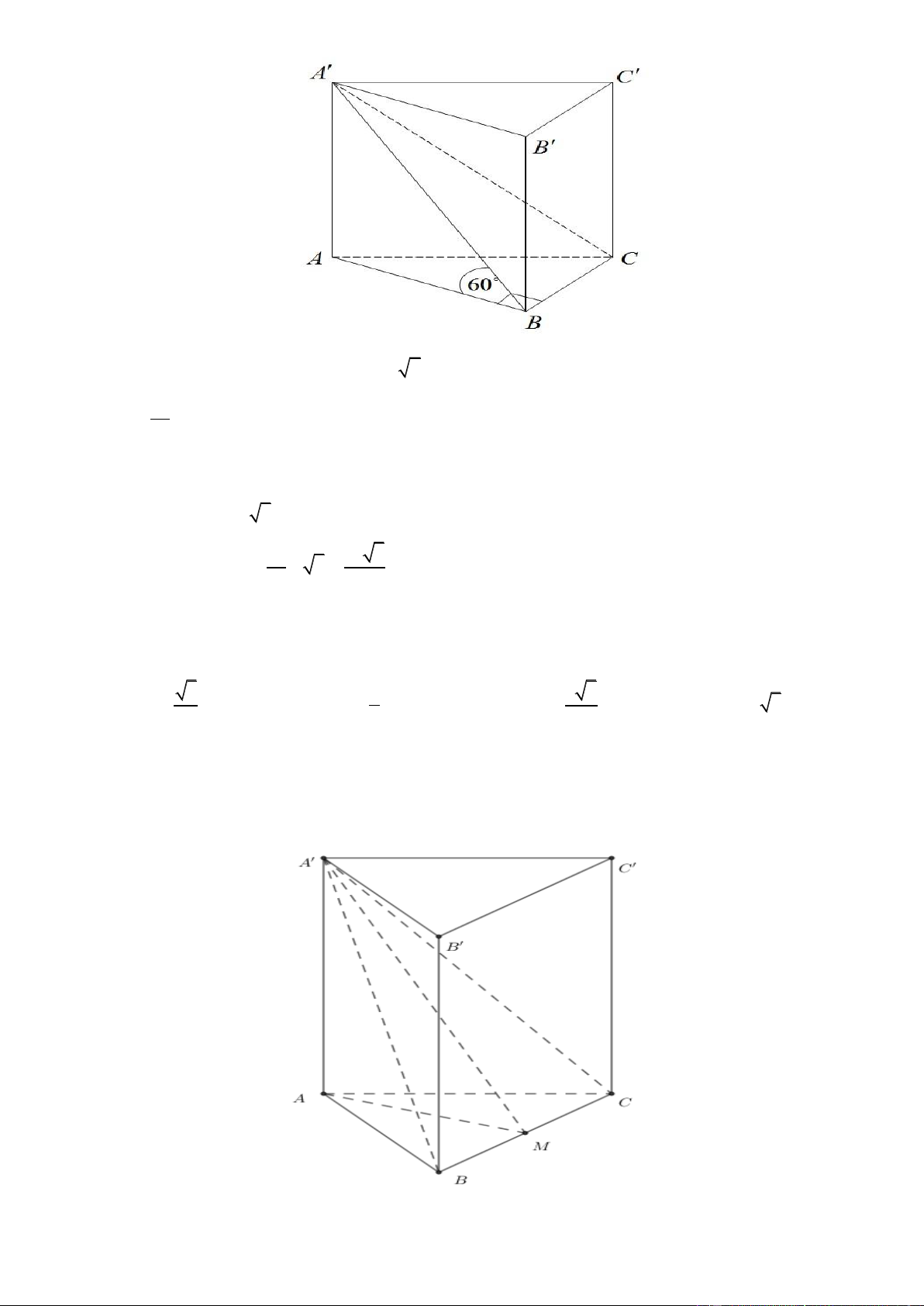
Câu 50. Cho hình lăng trụ đứng AB .
C A' B'C ' có đáy là tam giác đều cạnh a , A' B tạo với mặt phẳng đáy một góc o
60 . Thể tích khối lăng trụ AB .
C A' B'C ' bằng 3 3a 3 a 3 3a 3 3a A. . B. . C. . D. . 2 4 4 8 Lờigiải Chọn C 2
Đáy là tam giác đều cạnh a 3
a , có diện tích: S = . DABC 4 Vì AA ^ (ABC) 
Þ A BA = (A B (ABC)) o ' ' ' , = 60 , suy ra: o
AA' = AB tan 60 = a 3
Vậy thể tích khối lăng trụ: 2 3 a 3 3a V = S .AA' = .a 3 = .
ABC. A' B 'C ' DABC 4 4
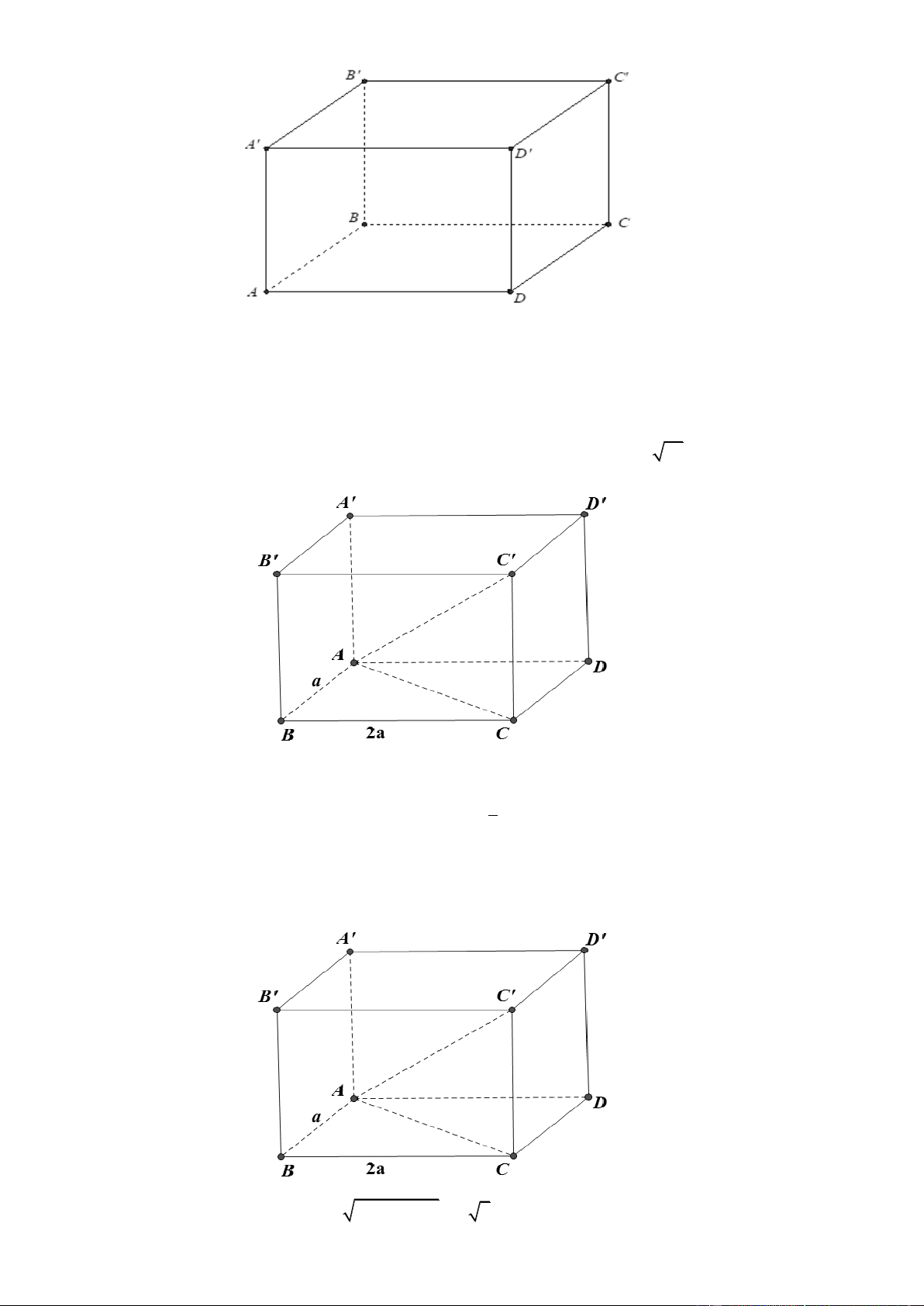
Câu 51. Cho hình lăng trụ đứng ABC .
D A' B'C ' D' , đáy là hình thang vuông tại A và D , có AB  2C ,
D AD CD a 2, AA'  2a . A' B' 2a C' D' A B a 2 D a 2 C
Thể tích khối lăng trụ đã cho bằng A. 3 12a . B. 3 6a . C. 3 2a . D. 3 4a . Lờigiải Trang23 Chọn B A' B' 2a C' D' A B a 2 D a 2 C
Diện tích hình thang ABCD là:
AB CD.AD 2CD CD.AD CD AD a a S   3 .  3. 2. 2  2  3a . ABCD 2 2 2 2
Thể tích khối lăng trụ đã cho: V S .AA 2  3a .2a 3  6a . ABCD
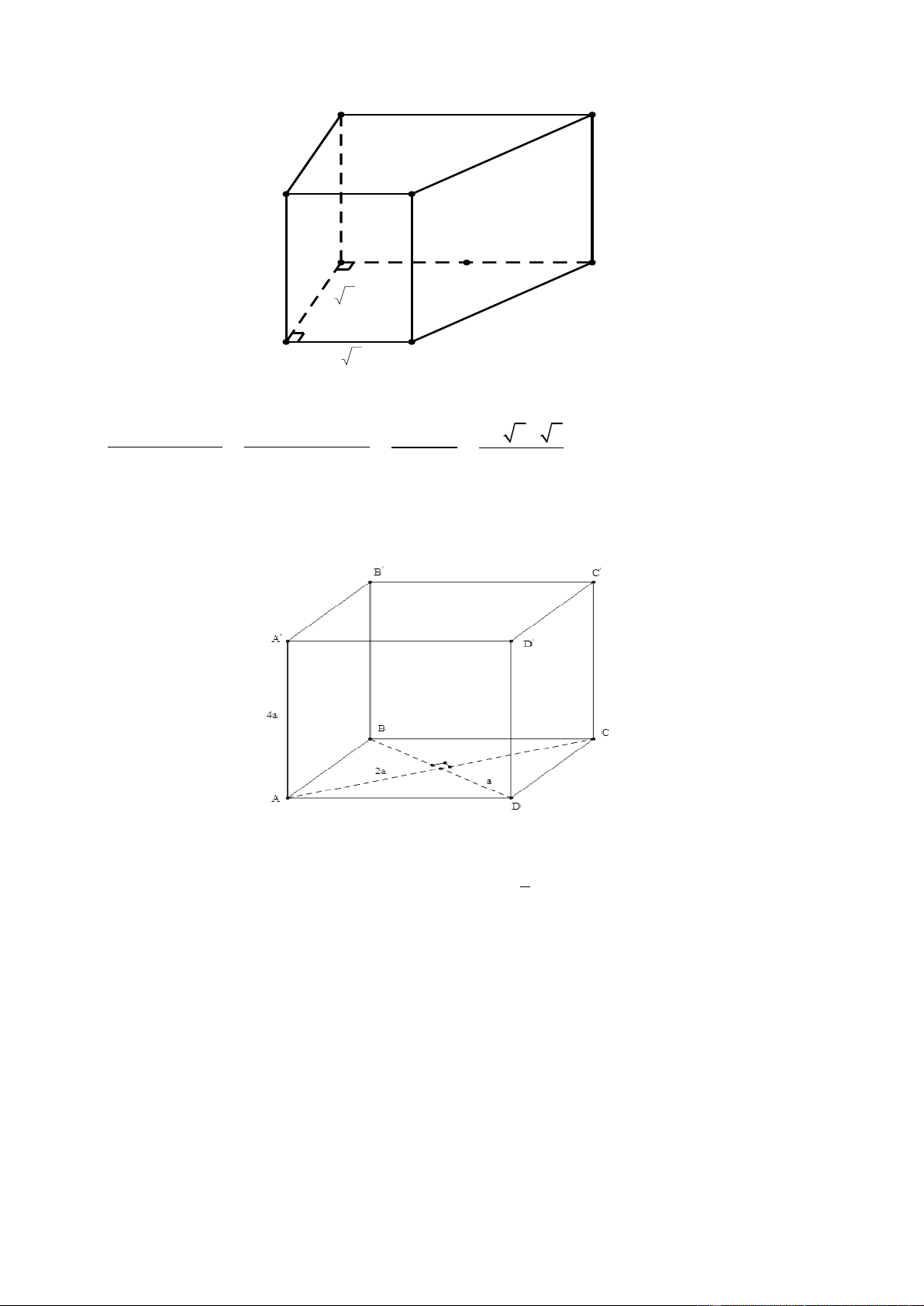
Câu 52. Cho hình lăng trụ đứng ABC . D A BCD
  có đáy là hình thoi, biết AA  4a, AC  2a, BD a .
Thể tích V của khối lăng trụ là 8 A. 3
V  8a . B. 3
V  2a . C. 3 V a . D. 3 V  4a . 3 Lờigiải Chọn D Trang24 1 1
Thể tích V của khối lăng trụ là: 3 V S .AA  .AC. . BD AA  .2 . a .4 a a  4a . ABCD 2 2
Câu 53. Tính thể tích khối lăng trụ đứng AB . C A BC
  biết AA  2 ; a AB  3 ;
a AC  4a và AB AC . A. 3 12a . B. 3 4a . C. 3 24a . D. 3 8a . Lờigiải Chọn A 1 1 Ta có: 2 S  . AB AC  3 .4 a a  6a . ABC 2 2 Vậy 3 V       AA .S 12a . ABC.A B C ABC
Câu 54. Cho hình hộp đứng có một mặt là hình vuông cạnh a và một mặt có diện tích là 2 3a . Thể tích khối hộp là A. 3 a . B. 3 3a . C. 3 2a . D. 3 4a . Lờigiải Chọn B Trang25
Giả sử mặt ABB' A' là hình vuông cạnh bằng a , mặt ABCD có diện tích bằng 2 3a .
Do đó chiều cao h AA' a, diện tích đáy là 2 B S  3a . ABCD
Suy ra thể tích của khối hộp đó là 2 3
V  3a a  3a .
Câu 55. Cho khối hộp chữ nhật ABCD . A BCD
 , biết AB a;BC  2a; AC  a 21 .
Tính thể tích V của khối hộp đó? 8 A. 3 4a . B. 3 16a . C. 3 a . D. 3 8a . 3 Lờigiải Chọn D
Xét tam giác vuông ABC , ta có: 2 2 AC
AB BC a 5 . Trang26
Xét tam giác vuông ACC , ta có: 2 2 CC 
AC  AC  4a .
Vậy thể tích của khối hộp hộp chữ nhật ABCD. A BCD   là: 3
V a.2a.4a  8a .
Câu 56. Cho hình hộp đứng có cạnh bên độ dài 3a , đáy là hình thoi cạnh a và có một góc 60 . Khi đó thể tích khối hộp là 3 3a 3 3 a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 4 3 2 2 Lờigiải Chọn D
Ta có chiều cao h  3a . 2 2
Hình thoi cạnh a và có một góc a 3 a 3
60 có diện tích S  2.  4 2 3 Thể tích khối hộp là 3a 3
V S.h  . 2
Câu 57. Cho khối hộp chữ nhật ABC . D A BCD
  có AA  a, AB  3a, AC  5a . Thể tích của khối hộp đã cho là A. 3 5a . B. 3 4a . C. 3 12a . D. 3 15a . Lờigiải ChọnC 2 2 Xét ABC
vuông tại B , ta có: 2 2 BC
AC AB  5a  3a  4a . 2 S
AB.BC  3a.4a 12a ABCD 2 3 V         S . AA
12a .a 12a . ABC . D A B C D ABCD
Câu 58. Cho hình lăng trụ đứng AB . C A BC
  có BB  a , đáy ABC là tam giác vuông cân tại ,
B AC a 2 . Tính thể tích lăng trụ Trang27 3 a 3 a 3 a A. . B. . C. 3 a . D. . 3 6 2 Lờigiải Chọn D Trong A
BC AC AB BC AB  a 2 2 2 2 2 : 2 2
AB BC  . a 3
Thể tích khối lăng trụ 1 a AB . C A BC   là: V         S .BB A . B BC.BB . ABC. A B C ABC 2 2
Câu 59. Cho hình lăng trụ đứng ABC . D A B ¢ C ¢ D
¢ ¢, có ABCD là hình vuông cạnh 2a , cạnh
AC¢= 2a 3 .Thể tích khối lăng trụ AB . C A B ¢ C ¢ ¢ bằng A. 3 4a . B. 3 3a . C. 3 2a . D. 3 a . Lờigiải Chọn A Ta có: 2 2 2 2 2 2
AC¢ = AB + AD + AA¢ Þ AA¢ = 4a Þ AA¢= 2a .
Thể tích khối lăng trụ AB . C A B ¢ C ¢ ¢là 1 1 3 V = . . AB . AD AA¢= .2 .2 a .2
a a = 4a . ABC. A B ¢ C ¢ ¢ 2 2
Câu 60. Cho lăng trụ đứng AB .
C A' B' C' có đáy ABC là tam giác vuông cân tại A với BC a và
mặt bên AA ' B ' B là hình vuông. Thể tích khối lăng trụ AB .
C A' B' C' bằng 2 2 1 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 8 4 4 12 Lờigiải Trang28 Chọn A. A B a C A' B' C' BC a 2 1 a
Tam giác ABC vuông cân tại 2 2 A AB   2  SAB  . ABC 2 2 2 4 Mặt bên a 2
AA ' B ' B là hình vuông  AA '  AB  . 2 2 3 a 2 a a 2 Vậy VAA'.S  .  .
ABC. A ' B ' C " ABC 2 4 8
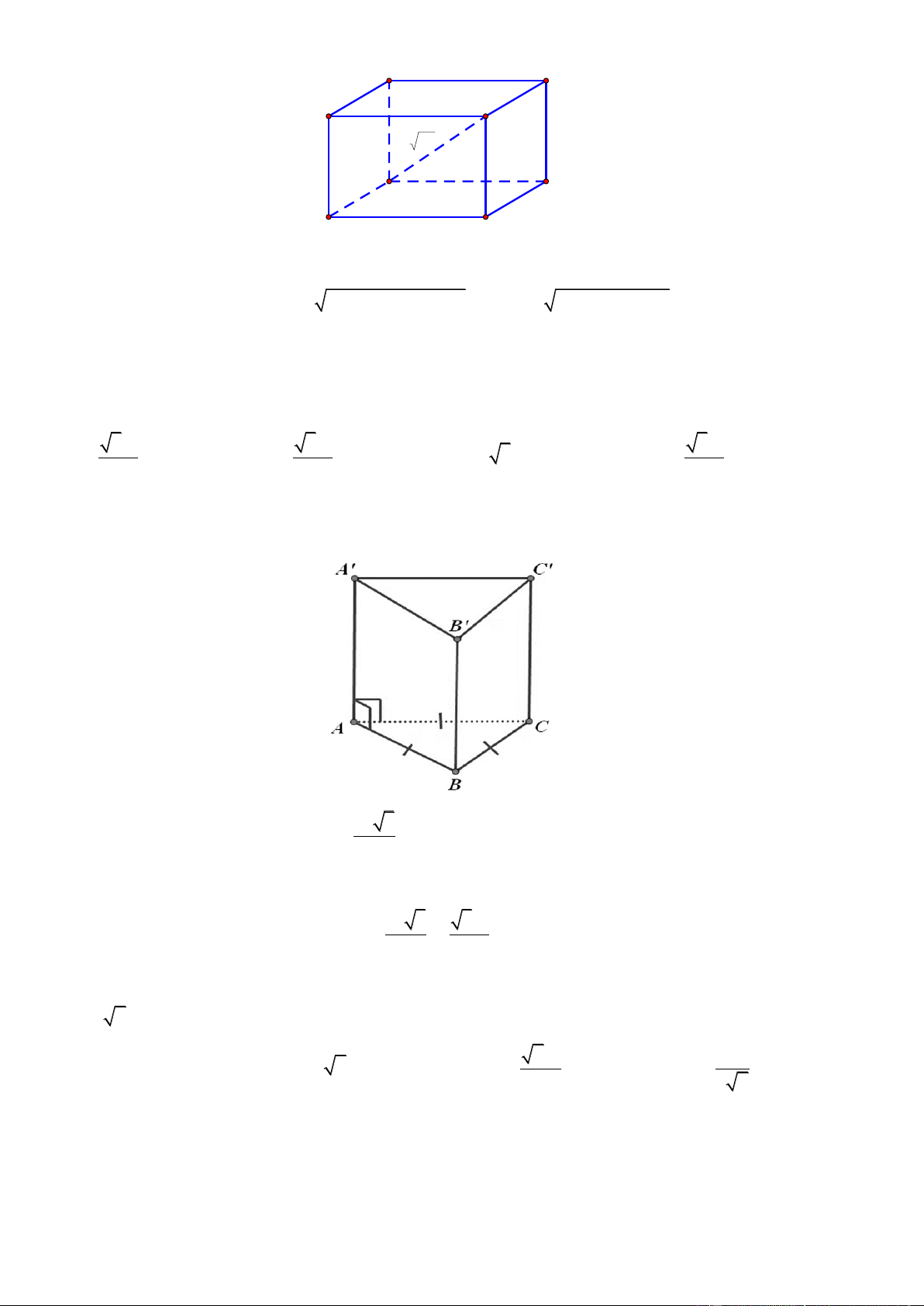
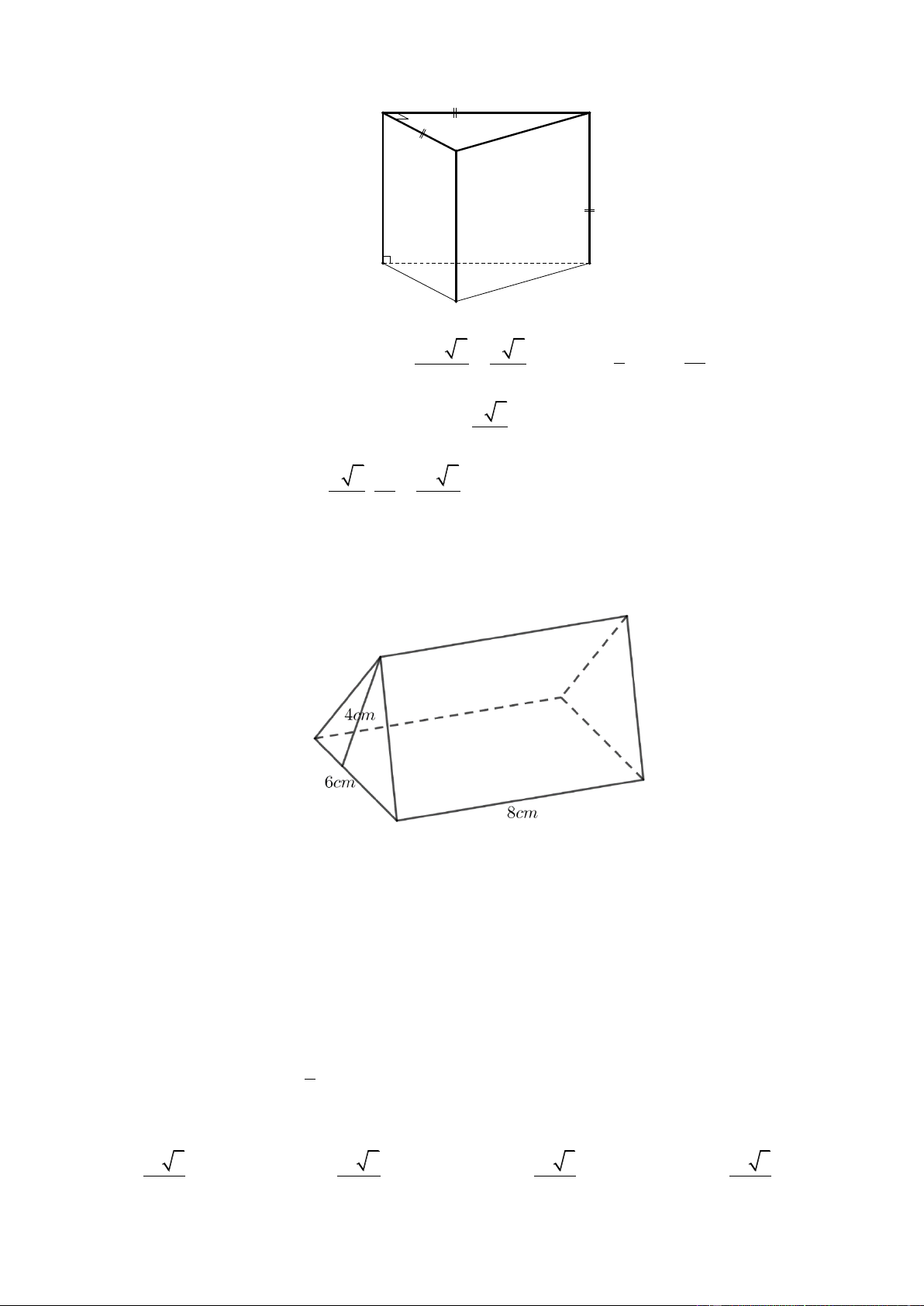
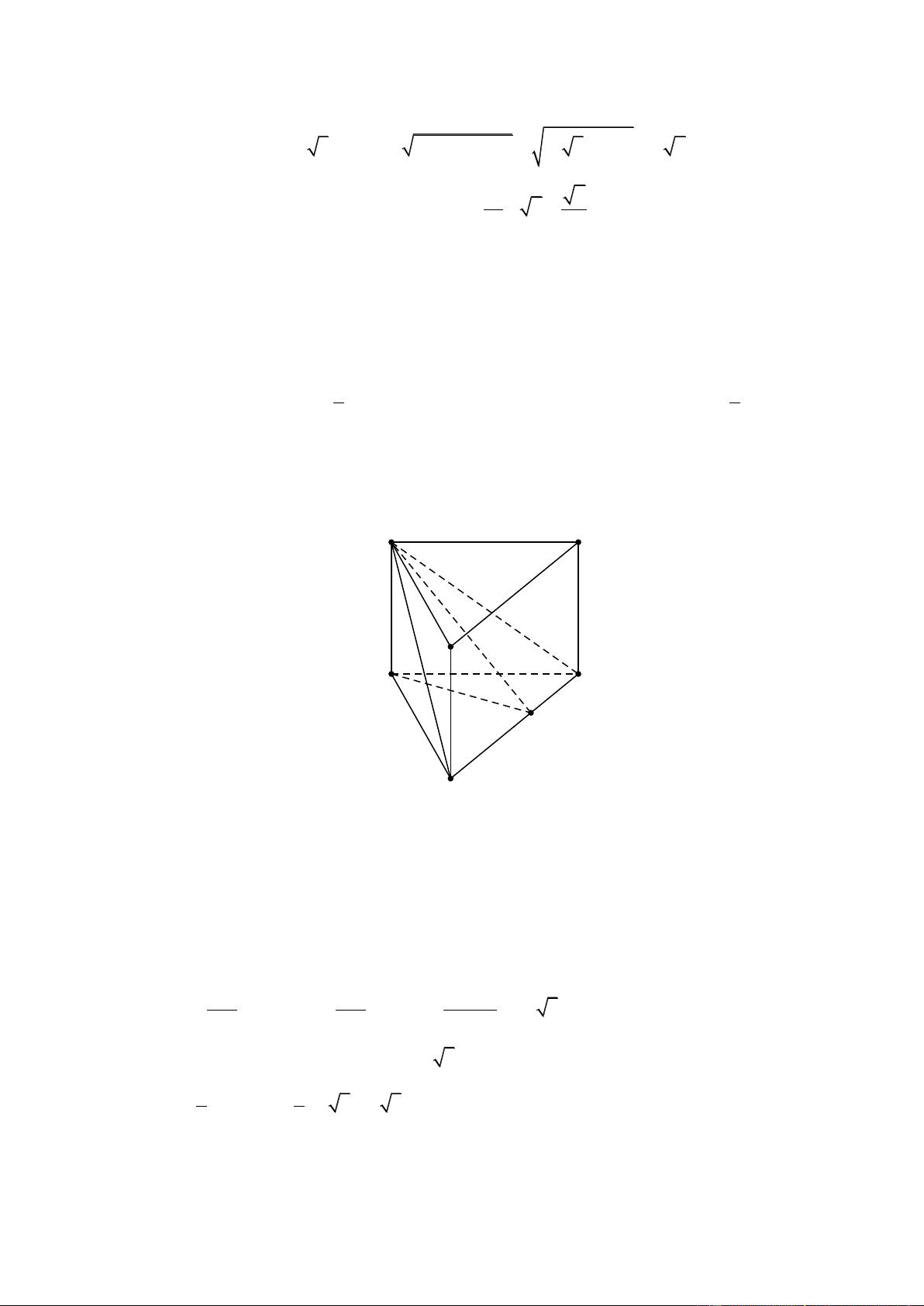
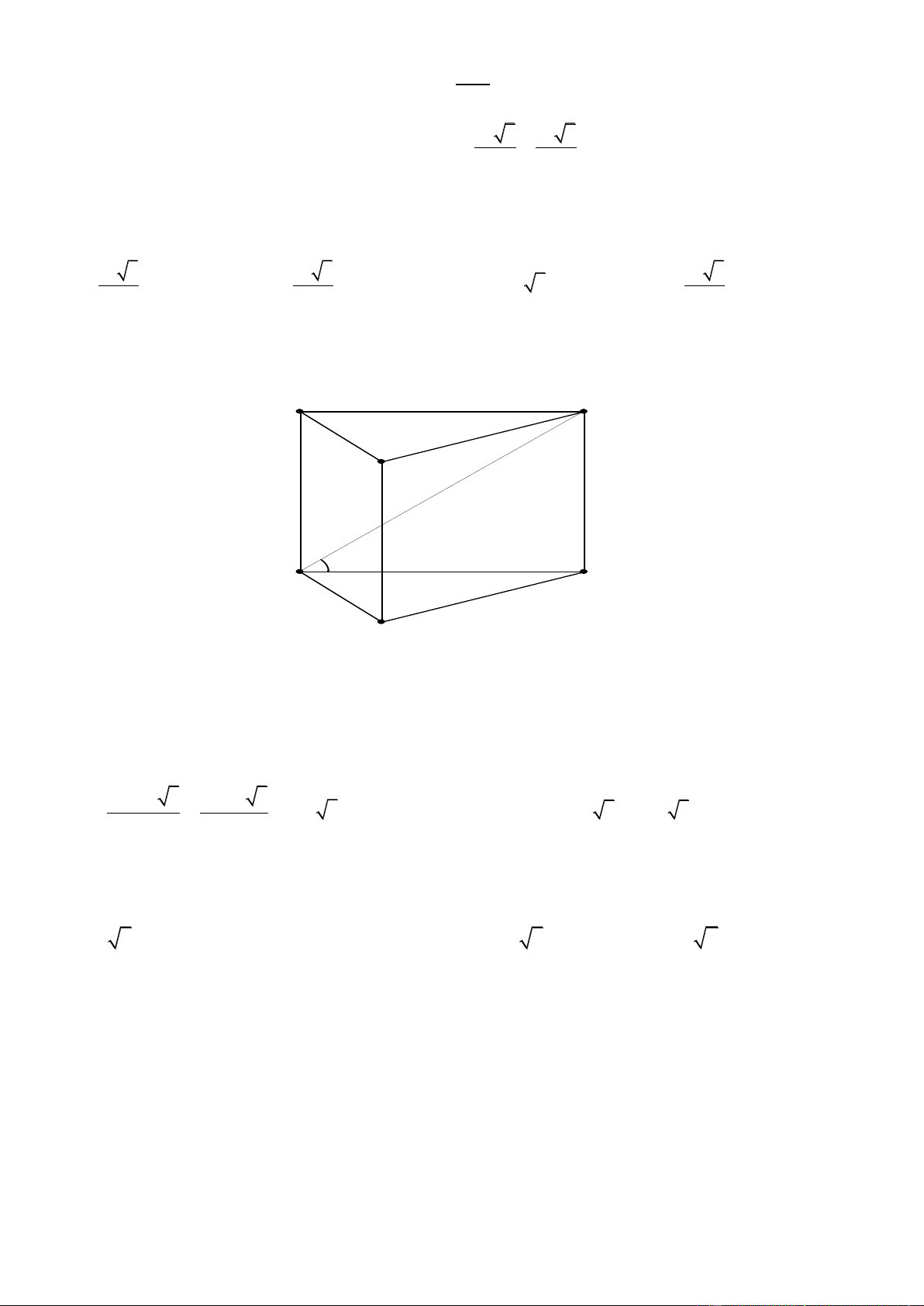
Câu 61. Cho khối đa diện (kích thước như hình vẽ bên) được tạo bởi ba hình chữ nhật và hai tam giác bằng nhau.
Tính thể tích khối đa diện đã cho. A. 3 48cm . B. 3 192cm . C. 3 32cm . D. 3 96cm . Lờigiải Chọn D
Từ giả thiết, suy ra khối đa diện là một khối lăng trụ đứng có đáy là tam giác và các mặt bên là hình chữ nhật.
Thể tích khối đa diện là 1 V  .6.4.8  96  3 cm  . 2
Câu 62. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a . Thể tích khối lăng trụ đó bằng 3 a 6 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 4 4 4 12 Lờigiải Trang29 Chọn C 2 2 3 Diện tích đáy a 3 a 3 a 3 S
, chiều cao h a . Khi đó V a  . 4 4 4
Câu 63. Cho hình lăng trụ tam giác đều AB . C A BC   có AB  2 ,
a AA  a 3 .
Tính thể tích khối lăng trụ AB . C A BC  . 3 a 3 3a A. 3 3a . B. . C. . D. 3 a . 4 4 Lờigiải Chọn A 2a2 3
Thể tích khối lăng trụ AB . C A BC  : 3
V AA .Sa 3.  3a . ABC 4
Câu 64. Cho khối lăng trụ đứng ABC . D A BCD
  có đáy là hình thoi cạnh a , BD a 3 và AA  4a
(minh họa như hình bên). Thể tích của khối lăng trụ đã cho bằng 3 2 3a 3 4 3a A. 3 2 3a . B. 3 4 3a . C. . D. . 3 3 Lờigiải Chọn A Trang30 Gọi BD a 3
I AC BD . Ta có: AC B , D BI  
. Xét tam giác vuông BAI vuông tại I : 2 2 2 2 2  a 3  3a a a 2 2 2 2 2
AI BA BI a     a  
AI   AC  . a   2 4 4 2   2
Diện tích hình bình hành 1 1 a 3 a 3 ABCD : S  2S
 2. BI.AC  2. .a  . ABCD ABC 2 2 2 2 2 Vậy: a 3 3 V         S .AA .4a 2 3a . ABCD.A B C D ABCD 2
MỨC ĐỘ KHÁ GIỎI
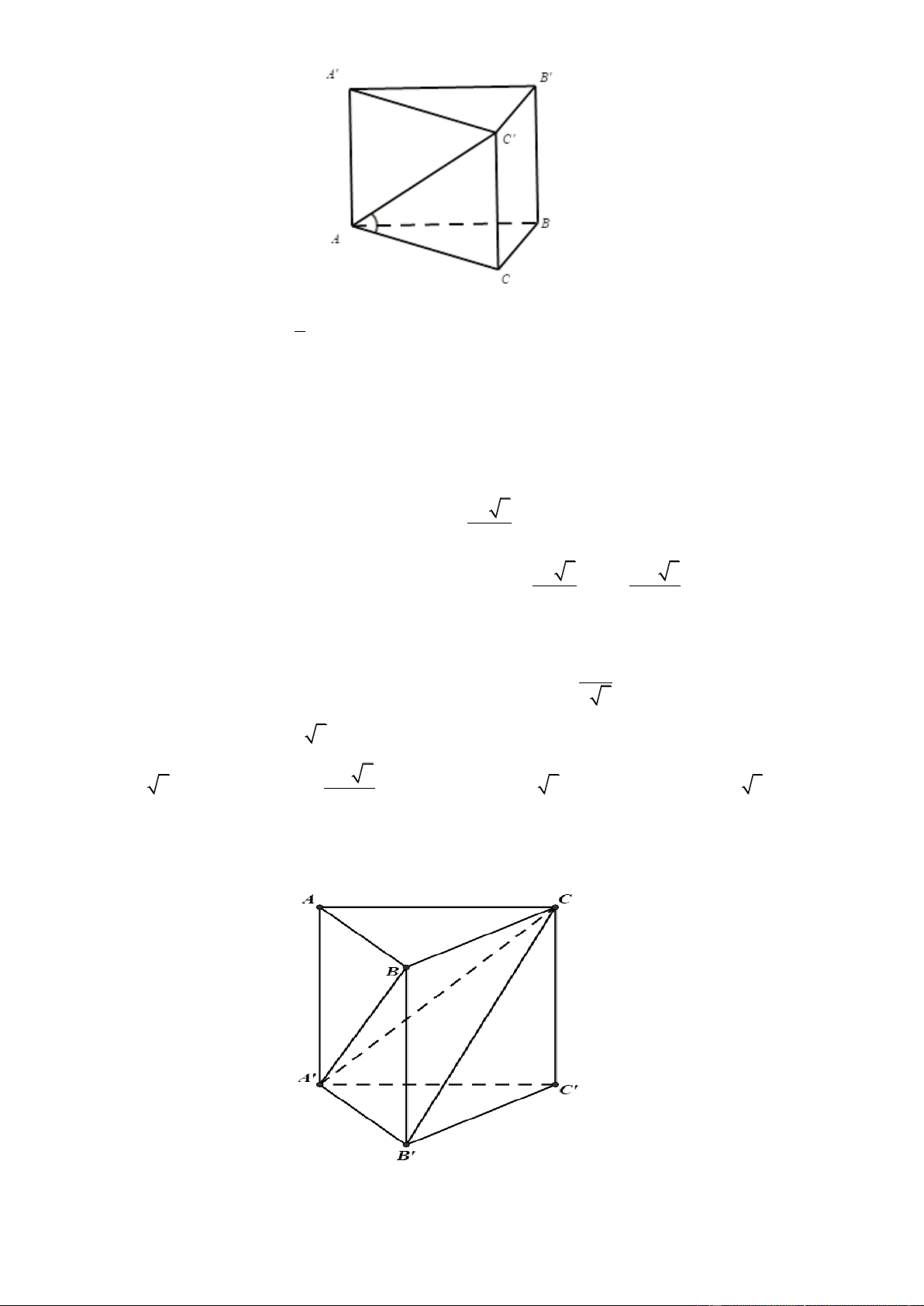
Câu 65. (Đề thi THPT Quốc Gia – Năm 2022 –Mã đề 101)
Cho khối lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại A , AB  2a. Góc giữa
đường thẳng BC và mặt phẳng  ACC A   bằng 0
30 . Thể tích của khối lăng trụ đã cho bằng A. 3 3a . B. 3 a . C. 3 12 2a . D. 3 4 2a . Lời giải Chọn D. Trang31 B' C' A' B C A
Ta có: BA BC và BA AA  BA   ACC A  .
Suy ra góc BC  ACC A
   BCC A    0 , ,  BC A   30 .
Ta giác ABC vuông tại A , có  AC  A . B cot AC B   2a 3 .
Tam giác CAC vuông tại C , có 2 2 CC 
AC  AC  2a 2 . 1
Thể tích khối lăng trụ là 3 V  . B h  .
AB AC.CC  4a 2 . 2
Câu 66. (Đề thi THPT Quốc Gia – Năm 2022 –Mã đề 102)
Cho khối lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại A , AB a . Góc giữa
đường thẳng BC và mặt phẳng  ACC A
  bằng 30. Thể tích của khối lăng trụ đã cho bằng 1 3 3 2 2 3 3 3 3 A. a . B. a . C. a . D. a . 8 8 2 2 Lời giải Chọn D. 2 1 a Diện tích đáy: S  . AB AC  . ABC 2 2 Trang32AB AC · Ta có: 
AB   ACC A
   BC ACC A   · ,  BC A   30. AB AA
Khi đó AC  AB   a
AA  AC  A C    a 2 2 2 2 .cot 30 3 3  a a 2 . 2 a 2
Vậy, thể tích khối lăng trụ đã cho là: 3 V S .AA  .a 2  .a . ABC 2 2
Câu 67. (Đề thi THPT Quốc Gia – Năm 2022 –Mã đề 103)
Cho khối lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông cân tại A , cạnh bên AA  2a ,
góc giữa hai mặt phẳng  A B
C  và  ABC bằng 30. Thể tích của khối lăng trụ đã cho bằng 3 8 3 8 A. 24a . B. 3 a . C. 8a . D. 3 a . 3 9 Lời giải Chọn A. A' C' B' A C H B
Kẻ AH BC , ta có AA   ABC nên AA'  BC .
AH BC và AA'  BC suy ra BC   AA H    A H   BC .
Suy ra góc giữa  A B
C  và  ABC là   A HA A HA  30 .
ΔA' AH vuông tại A có AAa a  2 2 tan AHA   tan 30   AH   2a 3. AH AH tan 30
ΔABC vuông cân tại A nên BC  2AH  4a 3 . 1 1 2  S
AH BC  2a 3  4a 3  12a . ABC 2 2
Vậy thể tích của khối lăng trụ đứng AB .
C A' B 'C ' là
Câu 68. (Đề thi THPT Quốc Gia – Năm 2022 –Mã đề 104) Trang33
Cho khối lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại A , cạnh bên AA  2a , góc
giữa hai mặt phẳng  A B
C và  ABC bằng 60. Thể tích của khối lăng trụ đã cho bằng 8 8 A. 3 a . B. 3 8a . C. 3 a . D. 3 24a . 9 3 Lời giải Chọn C. A' C' B' A C I B
Gọi I là trung điểm của BC .
Ta có: + ABC là tam giác vuông cân tại A nên AI BC + AB . C A BC
  là khối lăng trụ đứng nên AA  BC
suy ra BC   AA I
   BC A I .
Do đó, góc giữa hai mặt phẳng  A B
C và  ABC bằng góc giữa AI và AI , mà tam giác AAI vuông
tại A nên ta có 
AIA là góc nhọn.Suy ra góc giữa hai mặt phẳng  A B
C và  ABC bằng AIA  60. AA 2a
Trong tam giác vuông AAI , ta có AI   . tan 60 3 4a BC 2a 6
ABC là tam giác vuông cân tại A nên BC  2AI  , AB AC   . 3 2 3 2 3  
Vậy thể tích khối lăng trụ đã cho là 1 1 2 a 6 8a
V AA .SAA . A . B AC  .2 . a    . ABC    2 2 3 3  
Câu 69. (Đề thi THPT Quốc Gia – Đợt 1 - Năm 2021 –Mã đề 101)
Cho khối hộp chữ nhật ABCDAB C
 D có đáy là hình vuông, BD  2a , góc giữa hai mặt phẳng
ABD và (ABCD) bằng 30. Thể tích khối hộp chữ nhật đã cho bằng Trang34 2 3 2 3 A. 3 6 3a . B. 3 a C. 3 2 3a D. 3 a . 9 3 Lời giải Chọn D.
Gọi O AC BD . 2 2     Diện tích hình vuông BD 2a ABCD là 2 2 SAB    2a . ABCD      2   2 
Ta có:  ABD,(ABCD)   A ; O AO  30 3 Xét tam giác A O
A vuông tại A , ta có: AA  tan30 AO a 3
Thể tích khối hộp chữ nhật đã cho là 3 2 3 2 3
V AASa  2a a . ABCD 3 3
Câu 70. (Đề thi THPT Quốc Gia – Đợt 1 - Năm 2021 –Mã đề 102)
Cho khối hộp chữ nhật ABC .
D A' B'C ' D' có đáy là hình vuông, BD  4a , góc giữa hai mặt phẳng
A'BD và ABCD =30o . Thể tích của khối hộp chữ nhật đa cho bằng ? 16 3 16 3 A. 3 a B. 3 48 3a C. 3 a D. 3 16 3a 9 3 Lời giải Chọn C.
Gọi O là trung điểm của BD . Ta có: A  ' AB A
 ' AD suy ra A' B A' D suy ra A  ' BD cân. Trang35
A' BD  ABCD  BD  
Mà A'O BD
 ABD ABCD  ,
AOA  30 .  = 30o . AO BDA AA AA AA Aa Xét AO
A vuông tại A có: tan30o      2 3
A' A  2a tan 30  . AO AC BD 2a 3 2 2
Xét hình vuông ABCD có: BD AB 2  AB  2a 2.
Vậy thể tích của khối hình hộp chữ nhật bằng: 2 a 16 3 V A ' . A AB =  a 2 2 3 . 2 2 = 3 a . 3 3
Câu 71. (Đề thi THPT Quốc Gia – Đợt 1 - Năm 2021 –Mã đề 103)
Cho khối hộp chữ nhật ABCDAB C
 D có đáy là hình vuông, BD  2a , góc giữa hai mặt phẳng
ABD và (ABCD) bằng 60. Thể tích của khối hộp đã cho bằng 2 3 2 3 A. 3 a B. 3 6 3a C. 3 a D. 3 2 3a 9 3 Lời giải Chọn D.
Gọi O AC BD .
ABD(ABCD)  BD   0 
Ta có: A O BD
 60  AOA AC BD   
Tam giác AAO có: AA  tan 60 .OA  3a và 2 S  2a ABCD Vậy  3 V        AA S 2 3a . . ABCD ABCD A B C D
Câu 72. (Đề thi THPT Quốc Gia – Đợt 1 - Năm 2021 –Mã đề 104) Trang36
Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông BD  4a , góc giữa hai mặt phẳng  A BD và  ABCD bằng 0
60 . Thể tích của khối hộp chữ nhật đã cho bằng 16 3 16 3 A. 3 48 3a . B. 3 a . C. 3 a . D. 3 16 3a . 9 3 Lời giải Chọn D.
Ta có đáy ABCD là hình vuông có BD  4a AB  2 2a . Gọi I trung điểm .
BD Vì BD  4a BI AI  2a . AA
Tam giác AAI vuông tại A có: 0 tan 60 
AA  2 3a . AI
Thể tích của khối hộp chữ nhật đã cho bằng:V S A A    a2 3 . 2 2
.2 3a  16 3a . ABCD
Câu 73. Cho hình lăng trụ tam giác đều ABC.A' B 'C ' có AB a, góc giữa đường thẳng A'C và mặt
phẳng  ABC bằng 45. Thể tích khối lăng trụ ABC.A'B'C ' bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 2 12 6 Lời giải Chọn A. · ·
Có: (A 'C ,(A BC ))= A 'CA = 4 ° 5 . Trang37 · A A '
Xét tam giác A ' A C vuông tại A, ta có: t an A 'CA = Þ A A ' = a. A C 2 3 Thể tích khối lăng trụ a 3 a 3
ABC.A' B 'C ' là: V AA'.S  . a  . ABC  4 4
Câu 74. Cho hình lăng trụ tam giác đều AB . C A BC
  có AB  4a, góc giữa đường thẳng A C  và mặt
phẳng  ABC bằng o
45 . Thể tích khối lăng trụ AB . C A BC   bằng 3 a 3 3 a 3 3 a 3 A. . B. . C. 3 16a 3 . D. . 4 2 6 Lời giải ChọnC C' A' B' 45 0 C 4a A 4a 4a B AB . C A BC
  là lăng trụ tam giác đều  AB . C A BC
  là lăng trụ đứng và đáy là tam giác đều. Ta có: A A    ABC   A C   ABC  o ,  A C
A  45  AA
C vuông cân tại AA A
  AC  4a .
AB2 3 4a2 3 2 S    4a 3 2 3 VAA .S  4 . a 4a 3  16a 3 . ABC   4 4
ABC.A' B 'C ' ABC
Câu 75. Cho lăng trụ đều ABC.A BC
 . Biết rằng góc giữa  A B
C và  ABC là 30, tam giác A BC
có diện tích bằng 8 . Tính thể tích khối lăng trụ ABC.A BC  . A. 8 3 . B. 8 . C. 3 3 . D. 8 2 . Lời giải ChọnA Đặt AB  ,
x x  0 , gọi M là trung điểm BC .   A B
C   ABC  BC  
Ta có AM BC   A B
C  ABC  ,  A MA  30 . A M   BCTrang38 AM x 3 2 Xét AA
M , có AM   .  x cos 30 . 2 3 A' C' B' A 30° C x M B 1 2 S          8 A M .BC 8 x 16 x 4 A BC 2 4. 3 1 16. 3
Suy ra AA AM .tan 30  .  2 ; S   4 3 . 2 ABC 3 4 Vậy V        A . A S 2.4 3 8 3 . ABC. A B C ABC 2 a 3
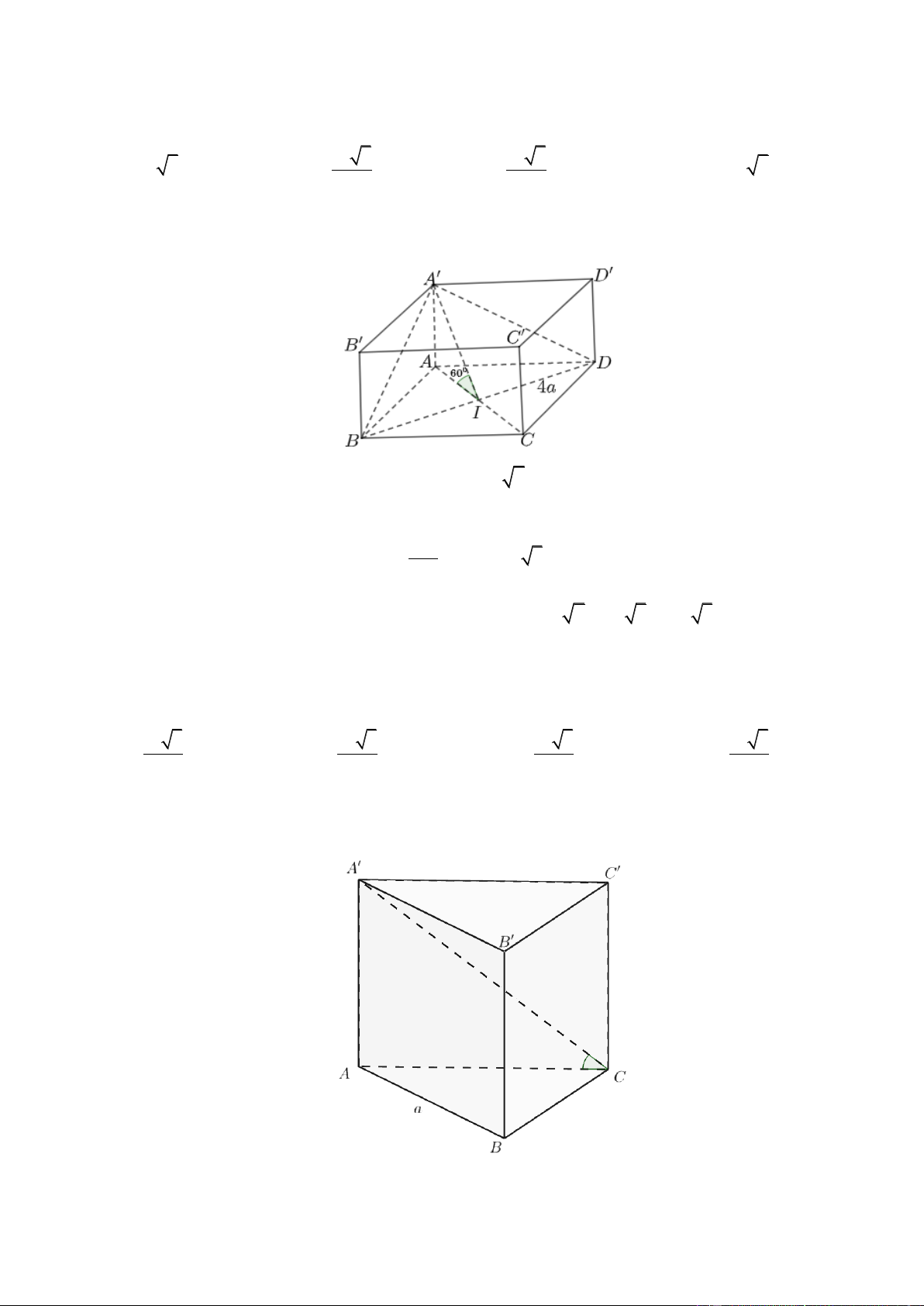
Câu 76. Cho lăng trụ tam giác đều AB .
C A' B 'C ' có diện tích đáy bằng
. Mặt phẳng  A' BC hợp 4
với mặt phẳng đáy một góc 0
60 . Tính thể tích khối lăng trụ AB .
C A' B 'C ' . 3 3 3 3a 3 3 a 3 5a 3 3a 2 A. B. C. D. 8 8 12 8 Lời giải ChọnA 2 Vì đáy a 3
ABC là tam giác đều có diện tích bằng
 cạnh đáy bằng a . 4 BC AM
Gọi M trung điểm BC , ta có 
BC A'M BC AA' Từ đó ta có 
A BC  ABC   A M AM   0 ' , ' ,
A'MA  60 . 3a Xét A  ' AM ta có 0
AA '  AM . tan 60  2 Trang39 3 Thể tích lăng trụ 3a 3 AB .
C A' B 'C ' là VAA'.S
ABC. A' B'C ' ABC 8
Câu 77. Cho lăng trụ tam giác đều AB . C A BC
  có cạnh đáy bằng a và AB vuông góc với BC . Tính
thể tích V của khối lăng trụ đã cho. 3 a 6 3 a 6 3 7a A. V  . B. V  . C. 3 V a 6 . D. V  . 4 8 8 Lời giải ChọnB
     Đặt x B
A , y BC , z BB
 , theo giả thiết AB  BC nên                
AB .BC  0   z x y z 2 2
 0  z.y z  . x y  .
x z  0  z  . x y 2  2   aa o 2  z x y o c s60   z  2 2 3 Vậy 1 a o 6 VA .
B AC.sin 60 .BB 
ABC.A' B'C ' 2 8
Câu 78. Cho lăng trụ đứng tam giác AB .
C A' B 'C ' có đáy ABC là tam giác vuông cân tại B với
BA BC a , biết A ' B tạo với mặt phẳng  ABC  một góc 0
60 . Thể tích khối lăng trụ đã cho bằng 3 a 3 3 a 3 3 a A. 3 2a . B. . C. . D. . 6 2 2 Lời giải ChọnC Trang40
Góc giữa đường thẳng A' B và mặt phẳng  ABC là  0 0
A' BA  60  A' A A .
B tan 60  a 3 . 2 3 1 a a 3 Có SB . A BC  V
S .A' A  . ABC
ABC.A'B 'C ' 2 2 ABC 2
Câu 79. Cho hình lăng trụ đứng AB .
C A' B'C ' có đáy ABC là tam giác vuông cân tại A , BC = a 2,
A ' B tạo với đáy một góc bằng 0
60 . Thể tích của khối lăng trụ bằng 3 3a 3 3a 3 3a 3 a A. . B. . C. . D. . 2 4 2 2 Lời giải ChọnA 1 1
ABC là tam giác vuông cân tại A , 2
BC = a 2 Þ AB = AC = a Þ S = . a a = a . D ABC 2 2
A ' B tạo với đáy một góc bằng 0  0
60 Þ BA' B ' = 60 .  BB '
D BA' B ' : tan BA' B ' = = 3 Þ BB ' =
3A ' B ' = a 3. v A ' B ' 3
Thể tích khối lăng trụ 1 3a AB .
C A' B'C 'là: 2 V = BB '.S = a 3. a = .
ABC. A' B'C ' DABC 2 2
Câu 80. Cho khối lăng trụ đứng tam giác AB . C A BC
  có đáy là một tam giác vuông tại A . Cho
AC AB  2a , góc giữa AC và mặt phẳng  ABC  bằng 30 . Tính thể tích khối lăng trụ AB . C A BC  . 3 2a 3 3 a 3 3 5a 3 3 4a 3 A. . B. . C. . D. . 3 3 3 3 Lời giải ChọnD Trang41 Diện tích tam giác 1 ABC : 2 S  . AB AC  2a . ABC 2
Hình chiếu vuông góc của AC lên  ABC là AC .
 Góc giữa AC và mặt phẳng  ABC là góc tạo bởi giữa đường thẳng AC và AC hay  C AC  Theo bài ra có  C AC  30. 2a 3 Xét tam giác C C
A vuông tại C có CC  AC.tan30  . 3 3
Thể tích của khối lăng trụ 2a 3 4a 3 AB . C A BC   là 2 V        CC .S .2a . ABC.A B C ABC 3 3
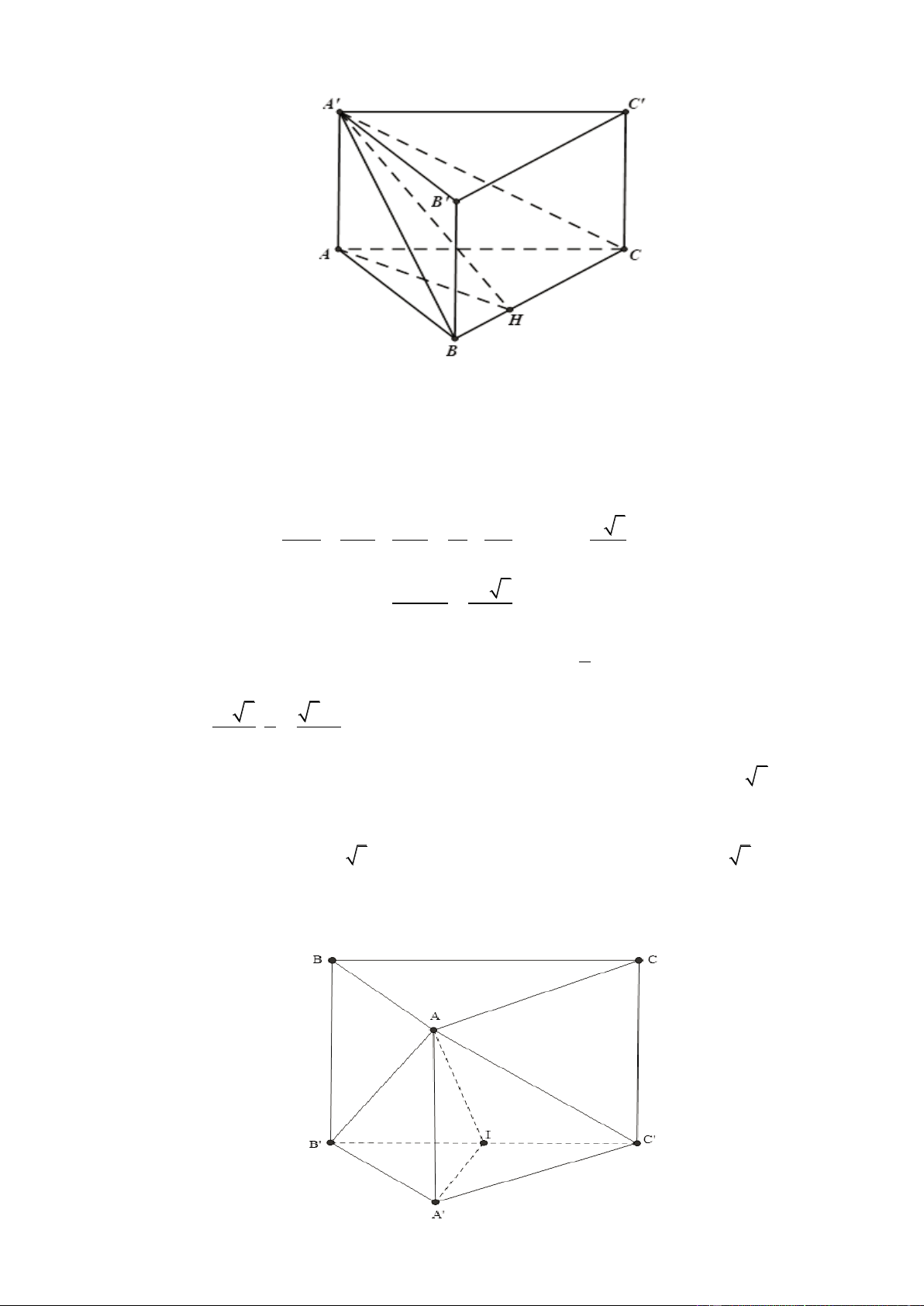
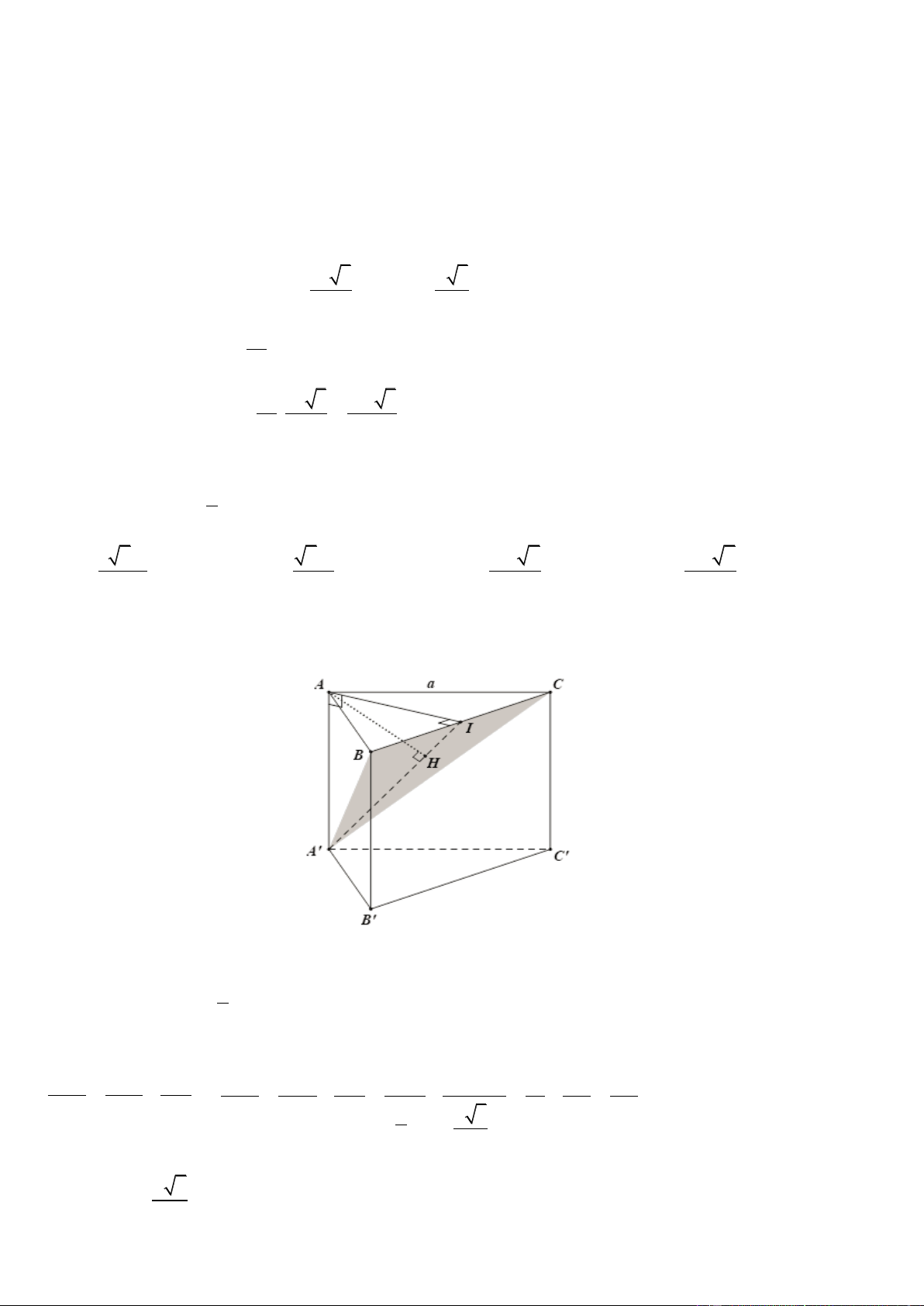
Câu 81. Cho hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông tại A ,  ACB  30 , biết
góc giữa B'C và mặt phẳng  ACC ' A' bằng  thỏa mãn 1 sin  
. Cho khoảng cách giữa hai 2 5
đường thẳng A' B và CC ' bằng a 3 . Tính thể tích V của khối lăng trụ AB .
C A' B 'C ' . 3 3a 6 A. 3 V a 6 . B. V  . C. 3 V a 3 . D. 3 V  2a 3 . 2 Lời giải ChọnD
* Ta có: CC//AA  CC//  AA BB   Trang42
Mà A' B   AA' B ' B, nên
d CC '; A' B  d CC '; AA' B ' B  C ' A'  a 3
* Ta có: AC A'C '  a 3 ; AB A' B '  a;
Diện tích đáy là B dt ABC 2 a 3  2
* Dễ thấy A' B '   ACC ' A'
Góc giữa B'C và mặt phẳng  ACC ' A' là  B 'CA '   A ' B ' 1 sin   
B 'C  2a 5 B 'C 2 5 2 2 2 2 CC ' 
B 'C B 'C ' 
20a  4a  4a 2 * Thể tích lăng trụ là a 3 V  .
B h với h CC ' 3 V  .4a  2a 3. 2
Câu 82. Cho khối lăng trụ đứng AB . C A BC
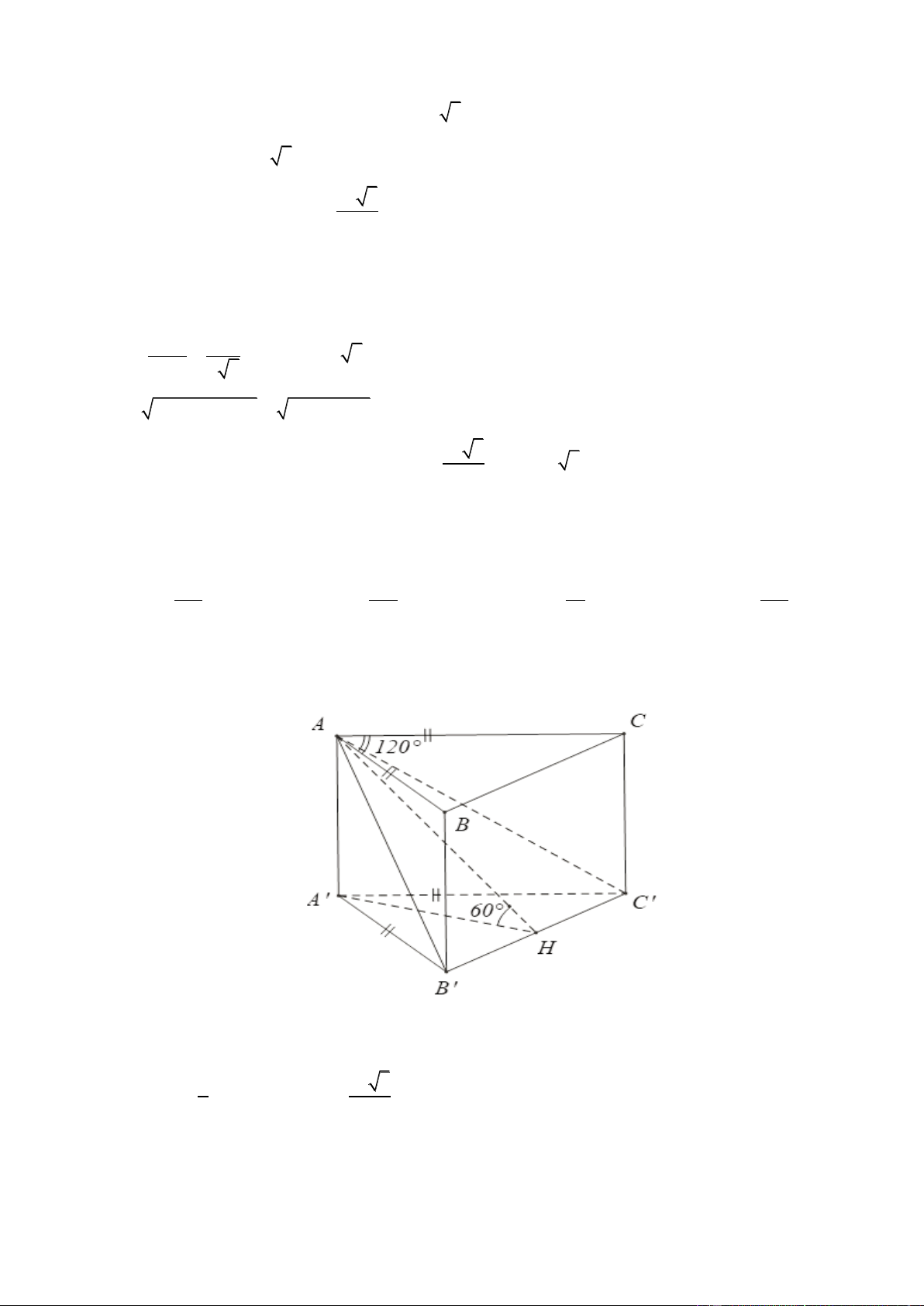
  có đáy ABC là tam giác cân với AB AC a , 
BAC  120 . Mặt phẳng ( AB C
 ) tạo với đáy một góc 60. Tính thể tích V của khối lăng trụ đã cho. 3 3a 3 9a 3 a 3 3a A. V B. V C. V D. V  8 8 8 4 Lời giải ChọnA
Gọi H là trung điểm của B C
 , khi đó góc giữa mp  AB C
  và đáy là góc  AHA  60 . 2 1 a 3 Ta có SAC.A . B sin120  . ABC  2 4 Trang43 1  S a 2 2 2 2 B C
   BC AB AC  2A .
B AC.cos120  a a  2. . a . a  2 a 3 ABCAH   2 B C   2 a 3
AA  A H  .tan 60  . 2 3 Vậy 3a V S .AA  . ACB 8
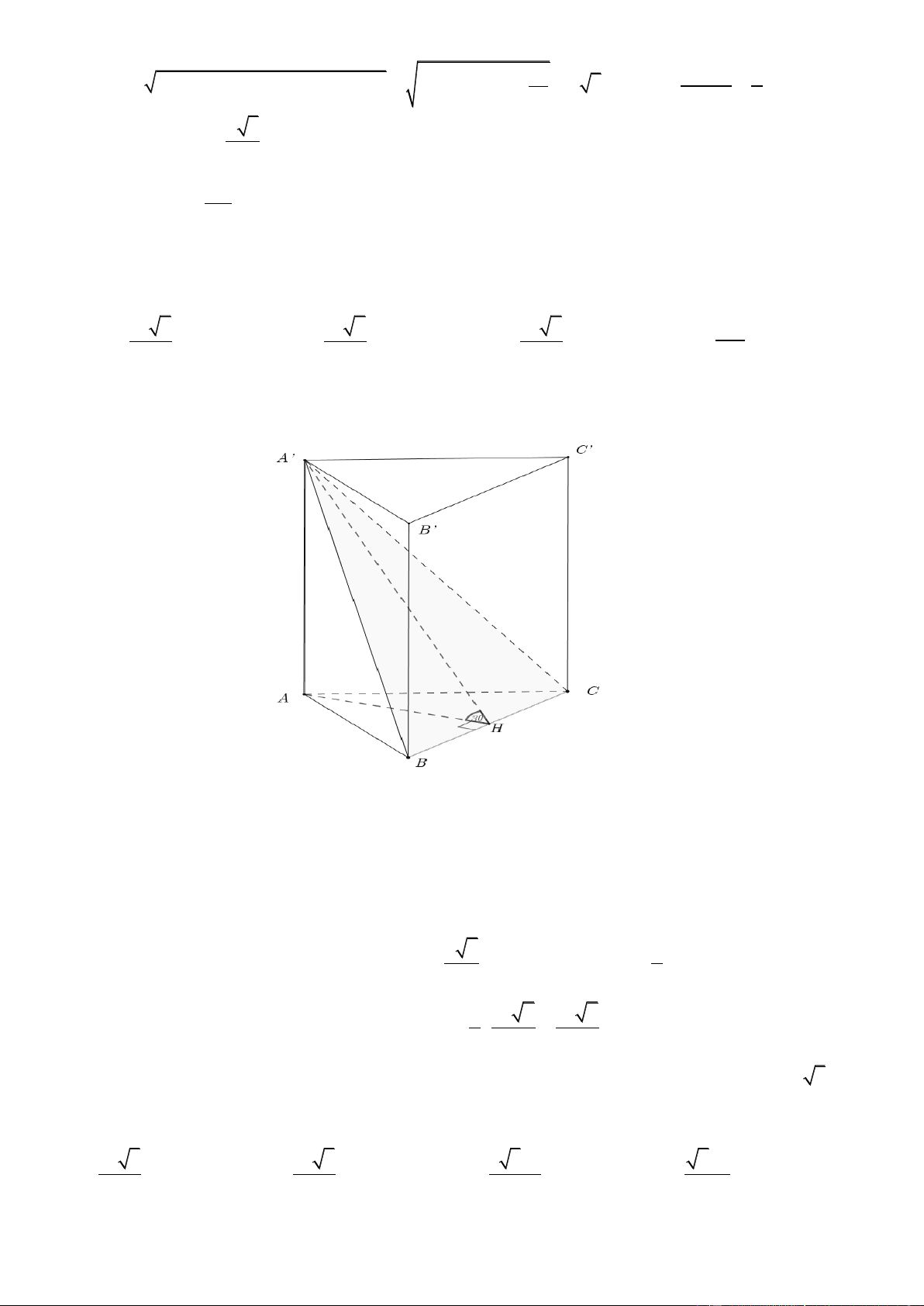
Câu 83. Cho hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác đều cạnh bằng a và  A' BC
hợp với mặt đáy ABC một góc 30 . Tính thể tích V của khối lăng trụ AB .
C A' B 'C ' . a3 3 a3 3 a3 3 a3 3 A. V  . B. V  . C. V  . D. V  . 8 12 24 8 Lời giải ChọnA
Gọi H là hình chiếu vuông góc của A trên BC . Suy ra AH BC .
A' H BC .
Mà  ABC    A' BC   BC
 Góc giữa  A'BC và  ABC bằng góc AH A H   ; '  AHA'   30 . a a
Ta có: ABC là tam giác đều cạnh bằng a nên AH
3 , A'A AH.tan30  . 2 2 a a2 a3 3 3
Thể tích khối lăng trụ AB .
C A' B'C ' là V A' A.S    . ABC  2 4 8
Câu 84. Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại A và AB a , AC a 3 , mặt phẳng  A B
C tạo với đáy một góc 30. Thể tích của khối lăng trụ AB . C A BC   bằng 3 a 3 3 a 3 3 3 3 a 3 3 a A. . B. . C. . D. . 12 3 4 4 Lời giải Trang44 ChọnD
* Xác định góc giữa mặt phẳng  A B
C và mặt phẳng đáy:
Trong mặt phẳng  ABC , dựng AH BC với H nằm trên cạnh BC . Theo định lý ba đường vuông 
góc, ta có: AH BC . Vậy  A B
C  ABC  ;  A HA  30 1 1 1 1 1 a 3
* Xét tam giác ABC có:      AH  . 2 2 2 2 2 AH AB AC a 3a 2 2 Diện tích A . B AC a 3
B của tam giác ABC là: B   . 2 2 a * Xét tam giác A H
A vuông tại A , ta có: AAAH.tan 30  . Thể tích khối lăng trụ AB . C A BC   2 2 3 a 3 a 3 a bằng V  . B h  .  . 2 2 4
Câu 85. Cho hình lăng trụ đứng, có đáy ABC là tam giác vuông cân tại A , AB = a 2 , góc giữa mp (AB 'C )
' và mp(ABC)bằng 600. Thể tích khối lăng trụ bằng A. 3 3a . B. 3 3 3a . C. 3 a . D. 3 3a . Lời giải ChọnD Trang45
Gọi I là trung điểm của cạnh B'C ' .
Ta có góc giữa mp(AB 'C )
' và mp(ABC) bằng góc giữa mp(AB 'C )
' và mp(A' B 'C ) '
Ta có B 'C ' = (AB 'C )
' Ç(A' B 'C ) '
Vì ABC là tam giác vuông cân tại A nên hai mặt bên ABB ' A' và ACC ' A' là hai hình chữ nhật bằng
nhau, do đó AC ' = AB' Þ DAB'C ' là tam giác cân tại A Þ AI ^ B'C '
Vì DA' B 'C ' là tam giác vuông cân tại A ' nên A' I ^ B'C ' . Như vậy góc giữa mp(AB 'C ) ' và mp (ABC) bằng  0 AIA' = 60 1 Ta có 0 A ' I =
BC = a Þ AA ' = A ' I. tan 60 = a 3 2 1 Þ V = AA'.S = a 3. a = a ABC A B C ABC ( 2)2 3 3 . ' ' ' 2
Câu 86. Cho hình lăng trụ đều AB . C A B ¢ C
¢ ¢. Biết khoảng cách từ điểm C đến mặt phẳng (ABC ) ¢ bằng 1
a , góc giữa hai mặt phẳng (ABC ) ¢ và (BCC B ¢ ) ¢ bằng  với cos =
. Tính thể tích khối lăng trụ 2 3 AB . C A B ¢ C ¢ ¢. 3 3a 2 3 3a 2 3 a 2 3 3a 2 A. V = . B. V = . C. V = . D. V = . 4 2 2 8 Lời giải ChọnB A' C' E y B' K α a A C M x B
Gọi M , N lần lượt là trung điểm của AB và BC ìï AB ^ CC¢ ï Do í Þ AB ^ (MCC ) ¢ Þ (ABC ) ¢ ^ (MCC ) ¢ . ï AB ^ CM ïî
Kẻ CK vuông góc với CM tại K thì ta được CK ^ (ABC )
¢ , do đó CK = d (C;(ABC ) ¢)= a . Trang46 Đặt x BC = ,
x CC¢= y,(x > 0, y > ) 0 , ta được: 3 CM = 2 1 1 1 4 1 1 + = Û + = ( ) 1 2 2 2 2 2 2 CM CC¢ . CK 3x y a KC a 12
Kẻ CE ^ BC¢ tại E , ta được  KEC =  , EC = = = a . sin 1 11 1- 12 1 1 1 11 Lại có + = = (2). 2 2 2 2 x y CE 12a Giải a ( ) 1 ,(2) ta được 6
x = 2a, y = . 2 2 2 3
Thể tích khối lăng trụ x 3 a 6 4a 3 3 2a AB . C A B ¢ C ¢ ¢ là: V = . y = . = 4 2 4 2
Câu 87. Cho khối lăng trụ tam giác đều AB . C A BC   có A B
  a 6 , đường thẳng A'B vuông góc với đường thẳng B C
 . Tính thể tích khối lăng trụ đã cho theo a . 3 a 6 3 3a 3 9a A. . B. 3 a 6 . C. . D. . 3 4 4 Lời giải ChọnA
Dựng hình hộp ABC .
D ABCD khi đó tứ giác ABCD là hình thoi.
Đặt AB x AD x
Tam giác ABD có góc BAD  120 áp dụng định lý côsin ta có: 2 2 2
BD AB AD  2 A . B A . D os c BAD 2 2
x x  2 . x . x cos120 2  3x
Ta có: A' B a 6  A D   a 6 Ta có: A D  //B C   A B   A D   AB
D vuông tại A 2 2 2
BD A' B A D  2 2  3x  12a 2 2
x  4a x  2a Chiều cao hình trụ 2 2 2 AA  A B   AB 2 2 2
 6a  4a  2a AA  a 2 Trang47 3 1 1 1 3 6aV        AA .S a 2. .2 . a 2 . a . ABC. A B C  3 ABC 3 2 2 3
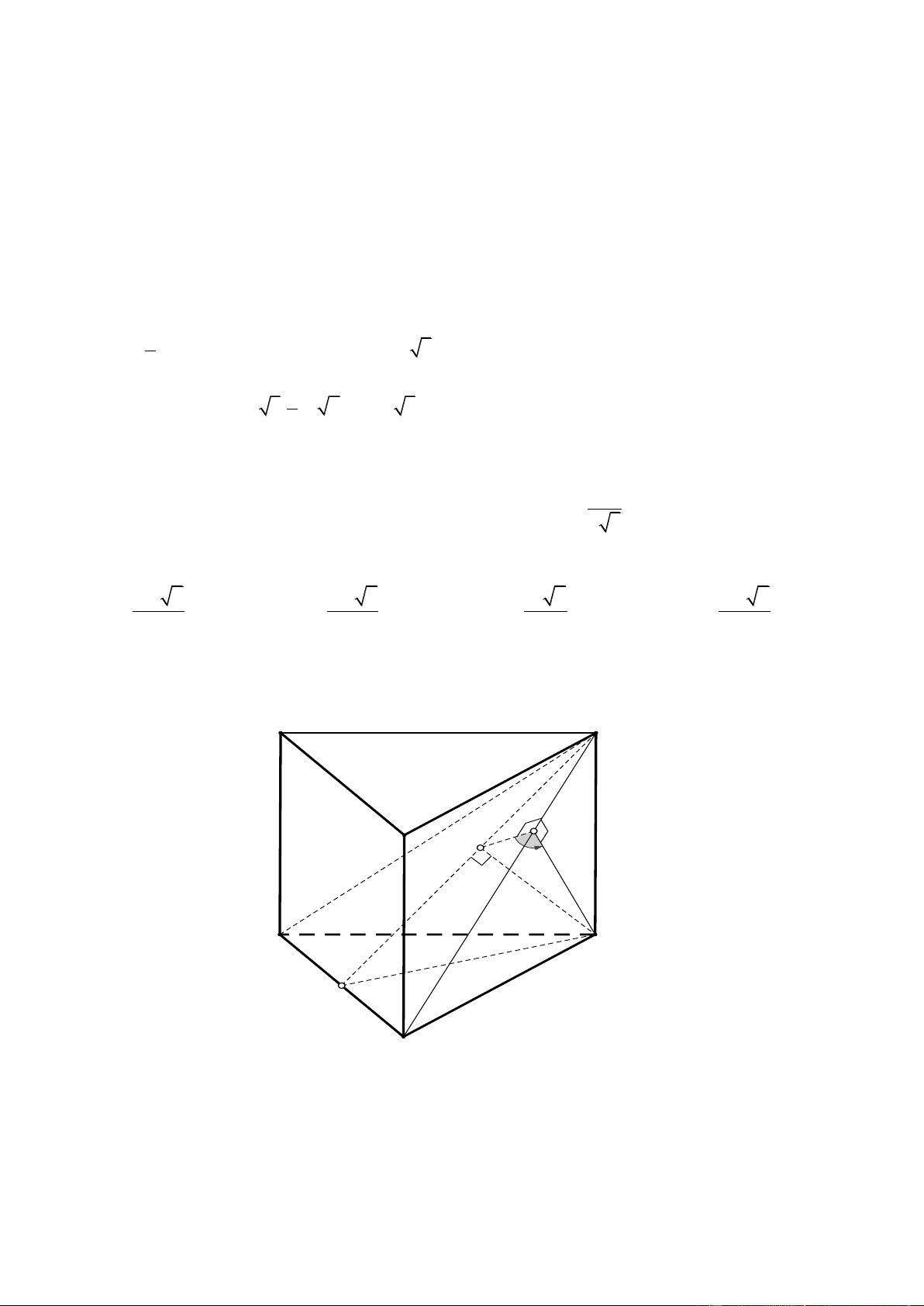
Câu 88. Cho khối lăng trụ đều AB .
C A' B 'C ' có cạnh đáy bằng a . Khoảng cách từ điểm A ' đến mặt phẳng  a
AB 'C ' bằng 2
3 . Thể tích của khối lăng trụ đã cho là 19 3 a 3 3 a 3 3 a 3 3 3a A. B. C. D. 4 6 2 2 Lời giải ChọnC
Gọi M là trung điểm của B'C ' .
AA'  B'C ' Ta có 
B 'C '   AA'M    AB'C '   AA'M  theo giao tuyến AM .
A'M B'C '
Kẻ A' H AM trong mặt phẳng  AA'M  , suy ra  A' H   AB'C ' . Vậy khoảng cách từ 2a 3
A ' đến mặt phẳng  AB 'C ' là A' H  . 19 1 1 1 1 1 1 1 Ta có      
A' A  2a . 2 2 2 2 2 2 2 A ' H A ' A A ' M A ' A A ' H A ' M 4a 2 3
Vậy thể tích khối lăng trụ là a 3 a 3
V AA'.S  2 . a  . A' B 'C ' 4 2
Câu 89. Cho lăng trụ đứng AB . C A
B C đáy là tam giác vuông cân tại B , AC a 2 , biết góc giữa  
A BC  và đáy bằng 60 . Tính thể tích V của khối lăng trụ. 3 3 3 3 3 3 3 6 A. a V . B. a V . C. a V . V a D. . 2 3 6 6 Lời giải ChọnA Trang48
Tam giác ABC vuông cân tại B , AC a 2  AB BC a . 2  a S . ABC 2 Góc giữa  
A BC  và đáy là góc   60 A BA .   . tan 60 A A ABa 3 . 2 3 a a 3 VSA A a  . ABCA BC . . 3 . ABC 2 2
Câu 90. Cho hình lăng trụ tam giác đều AB . C A BC
  có góc giữa hai mặt phẳng  A B
C và  ABC
bằng 60, cạnh AB a . Tính thể tích V của khối lăng trụ AB . C A BC  . 3 3 3 3 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V  3a . 4 4 8 Lời giải ChọnC Trang49
Gọi M là trung điểm của BC suy ra AM BC   1 BC AM Ta có   BC A M  2 BC AA
Mặt khác  ABC  A B
C  BC 3 Từ   
1 , 2 , 3 suy ra  ABC  A BC  ;  A MA  60 . 2 a 3 a 3
Vì tam giác ABC đều nên S  và AM  . ABC  4 2 3a
Ta có AA  AM . tan 60  . 2 2 3 Vậy 3a a 3 3a 3 V        AA .S . . ABC.A B C ABC 2 4 8
Câu 91. Cho khối lăng trụ tam giác đều AB . C A BC
  có cạnh đáy là a và khoảng cách từ A đến mặt a phẳng  A B
C bằng . Thể tích của khối lăng trụ bằng: 2 3 3 2a 3 2a 3 3a 2 3 3a 2 A. . B. . C. . D. . 12 16 16 48 Lời giải ChọnC
Gọi I là trung điểm của BC và H là hình chiếu vuông góc của A trên AI . Khi đó ta có:  a d ,
A ABC   AH  . 2
Trong tam giác vuông AAI ta có: 1 1 1   1 1 1 1 1 4 4 8         2 2 2 AH AAAI 2 2 2 2 2 2 2 2 AAAH AIa    a 3a 3 a 3 a      2  2   a 6 Suy ra: AA  . 4 Trang50 2 3
Thể tích khối lăng trụ là: a 3 a 6 3a 2 V S .AA    . ABC  4 4 16
Câu 92. Cho khối lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác cân với AB AC a, 
BAC  120 , mặt phẳng ( ABC )
 tạo với đáy một góc 60. Tính thể tích của khối lăng trụ đã cho 3 3a 3 9a 3 3a 3 3 3a A. V  . B. V  . C. . D. V  . 8 8 8 8 Lời giải ChọnD Hạ  B I   A C
  . Khi đó ta có ABC ABC  ,
B IB  60 B Ia 3 Vì  B A  C 120   B A
 I  60 . Do đó sin 60   B I  . B A  2 BBBBa 3 3a Suy ra  tan B IB       BB  . 3  B I  tan 60 B I  2 2 1 1 a 2 Mặt khác a 3 S
 .AI.BC  . .a 3  . ABC  2 2 2 4 2 3
Vậy thể tích khối chóp là a 3 a3 3 3a V  . B h  .  . 4 2 8
Câu 93. Cho hình lăng trụ đều AB . C A BC
  có cạnh đáy bằng a . Đường thẳng AB tạo với mặt phẳng BCC B
  một góc 30. Thể tích khối lăng trụ AB . C A BC   theo a . 3 3a 3 a 3 a 6 3 a 6 A. . B. . C. . D. . 4 4 12 4 Lời giải ChọnD Trang51
Gọi M là trung điểm của cạnh BC . Do AB . C A BC
  là hình lăng trụ tam giác đều nên ta có AM   BCC B
    AB BCC B    ,  AB M   30. AM AM 3a
Xét tam giác vuông AB M  ta có tan 30   AB   AB  . AB tan 30 2 2 2 9a a
Xét tam giác vuông B BM ta có 2 2 BB  B M   BM    a 2 . 4 4 1 3
Thể tích khối lăng trụ a 6 AB . C A BC   là V        . AB AC.sin 60 .BB . ABC. A B C 2 4
Câu 94. Cho hình lăng trụ đứng AB . C A BC
 , biết đáy ABC là tam giác đều cạnh a . Khoảng cách từ a
tâm O của tam giác ABC đến mặt phẳng  A B
C bằng . Tính thể tích khối lăng trụ AB . C A BC  . 6 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. . 8 28 4 16 Lời giải ChọnD 2 Diện tích đáy là a 3 B S  . ABC  4
Chiều cao là h d  ABC; A BC
   AA.
Do tam giác ABC là tam giác đều nên O là trọng tâm của tam giác ABC . Gọi I là trung điểm của BC ,
H là hình chiếu vuông góc của A lên AI ta có AH   A B
C  d  ; A A B
C  AH Trang52 d  ;
O ABC  IO 1 d  ; A A BC      AH a a d ; O A BC       AH d  ; A A BC IA 3 3 3 6 2
Xét tam giác AAI vuông tại A ta có: 1 1 1 3   1 1 1    a 3  a 3a 2 AA  3  h  V  . 2 2 2    AH AAAI 2 2 2 AAAH AI ABC.A B C 2 2 2 2 16
Câu 95. Cho một lăng trụ tam giác đều AB . C A BC
  có cạnh đáy bằng a , góc giữa A C  và mặt phẳng
đáy bằng 60. Tính diện tích xung quanh S của hình nón có đáy là đường tròn nội tiếp tam giác ABC xp
và đỉnh là trọng tâm của tam giác A BC   . B' A' C' A B C 2 a 333 2 a 333 2 a 111 2 a 111 A. S  . B. S  . C. S  . D. S  . xq 36 xq 6 xq 6 xq 36 Lời giải ChọnA Trang53 B' A' G' C' A B G M C  Ta có  A C   ABC  ;  A C
A  60 suy ra AA  AC.tan 60  3a . 1 1 3a 3 2 3a 111a Có r GM AM  .  a và 2 2 l G M   G G   GM 2  3a   . 3 3 2 6 36 6 2  Vậy 3 111 a 333 S  rl  . . a a  . xp 6 6 36 Trang54