







Preview text:
6 ĐT TỈ1 ẢI DƯƠNG
ĐỀ THI THỬ TỐT NGHIỆP THPT Năm họ 0 i Mã đề Kờ K K ể Kời gian phát đề ĐỀ BÀI
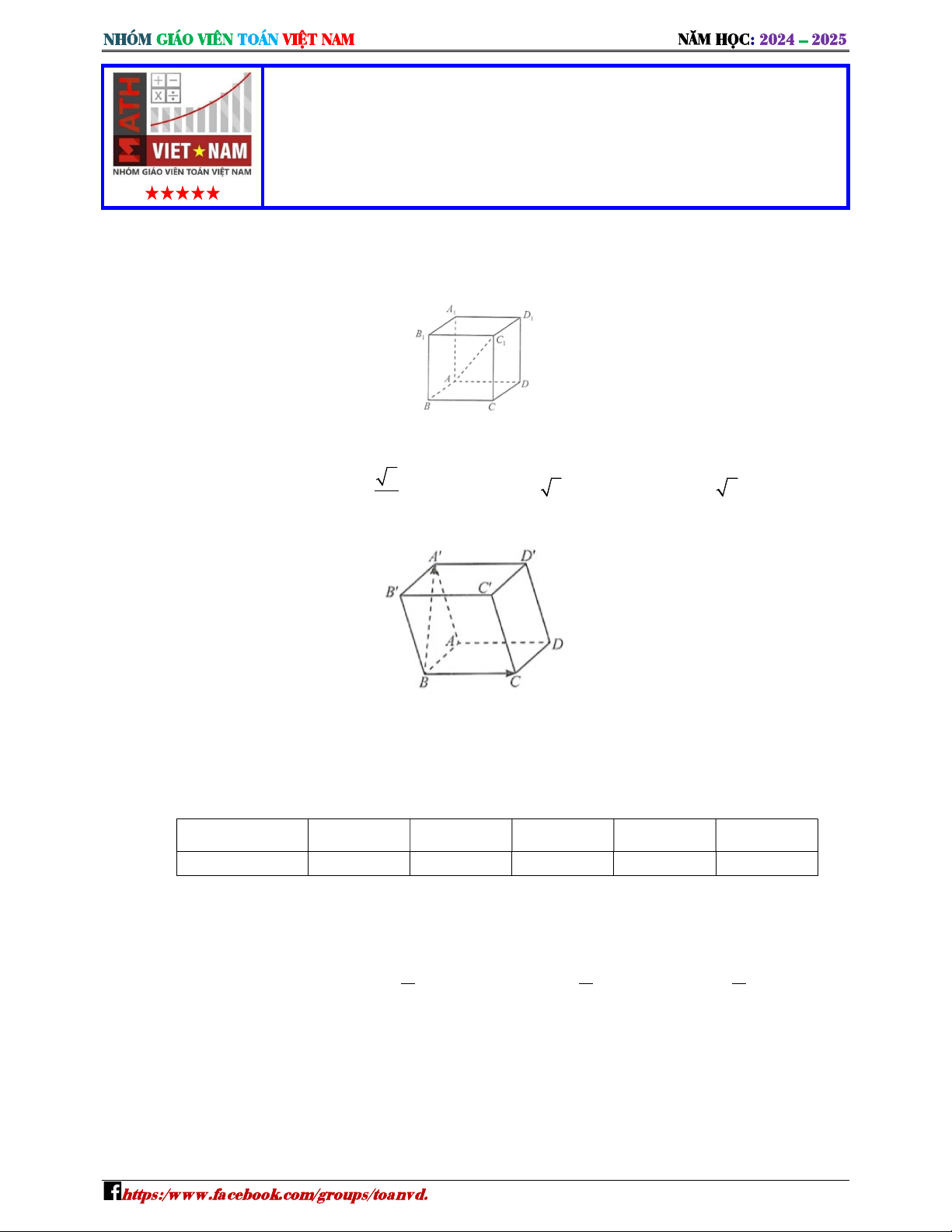
3 Ầ1 , T ắc nghiệm phương án lựa chọ K Ku K ập phương như hình vẽ
ọL ϕ là góc giữa đường thẳng ặt phẳng ( ) . Giá trị tanϕ ằng B − K Ku K KộS
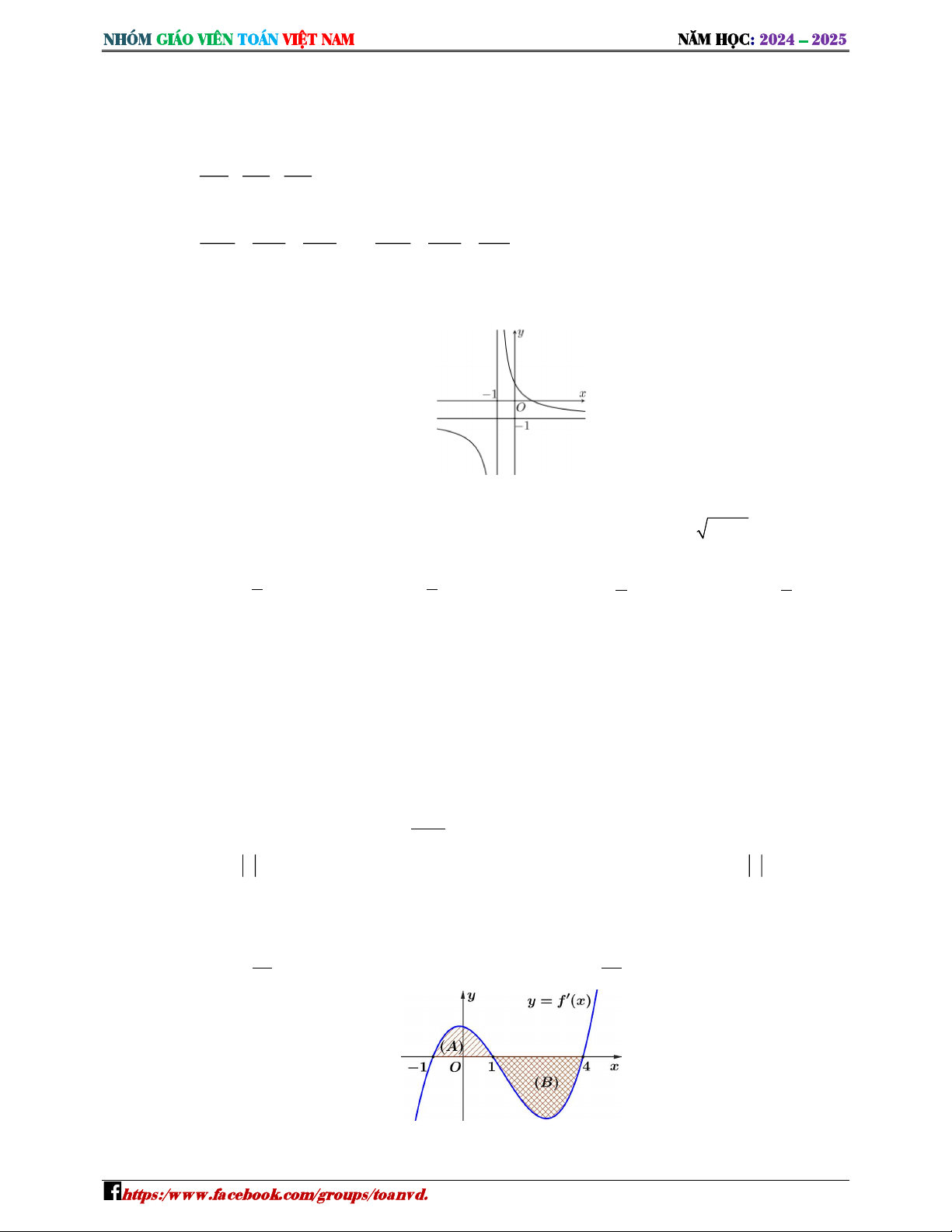
′ ′ ′ ′ như hình vẽ Khi đó, ′ + ằng B ′ ′ ′
7u KLểu thời gian hoàn thành một bài tập (đơn vị: phút) củD ột nhóm học sinh thu được kết T ả sau: 7Kời gian (phút) [ ) [ ) [ ) [ ) [ ) 6ố Kọc sinh
7Kời gian trung bình (đơn vị: phút) để hoàn thành bài tập của các em học sinh là 12,5. B 11,3. 10,4.
Phương trình sin =1 có một nghiệ π π π = π B = = − =
Trong không gian vớL Kệ trục tọa độ , cho các điể
(2;1;−1), (2;−2;−1) 7 ạ độ củD điể thoả m Kệ thức + = − − B − − − − −
Trong không gian vớL Kệ trục tọa độ , cho ba điể ( ), ( ), (− ).Phương
trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua và song song với đường thẳng = − + + + = = B = + − = + − − − + − − = = = = −
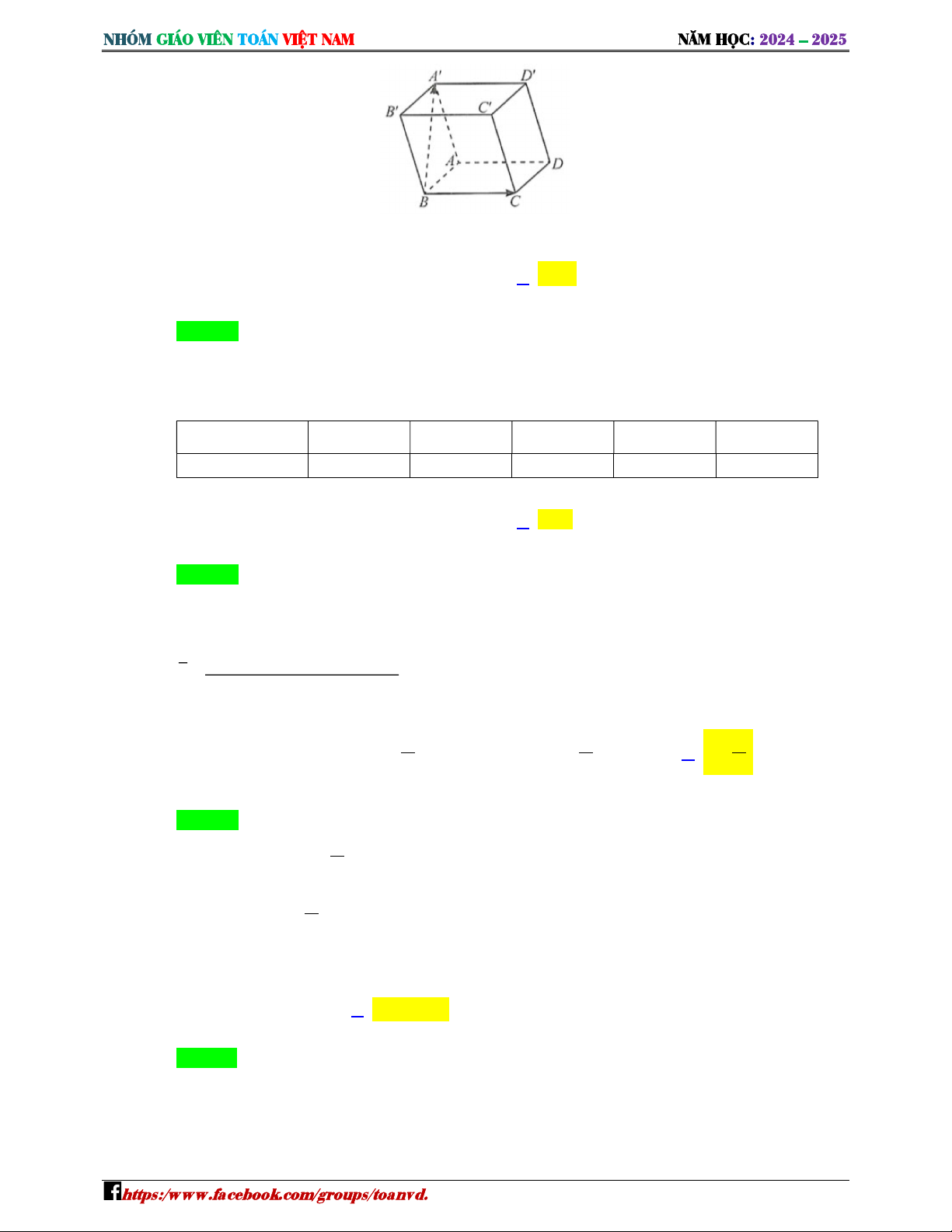
Cho hàm số = ( ) có đồ thị như hình vẽ. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số đã cho = B = = − = −
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường = H − , = , = , = xung quanh trục 5 H − H − B H − H − π H H − − 5 π H − H −
Cho cấp số cộng có và công sai . Giá trị củD ằng B − Nghiệm của phương trình = B = = =
6ố nghiệm nguyên củD ất phương trình log 1 1 B
Nguyên hàm của hàm số B
PHẦN II Trắc nghiệm chọn đúng sai
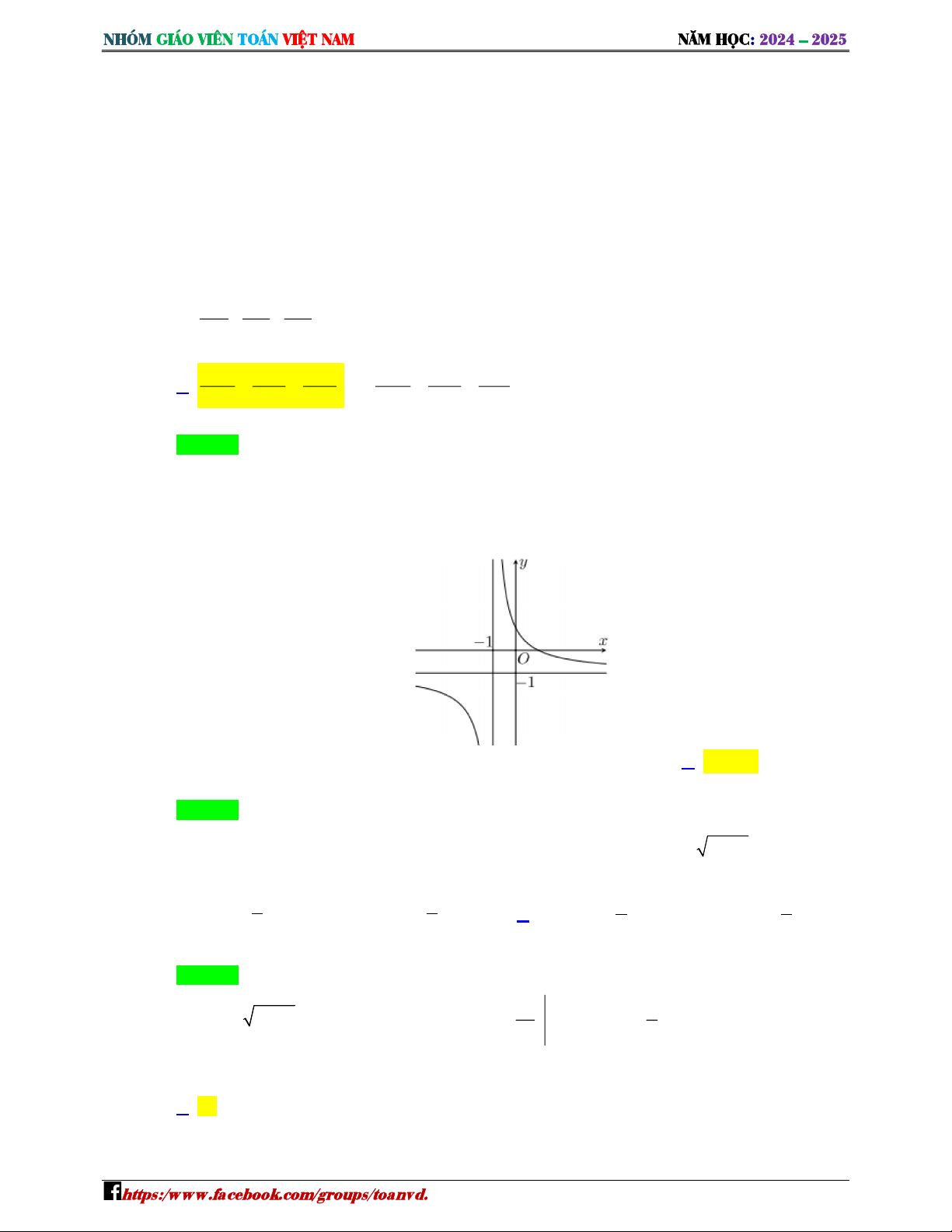
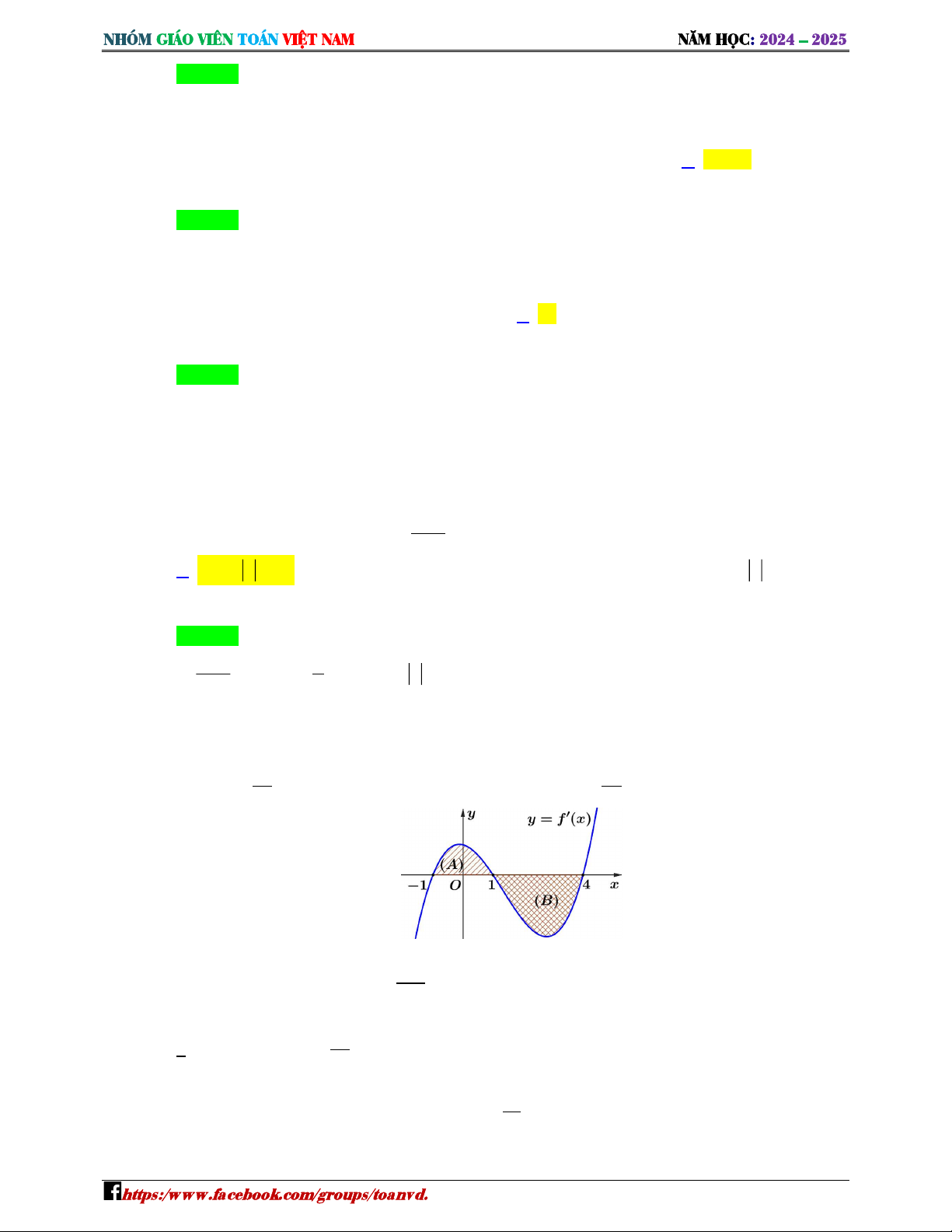
Cho hàm số = ( ) là hàm đa thức có đồ thị của hàm số = ′( ) như hình dưới đây, Biết (− ) 35 1 = −
, diện tích hình phẳng ( ),( ) ần lượt bằng D Giá trị củD ′ ∫ ( )d ằng 253 − Giá trị ( ) ằng
Hàm số đã cho có công thức là ( ) = − − + +
G Lện tích hình phẳng giớL Kạ ởi hai đồ thị hàm số = ( ) ( ) = − + tròn đến hàng đơn vị
Trong một cuộc thi bắn cung, mỗi cung thủ cần thực hiệ KDL ầ ắn liên tiếS 0ột cung thủ có
xác suất bắn trúng hồng tâm trong lầ ắn đầu tiên là 0,35. 1ế ầ ắn đầu tiên trúng hồng tâm
thì xác suất để cung thủ đó bắn trúng hồng tâm trong lầ ắt thứ KDL 0,45. 1ế ầ ắn đầ
tiên không trúng hồng tâm thì xác suất để cung thủ đó bắn trúng hồng tâm trong lầ ắn thứ KDL 0,25. ọL
Lến cố ầ ắn đầu tiên của cung thủ trúng hồng tâm” ọL
Lến cố ầ ắn thứ hai của cung thủ trúng hồng tâm” D ( ) = 0,65. ( | ) = 0,1575. ( ) = 0,68.
G Xác suất để ầ ắn đầu tiên của cung thủ trúng hồng tâm là 0,28 ết quả làm tròn đến
hàng phần trăm), biết rằng lầ ắn thứ hai của cung thủ không trúng hồng tâm
Trong không gian vớL Kệ trục tọD độ
, mỗi đơn vị trên trục có độ dài 10 km. Một trạm theo
dõi được đặt ở gốc tọa độ
và có thể phát hiện được các vật thể cách nó một khoảng không quá
30 km. Một vệ tinh do thám di chuyển từ ị trí đế ị trí − − ớL ận tốc 80
km/h theo một đường thẳng D Hai điể ,
ằm ngoài tầm phát hiện của trạm theo dõi = +
Phương trình đường thẳng = 2 + , ∈ = −
9ị trí đầu tiên vệ tinh do thám bị trạm theo dõi phát hiệ
G 9ệ tinh do thám bay qua vùng bị phát hiện trong khoảng thời gian ít hơn 15 phút
Cho hàm số ( ) = 3 − log ( −1) 5 D Đạo hàm của hàm số ′ = − , ∀ ∈ +∞ − Hàm số có một điểm cực tiể
Hàm số đồng biến trên khoảng +∞
G Giá trị Kỏ Kất của hàm số trên khoảng +∞ ớn hơn
3 Ầ1 ,,, Trắc nghiệm trả lời ngắ
Dân số trung bình sơ bộ năm của tỉ K ải Dương là người, tăng 1,04% so vớL năm
ỏL ới tốc độ tăng dân số được duy trì mức 1,04% ột năm thì đến năm bao nhiêu
dân số tỉ K ải Dương lần đầu vượt 3041975 ngườL
ệ thống đị K ị toàn cầu GPS (Global Positioning System) hiện tại có 24 vệ tinh, mỗL ệ tinh
cách Trái Đất 20000 km , ta coi Trái Đất là khối cầu có bán kính = (nghìn km). VớL ột hệ tọa độ đã chọn,
là tâm Trái Đất và đơn vị trên mỗi trục là nghìn km, hai vệ tinh có tọD độ , . Xét điể
thuộc bề ặt Trái Đất. Tính giá trị Kỏ Kất củD +
theo đơn vị nghìn km (Kết quả làm tròn đến hàng đơn vị
Nhà máy A chuyên sản xuất một loại sả SKẩm cung cấp cho nhà máy B Hai nhà máy thoả thuậ
rằng, hàng tháng nhà máy A cung cấp cho nhà máy B số lượng sả SKẩm theo đơn đặt hàng củD B (tối đa tấn sả SKẩ
1ếu số lượng đặt hàng là
tấn sả SKẩm thì giá bán cho mỗi tấ sả SKẩ
( ) = 45− 0,001 (triệu đồng). Chi phí để A sản xuất tấn sả SKẩm trong một tháng gồ
triệu đồng chi phí cố đị K
triệu đồng cho mỗi tấn sả SKẩ 1K iy A
cần bán cho nhà máy B bao nhiêu tấn sả SKẩ
ỗi tháng để ợL K ận thu được lớ Kất? (kết
T ả làm tròn đến hàng phần mườL
Hiện nay, nước ta đang trong quá trình tinh gọn bộ máy và thực hiện nghị quyết không tổ chức
công an cấp huyện. Do vậy, trong đợt điều động cán bộ công an từ huyện về công tác tại cơ sở
hoặc công tác tại công an tỉnh, phòng tổ chức cán bộ nhận thấy rằng: Có 60% cán bộ có nguyện
vọng về công tác tại cơ sở là các xã vùng sâu vùng xa, số còn lại nguyện vọng về công tác tại công an tỉnh
+ Trong số cán bộ có nguyện vọng về công tác tại cơ sở thì 70% có trình độ đại học và có trình độ trung cấp
+ Trong số cán bộ có nguyện vọng về công an tỉnh thì
có trình độ đại học và có trình độ trung cấp
Tuy nhiên, năng lực công tác cũng là một yếu tố quan trọng. Dựa trên hồ sơ đánh giá năng lực:
+ Trong số cán bộ có nguyện vọng về cơ sở thì tỷ lệ cán bộ được đánh giá có năng lực
“Tốt” trở lên với trình độ đại học là
và trình độ trung cấp là
+ Trong số cán bộ có nguyện vọng về công tác tại công an tỉnh thì tỷ lệ được đánh giá là
có năng lực “Tốt” trở lên với trình độ đại học là
và với trình độ trung cấp là
Chọn ngẫu nhiên một cán bộ công an. Tính xác suất để cán bộ này vừa có trình độ đại học, vừa
được đánh giá có năng lực “Tốt” và có nguyện vọng về công tác tại cơ sở là các xã vùng sâu
vùng xa. (Kết quả làm tròn đến hàng phần trăm) Cho hình chóp có đáy
là hình vuông tâm , cạ K P ạnh bên vuông
góc với đáy, góc = ° .K ảng cách giữa hai đường thẳng ằng bao nhiêu P
ết quả làm tròn đến hàng phần trăm) &k
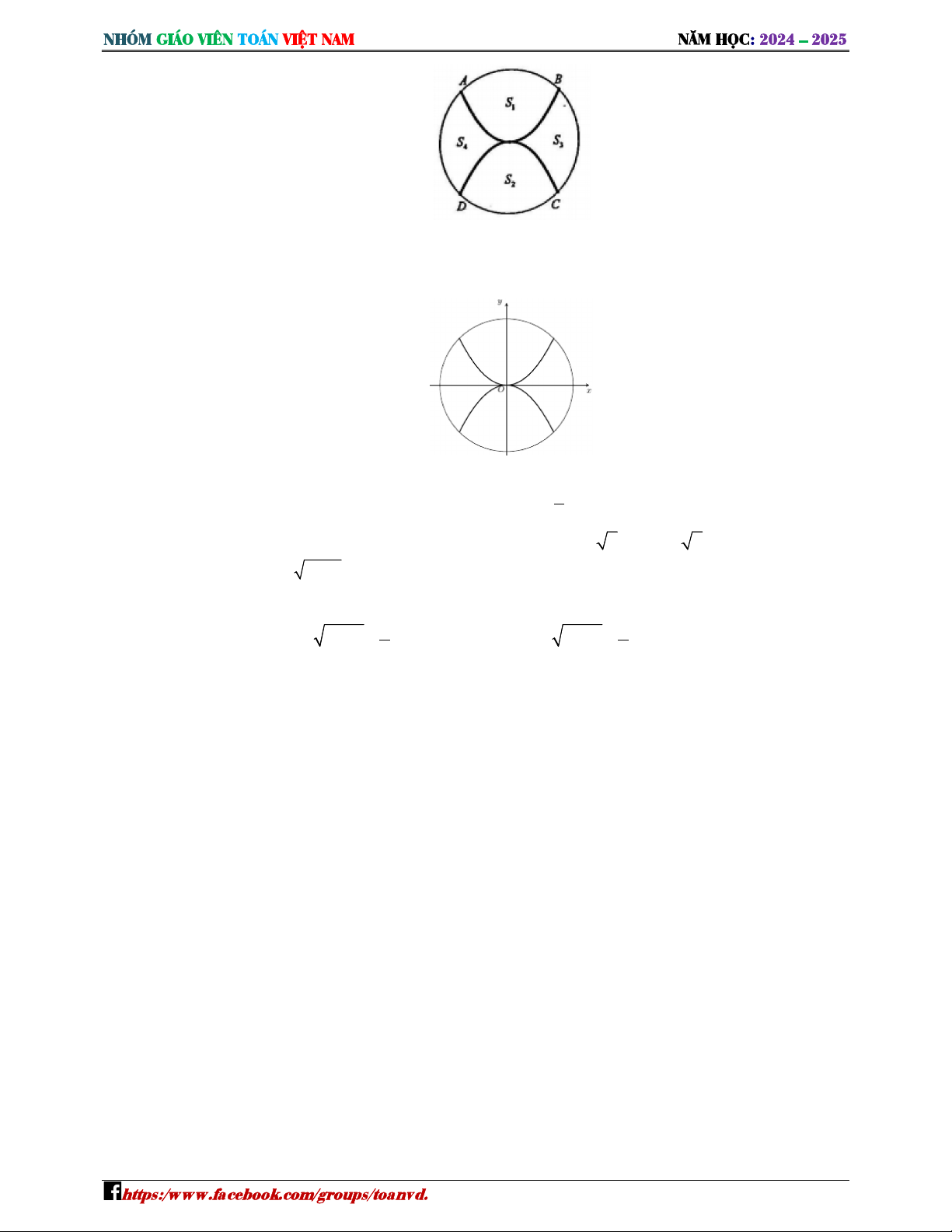
Sân trường có một bồn hoa hình tròn tâm . Một nhóm học sinh lớp 12 được giao thiết kế bồn
hoa, nhóm này định chia bồn hoa thành bốn phần bởi hai đường parabol có cùng đỉnh và đối xứng nhau qua
. Hai đường parabol này cắt đường tròn tại bốn điể , , , tạo thành một
hình vuông có cạnh bằng 4 m (như hình vẽ). Phần diện tích ,
dùng để trồng hoa, phần diện tích ,
dùng để trồng cỏ. Biết kinh phí trồng hoa là 150.000 đồng/m , kinh phí để trồng cỏ 100.000 đồng/m
ỏi nhà trường cần bao nhiêu triệu đồng để trồng bồn hoa đó? ết quả làm
tròn đến hàng phần trăm) ẾT 6 ĐT TỈ1 ẢI DƯƠNG
ĐỀ THI THỬ TỐT NGHIỆP THPT Năm họ 0 i Mã đề Kờ K K ể Kời gian phát đề BẢNG ĐÁP ÁN
3 Ầ1 , T ắc nghiệm phương án lựa chọ 1.B 5.B 9.A 12.A
PHẦN II. Trắc nghiệm chọn đúng sai. SĐSĐ ĐSSĐ ĐĐSS SĐĐĐ
3 ẦN III. Trắc nghiệm trả lời ngắ Trả lời HƯỚNG DẪN GIẢI
3 Ầ1 , T ắc nghiệm phương án lựa chọ K Ku K ập phương như hình vẽ
ọL ϕ là góc giữa đường thẳng ặt phẳng ( ) . Giá trị tanϕ ằng B − ời giải Chọn B. Ta có ∩( ) ={ } ⊥ ( ) Do đó ϕ = ( ( )) =
ọL D là độ dài cạ K Ku K ập phương. Khi đó = D , = D Xét tam giác vuông tạL có tan D = = = D K Ku K KộS
′ ′ ′ ′ như hình vẽ Khi đó, ′ + ằng B. ′ ′ ′ ời giải
Chọ
Ta có = ′ ′ . Khi đó ′ + = ′ + ′ ′ = ′
7u KLểu thời gian hoàn thành một bài tập (đơn vị: phút) củD ột nhóm học sinh thu được kết T ả sau: 7Kời gian (phút) [ ) [ ) [ ) [ ) [ ) 6ố Kọc sinh
7Kời gian trung bình (đơn vị: phút) để hoàn thành bài tập của các em học sinh là 12,5 B. 11,3 10,4. ời giải Chọ
Ta có giá trị đại diện của từng nhóm số Lệ ần lượt là: 2; 6; 10; 14; 18.
7Kời gian trung bình để hoàn thành bài tậS + + + + = = 10,4
Phương trình sin =1 có một nghiệ π π π = π B. = = − = ời giải Chọ π
Ta có sin =1⇔ = + 2π ( ∈) π 9ớL = thì =
Trong không gian vớL Kệ trục tọa độ , cho các điể
(2;1;−1), (2;−2;−1) 7 ạ độ củD điể thoả m Kệ thức + = − − B − − − − − ời giải Chọ B. = ( − − − − ) = ( − − − − − ) − + ( − ) = = ( ) + = ⇔ − + − − = ⇔ = − − − + (− − ) = = − 9ậy ( − − )
Trong không gian vớL Kệ trục tọa độ , cho ba điể ( ), ( ), (− ).Phương
trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua và song song với đường thẳng = − + + + = = B. = + − = + − − − + − − = = = = − ời giải Chọ
Đường thẳng song song vớL Kậ = (− ) làm vectơ chỉ phương.
Cho hàm số = ( ) có đồ thị như hình vẽ. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số đã cho = B. = = − = − ời giải Chọ
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường = H − , = , = , = xung quanh trục 5 H − H − B. H − H − π H H − − 5 π H − H − ời giải Chọ π ∫ ( H ) d π∫ (H )d π H π H H = − = − = − = − −
Cho cấp số cộng có và công sai . Giá trị củD ằng B. − ời giải Chọ Nghiệm của phương trình = B. = = = ời giải Chọ
6ố nghiệm nguyên củD ất phương trình log 1 1 B. ời giải Chọ Điều kiệ log 1 1 Suy ra 0 nên
Nguyên hàm của hàm số B. ời giải Chọ d 1
d ln
PHẦN II. Trắc nghiệm chọn đúng sai
Cho hàm số = ( ) là hàm đa thức có đồ thị của hàm số = ′( ) như hình dưới đây, Biết (− ) 35 1 = −
, diện tích hình phẳng ( ),( ) ần lượt bằng D Giá trị củD ′ ∫ ( )d ằng 253 − Giá trị ( ) ằng
Hàm số đã cho có công thức là ( ) = − − + +
G Lện tích hình phẳng giớL Kạ ởi hai đồ thị hàm số = ( ) ( ) = − + tròn đến hàng đơn vị ời giải D Sai. Ta có ′ ∫ ( ) = ′ ∫ ( ) + ′ ∫ ( ) 64 125 d d d = −63 = − . − − Đúng. Ta có ′ ∫ ( ) = ( )− (− ) 64 = ⇔ ( ) 35 64 − − = ⇔ ( ) 29 d 1 1 1 1 = . −
c) Sai. Ta thấy ′( ) = D( + )( − )( − ) = D( − )( − ) = D( − − + ) Suy ra ( ) = D − − + + ại có: (− ) 35 35 35 = − − D + = − D = ⇔ ⇔ ( ) = D = + = 9ậy ( ) = − − + =
d) Đúng. Xét phương trình ( ) ( ) − = ⇔ − = ⇔ =
9ậy diện tích hình phẳng giớL Kạ ởi hai đồ thị hàm số ( ) ( ) = ∫ ( )− ( ) d ≈ 216. −
Trong một cuộc thi bắn cung, mỗi cung thủ cần thực hiệ KDL ầ ắn liên tiếS 0ột cung thủ có
xác suất bắn trúng hồng tâm trong lầ ắn đầu tiên là 0,35. 1ế ầ ắn đầu tiên trúng hồng tâm
thì xác suất để cung thủ đó bắn trúng hồng tâm trong lầ ắt thứ KDL 0,45. 1ế ầ ắn đầ
tiên không trúng hồng tâm thì xác suất để cung thủ đó bắn trúng hồng tâm trong lầ ắn thứ KDL 0,25. ọL
Lến cố ầ ắn đầu tiên của cung thủ trúng hồng tâm”. ọL
Lến cố ầ ắn thứ hai của cung thủ trúng hồng tâm”. D ( ) = 0,65. ( | ) = 0,1575. ( ) = 0,68.
G Xác suất để ầ ắn đầu tiên của cung thủ trúng hồng tâm là 0,28 ết quả làm tròn đến
hàng phần trăm), biết rằng lầ ắn thứ hai của cung thủ không trúng hồng tâm. ời giải ( ) = 0,35
Theo dữ kiện đề cho, ta có ( | ) = 0,45. ( | ) = 0,25
D Đúng. 9u ( ) =1− ( ) = 0,35. Sai
c) Sai. 9u ( ) = ( ) ( | ) + ( ) ( | ) = 0,35.0,45+ 0,65.0,25 = 0,32. 0,35.(1−0,45) d) Đúng. 9u ( | ) ( ) ( ) = ( ) = = ≈ 0,28. 1− 0,32 272
Trong không gian vớL Kệ trục tọa độ
, mỗi đơn vị trên trục có độ dài 10 km. Một trạm theo
dõi được đặt ở gốc tọa độ
và có thể phát hiện được các vật thể cách nó một khoảng không quá
30 km. Một vệ tinh do thám di chuyển từ ị trí đế ị trí − − ớL ận tốc 80
km/h theo một đường thẳng. D Hai điể ,
ằm ngoài tầm phát hiện của trạm theo dõi. = +
Phương trình đường thẳng = 2 + , ∈ = −
9ị trí đầu tiên vệ tinh do thám bị trạm theo dõi phát hiệ
G 9ệ tinh do thám bay qua vùng bị phát hiện trong khoảng thời gian ít hơn 15 phút. ời giải a) Đúng b) Đúng c) Sai d) Sai D = + + = > , ( ) = − + − + = > 9ậy hai điể ,
ằm ngoài tầm phát hiện của trạm theo dõi. 5 5 5 = 5 − ;− ; = − (2;1; − )
1 . Do đó, phương trình tham số của đường thằng = + = 2 + , ∈ = − c) ọL ( + + − ) ∈
ị trí đầu tiên vệ tinh do thám bị trạm theo dõi phát hiệ Khi đó: = ⇔ ( + ) +( + ) +( − ) = ⇔ ( + ) + ( + ) + ( − ) = = − ⇔ + + = ⇔ =− 9ớL = − ⇒ ( ) ⇒ = 9ớL = − ⇒ ( ) ⇒ = 9u <
nên vị trí đầu tiên vệ tinh do thám bị trạm theo dõi phát hiệ ( ) d) 9u ( )
ị trí đầu tiên vệ tinh do thám bị trạm theo dõi phát hiệ nên ( )
ị trí cuối cùng ệ tinh do thám bị trạm theo dõi phát hiệ . Do đó quãng đường vệ tinh do thám bay qua vùng bị phát hiệ =
9ậy thời gian ệ tinh do thám bay qua vùng bị phát hiệ = = giờ ≈18, 4 Shút.
Cho hàm số ( ) = 3 − log ( −1) 5 D Đạo hàm của hàm số ′ = − , ∀ ∈ +∞ − Hàm số có một điểm cực tiể
Hàm số đồng biến trên khoảng +∞
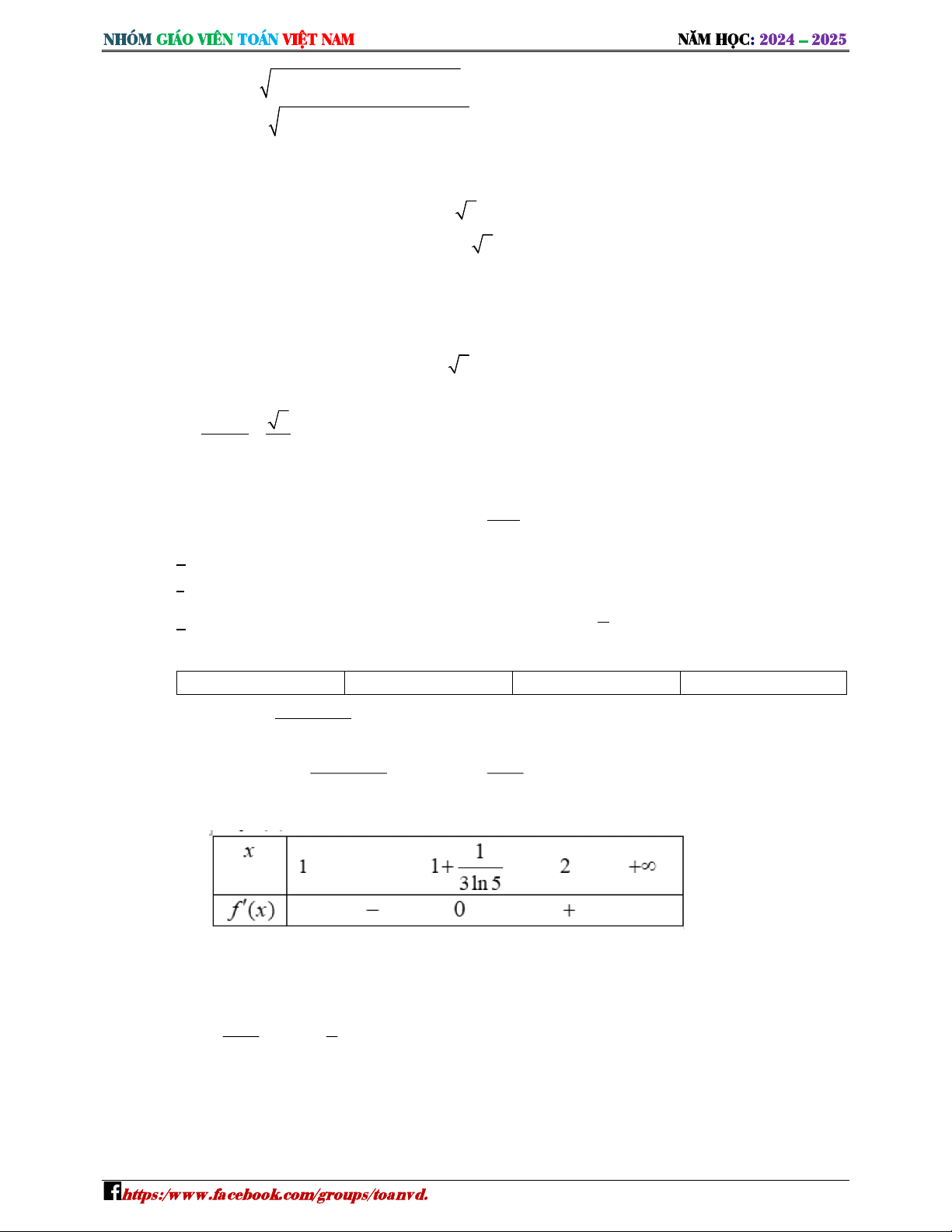
G Giá trị Kỏ Kất của hàm số trên khoảng +∞ ớn hơn ời giải a) Sai b) Đúng c) Đúng d) Đúng D ′ = − ( , ∀ ∈ +∞ − ) 1 .ln 5 ′ = ⇔ − ( ) = ⇔ = + < −1 .ln 5 3ln 5 Bảng xét dấ ′ Suy ra hàm số có một điểm cực tiể c) 7ừ ảng xét dấ ′ suy ra hàm số đồng biến trên khoảng +∞ d) 7ừ ảng xét dấ ′
suy ra giá trị Kỏ Kất của hàm số trên khoảng +∞ 1 + ≈ 4,6 > 3ln 5 2
3 ẦN III. Trắc nghiệm trả lời ngắ
Dân số trung bình sơ bộ năm của tỉ K ải Dương là người, tăng 1,04% so vớL năm
ỏL ới tốc độ tăng dân số được duy trì mức 1,04% ột năm thì đến năm bao nhiêu
dân số tỉ K ải Dương lần đầu vượt 3041975 ngườL ời giải Đáp án: ọL =
(người) là dân số của tỉ K ải Dương năm
ọL r =1,04% = 0,0104 là tốc độ tăng dân số Kằng năm. ọL
là dân số của tỉ K ải Dương sau năm kể từ cuối năm
Công thức tính dân số sau năm là P = P + r Ta cần tìm số năm
nguyên dương nKỏ Kất sao cho dân số ần đầu vượt $3041975$ ngườL
Ta có bất phương trình: > 3041975 ⇔ P (1+ r) > 3041975
⇔ 1936780⋅(1+ 0,0104) > 3041975
⇔ 1936780⋅(1,0104) > 3041975 ⇔ > 43,6369.
9u là số năm và phải là số nguyên (để đánh dấu năm dân số vượt ngưỡng), nên Kỏ Kất là năm kể từ năm
, dân số tỉ K ải Dương lần đầu vượt 3041975 ngườL Năm đó là: 2021+ 44 = 2065
Do đó, đến năm 2065 thì dân số tỉ K ải Dương lần đầu vượt 3041975 ngườL
ệ thống đị K ị toàn cầu GPS (Global Positioning System) hiện tại có 24 vệ tinh, mỗL ệ tinh
cách Trái Đất 20000 km , ta coi Trái Đất là khối cầu có bán kính = (nghìn km). VớL ột hệ tọa độ đã chọn,
là tâm Trái Đất và đơn vị trên mỗi trục là nghìn km, hai vệ tinh có tọD độ , . Xét điể
thuộc bề ặt Trái Đất. Tính giá trị Kỏ Kất củD +
theo đơn vị nghìn km (Kết quả làm tròn đến hàng đơn vị ời giải Đáp án:
Đơn vị được sử dụng trong bài toán là nghìn km.
Trái Đất được coi là khối cầu tâm bán kính =
9ậy phương trình mặt cầu Trái Đất là + + = = 7ọa độ các vệ tinh là Điể
thuộc bề ặt Trái Đất nên + + = Ta cần tính + = − + − + − = − + + = − 52 + 26 + + = ( + + ) −52 +26 + + = = , nên:
= 36 −52 + 676 = 712 −52 9ậy = 712 −52 Tương tự, = − + − + − = + − + = + − 52 + 26 + = ( + + ) −52 + 26
= 36 −52 + 676 = 712 −52 9ậy = 712 − 52
Ta cần tìm giá trị Kỏ Kất củD = + = 712 −52 + 712 −52 Do vai trò củD trong biểu thức
và trong phương trình mặt cầ + + =
đối xứng nhau qua các vệ tinh
ếu đổi vai trò ↔ , ↔ thì
bài toán không đổi), ta có thể dự đoán rằng giá trị Kỏ Kất đạt được khi = .KL = , điể thuộc mặt cầu nên + + = ⇔ + = Khi đó = 2 712 −52 Để
Kỏ Kất, thì 712 −52 SKảL Kỏ Kất. Vì hàm =
đồng biến, ta cầ 712 −52
Kỏ Kất. Điều này có nghĩa là 52 SKảL ớ Kất, hay SKảL ớ Kất. 7ừ + = , ta có = − 9u ≥ , nên ≤ ⇒ ≤ Do đó − ≤ ≤ Giá trị ớ Kất củD =
. Giá trị này đạt được khi = Khi đó = = = . Điể Giá trị Kỏ Kất củD = − = − PL 2 712 52(3 2) 2 712 156 2
6ử dụng máy tính: 2 ≈1,41421356
156 2 ≈156×1,41421356 ≈ 220,61731536 = − = PL
2 712 220,61731536 2 491,38268464 ≈ × ≈ PL 2 22,16715326 44,33430652
.ết quả làm tròn đến hàng đơn vị Đơn vị là nghìn km.
9ậy giá trị Kỏ Kất củD + nghìn km.
Nhà máy A chuyên sản xuất một loại sả SKẩm cung cấp cho nhà máy.B Hai nhà máy thoả thuậ
rằng, hàng tháng nhà máy A cung cấp cho nhà máy B số lượng sả SKẩm theo đơn đặt hàng củD B (tối đa tấn sả SKẩ
1ếu số lượng đặt hàng là
tấn sả SKẩm thì giá bán cho mỗi tấ sả SKẩ
( ) = 45− 0,001 (triệu đồng). Chi phí để A sản xuất tấn sả SKẩm trong một tháng gồ
triệu đồng chi phí cố đị K
triệu đồng cho mỗi tấn sả SKẩm. Nhà máy A
cần bán cho nhà máy B bao nhiêu tấn sả SKẩ
ỗi tháng để ợL K ận thu được lớ Kất? (kết
T ả làm tròn đến hàng phần mườL ời giải Đáp án:
ọL là số lượng sả SKẩm (tấn) mà nhà máy A cung cấp cho nhà máy B mỗi tháng. Điều kiệ ≤ ≤
Giá bán cho mỗi tấn sả SKẩ
( ) = 45− 0,001 (triệu đồng/tấ
Doanh thu khi bán tấn sả SKẩ
( ) = ⋅ ( ) = (45− 0,001 ) = 45 − 0,001 (triệu đồng). Chi phí để sản xuất tấn sả SKẩm gồ Chi phí cố đị K triệu đồng. Chi phí biến đổL triệu đồng (vì triệu đồng cho mỗi tấ 7ổng chi phí sản xuất tấn sả SKẩ = + (triệu đồng).
ợL K ận thu được khi bán tấn sả SKẩ = −
( ) = −0,001 +15 −100 (triệu đồng).
Để tìm số tấn sả SKẩ
sao cho lợL K ậ ớ Kất, ta tìm giá trị ớ Kất củD K trên đoạ Tính đạo hàm củD (′ ) = −0,003 +15 K ′ = ⇔ = 50 2 u ≥
Giá trị này nằm trong đoạ u 0 ≤ 70,710678 ≤ 100 Do đó,
. đạt cực đại tạL = 50 2 Ta so sánh giá trị củD tại các điể = , = = 50 2 = − = (50 2) = 500 2 −100
So sánh các giá trị, lợL K ậ ớ Kất là 500 2 −100 ≈ 607,10678 triệu đồng, đạt được khi = 50 2 tấ
Yêu cầu bài toán là làm tròn kết quả số tấn sả SKẩm đến hàng phần mườL = 50 2 ≈ 70,710678 tấ
Làm tròn đến hàng phần mười, ta được ≈ 70,7 tấ
9ậy, nhà máy A cần bán cho nhà máy B khoảng 70,7 tấn sả SKẩ
ỗi tháng để ợL K ận thu được lớ Kất.
Hiện nay, nước ta đang trong quá trình tinh gọn bộ máy và thực hiện nghị quyết không tổ chức
công an cấp huyện. Do vậy, trong đợt điều động cán bộ công an từ huyện về công tác tại cơ sở
hoặc công tác tại công an tỉnh, phòng tổ chức cán bộ nhận thấy rằng: Có 60% cán bộ có nguyện
vọng về công tác tại cơ sở là các xã vùng sâu vùng xa, số còn lại nguyện vọng về công tác tại công an tỉnh.
+ Trong số cán bộ có nguyện vọng về công tác tại cơ sở thì 70% có trình độ đại học và có trình độ trung cấp.
+ Trong số cán bộ có nguyện vọng về công an tỉnh thì
có trình độ đại học và có trình độ trung cấp.
Tuy nhiên, năng lực công tác cũng là một yếu tố quan trọng. Dựa trên hồ sơ đánh giá năng lực:
+ Trong số cán bộ có nguyện vọng về cơ sở thì tỷ lệ cán bộ được đánh giá có năng lực
“Tốt” trở lên với trình độ đại học là
và trình độ trung cấp là
+ Trong số cán bộ có nguyện vọng về công tác tại công an tỉnh thì tỷ lệ được đánh giá là
có năng lực “Tốt” trở lên với trình độ đại học là
và với trình độ trung cấp là
Chọn ngẫu nhiên một cán bộ công an. Tính xác suất để cán bộ này vừa có trình độ đại học, vừa
được đánh giá có năng lực “Tốt” và có nguyện vọng về công tác tại cơ sở là các xã vùng sâu
vùng xa. (Kết quả làm tròn đến hàng phần trăm) Lời giải Đáp án: 0,25 Gọi
là biến cố: “Cán bộ có nguyện vọng về công tác tại cơ sở là các xã vùng sâu vùng xa”.
là biến cố: “Cán bộ có nguyện vọng về công tác tại công an tỉnh”. Gọi
là biến cố: “Cán bộ có trình độ đại học”.
là biến cố: “Cán bộ có trình độ trung cấp”. Gọi
là biến cố: “Cán bộ được đánh giá là có năng lực “Tốt” trở lên”.
Ta có thể mô tả bằng sơ đồ cây như sau: 60% 70% 40% 60% 30% 30% 70% 85% 40% 80% 15% 20% 25% 75%
Từ đó, xác suất để cán bộ này vừa có trình độ đại học, vừa được đánh giá có năng lực “Tốt” và
có nguyện vọng về công tác tại cơ sở là các xã vùng sâu vùng xa.
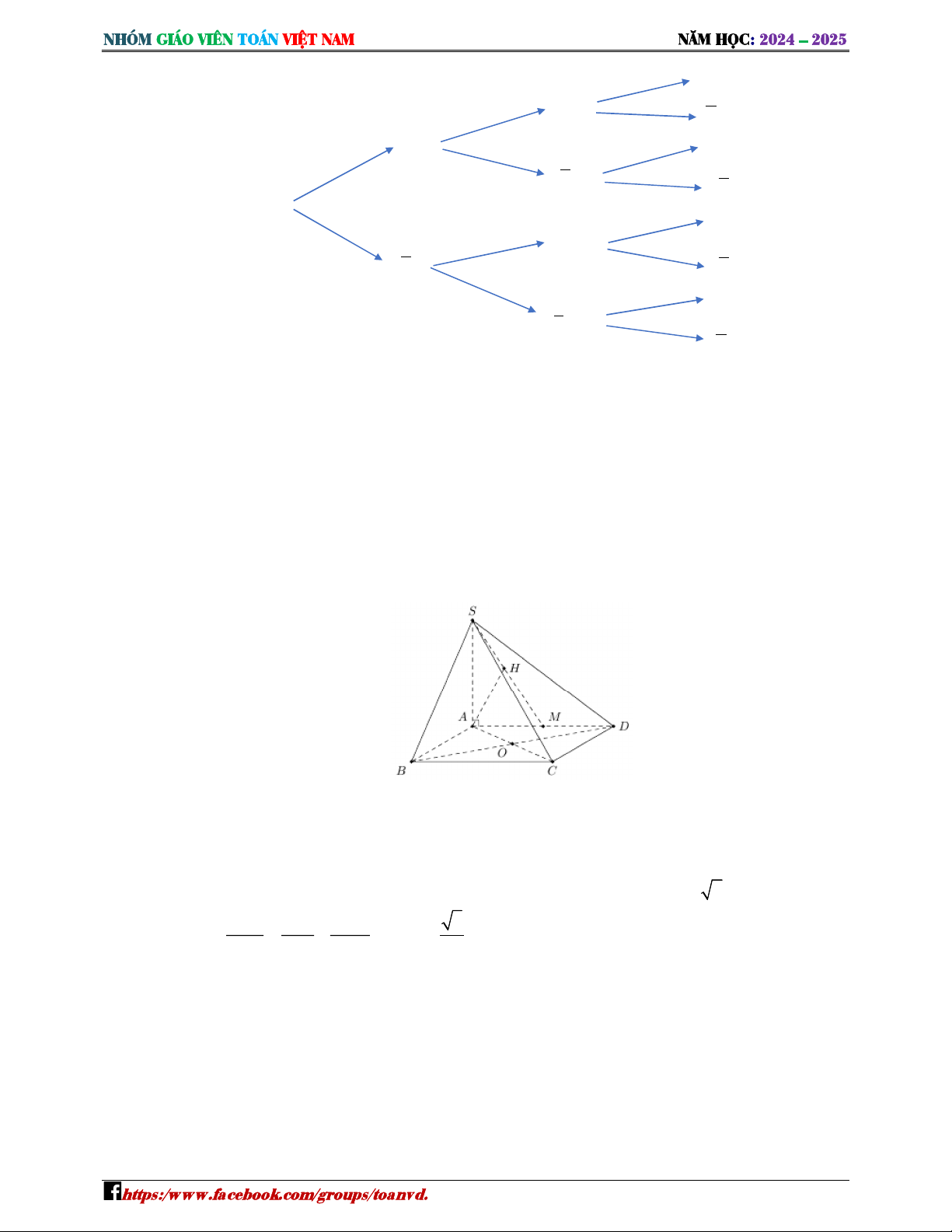
( . . ) = 0,6.0,7.0,6 = 0,252 ≈ 0,25 Cho hình chóp có đáy
là hình vuông tâm , cạ K P ạnh bên vuông
góc với đáy, góc = ° .K ảng cách giữa hai đường thẳng ằng bao nhiêu P
ết quả làm tròn đến hàng phần trăm) ờigiải Trả lời: 0,45 ọL là trung điểm củD .ẻ ( ∈ ) vuông góc vớL suy ra d( ,( )) = Khi đó d( , ) = d( ,( )) = d( ,( )) = Tam giác
cân và có góc = ° nên đều suy ra = = ⇒ = 1 1 1 5 Do đó = + ⇒ = ≈ 0,45 5 &k
Sân trường có một bồn hoa hình tròn tâm . Một nhóm học sinh lớp 12 được giao thiết kế bồn
hoa, nhóm này định chia bồn hoa thành bốn phần bởi hai đường parabol có cùng đỉnh và đối xứng nhau qua
. Hai đường parabol này cắt đường tròn tại bốn điểm , , , tạo thành một
hình vuông có cạnh bằng 4 m (như hình vẽ). Phần diện tích ,
dùng để trồng hoa, phần diện tích ,
dùng để trồng cỏ. Biết kinh phí trồng hoa là 150.000 đồng/m , kinh phí để trồng cỏ 100.000 đồng/m
ỏi nhà trường cần bao nhiêu triệu đồng để trồng bồn hoa đó? ết quả làm
tròn đến hàng phần trăm) ời giải Trả lời: 3,27
ắ Kệ trục tọa độ như Ku K ẽ
Parabol đi qua (−2;2), (2; 2) có phương trình =
Phương trình đường tròn có đường kính là = ⇒ = có phương trình + = ⇒ = −
Kinh phí để trồng bồ K D = 0,15⋅4⋅∫ 8− − d + 0,1⋅ 8
π − 4⋅ ∫ 8− −
d ≈ 3,27 triệu đồng ẾT

