20 Đề Học Sinh Giỏi Toán 6 Cấp Huyện 2025-2026 Có Đáp Án
Tìm số tự nhiên có ba chữ số biết rằng khi chia số đó cho các số 25, 28, 35 thì được các số dư lần lượt là 4, 7, 14. Một khu vườn hình chữ nhật ABCD có chu vi 120m, người ta mở rộng khu vườn như hình vẽ để được một vườn hình chữ nhật có diện tích lớn hơn như hình vẽ. Tài lieuejg iusp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 6 418 tài liệu
Môn: Toán 6 2.5 K tài liệu
Tác giả:
Preview text:
thuvienhoclieu.com
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI GIAO LƯU HỌC SINH GIỎI THIỆU HOÁ NĂM HỌC 2022-2023 Đề 1 Môn: Toán 6
Thời gian: 120 phút (không kể thời gian giao đề) Đề chính thức Ngày thi: 19/04/2023
(Đề gồm: 05 câu, 01 trang)
Câu 1: ( 4,0 điểm).
1. Tính giá trị các biểu thức sau: 2 2 9 2 6 2 14 4
5.(2 .3 ) .(2 ) 2.(2 .3) .3
a) A = 3.{5.[(52 + 23): 11] - 16} + 2026 b) B = 28 18 29 18 5.2 .3 7.2 .3 1 1 1 1 1 2. Chứng minh: ... 2 2 2 2 4 6 8 (2 ) n 4
Câu 2. (4,0 điểm) Tìm x biết: 1. 2 2 2 19x 2.5 :14 13 8 4 1 1 1 1 119 2. ... .x 1.2.3.4 2.3.4.5 3.4.5.6 7.8.9.10 720
3. Tìm số tự nhiên có ba chữ số biết rằng khi chia số đó cho các số 25, 28, 35 thì được
các số dư lần lượt là 4, 7, 14.
Câu 3: ( 4,0 điểm).
1. Cho a, b là các số tự nhiên thỏa mãn a + 4b chia hết 13.
Chứng minh (a + 4b).(10a +b) chia hết cho 169.
2. Tìm tất cả các số nguyên tố p, q sao cho 7p + q; pq + 11đều là số nguyên tố.
Câu 4: ( 6,0 điểm).
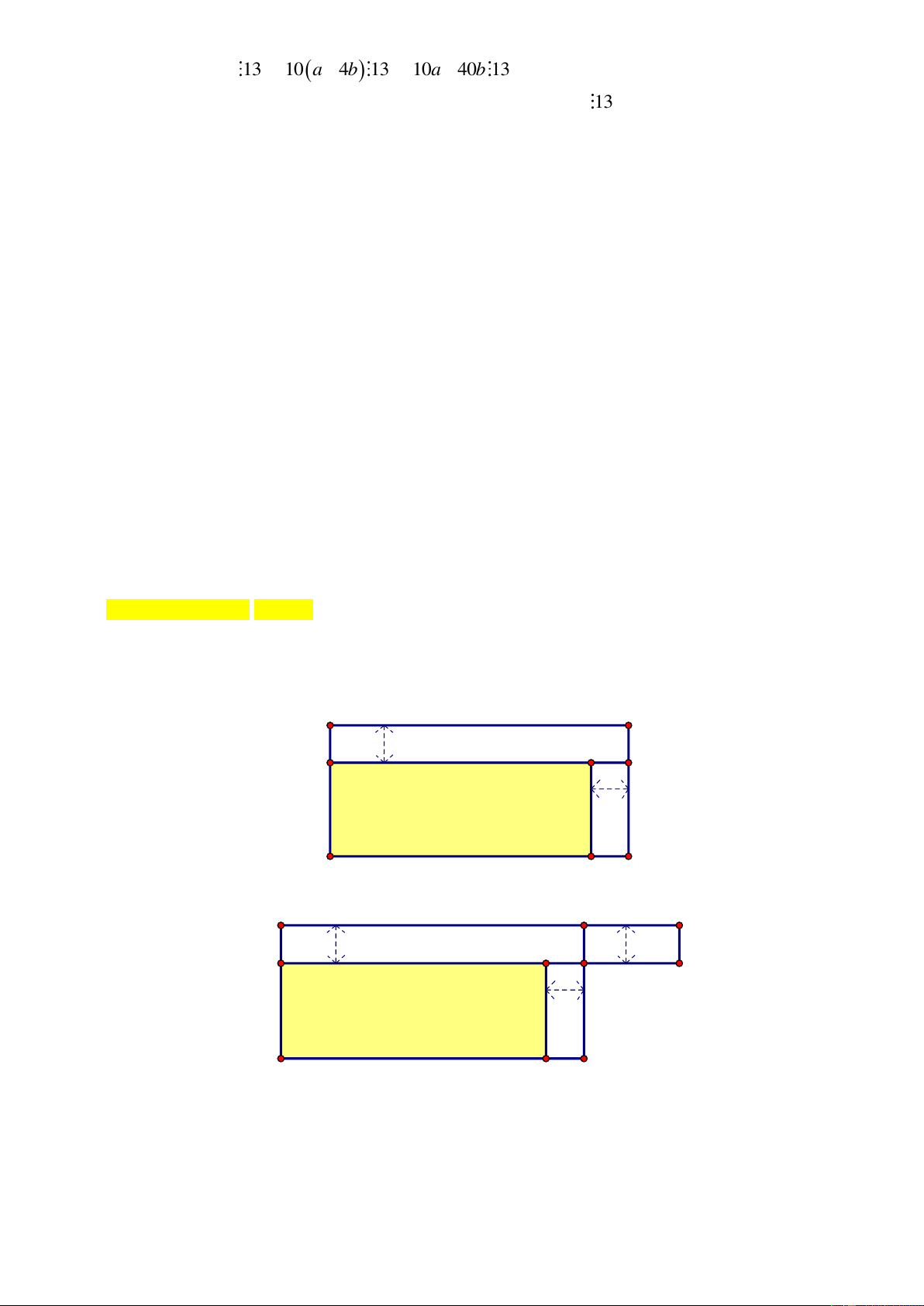
1) Một khu vườn hình chữ nhật ABCD có E
chu vi 120m, người ta mở rộng khu vườn F
như hình vẽ để được một vườn hình chữ nhật 10m B A G
có diện tích lớn hơn như hình vẽ. Hãy tính
diện tích phần mới mở thêm. 10m H D C
2) Đoạn thẳng AB = 36 cm được chia thành bốn đoạn thẳng có độ dài không bằng nhau
theo thứ tự là các đoạn thẳng AM, MN, NP và PB . Gọi E, F, G, H theo thứ tự là trung điểm
của các đoạn thẳng AM, MN, NP, PB . Biết độ dài của đoạn thẳng EH =30 cm. Tính độ dài
của đoạn thẳng FG.
3) Vẽ 101 đường thẳng đôi một cắt nhau. Hỏi số giao điểm (của hai đường thẳng hay nhiều
đường thẳng) ít nhất, nhiều nhất là bao nhiêu?
Câu 5: ( 2,0 điểm). Cho bốn số nguyên a, b, c, d sao cho 2b = a + c, 2c = b + d, c2 + d2 < 4. Tìm số nguyên a biết b = 2.
HƯỚNG DẪN GIẢI MÔN TOÁN 6
HUYỆN THIỆU HÓA NĂM HỌC 2022-2023
Câu 1: ( 4,0 điểm).
thuvienhoclieu.com Trang 1 thuvienhoclieu.com
1. Tính giá trị các biểu thức sau:
a) A = 3.{5.[(52 + 23): 11] - 16} + 2026 2 2 9 2 6 2 14 4
5.(2 .3 ) .(2 ) 2.(2 .3) .3 b) B = 28 18 29 18 5.2 .3 7.2 .3 1 1 1 1 1 2) Chứng minh: ... 2 2 2 2 4 6 8 (2 ) n 4 Lời giải 1. a)
3.{5.[(52 + 23): 11] - 16} + 2026 = 3.{5.[33 : 11] - 16} + 2026 =3.{15-16} + 2026 = 3.(-1) + 2026 = 2023 b) 2 2 9 2 6 2 14 4
5.(2 .3 ) .(2 ) 2.(2 .3) .3 B 28 18 29 18 5.2 .3 7.2 .3 18 18 12 28 14 4 5.2 .3 .2 2.2 .3 .3 28 18 29 18 5.2 .3 7.2 .3 30 18 29 18 5.2 .3 2 .3 28 18 2 .3 (5 7.2) 29 18 2 .3 (5.2 1) 2.9 2 28 18 2 .3 (5 14) 9 2.Ta có 1 1 1 1 A ... 2 2 2 2 4 6 8 (2 ) n 1 1 1 1 A ... 2 2 2 2 (2.2) (2.3) (2.4) (2. ) n 1 1 1 1 1 1 1 1 1 1 A ... 2 2 2 2 4 2 3 4 n
4 1.2 2.3 3.4 (n 1)n 1 1 1 1 1 1 1 1 1 A ... 4 1 2 2 3 3 4 (n 1) n 1 1 1 1 1 1 1 1 A 1 . Vậy ... 4 n 4 2 2 2 2 4 6 8 2n 4
Câu 2. (4,0 điểm) Tìm x biết: 1. 2 2 2 19x 2.5 :14 13 8 4 1 1 1 1 119 2. ... .x 1.2.3.4 2.3.4.5 3.4.5.6 7.8.9.10 720
3. Tìm số tự nhiên có ba chữ số biết rằng khi chia số đó cho các số 25, 28, 35 thì được
các số dư lần lượt là 4, 7, 14.
thuvienhoclieu.com Trang 2 thuvienhoclieu.com Lời giải 1. 2 2 2 19x 2.5 :14 13 8 4
19x 50:14 25 16 19x 50 9.14 126 19x 76 x 4 Vậy x = 4 2. 1 1 1 1 119 ... .x (1) 1.2.3.4 2.3.4.5 3.4.5.6 7.8.9.10 720 Ta có: 1 1 1 1 ... 1.2.3.4 2.3.4.5 3.4.5.6 7.8.9.10 1 1 1 1 1 1 1 ( ... ) 3 1.2.3 2.3.4 2.3.4 2.3.4 7.8.9 8.9.10 1 1 1 1 119 ( ) . 3 6 720 3 720 1 119 119 Nên từ (1) suy ra: . .x = > x=3 3 720 720
3. Ta gọi số cần tìm là x abc ,
0 a 9, 0 ,bc 9, ,a ,bcN
Theo bài ra số đó chia cho các số 25, 28, 35 thì được các số dư lần lượt là 4, 7, 14 nên Ta
x 25m 4 x 21 25
có: x 28n 7 , m ,
n p N x 21 28 x 35 p 14 x 21 35
Suy ra x + 21 là BC ( 25; 28; 35) mà BCNN ( 25; 28; 35) = 700 nên (x + 21) chia hết 700
Do: 100 x abc 999 121 x 21 1020=> x 21 700 x 679 Vậy x = 679.
Câu 3: ( 4,0 điểm).
1. Cho a, b là các số tự nhiên thỏa mãn a + 4b chia hết 13.
Chứng minh (a + 4b).(10a +b) chia hết cho 169.
2. Tìm tất cả các số nguyên tố p, q sao cho 7p + q; pq + 11đều là số nguyên tố. Lời giải: 1.
thuvienhoclieu.com Trang 3 thuvienhoclieu.com
Do a 4b 13 10a 4b 13 10a 40b 13
Lại có 10a 40b 10a b 10a 40b 10a b 39b 13 Suy ra 10a + b chia hết 13.
Vậy (a + 4b).(10a +b) chia hết cho 169 2.
Ta có p, q là số nguyên tố nên pq +11 là số nguyên tố lớn hơn 11
⇒ pq + 11 là số lẻ nên pq là số chẵn
Do 7p + q là số nguyên tố lớn hơn 7 nên p, q không thể cùng chẵn
*)Th1: p = 2 7p+ q =14 +q. Ta thấy 14 chia 3 dư 2
+)Nếu q chia hết cho 3, do q nguyên tố nên q = 3 7p+ q = 17;
pq +11=17 đều nguyên tố ( thỏa mãn).
+)Nếu q chia cho 3 dư 1⇒ 14+q chia hết cho 37p+ q là hợp số ( loại)
+)Nếu q chia cho 3 dư 2 thì 2q chia cho 3 dư 1 pq + 11 chia hết cho 3 nên pq +11 là hợp số
*)Th2: q = 2 7p + q= 7p+2 và pq + 11 = 2p +11
+)Nếu p chia hết cho 3 thì p = 3 khi đó 7p + q= 7p+2 = 23 và pq + 11 = 2p +11 = 17 đều nguyên tố ( thỏa mãn)
+)Nếu p chia 3 dư 1 thì 7p chia 3 dư 1 nên 7p + 2 chia hết cho 3 nên
7p + 2 là hợp số (loại)
+)Nếu p chia cho 3 dư 2 thì 2p chia 3 dư 1 ⇒ suy ra 2p + 11 chia hết cho 3 nên pq +11là hợp số ( loại)
Vậy ( p, q) là (2 ; 3) hoặc ( 3; 2)
Câu 4: ( 6,0 điểm). Lời giải 1. E F 10m B A G 10m D C H E F I 10m 10m B A G K 10m D C H
Nữa chu vi ABCD là AB + BC = 60m
Chuyển hình chữ nhật BGHC thành hình chữ nhật FIKG ( vì BG = FG = 10m)
Khi đó phần diện tích mở rộng chính là diện tích hình chữ nhật AEIK.
Chiều rộng AEIK là AE = 10m
Chiều dài AEIK là AK = AB + BG + GK = AB + BG + BC =70m
thuvienhoclieu.com Trang 4 thuvienhoclieu.com
Vậy diện tích phần mới mở thêm là : 70 x 10 = 700 (m2) 2. E F G H A B M N P
Do AB = 36cm mà EH = 30cm nên AE + BH = 6cm
Do E và H là trung điểm của AM và PB nên: AM + PB = 2 (AE + BH) = 12cm. Suy ra MP = 36 -12 = 24cm.
Lại có F, G là trung điểm của MN và NP nên:
FG = (MN + NP ): 2 = MP :2= 12cm.Vậy FG = 12cm
3.Số giao điểm ít nhất là khi 101 đường thẳng đó cùng đi qua 1 điểm ( đồng quy).
Khi đó số giao điểm là 1(giao điểm)
Số giao điểm nhiều nhất là khi 101 đường thẳng trong đó bất cứ hai đường thẳng nào cũng
cắt nhau và không có ba đường thẳng nào cùng đi qua một điểm. Khi đó:
Mỗi đường thẳng cắt 100 đường thẳng còn lại nên tạo ra 100 giao điểm.
Có 101 đường thẳng nên có: 101.100 = 10100 (giao điểm).
Do mỗi giao điểm được tính hai lần nên số giao điểm là:
10100 : 2 = 5050 (giao điểm).
Vậy số giao điểm ít nhất là 1, nhiều nhất là 5050 (giao điểm)
Câu 5: ( 2,0 điểm). Cho bốn số nguyên a, b, c, d sao cho 2b = a + c, 2c = b + d, c2 + d2 < 4. Tìm số nguyên a biết b = 2.
Lời giảiTa có: 2b = a + c nên b – a = c – b
2c = b + d nên d – c = c – b
Do đó d – c = b – a = c – b
Vì a, b, c, d là bốn số nguyên nên d – c, b – a, c – b là các số nguyên
Đặt d – c = b – a = c – b = k nguyên,
suy ra a = b – k, c = b + k, d = c + k = b + 2k = 2 +2k
Do c2 + d2 < 4 nên d2 < 4 (2 +2k)2 < 4 (1 +k)2 < 1 0 1 k 1 mà 1 + k nguyên nên
1 + k = 0 k = -1 a = 3, c = 1, d = 0.
Thử lại thấy a = 3, b = 2, c = 1, d = 0 thỏa mãn.Vậy a = 3
UBND HUYỆN LANG CHÁNH
ĐỀ GIAO LƯU HỌC SINH GIỎI LỚP 6
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
CẤP HUYỆN NĂM HỌC: 2022 - 2023 ĐỀ 2 Môn: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
Ngày thi: 01 tháng 4 năm 2023 ĐỀ CHÍNH THỨC
(Đề thi gồm có 01 trang)
Câu 1.(4,0 điểm). Tính giá trị các biểu thức sau: a) 2 01 3 .2014 1007.26 b) 3 3 3 8 6 0 2 .5
3. 400 673 2 .(7 : 7 7 ) 1 1 1 1 1 c) 2023 ... 2.6 4.9 6.12 36.57 38.60
Câu 2. (4.0 điểm). Tìm số nguyên x biết:
1) Tìm x biết: x 3 3 2 3 7 2 .3 53 1 1 1 2) ( ... 2021 2020 2 1 ). x = ... 2 3 2022 1 2 2020 2021
thuvienhoclieu.com Trang 5 thuvienhoclieu.com
Câu 3. (6,0 điểm).
1) Tìm tất cả các cặp số nguyên x, y sao cho: xy 2x y 1
2) Tìm số tự nhiên nhỏ nhất sao cho khi chia cho 11 dư 6 , chia cho 4 dư 1 và chia cho 19 dư 11.
3) Tìm các số nguyên tố x, y sao cho: x2 + 117 = y2
Câu 4.(4,0 điểm).
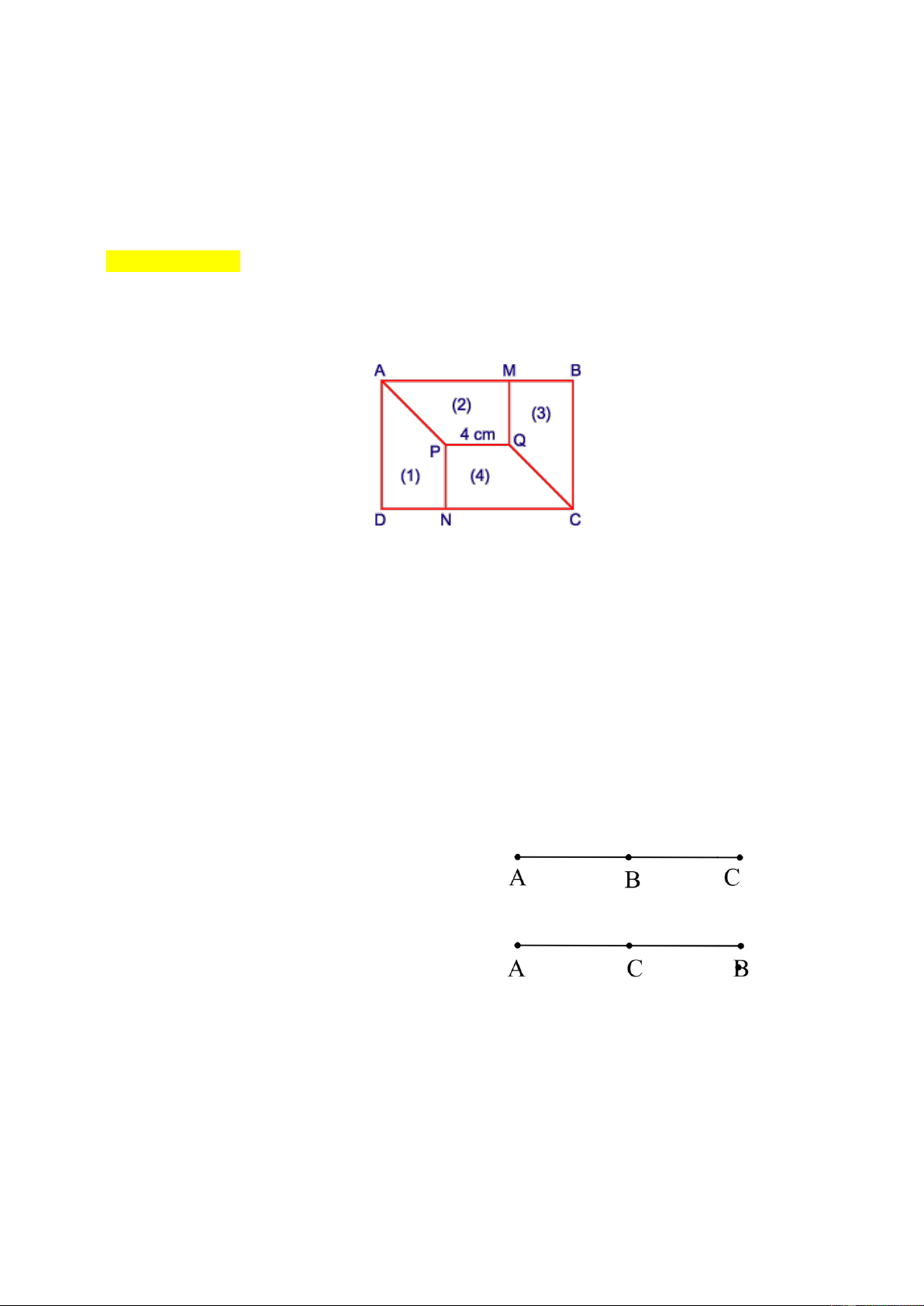
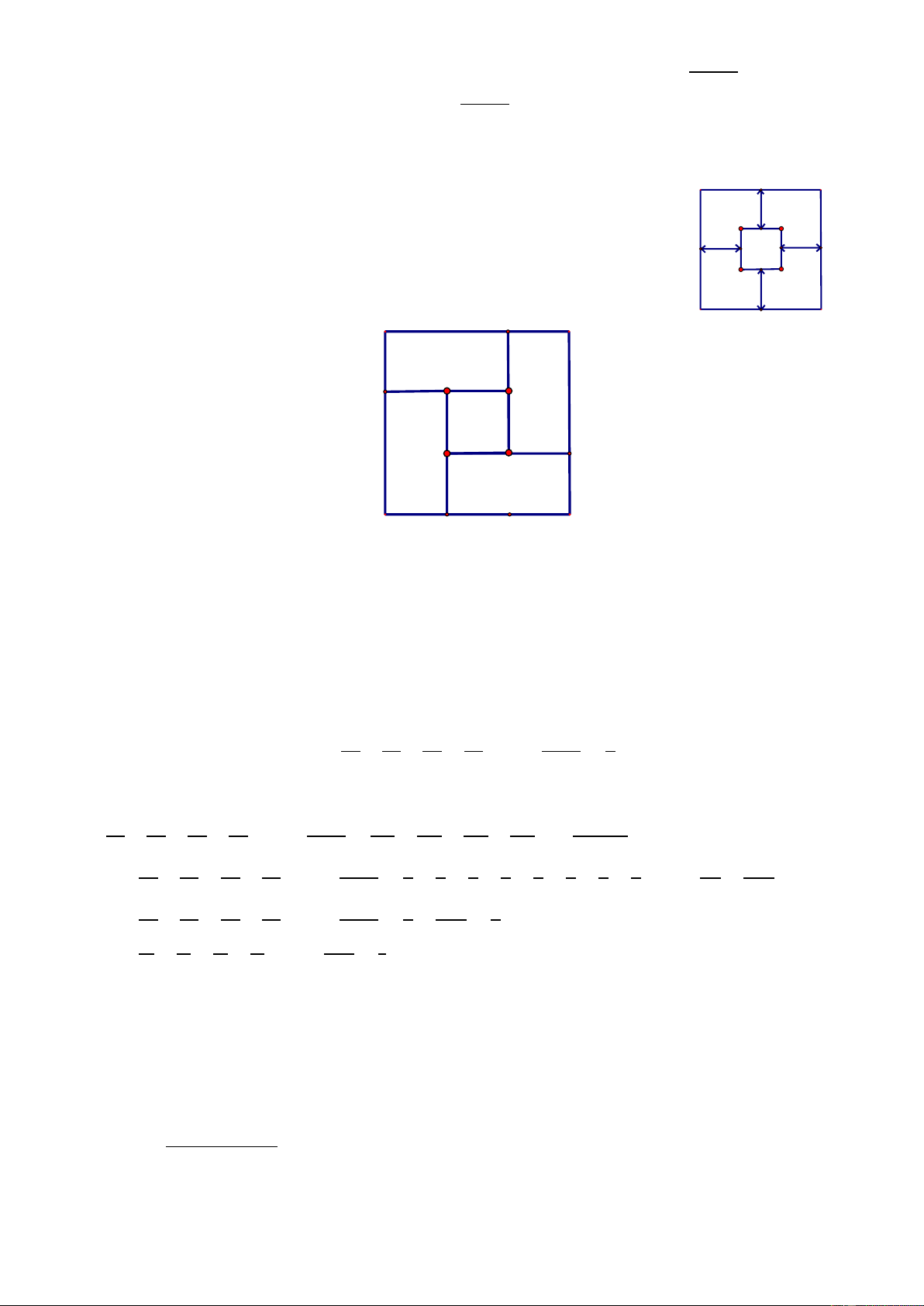
1) Cho (1), (2), (3), (4) là các hình thang vuông có kích thước bằng nhau.
Biết rằng PQ 4cm . Tính diện tích hình chữ nhật ABCD .
2) Cho đoạn thẳng AB 8cm . Điểm C thuộc đường thẳng AB sao cho BC 4cm . Tính độ dài đoạn thẳng AC .
3) Cho điểm Q không thuộc đường thẳng xy và lấy thêm 2019 điểm phân biệt khác thuộc đường
thẳng xy và không trùng với 4 điểm ,
A B, M , O . Hỏi có thể vẽ được bao nhiêu đoạn thẳng có 2
đầu mút là 2 điểm trong số các điểm đã cho? 1 1 1 1
Câu 5. (2,0 điểm). Chứng tỏ rằng: P 1 1 1 ... 1 3 2 3 200 2 2 2 2 -----HẾT----
Cán bộ coi thi không giải thích gì thêm
HƯỚNG DẪN GIẢI MÔN TOÁN 6
HUYỆN LANG CHÁNH NĂM HỌC 2022-2023
Câu 1.(4,0 điểm). Tính giá trị các biểu thức sau: 1. 2 01 3 .2014 1007.26 2. 3 3 3 8 6 0 2 .5
3. 400 673 2 .(7 : 7 7 ) 1 1 1 1 1 3. 2023 ... 2.6 4.9 6.12 36.57 38.60 Lời giải 1.
thuvienhoclieu.com Trang 6 thuvienhoclieu.com 2 013.2014 1007.26 2 013.2014 2014.13 2014. 2 01313 2014. 2 000 4028000
2. 23. 53 – 3.{400 – [673 – 23.(78 : 76 + 70)]}
= 8.125 – 3.{400 – [673 – 8.50]}
= 1000 – 3.{400 – 273}= 619 3. 1 1 1 1 1 2023 ... 2.6 4.9 6.12 36.57 38.60 1 1 1 1 1 1 2023 ... 2.3 1.2 2.3 3.4 18.19 19.20 1 1 1 1 1 1 1 1 1 1 2023 1 ... 2.3 2 2 3 3 4 18 19 19 20 1 1 2023 1 6 20 1 19 101 2023 . 2022 6 20 120
Câu 2. (4.0 điểm). Tìm số nguyên x biết:
1) Tìm x biết: x 3 3 2 3 7 2 .3 53 1 1 1 2) ( ... 2021 2020 2 1 ). x = ... 2 3 2022 1 2 2020 2021 Lời giải 1. Ta có x 3 3 2 3 7 2 .3 53 x 3 3 7 125 x 3 3 3 7 5 3x 7 5 3x 5 7 12 x 12 : 3 4 Vậy x 4 2. 1 1 1 ( ... 2021 2020 2 1 ). x = ... 2 3 2022 1 2 2020 2021 1 1 1 ( ... 2020 2019 2 1 ).x = 1 1 ... 1 1 1 2 3 2022 2 3 2020 2021
thuvienhoclieu.com Trang 7 thuvienhoclieu.com 1 1 1 ( ... 2022 2022 2022 2022 2022 2022 ).x = .... 2 3 2022 2 3 4 2020 2021 2022 1 1 1 ( ... 1 1 1 ).x = 2022. ... 2 3 2022 2 3 2022 x 2022 Vậy x = 202 2
Câu 3. (6,0 điểm).
1) Tìm tất cả các cặp số nguyên x, y sao cho: xy 2x y 1
2) Tìm số tự nhiên nhỏ nhất sao cho khi chia cho 11 dư 6 , chia cho 4 dư 1 và chia cho 19 dư 11.
3) Tìm các số nguyên tố x, y sao cho: x2 + 117 = y2 Lời giải
Ta có: xy 2x y 1
xy 2x y 2 2 1
x y 2 y 2 3 x
1 y 2 3 . Vì ;
x y Z nên x
1 ; y 2 là ước của 3. Ta có bảng sau: x 1 1 3 1 3 y 2 3 1 3 1 Suy ra x 0 2 2 4 y 1 1 5 3
Đối chiếu điều kiện ;
x y Z ; x y 0; 1; 2 ; 1 ;2;5;4; 3
2. Gọi số tự nhiên nhỏ nhất thỏa mãn đề bài là: a
Vì a chia cho 11 dư 6 nên ta có:
a 11.x 6 (x N )
a 27 11.x 6 27 (11.x 33) 11 M (a 27 )1 M 1 (1)
Vì a chia cho 4 dư 1 nên ta có:
a 4.y 1 ( y N )
a 27 (4.y 1) 27 (4.y 28) 4 M (a 27) 4 M (2)
Vì a chia cho 19 dư 11 nên ta có:
a 19.z 11 (z N )
a 27 (19.z 11) 27 (19.z 38) 19 M (a 27) 19 M (3)
Từ (1), (2), (3) (a 27) BC(11, 4,19) Mà a nhỏ nhất nên
a 27 BCNN (11, 4,19) a 27 836 a 809 Vậy a 809 .
thuvienhoclieu.com Trang 8 thuvienhoclieu.com 3.
* Với x = 2, ta có: 22 + 117 = y2 y2 = 121 y = 11 (là số nguyên tố)
* Với x > 2, mà x là số nguyên tố nên x lẻ y2 = x2 + 117 là số chẵn => y là số chẵn
kết hợp với y là số nguyên tố nên y = 2 (loại) Vậy x = 2; y = 11.
Câu 4.(4,0 điểm). Lời giải 1.
Vì các hình thang vuông PQMA , QMBC , QPNC , PNDA bằng nhau nên:
MQ NP QP 4 cm và CN AD .
Mặt khác AD NP QM 4 4 8cm . Do đó CN AD 8cm .
Diện tích hình thang vuông PQCN là: CN PQ NP 2 : 2 8 4 .4 : 2 24 cm
Suy ra diện tích hình chữ nhật ABCD là: 2 24.4 96 (cm ) . 2. Xét hai trường hợp : *TH 1:
C thuộc tia đối của tia BA.
Hai tia BA, BC là hai tia đối nhau B nằm giữa A và C
AC AB BC 8 + 4 = 12 (cm). *TH 2 : C thuộc tia BA.
C nằm giữa A và B (Vì B A BC )
AC BC AB AC AB BC 8 - 4 4 (cm). 3.
Tổng số điểm trên đường thẳng xy là 2023 điểm
Gọi tên các điểm đó là A, B, M, O, P1, P2, P3, ...., P2019
Từ Q vẽ được 2023 đoạn thẳng khi nối với các điểm còn lại
Từ A vẽ được 2022 đoạn thẳng khi nối với các điểm còn lại (trừ điểm Q)
Từ B vẽ được 2021 đoạn thẳng khi nối với các điểm còn lại (trừ điểm A, Q)
thuvienhoclieu.com Trang 9 thuvienhoclieu.com
................................................................................................................ ......
Vậy tổng số đoạn thẳng vẽ được là: 2023 2022 2021...3 2 1
= 2023.(2023 + 1) : 2 = 2 073 276 1 1 1 1
Câu 5. (2,0 điểm). Chứng tỏ rằng: P 1 1 1 ... 1 3 2 3 200 2 2 2 2 Lời giải
Ta có: 2n 2n 2 (n N) 1 1 1 1 1 1 2n 2n 2 2n 2n 2 1 2n 1 1 2n 2 n 1 2 1 Áp dụng vào P ta có: 1 1 1 1 P 1 1 1 ... 1 2 3 200 2 2 2 2 2 3 4 100 3 2 1 2 1 2 1 2 1 2 22 . 1 2 . ... 2 2 1 2 3 2 1 2 99 2 1 100 100 3 2 1 2 1 3 . 3. 3 3 dpcm 99 100 100 2 2 2 2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI HUYỆN HOÀI ĐỨC
NĂM HỌC: 2021 – 2022 ĐỀ 3 MÔN: TOÁN 6 6
Thời gian làm bài: 150 phút
ĐỀ THI CHÍNH THỨC
(Đề gồm 05 câu, 01 trang)
Câu 1 (4,0 điểm).Thực hiện các phép tính sau:
1) 𝐴 = 2011 − [39 − (23. 3 − 21)2]: (−3) + 20210 1 1 1 1 2) 𝐵 = + + + ⋯ + 4.9 9.14 14.19 64.69
3) 𝐶 = 1 − 2 − 3 + 4 + 5 − 6 − 7 + 8 + ⋯ + 993 − 994 − 995 + 996 + 997
Câu 2 ( 5,0 điểm). 1) So sánh: 7150 𝑣à 3775
2) Tìm hai số tự nhiên 𝑎 và 𝑏 biết 𝑎 > 𝑏; 𝑎 + 𝑏 = 96 𝑣à Ư𝐶𝐿𝑁 (𝑎; 𝑏) = 6.
3) Làm thế nào để lấy được 6 lít nước từ một bể nếu trong tay chỉ có một thùng dung tích
4 lít và một thùng dung tích 9 lít và không thùng nào có vạch chia dung tích?
Câu 3 ( 4,0 điểm).
1) Tìm các số nguyên 𝑥; 𝑦 biết : 𝑥𝑦 + 𝑥 + 𝑦 = 40 4𝑛+1 2) Cho phân số 𝐴 =
. Chứng minh A là phân số tối giản với mọi số tự nhiên n. 6𝑛+1
Câu 4 ( 6,0 điểm).
thuvienhoclieu.com Trang 10 thuvienhoclieu.com
1. Trên đường thẳng xy lấy điểm O. Trên tia Ox lấy điểm A; trên tia Oy lấy điểm B, C sao cho
OA = 2cm; OB = 7cm, C là trung điểm của đoạn thẳng OB.
a) Tính độ dài đoạn thẳng AC.
b) Điểm O có phải là trung điểm của đoạn thẳng AC không? Vì sao?
2. Vẽ n tia chung gốc, chúng tạo ra 66 góc. Tìm giá trị của n?
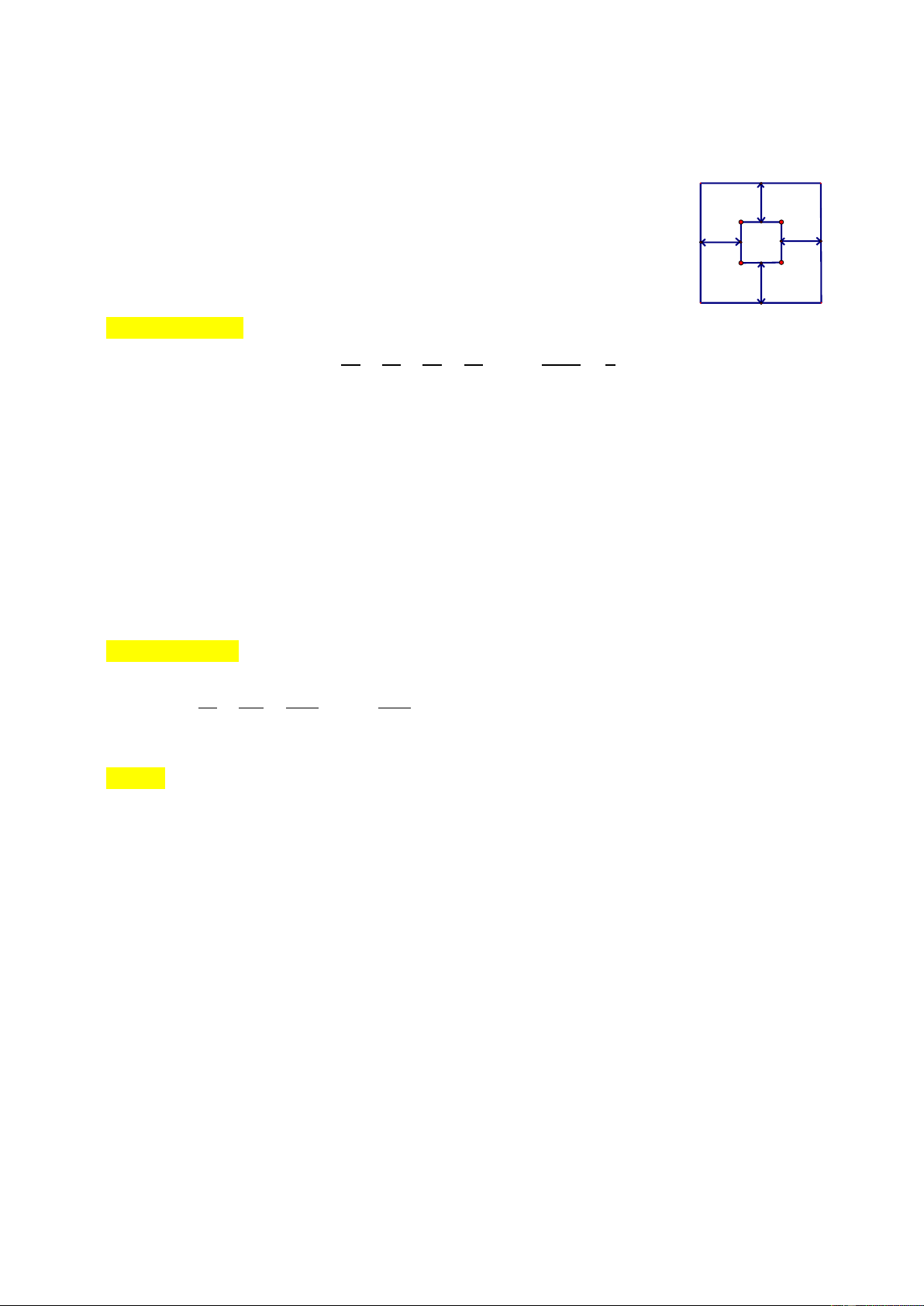
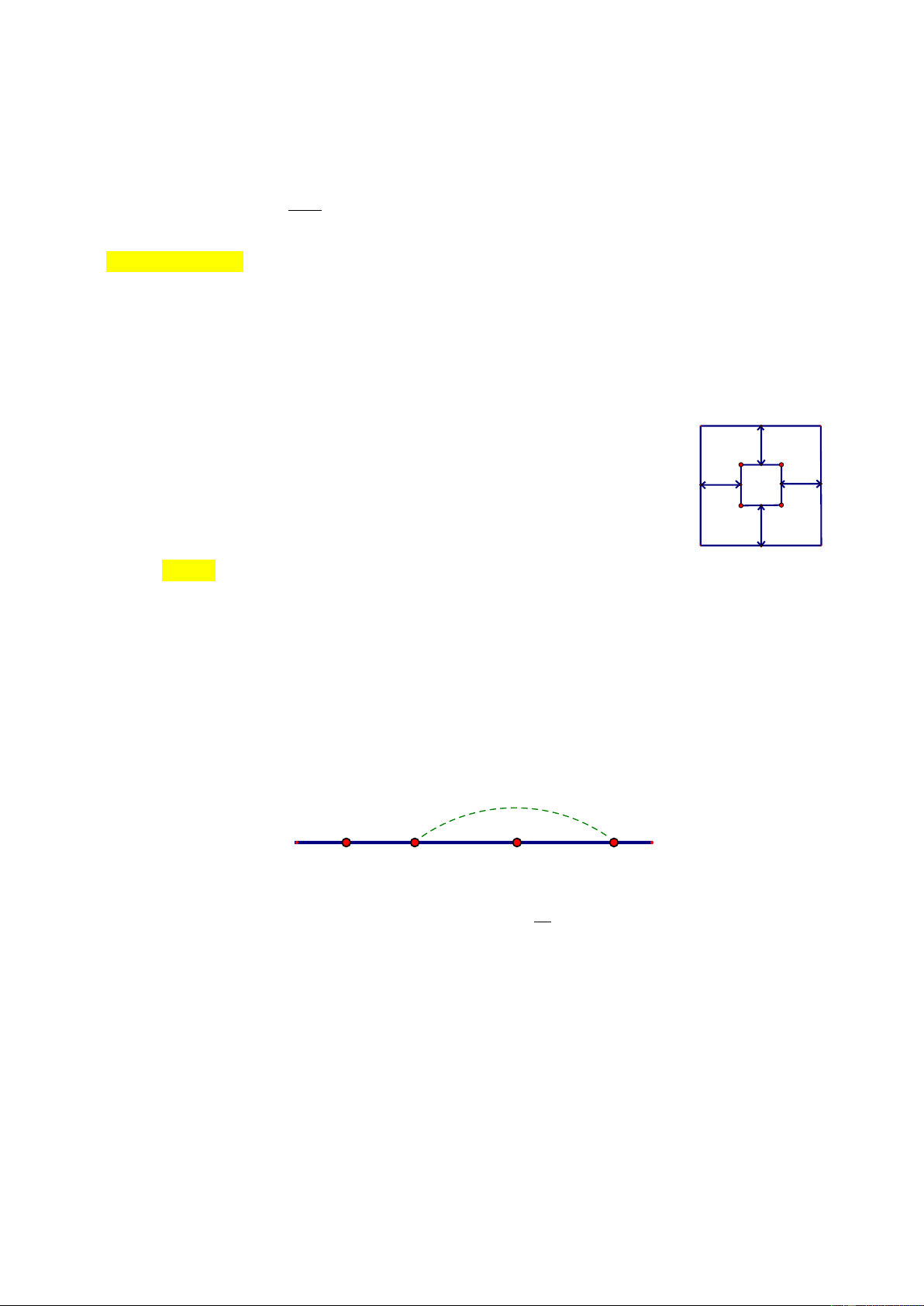
3. Người ta mở rộng một cái ao hình vuông về 4 phía như hình vẽ. Sau 4 m
khi mở rộng, diện tích ao tăng thêm 192 𝑚2. Tính diện tích ao trước khi mở rộng? 4 m 4 m 4 m
Câu 5 ( 1,0 điểm). Chứng minh rằng: 1 1 1 1 1 1 + + + + ⋯ + < 42 52 62 72 1002 3
----------Hết-----------
Họ và tên thí sinh:..................................................... Số báo danh:...............................................
HƯỚNG DẪN GIẢI MÔN TOÁN 6
HUYỆN HOÀI ĐỨC NĂM HỌC 2022-2023
Câu 1 (4,0 điểm).Thực hiện các phép tính sau:
1) 𝐴 = 2011 − [39 − (23. 3 − 21)2]: (−3) + 20210 1 1 1 1 2) 𝐵 = + + + ⋯ + 4.9 9.14 14.19 64.69
3) 𝐶 = 1 − 2 − 3 + 4 + 5 − 6 − 7 + 8 + ⋯ + 993 − 994 − 995 + 996 + 997 Lời giải 1.
𝐴 = 2011 − [39 − (23. 3 − 21)2]: (−3) + 20210
𝐴 = 2011 − [39 − (8.3 − 21)2]: (−3) + 1
𝐴 = 2011 + 1 − [39 − (24 − 21)2]: (−3)
𝐴 = 2012 − [39 − 32]: (−3)
𝐴 = 2012 − [39 − 9]: (−3) 𝐴 = 2012 − 30: (−3) 𝐴 = 2012 + 10 = 2022 Vậy A = 2022. 𝐴 = 2012 + 10 = 2022 Vậy A = 2022.
thuvienhoclieu.com Trang 11 thuvienhoclieu.com 2. 1 1 1 1 B = + + +. . . + 4.9 9.14 14.19 64.69 1 5 5 5 5 𝐵 = ( + + +. . . + ) 5 4.9 9.14 14.19 64.69 1 5 5 5 5 𝐵 = ( + + +. . . + ) 5 4.9 9.14 14.19 64.69 1 1 1 𝐵 = ( − ) 5 4 69 13 𝐵 = 276
3)𝐶 = 1 − 2 − 3 + 4 + 5 − 6 − 7 + 8 + ⋯ + 993 − 994 − 995 + 996 + 997
𝐶 = (1 − 2 − 3 + 4) + (5 − 6 − 7 + 8) + ⋯ + (993 − 994 − 995 + 996) + 997
𝐶 = 0 + 0 + ⋯ + 0 + 997 = 997. Vậy: C = 997
Câu 2 ( 5,0 điểm). 1) So sánh: 7150 𝑣à 3775
2) Tìm hai số tự nhiên 𝑎 và 𝑏 biết 𝑎 > 𝑏; 𝑎 + 𝑏 = 96 𝑣à Ư𝐶𝐿𝑁 (𝑎; 𝑏) = 6.
3) Làm thế nào để lấy được 6 lít nước từ một bể nếu trong tay chỉ có một thùng dung tích
4 lít và một thùng dung tích 9 lít và không thùng nào có vạch chia dung tích? Lời giải
1) (1,5 điểm) So sánh: 𝟕𝟏𝟓𝟎 𝒗à 𝟑𝟕𝟕𝟓 Ta có: 50 71 71 25 2 25 5041 (1) 75 37 37 25 3 25 50653 (2) Từ (1) và (2) suy ra 75 37 > 50 71
2) (2,0 điểm) Tìm hai số tự nhiên a và b biết 𝑎 > 𝑏; 𝑎 + 𝑏 = 96 và
ƯCLN(𝑎 ; 𝑏) = 6.
ƯCLN (a;b)= 6 nên a = 6m (m N*) và b = 6n (n N*)
(m > n và m; n là hai số nguyên tố cùng nhau)
thuvienhoclieu.com Trang 12 thuvienhoclieu.com
Vì a + b = 96 Nên 6m + 6n = 96. Suy ra m + n = 16 Ta có bảng m 15 13 11 9 n 1 3 5 7 a 90 78 66 54 b 6 18 30 42
Vậy (𝑎 ; 𝑏) ∈ {(90 ; 6) ;(78 ; 1 8) ;(66 ; 3 0) ;(54 ; 4 2)}
4) (1,5 điểm) Làm thế nào để lấy được 6 lít nước từ một bể nếu trong tay chỉ có một
thùng dung tích 4 lít và một thùng dung tích 9 lít và không thùng nào có vạch chia dung tích?
Kí hiệu (a,b) là trạng thái thùng 4 lít có a lít, và thùng 9 lít có b lít.
Khi đó việc lấy 6 lít nước được diễn tả qua các trạng thái sau:
(0 ; 0) → (0 ; 9) → (4 ; 5) → (0 ; 5) → (4 ; 1) → (0 ; 1) → (1 ; 9) → (4 ; 6)
Cuối cùng thùng có dung tích 9 lít chứa 6 lít nước.
(0 ≤ 𝑎 ≤ 4 ; 0 ≤ 𝑏 ≤ 9).
Câu 3 ( 4,0 điểm).
1) Tìm các số nguyên 𝑥; 𝑦 biết : 𝑥𝑦 + 𝑥 + 𝑦 = 40 4𝑛+1 2) Cho phân số 𝐴 =
. Chứng minh A là phân số tối giản với mọi số tự nhiên n. 6𝑛+1 Lời giải
1. (2,0 điểm) Tìm các số nguyên 𝑥; 𝑦 biết : 𝑥𝑦 + 𝑥 + 𝑦 = 40 xy + x + y = 40 x(y + 1) + y + 1 = 40 + 1 x(y + 1) + (y + 1) = 41
(x+1)(y+1) = 41 = 1.41=41.1= -1.(-41)= -41.(-1). Ta có bảng giá trị sau: x+1 1 41 -1 -41 y+1 41 1 -41 -1 x 0 40 -2 -42 y 40 0 -42 -2 t/m t/m t/m t/m
Vậy có các cặp (x;y) là {(0;40),(40;0),(-2;-42),(-42;-2)}.
2. (2,0 điểm) Cho phân số A = 4𝑛+1. Chứng minh A là phân số tối giản với mọi số tự 6𝑛+1 nhiên n.
Gọi d = ƯCLN(4n + 1; 6n + 1) 4𝑛 + 1 ⋮ 𝑑 ⇒ { 6𝑛 + 1 ⋮ 𝑑
thuvienhoclieu.com Trang 13 thuvienhoclieu.com 3. (4𝑛 + 1) ⋮ 𝑑 12𝑛 + 3 ⋮ 𝑑 ⇒ { ⇒ {
⇒ (12𝑛 + 3) − (12𝑛 + 2) ⋮ 𝑑 2. (6𝑛 + 1) ⋮ 𝑑 12𝑛 + 2 ⋮ 𝑑 ⇒ 1 ⋮ 𝑑 ⇒ 𝑑 = 1
Vậy phân số A =4𝑛+1 là phân số tối giản với mọi số tự nhiên 6𝑛+1
Câu 4 ( 6,0 điểm).
1. Trên đường thẳng xy lấy điểm O. Trên tia Ox lấy điểm A; trên tia Oy lấy điểm B, C sao cho
OA = 2cm; OB = 7cm, C là trung điểm của đoạn thẳng OB.
a) Tính độ dài đoạn thẳng AC.
b) Điểm O có phải là trung điểm của đoạn thẳng AC không? Vì sao?
2. Vẽ n tia chung gốc, chúng tạo ra 66 góc. Tìm giá trị của n?
3. Người ta mở rộng một cái ao hình vuông về 4 phía như hình vẽ. Sau 4 m
khi mở rộng, diện tích ao tăng thêm 192 𝑚2. Tính diện tích ao trước khi mở rộng? 4 m 4 m 4 m Lờ giải
1) (3,0 điểm) Trên đường thẳng xy lấy điểm O. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm
B, C sao cho OA = 2cm, OB = 7cm, C là trung điểm của đoạn thẳng OB.
a) Tính độ dài đoạn thẳng AC.
b) Điểm O có phải là trung điểm của đoạn thẳng AC không? Vì sao?
a) (2,0 điểm) Tính độ dài đoạn thẳng AC. 7 2 x A O C B y Vì C là trung điể 𝐵𝐶
m của đoạn thẳng OB nên 𝑂𝐶 = = 7 : 2 = 3,5𝑐𝑚 2
Điểm O nằm trên đường thẳng xy nên hai tia Ox, Oy đối nhau
Mà điểm A thuộc tia Ox, điểm C thuộc tia Oy => Điểm O nằm giữa 2 điểm A và C.
Do đó 𝐴𝑂 + 𝑂𝐶 = 𝐴𝐶
⇒ 𝐴𝐶 = 2 + 3,5 = 5,5𝑐𝑚 Vậy AC = 3,5 cm.
b)(1,0 điểm) Điểm O có phải là trung điểm của đoạn thẳng AC không? Vì sao?
Ta có OA = 2cm ; OC = 3,5 cm, ta thấy OC > OA
nên điểm O không là trung điểm của đoạn thẳng AC.
2) (1,5 điểm) Vẽ n tia chung gốc, chúng tạo ra 66 góc. Tìm giá trị của n?
Một tia bất kì trong số n tia chung gốc tạo thành với n -1 tia còn lại n-1 góc
Với n tia chung gốc tạo thành n.(n-1) góc
thuvienhoclieu.com Trang 14 thuvienhoclieu.com 𝑛.(𝑛−1)
Theo cách trên mỗi góc được vẽ 2 lần nên thực tế số góc tạo thành là: 2 𝑛.(𝑛−1)
Vì số góc tạo thành là 66 góc nên ta có: = 66 2 𝑛. (𝑛 − 1) = 132 𝑛. (𝑛 − 1) = 12.11
Vậy vẽ 12 tia chung gốc sẽ tạo thành 66 góc
3)Người ta mở rộng một cái ao hình vuông về 4 phía như hình vẽ. Sau khi
mở rộng, diện tích ao tăng thêm 4 m
192 𝑚2. Tính diện tích ao trước khi mở rộng? 4 m 4 m 4 m 4 m 4 m 4 m 4 m
Chia phần mở rộng thành 4 hình chữ nhật có diện tích bằng nhau và có chiều rộng là 4 m.
Vì diện tích tăng thêm 192 m2nên diện tích mỗi hình chữ nhâ ̣t là:192:448 (𝑚2).
Chiều dài của mỗi hình chữ nhâ ̣t là :48 : 4 = 12(𝑚).
Cạnh ao hình vuông là :12 − 4 = 8(𝑚).
Diện tích cái ao cũ là :8.8 = 64(𝑚2).
Vậy diện tích ao cũ là 64 m2
Câu 5 ( 1,0 điểm). Chứng minh rằng: 1 1 1 1 1 1 + + + + ⋯ + < 42 52 62 72 1002 3 Lời giải Ta có: 1 1 1 1 1 1 1 1 1 1 + + + + ⋯ + < + + + … + 42 52 62 72 1002 3.4 4.5 5.6 6.7 99.100 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 => + + + + ⋯ + < − + − + − + − + ⋯ + − 42 52 62 72 1002 3 4 4 5 5 6 6 7 99 100 1 1 1 1 1 1 1 1 => + + + + ⋯ + < − < 42 52 62 72 1002 3 100 3 1 1 1 1 1 1 => + + + + ⋯ + < ( Đpcm) 42 52 62 72 1002 3 PHÒNG GD&ĐT
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI HUYỆN TRIỆU SƠN Môn: Toán 6
Thời gian: 150 phút (không kể thời gian giao đề)
TRƯỜNG THCS THỌ BÌNH Ngày khảo sát: 25/02/2023 ĐỀ 4
(Đề gồm: 01 trang).
thuvienhoclieu.com Trang 15 thuvienhoclieu.com
Câu 1( 4 điểm) : Thực hiện phép tính 3 1 0,375 0,3 1,51 0,75 1980 1. 11 4 A : 100 5 5 5 2005 2,5 1,25 0 ,625 0,5 3 11 12 1 1 1 1 ... 2. 2 3 4 200 B 1 2 3 199 ... 199 198 197 1 1 1 1 1 3. C 1 1 1 ... 1 2 2 2 2 2 3 4 2023 Câu 2: ( 4 điểm): 2020 2024
1. Tìm x biết: 4x 3 4x 3 5 5 1 31 1
2. Tìm các số nguyên x thỏa mãn: 4
: 2 7 x 3 : 3, 2 4, 5.1 : 2 1 9 8 5 45 2
3. Tìm các số nguyên tố x,y thỏa mãn: 2 2 x 5y 29 Câu 3( 4 điểm )
1. Cho p,q là các số nguyên tố lớn hơn 5. Chứng minh rằng: 4 4
p 2019q Chia hết cho 20.
2. Tìm một số chính phương có 4 chữ số biết rằng số đó là bội của 147. Câu 4( 6 điểm)
1. Cho đường thẳng xy, trên đường thẳng xy lấy điểm O. Trên tia Ox lấy điểm A và B sao cho
OA = 2cm, OB = 6cm. Trên tia Oy lấy điểm C sao cho O là trung điểm của AC. a) Tính độ dài AB
b) Chứng minh A là trung điểm của BC 2.
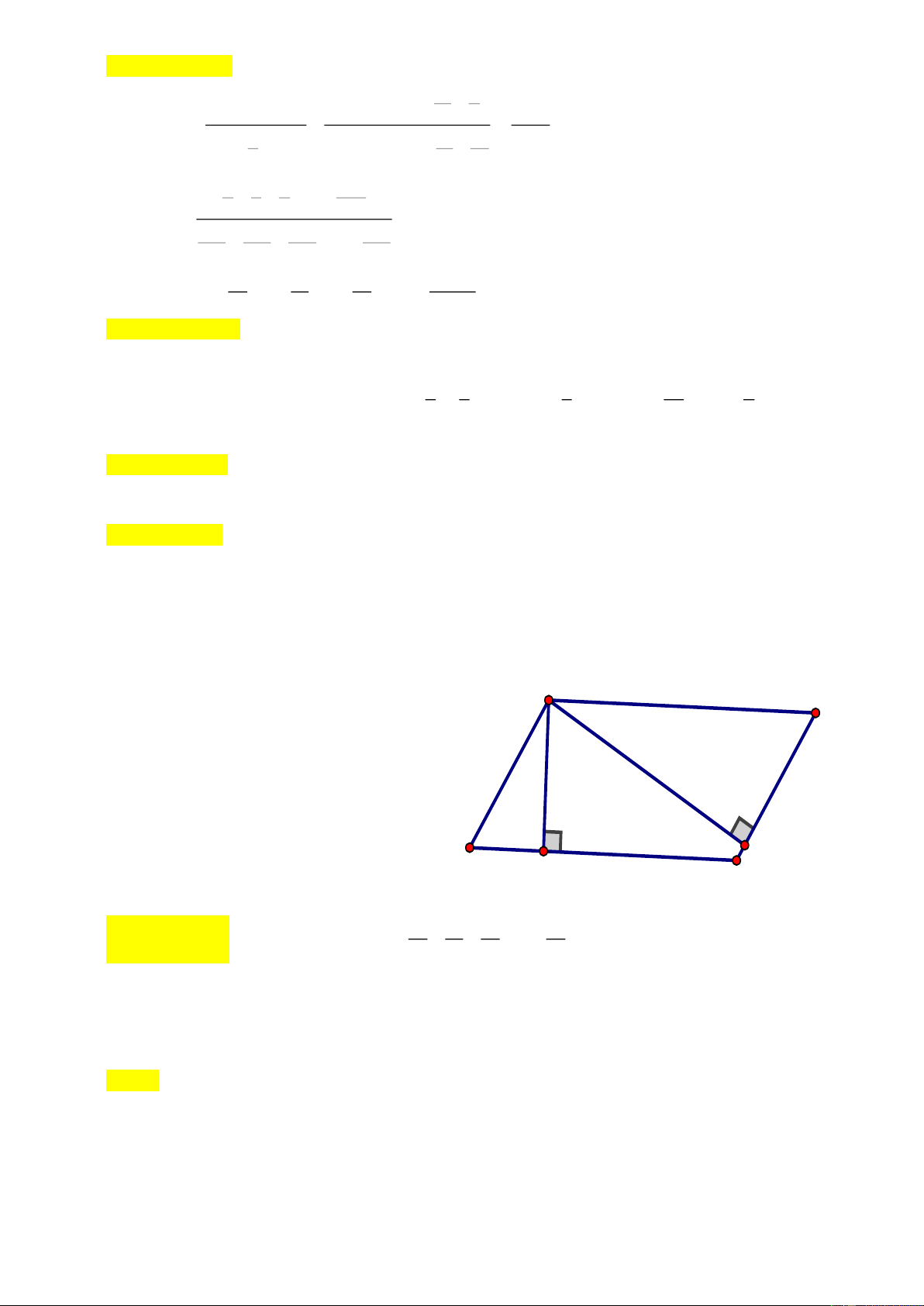
Cho hình bình hành ABCD như A
hình vẽ bên. Biết rằng AB = 8cm, B AD = 4cm và AH + AK = 9cm. Tính diện tích ABCD. D K H C Câu 5( 2 điểm): 1 1 1 1
Chứng minh rằng: S ... 1, * n N 2 2 2 2 2 3 4 n
_______________________________Hết____________________________
HƯỚNG DẪN CHẤM MÔN TOÁN 6
TRƯỜNG THCS THỌ BÌNH TRIỆU SƠN Câu 1:
thuvienhoclieu.com Trang 16 thuvienhoclieu.com 3 1 0, 375 0, 3 1,5 1 0,75 1980 11 4 A : 100 5 5 5 2005 2,5 1,25 0 ,625 0,5 3 11 12 3 3 3 3 3 3 3 396 1. 2 3 4 8 10 11 12 A : 100 5 5 5 5 5 5 5 401 2 3 4 8 10 11 12 3 3 396 A : 100 100 5 5 401 2. Xét: 1 2 3 199 1 2 3 198 ... 1 1 1 ... 1 1 199 198 197 1 199 198 197 2 200 200 200 200 200 1 1 1 1 ... 200. ... 199 198 197 2 200 2 3 4 200 1 1 1 1 ... Do đó: 1 2 3 4 200 B 1 1 1 1 200 200. ... 2 3 4 200 2 1 1 1 1 3 8 15 2023 1 C 1 1 1 ... 1 . . .... 2 2 2 2 2 2 3 4 2023 4 9 16 2023 1.3.2.4.3.5.....2022.2024
1.2.3.4...20223.4.5....2024 3. C
2.2.3.3.4.4.5.5.6.6....2023.2023
1.2.3...20231.2.3...2023 1 20 C 24 1012 . 2023 2 2023 Câu 2:
4x 32020 4x 32024 4x 32020 4x 32020 .4x 34 0
1. 4x 32020 1
4x 34 0 3 3 x x 4 4x 3 0 4 x x 1 4 4x 3 1 4 3 1 1 4x 3 1 x 2 5 5 1 31 1 4
: 2 7 x 3 : 3, 2 4,5.1 : 2 1 9 8 5 45 2 2. 8 ,737... x 0 , 4 x 8 , 7 , 6 , 5 , 4 ,3,2, 1 3. Ta có: 2 2 x 5y 29 +) Nếu x chẵn suy ra: 2 2 2 2
x 2 2 5y 29 5y 25 y 5 ( Không thoả mãn) 2 2 2
y 2 x 5.2 29 x 9 x 3(t / ) m
Câu 3( 4 điểm) Ta có: 4 4 4 4 4 p
q p q q 4 p 4 q 4 2019 2020 1 1 2020q
thuvienhoclieu.com Trang 17 thuvienhoclieu.com Ta chứng minh: 4
p 1 Chia hết cho 20. Chứng minh: 4
p 1 chia hết cho 5
Thật vậy vì P > 5 nên P các các dạng: P 5k 1; P 5k 2; P 5k 3; P 5k 4 +) 4 4
P k P
p mo 4 5 1 1(mod 5) 1 d5 p 1 5(1) 4 4
P k P
p mo 4 4 4 5 2 2(mod 5) 2
d5 p 16(mod 5) p 1(m d
o 5)5 p 1 5(2) 4 4
P k P
p mo 4 4 4 5 3 3(mod 5) 3
d5 p 81(mod 5) p 1(m d
o 5)5 p 1 5(3) 4 4
P k P
p mo 4 4 4 5 4 4(mod 5) 4
d5 p 256(mod 5) p 1(m d
o 5)5 p 1 5(4) Từ (1),(2),(3),(4): 4
p 1 5(*) Chứng minh: 4
p 1 chia hết cho 4.
Ta có p > 5 nên P là số lẻ 2 2 2 4 4
P 2k 1 p 1(m d
o 2) p 1 (m d o 2 ) 1(m d
o 4) p 1(m d
o 4) p 1 4(**) Vì 4
4;5 1 p 1 20 Chứng minh tương tự 4
q 1 20 . Mặt khác 4 4 4 4 4 4
2020q 20 ( p 1) (q 1) 2020q 20 p 2019q 20 (đpcm)
3. Gọi số đó là n. Ta có n là bội của 147 2
n 147.k 7 .3k là số chính phương do đó k là
lũy thừa bậc lẻ của 3. Mặt khác n lsf số có 4 chữ số nên 2
1000 147k 9999 6 k 86 k 27 n 63 3969 Câu 4: 1. x y C O A B a) Ta có: AB = 4cm
b) OA = OC = 2cm suy ra: AC = 4cm => AC = AB Nên A là trung điểm của BC. 1 1 S
.AH.CD .AK.BC AH.CD AK.BC 8AH 4AK 2. Ta có: D ABC 2 2 AK 2AH.
3. Mặt khác: AH AK 30 AH 2AH 9 AH 3cm AK 6c . m Do đó: 1 2 S .3.8 12cm ABCD 2 1 1 2 2 1.2 1 1 Câu 5: Ta có: 2 3 2.3 .......... 1 1 1 1 1 1 S ... 1 1 2 n (n 1).n 1.2 2.3 (n 1).n n
UBND HUYỆN VĨNH LỘC ĐỀ GIAO LƯU HỌC SINH GIỎI LỚP 6,7,8
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2021-2022 Môn: Toán 6 Đ Ề C H Í N H TH Ứ
C Thời gian làm bài 150 phút (không kể thời gian phát đề)
(Đề thi này gồm 01 trang, 5 câu) Đề 5
Câu I (4,0 điểm): Thực hiện phép tính:
A = 1800:{450:[450-(4.53-23.52)]} 15 9 20 9 4 . 5 9 . 3 . 4 8 . B= 10 19 29
6 ; 𝐶 = 1 + 32 + 34 + 36+. . . +32022 2 . 5 6 . 2 . 7 27 .
thuvienhoclieu.com Trang 18 thuvienhoclieu.com
Câu II (4,0 điểm): Tìm x ∈ Z biết: 2 2 1 3 0,4+ − a) 𝑥: (9 − ) =
9 11 b)( 2x – 15)5 = ( 2x – 15 )3 2 2 8 8 1,6+ − 9 11
Câu III (4,0 điểm): a) Tìm các số nguyên tố x,y,z thỏa mãn xy + 1 = z a 1 1
b) Tìm các số nguyên a, b biết rằng: 7 2 b 3
Câu IV (6,0 điểm):
1) Trên tia Ox lấy hai điểm M và N , sao cho OM 3 cm và ON 7 cm.
a) Tính độ dài đoạn thẳng MN .
b) Lấy điểm P trên tia Ox , sao cho MP 2 cm. Tính độ dài đoạn thẳng OP .
2) Cho 25 điểm trong đó có đúng 8 điểm thẳng hàng, ngoài ra không có ba điểm thẳng
hàng. Vẽ các đường thẳng đi qua các cặp điểm. Hỏi vẽ được tất cả bao nhiêu đường thẳng?
3) Một tờ giấy hình chữ nhật được gấp theo đường chéo như hình vẽ. Diện tích hình nhận
được bằng 5 diện tích hình chữ nhật ban đầu. Biết diện tích phần tô màu là 2 18 cm . Tính diện tích 8 tờ giấy ban đầu.
Câu V (2,0 điểm) : Tìm tất cả các bộ ba số nguyên tố a, b, c đôi một khác nhau thỏa mãn điều
kiện: 20abc 30(ab bc ca) 21abc
- Họ và tên thí sinh:…………………………………..; Số báo danh:
Chú ý: Cán bộ coi thi không được giải thích gì thêm.
thuvienhoclieu.com Trang 19 thuvienhoclieu.com
HƯỚNG DẪN CHẤM HỌC SINH GIỎI MÔN TOÁN 6 HUYỆN VĨNH LỘC
NĂM HỌC 2021 – 2022
Câu I (4,0 điểm): Thực hiện phép tính:
A = 1800:{450:[450-(4.53-23.52)]} 15 9 20 9 4 . 5 9 . 3 . 4 8 . B= 10 19 29
6 ; 𝐶 = 1 + 32 + 34 + 36+. . . +32022 2 . 5 6 . 2 . 7 27 . Lời giải: 1.
A = 1800:{450:[450-(4.53-23.52)]}
A = 1800 : { 450: [ 450 – (4 . 125 – 8 . 25)]}
A = 1800 : { 450:[450 – 300]}
A = 1800 : { 450 : 150} A = 1800 : 3 =600 2. 15 9 20 9 5.4 .9 4.3 .8 B 10 19 29 6 5.2 .6 7.2 .27 2.15 2.9 2 20 3.9 5.2 .3 2 .3 .2 B 10 19 19 29 3.6 5.2 .2 .3 7.2 .3 30 18 2 20 27 5.2 .3 2 .3 .2 B 29 19 29 18 5.2 .3 7.2 .3 29 18 2 2 .3 (5.2 3 ) B 29 18 2 .3 (5.3 7) 10 9 1 B 15 7 8 3.
𝐶 = 1 + 32 + 34 + 36+. . . +32022
Ta có: 𝐶 = 1 + 32 + 34 + 36+. . . +32022
=> 32𝐶 = 32(1 + 32 + 34 + 36+. . . +32022)
=> 9𝐶 = 32 + 34 + 36 + ⋯ + 32024
=> 9𝐶 − 𝐶 = (32 + 34 + 36+. . . +32024) − (1 + 32 + 34 + 36+. . . +32022) => 8𝐶 = 32024 − 1 32024 − 1 => 𝐶 = 8
Câu II (4,0 điểm): Tìm x ∈ Z biết: 2 2 1 3 0,4+ − a) 𝑥: (9 − ) =
9 11 b)( 2x – 15)5 = ( 2x – 15 )3 2 2 8 8 1,6+ − 9 11 Lời giải:
thuvienhoclieu.com Trang 20