20 Đề Ôn Thi HSG Toán 7 Cấp Huyện Năm 2025-2026 Có Đáp Án
Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI. Chứng minh tam giác FCH cân và AK = KI. Chứng minh ba điểm B, O, K thẳng hàng. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 7 264 tài liệu
Môn: Toán 7 2.3 K tài liệu
Tác giả:
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 1 2 2 2
Bài 1: (1 điểm) Tìm số x y z xyz biết: = = , và x – y + z = 4 4 9 25 2 2
Bài 2: (1 điểm) Biết 2 b 2 b a + ab + = 25 ;c + = 9 ; a2 + ac + c2 = 16 3 3
và a 0; c ≠ 0; a ≠ -c. Chứng minh rằng: c 2 b + c = . a a + c Bài 3: (2,5 điểm0
a/ Tìm giá trị của m để đa thức sau là đa thức bậc 3 theo biến x:
f (x) = (m2- 25) x4+ (20 + 4m) x3 + 7 x2 - 9
b/ Tìm giá trị nhỏ nhất của đa thức g(x) = 16 x4 - 72 x2 + 90.
Bài 4: (2 điểm) Tìm số chia và số dư biết rằng số bị chia bằng 112 và thương bằng 5.
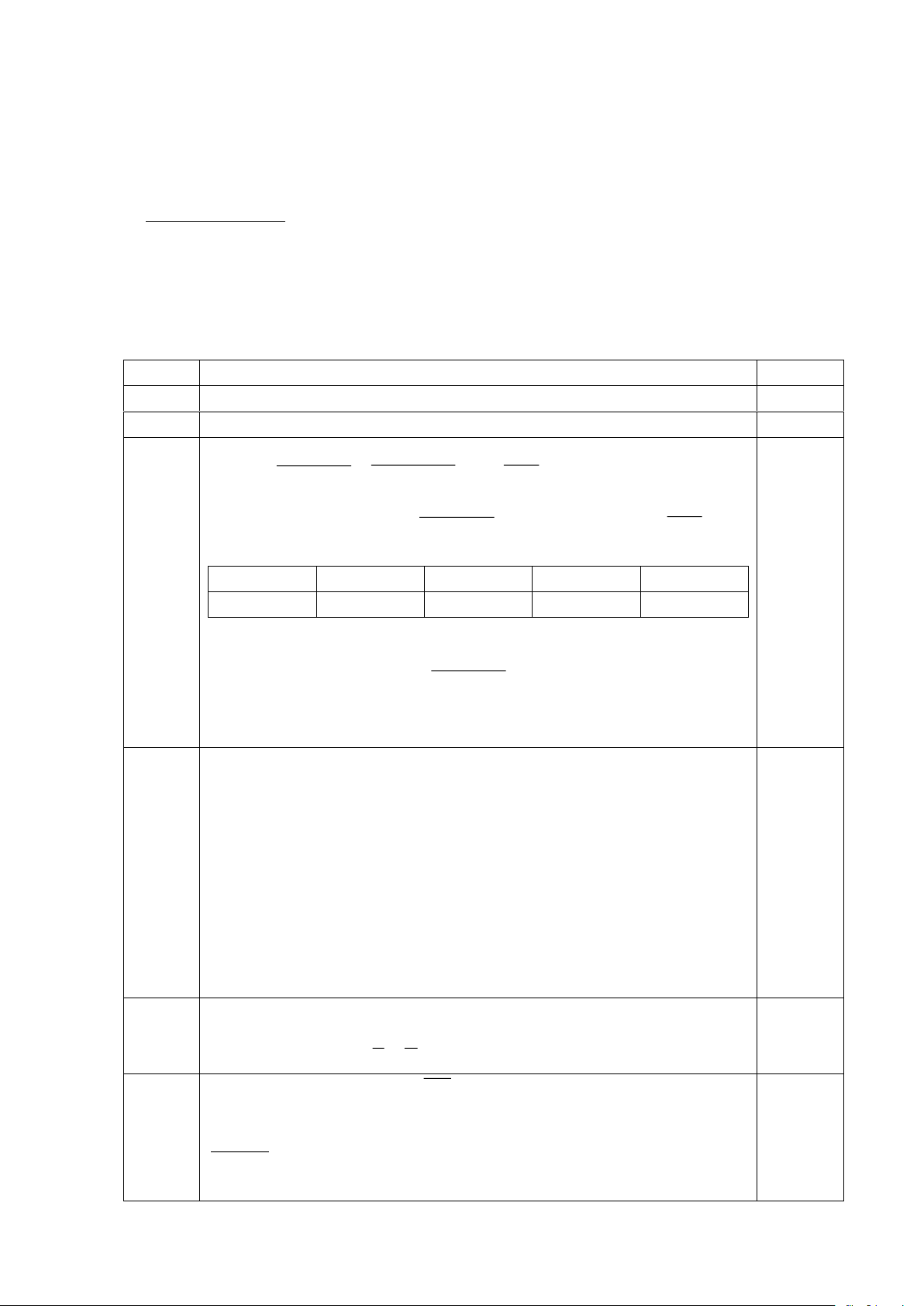
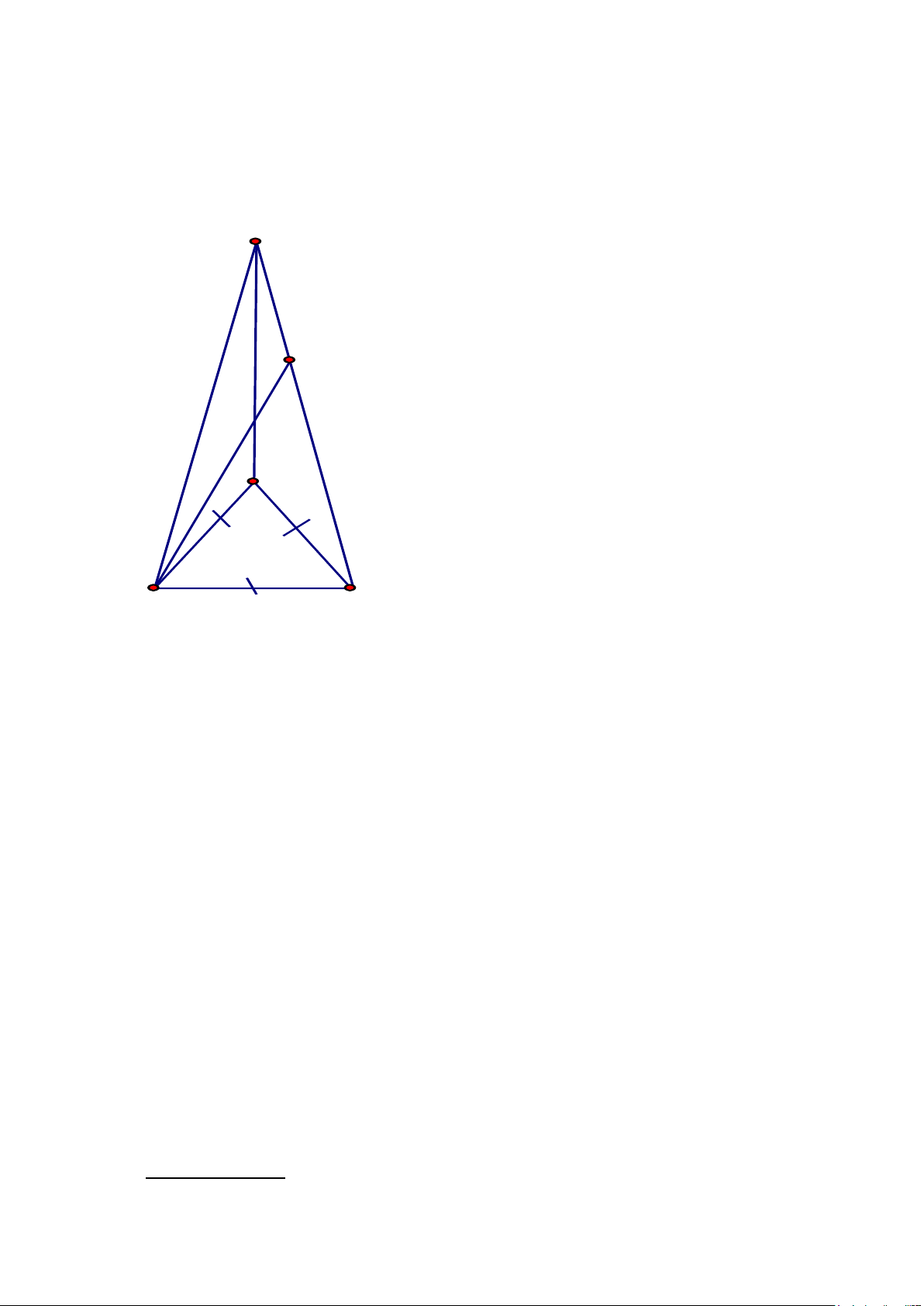
Bài 5: (3 điểm) Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của
góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O
trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI.
a/ Chứng minh tam giác FCH cân và AK = KI.
b/ Chứng minh ba điểm B, O, K thẳng hàng.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 1 Bài 1: (1điểm) x2 y2 z2 0,5đ = = x y z
và x, y, z N, x ≠ 0 = = 4 9 25 2 3 5 0,25đ 0,25đ x y z x − y + z 4 = = = = = 1 2 3 5 2 − 3 + 5 4
x = 2; y = 3; z = 5. Vậy xyz = 235 Bài 2: (1,5 điểm) 2 b 0,5đ 2 b2 Ta có: 2 c + + 2 a + ac + 2 c = a + ab + (vì 9 + 16 = 25) 3 3 0,25đ Suy ra: 2c2= a(b – c) 0,25đ c 2 b − c = (vì a ≠ 0; c ≠ 0) 0,5đ a c c 2 b − c c 2 + b − c b + c = = =
(vì a ≠ -c nên a + c ≠ 0) a c a + c a + c Trang 1 Bài 3: (2,5điểm) 0,5đ
a/ (1 điểm) f(x) = ( m2- 25)x4 + (20 + 4m)x3 + 7x2 - 9 là đa thức bậc 3 0,25đ
biến x khi: m2 - 25 = 0 và 20 + 4m ≠ 0 0,25đ m = 5 và m ≠ -5
Vậy m = 5 thì f(x) là đa thức bậc 3 biến x.
b/ (1,5 điểm) g(x) = 16 x4 - 72 x2 + 90 =(4x2 )2 - 2.4 x2.9 + 92 + 9 0,25đ g(x) = (4x2 – 9)2 + 9 0,25đ
Với mọi giá trị của x ta có: = (4x2 – 9)2 ≥ 0 g(x) = (4x2 – 9)2 + 9 ≥ 9.
Giá trị nhỏ nhất của g(x) là 9 0,25đ
Khi và chỉ khi (4x2 – 9)2 = 0 0,25đ 9 3
4x2 - 9 = 0 4x2 = 9 x2 = x = . 4 2 0,5đ Bài 4: (2 điểm)
Gọi số chia là a và số dư là r (a, r N*; a > r) Ta có: * 112 = 5a + r 0,5đ 5a < 112 a 22 (1)
*a > r 5a + r < 5a + a 112 < 6a 0,5đ a > 112 : 6 a ≥ 19 (2)
Từ (1) và (2) a = 19; 20; 21; 22 lập bảng số: a 19 20 21 22 0,5đ r = 112 – 5a 17 12 7 2 Bài 5: (3 điểm)
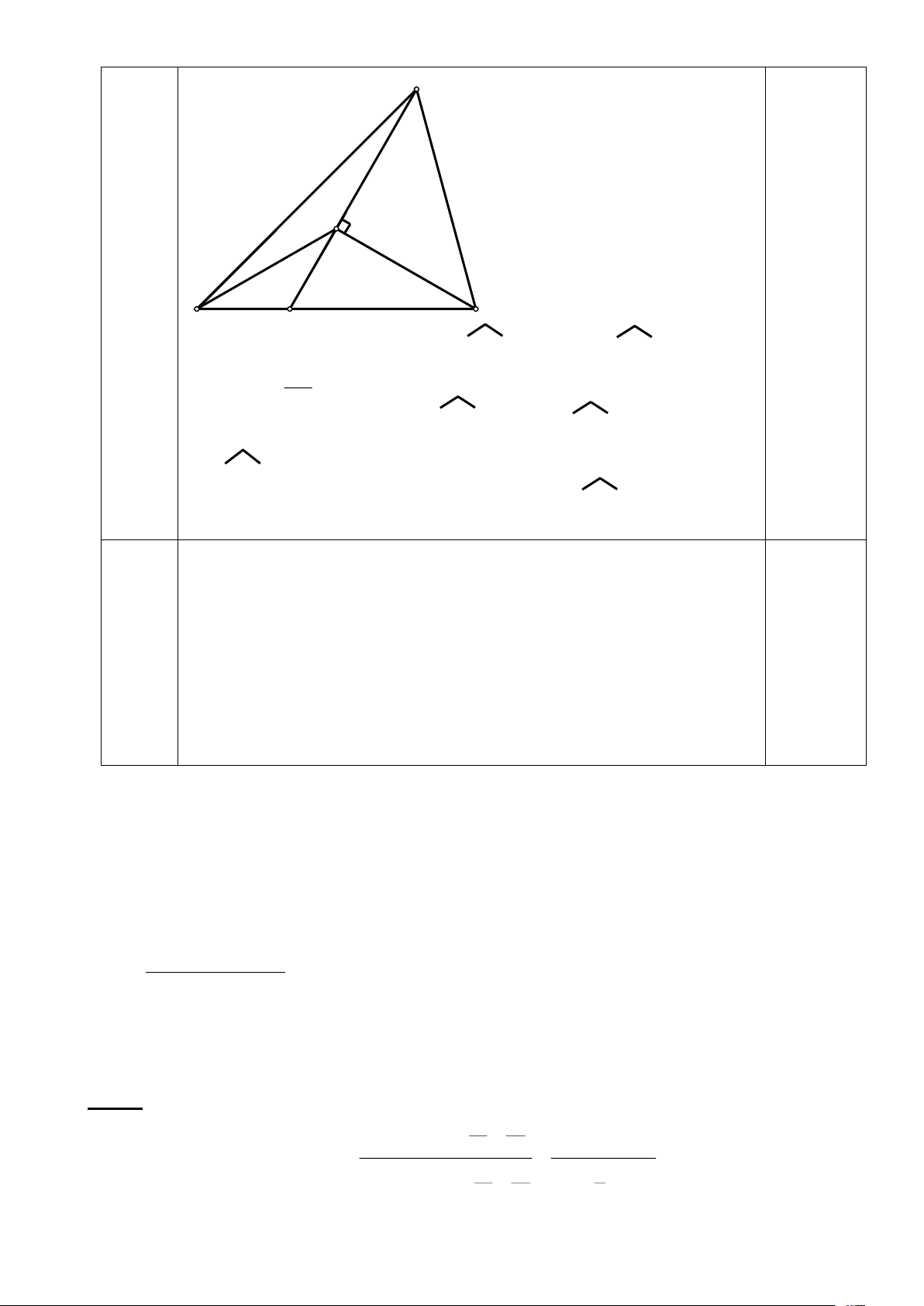
a/ (1,5 điểm) - Chứng minh CHO = CFO (cạnh huyền – góc nhọn) 0,25đ
suy ra: CH = CF. Kết luận FCH cân tại C. 0,25đ
-Vẽ IG //AC (G FH). Chứng minh FIG cân tại I. 0,25đ
- Suy ra: AH = IG, và IGK = AHK. 0,25đ
- Chứng minh AHK = IGK (g-c-g). 0,25đ - Suy ra AK = KI.. 0,25đ b/ (1,5 điểm)
Vẽ OE ⊥ AB tại E. Tương tự câu a ta có: AEH, BEF thứ tự cân tại A, B. Suy ra: BE = BF và AE = AH. 0,5đ
BA = BE + EA = BF + AH = BF + FI = BI. Suy ra: ABI cân tại B. 0,5đ
Mà BO là phân giác góc B, và BK là đường trung tuyến của ABI nên: B, O, K là ba điểm thẳng hàng. 0,5đ A E H K O G Trang 2 B F I C
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 2 Câu 1: ( 2 điểm)
Thực hiện phép tính : 2 a- 1 1 1
6.− − 3.− +1 : (− −1 ) 3 3 3 3 2 2 3
.− (.− )2003 1 b- 3 4 2 3 2 5 .− 5 12 Câu 2: ( 2 điểm) 2 a + a + a- Tìm số nguyên a để 3 là số nguyên a +1
b- Tìm số nguyên x,y sao cho x - 2xy + y = 0 Câu 3: ( 2 điểm)
a- Chứng minh rằng nếu a + c = 2b và 2bd = c (b+d) thì a c = với b,d khác 0 b d
b- Cần bao nhiêu số hạng của tổng S = 1+2+3+… để được một số có ba chữ số giống nhau . Câu 4: ( 3 điểm)
Cho tam giác ABC có góc B bằng 450 , góc C bằng 1200. Trên tia đối của tia CB lấy
điểm D sao cho CD = 2CB . Tính góc ADE Câu 5: ( 1điểm)
Tìm mọi số nguyên tố thoả mãn : x2 - 2y2 =1 Trang 3
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 2 CÂU HƯỚNG DẪN CHẤM ĐIỂM 1.a
Thực hiện theo từng bước đúng kết quả -2 cho điểm tối đa 1Điểm 1.b
Thực hiện theo từng bước đúng kết quả 14,4 cho điểm tối đa 1Điểm 2.a 2 a + a + 3 a(a + ) 1 + 3 3 0,25 Ta có : = = a + a +1 a +1 a +1 2 a + a + 3 3 vì a là số nguyên nên là số nguyên khi là số a +1 a +1
nguyên hay a+1 là ước của 3 do đó ta có bảng sau : 0,25 a+1 -3 -1 1 3 a -4 -2 0 2 0,25 2 a + a + Vậy với a− 3 , 4 − , 2 , 0 2 thì là số nguyên a +1 0,25 2.b Từ : x-2xy+y=0 Hay (1-2y)(2x-1) = -1 0,25
Vì x,y là các số nguyên nên (1-2y)và (2x-1) là các số nguyên
do đó ta có các trường hợp sau : 1− 2y = 1 x = 0 2x −1 = −1 y = 0 0,25 1− 2y = −1 x = 1 Hoặc 0,25 2x −1 = 1 y = 1
Vậy có 2 cặp số x, y như trên thoả mãn điều kiện đầu bài 0,25 3.a
Vì a+c=2b nên từ 2bd = c (b+d) Ta có: (a+c)d=c(b+d) 0,5 Hay ad=bc Suy ra a c = ( ĐPCM) b d 0,5 3.b
Giả sử số có 3 chữ số là aaa =111.a ( a là chữ số khác 0)
Gọi số số hạng của tổng là n , ta có : n(n + ) 1 = a 111 = a . 37 . 3 Hay n(n+1) =2.3.37.a 2 0,25
Vậy n(n+1) chia hết cho 37 , mà 37 là số nguyên tố và Trang 4
n+1<74 ( Nếu n = 74 không thoả mãn ) Do đó n=37 hoặc n+1 = 37 0,25 n n +
Nếu n=37 thì n+1 = 38 lúc đó ( ) 1 = 703 không thoả mãn 2 n n +
Nếu n+1=37 thì n = 36 lúc đó ( ) 1 = 666 thoả mãn 2
Vậy số số hạng của tổng là 36 0,5 4 A H B C D
Kẻ DH Vuông góc với AC vì ACD =600 do đó CDH = 300 0,5
Nên CH = CD CH = BC 2
Tam giác BCH cân tại C CBH = 300 ABH = 150 0,5
Mà BAH = 150 nên tam giác AHB cân tại H
Do đó tam giác AHD vuông cân tại H Vậy ADB = 1,0 450+300=750 1,0 5
Từ : x2-2y2=1suy ra x2-1=2y2 0,25
Nếu x chia hết cho 3 vì x nguyên tố nên x=3 lúc đó y= 2 0,25 nguyên tố thoả mãn
Nếu x không chia hết cho 3 thì x2-1 chia hết cho 3 do đó 2y2
chia hết cho 3 Mà(2;3)=1 nên y chia hết cho 3 khi đó x2=19 không thoả mãn 0,25
Vậy cặp số (x,y) duy nhất tìm được thoả mãn điều kiện đầu bài là (2;3) 0,25 Trang 5
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 3 Bài 1:(4 điểm) a) Thực hiện phép tính: 12 5 6 2 10 3 5 2 2 .3 − 4 .9 5 .7 − 25 .49 A = ( − 2 2 .3)6 4 5 + 8 .3 (125.7)3 9 3 + 5 .14
b) Chứng minh rằng : Với mọi số nguyên dương n thì : n+2 n+2 3
− 2 + 3n − 2n chia hết cho 10 Bài 2:(4 điểm) Tìm x biết: 1 4 2 a. x − + = ( 3 − ,2) + 3 5 5 x 1 + x 1 + 1 b. ( x − 7) − (x − 7) = 0 Bài 3: (4 điểm)
a) Số A được chia thành 3 số tỉ lệ theo 2 3 1
: : . Biết rằng tổng các bình phương của ba 5 4 6
số đó bằng 24309. Tìm số A. 2 2 b) Cho a c +
= . Chứng minh rằng: a c a = c b 2 2 b + c b Bài 4: (4 điểm)
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao
cho ME = MA. Chứng minh rằng: a) AC = EB và AC // BE
b) Gọi I là một điểm trên AC ; K là một điểm trên EB sao cho AI = EK . Chứng
minh ba điểm I , M , K thẳng hàng
c) Từ E kẻ EH ⊥ BC (H BC) . Biết HBE = 50o ; MEB =25o .
Tính HEM và BME Bài 5: (4 điểm)
Cho tam giác ABC cân tại A có 0
A = 20 , vẽ tam giác đều DBC (D nằm trong tam giác
ABC). Tia phân giác của góc ABD cắt AC tại M. Chứng minh: Trang 6
a) Tia AD là phân giác của góc BAC b) AM = BC
……………………………… Hết ………………………………
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 3 Bài 1:(4 điểm): Đáp án Thang điểm a) (2 điểm) 10 12 5 6 2 10 3 5 2 12 5 12 4 10 3 4 2 .3 − 4 .9 5 .7 − 25 .49 2 .3 − 2 .3 5 .7 − 5 .7 A = 0,5 điểm ( − = − 2 2 .3)6 4 5 + 8 .3 (125.7)3 9 3 12 6 12 5 9 3 9 3 3 + 5 .14 2 .3 + 2 .3 5 .7 + 5 .2 .7 12 4 2 .3 .(3 − ) 10 3 1 5 .7 .(1− 7) 0,5 điểm = − 12 5 2 .3 .(3 + ) 9 3 1 5 .7 .( 3 1+ 2 ) 0,5 điểm 12 4 10 3 2 .3 .2 5 .7 .( 6 − ) = − 12 5 9 3 2 .3 .4 5 .7 .9 0,5 điểm 1 10 − 7 = − = 6 3 2 b) (2 điểm)
3 n + 2 - Với mọi số nguyên dương n ta có: 0,5 điểm n+2 n+2 3
− 2 + 3n − 2n = n+2 n n+2 3 + 3 − 2 − 2n 1 điểm = n 2 n 2 3 (3 +1) − 2 (2 +1) 0,5 điểm = n n n n 1 3 10 2 5 3 10 2 − − = − 10 = 10( 3n -2n) Vậy n+2 n+2 3
− 2 + 3n − 2n 10 với mọi n là số nguyên dương. Bài 2:(4 điểm) Đáp án Thang điểm a) (2 điểm) 0,5 điểm 0,5 điểm Trang 7 1 4 − 0,5 điểm x − + = (− ) 2 1 4 16 2 3, 2 + x − + = + 3 5 5 3 5 5 5 1 4 14 x − + = 0,5 điểm 3 5 5 1 x− =2 1 3 x − = 2 1 3 x− = 2 − 0,5 điểm 3 1 7 0,5 điểm x=2+ = 3 3 1 5 x 2 − =− + = 3 3 0,5 điểm b) (2 điểm)
(x − 7)x 1+ − (x − 7)x 11 + = 0 ( x − 7)x 1+ 1
− (x − 7)10 = 0 0,5 điểm
(x − 7)(x+ )1 1
− (x − 7)10 = 0 x 1 + x 7 − 0 = 10 1 ( − x 7 − ) 0 = x 7 − 0 = x 7 = 10 (x 7 − ) 1 = x 8 = Bài 3: (4 điểm) Đáp án Thang điểm a) (2,5 điểm)
Gọi a, b, c là ba số được chia ra từ số A. 2 3 1 0,5 điểm
Theo đề bài ta có: a : b : c = : : (1) 5 4 6 và a2 +b2 +c2 = 24309 (2) 0,5 điểm a b c k Từ (1) = = = k 2 3
a = k;b = k;c = 2 3 1 5 4 6 5 4 6 0,5 điểm Do đó (2) 2 4 9 1 k ( + + ) = 24309 25 16 36 k = 180 và k = −180
+ Với k =180, ta được: a = 72; b = 135; c = 30. 0,5 điểm
Khi đó ta có số A = a + b + c = 237.
+ Với k = −180 , ta được: a = −72 ; b = −135 ; c = −30 0,5 điểm
Khi đó ta có só A = −72 +( −135 ) + ( −30 ) = −237 . b) (1,5 điểm) Trang 8 a c 0,5 điểm Từ = suy ra 2 c = . a b c b 2 2 2 a + c a + . a b 0,5 điểm khi đó = 2 2 2 b + c b + . a b 0,5 điểm a(a + b) a = = b(a + b) b Bài 4: (4 điểm) Đáp án Thang điểm Vẽ hình 0,5 điểm A I M B C H K E
a/ (1điểm) Xét AMC và EMB có : AM = EM (gt )
AMC = EMB (đối đỉnh ) BM = MC (gt )
Nên : AMC = EMB (c.g.c ) 0,5 điểm AC = EB
Vì AMC = EMB MAC = MEB
(2 góc có vị trí so le trong được tạo bởi đường thẳng AC và EB cắt đường thẳng AE ) Suy ra AC // BE . 0,5 điểm b/ (1 điểm )
Xét AMI và EMK có : AM = EM (gt )
MAI = MEK ( vì AM C = EMB ) AI = EK (gt )
Nên AMI = EMK ( c.g.c ) 0,5 điểm
Suy ra AMI = EMK
Mà AMI + IME = 180o ( tính chất hai góc kề bù ) EMK + IME = 180o
Ba điểm I;M;K thẳng hàng 0,5 điểm c/ (1,5 điểm )
Trong tam giác vuông BHE ( H = 90o ) có HBE = 50o
HBE = 90o - HBE = 90o - 50o =40o 0,5 điểm
HEM = HEB - MEB = 40o - 25o = 15o 0,5 điểm Trang 9
BME là góc ngoài tại đỉnh M của HEM
Nên BME = HEM + MHE = 15o + 90o = 105o
( định lý góc ngoài của tam giác ) 0,5 điểm Bài 5: (4 điểm) A 200 M D B C -Vẽ hình
a) Chứng minh ADB = ADC (c.c.c) 1 điểm
suy ra DAB = DAC 0,5 điểm Do đó 0 0 DAB = 20 : 2 = 10 0,5 điểm b) ABC cân tại A, mà 0 A = 20 (gt) nên 0 0 0
ABC = (180 − 20 ) : 2 = 80 ABC đều nên 0 DBC = 60 0,5 điểm
Tia BD nằm giữa hai tia BA và BC suy ra 0 0 0 ABD = 80 − 60 = 20 .
Tia BM là phân giác của góc ABD nên 0 ABM = 10 0,5 điểm
Xét tam giác ABM và BAD có: AB cạnh chung ; 0 0
BAM = ABD = 20 ; ABM = DAB = 10
Vậy: ABM = BAD (g.c.g)
suy ra AM = BD, mà BD = BC (gt) nên AM = BC 0,5 điểm
Lưu ý: Nếu học sinh làm theo cách khác đúng vẫn đạt điểm tối đa.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Trang 10 ĐỀ 4 Câu 1: ( 2 điểm)
Thực hiện phép tính : 2 a. 1 1 1
6.− − 3.− +1 : (− −1 ) 3 3 3 3 2 2 3
.− (.− )2003 1 b. 3 4 2 3 2 5 .− 5 12 Câu 2: ( 2 điểm) 2
a. Tìm số nguyên a để a + a + 3 là số nguyên a +1
b. Tìm số nguyên x, y sao cho x- 2xy + y = 0 Câu 3 : ( 2 điểm)
a. Chứng minh rằng nếu a + c = 2b và 2bd = c(b + d) thì a c = với b, d khác 0 b d
b. Cần bao nhiêu số hạng của tổng S = 1 + 2 + 3 +… để được một số có ba chữ số giống nhau . Câu 4 : ( 3 điểm)
Cho tam giác ABC có góc B bằng 450 , góc C bằng 1200. Trên tia đối của tia CB lấy
điểm D sao cho CD = 2CB . Tính góc ADE Câu 5 : ( 1điểm)
Tìm mọi số nguyên tố thoả mãn : x2- 2y2 = 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 4 CÂU HƯỚNG DẪN CHẤM ĐIỂM 1.a
Thực hiện theo từng bước đúng kết quả -2 cho điểm tối đa 1Điểm 1.b
Thực hiện theo từng bước đúng kết quả 14,4 cho điểm tối đa 1Điểm Trang 11 2.a 2 a + a + 3 a(a + ) 1 + 3 3 0,25 Ta có : = = a + a +1 a +1 a +1 2 a + a + 3 3 vì a là số nguyên nên là số nguyên khi là số a +1 a +1
nguyên hay a+1 là ước của 3 do đó ta có bảng sau : 0,25 a+1 -3 -1 1 3 a -4 -2 0 2 0,25 2 Vậy với a− a + a + 3 , 4 − , 2 , 0 2 thì là số nguyên a +1 0,25 2.b Từ : x- 2xy + y = 0 Hay (1- 2y)(2x - 1) = -1 0,25
Vì x,y là các số nguyên nên (1 - 2y)và (2x - 1) là các số nguyên
do đó ta có các trường hợp sau : 1− 2y = 1 x = 0 2x −1 = −1 y = 0 0,25 1− 2y = −1 x = 1 Hoặc 0,25 2x −1 = 1 y = 1
Vậy có 2 cặp số x, y như trên thoả mãn điều kiện đầu bài 0,25 3.a
Vì a + c = 2b nên từ 2bd = c(b + d) Ta có: (a + c)d =c(b + d) 0,5 Hay ad = bc Suy ra a c = ( ĐPCM) b d 0,5 3.b
Giả sử số có 3 chữ số là aaa =111.a ( a là chữ số khác 0)
Gọi số số hạng của tổng là n , ta có : n(n + ) 1 = a 111 = a . 37 . 3 Hay n(n + 1) =2.3.37.a 2 0,25
Vậy n(n+1) chia hết cho 37 , mà 37 là số nguyên tố và n + 1 < 74
( Nếu n = 74 không thoả mãn ) 0,25
Do đó n=37 hoặc n + 1 = 37 n n +
Nếu n =37 thì n + 1 = 38 lúc đó ( ) 1 = 703 không thoả mãn 2 n n +
Nếu n + 1=37 thì n = 36 lúc đó ( ) 1 = 666 thoả mãn 2 0,5
Vậy số số hạng của tổng là 36 4 Trang 12 A 0,5 H 0,5 B C D 1,0
Kẻ DH Vuông góc với AC vì ACD =600 do đó CDH = 300
Nên CH = CD CH = BC 1,0 2
Tam giác BCH cân tại C CBH = 300 ABH = 150
Mà BAH = 150 nên tam giác AHB cân tại H
Do đó tam giác AHD vuông cân tại H Vậy ADB = 450 + 300 =750 5
Từ : x2- 2y2 =1suy ra x2- 1 = 2y2 0,25
Nếu x chia hết cho 3 vì x nguyên tố nên x = 3 lúc đó y = 2 0,25 nguyên tố thoả mãn
Nếu x không chia hết cho 3 thì x2-1 chia hết cho 3 do đó 2y2 chia
hết cho 3 Mà(2;3) =1 nên y chia hết cho 3 khi đó x2 =19 không thoả mãn 0,25
Vậy cặp số (x,y) duy nhất tìm được thoả mãn điều kiện đầu bài là (2;3) 0,25
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 5 Câu 1: (1,5 điểm) 3 3 0,375 − 0,3 + + a. Thực hiện phép tính: 1,5 + 1− 0,75 11 12 + 5 5 5 0 − ,265 + 0,5 − − 2,5 + − 1,25 11 12 3 Trang 13
b. So sánh: 50 + 26 +1 và 168 . Câu 2: (4,0 điểm)
a. Tìm x biết: x − 2 + 3 − 2x = 2x +1
b. Tìm x; y Z biết: xy + 2x − y = 5
c. Tìm x; y; z biết: 2x = 3y; 4y = 5z và 4x - 3y + 5z = 7 Câu 3: (1,5 điểm)
a. Tìm đa thức bậc hai biết f(x) - f(x-1) = x. Từ đó áp dụng tính tổng S = 1+2+3+ ....+ n.
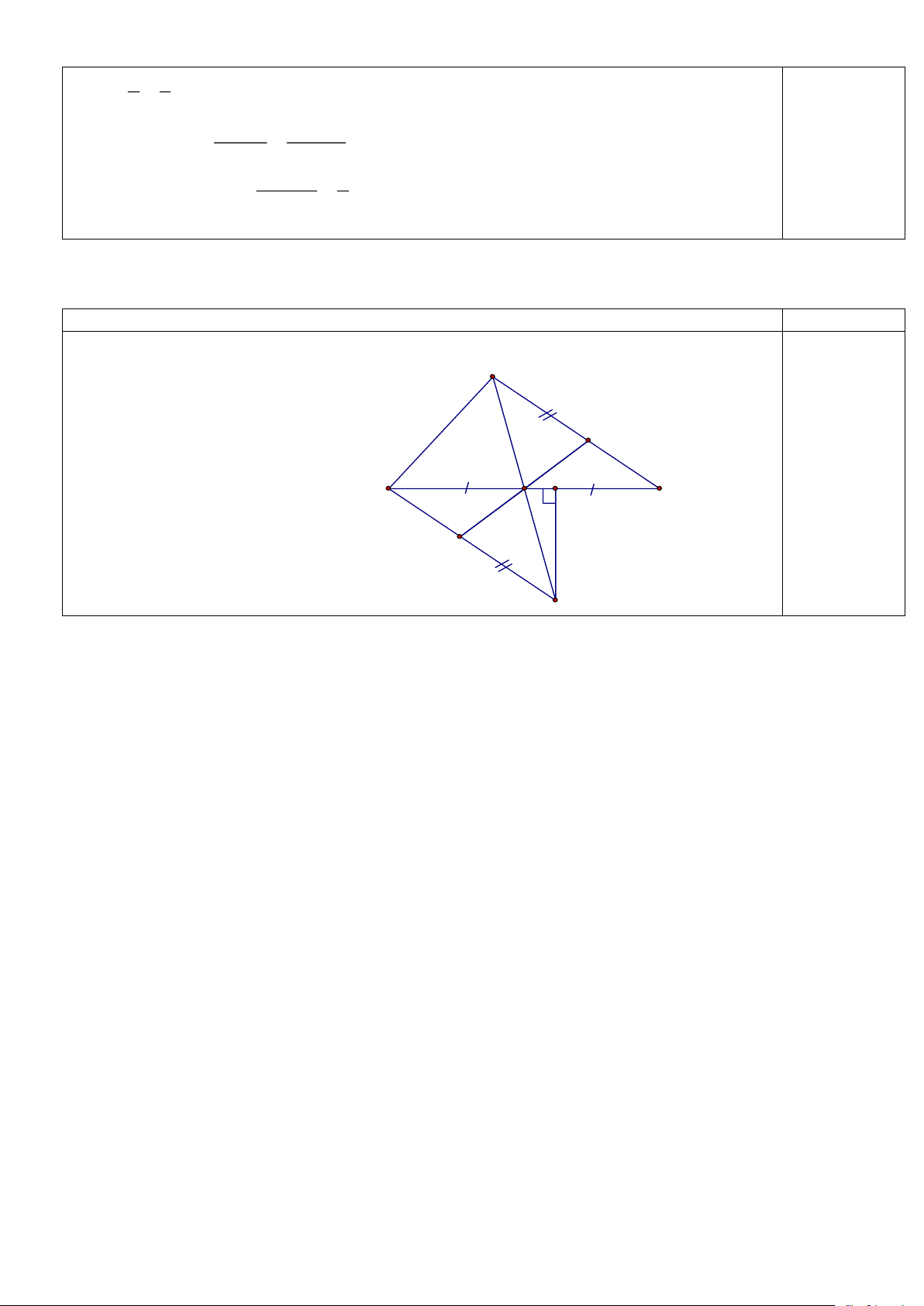
b. Cho 2bz −3cy 3cx − az ay − 2bx = = Chứng minh: x y z = = . a 2b 3c a 2b 3c Câu 4: (3,0 điểm) Cho tam giác ABC ( 90o BAC
), đường cao AH. Gọi E; F lần lượt là điểm đối xứng
của H qua AB; AC, đường thẳng EF cắt AB; AC lần lượt tại M và N. Chứng minh rằng: a. AE = AF;
b. HA là phân giác của MHN ; c. CM // EH; BN // FH. Hết./.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 5 Câu Ý Nội dung Điểm a. 0,5 3 3 3 3 3 3 3 0.25 điểm − + + + − A = 8 10 11 12 + 2 3 4 − 53 + 5 − 5 − 5 5 + 5 − 5 100 10 11 12 2 3 4 A= 1 1 1 1 1 1 1 165−132 +120 + − + + 3 + − 110 3 3( ) 8 10 11 12 2 3 4 3 Câu 1 + = 1320 + 1,5 −53 1 1 1 1 1 1 −53 −66+ 60+ 55 − 5 − + + 5 + − − 5 0.25 5( ) điểm 100 10 11 12 2 3 4 100 660 263 263 3. 3. 3 3 3945 3 − = + = + = + = 1881 1320 1320 −53 49 5 −1749 −1225 5 − − 5948 5 2 5. 9740 100 660 3300 b. 1
Ta có: 50 > 49 = 4; 26 > 25 = 5 0.5 điểm Vậy: 0,5
50 + 26 +1 7 + 5 +1 = 13 = 169 168 a. 1
Nếu x >2 ta có: x - 2 + 2x - 3 = 2x + 1 x = 6 0.25 điểm 0.25 Câu 2
Nếu 3 x 2 ta có: 2 - x + 2x - 3 = 2x + 1 x = - 2 loại 4 điểm 2 0.25
Nếu x< 3 ta có: 2 - x + 3 - 2x = 2x + 1 x = 4 2 5 Trang 14 Vậy: x = 6 ; x = 4 0.25 5 b. 1.5
Ta có: xy + 2x - y = 5 x(y+2) - (y+2) = 3 0. 5 điểm
(y+2)(x-1) = 3.1 =1.3 = (-1).(-3) = (-3).(-1) 0. 5 y + 2 3 1 -1 -3 x - 1 1 3 -3 -1 0.5 X 2 4 -2 0 Y 1 -1 -3 -5
c. 1.5 Từ: 2x= 3y; 4y = 5z 8x = 12y = 15z 0. 5 điểm x y z 4x 3y 5z − + = = = = =
= 4x 3y 5z 7 = = 12 1 1 1 1 1 1 1 1 1 7 0.5 − + 8 12 15 2 4 3 2 4 3 12 0. 5
x = 12. 1 = 3 ; y = 12. 1 = 1; z = 12. 1 4 = 8 2 12 15 5
a. 0.5 Đa thức bậc hai cần tìm có dạng: ( ) 2
f x = ax + bx + c (a 0). điểm
Ta có : f (x − ) = a(x − )2 1 1 + b( x − ) 1 + c . 0.25 2a =1 1 a =
f ( x) − f (x − )
1 = 2ax − a + b = x 2 b − a = 0 1 b = 2
Vậy đa thức cần tìm là: f (x) 1 2 1
= x + x + c (c là hằng số tùy ý). 2 2 Áp dụng:
+ Với x = 1 ta có : 1 = f ( ) 1 − f (0). 0.25
+ Với x = 2 ta có : 1 = f (2) − f ( ) 1 . Câu 3
…………………………………. 1.5
+ Với x = n ta có : n = f (n) − f (n − ) 1 . điểm 2 n n n(n + ) 1
S = 1+2+3+…+n = f (n) − f (0) = + + c − c = . 2 2 2 b. 1 2bz − 3cy 3cx − az ay − 2bx = = điểm a 2b 3c 2abz − 3acy 6bcx − 2abz 3acy − 6bcx 0.5 = = 2 2 2 a 4b 9c
2abz − 3acy + 6bcx − 2abz + 3acy − 6bcx = = 0 2 2 2
a + 4b + 9c 0.25 2bz - 3cy = 0 z y = (1) 3c 2b 0.25 3cx - az = 0 x z =
(2); Từ (1) và (2) suy ra: x y z = = a 3c a 2b 3c Trang 15 Câu 4 Hình 0.25 F 3 điểm vẽ 0. 5 đ A N M E B C H a. 1
Vì AB là trung trực của EH nên ta có: AE = AH (1) 0.25
điểm Vì AC là trung trực của HF nên ta có: AH = AF (2) 0.25
Từ (1) và (2) suy ra: AE = AF 0. 5 b. 1
Vì MAB nên MB là phân giác EMH MB là phân giác 0.25
điểm ngoài góc M của tam giác MNH 0.25
Vì NAC nên NC là phân giác FNH NC là phân giác
ngoài góc N của tam giác MNH 0.25
Do MB; NC cắt nhau tại A nên HA là phân giác trong góc H 0.25
của tam giác HMN hay HA là phân giác của MHN . c. 1
Ta có AH ⊥ BC (gt) mà HM là phân giác MHN HB là phân 0.25
điểm giác ngoài góc H của tam giác HMN
MB là phân giác ngoài góc M của tam giác HMN (cmt) 0.25 NB
là phân giác trong góc N của tam giác HMN 0.25
BN ⊥ AC ( Hai đường phân giác của hai góc kề bù thì vuông
góc với nhau). BN // HF ( cùng vuông góc với AC)
Chứng minh tương tự ta có: EH // CM
Lưu ý: Học sinh làm cách khác đúng thì vẫn cho điểm tối đa.
Học sinh không vẽ hình hoặc vẽ hình sai thì không chấm bài hình. Trang 16
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) ĐỀ 6
Bài 1: Thực hiện phép tính (6 điểm). a. 3 2 5 9 : − + .; 4 3 9 4 1 1 − 1 − − b. 45 1 1 1 − + + ; 19 2 3 4 15 9 20 9 c. 4 . 5 9 . − 3 . 4 8 . . 10 19 29 6 2 . 5 6 . − 2 . 7 27 . Bài 2: (6 điểm)
a. Tìm x, biết: 2(x-1) – 3(2x+2) – 4(2x+3) = 16; b. Tìm x, biết: 3 1 21 : 2x −1 = 2 22
c. Tìm x, y, z biết: 2x − y 3y − 2z = và x + z = 2y. 5 15
Bài 3: (1,5 điểm) Cho tỉ lệ thức a c = . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d).
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối
của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
c. Chứng minh: HMN cân.
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Hết
Họ và tên học sinh:.............................................................; SBD:............................
Học sinh trường:......................................................................................................... Trang 17
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
Môn: Toán – Lớp 7
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM ĐỀ 6
Bài 1: Thực hiện phép tính (6 điểm). Giải: a. 3 2 5 9 : − + . 4 3 9 4 3 2 5 9 3 1 9 : − + = : + 0,75đ 4 3 9 4 4 9 4 = 3 9 9 36 . + = = 9 0,75đ 4 1 4 4 1 1 − 1 − − b. 45 1 1 1 − + + 19 2 3 4 1 1 − − 45 1 1 1 1− 45 1 − + + = − 19 2 3 4 19 1 1 + 1,0đ 2 1 + 4 3 45 26 19 = − = = 1 1,0đ 19 19 19 15 9 20 9 c. 4 . 5 9 . − 3 . 4 8 . 10 19 29 6 2 . 5 6 . − 2 . 7 27 . 15 9 20 9 − 15 . 2 9 . 2 2 20 9 . 3 − 4 . 5 9 . 3 . 4 8 . = 2 . 5 3 . 2 3 . 2 . 01đ 10 19 29 6 2 . 5 6 . − 2 . 7 27 . 10 19 19 29 6 . 3 2 . 5 2 . 3 . − 2 . 7 3 . 229 3 . 18( 2 . 5 − 32 ) = 01đ 229 3 . 18( 3 . 5 − 7) 10 − 9 1 = = − 0,5đ 15 − 7 8 Bài 2: (6 điểm) Giải:
a. Tìm x, biết: 2(x-1) – 3(2x+2) – 4(2x+3) = 16.
2x – 2 – 6x – 6 – 8x – 12 = 16 0,25đ -12x – 20 = 16 0,25đ -12x = 16 + 20 = 36 0,50đ x = 36 : (-12) = -3 0,50đ b. Tìm x, biết: 3 1 21 : 2x −1 = 2 22 1
Nếu x . Ta có: (vì nếu x = ½ thì 2x – 1 = 0) 0,25đ 2 Trang 18 1 21 3 : 2x −1 = 2 22 7 21 : (2x – 1) = 0,25đ 2 22 7 21 7 22 11 2x – 1 = : = . = 0,25đ 2 22 2 21 3 11 14 2x = + 1 = 0,25đ 3 3 14 7 1 x = : 2 = > 0,25đ 3 3 2 1 Nếu x . Ta có: 0,25đ 2 1 21 3 : 2x −1 = 2 22 7 21 : (1 - 2x) = 0,25đ 2 22 11 8 -2x = - 1 = 0,25đ 3 3 8 4 1 x = : (-2) = − 0,25đ 3 3 2 7 4 Vậy x = hoặc x = − 0,25đ 3 3
c. Tìm x, y, z biết : 2x − y 3y − 2z = và x + z = 2y 5 15 Từ x + z = 2y ta có:
x – 2y + z = 0 hay 2x – 4y + 2z = 0 hay 2x – y – 3y + 2z = 0 0,25đ hay 2x – y = 3y – 2z 0,25đ 2x − y 3y − 2z Vậy nếu: =
thì: 2x – y = 3y – 2z = 0 (vì 5 15). 0,25đ 5 15 1
Từ 2x – y = 0 suy ra: x = y 0,25đ 2 1
Từ 3y – 2z = 0 và x + z = 2y. x + z + y – 2z = 0 hay y + y – z = 0 0,25đ 2 3 2 1
hay y - z = 0 hay y = z. suy ra: x = z. 0,25đ 2 3 3
Vậy các giá trị x, y, z cần tìm là: {x = 1 z; y = 2 z ; với z R } 3 3 0,5đ
hoặc {x = 1 y; y R; z = 3 y} hoặc {x R; y = 2x; z = 3x} 2 2
Bài 3: (1,5 điểm) Cho tỉ lệ thức a c = . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d)
Ta có: (a+2c)(b+d) = (a+c)(b+2d)
ab + ad + 2cb + 2cd = ab + 2ad + cb + 2cd 0,75đ a c cb = ad suy ra: = 0,75đ b d Trang 19
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối
của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
c. Chứng minh: HMN cân. Giải: B D K M N A C H
a/ Chứng minh CD song song với AB.
Xét 2 tam giác: ABK và DCK có: 0,25đ BK = CK (gt) A Kˆ B = D Kˆ C (đối đỉnh) 0,25đ AK = DK (gt) 0,25đ ABK = DCK (c-g-c) 0,25đ Cˆ D K = K Bˆ D ; mà 0 C Bˆ A + Cˆ A B = 90 0 Cˆ A D = Cˆ A B + Cˆ B D = 90 0,25đ Cˆ A D = 900 = C Aˆ B
AB // CD (AB ⊥ AC và CD ⊥ AC). 0,25đ
b. Chứng minh rằng: ABH = CDH
Xét 2 tam giác vuông: ABH và CDH có: 0,25đ BA = CD (do ABK = DCK) AH = CH (gt) 0,25đ ABH = CDH (c-g-c) 0,50đ
c. Chứng minh: HMN cân.
Xét 2 tam giác vuông: ABC và CDA có: 0,25đ AB = CD; Cˆ A D = 900 = C Aˆ B
; AC cạnh chung: ABC = CDA (c-g-c) Cˆ A B = D Aˆ C 0,25đ mà: AH = CH (gt) và Hˆ M A = Hˆ N C (vì ABH = CDH) 0,50đ AMH = CNH (g-c-g) 0,50đ
MH = NH. Vậy HMN cân tại H 0,50đ
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Giải:
Ta có: abcabc = a.105 + b.104 + c.103 + a.102 + b.10 + c 0,25đ
= a.102(103 + 1) + b.10(103 + 1) + c(103 + 1) 0,50đ
= (103 + 1)( a.102 + b.10 + c) 0,50đ Trang 20