80 Câu Trắc Nghiệm Min Max Của Hàm Số Theo Từng Mức Độ Có Đáp Án

80 câu trắc nghiệm Min Max của hàm số tùy theo từng mức độ được biên soạn dưới dạng file PDF gồm 10 trang. Tài liệu là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

64 32 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

10 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
TRẮC NGHIỆM TÌM MAX – MIN TRÊN ĐOẠN [a;b]
I. KIẾN THỨC CẦN NHỚ:
1. Định nghĩa
Cho hàm số
y f x
xác định trên tập
.D
Số M gọi là giá trị lớn nhất của hàm số
y f x
trên
D
nếu:
00
( ) ,
, ( )
f x M x D
x D f x M
.
Kí hiệu:
max ( )
xD
M f x
.
Số
m
gọi là giá trị nhỏ nhất của hàm số
y f x
trên
D
nếu:
00
( ) ,
, ( )
f x m x D
x D f x m
.
Kí hiệu:
min ( )
xD
m f x
.
2. Phƣơng pháp
Bƣớc 1. Tính đạo hàm
.
Bƣớc 2. Tìm tất cả các nghiệm
[ ; ]
i
x a b
của phương trình
( ) 0fx
và tất cả các điểm
[ ; ]
i
ab
làm
cho
không xác định.
Bƣớc 3. Tính
()fa
,
()fb
,
()
i
fx
,
()
i
f
.
Bƣớc 4. So sánh các giá trị tính được và kết luận
;
max ( )
ab
M f x
,
;
min ( )
ab
m f x
.
Chú ý:
Nếu
( )
fx
đồng biến trên
[ ]
;ab
thì
;
;
ax ( ) ;min ( )
ab
ab
M m f x f b f x f a
.
Nếu
( )
fx
nghịch biến trên
[ ]
;ab
thì
;
;
ax ( ) ;min ( )
ab
ab
M m f x f a f x f b
.
II. CÁC DẠNG BÀI TẬP TƢƠNG TỰ
Max – Min khi biết đồ thị, BBT.
Max – min của hàm số trên đoạn [a;b].
Max – min của hàm số trên K.
Max – min của hàm số chứa trị tuyệt đối.
Bài toán tham số về Max – min.
Max – min của biểu thức nhiều biến.
Ứng dụng Max – min giải toán tham số.
Bài toán thực tế, liên môn về Max – min.
Tìm Max – min của hàm hợp.
…
BÀI TẬP MẪU
(ĐỀ MINH HỌA LẦN 1-BDG 2020-2021)Gọi
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
hàm số
42
23f x x x
trên đoạn
0;2
. Tổng
Mm
bằng
A.
11
. B.
14
. C.
5
. D.
13
.
Phân tích hướng dẫn giải
1. DẠNG TOÁN:Đây là dạng toán tìm Max – min của hàm số trên đoạn
;ab
.
2. HƢỚNG GIẢI:
B1:
* Hàm số đã cho
y f x
xác định và liên tục trên đoạn
;.ab
*Tìm các điểm
12
, ,...,
n
x x x
trên khoảng
;ab
, tại đó
0fx
hoặc
fx
không xác định.
B2: Tính
12
, , ,..., , .
n
f a f x f x f x f b
B3:Khi đó:
*
12
,
max max , ,..., , , .
n
ab
f x f x f x f x f a f b
Trang2
*
12
,
min min , ,..., , , .
n
ab
f x f x f x f x f a f b
Từ đó, ta có thể giải bài toán cụ thể nhƣ sau:
Lờigiải
ChọnD
Ta có
3
( ) 4 4f x x x
¢
=-
và
( ) 0 0, 1f x x x
¢
= Û = = ±
.
Trên
[0;2],
ta xét các giá trị
(0) 3, (1) 2, (2) 11.f f f= = =
Do đó
11, 2Mm==
và
13.Mm+=
Bài tập tương tự và phát triển:
Mức độ 1
Câu 1. Giá trị lớn nhất của hàm số
32
8 16 9 f x x x x
trên đoạn
1;3
là
A.
1;3
max 5fx
.B.
1;3
max 6fx
. C.
1;3
13
max
27
fx
. D.
1;3
max 0fx
.
Câu 2. Giá trị lớn nhất của hàm số
42
8 16y f x x x
trên đoạn
1;3
.
A.
9
. B.
19
. C.
25
. D.
0
.
Câu 3. Cho hàm số
42
2 1.f x x x
Kí hiệu
0;2
max ,
x
M f x
0;2
min .
x
m f x
Khi đó
Mm
bằng.
A.
9
. B.
5
. C.
1
. D.
7
.
Câu 4. Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
2
2 3 4
3
x
y x x
trên
4;0
lần lượt là
M
và
m
. Giá trị của
Mm
bằng
A.
4
3
. B.
28
3
. C.
4
. D.
4
3
.
Câu 5. Giá trị nhỏ nhất của hàm số
42
45y x x
trên đoạn
2;3
bằng
A.
50
. B.
1
. C.
197
. D.
5
.
Câu 6. Gọi
M
,
N
lần lượt là GTLN, GTNN của hàm số
32
31y x x
trên
1;2
. Khi đó tổng
MN
bằng
A.
2
. B.
2
. C.
4
. D.
0
.
Câu 7. Tìm giá trị lớn nhất của hàm số
32
3 9 10f x x x x
trên
2; 2
.
A.
[ 2; 2]
max 5fx
.B.
[ 2; 2]
max 17fx
. C.
[ 2; 2]
max 15fx

. D.
[ 2; 2]
max 15fx
.
Câu 8. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
2 4 3y x x x
trên đoạn
4;0
lần lượt là
và Mm
. Giá trị của tổng
Mm
bằng bao nhiêu?
A.
2Mm
.B.
24Mm
. C.
4Mm
. D.
10Mm
.
Câu 9. Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
32
2 3 12 1y x x x
trên đoạn
1;3 .
Khi đó tổng
Mm
có giá trị là một số thuộc khoảng nào dưới đây?
A.
59;61
. B.
39;42
. C.
. D.
3;5
.
Câu 10. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
1
x
fx
x
trên đoạn
3;5
. Khi đó
Mm
bằng
A.
2
B.
3
8
C.
7
2
D.
1
2
Câu 11. Tìm giá trị lớn nhất của hàm số
32
2 4 1f x x x x
trên đoạn
1;3 .
A.
1;3
max 7fx
. B.
1;3
max 4fx
. C.
1;3
max 2fx
. D.
1;3
67
max
27
fx
.
Câu 12. Giá trị nhỏ nhất của hàm số
32
3y x x
trên đoạn
4; 1
bằng.
Trang3
A.
0
. B.
16
. C.
4
. D.
4
.
Câu 13. Cho hàm số
y f x
,
2;3x
có đồ thị như hình vẽ. Gọi
M
,
m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số
fx
trên đoạn
2;3
. Giá trị
Mm
là
A.
6
. B.
1
. C.
5
. D.
3
.
Câu 14. Cho hàm số
y f x
liên tục trên đoạn
3;2
và có bảng biến thiên như sau.
Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x
trên
đoạn
1;2
. Tính
Mm
.
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 15. Giá trị nhỏ nhất của hàm số
9
yx
x

trên đoạn
2;4
là:
A.
2;4
min 6y
. B.
2;4
13
min
2
y
. C.
2;4
25
min
4
y
. D.
2;4
min 6y 
.
Câu 16. Giá trị lớn nhất của hàm số
32
1
x
y
x
trên
0;2
bằng
A.
2
. B.
8
3
. C.
10
3
. D.
3
.
Câu 17. Giá trị lớn nhất của hàm số
5
7
x
y
x
trên đoạn
8;12
là
A.
15.
B.
17
.
5
C.
13.
D.
13
.
2
Câu 18. Cho hàm số
()y f x
xác định trên
3; 5


và có bảng biến thiên như hình vẽ:
Khẳng định nào sau đây là đúng?
A.
3; 5
min 0y
. B.
3; 5
max 2 5y
. C.
3; 5
max 2y
. D.
3; 5
min 2y

Câu 19. Giá trị nhỏ nhất của hàm số
x
ye
trên đoạn
1; 1
là:
2
5
-2
2
0
+
0
y
y'
x
+
1
-1
0
-
3
5
Trang4
A.
0
. B.
1
e
. C.
1
. D.
e
.
Câu 20. Cho hàm số
32
32y x x
.Gọi
,Mn
lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên
0;3
.Tính
Mn
.
A.
8
. B.
10
. C.
6
. D.
4
.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
C
C
A
B
A
C
D
A
B
D
11
12
13
14
15
16
17
18
19
20
C
B
B
A
A
B
C
D
B
D
Mức độ 2
Câu 1. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
22
2
xx
y
x

trên đoạn
2;1
lần lượt bằng:
A.
1
và
1
.
B.
2
và
0
.
C.
0
và
2
. D.
1
và
2
.
Câu 2. Giá trị nhỏ nhất của hàm số
9
yx
x

trên đoạn
2;4
là:
A.
2; 4
min 6y
. B.
2; 4
13
min
2
y
. C.
2; 4
min 6y 
. D.
2; 4
25
min
4
y
.
Câu 3. Tìm giá trị lớn nhất của hàm số
4
1
2
yx
x
trên đoạn [-1; 5].
A.
1;5
max 3y
. B.
1;5
max 4y
. C.
1;5
max 5y

. D.
1;5
46
max
7
y
.
Câu 4. Tìm giá trị lớn nhất (max) và giá trị nhỏ nhất (min) của hàm số
1
yx
x

trên đoạn
3
;3
2



.
A.
3
;3
2
10
max
3
y



,
3
;3
2
5
min
2
y



. B.
3
;3
2
10
max
3
y



,
3
;3
2
13
min
6
y



.
C.
3
;3
2
10
max
3
y



,
3
;3
2
min 2y



. D.
3
;3
2
16
max
3
y



,
3
;3
2
min 2y



.
Câu 5. Tìm giá trị nhỏ nhất của hàm số trên đoạn .
A.
0;3
min 1y 
. B.
0;3
3
min
7
y 
. C.
0;3
min 4y 
. D.
0;3
min 0y
.
Câu 6. Tìm giá trị nhỏ nhất của hàm số
2
32y x x
trên
1
;1
4



.
A.
1
2
. B.
0
. C.
1
. D.
2
.
Câu 7. Hàm số
2
2
41yx
có giá trị lớn nhất trên đoạn
1;1
là:
A.
12
. B.
14
. C.
17
. D.
10
.
Câu 8. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3x 6
()
1
x
fx
x

trên đoạn
2;4
lần lượt
là
,Mm
. Tính
.S M m
A.
6.S
B.
4.S
C.
7.S
D.
3.S
Câu 9. Tìm GTLN và GTNN của hàm số
5 4 3
5 5 1y x x x
trên
1;2 ?
2
4
21
xx
y
x
0;3
Trang5
A.
1;2
1;2
min 7, max 1
x
x
yy
. B.
1;2
1;2
min 10, max 2
x
x
yy
.
C.
1;2
1;2
min 2, max 10
x
x
yy
. D.
1;2
1;2
min 10, max 2
x
x
yy
.
Câu 10. Cho
2
2
1
4 5 4
x
f x x
xx

. Gọi
0;3
0;3
max ; minM f x m f x
, khi đó
M – m
bằng.
A.
9
5
. B.
3
5
. C.
7
5
. D.
1
.
Câu 11. Cho hàm số
( )
2
8
xm
fx
x
-
=
+
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để hàm số có giá trị nhỏ nhất trên đoạn
[ ]
0;3
bằng
3-
. Giá trị
0
m
thuộc khoảng nào trong các
khoảng cho dưới đây?
A.
2;5 .
B.
1;4 .
C.
6;9 .
D.
20;25 .
Câu 12. Tìm tất cả các giá trị của tham số
m
để hàm số
32
3y x x m= - +
có giá trị nhỏ nhất trên
[ ]
1;1-
bằng
2
.
A.
22m=+
. B.
42m=+
. C.
22
42
m
m
é
=+
ê
ê
=+
ê
ë
. D.
2m =
.
Câu 13. Giá trị lớn nhất của hàm số
42
cos cos 4y x x
bằng:
A.
5
. B.
1
2
. C.
4
. D.
17
4
.
Câu 14. Tìm
a
để giá trị lớn nhất của hàm số
32
31y x ax a
trên đoạn
1; a
bằng
10
, biết
0.a
A.
10a
. B.
5
2
a
. C.
3
2
a
. D.
11a
.
Câu 15. Gọi
A
,
B
là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
1
x m m
y
x

trên đoạn
2;3
. Tìm
tất cả các giá trị thực của tham số
m
để
13
2
AB
.
A.
1m
;
2m 
. B.
2m 
. C.
2m 
. D.
1m 
;
2m
.
Câu 16. Có một giá trị
0
m
của tham số
m
để hàm số
( )
32
11y x m x m= + + + +
đạt giá trị nhỏ nhất
bằng
5
trên đoạn
[ ]
0;1
. Mệnh đề nào sau đây là đúng?
A.
2
00
2018 0mm-³
. B.
0
2 1 0m -<
. C.
2
00
60mm-<
. D.
0
2 1 0m +<
.
Câu 17. Cho hàm số
y f x
có đạo hàm
2
1f x x
. Với các số thực dương
a
,
b
thỏa mãn
ab
, giá trị nhỏ nhất của hàm số
trên đoạn
;ab
bằng.
A.
f ab
. B.
2
ab
f



. C.
. D.
.
Câu 18. Cho hàm số
32
39y x x x m= - - +
có giá trị lớn nhất trên đoạn
[ ]
2;0-
bằng
2
, với
m
là
tham số thực. Mệnh đề nào dưới đây đúng?
A.
3m =-
. B.
4m =
. C.
2m =
. D.
3m =
.
Câu 19. Cho hàm số
xm
y
x
+
=
thỏa
[ ]
[ ]
1;2
1;2
min max 8yy+=
, với
m
là tham số thực. Mệnh đề nào dưới
đây đúng?
A.
4m>
. B.
02m<£
. C.
24m<£
. D.
0m £
.
Câu 20. Cho hàm số
2
,
8
xm
fx
x
với
m
là tham số. Giá trị lớn nhất của
m
để
0;3
min 2fx
là
Trang6
A.
5m
. B.
6m
. C.
4m
. D.
3m
.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
A
A
D
B
A
C
C
C
B
A
11
12
13
14
15
16
17
18
19
20
A
B
C
D
A
A
D
A
C
C
Mức độ 3
Câu 1. Tìm tập giá trị
T
của hàm số
2
4.y x x
.
A.
2;2T 
. B.
0;2T
. C.
0;2 2T


. D.
2;2 2T



.
Câu 2.
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
12f x x x
. Tính
Mm
?
A.
22Mm
. B.
22Mm
. C.
42Mm
. D.
22Mm
.
Câu 3. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2
34yx
lần lượt là.
A.
0;2
. B.
3; 1
. C.
3;0
. D.
2;2
.
Câu 4. Tìm
x
để hàm số
26y x x
đạt giá trị lớn nhất?
A.
2x
. B.
0x
. C.
2x 
. D.
4x
.
Câu 5. Tìm tất cả các giá trị thực của tham số
m
để giá trị nhỏ nhất của hàm số
2
2
3
x m m
y
x

trên
đoạn
0;1
bằng
2
.
A.
1m 
hoặc
3
2
m
. B.
2m
hoặc
3
2
m 
.
C.
1m
hoặc
1
2
m 
. D.
3m
hoặc
5
2
m 
.
Câu 6. Số các giá trị tham số
m
để hàm số
2
1xm
y
xm

có giá trị lớn nhất trên
0;4
bằng
6
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 7. Gọi
m
và
M
lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số
23
e
x
fx
trên
đoạn
0;2
. Mối liên hệ giữa
M
và
m
là
A.
M m e
. B.
1mM
. C.
2
1
.
e
mM
. D.
2
e
M
m
.
Câu 8. Hàm số
5mx
fx
xm
có giá trị nhỏ nhất trên đoạn
0;1
bằng
7
khi
A.
5
7
m
. B.
0m
. C.
1m
. D.
2m
.
Câu 9. Gọi
m
là giá trị để hàm số
2
8
xm
y
x
có giá trị nhỏ nhất trên
0;3
bằng
2
. Mệnh đề nào
sau đây là đúng?
A.
5m
. B.
5m
. C.
35m
. D.
2
16m
.
Câu 10. Chohàm số
3 2 2
1
2 2 9,
3
y x m x m m m
là tham số. Gọi
S
là tập tất cả các giá trị của
m
sao cho giá trị lớn nhất của hàm số trên đoạn
0;3
không vượt quá
3
. Tìm
?m
A.
; 3 1;S  
. B.
3;1S 
.
C.
; 3 1;S  
. D.
3;1S 
.
Trang7
Câu 11. Biết giá trị lớn nhất của hàm số
2
1
4
2
y x x m= - + - +
là
18
. Mệnh đề nào sau đây đúng?
A.
05m<<
. B.
10 15m<<
. C.
5 10m<<
. D.
15 20m<<
.
Câu 12. Cho hàm số
1
xm
y
x
(
m
là tham số thực) thoả mãn
1; 2
1; 2
16
min max
3
yy
. Mệnh đề nào dưới
đây đúng?
A.
0m
. B.
4m
. C.
02m
. D.
24m
.
Câu 13. Cho
;xy
là hai số thực bất kỳ thuộc đoạn
1;3 .
Gọi
, Mm
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
.
xy
S
yx
Tính
.Mm
A.
10
.
3
Mn
B.
3Mn
. C.
5Mn
. D.
16
3
Mn
.
Câu 14. Có một giá trị
0
m
của tham số
m
để hàm số
32
11y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây đúng?
A.
2
00
2018 0mm
. B.
0
2 1 0m 
. C.
2
00
60mm
. D.
0
2 1 0m 
Câu 15. Cho hàm số
y f x
liên tục trên
. Đồ thị của hàm số
y f x
như hình bên. Đặt
2
21g x f x x
. Mệnh đề nào dưới đây đúng?
A.
3;3
3Max g x g
. B.
3;3
1Min g x g
. C.
3;3
0Max g x g
. D.
3;3
1Max g x g
.
Câu 16. Cho hàm số
1 sin
cos 2
mx
y
x
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
0;10
đểgiá trị nhỏ nhất của hàm số nhỏ hơn
2
?
A.
1
. B.
9
. C.
3
. D.
6
.
Câu 17. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ dưới. Xét hàm số
3
21g x f x x m
. Tìm
m
để
0;1
max 10gx
.
A.
13m 
. B.
5m
. C.
3m
. D.
1m 
.
Câu 18. Cho hàm số
2
24y x x a
. Tìm
a
để giá trị lớn nhất của hàm số trên đoạn
2;1
đạt giá
trị nhỏ nhất?
A.
1a
. B.
2a
. C. Một giá trị khác. D.
3a
.
Câu 19. Biết rằng giá trị lớn nhất của hàm số
2
24y x x m= + + -
trên đoạn
[ ]
2;1-
đạt giá trị nhỏ
nhất, giá trị của tham số
m
bằng
Trang8
A.
1
. B.
3
. C.
4
. D.
5
.
Câu 20. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
xm
y
xm
trên đoạn
0;4
bằng
1
.
A.
0
. B.
2
. C.
3
. D.
1
.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
D
D
B
A
A
C
C
D
A
D
11
12
13
14
15
16
17
18
19
20
D
B
D
A
D
D
A
D
B
D
Mức độ 4
Câu 1. Biết rằng phương trình
2
224x x x m
có nghiệm khi
m
thuộc
;ab
với
a
,
b
. Khi đó giá trị của
22T a b
là?
A.
. B.
3 2 2T 
. C.
6T
. D.
8T
.
Câu 2. Hàm số
22
4 2 3 2y x x x x
đạt giá trị lớn nhất tại hai giá trị
x
mà tích của chúng là:
A.
1
. B.
1
. C.
0
. D.
2
.
Câu 3. Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2017 2019y x x
trên tập xác định của nó. Tính
Mm
.
A.
2019 2019 2017 2017
. B.
4036
.
C.
4036 2018
. D.
2019 2017
.
Câu 4. Giá trị nhỏ nhất, giá trị lớn nhất của hàm số
5 1 3 1 3f x x x x x
lần
lượt là
m
và
M
, tính
22
S m M
.
A.
170S
. B.
169S
. C.
172S
. D.
171S
.
Câu 5. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho
4 2 2
2;1
max 6 16x mx m
. Số
phần tử của
S
là ?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 6. Có tất cả bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2y x x m
trên
đoạn
1;2
bằng
5
.
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 7. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
22
3
1 3 1y x x
.
Hỏi điểm
;A M m
thuộc đường tròn nào sau đây?
A.
2
2
11xy
. B.
22
3 1 20xy
C.
22
3 1 2xy
. D.
22
1 1 1xy
.
Câu 8. Biết hàm số
y f x
liên tục trên
có
M
và
m
lần lượt là GTLN, GTNN của hàm số trên
đoạn
0;2
. Trong các hàm số sau, hàm số nào cũng có GTLN và GTNN tương ứng là
M
và
m
?.
A.
2
2y f x x
. B.
2
4
1
x
yf
x



.
C.
2 siny f x cosx
. D.
33
2 siny f x cos x
.
Trang9
Câu 9. Tìm các giá trị nguyên dương
2n
để hàm số
22
nn
y x x
với
2; 2x
có giá trị
lớn nhất gấp 8 lần giá trị nhỏ nhất.
A.
5n
. B.
6n
. C.
2n
. D.
4n
.
Câu 10. Đồ thị hàm số
'y f x
là đường cong nét đậm và
'y g x
là đường cong nét mảnh như
hình vẽ. Gọi ba giao điểm
,,A B C
của
'y f x
và
'y g x
trên hình vẽ lần lượt có hoành
độ
,,abc
. Tìm giá trị nhỏ nhất của hàm số
h x f x g x
trên đoạn
;ac
?
A.
;
min
ac
h x h a
. B.
;
min
ac
h x h b
.
C.
;
min
ac
h x h c
. D.
;
min 0
ac
h x h
.
Câu 11. Cho hàm số
( )
fx
có đạo hàm là
( )
fx
¢
. Đồ thị hàm số
( )
y f x
¢
=
được cho như hình vẽ bên.
Biết rằng
( ) ( ) ( ) ( )
0 2 1 3f f f f+ = +
. Giá trị lớn nhất của
( )
fx
trên đoạn
[ ]
0;3
là
A.
( )
1f
. B.
( )
0f
. C.
( )
2f
. D.
( )
3f
.
Câu 12. Cho hàm số
32
3 3 2 1 1y x mx m x
(với
m
là tham số). Tìm tất cả các giá trị của tham
số
m
để trên đoạn
2;0
hàm số trên đạt giá trị lớn nhất bằng
6.
A.
1.m
B.
0.m
C.
3.m
D.
1.m 
Câu 13. Để giá trị lớn nhất của hàm số
3
3 2 1y f x x x m
trên đoạn
0;2
là nhỏ nhất thì giá
trị của
m
thuộc
A.
0;1
. B.
1;0
. C.
1;2
. D.
2; 1
.
Câu 14. Cho hàm số
32
3 3 2 1 1y x mx m x
(với
m
là tham số). Tìm tất cả các giá trị của tham
số
m
để trên đoạn
2;0
hàm số trên đạt giá trị lớn nhất bằng
6.
A.
1.m
B.
0.m
C.
3.m
D.
1.m 
Câu 15. Xét hàm số
2
y x ax b
, với
,ab
là tham số. Gọi
M
là giá trị lớn nhất của hàm số trên
1;3
. Khi
M
nhận giá trị nhỏ nhất có thể được, tính
2ab
.
A.
5
. B.
4
. C.
2
. D.
3
.
Câu 16. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1

x mx m
y
x
trên
1;2
bằng
2
. Số phần tử của tập
S
là
A.
3
. B.
1
. C.
4
. D.
2
.
x
y
c
b
a
C
B
A
O
Trang10
Câu 17. Cho hàm số
y f x
có đạo hàm
fx
. Hàm số
y f x
liên tục trên tập số thực và có đồ
thị như hình vẽ.
Biết
13
1 , 2 6
4
ff
. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3g x f x f x
trên
1;2
bằng:
A.
1573
64
. B.
198
. C.
37
4
. D.
14245
64
.
Câu 18. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1
x mx m
y
x

trên
1;2
bằng
2
. Số phần tử của
S
là
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 19. Cho hàm số
42
( ) 8 . f x x x m
Có bao nhiêu giá trị nguyên của
[ 50;50]m
sao cho với
mọi số thực
, , [0;3]a b c
thì
( ), ( ), ( )f a f b f c
là độ dài ba cạnh của một tam giác.
A.
29.
B.
23.
C.
27
. D.
25.
Câu 20. Để giá trị lớn nhất của hàm số
2
2 3 4y x x m= - - +
đạt giá trị nhỏ nhất thì
m
thỏa
A.
3
2
m =
. B.
5
3
m =
. C.
4
3
m =
. D.
1
2
m =
.
Câu 21. Giá trị lớn nhất của hàm số
32
( ) 3 72 90f x x x x m
trên đoạn
5;5
là
2022.
Trong các
khẳng định dưới đây khẳng định nào đúng?
A.
1600 1700m
. B.
400m
. C.
1618m
. D.
1500 1600m
.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
C
A
C
D
D
C
C
B
D
B
11
12
13
14
15
16
17
18
19
20
D
D
A
D
B
D
A
D
D
A
21A
x
y
2
2
-1
1
4
O
| 1/10
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRẮC NGHIỆM TÌM MAX – MIN TRÊN ĐOẠN [a;b]
I. KIẾN THỨC CẦN NHỚ: 1. Định nghĩa
Cho hàm số y f x xác định trên tập . D
f (x)  M , x   D
Số M gọi là giá trị lớn nhất của hàm số y f x trên D nếu:  . x
  D, f (x )  M  0 0
Kí hiệu: M  max f (x) . x D   f (x)  , m x   D
Số m gọi là giá trị nhỏ nhất của hàm số y f x trên D nếu:  . x
  D, f (x )  m  0 0
Kí hiệu: m  min f (x) . x D2. Phƣơng pháp
Bƣớc 1. Tính đạo hàm f (  x).
Bƣớc 2. Tìm tất cả các nghiệm x [ ;
a b] của phương trình f (
x)  0 và tất cả các điểm  [a;b] làm i i cho f (
x) không xác định.
Bƣớc 3. Tính f (a) , f (b) , f (x ) , f ( ) . i i
Bƣớc 4. So sánh các giá trị tính được và kết luận M  max f (x) , m  min f (x) . a;b a;bChú ý:
Nếu f (x) đồng biến trên [ ;
a b] thì M m ax f (x)  f b; min f (x)  f a . a;b a;b
Nếu f (x) nghịch biến trên [ ;
a b] thì M m ax f (x)  f a; min f (x)  f b . a;b a;b
II. CÁC DẠNG BÀI TẬP TƢƠNG TỰ
Max – Min khi biết đồ thị, BBT.
Max – min của hàm số trên đoạn [a;b].
Max – min của hàm số trên K.
Max – min của hàm số chứa trị tuyệt đối.
Bài toán tham số về Max – min.
Max – min của biểu thức nhiều biến.
Ứng dụng Max – min giải toán tham số.
Bài toán thực tế, liên môn về Max – min.
Tìm Max – min của hàm hợp.  … BÀI TẬP MẪU
(ĐỀ MINH HỌA LẦN 1-BDG 2020-2021)Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
hàm số f x 4 2
x  2x  3 trên đoạn 0;2 . Tổng M m bằng A.11. B.14 . C. 5 . D.13 .
Phân tích hướng dẫn giải
1. DẠNG TOÁN:Đây là dạng toán tìm Max – min của hàm số trên đoạn  ; a b . 2. HƢỚNG GIẢI: B1:
* Hàm số đã cho y f x xác định và liên tục trên đoạn  ; a b.
*Tìm các điểm x , x ,..., x trên khoảng  ;
a b , tại đó f  x  0 hoặc f  x không xác định. 1 2 n
B2: Tính f a, f x , f x ,..., f x , f b . 1   2   n    B3:Khi đó:
* max f x  max f x , f x ,..., f x , f a , f b . 1   2 
n      a,bTrang1
* min f x  min f x , f x ,..., f x , f a , f b . 1   2 
n      a,b
Từ đó, ta có thể giải bài toán cụ thể nhƣ sau: Lờigiải ChọnD Ta có 3 f (
¢ x) = 4x - 4x và f (¢x) = 0 Û x = 0, x = ± 1 .
Trên [0; 2], ta xét các giá trị
f (0) = 3, f (1) = 2, f (2) = 11.
Do đó M = 11,m = 2 và M + m = 13.
Bài tập tương tự và phát triển: Mức độ 1 Câu 1.
Giá trị lớn nhất của hàm số f x 3 2
x 8x 16x 9 trên đoạn 1;  3 là 13
A. max f x  5 .B. max f x  6  .
C. max f x  .
D. max f x  0 . 1;  3 1;  3 1; 3 27 1;  3 Câu 2.
Giá trị lớn nhất của hàm số y f x 4 2
x 8x 16 trên đoạn  1  ;  3 . A. 9 . B. 19 . C. 25 . D. 0 . Câu 3.
Cho hàm số f x 4 2
x  2x 1. Kí hiệu M  max f x , m  min f x . Khi đó M m bằng. x   0;2 x   0;2  A. 9 . B. 5 . C. 1. D. 7 . 3 x Câu 4.
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y
 2x  3x  4 trên 4;0 lần lượt là 3
M và m . Giá trị của M m bằng 4 28 4 A. . B.  . C. 4  . D.  . 3 3 3 Câu 5.
Giá trị nhỏ nhất của hàm số 4 2
y  x  4x  5 trên đoạn 2;  3 bằng A. 50  . B. 1. C. 197  . D. 5  . Câu 6.
Gọi M , N lần lượt là GTLN, GTNN của hàm số 3 2
y x  3x 1 trên 1; 2. Khi đó tổng
M N bằng A. 2 . B. 2  . C. 4  . D. 0 . Câu 7.
Tìm giá trị lớn nhất của hàm số f x 3 2
x 3x 9x 10 trên  2  ; 2.
A. max f x  5.B. max f x  17.
C. max f x  1  5.
D. max f x  15. [ 2  ; 2] [ 2  ; 2] [ 2  ; 2] [ 2  ; 2] Câu 8.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y x  2x  4x  3 trên đoạn  4  ;0 lần lượt là
M và m . Giá trị của tổng M m bằng bao nhiêu?
A. M m  2
 .B. M m  24  .
C. M m  4  .
D. M m  10  . Câu 9.
Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 3 2
y  2x  3x 12x 1 trên đoạn  1  ; 
3 . Khi đó tổng M m có giá trị là một số thuộc khoảng nào dưới đây? A. 59;6  1 .
B. 39; 42 . C. 0; 2 . D. 3;5 . x
Câu 10. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 1  x trên đoạn 1
3; 5. Khi đó M m bằng 3 7 1 A. 2 B. C. D. 8 2 2
Câu 11. Tìm giá trị lớn nhất của hàm số f x 3 2
x  2x  4x 1 trên đoạn 1;  3 . 67
A. max f x  7  .
B. max f x  4  .
C. max f x  2  .
D. max f x  . 1; 3 1; 3 1; 3 1  ;3 27
Câu 12. Giá trị nhỏ nhất của hàm số 3 2
y x  3x trên đoạn  4  ;  1 bằng. Trang2 A. 0 . B. 16  . C. 4 . D. 4  .
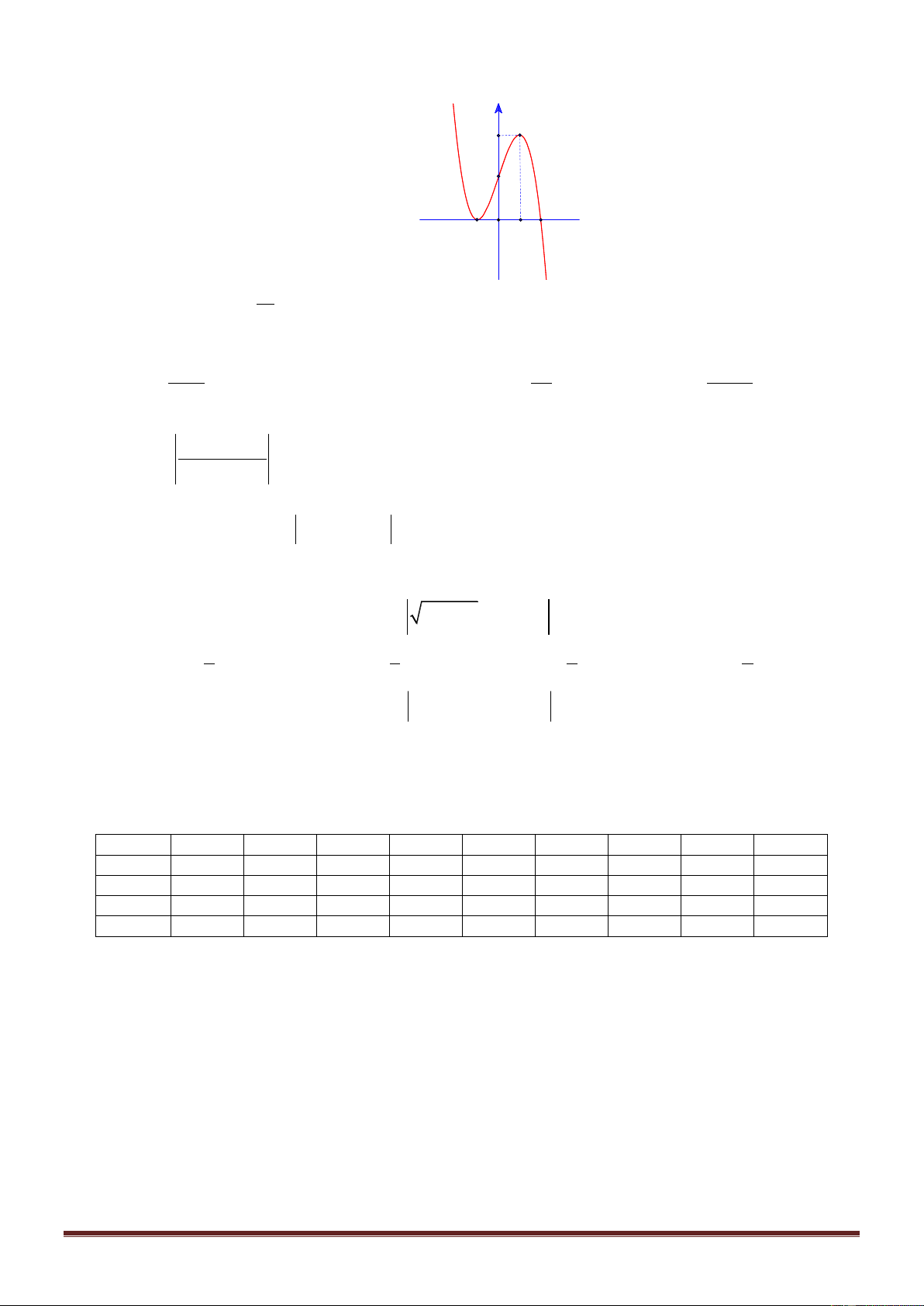
Câu 13. Cho hàm số y f x , x  2  ; 
3 có đồ thị như hình vẽ. Gọi M , m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số f x trên đoạn  2  ; 
3 . Giá trị M m là A. 6 . B. 1. C. 5 . D. 3 .
Câu 14. Cho hàm số y f x liên tục trên đoạn 3; 2 và có bảng biến thiên như sau.
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x trên đoạn  1
 ;2. Tính M m . A. 3 . B. 2 . C. 1. D. 4 .
Câu 15. Giá trị nhỏ nhất của hàm số 9 y x
trên đoạn 2;4 là: x 13 25
A. min y  6 . B. min y  . C. min y  . D. min y  6  . 2;4 2;4 2 2;4 4 2;  4 3x  2
Câu 16. Giá trị lớn nhất của hàm số y  trên 0;2 bằng x 1 8 10 A. 2 . B. . C. . D. 3 . 3 3 x
Câu 17. Giá trị lớn nhất của hàm số 5 y  trên đoạn 8;12 là x  7 17 13 A. 15. B. . C. 13. D. . 5 2
Câu 18. Cho hàm số y f (x) xác định trên  3; 5 
 và có bảng biến thiên như hình vẽ: x - 3 -1 1 5 y' + 0 0 + 2 5 2 y 0 -2
Khẳng định nào sau đây là đúng?
A. min y  0 .
B. max y  2 5 .
C. max y  2 . D. min y  2   3; 5    3; 5  3; 5      3; 5  
Câu 19. Giá trị nhỏ nhất của hàm số x
y e trên đoạn 1;  1 là: Trang3 1 A. 0 . B. . C. 1. D. e . e
Câu 20. Cho hàm số 3 2
y  x  3x  2 .Gọi M , n lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên
0; 3.Tính M n. A. 8 . B. 10 . C. 6 . D. 4 . ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 C C A B A C D A B D 11 12 13 14 15 16 17 18 19 20 C B B A A B C D B D Mức độ 2 2 2x x  2 Câu 1.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoạn  2  
;1 lần lượt bằng: 2  x A.1 và 1. B. 2 và 0 . C. 0 và 2  . D.1 và 2  . 9 Câu 2.
Giá trị nhỏ nhất của hàm số y x  trên đoạn 2;  4 là: x 13 25
A. min y  6 . B. min y  . C. min y  6  . D. min y  . 2; 4 2; 4 2 2; 4 2; 4 4 4 Câu 3.
Tìm giá trị lớn nhất của hàm số y x 1 trên đoạn [-1; 5]. x  2 46
A. max y  3.
B. max y  4 . C. max y  5  . D. max y  .  1  ;5  1  ;  5  1  ;5  1  ;  5 7 1 3  Câu 4.
Tìm giá trị lớn nhất (max) và giá trị nhỏ nhất (min) của hàm số y x  trên đoạn ;3   . x 2  10 5 10 13 A. max y  , min y  . B. max y  , min y  . 3  3  3  3  ;3 3 2 3 6   ;3 ;3 ;3        2  2  2  2  10 16 C. max y  , min y  2 . D. max y  , min y  2 . 3  3  3  3  ;3 3 3   ;3 ;3 ;3        2  2  2  2  2 x  4x Câu 5.
Tìm giá trị nhỏ nhất của hàm số y  trên đoạn 0;  3 . 2x 1 3 A. min y  1  .
B. min y   . C. min y  4  .
D. min y  0 . 0; 3 0  ;3 7 0  ;3 0;3 1  Câu 6.
Tìm giá trị nhỏ nhất của hàm số y x   x2 3 2 trên ;1   . 4  1 A. . B. 0 . C. 1. D. 2 . 2 Câu 7.
Hàm số y    x 2 2 4
1 có giá trị lớn nhất trên đoạn  1  ;  1 là: A. 12 . B. 14 . C. 17 . D. 10 . 2 x  3x  6 Câu 8.
Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x)  2; 4 lần lượt x  trên đoạn   1
là M , m . Tính S M  . m
A. S  6.
B. S  4.
C. S  7. D. S  3. Câu 9.
Tìm GTLN và GTNN của hàm số 5 4 3
y x  5x  5x 1 trên 1; 2? Trang4 A. min y  7
 , max y 1. B. min y  1
 0, max y  2 . x   1;2 x   1;2 x   1;2 x   1;2 C. min y  2
 , max y 10 . D. min y  1  0, max y  2  . x   1;2 x   1;2 x   1;2 x   1;2 1 x
Câu 10. Cho f x 2  
x . Gọi M  max f x;m  min f x , khi đó M – m bằng. 2 x  4x  5 4 0; 3 0; 3 9 3 7 A. . B. . C. . D.1. 5 5 5 2 x - m
Câu 11. Cho hàm số f (x)=
với m là tham số thực. Giả sử m là giá trị dương của tham số m x + 8 0
để hàm số có giá trị nhỏ nhất trên đoạn [0; ]
3 bằng - 3 . Giá trị m thuộc khoảng nào trong các 0 khoảng cho dưới đây? A. 2;5. B. 1; 4. C. 6;9. D. 20; 25.
Câu 12. Tìm tất cả các giá trị của tham số m để hàm số 3 2
y = x - 3x + m có giá trị nhỏ nhất trên [- 1; ] 1 bằng 2 . m é = 2+ 2 A. m = 2 + 2 . B. m = 4 + 2 . C. ê ê . D. m = 2 . m ê = 4 + 2 ë
Câu 13. Giá trị lớn nhất của hàm số 4 2
y  cos x  cos x  4 bằng: 1 17 A. 5 . B. . C. 4 . D. . 2 4
Câu 14. Tìm a để giá trị lớn nhất của hàm số 3 2
y x  3ax a 1 trên đoạn 1; a bằng 10 , biết a  0. 5 3 A. a 10 . B. a  . C. a  . D. a  11. 2 2 2
x m m
Câu 15. Gọi A , B là giá trị nhỏ nhất, giá trị lớn nhất của hàm số y  trên đoạn 2;  3 . Tìm x 1 13
tất cả các giá trị thực của tham số m để A B  . 2
A. m 1; m  2  . B. m  2  . C. m  2  . D. m  1  ; m  2 .
Câu 16. Có một giá trị m của tham số m để hàm số 3 y = x + ( 2 m + )
1 x + m + 1 đạt giá trị nhỏ nhất 0 bằng 5 trên đoạn [0 ]
;1 . Mệnh đề nào sau đây là đúng? A. 2
2018m - m ³ 0 .
B. 2m - 1< 0 . C. 2
6m - m < 0 .
D. 2m + 1< 0 . 0 0 0 0 0 0
Câu 17. Cho hàm số y f x có đạo hàm f  x 2
 x 1. Với các số thực dương a ,b thỏa mãn
a b , giá trị nhỏ nhất của hàm số f x trên đoạn  ; a b bằng.  a b
A. f ab . B. f   .
C. f a .
D. f b .  2 
Câu 18. Cho hàm số 3 2
y = x - 3x - 9x + m có giá trị lớn nhất trên đoạn [- 2;0] bằng 2 , với m là
tham số thực. Mệnh đề nào dưới đây đúng? A. m = - 3 . B. m = 4 . C. m = 2 . D. m = 3 . x + m
Câu 19. Cho hàm số y =
thỏa min y + max y = 8 , với m là tham số thực. Mệnh đề nào dưới x [1;2] [1;2] đây đúng? A. m > 4 .
B. 0 < m £ 2 .
C. 2 < m £ 4 . D. m £ 0 . x m
Câu 20. Cho hàm số f x 2  ,
min f x  2  là x
với m là tham số. Giá trị lớn nhất của m để 8 0  ;3 Trang5 A. m  5 . B. m  6 . C. m  4 . D. m  3 . ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 A A D B A C C C B A 11 12 13 14 15 16 17 18 19 20 A B C D A A D A C C Mức độ 3 Câu 1.
Tìm tập giá trị T của hàm số 2
y x  4  x . . A. T   2  ;2.
B.T  0; 2 .
C. T  0; 2 2       . D.T  2;2 2   . Câu 2.
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x 2
x 1 2  x . Tính
M m ?
A. M m  2 2 .
B. M m  2  2 .
C. M m  4  2 .
D. M m  2  2 . Câu 3.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2
y  3  4  x lần lượt là. A. 0; 2 . B. 3; 1. C. 3  ;0 . D. 2; 2 . Câu 4.
Tìm x để hàm số y
x  2  6  x đạt giá trị lớn nhất?
A. x  2 .
B. x  0 . C. x  2  .
D. x  4 . 2
x  2m m Câu 5.
Tìm tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y  trên x  3 đoạn 0  ;1 bằng 2  . 3 3 A. m  1
 hoặc m  .
B. m  2 hoặc m   . 2 2 1 5
C. m 1 hoặc m   .
D. m  3 hoặc m   . 2 2 2 x m 1 Câu 6.
Số các giá trị tham số m để hàm số y
có giá trị lớn nhất trên 0;4 bằng 6  là x m A. 0 . B. 2 . C.1. D. 3 . Câu 7.
Gọi m và M lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số   2 3 e x f x   trên
đoạn 0;2 . Mối liên hệ giữa M và m là 1 M
A. M m e.
B. m M 1. C. . m M  . D. 2  e . 2 e m mx Câu 8.
Hàm số f x 5  0;1 bằng 7  khi x
có giá trị nhỏ nhất trên đoạn   m 5 A. m  .
B. m  0 .
C. m 1.
D. m  2 . 7 2 x m Câu 9.
Gọi m là giá trị để hàm số y  0; 3 bằng 2  . Mệnh đề nào x
có giá trị nhỏ nhất trên   8 sau đây là đúng?
A. m  5 .
B. m  5 .
C. 3  m  5 . D. 2 m  16 . 1
Câu 10. Chohàm số 3 2 2 y
x m x  2m  2m  9, m là tham số. Gọi S là tập tất cả các giá trị của m 3
sao cho giá trị lớn nhất của hàm số trên đoạn 0; 
3 không vượt quá 3 . Tìm m?
A. S   ;    3 1; . B. S   3  ;  1 .
C. S   ;  3
 1;. D. S   3  ;  1 . Trang6 1
Câu 11. Biết giá trị lớn nhất của hàm số 2 y = 4- x + x -
+ m là 18 . Mệnh đề nào sau đây đúng? 2
A. 0 < m < 5.
B. 10 < m < 15.
C. 5 < m < 10 .
D. 15 < m < 20 . x m 16
Câu 12. Cho hàm số y
min y  max y  . Mệnh đề nào dưới x
( m là tham số thực) thoả mãn 1 1; 2 1; 2 3 đây đúng? A. m  0 . B. m  4 .
C. 0  m  2 .
D. 2  m  4 . Câu 13. Cho ;
x y là hai số thực bất kỳ thuộc đoạn 1; 
3 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức  x y S . Tính M  . m y x 10 16
A. M n  .
B. M n 3 .
C. M n 5 .
D. M n  . 3 3
Câu 14. Có một giá trị m của tham số m để hàm số 3
y x   2 m  
1 x m 1 đạt giá trị nhỏ nhất bằng 0 5 trên đoạn 0 
;1 . Mệnh đề nào sau đây đúng? A. 2
2018m m  0 .
B. 2m 1  0 . C. 2
6m m  0 .
D. 2m 1  0 0 0 0 0 0 0
Câu 15. Cho hàm số y f x liên tục trên  . Đồ thị của hàm số y f  x như hình bên. Đặt
g x  f x   x  2 2
1 . Mệnh đề nào dưới đây đúng?
A. Max g x  g 3 .
B. Min g x  g  
1 . C. Max g x  g 0 . D. Max g x  g   1 .  3  ;  3  3  ;  3  3  ;  3  3  ;  3 1 m sin x
Câu 16. Cho hàm số y
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 0;10 cos x  2
đểgiá trị nhỏ nhất của hàm số nhỏ hơn 2  ? A. 1. B. 9 . C. 3 . D. 6 .
Câu 17. Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ dưới. Xét hàm số
g x  f  3 2x x  
1  m . Tìm m để max g x  1  0 . 0; 1 A. m  13  . B. m  5 . C. m  3 . D. m  1  .
Câu 18. Cho hàm số 2
y x  2x a  4 . Tìm a để giá trị lớn nhất của hàm số trên đoạn  2   ;1 đạt giá trị nhỏ nhất? A. a 1. B. a  2 .
C. Một giá trị khác. D. a  3.
Câu 19. Biết rằng giá trị lớn nhất của hàm số 2
y = x + 2x + m- 4 trên đoạn [- 2 ] ;1 đạt giá trị nhỏ
nhất, giá trị của tham số m bằng Trang7 A. 1. B. 3 . C. 4 . D. 5 . 2 x m  2
Câu 20. Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y  trên đoạn x m 0;4 bằng 1. A. 0 . B. 2 . C. 3 . D. 1. ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 D D B A A C C D A D 11 12 13 14 15 16 17 18 19 20 D B D A D D A D B D Mức độ 4 Câu 1. Biết rằng phương trình 2
2  x  2  x  4  x m có nghiệm khi m thuộc  ; a b với
a , b   . Khi đó giá trị của T  a  2 2  b là?
A. T  0 .
B. T  3 2  2 .
C. T  6 .
D.T  8. Câu 2. Hàm số 2 2
y  4 x  2x  3  2x x đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là: A. 1. B.1. C. 0 . D. 2 . Câu 3.
Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y x  2
2017  2019  x
trên tập xác định của nó. Tính M m .
A. 2019 2019  2017 2017 . B. 4036 . C. 4036 2018 .
D. 2019  2017 . Câu 4.
Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f x  5 x 1  3 x   x   1 3 x lần
lượt là m và M , tính 2 2
S m M .
A. S 170 .
B. S 169 .
C. S 172 .
D. S  171. Câu 5.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho max  4 2 2
x  6mx m   16 . Số  2  ;  1
phần tử của S là ? A. 3 . B. 1. C. 0 . D. 2 . Câu 6.
Có tất cả bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số 2
y x  2x m trên đoạn  1  ;2 bằng 5. A. 3 . B. 1. C. 2 . D. 4 . Câu 7.
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   x    x 2 2 2 3 1 3 1 .
Hỏi điểm AM ; m thuộc đường tròn nào sau đây? 2 2
A. x   y  2 2 1 1.
B. x  3   y   1  20 2 2 2 2
C. x  3   y   1  2. D. x   1   y   1 1. Câu 8.
Biết hàm số y f x liên tục trên  có M và m lần lượt là GTLN, GTNN của hàm số trên
đoạn 0;2 . Trong các hàm số sau, hàm số nào cũng có GTLN và GTNN tương ứng là M và m ?.  4x
A. y f  2
x  2  x .
B. y f   . 2  x 1
C. y f  2sin x cosx  .
D. y f   3 3
2 sin x cos x . Trang8 n n Câu 9.
Tìm các giá trị nguyên dương n  2 để hàm số y  2  x  2  x với x  2  ; 2 có giá trị
lớn nhất gấp 8 lần giá trị nhỏ nhất. A. n  5.
B. n  6 .
C. n  2 .
D. n  4 .
Câu 10. Đồ thị hàm số y f ' x là đường cong nét đậm và y g ' x là đường cong nét mảnh như
hình vẽ. Gọi ba giao điểm ,
A B, C của y f ' x và y g ' x trên hình vẽ lần lượt có hoành
độ a,b, c . Tìm giá trị nhỏ nhất của hàm số hx  f x  g x trên đoạn  ; a c ? y a b c x O B C A
A. min h x  ha .
B. min h x  hb . a;c a;c
C. min h x  hc.
D. min h x  h0 . a;c a;c
Câu 11. Cho hàm số f (x) có đạo hàm là f (
¢ x). Đồ thị hàm số y = f (
¢ x) được cho như hình vẽ bên. Biết rằng f ( ) 0 + f ( ) 2 = f ( ) 1 + f ( )
3 . Giá trị lớn nhất của f (x) trên đoạn [0; ] 3 là A. f ( ) 1 . B. f (0). C. f ( ) 2 . D. f ( ) 3 .
Câu 12. Cho hàm số 3 2
y x  3mx  32m  
1 x 1 (với m là tham số). Tìm tất cả các giá trị của tham
số m để trên đoạn 2;0 hàm số trên đạt giá trị lớn nhất bằng 6. A. m  1. B. m  0. C. m  3. D. m  1. 
Câu 13. Để giá trị lớn nhất của hàm số y f x 3
x 3x  2m 1 trên đoạn 0;2 là nhỏ nhất thì giá trị của m thuộc A. 0;  1 . B.  1  ;0. C. 1; 2 . D.  2  ;  1 .
Câu 14. Cho hàm số 3 2
y x  3mx  32m  
1 x 1 (với m là tham số). Tìm tất cả các giá trị của tham
số m để trên đoạn 2;0 hàm số trên đạt giá trị lớn nhất bằng 6. A. m  1. B. m  0. C. m  3. D. m  1. 
Câu 15. Xét hàm số 2
y x ax b , với a, b là tham số. Gọi M là giá trị lớn nhất của hàm số trên  1  ; 
3 . Khi M nhận giá trị nhỏ nhất có thể được, tính a  2b . A. 5 . B. 4  . C. 2 . D. 3  .
Câu 16. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2 x mx   m y
trên 1; 2 bằng 2 . Số phần tử của tập S là x 1 A. 3 . B. 1. C. 4 . D. 2 . Trang9
Câu 17. Cho hàm số y f x có đạo hàm f  x . Hàm số y f  x liên tục trên tập số thực và có đồ thị như hình vẽ. y 4 2 O 2 -1 1 x 13 Biết f   1 
, f 2  6 . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 g x 3
f x 3 f x trên  1  ;2 bằng: 1573 37 14245 A. . B. 198. C. . D. . 64 4 64
Câu 18. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m y
1; 2 bằng 2 . Số phần tử của S là x  trên   1 A. 1. B. 4 . C. 3 . D. 2 .
Câu 19. Cho hàm số 4 2 f ( )
x x  8x m . Có bao nhiêu giá trị nguyên của 
m [  50;50] sao cho với mọi số thực , a ,
b c[0;3] thì f ( ) a , f ( ) b , f ( )
c là độ dài ba cạnh của một tam giác. A. 29. B. 23. C. 27 . D. 25.
Câu 20. Để giá trị lớn nhất của hàm số 2 y =
2x - x - 3m + 4 đạt giá trị nhỏ nhất thì m thỏa 3 5 4 1 A. m = . B. m = . C. m = . D. m = . 2 3 3 2
Câu 21. Giá trị lớn nhất của hàm số 3 2
f (x)  x  3x  72x  90  m trên đoạn  5  ;5 là 2022.Trong các
khẳng định dưới đây khẳng định nào đúng?
A. 1600  m 1700 . B. m  400 . C. m 1618 .
D. 1500  m 1600 . ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 C A C D D C C B D B 11 12 13 14 15 16 17 18 19 20 D D A D B D A D D A 21A Trang10