Ảnh màn hình 2025-10-29 lúc 211443

2.4 Phép cộng hệ lực phẳng
Khi xác định hợp lực của hệ nhiều hơn hai lực, dễ dàng hơn nếu ta xác định các thành
phần của mỗi lực dọc theo các trục cho trước, sau đó tính tổng đại số các thành phần này, cuối
cùng xác định hợp lực cần tìm. Cách phức tạp hơn là xác định hợp lực như đã trình bày ở mục
2.3 là áp dụng qui tắc hình bình hành.
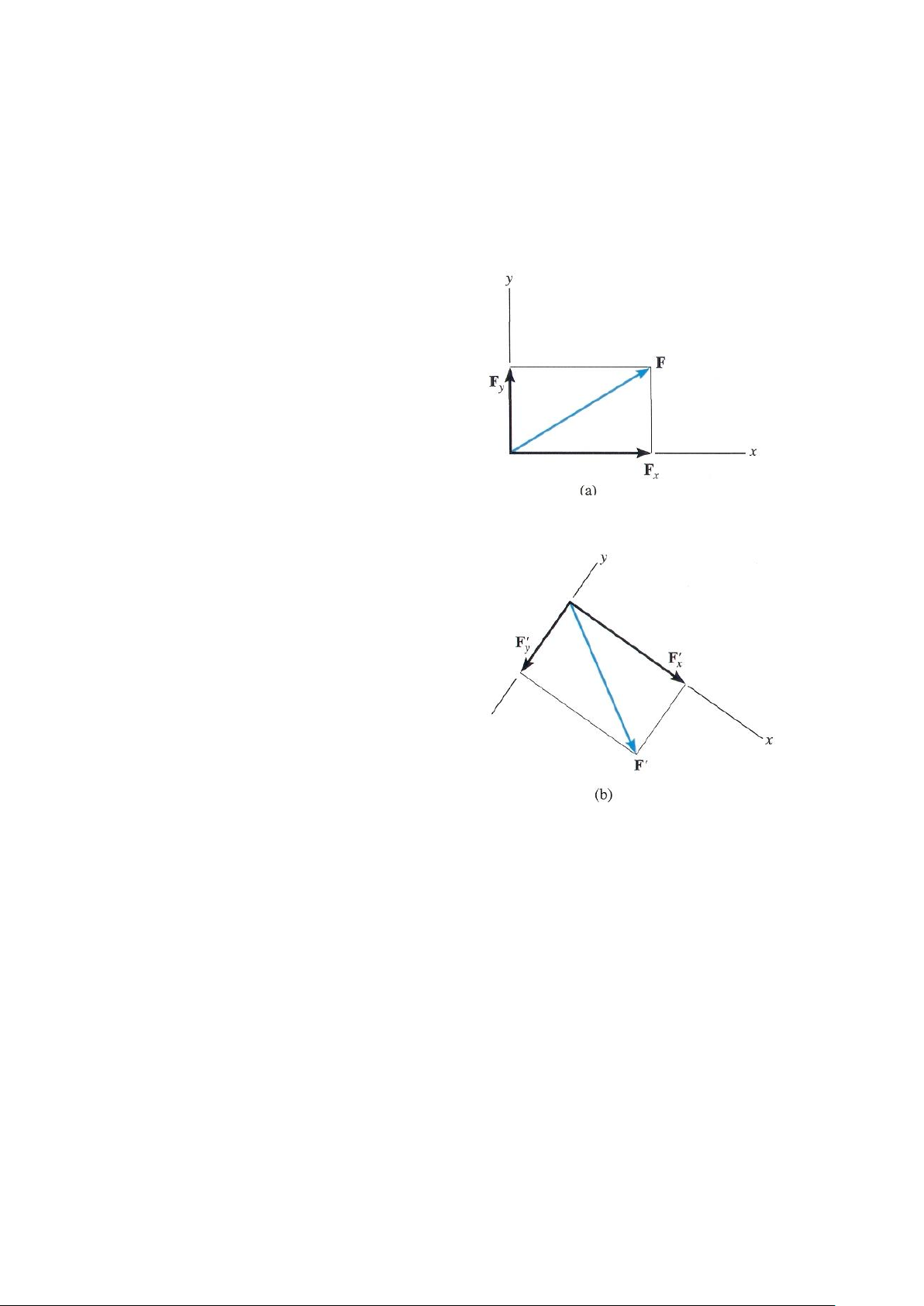
Trong mục này chúng ta sẽ phân tích các lực
thành các thành phần lực vuông góc với nhau Fx và
Fy, hai lực này tương ứng nằm dọc theo trục x và y
(hình 2-14a). Mặc dù các trục toạ độ là thẳng đứng
và nằm ngang, nhưng trong trường hợp tổng quát
chúng có thể nằm theo phương tùy ý miễn là vẫn
vuông góc với nhau (hình 2-14b). Trong mỗi
trường hợp, với qui tắc hình bình hành, ta có:
F = Fx + Fy và
F’ = F’x + F’y.
Theo hình 2-14 chiều của mỗi thành phần lực
được miêu tả bởi đoạn thẳng có mũi tên. Tuy nhiên,
để phân tích ta phải thiết lập các ký hiệu để biểu
diễn chiều của các thành phần lực đó. Để xây dựng
những ký hiệu đó chúng ta có thể làm theo một trong hai cách sau:
Ký hiệu vô hướng. Vì trục x, y đã được định
rõ chiều dương và chiều âm nên độ lớn và chiều
của các thành phần lực vuông góc có thể biểu diễn
theo dạng các đại lượng vô hướng. Ví dụ, những
thành phần của F (hình 2-14a) có thể được biểu Hình 2-14
diễn bởi các đại lượng vô hướng dương Fx và Fy, vì
chiều của chúng theo thứ tự hướng theo chiều dương của các trục x và y. Tương tự, các
thành phần của F’ (hình 2-14b) là F và -F . Ở đây thành phần chiếu lên phương y là âm, vì x y
F’y có hướng dọc theo chiều âm của trục y.
Quan trọng là phải nhớ những ký hiệu vô hướng dương và âm trên chỉ được sử dụng cho
mục đích tính toán chứ không được sử dụng với mục đích biểu diễn trên hình vẽ. Trong toàn
bộ quyển sách này, trên bất kỳ hình vẽ nào mũi tên ở đầu véc tơ cũng được dùng để chỉ rõ
chiều của véc tơ; các dấu đại số không được sử dụng cho mục đích này. Vì vậy các véctơ ở
các hình 2-14a và 2-14b được ký hiệu bởi các chữ in đậm (véctơ).* Trên các hình vẽ các chữ
in nghiêng được viết ở gần mũi tên của vectơ chúng biểu thị độ lớn của vectơ đó, và nó luôn luôn dương.
* Trên các hình vẽ dấu âm kết hợp với ký hiệu in đậm chỉ được sử dụng khi nó thể hiện các cặp véctơ bằng nhau
nhưng ngược chiều nhau như hình 2-2. 34
Ký hiệu véctơ Đề các. Ta cũng có thể biểu diễn các thành phần của lực dưới dạng các
véc tơ đơn vị Đề các. Khi chúng ta biểu diễn như vậy thì những phương pháp đại số véctơ sẽ
được áp dụng một cách dễ dàng hơn và chúng ta sẽ thấy việc biểu diễn lực bằng những véc tơ
sẽ trở nên đặc biệt thuận tiện khi giải các bài toán trong không gian.
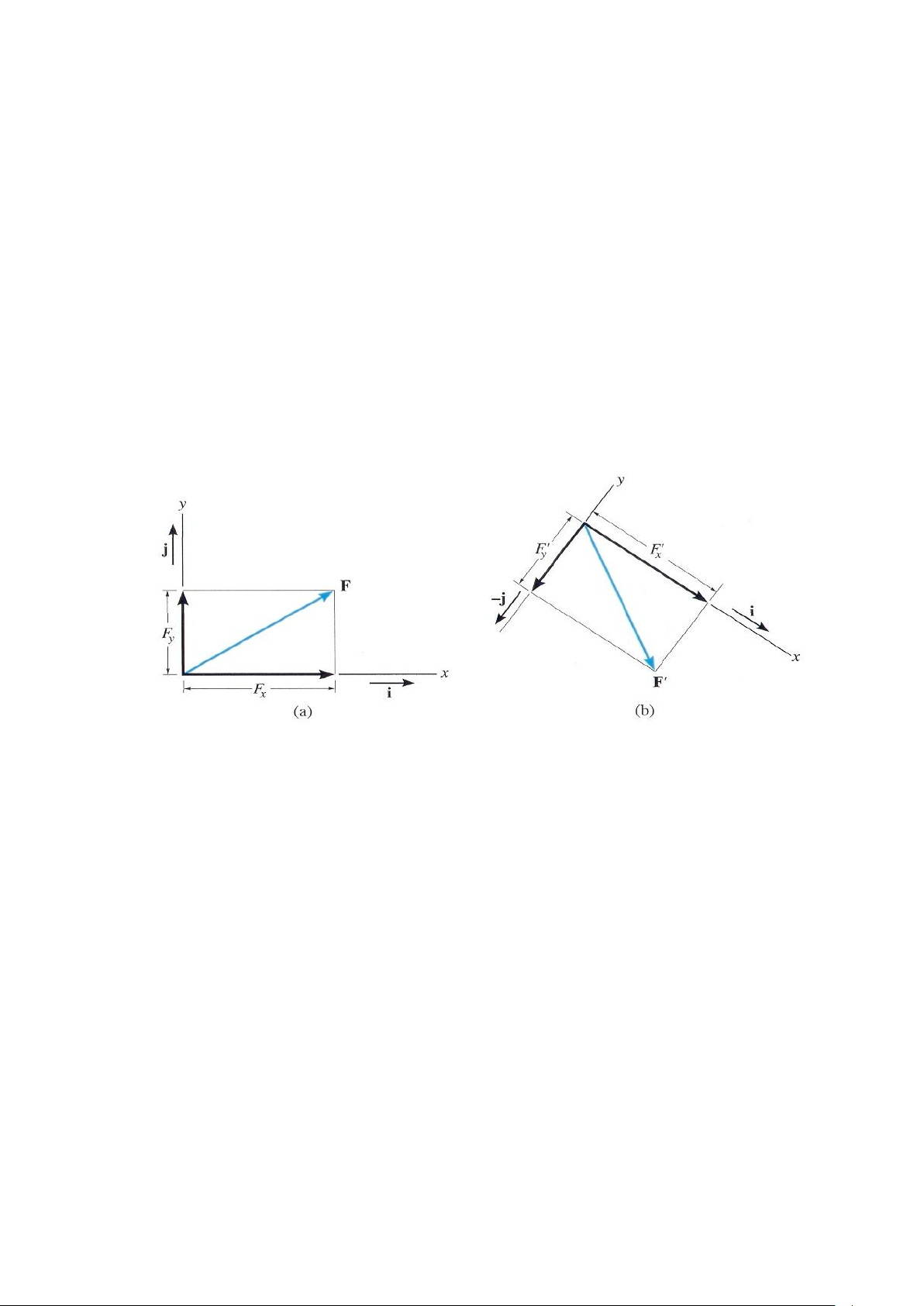
Trong mặt phẳng, véctơ đơn vị Đề các được ký hiệu là i, j, chúng tương ứng chỉ hướng
của trục x và y, hình 2-15a.*
Như trong hình 2-15a, độ lớn của mỗi thành phần của lực F là một đại lượng luôn dương
và vì vậy chúng được biểu diễn bằng các vô hướng dương Fx và Fy. Vì vậy với các ký hiệu đã
được thiết lập để biểu diễn độ lớn và chiều mỗi thành phần véc tơ, ta có thể biểu diễn F như
hình 2-15a bằng một véctơ Đề các: F = Fxi+ Fyj và cũng tương tự như vậy ở hình 2-15b ta
cũng có thể biểu diễn lực F’ như sau: F’ = F’xi+ F’y(- j ) hoặc chúng ta viết đơn giản là:
F’ = F’xi - F’y j Hình 2-15
Hợp lực của hệ lực đồng phẳng. Một trong hai phương pháp trình bày ở trên được dùng
để xác định hợp lực của hệ lực đồng phẳng. Để xác định hợp lực của hệ lực phẳng, trước tiên
mỗi lực được phân tích ra các thành phần theo trục x và trục y, sau đó với các thành phần lực
tuơng ứng cùng phương với nhau chúng ta sử dụng phép cộng đại số. Hợp lực được tạo bởi
cộng các lực tổng hợp của các lực thành phần trên trục x và trục y (sử dụng qui tắc hình bình
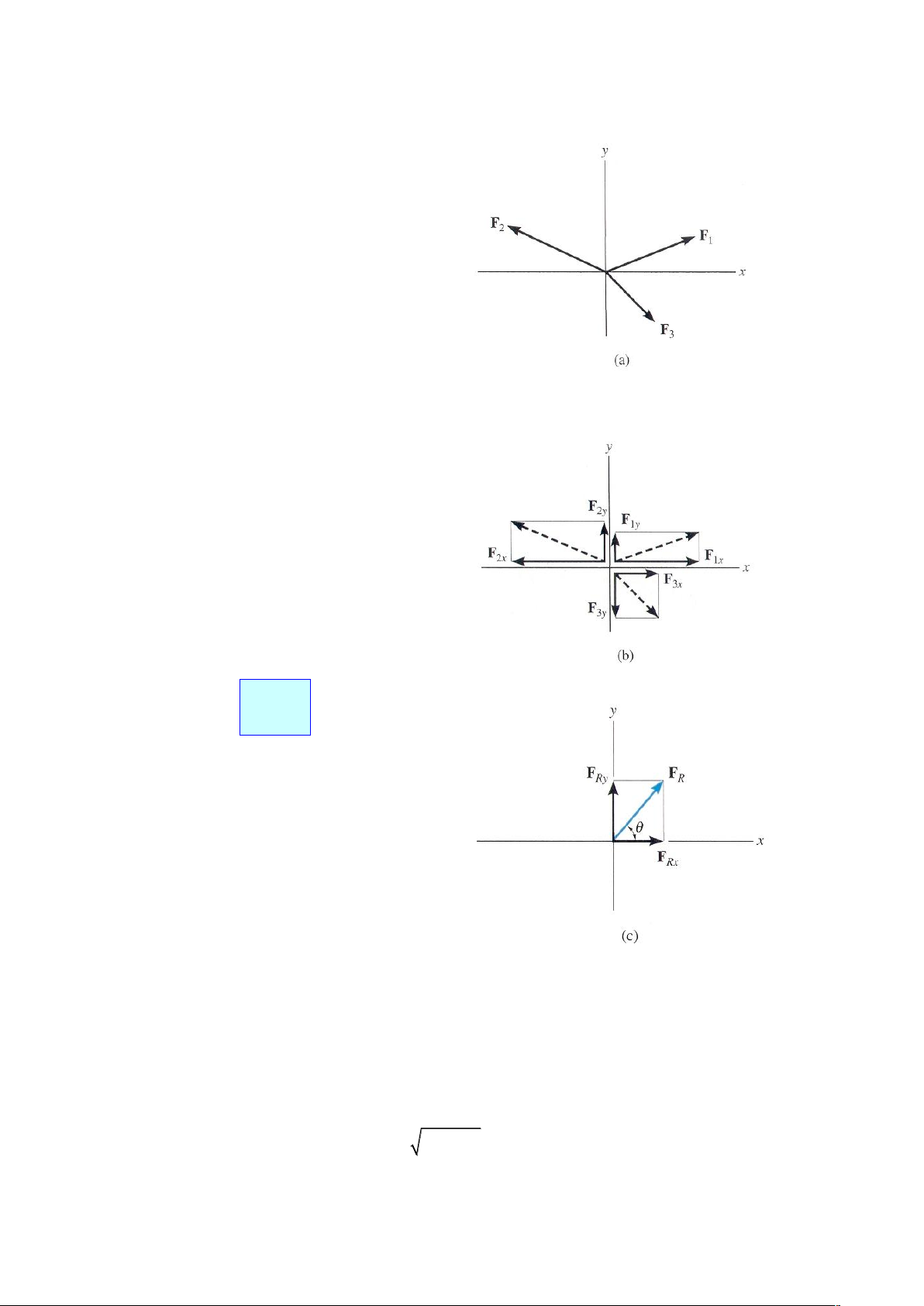
hành lực). Ví dụ: Xét hệ 3 lực đồng qui như hình 2-16a, với các thành phần lực theo phương x
và y như hình 2-16b. Để giải bài toán này chúng ta sử dụng ký hiệu véctơ Đề các, trước tiên
mỗi lực sẽ được biểu diễn theo véctơ Đề các như sau:
F1 = F1x i + F1yj
F2 =  F2x i + F2yj
F3 = F3x i  F3yj
* Để tính tay các véctơ đơn vị thường được ký hiệu bằng các dấu mũ, như là ˆi, ˆj . Những véc tơ này không có
thứ nguyên và có độ lớn là 1 dơn vị, và chiều của chúng ( hay chiều mũi tên) sẽ biểu diễn dấu cộng hoặc dấu trừ
phụ thuộc vào chúng nằm dọc theo chiều dương hay chiều âm của trục x và y. 35
Vì vậy véctơ hợp lực có dạng:
FR = F1 + F2 + F3
= F1x i + F1yj  F2x i + F2yj + F3x i  F3yj
= (F1x – F2x + F3x)i + (F1y + F2y – F3y)j
= (FRx)i + (FRy)j
Trên hình 2-16b sử dụng ký hiệu vô
hướng, khi chiều dương trục x hướng về phía bên
phải và chiều dương trục y hướng lên trên, ta có: (   )  F = F - F + F Rx 1x 2x 3x (+ )  F = F - F + F Rx 1x 2x 3x
Những kết quả này thì giống như những
thành phần theo phương i, j của FR đã xác định ở trên.
Trong trường hợp tổng quát, những thành
phần theo phương x, y của hợp lực của hệ lực
phẳng có thể được biểu diễn bằng tổng đại số các
thành phần chiếu lên trục x, y của tất cả các lực thuộc hệ, tức là: F = F  Rx x F = F  (2-1) Ry y
Khi áp dụng những công thức này, việc sử
dụng qui ước ký hiệu để thiết lập những thành
phần lực là rất quan trọng, và những thành phần
lực này có phương chiều dọc theo chiều dương
của các trục toạ độ thì được coi là các vô hướng
dương, ngược lại nếu chúng có phương chiều dọc
theo chiều âm của các trục toạ độ thì được coi là
các vô hướng âm. Nếu theo qui ước này thì: Dấu
của những thành phần hợp lực sẽ xác định chiều
của những thành phần này. Ví dụ, kết quả dương Hình 2-16
chỉ ra rằng thành phần lực có phương chiều theo
hướng dương của các trục toạ độ.
Một khi các thành phần lực đã được xác định, chúng được vẽ dọc theo các trục x, y theo
hướng thích hợp của chúng, và hợp lực có thể xác định được từ phép cộng véctơ, như hình 2-
16c. Từ hình vẽ này, độ lớn của FR sẽ tìm đựơc từ định lý Pitago: 2 2 F  F  F R Rx Ry 36
Ngoài ra, góc  chỉ rõ hướng của lực, được
xác định bằng công thức lượng giác: F 1  Ry   tan FRx
Những khái niệm trên được minh hoạ bằng các ví dụ sau.
NHỮNG ĐIỂM QUAN TRỌNG
 Hợp lực của một hệ lực phẳng có thể dễ Hợp lực của các lực của 4 dây cáp tác dụng vào
dàng được xác định nếu như hệ toạ độ x, y đã
rầm chìa có thể được xác định bởi phép cộng đại
được lập và lực đã được phân tích dọc theo các
số các thành phần lực của mỗi dây cáp chiếu lên trục toạ độ.
trên trục x và y. Hợp lực FR sinh ra tương đương
với lực kéo của cả bốn dây cáp tác dụng vào rầm
 Hướng của mỗi lực được chỉ rõ bởi góc chìa .
tạo bởi giữa đường tác dụng của lực với một
trong số các trục toạ độ hoặc là góc nghiêng của hình tam giác .
 Hướng của trục x và trục y bất kỳ, và chiều dương của chúng được chỉ rõ bởi các véctơ
đơn vị i, j.
 Các thành phần chiếu lên trục x và trục y của hợp lực được xác định đơn giản bởi phép
cộng đại số các thành phần của các lực đồng phẳng chiếu lên các trục.
 Độ lớn của hợp lực được xác định từ định lý Pitago , và khi những thành phần này
được vẽ trên trục x và trục y, hướng của chúng sẽ được xác định từ công thức lượng giác. 37
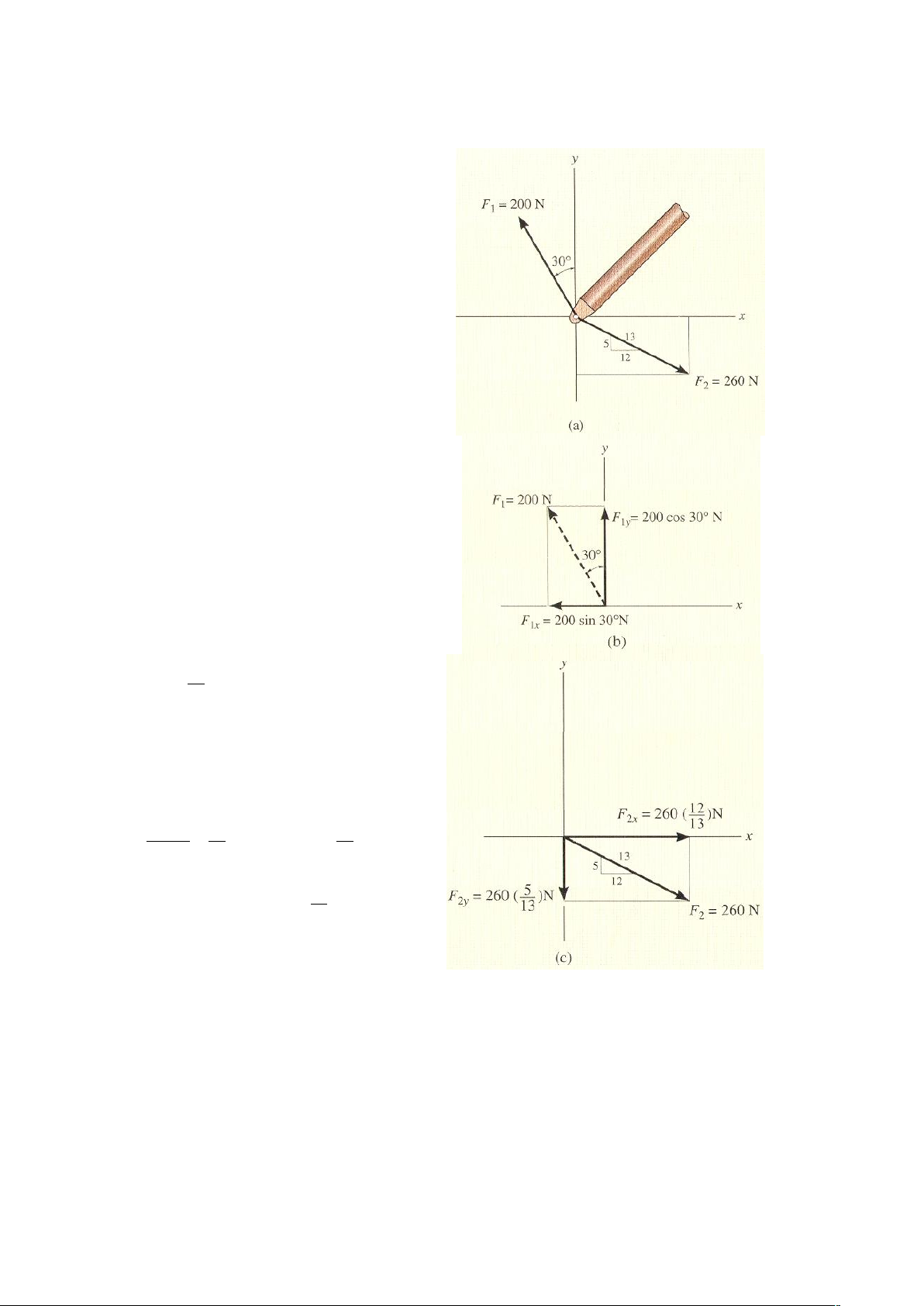
Ví dụ 2-5. Xác định thành phần theo
phương x, y của các lực F1, F2 tác dụng lên
thanh như hình 2-17a. Biểu diễn các lực đó
dưới dạng vectơ Đề các. Bài giải
Ký hiệu đại số. Theo qui tắc hình bình
hành, F1 được phân tích thành hai thành phần
theo phương x, y như hình 2-17b. Độ lớn của
mỗi thành phần được xác định bởi công thức
lượng giác. F1x có chiều theo chiều âm của
trục x, và F1y có chiều theo chiều dương của trục y, ta có: 0 F  2
 00sin30 N = - 100 N= 100 N  1x 0
F  200cos30 N = 173 N = 173 N  1y
Lực F2 được phân tích thành hai thành
phần theo phương x, y, như hình 2-17c. Ở
đây độ nghiêng của đường tác dụng của lực
đã được chỉ trên hình vẽ. Từ góc nghiêng của
tam giác lượng ta có thể xác định góc .   5 1 
  tan   và sau đó xác định độ lớn của 12 
các thành phần của lực như cách đã làm đối
với F1. Tuy nhiên có phương pháp tính dễ
hơn, khi sử dụng tỷ lệ thức của các tam giác đồng dạng. F 12 12  2x  ; F  260 N  240 N   260 N 13 2x 13   5  Tương tự: F  260 N 100 N 2y   13 
Sử dụng ký hiệu vô hướng ta có:
F  240 N  240 N  2x Hình 2-17 F  100  N 100 N  2 y
Ký hiệu véc tơ đề các. Khi đã xác định được độ lớn và chiều của các thành phần của mỗi
lực, ta có thể biểu diễn các lực đó dưới dạng vectơ Đề các như sau:
F1 = { 100i + 173j} N
F2 = {240i  100j} N 38
Chú ý: Độ lớn của thành phần lực nằm ngang F2x được xác định bởi phép nhân độ lớn của lực
với tỷ lệ giữa cạnh nằm ngang với cạnh huyền của tam giác (hình tam giác nhỏ trong hình 2-
17); Trong khi đó độ lớn của thành phần thẳng đứng F2y được xác định bởi phép nhân độ lớn
của lực với tỷ lệ giữa cạnh thẳng đứng với cạnh huyền của tam giác.
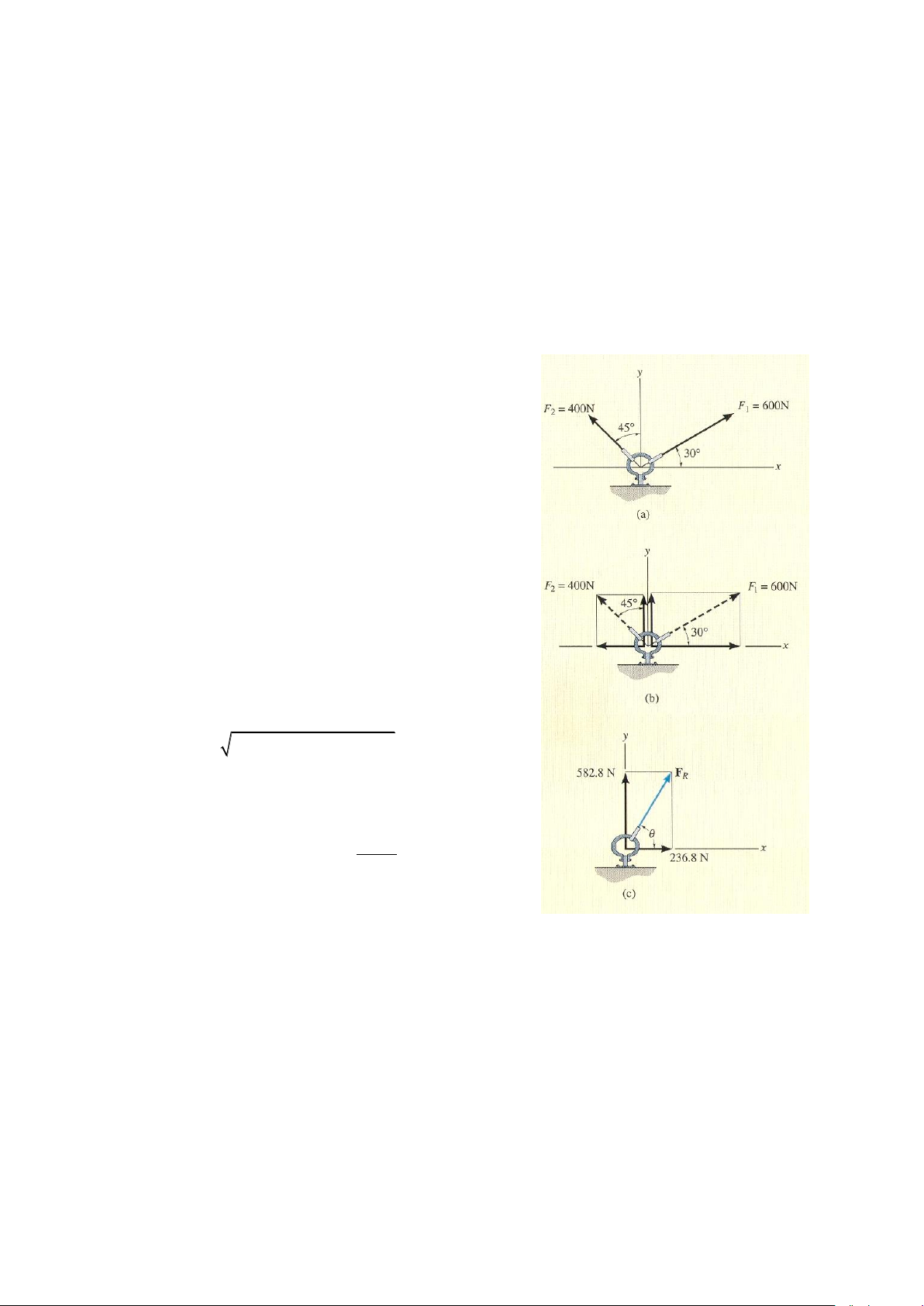
Ví dụ 2-6. Vòng nối chịu tác dụng của hai lực F1, F2 như hình 2-18a. Xác định độ lớn và
phương chiều của véc tơ hợp lực. Bài giải I
Ký hiệu đại số. Bài toán này có thể giải quyết
bằng cách sử dụng qui tắc hình bình hành; tuy nhiên,
ở đây ta sẽ phân tích các lực thành các thành phần
theo phương x và y như hình 2-18b và lấy tổng đại số
các lực thành phần đó. Bên cạnh các phương trình ta
chỉ rõ chiều dương của các thành phần lực theo phương x và y, ta có: 0 0  F  Rx
F ; F  600cos30 N400sin45 N  x Rx  236.8N  0 0
  F  F ; F  600sin30  400cos45 Ry y Ry  582.8N 
Hợp lực đuợc thể hiện trên hình 2-18c, có độ lớn là: 2 2
F  (236.8 N)  (582.8 N)  629N R
Từ phép cộng véctơ, hình 2-18c ta có góc  được tính như sau:   582.8  1 0   tan  67.9    236.8  Bài giải II
Ký hiệu véctơ Đề các. Từ hình 2-18b, các lưc Hình 2-18
F1, F2 được biểu diễn dưới dạng véc tơ Đề các như sau:
F1 = {600cos300i + 600sin300j}N
F2 = {- 400sin450i + 400cos450j}N Do đó:
FR = F1 + F2 = (600cos300 N – 400sin450 N)i + (600sin300 N + 400cos450 N)j
= {236.8i + 582.8j}N
Độ lớn và phương chiều của véctơ hợp lực FR được xác định tương tự như trên. 39
Chú ý: So sánh hai phương pháp thấy rằng: Sử dụng ký hiệu đại số hiệu quả hơn nhiều vì
các thành phần lực của hợp lực được xác định trực tiếp mà không cần phải biểu diễn các lực
dưới dạng véc tơ Đềcác trước khi cộng các lực thành phần. Tuy nhiên phân tích dưới dạng véc
tơ Đề các sẽ rất có lợi cho việc giải các bài toán không gian.
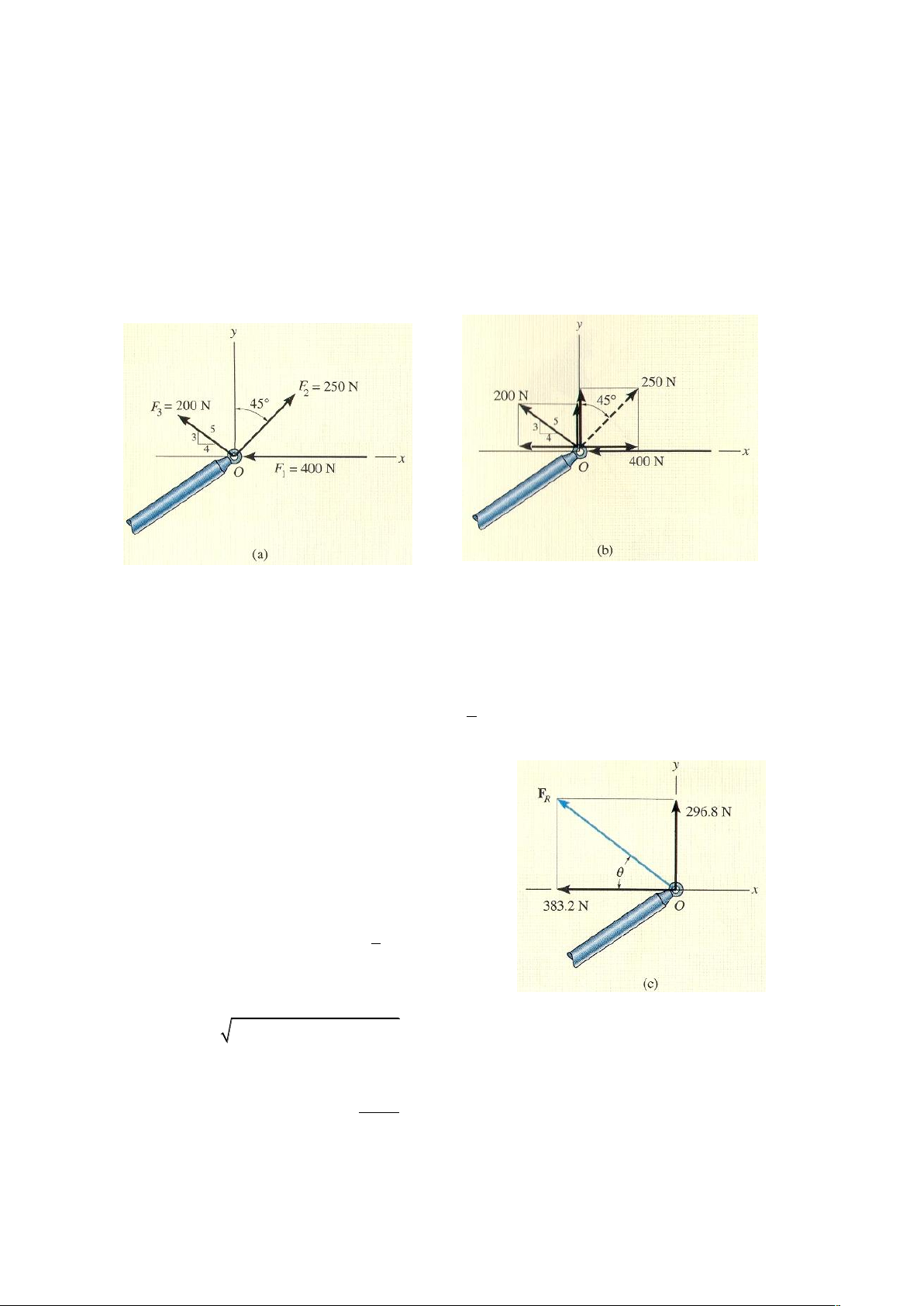
Ví dụ 2-7. Điểm cuối O của thanh chịu tác dụng của ba lực đồng qui phẳng như hình 2-
19a. Xác định độ lớn và hướng của hợp lực. Hình 2-19 Bài giải
Mỗi lực được phân tích thành các thành phần theo phương x, y như hình 2-19b. Tổng
hình chiếu của các lực lên trục x là:  4 0 
  F = F = -400N +250sin45 N-200. N = -383.2N = 383.2N  Rx x    5 
Dấu âm cho thấy FRx tác dụng hướng về phía trái là
hướng âm của trục x và nó đã được chỉ rõ chiều mũi tên
nhỏ. Rõ ràng điều này xảy ra do F1 và F3 như hình 2-
19b kéo sang trái nhiều hơn lực F2 kéo sang phải.
Tổng hình chiếu của các lực lên trục y là:   F  F  ; Ry y  3  0 F = 250cos45 N + 200. N = 296.8N  Ry    5 
Hợp lực được thể hiện như hình 2-19c có độ lớn là: 2 2
F = (-383.2 N) + (296.8 N) = 485N R
Từ phép cộng véc tơ trên hình 2-19c, góc  được xác định như sau:   296.8  1 0   tan  37.8    383.2 
Chú ý: Áp dụng phương pháp này thuận lợi hơn nhiều khi so với hai ứng dụng của qui tắc hình bình hành. 40 BÀI TẬP
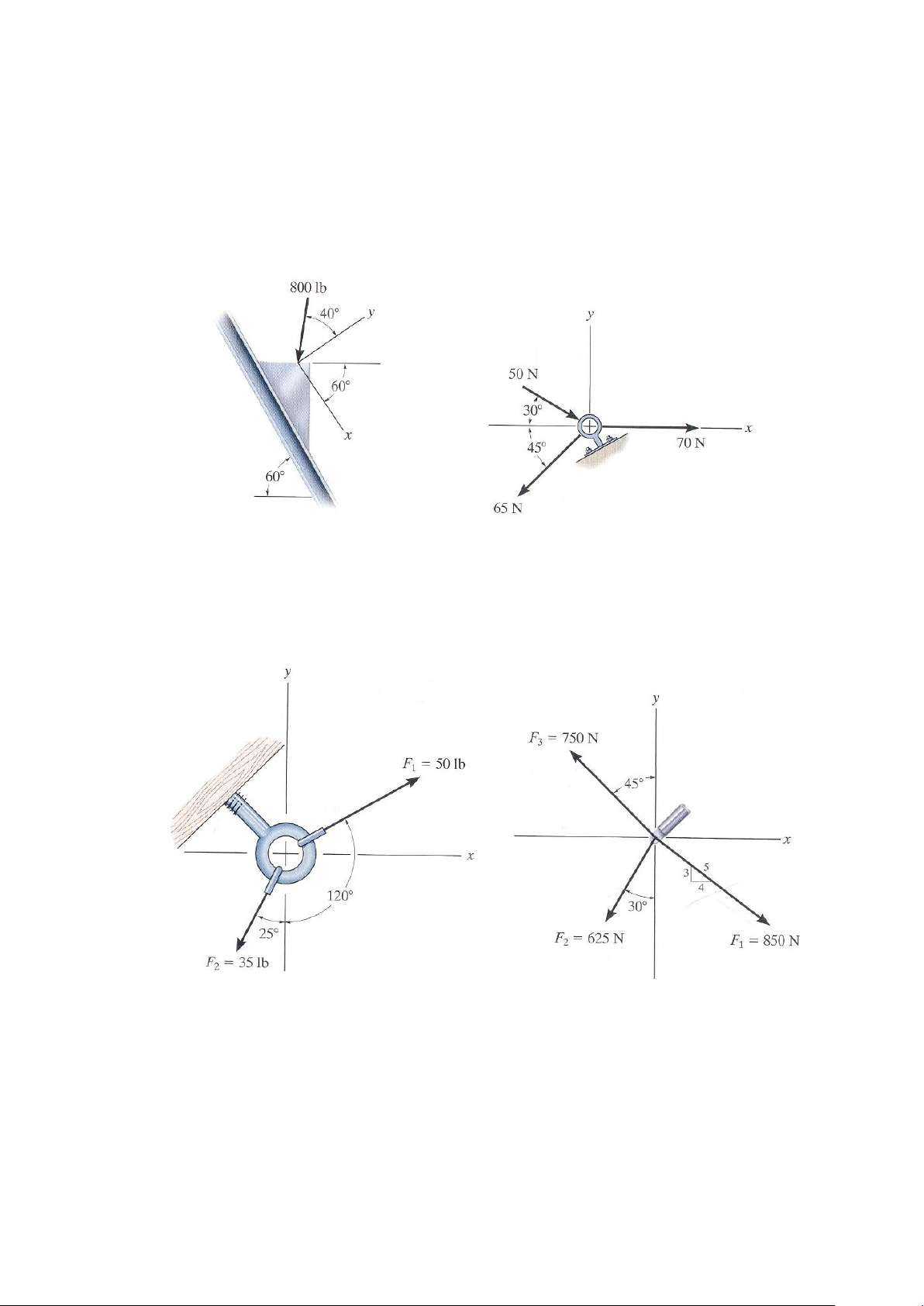
2-31. Xác định các thành phần theo phương x, y của lực có độ lớn 800 lb như trên hình vẽ.
*2-32. Xác định độ lớn lực tổng hợp của các lực cho trên hình vẽ và phương của nó tính
theo chiều thuận chiều kim đồng hồ tính từ chiều dượng trục x. Bài tập 2-31 Bài tập 2-32
2-33. Xác định độ lớn lực tổng hợp của các lực cho trên hình vẽ và phương của nó tính theo
chiều ngược chiều kim đồng hồ tính từ chiều dương trục x. Bài tập 2-33 Bài tập 2-34
2-34. Xác định độ lớn lực tổng hợp của các lực cho trên hình vẽ và phương của nó tính theo
chiều ngược chiều kim đồng hồ theo chiều dương trục x.
2-35. Cho ba lực tác dụng lên dầm côngxon như trên hình vẽ. Xác định độ lớn và
phương  của lực F1 sao cho véctơ lực tổng hợp có chiều theo chiều dương của trục x, có độ lớn 1 kN. 41
*2-36. Nếu F1 = 300 N và góc  = 200, hãy xác định độ lớn và phương chiều (theo chiều
ngược chiều kim đồng hồ từ với trục x’) của véctơ lực tổng hợp của ba lực tác dụng lên dầm. Bài tập 2-35/36 Bài tập 2-37
2-37. Xác định độ lớn lực tổng hợp của các lực cho trên hình vẽ và phương của nó tính theo
chiều ngược chiều kim đồng hồ theo chiều dương trục x.
2-38. Xác định độ lớn lực tổng hợp của các lực cho trên hình vẽ và phương của nó tính theo
chiều ngược chiều kim đồng hồ theo chiều dương trục x. Bài tập 2-38 Bài tập 2-39
2-39. Xác định độ lớn lực tổng hợp của các lực cho trên hình vẽ và phương của nó tính theo
chiều ngược chiều kim đồng hồ theo chiều dương trục x.
*2-40. Giải bài tập 2-1 bằng cách tính tổng của các thành phần vuông góc hoặc các thành
phần lực chiếu lên các trục x, y để xác định hợp lực.
2-41. Giải bài tập 2-2 bằng cách tính tổng của các thành phần vuông góc hoặc các thành
phần lực chiếu lên các trục x, y để xác định hợp lực. 42
2-42. Xác định độ lớn và phương (tính theo ngược chiều kim đồng hồ từ chiều dương
của trục y) của lực tổng hợp tác dụng lên dầm côngxon như hình vẽ. Cho FB = 600 N và góc  = 200. Bài tập 2-43 Bài tập 2-42
2-43. Nếu F1 = 300 N và góc  = 100, hãy xác định độ lớn và phương chiều (theo chiều
ngược chiều kim đồng hồ từ với trục x’) của véctơ lực tổng hợp của ba lực tác dụng lên dầm.
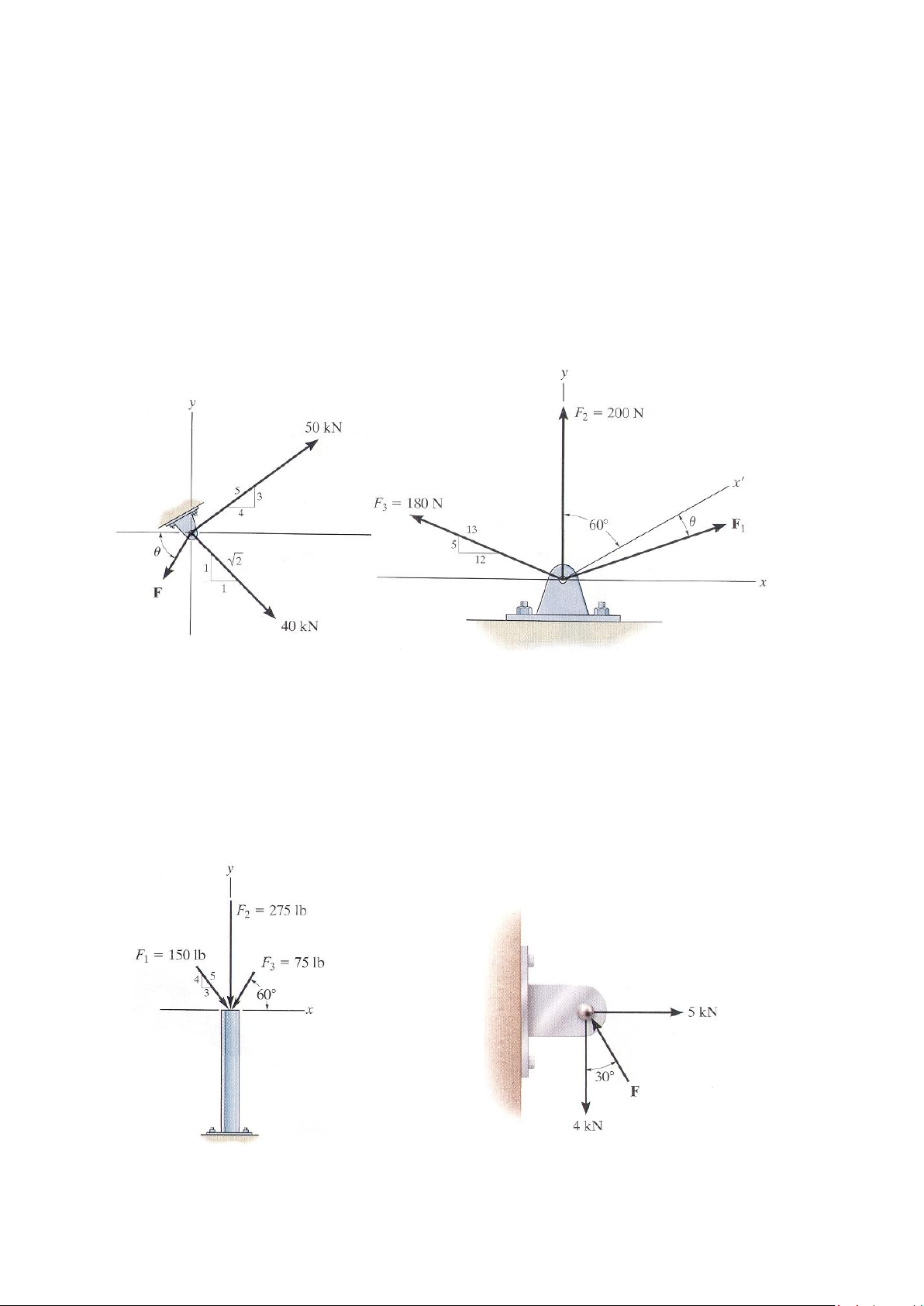
*2-44. Xác định các thành phần theo phương x, y của các lực F1 và F2 như trên hình vẽ.
2-45. Xác định độ lớn và phương chiều (theo chiều ngược chiều kim đồng hồ từ chiều
dương trục x) của véctơ lực tổng hợp của hai lực như trên hình vẽ.
2-46. Xác định các thành phần theo phương x, y của các lực tác dụng lên bản giằng của
giàn cầu như trên hình vẽ. Chứng minh rằng lực tổng hợp bằng không. Bài tập 2-44/45 Bài tập 2-46 43
2-47. Cho góc  = 600 và F = 20 kN, xác định độ lớn và phương chiều theo chiều cùng
chiều kim đồng tính từ chiều dương trục x của véctơ hợp lực.
*2-48. Cho ba lực tác dụng lên dầm côngxon như hình vẽ. Xác định độ lớn và phương 
của lực F1 sao cho véctơ lực tổng hợp của ba lực như trên hình vẽ có chiều theo chiều dương
của trục x và có độ lớn là 800N.
2-49. Nếu F1 = 300 N, góc  = 100, xác định độ lớn và phương chiều (theo chiều ngược
chiều kim đồng tính từ chiều dương trục x) của véctơ hợp lực của các lực tác dụng lên dầm
côngxon như trên hình vẽ. Bài tập 2-47 Bài tập 2-48/49
2-50. Hãy biểu diễn các lực tác dụng lên cột như trên hình vẽ dưới dạng véctơ đề các, và
xác định độ lớn của véctơ lực tổng hợp.
2-51. Xác định độ lớn của lực F sao cho véctơ lực tổng hợp FR của ba lực cho trên hình
vẽ là nhỏ nhất có thể. Hãy xác định giá trị nhỏ nhất của hợp lực FR. Bài tập 2-50 Bài tập 2-51 44
*2-52. Hãy biểu diễn các lực tác dụng lên dầm côngxon như trên hình vẽ dưới dạng véctơ
đề các tương ứng với các trục x, y. Xác định độ lớn và phương  của lực F1 sao cho véctơ lực
tổng hợp của chúng có chiều theo chiều dương của trục x và có độ lớn là FR = 600N. 1
2-53. Hệ ba lực đồng quy tác dụng lên cột có lực tổng hợp FR = 0. Nếu F  F và F 2 1 1 2
vuông góc với F2 như trên hình vẽ, hãy xác định độ lớn cần thiết của lực F3 được biểu diễn theo F1 và góc . Bài tập 2-52 Bài tập 2-53
2-54. Cho ba lực tác dụng lên dầm côngxon như hình vẽ. Xác định độ lớn và phương  của
lực F2 sao cho véctơ lực tổng hợp của chúng có chiều theo chiều dương của trục u và có độ lớn là 50 lb.
2-55. Cho F2 = 150 lb và góc  = 550. Xác định độ lớn và phương (theo chiều kim đồng
hồ tính từ chiều dương của trục x) của lực tổng hợp của ba lực tác dụng lên dầm côngxon như hình vẽ. Bài tập 2-54/55 Bài tập 2-56 45
*2-56. Cho ba lực tác dụng lên vòng như hình vẽ. Xác định khoảng giá trị độ lớn của P
sao cho độ lớn của véctơ lực tổng hợp không vượt quá 2500 N. Biết rằng lực P luôn luôn hướng sang phải. 46
2.5 Các véctơ Đề các
Sẽ đơn giản hơn rất nhiều nếu các vec tơ được
biểu diễn dưới dạng vectơ Đề các trước khi áp
dụng các phép toán của đại số véc tơ để giải bài
toán không gian ba chiều. Trong phần này chúng
ta sẽ trình bầy phương pháp tổng quát để làm điều
đó. Sang mục tiếp theo chúng ta sẽ áp dụng
phương pháp này để giải các bài toán bao gồm
phép cộng các lực. Ở các phần sau của quyển sách
các ứng dụng tương tự sẽ được minh hoạ cho các
véc tơ định vị và các véc tơ mô men.
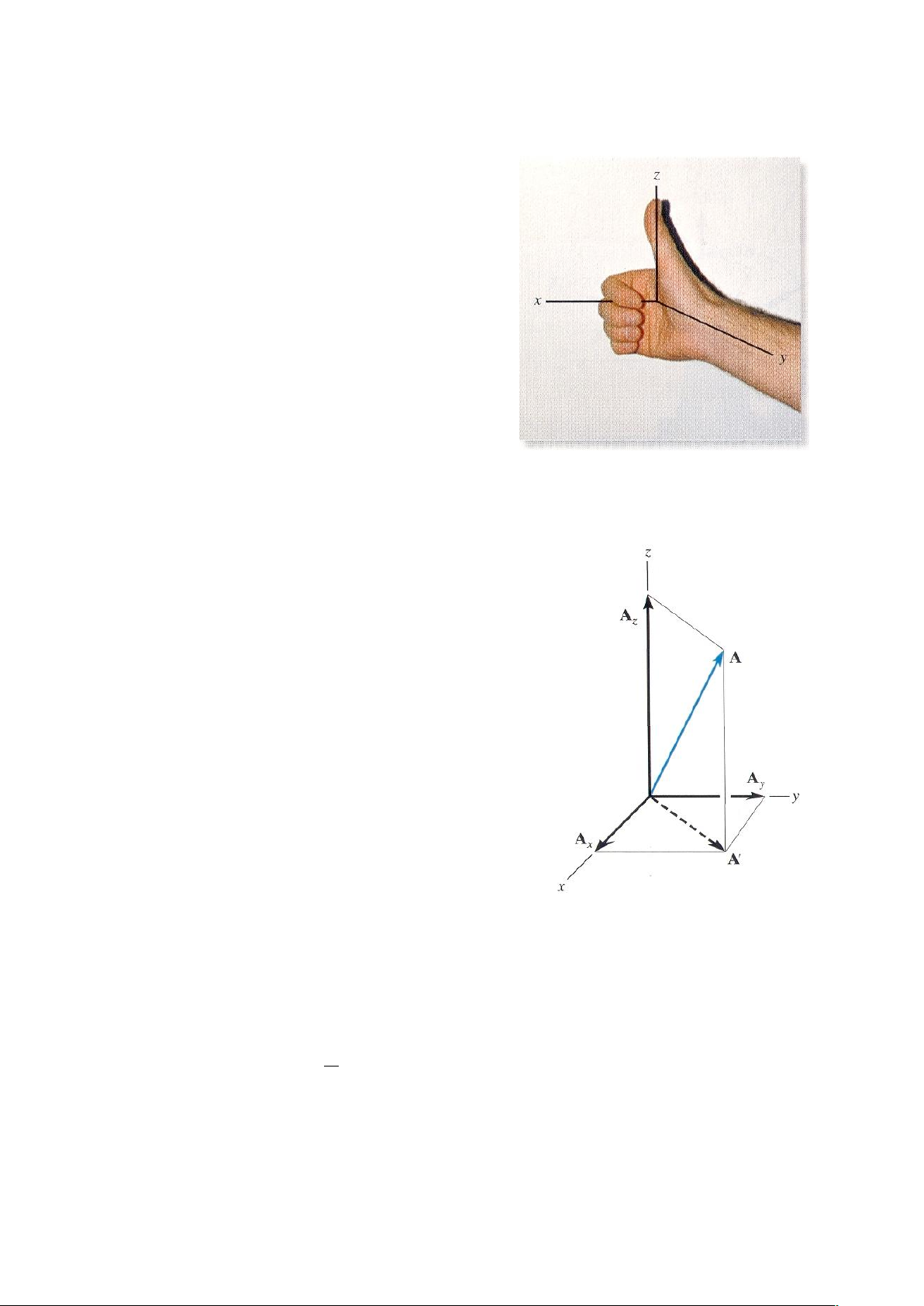
Hệ trục toạ độ bàn tay phải. Hệ trục tọa độ
bàn tay phải sẽ được sử dụng để phát triển lý
Hệ toạ độ bàn tay phải
thuyết đại số véctơ sau đây. Hệ trục toạ độ vuông Hình 2-20
góc hay hệ trục toạ độ Đề các, được gọi là hệ trục
toạ độ bàn tay phải nếu như ngón tay cái của bàn tay
phải chỉ hướng dương của trục z trong khi các ngón tay
còn lại của bàn tay phải cuộn quanh trục đó theo chiều
từ chiều dương của trục x đến chiều dương của trục y
như hình 2-20. Hơn nữa tuân theo qui tắc này trục z
trong các bài toán phẳng sẽ như trong hình 2-19 tức là
vuông góc với mặt phẳng giấy và hướng ra ngoài.
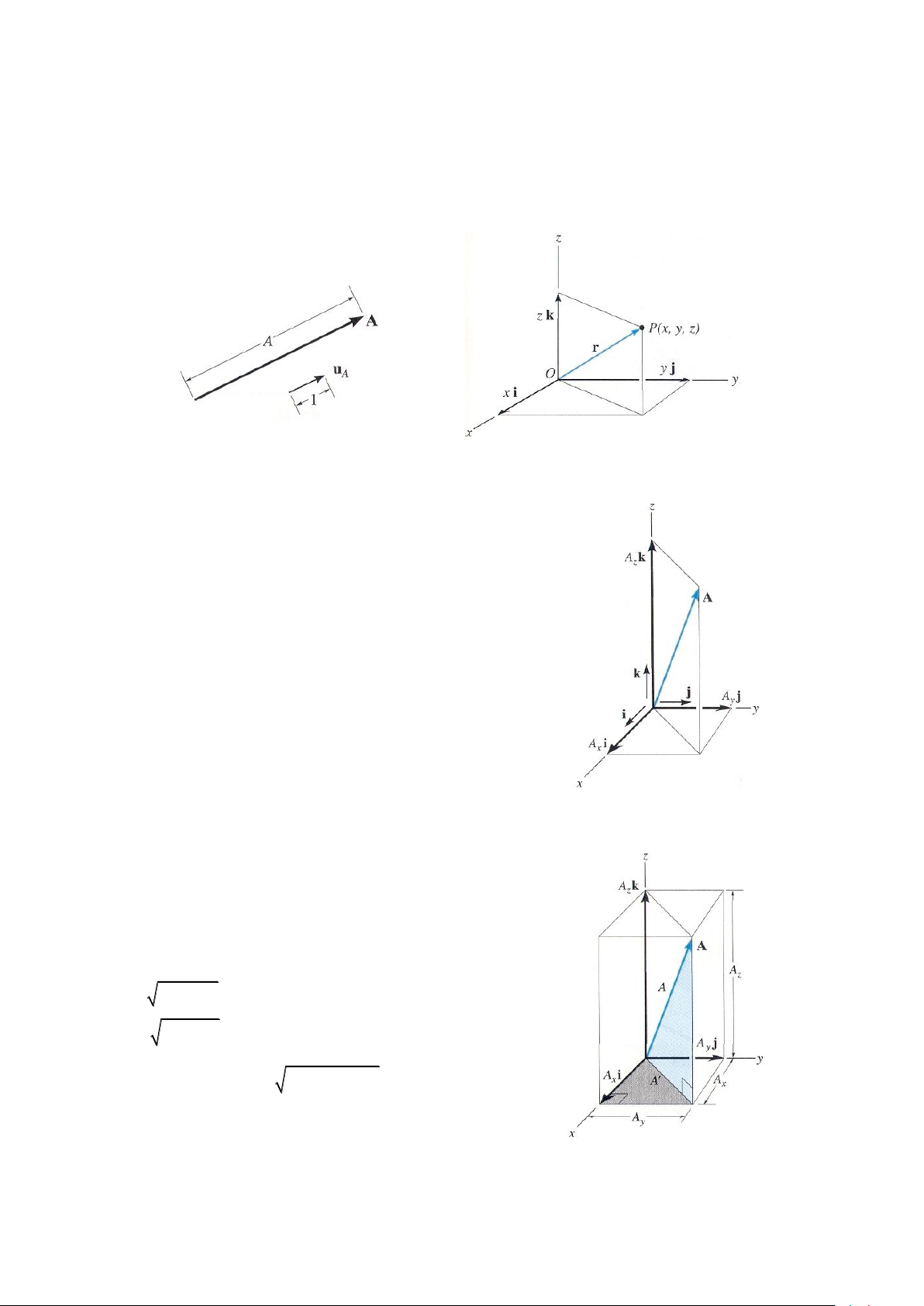
Các thành phần vuông góc của véctơ. Véctơ A
có thể có một, hai hoặc ba thành phần vuông góc
tương ứng với các trục toạ độ x, y, và z, phụ thuộc
vào véc tơ đó nằm như thế nào với các trục tọa độ.
Tuy nhiên, khi A chỉ nằm trong góc 1/8 của hệ trục
toạ độ x, y,z, hình 2-21 thì áp dụng qui tắc hình bình
hành hai lần ta có thể phân tích véctơ đó thành các
thành phần như sau A= A = A+ Az , và A = Ax+ Ay.
Kết hợp những công thức này, A được biểu diễn bởi Hình 2-21
tổng vectơ của ba thành phần vuông góc của nó.
A = Ax + Ay + Az (2-2)
Véctơ đơn vị. Sử dụng véctơ đơn vị để xác định chiều của A. Nếu A có độ lớn A  0, thì
khi đó véctơ đơn vị có cùng phương chiều với A và nó được biểu diễn như sau: A u  (2-3) A A
Do vậy: A = AuA (2-4)
Vì A là một véctơ cụ thể chẳng hạn là véctơ lực, thông thường sẽ sử dụng một hệ đơn vị
thích hợp cho việc mô tả nó. Độ lớn của A cũng có cùng đơn vị đó; do đó, từ phương trình 47
(2-3), véc tơ đơn vị sẽ không có thứ nguyên. Phương trình (2-4) cho thấy rằng A có thể được
biểu diễn cả về độ lớn và phương chiều cụ thể là: A (vô hướng dương) xác định độ lớn của A,
và uA( là một véc tơ không có thứ nguyên) xác định phương và chiều của A như hình 2-22. Hình 2-22 Hình 2-23
Véc tơ đơn vị Đề các. Trong không gian, thiết lập hệ véc
tơ đơn vị Đề các i, j, k. Hệ véc tơ đơn vị này được sử dụng để
xác định hướng tương ứng của các trục toạ độ x, y, z. Như đã
trình bầy trong phần 2-4, hướng ( chiều mũi tên) của những véc
tơ đó sẽ được biểu diễn theo công thức giải tích dấu cộng hoặc
dấu trừ phụ thuộc vào chúng nằm trên chiều dương hoặc chiều
âm của các trục x, y và z. Tất cả các véctơ đơn vị Đề các trong hình 2-23 đều dương .
Biểu diễn véc tơ Đề các. Vì ba thành phần của A trong
công thức (2-2) nằm theo chiều dương của các véc tơ đơn vị
Đề các i, j, k như hình 2-4, nên ta có thể viết lực A theo dạng
véc tơ Đề các như sau: A = Axi + Ayj + Azk (2-5)
Có thuận lợi khác khi biểu diễn các véc tơ theo cách này. Hình 2-24
Việc tách độ lớn và phương chiều của mỗi thành phần véc tơ
sẽ làm đơn giản hóa việc tính đại số véctơ, đặc biệt là đối với
các bài toán trong không gian.
Độ lớn của véc tơ Đề các. Luôn có thể xác định được độ
lớn của A khi nó được biểu diễn dưới dạng véctơ Đề các. Như
trong hình 2-25, từ tam giác màu xanh bên phải ta có: 2 2
A  A  A , và từ tam giác màu xám bên phải ta có: z 2 2
A  A  A . Kết hợp các phương trình đó ta có: x y 2 2 2 A  A  A  A (2-6) x y z
Vậy độ lớn của A sẽ bằng căn bậc hai của tổng bình
phương các giá trị lực thành phần (lấy giá trị dương).
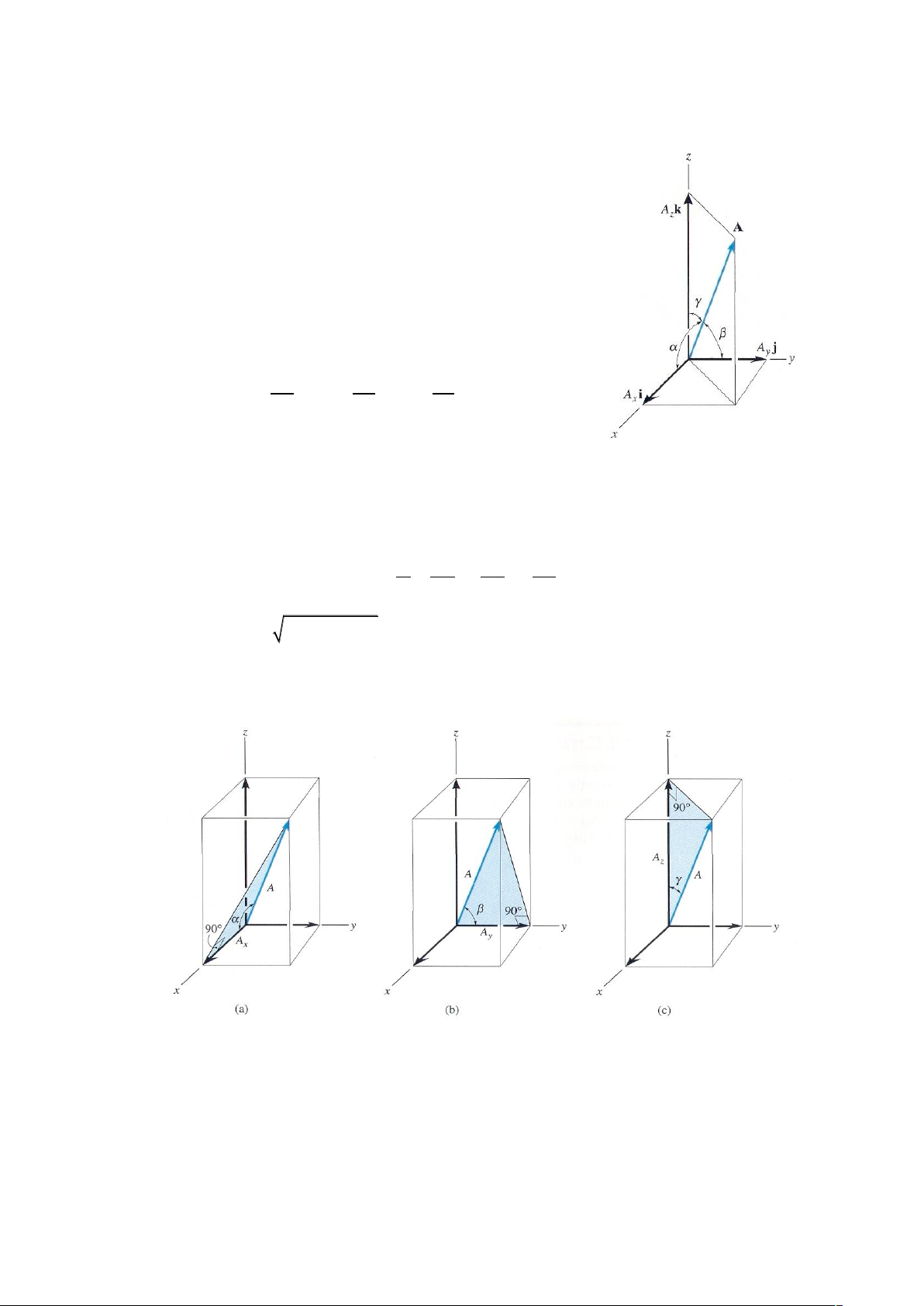
Hướng của các véctơ Đề các. Hướng của A được xác Hình 2-25 48
định bởi các góc chỉ phương ,  ,
  , là số đo các góc giữa
giá của A với chiều dương của các trục toạ độ x, y, z đặt tại
gốc của A, như hình 2-26.
Chú ý rằng, không quan tâm đến hướng của A, vì các
góc chỉ phương sẽ ở trong khoảng 00 đến 1800. Để xác định ,  ,
  , xét hình chiếu của A lên ba trục tọa
độ x, y, z, hình 2-27. Sử dụng các tam giác mầu xanh phía
bên phải trong mỗi hình vẽ, ta có: A A A x y z cosα = ;cosβ = ;cosγ = (2-7) A A A
Các công thức ở trên được gọi là các cosine chỉ phương
của A. Khi các đại lượng này đã được xác định, thì các góc Hình 2-26 ,  ,
  sẽ được xác định từ nghịch đảo của các giá trị cosine.
Một cách dễ dàng để xác định các cosine chỉ phương của A là tạo véctơ đơn vị theo phương của
A theo công thức (2- 3). Nếu A được biểu diễn dưới dạng véctơ Đề các: A = Axi + Ayj + Azk A A Ay A
(công thức 2-5), thì: u x   i  j z  k (2-8) A A A A A Ở đây: 2 2 2
A = A + A + A (công thức 2-6). So sánh với công thức (2-7), ta thấy các x y z
thành phần theo phương i, j, k của uA biểu diễn cosine chỉ phương của A, tức là:
uA = cos i + cos j + cos k (2-9) Hình 2-27
Độ lớn của véc tơ thì bằng căn bậc hai của tổng bình phương độ lớn của mỗi thành phần
của nó (lấy giá trị dương), và uA có độ lớn bằng 1. Vì vậy từ công thức (2-9) ta có mối liên hệ
quan trọng giữa các cosine chỉ phương theo công thức sau: 2 2 2
cos   cos   cos   1 (2-10) 49
Nếu A nằm trong góc 1/8 đã cho, thì công thức này sẽ được sử dụng để xác định một
trong những góc chỉ phương nếu đã biết hai góc.
Tóm lại, nếu độ lớn và các góc chỉ phương của A đã biết thì A sẽ được biểu diễn dưới
dạng véc tơ Đề các như sau:
A = AuA = Acos i +Acos j +Acos k = Axi + Ayj +Azk (2-11)
2.6 Cộng và trừ Véctơ Đề các
Phép tính cộng hay trừ của hai hay nhiều hơn
hai véctơ đã được đơn giản hoá đi rất nhiều nếu các
véc tơ này được biểu diễn dưới dạng toạ độ Đề các.
Ví dụ, nếu cộng hai véctơ A = Axi + Ayj +Azk và
B = Bxi + Byj +Bzk, như hình 2-28, thì sẽ được véctơ
tổng hợp là R, là véctơ có các thành phần tương ứng
tổng đại số các thành phần theo i, j, k của A và B, tức là:
R = A + B = (Ax + Bx)i + (Ay + By)j + (Az + Bz)k
Trừ véctơ là trường hợp đặc biệt của cộng véc tơ,
đơn giản là trừ đại số các thành phần tương ứng theo
i, j, k của A hoặc B. Ví dụ, Hình 2-28
R’ = A - B = (Ax - Bx)i + (Ay - By)j + (Az - Bz)k
Hệ lực đồng quy. Nếu các khái niệm về cộng véc tơ ở trên được khái quát hoá và áp
dụng vào hệ lực đồng quy thì lực tổng hợp là tổng véc tơ của tất cả các lực thuộc hệ và có thể
được biểu diễn như sau
FR = F = Fxi +Fyj + Fzk (2-12)
Ở đây: F , F và F tương ứng là tổng đại số của các lực thuộc hệ theo x y z
phương x, y, z hay là theo i, j, k .
Những ví dụ sau đây minh hoạ cho các phương pháp được dùng để áp dụng các lý thuyết
ở trên vào việc giải các bài toán có lực được coi là một đại lượng véc tơ.
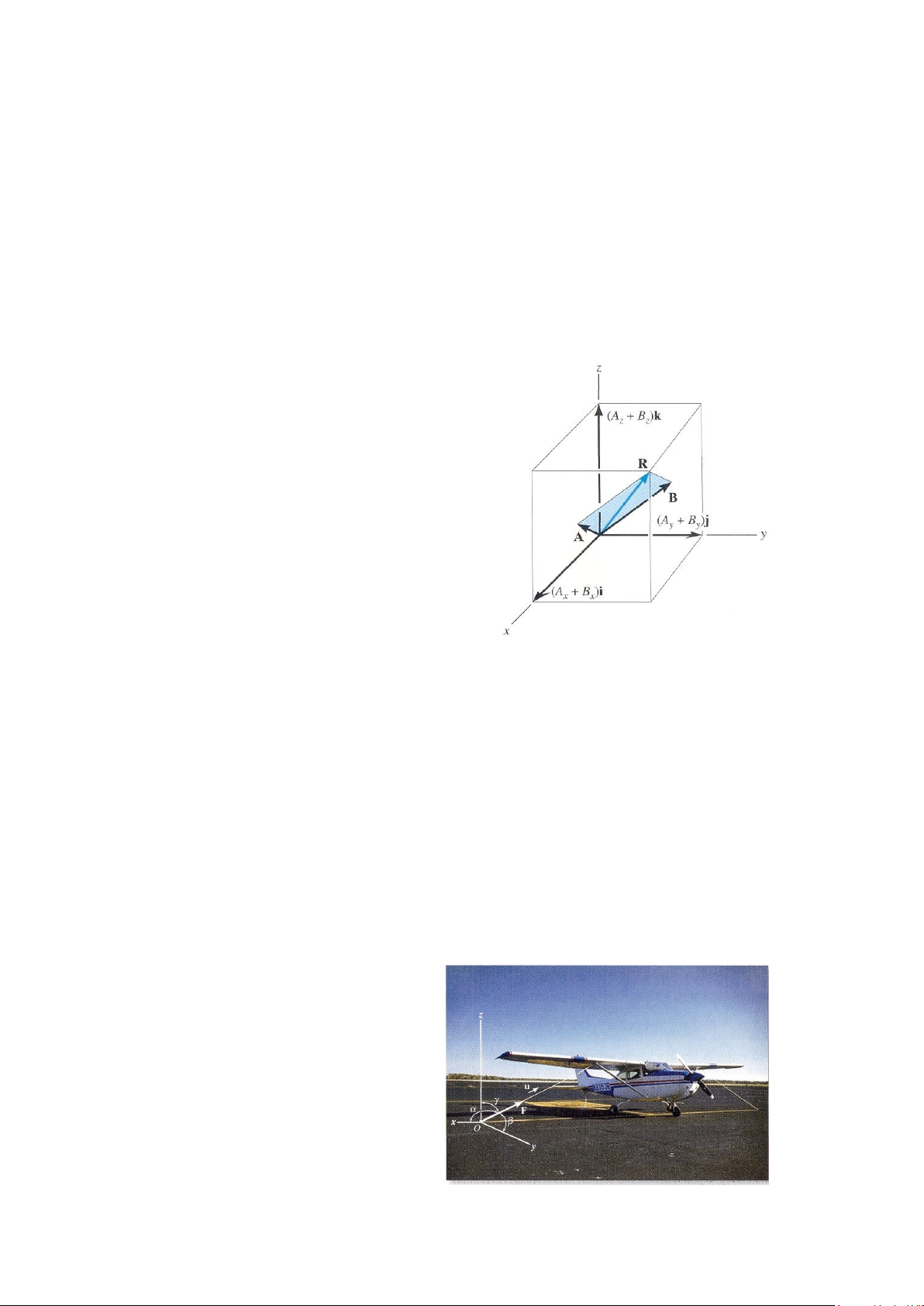
Lực F do dây buộc tác dụng lên nền tại O có phương
dọc theo dây. Có thể xác định được các góc chỉ
phương của lực , , , bằng cách sử dụng hệ trục tọa
độ địa phương x, y, z. Các giá trị cosine chỉ phương
chính là các thành phần theo phương x, y, z của véctơ
đơn vị u có phương dọc theo dây. Nếu lực có độ lớn
bằng F, thì lực có thể được biểu diễn theo dạng véctơ
đề các như sau F = Fu = Fcosi + Fcosj + Fcosk 50
NHỮNG ĐIỂM QUAN TRỌNG
 Phân tích véctơ Đề các thường được dùng để giải các bài toán trong hệ lực không gian.
 Chiều dương của các trục x, y, z được xác định tương ứng bởi các véctơ đơn vị Đề các
i, j, k .
 Độ lớn của véctơ Đề các là A= 2 2 2 A  A  A x y z
 Hướng của véctơ Đề các được xác định bởi các góc chỉ phương, là góc tạo bởi gốc của
véc tơ với chiều dương x, y, z tương ứng. Các thành phần của véctơ đơn vị u = A/A biểu diễn
các cosine chỉ phương , , . Nếu hai trong số các góc này đã biết, thì góc thứ 3 được xác
định nhờ quan hệ cos2+ cos2+ cos2 =1.
 Để tìm hợp lực của hệ lực đồng quy, ta biểu diễn các lực dưới dạng véc tơ Đề các và
lấy tổng các thành phần theo i, j, k của tất cả các lực thuộc hệ.
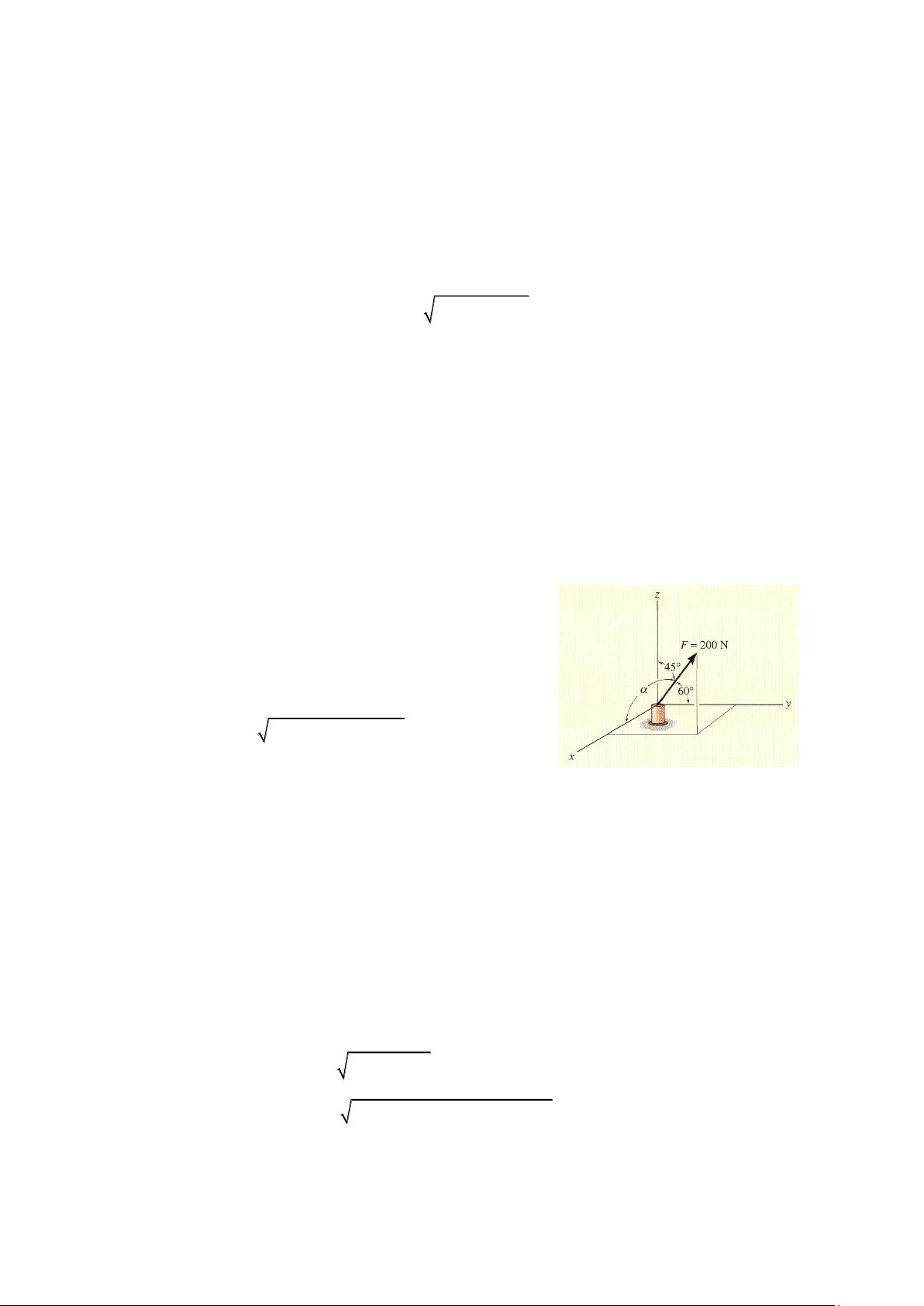
Ví dụ 2-8. Biểu diễn lực F cho trong hình 2-29 dưới dạng véc tơ Đề các. Bài giải
Vì hai góc chỉ phương đã biết nên góc thứ ba 
được xác định từ phương trình 2-10, cụ thể
cos2 + cos2 + cos2 =1
cos2 + cos260o + cos245o =1 cos = 2 2 1 (0.5)  (0.707)  0  .5
Vì vậy, có hai khả năng xảy ra, cụ thể:
 = cos1(0.5) = 60o hoặc  = cos1(0.5) = 120o Hình 2-29
Nghiên cứu hình 2-29, ta thấy  = 60o vì Fx nămg
theo chiều dương trục x.
Áp dụng phương trình 2-11, với F = 200 N, ta có:
F = Fcosi + Fcosj + Fcosk
= (200cos60o N)i + (200cos60oN)j + (200cos45oN)k
= (100.0i + 100.0j + 141.4k) N
Chú ý: Bằng cách áp dụng phương trình 2-6, và chú ý độ lớn của lực F = 200 N F = 2 2 2 F  F  F x y z = 2 2 2
(100.0)  (100.0)  (141.4)  200 N 51
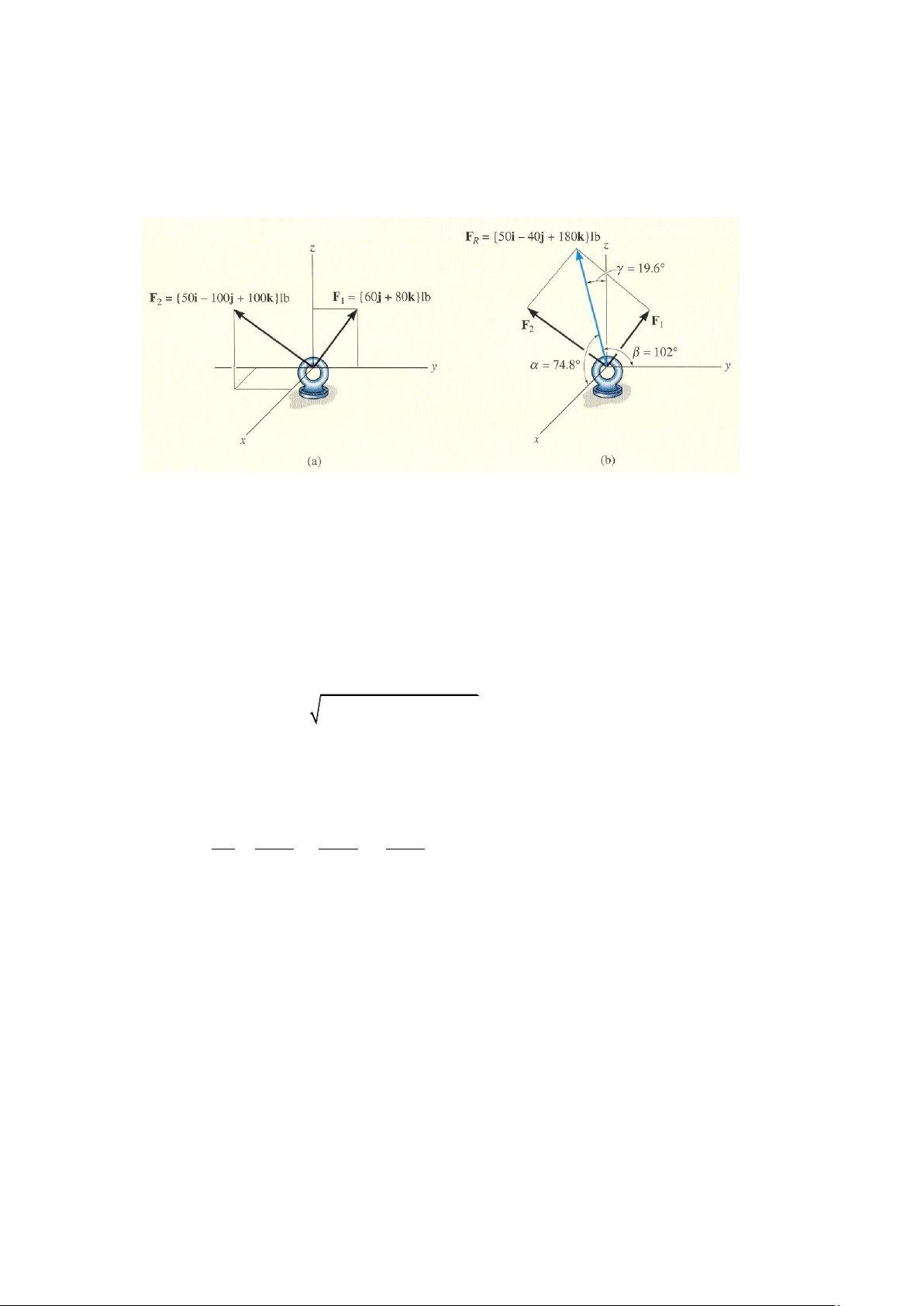
Ví dụ 2-9. Xác định độ lớn và các góc chỉ phương của hợp lực tác dụng lên vòng trên hình 2-30a Hình 2-30 Bài giải
Mỗi lực được biểu diễn dưới dạng véc tơ Đề các, hợp lực được thể hiện trên hình 2-30b
FR = F = F1 + F2 = {60j + 80k} lb + {50i – 100j + 100k} lb
= {50i – 40j + 180k} lb
Độ lớn của FR được tính theo công thức 2-6: F = 50 + -40 + 180 = 191.0 R  2  2  2 = 191 lb
Các góc chỉ phương , ,  được xác định từ các thành phần của véc tơ đơn vị theo hướng của FR F 50 40 180 u R   i  j  k R F F 0 . 191 0 . 191 0 . 191 R
= 0.2617i – 0.2094j + 0.9422k Vì vậy cos = 0.2617  = 74.8o cos = -0.2094  = 102o cos = 0.9422  = 19.6o
Những góc này được chỉ rõ trong hình 2-30b.
Chú ý: Nhớ rằng >90o thành phần theo j của uFR là âm. Có thể kiểm tra kết quả bằng cách
cộng F1 và F2 theo qui tắc hình bình hành. 52
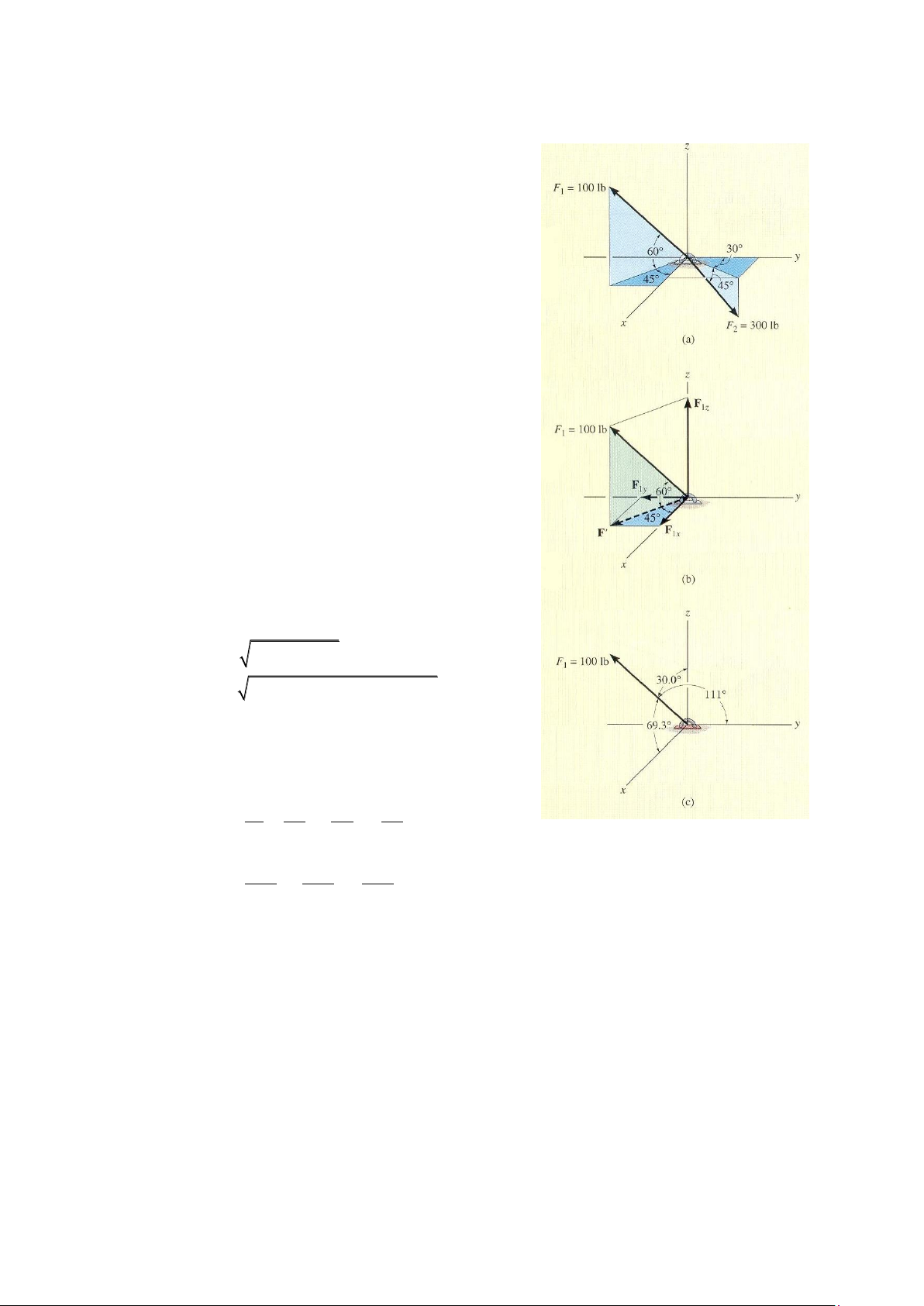
Ví dụ 2-10. Biểu diễn lực F1 như trong hình
2-31a dưới dạng véctơ đề các. Bài giải
Các góc 60o và 45o xác định hướng của F1 không
phải là các góc chỉ phương của nó. Áp dụng quy tắc
hình bình hành hai lần liên tiếp để phân tích F1 thành
các thành phần theo phương x, y, z thể hiện trong
hình 2-31b. Bằng lượng giác, độ lớn các thành phần này là: F1z = 100sin60o lb = 86.6 lb F' = 100cos60o lb = 50 lb F1x = 50cos45o lb = 35.4 lb F1y = 50sin45o lb = 35.4 lb
Nhận thấy rằng F1y có hướng theo –j , ta có:
F1 = {35.4i – 35.4j + 86.6k} lb
Để chứng minh độ lớn của véc tơ trên là 100 lb,
ta áp dụng phương trình 2-6: 2 2 2 F  F  F  F 1 1x 1y 1z 2 2 2  (35.4)  ( 3  5.4)  (86.6) 100lb
Nếu cần thiết, có thể xác định các góc chỉ
phương của F1 từ các thành phần của véc tơ đơn vị
dọc theo phương F1. Do đó F F F F u 1 1x   i 1y  j 1z  k 1 F F F F 1 1 1 1 Hình 2-31 4 . 35 4 . 35 6 . 86 = i  j  k 100 100 100
= 0.354i – 0.354j + 0.866k Kết quả là: 1 = cos-1(0.354) = 69.3o 1 = cos-1(-0.354) = 111o 1 = cos-1(0.866) = 30.0o
Các kết quả trên được được biểu diễn trong hình 2-31c.
Chú ý: Sử dụng theo cách trên, hãy chứng minh rằng F2 cho trong hình 2-31a ta có thể biểu
diễn dưới dạng véc tơ Đề các như sau:
F2 = {106i + 184j – 212k} N 53