





Preview text:
Microeconomics ASSIGNMENT 5 Group 8 – EBBA 13.2 Nguyen Khanh Hang Truong Van Phuc Tran Quynh Chi Le Phuc Anh Tuan Ha Anh Nguyet
Exercise 1: Suppose that a consumer who uses $60 to buy 2 goods: X and Y.
Given that price of the good X is $3 per unit and price of the good Y is $1
per unit. Suppose that the utility function of this consumer is TU=XY.
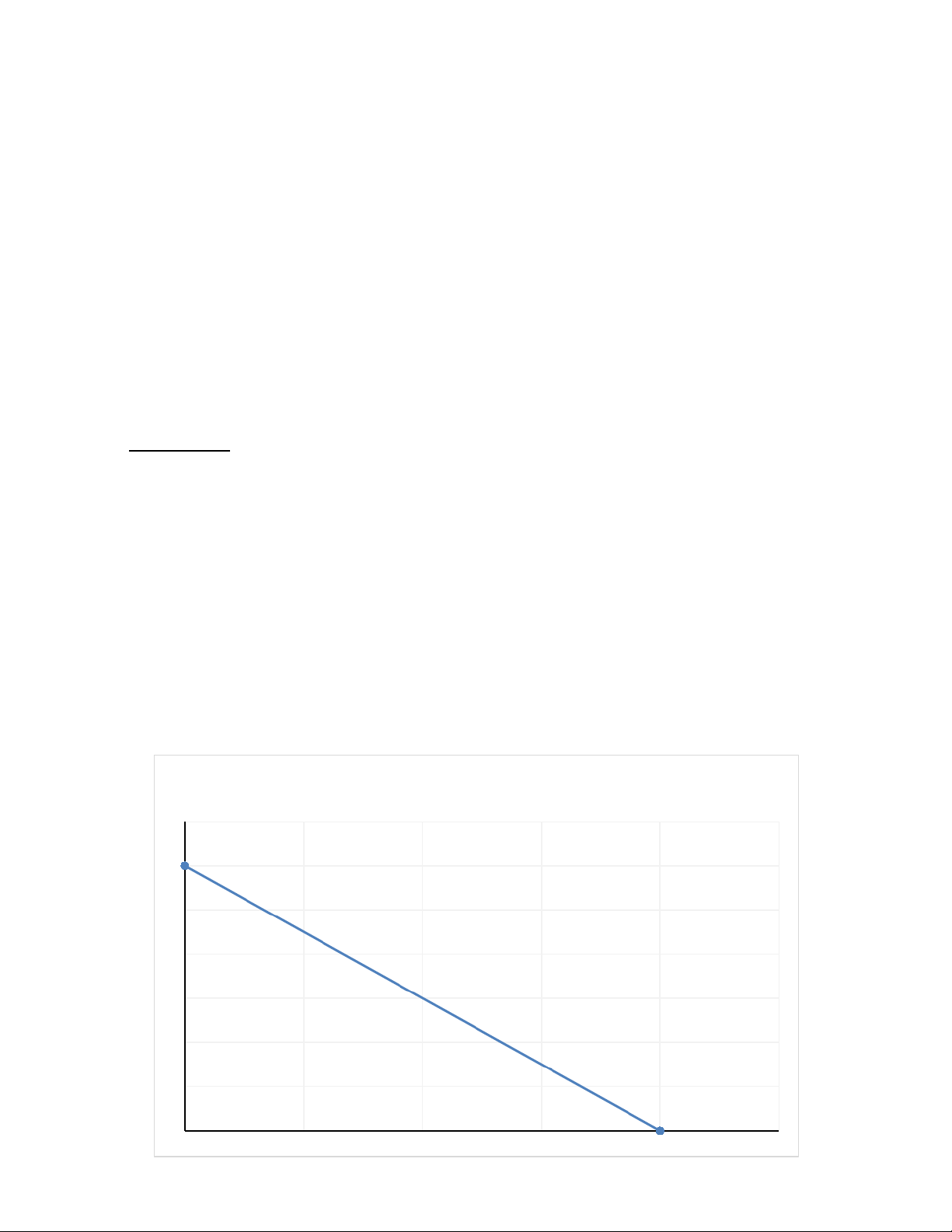
1) Identify the budget line equation for this consumer. −Px Py . x y = I Py I = $60, Px = $3, Py = $1 Px =3 Py
So the budget line equation for this consumer: y = 60 – 3x or 3x + y = 60 Budget Line Y 60 50 40 30 20 10 00 5 10 15 20 X
2) Identify MUx, MUy and MRSxy. We have: TU = XY MUx = (TU)’x = Y MUy = (TU)’y = X MUx Y So MRSxy = = MUy X
3) What are optimal quantity of good X (X*) and optimal quantity of
good Y (Y*) that he should buy to maximize his utility. MUx =Px
TU is max at the equilibrium point where: MUy Py Y =3 X Y=3X
System of equations: Y=3X
Y=60 –3X X = 10 and Y = 30 TU = 300
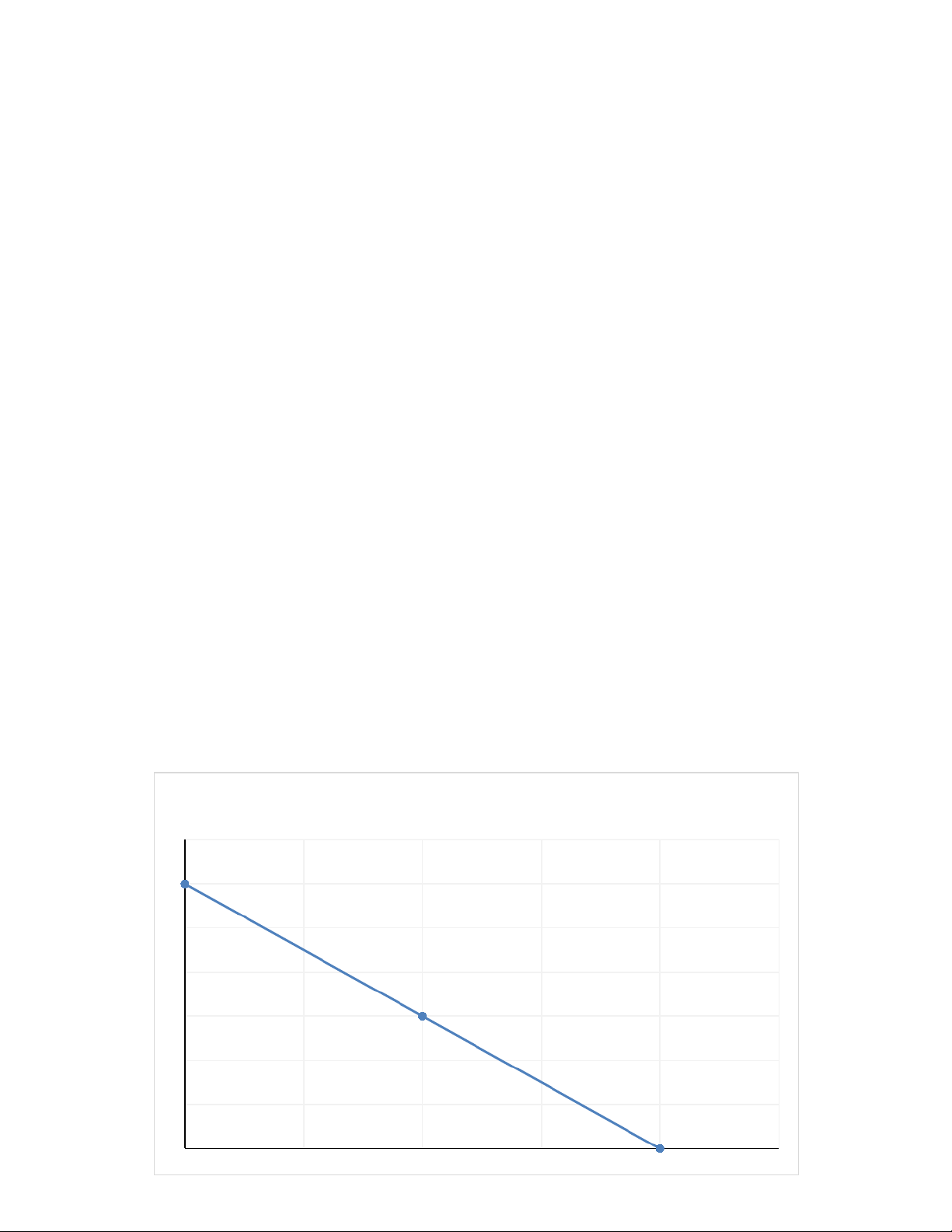
So the consumer should buy 10 units of good X and 30 units of good Y to
get the maximum utility by 300. Budget Line Y 60 50 40 E 30 20 U 10 0 0 5 10 15 20 X
Exercise 2: Monthly, Ms. Lan spends 1 million VND for buying meat (X)
and potato (Y). Price of meat is 20,000 dong/kg and price of potato is 5000 dong/kg.
a) Identify Lan’s budget line equation and draw that BL curve.
We have: I = 1,000,000 VND; Px = 20,000 VND; Py = 5,000 VND
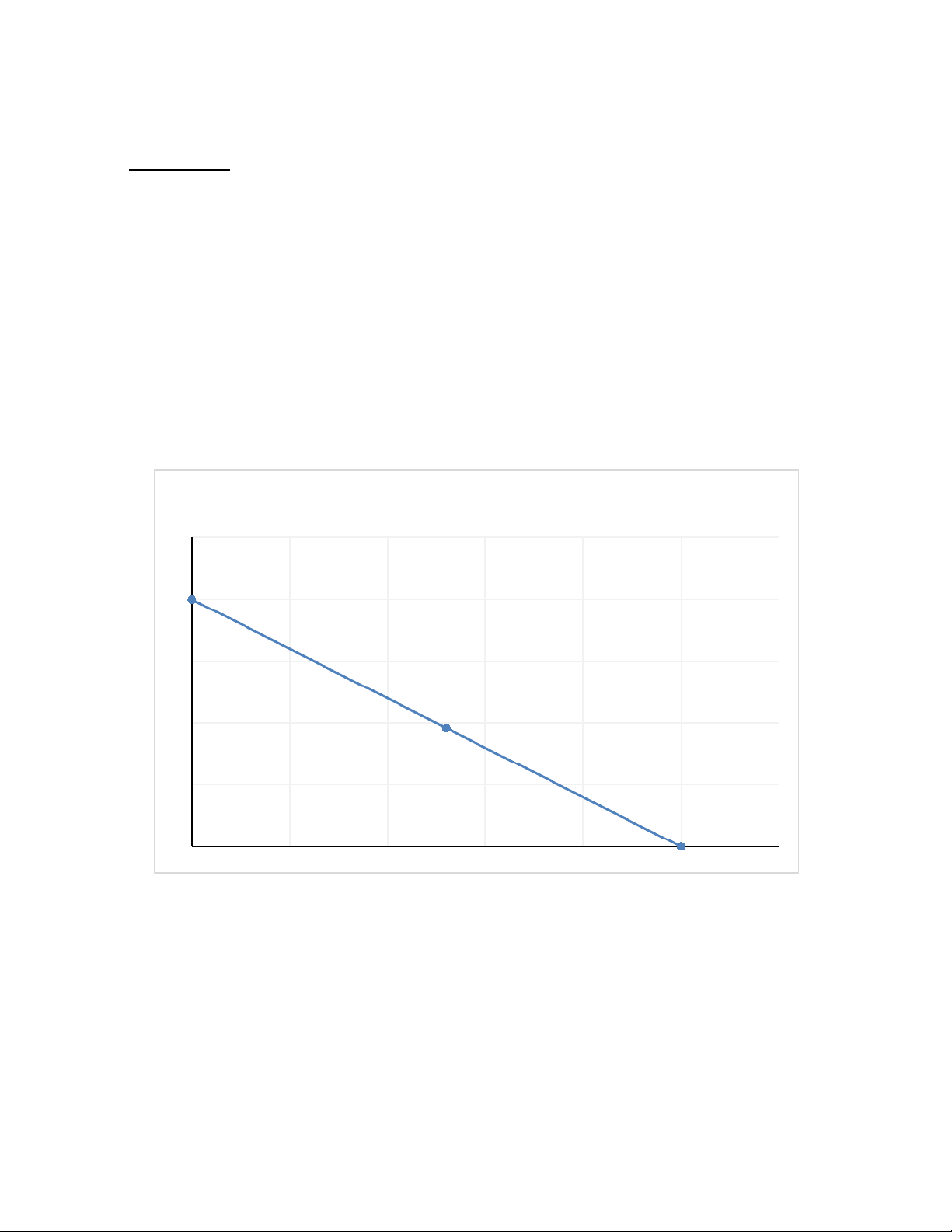
Budget Line Equation: X.Px + Y.Py = I 20000.x + 5000.y = 1000000
4x + y = 200 or y = 200 – 4x Budget Line Potato (Y) 0 200 150 E 100 96 50 U 20 00 10 20 30 40 50 26 45 Meat (X)
b) Assume that Lan’s utility function for meat and potato is TU = (X-2).Y,
what is Lan’s optimal choice between meat and potato to maximize her total utility?
We have TU = (X-2).Y = XY – 2Y MUx = (TU)’x = Y MUy = (TU)’y = X - 2 MUx
TU is max at the equilibrium point where: =Px MUy Py Y =20000 X−2 5000 Y=4X−8
System of equations: Y=4X−8
Y=200 –4X X = 26 and Y = 96 TU = 2304
So Lan should buy 26kg of meat and 96kg of potato to get the maximum utility by 2304.




