B5_

Chương 6 MẠNG HAI CỬA
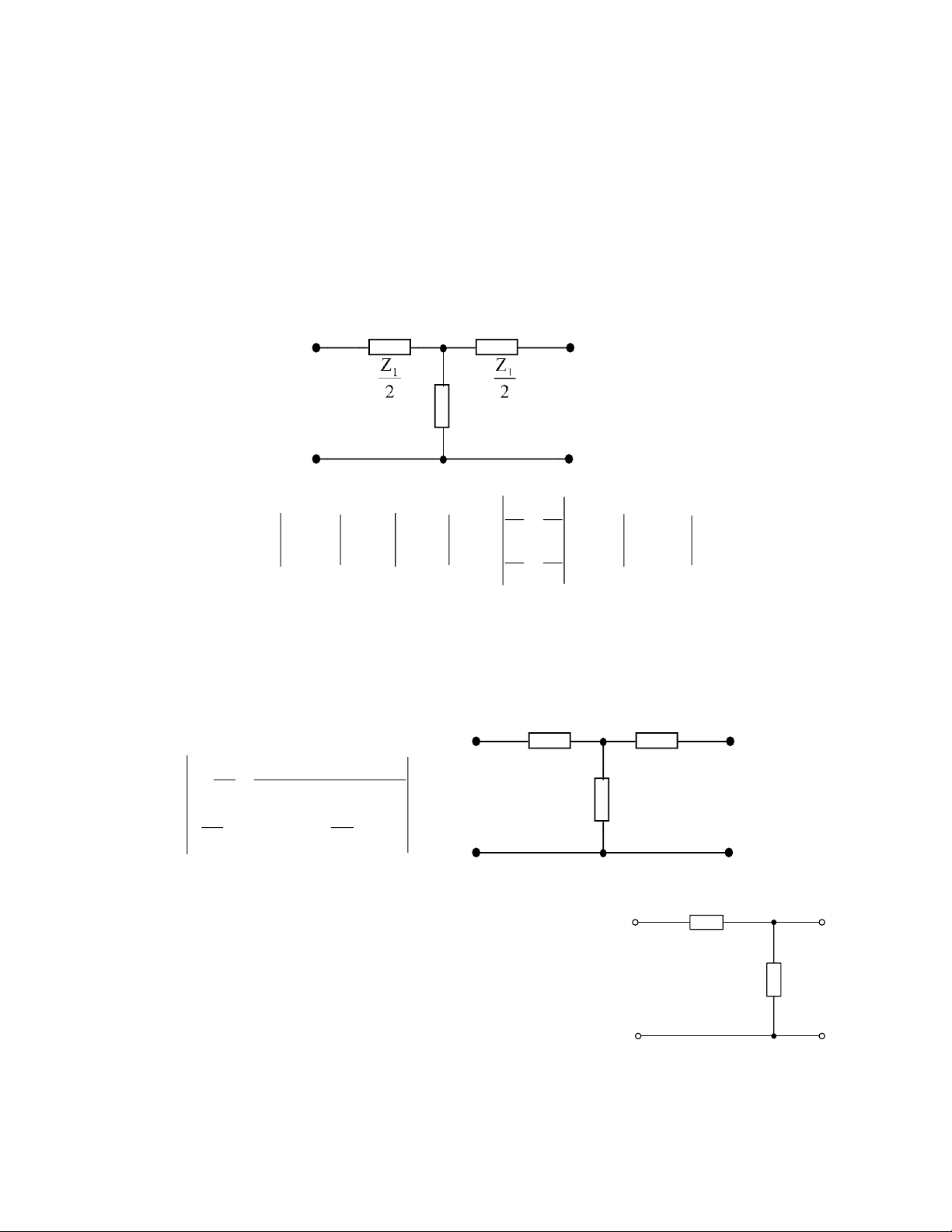
6.1. a. Xác định các phần tử của các ma trận A, Z, Y, H của mạch hình sau, với Z1 = 10, Z2 = 5.
b. Nếu cho Z1 = 8K, Z2 = 4K, xác định dòng cung cấp I1 và áp trên tải U2 khi
áp nguồn cung cấp là U1 = 48V với tải có tổng trở RL = , 6K, 0 Z2 Ů 1 Ů2 Hình 6.1 2 1 2 15 10 5 ĐS: 5 . 7 5 . 0 a. A = ; Z = ; 15 15 Y = ; H = 2 . 0 2 5 10 1 2 5 . 0 1 . 0 15 15 b. I1 = 6mA, U2 = 24V I1 = 7mA, U2 = 12V I1 = 8mA, U2 = 0
6.2. Xác định ma trận A Z1 Z2 1 2 Z Z Z + Z Z + Z Z 1 1 2 2 3 1 3 1 + ĐS: Z Z 3 3 A = Z3 1 Z2 1 + Z Z 3 3 1’ 2’ Hình 6.2
6.3. Cho mạng hai cửa hình Γ trên hình 6.3.
a) Hãy xác định hệ tham số A bằng phương pháp ngắn và hở 1 2 Z1 mạch 1-1’, 2-2’
b) Biến đổi về hệ tham số Y và Z. Z2
c) Kiểm chứng lại kết quả hệ tham số Y bằng phương pháp 2' ngắn hở mạch 1 1' -1’, 2-2’
d) Tính các trị số của tham số A tại tần số f=228kHz khi Z1 là H×nh 5.4 Hình 6.3 L27,95mH; Z2 là C24nF
6.4. Cho mạng hai cửa hình
“T” và hình “” trên hình a) b) 6.4. 1 2 1 2 Z2
a) Hãy xác định ma trận A Z1 Z3 của chúng. Z2 Z1 Z3 b) Nhận xét tính chất 1' 2' 1' 2'
“tương hỗ” của các ma trận trên H×nh 5.5 Hình 6.4
6.5. Tìm ma trận Y và Z của các mạng hai cửa hình T và hình  ở bài tập 6.5 và nhận xét
tính chất “tương hỗ” của các ma trận đó.
6.6. Cho mạng hai cửa hình 5.4. Hãy xác định hệ tham số H của mạng hai cửa này bằng
phương pháp ngắn và hở mạch 1-1’, 2-2’.
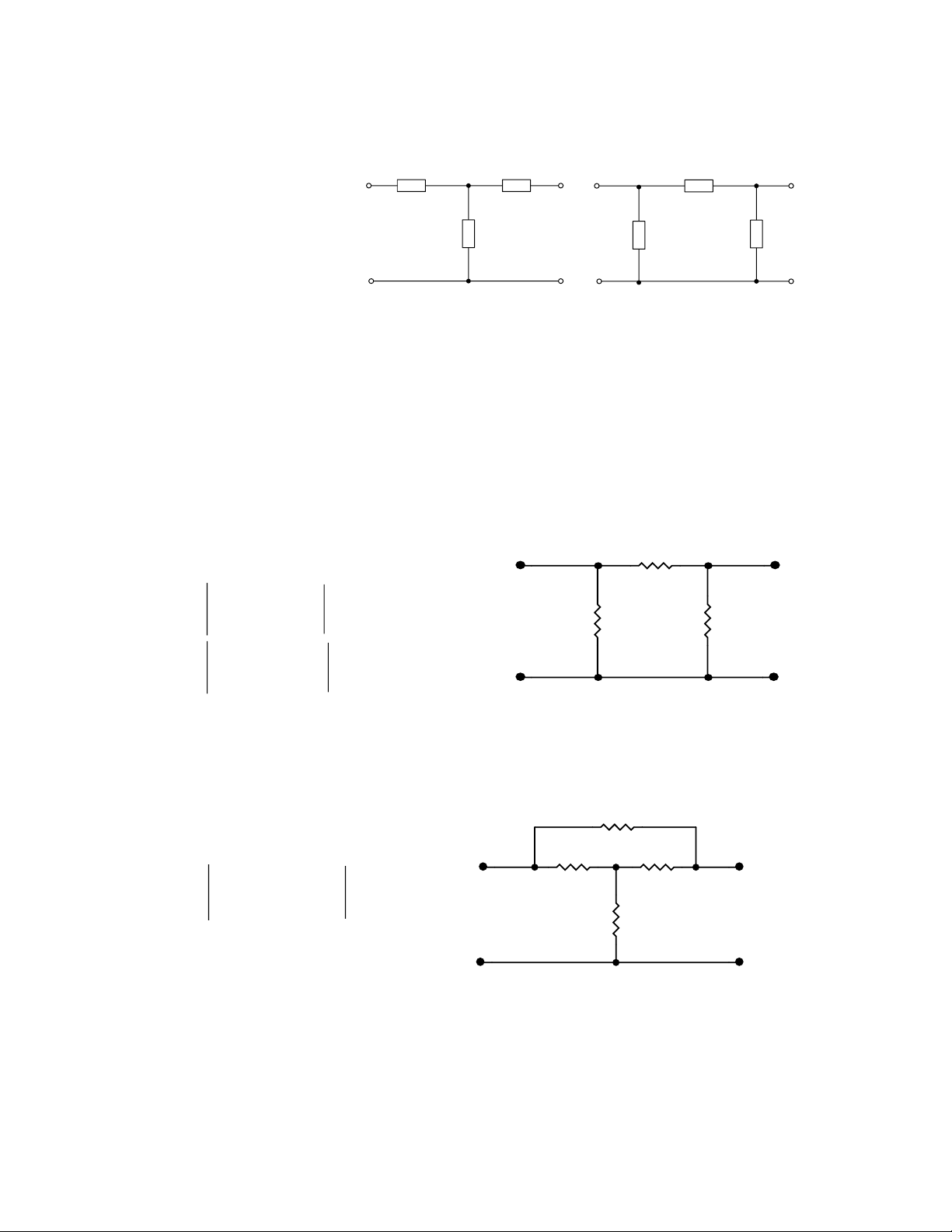
6.7. Xác định ma trận Y và H. Nghiệm lại các điều kiện đối xứng của mạng hai cửa. 20 ĐS: 1 2 06 . 0 − 05 . 0 Y = − 05 . 0 06 . 0 100 100 7 . 16 83 . 0 H = − 83 . 0 0183 . 0 1’ 2’ Hình 6.7 Y11 = Y22, Y12 = Y21 H12 = –H21, H = 1
6.8. Xác định ma trận A 1K ĐS: 5.55 545.45 1 2 A = 100 100 0.0545 5.55 10 1’ 2’ Hình 6.8
6.9. Xác định thông số ma trận A của mạng hai cửa trên hình 6.9. R R Z4 1 2 1 1 2 Za Z Z3 2 C C 1 Zb Z2 R 2C Zb 2 1' 2' 1' 2' 1' 2' Za H×nh 5.6 Hình 6.9 H×nh Hình 5.7 6.10 H×nh 5.8 Hình 6.11
6.10. Xác định thông số ma trận A của mạng hai cửa trên hình 6.10, biết Z1=(1 + j2) ,
Z2=-j, Z3=(-2-j5) , Z4= j.
6.11. Tìm hàm truyền đạt phức theo điện áp của mạng hai cửa hình 6.11.
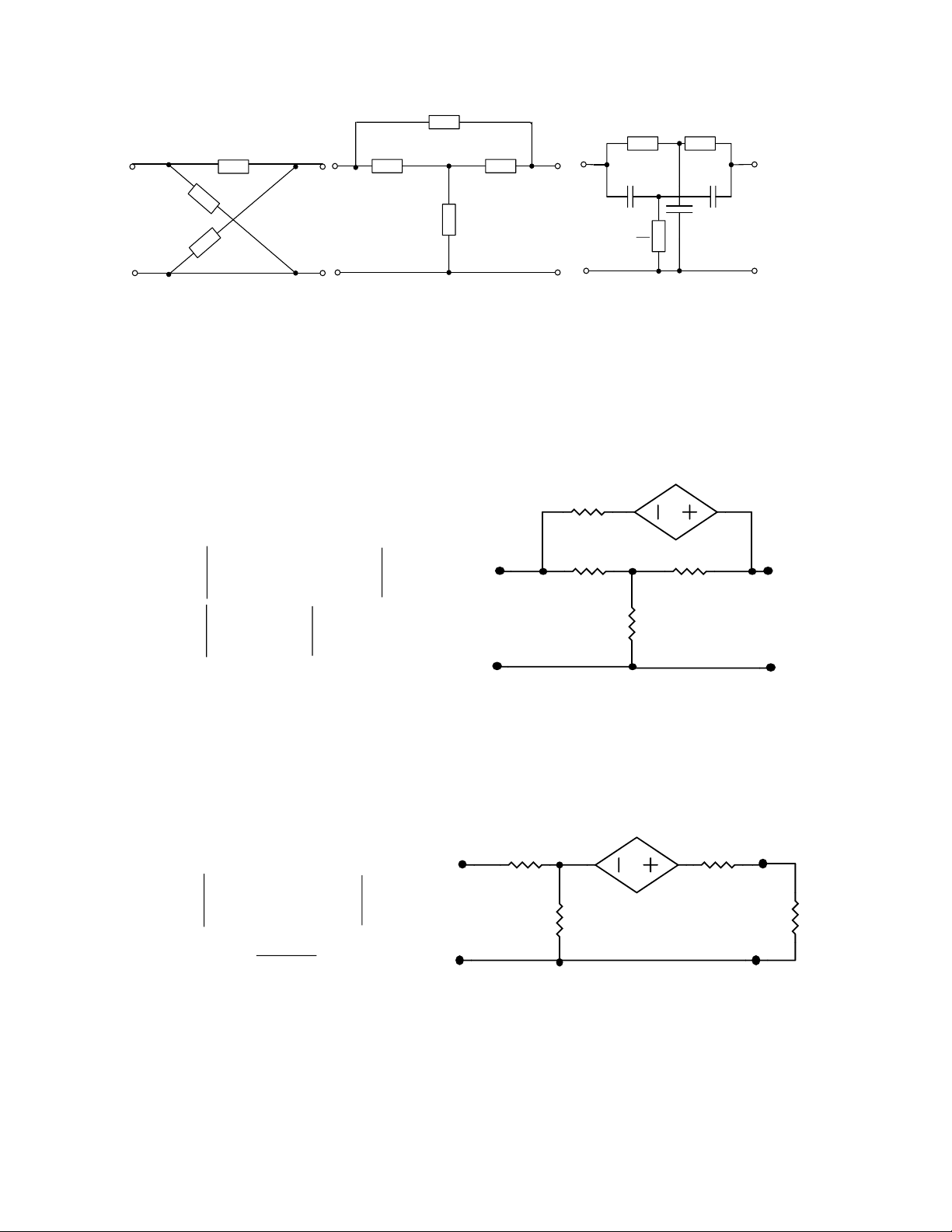
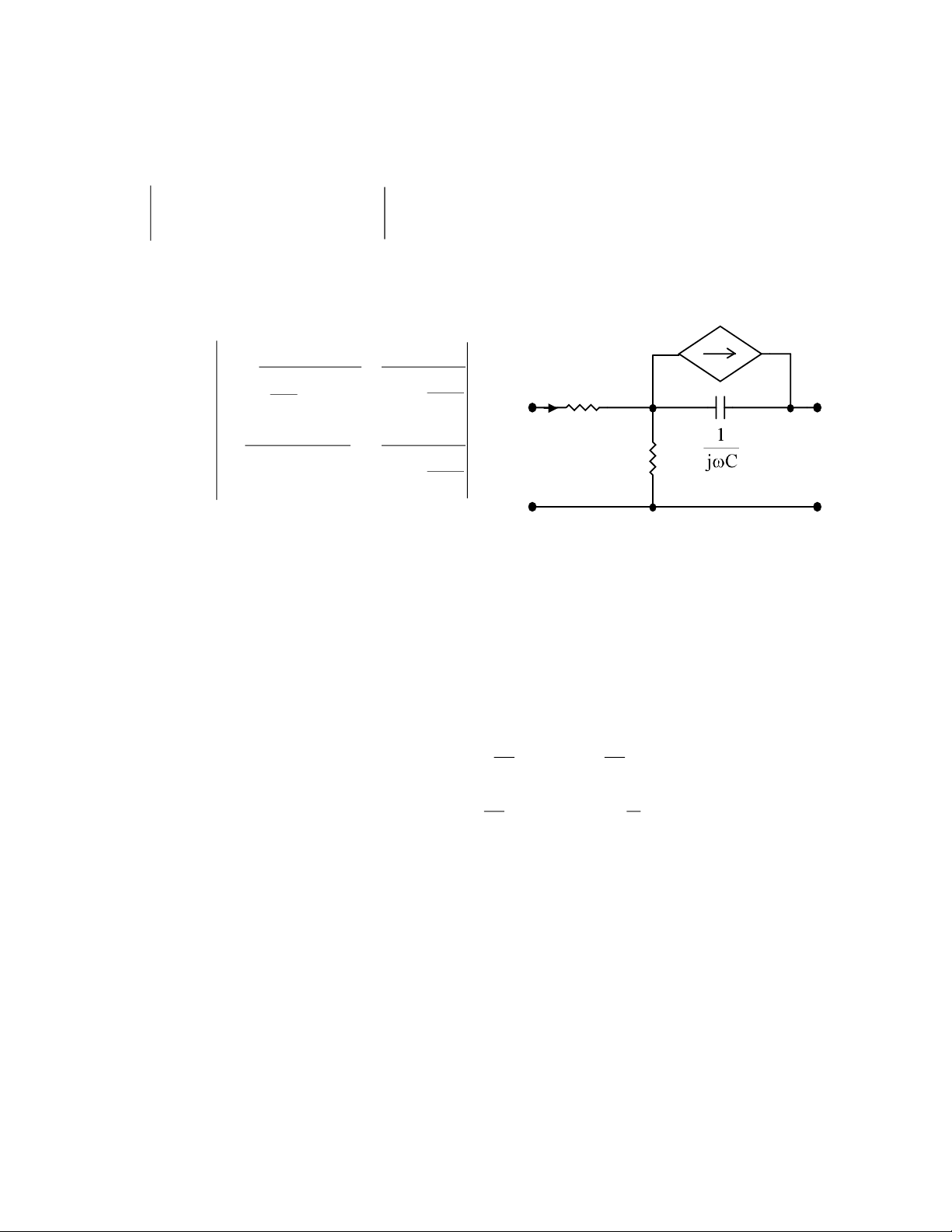
6.12. Xác định ma trận Y, A 0.15Ů x 150 ĐS: 01029 . 0 − 00828 . 0 + Ůx – Y = 2 − 1 00771 . 0 01 . 0 220 330 297 . 1 7 . 129 A = 100 005 . 0 335 . 1 1’ 2’ Hình 6.12
6.13. Cho mạng hai cửa như hình 6.13 a. Xác định ma trận Z
b. Tính trở kháng vào cửa 1 khi mắc cửa 2 một điện trở R ĐS: 1 R1 R2 2 R + R R + Ů 1 3 3 x – Z = R − R  R + R Ůx 3 1 2 3 R R3 Z Z . 12 21 1’ 2’ Z = Z − V 11 R + Z22 Hình 6.13
6.14. Xác định ma trận A trong mạch hình 6.14 20 j20 10 j10 10 1 2 1 2 -j40 -j10 -j40 1’ 2’ 1’ 2’ a b Hình 6.14 + + + + ĐS: 5 . 0 5 . 0 j 20 20 j 1 j 10 20 j a. A = b. = − A 012 . 0 5 + 037 . 0 j 5 5 . 0 + 5 . 0 j 02 . 0 − 04 . 0 j 2
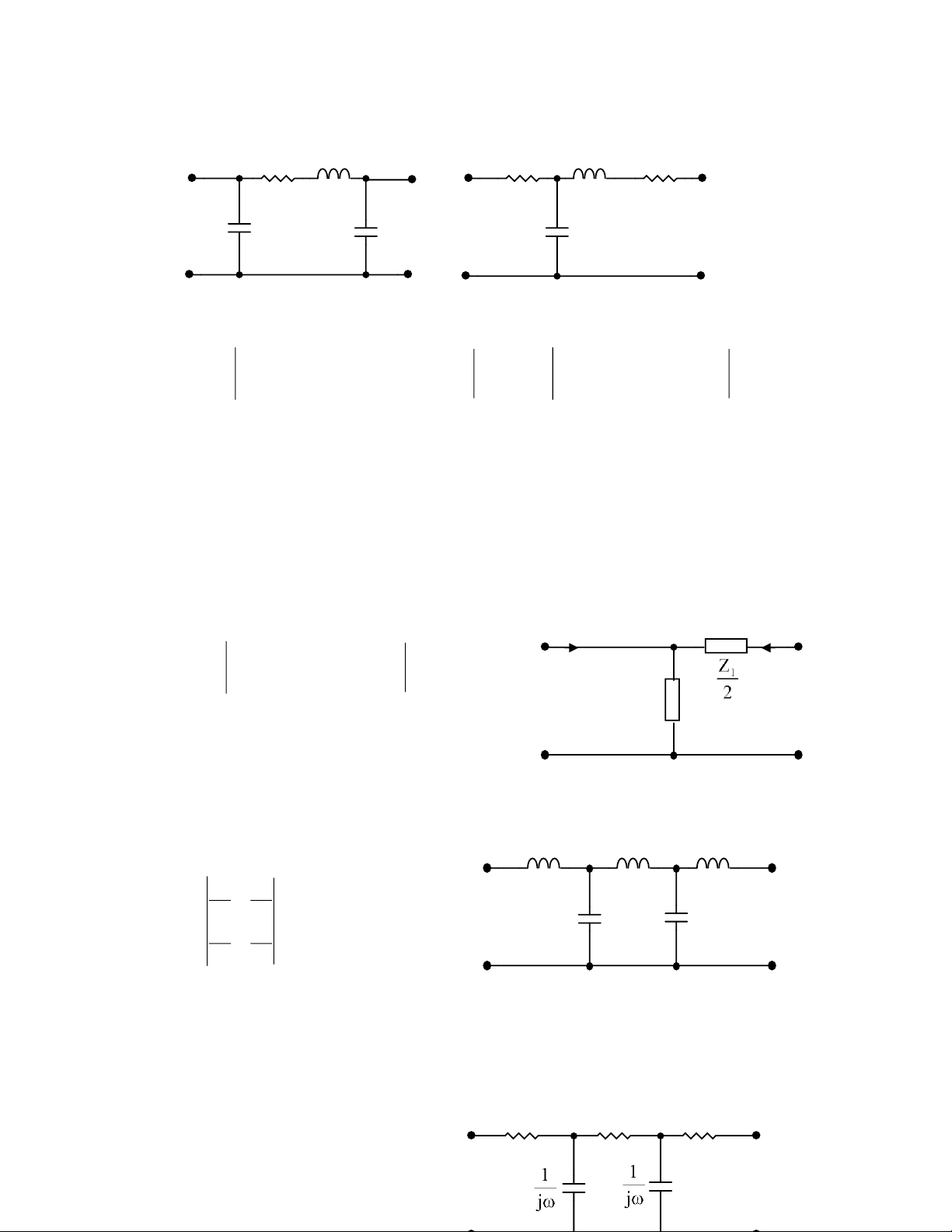
6.15. Cho mạng hai cửa với Z1/2 = 2Z2 = 10+j10 . a. Xác định ma trận A
b. Xác định áp đầu vào cửa (1-1’) để áp ngõ ra cửa (2-2’) là 20V
c. Giả sử khi ngắn mạch cửa vào (1-1’) và áp nguồn cung cấp ở cửa (2-2’) là 100mV,
xác định dòng của nguồn cấp cửa (2-2’)
d. Xác định chỉ số Waltmet khi dòng vào cuộn dòng là İ1 và áp hai đầu cuộn áp là Ů2
khi cho đầu ra hở mạch và áp tác dụng lên đầu vào là u(t) = 80sin(t+450)V ĐS: 1 İ1 İ2 2 10 10 + 20 j a. A = 02 . 0 − 04 . 0 j 2 2Z 2 b. 56.6 V c. 4.47 mA d. 64W 1’ 2’ Hình 6.15
6.16. Xác định ma trận Y j20 j40 j20 ĐS: 1 2 j j 60 30 Y = -j40 -j40 j j 30 60 1’ 2’ Hình 6.16
6.17. Xác định ma trận A 1 1 2 1 2 1’ 2’ ĐS: 1 − 22 + 4 j  4 − 22 +  A = 6 j − 22 + 2 j  1 − 22 + 4 j 
6.18. Xác định ma trận H İ 1 1 −  R2 1 R +  1  1  + jC R2 + 1 R1 2    ĐS: R2 j C H = ( + jCR 2) 1 İ − 1 1 + jCR 2 1 R2 R2 + jC 1’ 2’ Hình 6.18 1+ j 1 − 2 + j  
6.19. Cho mạng hai cửa với ma trận A =   j 1 − 2  a. Tìm ma trận [Z]
b. Xây dựng sơ đồ hình T ứng với ma trận [Z] vừa tìm và xác định trị số các thông số mạch.  1 1  1 + −  j j
6.20. Cho mạng hai cửa với ma trận Y =    1 1  − j( − )  j  
a. Xây dựng sơ đồ hình  ứng với ma trận trên và xác định trị số các thông số mạch. b. Tìm ma trận [Z]
6.21. Cho mạng hai cửa với ma trận [Y] trong bài tập 6.21. 1. Xác định ma trận A
2. Tìm hàm truyền đạt phức của mạch khi: a) Không mắc tải. b) Mắc tải là Zt=j.
3. Tìm tổng trở đầu vào của khi mắc tải Zt=j
6.22. Cho mạng hai cửa hình 6.21 với R=R1=1, L=1H, C=1F. Xác định hàm truyền đạt
phức theo điện áp và theo dòng điện . . I I 1 2 R1 L . C . R Zt u1(t) u2(t) U U 1 2 L H×nh 5.14 H×nh 5.15 Hình 6.21 Hình 6.22
6.23. Cho mạng hai cửa hình 6.22 với L = 10mH, R = 20. Tần số của tín hiệu tác động
là 2000 rad/s. Tại tần số này: a) Xác định ma trận A
b) Khi mắc tải Zt là điện trở Rt=10 nối tiếp với điện dung Ct=50F, hãy tính tổng trở
đầu vào của mạng hai cửa (tách riêng phần điện trở thuần và phần phản kháng: ZV=RV+jXV). . U
c) Tính hàm truyền đạt phức 2m T(j )  =
khi mắc tải như trên (viết dưới dạng . U m 1 j( )  T(j )  = T(j )  e ).
d) Theo biểu thức hàm truyền đạt phức vừa tìm trên hãy xác định công suất tác dụng ra
tải khi điện áp tác động ở đầu vào là:  u1(t)=10 sin (2000t+ ) (V) 4
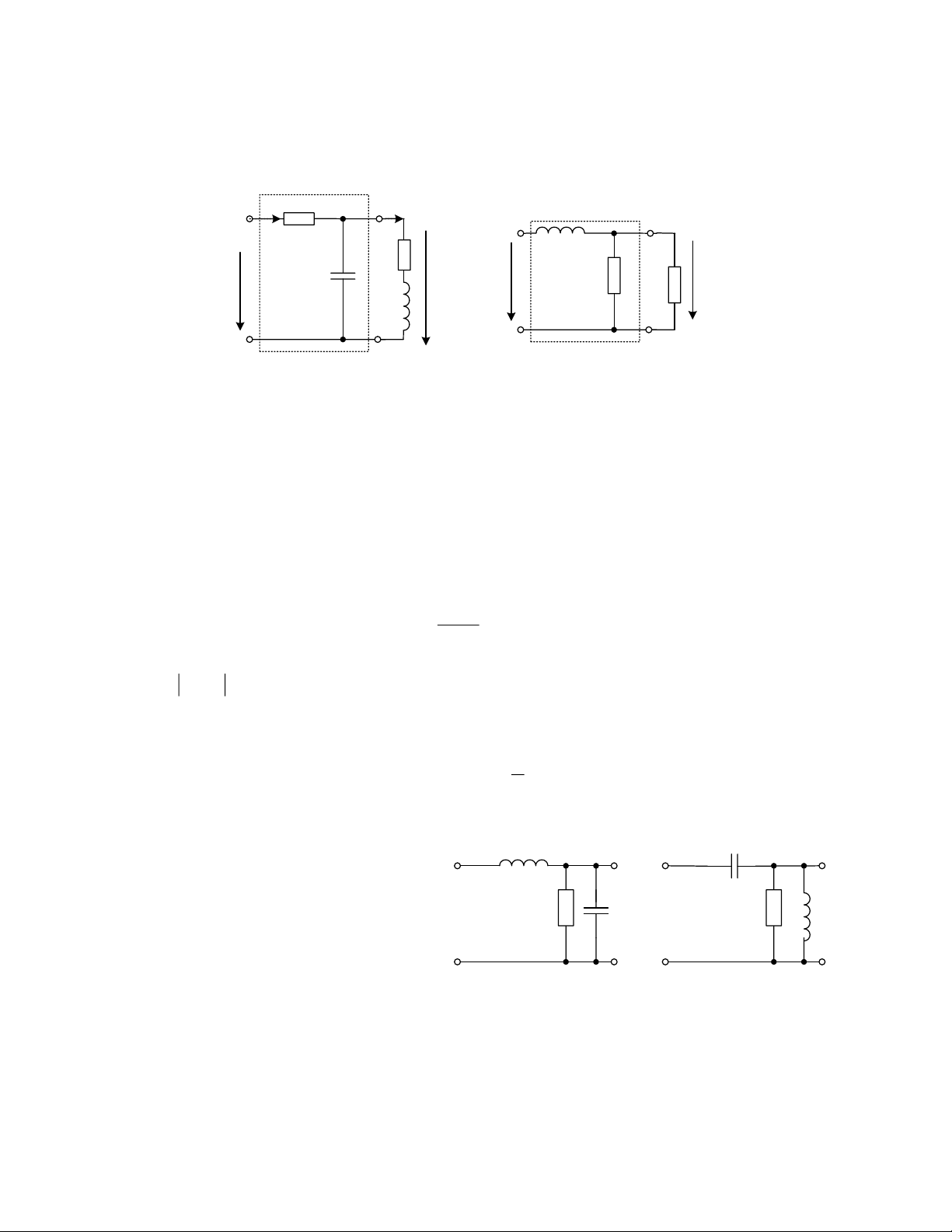
6.24. Tìm hàm truyền đạt phức theo a) b)
điện áp và vẽ đặc tính biên độ tần số L của các mạch hình 6.24. R C R L
6.25. Cho mạng hai cửa hình 6.24 với . H Hình 6. ×n 23 h.16
U1 =10 V, Z1=Z3=1, Z2=-j, Z4= j , Hình 6.22
Zt= 1 . Hãy xác định công suất tác dụng trên tải. Z4 I1 Z I2 1 Z3 1 Z2 2 1 Z3 2 T Z1 U1 Z U2 t U1 Z2 Zt 1' Z5 2' 1' 2' Z Z6 4  H×nh 5.17 H×nh 5.18. Hình 6.24 Hình 6.25
6.26. Cho mạng hai cửa hình 6.25 có Z1=Z3= Z5=Zt=5, Z2= Z4=Z6 = - j5 . Xác định I1, I2 và U2 biết U1=20V.
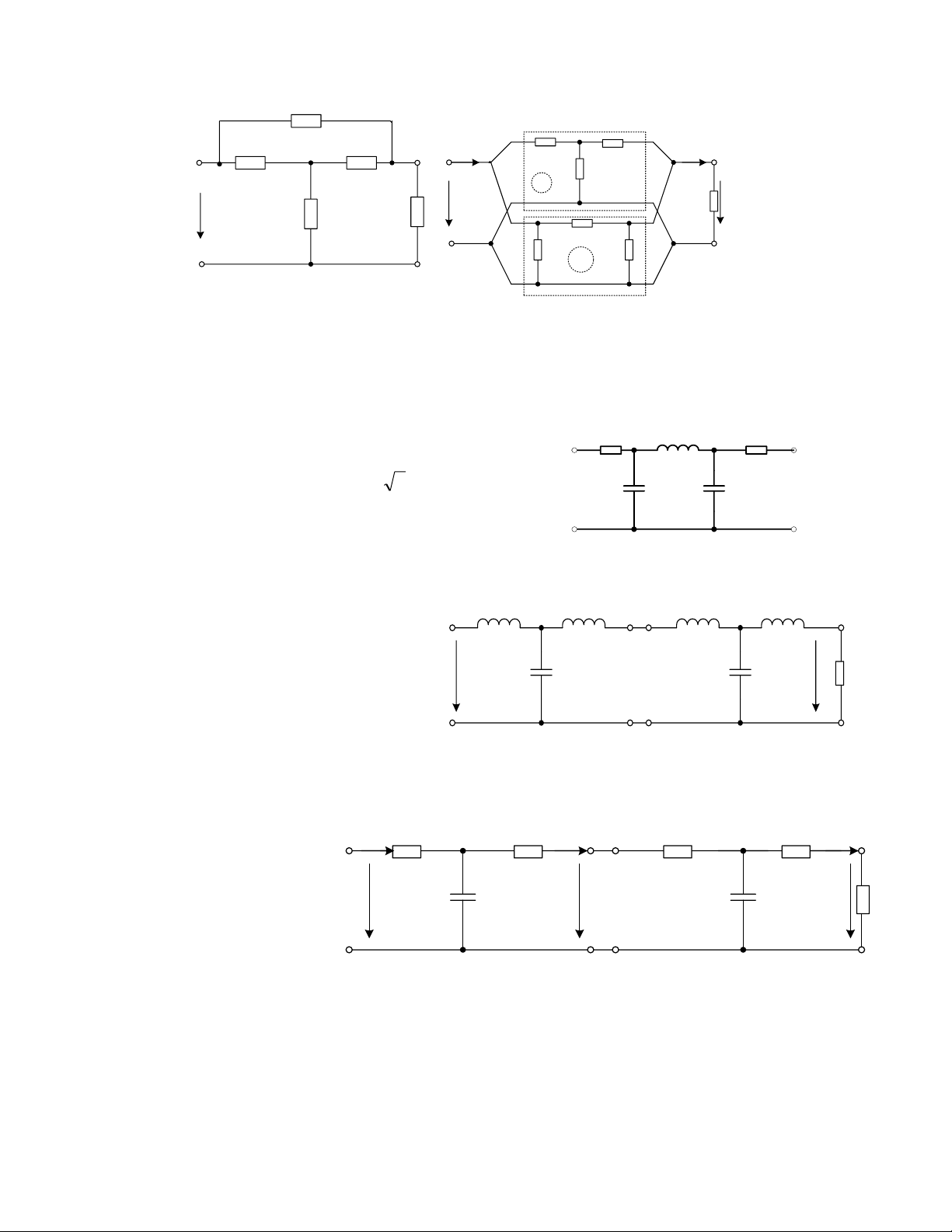
6.27. Cho mạng hai cửa hình 6.26 được mắc hoà hợp Z1 Z3 Z5
phụ tải, có Z1=Z5=1 , Z2=Z4 =-j , Z3=j , nguồn
tác động là điện áp : u1(t)= 10 2 sin t (V). Hãy Z2 Z4 xác định: a. Tổng trở đặc tính
b. Các giá trị hiệu dụng I1, U2, I2 H×nh 5.1 Hình 6. 9. 26 Hình 6.22 L L L L
6.28. Cho mạng hai cửa hình 6.27. Biết L=10mH, C=12,5F.
u1(t)=30sin(2000t+/2)[V]. Hãy xác U1 C C U2 định: Zt
a. Ma trận A và tổng trở đặc tính
b. Tính điện áp và dòng điện tức thời ở đầu ra. Hình 6.27 H×nh 5.20. Hình 6.22 . . .
6.29. Cho mạng hai cửa I I 1 2 I 3 hình 6.28 mắc hoà hợp Z Z1 Z phụ tải có Z 1 1 Z1 . 1=1 , U . . Z 1 U U 2=-j , U1=4V. Hãy 2 Z2 3 ZC xác định U Z2 2, U3, I1, I2 và I3. H×nh Hình 6. 5. 28 2 1. Hình 6.22
6.30. Cho mạng hai cửa hình 5.22 có C1 = C2 = 1F, C1 C2 C3
C3 = 0,5F, R1=0,5 , R2=Rt=1 . . Xác định : I2 . a. Ma trận A . 2 U R R R 2
b. Hàm truyền theo điện áp. 1 t 1 U
c. Tổng dẫn truyền đạt Y21. H×nh 5.22 Hình 6.29
6.31. Cho mạng hai cửa hình 6.30 khi mắc tải là Z 2 = Rt = 2  thì có:
- Hàm truyền đạt phức theo điện áp: Hình 6.22 . . T(j) = U 2 = 4 . . I1 3 + j2 I 2 U 1 . .
- Tổng trở truyền đạt U Mạng 1 MBC Z2 U 2 . hai cửa U 2 2 Z (j) = = 21 . Hình 1 + j4 I H×n 6. h 2 5 2 .2 Hình 6. 3. 30 1
Tìm tổng trở đầu vào Z V(j) và hàm truyền .
đạt phức theo dòng điện I 2 T (j )  = Hình 6.22 I . I1
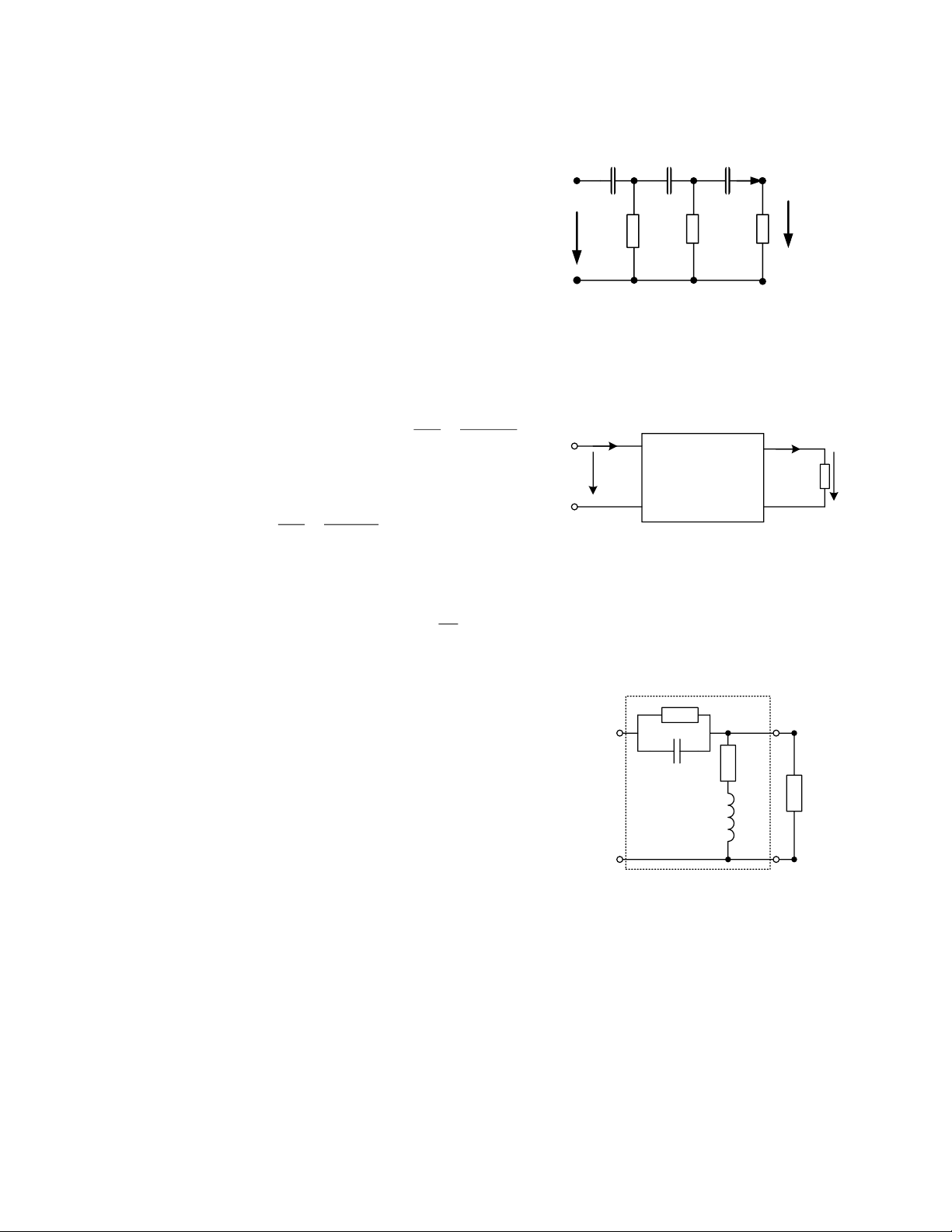
6.32. Cho mạng hai cửa hình 6.31 có R=1, C=1F, R
R1= 1, L=1 H. Xác định: a. Ma trận Y C R1
b. Hàm truyền đạt phức theo điện áp khi mắc tải Rt Rt =1  L H×nh.5.24 Hình 6.31 Hình 6.22