Bài 06: Mạch số môn Hệ thống máy tính | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

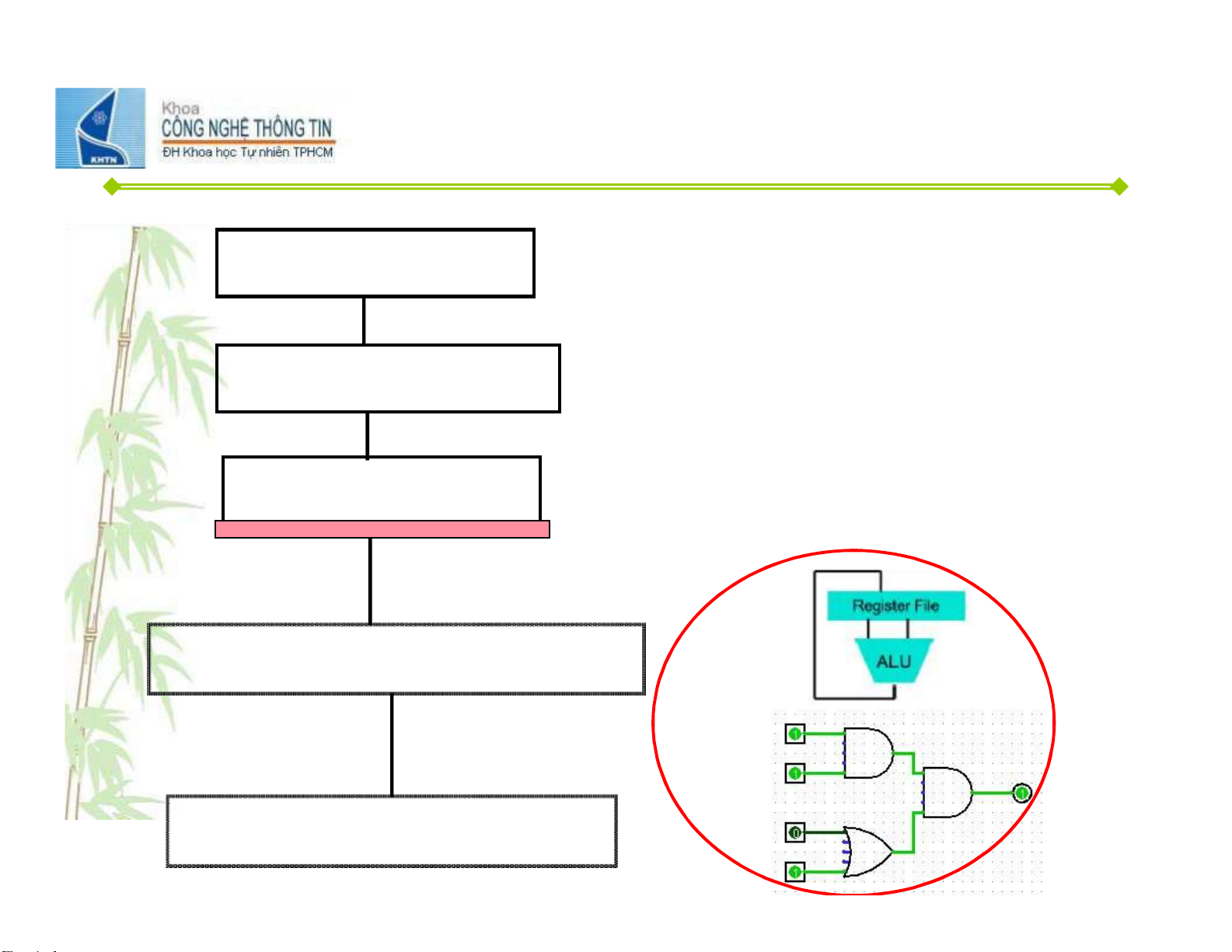
lOMoAR cPSD| 59994889 Bài 06: Mạch số Phạm Tuấn Sơn ptson@fit.hcmus.edu.vn lOMoAR cPSD| 59994889 Mô hình phân tầ ệ ử ng vi c x lý củ a máy tính temp = v[k]; High Level Language v[k] = v[k+1]; Program (e.g., C) v[k+1] = temp; Compiler lw $t0, 0($2) lw $t1, 4($2) Assembly Language sw $t1, 0($2) Program (e.g.,MIPS) sw $t0, 4($2) Assembler Machine Language
0000 1001 1100 0110 1010 1111 0101 1000
1010 1111 0101 1000 0000 1001 1100 0110 Program (MIPS)
1100 0110 1010 1111 0101 1000 0000 1001
0101 1000 0000 1001 1100 0110 1010 1111 Machine Interpretation
Hardware Architecture Description e
( .g. block diagrams ) Architecture Implementation
Logic Circuit Description
( Circuit Schematic Diagram ) 2 lOMoAR cPSD| 59994889
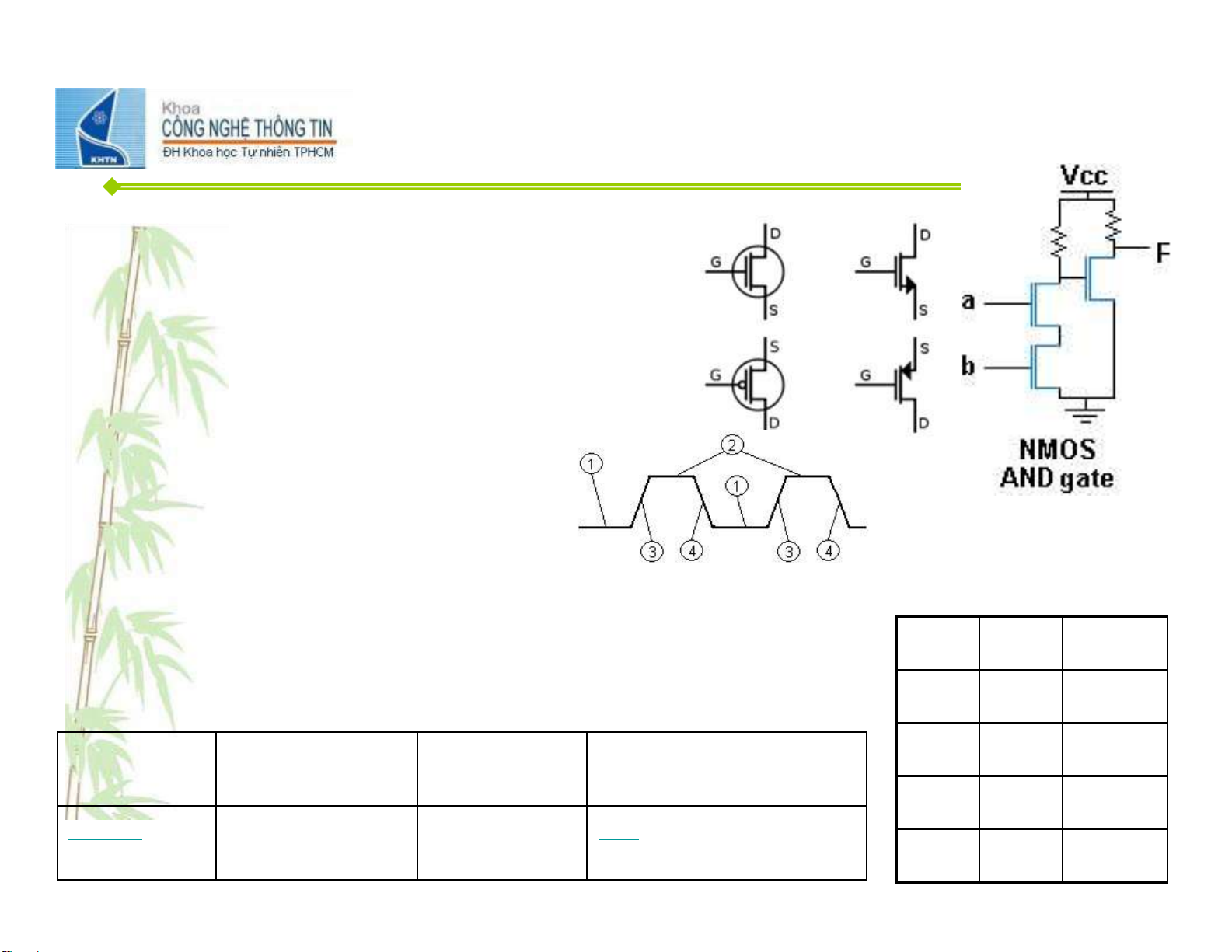
• Transistor là linh ki ệ n đ i ệ n t ử làm t ừ ch ấ t bán d ẫ n dùng để khu ế ch
đạ i và chuy ể n tín hi ệ u đ i ệ n
• MOSFET (metal-oxide-semiconductor field-effect transisto r) – NMOSFET (n-type)
• N ế u hi ệ u đ i ệ n th ế gi ữ a G và S đủ l ớ n,
thì D và S s ẽ đượ c n ố i transi (
stor s ẽ có tr ạ ng thái “on”) – PMOSFET (p-type)
• Ng ượ c l ạ i NMOSFET •
M ạ ch s ố là thi ế t b ị đ i ệ n t ử
k ế t n ố i các linh ki ệ n đ i ệ n t ử (nh
ư transistor) ho ạ t độ ng ở (1) low level, (2) high level
2 m ứ c đ i ệ n áp: cao và th ấ p (3) rising edge, (4) falling edge Mạch số a b F low low low Công nghệ high Điện áp thấp Điện áp Ghi chú low low cao low high low CMOS 0V  V VCC/2  VCCđiện áp nguồn high high high CC/2  VCC lOMoAR cPSD| 59994889 TTL 0V  0.8V 2V  VCC: 4.75V 5.25V  VCC ECL -1.175V  .75V  0V VEE:-5.2V VCC=Nối đất  -VEE lOMoAR cPSD| 59994889 Cổng logic
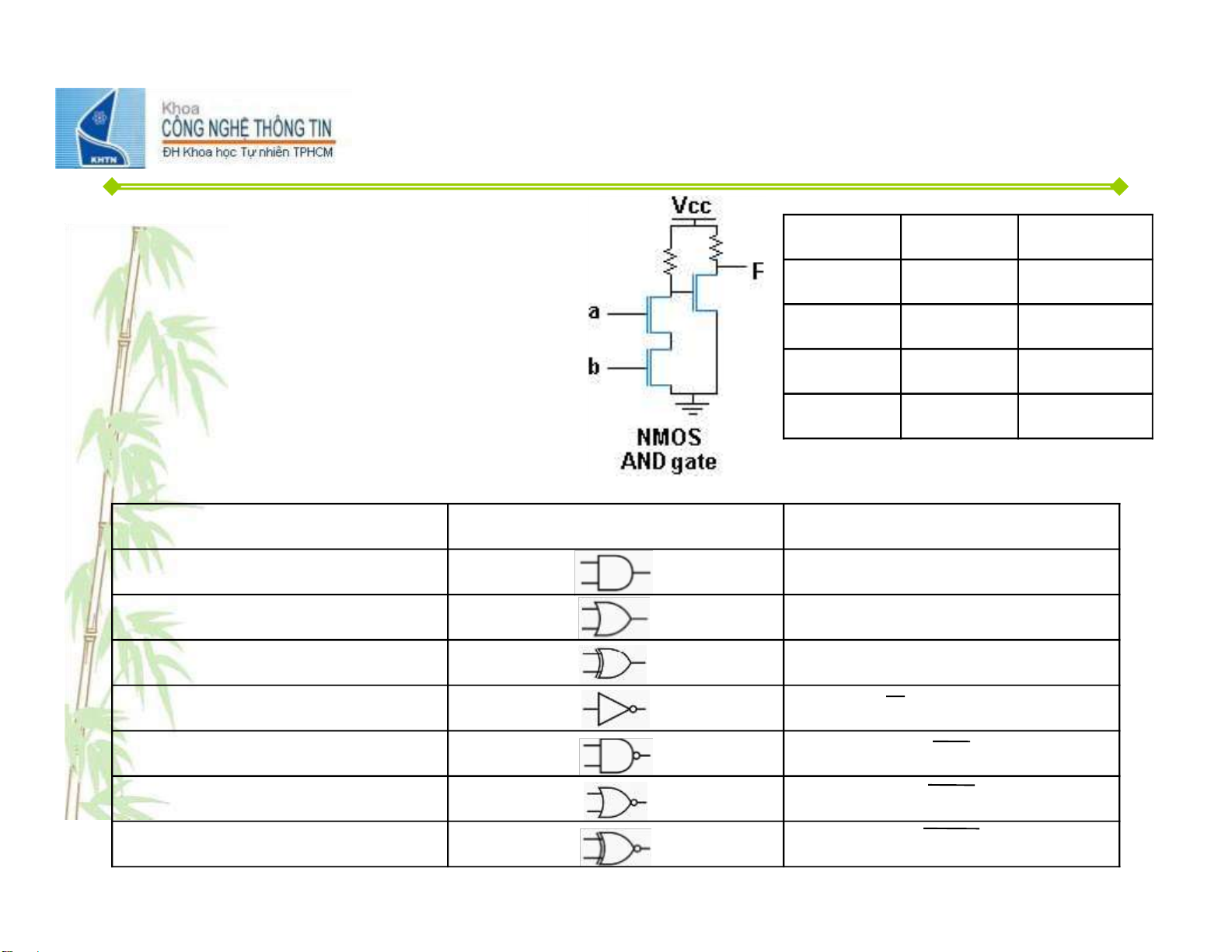
• Các linh ki ệ n đ i ệ n t ử th ườ ng a b F (AND)
k ế t n ố i v ớ i nhau thành các low (0) low (0) low (0) kh ố i c ơ b ả n high(1) low (0) • low (0)
Kh ố i c ơ b ả n nh ấ t là các c ổ ng low (0) logic v high(1) low (0)
ớ i các giá tr ị lu ậ n lý (qui ướ high(1) high(1) high(1)
c) 1 và 0 t ươ ng ứ ng v ớ i 2
m ứ c đ i ệ n th ế cao và th ấ p Tên ổ ẽ ệ c ng
Hình v
Ký hi u AND x.y OR x+y XOR x ⊕y NOT x (ho ặ c x’) NAND x.y NOR x+y NXOR x ⊕y 4 lOMoAR cPSD| 59994889 Thiết kế logic
• Các cổng logic thường được kết nối với nhau thành các khối cao cấp hơn
• Các mạch cao cấp này gồm 2 loại
– Mạch tổ hợp: kết nối các cổng logic sao cho kết quả của mạch
chỉ phụ thuộc vào giá trị đầu vào tại thời điểm đang xét. Ví dụ:
mạch adder, decoder, multiplexor, ALU,…
– Mạch tuần tự: kết nối các cổng logic sao cho kết quả của mạch
không chỉ phụ thuộc vào giá trị đầu vào tại thời điểm đang xét mà
còn phụ thuộc vào trạng thái tại thời điểm trước đó của mạch. Ví
dụ: mạch lật RS, JK, T, D,…
• Thông thường các mạch số (như mạch xử lý) được thiết
kế ở mức logic (kết nối các khối cao cấp và các khối cơ
bản), sau đó có thể sử dụng các kỹ thuật khác nhau để
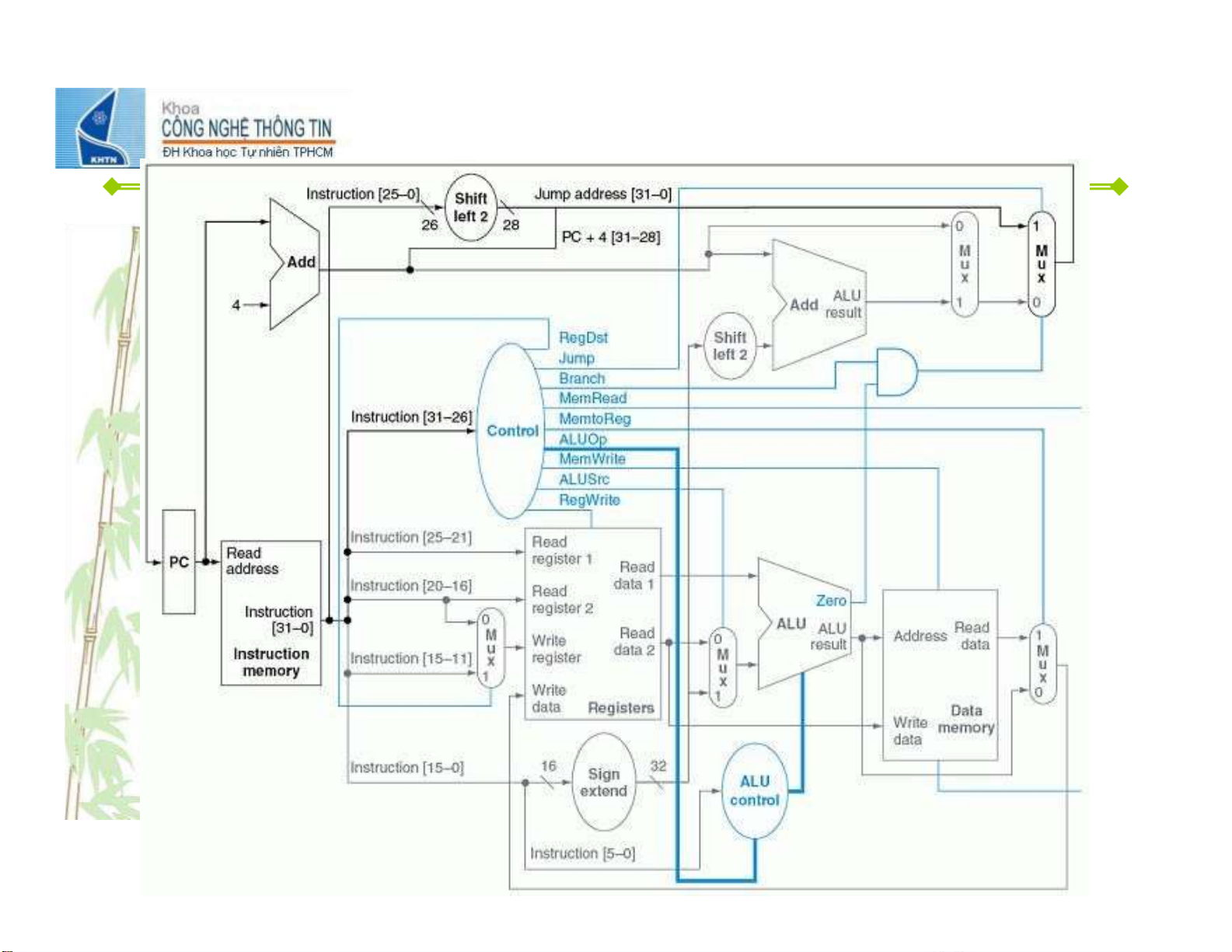
chuyển thành mạch số ở mức các linh kiện điện tử 6 lOMoAR cPSD| 59994889 Ví dụ ạ ố ế ế ở ứ m ch s thi t k m c logic 7 lOMoAR cPSD| 59994889 Mạch tổ hợp
• Kết nối các cổng logic sao cho kết quả của mạch
tại một thời điểm chỉ phụ thuộc vào giá trị đầu
vào tại thời điểm đó
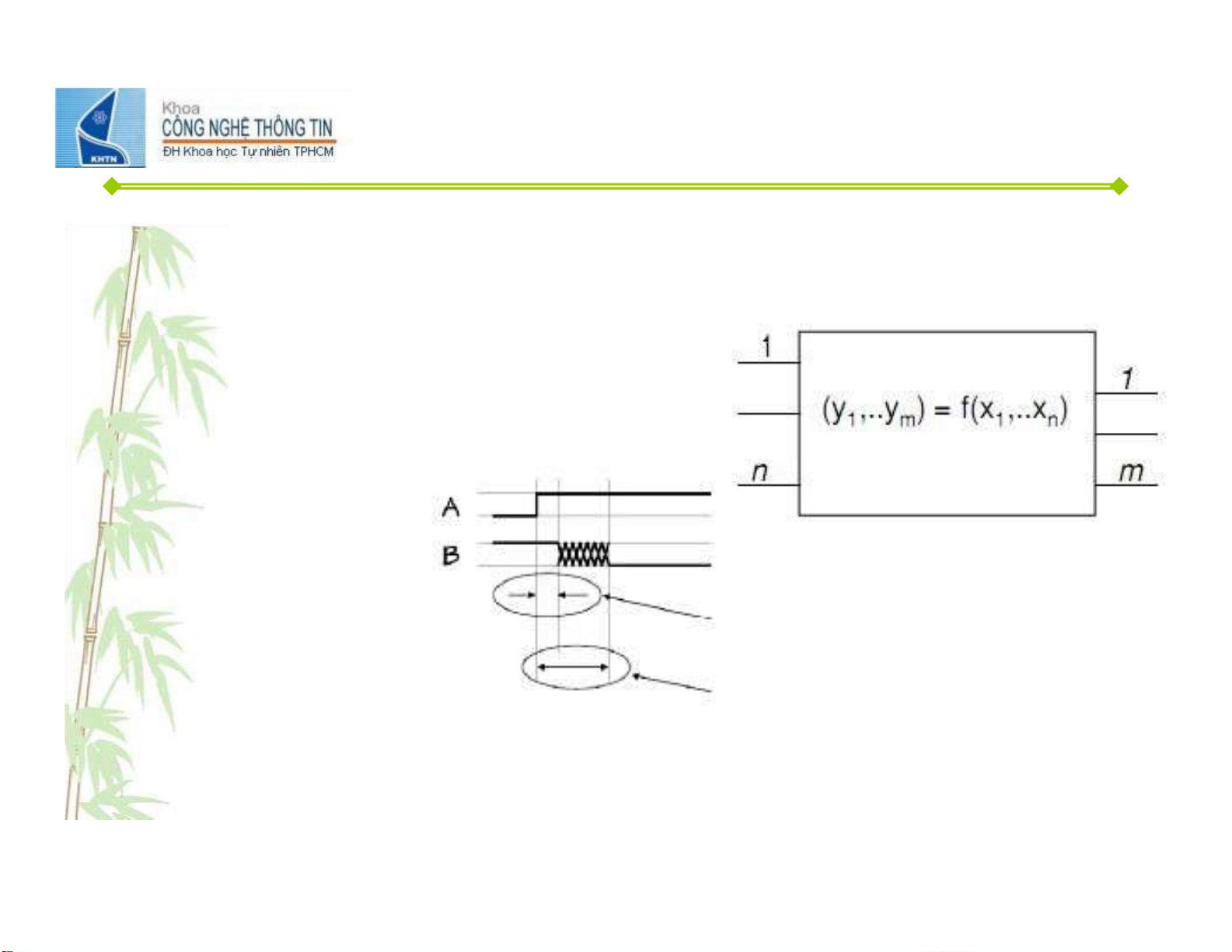
• Gồm n ngõ vào, m ngõ ra. Ngõ ra là một hàm luận lý của các ngõ vào • Luôn có một độ trễ giữa thời điểm tín hiệu vào ổn định với thời điểm tín hiệu ra ổn định (propagation delay) 8 lOMoAR cPSD| 59994889
Thiết kế mạch tổ hợp • ướ 3 b c – ậ ả ị ừ ầ L p b ng chân tr t yêu c u – ự ậ ừ ả ị Xây d ng hàm lu n lý t b ng chân tr – ẽ ơ đồ ạ ậ ử ệ V s m ch lu n lý và th nghi m 9 lOMoAR cPSD| 59994889 Lập bảng chân trị
• Từ yêu cầu, thiết lập tất cả các giá trị có thể có của các
đầu vào (n giá trị đầu vào sẽ có 2n trường hợp) và giá trị
tương ứng của các giá trị đầu ra cho từng trường hợp • Ví dụ x y z f
– Yêu cầu: thiết kế mạch tổ hợp có 3 đầu vào và 1 đầ 0 0 0 0 u ra, sao cho giá trị
logic ở đầu ra là giá trị nào chiếm đa 0 0 1 0 số trong các đầu vào 0 1 0 0
– Gọi x, y, z là các đầu vào; f là đầu ra 0 1 1 1
– Xét tất cả các khả năng có thể có của x, y, z 1 0 0 0 1 0 1 1 1 1 0 1 10 lOMoAR cPSD| 59994889
• Khó. Đôi khi phải tự đặt thêm nhiều 1 1 1 1
biến trạng thái mới có thể mô hình hóa được yêu cầu
Xây dựng hàm luận lý (1/2) • SOP (Sum Of Products)
– Với bảng chân trị cho mạch n đầu vào x1, …,
xn và một đầu ra f, ta dễ dàng thiết lập công
thức (hàm) logic theo thuật toán sau:
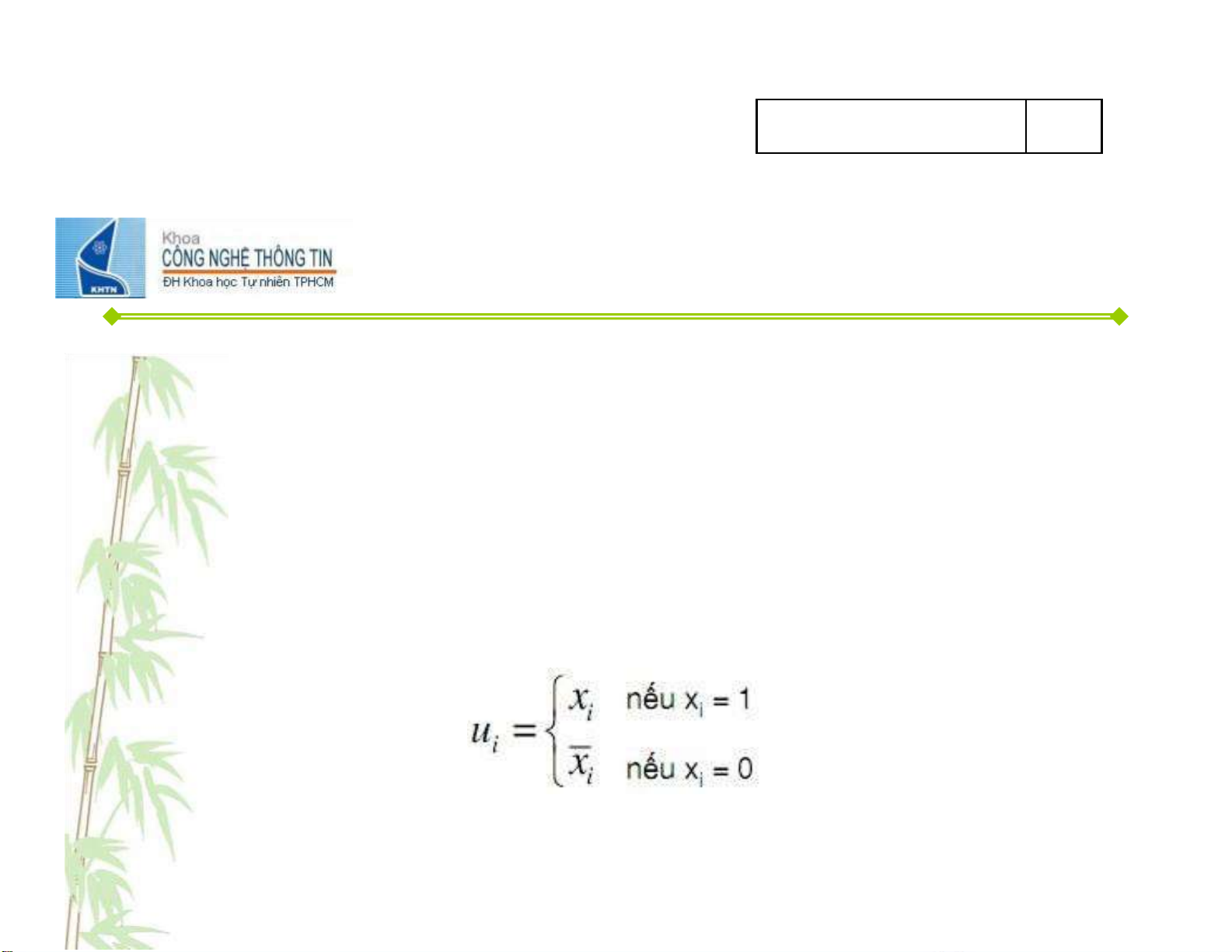
• Ứng với mỗi hàng của bảng chân trị có đầu ra bằng 1,
viết một tích dạng u1.u2…un trong đó 11 lOMoAR cPSD| 59994889
• Cộng các tích lại thành tổng, đó chính là công thức của f 12 lOMoAR cPSD| 59994889 Ví dụ SOP x y z f 0 0 0 0 0 0 1 0 0 1 0 0 0  1 1 1 x.y.z 1 0 0 0 1  0 1 1 x.y.z 1  1 0 1 x z .y. 1  1 1 1 x.y.z x f = .y.z + x. .z + x. y y. + x.y.z z 13 lOMoAR cPSD| 59994889
Xây dựng hàm luận lý (2/2) • POS (Product Of Sums) – Tr ườ đầ
ng h ợ p s ố hàng có giá tr ị u ra b ằ ng 1 nhi ề u h ơ đặ n b ằ ng 0, có th ể
t bi ế n g = NOT (f), sau đ ó vi ế t
công th ứ c d ạ ng SOP cho g, r ồ i l ấ y NOT để có công
th ứ c d ạ ng POS (tích c ủ a t ổ ng) c ủ a f – Ví d ụ 14 lOMoAR cPSD| 59994889
Rút gọn hàm luận lý (1/2)
• Mục đích: đơn giản hóa hàm logic để sơ đồ
mạch sử dụng ít cổng hơn
• Phương pháp đại số Bool 13 Downloaded by Bao Han (hanbao3006@gmail.com) lOMoAR cPSD| 59994889 Các luật cơ bản
A•B = B•A A+B = B+A Luật giao hoán
A•(B+C) = (A•B)+(A•C) A+(B•C) = (A+B)•(A+C) Luật phân phối 1•A = A 0+A = A Luật đồng nhất A•A = 0 A+A = 1 Phần tử nghịch đảo Other laws 0•A = 0 1+ A = 1 A•A = A A+A = A
A•(B•C) = (A•B)•C A+(B+C) = (A+B)+C Luật kết hợp
A•B = A+B A+B = A•B Luật DeMorgan 16
Downloaded by Bao Han (hanbao3006@gmail.com) lOMoAR cPSD| 59994889 Ví dụ ọ ằ đạ ố rút g n b ng i s Bool f = x
.y.z + x. y .z + x.y. z + x.y.z
= x .y.z + x.y.z + x. y .z + x.y.z + x.y. z + x.y.z = y.z x.z x.y = z.(x+y) + x.y 17 Downloaded by Bao Han (hanbao3006@gmail.com) lOMoAR cPSD| 59994889
Rút gọn hàm luận lý (2/2)
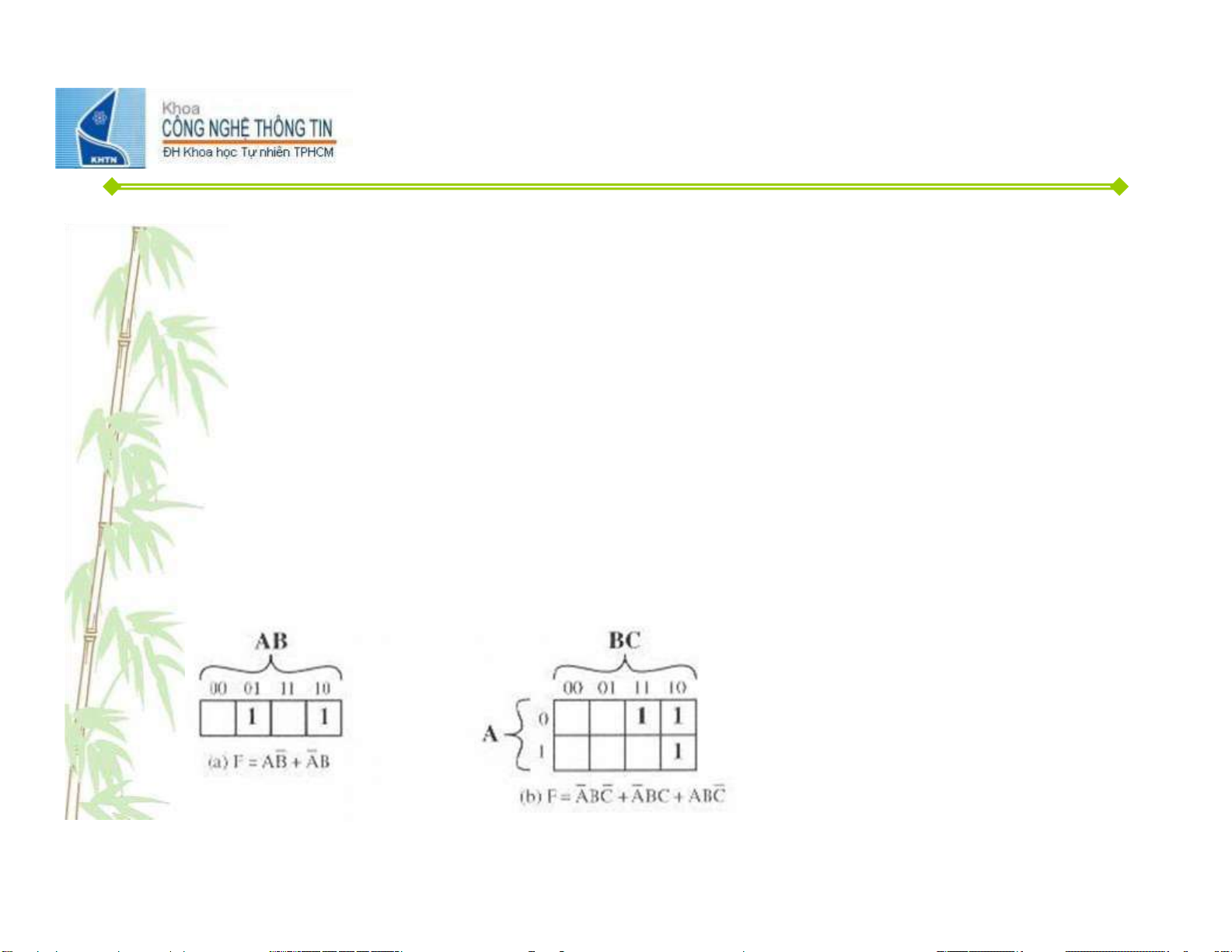
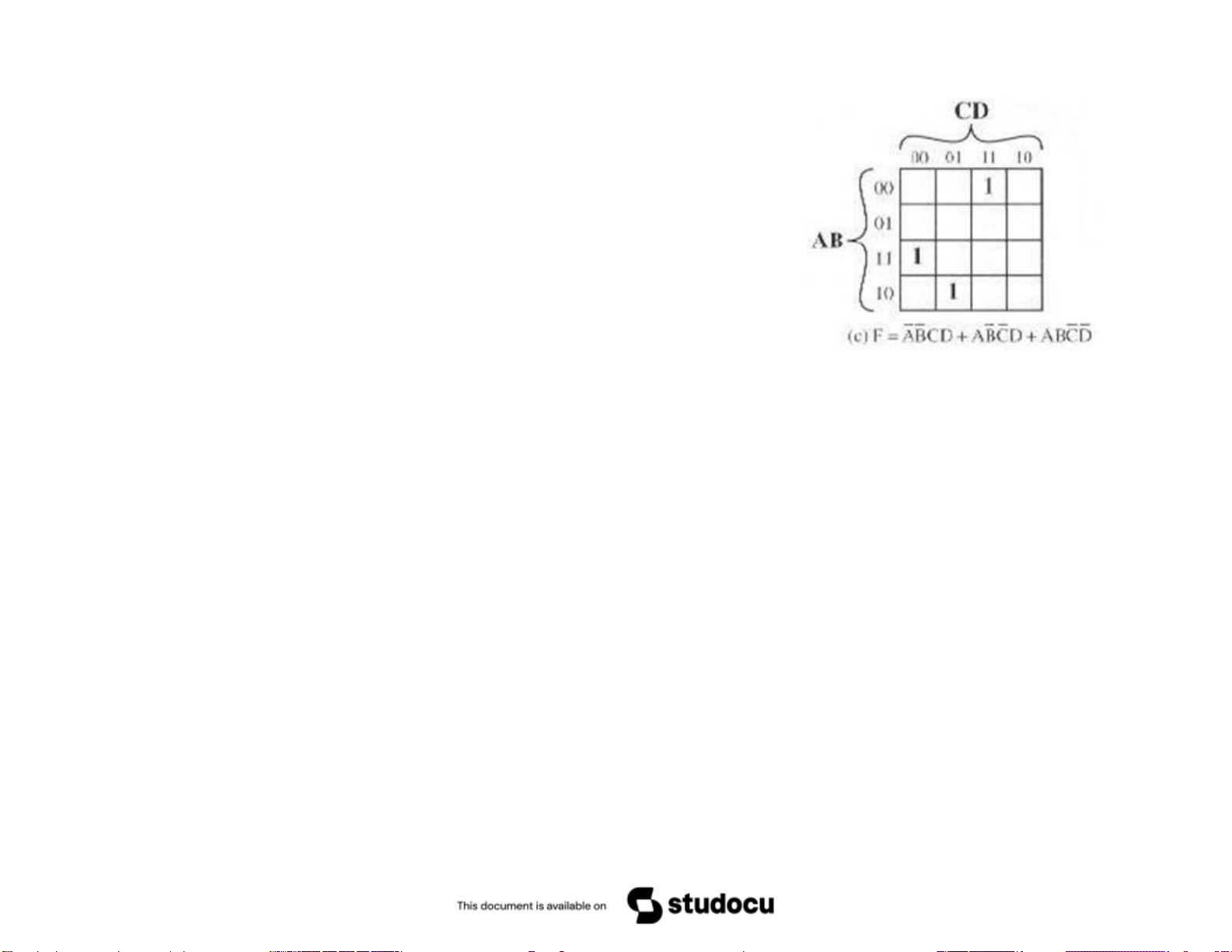
• Phương pháp biểu đồ Karnaugh
– Biểu đồ Karnaugh là một ma trận gồm 2n ô, tượng
trưng cho tất cả các trường hợp có thể có của n đầu vào
– Mỗi ô của biểu đồ Karnaugh sẽ mang giá trị hàm luận
lý của trường hợp tương ứng
– Phương pháp biểu đồ Karnaugh được sử dụng trong trường hợp n ≤ 4 18
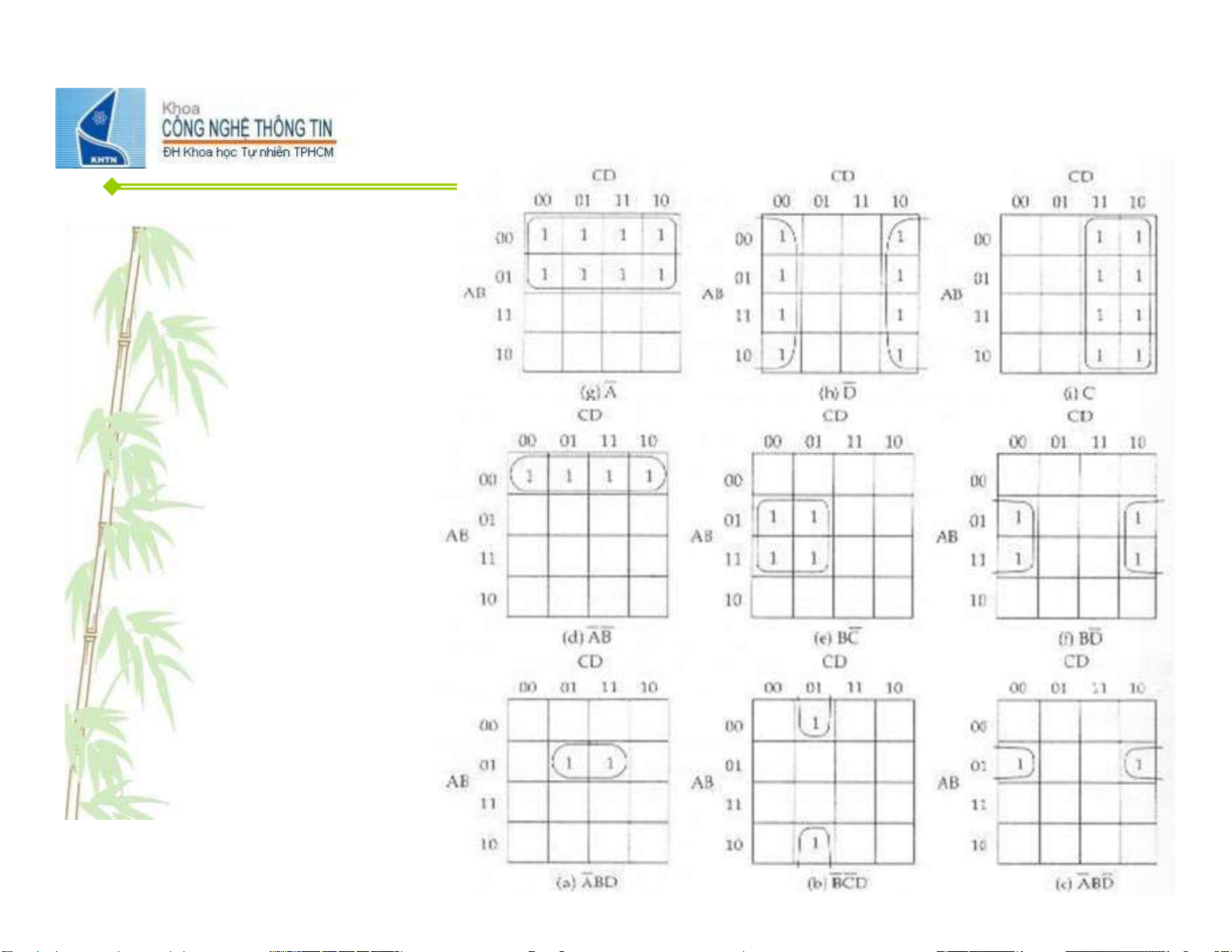
Downloaded by Bao Han (hanbao3006@gmail.com) lOMoAR cPSD| 59994889 19 Downloaded by Bao Han (hanbao3006@gmail.com) lOMoAR cPSD| 59994889 Nguyên tắ ọ ể đồ c rút g n bi u Karnaugh 1. Gom nhóm (2n , 8, 4, 2) các ô mang giá tr ị 1 2. …cho đế n khi nào không còn ô mang giá 1 nào ch ư a đượ c gom nhóm (1 ô có th ể thu ộ c nhi ề u nhóm khác nhau) 3. K ế t qu ả gom nhóm cu ố i cùng có th ể khác nhau 20
Downloaded by Bao Han (hanbao3006@gmail.com)