lOMoARcPSD| 45222017 lOMoAR cPSD| 45222017
§ 4. Ph n lớp dựa v o c y quyết định 4.1. Giới thiệu D XØt tập huấn luyện X n i , yi i
1 gồm n điểm trong kh ng gian d chiều, yi l nhªn của điểm Xi . Mỗi
điểm Xi l một bộ gồm d thuộc t nh, mỗi thuộc t nh c thể nhận giÆ trị l số hoặc category; số ph n lớp bằng k , tức l yi c c1 2, ,
,ck . Giả sử R l kh ng gian dữ liệu của D (kh ng gian chứa các điểm Xi ) .
C y quyết định sử dụng một siŒu phẳng song song với trục để chia R th nh hai miền
R1, R2 ; dẫn tới D cũng được chia th nh D1 , D2 . CÆc miền lại được chia (đệ quy) bởi cÆc siŒu phẳng
song song với cÆc trục cho đến khi cÆc miền nhận được l tinh khiết (pure), nghĩa là hầu hết các điểm
của cøng một miền đều thuộc về cøng một ph n lớp. Việc ph n chia c thứ tự miền D c thể được thể hiện
dưới dạng một c y (gọi l c y quyết định). Mỗi lÆ của c y quyết định được gÆn nhªn bởi một ph n lớp v
hầu hết cÆc phần tử tương ứng với miền đều thuộc ph n lớp đó. Để ph n lớp một điểm dữ liệu mới. Để
ph n lớp một điểm dữ liệu mới, xuất phÆt từ nœt gốc ta cần đánh giá liên tiếp xem điểm dữ liệu đó
thuộc nhÆnh n o của c y quyết định, cho đến khi đạt được nœt lÆ – nœt lÆ sẽ chỉ ra điểm dữ liệu thuộc ph n lớp n o.
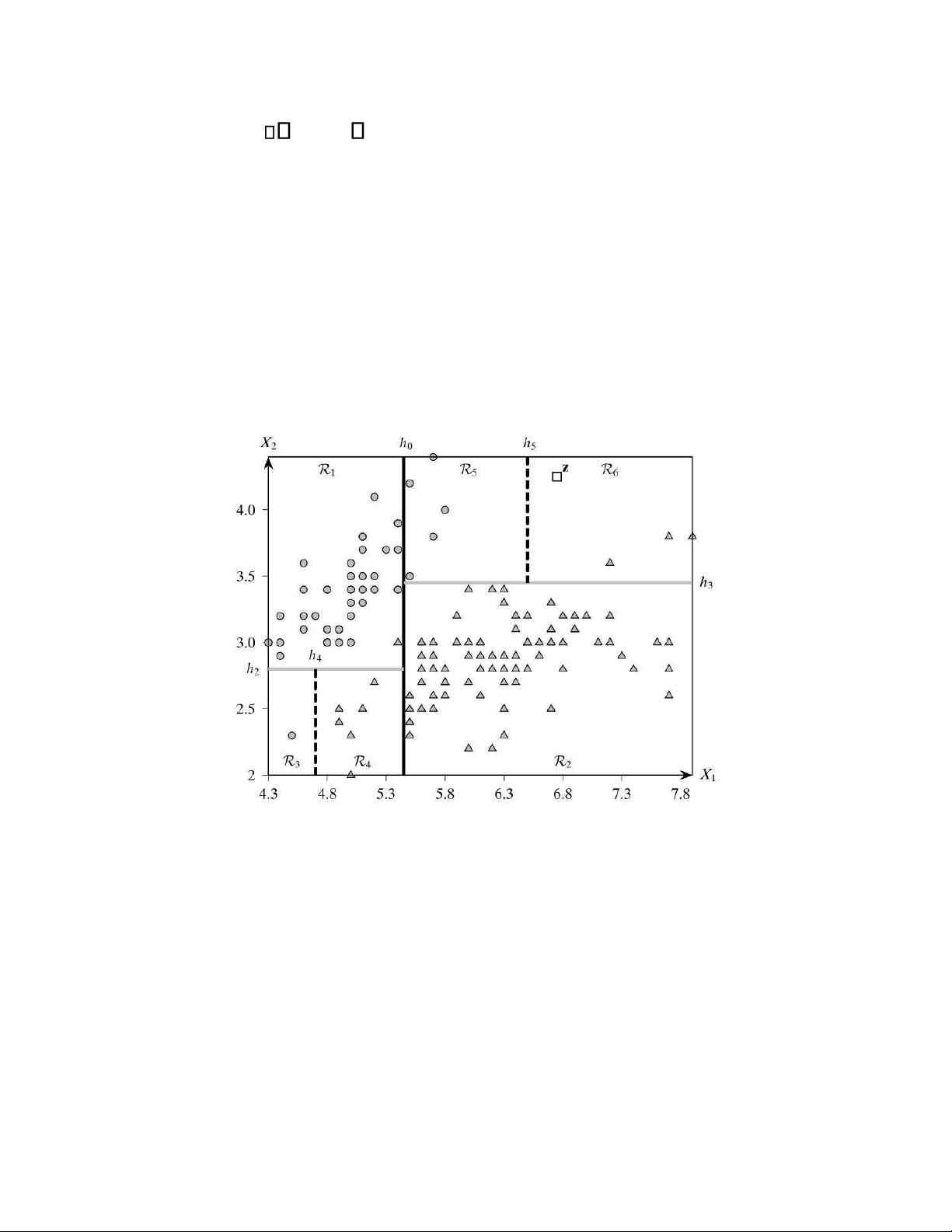
V dụ 4.1. XØt Iris dataset như hình 4.1. Ta quan tâm đến hai thuộc t nh sepal length ( x1) v sepal width (
x2 ). Ta muốn ph n dữ liệu th nh hai lớp: lớp c1 l iris-setosa (h nh tr n), lớp c2 gồm hai lo i c n lại (h nh tam
giÆc). D gồm 150 điểm dữ liệu nằm trong kh ng gian dữ liệu h nh chữ nhật R 4.3,7.9 2.0,4.4 .
Ta ph n hoạch R bởi cÆc siŒu phẳng song song với cÆc trục. Trong trường hợp hai chiều, cÆc siŒu
phẳng chính là các đường thẳng. Ta chia R (đệ quy) bởi 5 siŒu phẳng h0 , h2 , …, h5 . Tập hợp cÆc siŒu
phẳng v 6 miền tương ứng R1, R2 , …, R6 cho ta một c y quyết định. 1 lOMoARcPSD| 45222017 z XØt dữ liệu kiểm tra 6.75,4.25
T (h nh vu ng). Để dự đoán phân lớp của z , c y quyết định kiểm tra
z thuộc miền n o trong hai miền được chia ra bởi h0 . Ta thấy z thuộc nửa bŒn phải của miền được chia
ra bởi h0 . Quá trình này được lặp lại liŒn tiếp, ta thấy z thuộc miền ở ph a trŒn h3 v nằm ở miền bŒn
phải h5 . Và như vậy, z thuộc miền R6 ; ta dự đoán phân lớp của z l c2.
4.2. C y quyết định
Một c y quyết định bao gồm những nút trong dùng để biểu diễn cÆc quyết định tương ứng với siŒu
phẳng hay điểm chia. CÆc nœt lÆ biểu diễn những miền con của kh ng gian dữ liệu, được gÆn nhªn l
nhªn của những điểm dữ liệu chiếm đại bộ phận của miền.
H nh 4. 1. Iris dataset 2 lOMoARcPSD| 45222017
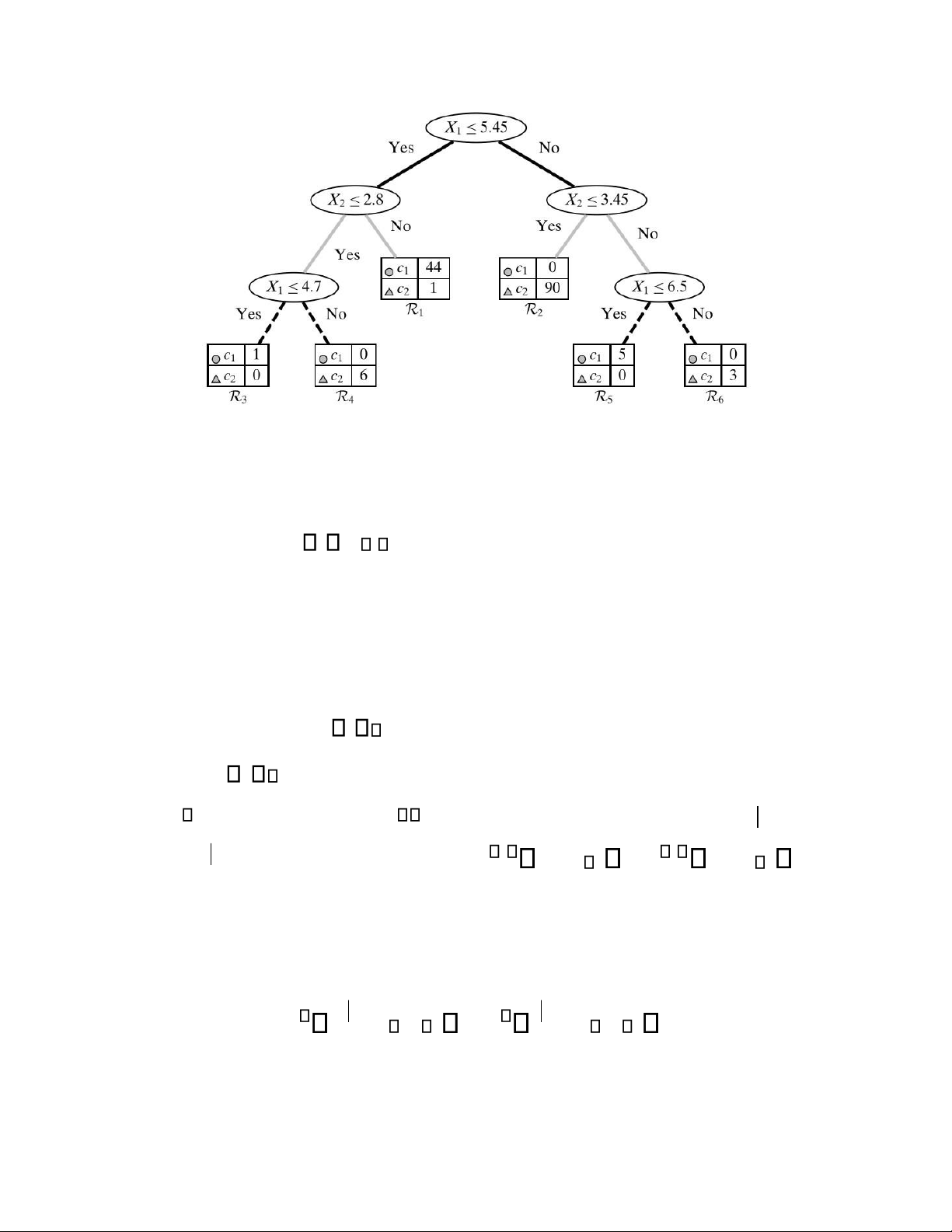
H nh 4. 2. C y quyết định tương ứng
SiŒu phẳng song song với trục
CÆc siŒu phẳng song song với trục có phương trình dạng: h X :x j b0. (4.1)
Trong đó, b là độ lệch tính đến gốc tọa độ. Mỗi cÆch chọn b cho ta một siŒu phẳng dọc theo chiều thứ j . Điểm chia
Mỗi siŒu phẳng cho ta một quyết định (tương ứng với điểm chia) giœp chia kh ng gian dữ liệu R th nh hai
nửa. Mọi điểm X thỏa mªn h X
0 nằm trŒn hoặc nằm về một ph a của siŒu phẳng, những điểm
X thỏa mªn h X
0 thuộc nửa c n lại. Để quyết định một điểm dữ liệu thuộc phần n o, ta cần so
sÆnh x bj với 0 ; tức l , so sÆnh xj với v
b . GiÆ trị v trŒn trục thứ j được gọi là điểm chia. Nhờ điểm
chia, kh ng gian dữ liệu R được chia th nh hai phần RY X R xj v v RN X R xj v .
Ph n hoạch dữ liệu
K hiệu DY v DN lần lượt là các điểm dữ liệu lần lượt thuộc về RY v RN , tức l : DY X X D x , j v
, DN X X D x , j v . 3 lOMoARcPSD| 45222017 Độ tinh khiết
Độ tinh khiết (purity) của miền Rj l tỷ lệ các điểm c nhªn chiếm đa số trong Rj : n putity D ji j maxi . (4.2) nj Trong đó, n j
Dj l tổng số điểm dữ liệu nằm trong miền Rj , nji l số lượng các điểm trong Dj v c nhªn l ci .
V dụ 2: H nh 4.2 biểu diễn diễn c y quyết định với quÆ tr nh ph n hoạch (đệ quy) dữ liệu ở h nh 4.1. Quá
trình đệ quy sẽ kết thœc khi thỏa mãn điều kiện dừng – điều kiện dừng liên quan đến kích thước v độ tinh
khiết của cÆc miền. Trong v dụ này, ta xét ngưỡng kích thước l 5 và ngưỡng tinh khiết l 0.95; tức l cÆc
miền sẽ tiếp tục được chia khi v chỉ khi c số điểm lớn hơn 5 và độ tinh khiết nhỏ hơn 0.95.
SiŒu phẳng đầu tiŒn l h X x 1
: 1 5.45 0 tương ứng với quyết định x1 5.45 ở nœt gốc của c y
quyết định. Hai nửa kh ng gian nhận được sẽ tiếp tục được chia (đệ quy) th nh cÆc nửa kh ng gian nhỏ hơn. Chẳng hạn, miền x 1
5.45 lại tÆch bởi biŒu phẳng h2 X : x2
2.8 0 tương ứng với quyết định x2
2.8 tương ứng với nœt con bŒn trÆi của nœt gốc. Ta thấy c 7 điểm thuộc miền x 2 2.8; trong
đó, c 1 điểm thuộc ph n lớp c
1 v 6 điểm thuộc ph n lớp c2. Độ tinh khiết của miền x2 2.8 l 6/7 0.857. Như vậy, miền x 2
2.8 c nhiều hơn 5 điểm và có độ tinh khiết nhỏ hơn 0.95 v do đó, miền n y sẽ được
tiếp tục chia bởi siŒu phẳng h 4 X : x1
4.7 0 tương ứng với quyết định x1 4.7 .
Ta quay lại xØt nửa kh ng gian bŒn phải siŒu phẳng h 2 , tức l miền x2
2.8. Miền n y chứa 45 điểm; tuy
nhiên độ tinh khiết l 44/ 45 0.98, vượt quÆ 0.95. Do đó, miền n y kh ng cần tÆch nữa. Miền x 2 2.8
trở th nh nœt lÆ của c y quyết định và được gÆn nhªn l c1. Các độ đo thường xuyŒn của nœt
lÆ cần được lưu lại để đánh giá tỷ lệ lỗi của luật ph n lớp tương ứng.
Categorical Attributes (thuộc t nh kh ng phải l số) 4 lOMoARcPSD| 45222017
C y quyết định cũng được sử dụng cho dữ liệu kh ng phải l số. Chẳng hạn, thuộc t nh xj kh ng phải l số v
nhận giÆ trị trŒn dom x j
. Khi đó, ta sử dụng cÆc quyết định c dạng xj V ; trong đó, V dom x j Luật quyết định
Một trong những ưu điểm của c y quyết định l cho ta một m h nh dễ h nh hiểu. Đặc biệt, một c y quyết
định c thể được xem l một tập luật quyết định. Mỗi luật quyết định gồm tiền tố v hậu tố: tiền tố bao gồm
cÆc quyết định trŒn cÆc nœt dọc theo đường đi đến lÆ, hậu tố l nhªn của lÆ.
V dụ 3: C y quyết ở hình 4.2 được biểu diễn bởi tập luật sau đây: R 1: If X1 5.45 and X2 2.8 and X1
4.7 , then class is c1; R 2 : If X1 5.45 and X2 2.8 and X1 4.7, then class is c2; R 3: If X1 5.45 and X2 2.8, then class is c1;
R4 : If X1 5.45 and X2 3.45 , then class is c2; R 5: If X1
5.45and X2 3.45 and X1
6.5 , then class is c1; R 6 : If X1
5.45 and X2 3.45and X1 6.5, then class is c2.
4.3. Thuật toÆn c y quyết định
Giả mª của thuật toÆn sinh c y quyết định được cho trong h nh 4.3. Đầu v o của thuật toÆn l tập huấn
luyện D, giÆ trị ngưỡng của leaf size , giÆ trị ngưỡng của độ tinh khiết . 5 lOMoARcPSD| 45222017
H nh 4. 3. Thuật toÆn sinh c y quyết định
4.3.1. Các độ đo được dùng để đánh giá điểm chia
Trong các trường hợp xj nhận giÆ trị số v xj nhận giÆ trị kh ng phải l số điều kiện quyết định (tương ứng
với điểm chia) c dạng x j v v x Vj
. Ta cần các phương pháp chấm điểm để biết điểm chia như thế n o l tốt. Entropy
Entropy đo độ hỗn độn hay độ kh ng chắc chắn của một hệ thống. Trong b i toÆn ph n lớp, mỗi một miền
sẽ c entropy c ng thấp nếu n c ng tinh khiết, nghĩa là chứa hầu hết cÆc điểm thuộc về cøng một lớp.
Entropy của tập dữ liệu c nhªn D được xác định như sau: k H D P c D i log2 P c D i . (4.3) i 1 6 lOMoARcPSD| 45222017 Trong đó, P c D i
l xÆc suất ph n lớp ci xuất hiện trong D; k l số lượng ph n lớp. Nếu một miền ho n
to n tinh khiết th sẽ c entropy bằng 0 . Một miền ho n to n hỗn độn sẽ c entropy bằng log2 k .
Giả sử một điểm chia thực hiện tÆch D th nh DY v DN . Ta định nghĩa split entropy l trung b nh c trọng số
entropy của cÆc nửa nhận được: H D D nY nN Y , N H D Y H D N . (4.4) n n n D Trong đó, , n Y DY v nN DN .
Tỷ lệ tăng th ng tin (information gain) của điểm chia được định nghĩa như sau: Gain D D , X ,DY H D
H D D Y ,N . (4.5)
Tỷ lệ tăng thông tin càng cao thì điểm chia c ng tốt. Do đó, ta có thể chọn điểm chia sao cho tỷ lệ tang th ng tin lớn nhất. Chỉ số Gini
Một phương pháp khác để đánh giá điểm chia l sử dụng chỉ số GINI. Chỉ số GINI được định nghĩa như sau: k G D 1 P c D 2 i . (4.6) i 1
Nếu một miền ho n to n tinh khiết th sẽ c chỉ số GINI bằng 0 . Một miền ho n to n hỗn độn sẽ c chỉ k 1 số GINI bằng . k
Chỉ số GINI c trọng số của điểm chia được định nghĩa như sau: Y N nY Y nN N G D D,
G D G D . n n n D Trong đó, , n Y DY v nN DN . 7 lOMoARcPSD| 45222017
Chỉ số GINI c ng thấp thì điểm chia c ng tốt.
Một độ đo khác có thể được dùng để thay thế cho entropy v chỉ số GINI l CART (Classification And
Regression Trees measure): CART D D Y ,N 2 nY nN k P c D iY P c D i N . (4.7) n n i 1
Độ đo CART càng cao thì điểm chia c ng tốt.
4.3.2. Xác định điểm chia
GiÆ trị của các độ đo được dùng để đánh giá điểm chia (entropy, chỉ số GINI, CART) phụ thuộc v o h m
khối xÆc suất (probability mass function, PMF) của cÆc ph n lớp trŒn D, trŒn DY , DN tức l các đại lượng P c D i , P c D
iY v P c D iN . Thuộc t nh l số
Giả sử X l thuộc t nh nhận giÆ trị l số. Ta cần đánh giá các điểm chia c dạng X v . Ta thấy rằng c v số
cÆch chọn v . C một cÆch hợp lý hơn là xét v l trung b nh cộng của hai giÆ trị kế tiếp khÆc nhau của D t
nh trŒn chiều X . Nếu D c n giÆ trị ph n biệt t nh theo chiều X th ta chỉ cần xØt n 1 giÆ trị của v .
Giả sử cÆc giÆ trị cần xØt của v l v v 1 2, , ,vm (v1
v2 vm ). Với mỗi v , ta cần t nh xÆc h m xÆc suất khối: P c D iY P c X v i , (4.8) P c D
iN P c X v i . (4.9) Theo định l Bayes: i P X vc P c i i P X vc P c i i P c X v k . (4.10) 8 lOMoARcPSD| 45222017 P X v P X vc P c j j j 1 Lại c : P cˆ 1 k I y c ni . (4.11) i n j 1 j i n n D
Trong đó, I l h m chỉ, y j l ph n lớp của X j ,
, ni l số điểm của D thuộc ph n lớp ci . K hiệu Nvi l số điểm
đồng thời thỏa mªn xj v v thuộc ph n lớp ci , trong đó xj l giÆ trị thuộc t nh X của X j : k Nvi I x j vand yj ci . (4.12) j 1 Do đó: P Xˆ v c i P Xˆ v iand ci 1 jn1 I x j v and yj c i ni P cˆ n n (4.13) Nvi . ni
Thay (4.11) v (4.13) v o (4.10): N (4.14) P c D vi iY P c X v i k . Nvj j 1 Ta c : 9 lOMoARcPSD| 45222017 . (4.15) P X vcˆ i 1 P X vcˆ i 1 N vi n Ni vi ni ni Từ (4.11) v (4.15) suy ra: P c D iN P c X v i k P X vc P c i i k n Ni vi . (4.16) P X vc P c j j n Nj vj j 1 j 1
H nh 4.4 l mª giả của thuật toán xác định điểm chia trong trường hợp thuộc t nh X nhận giÆ trị l số. Ta
thấy độ phức tạp của thuật toÆn l O n logn .
V dụ 4: XØt tiếp Iris dataset l tập dữ liệu D c số điểm dữ liệu l n 150 . Ta c n1 50 (iris-setosa) v n2 100 (c n lại). Do đó: P c 1 50 1 ; P c 2 100 2 . 150 3 150 3 10 lOMoARcPSD| 45222017
H nh 4. 4. Thuật toán xác định điểm chia trong trường hợp thuộc t nh X nhận giÆ trị l số
Do đó, theo c ng thức (4.3), entropy của D l : 1 2 H D 1 log 2 2 log2 0.918 . 3 3 3 3
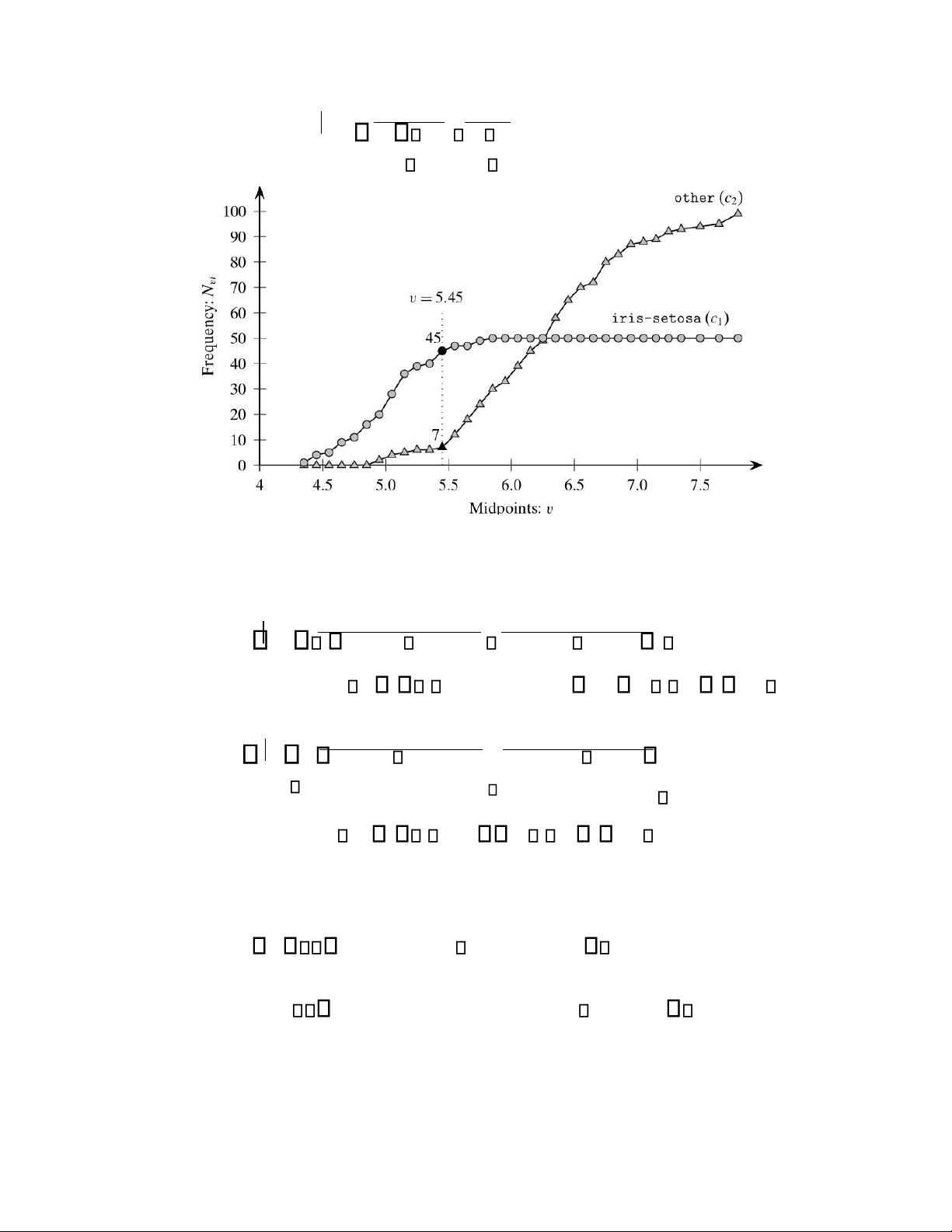
XØt thuộc t nh X1. Để đánh giá các điểm chia, ta cần t nh cÆc tần số Nvi (c ng thức 4.12) . CÆc giÆ trị Nvi
được thể hiện ở h nh 4.5. Xét điểm chia X1 5.45, ta c : N v1 45, Nv2 7.
Thay vào phương trình (4.14): P c D 1Y Nv1 45 0.865, Nv1 Nv2 45 7 11 lOMoARcPSD| 45222017 P c D Nv2 7 2Y 0.135 . Nv1 Nv2 45 7
H nh 4. 5. CÆc tần số N_{vi}
Từ phương trình (4.16), ta có: P c D 1N n N1 v1 50 45 0.051, n N 1 v1 n N2 v2 50 45 100 7 2N n2 Nv2 100 7 P c D 0.949 . n 1 Nv1 n2Nv2 50 45 100 7
Suy ra entropy của DY , DN : H D Y
0.865log2 0.865 0.135log2 0.135 0.571, H D( N ) 0.051log 0.051 0.949log2 2 0.949 0.291. Theo phương trình (4.4): 12 lOMoARcPSD| 45222017 H D D 52 Y ,N H D( Y ) 98 H D( N ) 0.388. 150 150
Suy ra tỷ lệ tăng th ng tin của điểm chia l :
Gain H D -H D D Y ,N 0.918 0.388 0.53.
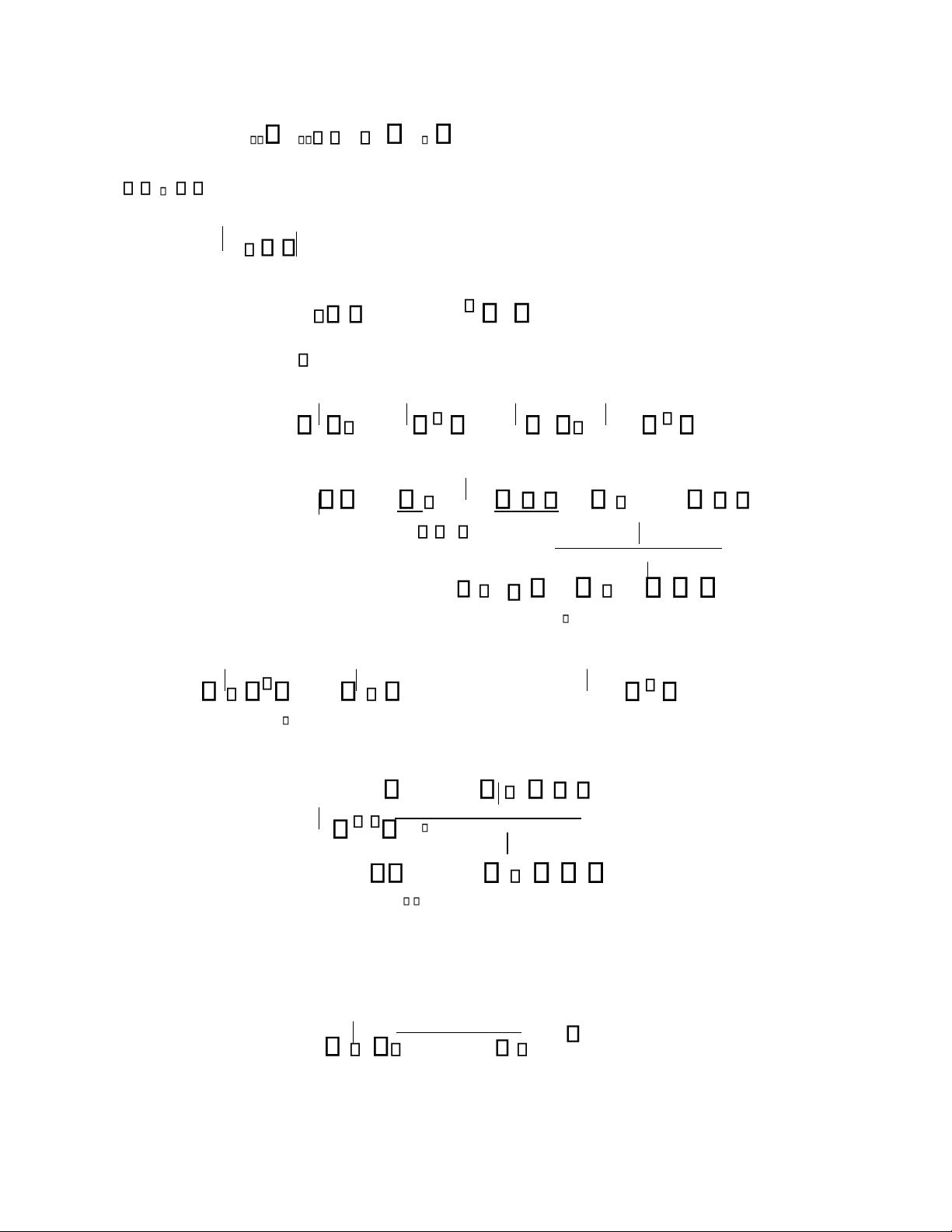
Tương tự, ta c thể tính được tỷ lệ tăng th ng tin cho tất cả các điểm chia trŒn cả thuộc t nh X1 , X2 như trong hình 4.6.
H nh 4. 6. Tỷ lệ tăng thông tin
Ta thấy rằng điểm chia X 5.45 l tốt nhất và được chọn l gốc của c y quyết định. Thuật toÆn lại tiếp diễn
một cách đệ quy v cuối cùng ta thu được c y quyết định.
Thuộc t nh kh ng l số
Nếu thuộc t nh X kh ng phải l số thì các điểm chia c dạng X V với V dom X v V . Khi X V
ph n hoạch bởi điểm chia X V ta được cøng kết quả khi ph n hoạch bởi điểm chia với
V dom X \V . Do đó, số cÆc ph n hoạch cần xØt l : 13 lOMoARcPSD| 45222017 m m/2 O 2m 1 . (4.17) i 1 i m dom X Trong đó,
. Ta thấy số cÆch ph n hoạch l một hàm mũ, dẫn đến khó khăn trong tính toÆn
khi m lớn. Một tiếp cận nhằm đơn giản h a vấn đề đã nêu là chỉ xét các trường hợp m V c một phần tử,
nghĩa là điểm chia c dạng X j v với v dom X j .
Để đánh giá điểm chia X V , ta cần t nh cÆc h m khối xÆc suất: P c D iY P c X V i , P c D iN P c X V i .
Sử dụng c ng thức Bayes, ta c : i P X V c P ci iP X V c P ci i
P c X V k .
P X V P X V c j P cj j 1 Ta c P X V c i P X vc
i . Suy ra, c ng thức t nh P c X V i được viết lại như sau: v V P X vc P c i i P c X V v V i k . (4.18) P X vc P c j j j 1 v V
K hiệu nvi l số phần tử thuộc D c giÆ trị thuộc t nh X bằng v v thuộc ph n lớp ci . Ta c : ˆ P X v c i P X vand cˆ i 14 lOMoARcPSD| 45222017 P cˆ i n vi ni n n n vi . (4.19) ni
Thay (4.19) v o (4.18), ta được: P Xˆ v c P c ˆ i i nvi P Xˆ v cj P cˆ j nvj P c D iY k v V kv V . (4.20) j 1 v V j 1 v V Tương tự, ta cũng có nvi P c D v V iY k . (4.21) nvj j 1 v V
H nh 4.7 l giả mª của thuật toán xác định điểm chia trong trường hợp thuộc t nh X kh ng phải l số. 1
Trong đó, l l số phần tử tối đa của V , do người dùng định nghĩa ( n m2 ). 15 lOMoARcPSD| 45222017
H nh 4. 7. Thuật toán xác định điểm chia cho thuộc t nh kh ng phải l số
4.3.3. Độ phức tạp
Ta chứng minh được độ phức tạp của thuật toÆn x y dựng c y quyết định l O dn 2 logn . 16