Bài giảng Chương 3: Phương trình Schrödinger môn Vật lý hiện đại | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

VẬT LÝ HIỆN ĐẠI CHƯƠNG 3
PHƯƠNG TRÌNH SCHRÖDINGER 1 Nội dung ➢ Phương trình Schrödinger ➢ Hạt chuyển động trong hố thế một chiều
➢ Hiệu ứng đường ngầm 2
Phần 1: Phương trình Schrödinger
➢ Được khám phá bởi nhà Vật lý học
người Áo - Erwin Schrödinger, vào năm 1925
➢ Đạt giải Nobel vào năm 1933
➢ Là một khám phá quan trọng trong cơ
học lượng tử – cũng giống như định
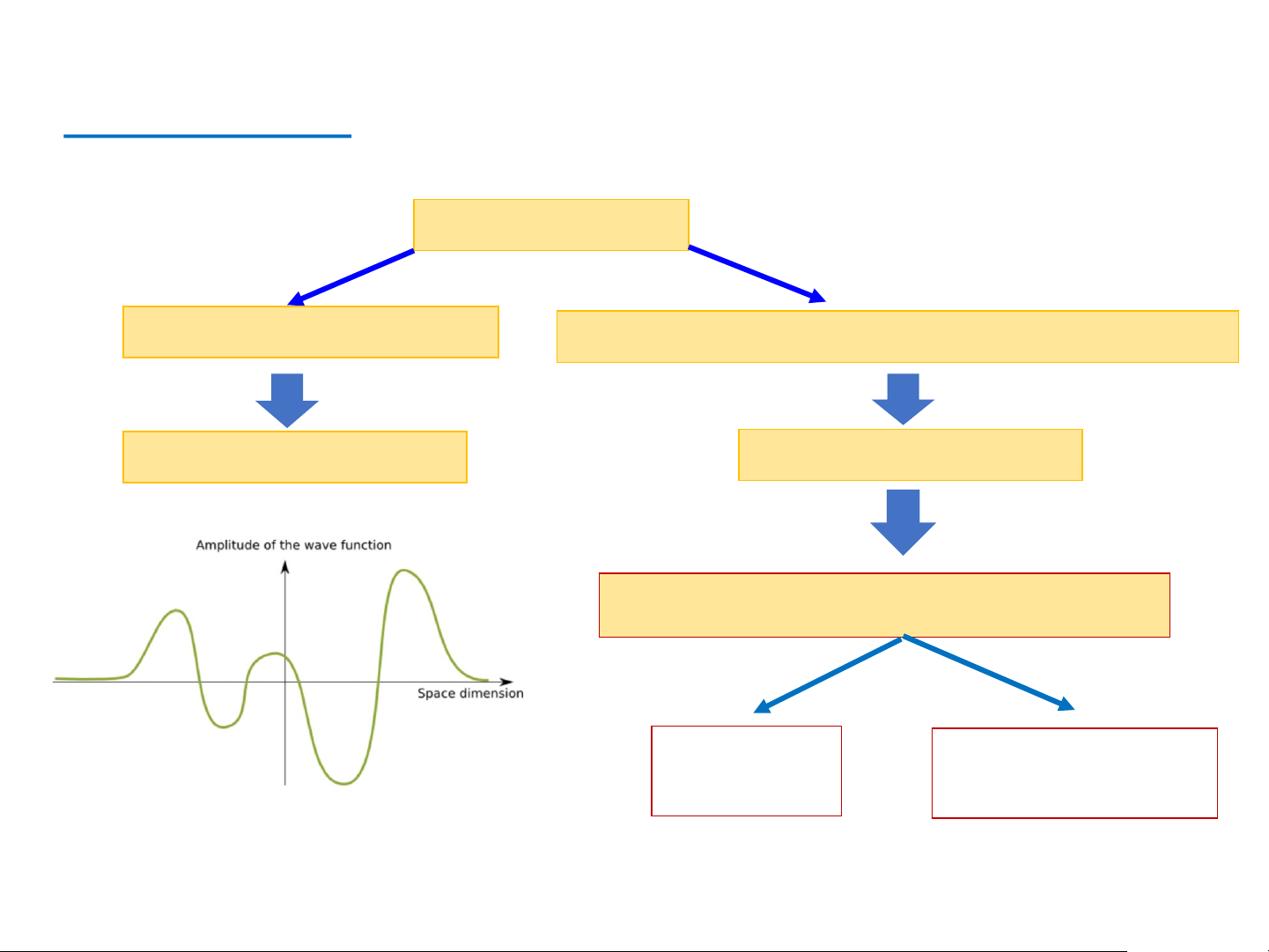
luật 2 Newton trong cơ học cổ điển 3 Hàm sóng HÀM SÓNG
Tính chất, khái niệm
Tìm như thế nào, dựa vào phương trình nào? Đã biết Chưa biết
Phương trình Schrödinger Phụ thuộc Không phụ thuộc thời gian thời gian 4
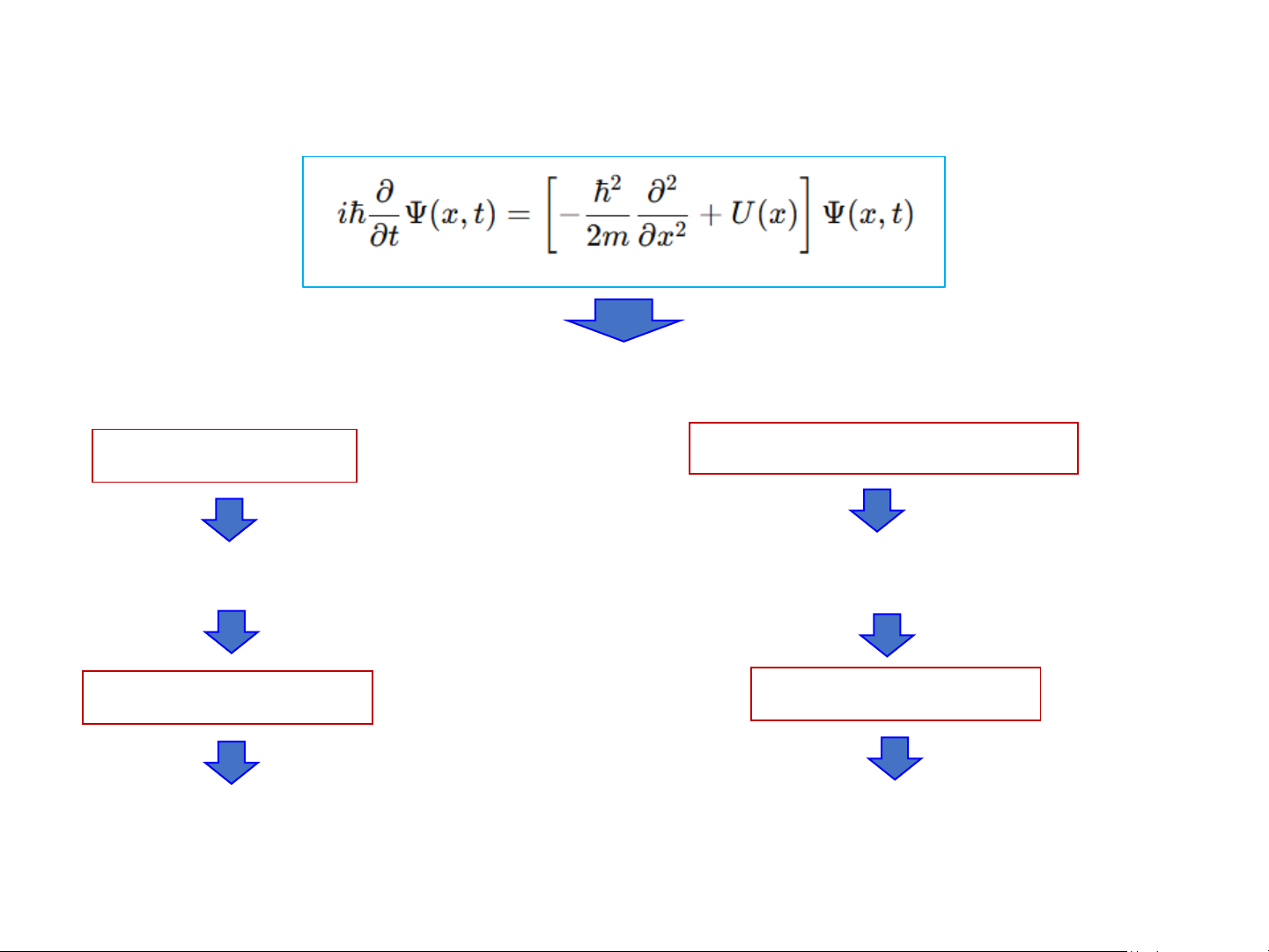
Phương trình Schrödinger phụ thuộc thời gian (1)
Phương trình Schrödinger cho hạt có khối lượng 𝑚 chuyển động một chiều 𝑥 Cơ học cổ điển Cơ học lượng tử Phương trình Newton
Phương trình Schrödinger F = ma (1)
Giải phương trình cho ta biết
Giải phương trình cho ta biết
vị trí của hạt theo thời gian
xác suất của hạt trong không gian theo thời gian 5
Phương trình schrödinger phụ thuộc thời gian
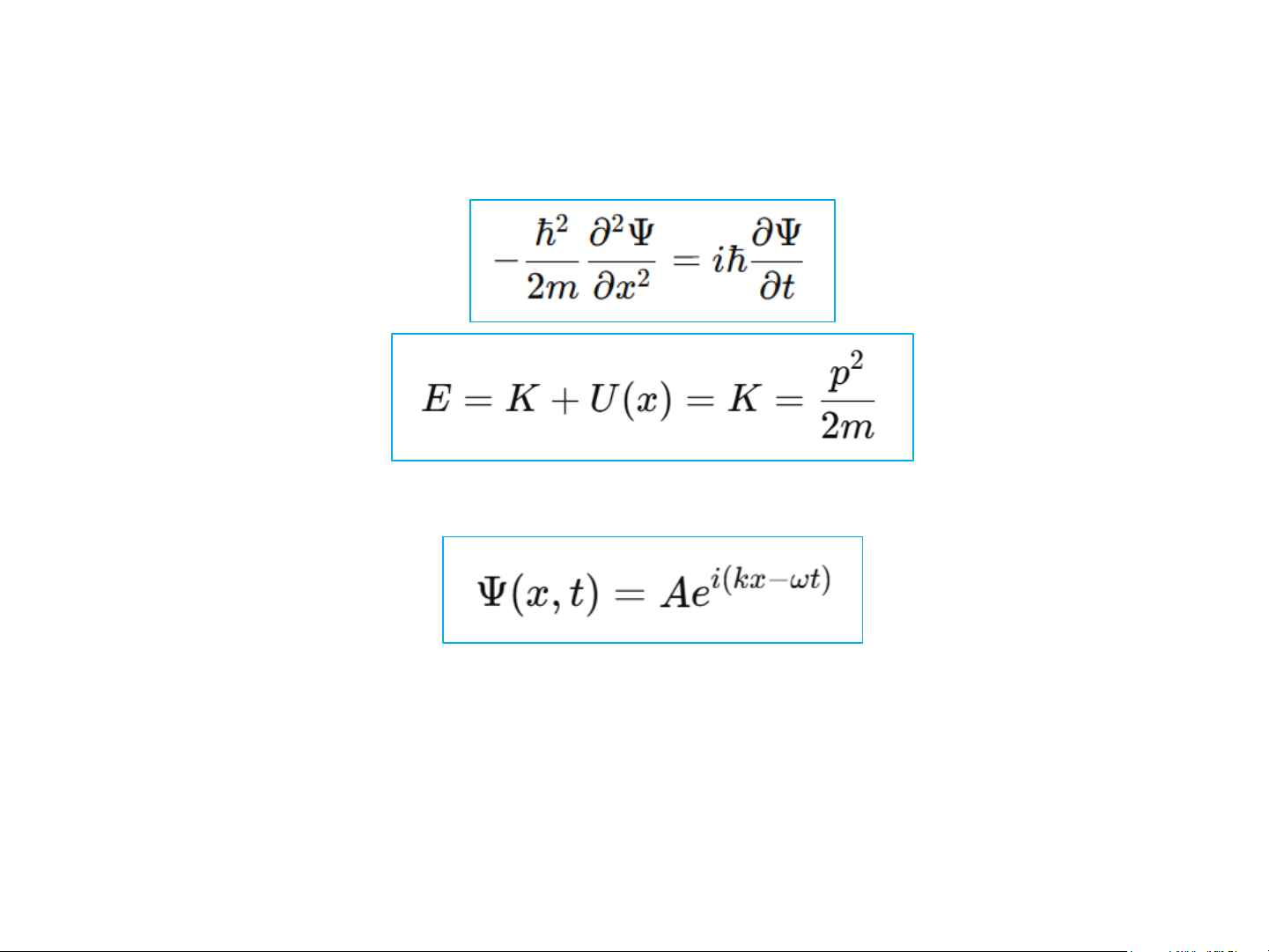
Đối với hạt tự do (𝑈(𝑥) = 0): (2) (3)
Hàm sóng có thể được biểu diễn dưới dạng: (4) • 𝑘 = 2 Τ 𝜋 𝜆 : số sóng
• 𝜔 = 2𝜋𝑓: tần số vòng 6
Phương trình Schrödinger không phụ thuộc thời gian i(kx−t) (x, t) = Ae (5)
Tách hàm sóng thành 2 hàm: phụ
thuộc không gian và thời gian −iEt /  (x, t) = (x)e (6) Phụ thuộc không gian Phụ thuộc thời gian 2 2 d (x) −iEt/ −iEt /  −iEt /  −iEt /  − e + U(x)(x)e = i( iE − / )e (x) = E(x)e 2 2m dx Rút gọn, ta thu được: 7
Phương trình Schrödinger không phụ thuộc thời gian 2 d2(x) −  + U(x)(x) = E(x) (7) 2m dx2 d2(x) 2m Sắp xếp lại: + E − U(x)(x) = 0 (8) dx2 2 
Phương trình Schrödinger cho hạt chuyển động một chiều
CHÚNG TA SẼ LÀM VIỆC TRÊN PHƯƠNG TRÌNH NÀY
Áp dụng giải nghiệm Dạng 1: Dạng 2:
cho phương trình vi y’’ - k2y = 0 y’’ + k2y = 0 phân ➔ Có nghiệm: ➔ Có nghiệm: y = Asinh(kx) + Bcosh(kx) y = Asin(kx) + Bcos(kx)
Hoặc y = Aexp(+kx) +Bexp(-kx) Hoặc y = Aexp(+ikx) +Bexp(-ikx) 8
Điều kiện của hàm sóng
Ngoài điều kiện chuẩn hoá của hàm sóng,
➢ Hữu hạn, nếu không thì điều kiện chuẩn hóa không được thỏa mãn,
➢ Đơn trị, vì ứng với mỗi trạng thái, tại một vị trí và tại một thời điểm chỉ có
một xác suất tìm thấy hạt,
➢  và đạo hàm bậc nhất của nó theo các tọa độ không gian phải liên tục.
Điều kiện này là do phương trình Schrödinger có chứa các đạo hàm bậc
hai của  theo các tọa độ không gian. Để phương trình có nghĩa, đạo hàm
bậc hai của  phải hữu hạn, muốn vậy thì  và đạo hàm bậc nhất của nó
theo tọa độ phải liên tục. 9
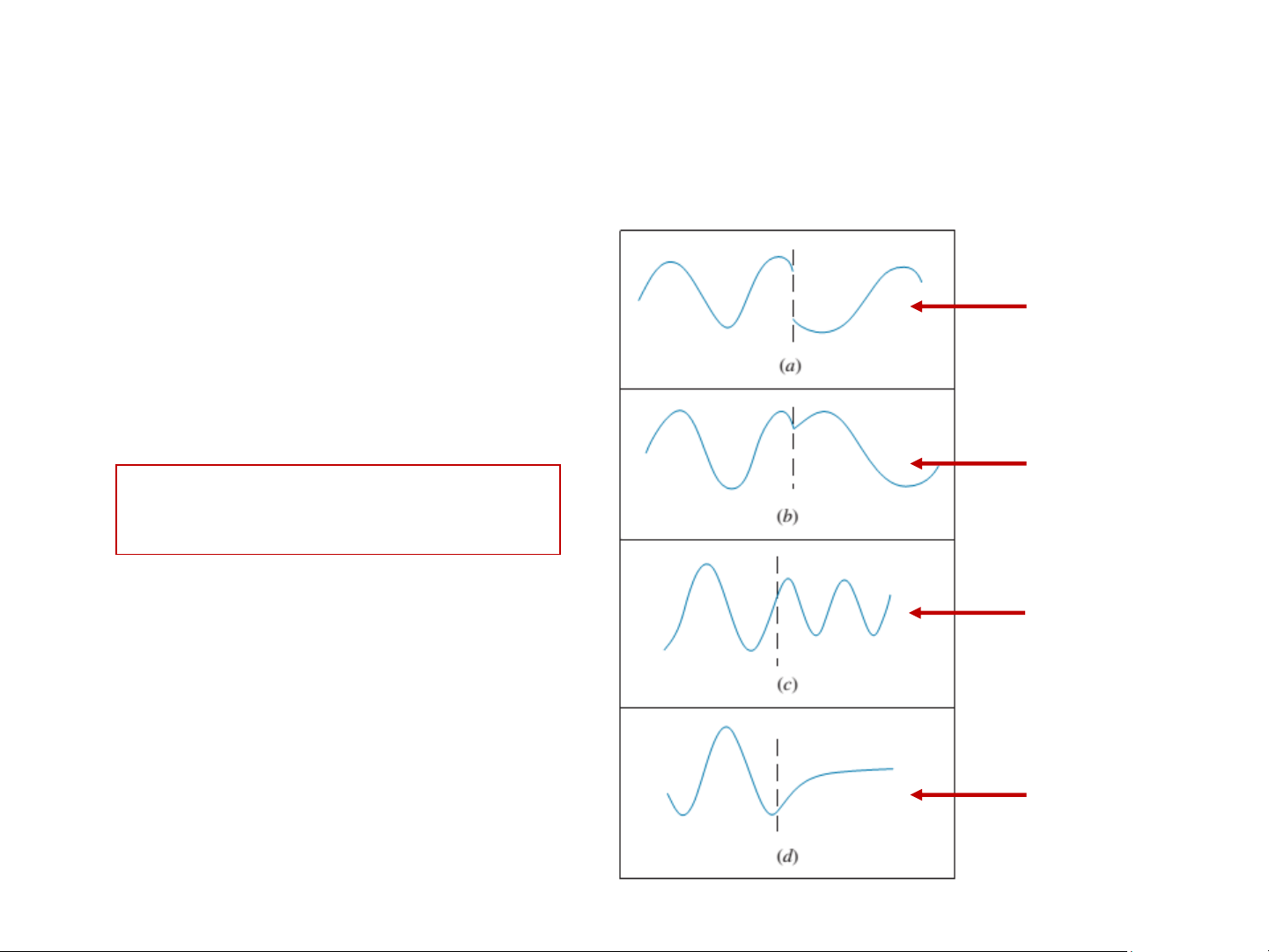
Thảo luận: Điều kiện của hàm sóng KHÔNG KHÔNG HÀM SÓNG NÀO THỎA ĐIỀU KIỆN LIÊN TỤC? THỎA THỎA 10
Phần 2: Hạt trong hố thế một chiều 11
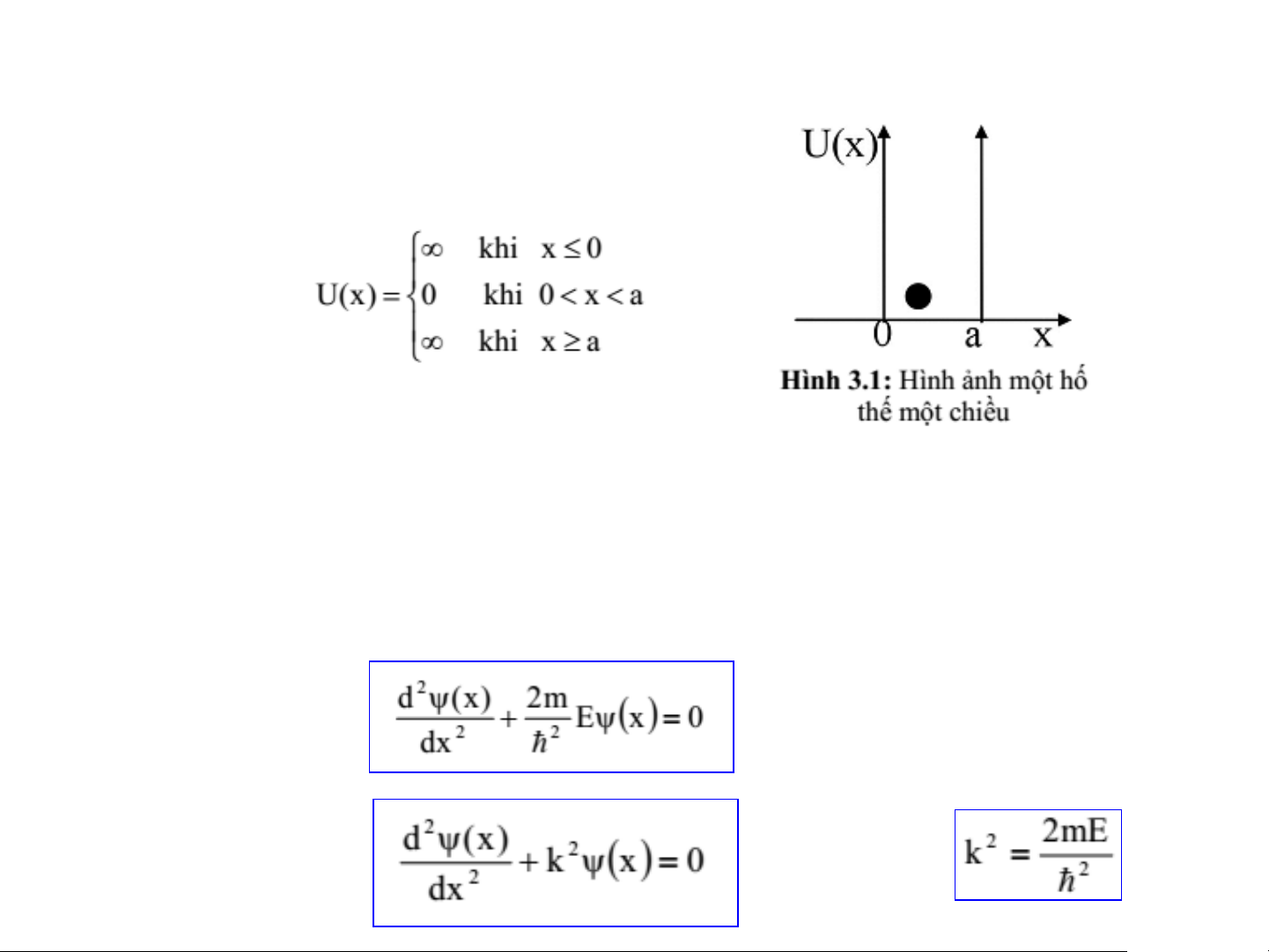
Hạt trong hố thế một chiều Thế năng:
• 0 < 𝑥 < 𝑎: 𝑈(𝑥) = 0 → hạt chuyển động tự do trong hố thế
• Bên ngoài: 𝑈(𝑥) lớn nên hạt không thể nhảy ra ngoài
❖ Phương trình Schrödinger trong trường hợp này: hay (9) với 12
Hạt trong hố thế một chiều
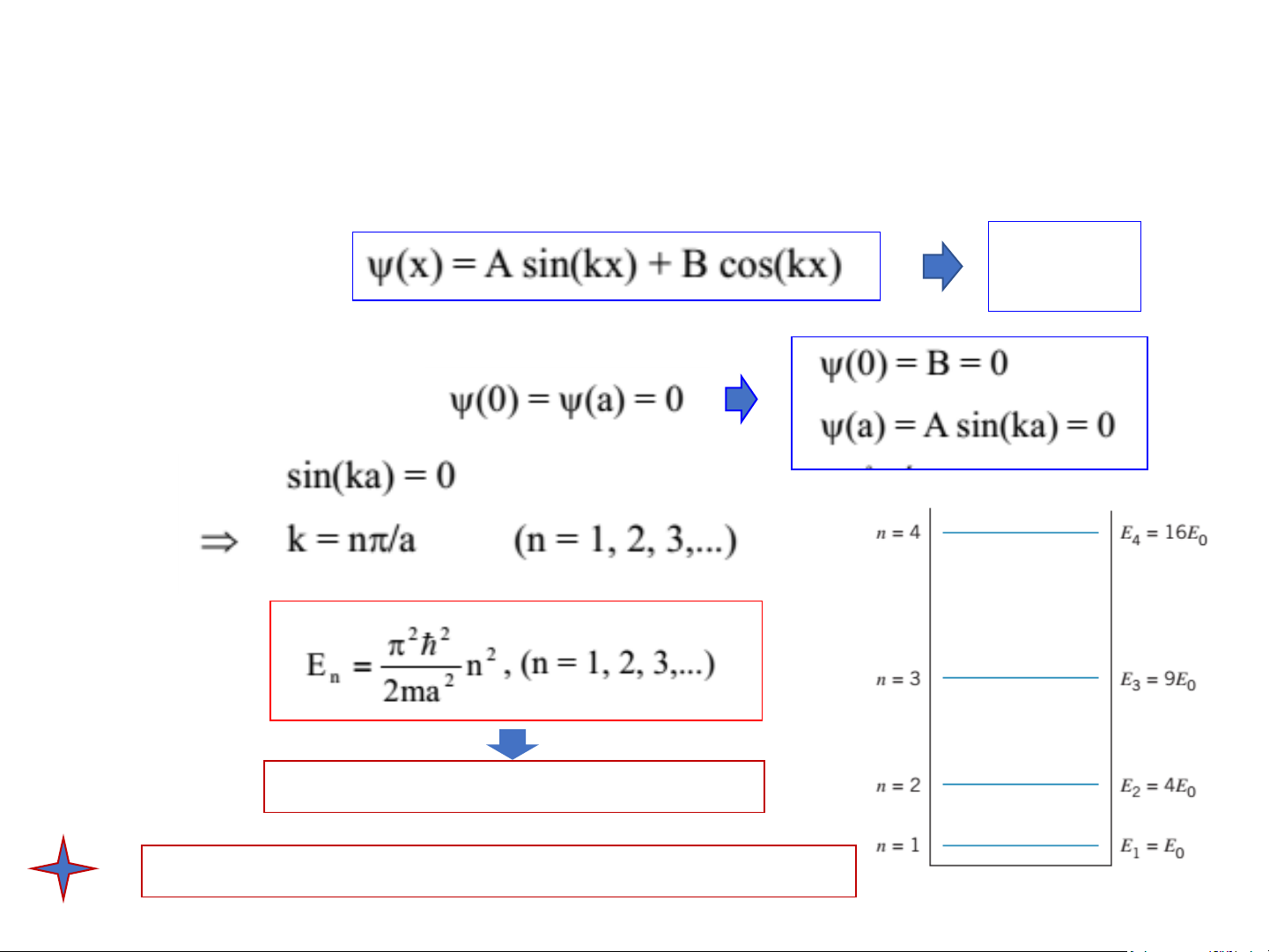
Phương trình (9) có nghiệm: A = ? B = ?
Dựa vào điều kiện biên: hay (10)
Năng lượng bị lượng tử hóa
Ở trạng thái lượng tử, hạt luôn chuyển động! 11/18/2025 13
Hạt trong hố thế một chiều: tìm A
Bây giờ ta tìm hằng số A?
Dựa vào điều kiện chuẩn hóa của hàm sóng
Vậy hàm sóng của hạt trong hố thế thu được là: (11)
Tuy nhiên, hàm sóng không có ý nghĩa vật lý, mà chỉ có mật độ xác suất mới có ý nghĩa vật lý. 11/18/2025 14
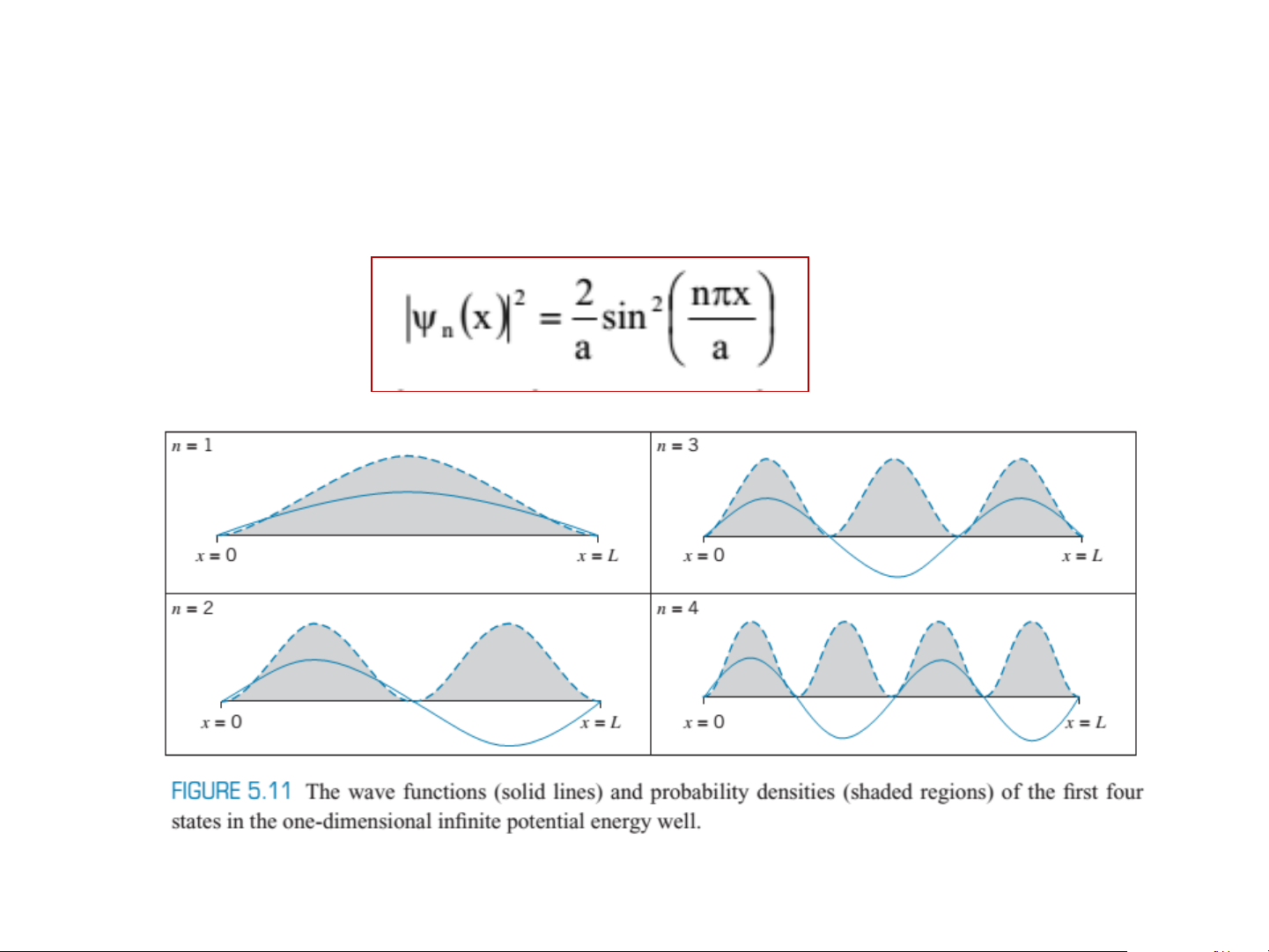
Hạt trong hố thế một chiều: mật độ xác suất
Mật độ xác suất tìm thấy hạt: (12) 11/18/2025 15
Hạt trong hố thế một chiều: xác suất cực đại và cực tiểu
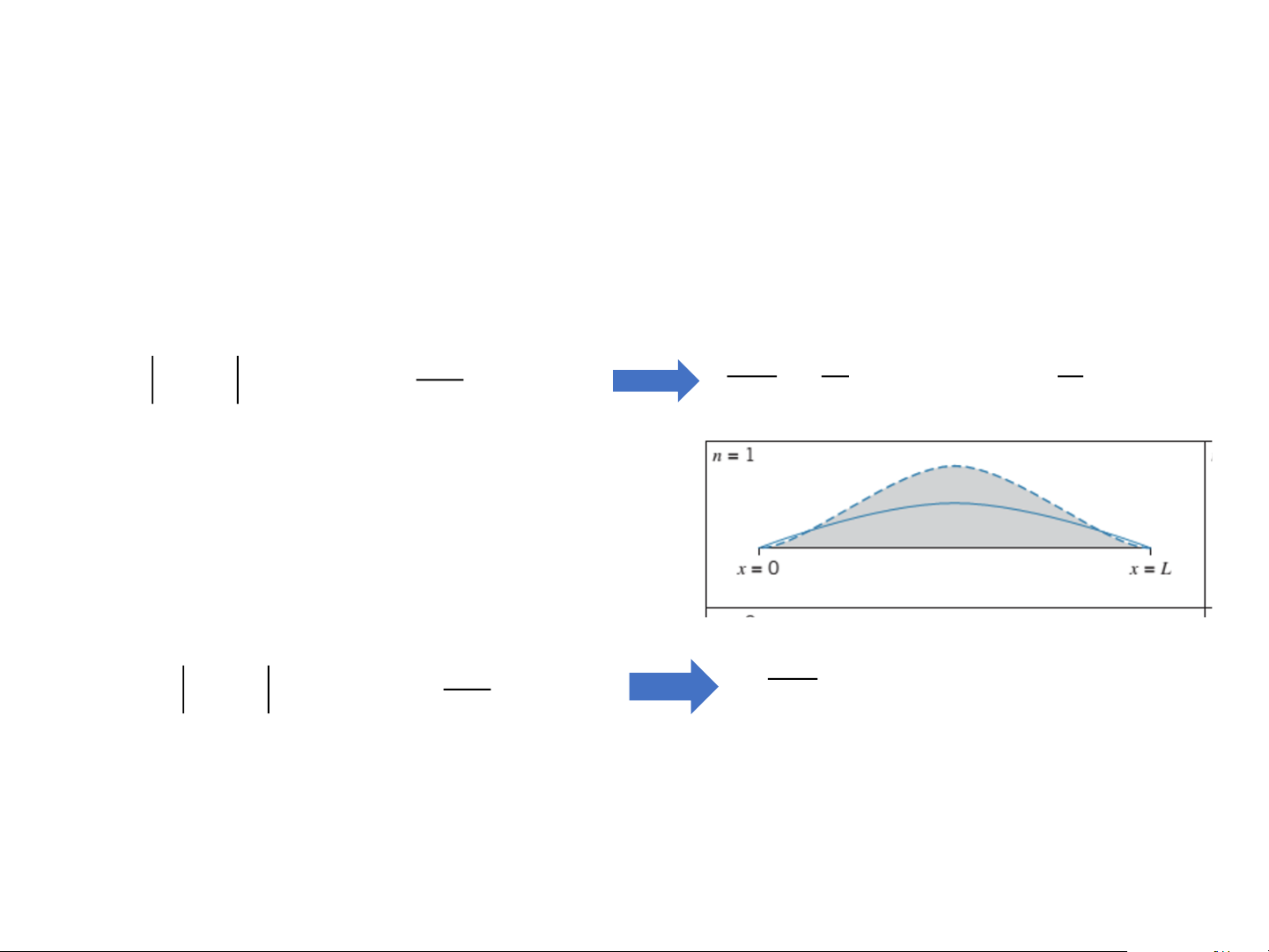
❑ Ở trạng thái cơ bản (n = 1), tìm vị trí mà hạt có:
➢ Xác suất phát hiện là cực đại   2  x   x a (x)  sin  = 1  = + k  x = + ka max  a  a 2 2 • k = 0 ➔ x = a/2
• k = 1 ➔ x = 3a/2 (loại)
➢ Xác suất phát hiện là cực tiểu x  2  x   (x)  sin  = 0 = k  x = ka min  a  a • k = 0 ➔ x = 0 • k = 1 ➔ x = a • k = 2 ➔ x = 2a (loại) 11/18/2025 16
Hạt trong hố thế một chiều: xác suất cực đại và cực tiểu
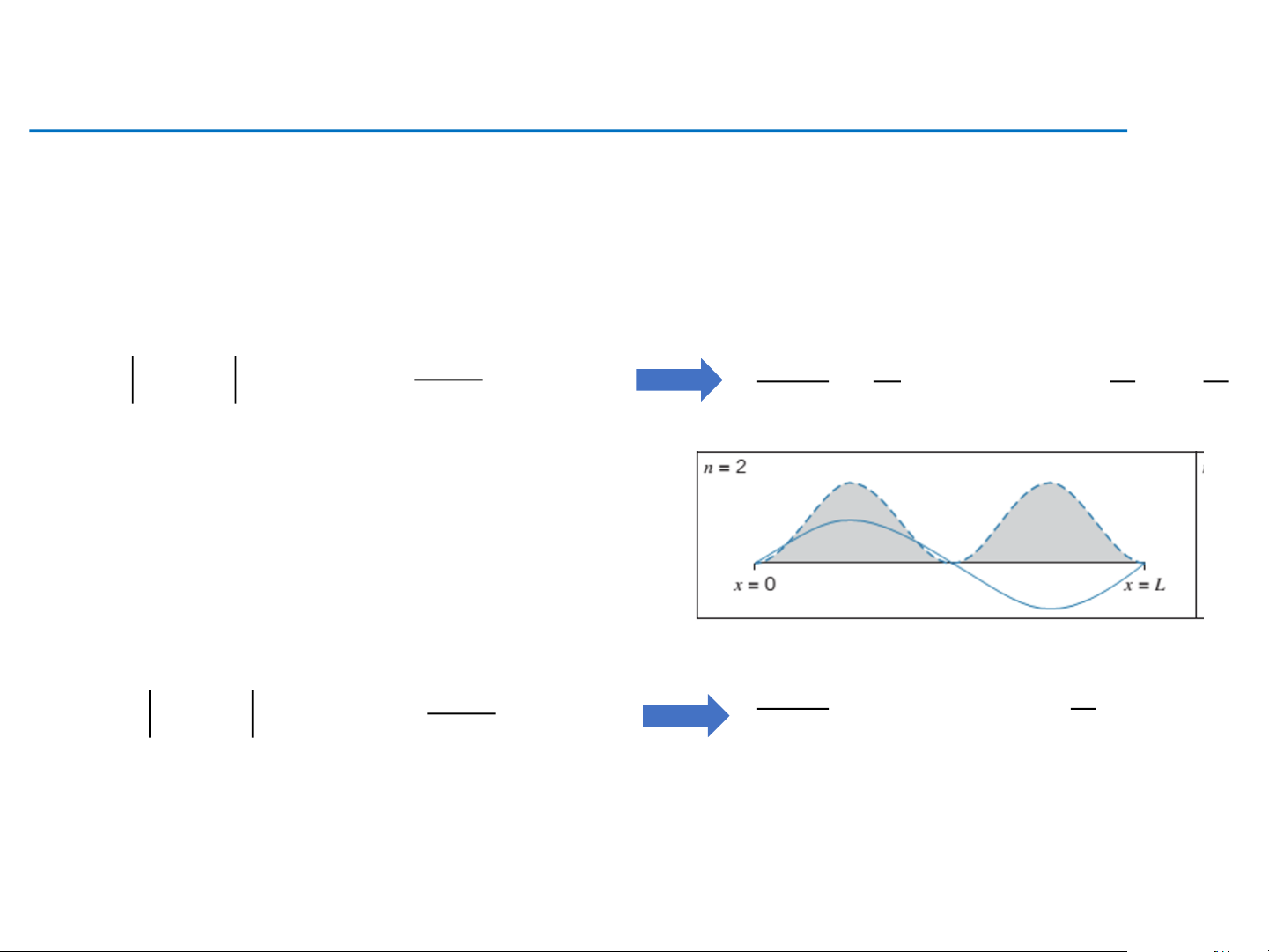
❑ Ở trạng thái kích thích thứ 1 (n = 2), tìm vị trí mà hạt có
➢ Xác suất phát hiện là cực đại 2  2 x      2 x a a (x)  sin  = 1  = + k  x = + k 2 max  a  a 2 4 2 • k = 0 ➔ x = a/4 • k = 1 ➔ x = 3a/4
➢ Xác suất phát hiện là cực tiểu 2 x  a 2  2 x    (x)  sin  = 0 = k  x = k 2 min  a  a 2 • k = 0 ➔ x = 0 • k = 1 ➔ x = a/2 11/18/2025 17 • k = 2 ➔ x = a
Bài tập ví dụ: Hạt trong hố thế một chiều
Ví dụ 3.1: Một vật nhỏ khối lượng 1,0 mg bị giam giữa hai bức tường cách nhau 1 cm.
(a) Tính vận tốc nhỏ nhất của vật.
(b) Nếu vật chuyển động với tốc độ 3 cm/s, hãy tính số lượng tử n. Bài giải:
a) Vận tốc nhỏ nhất ứng với trạng thái n = 1
Xem hạt chuyển động tự do: U = 0 2 2 1   2  E = K = mv = v =  = 3 , 3 .10−29 (m / s) 1 2 2 2ma ma 2 2  vma b) 1 2  2 E = K = mv = n 28 n = = 9.10 n 2 2 2ma  18
Bài tập ví dụ: Hạt trong hố thế một chiều
Ví dụ 3.2: Dùng mẫu hạt trong giếng thế hãy tính năng lượng cần thiết để
dịch chuyển electron từ trạng thái n = 1 lên trạng thái n = 2. Giả sử nguyên tử có bán kính 0,1 nm. Bài giải: 3π2ℏ2 ∆E = E2 − E1 = 2ma2 Trong đó: • m = me = 9,1x10-31 (kg)
• Bề rộng giếng thế =
= đường kính nguyên tử
= 2*bán kính nguyên tử = 0,2 nm ∆E = 28,2 (eV) 11/18/2025 19
Bài tập ví dụ: Hạt trong hố thế một chiều
Ví dụ 3.3: Một hạt chuyển động tự do trong hố thế vuông góc sâu vô hạn, bề
rộng a. Tính năng lượng của hạt ở trạng thái cơ bản trong các trường hợp sau:
a) Hạt là proton (m = 1,673.10-27 kg) và a = 0,1 nm.
b) Hạt là proton (m = 1,673.10-27 kg) và a = 1 fm. Bài giải: a)
Ở trạng thái cơ bản: n = 1 2 2  E =  = ,002(eV) 1 2ma2 b)
Ở trạng thái cơ bản: n = 1 2 2  E =  = 3 , 205 (MeV) 1 2ma2 11/18/2025 20