Bài giảng Chương 6: Nhiễu xạ sóng ánh sáng - Vật Lý đại cương | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

CHƯƠNG 6 NHIỄU XẠ SÓNG ÁNH SÁNG
1. Hiện tượng nhiễu xạ Ánh sáng
2. Nguyên lý Huygens-Fresnel
3. Nhiễu xạ Fresnel qua lỗ tròn
4. Nhiễu xạ Fresnel qua đĩa tròn
5. Nhiễu xạ Fraunhofer qua khe hẹp
6. Cách tử nhiễu xạ
2.1. GIỚI THIỆU VỀ NỀN NHIỄU XẠ
❑ Khi ánh sáng có bước sóng lớn hơn hay bằng
bề rộng của khe thì nó tán xạ qua mọi hướng
về phía trước khi nó truyền qua khe. Hiện
tượng này được gọi là nhiễu xạ.
❑ Nền nhiễu xạ gồm các vùng sáng – tối xen kẻ
nhau, tương tự như nền giao thoa
❑ Chính giữa nền nhiễu xạ sáng nhất gọi là cực đại chính giữa.
❑ Xung quanh cực đại chính giữa có những vùng
sáng yếu hơn, được gọi là cực đại thứ cấp.
❑ Những vùng tối được gọi là cực tiễu nhiễu xạ.
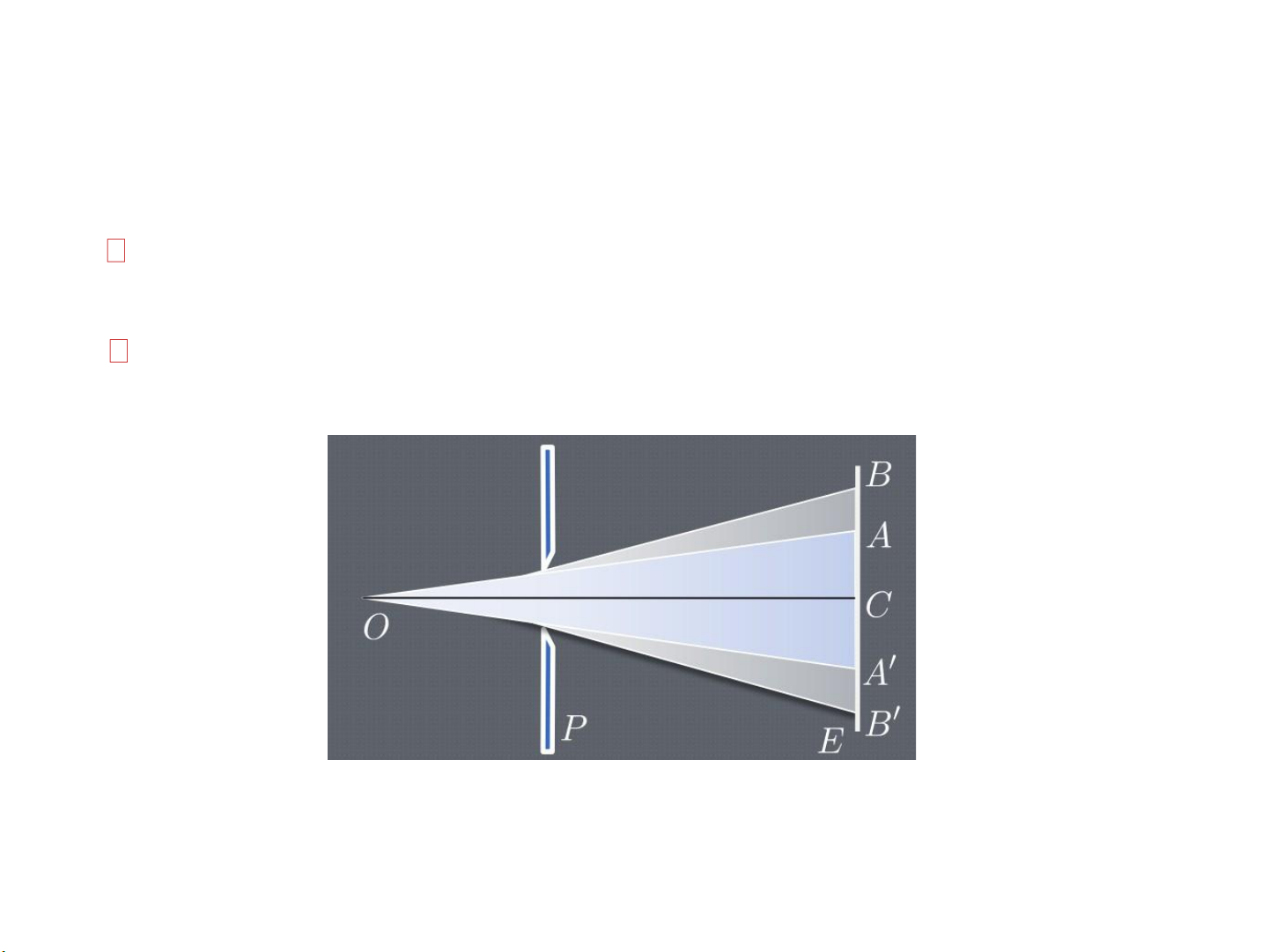
Nền nhiễu xạ qua khe hẹp
2.1. GIỚI THIỆU VỀ NỀN NHIỄU XẠ
 Hiện tượng nhiễu xạ ánh sáng là hiện tượng á n h s á n g bị lệch
khỏi phương truyền thẳng khi đi gần các vật cản.
 Nhiễu xạ gây bởi sóng phẳng gọi là nhiễu xạ Fraunhofer. Trái lại
nhiễu xạ gây bởi sóng cầu gọi là nhiễu xạ Fresnel.
Chúng ta sẽ tìm hiểu nhiễu xạ qua lỗ tròn và qua khe hẹp
2.2. NGUYÊN LÝ HUYGENS - FRESNEL 1 – Nội dung:
o Bất kì một điểm nào mà ánh sáng truyền đến đều
trở thành nguồn sáng thứ cấp, phát sóng cầu về phía trước nó.
o Biên độ và pha của nguồn thứ cấp là biên độ và pha
của nguồn thực gây ra tại vị trí nguồn thứ cấp.
2.2. NGUYÊN LÝ HUYGENS - FRESNEL 2 – Biểu thức sóng:
Đặt vấn đề: Giả sử dao động sáng tại nguồn O có dạng E = acost thì dao
động sáng tại M có dạng như thế nào? N
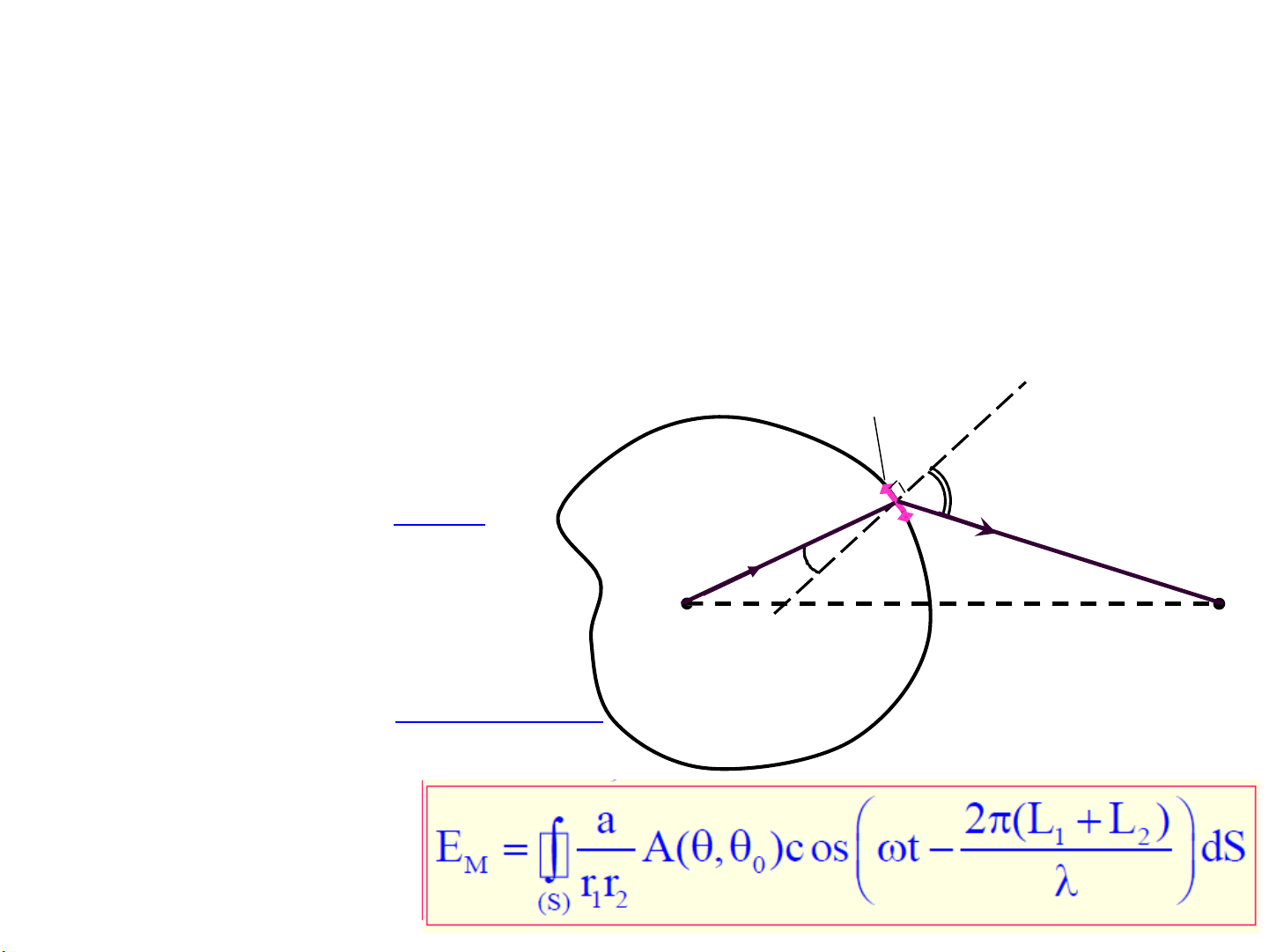
Giải quyết vấn đề: Chọn mặt kín (S) bao quanh O. dS
* Dđ sáng tại A do O truyền đến:  A  2L  r r2 E = a cos t − 1 1 A      o
* Dđ sáng tại M do dS truyền đến: O N’ M  2(L + L )  1 2 dE = a cos (S) M M t −    
* Dđ sáng tại M do mặt (S) a  2(L + L ) truyền đến: 1  2 E = A(,  )cos t − dS M  0   r r    (S) 1 2
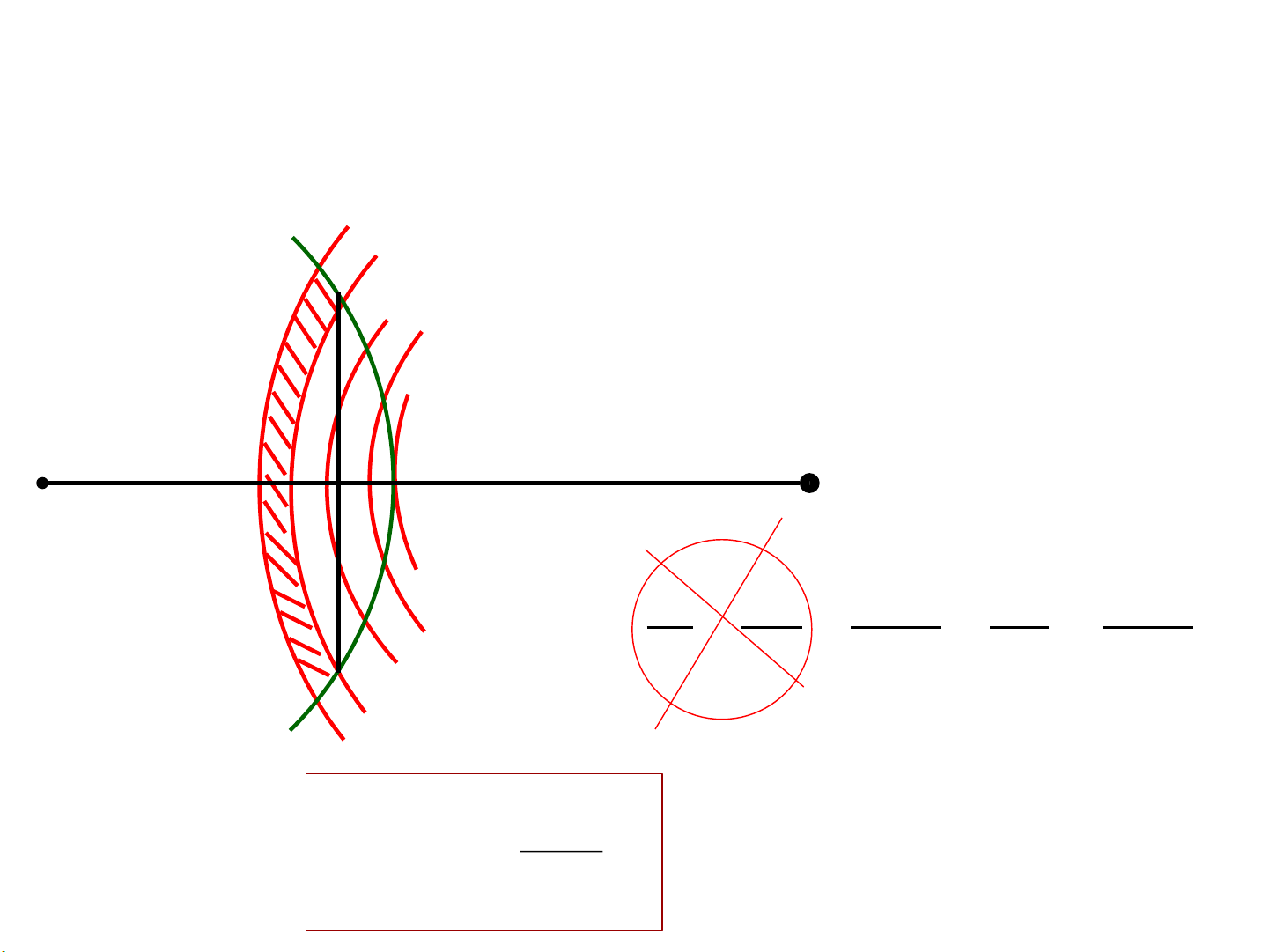
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
1 – Bố trí thí nghiệm: R O b R r b O M
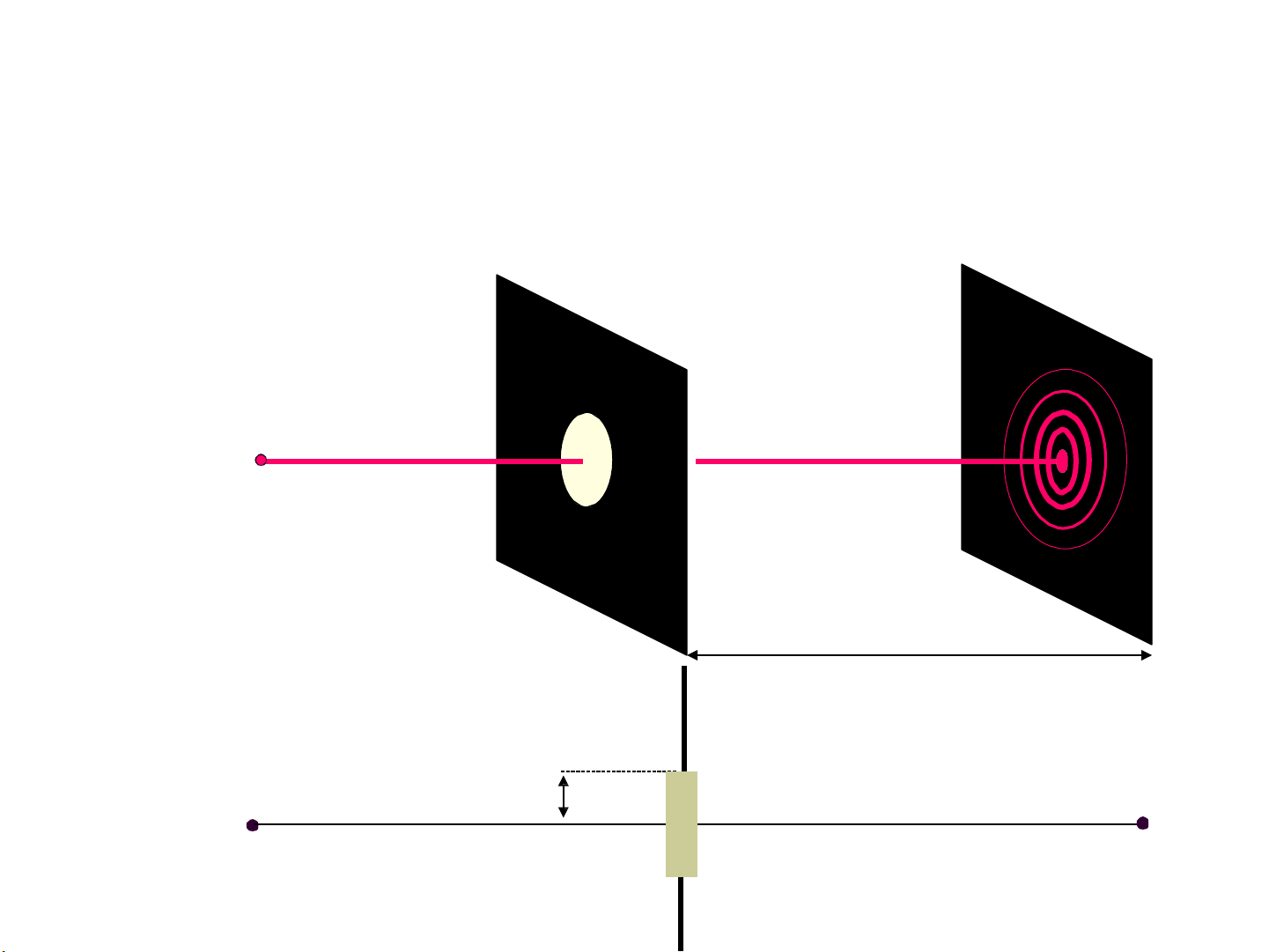
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
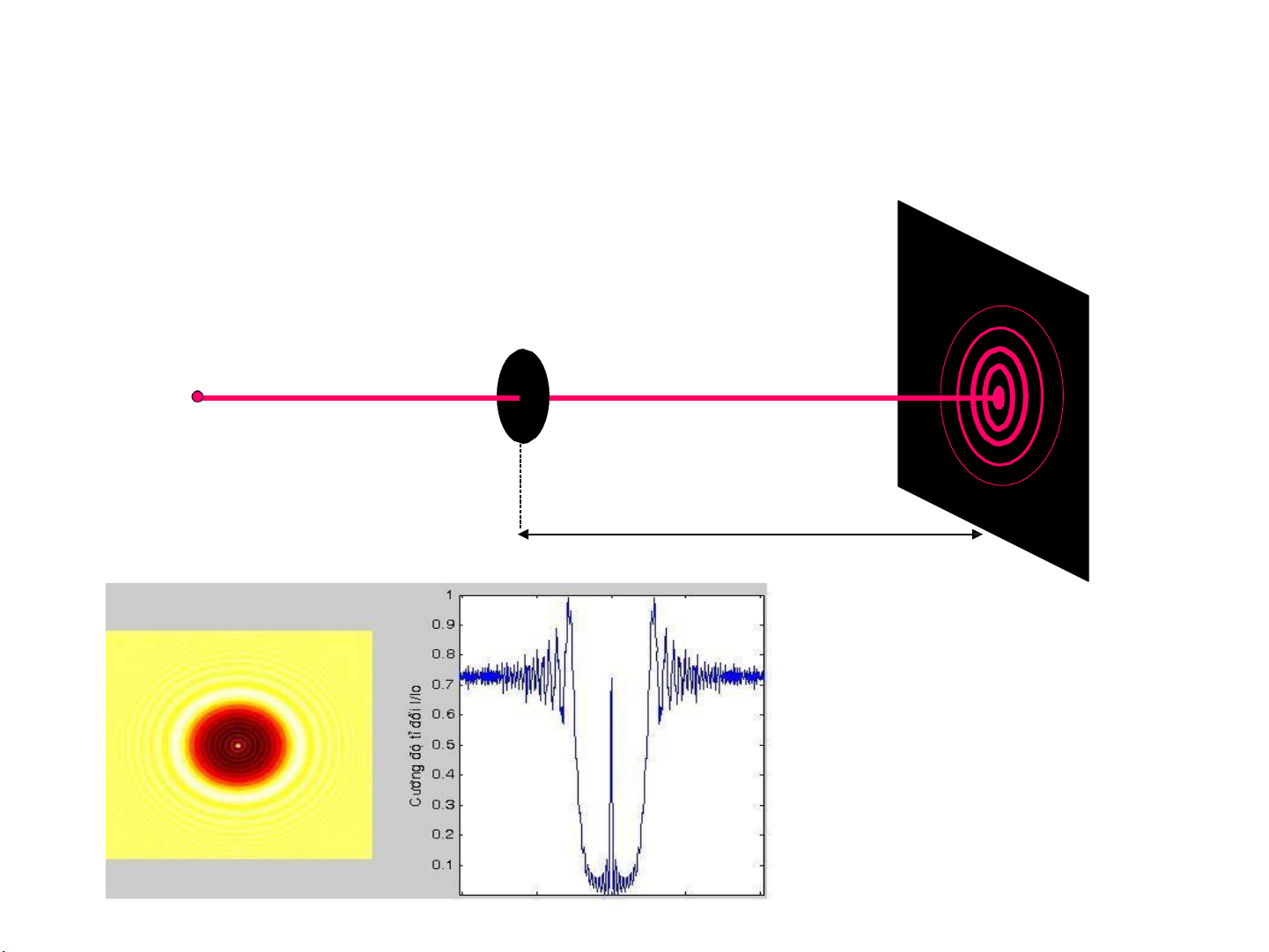
2 – Phân bố cường độ ảnh nhiễu xạ:
Ảnh nhiễu xạ có tính đối xứng tâm M.
Tâm M có lúc sáng, lúc tối,
tùy theo bán kính lỗ tròn và
khoảng cách từ lỗ tròn tới màn quan sát.
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN  b + 3
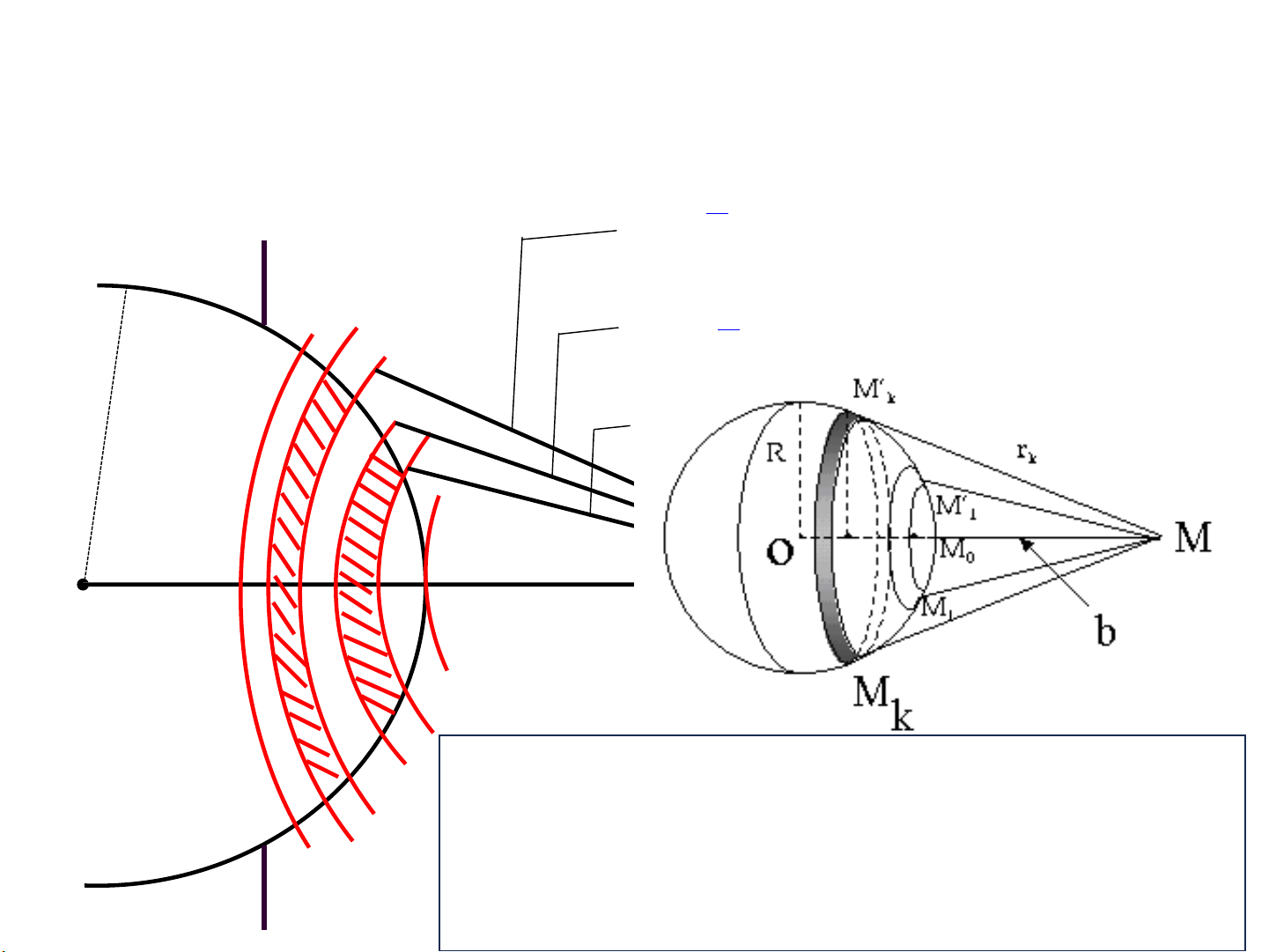
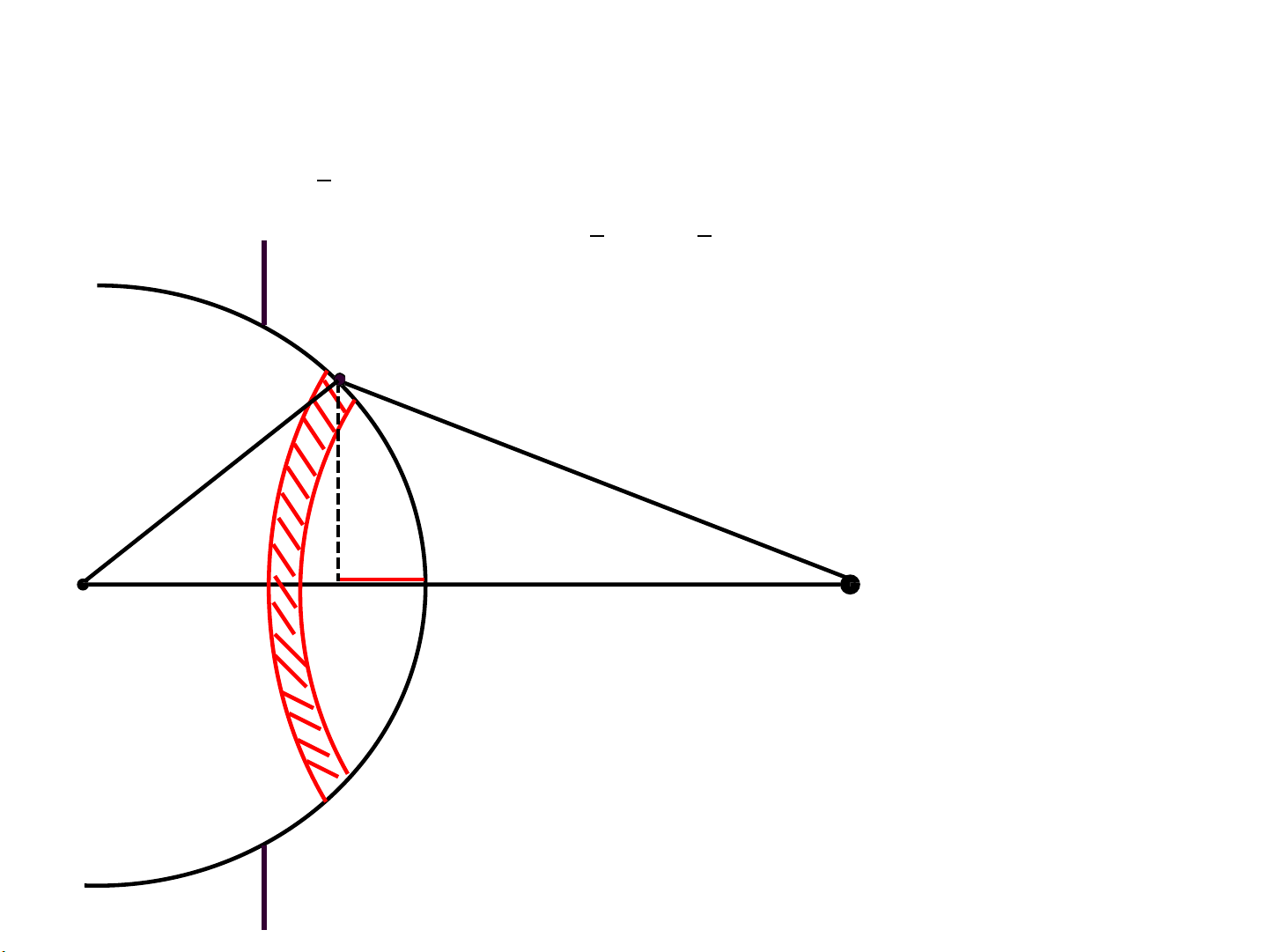
3 – Giải thích kết quả bằng pp đ2ới cầu Fresnel:  b + 2 2 R  b + 2 4 2 O 1 b M 3 5
- Nguồn (ghi 𝑆0 ,)tạo mặt sóng cầu )đường cong đen).
- Lỗ tròn (bán kính 𝑅) đặt trên mặt chắn )đường thẳng tím). S0
- xét điểm quan sát 𝑀ở phía sau, trên trục, cách lỗ một đoạn 𝑏(ghi trên trục ngang).
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
Ý tưởng: chia phần mặt sóng (hay vùng lỗ) thành các vành sao cho:
độ lệch đường đi từ mỗi vành đến 𝑀 so với tia trung tâm tăng đúng bội từng nửa bước sóng 𝜆. 2 𝜆 𝜆
Khoảng cách từ biên đới đến M: 𝑏 + 2 , 𝑏 + 3 2 2 Mk R rk
𝑏= khoảng cách từ tâm lỗ đến 𝑀(tia trung h tâm) k O M H 0 b k M k
Đới 1 gồm các điểm có pha quanh “gần cùng nhau” (so với 𝑀).
Sang đới 2 thì pha lệch thêm 𝜋 (vì thêm 𝜆/2).
Đới 3 lại lệch thêm 𝜋 nữa,… → đới lẻ và đới chẵn gần như ngược pha nhau.
Nếu lỗ cho qua số đới chẵn (1+2, hoặc 1+2+3+4…) → triệt tiêu mạnh S → 𝑀tối. 0
Nếu lỗ cho qua số đới lẻ (chỉ đới 1, hoặc 1+2+3…) → còn dư đáng kể → 𝑀sáng.
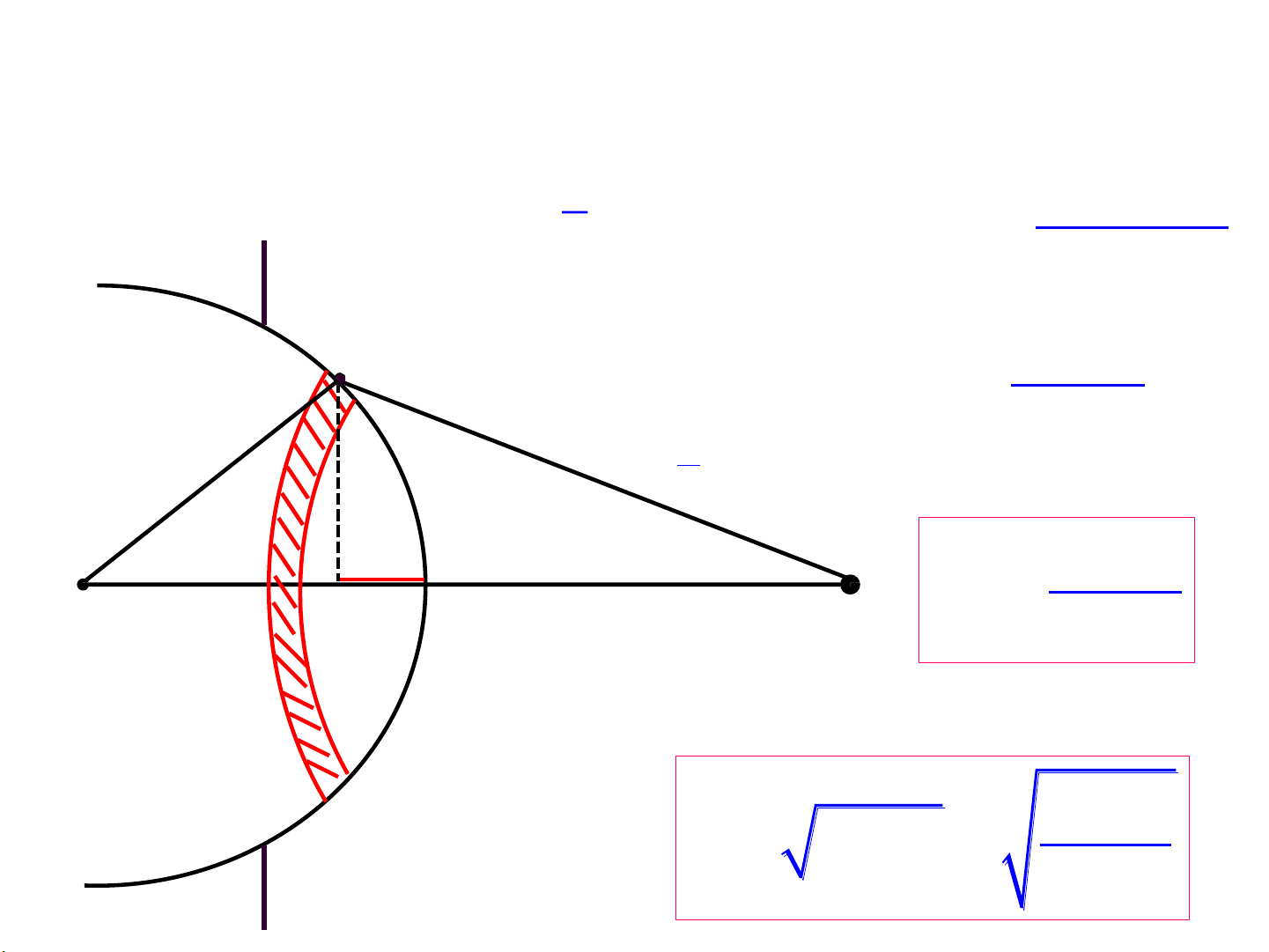
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN  kb 2 2 2 2 2
r = R − (R − h ) = (b + k ) − (b + h )  h =
k 3 – Giải thíchk kết quả bằ2ng pp đới ckầu Fresnk el: 2(R + b) Mk   S = h .2R = k. Rb k k  R + b R b + k rk
Diện tích của mỗi đới cầu: 2 hk S = Rb O M H 0 b k M R + b k
Bán kính của đới cầu thứ k: kRb S r  2Rh = 0 k k R + b
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
1. Diện tích đới cầu nói chung Về hình học thuần túy:
Một mặt cầu bán kính 𝑅, bị cắt bởi hai mặt phẳng song song, cách nhau một đoạn ℎ. Phần
mặt cầu nằm giữa hai mặt phẳng đó gọi là đới cầu (spherical zone).
Kết quả hình học cơ bản:
𝑆đới = 2𝜋𝑅ℎ
•𝑅 :bán kính cầu )ở đây là bán kính mặt sóng cầu từ nguồn 𝑂)
•ℎ: “chiều cao” đới cầu – khoảng cách giữa hai mặt phẳng cắt cầu
Cách hình dung: mở “vỏ bóng” ra, ta được một hình gần như hình chữ nhật:
chiều dài ≈ 2𝜋𝑅(chu vi “vòng bụng” của cầu), chiều rộng = ℎ, nên diện tích ≈ 2𝜋𝑅ℎ.
Trong slide, người ta viết:
𝑆𝑘 = ℎ𝑘 ⋅ 2𝜋𝑅
tức là diện tích từ cực đến hết 𝑘đới đầu tiên )hoặc dùng ℎ𝑘là tổng chiều cao từ cực đến
biên ngoài đới thứ 𝑘).
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
2. Từ 𝑆𝑘đến diện tích mỗi đới Fresnel
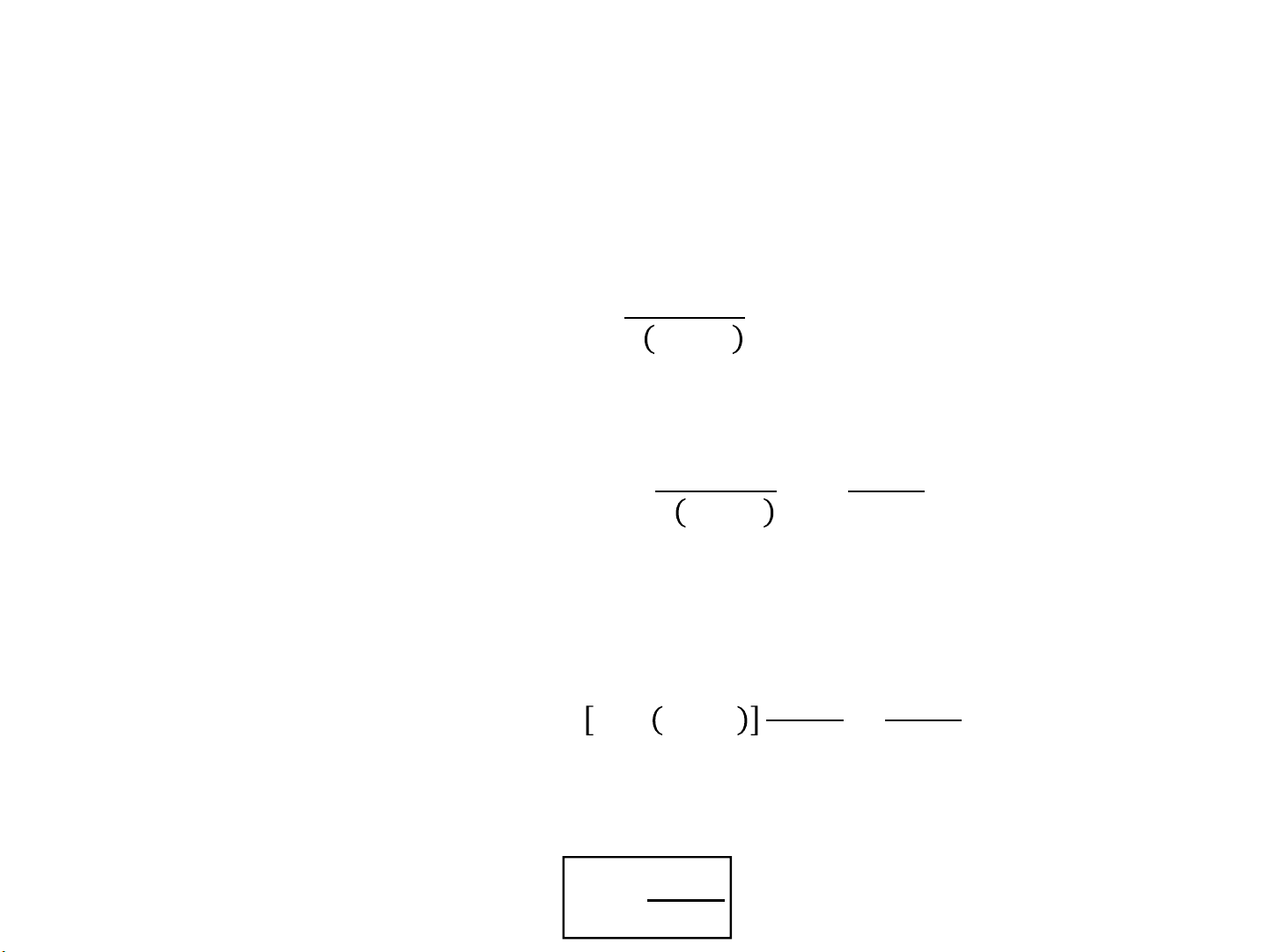
Từ điều kiện chênh lệch quang lộ Δ𝐿 = 𝑘𝜆/2 đã suy ra: 𝑘𝜆𝑏 ℎ𝑘 = 2 𝑅 + 𝑏 Thay vào: 𝑘𝜆𝑏 𝜋𝜆𝑅𝑏
𝑆𝑘 = 2𝜋𝑅ℎ𝑘 = 2𝜋𝑅 ⋅ = 𝑘 2 𝑅 + 𝑏 𝑅 + 𝑏
Đây là tổng diện tích của 𝑘 đới đầu tiên (từ cực đến hết đới thứ 𝑘).
Vậy diện tích riêng của mỗi đới là: 𝜋𝜆𝑅𝑏 𝜋𝜆𝑅𝑏
Δ𝑆 = 𝑆𝑘 − 𝑆𝑘−1 = 𝑘 − 𝑘 − 1 = 𝑅 + 𝑏 𝑅 + 𝑏 nên: 𝜋𝜆𝑅𝑏 Δ𝑆 = 𝑅 + 𝑏
Quan trọng: Δ𝑆 không phụ thuộc 𝑘→ tất cả các đới Fresnel trên mặt cầu đều có cùng diện tích.
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
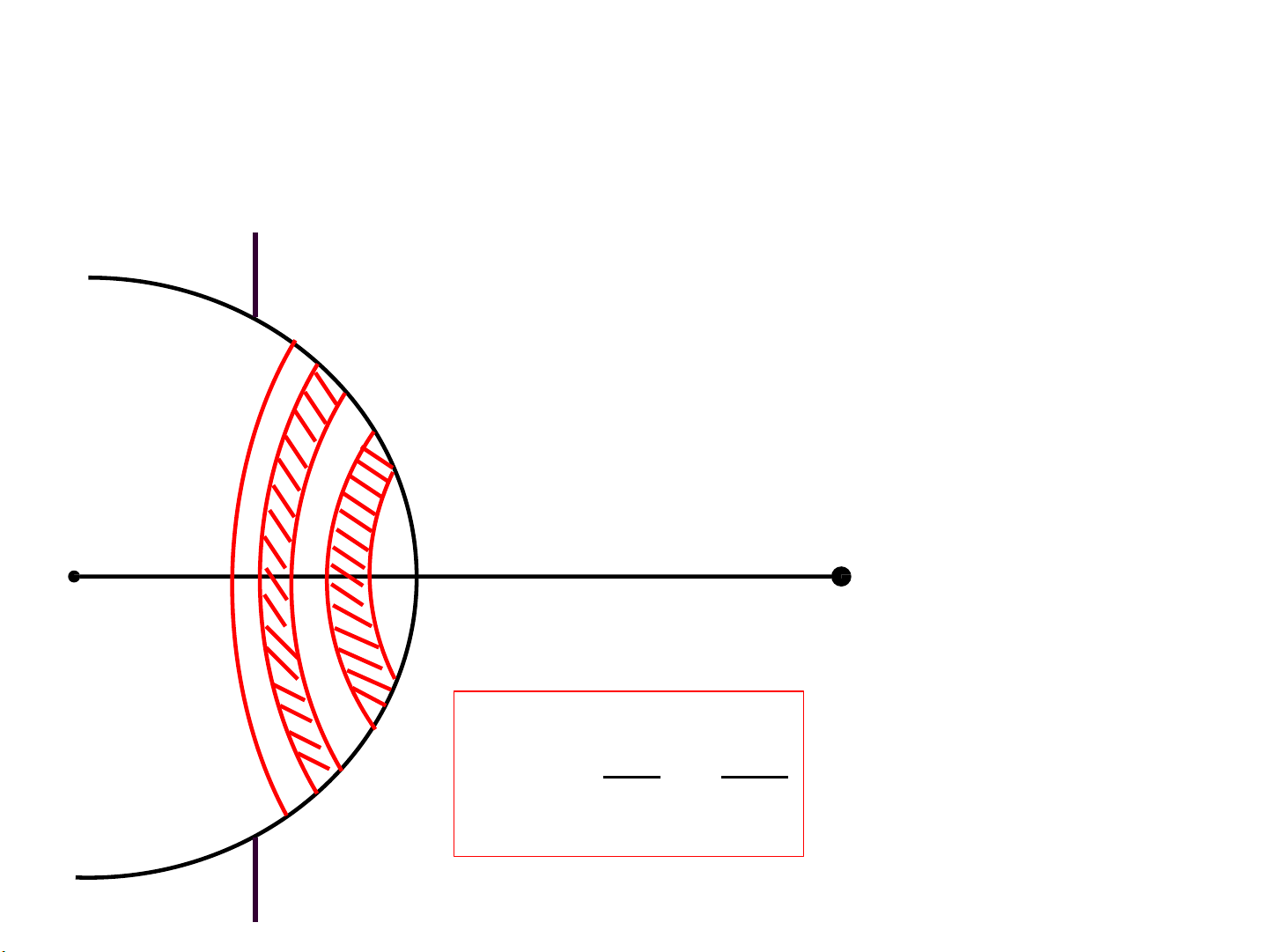
3 – Giải thích kết quả bằng pp đới cầu Fresnel:
Biên độ sóng ak do đới thứ k gửi tới M sẽ giảm dần
khi chỉ số k tăng, nhưng giảm chậm. Vì thế ta coi
ak là trung bình cộng của ak-1 và ak+1. Dao động sáng
tại M do hai đới kền hau
gửi tới sẽ ngược pha nhau. Vì thế, biên độ sóng tại M 4 2 là: a = a −a + a −a +...  a M 1 2 3 4 n O 1 b M 3 5
a = a1  an (Dấu “+” khi n lẻ; M 2 2 “-” khi n chẵn) S0
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN Kết luận:
Biên độ sóng và cường độ sáng tại M: a a  a a 2 a = 1  n  M I = a2 =  1  n  2 2 M  2 2 
o Nếu lỗ tròn quá lớn thì: 2 a2 I = a = 1 = I M 0 4
o Nếu lỗ tròn chứa số lẻ  a a 2 (M là điểm I = a2 = 1 + n  I
đới cầu Fresnel thì: M  sáng). 2 2  0  
o Nếu lỗ tròn chứa số  a a 2 (M là điểm
chẵn đới cầu Fresnel thì: I = a2 = 1 − n  I M  2 2  0   tối).
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
Ví dụ 2.1: Chiếu ánh sáng đơn sắc có bước sóng = 0,5m vào một lỗ tròn
có bán kính chưa biết. Nguồn sáng đặt tại điểm cách lỗ tròn 2m, sau lỗ tròn
2m đặt màn quan sát. Hỏi bán kính của lỗ tròn bằng bao nhiêu để tâm của
nền nhiễu xạ là tối nhất. Đáp số: r = 1 mm Bài giải
Tâm nền nhiễu xạ tối nhất khi lỗ tròn chứa 2 đới cầu
Vậy bán kính lỗ tròn phải bằng bán kính đới cầu thứ 2
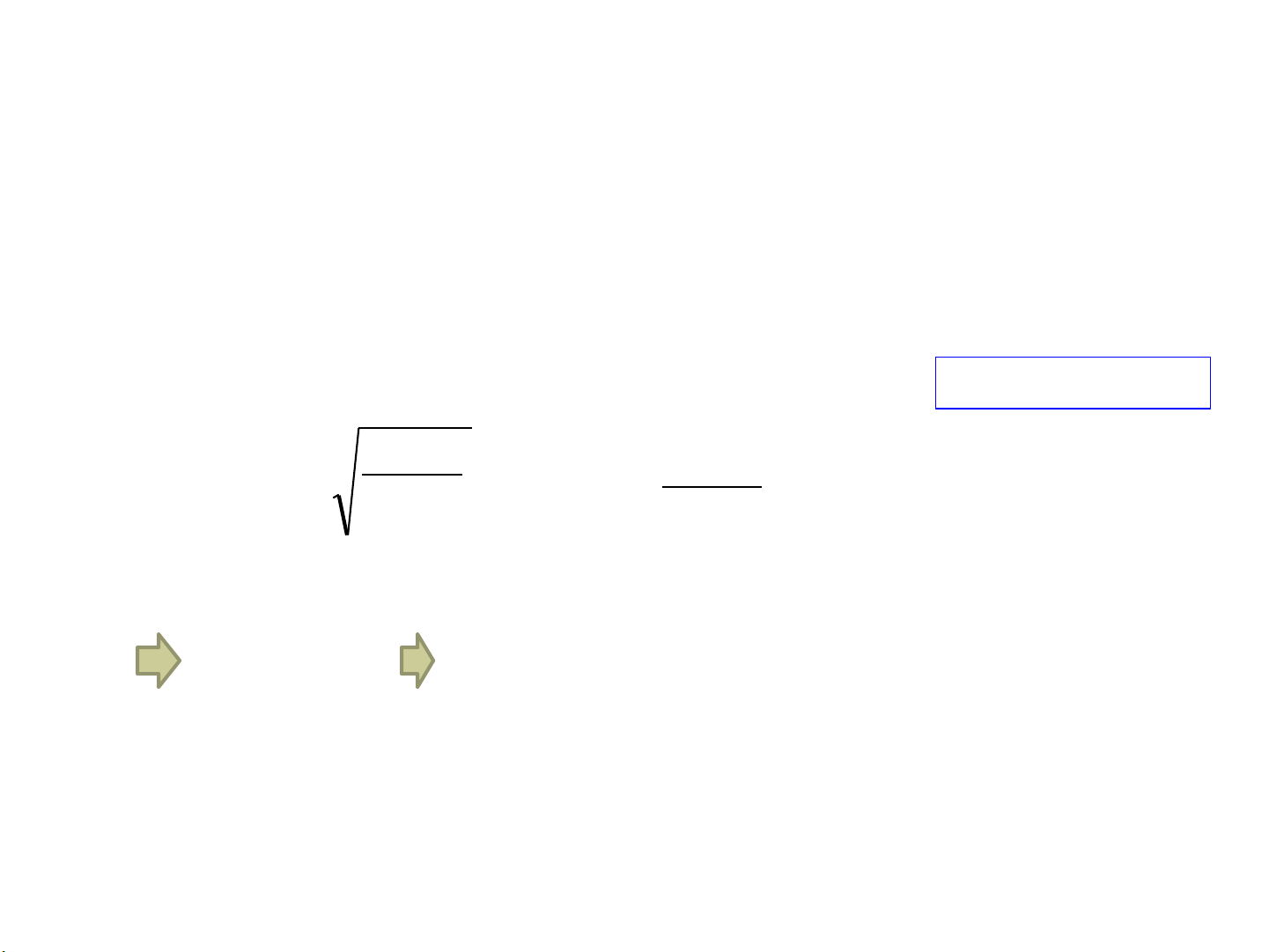
r = r = 2Rb = 0,001(m) =1(mm) 2 R + b
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
Ví dụ 2.2: Một màn đặt cách nguồn sáng ( = 0,5m) khoảng 2m. Chính
giữa màn và nguồn sáng là lỗ tròn đường kính 0,2cm. Tính số đới cầu
Fresnel mà lỗ tròn chứa được. Tâm của nền nhiễu xạ sáng hay tối? Bài giải Đáp số: k = 4
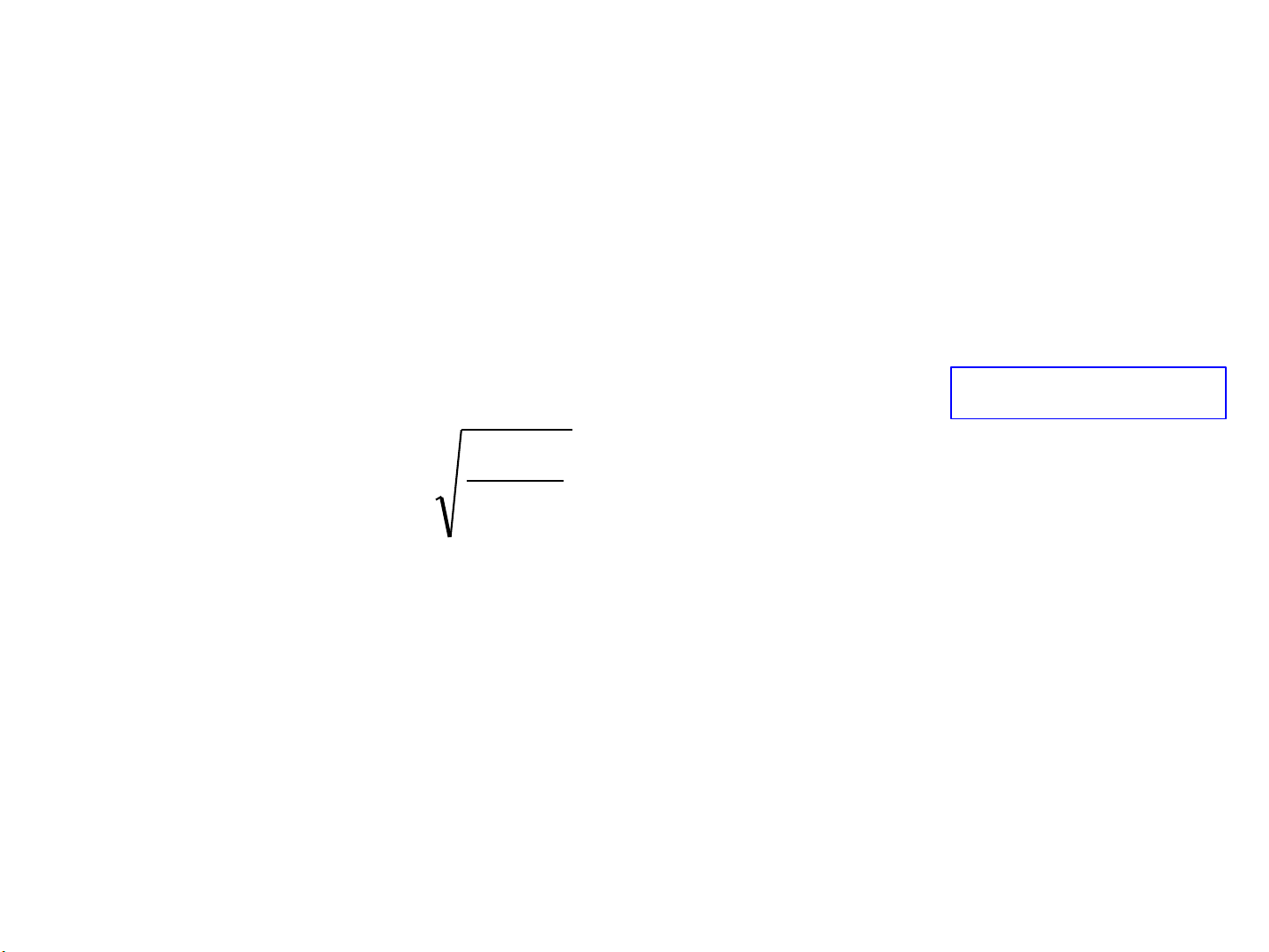
r = kRb  k = r2  R + b   R + b Rb    Với R + b = 2 m, R = b = 1 m k = 4
Tâm của nền nhiễu xạ là điểm tối
2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN
Ví dụ 2.3: Chiếu ánh sáng đơn sắc có bước sóng = 0,5m vào một lỗ tròn
có bán kính r = 1mm. Khoảng cách từ nguồn sáng đến lỗ tròn R= 1m. Tính
khoảng cách từ lỗ tròn đến màn để lỗ tròn chứa 3 đới cầu Fresnel. Bài giải Đáp số: b = 2 m r = r = 3Rb  b = ..... 3 R + b
2.4. NHIỄU XẠ FRESNEL QUA ĐĨA TRÒN
1 – Thí nghiệm: Đặt đĩa tròn chắn sáng, tại tâm vùng
bóng hình học trên màn lại xuất hiện một đốm sáng.
Điểm quan sát 𝑀chính là điểm nằm
đúng trên trục đối xứng (thẳng hàng nguồn–tâm đĩa–màn). O b Kết quả:
Tâm ảnh nhiễu xạ luôn có một chấm sáng (chấm sáng Fresnel)
2.4. NHIỄU XẠ FRESNEL QUA ĐĨA TRÒN
2 – Giải thích kết quả:
Giả sử đĩa tròn chắn hết m đới cầu
Fresnel thì biên độ sáng tại M chỉ do các
đới cầu thứ m +1, m +2, … gửi tới. O b M m+1
a = a1  am + am+1  a = am+1 M 2 2 2 2 2  a 2 m+1
Cường độ sáng I = a2 =
Vậy tại M luôn là điểm sáng. M    2 
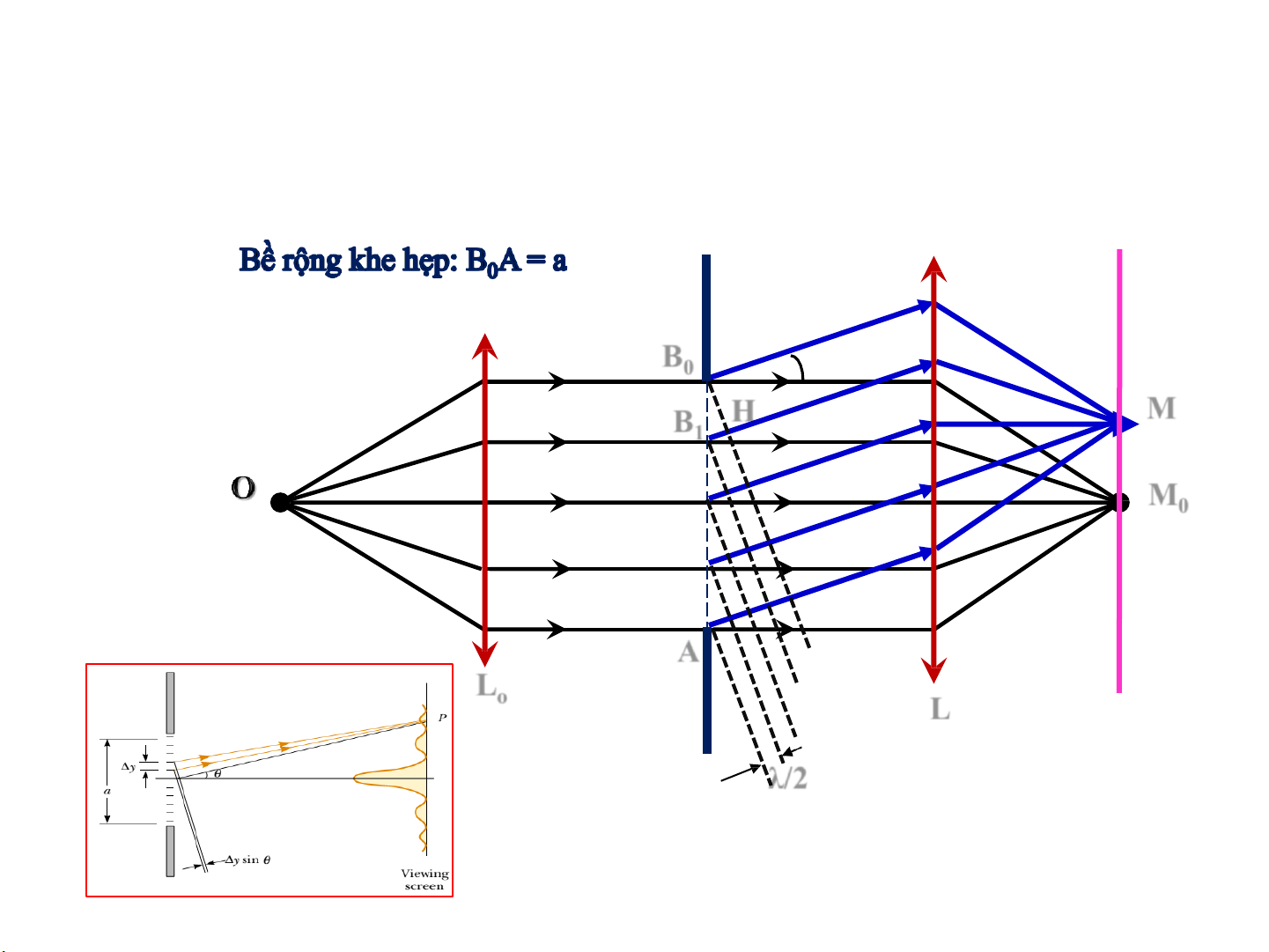
2.5. NHIỄU XẠ FRAUNHOFER QUA KHE HẸP B0 θ H M B1 M0 A o Lo 1 L λ/2