















Preview text:
Công thức truy hồi Trần Vĩnh Đức HUST Ngày 24 tháng 7 năm 2018 1 / 45 Nội dung Ví dụ Công thức truy hồi
Công thức truy hồi và hàm sinh Số Catalan
Công thức truy hồi tuyến tính Ví dụ
Một quần thể vi trùng có số lượng cá thể tăng gấp đôi sau mỗi giờ.
Nếu thoạt đầu có 5 cá thể hỏi sau 5 giờ số lượng của chúng là bao nhiêu? {an = 2an−1 a0 = 5 3 / 45 Bài tập
Hãy tìm công thức tường minh cho dãy {an = 2an a0 = 5 4 / 45 Ví dụ
Xét một cầu thang với n bậc thang. Có bao nhiêu cách để đi lên
cầu thang nếu chúng ta có thể leo lên 1 bậc hoặc 2 bậc trong mỗi bước? S1 = 1 S2 = 2
Sn+2 = Sn+1 + Sn với n ≥ 1 5 / 45 Ví dụ
Có bao nhiêu xâu nhị phân độ dài n không chứa hai bit 0 liên tiếp?
an+1 = an + an−1 a 1 = 2 a2 = 3 6 / 45 Bài tập
Hãy dùng kỹ thuật hàm sinh để tìm công thức tường minh cho dãy
an+1 = an + an−1 a 1 = 2 a2 = 3 7 / 45 Ví dụ
Có bao nhiêu xâu tam phân độ dài n không chứa dãy con ”012”?
an+3 = 3an+2 − an a 1 = 3 a2 = 9 8 / 45 Nội dung Ví dụ Công thức truy hồi
Công thức truy hồi và hàm sinh Số Catalan
Công thức truy hồi tuyến tính Công thức truy hồi Định nghĩa
Công thức truy hồi đối với dãy số ⟨an⟩ là công thức biểu diễn an
qua một hay nhiều số hạng đi trước của dãy. 10 / 45 Ví dụ
Xét dãy số ⟨an⟩ thỏa mãn công thức
{an = an−1 −an−2 a0 = 3a1 = 5
Từ công thức truy hồi ta có
a2 = a1 − a0 = 5 − 3 = 2
a3 = a2 − a1 = 2 − 5 = −3 11 / 45 Định nghĩa
Một dãy số được gọi là nghiệm của công thức truy hồi nếu các số
hạng của nó thỏa mãn công thức truy hồi này. 12 / 45 Ví dụ
▶ Xét công thức truy hồi
an = 2an−1 − an−2 với n ≥ 2.
▶ Dãy số ⟨an⟩ với an = 3n có phải là nghiệm của hệ thức truy hồi trên hay không?
▶ Còn dãy an = 2n? ▶ Còn dãy an = 5? 13 / 45 Ví dụ
Giả sử một người gửi 10, 000 đô la vào tài khoản của mình tại một
ngân hàng với lãi kép 11% mỗi năm. Hỏi sau 30 năm anh ta có
bao nhiêu tiền trong tài khoản ngân hàng.
{Pn = Pn−1 +0.11Pn−1 = 1.11Pn−1
P0 = 10, 000 đô la. 14 / 45 Ví dụ
▶ Một hệ máy tính coi một xâu các chữ số hệ thập phân là một
từ mã hợp lệ nếu nó chứa một số chẵn chữ số 0.
▶ Chẳng hạn, 1230407869 là hợp lệ, còn 120987045608 là không hợp lệ.
▶ Giả sử an là số các từ mã độ dài n.
▶ Hãy tìm công thức truy hồi cho an.
an = 9an−1 + (10n−1 − an−1)
= 8an−1 + 10n−1. 15 / 45 P1: JSN WB00623-07 WB00623-Tucker October 28, 2011 12:25
7.1 Recurrence Relation Models 285
Is there some systematic way to enumerate the ways to climb four stairs that
breaks the problem into parts involving the ways to climb three or fewer stairs?
Clearly, once the first step is taken there are three or fewer stairs remaining to climb.
Thus we see that after a first step of one stair, there are a3 ways to continue the climb
up the remaining three stairs. If the first step covers two stairs, then there are a2 ways
to continue up the remaining two stairs. So a4 = a3 + a2. We confirm that the values
for a4, a3, a2 satisfy this relation: 5 = 3 + 2. This argument applies to the first step
when climbing any number of stairs, as is shown in Figures 7.1b and 7.1c. Thus
an = an−1 + an−2.
In Section 7.3 we obtain an explicit solution to this recurrence relation. The rela-
tion an = an−1 + an−2 is called the Fibonacci relation. The numbers an generated by
the Fibonacci relation with the initial conditions a0 = a1 = 1 are called the Fibonacci
numbers. They begin 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. Fibonacci numbers arise natu-
rally in many areas of combinatorial mathematics. There is even a journal, Fibonacci
Quarterly, devoted solely to research involving the Fibonacci relation and Fibonacci
numbers. Fibonacci numbers have been applied to other fields of mathematics, such as
numerical analysis. They occur in the natural world—for example, the arrangements
of petals in some flowers. For more information about the occurrences of Fibonacci numbers in nature, see [1].
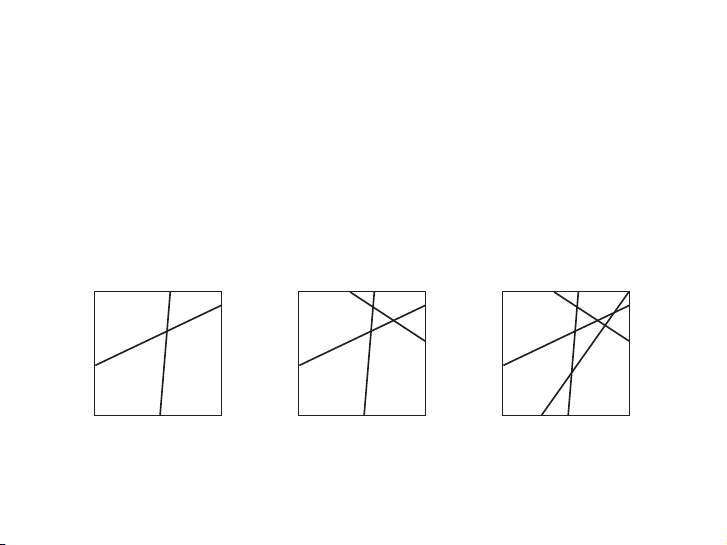
Example 3: Dividing the Plane
Suppose we draw n straight lines on a piece of paper so that every pair of lines intersect
(but no three lines intersect at a common point). Into how many regions do these n lines divide the plane?
Again we approach the problem initially by examining the situation for small
values of n. With one line, the paper is divided into two regions. With two lines,
we get four regions—that is, a2 = 4. See Figure 7.2a. From Figure 7.2b, we see that
a3 = 7. The skeptical reader may ask: how do we know that three intersecting lines will alw Ví ays dụ
create seven regions? Let us go back one step, then.
Clearly two intersecting lines will always yield four regions, as shown in Figure 7.2a. Now ▶ let Chúng us e ta vẽ xamine n the đường effect thẳng of dra trên wing giấ the y sao third cho line mọi cặp (labeled đường “3” in Figure 7.2b). It must thẳng cross đều each cắt of nhau the và other không two lines có (at ba dif đường ferent thẳng points). nào đồng Before, between, and after thesequy
tw .o intersection points, the third line cuts through three of the regions formed by ▶ the Các first đường two thẳng lines (this này chia action of mặt the phẳng third thành line does bao not nhiêu depend miền? on how it is
drawn, just that it intersects the other two lines). So in severing three regions, the third
line must form three new regions, actually creating six new regions out of three old
regions. Thus a3 = a2 + 3 = 4 + 3 = 7, independently of how the third line is drawn. 2 2 3 2 3 4 1 1 1 (a) (b) (c) Figure 7.2 16 / 45 Ví dụ (Chọn không lặp)
Đặt an,k là số cách chọn tập con k phần tử từ tập n phần tử. Hãy
tìm công thức truy hồi cho ak,n.
an,k = an−1,k + an−1,k−1 (Đẳng thức Pascal) 17 / 45 Ví dụ (Bỏ bóng)
Hãy tìm công thức truy hồi cho số cách bỏ n quả bóng giống nhau
và k chiếc hộp phân biệt sao cho mỗi hộp chỉ có 2 hoặc 3 hoặc 4 quả bóng.
an,k = an−2,k−1 + an−3,k−1 + an−4,k−1. 18 / 45
Ví dụ (Hệ thức truy hồi)
Tìm công thức truy hồi cho: Số xâu tam phân độ dài n với một số
chẵn 0 và một số lẻ 1.
an = bn−1 + cn−1 + an−1
bn = 3n−1 − cn−1
cn = 3n−1 − bn−1 19 / 45 Nội dung Ví dụ Công thức truy hồi
Công thức truy hồi và hàm sinh Số Catalan
Công thức truy hồi tuyến tính







