








Preview text:
Đồ thị Trần Vĩnh Đức HUST Ngày 24 tháng 7 năm 2018 1 / 57 Tài liệu tham khảo
▶ Norman L. Biggs, Discrete Mathematics, Oxford University Press, 2002. 2 / 57
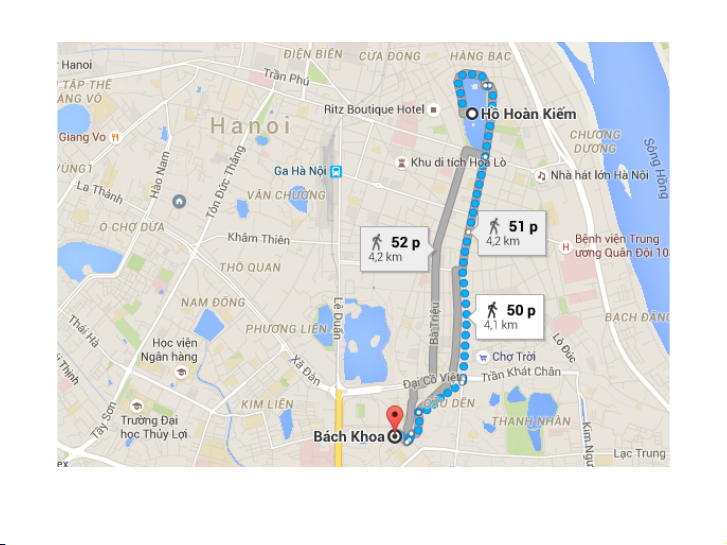
Hồ Hoàn Kiếm đến Bách Khoa, Hai Bà Trưng - Google Maps 1/26/16, 10:42 AM
Hồ Hoàn Kiếm đến Bách Khoa, Hai Bà Trưng Đi bộ 4,1 km, 50 p 3 / 57
Dữ liệu bản đồ ©2016 Google 1 ki lô mét via Phố Huế 50 p 4,1 km via Hàng Bài 51 p 4,2 km via Bà Triệu 52 p 4,2 km
https://www.google.com/maps/dir/Hồ+Hoàn+Kiếm,+Hàng+Trống,+Hoà…fe1abd:0x22b136bcf1c08e2a!2m2!1d105.8459098!2d21.0042694!3e2 Page 1 of 1 Nội dung Đồ thị và biểu diễn
Một số đồ thị đặc biệt Đẳng cấu Bậc Đường đi và chu trình Định nghĩa
Một đồ thị G là một cặp có thứ tự G = (V, E), ở đây V là một
tập, còn E là tập với các phần tử là các tập con hai phần tử của V.
Các phần tử của V được gọi là các đỉnh, còn các phần tử của E
gọi là các cạnh của G. Ví dụ a
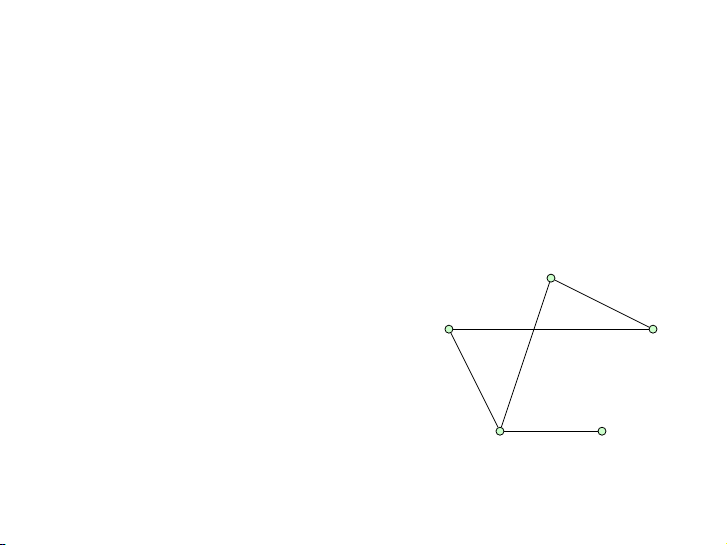
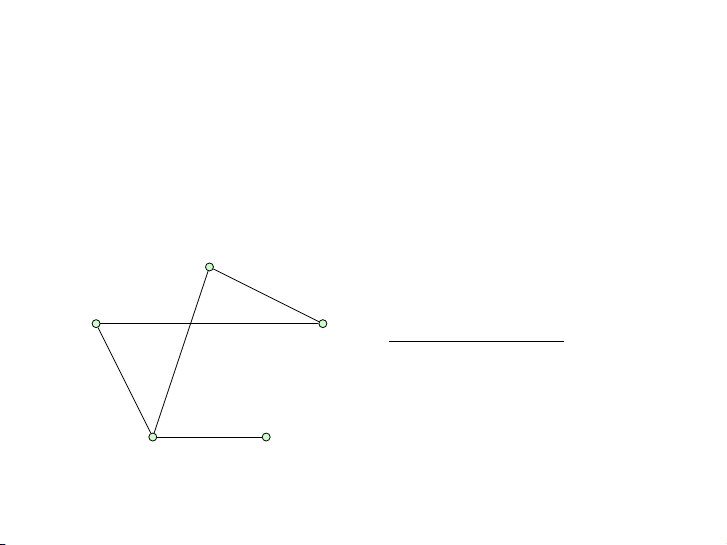
Xét đồ thị G = (V, E) trong đó z b
V = {a, b, c, d, z}
E = {{a, b}, {a, d}, {b, z}, {c, d}, {d, z}}. d c 5 / 57 Định nghĩa
▶ Hai đỉnh x và y gọi là kề nhau (hay hàng xóm) nếu {x, y} là
một cạnh của đồ thị.
▶ Ta biểu diễn đồ thị G = (V, E) bởi danh sách kề, trong đó
mỗi đỉnh v giữ một danh sách các đỉnh kề với v. Ví dụ a z b a b c d z b a d a b d z c d z d c 6 / 57 Bài tập
Có ba ngôi nhà A, B, C, mỗi ngôi nhà đều kết nối với cả ba nhà
cung cấp ga, nước, và điện: G, W, E.
1. Hãy viết danh sách kề cho đồ thị biểu diễn bài toán này và vẽ nó.
2. Liệu bạn có thể vẽ đồ thị này trên mặt phẳng để không có cạnh cắt nhau không? 7 / 57 Ví dụ
▶ GS Mc Brain và vợ là bà April tới một bữa tiệc ở đó có 4 đôi vợ chồng khác.
▶ Có một vài cặp bắt tay nhau nhưng không ai bắt tay với vợ hoặc chồng mình.
▶ GS hỏi mọi người khác xem họ bắt tay bao nhiêu người và
ông ấy nhận được 9 con số khác nhau.
▶ Hỏi có bao nhiêu người đã bắt tay April? 8 / 57 Nội dung Đồ thị và biểu diễn
Một số đồ thị đặc biệt Đẳng cấu Bậc Đường đi và chu trình Đồ thị đầy đủ
10.2 Graph Terminology and Special Types of Graphs 655 Định nghĩa Đồ thị đầy đủ
EXAMPLE 5 gồm n đỉnh, Complete ký Graphs hiệu A là K complete n là graph đồ on n thị v có ertices, đúng một
denoted by Kn, is a simple graph
cạnh nối mỗi cặp đỉnh that phân contains e biệt.
xactly one edge between each pair of distinct vertices. The graphs Kn, for
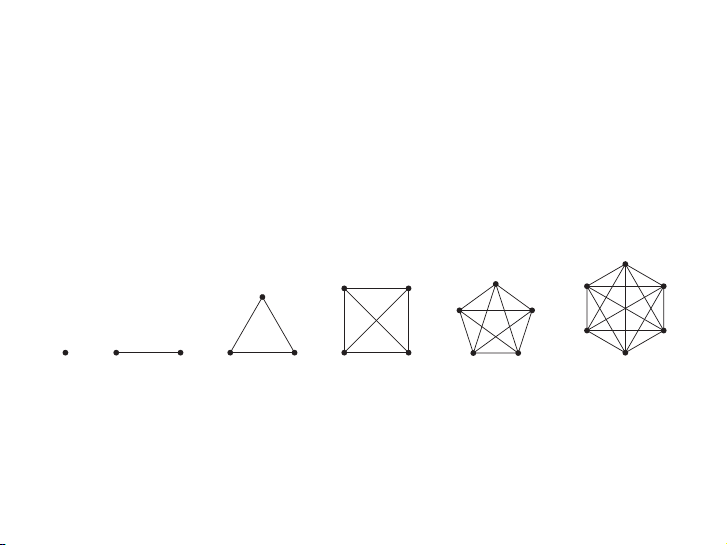
n = 1, 2, 3, 4, 5, 6, are displayed in Figure 3. A simple graph for which there is at least one
pair of distinct vertex not connected by an edge is called noncomplete. ▲ K1 K2 K3 K4 K5 K6
FIGURE 3 The Graphs Kn for 1 ≤ n ≤ 6.
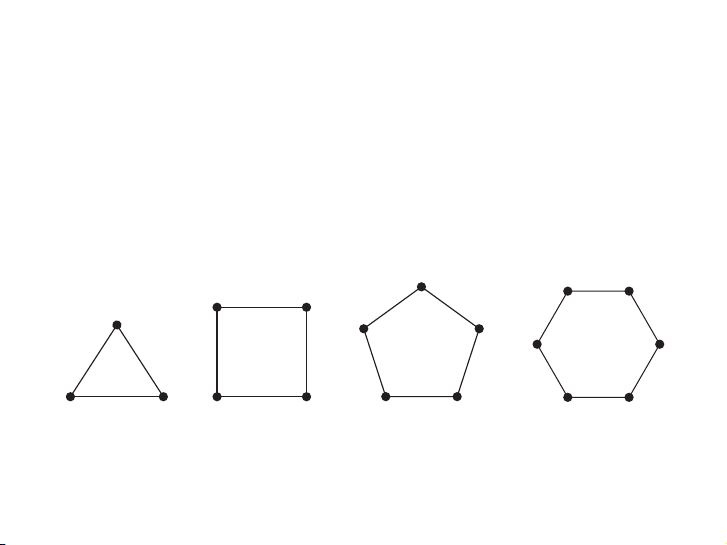
EXAMPLE 6 Cycles A cycle Cn, n ≥ 3, consists of n vertices v1, v2, . . . , vn and edges {v1, v2},
{v2, v3}, . . . , {vn−1, vn}, and {vn, v1}. The cycles C3, C4, C5, and C6 are displayed in Figure 4. ▲ 10 / 57 C3 C4 C5 C6
FIGURE 4 The Cycles C3, C4, C5, and C6.
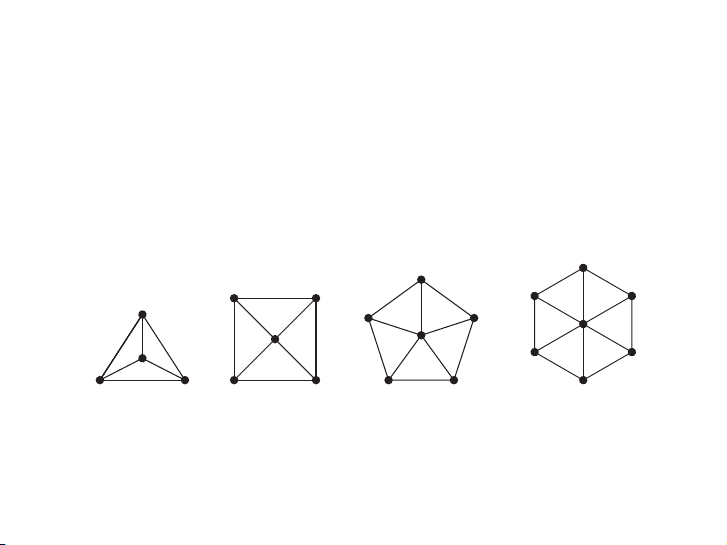
EXAMPLE 7 Wheels We obtain a wheel Wn when we add an additional vertex to a cycle Cn, for n ≥ 3,
and connect this new vertex to each of the n vertices in Cn, by new edges. The wheels W3, W4,
W5, and W6 are displayed in Figure 5. ▲ W3 W4 W5 W6
FIGURE 5 The Wheels W3, W4, W5, and W6.
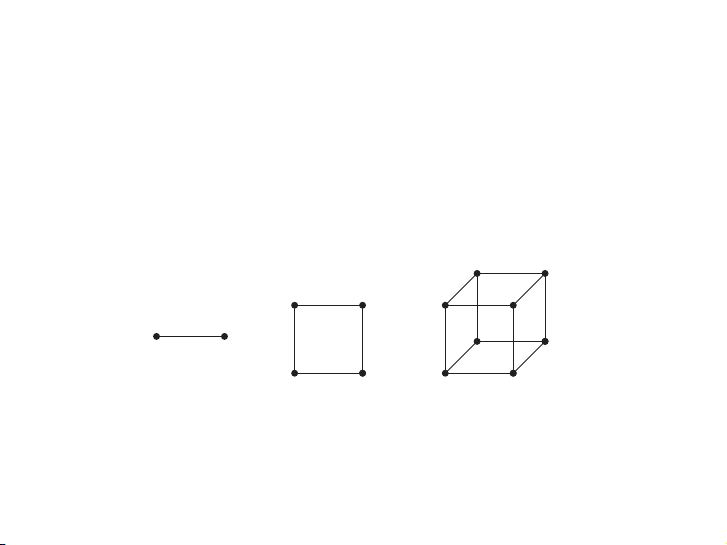
EXAMPLE 8 n-Cubes An n-dimensional hypercube, or n-cube, denoted by Qn, is a graph that has vertices
representing the 2n bit strings of length n. Two vertices are adjacent if and only if the bit strings
that they represent differ in exactly one bit position. We display Q1, Q2, and Q3 in Figure 6.
Note that you can construct the (n + 1)-cube Qn+1 from the n-cube Qn by making two
copies of Qn, prefacing the labels on the vertices with a 0 in one copy of Qn and with a 1 in the
other copy of Qn, and adding edges connecting two vertices that have labels differing only in
the first bit. In Figure 6, Q3 is constructed from Q2 by drawing two copies of Q2 as the top and
bottom faces of Q3, adding 0 at the beginning of the label of each vertex in the bottom face and
1 at the beginning of the label of each vertex in the top face. (Here, by face we mean a face of
a cube in three-dimensional space. Think of drawing the graph Q3 in three-dimensional space
with copies of Q2 as the top and bottom faces of a cube and then drawing the projection of the
resulting depiction in the plane.) ▲ Câu hỏi
Đồ thị Kn có bao nhiêu cạnh? 11 / 57
10.2 Graph Terminology and Special Types of Graphs 655
EXAMPLE 5 Complete Graphs A complete graph on n vertices, denoted by Kn, is a simple graph
that contains exactly one edge between each pair of distinct vertices. The graphs Kn, for
n = 1, 2, 3, 4, 5, 6, are displayed in Figure 3. A simple graph for which there is at least one
pair of distinct vertex not connected by an edge is called noncomplete. ▲ Đồ thị vòng K1 K2 K3 K4 K5 K6 Định nghĩa FIGURE 3 The Đồ thị Graphs vòng Kn f C
or 1 ≤ n ≤ 6.
n, với n ≥ 3 là một đồ thị có n đỉnh v1, v2, . . . , vn và các cạnh
EXAMPLE 6 Cycles {A cycle C v
n, n ≥ 3, consists of n vertices v1, v2, . . . , vn and edges {v1, v2},
1, v2}, {v2, v3}, · · · , {vn−1, vn}, và {vn, v1}
{v2, v3}, . . . , {vn−1, vn}, and {vn, v1}. The cycles C3, C4, C5, and C6 are displayed in Figure 4. ▲ C3 C4 C5 C6
FIGURE 4 The Cycles C3, C4, C5, and C6. EXAMPLE 7 12 / 57
Wheels We obtain a wheel Wn when we add an additional vertex to a cycle Cn, for n ≥ 3,
and connect this new vertex to each of the n vertices in Cn, by new edges. The wheels W3, W4,
W5, and W6 are displayed in Figure 5. ▲ W3 W4 W5 W6
FIGURE 5 The Wheels W3, W4, W5, and W6.
EXAMPLE 8 n-Cubes An n-dimensional hypercube, or n-cube, denoted by Qn, is a graph that has vertices
representing the 2n bit strings of length n. Two vertices are adjacent if and only if the bit strings
that they represent differ in exactly one bit position. We display Q1, Q2, and Q3 in Figure 6.
Note that you can construct the (n + 1)-cube Qn+1 from the n-cube Qn by making two
copies of Qn, prefacing the labels on the vertices with a 0 in one copy of Qn and with a 1 in the
other copy of Qn, and adding edges connecting two vertices that have labels differing only in
the first bit. In Figure 6, Q3 is constructed from Q2 by drawing two copies of Q2 as the top and
bottom faces of Q3, adding 0 at the beginning of the label of each vertex in the bottom face and
1 at the beginning of the label of each vertex in the top face. (Here, by face we mean a face of
a cube in three-dimensional space. Think of drawing the graph Q3 in three-dimensional space
with copies of Q2 as the top and bottom faces of a cube and then drawing the projection of the
resulting depiction in the plane.) ▲ Câu hỏi
Đồ thị Cn có bao nhiêu cạnh? 13 / 57
10.2 Graph Terminology and Special Types of Graphs 655
EXAMPLE 5 Complete Graphs A complete graph on n vertices, denoted by Kn, is a simple graph
that contains exactly one edge between each pair of distinct vertices. The graphs Kn, for
n = 1, 2, 3, 4, 5, 6, are displayed in Figure 3. A simple graph for which there is at least one
pair of distinct vertex not connected by an edge is called noncomplete. ▲ K1 K2 K3 K4 K5 K6
FIGURE 3 The Graphs Kn for 1 ≤ n ≤ 6.
EXAMPLE 6 Cycles A cycle Cn, n ≥ 3, consists of n vertices v1, v2, . . . , vn and edges {v1, v2},
{v2, v3}, . . . , {vn−1, vn}, and {vn, v1}. The cycles C3, C4, C5, and C6 are displayed in Figure 4. ▲ Đồ thị bánh xe C3 C4 C5 C6
FIGURE 4 The Cycles C3, C4, C5, and C6. Định nghĩa
Khi thêm một đỉnh vào vòng Cn với n ≥ 3 và nối đỉnh này với mỗi
EXAMPLE 7 Wheels We obtain a wheel Wn when we add an additional vertex to a cycle Cn, for n ≥ 3,
đỉnh trong Cn bằng một cạnh mới ta sẽ nhận được đồ thị bánh xe
and connect this new vertex to each of the n vertices in Cn, by new edges. The wheels W3, W4,
Wn. W5, and W6 are displayed in Figure 5. ▲ W3 W4 W5 W6
FIGURE 5 The Wheels W3, W4, W5, and W6.
EXAMPLE 8 n-Cubes An n-dimensional hypercube, or n-cube, denoted by Qn, is a graph that has vertices
representing the 2n bit strings of length n. Two vertices are adjacent14if / and 57 only if the bit strings
that they represent differ in exactly one bit position. We display Q1, Q2, and Q3 in Figure 6.
Note that you can construct the (n + 1)-cube Qn+1 from the n-cube Qn by making two
copies of Qn, prefacing the labels on the vertices with a 0 in one copy of Qn and with a 1 in the
other copy of Qn, and adding edges connecting two vertices that have labels differing only in
the first bit. In Figure 6, Q3 is constructed from Q2 by drawing two copies of Q2 as the top and
bottom faces of Q3, adding 0 at the beginning of the label of each vertex in the bottom face and
1 at the beginning of the label of each vertex in the top face. (Here, by face we mean a face of
a cube in three-dimensional space. Think of drawing the graph Q3 in three-dimensional space
with copies of Q2 as the top and bottom faces of a cube and then drawing the projection of the
resulting depiction in the plane.) ▲ Câu hỏi
Đồ thị Wn có bao nhiêu cạnh? 15 / 57 Các khối n chiều Định nghĩa
Các khối n chiều, ký hiệu Qn, là các đồ thị có 2n đỉnh, mỗi đỉnh
được biểu diễn bằng xâu nhị phân độ dài n. Hai đỉnh liền kề nếu và
chỉ nếu các xâu nhị phân biểu diễn chúng khác nhau đúng một bit. 656 10 / Graphs 110 111 10 11 100 101 010 0 1 011 00 01 000 001 Q1 Q2 Q3
FIGURE 6 The n-cube Qn, n = 1, 2, 3. Bipartite Graphs 16 / 57
Sometimes a graph has the property that its vertex set can be divided into two disjoint subsets
such that each edge connects a vertex in one of these subsets to a vertex in the other subset.
For example, consider the graph representing marriages between men and women in a village,
where each person is represented by a vertex and a marriage is represented by an edge. In this
graph, each edge connects a vertex in the subset of vertices representing males and a vertex in
the subset of vertices representing females. This leads us to Definition 5. DEFINITION 6
A simple graph G is called bipartite if its vertex set V can be partitioned into two disjoint
sets V1 and V2 such that every edge in the graph connects a vertex in V1 and a vertex in V2
(so that no edge in G connects either two vertices in V1 or two vertices in V2). When this
condition holds, we call the pair (V1, V2) a bipartition of the vertex set V of G.
In Example 9 we will show that C6 is bipartite, and in Example 10 we will show that K3 is not bipartite.
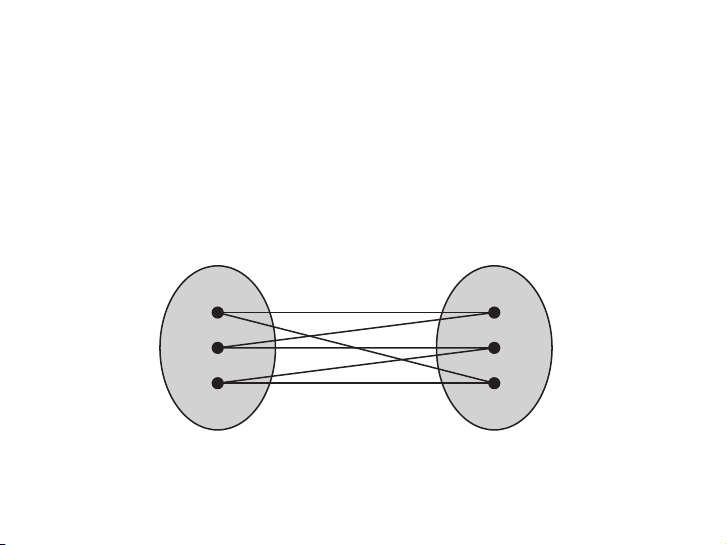
EXAMPLE 9 C6 is bipartite, as shown in Figure 7, because its vertex set can be partitioned into the two sets
V1 = {v1, v3, v5} and V2 = {v2, v4, v6}, and every edge of C6 connects a vertex in V1 and a vertex in V2. ▲
EXAMPLE 10 K3 is not bipartite. To verify this, note that if we divide the vertex set of K3 into two disjoint
sets, one of the two sets must contain two vertices. If the graph were bipartite, these two vertices
could not be connected by an edge, but in K3 each vertex is connected to every other vertex by an edge. ▲
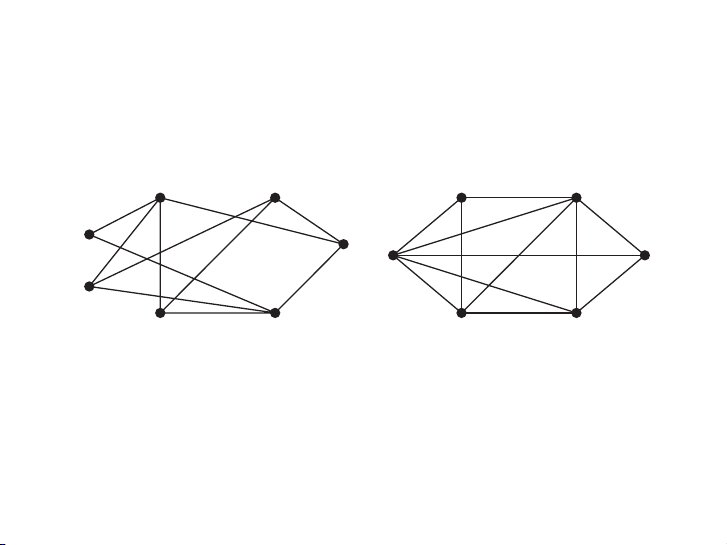
EXAMPLE 11 Are the graphs G and H displayed in Figure 8 bipartite? a b a b c g f c V1 V2 v f 1 v2 v3 v4 e d e d v5 v6 G H FIGURE 7
Showing That C6 Is
FIGURE 8 The Undirected Graphs G and H . Bipartite. Câu hỏi
Đồ thị Qn có bao nhiêu cạnh? 17 / 57 656 10 / Graphs 110 111 10 11 100 101 010 0 1 011 00 01 000 001 Q1 Q2 Q3
FIGURE 6 The n-cube Qn, n = 1, 2, 3. Bipartite Graphs
Sometimes a graph has the property that its vertex set can be divided into two disjoint subsets
such that each edge connects a vertex in one of these subsets to a vertex in the other subset.
For example, consider the graph representing marriages between men and women in a village,
where each person is represented by a vertex and a marriage is represented by an edge. In this
graph, each edge connects a vertex in the subset of vertices representing males and a vertex in
the subset of vertices representing females. This leads us to Definition 5. DEFINITION 6
A simple graph G is called bipartite if its vertex set V can be partitioned into two disjoint
sets V1 and V2 such that every edge in the graph connects a vertex in V1 and a vertex in V2
(so that no edge in G connects either two vertices in V1 or two vertices in V2). When this
condition holds, we call the pair (V1, V2) a bipartition of the vertex set V of G.
In Example 9 we will show that C6 is bipartite, and in Example 10 we will show that K3 is not bipartite.
EXAMPLE 9 C6 is bipartite, as shown in Figure 7, because its vertex set can be partitioned into the two sets
V1 = {v1, v3, v5} and V2 = {v2, v4, v6}, and every edge of C6 connects a vertex in V1 and a vertex in V2. ▲
EXAMPLE 10 K3 is not bipartite. To verify this, note that if we divide the vertex set of K3 into two disjoint
sets, one of the two sets must contain two vertices. If the graph were bipartite, these two vertices
could not be connected by an edge, but in K3 each vertex is connected to every other vertex by an edge. ▲ Đồ thị hai phần
EXAMPLE 11 Are the graphs G and H displayed in Figure 8 bipartite? Định nghĩa
Một đồ thị được gọi là hai phần nếu tập đỉnh V có thể phân hoạch
thành hai tập V1 và V2 sao cho mỗi cạnh của đồ thị nối một đỉnh a b a b
của V1 tới một đỉnh của V2. c g f c V1 V2 v f 1 v2 v3 v4 e d e d v5 v6 G H FIGURE 7
Showing That C6 Is
FIGURE 8 The Undirected Graphs G and H . Bipartite. 18 / 57 656 10 / Graphs 110 111 10 11 100 101 010 0 1 011 00 01 000 001 Q1 Q2 Q3
FIGURE 6 The n-cube Qn, n = 1, 2, 3. Bipartite Graphs
Sometimes a graph has the property that its vertex set can be divided into two disjoint subsets
such that each edge connects a vertex in one of these subsets to a vertex in the other subset.
For example, consider the graph representing marriages between men and women in a village,
where each person is represented by a vertex and a marriage is represented by an edge. In this
graph, each edge connects a vertex in the subset of vertices representing males and a vertex in
the subset of vertices representing females. This leads us to Definition 5. DEFINITION 6
A simple graph G is called bipartite if its vertex set V can be partitioned into two disjoint
sets V1 and V2 such that every edge in the graph connects a vertex in V1 and a vertex in V2
(so that no edge in G connects either two vertices in V1 or two vertices in V2). When this
condition holds, we call the pair (V1, V2) a bipartition of the vertex set V of G.
In Example 9 we will show that C6 is bipartite, and in Example 10 we will show that K3 is not bipartite.
EXAMPLE 9 C6 is bipartite, as shown in Figure 7, because its vertex set can be partitioned into the two sets
V1 = {v1, v3, v5} and V2 = {v2, v4, v6}, and every edge of C6 connects a vertex in V1 and a vertex in V2. ▲
EXAMPLE 10 K3 is not bipartite. To verify this, note that if we divide the vertex set of K3 into two disjoint
sets, one of the two sets must contain two vertices. If the graph were bipartite, these two vertices
could not be connected by an edge, but in K3 each vertex is connected to every other vertex by an edge. ▲ Câu hỏi
EXAMPLE 11 Are the graphs G and H displayed in Figure 8 bipartite?
Đồ thị nào dưới đây là đồ thị hai phần? a b a b c g f c V1 V2 v f 1 v2 v3 v4 e d e d v5 v6 G H FIGURE 7
Showing That C6 Is
FIGURE 8 The Undirected Graphs G and H . Bipartite. 19 / 57 Câu hỏi
Đồ thị C5 và C6 có phải là những đồ thị hai phần? 20 / 57






