Bài giảng động lực học hệ chất điểm - Vật lý đại cương 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Bài giảng động lực học hệ chất điểm - Vật lý đại cương 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Vật lý đại cương 2 (EPN1096)
Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Tác giả:
Tài liệu liên quan:
Preview text:
Ch−¬ng III
®éng lùc häc hÖ chÊt ®iÓm, ®éng lùc häc vËt r¾n
Bμi gi¶ng VËt lý ®¹i c−¬ng 1. Khèi t©m: G M G M 1 2 1.1. §Þnh nghÜa = − m g 1 + = m g 2
Khèi t©m cña hÖ chÊt ®iÓm M , M , 1 2 (m +m )g 1 2
...,M lÇn l−ît cã khèi l−îng m , m , n 1 2
..., m lμ ®iÓm G x¸c ®Þnh bëi ®¼ng n thøc: + + + = = ∑= 1.2. To¹ ®é khèi t©m M G M i 2 §èi víi mét gèc O r r r r = + r r = + O r ∑ r = ∑ + ∑ r = = = r ∑ r = ⇒ = ∑ r = ∑ ∑ = = = ∑ M (x ,y ,z ) i i i i = ⇒ = R (X ,Y ,Z ) ∑ G G G G = 1.3. VËn tèc khèi t©m r r r ∑ ∑ r r ∑ = = = = = ⇒ = ∑ ∑ ∑ = = = r r r r Tæng ®éng = ∑ ⇒ = ∑ = l−îng cña c¶ hÖ =
Tæng ®éng l−îng cña c¶ hÖ = ®éng l−îng cña
mét chÊt ®iÓm ®Æt t¹i khèi t©m, cã khèi l−îng
b»ng tæng khèi l−îng c¶ hÖ, cã vËn tèc b»ng vËn tèc cña khèi t©m cña hÖ
1.4.Ph−¬ng tr×nh chuyÓn ®éng cña khèi t©m HÖ chÊt ®iÓm M , M , ...,M 1 2 n cã khèi l−îng m , m , ..., m 1 2 n r r r ChÞu t¸c dông l−c r r r Cã gia tèc
§èi víi chÊt ®iÓm thø i: LÊy tæng cho c¶ hÖ: r r r r r = ∑ = ∑ = = = r ∑ r r ∑ r = = = = ∑ ∑ = = r ∑ r r r r = = = = ∑ ∑ ∑ = = =
Khèi t©m cña hÖ chuyÓn ®éng nh− chÊt ®iÓm cã
khèi l−îng b»ng khèi l−îng cña hÖ vμ chÞu t¸c
dông cña mét lùc b»ng tæng hîp ngo¹i lùc t¸c dông lªn hÖ.
2. ChuyÓn ®éng cña vËt r¾n
VËt r¾n lμ hÖ chÊt ®iÓm mμ vÞ trÝ t−¬ng ®èi gi÷a
c¸c chÊt ®iÓm ®ã kh«ng thay ®æi
2.1. ChuyÓn ®éng tÞnh tiÕn: T¹i mçi thêi ®iÓm tÊt
c¶ c¸c chÊt ®iÓm cña vËt r¾n cã cïng vÐc t¬ vËn tèc vμ vÐc t¬ gia tèc. r r HÖ chÊt ®iÓm M , M , ...,M m = 1 2 n 1 r r cã khèi l−îng m m = r , m r , ..., rm 1 2 n 2 ChÞu t¸c d ................ r ông lù r c r r r r Cã gia tèc = = = = m = n r r
ChØ cÇn kh¶o s¸t chuyÓn ®éng ∑ = = cña khèi t©m cña vËt r¾n 2.2. ChuyÓn ®éng quay Δr
§éng häc vËt r¾n quay quanh 1 trôc: r β ω r r
Mäi ®iÓm cã quÜ ®¹o trßn cïng r trôc Δ
Trong cïng kho¶ng thêi gian mäi ®iÓm cïng quay ®i gãc θ
Mäi ®iÓm cã cïng vËn tèc gãc
ω=dθ/dt vμ gia tèc gãc β=dω/dt= d2θ/dt2 r r r r r = ω × T¹i mäi thêi ®iÓm vμ r r r
cña mét ®iÓm ®−îc x¸c ®Þnh = β ×
3. Ph−¬ng tr×nh c¬ b¶n cña chuyÓn ®éng quay
cña vËt r¾n quanh mét trôc cè ®Þnh: Δ r 3.1.T¸c dông cña lùc r r r r r r r F = F + + r z r r r μ ®ång ph¼ng víi trôc v z F quay kh«ng g©y quay v× r r F Δ xuyªn t©m z
Trong chuyÓn ®éng quay cña vËt r¾n quanh r
mét trôc chØ cã thμnh phÇn tiÕp tuyÕn víi
quÜ ®¹o cña ®iÓm ®Æt míi cã t¸c dông thùc sù r r M«men cña lùc r M = r × M = r. α =
M«men cña lùc ®èi víi trôc quay r
chÝnh lμ m«men cña lùc ®èi víi O - Δr
giao ®iÓm cña trôc víi mÆt ph¼ng cña r quü ®¹o ®iÓm ®Æt lùc β r r O
3.2. Ph−¬ng tr×nh c¬ b¶n cña r mi chuyÓn ®éng quay r r ChÊt ®iÓm thø i m = i r r r r r r m r × = × β I = i i r r r r r r r r r r r r r r r × = × β × = β − β β = i r r r r r r 2 2 m r β = × = ∑m r β = i i ∑ i i r r M«men qu¸n tÝnh cña β I = ∑ 2 m r = i i vËt ®èi víi trôc quay r r ∑ =
Tæng hîp m«men cña c¸c lùc g©y quay r r
Gia tèc gãc ~M vμ ~ nghÞch víi I β = I <-> m vμ M<->F
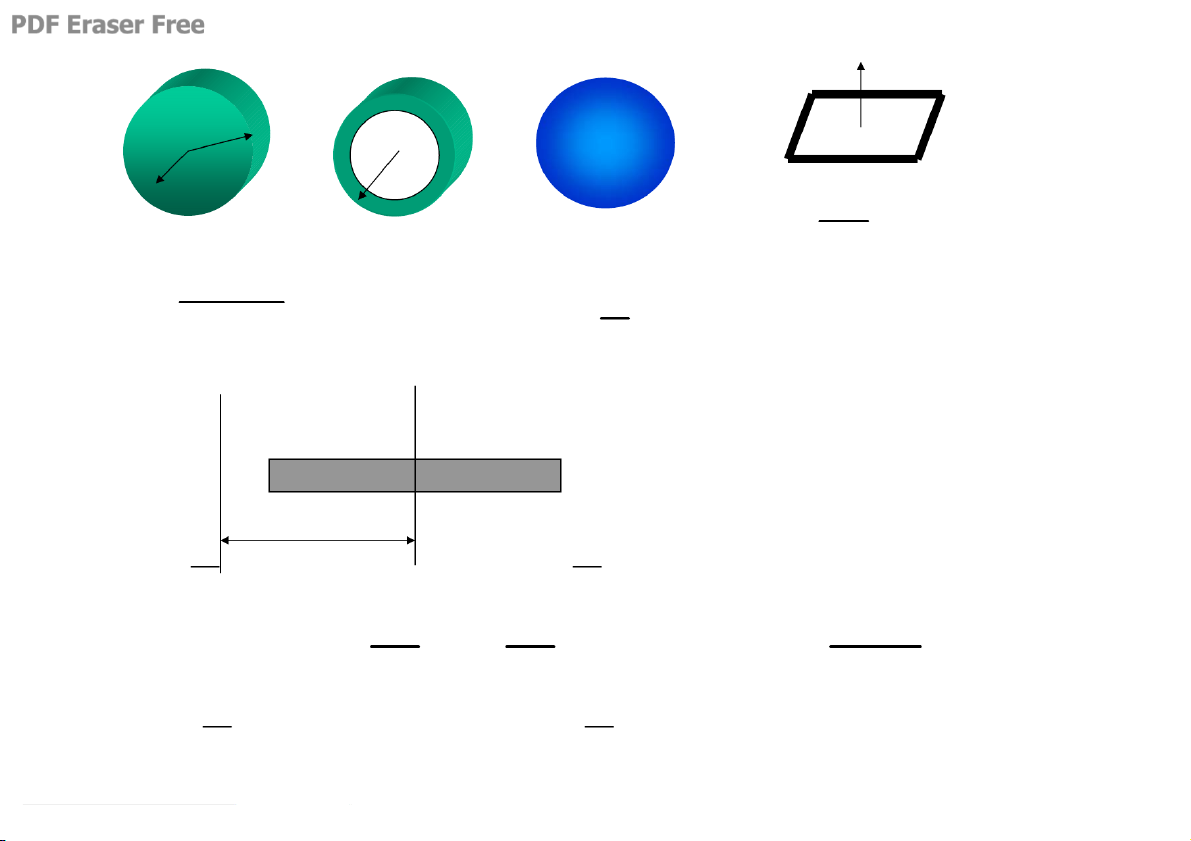
3.3. TÝnh m«men qu¸n tÝnh cña vËt ®èi víi trôc quay: Δ
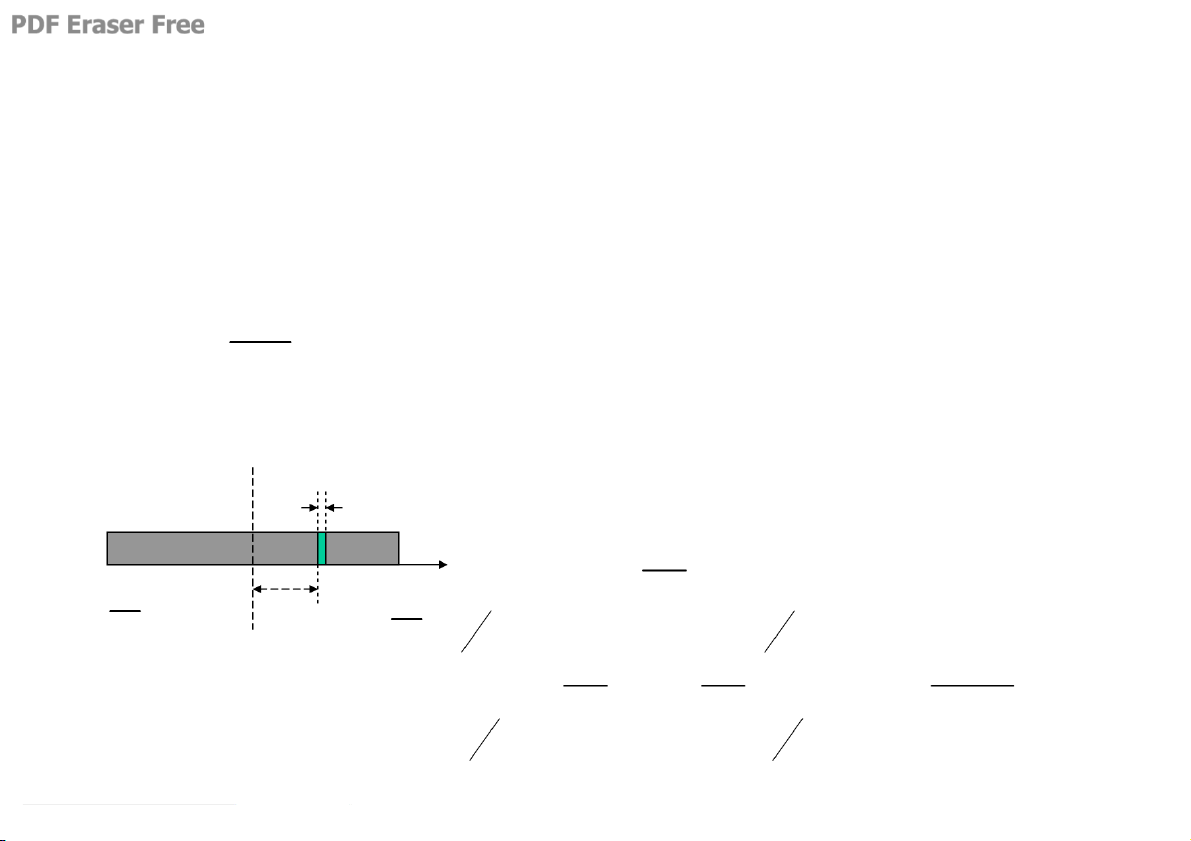
dx Thanh ®Òu: Khèi l−îng M, μ d i L dI x 2 = L - x 2 2 I = 2 x = 2 x = 0 ∫ ∫ − L L − Δ b R a Δ Δ I = + I = I = I = §Þnh lý Stene- Δ Δ = + Huyghen: M«men QT cña vËt r¾n d ®èi víi trôc bÊt kú =... I = (d + 2 x) = (d + 2 x) = + Δ ∫ L L ∫ − −
4. M«men ®éng l−îng cña hÖ chÊt ®iÓm
4.1. M«men ®éng l−îng cña hÖ chÊt ®iÓm ®èi víi gèc O HÖ chÊt ®iÓm M , M , ...,M 1 2 n cã khèi l−îng m , m , ..., m 1 2 n r r r VÞ trÝ ®èi víi gèc O r r r Cã vËn tèc
M«men ®éng l−îng cña hÖ ®èi víi O r r r r = ∑ = ∑ ×
M«men ®éng l−îng cña hÖ r r r = ∑ = ω
chÊt ®iÓm quay quanh trôc Δ ∑ M«men ®éng l r r −îng cña hÖ r = ∑ = ∑ ω
lμ vËt r¾n quay quanh trôc Δr r r r ω = ω = = ω = ω r r = ω = ω ∑ r = ∑ = ∑
4.2. §Þnh lý vÒ m«men ®éng l−îng cña hÖ chÊt ®iÓm r r r r r r Mét chÊt ®iÓm = μ ⇒ ∑ = ∑μ r r r r ∑ = ∑ = r = r r r μ = ∑
§¹o hμm theo thêi gian m«men ®éng
l−îng cña hÖ = tæng hîp c¸c m«men
ngo¹i lùc tdông lªn hÖ ®èi víi gèc O Tr−êng hîp hÖ lμ vËt r r = ∑ r ω = ω r¾n quay quanh trôc Δ r r ω r r r r r = = ⇒ Δ = − = ∫ r r r = ⇒ Δ = Δ
§é biÕn thiªn cña m«men ®éng l−îng trong
kho¶ng thêi gian Δt b»ng xung l−îng cña
m«men lùc trong kho¶ng thêi gian ®ã r r ω = r r ⇒ β = I=const
5. §Þnh luËt b¶o toμn m«men ®éng l−îng
5.1. ThiÕt lËp: HÖ chÊt ®iÓm chÞu t¸c dông
ngo¹i lùc víi m«men ®èi víi gèc O b»ng 0 r r r HÖ c« lËp, M =0 = = /O ⇒ = -> L=const
5.2. HÖ quay quanh mét trôc cè ®Þnh r r r r ω + ω + + ω = = r r r ω + ω + + ω =
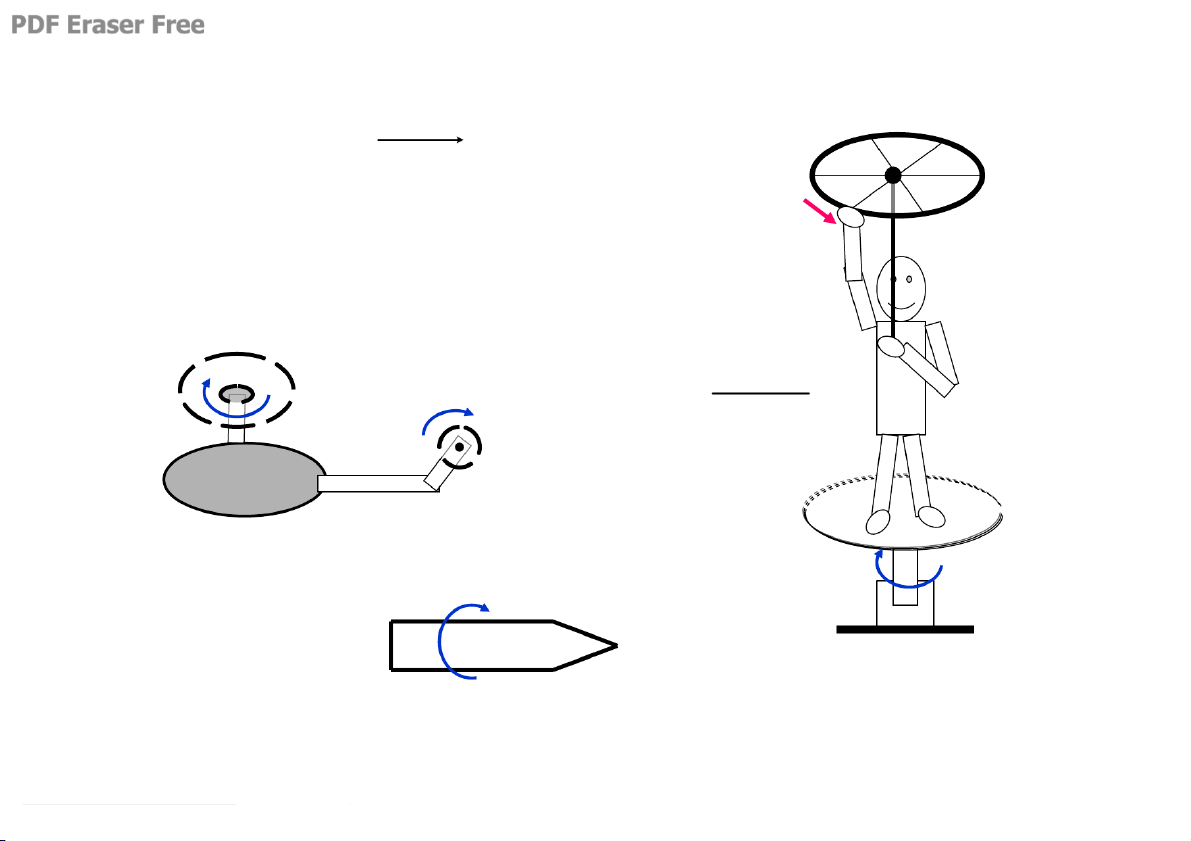
5.3. øng dông: HÖ quay quanh
mét trôc cè ®Þnh víi vËn tèc ω = gãc kh«ng ®æi
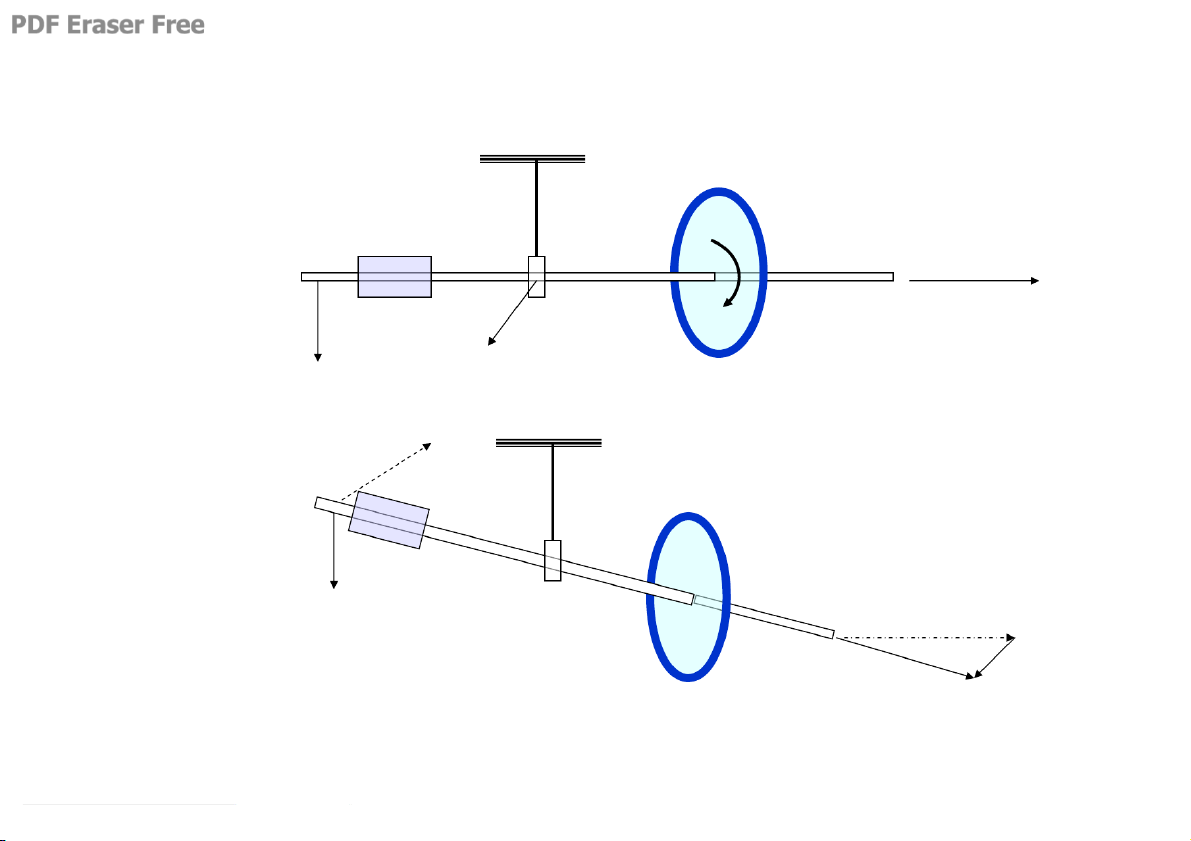
GhÕ Giukèpxki quay quanh mét trôc cè ®Þnh r r ω + ω = = r r ω ω cña b¸nh xe r ω cña ng−êi & ghÕ r r ω ω = − r ω 6. Con quay trôc quay tù do A C’ B B’ C A’ Con quay C¸c ®¨ng Con quay ®ang quay r r quay ngang r r r Δ
7. C«ng vμ ®éng n¨ng cña vËt r¾n
7.1. C«ng vμ c«ng suÊt cña lùc t¸c dông trong
chuyÓn ®éng quay cña vËt r¾n Δ = dα ds = r. dα r r = α = α ds α = = = ω r = ω r
7.2. §éng n¨ng trong tr−êng hîp vËt r¾n quay r r r r Δ = ω r = = ω ω dα r = βω = ω ω r ω ω ω = − W = ® ds
§éng n¨ng vËt r¾n l¨n kh«ng tr−ît = §éng
n¨ng chuyÓn ®éng tÞnh tiÕn + §éng n¨ng chuyÓn ®éng quay: ω W® = +