Bài giảng Đường đi trên đồ thị (Version 0.2) - Toán rời rạc thầy Trần Vĩnh Đức | Trường Đại học Bách khoa Hà Nội

 Đường đi đơn: Là đường đi mà mọi đỉnh trên đó, trừ đỉnh đầu và đỉnh cuối đều khác nhau. Một chu trình là một đường đi đơn mà đỉnh đầu và đỉnh cuối trùng nhau. Tài liệu được sưu tầm, giúp bạn ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán rời rạc (BKHN)

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

52 trang 2 tháng trước

Tác giả:

Profile Lân Nguyễn
Đường đi trên đồ thị (Version 0.2)
Trần Vĩnh Đức
HUST
Ngày 24 tháng 7 năm 2018
1 / 52
Tài liệu tham khảo
▶
S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani,
Algorithms, July 18, 2016.
▶
Chú ý: Nhiều hình vẽ trong tài liệu được lấy tùy tiện mà chưa
xin phép.
2 / 52
Nội dung
Khoảng cách và tìm kiếm theo chiều rộng
Thuật toán Dijkstra
Cài đặt hàng đợi ưu tiên
Đường đi ngắn nhất khi có cạnh độ dài âm
Đường đi ngắn nhất trong một DAG
DFS và đường đi
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4
Paths in graphs
4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
the vertices reachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest
paths to it. When S is held up, the strings along each of these paths become taut.
Figure 4.1
(a) A simple graph and (b) its depth-first search tree.
(a)
E
A
S
BD C
(b)
S
A
B
D
E
C
104
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4
Paths in graphs
4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
the vertices reachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest
paths to it. When S is held up, the strings along each of these paths become taut.
Figure 4.1
(a) A simple graph and (b) its depth-first search tree.
(a)
E
A
S
BD C
(b)
S
A
B
D
E
C
104
Đường đi trên cây DFS thường không phải là đường đi ngắn nhất.
4 / 52
Khoảng cách
Khoảng cách giữa hai đỉnh là độ dài của đường đi ngắn nhất giữa
chúng.
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4
Paths in graphs
4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
the vertices reachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest
paths to it. When S is held up, the strings along each of these paths become taut.
Figure 4.1
(a) A simple graph and (b) its depth-first search tree.
(a)
E
A
S
BD C
(b)
S
A
B
D
E
C
104
v Khoảng cách (S − v)
A
B
C
D
E
5 / 52
Mô hình vật lý của đồ thị
Giả sử rằng mọi cạnh có cùng độ dài. Ta nhấc đỉnh S lên:
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms
105
Figure 4.2 A physical model of a graph.
B
ES
D
C
A
D
E
C
B
A
S
On the other hand, edge (D, E ) plays no role in any shortest path and therefore
remains slack.
4.2 Breadth-first search
In Figure 4.2, the lifting of s partitions the graph into layers: s itself, the nodes at
distance 1 from it, the nodes at distance 2 from it, and so on. A convenient way
to compute distances from s to the other vertices is to proceed layer by layer. Once
we have picked out the nodes at distance 0, 1, 2,...,d, the ones at d + 1 are easily
determined: they are precisely the as-yet-unseen nodes that are adjacent to the layer
at distance d. This suggests an iterative algorithm in which two layers are active at
any given time: some layer d, which has been fully identified, and d + 1, which is
being discovered by scanning the neighbors of layer d.
Breadth-first search (BFS) directly implements this simple reasoning (Figure 4.3).
Initially the queue Q consists only of s, the one node at distance 0. And for each
subsequent distance d = 1, 2, 3,..., there is a point in time at which Q contains
all the nodes at distance d and nothing else. As these nodes are processed (ejected
off the front of the queue), their as-yet-unseen neighbors are injected into the end
of the queue.
Let’s try out this algorithm on our earlier example (Figure 4.1) to confirm that it does
the right thing. If S is the starting point and the nodes are ordered alphabetically,
they get visited in the sequence shown in Figure 4.4. The breadth-first search tree,
on the right, contains the edges through which each node is initially discovered.
Unlike the DFS tree we saw earlier, it has the property that all its paths from S are
the shortest possible. It is therefore a shortest-path tree.
Correctness and efficiency
We have developed the basic intuition behind breadth-first search. In order to check
that the algorithm works correctly, we need to make sure that it faithfully executes
this intuition. What we expect, precisely, is that
For each d = 0, 1, 2,..., there is a moment at which (1) all nodes at distance
≤ d from s have their distances correctly set; (2) all other nodes have their
distances set to ∞; and (3) the queue contains exactly the nodes at distance d.
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms
105
Figure 4.2 A physical model of a graph.
B
ES
D
C
A
D
E
C
B
A
S
On the other hand, edge (D, E ) plays no role in any shortest path and therefore
remains slack.
4.2 Breadth-first search
In Figure 4.2, the lifting of s partitions the graph into layers: s itself, the nodes at
distance 1 from it, the nodes at distance 2 from it, and so on. A convenient way
to compute distances from s to the other vertices is to proceed layer by layer. Once
we have picked out the nodes at distance 0, 1, 2,...,d, the ones at d + 1 are easily
determined: they are precisely the as-yet-unseen nodes that are adjacent to the layer
at distance d. This suggests an iterative algorithm in which two layers are active at
any given time: some layer d, which has been fully identified, and d + 1, which is
being discovered by scanning the neighbors of layer d.
Breadth-first search (BFS) directly implements this simple reasoning (Figure 4.3).
Initially the queue Q consists only of s, the one node at distance 0. And for each
subsequent distance d = 1, 2, 3,..., there is a point in time at which Q contains
all the nodes at distance d and nothing else. As these nodes are processed (ejected
off the front of the queue), their as-yet-unseen neighbors are injected into the end
of the queue.
Let’s try out this algorithm on our earlier example (Figure 4.1) to confirm that it does
the right thing. If S is the starting point and the nodes are ordered alphabetically,
they get visited in the sequence shown in Figure 4.4. The breadth-first search tree,
on the right, contains the edges through which each node is initially discovered.
Unlike the DFS tree we saw earlier, it has the property that all its paths from S are
the shortest possible. It is therefore a shortest-path tree.
Correctness and efficiency
We have developed the basic intuition behind breadth-first search. In order to check
that the algorithm works correctly, we need to make sure that it faithfully executes
this intuition. What we expect, precisely, is that
For each d = 0, 1, 2,..., there is a moment at which (1) all nodes at distance
≤ d from s have their distances correctly set; (2) all other nodes have their
distances set to ∞; and (3) the queue contains exactly the nodes at distance d.
6 / 52
Tìm kiếm theo chiều rộng (Breadth-First Search)
Chia đồ thị thành các mức:
▶
S là mức có khoảng cách 0.
▶
Các đỉnh có khoảng cách tới
S bằng 1.
▶
Các đỉnh có khoảng cách tới
S bằng 2
▶
...
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms
105
Figure 4.2 A physical model of a graph.
B
ES
D
C
A
D
E
C
B
A
S
On the other hand, edge (D, E ) plays no role in any shortest path and therefore
remains slack.
4.2 Breadth-first search
In Figure 4.2, the lifting of s partitions the graph into layers: s itself, the nodes at
distance 1 from it, the nodes at distance 2 from it, and so on. A convenient way
to compute distances from s to the other vertices is to proceed layer by layer. Once
we have picked out the nodes at distance 0, 1, 2,...,d, the ones at d + 1 are easily
determined: they are precisely the as-yet-unseen nodes that are adjacent to the layer
at distance d. This suggests an iterative algorithm in which two layers are active at
any given time: some layer d, which has been fully identified, and d + 1, which is
being discovered by scanning the neighbors of layer d.
Breadth-first search (BFS) directly implements this simple reasoning (Figure 4.3).
Initially the queue Q consists only of s, the one node at distance 0. And for each
subsequent distance d = 1, 2, 3,..., there is a point in time at which Q contains
all the nodes at distance d and nothing else. As these nodes are processed (ejected
off the front of the queue), their as-yet-unseen neighbors are injected into the end
of the queue.
Let’s try out this algorithm on our earlier example (Figure 4.1) to confirm that it does
the right thing. If S is the starting point and the nodes are ordered alphabetically,
they get visited in the sequence shown in Figure 4.4. The breadth-first search tree,
on the right, contains the edges through which each node is initially discovered.
Unlike the DFS tree we saw earlier, it has the property that all its paths from S are
the shortest possible. It is therefore a shortest-path tree.
Correctness and efficiency
We have developed the basic intuition behind breadth-first search. In order to check
that the algorithm works correctly, we need to make sure that it faithfully executes
this intuition. What we expect, precisely, is that
For each d = 0, 1, 2,..., there is a moment at which (1) all nodes at distance
≤ d from s have their distances correctly set; (2) all other nodes have their
distances set to ∞; and (3) the queue contains exactly the nodes at distance d.
Ý tưởng thuật toán: Khi mức d đã được xác định, mức d + 1 có
thể thăm bằng cách duyệt qua các hàng xóm của mức d.
7 / 52
Ý tưởng loang theo chiều rộng
Khởi tạo: Hàng đợi Q chỉ chứa đỉnh s, là đỉnh duy nhất ở mức 0.
Với mỗi khoảng cách d = 1, 2, 3, . . . ,
▶
sẽ có thời điểm Q chỉ chứa các đỉnh có khoảng cách d và
không có gì khác.
▶
Khi đó các đỉnh có khoảng cách d này sẽ được loại bỏ dần từ
đầu hàng đợi,
▶
và các hàng xóm chưa được thăm sẽ được thêm vào cuối
hàng đợi.
8 / 52
Bài tập
Chạy thuật toán BFS cho đồ thị dưới đây bắt đầu từ đỉnh S. Ghi
ra hàng đợi Q sau mỗi lần thăm đỉnh.
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4
Paths in graphs
4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
the vertices reachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest
paths to it. When S is held up, the strings along each of these paths become taut.
Figure 4.1
(a) A simple graph and (b) its depth-first search tree.
(a)
E
A
S
BD C
(b)
S
A
B
D
E
C
104
Đỉnh thăm Hàng đợi
S [S]
9 / 52
procedure bfs(G, s)
Input: đồ thị G = (V, E), có hướng hoặc vô hướng;
một đỉnh s ∈ V
Output: Với mỗi đỉnh u đến được từ s,
dist(u) = khoảng cách từ s tới u.
for all u ∈ V:
dist(u) = ∞
dist(s) = 0
Q = [s] (hàng đợi chỉ chứa s)
while Q khác rỗng:
u = eject(Q) (loại bỏ u khỏi hàng đợi)
for all edges (u, v) ∈ E:
if dist(v) = ∞:
inject(Q, v) (thêm v vào hàng đợi)
dist(v) = dist(u) + 1
10 / 52
Bài tập
Hãy chạy thuật toán BFS cho đồ thị dưới đây và ghi ra nội dung
của hàng đợi Q sau mỗi bước:
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4
Paths in graphs
4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
the vertices reachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest
paths to it. When S is held up, the strings along each of these paths become taut.
Figure 4.1
(a) A simple graph and (b) its depth-first search tree.
(a)
E
A
S
BD C
(b)
S
A
B
D
E
C
104
Thứ tự thăm đỉnh Hàng đợi
S [S]
11 / 52
Nội dung
Khoảng cách và tìm kiếm theo chiều rộng
Thuật toán Dijkstra
Cài đặt hàng đợi ưu tiên
Đường đi ngắn nhất khi có cạnh độ dài âm
Đường đi ngắn nhất trong một DAG
Độ dài của cạnh
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms
107
and extremely useful properties we saw in Chapter 3. But it also means that DFS
can end up taking a long and convoluted route to a vertex that is actually very
close by, as in Figure 4.1. Breadth-first search makes sure to visit vertices in in-
creasing order of their distance from the starting point. This is a broader, shal-
lower search, rather like the propagation of a wave upon water. And it is achieved
using almost exactly the same code as DFS—but with a queue in place of a
stack.
Also notice one stylistic difference from DFS: since we are only interested in dis-
tances from s, we do not restart the search in other connected components. Nodes
not reachable from s are simply ignored.
4.3 Lengths on edges
Breadth-first search treats all edges as having the same length. This is rarely true
in applications where shortest paths are to be found. For instance, suppose you
are driving from San Francisco to Las Vegas, and want to find the quickest route.
Figure 4.5 shows the major highways you might conceivably use. Picking the right
combination of them is a shortest-path problem in which the length of each edge
(each stretch of highway) is important. For the remainder of this chapter, we will
deal with this more general scenario, annotating every edge e ∈ E with a length l
e
.
If e = (u, v), we will sometimes also write l(u, v) or l
uv
.
Figure 4.5
Edge lengths often matter.
Francisco
San
Los
Angeles
Bakersfield
Sacramento
Reno
Las
Vegas
409
290
95
271
133
445
291
112
275
These l
e
’s do not have to correspond to physical lengths. They could denote time
(driving time between cities) or money (cost of taking a bus), or any other quantity
that we would like to conserve. In fact, there are cases in which we need to use
negative lengths, but we will briefly overlook this particular complication.
Trong các bài toán thực tế, mỗi cạnh e thường gắn với độ dài l
e
.
13 / 52
Câu hỏi
Liệu ta có thể sửa thuật toán BFS để nó chạy được trên đồ thị
tổng quát G = (V, E) trong đó mỗi cạnh có độ dài nguyên dương
l
e
?
14 / 52
Tách cạnh thành các cạnh với độ dài đơn vị
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
108
4.4 Dijkstra’s algorithm
4.4 Dijkstra’s algorithm
4.4.1 An adaptation of breadth-first search
Breadth-first search finds shortest paths in any graph whose edges have unit length.
Can we adapt it to a more general graph G = (V, E ) whose edge lengths l
e
are
positive integers?
A more convenient graph
Here is a simple trick for converting G into something BFS can handle: break G ’s
long edges into unit-length pieces by introducing “dummy” nodes. Figure 4.6 shows
an example of this transformation. To construct the new graph G
′
,
For any edge e = (u, v) of E , replace it by l
e
edges of length 1, by adding l
e
− 1
dummy nodes between u and v.
Graph G
′
contains all the vertices V that interest us, and the distances between
them are exactly the same as in G . Most importantly, the edges of G
′
all have unit
length. Therefore, we can compute distances in G by running BFS on G
′
.
Figure 4.6 Breaking edges into unit-length pieces.
C
A
B
E
D
C E
DB
A
1
2
2
4
2
3
1
Alarm clocks
If efficiency were not an issue, we could stop here. But when G has very long edges,
the G
′
it engenders is thickly populated with dummy nodes, and the BFS spends
most of its time diligently computing distances to these nodes that we don’t care
about at all.
To see this more concretely, consider the graphs G and G
′
of Figure 4.7, and imagine
that the BFS, started at node s of G
′
, advances by one unit of distance per minute. For
the first 99 minutes it tediously progresses along S − A and S − B, an endless desert
of dummy nodes. Is there some way we can snooze through these boring phases
and have an alarm wake us up whenever something interesting is happening—
specifically, whenever one of the real nodes (from the original graph G ) is reached?
We do this by setting two alarms at the outset, one for node A, set to go off at
time T = 100, and one for B, at time T = 200. These are estimated times of arrival,
based upon the edges currently being traversed. We doze off and awake at T = 100
to find A has been discovered. At this point, the estimated time of arrival for B is
adjusted to T = 150 and we change its alarm accordingly.
Thay cạnh e = (u, v) bởi l
e
cạnh độ dài 1, bằng cách thêm l
e
− 1
đỉnh tạm giữa u và v.
15 / 52
Vấn đề
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms
109
Figure 4.7 BFS on G
′
is mostly uneventful. The dotted lines show some early
“wavefronts.”
G:
A
B
S
200
100
50
G :
S
A
B
More generally, at any given moment the breadth-first search is advancing along
certain edges of G , and there is an alarm for every endpoint node toward which it
is moving, set to go off at the estimated time of arrival at that node. Some of these
might be overestimates because BFS may later find shortcuts, as a result of future
arrivals elsewhere. In the preceding example, a quicker route to B was revealed upon
arrival at A. However, nothing interesting can possibly happen before an alarm goes
off. The sounding of the next alarm must therefore signal the arrival of the wavefront
to a real node u ∈ V by BFS. At that point, BFS might also start advancing along
some new edges out of u, and alarms need to be set for their endpoints.
The following “alarm clock algorithm” faithfully simulates the execution of BFS on
G
′
.
!
Set an alarm clock for node s at time 0.
!
Repeat until there are no more alarms:
Say the next alarm goes off at time T, for node u. Then:
– The distance from s to u is T.
– For each neighbor v of u in G :
∗ If there is no alarm yet for v, set one for time T + l(u, v).
∗ If v’s alarm is set for later than T + l(u, v), then reset it to this earlier
time.
Dijkstra’s algorithm
The alarm clock algorithm computes distances in any graph with positive integral
edge lengths. It is almost ready for use, except that we need to somehow implement
the system of alarms. The right data structure for this job is a priority queue (usually
implemented via a heap), which maintains a set of elements (nodes) with associated
numeric key values (alarm times) and supports the following operations:
Insert. Add a new element to the set.
Decrease-key. Accommodate the decrease in key value of a particular element.
1
1
The name decrease-key is standard but is a little misleading: the priority queue typically does not itself
change key values. What this procedure really does is to notify the queue that a certain key value has
been decreased.
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms
109
Figure 4.7 BFS on G
′
is mostly uneventful. The dotted lines show some early
“wavefronts.”
G:
A
B
S
200
100
50
G :
S
A
B
More generally, at any given moment the breadth-first search is advancing along
certain edges of G , and there is an alarm for every endpoint node toward which it
is moving, set to go off at the estimated time of arrival at that node. Some of these
might be overestimates because BFS may later find shortcuts, as a result of future
arrivals elsewhere. In the preceding example, a quicker route to B was revealed upon
arrival at A. However, nothing interesting can possibly happen before an alarm goes
off. The sounding of the next alarm must therefore signal the arrival of the wavefront
to a real node u ∈ V by BFS. At that point, BFS might also start advancing along
some new edges out of u, and alarms need to be set for their endpoints.
The following “alarm clock algorithm” faithfully simulates the execution of BFS on
G
′
.
!
Set an alarm clock for node s at time 0.
!
Repeat until there are no more alarms:
Say the next alarm goes off at time T, for node u. Then:
– The distance from s to u is T.
– For each neighbor v of u in G :
∗ If there is no alarm yet for v, set one for time T + l(u, v).
∗ If v’s alarm is set for later than T +l(u, v), then reset it to this earlier
time.
Dijkstra’s algorithm
The alarm clock algorithm computes distances in any graph with positive integral
edge lengths. It is almost ready for use, except that we need to somehow implement
the system of alarms. The right data structure for this job is a priority queue (usually
implemented via a heap), which maintains a set of elements (nodes) with associated
numeric key values (alarm times) and supports the following operations:
Insert. Add a new element to the set.
Decrease-key. Accommodate the decrease in key value of a particular element.
1
1
The name decrease-key is standard but is a little misleading: the priority queue typically does not itself
change key values. What this procedure really does is to notify the queue that a certain key value has
been decreased.
Cả 99 bước di chuyển đầu tiên đều xử lý S − A và S − B trên các
đỉnh tạm.
16 / 52
Giải pháp: Đặt Alarm clock!
▶
Với đỉnh A, đặt hẹn T = 100
▶
Với đỉnh B, đặt hẹn T = 200
▶
Bị đánh thức khi A được thăm lúc
T = 100
▶
Ước lượng lại thời gian đến của B là
T = 150; và đặt lại Alarm cho B.
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms
109
Figure 4.7 BFS on G
′
is mostly uneventful. The dotted lines show some early
“wavefronts.”
G:
A
B
S
200
100
50
G :
S
A
B
More generally, at any given moment the breadth-first search is advancing along
certain edges of G , and there is an alarm for every endpoint node toward which it
is moving, set to go off at the estimated time of arrival at that node. Some of these
might be overestimates because BFS may later find shortcuts, as a result of future
arrivals elsewhere. In the preceding example, a quicker route to B was revealed upon
arrival at A. However, nothing interesting can possibly happen before an alarm goes
off. The sounding of the next alarm must therefore signal the arrival of the wavefront
to a real node u ∈ V by BFS. At that point, BFS might also start advancing along
some new edges out of u, and alarms need to be set for their endpoints.
The following “alarm clock algorithm” faithfully simulates the execution of BFS on
G
′
.
!
Set an alarm clock for node s at time 0.
!
Repeat until there are no more alarms:
Say the next alarm goes off at time T, for node u. Then:
– The distance from s to u is T.
– For each neighbor v of u in G :
∗ If there is no alarm yet for v, set one for time T + l(u, v).
∗ If v’s alarm is set for later than T + l(u, v), then reset it to this earlier
time.
Dijkstra’s algorithm
The alarm clock algorithm computes distances in any graph with positive integral
edge lengths. It is almost ready for use, except that we need to somehow implement
the system of alarms. The right data structure for this job is a priority queue (usually
implemented via a heap), which maintains a set of elements (nodes) with associated
numeric key values (alarm times) and supports the following operations:
Insert. Add a new element to the set.
Decrease-key. Accommodate the decrease in key value of a particular element.
1
1
The name decrease-key is standard but is a little misleading: the priority queue typically does not itself
change key values. What this procedure really does is to notify the queue that a certain key value has
been decreased.
17 / 52
Thuật toán Alarm Clock
Đặt một alarm clock cho đỉnh s tại thời điểm T = 0
Lặp lại cho đến khi không còn alarm:
Giả sử alarm kêu tại thời điểm T cho đỉnh u. Vậy thì:
- Khoảng cách từ s tới u là T.
- Với mỗi hàng xóm v của u trong G:
* Nếu vẫn chưa có alarm cho v,
đặt alarm cho v tại thời điểm T + l(u, v).
* Nếu alarm của v đã đặt, nhưng lại muộn hơn so với
T + l(u, v),
vậy thì đặt lại alarm cho v bằng T + l(u, v).
18 / 52
Ví dụ
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402
Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
108
4.4 Dijkstra’s algorithm
4.4 Dijkstra’s algorithm
4.4.1 An adaptation of breadth-first search
Breadth-first search finds shortest paths in any graph whose edges have unit length.
Can we adapt it to a more general graph G = (V, E ) whose edge lengths l
e
are
positive integers?
A more convenient graph
Here is a simple trick for converting G into something BFS can handle: break G ’s
long edges into unit-length pieces by introducing “dummy” nodes. Figure 4.6 shows
an example of this transformation. To construct the new graph G
′
,
For any edge e = (u, v) of E , replace it by l
e
edges of length 1, by adding l
e
− 1
dummy nodes between u and v.
Graph G
′
contains all the vertices V that interest us, and the distances between
them are exactly the same as in G . Most importantly, the edges of G
′
all have unit
length. Therefore, we can compute distances in G by running BFS on G
′
.
Figure 4.6 Breaking edges into unit-length pieces.
C
A
B
E
D
C E
DB
A
1
2
2
4
2
3
1
Alarm clocks
If efficiency were not an issue, we could stop here. But when G has very long edges,
the G
′
it engenders is thickly populated with dummy nodes, and the BFS spends
most of its time diligently computing distances to these nodes that we don’t care
about at all.
To see this more concretely, consider the graphs G and G
′
of Figure 4.7, and imagine
that the BFS, started at node s of G
′
, advances by one unit of distance per minute. For
the first 99 minutes it tediously progresses along S − A and S − B, an endless desert
of dummy nodes. Is there some way we can snooze through these boring phases
and have an alarm wake us up whenever something interesting is happening—
specifically, whenever one of the real nodes (from the original graph G ) is reached?
We do this by setting two alarms at the outset, one for node A, set to go off at
time T = 100, and one for B, at time T = 200. These are estimated times of arrival,
based upon the edges currently being traversed. We doze off and awake at T = 100
to find A has been discovered. At this point, the estimated time of arrival for B is
adjusted to T = 150 and we change its alarm accordingly.
Thời gian A B C D E
0 − − − −
0 0 2 1 − −
1 2 1 − 5
2 2 4 5
4 4 5
5 5
0 2 1 4 4
19 / 52
Hàng đợi ưu tiên
Tại sao cần hàng đợi ưu tiên? Để cài đặt hệ thống Alarm.
Hàng đợi ưu tiên là gì? Là một tập với mỗi phần tử được gắn với
giá trị số (còn gọi là khóa) và có các phép toán sau:
Insert. Thêm một phần tử mới vào tập.
Decrease-key. Giảm giá trị khóa của một phần tử cụ thể.
Delete-min. Trả lại phần tử có khóa nhỏ nhất và xóa nó khỏi tập.
Make-queue. xây dựng hàng đợi ưu tiên cho tập phần tử và giá trị
khóa cho trước.
Khóa của mỗi phần tử (đỉnh) ở đây chính là alarm của đỉnh đó.
Insert
và
Descrease-key
để đặt alarm;
Delete-min
để xác định
thời điểm alarm tiếp theo kêu.
20 / 52
| 1/52
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Đường đi trên đồ thị (Version 0.2) Trần Vĩnh Đức HUST Ngày 24 tháng 7 năm 2018 1 / 52 Tài liệu tham khảo
▶ S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani,
Algorithms, July 18, 2016.
▶ Chú ý: Nhiều hình vẽ trong tài liệu được lấy tùy tiện mà chưa xin phép. 2 / 52 Nội dung
Khoảng cách và tìm kiếm theo chiều rộng Thuật toán Dijkstra
Cài đặt hàng đợi ưu tiên
Đường đi ngắn nhất khi có cạnh độ dài âm
Đường đi ngắn nhất trong một DAG P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 Chapter 4 Paths in graphs 4.1 Distances Chapter 4 Depth-first search readily Pat
identifies halls i the nv gra ertices p of h a s graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS 4.1 tree Distances
shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
Path lengths allow us to talk quantitatively about the extent to which different
marized in its search tree (Figure 4.1). However, these paths might not be the most
vertices of a graph are separated from each other:
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
The distance between two nodes is the length of the shortest path between them.
algorithms for finding shortest paths in graphs.
To get a concrete feel for this Path lengths notion, allow us consider a to talk phy quantitativ sical r ely about ealization of the a gr extent aph to thatwhich different
vertices of a graph are separated from each other:
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other The distance balls that between get two pulled nodes up is the along length with of it the areshortest pr path ecisely between them. the vertices reachable from T s.o get a And concr to ete findfeel for their this notion, distancesconsider from a s, ph y ysical ou realization need only of a graph that
measure how far below s the has y a ball
hang. for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
In Figure 4.2, for example, v the ertex vertices B is at reachable distance from 2 fr s. omAnd S, to find and their there distances are two from s, shortest you need only
paths to it. When S is held measur up, the e how far strings below alongs they eachhang. of these paths become taut.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest DFS paths và to it. đường When S đi
is held up, the strings along each of these paths become taut.
Figure 4.1 (a) A simple graph and (b) its depth-first search tree.
Figure 4.1 (a) A simple graph and (b) its depth-first search tree. (a) (b) S (a) (b) S E S A E S A A D A D B E B E D C B D C B C C 104 104
Đường đi trên cây DFS thường không phải là đường đi ngắn nhất. 4 / 52 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 Chapter 4 Paths in graphs 4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely Khoảng the vertices r cách
eachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest
paths to it. When S is held up, the strings along each of these paths become taut.
Khoảng cách giữa hai đỉnh là độ dài của đường đi ngắn nhất giữa
Figure 4.1 (a) A simple graph and (b) its depth-first search tree. chúng. (a) (b) S v
Khoảng cách (S − v) E S A A A D B C B E D C B D E C 104 5 / 52 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 G das2340 TBL02 2 0-Dasgupta-v10 August 12, 2006 1:48 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Mô hình vật lý của đồ thị Chapter 4 Chapter 4 Algorithms Algorithms 105 105
Giả sử rằng mọi cạnh có cùng độ dài. Ta nhấc đỉnh S lên:
Figure 4.2 A Figur phy e 4.2 sical A ph model y of sical a gr model aph. of a graph. S S E A S A E S A C D E A C D E D C B D C B B B
On the other hand, edge (D, E ) plays no role in any shortest path and therefore On the other remains hand, slack.
edge (D, E ) plays no role in any shortest path and therefore remains slack.
4.2 Breadth-first search 6 / 52
4.2 Breadth-first search
In Figure 4.2, the lifting of s partitions the graph into layers: s itself, the nodes at In Figure 4.2, distance the lifting 1 fr of om s it, the nodes partitions the at gr distance aph into 2 layfrom ers: sit, and itself, so on. the A conv nodes at enient way distance 1 fromto compute it, the distances nodes at from distance s2tofr the om other it, v andertices so is on. to A proceed conv lay enient er w b a y y layer. Once to compute we ha distances ve fr pick om s ed to out the the nodes other v at distance ertices is to 0 pr , 1, 2, oceed. . . la ,y d, er the by ones layer. at d + Once 1 are easily we have picked determined: out the the nodes y at are precisely distance 0, the 1, 2 as-y , . . . et-unseen , d, the nodes ones at that d + ar 1 e ar adjacent e easily to the layer determined: the at y distance are pr d. This ecisely the suggests as-y an iter et-unseen ative algorithm nodes that are in which adjacent tw to o la the y laer y s er are active at at distance d. any This given time: suggests an some iter la ativ y e er d, which algorithm has in been which fully two identified, layers are and actived + at 1, which is
being discovered by scanning the neighbors of layer d.
any given time: some layer d, which has been fully identified, and d + 1, which is being discover Br ed eadth-fir by st sear scanning ch the (BFS) dir neighbors ectly of la implements yer d.
this simple reasoning (Figure 4.3).
Initially the queue Q consists only of s, the one node at distance 0. And for each
Breadth-first search (BFS) directly implements this simple reasoning (Figure 4.3).
subsequent distance d = 1, 2, 3, . . . , there is a point in time at which Q contains
Initially the queue Q consists only of s, the one node at distance 0. And for each
all the nodes at distance d and nothing else. As these nodes are processed (ejected subsequent distance d off the front
= 1, 2, 3, . . . , there is a point in time at which Q contains
of the queue), their as-yet-unseen neighbors are injected into the end
all the nodes at distance d and nothing else. As these nodes are processed (ejected of the queue.
off the front of the queue), their as-yet-unseen neighbors are injected into the end of the queue.
Let’s try out this algorithm on our earlier example (Figure 4.1) to confirm that it does
the right thing. If S is the starting point and the nodes are ordered alphabetically,
Let’s try out thisthey get visited algorithm on in our the sequence earlier ex sho ample wn in (FigureFigur 4.1) e 4.4. to The confirmbreadth-fir that it st does search tree, the right thing. on If the S is right, the contains starting the point edges and thr the ough nodes which are or each dered node is initially alphabetically, discovered. they get visited Unlik in e the the DFS tr sequence ee w sho e sa wn w in earlier Figure, it has 4.4. the The pr br operty that eadth-first all sear its ch paths tree, from S are on the right, the shortest contains the possible edges . thr It is ther ough efor whiche a shortest-path each node is tree. initially discovered.
Unlike the DFS tree we saw earlier, it has the property that all its paths from S are
Correctness and efficiency
the shortest possible. It is therefore a shortest-path tree.
We have developed the basic intuition behind breadth-first search. In order to check Correctness that and the algorithm efficiency
works correctly, we need to make sure that it faithfully executes We have dev this eloped intuition. the basic What we intuition expect, behind pr br ecisely, is eadth-firstthat search. In order to check that the algorithm F w or each orks d
correctly, we need to make sure that it faithfully executes
= 0, 1, 2, . . . , there is a moment at which (1) all nodes at distance
this intuition. What ≤wde freom s have xpect, pr their ecisely distances
, is that correctly set; (2) all other nodes have their distances set to For each d
∞; and (3) the queue contains exactly the nodes at distance d.
= 0, 1, 2, . . . , there is a moment at which (1) all nodes at distance
≤ d from s have their distances correctly set; (2) all other nodes have their
distances set to ∞; and (3) the queue contains exactly the nodes at distance d. P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 Chapter 4 Algorithms 105
Tìm kiếm theo chiều rộng (Breadth-First Search)
Figure 4.2 A physical model of a graph.
Chia đồ thị thành các mức: S
▶ S là mức có khoảng cách 0. E S A
▶ Các đỉnh có khoảng cách tới S bằng 1. A C D E
▶ Các đỉnh có khoảng cách tới D S C bằng 2 B ▶ ... B
Ý tưởng thuật toán: Khi mức d đã được xác định, mức d + 1 có
On the other hand, edge (D, E ) plays no role in any shortest path and therefore
thể thăm bằng cách duyệt qua các hàng xóm của mức d. remains slack. 4.2 Breadth-first search
In Figure 4.2, the lifting of s partitions the graph into layers: s itself, the nodes at7/52
distance 1 from it, the nodes at distance 2 from it, and so on. A convenient way
to compute distances from s to the other vertices is to proceed layer by layer. Once
we have picked out the nodes at distance 0, 1, 2, . . . , d, the ones at d + 1 are easily
determined: they are precisely the as-yet-unseen nodes that are adjacent to the layer
at distance d. This suggests an iterative algorithm in which two layers are active at
any given time: some layer d, which has been fully identified, and d + 1, which is
being discovered by scanning the neighbors of layer d.
Breadth-first search (BFS) directly implements this simple reasoning (Figure 4.3).
Initially the queue Q consists only of s, the one node at distance 0. And for each
subsequent distance d = 1, 2, 3, . . . , there is a point in time at which Q contains
all the nodes at distance d and nothing else. As these nodes are processed (ejected
off the front of the queue), their as-yet-unseen neighbors are injected into the end of the queue.
Let’s try out this algorithm on our earlier example (Figure 4.1) to confirm that it does
the right thing. If S is the starting point and the nodes are ordered alphabetically,
they get visited in the sequence shown in Figure 4.4. The breadth-first search tree,
on the right, contains the edges through which each node is initially discovered.
Unlike the DFS tree we saw earlier, it has the property that all its paths from S are
the shortest possible. It is therefore a shortest-path tree. Correctness and efficiency
We have developed the basic intuition behind breadth-first search. In order to check
that the algorithm works correctly, we need to make sure that it faithfully executes
this intuition. What we expect, precisely, is that
For each d = 0, 1, 2, . . . , there is a moment at which (1) all nodes at distance
≤ d from s have their distances correctly set; (2) all other nodes have their
distances set to ∞; and (3) the queue contains exactly the nodes at distance d.
Ý tưởng loang theo chiều rộng
Khởi tạo: Hàng đợi Q chỉ chứa đỉnh s, là đỉnh duy nhất ở mức 0.
Với mỗi khoảng cách d = 1, 2, 3, . . . ,
▶ sẽ có thời điểm Q chỉ chứa các đỉnh có khoảng cách d và không có gì khác.
▶ Khi đó các đỉnh có khoảng cách d này sẽ được loại bỏ dần từ đầu hàng đợi,
▶ và các hàng xóm chưa được thăm sẽ được thêm vào cuối hàng đợi. 8 / 52 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 Chapter 4 Paths in graphs 4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
the vertices reachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest
paths to it. When S is held up, the strings along each of these paths become taut. Bài tập
Figure 4.1 (a) A simple graph and (b) its depth-first search tree.
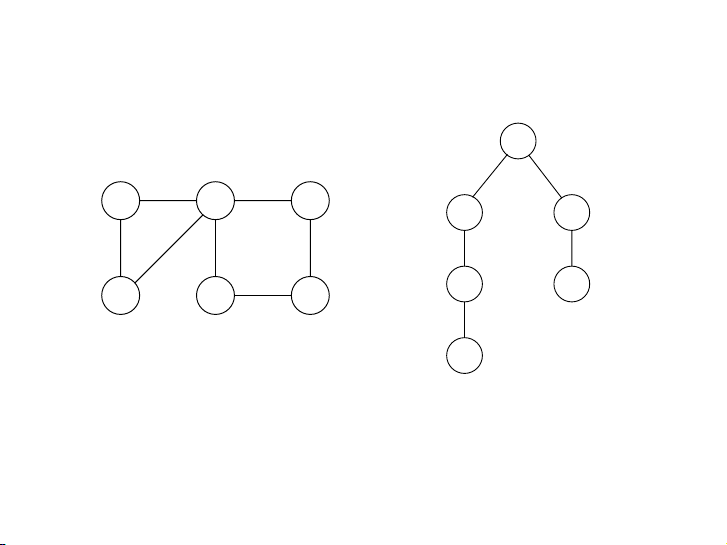
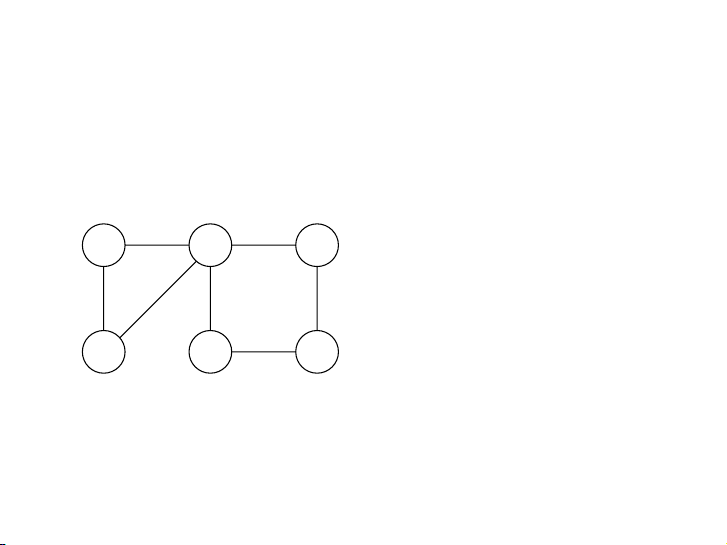
Chạy thuật toán BFS cho đồ thị dưới đây bắt đầu từ đỉnh S. Ghi
ra hàng đợi Q sau mỗi lần thăm đỉnh. (a) (b) S E S A Đỉnh thăm Hàng đợi A D S [S] B E D C B C 104 9 / 52 procedure bfs(G, s)
Input: đồ thị G = (V, E), có hướng hoặc vô hướng; một đỉnh s ∈ V
Output: Với mỗi đỉnh u đến được từ s,
dist(u) = khoảng cách từ s tới u. for all u ∈ V: dist(u) = ∞ dist(s) = 0 Q = [s]
(hàng đợi chỉ chứa s) while Q khác rỗng: u = eject(Q)
(loại bỏ u khỏi hàng đợi)
for all edges (u, v) ∈ E:
if dist(v) = ∞: inject(Q, v)
(thêm v vào hàng đợi)
dist(v) = dist(u) + 1 10 / 52 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 Chapter 4 Paths in graphs 4.1 Distances
Depth-first search readily identifies all the vertices of a graph that can be reached
from a designated starting point. It also finds explicit paths to these vertices, sum-
marized in its search tree (Figure 4.1). However, these paths might not be the most
economical ones possible. In the figure, vertex C is reachable from S by traversing
just one edge, while the DFS tree shows a path of length 3. This chapter is about
algorithms for finding shortest paths in graphs.
Path lengths allow us to talk quantitatively about the extent to which different
vertices of a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that
has a ball for each vertex and a piece of string for each edge. If you lift the ball for
vertex s high enough, the other balls that get pulled up along with it are precisely
the vertices reachable from s. And to find their distances from s, you need only
measure how far below s they hang.
In Figure 4.2, for example, vertex B is at distance 2 from S, and there are two shortest Bài paths tập
to it. When S is held up, the strings along each of these paths become taut.
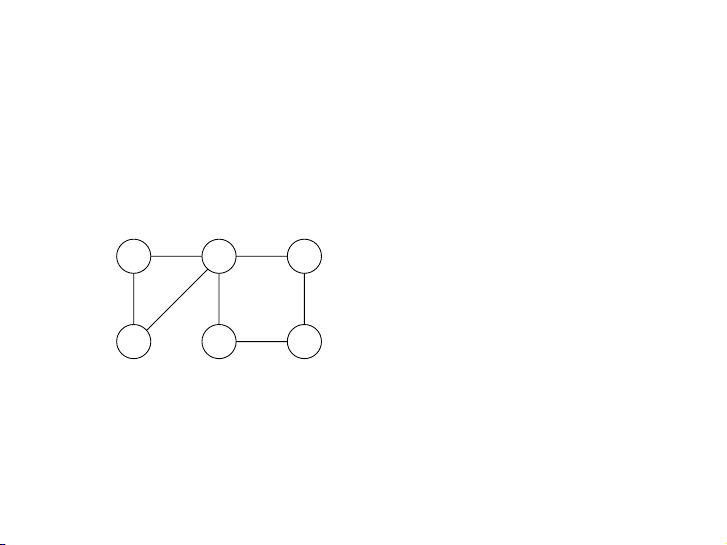
Hãy chạy thuật toán BFS cho đồ thị dưới đây và ghi ra nội dung của Figure hàng 4.1 đợi (a) Q A sau mỗi simple gr bướ aph c:
and (b) its depth-first search tree. (a) (b) S E S A Thứ tự thăm đỉnh Hàng đợi A S D [S] B E D C B C 104 11 / 52 Nội dung
Khoảng cách và tìm kiếm theo chiều rộng Thuật toán Dijkstra
Cài đặt hàng đợi ưu tiên
Đường đi ngắn nhất khi có cạnh độ dài âm
Đường đi ngắn nhất trong một DAG P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 Chapter 4 Algorithms 107
and extremely useful properties we saw in Chapter 3. But it also means that DFS
can end up taking a long and convoluted route to a vertex that is actually very
close by, as in Figure 4.1. Breadth-first search makes sure to visit vertices in in-
creasing order of their distance from the starting point. This is a broader, shal-
lower search, rather like the propagation of a wave upon water. And it is achieved
using almost exactly the same code as DFS—but with a queue in place of a stack.
Also notice one stylistic difference from DFS: since we are only interested in dis-
tances from s, we do not restart the search in other connected components. Nodes
not reachable from s are simply ignored. 4.3 Lengths on edges
Breadth-first search treats all edges as having the same length. This is rarely true
in applications where shortest paths are to be found. For instance, suppose you
are driving from San Francisco to Las Vegas, and want to find the quickest route.
Figure 4.5 shows the major highways you might conceivably use. Picking the right
combination of them is a shortest-path problem in which the length of each edge
(each stretch of highway) is important. For the remainder of this chapter, we will Độ dài của deal with cạnh
this more general scenario, annotating every edge e ∈ E with a length le.
If e = (u, v), we will sometimes also write l(u, v) or luv.
Figure 4.5 Edge lengths often matter. Sacramento 95 San 133 Francisco Reno 290 271 409 445 Bakersfield 291 112 Los Las Angeles 275 Vegas
These le’s do not have to correspond to physical lengths. They could denote time
(driving time between cities) or money (cost of taking a bus), or any other quantity
Trong các bài toán thực tế, mỗi cạnh e thường gắn với độ dài l
that we would like to conserve. In fact, there are cases in which we need to usee.
negative lengths, but we will briefly overlook this particular complication. 13 / 52 Câu hỏi
Liệu ta có thể sửa thuật toán BFS để nó chạy được trên đồ thị
tổng quát G = (V, E) trong đó mỗi cạnh có độ dài nguyên dương le? 14 / 52 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 108
4.4 Dijkstra’s algorithm 14.4 08 Dijkstra’s algorithm
4.4 Dijkstra’s algorithm
4.4.1 An adaptation of breadth-first search
4.4 Dijkstra’s algorithm
Breadth-first search finds shortest paths in any graph whose edges have unit length. Can 4.4.1 we An adapt it to adaptation a of more general breadth-first graph
search G = (V, E ) whose edge lengths le are positive Breadth-firinteger st sear s
ch?finds shortest paths in any graph whose edges have unit length.
Can we adapt it to a more general graph G = (V, E ) whose edge lengths l A more convenient graph e are positive integers?
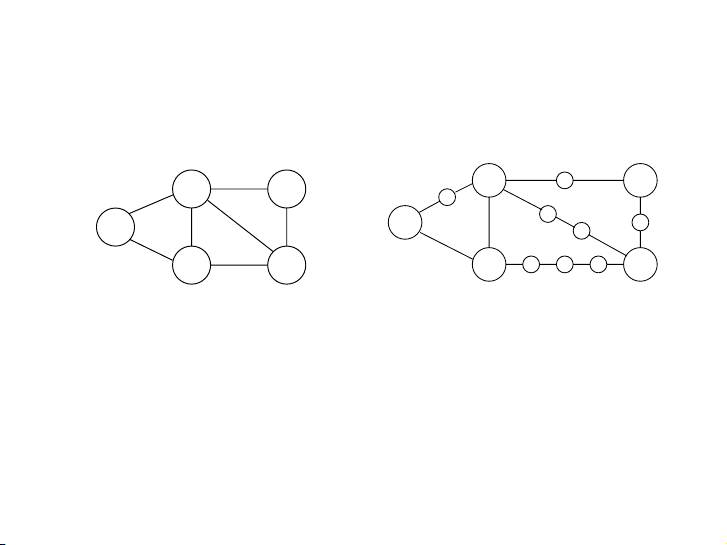
Here is a simple trick for converting G into something BFS can handle: break G ’s long A mor edges e conv into unit-length enient graph
pieces by introducing “dummy” nodes. Figure 4.6 shows an Here exisample a of simple this trick transformation. for converting G To into construct something the BFS new can graph
handle: Gbr′,eak G’s
long edges into unit-length pieces by introducing “dummy” nodes. Figure 4.6 shows an ex For any ample of edge this tr e = (u
ansformation. To construct the new graph G ′,
, v) of E , replace it by le edges of length 1, by adding le − 1 F dummy or any nodes edge e between u and v.
= (u, v) of E , replace it by le edges of length 1, by adding le − 1 Tách cạnh
dummy nodes between u and v. Graph thành G ′ các contains all cạnh the v với ertices độ V dài that đơn interest vị us, and the distances between them Graph ar G ′ e exactly contains the all same the v as ertices inV G . Most that inter importantly est us, and , the the edges distances of G betw′ all een have unit length. them are Ther ex efor actly e the , we samecan as compute
in G . Most distances in importantly, G the by running edges of G ′ BF all S havon e G unit′.
length. Therefore, we can compute distances in G by running BFS on G ′.
Figure 4.6 Breaking edges into unit-length pieces.
Figure 4.6 Breaking edges into unit-length pieces. 2 2 B D 2 2 B B D D B D A A 1 3 1 3 2 A 2 A 1 1 C C E 4 E C E 4 C E Alarm clocks Alarm If Thay clocks efficienc cạnhy w e ere = not (u, an v) issue bởi, w lee could cạnh stop độ here dài . But 1, when bằng G has cách very long thêm l edges e − , 1 If the đỉnh efficienc G ′ it tạm y giữawer engender u e s not is và v. an issue thickly , we could populated with stop her dummy e. But nodes, when and G the has BFS very long spends edges, the most G of ′ it its engender time s is diligently thickly populated computing distances with to dumm these y nodes nodes that , we and the don’t car BF e S spends most about of at its
all. time diligently computing distances to these nodes that we don’t care Tabout o see at this all.
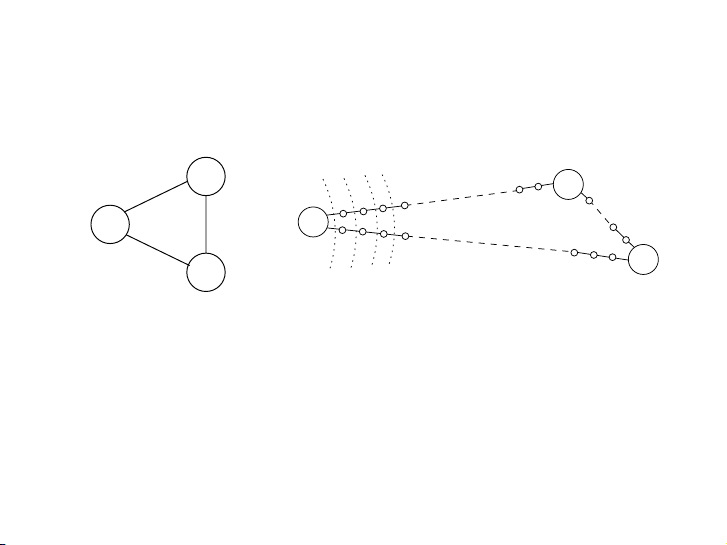
more concretely, consider the graphs G and G ′ of Figure 4.7, and imagine
that the BFS, started at node s of G ′, advances by one unit of distance per minute. For To the see first this 99 more minutes concr it etely tediously , consider progresses the gr along aphs S
G and G ′ of Figure 4.7, and imagine
− A and S − B, an endless desert that of the dummyBFS, started nodes. Is at there node some s of way G ′ w ,e adv can ances b snooze y one thr unit ough of these distance boring per minute phases . For the and fir ha st ve 99 an minutes alarm w it ak tediously e us up progr whenev esses er along something S − interA and esting S is − B, an endless happening— desert of dumm specifically, y nodes whenev .er Is ther one of e some the real way nodes w (fre can om thesnooze original thr gr ough aph G ) these is r boring eached? phases 15 / 52 and We dohave this an by alarm setting w twoake us alarms up at whene the ver outset, something one for node inter A, esting set to go is off happening— at specifically time T = 1 , 00, whene and onever for one B, at of the time T real = 2 nodes 00. (fr These om are the original estimated gr times aph of G ) arrival is , reached?
based upon the edges currently being traversed. We doze off and awake at T
We do this by setting two alarms at the outset, one for node A, set = 100to go off at
to find A has been discovered. At this point, the estimated time of arrival for B is time T adjusted = to 1
T 00, and one for B, at time T
= 150 and we change its alarm = 200. accor These dingly.
are estimated times of arrival,
based upon the edges currently being traversed. We doze off and awake at T = 100
to find A has been discovered. At this point, the estimated time of arrival for B is
adjusted to T = 150 and we change its alarm accordingly. P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 Chapter 4 Vấn đề Algorithms 109 Chapter 4
Figure 4.7 BFS on G′ is mostly uneventful. The dotted lines Algorithmssho 1 w 09 some early “wavefronts Figure .”
4.7 BFS on G′ is mostly uneventful. The dotted lines show some early “wavefronts.” G: G: A G : G : A 100 A A 100 S S 50 50 S S 200 200 B B B B
More generally, at any given moment the breadth-first search is advancing along
certain edges of G , and there is an alarm for every endpoint node toward which it Mor Cả e is gener mo 99 bướ ally ving,c set di, at to go an off chuy yat ển giv theen đầu moment estimated tiên time đều xửthe oflý br arriv S eadth-fir al − atAthat và Sst node. −sear B ch Some of trên is adv these các ancing along certain đỉnh edges might be ov tạm. of er G , and estimates there because is BFS an ma alarm y later for find every shortcuts endpoint , as a result node of to future ward which it is moving, arrivals set else to wher go e. In off the at pr the estimated eceding example, a time quicker of r arriv oute to al B w at as r that ev node ealed . upon Some of these might be arrival oatver A. estimates However, because nothing inter BFS esting ma can y later possibly find happen shortcuts before an , as alarm a goesresult of future
off. The sounding of the next alarm must therefore signal the arrival of the wavefront arrivals to a else real wher node u e. ∈ In V the by pr BFS. eceding At that example point, BFS , a quick might also er r start oute adv to B ancing was along revealed upon arrival at some A ne . w How edges ever out , of nothing u, and inter alarms esting need to be can set possibly for their happen endpoints. before an alarm goes off. The The sounding following “ of alarmthe ne clock xt alarm algorithm” must ther faithfully efore simulates signal the ex the arriv ecution of BFal S of on the wavefront to a r G eal ′.
node u ∈ V by BFS. At that point, BFS might also start advancing 16 / 52 along some ne ! w Set edges an out alarm of clock u, for and node salarms at time need 0. to be set for their endpoints.
! Repeat until there are no more alarms:
The following “alarm clock algorithm” faithfully simulates the execution of BFS on G ′.
Say the next alarm goes off at time T, for node u. Then:
– The distance from s to u is T. ! Set–anF alarm or each clock neighbor for v of node
u in G :s at time 0. ! Repeat ∗ until If there ther is noe are alarm no yet mor for v, e alarms:
set one for time T + l(u, v).
∗ If v’s alarm is set for later than T + l(u, v), then reset it to this earlier Say the ne timext .
alarm goes off at time T, for node u. Then: – The Dijkstra’s distance
algorithm from s to u is T.
The alarm clock algorithm computes distances in any graph with positive integral – edge For each lengths. It is neighbor almost r v eady of for u use in , ex G :
cept that we need to somehow implement the s ∗ y If stem ther of e is alarms. no The alarm right y data et for structur ve, set for one this job for is a time priority T +
queue l(u, v). (usually
implemented via a heap), which maintains a set of elements (nodes) with associated ∗ numeric If ke v y ’s v alarm alues is (alarm set for times) later and than supports the T + follo l(u wing, v), oper then
ations: reset it to this earlier time Insert. A . dd a new element to the set. Dijkstra’s Decr algorithm
ease-key. Accommodate the decrease in key value of a particular element.1
The1alarm clock algorithm computes distances in any graph with positive integral
The name decrease-key is standard but is a little misleading: the priority queue typically does not itself edge lengths change key v . It alues.is almost What this pr ready ocedure r for eally use does is ,to except notify the that queue w thatea need certain k to ey v someho alue has w implement the system been decr of alarms eased.
. The right data structure for this job is a priority queue (usually
implemented via a heap), which maintains a set of elements (nodes) with associated
numeric key values (alarm times) and supports the following operations:
Insert. Add a new element to the set.
Decrease-key. Accommodate the decrease in key value of a particular element.1
1The name decrease-key is standard but is a little misleading: the priority queue typically does not itself
change key values. What this procedure really does is to notify the queue that a certain key value has been decreased. P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Giải pháp: Đặt Alarm clock! Chapter 4 Algorithms 109
Figure 4.7 BFS on G′ is mostly uneventful. The dotted lines show some early “wavefronts.”
▶ Với đỉnh A, đặt hẹn T = 100 ▶ G: G :
Với đỉnh B, đặt hẹn T = 200 A A 100
▶ Bị đánh thức khi A được thăm lúc S 50 S T = 100
▶ Ước lượng lại thời gian đến của B là 200 B B
T = 150; và đặt lại Alarm cho B.
More generally, at any given moment the breadth-first search is advancing along
certain edges of G , and there is an alarm for every endpoint node toward which it
is moving, set to go off at the estimated time of arrival at that node. Some of these
might be overestimates because BFS may later find shortcuts, as a result of future
arrivals elsewhere. In the preceding example, a quicker route to B was revealed upon
arrival at A. However, nothing interesting can possibly happen before an alarm goes 17 / 52
off. The sounding of the next alarm must therefore signal the arrival of the wavefront
to a real node u ∈ V by BFS. At that point, BFS might also start advancing along
some new edges out of u, and alarms need to be set for their endpoints.
The following “alarm clock algorithm” faithfully simulates the execution of BFS on G ′.
! Set an alarm clock for node s at time 0.
! Repeat until there are no more alarms:
Say the next alarm goes off at time T, for node u. Then:
– The distance from s to u is T.
– For each neighbor v of u in G :
∗ If there is no alarm yet for v, set one for time T + l(u, v).
∗ If v’s alarm is set for later than T + l(u, v), then reset it to this earlier time. Dijkstra’s algorithm
The alarm clock algorithm computes distances in any graph with positive integral
edge lengths. It is almost ready for use, except that we need to somehow implement
the system of alarms. The right data structure for this job is a priority queue (usually
implemented via a heap), which maintains a set of elements (nodes) with associated
numeric key values (alarm times) and supports the following operations:
Insert. Add a new element to the set.
Decrease-key. Accommodate the decrease in key value of a particular element.1
1The name decrease-key is standard but is a little misleading: the priority queue typically does not itself
change key values. What this procedure really does is to notify the queue that a certain key value has been decreased. Thuật toán Alarm Clock
Đặt một alarm clock cho đỉnh s tại thời điểm T = 0
Lặp lại cho đến khi không còn alarm:
Giả sử alarm kêu tại thời điểm T cho đỉnh u. Vậy thì:
- Khoảng cách từ s tới u là T.
- Với mỗi hàng xóm v của u trong G:
* Nếu vẫn chưa có alarm cho v,
đặt alarm cho v tại thời điểm T + l(u, v).
* Nếu alarm của v đã đặt, nhưng lại muộn hơn so với
T + l(u, v),
vậy thì đặt lại alarm cho v bằng T + l(u, v). 18 / 52 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48 108
4.4 Dijkstra’s algorithm 4.4 Dijkstra’s algorithm
4.4.1 An adaptation of breadth-first search
Breadth-first search finds shortest paths in any graph whose edges have unit length.
Can we adapt it to a more general graph G = (V, E ) whose edge lengths le are positive integers? A more convenient graph
Here is a simple trick for converting G into something BFS can handle: break G ’s
long edges into unit-length pieces by introducing “dummy” nodes. Figure 4.6 shows
an example of this transformation. To construct the new graph G ′,
For any edge e = (u, v) of E , replace it by le edges of length 1, by adding le − 1
dummy nodes between u and v. Ví Gr dụ
aph G ′ contains all the vertices V that interest us, and the distances between
them are exactly the same as in G . Most importantly, the edges of G ′ all have unit
length. Therefore, we can compute distances in G by running BFS on G ′. Thời gian A B C D E
Figure 4.6 Breaking edges into unit-length pieces. 0 − − − − 0 0 2 1 − − 2 2 B D B D 1 2 1 − 5 A 1 3 2 A 2 2 4 5 1 C E 4 4 C E4 5 5 5 Alarm clocks 0 2 1 4 4
If efficiency were not an issue, we could stop here. But when G has very long edges,
the G ′ it engenders is thickly populated with dummy nodes, and the BFS spends
most of its time diligently computing distances to these nodes that we don’t care about at all.
To see this more concretely, consider the graphs G and G ′ of Figure 4.7, and imagine
that the BFS, started at node s of G ′, advances by one unit of distance per minute. For
the first 99 minutes it tediously progresses along S − A and S − B, an endless desert
of dummy nodes. Is there some way we can snooze through these boring phases 19 / 52
and have an alarm wake us up whenever something interesting is happening—
specifically, whenever one of the real nodes (from the original graph G ) is reached?
We do this by setting two alarms at the outset, one for node A, set to go off at
time T = 100, and one for B, at time T = 200. These are estimated times of arrival,
based upon the edges currently being traversed. We doze off and awake at T = 100
to find A has been discovered. At this point, the estimated time of arrival for B is
adjusted to T = 150 and we change its alarm accordingly. Hàng đợi ưu tiên
Tại sao cần hàng đợi ưu tiên? Để cài đặt hệ thống Alarm.
Hàng đợi ưu tiên là gì? Là một tập với mỗi phần tử được gắn với
giá trị số (còn gọi là khóa) và có các phép toán sau:
Insert. Thêm một phần tử mới vào tập.
Decrease-key. Giảm giá trị khóa của một phần tử cụ thể.
Delete-min. Trả lại phần tử có khóa nhỏ nhất và xóa nó khỏi tập.
Make-queue. xây dựng hàng đợi ưu tiên cho tập phần tử và giá trị khóa cho trước.
Khóa của mỗi phần tử (đỉnh) ở đây chính là alarm của đỉnh đó.
Insert và Descrease-key để đặt alarm; Delete-min để xác định
thời điểm alarm tiếp theo kêu. 20 / 52