





Preview text:
Ghép cặp trên đồ thị hai phần Trần Vĩnh Đức HUST Ngày 24 tháng 7 năm 2018 1 / 39
Ghép cặp trên đồ thị hai phần
▶ Eric Lehman, F Thomson Leighton & Albert R Meyer,
Mathematics for Computer Science, 2013 (Miễn phí) ▶ Albert R Meyer’s slides 2 / 39 Tìm bạn nhảy
▶ Tối thứ bảy, hội sinh viên tổ chức tiệc.
▶ Có 300 sinh viên tham gia.
▶ Họ không quen hết nhau!
▶ Trong 6 người luôn có ba người đôi một quen nhau hoặc ba
người đôi một lạ nhau! 3 / 39 Tìm bạn nhảy
▶ Tối thứ bảy, hội sinh viên tổ chức tiệc.
▶ Có 300 sinh viên tham gia.
▶ Họ không quen hết nhau!
▶ Nhưng mỗi cô gái quen đúng 50 chàng trai, và mỗi chàng trai quen đúng 50 cô gái!
▶ Liệu mọi sinh viên có thể nhảy đồng thời sao cho hai người
nhảy cùng nhau phải biết nhau? 4 / 39 Nội dung Ghép cặp Nam & Nữ Định lý Hall
Làm thế nào để tìm ghép cặp cực đại? Đồ thị Nam & Nữ
Nam & Nữ hợp nhau G B Hợp nhau Albert R Meyer. April 3, 2013 bipartite.2 6 / 39 Đồ thị Nam & Nữ
Compatible Boys & Girls G B Albert R Meyer. April 3, 2013 bipartite.3
Hãy tìm cách ghép cặp mỗi cô gái với chỉ một chàng trai phù hợp. 7 / 39 Đồ thị Nam & Nữ
Compatible Boys & Girls G B Albert R Meyer. April 3, 2013 bipartite.4 Hình: Một ghép cặp 8 / 39 Đồ thị Nam & Nữ
Compatible Boys & Girls G B suppose this edge was missing Albert R Meyer. April 3, 2013 bipartite.5
Giả sử không có cạnh này. 9 / 39 Đồ thị Nam & Nữ
Compatible Boys & Girls G B suppose this edge was missing Albert R Meyer. April 3, 2013 bipartite.6
Giả sử không có cạnh này. 10 / 39 Đồ thị Nam & Nữ
Compatible Boys & Girls G B 3 Albert R Meyer. April 3, 2013 bipartite.7 11 / 39 Không đủ số Nam No Compat t eno i u b gle B h boys & oys Gi fo r r ls these girls! G B 3 2 3 girls like only 2 boys Albert R Meyer. April 3, 2013 bipartite.8
Có 3 cô gái nhưng chỉ có 2 chàng trai phù hợp. 12 / 39
Không tồn tại cặp ghép cho Nữ No match is possible! G B 3 2 S E(S) Albert R Meyer. April 3, 2013 bipartite.9
|S| = 3 > 2 = |E(S)| 13 / 39 Tắc nghẽn No match is possible! a bottleneck G B S E(S) |S| > |E(S)| Albert R Meyer. April 3, 2013 bipartite.10 14 / 39 Tắc nghẽn
▶ Tắc nghẽn là một tập Nữ S không có đủ số Nam phù hợp.
E(S) ::= {chàng trai w |
w kề với ít nhất một cô cái trong S}
▶ Tập S là tắc nghẽn
|S| > |E(S)| 15 / 39 Bổ đề (Tắc nghẽn)
Nếu tồn tại tắc nghẽn, vậy không tồn tại cặp ghép. 16 / 39 Định lý (Hall)
Ngược lại, nếu không có tắc nghẽn, vậy có tồn tại cặp ghép. 17 / 39 Bài tập
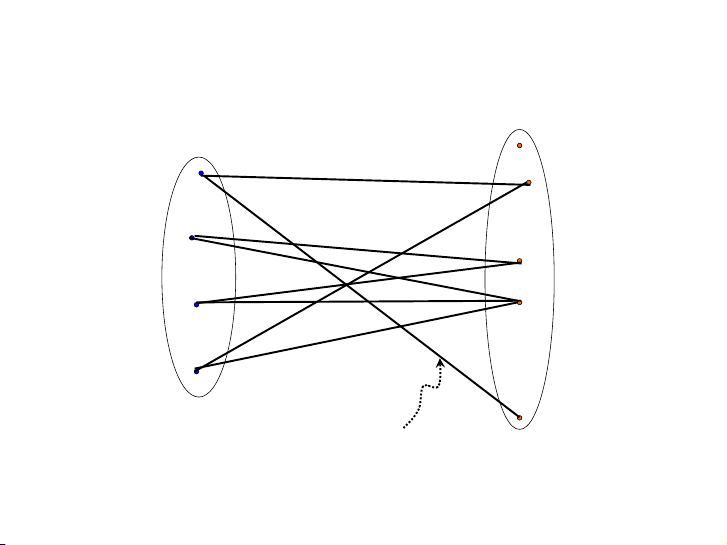
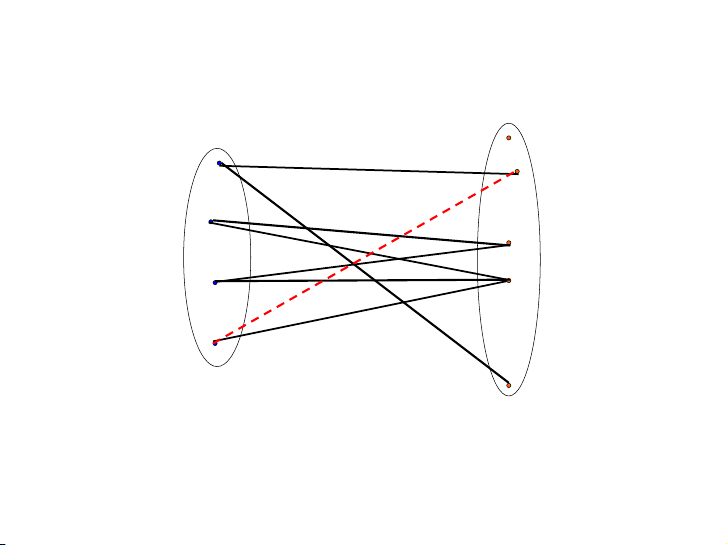
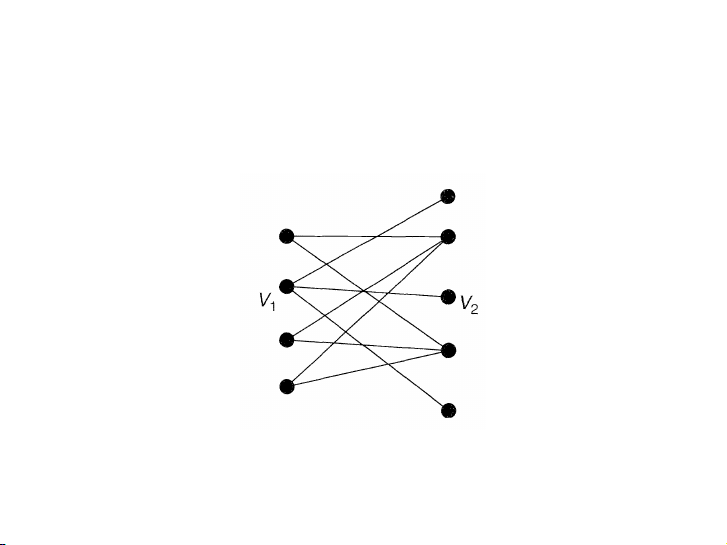
Tại sao đồ thị dưới đây không có cặp ghép nào phủ tập V1? 18 / 39 Nội dung Ghép cặp Nam & Nữ Định lý Hall
Làm thế nào để tìm ghép cặp cực đại?
Đồ thị hai phần H Bipartite graph H G B E(H) L(H) R(H) Albert R Meyer. April 3, 2013 Hall.2 20 / 39







