Bài giảng Luồng trên mạng V0.1 - Toán rời rạc thầy Trần Vĩnh Đức | Trường Đại học Bách khoa Hà Nội

Luồng trên mạng V0.1 Trần Vĩnh Đức HUST Ngày 20 tháng 11 năm 2019 1 / 34 Tài liệu tham khảo
▶ S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani,
Algorithms, July 18, 2006. 2 / 34 Nội dung
Bài toán luồng cực đại trên mạng Thuật toán Ford-Fulkerson
Luồng cực đại và lát cắt cực tiểu
Tính hiệu quả của thuật toán Network-flow algorithms 887 inflow equals outflow at every vertex con- (except the source and the sink) -
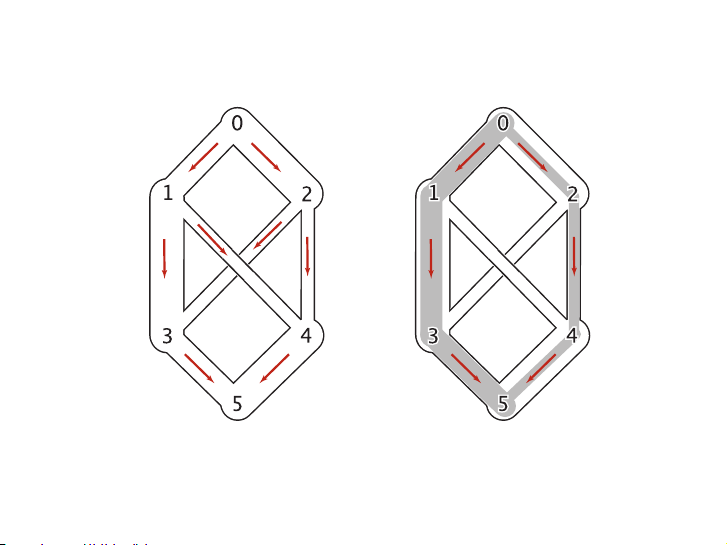
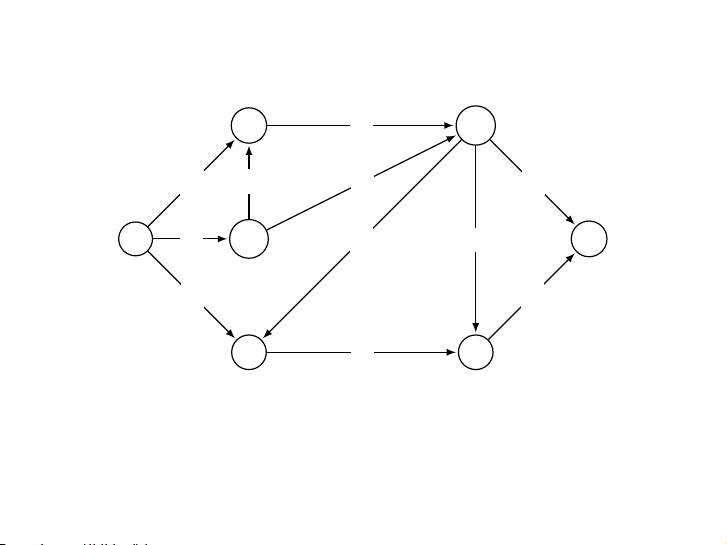
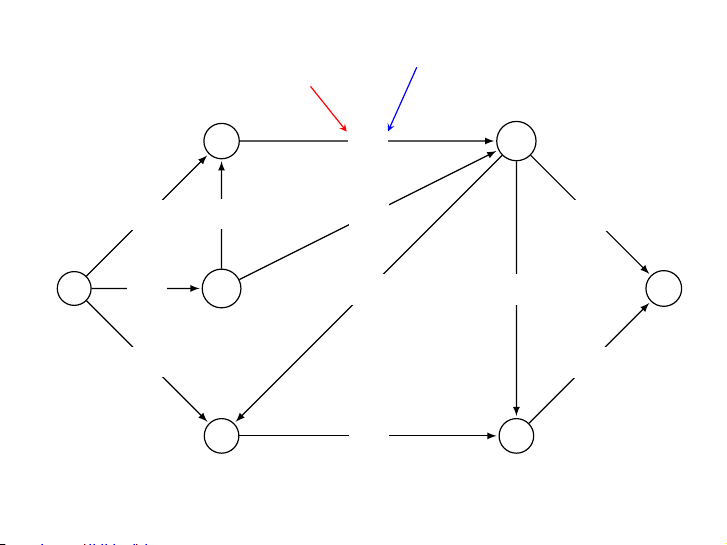
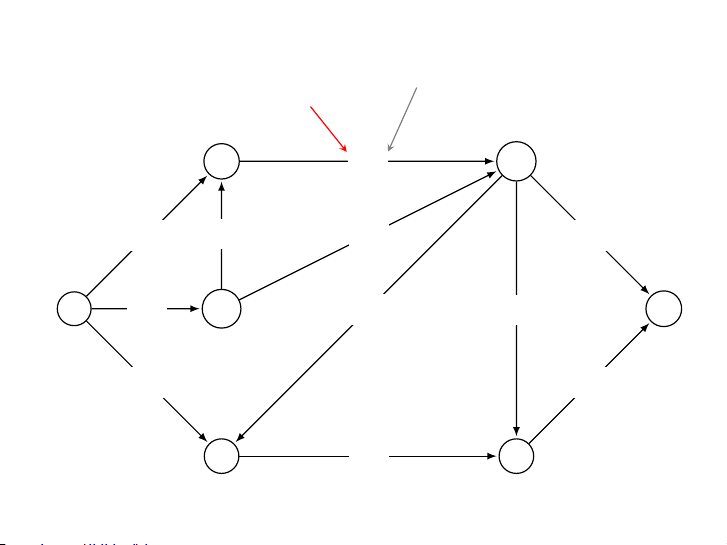
Local equilibrium in a flow network 0->1->3->5 0->2->4->5 0->1, 2->4, and 3->5 0 to 5 1 1->4 3->5 0->2->3->5 - ptg12441863 - Bài toán chuyển dầu tinyFN.txt standard drawing drawing with capacities drawing with flow flow representation source V 0 1 2.0 2.0 6 E 0 2 3.0 1.0 8 1 3 3.0 2.0 0 1 2.0 1 4 1.0 0.0 0 2 3.0 2 3 1.0 0.0 1 3 3.0 2 4 1.0 1.0 1 4 1.0 3 5 2.0 2.0 2 3 1.0 4 5 3.0 1.0 2 4 1.0 3 5 2.0 flow value 4 5 3.0 associated with each edge capacities sink
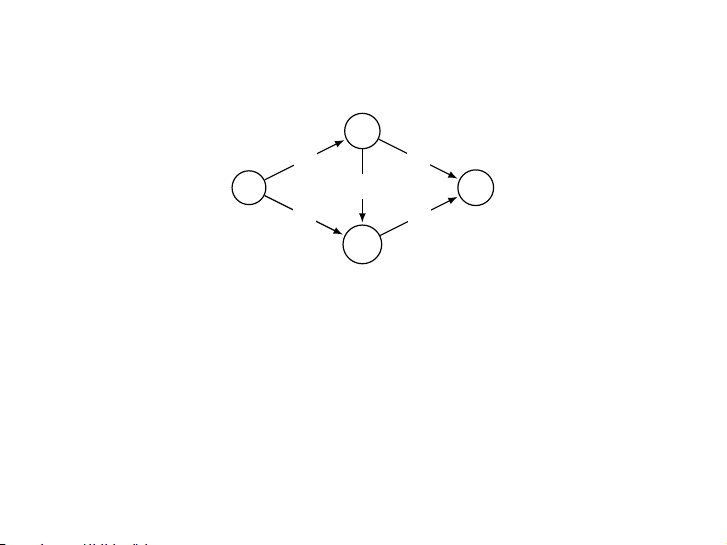
Anatomy of a network-flow problem 4 / 34 Mô hình bài bài toán a 2 d 3 10 1 2 s 3 b 1 1 t 4 5 c 5 e
▶ Đồ thị có hướng biểu diễn mạng đường ống, dầu có thể được
chuyển qua đường ống này
▶ Mục tiêu là chuyển dầu từ s đến t, nhiều nhất có thể. 5 / 34
Một luồng chuyển 7 đơn vị dầu từ s tới t luồng khả năng thông qua a 2/2 d 2/3 0/10 1/1 2/2 s 1/3 b 1/1 0/1 t 4/4 5/5 c 5/5 e
Liệu có cách nào làm tốt hơn? 6 / 34 Mạng Định nghĩa
Một mạng được định nghĩa là bộ G = (V, E, s, t, c), ở đây
▶ (V, E) là một đồ thị có hướng;
▶ s, t ∈ V, gọi là đỉnh nguồn và đỉnh đích; và
▶ c là một hàm gắn trên mỗi cạnh e của G một giá trị ce > 0
gọi là khả năng thông qua. Bài toán
Ta muốn chuyển nhiều dầu nhất có thể từ s tới t mà không vượt
quá khả năng thông qua trên mỗi cạnh. 7 / 34 Định nghĩa (Luồng)
Một luồng trên mạng G là một hàm
f : E −→ R+ ∪ {0},
gắn mỗi cạnh e của G với một giá trị số fe, sao cho:
1. Không vi phạm khả năng thông qua: 0 ≤ fe ≤ ce với mọi e ∈ E
2. Với mọi đỉnh u, ngoại trừ s và t, tổng luồng vào u bằng tổng luồng ra khỏi u: ∑ ∑ fwu = fuz. (w,u)∈E (u,z)
Nói cách khác, mạng là bảo toàn (theo luật Kirchhoff). 8 / 34
Luồng và lượng dầu chuyển luồng khả năng thông qua a 2/2 d 2/3 0/10 1/1 2/2 s 1/3 b 1/1 0/1 t 4/4 5/5 c 5/5 e 9 / 34 Định nghĩa
Giá trị của luồng là tổng lượng gửi từ s đến t. Theo luật bảo
toàn, size(f) bằng lượng rời khỏi s: ∑ size(f) = fsu. (s,u)∈E
▶ Mục đích của chúng ta là tìm được luồng có giá trị cực đại.
▶ Tương đương, tìm cách gán giá trị {fe : e ∈ E}
thỏa mãn một số ràng buộc.
▶ Đây là một bài toán quy hoạch tuyến tính. 10 / 34 Ví dụ
Bài toán tìm luồng cực đại trong mạng a 1 1 s 1 t 1 1 b
tương đương với bài toán quy hoạch tuyến tính max fsa + fsb
0 ≤ fsa, fsb, fab, fat, fbt ≤ 1
fsa = fat + fab
fsb + fab = fbt 11 / 34 Nội dung
Bài toán luồng cực đại trên mạng Thuật toán Ford-Fulkerson
Luồng cực đại và lát cắt cực tiểu
Tính hiệu quả của thuật toán Thuật toán tham lam
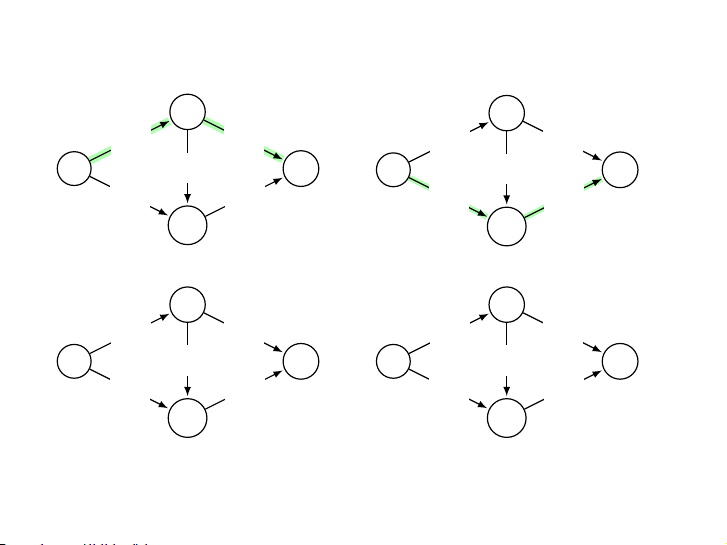
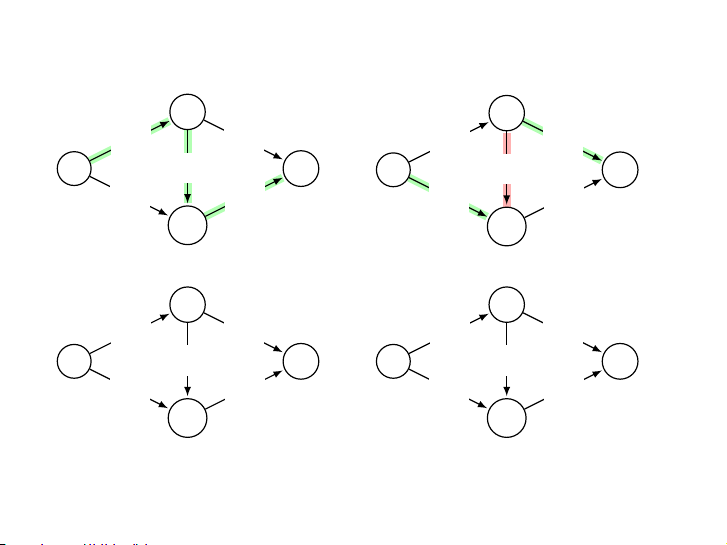
▶ Bắt đầu với luồng 0
▶ Lặp lại: Chọn một đường đi thích hợp từ s tới t và tăng
luồng nhiều nhất có thể dọc theo đường này. 13 / 34 Khởi tạo Tăng luồng a a 0/1 0/1 1/1 1/1 s 0/1 t s 0/1 t 0/1 0/1 0/1 0/1 b b Tăng luồng Luồng cực đại a a 1/1 1/1 1/1 1/1 s 0/1 t s 0/1 t 1/1 1/1 1/1 1/1 b b 14 / 34 Khởi tạo Tăng luồng a a 0/1 0/1 1/1 0/1 s 0/1 t s 1/1 t 0/1 0/1 0/1 1/1 b b
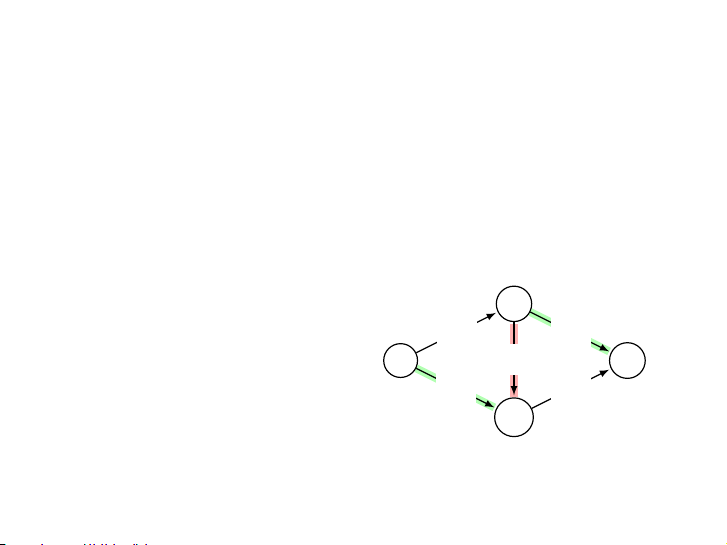
Hủy luồng trên cạnh a → b Luồng cực đại a a 1/1 1/1 1/1 1/1 s 0/1 t s 0/1 t 1/1 1/1 1/1 1/1 b b 15 / 34 Tìm đường tăng luồng
Tìm cạnh (u, v) có một trong hai kiểu
▶ (u, v) ∈ E và khả năng thông qua cuv vẫn chưa đầy. Khi đó
fuv có thể tăng thêm nhiều nhất là cuv − fuv.
▶ (v, u) ∈ E và có một luồng qua đó, tức là fvu > 0. Khi đó ta
có thể giảm một phần hoặc toàn bộ fvu. 16 / 34 Đường tăng luồng Cạnh gốc Cạnh ngược
▶ e = (u, v) ∈ E ▶ eR = (v, u) ▶ Luồng fe
▶ “Giảm” luồng fe đã gửi ▶ Khả năng ce
Khả năng thông qua còn lại Ví dụ a { 1/1 0/1 c s 1/1 t cf e − fe nếu e ∈ E (e) = f 0/1 e nếu eR ∈ E. 1/1 b 17 / 34 Đồ thị tăng luồng Định nghĩa
Đồ thị tăng luồng của mạng G với luồng f là đồ thị
Gf = (V, Ef, cf) với
Ef = {e : fe < ce} ∪ {eR : fe > 0}. Ví dụ
Mạng G với luồng f và đồ thị tăng luồng Gf tương ứng. a a 1/1 0/1 1 1 s 1/1 t s 1 t 0/1 1/1 1 1 b b 18 / 34 Đường tăng luồng Định nghĩa
▶ Một đường tăng luồng là một đường đi từ s đến t trong đồ thị tăng luồng Gf.
▶ Khả năng thông qua của đường tăng luồng P là
cf(P) = min{cf(e) : e ∈ P} Augment(f, c, P)
δ = cf(P) foreach cạnh e ∈ P:
if (e ∈ E) fe = fe + δ else
f(eR) = f(eR) − δ return f 19 / 34 Thuật toán Ford-Fulkerson Ford-Fulkerson (G)
foreach cạnh e ∈ E: fe = 0
Gf = đồ thị tăng luồng của G và f
while (còn đường tăng luồng P trong Gf):
f = Augment(f, c, P) Cập nhật Gf return f 20 / 34