Bài giảng môn Cấu trúc dữ liệu và giải thuật | Đại học Đồng Tháp

TRƯỜNG ĐẠI HỌC ĐỒNG THÁP
KHOA KỸ THUẬT – CÔNG NGHỆ
NGUYỄN HỮU DUYỆT
HUỲNH LÊ UYÊN MINH
LƯƠNG THÁI NGỌC BÀI GIẢNG
CẤU TRÚC DỮ LIỆU VÀ GIẢI THUẬT
Đồng Tháp, năm 2020
Lưu hành nội bộ LỜI NÓI ĐẦU
Cấu trúc dữ liệu và giải thuật đóng vai trò là môn học cơ sở rất quan trọng trong
chương trình đào tạo trình độ cao đẳng, đại học cho tất các ngành, chuyên ngành về công
nghệ thông tin và đào tạo giáo viên Tin học.
Dựa trên kinh nghiệm giảng dạy nhiều năm môn học Cấu trúc dữ liệu và giải thuật
và tham khảo các nguồn tài liệu đa dạng, phong phú của các giáo trình, bài giảng, tài liệu
tham khảo trong nước và ngoài nước, nhóm tác giả đã biên soạn bài giảng bám sát đề
cương môn học trong chương trình đào tạo ngành Khoa học máy tính và ngành Sư phạm
Tin học của Trường Đại học Đồng Tháp.
Mỗi mô đun bài giảng được trình bày theo thứ tự: Khái niệm kiểu dữ liệu trừu
tượng, mô tả các phép toán kèm theo là các ví dụ minh họa, ý tưởng giải thuật và việc cài
đặt giải thuật dựa vào ngôn ngữ lập trình C; đồng thời trong mỗi mô đun bài giảng chú
trọng liên hệ những ứng dụng thực tế.
Bài giảng được chia thành 6 chương, cụ thể gồm: -
Chương 1 trình bày những vấn đề mang tính tổng quan của môn học như
khái niệm mô hình dữ liệu và kiểu dữ liệu trừu tượng; các kiểu dữ liệu cơ bản và nâng cao;
giải thuật và kĩ thuật đánh giá độ phức tạp của giải thuật. -
Chương 2 trình bày các kiểu dữ liệu trừu tượng cơ bản, bao gồm kiểu dữ
liệu danh sách, ngăn xếp, hàng đợi và bảng băm. -
Chương 3 trình bày kiểu dữ liệu trừu tượng cây, bao gồm cây tổng quát và
cây nhị phân; các phép toán cơ bản trên cây. -
Chương 4 trình bày kiểu dữ liệu đồ thị được xem là kiểu dữ liệu tổng quát
nhất trong các kiểu dữ liệu được trình bày trong bài giảng này và kiểu dữ liệu này có nhiều
ứng dụng trong thực tế. -
Chương 5 trình bày các giải thuật sắp xếp trong, gồm các giải thuật sắp xếp
đơn giản, như sắp xếp chọn, chèn, nổi bọt, sắp xếp phức tạp như sắp xếp nhanh, vun đống
(Heap sort) và sắp xếp trộn. Riêng vấn đề sắp xếp ngoài sẽ là một nội dung được trình bày
trong một chủ đề khác. -
Chương 6 trình bày những kĩ thuật phổ biến trong thiết kế giải thuật, bao
gồm kĩ thuật tham ăn, quy hoạch động, chia để trị, quay lui.
Trong quá trình biên soạn bài giảng môn học Cấu trúc dữ liệu và giải thuật, mặc dù
nhóm tác giả đã nỗ lực hết sức, nhưng bài giảng chắc chắn sẽ không tránh khỏi những
thiếu sót. Nhóm tác giả mong muốn tiếp tục nhận được những ý kiến góp ý chân thành của độc giả. Nhóm tác giả MỤC LỤC
Chương 1. TỔNG QUAN ............................................................................................. 7
MỤC TIÊU ........................................................................................................ 7
1.1. GIỚI THIỆU CẤU TRÚC DỮ LIỆU ....................................................... 7
1.1.1. Từ bài toán đến chương trình .......................................................... 7
1.1.2. Kiểu dữ liệu trừu tượng (ADT – Abstract Data Type) ................... 9
1.1.3. Cấu trúc dữ liệu ............................................................................... 9
1.2. GIẢI THUẬT .......................................................................................... 10
1.2.1. Khái niệm giải thuật ...................................................................... 10
1.2.2. Đặc điểm của giải thuật ................................................................. 10
1.2.3. Mối quan hệ giữa cấu trúc dữ liệu và giải thuật ........................... 10
1.3. PHÂN TÍCH GIẢI THUẬT ................................................................... 11
1.3.1. Sự cần thiết phải phân tích giải thuật ................................................ 11
1.3.2. Tiêu chuẩn đánh giá giải thuật ...................................................... 11
1.3.3. Đo thời gian thực hiện chương trình ............................................. 12
1.3.4. Tỷ suất tăng ................................................................................... 12
1.3.5. Phương pháp đánh giá ................................................................... 13
1.4. TÓM TẮT CHƯƠNG ............................................................................. 22
1.5. CÂU HỎI VÀ BÀI TẬP ......................................................................... 23
Chương 2. CÁC KIỂU DỮ LIỆU TRỪU TƯỢNG CƠ BẢN ................................ 25
MỤC TIÊU ...................................................................................................... 25
2.1. DANH SÁCH (LIST) .............................................................................. 25
2.1.1. Khái niệm danh sách ......................................................................... 25
2.1.2. Các phép toán trên danh sách ............................................................ 25
2.1.3. Cài đặt danh sách .............................................................................. 26
2.2. NGĂN XẾP (STACK) ............................................................................. 40
2.2.1. Khái niệm ngăn xếp ......................................................................... 40
2.2.2. Các phép toán trên ngăn xếp ............................................................. 42
2.2.3. Cài đặt ngăn xếp ............................................................................... 42
2.2.4. Một số ứng dụng của ngăn xếp ..................................................... 48
2.3. HÀNG ĐỢI (QUEUE) ............................................................................ 52
2.3.1. Khái niệm hàng đợi. ...................................................................... 52
2.3.2. Các phép toán trên hàng đợi.......................................................... 53
2.3.3. Cài đặt hàng đợi ............................................................................ 53
2.3.4. Một số ứng dụng của cấu trúc hàng đợi ........................................ 57
2.4. BẢNG BĂM (HASH TABLE) ............................................................... 58
2.4.1. Lý thuyết về bảng băm ..................................................................... 58
2.4.2. Hàm băm (Hash Function) ............................................................... 60
2.4.3. Cài đặt từ điển bằng bảng băm...................................................... 61
2.5. TÓM TẮT CHƯƠNG ............................................................................. 68
2.6. CÂU HỎI VÀ BÀI TẬP ......................................................................... 68
Chương 3. KIỂU DỮ LIỆU TRỪU TƯỢNG CÂY ................................................. 72
MỤC TIÊU ...................................................................................................... 72
3.1. CÁC KHÁI NIỆM CƠ BẢN ................................................................... 72
3.1.1. Định nghĩa cây và các khái niệm liên quan ...................................... 72
3.1.2. Cây thứ tự .......................................................................................... 74
3.1.3. Duyệt cây .......................................................................................... 75
3.1.4. Cây có nhãn và cây biểu thức ........................................................... 76
3.2. CÁC PHÉP TOÁN CƠ BẢN ................................................................... 77
3.3. CÁC PHƯƠNG PHÁP CÀI ĐẶT ........................................................... 78
3.3.1. Cài đặt cây bằng mảng ...................................................................... 78
3.3.2. Cài đặt cây bằng danh sách các nút con ............................................ 80
3.3.3. Cài đặt cây theo phương pháp con trái nhất và anh em phải ............ 80
3.3.4. Cài đặt cây bằng con trỏ .................................................................... 82
3.4. CÂY NHỊ PHÂN ..................................................................................... 82
3.4.1. Định nghĩa cây nhị phân ................................................................... 82
3.4.2. Phép duyệt cây nhị phân ................................................................... 82
3.4.3. Cài đặt cây nhị phân .......................................................................... 83
3.4.4. Các giải thuật cơ bản trên cây nhị phân ............................................ 83
3.5. CÂY TÌM KIẾM NHỊ PHÂN (BINARY SEARCH TREE) ................... 85
3.5.1. Định nghĩa cây tìm kiếm nhị phân .................................................... 85
3.5.2. Cài đặt cây tìm kiếm nhị phân .......................................................... 86
3.5.3. Các giải thuật cơ bản trên cây tìm kiếm nhị phân ............................. 86
3.6. CÂY CÂN BẰNG (AVL) ........................................................................ 90
3.6.1. Định nghĩa cây cân bằng .................................................................. 90
3.6.2. Các phép quay cân bằng trên cây AVL ............................................ 91
3.6.3. Thêm nút vào cây AVL ................................................................. 94
3.6.4. Loại bỏ một nút khỏi cây AVL ..................................................... 96
3.7. TÓM TẮT CHƯƠNG ............................................................................. 96
3.8. CÂU HỎI VÀ BÀI TẬP ......................................................................... 96
Chương 4. KIỂU DỮ LIỆU ĐỒ THỊ ........................................................................ 99
MỤC TIÊU ...................................................................................................... 99
4.1. CÁC KHÁI NIỆM .................................................................................. 99
4.1.1. Đồ thị ............................................................................................. 99
4.1.2. Đỉnh kề (adjacent) ......................................................................... 99
4.1.3. Đường đi (path) và chu trình (cycle) .......................................... 100
4.1.4. Đồ thị không có chu trình (acyclic) ............................................ 100
4.2. BIỂU DIỄN ĐỒ THỊ ............................................................................. 100
4.2.1. Biểu diễn đồ thị bằng ma trận đỉnh kề ........................................ 100
4.2.2. Biểu diễn đồ thị bằng danh sách các đỉnh kề .............................. 101
4.3. SẮP XẾP TOPO (TOPOLOGICAL SORT) ........................................ 102
4.3.1. Khái niệm sắp xếp topo ............................................................... 102
4.3.2. Giải thuật tìm một sắp xếp topo .................................................. 102
4.4. CÁC PHÉP TOÁN ............................................................................... 103
4.4.1. Duyệt đồ thị ................................................................................. 104
4.4.2. Đường đi ngắn nhất từ một đỉnh nguồn – Giải thuật Dijkstra .... 106
4.4.3. Đường đi ngắn nhất giữa mọi cặp đỉnh – Giải thuật Floyd ........ 107
4.5. CÀI ĐẶT ............................................................................................... 108
4.5.1. Cài đặt kiểu dữ liệu đồ thị bằng Java .......................................... 108
4.5.2. Cài đặt kiểu dữ liệu đồ thị bằng C++ .......................................... 113
4.6. TÓM TẮT CHƯƠNG ........................................................................... 115
4.7. CÂU HỎI VÀ BÀI TẬP ....................................................................... 116
Chương 5. SẮP XẾP VÀ TÌM KIẾM .................................................................... 117
MỤC TIÊU .................................................................................................... 117
5.1. SẮP XẾP ............................................................................................... 117
5.1.1. Khái niệm .................................................................................... 117
5.1.2. Các giải thuật sắp xếp cơ bản ...................................................... 117
5.1.3. Các giải thuật sắp xếp nâng cao .................................................. 122
5.2. TÌM KIẾM ............................................................................................ 133
5.2.1. Tìm kiếm tuần tự ......................................................................... 133
5.2.2. Tìm kiếm nhị phân ...................................................................... 134
5.3. TÓM TẮT CHƯƠNG ........................................................................... 135
5.4. CÂU HỎI VÀ BÀI TẬP ........................................................................ 136
Chương 6. KỸ THUẬT THIẾT KẾ GIẢI THUẬT ............................................... 138
MỤC TIÊU .................................................................................................... 138
6.1. TỔNG QUAN ....................................................................................... 138
6.2. KỸ THUẬT THIẾT KẾ GIẢI THUẬT ............................................... 138
6.2.1. Phương pháp đệ qui..................................................................... 138
6.2.2. Đệ qui quay lui ............................................................................ 139
6.2.3. Phương pháp tham ăn .................................................................. 141
6.2.4. Phương pháp chia để trị ............................................................. 145
6.2.5. Phương pháp quy hoạch động ..................................................... 148
6.3. TÓM TẮT CHƯƠNG ........................................................................... 159
6.4. CÂU HỎI VÀ BÀI TẬP ....................................................................... 159
TÀI LIỆU THAM KHẢO ........................................................................................ 161
Chương 1. TỔNG QUAN MỤC TIÊU
Sau khi học xong chương này, người học có thể:
- Hiểu được ý nghĩa của các kiểu dữ liệu trừu tượng trong việc tổ chức dữ liệu
và thiết kế giải thuật;
- Đánh giá được hiệu quả giải thuật thông qua phương pháp tính thời gian thực
hiện chương trình, làm cơ sở lựa chọn giải thuật hiệu quả cho một bài toán.
1.1. GIỚI THIỆU CẤU TRÚC DỮ LIỆU
1.1.1. Từ bài toán đến chương trình
Để giải quyết một bài toán thực tế bằng máy tính điện tử, người ta thường thực hiện quy trình 5 bước:
Bước 1: Phân tích bài toán, nghĩa là xác định input, output và mối quan hệ giữa chúng
Bước 2: Mô hình hóa bài toán bằng một mô hình toán học phù hợp
Bước 3: Tìm kiếm giải thuật tối ưu cho mô hình toán học Bước 4: Xây dựng
chương trình Bước 5: Thử nghiệm.
Trong đó việc mô hình hóa bài toán bằng một mô hình toán học và tìm kiếm giải
thuật trên mô hình toán học là hai bước đặc biệt quan trọng và có mối quan hệ khăng khít với nhau.
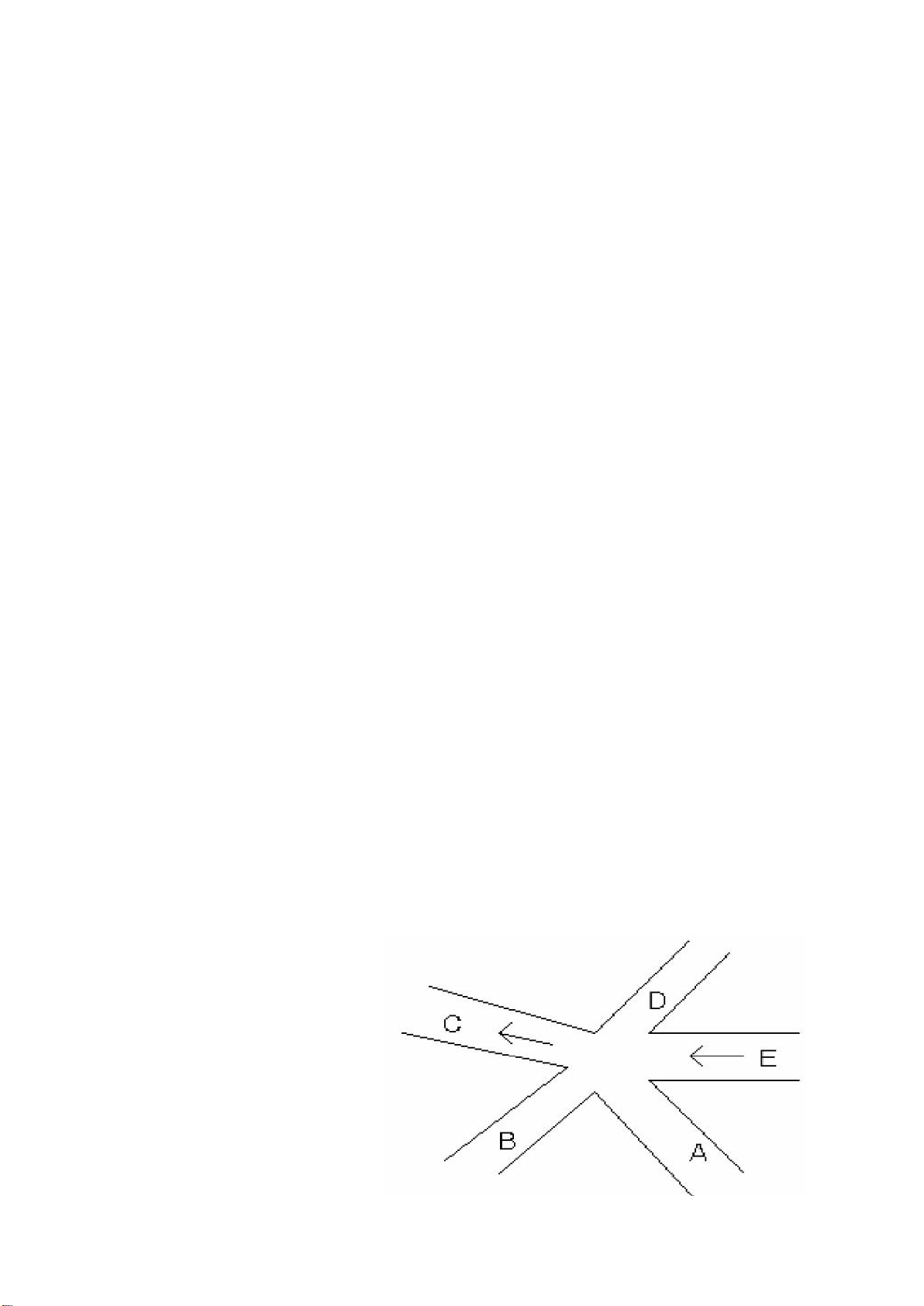
Ví dụ 1.1: Bài toán đèn giao thông
Cho một ngã năm giao thông như hình 1.1, trong đó C và E là các đường một
chiều theo chiều mũi tên, các đường khác là hai chiều. Hãy thiết kế một bảng đèn hiệu
điều khiển giao thông tại ngã năm này một cách hợp lý, nghĩa là: phân chia các lối đi
tại ngã năm này thành các nhóm, mỗi nhóm gồm các lối đi có thể cùng đi đồng thời
nhưng không xảy ra tai nạn giao thông (các hướng đi không cắt nhau), và số lượng
nhóm là ít nhất có thể được.
Hình 1.1. Hướng đi tại ngã 5
Ta có thể xem đầu vào (input) của bài toán là tất cả các lối đi tại ngã năm này, đầu
ra (output) của bài toán là các nhóm lối đi có thể đi đồng thời mà không xảy ra tai nạn
giao thông, mỗi nhóm sẽ tương ứng với một pha điều khiển của đèn hiệu, vì vậy ta phải
tìm kiếm lời giải với số nhóm là ít nhất để giao thông không bị tắc nghẽn vì phải chờ đợi quá lâu.
Trước hết ta nhận thấy rằng tại ngã năm này có 13 lối đi: AB, AC, AD, BA, BC,
BD, DA, DB, DC, EA, EB, EC, ED. Tất nhiên, để có thể giải được bài toán ta phải tìm
một cách nào đó để thể hiện mối liên quan giữa các lối đi này. Lối nào với lối nào
không thể đi đồng thời, lối nào và lối nào có thể đi đồng thời. Ví dụ cặp AB và EC có
thể đi đồng thời, nhưng AD và EB thì không, vì các hướng giao thông cắt nhau. Ở đây
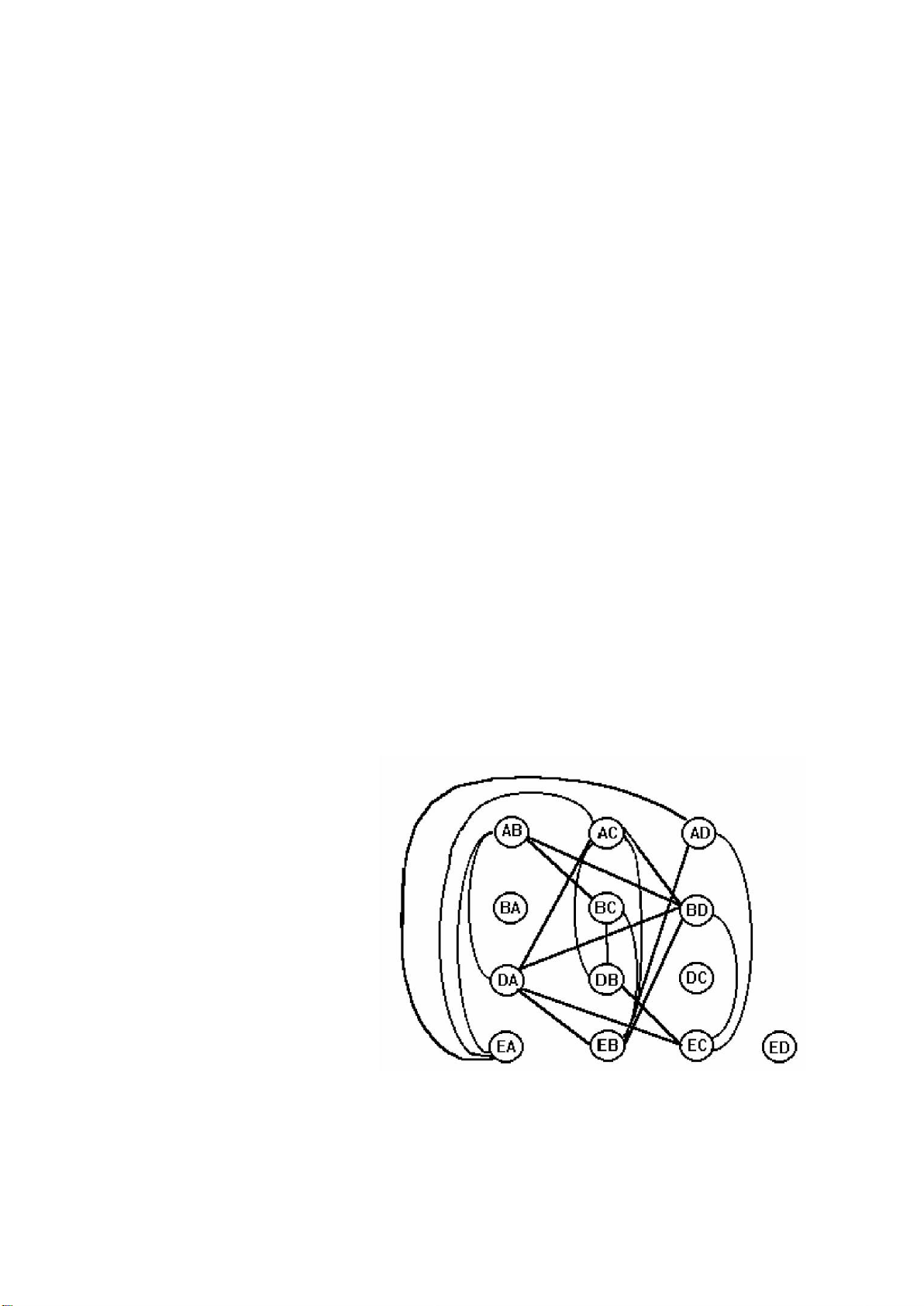
ta sẽ dùng một sơ đồ trực quan như sau: tên của 13 lối đi được viết lên mặt phẳng, hai
lối đi nào nếu đi đồng thời sẽ xảy ra đụng nhau (tức là hai hướng đi cắt qua nhau) ta
nối lại bằng một đoạn thẳng, hoặc cong, hoặc ngoằn ngoèo tuỳ thích. Ta sẽ có một sơ
đồ như hình 1.2. Như vậy, trên sơ đồ này, hai lối đi có cạnh nối lại với nhau là hai lối
đi không thể cho đi đồng thời.
Với cách biểu diễn như vậy ta đã có một đồ thị (Graph), tức là ta đã mô hình hoá
bài toán giao thông ở trên theo mô hình toán là đồ thị; trong đó mỗi lối đi trở thành một
đỉnh của đồ thị, hai lối đi không thể cùng đi đồng thời được nối nhau bằng một đoạn ta
gọi là cạnh của đồ thị. Bây giờ ta phải xác định các nhóm, với số nhóm ít nhất, mỗi
nhóm gồm các lối đi có thể đi đồng thời, nó ứng với một pha của đèn hiệu điều khiển
giao thông. Giả sử rằng, ta dùng màu để tô lên các đỉnh của đồ thị này sao cho: -
Các lối đi cho phép cùng đi đồng thời sẽ có cùng một màu. Dễ dàng nhận
thấy rằng hai đỉnh có cạnh nối nhau sẽ không được tô cùng màu. -
Số nhóm là ít nhất: Ta phải tính toán sao cho số màu được dùng là ít nhất.
Hình 1.2. Mô hình hóa cho bài toán đèn giao thông
Tóm lại, ta phải giải quyết bài toán: Tô màu cho đồ thị ở hình 1.2 sao cho hai
đỉnh có cạnh nối với nhau không cùng màu với tổng số màu được dùng là ít nhất.
1.1.2. Kiểu dữ liệu trừu tượng (ADT – Abstract Data Type)
Trong tin học, trừu tượng hóa nghĩa là đơn giản hóa, làm cho nó sáng sủa hơn và
dễ hiểu hơn. Hay nói cách khác, trừu tượng hóa là che đi những chi tiết, làm nổi bật
cái tổng thể. Trừu tượng hóa có thể thực hiện trên hai khía cạnh là trừu tượng hóa dữ
liệu và trừu tượng hóa chương trình.
Trừu tượng hóa chương trình là sự định nghĩa các chương trình con để tạo ra
các phép toán trừu tượng (sự tổng quát hóa của các phép toán nguyên thủy). Chẳng
hạn, ta có thể tạo ra một chương trình con matrixMult để thực hiện phép toán nhân hai
ma trận. Sau khi matrixMult đã được tạo ra, ta có thể dùng nó như một phép toán
nguyên thủy (chẳng hạn phép cộng hai số).
Trừu tượng hóa chương trình cho phép phân chia chương trình thành các chương
trình con. Sự phân chia này sẽ che dấu tất cả các lệnh cài đặt chi tiết trong các chương
trình con. Ở cấp độ chương trình chính, ta chỉ thấy lời gọi các chương trình con và điều
này được gọi là sự bao gói.
Định nghĩa 1.1: Một kiểu dữ liệu trừu tượng là một mô hình toán học cùng với
một tập hợp các phép toán (operator) trừu tượng được định nghĩa trên mô hình đó.
Ví dụ 1.2: Tập hợp số nguyên cùng với các phép toán kiểm tra phần tử có thuộc
tập hợp hay không, phép hợp, phép giao và phép hiệu là một kiểu dữ liệu trừu tượng.
Trong một ADT các phép toán có thể thực hiện trên các đối tượng (toán hạng)
không chỉ thuộc ADT đó, cũng như kết quả không nhất thiết phải thuộc ADT. Tuy nhiên
phải có ít nhất một toán hạng hoặc kết quả phải thuộc ADT đang xét.
Mục đích của việc đề xuất khái niệm kiểu dữ liệu trừu tượng là tách bạch việc
nghiên cứu về tổ chức dữ liệu và xây dựng phép toán trên dữ liệu với việc cài đặt dữ
liệu bằng một ngôn ngữ lập trình cụ thể.
Những kiểu dữ liệu trừu tượng phổ biến nhất sẽ được đề cập tới trong học phần này
là: Danh sách (List), Tập hợp (Set), Hàng đợi (Queue), Ngăn xếp (Stack), Cây (Tree), Đồ thị (Graph).
1.1.3. Cấu trúc dữ liệu
Như trên đã nói kiểu dữ liệu trừu tượng ADT mang tính khái quát, không phụ
thuộc vào một hệ thống cụ thể nào. Tuy nhiên, mục đích cuối cùng của việc giải quyết
bài toán bằng máy tính điện tử là các chương trình máy tính. Vì vậy, với mỗi kiểu dữ
liệu trừu tượng cần có một cách thể hiện cụ thể bằng một đối tượng dữ liệu cụ thể được
cài đặt trong máy tính, đó chính là cấu trúc dữ liệu.
Định nghĩa 1.2: Cấu trúc dữ liệu là một dữ liệu phức hợp, gồm nhiều thành phần
dữ liệu, mỗi thành phần hoặc là dữ liệu cơ sở hoặc là một cấu trúc dữ liệu đã được xây
dựng được liên kết với nhau theo một cách thức nào đó. 1.2. GIẢI THUẬT
1.2.1. Khái niệm giải thuật
Giải thuật, nhiều khi còn được gọi là thuật toán dùng để chỉ phương pháp hay
cách thức để giải quyết vần đề.
Giải thuật có thể được biểu diễn bằng ngôn ngữ tự nhiên, bằng lưu đồ hoặc bằng mã giả (pseudo code).
Giải thuật có tính độc lập tương đối với các ngôn ngữ lập trình, nghĩa là một giải thuật
có thể được cài đặt bằng một ngôn ngữ lập trình cụ thể. Trong thực tế, giải thuật thường
được biểu diễn bằng mã giả tựa trên một ngôn ngữ lập trình nào đó, chẳng hạn như C, Pascal.
Khi đã xác định được cấu trúc dữ liệu thích hợp, người lập trình sẽ bắt đầu tiến hành
xây dựng giải thuật tương ứng theo yêu cầu của bài toán đặt ra. Để giải quyết một vấn
đề có thể có nhiều phương pháp, do vậy sự lựa chọn phương pháp phù hợp là một việc
mà người lập trình phải cân nhắc và tính toán. Sự lựa chọn này cũng có thể góp phần
đáng kể trong việc giảm bớt công việc của người lập trình trong phần cài đặt thuật toán
trên một ngôn ngữ cụ thể.
Khi nói đến giải thuật ta quan tâm đến các vấn đề cơ bản sau:
- Tư tưởng (ý tưởng) của giải thuật.
- Nội dung của giải thuật và cách cài đặt giải thuật đó.
- Đánh giá độ phức tạp về thời gian và độ phức tạp về bộ nhớ.
1.2.2. Đặc điểm của giải thuật
Không phải tất cả các thủ tục có thể được gọi là một giải thuật. Một giải thuật
nên có các đặc điểm sau: -
Tính xác định: Giải thuật nên rõ ràng và không mơ hồ. Mỗi một giai đoạn
(hay mỗi bước) nên rõ ràng và chỉ mang một mục đích nhất định. -
Dữ liệu đầu vào xác định: Một giải thuật có thể không có hoặc có nhiều
dữ liệu đầu vào đã xác định. -
Kết quả đầu ra: Một giải thuật nên có một hoặc nhiều dữ liệu đầu ra đã
xác định, và nên kết nối với kiểu kết quả mong muốn. -
Tính dừng: Giải thuật phải kết thúc sau một số hữu hạn các bước. -
Tính hiệu quả: Một giải thuật nên thi hành được với các nguồn có sẵn,
tức là có khả năng giải quyết hiệu quả vấn đề trong điều kiện thời gian và tài nguyên cho phép. -
Tính phổ biến: Một giải thuật có tính phổ biến nếu giải thuật này có thể
giải quyết được một lớp các vấn đề tương tự.
1.2.3. Mối quan hệ giữa cấu trúc dữ liệu và giải thuật
Mối quan hệ giữa cấu trúc dữ liệu và giải thuật có thể minh họa bằng đẳng thức:
Cấu trúc dữ liệu + Giải thuật = Chương trình
Như vậy, khi đã có cấu trúc dữ liệu tốt, nắm vững giải thuật thực hiện thì việc thể hiện
chương trình bằng một ngôn ngữ cụ thể chỉ là vấn đề thời gian. Khi có cấu trúc dữ liệu
mà chưa tìm ra thuật giải thì không thể có chương trình và ngược lại không thể có giải
thuật khi chưa có cấu trúc dữ liệu. Một chương trình máy tính chỉ có thể được hoàn
thiện khi có đầy đủ cả cấu trúc dữ liệu để tổ chức dữ liệu và giải thuật xử lý dữ liệu
theo yêu cầu của bài toán đặt ra.
1.3. PHÂN TÍCH GIẢI THUẬT
1.3.1. Sự cần thiết phải phân tích giải thuật
Khi giải một bài toán chúng ta có thể có một số giải thuật khác nhau, vấn đề là
cần phải đánh giá các giải thuật đó để lựa chọn một giải thuật tốt nhất. Thông thường
thì ta sẽ căn cứ vào các tiêu chuẩn sau: (1) Giải thuật đúng đắn. (2) Giải thuật đơn giản. (3)
Giải thuật thực hiện nhanh. (4)
Tốn ít bộ nhớ (hoặc rộng hơn là tiêu tốn ít tài nguyên của hệ thống khi chạy chương trình).
Với yêu cầu (1), để kiểm tra tính đúng đắn của giải thuật chúng ta có thể cài đặt
giải thuật đó và cho thực hiện trên máy với một số bộ dữ liệu mẫu rồi lấy kết quả thu
được so sánh với kết quả đã biết. Cách làm này không chắc chắn bởi vì có thể giải thuật
đúng với tất cả các bộ dữ liệu chúng ta đã thử nhưng lại sai với một bộ dữ liệu nào đó.
Vả lại cách làm này chỉ phát hiện ra giải thuật sai chứ chưa chứng minh được là nó
đúng. Tính đúng đắn của giải thuật cần phải được chứng minh bằng toán học. Tất nhiên
điều này không đơn giản và do vậy chúng ta sẽ không đề cập đến ở đây. Khi chúng ta
viết một chương trình để sử dụng một vài lần thì yêu cầu (2) là quan trọng nhất. Chúng
ta cần một giải thuật dễ viết chương trình để nhanh chóng có được kết quả, thời gian
thực hiện chương trình không được đề cao vì dù sao thì chương trình đó cũng chỉ sử
dụng một vài lần mà thôi. Tuy nhiên khi một chương trình được sử dụng nhiều lần thì
yêu cầu tiết kiệm thời gian thực hiện chương trình lại rất quan trọng đặc biệt đối với
những chương trình mà khi thực hiện cần dữ liệu nhập lớn do đó yêu cầu (3) sẽ được
xem xét một cách kĩ càng. Ta gọi nó là hiệu quả thời gian thực hiện của giải thuật. Tiêu
chuẩn (4) cũng là tiêu chuẩn quan trọng khi cài đặt các bài toán thực tế.
1.3.2. Tiêu chuẩn đánh giá giải thuật
Một phương pháp để xác định hiệu quả thời gian thực hiện của một giải thuật là
lập trình nó và đo lường thời gian thực hiện của hoạt động trên một máy tính xác định
đối với tập hợp được chọn lọc các dữ liệu vào. Thời gian thực hiện không chỉ phụ thuộc
vào giải thuật mà còn phụ thuộc vào tập các chỉ thị của máy tính, chất lượng của máy
tính và kĩ xảo của người lập trình. Sự thi hành cũng có thể điều chỉnh để thực hiện tốt
trên tập đặc biệt các dữ liệu vào được chọn. Ðể vượt qua các trở ngại này, các nhà khoa
học máy tính đã chấp nhận tính phức tạp của thời gian được tiếp cận như một sự đo
lường cơ bản việc thực thi của giải thuật. Thuật ngữ tính hiệu quả sẽ đề cập đến việc
đo lường này và đặc biệt đối với độ phức tạp thời gian trong trường hợp xấu nhất.
1.3.3. Đo thời gian thực hiện chương trình
1.3.3.1. Đơn vị đo thời gian thực hiện
Khi ta nói một chương trình nào đó có thời gian thực hiện là T(n), thì đơn vị đo thời
gian của T(n) không phải là đơn vị đo thời gian bình thường như giờ, phút, giây... mà
thường được xác định bởi số các lệnh cơ bản, số chỉ thị được thực hiện trong một máy tính lý tưởng.
Ví dụ 1.3: Khi ta nói thời gian thực hiện của một chương trình là T(n) = Cn thì
có nghĩa là chương trình ấy cần Cn chỉ thị thực thi.
Đơn vị đo thời gian chạy của chương trình máy tính được xác định bằng các
lệnh đơn giản của máy tính, như lệnh gán, đọc, viết, goto, quan hệ.
1.3.3.2. Thời gian thực hiện chương trình
Một chương trình là một hàm của kích thước dữ liệu vào, ký hiệu T(n) trong đó n là
kích thước của dữ liệu vào.
Ví dụ 1.4: Chương trình tính tổng của n số có thời gian thực hiện là T(n) = C.n
trong đó C là một hằng số.
Thời gian thực hiện chương trình là một hàm không âm, tức là T(n) ≥ 0 n ≥ 0
1.3.3.3. Thời gian thực hiện trong trường hợp xấu nhất
Thời gian thực hiện chương trình không chỉ phụ thuộc vào kích thước mà còn phụ
thuộc vào tính chất của dữ liệu vào, nghĩa là dữ liệu vào có cùng kích thước nhưng thời
gian thực hiện chương trình có thể khác nhau. Chẳng hạn chương trình sắp xếp dãy số
nguyên tăng dần, khi ta cho vào dãy có thứ tự thì thời gian thực hiện khác với khi ta
cho vào dãy chưa có thứ tự, hoặc khi ta cho vào một dãy đã có thứ tự tăng thì thời gian
thực hiện cũng khác so với khi ta cho vào một dãy đã có thứ tự giảm. Vì vậy thường
ta coi T(n) là thời gian thực hiện chương trình trong trường hợp xấu nhất trên dữ liệu
vào có kích thước n, tức là T(n) là thời gian lớn nhất để thực hiện chương trình đối với
mọi dữ liệu vào có cùng kích thước n.
1.3.4. Tỷ suất tăng
Hàm T(n) không âm có tỷ suất tăng f(n) nếu tồn tại hằng số thực C > 0 và số tự
nhiên N0 sao cho T(n) ≤ Cf(n) với mọi n ≥ N0. Người ta đã chứng minh được: “Cho
một hàm không âm T(n) bất kỳ, luôn tồn tại tỷ suất tăng f(n) của nó”.
Ví dụ 1.5: Giả sử T(0) = 1, T(1) = 4 và tổng quát T(n) = (n+1)2. Ðặt N0 = 1 và C
= 4 thì với mọi n ≥1 chúng ta dễ dàng chứng minh được rằng T(n) = (n+1)2 ≤ 4n2 với
mọi n ≥ 1, tức là tỷ suất tăng của T(n) là n2.
Ví dụ 1.6: Tỷ suất tăng của hàm T(n) = 3n3 + 2n2 là n3. Thực vậy, cho N0 = 0 và C
= 5 ta dễ dàng chứng minh rằng với mọi n ≥ 0 thì 3n3 + 2n2 ≤ 5n3.
1.3.5. Phương pháp đánh giá
1.3.5.1. Độ phức tạp giải thuật
Cho 2 giải thuật P1, P2 có thời gian thực hiện tương ứng là T1(n) = 100n2 (với
tỷ suất tăng là n2) và T2(n) = 5n3 (với tỷ suất tăng là n3). Việc xét giải thuật nào thực
hiện nhanh hơn sẽ phụ thuộc vào kích thước dữ liệu vào như sau:
- Khi n < 20 thì P2 sẽ nhanh hơn P1 (T2số của 100n2 (5<100).
- Khi n > 20 thì ngược lại do số mũ của 100n2 nhỏ hơn số mũ của 5n3 (2<3).
Ở đây chúng ta chỉ nên quan tâm đến trường hợp n>20 vì khi n<20 thì thời gian
thực hiện của cả P1 và P2 đều không lớn và sự khác biệt giữa T1 và T2 là không đáng
kể. Như vậy một cách hợp lý là ta xét tỷ suất tăng của hàm thời gian thực hiện chương
trình hơn là so sánh trực tiếp các hàm T(n).
- Ký pháp “Ô lớn” (big O): Hàm T(n) gọi là có độ phức tạp f(n) nếu tồn tại
các hằng thực C, số tự nhiên N0 sao cho T(n) ≤ Cf(n) với mọi n ≥ N0 (tức là T(n) có
tỷ suất tăng là f(n)) và kí hiệu T(n) là O(f(n)) (đọc là “ô lớn của f(n)”).
Ví dụ 1.7: T(n) = (n + 1) n có độ phức tạp O(n2) - Tính chất:
O(c.f(n)) = O(f(n)), với c là hằng số O(c) = O(1). Nói cách
khác độ phức tạp tính toán của giải thuật là một hàm chặn trên của hàm
thời gian. Vì hằng số C trong hàm chặn trên không có ý nghĩa nên ta có thể bỏ qua, vì
vậy một số hàm thể hiện độ phức tạp có các dạng thường gặp sau: log2n, n, nlog2n, n2,
n3, 2n, n!, nn. Ba hàm cuối cùng ta gọi là dạng hàm mũ, các hàm khác gọi là hàm đa
thức. Một giải thuật mà thời gian thực hiện có độ phức tạp là một hàm đa thức thì chấp
nhận được tức là có thể cài đặt để thực hiện, còn các giải thuật có độ phức tạp hàm mũ
thì phải tìm cách cải tiến giải thuật.
Khi nói đến độ phức tạp của giải thuật là ta muốn nói đến hiệu quả về thời gian
thực hiện của chương trình nên ta có thể xem việc xác định thời gian thực hiện của
chương trình chính là xác định độ phức tạp của giải thuật.
1.3.5.2. Cách tính độ phức tạp giải thuật
Cho 2 chương trình: P1 có thời gian thực hiện T1(n) = O(f1(n)) và P2 có thời gian
thực hiện là T2(n) = O(f2(n))
Qui tắc cộng: Thời gian T(n) để thực hiện của đoạn hai chương trình P1, P2 nối tiếp nhau sẽ là: T(n)=O(max(f1(n).f2(n)))
Ví dụ 1.8: Lệnh gán x 15 tốn một hằng thời gian hay O(1), lệnh đọc dữ liệu scanf(x)
tốn một hằng thời gian hay O(1).Vậy thời gian thực hiện cả hai lệnh trên nối tiếp nhau là O(max(1,1)) = O(1).
Qui tắc nhân: Thời gian T(n) để thực thi P1 và P2 lồng nhau (ví dụ vòng lặp lồng nhau): T(n) = O(f1(n) × f2(n))
Ví dụ 1.9: for (i=1; i<= n; i++) for (j=1; j<=n; j++) { thực hiện công việc O(1) }
Ta tính được T1(n)= O(n), T2(n) = O(n) nên T(n) = O(n x n)= O(n2)
Qui tắc tổng quát: -
Đối với mỗi lệnh đọc (read, scanf), ghi (write, printf), lệnh gán, so sánh:
thời gian thực hiện là hằng số (hay O(1)). -
Thời gian thực hiện của một chuỗi tuần tự các lệnh được xác định bằng
quy tắc cộng. Như vậy thời gian này là thời gian thi hành một lệnh nào đó lâu nhất trong chuỗi lệnh. -
Thời gian thực hiện cấu trúc “if” là thời gian lớn nhất thực hiện lệnh sau
if, lệnh sau else (nếu có) và thời gian kiểm tra điều kiện (Quy tắc cộng). Thường thời
gian kiểm tra điều kiện là O(1). -
Thời gian thực hiện vòng lặp là tổng thời gian thực hiện thân vòng lặp.
Nếu thời gian thực hiện thân vòng lặp không đổi thì thời gian thực hiện vòng lặp là tích
của số lần lặp với thời gian thực hiện thân vòng lặp. (Trong trường hợp không xác định
được số lần lặp ta phải lấy số lần lặp trong trường hợp xấu nhất). Các ví dụ:
Ví dụ 1.10: Tính thời gian thực hiện của hàm sắp xếp dưới đây
void sapXep(int a[], int n){ int tam; {1}
for (int i = 0; i < n; i++) {2}
for (int j = i + 1; j < n; j++) {3} if (a[j] < a[i]) { {4} tam = a[i]; {5} a[i] = a[j]; {6} a[j] = tam; } }
Ở đây, chúng ta chỉ quan tâm đến độ phức tạp của giải thuật. Ta thấy toàn bộ chương
trình chỉ gồm một lệnh lặp {1}, lồng trong lệnh {1} là lệnh {2}, lồng trong lệnh {2} là
lệnh {3} và lồng trong lệnh {3} là 3 lệnh nối tiếp nhau {4}, {5} và {6}. Chúng ta sẽ
tiến hành tính độ phức tạp theo thứ tự từ trong ra ngoài.
Trước hết, cả ba lệnh gán {4}, {5} và {6} đều tốn O(1) thời gian, việc so sánh a[j] <
a[i] cũng tốn O(1) thời gian, do đó lệnh {3} tốn O(1) thời gian.
Vòng lặp {2} thực hiện (n-i) lần, mỗi lần O(1) do đó vòng lặp {2} tốn O((ni).1) = O(n-i).
Vòng lặp {1} lặp n lần, lần thứ i có thời gian chạy của thân vòng lặp là O(n-i)
tổng thời gian của giải thuật là: 𝑛−1 𝑛(𝑛 + 1) 2)
𝑇(𝑛) = ∑(𝑛 − 𝑖) = = 𝑂(𝑛 2 𝑖=0
Ví dụ 1.11: Tính thời gian thực hiện của hàm tìm kiếm tuần tự dưới đây
int timKiem(int x, int a[], int n){ int found, i; {1} i = 0; {2} found = 0; {3}
while (i < n && !found) {4} if (a[i] == x) found = 1; else i = i+1; {5} return i; }
Ta thấy các lệnh {1}, {2}, {3} và {5} nối tiếp nhau, do đó độ phức tạp của hàm
timKiem chính là độ phức tạp lớn nhất trong 4 lệnh này.
- Ba lệnh {1}, {2} và {5} đều có độ phức tạp O(1) do đó độ phức tạp của hàm
chính là độ phức tạp của lệnh {3}.
- Trong thân của lệnh {3} là lệnh {4}. Lệnh {4} có độ phức tạp O(1). Trong
trường hợp xấu nhất (tất cả các phần tử của mảng a đều khác x) thì vòng lặp {3} thực
hiện n lần, vậy ta có T(n) = O(n).
1.3.5.3. Ðộ phức tạp của chương trình có gọi chương trình con không đệ qui
int timKiem(int x, int a[], int n){ int found, i; {1} i = 0; {2} found = 0; {3}
while (i < n && !found) {4} if (a[i] == x) found = 1; else i = i+1; {5} return i; }
Đối với trường hợp này, ta áp dụng quy tắc tính từ trong ra ngoài. Nếu chúng ta có một
chương trình với các chương trình con không đệ quy, để tính thời gian thực hiện của
chương trình, trước hết chúng ta tính thời gian thực hiện của các chương trình con
không gọi các chương trình con khác. Sau đó chúng ta tính thời gian thực hiện của các
chương trình con chỉ gọi các chương trình con mà thời gian thực hiện của chúng đã
được tính. Tiếp tục quá trình đánh giá thời gian thực hiện của mỗi chương trình con
sau khi thời gian thực hiện của tất cả các chương trình con mà nó gọi đã được đánh giá.
Cuối cùng ta tính thời gian cho chương trình chính. Giả sử ta có một hệ thống các
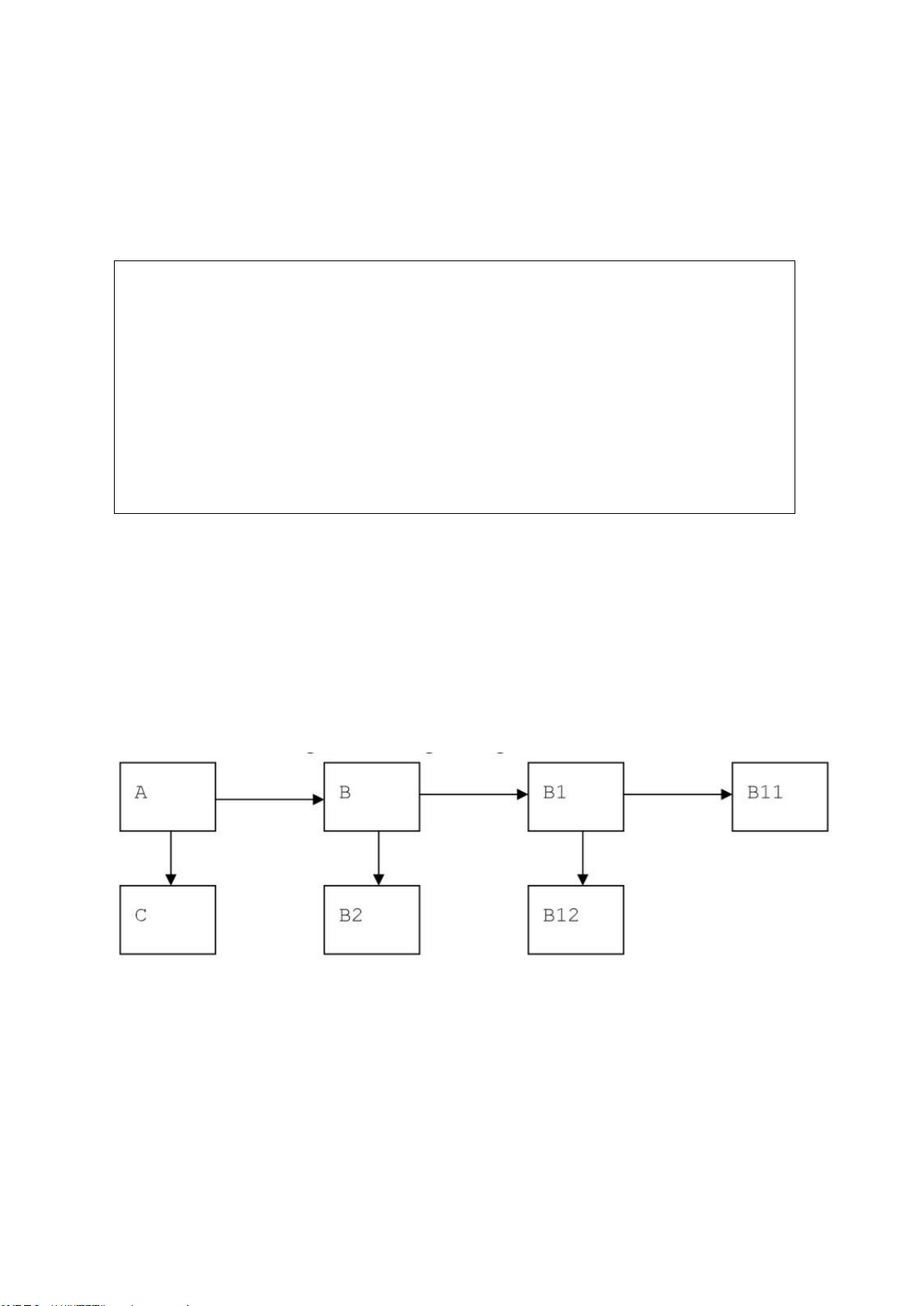
chương trình gọi nhau theo sơ đồ sau:
Hình 1.3. Sơ đồ gọi thực hiện các chương trình con không đệ quy
Chương trình A gọi hai chương trình con là B và C, chương trình B gọi hai
chương trình con là B1 và B2, chương trình B1 gọi hai chương trình con là B11 và
B12. Ðể tính thời gian thực hiện của A, ta áp dụng quy tắc tính từ trong ra ngoài theo các bước sau:
a. Tính thời gian thực hiện của C, B2, B11 và B12. Vì các chương trình con
này không gọi chương trình con nào cả.
b. Tính thời gian thực hiện của B1. Vì B1 gọi B11 và B12 mà thời gian thực
hiện của B11 và B12 đã được tính ở bước 1.
c. Tính thời gian thực hiện của B. Vì B gọi B1 và B2 mà thời gian thực hiện
của B1 đã được tính ở bước 2 và thời gian thực hiện của B2 đã được tính ở bước 1.
d. Tính thời gian thực hiện của A. Vì A gọi B và C mà thời gian thực hiện
của B đã được tính ở bước 3 và thời gian thực hiện của C đã được tính ở bước 1.
1.3.5.4. Độ phức tạp của chương trình đệ quy
Trong phạm vi này, chúng ta chỉ xét loại hàm đệ quy trực tiếp (hàm gọi trực tiếp chính bản thân nó).
Với các hàm đệ quy, ta không thể áp dụng cách tính như vừa trình bày trong
mục 1.3.5.3 bởi vì một hàm đệ quy sẽ gọi chính bản thân nó. Có thể thấy hình ảnh
chương trình đệ quy A như sau:
Hình 1.4. Sơ đồ chương trình con A đệ quy
Để tính độ phức tạp, trước hết chúng ta cần thành lập các phương trình đệ quy
T(n), sau đó giải phương trình đệ quy tìm nghiệm (nghiệm của phương trình đệ quy sẽ
là thời gian thực hiện của chương trình đệ quy), suy ra tỷ suất tăng f(n) hay O(f(n)).
Thành lập phương trình đệ quy
Phương trình đệ quy là một phương trình biểu diễn mối liên hệ giữa T(n) và
T(k), trong đó T(n) là thời gian thực hiện chương trình với kích thước dữ liệu nhập là
n, T(k) thời gian thực hiện chương trình với kích thước dữ liệu nhập là k, với k < n. Ðể
thành lập được phương trình đệ quy, ta phải căn cứ vào hàm đệ quy. Thông thường một
hàm đệ quy để giải bài toán kích thước n, phải có ít nhất một trường hợp dừng ứng với
một n cụ thể và lời gọi đệ quy để giải bài toán kích thước k (ktrình đệ quy, ta gọi T(n) là thời gian để giải bài toán kích thước n, ta có T(k) là thời
gian để giải bài toán kích thước k. Khi đệ quy dừng, ta phải xem xét khi đó chương
trình làm gì và tốn hết bao nhiêu thời gian, chẳng hạn thời gian này là C(n). Khi đệ quy
chưa dừng thì phải xét xem có bao nhiêu lời gọi đệ quy với kích thước k ta sẽ có bấy
nhiêu T(k). Ngoài ra ta còn phải xem xét đến thời gian để phân chia bài toán và tổng
hợp các lời giải, chẳng hạn thời gian này là d(n). Dạng tổng quát của một phương trình đệ quy sẽ là: 𝐶(𝑛) 𝑇(𝑛) = { 𝐹(𝑇(𝑘)) + 𝑑(𝑛)
Trong đó, C(n) là thời gian thực hiện chương trình ứng với trường hợp đệ quy dừng,
F(T(k)) là một hàm của các T(k), d(n) là thời gian để phân chia bài toán và tổng hợp các kết quả.
Ví dụ 1.12: Thành lập phương trình đệ quy của hàm tính giai thừa được viết
bằng giải thuật đệ quy như sau: int giaiThuat(int n) { if (n == 0) return 1; else
return (n * giaiThua (n – 1)); }
Gọi T(n) là thời gian thực hiện của hàm tính n!, thì T(n-1) là thời gian thực hiện
việc tính (n-1)!. Trong trường hợp n = 0 thì chương trình chỉ thực hiện một lệnh
giai_thua 1, nên tốn O(1), do đó ta có T(0) = C1. Trong trường hợp n>0 hàm phải
gọi đệ quy giai_thua(n-1), việc gọi đệ quy này tốn T(n-1), sau khi có kết quả của việc
gọi đệ quy, hàm phải nhân kết quả đó với n và trả kết quả về cho giai_thua. Thời gian
để thực hiện phép nhân và phép gán là một hằng C2. Vậy ta có phương trình đệ quy để
tính thời gian thực hiện của hàm đệ quy này là: 𝑇(𝑛) = { 𝐶1 𝑛ế𝑢 𝑛 = 0
(𝑇(𝑛 − 1)) + 𝐶2 𝑛ế𝑢 𝑛 > 0
Giải phương trình đệ quy
Hiện nay người ta chưa tìm được phương pháp tổng quát giải phương trình đệ
quy. Dưới đây là phương pháp giải phương trình đệ quy cho một số dạng:
• Phương pháp truy hồi:
Dùng phương pháp truy hồi, nghĩa là tính T(n) từ T(n-1), tính T(n-1) từ T(n-2), …,
và cuối cùng tính T(n0+ 1) từ T(n0) với n0 là giá trị nhỏ nhất, để từ đó tìm ra công thức
tổng quát cho hàm đệ quy.
Ví dụ 1.13: Giải phương trình đệ quy sau: 𝐶1 𝑛ế𝑢 𝑛 = 0 𝑇(𝑛) = {
(𝑇(𝑛 − 1)) + 𝐶2 𝑛ế𝑢 𝑛 > 0 Ta có: T(n) = T(n-1) + C2
T(n) = [T(n-2) + C2] + C2 = T(n-2) + 2C2
T(n) = [T(n-3) + C2] + 2C2 = T(n-3) + 3C2 ……
Tổng quát T(n) = T(n-i) + iC2
Quá trình trên kết thúc khi n - i = 0 hay i = n. Khi đó ta có:
T(n) = T(0) + nC2 = C1 + nC2 = O(n) Ví dụ 1.14: Giải phương trình đệ quy sau: 𝐶1 𝑛ế𝑢 𝑛 = 1 𝑇(𝑛) = { 𝑛
2𝑇 ( ) + 𝐶2𝑛 𝑛ế𝑢 𝑛 > 1 2 Ta có: T(n) = 2T(n/2) + C2n
T(n) = 2[2T(n/4) + C2(n/2)] + C2n = 4T(n/4) + 2C2n
T(n) = 4[2T(n/8) + C2(n/4)] + 2C2n = 8T(n/8) + 3C2n ………………
Tổng quát: T(n) = 2iT(n/2i) + iC2n
Quá trình suy rộng sẽ kết thúc khi n/2i = 1 hay 2i = n, do đó i = logn. Khi đó ta có:
T(n) = nT(1) + lognC2n = C1n + C2nlogn = O(nlogn).
• Phương pháp đoán nghiệm:
Ta đoán một nghiệm f(n) và dùng chứng minh quy nạp để chứng tỏ rằng T(n)≤
Cf(n) với mọi n. Thông thường f(n) là một trong các hàm quen thuộc như logn, n,
nlogn, n2, n3, 2n, n!, nn. Ðôi khi chúng ta chỉ đoán dạng của f(n) trong đó có một vài
tham số chưa xác định (chẳng hạn f(n) = an2 với a chưa xác định) và trong quá trình
chứng minh quy nạp ta sẽ suy diễn ra giá trị thích hợp của các tham số.
Ví dụ 1.15: Giải phương trình đệ quy: 𝐶1 𝑛ế𝑢 𝑛 = 1 𝑇(𝑛) = { 𝑛
2𝑇 ( ) + 𝐶2𝑛 𝑛ế𝑢 𝑛 > 1 2
Giả sử chúng ta đoán f(n) = anlogn. Với n = 1 ta thấy rằng cách đoán như vậy
không được bởi vì anlogn có giá trị 0 không phụ thuộc vào giá trị của a. Vì thế ta thử
tiếp theo f(n) = anlogn + b.
Với n = 1 ta có, T(1) = C1 và f(1) = b, muốn T(1) ≤ f(1) thì b ≥ C1 (*)
Giả sử rằng T(k) ≤ f(k), tức là T(k) ≤ aklogk + b với mọi k < n (giả thiết quy
nạp). Ta phải chứng minh T(n) ≤ anlogn + b với mọi n.
Giả sử n ≥ 2, từ phương trình đã cho ta có T(n) = 2T(n/2) + C2n Áp dụng giả
thiết quy nạp với k=n/2 < n ta có: T(n) = 𝑛𝐶2𝑛 𝑛 𝑛 𝐶2𝑛
T(n) ≤ (anlogn - an + 2b) + C2n
T(n) ≤ (anlogn + b) + [b + (C2 - a)n] . Nếu lấy a ≥ C2 + b (**) ta được
T(n) ≤ (anlogn + b) + [b +(C2 - C2 - b )n ]
T(n) ≤ (anlogn + b) + (1-n) b
T(n) ≤ anlogn + b = f(n). (do b>0 và 1-n<0)