Bài giảng Quy nạp - Toán rời rạc thầy Trần Vĩnh Đức | Trường Đại học Bách khoa Hà Nội

Nguyên lý quy nạp: Mọi con ngựa đều cùng màu. Đặt P(n) là mệnh đề ”Trong mọi tập gồm n con ngựa, các con ngựa đều cùng màu.” Tài liệu được sưu tầm, giúp bạn ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán rời rạc (BKHN)

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

37 trang 2 tháng trước

Tác giả:

Profile Lân Nguyễn
Quy nạp
Trần Vĩnh Đức
HUST
Ngày 24 tháng 7 năm 2018
1 / 37
Tài liệu tham khảo
▶
Eric Lehman, F Thomson Leighton & Albert R Meyer,
Mathematics for Computer Science, 2013 (Miễn phí)
▶
Kenneth H. Rosen, Toán học rời rạc ứng dụng trong tin học
(Bản dịch Tiếng Việt)
2 / 37
Nội dung
Nguyên lý quy nạp
Quy nạp mạnh
Nguyên lý quy nạp
Xét vị từ P(n) trên N. Nếu
▶
P(0) đúng, và
▶
với mọi n ∈ N, (P(n) ⇒ P(n + 1))
cũng đúng,
thì P(n) đúng với mọi n ∈ N.
88
87
86
85
84
83
82
81
80
79
78
77
76
75
74
73
72
71
70
69
68
67
66
65
64
63
62
61
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
4 / 37
Ví dụ
Định lý
Với mọi n ∈ N,
1 + 2 + · · · + n =
n(n + 1)
2
Đặt P(n) là mệnh đề
n
∑
i=1
i =
n(n + 1)
2
5 / 37
Chứng minh.
▶
Bước cơ sở: P(0) đúng.
▶
Bước quy nạp: Ta sẽ chứng minh: với mọi n ≥ 0, mệnh đề
P(n) ⇒ P(n + 1)
đúng.
Thật vậy, giả sử P(n) đúng, với n là một số nguyên bất kỳ. Vì
1 + 2 + · · · + n + (n + 1) = (1 + 2 + · · · + n) + (n + 1)
=
n(n + 1)
2
+ (n + 1)
=
(n + 1)(n + 2)
2
nên P(n + 1) đúng.
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N.
6 / 37
Ví dụ
Chứng minh rằng
1
2
+
1
4
+
1
8
+ · · · +
1
2
n
< 1
với mọi n ≥ 1.
7 / 37
Ví dụ
Định lý
Với mọi n ∈ N, ta có n
3
− n chia hết cho 3.
Đặt P(n) là mệnh đề
”n
3
− n chia hết cho 3.”
8 / 37
Chứng minh.
▶
Bước cơ sở: P(0) đúng vì 0
3
− 0 = 0 chia hết cho 3.
▶
Bước quy nạp: Ta sẽ chứng minh rằng, với mọi n ∈ N, mệnh
đề
P(n) ⇒ P(n + 1)
đúng.
Thật vậy, giả sử P(n) đúng, với n là một số nguyên bất kỳ. Vì
(n + 1)
3
− (n + 1) = n
3
+ 3n
2
+ 3n + 1 − n − 1
= n
3
+ 3n
2
+ 2n
= n
3
− n + 3n
2
+ 3n
= (n
3
− n) + 3(n
2
+ n)
chia hết cho 3 nên P(n + 1) đúng.
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N.
9 / 37
Ví dụ chứng minh sai
Định lý (Sai)
Mọi con ngựa đều cùng màu.
Đặt P(n) là mệnh đề
”Trong mọi tập gồm n con ngựa, các con ngựa đều
cùng màu.”
10 / 37
Đặt P(n) là mệnh đề
”Trong mọi tập gồm n con ngựa, các con ngựa đều
cùng màu.”
Chứng minh Sai.
▶
Bước cơ sở: P(1) đúng vì chỉ có một con ngựa.
▶
Bước quy nạp: Giả sử P(n) đúng để chứng minh P(n + 1)
đúng.
Xét tập gồm n + 1 con ngựa {h
1
, h
2
, · · · , h
n+1
}
▶
Các con h
1
, h
2
, . . . , h
n
có cùng màu (giả thiết quy nạp).
▶
Các con h
2
, h
3
, . . . , h
n+1
có cùng màu (giả thiết quy nạp).
Vậy
màu(h
1
) = màu(h
2
, . . . , h
n
) = màu(h
n+1
).
Vậy các con ngựa {h
1
, h
2
, · · · , h
n+1
} đều cùng màu. Có nghĩa
rằng P(n + 1) đúng.
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N.
11 / 37
Bài tập
1. Chứng minh rằng
n
∑
i=1
i
2
=
n(n + 1)(2n + 1)
6
2. Chứng minh rằng 2
n
> n
2
với n ≥ 5.
3. Chứng minh rằng với mọi n ≥ 1,
F(n − 1)F(n + 1) − F(n
2
) = (−1)
n
với F(i) là số Fibonacci thứ i.
12 / 37
Ví dụ lát gạch
Induction I 31
2.6 Courtyard Tiling
Induction served purely as a proof technique in the preceding examples. But induction
sometimes can serve as a more general reasoning tool.
MIT recently constructed a new computer science building. As the project went further
and further over budget, there were some radical fundraising ideas. One plan was to
install a big courtyard with dimensions 2
n
⇥ 2
n
:
2
n
2
n
One of the central squares would be occupied by a statue of a wealthy potential donor.
Let’s call him “Bill”. (In the special case n =0, the whole courtyard consists of a single
central square; otherwise, there are four central squares.) A complication was that the
building’s unconventional architect, Frank Gehry, insisted that only special L-shaped tiles
be used:
A courtyard meeting these constraints exsists, at least for n =2:
B
For larger values of n, is there a way to tile a 2
n
⇥ 2
n
courtyard with L-shaped tiles and a
statue in the center? Let’s try to prove that this is so.
Theorem 15. For all n 0 there exists a tiling of a 2
n
⇥ 2
n
courtyard with Bill in a central
square.
Hình: Sân
Induction I 31
2.6 Courtyard Tiling
Induction served purely as a proof technique in the preceding examples. But induction
sometimes can serve as a more general reasoning tool.
MIT recently constructed a new computer science building. As the project went further
and further over budget, there were some radical fundraising ideas. One plan was to
install a big courtyard with dimensions 2
n
⇥ 2
n
:
2
n
2
n
One of the central squares would be occupied by a statue of a wealthy potential donor.
Let’s call him “Bill”. (In the special case n =0, the whole courtyard consists of a single
central square; otherwise, there are four central squares.) A complication was that the
building’s unconventional architect, Frank Gehry, insisted that only special L-shaped tiles
be used:
A courtyard meeting these constraints exsists, at least for n =2:
B
For larger values of n, is there a way to tile a 2
n
⇥ 2
n
courtyard with L-shaped tiles and a
statue in the center? Let’s try to prove that this is so.
Theorem 15. For all n 0 there exists a tiling of a 2
n
⇥ 2
n
courtyard with Bill in a central
square.
Hình: Gạch
Induction I 31
2.6 Courtyard Tiling
Induction served purely as a proof technique in the preceding examples. But induction
sometimes can serve as a more general reasoning tool.
MIT recently constructed a new computer science building. As the project went further
and further over budget, there were some radical fundraising ideas. One plan was to
install a big courtyard with dimensions 2
n
⇥ 2
n
:
2
n
2
n
One of the central squares would be occupied by a statue of a wealthy potential donor.
Let’s call him “Bill”. (In the special case n =0, the whole courtyard consists of a single
central square; otherwise, there are four central squares.) A complication was that the
building’s unconventional architect, Frank Gehry, insisted that only special L-shaped tiles
be used:
A courtyard meeting these constraints exsists, at least for n =2:
B
For larger values of n, is there a way to tile a 2
n
⇥ 2
n
courtyard with L-shaped tiles and a
statue in the center? Let’s try to prove that this is so.
Theorem 15. For all n 0 there exists a tiling of a 2
n
⇥ 2
n
courtyard with Bill in a central
square.
Hình: Lát gạch và đặt
tượng Bill
13 / 37
Định lý
Với mọi n, luôn có cách lát gạch một sân 2
n
× 2
n
chỉ để lại một ô
trống ở giữa (để đặt tượng Bill).
14 / 37
Chứng minh thử.
Xét P(n) là mệnh đề
”Có cách lát gạch sân 2
n
× 2
n
để lại một ô ở giữa.”
▶
Bước cơ sở: P(0) đúng vì chỉ có một ô dành cho Bill.
▶
Bước quy nạp: !
15 / 37
Chứng minh.
Xét P(n) là mệnh đề
”Với mỗi vị trí đặt tượng Bill trong sân 2
n
× 2
n
, ta đều
có cách lát gạch kín sân.”
▶
Bước cơ sở: P(0) đúng vì chỉ có
một ô dành cho Bill.
▶
Bước quy nạp: Giả sử P(n) đúng,
ta chứng minh P(n + 1) đúng.
32 Induction I
Proof. (doomed attempt) The proof is by induction. Let P (n) be the proposition that there
exists a tiling of a 2
n
⇥ 2
n
courtyard with Bill in the center.
Base case: P (0) is true because Bill fills the whole courtyard.
Inductive step: Assume that there is a tiling of a 2
n
⇥ 2
n
courtyard with Bill in the center
for some n 0. We must prove that there is a way to tile a 2
n+1
⇥2
n+1
courtyard with Bill
in the center...
Now we’re in trouble! The ability to tile a smaller courtyard with Bill in the center does
not help tile a larger courtyard with Bill in the center. We can not bridge the gap between
P (n) and P (n +1). The usual recipe for finding an inductive proof will not work!
When this happens, your first fallback should be to look for a stronger induction hy-
pothesis; that is, one which implies your previous hypothesis. For example, we could
make P (n) the proposition that for every location of Bill in a 2
n
⇥2
n
courtyard, there exists
a tiling of the remainder.
This advice may sound bizzare: “If you can’t prove something, try to prove something
more grand!” But for induction arguments, this makes sense. In the inductive step, where
you have to prove P (n) ) P (n +1), you’re in better shape because you can assume P (n),
which is now a more general, more useful statement. Let’s see how this plays out in the
case of courtyard tiling.
Proof. (successful attempt) The proof is by induction. Let P (n) be the proposition that for
every location of Bill in a 2
n
⇥ 2
n
courtyard, there exists a tiling of the remainder.
Base case: P (0) is true because Bill fills the whole courtyard.
Inductive step: Asume that P (n) is true for some n 0; that is, for every location of Bill in
a 2
n
⇥2
n
courtyard, there exists a tiling of the remainder. Divide the 2
n+1
⇥2
n+1
courtyard
into four quadrants, each 2
n
⇥ 2
n
. One quadrant contains Bill (B in the diagram below).
Place a temporary Bill (X in the diagram) in each of the three central squares lying outside
this quadrant:
X
XX
B
2
n
2
n
2
n
2
n
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N.
16 / 37
15-Puzzle
“mcs-ftl” — 2010/9/8 — 0:40 — page 59 — #65
3.3. Invariants 59
252624
2221:
23
876
9
432
5
(a)
252624
2221:
23
876
9
432
5
(b)
Figure 3.5 The 15-puzzle in its starting configuration (a) and after the 12-block
is moved into the hole below (b).
262524
2221:
23
876
9
432
5
Figure 3.6 The desired final configuration for the 15-puzzle. Can it be achieved
by only moving one block at a time into an adjacent hole?
get all 15 blocks into their natural order. A picture of the 15-puzzle is shown in
Figure 3.5 along with the configuration after the 12-block is moved into the hole
below. The desired final configuration is shown in Figure 3.6.
The 15-puzzle became very popular in North America and Europe and is still
sold in game and puzzle shops today. Prizes were offered for its solution, but
it is doubtful that they were ever awarded, since it is impossible to get from the
configuration in Figure 3.5(a) to the configuration in Figure 3.6 by only moving
one block at a time into an adjacent hole. The proof of this fact is a little tricky so
we have left it for you to figure out on your own! Instead, we will prove that the
analogous task for the much easier 8-puzzle cannot be performed. Both proofs, of
course, make use of the Invariant Method.
⇒
252624
2221:
23
876
9
432
5
252624
2221:
23
876
9
432
5
262524
2221:
23
876
9
432
5
Chuyển hợp lệ: di chuyển một số sang ô trống cạnh nó.
17 / 37
15-Puzzle
Có thể chuyển từ
“mcs-ftl” — 2010/9/8 — 0:40 — page 59 — #65
3.3. Invariants 59
252624
2221:
23
876
9
432
5
(a)
252624
2221:
23
876
9
432
5
(b)
Figure 3.5 The 15-puzzle in its starting configuration (a) and after the 12-block
is moved into the hole below (b).
262524
2221:
23
876
9
432
5
Figure 3.6 The desired final configuration for the 15-puzzle. Can it be achieved
by only moving one block at a time into an adjacent hole?
get all 15 blocks into their natural order. A picture of the 15-puzzle is shown in
Figure 3.5 along with the configuration after the 12-block is moved into the hole
below. The desired final configuration is shown in Figure 3.6.
The 15-puzzle became very popular in North America and Europe and is still
sold in game and puzzle shops today. Prizes were offered for its solution, but
it is doubtful that they were ever awarded, since it is impossible to get from the
configuration in Figure 3.5(a) to the configuration in Figure 3.6 by only moving
one block at a time into an adjacent hole. The proof of this fact is a little tricky so
we have left it for you to figure out on your own! Instead, we will prove that the
analogous task for the much easier 8-puzzle cannot be performed. Both proofs, of
course, make use of the Invariant Method.
sang
“mcs-ftl” — 2010/9/8 — 0:40 — page 59 — #65
3.3. Invariants 59
252624
2221:
23
876
9
432
5
(a)
252624
2221:
23
876
9
432
5
(b)
Figure 3.5 The 15-puzzle in its starting configuration (a) and after the 12-block
is moved into the hole below (b).
262524
2221:
23
876
9
432
5
Figure 3.6 The desired final configuration for the 15-puzzle. Can it be achieved
by only moving one block at a time into an adjacent hole?
get all 15 blocks into their natural order. A picture of the 15-puzzle is shown in
Figure 3.5 along with the configuration after the 12-block is moved into the hole
below. The desired final configuration is shown in Figure 3.6.
The 15-puzzle became very popular in North America and Europe and is still
sold in game and puzzle shops today. Prizes were offered for its solution, but
it is doubtful that they were ever awarded, since it is impossible to get from the
configuration in Figure 3.5(a) to the configuration in Figure 3.6 by only moving
one block at a time into an adjacent hole. The proof of this fact is a little tricky so
we have left it for you to figure out on your own! Instead, we will prove that the
analogous task for the much easier 8-puzzle cannot be performed. Both proofs, of
course, make use of the Invariant Method.
không?
18 / 37
8-Puzzle
“mcs-ftl” — 2010/9/8 — 0:40 — page 60 — #66
Chapter 3 Induction60
GH
FED
CBA
(a)
G
H
FED
CBA
(b)
G
E
H
FD
CBA
(c)
Figure 3.7 The 8-Puzzle in its initial configuration (a) and after one (b) and
two (c) possible moves.
3.3.4 The 8-Puzzle
In the 8-Puzzle, there are 8 lettered tiles (A–H) and a blank square arranged in a
3 ⇥ 3 grid. Any lettered tile adjacent to the blank square can be slid into the blank.
For example, a sequence of two moves is illustrated in Figure 3.7.
In the initial configuration shown in Figure 3.7(a), the G and H tiles are out of
order. We can find a way of swapping G and H so that they are in the right order,
but then other letters may be out of order. Can you find a sequence of moves that
puts these two letters in correct order, but returns every other tile to its original
position? Some experimentation suggests that the answer is probably “no,” and we
will prove that is so by finding an invariant, namely, a property of the puzzle that is
always maintained, no matter how you move the tiles around. If we can then show
that putting all the tiles in the correct order would violate the invariant, then we can
conclude that the puzzle cannot be solved.
Theorem 3.3.3. No sequence of legal moves transforms the configuration in Fig-
ure 3.7(a) into the configuration in Figure 3.8.
We’ll build up a sequence of observations, stated as lemmas. Once we achieve
a critical mass, we’ll assemble these observations into a complete proof of Theo-
rem 3.3.3.
Define a row move as a move in which a tile slides horizontally and a column
move as one in which the tile slides vertically. Assume that tiles are read top-
to-bottom and left-to-right like English text, that is, the natural order, defined as
follows: So when we say that two tiles are “out of order”, we mean that the larger
letter precedes the smaller letter in this natural order.
Our difficulty is that one pair of tiles (the G and H) is out of order initially. An
immediate observation is that row moves alone are of little value in addressing this
19 / 37
8-Puzzle
Bài tập
Liệu có thể tìm được một dãy chuyển hợp lệ để chuyển từ
“mcs-ftl” — 2010/9/8 — 0:40 — page 60 — #66
Chapter 3 Induction60
GH
FED
CBA
(a)
G
H
FED
CBA
(b)
G
E
H
FD
CBA
(c)
Figure 3.7 The 8-Puzzle in its initial configuration (a) and after one (b) and
two (c) possible moves.
3.3.4 The 8-Puzzle
In the 8-Puzzle, there are 8 lettered tiles (A–H) and a blank square arranged in a
3 ⇥ 3 grid. Any lettered tile adjacent to the blank square can be slid into the blank.
For example, a sequence of two moves is illustrated in Figure 3.7.
In the initial configuration shown in Figure 3.7(a), the G and H tiles are out of
order. We can find a way of swapping G and H so that they are in the right order,
but then other letters may be out of order. Can you find a sequence of moves that
puts these two letters in correct order, but returns every other tile to its original
position? Some experimentation suggests that the answer is probably “no,” and we
will prove that is so by finding an invariant, namely, a property of the puzzle that is
always maintained, no matter how you move the tiles around. If we can then show
that putting all the tiles in the correct order would violate the invariant, then we can
conclude that the puzzle cannot be solved.
Theorem 3.3.3. No sequence of legal moves transforms the configuration in Fig-
ure 3.7(a) into the configuration in Figure 3.8.
We’ll build up a sequence of observations, stated as lemmas. Once we achieve
a critical mass, we’ll assemble these observations into a complete proof of Theo-
rem 3.3.3.
Define a row move as a move in which a tile slides horizontally and a column
move as one in which the tile slides vertically. Assume that tiles are read top-
to-bottom and left-to-right like English text, that is, the natural order, defined as
follows: So when we say that two tiles are “out of order”, we mean that the larger
letter precedes the smaller letter in this natural order.
Our difficulty is that one pair of tiles (the G and H) is out of order initially. An
immediate observation is that row moves alone are of little value in addressing this
sang
“mcs-ftl” — 2010/9/8 — 0:40 — page 61 — #67
3.3. Invariants 61
HG
FED
CBA
Figure 3.8 The desired final configuration of the 8-puzzle.
98
:
765
432
problem:
Lemma 3.3.4. A row move does not change the order of the tiles.
Proof. A row move moves a tile from cell i to cell i C 1 or vice versa. This tile
does not change its order with respect to any other tile. Since no other tile moves,
there is no change in the order of any of the other pairs of tiles. ⌅
Let’s turn to column moves. This is the more interesting case, since here the
order can change. For example, the column move in Figure 3.9 changes the relative
order of the pairs .G; H / and .G; E/.
Lemma 3.3.5. A column move changes the relative order of exactly two pairs of
tiles.
Proof. Sliding a tile down moves it after the next two tiles in the order. Sliding a
tile up moves it before the previous two tiles in the order. Either way, the relative
order changes between the moved tile and each of the two tiles it crosses. The
relative order between any other pair of tiles does not change. ⌅
These observations suggest that there are limitations on how tiles can be swapped.
Some such limitation may lead to the invariant we need. In order to reason about
swaps more precisely, let’s define a term referring to a pair of items that are out of
order:
20 / 37
| 1/37
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Quy nạp Trần Vĩnh Đức HUST Ngày 24 tháng 7 năm 2018 1 / 37 Tài liệu tham khảo
▶ Eric Lehman, F Thomson Leighton & Albert R Meyer,
Mathematics for Computer Science, 2013 (Miễn phí)
▶ Kenneth H. Rosen, Toán học rời rạc ứng dụng trong tin học (Bản dịch Tiếng Việt) 2 / 37 Nội dung Nguyên lý quy nạp Quy nạp mạnh Nguyên lý quy nạp 87 8685 8483 82 81 80 79 78 88 77 76 75 74 73 72 71 70 69 68 67 666564636261605958 57 56 55 54 53 52 51 50 49 48 47 46 45 44 4342414039383736353433 32 Xét vị từ P 31 (n) trên N. Nếu 30 29 28 27 ▶ 26 P 25 (0) đúng, và 24 23 22 21 ▶ 20
với mọi n ∈ N, (P(n) ⇒ P(n + 1)) 19181716 cũng đúng, 15141312 11
thì P(n) đúng với mọi n ∈ N. 10 9 8 7 6 5 4 3 2 1 4 / 37 Ví dụ Định lý Với mọi n ∈ N, n(n + 1)
1 + 2 + · · · + n = 2
Đặt P(n) là mệnh đề n ∑ n(n + 1) i = 2 i=1 5 / 37 Chứng minh.
▶ Bước cơ sở: P(0) đúng.
▶ Bước quy nạp: Ta sẽ chứng minh: với mọi n ≥ 0, mệnh đề
P(n) ⇒ P(n + 1) đúng.
Thật vậy, giả sử P(n) đúng, với n là một số nguyên bất kỳ. Vì
1 + 2 + · · · + n + (n + 1) = (1 + 2 + · · · + n) + (n + 1) n(n + 1) = + (n + 1) 2 (n + 1)(n + 2) = 2
nên P(n + 1) đúng.
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N. 6 / 37 Ví dụ Chứng minh rằng 1 1 1 1 + + + · · · + < 1 2 4 8 2n với mọi n ≥ 1. 7 / 37 Ví dụ Định lý
Với mọi n ∈ N, ta có n3 − n chia hết cho 3.
Đặt P(n) là mệnh đề
”n3 − n chia hết cho 3.” 8 / 37 Chứng minh.
▶ Bước cơ sở: P(0) đúng vì 03 − 0 = 0 chia hết cho 3.
▶ Bước quy nạp: Ta sẽ chứng minh rằng, với mọi n ∈ N, mệnh đề
P(n) ⇒ P(n + 1) đúng.
Thật vậy, giả sử P(n) đúng, với n là một số nguyên bất kỳ. Vì
(n + 1)3 − (n + 1) = n3 + 3n2 + 3n + 1 − n − 1
= n3 + 3n2 + 2n
= n3 − n + 3n2 + 3n
= (n3 − n) + 3(n2 + n)
chia hết cho 3 nên P(n + 1) đúng.
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N. 9 / 37 Ví dụ chứng minh sai Định lý (Sai)
Mọi con ngựa đều cùng màu.
Đặt P(n) là mệnh đề
”Trong mọi tập gồm n con ngựa, các con ngựa đều cùng màu.” 10 / 37
Đặt P(n) là mệnh đề
”Trong mọi tập gồm n con ngựa, các con ngựa đều cùng màu.” Chứng minh Sai.
▶ Bước cơ sở: P(1) đúng vì chỉ có một con ngựa.
▶ Bước quy nạp: Giả sử P(n) đúng để chứng minh P(n + 1) đúng.
Xét tập gồm n + 1 con ngựa {h1, h2, · · · , hn+1}
▶ Các con h1, h2, . . . , hn có cùng màu (giả thiết quy nạp).
▶ Các con h2, h3, . . . , hn+1 có cùng màu (giả thiết quy nạp). Vậy
màu(h1) = màu(h2, . . . , hn) = màu(hn+1).
Vậy các con ngựa {h1, h2, · · · , hn+1} đều cùng màu. Có nghĩa
rằng P(n + 1) đúng.
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N. 11 / 37 Bài tập 1. Chứng minh rằng n ∑
n(n + 1)(2n + 1) i2 = 6 i=1
2. Chứng minh rằng 2n > n2 với n ≥ 5.
3. Chứng minh rằng với mọi n ≥ 1,
F(n − 1)F(n + 1) − F(n2) = (−1)n
với F(i) là số Fibonacci thứ i. 12 / 37 Induction I 31 2.6 Courtyard Tiling
Induction served purely as a proof technique in the preceding examples. But induction
sometimes can serve as a more general reasoning tool.
MIT recently constructed a new computer science building. As the project went further
and further over budget, there were some Induction I
radical fundraising ideas. One plan 31 was to
install a big courtyard with dimensions 2.6 Courtyard Tiling 2n ⇥ 2n:
Induction served purely as a proof technique in the preceding examples. But induction
sometimes can serve as a more general reasoning tool.
MIT recently constructed a new computer science building. As the project went further
and further over budget, there were some radical fundraising ideas. One plan was to
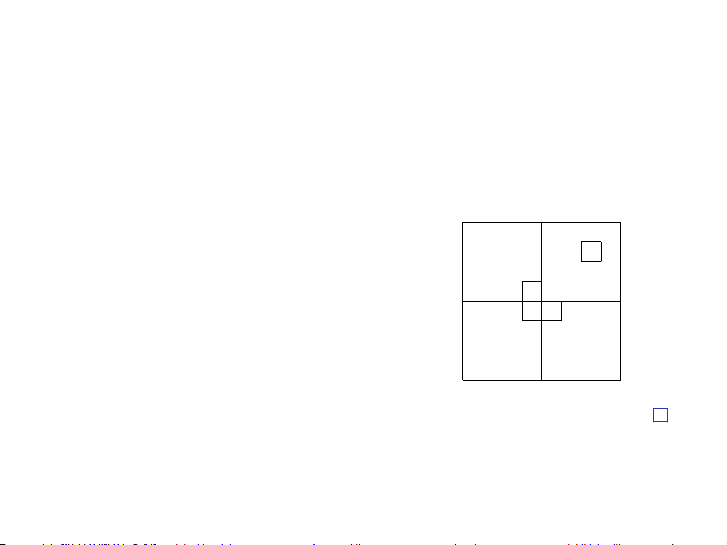
install a big courtyard with dimensions 2n ⇥ 2n: 2n 2n 2n 2n
One of the central squares would be occupied by a statue of a wealthy potential donor.
Let’s call him “Bill”. (In the special case n = 0, the whole courtyard consists of a single Induction I
central square; otherwise, there are four 31
central squares.) A complication was that the
building’s unconventional architect, Frank Gehry, insisted that only special L-shaped tiles 2.6 One of Courtyard the T central iling
squares would be occupied by a statue of a wealthy potential donor. be used:
Let’s call him “Bill”. (In the special case n = 0, the whole courtyard consists of a single
Induction served purely as a proof technique in the preceding examples. But induction
central square; otherwise, there are four central squares.) A complication was that the sometimes can serve as a Ví more dụ lát general r gạch easoning tool. MIT recently building’s constructed a new computer
unconventional ar sciencebuilding. chitect, As Frank theproject Gehry went , further
insisted that only special L-shaped tiles
and further over budget, there were some radical fundraising ideas. One plan was to be used:
install a big courtyard with dimensions
A courtyard meeting these constraints exsists, at least for 2n ⇥ 2n: n = 2: B 2n 2n
For larger values of n, is there a way to Hình: tile Lát a 2n ⇥ gạch 2n và courtyar đặt d with L-shaped tiles and a Hình: Sân Hình: Gạch
statue in the center? Let’s try to prove that tượng this Bill is so.
One of the central squares would be occupied by a statue of a wealthy potential donor. A Let’s call him courtyard“Bill”. (In the meetingspecial case these constraints Theorem exsists, 15. For all n at 0 least there exists for a n tiling of = a 2n 2:
n = 0, the whole courtyard consists of a single
⇥ 2n courtyard with Bill in a central
central square; otherwise, there are four central squar
square.es.) A complication was that the
building’s unconventional architect, Frank Gehry, insisted that only special L-shaped tiles be used: 13 / 37 B
A courtyard meeting these constraints exsists, at least for n = 2: B
For larger values of n, is there a way to tile a 2n ⇥ 2n courtyard with L-shaped tiles and a
statue in the center? Let’s try to prove that this is so.
For larger values of n, is there a way to tile a 2n ⇥ 2n courtyard with L-shaped tiles and a
statue in the center? Let’s try to prove that this is so. Theorem 15. For all n
0 there exists a tiling of a 2n ⇥ 2n courtyard with Bill in a central Theorem 15. For all n
0 there exists a tiling of a 2n ⇥ 2n courtyard with Bill in a central square. square. Định lý
Với mọi n, luôn có cách lát gạch một sân 2n × 2n chỉ để lại một ô
trống ở giữa (để đặt tượng Bill). 14 / 37 Chứng minh thử.
Xét P(n) là mệnh đề
”Có cách lát gạch sân 2n × 2n để lại một ô ở giữa.”
▶ Bước cơ sở: P(0) đúng vì chỉ có một ô dành cho Bill. ▶ Bước quy nạp: ! 15 / 37 32 Induction I
Proof. (doomed attempt) The proof is by induction. Let P (n) be the proposition that there
exists a tiling of a 2n ⇥ 2n courtyard with Bill in the center.
Base case: P (0) is true because Bill fills the whole courtyard.
Inductive step: Assume that there is a tiling of a 2n ⇥ 2n courtyard with Bill in the center for some n
0. We must prove that there is a way to tile a 2n+1 ⇥ 2n+1 courtyard with Bill in the center...
Now we’re in trouble! The ability to tile a smaller courtyard with Bill in the center does
not help tile a larger courtyard with Bill in the center. We can not bridge the gap between
P (n) and P (n + 1). The usual recipe for finding an inductive proof will not work!
When this happens, your first fallback should be to look for a stronger induction hy-
pothesis; that is, one which implies your previous hypothesis. For example, we could
make P (n) the proposition that for every location of Bill in a 2n ⇥2n courtyard, there exists a tiling of the remainder.
This advice may sound bizzare: “If you can’t prove something, try to prove something
more grand!” But for induction arguments, this makes sense. In the inductive step, where
you have to prove P (n) ) P (n + 1), you’re in better shape because you can assume P (n),
which is now a more general, more useful statement. Let’s see how this plays out in the case of courtyard tiling.
Proof. (successful attempt) The proof is by induction. Let P (n) be the proposition that for
every location of Bill in a 2n ⇥ 2n courtyard, there exists a tiling of the remainder. Chứng minh.
Base case: P (0) is true because Bill fills the whole courtyard. Xét P
Inductive step: Asume that P (n) is true for some n
0; that is, for every location of Bill in
(n) là mệnh đềa2n⇥2n courtyard, there exists a tiling of the remainder. Divide the 2n+1⇥2n+1 courtyard into four quadrants, each
”Với mỗi vị trí đặt tượng Bill trong
2n ⇥ 2n. One quadrant contains Bill (B in the diagram below). sân 2n
Place a temporary Bill (X in the diagram) × 2n, ta đều
in each of the three central squares lying outside
có cách lát gạch kín this sân.” quadrant: ▶ Bước cơ sở: P B (0) đúng vì chỉ có 2n một ô dành cho Bill. X ▶ X X
Bước quy nạp: Giả sử P(n) đúng,
ta chứng minh P(n + 1) đúng. 2n 2n 2n
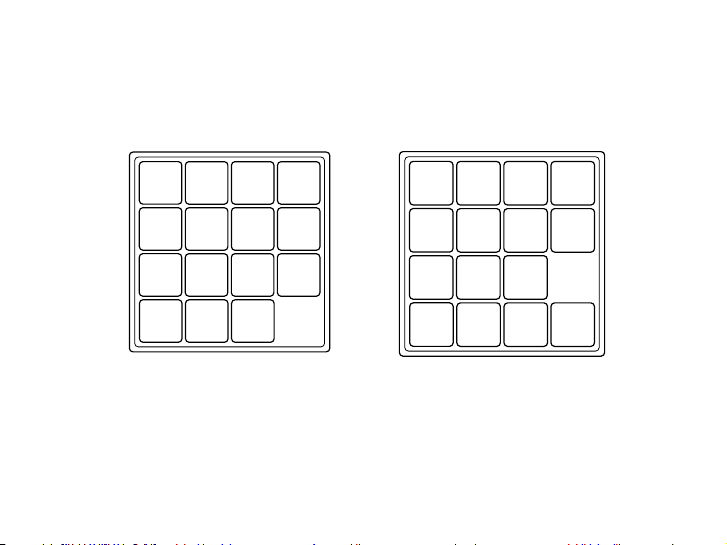
Theo quy nạp ta có P(n) đúng với mọi số n ∈ N. 16 / 37 15-Puzzle“mcs-ftl” “mcs-ftl” — — 2010/9/8 2010/9/8 — — 0:40 — page 59 — #65 3.3. 3.3. In In variants variants 59 59 2 2 3 3 4 4 5 5 2 3 4 5 6 6 7 7 8 8 9 9 6 7 8 9 ⇒ : : 21 21 22 22 23 23 : 21 22 24 26 25 24 26 25 23 24 26 25 24 26 25 23 (a) (b) (a) (b) Figur Chuy e ển 3.5 hợp The lệ: 15-puzzle di chuy in ển its starting một số configuration sang ô (a) trống and after cạnh the nó. 12-block
Figure 3.5 The 15-puzzle in its starting configuration (a) and after the 12-block
is moved into the hole below (b).
is moved into the hole below (b). 2 3 4 5 2 3 4 5 6 7 8 9 6 7 8 9 17 / 37 : 21 22 23 : 21 22 23 24 25 26 24 25 26
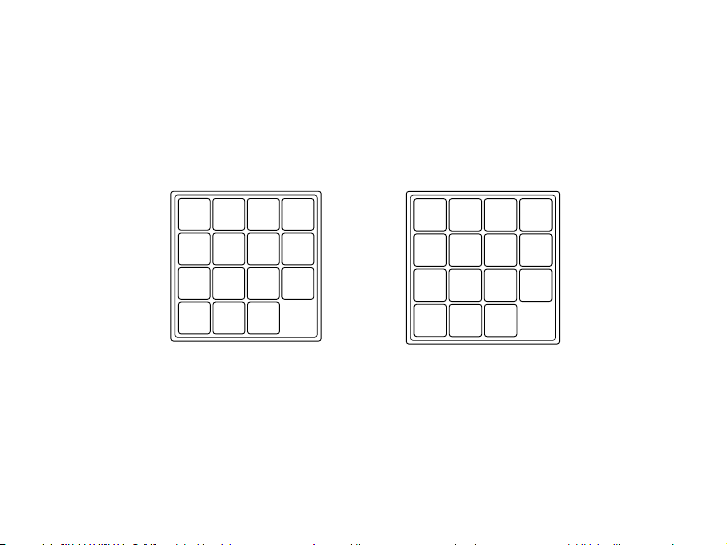
Figure 3.6 The desired final configuration for the 15-puzzle. Can it be achieved by only Figure mo 3.6 ving Theone block desired at a final time into an adjacent configuration for the hole? 15-puzzle. Can it be achieved
by only moving one block at a time into an adjacent hole?
get all 15 blocks into their natural order. A picture of the 15-puzzle is shown in Figure get all 3.5 15 along blocks with into the theirconfiguration natural orderafter . A the 12-block picture of the is moved into 15-puzzle is the sho hole wn in below Figure . The 3.5 desired along final with configuration the is configuration shown after in the Figure 3.6
12-block .is moved into the hole The below. 15-puzzle The became desired final very popular configuration is in North shown America in Figure and 3.6. Europe and is still sold Thein game and 15-puzzle puzzle became shops very today. popular Prizes in were North offered America for and its solution, Europe and is but still it is sold doubtful in game that and they were puzzle ev shopser awarded, today. since Prizes it is were impossible offered for to its get from solution, the but configuration it is doubtful in thatFigure they 3.5(a) were e to ver the aw configura arded, tion since itinis Figure 3.6 by impossible to only get moving from the one block at configuration a time in into Figure an 3.5 adjacent (a) to hole. the The proof configuration of in this fact Figure is 3.6 a little by trick only y mo so ving we one have block left at ait for time you into to anfigure out adjacent on your hole. o The wn! Instead, proof of this we factwill is a prove little that trick the y so analogous we have task left it for for the you much to easier figure out8-puzzle on your cannot own! be performed. Instead, we Both will pro proofs, ve that of the course, mak analogous e use task forof the the Invariant much Method.
easier 8-puzzle cannot be performed. Both proofs, of
course, make use of the Invariant Method.
“mcs-ftl” — 2010/9/8 — 0:40 — page 59 — #65 3.3. Invariants 59 2 3 4 5 2 3 4 5 15-Puzzle 6 7 8 9 6 7 8 9 : 21 22 23 : 21 22
“mcs-ftl” — 2010/9/8 — 0:40 24 — page 26 59 25 — #65 24 26 25 23 (a) (b) Có thể chuy 3.3. Inển từ variants 59
Figure 3.5 The 15-puzzle in its starting configuration (a) and after the 12-block
is moved into the hole below (b). 2 3 4 5 2 3 2 4 3 5 4 5 6 7 8 9 6 7 6 8 7 9 8 9 sang : 21 22 23 : 21 : 22 21 22 23 24 26 25 24 26 25 23 24 25 26 (a) (b) không? Figure 3.5
Figure 3.6 The desired final configuration for the 15-puzzle. Can it be achieved
The 15-puzzle in its starting configuration (a) and after the 12-block
by only moving one block at a time into an adjacent hole?
is moved into the hole below (b).
get all 15 blocks into their natural order. A picture of the 15-puzzle is shown in 2 3 4 5
Figure 3.5 along with the configuration after the 12-block is moved into the hole
below. The desired final configuration is shown in Figure 3.6. 6 The 7 15-puzzle 8 9
became very popular in North America and Europe and is still
sold in game and puzzle shops today. Prizes were offered for its solution, but it is : 21 doubtful 22 that they 23
were ever awarded, since it is impossible to get from the
configuration in Figure 3.5(a) to the configuration in Figure 3.6 by only moving one 18 / 37 24 block 25 at a 26
time into an adjacent hole. The proof of this fact is a little tricky so
we have left it for you to figure out on your own! Instead, we will prove that the
analogous task for the much easier 8-puzzle cannot be performed. Both proofs, of
Figure 3.6 The desired final configuration course, make use for of the the In15-puzzle. variant Can Method. it be achieved
by only moving one block at a time into an adjacent hole?
get all 15 blocks into their natural order. A picture of the 15-puzzle is shown in
Figure 3.5 along with the configuration after the 12-block is moved into the hole
below. The desired final configuration is shown in Figure 3.6.
The 15-puzzle became very popular in North America and Europe and is still
sold in game and puzzle shops today. Prizes were offered for its solution, but
it is doubtful that they were ever awarded, since it is impossible to get from the
configuration in Figure 3.5(a) to the configuration in Figure 3.6 by only moving
one block at a time into an adjacent hole. The proof of this fact is a little tricky so
we have left it for you to figure out on your own! Instead, we will prove that the
analogous task for the much easier 8-puzzle cannot be performed. Both proofs, of
course, make use of the Invariant Method. 8-Puzzle
“mcs-ftl” — 2010/9/8 — 0:40 — page 60 — #66 60 Chapter 3 Induction A B C A B C A B C D E F D E F D F H G H G H E G (a) (b) (c)
Figure 3.7 The 8-Puzzle in its initial configuration (a) and after one (b) and two (c) possible moves. 3.3.4 The 8-Puzzle
In the 8-Puzzle, there are 8 lettered tiles (A–H) and a blank square arranged in a
3 ⇥ 3 grid. Any lettered tile adjacent to the blank square can be slid into the blank.
For example, a sequence of two moves is illustrated in Figure 3.7. 19 / 37
In the initial configuration shown in Figure 3.7(a), the G and H tiles are out of
order. We can find a way of swapping G and H so that they are in the right order,
but then other letters may be out of order. Can you find a sequence of moves that
puts these two letters in correct order, but returns every other tile to its original
position? Some experimentation suggests that the answer is probably “no,” and we
will prove that is so by finding an invariant, namely, a property of the puzzle that is
always maintained, no matter how you move the tiles around. If we can then show
that putting all the tiles in the correct order would violate the invariant, then we can
conclude that the puzzle cannot be solved.
Theorem 3.3.3. No sequence of legal moves transforms the configuration in Fig-
ure 3.7(a) into the configuration in Figure 3.8.
We’ll build up a sequence of observations, stated as lemmas. Once we achieve
a critical mass, we’ll assemble these observations into a complete proof of Theo- rem 3.3.3.
Define a row move as a move in which a tile slides horizontally and a column
move as one in which the tile slides vertically. Assume that tiles are read top-
to-bottom and left-to-right like English text, that is, the natural order, defined as
follows: So when we say that two tiles are “out of order”, we mean that the larger
letter precedes the smaller letter in this natural order.
Our difficulty is that one pair of tiles (the G and H) is out of order initially. An
immediate observation is that row moves alone are of little value in addressing this 8-Puzzle
“mcs-ftl” — 2010/9/8 — 0:40 — page 60 — #66
“mcs-ftl” — 2010/9/8 — 0:40 — page 61 — #67 Bài tập 60 Chapter 3 Induction Liệu có thể tìm đượ 3.3. c In một
variants dãy chuyển hợp lệ để chuyển từ 61 A B C A B A C B A C B C D E F D sang E D F E D F F H G H G G H H E G (a) (b) (c)
Figure 3.8 The desired final configuration of the 8-puzzle.
Figure 3.7 The 8-Puzzle in its initial configuration (a) and after one (b) and two (c) possible moves. 2 3 4 3.3.4 The 8-Puzzle 5 6 7
In the 8-Puzzle, there are 8 lettered tiles (A–H) and a blank square arranged in a 20 / 37
3 ⇥ 3 grid. Any lettered tile adjacent to the blank square can be slid into the blank.
For example, a sequence of two moves is illustrated 8 in 9 Figure : 3.7.
In the initial configuration shown in Figure 3.7(a), the G and H tiles are out of
order. We can find a way of swapping G and H so that they are in the right order, but then other letters
problem: may be out of order. Can you find a sequence of moves that
puts these two letters in correct order, but returns every other tile to its original
Lemma 3.3.4. A row move does not change the order of the tiles.
position? Some experimentation suggests that the answer is probably “no,” and we will prove that Pr is oof. so A by ro finding w move an in movvariant, es a tilenamely from , a cell property i to cell of i the C 1 puzzle or that vice v is ersa. This tile always maintained, does not no matter change its how you order mo with ve the respect tiles to around. any other If we tile. can then Since no show other tile moves, that putting all the there is tiles no in the change correct in the order order w of ould any violate of the the other invar pairs iant, of then tiles. we can ⌅
conclude that the puzzle cannot be solved.
Let’s turn to column moves. This is the more interesting case, since here the Theorem 3.3.3. order No can sequence change. F of or le e gal mo xample, ves the transforms column mo the ve configur in Figure ation 3.9 in Fig- changes the relative ure 3.7(a) into the order of configur the ation pairs .G; in H F / igur and e 3.8 .G; . E/. We’ll build up a Lemma sequence 3.3.5. A of observ column ations move c , stated hanges as the lemmas. relative Once order w of ee achie xactlyvetwo pairs of a critical mass,
tiles. we’ll assemble these observations into a complete proof of Theo-
rem 3.3.3.Proof. Sliding a tile down moves it after the next two tiles in the order. Sliding a
Define a row move as a move in which a tile slides horizontally and a column
tile up moves it before the previous two tiles in the order. Either way, the relative
move as one in which the tile slides vertically. Assume that tiles are read top-
order changes between the moved tile and each of the two tiles it crosses. The
to-bottom and left-to-right like English text, that is, the natural order, defined as
relative order between any other pair of tiles does not change. ⌅
follows: So when we say that two tiles are “out of order”, we mean that the larger letter precedes the smaller These observ letter ations in this natural suggest that order there .
are limitations on how tiles can be swapped. Our difficulty Some is that such one pair limitation of tiles may (the lead to G and the in H) v is out ariant of we order need. initially In order . An to reason about immediate observ swaps ation more is that ro preciselyw , mo let’s ves alone define a are termof little value referring to ain addressing pair of items this that are out of order: