





Preview text:
Thuật toán tham lam Trần Vĩnh Đức HUST Ngày 1 tháng 9 năm 2019 1 / 64 Tài liệu tham khảo
I S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani,
Algorithms, July 18, 2006. 2 / 64 Nội dung Cây bao trùm nhỏ nhất Mã hóa Huffman Công thức Horn Phủ các tập P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Chapter 5
Greedy algorithms
A game like chess can be won only by thinking ahead: a player who is focused
entirely on immediate advantage is easy to defeat. But in many other games, such
as Scrabble, it is possible to do quite well by simply making whichever move seems
best at the moment and not worrying too much about future consequences.
This sort of myopic behavior is easy and convenient, making it an attractive algorith-
mic strategy. Greedy algorithms build up a solution piece by piece, always choosing
the next piece that offers the most obvious and immediate benefit. Although such
an approach can be disastrous for some computational tasks, there are many for
which it is optimal. Our first example is that of minimum spanning trees. 5.1 Minimum spanning trees
Suppose you are asked to network a collection of computers by linking selected
pairs of them. This translates into a graph problem in which nodes are computers,
undirected edges are potential links, and the goal is to pick enough of these edges that the Bài toán
nodes are connected. But this is not all; each link also has a maintenance
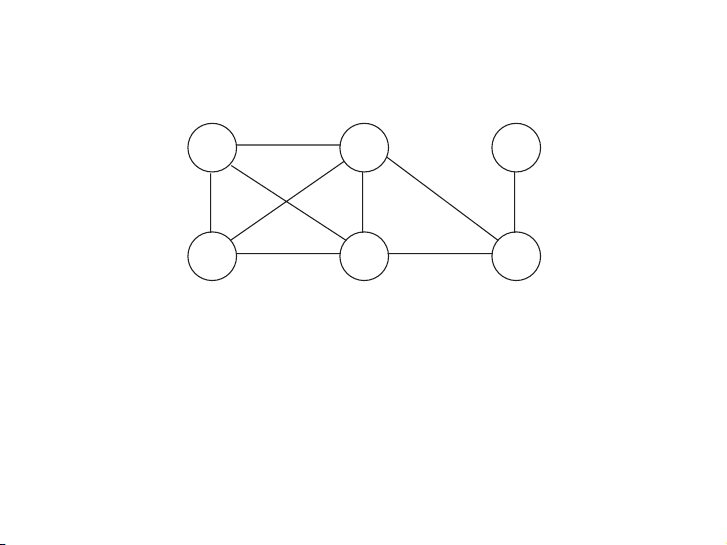
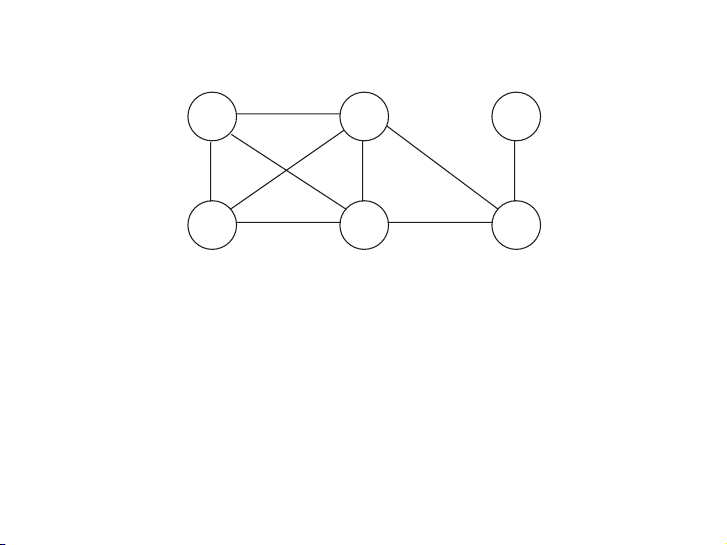
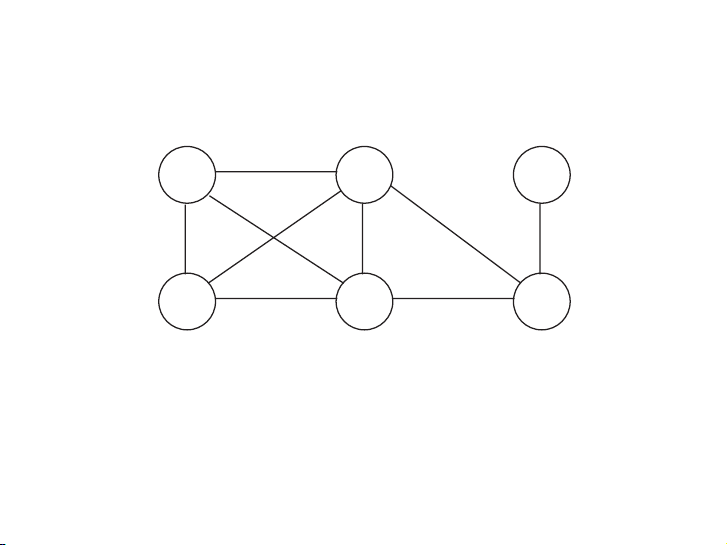
cost, reflected in that edge’s weight. What is the cheapest possible network? A 1 C E 4 3 4 4 2 5 B 4 D F 6
One immediate observation is that the optimal set of edges cannot contain a cycle,
I Bạn cần xây dựng mạng máy tính bằng cách kết nối từng cặp
because removing an edge from this cycle would reduce the cost without compro- máy. mising connectivity:
I Cần chọn một số kết nối để mạng liên thông; Property 1 Removing I nhưng a cycle không edge phải tất cannot cả các disconnect
cặp: Mỗi kết nốia gr tốn aph. một chi phí (tiền bảo trì). So the solution must I be Mạng vớiconnected chi phí nhỏ and nhất ac là yclic: gì?
undirected graphs of this kind are
called trees. The particular tree we want is the one with minimum total 4 / 64 weight,
known as the minimum spanning tree. Here is its formal definition. 127 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Chapter 5
Greedy algorithms
A game like chess can be won only by thinking ahead: a player who is focused
entirely on immediate advantage is easy to defeat. But in many other games, such
as Scrabble, it is possible to do quite well by simply making whichever move seems
best at the moment and not worrying too much about future consequences.
This sort of myopic behavior is easy and convenient, making it an attractive algorith-
mic strategy. Greedy algorithms build up a solution piece by piece, always choosing
the next piece that offers the most obvious and immediate benefit. Although such
an approach can be disastrous for some computational tasks, there are many for
which it is optimal. Our first example is that of minimum spanning trees. 5.1 Minimum spanning trees
Suppose you are asked to network a collection of computers by linking selected
pairs of them. This translates into a graph problem in which nodes are computers,
undirected edges are potential links, and the goal is to pick enough of these edges
that the nodes are connected. But this is not all; each link also has a maintenance
cost, reflected in that edge’s weight. What is the cheapest possible network? A 1 C E 4 3 4 4 2 5 B 4 D F 6
One immediate observation is that the optimal set of edges cannot contain a cycle, Tính chất
because removing an edge from this cycle would reduce the cost without compro-
Xóa một cạnh trên chu trình không làm mất tính liên thông của đồ mising connectivity: thị. Property 1
Removing a cycle edge cannot disconnect a graph.
Vậy, mạng với chi phí nhỏ nhất phải là một cây.
So the solution must be connected and acyclic: undirected graphs of this kind are
called trees. The particular tree we want is the one with minimum total weight,
known as the minimum spanning tree. Here is its formal definition. 5/64 127
Bài toán Cây bao trùm nhỏ nhất (Minimal Spaning Tree)
I Input: Đồ thị vô hướng G = (V, E); mỗi cạnh có trọng số we.
I Output: Một cây T = (V, E′) với E′ ⊆ E, với tổng trọng số ∑ weight(T) = we e∈E′ là nhỏ nhất. 6 / 64 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Chapter 5
Greedy algorithms
A game like chess can be won only by thinking ahead: a player who is focused
entirely on immediate advantage is easy to defeat. But in many other games, such
as Scrabble, it is possible to do quite well by simply making whichever move seems
best at the moment and not worrying too much about future consequences. P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
This sort of myopic behavior is easy and conv das23402 enient, Ch05 making GTBL02 it an attractiv 0-Dasgupta-v10 e algorith- August 10, 2006 22:46
mic strategy. Greedy algorithms build up a solution piece by piece, always choosing
the next piece that offers the most obvious and immediate benefit. Although such
an approach can be disastrous for some computational tasks, there are many for
which it is optimal. Our first example is that of minimum spanning trees. 128
5.1 Minimum spanning trees
5.1 Minimum spanning trees
Tìm cây bao trùm Input: An undirected graph G = (V, E); edge weights we.
Suppose you are asked to network a collection of computers by linking selected
pairs of them. This translates into a graph problem in Output: Awhich tree T nodes = (V, ar E ′ e ), computer
with E ′ ⊆ s,E, that minimizes !
undirected edges are potential links, and the goal is to pick enough of these weight(edges T) = we.
that the nodes are connected. But this is not all; each link also has a maintenancee∈E′
cost, reflected in that edge’s weight. What is In the the cheapest preceding e possible xample, netw the ork?
minimum spanning tree has a cost of 16: A 1 1 C E A C E 4 4 3 4 4 2 5 2 5 B B 4 D F 4 D F 6
One immediate observation is that the optimal Howe set ver, of edges this is cannot not the contain only a optimal cycle,
solution. Can you spot another?
because removing an edge from this cycle would reduce the cost without compro- mising connectivity: 5.1.1 A greedy approach
Đây có phải lời giải tối ưu không?
Kruskal’s minimum spanning tree algorithm starts with the empty graph and then Property 1
Removing a cycle edge cannot disconnect selects edges a fr gr om aph.
E according to the following rule.
So the solution must be connected and acyclic: R undirected epeatedly add graphs the nextof this lightestkind edge are
that doesn’t produce a cycle.
called trees. The particular tree we want is In the other one wor with ds, it minimum constructs total the tr w ee eight,
edge by edge and, apart from taking care to
known as the minimum spanning tree. Her a e v is oid its cy formal cles, definition.
simply picks whichever edge is cheapest at the moment. This is a greedy
algorithm: every decision it makes is the one with the most obvious immediate advantage. 127 7 / 64
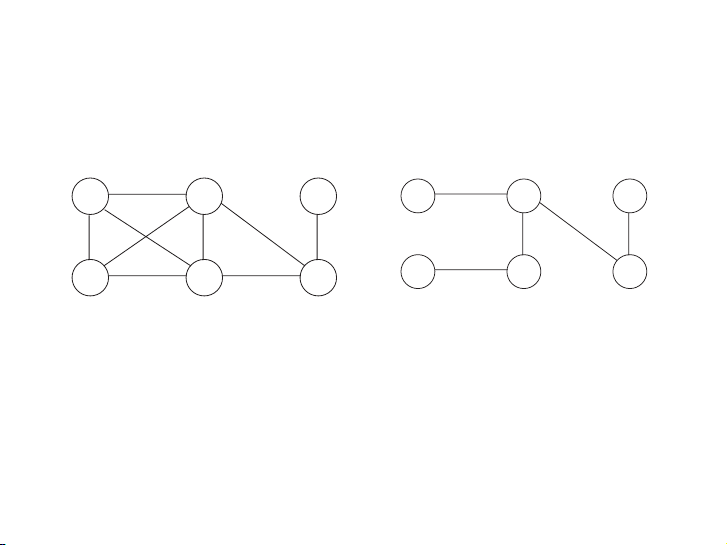
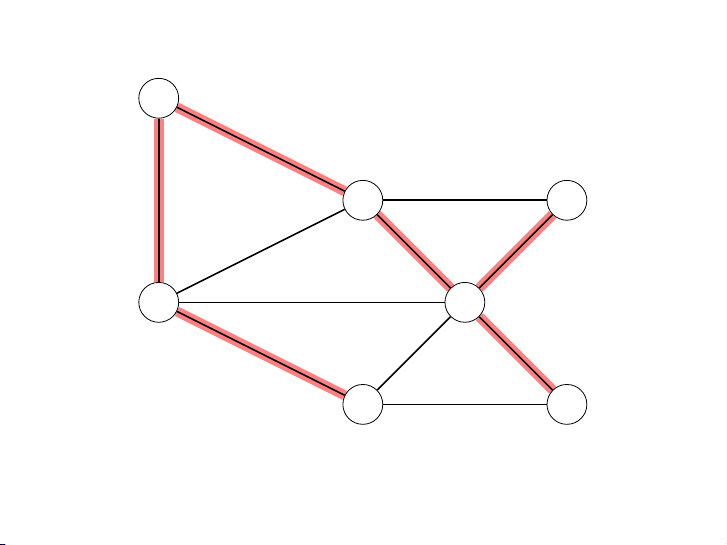
Figure 5.1 shows an example. We start with an empty graph and then attempt to
add edges in increasing order of weight (ties are broken arbitrarily):
B − C , C − D, B − D, C − F , D − F , E − F , A − D, A − B, C − E , A − C .
The first two succeed, but the third, B − D, would produce a cycle if added. So
we ignore it and move along. The final result is a tree with cost 14, the minimum possible.
Figure 5.1 The minimum spanning tree found by Kruskal’s algorithm. A 6 5 C E A C E 4 1 5 2 3 4 B 2 D F D F 4 B P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Chapter 5
Greedy algorithms
A game like chess can be won only by thinking ahead: a player who is focused
entirely on immediate advantage is easy to defeat. But in many other games, such
as Scrabble, it is possible to do quite well by simply making whichever move seems
best at the moment and not worrying too much about future consequences.
This sort of myopic behavior is easy and convenient, making it an attractive algorith-
mic strategy. Greedy algorithms build up a solution piece by piece, always choosing
the next piece that offers the most obvious and immediate benefit. Although such
an approach can be disastrous for some computational tasks, there are many for
which it is optimal. Our first example is that of minimum spanning trees. 5.1 Minimum spanning trees
Suppose you are asked to network a collection of computers by linking selected
pairs of them. This translates into a graph problem in which nodes are computers,
undirected edges are potential links, and the goal is to pick enough of these edges Thuật toán Kruskal
that the nodes are connected. But this is not all; each link also has a maintenance
cost, reflected in that edge’s weight. What is the cheapest possible network? A 1 C E 4 3 4 4 2 5 B 4 D F 6
One immediate observation is that the optimal set of edges cannot contain a cycle, because removing an Bắt edge đầu với fr đồ om thị this rỗng và cycle chọn w cạnh ould từ E reduce theo quy tắc the sau. cost without compro- mising connectivity:
Lặp lại việc thêm cạnh nhỏ nhất mà không tạo thành chu trình. Property 1
Removing a cycle edge cannot disconnect a graph. 8/64
So the solution must be connected and acyclic: undirected graphs of this kind are
called trees. The particular tree we want is the one with minimum total weight,
known as the minimum spanning tree. Here is its formal definition. 127
Ví dụ: Thuật toán Kruskal 1 7 8 5 2 3 7 9 5 15 4 5 6 9 8 11 6 7 Hình: Nguồn: tikz examples 9 / 64 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Nhát cắt 130
5.1 Minimum spanning trees Định nghĩa
Figure 5.2 T ∪ {e}. The addition of e (dotted) to T (solid lines) produces a cycle.Xét đồ This cythị cle G = must (V, E). containMột at nhát least cắt one là một other cách edge, chia shown tập here đỉnh as e′, across the thành cut (S, Vhai − nhóm: S). S và V − S. S V − S e e
Hình: Nhát cắt và các cạnh nối giữa hai phân hoạch.
The correctness of Kruskal’s method follows from a certain cut property, which
is general enough to also justify a whole slew of other minimum spanning tree algorithms. 10 / 64 5.1.2 The cut property
Say that in the process of building a minimum spanning tree (MST), we have already
chosen some edges and are so far on the right track. Which edge should we add
next? The following lemma gives us a lot of flexibility in our choice. Cut property
Suppose edges X are part of a minimum spanning tree of G = (V, E ).
Pick any subset of nodes S for which X does not cross between S and V − S, and let
e be the lightest edge across this partition. Then X ∪ {e} is part of some MST.
A cut is any partition of the vertices into two groups, S and V − S. What this property
says is that it is always safe to add the lightest edge across any cut (that is, between
a vertex in S and one in V − S), provided X has no edges across the cut.
Let’s see why this holds. Edges X are part of some MST T; if the new edge e also
happens to be part of T, then there is nothing to prove. So assume e is not in T. We
will construct a different MST T′ containing X ∪ {e} by altering T slightly, changing just one of its edges.
Add edge e to T. Since T is connected, it already has a path between the endpoints
of e, so adding e creates a cycle. This cycle must also have some other edge e′
across the cut (S, V − S) (Figure 5.2). If we now remove this edge, we are left with
T′ = T ∪ {e} − {e′}, which we will show to be a tree. T′ is connected by Property 1,
since e′ is a cycle edge. And it has the same number of edges as T; so by Properties 2 and 3, it is also a tree.
Moreover, T′ is a minimum spanning tree. Compare its weight to that of T:
weight(T′) = weight(T) + w(e) − w(e′). P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Chapter 5 Algorithms 131
Figure 5.3 The cut property at work. (a) An undirected graph. (b) Set X has
three edges, and is part of the MST T on the right. (c) If S = {A, B, C , D}, then
one of the minimum-weight edges across the cut (S, V − S) is e = {D, E}. X ∪ {e}
is part of MST T′, shown on the right. 1 3 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO (a) A C E das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 2 2 2 3 1 B D F 1 4 Tính chất Cắt Chapter 5
Giả sử các cạnh X là một
(b) phần của một MST nào đó Algorithms của 131 A C E A C E
G = (V, E). Chọn một tập đỉnh bất kỳ S sao cho không có cạnh Figure 5.3 The cut pr nào operty của at wX nối ork. giữa (a) S An và V − undir S Edg , và ected es xét gr X: e là aph. cạnh (b) có Set Xtrọng has số nhỏ MST T :
three edges, and is part of nhất the nối MSThai T phân on hoạch the nà right. y. Khi (c) If đó, S X = { ∪ A, B {e
B } là một phần của một , C , D}, then D F B D F MST nào đó.
one of the minimum-weight edges across the cut (S, V − S) is e = {D, E}. X ∪ {e}
is part of MST T′, shown on the right. (c) (a) 1 3 A C E A C E A C E 2 The cut: e MST 2 2 3 1 T : B D F B D F 1 4 B D F S V − S (b) A C E A C E Edges X: MST T : B D F Both e and B e′ cross D
between S Fand V − S,11/and 64
e is specifically the lightest edge of
this type. Therefore w(e) ≤ w(e′), and weight(T′) ≤ weight(T). Since T is an MST,
it must be the case that weight(T′) = weight(T) and that T′ is also an MST. (c) A C E Figure 5.3 A shows an C example E
of the cut property. Which edge is e′? The cut: e MST T : B D F 5.1.3 B Kruskal’s D algorithm F S V − S
We are ready to justify Kruskal’s algorithm. At any given moment, the edges it has
already chosen form a partial solution, a collection of connected components each
of which has a tree structure. The next edge e to be added connects two of these
components; call them T1 and T2. Since e is the lightest edge that doesn’t produce
Both e and e′ cross between S and V − S, anda ecis y specifically cle, it is the certainlightest to be edge the of
lightest edge between T1 and V − T1 and therefore
this type. Therefore w(e) ≤ w(e′), and weight(T′) ≤ weight( satisfies the T). cut Since pr T is operty. an MST,
it must be the case that weight(T′) = weight(T) and that T′ is also an MST.
Now we fill in some implementation details. At each stage, the algorithm chooses
Figure 5.3 shows an example of the cut property. Which edge is e′?
an edge to add to its current partial solution. To do so, it needs to test each candi-
date edge u − v to see whether the endpoints u and v lie in different components;
5.1.3 Kruskal’s algorithm
otherwise the edge produces a cycle. And once an edge is chosen, the correspond-
We are ready to justify Kruskal’s algorithm. At an ing y given moment, components the need edges to be it has
merged. What kind of data structure supports such
already chosen form a partial solution, a collection oper of connected ations? components each
of which has a tree structure. The next edge e to be added connects two of these
components; call them T1 and T2. Since e is the lightest edge that doesn’t produce
a cycle, it is certain to be the lightest edge between T1 and V − T1 and therefore satisfies the cut property.
Now we fill in some implementation details. At each stage, the algorithm chooses
an edge to add to its current partial solution. To do so, it needs to test each candi-
date edge u − v to see whether the endpoints u and v lie in different components;
otherwise the edge produces a cycle. And once an edge is chosen, the correspond-
ing components need to be merged. What kind of data structure supports such operations? P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Chapter 5 Algorithms 131
Figure 5.3 The cut property at work. (a) An undirected graph. (b) Set X has Chapter three 5
edges, and is part of the MST T on the right. (c) If S Algorithms 131
= {A, B, C , D}, then
one of the minimum-weight edges across the cut (S, V − S) is e = {D, E}. X ∪ {e}
Figure 5.3 The cut property at work. (a) An undirected graph. (b) Set X has
is part of MST T′, shown on the right.
three edges, and is part of the MST T on the right. (c) If S = {A, B, C , D}, then
one of the minimum-weight edges across the cut (S, V − S) is e = {D, E}. X ∪ {e} (a) is part of MST T′, 1 3 A shown on the right. C E 2 2 1 (a) 2 3 1 3 A C E B D F 1 2 4 2 2 3 1 B D F 1 4 (b) A C E A C E (b) Ví dụ A C E A C E Edges X: MST T : Edges X: MST T : B D F B D F B D F B D F (c) A (c) C A E C E A AC CE E The cut: The cut: e e MST T : MST T : B D F B D F B D F B D F S V − S S V − S
Nhát cắt S và V − S và một cây bao trùm nhỏ nhất.
Both e and e′ cross between S and V − S, and e is specifically the lightest edge of
this type. Therefore w(e) ≤ w(e′), and weight(T′) ≤ weight(T). Since T is an MST,
Both e and e′ cross between S and V − S, and e is specifically the lightest edge of
it must be the case that weight(T′) = weight(T) and that T′ is also an MST.
this type. Therefore w(e) ≤ w(e′), and weight(T′) ≤ weight(T). Since T is an MST, it must be the Figur case e that 5.3 w show eight( sT an
′) example of the cut property. Which edge is e′?
= weight(T) and that T′ is also an MST. 12 / 64
Figure 5.3 shows an example of the cut property. Which edge is e′? 5.1.3 Kruskal’s algorithm
We are ready to justify Kruskal’s algorithm. At any given moment, the edges it has
5.1.3 Kruskal’s already chosen
algorithm form a partial solution, a collection of connected components each
of which has a tree structure. The next edge e to be added connects two of these We are ready to components; justify Krusk call al’s them T
algorithm. At any given moment, the edges it has
1 and T2. Since e is the lightest edge that doesn’t produce already chosen a c form ycle a , it is partial certain to be solution, a the lightest collection edge of between
connectedTcomponents each
1 and V − T1 and therefore of which has a tr satisfies ee the structur cut e. property The ne .
xt edge e to be added connects two of these components; call Now them we T1 fill in and some T2. implementation Since e is the details lightest . At each edge stage that , the algorithm doesn’t pr chooses oduce a cycle, it is an certain edge to to be add the to its curr lightest ent partial edge betwsolution. een T1 To do and so, V − itTneeds 1 and to test ther each efore candi- satisfies the cut pr date edge
operty. u − v to see whether the endpoints u and v lie in different components;
otherwise the edge produces a cycle. And once an edge is chosen, the correspond- Now we fill in ing some components need implementation to be mer details. ged. At What each kind stage, of the data structur algorithm e supports chooses such an edge to add to oper its ations?
current partial solution. To do so, it needs to test each candi-
date edge u − v to see whether the endpoints u and v lie in different components;
otherwise the edge produces a cycle. And once an edge is chosen, the correspond-
ing components need to be merged. What kind of data structure supports such operations? P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 130
5.1 Minimum spanning trees Chứng Figure 5.2minh T ∪ { Tính e}. The chất Cắt
addition of e (dotted) to T (solid lines) produces a
cycle. This cycle must contain at least one other edge, shown here as e′, across
the cut (S, V − S). S V − S e e
Xét X là một phần của MST T; nếu cạnh e cũng là một phần của The corr T ectness thì Tính of Krusk chất al’s Cắt method đúng.
follows from a certain cut property, which
is general enough to also justify a whole slew of other minimum spanning tree algorithms. 5.1.2 The cut property 13 / 64
Say that in the process of building a minimum spanning tree (MST), we have already
chosen some edges and are so far on the right track. Which edge should we add
next? The following lemma gives us a lot of flexibility in our choice. Cut property
Suppose edges X are part of a minimum spanning tree of G = (V, E ).
Pick any subset of nodes S for which X does not cross between S and V − S, and let
e be the lightest edge across this partition. Then X ∪ {e} is part of some MST.
A cut is any partition of the vertices into two groups, S and V − S. What this property
says is that it is always safe to add the lightest edge across any cut (that is, between
a vertex in S and one in V − S), provided X has no edges across the cut.
Let’s see why this holds. Edges X are part of some MST T; if the new edge e also
happens to be part of T, then there is nothing to prove. So assume e is not in T. We
will construct a different MST T′ containing X ∪ {e} by altering T slightly, changing just one of its edges.
Add edge e to T. Since T is connected, it already has a path between the endpoints
of e, so adding e creates a cycle. This cycle must also have some other edge e′
across the cut (S, V − S) (Figure 5.2). If we now remove this edge, we are left with
T′ = T ∪ {e} − {e′}, which we will show to be a tree. T′ is connected by Property 1,
since e′ is a cycle edge. And it has the same number of edges as T; so by Properties 2 and 3, it is also a tree.
Moreover, T′ is a minimum spanning tree. Compare its weight to that of T:
weight(T′) = weight(T) + w(e) − w(e′). P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 130
5.1 Minimum spanning trees
Figure 5.2 T ∪ {e}. The addition of e (dotted) to T (solid lines) produces a c Chứng ycle. This minh cycle Tính must chất contain Cắt at least(2)
one other edge, shown here as e′, across
the cut (S, V − S). S V − S e e
I Giả sử e không thuộc MST T. Xét T ∪ {e}.
The correctness of Kruskal’s method follows from a certain cut property, which is general I enough Việc to thêm also justify
cạnh e vào aTwhole sẽ tạo sle raw of một other chu minimum trình. spanning tree algorithms
I .Chu trình này chứa ít nhất một cạnh e′ khác đi qua nhát cắt. 5.1.2 The cut property
Say that in the process of building a minimum spanning tree (MST), we have already 14 / 64
chosen some edges and are so far on the right track. Which edge should we add
next? The following lemma gives us a lot of flexibility in our choice. Cut property
Suppose edges X are part of a minimum spanning tree of G = (V, E ).
Pick any subset of nodes S for which X does not cross between S and V − S, and let
e be the lightest edge across this partition. Then X ∪ {e} is part of some MST.
A cut is any partition of the vertices into two groups, S and V − S. What this property
says is that it is always safe to add the lightest edge across any cut (that is, between
a vertex in S and one in V − S), provided X has no edges across the cut.
Let’s see why this holds. Edges X are part of some MST T; if the new edge e also
happens to be part of T, then there is nothing to prove. So assume e is not in T. We
will construct a different MST T′ containing X ∪ {e} by altering T slightly, changing just one of its edges.
Add edge e to T. Since T is connected, it already has a path between the endpoints
of e, so adding e creates a cycle. This cycle must also have some other edge e′
across the cut (S, V − S) (Figure 5.2). If we now remove this edge, we are left with
T′ = T ∪ {e} − {e′}, which we will show to be a tree. T′ is connected by Property 1,
since e′ is a cycle edge. And it has the same number of edges as T; so by Properties 2 and 3, it is also a tree.
Moreover, T′ is a minimum spanning tree. Compare its weight to that of T:
weight(T′) = weight(T) + w(e) − w(e′). P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 130
5.1 Minimum spanning trees
Figure 5.2 T ∪ {e}. The addition of e (dotted) to T (solid lines) produces a
cycle. This cycle must contain at least one other edge, shown here as e′, across Chứng the cut (S, minh V − S Tính ). chất Cắt (3) S V − S e e
I Xét đồ thị T′ = (T ∪ {e}) − {e′}.
The correctness of Kruskal’s method follows from a certain cut property, which is general I enough T′ là to một also cây. justify Tại a
sao? whole slew of other minimum spanning tree algorithms. 5.1.2 The G = (cut V, property
E) là một cây nếu và chỉ nếu G liên thông và |E| = |V| − 1;
Say that in the process of building a minimum spanning tree (MST), we have already
chosen some edges and are so far on the right track. Which edge should we 15 add / 64
next? The following lemma gives us a lot of flexibility in our choice. Cut property
Suppose edges X are part of a minimum spanning tree of G = (V, E ).
Pick any subset of nodes S for which X does not cross between S and V − S, and let
e be the lightest edge across this partition. Then X ∪ {e} is part of some MST.
A cut is any partition of the vertices into two groups, S and V − S. What this property
says is that it is always safe to add the lightest edge across any cut (that is, between
a vertex in S and one in V − S), provided X has no edges across the cut.
Let’s see why this holds. Edges X are part of some MST T; if the new edge e also
happens to be part of T, then there is nothing to prove. So assume e is not in T. We
will construct a different MST T′ containing X ∪ {e} by altering T slightly, changing just one of its edges.
Add edge e to T. Since T is connected, it already has a path between the endpoints
of e, so adding e creates a cycle. This cycle must also have some other edge e′
across the cut (S, V − S) (Figure 5.2). If we now remove this edge, we are left with
T′ = T ∪ {e} − {e′}, which we will show to be a tree. T′ is connected by Property 1,
since e′ is a cycle edge. And it has the same number of edges as T; so by Properties 2 and 3, it is also a tree.
Moreover, T′ is a minimum spanning tree. Compare its weight to that of T:
weight(T′) = weight(T) + w(e) − w(e′). P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 130
5.1 Minimum spanning trees
Figure 5.2 T ∪ {e}. The addition of e (dotted) to T (solid lines) produces a
cycle. This cycle must contain at least one other edge, shown here as e′, across Chứng the cut (S, minh V − S Tính ). chất Cắt (3) S V − S e e
I Xét đồ thị T′ = T ∪ {e} − {e′}.
The correctness of Kruskal’s method follows from a certain cut property, which is general I enough T′ là to một also
cây. justify a whole slew of other minimum spanning tree algorithms
I .Cây T′ cũng là cây bao trùm nhỏ nhất vì: 5.1.2 The cut property
weight(T′) = weight(T) + w(e) − w(e′) và w(e) ≤ w(e′).
Say that in the process of building a minimum spanning tree (MST), we have already
chosen some edges and are so far on the right track. Which edge should we 16 add / 64
next? The following lemma gives us a lot of flexibility in our choice. Cut property
Suppose edges X are part of a minimum spanning tree of G = (V, E ).
Pick any subset of nodes S for which X does not cross between S and V − S, and let
e be the lightest edge across this partition. Then X ∪ {e} is part of some MST.
A cut is any partition of the vertices into two groups, S and V − S. What this property
says is that it is always safe to add the lightest edge across any cut (that is, between
a vertex in S and one in V − S), provided X has no edges across the cut.
Let’s see why this holds. Edges X are part of some MST T; if the new edge e also
happens to be part of T, then there is nothing to prove. So assume e is not in T. We
will construct a different MST T′ containing X ∪ {e} by altering T slightly, changing just one of its edges.
Add edge e to T. Since T is connected, it already has a path between the endpoints
of e, so adding e creates a cycle. This cycle must also have some other edge e′
across the cut (S, V − S) (Figure 5.2). If we now remove this edge, we are left with
T′ = T ∪ {e} − {e′}, which we will show to be a tree. T′ is connected by Property 1,
since e′ is a cycle edge. And it has the same number of edges as T; so by Properties 2 and 3, it is also a tree.
Moreover, T′ is a minimum spanning tree. Compare its weight to that of T:
weight(T′) = weight(T) + w(e) − w(e′). P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch05 GTBL020-Dasgupta-v10 August 10, 2006 22:46 Chapter 5
Greedy algorithms
A game like chess can be won only by thinking ahead: a player who is focused
entirely on immediate advantage is easy to defeat. But in many other games, such
as Scrabble, it is possible to do quite well by simply making whichever move seems
best at the moment and not worrying too much about future consequences.
This sort of myopic behavior is easy and convenient, making it an attractive algorith-
mic strategy. Greedy algorithms build up a solution piece by piece, always choosing
the next piece that offers the most obvious and immediate benefit. Although such
an approach can be disastrous for some computational tasks, there are many for
which it is optimal. Our first example is that of minimum spanning trees. 5.1 Minimum spanning trees
Suppose you are asked to network a collection of computers by linking selected Tính pairs of đúng them. đắn This tr của Thuật anslates into a toán graph Kruskal?
problem in which nodes are computers,
undirected edges are potential links, and the goal is to pick enough of these edges
that the nodes are connected. But this is not all; each link also has a maintenance
cost, reflected in that edge’s weight. What is the cheapest possible network? A 1 C E 4 3 4 4 2 5 B 4 D F 6
One immediate observation is that the optimal set of edges cannot contain a cycle,
because removing an edge from this cycle would reduce the cost without compro-
Bắt đầu với đồ thị rỗng và chọn cạnh từ E theo quy tắc sau. mising connectivity:
Lặp lại việc thêm cạnh nhỏ nhất mà không tạo thành Property 1 Removing
chu trình. a cycle edge cannot disconnect a graph.
So the solution must be connected and acyclic: undirected graphs of this kind are
called trees. The particular tree we want is the one with minimum total weight,
known as the minimum spanning tree. Here is its formal definition. 17 / 64 127
Cài đặt thuật toán Kruskal
Sử dụng cấu trúc dữ liệu disjoint sets: mỗi tập là một thành phần liên thông.
Disjoint sets có ba phép toán:
I makeset(x): tạo ra một tập chỉ chứa phần tử x.
I find(x): x thuộc tập nào?
I union(x, y): hợp hai tập chứa x và y. 18 / 64 procedure kruskal(G, w)
Input: đồ thị liên thông vô hướng G = (V, E);
với trọng số cạnh we
Output: MST định nghĩa bởi tập cạnh X. for all u ∈ V: makeset(u) X = ∅
Sắp xếp các cạnh e theo trọng số
for all {u, v} ∈ E, lấy không giảm theo trọng số:
if find(u) ̸= find(v):
thêm cạnh {u, v} vào X union(u, v) 19 / 64
Cấu trúc dữ liệu Disjoint sets
I Lưu trữ tập dùng cây có hướng.
I Các nút là các phần tử của tập.
I Mỗi nút x có một con trỏ tới nút cha π(x) của nó.
I Ngoài ra mỗi nút có một rank để lưu trữ độ cao của cây con từ nút này.
I Phần tử ở gốc là đại diện, hoặc là tên, của tập.
I Cha của gốc là chính nó. 20 / 64





