Bài giảng Tìm kiếm trên đồ thị (Version 0.5) - Toán rời rạc thầy Trần Vĩnh Đức | Trường Đại học Bách khoa Hà Nội

Tìm kiếm trên đồ thị (Version 0.5) Trần Vĩnh Đức HUST Ngày 16 tháng 9 năm 2019 1 / 58 Tài liệu tham khảo
▶ S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani,
Algorithms, July 18, 2016.
▶ Chú ý: Nhiều hình vẽ trong tài liệu được lấy tùy tiện mà chưa xin phép. 2 / 58 Nội dung Biểu diễn đồ thị
Tìm kiếm theo chiều sâu trên đồ thị vô hướng
Tìm kiếm theo chiều sâu trên đồ thị có hướng
Thành phần liên thông mạnh Đồ thị
▶ Một đồ thị xác định bởi một tập đỉnh (còn gọi là nút) V và
bởi các cạnh E giữa các cặp đỉnh được chọn.
▶ Đồ thị có thể vô hướng: cạnh e = {u, v}
▶ hoặc có hướng e = (u, v). 4 / 58
Biểu diễn đồ thị dùng Ma trận kề
Nếu đồ thị có n = |V| đỉnh v1, v2, . . . , vn, thì ma trận kề là một
mảng n × n với phần tử (i, j) của nó là
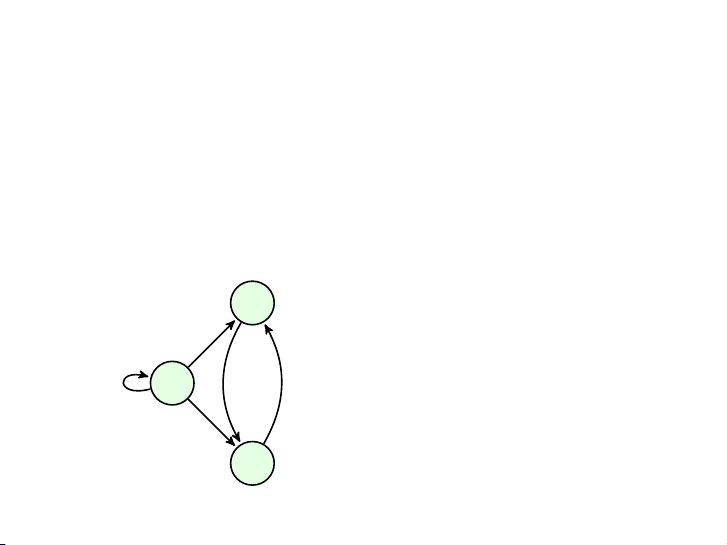
{1 nếu có cạnh từ v a i tới vj ij = 0 ngược lại. Ví dụ v2   1 1 1 v1 A = 0 0 1 0 1 0 v3 5 / 58
Dùng ma trận kề có hiệu quả?
▶ Có thể kiểm tra có cạnh nối giữa cặp đỉnh bất kỳ chỉ cần một lần truy cập bộ nhớ.
▶ Tuy nhiên, không gian lưu trữ là O(n2) 6 / 58
Biểu diễn đồ thị dùng danh sách kề
▶ Dùng một mảng Adj gồm |V| danh sách.
▶ Với mỗi đỉnh u ∈ V, phần tử Adj[u] lưu trữ danh sách các
hàng xóm của u. Có nghĩa rằng:
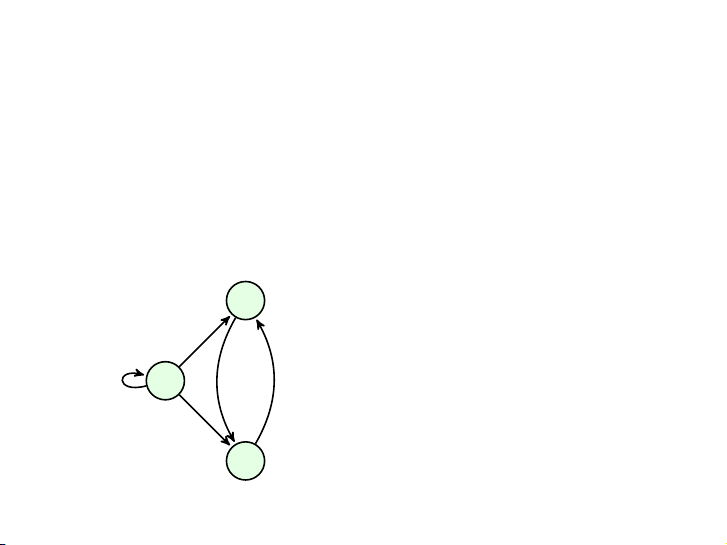
Adj[u] = {v ∈ V | (u, v) ∈ E}. Ví dụ 1
Adj[0] = {0, 1, 2} Adj[1] = {2} 0 Adj[2] = {1} 2 7 / 58
Dùng danh sách kề có hiệu quả?
▶ Có thể liệt kê các đỉnh kề với một đỉnh cho trước một cách hiệu quả.
▶ Nó cần không gian lưu trữ là O(|V| + |E|). Ít hơn O(|V|2) rất
nhiều khi đồ thị ít cạnh. 8 / 58 Nội dung Biểu diễn đồ thị
Tìm kiếm theo chiều sâu trên đồ thị vô hướng
Tìm kiếm theo chiều sâu trên đồ thị có hướng
Thành phần liên thông mạnh 4.1 n Undirected Graphs 525
Adjacency-lists data structure. 4HESTANDARDGRAPHREPRESENTATIONFORGRAPHSTHATARE
NOT DENSE IS CALLED THE adjacency-lists data structure WHERE WE KEEP TRACK OF ALL THE
VERTICESADJACENTTOEACHVERTEXONALINKEDLISTTHATISASSOCIATEDWITHTHATVERTEX7E
MAINTAINANARRAYOFLISTSSOTHATGIVENAVERTEXWECANIMMEDIATELYACCESSITSLIST4O
IMPLEMENTLISTSWEUSEOURBag!$4FROMSection 1.3WITHALINKEDLISTIMPLEMENTA-
TIONSOTHATWECANADDNEWEDGESINCONSTANTTIMEANDITERATETHROUGHADJACENTVERTI-
CESINCONSTANTTIMEPERADJACENTVERTEX4HEGraphIMPLEMENTATIONONPAGEISBASED
ONTHISAPPROACHANDTHElGUREONTHEFACINGPAGEDEPICTSTHEDATASTRUCTURESBUILTBY
THISCODEFORtinyG.txt4OADDANEDGECONNECTINGv and w, we add w to vSADJACENCY
list and v to wSADJACENCYLIST4HUSEACHEDGEAPPEARStwiceINTHEDATASTRUCTURE4HIS
GraphIMPLEMENTATIONACHIEVESTHEFOLLOWINGPERFORMANCECHARACTERISTICS n
3PACEUSAGEPROPORTIONALTOV + E n #ONSTANTTIMETOADDANEDGE n
4IMEPROPORTIONALTOTHEDEGREEOFvTOITERATETHROUGHVERTICESADJACENTTOv
CONSTANTTIMEPERADJACENTVERTEXPROCESSED
4HESECHARACTERISTICSAREOPTIMALFORTHISSETOFOPERATIONSWHICHSUFlCEFORTHEGRAPH
PROCESSINGAPPLICATIONSTHATWECONSIDER0ARALLELEDGESANDSELFLOOPSAREALLOWEDWE
DONOTCHECKFORTHEM Note)TISIMPORTANTTOREALIZETHATTHEORDERINWHICHEDGES
AREADDEDTOTHEGRAPHDETERMINESTHEORDERINWHICHVERTICESAPPEARINTHEARRAYOF
ADJACENCY LISTS BUILT BY Graph -ANY DIFFERENT AR- ptg12441863
RAYSOFADJACENCYLISTSCANREPRESENTTHESAMEGRAPH
7HENUSINGTHECONSTRUCTORTHATREADSEDGESFROM
ANINPUTSTREAMTHISMEANSTHATTHEINPUTFORMAT
AND THE ORDER IN WHICH EDGES ARE SPECIlED IN THE
lLE DETERMINE THE ORDER IN WHICH VERTICES APPEAR
INTHEARRAYOFADJACENCYLISTSBUILTBYGraph3INCE tinyG.txt Câu hỏi
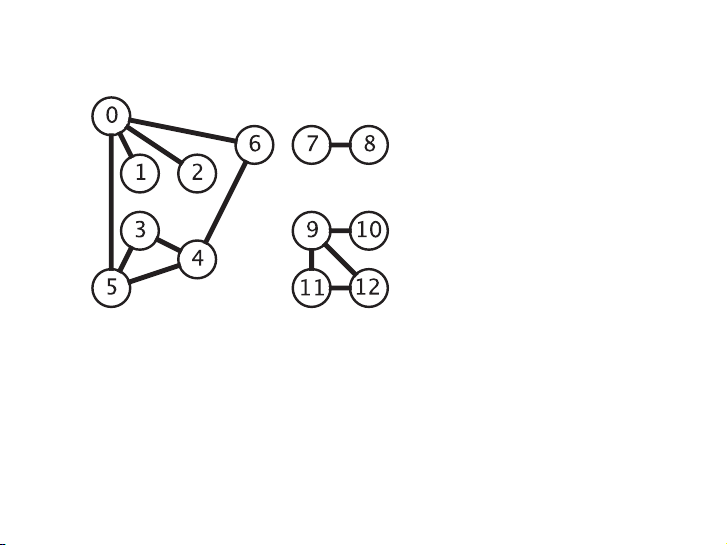
OURALGORITHMSUSEadj()ANDPROCESSALLADJACENT VTừ một đỉnh của đồ thị ta có thể đi tới những đỉnh nào? 13 % java Graph tinyG.txt
VERTICESWITHOUTREGARDTOTHEORDERINWHICHTHEY E 13 13 vertices, 13 edges 0: 6 2 1 5
APPEAR IN THE LISTS THIS DIFFERENCE DOES NOT AFFECT 0 5 4 3 1: 0
THEIR CORRECTNESS BUT IT IS IMPORTANT TO BEAR IT IN 0 1 2: 0 first adjacent 3: 5 4 vertex in input 10 / 58
MIND WHEN DEBUGGING OR FOLLOWING TRACES 4O FA- 9 12 6 4 4: 5 6 3 is last on list
CILITATETHESEACTIVITIESWEASSUMETHATGraphHASA 5 4 5: 3 4 0 6: 0 4
TESTCLIENTTHATREADSAGRAPHFROMTHEINPUTSTREAM 0 2 11 12 7: 8
NAMEDASCOMMANDLINEARGUMENTANDTHENPRINTS 9 10 8: 7 9: 11 10 12
ITRELYINGONTHEtoString()IMPLEMENTATIONON 0 6 second 7 8 10: 9 representation
PAGE TOSHOWTHEORDERINWHICHVERTICESAP- 9 11 11: 9 12 of each edge 12: 11 9 appears in red
PEARINADJACENCYLISTSWHICHISTHEORDERINWHICH 5 3
ALGORITHMSPROCESSTHEMSEEExercise 4.1.7
Output for list-of-edges input P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18 Tìm đường trong mê cung Chapter 3 Algorithms 83
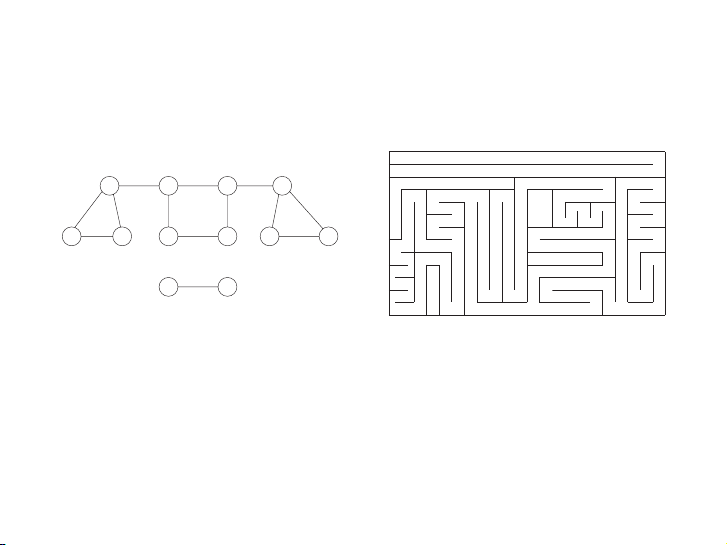
Figure 3.2 Exploring a graph is rather like navigating a maze. L K D A B E F H B G H C F I J C G E J K L I A D
Hình: Tìm kiếm trên đồ thị cũng giống tìm đường trong mê cung
3.2 Depth-first search in undirected graphs 3.2.1 Exploring mazes
Depth-first search is a surprisingly versatile linear-time procedure that reveals a
wealth of information about a graph. The most basic question it addresses is,
What parts of the graph are reachable from a given vertex? 11 / 58
To understand this task, try putting yourself in the position of a computer that has
just been given a new graph, say in the form of an adjacency list. This representation
offers just one basic operation: finding the neighbors of a vertex. With only this
primitive, the reachability problem is rather like exploring a labyrinth (Figure 3.2).
You start walking from a fixed place and whenever you arrive at any junction (vertex)
there are a variety of passages (edges) you can follow. A careless choice of passages
might lead you around in circles or might cause you to overlook some accessible
part of the maze. Clearly, you need to record some intermediate information during exploration.
This classic challenge has amused people for centuries. Everybody knows that all
you need to explore a labyrinth is a ball of string and a piece of chalk. The chalk
prevents looping, by marking the junctions you have already visited. The string
always takes you back to the starting place, enabling you to return to passages that
you previously saw but did not yet investigate.
How can we simulate these two primitives, chalk and string, on a computer? The
chalk marks are easy: for each vertex, maintain a Boolean variable indicating
whether it has been visited already. As for the ball of string, the correct cyber-
analog is a stack. After all, the exact role of the string is to offer two primitive
operations—unwind to get to a new junction (the stack equivalent is to push the
new vertex) and rewind to return to the previous junction (pop the stack).
Instead of explicitly maintaining a stack, we will do so implicitly via recursion
(which is implemented using a stack of activation records). The resulting algorithm procedure explore(G, v)
Input: đồ thị G = (V, E); v ∈ V
Output: visited(u)=true với mọi đỉnh u có thể đến được từ v visited(v) = true previsit(v)
for each edge (v, u) ∈ E: if not visited(u): explore(G, u) postvisit(v) 12 / 58 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL0 P1: 20-Dasgupta-v1 OSO/OVY 0 P2: OSO/OVY QC: OSO/OVY T1: OSO August 10, 2006 19:18 das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18
Ví dụ: Kết quả chạy explore(G, A) Chapter 3 Algorithms 83 Chapter 3 Algorithms 85 Figure 3.2 Exploring Figure a 3.4 graph The r is rather esult of like na explore( vigating A) on the a grmaze aph . of Figure 3.2. L A K D A B E F H B B D G H C F I J E F G C G E J I C H K L I A D J 3.2 Depth-first For search instance, in
while B undirected was being graphs
visited, the edge B − E was noticed and, since E
was as yet unknown, was traversed via a call to explore(E ). These solid edges 3.2.1 Exploring mazes
form a tree (a connected graph with no cycles) and are therefore called tree edges.
The dotted edges were ignored because they led back to familiar terrain, to vertices Depth-first search pre is a surprisingly viously visited. They ver are satile called linear-time back edges. procedur 13 e/58that reveals a
wealth of information about a graph. The most basic question it addresses is,
3.2.2 Depth-first search What parts of The the graph explore ar pr e reachable ocedure fr visits om only a given the vertex?
portion of the graph reachable from its
starting point. To examine the rest of the graph, we need to restart the procedure
elsewhere, at some vertex that has not yet been visited. The algorithm of Figure 3.5, To understand this task, called try depth-fir putting st search your (DF self S), in does the this position repeatedlyof a computer until the entire that graphhas been just been given a tr ne av w er gr
sed. aph, say in the form of an adjacency list. This representation
offers just one basic operation: finding the neighbors of a vertex. With only this primitive, the reachability Figure 3.5 problem Depth-fir is st rather
search. like exploring a labyrinth (Figure 3.2).
You start walking from a fixed place and whenever you arrive at any junction (vertex)
there are a variety of passages procedure (edges) dfs(G )
you can follow. A careless choice of passages
might lead you around in circles or might cause you to overlook some accessible for all v ∈ V: part of the maze. Clearly, you visited(v need )
to record some intermediate information during = false exploration. for all v
This classic challenge has amused ∈ V:
people for centuries. Everybody knows that all
if not visited(v): explore(v)
you need to explore a labyrinth is a ball of string and a piece of chalk. The chalk
prevents looping, by marking the junctions you have already visited. The string
always takes you back to the starting place, enabling you to return to passages that
The first step in analyzing the running time of DFS is to observe that each vertex is
you previously saw but did not yet investigate.
explore’d just once, thanks to the visited array (the chalk marks). During the How can we simulate explor these ation of atw v o primitiv ertex, there es ar ,e chalk the and follo string, wing steps: on a computer? The
chalk marks are easy: for each vertex, maintain a Boolean variable indicating
1. Some fixed amount of work—marking the spot as visited, and the whether it has been visited pre/ already
postvisit.. As for the ball of string, the correct cyber-
analog is a stack. After all, the exact role of the string is to offer two primitive
operations—unwind to get to a new junction (the stack equivalent is to push the
new vertex) and rewind to return to the previous junction (pop the stack).
Instead of explicitly maintaining a stack, we will do so implicitly via recursion
(which is implemented using a stack of activation records). The resulting algorithm Tìm kiếm theo chiều sâu procedure dfs(G) for all v ∈ V: visited(v) = false for all v ∈ V : if not visited(v): explore(G, v) 14 / 58 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18 86
3.2 Depth-first search in undirected graphs
2. A loop in which adjacent edges are scanned, to see if they lead somewhere new.
This loop takes a different amount of time for each vertex, so let’s consider all
vertices together. The total work done in step 1 is then O(|V|). In step 2, over
the course of the entire DFS, each edge {x, y} ∈ E is examined exactly twice, once
during explore(x) and once during explore(y). The overall time for step 2 is Ví dụ: ther Đồ efore O thị (|E |) và and Rừng so the DFS
depth-first search has a running time of O(|V| + |E |),
linear in the size of its input. This is as efficient as we could possibly hope for, since
it takes this long even just to read the adjacency list.
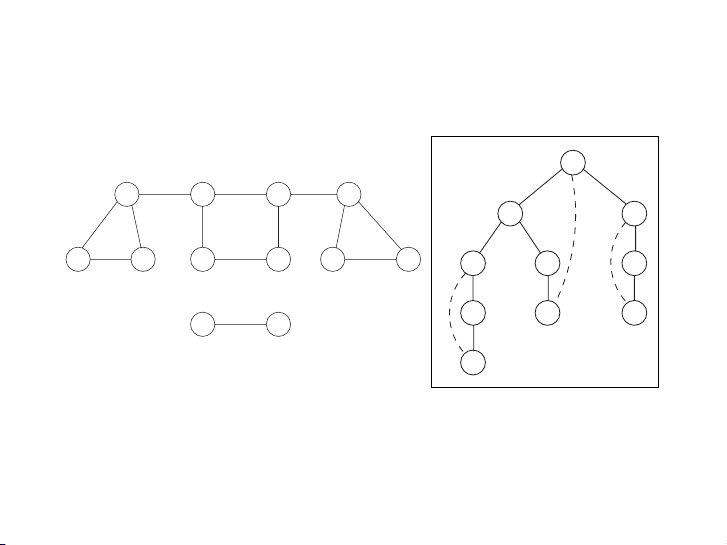
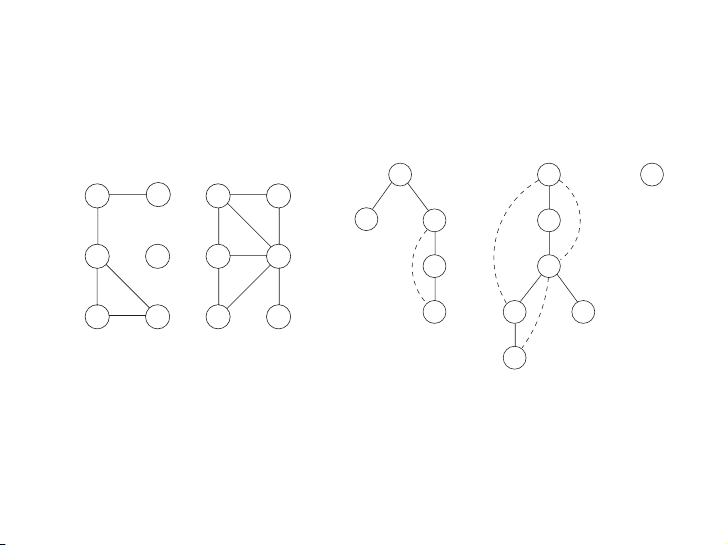
Figure 3.6 (a) A 12-node graph. (b) DFS search forest. 1,10 11,22 23,24 (a) (b) A C F A B C D B E 4,9 12,21 D 2,3 E F G H I 5,8 13,20 H I J K L J 14,17 G L 6,7 18,19 K 15,16
Figure 3.6 shows the outcome of depth-first search on a 12-node graph, once again
breaking ties alphabetically (ignore the pairs of numbers for the time being). The
outer loop of DFS calls explore three times, on A, C , and finally F . As a result,
there are three trees, each rooted at one of these starting points. Together they constitute a forest. 15 / 58
3.2.3 Connectivity in undirected graphs
An undirected graph is connected if there is a path between any pair of vertices. The
graph of Figure 3.6 is not connected because, for instance, there is no path from A
to K . However, it does have three disjoint connected regions, corresponding to the following sets of vertices:
{A, B, E , I, J }
{C , D, G, H, K , L} {F }.
These regions are called connected components: each of them is a subgraph that is
internally connected but has no edges to the remaining vertices. When explore
is started at a particular vertex, it identifies precisely the connected component
containing that vertex. And each time the DFS outer loop calls explore, a new
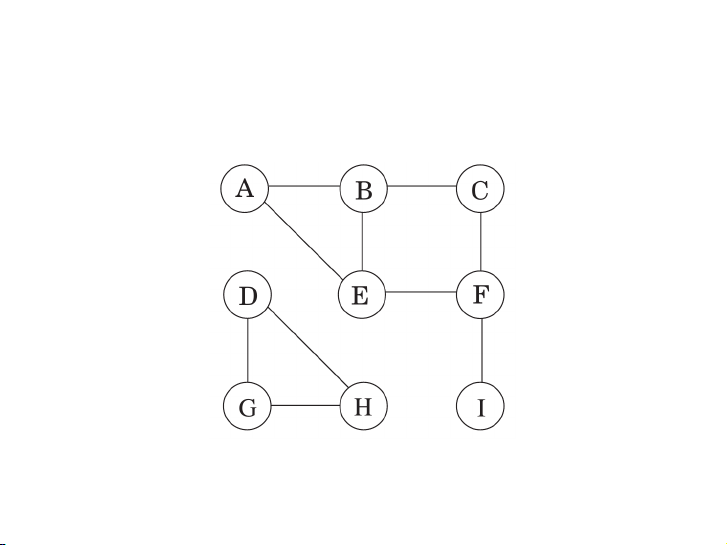
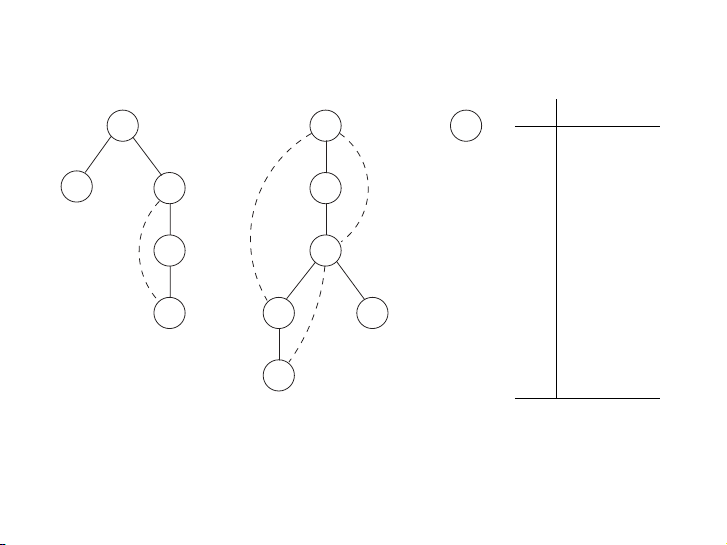
connected component is picked out. Bài tập
Xây dựng rừng DFS cho đồ thị sau với các đỉnh lấy theo thứ tự từ
điển. Vẽ cả những cạnh nét đứt. 16 / 58 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18 86
3.2 Depth-first search in undirected graphs
2. A loop in which adjacent edges are scanned, to see if they lead somewhere new.
This loop takes a different amount of time for each vertex, so let’s consider all
vertices together. The total work done in step 1 is then O(|V|). In step 2, over
the course of the entire DFS, each edge {x, y} ∈ E is examined exactly twice, once
during explore(x) and once during explore(y). The overall time for step 2 is
therefore O(|E |) and so the depth-first search has a running time of O(|V| + |E |),
linear in the size of its input. This is as efficient as we could possibly hope for, since
it takes this long even just to read the adjacency list.
Figure 3.6 (a) A 12-node graph. Rừng (b) DF DFS S sear và ch số for thành est. phần liên thông 1,10 11,22 23,24 (a) (b) v ccnum[v] A C F A 1 A B C D B 1 B E 4,9 12,21 D C 2 2,3 D 2 E F G H I 5,8 13,20 H E 1 F 3 G 2 I J K L J 14,17 G L H 6,7 18,19 2 I 1 K J 1 15,16
Biến ccnum[v] để xác định thành phần liên thông của đỉnh v.
Figure 3.6 shows the outcome of depth-first search on a 12-node graph, once again
breaking ties alphabetically (ignore the pairs of numbers for the time being). The
outer loop of DFS calls explore three times, on A, C , and finally F . As a result, 17 / 58
there are three trees, each rooted at one of these starting points. Together they constitute a forest.
3.2.3 Connectivity in undirected graphs
An undirected graph is connected if there is a path between any pair of vertices. The
graph of Figure 3.6 is not connected because, for instance, there is no path from A
to K . However, it does have three disjoint connected regions, corresponding to the following sets of vertices:
{A, B, E , I, J }
{C , D, G, H, K , L} {F }.
These regions are called connected components: each of them is a subgraph that is
internally connected but has no edges to the remaining vertices. When explore
is started at a particular vertex, it identifies precisely the connected component
containing that vertex. And each time the DFS outer loop calls explore, a new
connected component is picked out.
Tính liên thông trong đồ thị vô hướng procedure dfs(G) cc = 0
for all v ∈ V: visited(v) = false for all v ∈ V: if not visited(v): cc = cc + 1 explore(G, v) procedure explore(G, v) visited(v) = true previsit(v)
for each edge (v, u) ∈ E: if not visited(u): explore(G, u) postvisit(v) procedure previsit(v) ccnum[v] = cc 18 / 58 Bài tập
Hãy cài đặt chương trình tìm số thành phần liên thông của một đồ thị vô hướng. 19 / 58 previsit và postvisit
▶ Lưu thời gian lần đầu đến đỉnh trong mảng pre
▶ Lưu thời gian lần cuối rời khỏi đỉnh trong mảng post
▶ Để tính hai thông tin này ta dùng một bộ đếm clock, khởi
tạo bằng 1, và được cập nhật như sau: procedure previsit(v) pre[v] = clock clock = clock + 1 procedure postvisit(v) post[v] = clock clock = clock + 1 20 / 58