Bài tập Chương 2 - Kỹ Thuật Điện | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Bài tập Chương 2
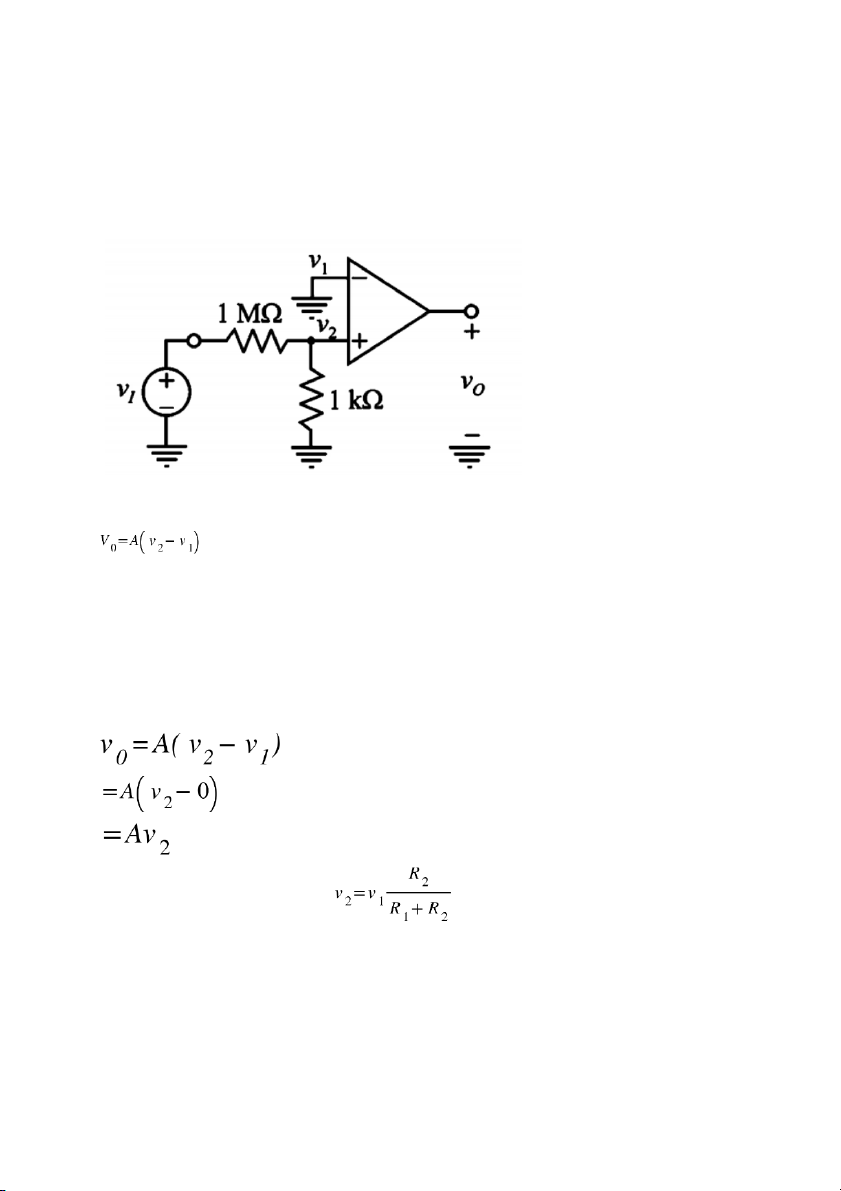
Bài 1: Mạch điện dưới đây sử dụng bộ khuếch đại thuật toán (OA) lý tưởng có hệ
số khếch đại A hữu hạn. Phép đo xác định được vo = 4V khi Vi = 2V. A=? Giải:
Áp dụng công thức điện áp đầu ra cho cấu hình vòng hở Trong đó: A: Hệ số khuếch đại
v2: Điện áp đầu vào không đảo
v1: Điện áp đầu vào đảo Từ hình vẽ ta có v1 = 0V
Áp dụng định luật chia áp Bài 2: Bài làm
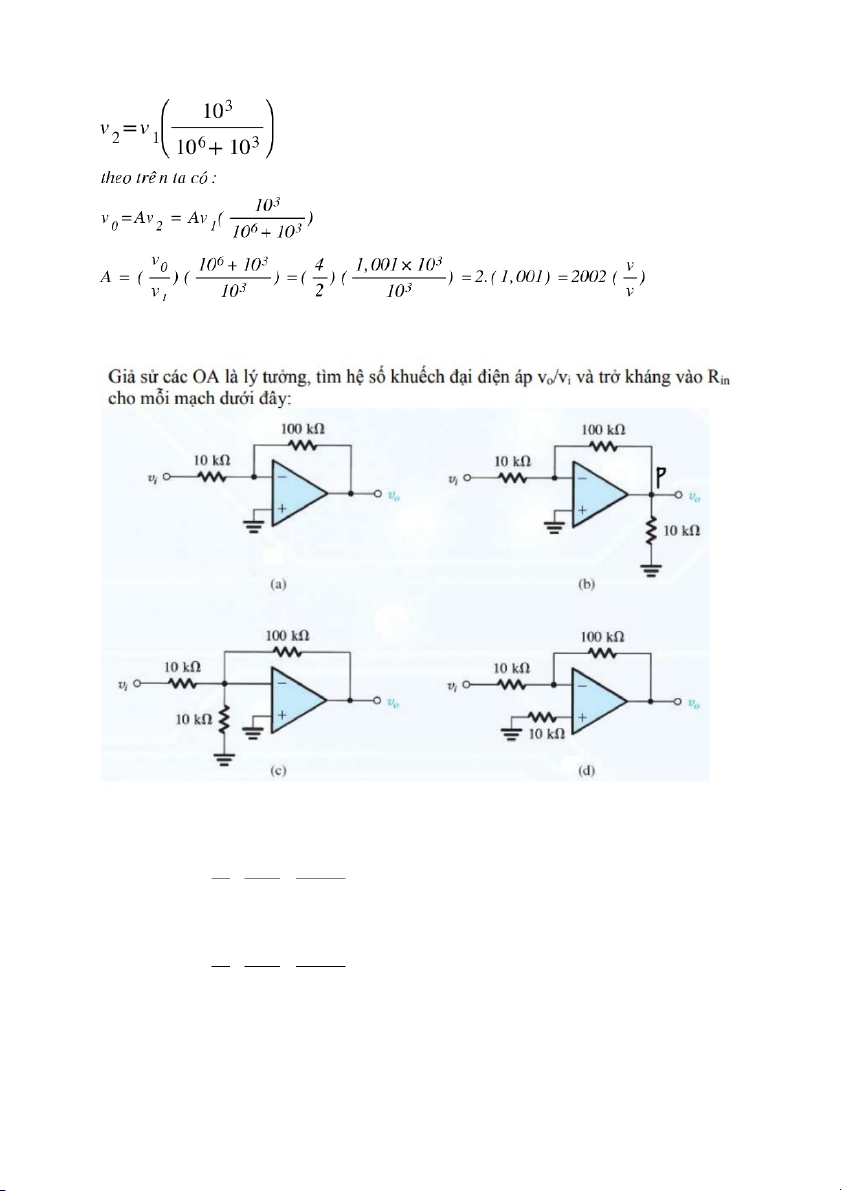
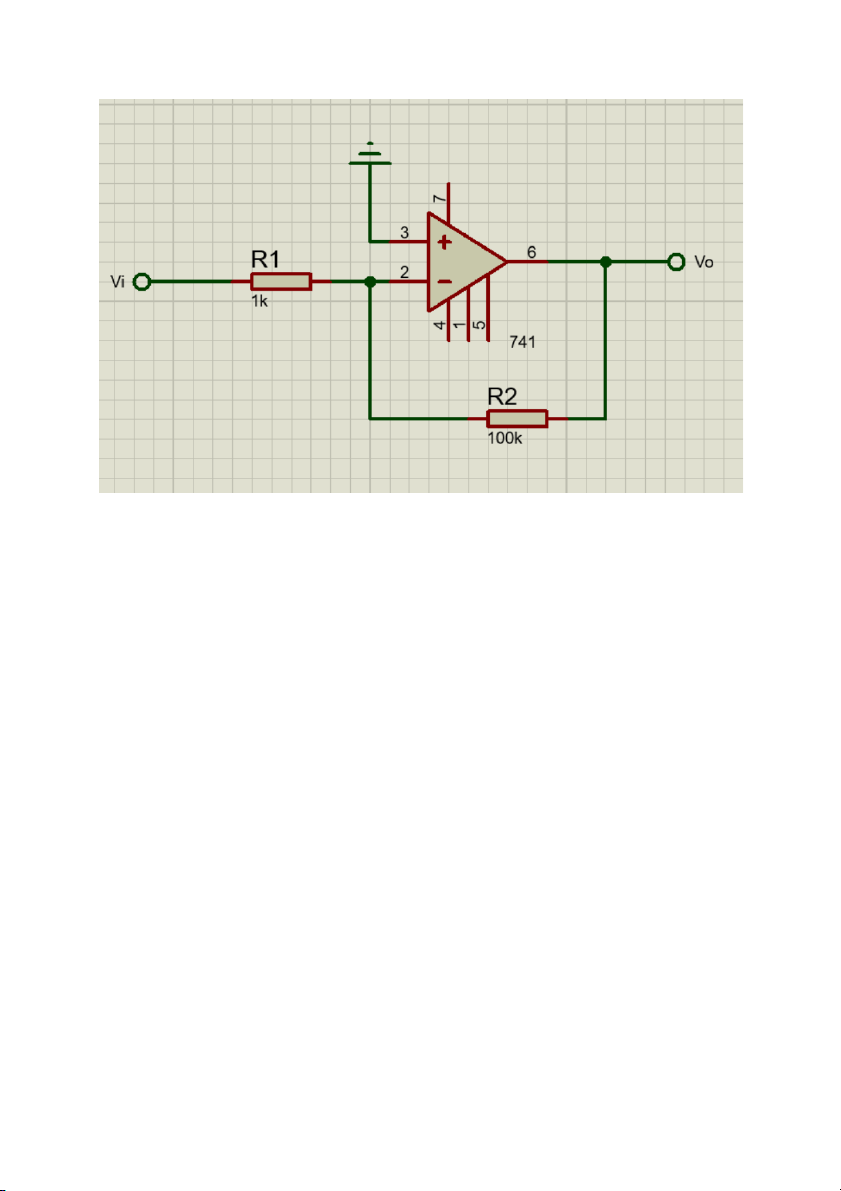
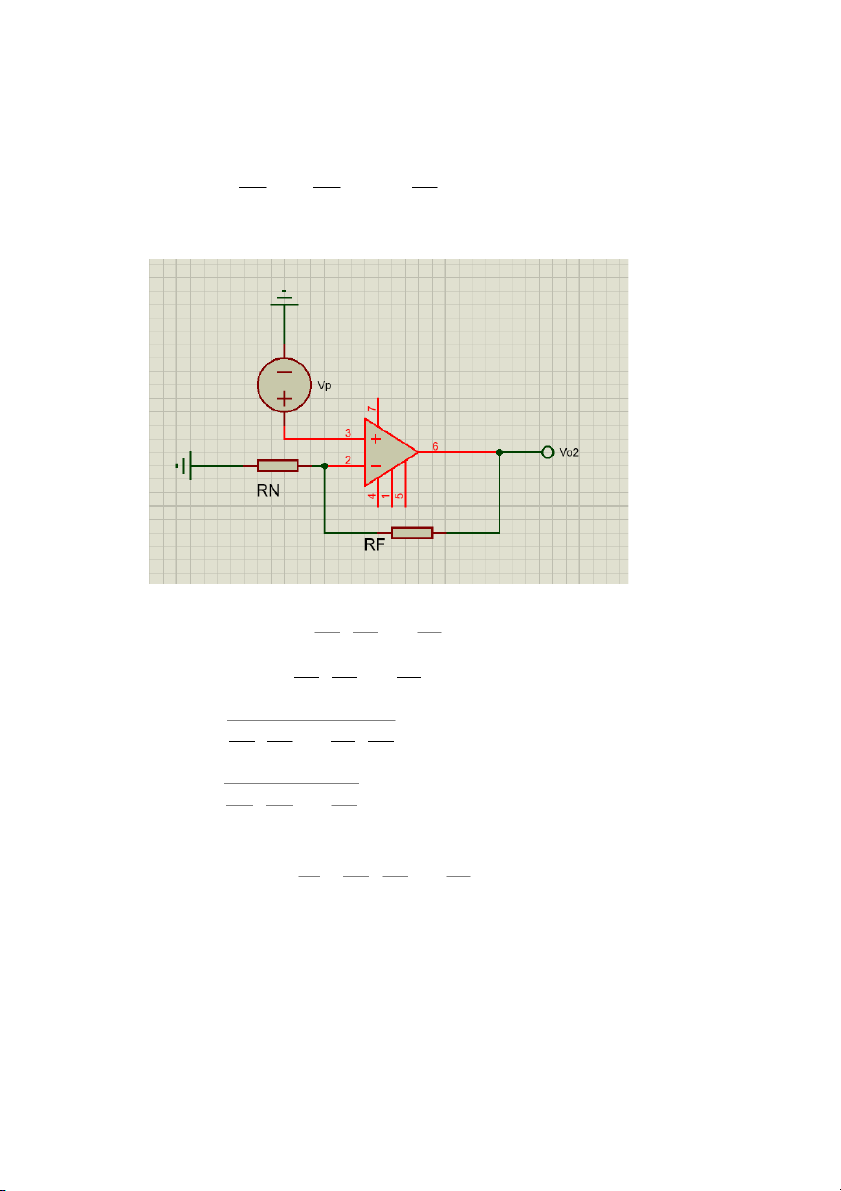
a. Đây là mạch khuếch đại đảo nên Vo − −100 = R 2= k =−10 Vi R 1 10 k
b. Từ hình ta thấy Vp = Vo nên R3 = 10k(ohm) không ảnh hưởng đến dòng
điện trong mạch nên đây là mạch khuếch đại đảo: Vo − −100 = R 2= k =−10 Vi R 1 10 k c.
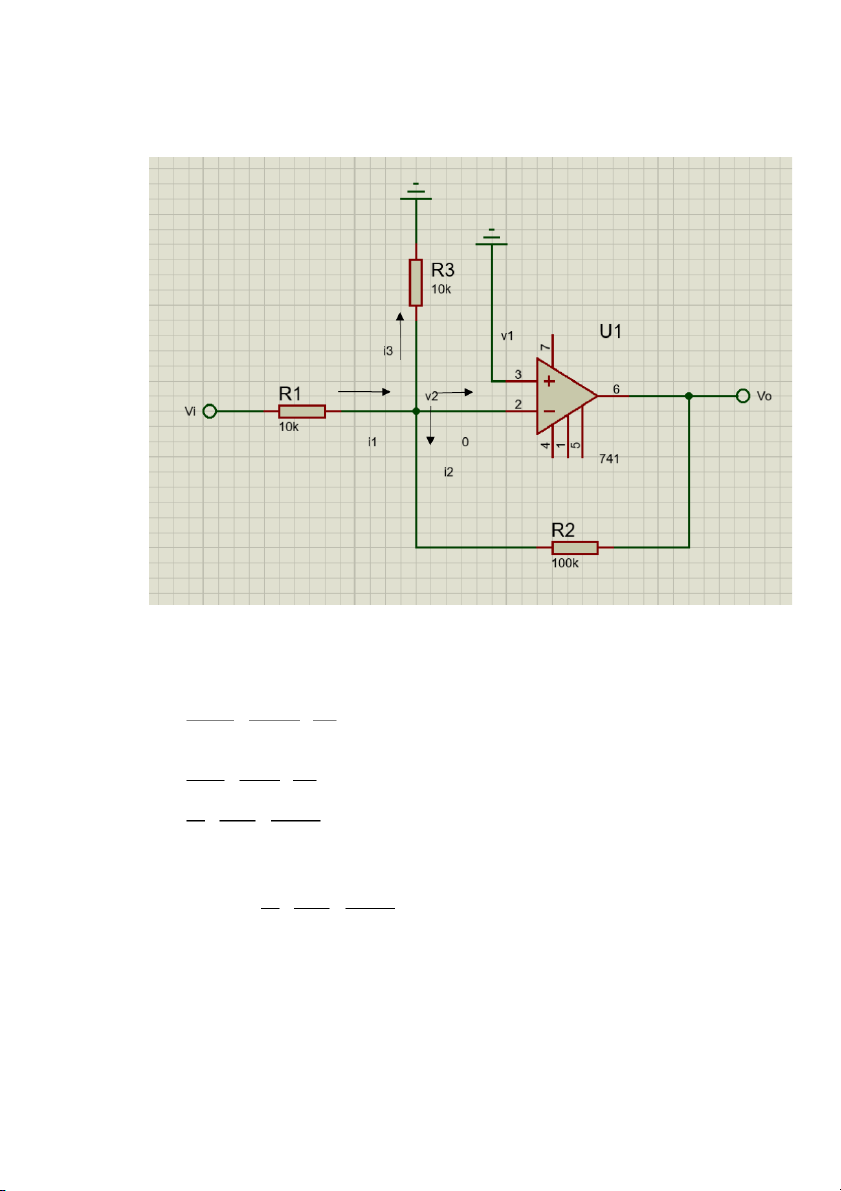
- Do A = ∞ nên Vo = A(v1 – v2) => v1 – v2 = 0 => v1 = v2 mà v1 = 0  v1 = v2 = 0
- Áp dụng định luật kirrchoff ta có: i1 = i2 + i3 + 0
 Vi−v2 = v 2−Vo + v2 R 1 R 2 R 3 mà v 2=0  Vi−0 0− 0 = Vo + R 1 R 2 R 3  Vo − −100 = R 2= k =−10 Vi R 1 10 k
d. Vì R3 = 10k(ohm) ở đầu vào + của mạch không có dòng điện nên đây là mạch khuếch đại đảo: Vo − −100 = R 2= k =−10 Vi R 1 10 k Bài 4: Bài làm
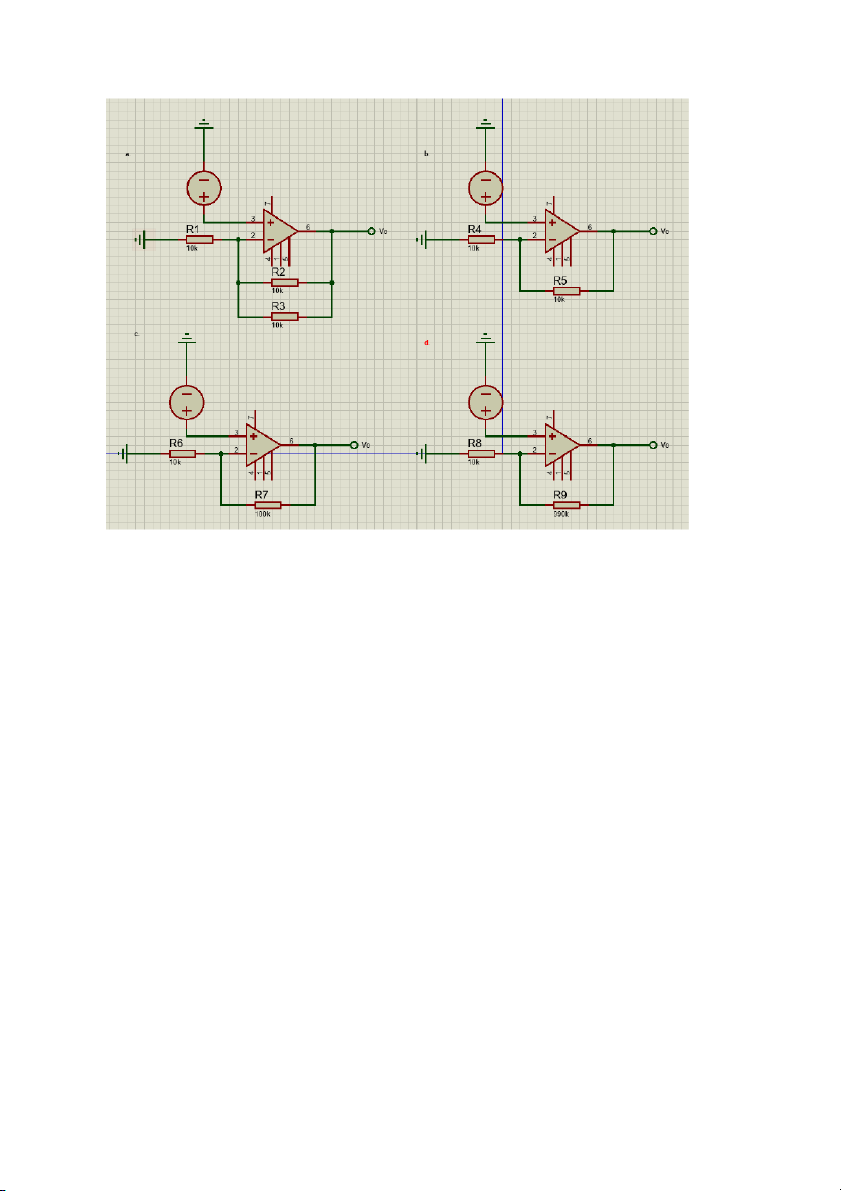
a. Vì sử dụng mạch khuếch đại đảo có Vo − =− R 2 1 mà Vo = Vi Vi R 1  R2 = R1 = 10k(ohm)
b. Tương tự câu a, R2 = 2R1 mà min R = 10k(ohm)
nên R1 = 10k(ohm) và R2 = 20k(ohm)
c. Vì sử dụng mạch khuếch đại đảo có Vo − =− Rtđ 0.5 mà Vo = Vi Vi R 1
Rtđ = 0.5R1.Chọn R1 = 10k(ohm) Rtđ = R23 = 5k(ohm)
d. Tương tự câu a, R2 = 100R1 mà min R = 10k(ohm)
nên R1 = 10k(ohm) và R2 = 1M(ohm)
Do đó ta có thể thiết kế mạch khuếch đại như hình vẽ dưới đây: Bài 7: Bài làm a. - Khi A = ∞ thì Vo − =− R 2 100 mà Vo =
và R 1=1 k (ohm ) Vi Vi R 1
 R 2=100 k (ohm) b.
- Nếu A = 2000 thì theo a, G =−100 ∞ −R 2/R 1 G −100 G = = ∞ = =−95.2 A 1+ R 2 / R 1 1−G 1+100 Bài 8: 1+ 1+ ∞ 1+ A A 2000 Bài làm R R
a. G = 1 ¿1+ tđ 2 → tđ2=0.Ta có thể vẽ mạchnhư sau: R R tđ 1 tđ 1 R R
b. G = 2 ¿1+ tđ 2 → tđ2=1.Tacó thể vẽ mạch như sau: R R tđ 1 tđ 1 R R
c. G = 11 ¿1+ tđ 2 → tđ2=10. Tacóthể vẽ mạch như sau: R R tđ 1 tđ 1 R R
d. G = 100 ¿1+ tđ 2 → tđ2=99. Tacó thể vẽ mạchnhư sau: R R tđ 1 tđ 1 S
Bài 9: Sử dụng cấu hình mạch khuếch đại không đảo để thiết kế một mạch có hệ số
khuếch đại là 1.5 V/V chỉ sử dụng các điện trở 10kΩ. Có thể ngắn mạch 1 điện trở
để thu được hệ số khuếch đại 1V/V hay 2V/V hay không? Bài làm V R - Ta có:
o =1.5=1+ Ry =¿ y =0.5 mà các điện trở trong mạch đều dùng V R i Rx x
điện trở R = 10kΩ nên R sẽ là 1 cặp điện trở mắc nối tiếp và R là một x y
điện trở đơn 10kΩ hoặc R là một điện trở đơn 10kΩ và R là 1 cặp x y điện trở mắc song song.
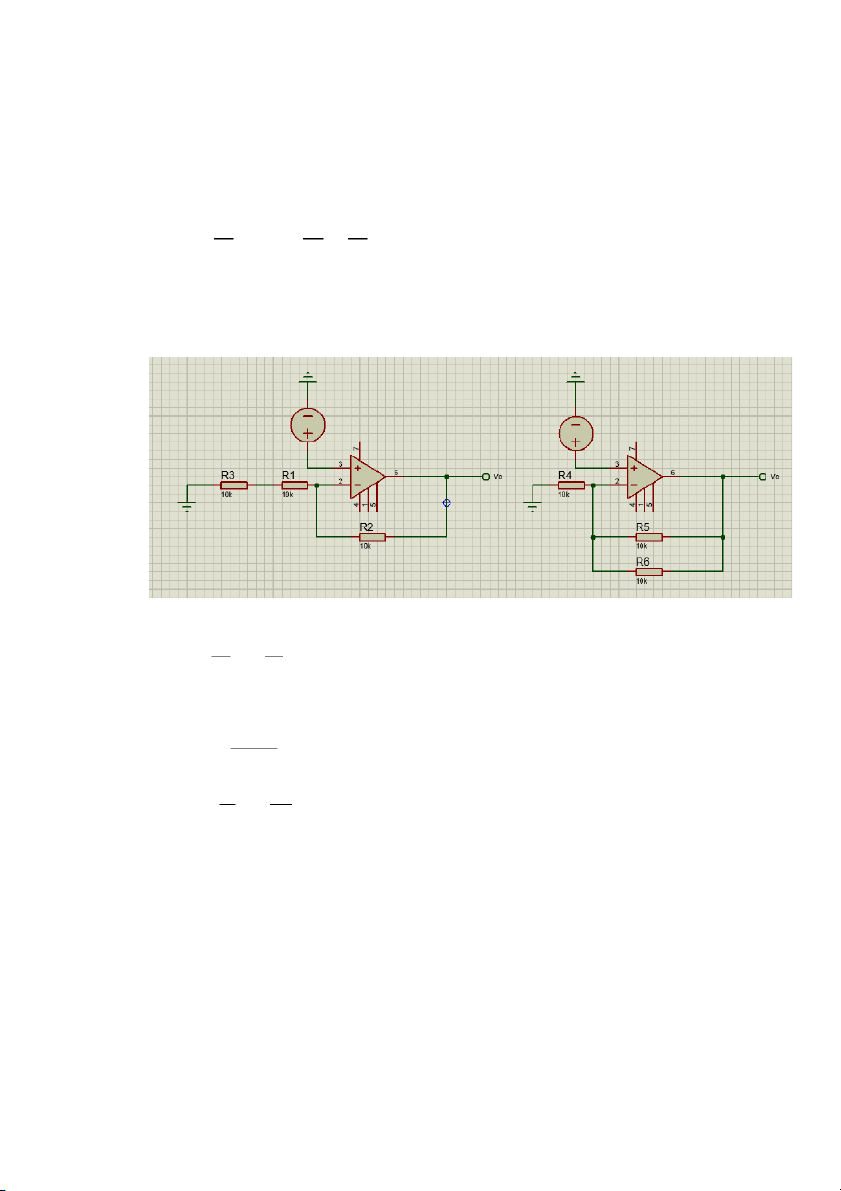
- Ta có mạch là 1 trong 2 TH sau:
- Xét hình bên trái : khi bỏ điện trở R ho c
ặ R thì mạch sẽ có 1 3 V R o = 2 1+ =1+ = 1 2 (V/V) v R i 1
- Xét hình bên phải khi ngắt bỏ điện trở R hoặc R thì ta có 5 6 R ∗R R =R = 5 6 =0 tđ 56 R + R 5 6 v R
Khi đó o =1+ tđ =1+0=1(V /V ) v R i 4
Vậy có thể ngắn mạch 1 điện trở để thu được hệ số khuếch đại 1V/V hay 2V/V Bài 10:
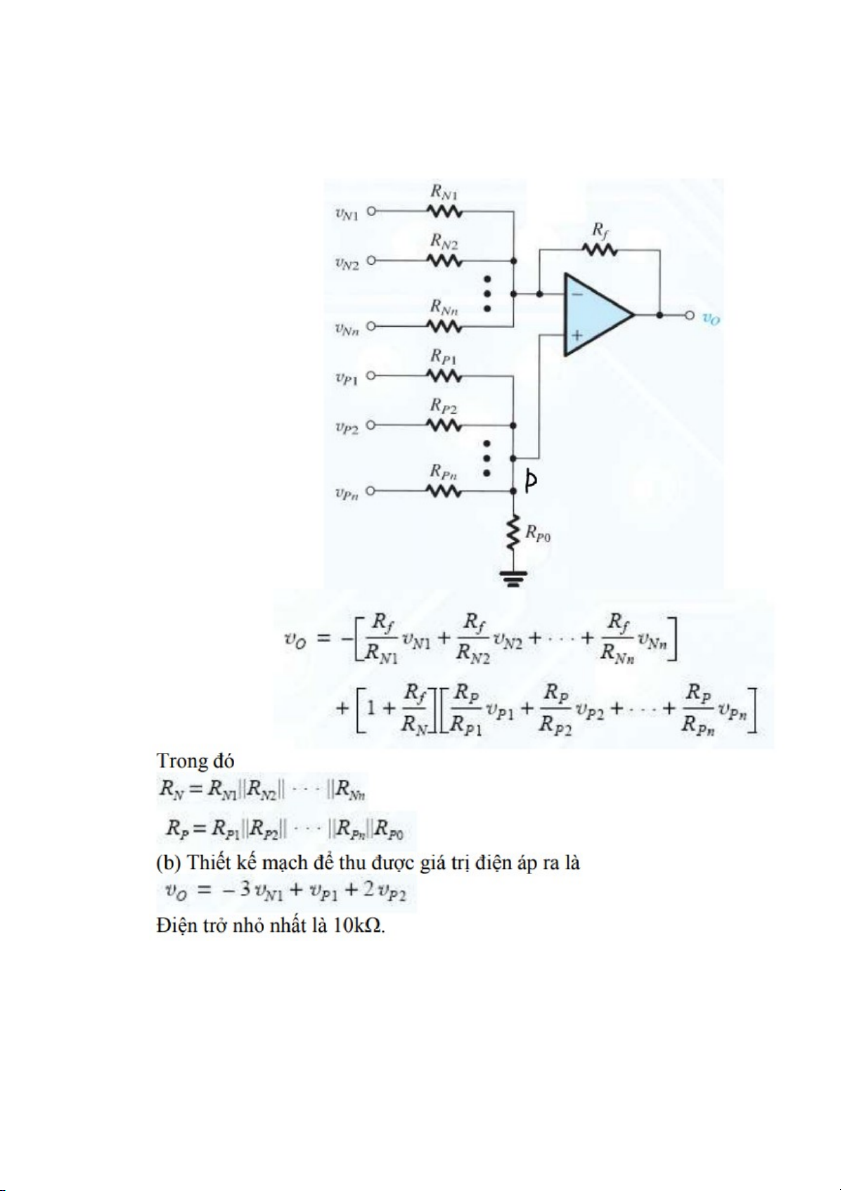
a. Sử dụng nguyên lý xếp chồng chứng minh rằng lối ra của mạch sau có giá trị là: Bài làm a.
- Khi v =v =…=v =0 khi đó mạch sẽ trở thành mạch khuếch đại đảo p 1 p 2 Pn R R R
Có v =−( f ∗v + f ∗v +…+ f ∗v ) o 1 R N 1 R N 2 R Nn N 1 N 2 Nn
- Khi v =v =…=v =0 N
khi đó mạch sẽ trở thành mạch khuếch đại không 1 N 2 Nn
đảo. Khi đó ta có thể viết mạch tương đương với Ta có: v v v
+ i =i +i +…+i = p1+ p2 +…+ pn p p 1 p 2 pn R R R p 1 p 2 pn v v v
+ v =i ∗R =R ∗( p1 + p2 +…+ pn ) p p P p R R R p 1 p 2 pn 1 R = Với p 1 1 1 1 + +…+ + R R R R p 1 p 2 pn p 0 1 R = N 1 1 1 + +…+ R R R N 1 N 2 Nn
Do là mạch khuếch đại không đảo nên lối ra là R v v v
v =R ∗(1+ f )∗( p1 + p2 +…+ pn ) o 2 p R R R R N p 1 p 2 pn
- Khi v ,v ,…, v ≠ 0 vàv ,v ,…,v ≠ 0 thì lối ra là; p 1 p 2 Pn N 1 N 2 Nn
v =v +v =đpcm o o 1 o 2 b.
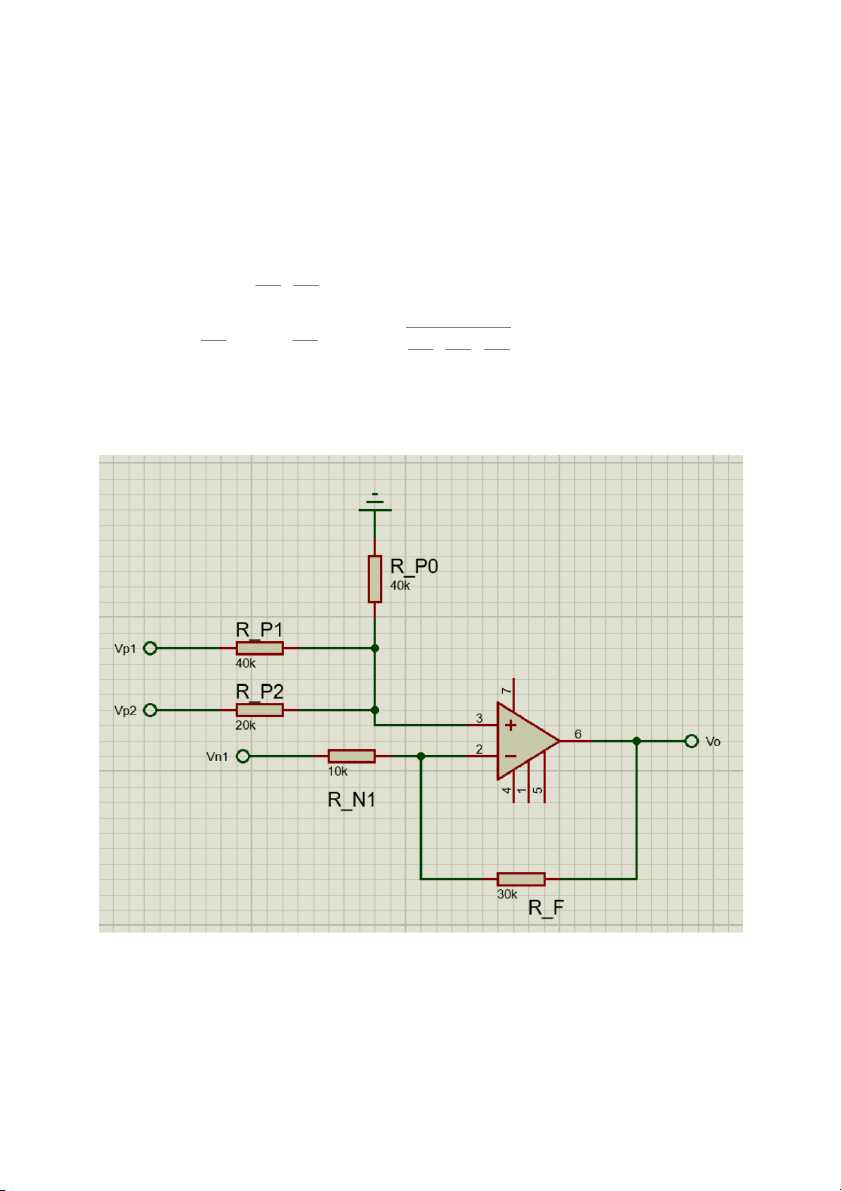
- Thiết kế mạch có v =−3v +v +2v o n 1 p 1 p 2 Khi đó + R =3 R chọn =10 =30 f n R
k (ohm) => R k ( ohm) 1 n 1 f  v v
v =4 R ( p1 + p2 ) o 2 p R R p 1 p 2 1 R R R =  4 p = p p 1 , 4 =2 , 1 1 1 R R + + p 1 p 2 R R R p 1 p 2 p 0
Chọn R =40k (ohm)=¿ R =10k(ohm)và R =20k (ohm) p 1 P p 2
Và R =40k(ohm) p 0
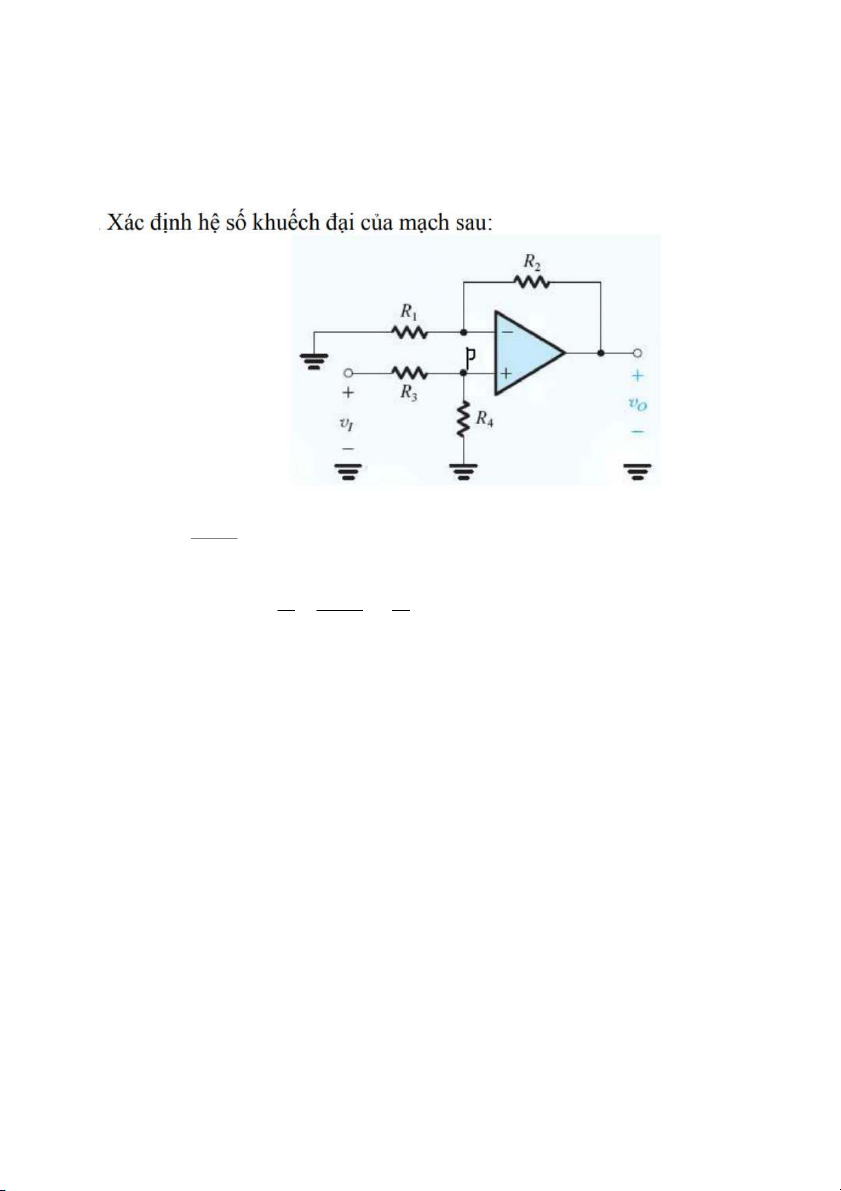
Ta thiết kế mạch vẽ như sau: Bài 11: R ∗v - v = 4 i P R + R 3 4
- Vì đây là mạch khuếch đại không đảo nên R R ∗v R v =v ( 2 4 i 2 1+ )= (1+ ) o i R R + R R 1 3 4 1
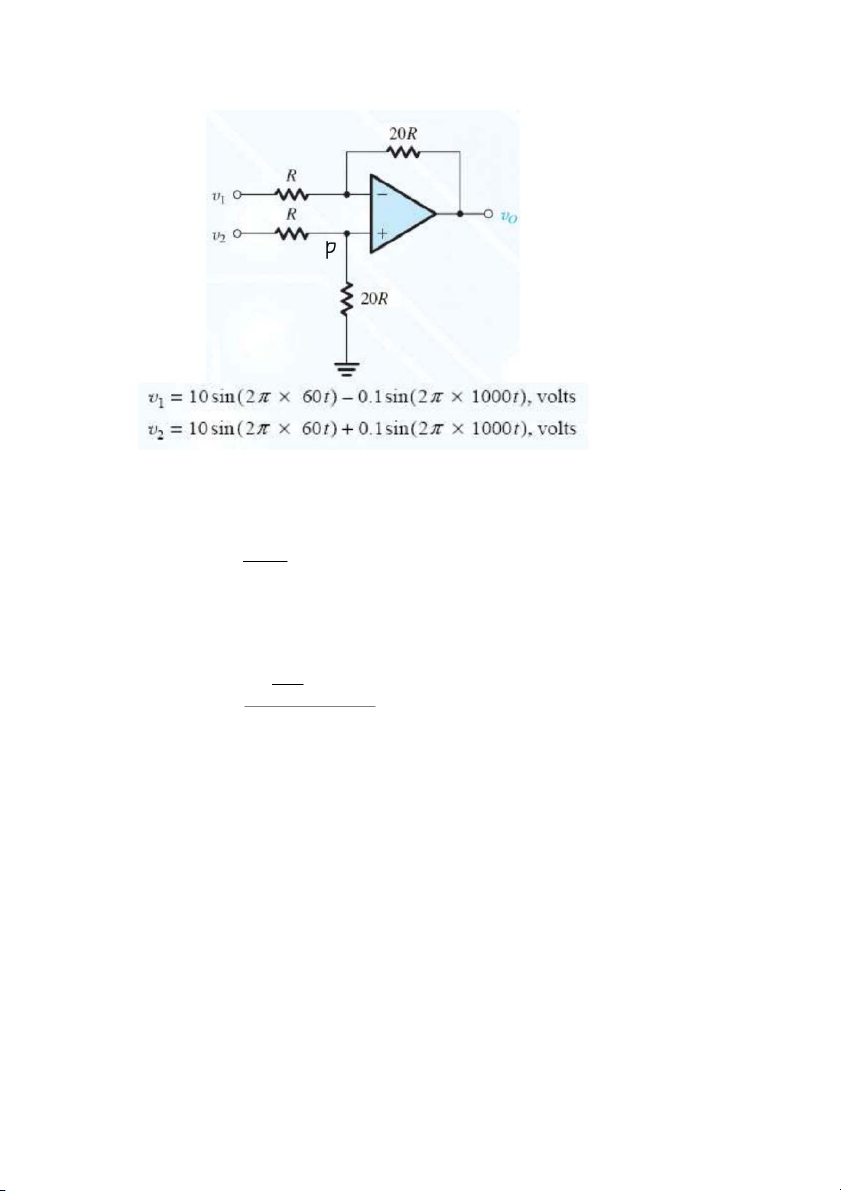
Bài 12: Cho mạch điện như hình dưới. Sử dụng nguyên lý xếp chồng tìm vo theo
điện áp lối vào v và v . Giả sử OA là lý tưởng. Tìm v nếu: 1 2 o Bài làm
- Với v =0 thì khi đó mạch sẽ là mạch khuếch đại đảo: 2 −20 R v =
v =−20( 10 sin (2 π∗60 t )−0.1 sin(2 π∗1000 t )) 01 R 1
= 2sin(2 π∗1000 t ) – 200 sin(2π∗60t) (V)
- Với v =0thì khi đó mạch sẽ là mạch khuếch đại không đảo: 1 ( 20R 1+ )∗v ∗20R R 2 v = =20 v o 2 20 R+ R 2
¿ 20( 10 sin (2 π∗60t)+0.1 sin (2 π∗1000t ) )
¿ 200 sin( 2π∗60t) + 2sin(2 π∗1000 t ) (V)
- Áp dụng nguyên lý chồng chất điện trường ta có:
v =v + v =400 sin(2 π∗60 t ) (V) o o 1 o 2
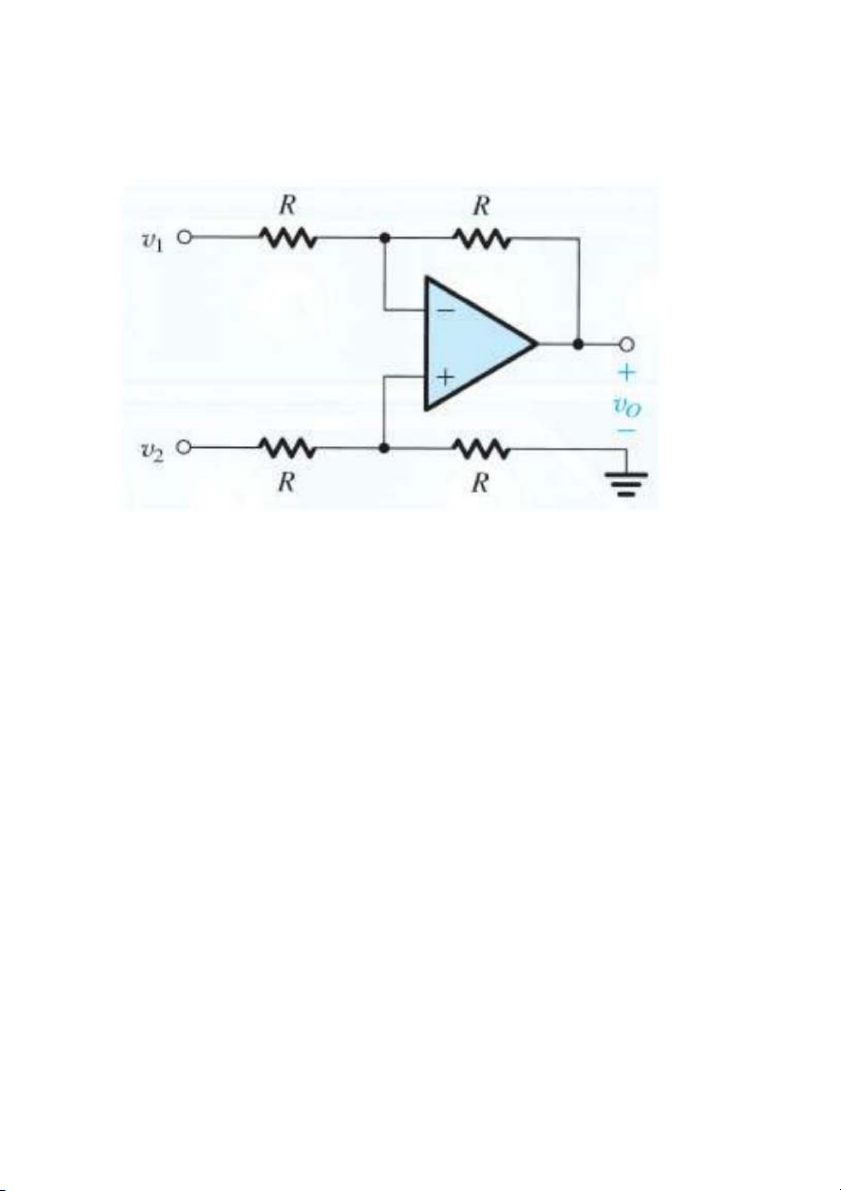
Câu 15: Cho mạch điện như hình dưới. Biểu diễn vo là hàm của v và v . Xác 1 2
định điện trở lối vào của mạch khi chỉ có v ? Khi chỉ có v ? Kết nối nguồn 1 2
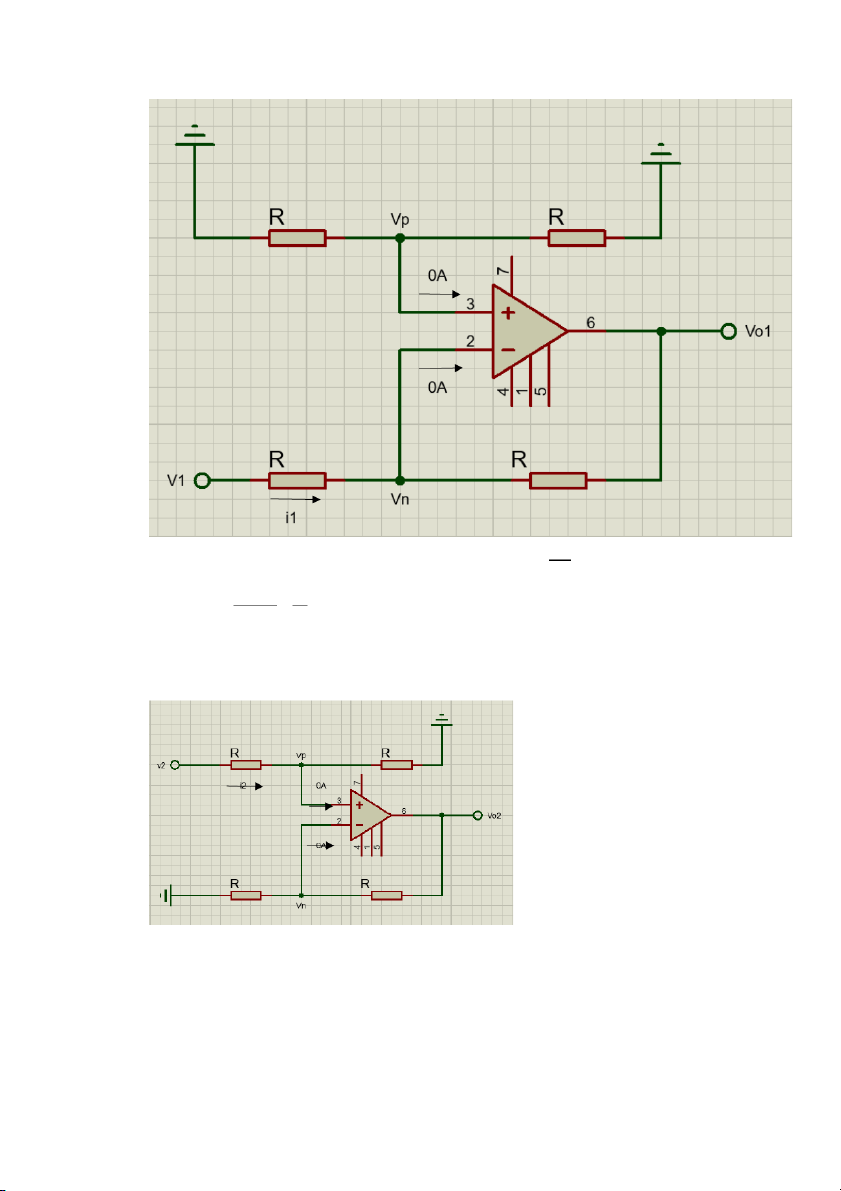
giữa hai lối vào? Kết nối nguồn tới đồng thời cả hai lối vào? Bài làm. a. Khi chỉ có v1 - Khi đó mạch có dạng: v
- Vì đây là mạch khuếch đại đảo nên v =v =0 và o1 =−1 n p v1 v −v v - Ta có 1 R= 1 n = =R i i ¿1 1 1 = > R = ¿ R 1 b. Khi chỉ có v 2
- Khi đó mạch vẽ có dạng :
- Xét tại điểm có điện áp Vp, ta có: v −v v v 2 p = p → v = 2 2 v → v = R R 2 p p 2
- Vì đây là mạch khuếch đại không đảo nên: vo2 =1+ R =1+1 2 = → v =v v R o 2 2 p
→ v =v +v =v − 2 v o o 1 o 2 1 - Ta có v − 2 v −v v2 2 v R i = 2 p=
→ R= 2 = ¿ 2 → R =2 R 2 R R 2 i 2 ¿ 2 2
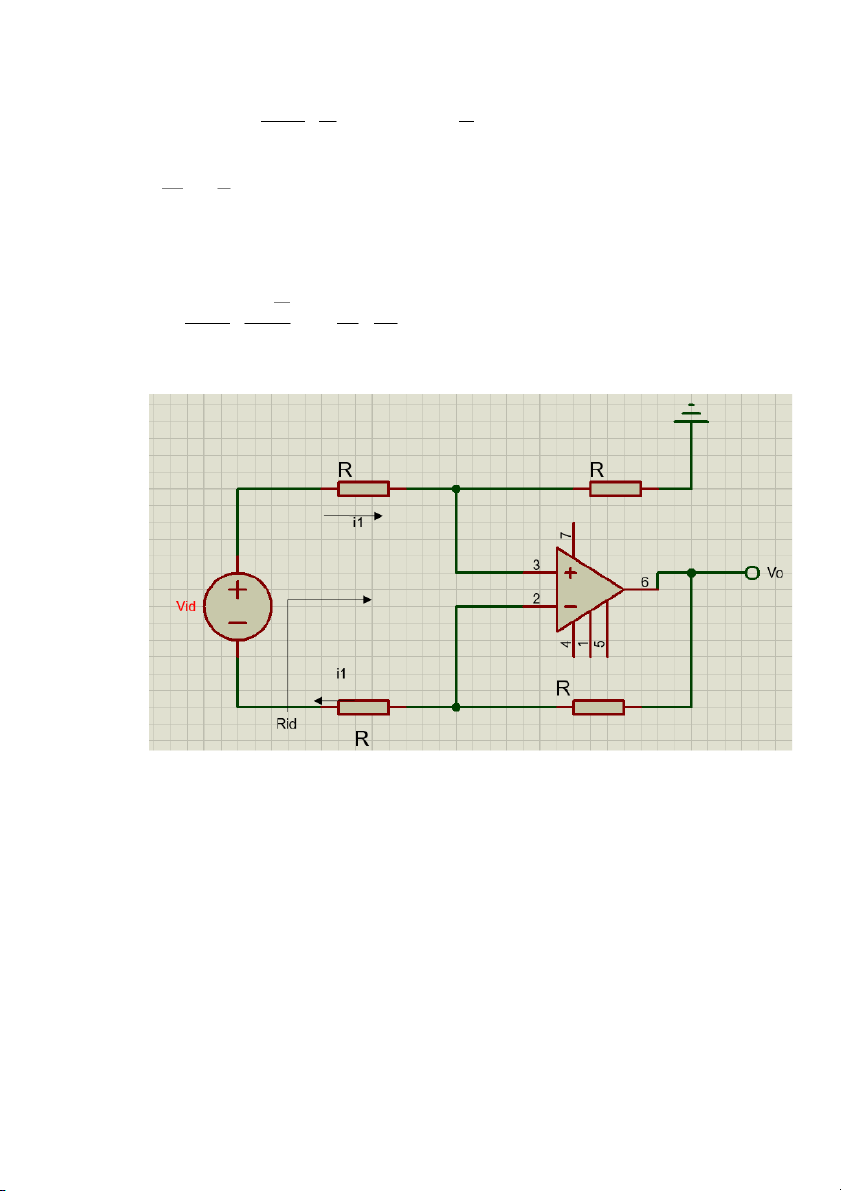
c. Kết nối nguồn giữa 2 lối vào. - Mạch vẽ có dạng :
- Xét định luật kirchoff ta có:
v −i ∗R−i ∗R=0 id 1 1
→ v =2 i1 R id →i R =2 R 1 i id 1
→R =2R hay R id ¿=2 R
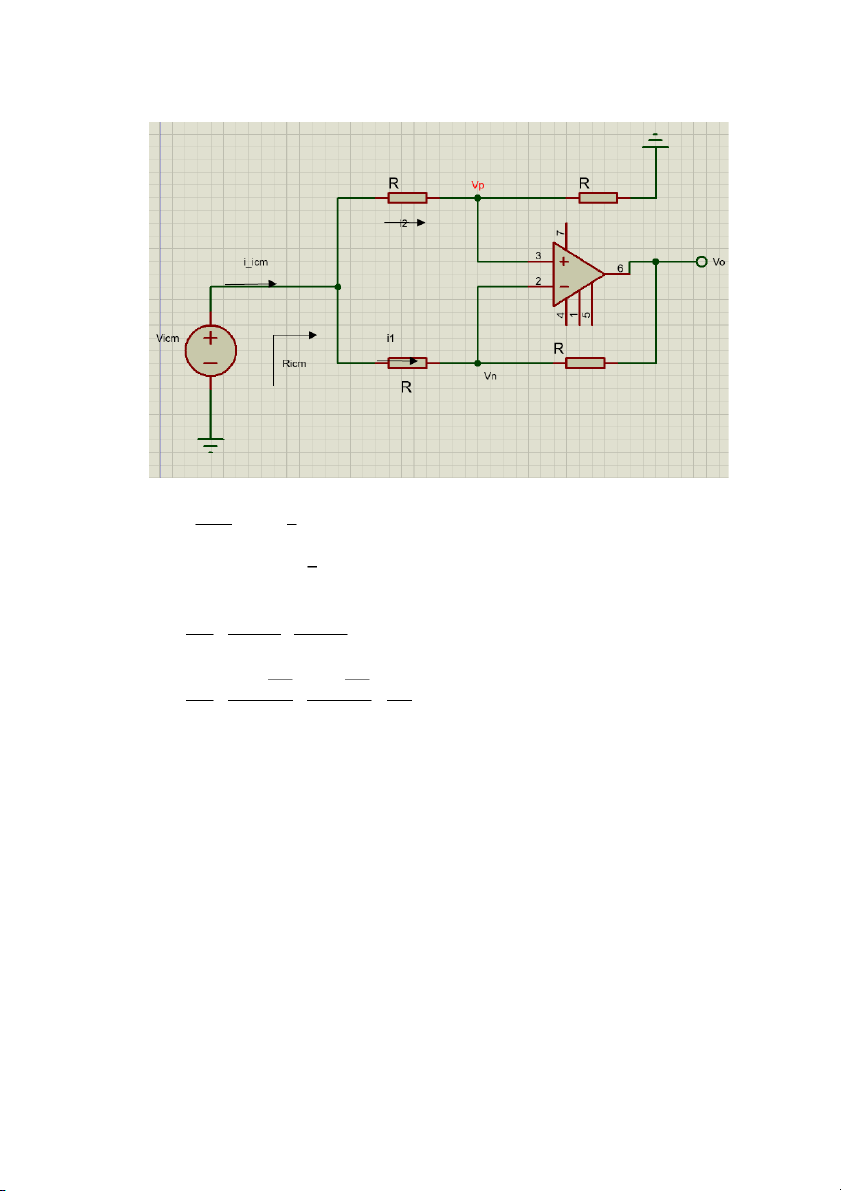
d. Kết nối đồng thời cả 2 lối vào. - Mạch vẽ có dạng:
- Áp dụng định luật chia áp ta có: 1
v =( R )∗v = v p R+ R icm 2 icm 1
- Tương tự ta có v = v n 2 icm - Ta có: i =i + 1 i icm 2 v v −v v −v → icm = icm n + icm p R R R icm v v − icm − icm → v v v icm icm v icm 2 2 = + = icm R R R R icm
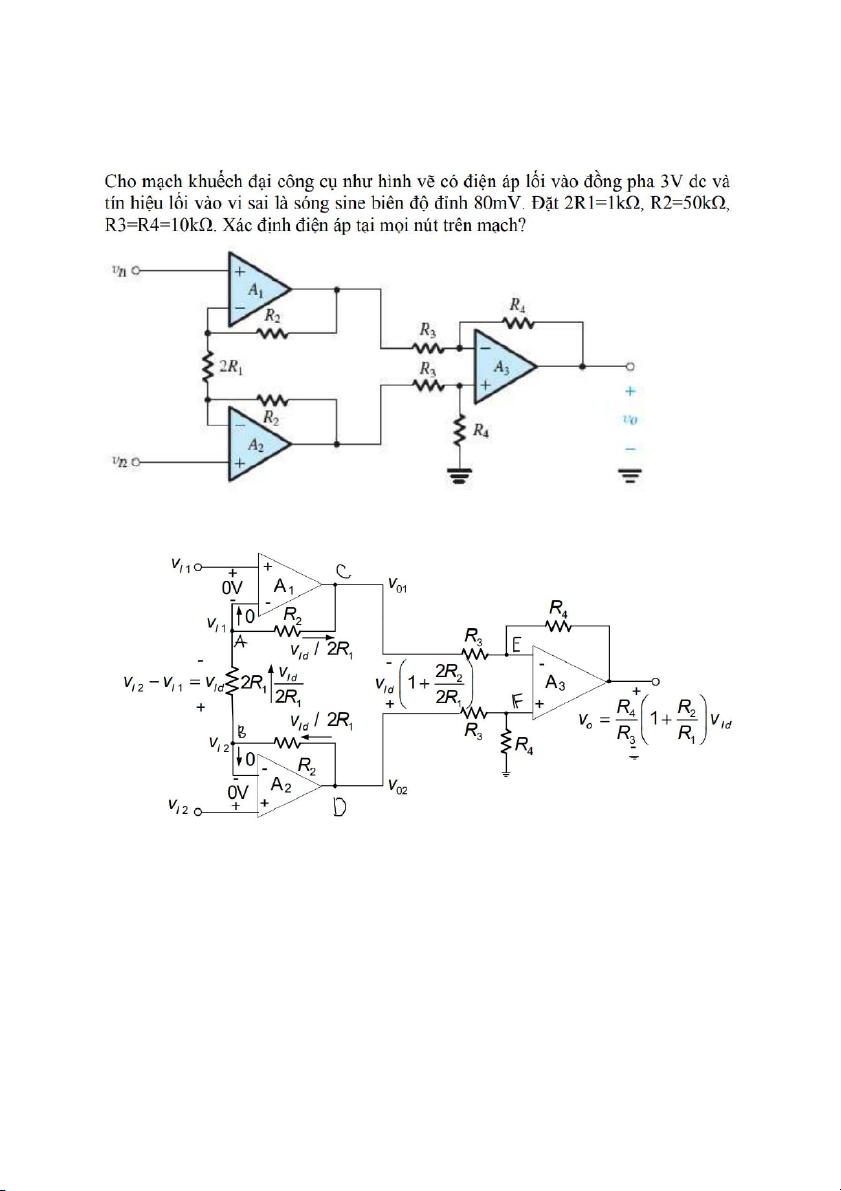
→ R =R=R icm ¿ Bài 16: Bài làm - Từ đầu bài ta có:
{v =3−0.04sinωt i 1
v =3+ 0.04 sinωt i 2 v =v − 2 v id 1
- Xét mạch khuếch đại A1, ta có v = A (v −v ) c 1 i 1 A
Vì đây là mạch khuếch đại lý tưởng nên A =∞ → v =v 1 A i 1
- Tương tự với mạch khuếch đại A2 → v =v B i2
- Giả sử xét chiều dòng điện đi từ điển D → B, và do mạch khuếch đại lý
tưởng nên dòng điện lối vào mạch khuếch đại = 0 hay i =0 do đó ta có i v −v v −v v dòng điện v =v =v mà v = B A = i2 i 1 = id D → B B → A A → C B → A 2 R 2 R 2 R 1 1 1 v → v =v =v = id D → B B → A A → C 2 R1 v −v v v ∗R Mà v = A
C = id → v =v =v − id 2 A →C R 2 R c o 1 i 1 2 R 2 1 1 v −v v v ∗R v = D
B= id → v =v =v + id 2 D → B R 2 R D o 2 i 2 2 R 2 1 1
- Sử dụng nguyên lý xếp chồng:
+ giả sử v =0 , khi đó mạch trở thành mạch khuếch đại đảo có v =0 o 2 e −R Và v = 4 ∗v o o1 R3 o 1 + giả sử v =0 o
khi đó mạch trở thành mạch khuếch đại không đảo có 1 R R R R 4 4 4 v = 4 ∗v và v =(1+ )v = ∗v (1+ ) F R + R o 2 o F o 2 o2 R R + R R 4 3 3 4 3 3 R R
+ Khi đó v =v +v = 4 ∗v ( 4 1+ )−R4∗v o o o o 2 o2 o1 R + R R R 4 3 3 3 o 1 R R v ∗R v ∗R
→ v = 4( v −v )= 4 (v + id 2 −v + id 2 ) o R o 2 o 1 R i 2 2 R i 1 2 R 3 3 1 1 R v ∗R v ∗R R → v = 4( 2 v + id 2 )= id 4(1+ ) o R id R R R 3 1 3 1 ¿ 80 m∗(1+ ) 100 = 8.08V Bài 18: Bài làm
- Do mạch vào có tần số nên tín hiệu lối v¿(t ) vào sẽ có dạng sóng hình sin
- Giả sử v (¿t )=¿ Asin( ωt )
- Ta có tín hiệu lối ra của mạch tích phân là: −1 −1 v (t )=
∫v (t )dt= ∫Asin (ωt ) dt out RC ¿ RC
- Ta có độ lớn của mạch khuếch đại là giá trị đỉnh của ngõ ra và giá trị đỉnh của ngõ vào nên : A
G=¿ | vout | = ωRC 1 (1) v = ¿ A ωRC
Với mỗi tín hiệu đầu vào khác nhau ta sẽ có hệ số khuếch đại điện áp tỉ lệ 1 1
nghịch với tần số như sau : G ↔G ω f
- Khi f = 1kHz thì G = -100V/V thì khi G = -1V/V thì
f ' =1k∗100=100 kHz
Vậy khi khi G = -1V/V thì f '=100 kHz
- Ta có t = RC, xét G = - 100V/V và f = 1kHz thay vào (1) ta được 1 1 100 = →t = =¿ 1.59* μs
2 π∗1 k∗t 2 π∗1000∗100