



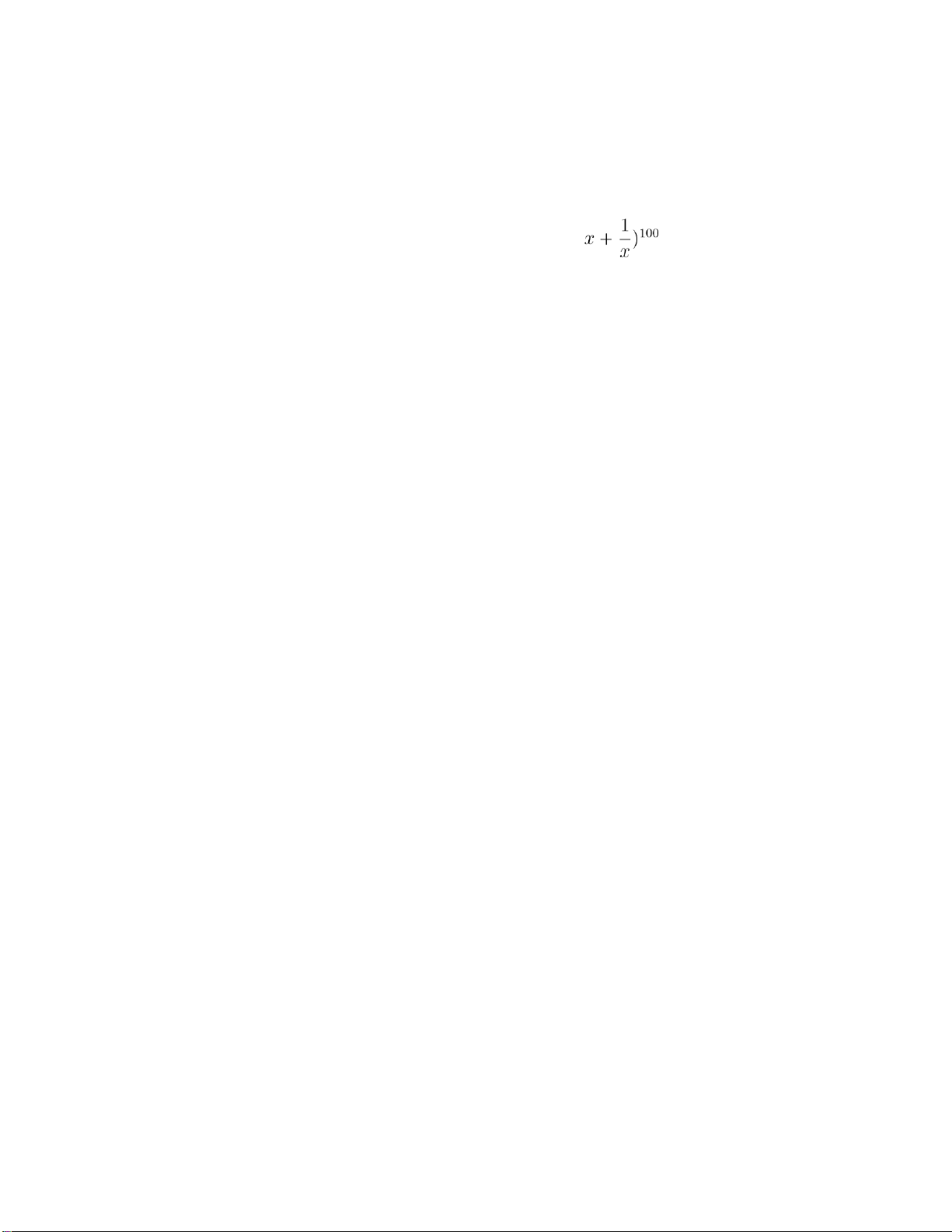
Preview text:
lOMoARcPSD| 40615933 Bài tập chương 3 lOMoAR cPSD| 40615933
Bài 1.1. Trong một lớp học có 12 sinh viên nam và 25 sinh viên nữ.
a. Có bao nhiêu cách chọn hai đại diện trong đó một là sinh viên nam, một là sinh viên nữ?
b. Có bao nhiêu cách chọn một đại diện hoặc là sinh viên nam hoặc là sinh viên nữ?
Bài 1.2. Một phiếu trắc nghiệm đa lựa chọn gồm 10 câu hỏi. Mỗi câu hỏi có 4 phương án trả lời.
a. Có bao nhiêu cách điền một phiếu trắc nghiệm nếu mọi câu hỏi đều được trả lời?
b. Có bao nhiêu cách điền một phiếu trắc nghiệm nếu có thể bỏ trống?
Bài 1.3. Có bao nhiêu người có họ tên viết tắt khác nhau bằng ba chữ cái trong bảng chữ cái tiếng Anh?
Bài 1.4. Có bao nhiêu người có họ tên viết tắt khác nhau bằng ba chữ cái trong bảng chữ cái
tiếng Anh mà không chữ nào bị lặp lại?
Bài 1.5. Có bao nhiêu xâu nhị phân có độ dài bằng 6?
Bài 1.6. Có bao nhiêu xâu tam phân có độ dài bằng 10 bắt đầu và kết thúc bởi số 1?
Bài 1.7. Có bao nhiêu xâu nhị phân (khác xâu rỗng) có độ dài ít hơn hoặc bằng n với n là một số nguyên dương?
Bài 1.8. Có bao nhiêu xâu chữ trong bảng chữ cái tiếng Anh có chiều dài bằng 4 và có chứa chữ x?
Bài 1.9. Trong những số nguyên dương có ba chữ số có bao nhiêu số a. chia hết cho 7?
b. có ba chữ số như nhau? c. chia hết cho 3 hoặc 4?
d. không chia hết cho 3 hoặc 4?
e. chia hết cho 3 nhưng không chia hết cho 4?
Bài 1.10. Có bao nhiêu xâu gồm ba chữ số trong hệ thập phân
a. không chứa cùng một chữ số ba lần?
b. bắt đầu bằng chữ số lẻ? lOMoARcPSD| 40615933
c. có đúng hai chữ số 2? d. có chứa chữ số 3?
Bài 1.11. Có bao nhiêu hàm khác nhau từ tập 10 phần tử đến tập a. có 3 phần tử? b. có 7 phần tử?
c. có n phần tử và là hàm đơn ánh với n là một số nguyên dương?
Bài 1.12. Có bao nhiêu hàm số từ tập t1,2,3,4,5,6u tới tập ta,b,c,du sao cho
a. đó là các hàm đơn ánh?
b. a là ảnh của 1 và 6?
c. b không là ảnh của 1 và d không là ảnh của 4?
Bài 1.13. Trong một đám cưới có 10 người kể cả cô dâu và chú rể. Để chụp ảnh người ta xếp 6
người thành một hàng. Hỏi có bao nhiêu cách xếp hàng nếu
a. mọi kiểu ảnh đều có cô dâu?
b. mọi kiểu ảnh đều có cô dâu và chú rể?
c. chỉ có cô dâu hoặc chú rể xuất hiện trong mọi kiểu ảnh?
d. mọi kiểu ảnh cô dâu đều đứng cạnh chú rể?
Bài 1.14. Có bao nhiêu xâu nhị phân độ dài bằng 8 bắt đầu bằng hai số 0 hoặc kết thúc bằng ba số 1?
Bài 1.15. Có bao nhiêu xâu nhị phân độ dài 10 và có năm số 0 hoặc năm số 1 liền nhau?
Bài 1.16. Dùng biểu đồ cây tìm số xâu nhị phân độ dài 4 không có ba số 0 liền nhau.
Bài 1.17. Có bao nhiêu cách xếp các chữ a,b,c,d sao cho chữ b không đi liền sau chữ a?
Bài 1.18. Dùng quy nạp toán học chứng minh quy tắc cộng cho m công việc từ quy tắc cộng cho hai việc.
Bài 1.19. Dùng quy nạp toán học chứng minh quy tắc nhân tính số cách làm một nhiệm vụ gồm
m việc từ quy tắc nhân cho hai việc.
Bài 1.20. Chứng tỏ rằng trong một lớp có 30 sinh viên thì ít nhất có 2 sinh viên có tên bắt đầu
bằng cùng một chữ cái.
Bài 1.21. Cho d là một số nguyên dương. Chứng tỏ rằng trong một nhóm tùy ý gồm d ` 1 số
nguyên có ít nhất hai số khi chia cho d có cùng số dư.
Bài 1.22. Cho S và T là hai tập hữu hạn và |S| ą |T|. Chứng minh rằng nếu f là một hàm từ tập
S đến tập T thì sẽ có ít nhất hai phần tử s1,s2 P S sao cho fps1q “ fps2q. lOMoARcPSD| 40615933
Bài 1.23. Mỗi sinh viên trong một trường đại học có quê ở một trong 26 tỉnh. Cần phải tuyển
ít nhất bao nhiêu sinh viên để chắc chắn có 50 sinh viên cùng tỉnh?
Bài 1.24. Cho pxi,yiq, i “ 1,2,3,4,5 là tập hợp gồm năm điểm khác nhau có các tọa độ nguyên
trên mặt phẳng Oxy. Chứng tỏ rằng có ít nhất một trung điểm của đoạn nối các cặp điểm này có tọa độ nguyên.
Bài 1.25. Cần có bao nhiêu cặp số nguyên pa,bq để chắc chắn có hai cặp số nguyên pa1,b1q và
pa2,b2q sao cho a1 mod 5 “ a2 mod 5 và b1 mod 5 “ b2 mod 5?
Bài 1.26. Chỉ ra rằng trong 5 số chọn từ 8 số nguyên dương đầu tiên nhất thiết có một cặp có tổng bằng 9.
Bài 1.27. Chỉ ra rằng trong 7 số chọn từ 10 số nguyên dương đầu tiên chắc chắn có hai cặp có tổng bằng 11.
Bài 1.28. Có 51 ngôi nhà trong một phố. Mỗi ngôi nhà có địa chỉ là một trong những con số
từ 1000 đến 1099. Chỉ ra rằng ít nhất có hai nhà có địa chỉ là hai số nguyên liên tiếp.
Bài 1.29. Chỉ ra rằng trong một nhóm có 5 người trong đó hai người bất kỳ hoặc là bạn hoặc là
thù không phải luôn có ba người là bạn của nhau hoặc là kẻ thù của nhau.
Bài 1.30. Một mạng máy tính gồm có 6 máy. Mỗi máy nối trực tiếp hoặc không nối với những
máy khác. Chỉ ra rằng có ít nhất hai máy mà số máy khác nối với chúng là bằng nhau.
Bài 1.31. Cho A là tập hợp có 10 phần tử mà mỗi phần tử là một trong những số nguyên từ 1
đến 50. Chứng minh rằng có ít nhất hai tập con gồm 5 phần tử của A có tổng các phần tử bằng nhau.
Bài 1.32. Liệt kê tất cả các hoán vị của tập ta,b,cu.
Bài 1.33. Có bao nhiêu hoán vị của tập ta,b,c,d,eu với phần tử cuối cùng là a?
Bài 1.34. Có bao nhiêu thứ tự có thể xảy ra trong cuộc thi chạy giữa 20 vận động viên?
Bài 1.35. Có bao nhiêu khả năng có thể xảy ra đối với những vị trí thứ nhất, thứ nhì và thứ ba
trong cuộc đua có 12 con ngựa, nếu mọi thứ tự đều có thể?
Bài 1.36. Một nhóm sinh viên gồm n nam và n nữ. Có bao nhiêu cách xếp
a. nam nữ đứng xen kẽ nhau thành một hàng?
b. nam nữ đứng xen kẽ nhau thành một vòng tròn?
c. cả nhóm thành hai hàng sao cho đối diện với một nam là một nữ?
Bài 1.37. Có bao nhiêu cách chọn một tập hợp 5 chữ từ bảng chữ cái tiếng Anh?
Bài 1.38. Có bao nhiêu xâu nhị phân độ dài 10 có: a. đúng 3 số 0?
b. số các số 0 bằng số các số 1? lOMoARcPSD| 40615933 c. ít nhất 7 số 1? d. ít nhất 3 số 1?
Bài 1.39. Một đội bóng gồm 15 cầu thủ.
b. Có bao nhiêu cách chọn 11 cầu thủ sao cho mỗi cầu thủ chơi ở một vị trí đã định?
c. Trong 15 cầu thủ có 4 cầu thủ dự bị. Có bao nhiêu cách chọn 11 cầu thủ sao cho có ít nhất một cầu thủ dự bị?
Bài 1.40. Có bao nhiêu cách rút 5 quân từ bộ bài gồm 52 quân thỏa mãn: a. Có tứ quý át?
b. Có cả 5 quân đều cùng một chất?
c. Có đúng một đôi (không nhất thiết cùng màu)?
d. Có ít nhất một đôi (không nhất thiết cùng màu)?
Bài 1.41. Một khách sạn có 10 tầng. Năm khách hàng cùng đi lên thang máy từ tầng một và
chọn tầng ra một cách ngẫu nhiên và độc lập. Hỏi có bao nhiêu cách để:
a. Tất cả cùng ra ở tầng năm?
b. Tất cả cùng ra ở một tầng?
c. Mỗi người ra ở một tầng khác nhau?
d. Năm người ra ở bốn tầng khác nhau?
Bài 1.42. Từ tập các số nguyên dương không vượt quá 100 có thể tạo được bao nhiêu chỉnh
hợp chập 4 chứa 3 số nguyên liên tiếp
a. Theo trật tự thông thường và có thể bị ngăn cách bởi các số khác của chỉnh hợp?
b. Tại những vị trí liên tiếp của chỉnh hợp?
Bài 1.43. Trong bảng chữ cái tiếng Anh có 21 phụ âm và 5 nguyên âm. Có bao nhiêu xâu gồm
6 chữ thường phân biệt chứa a. đúng một nguyên âm?
b. ít nhất hai nguyên âm? c. chữ a?
d. chữ a và chữ b?
Bài 1.44. Có bao nhiêu xâu nhị phân chứa đúng tám số 0 và mười số 1 và ngay sau mỗi số 0
nhất thiết là một số 1?
Bài 1.45. Có bao nhiêu xâu nhị phân độ dài 10 chứa ít nhất ba số 0 và ít nhất bốn số lOMoARcPSD| 40615933 1?
Bài 1.46. Tìm khai triển của p2x ´ 3yq5.
Bài 1.47. Tìm hệ số của x4y6 trong khai triển của px ` 2yq10
Bài 1.48. Tìm công thức tính hệ số của xk trong khai triển của p
với k là số tự nhiên.
Bài 1.49. Cho S là một tập hữu hạn. Chứng minh rằng số các tập con có số phần tử lẻ cũng bằng
số các tập con có số phần tử chẵn của S.
Bài 1.50. Có bao nhiêu cách chọn lần lượt có hoàn lại 5 phần tử từ tập gồm 3 phần tử? Bài
1.51. Có bao nhiêu xâu gồm 6 chữ cái trong bảng chữ cái tiếng Anh?
Bài 1.52. Có bao nhiêu cách phân 3 công việc cho 5 người làm nếu một người có thể làm được nhiều việc?
