Bài tập Định tuyến router | Trường Cao đẳng Công nghệ Thủ Đức

BÀI TẬP CHƯƠNG 4 Bài 1:
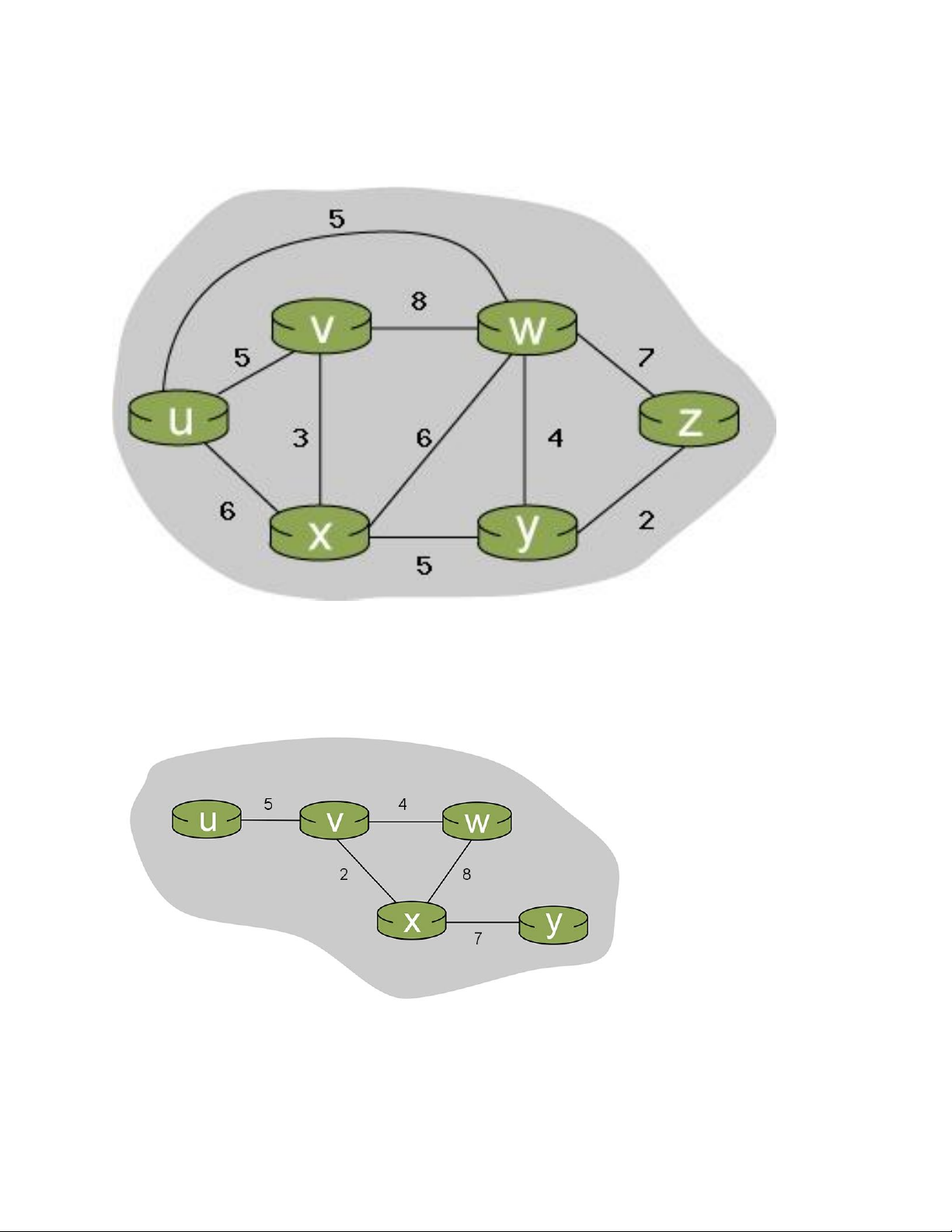
Cho mô hình mạng sau đây
a. Sử dụng thuật toán Dijsktra tìm đường đi ngắn nhất từ node u đến các node còn lại
b. Sử dụng thuật toán Dijsktra tìm đường đi ngắn nhất từ node y đến các node còn lại Bài 2:
Cho mô hình mạng sau đây:
Sử dụng thuật toán Bellman-Ford để xác định đường đi ngắn nhất với các bước sau:
a. Xác định vector ban đầu của mỗi node
b. Xác định vector của mỗi node sau mỗi lần trao đổi thông tin Bài 3:
Giả sử router có 4 links, được đánh số 0 đến 3 tương ứng với mỗi link là các network/địa chỉ đích như sau:
Destination Address Range Link Interface
11100000 00000000 00000000 00000000 through 0
11100000 00111111 11111111 11111111
_____________________________________________________________________
11100000 01000000 00000000 00000000 through 1
11100000 01000000 11111111 11111111
_____________________________________________________________________
11100000 01000001 00000000 00000000 through 2
11100001 01111111 11111111 11111111
_____________________________________________________________________ otherwise 3
Từ bảng forwarding trên, router sẽ xử lý các gói tin như thế nào nếu gói tin có địa chỉ đích như sau:
11001000 10010001 01010001 01010101
11100001 01000000 11000011 00111100
11100001 10000000 00010001 01110111
Bài 4: Cho tập hợp các router N = { u, v, w, x, y, z }, chi phí kết nối giữa các router như
sau: c(u,v) = 2;c(u,x) = 1;c(u,w) = 7;c(v,x) = 2; c(v,w) = 3;c(x,w) = 3,c(w,y) = 1;c(y,z) = 2; c(w,z) = 6;c(x,y)=1.
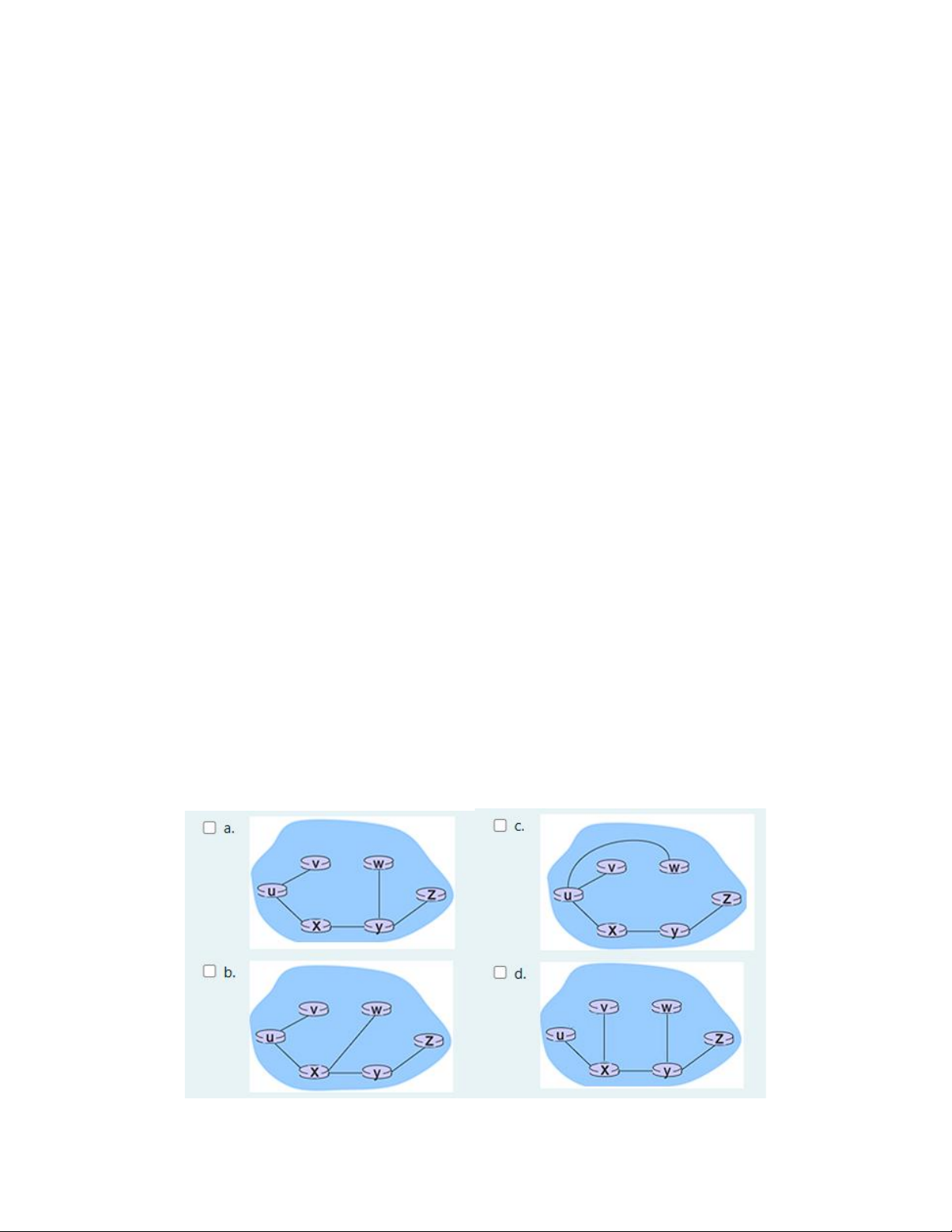
Dùng thuật toán Dijkstra để xác định đường đi ngắn nhất từ đỉnh u đến các đỉnh còn lại,
cây đường đi tìm được sẽ là:
Bài 5: Cho mô hình mạng như sau, giả sử các router sử dụng thuật toán Bellman-Ford,
hãy xác định vector khởi tạo ban đầu của x (trình bày dưới dạng u,v,x,y,w - nếu là ∞ thì viết là x.
Bài 6: Cho bảng forwarding như sau:
Giả sử router tiếp nhận và chuyển tiếp các gói tin có địa chỉ đích là địa chỉ 8bits và sử
dụng phương pháp "Longest match prefix" - So sánh phần đầu dài nhất.
Xác định địch chỉ đích và interface tương ứng cho các trường hợp dưới đây. 10000101 01010001 10001011