Chuyên đề: Giá trị lớn nhất – nhỏ nhất của hàm số. Bài tập tự luyện Câu 1: Gọi
và lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn . Tính . A. . B. . C. . D. .
Câu 2: Giá trị lớn nhất của hàm số trên đoạn bằng A. 1. B. 4. C. 5. D. 3.
Câu 3: Giá trị lớn nhất của hàm số trên đoạn bằng A. . B. . C. . D. .
Câu 4: Giá trị nhỏ nhất của hàm số trên đoạn là A. . C. . D. . B. .
Câu 5: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số A. B. C. D.
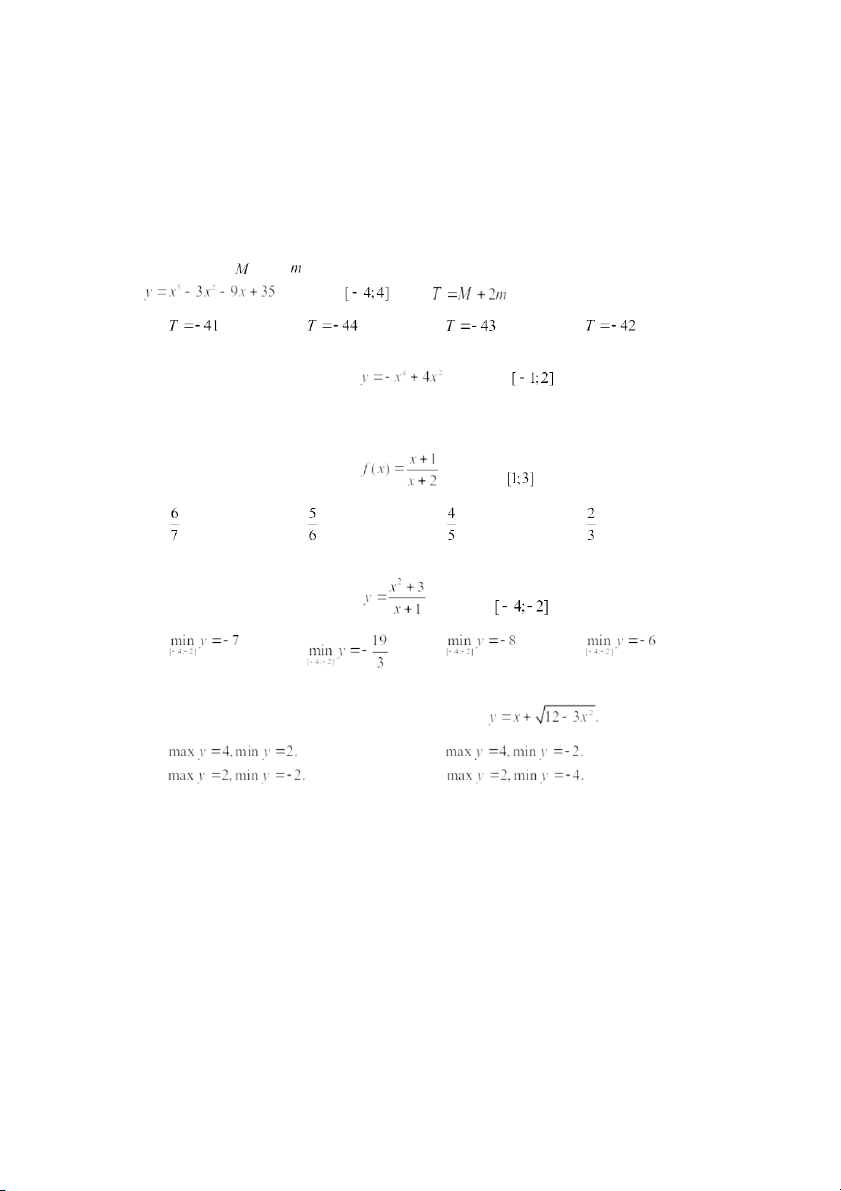
Câu 6: Cho hàm số có bảng biến thiên như hình bên. Xét ba khẳng định sau:
(1) Hàm số đồng biến trên khoảng
(2) Hàm số có một cực đại.
(3) Hàm số có giá trị lớn nhất bằng 3.
Số khẳng định đúng trong ba khẳng định trên là A. 1. B. 2. C. 3. D. 0.
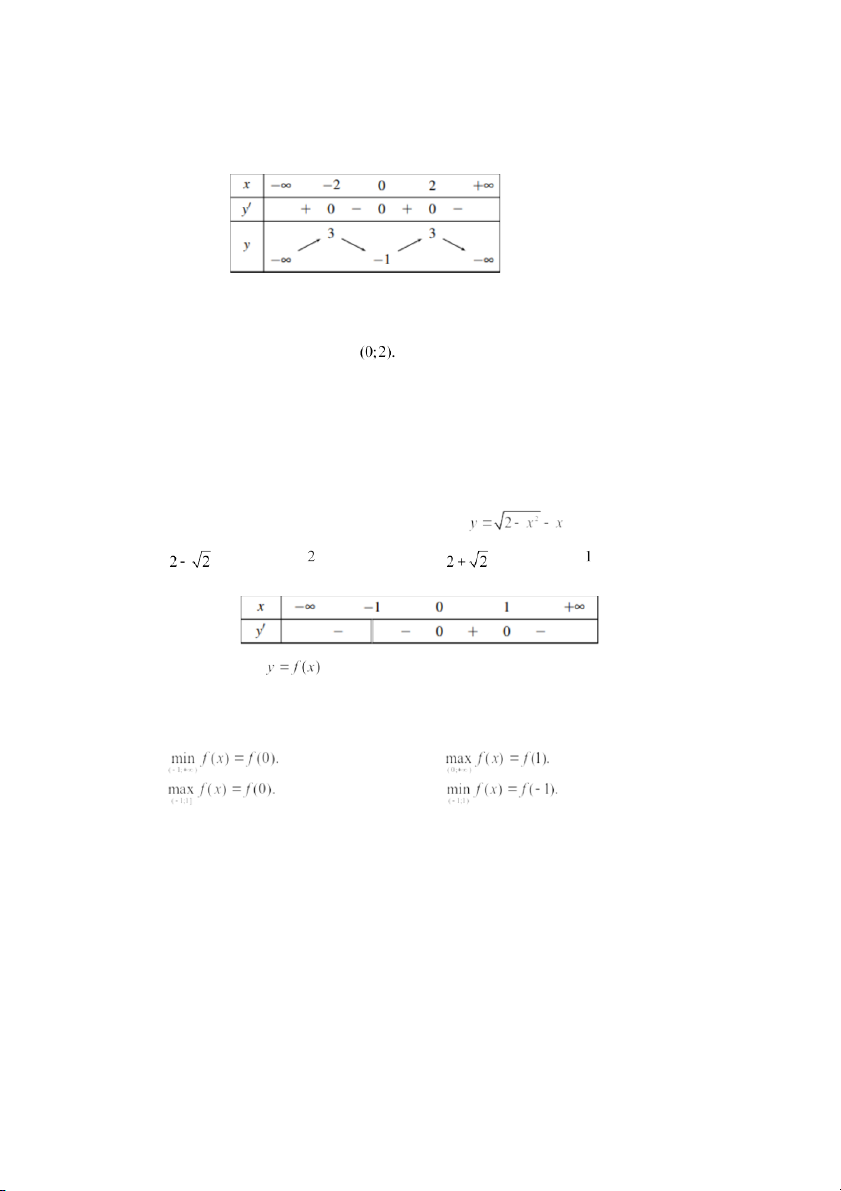
Câu 7: Tổng giá trị nhỏ nhất và lớn nhất của hàm số bằng bao nhiêu? A. . B. . C. . D. . Câu 8: Cho hàm số
có bảng xét dấu đạo hàm như sau:
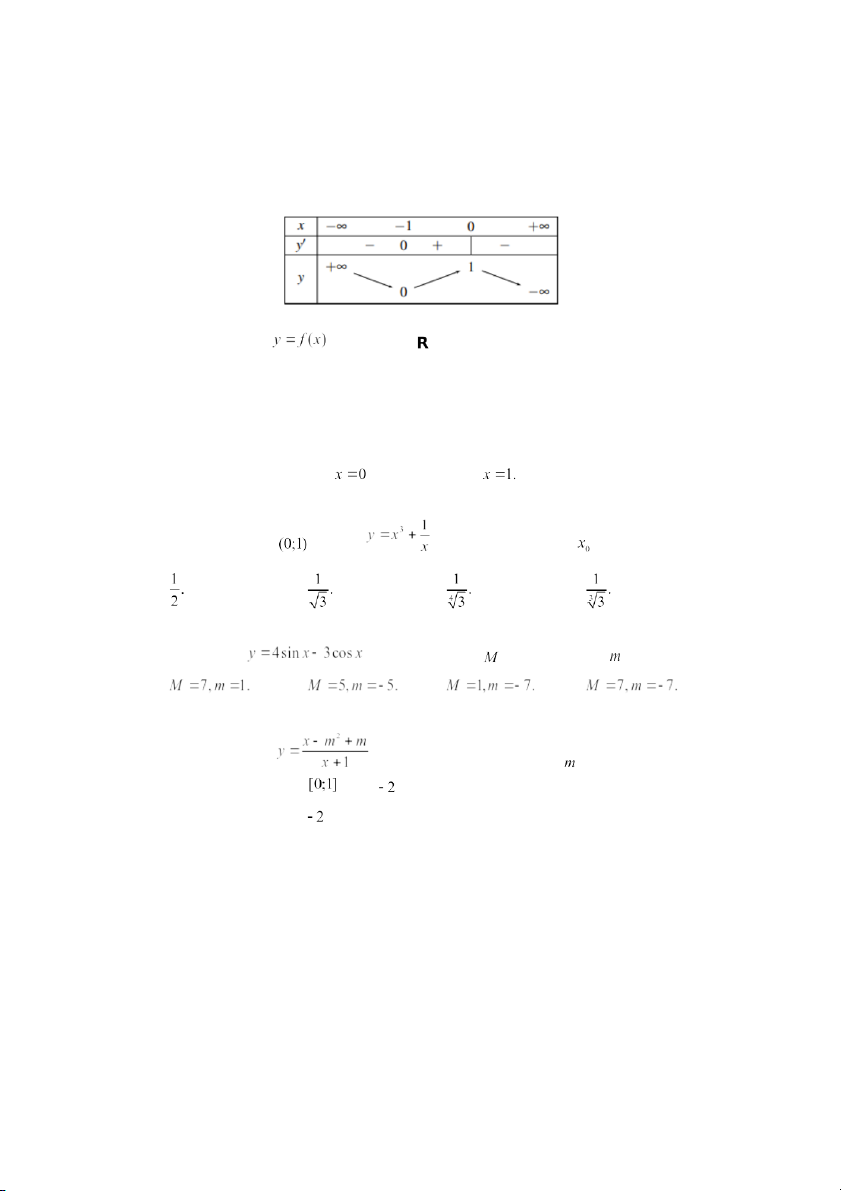
Mệnh đề nào sau đây đúng? A. B. C. D. Câu 9: Cho hàm số
liên tục trên và có bảng biến thiên như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 1.
C. Hàm số giá trị cực đại bằng 0.
D. Hàm số có đạt cực tiểu tại
và đạt cực đại tại Câu 10: Trên khoảng , hàm số
đạt giá trị nhỏ nhất tại bằng A. B. C. D. Câu 11: Hàm số có giá trị lớn nhất , giá trị nhỏ nhất là A. B. C. D. Câu 12: Cho hàm số
. Tổng các giá trị của tham số sao cho giá trị nhỏ
nhất của hàm số trên đoạn bằng là A. 2. B. . C. 0. D. 1.
Câu 13: Gọi là tập hợp tất cả giá trị của tham số để hàm số có giá trị lớn nhất
bằng . Tính tổng của các phần tử trong . C. . D. . A. . B. .
Câu 14: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số là B. . A. . C. . D. .
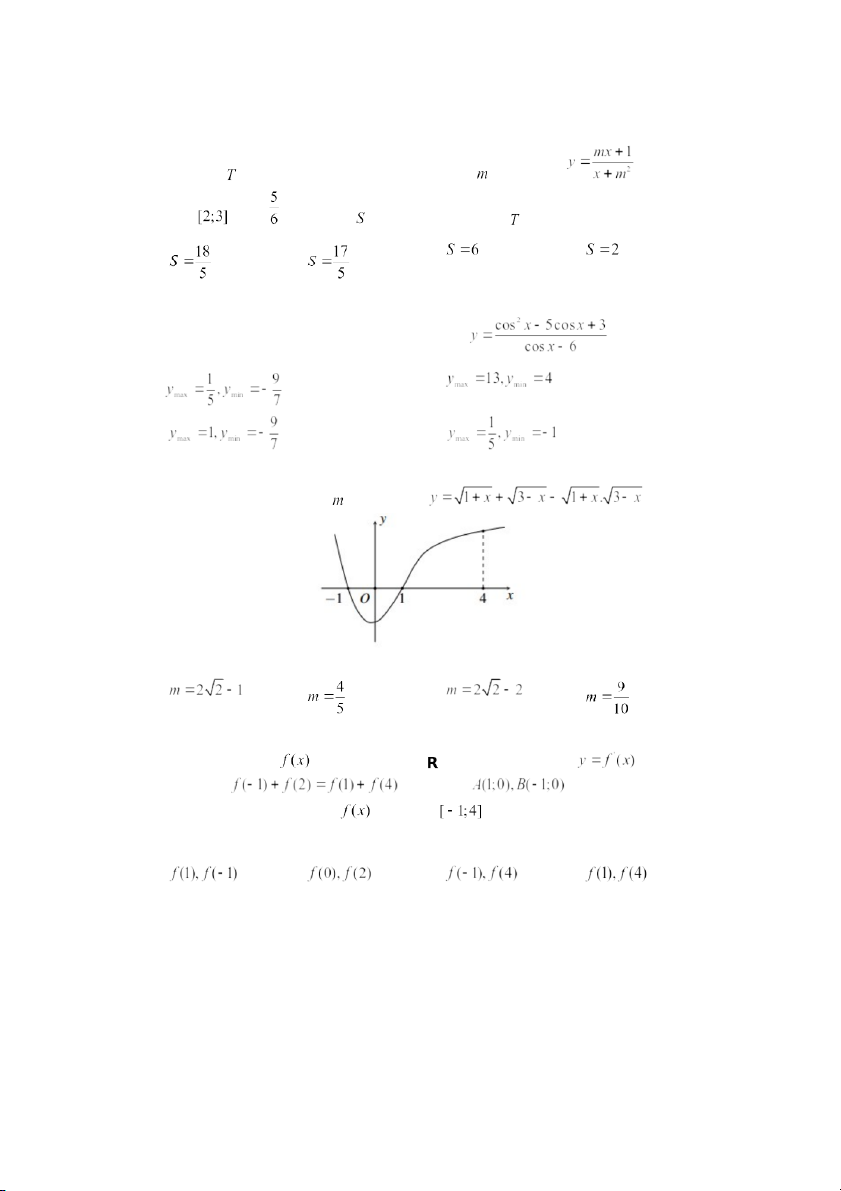
Câu 15: Tìm giá trị nhỏ nhất của hàm số trên tập xác định của nó. A. . C. . B. . D. . Câu 16: Cho hàm số
có đạo hàm trên và có đồ thị hàm số như hình vẽ. Biết rằng , các điểm
thuộc đồ thị. Giá trị
nhỏ nhất và giá trị lớn nhất của trên đoạn lần lượt là A. . B. . C. . D. .
Câu 17: Tìm để bất phương trình có nghiệm thực. A. . B. . C. . D. . Câu 18: Cho hàm số , với là tham số. Biết .
Hãy chọn kết luận đúng? A. . B. . C. . D. .
Câu 19: Tìm giá trị của tham số để bất phương trình nghiệm đúng với mọi . A. . D. . B. . C. . Câu 20: Cho
. Giá trị nhỏ nhất của biểu thức bằng A. . B. . C. . D. . Câu 21: Cho hai số thực
thay đổi thỏa mãn điều kiện . Gọi lần lượt
là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Giá trị của bằng A. . C. . D. . B. . Câu 22:
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số . Tìm . A. 9. B. . C. . D. . Câu 23: Cho biểu thức với
khác 0. Giá trị nhỏ nhất của bằng A. . B. 0. C. . D. 1.
Câu 24: Tìm giá trị nhỏ nhất của hàm số trên khoảng A. . B. . C. . D. . Câu 25: Gọi
lần lượt là giá trị nhỏ nhấy và giá trị lớn nhất của hàm số . Tính tích A. . B. . C. . D. .