 TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC
I. KIẾN THỨC CƠ BẢN
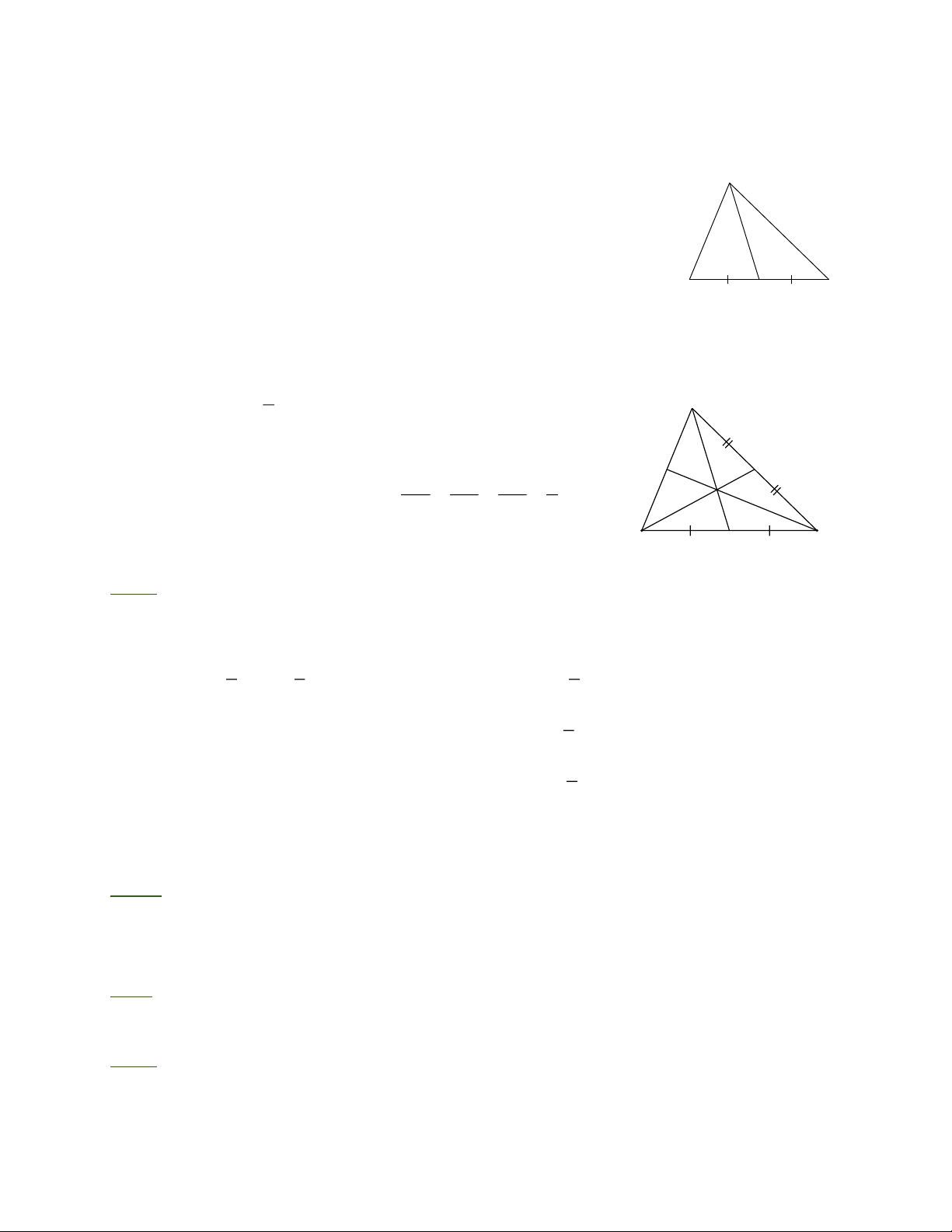
Đường trung tuyến của tam giác A
Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M
của cạnh BC gọi là đường trung tuyến của tam giác ABC .
 Mỗi tam giác có ba đường trung tuyến. B M C
Tính chất ba đường trung tuyến của tam giác
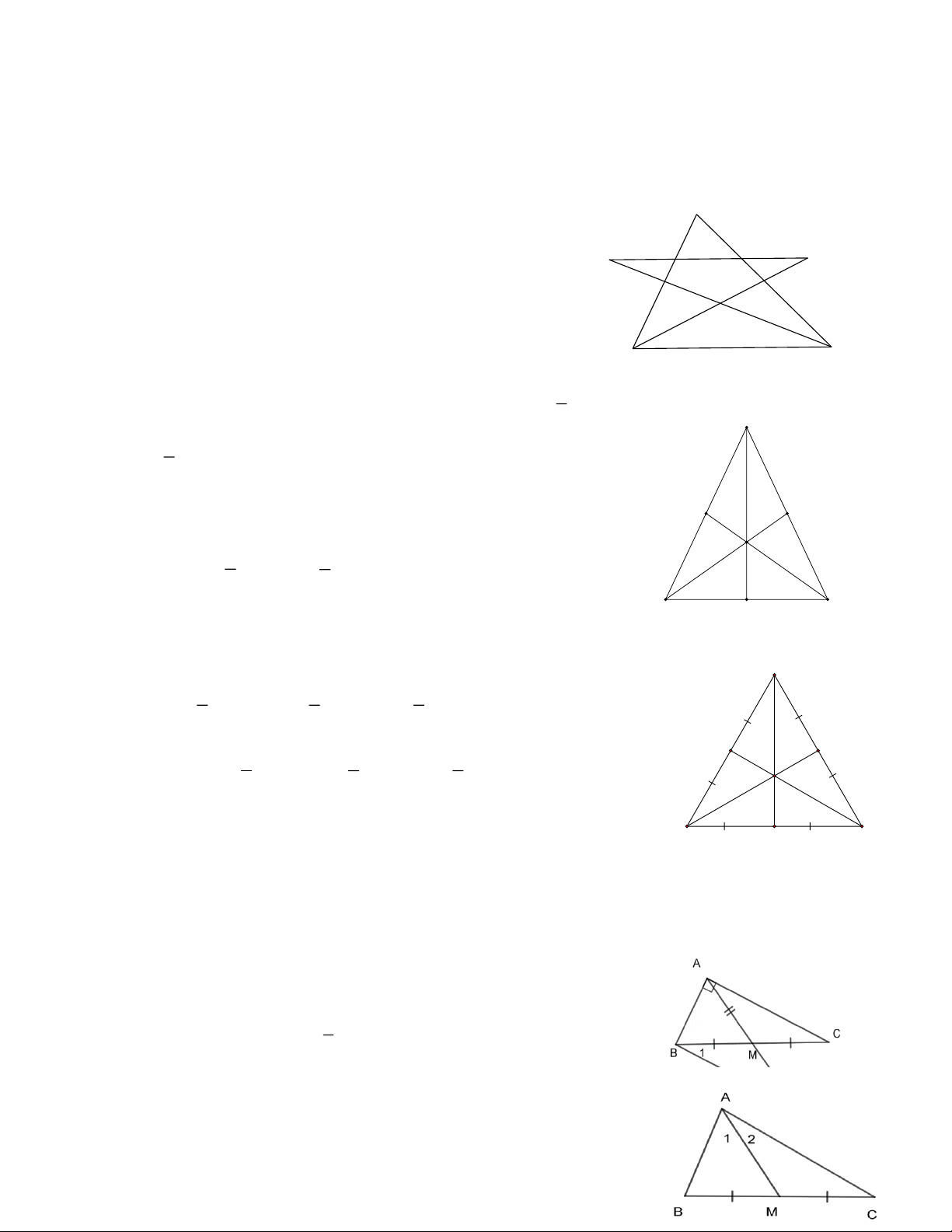
Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh 2
một khoảng bằng độ dài đường trung tuyến đi qua đỉnh A 3 ấy. F E  AG BG CG 2
G là trọng tâm tam giác ABC thì    . AD BE CF 3 G II. BÀI TẬP B D C Bài 1:
Từ các đẳng thức trên, hãy suy ra các đẳng thức khác: 1 1 2 GD = A D = ................... A G =
A D = ................................... 3 2 3 2 BG =
BE = .....................................
GE = ¼ ¼ ¼ ¼ = ¼ ¼ ¼ ¼ 3 2 CG =
CF = ....................................
GF = ¼ ¼ ¼ ¼ = ¼ ¼ ¼ ¼ 3
A D = ¼ ¼ ¼ = ¼ ¼ ¼ ; BE = ¼ ¼ ¼ = ¼ ¼ ¼ ; CF = ¼ ¼ ¼ = ¼ ¼ ¼
Bài 2: Cho tam giác ABC có hai đường trung tuyến BP,CQ cắt nhau tại .
G Trên tia đối của
tia PB lấy điểm E sao cho PE  P .
G Trên tia đối của tia QG lấy điểm F sao cho QF  Q .
G Chứng minh rằng: a) GB  GE,GC  GF;
b) EF  BC và EF // BC.
Bài 3: Tam giác ABC có các đường trung tuyến BD và CE bằng nhau. Chứng minh rằng A  BClà tam giác cân. Bài 4: Cho ABC Δ
có 3 đường trung tuyến A ,
D BE,CF đồng quy tại G . a) Nếu ABC Δ
đều hãy chứng minh: GD  GE  GF . Trang 1
b) Đảo lại, nếu có GD  GE  GF khi đó hãy chứng minh tam ABC Δ đều.
Bài 5: : Chứng minh rằng, trong một tam giác vuông, đường trung tuyến ứng với cạnh
huyền bằng một nửa cạnh huyền.
Bài 6: Chứng minh rằng nếu một tam giác có đường trung tuyến tương ứng với một cạnh
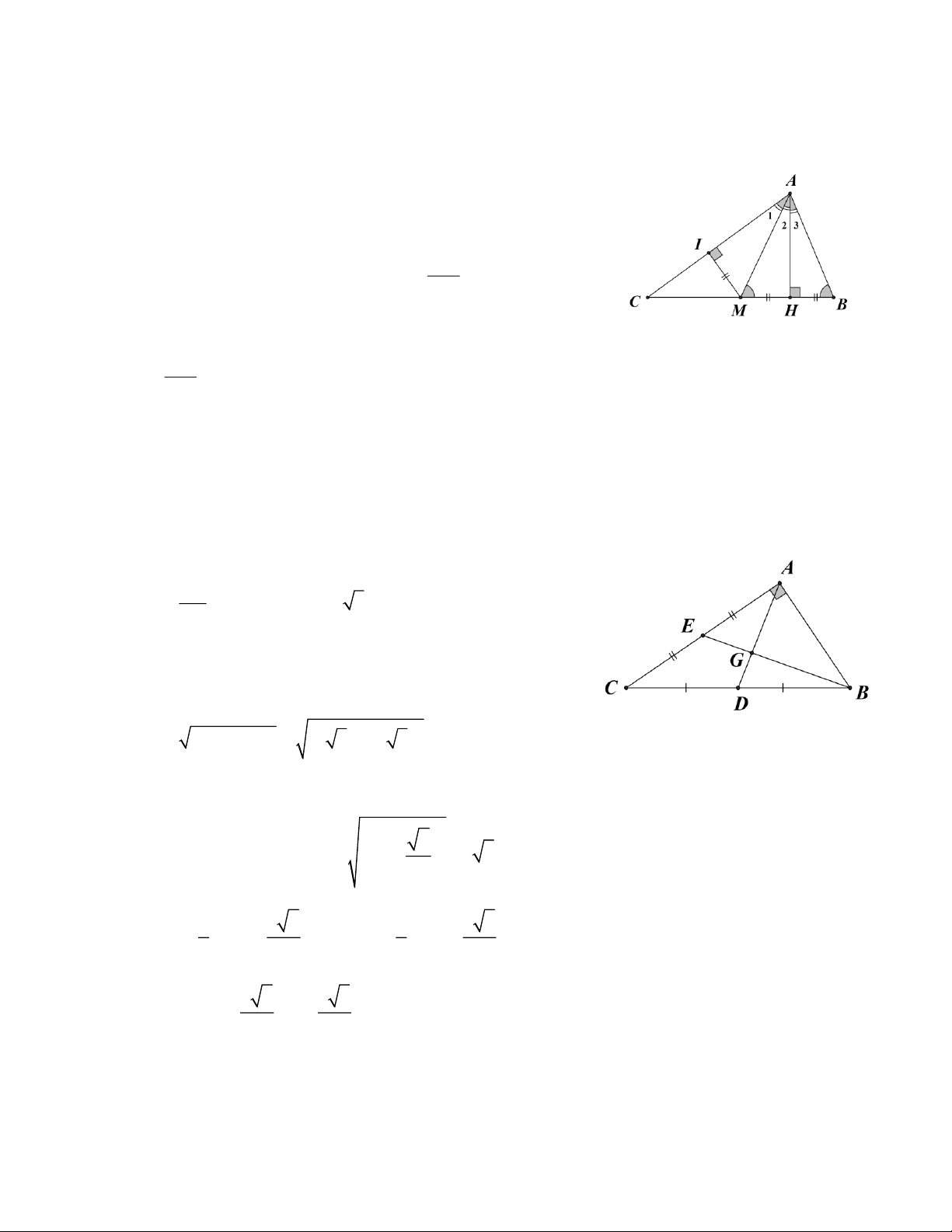
bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông. Bài 7: Cho ABC  cân ở ,
A AB  34c , m
BC  32cm và 3 trung tuyến AM , BN,CP đồng
quy tại trọng tâm G .
a) Chứng minh A M ^ BC
b) Tính độ dài AM , BN,CP . (làm tròn kết quả đến chữ số thập phân thứ hai). Bài 8: ABC Δ
có đường cao AH , trung tuyến AM (H n»m gi÷a M, B) . Cho biết · · ·
BA H = HA M = MA C .
a) Chứng minh MC  2MH
b) Vẽ MI  AC tại I. Chứng minh IMB  2.ABC .
c) Tính các góc của ABC Δ . Bài 9: Cho ABC Δ
vuông tại A có AD là trung tuyến. 1 a) Chứng minh A D = B C . 2
b) Biết AC  8 c ,
m AD  3 cm + Tính cạnh AB.
+ Trung tuyến BE của ABC Δ
cắt AD tại G. Tính BE và chứng minh A  GB là tam giác vuông.
Bài 10: Cho ABC Δ
có hai trung tuyến AM và BN vuông góc với nhau tại G. Chứng minh 2 2 2
BC  CA  5AB .
CÓ THỂ EM CHƯA BIẾT
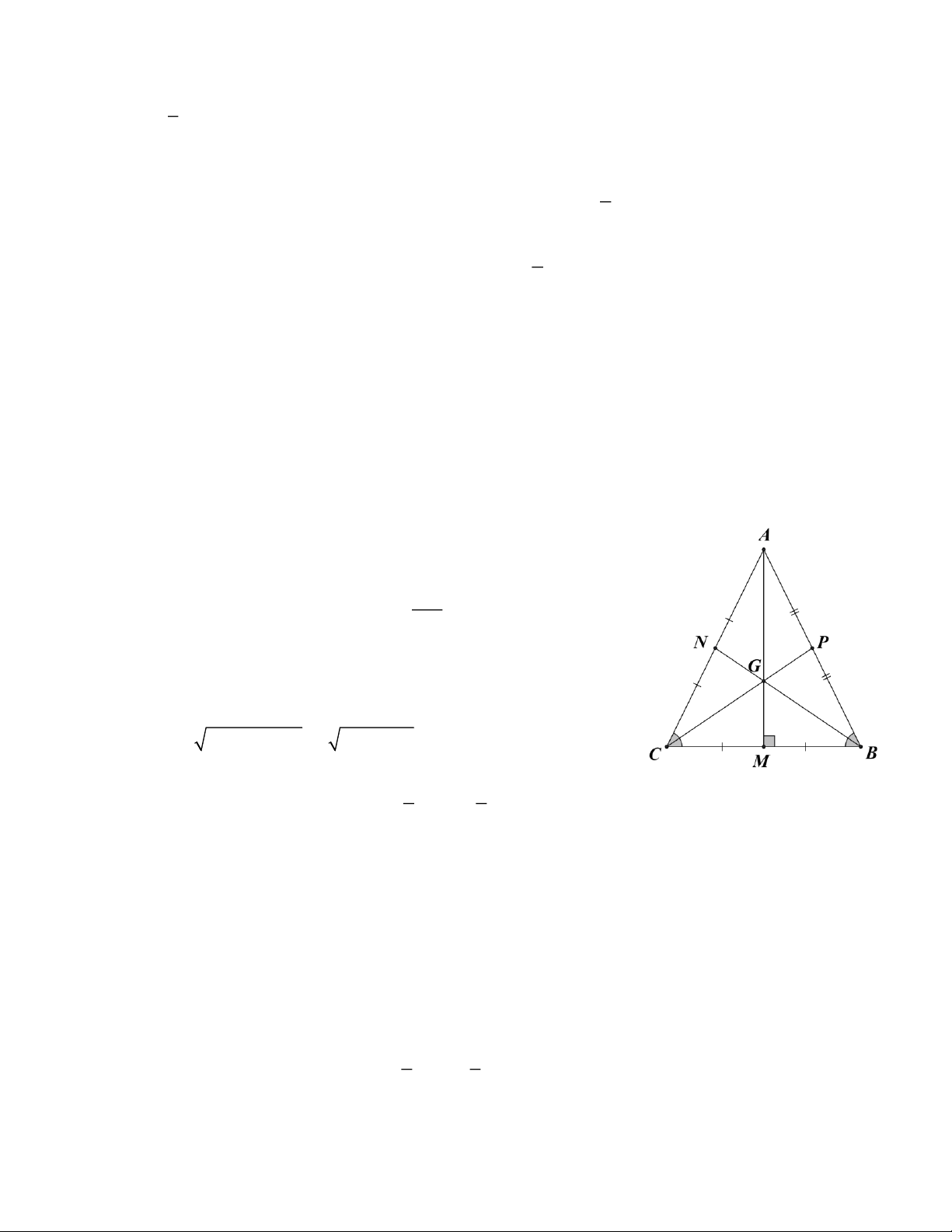
Mỗi trung tuyến chia thành 2 tam giác có diện tích bằng nhau.
Nối 3 đỉnh của tam giác với trọng tâm của nó ta được 3 tam giác nhỏ có diện tích bằng nhau.
3 trung tuyến của tam giác phân tam giác thành 6 tam giác nhỏ có diện tích bằng nhau. Hết Trang 2 HDG
Bài 1: Hs tự điền Bài 2: A
a) Vì G là trọng tâm ABC nên : BG  2GP,CG  2G . Q
Lại có PE  PG,QF  QG nên : GE  2GP,GF  2G . Q F E
Do đó BG  GE,CG  GF. Q G P
b) Suy ra : GBC  GEF (c.g.c)
Từ đó ta có EF  BC và GEF  GBC  EF // BC. B C 2
Bài 3: Gọi G là giao điểm của BD và CE, ta có BG = BD, 3 A 2
CG = CE . Do BD  CE nên BG  CG, GD  GE 3 B  GE  C
 GD  .cg.c  BE  CD E D G 1 Ta lại có BE  1 AB, CD 
AC nên AB  AC . Vậy ABC  là tam 2 2 giác cân. B C
Bài 4: a) Vì ABC Δ
đều nên AD  BE  CF A 1 1 1 mà EG = EB ; FG = CF ; DG =
A D Þ GE = GF = GD 3 3 3 E F 1 1 1 b) Ta có: EG = EB ; FG = CF ; DG = A D G 3 3 3
mà GE = GF = GD Þ A D = BE = CF C B D
BE  CF  AB  AC ( đã chứng minh bài 3 )
A D = BE Þ CA = CB
Þ AB = BC = CA Þ A Δ BC đều.
Bài 5: Xét ABC 
vuông tại A, đường trung tuyến AM. 1
Ta sẽ chứng minh A M = B C 2
Trên tia đối của tia MA lấy điểm D sao cho MD = MA . Ta có Trang 3 1 ¶ µ MA =
A D , cần chứng minh. Dễ thấy B  MD  C
 MA(c.g.c)Þ BD = AC, B = C do đó 2 1
BD//AC . Ta lại có BAC  90 nên ABD  90 . Do đó C  AB  D
 BA(vì cạnh AB chung, 1
CAB  DBA  90 , AC  BD ), suy ra BC  AD . Vậy AM  BC 2 1
Bài 6: Xét ABC 
, đường trung tuyến AM có AM  BC . 2
Ta sẽ chứng minh BAC  90 . Dễ thấy M
A  MB  MC .
Các tam giác MAB, MAC cân tại M nên: B  A , . C  A 1 2 µ µ µ ¶ ·
Do đó B + C = A + A = BA C 1 2
Ta lại có B  C  BAC  180 nên BAC  90 Bài 7: · ·
a) DA MB = DA MC (c. c. c) Þ A MB = A MC = 90° BC
b) Vì M là trung điểm BC Þ BM = = 16cm 2
Áp dụng định lí Pitago cho tam giác vuông ABM ta có: 2 2 2
A M + MB = A B 2 2 2 2 Þ A M = A B - MB = 34 - 16 = 30cm 1 1
Vì G là trọng tâm ΔA BC Þ GM = A M = .30 = 10cm 3 3 ìï µ µ
ï B = C (gt ) ïï
Xét ΔCBP và B
Δ CN có: í BC chung
Þ DCBP = DBCN (c. .
g c) Þ CP = B N ï
ïïCN = PB (AB = AC ) ïïî
Áp dụng định lí Pitago cho tam giác vuông GBM ta có: 2 2 2
GM + MB = MB 2 2 2
Þ MB = 10 + 16 = 356 Þ BM » 18, 87cm 3 3
Vì G là trọng tâm ΔA BC Þ BN = B G = .18, 87 = 28, 31cm 2 2
Vậy A M = 30cm; BN = CP = 28, 31cm Trang 4 Bài 8:
a) D A BH = D A MH (c.g.c) Þ BH = HM Þ BM = 2HM = MC b) Chỉ ra A Δ HM  A
Δ IM (ch  gn)  AMH  AMI
mà AMH  ABH (theo a)  BMI  2.ABC CM
c) Ta có: ΔAMI  ΔAMH  IM  MH  2
Trong tam giác vuông CMI có CM µ 0 · 0 · 0 µ 0 IM =
Þ C = 30 Þ CMI = 60 Þ IMB = 120 Þ B = 60 2 µ Þ µ µ
A = 90° . Vậy tam giác ABC có: C = 30 ; ° B = 60 ; ° µ A = 90°
Chứng minh bổ đề: Trong một tam giác vuông, góc đối diện với cạnh cạnh góc vuông bằng nửa
cạnh huyền thì bằng 30° Bài 9: BC a) AD 
 BC  2AD  2 3cm 2
b) Áp dụng định lí Pitago cho tam giác vuông ABC ta có: 2 2 2
BC  AB  AC
 AB  BC  AC   2  2 2 2 2 3 8  2cm
Áp dụng định lí Pitago cho tam giác vuông ABE ta có: 2 æ ö ç 8 ÷ 2 2 2 2
BE = A B + A E Þ BE = 2 + ç ÷ ç ÷ = 6 cm ç 2 ÷÷ è ø 2 2 3 2 2 6 mà A G = A D = cm ; BG = BE = cm 3 3 3 3 2 2 æ ö æ ö 2 ç 3 ÷ 2 ç 6 ÷ 2 2 2 A G + BG = ç ÷ ç ÷ + ç ÷ Þ D
vuông tại G ( Pitago đảo) ç ÷ ç ÷ = 4 = A B A GB ç 3 ÷ ç è ø 3 ÷ ÷ è ø
Bài 10: Vì AM  BN nên : Trang 5 2 2 2 2
BC + CA = (2BM ) + (2A N ) 2 2 2 2
= 4(BG + GM + GN + A G ) = ( 2 2 GB + A G )+ ( 2 2 4 4 GM + GN ) 2 2 é ù 1 æ ö ç ÷ 1 æ ö ê ç ÷ ú 2 2 = 4A B + 4 ç
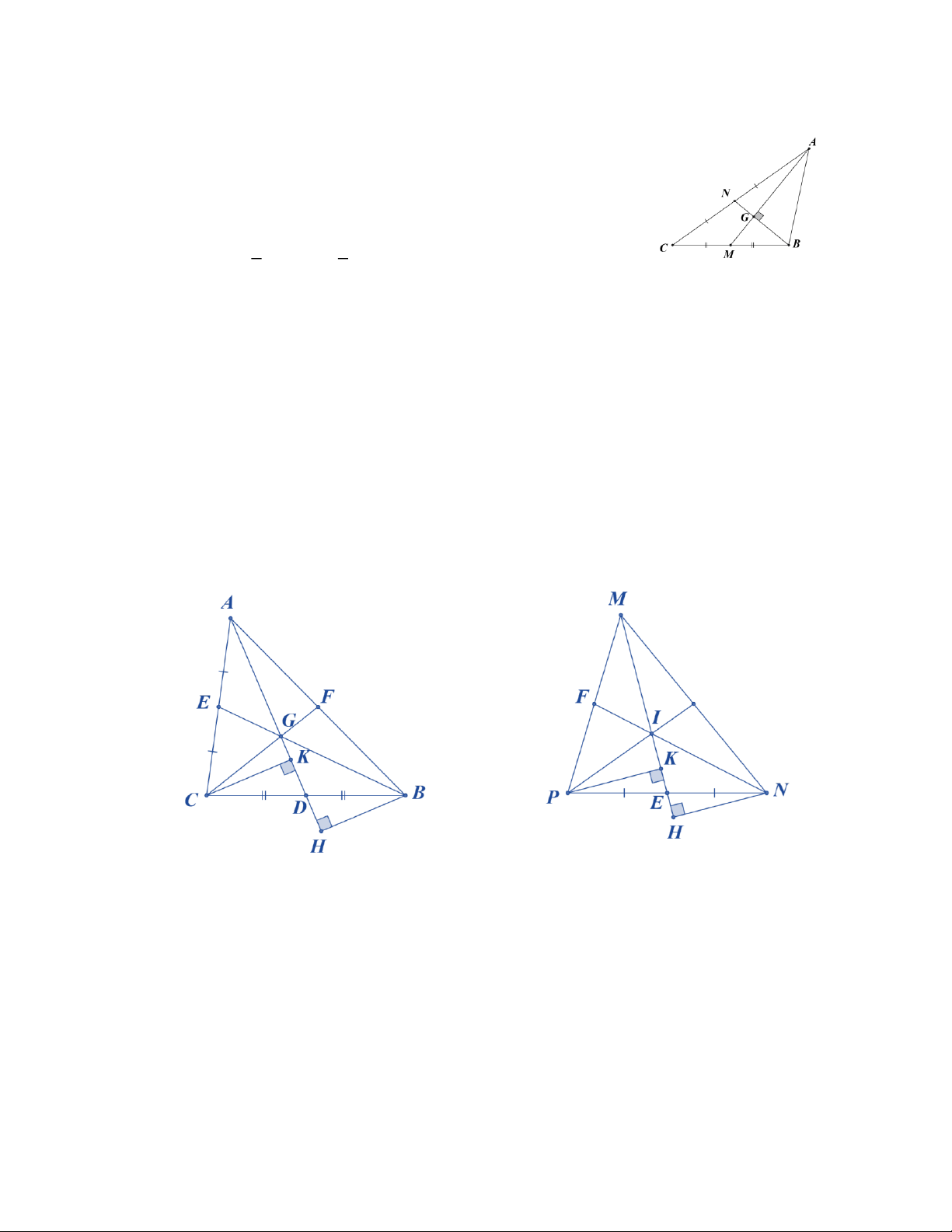
ê A G ÷ + ç BG ÷ = ç ÷ ç ÷ ç ÷ ú 5A B ê 2 è ø 2 ç ÷ è ø ú ë û Bài tập bổ sung: 1) Cho ABC Δ
có hai trung tuyến BE và CF cắt nhau tại G. Đường thẳng AG cắt BC tại D.
Kẻ BH  AD tại H và CK  AD tại K. Chứng minh: a) BH  CK b) S  S  S A  GB A  GC C
 GB ( S là diện tích) 2) Cho M
Δ NP . Gọi I là một điểm nằm trong tam giác. Chứng minh rằng nếu S  S  S Δ I  GN M  IP N
 IP thì I là trọng tâm của MNP
a) DBDH = DCKD(ch - gn ) Þ BH = CK
b) Xét ΔAGB và A
Δ GC có cạnh AG chung mà: ìï BH ^ AD
ïïïíCK ^ AD Þ S = S . Chứng minh tương tự ta được: S  S ΔA GB ΔA GC ï ΔBGC Δ AGC ïï BH = CK ïî Vậy S  S  S A  GB B  GC A  GC
2) Gọi MI  NP   
E ; NI  MP  F Trang 6
Kẻ NH  ME tại H, PK  ME tại K 1 1 Þ S = S Þ MI .NH = MI .PK D MNI D MIP 2 2
Þ NH = PK Þ DNHE = DPKE (cgv - gn) Þ NE = EP
 E là trung điểm NP . Chứng minh tương tự: F là trung điểm MP
mà ME  NF  I  I là trọng tâm M Δ NP Trang 7