. HAI TAM GIÁC BẰNG NHAU
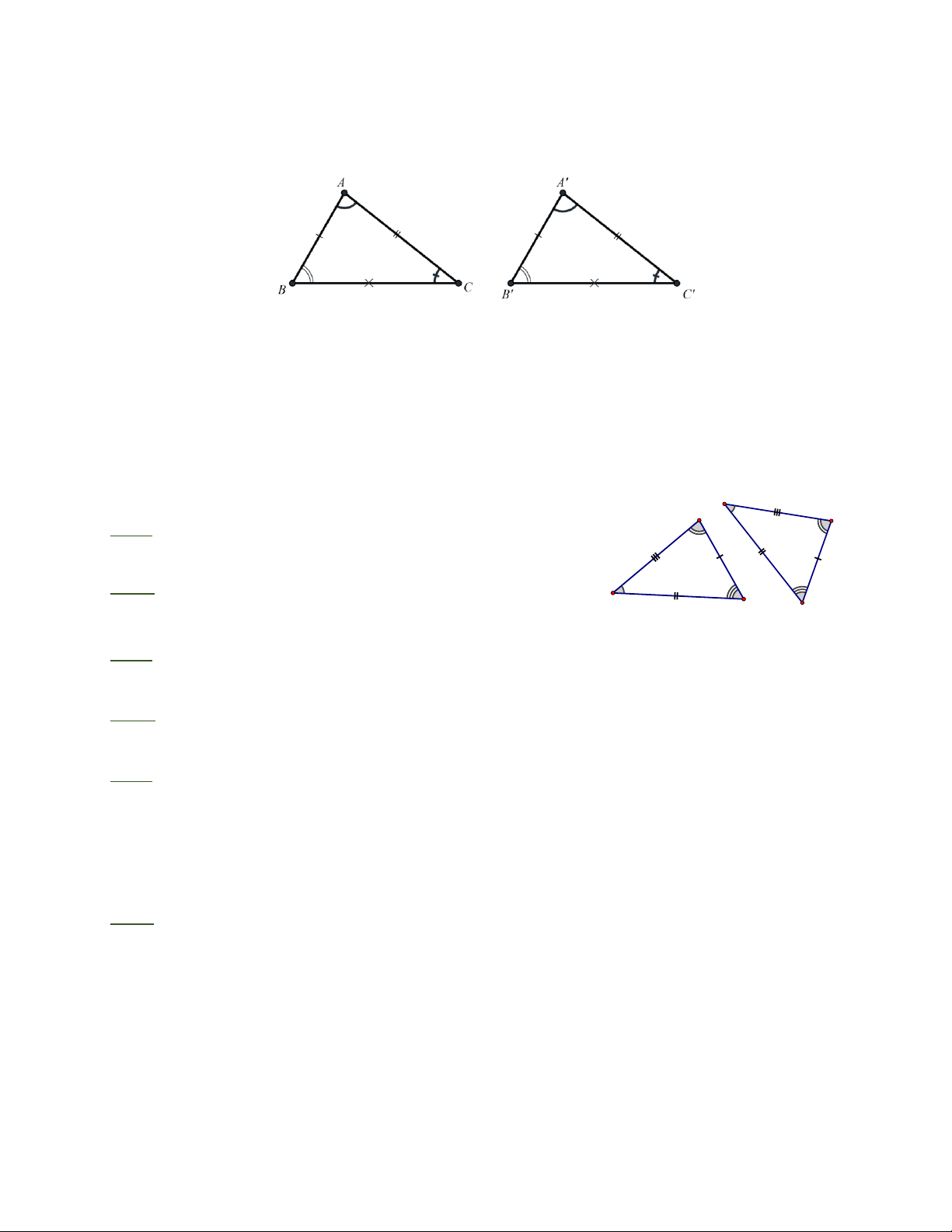
I. KIẾN THỨC CƠ BẢN ìï µ ¶ µ ¶ µ ¶ ï A = A ; ¢ B = B ; ¢ C = C ¢ ï
DA BC = DA 'B 'C ' Û í ï A B = A B ¢ ;¢ A C = A C ¢ ;¢ BC = B C ¢ ¢ ïïî
Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các
góc tương ứng bằng nhau. II. BÀI TẬP B E A
Bài 1: D DEF và D A BC có bằng nhau không? Vì sao? Nếu có
hãy viết kí hiệu bằng nhau theo 3 cách. Bài 2: A  MN  D
 EK . Hãy viết đẳng thức trên dưới F D C
một vài dạng khác. µ µ
Bài 3: Cho D A BC = D DHK , B = 35° , K = 100° .
Tính các góc còn lại của mỗi tam giác.
Bài 4: Cho D A BC = D DEI . Tính chu vi của mỗi tam giác trên, biết rằng A B = 5cm ,
A C = 6cm , EI = 8cm .
Bài 5: Cho hai tam giác bằng nhau : tam giác DEF ( không có hai góc nào bằng nhau,
không có hai cạnh nào bằng nhau) và một tam giác có ba đỉnh là G, H, K . Viết kí hiệu về
sự bằng nhau của hai tam giác đó, biết rằng : a) EF = GH, ED = GK b) ˆ ˆ ˆ ˆ
F = G, D = H
Bài 6: Cho hai tam giác bằng nhau : tam giác A B C (không có hai góc nào bằng nhau,
không có hai cạnh nào bằng nhau) và một tam giác có ba đỉnh là I ,J , K . Viết kí hiệu về sự
bằng nhau của hai tam giác đó, biết rằng : a) ˆ ˆ
A B = JI ,C = K b) AB = IK, AC = IJ c) ˆ ˆ ˆ ˆ
A = K , B = J Trang 1 HDG
Bài 1: D DEF = D BA C Bài 2: A  NM  D
 KE , M  AN  E
 DK , M  NA  E  KD , K  DE  N
 AM , K  ED  N  MA. Bài 3: ˆ ˆ D = D Þ = = 35o A BC DHK H B , ˆ ˆ = = 100o C K . Suy ra: ˆ o ˆ ˆ = 180 - -
= 180o - 35o - 100o = 45o A B C . Do đó ˆ ˆ = = 45o D A .
Bài 4: DA BC = DDEI Þ DE = A B = 5cm, DI = A C = 6cm, BE = EI = 8cm . Chu vi ABC 
bằng: 5  6  8  19(cm)
Chu vi DEI cũng bằng 19cm.
Bài 5: a) D DEF = D KGH ;
b) D DEF = D HKG
Bài 6: a) D A BC = D JIK ;
b) D A BC = D IKJ ; c) A V B C = D K JI Trang 2