 QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN TRONG MỘT TAM GIÁC
I. KIẾN THỨC CƠ BẢN
Định lý 1: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn. µ µ
DA BC , A C > A B Þ B > C . A
Định lý 2. Trong một tam giác cạnh đối diện
với góc lớn hơn là cạnh lớn hơn. B C µ µ
DA BC , B > C Þ A C > A B II. BÀI TẬP
Bài 1: So sánh các góc của ABC  biết:
a) A B = 4cm; BC = 6cm; CA = 5cm.
b) A B = 9cm; A C = 72cm; BC = 8cm.
c) Độ dài các cạnh A B, BC , CA lần lượt tỉ lệ nghịch với 2, 3, 4 . d) ABC 
vuông ở B và có A C = 6cm; A B = 19cm . µ 0 µ
e) Cho D DEF biết DE = DF < EF . Chứng minh D > 60 > E . 0 µ f) Cho $
D GHI biết IG = IH > GH . Chứng minh 0
90 > H > 60 > I .
Bài 2: So sánh các cạnh của ABC  , biết: µ 0 µ a) 0 A = 45 ;B = 55
b) Góc ngoài tại đỉnh A bằng 0 120 , 0 B  54 c) ABC  cân tại A, 0 A  60 . d) Số đo các góc ,
A B,C lần lượt tỉ lệ với 2,3, 4 . µ 1 1
e) A = 110° và số đo các góc B,C lần lượt tỉ lệ nghịch với ; 3 4 µ
f) A = 40° và số đo các góc B,C tỉ lệ với 3; 4
Bài 3: Cho tam giác ABC có AB < A .
C Tia phân giác góc A cắt cạnh BC tại . D Chứng
minh rằng DB < D . C Trang 1 Bài 4: Cho ABC 
có góc A tù. Trên cạnh AB lấy điểm D.
a) So sánh các đoạn thẳng , CA CD và CB .
b) Trên cạnh AC lấy điểm E. So sánh DE và BC.
Bài 5: Cho tam giác ABC có AB  A .
C Gọi M là trung điểm của .
BC Chứng minh rằng MAB  MA . C Bài 6: Cho ABC 
có AB  AC  BC . Tia phân giác góc A cắt cạnh BC tại D, tia phân giác
góc B cắt cạnh AC tại E, hai tia phân giác này cắt nhau tại I. So sánh: a) IA và IB
b) AEB và CEB c) DB và DC Bài 7: Cho ABC △
có góc A tù. Trên cạnh AB lấy điểm D.
a) So sánh các đoạn thẳng , CA CD và CB .
b) Trên cạnh AC lấy điểm E. So sánh DE và BC.
Bài 8: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D. Kẻ DH vuông
góc với BC  H  BC 
a. So sánh độ dài BA và BH
b. So sánh độ dài DA và DC Bài 9: Cho ABC 
có A B = A C . Trên cạnh BC lấy các điểm D, E sao cho BD = DE = EC · · · ·
. Chứng minh rằng trong ba góc: BA D, DA E , EA C thì góc DA E là góc lớn nhất. Trang 2 HDG
Bài 1: a) A B = 4cm; BC = 6cm; CA = 5cm.
 BC  CA  · · · µ µ µ
AB Þ BA C > CBA > A CB hay A > B > C (Định lý 1)
b) A B = 9cm; A C = 72cm » 8, 5cm; BC = 8cm.
Þ AB > AC > · · · µ µ µ
BC Þ A CB > A BC > BA C hay C > B > A (Định lý 1)
c) Độ dài các cạnh AB, BC, CA lần lượt tỉ lệ nghịch với 2,3, 4 .
Þ AB.2 = BC .3 = CA.4  AB  BC  AC
 ACB  BAC  ABC hay C  A  B (Định lý 1)
d) Tính được BC  17 (cm)  4,13 (cm)
A B = 19cm » 4, 35cm; BC = 17cm » 4,13cm; A C = 6cm.
Þ AC > AB > · · · µ µ µ
BC Þ A BC > A CB > BA C hay B > C > A (Định lý 1)
e) DEF cân tại D.  E  F (t/c tam giác cân)
DE  DF  EF  E  F  D (định lý 1) 0
D  E  F  180 (tổng 3 góc của một tam giác) 0 0  D  E 
 D  E  E 
 E  D  E   0 2 180 2 3 180 3 3 60  E  Mà 0 0
D  E D  E  0 60  E  0  60  E   1 0 0 0 0 0
D  2E  180  D  180  2E  180  2.60  60 (Vì 0 60  E ) 0  D  60 2 Từ (1) và (2) suy ra: 0
D  60  E (đpcm) f) GHI 
cân tại I.  H  G (t/c tam giác cân) µ µ
IG = IH > GH Þ H = G > $ I (định lý 1) $ µ µ 0
I + G + H = 180 (tổng 3 góc của một tam giác) $ µ 0 µ $ 0 $ µ Þ $ $ I + H = Û H - I = - I Þ (H - I )= ( 0 2 180 2 2 180 3 2 3 60 - I ) Trang 3 µ $ µ $ Mà $ $
H > I Þ H - I > 0 0 0
Þ 60 - I > 0 Û 60 > I ( ) 1 $ µ µ 0 $ 0 0 180 - I 180 - 60 0 0
I + 2H = 180 Þ H = > = 60 (Vì 0 60  I ) 0  H  60 2 2 2 0 0 180  I 180 Mặt khác: 0 H    90 3 (Vì 0 I  0 ) 2 2 Từ (1), (2) và (3) suy ra: 0 0
90  H  60  I (đpcm) µ µ µ Bài 2: a) 0
A + B + C = 180 (tổng 3 góc của một tam giác) µ 0 Þ C = - ( 0 0 + ) 0 180 45 55 = 80 µ µ µ
Þ C > B > A (Vì 0 0 0 80  55  45 )
Þ AB > AC > BC (Định lý 2) µ µ b) 0 0 0 A = 180 - 120 = 60 0 Þ C = - ( 0 0 + ) 0 180 60 54 = 66 µ µ µ
Þ C > A > B (Vì 0 0 0
66  60  54 )  AB  BC  AC (Định lý 2) c) ABC 
cân tại A.  B  C (t/c tam giác cân) 0
A  B  C  180 (tổng 3 góc của một tam giác) 0 0
 A  2B  180  A  180  2B µ 0 0 µ 0 0 µ µ Mà 0
A > 60 Þ 180 - 2B > 60 Þ 120 > 2B Þ B < 60 µ µ µ
Þ B = C < A (Vì 0
B  C  60  A ) ABC 
có B  C  A  AC  AB  BC (Định lý 2) µ µ µ 0 A B C A + B + C 180
d) Theo tính chất dãy tỉ số bằng nhau: 0 = = = = = 20 (tổng 3 góc 2 3 4 2 + 3 + 4 9 của một tam giác) µ 0 0 Þ µ µ A = 2.20 = 40 ; 0 0 B = 3.20 = 60 ; 0 0 C = 4.20 = 80 ABC 
có: C  B  A (Vì 0 0 0
80  60  40 )  AB  AC  BC (Định lý 2) e) 0 B  C  70 Trang 4 1 1
Vì số đo các góc B,C lần lượt tỉ lệ nghịch với ; 3 4 µ µ µ 1 µ 1 B C Þ B. = C . Þ = 3 4 3 4 µ µ µ µ 0 B C B + C 70
Theo tính chất dãy tỉ số bằng nhau: 0 = = = = 10 3 4 3 + 4 7 µ 0 0 Þ µ B = 3.10 = 30 ; 0 0 C = 4.10 = 40 ABC 
có: A  C  B (Vì 0 0 0 110  40  30 )
 BC  AB  AC (Định lý 2) B C f) 0
B  C  140 . Vì số đo các góc B,C lần lượt tỉ lệ với 3;4   3 4 µ µ µ µ 0 B C B + C 140
Theo tính chất dãy tỉ số bằng nhau: 0 = = = = 20 3 4 3 + 4 7 µ 0 0 Þ µ B = 3.20 = 60 ; 0 0 C = 4.20 = 80 ABC 
có: C  B  A (Vì 0 0 0
80  60  40 )  AB  AC  BC (Định lý 2) A
Bài 3: Trên cạnh AC lấy điểm E sao cho AB  AE,
chứng minh được ABD  AED (c-g-c). E
 DEC  xBD  ACB và DB  D . E B D C
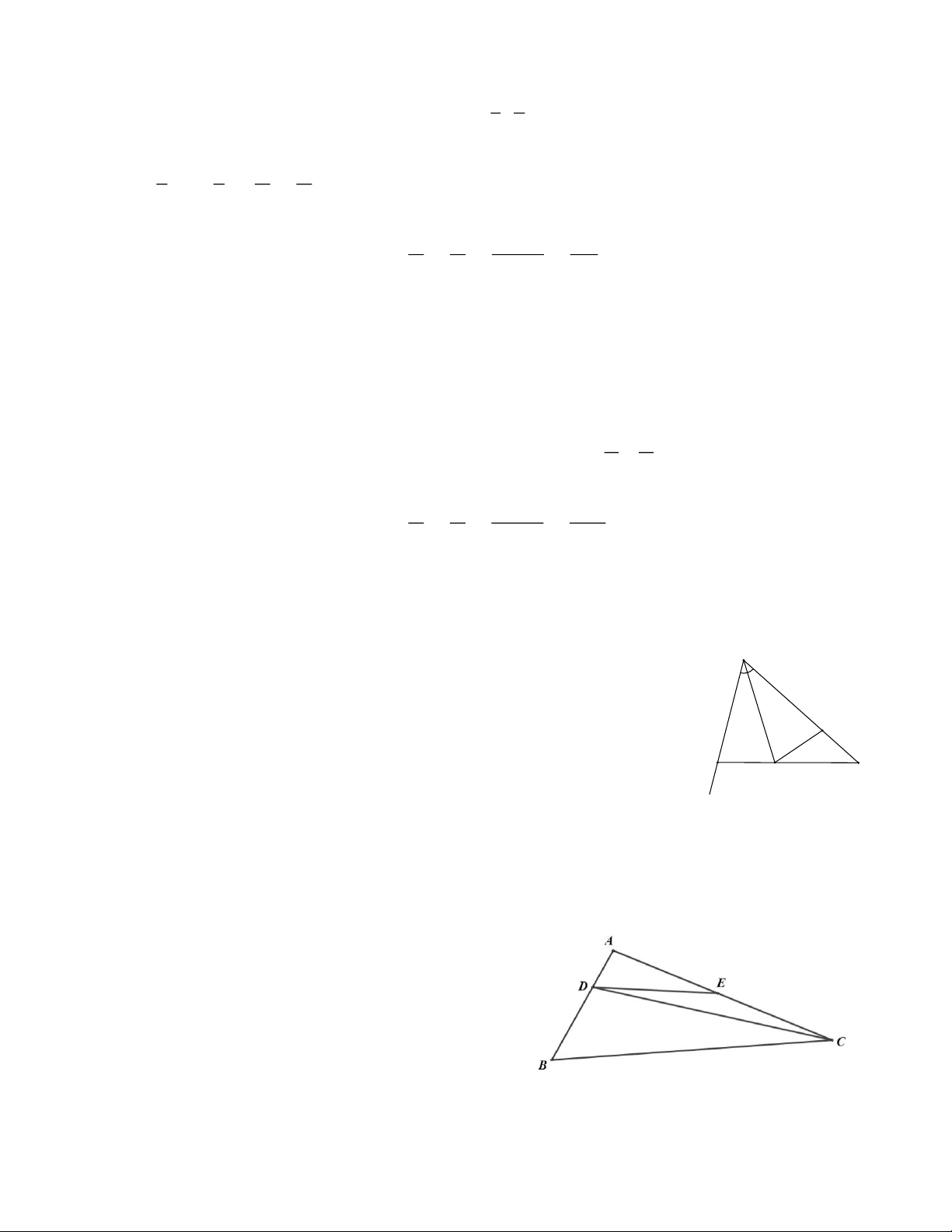
Từ đó DB  DE  D . C x Bài 4: a) A
 DC có DAC là góc tù nên CD > CA (1) và ADC là góc nhọn.
Mà ADC và BDC là 2 góc kề bù.  BDC là góc tù. B
 DC có BAC là góc tù nên BC > DC (2).
Từ (1) và (2) suy ra CB > CD > CA
b) ADE có DAE là góc tù nên AED là góc nhọn.
Mà AED và DEC là 2 góc kề bù.  DEC là góc tù. Trang 5 D
 EC có DEC là góc tù nên DC > DE .
Mặt khác: BC > DC (cmt)  BC  DE A
Bài 5: Trên tia đối của tia MA lấy điểm D sao cho MA  MD,
chứng minh được MAB  MDC (c-g-c).
 MAB  MDC, chú ý rằng CD  AB  AC  MAC  MD . C B M C
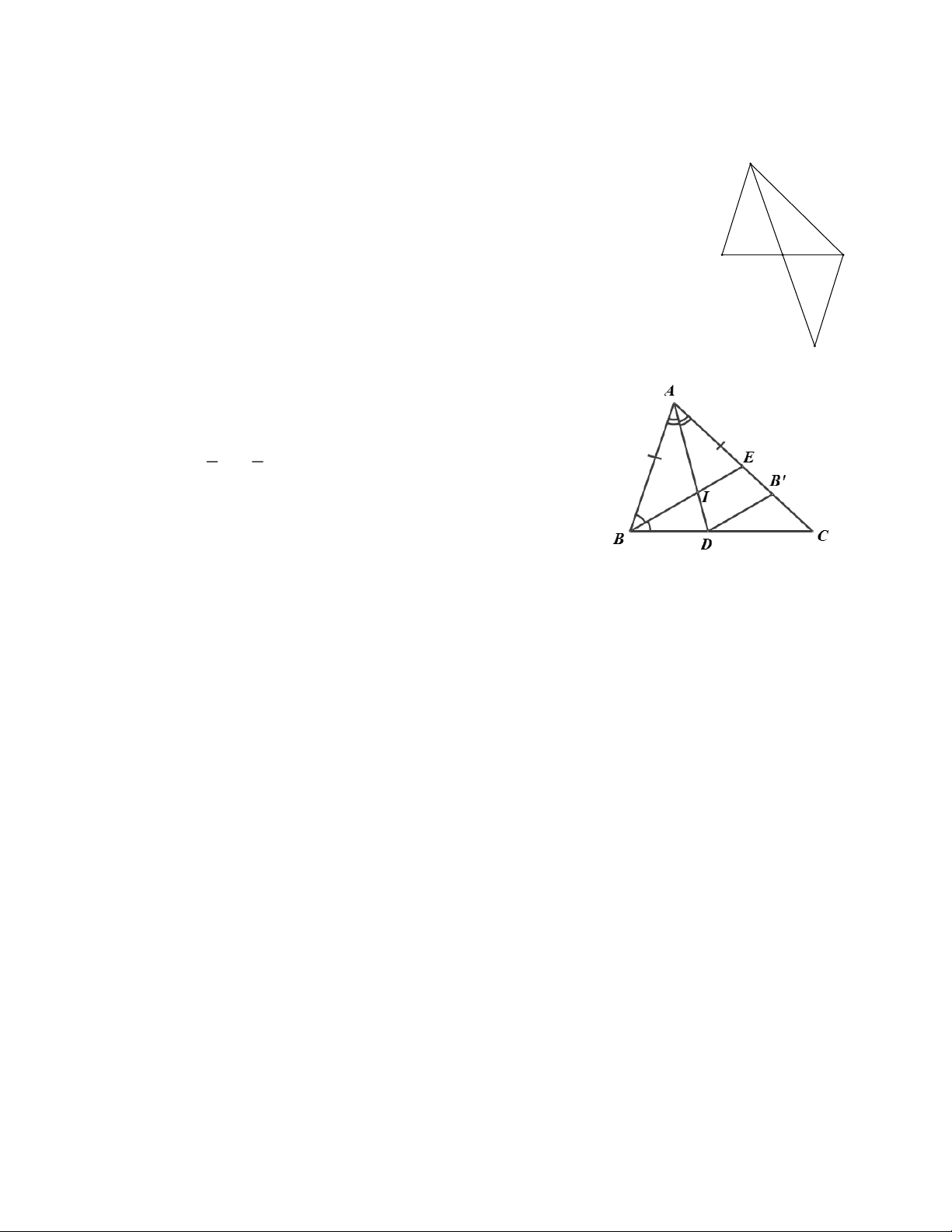
Do đó MAB  MA . C D Bài 6: a) ABC 
có AB  AC  BC
 C  B  A (định lý 1)  B  1 1 A  B 
A  ABI  BAI 2 2
ABI có ABI  BAI  AI  BI (định lý 2) b) ABC 
có BAC là góc lớn nhất (Do BC lớn nhất) nên
ABC; ACB là góc nhọn.  ABE 
có BAE là góc lớn nhất nên AEB là góc nhọn.
Mà AEB và CEB là 2 góc kề bù  CEB là góc tù  CEB > AEB
c)Trên AC lấy điểm B ' sao cho AB ' = AB
Xét AB ' D và ABD , có: AB  AB ' 
BAD  B ' AD  ABD   AB 
' D (c.g.c)  BD  B ' D và B '  B AD chung 
Ta có: B  C (gt)  B '  C Xét B
 ' DC có B '  C  DC  B'D  DC  BD (Vì BD  B ' D ) Trang 6