. TỔNG BA GÓC TRONG MỘT TAM GIÁC
I. KIẾN THỨC CƠ BẢN
1. Tổng ba góc của một tam giác.
Tổng ba góc của một tam giác bằng 180 . 
 ABC  A  B  C 180
2. Áp dụng vào tam giác vuông
a) Định nghĩa: Tam giác vuông là tam giác có một góc vuông.
b) Tính chất: Trong tam giác vuông, hai góc nhọn phụ nhau µ µ µ
D A BC ; A = 90° Þ B + C = 90°
3. Góc ngoài của tam giác
a) Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác.
b) Tính chất:
 Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó. ACD  A  . B
 Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó. ACD  ; A ACD  . B II. BÀI TẬP
Bài 1: Tính số đo x, y trong các hình vẽ sau: a) b) A A x x 0 20 y 0 0 60 40 B C x B C D
Bài 2: Tính các góc của tam giác ABC biết rằng A  B  C  2 : 3: 4.
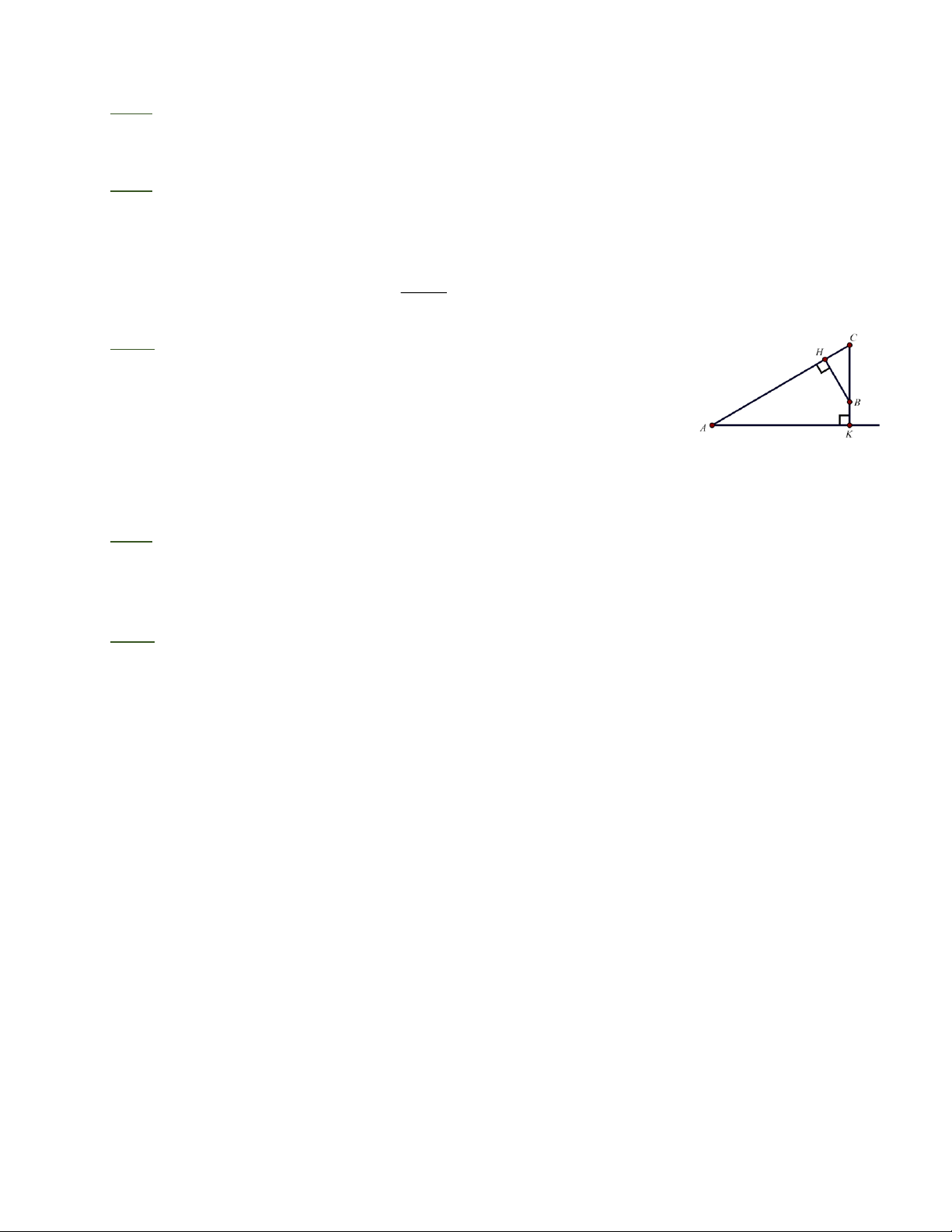
Bài 3: Cho tam giác vuông ABC tại A, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân
giác góc B và góc HAC cắt nhau tại I. Chứng minh rằng 0 AIB  90 . Trang 1
Bài 4: Cho tam giác ABC, tia phân giác AD (D thuộc BC). Tính ADB và ADC biết 0
B  C  40 .
Bài 5: Cho tam giác MNP có N > P . Vẽ phân giác MK.
a) Chứng minh MKP  MKN  N  . P
b) Đường thẳng chứa tia phân giác góc ngoài đỉnh M của tam giác MNP, cắt đường thẳng N  P
NP tại E. Chứng minh rằng MEP  . 2
Bài 6: Trên hình vẽ bên, các góc A và HBC có cạnh tương ứng
vuông góc  AH  BH , AK  BC , các góc A và HBK có cạnh
tương ứng vuông góc (A H ^ BH, A K ^ BK ). Hãy tìm mối liên hệ giữa: µ a) A và HBC ; b) A và HBK.
Bài 7: Cho tam giác ABC có A  90 .
 Gọi d là một đường thẳng đi qua C và vuông góc
với BC. Tia phân giác của góc B cắt AC ở D và cắt d ở E. Kẻ CH vuông góc với DE
H DE. Chứng minh rằng CH là tia phân giác của góc DC . E
Bài 8: Cho tam giác ABC, E là một điểm bất kì nằm trong tam giác. Chứng minh rằng:
BEC = A BE + A CE + BA C . Trang 2 HDG Bài 1: a) Ta có 0 0
A  180  (B  C)  80 . Vậy 0 x  80 .
b) Ta có ADC  BAD  ABD . Từ đó suy ra 0
y  ADC  110 .
Mà trong tam giác ADC có 0
y  2x  180 . Từ đó tính được 0 x  35 . µ µ µ µ µ µ A B C A + B + C 180o Bài 2: = = = = = 20o 2 3 4 2 + 3 + 4 9 µ o µ o µ Từ đó tính ra = 40 , = 60 , = 80 . o A B C A B HAC Bài 3: Ta có: 0 IBA  IAB   90  2 2 I Mà 0
HAC  90  BAH  B Từ đó suy ra 0
IBA  IAB  90 B H C 0
 AIB  90 (ĐPCM).
Bài 4: Sử dụng tính chất góc ngoài của tam giác A
Ta được: ADB  C  DAC  C  . 2 A A
Tương tự ADC  B  . 2 Suy ra 0
ADC  ADB  B  C  40 . Ta lại có : 0
ADC  ADB  180 . B D C Từ đó suy ra 0 0
ADC 110 , ADB  70 . x
Bài 5: a) Sử dụng tính chất góc ngoài. Ta được: M M M MKN  P  . MKP  N  . 2 2
Suy ra MKP  MKN  N  . P NMx
b) Ta có MEP  EMx  MPE   . P 2 E P K N N  P
Mà NMx  N  .
P Từ đó suy ra MEP  . 2 Bài 6: a) AKC có o A  C  90 ; H  BC có o HBC  C  90 . Suy ra, A  HBC. Trang 3 b) A  HBC mà o HBC  HBK  180 nên o A  HBK  180 . Bài 7:
B phụ D , C phụ D , mà D  D (hai góc đối đỉnh) nên B  C . d 1 1 1 2 1 2 1 1 E A ( ) H 1 1 D 1 2
B phụ E , C phụ E nên B  C . (2) 2 1 2 1 2 2 2 1 1 2 B C Từ ( )
1 ; (2)và B  B suy ra C  C . 1 2 1 2
Vậy CH là tia phân giác của góc DCE . Bài 8:
Kéo dài AE cắt BC tại K. A
Ta có: BEK  BAE  EB ; A
CEK  CAE  EC . A
Mà BEC  BEK  KEC. E B C
Từ đó ta có BEC = A BE + A CE + BA C . K Trang 4