. TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC:
GÓC – CẠNH - GÓC (G.C.G)
I. KIẾN THỨC CƠ BẢN
Trường hợp bằng nhau góc – cạnh – góc: A
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và
hai góc kề của tam giác kia thì hai tam giác đó bằng nhau. C B µ ¶ üï A' B = B ' ïïïï
BC = B 'C 'ý Þ DA BC = DA ' B 'C ' (g. c. g) ï µ ¶ ï C C ' ï = ïïþ C' B'
Trường hợp bằng nhau cạnh huyền – góc nhọn của tam giác vuông:
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng
cạnh huyền và một góc nhọn của tam giác vuông kia thì hai B B'
tam giác vuông đó bằng nhau. µ ¶ üï A = A ' = 90 ï °ïïï
BC = B 'C ' ý Þ DA BC = DA ' B 'C ' ï
(cạnh huyền – góc nhọn) µ ¶ ï B B ' ï = ï A C A' C' ïþ II. BÀI TẬP
Bài 1: Có những tam giác nào bằng nhau trong hình bên ? Vì sao? M P Q N O
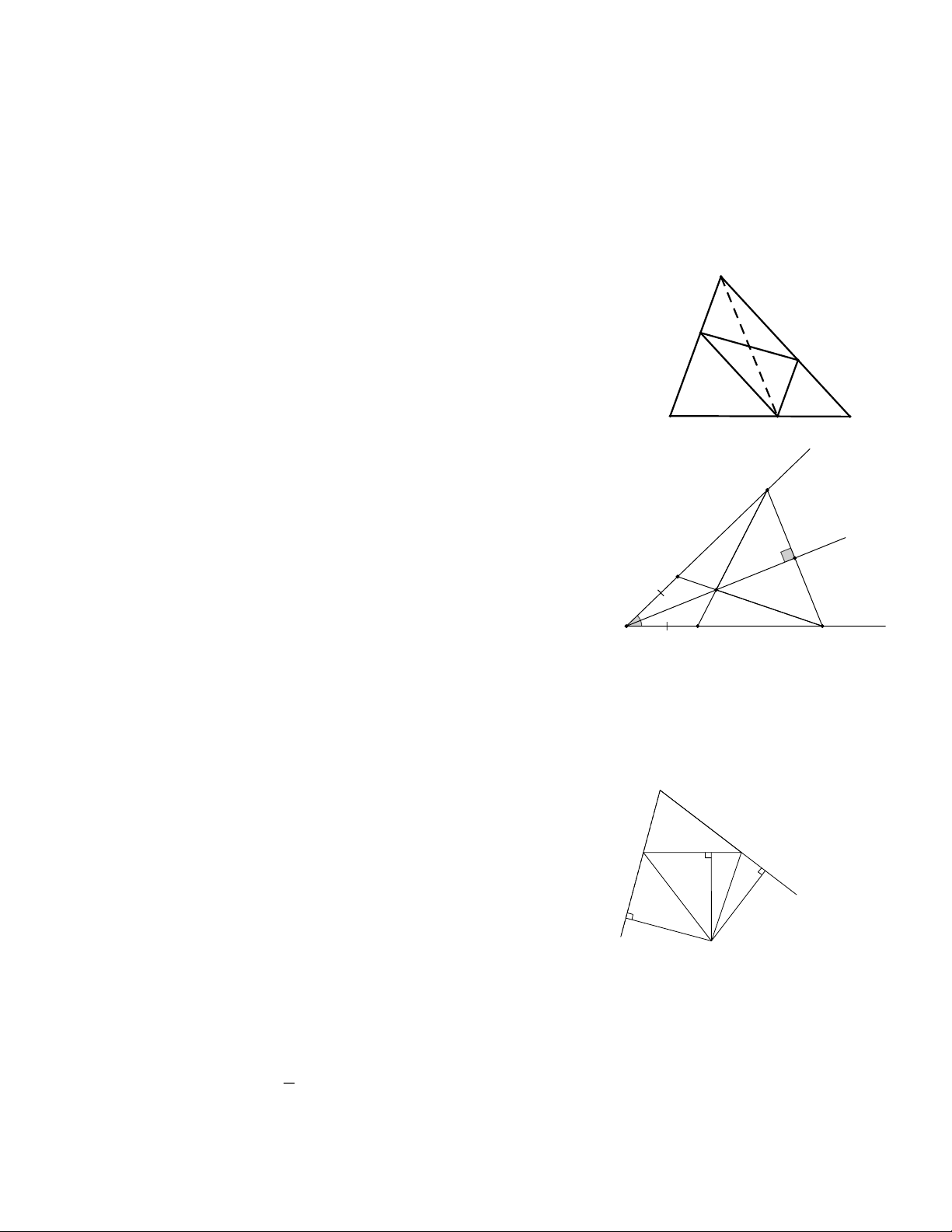
Bài 2: Cho tam giác ABC , Điểm D thuộc cạnh BC . Kẻ DE / / AC(E Î AB), kẻ
DF / / AB(F Î AC). Gọi I là trung điểm của EF . Chứng minh I là trung điểm của AD
Bài 3: Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường
vuông góc với Ot, nó cắt Ox và Oy theo thứ tự A và B
a. Chứng minh OA = OB
b. Lấy điểm C nằm giữa O và H. Chứng minh CA = CB Trang 1
c. AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD . Chứng minh B, C, E thẳng hàng.
Bài 4: Cho tam giác A B C . Các đường phân giác của các góc ngoài tại B và tại C cắt nhau
ở K. Qua K kẻ đường thẳng vuông góc với AB, cắt đường thẳng AB ở E. Qua K kẻ đường
thẳng vuông góc với AC, cắt đường thẳng AC ở F. Chứng minh rằng K E = K F . Bài 5: Cho ABC 
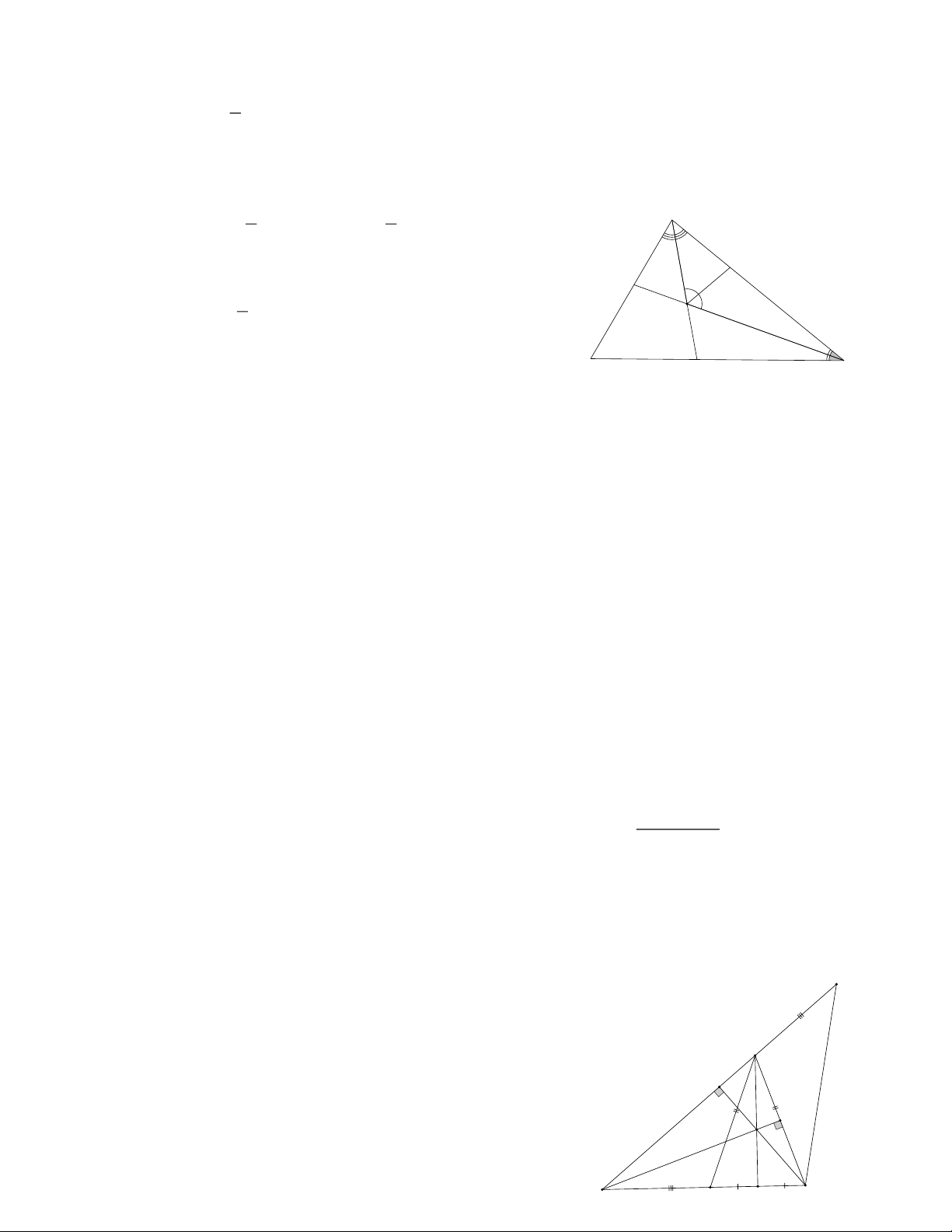
có A  60 . Tia phân giác của góc B cắt AC ở D, tia phân giác của góc C
cắt AB ở E và cắt BD ở I. Chứng minh IE = ID.
Bài 6: Cho tam giác ABC có 40o A 
, AB  AC , H là trung điểm của BC
a) Tính ABC, ACB và chứng minh AH  BC và AH là phân giác BAC
b) Đường thẳng d đi qua trung điểm của AC và vuông với với AC cắt tia CB tại M . · Tính MA H .
c) Trên tia đối của tia AM lấy điểm N sao cho AN  BM . Chứng minh AM  CN .
d) Vẽ CI  MN tại I .Chứng minh I là trung điểm MN .
e) AH cắt đường thẳng d tại K . Chứng minh C, I , K thẳng hàng . Hết Trang 2 HDG
Bài 1: DMPN = DMQO (g. c.g)
DPMO = DQMN (g. c.g) (HS có thể chỉ ra trường hợp c.c.c hoặc c.g.c dựa vào suy ra các cạnh và
góc tương ứng của DMPN = DMQO ) A Bài 2: AEF   DF 
E (g.c.g)  AE  DF E 2 1 I AIE   DIF 
(c.g.c)  AI  DI và I  I . 1 1 2 3 2 F 2 Ta lại có   180o I I nên   180o I I
, do đó A , I , D thẳng 2 3 1 3
hàng. Từ đó I là trung điểm của AD . B C D Bài 3: x
a) D A HO = D BHO ( cạnh huyền – góc nhọn) A
Þ OA = OB ; A H = HB · · t
b) D A HC = D BHC (c-g-c) Þ CA = CB và A CH = HCB H E · ·
c. DOEC = DODC (c. .
g c) Þ ECO = OCD C · · y
Ta có OCD = A CH ( đối đỉnh) O D B · · · ·
hay ECO = OCD = A CH = HCB · · ·
A,C , D thẳng hàng nên A CH + HCB + MCD = 180° · · ·
hay ECO + OCD + BCD = 180° hay E,C , B thẳng hàng.
Bài 4: Kẻ KD  BC A
KBE  KBD (cạnh huyền – góc nhọn) D
suy ra KE = KD (1) C B 2 1 1 2 F K  CD  K
 CF (cạnh huyền – góc nhọn) E
suy ra K D = K F (2) K
Từ (1) và (2) suy ra KE = KF
Bài 5: Kẻ IH là tia phân giác BIC 1
Ta có: CBD  ABD  ABC (BD là tia phân giác ABC ) 2 Trang 3 1
BCE  ACE  ACB (CE là tia phân giác ACB ) 2
Mà BAC  ABC  ACB  180 (định lí tổng 3 góc trong  )
 ABC  ACB 180  BAC 180  60 120 1       1 B CBD BCE ABC ACB  .120  60 2 2 B
 IC có: BIC 180  CBD BCE 18060 120 H E 1
 BIH  CIH  BIC  60 (IH là tia phân giác BIC ) I 2
BIE  180  BIC  180 120  60 60° · · A C D
Có: BIE = CID = 60° (2 góc đối đỉnh) Xét BIE và BIH có: · · üï B IE B IH 60 ï = = ° ïïï B I chung
ý Þ DBIE = DBIH ( . g c.g) ï · · · · ï EB I
HB I (A BD CBD)ï = = ïïïþ
 IE = IH (2 cạnh tương ứng) Xét D  IC và H  ICcó: · · üï DIC HIC 60 ï = = ° ïïï IC chung
ý Þ DDIC = DHIC ( . g c.g) ï · · · · ï ICH ICD (BCE A CE )ï = = ïïïþ
Þ ID = IH (2 c¹nh t­ ¬ng øn )ü g ïïý ID = IE (đpcm)
MµI E = IH (cmt ) ïïþ Bài 6: · · · · 180° - 40°
a) D A HB = D A HC (c.c.c) Þ A BH = A CH = A BC = A CB = = 70° 2 · · · · · ·
Þ A HB = A HC ; A HB + A HC = 180° Þ A HB = A HC = 90°
hay AH  BC · · ·
Þ HA B = HA C nên AH là phân giác BAC hay HAC = 20°
b) Gọi P là trung điểm của AC. N · · ·
D MPC = D MPA (c.g.c) Þ MA P = A CM = A CB = 70° · · ·
Ta có: MA H = MA C - HA C = 70° - 20° = 50° A · · · c) có MPC = 90 ;
° MCP = 70° Þ PMC = 20° I · Þ CA M = 40° P K Trang 4 B C H M · ·
D A NC = D B MA (c.g.c) Þ NC = MA và A NC = BMA = 40°
d) D MPC = D MPA (c.g.c) Þ MC = MA mà NC = MA (cmt) nên MC = NC
D CIM = D CIN (cạnh huyền – góc nhọn) Þ IM = IN
d) Hs có thể sử dụng cách cộng góc: · · ·
IKM + MKH + HKC = 70° + 70° + 40° = 180° từ đó suy ra C , I , K thẳng hàng. Trang 5