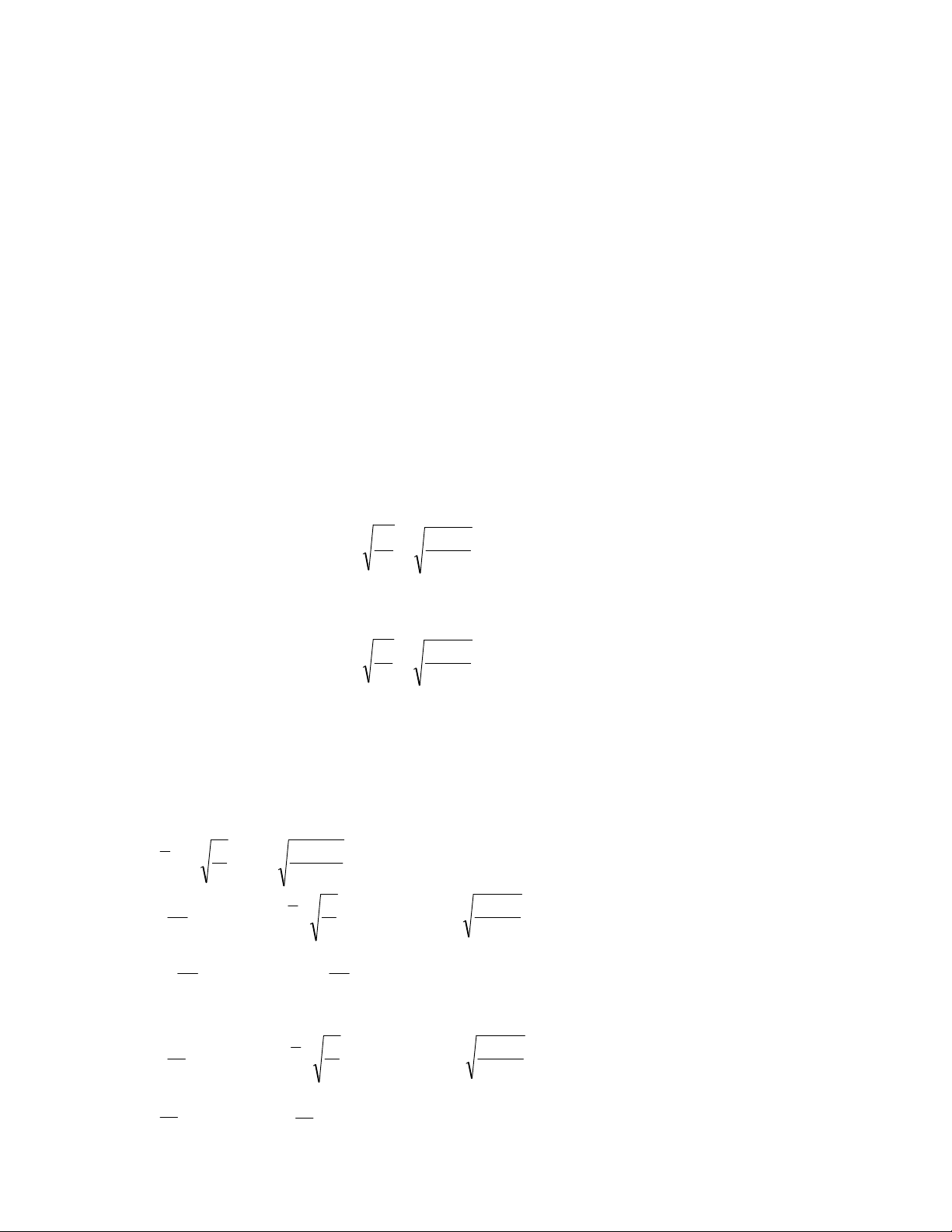




Preview text:
Chương 2: Liên kết VÝ dô 2.1:
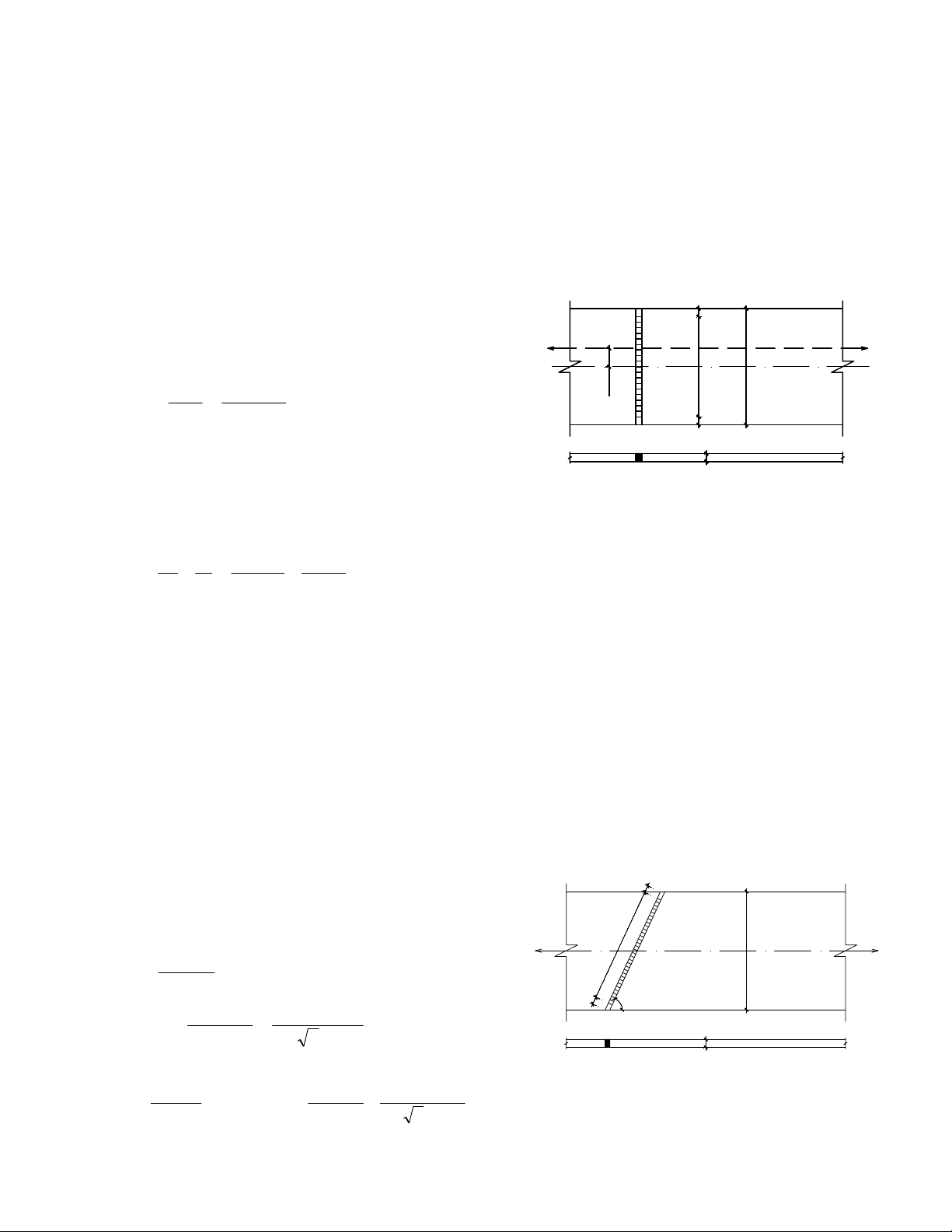
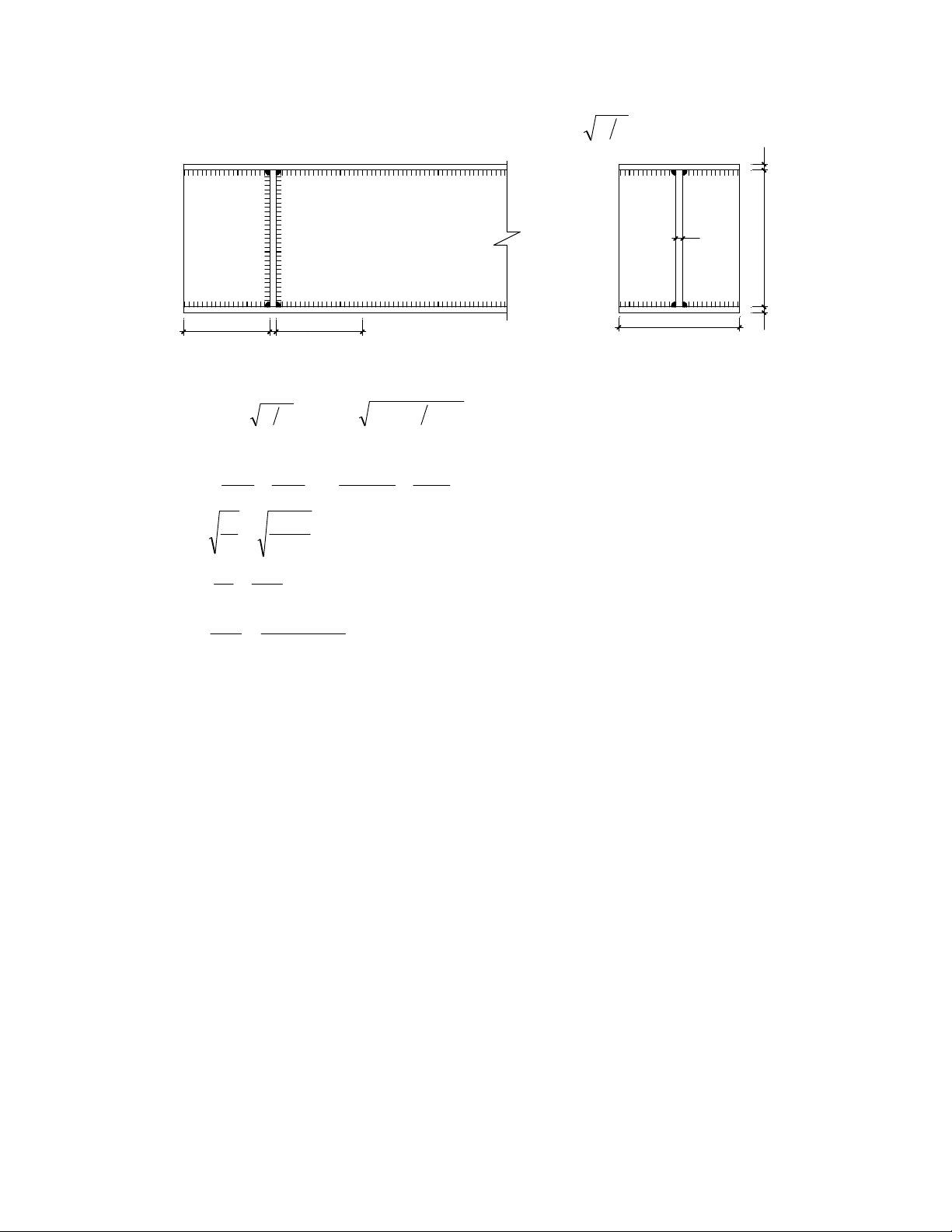
KiÓm tra kh¶ n¨ng chÞu lùc cho liªn kÕt hµn ®èi ®Çu nèi 2 b¶n thÐp cã kÝch th−íc (320x12)mm
nh− h×nh vÏ 2.12. BiÕt liªn kÕt chÞu lùc kÐo N=120KN ®−îc ®Æt lÖch t©m 1 ®o¹n e = 10cm. Sö dông vËt
liÖu thÐp CCT34s cã f=2100daN/cm2; que hµn N42 cã f = 1800 daN/cm2; γ =1; wt C Bµi lµm:
Do lùc trôc ®Æt lÖch t©m 1 ®o¹n e = 10cm, sinh ra m«men:
M = Ne = 120.10 = 1200 KNcm = 120000 daNcm.
ChiÒu dµi tÝnh to¸n cña ®−êng hµn: 2 1
l = b – 2t = 32 – 2.1,2 = 29,6 cm; w N=120KN N=120K 6 0 8 2
M«men kh¸ng uèn cña ®−êng hµn: 0 2 3 0 1 2 2 = l h e w 2 , 9 6 . , 1 2 W f = = = 17 , 5 2 ( 3 2 cm ) w 2 6 6 1
DiÖn tÝch cña ®−êng hµn: 2 1
A = l .t = 29,6.1,2 = 35,52 (cm2) w w H×nh 2.12
Kh¶ n¨ng chÞu lùc cña ®−êng hµn: M N 120000 12000 σ = + = + = , 1022 65 (daN / 2 cm ) < f γ = ( 1800 daN / 2 cm ) W A , 175 23 52 , 35 wt c
VËy liªn kÕt ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 2.2:
X¸c ®Þnh lùc lín nhÊt t¸c dông lªn liªn kÕt hµn ®èi ®Çu xiªn nèi 2 b¶n thÐp cã kÝch th−íc
(320x12)mm nh− h×nh vÏ 2.13. BiÕt gãc nghiªng α= 450. Sö dông vËt liÖu thÐp CCT34 cã f=2100
daN/cm2; que hµn N42 cã f =1800daN/cm2; γ =1; f =1250daN/cm2 wt C v Bµi lµm:
ChiÒu dµi thùc tÕ cña ®−êng hµn: l = (b/sin450) = 45,25 cm; tt
ChiÒu dµi tÝnh to¸n cña ®−êng hµn: l = l – 2t = 45,25 – 2.1,2 = 42,85 cm; w tt
DiÖn tÝch cña ®−êng hµn: 2 1
A = l .t = 42,85.1,2 = 51,42 (cm2) w w
øng suÊt ph¸p trªn ®−êng hµn ®èi ®Çu xiªn: .5 N 2 5 0 N=? 4 2 3 N cos = α σ ≤ f γ A wt c w 2 1 45 f γ .A 1800 1 . .5 , 1 42 ⇒ N wt c w ≤ =
= 130894daN ≈ 1309KN ) 1 ( 1 cosα 2 / 2 2 1
øng suÊt tiÕp trªn ®−êng hµn ®èi ®Çu xiªn: N sin α f γ .A 125 . 0 1.5 , 1 42 τ = f ⇒ ≤ γ N v c w ≤ =
= 90898daN ≈ 909KN (2) v c 2 A sin α w 2 / 2 1
Tõ (1) vµ (2), ta cã lùc lín nhÊt t¸c dông lªn liªn kÕt lµ: N = min (N , N ) = 909 KN max 1 2 VÝ dô 2.3:
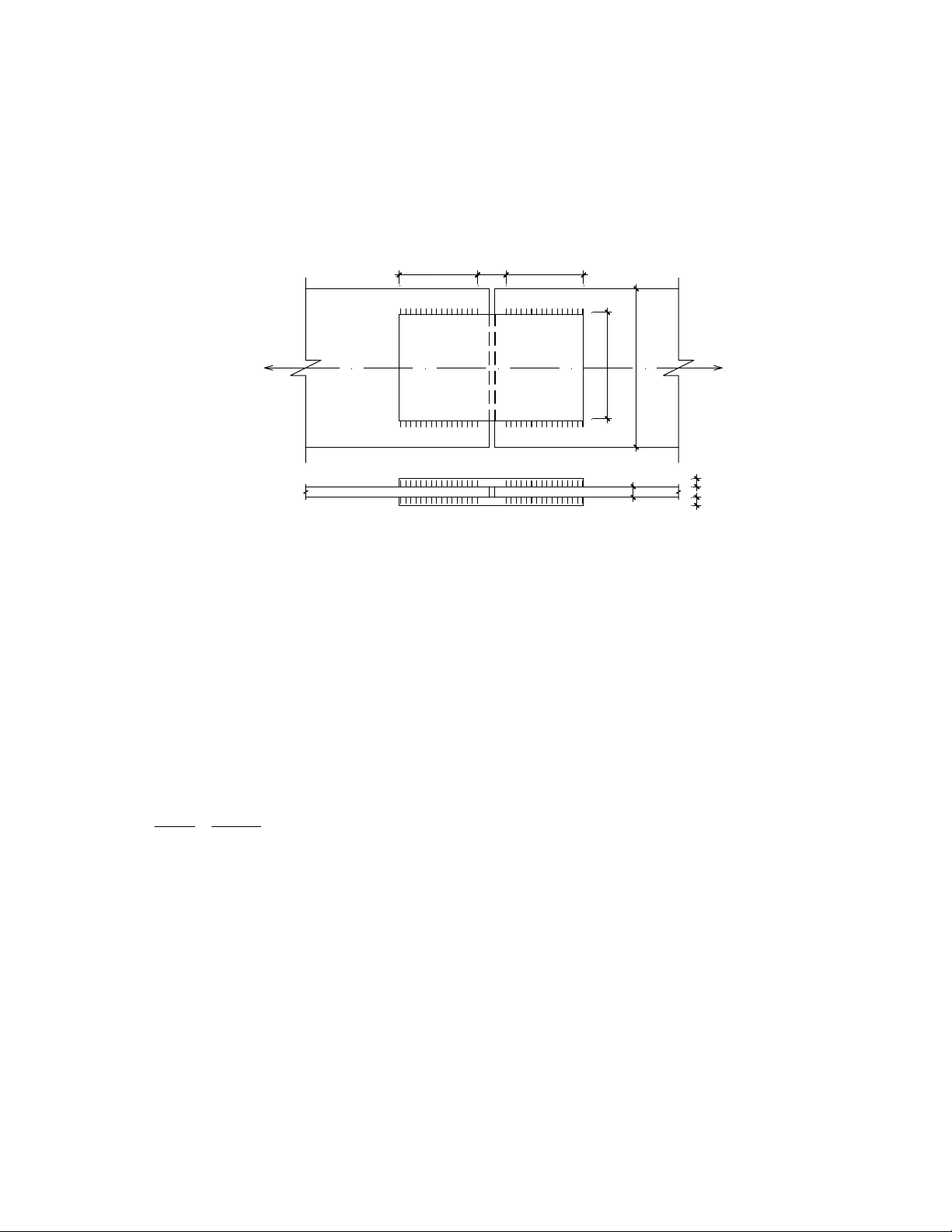
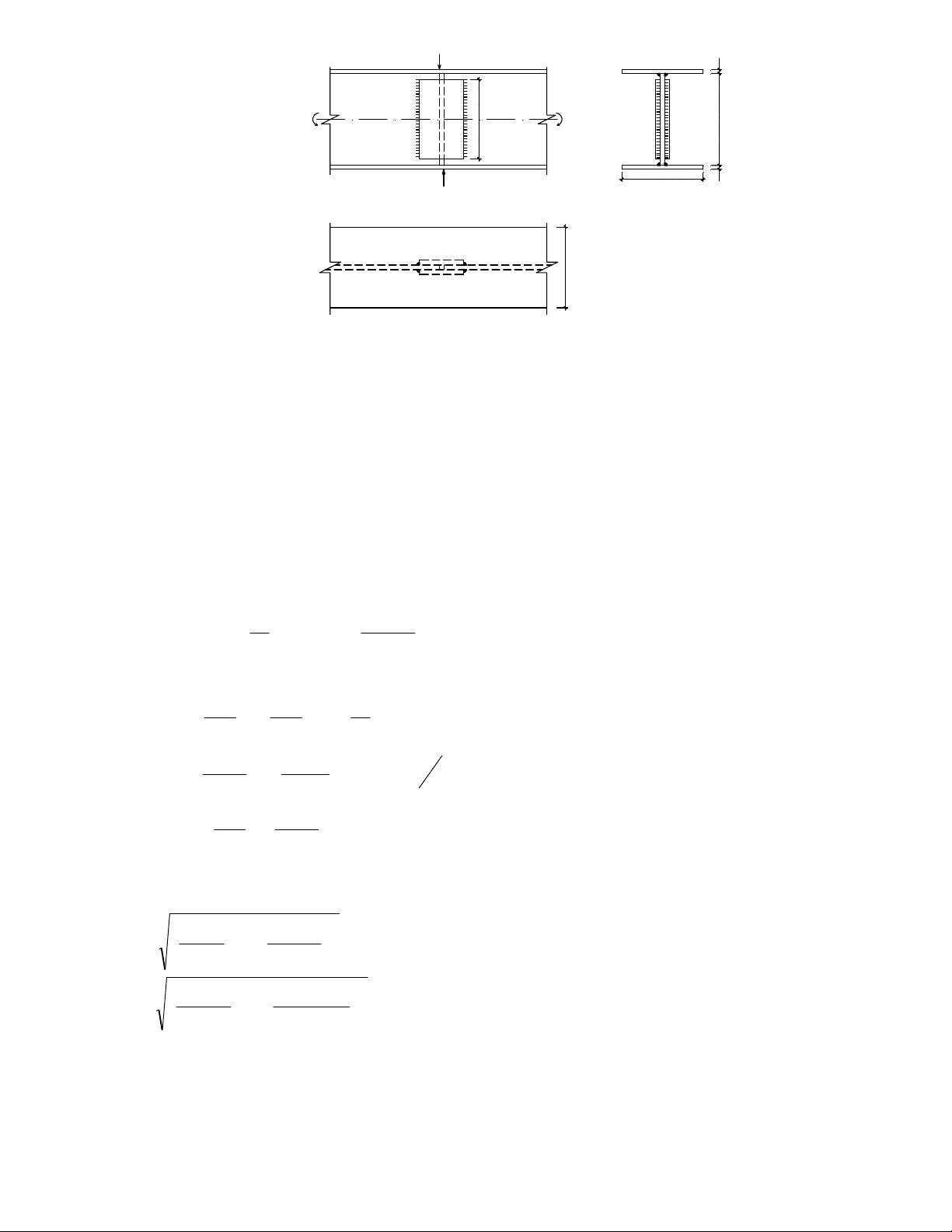
KiÓm tra kh¶ n¨ng chÞu lùc cho liªn kÕt hµn gãc c¹nh nèi 2 b¶n thÐp cã kÝch th−íc (320x12)mm,
liªn kÕt sö dông 2 b¶n ghÐp cã kÝch th−íc (300x8)mm nh− h×nh vÏ 2.13. BiÕt lùc kÐo tÝnh to¸n N = 1800
KN, chiÒu cao ®−êng hµn h =10mm; chiÒu dµi thùc tÕ cña ®−êng hµn l = 400mm; Sö dông vËt liÖu thÐp f tt
CCT34 cã f=2100 daN/cm2; que hµn N42 cã f = 1800 daN/cm2; f =1500daN/cm2; β =0,7; β = 1; γ =1; wf ws f s C ltt=400 50 ltt=400 0 0 N=180KN N 0 2 3= 3= 1 2 b b 0 2 1 1 = 1 t = 2 t 1 t H×nh 2.13 Bµi lµm:
a, KiÓm tra bÒn cho b¶n ghÐp:
∑A = 2.0,8.30 = 48 (cm2) > A = 32.1,2 = 38,4 (cm2) bg
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn.
b, KiÓm tra kh¶ n¨ng chÞu lùc cho liªn kÕt:
ChiÒu dµi tÝnh tãan cña 1 ®−êng hµn: l = l – 1 = 40 -1 = 39 (cm) f tt
DiÖn tÝch tÝnh to¸n cña c¸c ®−êng hµn:∑A = ∑l . h = 4.39.1 = 156 (cm2) f f f Ta cã: (βf )
= min (β f ; β f ) = min (1800.0,7; 1500.1) = 1260 (daN/cm2) w min f wf s ws
Kh¶ n¨ng chÞu lùc cña liªn kÕt: N 180000 σ = = =1153 8 , 5 (daN / 2 cm ) ≤ (βf γ = w ) 1260(daN / 2 cm ) ∑ A 156 min c f
VËy liªn kÕt ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 2.4:
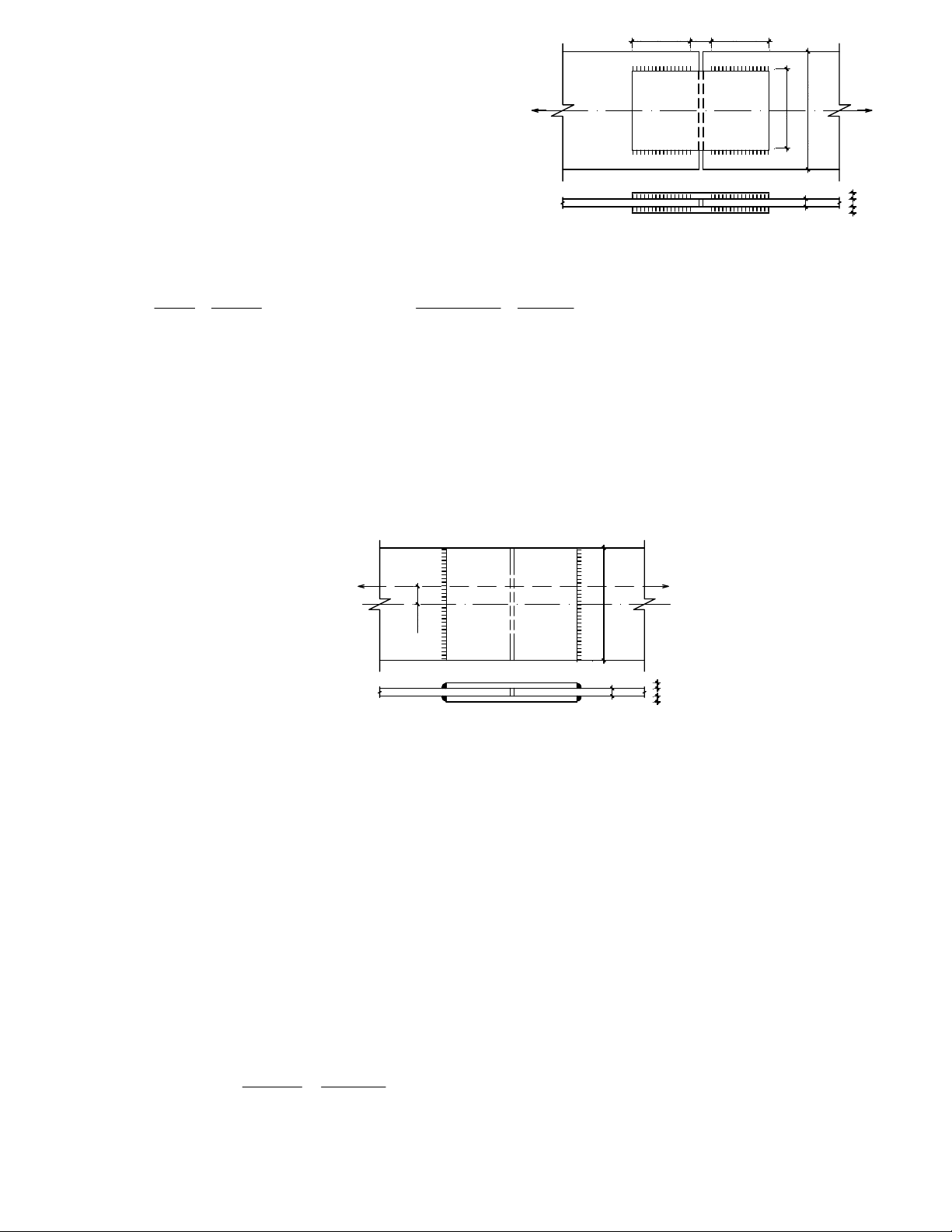
ThiÕt kÕ liªn kÕt hµn gãc c¹nh nèi 2 b¶n thÐp cã kÝch th−íc (320x12)mm, liªn kÕt sö dông 2 b¶n
ghÐp cã kÝch th−íc (300x10)mm nh− h×nh vÏ 2.14. BiÕt lùc kÐo tÝnh to¸n N = 1200 KN. Sö dông vËt
liÖu thÐp CCT34 cã f=2100 daN/cm2; que hµn N42 cã f = 1800 daN/cm2; f = 1500 daN/cm2; β =0,7; wf ws f β = 1; γ =1; s C Bµi lµm:
a, KiÓm tra bÒn cho b¶n ghÐp:∑A = 2.1.30 = 60 (cm2) > A = 32.1,2 = 38,4 (cm2) bg 2 ltt=? 50 ltt=?
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn.
b, X¸c ®Þnh chiÒu dµi ®−êng hµn: 0 0 N=120KN N 0 2 3= 3 1 = 2 b b
Víi chiÒu dµy tÊm thÐp c¬ b¶n lµ 12mm vµ thÐp b¶n
ghÐp lµ 10mm, chän chiÒu cao ®−êng hµn h = 10mm f ®¶m b¶o ®iÒu kiÖn: 0 2 1 1 = 1 t = 2 t 1 t h =6(mm) < h =10 (mm) < h =1,2t = 12 (mm). fmin f fmax min Ta cã: (βf )
= min (β f ; β f ) = min (1800.0,7; 1500.1) = 1260 (daN/cm2) H×nh 2.14 w min f wf s ws
Tæng chiÒu dµi cÇn thiÕt cña ®−êng hµn liªn kÕt: N N σ = = (βf ⇒ ≤ γ ∑ ≥ = = w ) N 120000 l cm min ∑ A ∑l h c f β γ f f f ( fw) 9 , 5 24( ) h 126 . 0 1.1 min c f
ChiÒu dµi thùc tÕ cña 1 ®−êng hµn: l = (∑l /4) + 1 =95,24/4 + 1 ≈ 25 (cm) f f VÝ dô 2.5:
X¸c ®Þnh lùc lín nhÊt t¸c dông lªn liªn kÕt hµn gãc ®Çu nèi 2 b¶n thÐp cã kÝch th−íc
(450x16)mm, liªn kÕt sö dông 2 b¶n ghÐp cã kÝch th−íc (450x12)mm nh− h×nh vÏ 2.15. BiÕt lùc kÐo
tÝnh to¸n N (KN) ®−îc ®Æt lÖch t©m 1 ®o¹n e = 10 cm. Sö dông vËt liÖu thÐp CCT34 cã f=2100 daN/cm2;
que hµn N42 cã f = 1800 daN/cm2; f = 1500 daN/cm2; β =0,7; β = 1; γ =1; wf ws f s C N N=? 0 5 4= 0 b 0 1 = e 2 6 1 1 = 1 t = 2 t 1 t H×nh 2.15 Bµi lµm:
a, KiÓm tra bÒn cho b¶n ghÐp:∑A = 2.1,2.45 = 108 (cm2) > A = 45.1,4 = 72 (cm2) bg
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn.
b, X¸c ®Þnh néi lùc lín nhÊt:
Víi chiÒu dµy tÊm thÐp c¬ b¶n lµ 16mm vµ thÐp b¶n ghÐp lµ 12mm, chän chiÒu cao ®−êng hµn h = f 14mm ®¶m b¶o ®iÒu kiÖn: h =6(mm) < h =14 (mm) < h =1,2t = 14,4 (mm). fmin f fmax min Ta cã: (βf )
= min (β f ; β f ) = min (1800.0,7; 1500.1) = 1260 (daN/cm2) w min f wf s ws
ChiÒu dµi thùc tÕ cña 1 ®−êng hµn:lw(tt) = b- 1 = 45 – 1 = 44 (cm)
DiÖn tÝch tÝnh to¸n cña c¸c ®−êng hµn trong liªn kÕt: ∑A =∑l =2.44.1,4 = 123,2 (cm2) f w hf
M«men kh¸ng uèn cña c¸c ®−êng hµn trong liªn kÕt: ∑ 2 l .h f f 2.442 , 1 . 4 ∑W f = = = 903 ( 5 , 3 cm ) 6 6
Do lùc trôc ®Æt lÖch t©m 1 ®o¹n e = 10cm, sinh ra m«men: 3
M = Ne = N.10 = 10N (KNcm) = 1000N (daNcm).
Tõ ®iÒu kiÖn bÒn cho liªn kÕt: N M N N e . σ = + = + ≤ (βf γ w )min c ∑ A ∑W ∑ A ∑W f f f f
Ta cã, lùc lín nhÊt t¸c dông lªn liªn kÕt: (βf γ w ) c 1260.1 min N ≤ =
≈ 65677 (daN) ≈ 657(KN) 1 e 1 10 + + ∑ A ∑W 12 , 3 2 + 903 5 , f f VÝ dô 2.6:
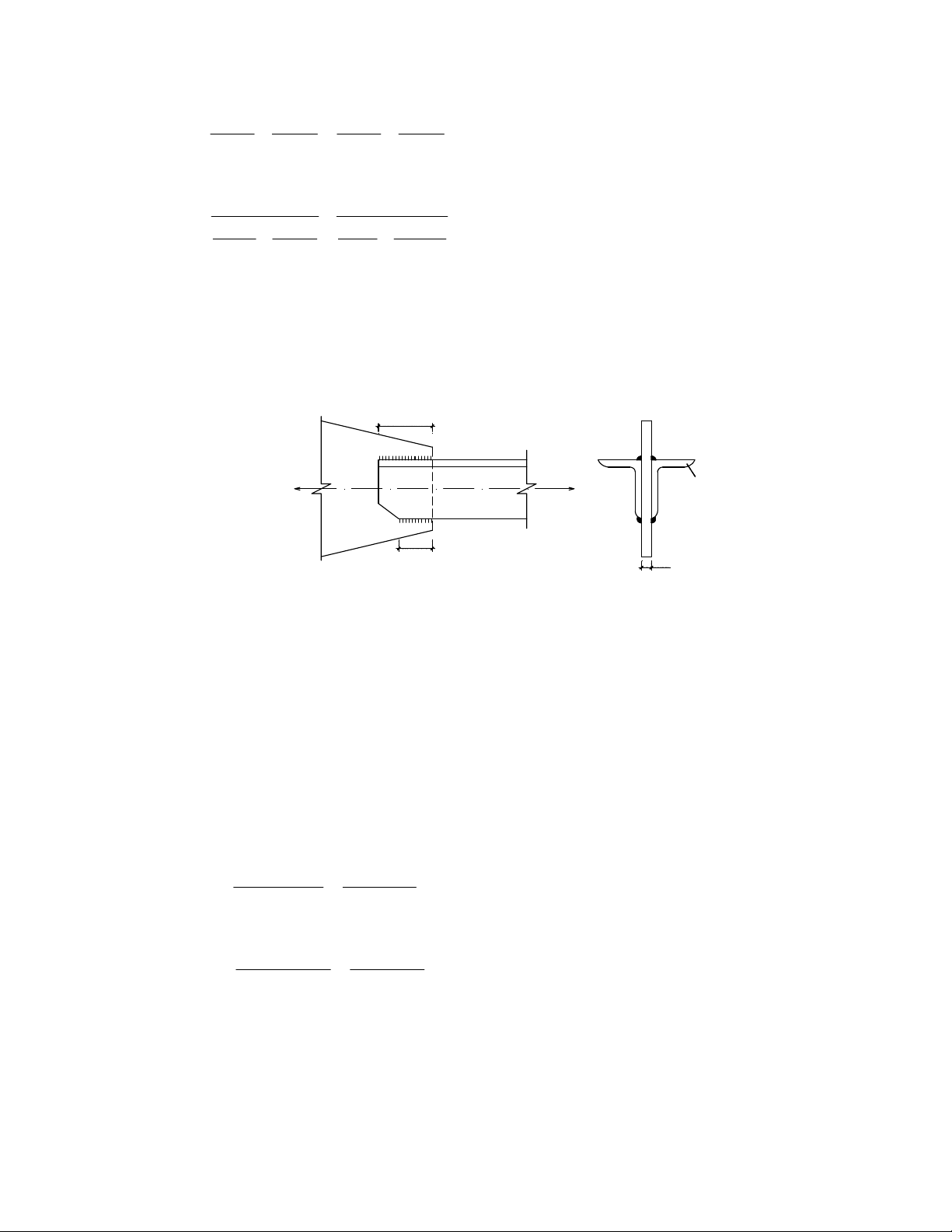
ThiÕt kÕ liªn kÕt hµn gãc c¹nh nèi 2 thÐp gãc L 100x75x8, liªn kÕt c¹nh dµi, víi b¶n thÐp cã
chiÒu dµy t=10mm. BiÕt lùc kÐo tÝnh to¸n N = 400(KN). Sö dông vËt liÖu thÐp CCT34 cã f=2100
daN/cm2; que hµn N42 cã f =1800daN/cm2; f = 1500 daN/cm2; β =0,7; β = 1; γ =1; wf ws f s C lsf N N=400KN L100x75x8 lmf t=10 H×nh 2.16 Bµi lµm:
Víi chiÒu dµy tÊm thÐp lµ 10mm vµ thÐp gãc ghÐp lµ 8mm, chän chiÒu cao ®−êng hµn h s = 8mm, h m = f f 6mm ®¶m b¶o ®iÒu kiÖn: h
=4(mm) < h s =8 (mm) < h =1,2t = 9,6 (mm). fmin f fmax min h
=4(mm) < h m =6 (mm) < h =1,2t = 9,6 (mm). fmin f fmax min Ta cã: (βf )
= min (β f ; β f ) = min (1800.0,7; 1500.1) = 1260 (daN/cm2) w min f wf s ws
Néi lùc ®−êng hµn sèng chÞu: N = kN = 0,6N = 240 (KN) s
Néi lùc ®−êng hµn mÐp chÞu: N = (1-k)N = 0,4N = 160 (KN) m
Tæng chiÒu dµi tÝnh to¸n cña ®−êng hµn sèng: 24000 s N ∑ l 40 f ≥ ( s β f γ . 1260 8 , 0 . 1 w ) = ≈ cm hs min c f
Tæng chiÒu dµi tÝnh to¸n cña ®−êng hµn mÐp: N 16000 ∑ l m 22 f ≥ m (βf γ 1260.1 6 , 0 . w ) = ≈ cm hm min c f
VËy, chiÒu dµi thùc tÕ cña 1 ®−êng hµn sèng:
l s = ∑( l s)/2 + 1 = 21 (cm) f f
ChiÒu dµi thùc tÕ cña 1 ®−êng hµn mÐp:
l m = ∑( l m)/2 + 1 = 12 (cm) f f VÝ dô 2.7:
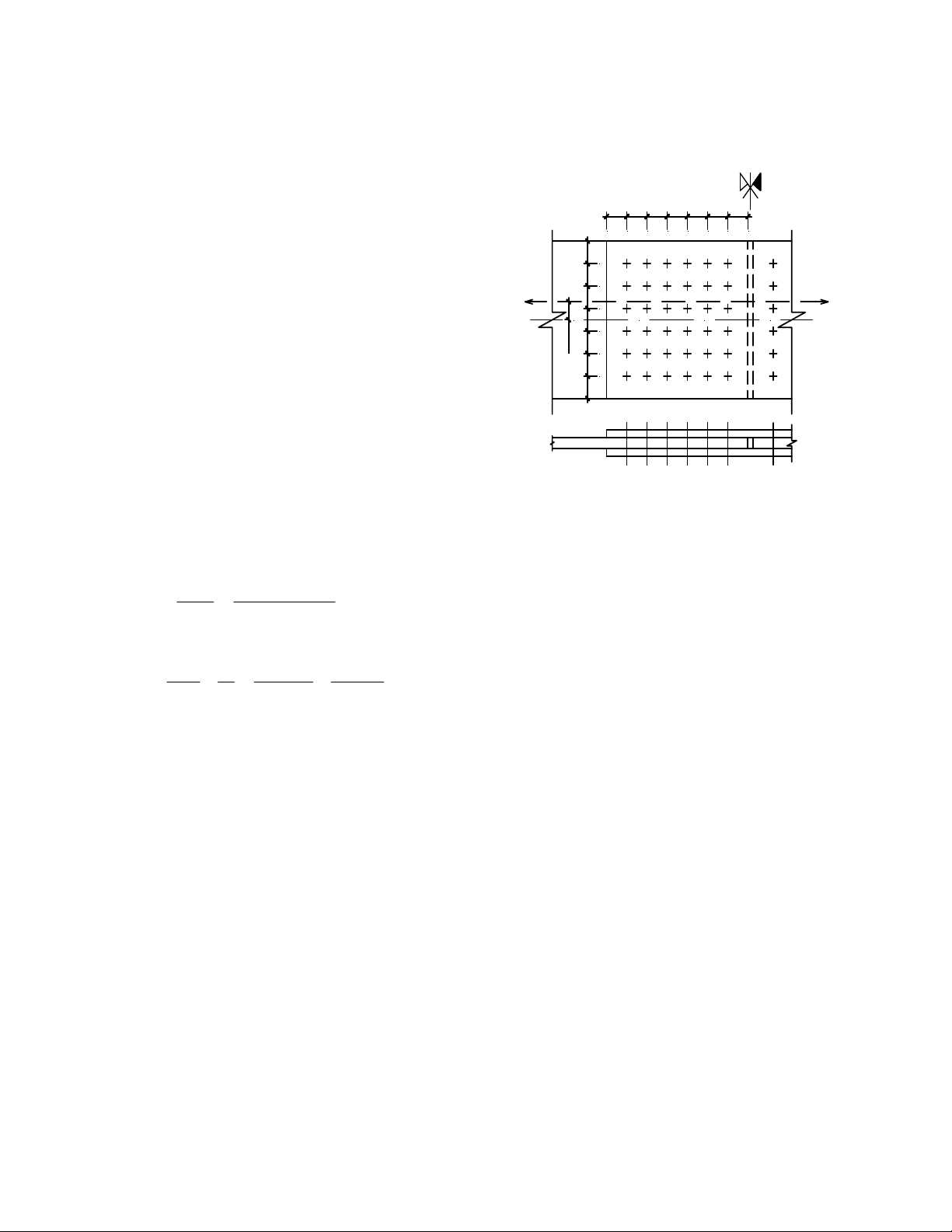
KiÓm tra kh¶ n¨ng chÞu lùc cho liªn kÕt bul«ng nèi 2 b¶n thÐp cã kÝch th−íc (400x16)mm, liªn
kÕt sö dông 2 b¶n ghÐp cã kÝch th−íc (400x12)mm nh− h×nh vÏ 2.17. BiÕt lùc kÐo tÝnh to¸n N = 2000 4
KN ®−îc ®Æt lÖch t©m 1 ®o¹n e=5cm. Sö dông vËt liÖu thÐp CCT34 cã f=2100 daN/cm2; sö dông bul«ng
th−êng cã cÊp ®é bÒn 4.6 cã f = 1500 daN/cm2; f = 3950 daN/cm2; ®−êng kÝnh bul«ng d=22mm; vb cb γ =1; C Bµi lµm: H×nh 2.17
a, KiÓm tra bÒn cho b¶n ghÐp: 60 60 60 60 60 60 60
∑A = 2.1,2.40 = 96 (cm2) > A = 1,6.40 = 64 (cm2) bg
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn. 0 5
b, KiÓm tra kh¶ n¨ng chÞu lùc cho liªn kÕt: 0 6 N 0 N=2000KN
Kh¶ n¨ng chÞu c¾t cña 1 bul«ng trong liªn kÕt: 6 0 6 0
[N] =n . A .γ . f =2.3,8.0,9.1500=10260 (daN) 5 0 vb v b b vb = e 6
Kh¶ n¨ng chÞu Ðp mÆt cña 1 bul«ng trong liªn kÕt: 0 6 0
[N] =d.∑(t) .γ . f =2,2.1,5.0,9.3950=11731,5(daN) 5 cb min b cb
Kh¶ n¨ng chÞu lùc nhá nhÊt cña bul«ng: [N]
= min([N] , [N] ) = 10260 (daN) bmin vb cb
Do lùc trôc ®Æt lÖch t©m 1 ®o¹n e = 5cm, sinh ra m«men:
M = Ne = N.5 = 2000.5 (KNcm) = 100000 (daNcm).
Lùc lín nhÊt t¸c dông lªn dgy bul«ng ngoµi cïng do m«men g©y ra: M l 1000000 3 . 0 N = 23809 ( 5 , daN ) bM = . 1 = ∑ 2 l 302 + 182 + 62 i
Lùc lín nhÊt t¸c dông lªn 1 bul«ng trong liªn kÕt: = N 23809 6 , 100000 N bM + = 952 (
4 daN ) < [N ] = 1026 ( 0 daN ) b + N = n n 6 36 b min 1
Trong ®ã: n – sè bul«ng trªn 1 dgy. 1
VËy, liªn kÕt ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 2.8:
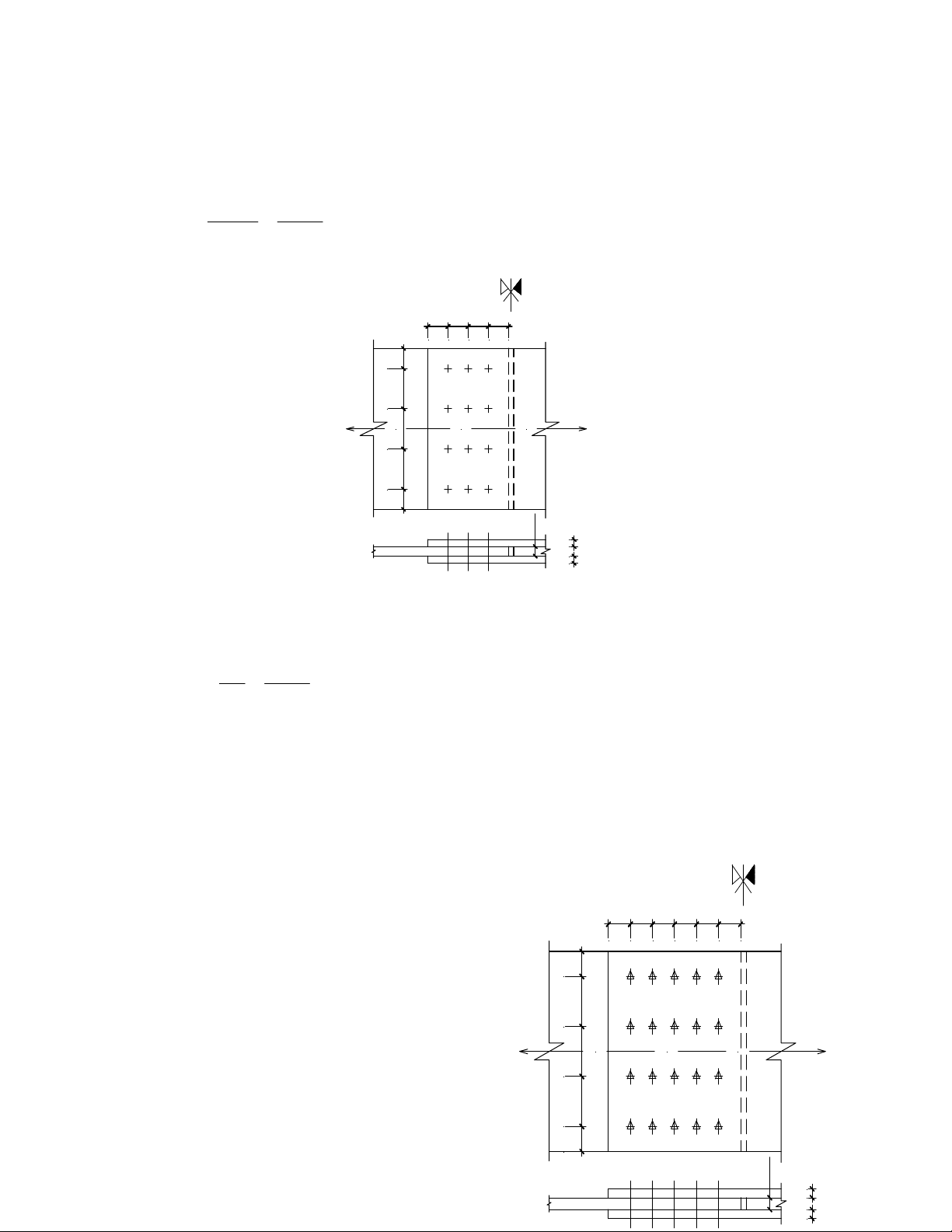
ThiÕt kÕ liªn kÕt bul«ng nèi 2 b¶n thÐp cã kÝch th−íc (400x16)mm, liªn kÕt sö dông 2 b¶n ghÐp,
chÞu lùc kÐo tÝnh to¸n N = 900 KN ®Æt ®óng t©m. Sö dông vËt liÖu thÐp CCT34 cã f=2100 daN/cm2; sö
dông bul«ng th−êng cÊp ®é bÒn 4.6 cã f = 1500 daN/cm2; f = 3950 daN/cm2; γ =1; vb cb C Bµi lµm:
a, KiÓm tra bÒn cho b¶n ghÐp:
Chän 2 b¶n ghÐp cã kÝch th−íc (400x12)mm ®¶m b¶o ®iÒu kiÖn:
∑A = 2.1,2.40 = 96 (cm2) > A = 1,6.40 = 64 (cm2) bg
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn. b, ThiÕt kÕ liªn kÕt:
Chän bul«ng cã ®−êng kÝnh d=20mm.
Kh¶ n¨ng chÞu c¾t cña 1 bul«ng trong liªn kÕt: 5
[N] = n . A .γ . f = 2.3,14.0,9.1500 = 8478 (daN) vb v b b vb
Kh¶ n¨ng chÞu Ðp mÆt cña 1 bul«ng trong liªn kÕt:
[N] = d.∑(t) .γ . f = 2.4.0,9.3950 = 28440 (daN) cb min b cb
Kh¶ n¨ng chÞu lùc nhá nhÊt cña bul«ng:
Sè l−îng bul«ng cÇn thiÕt trong liªn kÕt: N 90000 n = [ N ] = = 10 6 , 8478 b min
Chän 12 bul«ng vµ bè trÝ nh− h×nh vÏ. 50 50 50 50 0 5 0 0 1 N 0 N=1000KN 0 1 0 0 1 0 5 6 1=2t 2 1=1t 1 t H×nh 2.18
KiÓm tra bÒn cho b¶n ghÐp:
A = A -A = 40.1,6 – 4.2,2.1,6 = 49,92 (cm2) hn gy N 90000 σ = = = 1802 ( 9 , daN / 2
cm ) < fγ = 2100(daN / 2 cm ) A 49 9 , 2 c hn
VËy liªn kÕt bul«ng ®g chon ®¶m b¶o ®iÒu kiÖn bÒn. VÝ dô 2.9:
KiÓm tra kh¶ n¨ng chÞu lùc cho liªn kÕt bul«ng c−êng ®é cao nèi 2 b¶n thÐp cã kÝch th−íc
(400x16)mm, sö dông 2 b¶n ghÐp cã kÝch th−íc (400x12)mm nh− h×nh vÏ. BiÕt lùc kÐo tÝnh to¸n N =
2000 KN. Sö dông vËt liÖu thÐp CCT34 cã f=2100
daN/cm2; sö dông bul«ng c−êng ®é cao 40Cr cã f = ub 50 50 50 50 50 50
11000 daN/cm2; ®−êng kÝnh bul«ng d=20mm; γ =1; C Bµi lµm: 0 5
a, KiÓm tra bÒn cho b¶n ghÐp: 0 0 1
∑A = 2.1,2.40 = 96 (cm2) > A = 1,6.40 = 64 (cm2) bg N 0 N=4000KN
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn. 0 1
b, KiÓm tra kh¶ n¨ng chÞu lùc cho liªn kÕt: 0 0 1 0 5 6 6 1=2t 2 1 = 1 t 1 t
Kh¶ n¨ng chÞu kÐo cña 1 bul«ng c−êng ®é cao trong liªn kÕt: [N] = n . A .γ . f µ b f bn b1 hb γ b2
Ta cã: f = 0,7 f = 0,7.11000 = 7700 (daN/cm2) hb ub
γ =1 (do sè l−îng bul«ng trong liªn kÕt n >10); b1 a
γ =1,17; µ=0,35; n =2; A = 2,45 (cm2) b2 f bn 3 , 0 5 [N] = 2.2,45.1.7700. = 11287(daN) b 1 , 1 7
Lùc lín nhÊt t¸c dông lªn 1 bul«ng trong liªn kÕt: N 200000 N = =
= 10000(daN) <[N] = 11287 (daN) b n 20 b
VËy liªn kÕt ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 2.10:
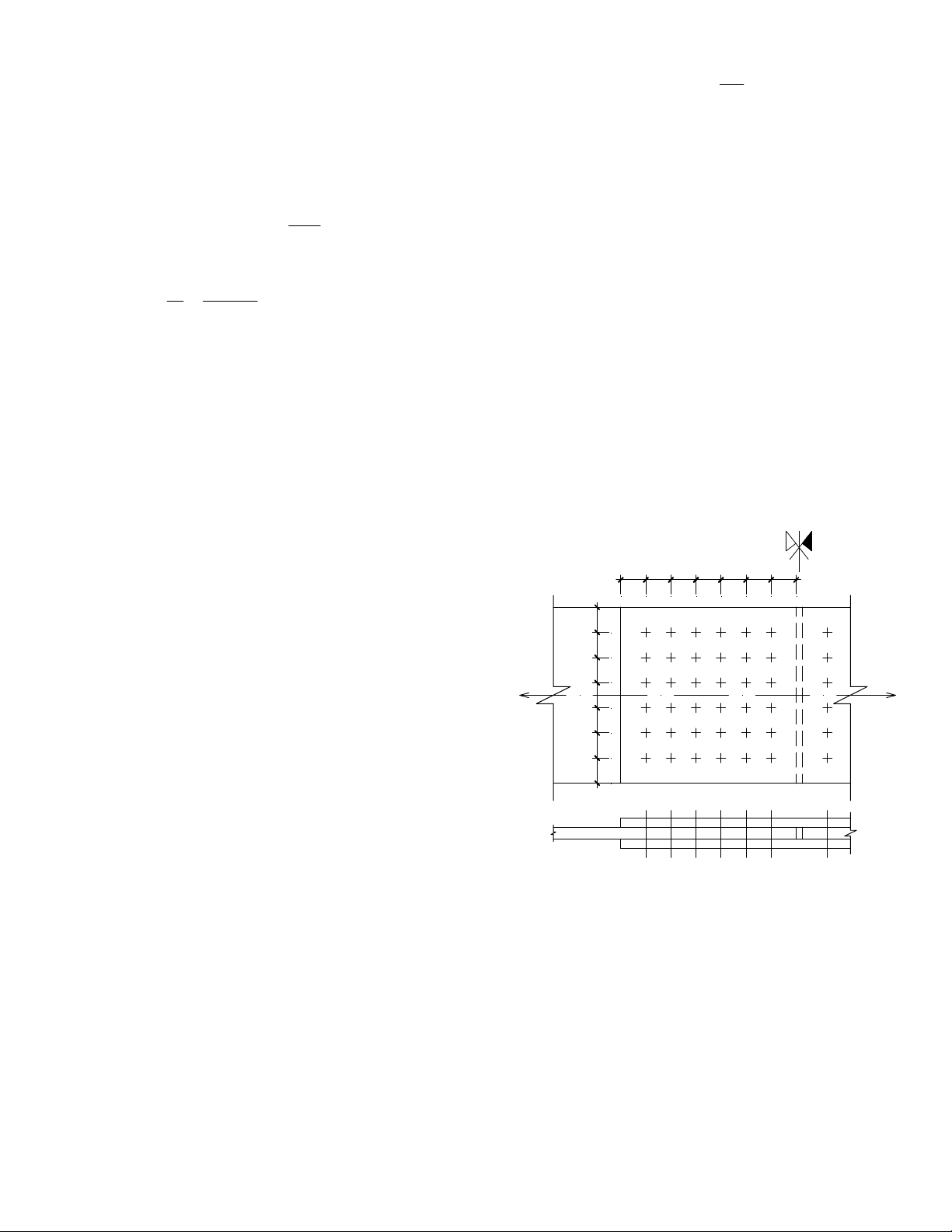
X¸c ®Þnh lùc lín nhÊt t¸c dông lªn liªn kÕt bul«ng nèi 2 b¶n thÐp cã kÝch th−íc (400x16)mm,
liªn kÕt sö dông 2 b¶n ghÐp cã kÝch th−íc (400x12)mm nh− h×nh vÏ 2.21. Sö dông vËt liÖu thÐp CCT34
cã f=2100 daN/cm2; bul«ng th−êng ®é bÒn líp 4.6 cã f = 1500 daN/cm2; f = 3950 daN/cm2; ®−êng vb cb kÝnh bul«ng d=20mm; γ =1; C Bµi lµm:
a, KiÓm tra bÒn cho b¶n ghÐp: 60 60 60 60 60 60 60
Chän 2 b¶n ghÐp cã kÝch th−íc (400x12)mm ®¶m b¶o 0 5 ®iÒu kiÖn: 0 6
∑A = 2.1,2.40 = 96 (cm2) > A = 1,6.40 = 64 (cm2) 0 bg 6 N N=?
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn. 0 6
b, X¸c ®Þnh lùc lín nhÊt t¸c dông lªn liªn kÕt: 0 6 0
Kh¶ n¨ng chÞu c¾t cña 1 bul«ng trong liªn kÕt: 6 0 5
[N] = n . A .γ . f = 2.3,14.0,9.1500 = 8478 (daN) vb v b b vb
Kh¶ n¨ng chÞu Ðp mÆt cña 1 bul«ng trong liªn kÕt:
[N] =d.∑(t) .γ . f = 2.1,5.0,9.3950 = 10665 (daN) cb min b cb
Kh¶ n¨ng chÞu lùc nhá nhÊt cña bul«ng: [N]
= min([N] , [N] ) = 8478 (daN) H×nh 2.21 bmin vb cb
Ngo¹i lùc lín nhÊt t¸c dông lªn liªn kÕt: N = [N ] .n = 8478 3
. 6 = 305208 (daN) ≈ 3052 (KN ) b min 7 Ch−¬ng 3: DÇm thÐp VÝ dô 3.1:
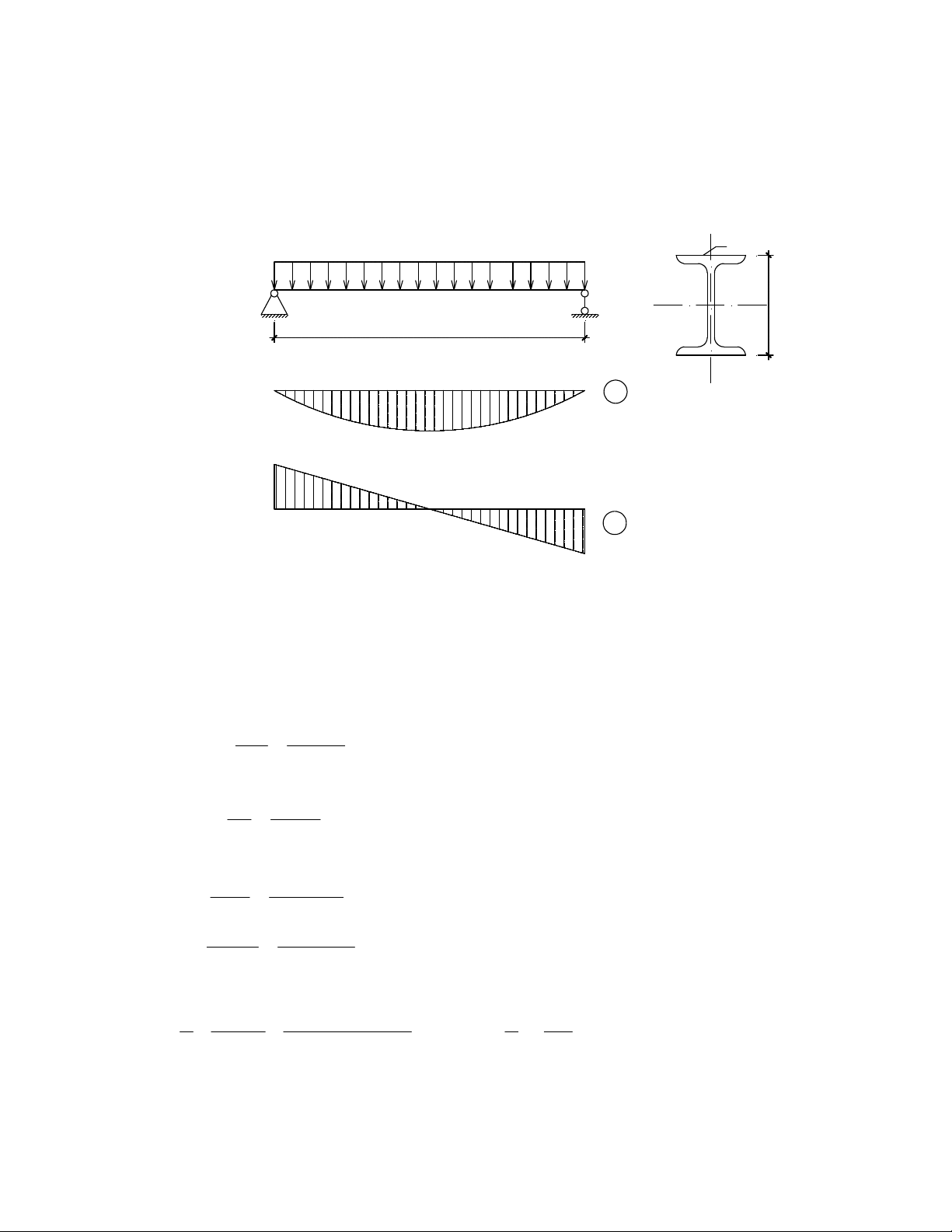
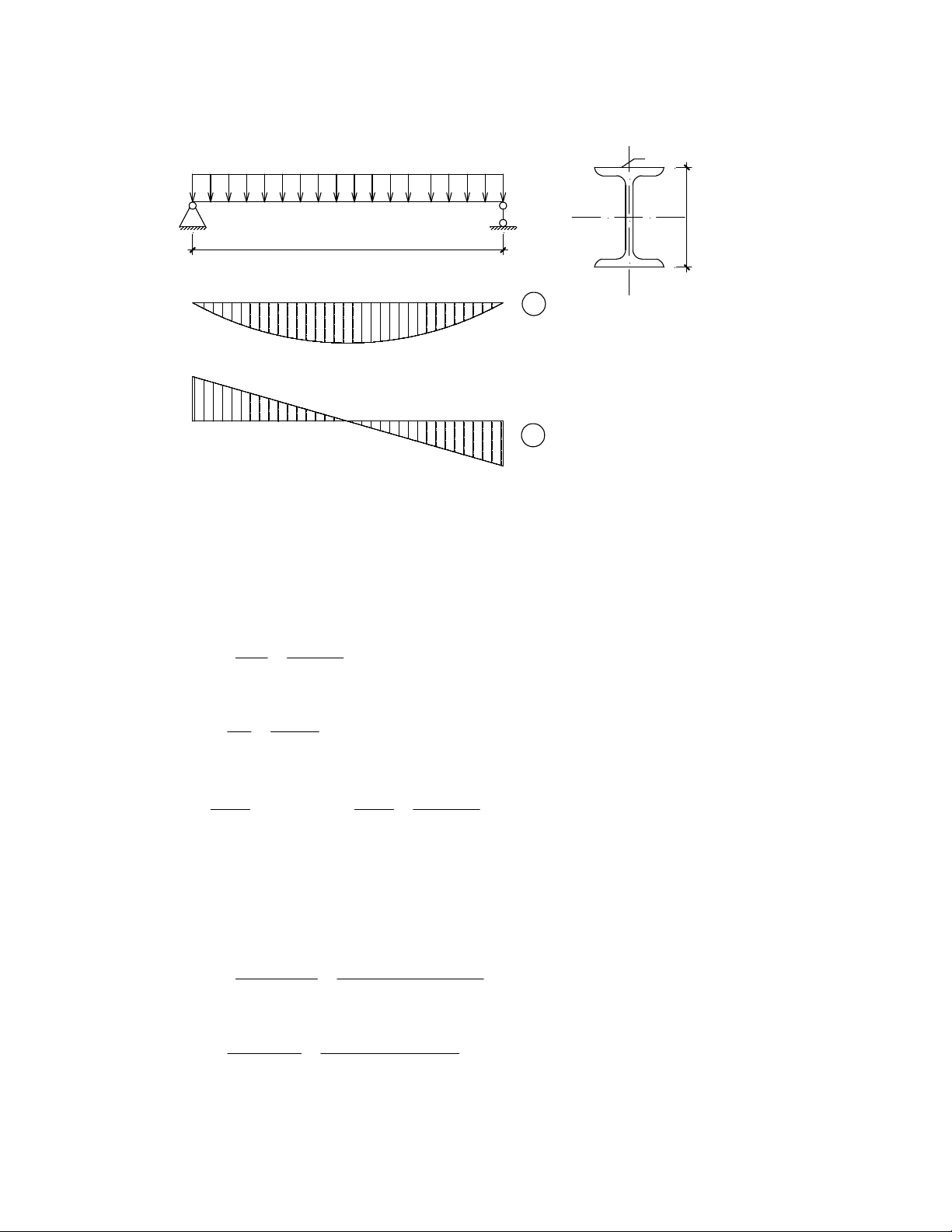
KiÓm tra kh¶ n¨ng chÞu lùc cho dÇm ch÷ IN 36 cã s¬ ®å dÇm ®¬n gi¶n nhÞp l = 6m, chÞu t¶i träng 0
ph©n bè ®Òu q = 2500 daN/m nh− h×nh vÏ 3.7. BiÕt c¸c ®Æc tr−ng h×nh häc cña thÐp IN 36: W = 743 c 0 x
cm3; I = 13380 cm4; h = 36cm; S = 423 cm3; t = 12,3 mm; bá qua träng l−îng b¶n th©n dÇm. Sö dông x x w
thÐp CCT34 cã f =2100 daN/cm2; f =1250 daN/cm2; ®é vâng [∆/l] = 1/250; γ =1; γ =1,2. V C q I No36 q x h l=6m y M ql /8 2 ql/2 V ql/2 H×nh 3.7 Bµi lµm:
T¶i träng tÝnh to¸n t¸c dông lªn dÇm:
q = q γ = 2500.1,2 = 3000 (daN/m) tt c q
M«men lín nhÊt t¸c dông lªn dÇm: 2 q l 300 . 0 62 M tt = = = 13500 (daNm) max 8 8
Lùc c¾t lín nhÊt t¸c dông lªn dÇm: q l 3000 6 . V tt = = = 9000 (daN) max 2 2
KiÓm tra bÒn cho dÇm h×nh: M 13500 1 . 02 max σ = = = 1817 (daN / 2
cm ) < fγ = 2100(daN / 2 cm ) W 743 c x V .S 9000.423 max x τ = = = 231 3 , (daN / 2
cm ) < f γ = 1250(daN / 2 cm ) I t 13380 , 1 . 23 v c x w
KiÓm tra ®é vâng cho dÇm h×nh: 3 ∆ 5. 3 q l 5.25 c (.6.102) ∆ 1 = = = 0 , 0 025 < = = , 0 004 l 384EI 384. 1 , 2 .106 1 . 3380 l 250 x
VËy dÇm thÐp ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 3.2: 8
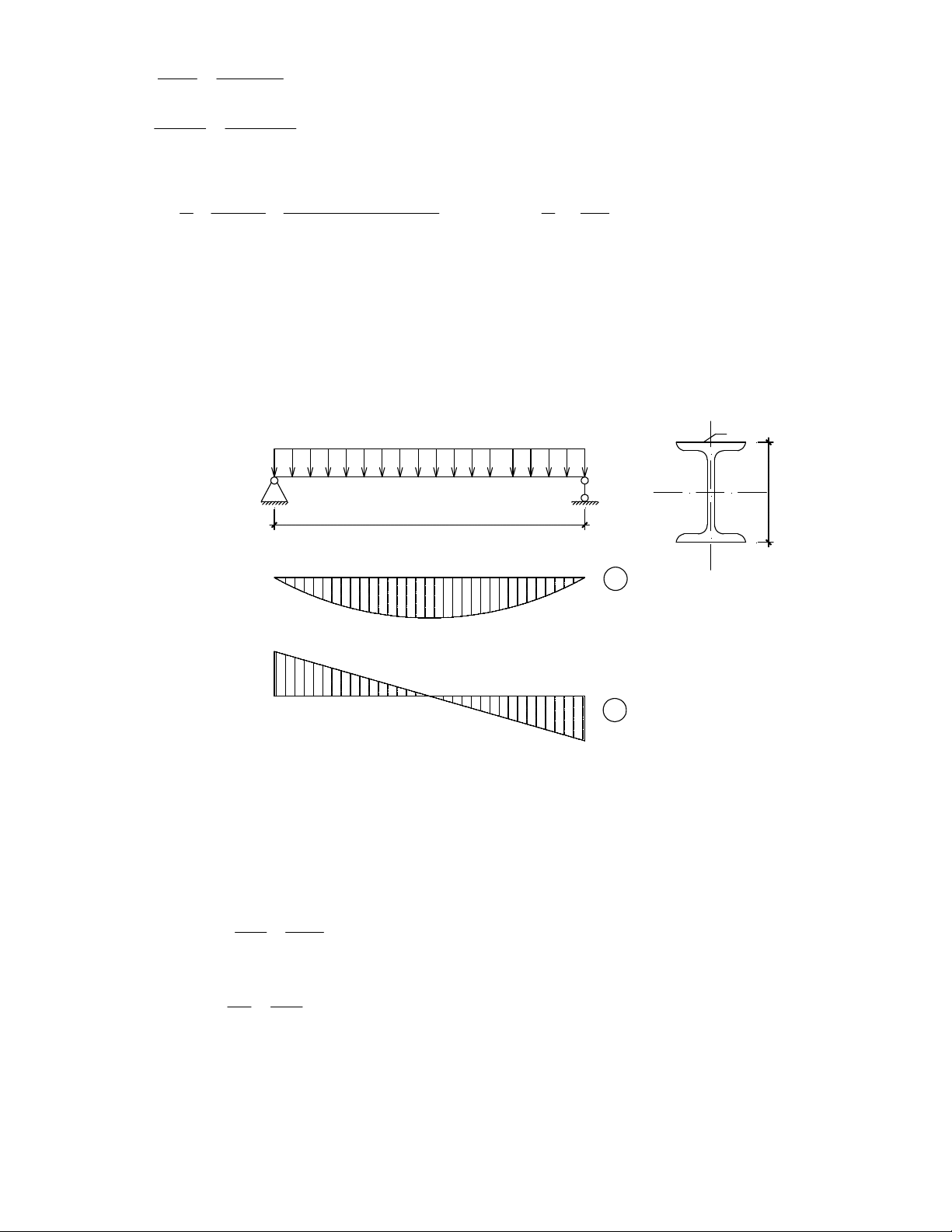
ThiÕt kÕ tiÕt diÖn dÇm ch÷ I ®Þnh h×nh cho dÇm cã s¬ ®å dÇm ®¬n gi¶n nhÞp l = 6m, chÞu t¶i träng
ph©n bè ®Òu q = 1000 daN/m nh− h×nh vÏ 3.8. Sö dông thÐp CCT34 cã f =2100 daN/cm2; f =1250 c V
daN/cm2; ®é vâng [∆/l]=1/250; γ =1; γ =1,2. C q I No? q x h l=6m y M ql 2/8 ql/2 V ql/2 H×nh 3.8 Bµi lµm:
T¶i träng tÝnh to¸n t¸c dông lªn dÇm:
q = q γ = 1000.1,2 = 1200 (daN/m) tt c q
M«men lín nhÊt t¸c dông lªn dÇm: 2 q l 120 . 0 62 M tt = = = 5400 (daNm) max 8 8
Lùc c¾t lín nhÊt t¸c dông lªn dÇm: q l 1200 6 . V tt = = = 3600 (daN) max 2 2
Tõ ®iÒu kiÖn ®¶m b¶o tra bÒn cho dÇm h×nh: M M 5400.102 max max σ = f ⇒ < γ W ≥ = = 257 ( 1 , 3 cm ) W c x fγ 2100 x c
Chän I N 24 cã c¸c ®Æc tr−ng h×nh häc: 0
W = 289 cm3; I = 3460 cm4; h = 24cm; S = 163 cm3; t = 9,5 mm; g =27,3(daN/m). x x x w bt
KiÓm tra l¹i tiÕt diÖn dÇm ®g chän:
M«men lín nhÊt t¸c dông lªn dÇm: (q + g + tt ) 2l (1200 27 .3 , , 1 05) 6 . 2 M bt = = ≈ 5529 (daNm) max 8 8
Lùc c¾t lín nhÊt t¸c dông lªn dÇm: (q + g + tt )l (1200 27 3, ,1 . 05).6 V bt = = ≈ 3686 (daN) max 2 2 KiÓm tra bÒn cho dÇm: 9 M 5529 1 . 02 max σ = = = 1913 (daN / 2
cm ) < fγ = 2100(daN / 2 cm ) W 289 c x V .S 3686.163 max x τ = = ≈ 182 8 , (daN / 2
cm ) < f γ = 1250(daN / 2 cm ) I t 3460. 9 , 0 5 v c x w
KiÓm tra ®é vâng cho dÇm h×nh: 3 ∆ 5. 3 q l 5. 1 ( 0 c + , 0 27 ) 3 (.6.102 ) ∆ 1 = = = 0 , 0 0398 < = = , 0 004 l 384EI 384 1 , 2 . .106 3 . 460 l 250 x
VËy dÇm thÐp ®g chän ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 3.3:
X¸c ®Þnh t¶i träng lín nhÊt t¸c dông lªn dÇm ®¬n gi¶n nhÞp l = 6m, cã tiÕt diÖn mÆt c¾t ngang
IN 24 nh− h×nh vÏ 3.9. BiÕt c¸c ®Æc tr−ng h×nh häc cña thÐp IN 24: W = 289 cm3; I = 3460 cm4; h = 0 0 x x
24cm; S = 163 cm3; t = 9,5 mm; bá qua träng l−îng b¶n th©n dÇm. Sö dông thÐp CCT34 cã f =2100 x w
daN/cm2; f =1250 daN/cm2; ®é vâng [∆/l] = 1/250; γ =1; γ =1,2. V C q I No24 q=? x h l=6m y M ql 2/8 ql/2 V ql/2 H×nh 3.9 Bµi lµm:
T¶i träng tÝnh to¸n t¸c dông lªn dÇm: q = q γ = q .1,2 (daN/m) tt c q C
M«men lín nhÊt t¸c dông lªn dÇm: 2 q l q 62 tt tt. M = = = 5 , 4 q (daNm) max 8 8 tt
Lùc c¾t lín nhÊt t¸c dông lªn dÇm: q l q .6 V tt tt = = = 3q (daN) max 2 2 tt
Tõ ®iÒu kiÖn ®¶m b¶o bÒn cho dÇm h×nh: 10 M fγ W max 2 . 2100 2 . 89 σ = < fγ
2100(daN / cm ) ⇒ = q c x ≤ = = daN m 1 134 , 8 7 ( / ) W c tt 5 , 4 5 , 4 1 . 02 x Tõ ®iÒu 1 q 1348 7 , q tt = = ≈ daN m 1 1124 ( / ) c γ , 1 2 q
kiÖn ®¶m b¶o ®é vâng cho dÇm h×nh: ∆ 5. 3 q l ∆ 1 ∆ EI c 2 384 1 1 , 2 .10 . 6 3460 3 . 84 = < = ⇒ q x ≤ = l 384EI l 250 c l 5. 3 l 250 Ta cã t¶i träng x ( 3 6 1 . 02 ) .5 = 10 3 , 3 (daN / c )
m = 1033 (daN / m)
tiªu chuÈn lín nhÊt t¸c dông lªn dÇm:
q max = min (q 1 vµ q 2) = 1033 (daN/m). c c c VÝ dô 3.4:
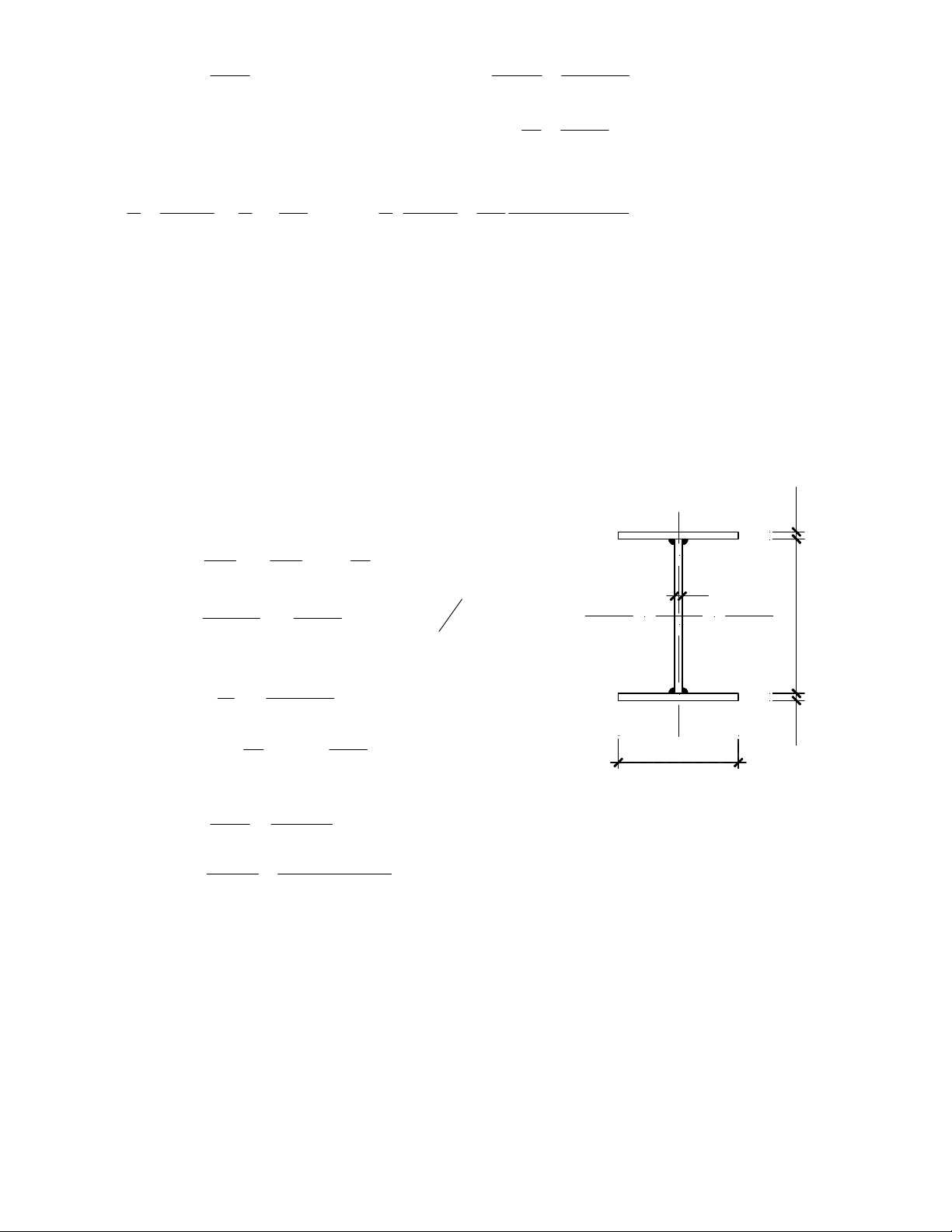
KiÓm tra kh¶ n¨ng chÞu lùc cho dÇm I tæ hîp hµn cã kÝch th−íc b¶n bông (1000x8)mm, b¶n c¸nh
(240x16)mm nh− h×nh vÏ 3.10. BiÕt M = 10000 daNm; V
= 130000 daN. Sö dông thÐp CCT34 cã f max max
=2100 daN/cm2; f =1250daN/cm2; V Bµi lµm: 6 1
C¸c ®Æc tr−ng h×nh häc cña dÇm: 3 h t 3 2 t b h I = w w f f f + 2 + b t f f 12 12 4 8 0 3 3 2 100 . 8 , 0 , 1 6 .24 x 0 = + 101 6 , 2 + , 1 6 2 . 4. 0 12 4 12 1 = 271168 (cm4) Ix 27116 . 8 2 W = .2 = = 525 , 5 2 (cm3) H×nh 3.10 x h 10 , 3 2 y 6 h 1 f 10 , 1 6 S = b t (cm3) 240 f f = 24 , 1 . 6. =192 , 3 07 x 2 2
KiÓm tra ®iÒu kiÖn bÒn cho dÇm: M 1000000 max σ = = = 1913 ( 8 , daN / 2
cm ) < fγ = 2100(daN / 2 cm ) W 525 , 5 2 c x V .S 130000.192 , 3 07 max x τ = = = 1152 ( 3 , daN / 2
cm ) < f γ = 1250(daN / 2 cm ) I .t 271168 8 , 0 . v c x w
VËy tiÕt diÖn dÇm ®g chän ®¶m b¶o ®iÒu kiÖn bÒn. VÝ dô 3.5:
X¸c ®Þnh kÝch th−íc s−ên gèi cho dÇm I tæ hîp hµn cã kÝch th−íc b¶n bông (1200x10)mm, b¶n
c¸nh (200x16)mm nh− h×nh vÏ 3.11. V = 1000 KN. Sö dông thÐp CCT34 cã f =2100 daN/cm2; max f =3200daN/cm2; c 11 18 f 6 1 10 0 0 2 1 6 1 0 2 200. 0 0 f t 2 C1 18 H×nh 3.11 Bµi lµm:
X¸c ®Þnh tiÕt diÖn s−ên gèi tõ ®iÒu kiÖn Ðp mÆt t× ®Çu: V V 100000 max max σ = f ⇒ ≤ γ A ≥ = ≈ 31 ( 3 , 2 cm ) A c c s f γ 3200 1 . s c c Chän b = b = 20 (cm) s f ChiÒu dµy s−ên gèi: A 31 3 , t s ≥ = ≈ , 1 6(cm) s b 20 s
KiÓm tra chiÒu dµy s−ên theo ®iÒu kiÖn æn ®Þnh: b E 1 , 2 .106 b 20 s ≤ = 3 , 1 6 ⇒ = t s ≥ = = 6 , 0 ( 5 cm) t f 2100 s 3 , 1 6 3 , 1 6 s
VËy, chän s−ên cã kÝch th−íc b .t = 20.1,8 (cm) S S
KiÓm tra æn ®Þnh tæng thÓ:
Ta cã: c = 0,65t . E f = 6 , 0 5.1. 1 , 2 .106 2100 = 20 5 , 4(cm) 1 W
A = A + A = 1,8.20 + 1.20,54 = 56,54 (cm2) S qu 3 t . 3 c b .t 13 2 . 0 5 , 4 20 . 3 1 I = w 1 s s + = + = 120 ( 2 4 cm ) Z 12 12 12 12 I 1202 i = z (cm) z = = 6 , 4 1 A 56 5 , 4 h 120 λ = w
. Tra b¶ng ta cã ϕ = 0,949. z = = 26 i , 4 61 z V 100000 max σ = = = 1864(daN / 2
cm ) < fγ = 2100(daN / 2 cm ) Aϕ 56 5 , 4 9 , 0 . 49 c
VËy, tiÕt diÖn s−ên gèi ®g chän ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 3.6: 12
KiÓm tra kh¶ n¨ng chÞu lùc cho vïng dÇm gÇn gèi tùa cña dÇm I tæ hîp hµn cã kÝch th−íc b¶n
bông (1200x10)mm, b¶n c¸nh (200x16)mm cã s¬ ®å nh− h×nh vÏ 3.12. V = 1500 KN. Sö dông thÐp max
CCT34 cã f =2100 daN/cm2; f =3200daN/cm2; BiÕt c = 0,65t . E f c 1 W 6 1 . 0 10 . 0. 2 1 6 . C 18 200. . C 1 1 1 H×nh 3.12 Bµi lµm:
TÝnh c = 0,65t . E f = 6 , 0 5.1. 1 , 2 .106 2100 = 20 5 , 4(cm) 1 W
A = A +2 A = 1,8.20 + 2.1.20,54 = 77,08 (cm2) S qu 3 t . 3 c b .t 13 2 . 0 5 , 4 203 1 . I = 2 w 1 s s + = . 2 + = 120 ( 4 4 cm ) Z 12 12 12 12 I 1204 i = z (cm) z = = 9 , 3 5 A 77,08 h 120 λ = w
. Tra b¶ng ta cã ϕ = 0,936. z = = 30 3 , 8 i 9 , 3 5 z V 150000 max σ = = = 208 ( 0 daN / 2
cm ) < fγ = 210 ( 0 daN / 2 cm ) Aϕ 7 , 7 08 9 , 0 . 36 c
VËy, tiÕt diÖn s−ên gèi ®g chän ®¶m b¶o kh¶ n¨ng chÞu lùc. VÝ dô 3.7:
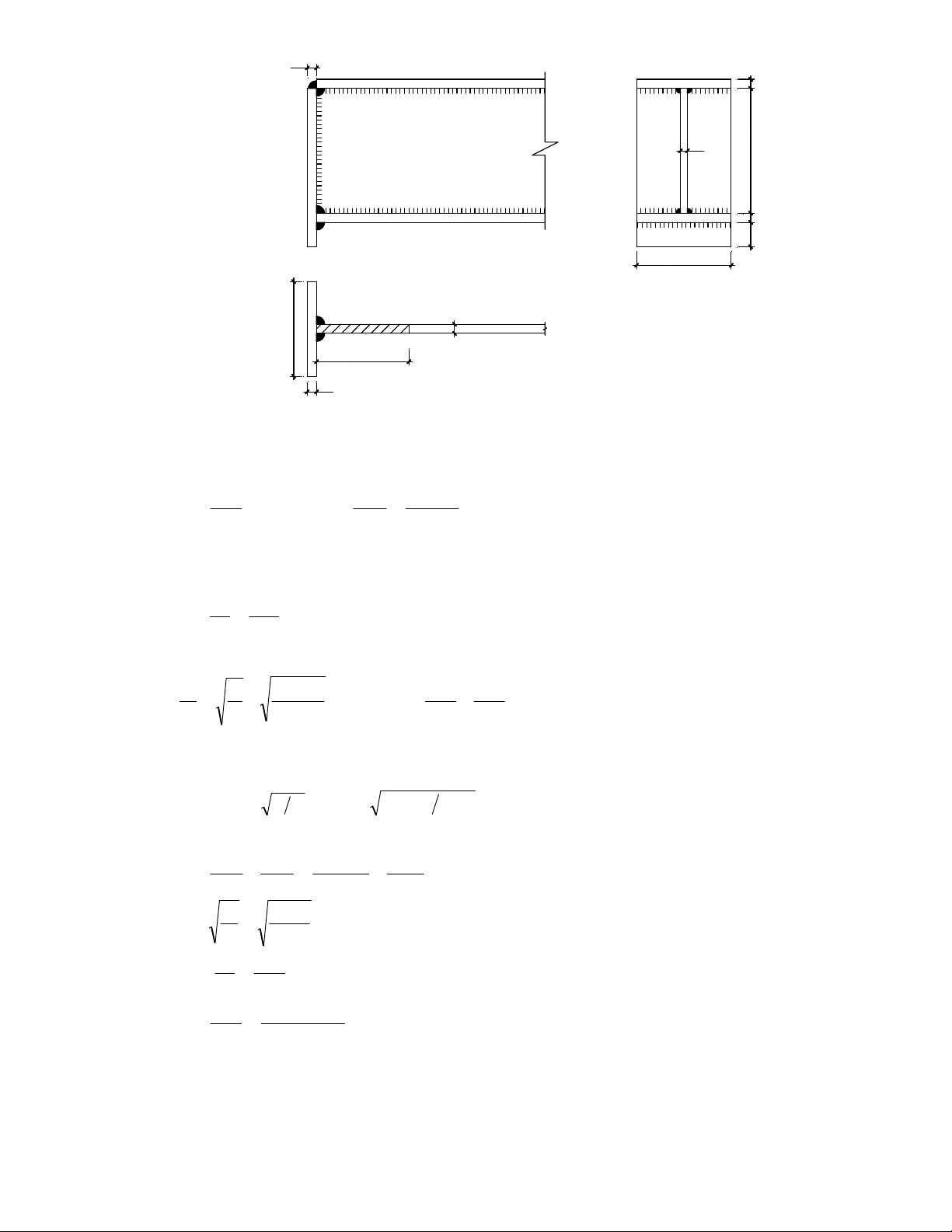
TÝnh mèi nèi b¶n bông cho dÇm I tæ hîp hµn cã kÝch th−íc b¶n bông (1200x10)mm, b¶n c¸nh
(200x16)mm nh− h×nh vÏ 3.14. BiÕt M = 300 KNm; V =2000 KN; Sö dông thÐp CCT34 cã f =2100 x x
daN/cm2; f =1250daN/cm2; que hµn N42 cã f = 1800 daN/cm2; f = 1500 daN/cm2; β =0,7; β = 1; V wf wf f s γ =1; C Bµi lµm:
Sö dông mèi nèi cã 2 b¶n ghÐp víi ®−êng hµn gãc ®Çu.
Chän b¶n ghÐp cã kÝch th−íc (1100x8x100)mm ®¶m b¶o ®iÒu kiÖn bÒn cho b¶n ghÐp:
∑A = 2.0,8.110 = 176 (cm2) > A = 1.120 = 120 (cm2) bg
VËy b¶n ghÐp ®¶m b¶o ®iÒu kiÖn bÒn. 13 6 V . x 1 Mx Mx 0 0 0 0. 1 2 1 1 . V 6 x 200 . 1 0 0. 2 H×nh 3.13
Chän chiÒu cao ®−êng hµn h =8(mm) tháa mgn ®iÒu kiÖn: f h = 6(mm) < h =8(mm) < h =1,2t = 9,6 (mm). fmin f fmax min
ChiÒu dµi tÝnh tãan cña 1 ®−êng hµn:
l = l – 1 = 110 -1 = 109 (cm) f tt
DiÖn tÝch tÝnh to¸n cña c¸c ®−êng hµn:
∑A = ∑l . h = 2.109.0,8= 174,4 (cm2) f f f
M« men kh¸ng uèn cña c¸c ®−êng hµn:
∑W = ∑l 2. h /6= 2.1092.0,8/6 = 3168,3 (cm2) f f f
M«men uèn mµ mèi hµn nèi bông ph¶i chÞu: I 144000 M = M
w +V .e = 300. + 2000 0 , 0 . 5 = 213 ( 5 , KNm) w x I x 380599 d Trong ®ã: 3 h t 3 2 t b h I = w w f f f + 2 + b t f f 12 12 4 3 3 2 120 .1 6 , 1 2 . 0 = + 121 6 , 2 + 2 2 . 0. = 380599 (cm4) 12 4 12 3 h t 1203 1 . I = w w = = 144000(cm4) W 12 12 Ta cã: (βf )
= min (β f ; β f ) = min (1800.0,7; 1500.1) = 1260 (daN/cm2) w min f wf s ws
Kh¶ n¨ng chÞu lùc cña liªn kÕt: 2 2 V M x w σ = + ∑ A W f ∑ f 2 2 200000 21350 1 . 00 = + = 1146 ( 8 , daN / 2 cm ) < (βf = w ) 1260(daN / 2 cm ) 17 , 4 4 3564 3 , min
VËy liªn kÕt ®¶m b¶o kh¶ n¨ng chÞu lùc. 14
Chương 4: Cột
Ví dụ 4.1.Chọn tiết diện cột đặc chịu nén đúng tâm (I định hình ). Biết cột có có chiều dài l = 5 m.
Cột có liên kết theo phương x hai đầu khớp; theo phương y 1 đầu ngàm, một đầu khớp. Tải trọng tác
dụng N = 3500 kN. Vật liệu là thép CCT38 có f = 2300 daN/cm2; [λ]= 120, γ =1 . Bài làm: f = 2300 daN/cm2=23 kN/cm2.
Chiều dài tính toán của cột
ly = 0,7.5= 3,5 (m); lx=1.5=5 (m)
Chọn sơ bộ độ mảnh λ=40 tra bảng được giá trị φ=0,900.
Diện tích tiết diện cột cần thiết là:
Ayc = N/(f. φ. γc)=3500/(23.0,9)= 169,1 (cm2). Bán kính quán tính
ixyc = lx/λ = 500/40= 12,5 (cm).
iyyc = ly/λ = 350/40= 8,75 (cm).
Chiều rộng và chiều cao tiết diện cột:
byc = iyyc/αy =8,75/0,24= 36,5 (cm);
hyc = ixyc/αx =12,5/0,42= 29,8 (cm).
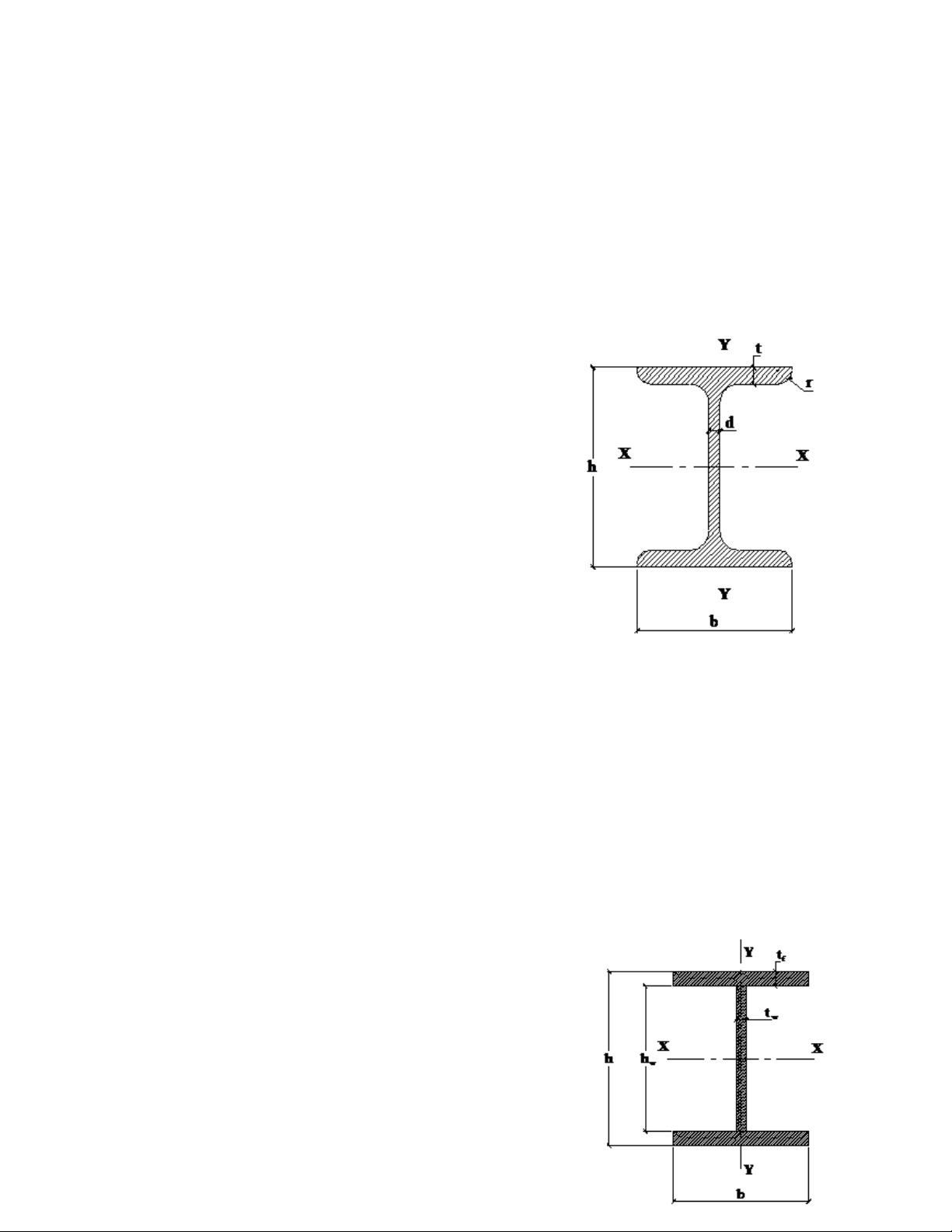
Từ bảng tra chọn thép I cánh rộng 40K1 có:
A=175,8 cm2; h= 393 mm; b= 400 mm; d=11mm; t=16,5
mm; r=22 mm; Ix= 52400 cm4; Wx =2664 cm3; ix= 17,26 cm; Sx=1457 cm3;
Iy= 17610 cm4; Wx =880 cm3; ix= 10 cm; g=138 kG/m. Độ mảnh λy= ly/ iy = 350/10= 35 ;
λx= lx/ ix = 500/17,26= 28,97→ λmax=35→ φ =0,918. Kiểm tra
σ= N/( A.φ)= 3500/(175,8.0,918)= 21,7 (kN/cm2) < f. γc = 23 kN/cm2.
Ổn định tổng thể cột đã chọn thỏa mãn. (kô cần kiểm tra ôđ cục bộ với tiết diện định hình)
Ví dụ 4.2. Chọn tiết diện cột đặc chịu nén đúng tâm (I tổ hợp ). Biết cột có có chiều dài l = 6,5 m.
Cột có liên kết theo phương x hai đầu khớp; theo phương y 1
đầu ngàm, một đầu khớp. Tải trọng tác dụng N = 4500 kN.
Vật liệu là thép CCT38 có f = 2300 daN/cm2; [λ]= 120, γ =1 . Bài làm: f = 2300 daN/cm2=23 kN/cm2.
Chiều dài tính toán của cột
ly = 0,7.6,5= 4,55 (m); lx=1.6,5=6,5 (m) 15
Chọn sơ bộ độ mảnh λ=40 tra bảng được giá trị φ=0,900.
Diện tích tiết diện cột cần thiết là:
Ayc = N/(f. φ)=4500/(23.0,9)= 217,3 (cm2). Bán kính quán tính
ixyc = lx/λ = 650/40= 16,25 (cm).
iyyc = ly/λ = 455/40= 11,35 (cm).
Chiều rộng và chiều cao tiết diện cột:
byc = iyyc/αy =11,35/0,24= 47,4 (cm);
hyc = ixyc/αx =16,25/0,42= 38,7 (cm). Chọn tiết diện cột: cánh- 2.48.1,8=172,8 (cm2)
bụng 217,3- 172,8= 44,5 (cm2)
hw =38,7-2.1,8=35,1 cm chọn 36 cm;
→ tw ≈44,5/36= 1,24 (cm); chọn hw =38 cm; tw= 1,2 cm. Kiểm tra ổn định
-đặc trưng hình học: Iy =2.1,8.483/12+38.1,23/12= 33183 cm4; A=2.1,8.48+1,2.38=218,4 (cm2) I y 33183 i = y = =12,3 (cm) A 21 , 8 4
λy= ly/ iy = 445/12,3= 36,2 ;
Ix =48.41,63/12- (48-1,2).383/12= 73964 cm4; I 73964 i x = x = =18,4 (cm) A 21 , 8 4
λx= lx/ ix = 650/18,4= 35,3→ λmax=36,2 → φ =0,912.
-kiểm tra ổn định tổng thể
σ= N/( A.φ)= 4500/(218,4.0,912)= 22,6 (kN/cm2) < f. γc = 23 kN/cm2.
(σ -f.γc)/ f.γc= 1,8%< 5% thỏa mãn.
-kiểm tra ổn định cục bộ bản bụng f 23 λ = λ = 3 , 6 2 =1,2 <2 4 E 1 , 2 1 . 0 h E 21000
w = (1,3+ 0,15 λ ) = (1,3+0,15.1,2) =44,7 t f 23 w h h
w =380/12= 31,6 < w =44,7 t tw w
-kiểm tra ổn định cục bộ bản cánh b0= (480-12)/2=234 (mm) b E 21000 0 = (0,36 + 0,1 λ ) = (0,36+0,1.1,2) =14,5 t f 23 f b b
0 =234/18= 13 < 0 =14,5. t t f f 16
Vậy tiết diện đã chọn thỏa mãn điều kiện ổn định tổng thể, ổn định cục bộ cánh và bụng.
Ví dụ 4.4. X¸c ®Þnh kh¶ n¨ng chÞu lùc cña cét chÞu nÐn ®óng t©m cã c¸c sè liÖu sau. Cét cã tiÕt
diÖn ch÷ I tæ hîp, b¶n c¸nh ( 480x18)mm, b¶n bông (450x12) mm. Cét cã chiÒu dµi l=6,5 m , hai ®Çu
liªn kÕt khíp. C−êng ®é thÐp f=2300daN/cm2, [λ] =120 Bài làm:
Chiều dài tính toán của cột lx=ly = 0,7.6,5= 4,55 (m). A=2.1,8.48+1,2.45=226,8 (cm2)
Iy =2.1,8.483/12 + 45.1,23/12= 33182 cm4;
Ix =48.48,63/12- (48-1,2).453/12= 103778 cm4; I y 33182 i = y =
=12,09 (cm); λy= ly/ iy = 445/12,09= 36,8 A 226 8 , I 103778 i x = x =
=21,4 (cm); λx= lx/ ix = 445/21,4=20,8 A 226 8 ,
λmax= λy=36,8 → φ =0,911.
Lực lớn nhất cột có thể chịu :
Nmax = A. φ .f. γc =226,8.0,911.23.1= 4752 kN. 17 Chương 5:Dàn
Ví dụ 5.1. Kiểm tra khả năng chịu lực của thanh dàn ghép từ hai thép góc có số hiệu L 125x90x10,
chịu lực nén N =500 KN. Biết chiều dài tính toán của thanh lx=250 cm, ly =400 cm. Diện tích tiết diện 1
thép góc Ag=20,6 cm2. Bán kính quán tính tra bảng ix =3,95 cm, iy = 2,6 cm; ix2 = 5,95 cm. Thép CCT34
cú f = 2100 daN/cm2, [λ ]=120.
Bài làm: ix= iy (tra báng) = 2,6 cm; iy = ix2 (tra bảng) = 5,95 cm f = 2100 daN/cm2 =21 kN/cm2.
λx= lx/ ix=250/2,6=96,2 <[λ] = 120;
λy= ly/ iy=400/5,95 = 67,2<[λ] = 120;
λmax= λx=96,2 (cm) → φ =0,611.
Kiểm tra ổn định thanh đã chọn
σ= N/( A.φ)= 500/(2.20,6.0,611)= 19,86 (kN/cm2) < f. γc = 21 kN/cm2.
Vậy tiết diện đã chọn đủ khả năng chịu lực.
Ví dụ 5.2. Chọn tiết diện thanh cánh trên của dàn mái bằng hai thép góc, chịu lực nén N =500 kN.
Biết chiều dài tính toán của thanh lx= 250 cm, ly =400 cm, chiều dầy bản mắt tbm =10 mm, f = 2100 daN/cm2 ;[λ] = 120. Bài làm:
f = 2100 daN/cm2 =21 kN/cm2. Chọn λ = 100→ φ =0,582
Diện tích tiết diện cần thiết:
Ayc = N/(φ .f. γc)= 500/(0,582.21.1)= 40,9 (cm2).
Bán kính quán tính cần thiết: ix=lx/λ=250/100=2,5 (cm) iy=ly/λ=400/100=4 (cm)
Ta chọn 2 thép góc không đều cạnh ghép cạnh ngắn (vì ix ≈0,5iy)
Từ bảng tra thép góc không đều cạnh chọn 2 thanh thép góc không đều cạnh L 100x90x13 có A=
2.23,1 cm2 =46,2 cm2 và với tbm=10 mm có ix2=4,7 > 4; ix=2,66 cm
λx= lx/ ix=250/2,66=94 <[λ] = 120;
λy= ly/ iy=400/4,7 = 85,1<[λ] = 120;
λmax= λx=94 (cm) → φ =0,625.
Kiểm tra ổn định thanh đã chọn
σ= N/( A.φ)= 500/(46,2.0,625)= 17,32 (kN/cm2) < f. γc = 21 kN/cm2. 18
Phần kết cấu gỗ
Nén đúng tâm
Bài 1: Kiểm tra một thanh nén đúng tâm 2 đầu liên kết khớp có kích thước như hình
vẽ. Biết lực nén tính toán Ntt= 10T; Rn= 130 kg/cm2; [λ]= 150.
Giải:
Kiểm tra về cường độ:
Theo công thức: σ = Ntt/Ath.
Ath= Ang - Agy= 18.15- 6.15= 180 cm2.
σ= Ntt/Ath= 10000/180= 55,6 kg/cm2 < Rn= 130 kg/cm2.
Vậy thanh gỗ thỏa mãn điều kiện chịu lực về cường độ.
b) Kiểm tra về ổn định Agy= 6.15= 80 cm2. Ang= 18.15= 270 cm2.
Agy/Ang= 80/270= 33%> 25% nên
Att= 4/3Ath= 4/3.180= 240 cm2.
rmin= 0,289.b= 0,289.15= 4,34 cm. l0= l=420 cm.
λmax= ltt/rmin= 420/4,34= 97 < [λ]= 150 thỏa mãn.
φ = 3100/ λ 2= 3100/ 972= 0,33.
σ = Ntt/(φ.Ath)= 10000/(0,33.240)= 126 kg/cm2< Rn= 130 kg/cm2.
Vậy thanh gỗ đảm bảo điều kiện về ổn định.
Từ các kết quả trên thấy rằng việc kiểm tra ổn định thường có tính chất quyết định.
Bài 2: Chọn tiết diện một cột gỗ chịu nén đúng tâm trong một kết cấu chịu lực lâu
dài biết chiều dài tính toán ltt= 5 m, tải trọng tính toán Ntt= 10 T.
Giải: Giả thiết λ>75. l N 500 10000 Dựng tiết diện tròn: A= tt 2 . = . = 278cm 15 7 , 5 R 1 , 5 75 130 n A 278 d= 1,135 = 1,135 = 18,9 cm. 19
Chọn gỗ có d= 20 cm, thử lại độ mảnh λ max = 500/(0,25.20)= 100 >75 dùng đúng công thức.
b) Nếu dựng tiết diện vuông : l N 500 10000 A= tt 2 . = . = 282cm 16 R 16 130 n A 282 a= = = 16,8 cm.
Dùng tiết diện vuông có cạnh 18x18 cm, thử lại độ mảnh λ max = 500/(0,289.18)=
93,7 >75 dùng đúng công thức.
Nếu λ max <75 ta giả thiết lại λ < 75 và dùng công thức tính toán tương ứng.
Uốn phẳng
Bài 1 : Chọn tiết diện một dầm gỗ biết l = 4,5m, tải trọng qtc = 400kG/m, qtt = 485 f 1 kG/m. =
, Gỗ nhóm VI, độ Nm 18%, nhiệt độ 20°C. Sơ đồ dầm đơn giản. l 250
Giải
Lấy các thông số đầu bài.
Gỗ nhóm VI, độ Nm 15%, nhiệt độ 20°C nên Ru = 120kG/cm2.
Tính toán nội lực. qtt l2 485 × , 4 52 M 1227 6 = = = max , kGm 8 8 qtt l 485 4 × ,5 Q 1091 3 = = = max , kG 2 2
Lựa chọn tiết diện.
Chọn tiết diện chữ nhật.
Giả thiết thanh gỗ có một cạnh > 15cm, h / b < 3,5, khi đó mu = 1,15. Giả thiết b = 0,8h. 20
