BÀI TẬP
1. Một bình có thể tích 0,625m3 chứa ôxi với 23 bar, nhiệt độ 280oC. Hãy xác định:
- Khối lượng ôxi trong bình, kg ;
- Thể tích riêng và khối lượng riêng của ôxi trong bình ở trạng thái đó và trạng thái tiêu chuẩn (p=760mmHg, t = 0oC).
- Thể tích ôxi chứa trong bình qui ra điều kiện tiêu chuẩn. Đáp số:
G = 10 kg, v = 0,0625 m3/kg, ρ=16 kg/m3,
vo =0,7m3/kg, ρo = 1,43 kg/m3 , Vo = 7 m3.tc GIẢI - Khối lượng không khí: V . p . 23 105 x 625 , 0 G = = =10kg R T . 8314 x(280+ ) 273 32
- Thể tích riêng v = V/G = 0,625/10 = 0,0625 m3/kg.
- Khối lượng riêng ρ = 1/v = 1/0,0625 = 16 kg/m3
- Điều kiện tiêu chuẩn: Po = 1,013 bar To = 273 oK R T . 287x273 v o = = = 7 , 0 o p , 1 1 . 013 05 o
ρo = 1/v = 1/0,7 = 1,43 kg/m3. Vo = G.vo = 10 x 0,7 = 7m3
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Bài 2. Một bình kín chứa không khí có thể tích không đổi 2 m3 áp suất ban đầu p1= 30 bar,
nhiệt độ t1= 27oC. Sau khi lấy một ít ra khỏi bình để sử dụng, áp suất trong bình còn 12 bar,
nhiệt độ không đổi. Cho biết không khí có µ=29 kg/kmol. Hãy xác định khối lượng không khí
đã lấy ra, thể tích riêng không khí trong bình trước và sau khi lấy ra sử dụng. Đáp số:
G1 = 70 kg, G2 = 28 kg , ∆G = 42kg
v1 = 0,029 m3/kg, v2 = 0,0714 m3/kg GIẢI 1
- Khối lượng không khí ban đầu trong bình p V . 1 . 30 05 x2 G 1 = = = 70kg 1 RT 287x(27 + 27 ) 3
- Khối lượng không khí trong bình sau khi đã sử dụng p V . 1 . 12 05 x2 G 2 = = = 28kg 2 RT 287x(27 + ) 273
- Khối lượng đã lấy đi
∆G = G1 – G2 = 70 – 28 = 42 kg
- Thể tích riêng ban đầu và cuối quá trình
v1 = V/G1 = 2/70 = 0,029 m3/kg.
v2 = V/G2 = 2/28 = 0,0714 m3/kg
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 3. Một bình kín chứa 0,5m3 không khí ở p1 = 2 bar, t1 = 20oC. Sau khi lấy một ít, trong
bình có độ chân không pck = 420mmHg mà nhiệt độ không đổi, biết áp suất khí quyển
768mmHg. Xác định lượng không khí trong bình trước và sau khi lấy ra, lượng khí đã lấy.
Đáp số: G1 = 1,19 kg, G2 = 0,28 kg , ∆G = 0,91kg GIẢI
- Ap suất tuyệt đối của không khí trong bình sau khi đã lấy một ít ra sử dụng: 348 p = B − p = 768 − 420 = mmHg 348 = bar = , 0 464bar 2 ck 750
- Lượng môi chất trong bình ban đầu p V . . 2 105 x 5 , 0 G 1 = = = 19 , 1 kg 1 RT 287x(20 + ) 273
- Khối lượng không khí trong bình sau khi đã sử dụng p V . , 0 464 10 . 5 x 5 , 0 G 2 = = = , 0 kg 28 2 RT 287x(20 + ) 273
- Khối lượng đã lấy đi
∆G = G1 – G2 = 1,19 – 0,28 = 0,91 kg
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 4. Một khinh khí cầu có thể tích 1000m3 chứa H2 thả vào khí quyển. Tính lực nâng
khinh khí cầu tại mặt đất nếu biết áp suất và nhiệt độ không khí và khí H2 trong khinh khí cầu
bằng nhau p=1bar và nhiệt độ t = 27oC. Biết gia tốc trọng trường g = 9,81 m/s2, coi khối lượng
vỏ khinh khí cầu không đáng kể.
Bií́t qui luật thay đổi mật độ theo độ cao : ρ=ρo – 0,0005.h (kg/m3)
ρo – Mật độ không khí tại mặt đất (h=0m) và h là độ cao (m). Xác định độ cao cực đại mà
khinh khí cầu đạt được. Đáp số: F=10.607 N GIẢI 2
Khinh khí cầu chịu tác động của hai lực
- Lực nâng F1: Có giá trị bằng trọng lực của không khí mà nó chiếm chổ
- Trọng lực F2 hướng xuống của khối không khí H2.  V . p V . p  g . V . p 1 1 F ∆ =F −F = (m −m ) g . = − g . = ( − ) 1 2 1 2  R T . R T .  T R R  1 2  1 2 Thay vào ta có: 105 1000 x x 81 , 9 29 2 F ∆ = ( − ) =10607N (27 + ) 273 8314 8314
- Khi đạt độ cao cực đại lực nâng và trọng lực cân bằng. Trọng lực luôn luôn không đổi,
nhưng lực nâng giảm dần theo độ cao vì mật độ không khí loãng dần. Ở độ cao cực đại: F’1 = F2 Từ đó suy ra: m’1 = m2 hay: ρ = ρH2 p p hay − , 0 h . 0005 = R T . R T . 1 2 1 p 1 1 1 105 29 2 hay h = . ( − ) = . ( − ) = m 2165 , 0 0005 T R R 0005 , 0 300 8314 8314 1 2
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
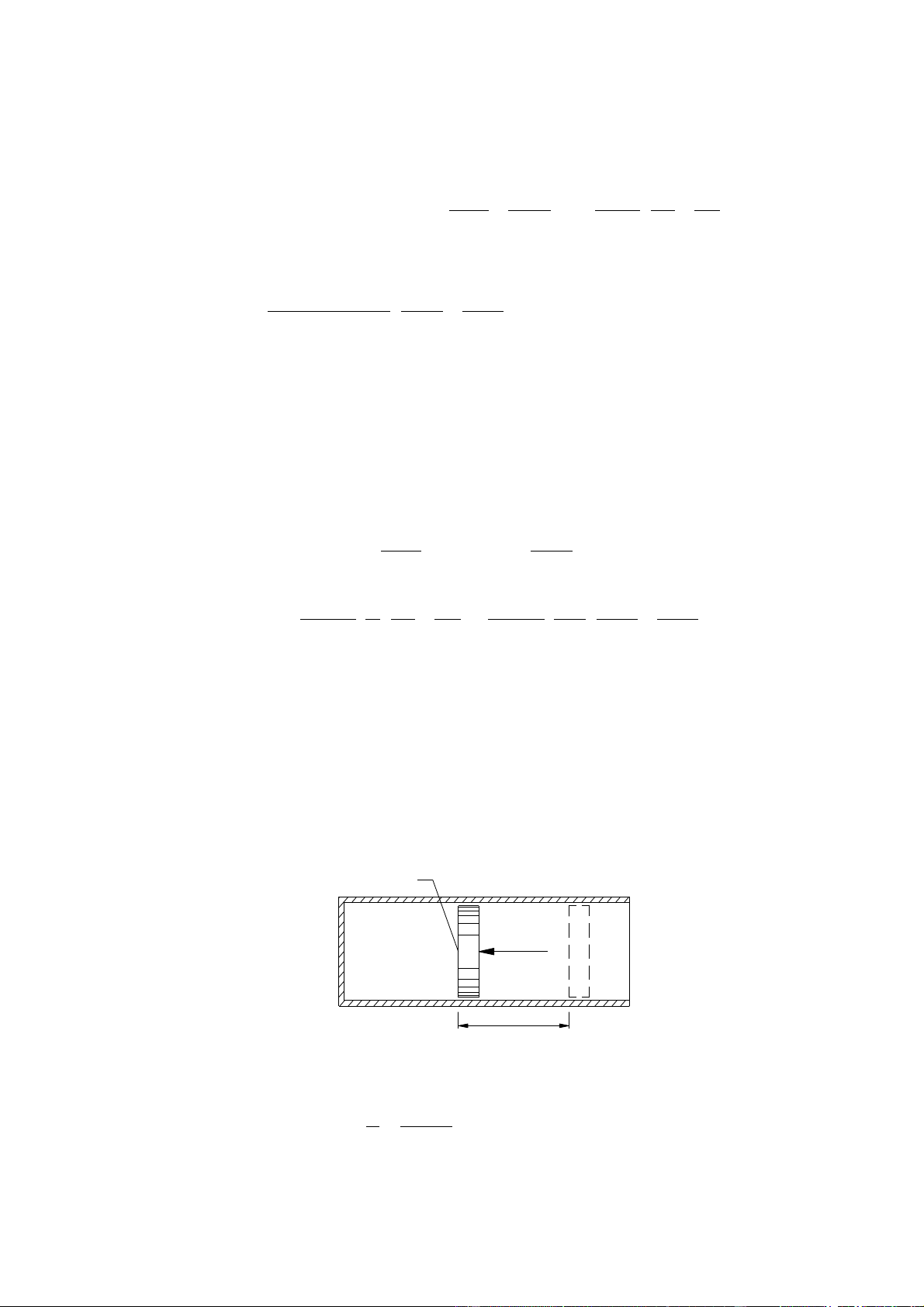
Cđu 4: Một xy lanh chứa không khí có thể tích ban đầu V1=3m3, nhiệt độ t1=27oC, diện tch
bề mặt tiết diện ngang xy lanh S=0,5m2. Lực tác động lên pittông không đổi F= 75000N.
Cung cấp cho không khí nhiệt lượng Q = 525 kJ. Hỏi:
- Áp suất và khối lượng không khí trong bnh.
- Nhiệt độ không khí sau khi cấp nhiệt .
- Quảng đường mà pittông dịch chuyển sau khi cấp nhiệt. 0,5m2 V=3m3 F=75000N t1=27oC x Giải: - Ap suất bên trong xi lanh F 75000 p = = = 5 , 1 1 . 05 N / m2 = 5 , 1 bar S 5 , 0
- Khối lượng không khí trong bình: 3 V . p . 150000 G = = R T . 1
Câu 4: Cho một chất khí lý tưởng có hằng số R=200 J/kg.K và số mủ đoạn nhiệt k = 1,4 ,
đựng trong một bình kín với thể tích 0,3m3 . Ở nhiệt độ t1 = 27oC, áp suất khối khí p1=3 bar.
Đốt nóng khối khí đến áp suất p2=6 bar.
a. Biểu thị quá trình thay đổi trạng thái trên đồ thị p-v và T-S;
b. Xác định khối lượng môi chất trong bình, G (kg);
c. Nhiệt độ cuối quá trình t2 (oC);
d. Nhiệt lượng cung cấp cho khối khí Q ;
e. Xác định độ biến thiên ∆U, ∆I, Lkt
Đáp sô : G = 1,5 kg ; t2 = 327oC ; Q = 225.000 J
∆U = Q = 225.000 J ; ∆I = 315.000 J ; Lkt = - 90.000 J GIẢI
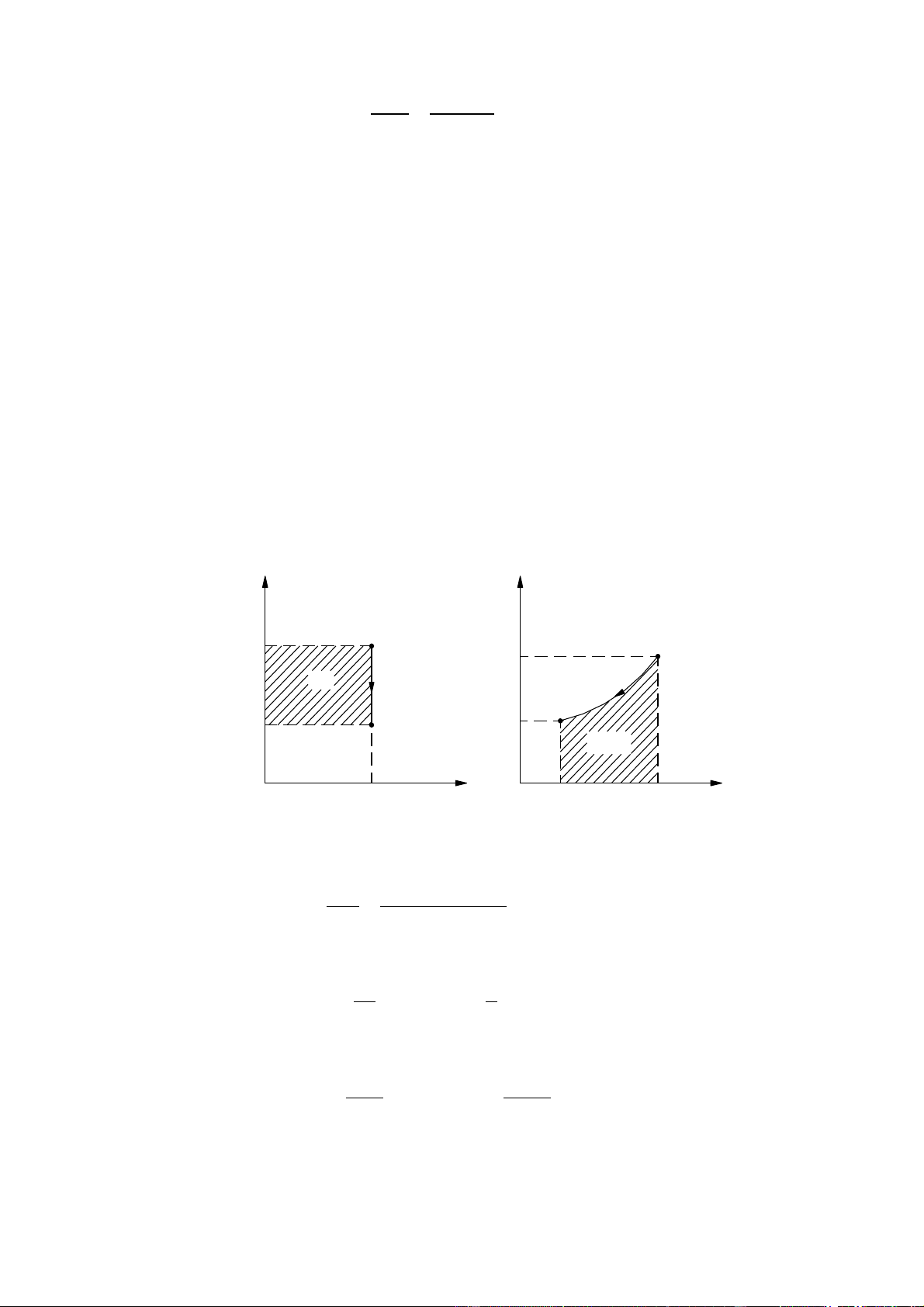
a). Biểu diễn trên đồ thị p-v và T-s
Đây là quá trình đẳng tích P, T, K N/m2 p1 1 1 T1 lKT 2 p2 2 T2 v, q=∆u s, m3/kg J/kg.K v1=v2 s2 s1
(Vẽ giống bản vẽ này nhưng đổi điểm 1 cho điểm 2 và ngược lại)
Khối lượng không khí trong bình : V . p 1 . 3 05 3 , 0 . G = = = 5 , 1 kg R T . 200x(27 + 27 ) 3
- Nhiệt độ cuối quá trình p 6 T = T . 2 = (27 + ) 273 . = 600o K 2 1 p 3 1 - Quá trình đẳng tích R 200 Q = ∆U = C . G (T − T ) = . G (T − T ) = . 5 , 1 (600 − ) 300 = 225000 v 2 1 ∆I = k.∆U = k −1 2 1 , 1 4 −1 1,4 x 225000 = 315000 J
Lkt = Q - ∆I = 225000 - 315000 = -90.000 J
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - 4
Câu 5: Một bóng đèn điện chứa N2 khi chưa sáng nhiệt độ bên trong đồng đều và bằng 25oC,
độ chân không 200 mmHg. Khi sáng ổn định nhiệt độ phần cầu 160oC, phần trụ 70oC. Biết
thể tích phần cầu 90cm3 và phần trụ 15cm3. Xác định áp suất lúc sáng, biết áp suất khí quyển 760mmHg. Giải: p V . - Lúc chưa sáng : p V . = G R . T . o G = o o hay R T . o - Lúc đốt sáng : V . p + Phần cầu V . p = G R . T . 1 G = 1 1 1 hay 1 R T . 1 V . p + Phần trụ V . p = G R . T . 2 G = 2 2 2 hay 2 R T . 2 Ta có: G = G1 + G2 V 105 T Suy ra o 298 p = p . = (760 − ) 200 . = 780mmHg o V V 90 15 1 2 + + T T 433 333 1 2
Câu 6. Đốt nóng 02 kg khí O2 (µ = 32 kg/kmol , k=1,4) trong điều kiện áp suất không đổi
p=5 bar từ nhiệt độ t1=27oC đến t2=127oC.
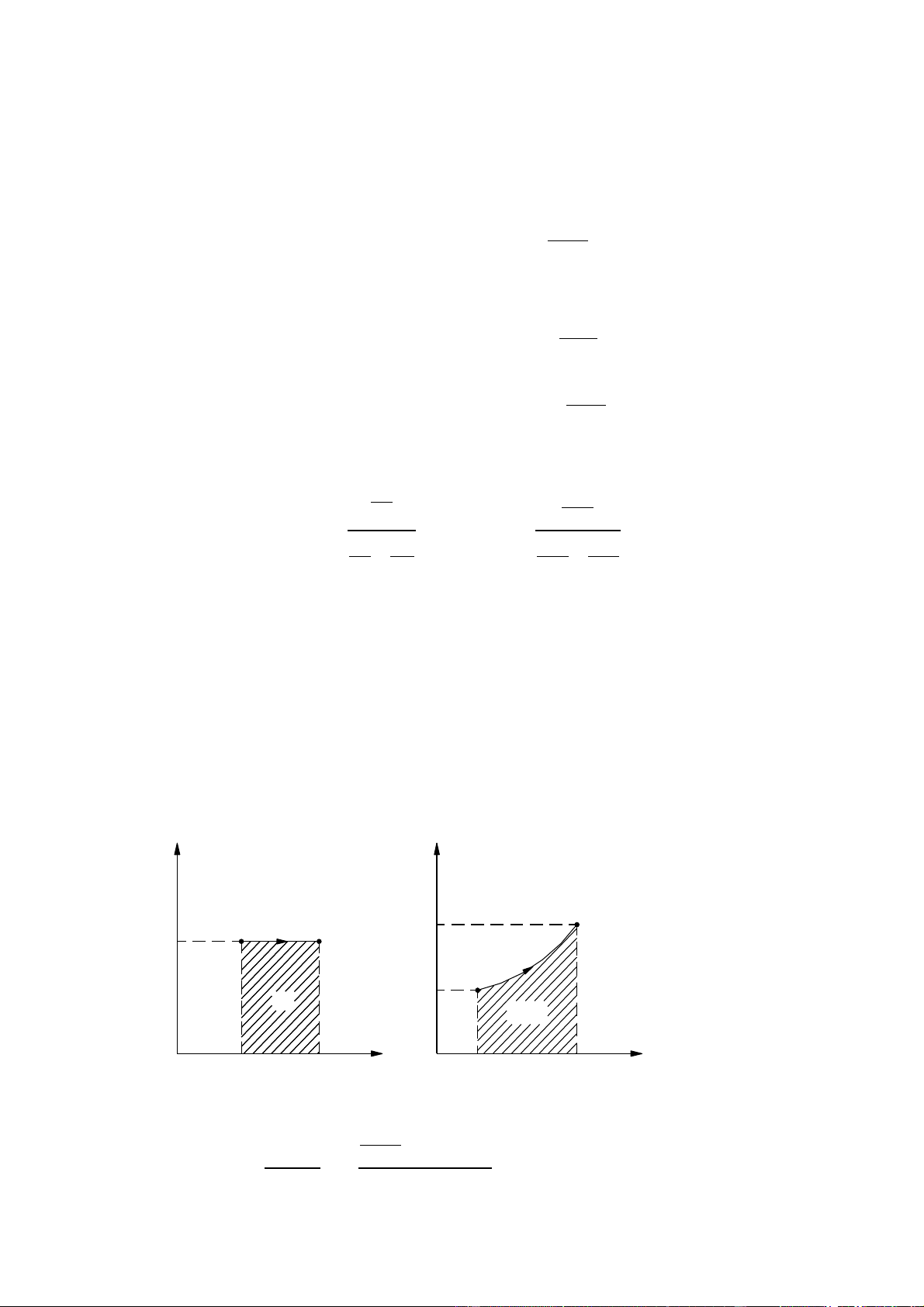
a. Biểu thị quá trình trên đồ thi p-v và T-S
b. Xác định thể tích của O2 ở trạng thái đầu và cuối
c. Xác định Q, ∆I , ∆U, Lkt, L
Đáp số : V1 = 0,312 m3 ; V2 = 0,416 m3
Q = ∆I = 182 000 J ; ∆U = 130 000 J ; Lkt = 0 ; L = 52 000 J GIẢI P, T, K N/m2 2 1 2 T2 p1=p2 1 T1 l12 v, q=∆i s, m3/kg J/kg.K v1 v2 s1 s2
- Thể tích riêng trạng thái đầu 8314 .(27 + ) 273 R . G T . 1 32 3 V = = . 2 = 31 , 0 2m 1 5 p . 5 10 5 T 127 + 273 2 3 V = V . = . 312 , 0 = , 0 416m 2 1 T 27 + 273 1 - Quá trình đẳng áp nên k , 1 4 8314 Q = ∆I = G C . .(T − T ) = G R . (T − T ) = . 2 . (400 − ) 300 p 2 1 k −1 2 1 , 1 4 −1 32 = 182.000 J I ∆ 182000 U ∆ = = =1 . 30 000J k , 1 4
L = Q - ∆U = 182.000 - 130.000 = 52.000 J Lkt = 0
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 7. Có 12 kg không khí ở nhiệt độ 27oC, áp suất tuyệt đối p = 6bar, giãn nở đẳng nhiệt để thể tích tăng 4 lần.
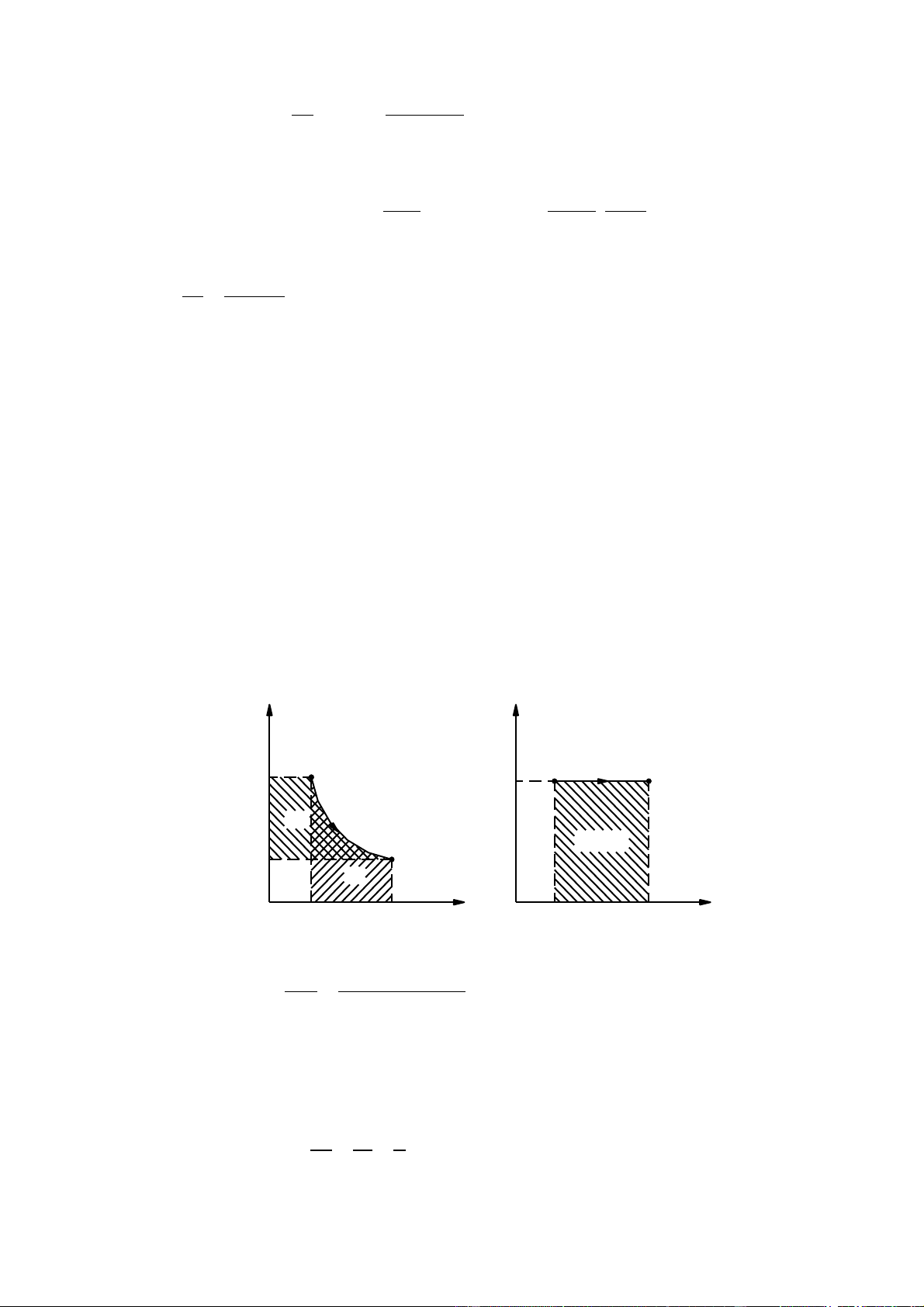
a. Biểu thị quá trình trên đồ thị p-v và T-S
b. Xác định các thông số trạng thái cuối
c. Xác định Q, ∆I , ∆U, Lkt, L, ∆S Đáp số :
v2 = 0,574 m3/kg ; p2 = 1,5 bar ; T2 = 300 oK
Q = L = Lkt = 1.432.319 J ; ∆U = ∆I = 0 ; ∆S = 4774 J/K GIẢI P, T, K N/m2 p 1 2 1 1 T1=T2 lKT q=T.∆s p2 2 v, s, l12 m3/kg J/kg.K v1 v2 s1 s2
- Thể tích riêng trạng thái đầu R T . 287x(27 + ) 273 v = = = 1435 , 0 m3 / kg 1 p 1 . 6 05 1
- Thể tích trạng thái cuối
v2 = 4.v1 = 4 x 0,1435 = 0,574 m3/kg
- Ap suất trạng thái cuối v p 6 p = p . 1 1 = = = 5 , 1 bar 2 1 v 4 4 2
- Quá trình đẳng nhiệt : 6 ∆U = ∆I = 0 v Q = L = L = G R . . T . ln 2 =12x287x(27 + ) 273 ln 4 = . 432 . 1 319 kt , J v1 v S ∆ = R .
G .ln 2 =12x287 ln 4 = 4774 , J/K v1
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 8. Giãn nở đoạn nhiệt 2kg không khí từ t1 = 327oC , p1 = 10 bar đến p2 = 1 bar.
a. Biểu diễn quá trình trên đồ thị p-v và T-S
b. Xác định các thông số trạng thái cơ bản trạng thái cuối
c. Xác định Q, ∆I , ∆U, Lkt, L, ∆S Đáp số :
v2 = 0,9 m3/kg ; T2 = 313oK ; Q = 0, ∆S = 0 L = - ∆U = 411.845 J Lkt = - ∆I = 576.583J GIẢI P, T, K N/m2 p1 1 T1 1 lKT T2 2 p2 2 l v, s, 12 m3/kg J/kg.K v1 v2 s1=s2 Ta có: k p T 2 2 k 1 ( ) − = p T 1 1 p k 1 − , 1 4 1 − Suy ra: T = T .( 2 ) k = 327 ( + ) 273 . 1 , 0 , 1 4 = 311o K 2 1 p1 RT 287x311 v 2 = = = 9 , 0 m3 / kg 2 p 105 2
Quá trình đoạn nhiệt nên Q = 0 và L = -∆U; Lkt = -∆I R 287 U ∆ = G C . (T − T ) = G (T − T ) = 2x 31 ( 1− ) 600 = 4 − 14.715 v 2 1 J k −1 2 1 , 1 4 −1 L = 414.715
∆I = k. ∆U = - 1,4 x 414.715 = -580.601 J = - Lkt 7
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 9. Nén đa biến 01 kg không khí n=1,2 từ t1=20oC , p1 = 0,981 bar đến p2= 7,845 bar
a. Biểu diễn quá trình trên đồ thị p-v và T-S
b. Xác định các thông số trạng thái cơ bản trạng thái cuối
c. Xác định Q, ∆I , ∆U, Lkt, L Đáp số :
v2 = 0,15 m3/kg ; T2 = 414oK , Q = -87 kJ L = - 174 kJ ; ∆U = 87 kJ
Lkt = - 208,8 kJ ; ∆I = 121,8 kJ GIẢI a). b).
- Nhiệt độ trạng thái cuối p n 1 − 7 845 , , 1 2 1 − T = T .( 2 ) n = (20 + ) 273 .( ) ,12 = 414o K 2 1 p 981 , 0 1
- Thể tích riêng trạng thái cuối R T . 287x414 v 2 = = = 1 , 0 5m3 / kg 2 p 7 . 845 , 105 2
- Biến thiên nội năng và entanpi R 287 U ∆ = G C . (T − T ) = G (T − T ) = x 1 (414 − ) 293 = 87.000 v 2 1 J k −1 2 1 , 1 4 −1
∆I = k. ∆U = 1,4 x 87.00 = 121.800 J - Nhiệt lượng Q, L, Lkt n − k R n − k Q = GC (T − T ) = GC (T − T ) = G . (T − T ) n 2 1 v n −1 2 1 k −1 n −1 2 1 287 , 1 2 − , 1 4 Q = x 1 . (414 − ) 293 = − 0 . 87 00 J , 1 4 −1 , 1 2 −1
L = Q - ∆U = -87.000 - 87.000 = -174.000 J
Lkt = Q - ∆I = -87.000 - 121.800 = -208.800 J
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 10: Cho 1,0 kg không khí (R=287 J/kg.K và k=1,4) thực hiện quá trình đa biến
từ trạng thái ban đầu với p1=10 bar và t1 = 307oC. Sau quá trình không khí nhận nhiệt
lượng q=200 kJ/kg và sinh công l = 400 kJ/kg.
- Xác định chỉ số đa biến n và các thông số trạng thái cơ bản (p, v và T) trạng thái cuối.
Tải bản FULL (file word 16 trang): bit.ly/3oMxDFi
Dự phòng: fb.com/TaiHo123doc.net 8
- Xác định biến thiên entrôpi ∆s.
- Biểu diễn quá trình trên đồ thị p-v và T-s. Đáp án: TT Nội dung
- Công và nhiệt lượng trong quá trình đa biến 1 1− k n − k l = C . .(T − T ) , q = C . .(T − T ) v n −1 2 1 v n −1 2 1 q 200 2
- Xác định chỉ số đa biến n = 1 .( − k) + k = 1 ( − , 1 ) 4 + , 1 4 = , 1 2 l 400 R 287
- Xác định nhiệt dung riêng đẳng tích C = = = 5 , 717 v J/kg.K k −1 , 0 4 3 q n −1 200 , 1 2 −1
- Nhiệt độ cuối quá trình: T = T + . = 580 + . = 301 2 1 oK C n − k 7175 , 0 , 1 2 − , 1 4 v T n 301 ,12 4 - Áp suất cuối p 2 n 1 − , 1 2 1 − 2: p = p .( ) = .( 10 ) = 195 , 0 bar 2 1 T 580 1
- Thể tích riêng trạng hái đầu và cuối : R T . 287x580 + v 1 = = = 166 , 0 1 6 m3/kg 5 p 10 1 T 1 580 1 + v = v .( 1 )n 1 − = .( 166 , 0 ) ,12 1 − = , 4 41 m3/kg 2 1 T 301 2 - Xác định ∆s : 6 n − k T , 1 2 − , 1 4 301 s ∆ = C ln 2 = . 7175 , 0 ln = , 0 471 v kJ/kg.K n −1 T , 1 2 −1 580 1 7
- Biểu diễn trên các đồ thị p-v và T-s
Câu 11: Cho vách phẳng 02 lớp
- Lớp 1 : Gạch thẻ có bề dày δ1=200mm, λ1=0,4 W/m.K ;
- Lớp 2 : Vửa xi măng có bề dày δ2=100mm, λ2=0,2 W/m.K;
- Nhiệt độ các bề mặt ngoài cùng : tW1 = 150oC và tW3 = 50oC Xác định :
- Mật độ dòng nhiệt qua vách q
- Nhiệt độ bề mặt tiếp xúc của 2 lớp tW2
- Nhiệt độ tâm của các lớp t1 và t2 Đáp số :
- Mật độ dòng nhiệt : q = 100 w/m2 , tw2 = 100oC, t1 = 125oC, t2= 75oC GIẢI
Tải bản FULL (file word 16 trang): bit.ly/3oMxDFi
Dự phòng: fb.com/TaiHo123doc.net 9 - Mật độ dòng nhiệt t − t 150 − 50 q w1 w3 = = =100 δ δ , 0 2 1 , 0 1 2 + + , w/m2 λ λ , 0 4 , 0 2 1 2 - Nhiệt độ vách tw2 δ , 0 2 t = t − . q 1 =150 − . 100 =100o C w 2 w1 λ , 0 4 1
- Nhiệt độ tâm lớp 1: t1 = (tw1+tw2)/2 = 125 oC
- Nhiệt độ tâm lớp 2: t2 = (tw2+tw3)/2 = 75 oC
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 12. Cho vách trụ 2 lớp
+ Lớp trong d1/d2 = 80/120 mm , λ1 = 0,5 w/m.K , tw1 = 200oC.
+ Lớp ngoài d2/d3 = 120/160 mm , λ2 = 0,2 w/m.K, tw3 = 50oC. Xác định :
- Dòng nhiệt qua 1 m chiều dài vách ql
- Nhiệt độ bề mặt tiếp xúc của 2 lớp tW2 Đáp số : + ql = 419 W/m , tw2 = 186oC GIẢI
- Dòng nhiệt tính cho 1m chiều dài t − t 200 − 50 q w1 w 3 = = = 419 l 1 d 1 d 1 ln120 / 80 ln160 /120 ln 2 + ln 3 [ + ] w/m 2πλ d 2πλ d 2x 1 , 3 4 5 , 0 , 0 2 1 1 2 2
- Nhiệt độ bề mặt ngăn cách 1 d 1 120 t = t − q . .ln 2 = 200 − . 419 ln =186o C w 2 w1 l . 2 πλ1 d 2x 1 , 3 4x 5 , 0 80 1
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Câu 13. Có một ống thép có đường kính d1/d2 = 100/110mm, hệ số dẫn nhiệt λ1 = 50 W/m.K,
được phủ hai lớp cách nhiệt có bề dày như nhau δ2 = δ3 = 50mm. Nhiệt độ mặt trong tw1 =
250oC và mặt ngoài của lớp cách nhiệt thứ hai tw4 = 50oC. Hệ số dẫn nhiệt của lớp thứ nhất và
thứ hai lần lượt là λ2 = 0,06 W/m.K và λ3 = 0,12 W/m.K
a). Xác định tổn thất nhiệt qua một mét ống và nhiệt độ trên bề mặt tiếp xúc giữa hai lớp cách nhiệt tw3
b). Nếu đổi vị trí hai lớp cách nhiệt thì tổn thất nhiệt và nhiệt độ tiếp xúc giữa hai lớp cách
nhiệt là bao nhiêu, nếu các điều kiện khác không đổi. Đáp số:
a). ql = 89 W/m ; tw3 = 97 oC ;
b). ql = 105,5 W/m ; tw3 = 159 oC ; 10 3446525