lOMoARcPSD| 40615933 BÀI TẬP
MÔN QUẢN TRỊ SẢN XUẤT VÀ TÁC NGHIỆP
Số ơn vị tín chỉ: 3
GV: TS. VƯƠNG THỊ THANH TRÌ BÀI
2. LẬP KẾ HOẠCH CÔNG SUẤT Bài tập 1.
Cho số liệu dưới ây. Giả sử các số liệu thể hiện LỢI NHUẬN
Trạng thái tự nhiên Giải pháp #1 (0,6) #2 (0,4) A 1 14 B 2 10 C 4 6
Hãy thực hiện các yêu cầu dưới:
1.1 Lựa chọn các giải pháp theo tiêu chí: Maximin, Maximax, Laplace
1.2 Giả sử xác suất xuất hiện của trạng thái tự nhiên (TTTN) #1= 0,6; #2= 0,4. Lựa chọn giải pháp
theo tiêu chí giá trị mong ợi của thông tin hoàn hảo (EVPI)
1.3 Lựa chọn giải pháp theo tiêu chí Minimax Regret: Sử dụng bảng Minimax Regret, xác ịnh giá
trị mong ợi của thông tin hoàn hảo (EVPI) với xác suất (TTTN) #1= 0,6; #2= 0,4 Bài tập 2.
Cho số liệu dưới ây. Giả sử các số liệu thể hiện CHI PHÍ
Trạng thái tự nhiên Giải pháp #1 (0,6) #2 (0,4) A 1 14 B 2 10 C 4 6
Hãy thực hiện các yêu cầu dưới:
2.1 Lựa chọn các giải pháp theo tiêu chí: Maximin, Minimin, Laplace
2.2 Với xác suất của TTTN #1= 0,6, lựa chọn giải pháp theo tiêu chí chi phí mong ợi nhỏ nhất.
Xác ịnh giá trị mong ợi của thông tin hoàn hảo (EVPI) có sử dụng số liệu vừa tính toán ược 2.3
Lựa chọn giải pháp theo tiêu chí Minimax Regret: Sử dụng bảng Minimax Regret, xác ịnh giá trị
mong ợi của thông tin hoàn hảo (EVPI) với xác suất (TTTN) #1= 0,6 lOMoARcPSD| 40615933
Bài tập 3. Nhà quản lý công ty VIT ang lựa chọn một trong 3 giải pháp A, B hoặc C, CHI PHÍ
của từng giải pháp khi môi trường kinh doanh thuận lợi (TTTN1) hoặc khó khăn (TTTN2) ược cho dưới ây:
Trạng thái tự nhiên Giải pháp #1 #2 A 8 7 B 4 14 C 1 9
Hãy thực hiện các yêu cầu dưới:
3.1 Hãy lựa chọn giải pháp theo tiêu chí: Maximin, Minimin, Laplace.
3.2 Giả sử xác suất hiện của TTTN#1 là 0,6, hãy lựa chọn giải pháp theo tiêu chí chi phí mong
ợi nhỏ nhất; Xác ịnh EVPI có sử dụng số liệu vừa tính toán ược.
3.3 Lựa chọn giải pháp theo tiêu chí Minimax Regret: Sử dụng bảng Minimax Regret, xác ịnh
EVPI với xác suất của TTTN#1 là 0,6 và xác suất của TTTN#2 là 0,4.
Bài tập 4. Một công ty muốn xây dựng một nhà máy mới cho một sản phẩm mới. Nếu xây nhà
máy nhỏ và nhu cầu là thấp, NPV ạt ược là $400.000, nếu nhu cầu là cao công ty có thể giữ nguyên
hoặc mở rộng sản xuất. Giữ nguyên NPV là $50.000, mở rộng cho NPV là $450.000. Nếu xây nhà
máy lớn và nhu cầu là cao thì NPV ạt ược là $800.000, còn nếu nhu cầu là thấp thì NPV là -
$10.000. Hãy phân tích dựa trên cây quyết ịnh nếu xác suất nếu xác suất của nhu cầu cao là 0,6; còn nhu cầu thấp là 0,4
Bài tập 5: Quyền thuê ất của 1 doanh nghiệp sắp hết hạn: DN ang lựa chọn chọn giữa việc thuê
tiếp thêm 5 năm nữa hoặc chuyển ến một mảnh ất mới ang chờ ược phê duyệt. Nếu thuê tiếp lợi
nhuận sẽ là $500.000 trong trường hợp mảnh ất mới ược phê duyệt và là $4.000.000 trong trường
hợp mảnh ất mới không ược phê duyệt. Còn nếu chuyển ịa iểm mới, lợi nhuận sẽ là $5.000.000
trong trường hợp mảnh ất ược phê duyệt và là $100.000 trong trường hợp mảnh ất bị huỷ bỏ.
Hãy thực hiện các yêu sau:Hãy ra quyết ịnh theo các tiêu chí Maximin, Maximax, Laplace và Minimax Regret
 Nếu DN có quyền thuê tiếp tạm thời trong khi chờ hội ồng thành phố phê duyệt và chi phí
thuê tạm thời là $24.000 thì DN có nên thuê tạm thời không? Biết khả năng ược phê duyệt là 0,35
Bài tập 6. Một công ty dự ịnh ầu tư dây chuyền máy móc theo 2 phương án A và B.
Phương án A có FC = $40.000; VCu = $10 và Rev = $15
Phương án B có FC = $30.000; VCu = $12 và Rev = $16
a. Xác ịnh iểm hoà vốn cho mỗi giải pháp
b. Xác ịnh số lượng ầu ra mà tại ó 2 phương án có lợi nhuận bằng nhau.
c. Nếu nhu cầu hàng năm là 12.000 ơn vị, phương án nào cho lợi nhuận lớn hơn.
7. Một nhà sản xuất ước tính nhu cầu cho tháng tới là 30.000 sản phẩm/tháng. FC cho
hoạt ộng sản xuất là $25.000/ tháng; VCu = $0,37.
a. Xác ịnh iểm hoà vốn nếu giá bán ơn vị là $1.
b. Xác ịnh giá bán ơn vị ể ạt ược lợi nhuận $15.000. lOMoARcPSD| 40615933 Bài tập
Bài tập 8. Doanh nghiệp sản xuất ồ gốm dự ịnh mở thêm một cửa hàng mới. Cửa hàng mới có
FC = $9.200/tháng; VCu = $0,7; Rev = $0,9.
a. Xác ịnh iểm hoà vốn
b. Xác ịnh lợi nhuận nếu nhu cầu hàng tháng là 61.000 sản phẩm; 87.000 sản phẩm.
c. Xác ịnh số lượng ể ạt ược lợi nhuận hàng tháng là $16.000; $23.000.
Bài tập 9. Một nhà quản lý ang cân nhắc giữa việc tự sản xuất và mua ngoài một loại sản phẩm.
Phương án tự sản xuất có FC = $150.000/ năm; VCu = $60.
Phương án mua ngoài có FC = $0/ năm; VCu = $80.
a. Nếu nhu cầu hàng năm là 12.000 sản phẩm, nhà quản lý nên mua hay tự sản xuất.
b. Xác ịnh số lượng mà tại ó 2 phương án có tổng chi phí bằng nhau.
Bài tập 10. Một nhà quản lý lựa chọn giữa 3 phương án A, B, C. Phương
án A: Mua sản phẩm từ bên ngoài với chi phí $7/1sản phẩm Phương
án B: FC = $160.000; VCu = $5.
Phương án C: FC = $190.000; VCu = $4.
Xác ịnh khoảng ầu ra tốt nhất cho mỗi phương án.
Bài tập 11. Một nhà quản lý lựa chọn giữa việc mua 1 hoặc hai máy. Mỗi máy có khả năng xử lý
100 sản phẩm/giờ. Một máy có chi phí cố ịnh là $2.000/ngày; Hai máy có chi phí cố ịnh là
$3.800/ ngày. VCu = $20; Rev =$45.
a. Xác ịnh iểm hoà vốn cho mỗi phương án.
b. Nếu nhu cầu trong khoảng từ 90 ến 120 sản phẩm/ giờ, nên lựa chọn phương án nào.
Bài tập 12. Một nhà sản xuất cân nhắc giữa việc sử dụng 1 hoặc hai dây chuyền. Một dây chuyền
có FC = $6.000/ tháng; Hai dây chuyền có FC = $10.500/ tháng. VCu = $3; Rev = $5,95.
Mỗi dây chuyền có khả năng xử lý 15 sản phẩm/ giờ. Nhà sản xuất hoạt ộng 300 giờ/ tháng. Nếu
nhu cầu trong khoảng từ 14 ến 18 sản phẩm/ giờ, nhà sản xuất nên ầu tư 1 hay 2 dây chuyền.
Bài tập 13. Một doanh nghiệp có 3 bộ phận: Thiết kế, sản xuất và hoàn thiện. Thời gian của từng
bộ phận ược cho như ở bên dưới: Bộ phận Thời gian sẵn có
Công suất hiệu quả Mức hữu dụng Thiết kế 93.600 0.92 0.95 Sản xuất 156.000 0.95 0.93 Hoàn thiện 62.400 0.96 0.95
Xác ịnh mức công suất thực sự ước tính. lOMoARcPSD| 40615933
Bài tập 14. Một doanh nghiệp sản xuất một sản phẩm với VC = $0,5; Rev = $1,00; FC = $14.000.
Số lượng sản phẩm bán ược hiện tại là 30.000 sản phẩm.
Doanh nghiệp có thể cải tiến chất lượng sản phẩm bằng cách ầu tư thêm một số thiết bị mới.
Lúc này VCu = $0,6; FC = $20.000 và số lượng sản phẩm bán ược lên ến 50.000 sản phẩm (do chất lượng cao).
Doanh nghiệp có nên mua thiết bị mới không?
Bài tập 15. Một nhà sản xuất ang cân nhắc giữa việc mua và tự sản xuất một loại sản phẩm Tự sản xuất Mua ngoài A B C D E P/án FC $200.000 $240.000 - - - VCu $17/sp $14/sp $20/sp 22 (0-1.000 sp) 21 (0-1.000 sp) 18 (>1001 sp) 19 (>1001 sp)
Xác ịnh phương án tối ưu nếu nhu cầu mong muốn là: a. 10.000 sản phẩm b. 20.000 sản phẩm
Bài tập 16. Một cửa hàng sản xuất và bán 4 loại thực phẩm với các số liệu sau: Thực phẩm Rev ($) VCu ($)
Số lượng ước tính/tháng A 1,50 0,75 30.000 B 10,00 5,00 10.000 C 2,50 1,00 10.000 D 6,25 3,25 20.000
Chi phí cố ịnh hàng tháng ước tính là $3.800
a. Xác ịnh doanh thu hoà vốn hàng tháng.
b. Xác ịnh số lượng hoà vốn theo ngày của sp B nếu cửa hàng hoạt ộng 360 ngày/năm.
c. Tổng doanh thu là bao nhiêu ể ạt ược 1 lượng lợi nhuận là $35.000/tháng.
Bài tập 17. Một doanh nghiệp ang sản xuất sản phẩm B với chi phí biến ổi ơn vị là $1, thu nhập
ơn vị là $1,5 và chi phí cố ịnh hàng tháng là $16.000. Số lượng sản phẩm bán ược hiện tại của
doanh nghiệp ó là 35.000 sản phẩm.
Doanh nghiệp ó dự ịnh cải tiến chất lượng sản phẩm bằng cách ầu tư thêm một số thiết bị
mới. Khi ó chi phí biến ổi ơn vị dự kiến là $1,2 và chi phí cố ịnh hàng tháng sẽ tăng thêm $5.000. lOMoARcPSD| 40615933 Bài tập
Với mức giá bán trên một ơn vị sản phẩm không ổi và số lượng sản phẩm dự tính bán ược lên ến 72.000 sản phẩm.
a. Tính iểm hoà vốn trong từng trường hợp.
b. Theo bạn, doanh nghiệp ó có nên mua thiết bị mới hay không. Tại sao?
Bài tập 18. Một doanh nghiệp ầu tư 3 dây chuyền sản xuất mới. Mỗi dây chuyền hoạt ộng 7 ngày
một tuần, 3 ca một ngày, 8 giờ một ca. Mỗi dây chuyền có công suất hiệu quả là 80%, mức hiệu
quả là 90%, Công suất lý thuyết của mỗi dây chuyền là 120 sp/một giờ.
Xác ịnh công suất thực tế ước tính theo tuần.
19. Một nhà sản xuất ang lựa chọn giữa 4 phương án: ầu tư 1 dây chuyền; 2 dây chuyền;
3 dây chuyền; 4 dây chuyền ( ơn vị tính: 1.000 VND). Chi phí cố ịnh hàng tháng cho 1 dây chuyền
(FC1) là 12.000; cho 2 dây chuyền (FC2) là 20.000; FC3 = 26.000; FC4 = 31.000. Công suất lý
thuyết của mỗi dây chuyền là 15 sản phẩm/giờ. Công suất hiệu quả = 80%. Mức hiệu dụng = 80%.
Nhà sản xuất hoạt ộng 300 giờ/tháng. Chi phí biến ổi ơn vị là 5 và giá bán ơn vị là 9.
a. Xác ịnh mức công suất thực tế ước tính của mỗi phương án.
b. Xác ịnh iểm hòa vốn của mỗi phương án. Phương án nào sẽ có iểm hòa vốn không khả thi.
c. Sử dụng kết quả tính toán ược từ câu a, hãy lựa chọn phương án ầu tư cho lợi nhuận lớn
nhất biết rằng thị trường có thể tiêu thụ bất cứ số lượng nào trong khoảng từ 2.000 ến 7.500 sản phẩm.
Bài tập 20. Tập oàn Hoa Sen ang lựa chọn giữa 4 phương án: ầu tư 1 dây chuyền; 2 dây chuyền,
3 dây chuyền; 4 dây chuyền ( ơn vị tính: 1.000 VND). Chi phí cố ịnh hàng tháng cho 1 dây chuyền
(FC1) là 28.000; cho 2 dây chuyền (FC2) là 70.000; FC3 = 90.000; FC4 = 130.000. Công suất lý
thuyết của mỗi dây chuyền là 30 sản phẩm/giờ. Mỗi dây chuyền có công suất hiệu quả 80%, mức
hiệu dụng 70% và doanh nghiệp hoạt ộng 25 ngày một tháng, 2 ca một ngày, 8 giờ một ca. Chi phí
biến ổi ơn vị 10 và giá bán ơn vị là 15.
a. Xác ịnh mức công suất thực tế ước tính của mỗi phương án.
b. Xác ịnh iểm hòa vốn của mỗi phương án. Phương án nào sẽ có iểm hòa vốn không khả thi.
c. Sử dụng kết quả tính toán ược từ câu a, hãy lựa chọn phương án ầu tư cho lợi nhuận lớn
nhất biết rằng thị trường có thể tiêu thụ bất cứ số lượng nào trong khoảng từ 5.500 ến 20.000 sản phẩm/tháng.
CHƯƠNG 3. BỐ TRÍ MẶT BẰNG (ĐIỀU KIỆN HẠ TẦNG)
Bài tập 1. Một dây chuyền có 17 nhiệm vụ thành phần. Nhiệm vụ thành phần dài nhất là 2,4 phút,
tổng thời gian của các nhiệm vụ là 18 phút. Thời gian làm việc 1 ngày là 450 phút.
a. Xác ịnh thời gian ngắn nhất của 1 chu kỳ; thời gian dài nhất của 1 chu kỳ.
b. Xác ịnh số lượng ầu ra tối a; số lượng ầu ra tối thiểu.
c. Xác ịnh số lượng tối thiểu các trạm công việc ể ạt ược số lượng sản phẩm ầu ra tối a. lOMoARcPSD| 40615933
d. Xác ịnh thời gian 1 chu kỳ ể ạt ược 125 sản phẩm ầu ra.
e. Xác ịnh số lượng sản phẩm ầu ra nếu thời gian 1 chu kỳ là 9 phút.
Bài tập 2. Các nhiệm vụ và thời gian ược cho như sau: Nhiệm vụ Thời gian (phút) Nhiệm vụ theo sau A 0,2 B B 0,4 D C 0,3 D D 1,3 G E 0,1 F F 0,8 G G 0,3 H H 1,2 -
Với giả thiết thời gian chu kỳ là ngắn nhất có thể a. Vẽ sơ ồ thứ tự
b. Phân các nhiệm vụ về các trạm công việc theo nguyên tắc: tổng thời gian lớn nhất của tất
cả các nhiệm vụ thành phần theo sau. Nếu có sự bằng nhau, giải quyết dựa trên số lượng
lớn nhất các nhiệm vụ theo sau:
c. Xác ịnh tỷ lệ thời gian nhàn rỗi
d. Tính toán mức sản phẩm ầu ra với ngày làm việc 420 phút.
Bài tập 3. Các nhiệm vụ và thời gian ược cho như ở bên dưới: Nhiệm vụ Thời gian (phút)
Nhiệm vụ ứng trước A 0,1 - B 0,2 A C 0,1 B D 0,2 - E 0,1 D F 0,6 C G 0,5 E, F
Với ngày làm việc 8 giờ và mức sản phẩm ầu ra 480 sản phẩm a. Vẽ sơ ồ thứ tự
b. Xác ịnh thời gian một chu kỳ và số trạm công việc tối thiểu
c. Phân các nhiệm vụ về các trạm công việc theo nguyên tắc: số lượng lớn nhất các
nhiệm vụ theo sau, nếu có sự bằng nhau, giải quyết dựa trên tổng thời gian lớn nhất của tất
cả các nhiệm vụ thành phần theo sau.
Tính tỷ lệ thời gian nhàn rỗi?
4. Các nhiệm vụ và thời gian ược cho như sau: lOMoARcPSD| 40615933 Bài tập Nhiệm vụ Thời gian (phút) Nhiệm vụ theo sau A 0,1 B B 0,2 C C 0,9 D D 0,6 F E 0,1 F F 0,2 G G 0,4 H H 0,1 I I 0,2 J J 0,7 K K 0,3 L L 0,2 -
Với thời gian một chu kỳ là 1,5 phút. a. Vẽ sơ ồ thứ tự b.
Phân các nhiệm vụ về các trạm công việc theo nguyên tắc: Tổng thời gian lớn nhất
của tất cả các nhiệm vụ theo sau. Nếu có sự bằng nhau, giải quyết dựa trên số lượng lớn nhất các nhiệm vụ theo sau. c.
Tính tỷ lệ thời gian nhàn rỗi
Bài tập 5. Một công việc bao gồm 8 nhiệm vụ thành phần. Thứ tự và thời gian các nhiệm vụ: Thời Thời Nhiệm Nhiệm vụ Nhiệm Nhiệm vụ TT gian gian vụ TT (phút) ứng trước vụ (phút) ứng trước 1 A 0,7 - 6 F 0,6 C, E 2 B 0,2 A 7 G 0,5 - 3 C 0,8 B 8 H 0,2 F, G 4 D 0,5 - 3,8 5 E 0,3 D
Nếu ầu ra mong ợi là 300 sản phẩm với một ngày làm việc 450 phút. a. Vẽ sơ ồ thứ tự b.
Xác ịnh thời gian một chu kỳ và số trạm công việc tối thiểu. c.
Phân các nhiệm vụ về các trạm công việc theo nguyên tắc: Số lượng lớn nhất các
nhiệm vụ theo sau. Nếu có sự bằng nhau, giải quyết dựa trên tổng thời gian lớn nhất của tất cả các nhiệm vụ theo sau.
Tính tỷ lệ thời gian nhàn rỗi. lOMoARcPSD| 40615933 TT Nhiệm Thời Nhiệmvụ vụ gian ứng Thời Nhiệmvụ (phút) trước TT Nhiệm vụ gian ứng 1 A 1,2 - (phút) trước 2 B 1,4 A 6 F 0,8 D,E 3 C 1,1 B 7 G 0,7 C,F 4 D 1,5 - 8 H 0,5 G 5 E 0,5 - 9 I 0,3 H d.
Cách phân nhiệm vụ về các trạm công việc
như trên ã tốt nhất chưa? Nếu chưa, bằng trực quan hãy phân lại các nhiệm vụ sao cho tỷ lệ thời
gian nhàn rỗi là nhỏ nhất. Tính tỷ lệ ó (chú ý: CT không ổi, số trạm không thay ổi)
Bài tập 6. Một công việc bao gồm 9 nhiệm vụ thành phần, thứ tự và thời gian thực hiện các nhiệm vụ như sau:
Nếu số sản phẩm mong ợi là 150 sản phẩm/ngày với ngày làm việc 450 phút.
a. Vẽ sơ ồ thứ tự. Xác ịnh thời gian một chu kỳ công việc và số trạm công việc tối thiểu.
b. Phân các nhiệm vụ về trạm công việc theo nguyên tắc: Số lượng lớn nhất các nhiệm vụ
theo sau. Nếu có sự bằng nhau, giải quyết dựa trên tổng thời gian lớn nhất của tất cả các
nhiệm vụ theo sau (kể cả nhiệm vụ thành phần ang xét). Tính tỷ lệ thời gian nhà rỗi.
c. Cách phân các nhiệm vụ như trên ã tốt nhất chưa? Nếu chưa, bằng trực quan hãy phân lại
các nhiệm vụ về các trạm công việc sao cho tỷ lệ thời gian nhàn rỗi là nhỏ nhất. Tính tỷ lệ
thời gian nhàn rỗi (nếu có); Xác ịnh mức hiệu quả ạt ược (nếu có)?
Bài tập 7. Một công việc bao gồm 9 nhiệm vụ thành phần, thứ tự và thời gian thực hiện các nhiệm vụ như sau: TT Nhiệm
Thời gian Nhiệmvụ TT Nhiệm
Thời gian Nhiệmv vụ (phút) theo sau vụ (phút) ụ theo sau 1 A 3 B 6 F 4 G 2 B 3 C 7 G 7 E 3 C 4 H 8 H 6 I 4 D 5 E 9 I 5 - 5 E 7 H 44
Nếu số sản phẩm mong ợi là 30 sản phẩm/ngày với ngày làm việc 420 phút; biết rằng tổng thời
gian của các nhiệm vụ thành phần là 44 phút.
a. Vẽ sơ ồ thứ tự; xác ịnh thời gian 1 chu kỳ và số trạm CV tối thiểu trên lý thuyết.
b. Phân công các nhiệm vụ về các trạm công việc theo nguyên tắc: Số lượng lớn nhất các
nhiệm vụ thành phần theo sau. Nếu có sự bằng nhau, giải quyết dựa trên tổng thời gian lớn
nhất của tất cả các nhiệm vụ theo sau (kể cả nhiệm vụ thành phần ang xét). Tính tỷ lệ thời gian nhàn rỗi. Bộ phận 1 A A E A X A A A I E A lOMoARcPSD| 40615933 Bài tập
c. Cách phân các nhiệm vụ như trên ã tốt chưa? Nếu chưa, bằng trực quan hãy phân lại các
nhiệm vụ về các trạm công việc sao cho tỷ lệ thời gian nhàn rỗi là nhỏ nhất (chú ý: các yếu
tố CT, Số trạm công việc không thay ổi). Tính tỷ lệ thời gian nhàn rỗi (nếu có).
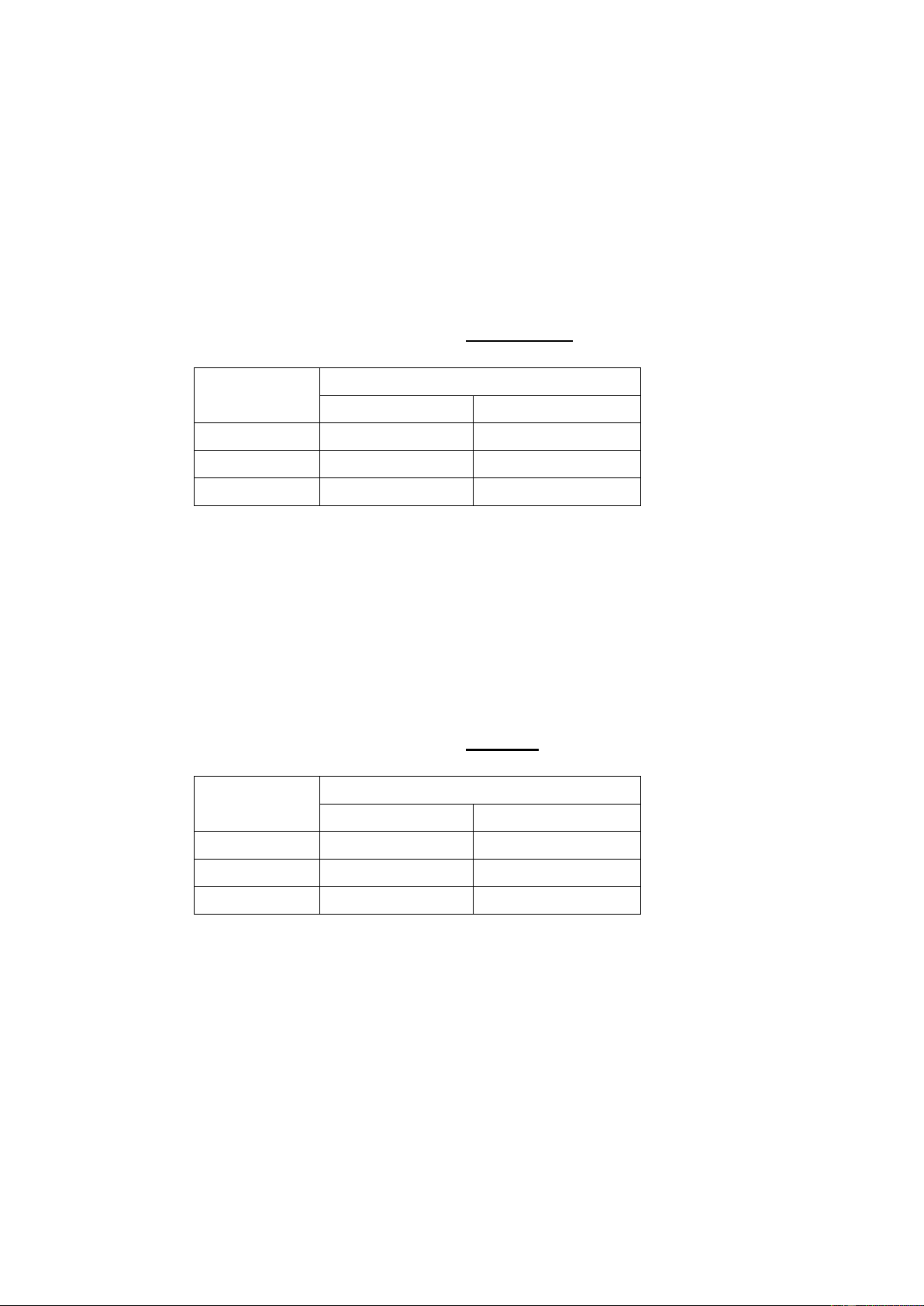
Bài tập 8. Sử dụng các thông tin dưới ây ể phân 9 bộ phận vào một hình vuông bao gồm 3 x 3 vị
trí. Bộ phận 4 phải ở góc trên bên phải lOMoARcPSD| 40615933 2 3 4 4 5 6 7 8 9
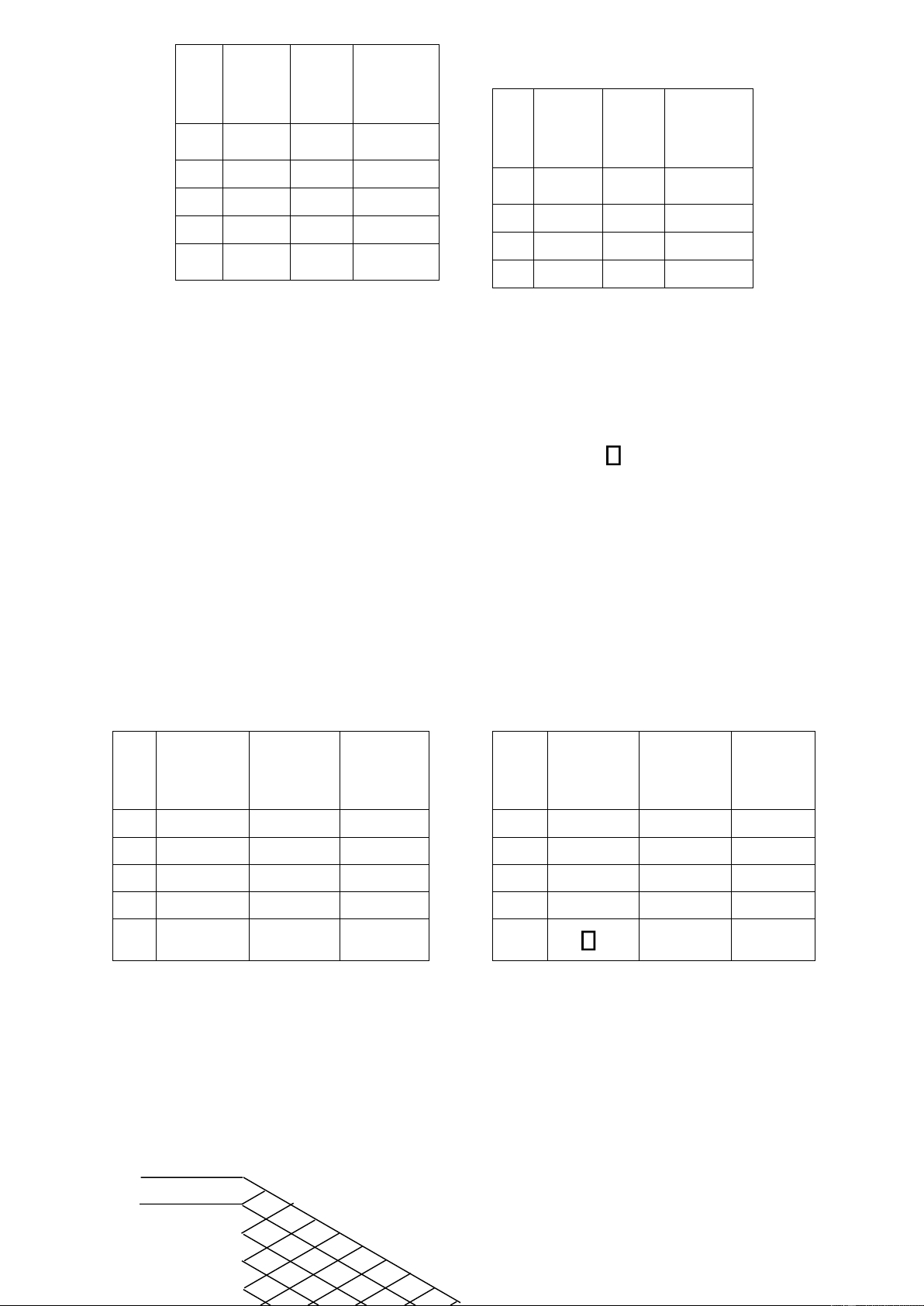
Bài tập 9. Tám bộ phận quan hệ với nhau như ở bên dưới. Xác ịnh liệu cách bố trí cho ở dưới ây ã
hợp lý chưa. Nếu chưa, hăy bố trí lại các bộ phận Department 1 2 X 2 5 4 A 3 O X O 4 O E 1 8 A E 6 5 A A A I 6 O A 7 3 A A 7 A A E 8 lOMoARcPSD| 40615933
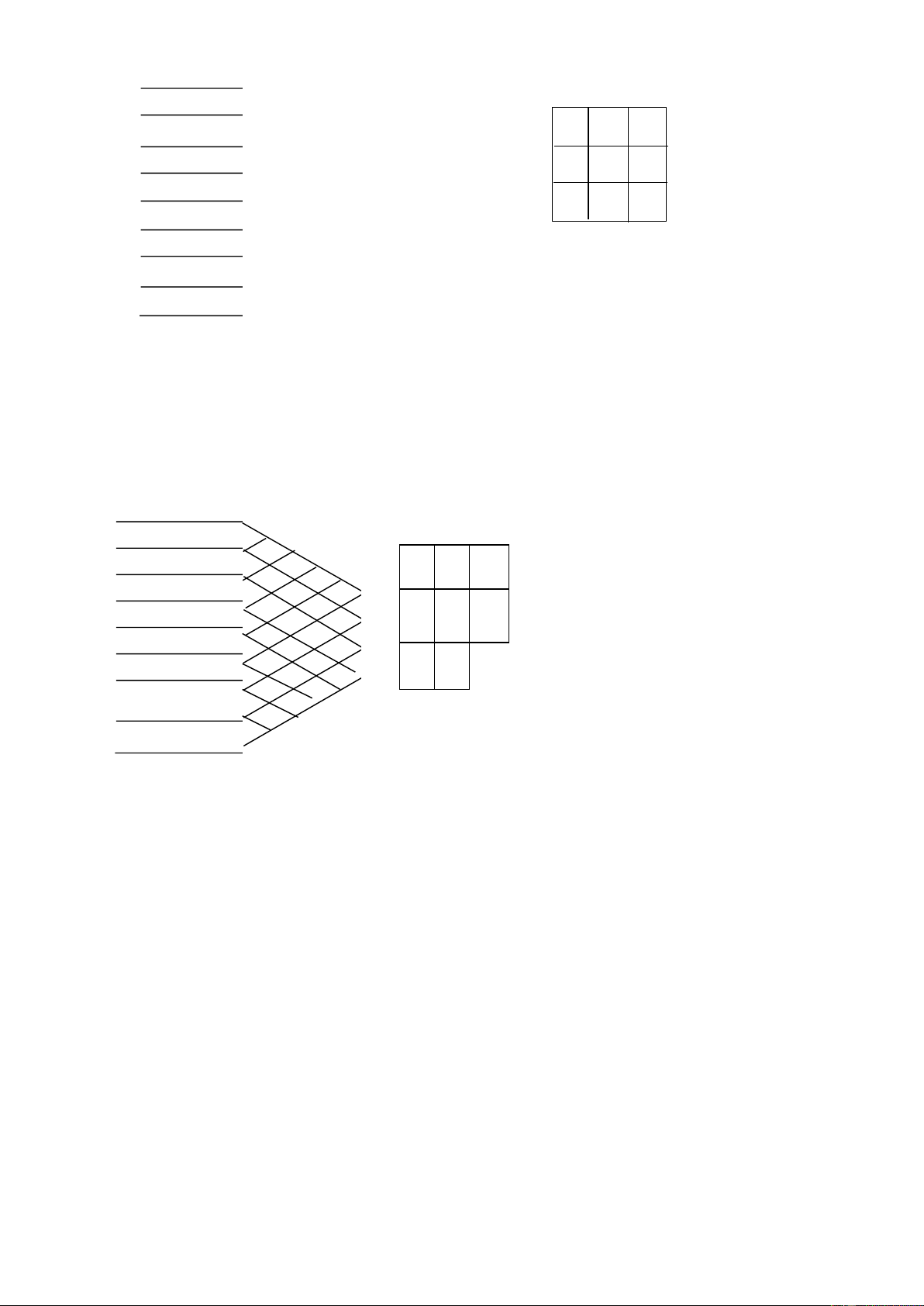
Bài tập 10. Sắp xếp 8 bộ phận dưới ây vào 1 hình chữ nhật bao gồm 2x4 vị trí với iều kiện bộ phận
1 buộc phải ở vị trí như ã cho sẵn Bộ phận 1 E 1 2 A A 3 E A E E U 4 A X U X 5 I X X A 6 O A E U 7 A A 8
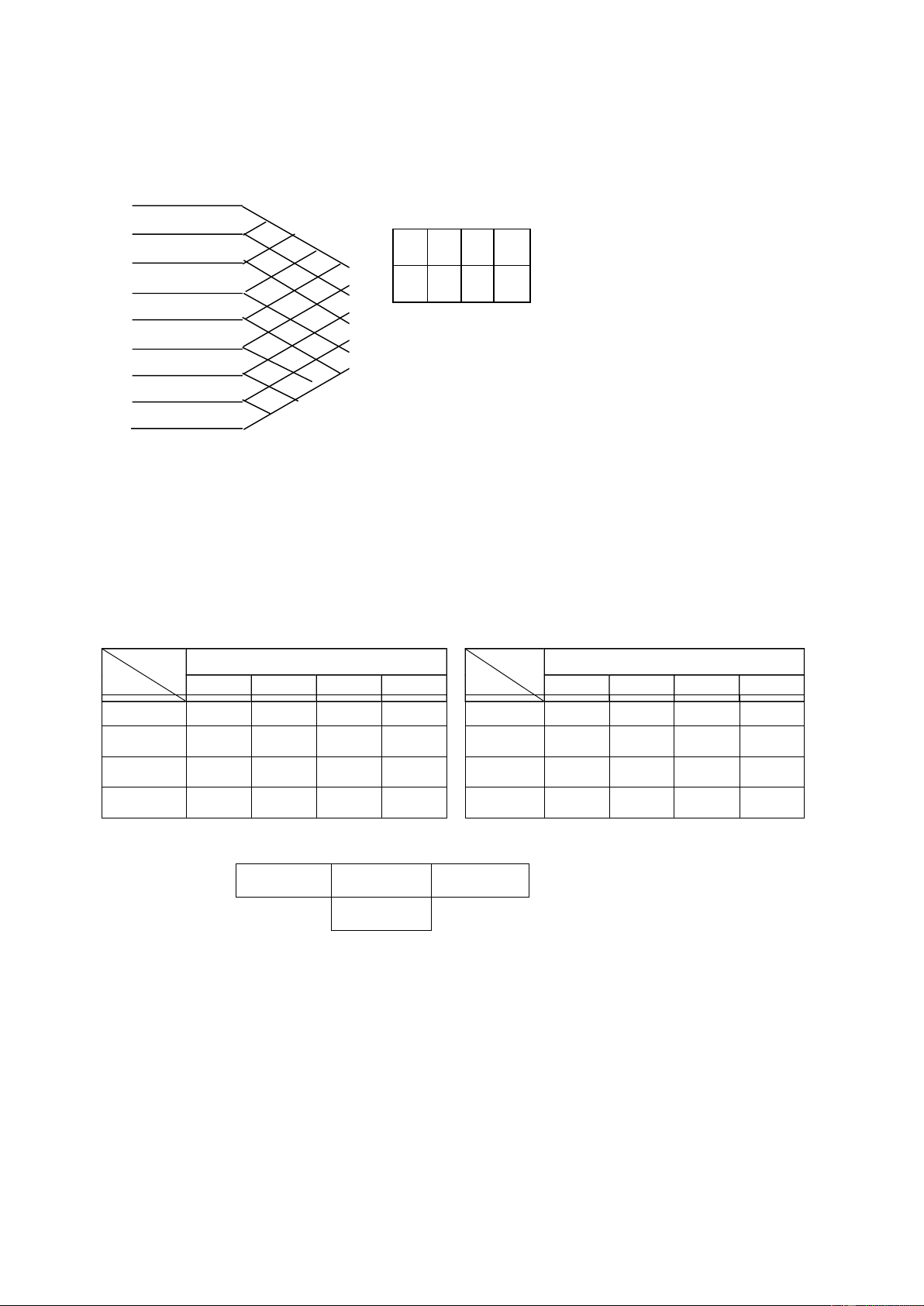
Bài tập 11. Khoảng cách giữa 4 vị trí ịa lý và khối lượng công việc trao ổi giữa 4 bộ phận ược cho như sau To
Vị trí ịa lý (mét)
To Các bộ phận From A B C D From 1 2 3 4 A - 40 80 70 1 - 10 20 30 B - 40 50 2 - 40 40 C - 60 3 - 25 D - 4 50 50 30 -
- Hãy phân 4 bộ phận vào 4 vị trí ịa lý dưới ây: A B C D
- Xác ịnh tổng chi phí của cách bố trí trên nếu chi phí vận chuyển = $1/m.
Bài tập 12. Khoảng cách giữa 4 vị trí ịa lý và khối lượng công việc trao ổi giữa 4 bộ phận cho như
ở bên dưới. Phân các bộ phận về các vị trí ịa lý sao cho khoảng cách và thời gian trao ổi khối
lượng công việc giữa các bộ phận là nhỏ nhất. lOMoARcPSD| 40615933
- Xác ịnh tổng chi phí của cách bố trí trên nếu chi phí vận chuyển = $2/m
BÀI 4. LỰA CHỌN ĐỊA ĐIỂM
Bài tập 1. Một công ty dự ịnh mở 1 nhà kho tại 1 trong 3 ịa iểm A, B, C, biết rằng:
Địa iểm A có chi phí cố ịnh $4.000/tháng, chi phí biến ổi ơn vị $4. Địa iểm
B có chi phí cố ịnh $3.500/tháng, chi phí biến ổi ơn vị $5.
Địa iểm C có chi phí cố ịnh $5.000/tháng, chi phí biến ổi ơn vị $6.
Chi phí vận chuyển ến A: $19.000, B: $22.000, C: $18.000 Địa
iểm nào sẽ cho chi phí thấp nhất với 800sp/tháng.
Bài tập 2. Một công ty ang lựa chọn giữa 2 ịa iểm A và B.
Địa iểm A có chi phí cố ịnh $8.000/tháng, chi phí biến ổi ơn vị $5.
Địa iểm B có chi phí cố ịnh $9.400/tháng, chi phí biến ổi ơn vị $4.
Nhu cầu ước tính là 8.800/tháng, giá bán ơn vị là $6. Xác
ịnh ịa iểm có lợi nhuận cao hơn.
Bài tập 3. Một công ty lựa chọn giữa 2 ịa iểm A và B. Thông tin về các ịa iểm này như sau: A B
Chi phí cố ịnh hàng năm $1.200.000 $1.400.000 Chi phí biến ổi ơn vị $36 $47
Nhu cầu mong ợi hàng năm 8.000 12.000
Giá bán ơn vị cho cả 2 ịa iểm là $185. Tìm ịa iểm cho lợi nhuận cao hơn.
Bài tập 4. Một công ty ang cân nhắc việc lựa chọn 1 trong 3 ịa iểm A,B và C. Cả 3 ịa iểm ều có
chi phí biến ổi ơn vị là $1,76. Giá bán ơn vị là $2,65. Chi phí cố ịnh lần lượt cho từng ịa iểm là $5.000, $5.500, $5.800.
a. Xác ịnh số lượng sản phẩm cần bán ể mỗi ịa iểm tạo ược lợi nhuận là $10.000
b. Nếu số lượng sản phẩm bán ược tại A là 21.000, B là 22.000, C là 23.000. Địa iểm nào cho lợi nhuận nhiều nhất? lOMoARcPSD| 40615933
Bài tập 5. Hãy lựa chọn một trong 2 ịa iểm sau: Địa iểm Yếu tố Trọng số A B Chi phí lao ộng 0,5 20 40 Chi phí nguyên vật liệu 0,3 10 30 Chi phí khác 0,2 50 10
Bài tập 6. Một nhà quản lý dự ịnh mở thêm 1 nhà máy mới, số lượng vận chuyển từ nhà máy này
ến các nhà kho của công ty là như nhau. Xác ịnh vị trí nên xây dựng nhà máy này bằng phương
pháp ịa iểm trung tâm, số liệu cho như sau: Địa iểm (x, y) A (3,7) B (8,2) C (4,6) D (4,1) E (6,4)
Bài tập 7. Một nhà quản lý dự ịnh mở thêm 1 cửa hàng mới, xác ịnh vị trí nên mở cửa hàng này
bằng phương pháp ịa iểm trung tâm, số liệu cho như sau: Địa iểm (x, y)
Số lượng hàng bán A (1,2) 900 B (2,4) 300 C (3,1) 700 D (4,2) 600 E (5,3) 800
Bài tập 8. Ủy ban nhân dân thành phố Hà Nội ịnh chọn một trong 3 ịa iểm ể xây 1 bệnh viện bình
dân là Hà Đông, Hoàng Mai và Đống Đa. Ủy ban nhân dân thành phố dựa vào 4 chỉ tiêu ể ánh giá
và ứng với mỗi chỉ tiêu tùy theo mức ộ quan trọng của nó có trọng số tương ứng như sau: Vị trí có khả năng Yếu tố Trọng số Hà Đông Hoàng Mai Đống Đa
1) Thuận ường cho nhiều người 5 9 7 7 2) Tiền ền bù ất ai 3 6 10 3
3) Địa iểm yên tĩnh trong lành 3 5 2 7
4) Dễ tìm cán bộ chuyên môn 2 3 6 2
Vậy ịa iểm nào có hy vọng ược chọn nhất?
BÀI 5. MÔ HÌNH VẬN TẢI lOMoARcPSD| 40615933
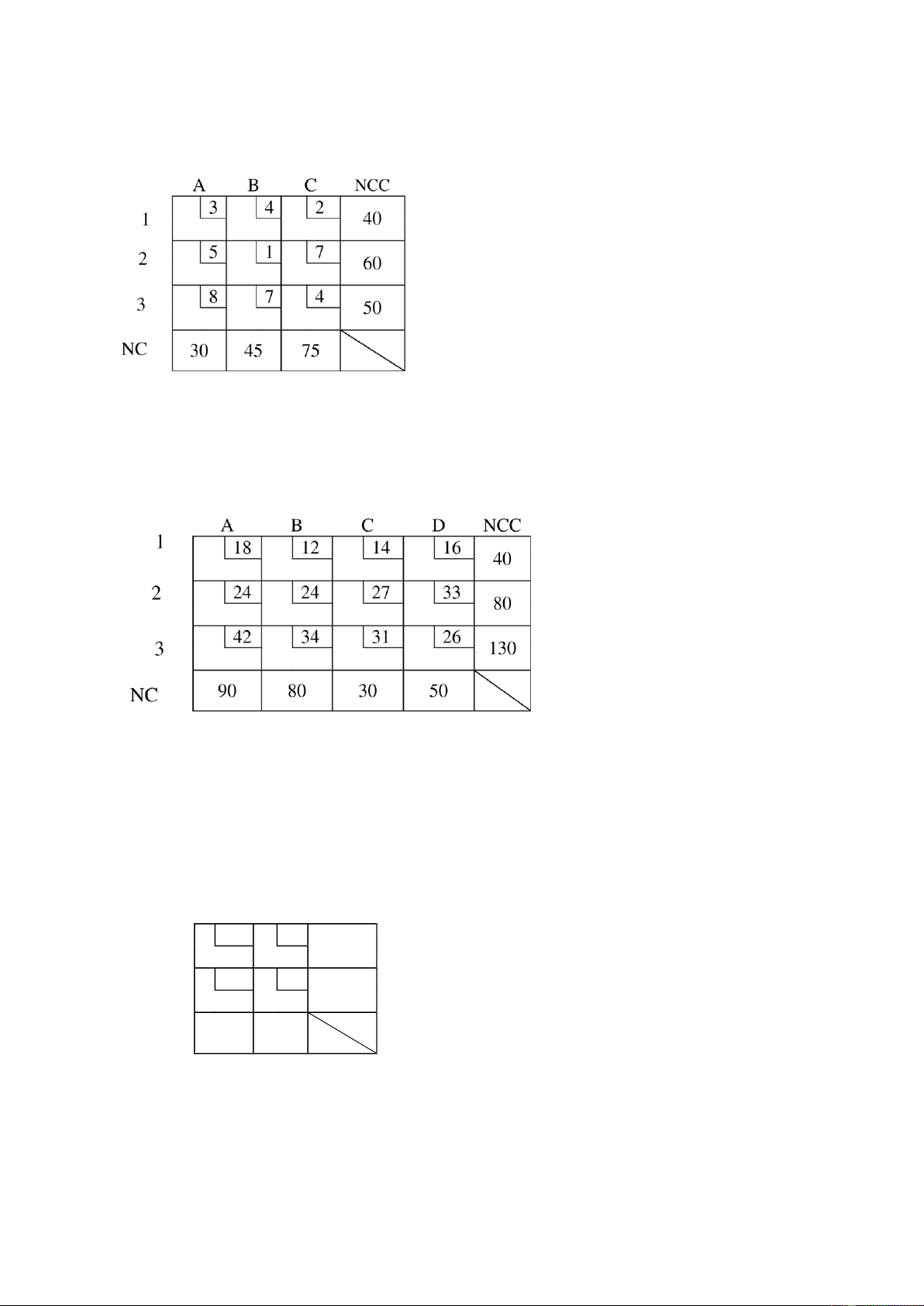
Bài tập 1. Xác ịnh giải pháp tối ưu và tính tổng chi phí cho hệ thống dưới ây, với: a. Sử
dụng phương pháp trực quan ể tiếp nhận giải pháp ban ầu.
b. Sử dụng VAM ể tiếp nhận giải pháp ban ầu.
Bài tập 2. Xác ịnh giải pháp tối ưu và tính tổng chi phí cho hệ thống sau:
a. Sử dụng VAM ể tiếp nhận giải pháp ban ầu và ánh giá các ô trống theo phương pháp MODI.
b. Sử dụng phương pháp trực quan ể tiếp nhận giải pháp ban ầu và ánh giá các ô trống dựa
trên phương pháp thế vị.
Bài tập 3. Xác ịnh giải pháp tối ưu cho hệ thống dưới ây. A B NCC 6 9 1 75 5 3 2 75 80 90 NC
Bài tập 4. Một công ty dự tính xây dựng một nhà máy mới tại một trong hai ịa iểm tại Chicago và
Detroit. Nhà máy mới có khả năng cung cấp 25.000 sản phẩm/ 1 tháng. Chi phí vận chuyển ơn vị
từ các ịa iểm này ến các nhà kho như sau: lOMoARcPSD| 40615933 Từ Detroit ến A: $ 10 Từ Chicago ến A: $ 12 B: $ 8 B: $ 13 C: $15 C: $ 5
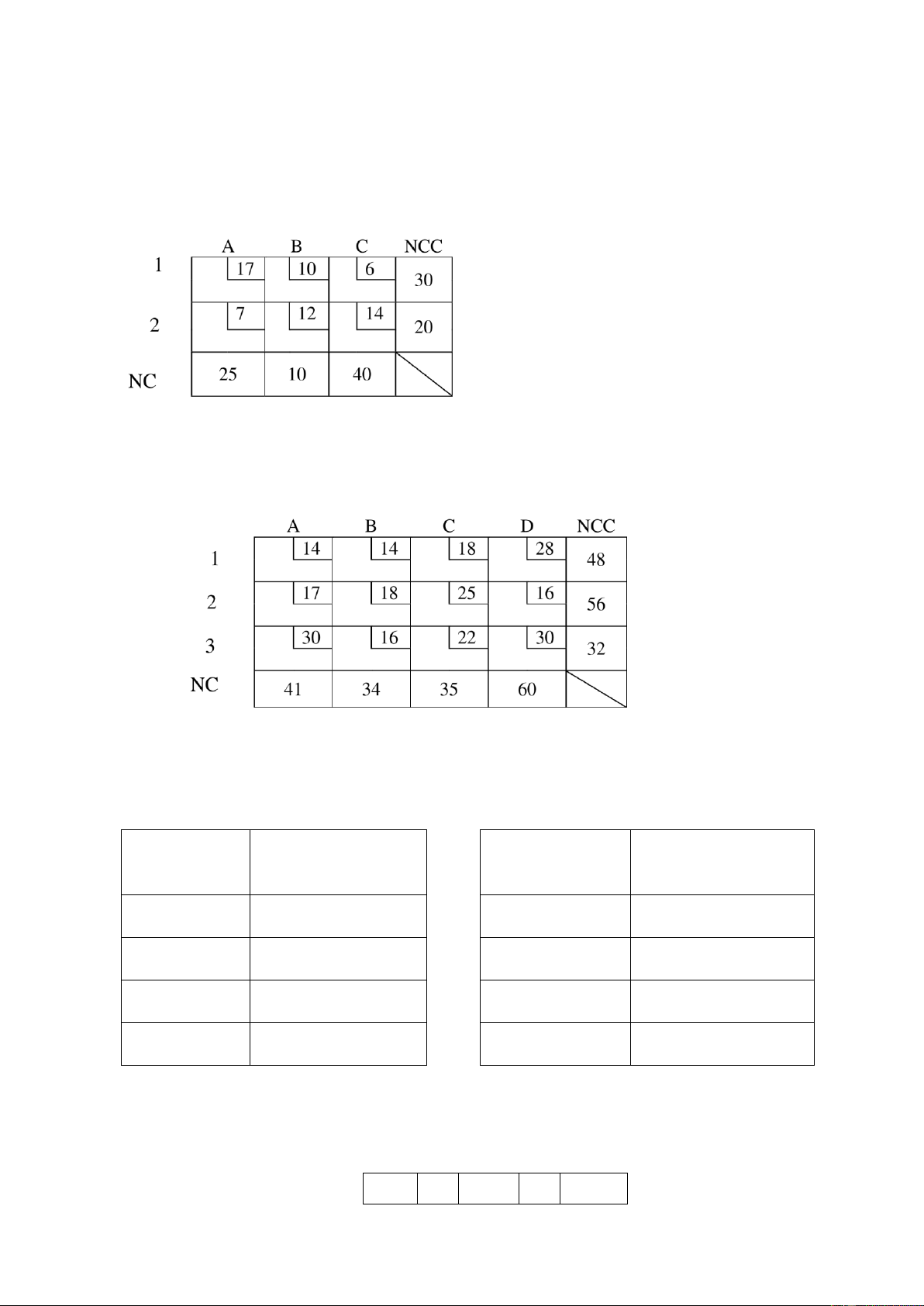
- Xác ịnh giải pháp tối ưu trên toàn bộ hệ thống sau: (Đơn vị tính: 1.000 sp)
Bài tập 5. Cho hệ thống sau ây:
Giả sử Công ty muốn mở thêm một nhà máy thứ 4 với khả năng cung cấp là 50 tại 1 trong 2 ịa iểm
là Baltimore và Philadelphia. Chi phí vận chuyển từ 2 ịa iểm trên tới A, B, C, D như sau: Từ Baltimore
Chi phí vận chuyển Từ Philadelphia
Chi phí vận chuyển tới ơn vị ($) tới ơn vị ($) A 18 A 31 B 16 B 25 C 22 C 19 D 27 D 20
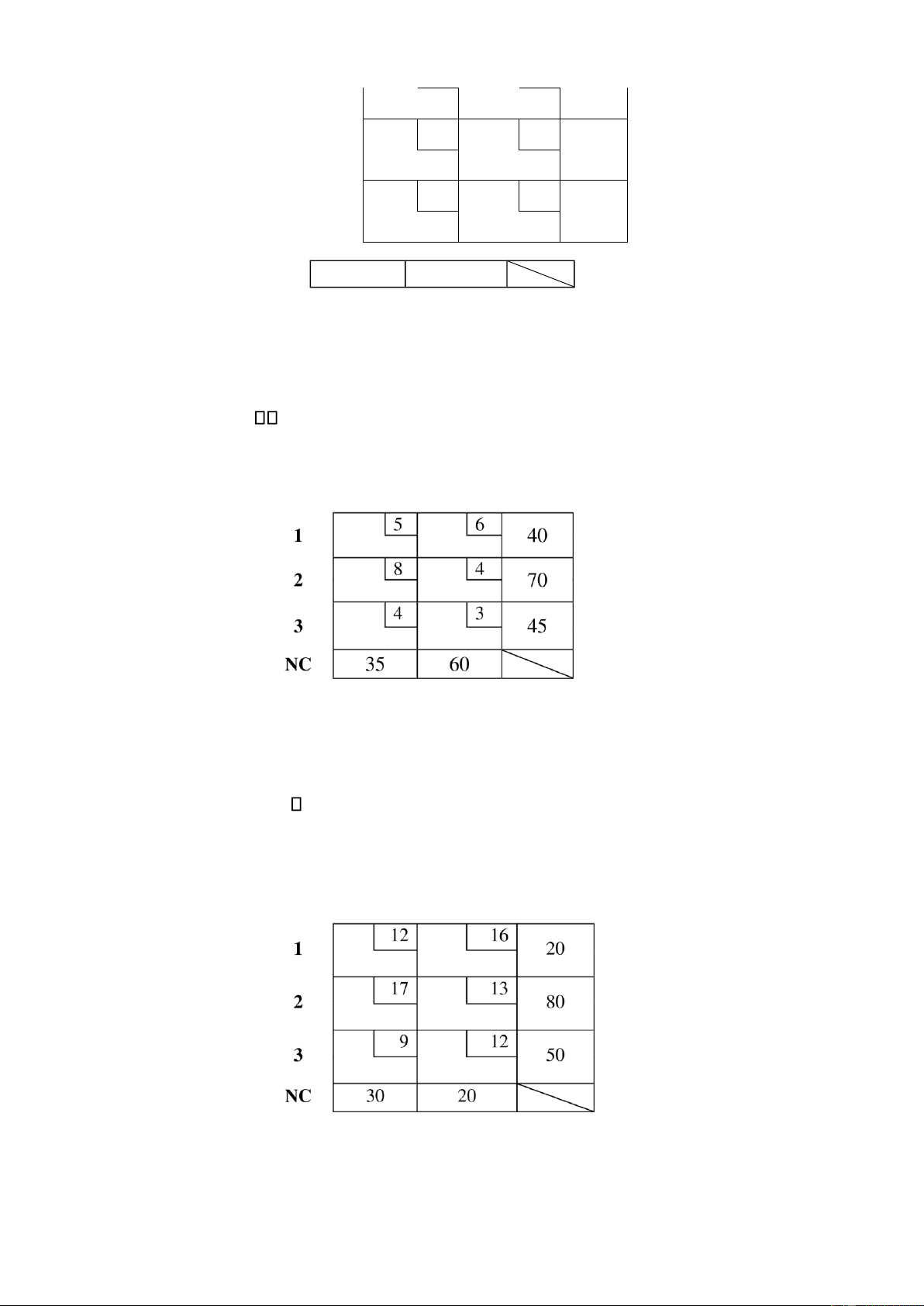
Bài tập 6. Một công ty bao gồm 3 nhà máy (1, 2, 3); 2 nhà kho (A, B) với khả năng cung cấp và
nhu cầu như sau (ơn vị tính: 1.000 sản phẩm): A B NCC 6 7 50 lOMoARcPSD| 40615933 1 9 5 80 2 5 4 55 3 NCC 45 70
Công ty dự ịnh mở thêm 1 nhà kho thứ 3 tại ịa iểm C với khả năng tiếp nhận 60.000 sản phẩm/
tháng. Biết rằng chi phí vận chuyển ơn vị từ các nhà máy 1, 2, 3 tới C lần lượt là $8, $11, $7.
Xác ịnh giải pháp tối ưu và tính tổng chi phí nếu xây dựng thêm nhà kho tại ịa iểm C? (Sử dụng
VAM và phương pháp MODI ể xác ịnh ịa iểm cho tổng chi phí vận chuyển nhỏ nhất xét trên toàn hệ thống (Nên gán
vào các ô 2-A, 2-C hoặc 3-B).
Bài tập 7. Một công ty bao gồm 3 nhà máy (1, 2, 3); 2 nhà kho (A, B) với khả năng cung cấp và
nhu cầu như sau (ơn vị tính: 1.000 sản phẩm): A B NCC
Công ty dự ịnh mở thêm 1 nhà kho thứ 3 tại ịa iểm C với khả năng tiếp nhận 50.000 sản
phẩm/tháng. Biết rằng chi phí vận chuyển ơn vị từ các nhà máy 1, 2, 3 tới C lần lượt là $7, $10, $6.
Xác ịnh giải pháp tối ưu và tính tổng chi phí nếu xây dựng thêm nhà kho tại ịa iểm C? (Sử
dụng VAM và phương pháp thế vị ể xác ịnh ịa iểm cho tổng chi phí vận chuyển nhỏ nhất xét trên
toàn hệ thống (Nên gán vào các ô 2-A, 2-C hoặc 3-B).
Bài tập 8. Một công ty bao gồm 3 nhà máy (1, 2, 3); 2 nhà kho (A, B) với khả năng cung cấp và
nhu cầu như sau (ơn vị tính: 1.000 sản phẩm): A B NCC
Công ty dự ịnh mở thêm 1 nhà kho thứ 3 tại ịa iểm C với khả năng tiếp nhận 70. Biết rằng chi phí
vận chuyển ơn vị từ các nhà máy 1, 2, 3 tới C lần lượt là $15, $14, $7. lOMoARcPSD| 40615933
Xác ịnh giải pháp tối ưu và tính tổng chi phí nếu xây dựng thêm nhà kho tại ịa iểm C? (Sử dụng
VAM và phương pháp thế vị ể xác ịnh ịa iểm cho tổng chi phí vận chuyển nhỏ nhất xét trên toàn hệ thống).
BÀI 6. THIẾT KẾ HỆ THỐNG CÔNG VIỆC
Bài tập 1. Một công việc bao gồm 4 nhiệm vụ thành phần ược nghiên cứu thời gian. Các kết quả
quan sát và mức ộ hoạt ộng trong 6 chu kỳ ược cho như sau: Thành Đánh giá mức ộ
Kết quả quan sát qua các chu kỳ (phút) phần hoạt ộng (%) 1 2 3 4 5 6 1 90 0,44 0,50 0,43 0,45 0,48 0,46 2 85 1,50 1,54 1,47 1,51 1,49 1,52 3 110 0,84 0,89 0,77 0,83 0,85 0,80 4 100 1,10 1,14 1,08 1,20 1,16 1,26
a. Xác ịnh thời gian trung bình cho mỗi thành phần.
b. Xác ịnh thời gian thông thường cho mỗi thành phần
c. Tính toán thời gian chuẩn cho toàn bộ công việc nếu % trì hoãn dựa trên công việc là 0,15.
Bài tập 2. Một doanh nghiệp cho phép người lao ộng nghỉ ngơi 48 phút; các hoạt ộng vệ sinh cá
nhân 20 phút và sự trì hoãn cho phép khác là 28 phút dựa trên ngày làm việc 8 giờ. Công việc ược
quan sát có thời gian trung bình là 6 phút với tốc ộ làm việc 95 %. Tính thời gian chuẩn.
Bài tập 3. Bao nhiêu quan sát cần tiến hành ể thời gian trung bình của chu kỳ chênh lệch khoảng
2 % so với trung bình mẫu với ộ tin cậy 99 %. 6 quan sát cho kết quả như sau: 5,2 phút; 5,5 phút;
5,6 phút; 5,3 phút; 5,5 phút; 5,3 phút.
Bài tập 4. Một nhà quản lý muốn ước tính tỷ lệ thời gian mà một công nhân trải qua ể iều chỉnh
máy móc với ộ tin cậy 90%. Dựa trên kinh nghiệm bản thân nhà quản lý tin rằng tỷ lệ này xấp xỉ 30%.
a. Nếu nhà quản lý sử dụng một kích thước mẫu là 400 quan sát thì mức sai lệch tối a cho phép là bao nhiêu?
b. Kích thước mẫu cần quan sát là bao nhiêu ể sai lệch tối a không quá 5%.
Bài tập 5. Một nhà phân tích muốn dự oán số các quan sát cần ể ạt ược mức sai lệch tối a cho phép
với ộ tin cậy 95,5%. Một nghiên cứu mở ầu nhận ược giá trị trung bình là 5,2 phút và ộ lệch chuẩn
của mẫu là 1,1 phút. Hãy xác ịnh tổng số quan sát cần thiết trong hai trường hợp sau:
a. Mức sai lệch tối a so với giá trị trung bình là 6%.
b. Mức sai lệch tối a cho phép e = 0,4 phút. lOMoARcPSD| 40615933
Bài tập 6. Một công ty nhỏ phải xây dựng 30 chiếc bể bơi. Nhà quản lý tin rằng hoạt ộng này có
ường cong kinh nghiệm là 85%. Thời gian ể hoàn thiện chiếc bể bơi ầu tiên ược ước tính là 8 ngày.
Hãy xác ịnh thời gian hoàn thiện cho: a. 10 chiếc ầu b. 10 chiếc thứ hai c. 10 chiếc cuối cùng
Bài tập 7. Sản phẩm thứ 5 trong một công việc bao gồm 25 sản phẩm chiếm khoảng 14,5 giờ ể hoàn
thành. Nếu ường cong kinh nghiệm là 90%, hãy:
a. Xác ịnh thời gian hoàn thiện sản phẩm cuối cùng.
b. Xác ịnh thời gian hoàn thiện sản phẩm thứ 10.
c. Xác ịnh thời gian hoàn thiện trung bình cho mỗi sản phẩm.
Bài tập 8. Sản phẩm thứ 5 trong một công việc bao gồm 10 sản phẩm mất khoảng 5 giờ ể hoàn
thiện. Sản phẩm thứ sáu ã thực hiện ược 2 giờ và chưa hoàn thiện. Xác ịnh thời gian cần thiết còn
lại ể hoàn thiện cả 10 sản phẩm nếu ường cong kinh nghiệm là 75%.
Bài tập 9. Một doanh nghiệp tuyển dụng và ào tạo người lao ộng. Chương trình ào tạo òi hỏi người
lao ộng phải hoàn thiện sản phẩm thứ 6 trong vòng 6 giờ hoặc nhỏ hơn. Ba người lao ộng ang thực
hiện công việc và ã hoàn thành ược 2 sản phẩm.
Người A hoàn thiện sản phẩm thứ nhất trong 9 giờ và sản phẩm thứ hai trong 8 giờ.
Người B hoàn thiện sản phẩm thứ nhất trong 10 giờ và sản phẩm thứ hai trong 8 giờ.
Người C hoàn thiện sản phẩm thứ nhất trong 12 giờ và sản phẩm thứ hai trong 9 giờ. Người
lao ộng nào sẽ ược tuyển dụng? Tại sao?
Bài tập 10. Một hoạt ộng lắp ráp có ường cong kinh nghiệm là 90%. Dây chuyền này thực hiện
sản xuất chi tiết mới; chi tiết ầu tiên mất 28 giờ lao ộng. Hãy xác ịnh thời gian hoàn thiện: a. 5 chi tiết ầu tiên.
b. Chi tiết thứ 20 ến chi tiết thứ 25.
Bài tập 11. Một nhà quản lý muốn xác ịnh tỷ lệ ường cong kinh nghiệm phù hợp cho một hoạt ộng
mới. Nhà quản lý ã xác ịnh ược thời gian hoàn thành cho 6 công việc lặp lại như sau: Sản phẩm Thời gian (phút) Sản phẩm Thời gian (phút) 1 15,9 4 9,1 2 12,0 5 8,4 3 10,1 6 7,5
Tỷ lệ ường cong kinh nghiệm là bao nhiêu sẽ phù hợp trong trường hợp này. lOMoARcPSD| 40615933
Bài tập 12. Thời gian thực hiện 6 sản phẩm ầu tiên là 15 giờ. Tính thời gian ể hoàn thành 25 sản
phẩm biết rằng hoạt ộng này có ường cong kinh nghiệm là 85%.
BÀI 7. KIỂM SOÁT CHẤT LƯỢNG TRONG QUY TRÌNH SẢN XUẤT
Bài tập 1. 11 mẫu ược quan sát. Số lượng sản phẩm hỏng của các mẫu cho như ở bên dưới. Xác
ịnh xem các biến ộng không ngẫu nhiên có tồn tại không qua việc kiểm soát chuỗi ặc thù. Biết
rằng ộ tin cậy là 95,5%. Mẫu 1 2 3 4 5 6 7 8 9 10 11 SL sp hỏng 22 17 19 25 18 20 21 17 23 23 24
Bài tập 2. Một quy trình óng chai tự ộng ược xác ịnh là tuân theo phân phối chuẩn với trung bình
là 1 lít với ộ lệch chuẩn 0,01 lít. Sản phẩm ầu ra ược kiểm soát theo các mẫu với kích thước mỗi mẫu là 25 quan sát.
a. Xác ịnh giới hạn kiểm soát trên và giới hạn kiểm soát dưới với ộ tin cậy 95,5%.
b. Nếu các mẫu lấy ược có các giá trị trung bình: 1,005; 1,001; 0,998; 1,002; 0,995; 0,999. Quy trình
có nằm trong sự kiểm soát không? Bài tập 3.
Một quy trình sản xuất ược kiểm soát với 6 mẫu; mỗi mẫu 20 quan sát ược cho như sau:
Mẫu Trung bình Khoảng mẫu
Mẫu Trung bình Khoảng mẫu 1 3,06 0,42 4 3,13 0,46 2 3,15 0,50 5 3,06 0,46 3 3,11 0,41 6 3,09 0,45
a. Xác ịnh giới hạn trên và dưới cho giá trị trung bình và cho ộ phân tán.
b. Quy trình có nằm trong sự kiểm soát không?
Bài tập 4. Một quy trình cắt nhựa với ộ dài trung bình là 80 cm ược kiểm tra. Các mẫu ược lấy, mỗi
mẫu có kích thước 5 quan sát như sau: Mẫu 1 Mẫu 2 Mẫu 3 Mẫu 4 Mẫu 5 Mẫu 6 79,2 80,5 79,8 78,9 80,5 79,7 78,8 78,7 79,4 79,4 79,6 80,6 80,0 81,0 80,4 79,7 80,4 80,5 78,4 80,4 80,3 79,4 80,8 80,0 81,0 80,1 80,8 80,6 78,8 81,1
Xây dựng sơ ồ trung bình và sơ ồ khoảng. lOMoARcPSD| 40615933
Bài tập 5. Số các vụ tai nạn giao thông qua các ơn vị thời gian ược cho như ở bên dưới. Xây dựng
sơ ồ kiểm soát với giới hạn 3 . GĐ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Số vụ tai nạn 4 10 14 8 9 6 5 12 13 7 6 4 2 10
Bài tập 6. Số các sản phẩm hỏng ược quan sát qua 16 mẫu (mỗi mẫu 100 quan sát) ược cho như ở
bên dưới. Hãy cho biết quy trình có nằm trong sự kiểm soát không với ộ tin cậy 95%.
Mẫu Số SP hỏng Mẫu Số SP hỏng 1 5 9 5 2 3 10 8 3 6 11 3 4 7 12 4 5 4 13 5 6 6 14 6 7 8 15 6 8 4 16 7
Bài tập 7. Cho 5 mẫu với kích thước mỗi mẫu là 4 sản phẩm, thông tin cụ thể như sau: Mẫu 1 Mẫu 2 Mẫu 3 Mẫu 4 Mẫu 5 5,25 5,21 5,31 5,27 5,29 5,56 5,24 5,23 5,35 5,47 5,41 5,35 5,29 5,43 5,46 5,26 5,48 5,41 5,35 5,22
a. Với ộ tin cậy 98,76% (z = 2,5), hãy xây dựng sơ ồ trung bình, sơ ồ khoảng và kết luận xem quy
trình có nằm trong sự kiểm soát không? Biết rằng ộ lệch chuẩn của quy trình là 0,1016.
b. Nếu R = 0,1272 thì quy trình có nằm trong sự kiểm soát không? Vì sao?
Bài tập 8. Một quy trình sản xuất phụ tùng ô tô tạo ra 5% sản phẩm sai hỏng. Nếu kiểm tra 100%
sản phẩm ầu ra thì chi phí kiểm tra là 0,4 $/SP. Nếu phụ tùng ược lắp vào ô tô mới phát hiện sai
hỏng, chi phí thay thế là 12 $/SP. Doanh nghiệp có nên kiểm tra 100% không?
Bài tập 9. Một dây chuyền lắp ráp có một tỷ lệ hỏng rất nhỏ. Doanh nghiệp ang cân nhắc giữa
việc kiểm tra trong dây chuyền hoặc kiểm tra sản phẩm cuối cùng. Nếu sản phẩm cuối cùng là
hỏng, chi phí thay thế là 30$. Chi phí kiểm tra ngay trong dây chuyền là 12 $/giờ. Một giờ kiểm tra ược 60 sản phẩm. lOMoARcPSD| 40615933
- Doanh nghiệp có nên kiểm tra 100% ngay trong dây chuyền không nếu tỷ lệ hỏng là 4%; 1%?
- Ở tỷ lệ hỏng nào thì hai loại kiểm tra trên là như nhau?
Bài tập 10. Một nhà sản xuất mua phụ tùng lắp ráp cho một dây chuyền. Nếu kiểm tra 100% thì
chi phí kiểm tra là 1 $/phụ tùng. Nếu không kiểm tra mà ưa vào dây chuyền lắp ráp thì chi phí thay
thế là 6,25 $/phụ tùng hỏng.
- Mức hỏng của lô hàng là bao nhiêu ể hai loại kiểm tra trên có chi phí bằng nhau?
- Nếu doanh nghiệp kiểm tra từng mẫu 15 sản phẩm, số phụ tùng hỏng trong một mẫu là bao
nhiêu ể lô hàng ược chấp nhận mà không phải kiểm tra 100% (có sử dụng kết quả từ câu trên). lOMoARcPSD| 40615933
BÀI 8, BÀI 9: TRONG SLIDE BÀI GIẢNG
BÀI 10. LẬP LỊCH TRÌNH CÔNG VIỆC
Bài tập 1. Hãy phân công công việc về các máy sao cho cực tiểu chi phí Máy Máy A B C D A B C 1 12 16 14 10 1 12 8 11 2 9 8 13 7 2 13 10 8 3 15 12 9 11 3 14 9 14 4 10 7 12
Bài tập 2. Số liệu dưới ây là lợi nhuận. Hãy phân công công việc ể tối a lợi nhuận Máy A B C D 1 8 6 2 4 2 6 7 11 10 3 3 5 7 6 4 5 10 12 9
Bài tập 3. Cho 5 máy (A, B, C, D, E) và 4 công việc (1, 2, 3, 4). Lợi nhuận xử lý công việc tương
ứng tại các máy cho ở bên dưới. Hãy phân công công việc về các máy ể tối a hóa lợi nhuận ( ơn
vị tính: $). Tính tổng lợi nhuận. Máy A B C D E 1 21 19 20 16 17 2 25 16 29 13 28 3 19 15 22 12 25 4 21 24 23 16 13
Bài tập 4. Năm công việc ang chờ ược xử lý tại 1 phân xưởng với thời gian xử lý và thời gian ến hạn như sau: Công việc
Thời gian xử lý (ngày)
Thời gian ÿến hạn (ngày) lOMoARcPSD| 40615933 A 12 15 B 6 24 C 14 20 D 3 8 E 7 6
Hãy sắp xếp trình tự xử lý theo FCFS, SPT, DD và tính hiệu quả của các cách sắp xếp trên.
Bài tập 5. Hãy phân công những công việc dưới ây về các máy sao cho cực tiểu chi phí trong những iều kiện sau:
a. Không ể công việc 2 ược xử lý ở máy D.
b. Không ể công việc 2 ược xử lý ở máy D và công việc 1 tại máy A. Máy A B C D E 1 16 18 20 17 18 2 14 15 19 20 17 3 12 16 15 14 17 4 11 13 14 12 14 5 10 16 15 14 13
Bài tập 6. Xác ịnh trình tự các công việc dưới ây theo FCFS và S/O. So sánh các thước o hiệu quả của 2 phương pháp trên. Thời gian Thời gian ÿến
Số các hoạt ÿộng Công việc xử lý (ngày) hạn (ngày) còn lại A 8 20 2 B 10 18 4 C 5 25 5 D 11 17 3 E 9 35 4
Bài tập 7. Sắp xếp trình tự cho các công việc dưới ây khi chúng ược xử lý tuần tự qua 2 trung tâm.
Tính tỷ lệ thời gian nhàn rỗi của trung tâm 2.
Thời gian tại trung Thời gian tại Công việc tâm 1 trung tâm 2 A 20 27 B 16 30 lOMoARcPSD| 40615933 C 43 51 D 60 12 E 35 28 F 42 24
Bài tập 8. Tám công việc ang chờ ược xử lý tại phân xưởng 1. Thời gian xử lý ược cho như ở bên dưới. Công Thời gian Thời gian
Công việc Thời gian Thời gian việc
xử lý (giờ) ến hạn (giờ)
xử lý (giờ) ến hạn (giờ) A 7 11 E 12 16 B 13 15 F 8 21 C 15 18 G 16 28 D 4 5 H 20 24
a. Hãy xác ịnh trình tự xử lý theo nguyên tắc DD (Due Date) và tính thời gian hoàn thành
trung bình; thời gian muộn trung bình.
b. Giả sử 8 công việc trên ược xử lý lần lượt qua hai phân xưởng: phân xưởng 1 (số liệu ã cho
ở trên) và phân xưởng 2. Thời gian xử lý công việc tại phân xưởng 2 ược cho cụ thể như sau: Công việc Thời gian Công việc Thời gian Công việc Thời gian xử lý (giờ) xử lý (giờ) xử lý (giờ) A 5 D 7 G 14 B 9 E 17 H 2 C 6 F 11
Hãy xác ịnh trình tự xử lý công việc tối ưu nhằm cực tiểu hóa thời gian nhàn rỗi tại hai phân
xưởng. Vẽ sơ ồ và xác ịnh tổng thời gian nhàn rỗi tại phân xưởng 2. Tính tỷ lệ thời gian nhàn rỗi ó.
----------HẾT----------