BÀI TẬP LỚN

CẤU TRÚC DỮ LIỆU VÀ GIẢI THUẬT

Ngành: Công nghệ thông tin

SINH VIÊN THỰC HIỆN: Bùi Đứa Toàn

MÃ SỐ SINH VIÊN: 20012030356

LỚP: K20.PR02

GV HƯỚNG DẪN: Thầy Quảng

1

BÀI TẬP LỚN

CẤU TRÚC DỮ LIỆU VÀ GIẢI THUẬT

Ngành: Công nghệ thông tin

SINH VIÊN THỰC HIỆN: Bùi Đức Toàn

MÃ SỐ SINH VIÊN: 20012030356

LỚP: K20.PR02

GV HƯỚNG DẪN MÔN HỌC: Thầy Quảng

NHẬN XÉT

Nhận xét của giảng viên hướng dẫn:

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

……………………………………………………………………………………….....

GIẢNG VIÊN HƯỚNG DẪN

LỜI CAM ĐOAN

Em xin cam đoan bài tập lớn môn Cấu trúc dữ liệu và giải thuật là kết quả thực hiện của bản thân em dưới sự hướng dẫn của thầy Quảng

Những phần sử dụng tài liệu tham khảo trong bài tập lớn đã được nêu rõ trong phần tài liệu tham khảo. Các kết quả trình bày trong bài tập lớn và chương trình xây dựng được hoàn toàn là kết quả do bản thân em thực hiện.

Nếu vi phạm lời cam đoan này, em xin chịu hoàn toàn trách nhiệm trước khoa và nhà trường.

Hà Nội, ngày … tháng … năm…..

Họ và tên sinh viên

LỜI CẢM ƠN

Để có thể hoàn thành bài tập lớn này, lời đầu tiên em xin phép gửi lời cảm ơn tới bộ môn Lập trình và phát triển ứng dụng web nâng cao, Khoa Công nghệ thông tin – Trường Cao đẳng Công nghệ Bách Khoa Hà Nội đã tạo điều kiện thuận lợi cho em thực hiện bài tập lớn môn học này.

Đặc biệt em xin chân thành cảm ơn thầy Quảng đã rất tận tình hướng dẫn, chỉ bảo em trong suốt thời gian thực hiện bài tập lớn vừa qua.

Em cũng xin chân thành cảm ơn tất cả các Thầy, các Cô trong Trường đã tận tình giảng dạy, trang bị cho em những kiến thức cần thiết, quý báu để giúp em thực hiện được bài tập lớn này.

Mặc dù em đã có cố gắng, nhưng với trình độ còn hạn chế, trong quá trình thực hiện đề tài không tránh khỏi những thiếu sót. Em hi vọng sẽ nhận được những ý kiến nhận xét, góp ý của các Thầy giáo, Cô giáo về những kết quả triển khai trong bài tập lớn.

Em xin trân trọng cảm ơn!

MỤC LỤC

CHƯƠNG I: CƠ SỞ LÝ THUYẾT 9

• 1. Khái niệm về giải thuật 9
     1. Giải thuật là gì? 9
  2. Cấu trúc dữ liệu mảng (Array) 18
     1. Khái niệm 18

Mảng (Array) là một trong các cấu trúc dữ liệu cũ và quan trọng nhất. Mảng có thể lưu giữ một số phần tử cố định và các phần tử này nền có cùng kiểu. Hầu hết các cấu trúc dữ liệu đều sử dụng mảng để triển khai giải thuật. Dưới đây là các khái niệm quan trọng liên quan tới Mảng. 18

Phần tử: Mỗi mục được lưu giữ trong một mảng được gọi là một phần tử 18

Chỉ mục (Index): Mỗi vị trí của một phần tử trong một mảng có một chỉ mục số được sử dụng để nhận diện phần tử 18

Mảng gồm các bản ghi có kiểu giống nhau, có kích thước cố định, mỗi phần tử được xác định bởi chỉ số 18

Mảng là cấu trúc dữ liệu được cấp phát lien tục cơ bản 18

• • 1. Ưu điểm 18
       • Truy câp phàn tử với thời gian hằng số O(1) 18

 Sử dụng bộ nhớ hiệu quả 18

• • • • Tính cục bộ về bộ nhớ 18
    1. Nhược điểm 18

Không thể thay đổi kích thước của mảng khi chương trình dang thực hiện 18

• • 1. Mảng động 18

Mảng động (dynamic aray) : cấp phát bộ nhớ cho mảng một cách động trong quá trình chạy chương trình trong C là malloc và calloc, trong C++ là new 18

Sử dụng mảng động ta bắt đầu với mảng có 1 phàn tử, khi số lượng phàn tử vượt qua khả năng của ảng thì ta gấp đôi kích thước mảng cuc và copy phàn tử mảng cũ vào nửa đầu của mảng mới 18

Ưu điểm: tránh lãng phí bộ nhớ khi phải khai báo mảng có kích thước lớn ngay từ đầu 18

Nhược điểm 18

• • • • Phải thực hiện them thao tác copy phần tử mỗi khi thay đổi kích thước 18
      • Một số thời gian thực hiện thao tác không còn là hằng số nữa 18
    1. Biểu diễn Cấu trúc dữ liệu mảng 18

Mảng có thể được khai báo theo nhiều cách đa dạng trong các ngôn ngữ lập trình. Để minh họa, chúng ta sử dụng phép khai báo mảng trong ngôn ngữ C 19

. 19

Hình minh họa phần tử và chỉ mục 19

. 19

Dưới đây là một số điểm cần ghi nhớ về cấu trúc dữ liệu mảng: 19

• • • • Chỉ mục bắt đầu với 0. 19
      • Độ dài mảng là 10, nghĩa là mảng có thể lưu giữ 10 phần tử 19
      • Mỗi phần tử đều có thể được truy cập thông qua chỉ mục của phần tử đó. Ví dụ, chúng ta có thể lấy giá trị của phần tử tại chỉ mục 6 là 27. 19
    1. Phép toán cơ bản được hỗ trợ bởi mảng 19
       • Duyệt: In tất cả các phần tử mảng theo cách in từng phần tử một 19
       • Chèn: Thêm một phần tử vào mảng tại chỉ mục đã cho. 19
       • Xóa: Xóa một phần tử từ mảng tại chỉ mục đã cho. 19
       • Tìm kiếm: Tìm kiếm một phần tử bởi sử dụng chỉ mục hay bởi giá trị 19
       • Cập nhật: Cập nhật giá trị một phần tử tại chỉ mục nào đó 19

Trong ngôn ngữ C, khi một mảng được khởi tạo với kích cỡ ban đầu, thì nó gán các giá trị mặc định cho các phần tử của mảng theo thứ tự sau: 19

Kiểu dữ liệu 19

Giá trị mặc định 19

bool 19

false 19

char 19

0 19

int 20

0 20

float 20

0.0 20

double 20

0.0f 20

void 20

wchar_t 20

0 20

• 1. Danh sách liên kết (Linked list) 20
     1. Khái niệm 20
     2. Khái niệm 35

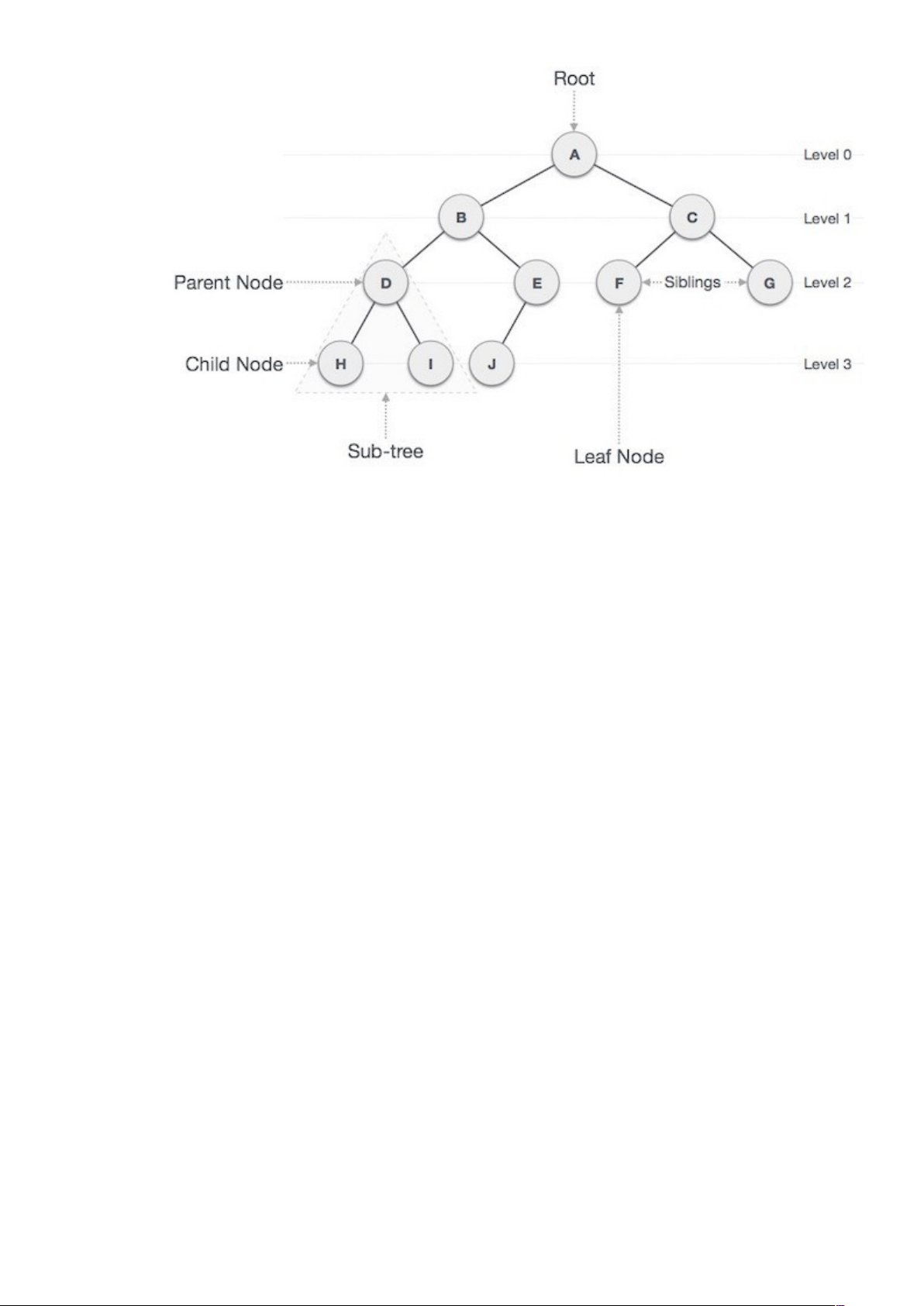
Cấu trúc dữ liệu cây biểu diễn các nút (node) được kết nối bởi các cạnh. Chúng ta sẽ tìm hiểu về Cây nhị phân (Binary Tree) và Cây tìm kiếm nhị phân (Binary Search Tree) trong phần này 35

Cây nhị phân là một cấu trúc dữ liệu đặc biệt được sử dụng cho mục đích lưu trữ dữ liệu. Một cây nhị phân có một điều kiện đặc biệt là mỗi nút có thể có tối đa hai nút con. Một cây nhị phân tận dụng lợi thế của hai kiểu cấu trúc dữ liệu: một mảng đã sắp thứ tự và một danh sách liên kết (Linked List), do đó việc tìm kiếm sẽ nhanh như trong mảng đã sắp thứ tự và các thao tác chèn và xóa cũng sẽ nhanh bằng trong Linked List 35

....35

Dưới đây là một số khái niệm quan trọng liên quan tới cây nhị phân: 35

• • • • Đường: là một dãy các nút cùng với các cạnh của một cây 35
      • Nút gốc (Root): nút trên cùng của cây được gọi là nút gốc. Một cây sẽ chỉ có một nút gốc và một đường xuất phát từ nút gốc tới bất kỳ nút nào khác. Nút gốc là nút duy nhất không có bất kỳ nút cha nào. 35
      • Nút cha: bất kỳ nút nào ngoại trừ nút gốc mà có một cạnh hướng lên một nút khác thì được gọi là nút cha. 35
      • Nút con: nút ở dưới một nút đã cho được kết nối bởi cạnh dưới của nó được gọi là nút con của nút đó. 35
      • Nút lá: nút mà không có bất kỳ nút con nào thì được gọi là nút lá. 35
      • Cây con: cây con biểu diễn các con của một nút 36
      • Truy cập: kiểm tra giá trị của một nút khi điều khiển là đang trên một nút đó. 36
      • Duyệt: duyệt qua các nút theo một thứ tự nào đó. 36

 Bậc: bậc của một nút biểu diễn số con của một nút. Nếu nút gốc có bậc là 0, thì nút con tiếp theo sẽ có bậc là 1, và nút cháu của nó sẽ có bậc là 2, 36

• • • • Khóa (Key): biểu diễn một giá trị của một nút dựa trên những gì mà một thao tác tìm kiếm thực hiện trên nút 36
    1. Hoạt động cơ bản trên cây tìm kiếm nhị phân 36
       • Chèn: chèn một phần tử vào trong một cây/ tạo một cây 36
       • Tìm kiếm: tìm kiếm một phần tử trong một cây 36
       • Duyệt tiền thứ tự: duyệt một cây theo cách thức duyệt tiền thứ tự (tham khảo chương sau) 36
       • Duyệt trung thứ tự: duyệt một cây theo cách thức duyệt trung thứ tự (tham khảo chương sau) 36
       • Duyệt hậu thứ tự: duyệt một cây theo cách thức duyệt hậu thứ tự (tham khảo chương sau) 36

PHẦN KẾT LUẬN 36

TÀI LIỆU THAM KHẢO 38

CHƯƠNG I: CƠ SỞ LÝ THUYẾT

Khái niệm về giải thuật

Giải thuật là gì?

Giải thuật (hay còn gọi là thuật toán - tiếng Anh là Algorithms) là một tập hợp hữu hạn các chỉ thị để được thực thi theo một thứ tự nào đó để thu được kết quả mong muốn. Nói chung thì giải thuật là độc lập với các ngôn ngữ lập trình, tức là một giải thuật có thể được triển khai trong nhiều ngôn ngữ lập trình khác nhau.

Xuất phát từ quan điểm của cấu trúc dữ liệu, dưới đây là một số giải thuật quan

trọng:

• Giải thuật Tìm kiếm: Giải thuật để tìm kiếm một phần tử trong một cấu trúc dữ liệu.
• Giải thuật Sắp xếp: Giải thuật để sắp xếp các phần tử theo thứ tự nào đó.
• Giải thuật Chèn: Giải thuật để chèn phần từ vào trong một cấu trúc dữ liệu.
• Giải thuật Cập nhật: Giải thuật để cập nhật (hay update) một phần tử đã tồn tại trong một cấu trúc dữ liệu.
• Giải thuật Xóa: Giải thuật để xóa một phần tử đang tồn tại từ một cấu trúc dữ liệu.

Đặc điểm của giải thuật

Không phải tất cả các thủ tục có thể được gọi là một giải thuật. Một giải thuật nên có các đặc điểm sau:

• • • • Tính xác định: Giải thuật nên rõ ràng và không mơ hồ. Mỗi một giai đoạn (hay mỗi bước) nên rõ ràng và chỉ mang một mục đích nhất định.
      • Dữ liệu đầu vào xác định: Một giải thuật nên có 0 hoặc nhiều hơn dữ liệu đầu vào đã xác định.
      • Kết quả đầu ra: Một giải thuật nên có một hoặc nhiều dữ liệu đầu ra đã xác định, và nên kết nối với kiểu kết quả bạn mong muốn.
      • Tính dừng: Các giải thuật phải kết thúc sau một số hữu hạn các bước.
      • Tính hiệu quả: Một giải thuật nên là có thể thi hành được với các nguồn có sẵn, tức là có khả năng giải quyết hiệu quả vấn đề trong điều kiện thời gian và tài nguyên cho phép.
      • Tính phổ biến: Một giải thuật có tính phổ biến nếu giải thuật này có thể giải quyết được một lớp các vấn đề tương tự.
      • Độc lập: Một giải thuật nên có các chỉ thị độc lập với bất kỳ phần code lập trình nào.

Giải thuật tiệm cận - Asymptotic Algorithms

Phân tích tiệm cận của một giải thuật là khái niệm giúp chúng ta ước lượng được thời gian chạy (Running Time) của một giải thuật. Sử dụng phân tích tiệm cận, chúng ta có thể đưa ra kết luận tốt nhất về các tình huống trường hợp tốt nhất, trường hợp trung bình, trường hợp xấu nhất của một giải thuật.

Phân tích tiệm cận tức là tiệm cận dữ liệu đầu vào (Input), tức là nếu giải thuật không có Input thì kết luận cuỗi cùng sẽ là giải thuật sẽ chạy trong một lượng thời gian cụ thể và là hằng số. Ngoài nhân tố Input, các nhân tố khác được xem như là không đổi.

Phân tích tiệm cận nói đến việc ước lượng thời gian chạy của bất kỳ phép tính nào trong các bước tính toán. Ví dụ, thời gian chạy của một phép tính nào đó được ước lượng là một hàm f(n) và với một phép tính khác là hàm g(n2). Điều này có nghĩa là thời gian chạy của

phép tính đầu tiên sẽ tăng tuyến tính với sự tăng lên của n và thời gian chạy của phép tính thứ hai sẽ tăng theo hàm mũ khi n tăng lên. Tương tự, khi n là khá nhỏ thì thời gian chạy của hai phép tính là gần như nhau.

Thường thì thời gian cần thiết bởi một giải thuật được chia thành 3 loại:

• • • • Trường hợp tốt nhất: là thời gian nhỏ nhất cần thiết để thực thi chương trình.
      • Trường hợp trung bình: là thời gian trung bình cần thiết để thực thi chương trình.
      • Trường hợp xấu nhất: là thời gian tối đa cần thiết để thực thi chương trình.

Asymptotic Notation trong Cấu trúc dữ liệu và giải thuật

Dưới đây là các Asymptotic Notation được sử dụng phổ biến trong việc ước lượng độ phức tạp thời gian chạy của một giải thuật:

• • • • Ο Notation
      • Ω Notation
      • θ Notation

Big Oh Notation, Ο trong Cấu trúc dữ liệu và giải thuật

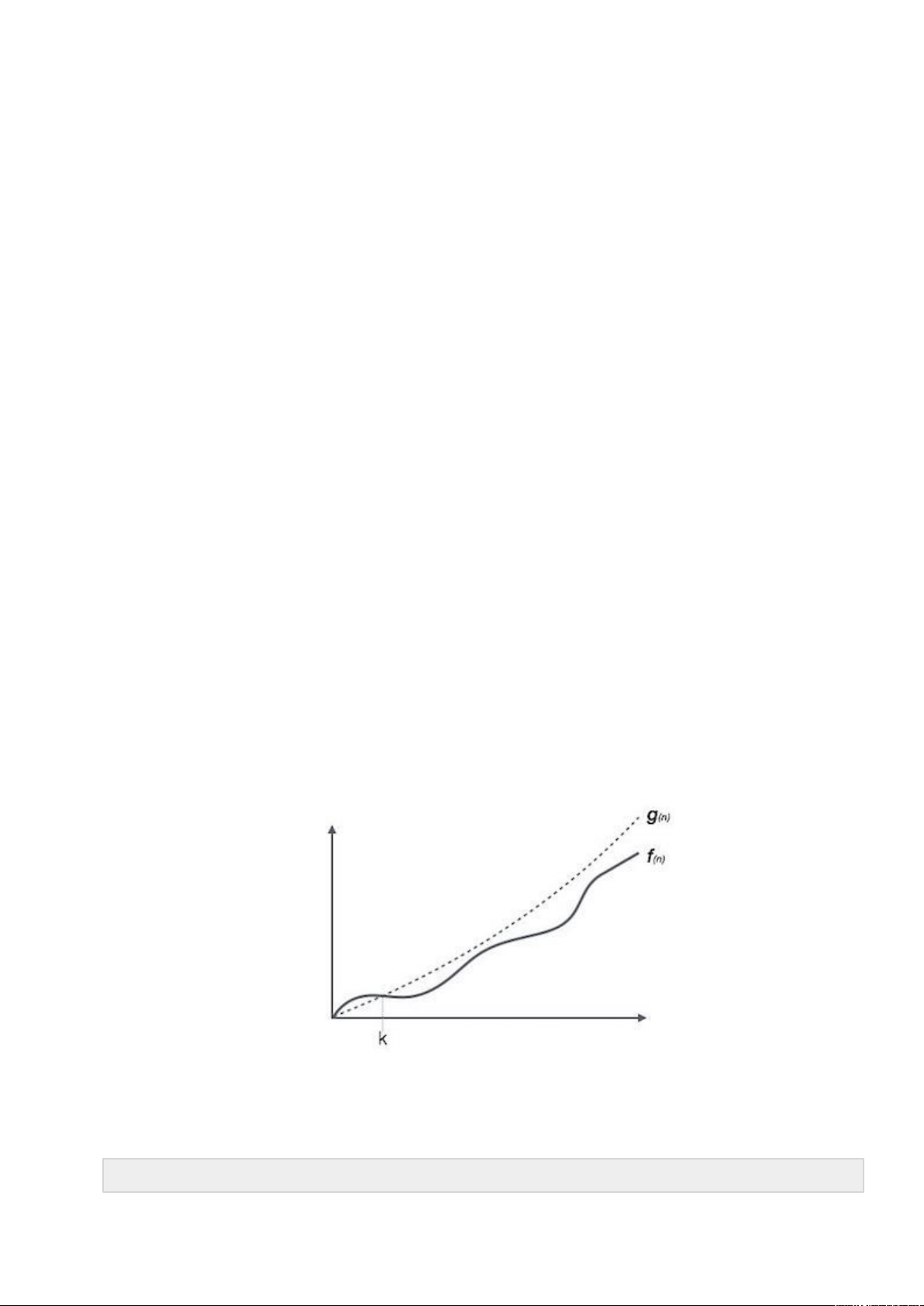
Ο(n) là một cách để biểu diễn tiệm cận trên của thời gian chạy của một thuật toán. Nó ước lượng độ phức tạp thời gian trường hợp xấu nhất hay chính là lượng thời gian dài nhất cần thiết bởi một giải thuật (thực thi từ bắt đầu cho đến khi kết thúc). Đồ thị biểu diễn như sau:

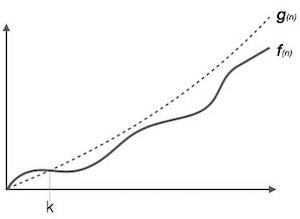
Ví dụ, gọi f(n) và g(n) là các hàm không giảm định nghĩa trên các số nguyên dương (tất cả các hàm thời gian đều thỏa mãn các điều kiện này):

Ο(f(n)) = { g(n) : nếu tồn tại c > 0 và n₀ sao cho g(n) ≤ c.f(n)

với mọi n > n₀. }

Omega Notation, Ω trong Cấu trúc dữ liệu và giải thuật

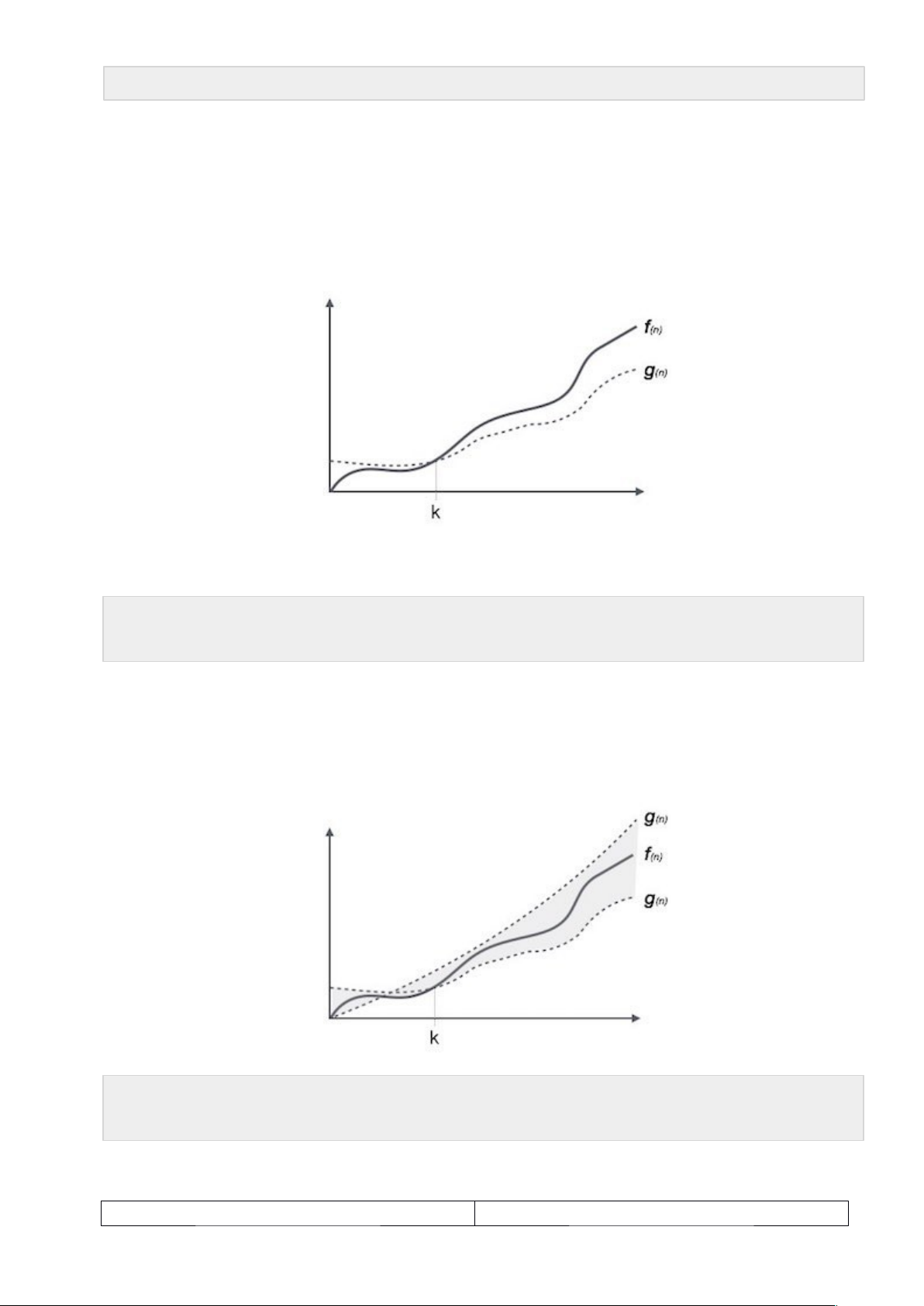
The Ω(n) là một cách để biểu diễn tiệm cận dưới của thời gian chạy của một giải thuật. Nó ước lượng độ phức tạp thời gian trường hợp tốt nhất hay chính là lượng thời gian ngắn nhất cần thiết bởi một giải thuật. Đồ thị biểu diễn như sau:

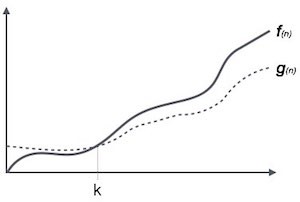
Ví dụ, với một hàm f(n):

Ω(f(n)) ≥ { g(n) : nếu tồn tại c > 0 và n₀ sao cho g(n) ≤ c.f(n)

với mọi n > n₀. }

Theta Notation, θ trong Cấu trúc dữ liệu và giải thuật

The θ(n) là cách để biểu diễn cả tiệm cận trên và tiệm cận dưới của thời gian chạy của một giải thuật. Bạn nhìn vào đồ thì sau:

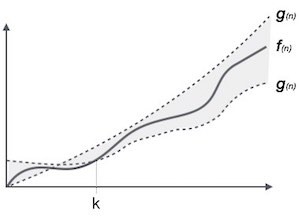
θ(f(n)) = { g(n) nếu và chỉ nếu g(n) = Ο(f(n)) và g(n) = Ω(f(n))

với mọi n > n₀. }

Một số Asymptotic Notation phổ biến trong cấu trúc dữ liệu và giải thuật

Ο(1)

hằng số

Giải thuật tham lam - Greedy Algorithms

Tham lam (hay tham ăn) là một trong những phương pháp phổ biến nhất để thiết kế giải thuật. Nếu bạn đã đọc truyện dân gian thì sẽ có câu chuyện như thế này: trên một mâm cỗ có nhiều món ăn, món nào ngon nhất ta sẽ ăn trước, ăn hết món đó ta sẽ chuyển sang món ngon thứ hai, và chuyển tiếp sang món thứ ba, …

Rất nhiều giải thuật nổi tiếng được thiết kế dựa trên ý tưởng tham lam, ví dụ như giải thuật cây khung nhỏ nhất của Dijkstra, giải thuật cây khung nhỏ nhất của Kruskal, …

Giải thuật tham lam (Greedy Algorithm) là giải thuật tối ưu hóa tổ hợp. Giải thuật tìm kiếm, lựa chọn giải pháp tối ưu địa phương ở mỗi bước với hi vọng tìm được giải pháp tối ưu toàn cục.

Giải thuật tham lam lựa chọn giải pháp nào được cho là tốt nhất ở thời điểm hiện tại và sau đó giải bài toán con nảy sinh từ việc thực hiện lựa chọn đó. Lựa chọn của giải thuật tham lam có thể phụ thuộc vào lựa chọn trước đó. Việc quyết định sớm và thay đổi hướng đi của giải thuật cùng với việc không bao giờ xét lại các quyết định cũ sẽ dẫn đến kết quả là giải thuật này không tối ưu để tìm giải pháp toàn cục.

Bạn theo dõi một bài toán đơn giản dưới đây để thấy cách thực hiện giải thuật tham lam và vì sao lại có thể nói rằng giải thuật này là không tối ưu.

Bài toán đếm số đồng tiền

Yêu cầu là hãy lựa chọn số lượng đồng tiền nhỏ nhất có thể sao cho tổng mệnh giá của các đồng tiền này bằng với một lượng tiền cho trước.

Nếu tiền đồng có các mệnh giá lần lượt là 1, 2, 5, và 10 xu và lượng tiền cho trước là 18 xu thì giải thuật tham lam thực hiện như sau:

Bước 1: Chọn đồng 10 xu, do đó sẽ còn 18 – 10 = 8 xu.

Bước 2: Chọn đồng 5 xu, do đó sẽ còn là 3 xu.

Bước 3: Chọn đồng 2 xu, còn lại là 1 xu.

Bước 4: Cuối cùng chọn đồng 1 xu và giải xong bài toán.

Bạn thấy rằng cách làm trên là khá ổn, và số lượng đồng tiền cần phải lựa chọn là 4 đồng tiền. Nhưng nếu chúng ta thay đổi bài toán trên một chút thì cũng hướng tiếp cận như trên có thể sẽ không đem lại cùng kết quả tối ưu.

Chẳng hạn, một hệ thống tiền tệ khác có các đồng tiền có mệnh giá lần lượt là 1, 7 và 10 xu và lượng tiền cho trước ở đây thay đổi thành 15 xu thì theo giải thuật tham lam thì số đồng tiền cần chọn sẽ nhiều hơn 4. Với giải thuật tham lam thì: 10 + 1 + 1 +1 + 1 + 1, vậy tổng cộng là 6 đồng tiền. Trong khi cùng bài toán như trên có thể được xử lý bằng việc chỉ chọn 3 đồng tiền (7 + 7 +1).

Do đó chúng ta có thể kết luận rằng, giải thuật tham lam tìm kiếm giải pháp tôi ưu ở mỗi bước nhưng lại có thể thất bại trong việc tìm ra giải pháp tối ưu toàn cục.

Có khá nhiều giải thuật nổi tiếng được thiết kế dựa trên tư tưởng của giải thuật tham lam. Dưới đây là một trong số các giải thuật này:

• Bài toán hành trình người bán hàng
• Giải thuật cây khung nhỏ nhất của Prim
• Giải thuật cây khung nhỏ nhất của Kruskal
• Giải thuật cây khung nhỏ nhất của Dijkstra
• Bài toán xếp lịch công việc
• Bài toán xếp ba lô

Giải thuật chia để trị - Divide and Conquer

Phương pháp chia để trị (Divide and Conquer) là một phương pháp quan trọng trong việc thiết kế các giải thuật. Ý tưởng của phương pháp này khá đơn giản và rất dễ hiểu: Khi cần giải quyết một bài toán, ta sẽ tiến hành chia bài toán đó thành các bài toán con nhỏ hơn. Tiếp tục chia cho đến khi các bài toán nhỏ này không thể chia thêm nữa, khi đó ta sẽ giải quyết các bài toán nhỏ nhất này và cuối cùng kết hợp giải pháp của tất cả các bài toán nhỏ để tìm ra giải pháp của bài toán ban đầu.

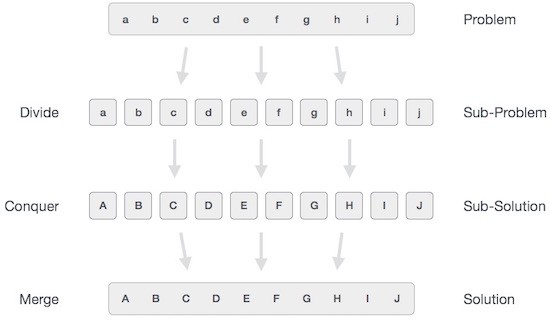
Nói chung, bạn có thể hiểu giải thuật chia để trị (Divide and Conquer) qua 3 tiến trình

sau:

Tiến trình 1: Chia nhỏ (Divide/Break)

Trong bước này, chúng ta chia bài toán ban đầu thành các bài toán con. Mỗi bài toán con nên là một phần của bài toán ban đầu. Nói chung, bước này sử dụng phương pháp đệ qui để chia nhỏ các bài toán cho đến khi không thể chia thêm nữa. Khi đó, các bài toán con được gọi là "atomic – nguyên tử", nhưng chúng vẫn biểu diễn một phần nào đó của bài toán ban đầu.

Tiến trình 2: Giải bài toán con (Conquer/Solve)

Trong bước này, các bài toán con được giải.

Tiến trình 3: Kết hợp lời giải (Merge/Combine)

Sau khi các bài toán con đã được giải, trong bước này chúng ta sẽ kết hợp chúng một cách đệ qui để tìm ra giải pháp cho bài toán ban đầu.

Hạn chế của giải thuật chia để trị (Devide and Conquer)

Giải thuật chia để trị tồn tại hai hạn chế, đó là:

Làm thế nào để chia tách bài toán một cách hợp lý thành các bài toán con, bởi vì nếu các bài toán con được giải quyết bằng các thuật toán khác nhau thì sẽ rất phức tạp.

Việc kết hợp lời giải các bài toán con được thực hiện như thế nào.

Dưới đây là một số giải thuật được xây dựng dựa trên phương pháp chia để trị (Divide and Conquer):

• Giải thuật sắp xếp trộn (Merge Sort)
• Giải thuật sắp xếp nhanh (Quick Sort)
• Giải thuật tìm kiếm nhị phân (Binary Search)
• Nhân ma trận của Strassen

Giải thuật qui hoạch động - Dynamic Programming

Giải thuật Qui hoạch động (Dynamic Programming) giống như giải thuật chia để trị (Divide and Conquer) trong việc chia nhỏ bài toán thành các bài toán con nhỏ hơn và sau đó thành các bài toán con nhỏ hơn nữa có thể. Nhưng không giống chia để trị, các bài toán con này không được giải một cách độc lập. Thay vào đó, kết quả của các bài toán con này được lưu lại và được sử dụng cho các bài toán con tương tự hoặc các bài toán con gối nhau (Overlapping Sub-problems).

Chúng ta sử dụng Qui hoạch động (Dynamic Programming) khi chúng ta có các bài toán mà có thể được chia thành các bài toán con tương tự nhau, để mà các kết quả của chúng có thể được tái sử dụng. Thường thì các giải thuật này được sử dụng cho tối ưu hóa. Trước khi giải bài toán con, giải thuật Qui hoạch động sẽ cố gắng kiểm tra kết quả của các bài toán con đã được giải trước đó. Các lời giải của các bài toán con sẽ được kết hợp lại để thu được lời giải tối ưu.

Do đó, chúng ta có thể nói rằng:

Bài toán ban đầu nên có thể được phân chia thành các bài toán con gối nhau nhỏ hơn.

Lời giải tối ưu của bài toán có thể thu được bởi sử dụng lời giải tối ưu của các bài toán con.

Giải thuật Qui hoạch động sử dụng phương pháp lưu trữ (Memoization) – tức là chúng ta lưu trữ lời giải của các bài toán con đã giải, và nếu sau này chúng ta cần giải lại chính bài toán đó thì chúng ta có thể lấy và sử dụng kết quả đã được tính toán.

Giải thuật tham lam và giải thuật qui hoạch động

Giải thuật tham lam (Greedy Algorithms) là giải thuật tìm kiếm, lựa chọn giải pháp tối ưu địa phương ở mỗi bước với hi vọng tìm được giải pháp tối ưu toàn cục.

Giải thuật Qui hoạch động tối ưu hóa các bài toán con gối nhau.

Giải thuật chia để trị và giải thuật Qui hoạch động

Giải thuật chia để trị (Divide and Conquer) là kết hợp lời giải của các bài toán con để tìm ra lời giải của bài toán ban đầu.

Giải thuật Qui hoạch động sử dụng kết quả của bài toán con và sau đó cố gắng tối ưu bài toán lớn hơn. Giải thuật Qui hoạch động sử dụng phương pháp lưu trữ (Memoization) để ghi nhớ kết quả của các bài toán con đã được giải.

Dưới đây là một số bài toán có thể được giải bởi sử dụng giải thuật Qui hoạch động:

• Dãy Fibonacci
• Bài toán tháp Hà Nội (Tower of Hanoi)
• Bài toán ba lô

Giải thuật định lý thợ - Master Theorem

Chúng ta sử dụng Định lý thợ (Master Theorem) để giải các công thức đệ quy dạng sau một cách hiệu quả :

T(n) =aT(n/b) + c.n^k trong đó a>=1 , b>1

Bài toán ban đầu được chia thành a bài toán con có kích thước mỗi bài là n/b, chi phí để tổng hợp các bài toán con là f(n).

Ví dụ : Thuật toán sắp xếp trộn chia thành 2 bài toán con , kích thước n/2. Chi phí tổng hợp 2 bài toán con là O(n).

Định lý thợ

a>=1, b>1, c, k là các hằng số. T(n) định nghĩa đệ quy trên các tham số không âm T(n) = aT(n/b) + c.n^k + Nếu a> b^k thì T(n) =O(n^ (logab)) + Nếu a= b^k thì

T(n)=O(n^k.lgn) + Nếu a< b^k thì T(n) = O(n^k)

Chú ý: Không phải trường hợp nào cũng áp dụng được định lý thợ

VD : T(n) = 2T(n/2) +nlogn a =2, b =2, nhưng không xác định được số nguyên k

Cấu trúc dữ liệu mảng (Array)

Khái niệm

Mảng (Array) là một trong các cấu trúc dữ liệu cũ và quan trọng nhất. Mảng có thể lưu giữ một số phần tử cố định và các phần tử này nền có cùng kiểu. Hầu hết các cấu trúc dữ

liệu đều sử dụng mảng để triển khai giải thuật. Dưới đây là các khái niệm quan trọng liên quan tới Mảng.

Phần tử: Mỗi mục được lưu giữ trong một mảng được gọi là một phần tử.

Chỉ mục (Index): Mỗi vị trí của một phần tử trong một mảng có một chỉ mục số được sử dụng để nhận diện phần tử.

Mảng gồm các bản ghi có kiểu giống nhau, có kích thước cố định, mỗi phần tử được xác định bởi chỉ số

Mảng là cấu trúc dữ liệu được cấp phát lien tục cơ bản

Ưu điểm

• • • • Truy câp phàn tử với thời gian hằng số O(1)
      • Sử dụng bộ nhớ hiệu quả
      • Tính cục bộ về bộ nhớ

Nhược điểm

Không thể thay đổi kích thước của mảng khi chương trình dang thực hiện

Mảng động

Mảng động (dynamic aray) : cấp phát bộ nhớ cho mảng một cách động trong quá trình chạy chương trình trong C là malloc và calloc, trong C++ là new

Sử dụng mảng động ta bắt đầu với mảng có 1 phàn tử, khi số lượng phàn tử vượt qua khả năng của ảng thì ta gấp đôi kích thước mảng cuc và copy phàn tử mảng cũ vào nửa đầu của mảng mới

Ưu điểm: tránh lãng phí bộ nhớ khi phải khai báo mảng có kích thước lớn ngay từ đầu

Nhược điểm:

• • • • Phải thực hiện them thao tác copy phần tử mỗi khi thay đổi kích thước.
      • Một số thời gian thực hiện thao tác không còn là hằng số nữa.

Biểu diễn Cấu trúc dữ liệu mảng

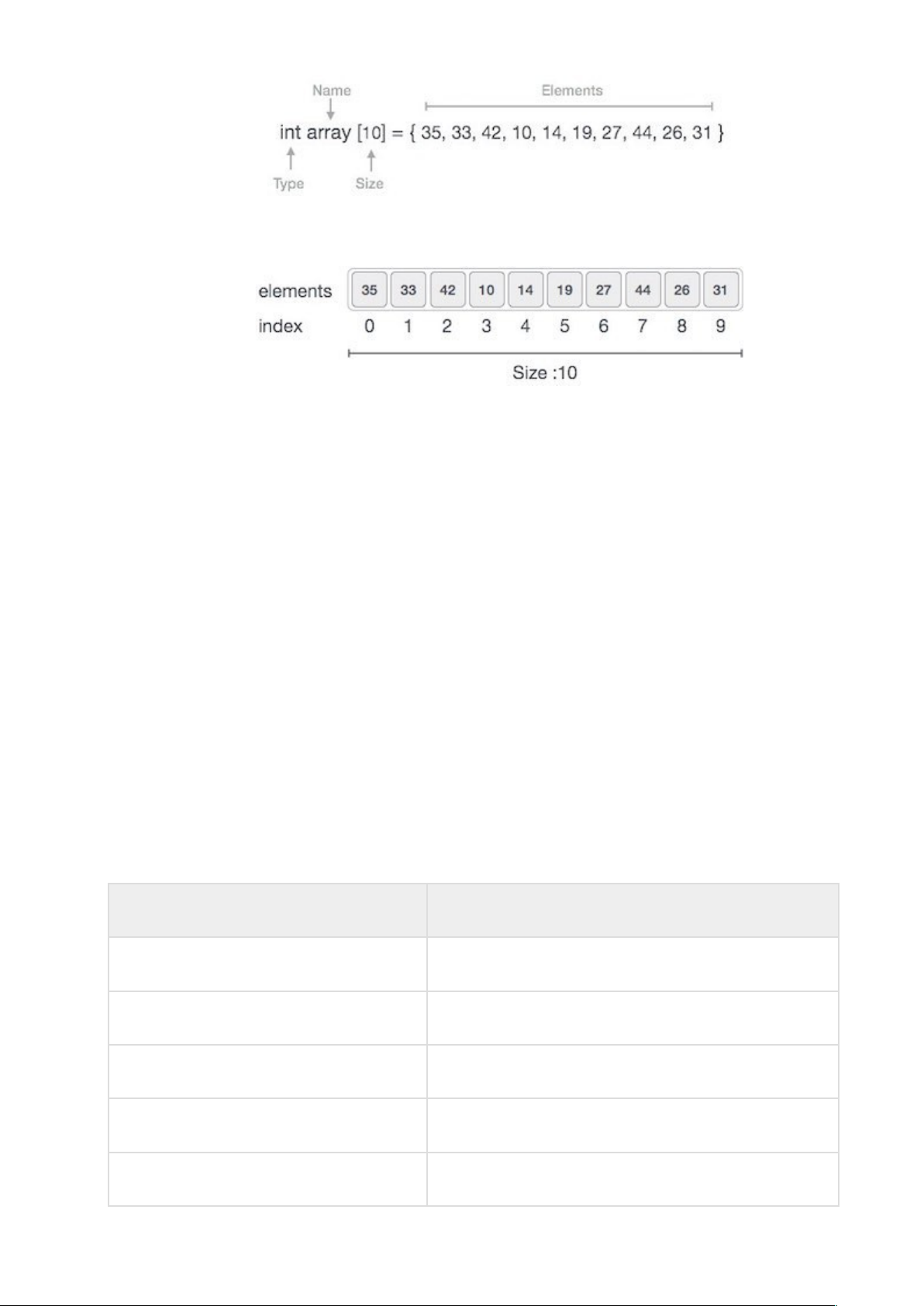
Mảng có thể được khai báo theo nhiều cách đa dạng trong các ngôn ngữ lập trình. Để minh họa, chúng ta sử dụng phép khai báo mảng trong ngôn ngữ C:

Hình minh họa phần tử và chỉ mục:

Dưới đây là một số điểm cần ghi nhớ về cấu trúc dữ liệu mảng:

• • • • Chỉ mục bắt đầu với 0.
      • Độ dài mảng là 10, nghĩa là mảng có thể lưu giữ 10 phần tử.
      • Mỗi phần tử đều có thể được truy cập thông qua chỉ mục của phần tử đó. Ví dụ, chúng ta có thể lấy giá trị của phần tử tại chỉ mục 6 là 27.
    1. Phép toán cơ bản được hỗ trợ bởi mảng
       • Duyệt: In tất cả các phần tử mảng theo cách in từng phần tử một.
       • Chèn: Thêm một phần tử vào mảng tại chỉ mục đã cho.
       • Xóa: Xóa một phần tử từ mảng tại chỉ mục đã cho.
       • Tìm kiếm: Tìm kiếm một phần tử bởi sử dụng chỉ mục hay bởi giá trị.
       • Cập nhật: Cập nhật giá trị một phần tử tại chỉ mục nào đó.

Trong ngôn ngữ C, khi một mảng được khởi tạo với kích cỡ ban đầu, thì nó gán các giá trị mặc định cho các phần tử của mảng theo thứ tự sau:

Danh sách liên kết (Linked list)

• • 1. Khái niệm

Một danh sách liên kết (Linked List) là một dãy các cấu trúc dữ liệu được kết nối với nhau thông qua các liên kết (link). Hiểu một cách đơn giản thì Danh sách liên kết là một cấu trúc dữ liệu bao gồm một nhóm các nút (node) tạo thành một chuỗi. Mỗi nút gồm dữ liệu ở nút đó và tham chiếu đến nút kế tiếp trong chuỗi.

Danh sách liên kết là cấu trúc dữ liệu được sử dụng phổ biến thứ hai sau mảng. Dưới đây là các khái niệm cơ bản liên quan tới Danh sách liên kết:

• • • • Link (liên kết): mỗi link của một Danh sách liên kết có thể lưu giữ một dữ liệu được gọi là một phần tử.
      • Next: Mỗi liên kết của một Danh sách liên kết chứa một link tới next link được gọi là Next.
      • First: một Danh sách liên kết bao gồm các link kết nối tới first link được gọi là First.

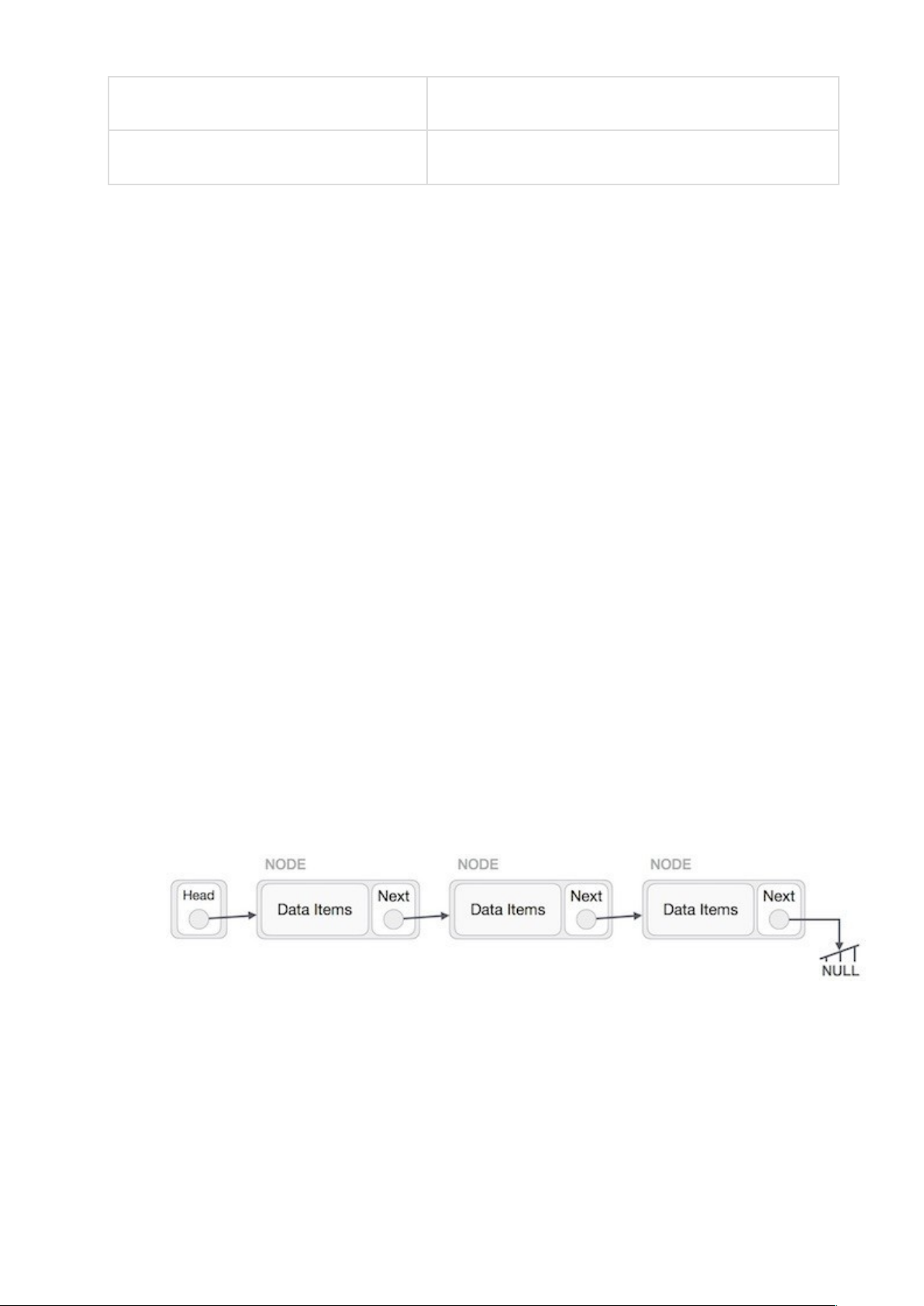
Danh sách liên kết có thể được biểu diễn như là một chuỗi các nút (node). Mỗi nút sẽ trỏ tới nút kế tiếp.

Dưới đây là một số điểm cần nhớ về Danh sách liên kết:

• • • • • Danh sách liên kết chứa một phần tử link thì được gọi là First.
        • Mỗi link mang một trường dữ liệu và một trường link được gọi là Next.
        • Mỗi link được liên kết với link kế tiếp bởi sử dụng link kế tiếp của nó.
        • Link cuối cùng mang một link là null để đánh dấu điểm cuối của danh sách.

Các loại danh sách Linked list

• • • • Danh sách liên kết đơn (Simple Linked List): chỉ duyệt các phần tử theo chiều về trước.
      • Danh sách liên kết đôi (Doubly Linked List): các phần tử có thể được duyệt theo chiều về trước hoặc về sau.
      • Danh sách liên kết vòng (Circular Linked List): phần tử cuối cùng chứa link của phần tử đầu tiên như là next và phần tử đầu tiên có link tới phần tử cuối cùng như là prev.
    1. Các hoạt động cơ bản trên Danh sách liên kết
       • Hoạt động chèn: thêm một phần tử vào đầu danh sách liên kết.
       • Hoạt động xóa (phần tử đầu): xóa một phần tử tại đầu danh sách liên kết.
       • Hiển thị: hiển thị toàn bộ danh sách.
       • Hoạt động tìm kiếm: tìm kiếm phần tử bởi sử dụng khóa (key) đã cung cấp.
       • Hoạt động xóa (bởi sử dụng khóa): xóa một phần tử bởi sử dụng khóa (key) đã cung cấp.

Hoạt động chèn trong Danh sách liên kết

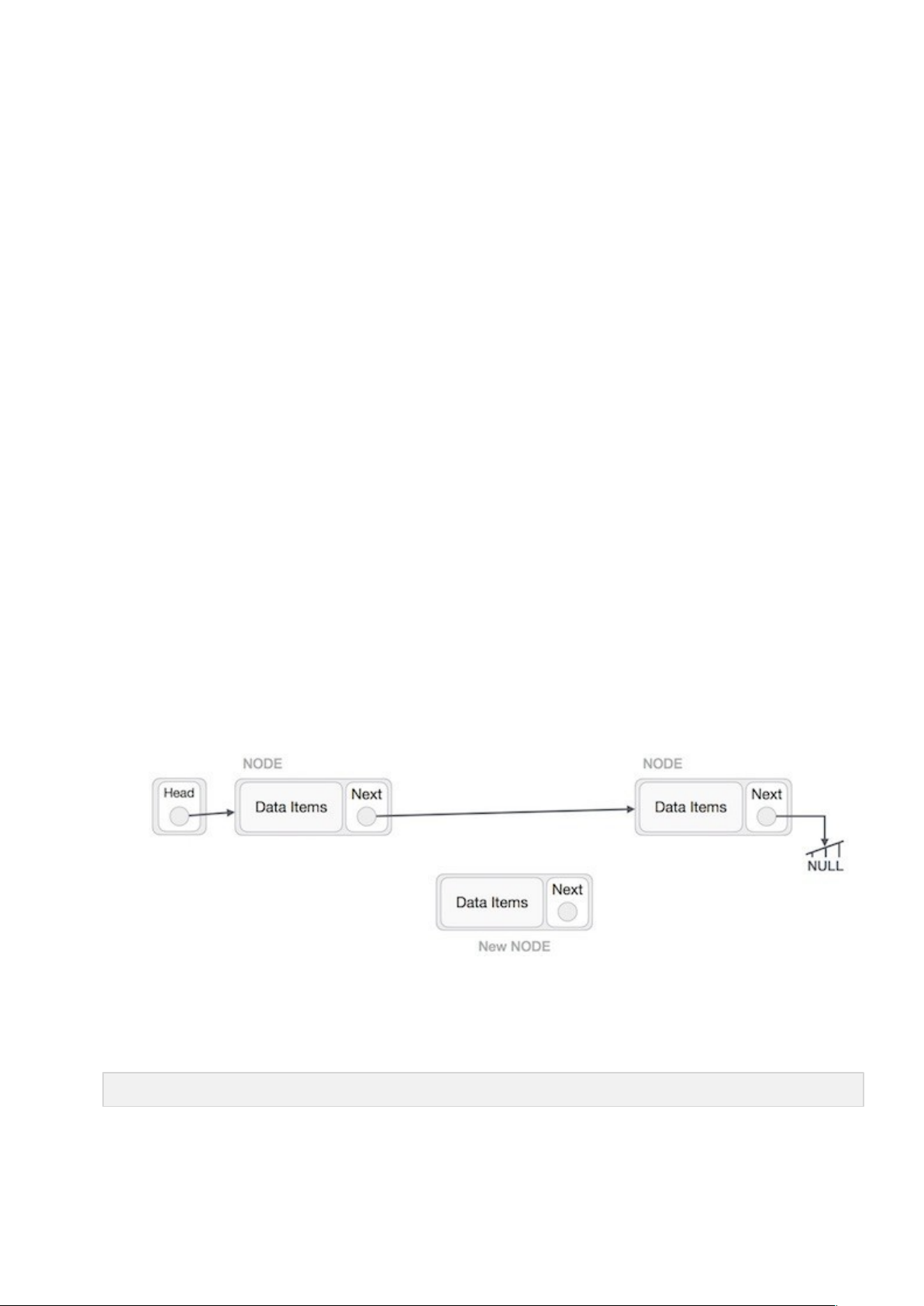
Việc thêm một nút mới vào trong danh sách liên kết không chỉ là một hoạt động thêm đơn giản như trong các cấu trúc dữ liệu khác (bởi vì chúng ta có dữ liệu và có link). Chúng ta sẽ tìm hiểu thông qua sơ đồ dưới đây. Đầu tiên, tạo một nút bởi sử dụng cùng cấu trúc và tìm vị trí để chèn nút này.

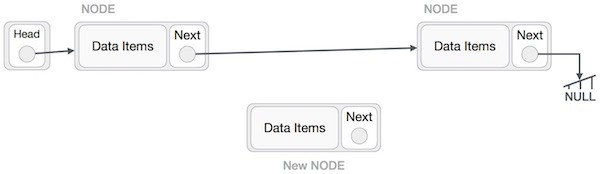
Giả sử chúng ta cần chèn một nút B vào giữa nút A (nút trái) và C (nút phải). Do đó: B.next trỏ tới C.

NewNode.next −> RightNode;

Hình minh họa như sau:

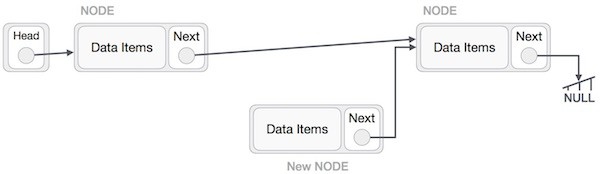
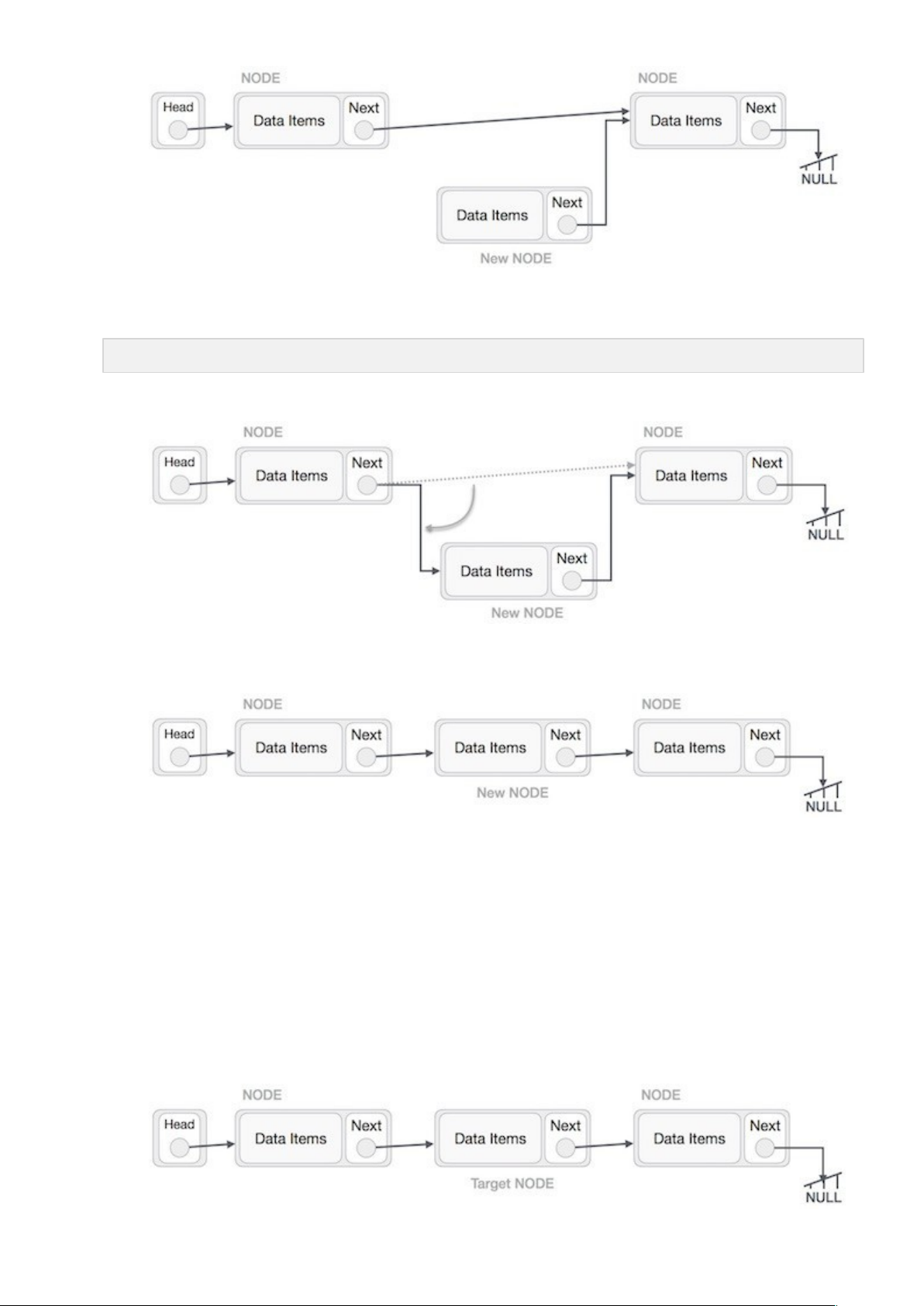
Bây giờ, next của nút bên trái sẽ trở tới nút mới.

LeftNode.next −> NewNode;

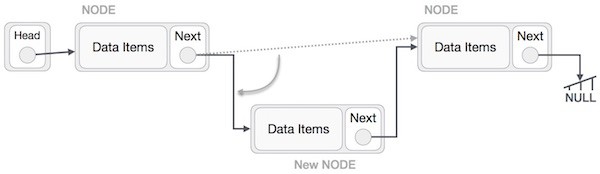
Quá trình trên sẽ đặt nút mới vào giữa hai nút. Khi đó danh sách mới sẽ trông như sau:

Các bước tương tự sẽ được thực hiện nếu chèn nút vào đầu danh sách liên kết. Trong khi đặt một nút vào vị trí cuối của danh sách, thìnút thứ hai tính từ nút cuối cùng của danh sách sẽ trỏ tới nút mới và nút mới sẽ trỏ tới NULL.

Hoạt động xóa trong Danh sách liên kết

Hoạt động xóa trong Danh sách liên kết cũng phức tạp hơn trong cấu trúc dữ liệu khác.

Đầu tiên chúng ta cần định vị nút cần xóa bởi sử dụng các giải thuật tìm kiếm.

Bây giờ, nút bên trái (prev) của nút cần xóa nên trỏ tới nút kế tiếp (next) của nút cần xóa.

LeftNode.next −> TargetNode.next;

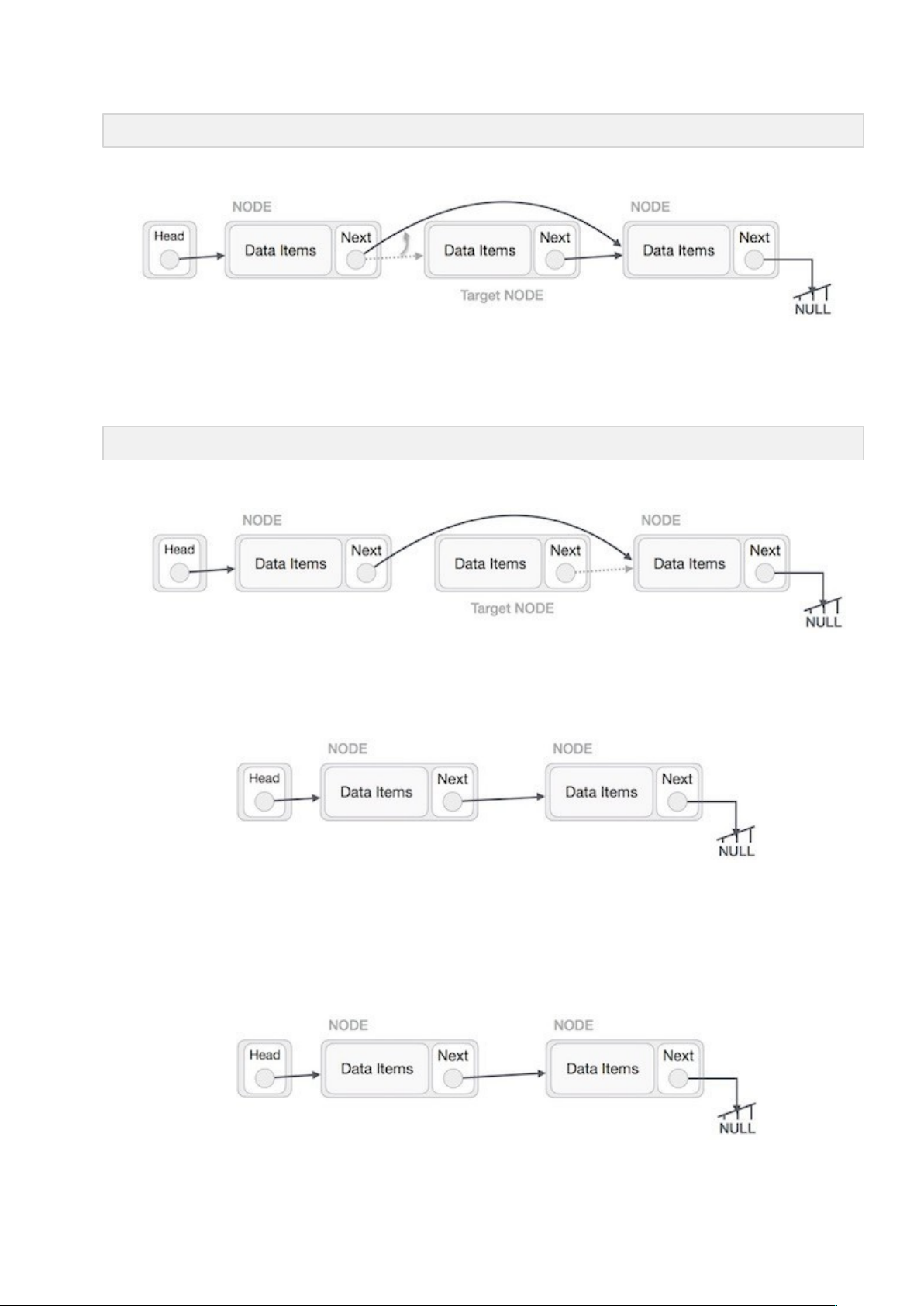
Quá trình này sẽ xóa link trỏ tới nút cần xóa. Bây giờ chúng ta sẽ xóa những gì mà nút cần xóa đang trỏ tới.

TargetNode.next −> NULL;

Nếu bạn cần sử dụng nút đã bị xóa này thì bạn có thể giữ chúng trong bộ nhớ, nếu không bạn có thể xóa hoàn toàn hẳn nó khỏi bộ nhớ.

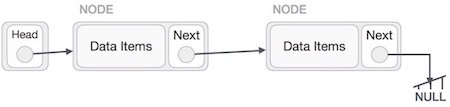
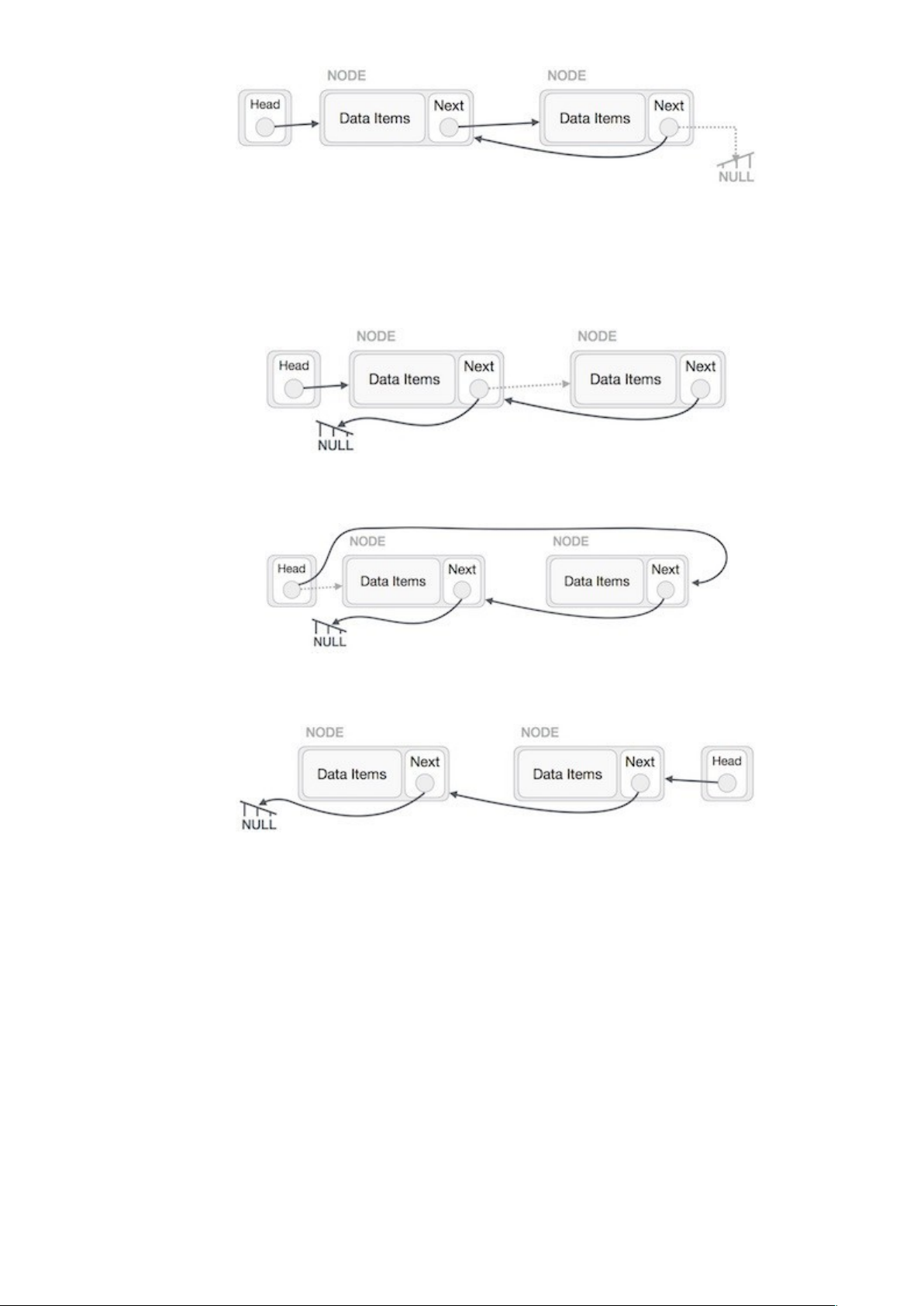
Hoạt động đảo ngược Danh sách liên kết

Với hoạt động này, bạn cần phải cẩn thận. Chúng ta cần làm cho nút đầu (head) trỏ tới nút cuối cùng và đảo ngược toàn bộ danh sách liên kết.

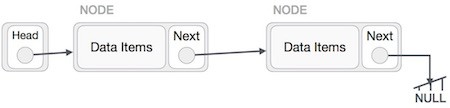
Đầu tiên, chúng ta duyệt tới phần cuối của danh sách. Nút này sẽ trỏ tới NULL. Bây giờ điều cần làm là làm cho nút cuối này trỏ tới nút phía trước của nó.

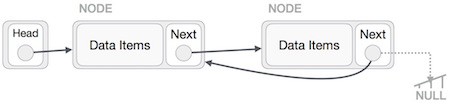
Chúng ta phải đảm bảo rằng nút cuối cùng này sẽ không bị thất lạc, do đó chúng ta sẽ sử dụng một số nút tạm (temp node – giống như các biến tạm trung gian để lưu giữ giá trị).

Tiếp theo, chúng ta sẽ làm cho từng nút bên trái sẽ trỏ tới nút trái của chúng.

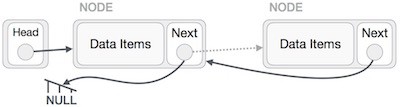
Sau đó, nút đầu tiên sau nút head sẽ trỏ tới NULL.

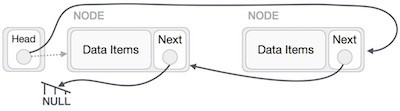
Chúng ta sẽ làm cho nút head trỏ tới nút đầu tiên mới bởi sử dụng các nút tạm.

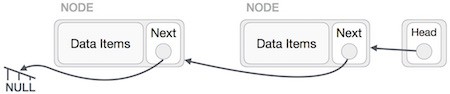
Bây giờ Danh sách liên kết đã bị đảo ngược.

Cấu trúc dữ liệu ngăn xếp (Stack)

• • 1. Khái niệm

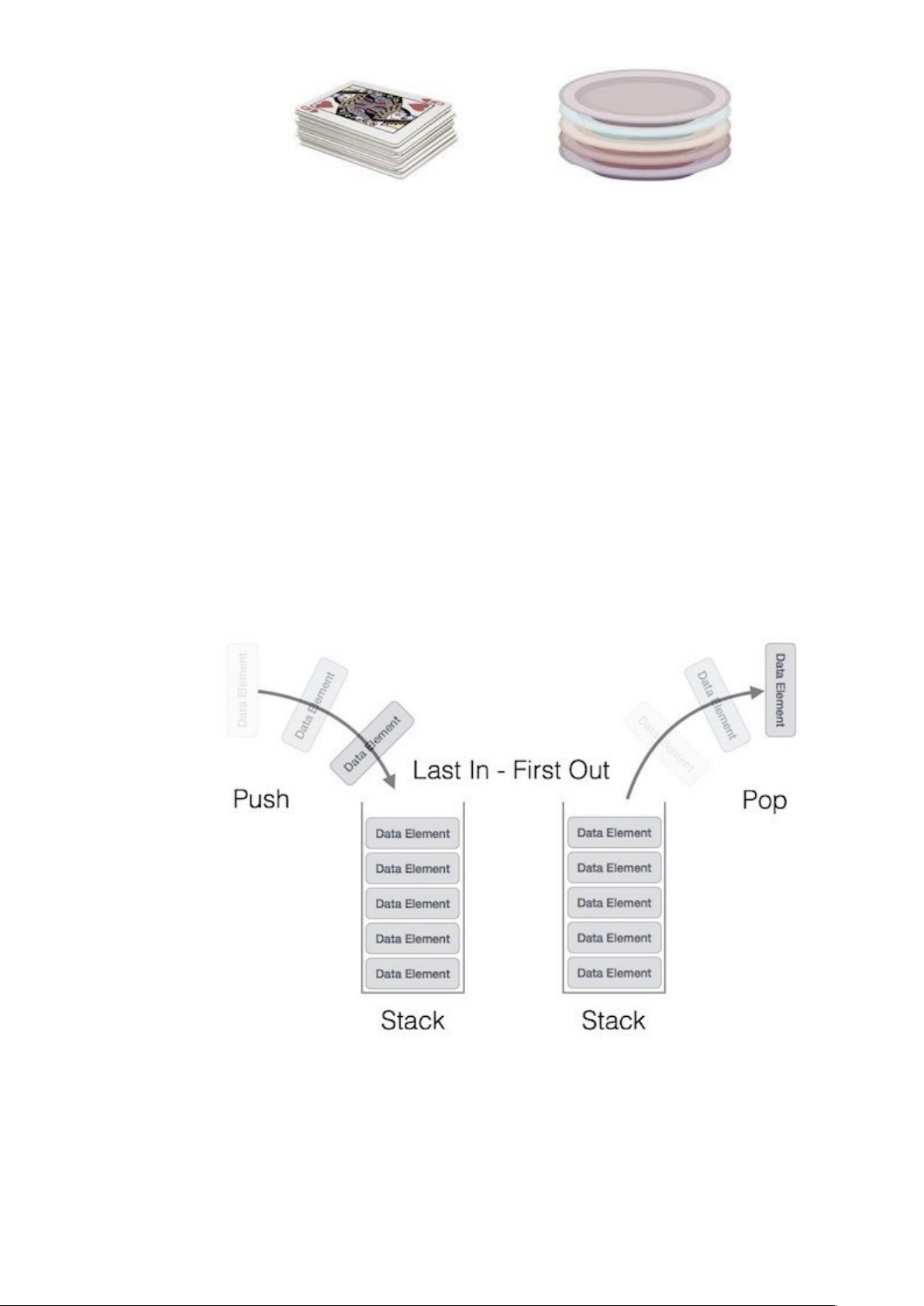
Một ngăn xếp là một cấu trúc dữ liệu trừu tượng (Abstract Data Type – viết tắt là ADT), hầu như được sử dụng trong hầu hết mọi ngôn ngữ lập trình. Đặt tên là ngăn xếp bởi vì nó hoạt động như một ngăn xếp trong đời sống thực, ví dụ như một cỗ bài hay một chồng đĩa, …

Trong đời sống thực, ngăn xếp chỉ cho phép các hoạt động tại vị trí trên cùng của ngăn xếp. Ví dụ, chúng ta chỉ có thể đặt hoặc thêm một lá bài hay một cái đĩa vào trên cùng của ngăn xếp. Do đó, cấu trúc dữ liệu trừu tượng ngăn xếp chỉ cho phép các thao tác dữ liệu tại vị trí trên cùng. Tại bất cứ thời điểm nào, chúng ta chỉ có thể truy cập phần tử trên cùng của ngăn xếp.

Đặc điểm này làm cho ngăn xếp trở thành cấu trúc dữ liệu dạng LIFO. LIFO là viết tắt của Last-In-First-Out. Ở đây, phần tử được đặt vào (được chèn, được thêm vào) cuối cùng sẽ được truy cập đầu tiên. Trong thuật ngữ ngăn xếp, hoạt động chèn được gọi là hoạt động PUSH và hoạt động xóa được gọi là hoạt động POP.

Dưới đây là sơ đồ minh họa một ngăn xếp và các hoạt động diễn ra trên ngăn xếp.

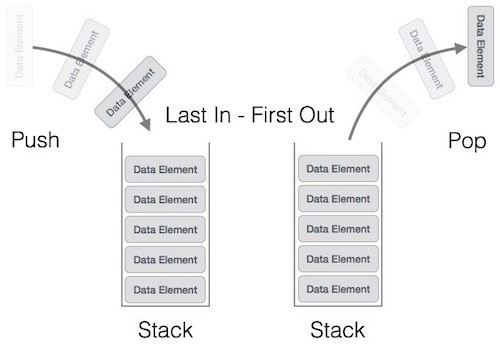
Một ngăn xếp có thể được triển khai theo phương thức của Mảng (Array), Cấu trúc (Struct), Con trỏ (Pointer) và Danh sách liên kết (Linked List). Ngăn xếp có thể là ở dạng kích cỡ cố định hoặc ngăn xếp có thể thay đổi kích cỡ. Phần dưới chúng ta sẽ triển khai ngăn xếp bởi sử dụng các mảng với việc triển khai các ngăn xếp cố định.

• • 1. Các hoạt động cơ bản trên cấu trúc dữ liệu ngăn xếp

Các hoạt động cơ bản trên ngăn xếp có thể liên quan tới việc khởi tạo ngăn xếp, sử dụng nó và sau đó xóa nó. Ngoài các hoạt động cơ bản này, một ngăn xếp có hai hoạt động nguyên sơ liên quan tới khái niệm, đó là:

• • • • Hoạt động push(): lưu giữ một phần tử trên ngăn xếp.
      • Hoạt động pop(): xóa một phần tử từ ngăn xếp.

Khi dữ liệu đã được PUSH lên trên ngăn xếp:

Để sử dụng ngăn xếp một cách hiệu quả, chúng ta cũng cần kiểm tra trạng thái của ngăn xếp. Để phục vụ cho mục đích này, dưới đây là một số tính năng hỗ trợ khác của ngăn xếp:

• • • • • Hoạt động peek(): lấy phần tử dữ liệu ở trên cùng của ngăn xếp, mà không xóa phần tử này.
        • Hoạt động isFull(): kiểm tra xem ngăn xếp đã đầy hay chưa.
        • Hoạt động isEmpty(): kiểm tra xem ngăn xếp là trống hay không.

Tại mọi thời điểm, chúng ta duy trì một con trỏ tới phần tử dữ liệu vừa được PUSH cuối cùng vào trên ngăn xếp. Vì con trỏ này luôn biểu diễn vị trí trên cùng của ngăn xếp vì thế được đặt tên là top. Con trỏ top cung cấp cho chúng ta giá trị của phần tử trên cùng của ngăn xếp mà không cần phải thực hiện hoạt động xóa ở trên (hoạt động pop).

Phần tiếp theo chúng ta sẽ tìm hiểu về các phương thức để hỗ trợ các tính năng của ngăn xếp.

• Phương thức peek() của cấu trúc dữ liệu ngăn xếp

Bắt đầu hàm peek return stack[top]

kết thúc hàm

• Phương thức isFull() của cấu trúc dữ liệu ngăn xếp

Bắt đầu hàm isfull

if top bằng MAXSIZE return true

else

return false

kết thúc if

kết thúc hàm

• Phương thức isEmpty() của cấu trúc dữ liệu ngăn xếp

bắt đầu hàm isempty

if top nhỏ hơn 1 return true

else

return false kết thúc if

kết thúc hàm

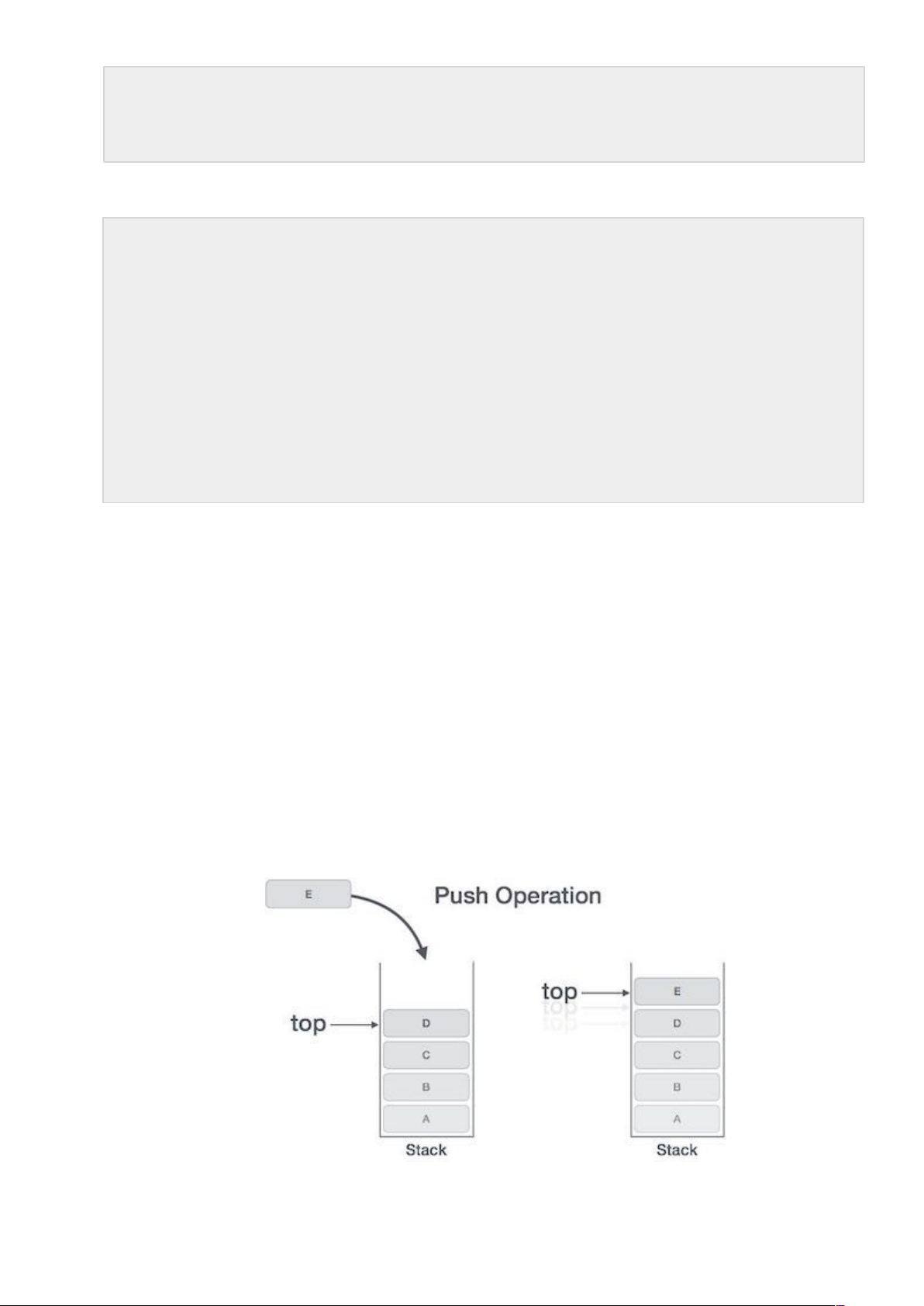
• Hoạt động PUSH trong cấu trúc dữ liệu ngăn xếp

Tiến trình đặt (thêm) một phần tử dữ liệu mới vào trên ngăn xếp còn được biết đến với tên Hoạt động PUSH. Hoạt động push bao gồm các bước sau:

Bước 1: kiểm tra xem ngăn xếp đã đầy hay chưa.

Bước 2: nếu ngăn xếp là đầy, tiến trình bị lỗi và thoát ra.

Bước 3: nếu ngăn xếp chưa đầy, tăng top để trỏ tới phần bộ nhớ trống tiếp theo. Bước 4: thêm phần tử dữ liệu vào vị trí nơi mà top đang trỏ đến trên ngăn xếp. Bước 5: trả về success.

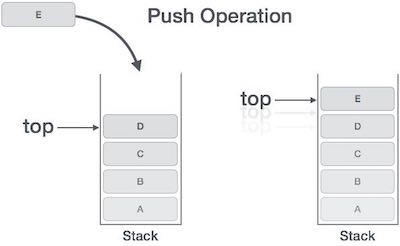
Nếu Danh sách liên kết được sử dụng để triển khai ngăn xếp, thì ở bước 3 chúng ta cần cấp phát một không gian động.

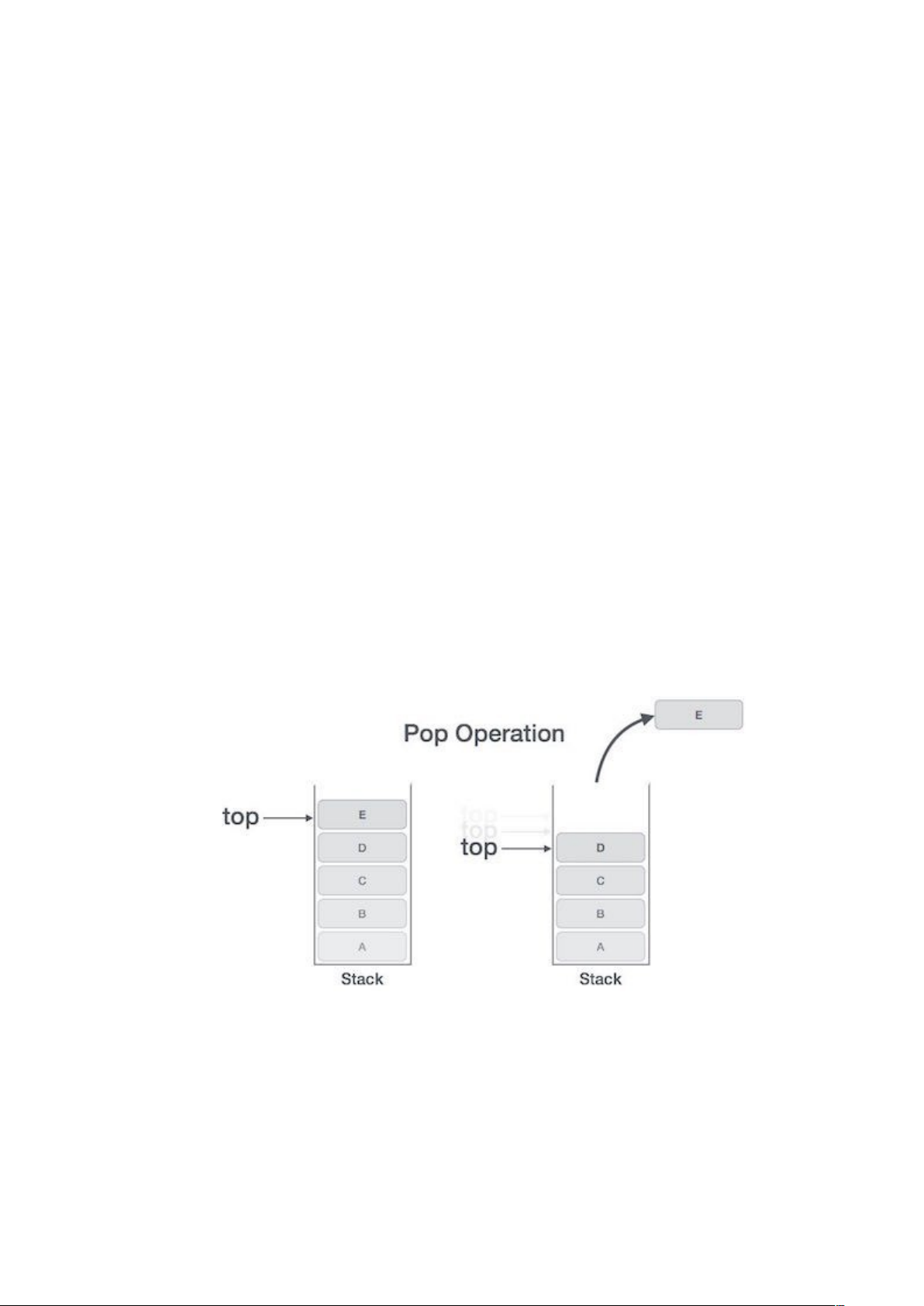
• Hoạt động POP của cấu trúc dữ liệu ngăn xếp

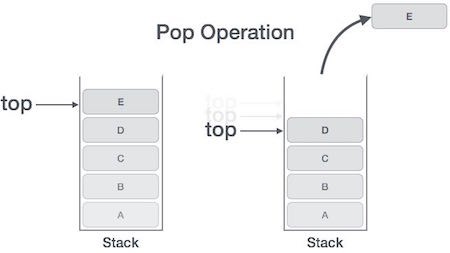
Việc truy cập nội dung phần tử trong khi xóa nó từ ngăn xếp còn được gọi là Hoạt động POP. Trong sự triển khai Mảng của hoạt động pop(), phần tử dữ liệu không thực sự bị xóa, thay vào đó top sẽ bị giảm về vị trí thấp hơn trong ngăn xếp để trỏ tới giá trị tiếp theo.

Nhưng trong sự triển khai Danh sách liên kết, hoạt động pop() thực sụ xóa phần tử xữ liệu và xóa nó khỏi không gian bộ nhớ.

Hoạt động POP có thể bao gồm các bước sau:

Bước 1: kiểm tra xem ngăn xếp là trống hay không.

Bước 2: nếu ngăn xếp là trống, tiến trình bị lỗi và thoát ra.

Bước 3: nếu ngăn xếp là không trống, truy cập phần tử dữ liệu tại top đang trỏ tới.

Bước 4: giảm giá trị của top đi 1.

Bước 5: trả về success.

• 1. Cấu trúc dữ liệu hàng đợi – Queue

Khái niệm

Hàng đợi (Queue) là một cấu trúc dữ liệu trừu tượng, là một cái gì đó tương tự như hàng đợi trong đời sống hàng ngày (xếp hàng).

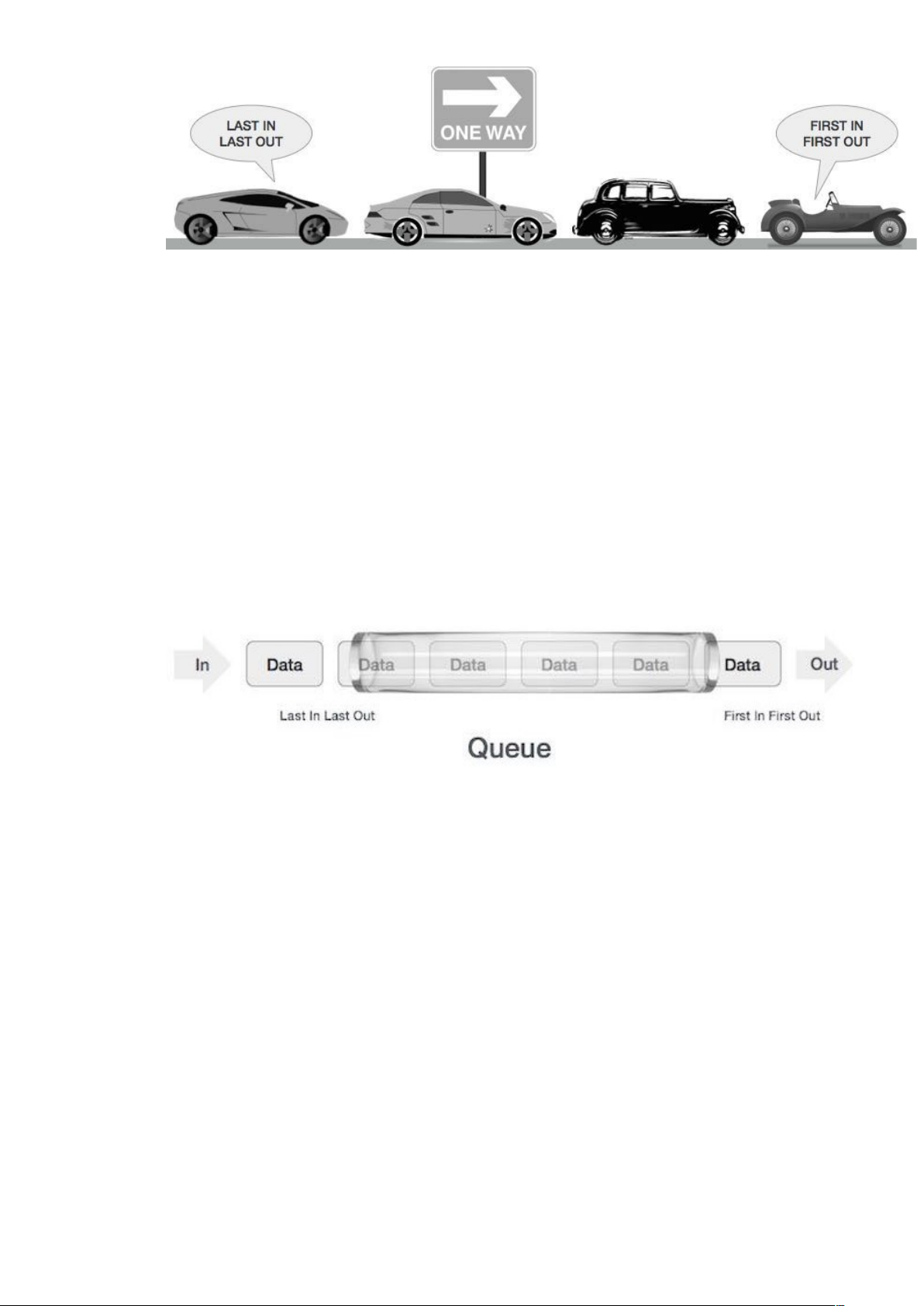
Khác với ngăn xếp, hàng đợi là mở ở cả hai đầu. Một đầu luôn luôn được sử dụng để chèn dữ liệu vào (hay còn gọi là sắp vào hàng) và đầu kia được sử dụng để xóa dữ liệu (rời hàng). Cấu trúc dữ liệu hàng đợi tuân theo phương pháp First-In-First-Out, tức là dữ liệu được nhập vào đầu tiên sẽ được truy cập đầu tiên.

Trong đời sống thực chúng ta có rất nhiều ví dụ về hàng đợi, chẳng hạn như hàng xe ô tô trên đường một chiều (đặc biệt là khi tắc xe), trong đó xe nào vào đầu tiên sẽ thoát ra đầu tiên. Một vài ví dụ khác là xếp hàng học sinh, xếp hàng mua vé, …

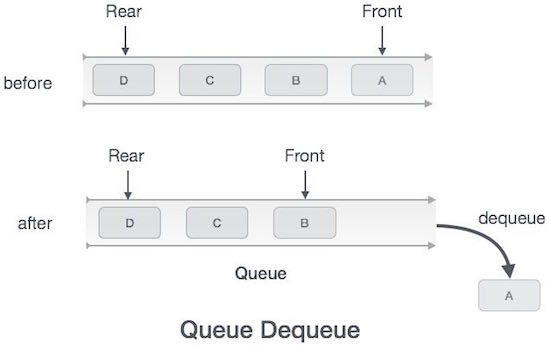
Giờ thì có lẽ bạn đã tưởng tượng ra hàng đợi là gì rồi. Chúng ta có thể truy cập cả hai đầu của hàng đợi. Dưới đây là biểu diễn hàng đợi dưới dạng cấu trúc dữ liệu:

Tương tự như cấu trúc dữ liệu ngăn xếp, thì cấu trúc dữ liệu hàng đợi cũng có thể được triển khai bởi sử dụng Mảng (Array), Danh sách liên kết (Linked List), Con trỏ (Pointer) và Cấu trúc (Struct). Để đơn giản, phần tiếp theo chúng ta sẽ tìm hiểu tiếp về hàng đợi được triển khai bởi sử dụng mảng một chiều.

1.4.2 Các hoạt động cơ bản trên cấu trúc dữ liệu hàng đợi

Các hoạt động trên cấu trúc dữ liệu hàng đợi có thể liên quan tới việc khởi tạo hàng đợi, sử dụng dữ liệu trên hàng đợi và sau đó là xóa dữ liệu khỏi bộ nhớ. Danh sách dưới đây là một số hoạt động cơ bản có thể thực hiện trên cấu trúc dữ liệu hàng đợi:

• Hoạt động enqueue(): thêm (hay lưu trữ) một phần tử vào trong hàng đợi.
• Hoạt động dequeue(): xóa một phần tử từ hàng đợi.

Để sử dụng hàng đợi một cách hiệu quả, chúng ta cũng cần kiểm tra trạng thái của hàng đợi. Để phục vụ cho mục đích này, dưới đây là một số tính năng hỗ trợ khác của hàng đợi:

• Phương thức peek(): lấy phần tử ở đầu hàng đợi, mà không xóa phần tử này.
• Phương thức isFull(): kiểm tra xem hàng đợi là đầy hay không.
• Phương thức isEmpty(): kiểm tra xem hàng đợi là trống hay hay không.

Trong cấu trúc dữ liệu hàng đợi, chúng ta luôn luôn: (1) dequeue (xóa) dữ liệu được trỏ bởi con trỏ front và (2) enqueue (nhập) dữ liệu vào trong hàng đợi bởi sự giúp đỡ của con trỏ rear.

Phương thức peek() của cấu trúc dữ liệu hàng đợi

bắt đầu hàm peek return queue[front]

kết thúc hàm

• Phương thức isFull() trong cấu trúc dữ liệu hàng đợi

Nếu khi chúng ta đang sử dụng mảng một chiều để triển khai hàng đợi, chúng ta chỉ cần kiểm tra con trỏ rear có tiến đến giá trị MAXSIZE hay không để xác định hàng đợi là đầy hay không. Trong trường hợp triển khai hàng đợi bởi sử dụng Danh sách liên kết vòng (Circular Linked List), giải thuật cho hàm isFull() sẽ khác.

bắt đầu hàm isfull

if rear equals to MAXSIZE return true

else

return false endif

kết thúc hàm

Phương thức isEmpty() trong cấu trúc dữ liệu hàng đợi

bắt đầu hàm isempty

if front là nhỏ hơn MIN OR front là lớn hơn rear

return true else

return false kết thúc if

kết thúc hàm

Nếu giá trị của front là nhỏ hơn MIN hoặc 0 thì tức là hàng đợi vẫn chưa được khởi tạo, vì thế hàng đợi là trống.

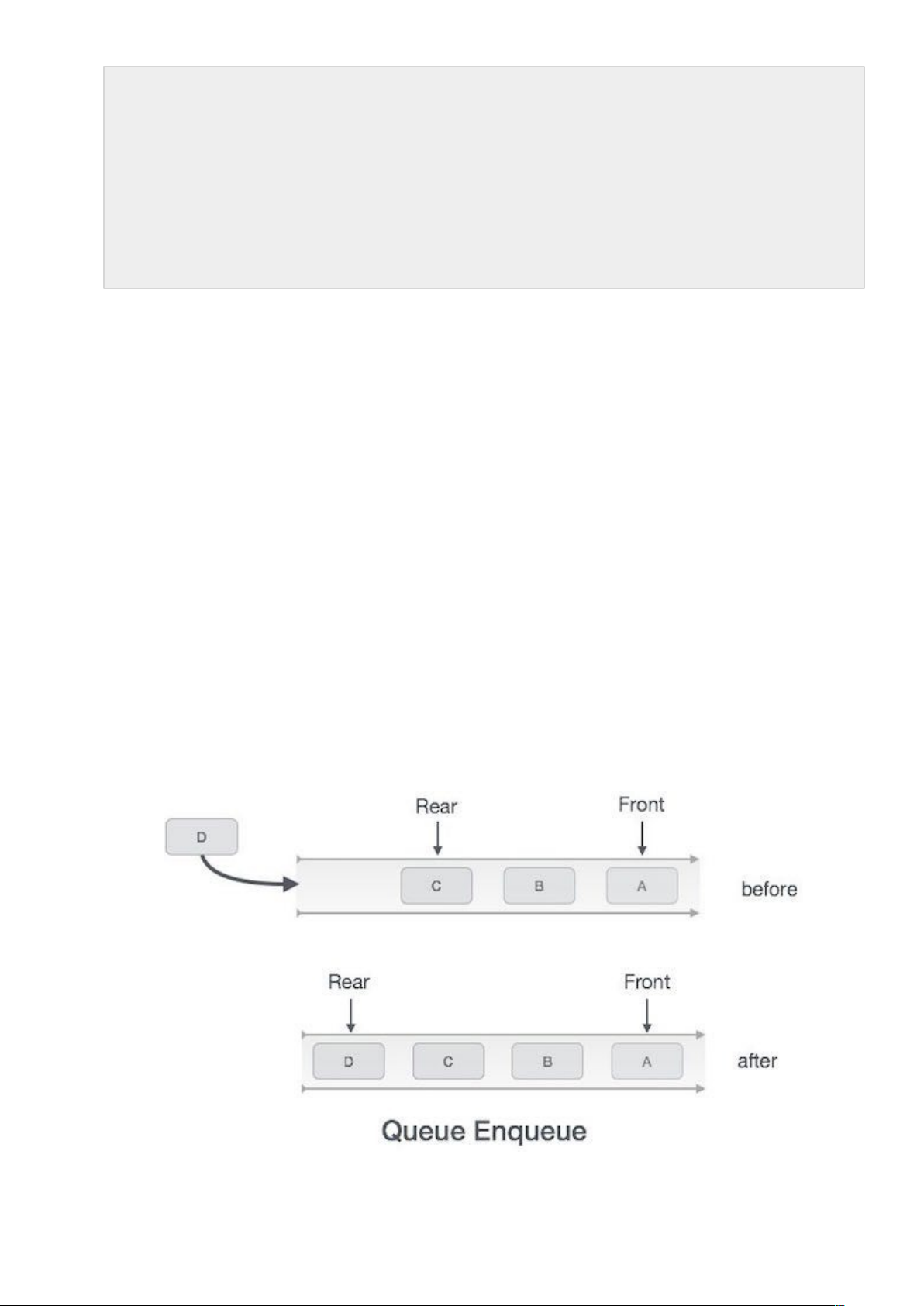
Hoạt động enqueue trong cấu trúc dữ liệu hàng đợi

Bởi vì cấu trúc dữ liệu hàng đợi duy trì hai con trỏ dữ liệu: front và rear, do đó các hoạt động của loại cấu trúc dữ liệu này là khá phức tạp khi so sánh với cấu trúc dữ liệu ngăn xếp.

Dưới đây là các bước để enqueue (chèn) dữ liệu vào trong hàng đợi:

Bước 1: kiểm tra xem hàng đợi là có đầy không.

Bước 2: nếu hàng đợi là đầy, tiến trình bị lỗi và bị thoát.

Bước 3: nếu hàng đợi không đầy, tăng con trỏ rear để trỏ tới vị trí bộ nhớ trống tiếp theo.

Bước 4: thêm phần tử dữ liệu vào vị trí con trỏ rear đang trỏ tới trong hàng đợi.

Bước 5: trả về success.

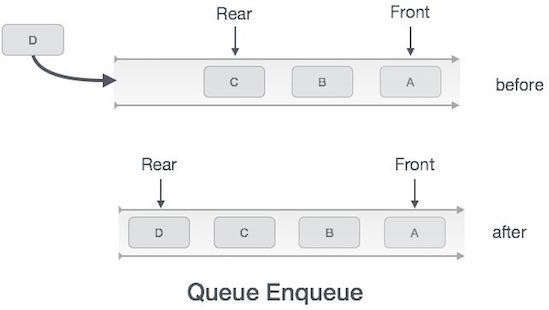
Đôi khi chúng ta cũng cần kiểm tra xem hàng đợi đã được khởi tạo hay chưa để xử lý các tình huống không mong đợi.

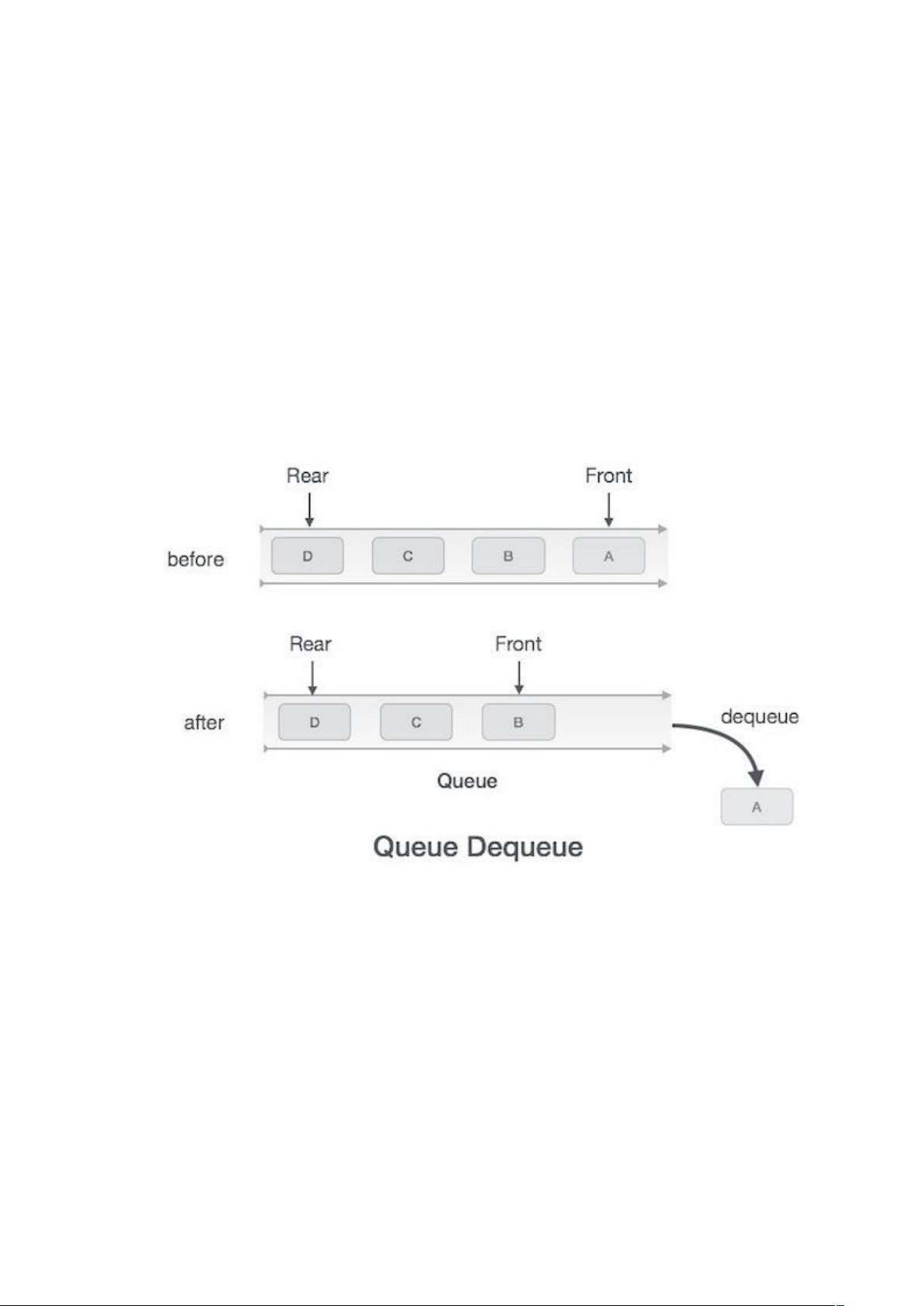
Hoạt động dequeue trong cấu trúc dữ liệu hàng đợi

Việc truy cập dữ liệu từ hàng đợi là một tiến trình gồm hai tác vụ: truy cập dữ liệu tại nơi con trỏ front đang trỏ tới và xóa dữ liệu sau khi đã truy cập đó. Dưới đây là các bước để thực hiện hoạt động dequeue:

Bước 1: kiểm tra xem hàng đợi là trống hay không.

Bước 2: nếu hàng đợi là trống, tiến trình bị lỗi và bị thoát.

Bước 3: nếu hàng đợi không trống, truy cập dữ liệu tại nơi con trỏ front đang trỏ.

Bước 4: tăng con trỏ front để trỏ tới vị trí chứa phần tử tiếp theo.

Bước 5: trả về success.

Cấu trúc dữ liệu đồ thị (Graph)

• • 1. Khái niệm

Một đồ thị (đồ thị) là một dạng biểu diễn hình ảnh của một tập các đối tượng, trong đó các cặp đối tượng được kết nối bởi các link. Các đối tượng được nối liền nhau được biểu diễn bởi các điểm được gọi là các đỉnh (vertices), và các link mà kết nối các đỉnh với nhau được gọi là các cạnh (edges).

Nói chung, một đồ thị là một cặp các tập hợp (V, E), trong đó V là tập các đỉnh và E là tập các cạnh mà kết nối các cặp điểm. Bạn theo dõi đồ thị sau:

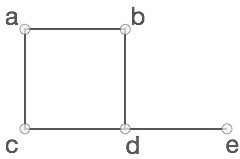
Trong đồ thị trên:

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Cấu trúc đồ thị

Các hình toán học có thể được biểu diễn trong cấu trúc dữ liệu. Chúng ta có thể biểu diễn một hình bởi sử dụng một mảng các đỉnh và một mảng hai chiều của các cạnh. Trước khi tiếp tục, chúng ta tìm hiểu một vài khái niệm quan trọng sau:

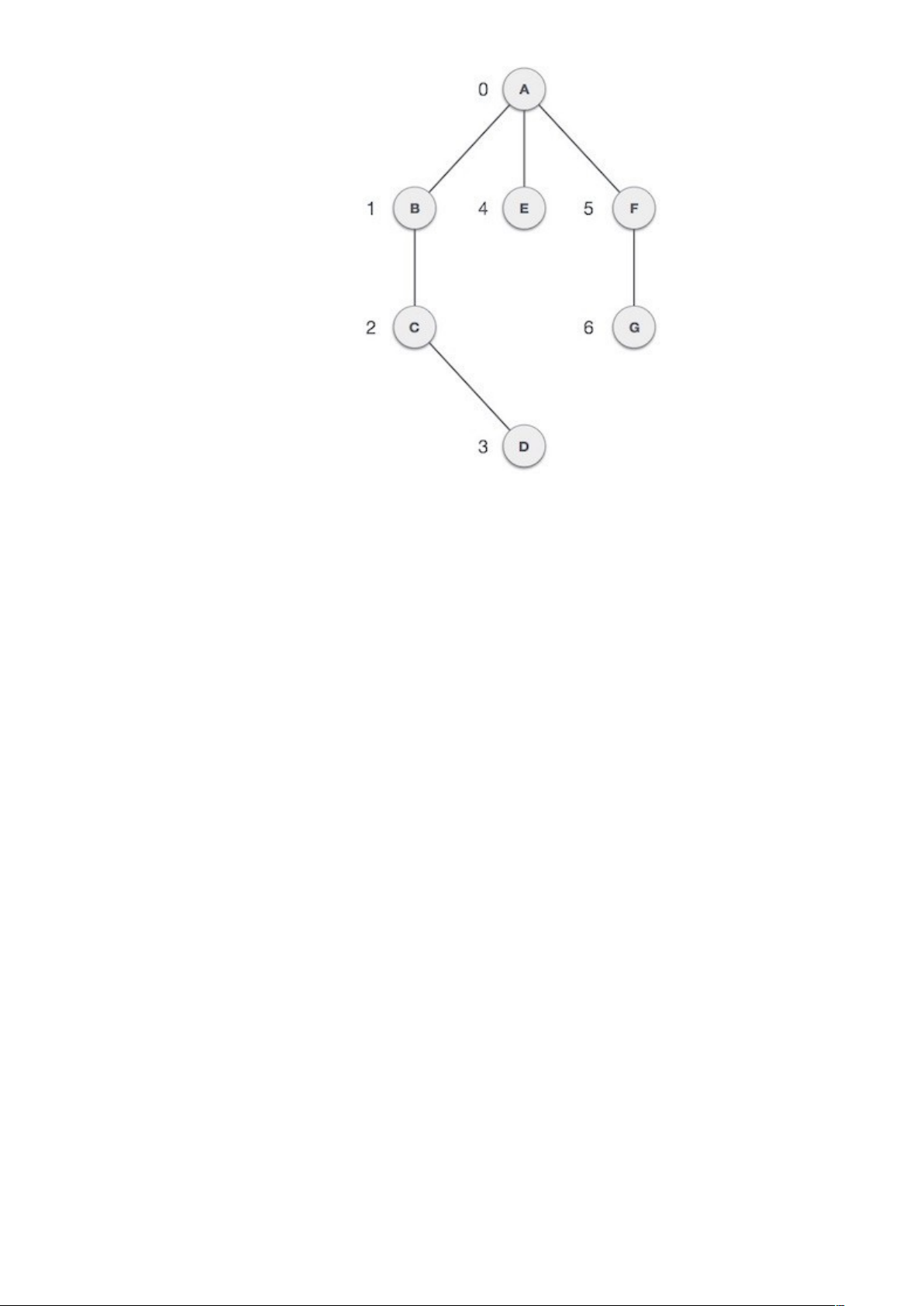
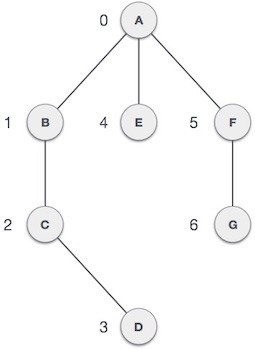
• • • • Đỉnh (Vertex): Mỗi nút của hình được biểu diễn như là một đỉnh. Trong ví dụ dưới đây, các hình tròn biểu diễn các đỉnh. Do đó, các điểm từ A tới G là các đỉnh. Chúng ta có thể biểu diễn các đỉnh này bởi sử dụng một mảng, trong đó đỉnh A có thể được nhận diện bởi chỉ mục 0, điểm B là chỉ mục 1, … như hình dưới.
      • Cạnh (Edge): Cạnh biểu diễn một đường nối hai đỉnh. Trong hình dưới, các đường nối A và B, B và C, … là các cạnh. Chúng ta có thể sử dụng một mảng hai chiều để biểu diễn các cạnh này. Trong ví dụ dưới, AB có thể được biểu diễn như là 1 tại hàng 0; BC là 1 tại hàng 1, cột 2, …
      • Kề nhau: Hai đỉnh là kề nhau nếu chúng được kết nối với nhau thông qua một cạnh. Trong hình dưới, B là kề với A; C là kề với B, …
      • Đường: Đường biểu diễn một dãy các cạnh giữa hai đỉnh. Trong hình dưới, ABCD biểu diễn một đường từ A tới D.

• Các thao tác cơ bản trên cấu trúc dữ liệu đồ thị
  • Thêm đỉnh: Thêm một đỉnh vào trong đồ thị.
  • Thêm cạnh: Thêm một cạnh vào giữa hai đỉnh của một đồ thị.
  • Hiển thị đỉnh: Hiển thị một đỉnh của một đồ thị.

Cấu trúc dữ liệu cây (tree)

• • 1. Khái niệm

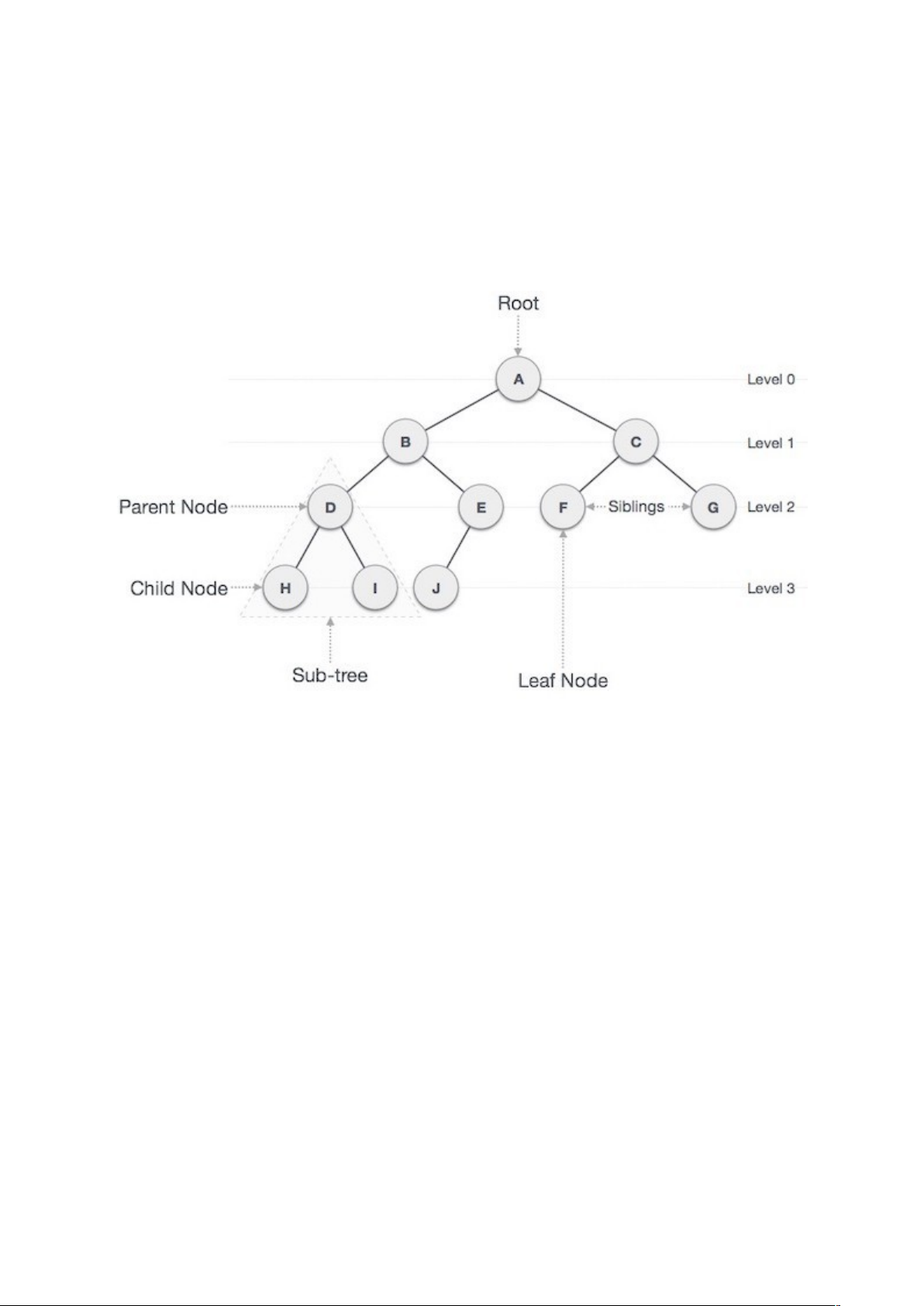
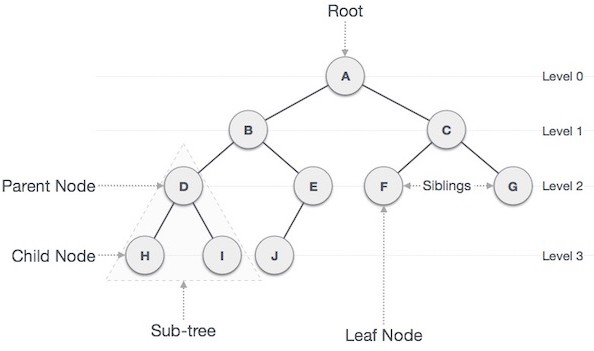
Cấu trúc dữ liệu cây biểu diễn các nút (node) được kết nối bởi các cạnh. Chúng ta sẽ tìm hiểu về Cây nhị phân (Binary Tree) và Cây tìm kiếm nhị phân (Binary Search Tree) trong phần này.

Cây nhị phân là một cấu trúc dữ liệu đặc biệt được sử dụng cho mục đích lưu trữ dữ liệu. Một cây nhị phân có một điều kiện đặc biệt là mỗi nút có thể có tối đa hai nút con. Một cây nhị phân tận dụng lợi thế của hai kiểu cấu trúc dữ liệu: một mảng đã sắp thứ tự và một danh sách liên kết (Linked List), do đó việc tìm kiếm sẽ nhanh như trong mảng đã sắp thứ tự và các thao tác chèn và xóa cũng sẽ nhanh bằng trong Linked List.

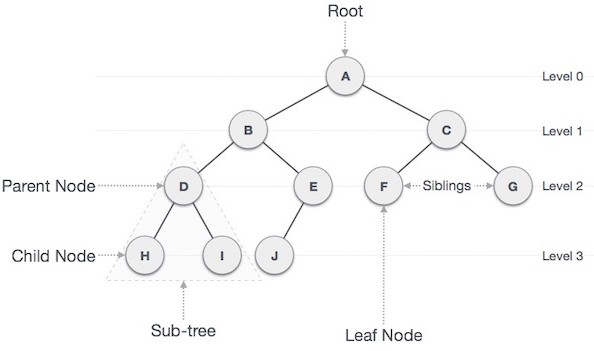
Dưới đây là một số khái niệm quan trọng liên quan tới cây nhị phân:

• • • • Đường: là một dãy các nút cùng với các cạnh của một cây.
      • Nút gốc (Root): nút trên cùng của cây được gọi là nút gốc. Một cây sẽ chỉ có một nút gốc và một đường xuất phát từ nút gốc tới bất kỳ nút nào khác. Nút gốc là nút duy nhất không có bất kỳ nút cha nào.
      • Nút cha: bất kỳ nút nào ngoại trừ nút gốc mà có một cạnh hướng lên một nút khác thì được gọi là nút cha.
      • Nút con: nút ở dưới một nút đã cho được kết nối bởi cạnh dưới của nó được gọi là nút con của nút đó.
      • Nút lá: nút mà không có bất kỳ nút con nào thì được gọi là nút lá.
      • Cây con: cây con biểu diễn các con của một nút.
      • Truy cập: kiểm tra giá trị của một nút khi điều khiển là đang trên một nút đó.
      • Duyệt: duyệt qua các nút theo một thứ tự nào đó.
      • Bậc: bậc của một nút biểu diễn số con của một nút. Nếu nút gốc có bậc là 0, thì nút con tiếp theo sẽ có bậc là 1, và nút cháu của nó sẽ có bậc là 2, …
      • Khóa (Key): biểu diễn một giá trị của một nút dựa trên những gì mà một thao tác tìm kiếm thực hiện trên nút.
    1. Hoạt động cơ bản trên cây tìm kiếm nhị phân
       • Chèn: chèn một phần tử vào trong một cây/ tạo một cây.
       • Tìm kiếm: tìm kiếm một phần tử trong một cây.
       • Duyệt tiền thứ tự: duyệt một cây theo cách thức duyệt tiền thứ tự (tham khảo chương sau).
       • Duyệt trung thứ tự: duyệt một cây theo cách thức duyệt trung thứ tự (tham khảo chương sau).
       • Duyệt hậu thứ tự: duyệt một cây theo cách thức duyệt hậu thứ tự (tham khảo chương sau).

CHƯƠNG 2: THỰC HÀNH

Đề bài

Viết hàm khai báo cac chương trình con cài đặt danh sách mảng. Dùng các chương trình con này để:

- Chương trình con nhận một dãy các số nguyên nhập từ bàn phím, lưu trữ nó trong danh sách thứ tự ngược với thú tự nhập vào

Phân tích

• • • Sử dụng cấu trúc Struct
    • Viết bằng ngôn ngữ C++
    • Dùng thư viện string để nhập

Code

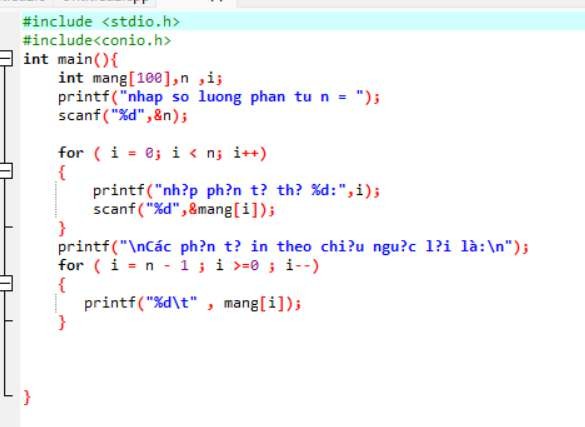
• 1. Giải thích

Hàm để nhập một dãy các phần tử vào danh sách

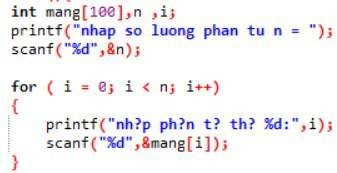
Hàmđể hiện thị ra danh sách trên Console

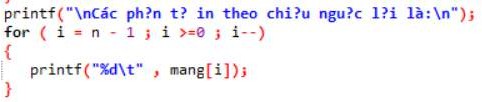
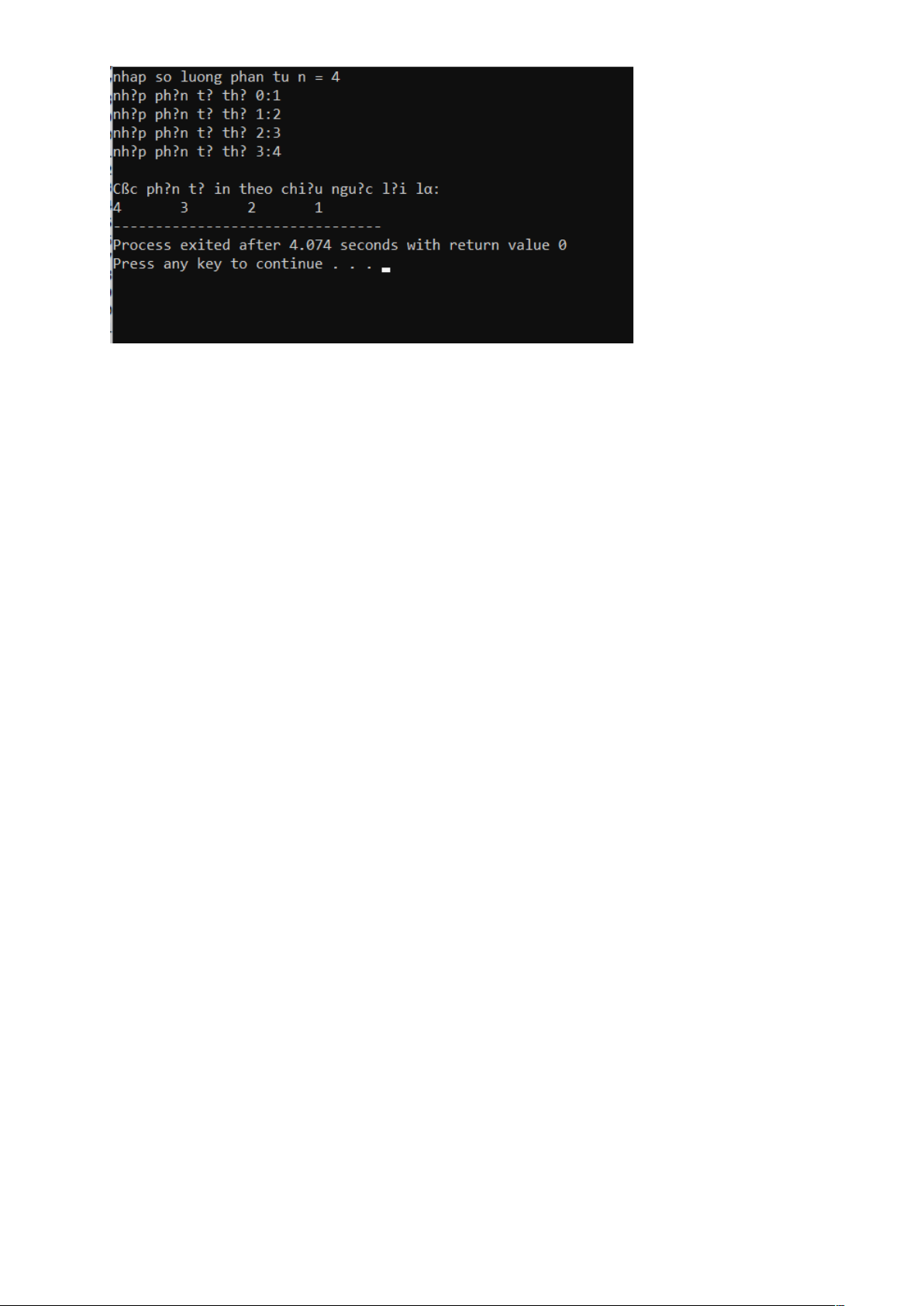
• 1. Kết quả

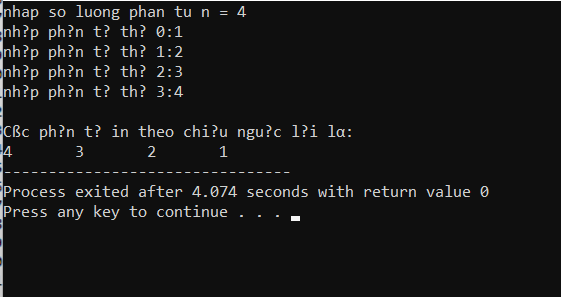
PHẦN KẾT LUẬN

Những việc đã hoàn thiện

• • Chương trình chạy ổn định
  • Kết quả theo đúng đề bài

Những việc chưa hoàn thiện

• • Còn thiếu nhiều trường hợp đặc biệt
  • Chưa tối ưu hoàn toàn

TÀI LIỆU THAM KHẢO

• W3School (https://www.w3schools.com)
• Stackoverflow (https://stackoverflow.com)
• Github (https://github.com)
• Vietjack (https://vietjack.com)