Bài tập lớn môn Kỹ thuật Điều khiển tự động | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Bài tập lớn Môn học Kỹ thuật Điều khiển tự động
Bài tập 1: Tìm tín hiệu có ảnh Laplace như các trường hợp dưới đây: 2 2s +13s +17 a, X(s) = ; 2 s + 4s + 3 b, c, d,
Bài tập 2: Tìm nghiệm của các phương trình vi phân sau: 2 d x + dx dx 4 + 5x =1; với (0) x(0) = 1, = 1 − 2 a, dt dt dt 2 d y dy + dy 2 + 5y = 3 ; với (0) y(0) = 0, = 0 2 b, dt dt dt
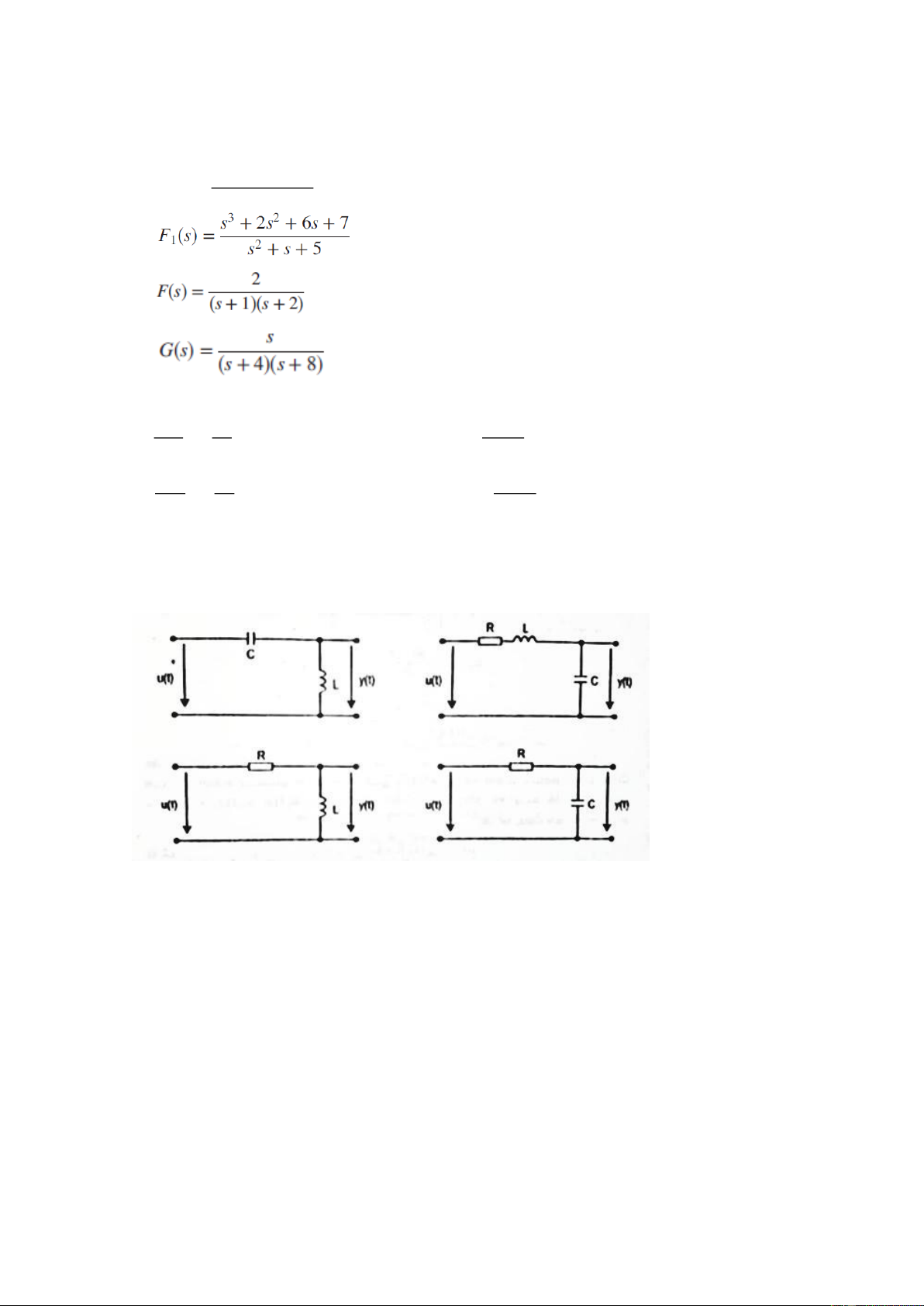
Bài tập 3: Viết phương trình vi phân mô tả mạch điện và tìm nghiệm của phương trình vi phân.
Bài tập 4: Cho sơ đồ mạch điện: 1
a.Viết phương trình vi phân mô tả mạch điện.
b.Viết hàm truyền mô tả mạch điện.
c.Viết phương trình trạng thái mô tả mạch điện.
Bài tập 5: Cho hệ thống có phương trình vi phân, viết phương trình trạng thái mô tả hệ thống 4 3 2 3 2 d y d y d y dy d u d u du + 3 + 2 +11 + 3y = 2 + 5 + 7 + 3u 4 3 2 3 2 a, dt dt dt dt dt dt dt 4 3 2 2 d y d y d y dy d u du + + 7 + 2 + 5y = 3 + 2 + 4u 4 3 2 2 b, dt dt dt dt dt dt 4 3 2 d y d y d y dy 3 + 5 + 4 + + 6y = 3u 4 3 2 c, dt dt dt dt 4 3 2 d y d y d y dy 6 + 9 + + + 3y = 12u 4 3 2 d, dt dt dt dt 4 3 2 d y d y d y dy du 4 + 3 + + 2 + 3y = 2 + u 4 3 2 e, dt dt dt dt dt Bài tập 6: 2 
Cho hệ thống được mô tả bằng phương trình trạng thái: X = A.X + B r .  .  c = C.X Cho hệ thống được x = A.x + B.r
mô tả bằng phương trình trạng thái: 
. r là tín hiệu vào, c là tín hiệu ra, x là  c = C.x
vector biến trang thái. Tìm hàm truyền của hệ thống, biết các ma trận trạng thái: 2 3 2 a, A = , B = ,C =     3 4 2 4 5 1 3 −  2 b, A = , B = ,C =     1 5 2 2  3 4 1 −  2 c, A = , B = ,C =     1 2 2 2  3
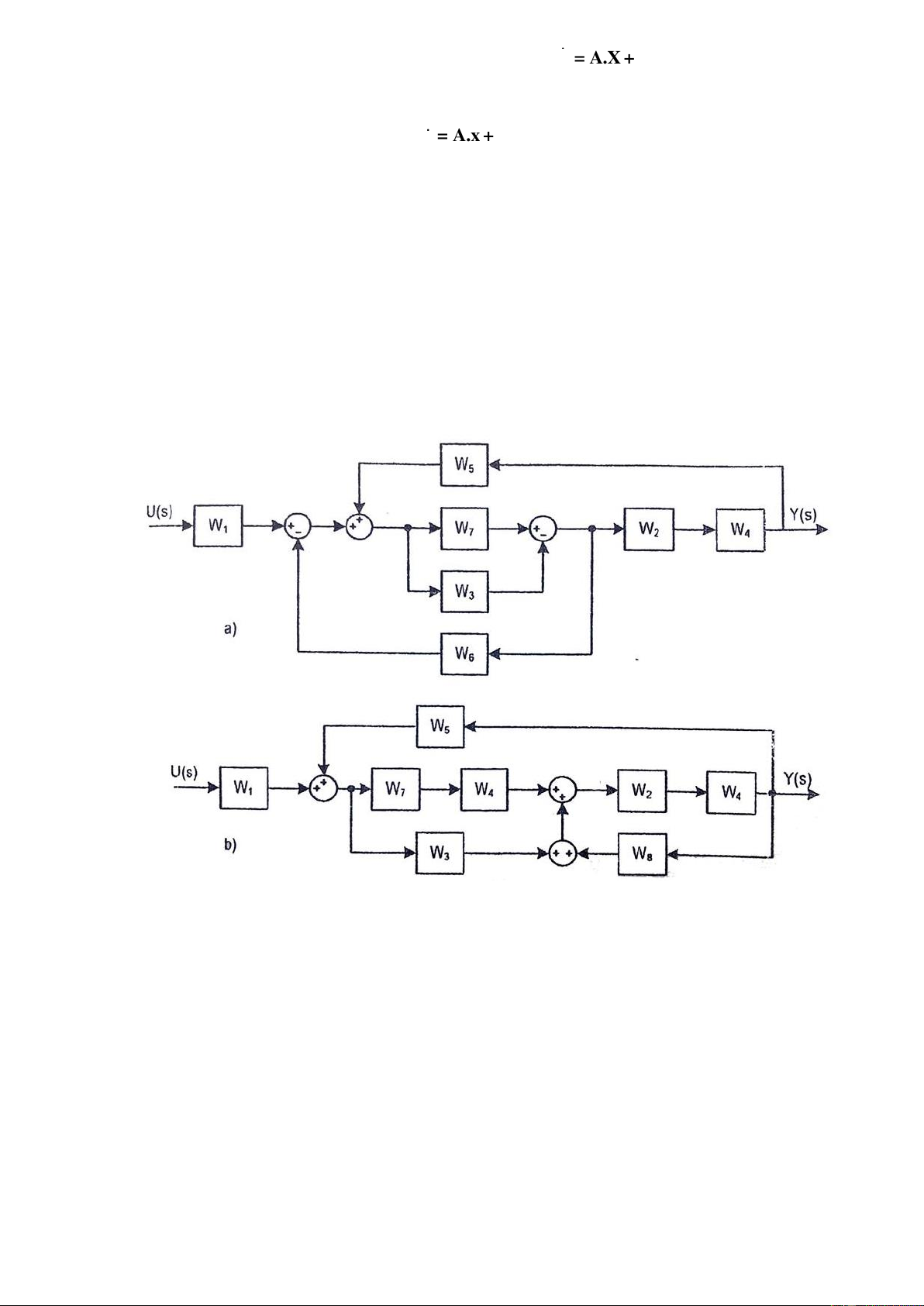
Bài tập 7: Đơn giản và viết hàm truyền của hệ thống sau: 3 4
Bài tập 7: Sử dụng công thức mason viết hàm truyền cho hệ thống sau:
Bài tập 8: Hãy xây dựng đặc tuyến tần số biên độ logarit của hàm truyền đạt sau: 50 4s + 2 1.W (s) ( ) = s (3s + ) 1 10s 2s + 4 2.W (s) ( ) = 3s +1 s 3.W (s) 2 10 = 2s +1 s 4s +1 4.W (s) ( ) = ( 2s + ) 1 (3s + ) 1 3s + 6 5.W (s) = ( 2s + )2 1 3s + 4 6.W (s) = ( 2s + ) 1 (5s + 4)
7.W (s) = 10(20s + 5) 2 s 4s +1 8.W (s) ( ) = ( 2s + ) 1 (3s + ) 1 1 9.W (s) = 100(5s + 3) 5
Bài tập 9: Sử dụng tiêu chuẩn Routh – Hurwitz để kiểm tra tính ổn định hệ có phương trình đặc tính. a) A(s) = 4 3 2
11.2s + 0.8s + 2.s + s + 0.5 b) A (s) 3 2
= s + 8s +10s + 5 c) A(s) = 5 4 2
2s + 3s + 4s + 0.3s + 20 d) A(s)= 5 4 2
s + 6s + s + s + 2
Bài tập 10: Cho hàm truyền đạt của hệ thống. Với giá trị nào của k thì hệ thống ổn định: 3 2 s + 2.s +1 a) W(s)= 4 3 2
s + 3.s + 4.k.s + 2.s + 2 3 2
2.s + 2.s + s + 5 b) W(s)= 4 3 2
k.s + 8.s + 4s + s +1 s +1 c) W(s)= 4 2.s + (k − ) 3 2
1 .s + s + s + 6 2 4s −1 d) W(s)= 3 4.s + ( 2 k − ) 2 1 .s + 2.s +1
Bài tập 11: Cho hệ thống hở có hàm truyền đạt: K W p = h (
) (s+ )1(2s+ )1(4s+ )1(5s+ )1
Xây dựng quỹ đạo nghiệm số cho hệ thống kín. Page 6