Bài tập lớn Xây dựng ứng dụng đánh cờ tướng người với máy môn Trí tuệ nhân tạo | Trường Đại học Kiến trúc Đà Nẵng

TRƯỜNG ĐẠI HỌC KIẾN TRÚC ĐÀ NẴNG KHOA CÔNG NGHỆ THÔNG TIN
TRƯỜNG ĐẠI HỌC KIẾN TRÚC ĐÀ NẴNG
DANANG ARCHITECTURE UNIVERSITY
BÀI TẬP LỚN TRÍ TUỆ NHÂN TẠO ĐỀ TÀI:
Xây dựng ứng dụng đánh Cờ tướng người với máy. Giảng Viên : Nguyễn Năng Hùng Vân
Sinh Viên : Đinh Xuân Hoàng
Mã Số Sinh Viên :2151220244
Sinh Viên : Đinh Cao Thanh Tùng
Mã Số Sinh Viên :2151220220
Đà Nẵng, Ngày 02 Tháng 01 Năm 2024 Giới thiệu
Cờ tướng là một môn thể thao khá phổ biến ở Việt Nam. Các bạn có thể bắt gặp các
bàn cờ ở các con hẻm của mỗi góc phố. Hoặc là khi các bộ bàn ghế đá thì người mua
cũng thường nhờ thợ khắc lên bàn cờ tướng để hàng xóm láng giềng giải trí ngày cuối
tuần. Trong bài viết này, mình sẽ hướng dẫn step by step ứng dụng chơi game cờ
tướng đơn giản với một chút AI. Hi vọng sẽ giúp được các bạn trên con đường thực hành học máy.
Các việc cần làm:
Tạo bàn cờ và sinh nước đi
Lượng giá bàn cờ Áp dụng minimax
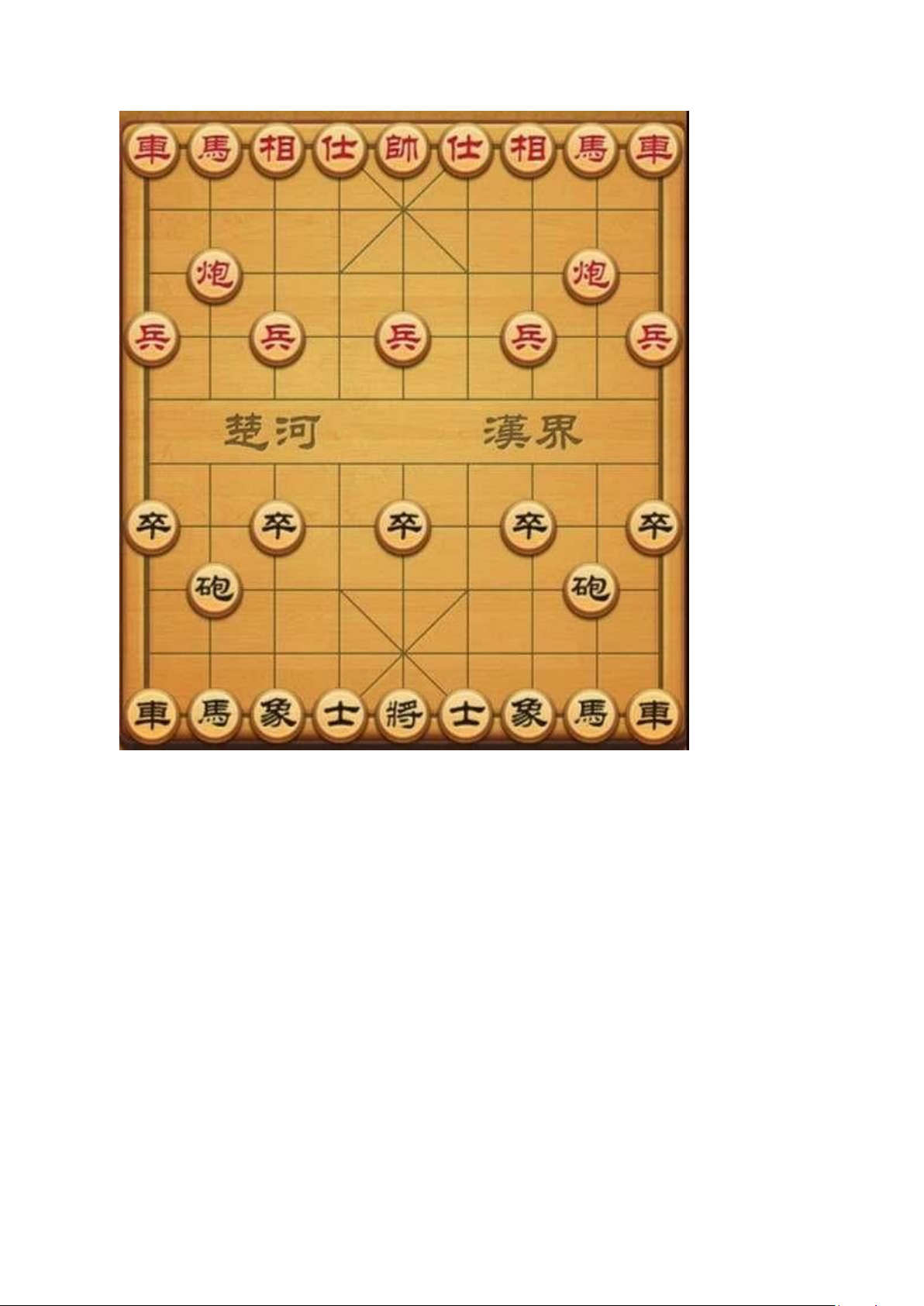
Bàn cờ được chia làm 2 đội, là đội đen (black, ký hiệu b) và đội đỏ (red , ký hiệu
r), mỗi đội gồm 16 quân, bao gồm 1 con tướng (General hoặc king , ký hiệu k), 2 con
sỹ (Advisor hoặc guards, ministers, ký hiệu là a), 2 con tượng (Elephants hoặc
bishops - ký hiệu là b), 2 con mã (Horses hoặc knights - ký hiệu là n, do chữ k trùng
với king là con tướng, nên người ta xài chữ n), 2 con xe (Chariot hoặc rooks - ký hiệu
là r), 2 con pháo (canons, ký hiệu là c ), 5 con chốt (Soldiers , ký hiệu là p ( do con
chốt ở cờ đen và cờ đỏ có phiên âm tiếng trung khác nhau, chốt cờ đen đọc gần giống
chữ “zú” (“pawn” hoặc “private” - tiếng anh), còn chốt cờ đỏ đọc là bing (“soldier” - tiếng anh) )).
Tổng cộng, ta có tướng, sỹ, tượng, mã, xe, pháo, chốt, 7 loại quân, tương đương với 7
ký hiệu, tổ hợp với 2 đội là đỏ và đen, tổ hợp với nhau, ta xác định được
Để bắt đầu, chúng ta sẽ code một hàm random bước đi đơn giản. Hàm có nhiệm vụ
lấy ngẫu nhiên một bước đi trong danh sách các bước có thể đi, sau đó máy sẽ đánh bước đi đó.
Bước 2: Hàm lượng giá
Dựa vào mức độ cơ động, tầm quang trọng của mỗi quân lính trên bàn cờ, chúng ta sẽ
gán cho mỗi quân cờ một trọng số khác nhau thể hiện điều đó.
Ví dụ, chúng ta set các trọng số như sau:
tướng của ta là 900 điểm, tướng của đối thủ là -900 điểm sỹ của ta là 20 điểm, sỹ của
đối thủ là -20 điểm tượng của ta là 20 điểm, tượng của đối thủ là -20 điểm mã của ta
là 40 điểm, mã của đối thủ là -40 điểm xe của ta là 90 điểm, xe của đối thủ là -90
điểm pháo của ta là 45 điểm, pháo của đối thủ là -45 điểm chốt của ta là 15 điểm,
chốt của đối thủ là -15 điểm
Hàm lượng giá ở trên khá ngây thơ, mọi quân cờ đều có điểm ngang nhau, không
quan tâm vị trí đứng của nó.
Trên thực tế, chúng ta thấy rằng, con tướng ở vị trí trung tâm thường là an toàn nhất,
một khi tướng leo lên lầu 1 hoặc leo lầu 2, nghĩa là con tướng có khả năng bị đột tử
cao hơn, nên chúng ta phải tinh chỉnh lại điểm của con tướng trong trường hợp này.
Một ví dụ nữa là vị trí con mã, mã gần với thành của tướng địch hơn thì khả năng con
Chúng ta sẽ duyệt lần lượt từ trái qua phải, từ trên xuống dưới, tính điểm của bàn cờ hiện tại.
Bây giờ, chúng ta chỉ cần duyệt qua toàn bộ các nước có thể đi, tính xem nước đi nào
có điểm số là lớn nhất, thì máy sẽ đi theo nước đi đó.
Vì vậy, ngoài việc xét điểm cho các loại quân, chúng ta sẽ có một bảng xét điểm cho các con
Kết quả có vẻ tốt hơn so với việc random bước đi trước đó, nhưng thuật toán vẫn còn
hơi dốt dốt xíu, do máy chỉ tính 1 nước đi và chọn ra nước đi tốt nhất. Nên máy chưa
có cái nhìn dài hơn. Có nhiều cách để cho máy có thể có góc nhìn xa hơn về thế cục
của bàn cờ, một trong các cách được giới thiệu ở đây là sử dụng minimax
Bước 3. Tìm kiếm cây sử dụng minimax
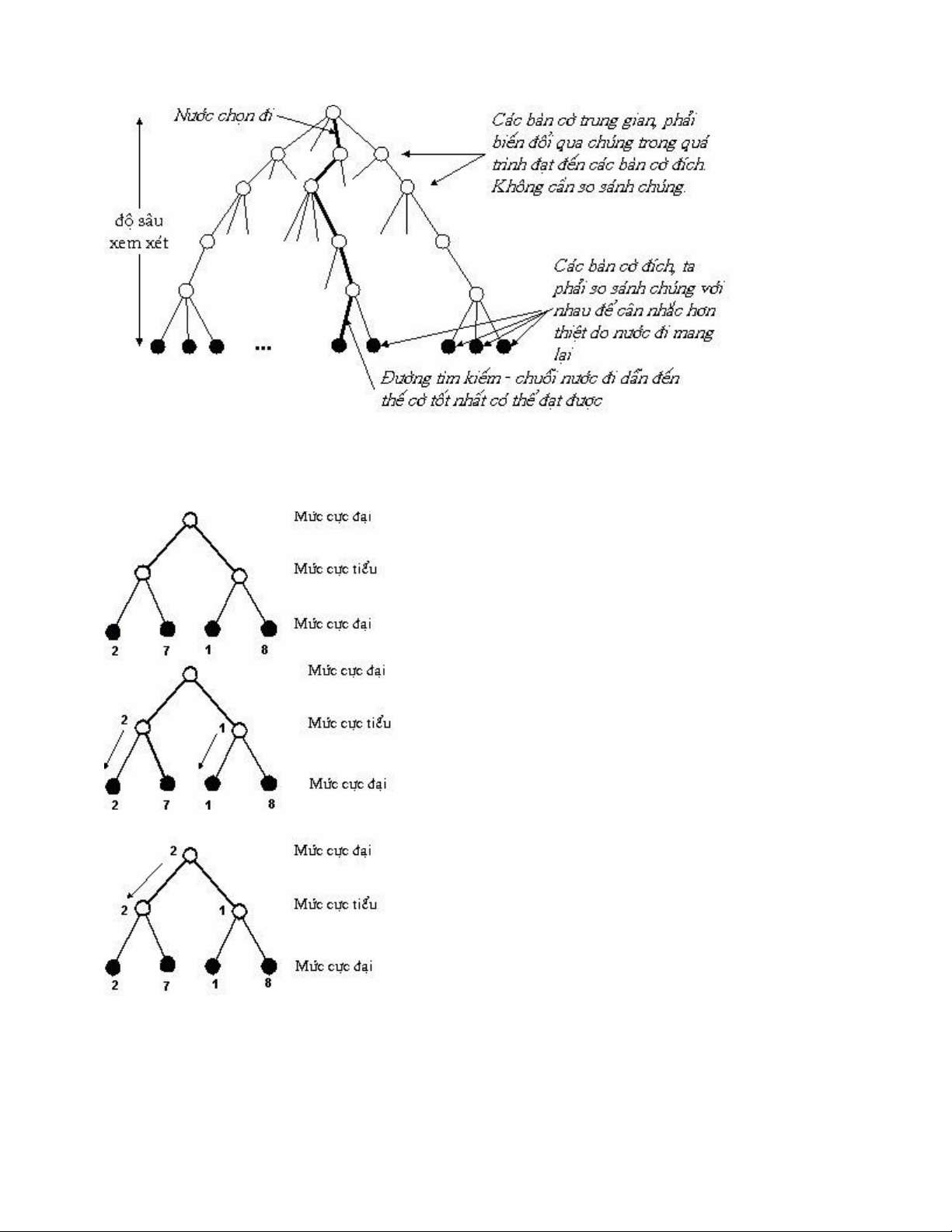
Thuật toán minimax thuộc nhóm duyệt theo chiều sâu (depth first search). Hai người
chơi, một người được gọi là MAX, người còn lại gọi là MIN. Thuật toán được thiết
kế để tìm nước đi tối ưu cho người MAX. Người MAX sẽ giữ node gốc, lần lượt
duyệt đệ quy qua tất cả các node con theo chiều sâu nhất định đến khi duyệt qua tất
cả các node hoặc là tìm được một đường đi mà đạt MAX.
Chi tiết hơn, người MAX sẽ đi đầu tiên. Nhiệm vụ của MAX là tìm nước đi sao cho
điểm số của mình là cao nhất, nhiệm vụ của MIN là tìm nước đi để cực tiểu hoá điểm số của MAX.
Thuật toán này hoạt động khá hiệu quả, nhưng có một điểm yếu là nó sẽ vét cạn toàn
bộ các trường hợp để tìm ra đường đi tối ưu nhất. Vì vậy, với giá trị độ sâu càng lớn
thì thuật toán chạy càng chậm.
Bước 4: Cắt tỉa Alpha - Beta
Cắt tỉa Alpha - Beta là một phương pháp tối ưu hoá của thuật toán minimax, phương
pháp này giúp chúng ta bỏ qua một vài nhánh trong quá trình tìm kiếm, làm giới hạn
phạm vi tìm kiếm, giúp mô hình hoạt động nhanh hơn.
Thuật toán sẽ hoạt động hiệu quả hơn nếu những bước tìm kiếm đầu tiên là những
nước đi tốt nhất :) Bài code được viết lại như sau:
import math import string import chess
class ChessBoard: def __init__(self):
self.board = [['R', 'N', 'B', 'Q', 'K', 'B', 'N', 'R'],
['P', 'P', 'P', 'P', 'P', 'P', 'P', 'P'],
[' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '],
[' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '],
[' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '],
[' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '],
['p', 'p', 'p', 'p', 'p', 'p', 'p', 'p'],
['r', 'n', 'b', 'q', 'k', 'b', 'n', 'r']] self.current_player = 'white'
def display(self): for row in self.board: print(' '.join(row)) print()
def is_valid_move(self, move): if self.is_stalemate():
print("Stalemate! The game is a draw.") return False
if len(move) != 2: print("Invalid move format. Enter move in the format 'e2e4'.") return False start, end = move try:
start_row, start_col = 8 - int(start[1]), ord(start[0].lower()) - ord('a')
end_row, end_col = 8 - int(end[1]), ord(end[0].lower()) - ord('a') except (ValueError, IndexError):
print("Invalid move format. Enter move in the format 'e2e4'.") return False
if not (0 <= start_row < 8 and 0 <= start_col < 8 and 0 <= end_row < 8 and 0 <=
end_col < 8): print("Invalid move. Out of board bounds.") return False
piece = self.board[start_row][start_col] if piece == ' ':
print("Invalid move. No piece at the starting position.") return False
if piece.isupper() and self.current_player != 'white':
print("Invalid move. It's not white's turn.") return False elif
piece.islower() and self.current_player != 'black':
print("Invalid move. It's not black's turn.") return False
if (end_row, end_col) not in self.get_legal_moves_from_position(start_row, start_col):
print("Invalid move. The piece cannot move to the specified position.") return False return True
def get_legal_moves_from_position(self, row, col):
piece = self.board[row][col] if piece == 'P':
return self.get_pawn_moves(row, col) elif piece == 'N':
return self.get_knight_moves(row, col) elif piece == 'B':
return self.get_bishop_moves(row, col) elif piece == 'R':
return self.get_rook_moves(row, col) elif piece == 'Q':
return self.get_queen_moves(row, col) elif piece == 'K':
return self.get_king_moves(row, col) return [] def get_legal_moves(self): legal_moves = []
for row in range(8): for col in range(8): if self.board[row][col].lower() == self.current_player[0]:
piece_moves = self.get_legal_moves_from_position(row, col)
legal_moves.extend([(row, col, end_row, end_col) for end_row, end_col in piece_moves])
return legal_moves def is_valid_move(self, move): if len(move) != 2: return False start, end = move try:
start_row, start_col = 8 - int(start[1]), ord(start[0].lower()) - ord('a')
end_row, end_col = 8 - int(end[1]), ord(end[0].lower()) - ord('a') except
(ValueError, IndexError): return False
if not (0 <= start_row < 8 and 0 <= start_col < 8 and 0 <= end_row < 8 and 0 <= end_col < 8): return False
# Implement additional validation logic based on the rules of chess
# For simplicity, you may want to start with basic checks like piece movement rules
# and make sure the start position contains a piece belonging to the current player return True
def make_move(self, move): if not self.is_valid_move(move): return False
start, end = move start_row, start_col = 8 - int(start[1]), ord(start[0].lower())
- ord('a') end_row, end_col = 8 - int(end[1]), ord(end[0].lower()) - ord('a')
piece = self.board[start_row][start_col] self.board[start_row][start_col] = ' '
self.board[end_row][end_col] = piece
self.current_player = 'black' if self.current_player == 'white' else 'white' return True
def undo_move(self): if hasattr(self, 'previous_state'): # Khôi phục lại
trạng thái trước đó self.board, self.current_player = self.previous_state
delattr(self, 'previous_state')
def get_legal_moves(self): legal_moves = []
for row in range(8): for col in range(8): if
self.board[row][col].lower() == self.current_player[0]:
piece_moves = self.get_piece_moves(row, col)
legal_moves.extend([(row, col, end_row, end_col) for end_row, end_col in piece_moves]) return legal_moves
def is_in_check(self, player):
king_position = self.find_king(player) opponent_moves =
self.get_opponent_moves(player) return king_position in opponent_moves
def is_checkmate(self, player): if not self.is_in_check(player): return False
legal_moves = self.get_legal_moves() for move in legal_moves:
# Try each legal move and check if the king is still in check
self.make_move(move) if not self.is_in_check(player):
self.undo_move() return False self.undo_move() return True
def get_piece_moves(self, row, col):
piece = self.board[row][col] if piece == 'P': return
self.get_pawn_moves(row, col) elif piece == 'N':
return self.get_knight_moves(row, col) elif piece == 'B':
return self.get_bishop_moves(row, col) elif piece == 'R':
return self.get_rook_moves(row, col) elif piece == 'Q':
return self.get_queen_moves(row, col) elif piece == 'K':
return self.get_king_moves(row, col) class ChessBoard: # ... (các phương thức khác)
def get_pawn_moves(self, row, col):
moves = [] direction = 1 if self.current_player == 'white' else -1 #
Forward move if 0 <= row + direction < 8 and self.board[row +
direction][col] == ' ': moves.append((row, col, row + direction, col))
# Double move from starting position if (row == 1 and
self.current_player == 'white') or (row == 6 and self.current_player == 'black'):
if self.board[row + 2 * direction][col] == ' ': moves.append((row, col, row + 2 * direction, col))
# Capture moves for d_col in [-1, 1]:
new_col = col + d_col if 0 <= row + direction < 8 and 0 <=
new_col < 8 and self.board[row + direction][new_col].lower() !=
self.current_player[0]: moves.append((row, col, row + direction, new_col)) return moves
def get_knight_moves(self, row, col): moves = []
for d_row in [-2, -1, 1, 2]: for d_col in [-2, -1, 1, 2]:
if abs(d_row) + abs(d_col) == 3:
new_row, new_col = row + d_row, col + d_col if 0 <=
new_row < 8 and 0 <= new_col < 8 and self.board[new_row] [new_col].lower() != self.current_player[0]:
moves.append((row, col, new_row, new_col)) return moves
def get_bishop_moves(self, row, col): moves = []
for d_row, d_col in [(-1, -1), (-1, 1), (1, -1), (1, 1)]: new_row,
new_col = row + d_row, col + d_col while 0 <= new_row < 8 and 0 <=
new_col < 8: if self.board[new_row][new_col] == ' ':
moves.append((row, col, new_row, new_col)) elif
self.board[new_row][new_col].lower() != self.current_player[0]:
moves.append((row, col, new_row, new_col)) break else: break
new_row, new_col = new_row + d_row, new_col + d_col return moves
def get_rook_moves(self, row, col): moves = []
for d_row, d_col in [(-1, 0), (1, 0), (0, -1), (0, 1)]: new_row, new_col
= row + d_row, col + d_col while 0 <= new_row < 8 and 0 <= new_col <
8: if self.board[new_row][new_col] == ' ':
moves.append((row, col, new_row, new_col)) elif
self.board[new_row][new_col].lower() != self.current_player[0]:
moves.append((row, col, new_row, new_col)) break else: break
new_row, new_col = new_row + d_row, new_col + d_col return moves
def get_queen_moves(self, row, col):
moves = [] moves.extend(self.get_bishop_moves(row, col))
moves.extend(self.get_rook_moves(row, col)) return moves
def get_king_moves(self, row, col): moves = []
for d_row in [-1, 0, 1]: for d_col in [-1, 0, 1]:
new_row, new_col = row + d_row, col + d_col if 0 <=
new_row < 8 and 0 <= new_col < 8 and self.board[new_row] [new_col].lower()
!= self.current_player[0]: moves.append((row, col, new_row, new_col)) return moves def find_king(self, player):
for row in range(8): for col in range(8): if
self.board[row][col] == 'K' and self.current_player[0] == player: return row, col
def get_opponent_moves(self, player):
opponent_moves = [] for row in range(8): for col in range(8):
if self.board[row][col].lower() != player[0]:
opponent_moves.extend(self.get_piece_moves(row, col)) return
opponent_moves def minimax(board, depth, maximizing_player, alpha, beta):
if depth == 0 or board.is_checkmate(board.current_player): return evaluate(board)
legal_moves = board.get_legal_moves()
if maximizing_player: max_eval = float('-inf') for move in
legal_moves: board.make_move(move) eval = minimax(board,
depth - 1, False, alpha, beta) max_eval = max(max_eval, eval)
alpha = max(alpha, eval) board.undo_move() if beta <= alpha: break return max_eval else:
min_eval = float('inf') for move in legal_moves:
board.make_move(move) eval = minimax(board, depth - 1, True, alpha,
beta) min_eval = min(min_eval, eval) beta = min(beta, eval)
board.undo_move() if beta <= alpha: break return min_eval
def get_best_move(board, depth):
legal_moves = board.get_legal_moves() best_move = None best_eval = float('-inf')
for move in legal_moves: board.make_move(move) eval =
minimax(board, depth - 1, False, float('-inf'), float('inf')) board.undo_move()
if eval > best_eval: best_eval = eval best_move = move return best_move def game_over(self):
return self.is_checkmate('white') or self.is_checkmate('black')
def evaluate(self): total_evaluation = 0
for row in range(8): for col in range(8):
piece = self.board[row][col] if piece == 'P':
total_evaluation += 10 if self.current_player == 'white' else -10 elif piece == 'N':
total_evaluation += 30 if self.current_player == 'white' else -30 elif piece == 'B':
total_evaluation += 30 if self.current_player == 'white' else -30 elif piece == 'R':
total_evaluation += 50 if self.current_player == 'white' else -50 elif piece == 'Q':
total_evaluation += 90 if self.current_player == 'white' else -90 elif piece == 'K':
total_evaluation += 900 if self.current_player == 'white' else -900 return total_evaluation
def display(self): for row in self.board: print(' '.join(row)) print() def main():
chess_board = ChessBoard() chess_board.display()
while not chess_board.game_over(): if chess_board.current_player == 'white':
move = get_best_move(chess_board, depth=3) else: move =
input("Enter your move (e.g., 'e2e4'): ")
if chess_board.is_valid_move(move): chess_board.make_move(move)
# Check for check and checkmate if
chess_board.is_in_check(chess_board.current_player):
print(f"{chess_board.current_player.capitalize()} is in check!")
if chess_board.is_checkmate(chess_board.current_player):
print(f"Checkmate! {chess_board.current_player.capitalize()} wins!")
chess_board.display() chess_board.current_player = 'black' if chess_board.current_player ==
'white' else 'white' else: print("Invalid move. Try again.")
if __name__ == "__main__": main() GIAO DIỆN CHƯƠNG TRÌNH 1.Giao diện khi vào game 2.Giao diện khi chơi