Bài tập tìm hai số khi biết tổng và hiệu của hai số đó | Toán 4

BÀI TẬP TÌM HAI SỐ KHI BIẾT TỔNG VÀ HIỆU CỦA HAI SỐ ĐÓ I. TRẮC NGHIỆM
Khoanh tròn vào chữ cái trước câu trả lời đúng:
Câu 1: Tổng của hai số là 320, hiệu của hai số đó là 28. Tìm hai số đó. A. 100 và 132 B. 146 và 174 C. 120 và 112 D. 125 và 107
Câu 2: Chiều cao trung bình của hai anh em là 127cm. Anh cao hơn em 8cm. Tính chiều cao của mỗi người.
A. Anh cao 132cm; em cao 122cm
B. Anh cao135cm; em cao118cm
C. Anh cao131cm; em cao123cm
D. Anh cao134cm; em cao120cm
Câu 3: Một lớp học có 38 học sinh. Số học sinh nam hơn số học sinh nữ là 6 em. Hỏi lớp học
đó có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?
A. Nữ: 14 học sinh; Nam: 24 học sinh
B. Nữ: 18 học sinh; Nam: 20 học sinh.
C.Nữ: 17 học sinh ; Nam: 21 học sinh
D. Nữ: 16 học sinh; Nam: 22 học sinh.
Câu 4: Một hình chữ nhật có chu vi là 180cm, chiều dài hơn chiều rộng 20cm. Tính diện tích hình chữ nhật đó. A. 2 1820cm B. 2 1925cm C. 2 1920cm D. 2 1825cm
Câu 5: Tôi đang nghĩ đến một số tự nhiên chẵn, biết tổng của số đó và số chẵn liền sau nó là
186. Hỏi tôi đang nghĩ tới số nào? A.92 B.94 C.96 D. 90
Câu 6: Tổng của hai số tròn chục liên tiếp là 190. Tìm hai số đó. A. 105 và 85 B. 110 và 90 C.110 và 100 D. 100 và 90
Câu 7: Trung bình cộng của ba số là 38. Một trong ba số đó là 35. Hai số còn lại có hiệu là 11. Tìm hai số đó. A. 47 và 32. B. 45 và 32. C. 45 và 34. D. 49 và 34.
Câu 8: Hai số lẻ liên tiếp có tổng là 272. Tìm hai số đó. A. 155 và 153 B. 139 và 137 C. 135 và 133 D. 137 và 135 II. TỰ LUẬN
Câu 1: Tìm 2 số biết tổng và hiệu của chúng lần lượt là: a) 56 và 8; b) 79 và 39 c) 125 và 53. 1
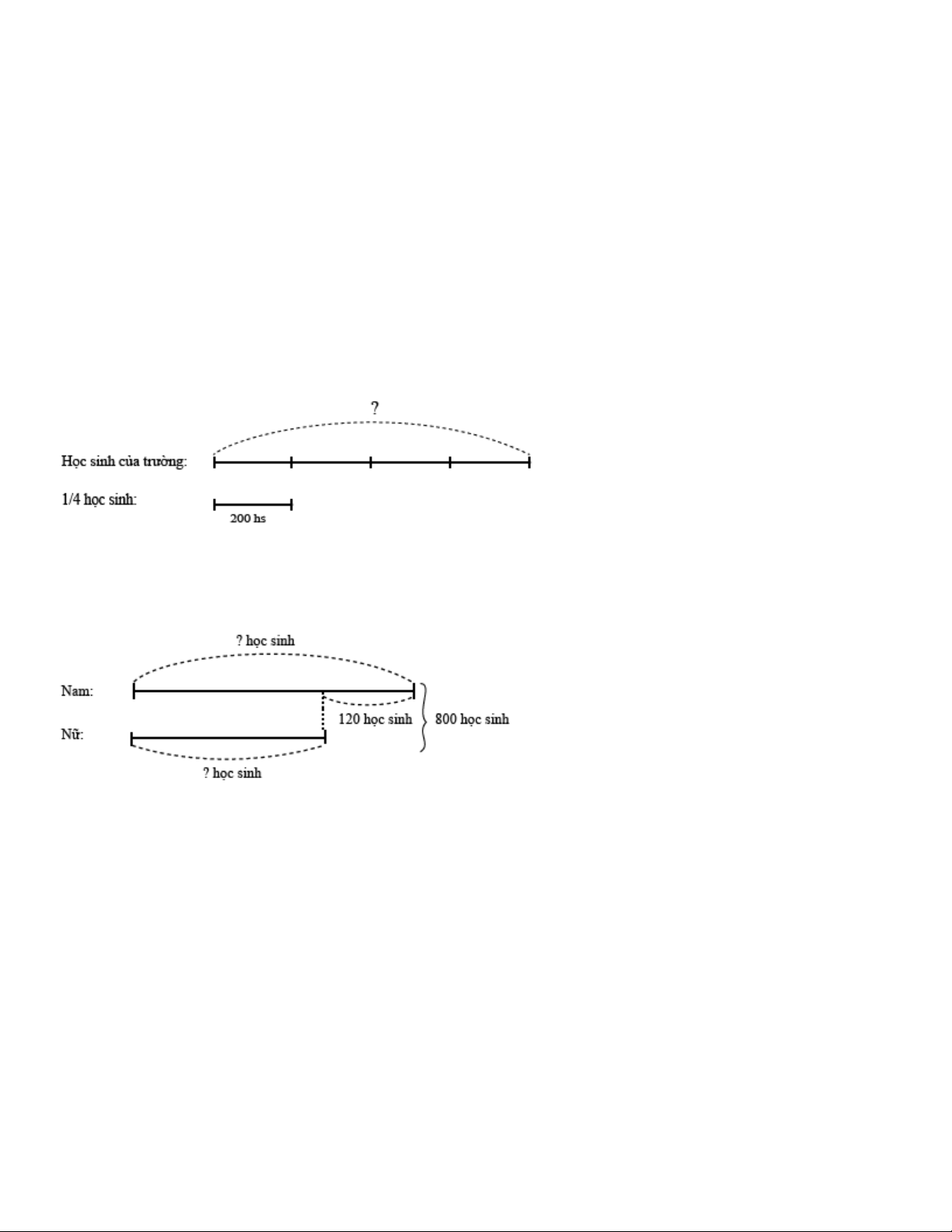
Câu 2: số học sinh của trường là 200 học sinh. Số học sinh nam nhiều hơn học sinh nữa là 4
120 học sinh. Hỏi có bao nhiêu học sinh nam và bao nhiêu học sinh nữ ? Câu 3:
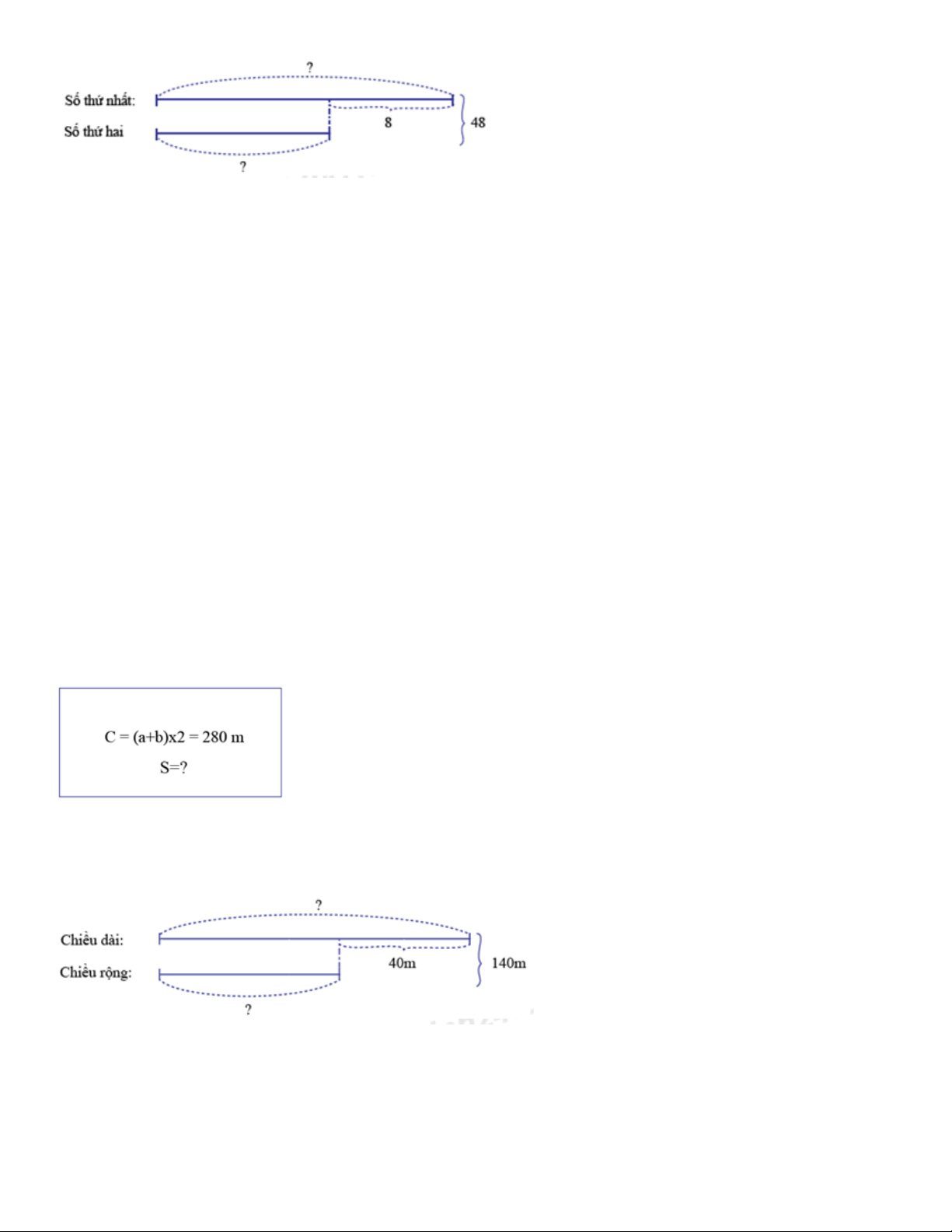
Tìm hai số biết rằng, số thứ hai bằng số thứ nhất cộng thêm 8. Số thứ nhất cộng số thứ hai bằng 48.
Câu 4: Một sân bóng chữ nhật có chu vi 280m chiều dài hơn chiều rộng 40m . Hỏi diện tích
của sân bóng là bao nhiêu 2 m
Câu 5: Trung bình cộng của ba số là 42. Số thứ hai đúng bằng trung bình cộng của ba số đó.
Tìm số thứ nhất và số thứ ba. Biết rằng số thứ ba lớn hơn số thứ nhất 14 đơn vị.
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN BỞI BAN CHUYÊN MÔN TUYENSINH247.COM I. TRẮC NGHIỆM. 1.B 2.C 3.D 4.B 5.A 6.D 7.C 8.D
Câu 1: Phương pháp: Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Số bé là: (232  32) : 2  146
Số lớn là: 146  28  174 Đáp số : Số bé : 146 Số lớn : 174 Chọn B
Câu 2: Phương pháp: Chiều cao trung bình của hai anh em được tính như sau : (tuổi anh + tuổi em) :2
- Khi biết chiều cao trung bình của hai anh em ta tính được tổng số tuổi của hai anh em.
- Từ đó tìm tuổi của mỗi người ta đi giải bài toán tìm hai số khi biết tổng và hiệu của hai số đó.
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Tổng chiều cao của hai anh em là: 127  2  254 cm
Chiều cao của anh là: 254  8 : 2 131 cm
Chiều cao của em là: 131  8  123cm
Đáp số : Anh cao131cm; emcao123cm Chọn C
Câu 3: Phương pháp: Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Số học sinh nữ là: 38  6 : 2 16 (học sinh)
Số học sinh nam là: 16  6  22 (học sinh)
Đáp số: Nữ: 16 học sinh; Nam: 22 học sinh. Chọn D
Câu 4: Phương pháp: Tìm nửa chu vi hình chữ nhật (chính là tổng chiều dài và chiều rộng của
hình chữ nhật đó). Sau đó tìm chiều dài và chiều rộng khi đã biết nửa chu vi của hình chữ nhật
và chiều dài hơn chiều rộng 20cm. Rồi tìm diện tích của hình chữ nhật đó.
Chú ý: Diện tích hình chữ nhật bằng chiều dài nhân với chiều rộng (cùng đơn vị đo) Cách giải:
Nửa chu vi là: 180 : 2  90cm
Chiều dài hình chữ nhật là: 90  20 : 2  55cm
Chiều rộng hình chữ nhật là: 55  20  35cm
Diện tích hình chữ nhật là:    2 55 35 1925 cm  Đáp số: 2 1925cm Chọn B
Câu 5: Phương pháp: Hai số tự nhiên chẵn hơn kém nhau 2 đơn vị, tổng của số đó và số chẵn
liền sau nó là 186.
Khi đó số chẵn mà tôi đang nghĩ tới là số bé.
Dựa vào cách tìm hai số khi biết tổng và hiệu của hai số đó có thể tìm được số mà tôi đang nghĩ tới. Cách giải:
Vì tổng hai số chẵn liên tiếp hơn kém nhau 2 đơn vị.
Nên ta có hiệu của số đó và số chẵn liền sau nó là 2.
Số đó là : 186  2 : 2  92 Chọn A
Câu 6 : Phương pháp: Hai số tròn chục liên tiếp hơn kém nhau 10 đơn vị. Nên hiệu của hai số đó là 10.
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Hai số tròn chục liên tiếp hơn kém nhau 10 đơn vị.
Số lớn là : 190 10 : 2  100
Số bé là : 100 10  90
Đáp số : Hai số đó là 100 và 90 Chọn D
Câu 7: Phương pháp: Từ trung bình cộng của ba số ta tìm được tổng của ba số đó, rồi tìm
được tổng của hai số còn lại, sau đó tìm hai số đó bằng cách giải bài toán khi biết tổng và hiệu của hai số đó.
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Tổng của ba số đó là : 38  3  114
Tổng của hai số còn lại là : 114  35  79 Số lớn là : 79   11 : 2  45
Số bé là : 45 11  34
Đáp số : hai số đó là 45 và 34. Chọn C
Câu 8: Phương pháp: Hai số lẻ liên tiếp hơn kém nhau 2 đơn vị. Từ đó tìm hai số lẻ liên tiếp
đề bài cho khi đã biết tổng và hiệu của hai số đó.
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Số lớn là : 272  2 : 2  137
Số bé là : 137  2  135
Đáp số : Số lớn : 137 ; số bé : 135 Chọn D II. TỰ LUẬN Câu 1: Phương pháp:
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải: a) 56 và 8;
Số lớn là: 56  8 : 2  32 Số bé là: 32  8  24 Hai số đó là: 24 và 32 b) 79 và 39
Số bé là: 79  39 : 2  20
Số lớn là: 20  39  59 Hai số đó là: 20 và 59 c) 125 và 53.
Số lớn là: 125  53 : 2  89
Số bé là: 89  53  36 Hai số đó là: 36 và 89. Câu 2: Phương pháp:
- Tìm số học sinh của trường. Sau đó tìm số học sinh nam, và số học sinh nữ chính là giải quyết
bài toán tìm hai số khi biết tổng và hiệu của hai số đó.
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Số học sinh của trường là: 200  4  800 (học sinh) Ta có sơ đồ:
Số học sinh nữ là : 800 120 : 2  340 (học sinh)
Số học sinh nam là : 340  120  460 (học sinh)
Đáp số : 340 học sinh nữ, 460 học sinh nam Câu 3:
Phương pháp: số thứ hai bằng số thứ nhất cộng thêm 8, hay hiệu của số thứ hai và số thứ nhất
bằng 8. Tổng của hai số bằng 48. Tìm hai số khi biết tổng và hiệu của hai số đó. Cách giải:
Số thứ nhất là: 48  8 : 2  20
Số thứ hai là: 20  8  28
Đáp số: số thứ nhất là 20, số thứ hai là 28. Câu 4: Phương pháp:
- Tổng chiều dài và chiều rộng của sân bóng chính là nửa chu vi của sân bóng.
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Nửa chu vi của sân bóng là: 280 : 2  140 m Ta có sơ đồ:
Chiều dài sân bóng là: 140  40 : 2  90m
Chiều rộng sân bóng là: 90  40  50m Diện tích sân bóng:    2 90 50 4500 m  Đáp số : 2 4500 m Câu 5:
Phương pháp: Tìm tổng của ba số đó, sau đó tìm tổng của số thứ nhất và số thứ ba.
Tìm số thứ nhất và số thứ ba biết tổng và hiệu của hai số đó.
- Tìm hai số khi biết tổng và hiệu: + Bước 1: Vẽ sơ đồ
+ Bước 2: Lựa chọn 1 trong hai cách giải: Cách 1: Cách 2:
Số bé = (tổng – hiệu) : 2
Số lớn = (tổng + hiệu) : 2
Số lớn = Số bé + hiệu
Số bé = Số lớn – hiệu Cách giải:
Tổng của ba số đó là: 42  3  126
Tổng của số thứ nhất và số thứ ba là:126  42  84 Ta có sơ đồ:
Số thứ nhất là: 84 14 : 2  35
Số thứ ba là: 35  14  49
Đáp số : Số thứ nhất là 35 ; số thứ hai là 49.