Bài tập Mạch điện 2 (có lời giải) hay, hấp dẫn nhất

mquanik@yahoo.com Bài tập: Mạch Điện 2 Bài 1:
Cho đường dây với các thông số sau: l = 100 km R = 6 /  m 0 -3 L = 1,6.10 H/km 0 -9 C = 6,4.10 F/km 0 6 G = 10 S/km 0 f = 100 Hz U = 1 kV 1 0 I = 500 -  15 A 1
1/ Xác định các hệ số: , Z , V,  C
2/ Xác định U và hệ số phản xạ sóng giữa đường dây Giải: a/Ta có:   2 f   2. .  100  200  (rad/s) I I 1 3 Z  R  j L  = 6 + j () o o o -6 -6 Y  G  j C  10 +4,0212.10 j (S) o o o U U 1 3
  Z .Y  0,0037 + 0,0034j (1/km) o o  = 0,0037 (neper/km)   = 0,0034 (rad/km) O x l/2 l Zo Z  1013,2 - 664,56j () C Yo  5 V=  1,8428.10 (km/s)  V 3 = 1,8428.10 (km) f b/ Ta có: 1 A  U  Z .I  5 4  2,8816.10 - 9,4922.10 j 1 1 C 1 2 1 A  U Z .I  5 4  -2,8716.10  9.4922.10 j 2 1 C 1 2 mquanik@yahoo.com Mặc khác:  x  x
U  A .e  A .e  U  U x 1 2 x x   A  A 1 x 2 x I  .e  .e  I  I  x x x Z Z  C C Tại điểm: x = l/2 thì .l/ 2 .l/ 2 U  U  A .e  A .e  U  U 3 l / 2 1 2 l/ 2 l/ 2 5 4
 -1,3683.10 - 6,4567.10 j (V)  -136,83 - 64,567j (kV) A  A 1 .l / 2 2 .l/ 2 I  I  .e  .e  I  I 3 l / 2 l/ 2 l/ 2 Z Z C C  479,95 144,69j (A) mquanik@yahoo.com Bài 2: l  30 km Z  500  c -3 =3.10 Neper/km Z  500  2
GTHD của điẹn áp ở dầu đường dây là U1 = 120V
a/ Xác định GTHD của U2;I2 cuối đường dây
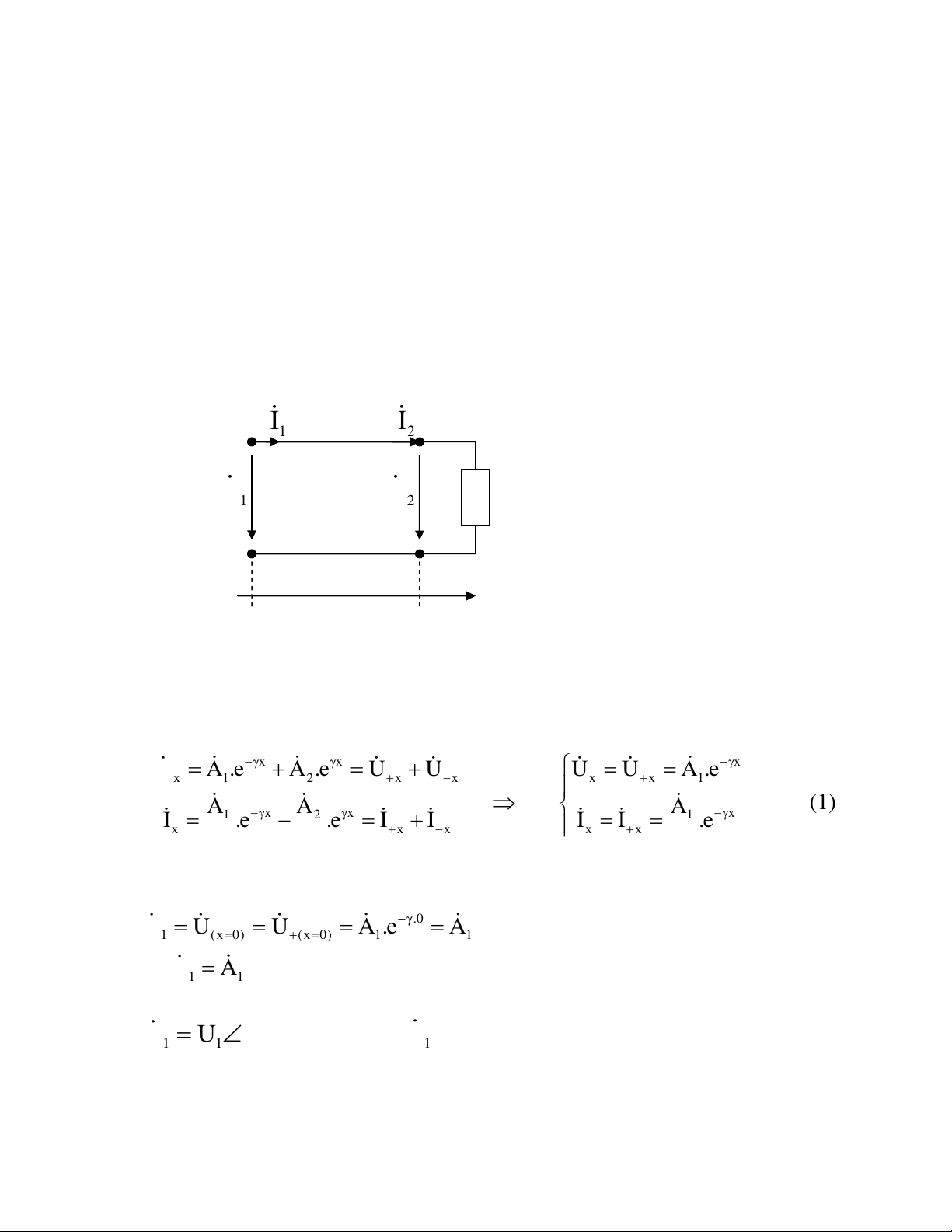
b/ Xác định hiệu suất truyền tải  của đường dây. Giải: I I 1 2 U U 1 2 Zc O l x
a/ Do: Z  R đường dây gần như vận hành ở chế đọ hoà hợp tải nên:   0 . Tức c c
là mọi điểm trên đường dây chỉ có ST mà không có SPX
Xây dựng công thức theo hệ trục như hình vẽ:  x  x   x
U  A .e  A .e  U  U U  U  A .e  x 1 2 x x x x 1      (1) A  A  A 1 x 2 x 1  x I  .e  .e  I  I I  I  .e   x x x  x x Z Z Z  C C  C Ta có .0 U  U  U  A .e  A 1 (x 0) (x0) 1 1  U  A 1 1 j.U1 U  U   U .e  A (2) 1 1 1 U 1 1
Thế (2) vào (1) ta được: mquanik@yahoo.com j.U    1 ( j ) x U  U .e .e x 1  j.U 1  U .e 1 ( j)x I  .e x Z  C  j(  U x ) x 1 U  U .e e x 1    U  j( x) 1 x U1 I  .e e  x Z  C  j(  U l) l 1 U  U  U .e e 2 ( x l) 1    U  j(  1 U l) l 1 I  I  .e e  2 ( x l) Z  C   l (30. 3
U  U .e 120.e 3.10 )  109.6717 (V) 2 1    3 U  120  1 l (30.3.10 ) I  .e  .e  0.2193 (A)  2 Z 500  C
b/ Hiệu suất truyền tải  : Ta có P2   .100% P1
P  U .I .cos(   )  2 2 2 U2 I2 Với:  P  U .I .cos(   )  1 1 1 1 U 1 I
Chế độ hoà hợp tải nên:  U  U ; I  I 1 1  1 1 U  U ; I  I  2 2  2 2   U U 1 1    Z  R  c c  I I 1 1   U U 2 2    Z  R c c  I I  2 2   U ;I cu`ng pha 1 1  U ;I cu`ng pha  2 2 cos(   )  1  U I 1 1  cos(  ) 1  U I 2 2 mquanik@yahoo.com l U  A 120 U  U .e 1 1 2 1    A  U ;  U 1 .0 1 1 l I  I  .e    I .e 1 ( x 0)   2 Z Z Z  C C  C  U l 1 l U .e . .e 1 U .I Z 2 2 C    .100%  100% U .I U1 1 1 U . 1 ZC 2  l  e .100%  85% mquanik@yahoo.com Bài 3:
Cho đường dây không tiêu tán có: l  100 km 3   3,4.10 rad / km U 110 2 sin( t  ) kV 2(t )
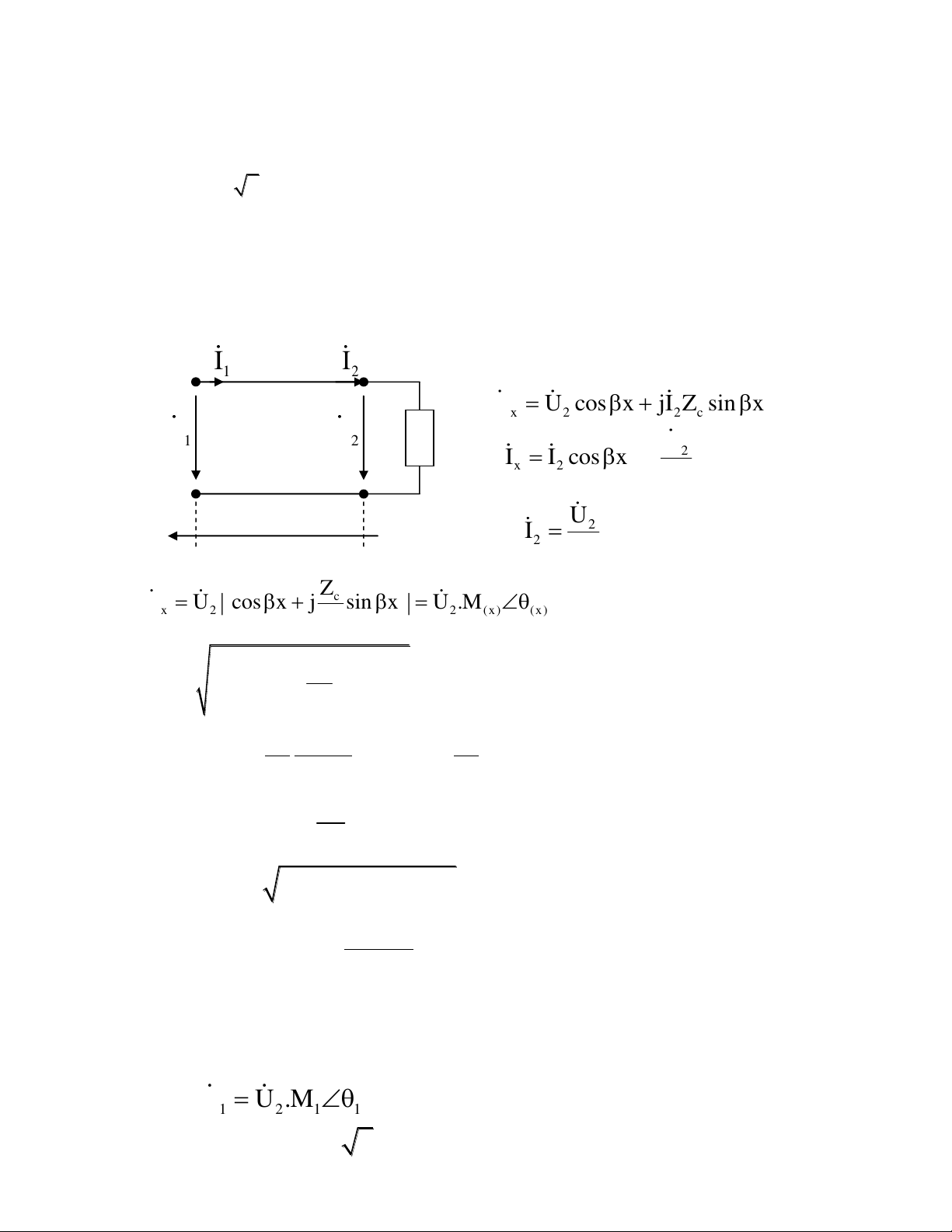
Xác địng U2(t) ở đầu đường dây trong các trường hợp có: a/ Z2 = Zc b/ Z2 = 0,5Zc Giải: I I 1 2 Ta có:
U  U cosx  jI Z sinx x 2 2 c U U  1 2 Z  U 2 2 I  I cos x  j sin x  x 2 Z  c U x l O 2  Mà I2 nên: Z2  Z  c U  U  cosx  j sin x   U .M  x 2 2 ( x ) ( x ) Z  2  2  Z  2 c M  cos x   sin x  x Z  2   Z sinx   Z  c c   arctan    arctan  tan x  ( x ) Z cos x Z  2   2  Zc   a/ Z = Z 1 2 C Z2 2 2
M  cos x  sin x  1 x  sinx    arctan  arctan tan x (x )      cosx  M  M 1 1 ( x l)   
 arctan tan l  0,34 (rad) 1 ( x l)   U  U .M   110.1 0  ,34 110 0  ,34 1 2 1 1  U 110 2 sin( t   0,34) (kV) 1( t ) mquanik@yahoo.com b/ Zc Z = 0,5.Z   2 2 C Z2
M  cos x  2sin x2 2 2 2  cos x  4sin x x  sinx    arctan 2.  arctan 2.tan x (x )      cosx  2 2 M  M
 cos l  4sin l  1,915 1 ( x l)   
 arctan tanl  0,616 (rad) 1 ( x l)  
U  U .M   110.1,915 0  .6157  210,62 0  ,616 1 2 1 1  U  210,62 2 sin( t   0,616 ) (kV) 1( t ) mquanik@yahoo.com Bài 4:
Một đường dây không tiêu tán. Có chiều dài l, ZC = RC, dòng điện có tần số f,
tải cuối đường dây là cuộn cảm L.
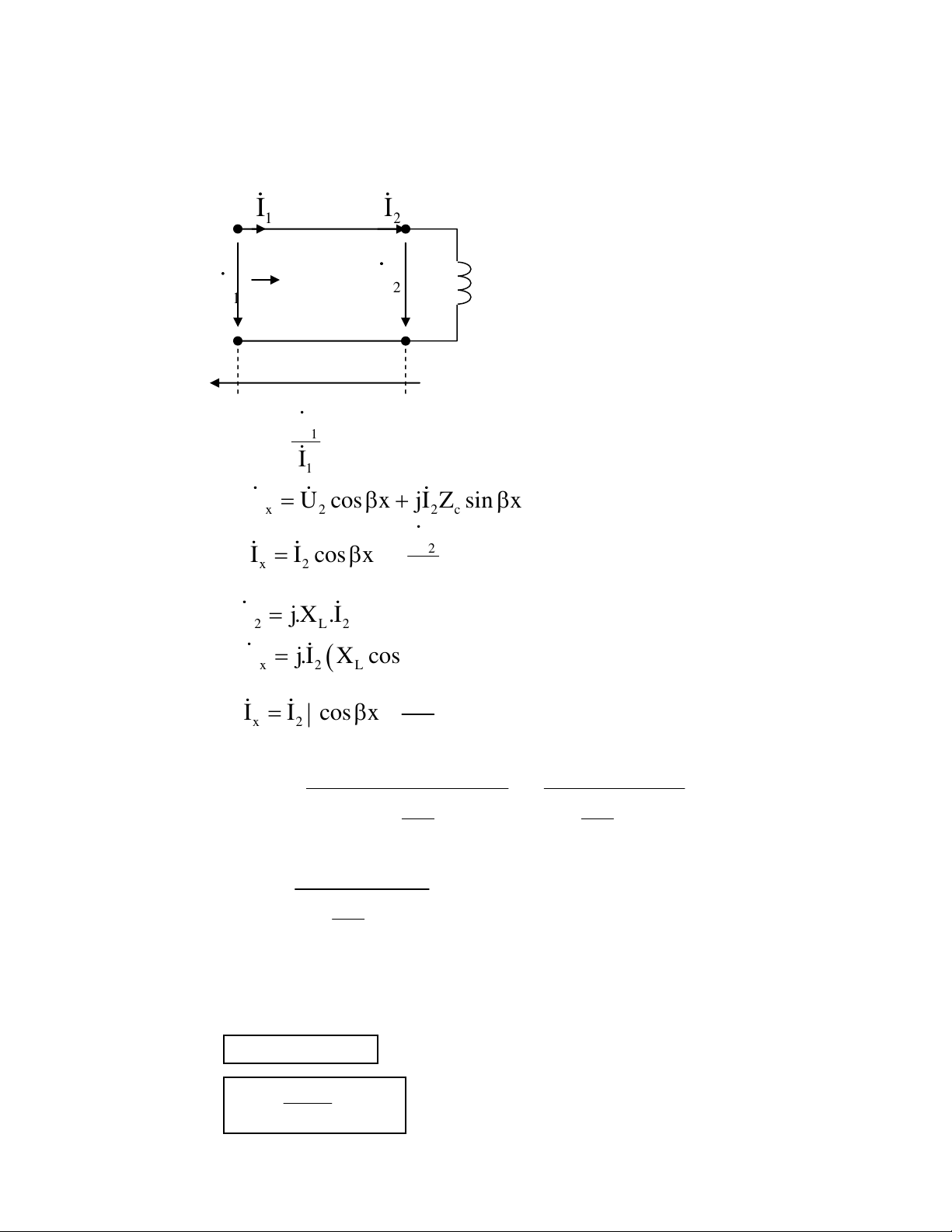
Xác định L để hệ đường dây và tải trở thành mạch cộng hưởng áp Giải: I I 1 2 U L 2 U1 Z 1V x l O U1 Z  V1 I1
U  U cosx  jI Z sin x x 2 2 c   U2 I  I cos x  j sin x  x 2 Z  c U  j.X .I 2 L 2
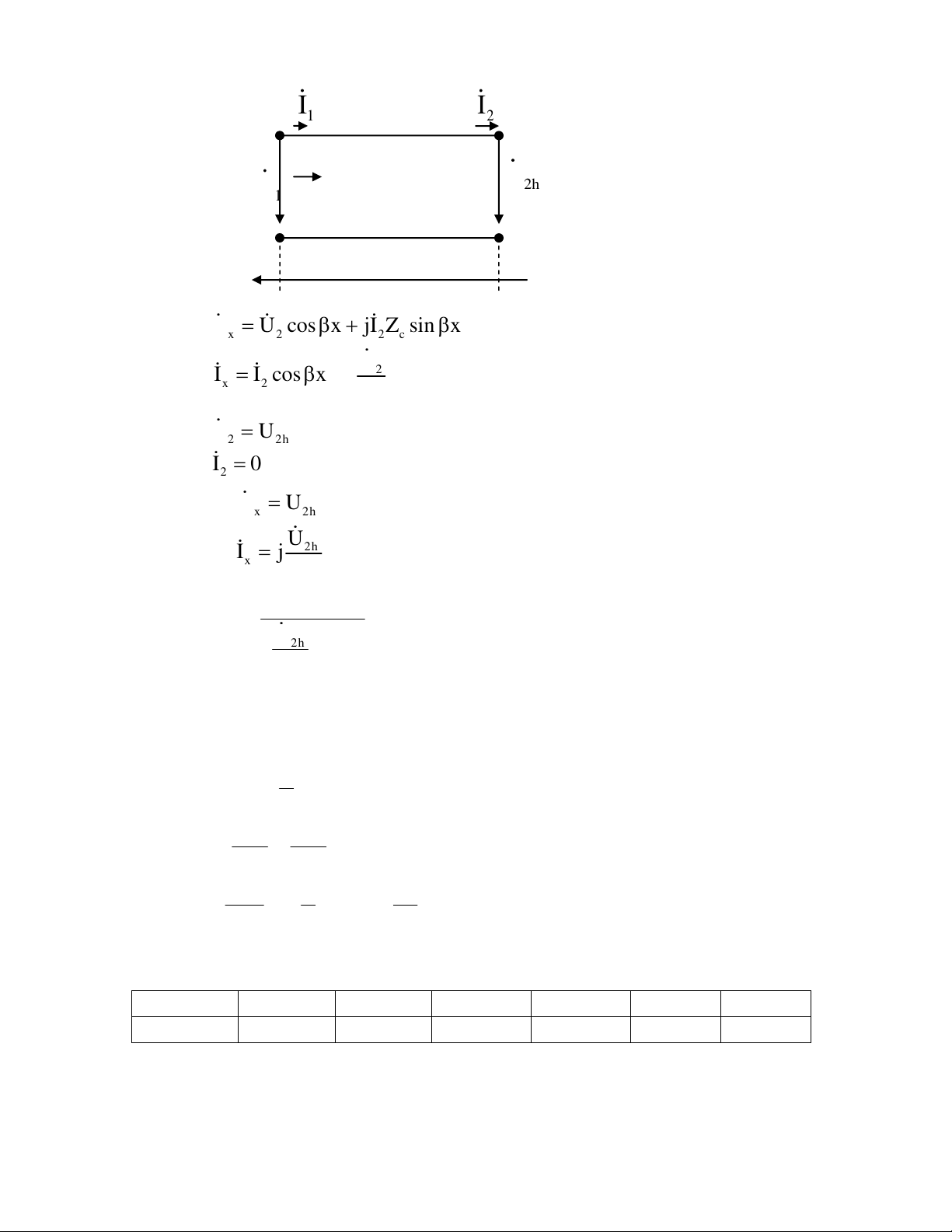
U  j.I X cosx  Z sin x x 2  L c     X  L I  I   cosx  sin x  x 2 Z   c  X cos x  Z sin x X  Z tan x L c  Z  j  L c j ( V x) X X L cos x  sin x L 1 tan x Z Z c c X  Z tan l L c  Z  j 1 V XL 1 tan l Zc  Z  0 1 V  X  Z tan l  0 L c  X  Z tan l L c Zc  L   tan l 2. .  f mquanik@yahoo.com Bài 5: I I 1 2 U2h U 1 Z 1V x l O
U  U cosx  jI Z sin x x 2 2 c   U2 I  I cos x  j sin x  x 2 Z  c U  U 2 2h I  0  2 U  U cosx x 2h    U2h I  j sin x  x Z  c U cos x 2h Z    j.Z .cotan x V c   ( x ) U2h j sin x Zc  Z   j.Z .cotan l V c   1 Z  0  cotan l  0 V   1 
 l  k k=1,3,5,....,2n+  1,.... 2 2 f  2 f     (dd tren ko: V=c) V c 2 f  l  c 6   k  f  k  2,5.10 k (Hz) c 2 4.l  2, 5.k (MHz) k 1 3 5 9 11 … f(MHz) 2.5 7.5 12.5 17.5 22.5 … mquanik@yahoo.com
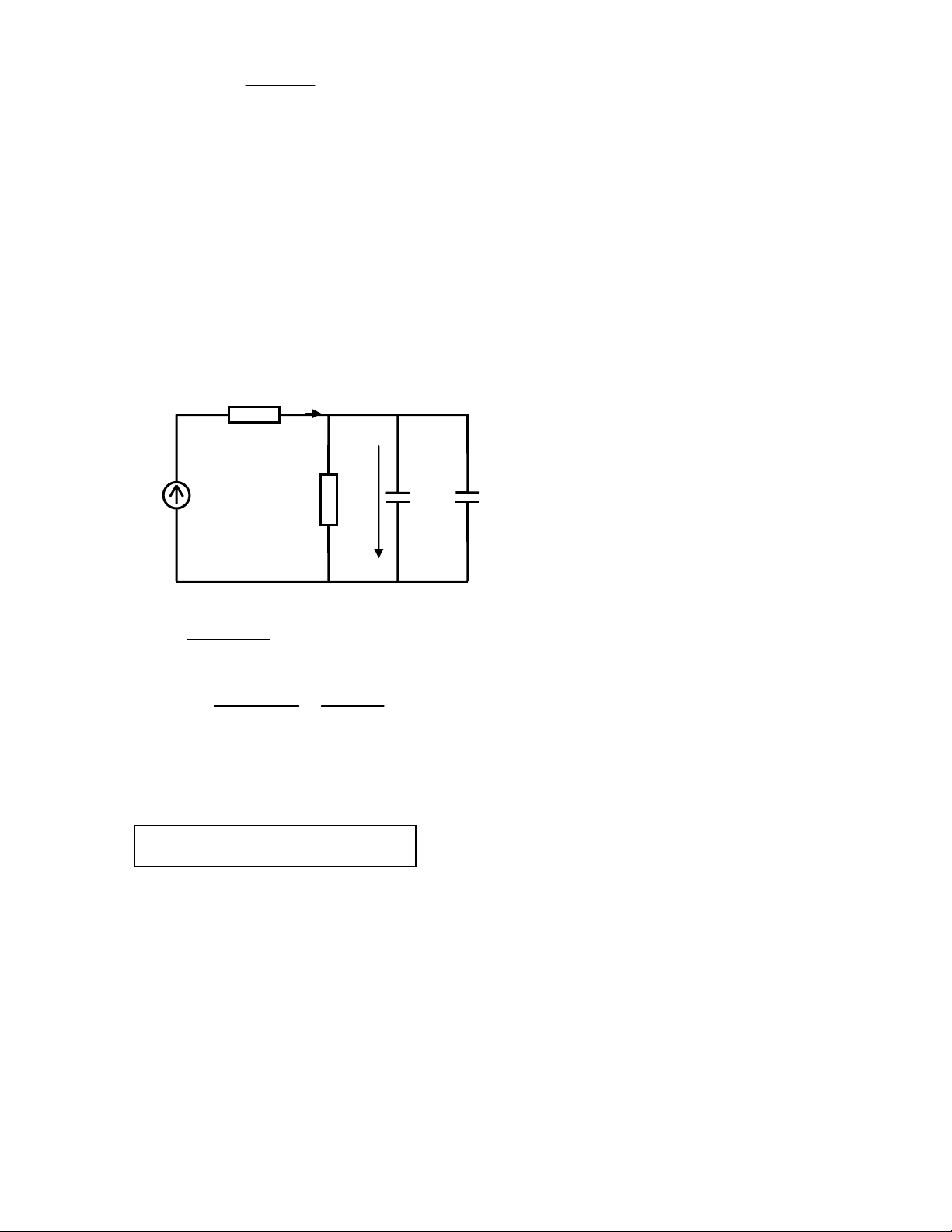
Bài tập 6 : Cho mạch điện như hình vẽ: L i i1 i2 K R1 e(t) R2 C
Đóng khoá K khi e  E sin( t   )
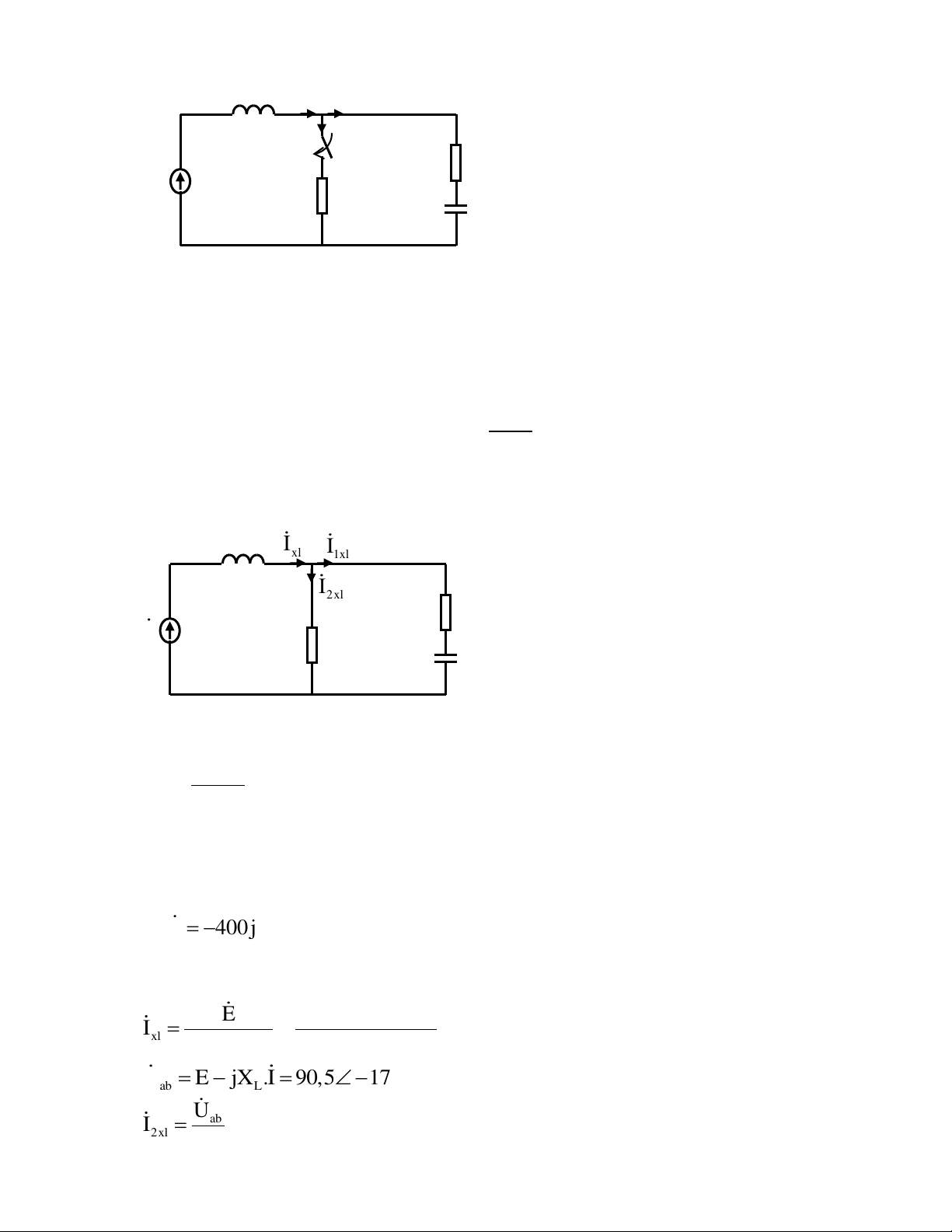
 (V) đạt giá trị cực đại âm (t ) m Xác định i biết: 2( t ) R  25 R  50 1 2 L  0.25H C  400 F  E  400V f  50Hz m Giải: Ta có: i  i i 2(t) 2td(t) 2xl(t)  Xác định i 2xl(t )
Mạch điện sau đóng mở ở chế độ xác lập XL I I xl a 1xl I2xl R1 E R2 XC b X  2 f  .L  78,5  L   1 X   7,96  C   2 f  .C
Tại thời điểm t = 0 thực hiện quá trình đóng cắt Nên o e
 E sin  E    9  0 (t ) m m o  e  400sin(314t  90 ) (t )  E  4  00j (V) Ta có:
Z  R //(R  j.X ) 17  3,5j ( )  ab 2 1 C E 4  00j o I    5,2 167,2 (A) xl j.X  Z 78,5j 17  3,5j L ab o
U  E  jX .I  90,5 178.8 (V) ab L Uab o I  1,8 178,8 (A) 2xl R2 mquanik@yahoo.com o  i
1,8sin(3,14t 178.8 ) (A) 2xl(t )  Xác định i 2td(t )
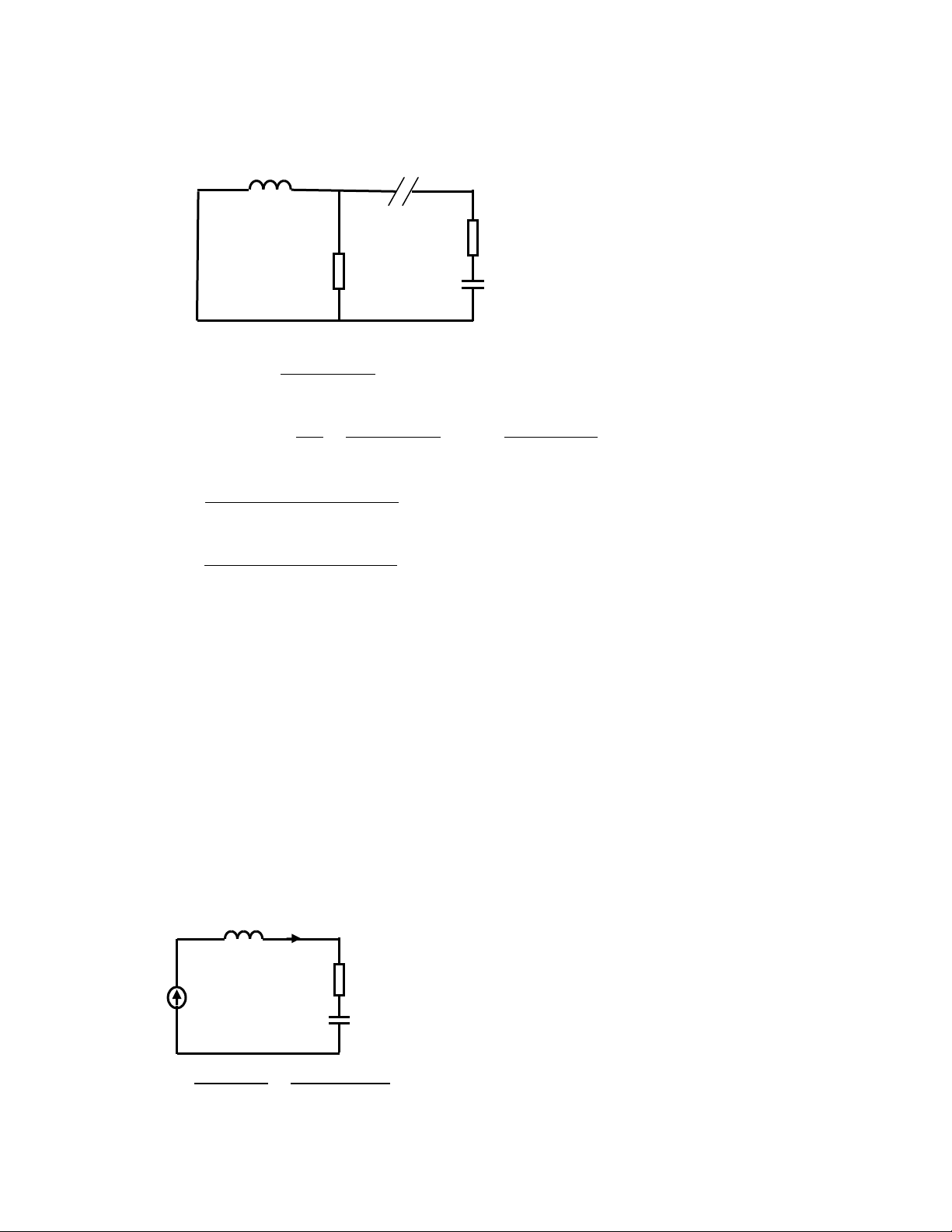
Xác định số mũ đặc tính p: pL a R1 R2 1/ pC b 12,5p Z  R // pL  ab 2 50  0, 25p 1 12,5p 1 Z  Z  R    25  v(p) ab 1 6 pC 50  0, 25p p.400.10 2 75p  7500p  50000  (200  p)p 2 75p  7500p  50000 Z   0 v(p) (200  p)p 2
 75p  7500p  50000  0 p  50   64,55j 1  p  50   64,55j  2 5  0t  i  2.A.e .cos(64,55t+) 2td(t )
Trong đó A và  là các hệ số cần xác định.
Xác định sơ kiện: vì trong biểu thức thành phần tự do có hai hệ số cần xác định nên
ta cần xác định 2 sơ kiện là i ;i’ 2(0) 2(0)  i  i (0) ( 0  )
Xác định: i(o),uc(o) theo luật đóng mở chỉnh:  u  u  c(0) c( 0  )
Xét mạch trước đóng mở (khi khoá K chưa mở) L i R1 e(t) C X  X 78,5  7,96 L c tg    2,8216 R 25 1 o    70,4 mquanik@yahoo.com E 400 m I    5,34(A) m 2 2 2 2 R  (X  X ) 25  (78,5  7,96) 1 L C o
 i  5,34.sin(314t 160,4 ) (A) (t ) U
 I .X  5,34.7,96  42,50 (V) Cm m C o  u
 42,50.sin(314t  250,4 ) (V) C(t ) o i   5,34.sin( 1  60,4 )  1  ,79 (A)  (0)   o u  42,50.sin( 2  50,4 )  40.03 (V)  C(0)
Hệ phương trình mô tả sau đóng mở: L i i1 i2 K R1 e(t) R2 C  i  i  i  0 ( t ) 1( t ) 2( t )   di L  i .R  e (I) 2( t ) 2 ( t ) dt   1 i .R  i .dt  i .R  0   2( t ) 2 1( t ) 1( t ) 1  C i  i  i  0 (0) 1(0) 2(0) 
Thay t = 0 vào hệ (I) ta được ' L.i  i .R  e (0) 2(0) 2 (0) i .R  u i .R  0  2(0) 2 C(0) 1(0) 1  1  ,79  i  i  0 i  i 1,79 1(0) 2(0)  1(0) 2(0)  '  0,25.i  50.i  4  00  25.i  50.i  4  0,03 (0) 2(0) 1(0) 2(0)   50.i  40,03  25.i  0  ' 0, 25.i  50.i  4  00 2(0) 1(0)  (0) 2(0) i  1,7272 (A) 1(0)   i  0  ,0628 (A) 2(0)  'i  1  578,44 (A /s)  (0)
Đạo hàm các vế của các phương trình trong hệ pt(I) mquanik@yahoo.com 
i  i  i  0
i  i  i  0 ( t ) 1( t ) 2( t )  ( t ) 1( t ) 2( t )  Li  i .R  e
 0,25.i  i .50  e ( t ) 2( t ) 2 ( t ) ( t ) 2( t ) ( t )   1      i .50 2500.i i .25  0 i .R  i  i .R  0  2(t) 1( t ) 1( t ) 2( t ) 2 1( t ) 1( t ) 1  C
i  i  i  0  1
 587,44  i  i  0 (0) 1(0) 2(0)  1(0) 2(0)  
0,25.i  i .50  e
 i .50  2500.1,7272  i .25  0 (0) 2(0) (0) 2(0) 1(0)   i .50  2500.i  i .25  0  0, 25.i  i .50  e 2(0) 1(0) 1(0)  (0) 2(0) (0) i    i  1  587,44 1(0) 2(0)  i    1  000,72 (A /s)   1(0) i .25  i .50  4318   1(0) 2(0)  i  5  86,72 (A / s)  2(0) 0, 25.i  i .50  e  (0) 2(0) (0) Ta có: i  i  i 2(t ) 2td(t ) 2xl(t ) o i
1,8sin(3,14t 178.8 ) (A) 2xl(t ) 5  0t i
 2.A.e .cos(64,55t+) (A) 2td(t ) i  i  i 2(0) 2td(0) 2xl(0)  0
 ,0628  2.A.cos()  0,0377  A.cos()  0  ,01255 (1) Ta có: i  i  i 2(t ) 2td(t ) 2xl(t ) o i
 314.1,8.cos(3,14t 178.8 ) (A/s) 2xl(t ) 5  0t i  2A.e 5
 0.cos(64,55t  )  64,55.sin(64,55t  ) (A/s) 2td(t )   i  i  i 2(0) 2td(0) 2xl(0)  5  86,72  2A 5
 0.cos  64,55.sin  o 314.1,8.cos( 1  78.8 )
 21,72 129,1.Asin  100Acos (2) Từ (1)(2) ta có Acos  0  ,54
  129,1.Asin100Acos 21,72 Acos  0  ,01255 tg  14  ,18      Asin   0,178 Asin   0,178 o   85,97  A  0,178 Vậy: o i
1,8sin(3,14t 178.8 ) (A) 2xl(t ) mquanik@yahoo.com 5  0t o i  0
 ,35e .cos(64,55t+85,97 ) (A) 2td(t ) o 5  0t o  i
1,8sin(3,14t 178.8 )  0,35e .cos(64,55t+85,97 ) (A) 2(t) mquanik@yahoo.com
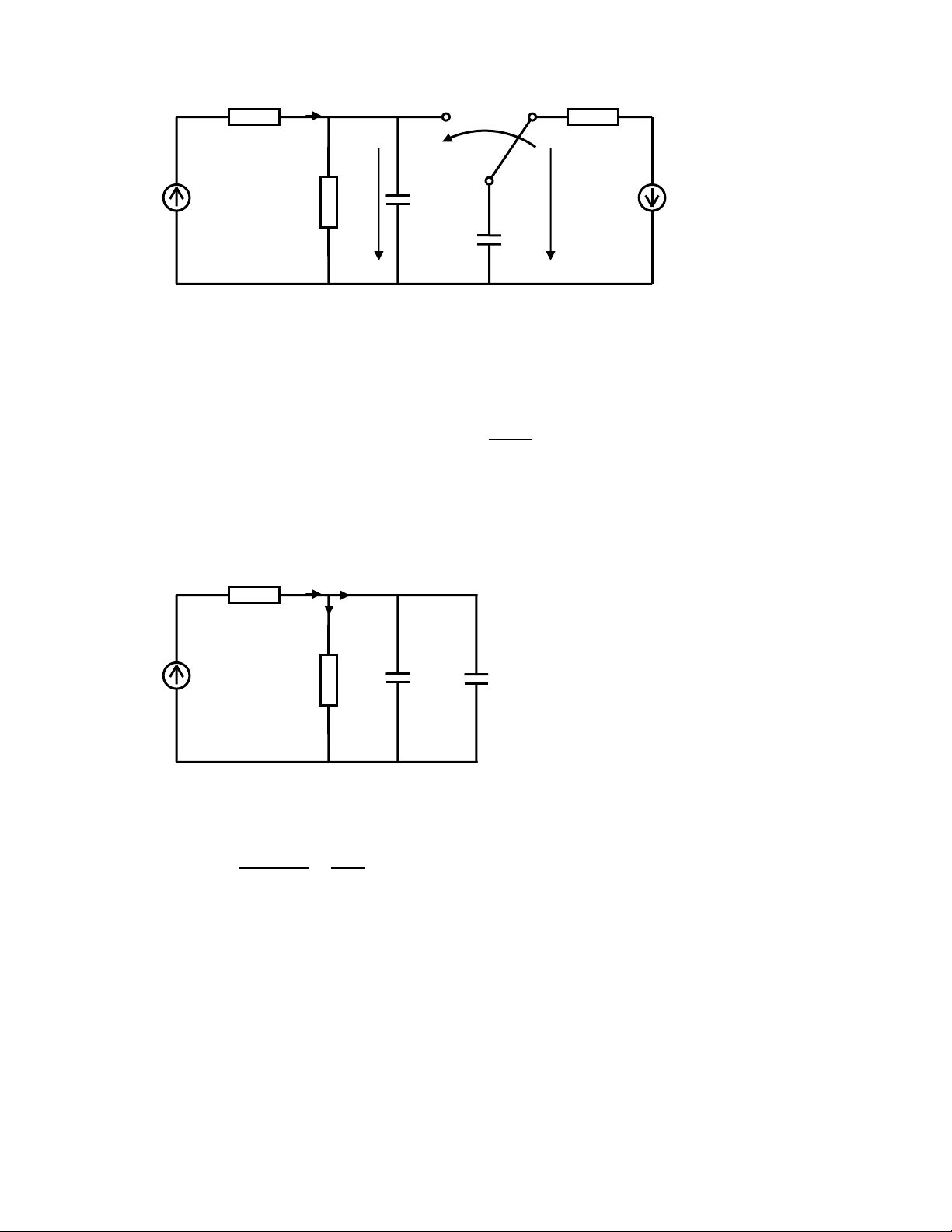
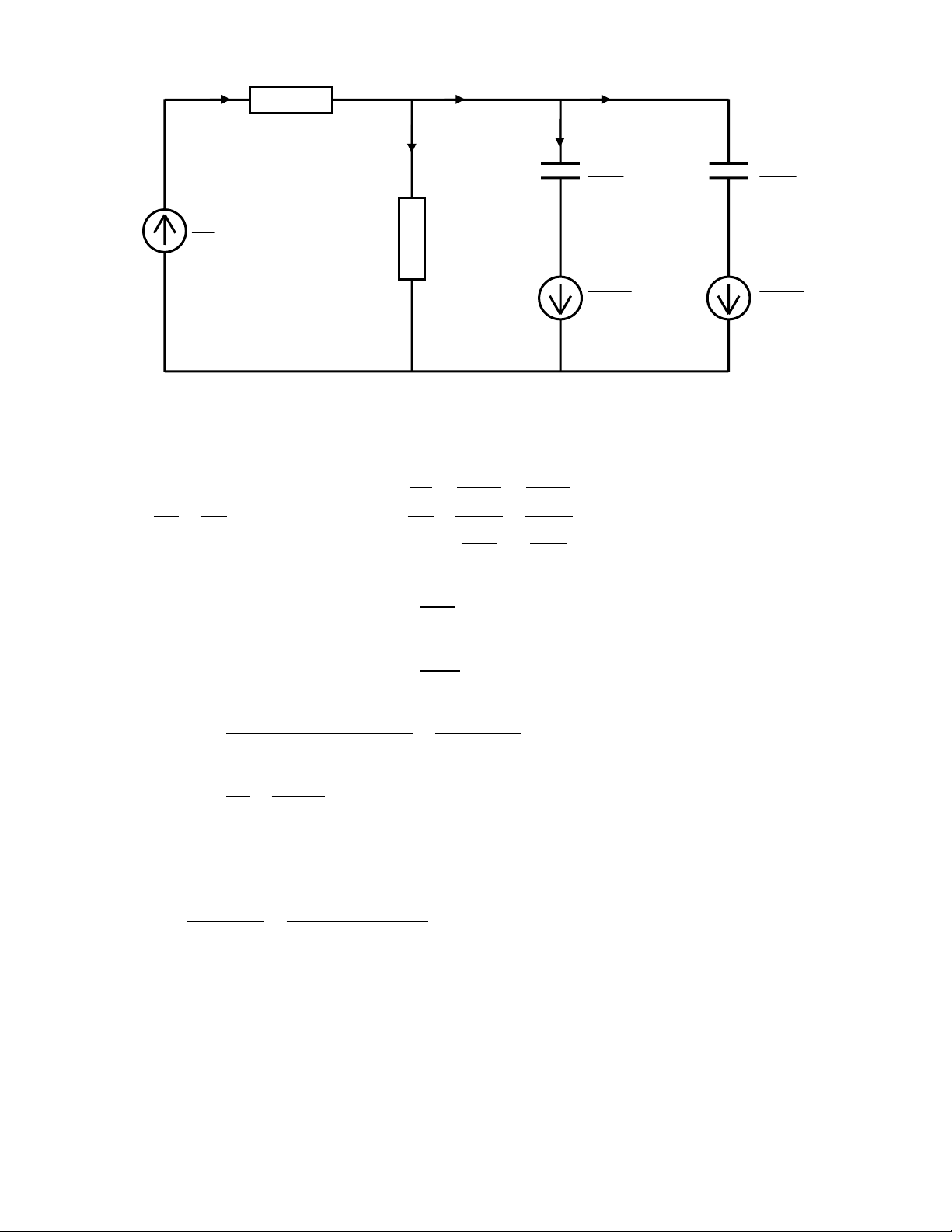
Bài tập 7: Cho mạch điện như hình vẽ: R R 1 i(t) 2 1 2 K E E 1 R C 2 3 3 C4 U U 3 4
Xác định i biết các nguồn trong mạch là nguồn hằng và các thông số sau: ( t )
R  300 R  R  600 1 2 3 C  300 F  C  200 F  3 4 E  36 V E  6 V 1 2 Giải:
A. Phương pháp tích phân kinh điển: Ta có: i  i i (t) td(t) xl(t)  Xác định i xl( t )
Mạch điện sau đóng mở ở chế độ xác lập R1 I  xl I 0 c Ixl E1 R C C 3 3 4
Vì nguồn E1 là nguồn hằng nên Ic = 0
Tại thời điểm trước đóng cắt E 36 1 i  I    0.04(A) xl(t ) xl R  R 900 1 3  Xác định i td( t )
Xác định số mũ đặc tính p:
Mạch điện sau đóng mở được đại số hóa theo p mquanik@yahoo.com Hở mạch R1 R 1 1 3 pC pC 3 4  1 1  Z  R // R     v(p)  1 3 pC pC  3 4  1 1  200   200  1 1 p(C  C ) 3 4  pC pC 3 4 1  200  4 5.10 p 1 Z  200   0 v(p) 4 5.10 p 1   200  4 5.10 p  p  10 
Dạng của thành phần tự do là: 10t i A.e   td(t )
Trong đó A hệ số cần xác định.
Xác định sơ kiện: vì trong biểu thức thành phần tự do có một hệ số cần xác định nên
ta cần xác định 1 sơ kiện là i(0)
Xác định: u3(o),u4(o) theo luật đóng mở không chỉnh:
Xét mạch trước đóng mở (khi khoá K chưa mở) R R 1 i(t) 2 E E 1 R C C 2 3 3 4 U U 3( 0  ) 4( 0  ) mquanik@yahoo.com E1 u  U   0.04 600  24V 3( t ) 3 R  R 1 3  u  24 3( 0  ) u  u  E  6  V 4(t ) 4 2  u  6  (V) 4( 0  )
Theo luật đóng mở không chỉnh: (C  C )U  C U  C U 3 4 3(0) 3 3( 0  ) 4 4( 0  )  500 U  300 24  200 6 3(0)  U  U 12 V 3(0) 4(0)
Hệ phương trình mô tả sau đóng mở: R1 i(t) E1 R C C 3 3 4 U3(t) E  U 1 3( t ) i  ( t ) R1 E  U  1 3(0) 36 12  i    0.08(A) (0) R 300 1 Xác định A: A  i  i  0.04 (0) xl(0) Vậy: 1  0t  i  0.04 (1 e ) 2(t )
B/ Giải bằng phương pháp toán tử LAPLACE
Các sơ kiện độc lập được tính như ở trên (phương pháp tích phân kinh điển): U  U 12 V 3(0) 4(0) Sơ đồ toán tử hóa: mquanik@yahoo.com R1 I I C(p) C4(p) 1 I1(p) I I C3(p) 3(p) 1 1 pC pC 3 4 E1 p R3 U U 3(0) 4(0) p p 2 Chọn   0 2(p)
Ta có điện thế đỉnh tạo điểm 1: E U U 3(0) 4(0) 1  1 1  p p p    pC  pC     3 4 1(p) R R R 1 1   1 2 1 pC pC 3 4     E 3 4 5 10  5 10  p 1    C .U  C .U 1(p) 3 3(0) 4 4(0) pR1     0.12 3 4
5 10  5 10  p   0.006 1(p) p 0.12  0.006p 240  12p     1(p) 4  3 p(5 10 p  5 10 ) p(p  10) 24 12     (V) 1(p) p p  10 Do đó: 1  0t   24 12e 1( t ) 1  0t E     1 1( t ) 36 24 12e i   ( t ) R 300 1 1  0t  i  0.04(1 e ) (t ) mquanik@yahoo.com Bài tập 8: L
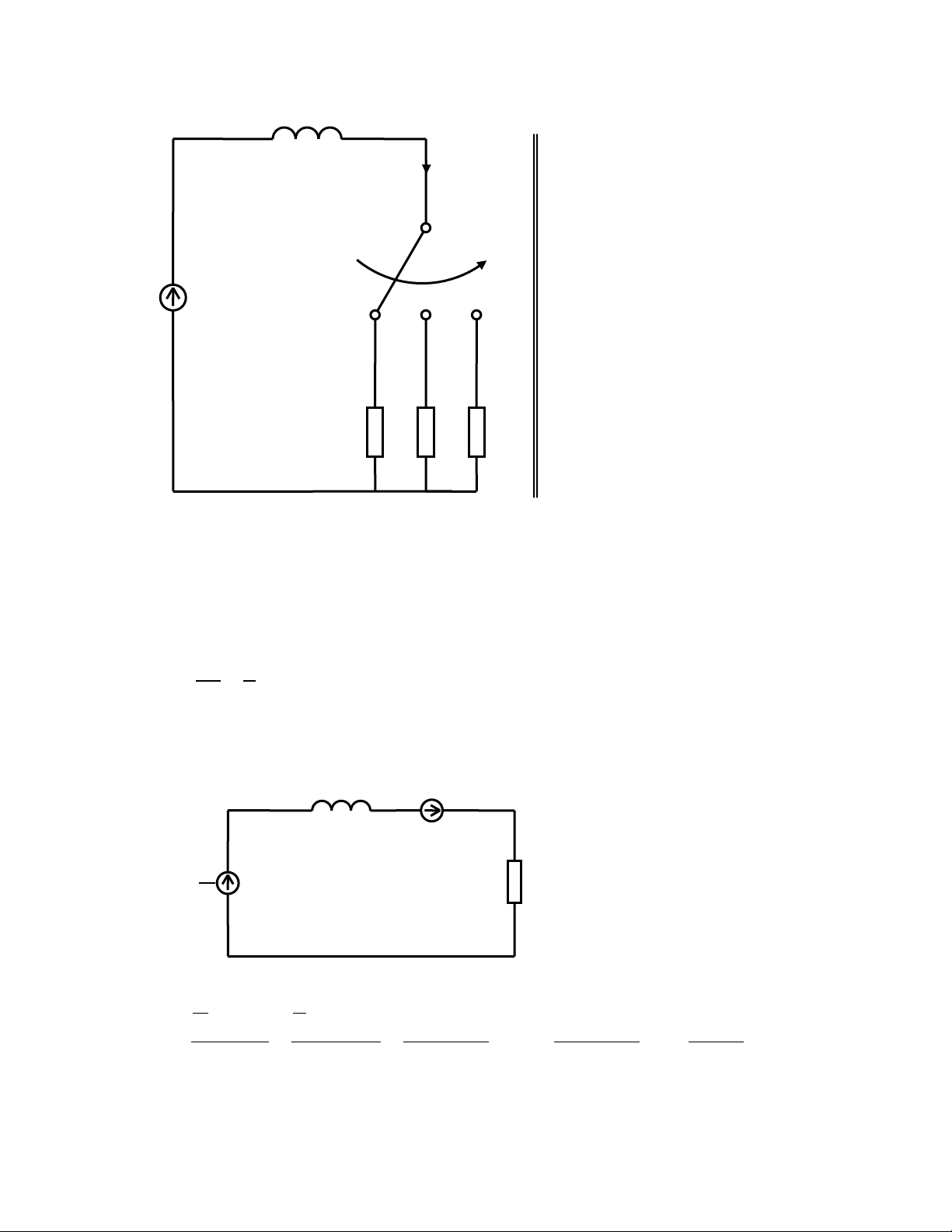
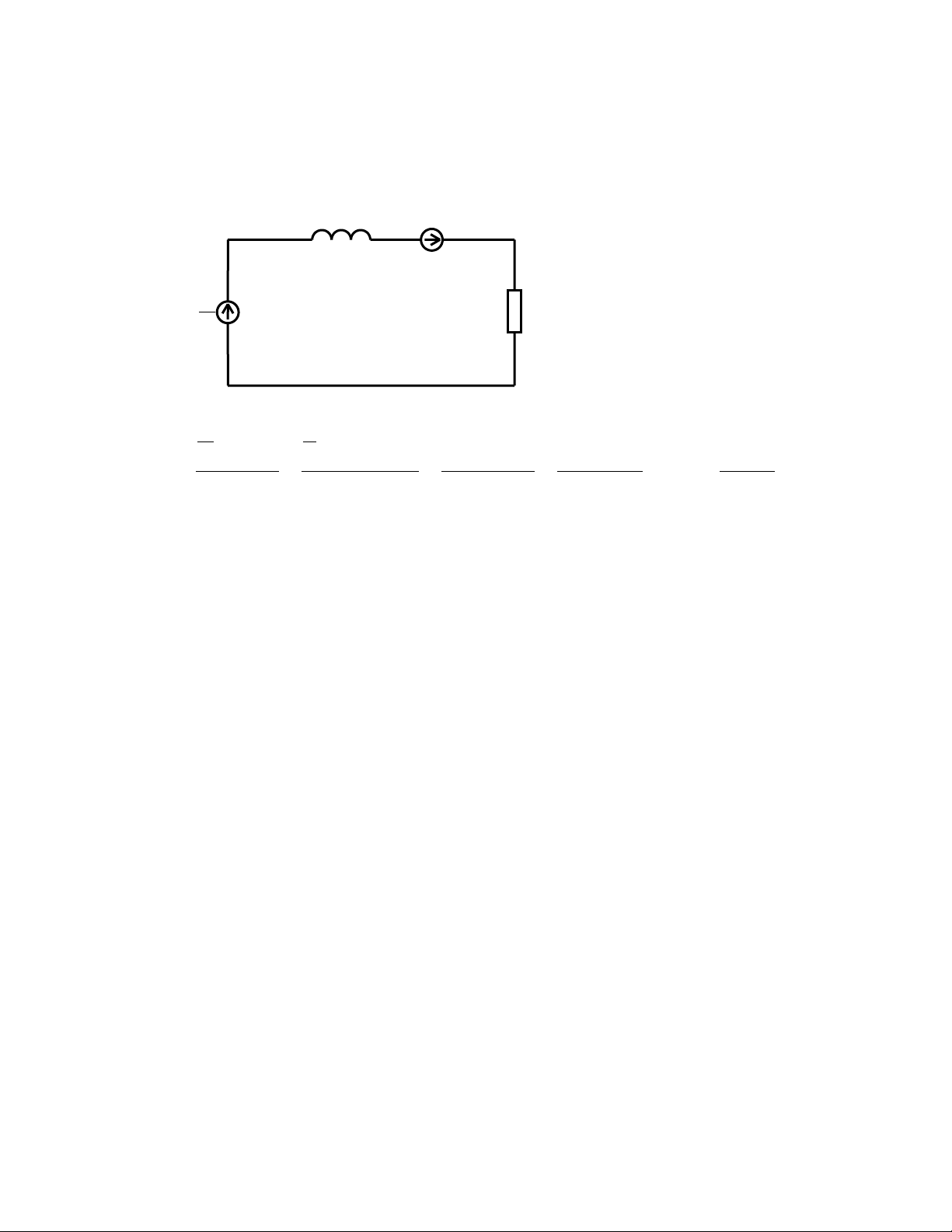
Cho mạch điện với các thông số i(t) sau: E  6 (E) L  100 mH E R  2  1 1 2 3 R  4  2 t = R 0 c  hu 6 yể  3 n K từ 1 sang 2
t = 25 ms chuyển K từ 2 sang 3 R R R 1 2 3
Hãy xác định dòng điện i(t) khi dịch chuyển K sang vị trí 3. Biết khi khóa K còn ở vị
trí 1 thì mạch ở chế độ xác lập Giải: A. Khi t < 25 ms
 Tính sơ kiện độc lập: i(0)
Trước khi khóa K chuyển từ vị trí 1 sang 2: E 6 i    3 (A) ( 0  ) R 2 1 Theo LDM chỉnh ta có: i  i  3 (A) L(0) L( 0  )  Sơ đồ phức hóa: pL Li(0) E R p 2 Ta có: E 6  Li  0.1 3 (0) p p 60  3p 40 p I    1.5  3 (p) pL  R p  0.1  4 p p  40 p p  40 p  40 2     4  0t 4  0t 4  0t  i 1.5(1 e )  3e 1.5(1 e ) (t ) mquanik@yahoo.com B. Khi t > 25ms
 Tính sơ kiện độc lập: i1(0)
Trước khi khóa K chuyển từ vị trí 2 sang 3: 3  4  0 2  5 1  0 i  i     1.5(1 e ) 2.05 (A) 3 1( 0  ) (t2.5 1  0 )  Sơ đồ phức hóa: pL Li(0) E R p 3 Ta có: E 6  Li  0.1 2.05 1(0) p p 60  2.05p 60 p I      2.05 (p)1 pL  R p  0.1  6 p p  60 p p  60 p  60 3     6  0t 6  0t 6  0t  i  (1 e )  2.05e 11.05e (t )1 mquanik@yahoo.com Bài tập 9: R i K 1 1 i i C 2 E C R2
Tính sơ kiện độc lập: uC(0) u  u  E 100 (V) C(0) C( 0  ) Sơ đồ phức hóa: R1 1 u E C(0) p p R2 1 pC 2 Chọn   0 2 Ta có: E uC(0)  1 1  p p     pC   1(p) R R R 1  1 2  1 pC  1 1  E     pC   Cu 1(p) C(0) R R pR  1 2  1    100 4 0.01  10 p 4  10 100 1(p) 200p    0.5 4 0.01  10 p   0.01 1(p)  p 0.5  0.01p 5000  100p 100 1     50 100 1(p) p 4 10 p   0.01 pp 100 pp 100 p 100 1  00t 1  00t 1  00t   50(1 e ) 100e  50(1 e ) 1(t ) mquanik@yahoo.com Ta có: 1  00t u        50(1 e ) C( t ) 1( t ) 2( t ) 1( t ) 1  00t u  C( t ) 50(1 e ) 1  00t i    0.25(1 e ) 2( t ) R 200 2