Bài tập nguyên lý kế toán | Đại học Văn Lang

BÀI TẬP CHƯƠNG 1
1.1 Trong một hộp có 20 sản phẩm, trong đó có 4 sản phẩm A, 6 sản phẩm B, 10 sản phẩm C. Từ hộp
a. Lấy ngẫu nhiên 1 sản phẩm. Tính xác suất lấy được sản phẩm A.
b. Lấy ngẫu nhiên 2 sản phẩm. Tính xác suất lấy được 2 sản phẩm A.
c. Lấy ngẫu nhiên 3 sản phẩm. Tính xác suất lấy được đúng 2 sản phẩm A.
d. Lấy ngẫu nhiên 3 sản phẩm. Tính xác suất lấy được ít nhất một sản phẩm A.
e. Lấy ngẫu nhiên 4 sản phẩm. Tính xác suất lấy được 4 sản phẩm cùng loại.
Đáp số: a. 1/5; b. 3/95; c. 48/95; d. 29/57; e. 77/1615
1.2 Một phòng có 21 nhân viên trong đó có 15 nhân viên nam và 6 nhân viên nữ. Tính xác suất
để chia các nhân viên này thành 3 nhóm sao cho mỗi nhóm có đúng 5 nhân viên nam và 2 nhân viên nữ. Đáp số: 441/2584.
1.3 Một hộp có 15 quả bóng bàn, trong đó có 4 quả màu trắng và 11 quả màu cam. Rút ngẫu
nhiên từ hộp ra 4 quả. Tính xác suất để lấy được a. 4 quả màu cam. b. đúng 2 quả màu cam.
c. ít nhất một quả màu cam.
Đáp số: a. 22/91; b. 22/91; c. 1364/1365.
1.4 Có 5 người lên 6 toa tàu điện (được đánh số 1, 2, 3, 4, 5, 6) một cách ngẫu nhiên. Tìm xác suất để a. 5 người lên toa số 1.
b. 5 người lên cùng 1 toa.
c. 5 người lên 5 toa khác nhau.
Đáp số: a. 1/7776; b. 1/1296; c. 5/54.
1.5 Có 3 sinh viên đi thi. Đặt
A là biến cố sinh viên 1 thi đậu
B là biến cố sinh viên 2 thi đậu
C là biến cố sinh viên 3 thi đậu
Hãy biểu diễn các biến cố sau theo A, B, C. a.
Cả ba sinh viên đều thi đậu. b.
Không có sinh viên nào thi đậu. c.
Có ít nhất một sinh viên thi đậu. d.
Chỉ có sinh viên 1 thi đậu. e.
Có nhiều nhất 1 sinh viên thi đậu.
1.6 Kiểm tra chất lượng 4 sản phẩm. Đặt
là biến cố sản phẩm thứ k tốt, k = 1, 2, 3, 4.
Hãy biểu diễn các biến cố sau theo .
a. Cả 4 sản phẩm đều tốt.
b. Chỉ có 3 sản phẩm tốt.
c. Có ít nhất một sản phẩm tốt.
1.7 Có tối đa 2 sản phẩm tốt.Cho A và B là
hai biến cố trong cùng không gian mẫu với , và . Tính . Đáp số:  , , .  , . 1.8 Cho A và B là
hai biến cố trong cùng không gian mẫu với và . Tìm . Đáp số: , .
1.9 Cho A và B là hai biến cố trong cùng không gian mẫu với và . Tính các xác suất sau: a. , b. , c. , d. . Đáp số: a. 0,6; 5/7; 0,5. b. 0,1; 0,4; 0,25. c. 0,75; 0,75; 0,9. d. 5/7; 8/13; 5/13
1.10 Một lô hàng có 10 sản phẩm trong đó có 4 phế phẩm. Lấy ngẫu nhiên lần lượt từng sản
phẩm cho đến khi lấy được 2 phế phẩm thì dừng. Tính xác suất để việc lấy bi dừng lại ở lần
thứ 4. Xét hai trường hợp: lấy có hoàn lại và lấy không hoàn lại. Đáp số: 108/625; 3/14.
1.11 Cho A, B là hai biến cố độc lập nhau. Chứng minh rằng ; ; cũng là các cặp biến cố độc lập.
1.12 Giả sử A, B là hai biến cố độc lập nhưng không xung khắc nhau, với ; . Tìm . Đáp số: .
1.13 Ba xạ thủ cùng bắn mỗi người một viên đạn vào một con thú. Xác suất bắn trúng con thú
của từng xạ thủ lần lượt là 0,4; 0,6; 0,8. Tính xác suất để
a. Cả ba xạ thủ bắn trúng.
b. Có đúng hai xạ thủ bắn trúng.
c. Có ít nhất một xạ thủ bắn trúng.
Đáp số: a. 0,192; b. 0,464; c. 0,952.
1.14 Một lô sản phẩm gồm hai loại chính phẩm và phế phẩm, trong đó số sản phẩm do máy I sản
xuất gấp 2 lần số sản phẩm do máy II sản xuất. Tỷ lệ phế phẩm do máy I sản xuất là 2%, do
máy II sản xuất là 3%. Lấy ngẫu nhiên một sản phẩm từ lô. a.
Tìm xác suất để sản phẩm lấy ra là phế phẩm. b.
Giả sử sản phẩm lấy ra là chính phẩm. Hỏi khả năng sản phẩm này được do nhà
máy nào sản xuất là cao nhất?
Đáp số: a. 7/300; b. máy 2.
1.15 Có hai chuồng thỏ: chuồng thứ nhất có 3 thỏ màu trắng và 3 con thỏ màu nâu, chuồng thứ
hai có 6 con thỏ màu trắng và 4 con thỏ màu nâu. Bắt ngẫu nhiên 4 con thỏ từ chuồng thứ
nhất bỏ vào chuồng thứ hai, rồi sau đó bắt ngẫu nhiên một con thỏ từ chuồng thứ hai ra.
Tính xác suất để bắt được con thỏ màu nâu từ chuồng thứ hai. Đáp số: 3/7
1.16 Bắn ba viên đạn một cách độc lập vào một mục tiêu. Xác suất trúng mục tiêu của từng viên
đạn tương ứng là 0,3; 0,4; 0,5. Nếu chỉ có một viên trúng thì mục tiêu bị phá hủy với xác
suất 0,4. Nếu có từ hai viên đạn trúng thì mục tiêu chắc chắn bị phá hủy. Tìm xác suất để
mục tiêu bị phá hủy khi bắn ba viên đạn như trên. Đáp số: 0,518.
1.17 Một bài thi trắc nghiệm gồm 12 câu hỏi, mỗi câu có 5 phương án trả lời trong đó chỉ có
một phương án đúng. Giả sử mỗi câu trả lời đúng thí sinh được 4 điểm, mỗi câu trả lời sai,
thí sinh bị trừ 1 điểm. Một thí sinh làm bài bằng cách chọn ngẫu nhiên các phương án trả
lời cho mọi câu hỏi. Tính xác suất để a. Thí sinh được 13 điểm. b. Thí sinh bị điểm âm.
Đáp số: a. 0,0532; b. 0,5584. Bài tập chương 2
2.1 Một đề thi trắc nghiệm có 2 câu, nội dung các câu độc lập, mỗi câu chỉ có hai thang điểm
nếu đúng thì được 5 điểm còn sai thì được 0 điểm. Khả năng làm đúng câu thứ nhất là 0,7 và khả
năng làm đúng câu thứ hai là 0,6.
a. Tính xác suất để một sinh viên nào đó dự thi đạt ít nhất 5 điểm.
b. Gọi X là số điểm sinh viên có thể đạt được. Lập bảng phân phối xác suất của X. c. Tính
2.2 Một trò chơi quay số trúng thưởng, vòng tròn quay số gồm có 11 ô chia đều được đánh số từ
0 đến 10. Nếu kim quay dừng ở ô nào thì số tiền được thưởng bằng chữ số ở ô đó nhân với 1
nghìn. Mỗi lần tham dự quay số người chơi phải trả tiền vé 6 nghìn đồng. Một người mua một vé để tham dự trò chơi.
a. Tính xác suất để người đó có lãi ít nhất 2 nghìn.
b. Gọi X là số tiền thưởng của người đó. Lập bảng phân phối xác suất của X. c. Tính
và giải thích ý nghĩa của kết quả tìm được. d. Tính
2.3 Một thiết bị gồm 3 bộ phận hoạt động độc lập với nhau, xác suất để các bộ phận bị hỏng
trong khoảng thời gian t tương ứng bằng 0,2; 0,3; 0,25. Gọi X là số bộ phận bị hỏng trong khoảng thời gian t.
a. Tìm phân phối xác suất của .
b. Tính xác suất để trong thời gian t có ít nhất một bộ phận bị hỏng.
2.4 Một xạ thủ đem theo 4 viên đạn để bắn kiểm tra trước ngày thi bắn. Anh ta bắn từng viên
vào bia với xác suất trúng vòng 10 trong mỗi lần bắn là 0,85. Nếu bắn được 2 viên liên tiếp trúng
vòng 10 thì anh ta thôi không bắn nữa.
a. Tính xác suất để người đó phải sử dụng ba viên.
b. Gọi X là số viên đạn phải sử dụng. Lập bảng phân phối xác suất của X.
2.5 Số tủ lạnh có khả năng bán được trong tuần tại một cửa hàng là biến ngẫu nhiên có bảng
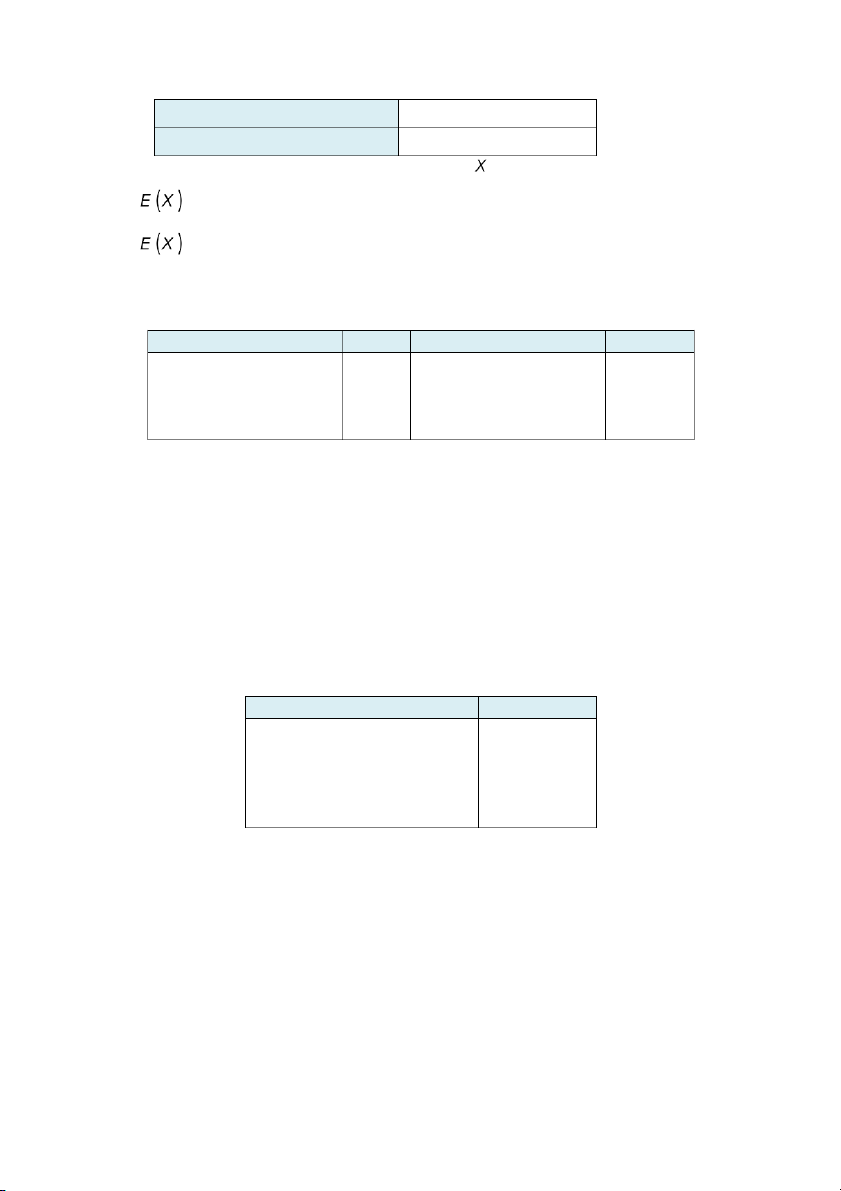
phân phối xác suất như sau: X 0 1 2 3 4 5 P 0,05 0,15 0,2 0,3 0,2 0,1
a. Tính xác suất để trong một tuần bán được ít nhất 4 chiếc tủ lạnh.
b. Khi bán một chiếc tủ lạnh thì cửa hàng lãi 300 nghìn đồng, chi phí của cửa hàng mỗi tuần là
500 nghìn. Tính tiền lãi trung bình của cửa hàng trong tuần.
2.6 Lợi nhuận (%) khi đầu tư vào hai ngành A và B trong một năm là các biến ngẫu nhiên độc
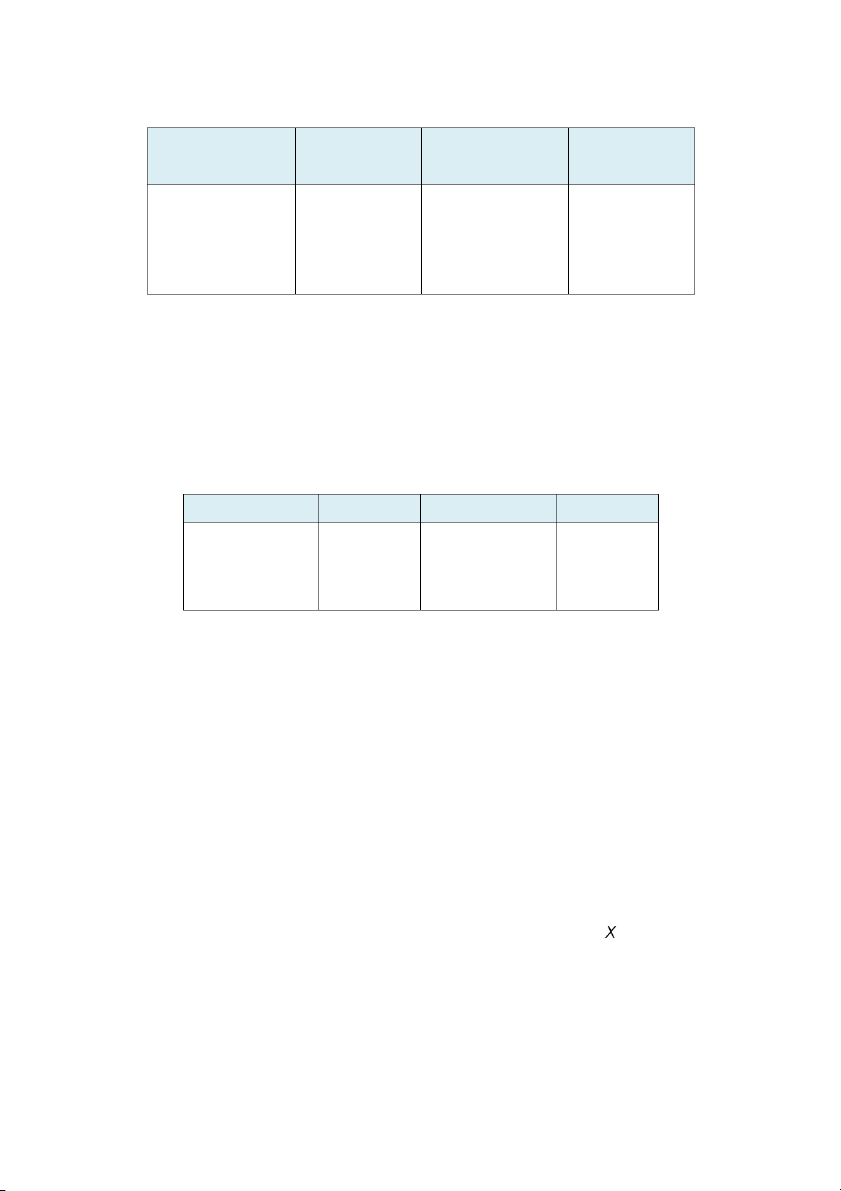
lập có bảng phân phối xác suất như sau: XA –5 0 10 20 XB –3 0 8 P 0,05 0,35 0,4 0,2 P 0.03 0,1 0,4
a. Muốn có lợi nhuận cao thì nên đầu tư vào ngành nào?
b. Muốn ổn định hơn thì nên đầu tư vào ngành nào?
c. Một người chia đều vốn đầu tư vào cả hai ngành A và B. Tính xác suất để người đó có lợi
nhuận trên 10%? Lợi nhuận trung bình của phương án này là bao nhiêu.
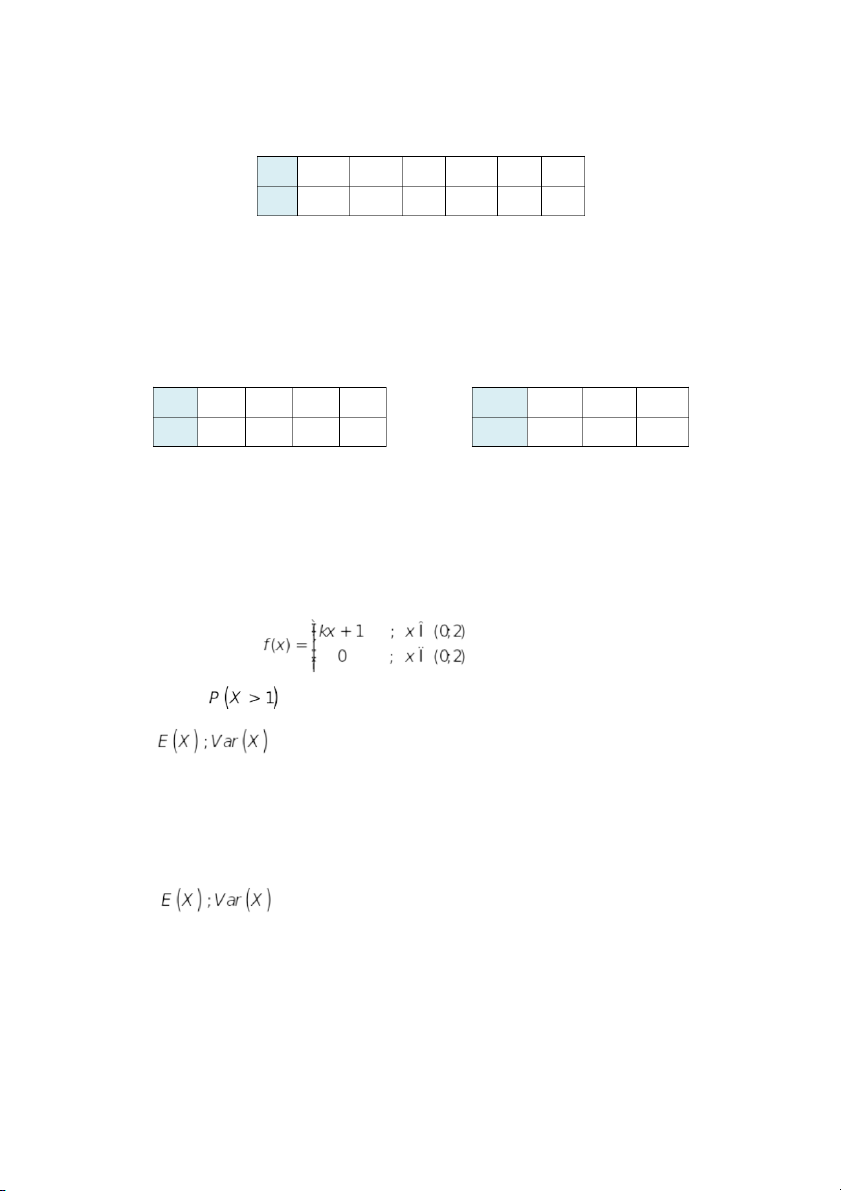
2.7 Biến ngẫu nhiên liên tục X có hàm mật độ xác suất như sau: a. Tìm k. Tính b. Tìm
2.8 Gieo 3 lần 1 đồng xu, xác suất hiện mặt sấp ở mỗi lần gieo là 0,5. Gọi X là biến ngẫu nhiên
chỉ số lần xuất hiện mặt sấp trong 3 lần gieo.
a. Lập bảng phân phối xác suất của X. c. Tính .
d. Tìm hàm phân phối xác suất của biến ngẫu nhiên X.
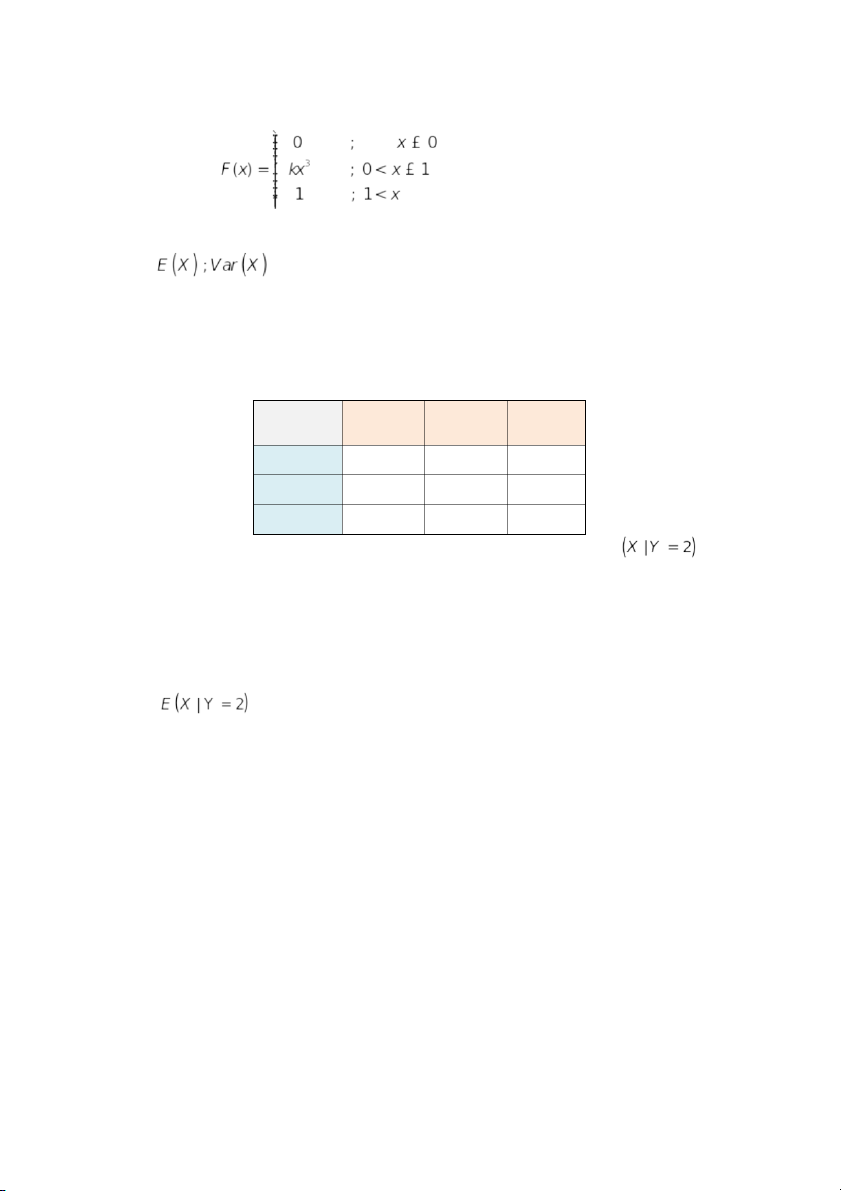
2.9 Biến ngẫu nhiên liên tục X có hàm phân phối xác suất như sau:
a. Xác hàm mật độ xác suất của biến ngẫu nhiên X. Tính k? b. Tính .
2.10 Cho bảng phân phối đồng thời của biến ngẫu nhiên hai chiều (X,Y), trong đó X là số người
trong độ tuổi lao động và Y là số người không trong độ tuổi lao động trong một gia đình ở một khu vực như sau: X 1 2 3 Y 0 0,05 0,12 0,07 1 0,11 0,25 0,14 2 0,1 p 0,1
a. Tìm p và lập bảng phân phối xác suất biên X, Y; và phân phối xác suất của .
b. Tính số người trung bình trong độ tuổi lao động và số người trung bình không trong độ tuổi
lao động trong một gia đình của vùng đó.
c. Tính xác suất để một hộ gia đình có ít nhất 4 người?
d. Tính số người trung bình trong một gia đình. e. Tính
? Nêu ý nghĩa của kết quả tìm được
f. X và Y có độc lập hay không? Bài tập chương 3
3.1. Tỷ lệ phế phẩm của sản phẩm A trước khi xuất xưởng là 30%. Trước khi đưa ra thị trường
người ta tiến hành kiểm tra bằng một thiết bị tự động. Thiết bị kiểm tra tự động có độ chính xác
90% đối với chính phẩm và 95% đối với phế phẩm. Sản phẩm A sẽ được đưa ra thị trường nếu
thiết bị kiểm tra tự động coi sản phẩm đó là chính phẩm.
a. Một người mua 3 sản phẩm A, hãy cho biết quy luật phân phối xác suất, kỳ vọng và phương
sai của số chính phẩm từ 3 sản phẩm này.
b. Xác suất để người đó mua được ít nhất một chính phẩm là bao nhiêu?
3.2. Tỷ lệ phế phẩm của sản phẩm Z là 30%. để đảm bảo chất lượng, người ta cho kiểm tra các
sản phẩm Z trước khi đưa ra thị trường. Thiết bị kiểm tra tự động có độ chính xác 90% đối với
chính phẩm, 95% đối với phế phẩm. Sản phẩm Z được đưa ra thị trường nếu thiết bị kiểm tra tự
động coi là chính phẩm.
a. Một người mua 3 sản phẩm Z, hãy cho biết quy luật phân phối xác suất, kỳ vọng và phương
sai của số chính phẩm từ 3 sản phẩm này.
b. Tính xác suất để trong 3 sản phẩm Z có ít nhất một chính phẩm.
3.3. Một người bắn 5 viên đạn vào bia, xác suất trúng đích mỗi lần bắn là 0,8 và độc lập với
nhau. Gọi X là số viên trúng đích.
a. Hãy cho biết X tuân theo quy luật gì? Tìm kỳ vọng và phương sai của X.
b. Tính xác suất để có ít nhất 4 viên trúng đích?
3.4. Tỷ lệ phế phẩm của 1 lô hàng là 20%, người ta lấy 10 sản phẩn từ lô hàng. Gọi X là số phế
phẩm trong 10 sản phẩm lấy ra.
a. Hãy cho biết X tuân theo quy luật gì? Tìm kỳ vọng và phương sai của X.
b. Tính xác suất để có nhiều nhất 1 sản phẩm xấu được lấy ra?
3.5. Hai người mỗi người ném 3 quả bóng vào rổ, xác suất ném trúng rổ mỗi lần của mỗi người
đều là 0,7. Gọi X1 là số lần ném trúng rổ của người thứ nhất. X2 là số lần ném trúng rổ của người
thứ hai. Đặt X = X + 1 X2 a. Hãy cho biết X , 1 X ,
2 X tuân theo quy luật gì? Tìm kỳ vọng và phương sai của X.
b. Tính xác suất để mỗi người đều ném trúng 2 quả.
c. Tính xác suất để tất cả chỉ có 4 quả bóng trúng rổ.
3.6. Một đề thi trắc nghiệm có 10 câu hỏi. Mỗi câu có 5 phương án trả lời, trong đó chỉ có 1
phương án trả lời đúng. Trả lời đúng mỗi câu được 1 điểm. Gọi X là số điểm đạt được.
a. Hãy cho biết X tuân theo quy luật gì? Tìm kỳ vọng và phương sai của X.
b. Tính xác suất để người đó đạt ít nhất 8 điểm.
3.7. Một cuộc thi tìm hiểu lịch sử, điểm của thí sinh dự thi tuân theo quy luật chuẩn với trung
bình là 500 điểm và độ lệch chuẩn là 50 điểm.
a. Tìm tỷ lệ thí sinh có số điểm từ 450 đến 600 điểm.
b. Người ta thưởng cho 10% số thí sinh dự thi đạt điểm cao. Muốn được thưởng thì số điểm phải đạt bao nhiêu?
3.8. Điểm tổng kết của một môn học tuân theo quy luật chuẩn với trung bình là 6 điểm và độ lệch
chuẩn là 2 điểm. Thí sinh dược xếp loại giỏi nếu có điểm tổng kết từ 8,5 trở lên, xếp loại khá nếu
điểm tổng kết từ 7 đến 8,5.
a. Tìm tỷ lệ thí sinh của trường xếp loại khá giỏi.
b. Tính xác suất để trong 3 em học sinh bất kỳ có đúng 1 em xếp loại giỏi.
3.9. Tỷ lệ người tham gia bảo hiểm y tế ở một vùng là 75%, điều tra 100 người trong vùng.
a. Tính xác suất để có ít nhất 80 người tham gia bảo hiểm.
b. Tính xác suất để tỷ lệ người tham gia bảo hiểm trong số 100 người nói trên không vượt quá 70%.
c. Với xác suất 0,9, biết trong 100 người có ít nhất bao nhiêu người tham gia bảo hiểm y tế?
3.10. Tuổi thọ của một loại sản phẩm là biến ngẫu nhiên phân với tuổi thọ trung bình là 1000
(giờ) và độ lệch chuẩn là 10(giờ). Một sản phẩm được bảo hành miễn phí nếu sản phẩm hỏng
trước 983,55 (giờ). Tính tỷ lệ sản phẩm nhà cung cấp phải bảo hành miễn phí.
3.11. Khi kinh doanh trong 2 ngành A, B có lợi nhuận hàng năm là các biến ngẫu nhiên XA, XB có
phân phối chuẩn và độc lập với nhau. Trung bình Độ lệch chuẩn XA 12% 3% XB 15% 4%
a. Muốn có lãi suất tối thiểu 10% thì nên chon đầu tư ở ngành nào?
b. Một người đầu tư vào cả 2 ngành theo tỷ lệ vốn đầu tư 30% vào ngành A và 70% vào ngành
B. Tính lợi nhuận trung bình và độ rủi ro (phương sai) của phương án đầu tư này.
c. Muốn đầu tư vào cả hai phương án, để độ rủi ro là nhỏ nhất thì chia tỷ lệ đầu tư vào 2 ngành A, B như thế nào? Bài tập chương 4
4.1 Nghiên cứu năng suất lúa vụ hè thu ở một địa phương người ta điều tra ngẫu nhiên 30 điểm
gặt, năng suất được thống kê ở bảng dưới đây Năng suất (kg) 58 - 59 59 - 60 60 - 61 61 -62 62 - 63 63 - 64 Số điểm 4 5 6 6 7 2
Tính năng suất trung bình, phương sai mẫu của năng suất.
4.2 Khi nghiên cứu thể lực của học sinh lớp 10 ở một địa phương, người ta tiến hành đo chiều
cao của một mẫu gồm 100 học sinh nam và thu được kết quả sau: Chiều cao(cm) 145 - 150 150 - 155 155 - 160 160 -165 165 - 170 170 - 175 Số học sinh 15 20 20 12 22 11
a. Tính trung bình mẫu, phương sai mẫu.
b. Tính tần suất học sinh nam có chiều cao từ 160 (cm).
4.3 Để đánh giá tình hình thu phí trên quốc lộ 5, người ta tiến hành điều tra ngẫu nhiên doanh
thu một số ngày ở một trạm thu phí, ta có bảng số liệu sau: Doanh thu 350-400 400-450 450-500 500-550 550-600 600-650 (triệu đồng) Số ngày 4 5 6 6 7 2
a. Tính trung bình mẫu, độ lệch chuẩn mẫu
b. Tính tẩn suất ngày có doanh thu nhỏ hơn 16 triệu.
4.4 Tại một trang trại chăn nuôi heo thương phẩm, người ta sử dụng một loai thức ăn mới trong
khẩu phần cho heo. Sau khi nuôi được ba tháng tuổi kiểm tra trọng lượng heo người ta thu được kết quả sau:
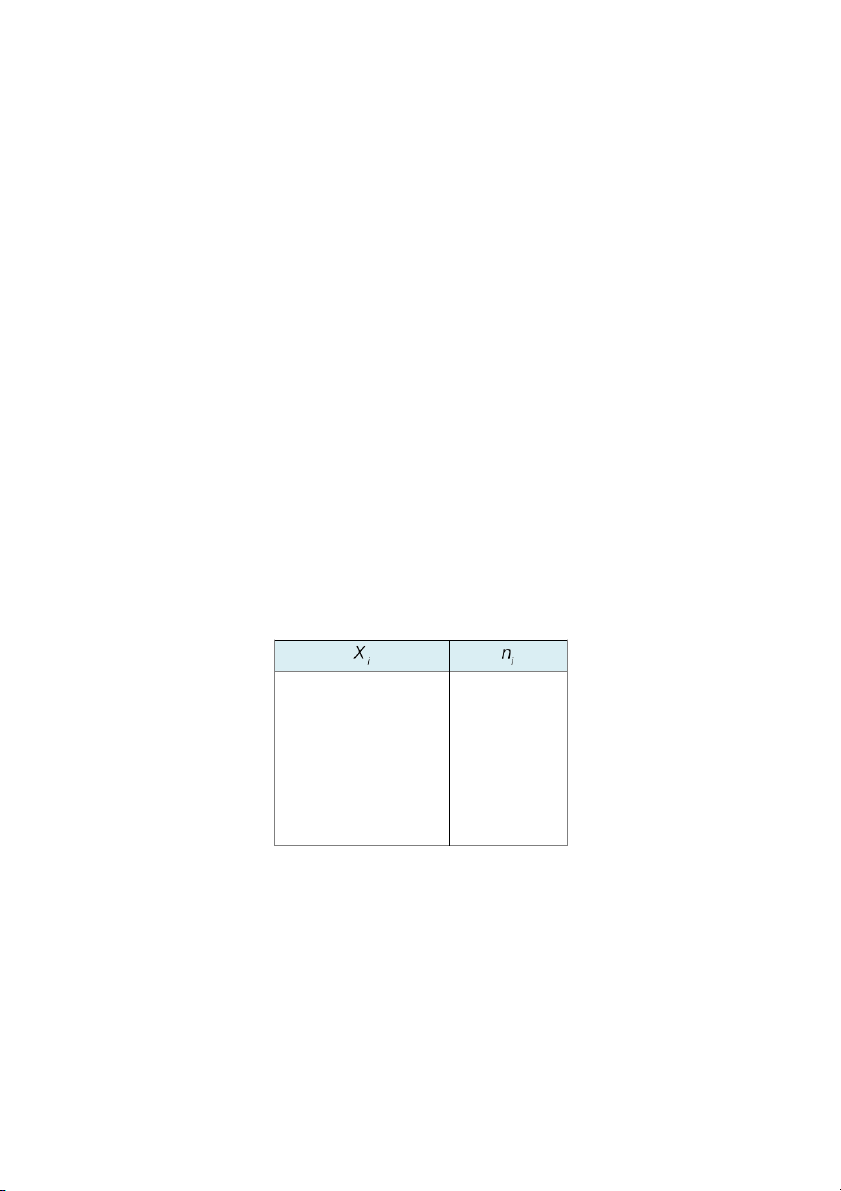
a. Lô heo có sử dụng thức ăn mới trong khẩu phần: xi (kg) 75 77 78 79 80 81 83 ni (số heo) 1 3 4 7 6 2 2
b. Lô heo không dùng thức ăn mới trong khẩu phần: xi (kg) 60 61 62 63 65 67 69 70 72 ni (số heo) 1 2 4 5 6 3 2 1 1
Hãy tìm trọng lượng trung bình, phương sai và độ lệch chuẩn mẫu của hai lô heo trên.
4.5 Baûng döôùi ñaây chæ keát quaû thu hoaïch Y (taï/ha) vaø löôïng phaân boùn X
(kg/ha) cuûa moät loaïi hoa maøu taïi 100 thöûa ruoäng gieo loaïi hoa maøu ñoù: Y X 14 15 16 17 18 i n 1 10 10 2 8 12 20 3 7 28 35 4 6 8 14 5 9 12 21 mj 18 19 34 17 22 n = 100 Haõy tính . Bài tập Chương 5
5.1 Một máy sản xuất hàng loạt. Người ta tiến hành một số mẫu kiểm tra. Kết quả cho trong bảng sau: Người kiểm tra Thời gian Kích thước mẫu Số sản phẩm loại A Nguyễn Văn A 1 – 5 8h 60 14 10h 50 03 14h 50 05 4 – 5 8h 60 09 16h 80 10 1 – 6 8h 80 18 9h 80 20 Lê Văn B 6 – 8 8h 40 17 10h 300 32
a. Tìm ước lượng cho tỉ lệ loại A với độ tin cậy 95%.
b. Ước lượng số sản phẩm loại A trong 20000 sản phẩm đã sản xuất với độ tin cậy 95%.
c. Muốn ước lượng tỉ lệ sản phẩm loại A với độ chính xác 3% thì đảm bảo độ tin cậy là bao nhiêu?
d. Muốn ước lượng tỉ lệ sản phẩm loại A với độ tin cậy 90% thì đảm bảo độ chính xác là bao nhiêu?
e. Muốn ước lượng số sản phẩm loại A với độ chính xác 500 sản phẩm thì phải điều tra thêm
bao nhiêu sản phẩm nếu muốn độ tin cậy là 92%?
5.2 Ở một cửa hàng chế biến thủy sản, theo dõi nhu cầu của mặt hàng nước mắm trong một số ngày, ta có kết quả: Số bán ra (lít) Số ngày 20 – 30 3 30 – 40 8 40 – 50 30 50 – 60 45 60 – 70 20 70 – 80 25 80 – 90 17 90 – 100 9 > 100 4
a. Hãy ước lượng lượng nước mắm trung bình bán một ngày với độ tin cậy 99% trong hai trường hợp: i. Biết phương sai ii. Chưa biết phương sai
b. Giả sử giá nhập một lít nước mắm là 6000đ. Với độ tin cậy 99% cửa hàng này phải dự trù
một món tiền trung bình bằng bao nhiêu để cung cấp nước mắm cho khách hàng?
5.3 Cân thử trọng lượng 15 con gia súc ở một trại chăn nuôi khi xuất chuồng, ta được các kết quả sau: 3,25; 2,5; 4; 3,75; 3,8; 3,9; 4,02; 3,8; 3,2; 3,82; 3,4; 3,6; 3,75; 4; 3,5;
Giả sử trọng lượng các con gia súc tuân theo luật phân phối chuẩn với phương sai 0,01.
Hãy ước lượng trọng lượng trung bình của một con gia súc với độ tin cậy 99%.
5.4 Đo đường kính của 20 trục máy do một máy tiện tự động sản xuất ra, ta được kết quả sau (tính bằng mm): 250; 249; 251; 253; 248; 250; 250; 252; 257; 245; 248; 247; 249; 250; 280; 250; 247; 253; 256; 249
Giả sử đường kính của các trục máy là đại lượng ngẫu nhiên có phân phối chuẩn. Hãy ước lượng
đường kính trung bình của các trục máy do máy tiện ra với độ tin cậy 95%.
5.5 X (đơn vị tính bằng %) là chỉ tiêu của một loại sản phẩm. Điều tra ở một số sản phẩm, ta có kết quả: 5 – 7 2 7 – 9 8 9 – 11 14 11 – 13 19 13 – 15 22 15 – 17 20 17 – 19 10 19 – 21 5
a. Để ước lượng trung bình chỉ tiêu X với độ tin cậy 92% và độ chính xác 0,3% thì cần điều
tra thêm bao nhiêu sản phẩm?
b. Sản phẩm có chỉ tiêu X càng lớn càng được ưa chuộng. Người ta xem các sản phẩm có chỉ
tiêu X dưới một mức qui định là loại II. Từ số liệu điều tra trên, bằng phương pháp ước
lượng khoảng cho tỉ lệ (loại II), người ta tính được khoảng tin cậy là . Tìm độ
chính xác và độ tin cậy của ước lượng này. c. Giả sử
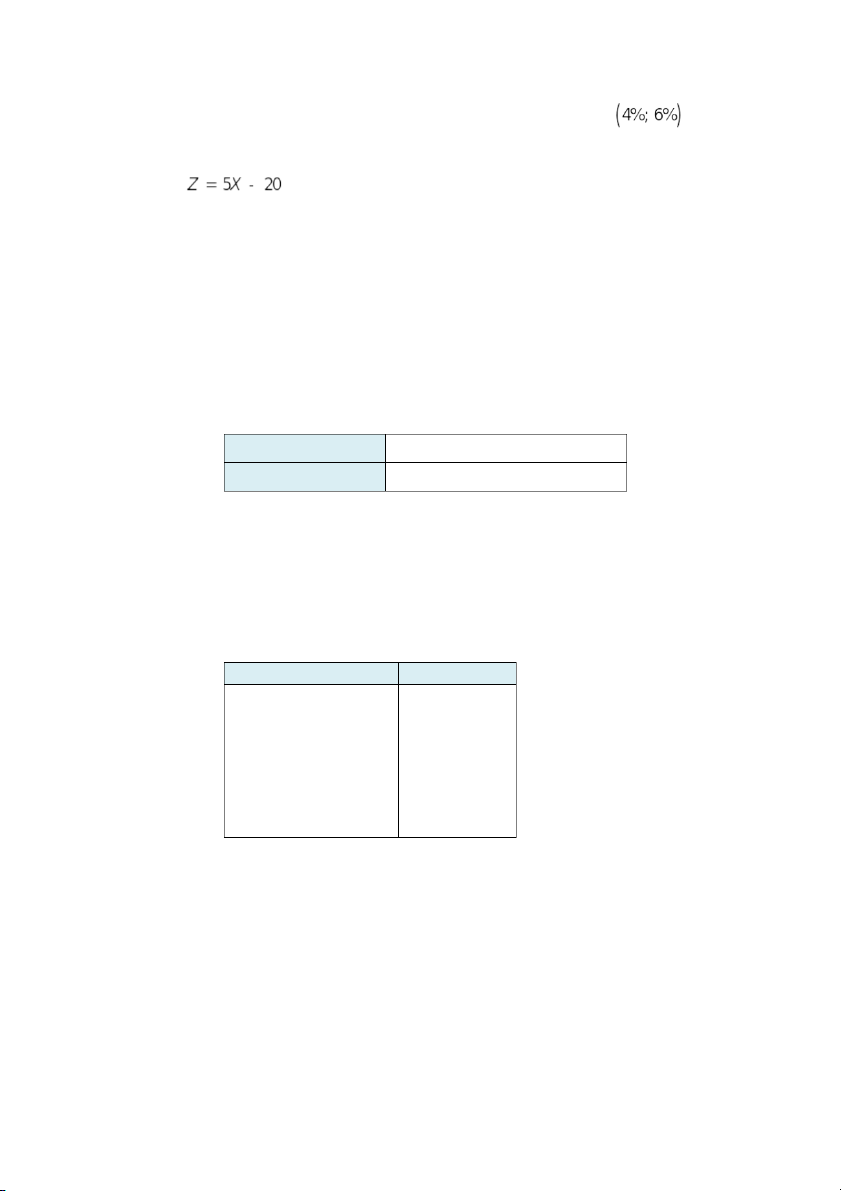
là một chỉ tiêu khác của sản phẩm. Tìm ước lượng không chệch cho
kỳ vọng và phương sai của Z.
d. Để ước lượng trung bình chỉ tiêu X với độ tin cậy 92% và độ chính xác 0,3% đồng thời ước
lượng tỉ lệ sản phẩm loại II với độ chính xác 2,8% và độ tin cậy 90% thì cần điều tra thêm bao nhiêu sản phẩm?
e. Hãy ước lượng trung bình chỉ tiêu X của các sản phẩm loại II.
5.6 Theo dõi số áo thun thể thao bán được ở một cửa hàng bán dụng cụ thể thao trong ngày
trong một tháng (30 ngày), ta có kết quả sau: Số áo bán được 12 14 18 21 25 28 Số ngày 1 4 7 9 4 5
a. Hãy ước lượng không chệch cho số áo thun trung bình bán được trong ngày.
b. Nếu ta qui ước những ngày bán được không quá 15 cái áo là ngày “ế hàng”, hãy ước lượng
không chệch cho tỉ lệ những ngày ế hàng.
5.7 Để tìm hiểu số lượng mũ cao su mỗi cây cao su cho ta trong một ngày trong năm đầu khai
thác (tính bằng gam), ghi nhận ở 100 cây ta có kết quả sau: Trọng lượng (gam) Số cây 200 – 210 2 210 – 220 8 220 – 230 14 230 – 240 30 240 – 250 25 250 – 260 12 260 – 270 9
a. Hãy ước lượng không chệch cho lượng mũ trung bình mỗi cây cho trong ngày.
b. Hãy ước lượng không chệch cho độ biến động của lượng mũ đó.
c. Giả sử ta qui định những cây cho một ngày trên 220g mũ là cây loại I, còn lại là cây loại II.
Hãy ước lượng không chệch cho tỉ lệ cây loại II.
5.8 Quan sát thu nhập của một số người ở một công ty ta có kết quả cho ở bảng sau: Thu nhập Thu nhập Số người Số người (triệu đồng/tháng) (triệu đồng/tháng) 5 – 5,5 5 7,5 – 8 47 5,5 – 6 9 8 – 8,5 24 6 – 6,5 12 8,5 – 9 18 6,5 – 7 35 9 – 9,5 6 7 – 7,5 6 9,5 – 10 3
a. Tìm ước lượng không chệch cho thu nhập trung bình trong một tháng của một người ở công ty này.
b. Những người có thu nhập trên 8 triệu đồng/tháng là những người có thu nhập cao. Tìm ước
lượng không chệch cho tỉ lệ những người có thu nhập cao.
5.9 Trọng lượng của các trái cây ở một nông trường là biến ngẫu nhiên có phương sai 400 gam .2
Cân thử 100 trái cây của nông trường đó ta có kết quả sau: Trọng lượng (g) Số trái Trọng lượng (g) Số trái 35 – 55 3 115 – 135 20 55 – 75 10 135 – 155 6 75 – 95 25 155 – 175 1 95 – 115 35
a. Ước lượng trọng lượng trung bình của các trái cây ở nông trường với độ tin cậy 99%.
b. Nếu độ chính xác của ước lượng là 2,35g thì độ tin cậy của ước lượng là bao nhiêu?
c. Với độ chính xác của ước lượng bé hơn 2,35g và độ tin cậy 99% thì phải cân thêm ít nhất bao nhiêu trái?
5.10 Một kỹ sư nông nghiệp muốn ước lượng tỉ lệ nảy mầm của một loại hạt giống. Người kỹ sư
đó đem gieo thử 1000 hạt giống thì thấy có 640 hạt nảy mầm.
a. Hãy ước lượng khoảng tin cậy 90% cho tỉ lệ những hạt nảy mầm.
b. Nếu muốn có độ tin cậy 90% và bán kính ước lượng không vượt quá 0,02 thì cần lấy mẫu
có kích thước bé nhất là bao nhiêu?
5.11 Mức hao phí nhiên liệu cho một đơn vị sản phẩm là biến ngẫu nhiên có luật phân phối
chuẩn. Quan sát 28 sản phẩm thu được kết quả sau:
Lượng nhiên liệu hao phí (g) 19 19,5 20 20,5 Số sản phẩm 5 6 14 3
Với độ tin cậy 90% hãy ước lượng phương sai của
trong hai trường hợp sau: a. chưa biết. b. = 20g .
5.12 Ở một nhà máy dệt, kiểm tra một số tấm vải (dài 30m), thấy kết quả như sau: Số khuyết tật/tấm Số tấm Số khuyết tật/tấm Số tấm 0 8 4 30 1 20 5 25 2 12 6 15 3 40
a. Hãy ước lượng số khuyết tật trung bình của mỗi tấm vải với độ tin cậy 95%.
b. Nếu độ chính xác của ước lượng là 0,14 (khuyết tật) thì độ tin cậy của ước lượng là bao nhiêu?
c. Với độ chính xác của ước lượng là bé hơn 0,14, độ tin cậy 95% thì phải kiểm tra thêm ít
nhất bao nhiêu tấm vải nữa?
d. Nếu gọi vải loại I là loại ở mỗi tấm vải có không quá 2 khuyết tật, hãy ước lượng tỉ lệ vải
loại I với độ tin cậy 99%.
5.13 Kiểm tra ngẫu nhiên khối lượng của 28 sản phẩm cùng loại do một máy sản xuất, ta thu được kết quả sau: Khối lượng (kg) Số sp 3,9 – 3,94 2 3,94 – 3,98 7 3,98 – 4,02 10 4,02 – 4,06 6 4,06 – 4,1 3
Biết rằng khối lượng sản phẩm có luật phân phối chuẩn.
a. Với độ tin cậy 0,95 hãy tìm khoảng ước lượng của khối lượng trung bình của sản phẩm.
b. Những sản phẩm có khối lượng lớn hơn 4,02 kg được xem là sản phẩm loại I. Hãy ước
lượng cho tỉ lệ sản phẩm loại I với mức ý nghĩa 1%.
c. Hãy ước lượng phương sai của khối lượng sản phẩm do máy sản xuất độ tin cậy 95%.
5.14 Để nghiên cứu nhu cầu của một loại hàng ở một khu vực người ta tiến hành điều tra về nhu
cầu của mặt hàng đó ở 400 gia đình (đơn vị tính: kg/tháng). Kết quả điều tra cho ở bảng sau: Nhu cầu Số gđ Nhu cầu Số gđ <1 10 4 – 5 78 1 – 2 35 5 – 6 31 2 – 3 86 6 – 7 18 3 – 4 132 7 – 8 10
a. Ước lượng nhu cầu trung bình về mặt hàng này của khu vực trong một năm với độ tin cậy 95%.
b. Khi ước lượng nhu cầu trung bình về mặt hàng này của khu vực trong một năm, nếu ta
muốn có độ tin cậy đạt được 95% và độ chính xác 4,8 kg thì cần điều tra về nhu cầu mặt
hàng này ở bao nhiêu hộ gia đình?
5.15 Giả sử trái cây của nông trường đã được đóng thành sọt, mỗi sọt có 10 trái. Kiểm tra 50 sọt được kết quả như sau: Số trái hỏng/sọt Số sọt Số trái hỏng/sọt Số sọt 0 0 6 4 1 2 7 7 2 3 8 0 3 7 9 0 4 20 10 1 5 6
a. Tìm ước lượng khoảng cho tỉ lệ trái cây hỏng trong nông trường với độ tin cậy 95%.
b. Tìm ước lượng khoảng cho tỉ lệ trái cây hỏng trung bình ở mỗi sọt với mức ý nghĩa 5%.
c. Tìm ước lượng khoảng tin cậy cho phương sai của tỉ lệ trái cây hỏng ở mỗi sọt với độ tin
cậy 95%. Biết tỉ lệ trái cây hỏng trung bình .
5.16 Đo đường kính của 100 chi tiết do một máy sản xuất, kết quả cho ở bảng sau: Đường kính (mm) Số chi tiết Đường kính (mm) Số chi tiết 19,80 - 19,85 3 20,00 - 20,05 23 19,85 - 19,90 5 20,05 - 20,10 14 19,90 - 19,95 16 20,10 - 20,15 7 19,95 - 20,00 28 20,15 - 20,20 4
Chi tiết có đường kính lớn hơn 19,9 mm đến 20,1 mm là chi tiết đạt tiêu chuẩn.
a. Hãy ước lượng đường kính trung bình của những chi tiết đạt tiêu chuẩn do máy này sản
xuất với độ tin cậy 95%.
b. Ước lượng tỉ lệ chi tiết đạt tiêu chuẩn của máy với độ tin cậy 96%.
c. Khi ước lượng tỉ lệ chi tiết đạt tiêu chuẩn, nếu ta muốn độ chính xác đạt được là 5% và độ
tin cậy 99% thì cần đo thêm bao nhiêu chi tiết nữa?
5.17 Quan sát thu nhập của một số người làm việc ở một công ty, ta có kết quả như sau: Thu nhập Thu nhập Số người Số người (triệu/tháng) (triệu/tháng) 2 - 5 5 13 - 15 47 5 - 7 9 15 - 17 24 7 - 9 12 17 - 19 18 9 - 11 35 19 - 23 6 11 - 13 66 23 - 25 3
a. Tìm ước lượng không chệch cho thu nhập trung bình của một người ở công ty này.
b. Những người có thu nhập từ 15 triệu đồng/tháng trở lên là những người có thu nhập cao.
Tìm ước lượng không chệch của tỉ lệ những người có thu nhập cao ở công ty này.
c. Ước lượng thu nhập trung bình của một người ở công ty này với độ tin cậy 95%.
d. Với mẫu đã cho, khi ước lượng thu nhập trung bình của một người ở công ty này, nếu
muốn độ tin cậy 99% thì độ chính xác đạt được là bao nhiêu?
e. Ước lượng phương sai của thu nhập.
5.18 Kết quả quan sát về hàm lượng Vitamin C của một loại trái cây cho ở bảng sau: Hàm lượng Vitamin C (%) Số trái 5 - 7 5 7 - 9 10 9 - 11 20 11 - 13 35 13 - 15 25 15 - 17 5
a. Hãy ước lượng hàm lượng vitamin C trung bình trong một trái với độ tin cậy 95%.
b. Quy ước những trái có hàm lượng Vitamin C trên 11% trở lên là trái loại I. Ước lượng tỉ lệ
trái loại I với độ tin cậy 98%.
c. Muốn độ chính xác khi ước lượng hàm lượng vitamin C trung bình là và độ
chính xác khi ước lượng tỉ lệ trái loại I là
với cùng độ tin cậy 95% thì cần quan
sát thêm bao nhiêu trái nữa?
5.19 Trong kho để rất nhiều sản phẩm của xí nghiệp A. Lấy ngẫu nhiên 100 sản phẩm, cân lên có kết quả: Khối lượng (g) Số sản phẩm Khối lượng (g) Số sản phẩm 800 - 850 5 1000 - 1050 15 850 - 900 10 1050 - 1100 10 900 - 950 20 1100 - 1150 10 950 - 1000 30
a. Các sản phẩm có trọng lượng trên 1050g là loại I. Hãy ước lượng trọng lượng trung bình
của các sản phẩm loại I với độ tin cậy 98% (giả thiết trọng lượng này có phân phối chuẩn).
b. Nếu muốn ước lượng tỷ lệ sản phẩm loại I với độ tin cậy 80% và độ chính xác 3% thì cần
điều tra thêm bao nhiêu sản phẩm nữa?
5.20 Giả sử trong kho để lẫn 1000 sản phẩm của xí nghiệp B và trong 100 sản phẩm lấy ra từ
kho có 9 sản phẩm của xí nghiệp B. Hãy ước lượng số sản phẩm của xí nghiệp A trong kho với độ tin cậy 82%.
a. Ước lượng giá trị trung bình của chỉ tiêu của những sản phẩm có chỉ tiêu trong
khoảng (35-40) với độ tin cậy 95% (biết là biến ngẫu nhiên có phân phối chuẩn).
b. Nếu muốn ước lượng giá trị trung bình của chỉ tiêu
với độ chính xác 0,5% thì độ tin cậy sẽ là bao nhiêu? Bài tập chương 6
6.1. Trọng lượng sản phẩm là biến ngẫu nhiên phân phối chuẩn với độ lệch chuẩn 1,5 (kg). Nghi
máy hoạt động không bình thường làm trọng lượng của sản phẩm giảm đi, người ta cân thử một
số sản phẩm và thu được kết quả sau: Trọng lượng(kg) 8,0-10 10-12 12-14 14-16 16-18 Số sản phẩm 5 30 35 25 5
Với mức ý nghĩa 5%, hãy cho kết luận về điều nghi ngờ trên. Biết rằng trọng lượng sản phẩm quy định là 14 (kg).
6.2. Định mức thời gian hoàn thành một sản phẩm là 10 (phút). Hỏi có cần thay đổi định mức
hay không, nếu theo dõi thời gian hoàn thành sản phẩm ở một số công nhân, ta có số liệu sau: Thời gian (phút) 8,0-8,5 8,5- 9,5-10 10-10,5 10,5-11 9,0 Số công nhân 6 7 8 7 8
Cho kết luận với mức ý nghĩa 5%, biết rằng thời gian hoàn thành một sản phẩm là biến ngẫu nhiên phân phối chuẩn.
6.3. Năm trước chi phí bình quân của mỗi sinh viên học tại Hà Nội là 1,4 triệu một tháng. Năm
nay điều tra mức chi phí của một số sinh viên, ta có kết quả: Chi phí (triệu/tháng)
1,2-1,3 1,3-1,4 1,4-1,6 1,6-1,8 1,8-2,0 Số sinh viên 6 9 8 10 8
Phải chăng mức chi tiêu hàng tháng của sinh viên đã tăng lên? Cho kết luận với mức ý nghĩa 5%,
biết rằng mức chi tiêu là biến ngẫu nhiên phân phối chuẩn.
6.4. Bình thường độ đồng đều của trọng lượng các gói mỳ chính được đóng gói tự động là 2
(gam). Do máy móc được cải tiến tốt hơn, nên có ý kiến cho rằng độ đồng đều của trọng lượng
các gói mỳ chính tăng lên, vì vậy người ta tiến hành cân thử một số gói và có kết quả sau: Trọng lượng (gam) 197 198 199 200 201 Số gói 20 15 17 33 15
Biết trọng lượng các gói mỳ chính là phân phối chuẩn. Cho kết luận về điều nghi ngờ trên với mức ý nghĩa 5%.
6.5. Trước đây định mức tiêu hao nhiên liệu của loại xe là 6 (lít). Do tình hình đường xá ngày
càng được tốt hơn, người ta theo dõi 41 chuyến và thu được các số liệu: Lượng tiêu hao (lít)
4,0-4,5 4,5-5,0 5,0-5,5 5,5-6,0 6,0-6,5 Số chuyến 7 8 11 7 8