











Preview text:
Đề 1
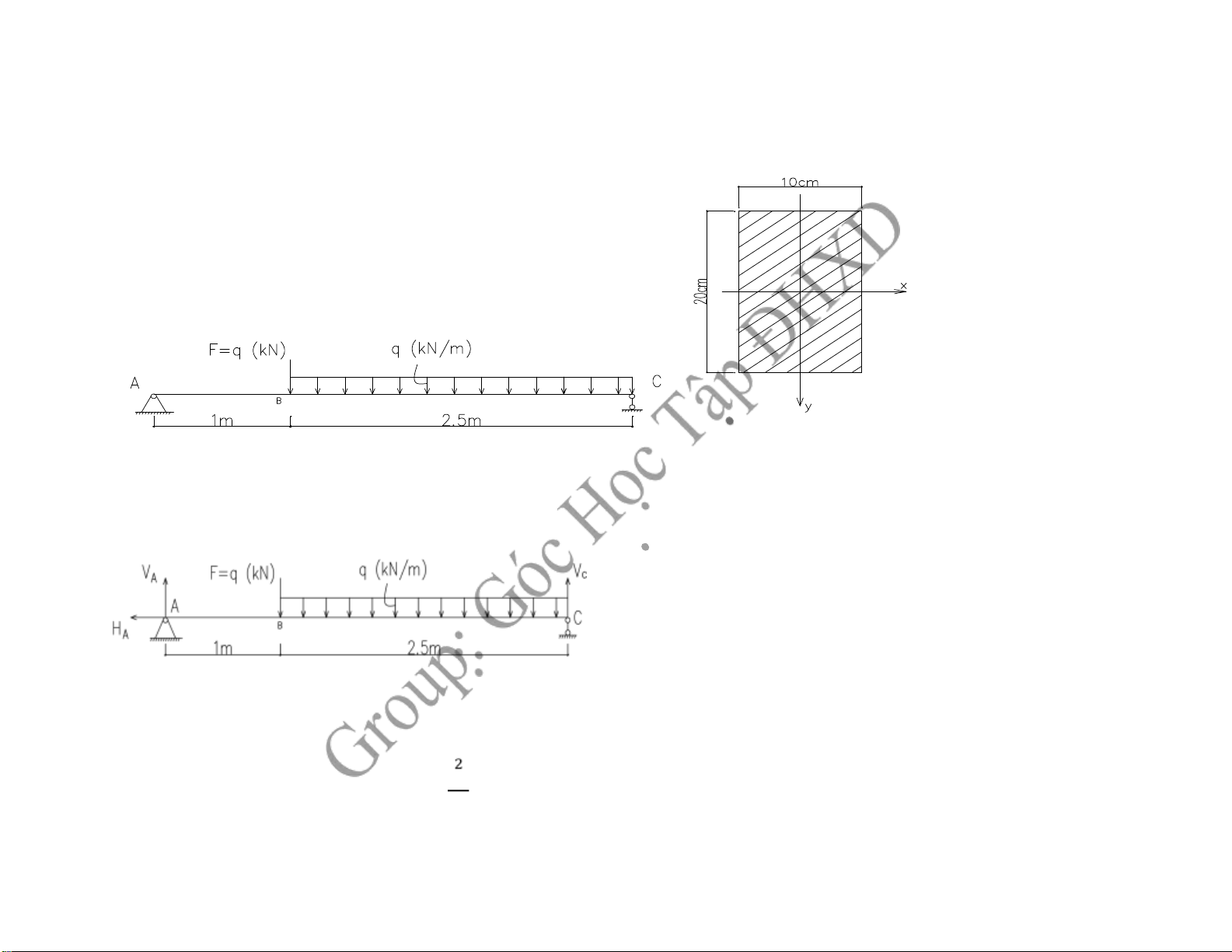
Câu 1 : Cho dầm có mặt cắt ngang là hình chữ nhật chịu lực như hình vẽ :
1. Vẽ biểu ồ ứng lực cho dầm theo tải trọng q
2. Xác ịnh tải trọng cho phép theo trạng thái ứng suất ơn. Biết [σ ] = 1,2 kN/m2 BÀI LÀM :
1, Vẽ biểu ồ ứng lực cho dầm
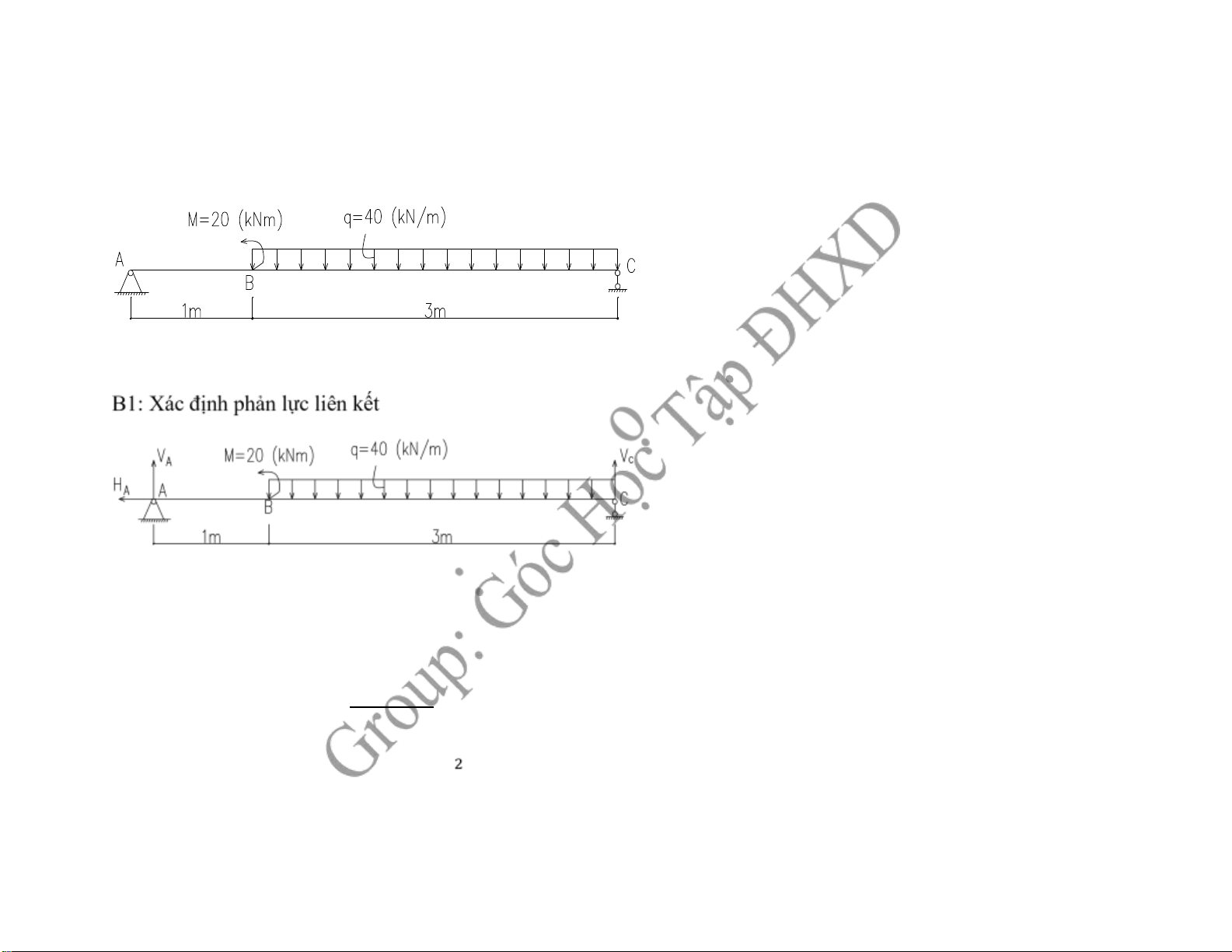
B1: Xác ịnh phản lực liên kết ∑ X= 0 → HA= 0 ∑ mA= 0
→ F.1+ q. 2,5. (1+ , ) - VC . 3,5 = 0
→VC. 3,5 = q. 1+ q. 2,5. 2,25 →VC = 1,89q
∑ Y= 0 → VA+ VC = F+ q. 2,5= q+ 2,5q →VA= 3,5q - 1,89q= 1,61q
B2: Chia oạn: 2 oạn AB, BC
B3: Viết biểu thức ứng lực cho từng oạn
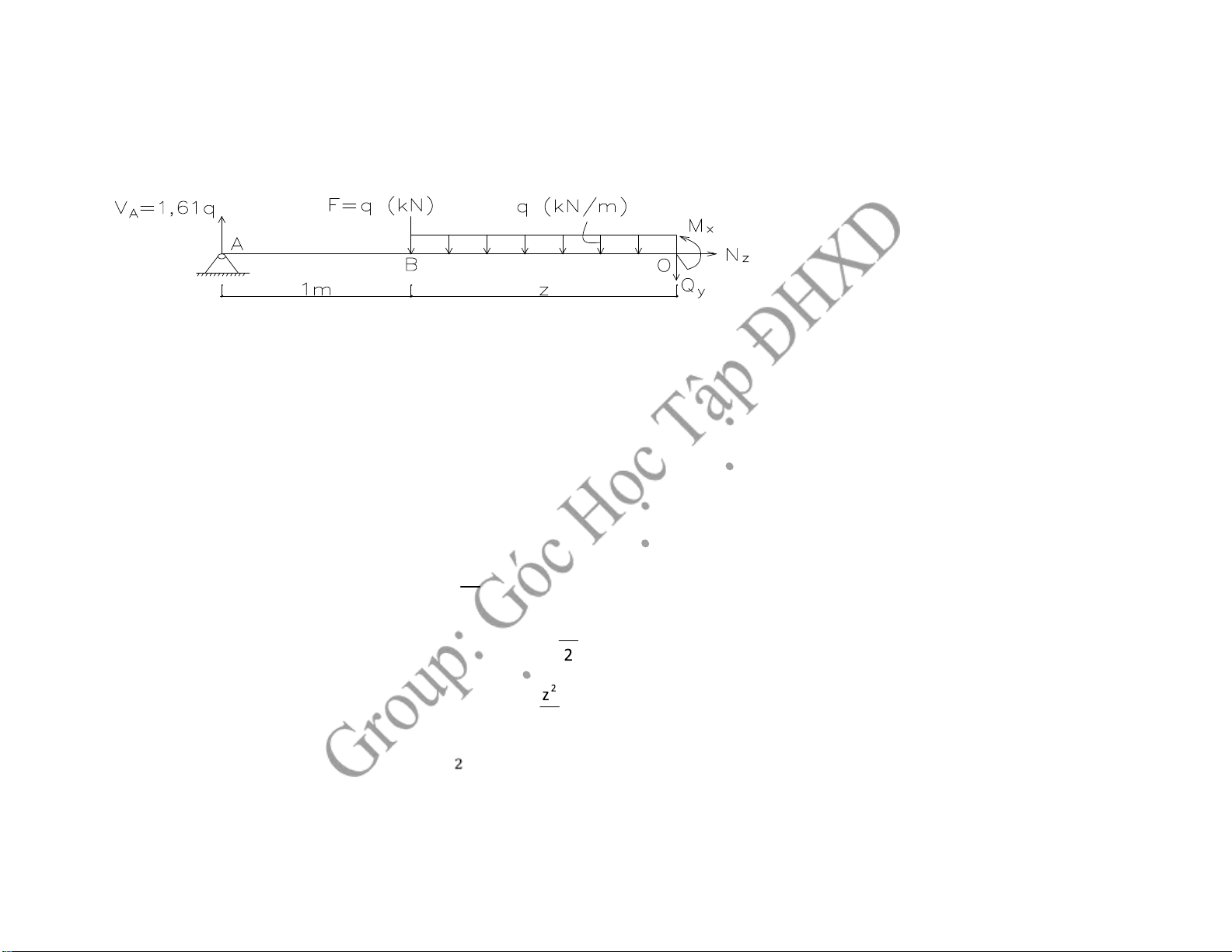
-Đoạn 1: AB với ( 0 ≤ z ≤ 1). Ta có q= 0 -> Mx : hàm bậc 1, Qy : hằng số ∑ X= 0 →NZ = 0 ∑ Y= 0 →VA = Qy =1,61.q ∑ mO= 0 →Mx = VA. z +) z= 0 → M A x = 0
+) z= 1 → M Bx = VA. 1 = 1,61q
-Đoạn 2: BC với ( 0 ≤ z ≤ 2,5 ). Ta có q > 0 → Mx : hàm bậc 2, Qy : hàm bậc 1 ∑ X= 0 → NZ = 0 ∑ Y= 0 → Qy = VA – F – q.z →Qy = 1,61.q – q – q.z
+) Tại B: z = 0 → Q By = 1,61.q – q = 0,61.q
+) Tại C: z = 2,5 → Q Cy = 1,61.q – q – 2,5.q = -1,89.q 2 ∑ mO = 0
→Mx = VA.( 1+ z ) – F.z – q. z 2
→ M = 1,61q (1+z ) – q.z – q z2 x
→ Mx = 1,61q + 0,61q.z – q 2
+) Tại B: z= 0 → M Bx = 1,61.q C 2,52
+) Tại C: z= 1 → M x =1,61.q + 0,61.q.2,5 – q. = 0 2
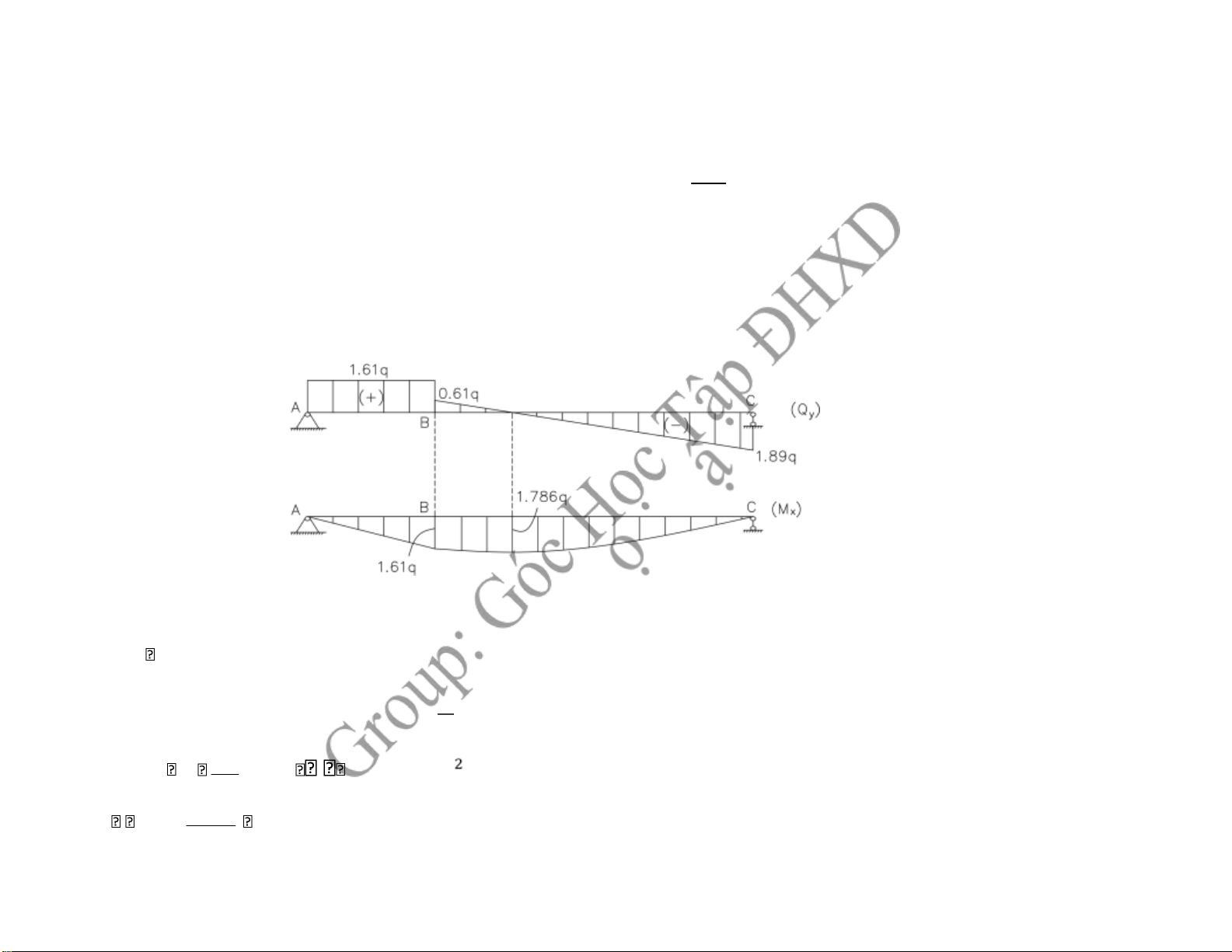
B4: Vẽ biểu ồ ứng lực Kiểm tra: Q B B ph
Qtr = - F = - q → 0,61q – 1,61q = - q (thỏa mãn)
3, Xác ịnh tải trọng cho phép theo TTƯS ơn. Biết [σ ] = 1,2 kN/m2 max Mx .ymax Ix Ix10.20 3 6666,667cm4 12 M max x 1,786 (q KN m. ) 178,6. (q KN cm. ) ymax 10cm 178,6q .10 1,2 q 4,5(KN cm/ ) 6666,667 Câu 2
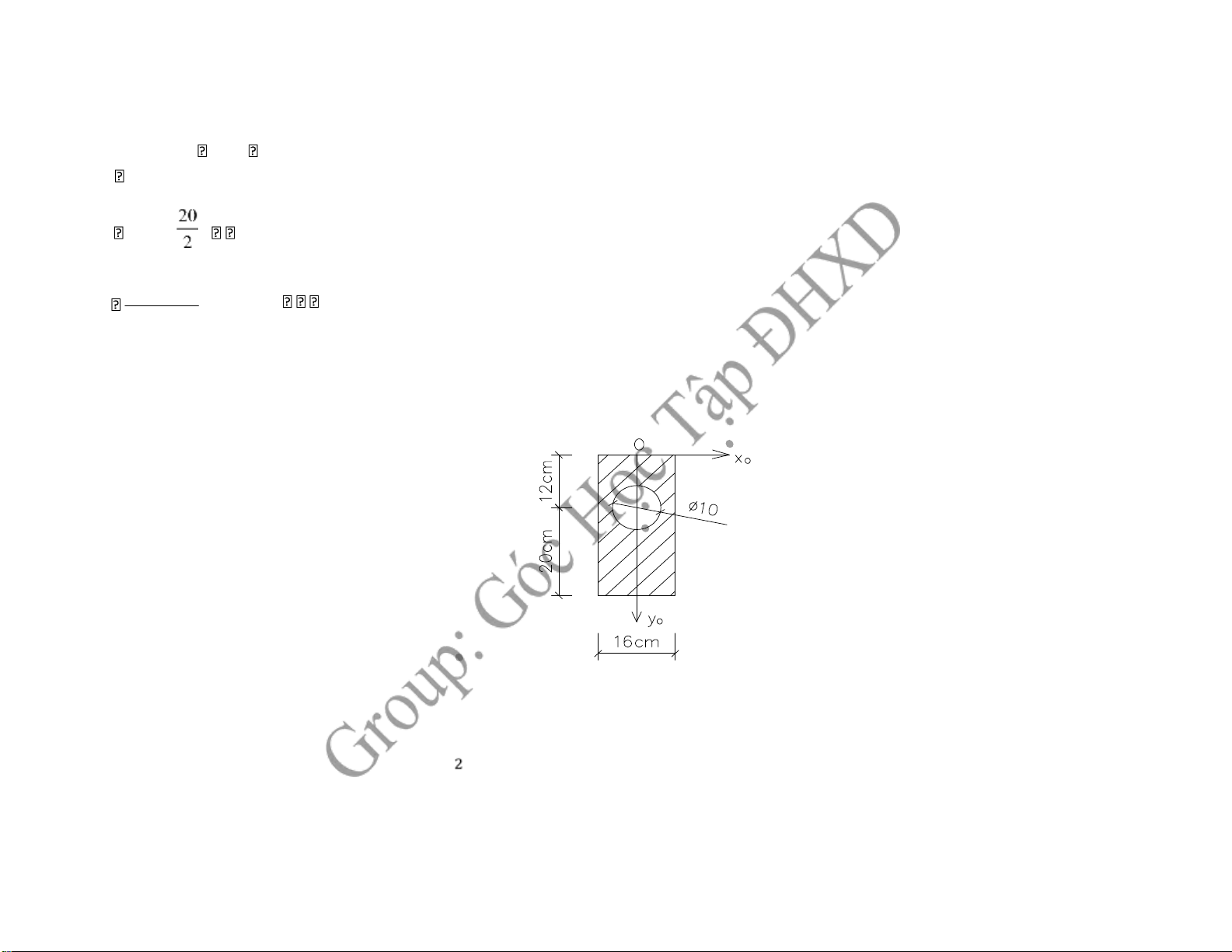
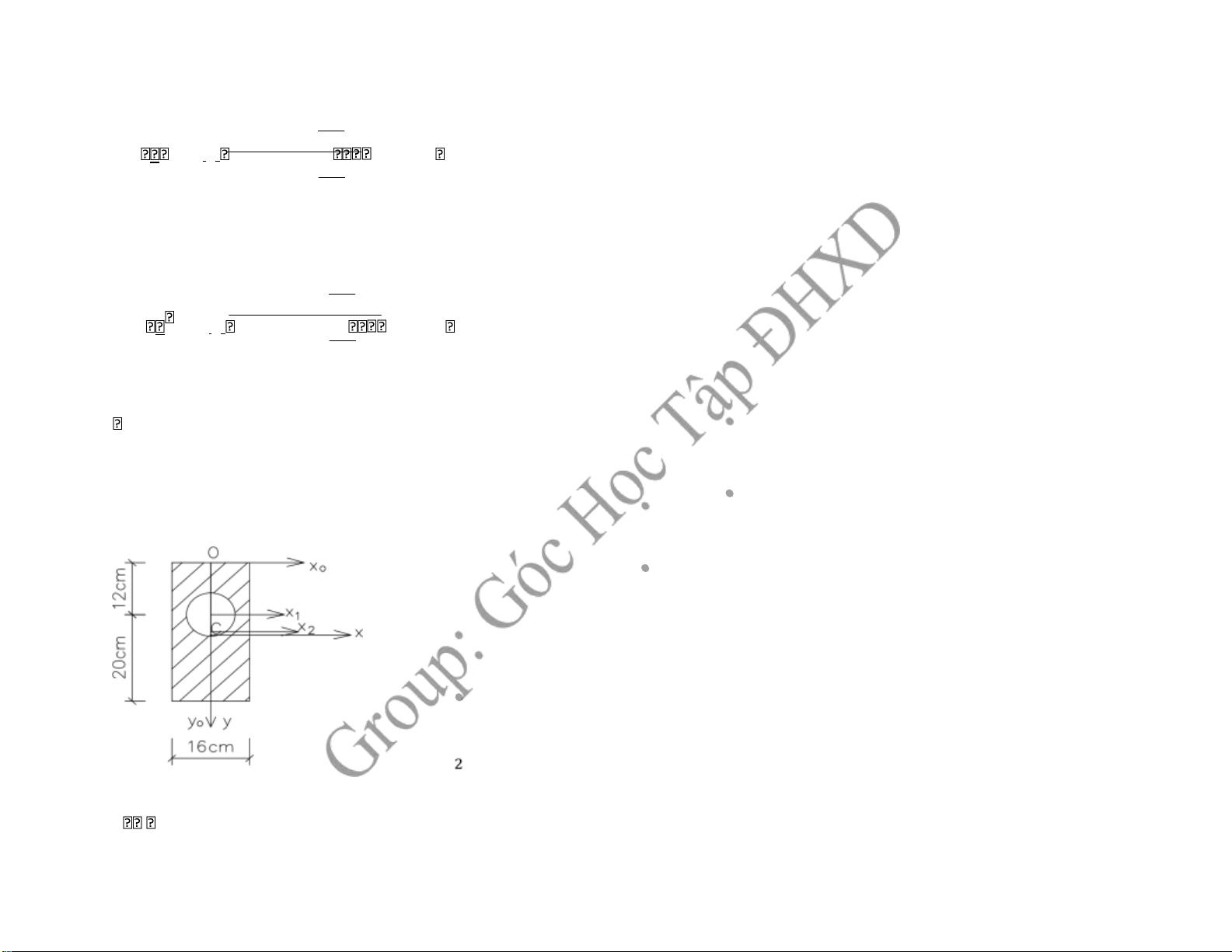
Hình phẳng có dạng và kích thước như sau: 1, Xác ịnh trọng tâm
2, Xác ịnh momen quán tính chính trung tâm Bài làm
1, Tìm trọng tâm của tiết diện
Chọn hệ trục Oxoyo như hình vẽ 102 +xc A xAi.i i 32.16.032.16 ..1042 .0 0 4 102 + yc A yAi.i i 32.16.1632.16 .. 42 .12 16,73 10 4 Tâm C(0;16,73)
2, Xác ịnh momen quán tính chính trung tâm
Dựng hệ trục Cxy //C x y1 1 1//C x y2 2 2
Áp dụng công thức chuyển trục song song ta ược Ix Ixi a Ai2. i Ix 16.32 12 3 0,73 .32.162 .1064 4 4,73 .2 .104 2 41715,474(cm4) Iy Iyi b Ai2. i Ix 16 .32123 0 .1064 4 0 4) 10431,793(cm Ixy a b Ai. .i i 0,73.0.16.32 4 ,73.0. .102 0(cm4) 4 y y I max/min Imax 41715,474(cm ) Imin 10431,793(cm4) ĐỀ 2 Câu 1:
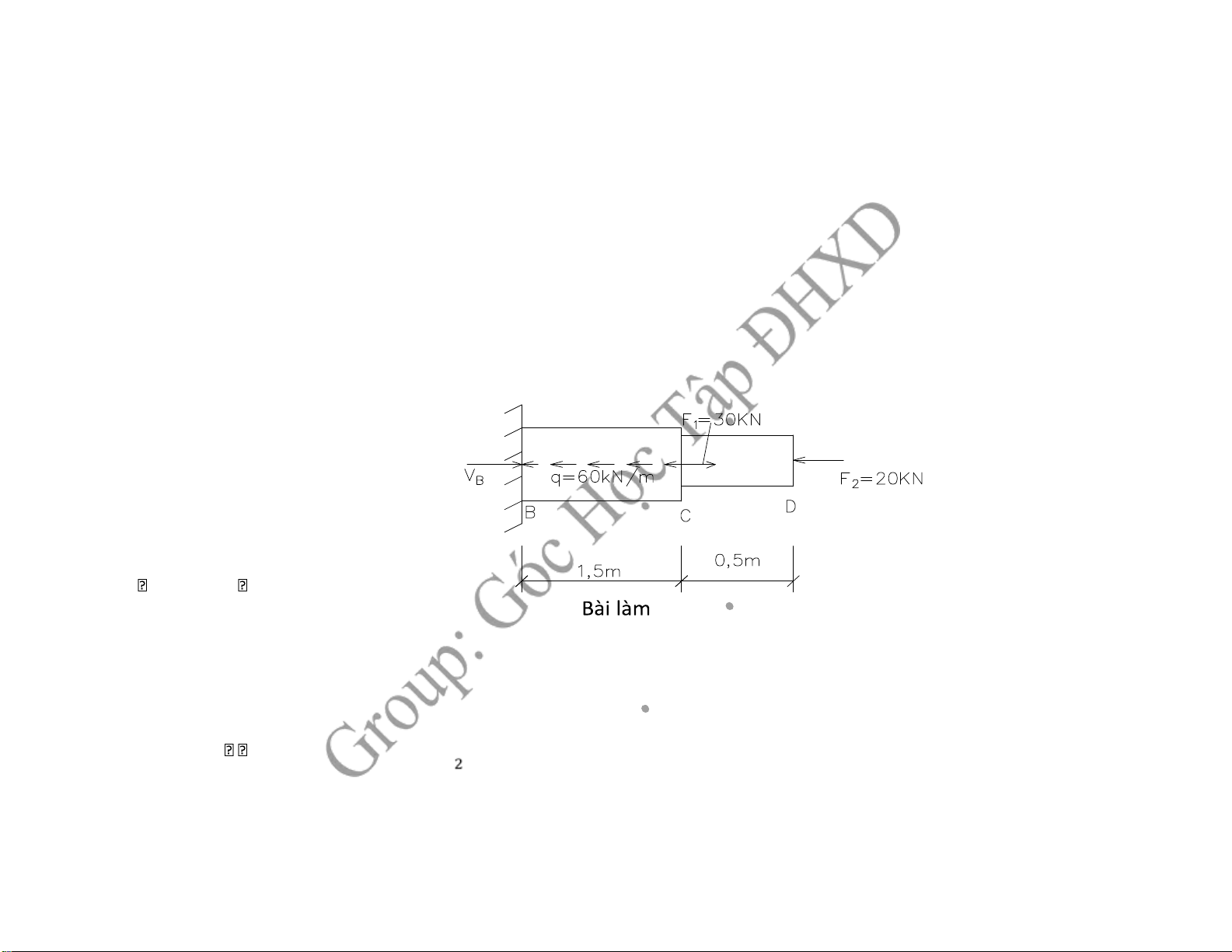
Cho hệ có tiết diện thay ổi như hình vẽ
1,Vẽ biểu ồ ứng lực cho thanh
2, Tính ứng suất lớn nhất trên tiết diện
3,Chuyển vị dọc trục C và D ABC 40cm A2; CD 20cm2
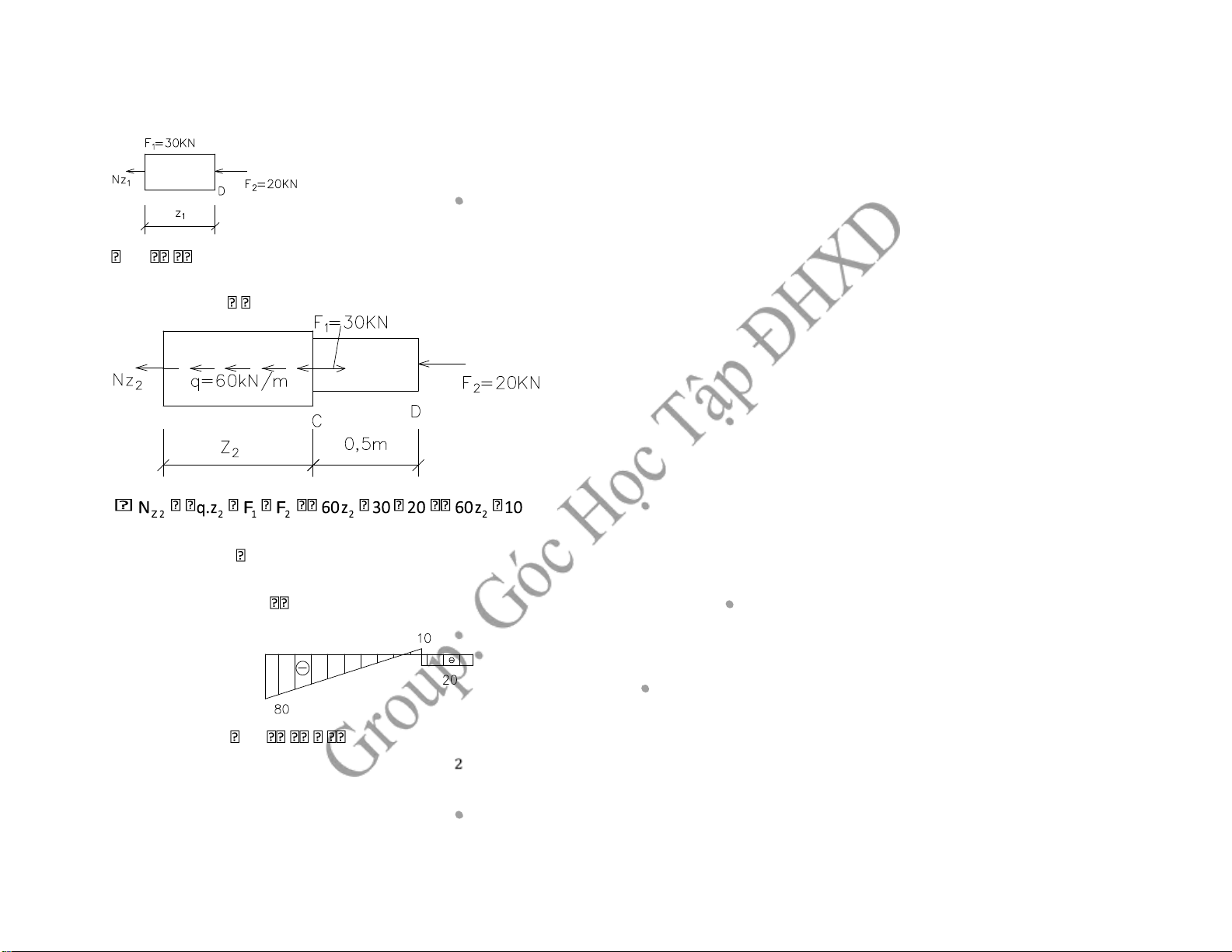
1, Vẽ biểu ồ ứng lực cho thanh -Chia oạn: 2 oạn +Đoạn CD:(0 z1 0,5 )m NZ1 F2 20KN
+Đoạn BC: (0 z1 1,5 )m ; q=const→NZ: bậc nhất Tại C: z=0→NZ 10KN Tại D: z=1,5m→NZ 80KN Kiểm tra: N ph tr Z NZ F 20 10 30 (thỏa mãn)
2, Tính ứng suất lớn nhất trên tiết diện -BC: N 80 Z 80KN Z1 2KN cm/ 2 40 -CD: N 20 Z 20KN Z 2 1KN cm/ 2 20 → max 2KN cm/ 2
3, Chuyển vị dọc trục của C và D SNZ BC WC LBC E A. BC 1 1 .80.1,333 .10.16,7 W 3 C 2 10 .403 0,13cm SNZCD 20.50 +WD LBDLBC LCDWC E A. CD 0,13 10 .203 0,18cm Câu 2 :
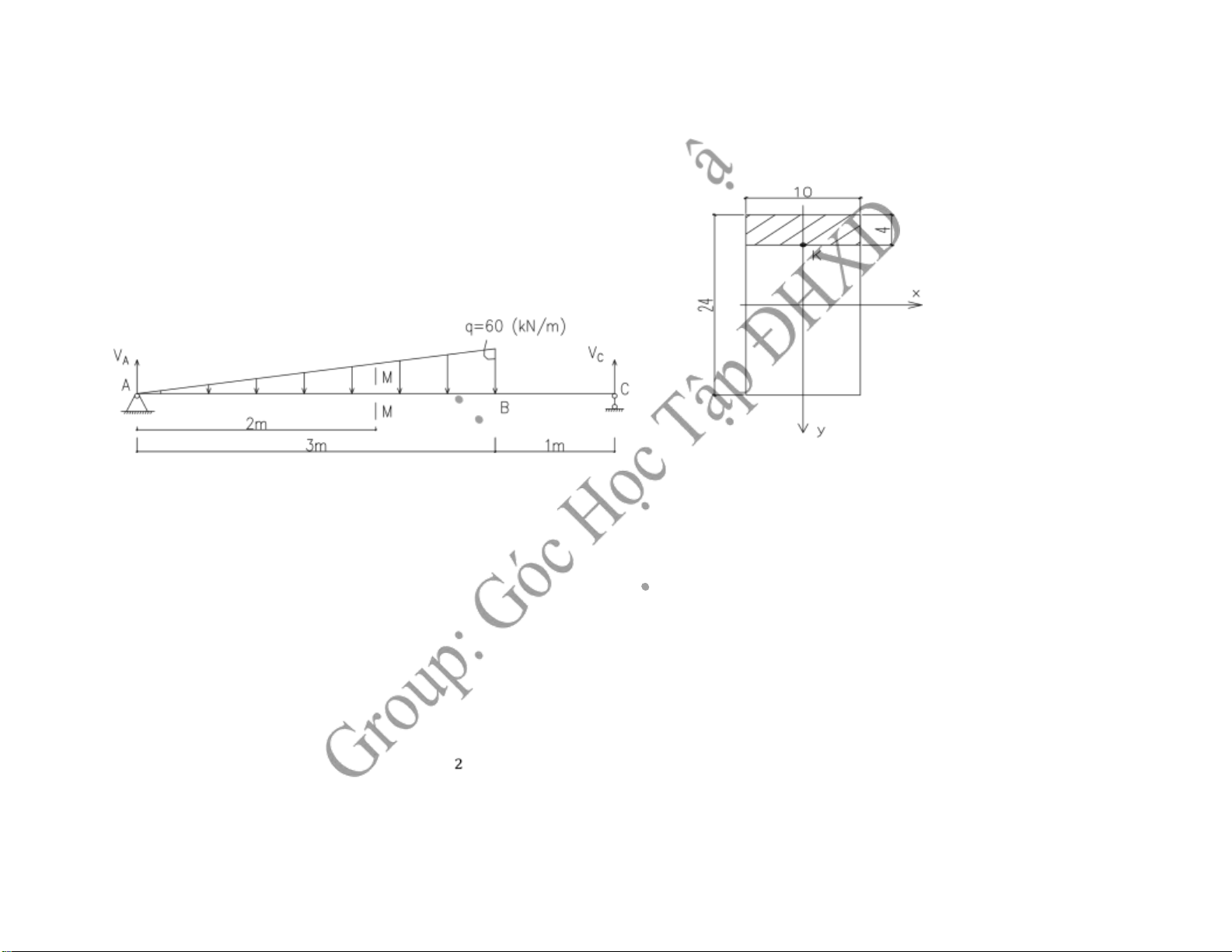
1, Tìm phản lực liên kết, ứng lực tại tiết diện M-M
2, Tính ứng suất pháp, ứng suất tiếp tại iểm K trên tiết diện M-M
3, Xác ịnh góc xoay A, ộ võng C Bài Làm:
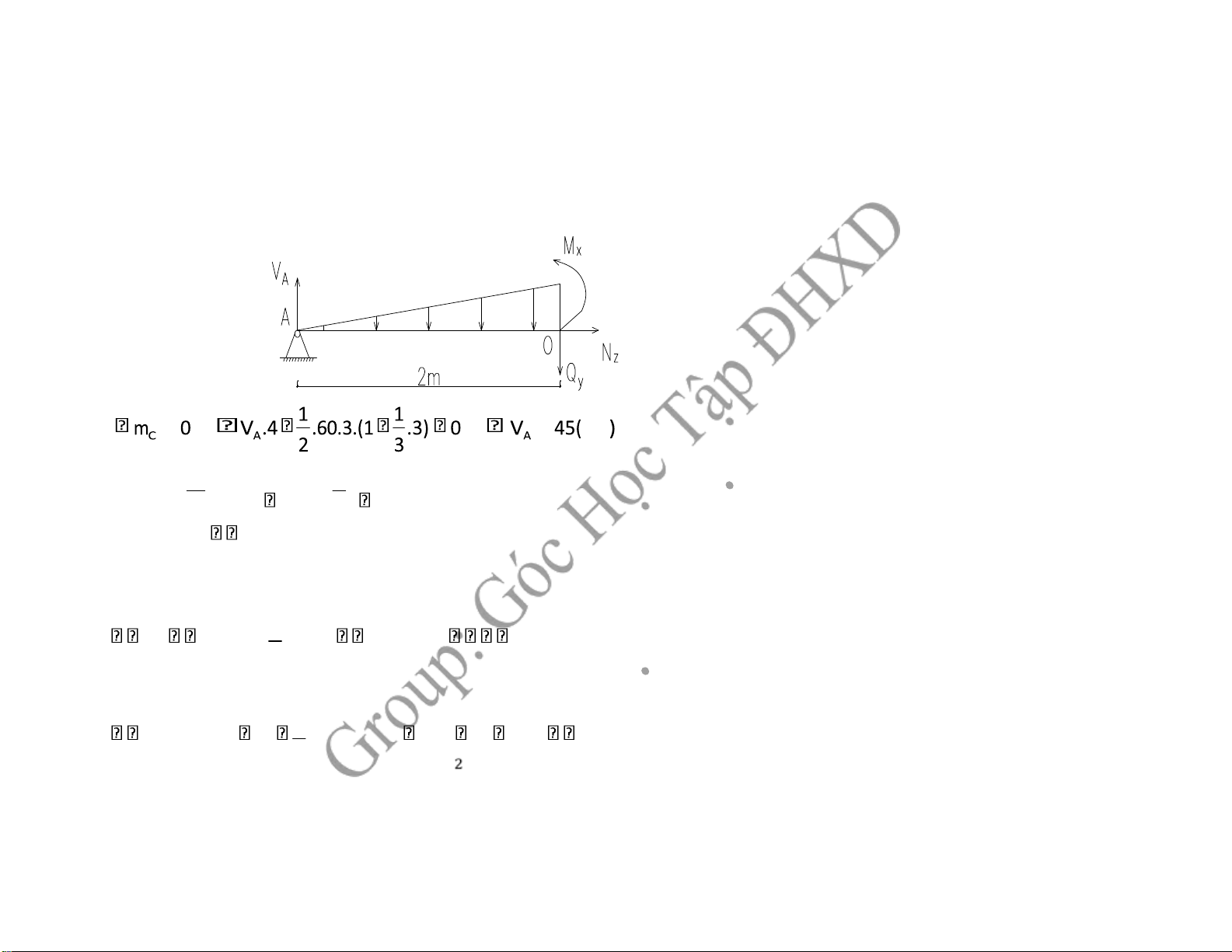
1, Xác ịnh phản lực liên kết, ứng lực tại tiết diện M-M: kN q'2 ' Ta có 2.60 40(kN m/ ) q q 3 3 y 0 V 1 A .40.2 Qy 0 Qy 45 40 5(kN) 2 mO
0 Mx 1.40.2. .21 VA.2 Mx 45.2 80 63,33(kN) 2 3 3
2, Tính ứng suất pháp, ứng suất tiếp tại iểm K trên tiết diện M-M
M > 0 → vùng tại K là vùng nén → yK = -8 (cm) xy
Q SI bxy.. CxC với: bC = 10 (cm) ; Qy = 5 (kN) Ta có : bh3 10.2434) Ix 11520(cm 12 12 S C x 10.4.10 400(cm3) 5.400 xy 0,02(kN cm/ 2) 11520.10 -Ứng suất pháp: ( )K z Mx .yK 63.33 .( 8) 0,04(kN cm/ 2) Ix 11520 +) Phương chính : 2 xy 2.0,02 0,009 tg(2 o) z( )K 4,4 o1 0,26o o2 90o o1 90o 0,26o 90,26o +) Ứng suất chính : (K) (K) 2 z max 2 2z ( zy(K))2 42,4 42,4 2 ( 0.02)2 min max 9.10 ( 5 kN cm/2) min 4,4(kN cm/2)
1 9.10 ( 5 kN cm/2); 2 0(kN cm/2); 3 4,4(kN cm/2)
3, Xác ịnh góc xoay tại A, ộ võng tại B Ta có : q q z( ) .z q' q l 3 EI
Phương trình ộ võng oạn 2 (BC): 1 60 y2 y1 . 4!.(z 3)4 205!.(z 3)5 EIx y2 o.z EI1x .
453!.z3 205!.z5 604!.(z 3)4 205!.(z 3)5 Điều kiện biên: yC y2 z 4 o.4 EI1 . 453!.43 205!.45 604!.(4 3) 4 205!.(4 3) 5 4. o 312EIx 0 x o 78 EIx EI78 EI1 45.z3 20.z5 y1 .z . 3! 5! x x 1 y1' EI78x EI1 . 453!.3.z2 205!.5.z4 x y y EI x x
Có E 2.10 (4 kN cm/ 2) 2.10 .10 (44 kN m/ 2) I
10.243 11520(cm4) 11520.10 ( 8 m4) x 12 A
2.10 .10 .11520.104 478 8 3,4.10 ( 3 rad) yB 4 478 8 .3 2.10 .10 .11520.104 4 1 8 . 453!.33 205!.35 3,125.10 ( ) 3 m 2.10 .10 .11520.10 ĐỀ 3 CÂU 1:
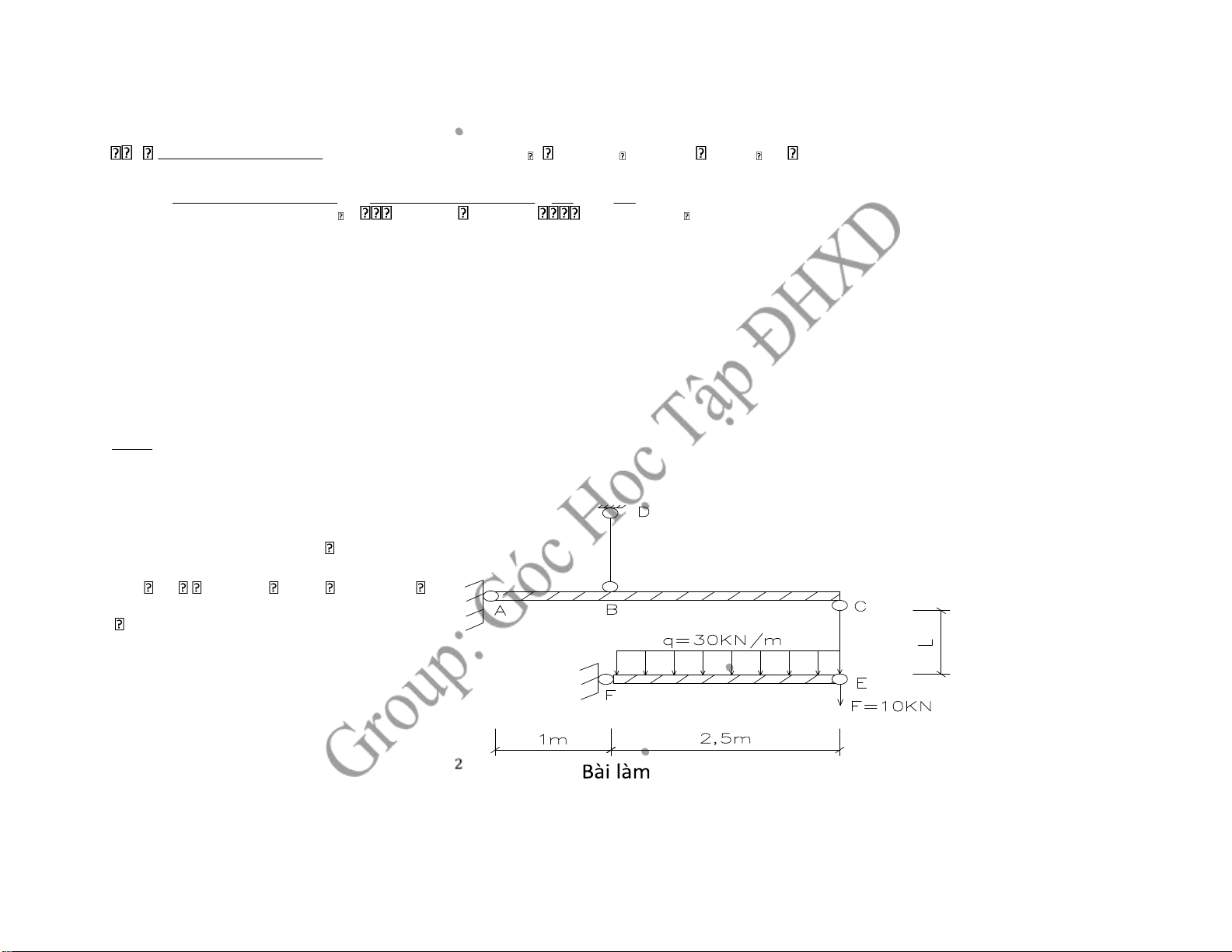
Cho hệ thanh chịu lực như hình vẽ
ABC; FE tuyệt ối cứng E 2.104 KN cm L/
2; BD LCE L 1,2m a 1m b; 2,5 ;m ABD ACE 4cm2
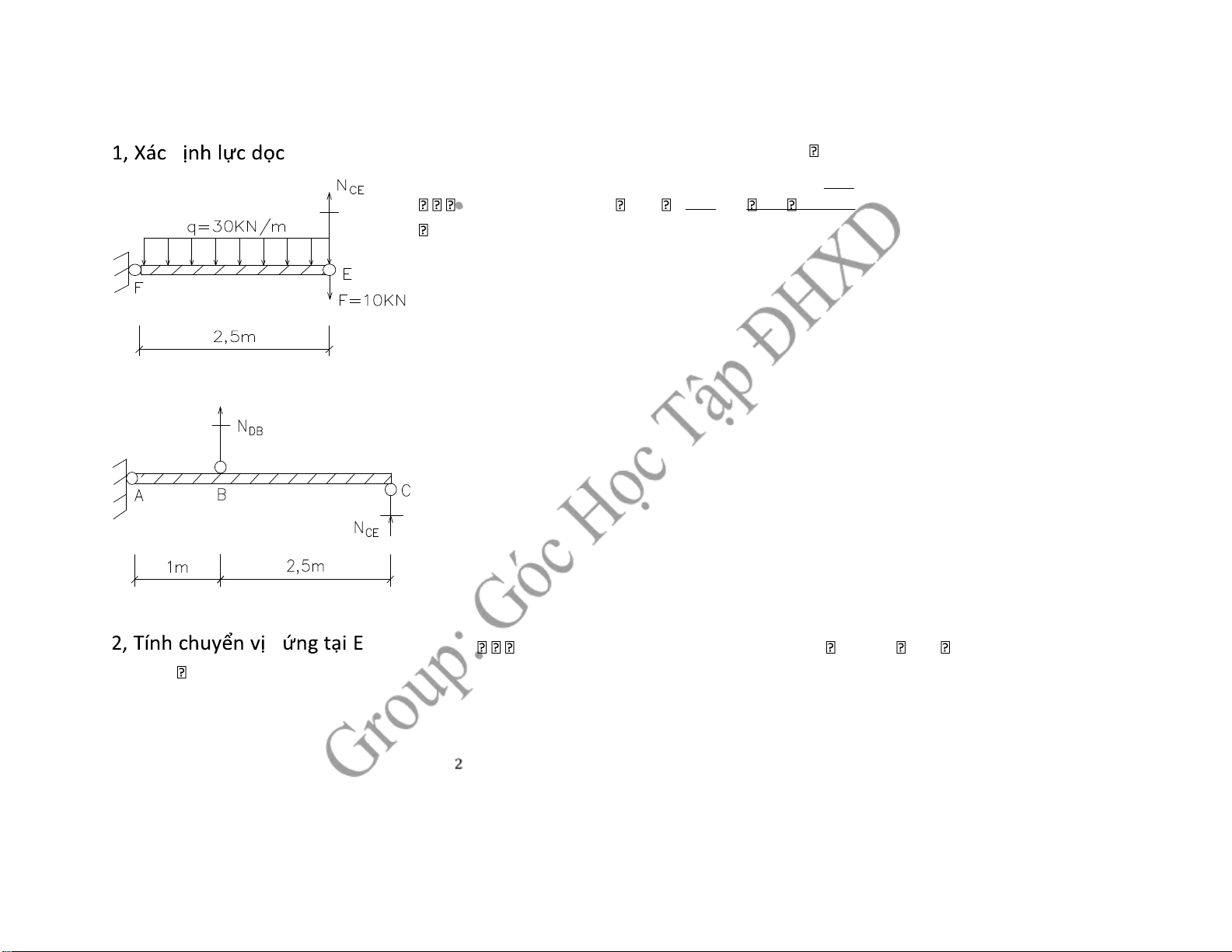
1, Xác ịnh Nz của BD và CE
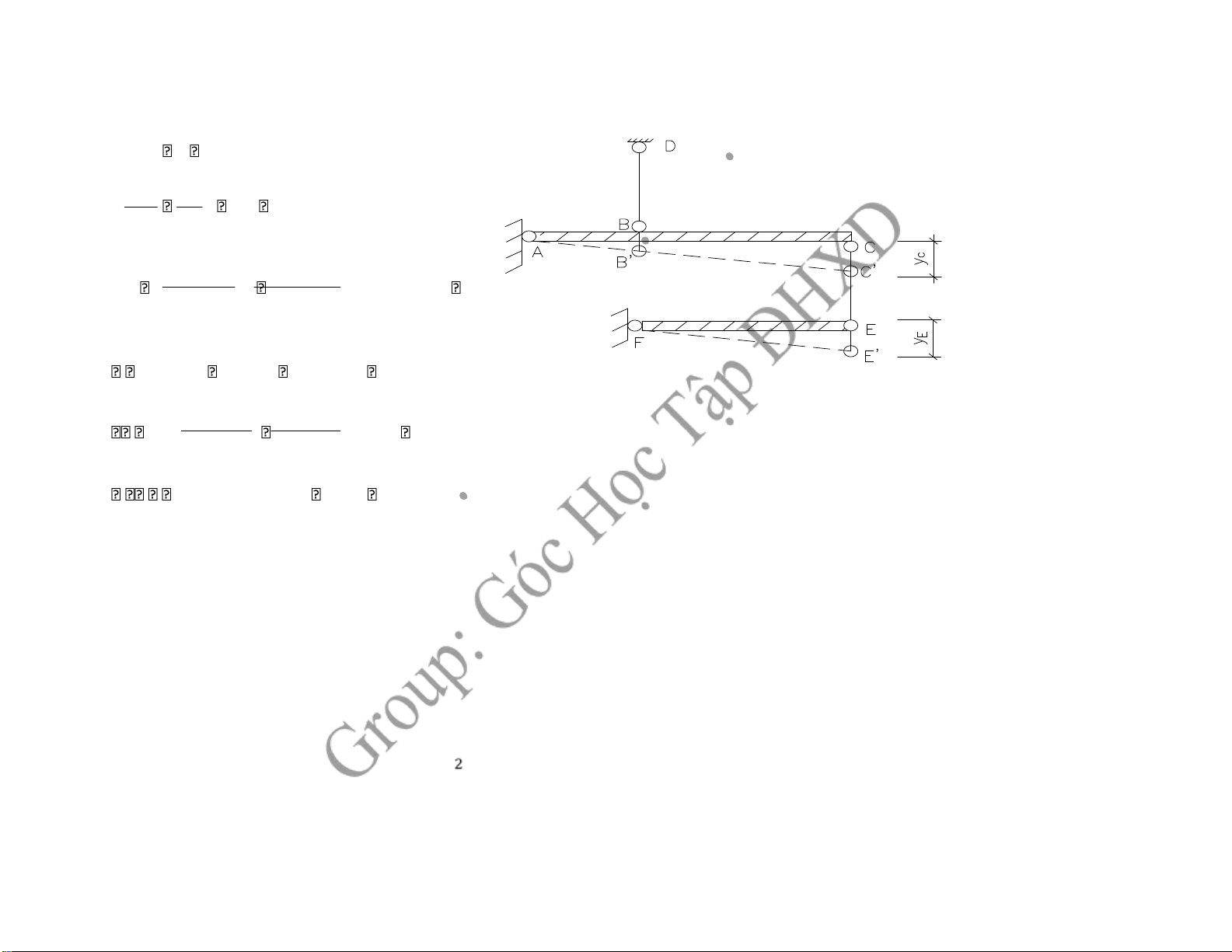
2, Tính chuyển vị tại E 2,52 m CE F 0 NZ .2,5 F.2,5 q. 2,52 NZCE 10.2,5 30. 2 47,5KN 2 2,5 m CE DB A 0 N DB.1 NZ .3,5 NZ 47,5.3,5 166,25KN EE' = L CE yc BB' 1 * CC ' 3,5.BB' CC' 3,5
BB' NE AZBD. .BDLBD 166,25.1202.10 .44 0,249cm yc CC' 3,5.BB' 3,5.0,249 0,872cm
LCENE AZCE. .CELCE 47,5.1202.10 .44 0,071cm yE LCE yc 0,872 0,071 0,943cm CÂU 2:
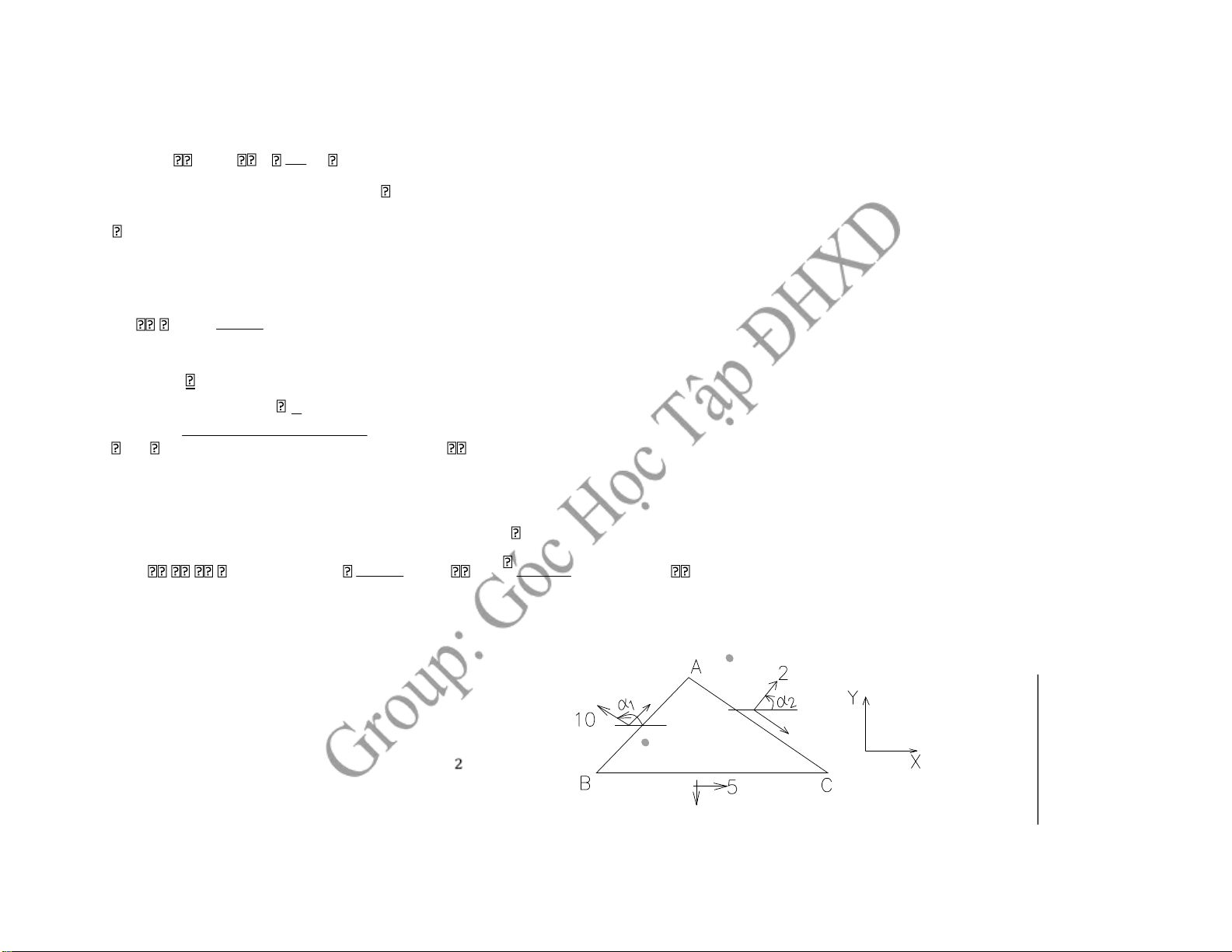
Cho phân tố ở trạng thái ứng suất phẳng như hình vẽ
1, Tính ứng suất pháp trên mặt ứng AC 2,
Xác ịnh các phương chính, ứng suất chính
3, Tính biến dạng dài tương ối theo
phương chính E = 2. 104 μ = 0,25 Bài làm 1, Ta có: τyx =3 τxy = -3 σ =6y σ =8u α(x;u)=150o σ +x σy σ -x σy Ta có: σ =u + .cos2α - τ .sin2αxy 2 2
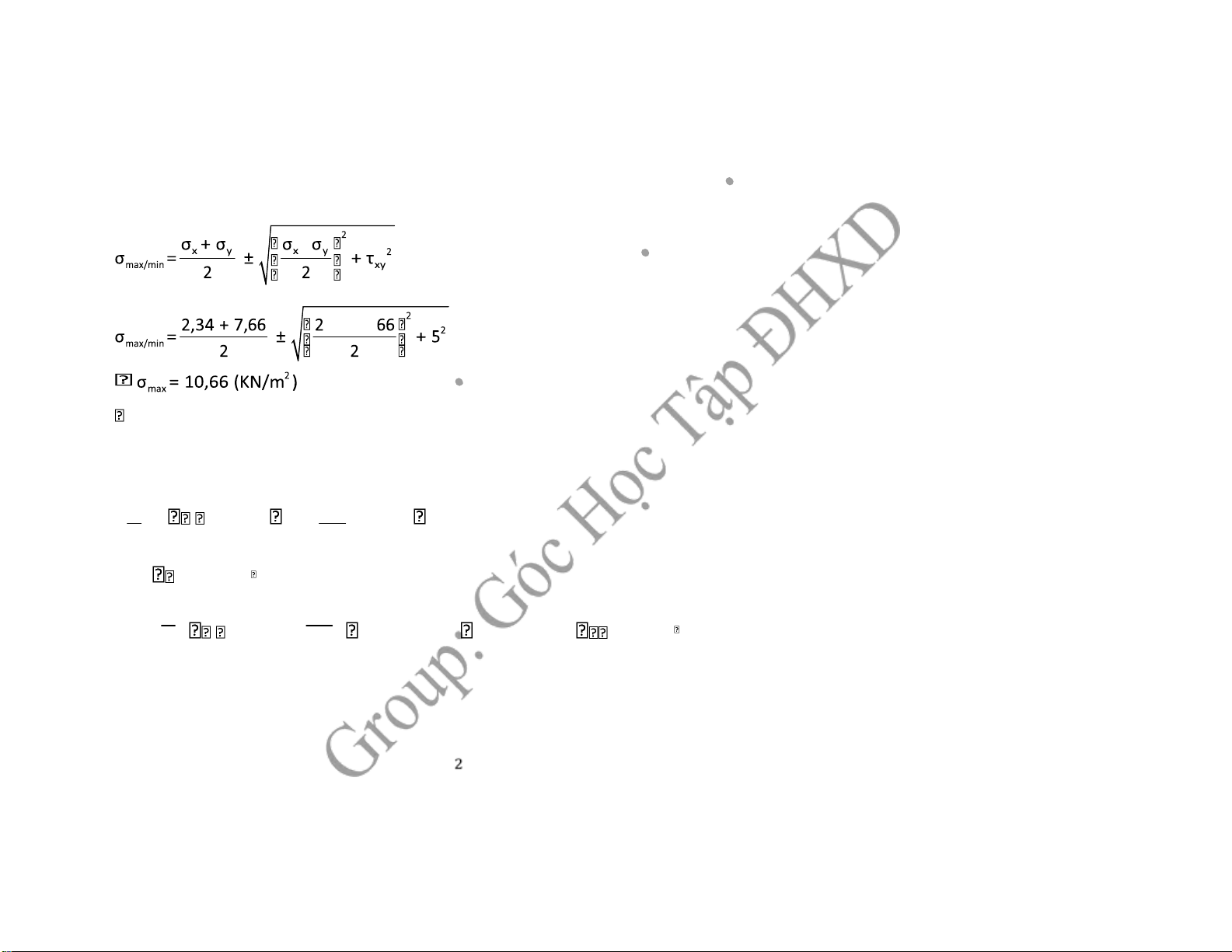
8 = σ +x 6 + σ -x 6.cos2.150 + 3.sin2.150o o 2 2 σ =12,13(x KN/m2 ) -2τ -2.(-3) xy 2, Ta có: tg2α =o = = 0,98 σ -σx y 12,13-6 α =o 22,2o o α =o1 α = 22,o 2 αo2 = 90 + α = 112,o o1 2o σmax/min = σ +x σy σ -x σy 2 2 2 ± 2 + τxy σmax/min =12,36 + 6 ± 12,36 - 2 6 2 + 32 2 σmax = 13,35 (KN/m2 ) σmin = 4,78 (KN/m2 )
Ứng suất chính: σ = 13,35 (KN/m2 ) 1 σ =2 4,78 (KN/m2 ) 2 ) σ =3 0 (KN/m
3, Biến dạng dài tương ối
ε =1 1 . α - μ(σ + σ ) = 1 2 3 1 4 . 13,35 - 0,25 . (4,78 + 0) 6,078.10 4 E 2.10
ε =2 1 . α - μ(σ + σ ) = 2 1 3
1 4 . 4 ,78 - 0,25 . (13,35 + 0) 7,21.10 5 E 2.10
ε =3 1 . α - μ(σ +σ ) = 3 2 1
1 4 . 0 - 0,25 . (4,78 + 13,35) 2,27.10 4 E 2.10 ĐỀ 4
CÂU 1 : Cho dầm chịu tải trọng như hình vẽ:
Vẽ biểu ồ nội lực cho dầm. BÀI LÀM: ∑ X= 0 → HA= 0 ∑ mA= 0 → M + VC.4 = q. 3. 2,25 → VC = . . , → VC = 70 (kN) ∑ Y= 0 → VA+ VC= q.3 → VA= 40.3 – 70 = 50 (kN) B2 : Chia oạn: 2 oạn
B3: Viết biểu thức ứng lực cho từng oạn
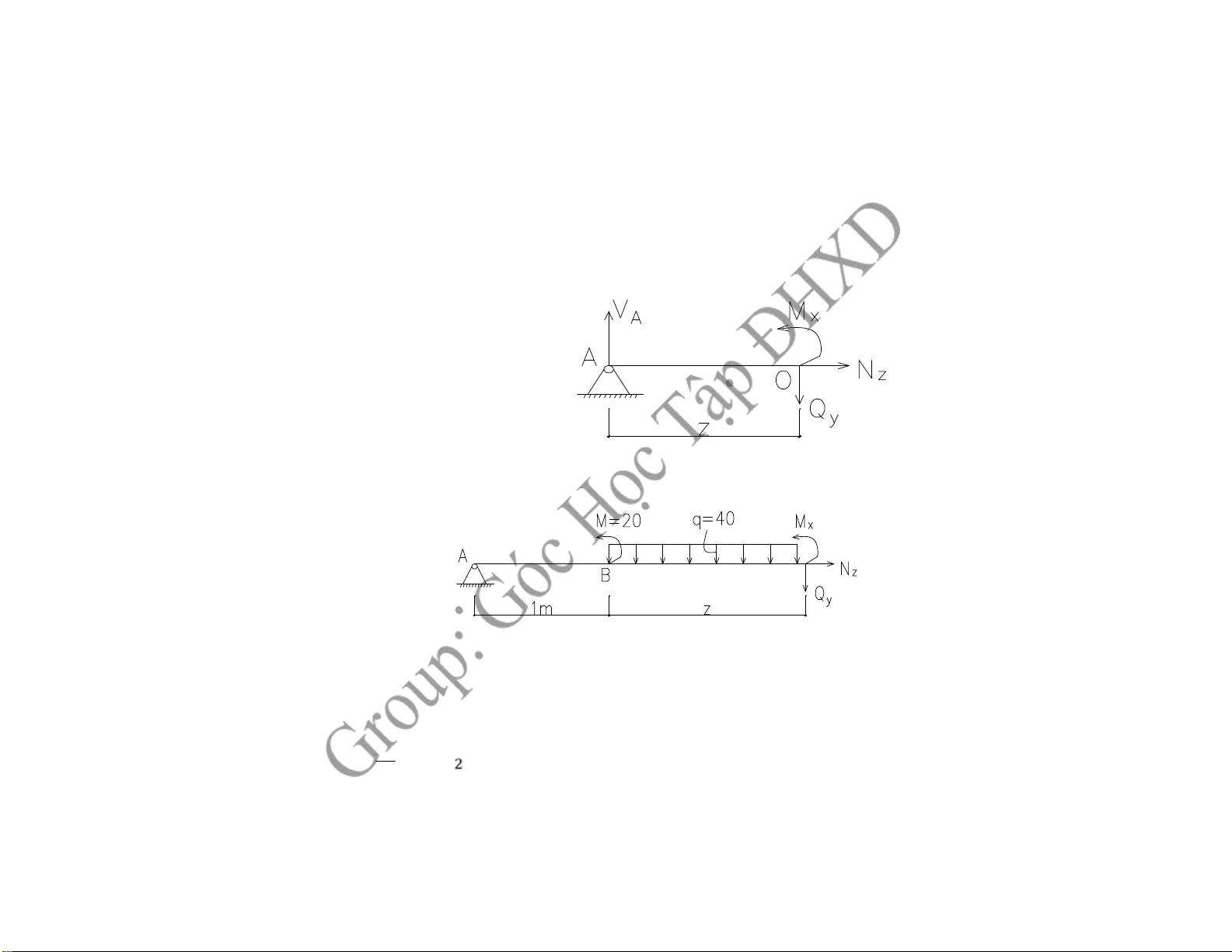
-Đoạn 1: AB ( z € [ 0 ; 1 ] ). Ta có q = 0 → Mx: bậc 1; Qy hằng số ∑ X= 0 → NZ = 0 ∑ Y= 0 →VA = Qy = 50(kN) ∑ mO= 0 → Mx = VA. z +) z= 0 → M A x = 0
+) z= 1 → M Bx = VA. 1= 50 (kN.m)
-Đoạn 2: BC ( z € [ 0 ; 3 ] ). Ta có q = const → Mx: hàm bậc 2; Qy hàm bậc 1 ∑ X= 0 → NZ = 0 ∑ Y= 0 → Qy = VA – q.z
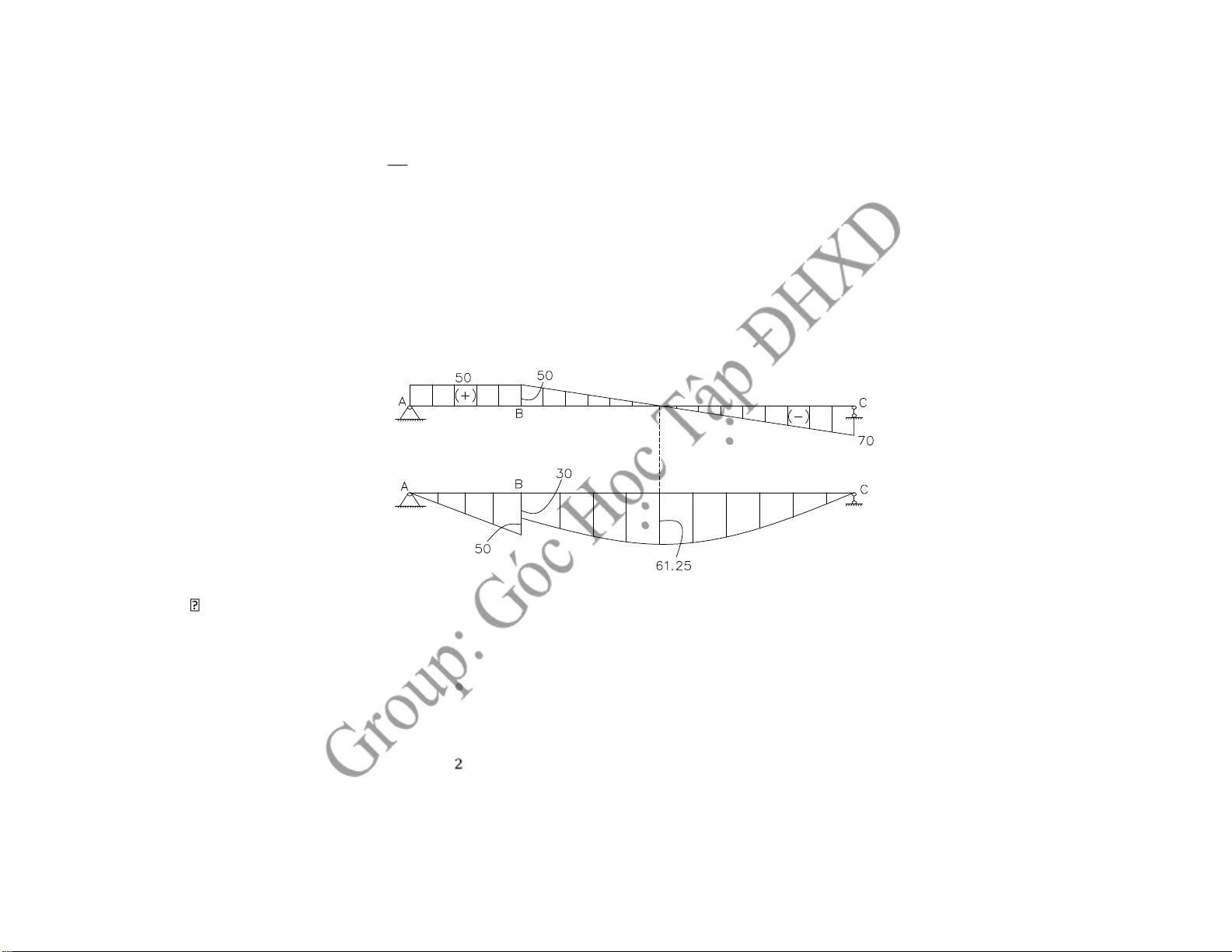
+) Tại B : z= 0 → Q By = VA = 50 (kN)
+) Tại C : z= 3 → Q Cy = VA – q.3 = 50 – 3.40 = -70 (kN) z2 O= 0 → Mx = - M - q. 2 + VA.( 1+ z ) ∑ m
→ Mx = -20 – 40. z2 + 50 .( 1+ z) 2
→ Mx = – 20.z2 + 50.z + 30
+) Tại B: z= 0 → M Bx = 30 (kN.m)
+) Tại C: z= 1 → M Cx = 0 (kN.m)
B4 : Vẽ biểu ồ nội lực (Qy) (Mx) Kiểm tra: +) M xB _ ph M xB tr_ = -M
→ 30 - 50 = -20 (thỏa mãn) Câu2 A = A = 6cm ; A 2 1 2 3 10cm2 E = 10 KN/cm ; F = 30KN4 2
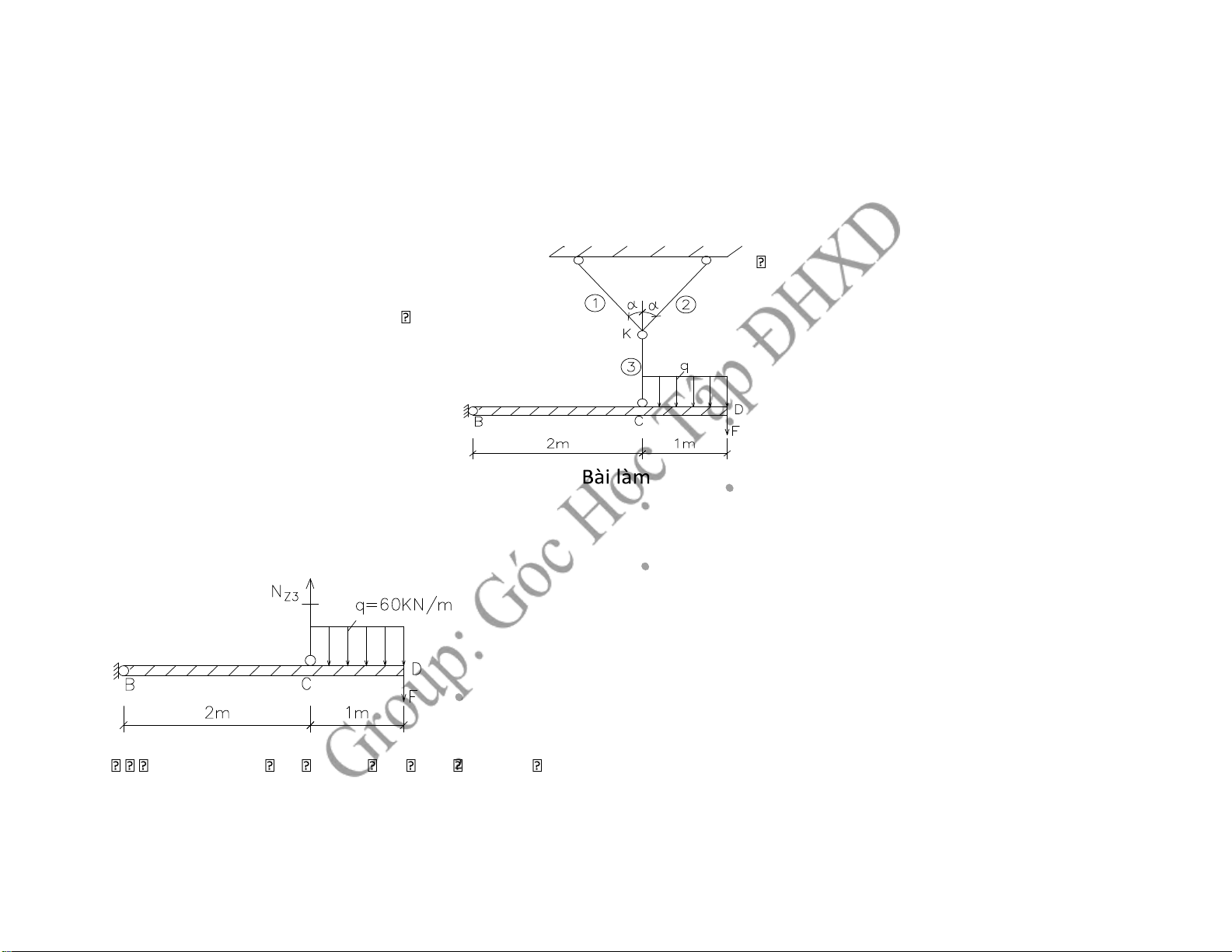
L = L = 1,5m; L = 1,2m1 2 3 q = 60KN/m; =30o
1, Xác ịnh lực dọc trong các thanh 2,
Tìm chuyển vị theo phương ứng của D
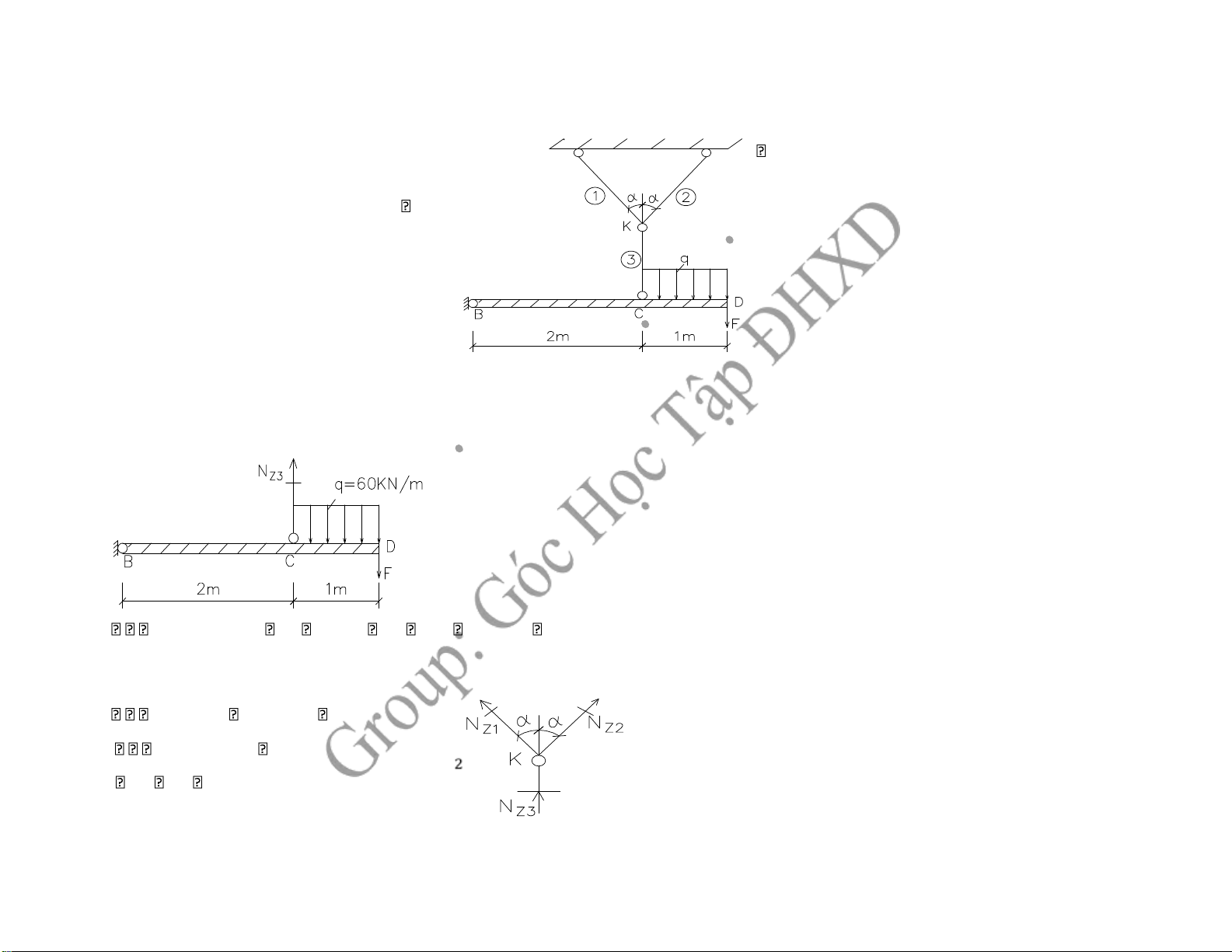
1, Xác ịnh lực dọc trong các thanh
Xét ngang qua thanh 3 ta xét phần dưới: mB0
NZ3.2 F.3 q.1.2,5 NZ3 30.3 60.1.2,5 120KN Xét hệ chính ta có: y 0
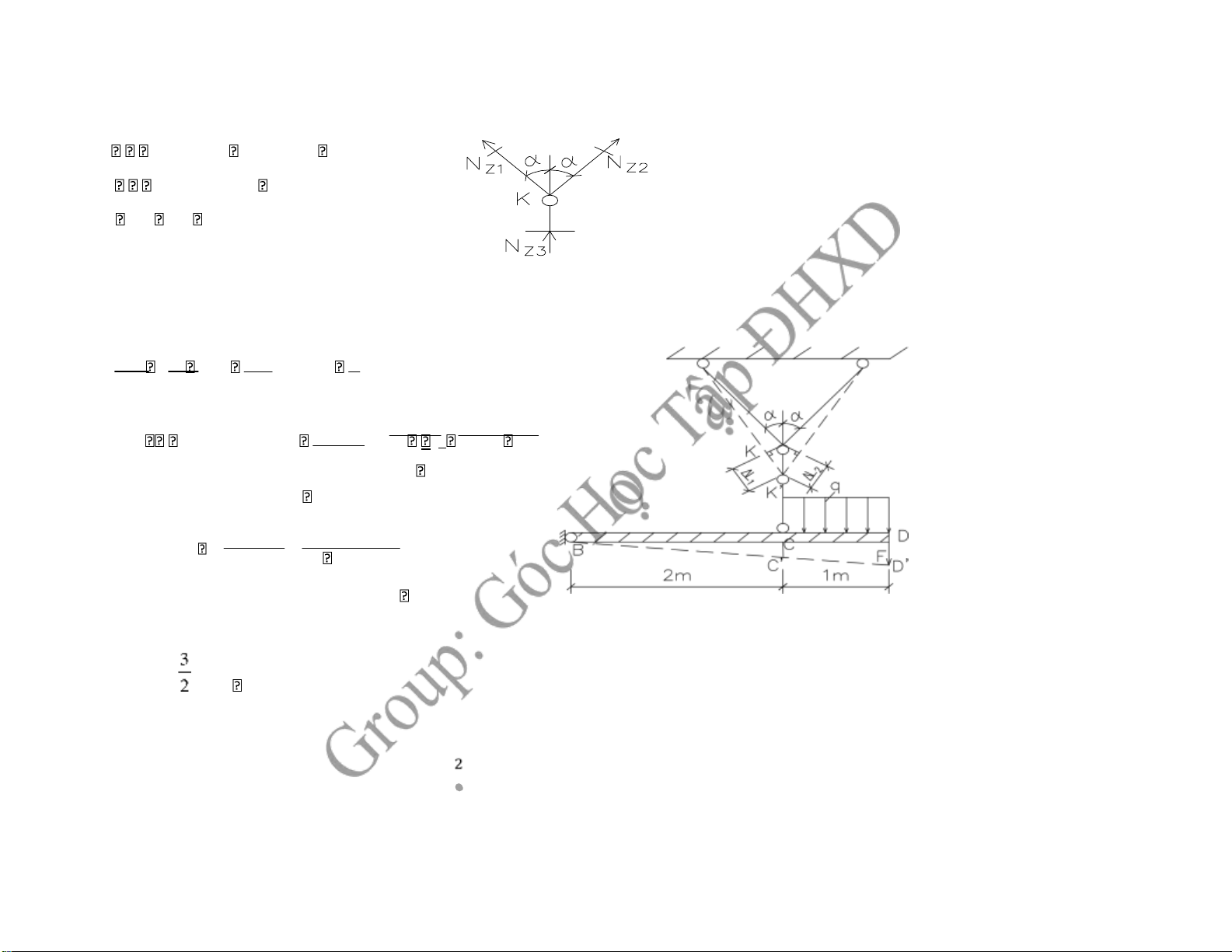
NZ3 NZ1.cos30o NZ 2.cos30 (1)o
x 0 NZ 2..sin30o NZ1.sin30 (2)o Từ (1,2) NZ1 NZ2 69,28KN
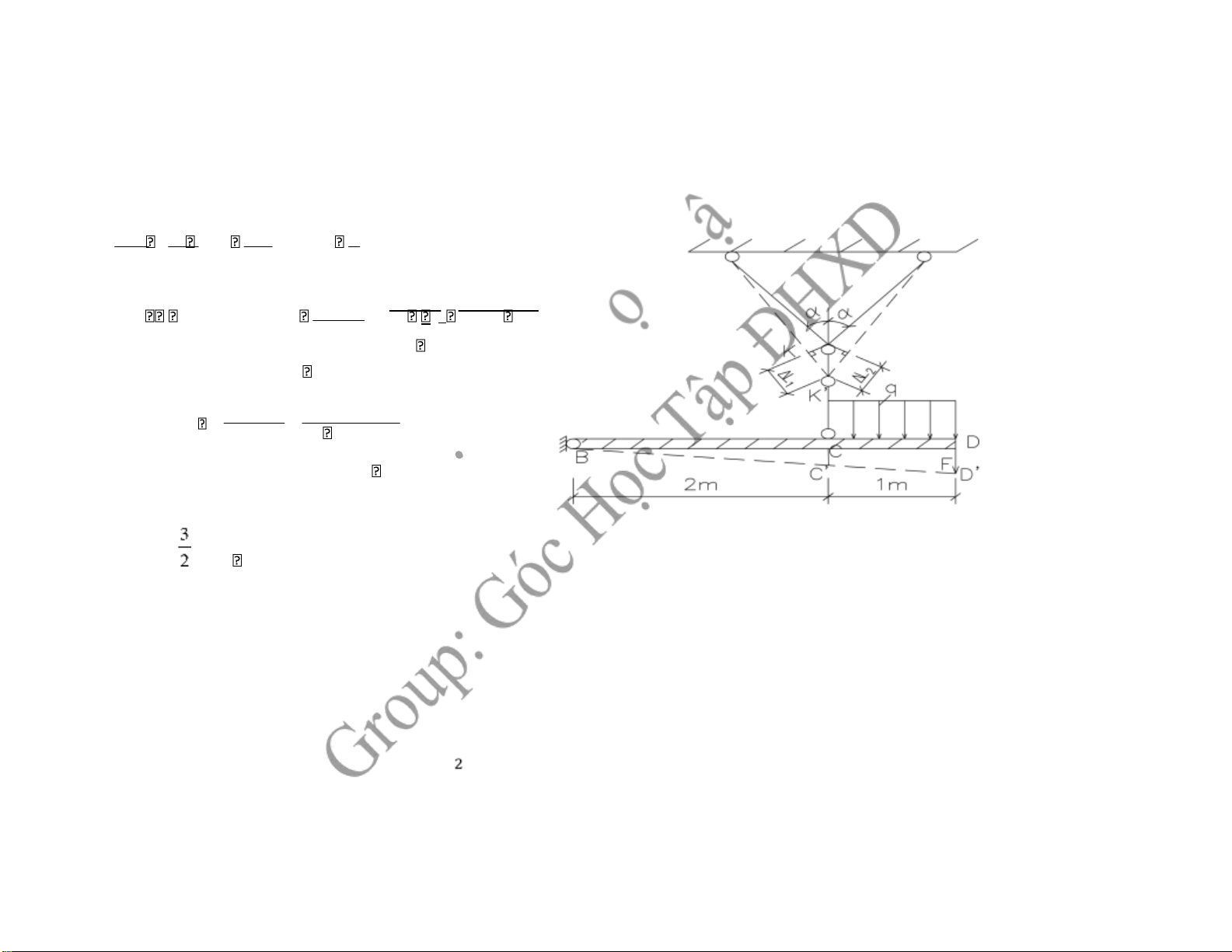
2, Tính chuyển vị theo phương ứng của D DD' BD DD' BD .CC ' 3 CC ' CC ' DC BC 2 CC ' L3 KK ' NZ3.L3 L1 NZ3.L3 N LZ1. 1 E A. 3 cos E A. 3 E A. 1.cos
→ CC ' 120.12010.104 10 .669,28.1504 .cos30o 0,34cm →DD’= .0,34 0,52cm ĐỀ 5 Câu1:
Cho hệ có tiết diện thay ổi như hình vẽ
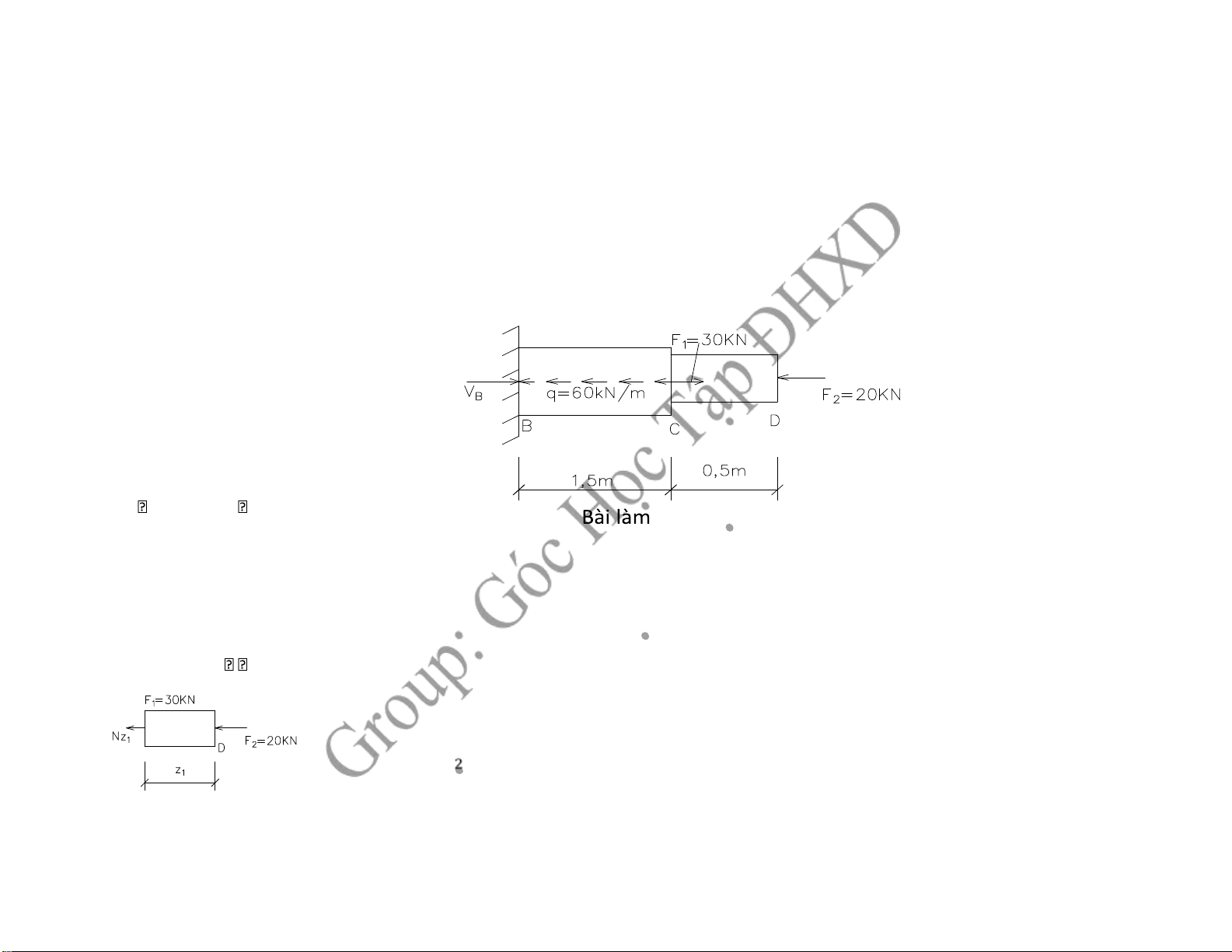
1,Vẽ biểu ồ ứng lực cho thanh
2, Tính ứng suất lớn nhất trên tiết diện
3,Chuyển vị dọc trục C và D ABC 40cm A2; CD 20cm2
1, Vẽ biểu ồ ứng lực cho thanh -Chia oạn: 2 oạn +Đoạn CD:(0 z1 0,5 )m NZ1 F2 20KN
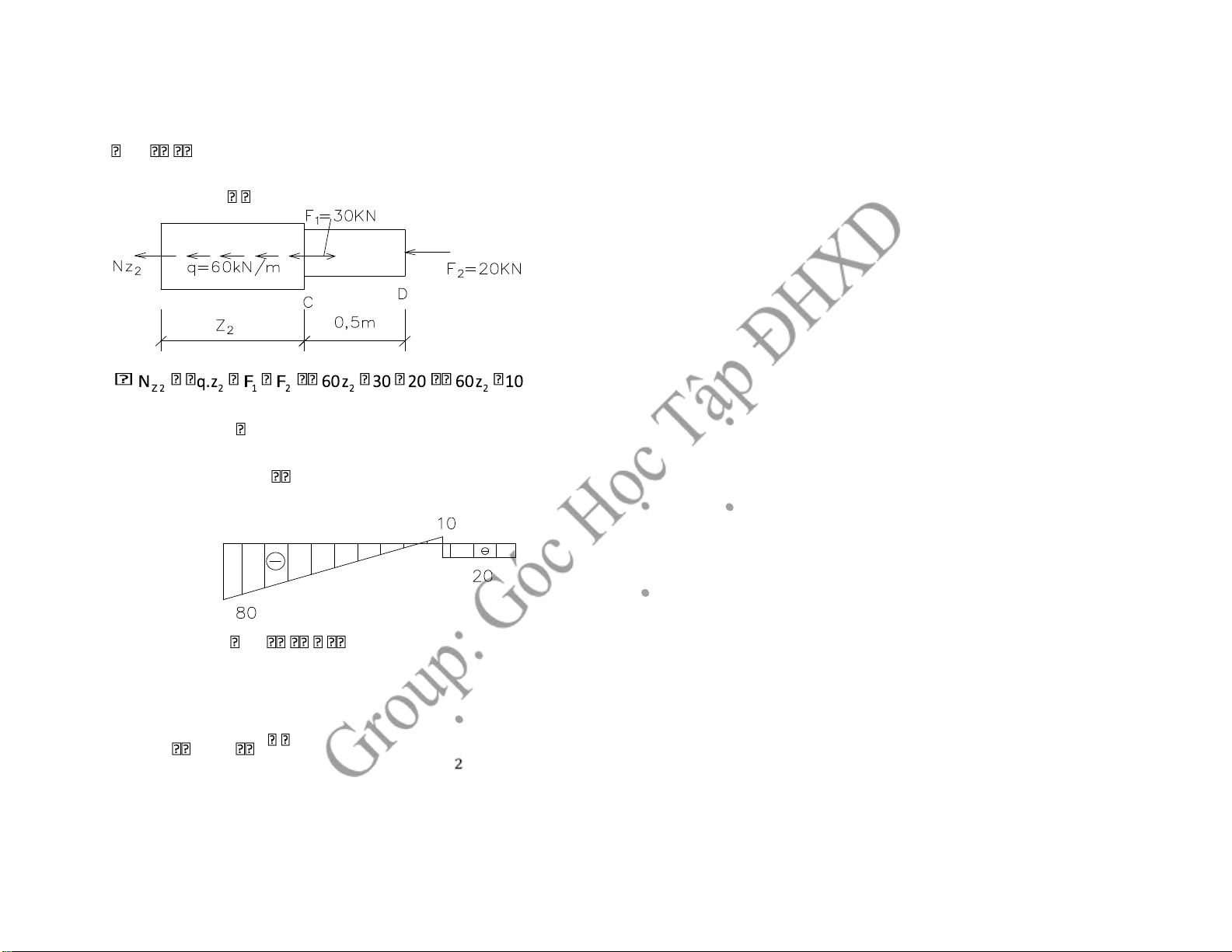
+Đoạn BC: (0 z1 1,5 )m ; q=const→NZ: bậc nhất Tại C: z=0→NZ 10KN Tại D: z=1,5m→NZ 80KN Kiểm tra: N ph tr Z NZ F 20 10 30 (thỏa mãn)
2, Tính ứng suất lớn nhất trên tiết diện -BC: N 80 Z 80KN Z1 2KN cm/ 2 40 -CD: NZ 20KN Z 2 20 1KN cm/ 2 20 → max 2KN cm/ 2
3, Chuyển vị dọc trục của C và D SNZ BC WC LBC E A. BC 1 1 .80.1,333 .10.16,7 W 3 C 2 10 .403 0,13cm SNZCD 20.50 +WD LBDLBC LCDWC E A. CD 0,13 10 .203 0,18cm Câu 2
Cho phân tố ở trạng thái ứng suất phẳng
1, Tính ứng suất σx; σy
2, Tính ứng suất pháp cực trị
3, Tính biến dạng dài tương ối theo ứng suất pháp
cực trị E = 2.104 μ = 0,25 Bài làm 1, Xét mặt phẳng nghiêng Xét mặt phẳng nghiêng Xét mặt phẳng BC ta có: AB ta có: AC ta có: σ =u1 10 (KN/m2 )σu2 = 2 (KN/m2 )σ =x ? (KN/m2) α = 135 o 1 α =2 60o σ =y ? (KN/m2)
τu v1 1 = ?τu v2 2 = ?τxy= τyx= -5 -Ta có:
⎧⎪10 = σ +σx 2 y + σ -x2 σy .cos270 - 5.sin270 σ = σ +σx
y + σ -x σy .cos2α - τ .sin2α→ u xy 2 2 ⎨ σ +σx y σ -x σy
⎪⎩ 2 = 2 + 2 .cos120 - 5.sin120 σ =x 2,34 (KN/m2 ) → σ = 2 y ) 7,66 (KN/m
2,Tính ứng suất pháp cực trị ,34 - 7, σmin = -0,66 (KN/m2 )
3, Biến dạng dài theo phương ứng suất pháp cực trị εmax = E1 . max - μ min = 10 14 . 10,66 - 0,25 . (- 0,66) 1,0825.10 3 E1 min - μ max = 1014 . -0,66 - 0,25 . 10,66 3,325.10 4 εmin = . Đề 6 Câu1 A = A = 6cm ; A 2 1 2 3 10cm2 E = 10 KN/cm ; F = 30KN4 2
L = L = 1,5m; L = 1,2m1 2 3 q = 60KN/m; =30o
1, Xác ịnh lực dọc trong các thanh 2,
Tìm chuyển vị theo phương ứng của D Bài làm
1, Xác ịnh lực dọc trong các thanh
Xét ngang qua thanh 3 ta xét phần dưới: mB0
NZ3.2 F.3 q.1.2,5 NZ3 30.3 60.1.2,5 120KN Xét hệ chính ta có: y 0
NZ3 NZ1.cos30o NZ 2.cos30 (1)o
x 0 NZ 2..sin30o NZ1.sin30 (2)o Từ (1,2) NZ1 NZ2 69,28KN
2, Tính chuyển vị theo phương ứng của D DD' BD DD' BD .CC ' 3 CC ' CC ' DC BC 2 CC ' L3 KK ' NZ3.L3 L1 NZ3.L3 N LZ1. 1 E A. 3 cos E A. 3 E A. 1.cos
→ CC ' 120.12010.104 10 .669,28.1504 .cos30o 0,34cm →DD’= .0,34 0,52cm Câu 2
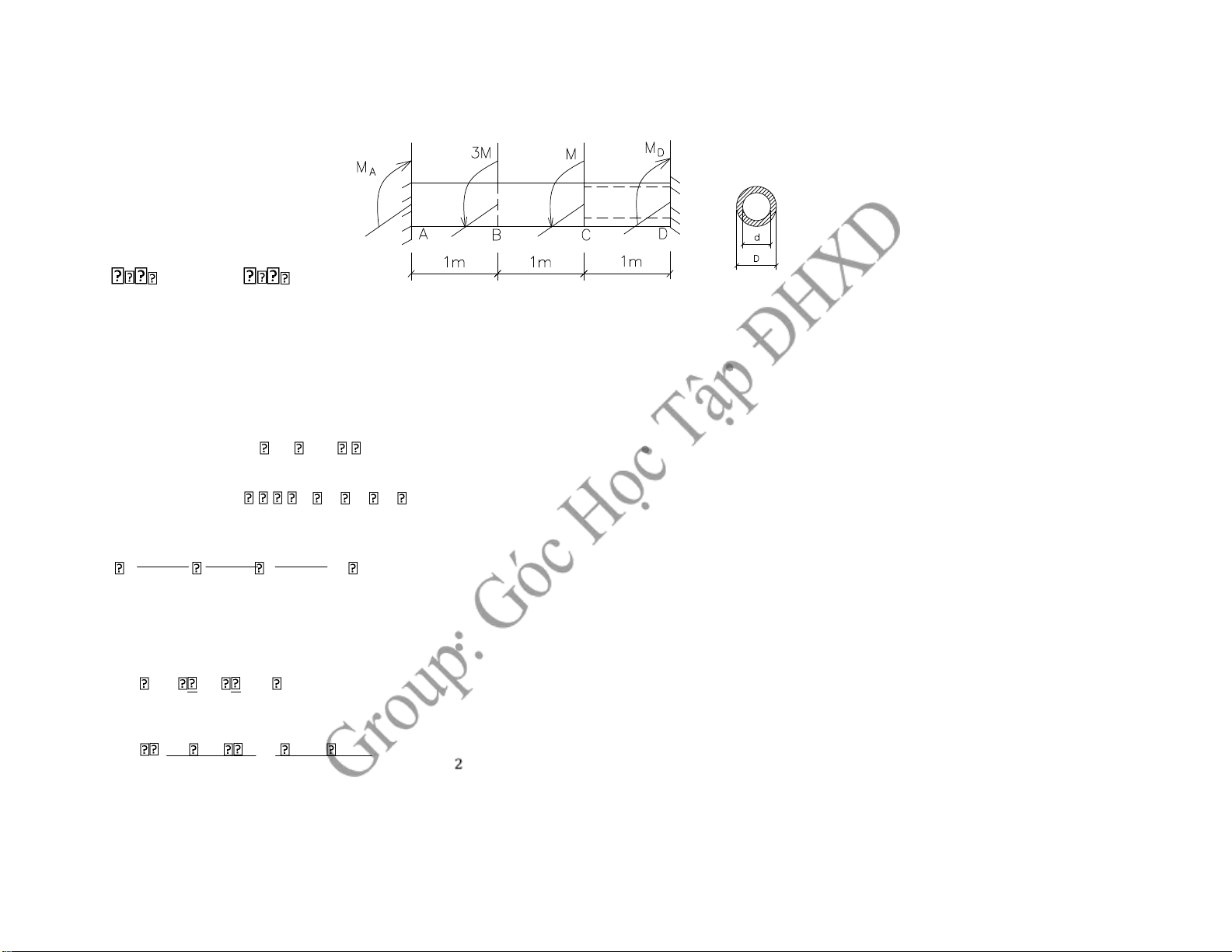
Cho hệ thay ổi tiết diện như hình vẽ D = 16cm; d = 12cm; G=8.103 kN/cm2 16KN cm/ 2; 2o / m
1, Vẽ biểu ồ nội lực 2, Xác ịnh M theo thuyết bền thế năng Và theo iều kiện cứng Bài làm 1, Vẽ biểu ồ -PT cân bằng: MA MD 3M M 4M
-PT biến dạng: AD AB BC CD 0
G IS.MZ AB SMZ BCBC G IS.MZPCDCD 0 AB G I. P P I AB BC P IP .D4 .164 6433,982 4 cm 32 32 I CD P .(D4 d4) .(164 12 )4 4398,23cm4 32 32 +Đoạn 1: M AB Z M A +Đoạn 2: M BC Z M A 3M +Đoạn 3: M CD Z 4M M A
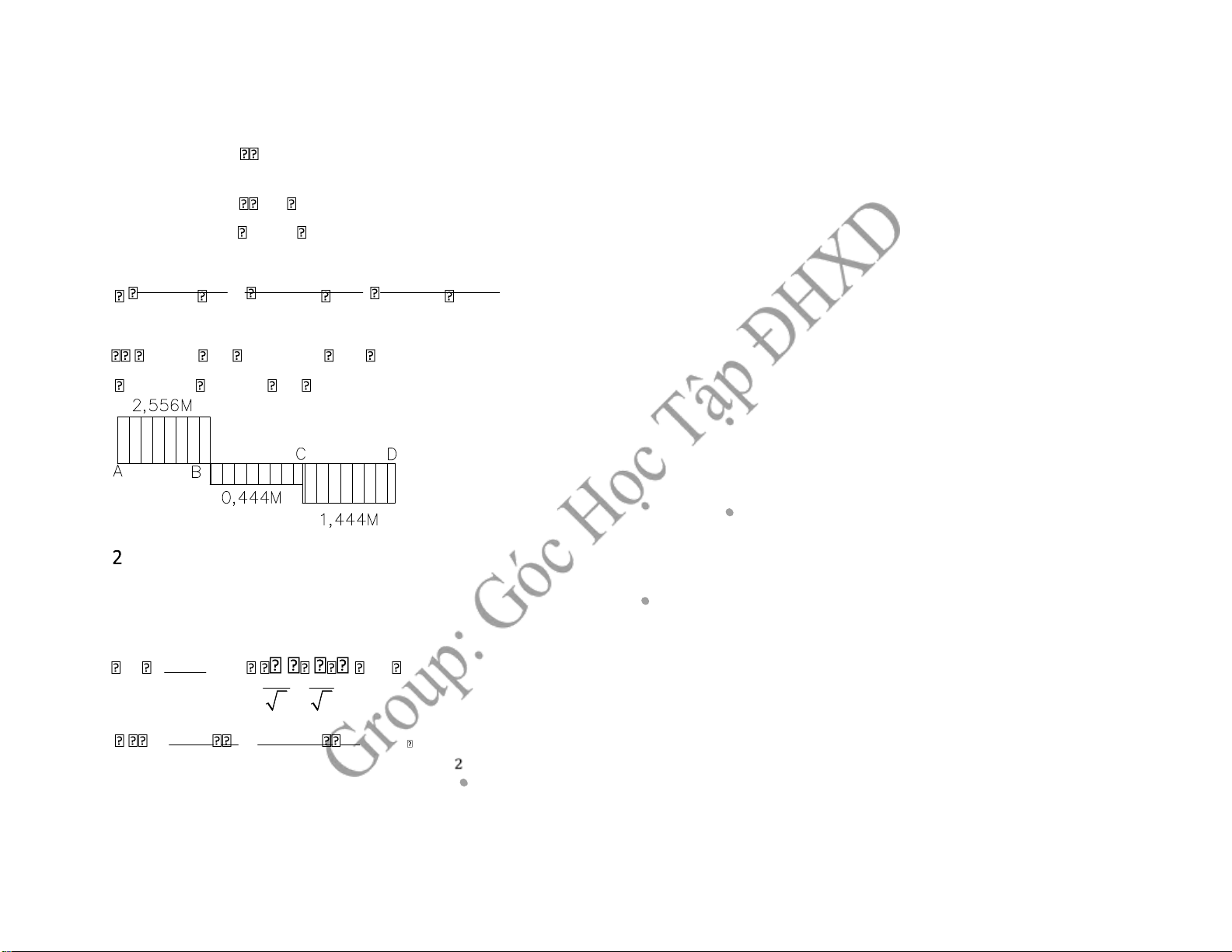
MA.100 (3M MA).100 (4M MA).100 0 G.6433,982 G.6433,982 G.4398,23 MA 3M MA 1,463.(4M MA) 0 3,463MA 8,852M MA 2,556M , Kiểm tra bền
-Theo thuyết bền thế năng: max | MZ | 16 9,24(kN cm/ 2) WP 3 3
MZAB . D 2,556M .16 3,178.10 3M AB IP 2 6433,982 2
MZBC . D 0,444M .16 5,52.10 4M BC IP 2 6433,982 2 CD
MZCD . D 1,444M .16 2,63.10 3M IP 2 4398,23 2 max 3,178.10 . 3 M
M 2906,74(kN cm. ) 29,0674(kN m. ) -Theo iều kiện cứng: max MZ G I. P AB 2,556M 3 8M 4,97.10 6433,982.8.10 CD 1,444M3 4,104.10 8M 4398,23.8.10 8 1 M 2. . 4,79.10 180 100 M 7287,4(kN cm.)




