Bài tập Portfolio môn học Optimal Engineering nội dung bằng tiếng Anh

lOMoARcPSD| 37054152 lOMoARcPSD| 37054152 LINEAR PROBLEM:
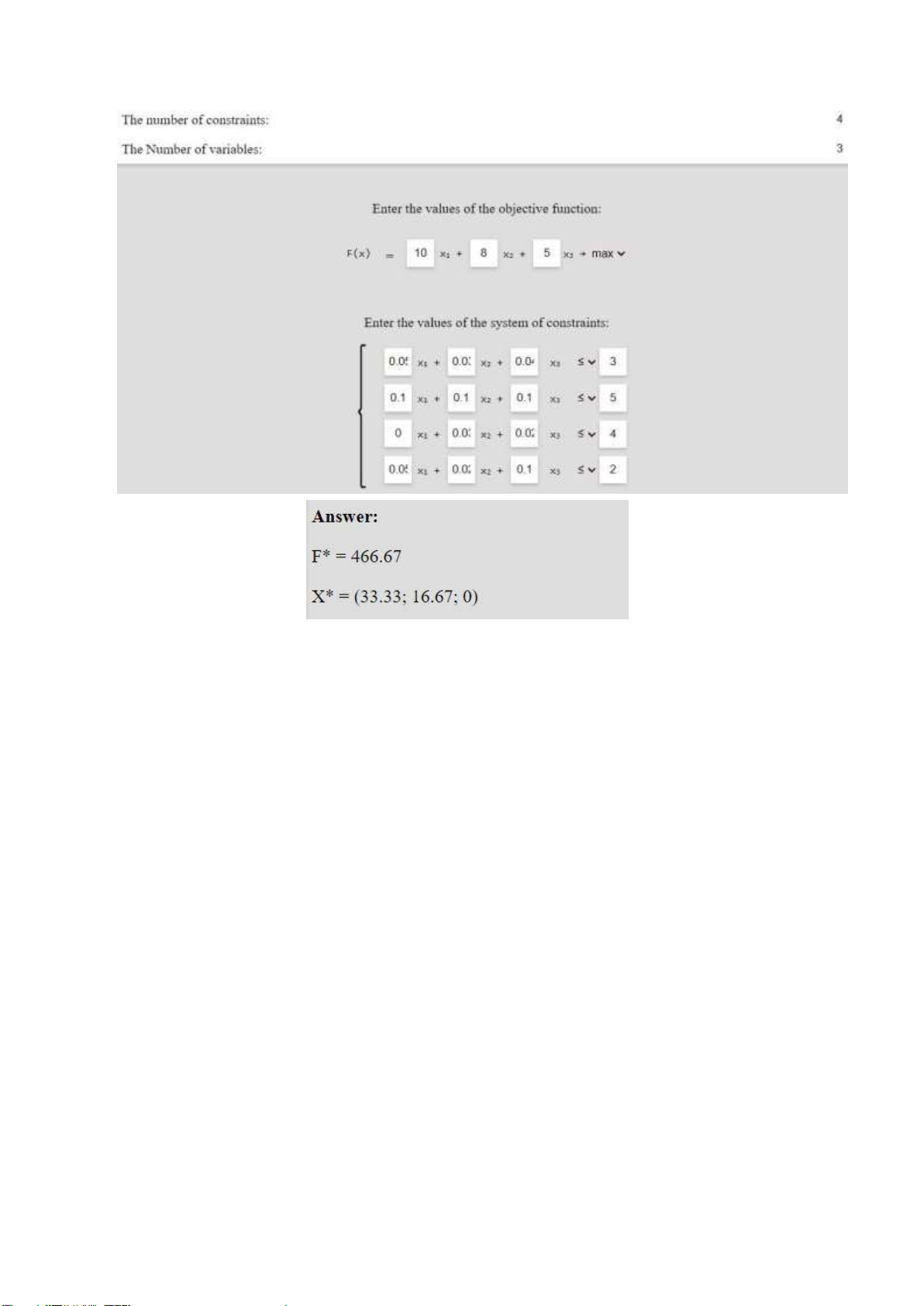
1. MANUFACTURING PROBLEM: 1.1 Problem:
Maximize profits of Coffee shop with limited materials in store. Coffee Milk tea Chocolate Stored Sugar 0,05 0,03 0,04 3 kg Ice 0,1 0,1 0,1 5 kg Milk 0 0,03 0,02 4 kg Cacao 0,05 0,02 0,1 2 kg Profit 10k 8k 5k 1.2 Modeling problem: Variable:
+ x1: number of cups of coffee made per day
+ x2: number of cups of milk tea made per day +
x3: number of cups of chocolate made per day Objective:
Z(x) = 10.x1 + 8.x2 + 5.x3 Maximum Constraint: Sugar: 0,05.x1 + 0,03.x2 + 0,04.x3 <=3kg Ice: 0,1.x1 + 0,1.x2 + 0,1.x3 <=5kg Milk: 0,03.x2 + 0,02.x3 <=4kg Sugar: 0,05.x1 + 0,02.x2 + 0,1.x3 <=2kg Condition: 0 < x1,x2,x3 < 40 1.3 Solving problem: lOMoARcPSD| 37054152 Result: F = 466.670 VNĐ
Number of cups of coffe x1 = 33 cups
Number of cups of milk tea x2 = 16 cups
Number of cups of chocolate x3 = 0 2. MIX MATERIAL: 2.1 Problem lOMoARcPSD| 37054152
Minimum cost to make a material. (20% Ag, 30% Cu, 50% Al) Ag Cu Al A B (%) Ag 1 0 0 0.5 0.5 0.2 Cu 0 1 0 1.4 0.6 0.3 Al 0 0 1 1.6 2.4 0.5 Price 150 75 50 40 60 2.2 Modeling problem: Variable: + x1: number of kilos Ag + x2: number of kilos Cu + x3: number of kilos Al + x4: number of kilos A + x5: number of kilos B Objective: T Zmin = C̅ X̅ 𝐶1 150 𝐶 2 75 C ̅ = 𝐶3 = 50 𝐶4 40 1 0 0 0.5 0.5 [𝐶5] [ 60 ] X = [0 1 0 1.4 0.6 ] 0 0 1 1.6 2.4 Constraint: A.x = b Condition: 0 < x1,x2,x3 < 40 3. TRANSPORTATION: 3.1 Problem:
Minimize the cost of transporting Cocacola to University canteen. lOMoARcPSD| 37054152 1. UTE (30) 2. BUH (25) 3. UFM (10) 1. Thu Duc (40) 7 3 5 2. Binh Duong (10) 6 5 8 3. Dong Nai (15) 2 4 6 Cost (x10,000 vnd)
3.2 Modeling problem Variable:
Xij is the number of Cocacola packs transports from i factory to j store. Objective:
Z(x) min = 7.x11 + 3.x12 + 5. x13 + 6.x21 + 5.x22 + 8.x23 +2.x31 + 4.x32 + 6.x33 Constraint: Factory: x11 + x12 + x13 ≤ 40 x21 + x22 + x23 ≤ 10 x31 + x32 + x33 ≤ 15 Store: x11 + x21 + x31 = 30 x12 + x22 + x32 = 25 x13
+ x23 + x33 = 10 Condition: Xij ≥ 0 3.3 Solving problem: lOMoARcPSD| 37054152 Result: F = 2,500,000 VNĐ From Thu Duc to HCMUTE: x11=5; From Thu Duc to BUH: x12= 25; From Thu Duc to UFM: x13=10; From Binh Duong to HCMUTE: x21=10; From Dong Nai to HCMUTE: x31= 15
4. COME BACK CITY WITH 4 BAGS: 4.1 Problem: lOMoARcPSD| 37054152
Maximize the value of products brought from the countryside to the city. With
limited number of bags and weight.
Soft drink Rice Meat Fruit Vegetable Left 15kg Right 20kg Back 30kg Front 10kg Price 40k 15k 50k 30k 10k VNĐ 4.2 Modeling problem: Variable:
Xij: Number of kilos j bring in bag i i: 1~4; j: 1~5 Objective: Zmax = C̅TX̅ T 𝐶1
40 40x1 + 15x2 + 50x3 + 30x4 + 10x5 = C̅ X̅ 𝐶 15 2 Constraint: C 50 ̅ = 𝐶3 A𝑥̅̅ 𝑏̅̅ 30 𝐶4 [10] 1 1
1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 15 [𝐶5]
0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 ̅ = [20] A = [ ] 𝑏̅
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 30
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 10 Condition: 0 20 4.3 Solving problem: lOMoARcPSD| 37054152 Result: F = 3,750,000 VNĐ
Number of kilos meet bring in left bag: x13 = 15kg
Number of kilos meet bring in right bag: x23 = 20kg
Number of kilos meet bring in back bag: x33 = 30kg
Number of kilos meet bring in front bag: x43 = 10kg 5. SHIPPING FRUIT: 5.1 Problem:
Watermelon Coconut Apple Orange Banana Motorbike (150kg) lOMoARcPSD| 37054152 Truck (1000kg) Train (800kg) Boat (500kg) Plane (300kg) 25k 30k 40k 50k 20k 5.2 Modeling problem: Variable: 𝑥̅1 𝑋̅̅ = 𝑥̅2 𝑥̅3 𝑥̅4 [𝑥̅5]
Number of kilos of watermelon on the transportation, x1
Number of kilos of coconut on the transportation, x2
Number of kilos of apple on the transportation, x3
Number of kilos of orange on the transportation, x4
Number of kilos of banana on the transportation, x5 Objective: Zmax = C̅TX̅ 𝐶1 25 C̅ = 𝐶2𝐶3 = 3040 𝐶4 50 [𝐶5] [20]
25x1 + 30x2 + 40x3 + 50x4 + 25x5= C̅TX̅ Constrant: lOMoARcPSD| 37054152 A𝑥̅̅ 𝑏̅̅
1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 150
0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1000 ̅ = 800
A = 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 𝑏̅
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 500
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1] [ 300 ] Condition: 50 500 100 300 20 50 30 70 0 150 lOMoARcPSD| 37054152
I. DEFINE REAL PROBLEM
Real problem description:
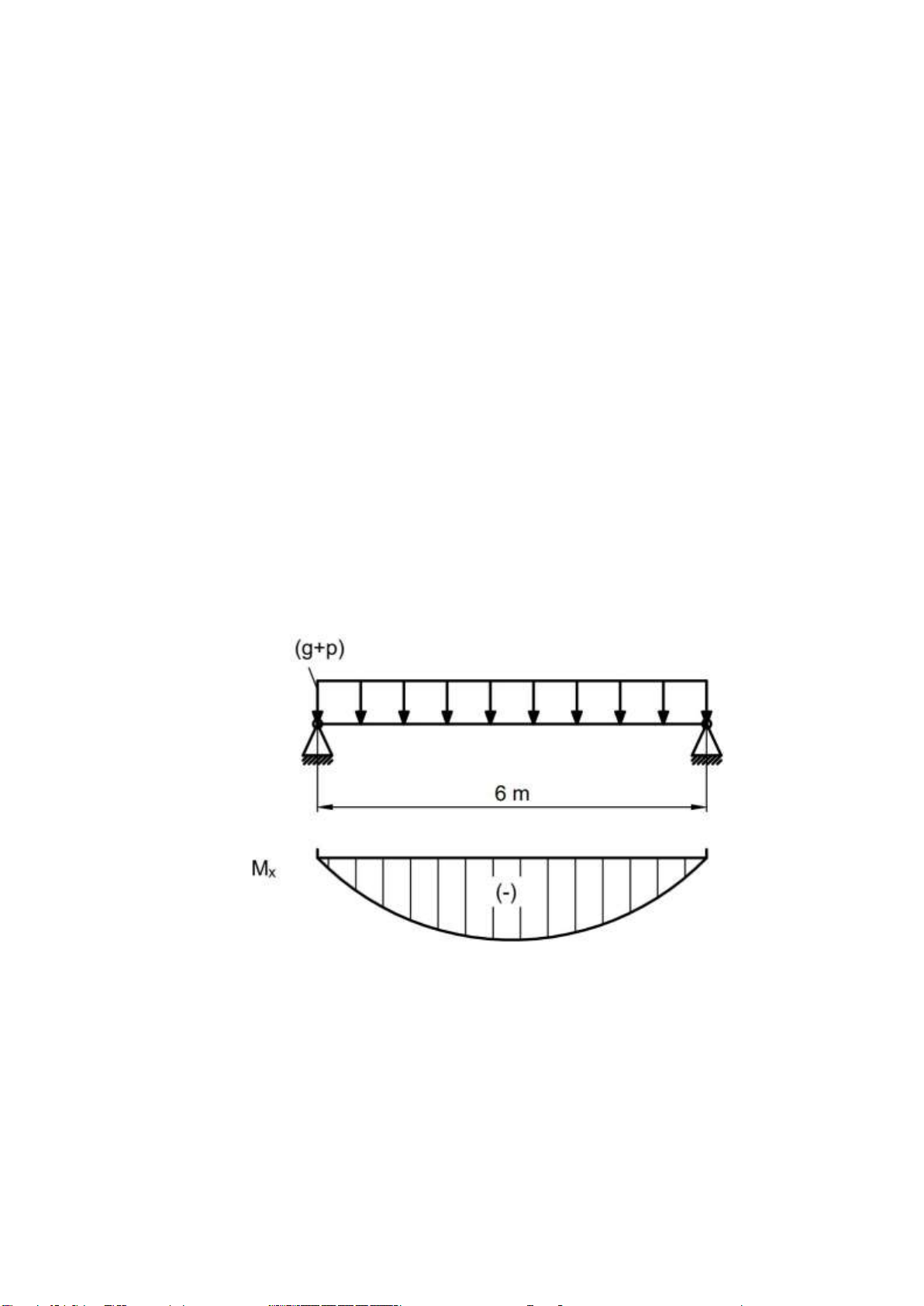
Beam structure is widely application in construction these days. In real working
condition, reinforced concrete beams load bearing including: self-weight, standard live
load p = 50kN/m as the figure 1.2 below. The problem posed is to minimize the mass of
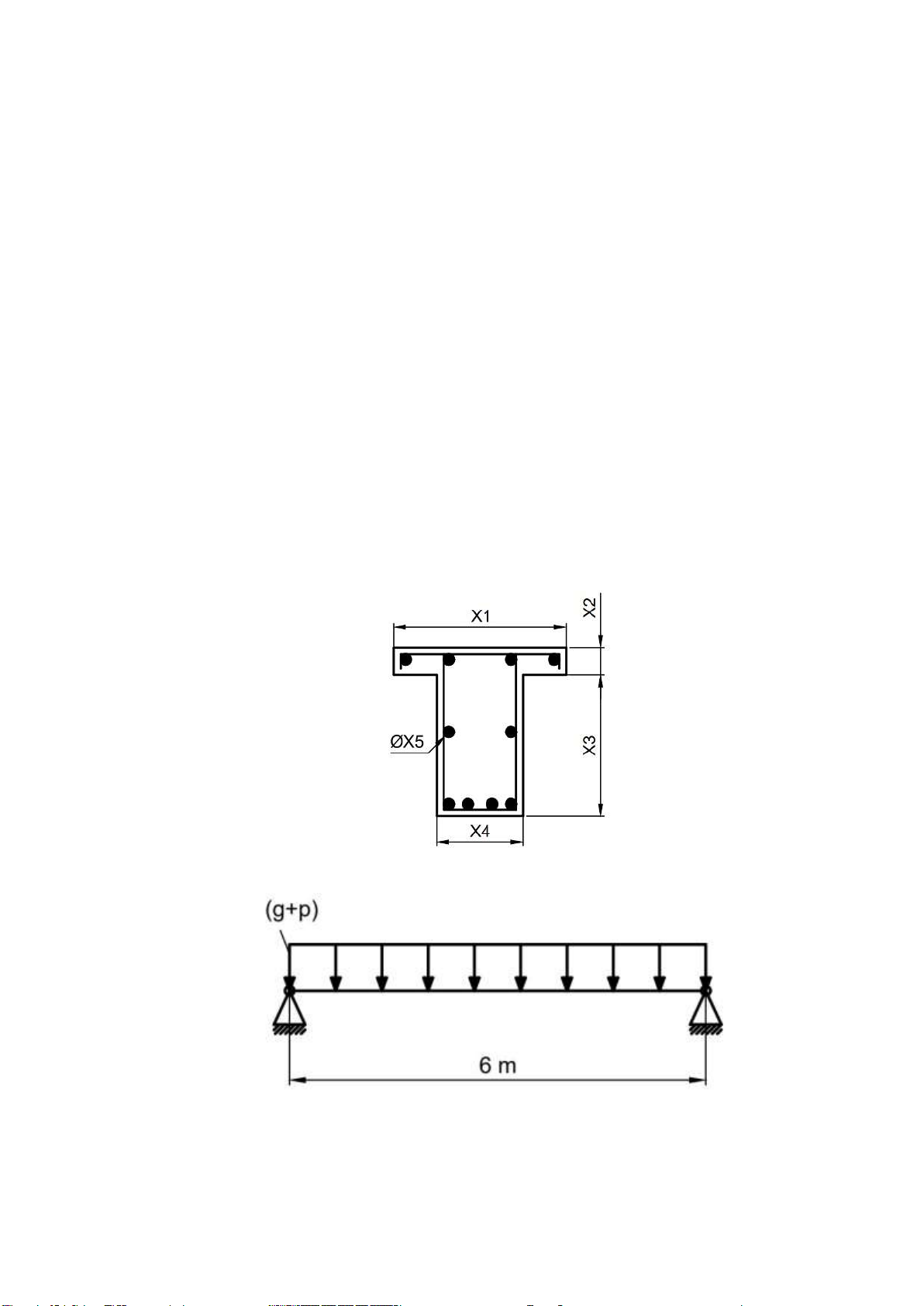
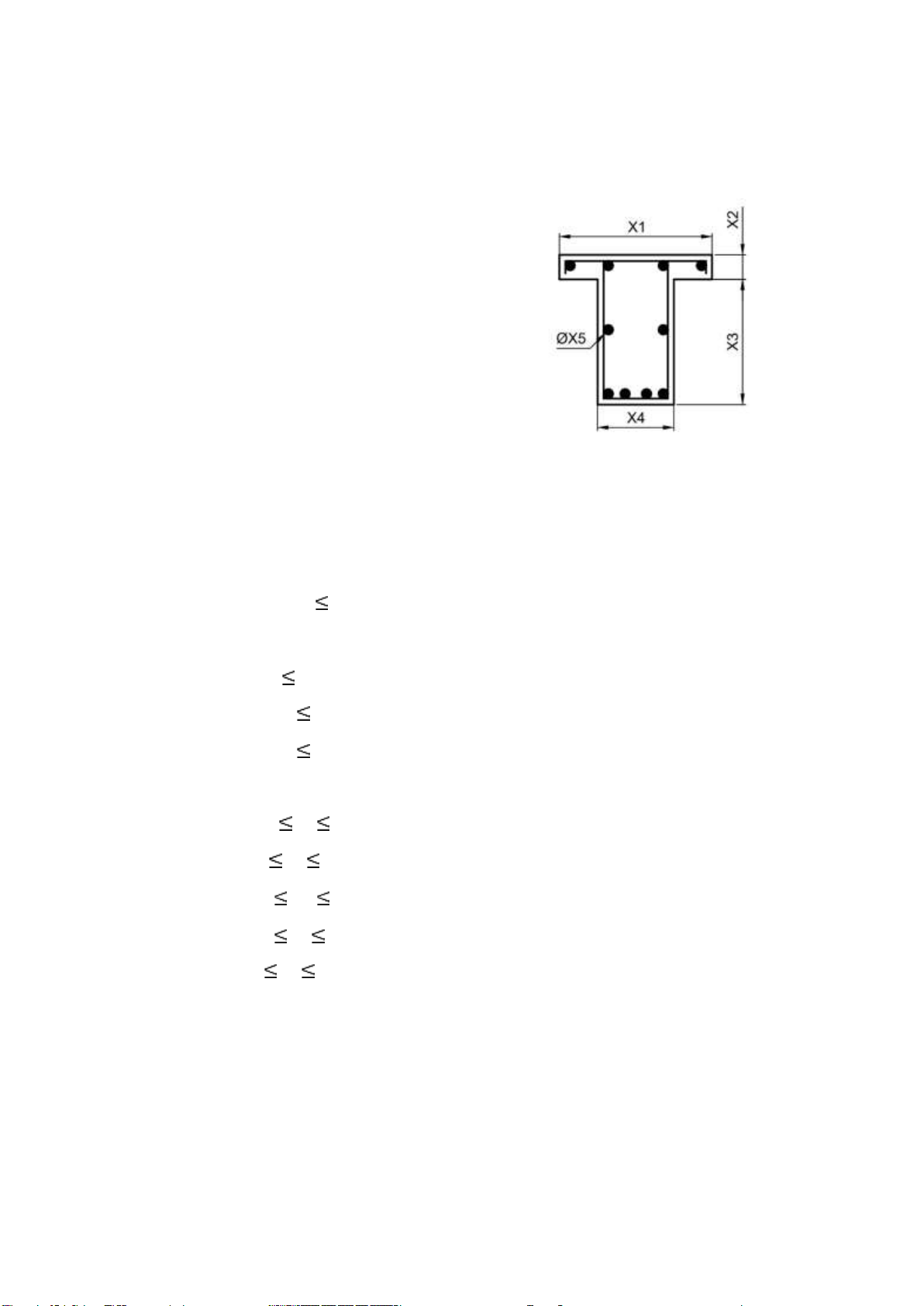
the beam. The cross-section of beam is T profile with the dimension as the figure 1.1. Given:
+ Reinforcement steel type CII, R s= Rsc = 280 MPa
+ Live load, p = 50kN/m, safety factor np = 1.2 + Length, L = 6 m
+ Weigh of beam, g, safety factor ng = 1.1
+ Thickness of protective concrete layer, a’ = 25 mm
+ Mass density of reinforced concrete, γ = 2,5 T/m3 = 0,000025 kg/mm3
Figure 1.1: Cross-section of beam
Figure 1.2: FBD diagram 1 Solution:
Distance from concrete edge to center of reinforcement steel: a = a’ + x5/2 (mm)
Area of tensile reinforcement steel: As = π.r2.n = π.(x5/2)2.4 (mm2)
Load capacity of reinforced concrete beam: [M] = Rs.As.((x2+x3)-2a) (kN.m) Moment caused by weight:
g = A.ng.γ = (x1.x2+x3.x4).1,1.2,5 (kN/m) Total load: q = g + p (kN/m) Moment diagram:
Figure 1.3: Moment diagram
Maximum moment at the cross section of beam: M = qL2/8 (kN.m)
Conditions for beams with sufficient load capacity: M ≤ 0.8[M] 2
II. ANOUNCEMENT PROBLEM 1. Introduction
In nowadays, reinforced concrete beams is widely use in most of the construction works:
houses, buildings, companies, … Therefore, the demand for reinforced concrete beam design is very high.
With the develop of technology, beside the required of the load capacity, the engineer also
need to minimize the weight of beam, it means save the material and reduce the cost.
To solve this problem, our group decided to address the T profile beam optimization
problem. Structural form which is widely used in construction today. 2. Method
The method we used is the Nonlinear Mathematical Optimization with function
fmincon on Matlab application. 3. Result
The beam has the dimension is:
x1 = 200; x2 = 50; x3 = 538.4; x4 = 100; x5 = 25; The mass: m = 965 kg 4. Conclusion
The results satisfied the initial requirements set out. In terms of load capacity as well as
optimized in mass. That saves costs and materials. 3 III. MODELING PROBLEM Variable:
x1 is the length of the beam x2 is the wing
thickness of the beam x3 is the height of
the beam x4 is the rib width of the beam
x5 is the diameter of reinforced steel Objective:
Minimize the mass of beam: Figure 3.1: Cross- section of beam f
= (x1.x2 + x3.x4 + pi.(x5/2)2).L.γ Constrain: - Loading constraint:
+ q.L2/8 0,8.Rs.As.((x2+x3)-2a) - Design constraint: + x5 25 + 4.x4 x3 + 2.x4 x1 Condition 150 x1 800 50 x2 200 200 x3 900 100 x4 600 15 x5 25 4 IV. SOLVING PROBLEM Define variables to use: P = 50; L = 6; R = 280; A = 4*pi*((x5/2)^2); w =
(x1*x2+x3*x4)*(10^-6)*1.1*2.5; d =
x5/2+25; Minimize the function:
f = (x1*x2 + x3*x4 + pi* (x5/2)2) *L*0,0000025 so that:
g (1) = (w+P) *L2/8 – 0,8*R*A* ((x2+x3)-2*d) 0 g (2) = x5 – 25 0 g (3) = 4*x4 - x3 0 g (4) = 2*x4 - x1 0 150 x1 800 50 x2 200 200 x3 900 100 x4 600 15 x5 25 Solving on Matlab: + Objective function opti.m: Figure 4.1: opti.m 5 Script: function f = opti(x)
x1 = x(1); x2 = x(2); x3 = x(3); x4 = x(4); x5 = x(5); L = 6000; rho = 0.0000025;
f = (x1*x2+x3*x4+((x5/2)^2*pi))*L*rho; + noncon.m: Figure 4.2: noncon.m Script:
function [g,h] = noncon(x) x1 = x(1); x2 = x(2); x3 = x(3); x4 = x(4); x5 = x(5); P = 50; L = 6; R = 280; A = 4*pi*((x5/2)^2);
w = (x1*x2+x3*x4)*(10^-6)*1.1*2.5; d = x5/2+25;
g(1) = (((P+w)*(L^2)/8)-0.8*(R*A*((x2+x3)-2*d))*(10^-6));
g(2) = x5-25; g(3) = 4*x4-x3; g(4) = x4*2-x1; h = []; + Command window: x0=[500,80,900,300,25];A=[]; Aeq=[]; b=[]; beq=[]; lb=[150;50;200;100;15]; ub=[800;200;900;600;25];
[x,f] = fmincon('opti',x0,[],[],[],[],lb,ub,'noncon') + Result: x =
200.0000 50.0000 538.3656 100.0000 25.0000 f = 964.9115
X1 = 200 mm; X2 = 50 mm; X3 = 538 mm; X4 = 100 mm; X5 = 25 mm F = 964.9 kg V. EVALUATION Result:
x1 = 200; x2 = 50; x3 = 538.4; x4 = 100; x5 = 25; f = 965 Check the load capacity: + M 0,8.[M]  q.L2/8 Rs.As.((x2+x3)-2a) M = 225,8 kN.M ;
[M] = 282,2 ; 282,2.0,8 = 225.8 => M 0,8.[M]
=> The load capacity is satisfied. Check the design constraint: + x5 – 25 0 25 – 25 0 (satisfied) + 4.x4 - x3 0 4*100 – 538,4 0 (satisfied) + 2.x4 - x1 0 2*100 – 200 0 (satisfied) Conclusion:
The results satisfied the initial requirements set out. In terms of load capacity as well as
optimized in mass. That saves costs and materials. GROUP PRESENTATION VIDEO LINK:
Optimal Presentation.mp4 - Google Drive
https://drive.google.com/file/d/1I7kSnh5WaLXT1okVTt O6cqpAG1ZNTtww/view