Bài tập Toán 10 học kì 2 – Nguyễn Văn Thanh

Tài liệu gồm 104 trang, được biên soạn bởi thầy giáo Nguyễn Văn Thanh, tuyển tập bài tập Toán 10 học kì 2 theo các dạng bài.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

104 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 1
ĐẠI SỐ 10 – Quyển 2- HỌC KỲ 2
CHƢƠNG IV. BẤT ĐẲNG THỨC. BẤT PHƢƠNG TRÌNH
BÀI 1 : BẤT ĐẲNG THỨC
DNG 1. TÍNH CHT CA BNG THC
Câu 1. Cho các bng thc
ab
và
cd
. Bng th
A.
a c b d
.
B.
a c b d
.
C.
ac bd
.
D.
ab
cd
.
Câu 2. Tìm m 
A.
a b ac bc
.
B.
a b ac bc
.
C.
a b a c b c
.
D.

ab
ac bd
cd
.
Câu 3. Trong các tính cht sau, tính cht nào sai?
A.
0
0
ab
cd


.
B.
ab
cd
a c b d
.
C.
ab
cd
a c b d
.
D.
0
0
ab
cd


ac bd
.
Câu 4. Nu
22a c b c
thì bt ng th
A.
33ab
.
B.
22
ab
.
C.
22ab
.
D.
11
ab
.
Câu 5. Khng 
A.
0x x x x
.
B.
2
33x x x
.
C.
2
1
0
x
x
.
D.
1
01x
x
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 2
Câu 6. Suy lu
A.
0
0
ab
ac bd
cd



. B.
ab
a c b d
cd
.
C.
ab
ac bd
cd

. D.
ab
ab
cd
cd

.
Câu 7. Cho
a
là s th i ?
A.
x a a x a
. B.
x a x a
.
C.
x a x a
. D.
xa
xa
xa


.
Câu 8. Bng thi mi s thc
a
?
A.
63aa
. B.
36aa
. C.
6 3 3 6 aa
. D.
63 aa
.
Câu 10. Cho
,ab
là các s thc bt kì. Trong các m sau, m nào sai?
A.
0a b a b
. B.
11
0ab
ab
. C.
33
a b a b
. D.
22
a b a b
.
Câu 11. Cho a > b kh
A.
22ab
. B. C.
.ab
D.
, ac cb c
.
Câu 12. Trong các m sau, m nào sai?
A.
a b a b
. B.
,x a a x a
0a
.
C.
,a b ac bc c
. D.
2a b ab
,
0, 0ab
.
Câu 13. Chuyên Lê Hồng Phong-Nam Định Trong các khnh sau, kh
A.
01
1
1
x
xy
y


. B.
1
1
1
x
xy
y

. C.
1
1
1
x
x
y
y

. D.
1
1
1
x
xy
y
.
Câu 14. Phát bi
A.
2
22
x y x y
. B.
0xy
thì
0x
hoc
0y
.
C.
xy
22
xy
. D.
0xy
thì
.0xy
.
DNG 2. BNG THC COSI và NG DNG
Câu 15. 
, ab

A.
2
2
ab
ab

. B.
2
2
ab
ab
. C.
2
ab
ab
. D.
2
2
ab
ab
.
Câu 16. Cho ba s không âm
,,abc
. Kh
A.
3
3a b c abc
. B.
3
3abc a b c
. C.
3a b c abc
. D.
3
4a b c abc
.
Câu 17. Cho hai s thc
a
và
b
tha mãn
4ab
. Kh?
A. Tích
.ab
có giá tr nh nht là
2
. B. Tích
.ab
không có giá tr ln nht.
C. Tích
.ab
có giá tr ln nht là
4
. D. Tích
.ab
có giá tr ln nht là
2
.
Câu 18. sai?
A.
ax
a b x y
by
. B.
1
20aa
a
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 3
C.
2 , 0a b ab a b
. D.
11
,0a b a b
ab
.
Câu 19. Cho các m sau
2
ab
I
ba

;
3
a b c
II
b c a
;
1 1 1 9
III
a b c a b c

Vi mi giá tr ca
a
,
b
,
c

A.
I

II
,
III
sai. B.
II

I
,
III
sai.
C.
III

I
,
II
sai. D.
I
,
II
,
III

Câu 20. Giá tr nh nht ca biu thc
2
16
,0P x x
x
bng
A.
4
. B.
24
. C.
8
. D.
12
.
Câu 21. Giá tr nh nht ca hàm s
3
2f x x
x

vi
0x
là
A.
43
. B.
6
. C.
26
. D.
23
.
Câu 22. 
24A x x
.
A.
2
. B.
2
. C.
22
. D.
0
.
Câu 23. Giá tr nh nht ca hàm s
42
2
4 3 9xx
y
x

;
0x
là
A.
9
. B.
3
. C.
12
. D.
10
.
Câu 24. Cho
a
là s thc bt kì,
2
2
1
a
P
a
. Bng thi mi
a
.
A.
1P 
. B.
1P
. C.
1P 
. D.
1P
.
Câu 25. Tìm giá tr nh nht ca
1
41
x
P
x

vi
1x
.
A.
7
4
. B.
1
. C.
1
4
. D.
5
4
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 4
Câu 26. Giá tr nh nht ca hàm s
2
21
x
fx
x

vi
1 x
là
A.
2
. B.
5
2
. C.
22
. D. 3.
Câu 27. Cho
2x
. Giá tr ln nht ca hàm s
2x
fx
x
bng
A.
1
22
. B.
2
2
. C.
2
2
. D.
1
2
.
Câu 28. Giá tr nh nht ca hàm s
2017
2018
x
y
x
là
A.
2
. B.
2017
2018
. C.
2018
2017
. D.
2019
.
Câu 29. Tìm giá tr ln nht
M
và giá tr nh nht
m
ca hàm s
6 2 3 2y x x
.
A.
M
không tn ti;
3m
. B.
3M
;
0m
.
C.
32M
;
3m
. D.
32M
;
0m
.
Câu 30. Chuyên Lê Hồng Phong-Nam Định Cho biu thc
1
x
fx
x
, vi
1x
. Giá tr nh nht
ca biu thc là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 31. Cho hai s thc
, xy
tha mãn:
3 1 3 2 .x x y y
Giá tr ln nht ca biu thc:
P x y
bng
A.
9 3 5
. B.
9 3 3
. C.
9 3 5
. D.
9 3 15
.
Câu 32. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Cho hai s thc
0x
,
0y
i và tha
u kin
22
x y xy x y xy
. Giá tr ln nht ca biu thc
33
11
M
xy

là
A. 9. B. 16. C. 18. D. 1.
Câu 33. Cho
,,x y z
là các s tha mãn
(3 ) 6 5 ( )x xy xz y z xz y z
. Giá tr nh nht
ca biu thc
36P x y z
là
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 5
A.
36
. B.
9
. C.
30
. D.
62
.
Câu 34. Cho ba s th     a mãn a+b+c=1. Tìm giá tr nh nht ca biu thc
1 4 9
P
a b c
?
A. 63. B. 36. C. 35. D. 34.
Câu 35. 
100m

    

A.
2
1350m
. B.
2
1250m
. C.
2
625m
. D.
2
1150m
.
Câu 36. Trong các hình ch nht có chu vi bng 300 m, hình ch nht có din tích ln nht bng
A.
2
22500m
. B.
2
900m
. C.
2
5625m
. D.
2
1200m
.
Câu 37. (NGÔ GIA TỰ_VĨNH PHÚC_LẦN 1_1819) Trong tt c các hình ch nht có cùng din tích
2
48m
, hình ch nht có chu vi nh nht là
A.
16 3
. B.
20 3
. C.
16
. D.
20
.
---------------------------------------------------------------------------------------------------------------------------------
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 6
BÀI 2: BẤT PHƢƠNG TRÌNH VÀ HỆ BẤT PHƢƠNG TRÌNH MỘT ẨN
DU KINH CA B
Câu 1. 
13
12xx


A.
1; 2xx
.
B.
1; 2xx
.
C.
1; 2xx
.
D.
1; 2xx
.
Câu 2. u kin ca b
2
1
2
4
x
x

là
A.
2x 
.
B.
2x
.
C.
2x
.
D.
0x
.
Câu 3. u kin ca b
23
1
23
x
x
x

.
A.
3
2
x 
.
B.
3
2
x
.
C.
2
3
x 
.
D.
2
3
x
.
Câu 4. u kin ca b
23
2
63
x
x
x

.
A.
2x
.
B.
2x
.
C.
2x
.
D.
2x
.
Câu 5. Giá tr
3x
thuc tp nghim ca b
A.
2
1
1
1
xx
x
x


.
B.
2
21xx
.
C.
22
16xx
.
D.
2
2 5 2 0xx
.
DNG 2. B B
Câu 6. sai?
A.
2
3
3
0
x
xx
x

. B.
3
0 3 0
4
x
x
x
.
C.
0x x x
. D.
2
11xx
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 7
Câu 7. Bi b
50x 
?
A.
2
50xx
. B.
5 5 0xx
.
C.
2
1 5 0xx
. D.
5 5 0xx
.
Câu 8. Kh
A.
2
3xx
3x
. B.
1
0
x
1x
.
C.
2
1
0
x
x
10x
. D.
x x x
.
Câu 9. Cp b 
A.
1xx
và
2 1 1 2 1x x x x
.B.
11
21
33
x
xx

và
2 1 0x 
.
C.
2
20xx
và
20x 
. D.
2
20xx
và
20x 
.
Câu 10. B
2 3 2xx
i:
A.
2
2 3 2xx
vi
3
2
x
. B.
2
2 3 2xx
vi
2x
.
C.
2 3 0
20
x
x


hoc
2
2 3 2
20
xx
x

.D. Tt c 
Câu 11. B
33
23
2 4 2 4
x
xx

i:
A.
23x
.
B.
3
2
x
và
2x
.
C.
3
2
x
.
D. Tt c 
DNG 3. S DNG CÁC PHÉP BI GII B
TRÌNH MT N
Câu 12. Tp nghim ca b
2
96xx
là
A.
3; 
.
B.
\3
.
C. .
D.
.
Câu 13. Bt 
3 9 0x
có tp nghim là
A.
3; 
.
B.
;3
.
C.
3; 
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 8
D.
;3
.
Câu 14. Tp nghim ca b
2 3 6xx
.
A.
1; 
.
B.
;1
.
C.
;1
.
D.
1; 
.
Câu 15. Cho
24f x x
, kh
A.
2;x 
.
B.
;2x 
C.
2;x 
.
D.
2x
.
Câu 16. Bt  trình
2
5 1 3
5
x
x
có nghim là
A.
2x
.
B.
5
2
x 
.
C.
x
.
D.
20
23
x
.
Câu 17. Tp nghim ca b
2 1 0x 
là
A.
1
;
2




.
B.
1
;
2




.
C.
1
;
2



.
D.
1
;
2




.
Câu 18. Chuyên Lê Hồng Phong-Nam Định B
3
1
x
có bao nhiêu nghim nguyên?
A.
3
.
B.
2
.
C. Vô s.
D.
4
.
Câu 19. Tp nghim ca b
11x 
là
A.
;2
.
B.
1;2
.
C.
0;2
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 9
D.
1;2
.
Câu 20. B
2 5 3
32
xx
có tp nghim là
A.
2;
.
B.
;1 2; 
.
C.
1; 
.
D.
1
;
4




.
Câu 21. Tp nghim ca b
2
3 2 1 1 0xx
là
A.
3
1;
2


B.
1; 
C.
2
;1
3


D.
2;3
Câu 22. Tp nghim ca b
2017 2017xx
là
A.
2017,
.
B.
,2017
.
C.
2017
.
D.
.
Câu 23. Tp nghim ca b
2
2
2 3 4
2
3
xx
x

là
A.
3 23 3 23
;
4 4 4 4





.
B.
3 23 3 23
;;
4 4 4 4

.
C.
2
;
3



.
D.
2
;
3




.
Câu 24. Tp nghim ca b
3 2 2 2x x x x
là
A.
1;2
.
B.
1;2
.
C.
;1
.
D.
1; 
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 10
Câu 25. Tp nghim ca b
1
1
3
x
x
là
A.
3;
.
B. .
C.
;3 3;
.
D.
;3
.
Câu 26. Tp nghim ca b
3
2 4 1
5
x
xx
.
A.
8
;
11
S



.
B.
8
;
11



.
C.
4
;
11
S



.
D.
2
;
11



.
Câu 27. Tp nghim ca b
2
21xx
.
A.
S 
.
B.
1
;
2
S


.
C.
1; 
.
D.
1
;
2



.
Câu 28. 
11
15
33
xx
xx

là
A.
1;5S
.
B.
1;5 \ 3S
.
C.
3;5S
.
D.
1;5 \ 3S
.
DNG 4. S DNG CÁC PHÉP BII H BT
N
Câu 32. (THPT NÔNG CỐNG - THANH HÓA LẦN 1_2018-2019)      

3 1 2 7
4 3 2 19
xx
xx
.
A.
6; .
B.
8; .
C.
6; .
D.
8; .
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 11
Câu 33. Tp nghim ca b
3 4 2
5 3 4 1
xx
xx
là
A.
;1
.
B.
4; 1
.
C.
;2
.
D.
1;2
.
Câu 34. 
40
20
x
x


là
A.
; 2 4;S  
.
B.
2;4S 
.
C.
.
D.
; 2 4;S  
.
Câu 35. Tp nghim ca h b
3 2 2 3
10
xx
x

là
A.
1
;1 .
5



B.
.
C.
1; 
.
D.
;1
.
Câu 36. H b
2 1 3 3
2
3
2
32
xx
x
x
x


có tp nghim là
A.
7;
.
B.
.
C.
7;8
.
D.
8
;8
3



.
Câu 37. Tp nghim ca h b
21
1
3
43
3
2
x
x
x
x

là
A.
4
2;
5



.
B.
4
2;
5



.
C.
3
2;
5



.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 12
D.
1
1;
3


.
DNG 5. B BT A THAM S
Câu 38. B
13mx
vô nghim khi
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Câu 39. B
2
3 2 2m m x m x
vô nghim khi
A.
1.m
B.
2.m
C.
1, 2.mm
D.
.m
Câu 40. Có bao nhiêu giá tr thc ca tham s
m
 b
2
m m x m
vô nghim.
A.
0.
B.
1.
C.
2.
D. Vô s.
Câu 41. Gi
S
là tp hp tt c các giá tr thc ca tham s
m
 b  
2
62m m x m x
vô nghim. Tng các phn t trong
S
bng:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 42. B
2
9 3 1 6m x m x
nghii mi
x
khi
A.
3.m
B.
3.m
C.
3.m 
D.
3.m 
Câu 43. B
22
4 2 1 4 5 9 12m x m m x m
nghii mi
x
khi
A.
1.m 
B.
9
.
4
m
C.
1.m
D.
9
.
4
m 
Câu 44. B
2
1 9 3m x x m
nghii mi
x
khi
A.
1.m
B.
3.m 
C.
.m 
D.
1.m 
Câu 45. Tìm tt c các giá tr thc ca tham s
m
 b  
34x m m x x
có tp
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 13
nghim là
2;m
.
A.
2.m
B.
2.m
C.
2.m
D.
2.m
Câu 46. Tìm tt c các giá tr thc ca tham s
m
 b
1m x m x
có tp nghim là
;1m
.
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Câu 47. Tìm tt c các giá tr ca tham s
m
 b
1 2 3m x x
có nghim.
A.
2m
.
B.
2m
.
C.
2m
.
D.
2m
.
Câu 48. Tìm tt c các giá tr ca tham s
m
 b
13m x x
có nghim.
A.
1m
.
B.
1m
.
C.
m
.
D.
3m
.
Câu 49. Gi
S
là tp nghim ca b
6 2 3mx x m
vi
2m
. Hi tp h
là phn bù ca tp
S
?
A.
3; 
.
B.
3; 
.
C.
;3
.
D.
;3
.
Câu 50. Tìm giá tr thc ca tham s
m
 b
2 2 11mxx 
có tp nghim là
1; .
A.
3m
B.
1m
C.
1m 
D.
2.m 
Câu 51. Tìm giá tr thc ca tham s
m
 b
2 3 1x m x
có tp nghim là
4; .
A.
1.m
B.
1.m
C.
1.m 
D.
1.m
Câu 52. Tìm tt c các giá tr ca tham s
m
 b
40mx 
nghii mi
8x
.
A.
11
;.
22
m




B.
1
;.
2
m



Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 14
C.
1
;.
2
m



D.
11
;0 0; .
22
m


Câu 53. Tìm tt c các giá tr thc ca tham s
m
 b
2
2 5 0m x mx x
nghim
i mi
2018;2x
.
A.
7
2
m
.
B.
7
2
m
.
C.
7
2
m
.
D.
m
.
Câu 54. Tìm tt c các giá tr thc ca tham s
m
 b
2
20m x m x
có nghim
1;2x
.
A.
2m 
.
B.
2m 
.
C.
1m 
.
D.
2m 
.
Câu 55. H b
2 1 0
2
x
xm


có nghim khi và ch khi:
A.
3
.
2
m 
B.
3
.
2
m 
C.
3
.
2
m 
D.
3
.
2
m 
Câu 56. H b
3 6 3
5
7
2
x
xm
có nghim khi và ch khi:
A.
11.m 
B.
11.m 
C.
11.m 
D.
11.m 
Câu 57. H b
2
10
0
x
xm


có nghim khi và ch khi:
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 15
Câu 58. Tìm tt c các giá tr thc ca tham s
m
 h b
2 1 3
0
x
xm


có nghim duy nht.
A.
2m
.
B.
2m
.
C.
2m
.
D.
1.m
.
Câu 59. Tìm tt c các giá tr ca tham s
m
 h b
2
6
3 1 5
m x x
xx

có nghim duy nht.
A.
1m
.
B.
1m 
.
C.
1m 
.
D.
1m
.
Câu 60. Tìm tt c các giá tr thc ca tham s
m
 h b  
2
2
3 7 1
2 8 5
x x x
mx

có
nghim duy nht.
A.
72
13
m
.
B.
72
13
m
.
C.
72
13
m
.
D.
72
13
m
.
Câu 61. Tìm giá tr thc ca tham s
m
 h b
3
39
mx m
m x m

có nghim duy nht.
A.
1.m
B.
2.m 
C.
2.m
D.
1.m 
Câu 62. H b
3 4 9
1 2 3 1
xx
x m x

vô nghim khi và ch khi:
A.
5
.
2
m
B.
5
.
2
m
C.
5
.
2
m
D.
5
.
2
m
Câu 63. H b
2 7 8 1
52
xx
mx

vô nghim khi và ch khi:
A.
3.m 
B.
3.m 
C.
3.m 
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 16
D.
3.m 
Câu 64. H b
2
2
3 7 1
2 8 5
x x x
mx

vô nghim khi và ch khi:
A.
72
.
13
m
B.
72
.
13
m
C.
1m
D.
1m
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 17
BÀI 3: DẤU CỦA NHỊ THỨC BẬC NHẤT
DNG 1. DU NH THC BC NHT
Câu 1. Cho nh thc bc nht
0f x ax b a
. Trong các m sau, m 
A. Nh thc
fx
có giá tr cùng du vi h s
a
khi
x
ly các giá tr trong khong
;
b
a




.
B. Nh thc
fx
có giá tr cùng du vi h s
a
khi
x
ly các giá tr trong khong
;
b
a




.
C. Nh thc
fx
có giá tr trái du vi h s
a
khi
x
ly các giá tr trong khong
;
b
a




.
D. Nh thc
fx
có giá tr cùng du vi h s
a
khi
x
ly các giá tr trong khong
;
b
a




.
Câu 2. Khng nh sai?
A. B
0ax b
có tp nghim là khi
0a
và
0b
.
B. Bc nht mt n luôn có nghim.
C. B
0ax b
vô nghim khi
0a
và
0b
.
D. B
0ax b
vô nghim khi
0a
.
Câu 3. Cho nh thc bc nht
23 20f x x
. Kh
A.
vi
20
;
23
x




. B.
vi
5
2
x
.
C.
vi
x
. D.
vi
20
;
23
x




.
Câu 4. Tìm  là nh thc bc nht.
A. .
B. .
C. .
D. .
Câu 5. 
1f x x

A.
01f x x
.
B.
01f x x
.
C.
01f x x
.
D.
01f x x
.
m
2 2 1f x m x m
2m
2
1
2
m
m

2m
2m
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 18
Câu 6. Chuyên Lê Hồng Phong-Nam Định Cho
fx
,
gx
 
:
p nghim ca b
0
fx
gx
là
A.
1;2
.
B.
1;2 3;
.
C.
1;2 3; 
.
D.
1;2 3; 
.
Câu 7. Hàm s có kt qu xét du
là hàm s
A.
3f x x
.
B.
3
x
fx
x
.
C.
3f x x x
.
D.
3f x x x
.
Câu 8. Bng xét du sau là ca biu thc nào?
x

2

fx
0
A.
2f x x
.
B.
24f x x
.
C.
16 8f x x
.
D.
2f x x
.
Câu 9. Vi
x
thuc tu thc
2
21
x
fx
x
không âm?
A.
1
;2
2
S




.
B.
1
;2
2
S



.
C.
1
; 2;
2
S



.
D.
1
; 2;
2
S



.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 19
Câu 10. Cho biu thc
2
1.
32
x
fx
x

Tp hp tt c các giá tr ca
x
tha mãn b  
là
A.
2
;1 .
3
x



B.
2
; 1; .
3
x

 


C.
2
;1 .
3
x


D.
2
;1 ; .
3
x




Câu 11. Cho biu thc
43
.
3 1 2
fx
xx


Tp hp tt c các giá tr ca
x
tha mãn b
là
A.
11 1
; 2; .
53
x




B.
11 1
; 2; .
53
x




C.
11 1
; ;2 .
53
x

D.
11 1
; ;2 .
53
x

Câu 12. Cho biu thc
2
32
.
1
xx
fx
x

Hi có tt c bao nhiêu giá tr nguyên âm ca
x
tha mãn
b
1fx
?
A.
1.
B.
2.
C.
3.
D.
4.
DNG 2. GII B
Câu 13. 
21f x x x

A.
0 1;2f x x
.
B.
0 1;2f x x
.
C.
0 1;2f x x
.
D.
0 ; 1 2;f x x 
.
Câu 14. Tp nghim ca b
1 3 0xx
A.
;1 3;
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 20
B.
3; 
.
C. .
D.
1;3
.
Câu 15. S nghim a b
2 1 3 0x x x
là
A.
1
.
B.
4
.
C.
2
.
D.
3
.
Câu 16. Tp nghim ca b
2 8 1 0xx
có dng
;.ab

ba
bng
A.
3.
B.
5.
C.
9.
D. không gii hn.
Câu 17. Tp nghim
4;5S 
là tp nghim ca b
A.
4 5 0.xx
B.
4 5 25 0.xx
C.
4 5 25 0.xx
D.
4 5 0.xx
Câu 18. Tng các nghim nguyên ca b
3 1 0xx
là
A.
1.
B.
4.
C.
5.
D.
4.
Câu 19. Tp nghim
0;5S
là tp nghim ca b
A.
5 0.xx
B.
5 0.xx
C.
5 0.xx
D.
5 0.xx
Câu 20. Hi b
2 1 3 0x x x
có tt c bao nhiêu nghi
A.
1.
B.
3.
C.
4.
D.
2.
Câu 21. Tích ca nghim nguyên âm ln nht và nghi nht ca b
3 6 2 2 1 0x x x x
là
A.
9.
B.
6.
C.
4.
D.
8.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 21
Câu 22. Tp nghim ca b
2 4 3 3 0x x x x
là
A. Mt khong
B. Hp ca hai khong.
C. Hp ca ba khong.
D. Toàn trc s.
Câu 23. Nghim nguyên nh nht tha mãn b
1 2 0x x x
là
A.
2.x 
B.
0.x
C.
1.x
D.
2.x
DNG 3. GII BA N MU
Câu 24. Tp nghim ca b
1
2
2
x
x
là
A.
1; 2 .
B.
1; 2 .
C.
3; 1 .
D.
1; 2 .
Câu 25. Tp nghim ca b
11
2 1 2 1xx

là
A.
11
;;
22



.
B.
1
;
2




.
C.
11
;
22



.
D.
11
;;
22

.
Câu 26. 
1
1
2x

S

A.
;3S 
.
B.
;3S 
.
C.
2;3S
.
D.
2;3
.
Câu 27. Tp nghim ca b
1
1
x
là
A.
0;1
.
B.
;1
.
C.
1; 
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 22
D.
;0 1;
.
Câu 28. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Tp nghim ca b
21
12
xx
xx


là
A.
1
1; 2;
2



.
B.
1
; 1 ;2
2




.
C.
1
; 1 ;2
2



.
D.
1
;
2



.
Câu 29. Tp nghim ca b  
1 2 5 1
0
4
x x x
x
là
;;S a b c d
  
a b c d
bng
A.
3
2
.
B.
1
.
C.
2
.
D.
5
2
.
Câu 30. Chuyên Lê Hồng Phong-Nam Định B
3
1
x
có bao nhiêu nghim nguyên?
A.
3
.
B.
2
.
C. Vô s.
D.
4
.
Câu 31. B
21
2
11
x
xx


có tp nghim là
A.
1
1; 1; .
3
S


B.
; 1 1; .S
C.
1
1; 1; .
3
S



D.
1
; 1 ;1 .
3
S




Câu 32. B
2
11
1
1
x
x
có tp nghim
S
là
A.
; 1 0;1 1;3 .T
B.
1;0 3; .T
C.
; 1 0;1 1;3 .T
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 23
D.
1;0 3; .T
DNG 4. GII B CHA DU GIÁ TR TUYI
Câu 33. Tp nghim ca b
2 1 1x 
.
A.
0;1S
.
B.
1
;1
2
S



.
C.
;1S 
.
D.
;1 1;S  
.
Câu 34. Tp nghim ca b
3 1 2x 
.
A.
1
; 1 ;
3
S

 


.
B.
S 
.
C.
1
1;
3
S




.
D.
1
;
3
S




.
Câu 35. S giá tr nguyên
x
trong
2017;2017
tha mãn b
2 1 3xx
là
A.
2016
.
B.
2017
.
C.
4032
.
D.
4034
.
Câu 36. Cho b
28
13 9x
. S nghim nguyên nh 
13
ca b
A.
0
.
B.
1
.
C.
2
.
D.
3
.
Câu 37. Nghim ca b
2
2
xx
x

là
A.
01x
.
B.
01x
.
C.
0
1
x
x
.
D.
1x
,
2x 
.
Câu 38. Vi
x
thuc t thc bc nht
2 5 3f x x

A.
1x
.
B.
5
2
x
.
C.
0x
.
D.
14x
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 24
Câu 39. B
54x 
có bao nhiêu nghim nguyên?
A.
10
.
B.
8
.
C.
9
.
D.
7
.
Câu 40. Tp hp nghim ca b
2 1 2 4xx
là
A.
3
;
2
S




.
B.
13
;
22
S




.
C.
3
;
2
S



.
D.
3
;
2



.
Câu 41. B
21xx
có tp nghim là
A.
1
; 1;
3

 


.
B.
1
;1
3



.
C. .
D. Vô nghim.
Câu 42. S nghim nguyên ca b
13xx
là
A.
4
.
B.
2
.
C.
3
.
D.
1
.
Câu 43. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) B  
2 3 1 6xx
có tp nghim là
A.
;2
.
B.
9
;
4



.
C.
9
;
4




.
D.
;2
.
Câu 44. S nghim nguyên tha mãn b
2 2 1 1x x x
là
A.
3.
B.
5.
C.
2.
D.
0.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 25
Câu 45. Bt  trình
3
21
2
x x x
có tp nghim là
A.
2; .
B.
1
;.
2



C.
3
;.
2



D.
9
;.
2




Câu 46. Tp nghim ca b
5 10
21xx

là
A. mt khong.
B. hai khong.
C. ba khong.
D. toàn trc s.
Câu 47. S nghim nguyên ca b
23
1
1
x
x
là
A.
1.
B.
2.
C.
0.
D.
3.
----------------------------------------------------------------------------------------------------------------------------
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 26
BÀI 4: BẤT PHƢƠNG TRÌNH BẬC NHẤT HAI ẨN
DNG 2. TÌM MIN NGHIM CA H BC NHT HAI N
Câu 1. Trong các cp s sau, cp nào không là nghim ca h b
20
2 3 2 0
xy
xy
là
A.
0;0
. B.
1;1
. C.
1;1
. D.
1; 1
.
Câu 2. c min nghim ca h b
2 5 1 0
2 5 0
10
xy
xy
xy
?
A.
0;0
. B.
1;0
. C.
0; 2
. D.
0;2
.
Câu 3. Min nghim ca h b
20
32
3
xy
xy
yx


ch
A.
1 ; 0A
. B.
2 ; 3B
. C.
0 ; 1C
. D.
1 ; 0 .D
DẠNG 3. TÌM GIÁ TRỊ NHỎ NHẤT- GIÁ TRỊ LỚN NHẤT
Câu 4. Giá tr nh nht ca biu thc
F y x
trên minh bi h
22
24
5
yx
yx
xy



là
A.
min 1F
khi
2x
,
3y
.
B.
min 2F
khi
0x
,
2y
.
C.
min 3F
khi
1x
,
4y
.
D.
min 0F
khi
0x
,
0y
.
Câu 5. Giá tr nh nht ca bit thc
F y x
trên minh bi h
22
2
54
xy
xy
xy


là
A.
min 3F 
khi
1, 2xy
.
B.
min 0F
khi
0, 0xy
.
C.
min 2F 
khi
42
,
33
xy
.
D.
min 8F
khi
2, 6xy
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 27
BÀI 5. DẤU CỦA TAM THỨC BẬC HAI
DNG 1. TAM THC BC HAI
Dng 1. Xét du tam thc bc hai
Câu 1. Cho tam thc
2
0 ,f x ax bx c a
2
4b ac
. Ta có
vi
x
khi và
ch khi:
A.
0
0
a

. B.
0
0
a

. C.
0
0
a

. D.
0
0
a

.
Câu 2. Cho tam thc bc hai
2
( ) 2 8 8f x x x
. Trong các m sau, m 
A.
( ) 0fx
vi mi
x
. B.
( ) 0fx
vi mi
x
.
C.
( ) 0fx
vi mi
x
. D.
( ) 0fx
vi mi
x
.
Câu 3. Tam thi mi giá tr ca
x
?
A.
2
10 2xx
. B.
2
2 10xx
. C.
2
2 10xx
. D.
2
2 10xx
.
Câu 4. Cho
2
f x ax bx c
,
0a
và
2
4b ac
. Cho bit du ca
khi
fx
luôn cùng du
vi h s
a
vi mi
x
.
A.
0
. B.
0
. C.
0
. D.
0
.
Câu 5. Cho hàm s
2
y f x ax bx c
 th t
2
4b ac
, tìm du ca
a
và
.
A.
0a
,
0
. B.
0a
,
0
. C.
0a
,
0
. D.
0a
,
, 0
.
Câu 6. Cho tam thc
2
8x 16f x x
. Kh
A. 
vô nghim. B.
vi mi
x
.
C.
vi mi
x
. D.
khi
4x
.
Câu 7. 
2
1f x x

A.
0;f x x 
. B.
01f x x
.
C.
0 ;1f x x 
. D.
0 0;1f x x
.
Câu 8. 
2
( ) ( 0)f x ax bx c a

A. Nu
0
thì
fx
luôn cùng du vi h s
a
, vi mi
x
.
B. Nu
0
thì
fx
luôn trái du vi h s
a
, vi mi
x
.
C. Nu
0
thì
fx
luôn cùng du vi h s
a
, vi mi
\
2
b
x
a


.
D. Nu
0
thì
fx
luôn cùng du vi h s
b
, vi mi
x
.
O
x
y
4
4
1
y f x
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 28
Dng 2. Gii bc hai và mt s bài toán liên quan
Câu 9. 
2
45f x x x

x

.
A.
; 1 5;x 
.
B.
1;5x
.
C.
5;1x
.
D.
5;1x
.
Câu 10. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Tp nghim ca b  
2
3 2 0xx
là
A.
1;2
.
B.
;1 2; 
.
C.
;1
.
D.
2;
.
Câu 11. (ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Tnh ca hàm s
2
23y x x
là:
A.
1;3
.
B.
; 1 3; 
.
C.
1;3
.
D.
; 1 3; 
.
Câu 12. Tìm tnh ca hàm s
2
2 5 2y x x
.
A.
1
; 2;
2



.
B.
2;
.
C.
1
;
2



.
D.
1
;2
2



.
Câu 13. Tp nghim ca b
2
96xx
là
A.
3; 
.
B.
\3
.
C. .
D.
.
DNG 2. B
Câu 14. B
2
1 7 6 0x x x
có tp nghim
S
là:
A.
;1 6; .S  
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 29
B.
6; .S 
C.
6; .
D.
6; 1 .S 
Câu 15. Tp nghim ca b
42
5 4 0xx
là
A.
1;4
.
B.
2; 1
.
C.
1;2
.
D.
2; 1 1;2
.
Câu 16. Gii b
2
5 2 2 .x x x
A.
1.x
B.
1 4.x
C.
;1 4; .x 
D.
4.x
Câu 17. Biu thc
2
3 10 3 4 5x x x
âm khi và ch khi
A.
5
;.
4
x



B.
15
; ;3 .
34
x
C.
15
; 3; .
34
x



D.
1
;3 .
3
x



Câu 18. Tp nghim ca b
32
3 6 8 0x x x
là
A.
4; 1 2; .x 
B.
4; 1 2; .x
C.
1; .x
D.
; 4 1;2 .x 
DNG 3. BA N MU
Câu 19. Cho biu thc
2
4 12
4
x
fx
xx
. Tp hp tt c các giá tr ca
x
tha mãn
fx

A.
0;3 4;x
.
B.
;0 3;4x
.
C.
;0 3;4x
.
D.
;0 3;4x
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 30
Câu 20. 
2
34
0
1
xx
x

.
A.
; 1 1;4T 
.
B.
; 1 1;4T 
.
C.
; 1 1;4T 
.
D.
; 1 1;4T 
.
Câu 21. Gi
S
là tp nghim ca b
2
2
3
1
4
xx
x


2;2S 
là t
A.
2; 1
.
B.
1;2
.
C.
.
D.
2; 1
.
Câu 22 Có bao nhiêu giá tr a
x
tha mãn
22
3 1 2
4 2 2
xx
x x x x

?
A.
0.
B.
2.
C.
1.
D.
3.
DNG 4. H BC HAI VÀ CÁC BÀI TOÁN LIÊN QUAN
Câu 23. Tp nghim ca h b
22
5 2 4 5
( 2)
xx
xx

có dng
;S a b
ng
ab
bng?
A.
1.
B.
6.
C.
8.
D.
7.
Câu 24. Tp nghim ca h b
2
1
1
24
4 3 0
x
x
xx
là
A.
2;3S
.
B.
;2 3; 
.
C.
2;3S
.
D.
;2 3; 
.
Câu 25. Tp nghim ca h b
2
2
6 5 0
8 12 0
xx
xx
là
A.
2;5
.
B.
1;6
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 31
C.
2;5
.
D.
1;2 5;6
.
Câu 26. H b
2
2
40
1 5 4 0
x
x x x

có s nghim nguyên là
A.
2
.
B.
1
.
C. Vô s.
D.
3
.
Câu 27. Tp nghim ca h b
2
4 3 0
6 12 0
xx
x
là
A.
1;2
.
B.
1; 4
.
C.
;1 3; 
.
D.
; 2 3; 
.
Câu 28. Tp nghim ca b
2
11
23
44
xx
xx

là
A.
3;1
.
B.
4; 3
.
C.
1; ; 3 
.
D.
1; 4; 3
.
Câu 29. Tìm tp nghim ca h b
2
4 3 0
2 5 0
xx
xx
.
A.
1;3
.
B.
2;5
.
C.
2;1 3;5
.
D.
3;5
.
Câu 30. 
5 6 0
2 1 3
xx
x

.
A.
51x
.
B.
1x
.
C.
5x 
.
D.
5x 
.
DNG 5. BÀI TOÁN CHA THAM S
D m
Câu 31. (ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Tìm tt c các giá tr ca
tham s  
2
40x mx
có nghim
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 32
A.
44m
.
B.
44m hay m
.
C.
22m hay m
.
D.
22m
.
Câu 32. Tìm
m
 
2
2 1 3 0x m x m
có hai nghim phân bit
A.
1;2
B.
; 1 2;
C.
1;2
D.
; 1 2; 
Câu 33. Giá tr nào ca
m

2
3 3 1 0m x m x m
1
có hai nghim phân
bit?
A.
\3m
.
B.
3
; 1; \ 3
5
m




.
C.
3
;1
5
m




.
D.
3
;
5
m



.
Câu 34. Tìm các giá tr ca tham s
m
 
2
40x mx m
vô nghim.
A.
0 16m
.
B.
44m
.
C.
04m
.
D.
0 16m
.
Câu 35. Tìm tt c các giá tr ca tham s
m
 
2
2 2 2 3 5 6 0m x m x m
vô nghim?
A.
0.m
B.
2.m
C.
3
.
1
m
m
D.
2
.
13
m
m

Câu 36. Hi có tt c bao nhiêu giá tr nguyên ca
m
 
22
2 2 2 3 4 0x m x m m
có nghim?
A.
3.
B.
4.
C.
2.
D.
1.
Câu 37. Tìm các giá tr ca
m
 
2
5 4 2 0m x mx m
có nghim.
A.
5.m
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 33
B.
10
1.
3
m
C.
10
.
3
1
m
m

D.
10
.
3
15
m
m


Câu 38. Các giá tr
m
 tam thc
2
2 8 1f x x m x m
i du 2 ln là
A.
0m
hoc
28.m
B.
0m
hoc
28.m
C.
0 28.m
D.
0.m
Câu 39. Tìm tt c các giá tr ca tham s
m

2
1 3 2 3 2 0m x m x m
có hai nghim phân bit?
A.
.m
B.
1m
C.
1 6.m
D.
1 2.m
Dạng 2. Tìm m để phƣơng trình bậc 2 có nghiệm thỏa mãn điều kiện cho trƣớc
Câu 40. Chuyên Lê Hồng Phong-Nam Định Tìm tt c các giá tr ca tham s
m
 
22
2 2 1 0mx x m m
có hai nghim trái du.
A.
0
1
m
m

.
B.
0m
.
C.
1m 
.
D.
0
1
m
m

.
Câu 41. nh
m
 
32
2 8 0mx x x m
có ba nghim phân bit l
1
.
A.
11
76
m
.
B.
11
26
m
.
C.
1
7
m
.
D.
0m
.
Câu 42. Vi giá tr nào ca
m

2
1 2 2 3 0m x m x m
có hai nghim
1
x
,
2
x
tha mãn
1 2 1 2
1x x x x
?
A.
13m
.
B.
12m
.
C.
2m
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 34
D.
3m
.
Câu 43. Cho  trình
2
5 2 1 0m x m x m
1
. Vi giá tr nào ca
m
thì
1
có
2
nghim
1
x
,
2
x
tha
12
2xx
?
A.
5m
.
B.
8
3
m
.
C.
8
5
3
m
.
D.
8
5
3
m
.
Câu 44. Tìm các giá tr thc ca tham s
m
 
2
1 2 0m x mx m
có mt nghim ln

1
và mt nghim nh 
1
?
A.
01m
.
B.
1m
.
C.
m
.
D.
0
1
m
m
.
Câu 45. Tìm tt c các giá tr ca tham s
m
 
2
2 2 0x mx m
có hai nghim
1
x
,
2
x
tha mãn
33
12
16xx
.
A. Không có giá tr ca
m
.
B.
2m
.
C.
1m 
.
D.
1m 
hoc
2m
.
Câu 46. Xác nh
m
 
2
1 2 3 4 12 0x x m x m


có ba nghim phân bit ln

1
.
A.
7
3
2
m
và
19
6
m 
.
B.
7
2
m 
.
C.
7
1
2
m
và
16
9
m 
.
D.
7
3
2
m
và
19
6
m 
.
Câu 47. Tìm
m
 
2
30x mx m
có hai nghit.
A.
6.m
B.
6.m
C.
6 0.m
D.
0.m
Câu 48. Tìm tt c các giá tr thc ca tham s
m

2
2 2 3 0m x mx m
có
hai nghit.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 35
A.
2 6.m
B.
3m 
hoc
2 6.m
C.
0m
hoc
3 6.m
D.
3 6.m
Câu 49. Tìm tt c các giá tr thc ca tham s
m

2
2 1 9 5 0x m x m
có hai nghim âm phân
bit.
A.
6.m
B.
hoc
6.m
C.
1.m
D.
1 6.m
Câu 50. 
2 2 2
2 1 2 3 5 0x m m x m m
có hai nghim phân bit trái du khi và ch
khi
A.
1m 
hoặc
5
.
2
m
B.
5
1.
2
m
C.
1m 
hoặc
5
.
2
m
D.
5
1.
2
m
Câu 51. Tìm tt c các giá tr thc ca tham s
m
  
2
1 2 0x m x m
có hai
nghim phân bit
12
,xx
khác
0
tha mãn
22
12
11
1.
xx

A.
; 2 2; 1 7; .m  
B.
11
; 2 2; .
10
m




C.
; 2 2; 1 .m 
D.
7; .m 
D BPT thu kic
Câu 52. Cho hàm s
2
2f x x x m
. Vi giá tr nào ca tham s
m
thì
0,f x x
.
A.
1m
.
B.
1m
.
C.
0m
.
D.
2m
.
Câu 53. Tìm tt c các giá tr ca tham s
m
 b
2
2 8 1 0x m x m
vô nghim.
A.
0;28m
.
B.
;0 28;m  
.
C.
;0 28;m  
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 36
D.
0;28m
.
Câu 54. Tam thc
22
2 1 3 4f x x m x m m
không âm vi mi giá tr ca
x
khi
A.
3m
.
B.
3m
.
C.
3m 
.
D.
3m
.
Câu 55. Có bao nhiêu giá tr nguyên ca tham s
m
 vi mi
x
biu thc
2
2 8 1f x x m x m
luôn nhn giá tr .
A.
27
.
B.
28
.
C. Vô s.
D.
26
.
Câu 56. Tìm các giá tr c biu thc
2
( ) ( 1) 2 7 0f x x m x m x
A.
2;6m
.
B.
( 3;9)m
.
C.
( ;2) (5; )m
.
D.
( 9;3)m
Câu 57. Tìm tt c các giá tr thc ca tham s  b
2
1 2 1 4 0m x m x
(1)
có tp nghim
SR
?
A.
1.m 
B.
1 3.m
C.
1 3.m
D.
1 3.m
Câu 58. B
2
40x x m
vô nghim khi
A.
4m
.
B.
4m
.
C.
4m
.
D.
4m
.
Câu 59.
(THPT
NGUYỄN
TRÃI-THANH
HOÁ
-
Lần
1.Năm
2018&2019)
B  
2
2 1 7 0mx m x m
vô nghim khi
A.
1
5
m
.
B.
1
4
m
.
C.
1
5
m
.
D.
1
25
m
.
Câu 60. Tìm tt c
m

2
2 1 0mx mx

A.
m
.
B.
1m 
.
C.
10m
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 37
D.
10m
.
Câu 61. Tìm tp hp các giá tr ca
m
 hàm s
2
10 2 2 1y m x m x
có t  nh
D
.
A.
1;6
.
B.
1;6
.
C.
; 1 6; 
.
D. .
Câu 62.  b
2
50x x m
vô nghim thì
m
thu ki
A.
1
5
m
.
B.
1
20
m
.
C.
1
20
m
.
D.
1
5
m
.
Câu 63.Có bao nhiêu giá tr nguyên ca tham s
m
 hàm s
2
2 2 3y x mx m
có tnh là
.
A.
4
.
B.
6
.
C.
3
.
D.
5
.
Câu 64. 
m

2
2 1 0x x m

A.
0m
.
B.
0m
.
C.
0m
.
D.
0m
.
Câu 65. B
2
1 2 1 3 0m x m x m
vi mi
x
khi
A.
1;m 
.
B.
2;m 
.
C.
1;m 
.
D.
2;7m
.
Câu 66. 
2
2 1 2 1f x x m x m
. Tìm tt c các giá tr ca tham s
m

,
0;1x
.
A.
1m
.
B.
1
2
m
.
C.
1m
.
D.
1
2
m
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 38
Dạng 4. Tìm m để hệ BPT bậc hai thỏa mãn điều kiện cho trƣớc
Câu 67. H b
5 3 0
3 2 0
xx
xm
vô nghim khi
A.
1m 
.
B.
1m 
.
C.
1m 
.
D.
1m 
.
Câu 68. Chuyên Lê Hồng Phong-Nam Định Tìm tt c các giá tr ca tham s
m
 h b
trình
2
2
2 5 2 0
2 1 1 0
xx
x m x m m
vô nghim.
A.
1
2
2
m
.
B.
1
2
2
m
m

.
C.
1
1
2
m
.
D.
1
2
2
m
m

.
Câu 69. Tìm tt c các giá tr ca tham s
m
 h b
2
2
45
10
xx
x m x m

có nghim.
A.
5
1
m
m

.
B.
5
1
m
m

.
C.
5
1
m
m

.
D.
5
1
m
m

.
Câu 70. H b
2
10
0
x
xm


có nghim khi
A.
1m
.
B.
1m
.
C.
1m
.
D.
1m
.
Câu 71. H b
2
2 0 1
3 4 0 2
xm
xx

vô nghim khi và ch khi:
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 39
A.
8
3
m 
.
B.
2m
.
C.
2m
.
D.
8
3
m 
.
Câu 72. H b
2
1 0 1
02
x
xm


có nghim khi:
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Câu 73. H b
3 4 0 1
12
xx
xm

có nghim khi và ch khi:
A.
5.m
B.
2.m 
C.
5.m
D.
5.m
Câu 74. Tìm
m

2
2
36
96
1
x mx
xx


nghii
x
.
A.
3 6.m
B.
3 6.m
C.
3.m 
D.
6.m
Câu 75. Tìm
m
sao cho h b
2
3 4 0 1
1 2 0 2
xx
mx
có nghim.
A.
3
1.
2
m
B.
3
.
2
m
C.
.m
D.
1.m 
Câu 76. Tìm tt c giá tr thc ca tham s
m
 h b
2
10 16 0 1
3 1 2
xx
mx m

vô nghim.
A.
1
.
5
m 
B.
1
.
4
m
C.
1
.
11
m 
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 40
D.
1
.
32
m
DNG 6. BA DU GIÁ TR TUYI và MT S BÀI TOÁN
LIÊN QUAN
Câu 77. (LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Tp nghim c  
2
3 1 2 0x x x

A. .
B.
4
.
C.
2
.
D.
3
.
Câu 78. Tìm tp nghim ca b
2
40xx
.
A.
.
B.
.
C.
0; 4
.
D.
; 0 4; 
.
Câu 79. Tìm
m

2
11
4 2 2
22
x m x x m
vi mi s thc
x
A.
23m
.
B.
3
2
m
.
C.
3m
.
D.
3
2
m
.
Câu 80. Tt c các giá tr ca
m
 b
2
2 2 2x m x mx
tha mãn vi mi
x
là
A.
m
.
B.
.
C.
2m
.
D.
22m
.
DNG 7. BT S BÀI TOÁN LIÊN QUAN
Câu 81. Tp nghim ca b
2
21xx
.
A.
S 
.
B.
1
;
2
S



.
C.
1; 
.
D.
1
;
2



.
Câu 82. B
2 1 2 3xx
có bao nhiêu nghim nguyên thuc khong
0;7
?
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 41
A. 4.
B. 5.
C. 2.
D. 6.
Câu 83. Tìm tp nghim
S
ca b
2
2 15 2 5x x x
.
A.
; 3 .S 
B.
; 3 .S 
C.
; 3 .S 
D.
; 3 .S 
Câu 84. B
2
16 3 0xx
có tp nghim là
A.
; 4 4; 
.
B.
3;4
.
C.
4;
.
D.
3 4; 
.
Câu 85. 
2
2017 2018xx
.
A.
;1T 
.
B.
;1T 
.
C.
1;T 
.
D.
1;T 
.
Câu 86. Tp nghim ca b
2xx
là
A.
2;
.
B.
;1
.
C.
2;2
.
D.
1;2
.
Câu 87. S nghim nguyên ca b
2
2 1 1xx
là:
A.
3
.
B.
1
.
C.
4
.
D.
2
.
Câu 88. Tp nghim
S
ca b
( 1) 1 0xx
là
A.
1;S 
.
B.
1 1;S 
.
C.
1 1;S 
.
D.
1;S 
.

Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 42
Chƣơng IV. CUNG VÀ GÓC LƢỢNG GIÁC. CÔNG THỨC LƢỢNG GIÁC
BÀI 1. CUNG VÀ GÓC LƢỢNG GIÁC
DNG 1. MI LIÊN H GI
Câu 1. S  a góc
315
là
A.
7
2
. B.
7
4
. C.
2
7
. D.
4
7
.
Câu 2. Cung tròn có s 
5
4
. Hãy chn s  c
A.
5
. B.
15
. C.
172
. D.
225
.
Câu 3. Góc có s 
0
108

A.
3
5
. B.
10
. C.
3
2
. D.
4
.
Câu 4. Góc có s 
9
 là:
A.
0
25 .
B.
0
15 .
C.
0
18 .
D.
0
20 .
Câu 5. Cho
2
2
ak

. Tìm
k

10 11a


A.
7k
. B.
5k
. C.
4k
. D.
6k
.
DNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN
Câu 6. Mng h ng, kim gi dài
10,57cm
và kim phút dài
13,34cm

gi v dài là
A.
2,78cm
. B.
2,77cm
. C.
2,76cm
. D.
2,8cm
.
Câu 7. Cung tròn bán kính bng
8,43cm
có s 
3,85rad
 dài là
A.
32,46cm
. B.
32,47cm
. C.
32,5cm
. D.
32,45cm
.
Câu 8. ng tròn bán kính
5r
 dài c
8
là:
A.
8
l
. B.
8
r
l
. C.
5
8
l
. D. kt qu khác.
Câu 9. Mng tròn có bán kính
10R cm
 dài cung
40
o
ng tròn gn bng
A.
11cm
. B.
13cm
. C.
7cm
. D.
9cm
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 43
Câu 10. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Trên hình v m
,MN
biu din các
cung có s 
A.
2
3
xk

. B.
3
xk
. C.
3
xk

. D.
.
32
xk


.
Câu 11. 
7
4
?
A.
4
. B.
4
. C.
3
4
. D.
3
4
.
Câu 12. 
M

A

2
63
k
AM


,
k
.
A.
6
. B.
4
. C.
3
. D.
8
.

Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 44
BÀI 2. GIÁ TRỊ LƢỢNG GIÁC CỦA MỘT CUNG
DNG 1. XÉT DU CA CÁC GIÁ TR NG GIÁC
Câu 1. Cho
2
a

. Kt qu là
A.
sin 0a
,
cos 0a
.
B.
sin 0a
,
cos 0a
.
C.
sin 0a
,
cos 0a
.
D.
sin 0a
,
cos 0a
.
Câu 2. Trong các giá tr sau,
sin
có th nhn giá tr nào?
A.
0,7
.
B.
4
3
.
C.
2
.
D.
5
2
.
Câu 3. Cho
5
2.
2
a
Chn kh
A.
tan 0, cot 0.aa
B.
tan 0, cot 0.aa
C.
tan 0, cot 0.aa
D.
tan 0, cot 0aa
.
Câu 4. góc ph nht cng giác. Hãy chn kt qu t qu sau

A.
cot 0
.
B.
sin 0
.
C.
.
D.
tan 0
.
Câu 5. góc ph ng giác. hãy chn kt qu t qu 
A.
cot 0
.
B.
tan 0
.
C.
sin 0
.
D.
.
Câu 6. Cho
7
2
4



A.
tan 0
.
B.
cot 0
.
C.
.
D.
sin 0
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 45
DNG 2. GIÁ TR NG GIÁC CC BIT
Câu 7. Cho hai góc nhn
và
ph nhau. H thsai?
A.
cot tan

. B.
cos sin

. C.
cos sin

. D.
sin cos


.
Câu 8. ng thng th
A.
0
  aa
. B.
0
  aa
.
C.
0
 si in saa
. D.
0
 si on caa
.
Câu 9. Chng thc sai ng thc sau
A.
sin cos
2
xx




. B.
sin cos
2
xx




.
C.
tan cot
2
xx




. D.
tan cot
2
xx




.
Câu 10. 
A.
cos cosxx
. B.
sin sinxx

.
C.
cos cosxx
. D.
sin cos
2
xx



.
Câu 11. Khsai?
A.
sin sin

. B.
cot cot

. C.
cos cos

. D.
tan tan

.
Câu 12. Kh
A.
sin sin .xx
B.
cos cos .xx
C.
cot cot .xx
D.
tan tan .xx
Câu 13. Chn h thc sai trong các h thc sau.
A.
3
tan cot
2
xx




. B.
sin 3 sin xx
.
C.
cos 3 cos xx
. D.
cos cosxx
.
Câu 14.
cos( 2017 )x

A.
cos x
. B.
sin x
. C.
sin x
. D.
cos x
.
DNG 3. TÍNH GIÁ TR NG GIÁC
Câu 15. Giá tr ca
cot1458
là
A.
1.
B.
1
. C.
0
. D.
5 2 5
.
Câu 16. Giá tr
cot
89
6
là
A.
3
. B.
3
. C.
3
3
. D.
3
3
.
Câu 17. Giá tr ca
tan180
là
A.
1
. B.
0
. C.

. D. nh.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 46
Câu 18. Cho bit
1
tan
2
. Tính
cot
A.
cot 2
.
B.
1
cot
4
.
C.
1
cot
2
.
D.
cot 2
.
Câu 19. Cho
và
2


. Giá tr ca
cos
là:
A.
4
5
.
B.
4
5
.
C.
4
5
.
D.
16
25
.
Câu 20. Cho
4
cos
5
vi
0
2

. Tính
sin
.
A.
.
B.
1
sin
5

.
C.
.
D.
3
sin
5

.
Câu 21.
Tính
bit
cos 1
A.
kk


.
B.
2kk


.
C.
2
2
kk

.
D.
2kk
.
Câu 22. Cho
tan 5
, vi
3
2



cos
bng:
A.
6
6
.
B.
6
.
C.
6
6
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 47
D.
1
6
.
Câu 23. Cho
3
sin 90 180
5

. Tính
cot
.
A.
3
cot
4
.
B.
4
cot
3
.
C.
4
cot
3

.
D.
3
cot
4

.
Câu 24. Cho
cot 3 2

vi
2



tan cot
22

bng:
A.
2 19
.
B.
2 19
.
C.
19
.
D.
19
.
Câu 25. Nu
3
sin cos
2


thì
sin2
bng
A.
5
4
.
B.
1
2
.
C.
13
4
.
D.
9
4
.
Câu 26. Cho
1
sin cos
2
xx
và
0
2
x

. Tính giá tr ca
sinx
.
A.
17
sin
6
x
.
B.
17
sin
6
x
.
C.
17
sin
4
x
.
D.
17
sin
4
x
.
Câu 27. Cho sinx =
1
2
. Tính giá tr ca
2
cos x
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 48
A.
2
3
cos
4
x
B.
2
3
cos
2
x
C.
2
1
cos
4
x
D.
2
1
cos
2
x
Câu 28. Cho
3sin cos
sin 2cos
xx
P
xx

tan 2x
. 
P

A.
8
9
.
B.
22
3
.
C.
8
9
.
D.
5
4
.
Câu 29. Cho
1
sinx
2
và cosx nhn giá tr âm, giá tr ca biu thc
sin cos
sin
xx
A
x cox
bng
A.
23
B.
23
C.
23
D.
23
Câu 30. Cho
tan 2x
.Giá tr biu thc
4sin 5cos
2sin 3cos
xx
P
xx
là
A.
2
.
B.
13
.
C.
9
.
D.
2
.
Câu 31. Cho tam giác
ABC
u. Tính giá tr ca biu thc
P cos , cos , cos ,AB BC BC CA CA AB
.
A.
3
P
2
.
B.
3
P
2

.
C.
33
P
2

.
D.
33
P
2
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 49
Câu 32. Cho
tan 2a
. Tính giá tr biu thc
2sin cos
sin cos
aa
P
aa
.
A.
2P
.
B.
1P
.
C.
5
3
P
.
D.
1P 
.
Câu 33. ng giác có s 
x
tha mãn
tan 2x
.Giá tr ca biu thc
3
3
sin 3cos
5sin 2cos
xx
M
xx
bng
A.
7
30
.
B.
7
32
.
C.
7
33
.
D.
7
31
.
Câu 34. Cho
1
sin
2
x
và
cos x
nhn giá tr âm, giá tr ca biu thc
sin cos
sin cos
xx
A
xx
bng
A.
23
.
B.
23
.
C.
23
.
D.
23
.
Câu 35. Cho
. Giá tr ca
3sin cos
sin cos
A


là:
A.
5
.
B.
5
3
.
C.
7
.
D.
7
3
.
Câu 36. Giá tr ca
2 2 2 2
3 5 7
A cos cos cos cos
8 8 8 8
bng
A.
0
.
B.
1
.
C.
2
.
D.
1
.
Câu 37. Bit
và
180 270

. Giá tr
cos sin

bng
A.
35
5
.
B.
 5
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 50
C.
35
2
.
D.
51
2
.
DNG 4. RÚT GN BIU THNG GIÁC
Câu 38. Trong các công thc sau, công thc nào sai?
A.
22
sin cos 1


.
B.
2
2
1
1 tan ,
cos 2
kk


.
C.
2
2
1
1 cot ,
sin
kk
.
D.
tan cot 1 ,
2
k
k


.
Câu 39. Biu thc rút gn ca A =
22
22
tan sin
cot cos
aa
aa
bng:
A.
6
tan a
.
B.
6
cos a
.
C.
4
tan a
.
D.
6
sin a
.
Câu 40. Biu thc
2 2 2 2 2
    D x x x x x
không ph thuc
x
và bng
A. 2.
B.

.
C. 3.
D.

.
Câu 41. n biu thc
2
2cos 1
sin cos
x
x
A
x
ta có
A.
cos sinA x x
.
B.
A x x
.
C.
 A x x
.
D.
 A x x
.
Câu 42. Bit
sin co
2
2
s


. Trong các kt qu sau, kt qu nào sai?
A.
 
1
4

.
B.
sin co
6
2
s


.
C.
44
7
sin cos
8


.
D.
22
tan cot 12


.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 51
Câu 43. n biu thc
2 2 2
   A x x x
ta có
A.
2
sinAx
.
B.
2
cosAx
.
C.
2
Ax
.
D.
2
Ax
.
Câu 44. n biu thc
A cos sin cos sin
2 2 2 2
, ta có:
A.
2sinAa
.
B.
2cosAa
.
C.
 A a a
.
D.
0A
.
Câu 45. Biu thc
3
sin cos cot 2 tan
22
P x x x x


có biu thc rút gn là
A.
2sinPx
.
B.
2sinPx
.
C.
0P
.
D.
2cotPx
.
Câu 46. Cho tam giác
ABC
ng thsai?
A.
A B C
.
B.
cos cosA B C
.
C.
sin cos
22
A B C
.
D.
sin sinA B C
.
Câu 47. n biu thc
A cos sin
2



, ta có
A.
sncos iA a a
.
B.
2sinAa
.
C.
ossin cA a a
.
D.
0A
.
Câu 48. Cho A, B, C là ba góc ca mt tam giác không vuông. M 
A.
tan cot
22
A B C



.
B.
cot tan
22
A B C



.
C.
cot cotA B C
.
D.
tan tanA B C
.
Câu 49. Tính giá tr ca biu thc
6 6 2 2
sin cos 3sin cosA x x xx
.
A.
A
.
B.
1A
.
C.
4A
.
D.
A
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 52
Câu 50. Biu thc
2
2
2 2 2
1 tan
1
4tan 4sin cos
x
x x x
A
không ph thuc vào
x
và bng
A.
1
.
B.

.
C.
1
4
.
D.
1
4
.
Câu 51. Biu thc
22
22
22
cos sin
cot .cot
sin .sin
xy
B x y
xy

không ph thuc vào
, xy
và bng
A.
2
.
B.

.
C.
1
.
D.

.
Câu 52. Nu
1
sin cos
2
xx
thì
3sin 2cosxx
bng
A.
57
4
hay
57
4
.
B.
55
7
hay
55
4
.
C.
23
5
hay
23
5
.
D.
32
5
hay
32
5
.
Câu 53. Vi mi , biu thc:
9
cos +cos ... cos
55
A

nhn giá tr bng:
A.

.
B.
10
.
C.
0
.
D.
5
.
Câu 54. Giá tr ca biu thc
2 2 2 2
3 5 7
sin sin sin sin
8 8 8 8
A
bng
A.
2
.
B.
2
.
C.
1
.
D.
0
.
Câu 55. Rút gn biu thc
3
cos sin tan .sin 2
22
A

c
A.
cosA
.
B.
cosA

.
C.
sinA
.
D.
3cosA
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 53
BÀI 3. CÔNG THỨC LƢỢNG GIÁC
DNG 1. ÁP DNG CÔNG THC CNG
Câu 1. Trong các công thc sau, công th
A.
cos cos .sin sin .sina b a b a b
. B.
sin sin .cos cos .sina b a b a b
.
C.
sin sin .cos cos .sina b a b a b
. D.
cos cos .cos sin .sina b a b a b
.
Câu 2. Trong các công thc sau, công th
A.
tan tan
tan .
1 tan tan
ab
ab
ab

B.
   a b a b
C.
tan tan
tan .
1 tan tan
ab
ab
ab

D.
tan tan tan .a b a b
Câu 3. Biu thc
sin cos cos sinx y x y
bng
A.
cos xy
. B.
cos xy
. C.
sin xy
. D.
sin yx
.
Câu 4. Chn khnh sai trong các khnh sau:
A.
cos( ) cos cos sin sina b a b a b
.
B.
sin( ) sin cos cos sina b a b a b
.
C.
sin( ) sin cos cos sina b a b a b
.
D.
2
cos2 1 2sinaa
.
Câu 5. (LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trong các khnh sau, khnh nào
sai?
A.
sin sin 2cos sin
22


a b a b
ab
. B.
cos cos cos sin sin a b a b a b
.
C.
sin sin cos cos sin a b a b a b
. D.
2cos cos cos cos a b a b a b
.
Câu 6. Biu thc
sin
sin
ab
ab
bng biu th s biu th
A.
sin
sin sin
.
sin sin sin
ab
ab
a b a b

B.
sin
sin sin
.
sin sin sin
ab
ab
a b a b

C.
sin
tan tan
.
sin tan tan
ab
ab
a b a b

D.
sin
cot cot
.
sin cot cot
ab
ab
a b a b

Câu 7. Rút gn biu thc:
       a a a a
c:
A.
sin2 .a
B.
cos2 .a
C.
1
.
2
D.
1
.
2
Câu 8. Giá tr ca biu thc
37
cos
12
bng
A.
62
.
4
B.
62
.
4
C.
62
.
4
D.
26
.
4
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 54
Câu 9. ng th
A.
1
cos cos
32




. B.
13
cos sin cos
3 2 2



.
C.
31
cos sin cos
3 2 2



. D.
13
cos cos sin
3 2 2



.
Câu 10. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Cho
tan 2
. Tính
tan
4



.
A.
1
3
.
B.
1
.
C.
2
3
.
D.
1
3
.
Câu 11.  
A.



sin cos 2 sin
4
x x x
.
B.



sin cos 2 cos
4
x x x
.
C.



sin 2 cos 2 2 sin 2
4
x x x
.
D.



sin 2 cos 2 2 cos 2
4
x x x
.
Câu 12. Cho
3
sin
5
x
vi
2
x


tan
4
x



bng.
A.
2
7
.
B.
1
7
.
C.
2
7
.
D.
1
7
.
Câu 13. Cho
sin
1
3
vi
0
2
. Giá tr ca
3
cos


bng
A.
26
26
.
B.
63
.
C.
11
2
6
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 55
D.
1
6
2
.
Câu 14. Cho hai góc
,

tha mãn
5
sin
13
,
2





và
3
cos
5
,
0
2




. Tính giá tr
a
cos

.
A.
16
65
.
B.
18
65
.
C.
18
65
.
D.
16
65
.
Câu 15. (THPT Cộng Hiền - Lần 1 - 2018-2019) Cho
33
sin , ;
5 2 2






   
21
cos
4



A.
2
10
.
B.
72
10
.
C.
2
10
.
D.
72
10
.
Câu 16. Cho hai góc nhn
a
và
b
vi
và
tan
3
4
b
. Tính
ab
.
A.
.
3
B.
.
4
C.
.
6
D.
2
.
3
Câu 17. Cho
, xy
là các góc nhn,
cot
3
4
x
,
. Tng
xy
bng:
A.
.
4
B.
3
.
4
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 56
C.
.
3
D.
.
Câu 18. Biu thc
2 2 2
cos cos cos
33
xxA x

không ph thuc
x
và bng:
A.
3
.
4
B.
4
.
3
C.
3
.
2
D.
2
.
3
Câu 19. Cho
;
sin 0a
;
3
sin
5
b
;
cos 0b
. Giá tr ca
cos .ab
bng:
A.
37
1.
54




B.
37
1.
54





C.
37
1.
54




D.
37
1.
54





Câu 20. Bit
1
cos
22
b
a




và
sin 0
2
b
a




;
3
sin
25
a
b




và
cos 0
2
a
b




. Giá tr
cos ab
bng:
A.
24 3 7
.
50
B.
7 24 3
.
50
C.
22 3 7
.
50
D.
7 22 3
.
50
Câu 21. Cho
3
sin
5
a
;
cos 0a
;
;
sin 0b
. Giá tr
sin ab
bng:
A.
19
7.
54




B.
19
7.
54




Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 57
C.
19
7.
54



D.
19
7.
54



DNG 2. ÁP DNG CÔNG TH H BC
Câu 22. ng thc nào không đúng vi mi
x
?
A.
2
1 cos6
cos 3
2
x
x
. B.
2
cos2 1 2sinxx
.
C.
sin2 2sin cosx x x
. D.
2
1 cos4
sin 2
2
x
x
.
Câu 23. Trong các công thc sau, công thc nào sai?
A.
2
cot 1
cot 2
2cot
x
x
x
. B.
2
2tan
tan 2
1 tan
x
x
x
.
C.
3
cos3 4cos 3cosx x x
. D.
3
sin3 3sin 4sinx x x
Câu 24. Trong các công thc sau, công thc nào sai?
A.
22
   a a a
B.
22
cos2 cos sin .a a a
C.
2
  aa
D.
2
  aa
Câu 25. M đúng?
A.
22
cos2 cos sina a a
. B.
22
cos2 cos sina a a
.
C.
2
cos2 2cos 1aa
. D.
2
cos2 2sin 1aa
.
Câu 26. ng giác
.a
Trong các khnh sau, khnh nào là khnh sai?
A.
2
cos2 1 2sinaa
. B.
22
cos2 cos sina a a
.
C.
2
cos2 1 2cosaa
. D.
2
cos2 2cos 1aa
.
Câu 27. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Kh
SAI?
A.
2
2sin 1 cos2aa
.
B.
cos2 2cos 1aa
.
C.
sin2 2sin cosa a a
.
D.
sin sin cos sin .cosa b a b b a
.
Câu 28. Ch
A.
sin2 2sin cosx x x
. B.
sin2 sin cosx x x
. C.
sin2 2cosxx
. D.
sin2 2sinxx
.
Câu 29. Cho
4
cos , ;0
52
xx




sin2x
là
A.
24
25
.
B.
24
25
.
C.
1
5
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 58
D.
1
5
.
Câu 30. Nu
1
sinx cos
2
x
thì sin2x bng
A.
3
4
.
B.
3
8
.
C.
2
2
.
D.
3
4
.
Câu 31. Bit rng
6 6 2
sin cos sin 2x x a b x
, vi
,ab
là các s thc. Tính
34T a b
.
A.
7T 
.
B.
1T
.
C.
0T
.
D.
7T
.
Câu 32. Cho
3
sin 2 .
4
Tính giá tr biu thc
tan cotA


A.
4
3
A
.
B.
2
3
A
.
C.
8
3
A
.
D.
16
3
A
.
Câu 33. Cho
,ab
là hai góc nhn. Bit
11
cos ,cos
34
ab
. Giá tr ca biu thc
cos cosa b a b
bng
A.
119
144
.
B.
115
144
.
C.
113
144
.
D.
117
144
.
Câu 34. (TOÁN HỌC TUỔI TRẺ SỐ 5) Cho s thc
tha mãn
. Tính
sin4 2sin 2 cos
A.
25
128
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 59
B.
1
16
.
C.
255
128
.
D.
225
128
.
DNG 3. ÁP DNG CÔNG THC BII TÍCH THÀNH TNG, TNG THÀNH TÍCH
Câu 35. M sai?
A.
1
cos cos cos cos
2
a b a b a b


. B.
1
sin cos sin cos
2
a b a b a b


.
C.
1
sin sin cos cos
2
a b a b a b


. D.
1
sin cos sin sin
2
a b a b a b


.
Câu 36. ng thng thc nào sai?
A.
( ) cos .cos sin .sincos a b a b a b
. B.
1
cos .cos ( ) ( )
2
a b cos a b cos a b
.
C.
sin( ) sin .cos sin .cosa b a b b a
. D.
cos cos 2 ( ). ( )a b cos a b cos a b
.
Câu 37. sai?
A.
cos cos 2cos .cos
22
a b a b
ab


. B.
cos cos 2sin .sin
22
a b a b
ab

.
C.
sin sin 2sin .cos
22
a b a b
ab


. D.
sin sin 2sin .cos
22
a b a b
ab


.
Câu 38. Rút gn biu thc
sin3 cos2 sin
sin2 0;2sin 1 0
cos sin2 cos3
x x x
A x x
x x x


c:
A.
cot6Ax
.
B.
cot3Ax
.
C.
cot2Ax
.
D.
tan tan2 tan3A x x x
.
Câu 39. Rút gn biu thc
sin sin
44
P a a

.
A.
3
cos2
2
a
.
B.
1
cos2
2
a
.
C.
2
cos2
3
a
.
D.
1
cos2
2
a
.
Câu 40. Bii biu thc
sin 1
thành tích.
A.
sin 1 2sin cos
22

.
B.
sin 1 2sin cos
2 4 2 4
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 60
C.
sin 1 2sin cos
22

.
D.
sin 1 2sin cos
2 4 2 4
.
Câu 41. Rút gn biu thc
cos 2cos3 cos5
sin 2sin3 sin 5
a a a
P
a a a


.
A.
.
B.
.
C.
cot3Pa
.
D.
tan3Pa
.
Câu 42. (THPT Phan Bội Châu - KTHK 1-17-18) Tính giá tr biu thc
sin30 .cos60 sin60 .cos30
o o o o
P 
.
A.
1P
.
B.
0P
.
C.
3P
.
D.
3P 
.
Câu 43. Giá tr a
2 4 6
cos cos cos
7 7 7

bng:
A.
1
.
2
B.
1
.
2
C.
1
.
4
D.
1
.
4
Câu 44. Tích s
cos10 .cos30 .cos50 .cos70
bng:
A.
1
.
16
B.
1
.
8
C.
3
.
16
D.
1
.
4
Câu 45. Tích s
45
cos .cos .cos
7 7 7
bng:
A.
1
.
8
B.
1
.
8
C.
1
.
4
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 61
D.
1
.
4
Câu 46. Cho hai góc nhn
a
và
b
. Bit
,
. Giá tr
cos .cosa b a b
bng:
A.
113
.
144
B.
115
.
144
C.
117
.
144
D.
119
.
144
Câu 47. Rút gn biu thc
sin sin 2 sin3
cos cos2 cos3
x x x
A
x x x


A.
tan6 .Ax
B.
tan3 .Ax
C.
tan2 .Ax
D.
tan tan2 tan3 .A x x x
Câu 48. Bii biu thc
sin 1a
thành tích.
A.
sin 1 2sin cos .
2 4 2 4
aa
a

B.
sin 1 2cos sin .
2 4 2 4
aa
a

C.
sin 1 2sin cos .
22
a a a

D.
sin 1 2cos sin .
22
a a a

DNG 4. KT HP CÁC CÔNG THNG GIÁC
Câu 49. Cho góc
tha mãn
2


và
2
sin
2
5
.Tính giá tr ca biu thc
tan
24





A
.
A.
1
3
A
.
B.
1
3
A 
.
C.
3A
.
D.
3A 
.
Câu 50. Cho
1
cos 0
32
xx



. Giá tr ca
tan2x
là
A.
5
2
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 62
B.
42
7
.
C.
5
2
.
D.
42
7
.
Câu 51. Cho
cos 0x
. Tính
22
sin sin
66
A x x

.
A.
3
2
.
B. 2.
C. 1.
D.
1
4
.
Câu 52. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Cho bit
2
os
3
c

. Giá tr ca biu thc
cot 3tan
2cot tan
P


bng bao nhiêu?
A.
19
.
13
P
B.
25
.
13
P
C.
25
.
13
P 
D.
19
.
13
P 
Câu 53. Cho
sin .cos sin

vi
2
k
,
2
l


,
,kl
. Ta có
A.
tan 2cot

.
B.
tan 2cot

.
C.
tan 2tan

.
D.
tan 2tan

.
Câu 54. Bit rng
2 2 2
cos
1 2.tan
,
cos sin 1 tan sin
ax
x
ab
x x x b ax
. Tính giá tr ca biu thc
P a b
.
A.
4P
.
B.
1P
.
C.
2P
.
D.
3P
.
Câu 55. Cho
2
cos2
3
. Tính giá tr ca biu thc
cos .cos3P

.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 63
A.
7
18
P
.
B.
7
9
P
.
C.
5
9
P
.
D.
5
18
.
Câu 56. Cho
tan 2x
3
2
x




. Giá tr ca
sin
3
x



là
A.
23
25
.
B.
23
25
.
C.
23
25
.
D.
23
25

.
Câu 57. Tng
     A
bng:
A.
4.
B.

C.
8.
D.

Câu 58. Cho hai góc nhn
a
và
b
vi
sin
1
3
a
,
sin
1
2
b
. Giá tr ca
sin2 ab
là:
A.
2 2 7 3
.
18
B.
3 2 7 3
.
18
C.
4 2 7 3
.
18
D.
5 2 7 3
.
18
Câu 59. Cho biu thc
2 2 2
   .nA a b a b
Hãy chn kt qu 
A.
2cos .sin .sin .A a b a b
B.
2sin .cos .cos .A a b a b
C.
2cos .cos .cos .A a b a b
D.
2sin .sin .cos .A a b a b
DNG 5. MIN-MAX
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 64
Câu 60. Giá tr nh nht ca
66
sin cosxx
là
A. 0.
B.
1
2
.
C.
1
4
.
D.
1
8
.
Câu 61. Giá tr ln nht ca
44
sin cosM x x
bng:
A.
4
.
B.
1
.
C.
2
.
D.
3
.
Câu 62. Cho
3sin 4cosxMx
. Chn kh
A.
55M
.
B.
5M
.
C.
5M
.
D.
5M
.
Câu 63. Giá tr ln nht ca
66
sin cosM x x
bng:
A.
2
.
B.
3
C.
0
.
D.
1
.
Câu 64. Cho biu thc
3
3
1 tan
1 tan
x
M
x
,
,,
42
x k x k k




, m nào trong các mnh
 sau đúng?
A.
1M
.
B.
1
4
M
.
C.
1
1
4
M
.
D.
1M
.
Câu 65. Cho
22
6cos 5sinM x x
 ln nht ca
M
là
A.
11
.
B.
1
.
C.
5
.
D.
6
.
Câu 66. Giá tr ln nht ca biu thc
22
7cos 2sinM x x
là
A.
2
.
B.
5
.
C.
7
.
D.
16
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 65
DNG 6. NHN DNG TAM GIÁC
Câu 67. Cho
,,A B C
là các góc ca tam giác
ABC
thì.
A.
sin2 sin2 2sinA B C
. B.
sin2 sin2 2sinA B C
.
C.
sin2 sin2 2sinA B C
. D.
sin2 sin2 2sinA B C
.
Câu 68. Mt tam giác
ABC
có các góc
,,A B C
tha mãn
33
sin cos sin cos 0
2 2 2 2
A B B A


c bit?
A.  B. u.
C.  D. c bit.
Câu 69. Cho
A
,
B
,
C
là các góc ca tam giác
ABC
(không là tam giác vuông) thì
cot .cot cot .cot cot .cotA B B C C A
bng :
A.
2
cot .cot .cotA B C
. B. Mt kt qu khác các kt qu 
C.
1
. D.
1
.
Câu 70. Cho
A
,
B
,
C
là ba là các góc nhn và
1
tan
2
A
;
1
tan
5
B
,
1
tan
8
C
. Tng
A B C
bng
A.
5
. B.
4
. C.
3
. D.
6
.
Câu 71. Bit
,,A B C
là các góc ca tam giác
,ABC
.
A.
cot cot .
22
A B C



B.
cos cos .
22
A B C



C.
cos cos .
22
A B C




D.
tan cot .
22
A B C



Câu 72.
,A
,B
,C
là ba góc ca mt tam giác. Hãy tìm h thc sai:
A.
sin sin 2A A B C
.
B.
3
sin cos
2
A B C
A


.
C.
3
cos sin
2
A B C
C

. D.
sin sin 2C A B C
.
Câu 73. Cho
A
,
B
,
C
là các góc ca tam giác
ABC
(không phi tam giác vuông) thì:
A.
tan tan tan tan .tan .tan A B C A B C
. B.
tan tan tan tan .tan .tan
2 2 2
A B C
A B C
.
C.
tan tan tan tan .tan .tan A B C A B C
. D.
tan tan tan tan .tan .tan
2 2 2
A B C
A B C
.
Câu 74. Bit
,,A B C
là các góc ca tam giác
,ABC
.
A.
sin cos .
22
A B C



B.
sin cos .
22
A B C




C.
sin sin .
22
A B C



D.
sin sin .
22
A B C




Câu 75. Nu
2ab
và
abc
. Hãy chn kt qu đúng.
A.
sin sin sin sin 2b b c a
. B.
2
sin sin sin sinb b c a
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 66
C.
2
sin sin sin cosb b c a
. D.
sin sin sin cos2b b c a
.
Câu 76. Cho
A
,
B
,
C
là các góc ca tam giác
ABC
thì:
A.
sin2 sin2 sin2 4sin .sin .sin A B C A B C
. B.
sin2 sin2 sin2 4cos .cos .cos A B C A B C
.
C.
sin2 sin2 sin2 4cos .cos .cos A B C A B C
. D.
sin2 sin2 sin2 4sin .sin .sin A B C A B C
.
Câu 77.
,A
,B
,C
là ba góc ca mt tam giác. Hãy ch h thc sai:
A.
43
cot tan
22
A B C A




. B.
2
cos sin
2
A B C
B





.
C.
3
sin cos2
2
A B C
C




. D.
65
tan cot
22
A B C C




.
Câu 78. Bit
,,A B C
là các góc ca tam giác
ABC

A.
cos cosC A B
. B.
tan tanC A B
.
C.
cot cotC A B
. D.
sin sinC A B
.
Câu 79. Cho
A
,
B
,
C
là ba góc ca mt tam giác. Hãy chn h th thc sau.
A.
222
cos cos cos 1 cos .cos .cos .A B C A B C
B.
222
      A B C A B C
C.
222
cos cos cos 1 2cos .cos .cos .A B C A B C
D.
222
      A B C A B C
Câu 80. Hãy ch ra công thc sai, nu
,,A B C
là ba góc ca mt tam giác.
A.
cos cos sin sin sin
2 2 2 2 2
B C B C A

. B.
cos .cos sin .sin cos 0B C B C A
.
C.
sin cos sin cos cos
2 2 2 2 2
B C C C A

.
D.
222
cos cos cos 2cos cos cos 1A B C A B C
.
---HT---
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 67
HÌNH HỌC 10 - Quyển 2- HỌC KỲ 2
CHƢƠNG III. PHƢƠNG PHÁP TOẠ ĐỘ TRONG MẶT PHẲNG.
BÀI 1. PHƢƠNG TRÌNH ĐƢỜNG THẲNG
D N CNG
THNG, H S GÓC CNG THNG
Câu 1. Trong mt phng
Oxy
ng thng
22
: 0, 0d ax by c a b
t
n cng thng
d
?
A.
;n a b
.
B.
;n b a
.
C.
;n b a
.
D.
;n a b
.
Câu 2. (THPT Cộng Hiền - Lần 1 - 2018-2019) Trong mt phng t    ng thng
: 2 3 0d x y
n cng thng
d
là
A.
1; 2n 
B.
2;1n
C.
2;3n 
D.
1;3n
Câu 3. ng thng
:3 2 10 0d x y
 a
d
?
A.
3;2u
.
B.
3; 2u 
.
C.
2; 3u 
.
D.
2; 3u
.
Câu 4. (THPT Quỳnh Lƣu- Nghệ An- 2019) ng thng
1
5
:
2
33
xt
yt

mn
cng thng
có t
A.
5; 3
.
B.
6;1
.
C.
1
;3
2



.
D.
5;3
.
Câu 5. 
Oxy

2
:
12
xt
d
yt
?
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 68
A.
2; 1n 
.
B.
2; 1n
.
C.
1;2n
.
D.
1;2n
.
Câu 6.  ng thng
d
:
14
23
xt
yt

là:
A.
4;3u 
.
B.
4;3u
.
C.
3;4u
.
D.
1; 2u 
.
Câu 7.  ng thng song song vi trc
Ox
:
A.
1;0u
.
B.
(1; 1)u 
.
C.
(1;1)u
.
D.
(0;1)u
.
Câu 8. ng thng
:7 3 1 0d x y
 a d?
A.
7;3u
.
B.
3;7u
.
C.
3;7u 
.
D.
2;3u
.
Câu 9. (THPT Yên Mỹ Hƣng Yên lần 1 - 2019) m
2;3M
và
2;5N
ng thng
MN
có m 
A.
4;2u
.
B.
4; 2u 
.
C.
4; 2u
.
D.
2;4u 
.
Câu 10. ng thng
d
có m 
3; 4u 
ng thng
vuông góc vi
d
có mt
n là:
A.
1
.4;3n
B.
2
4; 3 .n 
C.
3
.3;4n
D.
4
3; 4 .n
Câu 11. ng thng
d
có mn là
2; 5n
ng thng
vuông góc vi
d
có
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 69
m 
A.
1
.5; 2u
B.
2
5;2 .u
C.
3
.2;5u
D.
4
2; 5 .u
Câu 12. ng thng
d
có m 
3; 4u 
ng thng
song song vi
d
có mt
n là:
A.
1
.4;3n
B.
2
4;3 .n
C.
3
.3;4n
D.
4
3; 4 .n
Câu 13. ng thng
d
có mn là
2; 5n
ng thng
song song vi
d
có
m 
A.
1
.5; 2u
B.
2
5; 2 .u 
C.
3
.2;5u
D.
4
2; 5 .u
DNG 2. VING THNG VÀ CÁC BÀI TOÁN LIÊN QUAN
Dng 2.1 Ving thng khi bit VTPT hoc VTCP, H S 
qua
Câu 14. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) 

2; 1A
và
2;5B
là
A.
2
6
xt
yt

.
B.
2
56
xt
yt


.
C.
1
26
x
yt

.
D.
2
16
x
yt
.
Câu 15. tham s cng thm
3; 1 , 6;2AB
là
A.
13
2
xt
yt
.
B.
33
1
xt
yt

.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 70
C.
33
6
xt
yt

.
D.
33
1
xt
yt

.
Câu 16. Trong mt phng tm
3;0 , 0;2AB
ng thng
:0d x y
. L
trình tham s cng thng
qua
A
và song song vi
d
.
A.
3
xt
yt

.
B.
3
xt
yt

.
C.
3
xt
yt


.
D.
3
xt
yt


.
Câu 17. 
d

5
92
xt
yt

.


d
là
A.
2 1 0xy
.
B.
2 1 0xy
.
C.
2 1 0xy
.
D.
2 3 1 0xy
.
Câu 18. Trong mt phng
Oxy
 m
(1;2)M
. Gi
,AB
là hình chiu ca
M
lên
,Ox Oy
. Vit
ng thng
AB
.
A.
2 1 0xy
.
B.
2 2 0xy
.
C.
2 2 0xy
.
D.
30xy
.
Câu 19. Trong mt phng t Oxyng thng
35
: ( )
14
xt
dt
yt


ng quát ca
ng thng d là
A.
4 5 7 0.xy
.
B.
4 5 17 0.xy
.
C.
4 5 17 0.xy
.
D.
4 5 17 0.xy
Câu 20. Trong mt phng vi h trc t
Oxy
ng thng d ct hai trc
Ox
và
Oy
lt ti
m
;0Aa
và
0;Bb
0; 0ab
. Ving thng d.
A.
:0
xy
d
ab

.
B.
: 1.
xy
d
ab

Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 71
C.
: 1.
xy
d
ab

D.
: 1.
xy
d
ba

.
Câu 21. ng thm
0;4 , 6;0AB
là:
A.
1
64
xy

.
B.
1
46
xy

.
C.
1
46
xy

.
D.
1
64
xy

.
Dng 2.2 Ving thm vuông góc hoc vng thng cho
c
Câu 22. ng thng
d

1; 2A
và vuông góc vng thng
:3 2 1 0xy
là:
A.
3 2 7 0xy
.
B.
2 3 4 0xy
.
C.
3 5 0xy
.
D.
2 3 3 0xy
.
Câu 23. ng thng
:8 6 7 0d x y
. Nng thng
c ta  và vuông góc vi
ng thng d thì

A.
4 3 0xy
.
B.
4 3 0xy
.
C.
3 4 0xy
.
D.
3 4 0xy
.
Câu 24. ng thm
1;11A
và song song vng thng
35yx

A.
3 11yx
.
B.
3 14yx
.
C.
38yx
.
D.
10yx
.
Câu 25.
(HKI XUÂN PHƢƠNG - HN) L
2;5A
và song song vng
thng
: 3 4?d y x
A.
: 3 2yx
.
B.
: 3 1yx
.
C.
1
:1
3
yx
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 72
D.
: 3 1yx
.
Câu 26. 
Oxy

d
qua
1;1M

': 1 0d x y

A.
10xy
.
B.
0xy
.
C.
10xy
.
D.
20xy
.
Câu 27. Ving quát cng thm
1;2I
và vuông góc vng thng

2 4 0xy
.
A.
20xy
.
B.
2 3 0xy
.
C.
2 3 0xy
.
D.
2 5 0xy
.
Câu 28. Trong mt phng vi h t
Oxy
m
2;0A
¸
0;3B
và
3; 1C 
ng thng
m
B
và song song vi
AC
 là:
A.
5
.
3
xt
yt

B.
5
.
13
x
yt

C.
.
35
xt
yt

D.
35
.
xt
yt

Câu 29. Trong mt phng vi h t
Oxy
m
3;2A
¸
4;0P
và
0; 2Q
ng th
m
A
và song song vi
PQ
 là:
A.
34
.
22
xt
yt


B.
32
.
2
xt
yt


C.
12
.
xt
yt
D.
12
.
2
xt
yt
Câu 30. Trong mt phng vi h t
Oxy
, cho hình bình hành
ABCD
nh
A

ng thng cha cnh
CD
là
14
3
xt
yt

. Vi cng thng cha
cnh
AB
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 73
A.
23
22
xt
yt
.
B.
24
13
xt
yt

.
C.
23
14
xt
yt

.
D.
23
14
xt
yt

.
Câu 31. Vi cng thng
d
m
3;5M
và song song vng
phân giác ca góc ph nht.
A.
3
5
xt
yt

.
B.
3
5
xt
yt

.
C.
3
5
xt
yt

.
D.
5
3
xt
yt

.
Câu 32. Vi cng thng
d
m
4; 7M
và song song vi trc
Ox
.
A.
14
7
xt
yt


.
B.
4
7
x
yt
.
C.
7
4
xt
y
.
D.
7
xt
y

.
Câu 33.   ng quát c ng thng
d
 
O
và song song v ng thng
:6 4 1 0xx
là:
A.
3 2 0.xy
B.
4 6 0.xy
C.
3 12 1 0.xy
D.
6 4 1 0.xy
Câu 34. ng thng
d
m
1;2M
và vuông góc vng thng
:2 3 0xy
ng quát là:
A.
20xy
.
B.
2 3 0xy
.
C.
10xy
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 74
D.
2 5 0xy
.
Câu 35. Cho tam giác
ABC
có
A B C
ng thng
d

B
và song song vi
AC
ng quát là:
A.
xy
.
B.
xy
.
C.
 xy
.
D.
  xy
.
Câu 36. Ving quát cng thng
d
m
1;0M
và vuông góc vng
thng
:.
2
xt
yt

A.
2 2 0xy
.
B.
2 2 0xy
.
C.
2 1 0xy
.
D.
2 1 0xy
.
Câu 37. ng thng
d
m
2;1M
và vuông góc vng thng
13
:
25
xt
yt


trình tham s là:
A.
23
.
15
xt
yt

B.
25
.
13
xt
yt

C.
13
.
25
xt
yt


D.
15
.
23
xt
yt


Câu 38. Ving quát cng thng
d
m
3; 1M
và vuông góc vng
phân giác góc ph hai.
A.
40xy
.
B.
40xy
.
C.
40xy
.
D.
40xy
.
Câu 39. Vi cng thng
d
m
4;0M
và vuông góc vng
phân giác góc ph hai.
A.
4
xt
yt
.
B.
4xt
yt

.
C.
4
xt
yt

.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 75
D.
4
xt
yt

.
Câu 40. Ving quát cng thng
d
m
1;2M
và song song vi trc
Ox
.
A.
20y 
.
B.
10x 
.
C.
10x
.
D.
20y 
.
Dng 2.3 Ving cao, trung tuyn, phân giác ca tam giác
Dng cao ca tam giác
Câu 41. (ĐỘI CẤN VĨNH PHÚC LẦN 1 2018-2019) 
Oxy

ABC

1;2 , 3;1 , 5;4A B C

A


ABC
?
A.
2 3 8 0xy
.
B.
2 3 8 0xy
.
C.
3 2 1 0xy
.
D.
2 3 2 0xy
.
Câu 42. Cho
ABC
có
2; 1 , 4;5 , 3;2A B C
ng cao
AH
ca
ABC

A.
7 3 11 0xy
.
B.
3 7 13 0xy
.
C.
3 7 17 0xy
.
D.
7 3 10 0xy
.
Câu 43. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Trên mt phng t 
Oxy
, cho tam giác
ABC
có
1;2 , 3;1 , 5;4A B C
ng cao k t
A
ca tam
giác
ABC
?
A.
2 3 8 0xy
.
B.
2 3 8 0xy
.
C.
3 2 1 0xy
.
D.
2 3 2 0xy
.
Câu 44. Cho tam giác
ABC
có
1;1 , 0; 2 , 4 .() ;2A B C
Lng trung tuyn ca tam
giác
ABC
k t
.A
A.
2 0.xy
B.
2 3 0.xy
C.
2 3 0.xy
D.
0.xy
Câu 45. ng trung trc cn
AB
vi
1; 4A
và
5;2B

A.
2 3 3 0.xy
B.
3 2 1 0.xy
C.
3 4 0.xy
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 76
D.
1 0.xy
Câu 46. ng trung trc cn
AB
vi
4; 1A
và
1; 4B

A.
1.xy
B.
0.xy
C.
0.yx
D.
1.xy
Dng trung tuyn ca tam giác
Câu 47. Cho tam giác
ABC

1;1A
,
0; 2B
,
4;2C


B

ABC
là
A.
7 7 14 0 xy
.
B.
5 3 1 0xy
.
C.
3 2 0xy
.
D.
7 5 10 0xy
.
Câu 48. (THPT Yên Dũng 3 - Bắc Giang lần 1- 18-19) Trong h t
Oxy
, cho tam giác
ABC
có
2;3 , 1;0 , 1; 2A B C 
ng trung tuyn k t nh
A
ca tam giác
ABC
là:
A.
2 1 0xy
.
B.
2 4 0xy
.
C.
2 8 0xy
.
D.
2 7 0xy
.
Câu 49. (Nông Cống - Thanh Hóa - Lần 1 - 1819) Trong mt phng vi h t
Oxy
, cho tam giác
ABC
nh
AB
là
2 0,xy
nh
AC
là
2 5 0xy
. Bit
trng tâm ca tam giác  m
3;2G
   ng thng
BC
có dng
0.x my n
Tìm
.mn
A.
3
.
B.
2
.
C.
5
.
D.
4
.
Dng phân giác ca tam giác
Câu 50. Trong mt phng vi h t
Oxy
ng thng
:0ax by c
m
;
mm
M x y
,
;
nn
N x y
không thuc
. Chn khnh sau:
A.
, MN
khác phía so vi
khi
. 0.
m m n n
ax by c ax by c
B.
, MN
cùng phía so vi
khi
. 0.
m m n n
ax by c ax by c
C.
, MN
khác phía so vi
khi
. 0.
m m n n
ax by c ax by c
D.
, MN
cùng phía so vi
khi
. 0.
m m n n
ax by c ax by c
Câu 51. Trong mt phng vi h t
Oxy
, cng thng
:3 4 5 0d x y
và m
1;3A
,
2;Bm
. Tìm tt c các giá tr ca tham s
m

A
và
B
ni vi
d
.
A.
0m
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 77
B.
1
4
m 
.
C.
1m 
.
D.
1
4
m 
.
Câu 52. Trong mt phng vi h t 
Oxy
, c ng thng
2
:
13
xt
d
yt


và  m
1;2A
,
2;Bm
. Tìm tt c các giá tr ca tham s
m

A
và
B
ni vi
d
.
A.
13.m
B.
13m
.
C.
13.m
D.
13m
.
Câu 53. C ng th       a các góc hp bi hai ng thng
1
: 2 3 0xy
và
2
:2 3 0xy
.
A.
30xy
và
30xy
.
B.
30xy
và
3 6 0xy
.
C.
30xy
và
3 6 0xy
.
D.
3 6 0xy
và
3 6 0xy
.
DNG 3. V I CNG THNG
Câu 54. Trong mt phng
Oxy
 ng thng
: 2 1 0d x y
song song v ng th  

A.
2 1 0xy
.
B.
20xy
.
C.
2 1 0xy
.
D.
2 4 1 0xy
.
Câu 55. Tìm các giá tr thc ca tham s
m
 ng thng
2
3 3 1y m x m
song song vng
thng
5yx
.
A.
2m 
.
B.
2m 
.
C.
2m 
.
D.
2m
.
Câu 56. ng thng
12
: 5, : 9d mx y m d x my
ct nhau khi và ch khi
A.
1m 
.
B.
1m
.
C.
1m 
.
D.
2m
.
Câu 57. Vi giá tr nào ca
m
ng thng
1
:3 4 10 0d x y
và
2
2
: 2 1 10 0d m x m y
trùng nhau?
A.
2m
.
B.
1m 
.
C.
2m
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 78
D.
2m 
.
Câu 58. Trong mt phng vi h t 
Oxy
   ng th   
1
: 1 2 0d mx m y m
và
2
:2 1 0d x y
. Nu
1
d
song song
2
d
thì:
A.
2.m
B.
1.m 
C.
2.m 
D.
1.m
Câu 59. Tìm
m
 ng thng
1
:2 3 4 0d x y
và
2
23
:
14
xt
d
y mt


ct nhau.
A.
1
.
2
m 
B.
2.m
C.
1
.
2
m
D.
1
.
2
m
Câu 60. Vi giá tr nào ca
a
thì hai ng thng
1
d x y 
và
2
1
:
31
x at
d
y a t
vuông góc vi nhau?
A.
2.a 
B.
2.a
C.
1.a 
D.
1a
.
Câu 61. Vi giá tr nào ca
m
ng thng
1
22
:
3
xt
d
yt

và
2
2
:
6 1 2
x mt
d
y m t

trùng nhau?
A.
1
2
m
.
B.
2m 
.
C.
2m
.
D.
2m 
.
Câu 62. Tìm tt c các giá tr ca
m
 ng thng
1
22
:
1
xt
d
y mt


và
2
:4 3 0d x y m
trùng nhau.
A.
3m 
.
B.
1m
.
C.
4
3
m
.
D.
m
.
Câu 63. Vi giá tr nào ca
m
ng thng
1
:2 4 0d x y m
và
2
: 3 2 1 0d m x y m
song song?
A.
1.m
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 79
B.
1.m 
C.
2.m
D.
3.m
Câu 64. Tìm tt c các giá tr ca
m
 ng thng
1
:2 3 10 0x my
và
2
: 4 1 0mx y
ct nhau.
A.
1 10m
.
B.
1m
.
C. Không có
m
.
D. Vi mi
m
.
Câu 65. Vi giá tr nào ca
m
ng thng
1
: 19 0mx y
và
2
: 1 1 20 0m x m y
vuông góc?
A. Vi mi
m
.
B.
2m
.
C. Không có
m
.
D.
1m 
.
Câu 66. Vi giá tr nào ca
m
ng thng
1
:3 2 6 0d mx y
và
2
2
: 2 2 6 0d m x my
ct nhau?
A.
1m 
.
B.
1m
.
C.
m
.
D.
1 và 1mm
.
Câu 67. Tìm to  m cng thng
1
34
:
25
xt
d
yt

và
2
14
:.
75
xt
d
yt


A.
1;7 .
B.
3;2 .
C.
2; 3 .
D.
5;1 .
Câu 68.   ng thng
1
:2 3 19 0d x y
và
2
22 2
:
55 5
xt
d
yt


. Tìm to   m ca hai
ng th
A.
2;5 .
B.
10;25 .
C.
1;7 .
D.
5;2 .
Câu 69. Trong mt phng vi h t 
Oxy
   m
 AB
 ng thng
:
2
xt
d
yt


. Tìm t m cng thng
AB
và
d
.
A.
2;0
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 80
B.

.
C.
0;2
.
D.
.
Câu 70. nh
a
 ng thng
1
d ax y
và
2
1
:
33
xt
d
yt

ct nhau ti mm nm
trên trc hoành.
A.
1.a
B.
1.a 
C.
2.a
D.
2.a 
Câu 71. Tìm tt c các giá tr ca tham s
m
ng thng
2
1
d x my m
và
2
2
:
62
xt
d
yt


ct
nhau ti mm thuc trc tung.
A.
0m
hoc
6m 
.
B.
0m
hoc
2m
.
C.
0m
hoc
2m 
.
D.
0m
hoc
6m
.
Câu 72. Vi giá tr nào ca
m
ng thng
1
d x y
,
2
: 2 1 0d x y
và
3
d mx y
ng quy?
A.
6m 
.
B.
6m
.
C.
5m 
.
D.
5m
.
Câu 73. ng thng
:51 30 11 0d x y

A.
4
1; .
3
M




B.
4
1; .
3
N



C.
3
1; .
4
P



D.
3
1; .
4
Q




DNG 4. GÓC CNG THNG
Dng 4.1 Tính góc cng thc
Câu 74. (NGÔ GIA TỰ LẦN 1_2018-2019) Tính góc gi  ng thng
: 3 2 0xy
và
: 3 1 0xy
.
A.
90
.
B.
120
.
C.
60
.
D.
30
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 81
Câu 75. Góc ging thng
: 3 7 0a x y
và
: 3 1 0b x y
là:
A.
30
.
B.
90
.
C.
60
.
D.
45
.
Câu 76. ng thng
1
:2 5 2 0dxy
và
2
:3 7 3 0d x y
. Góc to bng thng
1
d
và
2
d
bng
A.
0
30
.
B.
0
135
.
C.
0
45
.
D.
0
60
.
Câu 77. Tìm côsin góc ging thng
1
:2 1 0xy
và
2
2
:
1
xt
yt


A.
10
10
.
B.
3
10
.
C.
3
5
.
D.
3 10
10
.
Câu 78. Tìm góc ging thng
1
: 2 15 0xy
và
2
2
:.
42



xt
t
yt
A.
5
.
B.
60
.
C.
0
.
D.
90
.
Câu 79. Tìm cosin góc gia
2
ng thng
12
: 2 7 0, :2 4 9 0d x y d x y
.
A.
3
5
.
B.
2
5
.
C.
1
5
.
D.
3
5
.
Câu 80. Tính góc to bi ging thng
1
:7 3 6 0d x y
và
2
:2 5 4 0.d x y
A.
4
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 82
B.
3
.
C.
2
3
.
D.
3
4
.
Câu 81. ng thng
1
2 2 0: xyd
và
2
0:d xy
. Tính cosin ca góc to bi ging
th
A.
10
10
.
B.
2
3
.
C.
3
3
.
D.
3
.

Câu 82. nh tt c các giá tr ca
a
 góc to bng thng
9
72
x at
yt


t
ng thng
3 4 2 0xy
bng
45
.
A.
1a
,
14a 
.
B.
2
7
a
,
14a 
.
C.
2a 
,
14a 
.
D.
2
7
a
,
14a
.
Câu 83. ng thng
   m c  ng thng
1
:2 3 0d x y
và
2
: 2 1 0d x y
ng thi to vng thng
3
: 1 0dy
mt góc
0
45

A.
(1 2) 0xy
hoc
: 1 0xy
.
B.
: 2 0xy
hoc
: 4 0xy
.
C.
:0xy
hoc
: 2 0xy
.
D.
:2 1 0x
hoc
5 0.y 
.
Câu 84. Trong mt phng vi h t
Oxy
ng thm
2;0A
và to vi
trc hoành mt góc
45 ?
A. Có duy nht.
B.
2
.
C. Vô s.
D. Không tn ti.
Câu 85. ng thng
to vng thng
: 2 6 0d x y
mt góc
0
45
. Tìm h s góc
k
cng
thng
.
A.
1
3
k
hoc
3.k 
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 83
B.
1
3
k
hoc
3.k
C.
1
3
k 
hoc
3.k 
D.
1
3
k 
hoc
3.k
Câu 86. Bit r      ca tham s
k
 ng thng
:d y kx
to v ng thng
: yx
mt góc
0
60
. Tng hai giá tr ca
k
bng:
A.
8.
B.
4.
C.
1.
D.
1.
DNG 5. KHONG CÁCH
Dng 5.1 Tính khong cách t m ng thc
Câu 87. Khong cách t m
1;1A
ng thng
5 12 6 0xy
là
A.
13
.
B.
13
.
C.
1
.
D.
1
.
Câu 88. Khong cách t m
5; 1M
ng thng
3 2 13 0xy
là:
A.
2 13
.
B.
28
13
.
C.
26
.
D.
13
2
.
Câu 89. Trong mt phng
Oxy
, khong cách t gc t
O
ng thng
:4 3 1 0d x y
bng
A.
3
.
B.
4
.
C.
1
.
D.
1
5
.
Câu 90. Mng tròn có tâm
3; 2I
tip xúc vng thng
: 5 1 0.xy
Hng
tròn bng bao nhiêu?
A.
14
.
26
B.
7
.
13
C.
26.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 84
D.
6.
Câu 91. Trong mt phng
Oxy
, khong cách t m
0;4M
 ng thng
: 4 2 0xcos y sin sin
bng
A.
8
.
B.
4sin
.
C.
4
cos sin
.
D.
8
.
Câu 92. Khong cách t m cng thng
3 4 0xy
và
2 3 1 0xy
ng thng
:3 4 0xy
bng:
A.
2 10
.
B.
3 10
5
.
C.
10
5
.
D.
2
.
Câu 93. Trong mt phng vi h t
Oxy
, cho tam giác
ABC
có
,1;2A
0;3B
và
4;0C
. Chiu
cao ca tam giác k t nh
A
bng:
A.
1
5
.
B.
3
.
C.
1
25
.
D.
3
5
.
Câu 94. Trong mt phng vi h t
Oxy
, cho tam giác
ABC
có
3; 4 ,A
1;5B
và
3;1C
. Tính
din tích tam giác
ABC
.
A.
10.
B.
5.
C.
26.
D.
2 5.
Câu 95. Khong cách t m
2;0M
ng thng
13
:
24
xt
yt


bng:
A.
2.
B.
2
.
5
C.
10
.
5
D.
5
.
2
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 85
Câu 96. Khong cách nh nht t m
15;1M
n mm bt kì thung thng
23
:
xt
yt

bng:
A.
10.
B.
1
.
10
C.
16
.
5
D.
5.
Câu 97. Tìm tt c các giá tr ca tham s
m
 khong cách t m
1;2A
 ng thng
: 4 0mx y m
bng
25
.
A.
2.m
B.
2
1
2
m
m

.
C.
1
2
m 
.
D. Không tn ti
m
.
Câu 98. Tìm tt c các giá tr ca tham s
m
 khong cách t  m c  ng thng
1
:
2
xt
d
yt

và
2
: 2 0d x y m
n gc to  bng
2
.
A.
4
.
2
m
m

B.
4
.
2
m
m


C.
4
.
2
m
m
D.
4
.
2
m
m

Câu 99. ng tròn
C
có tâm là gc t
0;0O
và tip xúc vng thng
:8 6 100 0xy
.
Bán kính
R
cng tròn
C
bng:
A.
4R
.
B.
6R
.
C.
8R
.
D.
10R
.
Câu 100. ng tròn
C
có tâm
2; 2I 
và tip xúc vng thng
:5 12 10 0xy
. Bán kính
R
cng tròn
C
bng:
A.
44
13
R
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 86
B.
24
13
R
.
C.
44R
.
D.
7
13
R
.
Câu 101. Tính khong cách ging thng
:7 3 0d x y
và
2
:
27
xt
yt

.
A.
32
2
.
B.
15
.
C.
9
.
D.
9
50
.
Câu 102. Khong cách ging thng song song
1
 dxy
và
2
d x y
bng:
A.
10,1
.
B.
1,01
.
C.
101
.
D.
101
.
Dng thn khong cách
Câu 103. Trong mt phng vi h t
Oxy
m
2;3A
và
1;4B
ng th
m
A
và
B
?
A.
2 0.xy
B.
2 0.xy
C.
2 2 10 0.xy
D.
100 0.xy
Câu 104. Trong mt phng vi h t
Oxy
m
,0;1A
12;5B
và
3;0 .C
ng thng
m
,A
B
và
C
.
A.
3 4 0xy
.
B.
10 0xy
.
C.
0xy
.
D.
5 1 0xy
.
Câu 105. Trong mt phng vi h t 
Oxy
   m
,1;1A
2;4B
 ng thng
: 3 0mx y
. Tìm tt c các giá tr ca tham s
m

m
, AB
.
A.
1
.
2
m
m

B.
1
.
2
m
m

Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 87
C.
1
.
1
m
m

D.
2
.
2
m
m

DM
Dnh ta hình chii xng
Câu 106.  ng thng
:3 5 15 0d x y
      m nào không thu ng
thng
d
A.
1
5;0M
.
B.
4
5;6M
.
C.
2
0;3M
.
D.
3
5;3M
.
Câu 107. Trong mt phng vi h trc t
Oxy
, cho tam giác
ABC
có
4;3A
,
2;7B
,
3; 8C 
.
T ng cao k t nh
A
xung cnh
BC
là:
A.
1;4
.
B.
1; 4
.
C.
1;4
.
D.
4;1
.
Câu 108. ng thng
: 3 5 0d x y
m
2;1M
. T hình chiu vuông góc ca
M
trên
d
là
A.
74
;
55



.
B.
74
;
55



.
C.
74
;
55




.
D.
54
;
75



.
Câu 109. 
1;2M

:0xy

A.
33
;
22



.
B.
1;1
.
C.
2;2
.
D.
33
;
22




Dn yu t khong cách, góc
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 88
Câu 110. m
3; 1 , 0;3AB
. Tìm t m
M
thuc
Ox
sao khong cách t
M
ng
thng
AB
bng
1
.
A.
7
;0
2
M



và
1;0M
.
B.
13;0M
.
C.
4;0M
.
D.
2;0M
.
Câu 111. Trong mt phng vi h t 
Oxy
,   m
1;1A
,
4; 3B
 ng thng
: 2 1 0d x y
m
M
thuc
d
có t nguyên và tha mãn khong cách t
M
n
ng thng
AB
bng
6
.
A.
3;7 .M
B.
7;3 .M
C.
43; 27 .M 
D.
.
27
11
3;M



Câu 112. Trong mt phng vi h t
Oxy
, m
0;1A
ng thng
2
:
2
3y
d
xt
t


m
M
thuc
d
và cách
A
mt khong bng
5
, bit
M
 âm.
A.
4;4 .M
B.
4;4
.
24 2
;
55
M
M




C.
24 2
;.
55
M




D.
4;4 .M
Câu 113. Bit rm thuc trng thng
:2 5 0xy
mt khong
bng
25
 cng:
A.
75
.
4
B.
25
.
4
C.
225
.
4
D.  khác.
Câu 114. Trong mt phng vi h t
Oxy
m
3; 1A
và
0;3B
. Tìm m
M
thuc trc
hoành sao cho khong cách t
M
ng thng
AB
bng
1
.
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 89
A.
7
;0
2
.
1;0
M
M



B.
14
;0
3
.
4
;0
3
M
M






C.
7
;0
2
.
1;0
M
M



D.
14
;0
3
.
4
;0
3
M
M






Câu 115. Trong mt phng vi h t
Oxy
m
3;0A
và
0; 4B
m
M
thuc trc
tung sao cho din tích tam giác
MAB
bng
6.
A.
0;0
.
0; 8
M
M
B.
0; 8 .M
C.
6;0 .M
D.
0;0
.
0;6
M
M
Câu 116. Trong mt phng vi h t 
Oxy
   m
1;2 ,A
3;2B
 ng thng
:2 3 0d x y
m
C
thuc
d
sao cho tam giác
ABC
cân ti
.C
A.
2; 1 .C 
B.
3
;0 .
2
C



C.
1;1 .C
D.
0;3C
Câu 117. Trong mt phng vi h t
Oxy
m
1;2 ,A
0;3B
ng thng
:2dy
.
m
C
thuc
d
sao cho tam giác
ABC
cân ti
.B
A.
1;2 .C
B.
4;2 .C
C.
1;2
.
1;2
C
C
D.
1;2 .C
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 90
Dn yu t cc tr
Câu 118. Trong mt phng t
Oxy
cho
: 1 0xy
m
2; 1 , 9; 6 .AB
m
;M a b
nng
sao cho
MA MB
nh nht. Tính
.ab
A.
7.
B.
9.
C.
7.
D.
9.
Câu 119. Trong mt phng vi h t
Oxy
ng thng
: 4 15 0d x y
m
2; 0A
. Tìm
t m
M
thuc
d
 n
AM
 dài nh nht.
A.
15;0M
.
B.
5; 5M
.
C.
0; 3M
.
D.
1; 4M
.
Câu 120. (Yên Định 1 - Thanh Hóa - 2018-2019) m  
  
A.
B.
C.
D.
Câu 121. Trong mt phng vi h t , cho tam giác nh , , .
m thuc trc tung sao cho nh nh là?
A. .
B. .
C. .
D. .
Câu 122. Trong mt phng t Oxy cho m , m
nng sao cho nh nht. Tính c kt qu là:
A. -9
.
B. 9.
C. -7.
D. 7
( 6;3); (0; 1); (3;2)A B C
M
:2 3 0d x y
MA MB MC
13 71
;
15 15
M



13 19
;
15 15
M



26 97
;
15 15
M



13 19
;
15 15
M



Oxy
ABC
2;2A
1; 3B
2;2C
M
MA MB MC
1
1
3
1
3
1
2
:x y 1 0
(2;1)A
(9;6)B
( ; )M a b
MA MB
ab
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 91
Dạng 6.4 Một số bài toán tổng hợp
Câu 123. Trong mt phng vi h trc t , cho hình vuông . Gi m ca
cnh , m trên cnh sao cho . Gi s ng thng
 . Tìm t m .
A. hoc .
B. hoc .
C. hoc .
D. hoc .
Câu 124. Trong mt phng vi h t    m   ng thng
m lt thung thng sao cho
m cn thng ng thng có m 
A. .
B. .
C. .
D. .
Câu 125. (TH&TT LẦN 1 – THÁNG 12) Trong mt phng t m ,
m C nng thng sao cho  m
C là
A. .
B. .
C. .
D. .
Câu 126. Trong mt phng vi h t  , cho  ng thng ,
ng thng ct ti . Tính t s .
A. 6.
B. 2.
C. 4.
D. 1.
Oxy
ABCD
M
BC
N
CD
2CN ND
11 1
;
22
M



AN
2 3 0xy
A
1; 1A
4; 5A
1; 1A
4; 5A 
1; 1A
4;5A
1;1A
4;5A
Oxy
1; 1I
12
: 3 0, : 2 6 0d x y d x y
,AB
12
,dd
I
AB
AB
1
1;2u
2
2;1u
3
1; 2u 
4
2; 1u 
Oxy
4;2A
2;6B
51
:
32
xy
d

CA CB
28
;
55



1 12
;
55



1 11
;
55



29
;
55



Oxy
3;5 , 1;3AB
:2 1 0d x y
AB
d
I
IA
IB
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 92
Câu 127. Trong mt phng vi h t , cho tam giác nh , , .
Trc tâm ca tam giác có t . Biu thc bng bao nhiêu?
A. .
B. .
C. .
D. .
DNG 7. MT S N DIN TÍCH
Câu 128. (THPT Quỳnh Lƣu- Nghệ An- 2019) ng thng to vi các trc t mt
tam giác có din tích bng bao nhiêu?
A. .
B. .
C. .
D. .
Câu 129. ng thng . Gi là tp hp các giá tr a
 tam giác to thành bi và trc hoành có din tích l . S phn t ca tp
là
A. .
B. .
C. .
D. .
Câu 130. ng thng Bing thng m và to vi
hai tia mt tam giác có din tích bng
A. .
B. .
C. .
D.
Câu 131. Chuyên Lê Hồng Phong-Nam Định Cho tam giác có , , .
ng thng  và chia tam giác thành hai phn có din tích b
trình ca là
A. .
B. .
C. .
D. .
------------------------------------------------------------------------------------------
Oxy
ABC
2;1A
2; 3B
2; 1C 
H
ABC
;ab
32S a b
0
1
5
1
:5 3 15xy
7,5
5
15
3
12
: 4; : 4d y mx d mx
S
m
12
,dd
8
S
1
3
2
4
:.d y ax b
d
1;3I
,Ox Oy
6?
9 72 72 6yx
9 72 72 6yx
36yx
3 6.yx
ABC
1; 3A
0;2B
2;4C
A
ABC
2 7 0xy
20xy
3 10 0xy
30xy
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 93
BÀI 2. PHƢƠNG TRÌNH ĐƢỜNG TRÒN
DNG 1. NHN DNG TRÒN
Câu 1. Tìm tt c các giá tr ca tham s   là
ng tròn.
A.
B. hoc .
C. hoc .
D. hoc .
Câu 2. Trong mt phng ng tròn?
A. .
B. .
C. .
D. .
Câu 3. ng tròn?
A. .
B. .
C. .
D. .
Câu 4. (Cụm liên trƣờng Hải Phòng-L1-2019)         a mt
ng tròn?
A. .
B. .
C. .
D. .
Câu 5. (THPT Quỳnh Lƣu- Nghệ An- 2019)   
u kin ca  ng tròn.
A. .
B. .
C. .
D. .
DNG 2. TÌM T NG TRÒN
Câu 6. Trong mt phng ng tròn có tâm là.
A. .
B. .
m
22
2 2 4 19 6 0x y m x my m
1 2.m
2m 
1m 
2m 
1m
1m
2m
Oxy
22
2 4 8 1 0x y x y
22
4 6 12 0x y x y
22
2 8 20 0x y x y
22
4 10 6 2 0x y x y
22
2 6 6 8 0x y x y
22
2 4 8 12 0x y x y
22
2 8 18 0x y x y
22
2 2 4 6 12 0x y x y
22
4 2 8 3 0x y xy x y
22
2 4 5 1 0x y x y
22
14 2 2018 0x y x y
22
4 5 2 0x y x y
22
2 4 2 6 0(1)x y mx m y m
m
(1)
2m
1
2
m
m
12m
1
2
m
m
Oxy
22
: 4 6 12 0C x y x y
2; 3I 
2;3I
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 94
C. .
D. .
Câu 7. ng tròn có bán kính bng bao nhiêu?
A. .
B. .
C. .
D. .
Câu 8. nh tâm và bán kính cng tròn
A. Tâm bán kính .
B. Tâm bán kính .
C. Tâm bán kính .
D. Tâm bán kính .
Câu 9. (ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Tìm t tâm và bán
kính cng tròn : .
A. .
B. .
C. .
D. .
Câu 10. Trong mt phng ng tròn ng tròn có tâm và bán
kính là
A. .
B. .
C. .
D. .
DNG 3. VING TRÒN
Dng 3.1 Khi bit tâm và bán kính
Câu 11.  và bán kính là
A. .
B. .
C. .
D. .
Câu 12. ng tròn tâm , bán kính 
A. .
B. .
4;6I
4; 6I 
22
10 24 0x y y
49
7
1
29
22
: 1 2 9.C x y
1;2 ,I
3R
1;2 ,I
9R
1; 2 ,I
3R
1; 2 ,I
9R
I
R
C
22
2 4 1 0x y x y
1;2 ; 4IR
1; 2 ; 2IR
1;2 ; 5IR
1; 2 ; 4IR
Oxy
22
: 2 3 9C x y
2;3 , 9IR
2; 3 , 3IR
3;2 , 3IR
2;3 , 3IR
1;2I
5R
22
2 4 20 0x y x y
22
2 4 20 0x y x y
22
2 4 20 0x y x y
22
2 4 20 0x y x y
1;2I
3R
22
2 4 4 0x y x y
22
2 4 4 0x y x y
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 95
C. .
D. .
Dng 3.2 Khi bi
Câu 13. ng tròn m , và có tâm thuc tr
là
A. .
B. .
C. .
D. .
Câu 14. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Trong mt phng vi h ta
 , tìm t tâm cm , , .
A. .
B. .
C. .
D. .
Câu 15. Cho tam giác có . To  ng tròn ngoi tip tam giác
là
A. .
B. .
C. .
D. .
Câu 16. Trong mt phng m , , là.
A. .
B. .
C. .
D. .
Câu 17. L        m và có tâm thu ng thng
.
A. .
22
2 4 4 0x y x y
22
2 4 4 0x y x y
C
1;1A
5;3B
I
2
2
4 10xy
2
2
4 10xy
2
2
4 10xy
2
2
4 10xy
Oxy
I
0;4A
2;4B
2;0C
1;1I
0;0I
1;2I
1;0I
ABC
1; 1 , 3;2 , 5; 5A B C
ABC
47 13
;
10 10



47 13
;
10 10



47 13
;
10 10




47 13
;
10 10



Oxy
1;2A
5;2B
1; 3C
22
25 19 49 0x y x y
22
2 6 3 0x y x y
22
6 1 0x y x y
22
6 1 0x y x xy
3;0 , 0;2AB
:0d x y
22
1 1 13
2 2 2
xy
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 96
B. .
C. .
D. .
Dng 3.3 S du kin tip xúc
Câu 18. (THPT Cộng Hiền - Lần 1 - 2018-2019) Trong mt phng t ng
tròn có tâm là gc t và tip xúc vng thng : là
A. .
B. .
C. .
D. .
Câu 19. (Trƣờng THPT Chuyên Lam Sơn_2018-2019) Trong mt phng t ng tròn
có tâm nng thng , bán kính và tip xúc vi các trc t. Lp
a , bi tâm là s 
A. .
B. .
C. .
D. .
Câu 20. M ng tròn có tâm tip xúc v ng thng . Hi bán kính
ng tròn bng bao nhiêu?
A. .
B. .
C. .
D. .
Câu 21. Trong h trc t m ng thng ng tròn
tâm và tip xúc vng thng 
A. .
B. .
C. .
22
1 1 13
2 2 2
xy
22
1 1 13
2 2 2
xy
22
1 1 13
2 2 2
xy
Oxy
O
20xy
22
2xy
22
2xy
22
1 1 2xy
22
1 1 2xy
Oxy
S
I
yx
3R
S
I
22
3 3 9xy
22
3 3 9xy
22
3 3 9xy
22
3 3 9xy
3;4I
:3 4 10 0xy
5
3
5
3
3
5
Oxy
1;1I
:3 4 2 0d x y
I
d
22
1 1 5xy
22
1 1 25xy
22
1 1 1xy
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 97
D. .
Câu 22. (LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trên h trc t ng tròn
có tâm và mt tip tuyn c . Vi
cng tròn .
A. .
B. .
C.
D. .
Câu 23. Trên mt phng to  m và ng tròn ni tip tam giác

A. .
B. .
C. .
D. .
Câu 24. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) m , ng tròn ni
tip tam giác 
A. .
B. .
C. .
D. .
DNG THNG TRÒN
Dp tuyn
Câu 25. ng tròn tip xúc vng thng th
A.
B.
C.
D.
Câu 26. p xúc vi trc Ox:
A. .
B. .
C. .
D. .
22
1
11
5
xy
Oxy
()C
3;2I
3 4 9 0xy
()C
22
3 2 2xy
22
3 2 2xy
22
3 2 4xy
22
3 2 4xy
Oxy
3;0A
0;4B
OAB
22
1xy
22
4 4 0x y x
22
2xy
22
1 1 1xy
3;0A
0;4B
OAB
22
1xy
22
2 2 1 0x y x y
22
6 8 25 0x y x y
22
2xy
22
10xy
3 4 5 0xy
0xy
3 4 1 0xy
10xy
22
10 0x y x
22
50xy
22
10 2 1 0x y x y
22
6 5 9 0x y x y
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 98
Câu 27. Trong mt phng vi h t ng tròn . Vi
trình tip tuyn c ng tròn bit tip tuy     ng thng
.
A. ; .
B. , .
C. , .
D. , .
Câu 28.  ng tròn  m  ng thng nào trong các
ng thp tuyn cng tròn tm .
A. .
B. .
C. .
D. .
Câu 29. ng tròn m ng thng thng
 và là tip tuyn cng tròn ?
A. .
B. .
C. .
D. .
Câu 30. Trong mt phng ng tròn p tuyn vi
ng tròn song song vng thng là
A. .
B. .
C. .
D. .
Câu 31. S tip tuyn chung c  ng tròn và
là
A. .
B. .
C. .
D. .
DNG 5. CÂU HI MIN-MAX
Câu 32.    
M
A. .
B. .
C. . D. .
Oxy
22
: 2 4 3 0C x y x y
d
()C
:3 4 1 0xy
3 4 5 2 11 0xy
3 4 5 2 11 0xy
3 4 5 2 11 0xy
3 4 5 2 11 0xy
3 4 5 2 11 0xy
3 4 5 2 11 0xy
3 4 5 2 11 0xy
3 4 5 2 11 0xy
22
: 2 4 4 0C x y x y
1;5A
C
A
50y 
50y 
50xy
50xy
22
: 4 0C x y
1;2A
A
C
4 3 10 0xy
6 4 0xy
3 4 10 0xy
3 4 11 0xy
Oxy
22
: 1 4 4C x y
C
:4 3 2 0xy
4 3 18 0xy
4 3 18 0xy
4 3 18 0;4 3 2 0x y x y
4 3 18 0;4 3 2 0x y x y
22
: 2 4 1 0C x y x y
22
' : 6 8 20 0C x y x y
1
2
4
3
22
: 2 4 4 0C x y x y
2;1M
C
6
7
37
27
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa 99
BÀI 3. PHƢƠNG TRÌNH ĐƢỜNG ELIP
DNG 1. TÌM CÁC YU T CA ELIP
Câu 1. ng Elip có tiêu c bng
A. .
B. .
C. .
D. .
Câu 2. Cho elip    . Kh nh nào sai trong các kh nh
sau?
A. có trc nh bng 8.
B. có tiêu c bng 3.
C. có trc nh bng 10.
D. m và .
Câu 3. Trong mt phng vi h t Oxy, cho elip . Tiêu c ca (E) bng
A. 10.
B. 16.
C. 4.
D. 8.
Câu 4. Mt elip có din tích hình ch nh là  dài tiêu c là . Tâm sai c
A. .
B. .
C. .
D. .
Câu 5. Cho elip . Din tích hình ch nh ca là
A. .
B. .
C. .
D. .
Câu 6. (Yên Định 1 - Thanh Hóa - 2018-2019) ng elip có tiêu c bng
A. .
B. .
C. .
D. .
22
1
16 7
xy

6
8
9
2;
E
22
16 25 400xy
E
E
E
E
1
3;0F
2
3;0F
22
:1
25 9
xy
E 
80
6
4
5
e
3
4
e
3
5
e
4
3
e
22
: 4 5 20E x y
E
25
80
85
40
22
1
16 7
xy

3
9
6
18
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa
100
Câu 7. c . Tính tâm sai ca elip.
A. .
B. .
C. .
D. .
Câu 8. (TH&TT LẦN 1 – THÁNG 12) Trong mt phng vi h t  , cho elip
(vi ) có m và M là mng trên .
Khđúng?
A. .
B.
C. .
D. .
Câu 9. Trong h trc cho Elip m và mm nm trên
. Bit rng chu vi ca tam giác bnh tâm sai e ca
A. .
B. .
C. .
D. .
Câu 10. Cho Elip m và có tâm sai . Tiêu c ca là
A. .
B. .
C. .
D. .
DNG 2. VI
Câu 11. Trong mt phng c ca mt elip?
22
1
41
xy

2
3
1
2
1
4
3
2
Oxy
22
22
:1
xy
E
ab

0ab
12
,FF
E
12
2MF MF b
2
22
12
4.MF MF b OM
2 2 2
12
.OM MF MF a b
2 2 2
12
.MF MF OM a b
,Oxy
E
12
4;0 , 4;0FF
M
E
12
MF F
.E
4
5
e
4
18
e
4
5
e 
4
9
e
E
3;0A
5
6
e
E
10
5
3
5
10
3
Oxy
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa
101
A. .
B. .
C. .
D. .
Câu 12.  , là
A. .
B. .
C. .
D. .
Câu 13. Trong mt phng t , vic ca elip bit mnh là và
mm là .
A. .
B. .
C. .
D. .
Câu 14. c c dài trc ln bng m :
A. .
B. .
C. .
D. .
Câu 15. 
và có tâm sai .
A. .
22
1
23
xy

22
1
98
xy

1
98
xy

22
1
91
xy

4a
3b
22
1
16 9
xy

22
1
9 16
xy

22
1
16 9
xy

22
1
9 16
xy

Oxy
1
5;0A
2
2;0F
22
1
25 21
xy
22
1
25 4
xy
22
1
29 25
xy
22
1
25 29
xy
4 10
0;6A
22
1
40 12
xy

22
1
160 36
xy

22
1
160 32
xy

22
1
40 36
xy

B
5
3
e
22
1
94
xy

Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa
102
B. .
C. .
D.
Câu 16.   là
A. .
B. .
C. .
D. .
Câu 17. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) c ca elip có tiêu c
bng và trc ln bng .
A.
B.
C.
D.
Câu 18. (LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Cho elip  dài trc ln gp hai ln
 dài trc nh và tiêu c bng . Vi
trình ca ?
A. .
B. .
C. .
D. .
Câu 19. c c dài trc ln bng  dài trc nh bng là:
A. .
22
1
32
xy

22
1
92
xy

22
1
93
xy

3;0
1;0
22
1
89
xy

22
1
98
xy

22
1
19
xy

22
1
91
xy

6
10
22
1.
25 9
xy

22
1.
16 25
xy

22
1.
100 81
xy

22
1.
25 16
xy

E
6
E
22
1
12 3

xy
22
1
12 3

xy
22
1
3 12

xy
22
1
48 12

xy
8
6
22
1
9 16
xy

Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa
103
B. .
C. .
D.
Câu 20. Elip có mm  dài trc ln vi trc bé bng . 
chính tc ca elip là:
A.
B.
C.
D.
Câu 21. Trong mt phng , vic ca elip bit 
và m i mt góc vuông.
A. .
B. .
C. .
D. .
DNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC
Câu 22. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho Elip m nm trên
Nm  bng 1 thì các
khong cách t M m ca (E) bng:
A. và .
B. .
C. và 5.
D. .
22
1
64 36
xy

22
1
86
xy

22
1
16 9
xy

2;0F
12 5
22
1.
95
xy
22
1.
45 16
xy
22
1.
144 5
xy
22
1.
36 20
xy
Oxy
E
E
34
;
55
M



M
12
,FF
22
:1
49
xy
E 
22
:1
94
xy
E 
22
:1
23
xy
E 
22
:1
32
xy
E 
22
( ): 1
16 12
xy
E 
M
( ).E
M
3,5
4,5
42
3
2
4
2
Nguy-GV chuyên Toán cp 3, Khu v.(0918)389.908
Facebook: Nguyc Tr Hàm Rng Biên Hòa
104
Câu 23. Trong mt phng vi h t  , cho elip  m sao cho
ng tròn ni tip tam giác
A.
B. .
C. .
D. .
….HẾT…
Oxy
22
:1
25 9
xy
E 
ME
0
12
90 .F MF
12
.MF F
2
4
1
1
2
| 1/104
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
ĐẠI SỐ 10 – Quyển 2- HỌC KỲ 2
CHƢƠNG IV. BẤT ĐẲNG THỨC. BẤT PHƢƠNG TRÌNH
BÀI 1 : BẤT ĐẲNG THỨC
DẠNG 1. TÍNH CHẤT CỦA BẤT ĐẲNG THỨC Câu 1.
Cho các bất đẳng thức a b và c d . Bất đẳng thức nào sau đây đúng
A. a c b d .
B. a c b d .
C. ac bd . a b D.  . c d Câu 2. Tìm mệnh đề đúng.
A. a b ac bc .
B. a b ac bc .
C. a b a c b c . a b D.   ac bd . c d Câu 3.
Trong các tính chất sau, tính chất nào sai? 0  a b a b A.    . 0  c d d ca b B.
a c b d . c da b C.
a c b d . c d
0  a b D.   ac bd . 0  c d Câu 4.
Nếu a  2c b  2c thì bất đẳng thức nào sau đây đúng? A. 3  a  3  b . B. 2 2 a b .
C. 2a  2b . 1 1 D.  . a b Câu 5.
Khẳng định nào sau đây đúng?
A. x x x x  0 . B. 2
x  3x x  3 . x 1 C.  0 . 2 x 1 D.  0  x  1. x
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 1
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 Câu 6.
Suy luận nào sau đây đúng? a b  0 a b A.   ac bd . B.
a c b d . c d  0 c da ba b a b C.
ac bd . D.    . c dc d c d Câu 7.
Cho a là số thực dƣơng. Mệnh đề nào dƣới đây đúng?
A. x a  a x a . B. x a x a . x  a
C. x a x a .
D. x a   . x a Câu 8.
Bất đẳng thức nào sau đây đúng với mọi số thực a ?
A. 6a  3a .
B. 3a  6a .
C. 6  3a  3  6a .
D. 6  a  3  a .
Câu 10. Cho a, b là các số thực bất kì. Trong các mệnh đề sau, mệnh đề nào sai? 1 1
A. a b a b  0 .
B. a b  0   . C. 3 3
a b a b . D. 2 2
a b a b . a b
Câu 11. Cho a > b khẳng định nào sau đây là đúng?
A. 2a  2b . B. C. a . b
D. ac c , b c  .
Câu 12. Trong các mệnh đề sau, mệnh đề nào sai?
A. a b a b .
B. x a  a x a, a  0 .
C. a b ac bc,  c    .
D. a b  2 ab , a  0,b  0 .
Câu 13. Chuyên Lê Hồng Phong-Nam Định Trong các khẳng định sau, khẳng định nào đúng? 0  x 1 x 1 x 1 xx 1 A.
xy 1. B.   xy 1. C.   1. D.
x y 1. y 1 y 1 y 1 yy 1
Câu 14. Phát biểu nào sau đây là đúng? A.   2 2 2 x y
x y . B. x y  0 thì x  0 hoặc y  0.
C. x y 2 2  x y .
D. x y  0 thì . x y  0 .
DẠNG 2. BẤT ĐẲNG THỨC COSI và ỨNG DỤNG
Câu 15. Bất đẳng thức Côsi cho hai số ,
a b không âm có dạng nào trong các dạng đƣợc cho dƣới đây? a b a b a b a b A.  2 a b . B.  2 ab . C. ab . D.  2 ab . 2 2 2 2
Câu 16. Cho ba số không âm a, ,
b c . Khẳng định nào sau đây đúng? A. 3
a b c  3 abc . B. 3
abc  3 a b c . C. a b c  3 abc . D. 3
a b c  4 abc .
Câu 17. Cho hai số thực a và b thỏa mãn a b  4 . Khẳng định nào sau đây đúng? A. Tích .
a b có giá trị nhỏ nhất là 2 . B. Tích .
a b không có giá trị lớn nhất. C. Tích .
a b có giá trị lớn nhất là 4 . D. Tích .
a b có giá trị lớn nhất là 2 .
Câu 18. Mệnh đề nào sau đây sai? a x 1 A.
a b x y . B. a   2 a   0 . b   y a
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 2
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 1
C. a b  2 ab  , a b  0 .
D. a b   a  ,b  0 . a b a b a b c 1 1 1 9
Câu 19. Cho các mệnh đề sau
  2 I  ;    3 II ;    III b a b c a a b c a b c
Với mọi giá trị của a , b , c dƣơng ta có
A. I  đúng và  II  ,  III  sai.
B. II  đúng và  I  ,  III  sai.
C. III  đúng và  I  ,  II  sai.
D. I  ,  II  ,  III  đúng. 16
Câu 20. Giá trị nhỏ nhất của biểu thức 2 P x  , x  0 bằng x A. 4 . B. 24 . C. 8 . D. 12 .
Câu 21. Giá trị nhỏ nhất của hàm số f x 3
 2x  với x  0 là x A. 4 3 . B. 6 . C. 2 6 . D. 2 3 .
Câu 22. Tìm giá trị nhỏ nhất của biểu thức A
x  2  4  x . A. 2 . B. 2 . C. 2  2 . D. 0 . 4 2 4x  3x  9
Câu 23. Giá trị nhỏ nhất của hàm số y  ; x  0 là 2 x A. 9 . B. 3  . C. 12 . D. 10 . 2a
Câu 24. Cho a là số thực bất kì, P  2
a  . Bất đẳng thức nào sau đây đúng với mọi a . 1 A. P  1. B. P  1 . C. P  1. D. P  1. x 1
Câu 25. Tìm giá trị nhỏ nhất của P   x  . 4 x  với 1 1 7 1 5 A. . B. 1. C. . D. . 4 4 4
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 3
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x
Câu 26. Giá trị nhỏ nhất của hàm số f x 2   với x 1  là 2 x 1 5 A. 2 . B. . C. 2 2 . D. 3. 2 x
Câu 27. Cho x  2 . Giá trị lớn nhất của hàm số f x 2  bằng x 1 2 2 1 A. . B. . C. . D. . 2 2 2 2 2 x
Câu 28. Giá trị nhỏ nhất của hàm số 2017 y  là x  2018 2017 2018 A. 2 . B. . C. . D. 2019 . 2018 2017
Câu 29. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y  6  2x  3  2x .
A. M không tồn tại; m  3 .
B. M  3 ; m  0 .
C. M  3 2 ; m  3 .
D. M  3 2 ; m  0 . x
Câu 30. Chuyên Lê Hồng Phong-Nam Định Cho biểu thức f x 
, với x  1. Giá trị nhỏ nhất x 1 của biểu thức là A. 2 . B. 3 . C. 1. D. 0 .
Câu 31. Cho hai số thực x, y thỏa mãn: x  3 x 1  3 y  2  .
y Giá trị lớn nhất của biểu thức:
P x y bằng A. 9  3 5 . B. 9  3 3 . C. 9  3 5 . D. 9  3 15 .
Câu 32. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Cho hai số thực x  0 , y  0 thay đổi và thỏa mãn điề 1 1 u kiện    2 2 x
y xy x y xy . Giá trị lớn nhất của biểu thức M   là 3 3 x y A. 9. B. 16. C. 18. D. 1.
Câu 33. Cho x, y, z là các số thực dƣơng thỏa mãn x(3  xy xz)  y  6z  5xz( y z) . Giá trị nhỏ nhất
của biểu thức P  3x y  6z là
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 4
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 A. 3 6 . B. 9 . C. 30 . D. 6 2 .
Câu 34. Cho ba số thực dƣơng a, b, c thỏa mãn a+b+c=1. Tìm giá trị nhỏ nhất của biểu thức 1 4 9 P    ? a b c A. 63. B. 36. C. 35. D. 34.
Câu 35. Ngƣời ta dùng 100 m rào để rào một mảnh vƣờn hình chữ nhật để thả gia súc. Biết một cạnh của
hình chữ nhật là bức tƣờng (không phải rào). Tính diện tích lớn nhất của mảnh để có thể rào đƣợc? A. 2 1350 m . B. 2 1250 m . C. 2 625 m . D. 2 1150 m .
Câu 36. Trong các hình chữ nhật có chu vi bằng 300 m, hình chữ nhật có diện tích lớn nhất bằng 2 2 2 2 A. 22500m . B. 900m . C. 5625m . D. 1200m .
Câu 37. (NGÔ GIA TỰ_VĨNH PHÚC_LẦN 1_1819) Trong tất cả các hình chữ nhật có cùng diện tích 2
48m , hình chữ nhật có chu vi nhỏ nhất là A. 16 3 . B. 20 3 . C. 16 . D. 20 .
---------------------------------------------------------------------------------------------------------------------------------
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 5
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 2: BẤT PHƢƠNG TRÌNH VÀ HỆ BẤT PHƢƠNG TRÌNH MỘT ẨN
DẠNG 1. TÌM ĐIỀU KIỆN XÁC ĐỊNH CỦA BẤT PHƢƠNG TRÌNH Câu 1. Bất phƣơng trình 1 3  x 1 x
có điều kiện xác định là 2 A. x  1  ; x  2 . B. x  1  ; x  2  .
C. x  1; x  2  .
D. x  1; x  2 . 1 Câu 2.
Điều kiện của bất phƣơng trình  x  2 2 x  là 4 A. x  2  . B. x  2 . C. x  2 . D. x  0 . x Câu 3.
Tìm điều kiện của bất phƣơng trình 2 3  x 1 2x  . 3 3 A. x   . 2 3 B. x  . 2 2 C. x   . 3 2 D. x  . 3 x Câu 4.
Tìm điều kiện của bất phƣơng trình 2 3  x  2 . 6  3x A. x  2 . B. x  2 . C. x  2 . D. x  2 . Câu 5.
Giá trị x  3 thuộc tập nghiệm của bất phƣơng trình nào sau đây? 2 x x 1 A. x 1 x  . 1 B. 2 2x 1  x . C. 2 2 x x 1  6 . D. 2
2x  5x  2  0 .
DẠNG 2. BẤT PHƢƠNG TRÌNH VÀ HỆ BẤT PHƢƠNG TRÌNH TƢƠNG ĐƢƠNG Câu 6.
hẳng định nào sau đây sai? x  3 x  3 A. 2 x  3x   . B.  0  x  3  0 x  0 x  . 4
C. x x  0  x  . D. 2
x  1  x  1.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 6
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 Câu 7.
Bất phƣơng trình nào sau đây không tƣơng đƣơng với bất phƣơng trình x  5  0 ? A. 2
x x  5  0 .
B. x  5  x  5  0 . 2 C. x  
1  x  5  0 .
D. x  5  x  5  0 . Câu 8.
Khẳng định nào sau đây đúng? 1 A. 2
x  3x x  3 . B.  0  x 1. x x 1 C.
 0  x 1 0 .
D. x x x x  0 . 2 x Câu 9.
Cặp bất phƣơng trình nào sau đây không tƣơng đƣơng 1 1
A. x 1  x và 2x   1
x 1  x 2x   1 .B. 2x 1  x   . x  3 x  và 2 1 0 3 C. 2
x x  2  0 và x  2  0. D. 2
x x  2  0 và  x  2  0 .
Câu 10. Bất phƣơng trình 2x  3  x  2 tƣơng đƣơng với: 3
A. x    x  2 2 3 2 với x  .
B. x    x  2 2 3 2 với x  2 . 2 2x  3  0
 x   x  2 2 3 2 C.  hoặc 
.D. Tất cả các câu trên đều đúng.  x  2  0  x  2  0
Câu 11. Bất phƣơng trình 3 3 2x   3 2x  4
2x  tƣơng đƣơng với: 4 A. 2x  3 . 3 B. x  và x  2 . 2 3 C. x  . 2
D. Tất cả đều đúng.
DẠNG 3. SỬ DỤNG CÁC PHÉP BIẾN ĐỔI TƢƠNG ĐƢƠNG ĐỂ GIẢI BẤT PHƢƠNG TRÌNH MỘT ẨN
Câu 12. Tập nghiệm của bất phƣơng trình: 2
x  9  6x là A. 3;  . B. \   3 . C. . D.  – ;  3 .
Câu 13. Bất phƣơng trình 3
x 9  0 có tập nghiệm là A. 3;   . B.   ;3  . C. 3;   .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 7
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D.  ;   3.
Câu 14. Tập nghiệm của bất phƣơng trình 2  3x x  6 .
A. 1;  . B.  ;    1 . C.   ;1  . D. 1;  .
Câu 15. Cho f x  2x  4 , khẳng định nào sau đây là đúng?
A. f x  0  x 2;  .
B. f x  0  x  ;  2  
C. f x  0  x  2;  .
D. f x  0  x  2  . 2x
Câu 16. Bất phƣơng trình 5x 1   3 có nghiệm là 5 A. x  2 . 5 B. x   . 2 C. x  . 20 D. x  . 23
Câu 17. Tập nghiệm của bất phƣơng trình 2x 1  0 là  1  A.  ;     .  2   1  B. ;    .  2   1  C.  ;     .  2   1  D. ;    .  2 
Câu 18. Chuyên Lê Hồng Phong-Nam Định Bất phƣơng trình 3  1 có bao nhiêu nghiệm nguyên? x A. 3 . B. 2 . C. Vô số. D. 4 .
Câu 19. Tập nghiệm của bất phƣơng trình x 1  1 là A. ; 2 . B. 1; 2 . C. 0; 2 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 8
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D. 1; 2 . x x
Câu 20. Bất phƣơng trình 2 5 3 
có tập nghiệm là 3 2
A. 2;  . B.   ;1  2;  .
C. 1;  .  1  D. ;   .  4 
Câu 21. Tập nghiệm của bất phƣơng trình  x    2 3 2 1 x 1  0 là  3  A. 1;    2  B. 1;  2  C. ;1   3  D. 2;  3
Câu 22. Tập nghiệm của bất phƣơng trình x  2017  2017  x là
A. 2017,  . B.  ,  2017 . C.   2017 . D.  . 2 2x  3x  4
Câu 23. Tập nghiệm của bất phƣơng trình  2 2 x  là 3  3 23 3 23  A.   ;     . 4 4 4 4    3 23   3 23  B.   ;      ;        . 4 4 4 4      2  C.  ;     .  3   2  D. ;    .  3 
Câu 24. Tập nghiệm của bất phƣơng trình 3  2x  2  x x  2  x là A. 1; 2 . B. 1; 2 . C.   ;1  . D. 1;  .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 9
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x
Câu 25. Tập nghiệm của bất phƣơng trình 1 1 x  là 3 A. 3;   . B. .
C. ;3  3;   . D. ;3 . x
Câu 26. Tập nghiệm của bất phƣơng trình 3 2x   4x 1. 5  8  A. S  ;    . 11   8  B. ;    .  11  4  C. S  ;    . 11   2  D. ;    .  11
Câu 27. Tập nghiệm của bất phƣơng trình 2
x  2  x 1. A. S   .  1  B. S   ;     .  2  C. 1;  . 1  D. ;    . 2 
Câu 28. Tập nghiệm của bất phƣơng trình 1 1
x 1  5  x   x  3 x  là 3
A. S  1;5 .
B. S  1;5 \   3 .
C. S  3;5 .
D. S  1;  5 \   3 .
DẠNG 4. SỬ DỤNG CÁC PHÉP BIẾN ĐỔI TƢƠNG ĐƢƠNG GIẢI HỆ BẤT PHƢƠNG TRÌNH MỘT ẨN
Câu 32. (THPT NÔNG CỐNG - THANH HÓA LẦN 1_2018-2019) Tìm tập nghiệm của hệ bất 3
x 1 2x  7 phƣơng trình:  .
4x  3  2x 19 A. 6; . B. 8; . C. 6; .
D. 8; .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 10
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
x  3  4  2x
Câu 33. Tập nghiệm của bất phƣơng trình  là 5
x  3  4x 1 A.  ;    1 . B.  4  ;  1 . C.  ;  2 . D. 1; 2 . 4  x  0
Câu 34. Tập nghiệm của hệ bất phƣơng trình  là x  2  0
A. S   ;  2  4; . B. S   2  ;4 .
C. S  2; 4 .
D. S   ;  2   4;. 3
x  2  2x  3
Câu 35. Tập nghiệm của hệ bất phƣơng trình  là 1   x  0  1  A. ;1 .    5  B. .  C. 1;  . D.   ;1  .
2x 1  3x  3  2  x
Câu 36. Hệ bất phƣơng trình sau   x  3 có tập nghiệm là 2   x  3  2  A. 7;  . B.  . C. 7;8 .  8  D. ;8   .  3 
2x 1  x 1  3
Câu 37. Tập nghiệm của hệ bất phƣơng trình  là 4  3x   3  x  2  4  A. 2;    .  5   4  B. 2;    .  5   3  C. 2;    .  5 
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 11
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908  1  D. 1  ;   .  3 
DẠNG 5. BẤT PHƢƠNG TRÌNH, HỆ BẤT PHƢƠNG TRÌNH CHỨA THAM SỐ
Câu 38. Bất phƣơng trình m  
1 x  3 vô nghiệm khi A. m  1. B. m 1. C. m  1. D. m  1.
Câu 39. Bất phƣơng trình  2
m  3mx m  2  2x vô nghiệm khi A. m  1. B. m  2.
C. m  1, m  2. D. m  .
Câu 40. Có bao nhiêu giá trị thực của tham số m để bất phƣơng trình  2
m mx m vô nghiệm. A. 0. B. 1. C. 2. D. Vô số.
Câu 41. Gọi S là tập hợp tất cả các giá trị thực của tham số m để bất phƣơng trình  2
m mx m  6x  2 vô nghiệm. Tổng các phần tử trong S bằng: A. 0. B. 1. C. 2. D. 3.
Câu 42. Bất phƣơng trình  2
m  9 x  3  m1 6x nghiệm đúng với mọi x khi A. m  3. B. m  3. C. m  3.  D. m  3. 
Câu 43. Bất phƣơng trình 2
m x     2 4 2 1
4m  5m  9 x 12m nghiệm đúng với mọi x khi A. m  1.  9 B. m  . 4 C. m  1. 9 D. m   . 4
Câu 44. Bất phƣơng trình 2 m x  
1  9x  3m nghiệm đúng với mọi x khi A. m  1. B. m  3.  C. m  .  D. m  1. 
Câu 45. Tìm tất cả các giá trị thực của tham số m để bất phƣơng trình  x mm x  3x  4 có tập
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 12
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
nghiệm là m  2; . A. m  2. B. m  2. C. m  2. D. m  2.
Câu 46. Tìm tất cả các giá trị thực của tham số m để bất phƣơng trình m x m  x 1 có tập nghiệm là  ;  m   1 . A. m  1. B. m  1. C. m 1. D. m 1.
Câu 47. Tìm tất cả các giá trị của tham số m để bất phƣơng trình m x  
1  2x  3 có nghiệm. A. m  2 . B. m  2 . C. m  2 . D. m  2 .
Câu 48. Tìm tất cả các giá trị của tham số m để bất phƣơng trình m x  
1  3  x có nghiệm. A. m  1. B. m  1. C. m . D. m  3 .
Câu 49. Gọi S là tập nghiệm của bất phƣơng trình mx  6  2x  3m với m  2 . Hỏi tập hợp nào sau đây
là phần bù của tập S ? A. 3;  . B. 3;  . C.  ;3   . D.   ;3  .
Câu 50. Tìm giá trị thực của tham số m để bất phƣơng trình m 2x  
1  2x 1 có tập nghiệm là 1; . A. m  3 B. m  1 C. m  1  D. m  2. 
Câu 51. Tìm giá trị thực của tham số m để bất phƣơng trình 2x m  3 x  
1 có tập nghiệm là 4; . A. m  1. B. m  1. C. m  1.  D. m  1.
Câu 52. Tìm tất cả các giá trị của tham số m để bất phƣơng trình mx  4  0 nghiệm đúng với mọi x  8 .  1 1 A. m   ; .    2 2  1  B. m   ;  .    2 
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 13
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908  1 
C. m   ;  .    2   1   1
D. m   ; 0  0; .      2   2
Câu 53. Tìm tất cả các giá trị thực của tham số m để bất phƣơng trình 2
m x  2  mx x  5  0 nghiệm
đúng với mọi x  2  018;2 . 7 A. m  . 2 7 B. m  . 2 7 C. m  . 2 D. m .
Câu 54. Tìm tất cả các giá trị thực của tham số m để bất phƣơng trình 2
m x  2  m x  0 có nghiệm x  1  ;2 . A. m  2  . B. m  2  . C. m  1  . D. m  2  . 2x 1  0
Câu 55. Hệ bất phƣơng trình 
có nghiệm khi và chỉ khi: x m  2 3 A. m   . 2 3 B. m   . 2 3 C. m   . 2 3 D. m   . 2 3  x  6  3  
Câu 56. Hệ bất phƣơng trình 5x m
có nghiệm khi và chỉ khi:   7  2 A. m  11.  B. m  11.  C. m  11.  D. m  11.  2 x 1  0
Câu 57. Hệ bất phƣơng trình 
có nghiệm khi và chỉ khi: x m  0 A. m  1. B. m  1. C. m  1. D. m  1.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 14
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2x 1 3
Câu 58. Tìm tất cả các giá trị thực của tham số m để hệ bất phƣơng trình  có nghiệm duy nhất. x m  0 A. m  2 . B. m  2 . C. m  2 . D. m  1. . 2
m x  6  x
Câu 59. Tìm tất cả các giá trị của tham số m để hệ bất phƣơng trình  có nghiệm duy nhất. 3
x 1  x  5 A. m  1. B. m  1  . C. m  1  . D. m  1.   x  2 2 3
x  7x 1
Câu 60. Tìm tất cả các giá trị thực của tham số m để hệ bất phƣơng trình  có
2m  8  5x nghiệm duy nhất. 72 A. m  . 13 72 B. m  . 13 72 C. m  . 13 72 D. m  . 13
mx m  3 
Câu 61. Tìm giá trị thực của tham số m để hệ bất phƣơng trình  có nghiệm duy nhất.  m  3   x m 9 A. m  1. B. m  2.  C. m  2. D. m  1.  3
x  4  x  9
Câu 62. Hệ bất phƣơng trình 
vô nghiệm khi và chỉ khi: 1
  2x m  3x 1 5 A. m  . 2 5 B. m  . 2 5 C. m  . 2 5 D. m  . 2
2x  7  8x 1
Câu 63. Hệ bất phƣơng trình 
vô nghiệm khi và chỉ khi:
m  5  2x A. m  3.  B. m  3.  C. m  3. 
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 15
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D. m  3.    x  2 2 3
x  7x 1
Câu 64. Hệ bất phƣơng trình 
vô nghiệm khi và chỉ khi:
2m  8  5x 72 A. m  . 13 72 B. m  . 13 C. m  1 D. m  1
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 16
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 3: DẤU CỦA NHỊ THỨC BẬC NHẤT
DẠNG 1. DẤU NHỊ THỨC BẬC NHẤT Câu 1.
Cho nhị thức bậc nhất f x  ax b a  0 . Trong các mệnh đề sau, mệnh đề nào đúng?  b
A. Nhị thức f x có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng  ;     .  a   b
B. Nhị thức f x có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng  ;    .  a   b
C. Nhị thức f x có giá trị trái dấu với hệ số a khi x lấy các giá trị trong khoảng ;    .  a   b
D. Nhị thức f x có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng ;    .  aCâu 2.
Khẳng định nào sau đây là khẳng định sai?
A. Bất phƣơng trình ax b  0 có tập nghiệm là
khi a  0 và b  0 .
B. Bất phƣơng trình bậc nhất một ẩn luôn có nghiệm.
C. Bất phƣơng trình ax b  0 vô nghiệm khi a  0 và b  0 .
D. Bất phƣơng trình ax b  0 vô nghiệm khi a  0 . Câu 3.
Cho nhị thức bậc nhất f x  23x  20 . Khẳng định nào sau đây đúng?  20  5
A. f x  0 với x    ;  
 . B. f x  0 với x    .  23  2  20 
C. f x  0 với x   .
D. f x  0 với x   ;   .  23  Câu 4.
Tìm m để f x  m  2 x  2m 1 là nhị thức bậc nhất. A. m  2 . m  2  B.  1 . m    2 C. m  2 . D. m  2 . Câu 5.
Cho nhị thức f x  x 1. Mệnh đề nào sau đây đúng?
A. f x  0  x  1.
B. f x  0  x  1.
C. f x  0  x  1.
D. f x  0  x  1.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 17
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 Câu 6.
Chuyên Lê Hồng Phong-Nam Định Cho f x , g x là các hàm số xác định trên , có bảng xét dấu nhƣ sau: f x
hi đó tập nghiệm của bất phƣơng trình  là g x 0 A. 1; 2.
B. 1; 2  3;   .
C. 1; 2 3;  .
D. 1; 23; . Câu 7.
Hàm số có kết quả xét dấu là hàm số
A. f x  x  3 . x
B. f x  x  . 3
C. f x  x 3  x .
D. f x  x x  3 . Câu 8.
Bảng xét dấu sau là của biểu thức nào? x  2  f x  0 
A. f x  x  2 .
B. f x  2  4x .
C. f x  16  8x .
D. f x  x  2 .  x Câu 9.
Với x thuộc tập nào dƣới đây thì biểu thức f x 2  2x không âm? 1  1  A. S   ; 2   .  2   1  B. S   ; 2   .  2   1  C. S   ;   2;     .  2   1  D. S   ;   2;     .  2 
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 18
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x
Câu 10. Cho biểu thức f x 2 1
. Tập hợp tất cả các giá trị của x thỏa mãn bất phƣơng trình 3x  2
f x  0 là  2  A. x  ;1 .    3   2  B. x   ;  1;   .  3   2  C. x  ;1 .    3   
D. x   2 ;1  ;  .    3  
Câu 11. Cho biểu thức f x 4 3   . 3x 1 2 
Tập hợp tất cả các giá trị của x thỏa mãn bất phƣơng trình x
f x  0 là  11 1  A. x   ;  2;   .  5 3   11 1  B. x   ;  2;   .  5 3   11  1  C. x   ;     ;2 .      5   3   11  1  D. x   ;     ;2 .      5   3  x  3 x  2
Câu 12. Cho biểu thức f x     . 2 x
Hỏi có tất cả bao nhiêu giá trị nguyên âm của x thỏa mãn 1
bất phƣơng trình f x  1 ? A. 1. B. 2. C. 3. D. 4.
DẠNG 2. GIẢI BẤT PHƢƠNG TRÌNH TÍCH
Câu 13. Cho biểu thức f x   x  2 x  
1 . Mệnh đề nào sau đây đúng?
A. f x  0  x  1  ;2.
B. f x  0  x  1  ;2 .
C. f x  0  x  1  ;2 .
D. f x  0  x  ;    1  2;  .
Câu 14. Tập nghiệm của bất phƣơng trình  x  
1  x  3  0 A.  
;1 3;   .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 19
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
B. 3;   . C. . D. 1;  3 .
Câu 15. Số nghiệm nguyên dƣơng của bất phƣơng trình 2  x x  
1 3  x  0 là A. 1. B. 4 . C. 2 . D. 3 .
Câu 16. Tập nghiệm của bất phƣơng trình 2x  81 x  0  có dạng  ;
a b. hi đó b a bằng A. 3. B. 5. C. 9.
D. không giới hạn.
Câu 17. Tập nghiệm S   4;5 là tập nghiệm của bất phƣơng trình nào sau đây?
A. x  4 x  5  0.
B. x  45x  25  0.
C. x  45x  25  0.
D. x  4 x  5  0.
Câu 18. Tổng các nghiệm nguyên của bất phƣơng trình  x  3 x   1  0 là A. 1. B.  4. C.  5. D. 4.
Câu 19. Tập nghiệm S  0;5 là tập nghiệm của bất phƣơng trình nào sau đây?
A. x x  5  0.
B. x x  5  0.
C. x x  5  0.
D. x x  5  0.
Câu 20. Hỏi bất phƣơng trình 2  x x  
1 3  x  0 có tất cả bao nhiêu nghiệm nguyên dƣơng? A. 1. B. 3. C. 4. D. 2.
Câu 21. Tích của nghiệm nguyên âm lớn nhất và nghiệm nguyên dƣơng nhỏ nhất của bất phƣơng trình
3x 6x  2x  2x   1  0 là A.  9. B.  6. C.  4. D. 8.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 20
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 22. Tập nghiệm của bất phƣơng trình 2x 4  x3  x3  x  0 là A. Một khoảng
B. Hợp của hai khoảng.
C. Hợp của ba khoảng. D. Toàn trục số.
Câu 23. Nghiệm nguyên nhỏ nhất thỏa mãn bất phƣơng trình  x   1
x x  2  0 là A. x   2. B. x  0. C. x  1. D. x  2.
DẠNG 3. GIẢI BẤT PHƢƠNG TRÌNH CHỨA ẨN Ở MẪU x
Câu 24. Tập nghiệm của bất phƣơng trình 1  2 là 2  x A. 1; 2. B. 1; 2. C.  3  ;  1 . D. 1; 2.
Câu 25. Tập nghiệm của bất phƣơng trình 1 1  2x 1 2x  là 1  1  1  A.  ;   ;      .  2  2   1  B. ;    .  2   1 1  C.  ;   .  2 2   1   1  D. ;   ;       .  2   2 
Câu 26. Bất phƣơng trình 1
 1 có tập nghiệm S là x  2
A. S    ;3 .
B. S  ;3 .
C. S  2;  3 . D. 2;  3 .
Câu 27. Tập nghiệm của bất phƣơng trình 1  1 là x A. 0  ;1 . B.   ;1  .
C. 1;   .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 21
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D.  ;  0 1;  . x x
Câu 28. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Tập nghiệm của bất phƣơng trình 2 1  x 1 x  là 2  1  A. 1  ; 2;    .  2    B.    1 ; 1  ; 2   .  2    C.    1 ; 1  ; 2   . 2   1  D. ;    .  2  x  
1 2x  5 x   1
Câu 29. Tập nghiệm của bất phƣơng trình  0 S  ; a b  ; c d . hi đó x  là     4
a b c d bằng 3 A.  . 2 B. 1. C. 2 . 5 D. . 2
Câu 30. Chuyên Lê Hồng Phong-Nam Định Bất phƣơng trình 3  1 có bao nhiêu nghiệm nguyên? x A. 3 . B. 2 . C. Vô số. D. 4 . x
Câu 31. Bất phƣơng trình 2 1   2 x 1 x  có tập nghiệm là 1  1 A. S  1  ; 1;  .   3
B. S   ;    1  1;  .  1  C. S  1  ; 1;   .  3   
D. S     1 ; 1  ;1 .    3  1 1
Câu 32. Bất phƣơng trình 
có tập nghiệm S là x 1 x  2 1
A. T   ;    1  0  ;1 1;  3 .
B. T  1;0  3;  .
C. T   ;    1  0  ;1  1;3.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 22
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
D. T  1;0 3;  .
DẠNG 4. GIẢI BẤT PHƢƠNG TRÌNH CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
Câu 33. Tập nghiệm của bất phƣơng trình 2x 1  1 .
A. S  0  ;1 . 1  B. S  ;1   . 2 
C. S    ;1 .
D. S    ;1 1;  .
Câu 34. Tập nghiệm của bất phƣơng trình 3x 1  2 .  
A. S     1 ; 1  ;    .  3  B. S   .  1  C. S  1  ;   .  3   1  D. S  ;    .  3 
Câu 35. Số giá trị nguyên x trong  2017; 2017 thỏa mãn bất phƣơng trình 2x 1  3x là A. 2016 . B. 2017 . C. 4032 . D. 4034 . 2 8
Câu 36. Cho bất phƣơng trình  x
. Số nghiệm nguyên nhỏ hơn 13 của bất phƣơng trình là 13 9 A. 0 . B. 1. C. 2 . D. 3 . x  2  x
Câu 37. Nghiệm của bất phƣơng trình  2 là x
A. 0  x  1.
B. 0  x  1. x  0 C.  . x 1
D. x  1, x  2  .
Câu 38. Với x thuộc tập nào dƣới đây thì nhị thức bậc nhất f x  2x  5  3 không dƣơng? A. x  1. 5 B. x  . 2 C. x  0 .
D. 1  x  4 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 23
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 39. Bất phƣơng trình x  5  4 có bao nhiêu nghiệm nguyên? A. 10 . B. 8 . C. 9 . D. 7 .
Câu 40. Tập hợp nghiệm của bất phƣơng trình 2x 1  2  4x là  3  A. S  ;   .  2   1 3 B. S   ;   .  2 2  3  C. S  ;   .  2  3  D. ;     . 2 
Câu 41. Bất phƣơng trình 2x 1  x có tập nghiệm là  1  A.  ;  1;    .  3   1  B. ;1   .  3  C. . D. Vô nghiệm.
Câu 42. Số nghiệm nguyên của bất phƣơng trình x 1  x  3 là A. 4 . B. 2 . C. 3 . D. 1.
Câu 43. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Bất phƣơng trình
2  x  3x 1  6 có tập nghiệm là A.  ;  2 .  9  B. ;    .  4   9  C. ;    .  4  D.  ;  2 .
Câu 44. Số nghiệm nguyên thỏa mãn bất phƣơng trình x  2  2
x 1  x 1 là A. 3. B. 5. C. 2. D. 0.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 24
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 3
Câu 45. Bất phƣơng trình x  2  x 1  x  có tập nghiệm là 2
A.  2;  .  1  B.  ;   .    2   3  C.  ;   .    2   9  D. ;   .    2  5  10
Câu 46. Tập nghiệm của bất phƣơng trình  x  2 x  là 1 A. một khoảng. B. hai khoảng. C. ba khoảng. D. toàn trục số. 2  3 x
Câu 47. Số nghiệm nguyên của bất phƣơng trình 1 là 1 x A. 1. B. 2. C. 0. D. 3.
----------------------------------------------------------------------------------------------------------------------------
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 25
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 4: BẤT PHƢƠNG TRÌNH BẬC NHẤT HAI ẨN
DẠNG 2. TÌM MIỀN NGHIỆM CỦA HỆ BẤT PHƢƠNG TRÌNH BẬC NHẤT HAI ẨN
x y  2  0 Câu 1.
Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phƣơng trình  là
2x  3y  2  0 A. 0;0 . B. 1;  1 . C.  1   ;1 . D.  1  ;  1 .
2x  5y 1  0  Câu 2.
Điểm nào sau đây thuộc miền nghiệm của hệ bất phƣơng trình  2x y  5  0 ?
x y 1 0  A. 0;0 . B. 1;0 . C. 0; 2   . D. 0; 2 .
x  2y  0  Câu 3.
Miền nghiệm của hệ bất phƣơng trình x  3y  2 chứa điểm nào sau đây?
y x  3 
A. A1 ; 0 . B. B  2  ; 3.
C. C 0 ;   1 . D. D  1  ; 0.
DẠNG 3. TÌM GIÁ TRỊ NHỎ NHẤT- GIÁ TRỊ LỚN NHẤT
y  2x  2  Câu 4.
Giá trị nhỏ nhất của biểu thức F y x trên miền xác định bởi hệ 2 y x  4 là
x y  5 
A. min F  1 khi x  2 , y  3 .
B. min F  2 khi x  0 , y  2 .
C. min F  3 khi x 1 , y  4 .
D. min F  0 khi x  0 , y  0 .
 2x y  2  Câu 5.
Giá trị nhỏ nhất của biết thức F y x trên miền xác định bởi hệ  x y  2 là
5x y  4  A. min F  3
 khi x 1, y  2  .
B. min F  0 khi x  0, y  0 . 4 2 C. min F  2
 khi x  , y   . 3 3
D. min F  8 khi x  2  , y  6 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 26
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 5. DẤU CỦA TAM THỨC BẬC HAI
DẠNG 1. TAM THỨC BẬC HAI
Dạng 1. Xét dấu tam thức bậc hai Câu 1.
Cho tam thức f x 2
ax bx ca  0, 2
  b  4ac . Ta có f x  0 với x   khi và chỉ khi: a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  .   0   0   0   0 Câu 2. Cho tam thức bậc hai 2 f (x)  2
x  8x 8. Trong các mệnh đề sau, mệnh đề nào đúng?
A. f (x)  0 với mọi x  .
B. f (x)  0 với mọi x  .
C. f (x)  0 với mọi x  .
D. f (x)  0 với mọi x  . Câu 3.
Tam thức nào dƣới đây luôn dƣơng với mọi giá trị của x ? A. 2
x 10x  2 . B. 2
x  2x 10 . C. 2
x  2x 10 . D. 2
x  2x 10. Câu 4. Cho   2
f x ax bx c , a  0 và 2
  b  4ac . Cho biết dấu của  khi f x luôn cùng dấu
với hệ số a với mọi x  . A.   0 . B.   0 . C.   0 . D.   0 . Câu 5. Cho hàm số    2 y
f x ax bx c có đồ thị nhƣ hình vẽ. Đặt 2
  b  4ac , tìm dấu của a và  . y
y f x 4 O x 1 4
A. a  0 ,   0 .
B. a  0 ,   0 .
C. a  0 ,   0 .
D. a  0 , ,   0 . Câu 6.
Cho tam thức f x 2
x  8x 16. Khẳng định nào sau đây là đúng?
A. phƣơng trình f x  0 vô nghiệm.
B. f x  0 với mọi x  .
C. f x  0 với mọi x  .
D. f x  0 khi x  4 . Câu 7.
Cho tam thức bậc hai f x 2
x 1. Mệnh đề nào sau đây đúng?
A. f x  0  x  ;   .
B. f x  0  x  1  .
C. f x  0  x   ;1 .
D. f x  0  x 0  ;1 . Câu 8. Cho tam thức bậc hai 2
f (x)  ax bx c (a  0) . Mệnh đề nào sau đây đúng?
A. Nếu   0 thì f x luôn cùng dấu với hệ số a , với mọi x  .
B. Nếu   0 thì f x luôn trái dấu với hệ số a , với mọi x  .  b
C. Nếu   0 thì f x luôn cùng dấu với hệ số a , với mọi x  \  .  2a
D. Nếu   0 thì f x luôn cùng dấu với hệ số b , với mọi x  .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 27
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Dạng 2. Giải bất phƣơng trình bậc hai và một số bài toán liên quan Câu 9.
Cho tam thức bậc hai f x 2
 x  4x  5. Tìm tất cả giá trị của x để f x  0 . A. x  ;    1 5;  . B. x  1  ;5. C. x  5   ;1 . D. x  5   ;1 .
Câu 10. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Tập nghiệm của bất phƣơng trình 2
x  3x  2  0 là A. 1; 2 . B.   ;1  2;    . C.   ;1  . D. 2;  .
Câu 11. (ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Tập xác định của hàm số 2
y  x  2x  3 là: A. 1;3 . B.  ;    1  3;  . C.  1  ;  3 . D.  ;    1 3; .
Câu 12. Tìm tập xác định của hàm số 2
y  2x  5x  2 .  1  A.  ;  2;     .  2  B. 2;   .  1  C. ;    .  2  1  D. ; 2   . 2 
Câu 13. Tập nghiệm của bất phƣơng trình: 2
x  9  6x là A. 3;  . B. \   3 . C. . D.  – ;  3 .
DẠNG 2. BẤT PHƢƠNG TRÌNH TÍCH
Câu 14. Bất phƣơng trình  x   2
1 x  7x  6  0 có tập nghiệm S là:
A. S   
;1 6; .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 28
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
B. S  6;. C. 6; .
D. S  6;   1 .
Câu 15. Tập nghiệm của bất phƣơng trình 4 2
x  5x  4  0 là A. 1; 4 . B.  2  ;  1 . C. 1; 2 . D.  2  ;  1  1; 2 .
Câu 16. Giải bất phƣơng trình x x     2 5 2 x  2. A. x  1.
B. 1  x  4.
C. x     ;1 4; . D. x  4.
Câu 17. Biểu thức  2
3x 10x  34x  5 âm khi và chỉ khi  5  A. x   ;  .    4   1   5  B. x   ;   ;3 .      3   4   1 5  C. x  ; 3;   .  3 4   1  D. x  ;3 .    3 
Câu 18. Tập nghiệm của bất phƣơng trình 3 2
x  3x  6x  8  0 là
A. x  4;   1 2; .
B. x   4;   1  2;  .
C. x 1; . D. x  ;   41;2.
DẠNG 3. BẤT PHƢƠNG TRÌNH CHỨA ẨN Ở MẪU 4x 12
Câu 19. Cho biểu thức f x 
f x không dƣơng là 2 x
. Tập hợp tất cả các giá trị của x thỏa mãn   4x
A. x  0;  3  4;  .
B. x   ;  03;4 .
C. x   ;  0 3;4. D. x  ;  0 3;4 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 29
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2 x  3x  4
Câu 20. Tìm tập nghiệm của bất phƣơng trình  0 . x 1
A. T   ;    1 1; 4.
B. T   ;    1  1; 4.
C. T   ;    1  1; 4 .
D. T   ;    1  1; 4 . 2 x x  3
Câu 21. Gọi S là tập nghiệm của bất phƣơng trình
1. hi đó S  2
 ;2 là tập nào sau đây? 2 x  4 A.  2  ;  1 . B. 1; 2 . C.  . D.  2  ;  1 . x  3 1 2x Câu 22
Có bao nhiêu giá trị nguyên dƣơng của x thỏa mãn   2 2 x  4 x  2 2x  ? x A. 0. B. 2. C. 1. D. 3.
DẠNG 4. HỆ BẤT PHƢƠNG TRÌNH BẬC HAI VÀ CÁC BÀI TOÁN LIÊN QUAN 5
x  2  4x  5
Câu 23. Tập nghiệm của hệ bất phƣơng trình  có dạng S   ;
a b . hi đó tổng a b 2 2
x  (x  2) bằng? A. 1.  B. 6. C. 8. D. 7.  1 xx   1
Câu 24. Tập nghiệm của hệ bất phƣơng trình  2 4 là 2
x 4x 3 0
A. S  2;3 . B.  ;  23; .
C. S  2;  3 . D.  ;  2 3; . 2
x  6x  5  0
Câu 25. Tập nghiệm của hệ bất phƣơng trình  là 2
x 8x 12  0 A. 2;5 . B. 1;6 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 30
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 C. 2;5 .
D. 1; 2 5;6. 2 x  4  0 
Câu 26. Hệ bất phƣơng trình 
có số nghiệm nguyên là x    1 
 2x 5x4  0 A. 2 . B. 1. C. Vô số. D. 3 . 2
x  4x  3  0
Câu 27. Tập nghiệm của hệ bất phƣơng trình  là  6  x 12  0 A. 1; 2 . B. 1; 4 . C.  ;   1  3;  . D.  ;  2 3; . 1 1
Câu 28. Tập nghiệm của bất phƣơng trình 2 x  2x   3  là x  4 x  4 A.  3   ;1 . B.  4  ; 3   .
C. 1;    ;  3   .
D. 1;    4  ; 3  . 2
x  4x  3  0
Câu 29. Tìm tập nghiệm của hệ bất phƣơng trình  .  x  2  x 5  0 A. 1;3 . B. 2;5 . C.  2   ;1  3;5 . D. 3;5 . 
 x  56  x  0
Câu 30. Giải hệ bất phƣơng trình  . 2x 1 3 A. 5   x 1. B. x  1. C. x  5  . D. x  5  .
DẠNG 5. BÀI TOÁN CHỨA THAM SỐ
Dạng 1. Tìm m để phƣơng trình có n nghiệm
Câu 31. (ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Tìm tất cả các giá trị của
tham số m để phƣơng trình 2
x mx  4  0 có nghiệm
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 31
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 A. 4   m  4 . B. m  4  hay m  4. C. m  2  hay m  2. D. 2   m  2 .
Câu 32. Tìm m để phƣơng trình 2
x  2m  
1 x m  3  0 có hai nghiệm phân biệt
A. 1; 2 B.  ;    1  2;  C.  1  ;2 D.  ;    1 2;
Câu 33. Giá trị nào của m thì phƣơng trình m   2
3 x  m  3 x  m   1  0   1 có hai nghiệm phân biệt? A. m  \   3 .  3  B. m   ;   1;     \  3 .  5   3  C. m   ;1   .  5   3 
D. m   ;     .  5 
Câu 34. Tìm các giá trị của tham số m để phƣơng trình 2
x mx  4m  0 vô nghiệm.
A. 0  m  16 . B. 4   m  4 .
C. 0  m  4 .
D. 0  m  16 .
Câu 35. Tìm tất cả các giá trị của tham số m để phƣơng trình m  2
2 x  22m  3 x  5m  6  0 vô nghiệm? A. m  0.
B. m  2. m  3 C. .  m 1 m  2 D.  . 1   m  3
Câu 36. Hỏi có tất cả bao nhiêu giá trị nguyên của m để phƣơng trình 2
x  m   2 2 2
2 x  3  4m m  0 có nghiệm? A. 3. B. 4. C. 2. D. 1.
Câu 37. Tìm các giá trị của m để phƣơng trình m   2
5 x  4mx m  2  0 có nghiệm.
A. m  5.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 32
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 10 B.   m  1. 3  10 m    C. 3 .  m 1  10 m    D. 3 .  1   m  5
Câu 38. Các giá trị m để tam thức f x 2
x  m  2 x  8m 1 đổi dấu 2 lần là
A. m  0 hoặc m  28.
B. m  0 hoặc m  28.
C. 0  m  28. D. m  0.
Câu 39. Tìm tất cả các giá trị của tham số m sao cho phƣơng trình m  2
1 x  3m  2 x  3  2m  0 có hai nghiệm phân biệt? A. m  . B. m  1 C. 1
  m  6. D. 1   m  2.
Dạng 2. Tìm m để phƣơng trình bậc 2 có nghiệm thỏa mãn điều kiện cho trƣớc
Câu 40. Chuyên Lê Hồng Phong-Nam Định Tìm tất cả các giá trị của tham số m để phƣơng trình 2 2
mx  2x m  2m 1  0 có hai nghiệm trái dấu. m  0 A.  . m  1  B. m  0 . C. m  1  . m  0 D.  . m  1 
Câu 41. Xác định m để phƣơng trình 3 2
mx x  2x  8m  0 có ba nghiệm phân biệt lớn hơn 1. 1 1 A. m  . 7 6 1 1 B.   m  . 2 6 1 C. m  . 7 D. m  0 .
Câu 42. Với giá trị nào của m thì phƣơng trình m   2
1 x  2m  2 x m  3  0 có hai nghiệm x , x 1 2
thỏa mãn x x x x  1? 1 2 1 2
A. 1  m  3.
B. 1  m  2 . C. m  2 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 33
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D. m  3 .
Câu 43. Cho phƣơng trình m   2
5 x  2 m  
1 x m  0  
1 . Với giá trị nào của m thì   1 có 2 nghiệm
x , x thỏa x  2  x ? 1 2 1 2 A. m  5 . 8 B. m  . 3 8 C. m  5 . 3 8 D. m  5 . 3
Câu 44. Tìm các giá trị thực của tham số m để phƣơng trình m   2
1 x  2mx m  0 có một nghiệm lớn
hơn 1 và một nghiệm nhỏ hơn 1?
A. 0  m  1. B. m  1. C. m . m  0 D.  . m  1
Câu 45. Tìm tất cả các giá trị của tham số m để phƣơng trình 2
x  2mx m  2  0 có hai nghiệm x , x 1 2 thỏa mãn 3 3 x x 16 . 1 2
A. Không có giá trị của m . B. m  2 . C. m  1  . D. m  1  hoặc m  2 .
Câu 46. Xác định m để phƣơng trình  x   2
1 x  2m  3 x  4m 12  0  
có ba nghiệm phân biệt lớn hơn 1  . 7 19 A.
m  3 và m   . 2 6 7 B. m   . 2 7 16 C.
m  1 và m   . 2 9 7 19 D.
m  3 và m   . 2 6
Câu 47. Tìm m để phƣơng trình 2
x mx m  3  0 có hai nghiệm dƣơng phân biệt. A. m  6. B. m  6.
C. 6  m  0. D. m  0.
Câu 48. Tìm tất cả các giá trị thực của tham số m sao cho phƣơng trình m   2
2 x  2mx m  3  0 có
hai nghiệm dƣơng phân biệt.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 34
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 A. 2  m  6. B. m  3
 hoặc 2  m  6.
C. m  0 hoặc 3  m  6. D. 3   m  6.
Câu 49. Tìm tất cả các giá trị thực của tham số m để 2
x  2m  
1 x  9m  5  0 có hai nghiệm âm phân biệt.
A. m  6. 5 B.
m 1 hoặc m  6. 9 C. m  1. D. 1  m  6.
Câu 50. Phƣơng trình 2 x   2 m m   2 2
1 x  2m  3m  5  0 có hai nghiệm phân biệt trái dấu khi và chỉ khi 5 A. m  1
hoặc m  . 2 5
B.  1  m  . 2 5 C. m  1
hoặc m  . 2 5
D.  1  m  . 2
Câu 51. Tìm tất cả các giá trị thực của tham số m để phƣơng trình 2
x  m  
1 x m  2  0 có hai 1 1
nghiệm phân biệt x , x khác 0 thỏa mãn  1. 1 2 2 2 x x 1 2 A. m  ;  2   2  ;  1  7;.  
B. m    11 ; 2  2  ; .    10 
C. m   ;  2    2  ;  1 .
D. m  7; .
Dạng 3. Tìm m để BPT thỏa mãn điều kiện cho trƣớc
Câu 52. Cho hàm số f x 2
x  2x m . Với giá trị nào của tham số m thì f x  0, x   . A. m  1. B. m  1. C. m  0 . D. m  2 .
Câu 53. Tìm tất cả các giá trị của tham số m để bất phƣơng trình 2
x  m  2 x  8m 1  0 vô nghiệm.
A. m 0; 2  8 .
B. m   ;
 0 28;. C. m  ;  028; .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 35
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
D. m  0; 28 .
Câu 54. Tam thức f x 2
x  m   2 2
1 x m  3m  4 không âm với mọi giá trị của x khi A. m  3 . B. m  3 . C. m  3  . D. m  3 .
Câu 55. Có bao nhiêu giá trị nguyên của tham số m để với mọi x  biểu thức f x 2
x  m  2 x 8m 1 luôn nhận giá trị dƣơng. A. 27 . B. 28 . C. Vô số. D. 26 .
Câu 56. Tìm các giá trị của m để biểu thức 2
f (x)  x  (m 1)x  2m  7  0 x  
A. m 2;6 . B. m ( 3  ;9) . C. m ( ;  2) (5; )  . D. m ( 9  ;3) .
Câu 57. Tìm tất cả các giá trị thực của tham số m để bất phƣơng trình: m   2
1 x  2m   1 x  4  0 (1)
có tập nghiệm S R ? A. m  1.     B. 1 m 3.    C. 1 m 3.    D. 1 m 3.
Câu 58. Bất phƣơng trình 2
x  4x m  0 vô nghiệm khi A. m  4 . B. m  4 . C. m  4 . D. m  4 .
Câu 59. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Bất phƣơng trình 2
mx  2 m  
1 x m  7  0 vô nghiệm khi 1 A. m  . 5 1 B. m  . 4 1 C. m  . 5 1 D. m  . 25
Câu 60. Tìm tất cả các giá trị của tham số m để bất phƣơng trình 2
mx  2mx 1  0 vô nghiệm.
A. m  . B. m  1  . C. 1   m  0 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 36
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D. 1   m  0 .
Câu 61. Tìm tập hợp các giá trị của m để hàm số y  m   2
10 x  2 m  2 x 1 có tập xác định D  . A.  1  ;6.
B. 1;6 . C.  ;    1  6;  . D. .
Câu 62. Để bất phƣơng trình 2
5x x m  0 vô nghiệm thì m thỏa mãn điều kiện nào sau đây? 1 A. m  . 5 1 B. m  . 20 1 C. m  . 20 1 D. m  . 5
Câu 63.Có bao nhiêu giá trị nguyên của tham số m để hàm số 2 y
x  2mx  2m  3 có tập xác định là . A. 4 . B. 6 . C. 3 . D. 5 .
Câu 64. Tìm tất cả giá trị của tham số m để bất phƣơng trình 2
x  2x m 1 0 vô nghiệm: A. m  0 . B. m  0 . C. m  0 . D. m  0 .
Câu 65. Bất phƣơng trình m   2
1 x  2 m  
1 x m  3  0 với mọi x  khi
A. m 1; .
B. m  2;  .
C. m  1;  . D. m  2  ;7 .
Câu 66. Cho hàm số f x 2
 x  2m  
1 x  2m 1. Tìm tất cả các giá trị của tham số m để f x  0 , x  0  ;1 . A. m  1. 1 B. m  . 2 C. m  1. 1 D. m  . 2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 37
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Dạng 4. Tìm m để hệ BPT bậc hai thỏa mãn điều kiện cho trƣớc
 x  53 x  0
Câu 67. Hệ bất phƣơng trình  vô nghiệm khi
x 3m  2  0 A. m  1  . B. m  1  . C. m  1  . D. m  1  .
Câu 68. Chuyên Lê Hồng Phong-Nam Định Tìm tất cả các giá trị của tham số m để hệ bất phƣơng 2
2x 5x  2  0 trình  vô nghiệm. 2 x   2m  
1 x m m   1  0 1 A. m  2 . 2  1 m   B.  2  . m  2 1 C. m  1. 2  1 m   D.  2  . m  2 2
x  4x  5
Câu 69. Tìm tất cả các giá trị của tham số m để hệ bất phƣơng trình  có nghiệm. 2 x   m   1 x m  0 m  5 A.  . m  1  m  5 B.  . m  1  m  5 C.  . m  1  m  5 D.  . m  1  2 x 1  0
Câu 70. Hệ bất phƣơng trình  có nghiệm khi x m  0 A. m  1. B. m  1. C. m  1. D. m  1.
2x m  0    1
Câu 71. Hệ bất phƣơng trình 
vô nghiệm khi và chỉ khi: 2
3x x  4  0  2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 38
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 8 A. m   . 3 B. m  2 . C. m  2 . 8 D. m   . 3 2
x 1 0  1
Câu 72. Hệ bất phƣơng trình  có nghiệm khi: x m  0  2 A. m  1. B. m  1. C. m  1. D. m  1.   x  3 
4 x  0  1
Câu 73. Hệ bất phƣơng trình 
có nghiệm khi và chỉ khi: x m 1  2 A. m  5. B. m  2.  C. m  5. D. m  5. 2 3x mx  6
Câu 74. Tìm m để 9    6 2 x x
nghiệm đúng với x   . 1 A. 3   m  6. B. 3   m  6. C. m  3.  D. m  6. 2
x 3x  4  0  1
Câu 75. Tìm m sao cho hệ bất phƣơng trình  có nghiệm. m   1 x  2  0 2 3 A. 1   m  . 2 3 B. m  . 2 C. m .  D. m  1.  2
x 10x 16  0  1
Câu 76. Tìm tất cả giá trị thực của tham số m để hệ bất phƣơng trình  vô nghiệm.
mx  3m 1  2 1
A. m   . 5 1 B. m  . 4 1 C. m   . 11
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 39
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 D. m  . 32
DẠNG 6. BẤT PHƢƠNG TRÌNH CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI và MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 77. (LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Tập nghiệm của phƣơng trình 2
x  3x 1 x  2  0 có tất cả bao nhiêu số nguyên? A. Vô số. B. 4 . C. 2 . D. 3 .
Câu 78. Tìm tập nghiệm của bất phƣơng trình: 2
x  4x  0 . A.  . B.    . C. 0; 4 . D.  ;  0 4;. 1 1
Câu 79. Tìm m để 2 4x  2m
 x  2x   m với mọi số thực x 2 2 A. 2
  m  3. 3 B. m  . 2
C. m  3 . 3 D. m  . 2
Câu 80. Tất cả các giá trị của m để bất phƣơng trình 2
2 x m x  2  2mx thỏa mãn với mọi x là A. m .
B. m   2 . C. m  2 .
D.  2  m  2 .
DẠNG 7. BẤT PHƢƠNG TRÌNH CHỨA CĂN và MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 81. Tập nghiệm của bất phƣơng trình 2
x  2  x 1. A. S   .  1  B. S   ;     .  2  C. 1;  . 1  D. ;    . 2 
Câu 82. Bất phƣơng trình 2x 1  2x  3 có bao nhiêu nghiệm nguyên thuộc khoảng 0;7 ?
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 40
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 A. 4. B. 5. C. 2. D. 6.
Câu 83. Tìm tập nghiệm S của bất phƣơng trình 2
x  2x 15  2x  5 .
A. S   ;    3 .
B. S   ;  3.
C. S   ;   3 .   D. S   ; 3.
Câu 84. Bất phƣơng trình  2
16  x x  3  0 có tập nghiệm là A.  ;  4
 4;. B. 3; 4 . C. 4;  . D.   3 4; .
Câu 85. Tìm tập nghiệm của bất phƣơng trình 2 x  2017  2018x .
A. T    ;1 .
B. T    ;1 .
C. T  1;  .
D. T  1;  .
Câu 86. Tập nghiệm của bất phƣơng trình x  2  x là A. 2;  . B.  ;    1 . C.  2  ;2. D.  1  ;2.
Câu 87. Số nghiệm nguyên của bất phƣơng trình  2 2 x  
1  x 1 là: A. 3 . B. 1. C. 4 . D. 2 .
Câu 88. Tập nghiệm S của bất phƣơng trình (x 1) x 1  0 là A. S   1  ; .
B. S    1  1;  .
C. S    1 1;  .
D. S  1;  .
………………………………………………………………………………………………………………
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 41
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Chƣơng IV. CUNG VÀ GÓC LƢỢNG GIÁC. CÔNG THỨC LƢỢNG GIÁC
BÀI 1. CUNG VÀ GÓC LƢỢNG GIÁC
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ Câu 1.
Số đo theo đơn vị rađian của góc 315 là 7 7 2 4 A. . B. . C. . D. . 2 4 7 7  Câu 2.
Cung tròn có số đo là 5 . Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây. 4 A. 5 . B. 15 . C. 172 . D. 225 . Câu 3. Góc có số đo 0
108 đổi ra rađian là: 3  3  A. . B. . C. . D. . 5 10 2 4  Câu 4. Góc có số đo
đổi sang độ là: 9 A. 0 25 . B. 0 15 . C. 0 18 . D. 0 20 . Câu 5. Cho     a
k2 . Tìm k để 10 a 11 2
A. k  7 .
B. k  5 .
C. k  4 .
D. k  6 .
DẠNG 2. ĐƢỜNG TRÕN LƢỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN Câu 6.
Một đồng hồ treo tƣờng, kim giờ dài 10,57cm và kim phút dài 13,34cm .Trong 30 phút mũi kim
giờ vạch lên cung tròn có độ dài là
A. 2, 78cm .
B. 2, 77cm .
C. 2, 76cm .
D. 2,8cm . Câu 7.
Cung tròn bán kính bằng 8, 43cm có số đo 3,85 rad có độ dài là
A. 32, 46cm .
B. 32, 47cm .
C. 32,5cm .
D. 32, 45cm . Câu 8.
Trên đƣờng tròn bán kính r  5 , độ dài của cung đo là: 8  r 5 A. l  . B. l  . C. l  .
D. kết quả khác. 8 8 8 Câu 9.
Một đƣờng tròn có bán kính R 10cm . Độ dài cung 40o trên đƣờng tròn gần bằng A. 11cm . B. 13cm . C. 7cm . D. 9cm .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 42
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
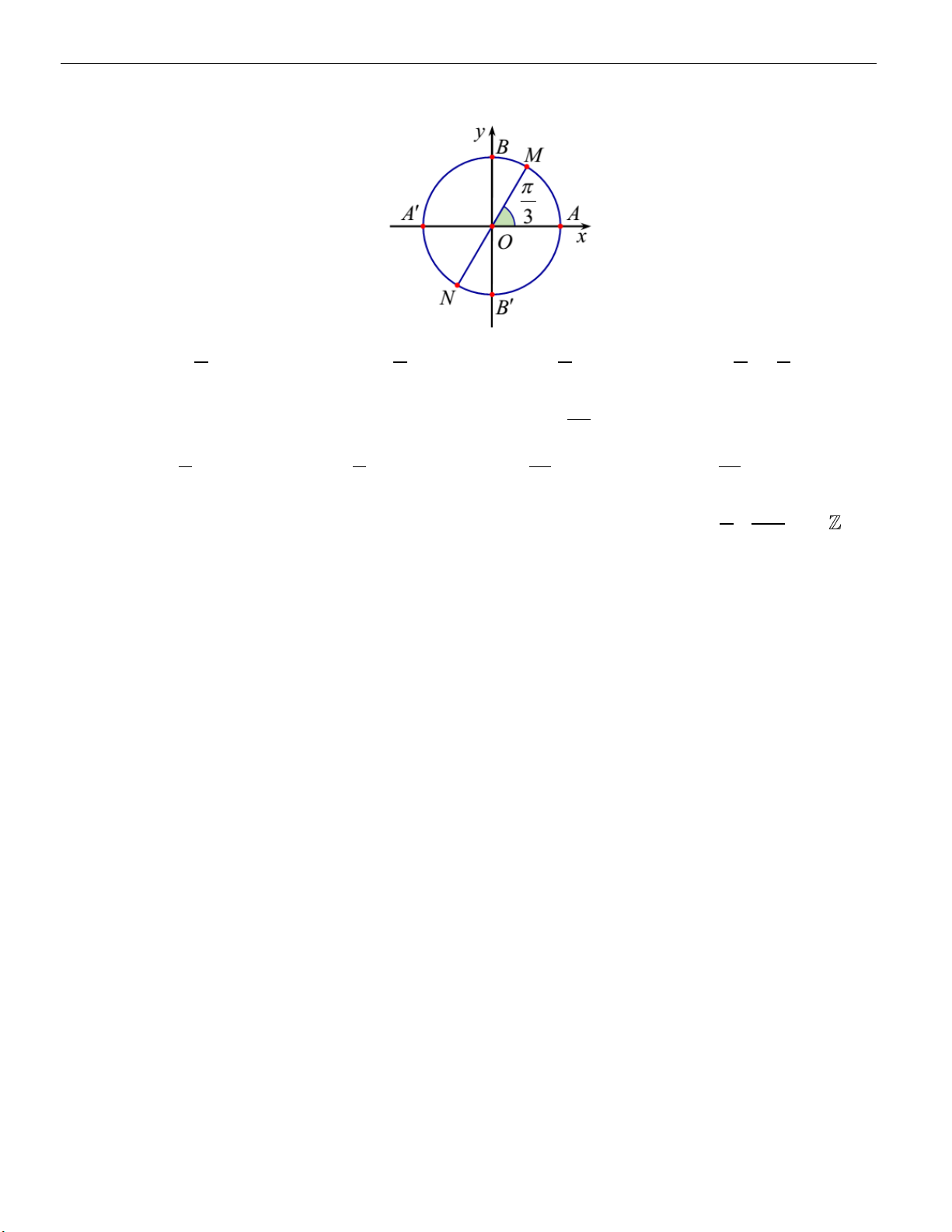
Câu 10. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Trên hình vẽ hai điểm M , N biểu diễn các cung có số đo là:      A. x   2k . B. x    k . C. x   k . D. x   k . . 3 3 3 3 2 
Câu 11. Góc lƣợng giác nào sau đây có cùng điểm cuối với góc 7 ? 4   3 3 A.  . B. . C. . D.  . 4 4 4 4  k
Câu 12. Có bao nhiêu điểm M trên đƣờng tròn định hƣớng gốc A thỏa mãn 2 AM   , k  . 6 3 A. 6 . B. 4 . C. 3 . D. 8 .
…………………………………………………………………………………
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 43
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 2. GIÁ TRỊ LƢỢNG GIÁC CỦA MỘT CUNG
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƢỢNG GIÁC  Câu 1. Cho
a   . Kết quả đúng là 2
A. sin a  0 , cos a  0 .
B. sin a  0 , cos a  0 .
C. sin a  0 , cos a  0 .
D. sin a  0 , cos a  0 . Câu 2.
Trong các giá trị sau, sin có thể nhận giá trị nào? A. 0  ,7 . 4 B. . 3 C.  2 . 5 D. . 2 5 Câu 3. Cho 2 a
. Chọn khẳng định đúng. 2 A. tan a 0, cot a 0. B. tan a 0, cot a 0. C. tan a 0, cot a 0. D. tan a 0, cot a 0 . Câu 4.
Ở góc phần tƣ thứ nhất của đƣờng tròn lƣợng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
A. cot  0 .
B. sin  0 .
C. cos  0 .
D. tan  0 . Câu 5.
Ở góc phần tƣ thứ tƣ của đƣờng tròn lƣợng giác. hãy chọn kết quả đúng trong các kết quả sau đây.
A. cot  0 .
B. tan  0.
C. sin  0 .
D. cos  0 . 7 Câu 6. Cho
   2 .Xét câu nào sau đây đúng? 4
A. tan  0.
B. cot  0 .
C. cos  0 .
D. sin  0 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 44
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
DẠNG 2. GIÁ TRỊ LƢỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT Câu 7.
Cho hai góc nhọn  và  phụ nhau. Hệ thức nào sau đây là sai?
A. cot  tan  .
B. cos  sin  .
C. cos   sin .
D. sin   cos  . Câu 8.
Trong các đẳng thức sau, đẳng thức nào đúng? A.  0
sin 180 – a  – cos a . B.  0
sin 180 – a  sin a . C. sin  0
180 – a  sin a. D. sin  0 180 – a  c s o a . Câu 9.
Chọn đẳng thức sai trong các đẳng thức sau       A. sin  x  cos x   . B. sin  x  cos x   .  2   2        C. tan  x  cot x   . D. tan  x  cot x   .  2   2 
Câu 10. Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos x   cos x .
B. sin  x    sin x .   
C. cos   x   cos x . D. sin
x  cos x   .  2 
Câu 11. Khẳng định nào sau đây là sai? A. sin  
   sin . B. cot  
   cot . C. cos 
   cos . D. tan      tan .
Câu 12. Khẳng định nào sau đây đúng?
A. sin x   s in . x
B. cos x   cos . x
C. cot x  cot . x
D. tan x  tan . x
Câu 13. Chọn hệ thức sai trong các hệ thức sau.  3  A. tan  x  cot x   .
B. sin 3  x  sin x .  2 
C. cos 3  x  cos x .
D. cos x  cos x .
Câu 14. cos(x  2017 ) bằng kết quả nào sau đây? A.  cos x . B. sin x . C. sin x . D. cos x .
DẠNG 3. TÍNH GIÁ TRỊ LƢỢNG GIÁC
Câu 15. Giá trị của cot1458 là A. 1. B. 1  . C. 0 . D. 5  2 5 . 89 cot Câu 16. Giá trị 6 là 3 A. 3 . B.  3 . C. . D. – 3 . 3 3
Câu 17. Giá trị của tan180 là A. 1. B. 0 . C. –1.
D. hông xác định.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 45
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1
Câu 18. Cho biết tan  . Tính cot  2 A. cot  2 . 1 B. cot   . 4 1 C. cot   . 2 D. cot   2 . 3 
Câu 19. Cho sin   và
    . Giá trị của cos là: 5 2 4 A. . 5 4 B.  . 5 4 C.  . 5 16 D. . 25 4  cos  0    Câu 20. Cho 5 với 2 . Tính sin . 1 A. sin   . 5 1 B. sin    . 5 3 C. sin   . 5 3 D. sin    . 5  
Câu 21. Tính  biết cos 1
A.   k k   .
B.   k 2 k   .  C.  
k2 k   . 2 D.   
  k2 k   . 3
Câu 22. Cho tan   5 , với     . hi đó cos bằng: 2 6 A.  . 6 B. 6 . 6 C. . 6
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 46
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 D. . 6 3 Câu 23. Cho sin 
90   180. Tính cot . 5 3 A. cot   . 4 4 B. cot   . 3 4 C. cot    . 3 3 D. cot    . 4   
Câu 24. Cho cot   3 2 với
    . hi đó giá trị tan  cot bằng: 2 2 2 A. 2 19 . B. 2  19 . C.  19 . D. 19 . 3
Câu 25. Nếu sin   cos  thì sin  2 bằng 2 5 A. . 4 1 B. . 2 13 C. . 4 9 D. . 4 1 
Câu 26. Cho sin x  cos x  và 0  x
. Tính giá trị của sin x . 2 2 1 7 A. sin x  . 6 1 7 B. sin x  . 6 1 7 C. sin x  . 4 1 7 D. sin x  . 4 1 Câu 27. Cho sinx = . Tính giá trị của 2 cos x . 2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 47
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 3 A. 2 cos x  4 3 B. 2 cos x  2 1 C. 2 cos x  4 1 D. 2 cos x  2 3sin x  cos x
Câu 28. Cho P
với tan x  2 . Giá trị của P bằng
sin x  2 cos x 8 A. . 9 2 2 B.  . 3 8 C. . 9 5 D. . 4 1 sin x  cos x Câu 29. Cho s inx 
và cosx nhận giá trị âm, giá trị của biểu thức A  bằng 2 sin x cox A. 2   3 B. 2  3 C. 2   3 D. 2  3
4 sin x  5 cos x
Câu 30. Cho tan x  2 .Giá trị biểu thức P  là
2 sin x  3cos x A. 2 . B. 13 . C. 9  . D. 2 .
Câu 31. Cho tam giác ABC đều. Tính giá trị của biểu thức P  cos  A ,
B BC   cos BC,CA  cos  , CA AB  . 3 A. P  . 2 3 B. P   . 2 3 3 C. P   . 2 3 3 D. P  . 2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 48
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2sin a  cos a
Câu 32. Cho tan a  2 . Tính giá trị biểu thức P  sin a  . cos a A. P  2 . B. P  1 . 5 C. P  . 3 D. P  1. 3 sin x  3cos x
Câu 33. Cho cung lƣợng giác có số đo x thỏa mãn tan x  2 .Giá trị của biểu thức M  3
5sin x  2 cos x bằng 7 A. . 30 7 B. . 32 7 C. . 33 7 D. . 31 1 sin x  cos x
Câu 34. Cho sin x
và cos x nhận giá trị âm, giá trị của biểu thức A  bằng 2 sin x  cos x A. 2   3 . B. 2  3 . C. 2   3 . D. 2  3 . 3sin   cos
Câu 35. Cho tan  2 . Giá trị của A  sin  là: cos A. 5 . 5 B. . 3 C. 7 . 7 D. . 3  3 5 7
Câu 36. Giá trị của 2 2 2 2 A  cos  cos  cos  cos bằng 8 8 8 8 A. 0 . B. 1. C. 2 . D. 1  .
Câu 37. Biết tan  2 và 180    270 . Giá trị cos  sin bằng 3 5 A.  . 5 B. 1– 5 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 49
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 3 5 C. . 2 5 1 D. . 2
DẠNG 4. RÚT GỌN BIỂU THỨC LƢỢNG GIÁC
Câu 38. Trong các công thức sau, công thức nào sai? A. 2 2 sin   cos   1 . 1    B. 2 1 tan  
   k,k    . 2 cos   2  1 C. 2 1 cot  
  k ,k  . 2   sin   k 
D. tan  cot   1   , k   .  2  2 2 tan a  sin a
Câu 39. Biểu thức rút gọn của A = 2 2 cot a  bằng: cos a A. 6 tan a . B. 6 cos a . C. 4 tan a . D. 6 sin a . Câu 40. Biểu thức 2 2 2 2 2 D  cos .
x cot x  3cos x – cot x  2sin x không phụ thuộc x và bằng A. 2. B. –2 . C. 3. D. –3 . 2 2 cos x 1
Câu 41. Đơn giản biểu thức A  ta có sin x  cos x
A. A  cos x  sin x .
B. A  cos x – sin x .
C. A  sin x – cos x .
D. A  sin x – cos x . 2
Câu 42. Biết sin  cos 
. Trong các kết quả sau, kết quả nào sai? 2
A. sin.cos  – 1 . 4 6
B. sin   cos   . 2 7 C. 4 4 sin   cos   . 8 D. 2 2 tan   cot   12 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 50
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 43. Đơn giản biểu thức A   2 x 2 x   2 1– sin .cot
1– cot x, ta có A. 2 A  sin x . B. 2 A  cos x . C. 2
A  – sin x . D. 2
A  – cos x .            
Câu 44. Đơn giản biểu thức A  cos   sin   cos  sin          , ta có:  2   2   2   2 
A. A  2sin a .
B. A  2cos a .
C. A  sin a – cos a .
D. A  0 .      
Câu 45. Biểu thức P    x  x       x 3 sin cos cot 2  tan  x
 có biểu thức rút gọn là  2   2 
A. P  2sin x . B. P  2  sin x . C. P  0 . D. P  2  cot x .
Câu 46. Cho tam giác ABC . Đẳng thức nào sau đây sai?
A. A B C   .
B. cos  A B  cos C . A B C C. sin  cos . 2 2
D. sin  A B  sin C .   
Câu 47. Đơn giản biểu thức A  cos    sin     , ta có  2 
A. A  cos a  s n i a .
B. A  2sin a .
C. A  sin a – os c a . D. A  0 .
Câu 48. Cho A, B, C là ba góc của một tam giác không vuông. Mệnh đề nào sau đây sai? A B C A. tan  cot   .  2  2  A B C B. cot  tan   .  2  2
C. cot  A B   cot C .
D. tan  A B  tan C .
Câu 49. Tính giá trị của biểu thức 6 6 2 2
A  sin x  cos x  3sin x cos x . A. A  –1. B. A  1 . C. A  4 . D. A  –4 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 51
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1tan x2 2 1
Câu 50. Biểu thức A  
không phụ thuộc vào x và bằng 2 2 2 4 tan x 4sin x cos x A. 1. B. –1. 1 C. . 4 1 D.  . 4 2 2 cos x  sin y Câu 51. Biểu thức 2 2 B   cot .
x cot y không phụ thuộc vào x, y và bằng 2 2 sin . x sin y A. 2 . B. –2 . C. 1. D. –1. 1
Câu 52. Nếu sin x  cos x
thì 3sin x  2cos x bằng 2 5  7 5  7 A. hay . 4 4 5  5 5  5 B. hay . 7 4 2  3 2  3 C. hay . 5 5 3  2 3  2 D. hay . 5 5     9 
Câu 53. Với mọi , biểu thức: A  cos + cos   ... cos       nhận giá trị bằng:  5   5  A. –10 . B. 10 . C. 0 . D. 5 .  3 5 7
Câu 54. Giá trị của biểu thức 2 2 2 2 A  sin  sin  sin  sin bằng 8 8 8 8 A. 2 . B. 2 . C. 1. D. 0 .     3 
Câu 55. Rút gọn biểu thức A  cos     sin   tan  .sin    
2   ta đƣợc  2   2 
A. A  cos .
B. A  cos .
C. A  sin .
D. A  3cos .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 52
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 3. CÔNG THỨC LƢỢNG GIÁC
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG Câu 1.
Trong các công thức sau, công thức nào đúng?
A. cos a b  cos .
a sin b  sin . a sin b .
B. sin a b  sin .
a cos b  cos .
a sin b .
C. sin a b  sin .
a cos b  cos .
a sin b .
D. cos a b  cos .
a cos b  sin . a sin b . Câu 2.
Trong các công thức sau, công thức nào đúng? a b A.
a b tan tan tan  .
tan a – b  tan a  tan . b 1 B.   tan a tan b a b C.
a b tan tan tan  .
tan a b  tan a  tan . b 1 D.   tan a tan b Câu 3.
Biểu thức sin x cos y  cos xsin y bằng
A. cos  x y .
B. cos  x y .
C. sin  x y .
D. sin  y x . Câu 4.
Chọn khẳng định sai trong các khẳng định sau: A. cos(a  )
b  cos a cos b  sin a sin b . B. sin(a  )
b  sin a cos b  cos a sin b . C. sin(a  )
b  sin a cos b  cos a sin b . D. 2
cos 2a  1 2sin a . Câu 5.
(LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trong các khẳng định sau, khẳng định nào sai?   A. sin  sin  a b a b a b 2 cos sin .
B. cos a b  cos a cos b  sin a sin b . 2 2
C. sin a b  sin a cosb  cos a sin b .
D. 2 cos a cos b  cos a b  cosa b .
sin a bCâu 6. Biểu thức
bằng biểu thức nào sau đây? (Giả sử biểu thức có nghĩa)
sin a b
sin a b sin a  sin b
sin a b sin a  sin b A.   B.  . a b . sin sin a  sin b
sin a b sin a  sin b
sin a b tan a  tan b
sin a b cot a  cot b C.   D.  . a b . sin tan a  tan b
sin a b cot a  cot b Câu 7.
Rút gọn biểu thức: sin a –17.cos a 13 – sin a 13.cos a –17 , ta đƣợc: A. sin 2 . a B. cos 2 . a 1 C.  . 2 1 D. . 2 37 Câu 8.
Giá trị của biểu thức cos bằng 12 6  2 6  2  2  6 A. . B. . C. – 6 2 . D. . 4 4 4 4
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 53
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 Câu 9.
Đẳng thức nào sau đây là đúng.    1    1 3 A. cos    cos    . B. cos    sin  cos   .  3  2  3  2 2    3 1    1 3 C. cos    sin   cos   . D. cos    cos  sin    .  3  2 2  3  2 2   
Câu 10. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Cho tan  2 . Tính tan     .  4  1 A.  . 3 B. 1. 2 C. . 3 1 D. . 3
Câu 11. ết quả nào sau đây sai?   
A. sin x  cos x  2 sin x    .  4    
B. sin x  cos x   2 cos x    .  4    
C. sin 2x  cos 2x  2 sin 2x    .  4    
D. sin 2x  cos 2x  2 cos 2x    .  4  3    
Câu 12. Cho sin x  với
x   khi đó tan x    bằng. 5 2  4  2 A. . 7 1 B. . 7 2 C. . 7 1 D. . 7 1   
Câu 13. Cho sin   với 0    . Giá trị của cos      bằng 3 2  3  2  6 A. . 2 6 B. 6  3. 1 1 C.  . 6 2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 54
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 D. 6  . 2 5    3   
Câu 14. Cho hai góc  ,  thỏa mãn sin   , 
     và cos   , 0     . Tính giá trị 13  2  5  2 
đúng của cos   . 16 A. . 65 18 B. . 65 18 C. . 65 16 D. . 65 3  3
Câu 15. (THPT Cộng Hiền - Lần 1 - 2018-2019) Cho sin ,     ;   . Tính giá trị 5  2 2   21  cos      4  2 A. . 10 7  2 B. . 10  2 C. . 10 7 2 D. . 10 1 3
Câu 16. Cho hai góc nhọn a và b với tan a  và tan b
. Tính a b . 7 4  A. . 3  B. . 4  C. . 6 2 D. . 3 3 1
Câu 17. Cho x, y là các góc nhọn, cot x  , cot y
. Tổng x y bằng: 4 7  A. . 4 3 B. . 4
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 55
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 C. . 3 D.  .       Câu 18. Biểu thức 2 2 2
A  cos x  cos  x  cos  x   
 không phụ thuộc x và bằng:  3   3  3 A. . 4 4 B. . 3 3 C. . 2 2 D. . 3 3 3
Câu 19. Cho cos a
; sin a  0 ; sin b
; cosb  0 . Giá trị của cos a b. bằng: 4 5 3  7  A. 1 .   5 4   3  7  B.  1 .   5 4   3  7  C. 1 .   5 4   3  7  D.  1 .   5 4    b  1  b   a  3  a
Câu 20. Biết cos a     và sin a   0   ; sin  b    và cos  b  0  
. Giá trị cos a b  2  2  2   2  5  2  bằng: 24 3  7 A. . 50 7  24 3 B. . 50 22 3  7 C. . 50 7  22 3 D. . 50 3 3
Câu 21. Cho sin a
; cos a  0 ; cos b
; sin b  0 . Giá trị sin a b bằng: 5 4 1  9  A.  7  .   5  4  1  9  B.  7  .   5  4 
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 56
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1  9  C. 7  .   5  4  1  9  D. 7  .   5  4 
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC
Câu 22. Đẳng thức nào không đúng với mọi x ? x A. 2 1 cos 6 cos 3x  . B. 2
cos 2x  1 2sin x . 2  x
C. sin 2x  2sin x cos x . D. 2 1 cos 4 sin 2x  . 2
Câu 23. Trong các công thức sau, công thức nào sai? 2 cot x 1 2 tan x A. cot 2x  . B. tan 2x  2 cot x 2 1 . tan x C. 3
cos 3x  4cos x  3cos x . D. 3
sin 3x  3sin x  4sin x
Câu 24. Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a  cos a – sin . a B. 2 2
cos 2a  cos a  sin . a C. 2
cos 2a  2cos a –1. D. 2 cos 2a 1– 2sin . a
Câu 25. Mệnh đề nào sau đây đúng? A. 2 2
cos 2a  cos a  sin a . B. 2 2
cos 2a  cos a  sin a . C. 2
cos 2a  2 cos a  1 . D. 2
cos 2a  2 sin a 1 .
Câu 26. Cho góc lƣợng giác a. Trong các khẳng định sau, khẳng định nào là khẳng định sai? A. 2
cos 2a  1 2sin a . B. 2 2
cos 2a  cos a  sin a . C. 2
cos 2a  1 2 cos a . D. 2
cos 2a  2 cos a 1.
Câu 27. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Khẳng định nào dƣới đây SAI? A. 2
2sin a  1 cos 2a .
B. cos 2a  2cos a 1.
C. sin 2a  2sin a cos a .
D. sin a b  sin a cos b  sin . b cos a .
Câu 28. Chọn đáo án đúng.
A. sin 2x  2sin x cos x . B. sin 2x  sin x cos x . C. sin 2x  2cos x .
D. sin 2x  2sin x . 4   
Câu 29. Cho cos x  , x   ; 0 
 . Giá trị của sin 2x là 5  2  24 A. . 25 24 B.  . 25 1 C.  . 5
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 57
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 D. . 5 1
Câu 30. Nếu s inx  cos x  thì sin2x bằng 2 3 A. . 4 3 B. . 8 2 C. . 2 3 D. . 4
Câu 31. Biết rằng 6 6 2
sin x  cos x a b sin 2x , với a, b là các số thực. Tính T  3a  4 b . A. T  7  . B. T  1. C. T  0 . D. T  7 . 3
Câu 32. Cho sin 2 
. Tính giá trị biểu thức A  tan  cot  4 4 A. A  . 3 2 B. A  . 3 8 C. A  . 3 16 D. A  . 3 1 1
Câu 33. Cho a,b là hai góc nhọn. Biết cos a  , cos b
. Giá trị của biểu thức cos a b cos a b 3 4 bằng 119 A.  . 144 115 B.  . 144 113 C.  . 144 117 D.  . 144 1
Câu 34. (TOÁN HỌC TUỔI TRẺ SỐ 5) Cho số thực  thỏa mãn sin   . Tính 4
sin 4  2sin 2 cos 25 A. . 128
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 58
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 B. . 16 255 C. . 128 225 D. . 128
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH
Câu 35. Mệnh đề nào sau đây sai? 1 1
A. cos a cos b
cosa b  cosa b   .
B. sin a cos b
sin a b  cosa b   . 2 2 1 1
C. sin a sin b
cosa b  cosa b   .
D. sin a cos b
sin a b  sin a b   . 2 2
Câu 36. Trong các đẳng thức sau, đẳng thức nào sai? 1
A. cos(a  ) b  cos .
a cos b  sin .
a sin b . B. cos . a cos b
cos(a b)  cos(a b). 2 C. sin(a  ) b  sin .
a cos b  sin . b cos a .
D. cos a  cos b  2cos(a  )
b .cos(a  ) b .
Câu 37. Công thức nào sau đây là sai? a b a b a b a b
A. cos a  cos b  2 cos .cos .
B. cos a  cos b  2  sin .sin . 2 2 2 2 a b a b a b a b
C. sin a  sin b  2sin .cos .
D. sin a  sin b  2sin .cos . 2 2 2 2
sin 3x  cos 2 x  sin x
Câu 38. Rút gọn biểu thức A
sin 2x  0;2sin x 1  0 ta đƣợc:
cos x  sin 2 x  cos 3x
A. A  cot 6x .
B. A  cot 3x .
C. A  cot 2x .
D. A  tan x  tan 2x  tan 3x .      
Câu 39. Rút gọn biểu thức P  sin a  sin a      .  4   4  3
A.  cos 2a . 2 1 B. cos 2a . 2 2 C.  cos 2a . 3 1 D.  cos 2a . 2
Câu 40. Biến đổi biểu thức sin 1 thành tích.      
A. sin 1  2sin   cos       .  2   2      B. sin     1  2sin  cos      .  2 4   2 4 
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 59
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908      
C. sin 1  2sin   cos       .  2   2      D. sin     1  2sin  cos      .  2 4   2 4 
cos a  2 cos 3a  cos 5a
Câu 41. Rút gọn biểu thức P  .
sin a  2 sin 3a  sin 5a
A. P  tan a .
B. P  cot a .
C. P  cot 3a .
D. P  tan 3a . Câu 42. (THPT Phan Bội Châu - KTHK 1-17-18) Tính giá trị biểu thức sin 30o.cos 60o sin 60o.cos 30o P   . A. P  1 . B. P  0 .
C. P  3 .
D. P   3 . 2 4 6
Câu 43. Giá trị đúng của cos  cos  cos bằng: 7 7 7 1 A. . 2 1 B.  . 2 1 C. . 4 1 D.  . 4
Câu 44. Tích số cos10 .  cos30 .  cos50 .  cos70 bằng: 1 A. . 16 1 B. . 8 3 C. . 16 1 D. . 4  4 5 Câu 45. Tích số cos .cos .cos bằng: 7 7 7 1 A. . 8 1 B.  . 8 1 C. . 4
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 60
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 D.  . 4 1 1
Câu 46. Cho hai góc nhọn a và b . Biết cos a  , cos b
. Giá trị cos a b.cos a b bằng: 3 4 113 A.  . 144 115 B.  . 144 117 C.  . 144 119 D.  . 144
sin x  sin 2x  sin 3x
Câu 47. Rút gọn biểu thức A  cos x cos2x  cos 3x A. A  tan 6 . x B. A  tan 3 . x C. A  tan 2 . x
D. A  tan x  tan 2x  tan 3 . x
Câu 48. Biến đổi biểu thức sin a 1 thành tích.  a    a  
A. sin a 1  2sin  cos  .      2 4   2 4   a    a  
B. sin a 1  2 cos  sin  .      2 4   2 4       
C. sin a 1  2sin a  cos a  .      2   2       
D. sin a 1  2 cos a  sin a  .      2   2 
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƢỢNG GIÁC   2    
Câu 49. Cho góc  thỏa mãn     và sin 
.Tính giá trị của biểu thức A  tan    . 2 2 5  2 4  1 A. A  . 3 1
B. A   . 3 C. A  3 . D. A  3  . 1   
Câu 50. Cho cos x    x  0 
 . Giá trị của tan 2x là 3  2  5 A. . 2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 61
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 4 2 B. . 7 5 C.  . 2 4 2 D.  . 7      
Câu 51. Cho cos x  0 . Tính 2 2 A  sin x   sin x      .  6   6  3 A. . 2 B. 2. C. 1. 1 D. . 4 2
Câu 52. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Cho biết os c
   . Giá trị của biểu thức 3 cot   3 tan  P  bằng bao nhiêu? 2 cot   tan  19 A. P  . 13 25 B. P  . 13 25 C. P   . 13 19 D. P   . 13  
Câu 53. Cho sin.cos      sin  với    
k ,    l , k,l   . Ta có 2 2
A. tan      2 cot .
B. tan      2 cot  .
C. tan      2 tan  .
D. tan      2 tan . 1 2.tan x cos ax
Câu 54. Biết rằng   a b
. Tính giá trị của biểu thức cos x  s in x 1 tan x
b  sin ax  ,  2 2 2 P a b . A. P  4 . B. P  1 . C. P  2 . D. P  3 . 2
Câu 55. Cho cos 2 
. Tính giá trị của biểu thức P  cos.cos3 . 3
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 62
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 7 A. P  . 18 7 B. P  . 9 5 C. P  . 9 5 D. . 18      
Câu 56. Cho tan x  3 2   x  
 . Giá trị của sin x    là  2   3  2  3 A. . 2 5 2  3 B.  . 2 5 2  3 C. . 2 5 2  3 D. . 2 5
Câu 57. Tổng A  tan 9  cot 9  tan15  cot15 – tan 27 – cot 27 bằng: A. 4. B. –4. C. 8. D. –8. 1 1
Câu 58. Cho hai góc nhọn a và b với sin a  , sin b
. Giá trị của sin 2 a b là: 3 2 2 2  7 3 A. . 18 3 2  7 3 B. . 18 4 2  7 3 C. . 18 5 2  7 3 D. . 18
Câu 59. Cho biểu thức 2 A  a b 2 2 sin – sin a – sin .
b Hãy chọn kết quả đúng: A. A  2 cos . a sin .
b sin a b. B. A  2sin . a cos .
b cos a b. C. A  2 cos . a cos .
b cos a b. D. A  2sin . a sin .
b cos a b. DẠNG 5. MIN-MAX
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 63
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 60. Giá trị nhỏ nhất của 6 6
sin x  cos x là A. 0. 1 B. . 2 1 C. . 4 1 D. . 8
Câu 61. Giá trị lớn nhất của 4 4
M  sin x  cos x bằng: A. 4 . B. 1. C. 2 . D. 3 .
Câu 62. Cho M  3sin x  4cosx . Chọn khẳng định đúng. A. 5
  M  5.
B. M  5 .
C. M  5 .
D. M  5 .
Câu 63. Giá trị lớn nhất của 6 6
M  sin x  cos x bằng: A. 2 . B. 3 C. 0 . D. 1. 3 1 tan x    
Câu 64. Cho biểu thức M           , x k , x k , k
 , mệnh đề nào trong các mệnh 1 tan x3  4 2 
đề sau đúng?
A. M  1. 1 B. M  . 4 1 C. M 1. 4
D. M  1. Câu 65. Cho 2 2
M  6 cos x  5sin x . hi đó giá trị lớn nhất của M là A. 11. B. 1. C. 5 . D. 6 .
Câu 66. Giá trị lớn nhất của biểu thức 2 2
M  7 cos x  2sin x là A. 2 . B. 5 . C. 7 . D. 16 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 64
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
DẠNG 6. NHẬN DẠNG TAM GIÁC Câu 67. Cho , A ,
B C là các góc của tam giác ABC thì.
A. sin 2A  sin 2B  2sin C .
B. sin 2A  sin 2B  2sin C .
C. sin 2A  sin 2B  2sin C .
D. sin 2A  sin 2B  2sin C . A B B A
Câu 68. Một tam giác ABC có các góc ,
A B, C thỏa mãn 3 3 sin cos  sin cos  0 thì tam giác đó 2 2 2 2 có gì đặc biệt?
A. Tam giác đó vuông. B. Tam giác đó đều.
C. Tam giác đó cân.
D. hông có gì đặc biệt.
Câu 69. Cho A , B , C là các góc của tam giác ABC (không là tam giác vuông) thì cot .
A cot B  cot .
B cot C  cot .
C cot A bằng : A. A B C 2 cot .cot .cot
. B. Một kết quả khác các kết quả đã nêu trên. C. 1. D. 1  . 1 1 1
Câu 70. Cho A , B , C là ba là các góc nhọn và tan A  ; tan B  , tan C
. Tổng A B C bằng 2 5 8     A. . B. . C. . D. . 5 4 3 6 Câu 71. Biết , A ,
B C là các góc của tam giác ABC, khi đó. A B CA B C A. cot  cot .   B. cos  cos .    2  2  2  2  A B CA B C C. cos  cos .   D. tan  cot .    2  2  2  2 Câu 72. , A ,
B C, là ba góc của một tam giác. Hãy tìm hệ thức sai:
3A B C
A. sin A   sin 2A B C  . sin A   cos B. 2 .
A B  3C C. cos C  sin .
D. sin C  sin  A B  2C  . 2
Câu 73. Cho A , B , C là các góc của tam giác ABC (không phải tam giác vuông) thì:
A. tan A  tan B  tan C  tan . A tan .
B tan C . B. tan  tan  tan   A B C A B C tan . tan . tan . 2 2 2
C. tan A  tan B  tan C   tan . A tan .
B tan C . D. tan  tan  tan  A B C A B C tan . tan . tan . 2 2 2 Câu 74. Biết , A ,
B C là các góc của tam giác ABC, khi đó. A B CA B C A. sin  cos .   B. sin  cos .    2  2  2  2  A B CA B C C. sin  sin .   D. sin  sin .    2  2  2  2 Câu 75. Nếu     a
2b và a b c  . Hãy chọn kết quả đúng.
A. sin b sin b  sin c  sin 2a . B. b b c 2 sin sin sin  sin a .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 65
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 C. b b c 2 sin sin sin  cos a .
D. sin b sin b  sin c  cos 2a .
Câu 76. Cho A , B , C là các góc của tam giác ABC thì:
A. sin 2A  sin 2B  sin 2C  4sin . A sin .
B sin C . B. sin 2A  sin 2B  sin 2C  4cos . A cos .
B cos C .
C. sin 2A  sin 2B  sin 2C  4  cos . A cos .
B cos C . D.
sin 2A  sin 2B  sin 2C  4sin . A sin .
B sin C . Câu 77. , A ,
B C, là ba góc của một tam giác. Hãy chỉ hệ thức sai:
 4A B C  3A
A  2B C A. cot   tan   . B. cos  sin B   .  2  2  2 
A B  3C
A B  6C  5C C. sin  cos 2C   . D. tan  cot   .  2   2  2 Câu 78. Biết ,
A B, C là các góc của tam giác ABC khi đó.
A. cos C  cos  A B . B. tan C  tan  A B .
C. cot C   cot  A B. D. sin C  sin  A B .
Câu 79. Cho A , B , C là ba góc của một tam giác. Hãy chọn hệ thức đúng trong các hệ thức sau. A. 2 2 2
cos A  cos B  cos C  1 cos . A cos . B cos . C B. 2 2 2
cos A  cos B  cos C 1– cos . A cos . B cos . C C. 2 2 2
cos A  cos B  cos C  1 2cos . A cos . B cos . C D. 2 2 2
cos A  cos B  cos C 1– 2cos . A cos . B cos . C
Câu 80. Hãy chỉ ra công thức sai, nếu , A ,
B C là ba góc của một tam giác. B C B C A A. cos cos  sin sin  sin . B. cos . B cosC  sin .
B sin C  cos A  0 . 2 2 2 2 2 B C C C A C. sin cos  sin cos  cos . 2 2 2 2 2 D. 2 2 2
cos A  cos B  cos C  2 cos Acos B cos C  1 . ---HẾT---
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 66
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
HÌNH HỌC 10 - Quyển 2- HỌC KỲ 2
CHƢƠNG III. PHƢƠNG PHÁP TOẠ ĐỘ TRONG MẶT PHẲNG.
BÀI 1. PHƢƠNG TRÌNH ĐƢỜNG THẲNG
DẠNG 1. XÁC ĐỊNH VÉCTƠ CHỈ PHƢƠNG, VÉC TƠ PHÁP TUYẾN CỦA ĐƢỜNG
THẲNG, HỆ SỐ GÓC CỦA ĐƢỜNG THẲNG Câu 1.
Trong mặt phẳng Oxy , đƣờng thẳng d ax by c   2 2 :
0, a b  0 . Vectơ nào sau đây là một
vectơ pháp tuyến của đƣờng thẳng d  ? A. n   ; a b   . B. n   ; b a . C. n   ;
b a . D. n   ; a b . Câu 2.
(THPT Cộng Hiền - Lần 1 - 2018-2019) Trong mặt phẳng tọa độ Oxy, cho đƣờng thẳng
d : x  2 y  3  0 . Vectơ pháp tuyến của đƣờng thẳng d là A. n  1; 2  
B. n  2;  1 C. n   2  ;3
D. n  1;3 Câu 3.
Cho đƣờng thẳng d  :3x  2y 10  0 . Véc tơ nào sau đây là véctơ chỉ phƣơng của d  ?
A. u  3; 2 .
B. u  3;  2 .
C. u  2;  3 . D. u   2  ;3 .  1 x  5  t Câu 4.
(THPT Quỳnh Lƣu- Nghệ An- 2019) Cho đƣờng thẳng  : 2 một vectơ pháp tuyến y  3   3t
của đƣờng thẳng  có tọa độ A. 5; 3 . B. 6  ;1 .  1  C. ;3   .  2  D. 5;3 . x  2   t Câu 5.
Trong hệ trục tọa độ Oxy , Véctơ nào là một véctơ pháp tuyến của đƣờng thẳng d :  ? y  1   2t
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 67
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 A. n  2  ;  1 .
B. n 2;   1 . C. n  1  ;2 .
D. n 1; 2 . x 1 4t Câu 6.
Vectơ chỉ phƣơng của đƣờng thẳng d :  là: y  2   3t A. u   4  ;3.
B. u  4;3 .
C. u  3;4 . D. u  1; 2   . Câu 7.
Vector nào dƣới đây là 1 vector chỉ phƣơng của đƣờng thẳng song song với trục Ox :
A. u  1;0 . B. u  (1; 1  ) .
C. u  (1;1) .
D. u  (0;1) . Câu 8.
Cho đƣờng thẳng d : 7x  3y 1  0. Vectơ nào sau đây là Vectơ chỉ phƣơng của d?
A. u  7;3 .
B. u  3;7 . C. u   3  ;7 .
D. u  2;3 . Câu 9.
(THPT Yên Mỹ Hƣng Yên lần 1 - 2019) Cho hai điểm M 2;3 và N  2  ;5 . Đƣờng thẳng
MN có một vectơ chỉ phƣơng là:
A. u  4;2 . B. u  4; 2   . C. u   4  ; 2   . D. u   2  ;4 .
Câu 10. Đƣờng thẳng d có một vectơ chỉ phƣơng là u  3; 4
  . Đƣờng thẳng  vuông góc với d có một vectơ pháp tuyến là: A. n  4;3 . 1   B. n  4  ; 3  . 2   C. n  3; 4 . 3   D. n  3; 4  . 4  
Câu 11. Đƣờng thẳng d có một vectơ pháp tuyến là n   2  ; 5
  . Đƣờng thẳng  vuông góc với d có
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 68
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
một vectơ chỉ phƣơng là: A. u  5; 2  . 1   B. u  5  ;2 . 2   C. u  2;5 . 3   D. u  2; 5  . 4  
Câu 12. Đƣờng thẳng d có một vectơ chỉ phƣơng là u  3; 4
 . Đƣờng thẳng  song song với d có một vectơ pháp tuyến là: A. n  4;3 . 1   B. n  4  ;3 . 2   C. n  3; 4 . 3   D. n  3; 4  . 4  
Câu 13. Đƣờng thẳng d có một vectơ pháp tuyến là n   2  ; 5
  . Đƣờng thẳng  song song với d có
một vectơ chỉ phƣơng là: A. u  5; 2  . 1   B. u  5  ; 2  . 2   C. u  2;5 . 3   D. u  2; 5  . 4  
DẠNG 2. VIẾT PHƢƠNG TRÌNH ĐƢỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
Dạng 2.1 Viết phƣơng trình đƣờng thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua
Câu 14. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Phƣơng trình tham số của đƣờng thẳng đi
qua hai điểm A2;  1 và B 2;5 là x  2t A.  . y  6tx  2  t B.  .
y  5  6tx  1 C.  . y  2  6t x  2 D.  . y  1   6t
Câu 15. Phƣơng trình tham số của đƣờng thẳng đi qua hai điểm A3;   1 , B  6  ;2 là
x  1 3t A.  . y  2t
x  3  3t B.  . y  1   t
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 69
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x  3 3t C.  . y  6   t
x  3  3t D.  . y  1   t
Câu 16. Trong mặt phẳng tọa độ, cho hai điểm A3;0, B 0; 2 và đƣờng thẳng d : x y  0 . Lập phƣơng
trình tham số của đƣờng thẳng  qua A và song song với d . x t A.  . y  3  tx t B.  . y  3 tx tC.  . y  3  t x tD.  . y  3 tx  5  t
Câu 17. Cho đƣờng thẳng d có phƣơng trình tham số 
. Phƣơng trình tổng quát của đƣờng y  9   2t thẳng d là
A. 2x y 1  0 . B. 2
x y 1 0 .
C. x  2 y 1  0 .
D. 2x  3y 1  0 .
Câu 18. Trong mặt phẳng Oxy cho điểm M (1; 2) . Gọi ,
A B là hình chiếu của M lên O , x Oy . Viết
phƣơng trình đƣờng thẳng AB .
A. x  2y 1  0 .
B. 2x y  2  0 .
C. 2x y  2  0 .
D. x y  3  0 . x  3 5t
Câu 19. Trong mặt phẳng tọa độ Oxy, cho đƣờng thẳng d : 
(t  ) . Phƣơng trình tổng quát của y 1 4t
đƣờng thẳng d là
A. 4x  5y  7  0. .
B. 4x  5y 17  0. .
C. 4x  5y 17  0. .
D. 4x  5y 17  0.
Câu 20. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng thẳng d cắt hai trục Ox và Oy lần lƣợt tại hai điểm A ;
a 0 và B 0;b a  0;b  0 . Viết phƣơng trình đƣờng thẳng d. x y A. d :   0 . a b x y B. d :  1. a b
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 70
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x y C. d :  1. a b x y D. d :  1. . b a
Câu 21. Phƣơng trình đƣờng thẳng đi qua hai điểm A0; 4, B  6  ;0 là: x y A.  1. 6 4 x y B.   1 4  . 6 x y C.  1 4 6  . x y D.  1. 6 4
Dạng 2.2 Viết phƣơng trình đƣờng thẳng đi qua một điểm vuông góc hoặc với đƣờng thẳng cho trƣớc
Câu 22. Phƣơng trình đƣờng thẳng d đi qua A1; 2
  và vuông góc với đƣờng thẳng  :3x  2y 1 0 là:
A. 3x  2 y  7  0 .
B. 2x  3y  4  0 .
C. x  3y  5  0 .
D. 2x  3y  3  0 .
Câu 23. Cho đƣờng thẳng d : 8x  6 y  7  0 . Nếu đƣờng thẳng  đi qua gốc tọa độ và vuông góc với
đƣờng thẳng d thì  có phƣơng trình là
A. 4x  3y  0 .
B. 4x  3y  0 .
C. 3x  4 y  0 .
D. 3x  4 y  0 .
Câu 24. Đƣờng thẳng đi qua điểm A1;1 
1 và song song với đƣờng thẳng y  3x  5 có phƣơng trình là
A. y  3x 11. B. y   3  x 14 .
C. y  3x  8 .
D. y x 10 .
(HKI XUÂN PHƢƠNG - HN) Lập phƣơng trình đƣờng đi qua A2;5 và song song với đƣờng Câu 25.
thẳng d  : y  3x  4?
A.  : y  3x  2 .
B.  : y  3x 1. C.  1 : y   x 1 . 3
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 71
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
D.  : y  3  x 1.
Câu 26. Trong hệ trục Oxy , đƣờng thẳng d qua M 1 
;1 và song song với đƣờng thẳng d ' : x y 1  0 có phƣơng trình là
A. x y 1  0 .
B. x y  0 .
C. x y 1  0 .
D. x y  2  0 .
Câu 27. Viết phƣơng trình tổng quát của đƣờng thẳng đi qua điểm I  1
 ;2 và vuông góc với đƣờng thẳng
có phƣơng trình 2x y  4  0 .
A. x  2y  0 .
B. x  2y  3  0 .
C. x  2y  3  0 .
D. x  2y  5  0 .
Câu 28. Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A2;0 ¸ B 0;3 và C  3  ;  1 . Đƣờng thẳng
đi qua điểm B và song song với AC có phƣơng trình tham số là: x  5t A.  . y  3 tx  5 B.  . y 1 3tx t C.  . y  3  5t
x  3  5t D.  . y t
Câu 29. Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A3; 2 ¸ P 4;0 và Q 0; 2
  . Đƣờng thẳng đi
qua điểm A và song song với PQ có phƣơng trình tham số là: x  3 4t A.  .
y  2  2t
x  3  2t B.  . y  2  tx  1   2t C.  . y t x  1   2t D.  . y  2   t
Câu 30. Trong mặt phẳng với hệ tọa độ Oxy , cho hình bình hành ABCD có đỉnh A –2;  1 và phƣơng x  1 4t
trình đƣờng thẳng chứa cạnh CD là 
. Viết phƣơng trình tham số của đƣờng thẳng chứa  y  3t cạnh AB .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 72
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x  2   3t A.  . y  2   2tx  2   4t B.  . y 1 3t
x  2  3t C.  . y  1 4t
x  2  3t D.  . y  1 4t
Câu 31. Viết phƣơng trình tham số của đƣờng thẳng d đi qua điểm M  3
 ;5 và song song với đƣờng
phân giác của góc phần tƣ thứ nhất. x  3   t A.  . y  5  tx  3   t B.  . y  5  tx  3 t C.  . y  5   tx  5  t D.  . y  3   t
Câu 32. Viết phƣơng trình tham số của đƣờng thẳng d đi qua điểm M 4; 7
  và song song với trục Ox . x  1 4t A.  .  y  7tx  4 B.  . y  7   tx  7   t C.  . y  4 x t D.  . y  7 
Câu 33. Phƣơng trình tổng quát của đƣờng thẳng d đi qua O và song song với đƣờng thẳng
 : 6x  4x 1 0 là:
A. 3x  2 y  0.
B. 4x  6y  0.
C. 3x 12 y 1  0.
D. 6x  4y 1  0.
Câu 34. Đƣờng thẳng d đi qua điểm M  1
 ;2 và vuông góc với đƣờng thẳng
 : 2x y  3  0 có phƣơng trình tổng quát là:
A. 2x y  0 .
B. x  2y  3  0 .
C. x y 1  0 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 73
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
D. x  2y  5  0 .
Câu 35. Cho tam giác ABC có A2;0, B 0;3, C –3 
;1 . Đƣờng thẳng d đi qua B và song song với
AC có phƣơng trình tổng quát là:
A. 5x – y  3  0 .
B. 5x y – 3  0 .
C. x  5y –15  0 .
D. x –15y 15  0 .
Câu 36. Viết phƣơng trình tổng quát của đƣờng thẳng d đi qua điểm M  1
 ;0 và vuông góc với đƣờng x t thẳng  :  . y  2  t
A. 2x y  2  0 .
B. 2x y  2  0 .
C. x  2y 1  0 .
D. x  2y 1  0 . x  1 3t
Câu 37. Đƣờng thẳng d đi qua điểm M  2  
;1 và vuông góc với đƣờng thẳng  :  có phƣơng
y  2  5t trình tham số là: x  2   3t A.  . y 1 5tx  2   5t B.  . y 1 3tx 1 3t C.  . y  2  5t
x 1 5t D.  .
y  2  3t
Câu 38. Viết phƣơng trình tổng quát của đƣờng thẳng d đi qua điểm M 3;  
1 và vuông góc với đƣờng
phân giác góc phần tƣ thứ hai.
A. x y  4  0 .
B. x y  4  0 .
C. x y  4  0 .
D. x y  4  0 .
Câu 39. Viết phƣơng trình tham số của đƣờng thẳng d đi qua điểm M  4
 ;0 và vuông góc với đƣờng
phân giác góc phần tƣ thứ hai. x t A.  . y  4   tx  4   t B.  . y t  x t C.  . y  4  t
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 74
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x t D.  . y  4  t
Câu 40. Viết phƣơng trình tổng quát của đƣờng thẳng d đi qua điểm M  1
 ;2 và song song với trục Ox .
A. y  2  0 .
B. x 1  0 .
C. x 1  0 .
D. y  2  0 .
Dạng 2.3 Viết phƣơng trình cạnh, đƣờng cao, trung tuyến, phân giác của tam giác
Dạng 2.3.1 Phƣơng trình đƣờng cao của tam giác
Câu 41. (ĐỘI CẤN VĨNH PHÚC LẦN 1 2018-2019) Trên mặt phẳng tọa độ Oxy , cho tam giác ABC
có A1;2, B3 
;1 , C 5;4 . Phƣơng trình nào sau đây là phƣơng trình đƣờng cao kẻ t A của tam giác ABC ?
A. 2x  3y  8  0 .
B. 2x  3y  8  0 .
C. 3x  2 y 1  0 .
D. 2x  3y  2  0 . Câu 42. Cho ABC  có A2;  
1 , B 4;5,C  3
 ;2 . Đƣờng cao AH của ABC  có phƣơng trình là
A. 7x  3y 11  0 . B. 3
x  7y 13  0 .
C. 3x  7 y 17  0 .
D. 7x  3y 10  0.
Câu 43. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Trên mặt phẳng tọa độ Oxy , cho tam giác ABC có
A1;2, B3; 
1 ,C 5;4 . Phƣơng trình nào sau đây là phƣơng trình đƣờng cao kẻ t A của tam giác ABC ?
A. 2x  3y  8  0 .
B. 2x  3y  8  0 .
C. 3x  2 y 1  0 .
D. 2x  3y  2  0 .
Câu 44. Cho tam giác ABC có A1  ;1 , B(0; 2
 ,) C 4;2. Lập phƣơng trình đƣờng trung tuyến của tam giác ABC kẻ t . A
A. x y  2  0.
B. 2x y  3  0.
C. x  2y  3  0.
D. x y  0.
Câu 45. Đƣờng trung trực của đoạn AB với A1; 4
  và B5;2 có phƣơng trình là:
A. 2x  3y  3  0.
B. 3x  2y 1  0.
C. 3x y  4  0.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 75
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
D. x y 1  0.
Câu 46. Đƣờng trung trực của đoạn AB với A4;   1 và B 1; 4
  có phƣơng trình là:
A. x y  1.
B. x y  0.
C. y x  0.
D. x y  1.
Dạng 2.3.2 Phƣơng trình đƣờng trung tuyến của tam giác
Câu 47. Cho tam giác ABC với A1 
;1 , B 0;  2 , C 4; 2 . Phƣơng trình tổng quát của đƣờng trung
tuyến đi qua điểm B của tam giác ABC là
A. 7x  7 y 14  0 .
B. 5x  3y 1  0 .
C. 3x y  2  0 . D. 7
x  5y 10  0.
Câu 48. (THPT Yên Dũng 3 - Bắc Giang lần 1- 18-19) Trong hệ tọa độ Oxy , cho tam giác ABC có
A2;3, B 1;0, C  1  ; 2
  . Phƣơng trình đƣờng trung tuyến kẻ t đỉnh A của tam giác ABC là:
A. 2x y 1  0 .
B. x  2 y  4  0 .
C. x  2y  8  0 .
D. 2x y  7  0 .
Câu 49. (Nông Cống - Thanh Hóa - Lần 1 - 1819) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác
ABC có phƣơng trình cạnh AB là x y  2  0, phƣơng trình cạnh AC là x  2y  5  0 . Biết
trọng tâm của tam giác là điểm G 3; 2 và phƣơng trình đƣờng thẳng BC có dạng
x my n  0. Tìm m  . n A. 3 . B. 2 . C. 5 . D. 4 .
Dạng 2.3.4 Phƣơng trình đƣờng phân giác của tam giác
Câu 50. Trong mặt phẳng với hệ tọa độ Oxy , cho đƣờng thẳng  : ax by c  0 và hai điểm M x ; y m m
, N x ; y không thuộc  . Chọn khẳng định đúng trong các khẳng định sau: n n
A. M , N khác phía so với  khi ax by c.ax by c  0. m m n n
B. M , N cùng phía so với  khi ax by c.ax by c 0. m m n n
C. M , N khác phía so với  khi ax by c.ax by c 0. m m n n
D. M , N cùng phía so với  khi ax by c.ax by c  0. m m n n
Câu 51. Trong mặt phẳng với hệ tọa độ Oxy , cho đƣờng thẳng d : 3x  4 y  5  0 và hai điểm A1;3 ,
B 2; m . Tìm tất cả các giá trị của tham số m để A và B nằm cùng phía đối với d . A. m  0 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 76
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 B. m   . 4 C. m  1  . 1 D. m   . 4 x  2  t
Câu 52. Trong mặt phẳng với hệ tọa độ Oxy , cho đƣờng thẳng d : 
và hai điểm A1; 2 , y 1 3t B  2;
m . Tìm tất cả các giá trị của tham số m để A và B nằm cùng phía đối với d . A. m  13. B. m  13 . C. m  13. D. m  13 .
Câu 53. Cặp đƣờng thẳng nào dƣới đây là phân giác của các góc hợp bởi hai đƣờng thẳng
 : x  2y  3  0 và  : 2x y  3  0 . 1 2
A. 3x y  0 và x  3y  0 .
B. 3x y  0 và x  3y  6  0 .
C. 3x y  0 và x  3y  6  0 .
D. 3x y  6  0 và x  3y  6  0 .
DẠNG 3. VỊ TRÍ TƢƠNG ĐỐI CỦA HAI ĐƢỜNG THẲNG
Câu 54. Trong mặt phẳng Oxy , đƣờng thẳng d : x  2y 1  0 song song với đƣờng thẳng có phƣơng trình nào sau đây?
A. x  2y 1  0 .
B. 2x y  0 .
C. x  2 y 1  0 . D. 2
x  4y 1 0 .
Câu 55. Tìm các giá trị thực của tham số m để đƣờng thẳng y   2
m  3 x  3m 1 song song với đƣờng
thẳng y x  5 . A. m  2  .
B. m   2 . C. m  2  . D. m  2 .
Câu 56. Hai đƣờng thẳng d :mx y m  5, d : x my  9 cắt nhau khi và chỉ khi 1 2 A. m  1  . B. m  1. C. m  1  . D. m  2 .
Câu 57. Với giá trị nào của m thì hai đƣờng thẳng
d : 3x  4 y 10  0 và d : 2m 1 x m y 10  0 trùng nhau? 2   2 1 A. m  2 . B. m  1  . C. m  2 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 77
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D. m  2  .
Câu 58. Trong mặt phẳng với hệ tọa độ Oxy , cho hai đƣờng thẳng có phƣơng trình
d : mx m 1 y  2m  0 và d : 2x y 1  0 . Nếu d song song d thì: 1   2 1 2 A. m  2. B. m  1.  C. m  2.  D. m  1.
x  2  3t
Câu 59. Tìm m để hai đƣờng thẳng d : 2x  3y  4  0 và d :  cắt nhau. 1 2 y 1 4mt 1 A. m   . 2 B. m  2. 1 C. m  . 2 1 D. m  . 2
Câu 60. Với giá trị nào của a thì hai đƣờng thẳng
x  1 at
d : 2x – 4 y 1  0 và d :  vuông góc với nhau? 1 2 y  3   a  1t A. a  2.  B. a  2. C. a  1.  D. a 1.
Câu 61. Với giá trị nào của m thì hai đƣờng thẳng x  2   2t
x  2  mtd :  và d :  trùng nhau? 1 y  3  t 2  y  6   1 2mt 1 A. m  . 2 B. m  2  . C. m  2 . D. m  2  .
Câu 62. Tìm tất cả các giá trị của m để hai đƣờng thẳng
x  2  2t d : 
và d : 4x  3y m  0 trùng nhau. 1 y 1 mt 2 A. m  3  . B. m  1. 4 C. m  . 3 D. m .
Câu 63. Với giá trị nào của m thì hai đƣờng thẳng
d : 2x y  4  m  0 và d : m  3 x y  2m 1  0 song song? 2   1 A. m  1.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 78
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 B. m  1.  C. m  2. D. m  3.
Câu 64. Tìm tất cả các giá trị của m để hai đƣờng thẳng
 : 2x  3my 10  0 và  : mx  4y 1  0 cắt nhau. 1 2
A. 1  m 10 . B. m  1.
C. Không có m .
D. Với mọi m .
Câu 65. Với giá trị nào của m thì hai đƣờng thẳng
 : mx y 19  0 và  : m 1 x m 1 y  20  0 vuông góc? 2     1
A. Với mọi m . B. m  2 .
C. Không có m . D. m  1  .
Câu 66. Với giá trị nào của m thì hai đƣờng thẳng
d : 3mx  2 y  6  0 và d :  2
m  2 x  2my  6  0 cắt nhau? 2  1 A. m  1  . B. m  1. C. m .
D. m  1 và m  1  .
Câu 67. Tìm toạ độ giao điểm của hai đƣờng thẳng x  3   4t
x 1 4td :  và d :  . 1
y  2  5t 2
y  7  5tA. 1;7. B.  3  ;2. C. 2; 3  . D. 5;  1 .
x  22  2t
Câu 68. Cho hai đƣờng thẳng d : 2x  3y 19  0 và d : 
. Tìm toạ độ giao điểm của hai 1 2
y  55  5t đƣờng thẳng đã cho. A. 2;5. B. 10; 25. C.  1  ;7. D. 5; 2.
Câu 69. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A –2;0, B 1; 4 và đƣờng thẳng x td : 
. Tìm tọa độ giao điểm của đƣờng thẳng AB và d . y  2  t A. 2;0 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 79
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 B.  –2;0 . C. 0; 2 . D. 0; – 2 . x  1   t
Câu 70. Xác định a để hai đƣờng thẳng d : ax  3y – 4  0 và d : 
cắt nhau tại một điểm nằm 1 2 y  3 3t trên trục hoành. A. a  1. B. a  1.  C. a  2. D. a  2.  x  2  t
Câu 71. Tìm tất cả các giá trị của tham số m để hai đƣờng thẳng 2
d : 4x  3my – m  0 và d :  cắt 1 2
y  6  2t
nhau tại một điểm thuộc trục tung.
A. m  0 hoặc m  6  .
B. m  0 hoặc m  2 .
C. m  0 hoặc m  2  .
D. m  0 hoặc m  6 .
Câu 72. Với giá trị nào của m thì ba đƣờng thẳng d : 2x y –1  0 , d : x  2y 1  0 và d : mx – y – 7  0 1 2 3 đồng quy? A. m  6  . B. m  6 . C. m  5  . D. m  5 .
Câu 73. Đƣờng thẳng d : 51x  30 y 11  0 đi qua điểm nào sau đây?  4  A. M 1  ; .    3   4  B. N 1  ; .    3   3  C. P 1; .    4   3  D. Q 1  ; .    4 
DẠNG 4. GÓC CỦA HAI ĐƢỜNG THẲNG
Dạng 4.1 Tính góc của hai đƣờng thẳng cho trƣớc
Câu 74. (NGÔ GIA TỰ LẦN 1_2018-2019) Tính góc giữa hai đƣờng thẳng  : x  3y  2  0 và 
 : x  3y 1 0. A. 90 . B. 120 . C. 60 . D. 30 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 80
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 75. Góc giữa hai đƣờng thẳng a : 3x y  7  0 và b : x  3y 1  0 là: A. 30 . B. 90 . C. 60 . D. 45 .
d : 2x  5y  2  0
d : 3x  7 y  3  0 d
Câu 76. Cho hai đƣờng thẳng 1 và 2
. Góc tạo bởi đƣờng thẳng 1 và d2 bằng A. 0 30 . B. 0 135 . C. 0 45 . D. 0 60 . x  2  t
Câu 77. Tìm côsin góc giữa hai đƣờng thẳng  : 2x y 1  0 và  :  1 2 y 1 t 10 A. . 10 3 B. . 10 3 C. . 5 3 10 D. . 10 x  2  t
Câu 78. Tìm góc giữa hai đƣờng thẳng  : x  2 y 15  0 và  : t  . 2   1
y  4  2t A. 5 . B. 60 . C. 0 . D. 90 .
Câu 79. Tìm cosin góc giữa 2 đƣờng thẳng d : x  2 y  7  0, d : 2x  4 y  9  0 . 1 2 3 A. . 5 2 B. . 5 1 C. . 5 3 D. . 5
Câu 80. Tính góc tạo bởi giữa hai đƣờng thẳng
d : 7x  3y  6  0 và d : 2x  5y  4  0. 1 2  A. . 4
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 81
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 B. . 3 2 C. . 3 3 D. . 4
Câu 81. Cho đƣờng thẳng d : x  2 y  2  0 và d : x y  0 . Tính cosin của góc tạo bởi giữa hai đƣờng 1 2 thẳng đã cho. 10 A. . 10 2 B. . 3 3 C. . 3 D. 3 .
Dạng 4.2 Viết phƣơng trình đƣờng thẳng liên quan đến góc
x  9  at
Câu 82. Xác định tất cả các giá trị của a để góc tạo bởi đƣờng thẳng 
t   và đƣờng thẳng
y  7  2t
3x  4 y  2  0 bằng 45 .
A. a  1, a  14  . 2 B. a  , a  14  . 7 C. a  2  , a  14  . 2 D. a  , a 14 . 7
Câu 83. Đƣờng thẳng  đi qua giao điểm của hai đƣờng thẳng d : 2x y  3  0 và d : x  2 y 1  0 1 2
đồng thời tạo với đƣờng thẳng d : y 1  0 một góc 0 45 có phƣơng trình: 3
A. x  (1 2) y  0 hoặc  : x y 1  0 .
B.  : x  2 y  0 hoặc  : x  4 y  0 .
C.  : x y  0 hoặc  : x y  2  0.
D.  : 2x 1  0 hoặc y  5  0. .
Câu 84. Trong mặt phẳng với hệ tọa độ Oxy , có bao nhiêu đƣờng thẳng đi qua điểm A2;0 và tạo với
trục hoành một góc 45? A. Có duy nhất. B. 2 . C. Vô số. D. Không tồn tại.
Câu 85. Đƣờng thẳng  tạo với đƣờng thẳng d : x  2 y  6  0 một góc 0
45 . Tìm hệ số góc k của đƣờng thẳng  . 1 A. k  hoặc k  3.  3
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 82
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 1 B. k  hoặc k  3. 3 1
C. k   hoặc k  3.  3 1
D. k   hoặc k  3. 3
Câu 86. Biết rằng có đúng hai giá trị của tham số k để đƣờng thẳng d : y kx tạo với đƣờng thẳng
 : y x một góc 0
60 . Tổng hai giá trị của k bằng: A. 8.  B. 4.  C. 1.  D. 1.  DẠNG 5. KHOẢNG CÁCH
Dạng 5.1 Tính khoảng cách t 1 điểm đến đƣờng thẳng cho trƣớc
Câu 87. Khoảng cách t điểm A1 
;1 đến đƣờng thẳng 5x 12 y  6  0 là A. 13 . B. 13  . C. 1  . D. 1.
Câu 88. Khoảng cách t điểm M 5; 1 đến đƣờng thẳng 3x 2 y 13 0 là: A. 2 13 . 28 B. . 13 C. 26 . 13 D. . 2
Câu 89. Trong mặt phẳng Oxy , khoảng cách t gốc tọa độ O đến đƣờng thẳng d : 4x  3y 1  0 bằng A. 3 . B. 4 . C. 1. 1 D. . 5
Câu 90. Một đƣờng tròn có tâm I 3;  2 tiếp xúc với đƣờng thẳng  :x  5y 1  0. Hỏi bán kính đƣờng tròn bằng bao nhiêu? 14 A. . 26 7 B. . 13 C. 26.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 83
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 D. 6. Câu 91. Trong mặt phẳng Oxy , khoảng cách t
điểm M 0;4 đến đƣờng thẳng
 : x cos  y sin  42  sin   0 bằng A. 8 .
B. 4sin . 4 C. .
cos  sinD. 8 .
Câu 92. Khoảng cách t giao điểm của hai đƣờng thẳng x  3y  4  0 và 2x  3y 1  0 đến đƣờng thẳng
 :3x y  4  0 bằng: A. 2 10 . 3 10 B. . 5 10 C. . 5 D. 2 .
Câu 93. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A1; 2, B 0;3 và C 4;0 . Chiều
cao của tam giác kẻ t đỉnh A bằng: 1 A. . 5 B. 3 . 1 C. . 25 3 D. . 5
Câu 94. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A3; 4
 , B1;5 và C 3  ;1 . Tính
diện tích tam giác ABC . A. 10. B. 5. C. 26. D. 2 5.  x 1 3t
Câu 95. Khoảng cách t điểm M 2;0 đến đƣờng thẳng  :  bằng:
y  2  4t A. 2. 2 B. . 5 10 C. . 5 5 D. . 2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 84
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
x  2  3t
Câu 96. Khoảng cách nhỏ nhất t điểm M 15 
;1 đến một điểm bất kì thuộc đƣờng thẳng  :  y t bằng: A. 10. 1 B. . 10 16 C. . 5 D. 5.
Câu 97. Tìm tất cả các giá trị của tham số m để khoảng cách t điểm A1; 2 đến đƣờng thẳng
 : mx y m  4  0 bằng 2 5 . A. m  2. m  2  B.  1  . m   2 1 C. m   . 2
D. Không tồn tại m .
Câu 98. Tìm tất cả các giá trị của tham số m để khoảng cách t giao điểm của hai đƣờng thẳng x t d : 
và d : x  2 y m  0 đến gốc toạ độ bằng 2 . 1 y  2  t 2 m  4 A. .  m  2 m  4 B. .  m  2 m  4 C. .  m  2 m  4 D. .  m  2
Câu 99. Đƣờng tròn C  có tâm là gốc tọa độ O 0;0 và tiếp xúc với đƣờng thẳng  :8x  6y 100  0 .
Bán kính R của đƣờng tròn C  bằng: A. R  4 . B. R  6 . C. R  8 . D. R  10 .
Câu 100. Đƣờng tròn C  có tâm I  2  ; 2
  và tiếp xúc với đƣờng thẳng  :5x 12y 10  0 . Bán kính R
của đƣờng tròn C  bằng: 44 A. R  . 13
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 85
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 24 B. R  . 13 C. R  44 . 7 D. R  . 13
x  2  t
Câu 101. Tính khoảng cách giữa hai đƣờng thẳng d : 7x y  3  0 và  :  .
y  2  7t 3 2 A. . 2 B. 15 . C. 9 . 9 D. . 50
Câu 102. Khoảng cách giữa hai đƣờng thẳng song song
d : 6x – 8y 101  0 và d : 3x – 4 y  0 bằng: 1 2 A. 10,1. B. 1, 01 . C. 101. D. 101 .
Dạng 5.2 Phƣơng trình đƣờng thẳng liên quan đến khoảng cách
Câu 103. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A2; 
3 và B 1; 4 . Đƣờng thẳng nào sau đây
cách đều hai điểm A và B ?
A. x y  2  0.
B. x  2y  0.
C. 2x  2y 10  0.
D. x y 100  0.
Câu 104. Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A0 
;1 , B 12;5 và C  3  ;0. Đƣờng thẳng
nào sau đây cách đều ba điểm ,
A B và C .
A. x  3y  4  0 .
B. x y 10  0 .
C. x y  0 .
D. 5x y 1  0 .
Câu 105. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1  ;1 , B  2
 ;4 và đƣờng thẳng
 : mx y  3  0 . Tìm tất cả các giá trị của tham số m để  cách đều hai điểm , A B . m  1 A. .  m  2 m  1  B. .  m  2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 86
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 m  1  C. .  m 1 m  2 D. .  m  2
DẠNG 6. XÁC ĐỊNH ĐIỂM
Dạng 6.1 Xác định tọa hình chiếu, điểm đối xứng
Câu 106. Cho đƣờng thẳng d : 3x  5y 15  0 . Trong các điểm sau đây, điểm nào không thuộc đƣờng thẳng d
A. M 5;0 . 1   B. M 5  ;6 . 4   C. M 0; 3 . 2   D. M 5;3 . 3  
Câu 107. Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có A4;3 , B 2;7 , C  3  ; 8   .
Tọa độ chân đƣờng cao kẻ t đỉnh A xuống cạnh BC là: A. 1; 4 . B. 1; 4   . C. 1; 4 . D. 4  ;1 .
Câu 108. Cho đƣờng thẳng d : 3x y  5  0 và điểm M  2  
;1 . Tọa độ hình chiếu vuông góc của M trên d là  7 4  A. ;    .  5 5   7 4  B.  ;   .  5 5   7 4  C.  ;   .  5 5   5 4  D.  ;   .  7 5 
Câu 109. Tọa độ hình chiếu vuông góc của điểm M 1; 2 lên đƣờng thẳng  : x y  0 là  3 3  A. ;   .  2 2  B. 1;  1 . C. 2; 2 .  3 3  D.  ;     2 2 
Dạng 6.2 Xác định điểm liên quan đến yếu tố khoảng cách, góc
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 87
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 110. Cho hai điểm A3;  
1 , B 0;3 . Tìm tọa độ điểm M thuộc Ox sao khoảng cách t M đến đƣờng thẳng AB bằng 1.  7  A. M ; 0 
 và M 1;0 .  2 
B. M  13;0 .
C. M 4;0 .
D. M 2;0 .
Câu 111. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1  ;1 , B 4; 3   và đƣờng thẳng
d : x  2 y 1  0 . Tìm điểm M thuộc d có tọa độ nguyên và thỏa mãn khoảng cách t M đến
đƣờng thẳng AB bằng 6 . A. M 3;7. B. M 7;3. C. M  4  3; 2  7.  27  D. M 3;  .    11 
x  2  2t
Câu 112. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm A0 
;1 và đƣờng thẳng d :  . Tìm điểm y  3  t
M thuộc d và cách A một khoảng bằng 5 , biết M có hoành độ âm.
A. M 4; 4. M 4;4  B. .   24 2  M  ;      5 5   24 2  C. M  ;  .    5 5  D. M  4  ;4.
Câu 113. Biết rằng có đúng hai điểm thuộc trục hoành và cách đƣờng thẳng  : 2x y  5  0 một khoảng
bằng 2 5 . Tích hoành độ của hai điểm đó bằng: 75 A.  . 4 25 B.  . 4 225 C.  . 4 D. Đáp số khác.
Câu 114. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A3;  
1 và B 0;3 . Tìm điểm M thuộc trục
hoành sao cho khoảng cách t M đến đƣờng thẳng AB bằng 1.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 88
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908   7  M ; 0    A.  2 .  M  1;0  14  M ; 0     3  B.  .   4  M ; 0      3    7  M  ; 0    C.  2 .  M   1  ;0   14  M  ; 0     3  D.  .   4  M  ; 0      3 
Câu 115. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A3; 0 và B 0; 4
  . Tìm điểm M thuộc trục
tung sao cho diện tích tam giác MAB bằng 6. M 0;0 A.  M    . 0; 8 B. M 0; 8  . C. M 6;0. M 0;0 D.  M   . 0; 6
Câu 116. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A 1  ;2, B 3
 ;2 và đƣờng thẳng
d : 2x y  3  0 . Tìm điểm C thuộc d sao cho tam giác ABC cân tại C. A. C  2  ;  1 .  3  B. C  ;0 .    2  C. C  1  ;  1 . D. C 0;3
Câu 117. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1; 2, B 0;3 và đƣờng thẳng d : y  2 .
Tìm điểm C thuộc d sao cho tam giác ABC cân tại . B
A. C 1; 2.
B. C 4; 2. C 1;2 C.  C   . 1; 2 D. C  1  ;2.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 89
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Dạng 6.3 Xác định điểm liên quan đến yếu tố cực trị
Câu 118. Trong mặt phẳng tọa độ Oxy cho  : x y 1  0 và hai điểm A2; 
1 , B 9; 6. Điểm M  ; a b
nằm trên đƣờng  sao cho MA MB nhỏ nhất. Tính a  . b A. 7.  B. 9.  C. 7. D. 9.
Câu 119. Trong mặt phẳng với hệ tọa độ Oxy , cho đƣờng thẳng d : x  4y  15  0 và điểm A 2; 0 . Tìm
tọa độ điểm M thuộc d để đoạn AM có độ dài nhỏ nhất. A. M  1  5;0 .
B. M 5; 5 .
C. M 0; 3 .
D. M 1; 4 .
Câu 120. (Yên Định 1 - Thanh Hóa - 2018-2019) Cho 3 điểm ( A 6  ;3); B(0; 1
 );C(3;2) . Tìm M trên
đƣờng thẳng d : 2x y  3  0 mà MA MB MC nhỏ nhất là 13 71 A. M ;   15 15  13 19  B. M ;   15 15   26 97  C. M ;    15 15   1  3 19  D. M ;    15 15 
Câu 121. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh A2; 2 , B 1; 3   , C  2  ;2 .
Điểm M thuộc trục tung sao cho MA MB MC nhỏ nhất có tung độ là? A. 1 . 1 B. . 3 1 C.  . 3 1 D. . 2
Câu 122. Trong mặt phẳng tọa độ Oxy cho  : x  y 1  0 và hai điểm (
A 2;1) , B(9;6) . Điểm M ( ; a b)
nằm trên đƣờng  sao cho MA MB nhỏ nhất. Tính a b ta đƣợc kết quả là: A. -9. B. 9. C. -7. D. 7
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 90
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Dạng 6.4 Một số bài toán tổng hợp
Câu 123. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hình vuông ABCD . Gọi M là trung điểm của  
cạnh BC , N là điểm trên cạnh CD sao cho CN  11 1
2ND . Giả sử M ; và đƣờng thẳng    2 2 
AN có phƣơng trình 2x y  3  0 . Tìm tọa độ điểm A .
A. A1;   1 hoặc A4; 5   .
B. A1;   1 hoặc A 4  ; 5   .
C. A1;  
1 hoặc A4;5 . D. A1 
;1 hoặc A4;5 .
Câu 124. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm I 1;   1 và hai đƣờng thẳng
d : x y  3  0, d : x  2 y  6  0 . Hai điểm ,
A B lần lƣợt thuộc hai đƣờng thẳng d , d sao cho 1 2 1 2
I là trung điểm của đoạn thẳng AB . Đƣờng thẳng AB có một véctơ chỉ phƣơng là A. u  1; 2 1  . B. u  2;1 2   . C. u  1; 2  3   . D. u  2; 1  4  .
Câu 125. (TH&TT LẦN 1 – THÁNG 12) Trong mặt phẳng tọa độ Oxy , cho điểm hai điểm A 4  ;2 , x  5 y 1
B 2;6 và điểm C nằm trên đƣờng thẳng d : 
sao cho CA CB . hi đó tọa độ điểm 3 2  C là  2 8  A. ; .    5 5   1  12  B. ;   .  5 5   1 11 C. ;   .  5 5   2 9  D. ;   .  5 5 
Câu 126. Trong mặt phẳng với hệ tọa độ Oxy , cho A 3
 ;5, B1;3 và đƣờng thẳng d :2x y 1 0 , IA
đƣờng thẳng AB cắt d tại I . Tính tỉ số . IB A. 6. B. 2. C. 4. D. 1.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 91
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 127. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh A2;  1 , B 2; 3   ,C  2  ;  1 . H ABC  ;ab
S  3a  2b Trực tâm của tam giác có tọa độ . Biểu thức bằng bao nhiêu? A. 0 . B. 1. C. 5 . D. 1  .
DẠNG 7. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN DIỆN TÍCH
Câu 128. (THPT Quỳnh Lƣu- Nghệ An- 2019) Đƣờng thẳng  :5x  3y  15 tạo với các trục tọa độ một
tam giác có diện tích bằng bao nhiêu? A. 7, 5 . B. 5 . C. 15 . D. 3 .
Câu 129. Cho hai đƣờng thẳng d : y mx  4; d : mx  4 . Gọi S là tập hợp các giá trị nguyên dƣơng của 1 2
m để tam giác tạo thành bởi d , d và trục hoành có diện tích lớn hơn 8 . Số phần tử của tập S 1 2 là A. 1 . B. 3 . C. 2 . D. 4 .
Câu 130. Tìm phƣơng trình đƣờng thẳng d : y ax  .
b Biết đƣờng thẳng d đi qua điểm I 1;3 và tạo với hai tia O ,
x Oy một tam giác có diện tích bằng 6?
A. y  9  72  x  72  6 .
B. y  9  72  x  72  6 .
C. y  3x  6 . D. y  3  x  6.
Câu 131. Chuyên Lê Hồng Phong-Nam Định Cho tam giác ABC có A1; 3
  , B0;2 , C  2  ;4 .
Đƣờng thẳng  đi qua A và chia tam giác ABC thành hai phần có diện tích bằng nhau. Phƣơng trình của  là
A. 2x y  7  0 .
B. x y  2  0 .
C. x  3y 10  0 .
D. 3x y  0 .
------------------------------------------------------------------------------------------
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 92
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 2. PHƢƠNG TRÌNH ĐƢỜNG TRÒN
DẠNG 1. NHẬN DẠNG PHƢƠNG TRÌNH ĐƢỜNG TRÒN Câu 1.
Tìm tất cả các giá trị của tham số m để phƣơng trình 2 2
x y  2m  2 x  4my 19m  6  0 là
phƣơng trình đƣờng tròn.
A. 1  m  2. B. m  2  hoặc m  1  . C. m  2  hoặc m 1.
D. m  1 hoặc m  2 . Câu 2.
Trong mặt phẳng Oxy , phƣơng trình nào sau đây là phƣơng trình của đƣờng tròn? A. 2 2
x  2 y  4x  8y 1  0 . B. 2 2
x y  4x  6 y 12  0 . C. 2 2
x y  2x  8y  20  0 . D. 2 2
4x y 10x  6 y  2  0 . Câu 3.
Phƣơng trình nào sau đây là phƣơng trình của đƣờng tròn? A. 2 2
2x y  6x  6 y  8  0 . B. 2 2
x  2 y  4x  8y 12  0 . C. 2 2
x y  2x  8y 18  0 . D. 2 2
2x  2 y  4x  6 y 12  0 . Câu 4.
(Cụm liên trƣờng Hải Phòng-L1-2019) Phƣơng trình nào sau đây là phƣơng trình của một đƣờng tròn? A. 2 2 x y 4xy 2x 8y 3 0 . B. 2 2 x 2 y 4x 5y 1 0 . C. 2 2 x y 14x 2 y 2018 0 . D. 2 2 x y 4x 5y 2 0 . Câu 5. (THPT Quỳnh Lƣu- Nghệ An- 2019) Cho phƣơng trình 2 2
x y  2mx  4m  2 y  6  m  0(1) . Điều kiện của m để (1) là phƣơng trình của đƣờng tròn. A. m  2 . m  1 B.  . m  2
C. 1  m  2 . m  1 D.  . m  2
DẠNG 2. TÌM TỌA ĐỘ TÂM, BÁN ÍNH ĐƢỜNG TRÒN Câu 6.
Trong mặt phẳng Oxy , đƣờng tròn C  2 2
: x y  4x  6 y 12  0 có tâm là. A. I  2  ; 3   .
B. I 2;3 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 93
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
C. I 4;6 . D. I  4  ; 6   . Câu 7. Đƣờng tròn 2 2
x y 10 y  24  0 có bán kính bằng bao nhiêu? A. 49 . B. 7 . C. 1 . D. 29 . 2 2 Câu 8.
Xác định tâm và bán kính của đƣờng tròn C :  x   1
  y  2  9. A. Tâm I  1
 ;2, bán kính R  3 . B. Tâm I  1
 ;2, bán kính R  9 .
C. Tâm I 1; 2
 , bán kính R  3 .
D. Tâm I 1; 2
 , bán kính R  9 . Câu 9.
(ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Tìm tọa độ tâm I và bán
kính R của đƣờng tròn C  : 2 2
x y  2x  4 y  1  0 . A. I  1  ; 2; R  4 . B. I 1; 2  ; R  2 . C. I  1  ; 2; R  5 . D. I 1; 2  ; R  4 . 2 2
Câu 10. Trong mặt phẳng Oxy , cho đƣờng tròn C  :  x  2   y  3  9 . Đƣờng tròn có tâm và bán kính là
A. I 2;3, R  9 . B. I 2; 3  , R  3. C. I  3  ;2, R  3. D. I  2  ;3, R  3 .
DẠNG 3. VIẾT PHƢƠNG TRÌNH ĐƢỜNG TRÒN
Dạng 3.1 Khi biết tâm và bán kính
Câu 11. Phƣơng trình đƣờng tròn có tâm I 1; 2 và bán kính R  5 là A. 2 2
x y  2x  4 y  20  0 . B. 2 2
x y  2x  4 y  20  0 . C. 2 2
x y  2x  4 y  20  0 . D. 2 2
x y  2x  4 y  20  0 .
Câu 12. Đƣờng tròn tâm I  1
 ;2 , bán kính R  3 có phƣơng trình là A. 2 2
x y  2x  4 y  4  0 . B. 2 2
x y  2x  4 y  4  0 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 94
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 C. 2 2
x y  2x  4 y  4  0 . D. 2 2
x y  2x  4 y  4  0 .
Dạng 3.2 Khi biết các điểm đi qua
Câu 13. Đƣờng tròn C  đi qua hai điểm A1 
;1 , B 5;3 và có tâm I thuộc trục hoành có phƣơng trình là
A. x  2 2 4  y  10 .
B. x  2 2 4  y 10 .
C. x  2 2 4  y  10 .
D. x  2 2 4  y  10 .
Câu 14. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Trong mặt phẳng với hệ tọa
độ Oxy , tìm tọa độ tâm I của đƣờng tròn đi qua ba điểm A0;4 , B 2;4 , C 2;0 . A. I 1;  1 .
B. I 0; 0 .
C. I 1; 2 .
D. I 1; 0 .
Câu 15. Cho tam giác ABC có A1;  
1 , B 3; 2, C 5; 5
  . Toạ độ tâm đƣờng tròn ngoại tiếp tam giác ABC là  47 13  A. ;  .    10 10   47 13  B. ; .    10 10   47 13  C.  ;  .    10 10   47 13  D.  ; .    10 10 
Câu 16. Trong mặt phẳng Oxy , đƣờng tròn đi qua ba điểm A1; 2 , B 5; 2 , C 1; 3
  có phƣơng trình là. A. 2 2
x y  25x 19 y  49  0 . B. 2 2
2x y  6x y  3  0 . C. 2 2
x y  6x y 1  0 . D. 2 2
x y  6x xy 1  0 .
Câu 17. Lập phƣơng trình đƣờng tròn đi qua hai điểm A3;0, B 0; 2 và có tâm thuộc đƣờng thẳng
d : x y  0 . 2 2  1   1  13 A. x   y       .  2   2  2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 95
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2 2  1   1  13 B. x   y       .  2   2  2 2 2  1   1  13 C. x   y       .  2   2  2 2 2  1   1  13 D. x   y       .  2   2  2
Dạng 3.3 Sử dụng điều kiện tiếp xúc
Câu 18. (THPT Cộng Hiền - Lần 1 - 2018-2019) Trong mặt phẳng tọa độ Oxy , phƣơng trình của đƣờng
tròn có tâm là gốc tọa độ O và tiếp xúc với đƣờng thẳng  : x y  2  0 là A. 2 2 x y 2 . B. 2 2 x y 2 . 2 2 C. x 1 y 1 2 . 2 2 D. x 1 y 1 2 .
Câu 19. (Trƣờng THPT Chuyên Lam Sơn_2018-2019) Trong mặt phẳng tọa độ Oxy , cho đƣờng tròn
S có tâm I nằm trên đƣờng thẳng y  x , bán kính R  3 và tiếp xúc với các trục tọa độ. Lập
phƣơng trình của S  , biết hoành độ tâm I là số dƣơng. 2 2
A. x  3   y  3  9 . 2 2
B. x  3   y  3  9 . 2 2
C. x  3   y  3  9 . 2 2
D. x  3   y  3  9 .
Câu 20. Một đƣờng tròn có tâm I 3; 4 tiếp xúc với đƣờng thẳng  :3x  4y 10  0 . Hỏi bán kính
đƣờng tròn bằng bao nhiêu? 5 A. . 3 B. 5 . C. 3 . 3 D. . 5
Câu 21. Trong hệ trục tọa độ Oxy , cho điểm I 1; 
1 và đƣờng thẳng d  : 3x  4y  2  0 . Đƣờng tròn
tâm I và tiếp xúc với đƣờng thẳng d  có phƣơng trình 2 2 A. x   1   y   1  5 . 2 2 B. x   1   y   1  25 . 2 2 C. x   1   y   1  1.
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 96
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2 2 1 D. x   1   y   1  . 5
Câu 22. (LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trên hệ trục tọa độ Oxy , cho đƣờng tròn (C) có tâm I  3
 ;2 và một tiếp tuyến của nó có phƣơng trình là 3x  4y 9  0 . Viết phƣơng trình
của đƣờng tròn (C) . 2 2
A. x  3   y  2  2 . 2 2
B. x  3   y  2  2 . 2 2
C. x  3   y  2  4 2 2
D. x  3   y  2  4 .
Câu 23. Trên mặt phẳng toạ độ Oxy , cho các điểm A3; 0 và B 0; 4 . Đƣờng tròn nội tiếp tam giác
OAB có phƣơng trình A. 2 2
x y  1. B. 2 2
x y  4x  4  0 . C. 2 2 x y  2 . 2 2 D. x   1   y   1  1.
Câu 24. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho hai điểm A3;0 , B 0;4 . Đƣờng tròn nội
tiếp tam giác OAB có phƣơng trình là A. 2 2 x y  1 . B. 2 2
x y  2x  2 y  1  0 . C. 2 2
x y  6x  8 y  25  0 . D. 2 2 x y  2 .
DẠNG 4. TƢƠNG GIAO CỦA ĐƢỜNG THẲNG VÀ ĐƢỜNG TRÒN
Dạng 4.1. Phƣơng trình tiếp tuyến
Câu 25. Đƣờng tròn 2 2
x y 1  0 tiếp xúc với đƣờng thẳng nào trong các đƣờng thẳng dƣới đây?
A. 3x  4 y  5  0
B. x y  0
C. 3x  4 y 1  0
D. x y 1  0
Câu 26. Đƣờng tròn nào sau đây tiếp xúc với trục Ox: A. 2 2
x y 10x  0 . B. 2 2
x y  5  0 . C. 2 2
x y 10x  2 y 1  0 . D. 2 2
x y  6x  5y  9  0 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 97
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
Câu 27. Trong mặt phẳng với hệ tọa độ Oxy , cho đƣờng tròn C  2 2
: x y  2x  4 y  3  0 . Viết phƣơng d (C) trình tiếp tuyến của đƣờng tròn
biết tiếp tuyến đó song song với đƣờng thẳng
 :3x  4y 1  0 .
A. 3x  4y  5 2 11  0 ; 3x  4y  5 2 11  0 .
B. 3x  4y  5 2 11  0 , 3x  4y  5 2 11  0 .
C. 3x  4y  5 2 11  0 , 3x  4y  5 2 11  0 .
D. 3x  4y  5 2 11  0 , 3x  4y  5 2 11  0 .
Câu 28. Cho đƣờng tròn C  2 2
: x y  2x  4 y  4  0 và điểm A1;5 . Đƣờng thẳng nào trong các
đƣờng thẳng dƣới đây là tiếp tuyến của đƣờng tròn C  tại điểm A .
A. y  5  0 .
B. y  5  0 .
C. x y  5  0 .
D. x y  5  0 .
Câu 29. Cho đƣờng tròn C  2 2
: x y  4  0 và điểm A1; 2 . Đƣờng thẳng nào trong các đƣờng thẳng
dƣới đây đi qua A và là tiếp tuyến của đƣờng tròn C  ?
A. 4x  3y 10  0 .
B. 6x y  4  0 .
C. 3x  4 y 10  0 .
D. 3x  4y 11  0 . 2 2
Câu 30. Trong mặt phẳng Oxy , cho đƣờng tròn C  :  x  
1   y  4  4 . Phƣơng trình tiếp tuyến với
đƣờng tròn C  song song với đƣờng thẳng  : 4x 3y  2  0 là
A. 4x  3y 18  0 .
B. 4x  3y 18  0 .
C. 4x  3y 18  0; 4x  3y  2  0 .
D. 4x  3y 18  0; 4x  3y  2  0 . Câu 31. Số tiếp tuyến chung của 2 đƣờng tròn C 2 2
: x y  2x  4 y 1  0 và C  2 2
' : x y  6x  8y  20  0 là A. 1 . B. 2 . C. 4 . D. 3 . DẠNG 5. CÂU HỎI MIN-MAX
Câu 32. Cho đƣờng tròn C  2 2
: x y  2x  4 y  4  0 và điểm M 2 
;1 . Dây cung của C  đi qua điểm
M có độ dài ngắn nhất là A. 6 . B. 7 .
C. 3 7 . D. 2 7 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 98
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908
BÀI 3. PHƢƠNG TRÌNH ĐƢỜNG ELIP
DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP 2 2 x y Câu 1. Đƣờng Elip   1 có tiêu cự bằng 16 7 A. 6 . B. 8 . C. 9 . D.  2;    . Câu 2.
Cho elip  E  có phƣơng trình 2 2
16x  25y  400 . Khẳng định nào sai trong các khẳng định sau?
A. E  có trục nhỏ bằng 8.
B. E  có tiêu cự bằng 3.
C. E  có trục nhỏ bằng 10.
D. E  có các tiêu điểm F 3  ;0 F 3; 0 2   1   và . x y Câu 3.
Trong mặt phẳng với hệ tọa độ Oxy, cho elip  E  2 2 : 
 1. Tiêu cự của (E) bằng 25 9 A. 10. B. 16. C. 4. D. 8. Câu 4.
Một elip có diện tích hình chữ nhật cơ sở là 80 , độ dài tiêu cự là 6 . Tâm sai của elip đó là 4 A. e  . 5 3 B. e  . 4 3 C. e  . 5 4 D. e  . 3 Câu 5.
Cho elip  E  2 2
: 4x  5y  20 . Diện tích hình chữ nhật cơ sở của E là A. 2 5 . B. 80 . C. 8 5 . D. 40 . 2 2 x y Câu 6.
(Yên Định 1 - Thanh Hóa - 2018-2019) Đƣờng elip 
 1 có tiêu cự bằng 16 7 A. 3 . B. 9 . C. 6 . D. 18 .
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 99
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2 2 x y Câu 7.
Cho elip có phƣơng trình chính tắc 
 1. Tính tâm sai của elip. 4 1 2 A. . 3 1 B. . 2 1 C. . 4 3 D. . 2 Câu 8.
(TH&TT LẦN 1 – THÁNG 12) Trong mặt phẳng với hệ tọa độ Oxy , cho elip   2 2 x y E : 
 1 (với a b  0 ) có F , F là các tiêu điểm và M là một điểm di động trên  E  . 2 2 a b 1 2
Khẳng định nào dƣới đây là đúng?
A. MF MF  2b . 1 2 2
B. MF MF   4 2 2 b OM . 1 2  C. 2 2 2
OM MF .MF a b . 1 2 D. 2 2 2
MF .MF OM a b . 1 2 Câu 9.
Trong hệ trục Oxy, cho Elip  E  có các tiêu điểm F 4  ;0 , F 4;0 M 1 
 2   và một điểm nằm trên
E. Biết rằng chu vi của tam giác MF F bằng 18. Xác định tâm sai e của E. 1 2 4 A. e  . 5 4 B. e  . 18 4 C. e   . 5 4 D. e  . 9
Câu 10. Cho Elip  E  đi qua điểm A 3  5
; 0 và có tâm sai e
. Tiêu cự của  E  là 6 A. 10 . 5 B. . 3 C. 5 . 10 D. . 3
DẠNG 2. VIẾT PHƢƠNG TRÌNH ELIP
Câu 11. Trong mặt phẳng Oxy , phƣơng trình nào sau đây là phƣơng trình chính tắc của một elip?
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 100
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2 2 x y A.   1. 2 3 2 2 x y B.   1. 9 8 x y C.  1. 9 8 2 2 x y D.   1. 9 1
Câu 12. Phƣơng trình chính tắc của đƣờng elip với a  4 , b  3 là 2 2 x y A.   1. 16 9 2 2 x y B.   1. 9 16 2 2 x y C.   1. 16 9 2 2 x y D.   1. 9 16
Câu 13. Trong mặt phẳng tọa độ Oxy , viết phƣơng trình chính tắc của elip biết một đỉnh là A 5  ;0 1   và
một tiêu điểm là F 2; 0 2   . 2 2 x y A. 1 . 25 21 2 2 x y B. 1 . 25 4 2 2 x y C. 1 . 29 25 2 2 x y D. 1 . 25 29
Câu 14. Tìm phƣơng trình chính tắc của Elip có độ dài trục lớn bằng 4 10 và đi qua điểm A0;6 : 2 2 x y A.  1. 40 12 2 2 x y B.   1 . 160 36 2 2 x y C.   1 . 160 32 2 2 x y D.  1. 40 36 5
Câu 15. Lập phƣơng trình chính tắc của Elip đi qua điểm B và có tâm sai e  . 3 2 2 x y A.   1 . 9 4
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 101
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2 2 x y B.   1. 3 2 2 2 x y C.   1. 9 2 2 2 x y D.   1 9 3
Câu 16. Phƣơng trình chính tắc của Elip có đỉnh 3;0 và một tiêu điểm là 1;0 là 2 2 x y A.   1 . 8 9 2 2 x y B.  1 . 9 8 2 2 x y C.   1 . 1 9 2 2 x y D.   1 . 9 1
Câu 17. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Tìm phƣơng trình chính tắc của elip có tiêu cự
bằng 6 và trục lớn bằng 10 . 2 2 x y A.   1. 25 9 2 2 x y B.   1. 16 25 2 2 x y C.   1. 100 81 2 2 x y D.   1. 25 16
Câu 18. (LƢƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Cho elip  E  có độ dài trục lớn gấp hai lần
độ dài trục nhỏ và tiêu cự bằng 6 . Viết phƣơng
trình của  E  ? 2 2 x y A.   1. 12 3 2 2 x y B.  1 . 12 3 2 2 x y C.  1 . 3 12 2 2 x y D.   1. 48 12
Câu 19. Phƣơng trình chính tắc của Elip có độ dài trục lớn bằng 8 , độ dài trục nhỏ bằng 6 là: 2 2 x y A.   1. 9 16
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 102
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 2 2 x y B.   1 . 64 36 2 2 x y C.   1. 8 6 2 2 x y D.   1 16 9
Câu 20. Elip có một tiêu điểm F
2;0 và tích độ dài trục lớn với trục bé bằng 12 5 . Phƣơng trình
chính tắc của elip là: 2 2 x y A. 1. 9 5 2 2 x y B. 1. 45 16 2 2 x y C. 1. 144 5 2 2 x y D. 1. 36 20  3 4 
Câu 21. Trong mặt phẳng Oxy , viết phƣơng trình chính tắc của elip  E  biết  E  đi qua M ;    5 5 
và M nhìn hai tiêu điểm F , F dƣới một góc vuông. 1 2 x y A. E  2 2 :  1. 4 9 x y B. E  2 2 :  1. 9 4 x y C. E  2 2 :  1. 2 3 x y D. E  2 2 :  1. 3 2
DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC 2 2 x y
Câu 22. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho Elip (E) : 
1 và điểm M nằm trên 16 12
(E). Nếu điểm M có hoành độ bằng 1 thì các
khoảng cách t M đến hai tiêu điểm của (E) bằng: A. 3, 5 và 4, 5 . B. 4  2 . C. 3 và 5. 2 D. 4  . 2
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 103
Nguyễn Văn Thanh -GV chuyên Toán cấp 3, Khu vực Cây Xăng 26, Biên Hòa –ĐT.(0918)389.908 x y
Câu 23. Trong mặt phẳng với hệ tọa độ Oxy , cho elip E 2 2 : 
1 . Điểm M E sao cho 25 9 0 F MF  90 . MF F . 1 2
Tìm bán kính đƣờng tròn nội tiếp tam giác 1 2 A. 2 B. 4 . C. 1 . 1 D. . 2 ….HẾT…
Facebook: Nguyễn Văn Thanh. FanPage: Toán Học Trẻ Hàm Rồng – Biên Hòa 104