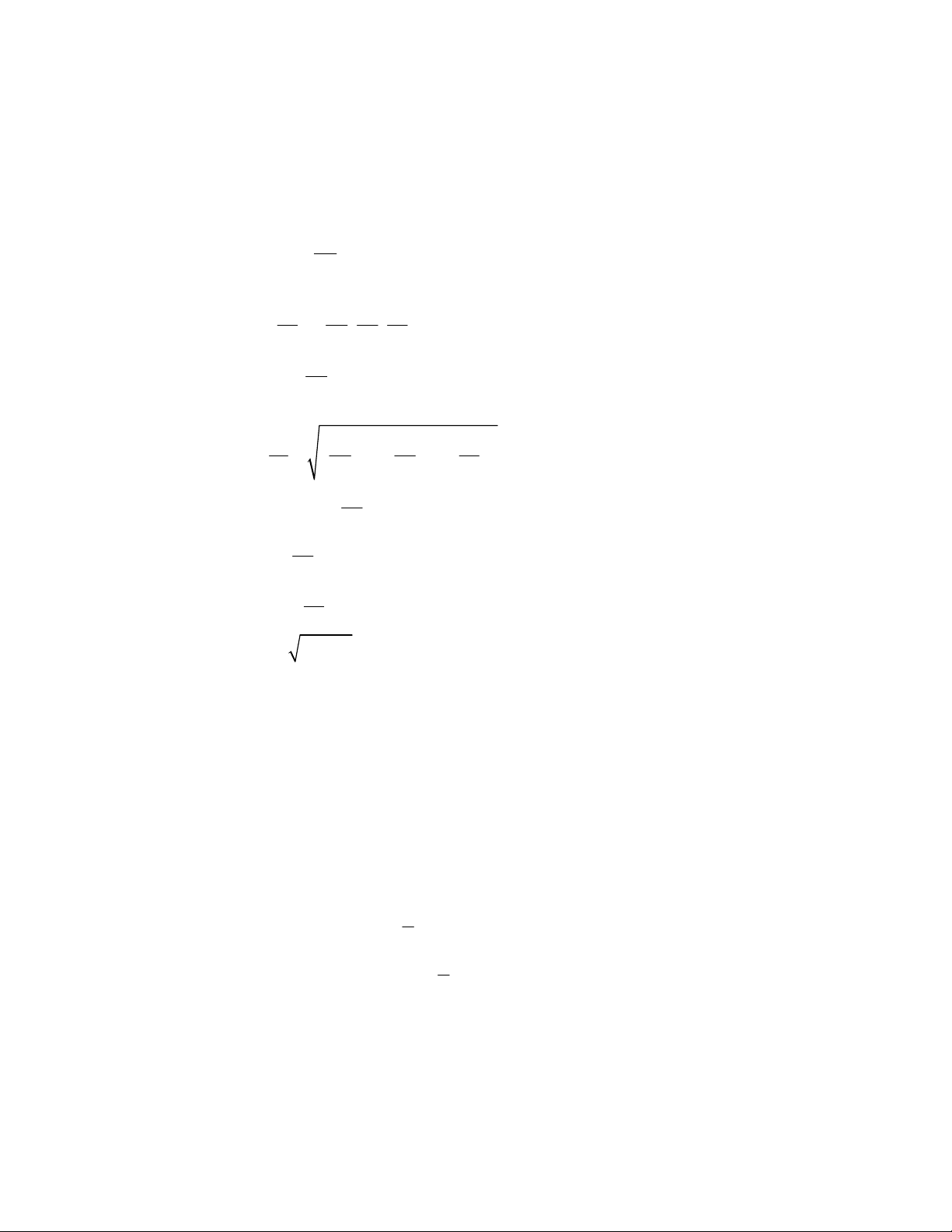













































Preview text:
lOMoARcPSD|36442750
Chương 1.1. Động học chất điểm
A. Tóm tắt lý thuyết
1. Các đại lượng đặc trưng trong chuyển động của chất điểm.
r - véc-tơ bán kính của chất điểm
r rx, y,z - x,y,z là các tọa độ của chất điểm trong hệ trục tọa độ Descartes vuông góc.
- vận tốc trung bình: r v tb t
Trong đó r là véc-tơ độ dời của chất điểm sau khoảng thời gian t .
- vận tốc tức thời: dr dx dy dz v ; ; dt dt dt dt
- tốc độ trung bình: s v tb t Trong đó s
là quãng đường mà chất điểm chuyển động được trong khoảng thời gian t . 2 2 2
- tốc độ tức thời: ds dx dy dz v dt
dt dt dt
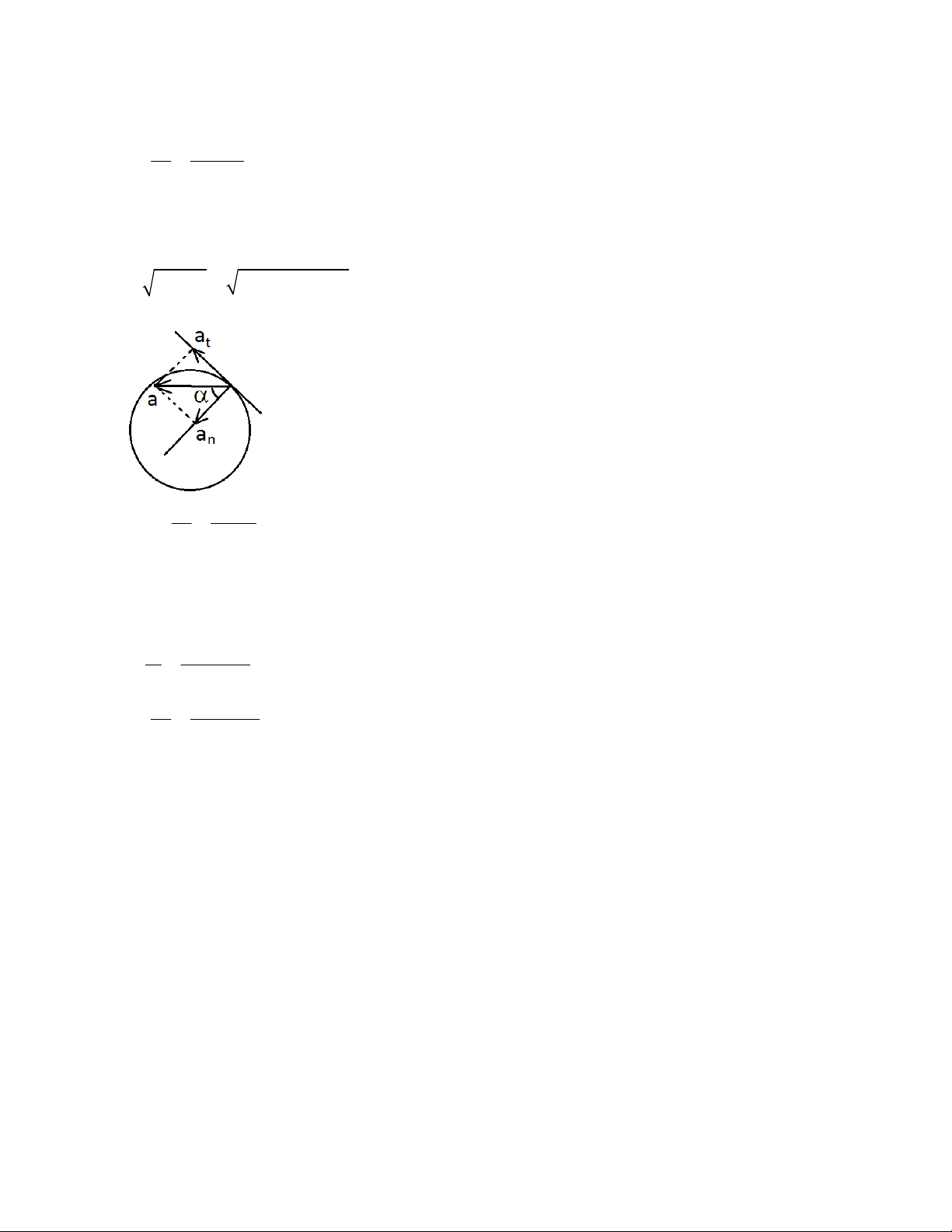
- véc-tơ gia tốc toàn phần: dv a a a t n dt
Gia tốc tiếp tuyến: dv a t dt 2
Gia tốc pháp tuyến: v a n R
Gia tốc toàn phần: 2 2 a a a t n
R – bán kính cong của quỹ đạo tại điểm đang xét.
2. Các dạng chuyển động
a. Chuyển động thẳng đều: - Gia tốc: a = 0;
- Vận tốc: v = const;
- Phương trình quãng đường: s = vt
- Phương trình chuyển động (phương trình tọa độ):
x = x0 + vt; trong đó x0 là tọa độ của chất điểm tại thời điểm ban đầu.
b. Chuyển động thẳng biến đổi đều:
- Gia tốc: a = const;
- Vận tốc: v = v0 + at; v0 là vận tốc ban đầu.
- Phương trình quãng đường: 1 2 s v t at 0 2
- Phương trình chuyển động: 1 2 x x v t at 0 0 2
- Công thức độc lập thời gian: 2 2 v v 2as 0 Chú ý:
Chuyển động thẳng nhanh dần đều a v
Chuyển động thẳng chậm dần đều a v
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
chứ không phải a>0 hay a<0 ! c. Sự rơi tự do
là trường hợp đặc biệt của chuyển động nhanh dần đều với:
v0 = 0; a = g = 9,81 m/s2
d. Chuyển động ném xiên a 0 - Gia tốc: x a a g y v v v cos - Vận tốc: x 0x 0 v
v v a t v sin gt y 0y y 0 x v t v cos . t 0x 0
- Phương trình chuyển động: 1 2 y v sin . t gt 0 2
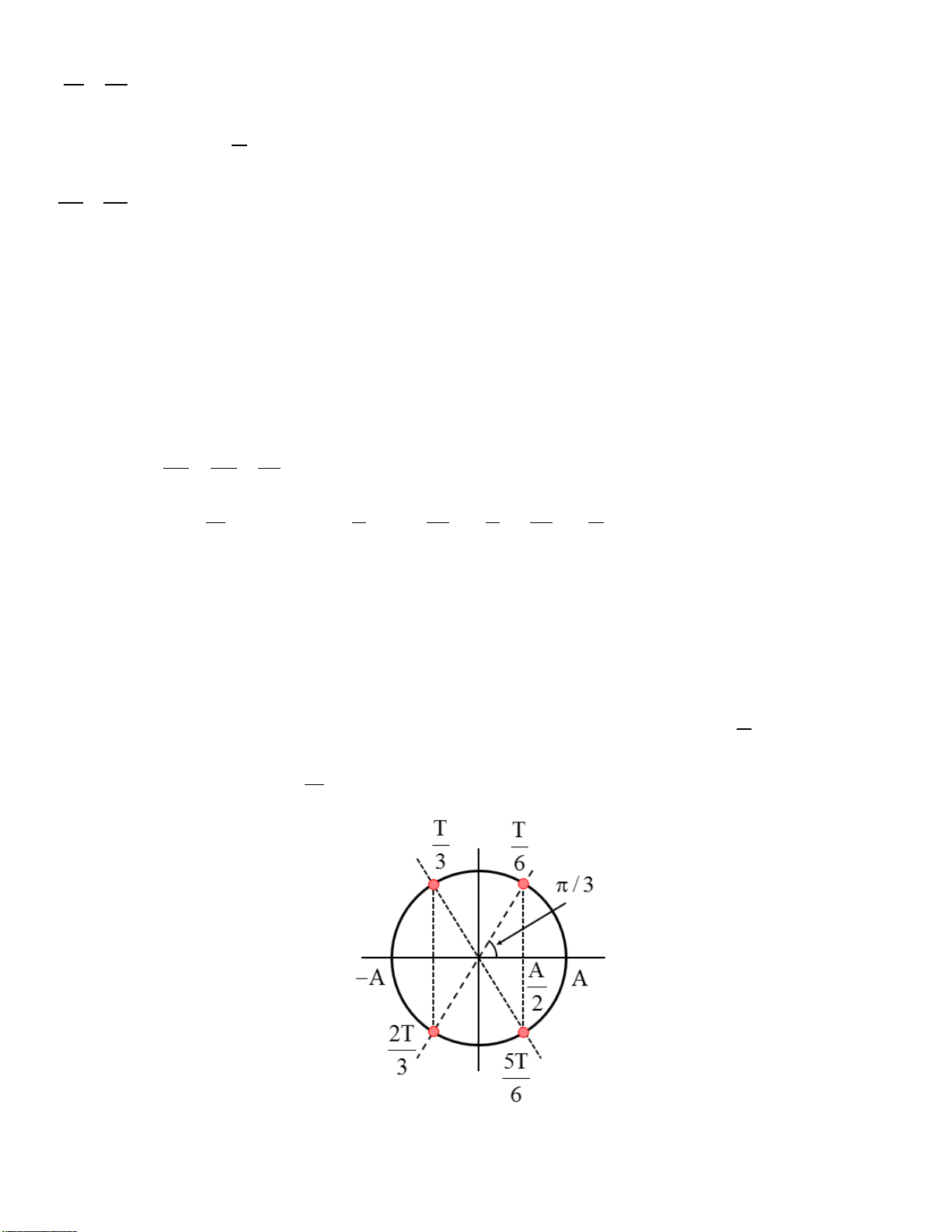
- Phương trình quỹ đạo: g 2 y x.tan .x Parabol 2 2 2v cos 0 2 2 - Độ cao cực đại: v sin 0 h max 2g 2 - Tầm xa: v sin 2 0 L x max g e. Chuyển động tròn - vận tốc góc: d
, trong đó là góc quay. dt 2 - gia tốc góc: d d 2 dt dt
Đối với chuyển động tròn đều:
const; 0. t - chu kỳ: 2 T - tần số: 1 T 2
Đối với chuyển động tròn biến đổi đều: const
- vận tốc góc: t 0
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 - góc quay: 1 2 t t 0 2
- công thức độc lập thời gian: 2 2 2 0
Liên hệ giữa vận tốc, gia tốc dài với vận tốc và gia tốc góc: 2 v R, a R , v 2 a R t n R
Bài 1.4. Một vật được thả rơi từ một khí cầu đang bay ở độ cao 300 m. Hỏi sau bao lâu vật rơi tới mặt đất, nếu:
a) Khí cầu đang bay lên (theo hướng thẳng đứng) với vận tốc 5 m/s;
b) Khí cầu hạ xuống (theo phương thẳng đứng) với vận tốc 5 m/s;
c) Khí cầu đang đứng yên. Bài giải:
Gốc tọa độ tại điểm thả vật, chiều dương hướng thẳng đứng xuống dưới. Vận tố của khí cầu là v0.
Có thể coi đây là chuyển động rơi tự do của 1 vật có vận tốc ban đầu. Ta có: 1 2
h v t gt , giải phương trình này ta được nghiệm: 0 2 2 v 2gh v 0 0 t g thay số:
a) v0 = - 5 m/s (chuyển động ngược chiều dương) g = 10 m/s2, h = 300 m 2 5 2.10.300 5 t 8,3s 10 b) v0 = 5 m/s, 2 5 2.10.300 5 t 7,3s 10
c) v0 = 0 m/s (khí cầu đứng yên) 2.10.300 t 7,7s 10
Bài 1.6. Thả rơi tự do từ độ cao h = 19,6 m. Tính:
a) Quãng đường mà vật rơi được trong 0,1 giây đầu tiên và 0,1 giây cuối của thời gian rơi.
b) Thời gian cần thiết để vật đi hết 1 m đầu và 1 m cuối của độ cao h. Bài giải:
Công thức quãng đường: 1 2 s gt 2
a) Quãng đương vật rơi được trong 0,1 giây đầu: 1 2 s .9,8.0,1 0,049 m 0,1s 2
Thời gian để vật rơi hết cả quãng đường h =19,6 m là:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2h 2.19,6 t 2 s 19,6m g 9,8
Như vậy quãng đường mà vật rơi được trong 0,1 giây cuối bằng quãng đường 19,6 m trừ đi quãng
đường vật rơi được trong 1,9 s đầu tiên.
Quãng đường vật rơi được trong 1,9 s đầu tiên: 1 2 1 2
s gt .9,8.1,9 17,7 m 1,9s 2 2
Quãng đường vật rơi được trong 0,1 s cuối cùng:
s0,1 giây cuối = 19,6 – 17,7 = 1,9 (m).
b) thời gian để vật rơi hết 1 m đầu tiên là: 2h 2.1 1 t 0,45 s 1m g 9,8
Thời gian để vật rơi hết 1 m cuối cùng bằng thời gian để vật rơi cả quãng đường 19,6 m trừ đi thời gian vật rơi 18,6 m:
Thời gian vật rơi 18,6 m: 2h 2.18,6 2 t 1,95 s 18,6m g 9,8
Như vậy thời gian rơi 1 m cuối:
t1m cuối cùng = 2 -1,95 = 0,05 (s).
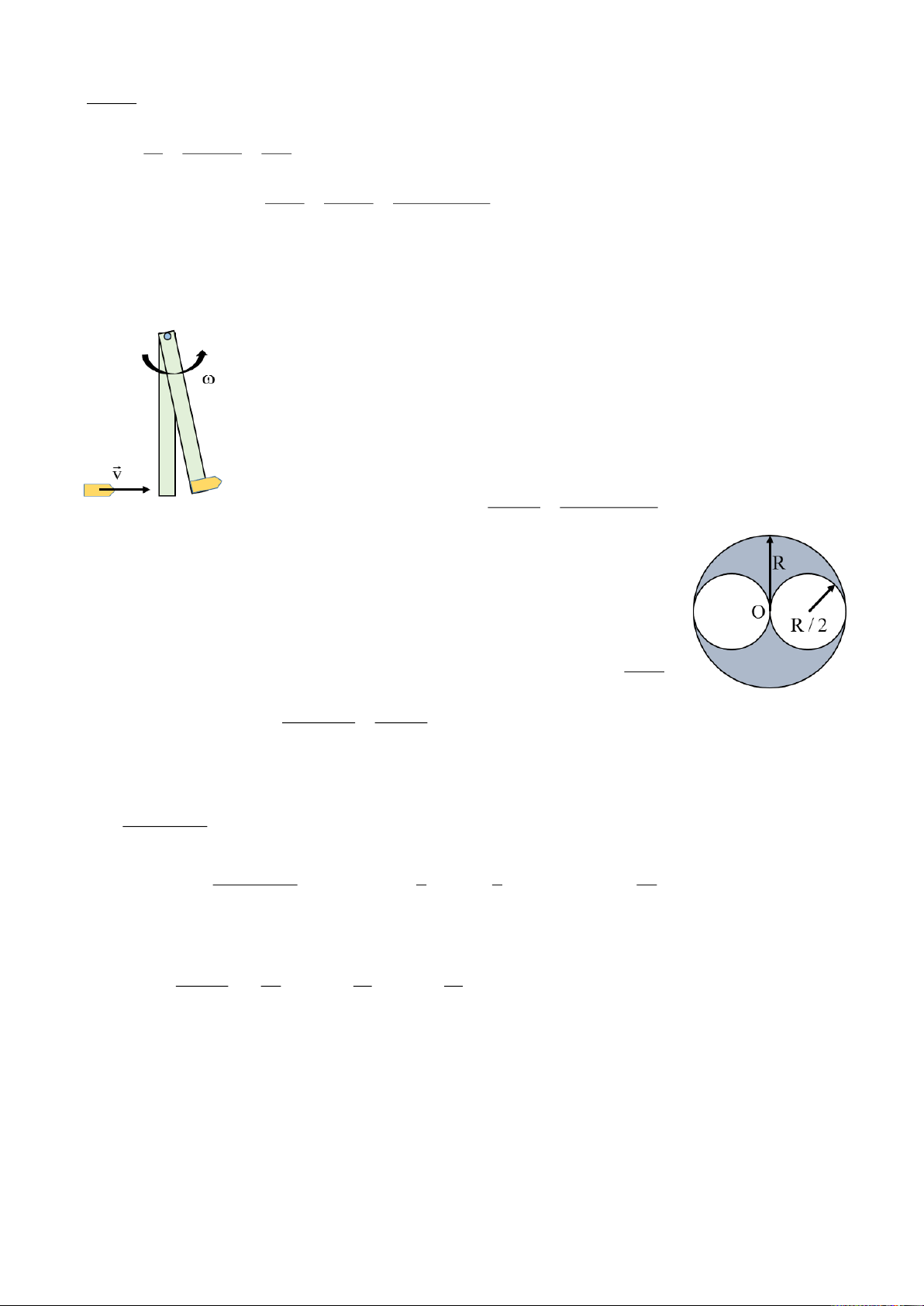
Bài 1.20. Một vô lăng sau khi bắt đầu quay được một phút thì thu được vận tốc 700 vòng/phút.
Tính gia tốc góc của vô lăng và số vòng mà vô lăng đã quay được trong phút ấy nếu chuyển động
của vô lăng là nhanh dần đều. Bài giải: Ta có: t = 1 phút = 60 giây, n 700 (vòng/phút) 70 700.2 / 60 rad / s 3 Gia tốc: 70 1 7 0 2 rad / s t 3 60 18 2 2 2 2 0
2 0 2 2 2 70 / 3
700rad 350 (vòng). 2 2.7 /18
Bài 1.22. Một bánh xe có bán kính R = 10 cm lúc đầu đứng yên, sau đó quay xung quanh trục của
nó với gia tốc góc bằng 3,14 rad/s2. Hỏi sau giây thứ nhất:
a) Vận tốc góc và vận tốc dài của một điểm trên vành bánh?
b) Gia tốc pháp tuyến, gia tốc tiếp tuyến và gia tốc toàn phần của một điểm trên vành bánh?
c) Góc giữa gia tốc toàn phần và bán kính của bánh xe (ứng với cùng một điểm trên vành bánh)? Bài giải:
a) vận tốc góc sau giây thứ nhất: 3,14rad / s
Vận tốc dài: v R 0,1.3,14 0,314m / s
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 b) gia tốc pháp tuyến: 2 2 v 0,314 a 0,99 2 m / s n R 0,1 Gia tốc tiếp tuyến:
a R 3,14.0,1 0,314 2 m / s t Gia tốc toàn phần: 2 2 2 2
a a a 0,99 0,314 1,1 2 m / s n t c) a 0,314 t 0 0 tan 17,6 17 36' a 0,99 n
Bài 1.25. Vận tốc của electron trong nguyên tử hydro bằng v =2,2.108 cm/s. Tính vận tốc góc và
gia tốc pháp tuyến của electron nếu xem quỹ đạo của nó là một vòng tròn bánh kính 0,5.10-8 cm. Bài giải: 6 v 2,2.10 16 4,4.10 rad / s 10 R 0,5.10 2 2 12 v 2,2 .10 22 a 9,68.10 2 rad / s n 10 R 0,5.10
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Chương 1.2. Động lực học chất điểm
A. Tóm tắt lý thuyết
Phương pháp giải một bài toán động lực học:
Bước 1: Xác định đầy đủ và chính xác các lực tác dụng lên vật.
Bước 2: Viết phương trình cơ bản của động lực học (phương trình định luật 2 Newton):
F ma , trong đó F là hợp lực tác dụng lên vật
Bước 3: Chiếu phương trình lên các phương, thu được phương trình đại số và giải.
1. Các loại lực: a) Lực ma sát nghỉ: F F F N , trong đó F là msn td msn max n
td là lực tác dụng, Fmsn max là lực ma sát nghỉ cực đại, n
hệ số ma sát nghỉ, N là áp lực vuông góc tác dụng lên vật.
b) Lực ma sát động (gồm ma sát trượt và lăn):
F N;F N , trong đó ; lần lượt là hệ số ma sát trượt và hệ số ma sát lăn. mst t msl l t l Chú ý: l t n c) Lực đàn hồi:
Định luật Hooke: F kl;F k l dh dh
Lực đàn hồi tỷ lệ thuận và ngược chiều với độ biến dạng.
2. Động lượng và định luật bảo toàn động lượng a) Động lượng
K mv, trong đó m là khối lượng của chất điểm, v là véc-tơ vận tốc. Đơn vị của K là kg.m/s
Các định lý động lượng:
Định lý 1: Đạo hàm động lượng của chất điểm theo thời gian có giá trị bằng tổng các ngoại lực
tác dụng lên chất điểm đó. dK F dt
- Định lý 2: Độ biến thiên động lượng của một chất điểm trong một khoảng thời gian nào đó có
giá trị bằng xung lượng của lực tác dụng lên chất điểm trong khoảng thời gian đó. t2 t2 K
K K dK Fdt 2 1 1 t 1 t
+ Hệ quả: Độ biến thiên động lượng của chất điểm theo thời gian có giá trị bằng lực tác dụng lên
chất điểm trong thời gian đó. K F F TB t
b) Định luật bảo toàn động lượng:
Tổng động lượng của hệ cô lập được bảo toàn. K const Chú ý:
- Viết trong hệ quy chiếu quán tính (có thể hiểu là hệ quy chiếu đứng yên hoặc chuyển động thẳng
đều, hay đơn giản là hệ quy chiếu gắn với mặt đất)
- Một số bài toán áp dụng được định luật bảo toàn động lượng:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
+ Hệ không có ngoại lực tác dụng;
+ Hệ có ngoại lực tác dụng nhưng tổng hợp ngoại lực bằng 0;
+ Hệ có nội lực rất lớn so với ngoại lực (bài toán viên đạn nổ);
+ Hệ có ngoại lực khác 0 nhưng hình chiếu lên 1 phương nào đó của lực bằng 0 thì định luật bảo
toàn động lượng có thể áp dụng theo phương đó, tức là:
Nếu F 0 thì K const . x x
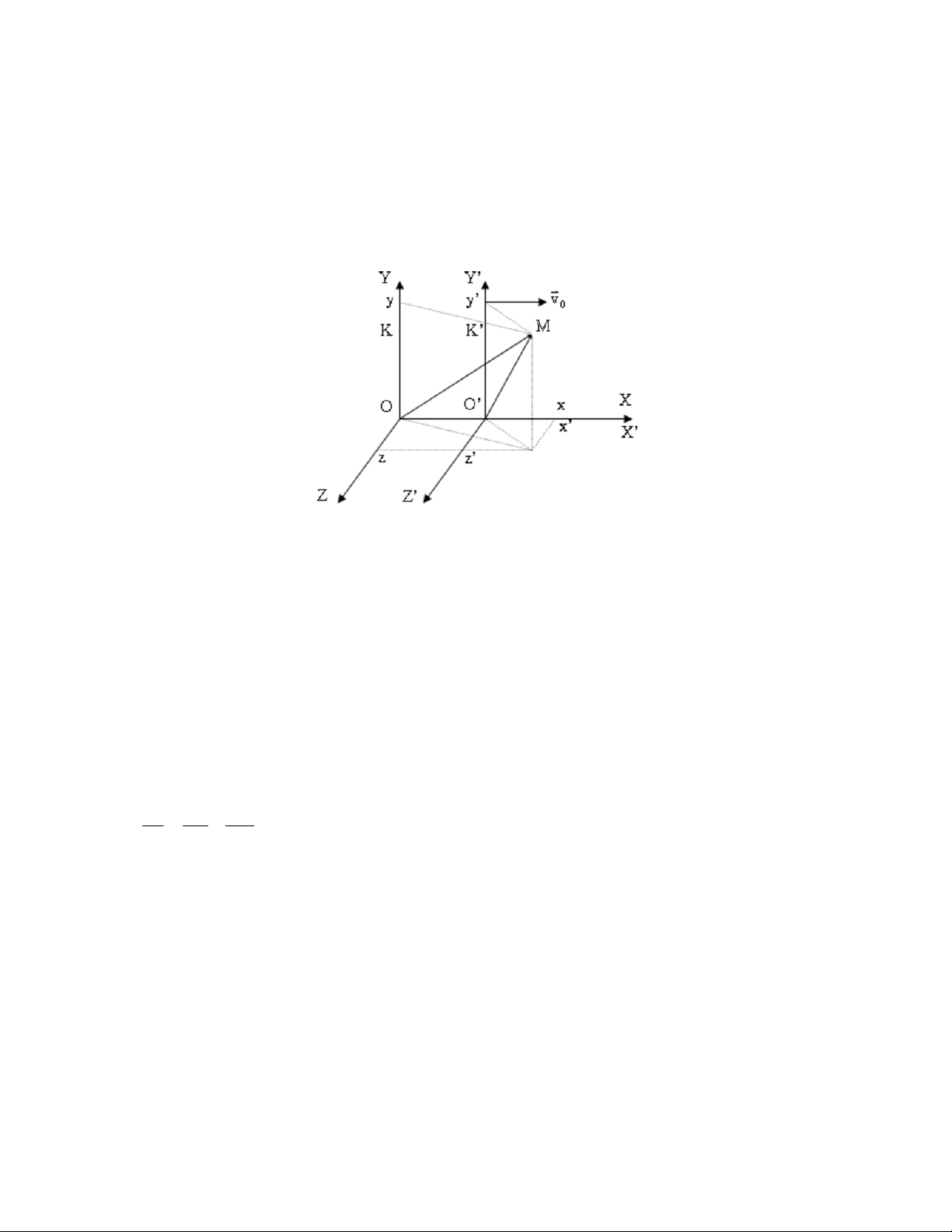
3. Phép biến đổi Galile Từ K’ sang K x = OO’+x’= x’+vot’ y = y’ z = z’ t = t’ Từ K sang K’ x’= x-vot’ y’= y z’= z t’= t Vận tốc:
vv ,v ,v v v ,v ,v v v ,0,0 x y z x y z 0 0 Gia tốc: dv dv dv 0 a a A dt dt dt
A là gia tốc của hệ K’ đối với hệ K.
Phương trình định luật 2 Newton trong hệ quy chiếu không quán tính:
ma F mA F F ; qt
trong đó: F mA là lực quán tính. qt B. Bài tập
Các bài tập thầy sẽ chữa trên lớp
2.1, 2.5, 2.9, 2.11,2.13, 2.15, 2.16, 2.22, 2.24, 2.34, 2.35
Bài tập phải làm để nộp:
2.3, 2.4, 2.6, 2.10, 2.12, 2.25, 2.31, 2.36
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bài 2.1. Một xe có khối lượng 20000 kg, chuyển động chậm dần đều dưới tác dụng của 1 lực bằng
6000 N, vận tốc ban đầu của xe bằng 15 m/s. Hỏi: a) Gia tốc của xe;
b) Sau bao lâu xe dừng lại;
c) Đoạn đường xe đã chạy được kể từ lúc hãm cho đến khi xe dừng hẳn. Tóm tắt: 4
m 2.10 kg;F 6000 N c v 15 m / s 0 a)a ? b)t ?v 0 c)s ? Bài giải: a) F 6000 c a 0,3 m / s 4 2 m 2.10 b) v v 0 15 0 v v at t 50 s 0 a 0 ,3 2 2 2 2 c) v v 0 15 0 s 375m 2a 2.0 ,3
Bài 2.5. Một vật có khối lượng m = 5 kg được đặt trên một mặt phẳng nghiêng hợp với mặt phẳng nằm ngang một góc 0
30 . Hệ số ma sát giữa vật và mặt phẳng nghiêng bằng k = 0,2. Tìm gia
tốc của vật trên mặt phẳng nghiêng. Tóm tắt: 0 m 5 kg ; 30 ;k 0,2 a ? Bài giải:
Phương trình định luật 2 Newton: P N F ma ms
Chiếu lên phương chuyển động:
Psin F ma mgsin kN ma 1 Chiếu lên phương vuông góc với phương chuyển ms động:
Pcos N 0 N mg cos
Thế biểu thức trên vào (1) ta được:
mgsin kmg cos ma mgsin kmg cos a m gsin kg cos Thay số: 0 0 2 a 10.sin 30 10.0,2.cos30 3,3 m / s
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
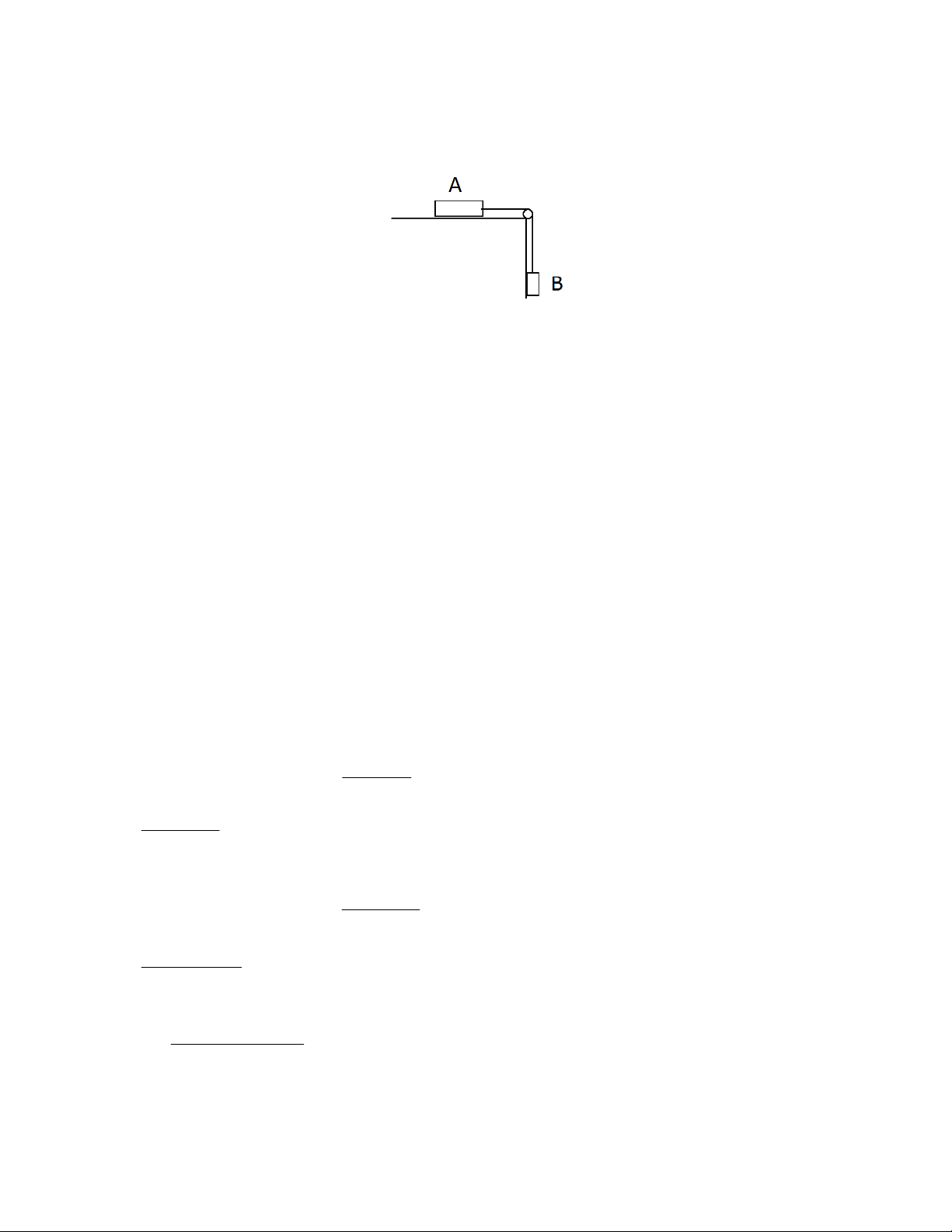
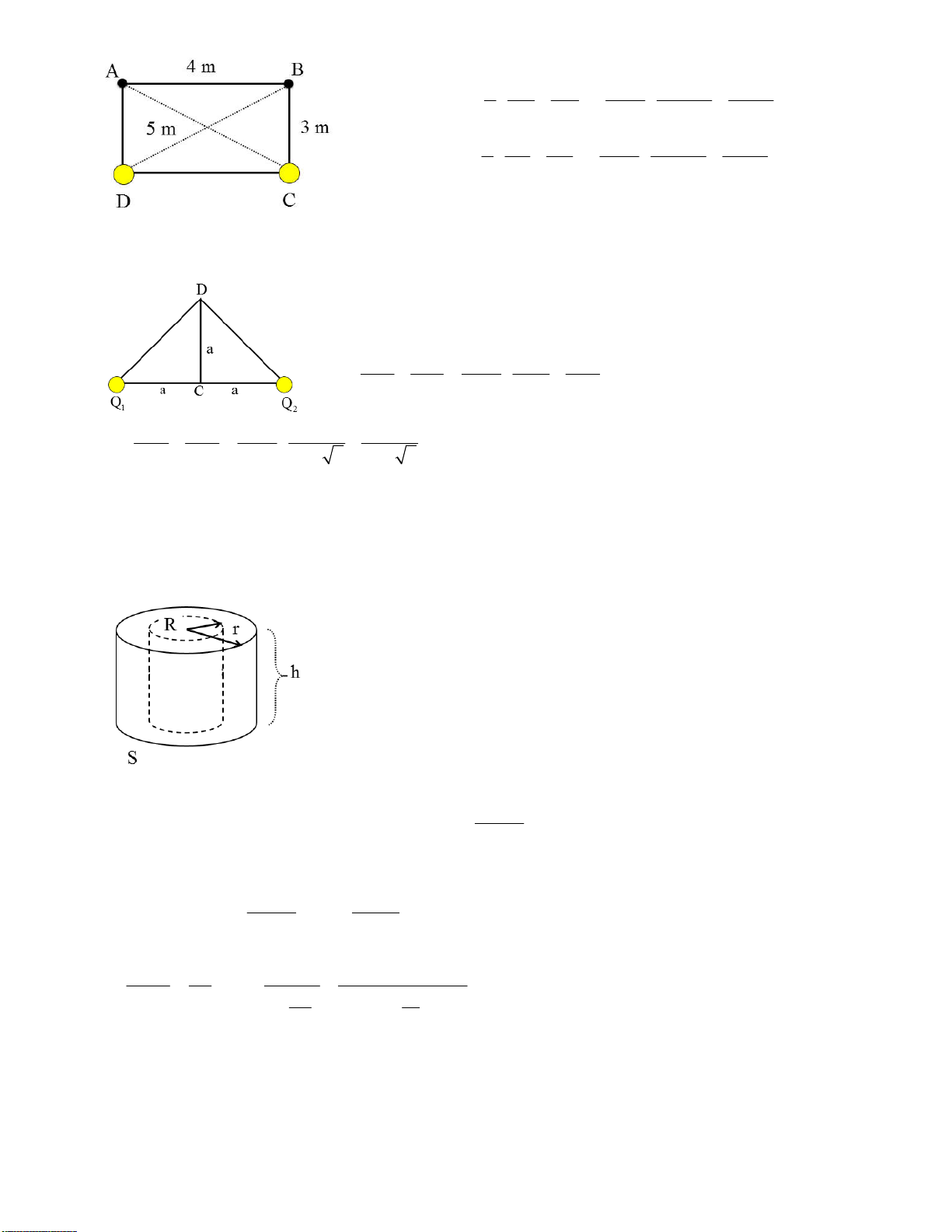
Bài 2.11. Một bản gỗ A được đặt trên một mặt phẳng nằm ngang. Bản A được nối với một bản gỗ
B khác bằng một sợi dây vặt qua một ròng rọc cố định. Khối lượng của ròng rọc và của dây coi như không đáng kể.
a) Tính lực căng của dây nếu cho mA = 200 g; mB = 300 g, hệ số ma sát giữa bản A và mặt phẳng nằm ngang là k = 0,25.
b) Nếu thay đổi vị trí của A và B thì lực căng của dây sẽ bằng bao nhiêu? Xem hệ số ma sát vẫn như cũ. Bài giải:
a) Các lực tác dụng vào vật A là: P , N ,T,F A A ms
Phương trình định luật 2 Newton:
P N T F m a A A ms A
Chiếu lên phương ngang, chiều dương là chiều chuyển động (giả sử vật B đi xuống):
T F m a T kN m a (1) ms A A A
Chiếu lên phương thẳng đứng ta được:
N P 0 F kN kP A A ms A A
Thay vào biểu thức (1) được: T kP m a A A
Đối với vật B, các lực tác dụng là P ,T , phương trình định luật 2 Newton: B P T m a B B
Chiếu lên phương thẳng đứng (chiều dương là chiều chuyển động) ta được: P T m a (2) B B
Cộng (1) và (2) ta được: P kP m m P kP B A a a B A A B m m A B m km B A g m m A B
Thay giá trị này của gia tốc a vào biểu thức (1) để tính lực căng T: m km B A
T km g m a m kg g A A A m m A B m m k 1 A B g (*) m m A B Thay số ta được: 0,25 1.0,2.0,3 T 10 1,5N 0,2 0,3
b) Từ biểu thức (*) tổng quát của lực căng T ta thấy vai trò của A và B có tính hoán vị, vì thế nếu
đổi vị trí A và B cho nhau thì lực căng T không đổi.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
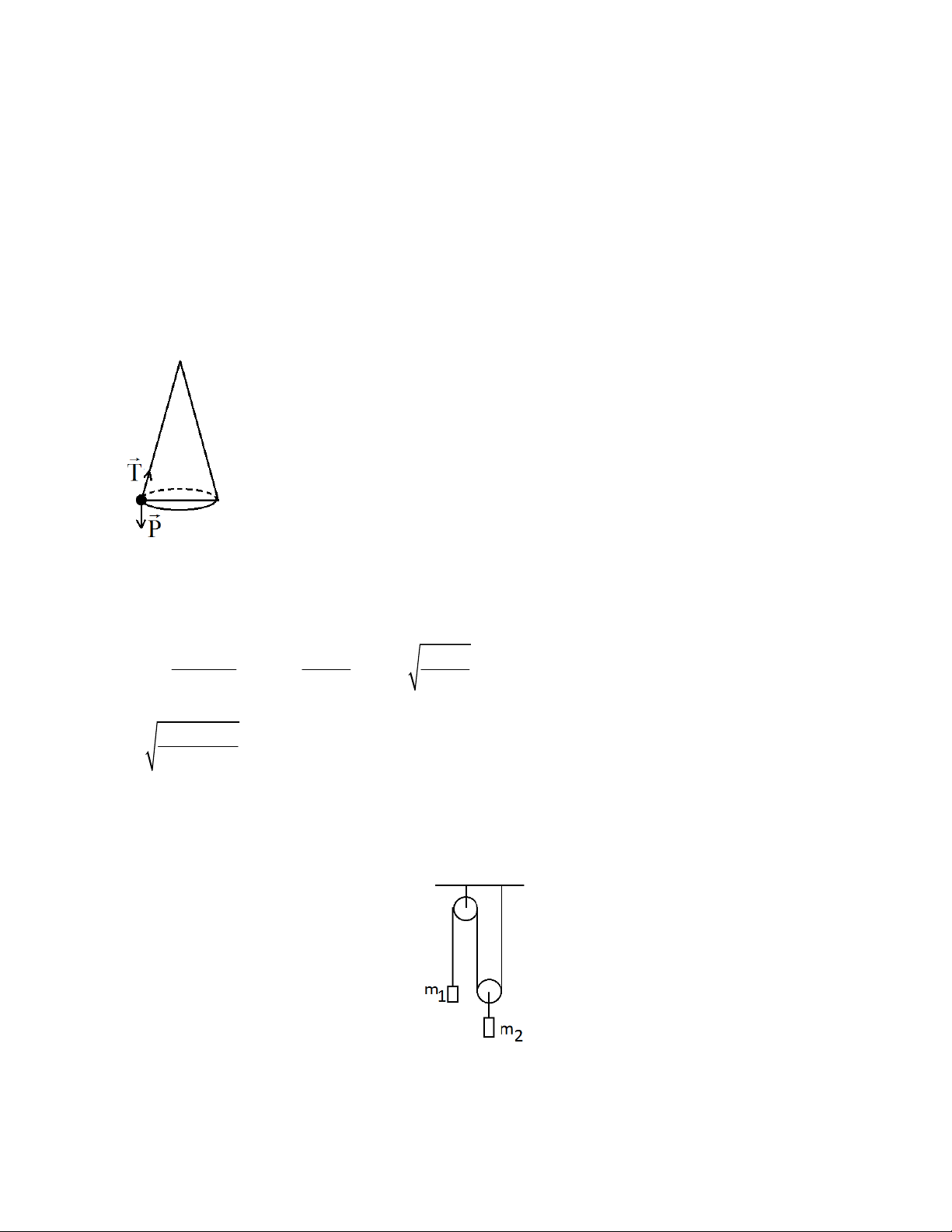
Bài 2.15. Một vật có khối lượng m = 200 g, được treo ở đầu một sợi dây dài l = 40 cm; vật quay
trong mặt phẳng nằm ngang với vận tốc không đổi sao cho sợi dây vạch một mặt nón. Giả sử khi
đó dây tạo với phương thẳng đứng một góc 0 36 .
Tìm vận tốc góc của vật và lực căng của dây. Tóm tắt:
m 200g 0,2kg;l 40cm 0,4m 0 36 v ? T ? Bài giải:
Các lực tác dụng vào vật gồm có: T,P
Phương trình định luật 2 Newton: T P ma
Chiếu lến phương bán kính
của quỹ đạo ta được: 2 2
Tsin ma m R m lsin ht
Chiếu lên phương thẳng đứng lại được:
T cos P 0 T cos mg
Chia vế với vế của 2 phương trình trên ta được 2 lsin 2 g g tan g lcos lcos Thay số ta được: 10 6,52 rad / s 0 0,4sin 36
Chú ý: bài này phải làm như trên, chứ đây không phải là 1 bài toán cân bằng lực nhé, cho nên
nguyên tắc là giải như 1 bài động lực học bình thường, gồm các bước xác định lực, viết phương
trình định luật 2 Newton, chiếu lên các phương và giải!
Bài 2.16. Xác định gia tốc của vật m1 trong hình vẽ. Bỏ qua ma sát, khối lượng của ròng rọc và
dây. Áp dụng cho trường hợp m1 = m2. Lời giải:
Chọn hệ quy chiếu hướng thẳng đứng xuống dưới.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Chứng minh a1 = 2a2 (đọc thêm để biết cách chứng minh cho những bài có cơ hệ phức tạp hơn),
tất nhiên có thể nói ngắn gọn là vì vật 1 chuyển động được quãng đường là s, thì vật 2 chỉ chuyển
động được quãng đường 0,5s nên nếu ban đầu hệ đứng yên, dễ dàng suy ra gia tốc của vật 1 lớn
gấp đôi gia tốc vật 2. Dưới đây là 1 cách thú vị để chứng minh cho những cơ hệ phức tạp (nghĩa
là gồm nhiều ròng rọc động hơn, nhiều vật hơn).
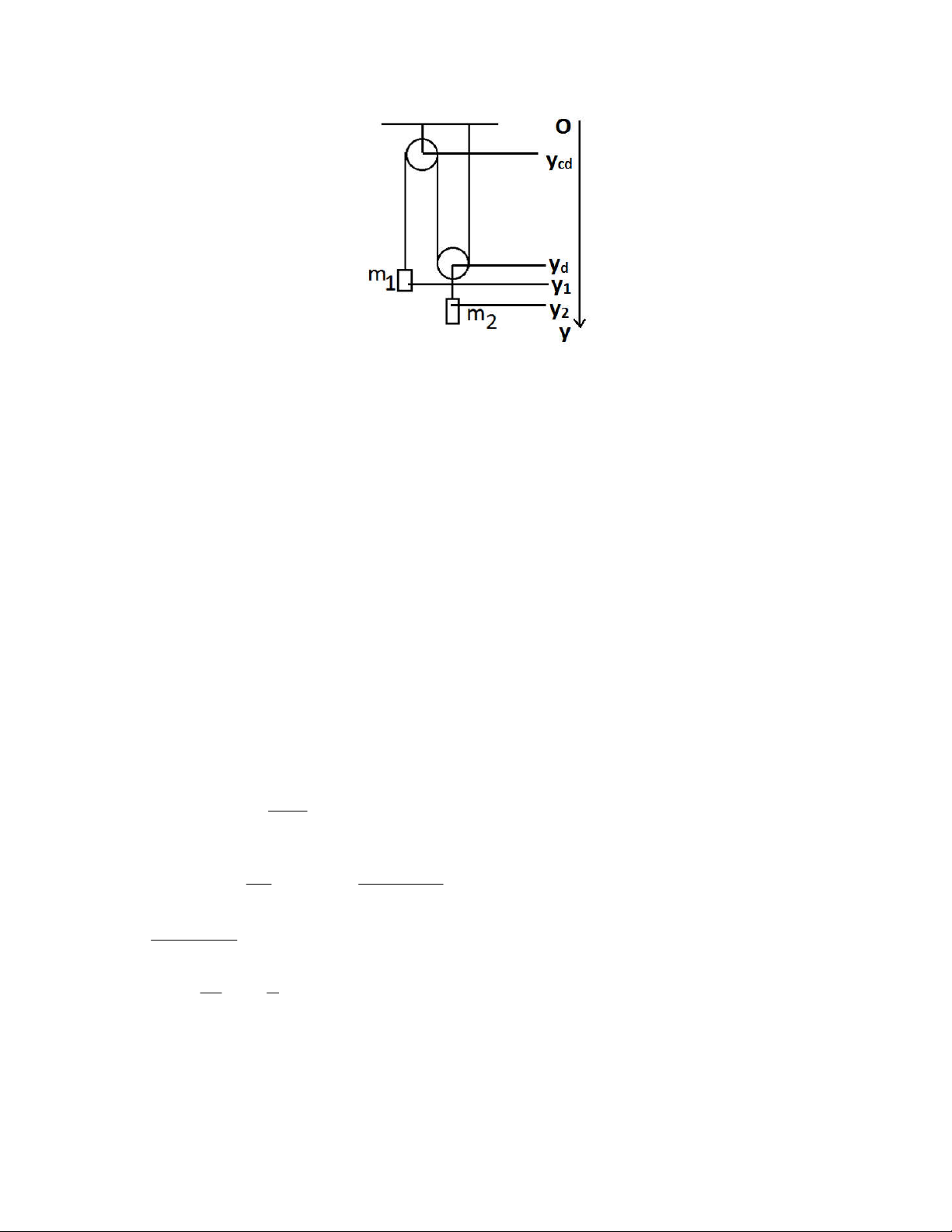
Gọi ycd là tọa độ của ròng rọc cố định,
yd là tọa độ ròng rọc động, y1 và y2 lần lượt là tọa độ của vật 1 và 2.
Chiều dài sợi dây trong thí nghiệm trên chính là:
y1 – ycd + (yd – ycd) + yd = const
đạo hàm biểu thức trên 2 lần và chú ý ycd = const, ta được:
a1 = - 2ad, tức là gia tốc của vật 1 gấp đôi và ngược chiều với gia tốc của ròng rọc động (tức là gia
tốc của vật 2), như vậy về độ lớn a1 = 2a2.
OK!, giờ bắt đầu vào bài toán của chúng ta:
Đối với vật 1, các lực tác dụng là P ,T , ta có: 1
P T m a , chiếu lên phương chuyển động ta được: P T m a (1) 1 1 1 1 1
Tương tự đối với vật 2:
P 2T m a (vì sợi dây không giãn, không có khối lượng nên lực căng ở chỗ nào cũng bằng 2 2 nhau).
Chiếu lên phương chuyển động: m a 2 1 P 2T m a (2) 2 2 2 2
Nhân 2 lần phương trình (1) rồi trừ đi (2) theo vế ta được: m 22P P 2 1 2 2P P 2m a a 1 2 1 1 1 2 4m m 1 2 2m m 1 2 2g
, với trường hợp m m m 4m m 1 2 1 2 Ta có: 2g g a ;a 1 2 5 5
Bài 2.22. Tính lực đẩy trung bình của hơi thuốc súng lên đầu đạn ở trong nòng một súng bộ binh,
biết rằng đầu đạn có khối lượng m = 10 g; thời gian chuyển động của đạn trong nòng là t = 0,001
giây, vận tốc của viên đạn ở đầu nòng là v = 865 m/s. Lời giải:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bài này nên áp dụng định lý về động lượng như sau: K mv 0 mv K F t F t t t 0,01.865 8650N 0,001
Bài 2.35. Xác định lực nén phi công vào ghế máy bay ở các điểm cao nhất và thấp nhất của vòng
nhào lộn nếu khối lượng của phi công bằng 75 kg, bán kính của vòng nhào lộn bằng 200 m, và vận
tốc của máy bay trong vòng nhào lộn luôn luôn không đổi và bằng 360 km/h. Lời giải:
Các lực tác dụng vào vật gồm có P; N . Ta có: P N ma
Xét tại vị trí thấp nhất của vòng nhào lộn, chiếu phương trình trên lên phương bán kính: 2 v N P ma m suy ra: ht R 2 2 mv 75.100 N P 75.10 4500N R 200
Xét tại vị trí cao nhất của vòng nhào lộn, chiếu phương trình trên lên phương bán kính: 2 2 mv mv N P ma N P ht R R Thay số: 2 2 mv 75.100 N P 75.10 3000N R 200
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Chương 2. Cơ học vật rắn A. Phần lý thuyết m r i i
- Khối tâm của hệ chất điểm: i r OG G mi i m v m v i i i i dr
- Vận tốc của khối tâm: G i i v G dt m m i i n n m a F i i i d v F
- Gia tốc của khối tâm: G i 1 i 1 a F ma G n dt m G m m i i 1
Phương trình chuyển động của khối tâm.
- Định luật bảo toàn động lượng của 1 hệ cô lập: F 0 m v const v const i i i G i i
- Vận tốc của 1 điểm trên vật rắn trong chuyển động phức tạp: v v R M G
- Mô-men quán tính của một chất điểm: 2 I
mr - r là khoảng cách từ chất điểm đến trục quay ;
- Mô-men quán tính của hệ chất điểm: n 2 I m r - r i i
i là khoảng cách từ chất điểm thứ i đến trục quay ; i 1
- Mô-men quán tính của 1 vật rắn: 2 I r dm
- r là khoảng cách từ khối lượng nguyên tố dm đến trục quay . vr
Đơn vị của mô-men quán tính: kgm2, thứ nguyên: ML2
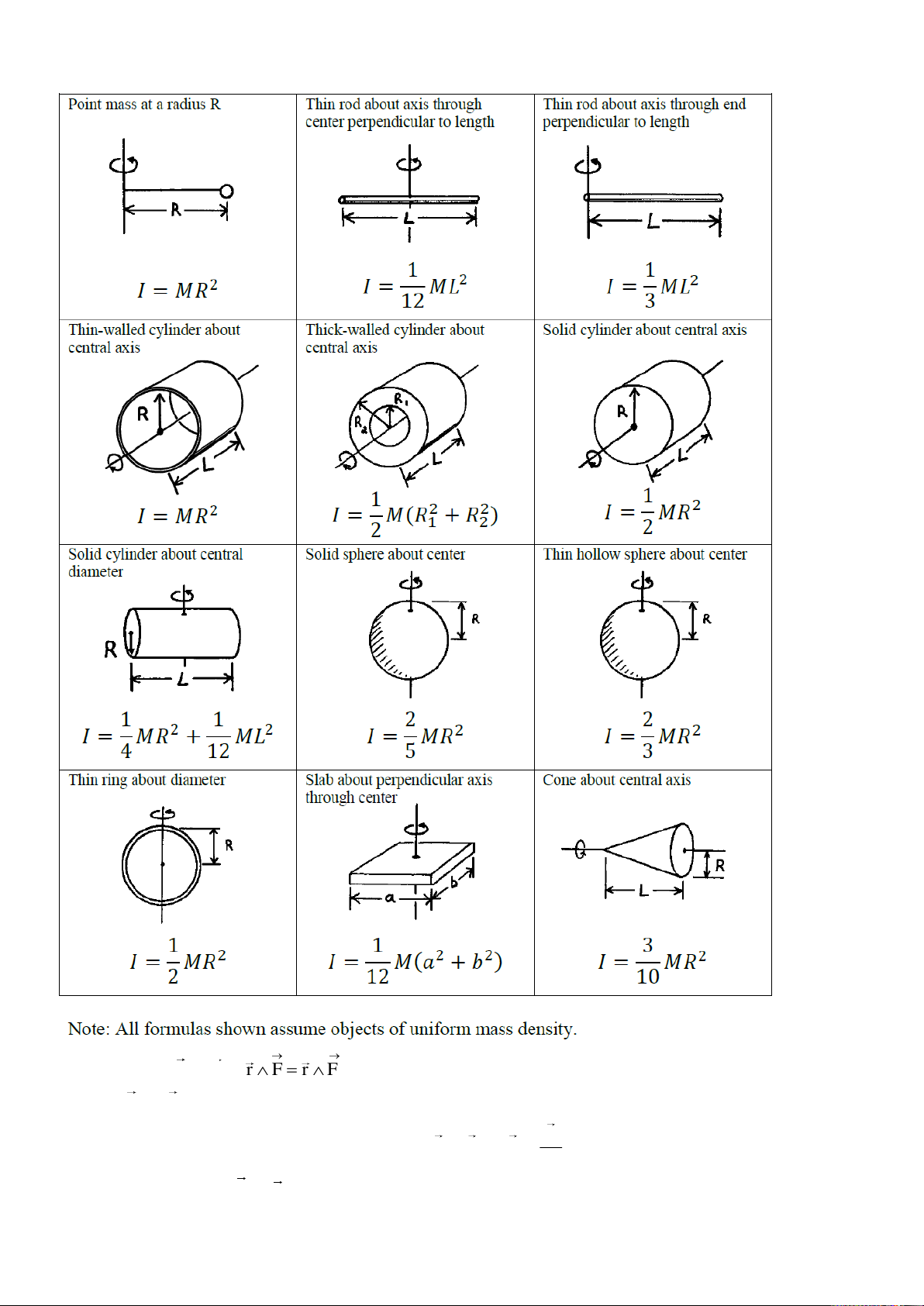
- Mô men quán tính đối với trục quay đi qua khối tâm của các vật rắn đồng chất 1
Khối trụ đặc, đĩa tròn 2 I mR 2
Khối trụ rỗng, vành tròn: 2 I mR 1
Thanh mảnh có chiều dài L: 2 I mL 12 2 Khối cầu đặc: 2 I mR 5 2 Quả cầu rỗng: 2 I mR 3 1 Mặt chữ nhật I m 2 2 a b 12
- Định lý Huygens-Steiner 2 I
I md , trong đó d là khoảng cách giữa 2 trục & . 0 0 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
- Mô-men quán tính của một số vật rắn thường gặp
- Mômen lực: M M r F r F t Độ lớn:|M| | M | rFsin rF t
- Phương trình cơ bản của chuyển động quay: I M M = I
- Mômen động lượng: L I 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 t2 t2 dL
- Định lý về mômen động lượng:
M L L L dL d M t (xung lượ 2 1
ng của mômen lực trong dt 1 t 1 t
khoảng thời gian . t .)
- Định luật bảo toàn mô men động lượng của hệ chất điểm. dL dL Ta có: i M dt dt n dL
Với hệ cô lập: M M 0
0 L const I const i i 1 dt B. Phần bài tập Bài tập cần làm:
3.2, 3.3, 3.4, 3.5, 3.6, 3.9, 3.11, 3.12, 3.13, 3.14, 3.19-3.22, 3.24
Bài tập cần trình bày ra giấy A4 & ghim vào nộp cho thầy
3.4, 3.5, 3.9, 3.12, 3.13, 3.20, 3.22, 3.24
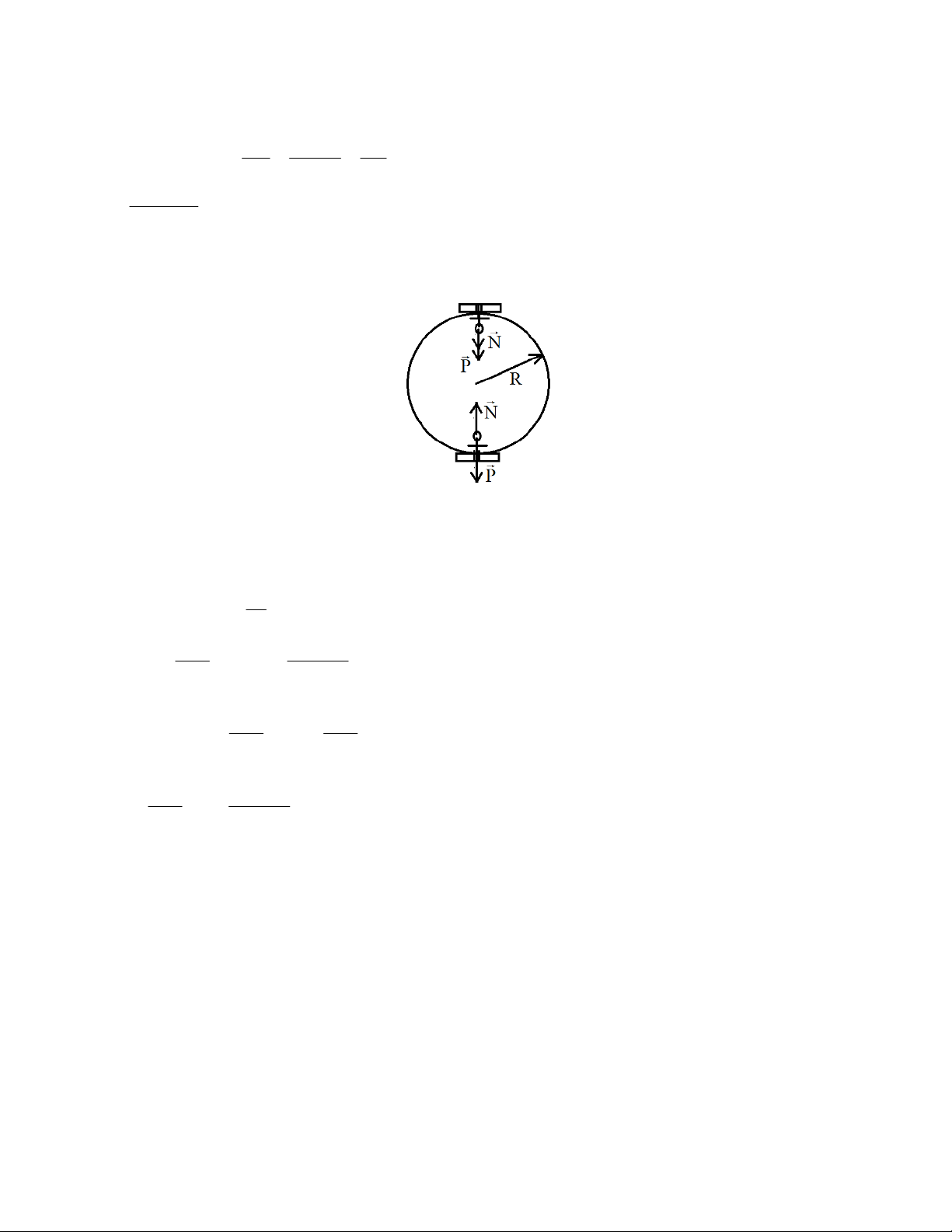
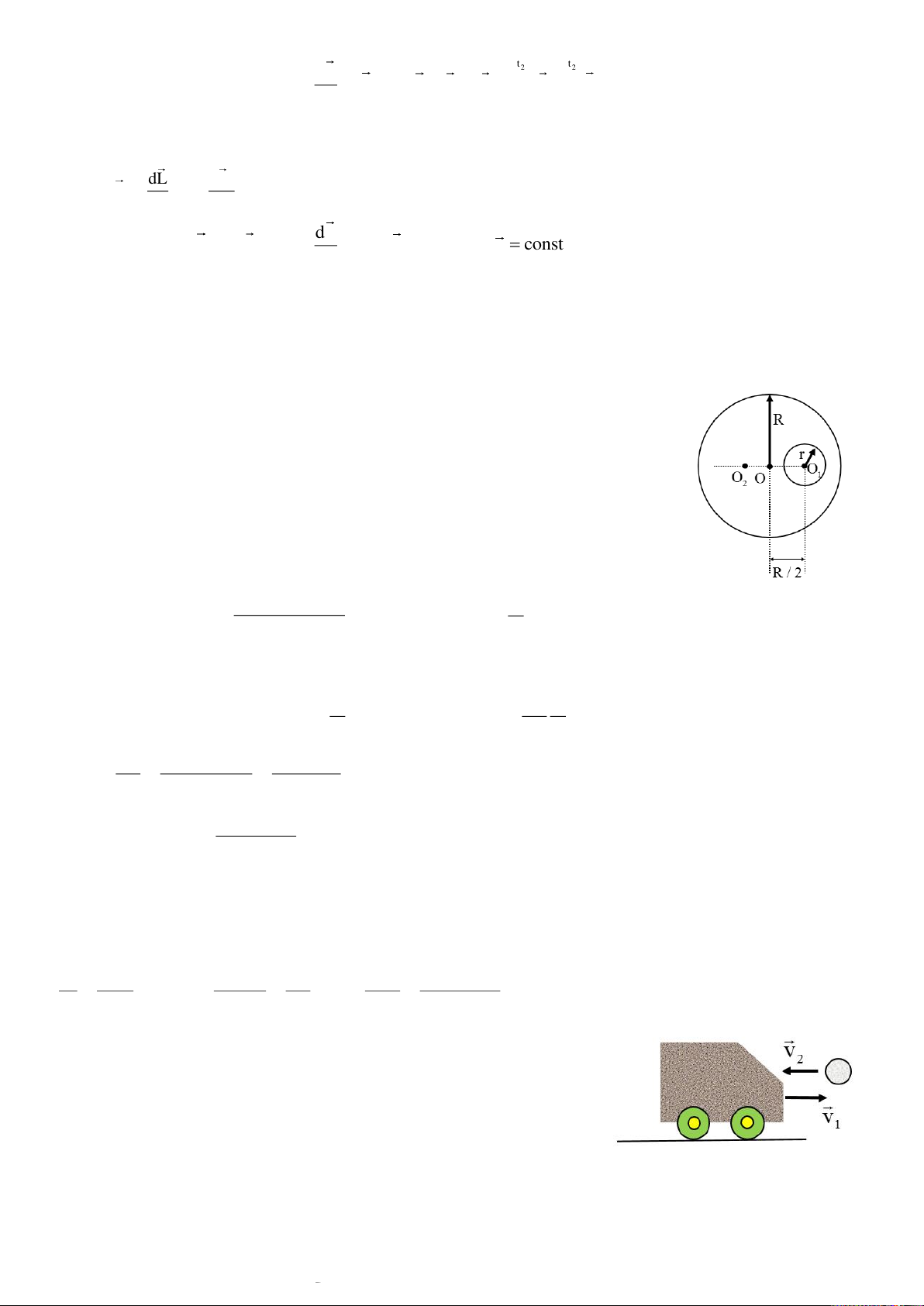
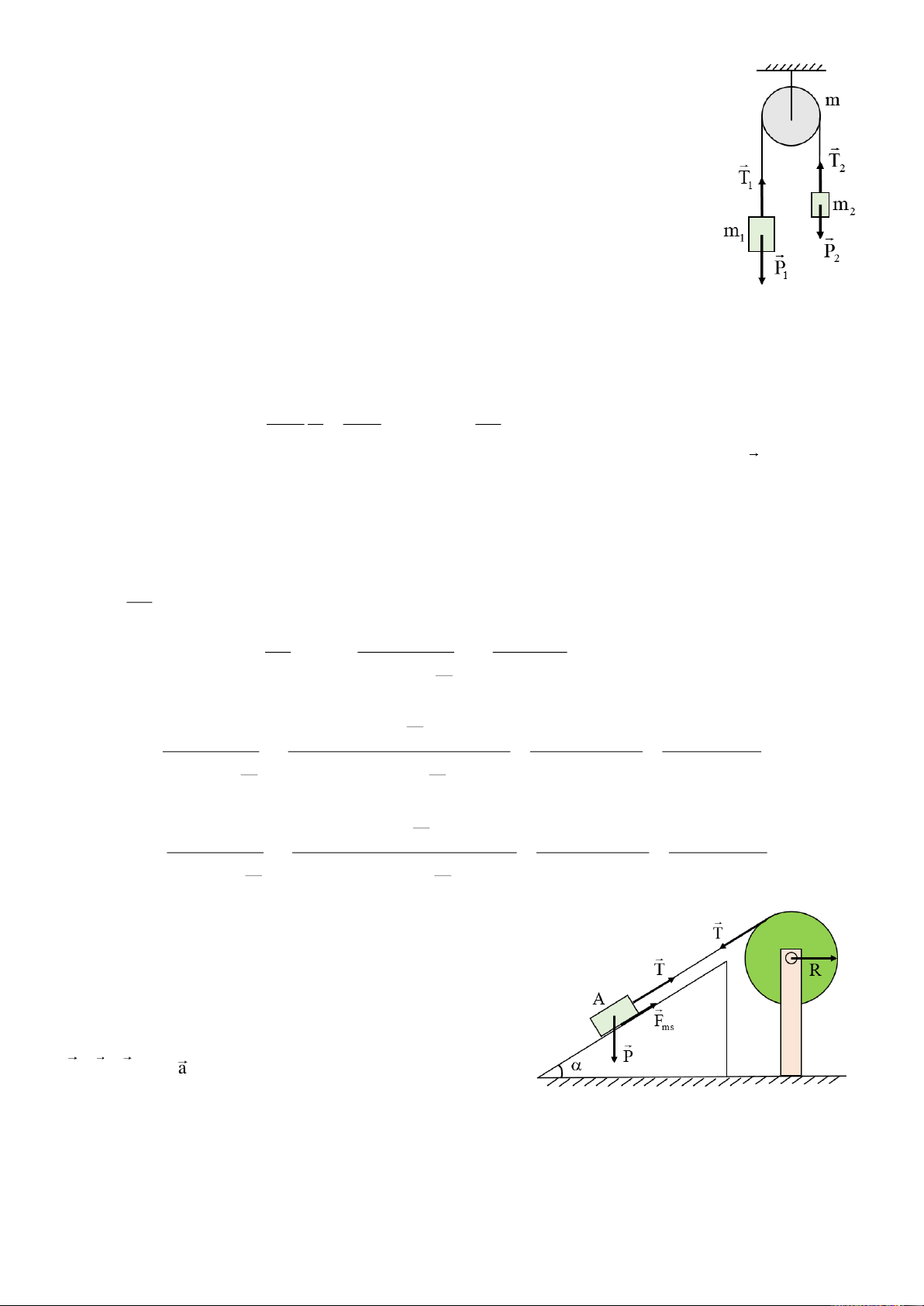
Bài 3.2. Trên một đĩa tròn đồng chất bán kính R có khoét 1 lỗ tròn nhỏ bán kính
r; tâm của lỗ khoét nằm cách tâm của đĩa một đoạn bằng R/2. Xác định vị trí khối tâm của đĩa trên. Bài giải:
Bài này có 2 cách, cách thứ nhất có thể áp dụng đúng định nghĩa về khối tâm và
sử dụng phương pháp tọa độ để giải.
Cách 1: Vì đĩa đối xứng qua đường nối tâm OO1 nên khối tâm cần tìm cũng nằm
trên đường OO1. Chọn O là gốc tọa độ, từ đó có tọa độ khối tâm của cái đĩa khi chưa bị khoét là: x 0 O m x m x Theo định nghĩa: 1 R 1 O 2 O2 x
0 , trong đó: x , x là khoảng cách chúng ta cần tìm, m O m m 1 là 1 O 2 O2 1 2
khối lượng của phần bị khoét đi (bán kính là r), m2 là khối lượng của phần đĩa còn lại (mà chúng ta đang đi tìm khối tâm). R m R
Thay vào biểu thức trên ta được: 1 m m x 0 x 1 2 O2 O2 2 m 2 2 2 2 m r r Lại có: 1
, có thể coi là khối lượng phân bố theo diện tích (kg/m2). m 2 2 R r 2 2 2 R r 2 r R Từ đó suy ra: x
, dấu “-” có nghĩa là O O
2 nằm ngược phía với O1. 2 2 2 2 R r
Cách 2. Làm theo kiểu thời phổ thông đã được học, chúng ta dùng quy tắc hợp lực song song chẳng hạn, khi
đó trọng lượng của cả cái đĩa chưa bị khoét bằng trọng lượng của cái đĩa (đang cần tìm khối tâm – m2) cộng
với trọng lượng phần đĩa bị khoét đi (m1), và đương nhiên khối tâm của cái đĩa đầy đủ nằm tại O. Theo quy tắc chia trong ta có: 2 P OO P .OO m m R r R 1 2 1 1 1 1 OO OO 2 1 P OO P m 2m 2 2 2 2 1 2 2 2 R r
Bài 3.4. Một xe chở đầy cát chuyển động không ma sát với vận tốc v1
= 1 m/s trên mặt đường nằm ngang. Toàn bộ xe cát có khối lượng M
= 10 kg. Một quả cầu khối lượng m = 2 kg bay theo chiều ngược lại
với vận tốc nằm ngang v2 = 7 m/s. Sau khi gặp xe, quả cầu nằm ngập
trong cát. Hỏi sau đó xe chuyển động theo chiều nào, với vận tốc bằng bao nhiêu? Tóm tắt: 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 v 1 m / s , M = 10 kg 1 m = 2 kg, v 7 m / s 2 v = ? Bài giải:
Đây là 1 bài toán va chạm mềm, áp dụng định luật bảo toàn động lượng. Mv mv M m Mv mv 10.1 2. 7 1 2 v v 0 ,33 m / s 1 2 M m 10 2
Dấu “ ” nghĩa là chuyển động ngược với chiều ban đầu.
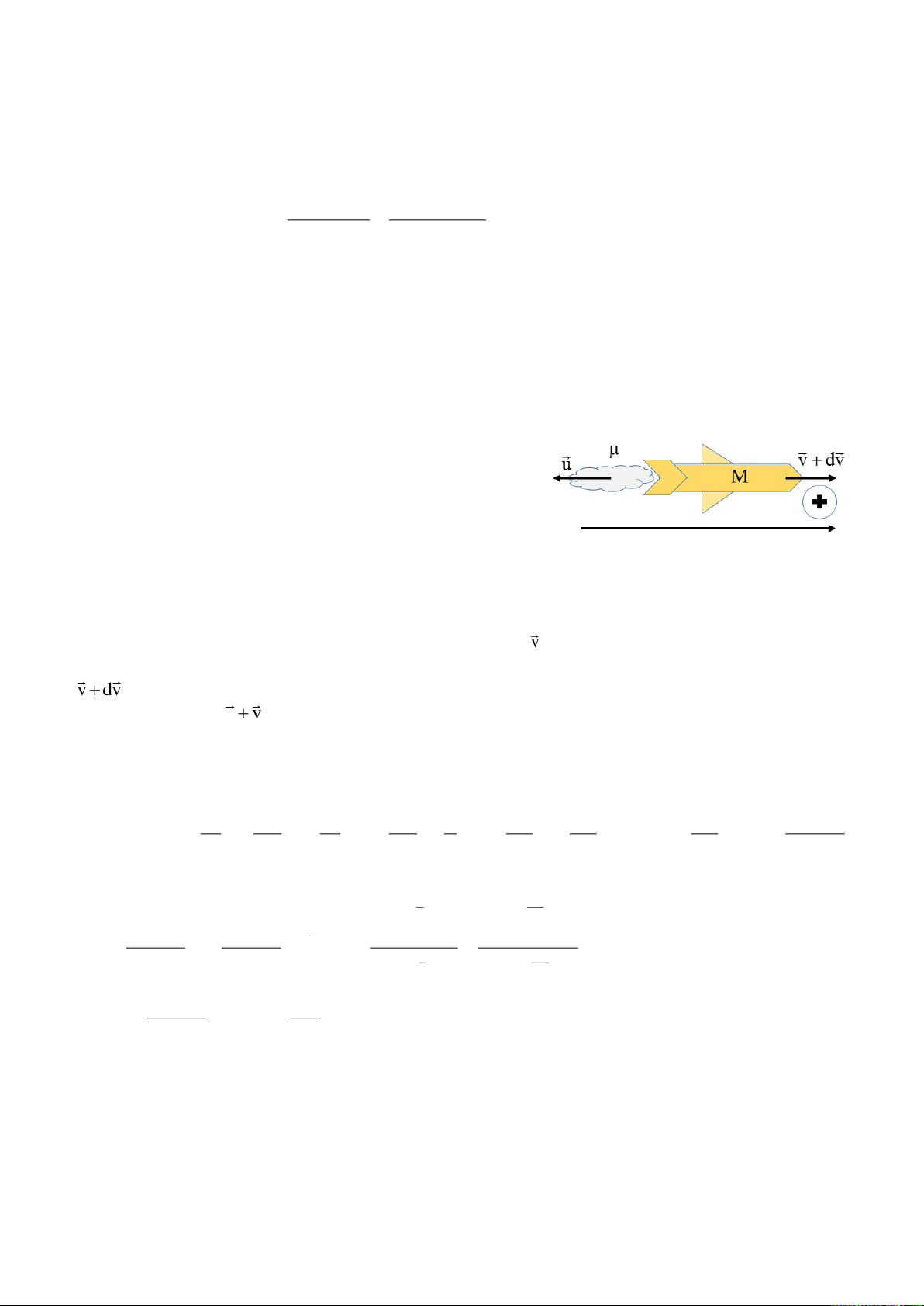
Bài 3.6. Một hỏa tiễn lúc đầu đứng yên, sau đó phụt khí đều đặn ra phía sau với vận tốc ko đổi u = 300 m/s
đối với hỏa tiễn. Trong mỗi giây, lượng khí phụt ra bằng μ = 90 g. Khối lượng tổng cộng ban đầu của hỏa tiễn bằng M0 = 270 g. Hỏi:
a) Sau bao lâu hỏa tiễn đạt tới vận tốc v = 40 m/s?
b) Khi khối lượng tổng cộng của hoả tiễn là 90 g thì vận tốc của hỏa tiễn là bao nhiêu? Bỏ qua sức cản của ko
khí và lực hút của Trái đất. Tóm tắt: u 300m / s
90g 0,09kg M 270 g 0, 27 kg 0
a)v 40m / s t ?
b)M 90g 0,09kg v ? Bài giải:
Tại thời điểm t bất kỳ, khối lượng của hỏa tiễn là M, vận tốc là v , chiếu lên phương chuyển động là v
Tại thời điểm t + dt, khối lượng của hỏa tiễn là M + dM (vì khối lượng hỏa tiễn giảm dần nên dM<0), vận tốc
là v dv , chiếu lên phương chuyển động là v + dv,
Vận tốc khí phụt ra là u v, chiếu lên phương chuyển động được v – u,
Áp dụng định luật bảo toàn động lượng theo phương chuyển động:
MdMvdv d
Mv u Mv , “ dM
” là khối lượng của lượng khí phụt ra.
Bỏ qua tích của dMdv ta được: v M dv dM dv dM v M M M M 0 0 0 Mdv udM 0 ln ln v u ln u ln u M u M u M M M M t 0 M 0 0 0 a) với v = 40 m/s v 40 u 300 M e 1 270e 1 0 v M M 0 0 u v u ln e t 0,374 s v 40 M t M t 0 0 u 300 e 90e M 270 b) 0 v u ln 300ln
300ln 3 329,6m / s M t 90 0
Bài 3.9. Một trụ đặc khối lượng m = 100 kg, bánh kính R = 0,5 m đang quay xung quanh trục của nó. Tác
dụng lên trụ một lực hãm F = 243,4 N, tiếp tuyến với mặt trụ và vuông góc với trục quay. Sau thời gian Δt =
31,4 giây, trụ dừng lại. Tính vận tốc góc của trụ lúc bắt đầu tác dụng lực hãm. Tóm tắt:
m 100kg,R 0,5m,F 2 43,4N, t
31,4s 0 ? 0 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Bài giải: 0 t 0 t M RF 2F Lại có: 2 I mR / 2 mR Thay vào ta đượ 2F t 2 F t 2.243, 4.31, 4 c: 305,7 rad / s 0 mR mR 100.0,5
Bài 3.11. Một thanh chiều dài l = 0,5 m có thể quay tự do xung quanh một trục nằm ngang đi qua một đầu của
thanh. Một viên đạn khối lượng m = 0,01 kg bay theo phương nằm ngang với vận tốc v = 400 m/s tới xuyên
vào đầu kia của thanh và mắc vào thanh. Tìm vận tốc góc của thanh ngay sau khi viên đạn đập vào thanh. Biết
răng mômen quán tính của thanh đối với trục quay bằng 5 kg.m2. Bài giải:
Tại vị trí va chạm, các lực tác dụng vào hệ “thanh + đạn” là trọng lực và lực đàn
hồi của thanh đều đi qua trục quay nên không gây ra mômen vì thế M 0 nên
mômen động lượng được bảo toàn.
Mômen trước: lmv (của viên đạn)
Mômen sau: I trong đó I là mômen quán tính của hệ “thanh + đạn”: 2 I I I I ml bar bullet lmv 0,5.0,01.400 Ta có: lmv 2 I ml 0,4 rad / s 2 2 I ml 5 0,01.0,5
Bài 3.14. Một đĩa bằng đồng (khối lượng riêng ρ = 8,9. 103 kg/m3 có bề dày b = 4.10-3 m, bán kính 2 R 5.10
m. Đĩa bị khoét thủng hai lỗ tròn bán kính R/2 như
trên hình. Tìm mômen quán tính của đĩa đã khoét đối với trục quay vuông góc với
đĩa và đi qua tâm O của đĩa. Bài giải: 2
Mômen quán tính đĩa tròn chưa bị MR
khoét đối với trục quay đi qua tâm là I 0 2 2 2 4 Trong đó: 2 R bR bR M R b I 0 2 2
Mômen quán tính của 2 đĩa tròn nhỏ có kích thước đúng bằng 2 lỗ tròn bán kính R/2 đối với trục quay đi qua tâm của chính chúng là: M R / 22 1 I I
, theo định lý Huygen-Steiner, mômen quán tính của 2 đĩa tròn nhỏ đối với trục quay đi 1 2 2 M R / 22 3 3 3 qua O là: I I
M R / 22 M R b R / 22 1 2 2 4 R bR 1O 2O 1 1 2 8 8 32
Suy ra mômen của đĩa bị khoét đi 2 lỗ có bán kính R/2 là: 4 b R 3 5 5 I I I I 2. b R b R
.8,9.10 .3,14.4.10 .5.10 4 4 4 3 3 2 4 2,2.10 2 kg.m 0 1 2 2 32 16 16 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bài 3.20. Hai vật có khối lượng lần lượt bằng m1 và m2 (m1 > m2), được nối với nhau
bằng một sợi dây vắt qua một ròng rọc (khối lượng của ròng rọc bằng m) (hình vẽ). Tìm:
a) Gia tốc của các vật;
b) Sức căng T1 và T2 của các dây treo. Coi ròng rọc là một đĩa tròn, ma sát không đáng
kể. Áp dụng bằng số m1 = 2 kg, m2 = 1 kg, m = 1 kg. Tóm tắt:
m m m 2kg, m 1kg, m 1kg 1 2 1 2 a)a ? b)T ?,T ? 1 2 Bài giải:
Dễ dàng viết được 2 phương trình theo định luật 2 Newton đối với mỗi vật: m g T m a (1), 1 1 1 T m g m a (2) 2 2 2
Phương trình đối với chuyển động quay của ròng rọc: 2 mR a maR ma
M I T R T R I T T (3) 1 2 1 2 2 R 2 2
(Ở đây chú ý, phương trình cơ bản của chuyển động quay được chiếu lên phương của véc-tơ , trong trường
hợp này véc-tơ này hướng từ bên trong mặt phẳng hình vẽ đi ra)
Từ các phương trình trên ta dễ dàng suy ra hệ phương trình:
m g T m a T m g m a 1 1 1 1 1 1
T m g m a T m g m a 2 2 2 2 2 2 ma T T 1 2 2
m m g m m ma m m 2 1 1 2 a a g 10 2,86 m / s 1 2 1 2 2 2 m 2 1 0,5 m m 1 2 2 m m g m m m m 1 1 2 1 2 m m 2 m g 4m m 2.10. 4.11 1 2 1 2 T m g g 14,3 N 1 1 m m 2m 2m m 2.2 2.11 1 2 m m m m 1 2 1 2 2 2 m m g m m m m 2 1 2 1 2 m m 2 m g 4m m 1.10. 4.2 1 1 2 2 1 T m g g 12,9 N 2 2 m m 2m 2m m 2.2 2.11 1 2 m m m m 1 2 1 2 2 2
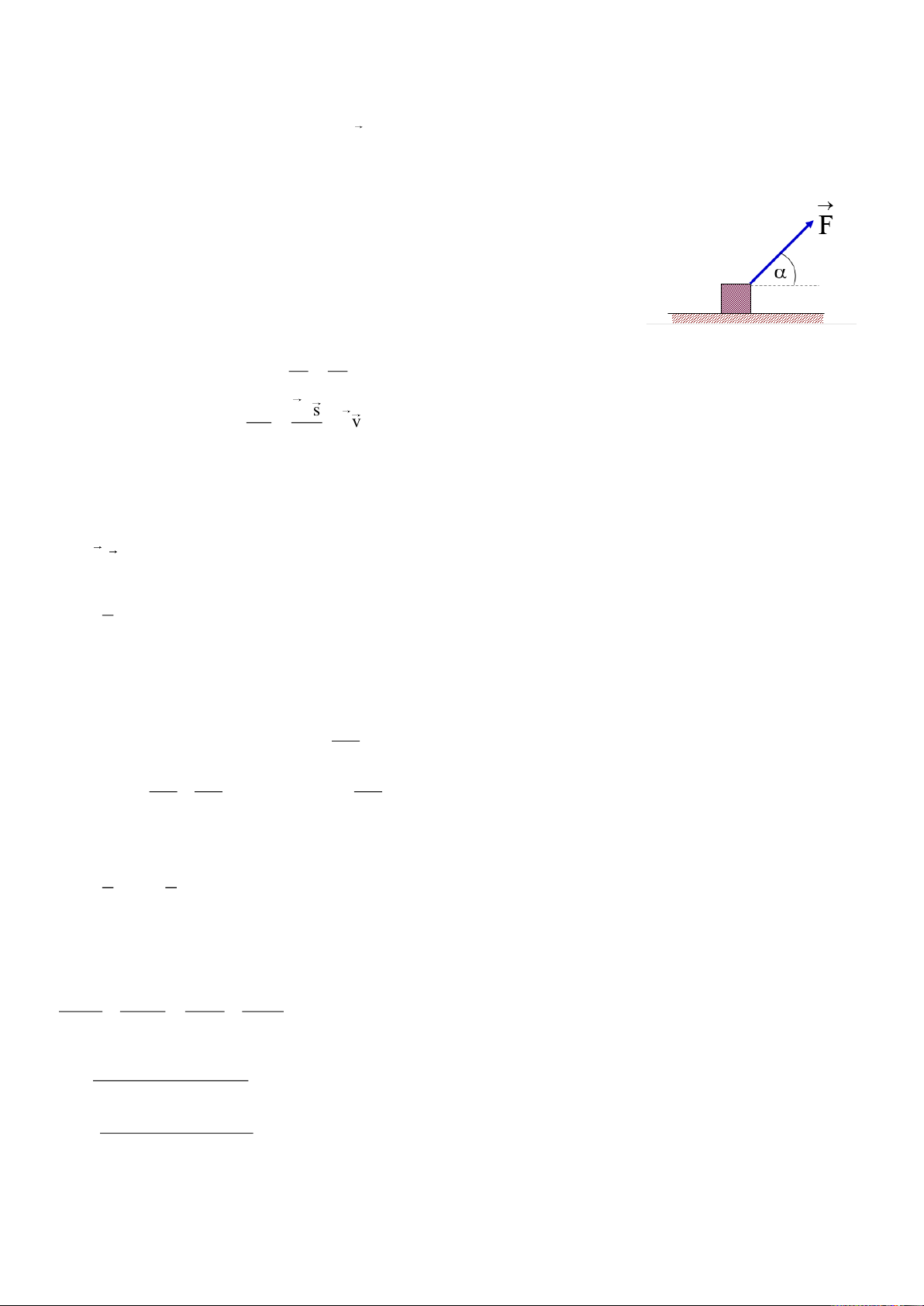
Bài 3.22. Một vật A khối lượng m trược trên mặt phẳng
nghiêng và làm quay một bánh xe có bán kính R (hình vẽ).
Mômen quán tính của bánh xe đối với trục quay bằng I. Khối
lượng của dây không đáng kể.Tìm gia tốc góc của bánh xe. Bài giải:
Đối với vật nặng ta có phương trình định luật 2 Newton như sau: T P F ma ms
Chiếu phương trình trên lên phương chuyển động và phương vuông góc với phương chuyển động ta được:
Psin T F ma và N P cos 0 N P cos F kmg cos ms ms
Suy ra mg sin T kmg cos ma mR 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Đố i với đĩa tròn ta có: I
M I TR I T R I mgR sin k cos
Thay vào phương trình phía trên ta được: mgsin
kmg cos mR 2 R I mR
Bài này chẳng rõ ràng gì sất, thứ nhất là chẳng nhắc gì đến lục ma sát cả, thứ 2 là từ công thức cuối cùng có
thể thấy, hệ này chỉ chuyển động khi mà sin k cos k tan , còn ngược lại thì hệ này cân bằng. Nên
về nguyên tắc, phải nói rõ mấy thứ này nữa. Và chú ý là trong sách giải của Trần Văn Quảng sai bét nhé. 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bài tập chương 4. Công và năng lượng
A. Phần tóm tắt lý thuyết 1. Công
Công nguyên tố (vi phân công) của lực F trên một đoạn đường vi phân ds
dA Fdscos Fd s Fd r
Trường hợp đặc biệt: Nếu lực F không đổi và luôn tạo với đường đi 1 góc
, ta có công thức: A Fscos
Trong hệ SI, đơn vị đo công là joule (jun), ký hiệu là (J), thứ nguyên là: [A] = ML2T-2 2. Công suất A Fs
- Công suất trung bình: P Fv tb tb t t dA Fds
- Công suất tức thời: P Fv dt dt
Đơn vị đo: Watt (oát), ký hiệu W = J/s
Một số đơn vị đo khác: 1 kW = 103 W, 1 MW = 106 W, 1 HP = 736 W
- Công và công suất trong chuyển động quay: dA Fds F rd d M t t P M
3. Động năng của chất điểm 1 2 W mv d 2
Định lý động năng: Độ biến thiên động năng của chất điểm trong một chuyển dời có giá trị bằng công của
ngoại lực tác dụng lên chất điểm trong chuyển dời đó. A W W d2 d1 2 I
- Động năng của vật rắn quay: W d 2 2 2 I I 2 I Suy ra: 2 1 A , trong đó W
gọi là động năng quay của vật rắn. 2 2 d 2
Trong trường hợp tổng quát, vật rắn lăn không trượt động năng toàn phần sẽ bằng tổng động năng tịnh tiến
cộng động năng quay: 1 2 1 2 W mv I d 2 2 4.Bài toán va chạm
- Va chạm đàn hồi xuyên tâm: động lượng và động năng được bảo toàn
m v m v m v m v 1 1 2 2 1 1 2 2 2 2 2 2 m v m v m v m v 1 1 2 2 1 1 2 2 2 2 2 2 Giải ra: 2m v (m m )v 2 2 1 2 1 v 1 m m 1 2 2m v (m m )v 1 1 2 1 2 v ' 2 m m 1 2
- Va chạm mềm: chỉ có động lượng được bảo toàn 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 m m m v m v 1 1 2 2 v m v m v v 1 2 1 1 2 2 m m 1 2
- Độ giảm động năng của hệ: 1 1 1 W
m v m v m m 1 m m v v v 2 2 2 2 1 2 d 1 1 2 2 1 2 1 2 2 2 2 2 m m 1 2 5. Thế năng
- Thế năng trọng trường:
Wt(h) = mgh + C; trong đó h là độ cao từ m tới mặt đất, C = 0 khi gốc thế năng ở mặt đất.
- Thế năng đàn hồi: 1 2
W kx C , trong đó x là độ biến dạng của lò xo, C = 0 khi gốc thế năng ở vị trí lò xo không biến dạng t 2
- Định lý về độ giảm thế năng: Công của trường lực (tức là công của trọng trường hoặc công của lực đàn hồi)
tác dụng lên chất điểm bằng độ giảm thế năng. A W M W N MN t t
6. Cơ năng & định luật bảo toàn cơ năng:
Tổng động năng và thế năng của chất điểm được gọi là cơ năng của chất điểm. Khi chất điểm chuyển động
trong một rường lực thế (mà không chịu tác dụng của 1 lực nào khác) thì cơ năng của chất điểm là một đại lượng bảo toàn. W W W const d t 2 mv W mgh const 2
- Từ định lý động năng và định lý thế năng dễ dàng thấy:
A W W và A W W , suy ra: W A d2 d1 t t1 t 2 #t
Bài tập cần làm: 4.2, 4.4, 4.8, 4.12, 4.13, 4.14, 4.16, 4.18, 4.20, 4.22, 4.26, 4.27, 4.30, 4.32.
Phải nộp: 4.2, 4.4, 4.14, 4.16, 4.20, 4.27, 4.32
Bài 4.2. Tính công cần thiết để kéo một lò xo giãn ra 20 cm, biết rằng lực kéo tỷ lệ với độ giãn của lò xo và
muốn lò xo giãn 1 cm phải cần một lực 30 N. Bài giải: Độ 30 N cứng của lò xo: k 3000 0,01 m
Công cần thiết để kéo lò xo giãn ra 20 cm = 0,2 m là: x x 2 2 k x 3000.0, 2 A Fdx kxdx 60 J 2 2 0 0
Bài 4.4. Một ôtô khối lượng 2 tấn, leo lên dốc có độ nghiêng 4%. Hệ số ma sát là 0,08. Tìm:
a) công thực hiện bởi động cơ ôtô trên quãng đường dài 3km;
b) Công suất của động cơ ôtô, biết rằng thời gian đi hết quãng đường trên mất 4 phút. Tóm tắt: m 2000kg; sin 4%; 0,08 a)s 3000m;A ? b)t 240s;P ? Bài giải: 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Ô tô chuyển động đều lên dốc, các lực tác dụng vào ô
tô thỏa mãn điều kiện:
F P F N 0 , dễ dàng suy ra: k ms
F P sin F 0 k ms
F mg sin kmg cos k
A F s mgsin k coss 2000.10.0,04 0,08. 6 1 .3000 7, 2.10 J k 6 A 7, 2.10
Công suất của động cơ: P 30000W t 240
Bài 4.13. Một vật khối lượng m trượt không ma sát từ đỉnh một mặt cầu xuống dưới (hình vẽ). Hỏi từ khoảng cách h
nào (tính từ đỉnh mặt cầu) vật bắt đầu rơi khỏi mặt cầu. Cho bán kính mặt cầu R = 90 cm.
Chú ý: Điều kiện của bài toán này là tìm khoảng cách để vật rơi
khỏi mặt cầu. Vật chỉ chịu tác dụng của trọng lực và áp lực, khi nào
áp lực bằng 0 thì…vật sẽ rời khỏi mặt cầu thôi
Xét tại thời điểm t vật ở vị trí như hình vẽ, khi đó theo định luật II Newton ta có: P N ma
Chiếu lên phương hướng tâm ta được phương trình: 2 2 mv mv Psin N ma N mgsin trong đó R h sin ht R R R
Mặt khác, áp dụng định luật bảo toàn cơ năng (cho vị trí cao nhất và vị trí thời điểm t): 2 2 mv 2 mv mv 2mg h mgR mg R h mg h
, thay giá trị này vào biểu thức trên ta được: 2 2 R R 2 mv R h 2mg h 3 h R N mgsin mg mg 1
, điều kiện N = 0, ta có: h 30cm R R R R 3
Bài 4.20. Để đo vận tốc của viên đạn người ta dùng con lắc thử đạn. Đó là một bì cát treo ở đầu một sợi dây
(hình vẽ). Khi viên đạn xuyên vào bì cát, nó bị mắc tại đó và bì cát được nâng lên một độ cao h nào đó. Tìm
vận tốc của đạn lúc nó sắp xuyên vào bì cát. Biết khối lượng của viên đạn là m, khối lượng của bì cát là M. Bài giải:
Định luật bảo toàn động lượng: mv M mV , trong đó V là vận
tốc của hệ bì cát và viên đạn sau va chạm mv V M m
Áp dụng định luật bảo toàn cơ năng: 2
m M V mMgh V 2gh 2 So sánh ta đượ mv m M c: 2gh v 2gh M m m
Bài 4.22. Một hòn bi khối lượng m chuyển động không ma sát trên một đường rãnh có dạng như hình vẽ. Hòn
bi được thả không có vận tốc ban đầu từ độ cao h = 2R, kích thước của bi nhỏ không đáng kể. Hỏi:
a) Ở độ cao nào bi rời khỏi đường rãnh?
b) Độ cao lớn nhất mà hòn bi sẽ đạt được sau khi rời khỏi rãnh? 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Cơ năng ban đầu tại A (chỉ gồm thế năng) W 2mgR A
Tại điểm B (là điểm mà tại đó vật rời khỏi rãnh) 2 mv W mgH B 1 2 2 2 mv mv H
Áp dụng định luật bảo toàn cơ năng: 1 mgH 2mgR 4mg 2mg (1) 1 2 R R
Tại B, phương trình định luật 2 Newton: P N ma , chiếu lên phương bán kính: 2 2 mv mv Psin N N mgsin R R 2 H R H mv H H H H 1 1 1 1 1 1 sin 1 N mg 1 4mg 2mg mg 1 5mg 3mg R R R R R R R 5
Tại đây vật rời khỏi rãnh nên áp lực N = 0, suy ra: N 0 H R 1 3
Thay vào 1 trong các phương trình trên để tìm vận tốc tại B: 2 2 2 mv 5 mv mv 1 2 mgH 2mgR mgR 2mgR mgR v gR 1 B 2 3 2 2 3 3
Tại điểm B ta có một chuyển động ném xiên với góc
Vận tốc theo phương ngang H 2 5 8 1 v cos v sin v 1 gR 1 gR B B B R 3 3 27
Cơ năng tại điểm cao nhất sau khi rời khỏi rãnh (khi đó chỉ còn vận tốc theo phương ngang): 1 2 1 8 4 W mgH mv mgH m gR mgH mgR C 2 2 2 2 2 27 27
So sánh với cơ năng tại A: 4 4 50 2mgR mgH mgR H 2 R R 2 2 27 27 27
Bài 4.27. Tính công cần thiết để làm cho một vô lăng hình vành tròn đường mình 1 m, khối lượng 500 kg,
đang đứng yên quay tới vận tốc 120 vòng/phút. Bài giải: 120.2
Phải đổi đơn vị: 120vßng / phót 4rad / s 60
Áp dụng định lý về độ biến thiên động năng ta có: 1 1 1 1 1 1 A W I 0 I mR md .500.1 .42 2 2 2 2 2 2 2 10000 J d 2 2 2 2 4 8
Bài 4.32. Một người ngồi trên ghế Giucôpxki và cầm trong tay hai quả tạ, mỗi quả có khối lượng 10 kg.
Khoảng cách từ mỗi quả tới trục quay là 0,75m. Ghế quay với vận tốc ω1 = 1 vòng/s. Hỏi công do người thực
hiện và vận tốc của ghế nếu người đó co tay lại để khoảng cách từ mỗi quả tạ đến trục quay chỉ còn là 0,20 m,
cho biết mômen quán tính của người và ghế đối với trục quay là I0 = 2,5kg.m2 . 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Bài giải:
Đổi đơn vị: 1 vßng / s 2 rad / s 1
Mômen quán tính của hệ trước: 2 2
I I 2md 2,5 2.10.0,75 13,75 2 kg.m 1 0 1 Của hệ sau: 2 2
I I 2md 2,5 2.10.0,20 3,30 2 kg.m 2 0 2
Áp dụng định luật bảo toàn mômen động lượng ta được: 2 2 I I 2md 2,5 2.10.0,75 1 1 0 1 I I .2 1 1 2 2 2 2 1 2 I I 2md 2,5 2.10.0, 20 2 0 2 26,2rad / s Động năng trướ 1 1
c và sau: W I .13,75.22 2 271,4 J d1 1 1 2 2 1 2 1 2
W I .3,3.26, 2 1132,6 J d2 2 2 2 2
Công của người đó phải thực hiện là: A W W 1132,6 271,4 861,2 J d1 d2 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bài tập chương 4. Trường hấp dẫn
A. Tóm tắt lý thuyết: 1. Lực hấp dẫn:
- của 2 chất điểm: m m 1 2 F = G hd 2 r
G: Hằng số hấp dẫn (G = 6,67.10-11 SI)
m1, m2: Khối lượng của hai chất điểm
r: khoảng cách giữa chúng
- của một vật lên một chất điểm: mdM Fhd = −G .r ∫ 3 r (M) Chú ý:
Lực hấp dẫn giữa 2 quả cầu đồng chất được tính
giống như 2 chất điểm đặt tại tâm của chúng.
2. Gia tốc rơi tự do
Là gia tốc rơi của các vật trong chân không, chỉ dưới tác dụng của trọng lực.
Ở sát bề mặt trái đất: M g = G ≈ 9,8( 2 m / s 0 2 ) R Ở độ cao h: 2 M R g = G = g 2 0 2 (R + h) (R + h)
3. Ứng dụng tính khối lượng của các thiên thể: 2 gR
- Khối lượng của Trái Đất: M = G 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
R – bán kính Trái Đất, = ( ) 6 R 6370 km ≈ 6,370.10 (m)
g – là gia tốc trọng trường trên mặt đất, ≈ ( 2 g 9,8 m / s ) 9,8(6,370.10 )2 6 24 M = ≈ 6.10 kg 11 ( ) 6,67.10−
- Khối lượng của Mặt Trời
Khi Trái Đất quay quanh Mặt Trời là do lực hấp dẫn của Mặt Trời đối với Trái Đất, lực này
đóng vai trò lực hướng tâm: 2 2 2 3 MM′ v M 2 R π ′ 4π R′ F = G = M. = → M′ = . , 2 2 R′ R′ R′ T T G
M′ - khối lượng của Mặt Trời, R′ - khoảng cách từ Trái Đất đến Mặt Trời, T – chu kỳ quay
của Trái Đất quanh Mặt Trời. 30 M′ ≈ 2.10 (kg)
4. Thế năng của trường hấp dẫn Mm W = −G
+ C , C là hằng số chọn tùy ý chọn từ giá trị thế năng tại vô cùng. t r
5. Bảo toàn cơ năng trong trường hấp dẫn
Trong trường hấp dẫn, cơ năng được bảo toàn: 2 mv Mm W = W + W = + −G =
const , để đơn giản, chọn: W ∞ = 0 t ( ) d t 2 r
6. Chuyển động của vệ tinh.
- Khi vận tốc vI = 7,9 km/s: Vận tốc vũ trụ cấp 1 Quỹ đạo tròn.
Tính vận tốc vũ trụ cấp 1:
Để vật trở thành vệ tinh nhân tạo chuyển động
tròn quanh Trái Đất thì lực hấp dẫn của đóng vai trò là lực hướng tâm: 2 GMm mv F = = mg = , h R , ta có: hd (R + h)2 R + h 2 mv mg ≈ mg = , suy ra: v = g R 0 R I 0
- Khi vận tốc 11,2 km/s > v > 7,9 km/s: Quỹ đạo là elip. 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
- Khi vận tốc vII = 11,2 km/s: Vận tốc vũ trụ cấp II Quỹ đạo parabol.
Tính vận tốc vũ trụ cấp 2:
Vận tốc vũ trụ cấp 2 gọi là vận tốc thoát ly, là giá trị
vận tốc tối thiểu một vật cần có để có thể thoát ra khỏi
trường hấp dẫn của một hành tinh. Vật chuyển động
quanh Mặt Trời. Định luật bảo toàn cơ năng: 2 mv Mm 2GM 0 + −G = 0 → v = = 0 2 R R = 2g R =11,2 km / s 0 ( )
- Khi vận tốc vIII = 16,7 km/s: Vận tốc vũ trụ cấp III Vệ tinh có thể thoát ra khỏi hệ Mặt Trời.
Bài tập cần làm: 5.1, 5.3, 5.5, 5.6, 5.7, 5.8, 5.9, 5.10, 5.11, 5.12
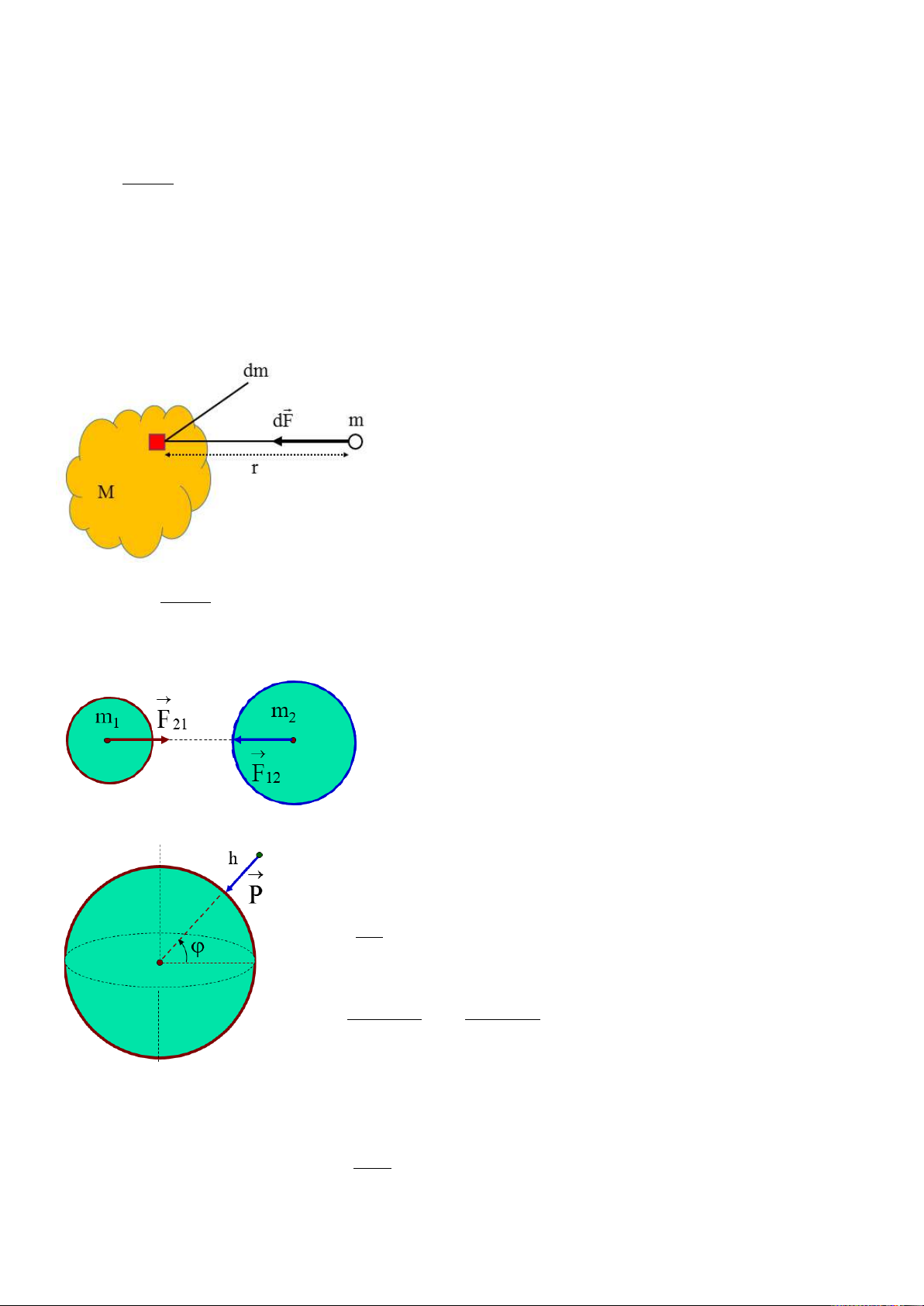
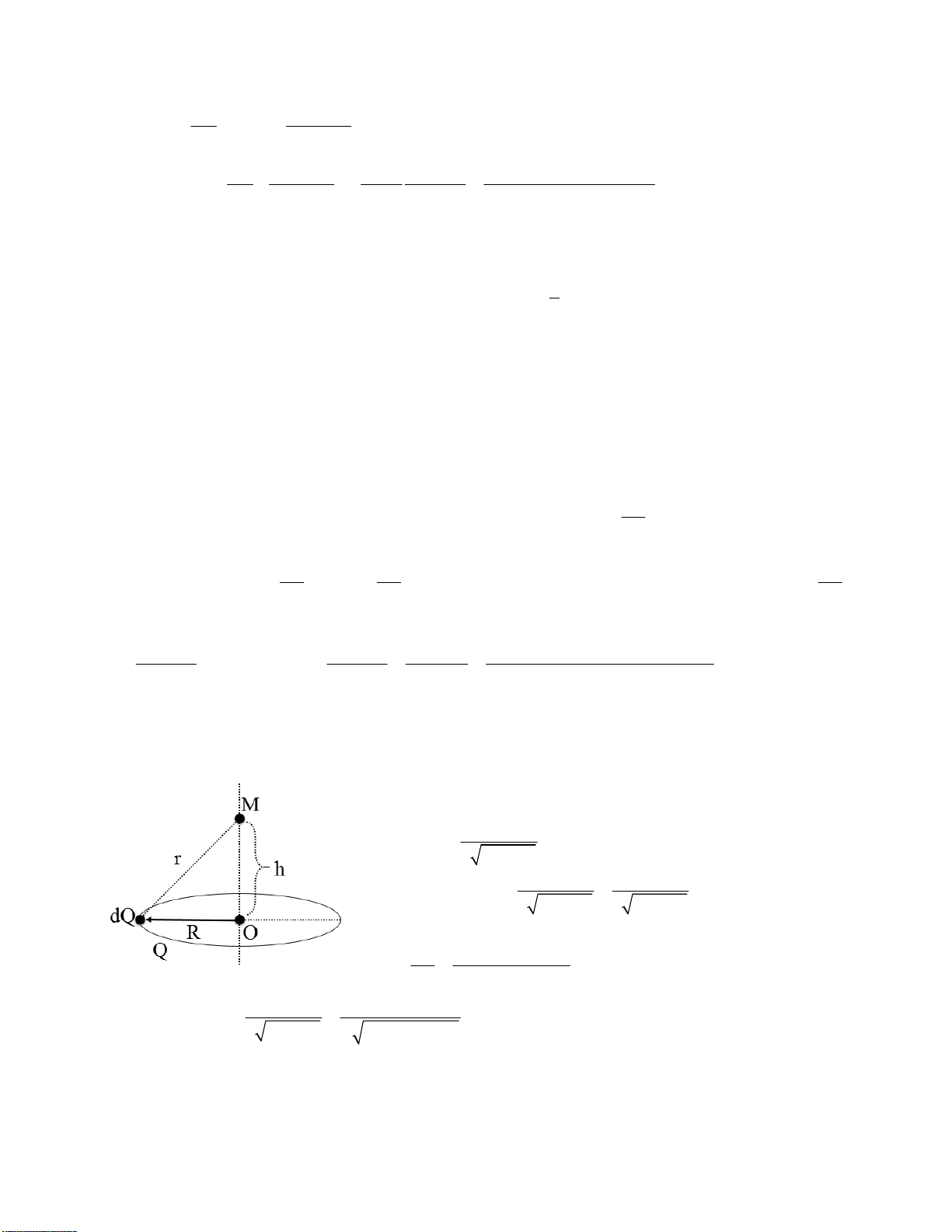
5-3. Một quả cầu khối lượng m1 đặt cách
đầu một thanh đồng chất một đoạn thẳng a trên
phương kéo dài của thanh. Thanh có chiều dài l,
khối lượng m2. Tìm lực hút của thanh lên quả cầu: Bài giải: 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Dạng thanh nên chia thanh thành từng đoạn nhỏ có kích thước dx và có khối lượng
dm, cách đầu O của thanh một khoảng x.
Giờ xác định dm theo dx, nhớ là đối với thanh dài thì ta chú ý đến khối lượng trên một
đơn vị độ dài λ. m2 dm = λdx = dx
Bài yêu cầu xác định lực hút, tức là sẽ phải sử dụng công thức liên quan tới lực hấp dẫn
giữa qủa cầu và đoạn dm. m dm m m dx 1 1 2 dF = G = ( + a − x) G 2 ( + a − x)2
Giờ lấy tích phân và tìm cận để xác định lực hút của thanh lên quả cầu. Khi quét từ trái
sang phải biến x thay đổi từ 0 đến . Đó chính là cận trên và cận dưới khi tính tích phân. m m dx Gm m Gm m 1 1 Gm m 1 2 1 2 1 2 1 2 F = G = = − = ∫ (
+ a − x)2 ( + a − x)2 a + a a a + 0 ( ) 0 Hình 5-2. 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bài tập chương 6. Trường tĩnh điện
A. Phần tóm tắt lý thuyết
1. Lực tương tác Coulomb 1 q q r q q r 1 q q q q 1 2 12 1 2 12 12 F . k . , độ lớn: 1 2 1 2 F k 2 2 4 r r r r 12 2 2 4 r r 0 0 12 2 2
8,86.10 C / Nm - hằng số điện môi (hằng số điện môi tuyệt đối của chân không), là hằng số điện 0
môi tỷ đối của môi trường.
2. Vectơ cường độ điện trường F E q
Cường độ điện trường gây ra bởi một điện tích điểm Q tại một điểm cách nó một khoảng r: Q r 1 Q r E k . . . , độ lớn: | Q | E k 2 2 r r 4 r r 2 r 0
Q>0: E hướng ra xa điện tích;
Q<0: E hướng vào điện tích.
3. Véc-tơ điện cảm (cảm ứng điện) D E 0
Véc-tơ điện cảm do một điện tích điểm gây ra: Q D . r 3 4 r
4. Cường độ điện trường gây bởi một sợi dây thẳng dài vô hạn mang điện đều tại một điểm cách dây một khoảng r: E
, trong đó là mật độ điện dài của dây. 2 r 0
5. Cường độ điện trường gây bởi một mặt phẳng mang điện đều: E
, trong đó là mật độ điện mặt. 2 0
6. Định lý Ostrogradski – Gauss:
Thông lượng cảm ứng điện gửi qua một mặt kín (S) bất kỳ bằng tổng đại số các điện tích có trong mặt kín. n DdS q i S i 1
7. Công của lực tĩnh điện khi dịch chuyển điện tích điểm q0 ừ điểm A đến điểm B trong điện trường: A q V V , trong đó V 0 A B
A và VB lần lượt là điện thế tại điểm A và B.
8. Tính chất thế của trường tĩnh điện
Lưu số của véc-tơ E theo một đường cong kín bằng 0: Edl 0
9. Hiệu điện thế giữa hai điểm A và B trong điện trường: B U V V Edl AB A B A
10. Mối liên hệ giữa cường độ điện trường và điện thế V E
hay E grad V s
Trong trường hợp điện trường đều: U E
, trong đó U V V là hiệu điện thế, d là khoảng cách giữa 2 d 1 2
mặt đẳng thế tương ứng.
11. Điện thế gây bở một điện tích điểm Q tại một điểm cách nó 1 khoảng r: 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Q V 4 r0
12. Hiệu điện thế giữa hai mặt cầu đồng tâm mang điện đều, bằng nhau, trái dấu: QR R 2 1 V V , trong đó R 1 2 R R
1 là bán kính của mặt cầu trong, R2 là bán kính của mặt cầu ngoài, Q là độ 0 1 2
lớn điện tích trên mỗi mặt cầu.
13. Hiệu điện thế giữa 2 mặt trụ đồng trục dài vô hạn mang điện đều bằng nhau và trái dấu: R2 V V ln , trong đó R 1 2 2 R
1 là bán kính mặt trong, R2 là bán kính mặt ngoài, là mật độ điện dài trên 0 1 mặt trụ. B. Phần bài tập
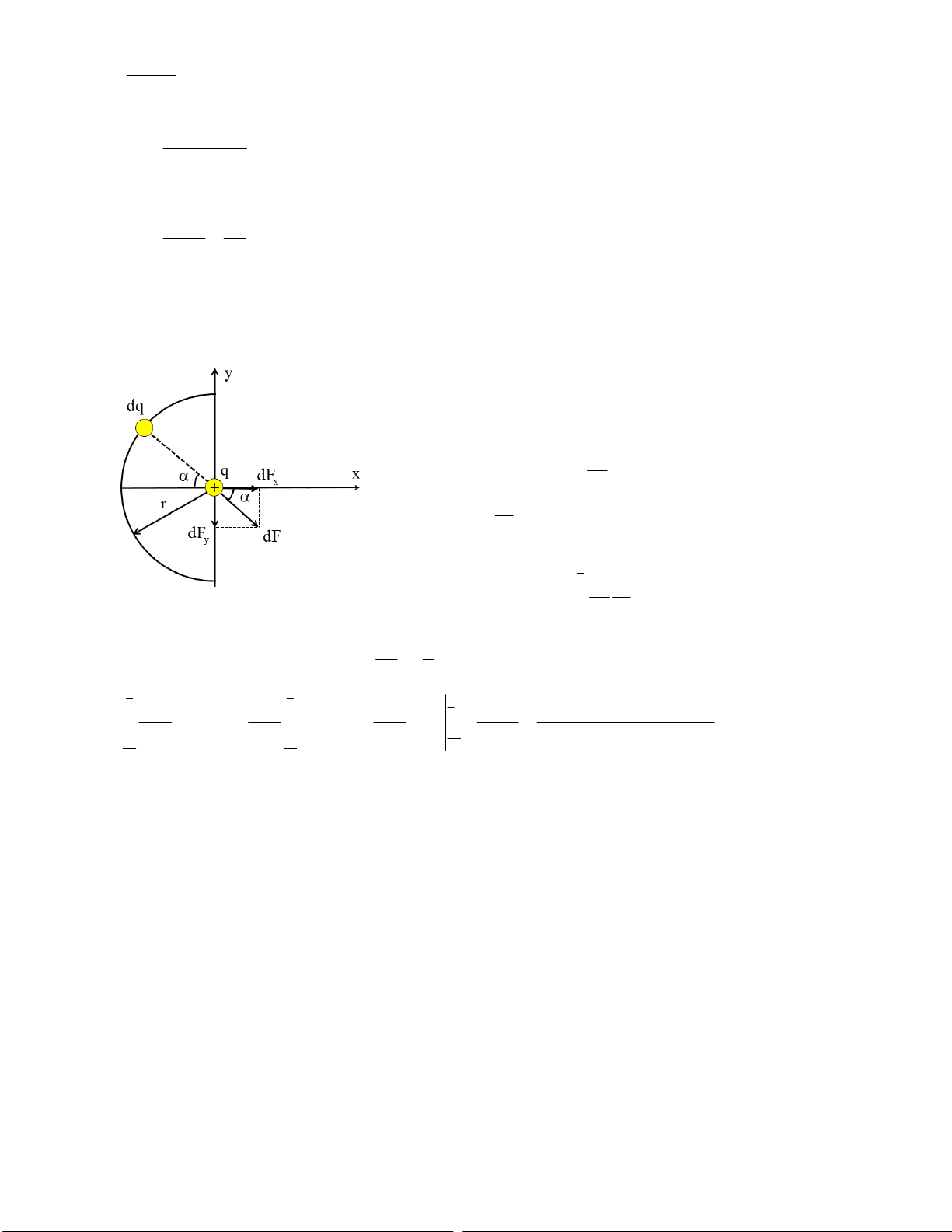
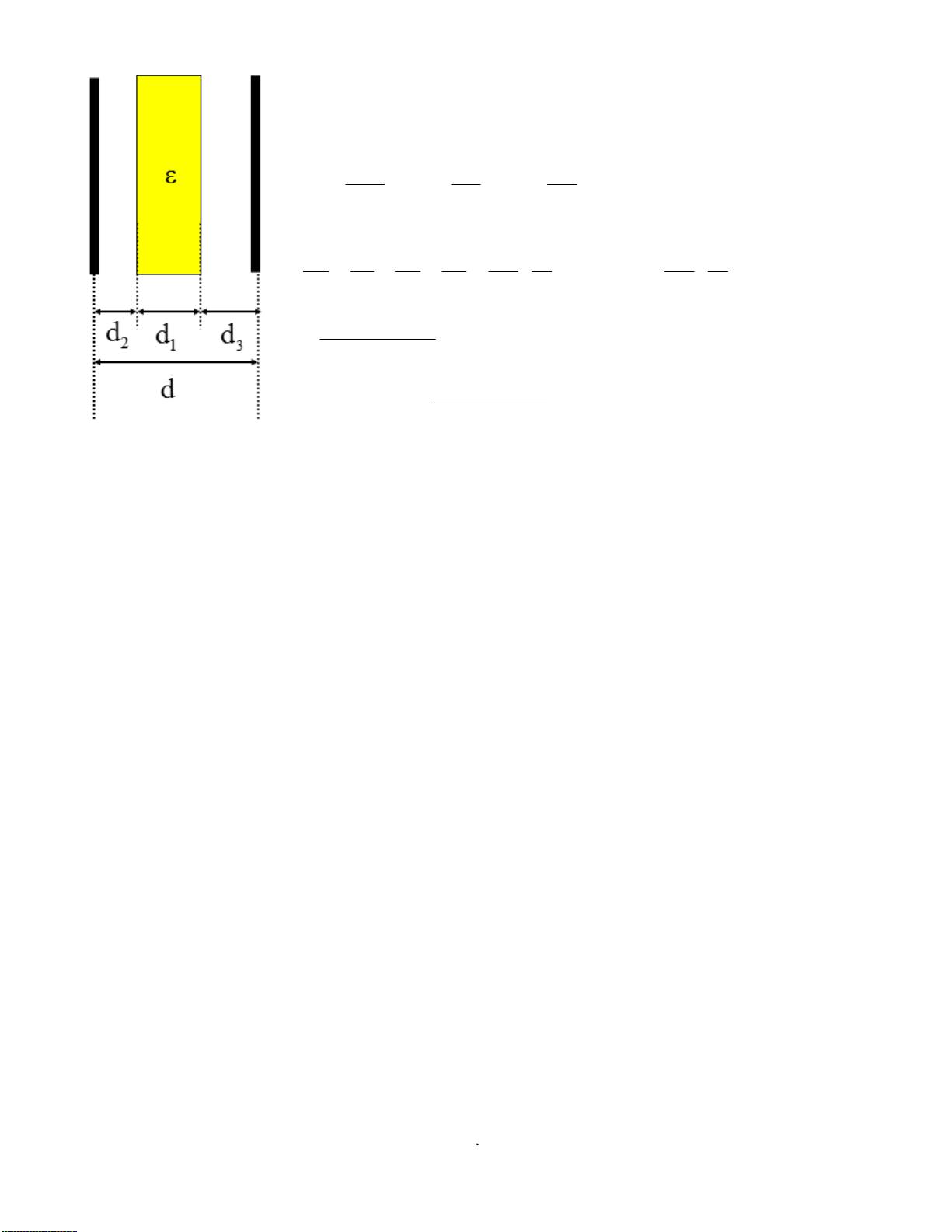
Bài 1.9. Tìm lực tác dụng lên một điện tích điểm q = (5/3).10-9 C đặt ở tâm nửa vòng xuyến bán kính r0 = 5
cm tích điện đều với điện tích Q = 3.10-7 C (đặt trong chân không). Bài giải:
Xét một điện tích nguyên tố dq gây ra cường độ điện trường dF cho
điện tích q. Phân tích dF theo phương x và y như trên hình vẽ. Dễ
dàng thấy do tính chất đối xứng nên các thành phần dFy triệt tiêu nhau. Như vậy: kq F dF dF dQcos x 2 r Trong đó: Q dQ
dl (điện tích chia đều theo độ dài r ), dl rd r
(độ dài cung bằng bán kính nhân với góc chắn cung). 2 Thay vào trên ta được: kq Q F rcosd 2 r r 2
Từ hình vẽ dễ thấy góc biến thiên từ
khi lấy tích phân trên toàn bộ nửa vòng xuyến. 2 2 2 2 kqQ kqQ kqQ 9 2kqQ 2.9.10 .5 / 3 9 7 2 .10 .3.10 F cosd cosd sin 3 1,146.10 N 2 2 2 2 = 2 r r r r .0,05 2 2 2
Bài 1.10. Có hai điện tích điểm 8 q 8.10 C và 8
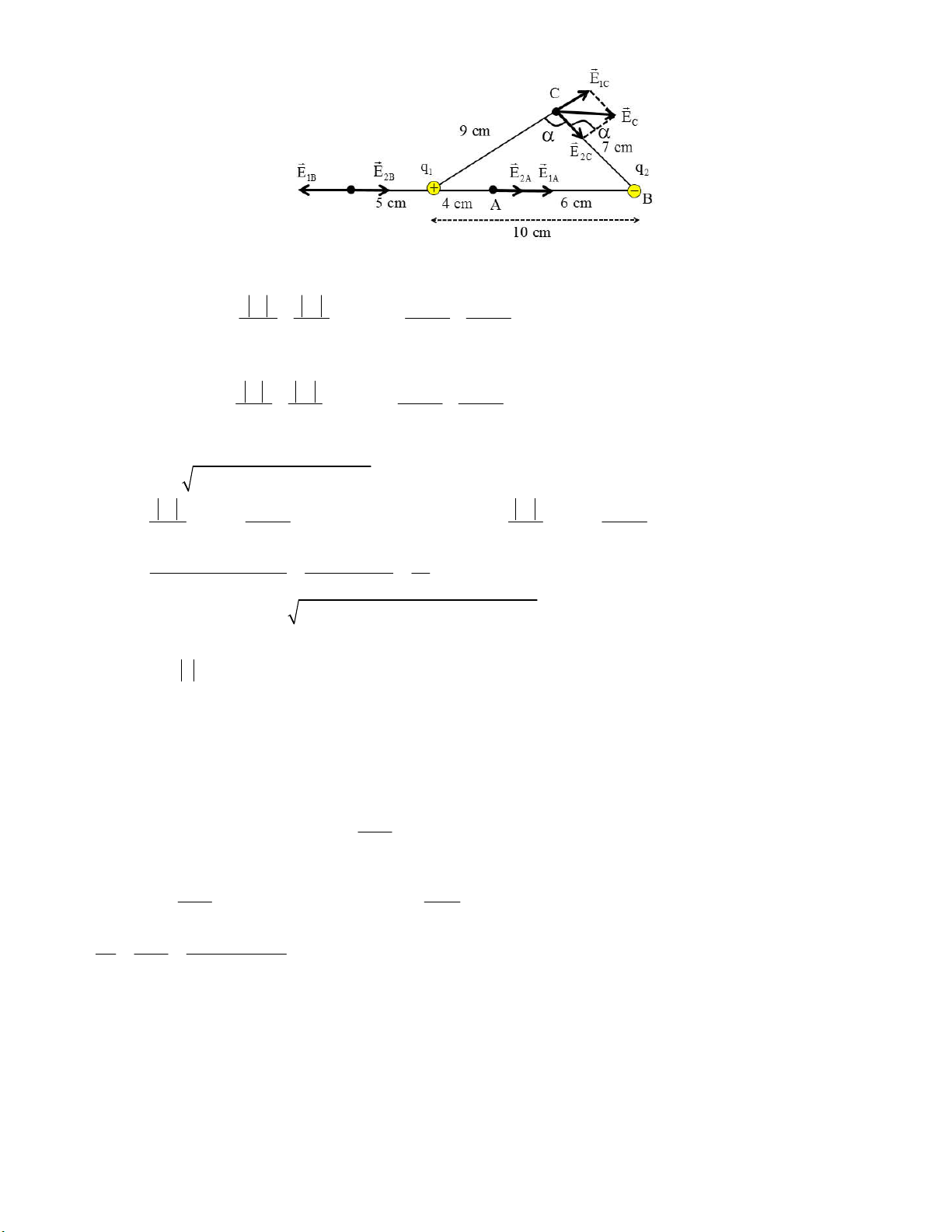
q 3.10 C đặt cách nhau một khoảng d = 10 cm trong 1 2 không khí. Tính:
a) Cường độ điện trường gây bởi các điện tích đó tại các điểm A, B, C. Cho biết: MN = d = 10 cm, MA = 4
cm, MB = 5 cm, MC = 9 cm, NC = 7 cm.
b) Lực tác dụng lên điện tích 10 q 5.10 C đặt tại C. Bài giải: 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Tại điểm A: E và E cùng chiều nhau như hình vẽ: 1A 2A 8 8 q q 1 2 9 8.10 3.10 3 E E E k 9.10 . 525.10 V / m A 1A 2A 2 2 2 2 MA NA 0,04 0,06
Tại điểm B: E và E ngược chiều nhau như hình vẽ: 1B 2B 8 8 q q 1 2 9 8.10 3.10 3 E E E k 9.10 . 276.10 V / m B 1B 2B 2 2 2 2 MB NB 0,05 0,15
Tại điểm C: E và E có chiều nhau như hình vẽ. 1C 2C Ta có: 2 2
E E E 2E E cos , trong đó: C 1C 2C 1C 2C 8 q 8 q 1 9 8.10 3 E k 9.10 . 88,9.10 V / m và 2 9 3.10 3 E k 9.10 . 55,1.10 V / m 2C 2 2 1C 2 2 MC 0,09 NC 0,07 2 2 2 2 2 2 MC NC MN 9 7 10 5 cos , 0 76,2 2MC.NC 2.9.7 21 Thay vào ta được: 3 2 2 3
E 10 88,9 55,1 2.88,9.55,1.(5 / 21) 92,8.10 V / m C
Cường độ điện trường tại C tạo với cạnh CN 1 góc: 0 0
90 90 76,2 13,8 b) Lực 1 0 3 5 F q E 5.10 .92,8.10 4,6.10 N C C
Lực này ngược chiều với EC.
Bài 1.20. Một mặt phẳng vô hạn mang điện đều có mật độ điện tích mặt là 2.10-9 C/cm2 = 2.10-5 C/m2. Hỏi
lực tác dụng lên một đơn vị chiều dài của một sợi dây dài vô hạn mang điện đều. Cho biết mật độ điện dài của dây là 8 6 3.10 C/cm 3.10 C/m . Bài giải:
Lực tác dụng của mặt phẳng lên sợi dây bằng tổng lực tác dụng lên các phần tử của sợi dây. Ta đã biết điện
trường do 1 mặt phẳng gây ra là E
không phụ thuộc vào khoảng cách từ mặt phẳng đến các phần tử 20
điện tích của sợi dây nên dù đặt sợi dây thế nào thì lực tác dụng lên 1 phần tử dq của sợi dây vẫn đều là dq dF Edq , trong đó dq dl dl nên dF
. Lực tác dụng lên mỗi đơn vị chiều dài của dây là: 2 2 0 0 5 6 dF 2.10 .3.10 3,4 N / m 12 dl 2 2.1.8,86.10 0
Bài 1.23. Cho 2 điện tích điểm 6 q 2.10 C , 6
q 10 C đặt cách nhau 10 cm. Tính công của lực tĩnh điện 1 2
khi điện tích q2 dịch chuyển trên đường thẳng nối hai điện tích đó xa thêm một đoạn 90 cm. Bài giải:
Ta coi đây là bài toán xác định công của lực tĩnh điện do điện tích q1 tác dụng để dịch chuyển điện tích điểm
q2 dịch chuyển trong điện trường mà nó gây ra. 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Như vậy: A q V V , trong đó V MN 2 M N
M và VN lần lượt là điện thế tại 2 điểm MN trên đường thẳng nối 2
điện tích và cách nhau 1 khoảng 90 cm. Giả sử: kq kq 1 V và 1 V M r N r r 9 6 kq kq kq q r 9.10 .2.10 . 6 10 .0,9 Suy ra: 1 1 1 2 A q 0 ,162 J MN 2 r r r r(r r ) 1.0,1. 0,10,9
Dấu “-” có nghĩa là lực điện trường là lực cản, tức là ta phải thực hiện 1 công là +0,162 J để thắng lực điện
trường. Trong bài toán này, 2 điện tích là trái dấu nên hút nhau, vì thế muốn đưa 1 điện tích ra xa thêm thì
đương nhiên là phải thực hiện công thắng lại lực hút này.
Bài 1.24. Tính công cần thiết để dịch chuyển một điện tích 1 7
q .10 C từ một điểm M cách quả cầu tích 3
điện bán kính r = 1 cm một khoảng R = 10 cm ra xa vô cực. Biết quả cầu có mật độ điện mặt là 1 1 2 7 2 10 C/cm 10 C/m . Bài giải:
Vẫn sử dụng công thức tính công của điện trường khi dịch chuyển điện tích từ điểm M đến N (trong trường
hợp này N ở vô cực): A q V V . Như vậy, cần phải tính điện thế tại các điểm M và N. MN M N
Nhân đây phải nói đến bài toán tính điện thế tại 1 điểm nằm bên ngoài và cách tâm quả cầu mang điện đều
1 khoảng là r>r0 (bài mà thầy chưa có dịp tính trên lớp trong giờ lý thuyết).
Ta có: dV Edr (mối liên hệ giũa điện trường và điện thế)
Mặt khác sử dụng định lý Ostrogradski – Gauss ta dễ dàng tính được: kQ E
, trong đó Q là điện tích của 2 r quả cầu. Thay vào ta được: kQ kQ dV dr V
C , chọn gốc điện thế tại vô cực ta có C = 0, suy ra: kQ V 2 r r r
Quay trở lại bài toán của chúng ta: A q V V MN M N 2 kQ kqQ kq4 r
9.10 .1/ 3.10 .40, 2 9 7 7 01 .10 7 V ;V 0 A 3,42.10 J , M r R N MN
r R r R 10,01 0, 1 trong đó 2 Q 4 r .
Bài 1.25. Một vòng dây tròn bán kính 4 cm tích điện đều với điện tích Q = (1/9).10-8 C. Tính điện thế tại: a) Tâm vòng dây;
b) Tại một điểm M trên trục vòng dây, cách tâm của vòng dây 1 đoạn là h = 3 cm.
Ta làm 1 bài tổng quát, tìm điện thế tại 1 điểm M trên trục vòng dây,
cách tâm vòng dây 1 đoạn là h. Ta có: kdQ dV 2 2 R h Suy ra: kdQ kQ V dV 2 2 2 2 R h R h
a) Điện thế tại tâm vòng dây h = 0 9 kQ 9.10 .1/ 9 8 .10 V 250 V O R 1.0,04 9 kQ 9.10 .1/ 9 8 .10 b) Tại điểm M: V 200 V H 2 2 2 2 R h 1. 0,04 0,03
Bài 1.32. Tại hai đỉnh C, D của một hình chữ nhật ABCD (có các cạnh AB = 4 m, BC = 3 m) người ta đặt hai điện tích điểm 8 q 3.10 C (tại C) và 8
q 3.10 C (tại D). Tính hiệu điện thế giữa A và B. 1 2 Bài giải: 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 AC = BD = 5 m 9 8 8 k q q 9.10 3. 10 3.10 1 2 V V V 36 V A CA DA CA DA 1 5 3 9 8 8 k q q 9.10 3.10 3.10 1 2 V V V 36 V B CB DB CB DB 1 3 5
Hiệu điện thế giữa A và B là: U V V 72 V AB A B
Bài 1.33. Tính công của lực điện trường khi chuyển dịch điện tích q = 10-9 C từ điểm C đến điểm D nếu a = 6
cm, Q1 = (10/3).10-9 C, Q2 = 2.10-9 C. Bài giải:
Nhớ là muốn tính công của lực điện trường thì có công thức: A q V V CD C D Ta có: 9 kQ kQ 9.10 10 / 3 2 1 2 9 V .10 200 V C A C B C 1 0,06 0,06 9 kQ kQ 9.10 10 / 3 2 1 2 9 V .10 141 V D A D B D 1 0,06 2 0,06 2
Công của lực điện khi đó: A qV V 9 10 200 14 9 1 59.10 J C D
Bài 1.37. Cho hai mặt trụ đồng trục mang điện đều bằng nhau và trái dấu có bán kính lần lượt là 3 cm và 10
cm, hiệu điện thế giữa chúng là 50 V. Tính mật độ điện dài trên mỗi mặt trụ và cường độ điện trường tại điểm
ở khoảng cách bằng trung bình cộng của hai bán kính. Bài giải:
Trước tiên quay trở lại bài toán tính điện trường gây ra bởi một mặt trụ dài vô hạn tích điện đều.
Xét 1 mặt Gauss có dạng mặt trụ có độ cao là h, diện tích đáy là S. Thông lượng điện: D dS D dS D dS e n n n mÆt trô mÆt bªn hai ®¸y trong đó D dS 0 vì D n n = 0 nên: hai ®¸y D dS D2 rh 2 Erh e n 0 mÆt bªn
Điện tích của khối trụ: Q h , trong đó là mật độ điện dài của khối trụ theo chiều cao.
Theo định lý O – G: Q
h 2 Erh E e 0 2 r 0
Đối với những điểm nằm giữa 2 mặt trụ thì chỉ có mặt trụ ở phía trong gây ra điện trường. Ta tính điện thế tại
1 điểm cách trục của mặt trụ trong 1 khoảng là r. dr ln r dV Edr dV V C 2 r 2 0 0
Như vậy hiệu điện thế giữa 2 mặt trụ R1 = 3 cm và R2 = 10 cm là: 1 2 R 2 V 2 1. , 86.10 .50 2 0 9 V ln 2,3.10 C 2 R R 10 0 1 2 ln ln R 3 1 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
BÀI TẬP CHƯƠNG VẬT DẪN – TỤ ĐIỆN
Tóm tắt lý thuyết
1. Điều kiện cân bằng tĩnh điện
- Véc-tơ cường độ điện trường tại mọi điểm bên trong vật dẫn phải bằng không: E 0 trong
- Thành phần tiếp tuyến E của véc-tơ cường độ điện trường tại mọi điểm trên mặt vật dẫn phải bằng không (tức t
là véc-tơ cường độ điện trường phải vuông góc với mặt vật dẫn): E 0, E E t n
2. Những tính chất của vật dẫn mang điện:
- Vật dẫn cân bằng tĩnh điện là một khối đẳng thế. Mặt vật dẫn là một mặt đẳng thế.
- Nếu truyền cho vật dẫn một điện tích q nào đó thì điện tích q chỉ được phân bố trên bề mặt của vật dẫn, bên
trong vật dẫn, điện tích bằng không (các điện tích âm và dương trung hòa nhau).
- Đối với một vật dẫn rỗng đã ở trạng thái cân bằng tĩnh điện, điện trường ở phần rỗng và trong thành của vật
rỗng cũng luôn luôn bằng không.
3. Hiện tượng điện hưởng
- Hiện tượng các điện tích cảm ứng xuất hiện trên một vật dẫn (lúc đầu không mang điện) khi đặt trong điện
trường ngoài được gọi là hiện tượng điện hưởng.
- Điện tích cảm ứng trên các phần tử tương ứng có độ lớn bằng nhau và trái dấu.
Trong trường hợp điện hưởng một phần, độ lớn của điện tích cảm ứng nhỏ hơn độ lớn điện tích trên vật mang điện.
Trong trường hợp điện hưởng toàn phần, độ lớn của điện tích cảm ứng bằng độ lớn điện tích trên vật mang điện.
4. Điện dung của một vật dẫn cô lập (về điện)
Điện dung của một vật dẫn cô lập là một đại lượng về giá trị bằng điện tích cân truyền cho vật dẫn để điện tích
của vật tăng lên một đơn vị điện thế.
(Điện dung của vật dẫn cô lập là một đại lượng về giá trị bằng điện tích mà vật dẫn tích được khi điện thế của
nó bằng một đơn vị điện thế). Q C V Đơn vị: 1 culomb 1 fara =
, các đơn vị ước của fara: 6 1 F = 10 F , 9 1 nF = 10 F , 1 2 1 pF = 10 F 1 von
Điện dung của 1 quả cầu bằng kim loại (cô lập)
Quả cầu là vật dẫn nên điện thế tại mọi điểm của quả cầu là như nhau và bằng điện thế do điện tích Q coi như đặt
tại tâm của quả cầu gây ra tại điểm cách tâm một khoảng bằng bán kính R: Q kQ V 4 R R 0
Theo định nghĩa, điện dung: Q R C 4 R 0 V k 5. Tụ điện
Tụ điện là hệ hai vật dẫn cô lập ở điều kiện điện hưởng toàn phần.
a. Tụ điện phẳng: là hệ hai bản kim loại phẳng cùng diện tích S đặt song song và cách nhau một đoạn d. Q Q C
, trong đó: U = Ed, E là điện trường đều giữa 2 bản tụ: Q E V V U S 1 2 0 0 Thay vào ta được: Q S 0 C U d
b. Tụ điện cầu: hai bản tụ là hai mặt cầu kim loại đồng tâm có bán kính R1 và R2 (R1 > R2)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Q 1 1 QR R kQ R R 1 2 1 2 Ta có: V V 1 2 4 R R 4 R R R R 0 1 2 0 1 2 1 2
Trong đó Q là giá trị tuyệt đối của điện thế mỗi bản, V V U là hiệu điện thế giữa hai bản tụ. Điện dung C 1 2 của tụ được tính: Q 4 R R R R 0 1 2 1 2 C U R R k R R 2 1 2 1
c. Tụ điện trụ: hai bản của tụ điện là hai mặt trụ kim loại đồng trục bán kính lần lượt là R1 và R2 (R1 < R2) có độ
cao là l, rất lớn so với R1 và R2. Ta có: Q R Q 2 l l 2 V V ln , do đó: 0 C 1 2 2 l R V V R R 0 1 1 2 2 2 ln 2k ln R R 1 1
6. Năng lượng vật dẫn cô lập 2 2 QV CV Q W 2 2 2C
7. Năng lượng của tụ điện 2 2 QU CU Q W 2 2 2C
8. Năng lượng điện trường của 1 tụ điện phẳng 1 2 W CU , 2 lại có: S 1 1 W 1 ED 0 C , U Ed suy ra: 2 2 2 W E Sd E V w E
- mật độ năng lượng điện d 0 0 0 2 2 V 2 2 trường. 2
Năng lượng của một điện trường bất kỳ: E ED 0 W dV dV 2 2 V V Phần bài tập
Bài 1.1. Cho 2 mặt cầu kim loại đồng tâm bán kính R1 = 4 cm, R2 = 2cm mang điện tích Q1 = -(2/3).10-9 C, Q2 =
3.10-9 C. Tính cường độ điện trường và điện thế tại những điểm cách tâm mặt cầu những khoảng lần lượt bằng 1 cm, 2 cm, 3 cm, 4 cm, 5 cm.
Bằng phép tính tích phân tính được: điện thế tại 1 điểm cách tâm quả cầu là x được tính theo công thức: kq (x R) R V kq (x R) x
Còn cường độ điện trường thì phía trong quả cầu E = 0, Phía ngoài vỏ cầu kq E 2 x
Bài 2.2. Một quả cầu kim loại bán kính 10 cm, điện thế 300 V. Tính mật độ điện mặt của quả cầu
Điện thế quả cầu được tính theo công thức: kq V , trong đó 2 q S 4 R , từ đó suy ra: R
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2 k4 R V 300 9 2 V 4k R 26,5.10 C/m 9 R 4k R 4.9.10 .0 ,1
Bài 2.8. Một quả cầu kim loại bán kính R = 1 m mang điện tích q =10-6 C. Tính:
a) Điện dung của quả cầu;
b) Điện thế của quả cầu;
c) Năng lượng trường tĩnh điện của quả cầu.
a) Ta có điện thế của quả cầu được tính theo công thức: kq V , suy ra: q R C R V k Thay số ta được: 1 10 C 1,1.10 F 9 9.10 6 b) Điện thế: q 10 V 9000 V 10 C 1,1.10 2 10 2
c) Năng lượng trường tĩnh điện của quả cầu: CV 1,1.10 .9000 3 W 4,5.10 J 2 2
Bài 2.9. Tính điện dung của Trái Đất, biết bán kính của Trái Đất là R = 6400 km. Tính độ biến thiên điện thế của
Trái Đất nếu tích thêm cho nó 1 C. 3
Coi như Trái Đất là 1 quả cầu, ta có điện dung của trái đất là: q R 6400.10 4 C 7,1.10 F 9 V k 9.10 Lại có q q 1 V V 1405 V 4 C C 7,1.10
Bài 2.11. Cho một tụ điện cầu bán kính hai bản là r = 1 cm và R = 4 cm, hiệu điện thế giữa hai bản là 3000 V.Tính
cường độ điện trường ở một điểm cách tâm tụ điện 3 cm.
Dùng định lý Gauss dễ dàng suy ra được cường độ điện trường chỉ do bản tụ phía trong gây ra. kq E
, điện thế tại một điểm nằm giữa 2 bản tụ là: 2 x kq kq V x dx const 2 x x
Hiệu điện thế giữa 2 bản tụ là: R kq kq R 1 1 U dx kq 2 x x r r R r Điện dung: q rR URr C q U k(R r) k R r Suy ra: kq kURr URr 3000.0,04.0,01 3 E 44,4.10 V/m 44,4 kV/m 2 x kR r 2 x R r 2 x 0,040,0 2 1 .0,03
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
BÀI TẬP CHƯƠNG 8. ĐIỆN MÔI
Tóm tắt lý thuyết:
- Liên hệ giữa cường độ điện trường và cảm ứng điện: D E 0
- Vector phân cực điện môi: P E 0
D E 1 E E P , trong đó 1 , gọi là hệ số phân cực điện môi. 0 0 0
- Mật độ điện tích liên kết trên mặt chất điện môi đặt trong điện trường: P E n 0 n
Trong đó Pn và En là hình chiếu của vector phân cực điện môi và vector cường độ điện
trường lên phương pháp tuyến ngoài của mặt có điện tích xuất hiện.
- Dạng toán liên quan đến tụ điện:
+ Mối quan hệ giữa hiệu điện thế U, cường độ điện trường E, khoảng cách giữa các bản tụ d: U Ed .
+ Cường độ điện trường gây bởi một mặt phẳng mang điện đều: E 2 0
+ Mật độ điện mặt trên hai bản tụ tích điện đều: E 0
+ Mật độ điện tích liên kết:
P E 1 E n 0 n 0 n
+ Điện dung của tụ điện phẳng: S 0 C d
Các bài tập cần làm: 3.1, 3.3, 3.4, 3.5, 3.8.
Bài 3.1. Xác định mật độ điện tích liên kết trên mặt một tấm mica dày 0,02 cm đặt vào giữa
và áp sát vào hai bản của một tụ điện phẳng được tích điện đến hiệu điện thế U = 400 V. Bài giải:
Cần nhớ, đây là xác định mật độ điện tích liên kết trên mặt một tấm điện môi (mica), ta nhớ đến công thức:
P E 1 E n 0 n 0 n
Đối với tụ điện, chúng ta chú ý, điện trường gây ra bởi 2 bản tụ là điện trường đều, hướng
vuông góc với các bản tụ, từ phía bản dương sang bản âm. Cho nên: U E E n d Nên ta có: 1 E U 1 7,5 1 2 400 4 1 .8,86.10 . 1,15.10 2 C / m 0 n 0 2 d 0,02.10
Chú ý: hằng số điện môi của mica có sách ghi là từ 5,7 đến 7, có sách ghi bằng 6, có sách ghì bằng 7,5.
Bài 3.3. Một tụ điện phẳng có chứa điện môi ( 6) khoảng cách giữa hai bản là 0,4 cm,
hiệu điện thế giữa hai bản là 1200 V. Tính:
1. Cường độ điện trường trong chất điện môi.
2. Mật độ điện mặt trên hai bản tụ điện.
3. Mật độ điện mặt trên chất điện môi. 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Tóm tắt:
6, d = 4 cm = 4.10-2 m, U = 1200 V. 1. E = ? 2. ? 3. ? Bài giải:
1. Đối với tụ điện bất kỳ, cường độ điện trường giữa các bản tụ (tức là cường độ điện trường
trong chất điện môi) là: U 1200 5 E 3.10 V / m 3 d 4.10
ở đây rất có thể chúng ta sẽ làm nhầm như sau:
Cường độ điện trường trong chất điện môi là E U 0 E
, trong đó E , tức là chúng ta 0 d
coi điện trường ngoài E0 là điện trường giữa 2 bản phẳng, nhưng nên nhớ, trong phần lý thuyết
E0 là điện trường giữa 2 bản phẳng lúc chưa đặt điện môi, có nghĩa là điện trường của 1 tụ điện
không khí. Còn trong trường hợp này, đây là một tụ điện có chứa điện môi 6 nên cường độ
điện trường giữa 2 bản tụ lúc này chính là cường độ điện trường trong lòng chất điện môi.
Để làm rõ hơn, tiếp tục chúng ta sẽ tính E0, tức là độ lớn của điện trường do các điện tích
tự do gây ra (tức là điện tích trên các bản tụ), theo lý thuyết: 5 5
E E 6.3.10 18.10 V / m 0
Ta tính luôn cả cường độ điện trường E gây ra do các điện tích liên kết trên bề mặt của chất điện môi: 5 5 5
E E E 18.10 3.10 15.10 V / m (đúng theo lý thuyết) 0
2. Mật độ điện mặt trên 2 bản tụ điện được suy ra từ công thức sau: 12 5 5
E 8,86.10 .18.10 1,59.10 2 C / m 0 0
3. Mật độ điện mặt trên chất điện môi cũng được tính từ công thức tương tự: 12 5 5
E 8,86.10 .15.10 1,33.10 2 C / m 0
Ngoài ra chúng ta có thể biến đổi để sử dụng công thức sau: 1
Thật vậy: E E E 0 0 0 Mặt khác: E 1 0 E nên ta có: 0 0 0 0
Bài 3.4. Cho một tụ điện phẳng, môi trường giữa hai bản ban đầu là không khí ( 1), 1
diện tích mỗi bản là 0,01 m2, khoảng cách giữa hai bản là 0,5 cm, hai bản được nối với một hiệu
điện thế 300 V. Sau đó bỏ nguồn đi rồi lấp đầy khoảng không gian giữa hai bản bằng một chất điện môi có 3. 2
1. Tính hiệu điện thế giữa hai bản tụ điện sau khi lấp đầy điện môi;
2. Tính điện tích trên mỗi bản. Bài giải: 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Đây là bài toán khá điển hình về tụ điện. Lúc đầu, đây là một tụ không khí và được tích
điện bằng một hiệu điện thế 300 vôn, sau khi các bản tụ đã tích điện xong thì ngắt nguồn và cho
điện môi vào giữa các bản tụ, khi đó điện tích không đổi, nhưng điện dung thay đổi thành ra hiệu
điện thế giữa hai bản tụ sẽ thay đổi. 12
Điện dung của tụ điện không khí là: S 8,86.10 .1.0,01 0 1 11 C 1,772.10 F 1 2 d 0,5.10 Suy ra: 1 1 9
Q C U 1,772.10 .300 5,3.10 C 1 1
Điện dung của tụ điện sau khi lấp đầy chất điện môi là: 12 S 8,86.10 .3.0,01 0 2 11 C 5,3.10 F 2 2 d 0,5.10 9 Khi đó Q 5,3.10 U 100 V 2 11 C 5,3.10 2
Bài 3.5. Cho một tụ điện phẳng, khoảng cách giữa hai bản là 0,01 m. Giữa hai bản đổ đầy
dầu có hằng số điện môi 4,5. Hỏi cần phải đặt vào các bản một hiệu điện thế bằng bao nhiêu
để mật độ điện tích liên kết trên dầu bằng 6,2.10-10 C/cm2. Bài giải: d = 0,01 m, 4,5, 1 0 2 6 2
6,2.10 C/cm 6,2.10 C/m U = ?
Cường độ điện trường giữa hai bản tụ: U E d
Mật độ điện tích liên kết được tính theo công thức: U
E E 1 1 0 0 0 0 d 6 Suy ra: d 6,2.10 .0,01 U 2000 V 1 8.86.10 .3,5 0 12
Bài 3.8. Trong một tụ điện phẳng có khoảng cách giữa các bản là d, người ta đặt một tấm
điện môi dày d1 < d song song với các bản của tụ điện. Xác định điện dung của tụ điện trên. Cho
biết hằng số điện môi của tấm điện môi là , diện tích của tấm đó bằng diện tích các bản của tụ điện và bằng S. Bài giải: 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Đây có thể coi như bài toán 3 tụ điện mắc nối tiếp, trong đó tụ 1 có
bề dầy d1, có chất điện môi . Hai tụ 2 và 3 lần lượt có bề dầy d2 và d3, là tụ không khí: Ta có: S S S 0 C , 0 C , 0 C 1 d 2 d 3 d 1 2 3
Đối với bộ tụ mắc nối tiếp ta có: 1 1 1 1 1 d 1 d 1 1 d d d d 2 3 1 C C C C S S b 1 2 3 0 0 d 1 d1 S 0 Ta suy ra: S 0 C d 1 d1 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
BÀI TẬP CHƯƠNG 8. TỪ TRƯỜNG
Tóm tắt lý thuyết: B
- Vector cường độ từ trường và vector cảm ứng từ: H = µµ0
- Định luật Biot – Savart – Laplace: vector cảm ứng từ gây bởi một phần tử dòng điện: → → → µµ0 d B = (Id l x r ) 3 4 r π
Trong đó dB là vector cảm ứng từ do phần tử dòng điện Idl gây ra tại điểm M xác định
bởi bán kinh vector r (vector nối từ phần tử dòng điện tới điểm M), 7 4 .10− µ = π H/m gọi là hằng 0
số từ, µ gọi là độ từ thẩm của môi trường.
+ có phương: vuông góc với mặt phẳng chứa phần tử dòng điện và điểm khảo sát.
+ có chiều: theo qui tắc đinh ốc hoặc nắm tay phải. + độ µµ Idl lớn: 0 dB = .sin θ 2 4 r π
- Nguyên lý chồng chất từ trường: → →
+ vector cảm ứng từ gây bởi một dòng điện bất kỳ: B = d B ∫ DD → →
vector cảm ứng từ gây bởi nhiều dòng điện: B = i ∑B i
- Vectơ cảm ứng từ của dòng điện thẳng: µµ I 0 B = (cosθ − cosθ ) 1 2 4 h π
+ có phương vuông góc với mặt phẳng chứa dòng điện và điểm khảo sát;
+ có chiều theo quy tắc cái đinh ốc, hoặc nắm tay phải; + độ µµ I lớn: 0 B = (cosθ − cosθ ) 1 2 4 h π µµ I I
- với sợi dây dài vô hạn: 0 B = → H = 2 h π 2 h π
- vector cảm ứng từ gây bởi dòng điện tròn tại một điểm trên trục của vòng dây: 2 µµ IR 0 B = 2 2 3/2 2(R + h ) µµ I
- vector cảm ứng từ gây bởi dòng điện tròn tại tâm vòng dây h = 0: 0 B = O 2R
- mômen từ của dòng điện tròn: p = I.S , p có phương vuông góc với mặt phẳng dòng m m
điện, co chiều xác định theo quy tắc cái đinh ốc hoặc nắm tay phải. N
- cảm ứng từ trong lòng ống dây: B = µµ nI = µµ . .I , trong đó n – là mật độ vòng dây. 0 0 L 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 → →
- từ thông: dΦ = BdScosα = Bd S (đơn vị là vêbe, Wb) m
- Từ thông của từ trường đều gởi qua một diện tích phẳng: Φ = BS.cosα m → →
- Định lý OG: Từ thông gửi qua một mặt kín bất kì thì luôn bằng không: Bd S = 0 ∫ , (S) → div B = 0
- Định lý Ampere: Lưu số của vectơ cường độ từ trường dọc theo một đường cong kín bất
kì thì bằng tổng đại số các dòng điện xuyên qua diện tích giới hạn bởi đường cong kín đó. → → → → Hd l = ∫ ∑I = k hay rot H j (C) k → → →
- Công thức Ampere: Lực từ tác dụng lên một phần tử dòng điện: d F = [Id l ,B]
+ phương vuông góc với mặt phẳng chứa phần tử dòng điện và vector cảm ứng từ;
+ chiều theo quy tắc bàn tay trái;
+ độ lớn: dF = BId .sinθ
- Từ trường đều tác dụng lên dây dẫn thẳng: F = BIl.sin θ F µµ I I
- Lực tương tác giữa 2 dòng điện thẳng song song (trên một mét dài): 0 1 2 f = = l 2 d π
- Lực từ tác dụng lên khung dây: → → →
+ Mômen của lực từ: M = p x B, độ lớn: M = p .B.sin θ = BIS.sin θ m m
- Công của lực từ: A = Fdx = BIl.dx = BIdS = I.dΦ ∫ ∫ ∫ ∫ . Suy ra: A = I.∆Φ m m → → → - Lực Lorentz: FL = q[v,B]:
+ phương vuông góc với mặt phẳng chứa vector ( v,B) ;
+ chiều đối với điện tích dương theo quy tắc bàn tay trái;
+ chiều đối với diện tích âm theo quy tắc bàn tay phải. F | = q | B.v.sinθ L
- Điện tích chuyển động trong từ trường đều: → → →
+ vector vận tốc ban đầu song song: v B ⇒ F = 0, suy ra điện tích chuyển động thẳng 0 L đều; → →
+ vector vận tốc ban đầu vuông góc v ⊥ B , điện tích chuyển động tròn đều, lực lorentz 0 2
đóng vai trò là lực hướ v ng tâm: F | = q | B.v = ma = m . L r π Bán kính quỹ đạo: mv r = , chu kỳ quay 2 m T = | q | B | q | B
- Điện tích chuyển động theo đường lò xo: khi vận tốc ban đầu tạo với B một góc nào đó,
thành phần song song không bị ảnh hưởng của từ trường, nên hạt chuyển động đều, thành phần 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
vuông góc thì chịu ảnh hưởng của chuyển động tròn đều. Như vậy, hạt vừa chuyển động tròn,
vừa chuyển động đều nên quỹ đạo có dạng lò xo: θ + bán kính xoắn: mv⊥ mv .sin 0 r = = | q | B | q | B π + chu kỳ: 2 m T = | q | B + Bướ π c xoắn: 2 m h = v .T = v .cos . θ 0 | q | B
Các bài tập cần làm: 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.10, 4.11, 4.13, 4.17, 4.18, 4.21,
4.26, 4.27, 4.29, 4.30, 4.37, 4.38, 4.40, 4.42, 4.43, 4.48.
Bài 4.1. Tính cường độ từ trường của một dòng điệnt hẳng dài vô hạn tại một điểm cách dòng
điện 2 cm. Biết cường độ dòng điện I = 5 A. Bài giải: Bài này trướ µ I µ
c khi giải phải nhớ công thức: 0 B =
và mối quan hệ giữa B và H: B = µ H µ 2 r π 0 Như vậ I 5 y: H = = ≈ 39,8 A / m 2 ( ) 2 r π 2 .2.10− π
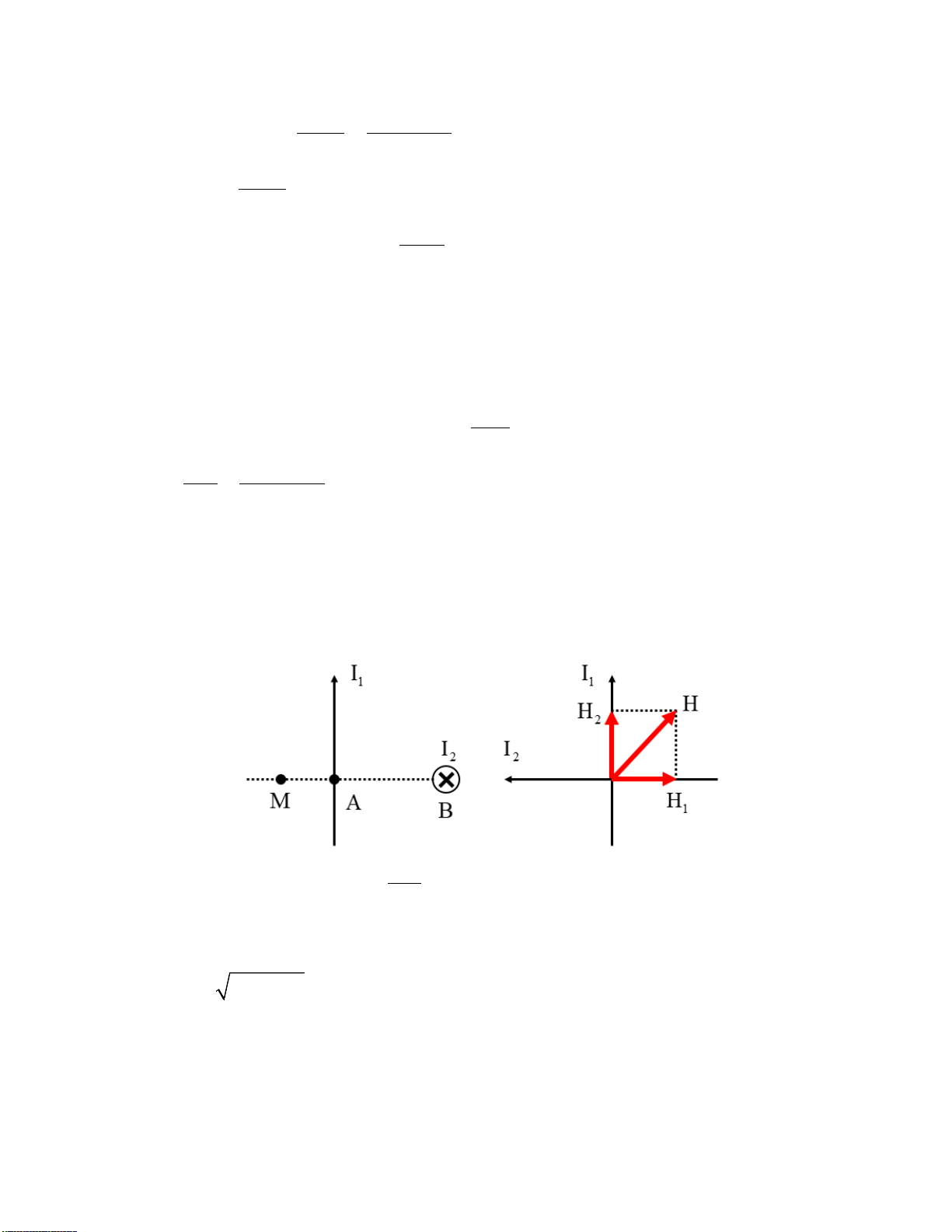
Bài 4.2. Hai dòng điện thẳng dài vô hạn, có cường độ dòng điện I = I = 5 A , được đặ 1 2 t vuông
góc với nhau và cách nhau một đoạn AB = 2 cm. Chiều các dòng điện như hình vẽ. Xác định
cường độ véc-tơ cường độ từ trường tại điểm M nằm trong mặt phẳng chứa I1 và vuông góc với
I2 , cách dòng điện I1 một đoạn MA = 1 cm. I
Bài này cần phải nhớ công thức: H =
giống ở bài trên. 2 r π
Tại điểm M, H1 xác định chiều theo quy tắc cái đinh ốc thì thấy đi ra, còn H2 theo quy tắc cái
đinh ốc hướng thẳng đứng lên trên. Và H ⊥ H , như vậ 1 2
y véc-tơ tổng sẽ hướng từ trong ra ngoài. Về độ lớn thì 2 2
H = H + H . Sau đó cần phải xác định góc hợp bởi H tổng hợp với 1 trong hai 1 2 véc-tơ H , như vậ 1 hoắc H2
y mới trả lời đủ câu hỏi H bằng bao nhiêu, và hướng đi đâu, theo phương nào.
Dòng điện I1 gây ra tại M từ trường H1 hướng từ trong ra ngoài (hình bên phải). 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 I 5 1 H = = ≈ 79,6 A / m 1 2 ( ) 2 . π AM 2 .10− π
Tương tự dòng I2 gây ra tại M từ trường H2 hướng lên trên (hình bên phải): I 5 2 H = = ≈ 26,5 A / m 2 2 ( ) 2 . π BM 2 .3.10− π Từ trường tổng hợp: 2 2 2 2
H = H + H = 79,6 + 26,5 ≈ 84 A / m 1 2 ( )
Góc lệch α so với phương H1: H 26,5 1 2 0 tan α = =
≈ ⇒ α ≈18 25′ H 79,6 3 1
Bài 4.3. Hình 4-8 vẽ mặt cắt vuông góc của hai dòng điện thẳng song song dài vô hạn ngược
chiều nhau. Khoảng cách giữa hai dòng điện AB = 10 cm. Cường độ của các dòng điện lần lượt bằng I = 20 A 1
, I2 = 30 A. Xác định vectơ cường độ từ trường tổng hợp tại các điểm M1, M2,
M3. Cho biết M1A = 2 cm, AM2 = 4 cm, BM3 = 3 cm.
Với bài này, tại mỗi điểm cần xác định rõ véc-tơ H1 (gây ra bởi dòng I1) và H2 (gây ra bởi dòng
I ) hướng đi đâu và độ 2
lớn của cái nào lớn hơn sẽ quyết định chiều của véc-tơ H tổng hợp. Trong
trường hợp này thì H1 và H2 luôn vuông góc với I1I2 nên H1 và H2 có 2 khả năng là cùng chiều hoặc ngược chiều.
• Tại điểm M1: H1 hướng xuống dưới như hình vẽ, độ lớn là: I 20 1 H = = =159,15 A / m 1 2 ( ) 2 . π AM 2 .2.10− π 1
H2 hướng từ dưới lên như hình vẽ, độ lớn là: I 30 1 H = = = 39,79 A / m 2 2 ( ) 2 . π BM 2 .12.10− π 1 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Từ trường tổng hợp tại M1: H =159,15 − 39,79 =119,36(A / m)
Vì H1 > H2 nên từ trường tổng hợp hướng theo H1, tức là hướng xuống dưới.
• Tại điểm M2: Từ trường H1 và H2 cùng hướng lên trên, tương tự ta có: I 20 1 H = = = 79,58 A / m 1 2 ( ) 2 . π AM 2 .4.10− π 2 I 30 1 H = = = 79,58 A / m 2 2 ( ) 2 . π BM 2 .6.10− π 1
Từ trường tổng hợp tại M2: H = 79,58*2=159,16(A/m)
Véc-tơ tổng hợp H hướng lên trên như H1 và H2
• Tại điểm M3: Từ trường H1 hướng lên trên và H2 hướng xuống dưới, tương tự ta có: I 20 1 H = = = 24,49 A / m 1 2 ( ) 2 . π AM 2 .13.10− π 2 I 30 1 H = = =159,16 A / m 2 2 ( ) 2 . π BM 2 .3.10− π 1
Từ trường tổng hợp tại M3: H = 159,16-24,49=134,67(A/m)
Vì H2 > H1 nên véc-tơ tổng hợp H hướng xuống dưới theo H2
Bài 4.4. Hình 4-9 biểu diễn tiết diện của ba dòng điện thẳng song song dài vô hạn. Cường độ các
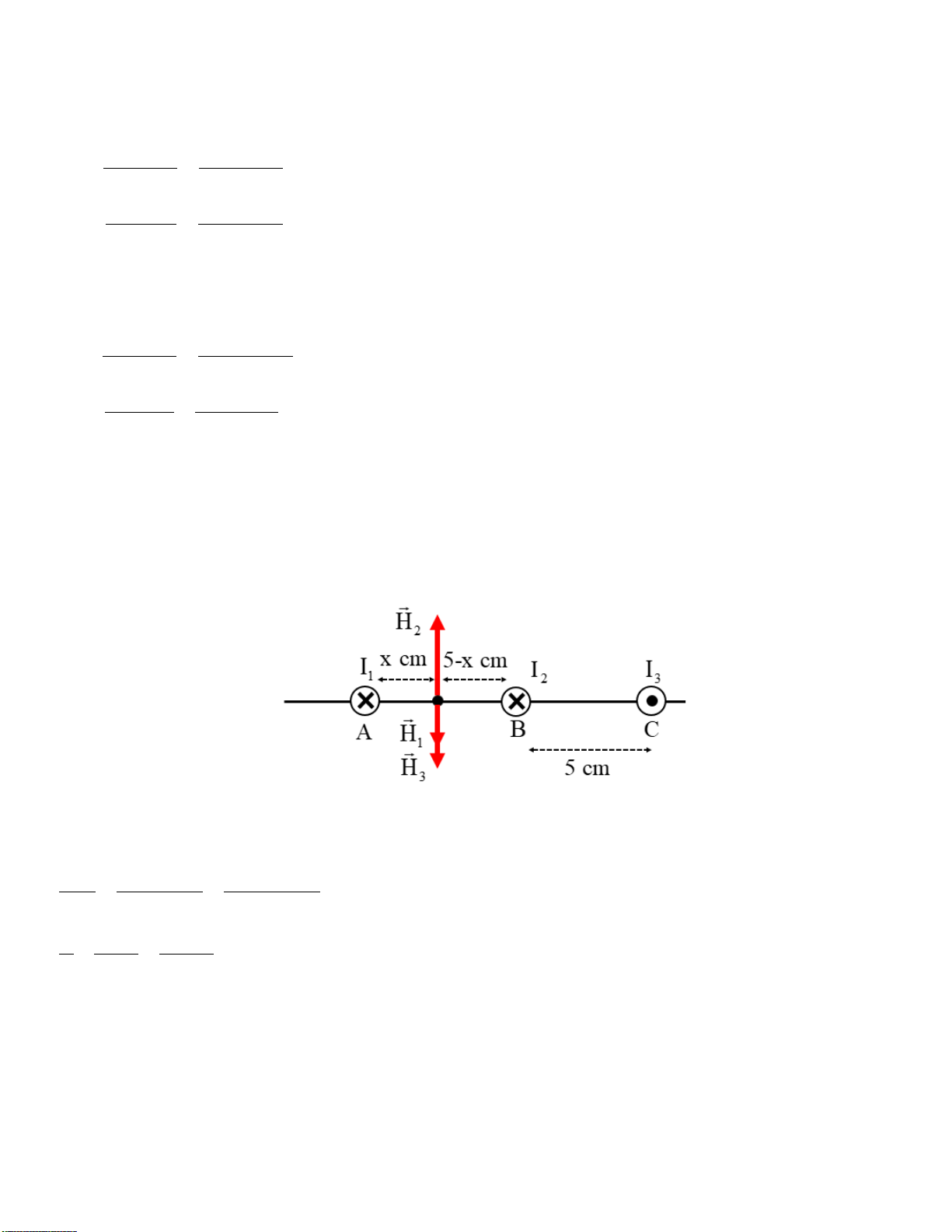
dòng điện lần lượt bằng: I = I = I;I = 2I. Biết AB = BC = 5 cm. Tìm trên đoạn AC điểm có 1 2 3
cường độ từ trường tổng hợp bằng không.
Dễ dàng suy luận được điểm cần tìm nằm trong đoạn AB vì nếu nằm trong đoạn BC, 3 véc-tơ
cường độ từ trường đều hướng xuống dưới và không thể triệt tiêu nhau được.
Ta có phương trình sau: H1 + H3 – H2 = 0 I I 2I − π π( − ) + π( − ) = 0 2 x 2 5 x 2 10 x 1 1 2 − + = 0 ⇒ x = 3,3(cm) x 5 − x 10 − x
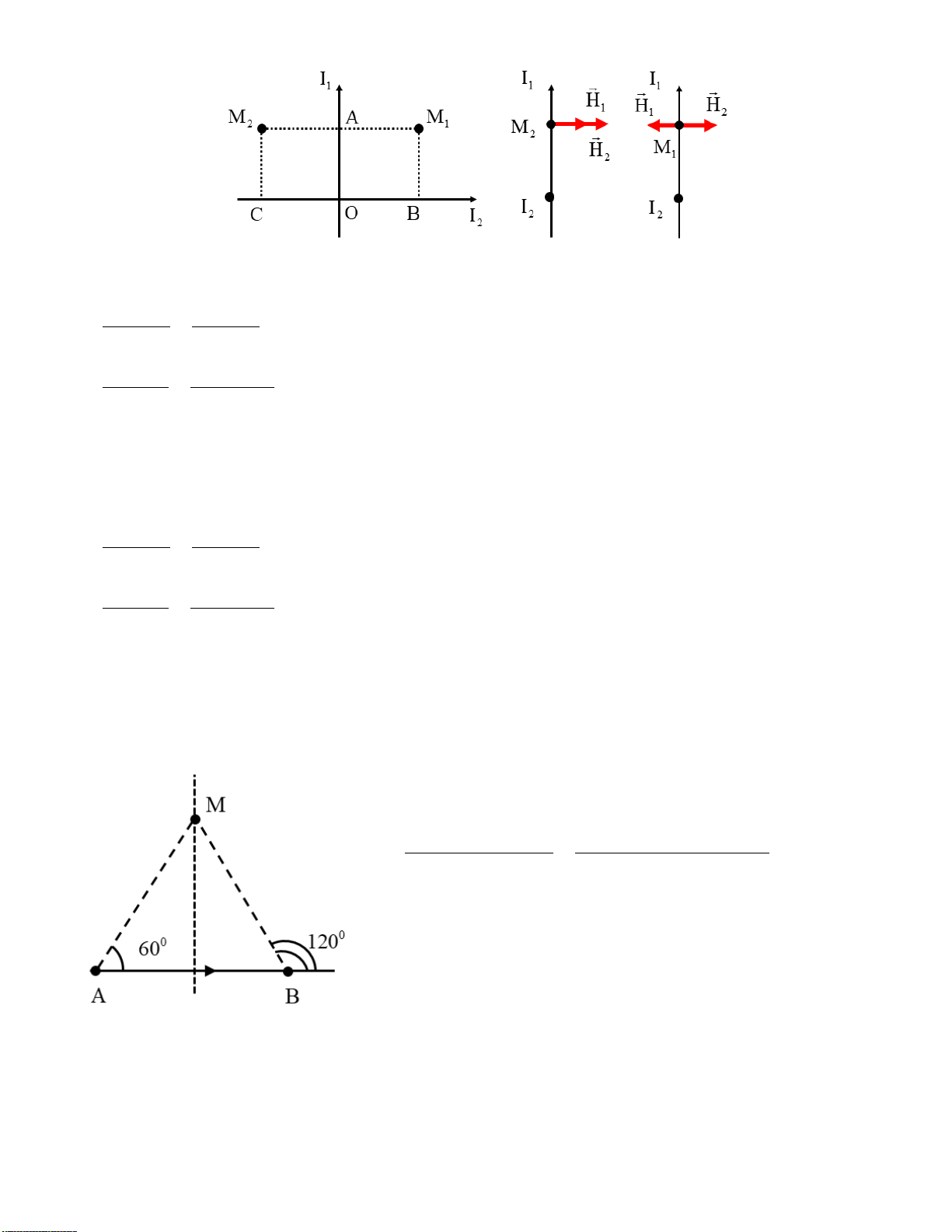
Bài 4.5. Hai dòng điện thẳng dài vô hạn đặt thẳng góc với nhau và nằm trong cùng một mặt phẳng
(hình 4-10). Xác định véc-tơ cường độ từ trường tổng hợp tại các điểm M1 và M2, biết rằng:
I1 = 2 A; I2 = 3 A; AM1 = AM2 = 1 cm; BM1 = CM2 = 2 cm; Giải: 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Tại điểm M1, cả 2 dòng điện gây ra các véc-tơ cường độ từ trường hướng vuông góc với mặt
phẳng hình vẽ nhưng ngược chiều nhau (và được quan sát lại trong hình chiếu cạnh). I 2 1 H = = = 31,83 A / m 1 2 ( ) 2 A π M 2 .10− π 1 I 3 2 H = = = 23,87 A / m 1 2 ( ) 2 B π M 2 .2.10− π 1
Cường độ từ trường tổng hợp là: H = 7,96 (A/m) hướng theo phương của H1 vì H1 > H2.
Tại điểm M2, cả 2 dòng điện gây ra các véc-tơ cường độ từ trường hướng vuông góc với mặt
phẳng hình vẽ theo cùng một chiều (và được quan sát lại trong hình chiếu cạnh). I 2 1 H = = = 31,83 A / m 1 2 ( ) 2 A π M 2 .10− π 1 I 3 2 H = = = 23,87 A / m 1 2 ( ) 2 B π M 2 .2.10− π 1
Cường độ từ trường tổng hợp là: H = 55,7 (A/m) hướng theo phương của H1 và H2.
Bài 4.6. Tìm cường độ từ trường gây ra tại điểm M bởi một đoạn dây dẫn thẳng AB có dòng điện
I = 20 A chạy qua, biết rằng tại điểm M nằm trên trung trực của AB, cách AB 5 cm và nhìn AB dưới góc 600. Bài giải:
Trong bài này ta áp dụng công thức tổng quát để tính cường
độ dòng điện gây ra bởi một đoạn dây dẫn: I(cosθ − cosθ ) 20( 0 0 cos60 − cos120 1 2 ) H = = ≈ 2 4 r π 4 5.10− π. ≈ 31,8(A / m) 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
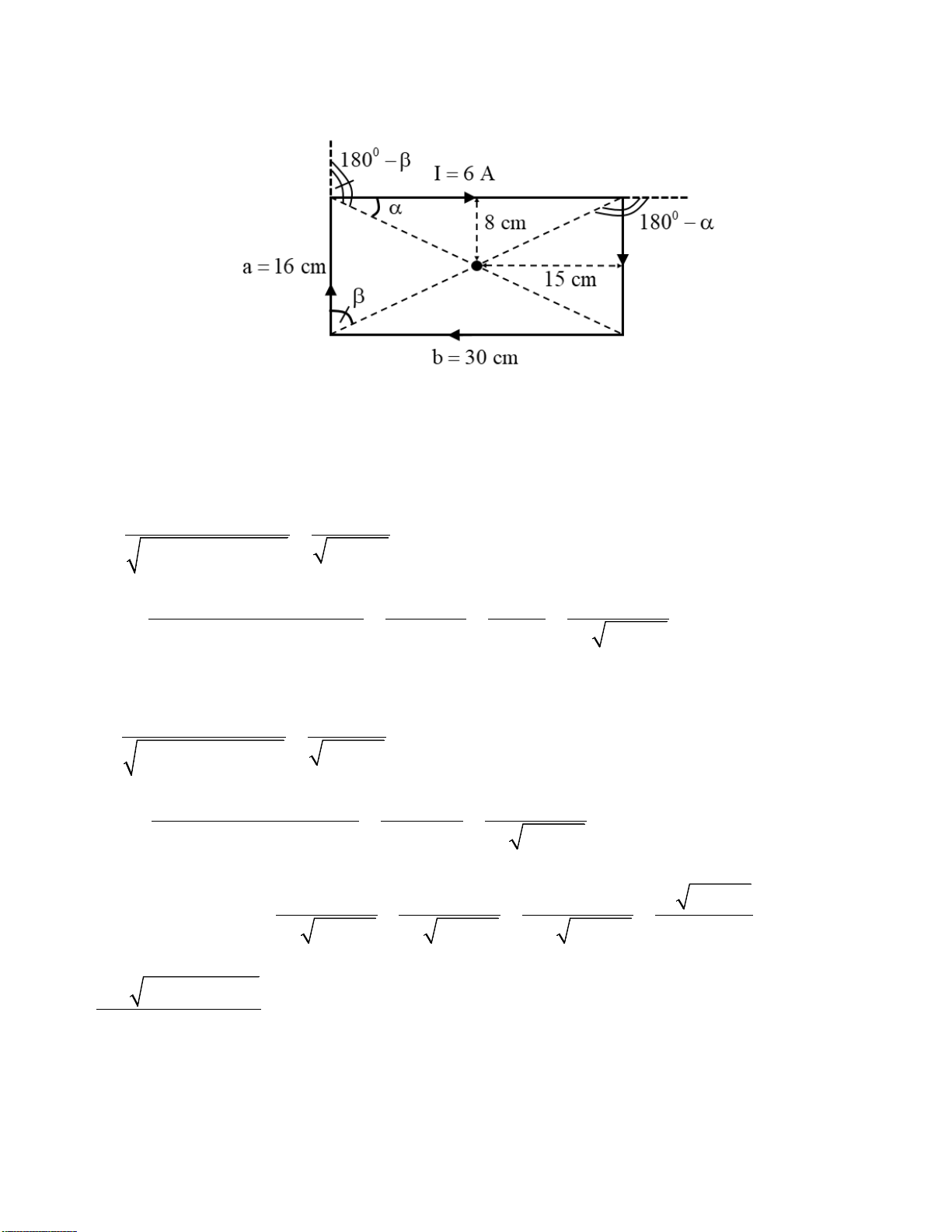
Bài 4.7. Một dây dẫn được uốn thành hình chữ nhật, có các cạnh a = 16 cm, b = 30 cm, có dòng
điện cường độ I = 6 A chạy qua. Xác định véc-tơ cường độ từ trường tại tâm của khung dây. Giải:
Từ hình vẽ trên dễ dàng suy ra, các véc-tơ cường độ từ trường gây ra tại tâm của hình chữ nhật
đều cùng phương, cùng chiều. Trong đó có 2 cặp bằng nhau (cùng do 2 cạnh dài và do 2 cạnh ngắn gây ra):
Cường độ từ trường gây ra bởi cạnh dài là cường độ từ trường gây ra bởi 1 đoạn thẳng mang dòng
điện 6 A được giới hạn bởi các góc α và 0
180 − α (như hình vẽ). Trong đó: b / 2 b cosα = = , ( 0 cos 180 − α) = −cosα (b / 2)2 + (a / 2)2 2 2 a + b I(cosα − cos( 0 180 − α) 2Icosα Icosα Ib H = H = = = = 1 3 4 r π 4π(a / 2) 2 2 a π 1 a π a + b
Cường độ từ trường gây ra bởi cạnh ngắn là cường độ từ trường gây ra bởi 1 đoạn thẳng mang
dòng điện 6 A được giới hạn bởi các góc β và 0
180 − β (như hình vẽ). Trong đó: a / 2 a cosβ = = , ( 0 cos 180 − β) = −cosβ (a / 2)2 + (b / 2)2 2 2 a + b I(cosβ − cos( 0 180 − β) 2Icosβ Ia H = H = = = 2 4 4 r π 4π(b / 2) 2 2 2 b π a + b
Cường độ từ trường tổng hợp có độ lớn: 2Ib 2Ia 2I( 2 2 a + b ) 2 2 2I a + b H = H + H + H + H = + = = 1 2 3 4 2 2 2 2 2 2 a π a + b b π a + b a π b a + b a π b Thay số vào ta được: 2 2 2.6. 0,16 + 0,30 H = ≈ 27, ( 1 A / m) .0 π ,16.0,30 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 8
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 9
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 10
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Giải:
Theo định lý Bio-Savart-Laplace, véc-tơ cảm ứng từ gây ra bởi một vòng dây tại tâm của nó là: 11
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 µ I µ I R IdN 0 B = → H = , suy ra: H = r r ∫
, trong đó dN là số vòng dây quấn quanh khi bán kính 2r 2r 2r d/2
thay đổi từ r đến r + dr.
Ta chia tỷ lệ, khi bán kính thay đổi từ d/2 đến R thì có N vòng dây, vậy nên: N dN = dr R − d / 2 2R R INln INdr Từ đó suy ra: d H = = ∫ 2r R − d / 2 2R − d d/2 ( ) ( )
Véc-tơ mômen từ có độ lớn: 2 p = I. r π m R R N I π N R − d / 8 2 ( 3 3 ) Suy ra: P = p dN = I r π dr = m ∫ m ∫ R − d / 2 3 R − d / 2 d/2 d/2 ( ) 12
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 13
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 14
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Giải:
- Do không có một công thức tổng quát tính lực tác dụng lên một nửa dòng điện tròn nên ta phải sử dụng tích phân.
- Giả sử ta chia vòng tròn thành các phần tử dây dẫn mang điện dl = (s / π)dα. Xét tại vị trí mà
Odl tạo với trục ON một góc α.
- Lực tác dụng của từ trường lên dây dẫn dl:
o Phương: qua tâm của dây dẫn tròn
o Chiều: như hình vẽ (được xác định bằng quy tắc bàn tay trái) o Độ lớn: dF = BIdl
- Lực tác dụng của từ trường lên toàn bộ dây dẫn là: F = dF = dF + dF ∫ ∫ n ∫ t
Do tính đối xứng nên dF = 0 ∫ t s π s BIs π 2BIs
F = dF = dFsin α = BIdlsin α = BI sin αdα = BI sin αdα = cosα = = 0,8 N ∫ n ∫ ∫ ∫ ∫ π π π 0 N 0 15
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 16
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 17
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 18
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 19
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
BÀI TẬP CHƯƠNG 9. CẢM ỨNG ĐIỆN TỪ
Tóm tắt lý thuyết:
Định luật cơ bản của hiện tượng cảm ứng điện từ:
Suất điện động cảm ứng luôn bằng về trị số, nhưng trái dấu với tốc độ biến thiên của từ
thông gửi qua diện tích của mạch điện: dΦm ε = − C dt
Suất điện động tự cảm. Hệ số tự cảm:
Từ thông gửi qua 1 ống dây có dòng điện chạy qua tỉ lệ thuận với cường độ dòng điện: Φ = LI m dΦ d (LI) dI m ε = − = − = −L tc dt dt dt
Trong đó L là hệ số tự cảm, đơn vị đo là H (henry).
Hệ số tự cảm của một ống dây điện thẳng dài: Vốn có: Φ NBS N m L = = , trong khi đó: B = µ nI µ = µ µ I I I 0 0 l 2 µ N µ S 0 2 2 L = = µ n µ Sl = µ n µ V 0 0 l
Trong đó: N là tổng số vòng dây, l và S là chiều dài và tiết diện ngang của ống dây. Năng lượ 1
ng của từ trường trong ống dây điện: 2 W = LI m 2 2
Mật độ năng lượng của từ trường: 1 B w = m 2 µ µ 0
Bài tập cần làm: 5.1, 5.2, 5.5, 5.6, 5.7, 5.10, 5.16, 5.17, 5.23.
Chú ý: điện trở suất của đồng là 1,72.10-8 m Ω 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2
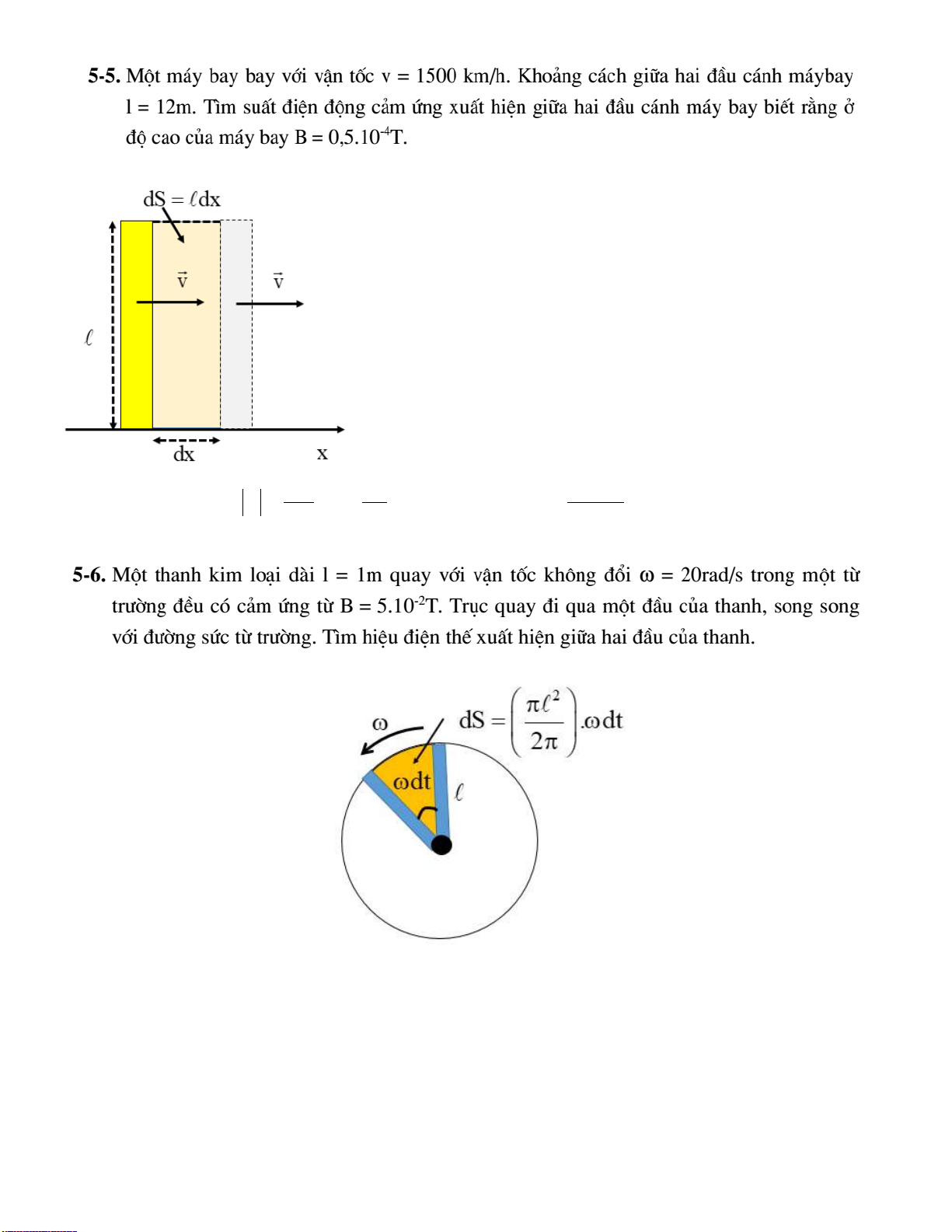
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Giải: 5 dΦ dx 4 − 15.10 dΦ = BdS = Bdx ⇒ E = = B = Bv = 0,5.10 .12. = 0,25(V) dt dt 3600 Giải:
Trong khoảng thời gian dt, thanh quét được 1 góc là ωdt ,
Diện tích của phần hình tròn được giới hạn bởi góc 2π chính là diện tích cả hình tròn: 2 S = π
Lấy tỷ lệ, tính được diện tích của phần hình tròn được giới hạn bởi góc ωdt là: 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2 π 1 2 1 2 dS =
ωdt = ω dt ⇒ dΦ = BdS = Bω dt ⇒ 2π 2 2 dΦ 1 2 1 2 − 2 E =
= Bω = .5.10 .20.1 = 0,5(V) dt 2 2
Chú ý: Bài này tương tự bài 5.6, tuy nhiên ở đây coi như 2 thanh, 1 thanh dài 25 cm, 1 thanh dài
95 cm. Sẽ đi tìm được hiệu điện thế giữa 2 đầu thanh so với gốc, rồi tìm giữa 2 đầu thanh với nhau. 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
BÀI TẬP CHƯƠNG 12. DAO ĐỘNG
Tóm tắt lý thuyết: 1. Dao động điều hòa
Phương trình dao động: x = Acos(ω t + ϕ , A > 0 0 ) x – li độ (độ dời); A – biên độ; ω - tần số góc; 0 ω t + ϕ - pha dao động; 0 ϕ - pha ban đầu; 2π T = - chu kỳ; 0 ω0 1 ω0 ν = =
- tần số. (chữ ν được phiên âm /nju:/ - đọc thế nào tùy các bạn) 0 T 2π 0 dx π Vận tốc: v =
= −ω Asin ω t + ϕ = ω Acos ω t + ϕ + 0 ( 0 ) 0 0 dt 2 dv Gia tốc: 2 a = = −ω Acos(ω t + ϕ) 2 2
= −ω x = ω Acos ω t + ϕ + π 0 0 0 0 ( 0 ) dt
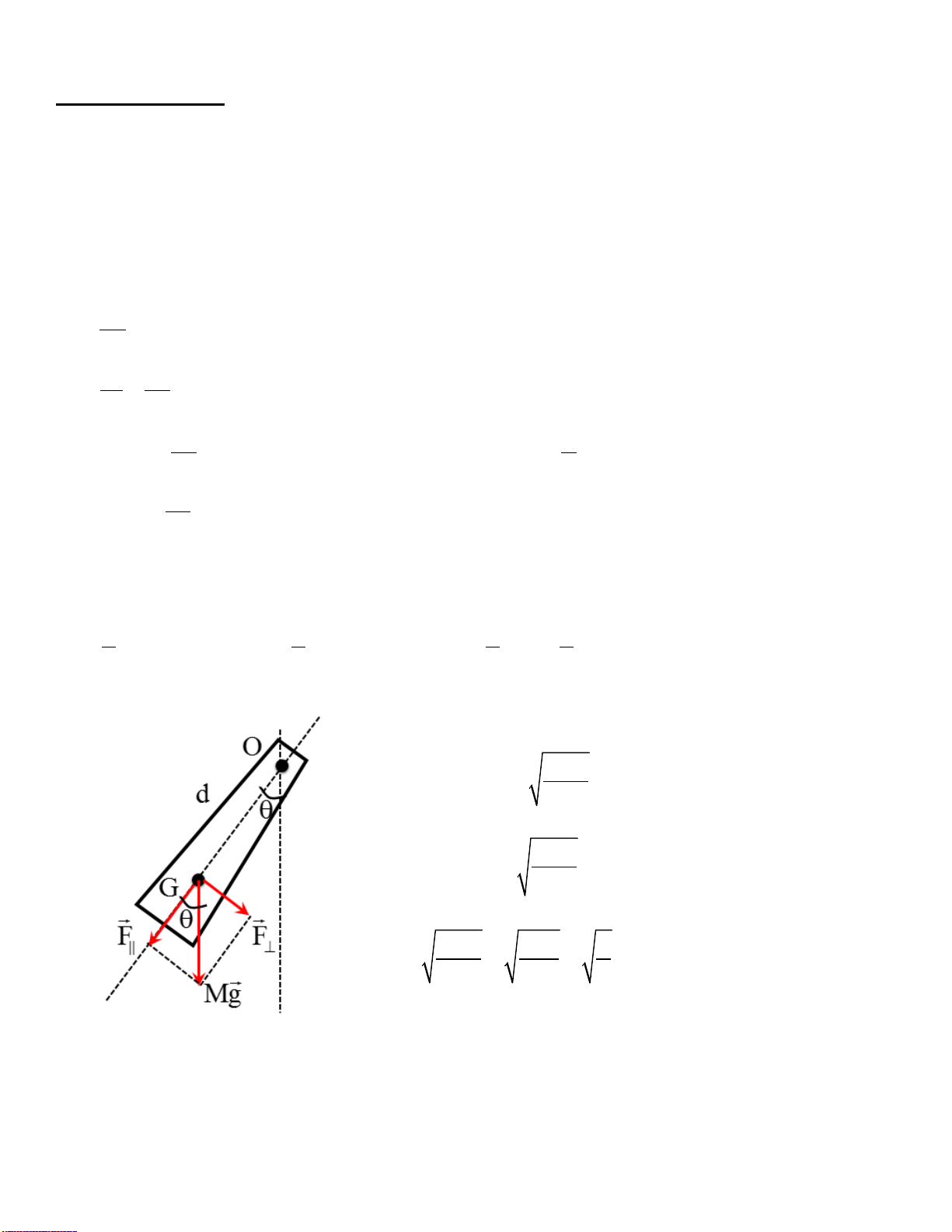
Năng lượng dao động điều hòa: Cơ năng: W = W + W d t Con lắc lò xo: 1 2 2 W = kA sin (ω t + ϕ) 1 2 2 + kA cos (ω t + ϕ) 1 2 1 2 2 = kA = mω A 0 0 0 2 2 2 2 Con lắc vật lý
Là một vật rắn khối lượng M, quay xung quanh một trục cố
định O nằm ngang. G là khối tâm, cách O một đoạn d. Mgd Tần số góc: ω = 0 I
I – là mômen quán tính của con lắc với trục O. I Chu kỳ: T = 2π 0 Mgd
Trường hợp riêng: con lắc đơn: Mgd Mgl g ω = = = 0 2 I Ml l
2. Dao động cơ tắt dần Phương trình dao động: −βt x = A e cos ωt + ϕ , 0 ( ) 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 trong đó: 2 2
ω = ω − β - tần số góc của dao động tắt dần 0 2π 2π T = =
- chu kỳ của dao động tắt dần 2 2 ω ω − β 0 t A A e−β =
- là biên độ của dao động tắt dần, giảm dần theo thời gian. 0 A(t) −βt A e Giảm lượng loga: 0 βT δ = ln = = = β A(t + T) ln ( ln e T −β t+T) A e 0
3. Dao động cơ cưỡng bức Phương trình: x = Acos( t Ω + Φ) Biên độ H : A = ; m (Ω − ω )2 2 2 2 2 + 4β Ω 0 Pha ban đâu: 2 − βΩ tan Φ = 2 2 Ω − ω0 Với điều kiện: 2 2 ω − 2β > 0 0
Tần gố góc cộng hưởng: Giá trị: 2 2
Ω = ω − 2β tại đó biên độ dao động cưỡng bức đạt trị số cực đại. ch 0 H A = max 2 2 2mβ ω − β 0
4. Dao động điện từ điều hòa
Phương trình dao động của dòng điện: I = I cos ω t + ϕ 0 ( 0 ) 1 Tần số góc riêng: ω = 0 LC 2π Chu kỳ riêng: T = = 2π LC ω0 Phương trình dao độ I π ng của điện tích: 0 q = cos ω t + ϕ − 0 ω 2 0 Phương trình dao độ q I π
ng của hiệu điện thế giữa 2 bản tụ: 0 u = = cos ω t + ϕ − 0 C Cω 2 0
5. Dao động điện từ tắt dần
Phương trình dao động của dòng điện: −βt I = I e cos ωt + ϕ 0 ( ) 2 1 R Tần số góc: 2 2 ω = ω − β = − o LC 2L 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2π 2π Chu kỳ: T = = 2 ω 1 R − LC 2L
6. Dao động điện từ cưỡng bức
Phương trình dao động của dòng điện: I = I cos t Ω + Φ 0 ( ) 1 ε L Ω − 0 I = và C cot Ω Φ = − 0 2 R 2 1 R + L Ω − C Ω 2 Đặ t 2 1 Z = R + L Ω −
- gọi là tổng trở của mạch dao động. C Ω Z = L Ω - cảm kháng L 1 Z = - dung kháng C C Ω
Cộng hưởng điện: 1 1 ε L Ω − = 0 → Ω = = ω 0 I = ch 0 C Ω LC 0 max R
7. Tổng hợp 2 dao động điều hòa cùng phương, cùng tần số x = a cos ωt + ϕ 1 1 ( 1 ) x = a cos ωt + ϕ 2 2 ( 2 ) 2 2 a = a + a + 2a a cos ∆ϕ 1 2 1 2 a sin ϕ + a sin ϕ 1 1 2 2 tan ϕ = a cosϕ + a cosϕ 1 1 2 2
8. Tổng hợp hai dao động điều hòa có phương vuông góc với nhau x = a cos ωt + ϕ 1 1 ( 1 ) x = a cos ωt + ϕ 2 2 ( 2 ) 2 2 x y xy + − 2 cos ϕ − ϕ = sin ϕ − ϕ 2 2 ( ) 2 2 1 ( 2 1) a a a a 1 2 1 2
Các trường hợp đặc biệt: a) ϕ − ϕ = 2kπ 2 1 x y −
= 0 đường thẳng trên góc phần tư 1 và 3 a a 1 2 b) ϕ − ϕ = 2k +1 π 2 1 ( ) 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 x y +
= 0 đường thẳng trên góc phần tư 2 và 4 a a 1 2 π c) ϕ − ϕ = 2k +1 2 1 ( ) 2 2 2 x y + = 0 đường elip vuông 2 2 a a 1 2 Nếu a1 = a2 đường tròn BÀI TẬP
8.1, 8.2, 8.3, 8.4, 8.7, 8.8, 8.12, 8.13, 8.14, 8.15, 8.17, 8.18, 8.19, 8.21, 8.23, 8.24, 8.26, 8.27
Bài 8.2. một chất điểm dao động điều hòa với T = 24 s, pha ban đầu bằng 0. Hỏi tại những thời
điểm nào (trong thời gian một chu kỳ đầu) li độ có giá trị tuyệt đối bằng 1/2 biên độ dao động. Bài giải:
Phương trình dao động: x = Acosω t 0 2π 2π π Ta có: ω = = = rad/s 0 T 24 12 A 1 t π 1 t π π x = Acosω t = ± ⇒ cosω t = ± ⇒ cos = ± ⇒ = ± + kπ ⇒ t = 4 ± +12k 0 0 2 2 12 2 12 3
Với điều kiện trong 1 chu kỳ, 0 ≤ t ≤ T = 24 s
Dễ thấy các giá trị sau đây thỏa mãn: t = 4 + 0 = 4 s. t = +4 + 12 = 16 s. t = -4 + 12 = 8 s t = -4 + 24 = 20 s.
Ngoài ra phương pháp đườ π
ng tròn (hình vẽ). Dễ dàng xác định được góc α = . Ta thấy có 4 vị 3 A
trí thỏa mãn điều kiện x = ± . 2 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bài 8.3. một chất điểm dao động điều hòa với chu kỳ T = 2 s, biên độ a = 50 mm. Tìm vận tốc
của chất điểm tại vị trí của li độ bằng 1/2 biên độ dao động. Bài giải: 2 v
Sử dụng hệ thức độc lập: 2 2 x + = A ω Suy ra: 2 2 v = ω A − x 1 1 3 3 2π 3 2π Với 2 2 x = A ⇒ v = ω A − A = ωA = A = 50 =136 mm/s 2 4 2 2 T 2 2 π
Bài 8.7. Một chất điểm dao động điều hòa với chu kỳ dao động T = 2 s, pha ban đầu ϕ = . Năng 3
lượng toàn phần W = 3.10-5 J và lực tác dụng lên chất điểm lúc lớn nhất bằng 1,5.10-3 N. Viết
phương trình dao động của chất điểm. Bài giải:
Phương trình dao động sẽ có dạng: x = Acos(ωt + ϕ) 2π 2π ω = = = π rad/s T 2 2 2 mω A Ta có: W = 2 Lực tác dụng: 2
F = ma = −mω x , lực tác dụng cực đại là 2 F = mω A max 5 2W 2.3.10− Suy ra: 2 A = = = 4.10− m = 4 cm. 3 F 1,5.10− max Phương trình dao độ π ng: x = 4cos t π + cm. 3
Bài 8.12. Biên độ dao động tắt dần sau thời gian t = 20 s giảm đi n 1
1 = 2 lần. Hỏi sau thời gian
t2 = 1 phút nó giảm đi bao nhiêu lần? Bài giải: −β −β A Ta có: t t A = A e ⇒ e = 0 A0 −β A 1 −β A Suy ra: 1 t 1 t2 2 e = = ;e = A 2 A 0 0
Ta có: t = 60 s,t = 20 s ⇒ t = 3t 2 1 2 1 A 3 −β − β −β 1 2 t2 3 1t = e = e = ( 1t e ) = A 8 0
Bài 8.13. Phương trình của một dao động tắt dần có dạng: 0 − ,2t x =10.2 .cos8 t π cm
Tìm biên độ dao động sau N = 10 dao động toàn phần. Bài giải: 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2π 2π Chu kỳ: T = = = 0,25 s ω 8π
Thời gian 10 dao động: t = 10T = 2,5 s Thay vào có: 0 − ,2.2,5 A =10.2 = 7,07 cm. 1
Bài 8.15. Cho hệ số tắt dần của dao động là 1 s− β =
. Tính thời gian để biên độ giảm đi e lần: 100 Bài giải: −βt A β 1 0 t A = A e ⇒
= e = e ⇒ βt =1⇒ t = =100 s 0 A β
Bài 8.17. Biết rằng vận tốc v = 20 m/s thì khi chạy qua các chỗ nối của đường ray xe lửa bị rung
nhiều nhất. Mỗi lò xo của toa xe chịu một khối lượng nén là M = 5 tấn. Chiều dài của mỗi thanh
ray là l = 12,5 m. Hãy xác định hệ số đàn hồi của lò xo? Bài giải:
Đây là một bài liên quan đến dao động cưỡng bức. Trong đó dao động riêng là dao động của lò
xo toa xe, lực cưỡng bức là do đường ray tác dụng lên mỗi lúc xe lửa qua chỗ nối. Xe lửa bị rung
nhiều nhất tức là xảy ra hiện tượng cộng hưởng, tức là tần số dao động riêng của lò xo toa xe với
tần số lực cưỡng bức của đường ray tác dụng lên toa xe là bằng nhau. l 12,5
Chu kỳ của lực cưỡng bức là: T = =
= 0,625 s , khi xảy ra cộng hưởng thì đây là chu kỳ v 20 của dao động riêng: 2 2 2π k 2π 4π M 4π .5000 ω = ⇒ = ⇒ k = = = 512000 N/m 2 2 T M T T 0,625
Bài 8.23. Một mạch dao động điện từ có điện dung C = 0,25 F
µ , hệ số tự cảm L = 1,015 H và
điện trở r = 0. Ban đầu hai cốt của tụ điện được tích điện đến 6 Q 2,5.10− = C 0
a) Viết phương rình dao động điện từ của mạch đối với điện tích Q và dòng điện i;
b) Năng lượng của mạch;
c) Tần số dao động của mạch. Bài giải: 1 1 3 ω = = ≈ 2.10 s 6 LC 1,015.0,25.10−
Phương trình dao động của q có dạng: q = Q cos ωt + ϕ 0 ( )
Tại thời điểm ban đầu t = 0: q = Q0 suy ra: cosϕ =1→ ϕ = 0 ( 3 ) ( ) 6 − = µ = ( 3 q 2,5cos 2.10 t C 2,5.10 cos 2.10 t) ( F) Dòng điệ dq n: 6 − 3 i = = 2 − ,5.10 .2.10 sin( 3 2.10 t) 3 − π 3 = 5.10 cos 2.10 t + ( A) dt 2 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Q 2,5.10− 0 ( )2 6 2 Năng lượng: 5 W = = =1,25.10− J 6 − ( ) 2C 2.0,25.10 3 ω 2.10 Tần số: ν = = ≈ 318,3 Hz 2π 2π
Bài 8.24. Một mạch dao động có hệ số tự cảm là 1 H, điện trở của mạch có thể bỏ qua. Điện tích
trên cốt của tụ điện biến thiên theo phương trình: 5 5 q = .10− cos 400 t π ( C) π Tìm:
a) Chu kỳ dao động của mạch; b) Điện dung của mạch;
c) Cường độ dòng điện trong mạch;
d) Năng lượng điện từ của mạch. Bài giải: 2π 2π a) chu kỳ dao động: T = = = 0,005 ( s) ω 400π b) điệ 1 1 1 n dung của mạch: 6 C 0,633.10− ω = ⇒ = = = F = 0,633 F µ 2 2 ( ) ( ) LC ω L (400π) .1
c) Cường độ dòng điện: dq 5 5 i = = 400 − π 10− π sin 400 t π = 0,02cos 400 t π + ( A) dt π 2
d) Năng lượng điện từ: 2 5 5 .10− 2 Q π 0 4 W = = = 2.10− J 6 − ( ) 2C 2.0,633.10
Bài 8.26. Một mạch dao động có điện dung C = 0,405 F
µ , hệ số tự cảm L = 10-2 H và điện trở R = 2 Ω . Tìm:
a) Chu kỳ dao động của mạch;
b) Sau thời gian một chu kỳ, hiệu điện thế giữa 2 cốt của tụ điện giảm bao nhiêu lần? Bài giải:
a) Chu kỳ dao động của mạch: 2π 2π 2π 2π 4 T = = = = = 4.10− ( s) 2 2 2 2 ω ω − β 0 1 R 1 2 − − 2 − 6 − 2 LC 2L 10 .0,405.10 2.10− b) ta có: U(t) −βt = U e ;U t + Τ = U e−β + 0 ( ) (t T) 0 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 − U(t) 4 RT 2.4.10 Suy ra: 2 T 2L 2.10− β ( (lần) + ) = e = e = e =1,04 U t T
Bài 8.27. Một mạch dao động có điện dung C = 1,1.10-9 F, hệ số tự cảm L = 5.10-5 H và giảm
lượng loga δ = 0,005. Hỏi sau thời gian bao lâu thì năng lượng điện từ trong mạch giảm đi 99%. Bài giải: 1 1 Chu kỳ dao động riêng: 6 ω = = = 4,264.10 rad/s 0 5 − 9 LC 5.10 .1,1.10− 2 2 2 − βt 2 2 2 − ( β t t +∆ ) Năng lượ Q Q e Q +∆ Q e ng: W(t) t 0 = = ;W(t + t ∆ ) t t 0 = = 2C 2C 2C 2C
Năng lượng giảm đi 99% nghĩa là: W(t + t ∆ ) 2 − ( β t t +∆ ) 1 e 1 2 − β t ∆ 1 = ⇒ = ⇒ = W(t) e 2 − βt 100 e 100 100 ln10 ⇒ β t ∆ = ln10 ⇒ t ∆ = β
Việc còn lại là đi tính β : 2π 2 2 2 δ = βT = β
⇒ δ ω − β = 2πβ ⇒ δ ( 2 2 ω − β ) 2 2 = 4π β 0 0 2 2 ω − β 0 2 2 6 δ ω δω 2 0,005.4,264.10 0 0 ⇒ β = ⇒ β = = = 3393 (s-1) 2 2 2 2 2 2 4π + δ 4π + δ 4π + 0,005 ln10 4 t 6,79.10− ∆ = = ( s) 3393 8
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
BÀI TẬP CHƯƠNG 13. SÓNG CƠ VÀ SÓNG ĐIỆN TỪ TÓM TẮT LÝ THUYẾT
1. Các đặc trưng của sóng
- Vận tốc sóng: là quãng đường mà sóng truyền được sau một đơn vị thời gian. Đố E i với sóng dọc: v =
, trong đó E – suất đàn hồi (suất Young), ρ là khối lượng riêng của ρ môi trường. Đố G i với sóng ngang: v =
, trong đó G – suất trượt của môi trường. ρ Đố F
i với ứng suất ta có công thức sau: G = , trong đó F là lực tác dụng, S là tiết diện. S
- Chu kỳ T và tân số ν của sóng: là chu kỳ và tần số của dao động của các phần tử môi trường.
- Bước sóng λ là quãng đường mà sóng truyền được sau một khoảng thời gian bằng một chu kỳ: v
λ = vT = (bước sóng là khoảng cách ngắn nhất giữa các điểm có dao động cùng pha). ν 2. Hàm sóng x u x,t = Acos ω t − + ϕ M ( ) v
Chọn ϕ = 0 ta có hàm sóng: x u = Acosω t − M v t x u = Acos 2π − M T λ 2 x π u = Acos ω t − M λ
3. Phương trình truyền sóng 2 1 ∂ u 2 2 2 ∂ ∂ ∂ M u ∆ = , trong đó ∆ = + + - toán tử Laplace M 2 2 v t ∂ 2 2 2 x ∂ y ∂ z ∂
4. Năng lượng sóng 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Năng lượng sóng trong phần thể tích vô cùng bé V
δ được tính theo biểu thức: π 2 2 2 2 x W δ = V δ ρω A sin ωt − λ
5. Mật độ năng lượng sóng
Là phần năng lượng có trong một đơn vị thể tích của môi trường, tức là: W δ π 2 2 2 2 x w = = ρω A sin ωt − V δ λ 1
Mật độ năng lượng trung bình: 2 2 w = ρω A 2 6. Năng thông sóng
Năng thông sóng P qua một mặt nào đó trong môi trường là một đại lượng về trị số bằng năng
lượng sóng gửi qua mặt đó trong một đơn vị thời gian: P = wSv 1
Giá trị trung bình của năng thông sóng: 2 2 P = wSv= ρω A Sv 2
7. Mật độ năng thông trung bình
Mật độ năng thông trung bình P là năng thông trung bình gửi qua một đơn vị diện tích: P P = = w.v S Dướ
i dạng véc-tơ: P = w.v - véc-tơ Umov – Poiting: là véc-tơ biểu diễn mật độ năng thông trung bình đượ
c truyền đi theo chiều của vận tốc v 8. Giao thoa sóng
Với 2 nguồn kết hợp, dao động cùng pha, thì những điểm thỏa mãn điều kiện: d − d = kλ là 2 1 những điểm cực đại. 1
Những điểm thỏa mãn: d − d = k +
λ là những điểm cực tiểu. 2 1 2
Trong đó k là những số nguyên, r và r lần lượt là khoảng cách từ điểm đang xét đến 2 nguồn. 1 2
Chú ý: ứng với k = 0, có cực đại chính – là đường trung trực của đoạn thẳng nối 2 nguồn. Các
cực đại ở hai bên đối xứng nhau, gọi là cực đại bậc 1 (k = ± ) 1 , bậc 2 (k = 2 ± ),… 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Không có cực tiểu giữa, ứng với cực tiểu bậc 1 ( k = 0 ), bậc 2 (k=1),… 1
Ghi nhớ: các kết quả kλ hay k + λ
đối với cực đại và cực tiểu chỉ đúng cho trường hợp này 2
(tức là trường hợp 2 nguồn dao động cùng pha), các trường hợp khác thì kết quả sẽ khác. Cụ thể,
nếu 2 nguồn dao động ngược pha. Các kết quả nêu trên đảo ngược lại, tức là tại những điểm hiệu 1
khoảng cách là kλ là những điểm cực tiểu, những điểm mà hiệu khoảng cách là k + λ là 2
những điểm cực đại. 9. Sóng dừng λ
Khoảng cách giữa 2 nút sóng liên tiếp, 2 bụng sóng liên tiếp là , khoảng cách giữa bụng và nút 2 λ sóng kề nhau là . 4 Điề kλ
u kiện của một sợi dây có 2 đầu cố định có sóng dừng là: l = 2 Điề 1 λ
u kiện của một sợi dây có 1 đầu cố định, 1 đầu tự do là: l = k + 2 2
10. Dao động âm và sóng âm Cường độ 1 âm: 2 2 I = P = va ρ ω 2 I
Mức cường độ âm: L =10lg (dB) I0 I0 là âm cơ sở.
11. Hiệu ứng Doppler v + u′ ′ ν = ν v − u Trong đó ′
ν là tần số mà máy thu nhận được,
ν là tần số mà máy phát phá ra.
u là vận tốc của máy phát. Quy ước nếu máy phát đang tiến đến máy thu thì u > 0 và ngược lại. 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
u′ là vận tốc của máy thu. Quy ước nếu máy thu đang tiến đến máy phát thì u′ > 0 và ngược lại.
Chú ý các dạng bài tập thường gặp:
- Dạng 1: cho hết các đại lượng và tính tần số máy thu nhận được.
- Dạng 2: bài toán của “con dơi” và mấy “cá vàng” bắn tốc độ. Tức là máy phát và máy thu là 1.
Phải xét 2 giai đoạn, giai đoạn 1 máy phát phát sóng, máy thu là “chướng ngại vật” hoặc các “quái
xế”. Giai đoạn 2 máy phát đóng vai trò máy thu, còn chướng ngại vật và quái xế đóng vai trò máy phát.
- Dạng 3: viên đạn “vọt” qua đầu người hoặc đoàn tàu vụt qua người đứng yên. Bài toán này có
2 giai đoạn, 1 giai đoạn “máy phát” đang tiến đến gần “máy thu”, giai đoạn 2 là máy phát đang “bye bye” máy thu. 12. Sóng điện từ
Xét sóng điện từ tự do, nghĩa là sóng điện từ trong môi trường không dẫn (không có dòng điện)
và không có điện tích (tức là j = 0;ρ = 0 )
Hệ phương trình Maxwell của sóng điện từ: B ∂ D ∂ rotE = − ; rotH = ; t ∂ t ∂ divD = 0; divB = 0 D = ε E ε ; B = µ H µ 0 0
- Vận tốc truyền sóng điện từ trong môi trường đồng chất, đẳng hướng: 1 c c v = =
= , ε và µ lần lượt là hằng số điện môi và độ từ thẩm của môi trường. ε εµ µ εµ n 0 0
Như vậy: εµ = n - là chiết suất tuyệt đối của môi trường. 1 1 8 c = =
≈ 3.10 m/s - vận tốc ánh sáng trong chân không. 12 − 7 − ε µ π 0 0 8,86.10 .4. .10
Phương trình sóng điện từ phẳng đơn sắc: x E = E cosω t − m v 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 x H = H cosω t − m v
- Hai véc tơ E và H luôn vuông góc với nhau
- Ba véc-tơ E , H và v theo thứ tự tạo thành một tam diện thuận.
- E và H luôn dao động cùng pha nhau, tức là trị số luôn tỷ lệ với nhau:
Mật độ năng lượng sóng điện từ: 1 2 1 2 w = ε E ε + µ H µ 0 0 2 2
Đối với sóng điện từ phẳng đơn sắc: 2 2 ε ε E = µ µ H ⇒ ε E ε = µ H µ 0 0 0 0 2 2 w = ε E ε = µ H µ = ε εE µ µH 0 0 0 0 BÀI TẬP
Các bài tập cần làm: 9.1, 9.2, 9.3, 9.5, 9.7, 9.8, 9.15, 9.16, 9.17, 9.18, 9.19, 9.20, 9.21.
Bài 9.2. Dao động âm, tần số 500 Hz, biên độ a = 0,25 mm, truyền trong không khí với bước sóng λ = 70 cm. tìm:
a) vận tốc truyền sóng âm;
b) vận tốc dao động cực đại của các phần tử không khí. Bài giải:
a) vận tốc v = λf = 0,7.500 − 350(m / s)
b) vận tốc dao động cực đại: 3 v a 2 fa 2.3,14.500.0,25.10− = ω = π = = 0,785(m / s)
Bài 9.3. Một nguồn sóng O dao động với phương trình x = 2,5sin t
π (cm) . Tìm li độ của một
điểm M cách nguồn 20 m tại thời điểm 1 s. Biết vận tốc truyền sóng v = 100 m/s. Bài giải:
Phương trình sóng có dạng: x x = sin 2,5π t − M v
Tại thời điểm t = 1, x = 20 m: 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 20 x = sin 2,5π 1− = sin 2π = 0 M 100
Tức là tại thời điểm đó tại điểm M dao động đang đi qua vị trí cân bằng.
Bài 9.8. một đoàn sóng có phương trình: x = 0,05sin(1980t − 6y)(cm) Tìm: a) tần số dao động
b) vận tốc truyền sóng và bước sóng
c) vận tốc cực đại của phần tử dao động bài giải: ω 1980 990 a) tần số: f = = = ≈ 315(Hz) 2π 2π π b) vận tốc truyền sóng 2π π π 990
so sánh hệ số ta thấy: 6 = ⇒ λ = (cm) ⇒ v = λf = . = 330(cm / s) λ 3 3 π
c) vận tốc cực đại của các phân tử dao động: v = ωa =1980.0,05 = 99 cm / s max ( )
Bài 9.16. Một con dơi bay theo hướng tới vuông góc với một bức tường với vận tốc 5 m/s. Dơi
phát ra một tia siêu âm có tần số 4,5.104 Hz. Hỏi dơi nhận được âm phản xạ có tần số là bao
nhiêu? Biết vận tốc truyền âm trong không khí là 340 m/s. Bài giải: Hiệu ứng Doppler: v + u′ ′ ν = ν v − u
Với bài toán này ta phải áp dụng 2 lần công thức trên, vì trong trường hợp này “máy thu” và “máy phát” là một.
1. Ta tính tần số do tường nhận được:
- ta có: “máy phát” – là con dơi có vận tốc u = + 5 m/s.
- “máy thu” – là tường có vận tốc u’ = 0; 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 v - suy ra: ν = ν 1 v − 6
2. Ta tính tần số do con dơi nhận được từ tường:
- máy phát – là tường có vận tốc u = 0;
- máy thu – là con dơi có vận tốc u’= +5m/s v + u′ v + 6 v v + 6 340 + 6 - suy ra: 4 4 ′ ν = ν = ν = ν = .4,5.10 = 4,66.10 Hz 1 ( ) v − u v − 0 v − 6 v − 6 340 − 6
Bài 9.18. Một tàu hỏa chuyển động với vận tốc 60 km/h và một người quan sát đứng yên. Khi đi
qua người quan sát, tàu kéo một hồi còi. Hỏi:
a) Người quan sát cảm giác gì về âm thanh khi tàu vụt qua?
b) Độ biến thiên của tần số so với khi tàu đứng yên? Cho vận tốc truyền âm trong không khí là 340 m/s. bài giải: v + u′
a) Vẫn với công thức ′ ν = ν v − u Ở đây có 2 giai đoạn:
- giai đoạn 1 lúc tàu đang tiến lại gần người quan sát: u’=0, u > 0 nên ta có: ′ ν > ν tức là người
quan sát thấy còi tàu có tần số cao hơn tần số phát ra.
- giai đoạn 2 lúc tàu vụt qua người, lúc này u’=0, u < 0 nên ta có ′
ν < ν tức là người quan sát thấy
còi tàu có tầm số thấp hơn tần số phát ra. Tức là đang nghe âm rất cao bị giảm xuống thấp đột ngột.
Các tính toán cũng chia làm 2 giai đoạn:
- giai đoạn khi tàu đang tiến đến, ta có: v ′ ν v ′ ν − ν ∆ν 60 / 3,6 60 1 ′ ν = ν ⇒ = ⇒ = = = v − 60 / 3,6 ν v − 60 / 3,6 ν ν v − 60 / 3,6 3,6v − 60
- giai đoạn khi tàu đang rời xa, ta có: v ′′ ν v ′′ ν − ν ∆ν 60 − / 3,6 60 − 2 ′′ ν = ν ⇒ = ⇒ = = = v + 60 / 3,6 ν v + 60 / 3,6 ν ν v + 60 / 3,6 3,6v + 60 Sai số tỏng hợp: 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 v ∆ 1 1 1 1 = 60 − = 60 − = 5% 3,6v 60 3,6v 60 3,6.340 60 3,6.340 60 ν − + − +
Bài 9.20. Một mạch phát sóng điện từ có điện dung C = 9.10-10 F, hệ số tự cảm L = 2.10-3 H.Tìm
bước sóng điện từ tương ứng. Bài giải: c 2 c π 8 3 − 10 − 3 λ = = = 2 c π LC = 2 .3.10 π 2.10 .9.10 = 2,5.10 (m) f ω
Bài 9.21. Một mạch dao động điện từ gồm một ống dây có hệ số tự cảm 5 L 3.10− = H mắc nối
tiếp với một tụ điện phẳng có diện tích các cốt 2
S =100 cm . Khoảng cách giữa các cốt là
d = 0,1 mm . Hằng số điện môi của môi trường chứa đầy trong khoảng không gian giữa hai cốt tụ
điện là bao nhiêu? Biết mạch dao động cộng hưởng với sóng có bước sóng 750 m Bài giải:
Xảy ra cộng hưởng nghĩa là tần số dao động của sóng điện từ bằng với tần số dao động riêng của mạch LC: 2 1 2 c π λ = ω = 2 f π = ⇒ C = 2 2 LC λ 4π c L εε S Lại có: 0 C = d 2 2 2 3 λ εε S λ d 750 .0,1.10− Suy ra: 0 C = = ⇒ ε = = = 5,96 2 2 2 2 12 − 2 4π c L d 4ε π c SL 4.8,86.10 .π .( 8 3.10 )2 4 − 5 − 0 100.10 .3.10 8
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)

