Bài tập trắc nghiệm nâng cao Toán 12 có đáp án và lời giải chi tiết – Đặng Việt Đông

Bài tập trắc nghiệm nâng cao Toán 12 có đáp án và lời giải chi tiết – Đặng Việt Đông được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

88 44 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay

MỤC LỤC

HÀM SỐ ............................................................................................................................................ 3

HÌNH ĐA DIỆN............................................................................................................................... 27

I – HÌNH CHÓP .......................................................................................................................... 27

II – HÌNH LĂNG TRỤ ................................................................................................................ 41

MŨ - LÔ GARIT ............................................................................................................................. 49

HÌNH NÓN - TRỤ - CẦU .............................................................................................................. 66

NGUYÊN HÀM , TÍCH PHÂN VÀ ỨNG DỤNG .......................................................................... 81

HÌNH HỌC TỌA ĐỘ KHÔNG GIAN OXYZ ............................................................................... 96

SỐ PHỨC ....................................................................................................................................... 123

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay

HÀM SỐ

Câu 1. Cho hàm số có đồ thị (C

). Tìm m để đồ thị (C

) cắt trục hoành tại một điểm

duy nhất.

A. B. C. D.

Hướng dẫn giải:

Số giao điểm của đồ thị (Cm) với Ox là số nghiệm của phương trình

Với m = 0 vô nghiệm nên không có giao điểm

Với



m ta có

Ta có bảng biến thiên của f(x) như sau:

0 1

+ + 0 -

-3

Số nghiệm phương trình (*) là số giao điểm của đồ thị hàm f(x) và đường thẳng y=m.

Dựa vào bảng biến thiên ta thấy

thì phương trình (*) có 1 nghiệm duy nhất.

Chọn đáp án B.

Câu 2. Cho hàm số: . Với giá trị nào của m thì đồ thị hám số có

cực đại và cực tiểu, đồng thời các điểm này tạo thành một tam giác đều

A. B. C. D.

Hướng dẫn giải:

Ta có:

Hàm số có CĐ, CT  PT có 3 nghiệm phân biệt  (*)

Khi đó toạ độ các điểm cực trị là: , , 

Do ABC luôn cân tại A, nên bài

toán thoả mãn khi

Chọn đáp án A.

Câu 3. Cho hàm số có đồ thị là (C). Tìm tất cả những điểm trên đồ thị (C) sao cho hệ

số góc của tiếp tuyến với đồ thị (C) tại những điểm đó là giá trị lớn nhất của hàm số

A. B. ;

y x mx

  



 





  

2 0

x mx

   

 

     

m x f x

f x x x

x x

2 2

( );(*)

2 2( 1)

'( ) 2 0 1





'( )

f x

( )

f x





 

4 2 2

2( 2) 5 5

y x m x m m

     

2 3

m  

2 3



3 2



3 2



' 4 4( 2)

y x m x

  

' 0

x m





 



 







' 0

f x









0, 5 5

A m m

 





2 ;1

B m m

 





2 ;1

C m m

  









2 2

2 ; 4 4 ; 2 ; 4 4

AB m m m AC m m m

            

 

 

60 cos

A A

  

0 2 3

AB AC

    

 

3 2

y = x x



4x +3

g(x) =

x +1

 

 

 

 

 

 

 

4 40

;

3 27

 

 

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay

C. ; D. ;

Hướng dẫn giải:

* Tìm giá trị lớn nhất của hàm số:

- Đặt t = x

, với ta có hàm số ;

- ; g’(t) = 0 ;

- Ta lại có: ; , bảng biến thiên của hàm số:

t –2 0

g’(t)

– 0 + + 0 –

g(t) 0

–1

- Vậy giá trị lớn nhất của hàm số là = 4, đạt được khi

* Tìm các điểm thuộc đồ thị (C)

- Ta có: y’ = 3x

– x, giả sử điểm M

, f(x

)) (C), thì hệ số góc tiếp tuyến của (C) tại M

là

f’(x

- Vậy: suy ra x

= –1; x

= , tung độ tương ứng f(–1) = – ; f( ) =

+ Có hai điểm thỏa mãn giải thiết ; .

Chọn đáp án B.

Câu 4. Cho hàm số có đồ thi điểm . Tìm để đường thẳng cắt

đồ thị tại hai điểm phân biệt và sao cho tứ giác là hình bình hành ( là gốc toạ

độ).

A. B. C. D.

Hướng dẫn giải:

Do các điểm và thuộc đường thẳng nên để là hình bình hành thì

Hoành độ của và là nghiệm của pt:

Vì ,nên luôn có hai nghiệm phân biệt, luôn cắt tại hai điểm

phân biệt

Giả sử là nghiệm của ta có:

Gọi

2 1 2

;

2 4

 



 

 

 

2 1 2

;

2 4

 

 

 

 

 

 

 





2; 10

 

4x +3

g(x) =

x +1

t 0



4 +3

g(t) =

t +1

2 2

4t 6t +4

g'(t) =

(t +1)

 

t = 2;t =



lim ( ) 0

g t





lim ( ) 0

g t









(x)

x  



0 0

3x x



0 0

3x x = 4



 

 

 

 

4 40

;

3 27

 

 

 

2 4











( 5;5)



y x m

  





OAMN



 

0; 2

m m



 

y x

  

OAMN

5 2

MN OA 

2 4

(3 ) ( 4) 0 ( 1) (1)

x m x m x m x



          



2 25 0,

m m m

     













1 2

x x





1 2

( 4)

x x m

  





  



2 2 2 2

1 1 2 2 1 2 1 2 1 2

( ; ), ( ; ) 2( ) 2 ( ) 4 2 4 50

M x x m N x x m MN x x x x x x m m

 

            

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay

+ thì thẳng hàng nên không thoã mãn.

+ thoã mãn.

Chọn đáp án C.

Câu 5. Cho hàm số: . Tìm sao cho từ A(0, ) kẻ được hai tiếp tuyến đến (C) nằm ở

hai phía trục Ox.

A. B. C. D.

Hướng dẫn giải:

Đường thẳng qua A(0, ) có hệ số góc k có phương trình tiếp xúc (C)

<=> có nghiệm kép <=> có nghiệm kép

<=> có nghiệm kép

có 2 nghiệm phân

biệt

Khi đó

Mà

Từ (1) và (2)

Chọn đáp án D.

Câu 6. Hai điểm M, N thuộc hai nhánh của đồ thị . Khi đó độ dài đoạn thẳng MN ngắn nhất

bằng?

A. 8 B. 4 C. D. .

Hướng dẫn giải:

Giả sử , , khi đó M , N với

5 2 2 4 50 50

MN m m





     









, , ,

O A M N



 

y C







;



 



 

 









2; \ 1

 





 

 

; \ 1



 



 

 

y kx a

 

kx a



 











1 2

kx a x x

   









1 2 0

kx k a x a

     

   

1 4 2 0

k a k a











      





   

( ) 2 5 1 0

h k k a k a











     









 

     

12 2 0

2; \ 1 1

(0) 1 0

h a

   





    



  













   

1 1

2 2

1 1

2 2

1 1

2 2

k a k a

x y

k a k a

x y

   

  





   



  













      

 

1 2 1 2

0 1 1 0

1 1 4 3 2 0

y y k a k a

k k a k k a a

         

   

         



 

 

; \ 1



 

  

 

 

3 1









8 2





3 ;3m

 

 

 

 

3 ;3n

 

 

 

 

, 0

m n



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay

. Kết luận MN ngắn nhất bằng 8

Chọn đáp án A.

Câu 7. Cho hàm số . Với giá trị nào của m thì đồ thị hàm số đã cho có cực

đại và cực tiểu đối xứng nhau qua đường thẳng

A. B. C. D.

Hướng dẫn giải:

+ . Đồ thị có 2 điểm cực trị khi:

+ Phương trình đường thẳng đi qua 2 điểm cực trị là: y = 2m

.x - 3m - 3

+ Trung điểm 2 điểm cực trị là

+ Điều kiện để 2 điểm cực trị đối xứng qua

+ Từ đó thấy m = 2 thỏa mãn hệ trên.

Chọn đáp án C.

Câu 8. Cho

 

2 2

1 1

 





f x e Biết rằng

       

1 . 2 . 3 ... 2017



f f f f e

với

m n

là các số tự nhiên

và

tối giản. Tính



m n

2018

 m n

. B.

2018

  m n

. C.

 

m n

. D.

  

m n

Hướng dẫn giải:

Xét các số thực



Ta có:

 

2 2

1 1 1 1 1 1

1 1 1

1 1

 

        

  

 

x x

x x x x x x x

x x x

Vậy,

       

1 1 1 1 1 1 1 1

1 2018 1

1 1 1 1

2018

1 2 2 3 3 4 2017 2018

2018 2018

1 . 2 . 3 ... 2017

       



           



       

      







  f f f f e e e ,

hay

2018 1

2018





Ta chứng minh

2018 1

2018



là phân số tối giản.

Giả sử

là ước chung của

2018 1



và

2018

Khi đó ta có

2018 1





2018 2018

d d



 

suy ra

1 1

  



d d

Suy ra

2018 1

2018



là phân số tối giản, nên

2018 1, 2018

  m n .

Vậy

  

m n

Chọn đáp án C.

2 2 2

8 8 1 1 64

( ) (2 ) 64 2 . 4 64

MN m n mn mn

m n m n mn

 

   

        

 

   

 

   

 

 

3 2

3 3 1

y x mx m

    

: 8 74 0

d x y

  



 



 

y' 0 3x 6mx 0

    

m 0



( ;2 3 1)

 

I m m m

: 8 74 0

d x y

  

2 .( ) 1

8(2 3 1) 74 0



  







    



m m m

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay

Câu 9. Cho hàm số ( )y f x có đồ thị ( )



y f x cắt trục

Ox tại ba điểm có hoành độ  a b c như hình vẽ. Mệnh

đề nào dưới đây là đúng?

A. ( ) ( ) ( ). f c f a f b

B. ( ) ( ) ( ). f c f b f a

C. ( ) ( ) ( ).f a f b f c 

D. ( ) ( ) ( ). f b f a f c

Hướng dẫn giải:

Đồ thị của hàm số ( )y f x



 liên tục trên các đoạn

 

;a b và

 

;b c , lại có ( )f x là một nguyên hàm

của ( )



f x .

Do đó diện tích của hình phẳng giới hạn bởi các đường:

( )

y f x

x a

x b























là:

     

( )d ( )d

 

      

 

b b

a a

S f x x f x x f x f a f b

. Vì

   

0  S f a f b

 

Tương tự: diện tích của hình phẳng giới hạn bởi các đường:

( )























y f x

x b

x c

là:

     

( )d ( )d

 

    

 

c c

b b

S f x x f x x f x f c f b

   

0  S f c f b

 

2 .

Mặt khác, dựa vào hình vẽ ta có:

           

1 2

S S f a f b f c f b f a f c      

 

3 .

(có thể so sánh

 

f a với

 

f b dựa vào dấu của ( )



f x trên đoạn

 

;a b và so sánh

 

f b với

 

f c

dựa vào dấu của ( )f x



trên đoạn

 

;b c ).

Từ (1), (2) và (3)

Chọn đáp án A.

Câu 10. Tìm tất cả các giá trị thực của tham số m để hàm số

   

2 1 3 2 cos   y m x m x nghịch

biến trên .

3 .

m    B.

3 .

   m C. 3. m D.

 m

Hướng dẫn giải:

TXĐ:  D

Ta có: (2 1) (3 2)sin



   y m m x

Để hàm số nghịch biến trên  thì 0,



 y x tức là: (2 1) (3 2)sin 0 (1) ,    m m x x

 m thì (1) thành

  x

 m thì (1) thành

1 2 1 2 5 1 2 1

sin 1 0

3 2 3 2 3 2 3 5

   

        

  

m m m

x m

m m m

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay

 

m thì (1) thành

1 2 1 2 3 2

sin 1 0 3

3 2 3 2 3 2 3

  

          

  

m m m

x m

m m m

Kết hợp được:

   

Chọn đáp án A.

Câu 11. Tìm tất cả các giá trị của m để hàm số:









3 2

2 3 1 6 2 3

     

y x m x m x nghịch biến trên

khoảng có độ dài lớn hơn 3



m hoặc



m B.



m C.



m D.



Hướng dẫn giải:

Dùng BBT để xét sự đồng biến và nghịch biến của hàm số trên các khoảng









' 6 6 1 6 2

    

y x m x m x

   

' 9 1 36 2 9 54 81 0

        

m m m m

Dấu bằng xảy ra khi



Gọi

1 2

x x

là 2 nghiệm của phương trình





1 2

' 0 

y x x

Theo viet:

1 2

. 2

  





 



x x m

Ta có BBT

Vậy hàm số đồng biến trên khoảng





1 2

, ' 0

 

x x pt y phải có 2 nghiệm phân biệt

 

Gọi Độ dài khoảng nghịch biến của hàm số là D

1 2

 

D x x

     

2 2

1 2

1 4 2 6 9

        

x x m m m m

3 9

  

D D

2 2

6 9 9 6 0

      

m m m m

m 0

 

hoặc



m (thỏa mãn)

Chọn đáp án A.

Câu 12. Cho hàm số







có đồ thị (C) và A là điểm thuộc (C). Tìm giá trị nhỏ nhất của tổng các

khoảng cách từ A đến các tiệm cận của (C).

2 2

B. 2 C. 3 D.

2 3

Hướng dẫn giải:

Gọi

  

; 1



 

 

 



 

M m C m

. Tổng khoảng cách từ M đến 2 đường tiệm cận



và



y là

1 2 2

1 1 1 2 1 . 2 2

1 1 1



         

  

S m m m

m m m

Dấu “=” xảy ra

1 1 2 1 2

        



m m m

Chọn đáp án A.

Câu 13. Cho hàm số

 

2x 1







y C

. Tìm k để đường thẳng

: x 2 1

  

d y k k

cắt (C) tại hai điểm

phân biệt

A B

sao cho khoảng cách từ

và

đến trục hoành bằng nhau.







y’ + 0 - 0 +

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Phương triình hoành độ giao điểm của (C) và d:

    

2x 1

x 2 1 2x 1 1 2 1 ; 1



          



k k x kx k x













x 3 1 2 0 1 ; 1

      

k k x k x

d cắt (C) tại hai điểm A, B phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt khác



    

6 1 0

3 2 2 3 2 2

1 3 1 1 2 0

k k

k k k









 

      

 

    







     





Khi đó:









1 1 2 2

; x 2 1 , ; x 2 1

   

A x k k B x k k với

1 2

x x

là nghiệm của (1).

Theo định lý Viet tao có

1 2

3 1

 



 











x x

Ta có









1 2

; ; x 2 1 x 2 1

      

d A Ox d B Ox k k k k

 

1 2

1 21 2

2 1 x 2 1

4 2 0

2 1 x 2 1



    



 



   

     



x x

kx k k k

k x x k

kx k k k

Do hai điểm A, B phân biệt nên ta loại nghiệm

1 2



x x

. Do đó





1 2

4 2 0 3

      

k x x k k .

Chọn đáp án C.

Câu 14. Nếu đồ thị hàm số







cắt đường thẳng ( ) :2

 

d x y m

tại hai đểm AB sao cho độ dài

AB nhỏ nhất thì

A. m=-1 B. m=1 C. m=-2 D. m=2

Hướng dẫn giải:

Phương trình hoành độ giao điểm

2 ( 1)

2 ( 3) 4 0



    



     

x m x

x m x m

( 1) 40 0,

      

m m R

Suy ra (d) luôn cắt dồ thị hàm số tại hai điểm A,B

3 4

; . ;

2 2

2 ; 2

2( )

  

  

     

   

A B A B

A A B B

B A B A

m m

x x x x

y x m y x m

y y x x

 

2 2 2

( ) ( ) 5( )

3 4 5

5 ( ) 4 5 4 1 40 5 2

2 2 4

     

 

  

 

 

        

 

 

 

 

 

 

B A B A B A

B A A B

AB x x y y x x

m m

x x x x m

Vậy AB nhỏ nhất khi m=-1

Chọn đáp án A.

Câu 15. Cho hàm số





3 2 2 2

3 3 1 1

     

y x mx m x m

. Tìm m để trên đồ thị hàm số có hai điểm đối

xứng qua gốc tọa độ

1 0

  

m hoặc



m B.

1 0

  

m hoặc



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay

1 0

 

m hoặc

 

m D.

1 0

 

m hoặc

 

Hướng dẫn giải:

Gọi hai điểm đối xứng nhau qua O là









0 0 0 0

, , , 

A x y B x y

Khi đó ta có





3 2 2 2

0 0 0 0

3 3 1 1

     

y x mx m x m

và





3 2 2 2

0 0 0 0

3 3 1 1

       

y x mx m x m

Từ đó suy ra:

2 2

6 2 2 0(*)

   mx m

Nếu



x thì

2 2 0

 

suy ra

1 0

  

y m . Vậy

 

A B O

Do đó: đồ thị hàm số có hai điểm đối xứng nhau qua gốc tọa độ O



phương trình (*) có nghiệm khác 0

 

2 2 0 1 0 hay 1

' 6 2 2 0







       





   





m m m

m m

Chọn đáp án B.

Câu 16. Cho hàm số

3 2 3

  

y x mx m

có đồ thị





và đường thẳng

2 3

: 2

 

d y m x m

. Biết rằng





1 2 1 2



m m m m

là hai giá trị thực của m để đường thẳng d cắt đồ thị





tại 3 điểm phân biệt có

hoành độ

1 2 3

, ,

x x x

thỏa

4 4 4

1 2 3

  

x x x . Phát biểu nào sau đây là đúng về quan hệ giữa hai giá trị

1 2

m m

1 2

 

m m . B.

1 2

2 4

 

m m . C.

2 1

2 4

 

m m . D.

1 2

 

m m .

Hướng dẫn giải:

 

3 2 2 3

3 3 0 : 0







       



 



x m

x mx m x m x m DK m

x m

4 4 4 4 4 4

1 2 3 1 2

83 81 83 1 0

             

ycbt x x x m m m m m m .

Chọn đáp án A.

Câu 17. Cho hàm số







có đồ thị là (C). Gọi I là giao điểm của 2 đường tiệm cận của (C). Tìm

tọa độ điểm M trên (C) sao cho độ dài IM là ngắn nhất ?





0 ; 3



M và





2 ; 5

M B.





1; 1



M và





3; 3

M

2 ;

 



 

 

M và

4 ;

 



 

 

M D.

1 5

;

2 3

 



 

 

M và

5 11

;

2 3

 



 

 

Hướng dẫn giải:

Gọi

;



 

 



 

M m

thuộc đồ thị, có I(–1 ; 1)

 

  



IM m

 

1 2 16

   



IM m

2 2



IM nhỏ nhất khi

2 2

IM . Khi đó (m + 1)

= 4. Tìm được hai điểm





1; 1



M và





3; 3

M .

Chọn đáp án B.

Câu 18. Giá trị của tham số m để diện tích hình phẳng giới hạn bởi đồ thị hàm số

, trục hoành, trục tung và đường thẳng x = 2 đạt giá trị nhỏ nhất là:

A. m = 2 B. m = 1 C. m = -1 D. m = - 2

Hướng dẫn giải:

Vì với m tùy ý ta luôn có nên diện tích hình phẳng cần tìm là

2 2

3 2 1

y x mx m

   

2 2

3 2 1 0

x mx m x

    

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay

S đạt giá trị nhỏ nhất bằng 8 khi m = - 1. (dùng casio thử nhanh hơn)

Chọn đáp án C.

Câu 19. Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số

2 3

 





x x

hợp với 2 trục tọa độ 1

tam giác có diện tích S bằng:

A. S=1,5 B. S=2 C. S=3 D. S=1

Ta có kết quả: Nếu đồ thị hàm số

( )



u x

v x

có điểm cực trị

( ; )

o o

x y

thì

( )



u x

v x

Suy ra phương trình đường thẳng đi qua 2 điểm cực trị là y=2x-2 (d)

(d) cắt 2 trục tọa độ tại 2 điểm A(0;-2) ,B(1;0) nên diện tích tam giác OAB bằng 1

Chọn đáp án D.

Câu 20. Cho hàm số có đồ thị . Giá trị của thì cắt trục

hoành tại 3 điểm phân biệt sao cho là

A. B. C. D.

Hướng dẫn giải:

Phương trình hoành độ giao điểm của (C) và trục hoành là

Chọn đáp án B.

Câu 21. Cho hàm số . Gọi M là điểm cực đại của đồ thị hàm số ứng với

một giá trị m thích hợp đồng thời là điểm cực tiểu của đồ thị hàm số ứng với một giá trị khác của

m. Số điểm M thỏa mãn yêu cầu đề bài là:

A. 1 B. 2 C. 3 D. 0

Hướng dẫn giải:

Ta có

Suy ra .

Vì nên hàm số đạt cực đại tại và giá trị cực đại là

Tương tự, ta có hàm số đạt cực tiểu tại và giá trị cực tiểu là .

Ta giả sử điểm M là điểm cực đạ của đồ thị hàm số ứng với giá trị và là điểm cực tiểu ứng của

đồ thị hàm số ứng với với giá trị .

   

 

2 2 3 2 2 2

3 2 1 1 2 4 10 2 1 8

S x mx m dx x mx m x m m m

 

             

 







3 2

2 1

y x x m x m

    









1 2 3

, ,

x x x

2 2 2

1 2 3

x x x

  





  











  

 





3 2

2 1 0

x x m x m

    

x x m









  













 









2 2 2

1 2 3 1 2 1 2

4 2 1 4 1 2 1 4 1

x x x x x x x m m

             

   

3 1

y x m x m   









   

3 3, 6

y x m y x m

 

    

x m

 





 



 







1, 1 0

x x m y m



    

x x m

  

3 2

y m m

  

x x m

  

3 2

y m m

  

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay

Q P

Từ YCBT suy ra hệ phương trình

Giải hệ ta tìm được nghiệm và suy ra tồn tại duy nhât một điêm thỏa

bài toán.

Chọn đáp án A.

Câu 21. Cho một tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN

nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định

giá trị lớn nhất của hình chữ nhật đó?

A. B. C. D.

Hướng dẫn giải:

Gọi H là trung điểm của BC  BH = CH =

Đặt BM = x , ta có:

Tam giác MBQ vuông ở M, và BM = x 

Hình chữ nhật MNPQ có diện tích:

S(x) = MN.QM =

S’

+ 0



Vậy khi x =

Chọn đáp án A.

Câu 22. Cho hàm số . Tìm để đường thẳng cắt tại hai điểm

phân biệt sao cho đạt giá trị nhỏ nhất với .



m B.



m C.

 

m D.



Hướng dẫn giải:

Phương trình hoành độ giao điểm của và :

cắt tại hai điểm phân biệt có 2 nghiệm phân biệt khác 1

Gọi là trung điểm của cố định.

1 2

2 2

1 1 2 2

1 1

3 2 3 2

m m

m m m m

  





    



1 2

3 1

2 2

m m

  

1 1

2 4

 



 

 

§iÒu kiÖn 0 x

 

 

 

 

MN 2MH 2(BH BM) 2 x a 2x

 

      

 

 



B 60



QM x 3



(a 2x)x 3 3(ax 2x )

   

a a

S'(x) 3(a 4x); S'(x) 0 x 0;

4 2

 

     

 

 

x 0;

maxS(x) a

 



 

 





( )

: 1

d y mx m

  

( )

M N

2 2

AM AN



( 1;1)



( )

2 1 0(1)

mx m

mx mx m







   





   





( )



(1)

 

(1; 1)

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay

Ta có:

Do nhỏ nhất nhỏ nhất

. Dấu “=” xảy ra

Vậy khi

Chọn đáp án C.

Câu 23. Cho hàm số bậc ba

 

y f x có đồ thị nhu hình vẽ bên. Tất cả

các giá trị của tham số m để hàm số





 

y f x m

có ba điểm cực trị là:

A. 1 m hoặc 3m B. 3 m hoặc 1m

C. 1 m hoặc 3m D. 1 3 m

Hướng dẫn giải:

Đồ thị hàm số là đồ thị hàm số tịnh tiến trên trục

Oy m đơn vị

Để đồ thị hàm số có ba điểm cực trị xảy

ra hai trường hợp sau:

+ Nằm phía trên trục hoành hoặc điểm cực tiểu thuộc trục Ox và cực đại dương

+ Nằm phía dưới trục hoành hoặc điểm cực đại thuộc trục Ox và cực tiểu dương

Khi đó hoặc là giá trị cần tìm.

Chọn đáp án A.

Câu 24. Tìm m để đồ thị hàm số có hai điểm cực trị A, B sao cho tam giác OAB

có diện tích bằng 1 (O là gốc tọa độ).

A. 1m B. 2m C. 1 m D. 3m

Hướng dẫn giải:

Ta có . Để đồ thị hàm số có hai điểm cực trị thì .

Khi đó hai điểm cực trị của đồ thị hàm số là (0;1)A và

(2 ; 4 1) B m m . Gọi H là hình chiếu

vuông góc của điểm B lên trục tung, ta có 2BH m . Diện tích của tam giác OAB là

1 1

. . 2

2 2

 S BH OA m

Theo đề bài S=1 nên ta có

. 2 1

m suy ra 1 m . Vậy m=±1 là giá trị cần tìm.

Chọn đáp án C.

Câu 25. Giá trị lớn nhất của hàm số là

A. 0 B. 4 C. 8 D. 2

Hướng dẫn giải:

TXĐ: , ta có .

2 2 2

AM AN AI  

2 2

AM AN





2 2 2

2 1

( ) (1 ) 4 8

MN x x m m

      

  

2 2

min( ) 20

AM AN

 

 





y f x m

 





y f x







y f x m

 





y f x m

  

m 3



m 1

 

3 2

y x 3mx 1

  





y' 3x 6mx 3x x 2m

   

m 0



 

4 4

2sin

sin cos

2 2

f x

x x









 

2 2 2

4 4 2

2sin 2sin 4sin

2 sin

sin cos 1 sin

2 2 2

x x x

f x

x x

  



 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay

Đặt , hàm số trở thành với , ta có

, suy ra hàm số đồng biến trên , vậy

, xảy ra khi

Chọn đáp án B.

Câu 26. Cho hàm số có đồ thị (C), với m là tham số. Giả sử đồ thị (C) cắt trục

hoành tại ba điểm phân biệt có hoành độ thỏa mãn

Khẳng định nào sau đây là đúng?

A. B.

C. D.

Hướng dẫn giải:

Khảo sát và vẽ đồ thị hàm số . Dựa vào đồ thị ta tìm được thì đồ thị

hàm số cắt Ox tại 3 điểm phân biệt.

Ta có do đó

Chọn đáp án B.

Câu 27. Tìm tất cả các giá trị thực của tham số m sao cho hàm số

tan 2

tan







x m

đồng biến trên khoảng

0; .



 

 

 

A. m  0 hoặc 1  m  2. B. m  0. C. 1  m  2. D. m  2.

Hướng dẫn giải:

2 2

2 2 2

1 1

(tan ) (tan 2)

cos cos

(tan ) cos (tan )

  



 

 

x m x

x x

x m x x m

Hàm số đồng biến trên 0;



 

 

 

khi và chỉ khi hàm số xác định trên 0;



 

 

 

và y’ ≥ 0 ∀ x ∈ 0;



 

 

 

tan , 0; 0

1 2

2 0

 

 

   





 

 

 





 





 



x x m

Chọn đáp án A.

2 Câu

28. Cho hàm số

4 2

  y ax bx c có đồ thị như hình vẽ

bên. Mệnh đề nào dưới đây đúng?

A. 0,a 0,b 0c

B. 0,a 0,b 0c

C. 0,a 0,b 0c

D. 0,a 0,b 0c

Hướng dẫn giải:

Do giới hạn của y khi x tiến tới vô cùng thì  nên 0a . Loại A và D





3 2

' 4 2 2 2

   

y ax bx x ax b









sin 0;1

x t t

 

 

g t



 





0;1



 





 

' 0 0;1

g t t

   

 





0;1





 









0;1

max ax 1 4

x t

f x m g t g

 

  



 

t x k k



    



3 2

6 9

y x x x m

   

1 2 3

x x x

 

1 2 3

1 3 4

x x x

    

1 2 3

0 1 3 4

x x x

     

1 2 3

0 1 3 4

x x x

     

1 2 3

1 3 4

x x x

    

3 2

6 9

y x x x

   

4 0

  

3 2

6 9

y x x x m

   

























0 . 1 0; 1 . 3 0; 3 . 4 0

y y y y y y

  

1 2 3

0 1 3 4

x x x

     

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay



a mà nếu



b thì phương trình



ax b

vô nghiệm

Nên



b thì hàm số mới có 3 cực trị.

Chọn đáp án B.

Câu 29. Cho hµm sè :

  



y x

( C ) T×m nh÷ng ®iÓm trªn ®å thÞ (C) cã hoµnh ®é lín h¬n 1

sao cho tiÕp tuyÕn t¹i diÓm ®ã t¹o víi 2 ®êng tiÖm cËn mét tam gi¸c cã chu vi nhá nhÊt .

4 4

1 1

1 ;2 2

2 2

 

   

 

 

4 4

1 1

2 2

 

 

 

 





1;2 2

 M

4 4

1 1

1 ;2 2

2 2

 

   

 

 

Hướng dẫn giải:

Gäi













; ; 0

  

M a y a C a th×

 

1 1

   

 

y a a

a a

PTTT cña ( C ) t¹i M lµ:

    

 

2 2



      



a a a

y y a y a x a y x a

(d)

TiÖm cËn ®øng x = 1 ; TiÖm cËn xiªn y = x + 1

Giao ®iÓm cña 2 tiÖm cËn lµ I=( 1 ; 2 )

Giao ®iÓm cña d víi tiÖm cËn ®øng x = 1 lµ

 



 



 

Víi tiÖm cËn xiªn lµ :





2 1;2

 

B a a

Ta cã

; 2 2 1

  



AI BI a

, nªn

. 4 2

AI BI v× a > 1

L¹i cã



 

AIB suy ra

2 2 2 2 2

2 . 2 .



     

AB AI BI AI BICos AI BI AI BI

Theo bÊt ®¼ng thøc C« si :





2 . 2 . 2 2 .

   

AB AI BI AI BI AI BI





2 2 2 1

  

(1)

§Æt p lµ chu vi tam gi¸c ABI th× :





2 . 2 2 2 1 4 2

       p AB AI BI AB AI BI

DÊu ®¼ng thøc x¶y ra

    AI BI a

VËy





2 2 2 1 4 2 1

     Minp a

Hay ®iÓm cÇn t×m lµ

4 4

1 1

1 ;2 2

2 2

 

   

 

 

Chọn đáp án D.

Câu 30. Cho hµm sè:

3 ( )

2 2

  

y x C

vµ ®iÓm M

( )



cã hoµnh ®é x

= a. Víi gi¸ trÞ nµo cña a

th× tiÕp tiÕp tuyÕn cña (C) t¹i M c¾t (C) 2 ®iÓm ph©n biÖt kh¸c M.









 



























 













 





Hướng dẫn giải:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay

§iÓm M

( )



, x

= a =>

2 2

  

y a ta cã Pt tiÕp tuyÕn víi (C) cã d¹ng

( )



( )  

x M M

y y x x y

víi

' 3

2 6

 

y a a

( )



3 2

(2 6 )( ) 3

2 2

     

y a a x a a

Hoµnh ®é giao ®iÓm cña

( )



vµ (C) lµ nghiÖm cña ph¬ng tr×nh

4 4

2 3 2 2 2 3

5 5

3 (2 6 )( ) 3 ( ) ( 2 3 6) 0

2 2 2 2

             

x a

x a a x a a x a x ax a

2 2

( ) 2 3 6 0









    



x a

g x x ax a

Bµi to¸n trë thµnh t×m a ®Ó g(x)=0 cã 2 nghiÖm ph©n biÖt kh¸c a

' 2 2

( )

(3 6) 0

3 0

( ) 6 6 0



    



 



  

  

  



 

  





g x

a a

g a a

Chọn đáp án A.

Câu 31. Cho hàm số:

2 3







. Viết phương trình tiếp tuyến của

( )

, biết tiếp tuyến đó cắt đường

tiệm cận đứng và tiệm cận ngang lần lượt tại

A B

sao cho



AB IB

, với

(2,2)

I .

  

y x ;

  

y x B.

 

y x ;

  

y x

  

y x ;

  

y x D.

 

y x ;

 

y x

Hướng dẫn giải:

Gọi

2 3

; ( )

 





 



 

M x C

. PTTT của (C) tại M:

   

0 0

2 2

0 0

1 2 6 6

2 2

 

  

 

x x

y x

x x



AB IB

và tam giác AIB vuông tại I  IA = IB nên hệ số góc của tiếp tuyến k = 1 hoặc k =

-1. vì

 



 



nên ta có hệ số góc tiếp tuyến k = -1.

 







   









 có hai phương trình tiếp tuyến

  

y x ;

  

y x

Chọn đáp án C.

Câu 32. Cho hàm số y = x

+ 2mx

+ (m + 3)x + 4 (m là tham số) có đồ thị là (C

), đường thẳng d có

phương trình y = x + 4 và điểm K(1; 3). Tìm các giá trị của tham số m để d cắt (C

) tại ba điểm phân

biệt A(0; 4), B, C sao cho tam giác KBC có diện tích bằng

8 2

1 37



m B.

1 137



m C.

1 7



m D.

1 142



m

Hướng dẫn giải:

Xét phương trình hoành độ giao điểm của (C) và d:

+ 2mx

+ (m + 3)x + 4 = x + 4  x(x

+ 2mx + m + 2) = 0

 

2 2 0 *









   



x mx m

d cắt (C) tại 3 điểm phân biệt  PT (*) có 2 nghiệm phân biệt khác 0

     

' 2

2 0

; 2 2; 1 2;

2 0



    

         



 



m m

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay

Khi đó B = (x

; x

+ 4), C = (x

; x

+ 4) với x

, x

là hai nghiệm của (*)

Theo Vi-ét ta có

1 2

  





 



x x m

   

 

2 2

1 2 1 2 1 2

2 2 8 2 2 2

        

BC x x x x x x m m

Ta có khoảng cách từ K đến d là h =

. Do đó diện tích KBC là:

 

2 2

1 1

. . 2.2 2 2 2 2

2 2

      

S h BC m m m m

1 137

8 2 2 2 8 2 ( )



      

S m m m TM

Chọn đáp án B.

Câu 33. Cho hàm số:

2009

 

y x x

có đồ thị là (C).

là điểm trên (C) có hoành độ



x . Tiếp

tuyến của (C) tại

cắt (C) tại điểm

khác

, tiếp tuyến của (C) tại

cắt (C) tại điểm

khác

, tiếp tuyến của (C) tại điểm



M cắt (C) tại điểm

khác



M (n = 4; 5;…), gọi





;

n n

x y

là tọa độ điểm

. Tìm n để :

2013

2009 2 0

  

n n

x y

685



n B.

627



675



n D.

672



Hướng dẫn giải:

Gọi





;

k k k

M x y

suy ra tiếp tuyến tại









: '  

k k k k

M y y y x x x









2 3

3 2009 2009

     

k k k k

y x x x x x

Tọa độ điểm



M được xác định:

















3 2 3 2 2

2009 3 2009 2009 . 2 0

          

k k k k k k k

x x x x x x x x x x x x x

2 2



       

k k k k

x x x x x x

Ta có :

 

1 2 3

1; 2; 4;...; 2



     

x x x x

   

2010 3 2010

3 3 2013

2013

2009 2 0 2009 2009 2 0

2 2 2 3 3 2013 672



       

          

n n n n n

x y x x x

n n

Chọn đáp án D.

Câu 34. Cho hàm số

3 2







x m

với

là tham số. Xác định m để đường thẳng

cắt các trục

Ox Oy

lần lượt tại

C D

sao cho diện tích



OAB

bằng 2 lần diện tích



OCD

 

m B.

 

m C.

 

m D.

 

Hướng dẫn giải:

Phương trình hoành độ giao điểm của

và đồ thị:

2 2

3 3 0,



   mx m x m x

Vì



m nên phương trình

3 3 1 0

   

x mx

(*). Ta có

9 12 0, 0

     

m m và

1 3

2 0, 0



 

    

 

 

f m

m m

(ở đây





f x

là vế trái của (*)) nên

luôn cắt đồ thị tại 2 điểm

A B

phân biệt

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay

Ta có









1 1 2 2

;3 3 , ;3 3

 

A x x m B x x m

với

1 2

x x

là 2 nghiệm của (*). Kẻ đường cao

của



OAB

ta có

 



 

OH d d

và

     

 

2 2 2

2 1 2 1 2 1

1 2 1 2

3 3 10

10 40 10

     

    

AB x x x x x x

x x x x m

(Định lý Viet đối với (*)).

Mặt khác ta có









;0 , 0; 3



C m D m

(để ý



m thì

, ,

C D O

phân biệt). Ta tìm

để

 



OAB OCD

S S hay

40 2

10 . 2 3

3 3



    

m m m m

Chọn đáp án C.

Câu 35. Cho hàm số

   

3 2

1 4 3 1

     

y mx m x m x

có đồ thị là





là tham số. Tìm các

giá trị của

để trên





có duy nhất một điểm có hoành độ âm mà tiếp tuyến của





tại điểm đó

vuông góc với đường thẳng

: 2 0

 

d x y .





















 

m D.

 









Hướng dẫn giải:

/ 2

2( 1) 4 3

    

y mx m x m

. Tiếp tuyến có hệ số góc bằng 2

Ta tìm

2( 1) 4 3 2

    

mx m x m





có đúng một nghiệm âm













1 3 2 0 1

      

x mx m x

hoặc

2 3

 

mx m



m : không thỏa yêu cầu



m , yêu cầu bài toán xảy ra khi

2 3









 







m m

Chọn đáp án C.

Câu 36. Cho hàm số

2 1







có đồ thị

(C)

và điểm





2;5

P . Tìm các giá trị của tham số

để

đường thẳng :

  

d y x m

cắt đồ thị





tại hai điểm phân biệt

và

sao cho tam giác

PAB

đều.

Phương trình hoành độ giao điểm của đường thẳng

và đồ thị

( )

là:

1, 5

  

m m B.

1, 4

 

m m C.

6, 5

  

m m D.

1, 8

  

m m

Hướng dẫn giải:

2 1



   



x m





( 3) 1 0 1

    x m x m , với

 

Đường thẳng

cắt đồ thị

(C)

tại hai điểm phân biệt khi và chỉ khi phương trình





có hai nghiệm

phân biệt khác



2 13 0

0. 3 0



  





 



m m

(đúng



)

Gọi

1 2

x x

là các nghiệm của phương trình (1), ta có:

1 2

  





  



x x m

Giả sử





1 1

; 

A x x m





2 2

; 

B x x m

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay

Khi đó ta có:

 

1 2

2 

AB x x

       

2 2 2 2

1 1 1 2

2 5 2 2

         PA x x m x x

       

2 2 2 2

2 2 2 1

2 5 2 2

         PB x x m x x

Suy ra



PAB

cân tại

Do đó



PAB

đều

2 2

 

PA AB

         

2 2 2 2

1 2 1 2 1 2 1 2 1 2

2 2 2 4 6 8 0

            

x x x x x x x x x x

4 5 0





    



 



m m

. Vậy giá trị cần tìm là

1, 5

  

m m .

Chọn đáp án C.

Câu 37. Cho hµm sè

4 3

4 2

    

y x mx x m . T×m tÊt c¶ c¸c gi¸ trÞ cña m ®Ó hµm sè ban ®Çu cã 3

cùc trÞ vµ träng t©m cña tam gi¸c víi 3 ®Ønh lµ to¹ ®é c¸c ®iÓm cùc trÞ trïng víi t©m ®èi xøng cña ®å thÞ

hµm sè





x m



m B.



m C.



m D.



Hướng dẫn giải:

Hµm sè ®· cho cã 3 cùc trÞ khi ph¬ng tr×nh y’(x) = 0 cã 3 nghiÖm ph©n biÖt

3 2

4 3 4 0

   

x mx

cã 3nghiÖm ph©n biÖt

XÐt g(x) =

3 2

4 3 4

 

x mx

cã g’(x) =

12 6 ( ) 0 0,



     

x mx g x x x

lim ( ) , lim ( )

 

   

x x

g x g x

vµ

(0) 4 0 , ( )

2 4



  

m m

g g nªn g(x) = 0

cã 3 nghiÖm ph©n biÖt

2 2







  













(häc sinh cã thÓ lËp b¶ng biÕn thiªn

cña hµm

( )



 

trªn





\ 0

R ®Ó t×m ra kÕt qu¶ trªn)

Khi ®ã t©m ®èi xøng cña ®å thÞ hµm sè





x m

lµ

( ;1)

Gäi

1 1 2 2 3 3

( ; ), ( ; ), ( ; )

A x y B x y C x y

lµ 3 ®iÓm cùc trÞ cña ®å thÞ hµm sè ®· cho th×

, x

lµ nghiÖm ph¬ng tr×nh :

3 2

4 3 4 0

  

x mx

nªn theo ®Þnh lý Viet ta cã

1 2 3

2 2 2 2

1 2 2 3 3 1

1 2 3 1 2 3 1 2 2 3 3 1

3 4

( ) 2( )

 









  

 



 

 

  

        







x x x m

x x x

x x x x x x

x x x x x x x x x x x x

ViÕt hµm sè ban ®Çu díi d¹ng:

2 2

3 5

( ) ( )( ) ( 3 2)

4 16 16 4



      

x m m x m

y x y x x , v× thÕ

2 2 2 2

3 5 3 5

( ) ( )( ) ( 3 2) 3 2

4 16 16 4 16 4

( ) 0 ( 1,2,3)



            



 

i i i

i i i i i

x m m x m m x m

y y x y x x x

do y x i

Tõ ®ã :

2 4

2 2 2

1 2 3

1 2 3 1 2 3

5 9 5

( ) ( ) 2 2

3 16 4 16 4

 

            

y y y m m m m

x x x x x x

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay

Träng t©m cña tam gi¸c ABC lµ G(

1 2 3 1 2 3

;

3 3

   

x x x y y y

)



( ;1)

I khi vµ chØ

khi :

1 2 3

 

 

y y y

3 2

9 5

2 1 ( 4)(9 36 144 64) 0

16 4

         

m m

m m m m

V×

2 2

m

nªn



m lµ gi¸ trÞ duy nhÊt cÇn t×m.

Chọn đáp án C.

Câu 38. Tìm tham số

để hàm số





3 2

3 3 1 2

    

y x mx m x nghịch biến trên một đoạn có độ dài

lớn hơn

1 21



m B.

1 21



m hoặc

1 21



m

1 21



m D.

1 21 1 21

2 2

 

 m

Hướng dẫn giải:

Ta có









2 2

, 3 6 3 1 3 2 1



        

D y x mx m x mx m

0 2 1 0



     

y x mx m





. Điều kiện cần và đủ để hàm số nghịch biến trên một đoạn có độ

dài lớn hơn 4



 

y trên đoạn có độ dài lớn hơn 4







có hai nghiệm





1 2 1 2

; 

x x x x

thoả mãn

1 2

 

x x

1 2

4 1 4

4 2 4



 





 



 



        

 



   









m m

x x

1 21 1 21

5 0

2 2

 

       m m m m .

Vậy hàm số





nghịch biến trên một đoạn có độ dài lớn hơn

1 21 1 21

2 2

 

   m m

Chọn đáp án B.

Câu 39. Đường thẳng :

 

d y x a

luôn cắt đồ thị hàm số

 

2 1

 





y H

tại hai điểm phân biệt

A B

. Gọi

1 2

k k

lần lượt là hệ số góc của các tiếp tuyến với





tại

và

. Tìm

để tổng

1 2



k k

đạt

giá trị lớn nhất.



a B.



 

a D.

 

Hướng dẫn giải:

Phương trình hoành độ giao điểm của

và





 

2 1

2 2 1 0 *





 



  







   



x a

x ax a

Đặt





2 2 1

   

g x x ax a

Vì

2 2 0,

1 1

2 2





     





 

   



 

 



a a a

g a

nên





có hai nghiệm phân biệt

1 2

x x

khác

với mọi

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay

Vậy

luôn cắt





tại hai điểm phân biệt

A B

với mọi

Gọi









1 1 2 2

; , ;

A x y B x y

với

1 2

x x

là hai nghiệm của





. Theo định lý Vi-ét ta có

1 2 1 2

 

   

x x a x x .

Tiếp tuyến tại

A v B

có hệ số góc là

   

1 2

2 2

1 2

1 1

;

2 1 2 1

 

 

 

k k

x x

Ta có

   

2 2

1 2

2 2 2 2

1 2 1 2

2 1 2 1

1 1

2 1 2 1 2 1 2 1

 

  

 

    

 

   

 

 

x x

k k

x x x x

       

2 2 2

1 2 1 2 1 2 1 2

4 8 4 2 ( 2 1 2 1 1)

 

         

 

x x x x x x do x x

 

4 1 2 2,

      

a a

. Dấu bằng xẩy ra

  

Vậy

1 2



k k

đạt giá trị lớn nhất bằng



khi

 

a .

Chọn đáp án D.

Câu 40. Tìm m để phương trình x

– ( 2m+3)x

+ m + 5 = 0 có 4 nghiệm x

, x

thoả mãn :

-2 < x

< -1 < x

< 0 < x

< 1 < x

< 3

A. Không có m B.



m C.



m D.



Hướng dẫn giải:

Đặt x

= X



, ta có phương trình: f(X) = X

– ( 2m+3).X + m + 5 = 0

(*)

để phương trình đã cho có 4 nghiệm phân biệt x

< x

thì phương trình (*) có hai nghiệm

thoả mãn: 0 < X

< X

. Khi đó

1 2 2 1 3 1 4 2

; ; ;     

x X x X x X x X

Do đó: -2<-

<-1< -

< 0 <

< 1 <

< 3

 

>1 >

> 0



4 > X

> 1 > X

> 0

(1) 0 3 0

(0) 0 5 0

(4) 0 7 9 0

   

 

 

    

 

 

   

 

af m









  











không tồn tại m thoả mãn bài toán .

Chọn đáp án A.

Câu 41. Cho hàm số: y = x

mmx  . Xác định m để đường thẳng y = x cắt đồ thị tại 3 điểm

phân biệt A, B, C sao cho AB = BC.

A. m = 0 ; m = 2 B. m = 0

C. m = 2 D. m = 0 ; m =

Hướng dẫn giải:

PT hoành độ giao điểm: x

- 0

 mxmx (1)

Đường thẳng y = x cắt đồ thị tại 3 điểm phân biệt A,B,C



pt (1) có 3 nghiệm phân biệt x

, x

. Theo Vi et ta có : x

+ x

m (2)

theo gt AB = BC



2 x

+ x

(3)

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay

Từ (2) và (3)



. Vậy x =

là một nghiệm của (1).

Chia f(x) =

323

mxmxx  cho

x  ta được:

f(x) = (x -

) (x

– mx – 1 -

) -

x =

là nghiệm của (1)



= 0



m=0, m = 2

Khi đó f(x) = (x -

) (x

– mx – 1 -

) có 3 nghiệm phân biệt

vì )(x



= x

– mx – 1 -

có 2 nghiệm trái dấu và có



(

) = -1 - 0



. m

Vậy: m = 0 ; m = 2

Chọn đáp án A.

Câu 42. Cho hàm số y=x

-(m+1)x

-(2m

-3m+2)x+2m(2m-1). Xác định m để hàm số đồng biến trên

(2;+ ) .

A. 3 2  m B. 2 2  m C. 3 1  m D. 3 2  m

Hướng dẫn giải:

Ta có:

)232()1(23)(

22,

 mmxmxxgy

∆

’

=7m

–7m +7 = 7(m

-m+1) > 0 , m

 0, );2( x

















0)2(

062













 m

Chọn đáp án D.

Câu 43. Bạn A có một đoạn dây dài 20m . Bạn chia đoạn dây thành hai phần. Phần đầu uốn thành một

tam giác đều. Phần còn lại uốn thành một hình vuông. Hỏi độ dài phần đầu bằng bao nhiêu để tổng

diện tích hai hình trên là nhỏ nhất?

9 4 3

180

9 4 3



120

9 4 3

Hướng dẫn giải:

Bạn A chia sợi dây thành hai phần có độ dài

 

x m và

 

20  x m , 0 20 x (như hình vẽ).

Phần đầu uốn thành tam giác đều có cạnh

 

m , diện tích

 

3 3

3 4 36

 

 

 

 

x x

S m

Phần còn lại uốn thành hình vuông có cạnh

 

 x

m , diện tích

 



 



 

 

S m

Tổng diện tích hai hình nhỏ nhất khi

 

3 20

36 4



 

 

 

 

x x

f x nhỏ nhất trên khoảng

 

0;20 .

Ta có:

 

3 20 180

' 0

18 8

4 3 9



    



x x

f x x .

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay

Bảng biến thiên:

180

4 3 9









f x



0 +





f x

Dựa vào bảng biến thiên ta được

180

4 3 9





Chọn đáp án D.

Câu 44. Cho các số thực

, ,

a b c

thỏa mãn

8 4 2 0

    





   



a b c

. Số giao điểm của đồ thị hàm số

3 2

   

y x ax bx c

và trục

là

. B.

. C.

. D.

Hướng dẫn giải:

Ta có hàm số

3 2

   

y x ax bx c

xác định và liên tục trên



Mà

lim



 

nên tồn tại số



sao cho







y M ;

lim



 

nên tồn tại số

 

m sao

Vậy đồ thị hàm số

3 2

   

y x ax bx c

và trục

có 3 điểm chung.

Chọn đáp án D.

Câu 45. Tập hợp các giá trị của

để đồ thị hàm số

  

2 2

2 1

2 1 4 4 1





   

mx x x mx

có đúng 1

đường tiệm cận là





0 .









; 1 1; .

   















; 1 0 1; .

    

Hướng dẫn giải:

Có

lim 0





. Nên hàm số luôn có 1 đường tiệm cận ngang



y . Vậy ta tìm điều kiện để hàm số

không có tiệm cận đứng .

Xét phương trình:

  

2 2

2 1 0 (1)

2 1 4 4 1 0

4 4 1 0 (2)



  

     



  



mx x

mx x x mx

x mx

TH1: Xét



m , ta được

 

2 1 1

4 1

2 1 4 1



  



  

x x

(thỏa ycbt)

TH2: Xét



m . Có:

  

và

4 4

  

Th2a. Cả 2 phương trình (1) và (2) đều vô nghiệm:

1 0

1 1

4 4 0

 





   

 

  

 



cho y





 0; y



2



 8 4a  2b  c  0 và y





 8  4a  2b  c  0.

Do y







2



 0 suy ra phương trình y  0 có ít nhất một nghiệm thuộc khoảng



m;2





2







 0 suy ra phương trình y  0 có ít nhất một nghiệm thuộc khoảng



2;2











 0 suy ra phương trình y  0 có ít nhất một nghiệm thuộc khoảng



2;M



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24

Facebook: https://www.facebook.com/dongpay

Th2b: (1) vô nghiệm, (2) có nghiệm kép



x : ta thấy trường hợp này vô lí (vì



m )

Th2c: (2) vô nghiệm, (1) có nghiệm kép



x : ta thấy trường hợp này vô lí (vì

1 1

  

m )

Chọn đáp án A.

Câu 46. Đường thẳng

: 4

 

d y x cắt đồ thị hàm số





3 2

2 3 4

    

y x mx m x tại 3 điểm phân

biệt





0;4 ,

A B

và

sao cho diện tích tam giác

MBC

bằng 4, với





1;3 .

M Tìm tất cả các giá trị của

thỏa mãn yêu cầu bài toán.



m hoặc



m B.

 

m hoặc



m C.



m D.

 

m hoặc

 

Hướng dẫn giải:

Phương trình hoành độ giao điểm của

và đồ thị









3 2

2 3 4 4

    

x mx m x

 

   

3 2

2 2 0

2 2 0 1





     



     



x mx m x

x x mx m

Với



x ta có giao điểm là





0;4 .

cắt





tại 3 điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác 0.





0 2 0

(*)

2 0

   









    





m m

Ta gọi các giao điểm của

và





lần lượt là









, ; 2 , ; 2

 

B B C C

A B x x C x x với

B C

x x

là nghiệm

của phương trình (1).

Theo định lí Viet, ta có:

. 2

  





 



B C

x x m

Ta có diện tích của tam giác

MBC

là

 

, 4.

   

S BC d M BC

Phương trình

được viết lại là:

: 4 4 0.

     

d y x x y

Mà

   

 

1 3 4

, , 2.

1 1

 

  

 

d M BC d M d

Do đó:

 

8 8

   

BC BC

d M BC

Ta lại có:

     

2 2 2

2 32

      

C B C B C B

BC x x y y x x

     

2 2

4 . 16 2 4 2 16

        

B C B C

x x x x m m

4 4 24 0 3 2.

        

m m m m

Đối chiếu với điều kiện, loại đi giá trị

 

Chọn đáp án C.

Câu 47. Cho các số thực x, y thỏa mãn





2 3 3

    

x y x y

. Giá trị nhỏ nhất của biểu thức





2 2

4 15

  

P x y xy

là:

min 83

 

P B.

min 63

 

P C.

min 80

 

P D.

min 91

 

Hướng dẫn giải:

Ta có





     

x y 2 x 3 y 3 x y 4 x y 8 x 3. y 3 4 x y

             

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25

Facebook: https://www.facebook.com/dongpay

. Mặt khác

Xét biểu thức và đặt

Lại có

Xét hàm số trên đoạn suy ra

Chọn đáp án A.

Câu 48. Gọi (C

) là độ thì hàm số

4 2

2 2017

   y x x m . Tìm m để (C

) có đúng 3 điểm chung

phân biệt với trục hoành, ta có kết quả:

2017



m B.

2016 2017

 

m C.

2017



m D.

2017



Hướng dẫn giải:

- Phương pháp: Tìm m để phương trình ẩn x tham số m có n nghiệm phân biệt thuộc khoảng K

+ Cô lập m, đưa phương trình về dạng m = f(x)

+ Vẽ đồ thị (hoặc bảng biến thiên) của y=f(x) trên K

+ Biện luận để đường thẳng y = m cắt đồ thị hàm số y =f(x) tại n điểm phân biệt trên K

- Cách giải:





cắt Ox tại 3 điểm phân biệt  Phương trình

4 2 4 2

2 2017 0 2 2017

       x x m m x x

có 3 nghiệm phân biệt.

Xét hàm số

4 2

2 2017

  y x x trên R

Có

' 4 4 0 0

    

y x x x hoặc

 

x . Bảng biến thiên:



0 0 1





0 + 0



0 +



2017



2016 2016

Dựa vào bảng biến thiên, ta thấy đường thẳng y = m cắt đồ thị hàm số y =f(x) tại 3 điểm phân biệt

khi và chỉ khi m =2017

Chọn đáp án A.

Câu 49. Tìm tất cả các giá trị thực của m để đồ thị hàm số







có hai đường tiệm cận

ngang.



m B.



m C.



m D.



Hướng dẫn giải:

Đồ thị hàm số







có hai đường tiệm cận ngang khi và chỉ khi các giới hạn









lim , lim

 

   

 

x x

y a a y b b tồn tại. Ta có:

+ với

m 0



ta nhận thấy

x x

lim y , lim y

 

   

suy ra đồ thị hàm số không có tiệm cận ngang.

x y 4

x y 0

 







 







 





x y 2 x 3 y 3 2 2 x y x y 8 x y 4;8

            





 

2 2

P 4 x y 15xy 4 x y 7xy

     





t x y 4;8 P 4t 7xy

     

        

x 3 y 3 0 xy 3 x y 9 P 4 x y 21 x y 63

             

4t 21t 63

  





f t 4t 21t 63

  





4;8





min

P f 7 83

  

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26

Facebook: https://www.facebook.com/dongpay

+ Với



m , khi đó hàm số có TXĐ

4 4

3 3

D ;

m m

 

   

 

 

, khi đó

x x

lim y, lim y

 

không tồn tại suy

ra đồ thị hàm số không có đường tiệm cận ngang.

+ Với



m , khi đó hàm số có TXĐ





suy ra

2 2

2 4

lim , lim

3 3

 

 



 

 



 

x x

x m x m

x x

suy ra

đồ thị hàm số có một đường tiệm cận ngang.

Vậy



m thỏa YCBT.

Chọn đáp án C.

Câu 50. Cho hàm số

2 4

   

y x x a . Tìm a để giá trị lớn nhất của hàm số trên đoạn





2;1

 đạt

giá trị nhỏ nhất.



a B.

a 2



a 1



D. Một giá trị khác

Hướng dẫn giải:

Ta có

 

2 4 1 5

       

y x x a x a . Đặt

 

 

u x khi đó





2;1

  x thì





u 0;4

 Ta

được hàm số





  

f u u a . Khi đó

   





















2;1 0;4

0 , 4 5 ; 1

  

    

x u

Max y Max f u Max f f Max a a

Trường hợp 1:

 





0;4

5 1 3 5 2 3



          

a a a Max f u a a

Trường hợp 2:

 





0;4

5 1 3 1 2 3



          

a a a Max f u a a

Vậy giá trị nhỏ nhất của

 

x 2;1

Max y 2 a 3

 

  

Chọn đáp án A.

Câu 51. Giá trị nhỏ nhất của hàm số:









3 3 3 3

2 1 1 2 1 1

       

y x x x x là:

A. 0 B. 1 C. 2 D. 3

Hướng dẫn giải:









3 3 3 3

2 1 1 2 1 1

       

y x x x x

   

2 2

3 3

1 1 1 1

      y x x

3 3

1 1 1 1

      

y x x

Điều kiện để hàm số xác định

 

Ta có

3 3

1 1 1 1

     

y x x

- Nếu

1 0

  

x thì

3 3 3

1 1 0 1 1 1 1 2

          

x x x y

- Nếu



x thì

3 2

1 1 0 2 1 2

      

x y x

Vậy:

2, 1, 2 0

      

y x y x

Chọn đáp án C.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27

Facebook: https://www.facebook.com/dongpay

z=17

y=9

x=8

HÌNH ĐA DIỆN

I – HÌNH CHÓP

Câu 1. Cho hình chóp có chân đường cao nằm trong tam giác ; các mặt phẳng ,

và cùng tạo với mặt phẳng một góc bằng nhau. Biết , ,

; đường thẳng tạo với mặt đáy một góc bằng . Tính thể tích của khối chóp

A. B. C. D.

Hướng dẫn giải:

Gọi J là chân đường cao của hình chóp S.ABC; H, K và L

lần lượt là hình chiếu của J trên các cạnh AB, BC và CA.

Suy ra, , và lần lượt là góc tạo bởi

mặt phẳng với các mặt phẳng , và

Theo giả thiết, ta có ,

suy ra các tam giác vuông và bằng nhau.

Từ đó, . Mà J nằm trong tam giác ABC nên J là

tâm đường tròn nội tiếp tam giác ABC.

Áp dụng công thức Hê-rông, ta tính được diện tích của tam giác

ABC là . Kí hiệu là nửa chu vi tam giác ABC, là

bán kính đường tròn nội tiếp của ABC. Ta có . Đặt , ,

Ta có hệ phương trình .

Giải ra được

Ta có , suy ra SJB là tam giác

vuông cân tại J. .

Thể tích V của khối chóp S.ABC là

Chọn đáp án A.

Câu 2. Cho tứ diện lần lượt thuộc

sao cho

, mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số

thể tích hai phần khối tứ diện ABCD bị chia bởi mặt

phẳng (MNP).

A. B.

C. D. .

Hướng dẫn giải:

S ABC

ABC

( )

SAB

( )

SAC

( )

SBC

( )

ABC





S ABC

680



408



578



600





SHJ



SLJ



SKJ

( )

ABC

(S )

( )

SBC

( )

SAC



SHJ SLJ SKJ

 

SJH SJL

SJK

JH JL JK

 

204



204

  

x BH BL

 

y CL CK

 

z AH AK

 

x y

x z

y z



 



 





 





( ; ; ) (8;9;17)

x y z



2 2 2 2

6 8 10

JB JH BH

    



( ,( )) 45

SBJ SB ABC

  

SJ JB

 

. 680

ABC

V SJ S 

, , ,

ABCD M N P

, ,

BC BD AC

4 , 2 ,

BC BM BD BN

 

AC AP



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28

Facebook: https://www.facebook.com/dongpay

Gọi , kẻ

đồng dạng

Đặt Ta có:

Chọn đáp án B.

Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = a, hình chiếu

vuông góc của đỉnh S trên mặt phẳng (ABCD) là điểm H thuộc đoạn AC, . Gọi CM là

đường cao của tam giác SAC. Tính thể tích khối tứ diện SMBC theo a.

A. B. C. D.

Hướng dẫn giải:

Gọi O là tâm của hình vuông ABCD.

Ta có:

Chọn đáp án A.

Câu 4. Cho hình chóp tứ giác đều có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên và

mặt phẳng đáy là thoả mãn . Mặt phẳng qua AC và vuông góc với mặt phẳng

chia khối chóp thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị

nào trong các giá trị sau

A. 0,11 B. 0,13 C. 0,7 D. 0,9

I MN CD Q PI AD

   









/ / , / /

DH BC H IM DK AC K IP

 

ID DH BM

NMB NDH

IC CM CM

      

1 1 2

3 2 3 3

IK DK ID DK DK

IP CP IC AP AP

      

APQ



DKQ



3 3

2 5

AQ AP AQ

DQ DK AD

    

ABCD

V V



1 1 1

. ,

5 2 10

ANPQ

ANCD DACN

ANPQ

ANCD ABCD DABC

V VAP AQ DN

V V

V AC AD V V DB

      

 

1 1 1 1 1

2 2 2 2 4

CDMP

CDMP N ABMP DABMP CDMP

CDBA

V CM CP

V V V V V V V

V CB CA

        

7 7

20 13

ABMNQP

ABMNQP ANPQ N ABMP

CDMNQP

V V V V

     

AH 

. 2

AM AH AH AC a

AC SA SA a

    

 

2 2

a a

MC AC AM a

 

     

 

 

1 1 7 7

2 2 2 2 8

SMC

a a a

S SM MC   

2 3

1 1 2 7 14

3 3 2 8 48

SMAC SMC

a a a

V BO S   

S ABCD



cos =











SAD

S ABCD

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

là hình chóp tứ giác đều . Gọi N là trung điểm CD

Kẻ . Ta có

nên mặt phẳng

là

+ Xét tam giác SON vuông tại N có :

+ Xét tam giác SOD vuông tại O có :

Ta có

- Xét tam giác MCD vuông tại M có :

Ta có :

. Mặt phẳng

chia khối chóp S.ABCD thành 2 khối và

. Do đó :

Chọn đáp án A.

Câu 5. Cho hình chóp , có đáy là tam giác đều cạnh . Các mặt bên , ,

lần lượt tạo với đáy các góc lần lượt là . Tính thể tích của khối chóp .

Biết rằng hình chiếu vuông góc của trên mặt phẳng nằm bên trong tam giác .

A. . B. . C. . D. .

S ABCD







SO ABCD

   

,  







 





CD SN CD ON

SCD ABCD CD

   









, 

SCD ABCD SNO



CM SD

 

 

   







AC BD

AC SBD AC SD

AC SO













   

SD ACM ACM SAD









ACM



cos

  

ON a

SNO

2 2

   

    

   

   

a a

SO SN ON a

 

2 2

2 10

2 2

 

    

 

 

a a

SD SO OD a

1 1

. .

2 2



 

SCD

S CM SD SN CD

. 3 10

   

SN CD a

2 2 2

3 10 10

10 10

 

    

 

 

a a

DM CD CM a

1 1 1 1

. . . . .

2. 2 2 2 10

    

MACD MACD

SABCD SACD

V V

DM DA DC DM

V V DS DA DA DS

 

MACD SABCD

V V





MACD

SABCM

  

SABCD MACD SABCM

V V V

 

SABCM SABCD

V V

0,11

 

MACD

SABCM

S ABC

ABC





SAB





SAC





SBC

0 0 0

30 ,45 ,60

S ABC





ABC

 

4 3

V 



 

2 4 3

V 



 

4 4 3

V 



 

8 4 3

V 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Gọi là hình chiếu vuông góc của trên mặt phẳng

. Kẻ , ,

. Khi đó ta có

, ,

. Ta có suy ra

Vậy .

Chọn đáp án D.

Câu 6. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, góc giữa SC và mp(ABC) là 45 . Hình

chiếu của S lên mp(ABC) là điểm H thuộc AB sao cho HA = 2HB. Biết . Tính khoảng cách

giữa 2 đường thẳng SA và BC:

A. B. C. D.

Hướng dẫn giải:

+ D là đỉnh của hình bình hành ABCD thì d(SA;BC)=d(B;(SAD))=1,5.d(H;(SAD))

+ Kẻ HE vuông AD, E thuộc AD. Kẻ HI vuông SE, I thuộc AE thì d(H;(SAD))=HI

+ Tính

Chọn đáp án B.

Câu 7. Cho khối chóp S.ABC có đáy là tam giác vuông ở A,

AB = a, AC = 2a. Đỉnh S cách đều A, B, C; mặt bên (SAB)

hợp với mặt đáy (ABC) góc 60

. Tính thể tích khối chóp

S.ABC.

A. V=

B. V= a

C. V=

D. V=

Hướng dẫn giải:

Gọi M, N, H lần lượt là trung điểm của AB, AC, và BC

Ta có tam giác SAB cân suy ra SM AB

HM // AC HM  AB



   

1SMH AB SH  

Và [(SAB), (ABC)] = SMH = 60

Tương tự AC  (SNH) AC  SH (2)

Từ (1) và (2) SH  (ABC)

Ta có SH = MH. tan 60

= 3

= a 3





ABC





HD AB D AB

 





HE AC E AC

 





HF BC E BC

 

tan30

HD SH 

tan45

HE SH

 

tan 60

SH SH

HF  

ABC





 

1 1 3 3

1 3

2 4

2 4 3

a a

SH a SH

 

    

 



 

   

2 3

1 3 3 3

. .

3 4

2 4 3 8 4 3

a a a

V  

 



CH 

210



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31

Facebook: https://www.facebook.com/dongpay

ABC

AC.AB = a

. Vậy V =

.SH. S

ABC

(đvdt)

Chọn đáp án A.

Câu 8. Cho hình chóp S.ABCD có SA=x, các cạnh còn lại bằng 2. Tìm giá trị của x để thể tích khối

chóp lớn nhất

A. 6 B. 2 C. 7 D. 2 6

Hướng dẫn giải:

Gọi O là giao điểm của AC và BD.

Ta có OD=OB và SB=SD nên SO BD , do đó

 

BO SAC .

Mặt khác

2 2 2 2 2 2

SO SB OB AB OB OA    

nên SO OA OC  . Do đó tam giác SAC vuông

tại S.

Ta có

2 2 2 2

4 4 4

AC x OA x

    

Do đó

2 2

4 12 0 2 3OB x x     .

Và

 

2 2 2 2 2

16 4 4

SOA

S x OA x x   .

Để

.S ABCD

V đạt giá trị lớn nhất khi và chỉ khi

SOAB

V đạt giá trị lớn nhất .

Do đó

.S ABCD

V đạt giá trị lớn nhất khi và chỉ khi

 

2 2

12x x đạt giá trị lớn nhất.

Suy ra

2 2 2

12 6 6x x x x      .

Chọn đáp án A.

Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của AD. Gọi S’ là

giao của SC với mặt phẳng chứa BM và song song với SA. Tính tỉ số thể tích của hai khối chóp

S’.BCDM và S.ABCD.

Hướng dẫn giải:

Trong

 

ABCD , gọi

 

I AC BM  , trong

 

SAC , kẻ đường thẳng qua I,

/ / SA

, cắt

tại S’



S’ là giao điểm của SC với mp chứa BM, //SA.

Do M là trung điểm của AD nên

   

'. '.

3 3

4 4

S BCDM S ABCD

dt BCDM dt ABCD V V  

Gọi H, H’ lần lượt là hình chiếu của S, S’ trên ABCD

' ' ' 2

S H CS CI

SH CS CA

   

'. '. . .

3 3 2 1

4 4 3 2

S BCDM S ABCD S ABCD S ABCD

V V V V    

Chọn đáp án A.

Câu 10. Đáy của hình chóp SABC là tam giác cân ABC có AB AC a  và



B C



 

. Các cạnh bên

cùng tạo với đáy một góc



. Tính thể tích hình chóp SABC.

tan



 B.

cos tan

 

 C.

cos tan

 

 D.

sin 2





Hướng dẫn giải:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32

Facebook: https://www.facebook.com/dongpay

Kẻ

 

SO ABC OA là hình chiếu vuông góc của SA lên (ABC)

Do đó

 



;SA ABC SAO



  . Tương tự ta cũng có



SBO SCO



  .

Nên SAO SBO SCO     AO BO CO   .

Theo định lí sin ta có: 2O

sin sin 2sin

AC a a

A OA

 

    .

Nên

tan

.tan

2sin

SO OA





  .

Mặt khác

 

1 1 sin

. .sin A sin 180 2

2 2 2

ABC

S AB AC a







    .

Vậy

2 3

1 1 sin tan cos tan

. .

3 6 2 2sin 6

ABC

a a a

V S SO

   







   .

Chọn đáp án B.

Câu 11. Cho hình chop S.ABCD, đáy là hình thang vuông tại A và B. AB = BC = a, AD = 2a,

 

SA ABCD . Gọi M, N là trung điểm của SB và SD. Tính V hình chop biết rằng (MAC) vuông góc

với (NAC).

3 3

Hướng dẫn giải:

Gọi I, H lần lượt là trung điểm AD và AB, O là giao điểm của AC và BI, vẽ HK // BI (K thuộc AC)

Ta có ABCI là hình vuông nên AC vuông góc với BI

Mà AC vuông góc NI (do NI // SA)

Suy ra

     

 

,AC NIO NOI NAC ACD



    

Tương tự ta có

   

 

,MKH MAC ACB



  

Theo đề ta có

tan cot90

NI HK

NO MH

  



    

Suy ra

2 2

. . .

2 2 2 4

SA SA a a

NI MH OI HK SA a    

Mà

2 3

3 1

2 3 2

ABCD ABCD

a a

S V S SA   

Chọn đáp án C.

Câu 12. Cho tứ diện .S ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho 2MA SM ,

2SN NB , ( )



là mặt phẳng qua MN và song song với SC . Kí hiệu

( )H và

( )H là các khối đa

diện có được khi chia khối tứ diện .S ABC bởi mặt phẳng ( )



, trong đó,

( )H chứa điểm S ,

( )H

chứa điểm A ;

V và

V lần lượt là thể tích của

( )H và

( )H . Tính tỉ số

Hướng dẫn giải:

Kí hiệu V là thể tích khối tứ diện SABC .

Gọi P , Q lần lượt là giao điểm của ( )



với các đường thẳng BC , AC .

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33

Facebook: https://www.facebook.com/dongpay

Ta có

// //

NP MQ SC

. Khi chia khối

( )

bởi mặt phẳng

( )

QNC

, ta được hai khối chóp .

N SMQC

và .

N QPC

Ta có:

( ,( ))

(B,( ))

N SMQC SMQC

B ASC SAC

V S

d N SAC

V d SAC S

 

;

( ,( )) 2

(B,( )) 3

d N SAC NS

d SAC BS

 

;

4 5

9 9

AMQ SMQC

ASC ASC

S S

S AS S

 

   

 

 

Suy ra

2 5 10

3 9 27

N SMQC

B ASC

  

.QP

( ,(QP ))

(S,(A ))

1 1 2 2

3 3 3 27

QPCN C

S ABC ABC

d N C

V d BC S

NB CQ CP

SB CA CB

 

      

. .QP

1 1

1 2

. . 1 2

10 2 4 4

5 4

27 27 9 9

N SMQC N C

B ASC S ABC

V V

V V V V V

        



 

Chọn đáp án A.

Câu 13. Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là

. Để làm

thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng

x V



x V

 C.

x V



x V



Hướng dẫn giải:

Gọi

là độ dài cạnh đáy,

là độ dài đường cao của thùng đựng đồ





a,x 0



Khi đó,

2 2

V V

V a x a S 2a 4ax 2 4 Vx

x x

       

Để làm thùng hàng tốn ít nguyên liệu nhất thì

nhỏ nhất

2 4 Vx

 

nhỏ nhất.

Cách 1 : Xét hàm số

 

f x 2 4 Vx

 

trên







Ta có

   

2V 2 V

f' x ; f' x 0 x V V x x V



      

Từ BBT ta thấy để làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng

f x( )

f' x( )

f (V

)

+ ∞

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34

Facebook: https://www.facebook.com/dongpay

Cách 2: ta có

V V

2 4 Vx 2 2 Vx 2 Vx 6 V

x x

    

Dấu " " xảy ra tại

Vx x V x V

    

Chọn đáp án B.

Câu 14. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

SAD

là tam giác đều và nằm trong

mặt phẳng vuông góc với mặt phẳng đáy. Biết rằng diện tích mặt cầu ngoại tiếp khối chóp

.ABCDS

là

 



. Khoảng cách giữa hai đường thẳng

và

gần với giá trị nào nhất sau đây ?

dm . B.

dm. C.

dm . D.

dm .

Hướng dẫn giải:

Gọi

0x

là cạnh của hình vuông

ABCD

và

là

trung điểm cạnh

Dễ dàng chứng minh

 

 

SH ABCD SH .

Gọi

 O AC BD

và

là trọng tâm

SAD

, đồng

thời

1 2

,d d lần lượt là 2 trục đường tròn ngoại tiếp

,ABCD SAD

 

1 2

qua O va / / , qua G va / /d SH d AB

1 2

  I d d là tâm mặt cầu ngoại tiếp khối chóp

.S ABCD

 R SI

 

2 2 2

2 21

4 1

2 7



 

         

 

 

x x

S R R SI SG GI x dm

Gọi

là điểm thỏa

ADEC

là hình bình hành

   

 

/ / ; ;  ED AC d AC SD d AC SDE

   

 

; ; 2 ; 2   d AC SD d A SDE d H SDE HP

(phần chứng minh

 

HP SDE

xin

dành cho bạn đọc)

 

2 2 2 2 2

1 1 1 1 1

3 2

2 4

21 3 6

;SD

14 7 7

SKH

HP SH KH

x x

HP dm d AC dm

    

   

   

   

    

Chọn đáp án D.

Câu 15. Cho hình chóp có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm

của , một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N.Gọi là thể tích của khối

chóp . Tìm giá trị nhỏ nhất của ?

S ABCD

S AMPN

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35

Facebook: https://www.facebook.com/dongpay

A. B. C. D.

Hướng dẫn giải:

Đặt khi đó ta có :

Ta có :

Lại có :

Từ (1) và (2) suy ra : do

Từ (2) suy ra

Khảo sát hàm số

Chọn đáp án B.

Câu 16. Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ diện đó lớn nhất là

bao nhiêu?

A. B. C. D.

Hướng dẫn giải:

Giả sử tứ diện ABCD có cạnh lớn nhất là AB, suy ra các tam giác

ACD và BCD có tất cả các cạnh đều không lớn hơn 1. Các chiều

cao AF và BE của chúng không lớn hơn , trong đó

Chiều cao của hình tứ diện

(do tam giác AHF vuông tại H có AF là cạnh huyền)

Thể tích của khối tứ diện là:

; ,(0 , 1)

SM SN

x y x y

SD SB

   

SABC SADC SABD SBCD

V V V V

   

   

1 1

. 1

2 2 2 4

SAMPN SAMP SANP SAMP SANP

SADC SABC

V V V V V V

SM SP SN SP

x y

V V V V V SD SC SB SC

 









       











 

 

1 1 3

2 2 2 2 4

SAMPN SAMN SMNP

SABD SBCD

V V V V

xy xy xy

V V V V

 







     











 

 

1 3

4 4 3 1

x y xy y

   



0 1 1

3 1 2

y x

     







3 3 3 3 1

. . ( ), 1

4 4 3 1 4 2

4 3 1

x x

xy x f x x

V x

 







     













 

1 2 4 1

( ), 1 min ( )

2 3 9 3

x x

y f x x f x f

 







  









 

   

 

 

 

       

 

 

 

 

 

   



CD a

 

AH AF  

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36

Facebook: https://www.facebook.com/dongpay

Để tìm giá trị lớn nhất của V ta xét biểu thức .

Vì nên và .

Chọn đáp án C.

Câu 17. Cho hình chóp có đáy là hình vuông cạnh vuông góc với mặt

phẳng đáy và góc giữa với mặt phẳng bằng Gọi là điểm di động trên cạnh và

là hình chiếu vuông góc của trên đường thẳng Khi điểm di động trên cạnh thì thể

tích của khối chóp đạt giá trị lớn nhất bằng?

A. B. C. D.

Hướng dẫn giải:

Ta có góc giữa SC và mặt phẳng (SAB) là

Trong tam giác SBC có

Trong tam giác SAB có

Thể tích khối chóp S.ABH là:

Ta có và theo bất đẳng thức AM-GM ta có

Đẳng thức xảy ra khi

Khi đó

3 3

3cos

4(cot cot )



 





g g

3 3

3cos

2(cot cot )

g g



 





3cos

2(cot cot )

g g



 





5cos

4(cot cot )

g g



 





Hướng dẫn giải:

Đặt 2 hình chóp tam giác đều là : O.ABC và O’.A’B’C’ với O là tâm của tam giác ABC và O’ là tâm

của tam giác A’B’C’.

Theo bài ra thì OO’ là đường cao chung của 2 hình chóp .

Đặt D,E,F là các giao điểm của các cặp cạnh bên tương ứng của 2 hình chóp . Phần thể tích chung

của 2 hình chóp là thẻ tích của khối đa diện ODEFO’. Ký hiệu V là thể tích đó thì





DEF

V OO S

 

1 1 1 1 1 1

. . . . . . . . 1 4

3 3 2 3 2 4 24

V S AH BE CD AH a a a

 

     

 

 





a a



0 1

 





4 3

a a

 

 

1 1

24 8

V a a

  

S ABCD

ABCD

( )

SAB

30 .

S ABH





CSB

 

. 30 3

SB BC cot a

  

2 2

SA SB AB a

  

1 1 1 2

. . . . 2 .

3 3 2 6

S ABH ABH

V S SA HAHB a HAHB

  

2 2 2 2

HA HB AB a

    

2 2 2

2. . .

a HA HB HAHB HAHB



    

HA HB ABM M D

  

2 3

2 2 2

. .

6 6 2 12

S ABH

a a a a

V HAHB

Chọn đáp án D.

Câu 18. Hai hình chóp tam giác đều có chung chiều cao , đỉnh của hình chóp này trùng với tâm của

đáy hình chóp kia. Mỗi cạnh bên của hình chóp này đều cắt một cạnh bên của hình chóp kia. Cạnh bên

l của hình chóp thứ nhất tạo với đường cao một góc



.Cạnh bên của hình chóp thứ 2 tạo với đường

cao một góc



. Tìm thể tích phần chung của hai hình chóp .

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37

Facebook: https://www.facebook.com/dongpay



OO C

vuông tại O’ nên

' cos





OO l

Do tính đối xứng nên OO’ đi qua tâm I của



DEF

Trong



IOE

ta có :

cot





OI IE g

Trong



IO E

có:

' cot





O I IE g

Suy ra

' (cot cot )

OO IE g g

 

 

' cos

cot cot cot cot

OO l

g g g g



   

  

 

Tam giác DEF đều , đường cao



EJ EI

Diện tích





DEF

với

2 3

 

DE EI

Do đó

2 2

3 3cos

4(cot cot )



 







DEF

g g

Vậy thể tích phần chung của 2 hình chóp là :

3 3

3cos

4(cot cot )



 





g g

Chọn đáp án A.

Câu 19. Cho hình chóp S.ABCD có đáy là nửa lục giác đều với cạnh a (a> 0). Cạnh SA vuông góc với

đáy và SA =

. M là một điểm khác B trên SB sao cho AM  MD. Tính tỉ số

Hướng dẫn giải:

Đặt hình chóp vào hệ trục toạ độ như hình vẽ.

Suy ra ta có: A = (0; 0; 0), D = (2a; 0; 0), S =

(0; 0; a

) và

B =

; ;0

2 2

 

 

 

a a

. Suy ra phương trình của

SB là:

2 2 3

3 3



 



x y z a

a a

Gọi M(x

; y

; z

) thuộc cạnh SB, ta có:

0 0

3 2 3









 





y x

z a x

Mặt khác AMDN 

. 0



 

AM DM

 x

– 2ax

+ y

+ z

= 0

 

3 3 3 3

; ;

8 8 4

 

 

 

 

a a a





 

SM SB

hay



Chọn đáp án A.

Câu 20. Cho khối tứ diện ABCD có cạnh AB > 1, các cạnh còn lại có độ dài không lớn hơn 1. Gọi V là thể

tích của khối tứ diện. Tìm giá trị lớn nhất của V.

This image cannot currently be displayed.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Theo giả thiết



ACD

và



BCD

có tất cả các cạnh không lớn hơn 1.

Đặt CD = a (

0 1

 

Gọi AM, BN lần lượt là chiều cao của



ACD

và



BCD

Ta có

 

AM ;

 

BN .

Gọi AH là chiều cao của tứ diện, ta có

  

AH AM .

Thể tích của tứ diện ABC

1 1

. . . . . (1 )

3 6 6 4



   

BCD

a a

V S AH BN CD AH

Xét

( ) (4 )

 

f a a a

trên (0, 1]. Ta có f(a) liên tục trên (0, 1].

' 2 '

( ) 4 3 , ( ) 0

   

f a a f a





0;1

  a

Vậy





0,1

max ( ) (1) 3

 

f a f .

Suy ra

max



khi



ACD

và



BCD

là hai tam giác đều cạnh bằng 1, hai mặt phẳng (ACD) và

(BCD) vuông góc với nhau. Khi đó tính được

 

Chọn đáp án B.

Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA =

và SA vuông góc

với mặt phẳng đáy. Mặt phẳng (P) đi qua điểm A và vuông góc với SC cắt SB, SC, SD lần lượt tại B’,

C’, D’. Tính thể tích khối chóp S.AB’C’D’ theo a.

3 3

3 5

Hướng dẫn giải:

, ( ) '

     

BC AB BC SA BC SAB BC AB

( ) ' ' ( ) '

      

SC P SC AB AB SBC AB SB

Tương tự '



AD SD

. ' ' ' . ' ' . ' '

 

S AB C D S AB C S AD C

V V V

2 2

. ' '

2 2 2 2

' ' '. '. 3 3 9

. . . .

4 5 20

    

S AB C

S ABC

SB SC SB SB SC SC SA SA

V SB SC SB SC SB SC

(1)

f(a)

f'(a)

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39

Facebook: https://www.facebook.com/dongpay

2 2

. ' '

2 2 2 2

' ' '. '. 3 3 9

. . . .

4 5 20

    

S AD C

S ADC

SD SC SD SD SC SC SA SA

V SD SC SD SC SD SC

(2)

. .

1 1 3

. . 3

3 2 6

  

S ABC S ADC

V V a a

Cộng (1) và (2) theo vế ta được

3 3

. ' ' . ' '

. ' ' '

3 3

9 9 9 3 3 3

20 20 10 6 20

3 3

     

S AB C S AD C

S AB C D

V V

a a

Hướng dẫn giải:

Xét



SAC

ta có

2 2 2 2

2 2 2, 1 2

         

AC SA SC OC OD CD OC BD

Thể tích

. .

1 1 1 1 15

2 5 3

4 12 12 2 12



         

S CMD S ABCD SAC

V V BD S

Gọi

là trung điểm của

nên





/ /

CD SMN

Suy ra

 

( , ) ( ,( )) ( ,( ))





   

C SMN

SMN

d CD SM d CD SMN d C SMN

Thể tích

. .

 

C SMN S MCD

V V

(1).

Ta có

3 13

3, ,

2 2

  MN SM SN

( sử dụng công thức

đường trung tuyến)

Theo định lý hàm số cosin trong



SMN

ta có

 

2 23

cos sin

3 3 3 3

  SMN SMN

Vậy



1 23

sin

2 4

    

SMN

S SM MN SMN

(2).

Thay (1), (2) vào







ta được

3 15

( , )





  

C SMN

SMN

d CD SM

6 6

Chọn đáp án A.

Câu 22. Cho hình chóp S.ABCD thỏa mãn SA  5,SB  SC  SD  AB  BC  CD  DA  3.

Gọi

là trung điểm của cạnh BC . Tính thể tích khối chóp S.MCDvà khoảng cách giữa hai

đường thẳng

SM,CD

Ta thấy ABCD là hình thoi, tam giác SBD cân tại S suy ra

BD 



SAC



Gọi O là giao điểm của

và

, ta thấy

SBD  ABD  CBD



c.c.c



Suy ra

OA  OC  OS 

 AC

nên SAC vuông tại S .

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40

Facebook: https://www.facebook.com/dongpay

Chọn đáp án A.

Câu 23. Cho tứ diện đều ABCD cạnh a. Mặt phẳng (P) chứa cạnh BC cắt cạnh AD tại E. Biết góc giữa

hai mặt phẳng (P) và (BCD) có số đo là



thỏa mãn

5 2

tan





. Gọi thể tích của hai tứ diện ABCE

và tứ diện BCDE lần lượt là

và

. Tính tỷ số

Hướng dẫn giải:

+) Gọi M là trung điểm BC.

Khi đó BC



(MAD) nên (P)(AMD);

(P)(AMD)=ME.

Kẻ AHME thì AH(BCE) ( do AH



(AMD) )

Kẻ DKME nên DK(BCE) (do DK



(AMD) ).

Hiển nhiên AH song song DK

Khi đó

2 .

 

A BCE

D BCE

V V DK

+) Gọi  là góc giữa (P) và (ABC) (





 

Hiển nhiên







DME

;







AME

Vì AM = DM nên:

sin

sin .sin .sin

sin



  



   

VAH

DK V

(1)

+) Trong tam giác OMA:

1 1

os( ) os cos sin

3 3

     

     

c c sin

. (2)

Từ (1) có:

2 2 2 2

os 1 sin 1 .sin 1 .

  

     

c t t x

; với x=sin

.

Thay vào (2) ta có:

2 2

1 1

1 . 1 . (1 )(1 ) .

3 3

        

t x x t x t x x t x

+) Giải phương trình có:

(9 6 9)



 

t t

Vì

2 2

2 2 2

8 9 6 9 8

sin tan .

1 9 6 9 9 6 1 9 6 1

 

 

    

      

x t t

x t t t t t t

Theo giả thiết suy ra

2 2

8 50 196 171

9 6 1 9 6 0

9 6 1 49 25 25







         





 









t t t t

t t

Vậy



ABCE

DBCE

Chọn đáp án C.

Câu 24. Cho khối chóp .

S ABC

có

SA a



SB a

 ,

SC a

 . Thể tích lớn nhất của khối chóp là

a . B.

. C.

. D.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Gọi

là hình chiếu của

lên

( ) .

SBC

SBC V AH S

 

Ta có

AH SA



; dấu “=” xảy ra khi





AS SBC





1 1

. .sin .

2 2

SBC

S SB SC SBC SB SC

 

, dấu “=” xảy ra khi

SB SC



Khi đó,

1 1 1 1

3 3 2 6

SBC

V AH S AS SB SC SA SB SC

      

Dấu “=” xảy ra khi

, ,

SA SB SC

đôi một vuông góc với nhau.

Suy ra thể tích lớn nhất của khối chóp là

1 6

. .

6 6

V SA SB SC 

Chọn đáp án D.

Câu 25. Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông cân,

 

AB AC a







SC ABC

và



SC a

. Mặt phẳng qua

, vuông góc với

cắt

SA SB

lần lượt tại

và

. Tính thể tích khối

chóp .

S CEF



SCEF

. B.



SCEF

V . C.



SCEF

V . D.



SCEF

Hướng dẫn giải: Từ

hạ





, 

CF SB F SB





, 

CE SA E SA

Ta có

 





   







   

AB AC

AB SAC AB CE

AB SC

CE SAB CE SB

Vậy mặt phẳng qua

và vuông góc

là mặt





CEF

Ta có



SCEF

SCAB

SE SF

V SA SB

Tam giác vuông

SAC

vuông tại

ta có:

2 2

  

SA SC AC a

và

2 2

   

SE SC a SE

SA SA

SA a

Tam giác vuông

SBC

vuông tại

ta có:

2 2

  

SB SC BC a

và

2 2

   

SF SC a SF

SB SC

SB a

Do đó

1 1 1 1 1 1 1

. . .

2 3 6 6 6 3 36

     

SCEF

SCEF SABC ABC

SCAB

V V SAS a

Chọn đáp án C.

II – HÌNH LĂNG TRỤ

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42

Facebook: https://www.facebook.com/dongpay

Câu 24. Một hình hộp có 6 mặt đều là các hình thoi có góc bằng 60

và cạnh bằng a. Tính thể tích của

hình hộp đó.

A. B.

C. D.

Hướng dẫn giải:

Ta có: AB = AD = BD = a; AA’ = A’B = A’D = a

A’ABCD là tứ diện đều

Chân đường cao A’H trùng với tâm của ABD

HA = HB = HD = AO =

A’H2 = AA’2 – AH2 = a

- =

A’H = Từ đó tìm được

Chọn đáp án B.

Câu 25. Cho khối lập phương .

   

ABCD A B C D

cạnh

. Các điểm

và

lần lượt là trung điểm

của

 

C B và

 

C D . Mặt phẳng

 

AEF

cắt khối lập phương đã cho thành hai phần, gọi

V là thể tich

khối chứa điểm



và

V là thể tich khối chứa điểm 'C . Khi đó

là

. B. 1. C.

. D.

Hướng dẫn giải:

  

AQEFPB A D

Gọi

   



ABCD A B C D

V V ,

3 .





A A MN

V V ,

4 4

 

 

PFD N QMB E

V V V V

Do tính đối xứng của hình lập phương nên ta có

4 5

V V .

1 1 3 3 3

. . . .

6 6 2 2 8

  

  

a a a

V AA A M A N a

1 1

. . . . .

6 6 3 2 2 72

  

  

a a a a

V PD D F D N

1 3 4

  

V V V

2 1

  

V V V

. Vậy



Chọn đáp án A.

Câu 26. Cho lăng trụ đứng

  

ABCA B C

có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa

mặt phẳng

( )



AB C

và mặt phẳng

( )



BB C

bằng

60 .Tính thể tích lăng trụ

  

ABCA B C .

2 2







3 3

2 3

a a





V 

Đường thẳng

cắt



tại N , cắt



tại

, AN cắt



tại

cắt



tại

Từ đó mặt phẳng



AEF



cắt khối lăng trụ thành

hai khối đó là

ABCDC



QEFP

và

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43

Facebook: https://www.facebook.com/dongpay

a B.

a D.

Hướng dẫn giải:

Từ A kẻ AI





I là trung điểm BC



(BC

 

C B

)







C (1)

Từ I kẻ IM





C (2)

Từ (1), (2)







(IAM)

Vậy góc giữa (A



C) và (



CB) là



AMI

= 60

Ta có AI=



BC a

; IM=

tan60



AI a

 

BH IM

;

2 2 2 2 2 2

1 1 1 3 1 1

' 4 4 2

    

B B BH BC a a a

Suy ra



;

1 1

. .2

2 2



  

ABC

S AI BC a a a

2 3

2. 2

  

 

ABC A B C

V a a a

Chọn đáp án A.

Câu 27. Cho lăng trụ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm

lên mặt phẳng trùng với trọng tâm tam

giá . Biết khoảng cách giữa hai đường

thẳng và bằng . Khi đó thể tích

của khối lăng trụ là

A. B.

C. D.

Hướng dẫn giải:

Gọi là trung điểm BC, dựng MH vuông

góc với A’A. suy ra

Đặt AH=x, ta có

Từ A’A. MH=A’G.AM, suy ra



. Vậy .

Chọn đáp án A.

ABC.A'B'C'

(ABC)

ABC

AA'

a 3

 

, '

MH d BC A A 

A A x 

2 3

3 3

3 4 12

a a a

V  

B’

A’

C’

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44

Facebook: https://www.facebook.com/dongpay

Câu 28. Cho hình lăng trụ có đáy là tam giác đều cạnh , hình chiếu vuông

góc của lên măt phẳng trùng với tâm của tam giác . Biết khoảng cách giữa

và là . Tính thể tích của khối lăng trụ .

A. B. C. D.

Hướng dẫn giải:

Gọi M là trung điểm B

Gọi H,K lần lượt là hình chiếu vuông góc của G,M trên AA’

Vậy KM là đọan vuông góc chung củaAA’và BC, do đó .

AA’G vuông tại G,HG là đường cao,

Chọn đáp án C.

Câu 29. Cho khối lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt thuộc các cạnh bên AA’, CC’ sao

cho

MA MA'



và

NC 4NC'



. Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ diện GA’B’C’,

BB’MN, ABB’C’ và A’BCN, khối tứ diện nào có thể tích nhỏ nhất?

A. Khối A’BCN B. Khối GA’B’C’ C. Khối ABB’C’ D. Khối BB’MN

Hướng dẫn giải:

+ Nhận thấy khoảng cách từ G và A xuống mặt phẳng (A’B’C’) là

bằng nhau ( do G,A thuộc mặt phẳng (ABC)//(A’B’C’)

GA'B'C' A.A 'B'C'

V V

Mà

A.A'B'C' ABB'C'

V V (Do 2 hình chóp này có 2 đáy AA’B’ và ABB’

diện tích bằng nhau;chung đường cao hạ từ C’)

GA'B'C' ABB'C'

V V 

=> Không thế khối chóp GA’B’C’hoặc ABB’C’ thể thích nhỏ nhất

→ Loại B,C

+ So sánh Khối A’BCN và Khối BB’MN

Nhận thấy khoảng cách từ M và A’ xuống mặt BBCC’ là bằng nhau

→ Khối A’BCN và Khối BB’MN có đường cao hạ từ M và A’ bằng

nhau. Mặt khác Diện tích đáy BNB’ > Diện tích đáy BCN

=> Khối A’BCN < Khối BB’MN.

=> Khối A’BCN có diện tích nhỏ hơn.

Chọn đáp án A.

. ' ' '

ABC A B C

ABC





ABC

. ' ' '

ABC A B C



( ' )

BC A AM

 

( A',BC)

d A KM 

AGH AMH

   



2 3

3 6

GH KH  



A G



. ' ' '

. '

ABC A B C ABC

V S A G

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45

Facebook: https://www.facebook.com/dongpay

Câu 30. Cho hình lăng trụ đứng

ABC.A'B'C'

có đáy

ABC

là tam giác cân tại

, góc



BAC

nhọn.

Góc giữa

AA'

và

BC'

là

, khoảng cách giữa

AA'

và

BC'

là

. Góc giữa hai mặt bên





AA'B'B

và





AA'C'C

là

. Thể tích lăng trụ

ABC.A'B'C'

là

2a 3

a 3

a 6

Hướng dẫn giải:

Ta có góc giữa hai mặt bên





AA'B'B

và





AA'C'C

là



BAC 60



ABC





đều.

Vì















AA'/ /CC' AA';BC' CC';BC' BC'C 30

   

Kẻ





AI BC AI BB'C'C

  













  

      

ABC.A'B'C '

d AA';BC' d AA'; BB'C'C AI a

2a BC 1 2a 2a 3

BC ,CC' 2a V 2a. .a.

2 3

tan30

3 3

Chọn đáp án A.

Câu 31. Cho hình lăng trụ tam giác đều ABC. A’B’C’, có cạnh đáy bằng và cạnh bên bằng .

Lấy M, N lần lượt trên cạnh AB’, A’C sao cho . Tính thể tích V của khối BMNC’C.

A. B. C. D.

Hướng dẫn giải:

Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ và AA’C’C.

Ta có: (Do G trung điểm AB’).

Xét tam giác ABA’ có AG là trung tuyến và . Suy ra

là trọng tâm tam giác ABA’. Do đó BM đi qua trung điểm I

của AA’.

Ta có: (Do K là trung điểm A’C).

Xét tam giác AA’C’ có A’K là trung tuyến và . Suy ra

N là trọng tâm của tam giác AA’C’. Do đó C’N đi qua trung

điểm I của AA’.

Từ là trọng tâm tam giác ABA’ và N là trọng tâm của tam

giác AA’C’. Suy ra:

Gọi lần lượt là thể tích các khối chóp IMNC; IBCC’. Ta có:

. Mà . Suy ra .

' 1

' ' 3

AM A N

AB A C

 

108

2 6

3 6

108

1 2

' 3 3

AM AM

AB AG

  



' 1 ' 2

' 3 ' 3

A N A N

A C A K

  

' 2

' 3

A N

A K



' 3

IM IN

IB IC

 

1 2

;

V V

. .

' 9

IM IN IC

V IB IC IC

 

1 2

V V V

 

V V



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46

Facebook: https://www.facebook.com/dongpay

Hạ AH vuông góc với BC tại H thuộc BC. Ta được AH vuông góc với mặt phẳng (BB’C’C). AA’

song song với mặt phẳng nên khoẳng cách từ I đến mặt phẳng (BB’C’C) bằng khoẳng

cách từ A đến (BB’C’C) và bằng AH. Ta có: .

. Suy ra .

Chọn đáp án B.

Câu 32. Cho hình lập phương

D. ' ' ' 'ABC A B C D

có khoảng cách giữa

'A C

và

' 'C D

là 1 cm. Thể

tích khối lập phương

D. ' ' ' 'ABC A B C D

là:

8 cm

. B.

2 2

. C.

3 3

. D.

27 cm

Hướng dẫn giải:

Để tìm khoảng cách giữa A’C và C’D’, ta dựng một mặt phẳng chứa A’C và song song với C’D’.

Dễ thấy đó là mặt phẳng (CA’B’).

Gọi a là độ dài cạnh của khối lập phương, lúc này ta có:

     

' ', ' ' ', ' ' ', ' ' 

   

   

d C D A C d C D CA B d D CA B

Để tính khoảng cách từ điểm D’ đến mặt phẳng (CA’B’), ta xét

khối tứ diện D’CA’B’.

 

2 3

' ' ' ' ' '

1 1

. '. . .

3 3 2 6

  

D CA B B A D

a a

V CC S a cm

 

2 2

' '

1 1 2

S .CB'.B'A' . 2.

2 2 2

  

CA B

a a a cm (do tam giác

CA’B’ vuông tại B’)

Suy ra:

   

' ' '

2' '

', ' ' 2

    

 

 

D CA B

CA B

d D CA B a cm a

(cm).

Do đó

3 3

2 2 

V a cm

Chọn đáp án B.

Câu 33. Cho hình hộp ABCDA’B’C’D’. Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng thời

song song với B’D’. Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V

, V

( Trong đó

là thể tích khối chứa A). Tính tỉ số



. B. 1. C.

. D.

Hướng dẫn giải:

*Gọi N là trung điể A’D’. Khi đó (P)BDNM).

Thấy BMDNAA’=I.

Khi đó: V

=V(A’MNABD); V

=V-V

. (Với V là thể tích hình hộp)

* Ta có:

( ' ) ( ) 1

( A'B'D') ( ' ' ') 4

 

V IA MN S AMN

V A S A B D





' '

BB C C

AH 

 

2 3

2 '

1 1 3 2 6

. ; ' ' . . .

3 3 2 2 12

BCC

a a a

V d I BB C C S



 

  

 

 

8 2 6

9 27

V V

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47

Facebook: https://www.facebook.com/dongpay

* Mà:

(AA'B'D') 1



nên có:

( ' )



V IA MN V

* Lại có:

( ' ) '. . 1

( ) . . 8

 

V IA MN IA IM IN

V IABD IA IB ID

*Vậy:

( )



V IABD V

* Do đó:

1 1 7

3 24 24

  

V V V V

nên

2 1

  

V V V V

. Vậy:



Chọn đáp án A.

Câu 34. Cho khối lăng trụ tam giác ABC.A’B’C’. Gọi I, J, K lần lượt là trung điểm của các

cạnh AB, AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích

của hai phần đó.

. B. 1. C.

. D.

Hướng dẫn giải:

Chứng minh EI = IJ = JF. Từ đó suy ra

' 1

' ' 3

  

EB EM FA

EB EK FB

. Lại từ đó suy ra



Ta có: d(K, A'B') = (1/2)d(C', A'B'), FB' = (3/2)A'B'. Suy ra S

KFB’

(3/4)S

A’B’C’

Mặt khác vì

' 3



nên suy ra d(E, (KFB’)) = (3/2)h (h là chiều

cao lăng trụ).

Do đó V

EKFB’

= (3/8)V (V là thể tích lăng trụ) .

1 1 1 1

. . . .

' 3 3 3 27

  

EBIM

EB FK

V EI EM EB

V EF EK EB

nên V

EBIM

1 3 1

27 8 72



V V

' 1 1 1 1

. . . .

' 3 3 2 18

  

FA JN

FB EK

V FJ FA FN

V FE FB FK

nên V

FA’JN

1 3 1

18 8 48



V V

Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Gọi V

là thể tích phần chứa điểm B' và

là thể tích phần chứa điểm C.

Ta có V

= (3/8 – 1/72 – 1/48)V = (49/144)V nên V

= (95/144)V.

Do đó V

Chọn đáp án C.

Câu 35. Cho hình lăng trụ .

ABC A B C

  

có đáy là tam giác đều cạnh

Hình chiếu vuông góc của

điểm



lên mặt phẳng





ABC

trùng với trọng tâm tam giác

ABC

Biết khoảng cách giữa hai đường

thẳng



và

bằng

Tính thể tích

của khối lăng trụ

. .

ABC AB C

  

V 

. B.

V 

. C.

V 

. D.

V 

Hướng dẫn giải:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48

Facebook: https://www.facebook.com/dongpay

là trung điểm của

thì





BC AA M





Gọi

là đường cao của tam giác

A AM



thì

MH A A





và

HM BC



nên

là khoảng cách



và

Ta có . .AAHM A G AM

 

 

3 3

4 2 3

a a a

A A A A

 

 

Đường cao của lăng trụ là

2 2

4 3

9 9 3

a a a

A G



  

Thể tích

2 3

3 3

3 4 12

a a a

V  

Chọn đáp án B.

Câu 36. Cho hình lăng trụ có tất cả các cạnh đều bằng

, đáy là lục giác đều, góc tạo bởi cạnh bên và

mặt đáy là



. Tính thể tích khối lăng trụ

V a



. B.

V a



. C.

V a



. D.

Hướng dẫn giải:

Ta có

ABCDEF

là lục giác đều nên góc ở đỉnh bằng

120



ABC

là tam giác cân tại

DEF

là tam giác cân tại

1 3

. .sin120

2 4

ABC DEF

S S a a   

2 2

2. . .cos

AC AB BC AB BC B

  

2 2

2. . . 3

a a a a a

 

    

 

 

. 3. 3

ACDF

S AC AF a a a  

2 2 2

3 3 3 3

4 4 2

ABCDEF ABC ACDF DEF

a a a

S S S S a      



' 60 ' '.sin60

B BH B H BB     

Chọn đáp án D.

3 3 9

'. 3.

4 4

ABCDEF

V BH S a a

  

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49

Facebook: https://www.facebook.com/dongpay

MŨ - LÔ GARIT

Câu 1. Cho phương trình . Tìm m để phương trình vô nghiệm?

A. B. C. D.

Hướng dẫn giải:

+Phương trình tương đương:

+ Do hàm f(t)=5

+ t đồng biến trên R nên ta có:

+ Từ đó điều kiện để pt vô nghiệm là C.

Chọn đáp án C.

Câu 2. Tìm tất cả các giá trị thực của tham số m để phương trình sau có hai nghiệm thực phân biệt:

3 1

log (1 ) log ( 4) 0

    

x x m



 

. B.

5 .

 m

5 .

 m



 

Hướng dẫn giải:





3 1

3 3

1;1

1 0

log (1 ) log ( 4) 0

log (1 ) log ( 4)

1 4

  



 

 

      

 

   





x x m

Yêu cầu bài toán





5 0

     

f x x x m

có 2 nghiệm phân biệt





1;1

 

Cách 1: Dùng định lí về dấu tam thức bậc hai.

Để thỏa yêu cầu bài toán ta phải có phương trình







f x

có hai nghiệm thỏa:

1 2

1 1

   

x x





 

. 1 0

5 0

. 1 0

3 0 5

21 4 0

1 1

 



 







 

      

 

 

 

 





  





a f

m m

Cách 2: Dùng đạo hàm

Xét hàm số

   

5 2 1 0



         

f x x x f x x x

Có

   

1 21

; 1 3; 1 5

2 4

 

       

 

 

f f f

Ta có bảng biến thiên

Dựa vào bảng biến thiên, để có hai nghiệm phân biệt trong khoảng





1;1



khi

21 21

5 5

4 4

       

m m

2 2

2 2 2 4 2 2

5 5 2 0

x mx x mx

x mx m

   

    





0 1

 

 







   

      

2 2

2 2 2 2 4 2 2

5 ( 2 2) 5 (2 4 2)

x mx x mx

    

2 2

( 2 2) (2 4 2)

x mx x mx

–

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50

Facebook: https://www.facebook.com/dongpay

Cách 3: Dùng MTCT

Sau khi đưa về phương trình

5 0

   

x x m , ta nhập phương trình vào máy tính.

* Giải khi

0,2

 

: không thỏa



loại A, D.

* Giải khi



m : không thỏa



loại B.

Chọn đáp án C.

Câu 3. Tìm tất cả các giá trị của tham số sao cho bất phương trình sau có tập nghiệm là :

A. . B. . C. . D. .

Hướng dẫn giải:

Phương trình đã cho tương đương

. Đặt ta được:

. Bất phương trình nghiệm đúng

nên bất phương trình có nghiệm , suy ra phương trình có 2 nghiệm

thỏa . Vậy

thỏa mãn

Chọn đáp án C.

Câu 4. Tính giá trị của biểu thức

















ln tan1° ln tan2 ln tan3 ... ln tan89

       



P B.



P D.



Hướng dẫn giải:

















 

ln tan1° ln tan2 ln tan3 ... ln tan89

ln tan1 .tan2 .tan3 ...tan89

ln tan1 .tan2 .tan3 ...tan45 .cot44 .cot 43 ...c

ot1

       

    

       





ln tan45 ln1 0.

   

(vì

tan .cot 1

  

)

Chọn đáp án C.

Câu 5. Cho phương trình : . Tìm để PT có 4 nghiệm phân biệt.



 

. B.

5 .

 m

0 2.

1 1

8 256

 







 





m m



 

Hướng dẫn giải:

Viết lại PT dưới dạng :







 









2 2 1 3 5 3 5 0

x x

m m



     

 





 

   

3 5 3 5

2 2 1 0 1

2 2

x x

m m

   

 

   

   

   

3 5

 



 

 

 

     

2 2 1 0 2 2 1 0 2

m m t f t t mt m

         





 





0 1

 





f t



1 2

t t

1 2

0 1

t t

  





 

0 0

2 1 0

4 2 0

1 0



 





 

 

 









0,5

 







 



 

2 2

5 6 1 6 5

.2 2 2.2 (1)

x x x x

m m

   

  

(1)

2 2

5 6 1 6 5

.2 2 2.2

x x x x

m m

   

  

2 2 2 2

5 6 1 ( 5 6) (1 )

.2 2 2

x x x x x x

m m

      

   

2 2 2 2

5 6 1 5 6 1

.2 2 2 .2

x x x x x x

m m

     

   

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51

Facebook: https://www.facebook.com/dongpay

Đặt : . Khi đó PT tương đương với :

Để có 4 nghiệm phân biệt có 2 nghiệm phân biệt khác 2 và 3.

(*) . Khi đó điều kiện là :

Vậy với thỏa điều kiện đề bài.

Chọn đáp án C.

Câu 6. Tìm tất cả các giá trị của m để phương trình





3 3

log 2 .log 3 1 0

    

x m x m

có 2 nghiệm

1 2

x x

sao cho

1 2

. 27



x x



m C.

m



Hướng dẫn giải:

     

3 3

log 2 .log 3 1 0 1

    x m x m

Đặt

log



x t

1 2

1 2 1 2

Theo Vi-et:

1 2

  

t t m . Suy ra



Chọn đáp án D.

Câu 7. Trong tất cả các cặp





;

x y

thỏa mãn





2 2

log 4 4 4 1

 

  

x y

x y . Tìm

để tồn tại duy

nhất cặp





;

x y

sao cho

2 2

2 2 2 0

     

x y x y m .





10 2

 . B.

10 2

 và

10 2

 .





10 2

 và





10 2

 . D.

10 2

 .

5 6

, , 0

x x

u v

 



















5 6

1 2 1

( 1)( ) 0 2

2 (*)

x x

mu v uv m u v m x

v m

 









 



          

















(1)

(*)



2 2

0 0

1 log 1 log

m m

x m x m

 

 

 

 

 

   

 

 

1 log 0

1 1

(0;2)\ ;

1 log 4

8 256

1 log 9

256















 

 

 

  

   



 

 

 

 









1 1

(0;2)\ ;

8 256

 



 

 

Phương trình trở thành:





m  2



t 3m1 0





Phương trình (1) nghiệm phân biệt khi và chỉ khi (2) có 2 nghiệm phân biệt.

   0 



m  2



 4



3m 1



 m

8m 8  0

(đúng)

Gọi t

là 2 nghiệm của phương trình (2)

 x  3

,x  3

 3

 27  t  t  3

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Ta có





2 2

log 4 4 4 1

 

  

x y

2 2

4 4 6 0

     

x y x y





Giả sử





;

M x y

thỏa mãn pt





, khi đó tập hợp điểm

là hình tròn





tâm





2;2

bán

kính

R

Các đáp án đề cho đều ứng với



m . Nên dễ thấy

2 2

2 2 2 0

     

x y x y m là phương

trình đường tròn





tâm





1;1

J

bán kính



R m

Vậy để tồn tại duy nhất cặp





;

x y

thỏa đề khi chỉ khi





và





tiếp xúc ngoài





1 2

10 2 10 2

        IJ R R m m .

Chọn đáp án A.

Câu 8. Cho n là số nguyên dương, tìm n sao cho

2 2 2 2 2

log 2019 2 l g 2019 3 log 2019 ... log 2019 1008 2017

log 2019

     

a a

a a a

o n

A. n=2017 B. n=2018 C. n=2019 D. n=2016

Hướng dẫn giải:

2 2 2 2 2

3 3 3 2 2

3 3 3 3 2 2

log 2019 2 l g 2019 3 log 2019 ... log 2019 1008 2017

log 2019

log 2019 2 l g 2019 3 log 2019 ... log 2019 1008 2017

log 2019

(1 2 3 ... )log 2019 1008 2017 log 2019

( 1) 2016.

     

      



 

 

 

 

a a

a a a

a a a a a

a a

o n

n n

2017

 

 

 

 

Chọn đáp án A.

Câu 9. Phương trình









3 2

log 6 2log 14 29 2 0

     

mx x x x

có 3 nghiệm thực phân biệt khi:



m B.



m C.

 m

19 39

 

Hướng dẫn giải:









3 2

log 6 2log 14 29 2 0

     

mx x x x









3 2

2 2

log 6 log 14 29 2 0

      

mx x x x

3 2

6 14 29 2

  

       

x x x

mx x x x m

   

3 2

6 14 29 2 2

12 14

  



    

x x x

f x f x x

x x

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 53

Facebook: https://www.facebook.com/dongpay

 

1 1 19

1 1 39

2 2 2

1 1 121

3 3 3





  



 



    



 

 



 

    



 

 



x f

f x x f

x f

Lập bảng biến thiên suy ra đáp án

Chọn đáp án C.

Câu 10. Biết phương trình

5 3

2 1 1

log 2log

 



 

 

 

x x

có nghiệm duy nhất

 

x a b

trong

đó

a b

là các số nguyên. Tính



a b



Hướng dẫn giải:

5 3 5 3

2 1 1 2 1 1

log 2log log 2log

2 2

 

  

   

 

 

x x x x

x x

Đk:

1 0





 



 







 

5 5 3 3

5 3 5 3

Pt log 2 1 log log ( 1) log 4

log 2 1 log 4 log log ( 1) (1)

     

     

x x x x

Đặt

 

2 1 4 1

    

t x x t

(1)

có dạng

2 2

5 3 5 3

log log ( 1) log log ( 1) (2)

    t t x x

Xét

5 3

( ) log log ( 1)

  

f y y y

, do

1 3 1

    

x t y

Xét



1 1

'( ) .2( 1) 0

ln5 ( 1) ln3

   



f y y

y y

( )



f y

là hàm đồng biến trên miền







(2)

có dạng

( ) ( ) 2 1 2 1 0

         

f t f x t x x x x x

1 2

3 2 2 ( )

1 2 (vn)



 

   



 





x tm

Chọn đáp án C.

Câu 11. Phương trình sau có bao nhiêu nghiệm :

   

2 3

4 8

log 1 2 log 4 log 4     

x x x

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. Vô nghiệm

Hướng dẫn giải:

   

2 3

4 8

log 1 2 log 4 log 4     

x x x

(2) Điều kiện:

1 0

4 4

4 0

 



  





  

 

 





 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 54

Facebook: https://www.facebook.com/dongpay













 

2 2 2 2 2

2 2

(2) log 1 2 log 4 log 4 log 1 2 log 16

log 4 1 log 16 4 1 16

           

       

x x x x x

x x x x

+ Với

1 4

  

x ta có phương trình

4 12 0 (3)

  x x ;

 

(3)









 



lo¹i

+ Với

4 1

   

x ta có phương trình

4 20 0

  

x x (4);

 

2 24



 





 





lo¹i

Vậy phương trình đã cho có hai nghiệm là



x hoặc





2 1 6

 x

Chọn đáp án B.

Câu 12. Cho phương trình









2 2

2 5 3.3 15 5 0

    

x x

m m x

. Tìm tập hợp tất cả các giá trị thực của

tham số m để phương trình có nghiệm trong khoảng





0;2







2;3















Hướng dẫn giải:

Vậy







f x

có nghiệm trên khoảng





0;2

với mọi giá trị thực của m.

Chọn đáp án A.

Câu 13. PHương trình









3 3

log 1 2 log

    

x x x x x

có bao nhiêu nghiệm

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. Vô nghiệm

Hướng dẫn giải:

điều kiện x > 0

Phương trình tương đương với

log 2

 

 

 

 

 

x x

Ta có

 

2 1 1 1

    

x x x

Và

3 3 3 3

1 1 1

log log 1 log 3 log 3 1

 

 

 

       

 

 

x x

Do đó

 

1 0

log 2 1



 

 

 



    



 

 

 





x x

x x x

Chọn đáp án A.

Câu 14. Cho hàm số

( ) ,

9 3

  





f x x . Tính

2 2 2

(sin 10 ) (sin 20 ) ..... (sin 80 )

      

P f f f

B. 8 C. 9 D. 3

Hướng dẫn giải:

Đặt









2  m



 3.3

 m



15x  5



. Do f liên tục trên



nên f cũng liên tục trên đoạn



0;2



Ta có









2  m



 3.3

 m



15.0  5



 6m

1 0,m









2  m



 3.3

 m



15.2  5



13  0

Khi đó









 0, m

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 55

Facebook: https://www.facebook.com/dongpay

Nếu

 

a b

thì

( ) ( ) 1

 

f a f b

. Do đó

1 1 1 1 4

    

Chọn đáp án A.

Câu 15. Phương trình

3 3 3 3 4 4 3

3 3 3 3 10

   

   

x x x x

có tổng các nghiệm là ?

A. 0. B. 2. C. 3. D. 4.

Hướng dẫn giải:

3 3 3 3 4 4 3

3 3 3 3 10

   

   

x x x x





   

3 3 3 3

3 3

27 81 1 1

7 27.3 81.3 10 27. 3 81. 3 10 7

3 3 3 3

   



         

   

   

x x x x

Đặt

1 1

3 2 3 . 2

3 3

   

x x

Côsi

3 3 2 3 3

2 3 3

1 1 1 1 1

3 3 3.3 . 3.3 . 3 3

3 3 3 3 3

 

          

 

 

x x x x x

t t t

Khi đó:

 

3 3 3

10 10

7' 27 3 81 10 2

27 3

        

t t t t t N

Với

 

10 1 10

3 7

3 3 3



   

Đặt

3 0

 

y . Khi đó:

 





 

1 10

7 3 10 3 0







       









y N

y y y

y N

Với

3 3 3 1

    

y x

Với

1 1

3 1

3 3

     

y x

Chọn đáp án A.

Câu 16. Gọi





1 2 1 2

, 

x x x x

là hai nghiệm của phương trình









5 1 5 1 5.2



   

x x

. Trong các

khẳng định dưới đây, khẳng định nào sai?













, 1,1 1,1

    x













, 1,1 1,1

    x













1 2

, 1,0 1,0

   x x













1 2

, 1,1 1,1

   x x

Hướng dẫn giải:

   

 

5 1 5 1 5

5 1 5 1 5.2 1

2 2 2



   

 

      

   

   

x x

Nhận xét:

5 1 5 1 5 1 5 1

1 1

2 2 2 2



       

   

   

       

       

x x x x

+ Đặt

 

1 2

5 1 5 1

2 2

5 1 1 5 1

0, 1 log 2, log

2 2 2

 

 



       

 

 

t t x x

Câu 17. Phương trình

9 9 3

1 log 3log log 1

   

x x x

có bao nhiêu nghiệm nguyên ?

A. 0 B. 1 C. 2 D. 3

Hướng dẫn giải:

Giải phương trình:

9 9 3

1 log 3log log 1

   

x x x

. Điều kiện xác định: x ≥ 1

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 56

Facebook: https://www.facebook.com/dongpay

9 9 3

1 log 3log log 1

   

x x x



9 9 9

1 log 3log 2log 1

   

x x x



 





9 9 9 9

1 2log 2log 1 1 log 3 log    

x x x x



 





9 9 9

2log 1 1 log 3 log 1 0

    

x x x



2log 1



x vì:

9 9

1 log 3log 1 0

   

x x  x = 3.

Vậy nghiệm phương trình đã cho: x = 3.

Chọn đáp án B.

Câu 18. Tìm

để bất phương trình









2 2

5 5

1 log 1 log 4    

x mx x m

thoã mãn với mọi





x .

1 0

  

m . B.

1 0

  

m . C.

2 3

 

m . D.

2 3

 

m .

Hướng dẫn giải:

BPT thoã mãn với mọi





x .

 

2 2

4 0

5 1 4



  



 



   







mx x m

x mx x m



 

4 0

5 4 5 0



  



 



    







mx x m

m x x m



 

16 4 0

5 0

16 4 5 0







 





 



  











 





































2 3

 

m .

Chọn đáp án C.

Câu 19. Cho là các số thực thỏa mãn . Giá trị biểu thức là:

A. 0 B. 1 C. 6 D. 3

Hướng dẫn giải:

Khi một trong ba số bằng 0 thì các số còn lại bằng 0. Khi đó M=0

Khi ta đặt suy ra .

Do 2.3=6 nên hay

Từ đó suy ra M=0

Chọn đáp án A.

Câu 20. Cho , với và là các số hữu tỷ. Các khẳng định sau đây,

khẳng định nào đúng?

A. B. C. D.

Hướng dẫn giải:

Do a, b, c là các số hữu tỷ nên

Chọn đáp án A.

Câu 21. Với , cho biết : . Chọn khẳng định đúng :

, ,

x y z

2 3 6

x y z



 

M xy yz xz

  

, ,

x y z

, , 0

x y z



2 3 6

x y z



  

2 ,3 ,6

k k k



  

k k k





1 1 1

x y z

  

55log2log3log

666

 cba

ba,





bac



log 3 2 5 5

a b c

 

5 5 5 0

3 .2 .5 6 3 .2 .5

a b c

  

a b

 









0, 1

a a

 

1 1

1 log 1 log

;

a a

u t

t a v a

 

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 57

Facebook: https://www.facebook.com/dongpay

A. B. C. D.

Hướng dẫn giải:

Từ giả thiết suy ra:

Chọn đáp án D.

Câu 22. Có bao nhiêu giá trị của tham số m để phương trình có

3 nghiệm phân biệt.

A. 1 B. 2 C. 3 D. 4

Hướng dẫn giải:

Vậy, có 3 giá trị của m thỏa mãn.

Chọn đáp án C.

Câu 23. Tìm tất cả các giá trị thực của tham số để phương trình

có nghiệm thuộc ?

A. . B. . C. . D. .

Hướng dẫn giải:

Điều kiện: Khi đó phương trình tương đương: .

Đặt với hay

Phương trình có dạng .

Khi đó bài toán được phát biểu lại là: “Tìm để phương trình (*) có nghiệm ”

Với thì

1 log

u a





1 log

u a





1 log

u a





1 log

u a





1 1

log .log

1 log 1 log

a a

t a

u u

 

 

1 log

1 1 1

log .log

1 log 1 log log

1 log

a a

a a a

v a

t t u



   

  



1 log

log log 1 log log (1 log ) 1 log

1 log

a a a a a a

v u u u v u u a



          



2 2

5 6 1 6 5

.2 2 2.2

x x x x

m m

   

  

















2 2 2 2 2

5 6 1 5 6 5 6 1

2 1 2 1 2 2 1 2 0

x x x x x x x x

Pt m m

       

       

 

5 6

2 2 0

2 *

x x

 











 

  



















2 2 2

2 1 4

log log 3 log 3

x x m x

   





32;





1; 3











1; 3











1; 3



 







3;1



 











2 2 2

log 2log 3 log 3

x x m x

   

log

t x



2 2

32 log log 32 5

x x

   











2 3 3 *

t t m t   



















(*) 3 . 1 3 3. 1 3 0

t t m t t t m t

          

1 3 0

t m t m



      



TH1: (*) có nghiệm duy nhất ( nghiệm x =0)

 m  2.

TH2: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 2 và nghiệm còn lại khác 3

 m  2

3

TH3: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 3 và nghiệm còn lại khác 2

 m  2

8

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 58

Facebook: https://www.facebook.com/dongpay

Ta có Với hay

suy ra Vậy phương trình có nghiệm với

Chọn đáp án A.

Câu 24. Tập các giá trị của m để bất phương trình nghiệm đúng với mọi x > 0 bằng

A. B. C. D.

Hướng dẫn giải:

Đặt . Khi đó ta có

Bất phương trình ban đầu có nghiệm với mọi x > 0 nghiệm đúng với mọi t > 1

Xét hàm số trên

BBT

Từ BBT ta có kết luận bất phương trình có nghiệm với mọi t > 1

Chọn đáp án A.

Câu 25. Giả sử p và q là các số thực dương sao cho: . Tìm giá trị của

A. B. C. D.

Hướng dẫn giải:

Đặt: thì: , , (1)

Chia hai vế của (1) cho ta được: , đặt đưa về phương trình:

 do , suy ra .

Chọn đáp án D.

Câu 26. Tập nghiệm của bất phương trình: là

1 4

1 .

3 3

t t



 

 

4 4

5 1 1 1 3

3 5 3

      

 

1 1

1 3 1 3

3 3

t t

 

    

 

1 3.

 

1 3.

 

log

log 1





( ;1]



[1; )







5;2



[0;3)





t log 1

x t

 

 











 

f t











 

f t











' 0 2

f t t

  





lim

f t



 





lim

f t



 

+∞

f(t)

f'(t)

t +∞

 





9 12 16

log log log

p q p q

  





1 3







1 5







9 12 16

log log log

t p q p q

   



q 

16 9 12

t t t

p q   

4 4

3 3

t t

   

 

   

   

 

  

 

 

1 0

x x

  





1 5

x  







1 5

 

2 2 1

81.9 3 .3 0

x x x x  

  

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 59

Facebook: https://www.facebook.com/dongpay

A. B. C. D.

Hướng dẫn giải:

ĐKXĐ:

BPT đã cho

(vì )

Vậy tập nghiệm của BPT đã cho là

Chọn đáp án A.

Câu 27. Cho là cấp số nhân với số hạng tổng quát . Khi đó khẳng định nào sau

đây là đúng?

Hướng dẫn giải:

Vì là cấp số nhân nên

Chọn đáp án A.

Câu 28. Số nghiệm của phương trình





2 2

3 5

log 2 log 2 2

   

x x x x

là

Hướng dẫn giải:

ĐK:

0; 2

 x x .

Đặt

 

t x x

2 2 2

    

x x t





3 5

log log 2

  

t t









1; 0 .

S   





1; .

 





0; .

 









2; 0 .

S   



9 2

81. 3 .3 .3.3 0

81 3

x x x

   

2 2

3 3 .3 2.3 0

x x x x

   









3 3 3 2.3 0

x x x x

   

3 3 0

x x

  

3 2.3 0, 0.

x x

   

1 1

3 3

x x



 



     





















1; 0 .

S   





0; 1

n n

u u

 

1 1

log 2017 log 2017 log 2017

k k k

u u u

 

 







1 1

log 2017 log 2017 log 2017

k k k

u u u

 

 







1 1

log 2017 log 2017 log 2017

k k k

u u u

 

 







1 1

log 2017 log 2017 log 2017

k k k

u u u

 

 











1 1

k k k

u u u

 



2017 2017 1 2017 1

2log log log

k k k

u u u

 

  

1 1

1 1 1 1

log 2017 log 2017 log 2017 log 2017

log 2017 log 2017 log 2017

k k k k

k k k

u u u u

u u u

 

 

 

   



 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 60

Facebook: https://www.facebook.com/dongpay

Đặt





3 5

log log 2

t t u

  

 

log

log 2

 







 





t u

2 5









 





5 2 3

  

u u



5 2 3

u u



 



  



5 3 2

3 2 5



 





 



u u

5 3 2 (1)

3 1

2 1 (2)

5 5



 





   



 

   



   



u u

Xét





1 :5 3 2

 

u u

Ta thấy



u là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm



là duy nhất.

Với

0 1 2 1 0

u t x x

       

, phương trình này vô nghiệm.

Xét

 

3 1

2 : 2 1

5 5

u u

   

 

   

   

Ta thấy



u là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm



u là duy nhất.

Với

0 3 2 3 0

      

u t x x , phương trình có 2 nghiệm phân biệt thỏa

0; 2

 x x .

Chọn đáp án B.

Câu 29. Cho

 

2 2

1 1

f x e

 





Biết rằng

       

1 . 2 . 3 ... 2017



f f f f e

với

m n

là các số tự

nhiên và

tối giản. Tính



m n

2018

 m n . B.

2018

  m n . C.

 

m n . D.

  

m n .

Hướng dẫn giải:

Xét các số thực



Ta có :

 

2 2

1 1 1 1 1 1

1 1 1

1 1

x x

x x x x x x x

x x x

 

        

  

 

Vậy,

       

1 1 1 1 1 1 1 1

1 2018 1

1 1 1 1

2018

1 2 2 3 3 4 2017 2018

2018 2018

1 . 2 . 3 ... 2017

       



           



       

      







  f f f f e e e ,

hay

2018 1

2018





Ta chứng minh

2018 1

2018



là phân số tối giản.

Giả sử

là ước chung của

2018 1



và

2018

Khi đó ta có

2018 1





2018 2018

 

d d

suy ra

1 1

  



d d

Suy ra

2018 1

2018



là phân số tối giản, nên

2018 1, 2018

  m n .

Vậy

  

m n .

Chọn đáp án D.

Câu 30. Hỏi phương trình

3.2 4.3 5.4 6.5

  

x x x x

có tất cả bao nhiêu nghiệm thực?

. B.

. C.

. D.

Hướng dẫn giải:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 61

Facebook: https://www.facebook.com/dongpay

2 3 4

3. 4. 5. 6 0

5 5 5

     

    

     

     

x x x

Xét hàm số

 

2 3 4

3. 4. 5. 6

5 5 5

     

   

     

     

x x x

f x

liên tục trên



Ta có:

 

2 2 3 3 4 4

3 ln 4 ln 5 ln 0,

5 5 5 5 5 5

     



           

     

     



x x x

f x x

Do đó hàm số luôn nghịch biến trên



mà





0 6 0

 





2 22 0

  

nên phương trình

tùy ý. B.

 

 

 

Hướng dẫn giải:

Đặt

3 , 0

 

t t

ycbt





2 1 3 2 0, 0

       

t m t m t

2 3

, 0

2 2

 

   



t t

m t

 

3 , 0

    

m t t

     

1 1

3 , 0, 0

2 2

f t t f t t



     



hàm số đồng biến trên







Vậy

   

, 0 0

       

ycbt m f t t m f

Chọn đáp án D.

Câu 32. Tìm tập hợp tất cả các tham số

sao cho phương trình

2 2

2 1 2 2

4 .2 3 2 0

   

   

x x x x

m m

có

bốn nghiệm phân biệt.







. B.









;1 2;

  

. C.







. D.







Hướng dẫn giải:

Đặt

 

( 1)

2 1



 

t t

Phương trình có dạng:





2 3 2 0 *

t mt m   

Phương trình đã cho có 4 nghiệm phân biệt



phương trình (*) có hai nghiệm phân biệt lớn hơn 1

2 2

1,2

3 2 0

1 0 2

3 2 1

3 2 2 1



  



  



  

 

      

 

    

   





    



m m

x m m m

m m m

m m m m

Chọn đáp án D.

Câu 33. Cho

x y

là số thực dương thỏa mãn





ln nln l

 

 y xx

. Tìm giá trị nhỏ nhất của

 

P x y



P . B.

2 2 3

 

P . C.

2 3 2

 P . D.

17 3

 P .

Hướng dẫn giải:

Từ





2 2

l nn ln l

   

 x y xy xx y

. Ta xét:





 0

có nghiệm duy nhất.

Chọn đáp án C.

Câu 31. Tìm tất cả các giá trị thực của tham số

để bất phương trình

 2



m1



3 2m  0

nghiệm đúng với mọi x.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 62

Facebook: https://www.facebook.com/dongpay

Nếu 0





thì

2 2

    

xy yy

x mâu thuẫn.

Nếu



thì

 

2 2

      



xy x y y x x

y . Vậy

  



x y .

Ta có

 

 



f x x

xét trên









Có

 

2 2

( )

' 0

2 2

( )

4 1









  

 

  









x loai

f x

x an

Vậy

 

2 2

min 2 2 3



 



  

 

 

f x f

Chọn đáp án B.

Câu 34. Tìm tất cả các giá trị thực của tham số m để bất phương trình

5 4

12 .log 3

 

  

x x x m

có nghiệm.

2 3

m B.

2 3

m

12log 5

m D.

2 12log 5

 m

Hướng dẫn giải:

Điều kiện:





0;4

x

. Ta thấy

5 4

4 4 5 4 3 log 3 0

 

       

x x

Khi đó bất phương trình đã cho trở thành

 









 

12 .log 5 4 *

     m f x x x x x

Với

3 1

12 '

2 12

     



u x x x u

và





 

log 5 4 '

2 4 5 4 .ln3

    

  

v x v

x x

Suy ra













f ' x 0; x 0;4 f x

   

là hàm số đồng biến trên đoạn





0;4

Để bất phương trình (*) có nghiệm

 









0;4

min 0 2 3

   m f x f

Chọn đáp án A.

Câu 35. Tìm giá trị của a để phương trình





 





2 3 1 2 3 4 0

     

x x

a có 2 nghiệm phân biệt

thỏa mãn:

1 2

2 3

log 3



 

x x

, ta có a thuộc khoảng:





; 3

 





 













Hướng dẫn giải:

Ta có













 

2 3 2 3 1 2 3

2 3

     



x x x

. Đặt

 

2 3











, phương trình

đã cho trở thành

 

4 0 4 1 0 *



       

t t t a

Phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân

biệt

1 2

4 0

1 0

  



  



  



t t

t t a

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 63

Facebook: https://www.facebook.com/dongpay

Ta có

 





 

1 2

2 3

log 3 2 3 3 3 3

2 3





        



x x

Vì

1 2

 

t t nên điều này xảy ra khi và chỉ khi phương trình (*) có 2 nghiệm t=3 và t=1

Khi đó

1 3.1 3 2

     

a a .

Chọn đáp án B.

Câu 36. Gọi m là số chữ số cần dùng khi viết số

trong hệ thập phân và n là số chữ số cần dùng khi

viết số

trong hệ nhị phân. Ta có tổng m + n bằng

A. 18 B. 20 C. 19 D. 21

Hướng dẫn giải:

- Phương pháp: Số chữ số cần dùng khi viết số A trong hệ thập phân là





log 1



với





là số

nguyên lớn nhất nhỏ hơn hoặc bằng x.

Tổng quát: số chữ số cần dùng khi viết số A trong hệ n-phân là





log 1



Dựa vào 2 kết quả trên ta có





 

2 2

log2 1 30log2 1 10

log 30 1 2log 30 1 10

 

    

 

 

    

 

  

m n

Chọn đáp án B.

Câu 37. Cho hàm số

2 4

   

y x x a

. Tìm a để giá trị lớn nhất của hàm số trên đoạn





2;1



đạt

giá trị nhỏ nhất.



a B.



a C.



a D. Một giá trị khác

Hướng dẫn giải:

Ta có

 

2 4 1 5

       

y x x a x a

. Đặt

 

 

u x

khi đó





2;1

  x

thì





0;4

u

được hàm số





  

f u u a

. Khi đó

   





















2;1 0;4

0 , 4 5 ; 1

  

    

x u

Max y Max f u Max f f Max a a

Trường hợp 1:

 





0;4

5 1 3 5 2 3



          

a a a Max f u a a

Trường hợp 2:

 





0;4

5 1 3 1 2 3



          

a a a Max f u a a

Vậy giá trị nhỏ nhất của

 

2;1

2 3

 

  

Max y a

Chọn đáp án A.

Câu 38. Cho phương trình









3 2

2log cotx log cos



. Phương trình này có bao nhiêu nghiệm trên

khoảng

;

6 2

 

 

 

 

A. 4 B. 3 C. 2 D. 1

Hướng dẫn giải:

Điều kiện

sin 0,cos 0

 

x x

. Đặt





log cos



u x

khi đó

cot 3

cos 2















Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 64

Facebook: https://www.facebook.com/dongpay

Vì

cos

cot

1 cos





suy ra





 

u u

3 f u 4 1 0

1 2

 

     

 

 



 

4 4

' ln 4 ln4 0,

3 3

   

    

   

   



f u u

. Suy ra hàm số f(u) đồng biến trên R, suy ra phương

trình







f u

có nhiều nhất một nghiệm, ta thấy





1 0

 

suy ra

 

cos 2

2 3



      



x x k k

Theo điều kiện ta đặt suy ra nghiệm thỏa mãn là



  

x k

. Khi đó phương trình nằm trong khoảng

;

6 2

 

 

 

 

là

3 3

 

 x x

. Vậy phương trình có hai nghiệm trên khoảng

;

6 2

 

 

 

 

Chọn đáp án C.

Câu 39. Trong các nghiệm

( ; )

x y

thỏa mãn bất phương trình

2 2

log (2 ) 1



 

x y

x y . Giá trị lớn nhất của

biểu thức

 

T x y

bằng:

. B.

. C.

. D. 9.

Hướng dẫn giải:

Bất PT

2 2

2 2 2 2

2 1 0 2 1

log (2 ) 1 ( ), ( )

2 2 0 2 2

x y

x y x y

x y I II

x y x y x y x y



 

    

 

   

 

      

 

 

Xét T=



x y

TH1: (x; y) thỏa mãn (II) khi đó

2 2

0 2 2 1

     

T x y x y

TH2: (x; y) thỏa mãn (I)

2 2 2 2

1 9

2 2 ( 1) ( 2 )

2 2

       

x y x y x y

. Khi đó

2 2 2

1 1 9 1 1 9 9 9 9 9

2 2( 1) ( 2 ) (2 ) ( 1) ( 2 ) .

4 2 4 2 8 4 2

2 2 2 2 2

 

              

 

 

x y x y x y

Suy ra :

max



( ;y) (2; )

 x

Chọn đáp án B.

Câu 40. Xét các số thực thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức

 

2 2

log 3log

 

 

 

 

a b

P a

min



P B.

min



P C.

min



P D.

min



Hướng dẫn giải:

 

2 2

1 4

3 log 1 3 log 1

1 log

log

     



 

 

 

b b

P a a

Đặt

log



t b

 

a b

nên

0 1

 

 

4 3

  



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 65

Facebook: https://www.facebook.com/dongpay

Xét

 

4 3

  



f t

trên





0;1

ta thấy GTNN của f(t) là

 



 

 

Chọn đáp án D.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 66

Facebook: https://www.facebook.com/dongpay

HÌNH NÓN - TRỤ - CẦU

Câu 1. Cho hình chóp S.ABCD có SA vuông góc với đáy, . Đáy ABCD là hình thang vuông

tại A và B, Gọi E là trung điểm của AD. Tính bán kính mặt cầu ngoại tiếp hình

chóp S.ECD.

A. B. C. D.

Hướng dẫn giải:

Gọi H là trung điểm của CD và d là đường thẳng qua H và

vuông góc với đáy. Gọi I và R là tâm và bán kính mặt cầu

ngoại tiếp S.CDE. Suy ra I thuộc d. Đặt

Trong mp(ASIH) kẻ đường thẳng qua I và song song với

AH cắt AS tại K.

Ta có:

Suy ra: Vậy bán kính mặt cầu bằng

Chọn đáp án C.

Câu 2. Cho tứ diện với ,các cạnh còn lại đều bằng và là góc tạo bởi hai mặt

phẳng và . Gọi I,J lần lượt là trung điểm các cạnh . Giả sử hình cầu đường IJ

kính tiếp xúc với CD. Giá trị là:

A. B. C. D.

Hướng dẫn giải:

Gọi O là trung điểm IJ và F là điểm tiếp xúc giữa hình cầu đường kính IJ và đường thẳng CD. Hình

cầu đường kính IJ tiếp xúc với CD khi và chỉ khi khoảng cách từ O đến CD bằng nữa độ dài IJ.

Ta có .

Vì FC và CI là hai tiếp tuyến xuất phát từ một điểm nên

Tương tự ta có

Tam giác ADI cân có IJ là đường trung tuyến nên tam giác IDJ vuông tại J.

Suy ra



SA a

  

AB BC AD a



R a



IH x

2 2 2 2

   

ID IH HD x

2 2 2 2 2 2 2 2 2 2

IS 2 ( 6 )

          

IK KS AH KS AC CH KS a a x

2 2

2 2 2

2 6

2 ( 6 ) .

2 2 3

      

a a a

x a a x x



ABCD

BC a









ABC





BCD

BC AD

cos



3 2 3



2 3 3



2 3



AI DI 

FC CI

 

2 2

a a

DJ DF

  



 

3 1

6 2

sin sin

2 2

JID





   

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 67

Facebook: https://www.facebook.com/dongpay

Do vậy nên

Chọn đáp án B.

Câu 3. Cho hình vẽ bên. Tam giác

SOA

vuông tại O có

MN SO

€

với

M N

lần lượt nằm trên cạnh SA, OA. Đặt



SO h

không đổi. Khi quay hình vẽ

quanh

thì tạo thành một hình trụ nội tiếp hình nón đỉnh

có đáy là hình

tròn tâm O bán kính



R OA

. Tìm độ dài của MN để thể tích khối trụ là lớn

nhất.



Hướng dẫn giải :

Ta thấy khi quay quanh trục SO sẽ tạo nên một khối trụ nằm trong khối

chóp. Khi đó thiết diện qua trục của hình trụ là hình chữ nhật MNPQ. Ta

có hình sau:

Ta có



SO h

;



OA R

. Khi đó đặt

 

OI MN x

Theo định lí Thales ta có







   

R h x

IM SI OA SI

OA SO SO h

. Thể

tích khối trụ

 

. .



   

V IM IH x h x

Áp dụng bất đẳng thức Cauchy ta có:

 

2 2

 

 

 

 

 

x h x

Vậy





R h

V . Dấu

'' ''



xảy ra khi



. Hay



Chọn đáp án B.

Câu 4. Một hình nón bị cắt bởi mặt phẳng





song song với đáy.

Mặt phẳng





chia hình nón làm hai phần





và





. Cho hình

cầu nội tiếp





như hình vẽ sao cho thể tích hình cầu bằng một nửa

thể tích của





. Một mặt phẳng đi qua trục hình nón và vuông góc

với đáy cắt





theo thiết diện là hình thang cân, tang góc nhọn của

hình thang cân là

Hướng dẫn giải:

Giả sử ta có mặt cắt của hình nón cụt và các đại lượng như hình vẽ.

Gọi



là góc cần tìm.

Xét



AHD

vuông tại

có

  

DH h AH R r









2 .tan tan 1

      h r AH R r

Thể tích khối cầu là

1 0

3 6



  

V r

cos 2 3 3



 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 68

Facebook: https://www.facebook.com/dongpay

Thể tích của





là

 

2 2

   

V h R r Rr

 

2 2 2

    

h R r Rr

Ta có

 

BC R r

(tính chất hai tiếp tuyến cắt nhau)

Mà

   

2 2

4 3

   h BC R r Rr

Từ

       

2 , 3 4

  R r Rr

Từ

         

2 2

1 , 3 , 4 .tan 4     

h R r R r

(vì



là góc nhọn)

tan 4 tan 2

     

Chọn đáp án A.

Câu 5. Cho tam giác ABC có độ dài cạnh huyền 5. Người ta quay tam giác ABC quanh một cạnh góc

vuông để sinh ra hình nón. Hỏi thể tích V khối nón sinh ra lớn nhất là bao nhiêu.

250 3



V

25 2



V

20 3



V

250 6



V

Hướng dẫn giải:

Ta có

 

2 2 2 3

1 1 1 25 1

3 3 3 3 3

          

V r h x y y y y y

Xét hàm số

25 1

3 3

   

V y y

với

0 5

 

Ta có

25 5

' 0

      V y y

Khi đó thể tích lớn nhất là

250 3



V

Chọn đáp án A.

Câu 6. Một công ty sản xuất một loại cốc giấy hình nón có thể tích 27cm

. Vói chiều cao h và bán

kính đáy là r. Tìm r để lượng giấy tiêu thụ ít nhất.





r B.





r C.





r D.





Hướng dẫn giải:

Ta có:

1 3

   



V r h h

=> độ dài đường sinh là:

2 2 2 2 2 2 2

2 2 2 4

3 81 3

( ) ( )

       

  

l h r r r r

r r r

Diện tích xung quanh của hình nòn là:

8 8

2 4

2 4 2 2

3 3

       

 

S rl r r r

r r

Áp dụng BĐT Cauchy ta được giá trị nhỏ nhất là khi





r .

Chọn đáp án B.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 69

Facebook: https://www.facebook.com/dongpay

Câu 7. Cho một khối trụ có bán kính đáy

r a

và chiều cao 2h a . Mặt phẳng

( )P

song song với

trục 'OO của khối trụ chia khối trụ thành 2 phần, gọi

V là thể tích phần khối trụ chứa trục 'OO ,

V là

thể tích phần còn lại của khối trụ. Tính tỉ số

, biết rằng

( )P

cách 'OO một khoảng bằng

3 2

 

 

. B.

3 2

 

. C.

2 3

 

 

. D.

2 3

 

Hướng dẫn giải:

Thể tích khối trụ

2 2 3

.2 2

     

V r h a a a

Gọi thiết diện là hình chữ nhật

' 'ABB A

Dựng lăng trụ ABCD. A’B’C’D’ như hình vẽ.

Gọi H là trung điểm AB.

Ta có

( ' ')  OH AB OH ABB A







  

AH BH OH

 OAB vuông cân tại O  ABCD là hình vuông.

Từ đó suy ra:

 

3 2

2 . ' ' ' '

1 1 ( 2)

2 ( 2) .2

4 4 2

 

     

ABCD A B C D

V V V a a a .

3 3

1 2

( 2) (3 2)

2 2

   

     

a a

V V V a . Suy ra

3 2

 



 

Chọn đáp án A.

Câu 8.

Trong số các khối trụ có thể tích bằng V, khối trụ có diện tích toàn phần bé nhất thì có bán kính

đáy là





4

R



R





Hướng dẫn giải:

.    



V R h l h

2 2

2 2 2 2        

TP Xq d

S S S Rl R R

Xét hàm số

( ) 2  

f R R

với R>0,

2 4

'( ) , '( ) 0

  

   



V R V

f R f R R

Bảng biến thiên

2



( )

f R

+ 0 - 0

( )

f R



Từ bảng biến thiên ta thấy diện tích toàn phần nhỏ nhất khi





Chọn đáp án A.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 70

Facebook: https://www.facebook.com/dongpay

Câu 9. Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông cân AB=BC=a. Mặt phẳng

(AB’C) tạo với (BCC’B’) một góc



với

tan

 

. Gọi M là trung điểm của BC. Tính bán kính mặt

cầu ngoại tiếp hình chóp B’ACM.

3 10

3 13

Trục không có tính chất đặc

biệt, ta sử dụng phương pháp 4

để giải

= B’O

= NO

+ B’N

2 2

( ' )

 

 

BJ BB JO

= OM

= OJ

+ JM

Chú ý



CBJ

Giải phương trình ta tìm được

OJ =

5 2

R =

3 10

Xác định tâm đáy: giao của hai

đường thẳng trung trục MC và

BI.

Dựng góc: chú ý BA vuông góc

với giao tuyến CB’

Từ tam giác vuông BIA và góc



, tính được BI. Từ BI sử dụng

2 2 2

1 1 1

 

BI BC B B

tính được

' 2



B B a

Chọn đáp án A.

Câu 10. Cho hình nón có bán kính đáy là a, đường sinh tạo với mặt phẳng đáy góc



. Tính thể tích

khối cầu ngoại tiếp hình nón.

4sin 2







V B.

3sin 3







V C.

3sin 2







V D.

3sin







Hướng dẫn giải:

Nếu mặt phẳng





qua trục của hình nón thì (P) cắt hình nón theo tam giác cân SMN, (P) cắt mặt

cầu ngoại tiếp hình nón theo đường tròn có bán kính là R. Gọi I là tâm mặt cầu ngoại tiếp hình nón,

O là tâm đường tròn đáy của hình nón.

Ta có

. . .tan tan



    

SMN

S MO SO a a a

Mặt khác

2 3

.2a

. . .2a

cos

4R 4R 4R 2Rcos



 

 



 

   



SMN

SM SN MN SM a

Do đó

2 2

tan

2R cos 2cos tan sin2

    

   

a a a

a R

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 71

Facebook: https://www.facebook.com/dongpay

R cũng là bán kính của mặt cầu ngoại tiếp.

4 4

3 3 sin 2

   



V .

Chọn đáp án C.

Câu 11. Cho hình nón có chiều cao h, đường tròn đáy bán kính R. Một mặt phẳng (P) song song với

đáy cách đáy một khoảng bằng d cắt hình nón theo đường tròn (L). Dựng hình trụ có một đáy là (L),

đáy còn lại thuộc đáy của hình nón và trục trùng với trục hình nón. Tìm d để thể tích hình trụ là lớn

nhất.



Hướng dẫn giải:

Gọi r là bán kính của (L).

Ta có

 



   

r h d R

r h d

R h h

    

   

2 2 2 2

2 2 2

. .2

2 2 3 27

    



          

 

 

h d h d d

R R R R h

V h d d h d h d d

h h h

Dấu bằng xảy ra khi

   

h d d d

Chọn đáp án A.

Câu 12. Trong số các hình trụ có diện tích toàn phần đều bằng

thì bán kính

và chiều cao

của

khối trụ có thể tích lớn nhất là:

;

2 2 2

 

 

S S

R h

. B.

;

4 4

 

 

S S

R h

2 2

; 4

3 3

 

 

S S

R h

. D.

; 2

6 6

 

 

S S

R h

Hướng dẫn giải:

Gọi thể tích khối trụ là

, diện tích toàn phần của hình trụ là

Ta có:

2 2

     

day xq

S S S R Rh

. Từ đó suy ra:

2 2 2

2 2 2 2 4

       

     



Cauchy

S S V V V V

R Rh R R

R R R

hay

2 3

4 2 54

 

  

 

  

 

V S S

Vậy

max





V . Dấu “=” xảy ra



2 2 2



  

 

V R h Rh

R R

hay



h R

Khi đó

   



S R R

và

2 2

 



h R

Chọn đáp án D.

Câu 13. Một bình đựng nước dạng hình nón (không đáy) đựng đầy nước. Biết rằng chiều cao của bình

gấp 3 lần bán kính đáy của nó. Người ta thả vào đó một khối trụ và đo dược thể tích nước tràn ra ngoài

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 72

Facebook: https://www.facebook.com/dongpay

là



. Biết rằng một mặt của khối trụ nằm trên mặt trên của hình nón, các điểm trên đường tròn

đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ có chiều cao bằng đường

kính đáy của hình nón. Diện tích xung quanh

của bình nước là:

9 10





S dm

. B.

4 10 

S dm

. C.

4 

S dm

. D.





S dm

Hướng dẫn giải:

Xét hình nón :

 

h SO r

 

r OB l SA

. Xét hình trụ :

2 

h r NQ

 

r ON QI

 



SQI SBO

3 3

    

QI SI r

BO SO



Thể tích khối trụ là :

1 1

2 16

2 6

9 9

 

       

V r h r h

2 2

2 10

   l h r

4 10    

S rl dm

Chọn đáp án B.

Câu 14. Cho một miếng tôn hình tròn có bán kính

. Biết hình nón có thể tích lớn nhất khi diện

tích toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy là

10 2

50 2

Hướng dẫn giải:

Đặt



a cm

. Gọi bán kính đáy và chiều cao của hình nón lần

lượt là





, , 0



x y x y

. Ta có

2 2 2 2

   

SA SH AH x y

Khi đó diện tích toàn phần của hình nón là

2 2 2

    

S x x x y

Theo giả thiết ta có:

2 2 2 2 2 2 2 2

         

x x x y a x x y x a

 

2 2 2 2

2 2 2 4 4 2 2 2

2 2

2 , :

    

      



x x y a x

x x y a x a x DK x a x

y a

Khi đó thể tích khối nón là:

2 2 2 2

1 1

. . .

3 2 3 2

   

 

a y

V y a

y a y a

Q P

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 73

Facebook: https://www.facebook.com/dongpay

đạt giá trị lớn nhất khi và chỉ khi

2 2



y a

đạt giá trị nhỏ nhất

Ta có

2 2 2 2

2 2 2

2 . 2 2



   

y a a a

y y a

y y y

Vậy

đạt giá trị lớn nhất khi và chỉ khi



, tức là

2 25

   

y a x cm

Chọn đáp án D.

Câu 15. Thiết diện qua trục của một hình nón là một tam giác vuông có cạnh góc vuông bằng a. Tính

diện tích của thiết diện qua đỉnh tạo với đáy một góc 60

Hướng dẫn giải:

Gọi thiết diện qua trục là



SAB vuông cân tại S,

 

SA SB a

Gọi O là tâm của đáy, SO =

Gọi thiết diện qua đỉnh, tạo với đáy góc 60

là



SAC.

Gọi M là trung điểm AC, góc giữa mặt phẳng (SAC) với mặt

đáy là



SMO

= 60

sin60 3

 

SO a

(



SMO vuông tại O).



2 2

2 2  

AC AM OA OM

2 3

* S

SAC

SM.AC =

2 3

Chọn đáp án C.

Câu 16. Cho hình chóp SABC với SA vuông góc với mặt phẳng (ABC) và

BC= a, . Gọi H, K lần lượt là hình chiếu của A lên SB và

SC. Mặt cầu qua các điểm A, B, C, H, K có bán kính bằng:

A. 1 B. 2

C. D. Không đủ dữ kiện để tính

Hướng dẫn giải:

Gọi AD là đường kính của đường tròn (ABC)

Suy ra, , suy ra hay

Tương tự, . Suy ra mặt cầu qua các điểm A, B, C, H, K có

đường kính AD .

Chọn đáp án B.





BAC

AC DC



( )

CD SAC



AE DE



AH HD



sin60

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 74

Facebook: https://www.facebook.com/dongpay

Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S

trên mặt phẳng (ABC) là trung điểm cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng

. Gọi G là trọng tâm tam giác SAC. Bán kính mặt cầu tâm G và tiếp xúc với mặt phẳng (SAB) là:

A. B. C. D.

Hướng dẫn giải:

+ Gọi H là trung điểm BC

+ Bán kính mặt cầu là:

+ Gọi E là hình chiếu của H trên AB và K là hình chiếu của H

trên SE.

Chứng minh: HK  (SAB)

+ Tính được:

Chọn đáp án A.

Câu 18. Cho nửa đường tròn đường kính



AB R

và điểm

thay đổi trên nửa đường tròn đó, đặt



CAB





và gọi

là hình chiếu vuông góc của

lên

. Tìm



sao cho thể tích vật thể tròn xoay

tạo thành khi quay tam giác

ACH

quanh trục

đạt giá trị lớn nhất.

  

. B.

  

. C.

arctan

. D.

  

Hướng dẫn giải:

. cos 2 .cos

.sin 2 .cos .sin ; .cos 2 .cos

   

        

AC AB R

CH AC R AH AC R

Thể tích vật thể tròn xoay tạo thành khi quay tam giác

ACH

quanh trục

là

2 3 4 2

1 8

. .cos .sin

3 3

    

V AH CH R

Đặt





cos 0 1

   

t t

 

3 2

  

V R t t

 

3 3

8 8 2 2

. . 2 2

6 6 3

  

 

  

 

 

t t t

R t t t R

Vậy

lớn nhất khi



khi

arctan

 

Chú ý: có thể dùng PP hàm số để tìm GTNN của hàm









 

f t t t

Chọn đáp án C.

3 13



( ,( )) 60

SA ABC SAH 

3 3

, tan60

2 2

a a

AH SH AH  

1 2

( ,( )) ( ,( )) ( ,( ))

3 3

R d G SAB d C SAB d H SAB

  

3 3

;

2 13

a a

HE HK 

R HK 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 75

Facebook: https://www.facebook.com/dongpay

Câu 19. Cho hình chóp .

S ABCD

có đáy

ABCD

là hình vuông cạnh

2 2,

cạnh bên

vuông góc

với mặt phẳng đáy và



SA Mặt phẳng







qua

và vuông góc với

cắt các cạnh

lần lượt tại các điểm

. Tính thể tích

của khối cầu ngoại tiếp tứ diện

CMNP



V

. B.

64 2



V

108



V

. D.

125



V

Hướng dẫn giải:

Ta có:













, 1

   CB SAD AM SAB AM CB













, 2

     SC AM AM SC

 



      

AM SBC AM MC AMC

Chứng minh tương tự ta có



 

APC

Có



   

AN SC ANC

. Ta có:



AMC APC APC

   



mặt cầu đường kính

là mặt cầu ngoại tiếp tứ

diện

CMNP

Bán kính cầu này là

 

. Thể tích khối cầu:

4 32

3 3



  V r

Chọn đáp án A.

Câu 20. Cho tứ diện ABCD có ABC và ABD là các tam giác đều cạnh a và nằm trong hai mặt phẳng

vuông góc với nhau. Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD theo a.



Hướng dẫn giải:

;



 









 





H CM CH CM

G DM DG DM

Kẻ Đường vuông góc với đáy (ABC) từ H và Đường vuông góc với (ABD) từ G.

Do hai đường vuông góc này đều thuộc (DMC) nên chúng cắt nhau tại O.

Gọi M là Trung điểm của AB

Vì Tam giác ADB và tam giác ABC là tam giác đều

 DM  AB;CM  AB

Do có ABC và ABD là các tam giác đều cạnh a và nằm

trong hai mặt phẳng vuông góc với nhau => Góc



MC  90

Gọi H là tâm đường tròn ngoại tiếp Tam giác ABC

G là tâm đường tròn ngoại tiếp Tam giác ABD

=> H,G đồng thời là trọng tâm của tam giác ABC và

ABD

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 76

Facebook: https://www.facebook.com/dongpay

=> O chính là tâm mặt cầu ngoại tiếp tứ diện ABCG và R = OC.

Tam giác ABC đều

 

3 3 3

.sin 60 ;

2 3 6

     CM CB a CH a HM a

CMTT ta có

GM a



Từ đó nhận thấy OGMH là hình vuông

 OH a

Tam giác OHC vuông tại H → Áp dụng định lý Pitago ta có:

 

3 3 3

.sin 60 ;

2 3 6

    

CM CB a CH a HM a

2 2

   OC CH OH a R

2 2

    V R a

Chọn đáp án A.

Câu 21. Cho một mặt cầu bán kính bằng

. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên.

Hỏi thể tích nhỏ nhất của chúng là bao nhiêu?

A. min 8 3V . B. min 4 3V . C. min 9 3V . D. min 16 3V .

Hướng dẫn giải:

Gọi cạnh đáy của hình chóp là

Ta có  SIJ SMH

 

   

2 2

2 2 2

2 2 2 2

12 2 0 12

     

   

      



SI IJ

MH SH IH IJ SH HM

SM MH

MH SH SH HM

a SH a SH SH a

2 4

1 3 2 3 1

1 12

3 6 12 6

  



ABC

S S SH

a a

Ta có

2 4

1 12 1

 

a a

8 3 S

Chọn đáp án A.

Câu 22. Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm, cần xả thành một chiếc xà có tiết

diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng x

của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 77

Facebook: https://www.facebook.com/dongpay

 

3 34 17 2





x cm

 

3 34 19 2





x cm

 

5 34 15 2





x cm

 

5 34 13 2





x cm

Hướng dẫn giải:

Diện tích sử dụng theo tiết diện ngang là

 

MNPQ

S S xy

Cạnh hình vuông

 

20 2

2 2

  

MN cm





20 2 4 800 4

    

S xy xy

(1)

Ta có

2 20 2 20 2 40 20 2

       x AB MN AB BD

0 20 10 2

   x

Lại có





2 2 2 2 2

40 2 20 2 1600

      AB AD BD x y

2 2 2

800 80 2 4 800 80 2 4

       

y x x y x x

Thế vào

 

2 2 3 4

1 800 4 800 80 2 4 800 4 800 80 2 4

        

S x x x x x x

Xét hàm số





2 3 4

800 80 2 4

  

f x x x x

, với





0;20 10 2

 x

có

 





2 3 2

' 1600 240 2 16 16 100 15 2     

f x x x x x x x

Ta có





 





 

0;20 10 2

5 34 15 2

' 0 16x 100 15x 2 0



 

 



 

  

 

   

 



f x x

Khi đó

5 34 15 2



x

chính là giá trị thỏa mãn bài toán.

Chọn đáp án C.

Câu 23. Một hình trụ có bán kính đáy bằng 50cm và có chiều cao là 50cm. Một đoạn thẳng AB có

chiều dài là 100cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng

đó đến trục hình trụ.



d cm

50 3



d cm



d cm

25 3



d cm

Hướng dẫn giải:

Kẻ AA

vuông góc với đáy, A

thuộc đáy. Suy ra:

























1 1 1 1 1 1 1 1 1

/ / / / , , ,   

OO AA OO AAB d OO AB d OO AAB d O AAB

Tiếp tục kẻ

1 1



O H A B

tại H, vì O

H nằm trong đáy nên cũng

vuông góc với A

A suy ra:





1 1



O H AAB

. Do đó





















1 1 1 1 1 1

, , ,  

d OO AB d OO AAB d O AAB O H

Xét tam giác vuông

AA B

ta có

2 2

1 1

A B AB AA 50 3

  

Vậy

2 2

1 1 1 1

O H O A A H 25cm

  

Chọn đáp án C.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 78

Facebook: https://www.facebook.com/dongpay

Câu 24. Một công ty sản xuất một loại cốc giấy hình nón có thể tích 27cm

với chiều cao là h và bán

kính đáy là r. để lượng giấy tiêu thụ là ít nhất thì giá trị của r là:









r C.





r D.





Hướng dẫn giải:

Thể tích của cốc:

2 2

1 81 81 1

27 .

      

  

V r h r h h

Lượng giấy tiêu thụ ít nhất khi và chỉ khi diện tích xung quanh nhỏ nhất.

2 2

2 2 2 4

2 4 2 2

81 1 81 1

2 2 2 2          

 

S rl r r h r r r

r r

2 2 2 2

4 4

2 2 2 2 2 2 2 2

81 1 81 1 81 1 81 1

2 2 3 . .

2 2 2 2

     

   

r r

r r r r

2 3

 



(theo BĐT Cauchy)

nhỏ nhất

2 8 8

4 6

2 2 2 2

81 1 3 3

2 2 2

     

  

r r r

Chọn đáp án B.

Câu 25. Cho một hình lăng trụ đứng có đáy là tam giác đều .Thể tích của hình lăng trụ là V. Để diện

tích toàn phần của hình lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ là:

Hướng dẫn giải:

Gọi cạnh đáy của lăng trụ là a, chiều cao lăng trụ là h.

Theo bài ra ta có

3 4

  

a V

V h h

Diện tích toàn phần của lăng trụ là:

3 4

3 .

   

toan phan day xung quanh

a V

S S S a

Áp dụng bất đẳng thức AM - GM ta có:

3 4 3

 

toan phan

a V

2 2

3 2 3 2 3 2 2 3 2 3

3 . .

2 2

   

a V V a V V

a a a a

Dấu bằng xảy ra khi

3 2 3 2 3

 

a V V

a a

hay



a V

Chọn đáp án A.

Câu 26. Trong không gian cho hai điểm phân biệt A, B cố định. Tìm tập hợp tất cả các điểm M trong

không gian thỏa mãn



 

MA MB AB

A. Mặt cầu đường kính AB.

B. Tập hợp rỗng (tức là không có điểm M nào thỏa mãn điều kiện trên).

C. Mặt cầu có tâm I là trung điểm của đoạn thẳng AB và bán kính R =AB.

D. Mặt cầu có tâm I là trung điểm của đoạn thẳng AB và bán kính



R AB

Hướng dẫn giải:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 79

Facebook: https://www.facebook.com/dongpay

+ Tam giác MAB có đường trung tuyến IM

MA MB



 

 







 



MA MB

 

   

 

2 2

4. .

4 .

4 4 4



  

    



     



BA AB

MA MB MA MB MA MB

MI AB

MI AB

Vậy Tập hợp điểm M trong không gian là Mặt cầu có tâm I là trung điểm của đoạn thẳng AB và bán

kính

R AB

Chọn đáp án C.

Câu 27. Gọi

và h lần lượt là bán kính đáy và chiều cao của một hình nón. Kí hiệu

V ,

V lần lượt là

thể tích của hình nón và thể tích của khối cầu nội tiếp hình nón. Giá trị bé nhất của tỉ số

là

. B.

. C. 3. D.

Hướng dẫn giải:

Ta có: Thể tích khối nón là

 V r h

Xét mặt cắt qua tâm

,SAB

kẻ tia phân giác của góc



SBO

, cắt SO

tại .I

Ta có:

2 2



    



IO OB r r h

IS IO

IS SB r

r h

Mặt khác:  IO IS h

Do đó ta có bán kính của mặt cầu nội tiếp hình chóp là

2 2

 

 

R IO

r h r

Thể tích khối cầu là

 

3 3

2 2

4 4

3 3

   

 

r h

V R

r h r





2 2

1 1

 

 

 

 

 

  

r r h

V rh

. Đặt

1 

( 1t )

 

3 2

1 1

4 1

 

  



t t

V t

Đặt

 







f t

, Điều kiện: 1t ,

 

2 3

 







t t

f t

 

0 3



  f t t

 

3 8f

BBT

 

8 1   f t t

2 

Chọn đáp án D.

Câu 28. Giá trị lớn nhất của thể tích khối nón nội tiếp trong khối cầu có bán kính

là

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 80

Facebook: https://www.facebook.com/dongpay



. B.



. C.

4 2



. D.



Hướng dẫn giải:

Rõ ràng trong hai khối nón cùng bán kính đáy nội tiếp trong một

khối cầu thì khối nón có chiều cao lớn hơn thì thể tích lớn hơn, nên

ta chỉ xét khối nón có chiều cao lớn hơn trong hai khối nón đó.

Giả sử rằng khối nón có đáy là hình tròn





bán kính

. Gọi

với







f x

là khoảng cách giữa tâm khối cầu đến đáy khối nón. Khi

đó chiều cao lớn nhất của khối nón nội tiếp khối cầu với đáy là

hình tròn





sẽ là

 

h R x

. Khi đó bán kính đáy nón là

2 2

 

r R x

, suy ra thể tích khối nón là

 

       

2 2 2

1 1 1 1

2 2

3 3 3 6

               

V r h R x R x R x R x R x R x R x R x

Áp dụng BĐT Cô-si ta có

 

2 2

1 32

6 27 81

    



  

R x R x R x

Chọn đáp án D.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 81

Facebook: https://www.facebook.com/dongpay

NGUYÊN HÀM , TÍCH PHÂN VÀ ỨNG DỤNG

Câu 1. Cho tích phân trong đó a là nghiệm của phương trình , b là một số

dương và . Gọi . Tìm chữ số hàng đơn vị của b sao cho .

A. 3 B. 2 C. 4 D. 5

Hướng dẫn giải:

Giải phương trình

Tính tích phân C. Đặt:

Tính tích phân A ta có

Theo giả thiết

Chọn đáp án A.

Câu 2. Cho biết tích phân với là các ước nguyên của 4.

Tổng

A. 2 B. 4 C. 3 D. 1

Hướng dẫn giải:

Ta có

Chọn đáp án A.

Câu 3. Cho hàm số . Biết rằng và . Khi đó tổng

bằng?

A. B. C. D. .

Hướng dẫn giải:







C dx

2 2







b a





A x dx



C A

2 2 0 0



    

x a

3 3

    

x x

t e t e

2 

tdt e dx







C dt

= 2 2 2 3 4



   



dt t e



7 11 109 109

3 2 3 4 3. 3 ln 3,305053521

3 2 4 4

            

b b b

C A e e e b

 

4 2

. .

2 ln

a e b e c

I x x x dx

 

  



, ,

a b c

  

 

2 3

1 1 1

2 ln 2 ln

e e e

I x x x dx x dx x xdx

   

  

 

3 4 4

1 1

2 1

2 2

x dx x e

  



2 2 2 2

1 1

1 1 1 1 1

ln ln

1 1

2 2 2 4

e e

x xdx x x x dx e x

 



    

 

 

 

   

2 4 2

2 4

1 1 2e 1

2 ln 1

2 4 4

e e

I x x x dx e

  

     



( ) .

(x 1)

f x b xe

 



'(0) 22

 

( ) 5

f x dx





a b



146



146

'(x) (1 )

(x 1)

'(0) 22 3a b 22 (1)

f be x



  



      

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 82

Facebook: https://www.facebook.com/dongpay

Giải hệ (1) và (2) ta được: .

Chọn đáp án D.

Câu 4.

Cho

( ) 5

f x dx





. Tính

(1 )

I f x dx

 



Hướng dẫn giải:

Đặt

t x dt dx

   

0 1

1 0

x t

  

( ) 5

I f t dt

  



Chọn đáp án A.

Câu 5. Biết tích phân

1 .

1 2 8

x a b





 







trong đó

,a b





. Tính tổng

a b



A. 0 B. 1 C. 3 D. -1

Hướng dẫn giải:

2 2 2

0 0

2 2

1 1 1

1 2 1 2 1 2

x x x

I dx dx dx x dx

 

  

    

  

   

Đặt

sin

x t







 

Chọn đáp án C.

Câu 6. Trong không gian với hệ trục tọa độ Oxyz, gọi d là đường thẳng đi qua điểm





1;0; 1

 

, cắt

1 2 2

2 1 1

x y z

  

 



, sao cho





cos ;d



là nhỏ nhất, biết phương trình của đường thẳng

3 2 3

1 2 2

x y z

  

  



. Phương trình đường thẳng d là?

1 1

2 2 1

x y z

 

 



1 1

4 5 2

x y z

 

 



1 1

4 5 2

x y z

 

 

 

1 1

2 2 1

x y z

 

 

Hướng dẫn giải:

Gọi





1 2 ;2 ; 2

M d M t t t

      

d có vectơ chỉ phương là





2 2; 2; 1

u AM t t t

     

 



có vectơ chỉ phương





1;2;2

u  



1 1 1

0 0 0

( ) 5 5

(x 1)

5 (2)

f x dx a dx b xe dx

   



  

  

108 38

13 13

a b 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 83

Facebook: https://www.facebook.com/dongpay

 

cos ;

3 6 14 9

t t

 

 

Xét hàm số

 

6 14 9

f t

t t



 

, ta suy ra được









min 0 0

f t f

 

Do đó





min cos ; 0

 

 

 

khi



. Nên





2;2; 1

 



Vậy phương trình đường thẳng d là:

1 1

2 2 1

x y z

 

 



Chọn đáp án A.

Câu 7. Cho F(x) là một nguyên hàm của

 

tan

cos 1 cos

f x

x a x





, biết





0 0





 



 

 

. Tính

3 4

F F

 

   



   

   

5 3

 B.

5 1



3 5

 D.

5 2



Hướng dẫn giải:

 

4 4 4 4

2 2 2 2

0 0 0 0

tan tan 1

tan 1

cosx 1 cos cos tan 1 2 tan 1

x x

f x dx dx dx d x a

a x x x a x a

   

    

    

   

2 2

tan 1 tan 0 1 3 2

a a



       

2 1 3 2

a a     





2 1 2 1 3 2 5 2 6

3 6

1 1

3 2

a a a

a a

        



    



Do đó

tan

3 4

cos 1 cos

F F dx

x x



 

   

  

   

   





2 2

tan 2 tan 2 5 3

3 4

 

    

Chọn đáp án A.

Câu 8. Cho

( )

f x

là hàm liên tục và



. Giả sử rằng với mọi

[0; ]

x a



, ta có

( ) 0

f x



và

( ) ( ) 1

f x f a x

 

. Tính

1 ( )

f x





ln( 1)

a a



Hướng dẫn giải:

Đặt

t a x

 

ta có:

0 0

( )

1 ( ) 1 ( ) ( ) 1

a a

dx dt f t dt

f x f a t f t

  

   

  

Suy ra:

1 ( ) 2

dx a

f x







Chọn đáp án A.

Câu 9. Tích phân

2001

2 1002

(1 )







I dx

có giá trị là

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 84

Facebook: https://www.facebook.com/dongpay

1001

2002.2

. B.

1001

2001.2

. C.

1002

2001.2

. D.

1002

2002.2

Hướng dẫn giải:

2 2

2004

1002

3 2 1002

31 1

. .

(1 )

 



 



 

 

 

I dx dx

x x

. Đặt

2 3

1 2

1     

t dt dx

x x

Câu 10. Trong chương trình nông thôn mới, tại một xã X có xây một cây cầu bằng bê tông như hình

vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu. (Đường cong trong hình vẽ là các đường Parabol).

. B.

. C.

18 .

Hướng dẫn giải:

Chọn hệ trục

Oxy

như hình vẽ.

Ta có

Gọi





P y ax c

 

là Parabol đi qua hai điểm

 

;0 , 0;2

A B

 

 

 

Nên ta có hệ phương trình sau:

 

0 . 2

: 2

361

P y x



 

 

 

 

 

    

 

 

 



 



Gọi





P y ax c

 

là Parabol đi qua hai điểm

 

10;0 , 0;

C D

 

 

 

0,5

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 85

Facebook: https://www.facebook.com/dongpay

Câu 11. Cho

là hai hàm liên tục trên





1;3

thỏa:

   

3 d 10

f x g x x

 

 

 

   

2 d 6

f x g x x

 

 

 

. Tính

   

f x g x x



 

 



A. 8. B. 9. C. 6. D. 7.

Hướng dẫn giải:

+ Ta có

       

3 3 3

1 1 1

3 d 10 d 3 d 10

f x g x x f x x g x x

    

 

   

+ Tương tự

       

3 3 3

1 1 1

2 d 6 2 d d 6

f x g x x f x x g x x

    

 

   

+ Xét hệ phương trình

3 10 4

2 6 2

u v u

u v v

  

 



 

  

 

, trong đó

 

u f x x





 

v g x x





+ Khi đó

       

3 3 3

1 1 1

d d d 4 2 6

f x g x x f x x g x x

     

 

   

Nên ta có hệ phương trình sau:

 

0 . 10

1 5

402

40 2

2 2

P y x

b b



  



 

    

 

 

 



 

Ta có thể tích của bê tông là:

2 2 3

0 0

1 5 8

5.2 2 40

40 2 361

V x dx x dx m

 

   

      

 

   

   

 

 

Câu 12. Gọi là diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Ox và đường

thẳng với . Kết quả giới hạn là:

A. 1 B. 2 C. 3 D. 4

Hướng dẫn giải:

Ta có

Suy ra , chọn đáp án B.

Câu 13. Một khối cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông góc bán kính

và cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được.

A. (dm

) B. (dm

)

C. (dm

) D. (dm

)

Hướng dẫn giải:

Đặt hệ trục với tâm O, là tâm của mặt cầu; đường thẳng đứng là Ox,

đường ngang là Oy; đường tròn lớn có phương trình .

Thể tích là do hình giới hạn bởi Ox, đường cong ,

quay quanh Ox.

= (bấm máy)

x x

y e e

 

x a



ln2



lim



 

ln2

2 2

2 2 2

x x a a

S e e dx e e

    



lim 2





132



100



2 2

x y

 

y x

 

3, 3

x x

  

(25 )

V x dx





 



132



5dm

3dm

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 86

Facebook: https://www.facebook.com/dongpay

Câu 14. Một vật di chuyển với gia tốc . Khi thì vận tốc của vật là

. Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).

A. . B. . C. . D. .

Hướng dẫn giải:

Ta có . Theo đề ta có

. Vậy quãng đường vật đó đi được sau 2 giây là:

Câu 15. Tìm giá trị của tham số m sao cho: và y = m(x+2) giới hạn bởi hai hình

phẳng có cùng diện tích

A. 0 < m < 1 B. m = 1 C. D. m = 9

Hướng dẫn giải:

Phương trình hoành độ giao điểm:

Điều kiện d: y = m(x+2) và (C): giới hạn 2 hình phẳng:

Gọi S

, S

lần lượt là diện tích các hình phẳng nhận được theo thứ tự từ trái sang phải.

Nếu m = 1: d đi qua điểm uốn (0;2) của (C). Khi đó S

= S

Nếu 0 < m < 1: S

> 4 > S

Nếu 1 < m < 9: S

< 4 < S

Nếu m > 9  Khi đó:

 S

= 2m

Vậy m = 1 thỏa yêu cầu bài toán

Câu 16. Cho , , . Khẳng định nào sau đây đúng?

A. B. C. D.

Hướng dẫn giải:

Với .

Đặt .

chọn .

   

20 1 2

a t t



  





m s



30 /

m s

106

S m



107

S m



108

S m



109

S m



     

20 1 2

1 2

v t a t dt t dt C



     



 





0 30 10 30 20

v C C

     

 

20 5ln 1 2 20 5ln5 100 108

1 2

S dt t t m

 

       

 



 



y x 3x 2

  

1 m 9

 

x 3x 2 m(x 2)

   

x 2 hoÆc x 1 m, m 0.

     

y x 3x 2

  

0 m 9.

 

(x 4x)dx 4



 



1 m 2;1 m 4.

    

2 1 m

3 3

1 2

1 m

S x 3x 2 m(x 2) dx; S x 3x 2 m(x 2) dx

 



         

 

m 0



cos

I xdx













n n

I I





n n

I I





n n

I I





n n

I I





0 1

; cos 1

I I xdx



  







1 2

cos 1 cos .sin

n n

u x du n x xdx

 

    

cos

dv xdx



sin

v x



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 87

Facebook: https://www.facebook.com/dongpay

Suy ra

Do đó .

Chọn đáp án C.

Câu 17. Cho hàm số có đồ thị (C). Tìm sao cho hình

phẳng giới hạn bởi đồ thị (C) và các đường thẳng và có diện tích bằng 4.

A. B. C. D.

Hướng dẫn giải:

Xét hàm số trên . Ta có ,

. Do nên

và

Ta có bảng biến thiên trong

0 2



Dựa vào BBT suy ra

Gọi S là diện tích hình phẳng cần tìm. Ta có:

Chọn đáp án C.

 

2 2

1 2 2

0 0

cos cos .sin 1 cos .sin

n n n

xdx x x n x xdx

 



 

  

 

 

2 2

1 cos . 1 cos

n x x dx





  



   

2 2

0 0

1 cos . 1 cos .

n n

n x dx n x dx

 



   

 

2 2

0 0

cos . cos .

n n

x dx x dx

 





 

3 2

1 1

2 2

3 3

y x mx x m

    

 















 

0, 2, 0

x x y

  



3 2

1 1

2 2

3 3

y x mx x m

    





0;2

2 2

y x mx



  

x m m



  





 



  



 















 

2 2

2 0, 0 2 2

m m m m

       

   

1 5

0 2 0, 2 2 0.

3 3

y m y m

     





0;2

m m

  

















0, 0;2

y x

  

3 2

1 1

4 2 2 4

3 3

1 1 4 10 1

2 2 4 4

3 3 3 2

S x mx x m dx

x mx x m dx m

      

 







          









 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 88

Facebook: https://www.facebook.com/dongpay

Câu 18. Trong hệ trục Oxy, cho tam giác OAB vuông ở A, điểm B nằm trong góc phàn tư thứ nhất.

A nằm trên trục hoành, OB = 2017. Góc Khi quay tam giác đó quanh trục Ox

ta được khối nón tròn xoay. Thể tích của khối nón lớn nhất khi:

A. B. C. D.

Hướng dẫn giải:

Phương trình đường thẳng

Khi đó thể tích nón tròn xoay là:

Đặt Xét hàm số .

Ta tìm được lớn nhất khi

Chọn đáp án A.

Câu 19. Từ một khúc gõ hình trụ có đường kính 30cm, người ta cắt khúc gỗ bởi một mặt phẳng đi

qua đường kính đáy và nghiêng với đáy một góc để lấy một hình nêm (xem hình minh họa dưới

đây)

Hình 1 Hình 2

Kí hiệu là thể tích của hình nêm (Hình 2). Tính .

A. B. C. D.

Hướng dẫn giải:

Chọn hệ trục tọa độ như hình vẽ.Khi đó hình nêm

có đáy

là nửa hình tròn có phương trình:

Một một mặt phẳng cắt vuông góc với trục Ox tại

điểm có hoành độ ,



, 0 .

AOB



 

 

  

 

 

sin





cos





cos





sin





: .tan ; 2017cos .

OB y x OA

 

 

 

2017.cos

3 3

2 2 2 2

2017 . 2017 .

tan . .cos .sin .cos 1 cos .

3 3

V x dx



 

     

   



cos 0; .

t t



 

  

 

 

 

1 , 0;

f t t t t

 

  

 

 





f t

3 3 6

cos sin .

3 3 3

 

    





V cm

2250

 

V cm

225









V cm

1250





V cm

1350

y x x

225 , 15;15

 

   

 





15;15

 

 

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 89

Facebook: https://www.facebook.com/dongpay

cắt hình nêm theo thiết diện có diện tích là (xem hình).

Dễ thấy và khi đó

suy ra thể tích hình nêm là:

Câu 20. Tìm tham số để đồ thị hàm số cắt trục tại bốn điểm phân

biệt và thỏa mãn hình phẳng giới hạn bởi đồ thị (C) và trục của phần nằm phía trên trục có diện

tích bằng diện tích hình phẳng giới hạn bởi đồ thị (C) và trục của phần nằm phía dưới trục .

A. 3 B. -3 C. 2 D. 4

Hướng dẫn giải:

Điều kiện để (C) cắt trục ox tại 4 điểm phân biệt là

Do tính đối xứng của đồ thị qua trục tung nên bài toán xảy ra khi

Suy ra là nghiệm của hệ

Chọn đáp án A.

Câu 21. Cho hàm số có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ

thị (C) với y<0 và trục hoành, S’ là diện tích hình phẳng giới hạn bởi đồ thị (C) với y>0 và trục hoành.

Với giá trị nào của m thì ?

A. B. C. D.

Hướng dẫn giải: Phương trình hoành độ giao điểm (*)

Đặt , phương trình trở thành: (**)

Để S>0, S’>0 thì 0<m<4. Khi đó (*) có 4 nghiệm phân biệt với

là hai nghiệm dương phân biệt của (**)

Do ĐTHS hàm bậc 4 nhận Oy làm trục đối xứng nên

Kết hợp với (**) ta được .

Chọn đáp án C.





S x



NP y

   

0 2

tan45 15

MN NP y x

 

  

1 1

. . 225

2 2

S x MN NP x

 







V S x dx

   

x dx cm

2 3

. 225 2250



  







4 2

2 2

y x mx m C

   



   

3 4

4 2 4 2

2 2 2 2

x x

x mx m dx x mx m dx

       

 

 

4 2 4 2

4 4

2 2 0 3 10 15 2 0

x mx m dx x mx m

         



 

4 2

4 4

4 2

4 4

2 2 0

3 6

3 10 15 2 0

x mx m

x m

x mx m



   





   



   





4 2

y x x m

  

S S



m 



4 2

4 0

x x m

  

; 0

x t t

 

4 0

t t m

  

2 1 1 2

; ; ;

t t t t

 





1 2 1 2

; ,

t t t t



   

 

1 1

4 2 4 2

4 2

2 2

' 4 4

4 0 0

5 3

t t

S S x x m dx x x m dx

t t

x x m dx m

      

       

 



m 





y f x





Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 90

Facebook: https://www.facebook.com/dongpay

Câu 22. Cho









3 2

, , , , , 0

y f x ax bx cx d a b c d a

      



có đồ thị





. Biết rằng đồ thị





tiếp xúc với đường thẳng



tại điểm có hoành độ âm và đồ thị của hàm số





y f x





cho bởi hình

vẽ bên. Tính diện tích

của hình phẳng giới hạn bởi đồ thị





và trục hoành.



. B.

S 

. D.



Hướng dẫn giải:

Từ đồ thị suy ra





3 3

f x x



 













2 3

d 3 3 d 3

f x f x x x x x x C



     

 





tiếp xúc với đường thẳng



tại điểm có hoành độ

âm nên





0 0 0

0 3 3 0 1

f x x x



      

Vậy





1 4

 

nên có ngay



. Vậy phương trình đường cong





là

3 2

y x x

  

Xét phương trình

3 2 0

x x

 



   







Diện tích hình phẳng cần tìm là

 

3 2 d

x x x



  



Chọn đáp án B.

Câu 23. Cho





y f x



là hàm số chẵn, có đạo hàm trên đoạn





6;6 .



Biết rằng

 

d 8

f x x







và

 

2 d 3.

f x x

 



Tính

 

d .

f x x







. B.



. C.



. D.



Hướng dẫn giải:

Xét tích phân

 

2 d

K f x x

 



Đặt

2 d 2d d

u x u x x       

Đổi cận: Khi

1 2

x u

   

;

3 6

x u

   

Vậy,

   

6 2

2 6

1 1

d d

2 2

K f u u f x x

 

  

 

. Mà



, nên

 

d 6

f x x







Vì

là hàm chẵn trên





6;6

 nên

   

6 2

2 6

d d 6

f x x f x x



 

 

Từ đó suy ra

     

6 2 6

1 1 2

d d d 8 6 14

I f x x f x x f x x

 

     

  

Chọn đáp án D.

Câu 24. Biết

 

x x 4 2

e 2x e dx a.e b.e c

   



với a, b, c là các số hữu tỷ. Tính

S a b c

  

S 2



S 4

 

S 2

 

S 4



Hướng dẫn giải:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 91

Facebook: https://www.facebook.com/dongpay

Ta có

 

2x x

2 2 2 2 2

x x 2x x x x

0 0 0 0 0

e e 1

I e 2x e dx e dx 2x.e dx 2 xe dx 2 xe dx

2 2 2

        

    

Đặt

     

4 4 4

2 2 2

x x 2 x 2

x x

0 0 0

u x du dx

e 1 e 1 e 3

I 2x.e 2 e dx 2x.e 2e 2e

2 2 2 2 2 2

dv e dx v e

 

 

            



 

 

 

1 3

a ;c

S a b c 4

2 2

b 2



 



     









Chọn đáp án D.

Câu 25. Rút gọn biểu thức:      





0 1 2 *

1 1 1

... , .

2 3 1

n n n n

T C C C C n

A. 











2 1









2 1

Hướng dẫn giải:

Ta có

0 1

1 1

...

2 1

n n n

T C C C

   



. Nhận thấy các số

1 1 1 1

; ; ;...;

1 2 3 1



thay đổi ta nghĩ ngay đến biểu thức

n n

x dx x c



 





Ở đây ta sẽ có lời giải như sau:





0 1 2 2 3 3

1 ...

n n

n n n n n

x C xC x C x C x C

      

Khi đó ta suy ra

 

1 1

0 1 2 2 3 3

0 0

1 ...

n n

n n n n n

x dx C xC x C x C x C dx

      

 

 

2 3 1

0 1 3

1 1

1 ...

0 0

1 2 3 1

n n n n

x x x

x C x C C C

n n



 

      

 

 

 

0 1 2

2 1 1 1 1

...

1 2 3 1

n n n n

C C C C

n n





     

 

Chọn đáp án D.

Câu 26. Hàm số nào dưới đây là nguyên hàm của hàm số

 





f x

trên khoảng





 

;

 





   

ln 1

F x x x C

 





   

ln 1 1

F x x C





  

F x x C

 

 



F x C

Hướng dẫn giải:

Ta có bài toán gốc sau:

Bài toán gốc: Chứng minh

 

x x a c a

x a

    







Đặt

2 2

x x x a

t x x a dt dx dt dx

x a x a

 

 

       

 

 

 

tdx

x a

 



dt dx

x a

 



Vậy khi đó

ln ln

dx dt

t c x x a c

x a

      



 

( điều phải chứng minh).

Khi đó áp dụng công thức vừa chứng minh ta có

 





2 2

ln 1 ln 1

F x dx x x c x x c

        





Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 92

Facebook: https://www.facebook.com/dongpay

Chọn đáp án A.

Câu 27. Trong các số dưới đây, số nào ghi giá trị của

x 1

2 .cosx

1 2













B. 0 C. 2 D. 1

Hướng dẫn giải:

Ta có:

   

 

x 1 x x

2 2 2

x x

0 0

2 cosx 2 cos x 2 cosx

dx dx dx 1

1 2

1 2 .2 1 2 .2

  







 



 

  

Đặt

x t

 

ta có

x 0



thì

t 0,x



 

thì





và

dx dt

 

 

   

2 2 2 2

x t t x

0 0 0 0

2 cos t

2 cosx cost cos x

dx d t dt dx

1 2 .2 1 2 .2 1 2 .2 1 2 .2

   



     

   

   

Thay vào (1) có

   

 

x 1 x

2 2 2 2 2

x x x

0 0 0 0

1 2 cosx

2 cosx 2 cosx cos x cos x sin x 1

dx dx dx dx dx

1 2 2 2 2

1 2 .2 1 2 .2 1 2 .2

    











     



  

    

Vậy

x 1

2 cosx 1

1 2 2















Chọn đáp án A.

Câu 28. Người ta dựng một cái lều vải





có dạng hình “chóp lục giác cong đều” như hình vẽ bên.

Đáy của





là một hình lục giác đều cạnh

. Chiều cao

SO m



(

vuông góc với mặt phẳng

đáy). Các cạnh bên của





là các sợi dây

nằm trên các đường parabol có trục đối xứng song

135 3

(

). B.

96 3

(

135 3

(

). D.

135 3

(

Hướng dẫn giải:

Đặt hệ trục tọa độ như hình vẽ, ta có parabol cần tìm đi qua 3 điểm có tọa độ lần lượt là





0;6





1;3





3;0

nên có phương trình là

1 7

2 2

y x x

  

song với

. Giả sử giao tuyến (nếu có) của





với

mặt phẳng





vuông góc với

là một lục giác đều và

khi





qua trung điểm của

thì lục giác đều có cạnh

1 m

. Tính thể tích phần không gian nằm bên trong cái lều





đó.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 93

Facebook: https://www.facebook.com/dongpay

Theo hình vẽ ta có cạnh của “thiết diện lục giác” là

Nếu ta đặt

t OM

thì

7 1

2 4

BM t  

(chú ý là ta phải

lấy giá trị có dấu “



” trước dấu căn và cho

chạy từ

đến

Khi đó, diện tích của “thiết diện lục giác” bằng

 

3 3 3 7 1

6. 2

4 2 2 4

S t t

 

   

 

 

với

 

0;6t

Vậy thể tích của “túp lều” theo đề bài là:

 

6 6

0 0

3 3 7 1 135 3

d 2 d ...

2 2 4 8

V S t t t t

 

     

 

 

 

Chọn đáp án D.

Câu 29. Xét hàm số





y f x



liên tục trên miền





;

D a b



có đồ thị là một đường cong

. Gọi

là

phần giới hạn bởi

và các đường thẳng

x a

x b

. Người ta chứng minh được rằng diện tích mặt

cong tròn xoay tạo thành khi xoay

quanh

bằng

   

 

2 1 d

S f x f x x





 



. Theo kết quả

trên, tổng diện tích bề mặt của khối tròn xoay tạo thành khi xoay phần hình phẳng giới hạn bởi đồ thị

hàm số

 

2 ln

x x

f x



 và các đường thẳng

1x 

x e

quanh

là

2 1





. B.

4 9





. C.

4 2

4 16 7

e e



 

. D.

4 9





Hướng dẫn giải:

Ta có

     

 

2 ln ln 1 1 1 1

4 2 4 4 4 16 2

x x x x

f x f x x f x x x

x x x



 

 

           

 

 

Lại có

   

0, 1;

f x x x e



    

, nên

 

f x

đồng biến trên

 

1;e

. Suy ra

   

 

1 0, 1;

f x f x e    

Từ đây ta thực hiện phép tính như sau

   

 

ln 1 1

2 1 d 2 1 d

2 4 16 2

b e

x x

S f x f x x x x

 

 



      

 

 

 

 

2 2

1 1

1 2 3

ln 1 1 ln 1

2 d 2 d

2 4 16 2 2 4 4

ln 1

2 d

2 4 4

1 1 1 1 ln

2 ln d

2 8 4 16

e e

x x x x

S x x x x

x x

x x x x x

I I I

 



   

 

      

   

 

 

   

 

  

 

 

 

   

 

 

  

 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 94

Facebook: https://www.facebook.com/dongpay

Với

4 2 4 2

1 1 2 3

2 8 8 16 16

x x e e

I x x x

 

 

 

    

 

 



 

2 2

1 1 1 1 1

ln d 2ln 1

4 4 4 16 16

I x x x x x e

 

      

 

 



1 ln 1 1

d ln

16 32 32

I x x

 

    

 

 



Chọn đáp án D.

Câu 30. Cho hàm số

2 2

y m x

  

. Tập hợp tất cả các giá trị của tham số thực

sao cho đồ thị

của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua

điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng

là



. B.







. C.

; 1

 

 

 

 

 

 

. D.

; 1

 

 

 

 

Hướng dẫn giải:

Tập xác định









3 2 2 2

2 4 2 2

y x m x x x m



   

;

0 2

y x m

x m









  



 



Đồ thị của hàm số đã cho có cực đại và cực tiểu

 

Vì

 

nên hàm số đạt cực đại tại



suy ra điểm cực đại của đồ thị hàm số là





0;2

Đường thẳng cùng phương với trục hoành qua điểm cực đại có phương trình là

: 2

d y



Phương trình hoành độ giao điểm của





và

là:

2 2

2 2 2 2

m x x m

x m







 

     









 



Diện tích hình phẳng cần tìm là: (chú ý rằng hàm số đã cho là hàm chẵn)

2 2 2

4 4 4

2 2 2 2 2 2

2 0 0

2 3

2 d 2 2 d 2 2 d

2 2 2

2 64

10 3 15

m m m

x x x

S m x x m x x m x x

m x m



 

     

 

 

 

  

 

 

  

Ta có

S m





   



 



Chọn đáp án B.

Câu 31. Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta định xây cầu có

10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau 40m,biết 2 bên đầu cầu và giữa mối nhịp nối người

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 95

Facebook: https://www.facebook.com/dongpay

ta xây 1 chân trụ rộng 5m. Bề dày nhịp cầu không đổi là 20cm. Biết 1 nhịp cầu như hình vẽ. Hỏi lượng

bê tông để xây các nhịp cầu là bao nhiêu (bỏ qua diện tích cốt sắt trong mỗi nhịp cầu)

A. B. C. D.

Hướng dẫn giải:

Chọn hệ trục tọa độ như hình vẽ với gốc O(0;0) là chân cầu (điểm tiếp xúc Parabol trên), đỉnh I(25;

2), điểm A(50;0) (điểm tiếp xúc Parabol trên với chân đế)

Gọi Parabol trên có phương trình ( ): (do (P) đi qua O)

là phương trình parabol dưới

Ta có ) đi qua I và A

Khi đó diện tích mỗi nhịp cầu là với là phần giới hạn bởi trong khoảng

Vì bề dày nhịp cầu không đổi nên coi thể tích là tích diện tích và bề dày

số lượng bê tông cần cho mỗi nhip cầu

Vậy 10 nhịp cầu 2 bên cần bê tông.

Chọn đáp án C.

100

2 2

y ax bx c ax bx

    

2 2

20 1

100 5

y ax bx ax bx

      

(

2 2

1 1 2

2 4 2 4 1

( ):

625 25 625 25 5

P y x x y x x

        

S S



1 2

;

y y

(0;25)

0,2

0 0,2

2 4 1

2 ( )

625 25 5

( )

S x x dx dx

   

 

9,9



.0,2 9,9.0,2 1,98

V S m

  





Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 96

Facebook: https://www.facebook.com/dongpay

HÌNH HỌC TỌA ĐỘ KHÔNG GIAN OXYZ

Câu 1. Trong không gian với hệ tọa độ , cho hai điểm , và đường thẳng

có phương trình tham số . Một điểm thay đổi trên đường thẳng , xác định vị

trí của điểm để chu vi tam giác đạt giá trị nhỏ nhất. Khi đó toạ độ của điểm M là:

A. B. C. D.

Hướng dẫn giải:

Gọi là chu vi của tam giác thì

Vì không đổi nên nhỏ nhất khi và chỉ khi nhỏ nhất.

Điểm nên ;

Trong mặt phẳng tọa độ , ta xét hai vectơ và .

Ta có  và

Mặt khác, ta luôn có Như vậy

Đẳng thức xảy ra khi và chỉ khi cùng hướng

và . Vậy khi thì

Chọn đáp án A.

Câu 2. Trong không gian tọa độ Oxyz, cho các phương trình mặt phẳng

Xét các mệnh đề sau:

(I) Với mọi thì các mặt phẳng luôn tiếp xúc với một mặt cầu không đổi.

(II) Với mọi thì các mặt phẳng luôn cắt mặt phẳng (Oxz).

(III) .

Khẳng định nào sau đây đúng?

A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III) D. Cả 3 đều đúng.

Hướng dẫn giải:

+ Ta có , với mọi .

Do đó với mọi m thay đổi trên thì các mặt phẳng luôn tiếp xúc với mặt cầu tâm O, bán

kính . Khẳng đinh (I) đúng.

+ Vectơ pháp tuyến của mặt phẳng là và vectơ pháp tuyến của mặt

phẳng (Oxz) là .

Oxyz





1;5;0





3;3;6



 

1 2

x t

y t t

z t

  





  













MAB





1;0;2





2;4;3





3;2; 2

 





1;4;3

MAB

P AB AM BM

  

AM BM











1 2 ;1 ;2

  

M t t t

2 2 2 2

(3 ) (2 5) (3 6) (2 5)

     AM BM t t

Oxy





3 ;2 5





u t





3 6;2 5

  



v t

 

| | 3 2 5

| | 3 6 2 5



 







  







u t

v t

| | | |

  

 

AM BM u v





6;4 5 | | 2 29

    

   

u v u v

| | | | | |

  

   

u v u v

2 29

 AM BM

 

u v

3 2 5

3 6

2 5

   

 





1;0;2

 M





min 2 29

 AM BM





1;0;2





min 2 11 29

P  





: 3 5 1 4 20 0, 1;1

mx m y mz m

 

      

 

 

1;1

 

 

 

 



















; 5, 1;1

d O m

 

   

 

 

 





2 2 2

; 4

9 25 1 16

d O

m m m



 

  

 

 

  

1;1

 

 

 

 

1;1

 



 

 



















3 ;5 1 ;4

n m m m

 







0;1;0

j 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 97

Facebook: https://www.facebook.com/dongpay

cắt (Oxz) khi và chỉ khi . Khẳng đinh (II) đúng.

+ Khẳng đinh (III) sai.

Chọn đáp án A.

Câu 3. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng:

, và mặt cầu

Viết phương trình mặt phẳng song song với hai đường thẳng và cắt mặt cầu (S) theo giao

tuyến là đường tròn (C) có chu vi bằng .

Chọn đáp án B.

Hướng dẫn giải:

+ qua và có vectơ chỉ phương .

qua và có vectơ chỉ phương .

+ Mặt phẳng () song song với nên có vectơ pháp tuyến:

Phương trình mặt phẳng () có dạng:

+ Mặt cầu (S) có tâm và bán kính .

Gọi r là bán kính đường tròn (C), ta có:

Khi đó:

+ Phương trình mặt phẳng .

Vì nên M

và M

không thuộc loại (1).

Vậy phương trình mặt phẳng () cần tìm là: .

Chọn đáp án B.

Câu 4. Trong không gian Oxyz, cho 2 đường thẳng d: và d’:

Viết phương trình mặt phẳng () chứa (d) và tạo với mặt phẳng Oyz một góc nhỏ nhất.

A. . B. .

C. . D. .

Hướng dẫn giải:

Giả sử (β): (đk: ), (β) có vtpt là

d  (β)   







; 0 0

n j m

 

  

 

 

 

2 1 1

1 2 3

x y z

  

  



: 2

1 2

x t

y t

z t







  





 



2 2 2

( ): 2 2 6 5 0

S x y z x y z

      

( )



1 2

 

2 365



5 3 4 0; 5 3 10 0

x y z x y z

       

5 3 10 0

x y z

   

5 3 3 511 0; 5 3 3 511 0

x y z x y z

         

5 3 4 0

x y z

   



(2; 1;1)

M 

(1;2; 3)

 





(0;2;1)

(1; 1;2)

u  



1 2

 

1 2

, (1; 5; 3)

u u

 

  

 

 



5 3 0

x y z D

   

I(1; 1;3)





2 365 365

5 5

r r



  

 

2 2

,( )

d I R r



  

 





  







( ) : 5 3 4 0 (1) hay 5 3 10 0 (2)

x y z x y z



       

1 2

/ /( ), / /( )

 

 

( )





5 3 10 0

x y z

   



 



  









x t

y t

z t

5 '

2 ' 3 2 5







 





  



x t

y t

z t

3 2 7 0

   

x y z

3 2 7 0

   

x y z

3 2 7 0

    

x y z

3 2 7 0

   

x y z

   

Ax By Cz D

2 2 2

  

A B C

( ; ; )





n A B C

( )

. 0

 















n a



3 2 0

2 0

  







  





A B D

A B C

2 2



  





 





D A C

B A C

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 98

Facebook: https://www.facebook.com/dongpay

TH 1: A = 0 (không thoả đb hoặc không nhỏ nhất)

TH 2: A ≠ 0, ta có:

= = =

nhỏ nhất  lớn nhất  nhỏ nhất 

 nên . Vậy: (β):

Chọn đáp án D.

Câu 5. Trong không gian tọa độ Oxyz cho đường thẳng và mp

. Viết phương trình mặt phẳng qua d và tạo với một góc nhỏ nhất.

A. B.

C. D.

Hướng dẫn giải:

Đường thẳng d là giao tuyến của hai mặt phẳng: .

Do vậy mặt phẳng qua d thì thuộc chùm mặt phẳng: .

Hay mp : (*). Mp có .

Vậy:

Do nhỏ nhất cho nên lớn nhất khi .

Vậy thay vào (*) ta có mp .

Chọn đáp án B.

Câu 6. Trong không gian với hệ toạ độ , gọi là mặt phẳng qua hai điểm và

đồng thời hợp với mặt phẳng một góc . Khoảng cách từ O tới là:



cos(( ),( )) cos( , )

 



Oyz n i



2 2 2

( 2)  

A A C C



( ),( )

Oyz





cos(( ),( ))

Oyz



2 2

1 (1 2) ( )

  

C C

A A

2 2

6 12

( 3) 2. 2 ( )

3 9

  

C C

A A

6 12

( 3 )

3 9

 



( ),( )

Oyz





cos(( ),( ))

Oyz



( 3 )



3 0

 

1 (choïn)









 















 





3 2 7 0

   

x y z

: 1 2

x t

d y t

z t



 



  





 









: 2 2 2 0

P x y z

   









3 0

x y z

   

3 0

x y z

   

3 0

x y z

   

3 0

x y z

   

2 1 0

1 2

2 2 0

1 1

x y

x z x z













  





 



 

 

   





























2 1 2 0

x y m x z

     









2 1 2 0

m x y mz m

     













2;1; ; 2; 1; 2

n m m n

    

 





   

2 2 2

2 2 1 2

5 5 1 5

cos

3 3

3 2 4 5

2 1 4 1 4 2 1 3

m m

n n

m m

n n

m m m



  

    

 

      

 





cos









: 3 0

R x y z

   

Oxyz











2;0;1





2;0;5







Oxz







Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 99

Facebook: https://www.facebook.com/dongpay

A. B. C. D.

Hướng dẫn giải:

Gọi lần lượt là hình chiếu vuông góc điểm lên đường thẳng và mặt phẳng

Ta có:

Suy ra tam giác vuông cân tại

Khi đó:

Mặt khác:

Khi đó:

Chọn đáp án A.

Câu 7. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 2x – y + z + 1 =

0 và hai điểm M(3; 1; 0), N(- 9; 4; 9). Tìm điểm I(a; b; c) thuộc mặt phẳng (P) sao cho đạt

giá trị lớn nhất. Biết a, b, c thỏa mãn điều kiện:

A. B. C. D.

Hướng dẫn giải:

Nhận thấy 2 điểm M, N nằm về hai phía của mặt phẳng (P).

Gọi R là điểm đối xứng của M qua mặt phẳng (P), khi đó đường thẳng MR đi qua điểm M(3; 1; 0)

và vuông góc với mặt phẳng (P) có phương trình: . Gọi

Ta có . Đẳng thức xảy ra khi I, N, R thẳng hàng. Do đó tọa độ điểm I là

giao điểm của đường thẳng NR: (t là tham số ) và mặt phẳng (P).

Dễ dàng tìm được I(7; 2; 13).

Chọn đáp án A.

Câu 8. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng và hai điểm

. M là một điểm trên mặt phẳng . Giá trị lớn nhất của là:

A. B. C. D.

Hướng dẫn giải:

Ta có: A, B nằm khác phía so với (P). Gọi B’ là điểm đối xứng với B qua (P). Suy ra .

;

K H











A B Oxz











Oxz AB



  





HK AB

OK AB













 







   















, ,

Oxz KH OK OKH



  

OHK

 

, .

d O OH



 

 

, .

OA AB

OK d O AB



  

 



 

, .

d O OH



  

IM IN



a b c

  

a b c

  

a b c

  

19.

a b c

  

3 1

2 1 1

x y z

 

 



(P) (1;2; 1) ( 1;3; 2)

H MR H R

      

IM IN IR IN RN

   

1 8

2 11

x t

y t

z t

  





 





  



( ): 1 0

P x y z

   





(1; 3;0), 5; 1; 2

A B

  

( )

T MA MB

 

2 5.

T 

2 6.

T 

4 6

T 

2 3

T 

'( 1; 3;4)

 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 100

Facebook: https://www.facebook.com/dongpay

Đẳng thức xảy ra khi M, A, B’ thẳng hàng.

Chọn đáp án A.

Câu 9. Cho hai điểm A(-1, 3, -2); B(-9, 4, 9) và mặt phẳng (P): 2x-y+z+1=0. Điểm M thuộc (P). Tính

GTNN của AM + BM.

A. B. C. D.

Hướng dẫn giải:

Ta có: (2.(-1)-3+(-2)+1)(2.(-9)-4+9+1)=72 > 0 => A,B nằm cùng phía so với mặt phẳng (P).

Gọi A’ là điểm đối xứng của A qua (P). Mặt phẳng (P) có vtpt

Đường thẳng AA’ đi qua A(-1, 3, -2) có vtcp có pt:

Gọi H là giao của AA’ và (P) ta có: 2(-1+2t) - (3-t) + (-2 + t) + 1 =0 => t=1 => H(1, 2, -1).

Ta có H là trung điểm của AA’ => A’(3, 1, 0).

Đường A’B đi qua A’(3, 1, 0) có vtcp có pt:

Gọi N là giao điểm của A’B và mặt phẳng (P) ta có:

2.(3-4t) – (1+t) + 3t +1 =0 => t=1 => N(-1, 2, 3).

Để MA+MB nhỏ nhất thì khi đó MA+MB = A’B =

Chọn đáp án D.

Câu 10. Trong không gian với hệ tọa độ , cho hai đường thẳng và

. Viết phương trình mặt phẳng chứa sao cho góc giữa mặt phẳng và

đường thẳng là lớn nhất.

6 0

   

x y z

. B.

7 5 9 0

   

x y z

. C.

6 0

x y z

   

. D.

3 0

   

x y z

Hướng dẫn giải:

Ta có: đi qua và có .

Phương trình mặt phẳng có dạng: .

Ta có:

Gọi

Với

Với . Đặt , ta được

Xét hàm số . Ta có:

' ' 2 5.

T MA MB MA MB AB     

6 204



7274 31434



2004 726



3 26





2, 1,1

n 







2, 1,1

n 



1 2

x t

y t

z t

  





 





  







' 12,3,9

A B 



3 4

x t

y t

z t

 





 









M N



 

2 2

12 3 9 234 3 26

    

Oxyz

1 2

1 2 1

x y z

 

 



2 1

2 1 2

x y z

 

 



( )

(1; 2;0)



(1;2; 1)

VTCPu

 



( )

2 2 2

( 1) ( 2) 0,( 0)

A x B y Cz A B C

       

( ) . 0 2

d P u n C A B

     

 

2 2

4 3

1 (4 3 )

(( ), ) sin .

2 4 5

3 2 4 5

A B

P d

A AB B

 



   

 



2 2

sin



 





1 (4 3)

sin .

2 4 5

t t







 

(4 3)

( )

2 4 5

f t

t t





 

2 2

16 124 84

'( )

(2 4 5)

t t

f t

t t

 



 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 101

Facebook: https://www.facebook.com/dongpay

BBT: -7

+ 0 - 0 +

Dựa vào BBT ta có: khi

Khi đó:

Vậy khi Phương trình mặt phẳng

Chọn đáp án B.

Câu 11. Cho đường thẳng d là giao tuyến của hai mặt phẳng

và mặt cầu S có phương trình . Tìm m để

đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho AB = 8.

A. 9 B. 12 C. 5 D. 2

Hướng dẫn giải:

Ta có lần lượt là VTPT của (α) và (β)

Suy ra VTCP của đường thẳng d là

Ta có A(6;4;5) là điểm chung của hai mặt phẳng (α) và (β) nên Ad.

Mặt cầu (S) có tâm I(-2;3;0), bán kính với m < 13.

Gọi H là trung điểm của AB  .

Trong tam giác vuông IHA ta có:

. Vậy m = 12 là giá trị cần tìm.

Chọn đáp án B.

Câu 12. Trong không gian tọa độ , cho tám điểm , , ,

, , , , . Hỏi hình đa diện tạo bởi tám điểm

đã cho có bao nhiêu mặt đối xứng.

A. 3. B. 6. C. 8. D. 9

Hướng dẫn giải:

Vì tám điểm đã chõ tạo nên một hình lập phương, nên hình đa diện tạo bởi tám điểm này có 9 mặt

đối xứng.

Chọn đáp án D.

'( ) 0

f t



 



 



 











'( )

f t

( )

f t

max ( )

f t 

 

  

5 3

sin ( 7)



  

5 3

sin





 



( ):7 5 9 0

P x y z

   

( ):x 2y 2z 4 0

    

( ):2x 2y z 1 0,

    

2 2 2

x y z 4x 6y m 0

     

1 2

n (2; 2; 1), n (1;2; 2)

    

 

1 2

u n ;n (2;1;2),

 

 

 

  

R 13 m

 

IA (8;1;5) IA,u ( 3; 6;6) d(I,d) 3

 

      

 

  

AH 4 vµ IH 3

  

2 2 2 2

IA IH AH R 9 16

    

13 m 25 m 12

     

Oxyz





2; 2;0

A  





3; 2;0

B 





3;3;0





2;3;0

D 





2; 2;5

M  





2; 2;5

N  





3; 2;5

P 





2;3;5

Q 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 102

Facebook: https://www.facebook.com/dongpay

Câu 13. Trong không gian với hệ toạ độ Oxyz cho A(2;



1;6), B(



1;2;4) và I(



3;2). Viết

phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ I đến (P) lớn nhất.

3 7 6 35 0   x y z

. B.

7 5 9 0   x y z

. C.

6 0x y z   

. D.

3 0   x y z

Hướng dẫn giải:

Ta có

2 2 2

3 2 4 29

   IA

và

2 2 2

0 5 2 29

   IB

. Gọi M là trung điểm của đoạn thẳng

AB, vì IA=IB nên IM



AB, ta có

1 1

; ;5 ;

2 2

 

 

 

IM

Gọi H là hình chiếu vuông góc của I lên mặt phẳng (P):

Nếu H, M là hai điểm phân biệt thì tam giác IHM vuông tại H, IH<IM hay

IH

Nếu H trùng với M thì

 IH IM

. Vậy ta có

IH

, IH lớn nhất khi H



Khi đó (P) có vectơ pháp tuyến là

3 7

; ;3

2 2

 

  

 

 

  

n IH IM

. Vậy phương trình mặt phẳng (P) là

     

3 7

2 1 3 6 0

2 2

     x y z

hay

3 7 6 35 0   x y z

Chọn đáp án A.

Câu 14. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt phẳng (P):

2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) saocho MA

+ MB

nhỏ nhất là:

A. (-1;3;2) B. (2;1;-11) C. (-1;1;5) D. (1;-1;7)

Hướng dẫn giải:

+ Kiểm tra phương án A không thuộc (P).

+ Tính trực tiếp MA

+ MB

trong 3 phương án B,C,D và so sánh. Chọn C.

Câu 15. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm và . Mặt phẳng

(P) đi qua M, N sao cho khoảng cách từ đến (P) đạt giá

trị lớn nhất. (P) có vectơ pháp tuyến là:

A. B.

C. D.

Hướng dẫn giải:

- Khoảng cách từ K đến (P) lớn nhất bằng KH, khi H’ trùng H

- Vậy mặt phẳng (P) qua MN và vuông góc với KH.

- Tìm H và viết (P) hoặc:

- (P) chứa MN và vuông góc với (MNP).

Gọi H, H’ là hình chiếu của K lên MN và (P).

(0; 1;2)



( 1;1;3)







0;0;2

(1;1; 1)



(1; 1;1)



(1; 2;1)



(2; 1;1)



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 103

Facebook: https://www.facebook.com/dongpay

Ta có: không đổi.

Vậy lớn nhất khi và chỉ khi H’ trùng H hay (P) vuông góc với KH.

;

(MNK) có vtpt là

Do nên HK có vtcp là .

Chọn đáp án A.

Câu 16. Trong không gian tọa độ Oxyz, cho điểm và mặt cầu (S) có

phương trình: . Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện ABCD có thể

tích lớn nhất.

A. B. C. D. D(1; - 1; 0)

Hướng dẫn giải:

Ta thấy câu C và D có điểm D không thuộc (S). Loại C,D.

Ta tính thể tích cho điểm D ở câu A và câu B. Điểm B ở câu B có thể tích lớn hơn.

Chọn đáp án B.

Câu 1.5. Phương trình nào sau đây không phải là phương trình hình chiếu vuông góc của đường thẳng

d: trên mặt phẳng (Oxy):

A. B. C. D.

Hướng dẫn giải:

A(1;-2;3), B(3;1;4) thuộc d. Hình chiếu của A,B trên mặt phẳng (Oxy) là A

(1;-2;0), B

(3;1;0)

Phương trình hình chiếu đi qua hoặc và nhận véc tơ cùng phương với làm

véc tơ chỉ phương.

Chọn đáp án C.

Câu 17. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng và hai điểm

. M là một điểm trên mặt phẳng . Giá trị lớn nhất của là:

A. B. C. D.

Hướng dẫn giải:

Ta có: A, B nằm khác phía so với (P). Gọi B’ là điểm đối xứng với B qua (P). Suy ra .

Đẳng thức xảy ra khi M, A, B’ thẳng hàng.

Chọn đáp án A.

 

( ,( )) '

d k P KH KH

( ,( ))

d K P

   

 

(0;1;0); (1; 1; 1)

MK NK  



( 1;2;1)

 

   

 

  

, ( 1;0; 1)

n MK NK











( )

HK MNK

HK MN

 

 

 

 

, (2;2; 2)

MN n

A B C

(0;1;1), (1;0; 3), ( 1; 2; 3)

   

x y z x z

2 2 2

2 2 2 0

     





1;0;1

7 4 1

; ;

3 3 3

 

 

 

 

 

 

 

 

1 4 5

; ;

3 3 3

1 2

2 3 ,

x t

y t t R

z t

 





   





 



3 2 '

1 3 ' , '

x t

y t t R

 





  









1 4 '

2 6 ', '

x t

y t t R

 





   









1 2 '

2 3 ', '

x t

y t t R

 





  









5 2 '

4 3 ', '

x t

y t t R

 





  









 

/ /

2;3;0

A B 



( ): 1 0

P x y z

   





(1; 3;0), 5; 1; 2

A B

  

( )

T MA MB

 

2 5.

T 

2 6.

T 

4 6

T 

2 3

T 

'( 1; 3;4)

 

' ' 2 5.

T MA MB MA MB AB     

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 104

Facebook: https://www.facebook.com/dongpay

Câu 18. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm





2; 2;1

 M





1;2; 3



và đường thẳng

1 5

2 2 1

 

 



x y z

. Tìm véctơ chỉ phương



của đường thẳng



đi qua

, vuông góc với đường

thẳng

đồng thời cách điểm

một khoảng bé nhất.





2;1;6





u . B.





1;0;2





u . C.





3;4; 4

 



u . D.





2;2; 1

 



u .

Hướng dẫn giải:

Gọi





là mặt phẳng qua

và vuông góc với

. Phương trình của





:2 2 9 0

   

P x y z

Gọi

H K

lần lượt là hình chiếu vuông góc của

trên







Ta có





3; 2; 1

  

( , )

  

d A AH AK

Vậy khoảng cách từ

đến



bé nhất khi



đi qua

M K



có véctơ chỉ phương





1;0;2





Chọn đáp án B.

Câu 19. Trong không gian với hệ trục toạ độ Oxyz, cho điểm và đường thẳng

. Gọi

(



)

là mặt phẳng chứa đường thẳng  sao cho khoảng cách từ  đến

(



)

lớn

nhất. Tính khoảng cách từ điểm đến mặt phẳng

(



)

A. B. C. D.

Hướng dẫn giải:

Vậy .

Chọn đáp án A.

Câu 20. Trong không gian với hệ tọa độ

Oxyz

xét các điểm





0;0;1





;0;0

B m





0; ;0

C n





1;1;1

với

0; 0

 

m n

và

 

m n Biết rằng khi

thay đổi, tồn tại một mặt cầu cố định tiếp

xúc với mặt phẳng





ABC

và đi qua

. Tính bán kính

của mặt cầu đó?





2;5;3

1 2

2 1 2

x y z

 

 





1;2; 1



11 18

3 2

 

11 18

d M P 



Gọi H là hình chiếu của A trên d; K là hình chiếu của A trên

(

)

Ta có d



(

)



=AK ≤ AH(khôngđổi)

⟹ GTLNcủad



(

)



làAH

⟹ d



(

)



lớn nhất khi K ≡ H.

Ta có H

(

3;1;4

)

(

)

qua H và ⊥ AH







:x  4y  z 3  0

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 105

Facebook: https://www.facebook.com/dongpay



. B.

R

. C.



. D.

R

Hướng dẫn giải:

Gọi

(1;1;0)

là hình chiếu vuông góc của

lên mặt phẳng

( )

Oxy

Ta có: Phương trình theo đoạn chắn của mặt phẳng

( )

ABC

là:

  

x y

m n

Suy ra phương trình tổng quát của

( )

ABC

là

   

nx my mnz mn

Mặt khác

2 2 2 2

( ,( )) 1



 

 

d I ABC

m n m n

(vì

 

m n

) và

1 ( ,( ))

 

ID d I ABC

Nên tồn tại mặt cầu tâm

(là hình chiếu vuông góc của

lên mặt phẳng

Oxy

) tiếp xúc với

( )

ABC

và đi qua

Chọn đáp án A.

Câu 21. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình:

. Viết phương trình mặt phẳng (P) song song với giá của véc tơ

, vuông góc với mặt phẳng và tiếp xúc với (S).

2 2 3 0

2 2 21 0

   





   



x y z

. B.

2 2 3 0

2 2 21 0

   





   



x y z

2 3 0

2 1 0

   





   



x y z

. D.

2 13 0

2 1 0

   





   



x y z

Hướng dẫn giải:

Vậy: (P): hoặc (P):

(S) có tâm I(1; –3; 2) và bán kính R = 4. VTPT của là .

 VTPT của (P) là:  PT của (P) có dạng: .

Vì (P) tiếp xúc với (S) nên .

Vậy: (P): hoặc (P): .

Chọn đáp án B.

Câu 22. Trong không gian với hệ tọa độ

Oxyz

, cho bốn điểm





1; 2;0 ,

A





0; 1;1 ,

B





2;1; 1 ,







3;1;4

. Hỏi có bao nhiêu mặt phẳng cách đều bốn điểm đó?

D. Vô số.

Hướng dẫn giải:

Ta có





1;1;1 ,

 







1;3; 1 ,

 







2;3;4





AD .

Khi đó

 

, 4;0; 4

 

  

 

 

AB AC

suy ra

, . 24 0

 

  

 

  

AB AC AD

Do đó

, , ,

A B C D

không đồng phẳng và là 4 đỉnh của một tứ diện.

Khi đó sẽ có 7 mặt phẳng cách đễu bốn đỉnh của tứ diện. Bao gồm: 4 mặt phẳng đi qua trung điểm

của ba cạnh tứ diện và 3 mặt phẳng đi qua trung điểm bốn cạnh tứ diện (như hình vẽ).

2 2 2

2 6 4 2 0

x y z x y z

      

(1;6;2)





( ): 4 11 0

x y z



   

2 2 3 0

x y z

   

2 2 21 0

x y z

   

( )



(1;4;1)









, (2; 1;2)

n n v  

  

2 2 0

x y z m

   

( ,( )) 4

d I P



 











2 2 3 0

x y z

   

2 2 21 0

x y z

   

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 106

Facebook: https://www.facebook.com/dongpay

Chọn đáp án C.

Câu 23. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; –2; 0), B(0; –1; 1), C(2; 1; –1) và

D(3; 1; 4). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ?

A. 1 mặt phẳng. B. 4 mặt phẳng. C. 7 mặt phẳng. D. Có vô số mặt

phẳng.

Hướng dẫn giải:

Ta có:

( 1;1;1); (1;3; 1); (2;3;4)

    

  

AB AC AD

Khi đó:

; . 24 0

 

  

 

  

AB AC AD

do vậy A,B,C,D không đồng phẳng

Chọn đáp án C.

Câu 24. Đường thẳng



song song với

4 5 2

3 4 1

x y z

  

 



và cắt cả hai đường thẳng

1 1 2

3 1 2

  

 

x y z

và

2 3

2 4 1

 

 

x y z

. Phương trình nào không phải đường thẳng



4 1 1

3 4 1

  

  



x y z

7 2

3 3

3 4 1

 



  



y z

Do đó có 7 mặt phẳng cách đều 4 điểm đã cho bao gồm.

+) Mặt phẳng qua trung điểm của AD và song song với mặt phẳng (ABC)

+) Mặt phẳng qua trung điểm của AB và song song với mặt phẳng (ACD)

+) Mặt phẳng đi qua trung điểm của AC và song song với mặt phẳng (ABD)

+) Mặt phẳng đi qua trung điểm của AB và song song với mặt phẳng (BCD)

+) Mặt phẳng qua trung điểm của AB và CD đồng thời song song với BC và AD

+) Mặt phẳng qua trung điểm của AD và BC đồng thời song song với AB và CD

+) Mặt phẳng qua trung điểm của AC và BD đồng thời song song với BC và AD

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 107

Facebook: https://www.facebook.com/dongpay

9 7 2

3 4 1

  

  



x y z

4 1 1

3 4 1

  

  



x y z

Hướng dẫn giải:

Giải: Gọi M, N là giao điểm của



và

1 2

d d

Khi đó M, N thuộc

1 2

d d

nên

2 2 '

1 3

1 , 3 4 '

2 2

  

 



 

    

 

 

 



 

M N

x t

y t y t

z t

Vector chỉ phương của



là





3 2 ' 3 ;4 4 ' ; 2 ' 2

        



MN t t t t t t



song song với

4 5 2

3 4 1

  

 



x y z

nên

3 2 ' 3 4 4 ' 2 ' 2

3 4 1

       

 



t t t t t t

Giải hệ ta được

' 1;

   

t t

. Vậy

 

7 2

4; 1; 1 , 3; ;

3 3

 

     

 

 

N M

Vậy

4 1 1

3 4 1

  

  



x y z

Chọn đáp án A.

Câu 25. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng



có

phương trình tham số

1 2

  





 









x t

y t

z t

. Một điểm M thay đổi trên đường thẳng



sao cho chu vi tam giác

MAB đạt giá trị nhỏ nhất. Tọa đô điểm M và chu vi tam giác ABC là

A. M(1;0;2) ; P =

2( 11 29)

 B. M(1;2;2) ; P =

2( 11 29)



C. M(1;0;2) ; P =

11 29

 D. M(1;2;2) ; P =

11 29



Hướng dẫn giải:

 Gọi P là chu vi của tam giác MAB thì P = AB + AM + BM.

Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM + BM nhỏ nhất.

Điểm



nên





1 2 ;1 ;2

  

M t t t

2 2 2 2

(3 ) (2 5) (3 6) (2 5)

     AM BM t t

Trong mặt phẳng tọa độ Oxy, ta xét hai vectơ





3 ;2 5





u t

và





3 6;2 5

  



v t

Ta có

2 2 2 2

(3 ) (2 5) ; (3 6) (2 5)

    

 

u t v t



| | | |

  

 

AM BM u v

và

(6;4 5) | | 2 29

    

   

u v u v

Mặt khác, ta luôn có

| | | | | |

  

   

u v u v

Như vậy

2 29

 AM BM

Đẳng thức xảy ra khi và chỉ khi

 

u v

cùng hướng

3 2 5

3 6

2 5

   

 

(1;0;2)



và

min( ) 2 29

 AM BM . Vậy khi M(1;0;2) thì minP =

2( 11 29)



Chọn đáp án A.

Câu 26. Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;2; -1), B(7; -2; 3) và đường thẳng d

có phương trình

2 3

2 (t R)

4 2

 





  





 



x t

y t

z t

. Điểm M trên

sao cho tổng khoảng cách từ M đến A và B là

nhỏ nhất có tổng các tọa độ là:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 108

Facebook: https://www.facebook.com/dongpay

A. M=(2;0;4 ). B. M=(2;0;1). C. M=(1;0;4 ). D. M=(1;0;2 ).

Hướng dẫn giải:

Nếu M nằm trên d thì điểm I có tọa độ là M=(2+3t;-2t;4+2t). Từ đó ta có:

       

2 2 2

3 1; 2 2 ;2 5 3 1 2 2 2 5

            



AM t t t AM t t t

Tương tự:

       

2 2 2

3 5;2 2 ;2 1 3 5 2 2 2 1

           



BM t t t BM t t t

Từ (*): MA=MB =

     

2 2 2

3 1 2 2 2 5

    t t t

     

2 2 2

3 5 2 2 2 1

    t t t

Hay:

2 2

17 34 30 17 36 30 34 36 0 11 70 0 0

             

t t t t t t t t

Tọa độ M thỏa mãn yêu cầu là: M=(2;0;4 ).

Chọn đáp án A.

Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): và đường thẳng

. Phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt phẳng (Q)

một góc nhỏ nhất là

A. B.

C. D.

Hướng dẫn giải:

PT mặt phẳng (P) có dạng: . Gọi .

Chọn hai điểm . Ta có:

 (P): 

TH1: Nếu a = 0 thì  .

TH2: Nếu a  0 thì . Đặt và

Xét hàm số .

Dựa vào BBT, ta thấy

Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn .

Vậy: (P): .

Chọn đáp án A.

Câu 28. Trong không gian với hệ tọa độ

Oxyz

gọi

đi qua điểm





1; 1;2

A

, song song với





:2 3 0

   

P x y z

, đồng thời tạo với đường thẳng

1 1

1 2 2

 

  



x y z

một góc lớn nhất. Phương

trình đường thẳng

là.

x y z

2 5 0

   

x y z

1 1 3

2 1 1

  

 





  

: 4 0

P y z





  

:x 4 0

P z





   

:x 4 0

P y z





  

: 4 0

P y z

ax by cz d a b c

2 2 2

0 ( 0)

      



P Q

(( ),( ))

a

M N d

( 1; 1;3), (1;0;4)

  

M P c a b

N P d a b

( )

( ) 7 4

 

   



 

  

 

ax by a b z a b

( 2 ) 7 4 0

      

a b

a ab b

2 2

cos .

5 4 2







 

3 3

cos .



 

a

b b

a a

cos .

5 4 2







 

 

 

 



f x

( ) cos





x x

f x

x x

9 2 1

( ) .

5 4 2

 



 

f x

0 0

min ( ) 0 cos 0 90 30



     a

b c d

1, 1, 4

  

y z

4 0

  

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 109

Facebook: https://www.facebook.com/dongpay

1 1 2

1 5 7

  

 



x y z

1 1 2

4 5 7

  

 



x y z

1 1 2

4 5 7

  

 

x y z

1 1 2

1 5 7

  

 

 

x y z

Hướng dẫn giải:



có vectơ chỉ phương





1; 2;2



 



có vectơ chỉ phương





; ;





a a b c





có vectơ pháp tuyến





2; 1; 1

  



Vì





d P

€

nên

. 0 2 0 2

         

   

d P d P

a n a n a b c c a b

 

2 2

5 4 5 4

cos ,

3 5 4 2

 

  

 

a b a b

a ab b

Đặt



, ta có:

 

5 4

cos ,

3 5 4 2



 

 

t t

Xét hàm số

 

5 4

5 4 2





 

f t

t t

, ta suy ra được:

 

1 5 3

max

5 3

 

  

 

 

f t f

Do đó:

 

5 3 1 1

max cos ,

27 5 5

       

 

 

d t

Chọn

1 5, 7

    

a b c

Vậy phương trình đường thẳng

là

1 1 2

1 5 7

  

 



x y z

Chọn đáp án A.

Câu 29. Trong không gian với hệ toạ độ

Oxyz

,cho





: 4 2 6 0

   

P x y z





: 2 4 6 0

   

Q x y z

Lập phương trình mặt phẳng







chứa giao tuyến của









P Q

và cắt các trục tọa độ tại các điểm

, ,

A B C

sao cho hình chóp .

O ABC

là hình chóp đều.

6 0

   

x y z

. B.

6 0

   

x y z

. C.

6 0

   

x y z

. D.

3 0

   

x y z

Hướng dẫn giải:

Chọn









6;0;0 , 2;2;2

M N

thuộc giao tuyến của









P Q

Gọi













;0;0 , 0; ;0 , 0;0;

A a B b C c

lần lượt là giao điểm của







với các trục

, ,

Ox Oy Oz



   

: 1 , , 0

    

x y z

a b c







chứa

M N

2 2 2













  





a b c

Hình chóp .

O ABC

là hình chóp đều

     

OA OB OC a b c

Vây phương trình

6 0

   

x y z

Chọn đáp án B.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 110

Facebook: https://www.facebook.com/dongpay

Câu 30. Trong không gian với hệ tọa độ

2 2 2 0







   



x y z

Oxyz

cho điểm





1;0;0

và





0;0; 1



, mặt phẳng





qua điểm

M N

và tạo với mặt phẳng





: 4 0

  

Q x y

một góc bằng

. Phương trình mặt phẳng





là

2 2 2 0







   



x y z

. B.

2 2 2 0







   



x y z

2 2 2 0

   





   



x y z

. D.

2 2 2 0

  





  



x z

Hướng dẫn giải:

Gọi vectơ pháp tuyến của mp





và





lần lượt là





; ;



n a b c





2 2 2

  

a b c



















qua 1;0;0 : 1 0

    

P M P a x by cz





qua





0;0; 1



  

a c





hợp với





góc

 

2 2

, 45

2 2







    



 





 

P Q

a b

cos n n cos

a b

Với

0 0

  

a c chọn



phương trình





: 0



P y

1 1

2 1 3

 

 

x y z

. Gọi





là mặt phẳng đi qua điểm

, song song với đường thẳng

sao cho

khoảng cách giữa

và





lớn nhất. Khoảng cách từ điểm





1;2;3

M

đến mp





là

97 3

76 790

790

2 13

3 29

Hướng dẫn giải:











d d P

lớn nhất khi

vuông góc với





Khi đó, nếu gọi





là mặt phẳng chứa

và

thì





vuông góc với





Với a  2b chọn b  1 a  2 phương trình mặt phẳng





: 2x  y  2z  2  0

Chọn đáp án A.

Câu 31. Trong không gian với hệ trục toạ độ Oxyz, cho điểm



10;2;1



và đường thẳng





là mặt phẳng đi qua điểm

và song song với

đường thẳng d nên





chứa đường thẳng d



đi qua

điểm

và song song với đường thẳng d .

Gọi

là hình chiếu của

trên d ,

là hình chiếu

của

trên





Ta có





 HK  AH

( AH không đổi)



GTLN của

d(d, (P))

là

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 111

Facebook: https://www.facebook.com/dongpay

 

   

 

, 98;14; 70

97 3

:7 5 77 0 , .

 

   

 

      

  

P d Q

n u n

P x y z d M P

Chọn đáp án A.

Câu 32. Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng d:

. Mặt phằng (P) chứa đường thẳng d và có khoảng cách từ A đến (P) là lớn nhất. Khi

đó (P) có một véctơ pháp tuyến là

A. B. C. D.

Hướng dẫn giải:

Gọi H,K lần lươt là hình chiếu vuông góc của A lên d và (P)

Khi đó: d(A,(P)) = AK AH hay d(A,(P)) lớn nhất khi và chỉ khi

Ta có: và

Suy ra:

Hay một véctơ pháp tuyến của (P) là

Chọn đáp án A.

Câu 33. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

(2; 2;0)



, đường thẳng

1 2

1 3 1

 

  



x y z

. Biết mặt phẳng

( )

có phương trình

   

ax by cz d

đi qua

, song song

với



và khoảng cách từ



tới mặt phẳng

( )

lớn nhất. Biết

a b

là các số nguyên dương có ước

chung lớn nhất bằng 1. Hỏi tổng

  

a b c d

bằng bao nhiêu?

. B.

. C.

. D.



Hướng dẫn giải:

Gọi

là hình chiếu vuông góc của

trên đường thẳng



( 1 ;3 ;2 )

    

H H t t t

( 3;3 2; 2)

     



AH t t t

. 0



   

 

AH AH u

với

( 1;3;1)



 



1.( 3) 3.(3 2) 1.( 2) 0 11 11

           

t t t t

  





0; 3;1

 H

Gọi

là hình chiếu vuông góc của

trên

( )

, khi đó:

( ,( )) ( ,( ))

   

d P d H P HF HA

Suy ra

max

( ,( )) 

d P HA

. Dấu “=” xảy ra khi



F A

( )

 

AH P

, hay bài toán được phát biểu lại

là:

“ Viết phương trình mặt phẳng

( )

đi qua

và vuông góc với

”

Ta có





2; 1;1 (2;1; 1)

     



AH , suy ra

( )

(2;1; 1)

 



Suy ra phương trình mặt phẳng

( )

là:

2( 2) 2 0 2 2 0

         

x y z x y z

, * 2, 1

( , ) 1 1, 2

  

 

     

 

    

 



a b a b

a b c d

Chọn đáp án B.

3 1

2 1 1

 

 



x y z

4 5 13

( ; ; )

n 



4 5 13

( ; ; )

 



4 5 13

( ; ; )

n  



4 5 13

( ; ; )

n  





H K



3 2 1 2 1 1

( ; ; ); ( ; ; )

H t t t a

      



.AH a t

  

 

4 5 13

3 3 3

( ; ; )

AH    



4 5 13

( ; ; )

n 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 112

Facebook: https://www.facebook.com/dongpay

Câu 34. Trong không gian tọa độ Oxyz cho M(2;1;0) v đường thẳng d có phương trình:

1 1

2 1 1

 

 



x y z

. Gọi



là đường thẳng đi qua M, cắt và vuông góc với d. Viết phương trình đường

thẳng



1 4

 





 





 



x t

y t

z t

1 4

3 2

 





 





 



x t

y t

z t

1 4

 





 





 



x t

y t

z t

1 4

 





 





 



x t

y t

z t

Hướng dẫn giải:

PTTS của d là

1 2

 





  





 



x t

y t

z t

Gọi H là hình chiếu vuông góc của M lên d, đường thẳng



cần tìm là đường thẳng MH.

Vì H thuộc d nên





1 2 ; 1 ;

   

H t t t

suy ra

(2 1; 2 ; )

    



MH t t t

Vì



MH d

và d có 1 VTCP là

(2;1; 1)

 



u nên

. 0

MH u



 





. Do đó

1 4 2

; ;

3 3 3

 

 



 

 



Vậy PTTS của



là:

1 4

 





 





 



x t

y t

z t

Chọn đáp án A.

Câu 35. Cho đường thẳng

( ): 1

 





 









x t

d y t

z t

và mp (P):

2 0

  

x y

. Tìm phương trình đường thẳng

nằm trong mặt phẳng (P) cắt và vuông góc với (d).

1 2

 





 









x t

y t

1 3

 





 









x t

y t

1 2

 





 









x t

y t

 





 









x t

y t

Hướng dẫn giải:

Gọi I là giao điểm của (d) và (P)

(1 ;1 ;2 ), ( ) 0 (1;1;0)

     

I t t t I P t I

(d) có vectơ chỉ phương

( 1; 1;2)

  



(P) có vectơ pháp tuyến

(1;1;0)





Vecstơ pháp tuyến của mặt phẳng cần tìm là



 



 

  

u u v

= (-2 ;2 ;0)

Phương trình mặt phẳng cần tìm là

1 2

 





 









x t

y t

Chọn đáp án A.

Câu 36. Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật .

   

ABCD A BCD

có điểm A

trùng với gốc tọa độ,

( ;0;0), (0; ;0), (0;0; )



B a D a A b

với

( 0, 0)

 

a b

. Gọi M là trung điểm của cạnh



. Giả sử

 

a b , hãy tìm giá trị lớn nhất của thể tích khối tứ diện



A BDM

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 113

Facebook: https://www.facebook.com/dongpay

max





A MBD

max 1





A MBD

max



 

A MBD

max





A MBD

Hướng dẫn giải:

Ta có:

( ; ;0), ( ;0; ), (0; ; ), ( ; ; ) ; ;

 

  



 

 

C a a B a b D a b C a a b M a a

Suy ra:

( ;0; ), (0; ; ), ; ;

 

 

     

 

 

  

A B a b A D a b AM a a

2 2

, ( ; ; ) , .

2 4



   

    

     

   

    

A MBD

a b a b

A B A D ab ab a A B A D A M V

, 0



a b

nên áp dụng BĐT Côsi ta được:

2 2

1 1 1 64

4 3

2 2 4 27

       a b a a b a b a b

Suy ra:

max





A MBD

Chọn đáp án A.

Câu 37. Cho













1;3;5 , 2;6; 1 , 4; 12;5

   A B C

và điểm





: 2 2 5 0

   

P x y z

. Gọi M là điểm

thuộc





sao cho biểu thức

4    

    

S MA MB MA MB MC

đạt giá trị nhỏ nhất. Tìm hoành độ

điểm M.



x B.

 

x C.



x D.

 

Hướng dẫn giải:

Gọi I là điểm





4 0 3;7; 3

   

  

IA IB I

Gọi G là trọng tâm ta m giác ABC





1; 1;3

  G

Nhận thấy, M,I nằm khác phía so với mp(P).

Có





3 3

  

S MI MG GI

. Dấu bằng xảy ra khi M là giao điểm của GI và (P)





1;3;1

 M

Chọn đáp án C.

Câu 38. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm





2;1; 1







0;3;1

và mặt phẳng





: 3 0

   

P x y z

. Tìm tọa độ điểm

thuộc

( )

sao cho

2 

 

MA MB

có giá trị nhỏ nhất.





4; 1;0

 M

. B.





1; 4;0

 M

. C.





4;1;0

. D.





1; 4;0

M

Hướng dẫn giải:

Gọi





; ;

I a b c

là điểm thỏa mãn

2 0

IA IB

 

 



, suy ra





4; 1; 3

 

Ta có

2 2 2 .

     

      

MA MB MI IA MI IB MI

Suy ra

2   

  

MA MB MI MI

Do đó

2 

 

MA MB

nhỏ nhất khi

nhỏ nhất hay

là hình chiếu của

trên mặt phẳng





Đường thẳng đi qua

và vuông góc với





có là

4 1 3

1 1 1

  

 



x y z

Tọa độ hình chiếu

của

trên





thỏa mãn

 

4 1 3

1 1

1; 4 0

;

3 0



 

  



 

















x z

x y

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 114

Facebook: https://www.facebook.com/dongpay

Chọn đáp án D.

Câu 39. Trong không gain Oxyz, cho hai đường thẳng

1 2 1

  

 



x y z

và

: 3

 





 





 



x t

d y t

. Mặt

phẳng





: 0

   

P ax by cz d

(với

; ; ;





a b c d

) vuông góc với đường thẳng

và chắn

1 2

d d

đoạn thẳng có độ dài nhỏ nhất. Tính

  

a b c d



Hướng dẫn giải:

Ta có mặt phẳng (P) vuông dóc với đường thẳng

nên (P) có véctơ pháp tuyến





1;2;1





n .

Phương trình (P) có dạng





: 2 0

   

P x y z d

Gọi M là giáo điểm của (P) với

và N là giao của (P) với

suy ra

2 2 10

; ;

6 3 6

  

 

 

 

d d d

4 1

; ; 2

3 3

   

 



 

 

d d

Ta có

16 155

18 9 9

  

d d

MN .

Để MN nhỏ nhất thì

nhỏ nhất, nghĩa là

 

d .

Khi đó

    

a b c d .

Chọn đáp án A.

Câu 40. Trong không gian với hệ trục tọa độ

Oxyz

, cho hai đường thẳng

1 2

1 2 1

 

 



x y z

và

2 1

2 1 2

 

 



x y z

. Gọi





là mặt phẳng chứa

sao cho góc giữa mặt phẳng





và đường

thẳng

là lớn nhất. Chọn mệnh đề đúng trong các mệnh đề sau:



Hướng dẫn giải:

qua





1; 2;0

M

và có VTCP





1;2; 1

 



u . Vì







d P

nên





M P



Pt mặt phẳng





có dạng:













2 2 2

1 2 0 0

       

A x B y Cz A B C

Ta có:





. 0 2

     

 

d P u n C A B

Gọi

 



 

2 2

4 3 4 3

, sin

3 2 4 5

 

     

 

A B A B

P d

A AB B

TH1: Với



B thì

2 2

sin

 

TH2: Với



B . Đặt



, ta được:

 

4 3

sin

3 2 4 5



 

 

t t





có vectơ pháp tuyến là 



1;1;2







qua điểm



0;2;0







song song với mặt phẳng





:7x  y  5z 3  0





cắt d

tại điểm



2;1;4



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 115

Facebook: https://www.facebook.com/dongpay

Xét hàm số

 

4 3

2 4 5





 

f t

t t

. Dựa vào bảng biến thiên ta có:

 

max

f x

khi

 

t khi

 

. Khi đó

 

5 3

sin 7

   f

So sánh TH1 và TH2

 

lớn nhất với

5 3

sin

 

khi

 

Vậy phương trình mặt phẳng





:7 5 9 0

   

P x y z

Chọn đáp án B

Câu 41. Trong không gian với hệ trục tọa độ Oxyz, cho

(1;0;2), (3;1;4), (3; 2;1)



A B C

. Tìm tọa độ điểm

S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng

3 11

và S có cao

độ âm.

( 4; 6;4)

 

. B.

(3;4;0)

. C.

(2;2;1)

. D.

(4;6; 4)



Hướng dẫn giải:

Ta có

(2;1;2); (2; 2; 1)

   

 

AB AC , suy ra 

 

AB AC

Tam giác ABC vuông nên I và S có thể sử dụng các tính chất của phép dụng tâm để tính.

Tính được IM.

( ) ,

 

   

 

  

MI ABC MI k AB AC k



 

AS MI

, tìm S.

, (3;6; 6)

 

 

 

 

AB AC

Gọi

1 5

3; ;

2 2



 

 

 

là trung điểm BC. Ta có:

2 2 2

3 11 9 81 9

2 2 4 2

 

      

 

 

IM IB BM IM

( ) , (3;6; 6) 9 .

      

MI ABC MI k AB AC k MI k

Suy ra

9 1

2 2

   

k k



thì









2 3;6; 6 4;6; 4

    

 

AS MI S

Chọn đáp án D.

Câu 42. Trong không gian với tọa độ

Oxyz

, cho đường thẳng

: 1 3



   

d y z

và mặt phẳng





: 2 5 0

   

P x y z

. Mặt phẳng





chứa đường thẳng

và tạo với





một góc nhỏ nhất có

phương trình

3 0.

  

x z B.

2 0.

   

x y z

3 0.

   

x y z

4 0.

  

y z

Hướng dẫn giải:

Gọi



là giao tuyến giữa





và





. Khi đó, góc giữa









P Q

nhỏ nhất khi chỉ khi

 

Đường thẳng

đi qua điểm





1; 1;3

M  

và có vectơ chỉ phương là





2;1;1





Vectơ chỉ phương của



là





3; 3; 3



    

  

u n u

Vectơ pháp tuyến của





là.





0;9; 9



   

  

Q d

n u u

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 116

Facebook: https://www.facebook.com/dongpay

Mặt phẳng





đi qua





1; 1;3

 M

và nhận vectơ pháp tuyến





0;1; 1

 



có phương trình

4 0

  

y z

Chọn đáp án D.

Câu 43. Trong không gian Oxyz, cho điểm và mặt phẳng . Mặt cầu S

có tâm I nằm trên mặt phẳng , đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng

. Phương trình mặt cầu S là:

A. hoặc

B. hoặc

C. hoặc

D. hoặc

Hướng dẫn giải:

Gọi là tâm của S.

Khi đó nên ta suy ra hệ

Giải hệ ta tìm được hoặc

Chọn đáp án D.

Câu 44. Trong không gian với hệ trục tọa độ , cho ba điểm và .

Mặt cầu tâm I đi qua và độ dài

(biết tâm I có hoành độ nguyên, O là gốc tọa

độ). Bán kính mặt cầu là

A. B. C. D.

Hướng dẫn giải:

Phương trình mặt cầu (S) có dạng:

Vì điểm thuộc mặt cầu (S) nên ta có hệ:

Suy ra

Chọn đáp án B.

Câu 45. Cho hình chóp O.ABC có OA=a, OB=b, OC=c đôi một vuông góc với nhau. Điểm M cố định

thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC), (OCA), (OAB) là 1,2,3. Khi

tồn tại a,b,c thỏa thể tích khối chóp O.ABC nhỏ nhất, giá trị nhỏ nhất của thể tích khối chóp O.ABC là

A. 18 B. 27

C. 6 D. Không tồn tại a,b,c thỏa yêu cầu bài toán





1,0, 1







: 3 0

P x y z

   





6 2



     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

2 2 1 9.

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

1 2 2 9

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

1 2 2 9

x y z

     





, ,

I x y z





, , 6 2

I P IO IA IO IA AO     

   

2 2

2 2 2 2

2 2 2 2 2 2

1 1

1 0

2 2 6 2 9

3 0

x y z x y z

x z

x y z x y z

x y z



      

   







        

 

 

   











2,2,1





1,2, 2

 

Oxyz









0;2;0 , 1;1;4

A B 





3; 2;1

C 





, ,

A B C

OI 







R 

2 2 2

2 2 2 0

x y z ax by cz d

      

, , ,

O A B C

( ) 4 4 0

( ) 2 2 8 18 0

( ) 6 4 2 14 0

A S b d

B S a b c d

C S a b c d

   

 

 

       

 

 

     

 

2 2 2 2

5 5 5

OI OI a b c

      

1; 0; 2; 4 3

a b c d R

        

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 117

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Chọn hệ trục tọa độ thỏa O(0,0,0), A(a,0,0), B(0,b,0), C(0,0,c)

Điểm M cố định thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC), (OCA),

(OAB) là 1,2,3 nên tọa độ điểm M là (1,2,3)

Phương trình mặt phẳng (ABC) là

Vì M thuộc mặt phẳng (ABC) nên

OABC

Áp dụng bất đẳng thức Cauchy ta có

Chọn đáp án B.

Câu 46. Cho hai điểm và hai mặt phẳng

. Viết phương trình đường thẳng qua cắt lần lượt tại sao

cho tam giác cân tại và nhận là đường trung tuyến.

A. B.

C. D.

Hướng dẫn giải:

Gọi , từ giả thiết suy ra là trung điểm của , suy ra .

nên có hai pt:

Tam giác cân tại nên:

Từ và có hệ:

Đường thẳng qua và có pt .

Chọn đáp án D.

Câu 47. Trong không gian với hệ tọa độ , cho đường thẳng hai điểm

và . Biết điểm thuộc thì nhỏ nhất.Tìm

A. B. C. D.

Hướng dẫn giải:

x y z

a b c

  

1 2 3

a b c

  

abc

1 2 3 1 1 1 1

1 3 . . 27

abc

a b c a b c

     









1;2;3 , 2;4;4

M A





: 2 1 0,

P x y z

   





: 2 4 0

Q x y z

   











B C

ABC

1 2 3

1 1 1

x y z

  

  

 

1 2 3

2 1 1

x y z

  

  



1 2 3

1 1 1

x y z

  

  

1 2 3

1 1 1

x y z

  

  







; ;

B a b c





2 ;4 ;6

C a b c

  









B P C Q

 









2 1 0 1 2 8 0 2 .

a b c a b c         ;









1; 2; 1 , 2 2 ;4 2 ;6 2 .

AM BC a b c

     

 

ABC





. 0 2 8 0 3 .

AM BC a b c     

 









1 , 2





   

2 1 0 0

2 8 0 3 0;3;2 , 2;1;4 .

2 8 0 2

a b c a

a b c b B C

a b c c

    

 

 

       

 

 

    

 



1 2 3

1 1 1

x y z

  

  



Oxyz

 

x t

y t t

z t

: 1 2



 



    















2;0;3





2; 2; 3

 





M x y z

0 0 0

; ;



MA MB

4 4





Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 118

Facebook: https://www.facebook.com/dongpay

Phương trình đường thẳng AB là: . Dễ thấy đường thẳng và AB cắt nhau tại

điểm suy ra AB và đồng phẳng.

Lại có .

Ta có: .

Do đó nhỏ nhất khi trùng với điểm

Chọn đáp án C.

Câu 48. Trong hệ trục tọa độ Oxyz cho 3 điểm với .Giả sử

thay đổi nhưng thỏa mãn không đổi. Diện tích tam giác ABC đạt giá trị lớn

nhất bằng

A. B. C. D.

Hướng dẫn giải:

Phương trình (ABC):

Gọi là hình chiếu vuông góc của O lên

Khi đó

Ta có

Áp dụng bất đẳng thức Cosi ta có

Dấu “=” xảy ra khi và chỉ khi

Vậy

Chọn đáp án B.

 

y t t

z t

1 1

3 3







 





 











2; 1;0













IA IB IA IB IA IB AB

0;1;3 , 0; 1; 3       

   

 

   

MA MB MA MB MA MB AB IA IB

2 4

4 4 2 2 4

1 1 1 1 1

2 2 2 8 8

 

       

 

 

MA MB

4 4







2; 1;0















;0;0 , 0; ;0 , 0;0;

A a B b C c

, , 0

a b c



, ,

a b c

2 2 2 2

a b c k

  

x y z

a b c

  





; ;

H x y z





ABC

 

     

2 2

2 2 2

2 2

2 2 2

2 2

2 2 2

ab c

ab bc ca

H ABC

bcx cay abz abc

a bc

OH AB ax by y

ab bc ca

OH AC ax cz

a b c

ab bc ca







 





  





  

      

  

 

   

 









 





     

2 2 2

abc

ab bc ca

 

 

1 1

. .

6 6

OABC

V OAOB OC abc

 

     

2 2 2

3 1

ABCD

ABC

S ab bc ca



    

4 4 4 4 4 4

2 2 2 2 2 2 4 4 4

2 2 2

a b b c c a

a b b c c a a b c

  

       

a b c

 

4 2

1 3

max

2 3 6

k k

S  

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 119

Facebook: https://www.facebook.com/dongpay

Câu 49. Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi qua điểm , cắt

các tia Ox, Oy, Oz tại A, B, C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất là

A. B. C. D.

Hướng dẫn giải:

Giá sử .

Khi đó PT mặt phẳng (P) có dạng: .

Ta có:  (1); (2)

(1)  ≥ 

Dấu "=" xảy ra   (P): .

Chọn đáp án B.

Câu 50. Trong không gian Oxyz cho 4 điểm , , , . Gọi M

là một điểm nằm trên đường thẳng CD sao cho tam giác MAB có chu vi bé nhất. Khi đó toạ độ điểm M

là:

A. B. C. D.

Hướng dẫn giải:

Tam giác MAB có độ dài cạnh không đổi, do đó chu vi bé nhất khi và chỉ khi

bé nhất.

; . Vì nên , suy ra điểm M cần tìm là hình

chiếu vuông góc của A, cũng là hình chiếu vuông góc của B lên đường thẳng

. Từ đó tìm ra

điểm .

Chọn đáp án A.

Câu 51. Trong không gian tọa độ Oxyz cho điểm và mặt cầu (S) có

phương trình: .Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện ABCD có thể

tích lớn nhất.

A. B. C. D.

Hướng dẫn giải:

Ta có (S) suy ra (S) có tâm I(1;0;-1), bán kính

Và

Mặt phẳng (ABC) có một vectơ pháp tuyến là

Suy ra mp(ABC) có phương trình:

Ta có nên lớn nhất khi và chỉ khi lớn nhất. Gọi

là đường kính của mặt cầu (S) vuông góc với mp(ABC). Ta thấy với D là 1 điểm bất kỳ

thuộc (S) thì .

(9;1;1)

  

7 3 3

x y z

  

27 3 3

x y z

  



27 3 3

x y z

   

27 3 3

x y z

A a Ox B b Oy C c Oz

( ;0;0) , (0; ;0) , (0;0; )

  

a b c

( , , 0)



x y z

a b c

  

M P

(9;1;1) ( )



a b c

9 1 1

  

OABC

V abc



abc bc ac ab

  

abc

3 9( )

abc abc abc

3 2

( ) 27.9( ) 243

  

bc ac ab

a b c

9 1 1







 



 



  







x y z

27 3 3

  





2;3;2





6; 1; 2

 





1; 4;3

C  





1;6; 5







0;1; 1







2;11; 9







3;16; 13

M 





1; 4;3

M  

4 3

AB 

MA MB







4; 4; 4

  







2;10; 8

 



. 0

ABCD



 

AB CD







0;1; 1



(0;1;1), (1;0; 3), ( 1; 2; 3)

A B C

   

2 2 2

2 2 2 0

x y z x z

     

7 4 1

; ;

3 3 3

 

 

 

 

1 4 5

; ;

3 3 3

 

 

 

 

7 4 1

; ;

3 3 3

 

 

 

7 4 1

; ;

3 3 3

 



 

 

2 2 2

:( 1) ( 1) 4

    

x y z

R 2



(1; 1; 4); ( 1; 3; 4)

AB AC

      

 

, ( 8;8; 4)

n AB AC

 

   

 

  

8x 8(y 1) 4(z 1) 0 2x 2y z 1 0

          

( ;( )).

ABCD ABC

V d D ABC S



ABCD

( ;( ))

d D ABC

1 2

D D





1 2

( ;( )) max ( ;( )); ( ;( ))

d D ABC d D ABC d D ABC



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 120

Facebook: https://www.facebook.com/dongpay

Dấu “=” xảy ra khi D trùng với D

hoặc D

Đường thẳng đi qua I(1;0;-1), và có VTCP là

Do đó (D

) có phương trình: .

Tọa độ điểm D

và D

thỏa mãn hệ:

Ta thấy: . Vậy điểm là điểm cần tìm

Chọn đáp án D.

Câu 52. Trong không gian

Oxyz

, cho điểm

1 3

; ;0

2 2

 

 

 

và mặt cầu





2 2 2

: 8.

  

S x y z

Đường

thẳng

thay đổi, đi qua điểm

cắt mặt cầu





tại hai điểm phân biệt. Tính diện tích lớn nhất

của tam giác

OAB

S . B.



S . C.

2 7

S . D.

2 2

S .

Hướng dẫn giải:

2 2 2

  

OH

HA R x

. Vậy diện tích tam giác

OAB

là

. . 8

  



OAB

S OH AB OH HA x x

Khảo sát hàm số

( ) 8

 

f x x x

trên





0;1

, ta được













0;1

max 1 7

 f x f

Vậy giá trị lớn nhất của





OAB

, đạt được khi



hay



H M

, nói cách khác là



d OM

Chọn đáp án A.

Câu 53. Cho mặt cầu





2 2 2

: 2 4 1 0

     

S x y z x z

và đường thẳng

: .

 











 



x t

d y t

z m t

Tìm

để

cắt





tại hai điểm phân biệt

A B

sao cho các mặt phẳng tiếp diện của





tại

và tại

vuông

góc với nhau.

1 2

D D

(2; 2;1)

ABC

n  



1 2

 





 





  



x t

y t

z t

2 2 2

1 2

( 1) ( 1) 4

x t

y t

z t

x y z

 











 









   













    



1 2

7 4 1 1 4 5

; ; & ; ;

3 3 3 3 3 3

   

   



   

   

D D

1 2

( ;( )) ( ;( ))

d D ABC d D ABC



7 4 1

; ;

3 3 3

 

 

 

 

Mặt cầu





có tâm



0;0;0



và bán kính R  2 2 .

Vì OM 1 R nên

thuộc miền trong của mặt cầu





. Gọi

là giao điểm của đường thẳng với mặt

cầu. Gọi

là chân đường cao hạ từ O của tam giác

OAB.

Đặt x  OH , ta có 0  x  OM 1, đồng thời

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 121

Facebook: https://www.facebook.com/dongpay

A. 1 m hoặc 4 m B. 0m hoặc 4 m

 

m hoặc



m D. Cả A, B, C đều sai

Hướng dẫn giải:

Để thỏa mãn yêu cầu đề bài thì trước tiên d phải cắt mặt cầu, tức là phương trình

       

2 2

2 2. 2 4. 1 0         t t m t t m t

có hai nghiệm phân biệt.

 

2 2

3 2 1 4 1 0      t m t m m

Phương trình có hai nghiệm phân biệt khi

 

' 0 1 3 12 3 0

       

m m m

5 1 0   m m .

Với phương trình có hai nghiệm phân biệt , áp dụng định lí Viet ta có

 

1 2 1 2

4 1 2

; 1

3 3

  

   

m m

t t t t m

Khi đó

   

1 1 1 2 2 2

1 ; ; 2 , 1 ; ; 2       

 

IA t t m t IB t t m t .

Vậy

















1 2 1 2 1 2

. 1 1 2 2 0

         

 

IA IB t t t t m t m t

    

1 2 1 2

3 1 2 1 0       t t m t t m

   

2 2

4 1 1 2 1 0

        m m m m

 







 



(TM).

Chọn đáp án A.

Câu 54. rong không gian với hệ tọa độ Oxyz cho ba điểm

     

1;01;1 , 1;2;1 , 4;1; 2A B C

và mặt

phẳng





: 0

  

P x y z

. Tìm trên (P) điểm M sao cho

2 2 2

 MA MB MC đạt giá trị nhỏ nhất. Khi

đó M có tọa độ





1;1; 1







1;1;1





1;2; 1







1;0; 1



Hướng dẫn giải:

phương trình tham số là

 





 









x t

y t

z t

Tọa độ M là nghiệm của hệ phương trình

 

2 1

1 1

1;0; 1

0 1

   

 

 

  

 

  

 

 

 

    

 

x t t

y t x

z t y

x y z z

Chọn đáp án D.

Câu 55. Trong không gian Oxyz, cho mặt cầu

 

2 2 2

: 4 6 0     S x y z x y m

và đường thẳng

 

1 1

2 1 2

 

 

x y z

. Tìm m để (d) cắt (S) tại hai điểm M, N sao cho độ dài MN bằng 8.

Gọi G là trọng tâm của tam giác ABC, ta có



2;1;0



, ta có

 MB

 MC

 3MG

GA

 GB

 GC





Từ hệ thức (1) ta suy ra :

 MB

 MC

đạt GTNN  MG đạt GTNN  M là hình

chiếu vuông góc của G trên (P).

Gọi (d) là đường thẳng qua G và vuông góc với (P) thì (d) có

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 122

Facebook: https://www.facebook.com/dongpay

 

m B.



m C.



m D.

 

Hướng dẫn giải:

(S) có tâm





2;3;0

I

và bán kính

   

2 2

2 3 0 13 13

       R m m m

Gọi H là trung điểm M, N

 

Đường thẳng (d) qua





0;1; 1



và có vectơ chỉ phương

   

2;1;2 ; 3

 

 

   

 



u AI

u d I d

Suy ra

 

2 2 2 2

; 4 3 5

    

R MH d I d

Ta có

13 5 13 25 12

       

m m m

Chọn đáp án D.

Câu 56. Trong không gian Oxyz, cho điểm













2;0; 2 , 3; 1; 4 , 2;2;0

   A B C

. Điểm D trong mặt

phẳng (Oyz) có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến

mặt phẳng (Oxy) bằng 1 có thể là:





0; 3; 1

 





0;2; 1







0;1; 1







0;3; 1



Hướng dẫn giải:









0; ;

 

D Oyz D b c

với



Theo giả thiết:

 





 

, 1 1 0; ; 1



     

 



 

 



c loai

d D Oxy c D b

Ta có













1; 1; 2 , 4;2;2 , 2; ;1

      

  

AB AC AD b

Suy ra

 

, 2;6; 2 , . 6 6

   

    

   

    

AB AC AB AC AD b

Cũng theo giả thiết, ta có:

, . 1 2





 

    



 

 



  

ABCD

V AB AC AD b

Chọn đáp án D.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 123

Facebook: https://www.facebook.com/dongpay

SỐ PHỨC

Câu 1. Cho hai số phức phân biệt thỏa điều kiện là số ảo. Khẳng định nào sau đây là

đúng?

A. B. C. D.

Hướng dẫn giải:

Thì là số ảo .

. .

Chọn đáp án A.

Câu 2. Gọi là 4 nghiệm phức của phương trình . Tìm tất cả các giá

trị m để .

A. B. C. D.

Hướng dẫn giải:

nếu hoặc

nếu

Khi đó

hoặc

Kết hợp lại thì thoả mãn bài toán.

Chọn đáp án D.

Câu 3. Tìm số phức z biết z thỏa mãn phương trình

A. 1 B. 1+i C. 1-i D. i

Hướng dẫn giải:

1 2

;

z z

1 2

z z





1 2

1; 1

z z

 

1 2

z z



1 2

z z



1 2

z z

 

2 1 2

z z z

   

1 2

z z





1 2 1 2

z z z z

 

 









  









 

 

1 2 1 2

1 2

z z z z

z z

 

  



















1 2 1 2 1 2 1

z z z z z z z z

      





1 1 2 2

2 0

z z z z

  

1 1 2 2

z z z z

  

1 2

z z

  

1 2 3 4

; ; ;

z z z z





4 2

4 4 0

z m z m

   

1 2 3 4

z z z z

   

 

 

 

  

1;2

4 2 2 2

3;4

4 4 0 4 0

z i

z m z m z z m

z m



 



        



 







1;2

3;4

z i

z i m



 







 







1 2 3 4

6 4 2

z z z z m





      



  











1 2 3 4

6 4 2

z z z z m





     



 











 

z 2

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 124

Facebook: https://www.facebook.com/dongpay

Chọn đáp án A.

Câu 4. Trong các số phức thỏa điền kiện , modun nhỏ nhất của số phức z bằng?

A. B. 2 C. 1 D. .

Hướng dẫn giải:

Giả sử số phức

Theo đề

Mà (thay (1) vào)

Chọn đáp án A.

Câu 5. Cho số phức thỏa mãn . Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

A. . B. . C. . D. .

Hướng dẫn giải:

Ta có . Mặt khác suy ra

Suy ra giá trị lớn nhất và giá trị nhỏ nhất là . Vậy tổng tổng giá trị lớn nhất và giá trị nhỏ nhất

của biểu thức là .

Chọn đáp án B.

Câu 6. Số phức z có mô đun lớn nhất và thỏa mãn điều kiện là:

A. B. C. D.

Hướng dẫn giải:

+ Gọi z=x+yi. Từ giả thiết ta có:

2 2

( 3) ( 2)

     

x y x y

2 2

2 2 2

z 2 z z.z 2z

a bi a b 2(a bi)

(a a b ) bi 2a 2bi

a 1

z 1

b 0

a a b 2a a a 0

b 2b b 0 a 0

z 0(loai)

b 0

    

     

 



 







 

    





 

 



   



 



 











4 2 2

z i i z

   

2 2

3 2

z x yi x y R

  

4 2 2

z i i z

   

2 2 2 2

(x 2) (y 4) (y 2)

4 0

4 (1)

x y

y x

      

   

  

2 2 2 2

(4 x)

z x y x    

2( 2) 8 2 2

x   





z i





1 1

1 1 1 1 1 1

i i i i

z z z z z z

          

1 1

  

1 3

2 2

 

3 1

2 2

 

1 3 2

Z i i   

1 3

z i

 

2 1

2 2

z i

 

3 1

2 2

z i

 

3 15

4 4

z i

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 125

Facebook: https://www.facebook.com/dongpay

+ Đồng thời

2 2

| | 

z x y

lớn nhất.

Chọn đáp án A.

Câu 7. Tính tổng mô-đun tất cả các nghiệm của phương trình:

A. 3 B. 4 C. 6 D. 8

Hướng dẫn giải:

Suy ra tổng mô-đun các nghiệm bằng 6.

Chọn đáp án C.

Câu 8. Gọi A, B, C lần lượt là các điểm biểu diễn của 3 số phức: .Diện

tích của tam giác ABC bằng:

A. B. C. D.

Hướng dẫn giải:

Dùng máy tính casio ta có A(1;2), B(3;1) ,C(0;2)

Dùng công thức Với

Dùng máy tính ta có kết quả B: S=1/2

(Có thể dùng công thức tính diện tích phần Oxy tính nhanh hơn)

Chọn đáp án B.

Câu 9. Cho số phức

 

1 2 1



 

 



z m

m i

. Số các giá trị nguyên của

để

 

z i

là



D. Vô số

Hướng dẫn giải:

Ta có

 





 





1 1 2 3 1 1

1 2 1 1 2 1 1 2

      



    

     

m i mi m m m i

z i i

m i m i m mi









       

2 2 2

3 1 1

1 2 1 2

3 1 1 1 2 3 1 1 1 4

5 6 1 0 1

  

    

   

             

        

m m i

z i

m mi m mi

m m i m mi m m m m

m m m

Vì

 



m Không có giá trị của

thỏa mãn.

Chọn đáp án A.

Câu 10. Cho hai số phức

1 2

;

z z

thỏa mãn

 

và

2 1



z iz

. Tìm giá trị nhỏ nhất của biểu thức

1 2



z z













2 3

1 0

z i z z i

   

 

  

2 3

3 3

1 0 1

1 0

z i

z i z z i z

z i

z iz

 



 







 

 



 



        











 

 





  











  



2 6

1 2i; (1 )(1 2 );

i i

S AB AC

 



 

 









2; 1;0 , 1;0;0

AB AC   

 

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 126

Facebook: https://www.facebook.com/dongpay









Hướng dẫn giải:

Bài toán này, thực chất là dựa trên kiến thức “ Biểu diễn

hình học số phức”. Ta thấy nếu đặt





1 1 1 1 1

;  



z x y i x y

. Khi đó điểm





1 1

;

M x y

là điểm

biểu diễn số phức

z thỏa mãn:

 

1 1

  i x y i

1 1

   ix y

 

1 1

   x y

. Suy ra tập hợp các điểm M biểu

diễn

z là đường trong

 

có tâm

 

0; 2I

và bán kính

R

Khi đó nếu N là điểm biểu diễn của số phức

z thì việc tìm GTNN của

1 2

z z

là việc tìm GTNN

của MN.

Theo đề thì

 

2 1 1 1 1 1

;     z iz y xi N y x

là điểm biểu diễn

z . Ta nhận thấy rõ ràng

1 1 1 1

. 0   

 

OM ON x y x y

 OM ON . Dễ nhận thấy

2 2

1 1

  OM ON x y

Ta có hình vẽ sau:

Do OMN là tam giác vuông cân tại O nên 2MN OM , do đó để MN nhỏ nhất thì OM nhỏ nhất.

Dễ thấy, OM nhỏ nhất khi

'M M

(M’ là giao điểm của OI với đường tròn như hình vẽ) Tức là

0; 2

 



 

 

. Khi đó

1 1

2 2 2 2

 

    

 

 

MN OM

Chọn đáp án A.

Câu 11. Trong mặt phẳng phức

Oxy

, trong các số phức

thỏa

1 1

  

z i

. Nếu số phức

có

môđun lớn nhất thì số phức

có phần thực bằng bao nhiêu ?

2 2

 

. B.

2 2



. C.

2 2



. D.

2 2



Hướng dẫn giải:

Gọi

 

,M x y

là điểm biểu diễn số phức

 

,  z x yi x y R

Gọi

là điểm biểu diễn số phức

 

Ta có:

1 1 1    z i MA

. Vậy tập hợp điểm biểu diễn số phức là hình tròn tâm

 

1,1 , 1 A R

như hình vẽ

Để

max z

 

max OM

 M thỏa hệ:

   

2 2

1 1 1



   





 





x y

y x

M’

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 127

Facebook: https://www.facebook.com/dongpay

2 2 2 2

2 2

 

   x x

Chọn đáp án A.

Câu 12. Trong mặt phẳng phức

Oxy

, các số phức

thỏa

2 1

   

z i z i

. Tìm số phức

được

biểu diễn bởi điểm

sao cho

ngắn nhất với





1,3



. B.

1 3



. C.

2 3



. D.

2 3

 

Hướng dẫn giải:

Gọi





M x y

là điểm biểu diễn số phức





,  

z x yi x y R

Gọi





1, 2



là điểm biểu diễn số phức

1 2



Gọi





0, 1



là điểm biểu diễn số phức



Ta có:

2 1     

z i z i ME MF



Tập hợp điểm biểu diễn số phức

là đường trung trục

: 2 0

  

EF x y

Để

ngắn nhất khi



MA EF

tại





3,1 3

   

M z i

Chọn đáp án A.

Câu 13. Trong các số phức z thỏa mãn







z i

. Tìm giá trị lớn nhất của

A. 1. B. 2. C.

Hướng dẫn giải:

Ta có:

(2 )(2 ) (2 )(2 )

2 2 2

1 . 1 . 1

2 0

2 2 2

    

  

     



 

  



z i z i iz iz

z i z i z i

z z

iz iz iz

Chọn đáp án A.

Câu 14. Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều

kiện sau:

3 4

  

z z i

3 4 0

  

x y

3 4 25 0

  

x y

3 4 0

  

x y

3 4 25 0

  

x y

Hướng dẫn giải:

Vì



z z

nên

3 4 3 4 3 4

       

z i z i z i

suy ra

3 4

  

z z i

3 4

   

z z i

3 4

 

 

z i

Tập hợp điểm có tọa vị z thỏa mãn

3 4

 



z i

là đường trung trực của đoạn thẳng OA, với





và





3 4



A i

. Đường trung trực này đi qua trung điểm

 



 

 

K i

của đoạn thẳng OA và

nhận véctơ





3 4





OA i

làm véctơ pháp tuyến nên có phương trình là:

 

3 4 2 0

 

   

 

 

x y

3 4 0

   

x y

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 128

Facebook: https://www.facebook.com/dongpay

Chọn đáp án A.

Câu 15. Điểm M biểu diễn số phức



z và điểm M’ biểu diễn số phức



. Nếu điểm M di động

trên đường tròn tâm A(-1;1) bán kính

R thì M’ di động trên đường nào?

2 2

2 2 0

   

x y x y B.

2 2 1 0

  

x y

2 2 1 0

  

x y

2 2 1 0

  

x y

Hướng dẫn giải:

Ta có

'  

. Do đó

2 2























x y

M di động trên đường tròn tâm A(-1;1) bán kính

R nên









2 2

2 2 2 2

1 1 2

2 2

2 2 0 0

2 2

1 0 2 ' 2 ' 1 0

   

  

      



       

 

x y

x y x y

x y

x y x y

Chọn đáp án C.

Câu 16. Tìm số thực

 m a b (a, b là các số nguyên khác 0) để phương trình

2 2( 1) (2 1) 0

    

z m z m có hai nghiệm phức phân biệt z

, z

thỏa mãn

1 2

 z z . Tìm a.

A. 1 B. 2 C. 3 D. 4

Hướng dẫn giải:

' 6 1

    

m m



TH1:

' 0 hay ( ;3 10) (3 10; )

       

Khi đó

2 2

1 2 1 2 1 2

10 2 10

     

z z z z z z

2 1 0

(1 ) 10

1 10 ( )

(1 ) (2 1) 2 1 10

2 1 0

3 20

6 11 0

  







 

 





        



 



 











  





m loai

m m m

m m

TH2:

' 0 hay (3 10;3 10)

    m

Khi đó:

2 2

1 2

1 ( 6 1) 1 ( 6 1)

10 10

2 2

         

    

m i m m m i m m

z z

Hay

2 2

(1 ) ( 6 1) 10 2

       

m m m m

Vậy m = 2 hoặc

3 20

 m

Chọn đáp án C.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 129

Facebook: https://www.facebook.com/dongpay

Câu 17. Cho các số phức z thỏa mãn



.Biết rằng tập hợp các điểm biểu diễn các số phức





3 2 2   

w i i z

là một đường tròn.Tính bán kính r của đường tròn đó.

A. 20 B.

D. 7

Hướng dẫn giải:

Đặt





, ,  



w x yi x y





 

   

2 2

3 2 2

3 2

2 8 2 1

2 5 5

2 8 2 1

5 5

6 4 7 0

3 2 20

   

     

  

   

   



   

   

  

   

   

     

    

w i i z

x yi i i z

x y i

x y x y

z i

x y x y

x y

Bán kính của đường tròn là

r

Chọn đáp án B.

Câu 18. Cho hai số phức u,v thỏa mãn

 

u v

và

3 4 2016

 u v . Tính

4 3

 

M u v

2984

2884

2894

Hướng dẫn giải:

Ta có



z z z

. Đặt

3 4

 

N u v

Khi đó

 









2 2

3 4 3 4 9 16 12      

N u v u v u v uv vu

Tương tự ta có





2 2

16 9 12   

M u v uv vu

Do đó





2 2

25 5000

   M N u v

Suy ra

2 2

5000 5000 2016 2984 2984

      M N M .

Chọn đáp án A.

Câu 19. Cho số phức z thoả mãn:

6 7

1 3 5









z i

. Tìm phần thực của số phức

2017

1008



1008

504

2017

Hướng dẫn giải:

Cho số phức z thoả mãn:

6 7

1 3 5









z i

. Tìm phần thực của số phức

2013

Gọi số phức ( , )

     



z a bi a b z a bi

thay vào (1) ta có

6 7

1 3 5

 

 





a bi i

a bi

( )(1 3 ) 6 7

10 10 3 ( 3 ) 12 14

10 5

9 3 (11 3 ) 12 14

  

         

     



a bi i i

a bi a bi a b i b a i

a b i b a i

9 3 12 1

11 3 14 1

  

 

 

 

  

 

a b a

b a b

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 130

Facebook: https://www.facebook.com/dongpay





     

504

2017 4 1008 1008

1 1 (1+i) 1 4 1 2 2            

a b z i z i i i

Chọn đáp án B.

Câu 20. Cho số phức

có mô đun bằng

2017

và

là số phức thỏa mãn biểu thức

1 1 1

 



z w z w

Môđun của số phức

bằng:

A. 1 B. 2 C. 2016 D. 2017

Hướng dẫn giải:

Từ

 

1 1 1 1

0 0

 



      

  

z w zw

z w

z w z w zw z w zw z w

2 2

2 2 2 2 2 2

1 3 1 3 1 3

0 0

4 4 2 4 2 2

 

   

               

 

   

 

   

 

i w

z w zw z zw w w z w w z w

Từ

w 3w 1 3

w w=

2 2 2 2

1 3

2 2

   

 

      

   

 

   

 

 

   

 

 

 

i i z

z z

Suy ra:

2017

w 2017

1 3

4 4

 



Chọn đáp án D.

Câu 21.

Biết số phức Z thỏa điều kiện

3 3 1 5

   

z i

. Tập

hợp

các điểm biểu diễn của Z tạo thành một hình phẳng. Diện tích của

hình phẳng đó bằng



Hướng dẫn giải:

Đặt z=x+yi

2 2

3 1 1 ( 3) ( 1) ( 3)

         z i x y i x y

Do đó

2 2

3 3 1 5 9 ( 1) ( 3) 25

         

z i x y

Tập hợp các điểm biểu diễn của Z là hình phẳng nằm trong

đường tròn

Tâm I (1 ;3) với bán kính bằng R=5 đồng thời nằm ngoài

đường tròn tâm I (1 ;3) với bán kính r=3

Diện tích của hình phẳng đó là

2 2

.5 .3 16

     

Chọn đáp án A.

Câu 22. Số Phức cho ba số phức

1 2 3

, ,

z z z

thỏa mãn

1 2 3

  

z z z

và

1 2 3

  

z z z . Mệnh đề

nào sau đây là sai.

A. Trong ba số đó có hai số đối nhau.

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 131

Facebook: https://www.facebook.com/dongpay

B. Trong ba số đó phải có một số bằng 1.

C. Trong ba số đó có nhiều nhất hai số bằng 1.

D. Tích của ba số đó luôn bằng 1.

Hướng dẫn giải:

Ta có:

1 2 3 1 2 3

1 1

      

z z z z z z

Nếu

1 0

 

z thì

2 3 2 3

    

z z z z

Nếu

1 0

 

z thì điểm P biểu diễn số phức

1 2 3

  

z z z

không trùng với góc tọa độ O.

Gọi M là điểm biểu diễn của số phức



và A là điểm biểu diễn của số 1.

Khi đó ta có  

  

OA OM OP

(do P là điểm biểu diễn của số





 

) nên OAPM là hình bình

hành. Mà

1 2 3

  

z z z

nên các điểm biểu diễn cho ba số

1 2 3

, ,

z z z

đều nằm trên đường tròn

đơn vị. Ta cũng có

 

OA OM nên OAPM là hình thoi. Khi đó ta thấy M, A là giao điểm của

đường trung trực đoạn OP với đường tròn đơn vị.

Tương tự do P cũng là điểm biểu diễn của

2 3



z z

, nếu M’ và A’ là hai điểm biểu diễn của số

2 3

z z

thì ta cũng có M’, A’ là giao điểm đường trung trực của OP và đường tròn đơn vị.

Vậy

' , '

 

M M A A

hoặc ngược lại. Nghĩa là

2 3 1

  

z z z

hoặc

3 2 1

  

z z z

Do đó A, B là mệnh đề đúng.

C đúng là hiển nhiên, vì nếu ba số đều 1 một thì tổng bằng 3.

D sai vì với

1 2 3

2 2 2 2

1, ,

2 2 2 2

     

z z i z i

thỏa hai tính chất trên của đề bài nhưng

1 2 3



z z z .

Chọn đáp án D.

Câu 23. Cho là số phức có mô đun bằng 2017 và là số phức thỏa mãn . Mô đun

của số phức là

A. 2015 B. 1 C. 2017 D. 0

Hướng dẫn giải:

Từ ta suy ra

Lấy mô đun hai vế ta có .

Chọn đáp án C.

Câu 24. Cho số phức z thoả mãn điều kiện . Tìm giá trị nhỏ nhất của

A. B. 2 C. D. 2

Hướng dẫn giải:

Các điểm M biểu diễn số phức z thoả mãn nằm trên đường tròn (C) tâm I(2; −3) và

bán kính R = .

(Ý nghĩa hình học của : độ dài OM)

Ta có |z| đạt giá trị nhỏ nhất  điểm M(C) và OM nhỏ nhất.

(Bài toán hình học giải tích quen thuộc)

Ta có: OM OI – IM = OI – R = .

Dấu « = » xảy ra khi M là giao điểm của (C) và đoạn thẳng OI.

1 1 1

w w

z z

 



1 1 1

w w

z z

 



2 2

w w 0

z z

  

w 3w 1 3

2 2 2 2

i i

z z

   

 

      

   

 

   

 

   

w 2017

z  

2 3 3

z i

  

13 3



13 2



2 3 3

z i

  





13 3

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 132

Facebook: https://www.facebook.com/dongpay

Vậy GTNN của là: .

Chọn đáp án A.

Câu 25. Cho số phức thỏa mãn: . Tìm giá trị nhỏ nhất của .

A. 1 B. 2 C. 3 D. 4

Hướng dẫn giải:

Giả sử , ta có:

Đặt

Đặt .

Dấu “=” xảy ra khi .

Vậy .

Chọn đáp án A.

Câu 26. Tìm phần thực của số phức thỏa mãn phương trình

A. 5 B. 6 C. 7 D. 8

Hướng dẫn giải:

Điều kiện n > 3,

Phương trình (so đk)

Vậy phần thực của số phức z là 8.

Chọn đáp án D.

Câu 27. Cho số phức thỏa mãn và số phức . Khi đó mô đun của số phức là:

A. B. C. D.

Hướng dẫn giải:

Giả sử

Xét (vô lí)

Nên



13 3

3 4 4

z i

  

z a bi

 









2 2

3 4 4 3 4 16

a bi i a b

        

3 4sin 3 4sin

4 4cos 4cos 4

a a

b b

 

   

 



 

   

 

2 2 2 2

9 16sin 24sin 16cos 16 32cos

41 24sin 32cos

3 4

41 40( sin cos )

5 5

z a b

   

 

        

  

3 4

cos ,sin

5 5

 

 

2 2

41 40sin( ) 1

z a b

 

      

2 2

k k

 

     

        

Min z



z (1 i) , n

  



4 4

log (n 3) log (n 9) 3

   





4 4 4

log (n 3) log (n 9) 3 log (n 3)(n 9) 3 n 7

         

 

7 3

z (1 i) (1 i). 1 i (1 i)(2i) 8 8i

 

        

 



2 1







w 2



1 w 2.

 

w 1



w 2







, .

z a bi a b

  



2 2

1 1.

z a b

   

 

4 2 1

2 1

a b

b a

 







 

 

2 2

4 2 1

2 1

1 1 ... 1.

a b

b a

 



      



 



Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 133

Facebook: https://www.facebook.com/dongpay

Chọn đáp án C.

Câu 28. Cho các số phức thỏa mãn . Biết rằng tập hợp các điểm biểu diễn các số phức

là một đường tròn. Tính bán kính của đường tròn đó?

A. B. C. D.

Hướng dẫn giải:

Giả sử

Theo đề

suy ra bán kính đường tròn là .

Chọn đáp án A.

Câu 29. Tìm phần ảo của số phức , biết số phức z thỏa mãn

A. B. C. D.

Hướng dẫn giải:

Ta thấy lập thành một cấp số nhân gồm 2018 số hạng với công bội

Suy ra

Vậy phần ảo của z là .

Chọn đáp án B.

Câu 30. Cho các số phức

thỏa mãn



. Biết rằng tập hợp các điểm biểu diễn các số phức

(3 4 )

  

w i z i

là một đường tròn. Tính bán kính r của đường tròn đó.

A. r  4. B. r  5. C. r  20. D. r  22.

Hướng dẫn giải:

Gọi

 

w a bi

, ta có





( 1) (3 4 )

( 1)

(3 4 )

3 4 9 16

  

 

       

 

a b i i

a b i

w a bi i z i z

i i

2 2

(3 4 4) (3 4 3)

3 4 4 (3 4 3)

25 25 25

    

   

   

a b b a

i z

Mà

= 4 nên

2 2 2 2 2

(3 4 4) (3 4 3) 100 2 399

          a b b a a b b

Theo giả thiết, tập hợp các điểm biểu diễn các số phức

(3 4 )

  

w i z i

là một đường tròn nên ta có

2 2 2 2

2 399 ( 1) 400 400 20

         

a b b a b r

1 2

 





w i z

1 3 2

  







 

z a bi w x yi a b x y a b

; ; , , , 1 4

        











 

x a b x a b

w i z x yi i z

y b a y b a

2 3 3 1 3

1 3 2 1 3 2

3 3 3 1

 

      

 

         

 

     

 

 

 









 





 

x y a b b a a b

2 2 2

2 2

3 3 1 3 1 3 4 1 16

 

             

 

 

 





x y

3 3 16

    

16 4

 

   

2 2017

. 2 1 ... 1 .

i z i i i      

1009



1009

   

2 2017

1; 1 ; 1 ; ........; 1i i i  



q i

 

 

2018

2018 1

1 1

. 1

i z S u i i i

q i

 



     



     

1009

2018 2 1009

1009

1 1 1 1 1 2 1 2

1 2

z i i i i

z i

 

          

 

  

1009

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 134

Facebook: https://www.facebook.com/dongpay

Chọn đáp án C.

Câu 31. Với hai số phức

z và

z thỏa mãn

1 2

8 6  z z i và

1 2

 

z z

. Tìm giá trị lớn nhất của

1 2

 P z z

A. 5 3 5 P . B. 2 26P . C. 4 6P . D. 34 3 2 P .

Hướng dẫn giải:

Đặt

1 2

, 

OA z OB z

( với O là gốc tọa độ,

,A B

là điểm biểu diễn của

1 2

,z z ).

Dựng hình bình hành OACB, khi đó ta có

1 2 2 1

2, 10, 5      AB z z OC z z OM

Theo định lý đường trung tuyến ta có

 

2 2 2

2 2

2 2 2

1 2

52 52

 

      

OA OB AB

OM OA OB z z

Ta có

 

2 2

1 2 1 2 max

2 2 26 2 26     z z z z P

Chọn đáp án B.

Bấm Tải xuống để xem toàn bộ.

| 1/134

| | Tải xuống

Preview text:

Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 MỤC LỤC
HÀM SỐ ............................................................................................................................................ 3
HÌNH ĐA DIỆN............................................................................................................................... 27
I – HÌNH CHÓP .......................................................................................................................... 27
II – HÌNH LĂNG TRỤ ................................................................................................................ 41
MŨ - LÔ GARIT ............................................................................................................................. 49
HÌNH NÓN - TRỤ - CẦU .............................................................................................................. 66
NGUYÊN HÀM , TÍCH PHÂN VÀ ỨNG DỤNG .......................................................................... 81
HÌNH HỌC TỌA ĐỘ KHÔNG GIAN OXYZ ............................................................................... 96
SỐ PHỨC ....................................................................................................................................... 123
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 HÀM SỐ
Câu 1. Cho hàm số y  x3  mx  2 có đồ thị (Cm). Tìm m để đồ thị (Cm) cắt trục hoành tại một điểm duy nhất. A. m  3 B. m  3 C. m  3 D. m  3 Hướng dẫn giải: 3
Số giao điểm của đồ thị (Cm) với Ox là số nghiệm của phương trình x  mx  2  0
Với m = 0 vô nghiệm nên không có giao điểm Với m  0 ta có 2 m  x2   f (x);(*) x 2 2(x3  1)
f '(x)  2x   0  x  1 x2 x2
Ta có bảng biến thiên của f(x) như sau: x  0 1  f '(x) + + 0 - f (x)  -3   
Số nghiệm phương trình (*) là số giao điểm của đồ thị hàm f(x) và đường thẳng y=m.
Dựa vào bảng biến thiên ta thấy m  3 thì phương trình (*) có 1 nghiệm duy nhất. Chọn đáp án B. Câu 2. Cho hàm số: 4 2 2
y  x  2(m  2) x  m  5m  5 . Với giá trị nào của m thì đồ thị hám số có
cực đại và cực tiểu, đồng thời các điểm này tạo thành một tam giác đều A. 3 m  2  3 B. 2  3 C. 3  2 D. 3 3  2 Hướng dẫn giải: Ta có: 3
y '  4 x  4(m  2) x x  0 y '  0   2 x  2  m 
Hàm số có CĐ, CT  PT f ' x  0 có 3 nghiệm phân biệt  m  2 (*)
Khi đó toạ độ các điểm cực trị là: 2
A 0, m  5m  5 , B
2  m;1 m , C  2  m;1 m          2 2 AB 
2  m;  m  4m  4 ; AC   2  m;  m  4m  4 Do ABC luôn cân tại A, nên bài       1 A . B AC toán thoả mãn khi  0 
A  60  cos A  3
    0  m  2  3 2 AB AC Chọn đáp án A. 1 Câu 3. Cho hàm số 3 2
y = x  x có đồ thị là (C). Tìm tất cả những điểm trên đồ thị (C) sao cho hệ 2 2 4x + 3
số góc của tiếp tuyến với đồ thị (C) tại những điểm đó là giá trị lớn nhất của hàm số g(x) = 4 x +1  1   3   4 40  A. ; 0 B. 1  ;  ;     ;    2   2   3 27 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  2 1 2   2 1   2   1  C.   ;   ;  ;  D. ; 0 ;  2  ; 1  0    2 4      2 4    2  Hướng dẫn giải: 2 4x + 3
* Tìm giá trị lớn nhất của hàm số: g(x) = 4 x +1 t 4 + 3
- Đặt t = x2, với t  0 ta có hàm số g(t) = ; 2 t +1 2 4  t  6t + 4 1 - g'(t) = ; g’(t) = 0  t = 2  ; t = ; 2 2 (t +1) 2
- Ta lại có: lim g(t)  0 ; lim g(t)  0 , bảng biến thiên của hàm số: t  t  t  –2 0 1  2 g’(t) – 0 + + 0 – 4 g(t) 0 3 0 –1 2
- Vậy giá trị lớn nhất của hàm số là g(x) = 4, đạt được khi x   2
* Tìm các điểm thuộc đồ thị (C)
- Ta có: y’ = 3x2 – x, giả sử điểm M0(x0, f(x0))(C), thì hệ số góc tiếp tuyến của (C) tại M0 là f’(x 2 0)= 3x  x 0 0 2 4 3 4 40
- Vậy: 3x  x = 4 suy ra x0 = –1; x0 =
, tung độ tương ứng f(–1) = – ; f( ) = 0 0 3 2 3 27  3   4 40 
+ Có hai điểm thỏa mãn giải thiết 1  ;  ; ; .      2   3 27  Chọn đáp án B. 2x  4
Câu 4. Cho hàm số y 
có đồ thi C  điểm ( A 5
 ;5) . Tìm mđể đường thẳng y  x  m cắt x 1
đồ thị C  tại hai điểm phân biệt M và N sao cho tứ giác OAMN là hình bình hành (O là gốc toạ độ). A. m  0
B. m  0; m  2 C. m  2 D. m  2 Hướng dẫn giải:
Do các điểm O và Athuộc đường thẳng  : y  x nên để OAMN là hình bình hành thì
MN  OA  5 2 2x  4
Hoành độ của M và N là nghiệm của pt: 2
 x  m  x  (3  )
m x  (m  4)  0 (x  1  ) (1) x  1 Vì 2
  m  2m  25  0, m  ,nên  
1 luôn có hai nghiệm phân biệt, dluôn cắt C tại hai điểm phân biệt
x  x  m  3
Giả sử x , x là nghiệm của   1 1 2 ta có:  1 2
x x  (m  4)  1 2 Gọi 2 2 2 2
M ( x ; x  m), N (x ; x  m)  MN  2( x  x )  2 (x  x )  4x x   2m  4m  50 1 1 2 2 1 2 1 2 1 2  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 m  2 2
MN  5 2  2m  4m  50  50  m  0  + m  0 thì , O ,
A M,N thẳng hàng nên không thoã mãn. + m  2 thoã mãn. Chọn đáp án C. x  2
Câu 5. Cho hàm số: y 
C . Tìm a sao cho từ A(0, a ) kẻ được hai tiếp tuyến đến (C) nằm ở x 1 hai phía trục Ox.  2    2   A. ;  B.  2  ;  \  1 C.  2  ;  D. ;  \     1    3   3  Hướng dẫn giải:
Đường thẳng qua A(0, a ) có hệ số góc k có phương trình y  kx  a tiếp xúc (C) x  2
<=> kx  a 
có nghiệm kép <=> kx  a x  
1  x  2 có nghiệm kép x 1 <=> 2
kx  k  a  
1 x  a  2  0 có nghiệm kép k  0  k  0     
có 2 nghiệm k phân   
k  a  2
1  4k a  2  0 
h(k )  k  2 
a  5 k  a  2 2 1  0  biệt
  12 a  2  0   
 a 2;  \  1   1
h(0)   a  2 1  0   k  a 1 k  a  1 1   1   x   y   1 1  2k 2 Khi đó 1  k  a 1 k  a 1  2   2   x   y  2 2  2k 2  2 Mà
y y  0  k  a 1  k  a 1   0 1 2  1    2  
 k k  a  
1 k  k   a  2 1  4  3a  2  0 1 2 1 2   2   a  2 3  2  
Từ (1) và (2)  a  ;  \     1  3  Chọn đáp án D. 3x 1
Câu 6. Hai điểm M, N thuộc hai nhánh của đồ thị y 
. Khi đó độ dài đoạn thẳng MN ngắn nhất x  3 bằng? A. 8 B. 4 C. x  3 D. 8 2 . M Hướng dẫn giải:  8   8 
Giả sử x  3 , x  3 , khi đó M 3  ; m 3  , N 3  n;3 
với m, n  0 M N      m   n 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2 8 8  1 1     64 2 2 2 
MN  (m  n)    (2 mn )  64    2 .   4 mn   64   m n  m n     mn   
 MN  8 . Kết luận MN ngắn nhất bằng 8 Chọn đáp án A. Câu 7. Cho hàm số 3 2
y  x  3mx  3m 1 . Với giá trị nào của m thì đồ thị hàm số đã cho có cực
đại và cực tiểu đối xứng nhau qua đường thẳng d : x  8 y  74  0 A. m  1 B. m  2  C. m  2 D. m  1  Hướng dẫn giải: + 2 y '  0  3x 
 6mx  0 . Đồ thị có 2 điểm cực trị khi: m  0
+ Phương trình đường thẳng đi qua 2 điểm cực trị là: y = 2m2.x - 3m - 3
+ Trung điểm 2 điểm cực trị là 3 I ( ;
m 2m  3m 1)
+ Điều kiện để 2 điểm cực trị đối xứng qua d : x  8 y  74  0  1 2 2m .( )  1   8 3
m  8(2m  3m 1)  74  0 
+ Từ đó thấy m = 2 thỏa mãn hệ trên. Chọn đáp án C. 1 1 1  m 2 2 x
Câu 8. Cho f  x  x  1  e . Biết rằng  
1 . 2. 3... 2017  n f f f f
e với m, n là các số tự nhiên m và tối giản. Tính 2 m  n . n A. 2
m  n  2018 . B. 2 m  n  2  018 . C. 2 m  n  1. D. 2 m  n  1  . Hướng dẫn giải:
Xét các số thực x  0
x  x  2 2 2 1 1 1 x  x  1 1 1 1 Ta có: 1      1   1   . 2 x  x  2 1 x  x  2 2 2 1 x  x x  x   1 x x  1 2  1 1   1 1   1 1   1 1  1 2018 1 1   1   1    1          2018
Vậy, f   f   f   f    1 2   2 3   3 4   2017 2018  2018 2018 1 . 2 . 3 ... 2017  e  e  e , 2 m 2018  1 hay  n 2018 2 2018  1 Ta chứng minh là phân số tối giản. 2018
Giả sử d là ước chung của 2 2018  1 và 2018 Khi đó ta có 2 2018  1d , 2
2018d  2018  d suy ra 1d  d  1 2 2018  1 Suy ra
là phân số tối giản, nên 2
m  2018  1, n  2018 . 2018 Vậy 2 m  n  1  . Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
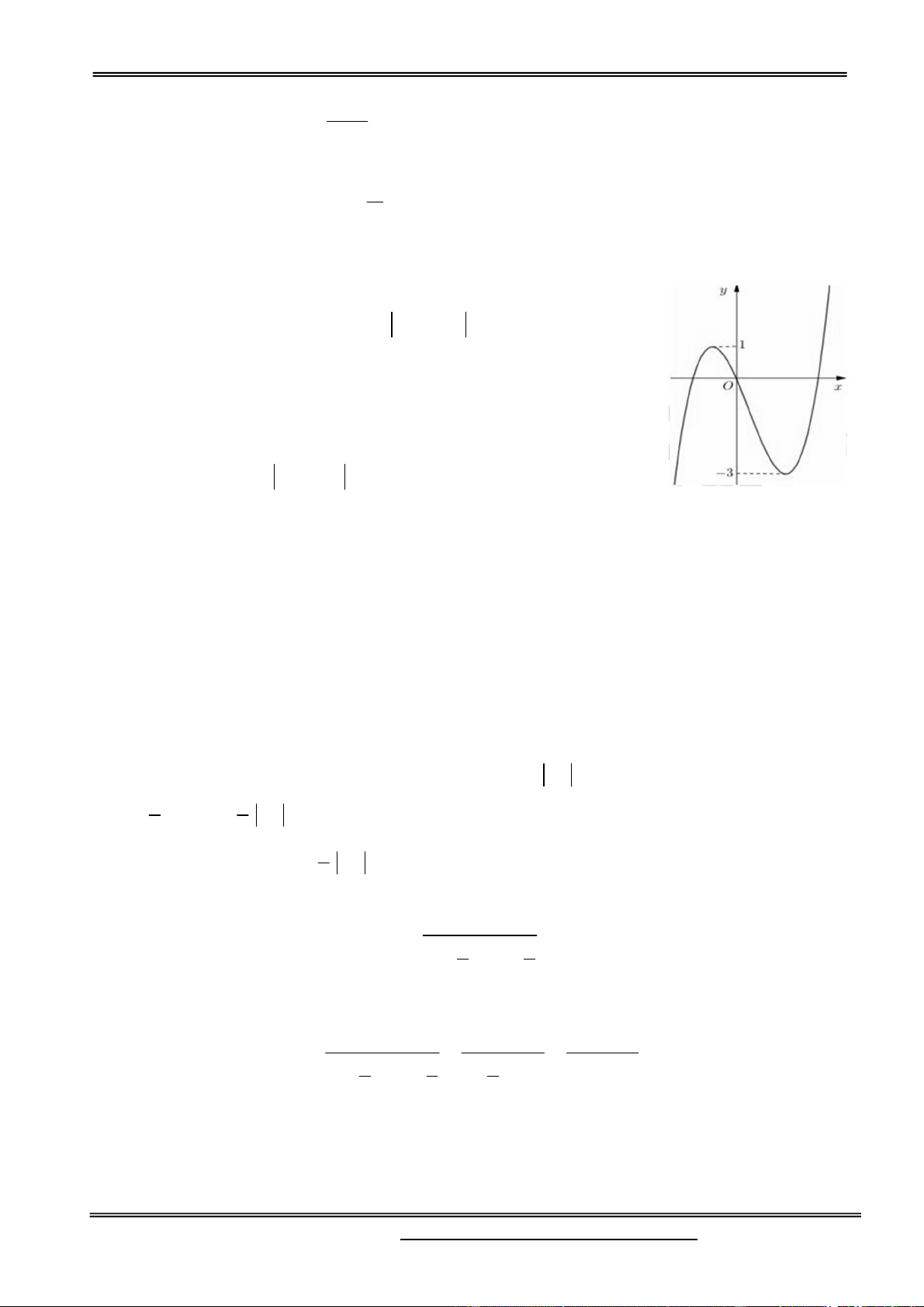
Câu 9. Cho hàm số y  f (x) có đồ thị y  f (  x) cắt trục
Ox tại ba điểm có hoành độ a  b  c như hình vẽ. Mệnh
đề nào dưới đây là đúng?
A. f (c)  f (a)  f (b).
B. f (c)  f (b)  f (a).
C. f (a)  f (b)  f (c).
D. f (b)  f (a)  f (c). Hướng dẫn giải:
Đồ thị của hàm số y  f (
 x) liên tục trên các đoạn ; a b và  ;
b c , lại có f (x) là một nguyên hàm của f (  x) .  y  f (  x)   y  0
Do đó diện tích của hình phẳng giới hạn bởi các đường:  là: x  a  x  b  b b b S  f (
 x) dx   f (
 x)dx   f x
 f a  f b . Vì S  0  f a  f b   1 1     1         a a a  y  f (  x)   y  0
Tương tự: diện tích của hình phẳng giới hạn bởi các đường:  là: x   b x   c c c c S  f (  x) dx  f (
 x)dx  f x
 f c  f b . S  0  f c  f b 2 . 2     2         b b b
Mặt khác, dựa vào hình vẽ ta có: S  S  f a  f b  f c  f b  f a  f c 3 . 1 2            
(có thể so sánh f a với f b dựa vào dấu của f (
 x) trên đoạn  ;
a b và so sánh f b với f c
dựa vào dấu của f (
 x) trên đoạn  ; b c ). Từ (1), (2) và (3) Chọn đáp án A.
Câu 10. Tìm tất cả các giá trị thực của tham số m để hàm số y  2m  
1 x  3m  2cos x nghịch biến trên .  1 1 1 A. 3   m   . B. 3   m   . C. m  3  . D. m   . 5 5 5 Hướng dẫn giải: TXĐ: D  
Ta có: y  (2m  1)  (3m  2) sin x
Để hàm số nghịch biến trên  thì y  0,x tức là: (2m  1)  (3m  2)sin x  0 (1) ,x 2 7 +) m   thì (1) thành   0,x 3 3 2 1  2m 1  2m 5m  1 2 1 +) m  
thì (1) thành sin x    1   0    m  3 3m  2 3m  2 3m  2 3 5
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 1  2m 1  2m m  3 2
+) m   thì (1) thành sin x    1    0  3   m   3 3m  2 3m  2 3m  2 3 1 Kết hợp được: 3   m   5 Chọn đáp án A.
Câu 11. Tìm tất cả các giá trị của m để hàm số: 3
y  x  m   2 2 3
1 x  6m  2 x  3 nghịch biến trên
khoảng có độ dài lớn hơn 3
A. m  0 hoặc m  6 B. m  6 C. m  0 D. m  9 Hướng dẫn giải:
Dùng BBT để xét sự đồng biến và nghịch biến của hàm số trên các khoảng 2
y '  6x  6m  
1 x  6m  2 x
  m  2  m   2 ' 9 1 36
2  9m  54m  81  0
Dấu bằng xảy ra khi m  3
Gọi x , x là 2 nghiệm của phương trình y '  0 x  x 1 2  1 2
x  x  1  m Theo viet: 1 2
x .x  m  2  1 2 Ta có BBT t  x1 x2  y’ + 0 - 0 + y
Vậy hàm số đồng biến trên khoảng  x , x  pt y '  0 phải có 2 nghiệm phân biệt  m  3 1 2 
Gọi Độ dài khoảng nghịch biến của hàm số là D 2 2
D  x  x   x  x  1  m
 4 m  2  m  6m  9 1 2      2 1 2 2
D  3  D  9 2 2
 m  6m  9  9  m  6m  0  m  0 hoặc m  6 (thỏa mãn) Chọn đáp án A. x  1
Câu 12. Cho hàm số y 
có đồ thị (C) và A là điểm thuộc (C). Tìm giá trị nhỏ nhất của tổng các x 1
khoảng cách từ A đến các tiệm cận của (C). A. 2 2 B. 2 C. 3 D. 2 3 Hướng dẫn giải:  m  1 Gọi M ; m
 C m    
1 . Tổng khoảng cách từ M đến 2 đường tiệm cận x  1 và y  1 là  m  1  m  1 2 2 S  m 1  1  m 1   2 m  1 .  2 2 m 1 m 1 m 1 2
Dấu “=” xảy ra  m 1   m 1  2  m  1  2 m 1 Chọn đáp án A. 2x  1
Câu 13. Cho hàm số y 
C  . Tìm k để đường thẳng d : y  kx  2k 1 cắt (C) tại hai điểm x  1 phân biệt ,
A B sao cho khoảng cách từ A và B đến trục hoành bằng nhau. A. 12 B. 4 C. 3  D. 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải:
Phương triình hoành độ giao điểm của (C) và d:
2x  1  kx  2k 1 2x 1  x  1kx  2k  1; x   1 x  1 2  x k  3k  
1 x  2k  0   1 ;  x    1
d cắt (C) tại hai điểm A, B phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt khác 1. k  1  k  0  2 
   k  6k 1  0   . 
k  3  2 2  k  3  2 2  k   2 1  3k   1   1  2k  0 
Khi đó: A x ; x k
 2k  1 , B x ; x k
 2k  1 với x , x là nghiệm của (1). 1 1   2 2  1 2  3  k  1 x  x  Theo định lý Viet tao có 1 2  k . x x  2  1 2 Ta có d  ;
A Ox  d  B;Ox  x k  2k 1  x k  2k  1 1 2
kx  2k  1  x k  2k  1 x  x 1 2 1 2     .
kx  2k  1   x k  2k  1 k x  x  4k  2  0  1 2   1 2 
Do hai điểm A, B phân biệt nên ta loại nghiệm x  x . Do đó k  x  x  4k  2  0  k  3  . 1 2  1 2 Chọn đáp án C. x  4
Câu 14. Nếu đồ thị hàm số y 
cắt đường thẳng (d ) : 2x  y  m tại hai đểm AB sao cho độ dài x  1 AB nhỏ nhất thì A. m=-1 B. m=1 C. m=-2 D. m=2 Hướng dẫn giải:
Phương trình hoành độ giao điểm
x  4  2x  m (x  1  ) x  1 2
 2x  (m  3)x  m  4  0 2
  (m  1)  40  0,m  R
Suy ra (d) luôn cắt dồ thị hàm số tại hai điểm A,B m  3 m  4 x  x  ; x .x  ; A B 2 A B 2 y  2x  ; m y  2  x  m A A B B y  y  2  (x  x ) B A B A 2 2 2 AB 
(x  x )  ( y  y )  5(x  x ) B A B A B A 2  m 3  m 4     5 
5  (x  x )  4x x   5 m B A A B   4          2 2 1  40  5 2 2 2 4       
Vậy AB nhỏ nhất khi m=-1 Chọn đáp án A. Câu 15. Cho hàm số 3 2
y  x  mx   2 m   2 3 3
1 x  1  m . Tìm m để trên đồ thị hàm số có hai điểm đối xứng qua gốc tọa độ A. 1
  m  0 hoặc m  1 B. 1
  m  0 hoặc m  1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
C. 1  m  0 hoặc m  1 
D. 1  m  0 hoặc m  1  Hướng dẫn giải:
Gọi hai điểm đối xứng nhau qua O là A x , y , B x ,  y 0 0   0 0  Khi đó ta có 3 2
y  x  3mx  3 2 m   2
1 x  1  m và 3 2
 y  x  3mx  3 m  1 x  1  m 0 0 0  2  2 0 0 0 0 0 Từ đó suy ra: 2 2 6  mx  2  2m  0(*) 0 Nếu x  0 thì 2 2  2m  0 suy ra 2
y  1  m  0 . Vậy A  B  O 0 0
Do đó: đồ thị hàm số có hai điểm đối xứng nhau qua gốc tọa độ O m  0  
 phương trình (*) có nghiệm khác 0 2  2  2m  0  1
  m  0 hay m  1 '  6  m  2 2  2m   0  Chọn đáp án B. Câu 16. Cho hàm số 3 2 3
y  x  3mx  m có đồ thị C và đường thẳng 2 3
d : y  m x  2m . Biết rằng m  m , m m  m
là hai giá trị thực của m để đường thẳng d cắt đồ thị C
tại 3 điểm phân biệt có m  1 2  1 2 
hoành độ x , x , x thỏa 4 4 4 x  x  x
 83 . Phát biểu nào sau đây là đúng về quan hệ giữa hai giá trị 1 2 3 1 2 3 m , m ? 1 2
A. m  m  0 . B. 2
m  2m  4 . C. 2 m
 2m  4 . D. m  m  0 . 1 2 1 2 2 1 1 2 Hướng dẫn giải:  x  m 3 2 2 3 
x  3mx  m x  3m  0  x  m  DK : m  0   x  3  m 4 4 4 4 4 4
ycbt  x  x  x
 83  m  m  81m  83  m  1  m  m  0 . 1 2 3 1 2 Chọn đáp án A. x  3
Câu 17. Cho hàm số y 
có đồ thị là (C). Gọi I là giao điểm của 2 đường tiệm cận của (C). Tìm x  1
tọa độ điểm M trên (C) sao cho độ dài IM là ngắn nhất ?
A. M 0 ;  3 và M 2 ; 5
B. M 1 ; 1 và M 3 ; 3 2   1   2   1    1   7   1 5   5 11  C. M 2 ;  và M 4 ; D. M ;  và M  ; 1   2   1   2    3   3   2 3   2 3  Hướng dẫn giải:  m  3  Gọi M m ; 
 thuộc đồ thị, có I(–1 ; 1)  m  1  16 2 16
IM  m  2 1 
, IM  m   1   2 16  2 2  2 m  2 1 m   1
IM nhỏ nhất khi IM  2 2 . Khi đó (m + 1)2 = 4. Tìm được hai điểm M 1 ; 1 và M 3 ; 3 . 2   1   Chọn đáp án B.
Câu 18. Giá trị của tham số m để diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 2
y  3x  2mx  m 1 , trục hoành, trục tung và đường thẳng x = 2 đạt giá trị nhỏ nhất là: A. m = 2 B. m = 1 C. m = -1 D. m = - 2 Hướng dẫn giải:
Vì với m tùy ý ta luôn có 2 2
3x  2mx  m 1  0 x
 nên diện tích hình phẳng cần tìm là
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 10
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2
S  3x  2mx  m  
1 dx  x  mx  m  
1 x  2m  4m 10  2m  2 2 2 3 2 2 2 1  8   0 0
S đạt giá trị nhỏ nhất bằng 8 khi m = - 1. (dùng casio thử nhanh hơn) Chọn đáp án C. 2 x  2x  3
Câu 19. Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số y 
hợp với 2 trục tọa độ 1 x 1
tam giác có diện tích S bằng: A. S=1,5 B. S=2 C. S=3 D. S=1 u(x) / u (x )
Ta có kết quả: Nếu đồ thị hàm số y 
có điểm cực trị (x ; y ) thì y  o v(x) o o o / v (x ) o
Suy ra phương trình đường thẳng đi qua 2 điểm cực trị là y=2x-2 (d)
(d) cắt 2 trục tọa độ tại 2 điểm A(0;-2) ,B(1;0) nên diện tích tam giác OAB bằng 1 Chọn đáp án D.
Câu 20. Cho hàm số 3 2
y  x  2x  1 m x  m có đồ thị C . Giá trị của m thì C  cắt trục
hoành tại 3 điểm phân biệt x , x , x 2 2 2
sao cho x  x  x  4 là 1 2 3 1 2 3  1   m  1 1 1 A. m  1 B.  4
C.   m  1 D.  m  1  4 4 m   0 Hướng dẫn giải:
Phương trình hoành độ giao điểm của (C) và trục hoành là x  1 3 2
x  2x  1 m x  m  0   2
x  x  m  0  m  0 
(C) và trục hoành cắt nhau tại 3 điểm phân biệt:   1 m     4
x  x  x  4   x  x 2 2 2 2
 2x x 1  4  1 2m 1  4  m  1 1 2 3 1 2 1 2 Chọn đáp án B. 3
Câu 21. Cho hàm số y   x  m 2
 3x  m  
1 . Gọi M là điểm cực đại của đồ thị hàm số   1 ứng với
một giá trị m thích hợp đồng thời là điểm cực tiểu của đồ thị hàm số  
1 ứng với một giá trị khác của
m. Số điểm M thỏa mãn yêu cầu đề bài là: A. 1 B. 2 C. 3 D. 0 Hướng dẫn giải: 2
Ta có y  3 x  m  3, y  6  x  m  x  m 1 Suy ra y  0  .  x  m 1 
Vì x  x  m 1, y m 1  0
x  x  m 1 1  
nên hàm số đạt cực đại
tại và giá trị cực đại là 1 2
y  m  3m  2 . 1
Tương tự, ta có hàm số đạt cực tiểu tại x  x  m 1 và giá trị cực tiểu là 2
y  m  3m  2 . 2 2
Ta giả sử điểm M là điểm cực đạ của đồ thị hàm số ứng với giá trị m và là điểm cực tiểu ứng của 1
đồ thị hàm số ứng với với giá trị m . 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 11
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
m 1  m 1 1 2
Từ YCBT suy ra hệ phương trình  2 2
m  3m  2  m  3m  2  1 1 2 2 3 1  1 1 
Giải hệ ta tìm được nghiệm m  , m  
và suy ra tồn tại duy nhât một điêm M ,  thỏa 1 2   2 2  2 4  bài toán. Chọn đáp án A.
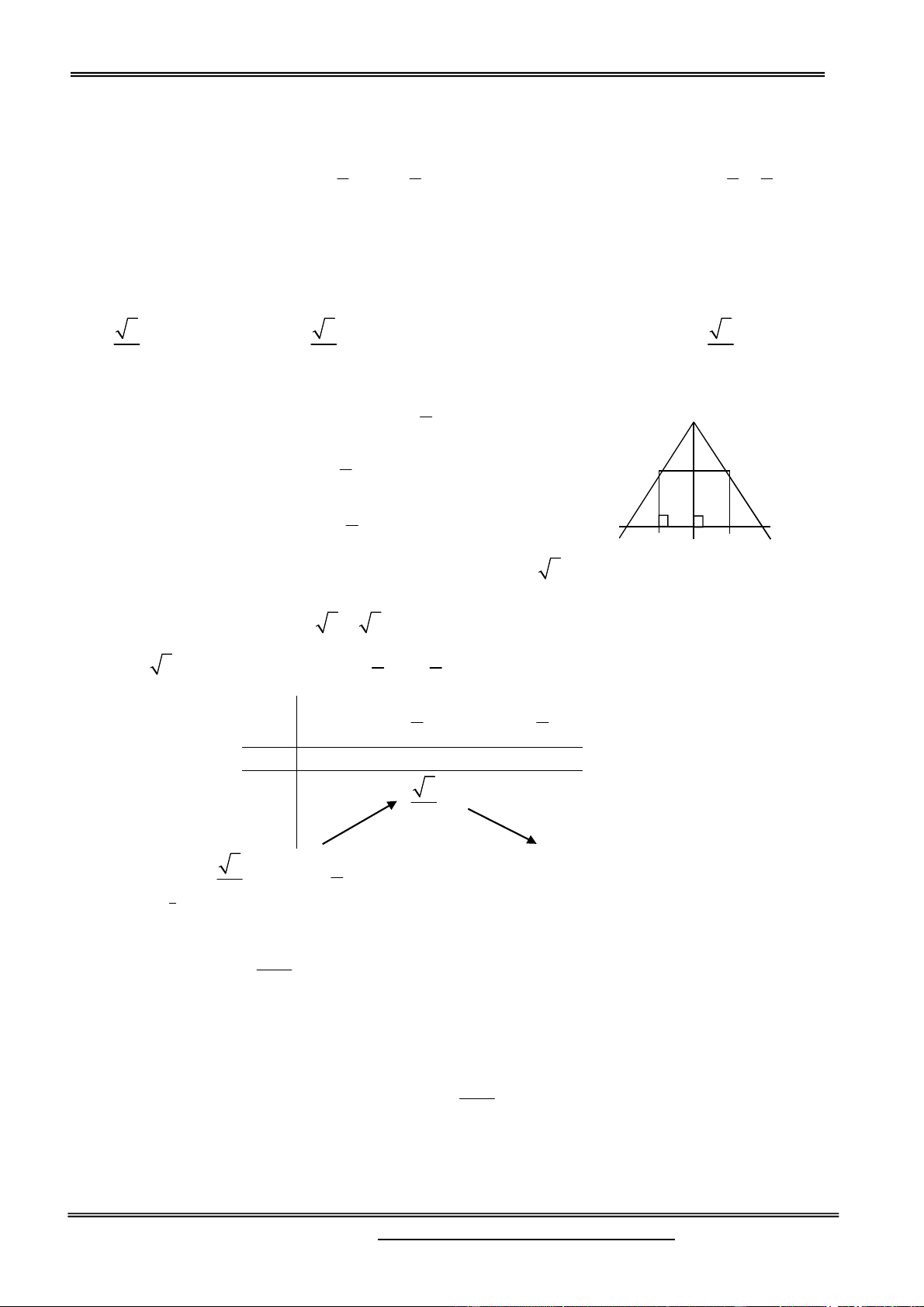
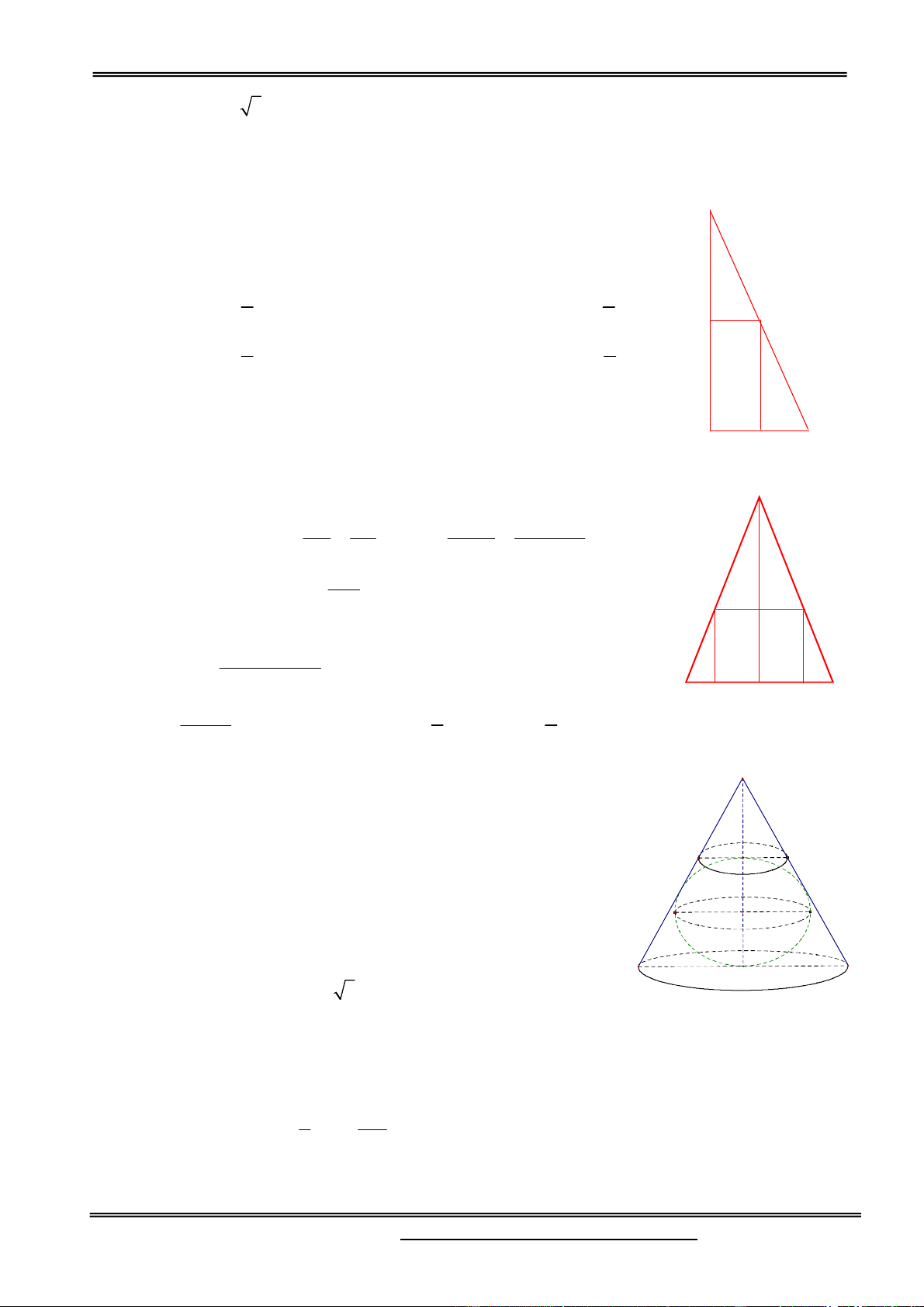
Câu 21. Cho một tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN
nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định
giá trị lớn nhất của hình chữ nhật đó? 3 3 3 A. 2 a B. 2 a C. 0 D. 2 a 8 4 2 Hướng dẫn giải: a A
Gọi H là trung điểm của BC  BH = CH = 2  a 
Đặt BM = x § iÒu kiÖn 0  x  , ta có: Q P    2   a 
MN  2MH  2(BH  BM)  2  x  a  2x    2  M H N C B
Tam giác MBQ vuông ở M,  0
B  60 và BM = x  QM  x 3
Hình chữ nhật MNPQ có diện tích: S(x) = MN.QM = 2
 (a  2x)x 3  3(ax  2x ) a  a 
S'(x)  3(a  4x); S'(x)  0  x   0;   4  2  x a a 0 4 2 S’ + 0  3 2 a S 8 3 a Vậy 2 max S(x)  a khi x =  a  8 4 x 0;    2  Chọn đáp án A. x
Câu 22. Cho hàm số y 
(C) . Tìm m để đường thẳng d : y  mx  m 1 cắt (C) tại hai điểm 1 x
phân biệt M, N sao cho 2 2
AM  AN đạt giá trị nhỏ nhất với ( A 1;1) . A. m  1 B. m  2 C. m  1 D. m  3 Hướng dẫn giải: x  x  1
Phương trình hoành độ giao điểm của (C) và d :
 mx  m  1   2 1 x
mx  2mx  m  1  0(1) 
d cắt (C) tại hai điểm phân biệt  (1) có 2 nghiệm phân biệt khác 1  m  0
Gọi I là trung điểm của MN  I(1; 1  ) cố định.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 12
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 MN Ta có: 2 2 2
AM  AN  2AI  2 Do 2 2
AM  AN nhỏ nhất  MN nhỏ nhất 4 2 2 2
MN  (x  x ) (1 m)  4  m 
 8 . Dấu “=” xảy ra  m  1  2 1 m Vậy 2 2
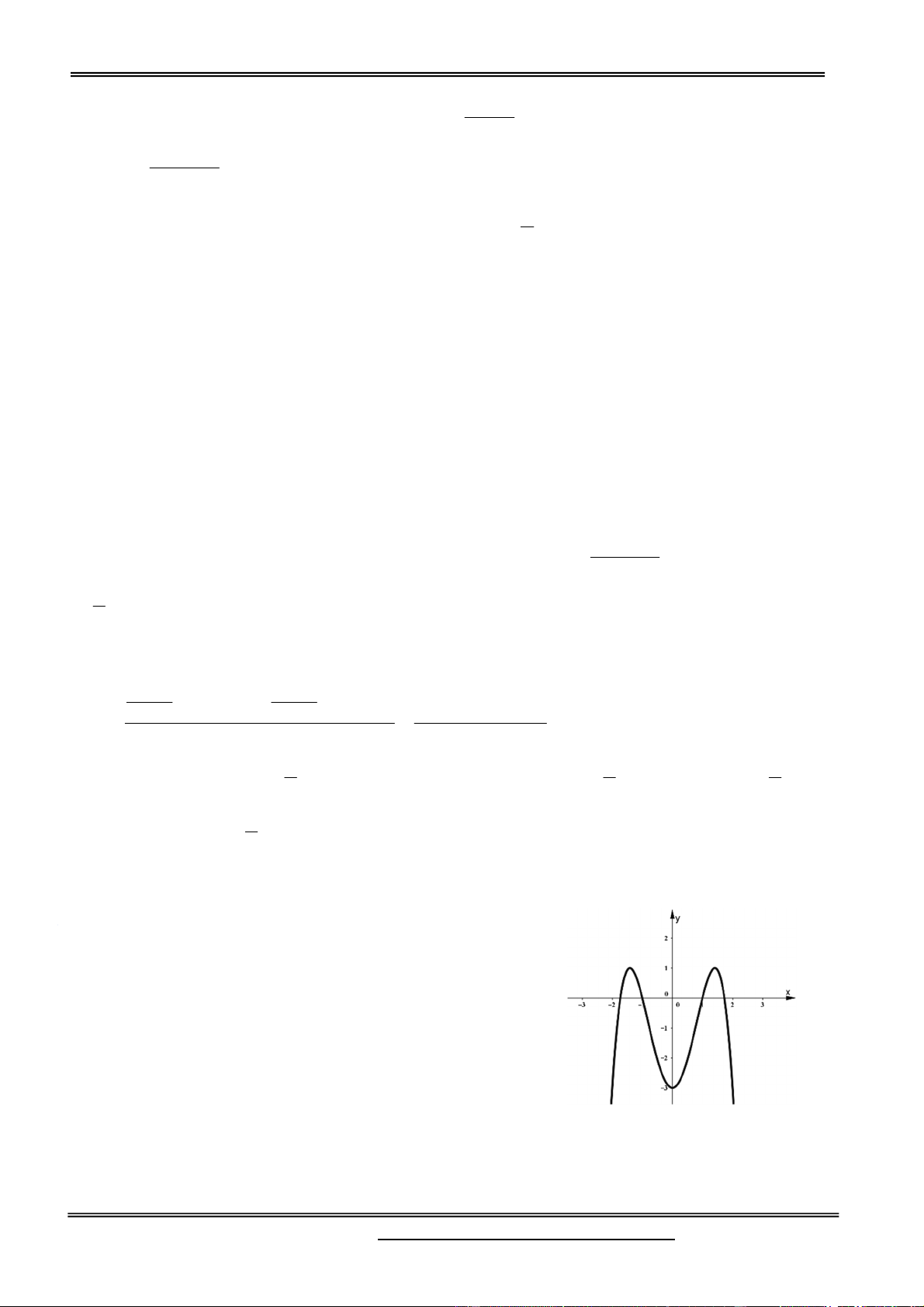
min(AM  AN )  20 khi m  1  Chọn đáp án C.
Câu 23. Cho hàm số bậc ba y  f  x có đồ thị nhu hình vẽ bên. Tất cả
các giá trị của tham số m để hàm số y  f  x  m có ba điểm cực trị là: A. m  1  hoặc m  3 B. m  3  hoặc m  1
C. m  1 hoặc m  3 D. 1  m  3 Hướng dẫn giải:
Đồ thị hàm số y  f x  m là đồ thị hàm số y  f  x tịnh tiến trên trục Oy m đơn vị
Để đồ thị hàm số y  f x  m có ba điểm cực trị  y  f x  m xảy ra hai trường hợp sau:
+ Nằm phía trên trục hoành hoặc điểm cực tiểu thuộc trục Ox và cực đại dương
+ Nằm phía dưới trục hoành hoặc điểm cực đại thuộc trục Ox và cực tiểu dương
Khi đó m  3 hoặc m  1
 là giá trị cần tìm. Chọn đáp án A.
Câu 24. Tìm m để đồ thị hàm số 3 2
y  x  3mx 1 có hai điểm cực trị A, B sao cho tam giác OAB
có diện tích bằng 1 (O là gốc tọa độ). A. m  1 B. m  2 C. m  1 D. m  3 Hướng dẫn giải: Ta có 2
y '  3x  6mx  3x  x  2m . Để đồ thị hàm số có hai điểm cực trị thì m  0 .
Khi đó hai điểm cực trị của đồ thị hàm số là ( A 0;1) và 3 B(2 ; m 4
 m  1) . Gọi H là hình chiếu
vuông góc của điểm B lên trục tung, ta có BH  2m . Diện tích của tam giác OAB là 1 1 S  BH.OA  . 2m 2 2 1
Theo đề bài S=1 nên ta có . 2m  1suy ra m  1. Vậy m=±1 là giá trị cần tìm. 2 Chọn đáp án C. 2 2 sin x
Câu 25. Giá trị lớn nhất của hàm số f x  là 4 x 4 x sin  cos 2 2 A. 0 B. 4 C. 8 D. 2 Hướng dẫn giải: 2 2 2 2 sin x 2sin x 4sin x
TXĐ: D   , ta có f x    . 2  4 x 4 x 1 2 2 sin x sin  cos 1 sin x 2 2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 13
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 t Đặt 2
sin x  t t  0; 
1  , hàm số trở thành g t 4  với t 0;  1 , ta có t   2 g t 8 '   0t 0; 
1 , suy ra hàm số đồng biến trên 0;  1 , vậy  t   22 
max f x  a
m x g t  g  
1  4 , xảy ra khi t 1 x 
 kk   x t   0;  1 2 Chọn đáp án B. Câu 26. Cho hàm số 3 2
y  x  6x  9x  m có đồ thị (C), với m là tham số. Giả sử đồ thị (C) cắt trục
hoành tại ba điểm phân biệt có hoành độ thỏa mãn x  x  x . 1 2 3
Khẳng định nào sau đây là đúng?
A. 1  x  x  3  x  4
B. 0  x  1  x  3  x  4 1 2 3 1 2 3
C. x  0  1  x  3  x  4
D. 1  x  3  x  4  x 1 2 3 1 2 3 Hướng dẫn giải:
Khảo sát và vẽ đồ thị hàm số 3 2
y  x  6x  9x . Dựa vào đồ thị ta tìm được 4
  m  0 thì đồ thị hàm số 3 2
y  x  6x  9x  m cắt Ox tại 3 điểm phân biệt.
Ta có y 0 .y 1  0; y 1 .y 3  0; y 3 .y 4  0 do đó 0  x  1  x  3  x  4             1 2 3 Chọn đáp án B. tan x  2
Câu 27. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y 
đồng biến trên khoảng tan x  m    0; .    4 
A. m  0 hoặc 1  m  2. B. m  0.
C. 1  m  2. D. m  2. Hướng dẫn giải: 1 1
(tan x  m)  (tan x  2) 2 2 2 cos x cos  m '  x y  2 2 2 (tan x  m)
cos x(tan x  m)         
Hàm số đồng biến trên 0; 
 khi và chỉ khi hàm số xác định trên 0; 
 và y’ ≥ 0 ∀ x ∈ 0;    4   4   4     
tan x ,x  0;   m  0   
4   1 m  2   2  m  0  Chọn đáp án A.
2 Câu 28. Cho hàm số 4 2
y  ax  bx  c có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c  0
B. a  0, b  0, c  0
C. a  0, b  0, c  0
D. a  0, b  0, c  0 Hướng dẫn giải:
Do giới hạn của y khi x tiến tới vô cùng thì  nên a  0 . Loại A và D 3
y  ax  bx  x  2 ' 4 2 2 2ax  b
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 14
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Do a  0 mà nếu b  0 thì phương trình 2
2ax  b vô nghiệm
Nên b  0 thì hàm số mới có 3 cực trị. Chọn đáp án B. 1
Câu 29. Cho hµm sè : y  x  1 
( C ) T×m nh÷ng ®iÓm trªn ®å thÞ (C) cã hoµnh ®é lín h¬n 1 x  1
sao cho tiÕp tuyÕn t¹i diÓm ®ã t¹o víi 2 ®êng tiÖm cËn mét tam gi¸c cã chu vi nhá nhÊt .  1 1   1 1  A. M  1  ;2  2   B. M  ; 2  4 4     2 2  4 4  2 2   1 1 
C. M  1;2  2  D. M  1  ;2  2   4 4   2 2  Hướng dẫn giải: 2 1 a Gäi M   ;
a y a  C;a  0 th× y a  a 1  a 1 a 1 2 2 a  2a a
PTTT cña ( C ) t¹i M lµ: y  y a  y 'a x  a  y  x  a  (d) 2   a   1 a 1
TiÖm cËn ®øng x = 1 ; TiÖm cËn xiªn y = x + 1
Giao ®iÓm cña 2 tiÖm cËn lµ I=( 1 ; 2 )  2a 
Giao ®iÓm cña d víi tiÖm cËn ®øng x = 1 lµ A  1;    a  1 
Víi tiÖm cËn xiªn lµ : B  2a 1;2a 2 Ta cã AI 
; BI  2 2 a 1 , nªn AI.BI  4 2 v× a > 1 a 1   L¹i cã AIB  suy ra 2 2 2 2 2
AB  AI  BI  2 AI.BICos
 AI  BI  2 AI .BI 4 4
Theo bÊt ®¼ng thøc C« si : 2
AB  2 AI.BI  2AI.BI  2  2  AI.BI
 AB  2 2 2   1 (1)
§Æt p lµ chu vi tam gi¸c ABI th× : p  AB  AI  BI  AB  AI BI     4 2 . 2 2 2 1  4 2 1
DÊu ®¼ng thøc x¶y ra  AI  BI  a  1  4 2 1
VËy Minp  2 2 2   4
1  4 2  a  1  4 2  1 1 
Hay ®iÓm cÇn t×m lµ M  1  ;2  2   4 4   2 2  Chọn đáp án D. 4 x 5 Câu 30. Cho hµm sè: 2 y   3x 
(C) vµ ®iÓm M  (C) cã hoµnh ®é x = a. Víi gi¸ trÞ nµo cña a M 2 2
th× tiÕp tiÕp tuyÕn cña (C) t¹i M c¾t (C) 2 ®iÓm ph©n biÖt kh¸c M.   a  3   a  3  a  3   a  7 A.  B.  C.  D.  a  1   a  1  a  1   a  2   Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 15
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 4 a 5
§iÓm M (C) , x = a => 2 y   3a 
ta cã Pt tiÕp tuyÕn víi (C) cã d¹ng M M 2 2 () : '
y  y (x  x )  y víi ' 3 y  2a  6a xM M M M 4 a 5 => () 3 2
y  (2a  6a)(x  a)   3a  2 2
Hoµnh ®é giao ®iÓm cña () vµ (C) lµ nghiÖm cña ph¬ng tr×nh 4 4 x 5 a 5 2 3 2 2 2 3  3x 
 (2a  6a)(x  a)   3a 
 (x  a) (x  2ax  3a  6)  0 2 2 2 2 x  a   2 2
g(x)  x  2ax  3a  6  0 
Bµi to¸n trë thµnh t×m a ®Ó g(x)=0 cã 2 nghiÖm ph©n biÖt kh¸c a ' 2 2 2 
 a  (3a  6)  0   a g x   3  0  ( )  a  3       2 2
g(a)  6a  6  0 a  1   a  1   Chọn đáp án A. 2x  3
Câu 31. Cho hàm số: y 
. Viết phương trình tiếp tuyến của (C) , biết tiếp tuyến đó cắt đường x  2
tiệm cận đứng và tiệm cận ngang lần lượt tại ,
A B sao cho AB 
2IB , với I (2, 2) .
A. y  x  2 ; y  x  3
B. y  x  2 ; y  x  6
C. y  x  2 ; y  x  6
D. y  x  2 ; y  x  6 Hướng dẫn giải:  2x  3  2 1 2x  6x  6 Gọi 0 M x ;  (C) 0 0 
. PTTT của (C) tại M: y   x  0  x  2 2 2  0   x  2 x  2 0   0 
Do AB  2IB và tam giác AIB vuông tại I  IA = IB nên hệ số góc của tiếp tuyến k = 1 hoặc k = 1  -1. vì / y 
 0 nên ta có hệ số góc tiếp tuyến k = -1.  x  22 1   x  1 0   1     x  2 1 x  3  0 0
 có hai phương trình tiếp tuyến y  x  2 ; y  x  6 Chọn đáp án C.
Câu 32. Cho hàm số y = x3 + 2mx2 + (m + 3)x + 4 (m là tham số) có đồ thị là (Cm), đường thẳng d có
phương trình y = x + 4 và điểm K(1; 3). Tìm các giá trị của tham số m để d cắt (Cm) tại ba điểm phân
biệt A(0; 4), B, C sao cho tam giác KBC có diện tích bằng 8 2 . 1  37 1  137 1  7 1  142 A. m  B. m  C. m  D. m  2 2 2 2 Hướng dẫn giải:
Xét phương trình hoành độ giao điểm của (C) và d:  x  0
x3 + 2mx2 + (m + 3)x + 4 = x + 4  x(x2 + 2mx + m + 2) = 0   2
x  2mx  m  2  0 * 
d cắt (C) tại 3 điểm phân biệt  PT (*) có 2 nghiệm phân biệt khác 0 ' 2
  m  m  2  0    m   ;  2     2  ;   1  2; m  2  0 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 16
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Khi đó B = (x1; x1 + 4), C = (x2; x2 + 4) với x1, x2 là hai nghiệm của (*). x  x  2  m Theo Vi-ét ta có 1 2
x x  m  2  1 2
 BC  2 x  x 2  2 x  x 2  8x x  2 2 2 m  m  2 1 2 1 2 1 2 
Ta có khoảng cách từ K đến d là h = 2 . Do đó diện tích KBC là: 1 1 S  . . h BC  2.2 2 2 m  m  2 2
 2 m  m  2 2 2 1  137 2
S  8 2  2 m  m  2  8 2  m  (TM ) . 2 Chọn đáp án B.
Câu 33. Cho hàm số: 3
y  x  2009x có đồ thị là (C). M là điểm trên (C) có hoành độ x  1 . Tiếp 1 1
tuyến của (C) tại M cắt (C) tại điểm M khác M , tiếp tuyến của (C) tại M cắt (C) tại điểm M 1 2 1 2 3
khác M , tiếp tuyến của (C) tại điểm M
cắt (C) tại điểm M khác M
(n = 4; 5;…), gọi  x ; y n n  2 n1 n n1
là tọa độ điểm M . Tìm n để : 2013
2009x  y  2  0 n n n A. n  685 B. n  627 C. n  675 D. n  672 Hướng dẫn giải:
Gọi M  x ; y suy ra tiếp tuyến tại M : y  y  y ' x  x  x k k k k  k k k   y   2 x  x x x x k   k  3 3 2009   2009 k k Tọa độ điểm M được xác định: k 1 3 x  x   2 x  x x x x x x x x x x k   k  3    k k   k  2 2 2009 3 2009 2009  .  2 k k   0
 x  x  x  2  x  x  2  x k k k 1 k n 
Ta có : x  1; x  2; x  4;...; x  n 2 1 1 2 3 2010 3 2010
2009x  y  2
 0  2009x  x  2009x  2  0 n n n n n n    2  3 3  2   2  2013 2013
 3n  3  2013  n  672 Chọn đáp án D. 3x  2m
Câu 34. Cho hàm số y 
với m là tham số. Xác định m để đường thẳng d cắt các trục mx  1
Ox, Oy lần lượt tại C, D sao cho diện tích OAB bằng 2 lần diện tích OCD . 5 2 1 A. m   B. m  3  C. m   D. m   3 3 3
Hướng dẫn giải: 1 
Phương trình hoành độ giao điểm của d và đồ thị: 2 2
3mx  3m x  m  0, x  m
Vì m  0 nên phương trình 2
 3x  3mx  1  0 (*). Ta có 2
  9m  12  0,m  0 và  1  3 f   2  0,m  0  
(ở đây f  x là vế trái của (*)) nên d luôn cắt đồ thị tại 2 điểm , A B 2  m  m phân biệt m  0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 17
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Ta có A x ;3x  3m , B x ;3x  3m với x , x là 2 nghiệm của (*). Kẻ đường cao OH của 1 1   2 2  1 2
AB   x  x  3x  3x  10 x  x 2 1 2  2 1 2  2 1 2 3  m
OAB ta có OH  d 0;d   và 10 40
 10 x  x 2 2
 40x x  10m  1 2 1 2 3
(Định lý Viet đối với (*)).
Mặt khác ta có C  ; m 0, D0; 3
 m (để ý m  0 thì C, D,O phân biệt). Ta tìm m để 40 3  m 2 S  2S hay 2 10m  .
 2 m 3m  m   OAB OCD 3 10 3 Chọn đáp án C. 1 Câu 35. Cho hàm số 3 y 
mx  m   2
1 x  4  3m x  1 có đồ thị là C
, m là tham số. Tìm các m  3
giá trị của m để trên C
có duy nhất một điểm có hoành độ âm mà tiếp tuyến của C tại điểm đó m  m 
vuông góc với đường thẳng d : x  2 y  0 . m  0 m  1  m  0 1 A.   2 B. C. 0  m  D. 5   m  m  1  3 m   3  3 Hướng dẫn giải: / 2
y  mx  2(m  1)x  4  3m . Tiếp tuyến có hệ số góc bằng 2 Ta tìm m : 2
mx  2(m  1)x  4  3m  2  
* có đúng một nghiệm âm   *   x  
1 mx  3m  2  0  x  1 hoặc mx  2  3m
m  0 : không thỏa yêu cầu m  0 2  3m
m  0 , yêu cầu bài toán xảy ra khi 0    2 m m   3 Chọn đáp án C. 2x  1
Câu 36. Cho hàm số y 
có đồ thị (C) và điểm P 2;5 . Tìm các giá trị của tham số m để x  1
đường thẳng d : y  x  m cắt đồ thị C  tại hai điểm phân biệt A và B sao cho tam giác PAB đều.
Phương trình hoành độ giao điểm của đường thẳng d và đồ thị (C) là:
A. m  1, m  5 
B. m  1, m  4
C. m  6, m  5 
D. m  1, m  8  Hướng dẫn giải:
2x  1  x  m  2
x  (m  3)x  m 1  0   1 , với x  1  x  1
Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình   1 có hai nghiệm phân biệt khác 1 2
m  2m  13  0   (đúng m ) 0.m  3  0 
x  x  m  3
Gọi x , x là các nghiệm của phương trình (1), ta có: 1 2 1 2
x x  m 1  1 2
Giả sử A x ; x  m , B  x ; x  m 2 2  1 1 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 18
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Khi đó ta có: AB  2 x  x 2 1 2
PA   x  22  x  m  52   x  22   x  22 , 1 1 1 2
PB   x  22  x  m  52   x  22   x  22 2 2 2 1
Suy ra PAB cân tại P
Do đó PAB đều 2 2  PA  AB
  x  22   x  22  2 x  x 2   x  x 2  4 x  x  6x x  8  0 1 2 1 2 1 2  1 2  1 2  m  1 2
 m  4m  5  0  
. Vậy giá trị cần tìm là m  1, m  5  . m  5   Chọn đáp án C. Câu 37. Cho hµm sè 4 3
y  x  mx  4x  m  2 . T×m tÊt c¶ c¸c gi¸ trÞ cña m ®Ó hµm sè ban ®Çu cã 3
cùc trÞ vµ träng t©m cña tam gi¸c víi 3 ®Ønh lµ to¹ ®é c¸c ®iÓm cùc trÞ trïng víi t©m ®èi xøng cña ®å thÞ 4x hµm sè y  . 4x  m A. m  2 B. m  1 C. m  4 D. m  3 Hướng dẫn giải:
Hµm sè ®· cho cã 3 cùc trÞ khi ph¬ng tr×nh y’(x) = 0 cã 3 nghiÖm ph©n biÖt 3 2
 4x  3mx  4  0 cã 3nghiÖm ph©n biÖt m XÐt g(x) = 3 2
4x  3mx  4 cã g’(x) = 2
12x  6mx  g (
 x)  0  x  0, x  2 3 m 16  m
Do lim g(x)   , lim g(x)   vµ g(0)  4  0 , g( )  nªn g(x) = 0 x   x  2 4  m  0   2 cã 3 nghiÖm ph©n biÖt 3  
 m  2 2 (häc sinh cã thÓ lËp b¶ng biÕn thiªn 3 16   m  0   4 3 x 1 cña hµm (x)  trªn R \  
0 ®Ó t×m ra kÕt qu¶ trªn) 2 x 4x m
Khi ®ã t©m ®èi xøng cña ®å thÞ hµm sè y  lµ I ( ; 1) 4x  m 4 Gäi (
A x ; y ), B(x ; y ),C(x ; y ) lµ 3 ®iÓm cùc trÞ cña ®å thÞ hµm sè ®· cho th× 1 1 2 2 3 3
x , x , x lµ nghiÖm ph¬ng tr×nh : 3 2
4x  3mx  4  0 nªn theo ®Þnh lý Viet ta cã 1 2 3
 x  x  x m 1 2 3  3m  
x  x  x  1 2 3  3 4  4   2 9m 2 2 2 2 x x x x x x 0      1 2 2 3 3 1
x  x  x  (x  x  x )  2(x x  x x  x x )  1 2 3 1 2 3 1 2 2 3 3 1   16 2 2 x m 3m x 5m
ViÕt hµm sè ban ®Çu díi d¹ng: y(x)  y (  x)(  )  (  3x   2) , v× thÕ 4 16 16 4 2 2 2 2 x m 3m x 5m 3m x 5m
y  y(x )  y (  x )( i  )  ( i  3x   2)   i  3x   2 i i i 4 16 16 i 4 16 i 4 do y (  x )  0 (i  1, 2,3) i 2 4
y  y  y m 5m 9m 5m Tõ ®ã : 1 2 3 2 2 2  
(x  x  x )  (x  x  x )   2     2 1 2 3 1 2 3 2 3 16 4 16 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 19
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
x  x  x
y  y  y m
Träng t©m cña tam gi¸c ABC lµ G( 1 2 3 1 2 3 ; )  I ( ; 1) khi vµ chØ 3 3 4
y  y  y 4 9m 5m khi : 1 2 3  1  3 2  
 2  1  (m  4)(9m  36m  144m  64)  0 3 2 16 4 V× 3
m  2 2 nªn m  4 lµ gi¸ trÞ duy nhÊt cÇn t×m. Chọn đáp án C.
Câu 38. Tìm tham số m để hàm số 3 2
y  x  3mx  3m  
1 x  2 nghịch biến trên một đoạn có độ dài lớn hơn 4 . 1  21 1  21 1  21 A. m  B. m  hoặc m  2 2 2 1  21 1  21 1  21 C. m  D.  m  2 2 2 Hướng dẫn giải: Ta có 2 D  
y  x  mx  m     2 , 3 6 3 1
3 x  2mx  m   1 2
y  0  x  2mx  m  1  0  
1 . Điều kiện cần và đủ để hàm số nghịch biến trên một đoạn có độ
dài lớn hơn 4  y  0 trên đoạn có độ dài lớn hơn 4   
1 có hai nghiệm x ; x x  x thoả mãn 1 2  1 2  x  x  4 1 2     0 0   2    
   4  m  m  1  4 x  x  4 2   4   1 2   1  21 1  21 2
 m  m  5  0  m   m  . 2 2 Vậy hàm số  
1 nghịch biến trên một đoạn có độ dài lớn hơn 4 1  21 1  21  m   m  2 2 Chọn đáp án B.  x  1
Câu 39. Đường thẳng d : y  x  a luôn cắt đồ thị hàm số y 
H  tại hai điểm phân biệt , A B 2x  1
. Gọi k ,k lần lượt là hệ số góc của các tiếp tuyến với  H  tại A và B . Tìm a để tổng k  k đạt 1 2 1 2 giá trị lớn nhất. A. a  1 B. a  2 C. a  5  D. a  1  Hướng dẫn giải:
Phương trình hoành độ giao điểm của d và  H  :  1 x  1 x    x  a  2  2x  1 2
2x  2ax  a 1  0 * 
Đặt g  x 2
 2x  2ax  a 1 2  
  a  2a  2  0, a g  1 Vì   1  1 nên  
* có hai nghiệm phân biệt x , x khác với mọi a . 1 2 g    0,    a 2   2  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 20
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Vậy d luôn cắt  H  tại hai điểm phân biệt ,
A B với mọi a .
Gọi A x ; y , B x ; y với x , x là hai nghiệm của  
* . Theo định lý Vi-ét ta có 1 1   2 2  1 2 a  1
x  x  a , x x  . 1 2 1 2 2 1  1 
Tiếp tuyến tại A à
v B có hệ số góc là k  ; k  1 2x  2 2 1 2x  2 1 1 2 1  1   2x 1 2x 1     1 2  2 2
Ta có k  k       1 2 2x  2 1 2x  2 1  2x  2 1 2x  2 1  1 2  1 2  4 x x 2 8x x 4 x x  2       
(do 2x  2 1 2x  2 1  1) 1 2 1 2 1 2 1 2     a  2 4 1  2  2
 ,a . Dấu bằng xẩy ra  a  1 
Vậy k  k đạt giá trị lớn nhất bằng 2 khi a  1  . 1 2 Chọn đáp án D.
Câu 40. Tìm m để phương trình x4 – ( 2m+3)x2 + m + 5 = 0 có 4 nghiệm x1, x2, x3, x4 thoả mãn :
-2 < x1 < -1 < x2 < 0 < x3 < 1 < x4 < 3 A. Không có m B. m  1 C. m  4 D. m  3 Hướng dẫn giải:
Đặt x2 = X  0 , ta có phương trình: f(X) = X2 – ( 2m+3).X + m + 5 = 0 (*)
để phương trình đã cho có 4 nghiệm phân biệt x1 < x2 < x3 < x4 thì phương trình (*) có hai nghiệm
thoả mãn: 0 < X1 < X2. Khi đó x   X ; x   X ; x  X ; x  X 1 2 2 1 3 1 4 2 Do đó: -2<- X <-1< - X < 0 < X < 1 < X < 3 2 1 1 2  2  X >1 > X > 0  4 > X 2 1 2 > 1 > X1 > 0   af (1)  0  m  3  0  m  3   
 af (0)  0   m  5  0  m  5  af (4) 0   7m  9  0    9  m   7
 không tồn tại m thoả mãn bài toán . Chọn đáp án A. 3 1
Câu 41. Cho hàm số: y = x3 - 2 3 mx 
m . Xác định m để đường thẳng y = x cắt đồ thị tại 3 điểm 2 2
phân biệt A, B, C sao cho AB = BC. A. m = 0 ; m =  2 B. m = 0 C. m =  2 D. m = 0 ; m = 2 Hướng dẫn giải: 3 2 1
PT hoành độ giao điểm: x3 - 3 mx  x  m  0 (1) 2 2
Đường thẳng y = x cắt đồ thị tại 3 điểm phân biệt A,B,C  pt (1) có 3 nghiệm phân biệt xA, xB, 3
xC. Theo Vi et ta có : xA + xB +xC = m (2) 2
theo gt AB = BC  2 xB =xA + xC (3)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 21
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 m m Từ (2) và (3)  xB = . Vậy x = là một nghiệm của (1). 2 2 3 1 m Chia f(x) = 3 2 3 x  mx  x  m cho x  ta được: 2 2 2 m 2 m m 3 m f(x) = (x - ) (x2 – mx – 1 - ) - + . 2 2 2 4 m m 3 m x = là nghiệm của (1)  - + = 0  m=0, m =  2 2 2 4 m 2 m Khi đó f(x) = (x - ) (x2 – mx – 1 - ) có 3 nghiệm phân biệt 2 2 2 m m 3 2 m
vì (x) = x2 – mx – 1 -
có 2 nghiệm trái dấu và có  ( ) = -1 -  0 . m  2 2 4 Vậy: m = 0 ; m =  2 Chọn đáp án A.
Câu 42. Cho hàm số y=x3-(m+1)x2-(2m2-3m+2)x+2m(2m-1). Xác định m để hàm số đồng biến trên (2;+  ) . A. 3   m  2 B. 2   m  2 C. 3   m  1 D. 3   m  2 Hướng dẫn giải: Ta có: ,
y  g(x)  3 2 x  2(m  ) 1 x  (2 2 m  3m  2)
∆’ =7m2 –7m +7 = 7(m2-m+1) > 0 , m  g(2)  0  2 2
 m  m  6  0 y,  0, x  ( ; 2 )   S    3   m  2   2  0 m  5  0   2 Chọn đáp án D.
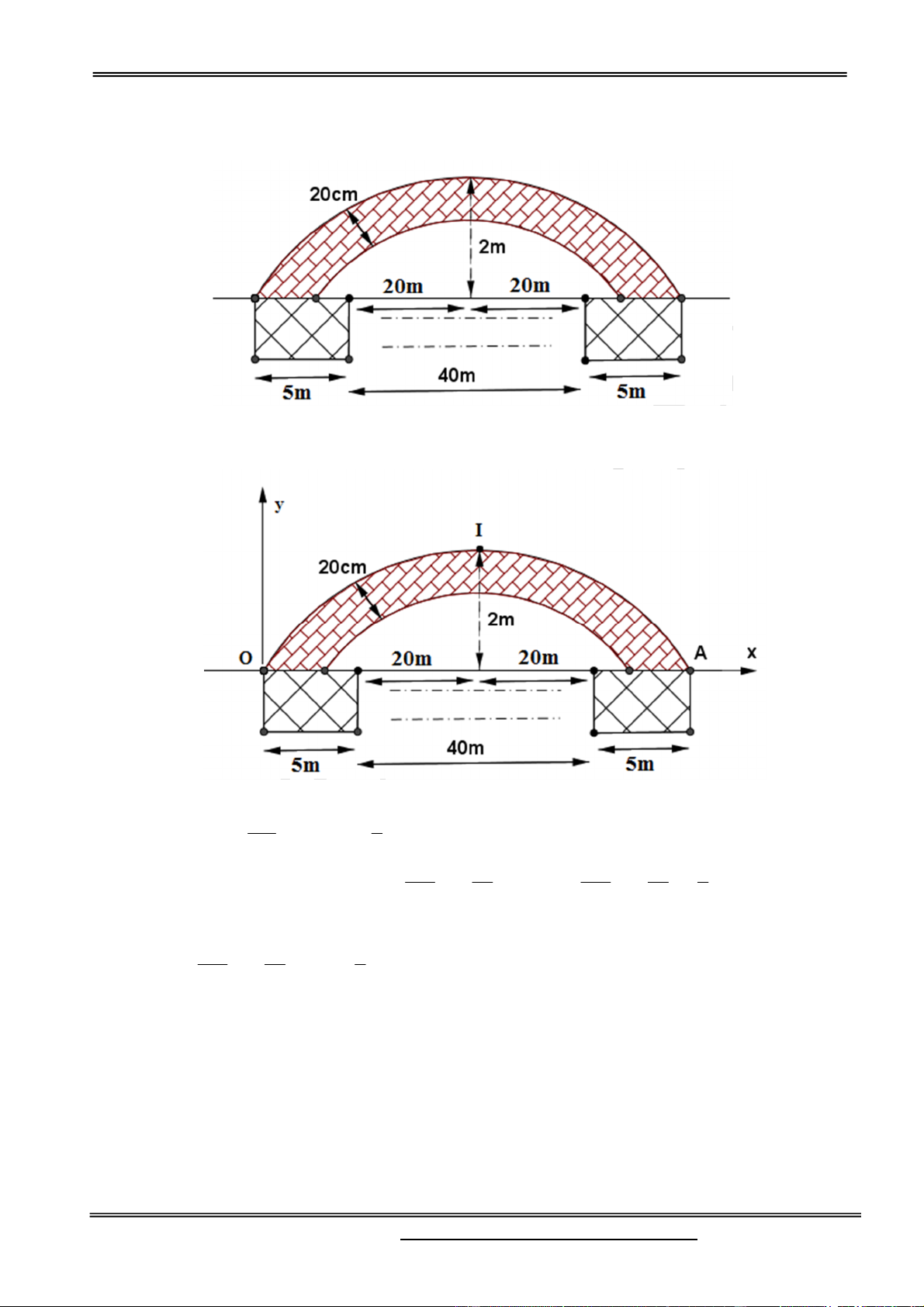
Câu 43. Bạn A có một đoạn dây dài 20m . Bạn chia đoạn dây thành hai phần. Phần đầu uốn thành một
tam giác đều. Phần còn lại uốn thành một hình vuông. Hỏi độ dài phần đầu bằng bao nhiêu để tổng
diện tích hai hình trên là nhỏ nhất? 40 180 120 60 A. . m B. . m C. . m D. . m 9  4 3 9  4 3 9  4 3 9  4 3 Hướng dẫn giải:
Bạn A chia sợi dây thành hai phần có độ dài x m và 20  xm , 0  x  20 (như hình vẽ). 2 x 2  x  3 x 3
Phần đầu uốn thành tam giác đều có cạnh
m , diện tích S  .     2 m 1  3  3  4 36 2 20  x  20  x 
Phần còn lại uốn thành hình vuông có cạnh
m , diện tích S     2 m 2  4  4  2 2 x 3  20  x 
Tổng diện tích hai hình nhỏ nhất khi f  x   
 nhỏ nhất trên khoảng 0;20 . 36  4  x 3 20  x 180
Ta có: f ' x    0  x  . 18 8 4 3  9
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 22
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Bảng biến thiên: 180 x 0 20 4 3  9 f  x  0 + f  x 180
Dựa vào bảng biến thiên ta được x  . 4 3  9 Chọn đáp án D.  8
  4a  2b  c  0
Câu 44. Cho các số thực a, b, c thỏa mãn 
. Số giao điểm của đồ thị hàm số
8  4a  2b  c  0  3 2
y  x  ax  bx  c và trục Ox là A. 0 . B.1. C. 2 . D. 3 . Hướng dẫn giải: Ta có hàm số 3 2
y  x  ax  bx  c xác định và liên tục trên  .
Mà lim y   nên tồn tại số M  2 sao cho y  M   0 ; lim y   nên tồn tại số m  2  sao x   x  
cho y m  0 ; y 2  8  4a  2b  c  0 và y 2  8  4a  2b  c  0 .
Do y m.y 2  0 suy ra phương trình y  0 có ít nhất một nghiệm thuộc khoảng m;2 .
y 2.y 2  0 suy ra phương trình y  0 có ít nhất một nghiệm thuộc khoảng 2;2 .
y 2.y M   0 suy ra phương trình y  0 có ít nhất một nghiệm thuộc khoảng 2;M  . Vậy đồ thị hàm số 3 2
y  x  ax  bx  c và trục Ox có 3 điểm chung. Chọn đáp án D. 2x  1
Câu 45. Tập hợp các giá trị của m để đồ thị hàm số y  có đúng 1  2
mx  2x   1  2
4x  4mx   1 đường tiệm cận là A.   0 . B.  ;    1  1;. C.  D.  ;    1   0  1;. Hướng dẫn giải:
Có lim y  0 . Nên hàm số luôn có 1 đường tiệm cận ngang y  0 . Vậy ta tìm điều kiện để hàm số x
không có tiệm cận đứng . 2
mx  2x 1  0 (1) Xét phương trình:  2
mx  2x   1  2
4x  4mx   1  0   2
4x  4mx  1  0 (2)  2x  1 1
TH1: Xét m  0 , ta được y    (thỏa ycbt) 2x   1  2 4x   2 1 4x  1
TH2: Xét m  0 . Có:   1  m và 2   4m  4 1 2 1   m  0 m  1
Th2a. Cả 2 phương trình (1) và (2) đều vô nghiệm:      m   2 4m  4  0 1   m  1  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 23
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1
Th2b: (1) vô nghiệm, (2) có nghiệm kép x 
: ta thấy trường hợp này vô lí (vì m  1 ) 2 1
Th2c: (2) vô nghiệm, (1) có nghiệm kép x 
: ta thấy trường hợp này vô lí (vì 1   m  1) 2 Chọn đáp án A.
Câu 46. Đường thẳng d : y  x  4 cắt đồ thị hàm số 3 2
y  x  2mx  m  3 x  4 tại 3 điểm phân
biệt A0;4, B và C sao cho diện tích tam giác MBC bằng 4, với M 1;3. Tìm tất cả các giá trị của
m thỏa mãn yêu cầu bài toán.
A. m  2 hoặc m  3. B. m  2
 hoặc m  3. C. m  3. D. m  2  hoặc m  3  . Hướng dẫn giải:
Phương trình hoành độ giao điểm của d và đồ thị C  : 3 2
x  2mx  m  3 x  4  4 x  0 3 2
 x  2mx  m  2 x  0    x 2
 x  2mx  m  2  0   1 
Với x  0, ta có giao điểm là A0;4.
d cắt C  tại 3 điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác 0. 
 0  m  2  0   (*) 2
  m  m  2  0 
Ta gọi các giao điểm của d và C  lần lượt là ,
A B x ; x  2 C x x
với x , x là nghiệm B B ,  ;  2 C C  B C của phương trình (1). x  x  2  m
Theo định lí Viet, ta có: B C x .x  m  2  B C 1
Ta có diện tích của tam giác MBC là S 
 BC  d  M , BC   4. 2
Phương trình d được viết lại là: d : y  x  4  x  y  4  0. 1  3  4
Mà d M , BC   d  M , d    2. 1   2 2 1 8 8 Do đó: 2 BC    BC  32
d  M , BC  2 2 2 2 Ta lại có: 2
BC   x  x y y x x C B     C B   2  C B   32   x  x x x m m B C 2    B C  2 4 . 16 2  4  2  16 2
 4m  4m  24  0  m  3  m  2.
Đối chiếu với điều kiện, loại đi giá trị m  2  . Chọn đáp án C.
Câu 47. Cho các số thực x, y thỏa mãn x  y  2 x  3  y  3 . Giá trị nhỏ nhất của biểu thức P   2 2
4 x  y  15xy là:
A. min P  83
B. min P  63
C. min P  80 D. min P  9  1 Hướng dẫn giải: 2 Ta có x  y  2
x  3  y  3  x  y
 4 x  y  8 x  3. y  3  4 x  y        
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 24
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  y  4  . Mặt khác x  y  0 
x  y  2 x  3  y  3  2 2x  y  x  y  8  x  y4;8 Xét biểu thức         2 2 2 P 4 x y 15xy 4 x y  7xy và đặt     2 t x y 4;8  P  4t  7xy . 2
Lại có x  3 y  3  0  xy  3
 x  y  9  P  4 x  y  21 x  y  63 2  4t  21t  63 . Xét hàm số   2
f t  4t  21t  63 trên đoạn 4;  8 suy ra P  f 7  8  3 min   Chọn đáp án A.
Câu 48. Gọi (Cm) là độ thì hàm số 4 2
y  x  2x  m  2017 . Tìm m để (Cm) có đúng 3 điểm chung
phân biệt với trục hoành, ta có kết quả: A. m  2017
B. 2016  m  2017 C. m  2017 D. m  2017 Hướng dẫn giải:
- Phương pháp: Tìm m để phương trình ẩn x tham số m có n nghiệm phân biệt thuộc khoảng K
+ Cô lập m, đưa phương trình về dạng m = f(x)
+ Vẽ đồ thị (hoặc bảng biến thiên) của y=f(x) trên K
+ Biện luận để đường thẳng y = m cắt đồ thị hàm số y =f(x) tại n điểm phân biệt trên K - Cách giải: C
cắt Ox tại 3 điểm phân biệt  Phương trình m  4 2 4 2
x  2x  m  2017  0  m  x  2x  2017 có 3 nghiệm phân biệt. Xét hàm số 4 2
y  x  2x  2017 trên R Có 3
y '  4x  4x  0  x  0 hoặc x  1  . Bảng biến thiên: x  0 0 1  y'  0 + 0  0 + y  2017  2016 2016
Dựa vào bảng biến thiên, ta thấy đường thẳng y = m cắt đồ thị hàm số y =f(x) tại 3 điểm phân biệt khi và chỉ khi m =2017 Chọn đáp án A. 2 x  2
Câu 49. Tìm tất cả các giá trị thực của m để đồ thị hàm số y 
có hai đường tiệm cận 4 mx  3 ngang. A. m  0 B. m  0 C. m  0 D. m  3 Hướng dẫn giải: 2 x  2
Đồ thị hàm số y 
có hai đường tiệm cận ngang khi và chỉ khi các giới hạn 4 mx  3
lim y  a a  , lim y  bb   tồn tại. Ta có: x  x
+ với m  0 ta nhận thấy lim y  , lim y   suy ra đồ thị hàm số không có tiệm cận ngang. x  x 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 25
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  3 3 
+ Với m  0 , khi đó hàm số có TXĐ 4 4 D     ; 
 , khi đó lim y, lim y không tồn tại suy  m m    x  x 
ra đồ thị hàm số không có đường tiệm cận ngang. 2  2  2 x 1   2  1  2  x  1
+ Với m  0 , khi đó hàm số có TXĐ D   suy ra lim , lim x  suy ra x  3 x 3 m 2 2 x m  x m  2 4 x x
đồ thị hàm số có một đường tiệm cận ngang.
Vậy m  0 thỏa YCBT. Chọn đáp án C. Câu 50. Cho hàm số 2
y  x  2x  a  4 . Tìm a để giá trị lớn nhất của hàm số trên đoạn  2  ;  1 đạt giá trị nhỏ nhất. A. a  3 B. a  2 C. a  1
D. Một giá trị khác Hướng dẫn giải:
Ta có y  x  x  a    x  2 2 2 4 1
 a  5 . Đặt u   x  2
1 khi đó x  2  ;  1 thì u 0;4 Ta
được hàm số f u  u  a  5 . Khi đó
Max y  Max f u  Max f 0, f 4  Max a  5 ; a 1 x   2;  1 u   0;  4
Trường hợp 1: a  5  a  1  a  3  Max f u   5  a  2  a  3 u   0;4
Trường hợp 2: a  5  a  1  a  3  Max f u   a 1  2  a  3 u   0;4
Vậy giá trị nhỏ nhất của Max y  2  a  3 x   2;  1 Chọn đáp án A.
Câu 51. Giá trị nhỏ nhất của hàm số: 3 y  x   3  x   3  x   3 2 1 1 2 1  x  1 là: A. 0 B. 1 C. 2 D. 3 Hướng dẫn giải: 3 y  x   3  x   3  x   3 2 1 1 2 1  x  1
 y   x   2   x   2 3 3 1 1 1 1 3 3  y  x  1  1  x  1  1
Điều kiện để hàm số xác định x  1  Ta có 3 3 y  x  1  1  x  1  1 - Nếu 1   x  0 thì 3 3 3 x  1  1  0  x  1  1  1 
x  1  y  2 - Nếu x  0 thì 3 2
x  1 1  0  y  2 x  1  2
Vậy: y  2,x  1
 , y  2  x  0 Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 26
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 HÌNH ĐA DIỆN I – HÌNH CHÓP
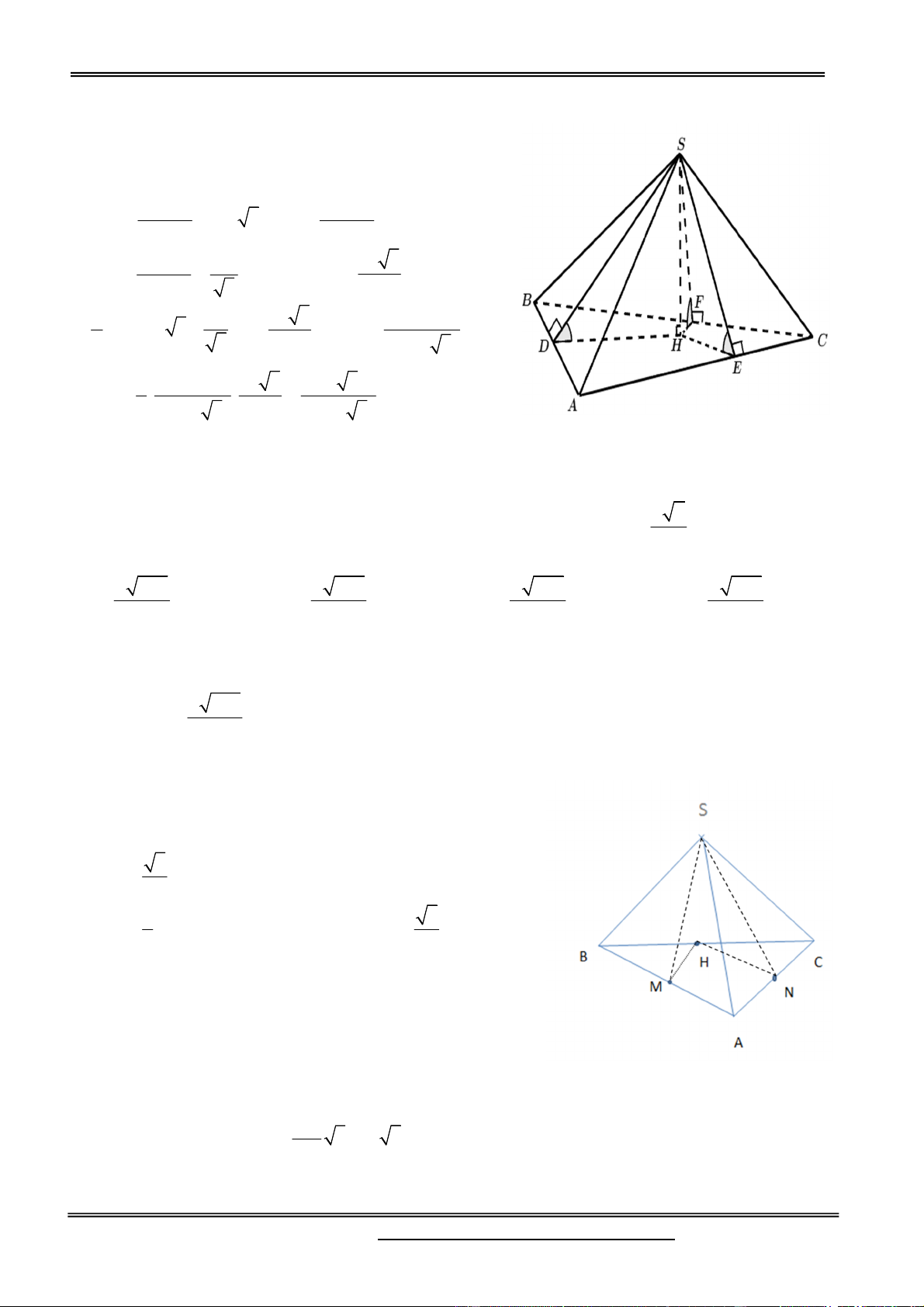
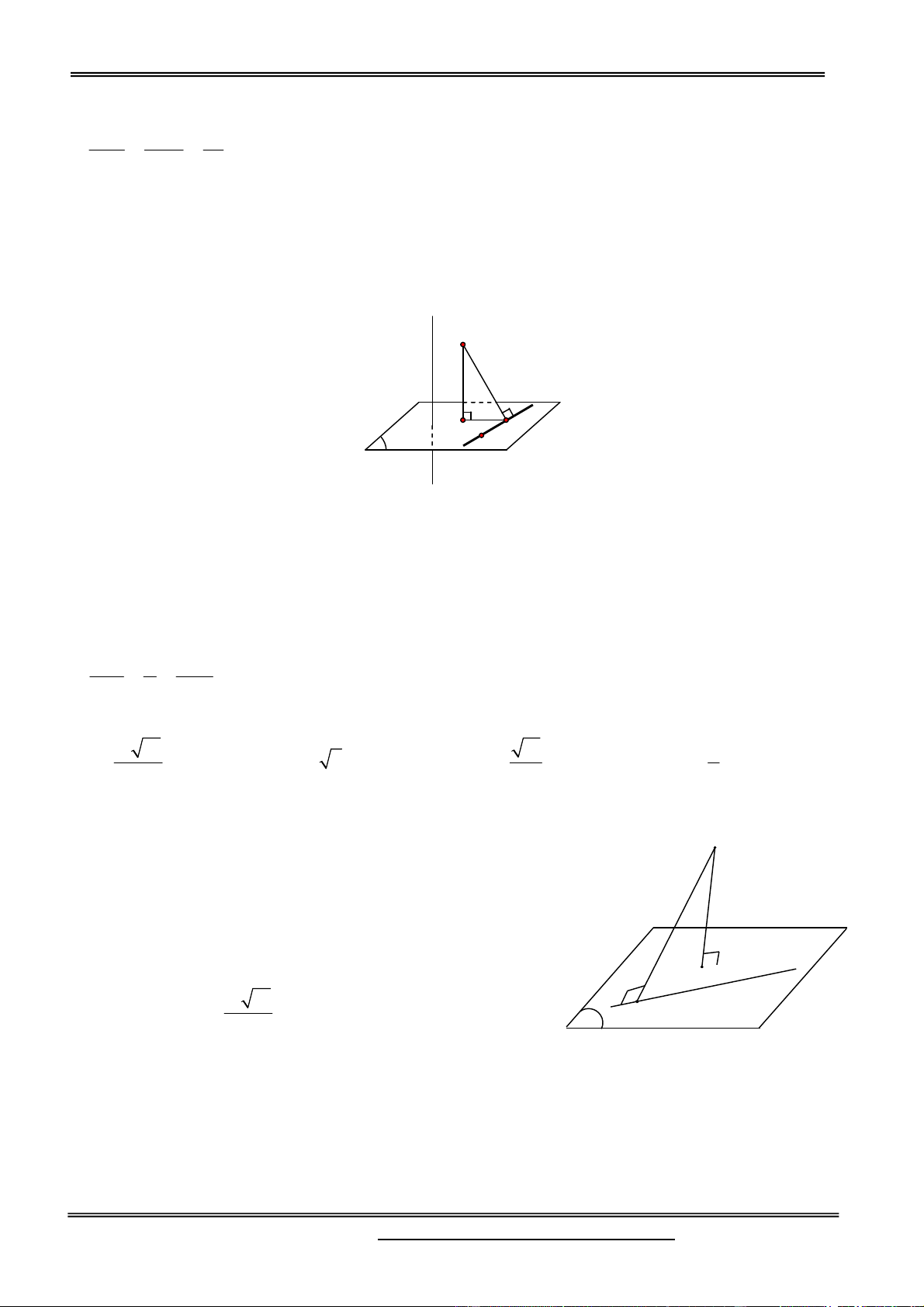
Câu 1. Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC ; các mặt phẳng (SAB),
(SAC ) và (SBC) cùng tạo với mặt phẳng (ABC ) một góc bằng nhau. Biết AB  25, BC  17 ,
AC  26 ; đường thẳng SB tạo với mặt đáy một góc bằng 45 . Tính thể tích V của khối chóp S.ABC . A. V  680 B. V  408 C. V  578 D. V  600 Hướng dẫn giải:
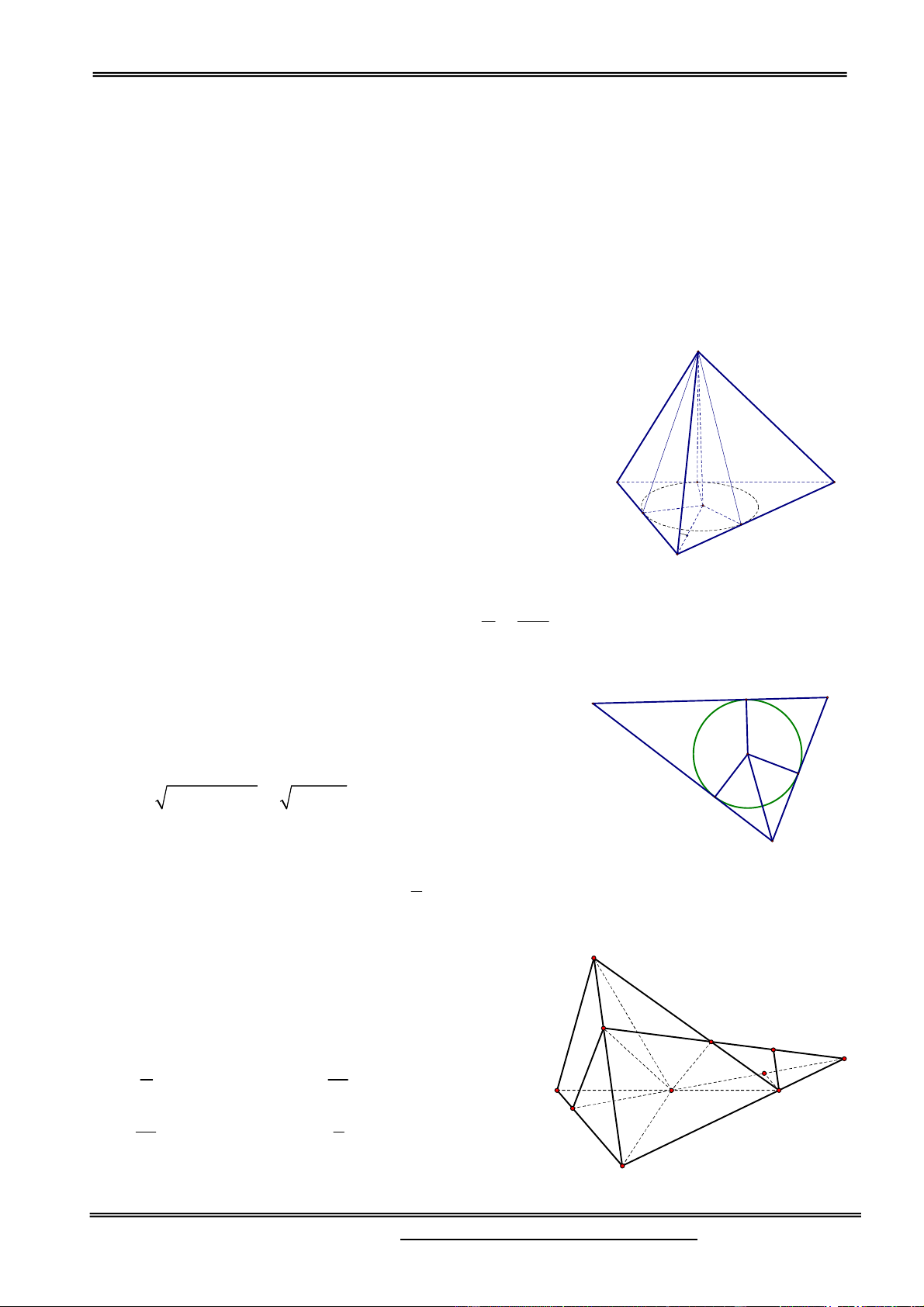
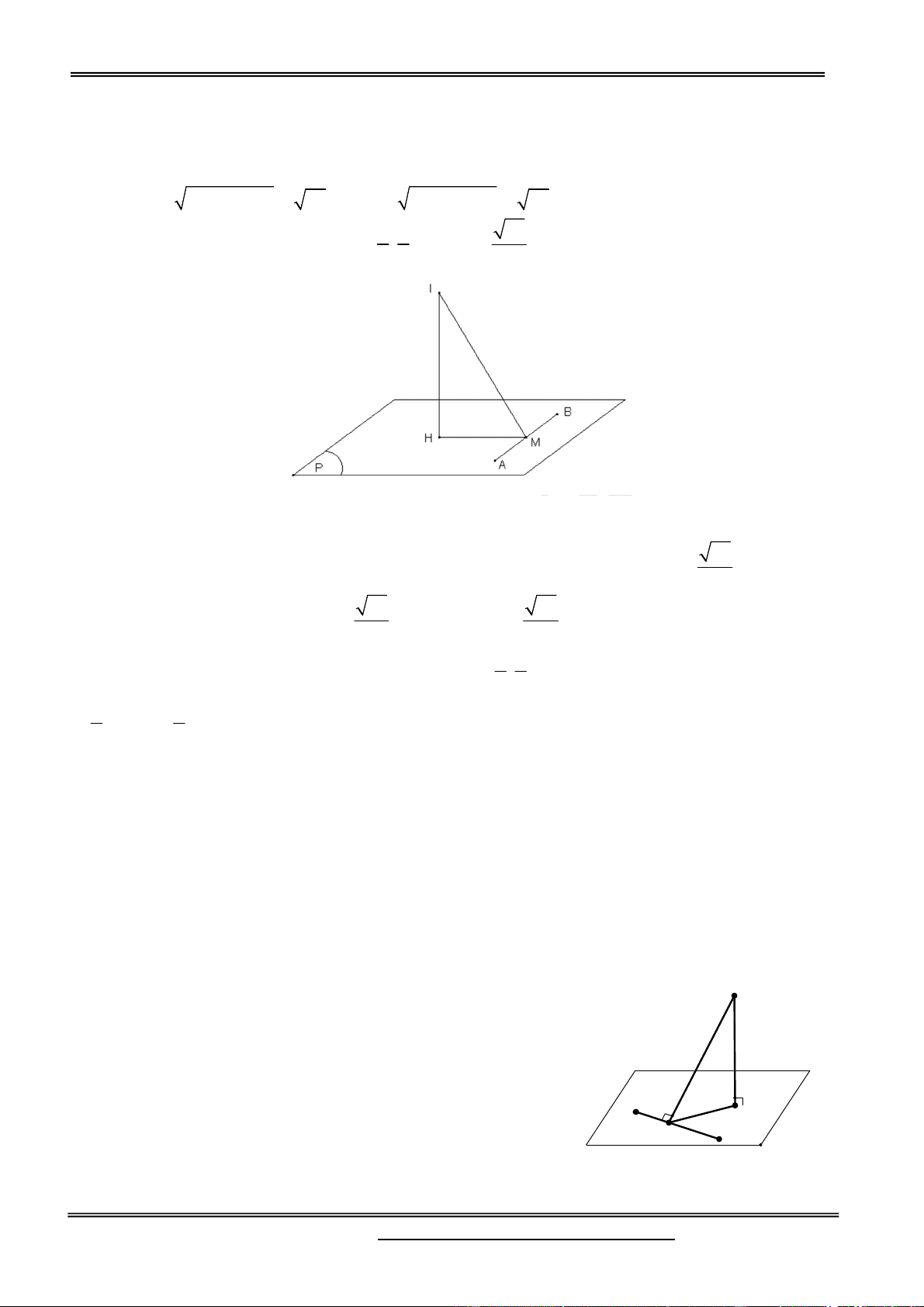
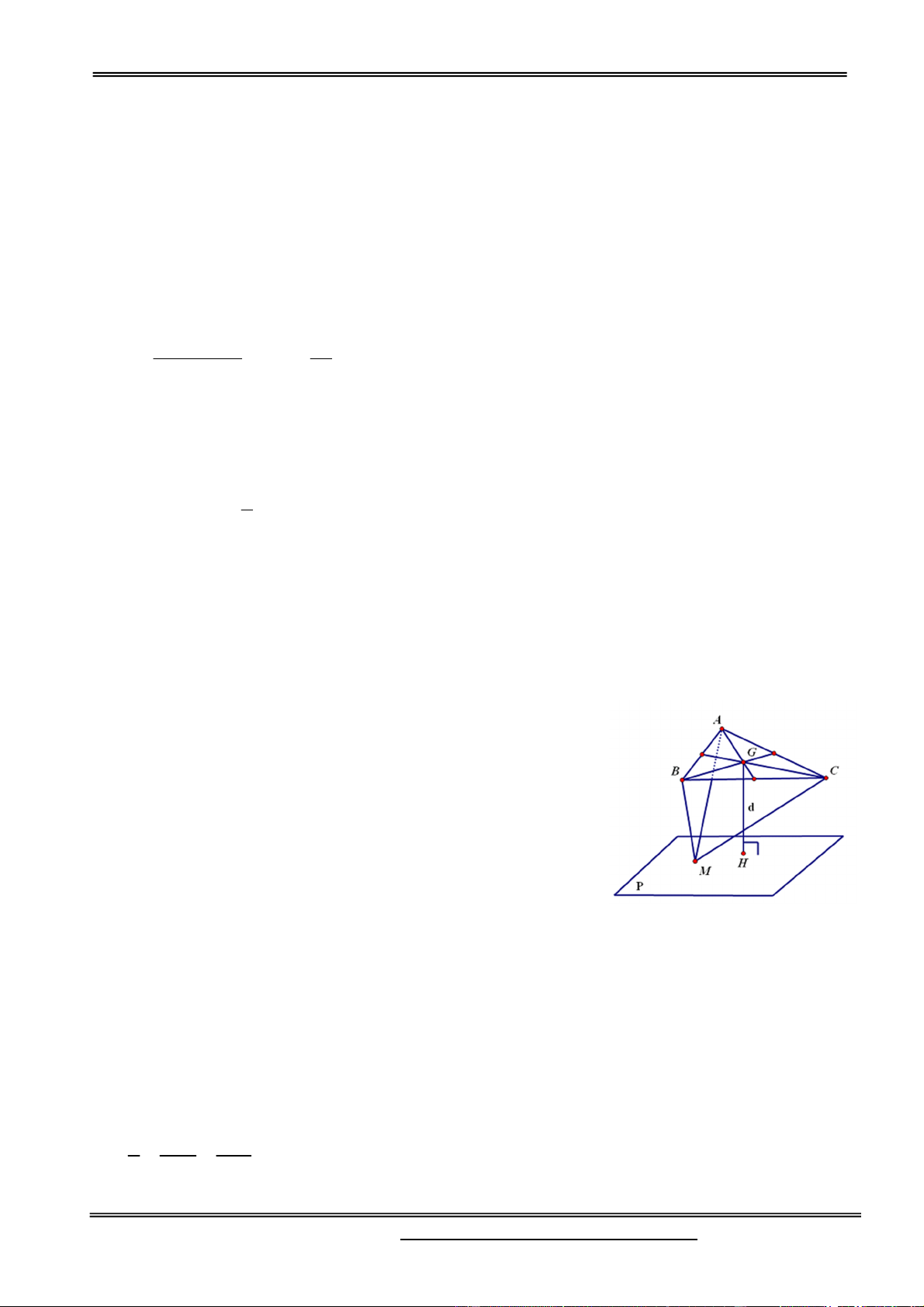
Gọi J là chân đường cao của hình chóp S.ABC; H, K và L S
lần lượt là hình chiếu của J trên các cạnh AB, BC và CA.  Suy ra, SHJ  , SLJ 
và SKJ lần lượt là góc tạo bởi
mặt phẳng (ABC ) với các mặt phẳng (S AB) , (SBC ) và (SAC ) . Theo giả thiết, ta có   
SHJ  SLJ  SKJ , z=17 K y=9 A C
suy ra các tam giác vuông SJH ,SJL và SJK bằng nhau. z=17 J y=9 H
Từ đó, JH  JL  JK . Mà J nằm trong tam giác ABC nên J là L x=8
tâm đường tròn nội tiếp tam giác ABC. x=8
Áp dụng công thức Hê-rông, ta tính được diện tích của tam giác B
ABC là S  204 . Kí hiệu p là nửa chu vi tam giác ABC, r là S 204
bán kính đường tròn nội tiếp của ABC. Ta có r  
 6 . Đặt x  BH  BL , y CL CK , p 34
z  AH  AK .
x  y 17 z y K C  A
Ta có hệ phương trình x  z  25 .  y
y  z  26  z J
Giải ra được (x; y; z)  (8;9;17) L 2 2 2 2
JB  JH  BH  6 8  10 . H x   x
Ta có SBJ  (SB,( ABC ))  45 , suy ra SJB là tam giác B
vuông cân tại J. SJ  JB  10 . 1
Thể tích V của khối chóp S.ABC là V  SJ .S  680 3 ABC Chọn đáp án A.
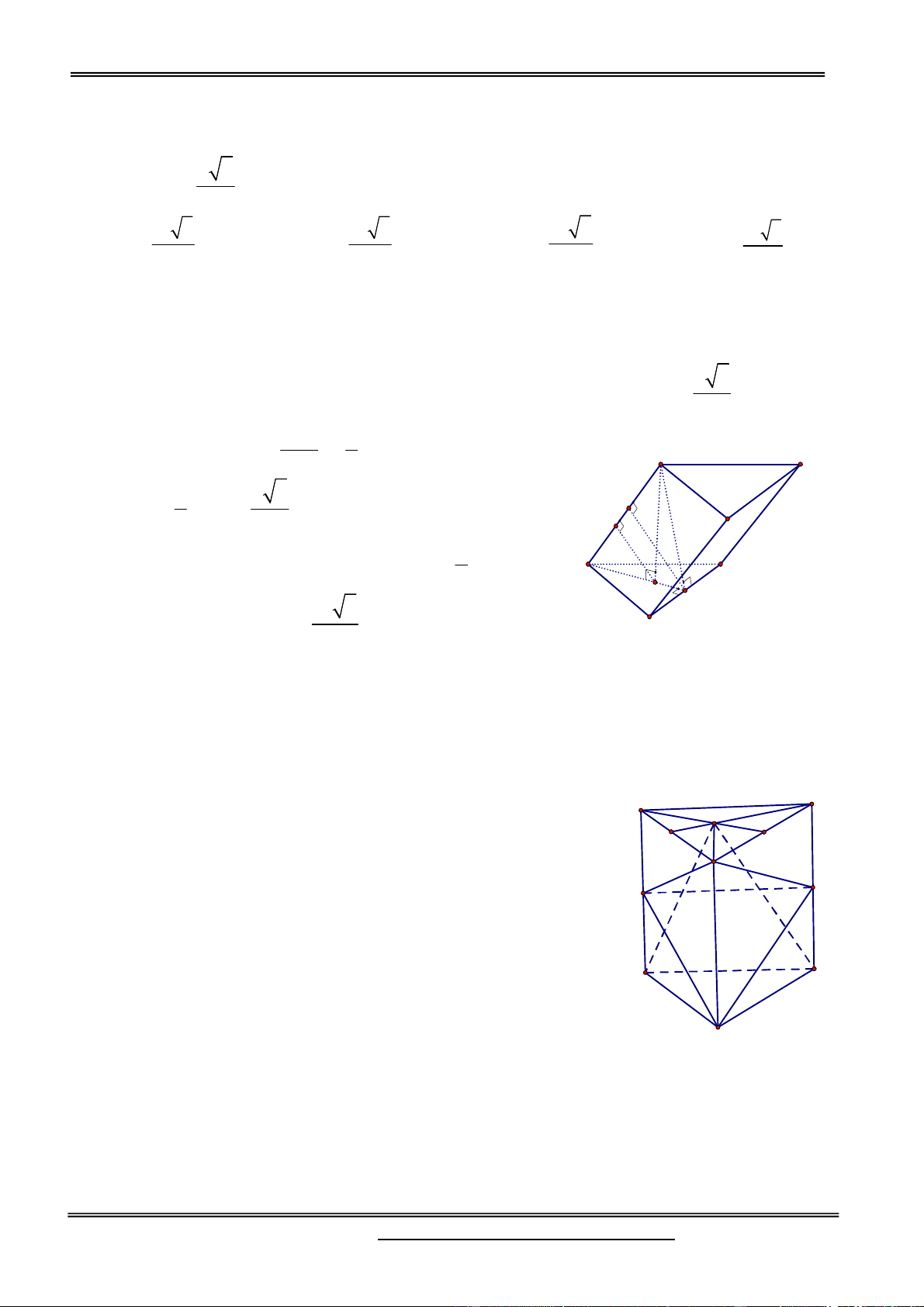
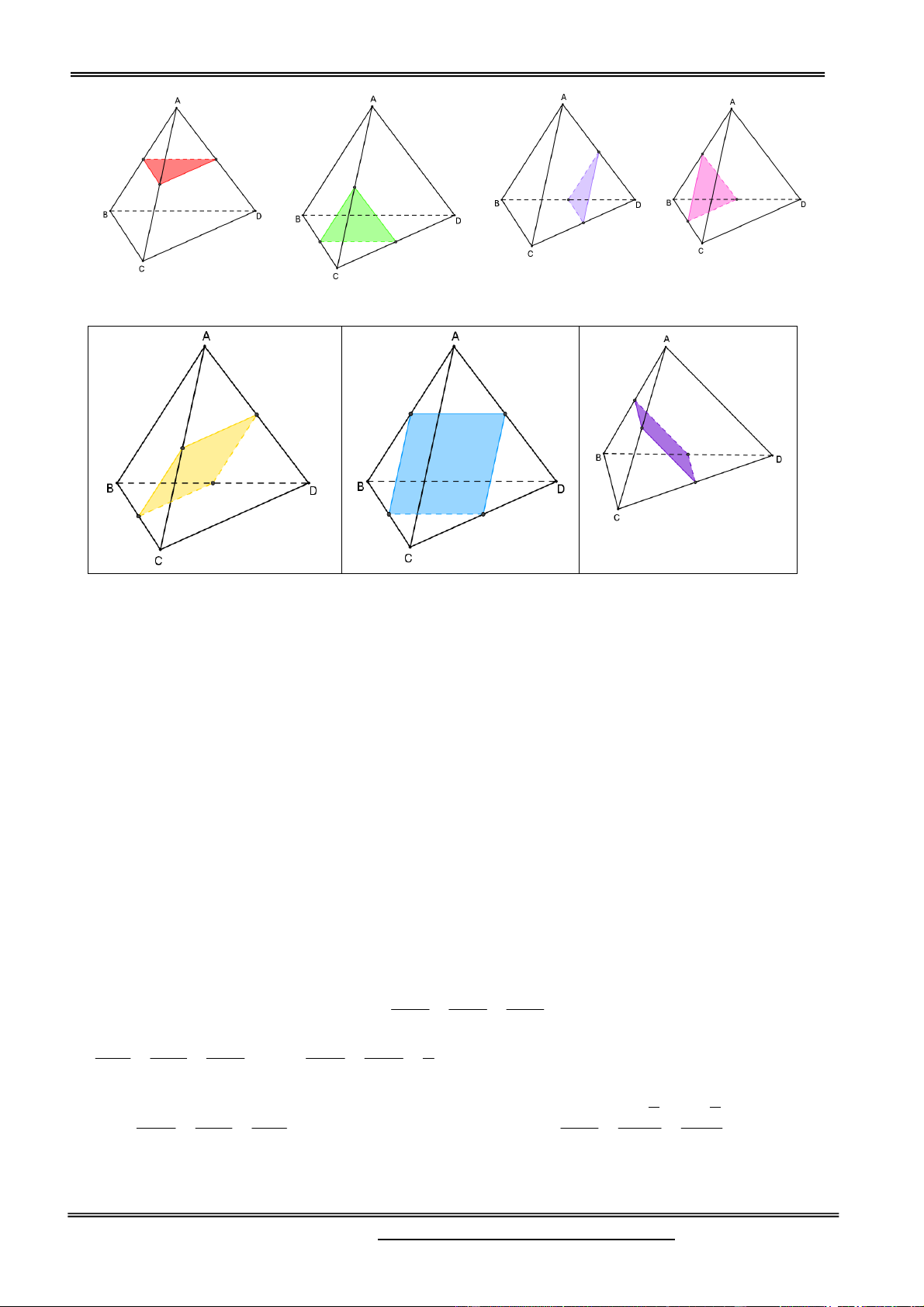
Câu 2. Cho tứ diện ABC ,
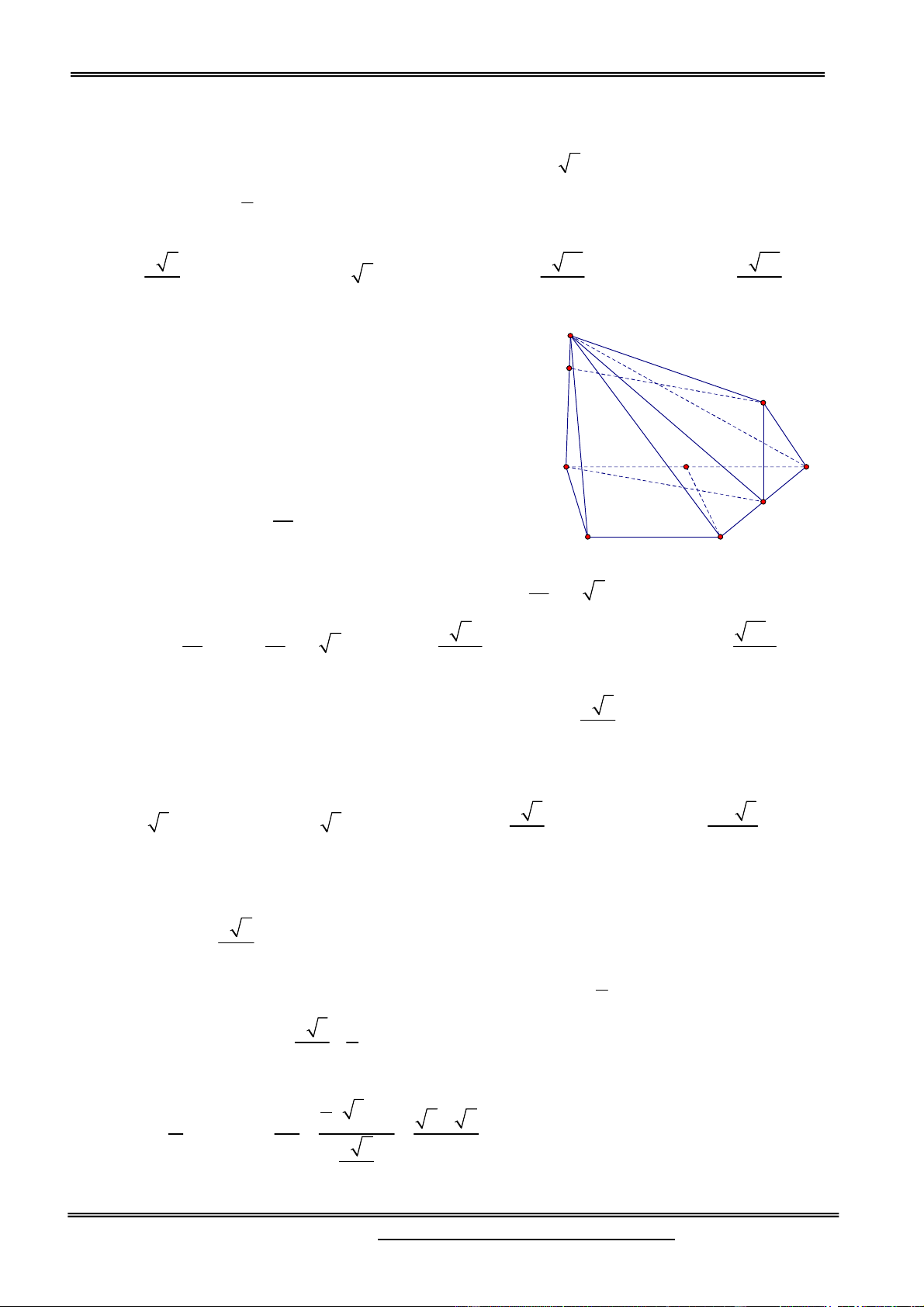
D M , N, Plần lượt thuộc A BC, B , D AC sao
cho BC  4BM , BD  2BN,
AC  3AP , mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số
thể tích hai phần khối tứ diện ABCD bị chia bởi mặt P Q K phẳng (MNP). I H 2 7 A. B. B 3 13 N D M 5 1 C. D. . 13 3
Hướng dẫn giải: C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 27
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Gọi I  MN  C ,
D Q  PI  AD , kẻ DH / / BC  H  IM , DK / / AC K  IP ID DH BM 1 NMB  N  DH     IC CM CM 3 IK DK ID 1 DK 1 DK 2        IP CP IC 3 2 AP 3 AP 3 A
 PQ đồng dạng D  KQ AQ AP 3 AQ 3      DQ DK 2 AD 5 Đặt V  V Ta có: ABCD VANPQ AP AQ 1 V V DN 1 1  .  , ANCD DACN     V  V V AC AD 5 V V DB 2 ANPQ 10 ANCD ABCD DABC V CM CP 1 1 1 1 1 CDMP  .   V  V  V  V  V V  V CDMP N . ABMP DABMP  CDMP  V CB CA 2 2 2 2 4 CDBA 7 VABMNQP 7  V  V  V  V   ABMNQP ANPQ N . ABMP 20 V 13 CDMNQP Chọn đáp án B.
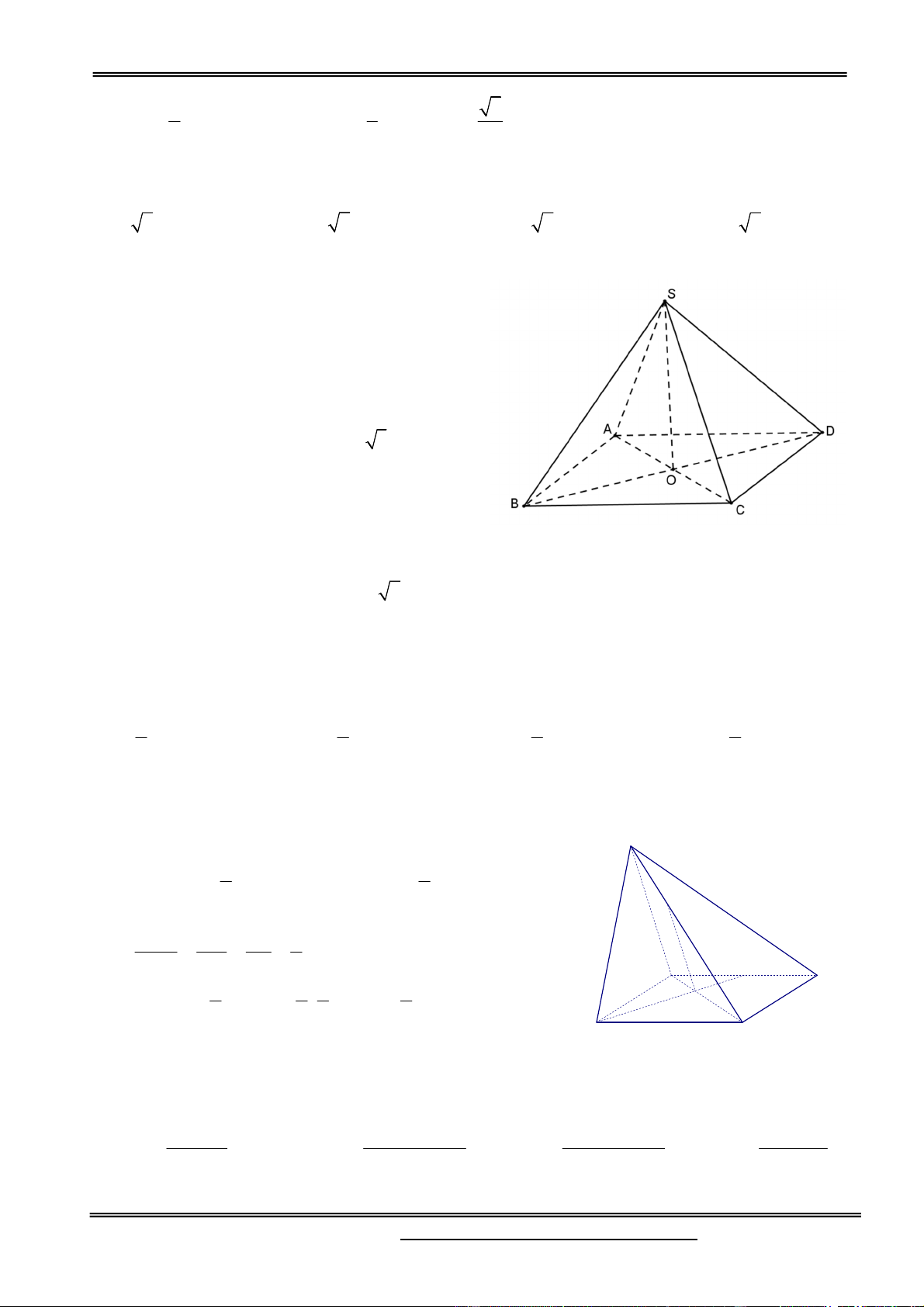
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = a, hình chiếu AC
vuông góc của đỉnh S trên mặt phẳng (ABCD) là điểm H thuộc đoạn AC, AH  . Gọi CM là 4
đường cao của tam giác SAC. Tính thể tích khối tứ diện SMBC theo a. 3 a 14 3 a 14 3 a 14 3 a 14 A. B. C. D. 48 24 16 8 Hướng dẫn giải:
Gọi O là tâm của hình vuông ABCD. S a 2 .a 2 AM AH AH .AC a M Ta có: 4   AM    AC SA SA a 2 A D 2 H       a  a MC AC AM a 2 2 7 2 2     O  2  2 2 1 1 a a 7 a 7 C B  S  SM .MC   SMC 2 2 2 2 8 2 3 1 1 a 2 a 7 a 14  V  B . O S   SMAC 3 SMC 3 2 8 48 Chọn đáp án A.
Câu 4. Cho hình chóp tứ giác đều .
S ABCDcó đáy là hình vuông ABCD cạnh a, góc giữa mặt bên và 1
mặt phẳng đáy là  thoả mãn cos =
. Mặt phẳng P qua AC và vuông góc với mặt phẳng SAD 3 chia khối chóp .
S ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị
nào trong các giá trị sau A. 0,11 B. 0,13 C. 0,7 D. 0,9
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 28
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: .
S ABCD là hình chóp tứ giác đều SO   ABCD. Gọi N là trung điểm CD
CD  SN,CD   ON 
 SCD  ABCD     ,  SNO 
 SCDABCD    CD
Kẻ CM  SD . Ta có AC  BD 
 AC  SBD  AC  SD AC   SO S
 SD   ACM    ACM   SAD nên mặt phẳng
P là ACM
+ Xét tam giác SON vuông tại N có : M a ON 3 2 a SN     1 A cosSNO 2 D 3 2 2 O N  3a   a  2 2
SO  SN  ON    a 2     B  2   2  C 2 2  a 2  a 10
+ Xét tam giác SOD vuông tại O có : 2 2
SD  SO  OD  a 2       2  2   3a 1 1 .a SN.CD 3a 10 Ta có S 
CM.SD  SN.CD 2  CM    SCD 2 2 SD a 10 10 2 2   a a
- Xét tam giác MCD vuông tại M có : 2 2 2 3 10 10
DM  CD  CM  a      10  10   a 10 V V 1 DM DA DC 1 DM 1 1 Ta có : MACD MACD 10   . . .  .  .  V 2.V 2 DS DA DA 2 DS 2 SABCD SACD a 10 10 2 1  V  V
. Mặt phẳng P chia khối chóp S.ABCD thành 2 khối MACD và SABCM MACD 10 SABCD 9 V 1  V  V  V  V  V . Do đó : MACD   0,11 SABCD MACD SABCM SABCM 10 SABCD V 9 SABCM Chọn đáp án A.
Câu 5. Cho hình chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Các mặt bên SAB,  SAC  ,
SBC  lần lượt tạo với đáy các góc lần lượt là 0 0 0
30 , 45 , 60 . Tính thể tích V của khối chóp S.ABC .
Biết rằng hình chiếu vuông góc của S trên mặt phẳng  ABC  nằm bên trong tam giác ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 4  3 24  3 4 4  3 84  3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 29
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải:
Gọi H là hình chiếu vuông góc của S trên mặt phẳng
 ABC  . Kẻ HD  AB D  AB, HE  AC E  AC  ,
HF  BC  E  BC . Khi đó ta có SH SH HD 
 SH 3 , HE   SH , 0 tan 30 0 tan 45 SH SH 2 a 3 HF   . Ta có S  suy ra 0 ABC tan 60 3 4 2 1  1  a 3 3a SH 1 3  a   SH  .   2  3  4 24  3 2 3 1 3a a 3 a 3 Vậy V  . .  . 3 24  3 4 84  3 Chọn đáp án D.
Câu 6. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, góc giữa SC và mp(ABC) là 45  . Hình a 7
chiếu của S lên mp(ABC) là điểm H thuộc AB sao cho HA = 2HB. Biết CH  . Tính khoảng cách 3
giữa 2 đường thẳng SA và BC: a 210 a 210 a 210 a 210 A. B. C. D. 30 20 45 15 Hướng dẫn giải:
+ D là đỉnh của hình bình hành ABCD thì d(SA;BC)=d(B;(SAD))=1,5.d(H;(SAD))
+ Kẻ HE vuông AD, E thuộc AD. Kẻ HI vuông SE, I thuộc AE thì d(H;(SAD))=HI a 210 + Tính HI  30 Chọn đáp án B.
Câu 7. Cho khối chóp S.ABC có đáy là tam giác vuông ở A,
AB = a, AC = 2a. Đỉnh S cách đều A, B, C; mặt bên (SAB)
hợp với mặt đáy (ABC) góc 600. Tính thể tích khối chóp S.ABC. 3 A. V= a3 B. V= a3 3 1 3 C. V= a3 D. V= 3. a3 3 3 Hướng dẫn giải:
Gọi M, N, H lần lượt là trung điểm của AB, AC, và BC
Ta có tam giác SAB cân suy ra SM  AB
HM // AC  HM  AB  AB  SMH   AB  SH   1
Và [(SAB), (ABC)] = SMH = 600
Tương tự AC  (SNH)  AC  SH (2)
Từ (1) và (2)  SH  (ABC) AC Ta có SH = MH. tan 600 = 3 = a 3 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 30
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1 1 3 SABC = AC.AB = a2 . Vậy V = .SH. SABC = a3 (đvdt) 2 3 3 Chọn đáp án A.
Câu 8. Cho hình chóp S.ABCD có SA=x, các cạnh còn lại bằng 2. Tìm giá trị của x để thể tích khối chóp lớn nhất A. 6 B. 2 C. 7 D. 2 6 Hướng dẫn giải:
Gọi O là giao điểm của AC và BD.
Ta có OD=OB và SB=SD nên SO  BD , do đó
BO  SAC  . Mặt khác 2 2 2 2 2 2
SO  SB  OB  AB  OB  OA
nên SO  OA  OC . Do đó tam giác SAC vuông tại S. Ta có 2 2 2 2
AC  x  4  4OA  x  4 . Do đó 2 2
4OB  12  x  0  x  2 3 . Và 2 2 S  x  2 2 OA  x  2 16 4  4x . SOA Để V
đạt giá trị lớn nhất khi và chỉ khi S . ABCD V
đạt giá trị lớn nhất . SOAB Do đó V
đạt giá trị lớn nhất khi và chỉ khi 2 x  2
12  x  đạt giá trị lớn nhất. S . ABCD Suy ra 2 2 2
x  12  x  x  6  x  6 . Chọn đáp án A.
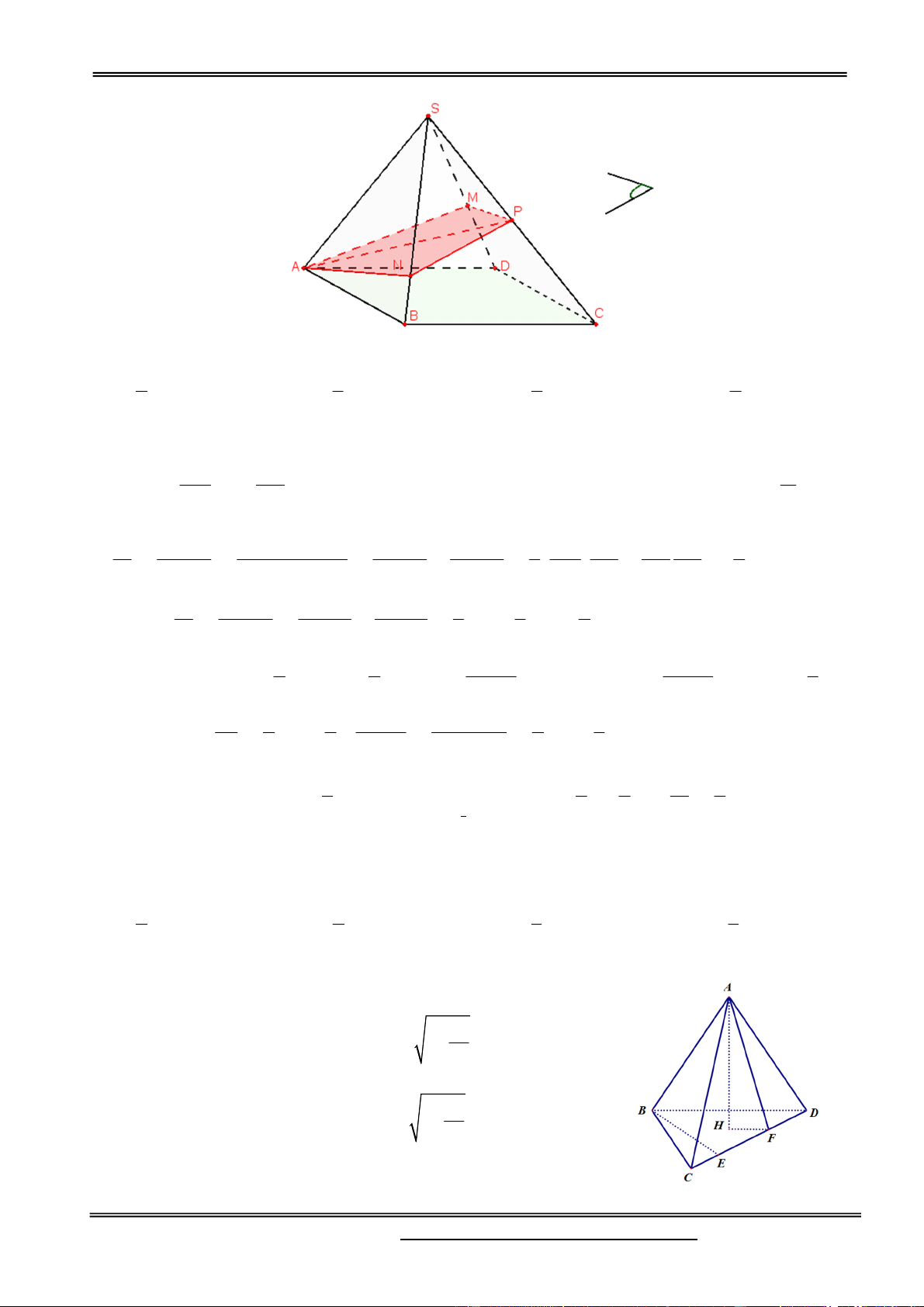
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của AD. Gọi S’ là
giao của SC với mặt phẳng chứa BM và song song với SA. Tính tỉ số thể tích của hai khối chóp S’.BCDM và S.ABCD. 1 2 3 1 A. B. C. D. 2 3 4 4 Hướng dẫn giải:
Trong  ABCD , gọi I  AC  BM , trong  SAC  , kẻ đường thẳng qua I, / / SA , cắt SC tại S’ 
S’ là giao điểm của SC với mp chứa BM, //SA. S
Do M là trung điểm của AD nên 3 3
dt  BCDM   dt  ABCD  V  V S '.BCDM S '. 4 4 ABCD S'
Gọi H, H’ lần lượt là hình chiếu của S, S’ trên ABCD S ' H ' CS ' CI 2     SH CS CA 3 A M D 3 3 2 1 I  V  V   V  V S '.BCDM S '. ABCD S . ABCD S. 4 4 3 2 ABCD B C Chọn đáp án A.  
Câu 10. Đáy của hình chóp SABC là tam giác cân ABC có AB  AC  a và B  C   . Các cạnh bên
cùng tạo với đáy một góc  . Tính thể tích hình chóp SABC. 3 a tan  3
a cos tan  3
a cos tan  3 a sin 2 A. V  B. V  C. V  D. V  6 6 3 6 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 31
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Kẻ SO   ABC   OA là hình chiếu vuông góc của SA lên (ABC)
Do đó SA  ABC   ;
 SAO   . Tương tự ta cũng có  
SBO  SCO   . Nên S
 AO  SBO  S
 CO  AO  BO  CO . AC a a Theo định lí sin ta có: 
 2OA  OA  . sin B sin  2 sin  a tan  Nên SO  O . A tan   . 2sin  2 1 1 a sin   Mặt khác 2 S  A . B AC.sin A  a sin    . ABC 180 2  2 2 2 2 3 1 1 a sin   a tan 
a cos tan  Vậy V  S .SO  .  . 3 A  BC 6 2 2sin  6 Chọn đáp án B.
Câu 11. Cho hình chop S.ABCD, đáy là hình thang vuông tại A và B. AB = BC = a, AD = 2a,
SA   ABCD . Gọi M, N là trung điểm của SB và SD. Tính V hình chop biết rằng (MAC) vuông góc với (NAC). 3 3a 3 3a 3 3 a 3 a 3 A. B. C. D. 2 2 2 2 Hướng dẫn giải:
Gọi I, H lần lượt là trung điểm AD và AB, O là giao điểm của AC và BI, vẽ HK // BI (K thuộc AC)
Ta có ABCI là hình vuông nên AC vuông góc với BI
Mà AC vuông góc NI (do NI // SA)
Suy ra AC   NIO  N
 OI   NAC, ACD   Tương tự ta có MK 
H  MAC, ACB    NI HK
Theo đề ta có     90  tan   cot    NO MH Suy ra SA SA a 2 a 2
NI.MH  OI.HK  .   SA  a 2 2 2 4 2 3 3a 1 a Mà S   V  S .SA  ABCD 2 3 ABCD 2 Chọn đáp án C.
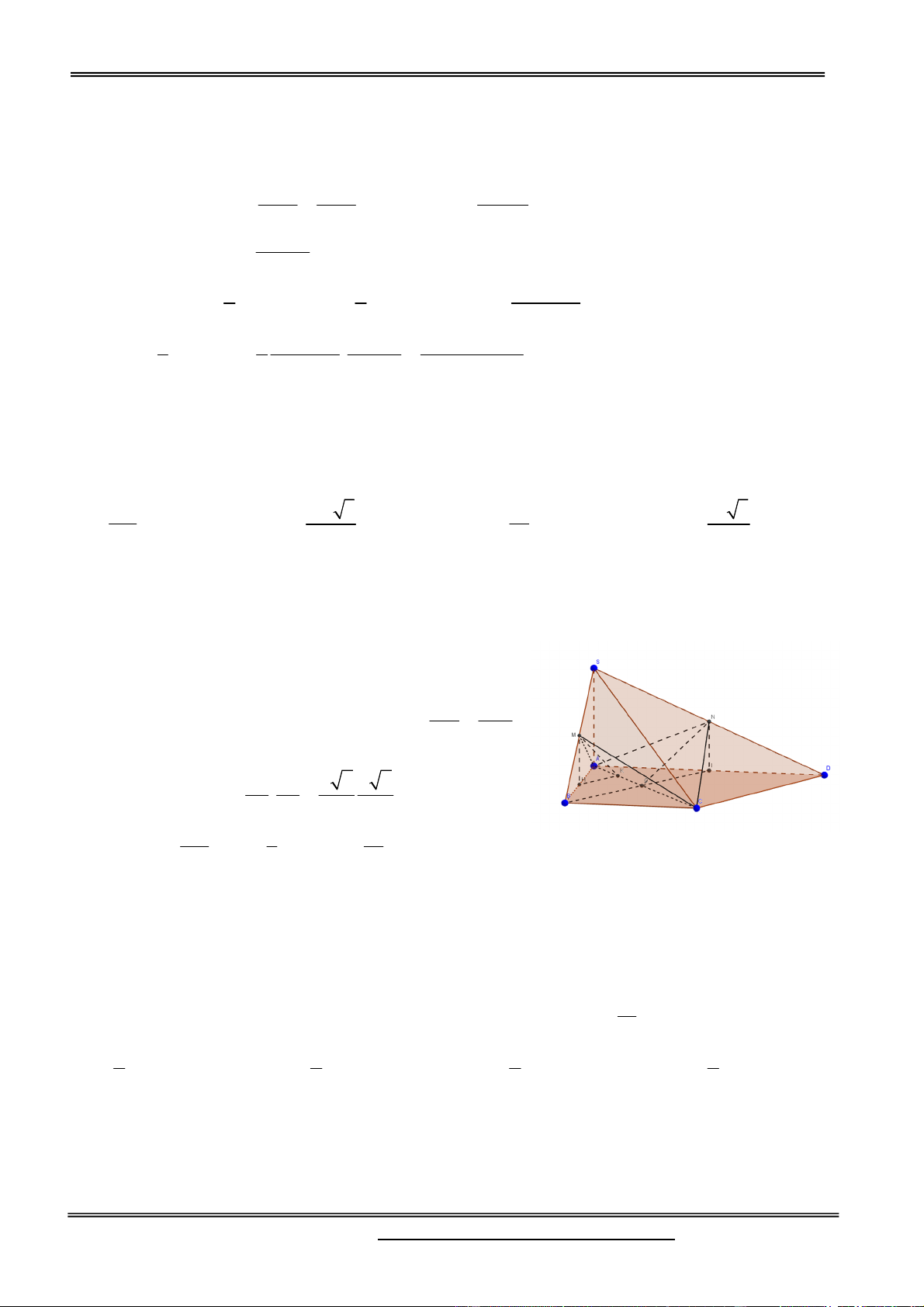
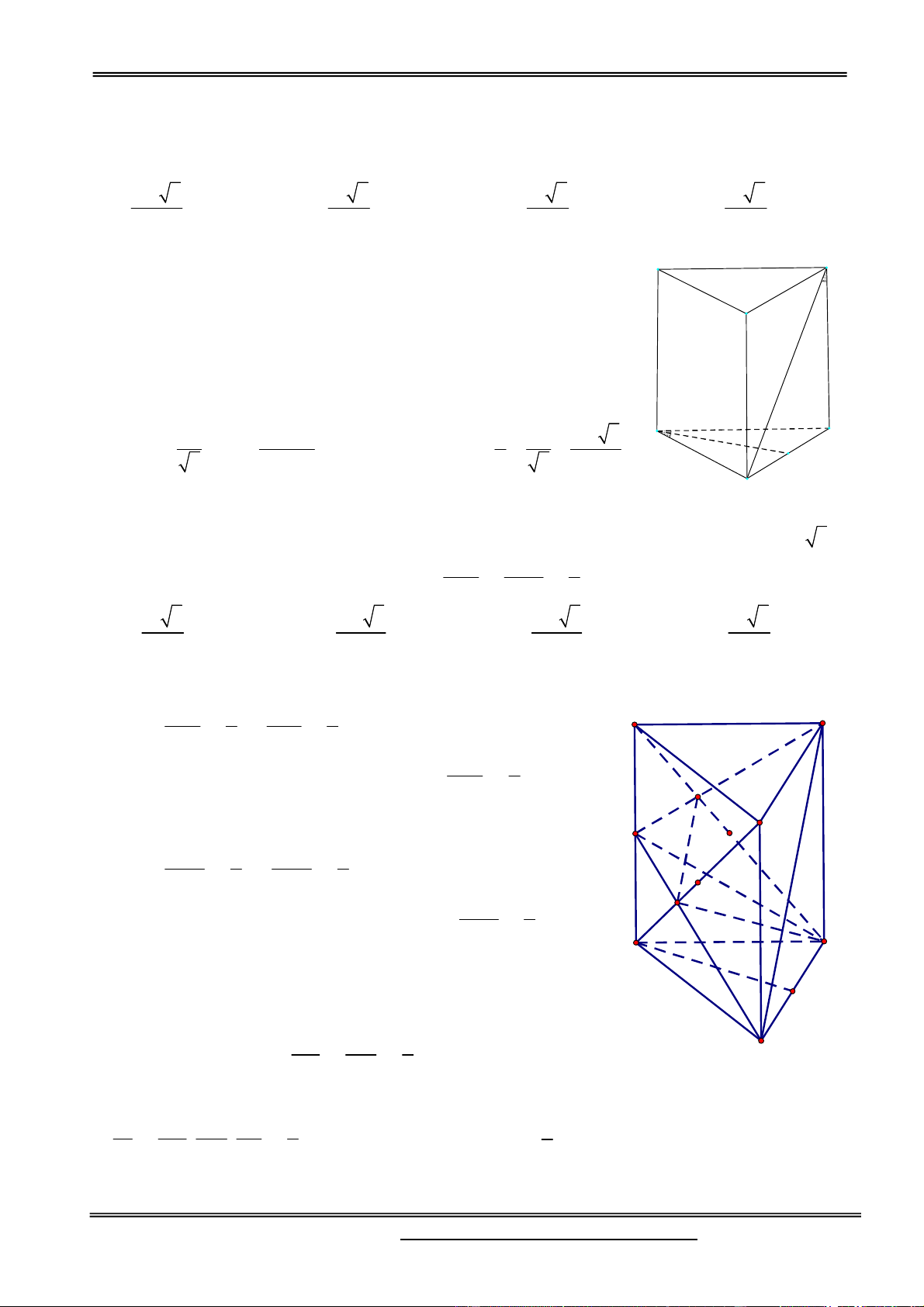
Câu 12. Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA  2SM ,
SN  2NB , ( ) là mặt phẳng qua MN và song song với SC . Kí hiệu (H ) và (H ) là các khối đa 1 2
diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng ( ) , trong đó, (H ) chứa điểm S , (H ) 1 2 V
chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . Tính tỉ số 1 . 1 2 1 2 V2 4 5 3 4 A. B. C. D. 5 4 4 3 Hướng dẫn giải:
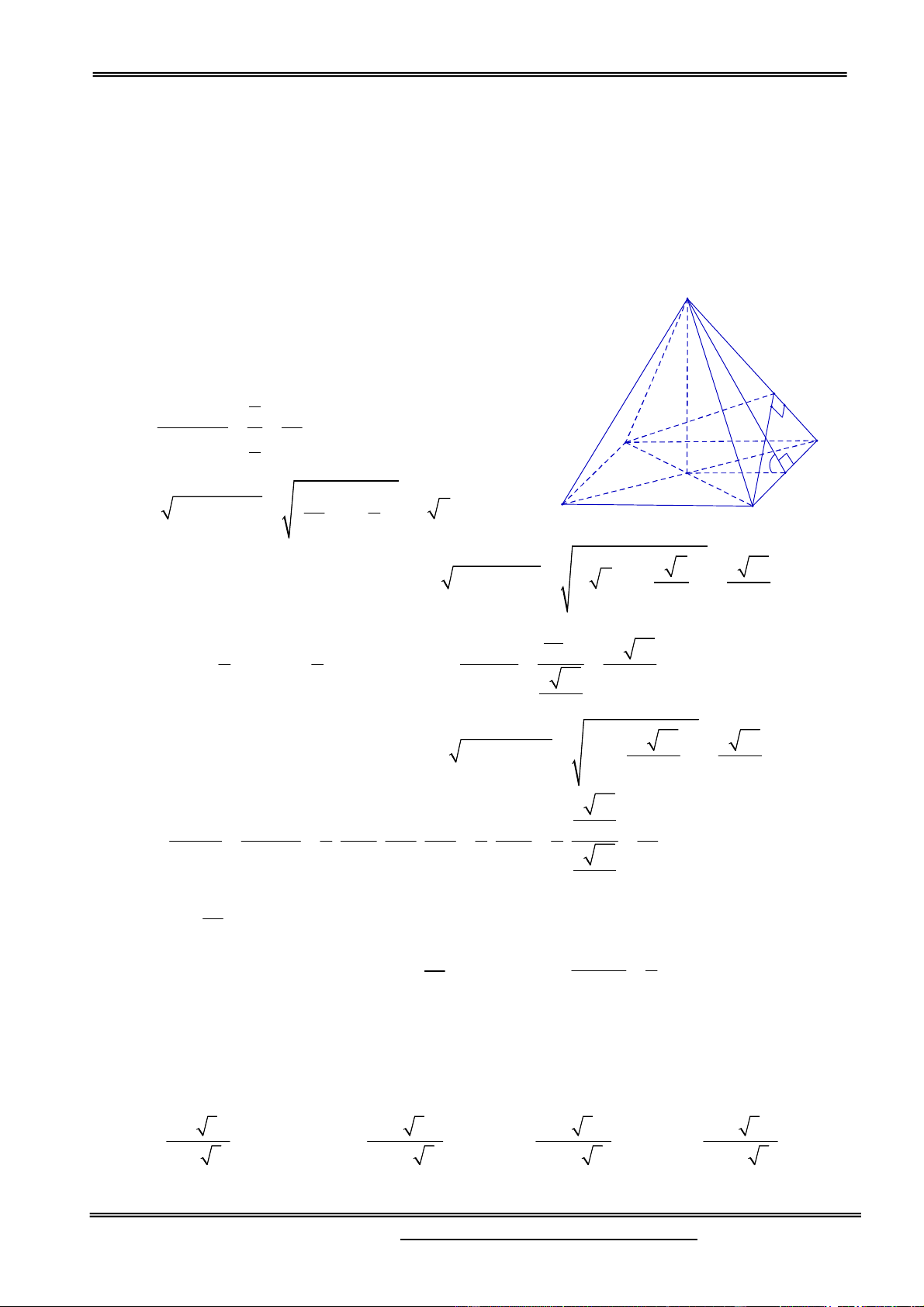
Kí hiệu V là thể tích khối tứ diện SABC .
Gọi P , Q lần lượt là giao điểm của ( ) với các đường thẳng BC , AC .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 32
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Ta có NP//MQ//SC . Khi chia khối (H ) bởi mặt phẳng (QNC) , ta được hai khối chóp N.SMQC 1
và N.QPC . V d N SAC S N SMQC ( , ( )) Ta có: . SMQC   ; V d (B, (SAC)) S B. ASC SAC S
d (N, (SAC)) NS 2   ; d (B, (SAC)) BS 3 2 S  AM S M AMQ  4 SMQC 5       . S  AS  9 S 9 ASC ASC VN SMQC 2 5 10 Suy ra .    V 3 9 27 N B. ASC V d N C S N .QPC ( , (QP )) QPC C   A Q V
d (S, (A BC)) S S . ABC ABC P NB CQ CP 1 1 2 2 B        SB CA CB 3 3 3 27 V V V N .SMQC N .QPC 10 2 4 V 4 V 4 1 1         5V  4V 1   1 2 V V V 27 27 9 V V 9 V 5 B. ASC S . ABC 1 2 2 Chọn đáp án A.
Câu 13. Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là V . Để làm
thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng 2 1 A. 3 x  V B. 3 x  V C. 4 x  V D. x  V Hướng dẫn giải:
Gọi a là độ dài cạnh đáy, x là độ dài đường cao của thùng đựng đồ a,x  0 V V Khi đó, 2 2 V  a x  a   S  2a  4ax  2  4 Vx tp x x V
Để làm thùng hàng tốn ít nguyên liệu nhất thì S nhỏ nhất  2  4 Vx nhỏ nhất. tp x
Cách 1 : Xét hàm số   V f x  2  4 Vx trên 0; x 1 2  V 2 V Ta có f 'x   ; f 'x 2 3  0  x V  V x  x  V 2 x x 1 x 0 V 3 + ∞ f' x ( ) 0 + f x ( ) 1 f (V 3 ) 1
Từ BBT ta thấy để làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng 3 V .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 33
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 V V Cách 2: ta có 3 2 2  4 Vx  2  2 Vx  2 Vx  6 V x x V Dấu "  " xảy ra tại 3 3  Vx  x  V  x  V x Chọn đáp án B.
Câu 14. Cho hình chóp S. ABCD có đáy ABCD là hình vuông, SAD là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Biết rằng diện tích mặt cầu ngoại tiếp khối chóp S. ABCD là  2
4 dm  . Khoảng cách giữa hai đường thẳng SD và AC gần với giá trị nào nhất sau đây ? 2 3 4 6 A. dm . B. dm . C. dm . D. dm . 7 7 7 7
Hướng dẫn giải:
Gọi x  0 là cạnh của hình vuông ABCD và H là
trung điểm cạnh AD x 3
Dễ dàng chứng minh SH   ABCD, SH  . 2
Gọi O  AC  BD và G là trọng tâm SAD , đồng
thời d , d lần lượt là 2 trục đường tròn ngoại tiếp 1 2 ABC , D SAD
d qua O va / /SH , d qua G va / / AB 1 2 
 I  d  d là tâm mặt cầu ngoại tiếp khối chóp 1 2
S. ABCD  R  SI 2 2  x   x  2 21 2 2 2
S  4 R  R  1  SI  SG  GI    x      dm  3   2  7
Gọi E là điểm thỏa ADEC là hình bình hành  ED / / AC  d  AC; SD  d  AC;SDE 
 d  AC; SD  d  ;
A SDE  2d H;SDE  2HP (phần chứng minh HP  SDE  xin dành cho bạn đọc) 1 1 1 1 1 S  KH :     2 2 2 2 2 HP SH KH  x 3   x 2      2 4     x 21 3 6  HP  
dm  d  AC;SD  dm 14 7 7 Chọn đáp án D.
Câu 15. Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm
của SC , một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N.Gọi V là thể tích của khối 1 V
chóp S.AMPN . Tìm giá trị nhỏ nhất của 1 ? V
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 34
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3 1 2 1 A. B. C. D. 8 3 3 8 Hướng dẫn giải: SM SN V Đặt x  ;y 
,(0  x,y  1) khi đó ta có : V V V V  SD SB SABC SADC SABD SBCD 2 Ta có : V V V V V V 1 SM SP SN SP    1 1 SAMPN SAMP SANP SAMP SANP       .     
x  y  1 V V V 2V 2V 2  SD SC SB SC  4 SADC SABC V V V V 1  1    3 Lại có : 1 SAMPN SAMN SMNP     x
 y  xy  xy     2 V V 2V 2V 2  2  4 SABD SBCD 1 3 x x 1
Từ (1) và (2) suy ra : x  y  xy  y 
do 0  y  1   1  x  4 4 3x  1 3x  1 2 2 V   1 3 3 x 3x 3 1   Từ (2) suy ra  .xy  .x  
f x   x   V x    43x   ( ), 1 4 4 3 1 1 4 2  1  2     4 V 1 Khảo sát hàm số 1
y  f (x),  x  1  min f (x)  f            1 2              V x x 3 9 3 1   2  Chọn đáp án B.
Câu 16. Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ diện đó lớn nhất là bao nhiêu? 1 3 1 5 A. B. C. D. 4 4 8 8 Hướng dẫn giải:
Giả sử tứ diện ABCD có cạnh lớn nhất là AB, suy ra các tam giác
ACD và BCD có tất cả các cạnh đều không lớn hơn 1. Các chiều 2 a
cao AF và BE của chúng không lớn hơn 1 , trong đó 4 CD  a  1. 2 a
Chiều cao của hình tứ diện AH  AF  1 4
(do tam giác AHF vuông tại H có AF là cạnh huyền)
Thể tích của khối tứ diện là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 35
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 1 1 1 1 1  a  1 V  S
.AH  . .BE.C . D AH  . . . a 1  a  a BC    2 4 D  3 3 2 3 2 4 24  
Để tìm giá trị lớn nhất của V ta xét biểu thức a  2 4  a  . 1 1
Vì 0  a  1 nên a  2
4  a   3 và V  a  2 4  a   . 24 8 Chọn đáp án C.
Câu 17. Cho hình chóp S .ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt
phẳng đáy và góc giữa SC với mặt phẳng (SAB) bằng 0
30 . Gọi M là điểm di động trên cạnh CD và
H là hình chiếu vuông góc của S trên đường thẳng BM. Khi điểm M di động trên cạnh CD thì thể
tích của khối chóp S.ABH đạt giá trị lớn nhất bằng? 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 2 6 12 Hướng dẫn giải: 
Ta có góc giữa SC và mặt phẳng (SAB) là CSB  0 30
Trong tam giác SBC có SB  0
BC.cot30  a 3
Trong tam giác SAB có SA  2 SB  2 AB  a 2 1 1 1 a 2
Thể tích khối chóp S.ABH là: V  S .SA  . H . A HB.a 2  H . A HB S .ABH 3 ABH 3 2 6 Ta có 2  2  2  2 HA HB AB
a và theo bất đẳng thức AM-GM ta có 2 a 2 a  2 HA  2 HB  2. . HA HB  H . A HB  2 
Đẳng thức xảy ra khi HA  HB  ABM  0 45  M  D 2 3 a 2 a 2 a a 2 Khi đó V  H . A HB  .  S .ABH 6 6 2 12 Chọn đáp án D.
Câu 18. Hai hình chóp tam giác đều có chung chiều cao , đỉnh của hình chóp này trùng với tâm của
đáy hình chóp kia. Mỗi cạnh bên của hình chóp này đều cắt một cạnh bên của hình chóp kia. Cạnh bên
l của hình chóp thứ nhất tạo với đường cao một góc  .Cạnh bên của hình chóp thứ 2 tạo với đường
cao một góc  . Tìm thể tích phần chung của hai hình chóp . 3 3 l 3 cos  3 3 l 3 cos  A. V  B. V  2
4(cot g  cot g ) 2
2(cot g  cot g ) 3 l 3 cos  3 l 5 cos C. V  D. V  2
2(cot g  cot g ) 2
4(cot g  cot g ) Hướng dẫn giải:
Đặt 2 hình chóp tam giác đều là : O.ABC và O’.A’B’C’ với O là tâm của tam giác ABC và O’ là tâm của tam giác A’B’C’.
Theo bài ra thì OO’ là đường cao chung của 2 hình chóp .
Đặt D,E,F là các giao điểm của các cặp cạnh bên tương ứng của 2 hình chóp . Phần thể tích chung 1
của 2 hình chóp là thẻ tích của khối đa diện ODEFO’. Ký hiệu V là thể tích đó thì V  OO '.S 3 DEF
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 36
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
OO'C vuông tại O’ nên OO'  l cos C'
Do tính đối xứng nên OO’ đi qua tâm I của DEF . A'
Trong IOE ta có : OI  IE cot  g O
Trong IO ' E có: O ' I  IE cot  g B'
Suy ra OO '  IE(cot g  cot g ) D OO ' l cos F  IE   I
cot g  cot g
cot g  cot g E 3
Tam giác DEF đều , đường cao EJ  EI 2 2 C DE 3 2EJ 3 Diện tích S  với DE   EI 3 A DEF 4 3 O' 2 2 3l 3 cos  Do đó S  DEF 2
4(cot g  cot g ) B
Vậy thể tích phần chung của 2 hình chóp là : 3 3 l 3 cos  V  2
4(cot g  cot g ) Chọn đáp án A.
Câu 19. Cho hình chóp S.ABCD có đáy là nửa lục giác đều với cạnh a (a> 0). Cạnh SA vuông góc với SM
đáy và SA = a 3 . M là một điểm khác B trên SB sao cho AM  MD. Tính tỉ số . SB 3 1 3 5 A. B. C. D. 4 4 5 4 Hướng dẫn giải:
Đặt hình chóp vào hệ trục toạ độ như hình vẽ.
Suy ra ta có: A = (0; 0; 0), D = (2a; 0; 0), S =
This image cannot currently be display ed. (0; 0; a 3 ) và  a a 3  B =  ;
; 0  . Suy ra phương trình của  2 2    2x 2 y z  a 3 SB là:   a a 3 a 3
Gọi M(x0; y0; z0) thuộc cạnh SB, ta có:   y  3x 0 0  .
z  a 3  2 3  x 0 0
 
Mặt khác AMDN  AM.DM  0 3a  x 2 2 2
0 – 2ax0 + y0 + z0 = 0  x  0 8
 3a 3a 3 a 3   3  SM 3  M   ; ;   SM  SB hay  .  8 8 4    4 SB 4 Chọn đáp án A.
Câu 20. Cho khối tứ diện ABCD có cạnh AB > 1, các cạnh còn lại có độ dài không lớn hơn 1. Gọi V là thể
tích của khối tứ diện. Tìm giá trị lớn nhất của V.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 37
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3 1 3 5 A. B. C. D. 8 8 5 8 Hướng dẫn giải:
Theo giả thiết ACD và BCD có tất cả các cạnh không lớn hơn 1. A
Đặt CD = a ( 0  a 1).
Gọi AM, BN lần lượt là chiều cao của ACD và BCD . 2 a 2 a Ta có AM  1 ; BN  1 . 4 4 D 2 a B H M
Gọi AH là chiều cao của tứ diện, ta có AH  AM  1 . 4 N C 2 1 1 a a
Thể tích của tứ diện ABCV  .S .AH  .BN.C . D AH  (1 ) 3 BCD 6 6 4 Xét 2
f (a)  a(4  a ) trên (0, 1]. Ta có f(a) liên tục trên (0, 1]. 2 ' 2 '
f (a)  4  3a , f (a)  0  a    0;  1 . 3 a 0 1 + f'(a) 3 f(a) 0
Vậy m ax f (a)  f (1)  3 . 0,  1 1 Suy ra maxV 
khi ACD và BCD là hai tam giác đều cạnh bằng 1, hai mặt phẳng (ACD) và 8 6
(BCD) vuông góc với nhau. Khi đó tính được AB   1. 2 Chọn đáp án B.
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a 3 và SA vuông góc
với mặt phẳng đáy. Mặt phẳng (P) đi qua điểm A và vuông góc với SC cắt SB, SC, SD lần lượt tại B’,
C’, D’. Tính thể tích khối chóp S.AB’C’D’ theo a. S 3 3 3a 3 3a A. B. 20 20 C' 3 3 3a 3 3 5a C. D. 10 10 D' Hướng dẫn giải: B' BC  A ,
B BC  SA  BC  (SAB)  BC  AB '
SC  (P)  SC  AB '  AB '  (SBC)  AB '  SB
Tương tự AD '  SD D C V  V V
S . AB 'C ' D '
S. AB 'C '
S. AD 'C ' 2 2 V SB ' SC '
SB '.SB SC '.SC SA SA 3 3 9
S . AB 'C '  .  .  .  A .  2 2 2 2 V SB SC SB SC SB SC 4 5 20 B S. ABC (1)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 38
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2 V SD ' SC '
SD '.SD SC '.SC SA SA 3 3 9
S . AD 'C '  .  .  .  .  (2) 2 2 2 2 V SD SC SD SC SD SC 4 5 20 S. ADC 3 1 1 a 3 Do 2 V  V  . a .a 3  S . ABC S. ADC 3 2 6
Cộng (1) và (2) theo vế ta được 3 3 V V 9 9 9 a 3 3 3a
S . AB 'C '
S . AD 'C '     V  . 
S . AB 'C ' D ' 3 3 a 3 a 3 20 20 10 6 20 6 6 Chọn đáp án A.
Câu 22. Cho hình chóp S.ABCD thỏa mãn SA  5, SB  SC  SD  AB  BC  CD  DA  3 .
Gọi M là trung điểm của cạnh BC . Tính thể tích khối chóp S.MCD và khoảng cách giữa hai
đường thẳng SM , CD . 15 5 15 13 A. B. C. D. 23 23 29 23 Hướng dẫn giải:
Ta thấy ABCD là hình thoi, tam giác SBD cân tại S suy ra BD   SAC
Gọi O là giao điểm của AC và BD , ta thấy SBD  ABD  CBD c.c.c 1
Suy ra OA  OC  OS  2  AC nên SAC vuông tại S . Xét SAC ta có 2 2 2 2 AC 
SA  SC  2 2  OC 
2,OD  CD  OC  1  BD  2 Thể tích 1 1 1 1 15 V  V   BD  S   2  5  3  S .CMD S. 4 ABCD 12 SAC 12 2 12 S
Gọi N là trung điểm của AD nên CD / /  SMN  Suy ra 3VC.
d (CD, SM )  d (CD, (SMN ))  d (C, (SMN ))  SMN  SSMN 15 Thể tích V  V  (1). C.SMN S.MCD 12 B A 3 13 M O N
Ta có MN  3, SM  , SN  ( sử dụng công thức 2 2 C D đường trung tuyến) 2 23 Theo định lý h  
àm số cosin trong SMN ta có cos SMN   sin SMN  3 3 3 3 1  23 Vậy S 
 SM  MN sin SMN  (2). SMN 2 4 3 15 3V 15 Thay (1), (2) vào    ta được C.SMN 12
d (CD, SM )    . S 23 23 SMN 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 39
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án A.
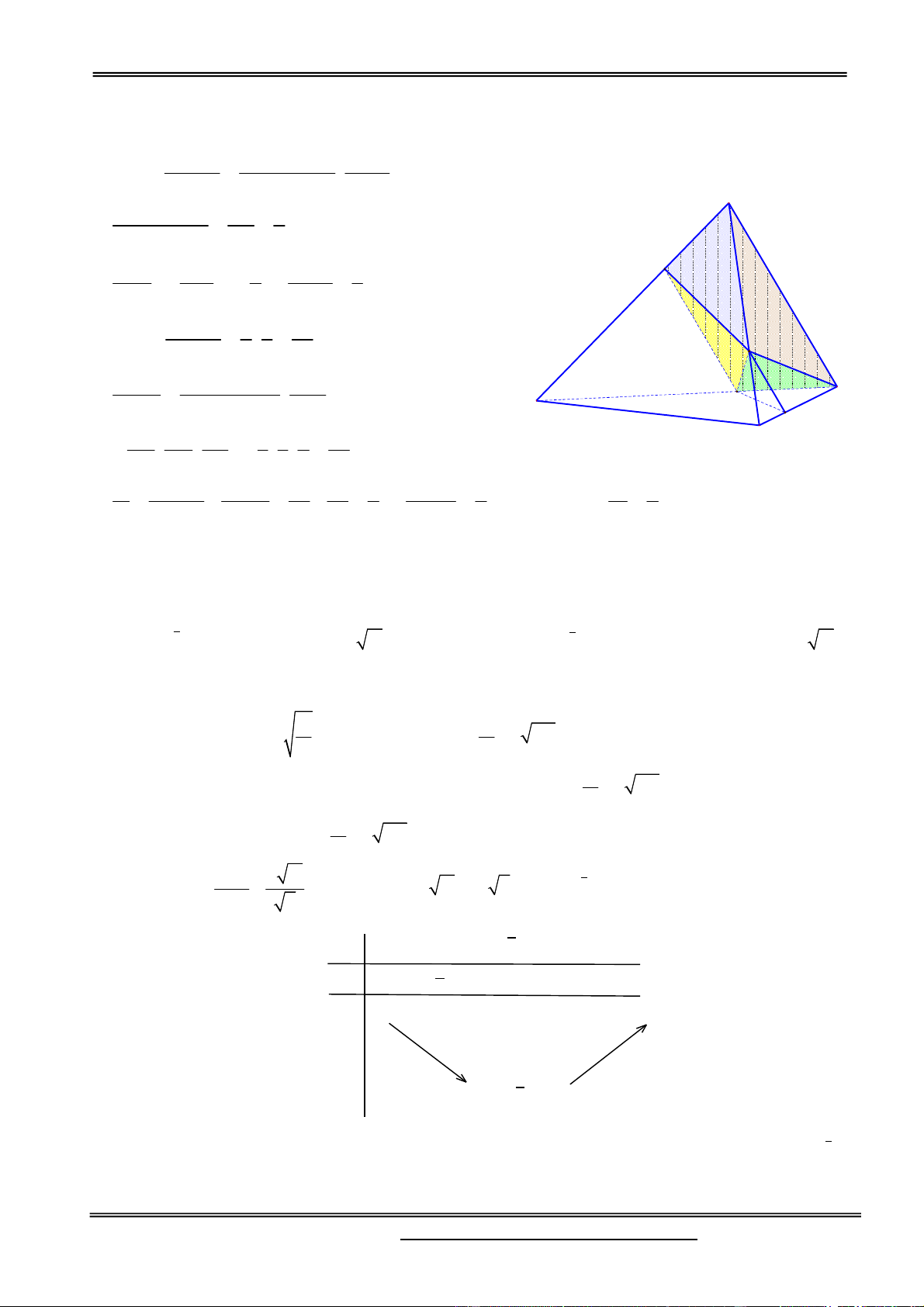
Câu 23. Cho tứ diện đều ABCD cạnh a. Mặt phẳng (P) chứa cạnh BC cắt cạnh AD tại E. Biết góc giữa 5 2
hai mặt phẳng (P) và (BCD) có số đo là  thỏa mãn tan 
. Gọi thể tích của hai tứ diện ABCE 7 V
và tứ diện BCDE lần lượt là V và V . Tính tỷ số 1 . 1 2 V2 3 1 3 5 A. B. C. D. 8 8 5 8 Hướng dẫn giải:
+) Gọi M là trung điểm BC. A
Khi đó BC  (MAD) nên (P)(AMD); H (P)(AMD)=ME.
Kẻ AHME thì AH(BCE) ( do AH  (AMD) ) E
Kẻ DKME nên DK(BCE) (do DK  (AMD) ). Hiển nhiên AH song song DK K V V AH Khi đó 1 A.  BCE  V V DK 2 D.BCE B D 
+) Gọi  là góc giữa (P) và (ABC) ( 0    ). 2 M  
Hiển nhiên DME   ; AME   . Vì AM = DM nên: C sin  AH V1   sin  
.sin   t.sin (1) sin DK V2 MO 1 1 +) Trong tam giác OMA: o
c s(   )    o
c s cos   sin sin  . (2) MA 3 3 Từ (1) có: 2 2 2 2 o
c s  1 sin   1 t .sin   1 t .x ; với x=sin2. 1 1 Thay vào (2) ta có: 2 2
1 t x. 1 x  t.x 
 (1 t x)(1 x)  . t x  . 3 3 8
+) Giải phương trình có: x  . 2
(9t  6t  9) 2 x 8 9t  6t  9 8 Vì 2 2
sin   x  tan    .  2 2 2 1 x
9t  6t  9 9t  6t 1 9t  6t 1  3 t  8 50 196 171  5 Theo giả thiết suy ra 2 2 
 9t  6t  1 
 9t  6t   0   2 9t  6t 1 49 25 25 19  t   15 V 3 Vậy ABCE  V 5 DBCE Chọn đáp án C.
Câu 24. Cho khối chóp S.ABC có SA  a , SB  a 2 , SC  a 3 . Thể tích lớn nhất của khối chóp là 3 a 6 3 a 6 3 a 6 A. 3 a 6 . B. . C. . D. . 2 3 6
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 40
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: 1 A
Gọi H là hình chiếu của A lên (SBC)  V  AH.S . 3 SBC
Ta có AH  SA; dấu “=” xảy ra khi AS  SBC . 1  1 S  S . B SC.sin SBC  S .
B SC , dấu “=” xảy ra khi SBC a 2 2 SB  SC . a 3 1 1 1 1 Khi đó, V  AH.S  AS  SB  SC 
SA SB  SC . S C 3 SBC 3 2 6 H
Dấu “=” xảy ra khi S , A S ,
B SC đôi một vuông góc với nhau. Suy ra thể tích lớn nhất của khối chóp là a 2 3 1 a 6 V  S . A S . B SC  . B 6 6 Chọn đáp án D.
Câu 25. Cho hình chóp SABC có đáy ABC là tam giác vuông cân, AB  AC  a , SC   ABC và
SC  a . Mặt phẳng qua C , vuông góc với SB cắt S ,
A SB lần lượt tại E và F . Tính thể tích khối chóp S.CEF . 3 2a 3 a 3 a 3 2a A. V  . B. V  . C. V  . D. V  . SCEF 36 SCEF 18 SCEF 36 SCEF 12
Hướng dẫn giải: Từ C hạ CF  S ,
B  F  SB , CE  S ,
A  E  S  A  AB  AC S 
 AB   SAC   AB  CE Ta có AB   SC
 CE   SAB  CE  SB F
Vậy mặt phẳng qua C và vuông góc SB là mặt CEF . a V SE SF Ta có SCEF  . V SA SB E SCAB
Tam giác vuông SAC vuông tại C ta có: B C 2 2
SA  SC  AC  a 2 a a 2 2 SE SC a SE 1 và     2 2 SA SA 2a SA 2 A
Tam giác vuông SBC vuông tại C ta có: 2 2
SB  SC  BC  a 3 2 2 SF SC a SF 1 và     2 2 SB SB 3a SC 3 V 1 1 1 1 1 1 1 Do đó SCEF 3  .   V  V  . S . A S  a . V 2 3 6 SCEF 6 SABC 6 3 ABC 36 SCAB Chọn đáp án C.
II – HÌNH LĂNG TRỤ
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 41
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 24. Một hình hộp có 6 mặt đều là các hình thoi có góc bằng 600 và cạnh bằng a. Tính thể tích của hình hộp đó. D' C' 3 a 3 2a A. B. 2 2 3 2a 3 2 2a 600 C. D. A' B' 3 3 Hướng dẫn giải:
Ta có: AB = AD = BD = a; AA’ = A’B = A’D = a
 A’ABCD là tứ diện đều
 Chân đường cao A’H trùng với tâm của  ABD D 2 2 a 3 a 3 C  HA = HB = HD = AO =  3 3 2 3 O 2 600 600 3a 2 6a H
 A’H2 = AA’2 – AH2 = a2 - = 9 9 A a B a 6 3 2a  A’H =
Từ đó tìm được V  3 2 Chọn đáp án B.
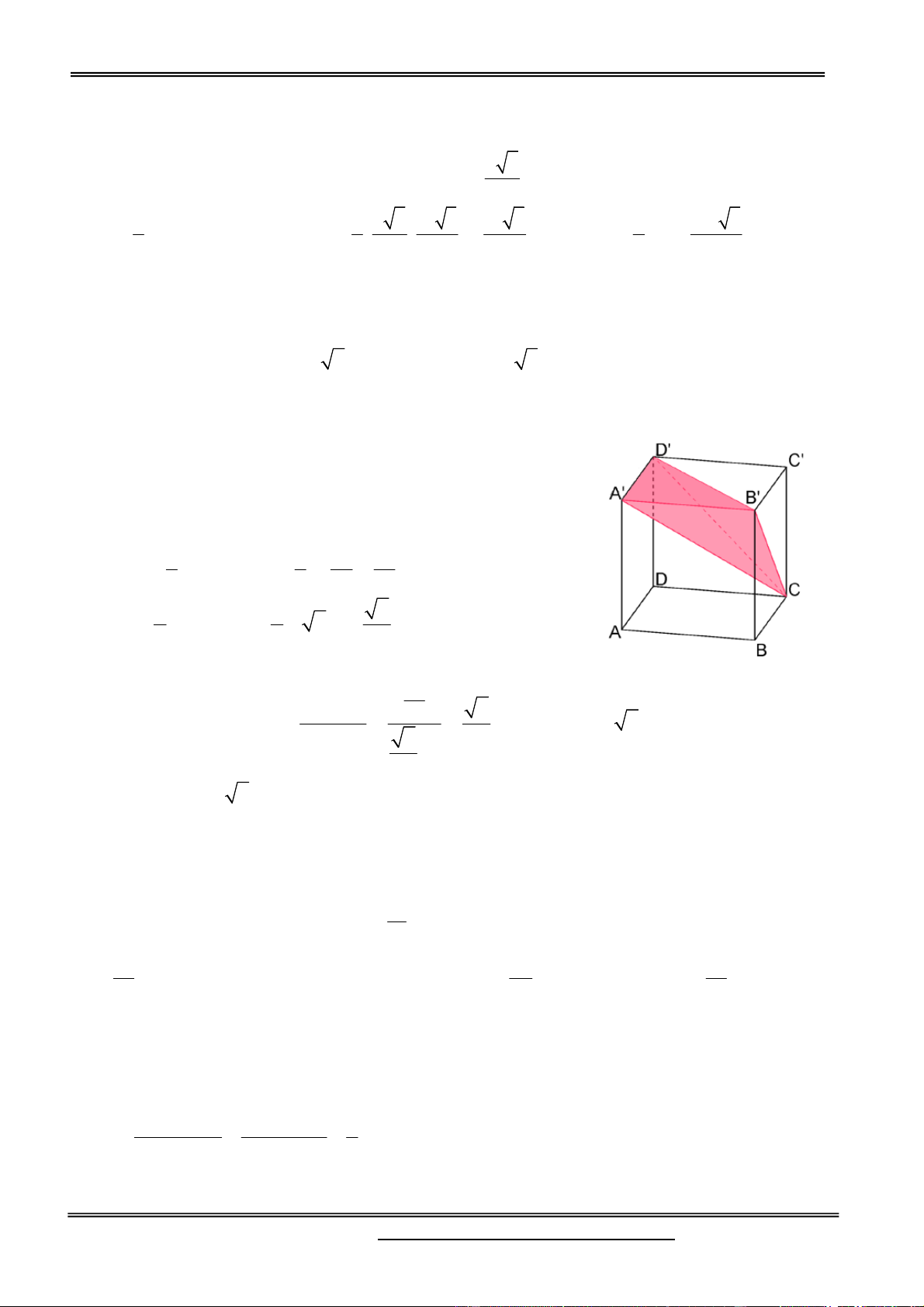
Câu 25. Cho khối lập phương ABC . D  A BC 
D cạnh a . Các điểm E và F lần lượt là trung điểm
của CB và C 
D . Mặt phẳng  AEF  cắt khối lập phương đã cho thành hai phần, gọi V là thể tich 1 V khối chứa điểm 
A và V là thể tich khối chứa điểm C ' . Khi đó 1 là 2 V2 25 17 8 A. . B. 1. C. . D. . 47 25 17 Hướng dẫn giải:
Đường thẳng EF cắt AD tại N , cắt AB tại
M , AN cắt DD tại P , AM cắt BB tại Q .
Từ đó mặt phẳng  AEF  cắt khối lăng trụ thành
hai khối đó là ABCDCQEFP và AQEFP  B  A  D . Gọi V  V , V  V , ABCD.  A  B CD 3 . A  A MN V  V , V  V . 4 PFDN 4 QMBE
Do tính đối xứng của hình lập phương nên ta có V  V . 4 5 3 1 1 3a 3a 3a 3 1 1 a a a a V  AA .  A M .  A N  . a .  , V  PD .  D F.  D N  . . .  3 6 6 2 2 8 4 6 6 3 2 2 72 3 25a 3 47a V 25
V  V  2V 
, V  V V  . Vậy 1  . 1 3 4 72 2 1 72 V 47 2 Chọn đáp án A.
Câu 26. Cho lăng trụ đứng ABC  A 
B C có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa
mặt phẳng ( ABC) và mặt phẳng (BBC) bằng 0
60 .Tính thể tích lăng trụ ABC  A  B C .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 42
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. 3 a 2 B. 3 2a C. 3 a 6 D. 3 3a Hướng dẫn giải:
Từ A kẻ AI  BC  I là trung điểm BC A' B C'
AI  (BC C  B )  AI   C (1)
Từ I kẻ IM  B C (2) B'
Từ (1), (2)  B C  (IAM)
Vậy góc giữa (A B C) và ( B CB) là B' H  AMI = 600 M 1 Ta có AI=
BC  a ; IM= M 2 B C 600 AI a I A  C 0 tan 60 3 2a I BH  2IM  ; 3 B 1 1 1 3 1 1      2 2 2 2 2 2 B ' B BH BC 4a 4a 2a . 1 1
Suy ra BB = a 2 ; 2 S  AI.BC  .
a 2a  a ABC 2 2 2 3 V
 a 2.a  a 2 ABC  A BC Chọn đáp án A.
Câu 27. Cho lăng trụ ABC.A 'B'C ' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A'
lên mặt phẳng (ABC) trùng với trọng tâm tam
giá ABC . Biết khoảng cách giữa hai đường C’ B’ thẳng a 3 AA' và BC bằng . Khi đó thể tích 4 của khối lăng trụ là A’ 3 a 3 3 a 3 A. B. 12 6 3 a 3 3 a 3 C. D. 3 24 H M
Hướng dẫn giải:
Gọi M là trung điểm BC, dựng MH vuông C B góc với A’A. suy ra G a 3
MH  d  BC, A' A  4 A 2 a Đặt AH=x, ta có 2 A' A  x  3 a 2 3 a a 3 a 3
Từ A’A. MH=A’G.AM, suy ra x  . Vậy V  .  . 3 3 4 12 Chọn đáp án A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 43
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 28. Cho hình lăng trụ ABC .A ' B 'C ' có đáy ABC là tam giác đều cạnh a , hình chiếu vuông
góc của A ' lên măt phẳng ABC  trùng với tâm G của tam giác ABC . Biết khoảng cách giữa a 3
AA ' và BC là
. Tính thể tích V của khối lăng trụ ABC .A ' B 'C ' . 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V  B. V  C. V  D. V  3 6 12 36 Hướng dẫn giải:
Gọi M là trung điểm B  BC  (A ' AM )
Gọi H,K lần lượt là hình chiếu vuông góc của G,M trên AA’ a 3
Vậy KM là đọan vuông góc chung củaAA’và BC, do đó d( A
A ',BC)  KM  . 4 KM 3 A  GH  A  MH   GH 2 A' C' 2 a 3
 GH  KH  K 3 6 H B' a
 AA’G vuông tại G,HG là đường cao, A'G  A 3 C G 3 a 3 M V  S .A 'G 
ABC .A' B 'C ' ABC 12 B Chọn đáp án C.
Câu 29. Cho khối lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt thuộc các cạnh bên AA’, CC’ sao
cho MA  MA ' và NC  4NC' . Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ diện GA’B’C’,
BB’MN, ABB’C’ và A’BCN, khối tứ diện nào có thể tích nhỏ nhất? A. Khối A’BCN B. Khối GA’B’C’ C. Khối ABB’C’ D. Khối BB’MN Hướng dẫn giải: C A
+ Nhận thấy khoảng cách từ G và A xuống mặt phẳng (A’B’C’) là G
bằng nhau ( do G,A thuộc mặt phẳng (ABC)//(A’B’C’) V  V B GA 'B 'C ' A.A 'B 'C ' Mà V  V
(Do 2 hình chóp này có 2 đáy AA’B’ và ABB’ A.A ' B 'C ' ABB 'C ' N M
diện tích bằng nhau;chung đường cao hạ từ C’)  V  V GA ' B 'C ' ABB 'C '
=> Không thế khối chóp GA’B’C’hoặc ABB’C’ thể thích nhỏ nhất C' A' → Loại B,C
+ So sánh Khối A’BCN và Khối BB’MN
Nhận thấy khoảng cách từ M và A’ xuống mặt BBCC’ là bằng nhau B'
→ Khối A’BCN và Khối BB’MN có đường cao hạ từ M và A’ bằng
nhau. Mặt khác Diện tích đáy BNB’ > Diện tích đáy BCN
=> Khối A’BCN < Khối BB’MN.
=> Khối A’BCN có diện tích nhỏ hơn. Chọn đáp án A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 44
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 
Câu 30. Cho hình lăng trụ đứng ABC.A' B'C' có đáy ABC là tam giác cân tại A , góc BAC nhọn. Góc giữa AA' và BC' là 0
30 , khoảng cách giữa AA' và BC' là a . Góc giữa hai mặt bên
AA'B'B và AA'C'C là 0
60 . Thể tích lăng trụ ABC.A' B'C' là 3 2a 3 3 a 3 3 a 6 3 a 6 A. B. C. D. 3 3 6 3 Hướng dẫn giải:  A' C'
Ta có góc giữa hai mặt bên AA'B'B và AA'C'C là 0 BAC  60  A  BC đều. B'  300 Vì         0 AA'/ /CC' AA'; BC' CC'; BC'  BC'C  30
Kẻ AI  BC  AI  BB'C'C
dAA'; BC'  dAA';BB'C'C  AI  a 3 2a BC 1 2a 2a 3 600 C  BC  ,CC'   2a  V  2a. .a.  A 0 ABC.A ' B ' C ' 3 tan 30 2 3 3 I Chọn đáp án A. B
Câu 31. Cho hình lăng trụ tam giác đều ABC. A’B’C’, có cạnh đáy bằng a và cạnh bên bằng a 2 . AM A ' N 1
Lấy M, N lần lượt trên cạnh AB’, A’C sao cho 
 . Tính thể tích V của khối BMNC’C. AB ' A'C 3 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. 108 27 108 27 Hướng dẫn giải:
Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ và AA’C’C. AM 1 AM 2 A' C' Ta có:  
 (Do G trung điểm AB’). AB ' 3 AG 3 AM 2
Xét tam giác ABA’ có AG là trung tuyến và  . Suy ra AG 3 N
M là trọng tâm tam giác ABA’. Do đó BM đi qua trung điểm I K của AA’. B' I A ' N 1 A ' N 2 Ta có:   
(Do K là trung điểm A’C). A 'C 3 A ' K 3 G A ' N 2 M
Xét tam giác AA’C’ có A’K là trung tuyến và  . Suy ra A ' K 3
N là trọng tâm của tam giác AA’C’. Do đó C’N đi qua trung A C điểm I của AA’.
Từ M là trọng tâm tam giác ABA’ và N là trọng tâm của tam H giác AA’C’. Suy ra: IM IN 1   . B IB IC ' 3
Gọi V ; V lần lượt là thể tích các khối chóp IMNC; IBCC’. Ta có: 1 2 V IM IN IC 1 8 1  . .
 . Mà V V V . Suy ra V  V . V IB IC ' IC 9 1 2 2 9 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 45
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Hạ AH vuông góc với BC tại H thuộc BC. Ta được AH vuông góc với mặt phẳng (BB’C’C). AA’
song song với mặt phẳng BB 'C 'C  nên khoẳng cách từ I đến mặt phẳng (BB’C’C) bằng khoẳng a 3
cách từ A đến (BB’C’C) và bằng AH. Ta có: AH  . 2 1 1 a 3 a 2 a 6 3 8 2a 6 V
.d I; BB 'C 'C   .S  . .  V  V  2    2 3 . Suy ra .   B  CC ' 3  3 2 2 12 2 9 27 Chọn đáp án B.
Câu 32. Cho hình lập phương ABCD. A ' B ' C ' D ' có khoảng cách giữa A ' C và C ' D ' là 1 cm. Thể
tích khối lập phương ABCD. A ' B ' C ' D ' là: A. 3 8 cm . B. 3 2 2 cm . C. 3 3 3 cm . D. 3 27 cm . Hướng dẫn giải:
Để tìm khoảng cách giữa A’C và C’D’, ta dựng một mặt phẳng chứa A’C và song song với C’D’.
Dễ thấy đó là mặt phẳng (CA’B’).
Gọi a là độ dài cạnh của khối lập phương, lúc này ta có:
d C ' D ', A'C   d C ' D ', CA' B '  d D ',CA' B '    
Để tính khoảng cách từ điểm D’ đến mặt phẳng (CA’B’), ta xét
khối tứ diện D’CA’B’. 2 3 1 1 a a V  .CC '.S  .a.  cm D CA B B A D  3 ' ' ' ' ' '  3 3 2 6 1 1 2 2 S  . CB'. B'A'  .a 2.a  a cm (do tam giác CA B  2 ' '  2 2 2 CA’B’ vuông tại B’) 3 a 3V 2
Suy ra: d D CA B  D 'CA' B' 2 ', ' '    
a cm  a  2   (cm). SCA B 2 2 ' ' 2 a 2 Do đó 3 3
V  a  2 2 cm Chọn đáp án B.
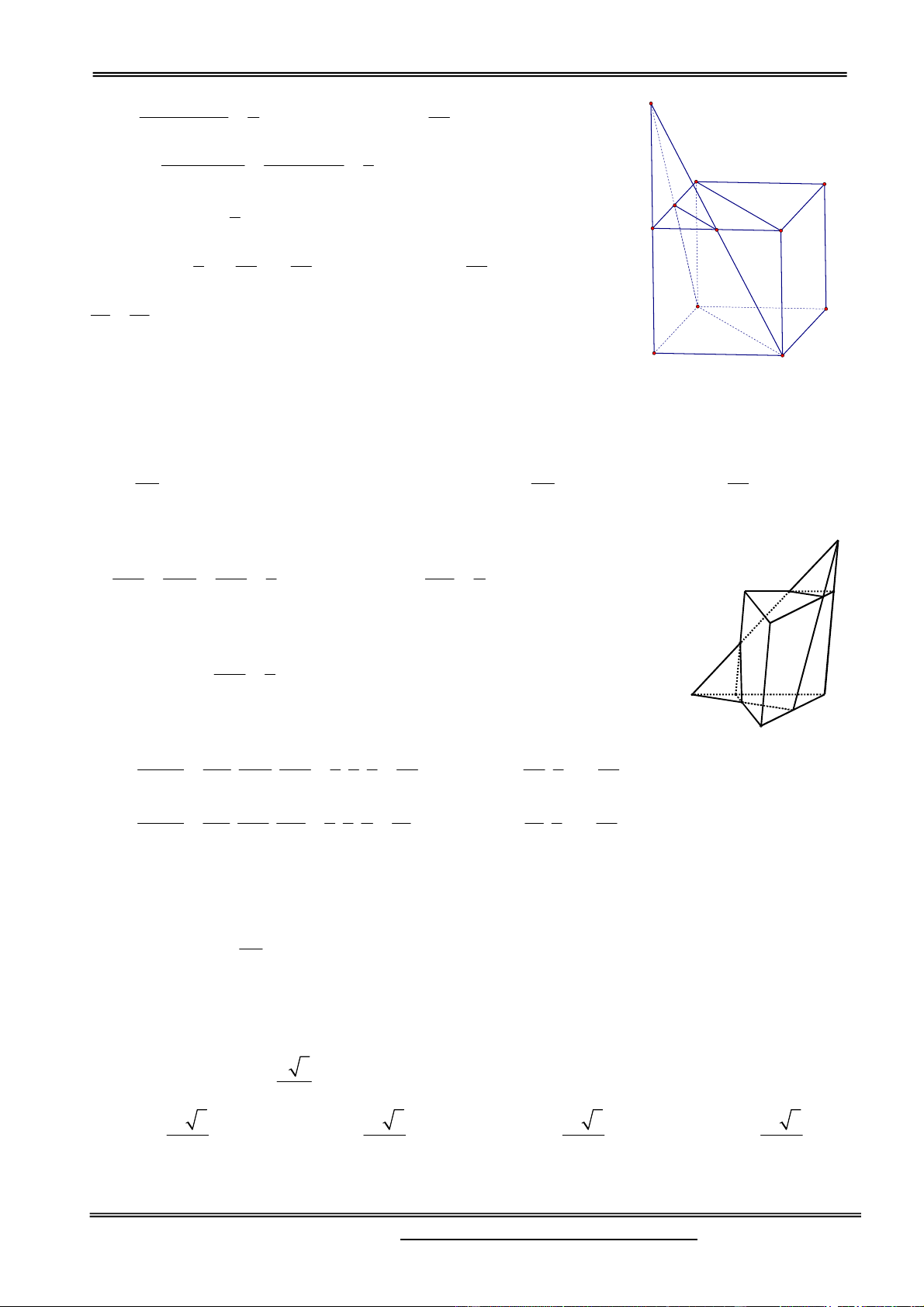
Câu 33. Cho hình hộp ABCDA’B’C’D’. Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng thời
song song với B’D’. Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V1, V2 ( Trong đó V
V1 là thể tích khối chứa A). Tính tỉ số 1 F  . V2 7 17 8 A. . B. 1. C. . D. . 17 25 17 Hướng dẫn giải:
*Gọi N là trung điể A’D’. Khi đó (P)BDNM). Thấy BMDNAA’=I.
Khi đó: V1=V(A’MNABD); V2=V-V1. (Với V là thể tích hình hộp)
V (IA' MN ) S ( AMN ) 1 * Ta có:   V ( AA'B'D')
S ( A ' B ' D ') 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 46
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 V (AA'B'D') 1 1 I * Mà: 
nên có: V (IA ' MN )  V V 6 24
V (IA' MN )
IA'.IM .IN 1 * Lại có:   D' V (IABD) I . A I . B ID 8 C' 1 N
*Vậy: V (IABD)  V M 3 A' B' 1 1 7 17
* Do đó: V  V  V 
V nên V  V V  V . Vậy: 1 3 24 24 2 1 24 V 7 D 1  C V 17 2 Chọn đáp án A. A B
Câu 34. Cho khối lăng trụ tam giác ABC.A’B’C’. Gọi I, J, K lần lượt là trung điểm của các
cạnh AB, AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó. 25 49 8 A. . B. 1. C. . D. . 47 95 17 Hướng dẫn giải:
Chứng minh EI = IJ = JF. Từ đó suy ra E EB EM FA' 1 FN 1    . Lại từ đó suy ra  . EB ' EK FB ' 3 FK 2 I A B M
Ta có: d(K, A'B') = (1/2)d(C', A'B'), FB' = (3/2)A'B'. Suy ra SKFB’ = C (3/4)SA’B’C’. J EB 1 Mặt khác vì 
nên suy ra d(E, (KFB’)) = (3/2)h (h là chiều EB ' 3 F A' B' cao lăng trụ). N K
Do đó VEKFB’ = (3/8)V (V là thể tích lăng trụ) . C' V EI EM EB 1 1 1 1 1 3 1 EBIM  . .  . .  nên VEBIM = . V  V . V EF EK EB ' 3 3 3 27 27 8 72 EB ' FK V FJ FA' FN 1 1 1 1 1 3 1 FA' JN  . .  . .  nên VFA’JN = . V  V . V FE FB ' FK 3 3 2 18 18 8 48 FB ' EK
Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Gọi V1 là thể tích phần chứa điểm B' và
V2 là thể tích phần chứa điểm C.
Ta có V1 = (3/8 – 1/72 – 1/48)V = (49/144)V nên V2 = (95/144)V. 49 Do đó V1/V2 = . 95 Chọn đáp án C.
Câu 35. Cho hình lăng trụ AB . C A B  C
  có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của
điểm A lên mặt phẳng  ABC trùng với trọng tâm tam giác AB .
C Biết khoảng cách giữa hai đường a 3
thẳng AA và BC bằng
. Tính thể tích V của khối lăng trụ AB . C A B  C  . 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 24 12 3 6 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 47
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
M là trung điểm của BC thì BC   AA M   . A C
Gọi MH là đường cao của tam giác AAM thì
MH  AA và HM  BC nên HM là khoảng cách AA và BC . H B 2 a 3 a 3 a Ta có A . A HM  A . G AM  2 .AA  AA  4 2 3 A 2 2 C 4a 3a a
Đường cao của lăng trụ là AG    . G 9 9 3 M 2 3 a 3a a 3 B Thể tích V  .  . LT 3 4 12 Chọn đáp án B.
Câu 36. Cho hình lăng trụ có tất cả các cạnh đều bằng a , đáy là lục giác đều, góc tạo bởi cạnh bên và
mặt đáy là 60 . Tính thể tích khối lăng trụ 27 3 3 9 A. 3 V  a . B. 3 V  a . C. 3 V  a . D. 3 a . 8 4 2 4 Hướng dẫn giải: A' F'
Ta có ABCDEF là lục giác đều nên góc ở đỉnh bằng 120 .
ABC là tam giác cân tại B , DEF là tam giác cân tại E . B' E' 2 1 a 3 S  S  . a . a sin120  ABC DEF 2 4 C' D' 2 2 A AC 
AB  BC  2.A . B B . C cos B F  1 2 2 
 a  a  2. . a . a   a 3    2  B E H 2 S  A .
C AF  a 3.a  a 3 ACDF C 2 2 2 D a 3 a 3 3a 3 2 S  S  S  S   a 3   ABCDEF ABC ACDF DEF 4 4 2  a 3
B ' BH  60  B ' H  BB '.sin 60  2 2 3a 3 9 3
V  BH '.S  a 3.  a ABCDEF 4 4 Chọn đáp án D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 48
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 MŨ - LÔ GARIT 2 2
Câu 1. Cho phương trình x 2mx2 2x 4 mx2 2 5  5
 x  2mx  m  0 . Tìm m để phương trình vô nghiệm? m  1 A. m  0 B. m  1
C. 0  m  1 D. m  0  Hướng dẫn giải: 2 2
+Phương trình tương đương: x 2mx2 2 2x 4mx  x  mx   2  2 5 ( 2 2) 5
(2x  4mx  2) 2 2
+ Do hàm f(t)=5t + t đồng biến trên R nên ta có: (x  2mx  2)  (2x  4mx  2)
+ Từ đó điều kiện để pt vô nghiệm là C. Chọn đáp án C.
Câu 2. Tìm tất cả các giá trị thực của tham số m để phương trình sau có hai nghiệm thực phân biệt: 2
log (1 x )  log (x  m  4)  0 . 3 1 3 1 21 21 1 A.  m  0 . B. 5  m  . C. 5  m  . D.  m  2 . 4 4 4 4 Hướng dẫn giải: 2 1    x  0 x   1;  1 2
log (1  x )  log (x  m  4)  0    3 1  2 2 l
 og (1  x )  log (x  m  4) 
  x  x  m  3 1 4 3 3 
Yêu cầu bài toán  f  x 2
 x  x  m  5  0 có 2 nghiệm phân biệt  1  ;  1
Cách 1: Dùng định lí về dấu tam thức bậc hai.
Để thỏa yêu cầu bài toán ta phải có phương trình f  x  0 có hai nghiệm thỏa: 1
  x  x  1 1 2  . a f   1  0  m a f      5  0 . 1 0   21      m  3  0  5 0  m  . 4  21 4m  0 S  1 1   2
Cách 2: Dùng đạo hàm 1
Xét hàm số f  x 2
 x  x  5  f  x  2x 1  0  x   2  1  21 Có f    ; f   1  3  ; f   1  5     2  4 Ta có bảng biến thiên –
Dựa vào bảng biến thiên, để có hai nghiệm phân biệt trong khoảng  1  ;  1 khi 21 21   m  5   m  5 . 4 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 49
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Cách 3: Dùng MTCT
Sau khi đưa về phương trình 2
x  x  m  5  0 , ta nhập phương trình vào máy tính. * Giải khi m  0
 , 2 : không thỏa  loại A, D.
* Giải khi m  5: không thỏa  loại B. Chọn đáp án C.
Câu 3. Tìm tất cả các giá trị của tham số m sao cho bất phương trình sau có tập nghiệm là  ;   0 : x x x 1
m2   2m   1 3  5  3  5  0 .     1 1 1 1 A. m   . B. m  . C. m  . D. m   . 2 2 2 2 Hướng dẫn giải:
Phương trình đã cho tương đương x x x  3  5   3  5   3  5 
2m  2m   1       0   1 . Đặt t     0 ta được:  2   2        2   1
2m  2m   1
 t  0  f t  2
 t  2mt  2m 1  0 2 . Bất phương trình   1 nghiệm đúng t x
  0 nên bất phương trình 2 có nghiệm 0  t  1, suy ra phương trình f t   0 có 2 nghiệm  f  0  0 2m 1  0 m  0, 5 1
t , t thỏa t  0  1  t      . Vậy m   thỏa mãn 1 2 1 2  f    1  0 4m  2  0     m 0, 5  2 Chọn đáp án C.
Câu 4. Tính giá trị của biểu thức P  ln tan1°  lntan 2  lntan3  ...  lntan89 . 1 A. P  1. B. P  . C. P  0. D. P  2. 2 Hướng dẫn giải:
P  ln tan1°  ln tan 2  ln tan 3  ...  ln tan89  ln  tan1 .  tan 2.tan 3 .  ..tan 89  ln  tan1 .  tan 2.tan 3 .  ..tan 45 .  cot 44.cot 43 .  ..cot1
 lntan 45  ln1  0. (vì tan .  cot   1) Chọn đáp án C. 2 2
Câu 5. Cho phương trình : x 5x6 1x 65 .2  2  2.2 x m  (
m 1) . Tìm m để PT có 4 nghiệm phân biệt. 0  m  2. 1 21  1 A.  m  0 . B. 5  m  . C.  1 1 D.  m  2 . 4 4 m  , m   4  8 256 Hướng dẫn giải:
Viết lại PT (1) dưới dạng : 2 2 x 5x6 1x 65 2 2 2 2 .2  2  2.2 x m  m x 5x6 1x
( x 5x6)(1x )  . m 2  2  2  m 2 2 2 2 x 5x6 1x x 5x6 1  .2  2  2 .2 x m  m
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 50
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 x 5x6  u  2 Đặt :  , ,
u v  0 . Khi đó PT tương đương với : 2 1 v  2 x   x  3 2 x 5 x 6 u 1    2  1 
mu  v  uv  m  (u 1)(v  m)  0     x  2  2  1 v  m  2 x  m 2   1 2 x  m(*) 
Để (1) có 4 nghiệm phân biệt  (*) có 2 nghiệm phân biệt khác 2 và 3. m   0 m   0 (*)    
. Khi đó điều kiện là : 2 2 1
  x  log m x    1 log m 2  2 m  0 m  0 m  2   1 log m  0  2  1 1 1      m  (0; 2) \   ; m  1 log m  4 8 256  2  8   1  log m 9    1  2 m   256 1 1 
Vậy với m  (0; 2) \  ;
thỏa điều kiện đề bài.  8 256   Chọn đáp án C.
Câu 6. Tìm tất cả các giá trị của m để phương trình 2
log x  m  2 .log x  3m 1  0 có 2 nghiệm 3   3
x , x sao cho x .x  27 1 2 1 2 4 28 A. m  B. m  25 C. m  D. m  1 3 3 Hướng dẫn giải:
log x2  m  2 .log x  3m 1  0 1 3   3  
Đặt log x  t 3
Phương trình trở thành: t2  m  2t  3m 1  02
Phương trình (1) nghiệm phân biệt khi và chỉ khi (2) có 2 nghiệm phân biệt.
   0  m  22  43m 1  m2  8m  8  0 (đúng)
Gọi t ,t là 2 nghiệm của phương trình (2) 1 2 1 2
 x  3t1 , x  3t2  3t 3t  27  t  t  3 1 2 1 2
Theo Vi-et: t  t  m  2 . Suy ra m  1 1 2 Chọn đáp án D.
Câu 7. Trong tất cả các cặp  ; x y thỏa mãn log
4x  4 y  4  1. Tìm m để tồn tại duy 2 2   x  y  2 nhất cặp  ; x y sao cho 2 2
x  y  2x  2 y  2  m  0 . A.   2 10 2 .
B. 10  2 và 10  2 . C.   2 10 2 và   2 10 2 . D. 10  2 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 51
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: Ta có log
4x  4 y  4  1 2 2
 x  y  4x  4 y  6  0   1 . 2 2   x  y  2 Giả sử M  ;
x y thỏa mãn pt  
1 , khi đó tập hợp điểm M là hình tròn C tâm I 2;2 bán 1  kính R  2 . 1
Các đáp án đề cho đều ứng với m  0 . Nên dễ thấy 2 2
x  y  2x  2 y  2  m  0 là phương
trình đường tròn C tâm J  1  ; 
1 bán kính R  m . 2  2
Vậy để tồn tại duy nhất cặp  ;
x y thỏa đề khi chỉ khi C và C tiếp xúc ngoài 2  1 
 IJ  R  R  10  m  2  m   10  22 . 1 2 Chọn đáp án A.
Câu 8. Cho n là số nguyên dương, tìm n sao cho 2 2 2 2 2 log 2019  2 lo g 2019  3 log
2019  ...  n logn 2019  1008  2017 log 2019 3 a a a a a A. n=2017 B. n=2018 C. n=2019 D. n=2016 Hướng dẫn giải: 2 2 2 2 2 log 2019  2 lo g 2019  3 log
2019  ...  n logn 2019  1008  2017 log 2019 3 a a a a a 3 3 3 2 2
 log 2019  2 l o g 2019  3 log 2019  ...  n log 2019  1008  2017 log 2019 a a a a a 3 3 3 3 2 2
 (1  2  3  ...  n ) log 2019  1008  2017 log 2019 a a 2 2
 n(n  1)   2016.2017         2   2   n  2017 Chọn đáp án A.
Câu 9. Phương trình log  3
mx  6x   2log  2 1
 4x  29x  2  0 có 3 nghiệm thực phân biệt khi: 1 2  2 39 A. m  19 B. m  39 C. 19  m 
D. 19  m  39 2 Hướng dẫn giải: log  3
mx  6x   2log  2 1
 4x  29x  2  0  log  3
mx  6x   log  2 1
 4x  29x  2  0 2 2  1 2  2 3 2
6x 14x  29x  2 3 2
 mx  6x  1
 4x  29x  2  m  x 3 2
6x 14x  29x  2 2 f  x 
 f  x  12x 14  2 x x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 52
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 
 x  1 f   1  19   1  1  39
f  x  0  x   f     2  2  2   1  1  121  x    f      3  3  3
Lập bảng biến thiên suy ra đáp án Chọn đáp án C. 2 x  1  x 1 
Câu 10. Biết phương trình log  2log  
có nghiệm duy nhất x  a  b 2 trong 5 3   x 2 2   x 
đó a,b là các số nguyên. Tính a  b ? A. 5 B. 1  C. 1 D. 2 Hướng dẫn giải: 2 x  1  x 1  2 x  1 x 1 log  2log     log  2log 5 3 5 3  x 2 2  x x 2   x x  0 Đk:   x  1 x  1  0 
Pt  log 2 x   2
1  log x  log (x 1)  log 4x 5 5 3 3  log 2 x   2
1  log 4x  log x  log (x 1) (1) 5 3 5 3 Đặt t 
x   x  t  2 2 1 4 1 (1) có dạng 2 2
log t  log (t 1)  log x  log (x 1) (2) 5 3 5 3 Xét 2
f ( y)  log y  log ( y 1) , do x  1  t  3  y  1. 5 3 1 1
Xét y  1 : f '( y)   .2( y 1)  0 2 y ln 5 ( y 1) ln 3
 f ( y) là hàm đồng biến trên miền 1;
(2) có dạng f (t)  f (x)  t  x  x  2 x  1  x  2 x 1  0  x  1 2  
 x  3  2 2 (tm) .  x  1  2 (vn)  Chọn đáp án C.
Câu 11. Phương trình sau có bao nhiêu nghiệm : log  x  2 1  2  log
4  x  log 4  x 3 4 8 2 A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. Vô nghiệm Hướng dẫn giải: x  1  0   4   x  4 log  x  2 1  2  log
4  x  log 4  x3 (2) Điều kiện: 4  x  0  4 8  2 x  1    4  x  0 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 53
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
(2)  log x  1  2  log 4  x  log 4  x  log x  1  2  log  2 16  x 2 2 2 2 2 
 log 4 x  1  log  2 16  x  2
 4 x  1  16  x 2 2 x  2 + Với 1
  x  4 ta có phương trình 2
x  4x  12  0 (3) ; (3)   x  6  lo¹i  x  2  24 + Với 4   x  1  ta có phương trình 2
x  4x  20  0 (4); 4  x  2 24lo¹i 
Vậy phương trình đã cho có hai nghiệm là x  2 hoặc x  21 6 , Chọn đáp án B.
Câu 12. Cho phương trình  2  m  x x 2 2
5  3.3  m 15x  5  0 . Tìm tập hợp tất cả các giá trị thực của
tham số m để phương trình có nghiệm trong khoảng 0;2 . A.  B. 2;3 C. 0; D.  ;   1 Hướng dẫn giải:
Đặt f  x  2  m2 5x  3.3x  m2 15x  5 . Do f liên tục trên  nên f cũng liên tục trên đoạn 0;2.
Ta có f 0  2  m2 50  3.30  m2 15.0  5  6m2 1  0,m .
f 2  2  m2 52  3.32  m2 15.2  5  13  0 .
Khi đó f 0. f 2  0, m .
Vậy f  x  0 có nghiệm trên khoảng 0;2 với mọi giá trị thực của m. Chọn đáp án A.
Câu 13. PHương trình log  2
x  x  1  x 2  x  log x có bao nhiêu nghiệm 3    3 A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. Vô nghiệm Hướng dẫn giải: điều kiện x > 0 2
 x  x 1
Phương trình tương đương với 2 log  2x  x 3    x 
Ta có x  x    x  2 2 2 1 1  1 2 2 x  x  1  1    1     Và log  log x   1  log  x   3  log 3  1 3   3   3   3    x   x   x      x  2 1  0 2
 x  x  1  Do đó 2 log  2x  x      x  1 3 1  x  x   0   x Chọn đáp án A. 9x
Câu 14. Cho hàm số f (x)  ,x   . Tính 2 2 2
P  f (sin 10 )
  f (sin 20)  .....  f (sin 80) 9x  3 A. 4 B. 8 C. 9 D. 3 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 54
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Nếu a  b 1 thì f (a)  f (b)  1. Do đó P  1  1  1  1  4 Chọn đáp án A.
Câu 15. Phương trình 33x 33x 4 x 4 x 3 3  3  3  3
 10 có tổng các nghiệm là ? A. 0. B. 2. C. 3. D. 4. Hướng dẫn giải: 33x 33x 4 x 4 x 3 3  3  3  3  10 7 27 81 x x  1 x   1  x  7 3 3 3 3  27.3   81.3   10  27. 3   81. 3   10 x x  x   x  7 3 3 3 3  3   3  Côsi x 1 x 1 Đặt t  3   2 3 .  2 3x 3x 3  x 1  x x 1 x 1 1 x 1 3 3 2 3 3  t  3   3  3.3 .  3.3 .   3   t  3  t x  x 2 x 3x 3x  3  3 3 3 3 3 10 10 Khi đó: 7'  27 3 t  3t  3 3
 81t  10  t   t   2  N  27 3 10 1 10 Với t   3x   7  3 3x 3
 y  3  N  1 10 Đặt  3x y  0 . Khi đó: 7  2 y 3y 10 y 3 0           1 y 3
 y  N   3 Với  3  3x y  3  x  1 1 1 Với   3x y   x  1 3 3 Chọn đáp án A. x x
Câu 16. Gọi x , x x  x là hai nghiệm của phương trình     x 1 5 1 5 1 5.2      . Trong các 1 2  1 2 
khẳng định dưới đây, khẳng định nào sai?
A.  x ,  1  ,1  1  ,1
B.  x ,  1  ,1  1  ,1 2      1     
C.  x , x  1  ,0  1  ,0
D.  x , x  1  ,1  1  ,1 1 2      1 2      Hướng dẫn giải: x x  x x       5   1   5   5 1 5 1 5 x 1 1  5.2          1 .  2   2  2     x x x  x  5 1  5  1  5 1  5  1 Nhận xét: x      1  1        2   2   2   2          x  5 1 1 5 1 + Đặt t     0,  1  t    x  log 2, x  log . 1 2 5 1  5 1  2  t 2 2   2 2
Câu 17. Phương trình 1  log x  3log x  log x 1 có bao nhiêu nghiệm nguyên ? 9 9 3 A. 0 B. 1 C. 2 D. 3 Hướng dẫn giải:
Giải phương trình: 1  log x  3log x  log x 1 . Điều kiện xác định: x ≥ 1 9 9 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 55
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
1  log x  3log x  log x 1  1  log x  3log x  2log x 1 9 9 3 9 9 9
 1  2log x  2 log x 1
1  log x  3 log x  9  9  9 9  2log x 1
1  log x  3 log x  1  0 9  9 9 
 2log x  1 vì: 1  log x  3log x  1  0  x = 3. 9 9 9
Vậy nghiệm phương trình đã cho: x = 3. Chọn đáp án B.
Câu 18. Tìm m để bất phương trình 1  log  2 x   1  log  2
mx  4x  m thoã mãn với mọi x  . 5 5 A. 1
  m  0 . B. 1   m  0 .
C. 2  m  3 .
D. 2  m  3 . Hướng dẫn giải: 2
mx  4x  m  0 
BPT thoã mãn với mọi x  .   x    5 2  x   2
1  mx  4x   m m  0  m  0 m  2   2   2
mx  4x  m  0 16  4m  0  m  2     x        2  m  3 .   5  m 2
x  4x  5  m  0  5  m  0  m  5  16 
 45  m2  0   m  3   m  7  Chọn đáp án C. Câu 19. Cho ,
x y, z là các số thực thỏa mãn 2x  3y  6z . Giá trị biểu thức M  xy  yz  xz là: A. 0 B. 1 C. 6 D. 3 Hướng dẫn giải: Khi một trong ba số ,
x y, z bằng 0 thì các số còn lại bằng 0. Khi đó M=0 1 1 1 
Khi x, y, z  0 ta đặt 2x  3y  6z  k suy ra 2  , 3 y x  , 6 z k k  k . 1 1 1  1 1 1
Do 2.3=6 nên x . y z k k  k hay    x y z Từ đó suy ra M=0 Chọn đáp án A.
Câu 20. Cho a log 3  b log 2  c log 5  5 , với a, b và c là các số hữu tỷ. Các khẳng định sau đây, 6 6 6 khẳng định nào đúng?
A. a  b
B. a  b
C. b  a
D. c  a  b Hướng dẫn giải:
log 3a2b5c   5 6 a b c 5 5 5 0  3 .2 .5  6  3 .2 .5 a  b  5
Do a, b, c là các số hữu tỷ nên c  0  Chọn đáp án A. 1 1
Câu 21. Với a  0, a  1, cho biết : 1log u 1log t a t  a ; a v  a
. Chọn khẳng định đúng :
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 56
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1  1 1 1 A. 1loga v u  a B. 1 loga t u a   C. 1 loga v u a   D. 1 loga v u a   Hướng dẫn giải: 1 1
Từ giả thiết suy ra: log t  .log a  a 1 log a u 1 log u a a 1 1 1 1 log u log v  .log a a    a 1 log a t 1 log t 1  log u a a 1 a  1log u a 1 1 1log
  log v log u  1 log u  log u(1 log v)  1  log v a u   u  a a a a a a a 1 log v a Chọn đáp án D. 2 2 x 5x6 1 x 65x
Câu 22. Có bao nhiêu giá trị của tham số m để phương trình . m 2  2  2.2  m có
3 nghiệm phân biệt. A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải: 
 2x x   2 x   2 x  x 
   2x x   2 5 6 1 5 6 5 6 1 2 1 2 1 2 2 1  2 x Pt m m   0  2 x  2 x 5x6 2  2  0     x  3 2 1 2 x  m 2   1
2 x  m * 
TH1: (*) có nghiệm duy nhất ( nghiệm x =0)  m  2.
TH2: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 2 và nghiệm còn lại khác 3  m  23.
TH3: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 3 và nghiệm còn lại khác 2  m  28.
Vậy, có 3 giá trị của m thỏa mãn. Chọn đáp án C.
Câu 23. Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x  log x 3  m 2 log x  3 32;   2 1 4  có nghiệm thuộc ? 2   
A. m  1; 3 . B. m  1; 3  . C. m   1; 3  .
D. m   3;1 .     Hướng dẫn giải:
Điều kiện: x  0. Khi đó phương trình tương đương: 2
log x  2 log x 3  m log x 3 2 2  2 .
Đặt t  log x với x  32  log x  log 32  5 hay t  5. 2 2 2 Phương trình có dạng 2
t  2t 3  mt   3 * .
Khi đó bài toán được phát biểu lại là: “Tìm m để phương trình (*) có nghiệm t  5 ”
Với t  5 thì (*)  t   3 .t  
1  mt  
3  t 3. t 1m t 3 0 t 1
 t 1m t 3  0  m  t3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 57
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 t 1 4 4 4 Ta có 1
. Với t  5 1 1 1  3 hay t 3 t 3 t 3 53 t 1 t 1 1  3 1  3 t 3 t 3
suy ra 1  m  3. Vậy phương trình có nghiệm với 1  m  3. Chọn đáp án A. 2 log x
Câu 24. Tập các giá trị của m để bất phương trình 2
 m nghiệm đúng với mọi x > 0 bằng 2 log x 1 2 A. ( ;  1] B. [1; ) C.  5  ; 2 D. [0;3) Hướng dẫn giải: t Đặt 2 t  log x t  1 2   . Khi đó ta có  m * t  1
Bất phương trình ban đầu có nghiệm với mọi x > 0   
* nghiệm đúng với mọi t > 1 t
Xét hàm số f t   trên 1; t 1 t  2 f 't  
, f 't   0  t  2  t 13
lim f t  
lim f t    t  t 1  BBT 1 2 t +∞ 0 f'(t) +∞ +∞ f(t) 1
Từ BBT ta có kết luận bất phương trình có nghiệm với mọi t > 1  m  1 Chọn đáp án A.
Câu 25. Giả sử p và q là các số thực dương sao cho: log p  log q  log p  q 9 12 16   . Tìm giá trị của p q 4 8 1 1 A. B. C. 1 3 D.   1 5 3 5 2 2 Hướng dẫn giải:
Đặt: t  log p  log q  log p  q 9t p  12t q  16t    9t 12t p q 9 12 16   thì: , , (1) 2t t t  4   4   4  q
Chia hai vế của (1) cho 9t ta được:  1 , đặt x  
 0 đưa về phương trình:        3   3   3  p 1 2 q 1
x  x 1  0  x 
1 5 do x  0 , suy ra  1 5 .     2 p 2 Chọn đáp án D. 2
Câu 26. Tập nghiệm của bất phương trình: x2 x x 2 x 1 81.9 3 .3     0 là 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 58
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
A. S  1;    0 .
B. S  1; .
C. S  0;.
D. S  2;   0 . Hướng dẫn giải: ĐKXĐ: x  0. 9x x x 2 2 x BPT đã cho  81.  3 .3  .3.3  0 2 x x x 2 3 3 .3 2.3 x     0 81 3
3x 3 x 3x 2.3 x      0 3x 3 x  
 0 (vì 3x  2.3 x  0, x   0.)  x  1 x  1
 3x  3 x  x  x    x  0  x  0  
Vậy tập nghiệm của BPT đã cho là S  1;    0 . Chọn đáp án A.
Câu 27. Cho u u  0; u  1
n  là cấp số nhân với số hạng tổng quát
. Khi đó khẳng định nào sau n n đây là đúng? log 2017 log 2017  log 2017 A. u u u k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 B. u u u k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 C. u u u k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 D. u u u k 1  k k 1   log 2017 log 2017  log 2017 u u u k 1  k k 1  Hướng dẫn giải: Vì u 2
u  u .u
n  là cấp số nhân nên k k 1  k 1   2log u  log u  log u 2017 k 2017 k 1  2017 k 1  1 1 1 1     log 2017 log 2017 log 2017 log 2017 u u u u k k 1  k 1  k log 2017 log 2017  log 2017 u u u k 1  k 1  k   log 2017 log 2017  log 2017 u u u k 1  k k 1  Chọn đáp án A.
Câu 28. Số nghiệm của phương trình 2
log x  2x  log  2
x  2x  2 là 3 5  A. 3. B. 2. C. 1. D. 4. Hướng dẫn giải:
ĐK: x  0; x  2 . Đặt 2
t  x  2x 2
 x  2x  2  t  2  log t  log t  2 . 3 5  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 59
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 log t  u  u  t  3 3 
Đặt log t  log t  2  u , u u    5  2  3 3 5    log t  2   u  u t   5   2 5  5
 u  3u  2 (1)
5u  2  3u
5u  3u  2       u u .   3   1  5u  2  3u  u u  3  2  5   2  1 (2)        5   5  Xét  
1 : 5u  3u  2
Ta thấy u  0 là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm u  0 là duy nhất. Với 2
u  0  t  1
  x  2x 1  0, phương trình này vô nghiệm. u u  3   1  Xét 2 :  2  1      5   5 
Ta thấy u  1 là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm
u  1 là duy nhất. Với 2
u  0  t  3  x  2x  3  0 , phương trình có 2 nghiệm phân biệt thỏa x  0; x  2 . Chọn đáp án B. 1 1 1  m 2 2 x x 1 
Câu 29. Cho f  x    e . Biết rằng  
1 . 2. 3... 2017  n f f f f e với ,
m n là các số tự m nhiên và tối giản. Tính 2 m  n . n A. 2
m  n  2018 . B. 2 m  n  2  018 . C. 2 m  n  1. D. 2 m  n  1  . Hướng dẫn giải:
Xét các số thực x  0 x  x 1 1 1 2 2 2 x  x  1 1 1 1 Ta có : 1     1  1  . 2 x  x  2 1 x  x  2 2 2 1 x  x x  x   1 x x  1 2  1 1   1 1   1 1   1 1  1 2018 1 1   1   1    1          2018
Vậy, f   f   f   f    1 2   2 3   3 4   2017 2018  2018 2018 1 . 2 . 3 ... 2017  e  e  e , 2 m 2018  1 hay  n 2018 2 2018 1 Ta chứng minh là phân số tối giản. 2018
Giả sử d là ước chung của 2 2018 1 và 2018 Khi đó ta có 2 2018 1d , 2
2018d  2018 d suy ra 1d  d  1 2 2018 1 Suy ra
là phân số tối giản, nên 2
m  2018  1, n  2018 . 2018 Vậy 2 m  n  1  . Chọn đáp án D.
Câu 30. Hỏi phương trình 3.2x  4.3x  5.4x  6.5x có tất cả bao nhiêu nghiệm thực? A. 2 . B. 4 . C. 1. D. 3 . Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 60
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x x x  2   3   4  pt  3.  4.  5.  6  0        5   5   5  x x x  2   3   4 
Xét hàm số f  x  3.  4.  5.  6       liên tục trên  .  5   5   5  x x x  2  2  3  3  4  4
Ta có: f  x  3  ln  4   ln  5   ln  0,x          5  5  5  5  5  5
Do đó hàm số luôn nghịch biến trên  mà f 0  6  0 , f 2  2
 2  0 nên phương trình
f  x  0 có nghiệm duy nhất. Chọn đáp án C.
Câu 31. Tìm tất cả các giá trị thực của tham số m để bất phương trình 9x  2m 1.3x  3  2m  0
nghiệm đúng với mọi x  . 4 3 3 A. m tùy ý. B. m   . C. m   . D. m   . 3 2 2 Hướng dẫn giải: Đặt  3x t , t  0 2 t  2t  3 1 ycbt 2
 t  2m  
1 t  3  2m  0,t  0  m 
,t  0  m 
t  3,t  0 2t  2 2 1 1
f t  t  3, f t   0, t
  0  hàm số đồng biến trên 0,  2 2 3
Vậy ycbt  m  f t ,t  0  m  f 0   . 2 Chọn đáp án D. 2 2
Câu 32. Tìm tập hợp tất cả các tham số m sao cho phương trình x 2x1 x  2 x  2 4  . m 2  3m  2  0 có bốn nghiệm phân biệt. A.  ;   1 . B.  ;   1  2; . C. 2; . D. 2;  . Hướng dẫn giải: 2 Đặt ( x 1  ) t  2 t   1 Phương trình có dạng: 2
t  2mt  3m  2  0  *
Phương trình đã cho có 4 nghiệm phân biệt
 phương trình (*) có hai nghiệm phân biệt lớn hơn 1 2  2
m  3m  2  0 2
m  3m  2  0
m  3m  2  0         m 1  0  m  2 2 2 x
 m  m  3m  2  1 
 m  3m  2  m 1 1,2    2 2
m  3m  2  m  2m  1  Chọn đáp án D.
Câu 33. Cho x, y là số thực dương thỏa mãn
x  ln y  l  2 ln
n x  y . Tìm giá trị nhỏ nhất của
P  x  y A. P  6 .
B. P  2 2  3 .
C. P  2  3 2 .
D. P  17  3 . Hướng dẫn giải:
Từ n x  ln y  l  2 x  y 2 l n
 xy  x  y . Ta xét:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 61
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Nếu 0  x  1 thì 2 2 y  y
x  x  y  0  x mâu thuẫn. 2 x 2 x Nếu x  1 thì 2
xy  x  y  y  x   2
1  x  y 
. Vậy P  x  y  x  . x 1 x 1 2 x
Ta có f  x  x  xét trên 1; . x  1  2  2  x  (loai) 2 2x  4x  1 2
Có f ' x   0   2 x  2x  1  2  2  x  (n a h n)  2  2  2 
Vậy min f  x  f    2 2  3 . 1;     2    Chọn đáp án B.
Câu 34. Tìm tất cả các giá trị thực của tham số m để bất phương trình x x  x 12  . m log 3 5 4 x có nghiệm. A. m  2 3 B. m  2 3
C. m  12 log 5
D. 2  m  12log 5 3 3 Hướng dẫn giải:
Điều kiện: x 0; 
4 . Ta thấy 4  x  4  5  4  x  3  log 3  0 5 4 x
Khi đó bất phương trình đã cho trở thành m  f  x   x x  x 12 .log 5  4  x * 3     3 x 1
Với u  x x 
x  12  u '   và 2 2 x  12 1
v  log 5  4  x  v '  3  
2 4  x 5  4  x .ln3
Suy ra f ' x   0;x  0; 4  f  x  là hàm số đồng biến trên đoạn 0;  4
Để bất phương trình (*) có nghiệm  m  min f  x  f 0  2 3 0;  4 Chọn đáp án A. x x
Câu 35. Tìm giá trị của a để phương trình 2  3  1 a2  3  4  0 có 2 nghiệm phân biệt
thỏa mãn: x  x  log 3, ta có a thuộc khoảng: 1 2 2 3 A.  ;  3   B.  3  ; C. 3; D. 0; Hướng dẫn giải: x x x 1 1
Ta có 2  3 2  3  1 2  3  . Đặt t 
t  0 , phương trình  x x 2  3  2  3 1  a đã cho trở thành 2 t 
 4  0  t  4t  1  a  0 * t
Phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân
t  t  4  0 biệt 1 2    a  1
t t  1 a  0  1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 62
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x x  x 2  3 1 1 2 t
Ta có x  x  log 3         2 3 1 3 3 3 1 2 2 3  x 2  3  2 t2
Vì t  t  4 nên điều này xảy ra khi và chỉ khi phương trình (*) có 2 nghiệm t=3 và t=1 1 2
Khi đó 1 a  3.1  3  a  2  . Chọn đáp án B.
Câu 36. Gọi m là số chữ số cần dùng khi viết số 30
2 trong hệ thập phân và n là số chữ số cần dùng khi viết số 2
30 trong hệ nhị phân. Ta có tổng m + n bằng A. 18 B. 20 C. 19 D. 21 Hướng dẫn giải:
- Phương pháp: Số chữ số cần dùng khi viết số A trong hệ thập phân là log 
A 1 với  x là số
nguyên lớn nhất nhỏ hơn hoặc bằng x.
Tổng quát: số chữ số cần dùng khi viết số A trong hệ n-phân là log A n  1
Dựa vào 2 kết quả trên ta có 30
m  log 2   1  30log 2  1  10   2
n  log 30   1  2 log 30  1  10 2  2   
 m  n  20 Chọn đáp án B. Câu 37. Cho hàm số 2
y  x  2x  a  4 . Tìm a để giá trị lớn nhất của hàm số trên đoạn 2;  1 đạt giá trị nhỏ nhất. A. a  3 B. a  2 C. a  1
D. Một giá trị khác Hướng dẫn giải:
Ta có y  x  x  a    x  2 2 2 4
1  a  5 . Đặt u   x  2
1 khi đó x  2  ;  1 thì u 0;  4 Ta
được hàm số f u  u  a  5 . Khi đó
Max y  Max f u  Max f 0, f 4  Max a  5 ; a 1 x   2  ;  1 u   0;  4
Trường hợp 1: a  5  a 1  a  3  Max f u  5  a  2  a  3 u   0;4
Trường hợp 2: a  5  a 1  a  3  Max f u  a 1  2  a  3 u   0;4
Vậy giá trị nhỏ nhất của Max y  2  a  3 x   2  ;  1 Chọn đáp án A.
Câu 38. Cho phương trình 2log cotx  log cos x . Phương trình này có bao nhiêu nghiệm trên 3   2       khoảng ;    6 2  A. 4 B. 3 C. 2 D. 1 Hướng dẫn giải: 2 c  u  ot x  3
Điều kiện sin x  0,cos x  0 . Đặt u  log cos x khi đó 2   c  os x  2u 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 63
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2 u u cos x 2   4  Vì 2 cot x  suy ra u  3  f u   4 1  0 2   u 2   1  cos x   u   3 1 2  u  4   4  '   ln  4u f u ln 4  0,u     
 . Suy ra hàm số f(u) đồng biến trên R, suy ra phương  3   3 
trình f u  0 có nhiều nhất một nghiệm, ta thấy f   1  0 suy ra 1  cos x   x  
 k 2k   . 2 3 
Theo điều kiện ta đặt suy ra nghiệm thỏa mãn là x 
 k 2 . Khi đó phương trình nằm trong khoảng 3   9   7   9  ;   là x  , x 
. Vậy phương trình có hai nghiệm trên khoảng ;   .  6 2  3 3  6 2  Chọn đáp án C.
Câu 39. Trong các nghiệm (x; y) thỏa mãn bất phương trình log
(2x  y)  1 . Giá trị lớn nhất của 2 2 x  2 y
biểu thức T  2x  y bằng: 9 9 9 A. . B. . C. . D. 9. 4 2 8 Hướng dẫn giải: 2 2 2 2 
x  2 y  1 0 
  x  2 y  1 Bất PT  log
(2x  y)  1   (I ),  (II ) . 2 2 x 2 y 2 2 2 2
2x  y  x  2 y 0 
  2x  y  x  2 y 
Xét T= 2x  y
TH1: (x; y) thỏa mãn (II) khi đó 2 2
0  T  2x  y  x  2 y  1 1 9 TH2: (x; y) thỏa mãn (I) 2 2 2 2
x  2 y  2x  y  (x 1)  ( 2 y  )  . Khi đó 2 2 8 1 1 9 1  1  9 9 9 9 9 2 2 2
2x  y  2(x 1)  ( 2 y  ) 
 (2  ) (x 1)  ( 2 y  )   .     2 2 2 4 2  2 2  4 2 8 4 2 9 1 Suy ra : maxT   ( ; x y)  (2; ) 2 2 Chọn đáp án B.  a 
Câu 40. Xét các số thực
thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức 2 P  a a  2 log   3logb   b b   A. P  19 B. P  13 C. P  14 D. P  15 min min min min Hướng dẫn giải: 1 4 P   3 log a 1   3 log a 1 2  b  2  b   a  1 log b a  log 2  a   b 
Đặt t  log b do a  b  1 nên 0  t  1 a 4 3 P    3 1 t2 t
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 64
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 4 3  1 
Xét f t    3 trên 0; 
1 ta thấy GTNN của f(t) là f  15   1 t2 t  3  Chọn đáp án D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 65
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
HÌNH NÓN - TRỤ - CẦU
Câu 1. Cho hình chóp S.ABCD có SA vuông góc với đáy, SA  a 6 . Đáy ABCD là hình thang vuông 1
tại A và B, AB  BC  AD  .
a Gọi E là trung điểm của AD. Tính bán kính mặt cầu ngoại tiếp hình 2 chóp S.ECD. a 2 a 30 a 26 A. R  .
B. R  a 6. C. R  . D. R  . 2 3 2 Hướng dẫn giải: . S
Gọi H là trung điểm của CD và d là đường thẳng qua H và R
vuông góc với đáy. Gọi I và R là tâm và bán kính mặt cầu K
ngoại tiếp S.CDE. Suy ra I thuộc d. Đặt IH  . x I
Trong mp(ASIH) kẻ đường thẳng qua I và song song với R x AH cắt AS tại K. E A D Ta có: 2 a a 2 2 2 2 H
ID  IH  HD  x  . 2 B a C 2 a 2 2 2 2 2 2 2 2 2 2
IS  IK  KS  AH  KS  AC  CH  KS  2a   (a 6  x) 2 2 2 a a 2 6a 30a Suy ra: 2 2 2 x   2a 
 (a 6  x)  x 
. Vậy bán kính mặt cầu bằng R  . 2 2 3 3 Chọn đáp án C. a 3
Câu 2. Cho tứ diện ABCD với BC  a ,các cạnh còn lại đều bằng
và  là góc tạo bởi hai mặt 2
phẳng  ABC  và  BCD . Gọi I,J lần lượt là trung điểm các cạnh BC, AD . Giả sử hình cầu đường IJ
kính tiếp xúc với CD. Giá trị cos là: 2 3 2  3 A. 3  2 3 B. 2 3  3 C. D. 3 3 Hướng dẫn giải:
Gọi O là trung điểm IJ và F là điểm tiếp xúc giữa hình cầu đường kính IJ và đường thẳng CD. Hình
cầu đường kính IJ tiếp xúc với CD khi và chỉ khi khoảng cách từ O đến CD bằng nữa độ dài IJ. a 2
Ta có AI  DI  . 2 a
Vì FC và CI là hai tiếp tuyến xuất phát từ một điểm nên FC  CI  2 a 3 a
Tương tự ta có DJ  DF   2 2
Tam giác ADI cân có IJ là đường trung tuyến nên tam giác IDJ vuông tại J. a   JD  3 1 6  2 Suy ra  2 sin  sin JID    2 DI a 2 2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 66
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Do vậy cos  2 3  3 nên Chọn đáp án B.
Câu 3. Cho hình vẽ bên. Tam giác SOA vuông tại O có MN S
€ O với M , N
lần lượt nằm trên cạnh SA, OA. Đặt SO  h không đổi. Khi quay hình vẽ S
quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình
tròn tâm O bán kính R  OA. Tìm độ dài của MN để thể tích khối trụ là lớn nhất. h h A. MN  B. MN  2 3 M h h C. MN  D. MN  4 6
Hướng dẫn giải :
Ta thấy khi quay quanh trục SO sẽ tạo nên một khối trụ nằm trong khối
chóp. Khi đó thiết diện qua trục của hình trụ là hình chữ nhật MNPQ. Ta A O có hình sau: N S
Ta có SO  h ; OA  R . Khi đó đặt OI  MN  x . IM SI O . A SI .
R h  x
Theo định lí Thales ta có   IM   . Thể OA SO SO h 2 R 2 tích khối trụ 2
V  IM .IH  .x h  x 2   h Q I M
Áp dụng bất đẳng thức Cauchy ta có: 2
 2x  2h  x 3 
2xh  x    3   B A P O N 2 4R h h h Vậy V 
. Dấu '  ' xảy ra khi x  . Hay MN  . 27 3 3 Chọn đáp án B.
Câu 4. Một hình nón bị cắt bởi mặt phẳng  P song song với đáy.
Mặt phẳng  P chia hình nón làm hai phần  N và  N . Cho hình 2  1  N1
cầu nội tiếp  N như hình vẽ sao cho thể tích hình cầu bằng một nửa 2 
thể tích của  N . Một mặt phẳng đi qua trục hình nón và vuông góc 2 
với đáy cắt  N theo thiết diện là hình thang cân, tang góc nhọn của 2  hình thang cân là A. 2 B. 4 N2 C. 1 D. 3 Hướng dẫn giải:
Giả sử ta có mặt cắt của hình nón cụt và các đại lượng như hình vẽ.
Gọi  là góc cần tìm.
Xét AHD vuông tại H có DH  h, AH  R  r  h  2r  AH.tan   R  r tan  1 0     3 4 h Thể tích khối cầu là 3 V  r  1 0 3 6
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 67
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1
Thể tích của  N là V  h 2 2
R  r  Rr 2  2  D r C 3 V 1 1 2 2 2 
 h  R  r  Rr 2 r0 V 2 2
Ta có BC  R  r (tính chất hai tiếp tuyến cắt nhau) h O 2 Mà 2 2
h  BC   R  r  4Rr 3 2
Từ 2,3   R  r   Rr 4 2 2 K Từ       2
 h   R  r  2 1 , 3 , 4
.tan   4 R  r α H A B R (vì  là góc nhọn) 2
 tan   4  tan   2 Chọn đáp án A.
Câu 5. Cho tam giác ABC có độ dài cạnh huyền 5. Người ta quay tam giác ABC quanh một cạnh góc
vuông để sinh ra hình nón. Hỏi thể tích V khối nón sinh ra lớn nhất là bao nhiêu. 250 3 25 2 20 3 250 6 A. V  B. V  C. V  D. V  27 27 27 27 Hướng dẫn giải: 1 1 1 25 1 Ta có 2 2 V  r h  x y   2 25  y  3 y  y  y . 3 3 3 3 3 25 1 Xét hàm số 3 V 
y  y với 0  y  5 . 3 3 25 5 Ta có 2 V ' 
  y  0  y  . 3 3 250 3
Khi đó thể tích lớn nhất là V  . 27 Chọn đáp án A.
Câu 6. Một công ty sản xuất một loại cốc giấy hình nón có thể tích 27cm3. Vói chiều cao h và bán
kính đáy là r. Tìm r để lượng giấy tiêu thụ ít nhất. 6 3 8 3 8 3 6 3 A. 4 r  B. 6 r  C. 4 r  D. 6 r  2 2 2 2 2 2 2 2 Hướng dẫn giải: 1 3V Ta có: 2 V 
r h  h 
=> độ dài đường sinh là: 2 3 r 8 3V 81 3 2 2 2 2 2 2 2 l  h  r  ( )  r  ( )  r   r 2 2 2 4 r r  r 8 8 3 3
Diện tích xung quanh của hình nòn là: 2 4 S
 rl  r  r    r xq 2 4 2 2  r  r 8 3
Áp dụng BĐT Cauchy ta được giá trị nhỏ nhất là khi 6 r  . 2 2 Chọn đáp án B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 68
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 7. Cho một khối trụ có bán kính đáy r  a và chiều cao h  2a . Mặt phẳng (P) song song với
trục OO' của khối trụ chia khối trụ thành 2 phần, gọi V là thể tích phần khối trụ chứa trục OO' , V là 1 2 V a 2
thể tích phần còn lại của khối trụ. Tính tỉ số 1 , biết rằng (P) cách OO' một khoảng bằng . V 2 2 3  2 3  2 2  3 2  3 A. . B. . C. . D. .   2   2   2   2 Hướng dẫn giải: Thể tích khối trụ 2 2 3
V  r h  a .2a  2a .
Gọi thiết diện là hình chữ nhật ABB ' A' .
Dựng lăng trụ ABCD. A’B’C’D’ như hình vẽ.
Gọi H là trung điểm AB. a 2
Ta có OH  AB  OH  ( ABB ' A')  OH  2 a 2
 AH  BH   OH . 2
 OAB vuông cân tại O  ABCD là hình vuông. Từ đó suy ra: 3 1 1 a (  2) V  V V a a a . ABCD A B C D    3 2 2  ( 2) .2  2 . ' ' ' '  4 4 2 3 3 a (  2) a (3  2) V 3  2 3
V  V  V  2a   . Suy ra 1  . 1 2 2 2 V   2 2 Chọn đáp án A.
Câu 8. Trong số các khối trụ có thể tích bằng V, khối trụ có diện tích toàn phần bé nhất thì có bán kính đáy là V 4  V A. 3 R  . B. 3 R  C. 3 R  D. 3 R  2 V V  Hướng dẫn giải: V 2V 2
V  R .h  l  h  , 2 2 S  S
 2S  2Rl  2R   2R 2 R TP Xq d R 2V 3 2  V  4R V Xét hàm số 2 f (R) 
 2R với R>0, 3 f '(R) 
, f '(R)  0  R  R 2 R 2 Bảng biến thiên R V 0 3 +  2 , f (R) + 0 - 0 f (R)   V
Từ bảng biến thiên ta thấy diện tích toàn phần nhỏ nhất khi 3 R  2 Chọn đáp án A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 69
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 9. Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông cân AB=BC=a. Mặt phẳng 3
(AB’C) tạo với (BCC’B’) một góc  với tan  
. Gọi M là trung điểm của BC. Tính bán kính mặt 2
cầu ngoại tiếp hình chóp B’ACM. 3 10a 3 10a 3 13a 13a A. B. C. D. 8 4 8 2 B' A' B' A' B' A' C' C' N C' O B I a A B α A M a K M K a B A J C J M C
Trục không có tính chất đặc
Xác định tâm đáy: giao của hai
biệt, ta sử dụng phương pháp 4 C
đường thẳng trung trục MC và để giải
Dựng góc: chú ý BA vuông góc BI.
R2 = B’O2 = NO2 + B’N2
với giao tuyến CB’  
Từ tam giác vuông BIA và góc = 2 2
BJ  (BB '  JO)
 , tính được BI. Từ BI sử dụng = OM2 = OJ2 + JM2 1 1 1  Chú ý 0 CBJ  45   tính được 2 2 2 BI BC B ' B
Giải phương trình ta tìm được
B' B  a 2 . 5 2a OJ = 8 3 10a R = 8 Chọn đáp án A.
Câu 10. Cho hình nón có bán kính đáy là a, đường sinh tạo với mặt phẳng đáy góc  . Tính thể tích
khối cầu ngoại tiếp hình nón. 3 3a 3 4a 3 4a 3 4a A. V  B. V  C. V  D. V  3 4sin 2 3 3sin 3 3 3sin 2 3 3sin  Hướng dẫn giải:
Nếu mặt phẳng  P qua trục của hình nón thì (P) cắt hình nón theo tam giác cân SMN, (P) cắt mặt
cầu ngoại tiếp hình nón theo đường tròn có bán kính là R. Gọi I là tâm mặt cầu ngoại tiếp hình nón,
O là tâm đường tròn đáy của hình nón. Ta có 2 S  M . O SO  . a .
a tan   a tan  . SMN 2  a  .2a 2   3 SM .SN.MN SM .2a  cos   a Mặt khác S     . SMN 2 4R 4R 4R 2R cos  3 a a a Do đó 2
 a tan   R   . 2 2 2R cos  2 cos  tan  sin 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 70
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
R cũng là bán kính của mặt cầu ngoại tiếp. 3 4 4 a 3 V  R    . 3 3 3 sin 2 Chọn đáp án C.
Câu 11. Cho hình nón có chiều cao h, đường tròn đáy bán kính R. Một mặt phẳng (P) song song với
đáy cách đáy một khoảng bằng d cắt hình nón theo đường tròn (L). Dựng hình trụ có một đáy là (L),
đáy còn lại thuộc đáy của hình nón và trục trùng với trục hình nón. Tìm d để thể tích hình trụ là lớn nhất. h h h h A. d  B. d  C. d  D. d  3 2 6 4 Hướng dẫn giải:
Gọi r là bán kính của (L). r h  d R Ta có   r  h  d  R h h R 2 R
R  h  d   h  d  3 2 2 2 2  2d  4R h  V  
h  d  .d  
h  d h  d .2d    2 2 2   h 2h 2h 3 27   h
Dấu bằng xảy ra khi h  d  2d  d  . 3 Chọn đáp án A.
Câu 12. Trong số các hình trụ có diện tích toàn phần đều bằng S thì bán kính R và chiều cao h của
khối trụ có thể tích lớn nhất là: S 1 S S S A. R  ; h  . B. R  ;h  . 2 2 2 4 4 2S 2S S S C. R  ;h  4 . D. R  ; h  2 . 3 3 6 6 Hướng dẫn giải:
Gọi thể tích khối trụ là V , diện tích toàn phần của hình trụ là S . Ta có: 2 S  S
 S  2R  2Rh . Từ đó suy ra: 2day xq Cauchy 2 S S V V V V 2 2 2 3  R  Rh   R   R   3  2 2 2 R 2R 2R 4 3 2 3 V  S  S hay 27   V  . 2   4  2  54 3 S 2 V R h Rh Vậy V  . Dấu “=” xảy ra  2 R    hay h  2R . max 54 2R 2R 2 S S Khi đó 2
S  6R  R 
và h  2R  2 . 6 6 Chọn đáp án D.
Câu 13. Một bình đựng nước dạng hình nón (không đáy) đựng đầy nước. Biết rằng chiều cao của bình
gấp 3 lần bán kính đáy của nó. Người ta thả vào đó một khối trụ và đo dược thể tích nước tràn ra ngoài
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 71
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 16 là 3
dm . Biết rằng một mặt của khối trụ nằm trên mặt trên của hình nón, các điểm trên đường tròn 9
đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ có chiều cao bằng đường
kính đáy của hình nón. Diện tích xung quanh S của bình nước là: xq M N A O B I P Q S 9 10 3 A. 2 S  dm . B. 2 S  4 10 dm . C. 2 S  4dm . D. 2 S  dm . xq 2 xq xq xq 2 Hướng dẫn giải:
Xét hình nón : h  SO  3r , r  OB, l  SA . Xét hình trụ : h  2r  NQ , r  ON  QI 1 1 QI SI 1 r
SQI  SBO     r 
 Thể tích khối trụ là : 1 BO SO 3 3 3 2r 16 2 V  r h  
 r  2  h  6 2 2
 l  h  r  2 10 2  S
 rl  4 10 dm t 1 1 9 9 xq Chọn đáp án B.
Câu 14. Cho một miếng tôn hình tròn có bán kính 50cm . Biết hình nón có thể tích lớn nhất khi diện
tích toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy là A. 10 2cm B. 20cm C. 50 2cm D. 25cm Hướng dẫn giải:
Đặt a  50cm . Gọi bán kính đáy và chiều cao của hình nón lần S lượt là , x y , x y  0 . Ta có 2 2 2 2
SA  SH  AH  x  y
Khi đó diện tích toàn phần của hình nón là 2 2 2
S  x  x x  y tp I Theo giả thiết ta có: J 2 2 2 2 2 2 2 2
x  x x  y  a  x x  y  x  a O 2 2 2 2
 x x  y  a  x  A 4 a H 2 x  2 2 x  y  4 4 2 2
 a  x  2a x , DK : x  a 2  x  2 2 y  2a
Khi đó thể tích khối nón là: 4 1 a 1 y 4 V  .  .y  a . 2 2 2 2 3 y  2a 3 y  2a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 72
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2 y  2a
V đạt giá trị lớn nhất khi và chỉ khi
đạt giá trị nhỏ nhất y 2 2 2 2 y  2a 2a 2a Ta có  y   2 . y  2 2a y y y 2 2a a
Vậy V đạt giá trị lớn nhất khi và chỉ khi y 
, tức là y  a 2  x   25cm y 2 Chọn đáp án D.
Câu 15. Thiết diện qua trục của một hình nón là một tam giác vuông có cạnh góc vuông bằng a. Tính
diện tích của thiết diện qua đỉnh tạo với đáy một góc 600. 2 a 2 a 3 2 a 2 2 a A. B. C. D. 2 2 3 3 Hướng dẫn giải:
Gọi thiết diện qua trục là  SAB vuông cân tại S,
SA  SB  a S a
Gọi O là tâm của đáy, SO = 2
Gọi thiết diện qua đỉnh, tạo với đáy góc 600 là  SAC.
Gọi M là trung điểm AC, góc giữa mặt phẳng (SAC) với mặt a đáy là  SMO = 600 SO a 6 * SM   (  SMO vuông tại O). 0 sin 60 3 45 a 6 A B O * OM  M 6 C 2a 3 * 2 2
AC  2AM  2 OA  OM = 3 1 1 a 6 2a 3 2 a 2 * SSAC = SM.AC = . . = 2 2 3 3 3 Chọn đáp án C.
Câu 16. Cho hình chóp SABC với SA vuông góc với mặt phẳng (ABC) và S  BC= 3 a,  60o BAC
. Gọi H, K lần lượt là hình chiếu của A lên SB và K
SC. Mặt cầu qua các điểm A, B, C, H, K có bán kính bằng: A. 1 B. 2 C. 3
D. Không đủ dữ kiện để tính H 3 Hướng dẫn giải: A C 600
Gọi AD là đường kính của đường tròn (ABC) 2
Suy ra, AC  DC , suy ra CD  (SAC) hay AE  DE
Tương tự, AH  HD . Suy ra mặt cầu qua các điểm A, B, C, H, K có B BC S đường kính AD   2 . 0 sin 60 K Chọn đáp án B. H A C 600
File Word liên h D
ệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com B
Trang 73
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S
trên mặt phẳng (ABC) là trung điểm cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng
600. Gọi G là trọng tâm tam giác SAC. Bán kính mặt cầu tâm G và tiếp xúc với mặt phẳng (SAB) là: 13a 13a 3 13a 13a A. B. C. D. 13 39 26 26 Hướng dẫn giải: + Gọi H là trung điểm BC +   ( , ( ))   60o SA ABC SAH a 3 3a + 0 AH 
, SH  AH tan 60  2 2 + Bán kính mặt cầu là: S 1 2
R  d(G, (SAB)) 
d (C, (SAB)) 
d (H , (SAB)) 3 3
+ Gọi E là hình chiếu của H trên AB và K là hình chiếu của H trên SE. M K G Chứng minh: HK  (SAB) H C B a 3 3a
+ Tính được: HE  ; HK  E 4 2 13 2 a A + R  HK  3 13 Chọn đáp án A.
Câu 18. Cho nửa đường tròn đường kính AB  2R và điểm C thay đổi trên nửa đường tròn đó, đặt 
  CAB và gọi H là hình chiếu vuông góc của C lên AB . Tìm  sao cho thể tích vật thể tròn xoay
tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất. 1 A.   60 . B.   45. C. arctan . D.   30 . 2 Hướng dẫn giải: AC  A . B cos   2 . R cos 2
CH  AC.sin   2 . R cos .  sin ;
 AH  AC.cos   2 . R cos 
Thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB là 1 8 2 3 4 2 V  AH.CH  R .cos .  sin  . 3 3 8 Đặt 2
t  cos  0  t   1 3 2  V  R t 1 t 3 3 8 8
 t  t  2  2t 3  
R .t.t 2  2t 3  R   6 6  3  2 1
Vậy V lớn nhất khi t  khi   arctan . 3 2
Chú ý: có thể dùng PP hàm số để tìm GTNN của hàm f t 2
 t 1 t Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 74
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2, cạnh bên SA vuông góc
với mặt phẳng đáy và SA  3. Mặt phẳng  qua A và vuông góc với SC cắt các cạnh SB , SC ,
SD lần lượt tại các điểm M , N , P . Tính thể tích V của khối cầu ngoại tiếp tứ diện CMN . P 32 64 2 A. V  . B. V  . 3 3 108 125 C. V  . D. V  . 3 6 Hướng dẫn giải:
Ta có: CB  SAD, AM   SAB  AM  CB   1 S
  SC, AM    AM  SC 2 N P
 AM   SBC  
 AM  MC  AMC  90 .
Chứng minh tương tự ta có  APC  90 
Có AN  SC  ANC  90 . Ta có: M   
AMC  APC  APC  90 D
 mặt cầu đường kính AC là mặt cầu ngoại tiếp tứ A diện CMNP . AC
Bán kính cầu này là r 
 2 . Thể tích khối cầu: 2 B C 4 32 3 V  r  3 3 Chọn đáp án A.
Câu 20. Cho tứ diện ABCD có ABC và ABD là các tam giác đều cạnh a và nằm trong hai mặt phẳng
vuông góc với nhau. Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD theo a. 5 11 4 A. 2 a B. 2 a C. 2 2a D. 2 a 3 3 3 Hướng dẫn giải:
Gọi M là Trung điểm của AB D
Vì Tam giác ADB và tam giác ABC là tam giác đều
 DM  AB;CM  AB
Do có ABC và ABD là các tam giác đều cạnh a và nằm
trong hai mặt phẳng vuông góc với nhau => Góc  DMC  900 O
Gọi H là tâm đường tròn ngoại tiếp Tam giác ABC G
G là tâm đường tròn ngoại tiếp Tam giác ABD
=> H,G đồng thời là trọng tâm của tam giác ABC và A C H ABD  2
H  CM ;CH  M  CM  3   2 B
G  DM ; DG  DM   3
Kẻ Đường vuông góc với đáy (ABC) từ H và Đường vuông góc với (ABD) từ G.
Do hai đường vuông góc này đều thuộc (DMC) nên chúng cắt nhau tại O.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 75
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
=> O chính là tâm mặt cầu ngoại tiếp tứ diện ABCG và R = OC. 3 3 3
Tam giác ABC đều  CM  C . B sin  0 60   a  CH  ; a HM  a 2 3 6 3 CMTT ta có GM  a 6 3
Từ đó nhận thấy OGMH là hình vuông  OH  a 6
Tam giác OHC vuông tại H → Áp dụng định lý Pitago ta có: 3 3 3 CM  C . B sin 60  a  CH  a; HM  a 2 3 6 5 5 2 2
OC  CH  OH  a  R 2 2
 V  4R  a 12 3 Chọn đáp án A.
Câu 21. Cho một mặt cầu bán kính bằng 1. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên.
Hỏi thể tích nhỏ nhất của chúng là bao nhiêu?
A. minV  8 3 .
B. minV  4 3 .
C. minV  9 3 .
D. minV  16 3 . Hướng dẫn giải:
Gọi cạnh đáy của hình chóp là a S
Ta có SIJ ~ SMH SI IJ  
 MH  SH  IH  2 2  IJ SH  HM SM MH
 MH SH  2 2 2 2 1  SH  HM 2 2a 2 2 2 2 J
 a  12 SH  2a SH  0  SH  a  12 I 2 a  12 4 A B 1 3 2a 3 1 S  S .SH   ABC 2 H 3 6 a 12 6 1 12 M  2 4 a a C 1 12 1 Ta có    S  8 3 2 4 a a 48 Chọn đáp án A.
Câu 22. Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm, cần xả thành một chiếc xà có tiết
diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng x
của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 76
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3 34 17 2 3 34 19 2 A. x  cm B. x  cm 2 2 5 34  15 2 5 34 13 2 C. x  cm D. x  cm 2 2 Hướng dẫn giải:
Diện tích sử dụng theo tiết diện ngang là S  S  4xy MNPQ MP 40
Cạnh hình vuông MN    20 2 cm 2 2  S   2 20 2
 4xy  800  4xy (1)
Ta có 2x  AB  MN  AB  20 2  BD  20 2  40  20 2  0  x  20 10 2
Lại có AB  AD  BD    x  2 2 2 2 2 2 40 2 20 2  y  1600 2 2 2
 y  800  80x 2  4x  y  800  80x 2  4x Thế vào   2 2 3 4
1  S  800  4x 800  80x 2  4x  800  4 800x  80x 2  4x
Xét hàm số f  x 2 3 4  800x  80x
2  4x , với x  0;20 10 2  có f  x 2 3  x  x  x  x  2 ' 1600 240 2 16 16
100  15x 2  x  x  x        0;20 10 2 0; 20 10 2  5 34 15 2 Ta có     x 
 f  x     2   x  2 ' 0 16x 100 15x 2  0  5 34 15 2 Khi đó x 
chính là giá trị thỏa mãn bài toán. 2 Chọn đáp án C.
Câu 23. Một hình trụ có bán kính đáy bằng 50cm và có chiều cao là 50cm. Một đoạn thẳng AB có
chiều dài là 100cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng
đó đến trục hình trụ.
A. d  50cm
B. d  50 3cm
C. d  25cm
D. d  25 3cm Hướng dẫn giải: A O
Kẻ AA1 vuông góc với đáy, A1 thuộc đáy. Suy ra:
OO / / AA  OO / / AA B  d OO , AB  d OO , AA B  d O , AA B 1 1 1  1   1   1  1   1  1 
Tiếp tục kẻ O H  A B tại H, vì O 1 1
1H nằm trong đáy nên cũng vuông góc với A1A suy ra: I
O H  AA B . Do đó K 1  1 
d OO , AB  d OO , AA B  d O , AA B  O H 1   1  1   1  1  1
Xét tam giác vuông AA B ta có 2 2 A B  AB  AA  50 3 A1 1 1 1 O1 Vậy 2 2 O H  O A  A H  25cm H 1 1 1 1 Chọn đáp án C. B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 77
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 24. Một công ty sản xuất một loại cốc giấy hình nón có thể tích 27cm3 với chiều cao là h và bán
kính đáy là r. để lượng giấy tiêu thụ là ít nhất thì giá trị của r là: 6 3 8 3 8 3 6 3 A. 4 r  B. 6 r  C. 4 r  D. 6 r  2 2 2 2 2 2 2 2 Hướng dẫn giải: 1 81 81 1 Thể tích của cốc: 2 2 V 
r h  27  r h   h  . 2    r
Lượng giấy tiêu thụ ít nhất khi và chỉ khi diện tích xung quanh nhỏ nhất. 2 2 81 1 81 1 2 2 2 4 S
 2rl  2r r  h  2r r   2 r  xq 2 4 2 2  r  r 2 2 2 2 81 1 81 1 81 1 81 1 4 4 4 81 3  2 r    2 3 r . . 6  2 3 (theo BĐT Cauchy) 2 2 2 2 2 2 2 2 2 r 2 r 2 r 2 r 4 4 2 8 8 81 1 3 3 S nhỏ nhất 4 6 6  r   r   r  xq 2 2 2 2 2 r 2 2 Chọn đáp án B.
Câu 25. Cho một hình lăng trụ đứng có đáy là tam giác đều .Thể tích của hình lăng trụ là V. Để diện
tích toàn phần của hình lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ là: A. 3 4V B. 3 V C. 3 2V D. 3 6V Hướng dẫn giải:
Gọi cạnh đáy của lăng trụ là a, chiều cao lăng trụ là h. 2 a 3 4V
Theo bài ra ta có V  .h  h  2 4 a 3 2 a 3 4V
Diện tích toàn phần của lăng trụ là: S  S  S   3a. toan phan 2 day xung quanh 2 2 a 3 2 a 3 4 3V
Áp dụng bất đẳng thức AM - GM ta có: S   toan phan 2 a 2 2 a 3 2 3V 2 3V a 2 2 3V 2 3V 3     3 . . 2 a a 2 a a 2 a 3 2 3V 2 3V Dấu bằng xảy ra khi   hay 3 a  4V . 2 a a Chọn đáp án A.
Câu 26. Trong không gian cho hai điểm phân biệt A, B cố định. Tìm tập hợp tất cả các điểm M trong   3 không gian thỏa mãn 2 M . A MB  AB 4
A. Mặt cầu đường kính AB.
B. Tập hợp rỗng (tức là không có điểm M nào thỏa mãn điều kiện trên).
C. Mặt cầu có tâm I là trung điểm của đoạn thẳng AB và bán kính R =AB. 3
D. Mặt cầu có tâm I là trung điểm của đoạn thẳng AB và bán kính R  AB 4 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 78
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12    MA  MB
+ Tam giác MAB có đường trung tuyến IM  MI  2    MA  MB MI  2        3  4. .  BA AB 2
MA  MB MA  MB  4M . A MB  2 2 2 2  MI  4 2     AB 4 4 4 MI  AB
Vậy Tập hợp điểm M trong không gian là Mặt cầu có tâm I là trung điểm của đoạn thẳng AB và bán kính R  AB Chọn đáp án C.
Câu 27. Gọi r và h lần lượt là bán kính đáy và chiều cao của một hình nón. Kí hiệu V , V lần lượt là 1 2 V
thể tích của hình nón và thể tích của khối cầu nội tiếp hình nón. Giá trị bé nhất của tỉ số 1 là V2 5 4 A. . B. . C. 3 . D. 2 . 4 3 Hướng dẫn giải: 1
Ta có: Thể tích khối nón là 2 V  r h . 1 3 
Xét mặt cắt qua tâm SAB, kẻ tia phân giác của góc SBO , cắt SO tại I. 2 2 IO OB r r  h Ta có:  
 IS  IO  2 2 IS SB  r r h
Mặt khác: IO  IS  h
Do đó ta có bán kính của mặt cầu nội tiếp hình chóp là rh R  IO  2 2
r  h  r 3 3 4 4 r h Thể tích khối cầu là 3 V  R   . 2 3
3 r  h  r 3 2 2 3 2   h
r  r  h 3 1 1 2 2  2   r 3 2 V 2 h V 1  t t  1 1     1      . Đặt t  1  ( t  1 )    2 2 V 4rh h 2 r V 4 2 t  1 4 t  1 2    2 4 2 r t  2 1 2 t  2t  3
Đặt f t  
, Điều kiện: t  1, f t  
, f t   0  t  3 , f   3  8 t  1 t  2 1 V
BBT  f t   8t  1 1   2 V2 Chọn đáp án D.
Câu 28. Giá trị lớn nhất của thể tích khối nón nội tiếp trong khối cầu có bán kính R là
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 79
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1 4 4 2 32 A. 3 R . B. 3 R . C. 3 R . D. 3 R . 3 3 9 81 Hướng dẫn giải:
Rõ ràng trong hai khối nón cùng bán kính đáy nội tiếp trong một
khối cầu thì khối nón có chiều cao lớn hơn thì thể tích lớn hơn, nên
ta chỉ xét khối nón có chiều cao lớn hơn trong hai khối nón đó.
Giả sử rằng khối nón có đáy là hình tròn C bán kính r . Gọi x R
với f  x là khoảng cách giữa tâm khối cầu đến đáy khối nón. Khi O
đó chiều cao lớn nhất của khối nón nội tiếp khối cầu với đáy l R à x
hình tròn C sẽ là h  R  x . Khi đó bán kính đáy nón là r 2 2
r  R  x , suy ra thể tích khối nón là 1 1 1 1 2 V  r h 
 R  x 2 2
R  x   R  xR  xR  x  R  xR  x2R  2x 3 3 3 6 1
R  x  R  x  R  x3 3 2 2 32R
Áp dụng BĐT Cô-si ta có V    6 27 81 Chọn đáp án D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 80
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
NGUYÊN HÀM , TÍCH PHÂN VÀ ỨNG DỤNG b x e 2
Câu 1. Cho tích phân C 
dx trong đó a là nghiệm của phương trình x 1
2   2 , b là một số  x a e  3 2
dương và b  a . Gọi 2
A  x dx . Tìm chữ số hàng đơn vị của b sao cho C  3A.  1 A. 3 B. 2 C. 4 D. 5 Hướng dẫn giải: 2
Giải phương trình x 1
2   2  x  0  a  0
Tính tích phân C. Đặt: x 2   3   x t e t e  3  2  x tdt e dx b e 3 b 2t e 3 b e 3 C   dt = 2  2  2 b dt t e  3  4  t 2 2 2 7
Tính tích phân A ta có A  3 Theo giả thiết b 7 b 11 b 109 109
C  3A  2 e  3  4  3.  e  3   e   b  ln  3,305053521 3 2 4 4 Chọn đáp án A. e 4 2 . a e  . b e  c
Câu 2. Cho biết tích phân I  x   2
2x  ln xdx  với , a ,
b c là các ước nguyên của 4. 4 1
Tổng a  b  c  ? A. 2 B. 4 C. 3 D. 1 Hướng dẫn giải: e e e I  x   2 2x  ln x 3
dx  2 x dx  x ln xdx .   1 1 1 e e 1 1 3 4 2 x dx  x   4 e    1 2 2 1 1 e e 2 1  e 1  1  1 e e 1 Ta có 2 2 2 2 x ln xdx 
x ln x  x dx  e  x      2 1 x 2 2 1 4 1  1    e 2 4 2    I  x  1 e 1 2e e 1 2
2x  ln xdx   4 e   1    2 4 4 1 Chọn đáp án A. 1 a
Câu 3. Cho hàm số f (x)   . x
b xe . Biết rằng f '(0)  22 và
f (x)dx  5 . Khi đó tổng  3  a b (x1) 0 bằng? 1  46 26 2  6 146 A. B. C. D. . 13 11 11 13 Hướng dẫn giải: 3a f '(x) x   be (1 x) 4 (x1) f '(0)  2  2  3  a b  2  2 (1)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 81
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1 1 1 1 ( )  5 x f x dx  a
dx  b xe dx  5   3  (x 1) 0 0 0 a   b  5 (2) 4 108 38
Giải hệ (1) và (2) ta được: a  , b  . 13 13 Chọn đáp án D. 1 1 Câu 4. Cho
f (x)dx  5 
. Tính I  f (1 x)dx  0 0 1 A. 5 B. 10 C. D. 5 5 Hướng dẫn giải:
x  0  t  1
Đặt t  1 x  dt  dx , x 1 t  0 0
I   f (t)dt  5  1 Chọn đáp án A. 2 2 2 1 x . a   b
Câu 5. Biết tích phân dx   trong đó ,
a b   . Tính tổng a  b ? 1 2x 8 2  2 A. 0 B. 1 C. 3 D. -1 Hướng dẫn giải: 2 2 2 2 2 0 2 2 2 2 1 x 1 x 1 x 2 I  dx  dx  dx  1 x dx     1 2x 1 2x 1 2x 2 2 0 0   2 2   2
Đặt x  sin t  I  . 8 Chọn đáp án C.
Câu 6. Trong không gian với hệ trục tọa độ Oxyz, gọi d là đường thẳng đi qua điểm A 1  ;0;  1 , cắt x 1 y  2 z  2  
, sao cho cosd;  là nhỏ nhất, biết phương trình của đường thẳng 2  2 1 1 x  3 y  2 z  3  :  
. Phương trình đường thẳng d là? 2 1  2 2 x 1 y z 1 x 1 y z 1 A.   B.   2 2 1 4 5 2 x 1 y z 1 x 1 y z 1 C.   D.   4 5 2  2 2 1 Hướng dẫn giải:
Gọi M  d    M 1 2t; 2  t; 2   t . 1    
d có vectơ chỉ phương là ud  AM  2t  2;t  2; 1   t  . 
 có vectơ chỉ phương u2  1; 2; 2 . 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 82
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2 t cos d;   . 2  2 3 6t 14t  9 2 t
Xét hàm số f t  
, ta suy ra được min f t  f 0  0 . 2 6t 14t  9 
Do đó min cos d;    0 
t  . Nên AM  2; 2;   1 . 2  khi 0 x 1 y z 1
Vậy phương trình đường thẳng d là:   . 2 2 1 Chọn đáp án A. tan x   
Câu 7. Cho F(x) là một nguyên hàm của f  x 
, biết F 0  0 , F  1   . Tính 2
cos x 1 a cos x  4        F  F     ?  3   4  A. 5  3 B. 5 1 C. 3  5 D. 5  2 Hướng dẫn giải:     4 4 4 4 tan x tan x 1 f  x 2 dx  dx  dx 
d tan x 1 a     2 2 2 2 0 0 cos x 1 a cos x 0 cos
x tan x 1 a 0 2 tan x 1 a  2 2  tan
1 a  tan 0 1 a  3  2 . 4  a  2  a  1  3  2
 a  2  a 1 2 a 1 3  2   5  2 6 3  6 
 a 1  a  1 3  2  3       tan x   Do đó F  F  dx       2 2 tan  2  tan  2  5  3 . 2  3   4  3 4
 cos x 1  cos x 4 Chọn đáp án A.
Câu 8. Cho f (x) là hàm liên tục và a  0 . Giả sử rằng với mọi x [0; a] , ta có f (x)  0 và a dx
f (x) f (a  x)  1 . Tính 1 f (x) 0 a a A. B. 2a C.
D. a ln(a 1) 2 3 Hướng dẫn giải: a 0 a dx dt f (t)dt
Đặt t  a  x ta có:       1 f (x)
1 f (a  t) f (t) 1 0 a 0 a dx a Suy ra:   1 f (x) 2 0 Chọn đáp án A. 2 2001 x
Câu 9. Tích phân I   dx có giá trị là 2 1002 (1  x ) 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 83
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1 1 1 1 A. . B. . C. . D. . 1001 2002.2 1001 2001.2 1002 2001.2 1002 2002.2 Hướng dẫn giải: 2 2004 2 x 1 1 2 I  .dx  . 
dx . Đặt t   1  dt   dx . 3 2 1002  1002 x (1  x ) 2 3  1 x x 1 1 3  x  1  2   x 
Câu 10. Trong chương trình nông thôn mới, tại một xã X có xây một cây cầu bằng bê tông như hình
vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu. (Đường cong trong hình vẽ là các đường Parabol). 0, 5m 2m 5m 0, 5m 19m 0, 5m A. 3 19m . B. 3 21m . C. 3 18m . D. 3 40m . Hướng dẫn giải:
Chọn hệ trục Oxy như hình vẽ. y O x Ta có 19  Gọi  P  2
: y  ax  c là Parabol đi qua hai điểm A ; 0 , B   0;2 1  2  2   19   8 0   . a  2 a   8  
Nên ta có hệ phương trình sau:   2    361   P  2 : y   x  2 1 361  b   2 2  b    5  Gọi  P  2
: y  ax  c là Parabol đi qua hai điểm C 10;0 , D 0; 2    2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 84
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3 Câu 11. Cho
f , g là hai hàm liên tục trên 1; 
3 thỏa:  f  x  3g  x dx  10    . 1 3 3
2 f  x  g  x dx  6    . Tính
 f  x  g  x dx    . 1 1 A. 8. B. 9. C. 6. D. 7. Hướng dẫn giải: 3 3 3 + Ta có
 f  x  3g  x dx  10  f  x dx  3 g  x dx  10      . 1 1 1 3 3 3 + Tương tự
2 f  x  g  x dx  6  2 f  x dx  g  x dx  6      . 1 1 1 u   3v  10 u   4 3 3
+ Xét hệ phương trình    , trong đó u 
f  x dx 
, v  g  x dx  . 2u  v  6 v  2   1 1 3 3 3 + Khi đó
 f  x  g  x dx  f  x dx  g  x dx  4  2  6      . 1 1 1  5  1 0  . a 102  a     2   40 1 5
Nên ta có hệ phương trình sau:      P  2 : y   x  2 5 5 40 2  b   b    2   2 19  10  1 5   8  
Ta có thể tích của bê tông là: 2 2 3 2 V  5.2  x  dx  
x  2 dx  40m        0 0   40 2   361  
Câu 12. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 x   2 x y e
e , trục Ox và đường a
thẳng x  a với a  ln 2 . Kết quả giới hạn lim S là: a a A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải: ln 2 x x 1 Ta có S  e  e dx  e  e  a   2 2  2a 2 a 2 2 a
Suy ra lim S  2 , chọn đáp án B. a a
Câu 13. Một khối cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông góc bán kính
và cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được.
A. 132 (dm3)
B. 41 (dm3) 100 C.  (dm3)
D. 43 (dm3) 3 3dm Hướng dẫn giải: 5dm
Đặt hệ trục với tâm O, là tâm của mặt cầu; đường thẳng đứng là Ox,
đường ngang là Oy; đường tròn lớn có phương trình 2 2
x  y  25 . 3dm
Thể tích là do hình giới hạn bởi Ox, đường cong 2 y  25  x , x  3, x  3  quay quanh Ox. 3 2
V   (25  x )dx = (bấm máy)  132 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 85
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 
Câu 14. Một vật di chuyển với gia tốc a t     t 2 20 1 2  2
m / s  . Khi t  0 thì vận tốc của vật là
30m / s . Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).
A. S  106m .
B. S  107m .
C. S  108m .
D. S  109m . Hướng dẫn giải: 
Ta có v t   a t dt     t  2 10 20 1 2 dt 
 C . Theo đề ta có   1 2t
v 0  30  C  10  30  C  20 . Vậy quãng đường vật đó đi được sau 2 giây là: 2  10  S   20 dt     2
5 ln 1 2t   20t   5ln 5 100  108m . 0  1 2t  0
Câu 15. Tìm giá trị của tham số m sao cho: 3
y  x  3x  2 và y = m(x+2) giới hạn bởi hai hình
phẳng có cùng diện tích A. 0 < m < 1 B. m = 1 C. 1  m  9 D. m = 9 Hướng dẫn giải:
Phương trình hoành độ giao điểm: 3 x  3x  2  m(x  2)
 x  2 hoÆc x  1  m , m  0.
Điều kiện d: y = m(x+2) và (C): 3
y  x  3x  2 giới hạn 2 hình phẳng: 0  m  9.
Gọi S1, S2 lần lượt là diện tích các hình phẳng nhận được theo thứ tự từ trái sang phải. 0
Nếu m = 1: d đi qua điểm uốn (0;2) của (C). Khi đó S 3 1 = S2 = (x  4x)dx  4  2 
Nếu 0 < m < 1: S1 > 4 > S2
Nếu 1 < m < 9: S1 < 4 < S2 Nếu m > 9  1  m  2
 ; 1  m  4. Khi đó: 2 1 m 3 3 S 
x  3x  2  m(x  2) dx; S 
x  3x  2  m(x  2) dx 1 2   1 m 2 S2  S1 = 2m m  0
Vậy m = 1 thỏa yêu cầu bài toán  2
Câu 16. Cho I  cosn xdx , , n 
. Khẳng định nào sau đây đúng?  n   2 n 0 n  1 n  2 n  1 A. I  I B. I  I C. I  I
D. I  2I n n 1 n  n n 2 n  n n 2 n  n n 2  Hướng dẫn giải:  2  Với I  ; I  cos xdx  1.  0 1 2 0   Đặt n 1 u 
x  du  n   n 2 cos 1 cos x.sin xdx .
dv  cos xdx chọn v  sin x .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 86
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12   2  2   Suy ra n n 1 2 cos xdx  cos
x.sin x  n    n 2 2 1 cos x.sin xdx  0 0 0    2 2 2 n  n 2 1 cos    x.   2 1  cos xdx   n 2 1 cos    .     1 cosn n x dx n x.dx .  0 0 0   2 2 n  n 1 n 2  Do đó cos x.dx  cos x.dx .   n 0 0 Chọn đáp án C. 1 1   Câu 17. Cho hàm số 3 2 y 
x  mx 2x 2m  5
có đồ thị (C). Tìm m  0;  sao cho hình   3 3  6
phẳng giới hạn bởi đồ thị (C) và các đường thẳng x  0, x  2, y  0 và có diện tích bằng 4. 1 A. m  1 B. m  1 C. m  D. m  1 4 3 2 Hướng dẫn giải: 1 1 Xét hàm số 3 2 y 
x  mx 2x 2m  trên 0;2. Ta có 2
y  x  2mx 2 , 3 3  2 x  m   m 2   5 y  0  
. Do m  0;  nên 2 2   m
  m  2  0, 0  m   m  2  2 2    x  m   m 2  6 1 5 và y 0  2
 m  0, y2 2m  0. 3 3
Ta có bảng biến thiên trong 0;2 x 0 2 2 m   m 2  y 0  y y0 y2
Dựa vào BBT suy ra y  0, x  0;2
Gọi S là diện tích hình phẳng cần tìm. Ta có: 2 1 1 3 2 S  4 
x  mx  2x  2m  dx  4  3 3 0 2 1 1  4m 10 1 3 2
   x  mx 2x 2m  dx     4   4  m  3 3  3 2 0 Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 87
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 18. Trong hệ trục Oxy, cho tam giác OAB vuông ở A, điểm B nằm trong góc phàn tư thứ nhất.    
A nằm trên trục hoành, OB = 2017. Góc AOB   , 0   
. Khi quay tam giác đó quanh trục Ox    3 
ta được khối nón tròn xoay. Thể tích của khối nón lớn nhất khi: 6 3 1 2 A. sin  B. cos  C. cos  D. sin  3 2 2 3 Hướng dẫn giải:
Phương trình đường thẳng OB : y  .
x tan; OA  2017 cos.
Khi đó thể tích nón tròn xoay là: 2017.cos 3 3 2 2 2017 . 2 2017 . V  
x tan .dx 
.cos.sin   .cos   2 1  cos  . 3 3 0  1  2  1 
Đặt t  cos  t  0;
. Xét hàm số f t   t 1 t , t  0; .        2   2  3 3 6
Ta tìm được f t  lớn nhất khi t   cos   sin  . 3 3 3 Chọn đáp án A.
Câu 19. Từ một khúc gõ hình trụ có đường kính 30cm, người ta cắt khúc gỗ bởi một mặt phẳng đi
qua đường kính đáy và nghiêng với đáy một góc 0
45 để lấy một hình nêm (xem hình minh họa dưới đây) Hình 1 Hình 2
Kí hiệuV là thể tích của hình nêm (Hình 2). Tính V . 225 A. V  cm3 2250 B. V  cm3 C. V  cm3 1250 D.       V  cm3 1350  4 Hướng dẫn giải:
Chọn hệ trục tọa độ như hình vẽ.Khi đó hình nêm có đáy
là nửa hình tròn có phương trình: y   x 2 225 ,x  15;15  
Một một mặt phẳng cắt vuông góc với trục Ox tại
điểm có hoành độ x , x   15  ;15   
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 88
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
cắt hình nêm theo thiết diện có diện tích là S x (xem hình).   1 1
Dễ thấy NP  y và MN  0 NP  y   2 tan 45
15 x khi đó S x   MN.NP  .225  2 x  2 2 15 15 1 2 3
suy ra thể tích hình nêm là: V   S x dx  .
 225  x dx  2250cm  2 15 1  5
Câu 20. Tìm tham số 4 2
m để đồ thị hàm số y  x  2mx  m  2C  cắt trục ox tại bốn điểm phân
biệt và thỏa mãn hình phẳng giới hạn bởi đồ thị (C) và trục ox của phần nằm phía trên trục ox có diện
tích bằng diện tích hình phẳng giới hạn bởi đồ thị (C) và trục ox của phần nằm phía dưới trục ox . A. 3 B. -3 C. 2 D. 4 Hướng dẫn giải:
Điều kiện để (C) cắt trục ox tại 4 điểm phân biệt là m  2
Do tính đối xứng của đồ thị qua trục tung nên bài toán xảy ra khi x x 3 4   4 2
x  2mx  m  2 dx     4 2
x  2mx  m  2dx 0 x3 x4    4 2
x  2mx  m  2 4 2
dx 0  3x 10mx 15 m  2  0 4 4   0 4 2
x  2mx  m  2  0  3m  6
Suy ra x là nghiệm của hệ 4 4 2   x   m  3 4 3x 10mx 15  m  2 4 4 2  0 m 4 4  Chọn đáp án A. Câu 21. Cho hàm số 4 2
y  x  4x  m có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ
thị (C) với y<0 và trục hoành, S’ là diện tích hình phẳng giới hạn bởi đồ thị (C) với y>0 và trục hoành.
Với giá trị nào của m thì S  S ' ? 2 20 A. m  2 B. m  C. m  D. m  1 9 9
Hướng dẫn giải: Phương trình hoành độ giao điểm 4 2
x  4x  m  0 (*) Đặt 2
x  t; t  0, phương trình trở thành: 2
t  4t  m  0 (**)
Để S>0, S’>0 thì 0t ;  t ; t ; t với t ; t , t  t 1 2  1 2  2 1 1 2
là hai nghiệm dương phân biệt của (**)
y  f  x
Do ĐTHS hàm bậc 4 nhận Oy làm trục đối xứng nên y t t 1 1
S  S '    4 2
x  4x  mdx    4 2
x  4x  mdx 0 t O 2 t 2 1  1 x 2    t 4t 4 2
x  4x  m 2 2 dx  0    m  0 0 5 3 20
Kết hợp với (**) ta được m  . 9 Chọn đáp án C. 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 89
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 22. Cho y  f  x 3 2
 ax  bx  cx  d,  , a , b , c d  ,
 a  0 có đồ thị C. Biết rằng đồ thị C
tiếp xúc với đường thẳng y  4 tại điểm có hoành độ âm và đồ thị của hàm số y  f  x cho bởi hình
vẽ bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị C và trục hoành. 27 A. S  9 . B. S  . 4 21 5 C. S  . D. S  . 4 4 Hướng dẫn giải:
Từ đồ thị suy ra f  x 2  3x  3.
f  x  f  x x    2 x   3 d 3
3 dx  x  3x  C .
Do C tiếp xúc với đường thẳng y  4 tại điểm có hoành độ x âm nên 0 f  x  2
 0  3x  3  0  x  1  . 0 0 0 Vậy f  
1  4 nên có ngay C  2 . Vậy phương trình đường cong C là 3
y  x  3x  2 .  x  2 Xét phương trình 3
x  3x  2  0   . x  1  1 27
Diện tích hình phẳng cần tìm là  3
x  3x  2dx   . 2  4 Chọn đáp án B. 2
Câu 23. Cho y  f  x là hàm số chẵn, có đạo hàm trên đoạn  6  ;6. Biết rằng
f  x dx  8  và 1 3 6
f 2x dx  3.  Tính f  x d . x  1 1 A. I  11. B. I  5 . C. I  2 . D. I  14 . Hướng dẫn giải: 3
Xét tích phân K  f  2  xdx  1 du Đặt u  2
 x  du  2
 dx  dx   2
Đổi cận: Khi x 1 u  2
 ; x  3  u  6  6 2 1 1 2  Vậy, K  
f udu 
f  xdx   . Mà K  3 , nên
f  x dx  6  . 2 2 2 6 6  6 2
Vì f là hàm chẵn trên  6
 ;6 nên f  x dx 
f  xdx  6   . 2 6 6 2 6 Từ đó suy ra I 
f  x dx 
f  x dx  f  xdx  8  6 14    . 1  1  2 Chọn đáp án D. 2 Câu 24. Biết x  e  x 2x  e  4 2
dx  a.e  b.e  c với a, b, c là các số hữu tỷ. Tính S  a  b  c 0 A. S  2 B. S  4  C. S  2  D. S  4 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 90
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2x x 2 2 2 2 2 e e 1 Ta có x I   e  x 2x  e  2x x x x
dx  e dx   2x.e dx   2 xe dx    2 xe dx 0 0 0 2 0 2 2 0 0 Đặt 4 4 4 u  x d  u  dx 2 2 e 1     I    2x.e  e 1  2 e dx  
 2x.e  2  2e  2 e 3 x x 2 x 2   2e  x x 0 0 0 dv  e dx v  e 2 2 0 2 2 2 2    1 3 a  ;c    2
2  S  a  b  c  4 b  2  Chọn đáp án D. 1 1 1
Câu 25. Rút gọn biểu thức: T  0 C  1 C  2 C  ...  n C ,n * . n 2 n 3 n n  1 n 2n 2n  1 n1 2  1 A. T  B.   1 2n T C. T  D. T  n  1 n  1 n  1 Hướng dẫn giải: Ta có 0 1 1 1 1 1 1 1 T  C  C  ... n 
C . Nhận thấy các số ; ; ; ...;
thay đổi ta nghĩ ngay đến biểu thức n 2 n n  1 n 1 2 3 n  1 n 1 n1 x dx  x  c  . n  1 n
Ở đây ta sẽ có lời giải như sau:   x 0 1 2 2 3 3 1
 C  xC  x C  x C  ... n n  x C . n n n n n 1 1 n
Khi đó ta suy ra  1  x dx    0 1 2 2 3 3
C  xC  x C  x C  ... n n  x C dx n n n n n  0 0 2 3 n1 1 n1 n 1  x x x  1 2  1 1 1 1  x  1 1 0 1 3  0 1 2 n C x  C  C  ... n  C  
 C  C  C  ...  C . n  1 0 n 2 n 3 n n  1 n 0 n n n n   n  1 2 3 n  1 Chọn đáp án D. 1
Câu 26. Hàm số nào dưới đây là nguyên hàm của hàm số f x 
trên khoảng ;  ? 1  2 x
A. F x  x  2 ln 1 x  C
B. F x     2 ln 1 1 x  C 2x
C. F x   2 1 x  C
D. F x   C 1  2 x Hướng dẫn giải: Ta có bài toán gốc sau: dx
Bài toán gốc: Chứng minh 2
 ln x  x  a  c  a   2 x  a 2  2x 
x  x  a tdx dt dx Đặt 2
t  x  x  a  dt  1 
 dx  dt  dx   dt    2  2  2 x  a  x  a 2 x  a 2 t x  a dx dt Vậy khi đó 2 
 ln t  c  ln x  x  a  c  
( điều phải chứng minh). 2 t x  a
Khi đó áp dụng công thức vừa chứng minh ta có F x 1 2 
dx  ln x  1  x  c  ln   2 x  1  x  c . 2  1  x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 91
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án A.  2 x 1 2  .cos x
Câu 27. Trong các số dưới đây, số nào ghi giá trị của dx  x 1 2   2 1 A. B. 0 C. 2 D. 1 2 Hướng dẫn giải:     2 x 1  2 x 2 x 2 cosx 2 cos x 2 cos x Ta có: dx  dx  dx 1  x     1 2   x 1 2 .2  x 1 2 .2 0 0   2  
Đặt x  t ta có x  0 thì t  0, x  thì t  và dx  d  t 2 2     2 x 2  t 2 cos x 2 cos t 2 2 cos t cos x dx  d t   dt   dx      x 1 2 .2   t 1 2 .2  t 1 2 .2  x 1 2 .2 0 0 0 0  Thay vào (1) có       2  2 2 2 2 cosx 2 cos x cos x  x x 1 x 1 2  2 cos x 2 cos x sin x 1 dx  dx  dx  dx  dx    x     1 2  1 2 .2 1 2 .2 1 2 .2 2 2 2 0  x  0  x  0  x  0 0  2  2 x 1 2  cosx 1 Vậy dx   x 1 2 2   2 Chọn đáp án A.
Câu 28. Người ta dựng một cái lều vải  H  có dạng hình “chóp lục giác cong đều” như hình vẽ bên.
Đáy của  H  là một hình lục giác đều cạnh 3 m . Chiều cao SO  6 m ( SO vuông góc với mặt phẳng
đáy). Các cạnh bên của  H  là các sợi dây c , c , c , c , 1 2 3 4 S
c , c nằm trên các đường parabol có trục đối xứng song 5 6
song với SO . Giả sử giao tuyến (nếu có) của  H  với
mặt phẳng  P vuông góc với SO là một lục giác đều và
khi  P qua trung điểm của SO thì lục giác đều có cạnh c6 c5
1 m . Tính thể tích phần không gian nằm bên trong cái lều c 1m 1 H  đó. c 135 3 96 3 2 c3 c A. ( 3 m ). B. ( 3 m ). 4 5 5 O 135 3 135 3 C. ( 3 m ). D. ( 3 m ). 4 8 3m Hướng dẫn giải:
Đặt hệ trục tọa độ như hình vẽ, ta có parabol cần tìm đi qua 3 điểm có tọa độ lần lượt là A0;6 , 1 7 B1; 
3 , C 3;0 nên có phương trình là 2 y  x  x  6 2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 92
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Theo hình vẽ ta có cạnh của “thiết diện lục giác” là BM . 7 1
Nếu ta đặt t  OM thì BM   2t  (chú ý là ta phải 2 4
lấy giá trị có dấu “  ” trước dấu căn và cho B chạy từ C đến A ).
Khi đó, diện tích của “thiết diện lục giác” bằng 2 2 BM 3 3 3  7 1 
S t   6.    2t 
 với t 0;  6 . 4 2  2 4   
Vậy thể tích của “túp lều” theo đề bài là: 2 6 6 3 3  7 1  135 3
V  S t  dt    2t   dt  ...    2  2 4  8 0 0   Chọn đáp án D.
Câu 29. Xét hàm số y  f  x liên tục trên miền D   ;
a b có đồ thị là một đường cong C . Gọi S là
phần giới hạn bởi C và các đường thẳng x  a , x  b . Người ta chứng minh được rằng diện tích mặt b
cong tròn xoay tạo thành khi xoay S quanh Ox bằng S   f  x  
 f x2 2 1 dx . Theo kết quả a
trên, tổng diện tích bề mặt của khối tròn xoay tạo thành khi xoay phần hình phẳng giới hạn bởi đồ thị 2 2x  ln x
hàm số f  x 
và các đường thẳng x  1 , x  e quanh Ox là 4 2 2e 1 4 4e  9 4 2 4e 16e  7 4 4e  9 A.  . B.  . C.  . D.  . 8 64 16 16 Hướng dẫn giải: 2 2 2 2x  ln x x ln x 1 2  1  1 1
Ta có f  x   
 f  x  x 
  f  x 2  x   x     2 4 2 4 4x  4x  16x 2 1
Lại có f  x  x   0, x
 1;e , nên f  x đồng biến trên 1;e . Suy ra 4x 1
f  x  f   1   0, x  1;e . 2
Từ đây ta thực hiện phép tính như sau b e 2  x ln x   1 1  S  2 f  x 1 
 f x2 2 dx  2  1 x   dx    2  2 4    16x 2  a 1 e e 2 2 2  x ln x  1 1  x ln x   1 2  S  2  x   dx  2  x  dx   2     2 4 16x 2 2 4      4x  1 1 e 2  x ln x   1   2  x  dx     2 4    4x  1 e  1 1 1 1 ln x 3   2 x  x  x ln x  dx    2 8 4 16 x  1
 2  I  I  I 1 2 3 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 93
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 e 4 2 4 2 e  1 1   x x  2e  e  3 Với 3 I  x  x dx    1      1  2 8  8 16 16   1 e e  1  1 1 1 1 2 I  
x ln x dx   x    2ln x   2 1   e  2 1  4  4 4 16 16 1 e e  1 ln x  1 1 2 I   dx   ln x   . 3    1  16 x  32 32 1 Chọn đáp án D. 4 x Câu 30. Cho hàm số 2 2 y 
 2m x  2 . Tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị 2
của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua 64
điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng là 15  2     1  A.  . B.   1  . C.   ; 1   . D.  ; 1 .  2     2  Hướng dẫn giải:
Tập xác định D    x  0  3 2
y  x  m x  x  2 2 2 4 2
x  2m  ; y  0  x  2m   x   2m 
Đồ thị của hàm số đã cho có cực đại và cực tiểu  m  0 1 Vì a 
 0 nên hàm số đạt cực đại tại x  0 suy ra điểm cực đại của đồ thị hàm số là A0;2 2
Đường thẳng cùng phương với trục hoành qua điểm cực đại có phương trình là d : y  2 .
Phương trình hoành độ giao điểm của C và d là: m  x  0 4 2 x x  0  2 2
 2m x  2  2    x  2 m  2 2 2 x  4m  x  2  m 
Diện tích hình phẳng cần tìm là: (chú ý rằng hàm số đã cho là hàm chẵn) 2 m 2 m 2 4 4 m 4 x x  x  2 2 2 2 2 2 S 
 2m x dx  2
 2m x dx  2  2m x dx      2 2 2 2  m 0 0   5  x 2  2 m 64 5 2 3  2  m x  m   10 3   0 15 64 m  1 Ta có S   m  1   15 m  1   Chọn đáp án B.
Câu 31. Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta định xây cầu có
10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau 40m,biết 2 bên đầu cầu và giữa mối nhịp nối người
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 94
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
ta xây 1 chân trụ rộng 5m. Bề dày nhịp cầu không đổi là 20cm. Biết 1 nhịp cầu như hình vẽ. Hỏi lượng
bê tông để xây các nhịp cầu là bao nhiêu (bỏ qua diện tích cốt sắt trong mỗi nhịp cầu) A. 3 20m B. 3 50m C. 3 40m D. 3 100m Hướng dẫn giải:
Chọn hệ trục tọa độ như hình vẽ với gốc O(0;0) là chân cầu (điểm tiếp xúc Parabol trên), đỉnh I(25;
2), điểm A(50;0) (điểm tiếp xúc Parabol trên với chân đế)
Gọi Parabol trên có phương trình ( P ): 2 2
y  ax  bx  c  ax  bx (do (P) đi qua O) 1 1 20 1 2 2
 y  ax  bx 
 ax  bx 
là phương trình parabol dưới 2 100 5 2 4 2 4 1
Ta có (P ) đi qua I và A 2 2
 (P ) : y   x  x  y   x  x  1 1 1 2 625 25 625 25 5
Khi đó diện tích mỗi nhịp cầu là S  2S với S là phần giới hạn bởi y ; y trong khoảng (0; 25) 1 1 1 2 0,2 25 2 4 1 2 S  2( ( x  x)dx  d ) x   2  9,9m 625 25 5 0 0,2
Vì bề dày nhịp cầu không đổi nên coi thể tích là tích diện tích và bề dày 3
V  S.0, 2  9,9.0, 2  1,98m  số lượng bê tông cần cho mỗi nhip cầu 3  2m
Vậy 10 nhịp cầu 2 bên cần 3  40m bê tông. Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 95
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
HÌNH HỌC TỌA ĐỘ KHÔNG GIAN OXYZ
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 5; 0, B 3;3; 6 và đường thẳng  x  1   2t 
có phương trình tham số  y  1 t
t   . Một điểm M thay đổi trên đường thẳng , xác định vị z  2t 
trí của điểm M để chu vi tam giác MAB đạt giá trị nhỏ nhất. Khi đó toạ độ của điểm M là:
A. M 1; 0; 2
B. M 2; 4;3 C. M  3  ; 2; 2
D. M 1; 4;3
Hướng dẫn giải:
Gọi P là chu vi của tam giác MAB thì P  AB  AM  BM
Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM  BM nhỏ nhất.
Điểm M   nên M  1
  2t;1  t; 2t  ; 2 2 2 2 AM  BM 
(3t)  (2 5)  (3t  6)  (2 5)  
Trong mặt phẳng tọa độ Oxy , ta xét hai vectơ u  3t;2 5 và v   3  t  6;2 5 .  2
|u | 3t2   2 5        Ta có   AM  BM |
 u |  | v | và 
u  v  6;4 5 |
 u  v | 2 29 2 |
 v | 3t  62   2 5     
Mặt khác, ta luôn có | u |  | v | |
 u  v | Như vậy AM  BM  2 29   3t 2 5
Đẳng thức xảy ra khi và chỉ khi u, v cùng hướng    t  1 3  t  6 2 5
 M 1;0; 2 và min  AM  BM   2 29 . Vậy khi M 1;0;2 thì min P  2 11  29  Chọn đáp án A.
Câu 2. Trong không gian tọa độ Oxyz, cho các phương trình mặt phẳng  mx m y mz m          m  2 : 3 5 1 4 20 0, 1;1 .   Xét các mệnh đề sau: (I) Với mọi m  1;1  
thì các mặt phẳng 
luôn tiếp xúc với một mặt cầu không đổi.    m
(II) Với mọi m  0 thì các mặt phẳng m  luôn cắt mặt phẳng (Oxz).   (III) d O;   m       m  5, 1;1 .      
Khẳng định nào sau đây đúng? A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III)
D. Cả 3 đều đúng. Hướng dẫn giải: 20 20  
+ Ta có d O;      m   1;1 m  4 , với mọi .     2 9m  25 2 1  m  2  16m 25
Do đó với mọi m thay đổi trên  1;1 
thì các mặt phẳng 
luôn tiếp xúc với mặt cầu tâm O, bán    m
kính R  4 . Khẳng đinh (I) đúng.  2
+ Vectơ pháp tuyến của mặt phẳng 
n  3m;5 1m ;4m m  là
và vectơ pháp tuyến của mặt 
phẳng (Oxz) là j  0;1;  0 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 96
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12       n
 ; j  0  m  0
m  cắt (Oxz) khi và chỉ khi . Khẳng đinh (II) đúng.   + Khẳng đinh (III) sai. Chọn đáp án A.
Câu 3. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng: x  t x  2 y 1 z 1   :   ,  : 2 2 2
 y  2  t và mặt cầu (S ) : x  y  z  2x  2 y  6z  5  0 1 1 2 3  2 z 1 2t 
Viết phương trình mặt phẳng ( ) song song với hai đường thẳng  ,  và cắt mặt cầu (S) theo giao 1 2 2 365
tuyến là đường tròn (C) có chu vi bằng . 5
A. x  5y  3z  4  0; x  5y  3z 10  0
B. x  5y  3z 10  0
C. x  5 y  3z  3  511  0; x  5 y  3z  3  511  0
D. x  5y  3z  4  0 Chọn đáp án B. Hướng dẫn giải:  +  qua M (2; 1
 ;1) và có vectơ chỉ phương u  (1; 2; 3  ) . 1 1 1 
 qua M (0; 2;1) và có vectơ chỉ phương u  (1; 1; 2) . 2 2 2  
+ Mặt phẳng () song song với  ,  nên có vectơ pháp tuyến: u ,u   (1; 5; 3  ) 1 2 1 2  
 Phương trình mặt phẳng () có dạng: x  5y  3z  D  0
+ Mặt cầu (S) có tâm I(1; 1
 ;3) và bán kính R  4 . 2 365 365
Gọi r là bán kính đường tròn (C), ta có: 2 r   r  5 5 35 D  3 35 D  4
Khi đó: d  I , ( ) 2 2  R  r      5 35 5 D  10 
+ Phương trình mặt phẳng () : x  5y  3z  4  0 (1) hay x  5y  3z 10  0 (2) .
Vì  / /( ),  / /( ) nên M1 và M2 không thuộc ( )  loại (1). 1 2
Vậy phương trình mặt phẳng () cần tìm là: x  5y  3z 10  0 . Chọn đáp án B.
 x  3  t  x  t '  
Câu 4. Trong không gian Oxyz, cho 2 đường thẳng d:  y  2  t và d’:  y  5  t '   z  2  t z  2t ' 3 2  5 
Viết phương trình mặt phẳng () chứa (d) và tạo với mặt phẳng Oyz một góc nhỏ nhất.
A. 3x  y  2z  7  0 .
B. 3x  y  2z  7  0 . C. 3
 x  y  2z  7  0 .
D. 3x  y  2z  7  0 . Hướng dẫn giải: 
Giả sử (β): Ax  By  Cz  D  0 (đk: 2 2 2
A  B  C  0), (β) có vtpt là n  ( ; A ; B C)  A( ) 
3A  2B  D  0  
D   A  2C 2 d  (β)        n . a  0 
 A  B  C 2  0 
B  A  C 2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 97
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12    A
cos(( ),(Oyz))  cos(n, i ) = 2 2 2
A  ( A  C 2 )  C
TH 1: A = 0 (không thoả đb hoặc 
( ), (Oyz) không nhỏ nhất) TH 2: A ≠ 0, ta có:  1 1
cos(( ),(Oyz)) = = = C 2 C 2 1 (1  2 )  ( ) C C 6 12 2 2 ( 3)  2. 2  ( )  A A A A 3 9 1 C 6 12 2 ( 3  )  A 3 9  C 6 C 6
( ), (Oyz) nhỏ nhất  
cos(( ),(Oyz)) lớn nhất  2 ( 3  ) nhỏ nhất  3   0 A 3 A 3  1  A  1 (choïn) B     3   nên 
. Vậy: (β): 3x  y  2z  7  0 2 C    7   3 D     3 Chọn đáp án D. x  t  
Câu 5. Trong không gian tọa độ Oxyz cho đường thẳng d :  y  1 2t và mp
z 2t 
P: 2x  y2z 2  0 . Viết phương trình mặt phẳng R qua d và tạo với P một góc nhỏ nhất.
A. x  y  z  3  0
B. x  y  z  3  0
C. x  y  z  3  0
D. x  y  z  3  0 Hướng dẫn giải:  x y 1    2  
 x  y 1 0 1 2 
Đường thẳng d là giao tuyến của hai mặt phẳng:    .  x z  2
x  z 2  0     1 1
Do vậy mặt phẳng R qua d thì R thuộc chùm mặt phẳng: 2x  y 1 mx  z  2  0 .  
Hay mp R : 2  m x  y  mz 12m  0 (*). Mp R có n  m  2;1;m ;n  2; 1  ; 2  1   P  .  Vậy:  n .n
2m  21 2m 5 5 1 5 1 cos P        n n m    m   m  m    P  22 2 3 1 4 1 4 3 2 4 5 2m 2 2 3 3 1 1 3
Do  nhỏ nhất cho nên cos  lớn nhất khi m  1  .
Vậy thay vào (*) ta có mp R: x  y  z 3  0 . Chọn đáp án B.
Câu 6. Trong không gian với hệ toạ độ Oxyz , gọi   là mặt phẳng qua hai điểm A2; 0;1  và B 2  ;0; 
5 đồng thời hợp với mặt phẳng Oxz một góc 0
45 . Khoảng cách từ O tới   là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 98
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3 3 1 2 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải:
Gọi K; H lần lượt là hình chiếu vuông góc điểm O lên đường thẳng AB và mặt phẳng . Ta có: , A B Oxz
    Oxz  AB O O 
 H    HK  AB    O  K  AB OK  AB  
 Oxz         KH OK   , ,  OKH K 450
Suy ra tam giác OHK vuông cân tại H OK Khi đó: d  ,
O    OH  . H 2  OA  AB 3 
Mặt khác: OK  d  , O AB    . AB 2 OK
Khi đó: d O   3 ,  OH   . 2 2 Chọn đáp án A.
Câu 7. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 2x – y + z + 1 =
0 và hai điểm M(3; 1; 0), N(- 9; 4; 9). Tìm điểm I(a; b; c) thuộc mặt phẳng (P) sao cho IM  IN đạt
giá trị lớn nhất. Biết a, b, c thỏa mãn điều kiện:
A. a  b  c  21
B. a  b  c  14
C. a  b  c  5
D. a  b  c  19. Hướng dẫn giải:
Nhận thấy 2 điểm M, N nằm về hai phía của mặt phẳng (P).
Gọi R là điểm đối xứng của M qua mặt phẳng (P), khi đó đường thẳng MR đi qua điểm M(3; 1; 0) x  3 y 1 z
và vuông góc với mặt phẳng (P) có phương trình:   . Gọi 2 1 1
H  MR  (P)  H (1; 2; 1
 )  R(1;3; 2) .
Ta có IM  IN  IR  IN  RN . Đẳng thức xảy ra khi I, N, R thẳng hàng. Do đó tọa độ điểm I là x  1   8t 
giao điểm của đường thẳng NR: y  3  t
(t là tham số ) và mặt phẳng (P).
z  2 11t 
Dễ dàng tìm được I(7; 2; 13). Chọn đáp án A.
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x  y  z 1  0 và hai điểm (
A 1;3;0), B 5; 1
 ;2 . M là một điểm trên mặt phẳng (P) . Giá trị lớn nhất của T  MA  MB là: 4 6 2 3 A. T  2 5. B. T  2 6. C. T  . D. T  . 2 3 Hướng dẫn giải:
Ta có: A, B nằm khác phía so với (P). Gọi B’ là điểm đối xứng với B qua (P). Suy ra B '(1; 3  ; 4) .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 99
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
T  MA  MB  MA  MB '  AB '  2 5. Đẳng thức xảy ra khi M, A, B’ thẳng hàng. Chọn đáp án A.
Câu 9. Cho hai điểm A(-1, 3, -2); B(-9, 4, 9) và mặt phẳng (P): 2x-y+z+1=0. Điểm M thuộc (P). Tính GTNN của AM + BM. 7274  31434 2004  726 A. 6  204 B. C. D. 3 26 6 3 Hướng dẫn giải:
Ta có: (2.(-1)-3+(-2)+1)(2.(-9)-4+9+1)=72 > 0 => A,B nằm cùng phía so với mặt phẳng (P). 
Gọi A’ là điểm đối xứng của A qua (P). Mặt phẳng (P) có vtpt n 2, 1  ,  1 
x  1 2t 
Đường thẳng AA’ đi qua A(-1, 3, -2) có vtcp n 2, 1, 
1 có pt:  y  3  t z  2   t 
Gọi H là giao của AA’ và (P) ta có: 2(-1+2t) - (3-t) + (-2 + t) + 1 =0 => t=1 => H(1, 2, -1).
Ta có H là trung điểm của AA’ => A’(3, 1, 0). 
x  3  4t 
Đường A’B đi qua A’(3, 1, 0) có vtcp A' B  1
 2,3,9 có pt:  y  1 t z  3t 
Gọi N là giao điểm của A’B và mặt phẳng (P) ta có:
2.(3-4t) – (1+t) + 3t +1 =0 => t=1 => N(-1, 2, 3).
Để MA+MB nhỏ nhất thì M  N khi đó MA+MB = A’B =  2 2 2 12  3  9  234  3 26 Chọn đáp án D. x 1 y  2 z
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d :   và 1 1 2 1 x  2 y 1 z d :  
. Viết phương trình mặt phẳng (P) chứa d sao cho góc giữa mặt phẳng (P) và 2 2 1  2 1
đường thẳng d là lớn nhất. 2
A. x  y  z  6  0 .
B. 7x  y  5z  9  0 .
C. x  y  z  6  0 .
D. x  y  z  3  0 . Hướng dẫn giải: 
Ta có: d đi qua M(1; 2
 ; 0) và có VTCPu  (1;2;1) . 1
Phương trình mặt phẳng (P) có dạng: 2 2 2 (
A x 1)  B(y  2)  Cz  0,(A  B  C  0) .  
Ta có: d  (P)  .
u n  0  C  A  2B 2 4A  3B 1 (4A  3B)
Gọi   ((P),d )  sin   . 2 2 2 2 2 3 2A  4AB  5 3 2  4  5 B A AB B 2 2
Với B  0  sin  3 A 2 1 (4t  3)
Với B  0 . Đặt t 
, ta được sin  . B 2 3 2t  4t  5 2 (4t  3) 2
16t 124t  84
Xét hàm số f (t) 
. Ta có: f '(t)  2 2t  4t  5 2 2
(2t  4t  5)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 100
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  3 t   f '(t) 0    4  t  7   3 BBT: t  -7   4 f '(t) + 0 - 0 + 25 f (t) 3 25 A
Dựa vào BBT ta có: max f (t)  khi t  7   7 3 B 5 3
Khi đó: sin  f (7)  9 5 3 A Vậy sin  khi  7
  Phương trình mặt phẳng (P) : 7x  y  5z  9  0 9 B Chọn đáp án B.
Câu 11. Cho đường thẳng d là giao tuyến của hai mặt phẳng ( )
 : x  2y  2z  4  0
() : 2x  2y  z  1  0, và mặt cầu S có phương trình 2 2 2
x  y  z  4x  6y  m  0 . Tìm m để
đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho AB = 8. A. 9 B. 12 C. 5 D. 2 Hướng dẫn giải:   Ta có n  (2; 2; 1
 ), n  (1;2;2) lần lượt là VTPT của (α) và (β) 1 2  1  
Suy ra VTCP của đường thẳng d là u  n ;n   (2;1; 2), 1 2 3  
Ta có A(6;4;5) là điểm chung của hai mặt phẳng (α) và (β) nên Ad.
Mặt cầu (S) có tâm I(-2;3;0), bán kính R  13  m với m < 13.   
IA  (8;1;5)  IA, u  ( 3
 ; 6; 6)  d(I, d)  3   AB
Gọi H là trung điểm của AB  AH   4 vµ IH  3 . 2
Trong tam giác vuông IHA ta có: 2 2 2 2
IA  IH  AH  R  9  16
 13  m  25  m  1
 2 . Vậy m = 12 là giá trị cần tìm. Chọn đáp án B.
Câu 12. Trong không gian tọa độ Oxyz , cho tám điểm A 2; 2; 0 , B 3; 2; 0 , C 3;3; 0 ,
D 2; 3; 0 , M  2; 2; 5 , N 2; 2; 5 , P 3; 2; 5, Q  2;3;5 . Hỏi hình đa diện tạo bởi tám điểm
đã cho có bao nhiêu mặt đối xứng. A. 3. B. 6. C. 8. D. 9 Hướng dẫn giải:
Vì tám điểm đã chõ tạo nên một hình lập phương, nên hình đa diện tạo bởi tám điểm này có 9 mặt đối xứng. Chọn đáp án D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 101
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 13. Trong không gian với hệ toạ độ Oxyz cho A(2;  1;6), B(  1;2;4) và I(  1;  3;2). Viết
phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ I đến (P) lớn nhất.
A. 3x  7 y  6z  35  0 . B. 7x  y  5z  9  0 .
C. x  y  z  6  0 .
D. x  y  z  3  0 . Hướng dẫn giải: Ta có 2 2 2
IA  3  2  4  29 và 2 2 2
IB  0  5  2  29 . Gọi M là trung điểm của đoạn thẳng  1 1  94
AB, vì IA=IB nên IM  AB, ta có M ; ;5 ;   IM  .  2 2  2
Gọi H là hình chiếu vuông góc của I lên mặt phẳng (P): 94
Nếu H, M là hai điểm phân biệt thì tam giác IHM vuông tại H, IHIH  . 2 94 94
Nếu H trùng với M thì IH  IM  . Vậy ta có IH 
, IH lớn nhất khi H  M. 2 2
    3 7 
Khi đó (P) có vectơ pháp tuyến là n  IH  IM 
; ;3 . Vậy phương trình mặt phẳng (P) là P    2 2  3 7
 x  2   y  
1  3 z  6  0 hay 3x  7 y  6z  35  0 2 2 Chọn đáp án A.
Câu 14. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt phẳng (P):
2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) saocho MA2 + MB2 nhỏ nhất là: A. (-1;3;2) B. (2;1;-11) C. (-1;1;5) D. (1;-1;7) Hướng dẫn giải:
+ Kiểm tra phương án A không thuộc (P).
+ Tính trực tiếp MA2 + MB2 trong 3 phương án B,C,D và so sánh. Chọn C.
Câu 15. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(0;1;2) và N(1;1; 3). Mặt phẳng
(P) đi qua M, N sao cho khoảng cách từ K 0;0; 
2 đến (P) đạt giá
trị lớn nhất. (P) có vectơ pháp tuyến là: K A. (1;1; 1  ) B. (1; 1  ;1) C. (1; 2  ;1) D. (2; 1  ;1) Hướng dẫn giải:
- Khoảng cách từ K đến (P) lớn nhất bằng KH, khi H’ trùng H
- Vậy mặt phẳng (P) qua MN và vuông góc với KH. H'
- Tìm H và viết (P) hoặc: M N P H
- (P) chứa MN và vuông góc với (MNP).
Gọi H, H’ là hình chiếu của K lên MN và (P).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 102
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Ta có: d(k,(P))  KH  KH ' không đổi.
Vậy d(K,(P)) lớn nhất khi và chỉ khi H’ trùng H hay (P) vuông góc với KH.   
MK  (0;1;0); NK  (1; 1; 1); MN  (1;2;1)    (MNK) có vtpt là  
n  MK, NK  (1;0;1)     HK  (MNK) Do nên HK có vtcp là  
MN,n  (2;2;2). HK     MN Chọn đáp án A.
Câu 16. Trong không gian tọa độ Oxyz, cho điểm A(0;1;1), B(1; 0; 3  ),C( 1  ; 2  ; 3  ) và mặt cầu (S) có
phương trình: x2  y2  z2  2x  2z  2  0 . Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện ABCD có thể tích lớn nhất.  7 4 1   1 4 5 
A. D 1; 0;  1 B. D ; ; C. D ; ; D. D(1; - 1; 0)  3 3 3      3 3 3  Hướng dẫn giải:
Ta thấy câu C và D có điểm D không thuộc (S). Loại C,D.
Ta tính thể tích cho điểm D ở câu A và câu B. Điểm B ở câu B có thể tích lớn hơn. Chọn đáp án B.
Câu 1.5. Phương trình nào sau đây không phải là phương trình hình chiếu vuông góc của đường thẳng x  1 2t  d:  y  2
  3t , t  R trên mặt phẳng (Oxy): z  3  t 
x  3  2t '
x  1 4t '
x  1 2t '
x  5  2t '    
A. y  1 3t ' ,t ' R B. y  2
  6t ',t ' R
C. y  2  3t ',t ' R D. y  4  3t ',t ' R z  0     z  0  z  0  z  0  Hướng dẫn giải:
A(1;-2;3), B(3;1;4) thuộc d. Hình chiếu của A,B trên mặt phẳng (Oxy) là A/(1;-2;0), B/(3;1;0) 
Phương trình hình chiếu đi qua / A hoặc /
B và nhận véc tơ cùng phương với / /
A B  2;3;0 làm véc tơ chỉ phương. Chọn đáp án C.
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x  y  z 1  0 và hai điểm (
A 1;3;0), B 5; 1
 ;2 . M là một điểm trên mặt phẳng (P) . Giá trị lớn nhất của T  MA  MB là: 4 6 2 3 A. T  2 5. B. T  2 6. C. T  . D. T  . 2 3 Hướng dẫn giải:
Ta có: A, B nằm khác phía so với (P). Gọi B’ là điểm đối xứng với B qua (P). Suy ra B '( 1  ; 3  ;4) .
T  MA  MB  MA  MB '  AB '  2 5. Đẳng thức xảy ra khi M, A, B’ thẳng hàng. Chọn đáp án A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 103
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho hai điểm M  2  ; 2  ;  1 , A1;2;  3  và đường thẳng x  1 y  5 z  d :  
. Tìm véctơ chỉ phương u của đường thẳng  đi qua M , vuông góc với đường 2 2 1
thẳng d đồng thời cách điểm A một khoảng bé nhất.    
A. u  2;1;6 .
B. u  1;0;2 .
C. u  3;4; 4   .
D. u  2;2;  1 . Hướng dẫn giải:
Gọi  P là mặt phẳng qua M và vuông góc với d . Phương trình của  P : 2x  2y  z  9  0 .
Gọi H , K lần lượt là hình chiếu vuông góc của A trên ,   P . d A K H P  M Ta có K  3  ; 2  ;  1 d( ,
A )  AH  AK 
Vậy khoảng cách từ A đến  bé nhất khi  đi qua M , K .  có véctơ chỉ phương u  1;0;2 Chọn đáp án B.
Câu 19. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A2;5;3 và đường thẳng x 1 y z  2 d :  
. Gọi ( ) là mặt phẳng chứa đường thẳng sao cho khoảng cách từ đến ( ) lớn 2 1 2
nhất. Tính khoảng cách từ điểm M 1; 2;  
1 đến mặt phẳng ( )? 11 18 11 4 A. B. 3 2 C. D. 18 18 3 Hướng dẫn giải:
Gọi H là hình chiếu của A trên d; K là hình chiếu của A trên A (P).
Ta có d A, (P) = AK ≤ AH ( không đổi)
⟹ GTLN của d A, (P) là AH
⟹ d A, (P) lớn nhất khi K ≡ H.
Ta có H(3; 1; 4), (P) qua H và ⊥ AH d' K
  P :x  4y  z  3  0
Vậy d M  P 11 18 ,  . H 18 P Chọn đáp án A.
Câu 20. Trong không gian với hệ tọa độ Oxyz, xét các điểm A0;0;  1 , B ;
m 0;0 , C 0; ; n 0 , D1;1; 
1 với m  0;n  0 và m  n  1. Biết rằng khi m , n thay đổi, tồn tại một mặt cầu cố định tiếp
xúc với mặt phẳng  ABC và đi qua d . Tính bán kính R của mặt cầu đó?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 104
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 3 3 A. R  1 . B. R  . C. R  . D. R  . 2 2 2 Hướng dẫn giải:
Gọi I (1;1;0) là hình chiếu vuông góc của D lên mặt phẳng (Oxy) x y
Ta có: Phương trình theo đoạn chắn của mặt phẳng ( ABC) là:   z  1 m n
Suy ra phương trình tổng quát của ( ABC) là nx  my  mnz  mn  0 1  mn
Mặt khác d (I ,( ABC)) 
 1 (vì m  n 1) và ID  1  d(I ,( ABC)) 2 2 2 2
m  n  m n
Nên tồn tại mặt cầu tâm I (là hình chiếu vuông góc của D lên mặt phẳng Oxy ) tiếp xúc với
( ABC) và đi qua D Chọn đáp án A.
Câu 21. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình: 2 2 2
x  y  z  2x  6 y  4z  2  0 . Viết phương trình mặt phẳng (P) song song với giá của véc tơ
v  (1;6;2), vuông góc với mặt phẳng(): x 4y  z 11 0 và tiếp xúc với (S).
2x  y  2z  3  0
2x  y  2z  3  0 A.  . B.  .
2x  y  2z  21  0 
2x  y  2z  21  0 
2x  y  z  3  0
2x  y  z  13  0 C.  . D. 
2x  y  z  1  0 
2x  y  z  1  0  Hướng dẫn giải:
Vậy: (P): 2x  y  2z  3  0 hoặc (P): 2x  y  2z  21  0 
(S) có tâm I(1; –3; 2) và bán kính R = 4. VTPT của ( ) là n  (1; 4;1) .   
 VTPT của (P) là: n  n,v   (2; 1
 ;2)  PT của (P) có dạng: 2x  y  2z  m  0. P m  2  1
Vì (P) tiếp xúc với (S) nên d(I ,(P))  4  . m  3 
Vậy: (P): 2x  y  2z  3  0 hoặc (P): 2x  y  2z  21  0 . Chọn đáp án B.
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho bốn điểm A1; 2  ;0, B0; 1  ;  1 , C 2;1;  1 ,
D3;1;4 . Hỏi có bao nhiêu mặt phẳng cách đều bốn điểm đó? A. 1. B. 4. C. 7. D. Vô số. Hướng dẫn giải:   
Ta có AB  1;1; 
1 , AC  1;3; 
1 , AD  2;3;4 .  
  
Khi đó  AB, AC    4  ;0; 4
  suy ra  AB AC  AD    .   , . 24 0   Do đó ,
A B,C, D không đồng phẳng và là 4 đỉnh của một tứ diện.
Khi đó sẽ có 7 mặt phẳng cách đễu bốn đỉnh của tứ diện. Bao gồm: 4 mặt phẳng đi qua trung điểm
của ba cạnh tứ diện và 3 mặt phẳng đi qua trung điểm bốn cạnh tứ diện (như hình vẽ).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 105
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án C.
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; –2; 0), B(0; –1; 1), C(2; 1; –1) và
D(3; 1; 4). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ? A. 1 mặt phẳng. B. 4 mặt phẳng. C. 7 mặt phẳng. D. Có vô số mặt phẳng. Hướng dẫn giải:    Ta có: AB  ( 1
 ;1;1); AC  (1;3;1); AD  (2;3;4)
  
Khi đó:  AB; AC .AD  24  0 do vậy A,B,C,D không đồng phẳng  
Do đó có 7 mặt phẳng cách đều 4 điểm đã cho bao gồm.
+) Mặt phẳng qua trung điểm của AD và song song với mặt phẳng (ABC)
+) Mặt phẳng qua trung điểm của AB và song song với mặt phẳng (ACD)
+) Mặt phẳng đi qua trung điểm của AC và song song với mặt phẳng (ABD)
+) Mặt phẳng đi qua trung điểm của AB và song song với mặt phẳng (BCD)
+) Mặt phẳng qua trung điểm của AB và CD đồng thời song song với BC và AD
+) Mặt phẳng qua trung điểm của AD và BC đồng thời song song với AB và CD
+) Mặt phẳng qua trung điểm của AC và BD đồng thời song song với BC và AD Chọn đáp án C. x  4 y  5 z  2
Câu 24. Đường thẳng  song song với d :  
và cắt cả hai đường thẳng 3 4  1 x 1 y 1 z  2 x  2 y  3 z d :   và d :  
. Phương trình nào không phải đường thẳng  1 3 1 2 2 2 4 1 7 2 y  z  x  4 y  1 z  1 x  3 A.  :   B. 3 3  :   3 4  1 3 4 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 106
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  9 y  7 z  2 x  4 y 1 z  1 C.  :   D.  :   3 4  1 3 4 1 Hướng dẫn giải:
Giải: Gọi M, N là giao điểm của  và d , d . 1 2 x  1 3t x t M   2  2 ' N  
Khi đó M, N thuộc d , d nên  y  1  t , y t . M   3  4 ' 1 2 N z 2 2    t z  t '  M  N 
Vector chỉ phương của  là MN   3
  2t ' 3t; 4  4t ' t; 2
  t ' 2t  x  4 y  5 z  2 3
  2t ' 3t 4  4t ' t
2  t ' 2t  song song với d :   nên   3 4 1 3 4 1 4  7 2 
Giải hệ ta được t '  1;t   . Vậy N  4  ; 1  ;   1 , M 3; ;   3  3 3  x  4 y  1 z  1 Vậy  :   3 4  1 Chọn đáp án A.
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng  có x  1   2t 
phương trình tham số  y  1 t
. Một điểm M thay đổi trên đường thẳng  sao cho chu vi tam giác z  2  t
MAB đạt giá trị nhỏ nhất. Tọa đô điểm M và chu vi tam giác ABC là
A. M(1;0;2) ; P = 2( 11  29)
B. M(1;2;2) ; P = 2( 11  29) C. M(1;0;2) ; P = 11  29 D. M(1;2;2) ; P = 11  29 Hướng dẫn giải:
 Gọi P là chu vi của tam giác MAB thì P = AB + AM + BM.
Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM + BM nhỏ nhất.
Điểm M   nên M  1
  2t;1 t;2t  . 2 2 2 2
AM  BM  (3t)  (2 5)  (3t  6)  (2 5)  
Trong mặt phẳng tọa độ Oxy, ta xét hai vectơ u  3t;2 5 và v   3  t  6; 2 5  .   Ta có 2 2 2 2
u  (3t)  (2 5) ; v  (3t  6)  (2 5)        AM  BM |
 u |  | v | và u  v  (6;4 5) |
 u  v | 2 29    
Mặt khác, ta luôn có | u |  | v | |
 u  v | Như vậy AM  BM  2 29   3t 2 5
Đẳng thức xảy ra khi và chỉ khi u, v cùng hướng    t  1 3  t  6 2 5
 M (1;0;2) và min( AM  BM )  2 29 . Vậy khi M(1;0;2) thì minP = 2( 11  29) Chọn đáp án A.
Câu 26. Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;2; -1), B(7; -2; 3) và đường thẳng d
x  2  3t 
có phương trình  y  2t (t  R) . Điểm M trên d sao cho tổng khoảng cách từ M đến A và B là z  4  2  t
nhỏ nhất có tổng các tọa độ là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 107
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. M=(2;0;4 ). B. M=(2;0;1). C. M=(1;0;4 ). D. M=(1;0;2 ). Hướng dẫn giải:
Nếu M nằm trên d thì điểm I có tọa độ là M=(2+3t;-2t;4+2t). Từ đó ta có: 
 AM   t    t t    AM   t  2    t2   t  2 3 1; 2 2 ;2 5 3 1 2 2 2 5  2 2 2
Tương tự:  BM  3t  5;2  2t;2t  
1  BM  3t  5  2  2t   2t   1 2 2 2 2 2 2
Từ (*): MA=MB = 3t  
1  2  2t   2t  5 = 3t  5  2  2t   2t   1 Hay: 2 2
 17t  34t  30  17t  36t  30  34t  36t  0 11  70t  0  t  0
Tọa độ M thỏa mãn yêu cầu là: M=(2;0;4 ). Chọn đáp án A.
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x  2y  z  5  0 và đường thẳng x  1 y 1 z  3 d :  
. Phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt phẳng (Q) 2 1 1 một góc nhỏ nhất là
A. P  : y  z  4  0
B. P  : x z  4  0
C. P  : x y  z  4  0
D. P  : y  z  4  0 Hướng dẫn giải: 
PT mặt phẳng (P) có dạng: ax  by  cz  d 
a2  b2  c2 0 (
 0) . Gọi a  ((P), Q ( )) . M (P)
c  a  b
Chọn hai điểm M(1; 1;3), N (1; 0; 4)  d . Ta có:   N (P)   d  a 7  4b   3 a  b
 (P): ax  by  (2a  b)z  7a  4b  0  cos  . 6 a2 5  4ab  2b2 3 b 3
TH1: Nếu a = 0 thì cos  .  0  a  30 . 6 2b2 2 b 1 3 a b
TH2: Nếu a  0 thì cos  . . Đặt x  và f x 2 ( )  cos  2 6 a b  b  5  4  2  a  a 
9 x2  2x  1
Xét hàm số f (x)  . .
6 5  4x  2x2 Dựa vào BBT, ta thấy f x 0 0
min ( )  0  cos  0  a  90  30
Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn b  1,c  1,d  4 .
Vậy: (P): y  z  4  0 . Chọn đáp án A.
Câu 28. Trong không gian với hệ tọa độ Oxyz, gọi d đi qua điểm A1; 1  ;2 , song song với  x  1 y 1 z
P : 2x  y  z  3  0 , đồng thời tạo với đường thẳng  :  
một góc lớn nhất. Phương 1 2  2
trình đường thẳng d là.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 108
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x 1 y  1 z  2 x 1 y  1 z  2 A.   . B.   . 1 5  7 4 5  7 x 1 y  1 z  2 x 1 y  1 z  2 C.   . D.   . 4 5 7 1 5  7  Hướng dẫn giải: 
 có vectơ chỉ phương a  1; 2  ; 2   
d có vectơ chỉ phương a  a b c d  ; ;  
P có vectơ pháp tuyến n  P 2; 1  ;   1     Vì d 
€ P nên a  n  a .n  0  2a  b  c  0  c  2a  b d P d P 5a  4b 1 5a  4b2 cos ,  d    2 2 2 2
3 5a  4ab  2b
3 5a  4ab  2b a 1 5t  42 Đặt t 
, ta có: cos, d   b 2
3 5t  4t  2 5t  42  1  5 3
Xét hàm số f t 
, ta suy ra được: max f t   f   2   5t  4t  2  5  3 5 3 1 a 1 Do đó: max cos ,  d    t        27 5 b 5
Chọn a  1  b  5  ,c  7 x 1 y  1 z  2
Vậy phương trình đường thẳng d là   1 5  7 Chọn đáp án A.
Câu 29. Trong không gian với hệ toạ độ Oxyz ,cho  P : x  4y  2z  6  0 , Q : x  2y  4z  6  0 .
Lập phương trình mặt phẳng  chứa giao tuyến của  P,Q và cắt các trục tọa độ tại các điểm ,
A B,C sao cho hình chóp .
O ABC là hình chóp đều.
A. x  y  z  6  0 .
B. x  y  z  6  0 .
C. x  y  z  6  0 .
D. x  y  z  3  0 . Hướng dẫn giải:
Chọn M 6;0;0, N 2;2;2 thuộc giao tuyến của  P,Q Gọi A ;
a 0;0, B0; ;
b 0,C0;0;c lần lượt là giao điểm của  với các trục O , x Oy,Oz x y z   :     1 a, , b c  0 a b c  6 1     a
chứa M , N  2 2 2     1   a b c Hình chóp .
O ABC là hình chóp đều  OA  OB  OC  a  b  c
Vây phương trình x  y  z  6  0 . Chọn đáp án B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 109
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  y  0
Câu 30. Trong không gian với hệ tọa độ 
Oxyz cho điểm M 1;0;0 và
2x  y  2z  2  0  N 0;0;  1
 , mặt phẳng P qua điểm M , N và tạo với mặt phẳng Q : x  y  4  0 một góc bằng O
45 . Phương trình mặt phẳng  P là  y  0  y  0 A.  . B.  .
2x  y  2z  2  0 
2x  y  2z  2  0 
2x  y  2z  2  0
2x  2z  2  0 C.  . D. . 
2x  y  2z  2  0 
2x  2z  2  0  Hướng dẫn giải:  
Gọi vectơ pháp tuyến của mp  P và Q lần lượt là n a b c  2 2 2
a  b  c  0 , n P  ; ;  Q
P qua M 1;0;0  P : a x  
1  by  cz  0
P qua N 0;0;  1
  a  c  0   a  b 1 a  0
P hợp với Q góc O
45  cos n ,n cos P Q  O  45     2 2 2 2 2 a  2    b a b
Với a  0  c  0 chọn b  1 phương trình  P : y  0
Với a  2b chọn b  1 a  2 phương trình mặt phẳng  P  : 2x  y  2z  2  0 . Chọn đáp án A.
Câu 31. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A10;2;1 và đường thẳng x 1 y z 1 d :  
. Gọi  P là mặt phẳng đi qua điểm A , song song với đường thẳng d sao cho 2 1 3
khoảng cách giữa d và  P lớn nhất. Khoảng cách từ điểm M  1  ;2; 
3 đến mp  P là 97 3 76 790 A. . B. . 15 790 d 2 13 3 29 C. . D. . H 13 29 Hướng dẫn giải:
P là mặt phẳng đi qua điểm A và song song với d' K
đường thẳng d nên  P chứa đường thẳng d đi qua
điểm A và song song với đường thẳng d . A P
Gọi H là hình chiếu của A trên d , K là hình chiếu
của H trên  P .
Ta có d d, P  HK  AH ( AH không đổi)
 GTLN của d(d, (P)) là AH
 d d, P lớn nhất khi AH vuông góc với  P .
Khi đó, nếu gọi Q là mặt phẳng chứa A và d thì  P vuông góc với Q .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 110
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12   
 nP  ud , nQ   98;14; 70   97 3
  P :7x  y  5z  77  0 d M , P . 15 Chọn đáp án A.
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng d: x  3 y 1 z  
. Mặt phằng (P) chứa đường thẳng d và có khoảng cách từ A đến (P) là lớn nhất. Khi 2 1 1 
đó (P) có một véctơ pháp tuyến là    
A. n  (4; 5;13)
B. n  (4; 5; 1  3)
C. n  (4; 5;13) D. n  ( 4  ; 5;13) Hướng dẫn giải:
Gọi H,K lần lươt là hình chiếu vuông góc của A lên d và (P)
Khi đó: d(A,(P)) = AK  AH hay d(A,(P)) lớn nhất khi và chỉ khi H  K    4 Ta có: H( 3   2t; 1   t; t  ); a  (2;1; 1
 ) và AH.a  0  t  3  4 5 13
Suy ra: AH  ( ;  ;  ) 3 3 3 
Hay một véctơ pháp tuyến của (P) là n  (4; 5;13) Chọn đáp án A.
Câu 33. Trong không gian với hệ tọa độ Oxyz , cho điểm ( A 2; 2  ;0) , đường thẳng x  1 y z  2  :  
. Biết mặt phẳng (P) có phương trình ax  by  cz  d  0 đi qua A , song song 1 3 1
với  và khoảng cách từ  tới mặt phẳng (P) lớn nhất. Biết a,b là các số nguyên dương có ước
chung lớn nhất bằng 1. Hỏi tổng a  b  c  d bằng bao nhiêu? A. 3 . B. 0 . C. 1 . D. 1  . Hướng dẫn giải:
Gọi H là hình chiếu vuông góc của A trên đường thẳng  . 
Do H    H ( 1
  t;3t;2  t)  AH  (t  3;3t  2;t  2)   
Do AH    AH.u  0 với u  ( 1  ;3;1)    1
 .(t  3)  3.(3t  2) 1.(t  2)  0  11t  1  1  t  1   H 0; 3  ;  1
Gọi F là hình chiếu vuông góc của H trên (P) , khi đó: d(,(P))  d (H ,(P))  HF  HA
Suy ra d (,(P))
 HA . Dấu “=” xảy ra khi F  A  AH  (P) , hay bài toán được phát biểu lại max là:
“ Viết phương trình mặt phẳng (P) đi qua A và vuông góc với AH ”  
Ta có AH  2;1;  1  (2;1; 1  ) , suy ra n  (2;1; 1) ( P)
Suy ra phương trình mặt phẳng (P) là: 2(x  2)  y  2  z  0  2x  y  z  2  0 . a,b   *
a  2,b  1 Do   
 a  b  c  d  0 . (a,b)  1 c  1  , d  2    Chọn đáp án B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 111
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 34. Trong không gian tọa độ Oxyz cho M(2;1;0) v đường thẳng d có phương trình: x  1 y  1 z  
. Gọi  là đường thẳng đi qua M, cắt và vuông góc với d. Viết phương trình đường 2 1 1 thẳng  ? x  2  t x  2  t x  1 t x  2  t    
A. y  1  4t
B. y  1  4t
C. y  1  4t
D. y  1  4t z  2      t z  3  2  t z  2   t z  2   t Hướng dẫn giải:
x  1  2t 
PTTS của d là  y  1  t . z    t
Gọi H là hình chiếu vuông góc của M lên d, đường thẳng  cần tìm là đường thẳng MH. 
Vì H thuộc d nên H 1 2t; 1
  t;t  suy ra MH  (2t 1; 2
  t;t) .    2   1 4  2  
Vì MH  d và d có 1 VTCP là u  (2;1; 1
 ) nên MH .u  0  t  . Do đó MH  ; ;   3  3 3 3  x  2  t 
Vậy PTTS của  là: y  1  4t . z  2   t Chọn đáp án A. x  1 t 
Câu 35. Cho đường thẳng (d ) :  y  1  t và mp (P): x  y  2  0 . Tìm phương trình đường thẳng z  2  t
nằm trong mặt phẳng (P) cắt và vuông góc với (d). x  1 2t x  1 3t x  1 2t x  1 t    
A. y  1  2t
B. y  1  3t
C. y  1  2t
D. y  1  t z  0     z  5  z  0  z  5  Hướng dẫn giải:
Gọi I là giao điểm của (d) và (P)
I (1 t;1  t;2t), I  (P)  t  0  I (1;1;0) 
(d) có vectơ chỉ phương u  ( 1  ; 1  ; 2) 
(P) có vectơ pháp tuyến n  (1;1;0)   
Vecstơ pháp tuyến của mặt phẳng cần tìm là u  u v  , = (-2 ;2 ;0)   x  1 2t 
Phương trình mặt phẳng cần tìm là y  1  2t z  0  Chọn đáp án A.
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABC . D  A  B  C  D có điểm A
trùng với gốc tọa độ, ( B ; a 0;0), ( D 0; ; a 0), A (  0;0; )
b với (a  0,b  0) . Gọi M là trung điểm của cạnh
CC . Giả sử a  b  4 , hãy tìm giá trị lớn nhất của thể tích khối tứ diện  A BDM ?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 112
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 64 A. maxV  B. maxV  1 AMBD A 27 MBD 64 27 C. maxV   D. maxV  AMBD A 27 MBD 64 Hướng dẫn giải:  b  Ta có: C( ; a ; a 0), B (  ;
a 0;b), D (  0; ; a b),C (  ; a ; a b)  M ; a ;  a   2      b  Suy ra:  A B  ( ; a 0; b),  A D  (0; ;
a b), AM  ; a ; a     2  2 2  
   3a b a b 2    A B,  A D  (a ; b a ; b a )    A B,  A D.  A M   V  A     2 MBD 4 1 1 1 64
Do a,b  0 nên áp dụng BĐT Côsi ta được: 2 2 3
4  a  b  a  a  b  3 a b  a b  2 2 4 27 64 Suy ra: maxV  . AMBD 27 Chọn đáp án A.
Câu 37. Cho A 1
 ;3;5, B2;6;  1 ,C  4  ; 1
 2;5 và điểm  P : x  2y  2z  5  0 . Gọi M là điểm  
  
thuộc  P sao cho biểu thức S  MA  4MB  MA  MB  MC đạt giá trị nhỏ nhất. Tìm hoành độ điểm M. A. x  3 B. x  1  C. x  1 D. x  3  M M M M
Hướng dẫn giải:   
Gọi I là điểm IA  4IB  0  I 3;7; 3  
Gọi G là trọng tâm ta m giác ABC  G 1  ; 1  ;  3
Nhận thấy, M,I nằm khác phía so với mp(P).
Có S  3MI  MG  3GI . Dấu bằng xảy ra khi M là giao điểm của GI và (P)  M 1;3;  1 Chọn đáp án C.
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;1;  1  , B0;3;  1 và mặt phẳng  
P : x  y  z  3  0 . Tìm tọa độ điểm M thuộc (P) sao cho 2MA  MB có giá trị nhỏ nhất. A. M  4  ; 1  ;0 . B. M  1  ; 4  ;0 .
C. M  4;1;0 . D. M 1; 4  ;0 . Hướng dẫn giải:    Gọi I  ; a ;
b c là điểm thỏa mãn 2IAIB  0 , suy ra I 4; 1  ;  3 .   
      
Ta có 2MA  MB  2MI  2IA  MI  IB  MI. Suy ra 2MA  MB  MI  MI .  
Do đó 2MA  MB nhỏ nhất khi MI nhỏ nhất hay M là hình chiếu của I trên mặt phẳng  P . x  4 y  1 z  3
Đường thẳng đi qua I và vuông góc với  P có là d :   . 1 1 1
Tọa độ hình chiếu M của I trên  P thỏa mãn  x  4 y  1 z  3     1 1 1   M 1; 4  ;0 .
x  y  z  3  0 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 113
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án D. x  2  t x 1 y  2 z 1 
Câu 39. Trong không gain Oxyz, cho hai đường thẳng d :  
và d :  y  3  t . Mặt 1 2 1 2 1 z  2  
phẳng  P : ax  by  cz  d  0 (với ; a ; b ;
c d   ) vuông góc với đường thẳng d và chắn d , d 1 1 2
đoạn thẳng có độ dài nhỏ nhất. Tính a  b  c  d . A. 1  4 B. 1 C. 8  D. 1  2 Hướng dẫn giải: 
Ta có mặt phẳng (P) vuông dóc với đường thẳng d nên (P) có véctơ pháp tuyến n  1;2;  1 . 1
Phương trình (P) có dạng  P : x  2y  z  d  0 .
 2  d 2  d 10  d 
Gọi M là giáo điểm của (P) với d và N là giao của (P) với d suy ra M ; ; , 1 2    6 3 6   4
  d 1 d  N ; ; 2    .  3 3  2 d 16d 155 Ta có 2 MN    . 18 9 9 Để MN nhỏ nhất thì 2
MN nhỏ nhất, nghĩa là d  1  6 .
Khi đó a  b  c  d  1  4 . Chọn đáp án A. x 1 y  2 z
Câu 40. Trong không gian với hệ trục tọa độ Oxyz , cho hai đường thẳng d :   và 1 1 2 1 x  2 y 1 z d :  
. Gọi  P là mặt phẳng chứa d sao cho góc giữa mặt phẳng  P và đường 2 2 1  2 1
thẳng d là lớn nhất. Chọn mệnh đề đúng trong các mệnh đề sau: 2 
A.  P có vectơ pháp tuyến là n  1;1;2 .
B.  P qua điểm A0;2;0 .
C.  P song song với mặt phẳng Q : 7x  y  5z  3  0 .
D.  P cắt d tại điểm B2;1;4 . 2 Hướng dẫn giải:  d qua M 1; 2
 ;0 và có VTCP u  1;2; 
1 . Vì d  P nên M  P . 1   1
Pt mặt phẳng  P có dạng: A x    B y    Cz   2 2 2 1 2
0 A  B  C  0 .  
Ta có: d  P  .
u n  0  C  A  2B . 1   4A  3B 1 4A  3B Gọi    P   ,d   2  sin    . 2 2 2 2 2
3 2A  4AB  5B
3 2A  4AB  5B 2 2
TH1: Với B  0 thì sin   . 3 A 1 4t  32
TH2: Với B  0 . Đặt t  , ta được: sin   . B 2 3 2t  4t  5
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 114
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 4t  32 25
Xét hàm số f t  
. Dựa vào bảng biến thiên ta có: max f  x  khi t  7  khi 2 2t  4t  5 7 A 5 3
 7 . Khi đó sin   f  7    . B 9 5 3 A
So sánh TH1 và TH2   lớn nhất với sin   khi  7 . 9 B
Vậy phương trình mặt phẳng  P : 7x  y  5z  9  0 . Chọn đáp án B .
Câu 41. Trong không gian với hệ trục tọa độ Oxyz, cho (
A 1;0;2), B(3;1;4),C(3; 2
 ;1) . Tìm tọa độ điểm 3 11
S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng và S có cao 2 độ âm. A. S( 4  ; 6  ;4) . B. S(3;4;0) . C. S(2; 2;1) . D. S(4;6; 4  ) . Hướng dẫn giải:    
Ta có AB  (2;1; 2); AC  (2; 2  ; 1
 ) , suy ra AB  AC .
Tam giác ABC vuông nên I và S có thể sử dụng các tính chất của phép dụng tâm để tính. Tính được IM. S   
MI  ( ABC)  MI  k  AB, AC     k  
AS  2MI , tìm S. N  
 AB, AC   (3;6;6)   I  1 5  A C Gọi M 3; ; 
 là trung điểm BC. Ta có:  2 2  M 2  3 11  9 81 9 2 2 2 B
IM  IB  BM       IM 
MI  ( ABC)  MI  k AB, AC  k (3;6;6)  MI  9 k .  2  2 4 2   9 1 Suy ra
 9 k  k   2 2 1   k 
thì AS  2MI  3;6;6  S 4;6; 4   2 Chọn đáp án D. x  1
Câu 42. Trong không gian với tọa độ Oxyz , cho đường thẳng d :
 y  1  z  3 và mặt phẳng 2
P : x  2y  z  5  0 . Mặt phẳng Q chứa đường thẳng d và tạo với P một góc nhỏ nhất có phương trình
A. x  z  3  0.
B. x  y  z  2  0.
C. x  y  z  3  0.
D. y  z  4  0. Hướng dẫn giải:
Gọi  là giao tuyến giữa  P và Q . Khi đó, góc giữa  P,Q nhỏ nhất khi chỉ khi   d . 
Đường thẳng d đi qua điểm M  1  ; 1  ; 
3 và có vectơ chỉ phương là u  . d 2;1;  1   
Vectơ chỉ phương của  là u  n  u  . d 3; 3  ;  3   
Vectơ pháp tuyến của Q là. n  u  u  . Q d 0;9; 9   
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 115
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 
Mặt phẳng Q đi qua M  1  ; 1  ; 
3 và nhận vectơ pháp tuyến n  0;1;  1 có phương trình
y  z  4  0 Chọn đáp án D.
Câu 43. Trong không gian Oxyz, cho điểm A1, 0,  
1 và mặt phẳng  P : x  y  z  3  0 . Mặt cầu S
có tâm I nằm trên mặt phẳng  P , đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng
6  2 . Phương trình mặt cầu S là: 2 2 2 2 2 2
A.  x  2   y  2   z   1
 9 hoặc  x  2   y  2   z   1  9. 2 2 2 2 2 2
B.  x  2   y  2   z   1
 9 hoặc  x   1
  y  2   z  2  9 2 2 2 2 2 2
C.  x  2   y  2   z   1
 9 hoặc  x  2   y  2   z   1  9 2 2 2 2 2 2
D.  x  2   y  2   z   1
 9 hoặc  x  
1   y  2   z  2  9 Hướng dẫn giải: Gọi I  ,
x y, z  là tâm của S.
Khi đó I   P, IO  I ,
A IO  IA  AO  6  2 nên ta suy ra hệ  x  2
1  y   z  2 2 2 2 2 1 
x  y  z 
x  z 1  0  2 2 2  2 2 2
2 x  y  z  2  6  2
 x  y  z  9
x  y  z 3  0
x  y  z  3  0   
Giải hệ ta tìm được I 2, 2, 
1 hoặc I 1, 2, 2 Chọn đáp án D.
Câu 44. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A0; 2;0, B  1
 ;1;4 và C 3;2  ;1 .
Mặt cầu  S  tâm I đi qua , A ,
B C và độ dài OI  5 (biết tâm I có hoành độ nguyên, O là gốc tọa
độ). Bán kính mặt cầu  S  là A. R  1 B. R  3 C. R  4 D. R  5 Hướng dẫn giải:
Phương trình mặt cầu (S) có dạng: 2 2 2
x  y  z  2ax  2by  2cz  d  0 Vì 4 điểm , O , A ,
B C thuộc mặt cầu (S) nên ta có hệ:  A  (S)
4b  d  4  0  
B  (S)  2a  2b  8c  d 18  0 C  (S )  
6a  4b  2c  d  14  0   2 2 2 2
OI  5  OI  5  a  b  c  5 Suy ra a  1
 ;b  0;c  2  ;d  4   R  3 Chọn đáp án B.
Câu 45. Cho hình chóp O.ABC có OA=a, OB=b, OC=c đôi một vuông góc với nhau. Điểm M cố định
thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC), (OCA), (OAB) là 1,2,3. Khi
tồn tại a,b,c thỏa thể tích khối chóp O.ABC nhỏ nhất, giá trị nhỏ nhất của thể tích khối chóp O.ABC là A. 18 B. 27 C. 6
D. Không tồn tại a,b,c thỏa yêu cầu bài toán
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 116
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải:
Chọn hệ trục tọa độ thỏa O(0,0,0), A(a,0,0), B(0,b,0), C(0,0,c)
Điểm M cố định thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC), (OCA),
(OAB) là 1,2,3 nên tọa độ điểm M là (1,2,3) x y z
Phương trình mặt phẳng (ABC) là    1 a b c 1 2 3
Vì M thuộc mặt phẳng (ABC) nên    1 a b c 1 VOABC= abc 6 1 2 3 1 1 1 1
Áp dụng bất đẳng thức Cauchy ta có 3 1     3 . .  abc  27 a b c a b c 6 Chọn đáp án B.
Câu 46. Cho hai điểm M 1; 2;3, A
2; 4; 4 và hai mặt phẳng P : x  y  2z 1  0,
Q : x  2y  z  4  0 . Viết phương trình đường thẳng  qua M cắt  P, Q lần lượt tại , B C sao
cho tam giác ABC cân tại A và nhận AM là đường trung tuyến. x 1 y  2 z  3 x 1 y  2 z  3 A.  :   B.  :   1  1  1 2 1  1 x 1 y  2 z  3 x 1 y  2 z  3 C.  :   D.  :   1 1 1 1 1  1 Hướng dẫn giải: Gọi B  ; a ;
b c , từ giả thiết suy ra M là trung điểm của BC , suy ra C 2  ; a 4  ; b 6  c.
B  P, C
 Q nên có hai pt: a  b  2c 1  0  
1 ;  a  2b  c  8  0 2.   AM 1; 2  ;   1 , BC 2  2 ; a 4  2 ; b 6  2c.  
Tam giác ABC cân tại A nên: AM .BC  0  a  2b  c  8  0 3.
a  b  2c 1  0 a  0   Từ  
1 , 2 và 3 có hệ: a  2b  c 8  0  b
  3  B 0;3; 2, C 2;1; 4. a 2b c 8 0      c  2   x 1 y  2 z  3
Đường thẳng  qua B và C có pt  :   . 1 1  1 Chọn đáp án D. x   2  t 
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  : y   1   t
2 t   hai điểm   z   t 3 
A 2;0;3 và B 2; 2; 3 
. Biết điểm M x ;y ;z thuộc  thì MA4 MB4  nhỏ nhất.Tìm      x 0 0 0  0 A. x  0 B. x  1 C. x  2 D. x  3 0 0 0 0 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 117
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x   2 
Phương trình đường thẳng AB là: y   t
t   . Dễ thấy đường thẳng  và AB cắt nhau tại 1  1  z   3  t 3 1 
điểm I 2; 1;0 suy ra AB và  đồng phẳng.    
Lại có IA0;1;3,IB 0; 1  ; 3
   IA  I
 B  IA  IB  AB . 2 2  2  4 1 1 1 1 1
Ta có: MA4  MB4  MA2  MB2  MA  MB  AB4  IA  IB .         2 2 2 8 8   Do đó MA4 MB4 
nhỏ nhất khi M trùng với điểm I 2; 1;0 Chọn đáp án C.
Câu 48. Trong hệ trục tọa độ Oxyz cho 3 điểm A ;
a 0; 0, B0; ;
b 0 ,C 0;0;c với a, , b c  0 .Giả sử , a ,
b c thay đổi nhưng thỏa mãn 2 2 2 2
a  b  c  k không đổi. Diện tích tam giác ABC đạt giá trị lớn nhất bằng 2 k 3 2 k 3 A. B. C. 2 k 3 D. 2 k 2 6 Hướng dẫn giải: x y z Phương trình (ABC):    1 a b c Gọi H  ; x ;
y z  là hình chiếu vuông góc của O lên  ABC  2 2  ab c x  
ab2  bc2  ca2
H   ABC  b
 cx  cay  abz  abc 2 2     a bc Khi đó O
 H  AB  ax  by  0  y  O  H  AC
ax  cz  0   
ab2  bc2  ca2 2 2  a b c z   
ab2  bc2  ca2  abc  OH 
ab2  bc2  ca2 1 1 Ta có V  O . A O . B OC  abc OABC 6 6 3V 1 ABCD  S   ab  bc  ca ABC  2  2  2 OH 2
Áp dụng bất đẳng thức Cosi ta có 4 4 4 4 4 4 a  b b  c c  a 2 2 2 2 2 2 4 4 4
a b  b c  c a   
 a  b  c 2 2 2
Dấu “=” xảy ra khi và chỉ khi a  b  c 4 2 1 k k 3 Vậy max S   2 3 6 Chọn đáp án B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 118
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 49. Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M(9;1;1) , cắt
các tia Ox, Oy, Oz tại A, B, C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất là x y z x y z x y z x y z A.    1 B.    1 C.    1 D.    1 7 3 3 27 3 3 27 3 3 27 3 3 Hướng dẫn giải:
Giá sử A(a;0;0)Ox,B(0;b;0)Oy,C(0;0;c)Oz a ( ,b,c  0) . x y z
Khi đó PT mặt phẳng (P) có dạng:    1 . a b c 9 1 1 1
Ta có: M(9;1;1) (P)     1 (1); V  abc (2) a b c OABC 6 3
(1)  abc  9bc  ac  ab ≥ 3 9 a ( bc 2 )  abc 3  abc 2 ( ) 27.9( )  abc  243
9bc  ac  ab a  27   x y z Dấu "=" xảy ra  9 1 1
 b  3  (P):    1.    1  c 27 3 3  a b c  3  Chọn đáp án B.
Câu 50. Trong không gian Oxyz cho 4 điểm A2;3;2 , B 6; 1
 ; 2 , C 1; 4;3 , D1;6; 5  . Gọi M
là một điểm nằm trên đường thẳng CD sao cho tam giác MAB có chu vi bé nhất. Khi đó toạ độ điểm M là:
A. M 0;1;   1 B. M 2;11; 9   C. M 3;16; 1   3 D. M  1  ; 4;3 Hướng dẫn giải:
Tam giác MAB có độ dài cạnh AB  4 3 không đổi, do đó chu vi bé nhất khi và chỉ khi MA  MB bé nhất.     AB  4; 4  ; 4
  ; CD  2;10; 8   . Vì .
AB CD  0 nên AB  CD , suy ra điểm M cần tìm là hình
chiếu vuông góc của A, cũng là hình chiếu vuông góc của B lên đường thẳng CD . Từ đó tìm ra
điểm M 0;1;   1 . Chọn đáp án A.
Câu 51. Trong không gian tọa độ Oxyz cho điểm (
A 0;1;1) , B(1;0; 3  ), C( 1  ; 2  ; 3  ) và mặt cầu (S) có phương trình: 2 2 2
x  y  z  2x  2z  2  0 .Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện ABCD có thể tích lớn nhất.  7 4 1   1  4 5   7 4 1   7 4 1  A. D ;  ;  B. D ; ; C. D ; ; D.       D ;  ;    3 3 3   3 3 3   3 3 3   3 3 3  Hướng dẫn giải: Ta có (S) 2 2 2
: (x 1)  y  (z 1)  4 suy ra (S) có tâm I(1;0;-1), bán kính R  2  
Và AB  (1; 1; 4); AC  (1; 3; 4)   
Mặt phẳng (ABC) có một vectơ pháp tuyến là n   AB, AC   (8;8; 4)   
Suy ra mp(ABC) có phương trình: 8
 x  8(y 1)  4(z 1)  0  2x  2y  z 1  0 1 Ta có V  d( ;
D ( ABC)).S nên V
lớn nhất khi và chỉ khi d( ;
D ( ABC)) lớn nhất. Gọi ABCD 3 ABC ABCD
D D là đường kính của mặt cầu (S) vuông góc với mp(ABC). Ta thấy với D là 1 điểm bất kỳ 1 2 thuộc (S) thì d ( ;
D ( ABC))  max d (D ;( ABC)); d(D ;( ABC)) 1 2  .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 119
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Dấu “=” xảy ra khi D trùng với D1 hoặc D2 
Đường thẳng D D đi qua I(1;0;-1), và có VTCP là nABC  (2; 2  ;1) 1 2 x  1 2t 
Do đó (D1D2) có phương trình:  y  2  t . z  1    t x  1 2t  2  t   y  2  t  3
Tọa độ điểm D1 và D2 thỏa mãn hệ:    z  1 t 2  t   2 2 2
 (x 1)  y  (z 1)  4  3   7 4  1    1  4 5   D ; ; & D ; ; 1   2    3 3 3   3 3 3   7 4 1 
Ta thấy: d (D ; ( ABC))  d (D ; ( ABC)) . Vậy điểm D ;  ;  là điểm cần tìm 1 2    3 3 3  Chọn đáp án D.  1 3 
Câu 52. Trong không gian Oxyz , cho điểm M  ;
;0  và mặt cầu  S  2 2 2
: x  y  z  8. Đường  2 2   
thẳng d thay đổi, đi qua điểm M , cắt mặt cầu  S  tại hai điểm phân biệt. Tính diện tích lớn nhất S của tam giác OA . B A. S  7 . B. S  4 . C. S  2 7 . D. S  2 2 . Hướng dẫn giải: A
Mặt cầu  S  có tâm O0;0;0 và bán kính R  2 2 .
Vì OM  1 R nên M thuộc miền trong của mặt cầu
S  . Gọi A , B là giao điểm của đường thẳng với mặt H
cầu. Gọi H là chân đường cao hạ từ O của tam giác OAB .
Đặt x  OH , ta có 0  x  OM 1, đồng thời O M 2 2 2
HA  R  OH  8  x . Vậy diện tích tam giác B OAB là 1 2 S 
OH.AB  OH.HA  x 8  x . OAB 2 Khảo sát hàm số 2
f (x)  x 8  x trên 0;  1 , ta được
max f  x  f   1  7 . 0;  1
Vậy giá trị lớn nhất của S
 7 , đạt được khi x  1 hay H  M , nói cách khác là d  OM . OAB Chọn đáp án A.
 x  2  t 
Câu 53. Cho mặt cầu  S  2 2 2
: x  y  z  2x  4z 1  0 và đường thẳng d :  y  t . Tìm m để d z  m   t
cắt  S  tại hai điểm phân biệt ,
A B sao cho các mặt phẳng tiếp diện của  S  tại A và tại B vuông góc với nhau.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 120
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. m  1  hoặc m  4 
B. m  0 hoặc m  4  C. m  1  hoặc m  0
D. Cả A, B, C đều sai Hướng dẫn giải:
Để thỏa mãn yêu cầu đề bài thì trước tiên d phải cắt mặt cầu, tức là phương trình
  t2  t  m  t2 2 2
 2.2  t  4.m  t  1  0 có hai nghiệm phân biệt. 2
 t  m   2 3 2
1 t  m  4m 1  0
Phương trình có hai nghiệm phân biệt khi    m  2 2 ' 0
1  3m 12m  3  0 2
 m  5m 1  0 .
Với phương trình có hai nghiệm phân biệt , áp dụng định lí Viet ta có 2 m  4m  1 2  t t  ;t  t  m  1 1 2 1 2   3 3  
Khi đó IA  1 t ;t ;m  2  t , IB  1  t ;t ;m  2  t . 1 1 1   2 2 2    Vậy I .
A IB  1 t 1  t
 t t  m  2  t m  2  t  0 1   2  1 2  1   2 
 3t t  m  
1 t  t   m  22 1  0 1 2 1 2 2 m  1 
 m  4m  1  m  2 1  m  22 2  1  0   (TM). 3 m  4   Chọn đáp án A.
Câu 54. rong không gian với hệ tọa độ Oxyz cho ba điểm A1;01;  1 , B1;2;  1 ,C 4;1; 2   và mặt
phẳng  P : x  y  z  0 . Tìm trên (P) điểm M sao cho 2 2 2
MA  MB  MC đạt giá trị nhỏ nhất. Khi đó M có tọa độ A. M 1;1;  1  B. M 1;1;  1 C. M 1;2;  1  D. M 1;0;  1  Hướng dẫn giải:
Gọi G là trọng tâm của tam giác ABC, ta có G 2;1;0 , ta có
MA2  MB2  MC2  3MG2  GA2  GB2  GC2 1
Từ hệ thức (1) ta suy ra :
MA2  MB2  MC2 đạt GTNN  MG đạt GTNN  M là hình
chiếu vuông góc của G trên (P).
Gọi (d) là đường thẳng qua G và vuông góc với (P) thì (d) có x  2  t 
phương trình tham số là  y  1  t z   t x  2  t t  1   
 y  1  t x  1
Tọa độ M là nghiệm của hệ phương trình     M 1;0;  1 z  t y  0  
x  y  z  0 z  1   Chọn đáp án D.
Câu 55. Trong không gian Oxyz, cho mặt cầu  S  2 2 2
: x  y  z  4x  6y  m  0 và đường thẳng x y  1 z  1 d  :  
. Tìm m để (d) cắt (S) tại hai điểm M, N sao cho độ dài MN bằng 8. 2 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 121
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. m  2  4 B. m  8 C. m  16 D. m  1  2 Hướng dẫn giải: 2 (S) có tâm I  2
 ;3;0 và bán kính R    2 2 2
 3  0  m  13  m m  13
Gọi H là trung điểm M, N  MH  4     u, AI   
Đường thẳng (d) qua A0;1;  1 
và có vectơ chỉ phương u  2;1;2  d  I;d     3 u Suy ra 2 2 R 
MH  d  I d  2 2 ;  4  3  5
Ta có 13  m  5  13  m  25  m  12  Chọn đáp án D.
Câu 56. Trong không gian Oxyz, cho điểm A2;0; 2  , B3; 1  ; 4  ,C  2
 ;2;0 . Điểm D trong mặt
phẳng (Oyz) có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến
mặt phẳng (Oxy) bằng 1 có thể là: A. D0; 3  ;  1 B. D0;2;  1  C. D0;1;  1  D. D0;3;  1  Hướng dẫn giải:
Do D Oyz  D0; ;
b c với c  0 c   1 loai
Theo giả thiết: d D,Oxy  1  c  1       D 0; ; b   1 c  1     Ta có AB  1; 1  ; 2
 , AC  4;2;2, AD   2  ; ; b  1  
  
Suy ra  AB, AC   2;6; 2   
  AB, AC .AD  6b  6    
1    b  3
Cũng theo giả thiết, ta có: V 
 AB, AC .AD  b  1  2  ABCD    6 b  1  Chọn đáp án D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 122
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 SỐ PHỨC z  z
Câu 1. Cho hai số phức phân biệt z ; z thỏa điều kiện 1
2 là số ảo. Khẳng định nào sau đây là 1 2 z  z 1 2 đúng?
A. z  1; z  1
B. z  z
C. z  z D. z  z  1 2 1 2 1 2 1 2 Hướng dẫn giải:
z  z  z  z  0 . 1 2 1 2 z  z z z z z      z  z z  z Thì 1 2 là số ảo 1 2 1 2      0   . 1 2 1 2    0 z  z z  z
z  z  z  z  1 2 1 2 1 2 1 2 z z 1 2
 z  z z  z  z  z z  z  0  2z z z z  0 1 1 2 2  1 2  1 2   1 2 1  .
 z z  z z  0 .  z  z  0. 1 1 2 2 1 2 Chọn đáp án A.
Câu 2. Gọi z ; z ; z ; z là 4 nghiệm phức của phương trình 4
z    m 2 4
z  4m  0 . Tìm tất cả các giá 1 2 3 4
trị m để z  z  z  z  6 . 1 2 3 4 A. m  1 B. m  2 C. m  3 D. m  1 Hướng dẫn giải:     z i  z 4  
m z  4m  0  z  4z  m 2 1;2 4 2 2 2  0  
nếu m  0 hoặc z   m   3;4 z  2  i 1;2    nếu m  0 z  i  m  3;4 6   
z  z  z  z  4  2 m  Khi đó 1 2 3 4   m  1  m  0  6
  z  z  z  z  4  2 m  hoặc 1 2 3 4   m  1 m 0 
Kết hợp lại thì m  1 thoả mãn bài toán. Chọn đáp án D. z
Câu 3. Tìm số phức z biết z thỏa mãn phương trình  z  2 z A. 1 B. 1+i C. 1-i D. i Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 123
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
z  z  2  z  z.z  2z z 2 2
 a  bi  a  b  2(a  bi) 2 2
 (a  a  b )  bi  2a  2bi . a  1   z  1 2 2 2 a  a  b  2a a  a  0 b  0      b 2b b 0       a  0   z  0(loai)  b  0  Chọn đáp án A.
Câu 4. Trong các số phức thỏa điền kiện z  4i  2  2i  z , modun nhỏ nhất của số phức z bằng? A. 2 2 B. 2 C. 1 D. 3 2 . Hướng dẫn giải:
Giả sử số phức z  x  yi
x, y  R
Theo đề z  4i  2  2i  z 2 2 2 2  (x 2)  (y 4)  x  (y 2)
 x  y  4  0
 y  4  x (1) Mà 2 2 2 2 z  x  y  x  (4  x) (thay (1) vào) 2
 2(x  2)  8  2 2 . Chọn đáp án A.
Câu 5. Cho số phức z  0 thỏa mãn z  2 . Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức z  i P  . z A. 1 . B. 2 . C. 3. D. 4 . Hướng dẫn giải: i i i 1 i 1 1 1 1 3 Ta có 1  1  1  1  1  1
. Mặt khác z  2   suy ra  P  z z z z z z z 2 2 2 3 1
Suy ra giá trị lớn nhất và giá trị nhỏ nhất là ,
. Vậy tổng tổng giá trị lớn nhất và giá trị nhỏ nhất 2 2
của biểu thức P là 2 . Chọn đáp án B. 13
Câu 6. Số phức z có mô đun lớn nhất và thỏa mãn điều kiện Z 1 i  3  2i  là: 2 2 1 3 1 3 15
A. z  1 3i B. z   i C. z   i D. z   i 2 2 2 2 4 4 Hướng dẫn giải: 13
+ Gọi z=x+yi. Từ giả thiết ta có: 2 2
(x  y  3)  (x  y  2)  4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 124
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 + Đồng thời 2 2 | z |
x  y lớn nhất. Chọn đáp án A.
Câu 7. Tính tổng mô-đun tất cả các nghiệm của phương trình:  z  i  2 z   3
1 z  i  0 A. 3 B. 4 C. 6 D. 8 Hướng dẫn giải:  z  i   z  i  z i      z  1  z  1     z i 2 z  1  3 z i 0 z 1            z  i   z  i  3 3
 z  i  0   2  i   5
z  iz 1  0  z   2
Suy ra tổng mô-đun các nghiệm bằng 6. Chọn đáp án C. 2  6i
Câu 8. Gọi A, B, C lần lượt là các điểm biểu diễn của 3 số phức:1 2 i; (1 i)(1 2i); .Diện 3  i
tích của tam giác ABC bằng: 1 1 5 5 A. B. C. D. 4 2 5 2 Hướng dẫn giải:
Dùng máy tính casio ta có A(1;2), B(3;1) ,C(0;2) 1    
Dùng công thức S   A ,
B AC Với AB  2; 1
 ; 0, AC   1  ; 0; 0 2  
Dùng máy tính ta có kết quả B: S=1/2
(Có thể dùng công thức tính diện tích phần Oxy tính nhanh hơn) Chọn đáp án B. m  1
Câu 9. Cho số phức z 
m  . Số các giá trị nguyên của m để z  i 1 là
1  m2i   1 A.  B. 1 C. 4 D. Vô số Hướng dẫn giải: m  1
m  1  i 1  2mi  m
3m  1  m   1 i
Ta có z  i   i  
1  m2i   1
1  m2i   1 1  m  2mi
3m 1  m   1 i
3m  1  m   1 i  z  i    1 1  m  2mi 1  m  2mi
 3m  1  m  
1 i  1  m  2mi  3m  2 1  m  2 1  1 m2 2  4m 1 2
 5m  6m  1  0  1  m   5
Vì m  Không có giá trị của m thỏa mãn. Chọn đáp án A. 1
Câu 10. Cho hai số phức z ; z thỏa mãn iz  2 
và z  iz . Tìm giá trị nhỏ nhất của biểu thức 1 2 1 2 2 1 z  z . 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 125
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1 1 A. 2  B. 2  C. y 2 2 1 1 2  D. 2  2 2 Hướng dẫn giải:
Bài toán này, thực chất là dựa trên kiến thức “ Biểu diễn
hình học số phức”. Ta thấy nếu đặt I M
z  x  y i
x ; y  . Khi đó điểm M  x ; y là điểm N 1 1  1 1 1  1 1  M’
biểu diễn số phức z thỏa mãn: x 1 1 1 O
i  x  y i  2 
 ix  y  2  1 1  2 1 1 2
 x   y  22 1 2 
. Suy ra tập hợp các điểm M biểu 1 1 4
diễn z là đường trong C có tâm I 0; 2  và bán kính 1 1 R  . 2
Khi đó nếu N là điểm biểu diễn của số phức z thì việc tìm GTNN của z  z là việc tìm GTNN 2 1 2 của MN.
Theo đề thì z  iz   y  x i  N y ; x là điểm biểu diễn z . Ta nhận thấy rõ ràng 2 1 1 1  1 1 2  
OM.ON  x y  x y  0  OM  ON . Dễ nhận thấy 2 2 OM  ON  x  y 1 1 1 1 1 1 Ta có hình vẽ sau:
Do OMN là tam giác vuông cân tại O nên MN  OM 2 , do đó để MN nhỏ nhất thì OM nhỏ nhất.
Dễ thấy, OM nhỏ nhất khi M  M ' (M’ là giao điểm của OI với đường tròn như hình vẽ) Tức là  1   1  1 M 0; 2  
 . Khi đó MN  OM 2  2  2  2    .  2   2  2 Chọn đáp án A.
Câu 11. Trong mặt phẳng phức Oxy , trong các số phức z thỏa z 1  i  1 . Nếu số phức z có
môđun lớn nhất thì số phức z có phần thực bằng bao nhiêu ?  2  2 2  2 2  2 2  2 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải: Gọi M  ,
x y là điểm biểu diễn số phức z  x  yi , x y  R
Gọi A là điểm biểu diễn số phức 1   i
Ta có: z 1  i  1  MA  1. Vậy tập hợp điểm biểu diễn số phức là hình tròn tâm A 1  ,  1 , R  1 như hình vẽ
Để max z  max OM   
 x  2   y  2 1 1  1  M thỏa hệ:   y    x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 126
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2  2 2  2  x  , x   2 2 Chọn đáp án A.
Câu 12. Trong mặt phẳng phức Oxy , các số phức z thỏa z  2i 1  z  i . Tìm số phức z được
biểu diễn bởi điểm M sao cho MA ngắn nhất với A1,3 . A. 3  i . B. 1 3i . C. 2  3i . D. 2   3i . Hướng dẫn giải: Gọi M  ,
x y là điểm biểu diễn số phức z  x  yi , x y  R Gọi E 1, 2
  là điểm biểu diễn số phức 1 2i Gọi F 0,  1 
là điểm biểu diễn số phức i
Ta có: z  2i 1  z  i  ME  MF  Tập hợp điểm biểu diễn số phức z là đường trung trục
EF : x  y  2  0 .
Để MA ngắn nhất khi MA  EF tại M  M 3, 
1  z  3  i Chọn đáp án A. 2z  i
Câu 13. Trong các số phức z thỏa mãn
 1. Tìm giá trị lớn nhất của z . 2  iz A. 1. B. 2. C. 2 D. 3 Hướng dẫn giải: Ta có: 2z  i
2z  i 2z  i
(2z  i)(2z  i)  (2  iz)(2  iz )  1  .  1    z.z  1 2  iz
2  iz 2  iz 2  iz  0  Chọn đáp án A.
Câu 14. Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều
kiện sau: z  z  3  4i . 25
A. 3x  4 y   0
B. 3x  4y  25  0 2 25
C. 3x  4 y   0
D. 3x  4 y  25  0 2 Hướng dẫn giải:
Vì z  z nên z  3  4i  z  3  4i  z  3  4i , z  3  4i
suy ra z  z  3  4i  z  z  3  4i   1 z z  3  4i
Tập hợp điểm có tọa vị z thỏa mãn
 1 là đường trung trực của đoạn thẳng OA, với z  3 
O 0 và A3  4i . Đường trung trực này đi qua trung điểm K  2 
i  của đoạn thẳng OA và  2  
nhận véctơ OA3  4i làm véctơ pháp tuyến nên có phương trình là:  3  25 3 x   4  
 y  2  0  3x  4y   0 .  2  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 127
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án A. 1
Câu 15. Điểm M biểu diễn số phức z  0 và điểm M’ biểu diễn số phức z '  . Nếu điểm M di động z
trên đường tròn tâm A(-1;1) bán kính R  2 thì M’ di động trên đường nào? A. 2 2
x  y  2x  2 y  0
B. 2x  2 y  1  0
C. 2x  2 y  1  0
D. 2x  2 y  1  0 Hướng dẫn giải:  x x '   1 z 2 2  x  y Ta có z '   . Do đó  2 z z  y y '  2 2  x   y
M di động trên đường tròn tâm A(-1;1) bán kính R  2 nên  x  2 1   y  2 1  2 2 2
x  y  2x  2 y 2 2
 x  y  2x  2 y  0   0 2 2 x  y 2x 2 y  1  
 0  2x ' 2 y '1  0 2 2 2 2 x  y x  y Chọn đáp án C.
Câu 16. Tìm số thực m  a  b 20 (a, b là các số nguyên khác 0) để phương trình 2
2z  2(m  1)z  (2m  1)  0 có hai nghiệm phức phân biệt z1, z2 thỏa mãn z  z  10 . Tìm a. 1 2 A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải: 2
'  m  6m 1 
TH1:  '  0 hay m  ( ;
 3  10)  (3  10;) Khi đó 2 2
z  z  10  z  z  2 z z  10 1 2 1 2 1 2 2m  1  0  2 (1  m)  10   m  1  10 (loai) 2  (1 ) m
 (2m  1)  2m  1  10    2m 1 0 m  3  20    2
 m  6m 11  0 
TH2:  '  0 hay m  (3  10;3  10) 2 2 1 m  i (
 m  6m 1) 1 m  i (
 m  6m 1)
Khi đó: z  z  10    10 1 2 2 2 Hay 2 2 (1  ) m
 (m  6m  1)  10  m  2
Vậy m = 2 hoặc m  3  20 Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 128
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 17. Cho các số phức z thỏa mãn z  2 .Biết rằng tập hợp các điểm biểu diễn các số phức
w  3  2i  2  i z là một đường tròn.Tính bán kính r của đường tròn đó. A. 20 B. 20 C. 7 D. 7 Hướng dẫn giải:
Đặt w  x  yi, , x y  
w  3  2i  2  i z
 x  yi  3  2i  2  i z
x  3   y  2i 2x  y  8 x  2 y 1  z    i 2  i 5 5 2 2
 2x  y  8 
 x  2 y 1     2      5   5  2 2
 x  y  6x  4 y  7  0
  x  32   y  22  20
Bán kính của đường tròn là r  20 Chọn đáp án B.
Câu 18. Cho hai số phức u,v thỏa mãn u  v  10 và 3u  4v 
2016 . Tính M  4u  3v . A. 2984 B. 2884 C. 2894 D. 24 Hướng dẫn giải: 2
Ta có z  z.z . Đặt N  3u  4v . 2 2 Khi đó 2
N  3u  4v3u  4v  9 u 16 v 12uv  vu . 2 2 Tương tự ta có 2
M  16 u  9 v  12uv  vu . 2 2 Do đó 2 2
M  N  25 u  v   5000. Suy ra 2 2
M  5000  N  5000  2016  2984  M  2984 . Chọn đáp án A. z 6  7i
Câu 19. Cho số phức z thoả mãn: z  
. Tìm phần thực của số phức 2017 z . 1  3i 5 A. 1008 2  B. 1008 2 C. 504 2 D. 2017 2 Hướng dẫn giải: z 6  7i
Cho số phức z thoả mãn: z  
. Tìm phần thực của số phức 2013 z . 1  3i 5 a  bi 6  7i
Gọi số phức z  a  bi (a,b  )  z  a  bi thay vào (1) ta có a  bi   1  3i 5
(a  bi)(1 3i) 6  7i a  bi  
 10a  10bi  a  3b  i(b  3a)  12  14i 10 5
 9a  3b  i(11b  3a)  12  14i
9a  3b  12 a  1    
11b  3a  14 b  1  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 129
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
a  b   z   i  z  
504   i   504 2017 4   i 1008 1008 1 1 (1+i) 1 4 1  2  2 i Chọn đáp án B. 1 1 1
Câu 20. Cho số phức z có mô đun bằng 2017 và w là số phức thỏa mãn biểu thức   . z w z  w
Môđun của số phức w bằng: A. 1 B. 2 C. 2016 D. 2017 Hướng dẫn giải: z  w  z  w2 1 1 1 1  zw Từ      0   0 z w z  w zw z  w
zw z  w 2 2 2 1 3 1 3 1  i 3w      2 2 2 2 2 2
 z  w  zw  0  z  zw  w 
w  0  z  w
  w  z  w        4 4 2 4 2  2        2 2 w  i 3w   1 i 3    z Từ z        z      w  w=  2   2   2 2       1 i 3      2 2   2017 Suy ra: w   2017 1 3  4 4 Chọn đáp án D.
Câu 21. Biết số phức Z thỏa điều kiện 3  z  3i 1  5 . Tập hợp
các điểm biểu diễn của Z tạo thành một hình phẳng. Diện tích 8 của hình phẳng đó bằng A. 16 B. 4 6 C. 9 D. 25 Hướng dẫn giải: Đặt z=x+yi 4 2 2
z  3i 1  x 1 (y  3)i  (x 1)  (y  3) 2 Do đó 2 2
3  z  3i 1  5  9  (x 1)  ( y  3)  25
Tập hợp các điểm biểu diễn của Z là hình phẳng nằm trong 5 O đường tròn
Tâm I (1 ;3) với bán kính bằng R=5 đồng thời nằm ngoài 2
đường tròn tâm I (1 ;3) với bán kính r=3
Diện tích của hình phẳng đó là 2 2 S  .  5  .  3  16 Chọn đáp án A.
Câu 22. Số Phức cho ba số phức z , z , z thỏa mãn z  z  z  1 và z  z  z  1. Mệnh đề 1 2 3 1 2 3 1 2 3 nào sau đây là sai.
A. Trong ba số đó có hai số đối nhau.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 130
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
B. Trong ba số đó phải có một số bằng 1.
C. Trong ba số đó có nhiều nhất hai số bằng 1.
D. Tích của ba số đó luôn bằng 1. Hướng dẫn giải:
Ta có: z  z  z  1  1  z  z  z . 1 2 3 1 2 3
Nếu 1  z  0 thì z  z  0  z  z . 1 2 3 2 3
Nếu 1  z  0 thì điểm P biểu diễn số phức 1  z  z  z không trùng với góc tọa độ O. 1 1 2 3
Gọi M là điểm biểu diễn của số phức  z và A là điểm biểu diễn của số 1. 1
  
Khi đó ta có OA  OM  OP (do P là điểm biểu diễn của số 1 z ) nên OAPM là hình bình 1 
hành. Mà z  z  z  1 nên các điểm biểu diễn cho ba số z , z , z đều nằm trên đường tròn 1 2 3 1 2 3
đơn vị. Ta cũng có OA  OM  1 nên OAPM là hình thoi. Khi đó ta thấy M, A là giao điểm của
đường trung trực đoạn OP với đường tròn đơn vị.
Tương tự do P cũng là điểm biểu diễn của z  z , nếu M’ và A’ là hai điểm biểu diễn của số z , z 2 3 2 3
thì ta cũng có M’, A’ là giao điểm đường trung trực của OP và đường tròn đơn vị.
Vậy M '  M , A'  A hoặc ngược lại. Nghĩa là z  1, z   z hoặc z  1, z   z . 2 3 1 3 2 1
Do đó A, B là mệnh đề đúng.
C đúng là hiển nhiên, vì nếu ba số đều 1 một thì tổng bằng 3. 2 2 2 2
D sai vì với z  1, z   i, z   
i thỏa hai tính chất trên của đề bài nhưng 1 2 3 2 2 2 2 z z z  1. 1 2 3 Chọn đáp án D. 1 1 1
Câu 23. Cho z là số phức có mô đun bằng 2017 và w là số phức thỏa mãn   . Mô đun z w z  w của số phức w là A. 2015 B. 1 C. 2017 D. 0 Hướng dẫn giải: 1 1 1 Từ   ta suy ra 2 2
z  w  zw  0 z w z  w 2 2 w  i 3w   1 i 3     z        z      w 2  2   2 2       
Lấy mô đun hai vế ta có z  w  2017 . Chọn đáp án C.
Câu 24. Cho số phức z thoả mãn điều kiện z  2  3i  3 . Tìm giá trị nhỏ nhất của z A. 13  3 B. 2 C. 13  2 D. 2 Hướng dẫn giải:
Các điểm M biểu diễn số phức z thoả mãn z  2  3i  3 nằm trên đường tròn (C) tâm I(2; −3) và y bán kính R = 3.
(Ý nghĩa hình học của z : độ dài OM) x O
Ta có |z| đạt giá trị nhỏ nhất  điểm M(C) và OM nhỏ nhất. z
(Bài toán hình học giải tích quen thuộc) M C
Ta có: OM  OI – IM = OI – R = 13  3.
Dấu « = » xảy ra khi M là giao điểm của (C) và đoạn thẳng OI. I
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 131
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Vậy GTNN của z là: 13  3 . Chọn đáp án A.
Câu 25. Cho số phức z thỏa mãn: z  3  4i  4 . Tìm giá trị nhỏ nhất của z . A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải: 2 2
Giả sử z  a  bi , ta có: a  bi  3  4i  4   a  3  b  4  16
a  3  4sin
a  3  4sin Đặt   
b  4  4 cos
b  4 cos  4   2 2 2 2 2
 z  a  b  9 16sin   24sin  16cos  16  32cos
 41 24sin  32cos 3 4
 41 40( sin  cos ) 5 5 3 4 2 2 2 Đặt cos  ,sin 
 z  a  b  41 40sin(   )  1. 5 5  
Dấu “=” xảy ra khi     
 k 2    
   k 2 . 2 2 Vậy Min z  1. Chọn đáp án A.
Câu 26. Tìm phần thực của số phức n z  (1  i) , n   thỏa mãn phương trình
log (n  3)  log (n  9)  3 4 4 A. 5 B. 6 C. 7 D. 8 Hướng dẫn giải:
Điều kiện n > 3, n  
Phương trình log (n  3)  log (n  9)  3  log (n  3)(n  9)  3  n  7 (so đk) 4 4 4 3   2 7 3 z (1 i) (1 i). 1 i      
 (1  i)(2i)  8  8i  
Vậy phần thực của số phức z là 8. Chọn đáp án D. 2z 1
Câu 27. Cho số phức z thỏa mãn z  1 và số phức w 
. Khi đó mô đun của số phức w là: 2  iz A. w  2 B. 1  w  2. C. w  1 D. w  2 Hướng dẫn giải:
Giả sử z  a  bi a,b  . 2 2
z  1  a  b  1. 2 2 2z 1
4a  2b  2 2 1 2z 1
4a  2b   1 Xét 2 2        (vô lí)  . 1 1 ... a b 1. 2  iz  2 2  b2 2  a 2  iz 2  b 2  a Nên w  1.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 132
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án C.
Câu 28. Cho các số phức z thỏa mãn z  1  2 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  1  i 3 z  2 là một đường tròn. Tính bán kính r của đường tròn đó?   A. r  4 B. r  2 C. r  16 D. r  25 Hướng dẫn giải: 2
Giả sử z  a  bi
w  x  yi a b x y    a    b2 ; ; , , , 1  4 Theo đề           1 3  2 1 3  x a 2 b 3 x 3 a 1 b 3 w i z x yi i z 2              
y  b  a 3
y  3  b  3   a  1   2 2 2  2 2 x  y  a b
 b a     a  b2 3 3 1 3 1 3 4 1                 16   2   2
x  3  y  3  16 suy ra bán kính đường tròn là r  16  4 .   Chọn đáp án A. 2 2017
Câu 29. Tìm phần ảo của số phức z , biết số phức z thỏa mãn .
i z  2  i  1 i  ...  1 i . A. 1 B. 1009 2 C. 1009 2  D. 1009 2 i Hướng dẫn giải: 2 2017
Ta thấy 1; 1 i; 1 i ; ........;1 i
lập thành một cấp số nhân gồm 2018 số hạng với u  1 công bội 1 q 1 i . q 1 1 i2018 2018 1 2018 Suy ra . i z  S  u 
 i  i 1 i 2018 1   q 1 i 1009
 z  1 1 i2018  1 1 i2   1 2i1009 1009  1 2 i   1009  z  1 2 i
Vậy phần ảo của z là 1009 2 . Chọn đáp án B.
Câu 30. Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  (3  4i)z  i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  4. B. r  5. C. r  20. D. r  22. Hướng dẫn giải:
a  (b 1)i
a  (b 1)i(3  4i)
Gọi w  a  bi , ta có w  a  bi  (3  4i)z  i  z   2 3  4i 9 16i 2 2 3a  4b  4
(3b  4a  3)
(3a  4b  4)  (3b  4a  3)   .i  z  25 25 25 Mà z = 4 nên 2 2 2 2 2
 (3a  4b  4)  (3b  4a  3)  100  a  b  2b  399
Theo giả thiết, tập hợp các điểm biểu diễn các số phức w  (3  4i)z  i là một đường tròn nên ta có 2 2 2 2
a  b  2b  399  a  (b 1)  400  r  400  20
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 133
Facebook: https://www.facebook.com/dongpay
Giáo viên: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án C.
Câu 31. Với hai số phức z và z thỏa mãn z  z  8  6i và z  z  2 . Tìm giá trị lớn nhất của 1 2 1 2 1 2
P  z  z 1 2
A. P  5  3 5 . B. P  2 26 . C. P  4 6 .
D. P  34  3 2 . Hướng dẫn giải:
Đặt OA  z ,OB  z ( với O là gốc tọa độ, ,
A B là điểm biểu diễn của z , z ). 1 2 1 2
Dựng hình bình hành OACB , khi đó ta có AB  z  z  2,OC  z  z  10,OM  5 1 2 2 1
Theo định lý đường trung tuyến ta có 2 2 2 OA  OB  2  AB 2 2 2 2 2 OM 
 OA  OB  52  z  z  52 1 2 4 2 2
Ta có z  z  2 z  z  2 26  P  2 26 1 2  1 2  max Chọn đáp án B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 134
Facebook: https://www.facebook.com/dongpay

Bài tập trắc nghiệm nâng cao Toán 12 có đáp án và lời giải chi tiết – Đặng Việt Đông

Thông tin :

Tài liệu liên quan:

Hình nón là gì? Công thức tính diện tích xung quanh hình nón | Toán 12

Đề tham khảo kỳ thi tốt nghiệp THPT từ năm 2025 môn Toán

Đề thi thử TN THPT 2025 lần 1 môn Toán trường THPT Lương Tài 2 – Bắc Ninh

Lời giải chi tiết đề tham khảo kỳ thi tốt nghiệp THPT môn Toán từ năm 2025

Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2024 – 2025 sở GD&ĐT Bắc Giang