Bài tập trắc nghiệm Toán 12 – Nguyễn Văn Lực (Tập 1)

Bài tập trắc nghiệm Toán 12 – Nguyễn Văn Lực (Tập 1) được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

125 63 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

129 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
4. SỐ PHỨC
3. NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG
2. HÀM SỐ LŨY THỪA – MŨ - LÔGARIT
ĐỀ CƯƠNG TRẮC NGHIỆM 12 – TẬP 1
Nguyễn Văn Lực
www.facebook.com/VanLuc168
CẦN THƠ – 01/2017
1. ỨNG DỤNG ĐẠO HÀM
1A. Sự đồng biến, nghịch biến của hàm số
1
HÀM BẬC BA
Tìm các khoảng đơn điệu của hàm số
Câu 1. Hàm số

32
3y x x
nghịch biến trên khoảng nào?
A.
 ;2
B.
C.
2;0
D.
0;4
Câu 2. Cho hàm số
32
3 9 12,y x x x
trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số đồng biến trên khoảng
 ;2
B. Hàm số nghịch biến trên khoảng
1;2
C. Hàm số đồng biến trên khoảng
5;
D. Hàm số nghịch biến trên khoảng
2;5
Câu 3. Hàm số
32
3 3 5y x x x
đồng biến trên khoảng nào?
A.
( ;1)
B.
(1; )
C.
( ; ) 
D.
( ;1)
và
(1; )
Câu 4. Các khoảng nghịch biến của hàm số:

3
34y x x
là
A.
 
11
; ; ;
22
B.



11
;
22
C.




1
;
2
D.




1
;
2
Câu 5. Cho hàm số
593
23
xxxy
. Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên
)3;1(
B. Hàm số nghịch biến trên khoảng
)1;( 
.
C. Hàm số đồng biến trên mỗi khoảng
)1;( 
,
);3( 
D. Hàm số chỉ đồng biến trên khoảng
);3( 
.
Câu 6. Hàm số
32
39y x x x
nghịch biến trên khoảng nào sau đây?
A. B.
( ; 1);(3; )
C.
(3; )
D.
( 1;3)
Câu 7. Hàm số
3
2
3
x
y x x
đồng biến trên khoảng nào?
A. B.
;1
C.
1;
D.
;1
và
1;
Câu 8. Khoảng nghịch biến của hàm số
32
15
3
33
y x x x
là
A.
 ;1
B.
1;3
C.
3;
D.
 ;1
và
3;
Câu 9. Cho hàm số
32
42
6 9 .
33
y x x x
Khoảng đồng biến của hàm số là:
A.
;3
B.
2;
C. D. Không có.
SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
1A. Sự đồng biến, nghịch biến của hàm số
2
Câu 10. Cho hàm số
22
1
2 10.
3
y x x x
Khoảng đồng biến của hàm số là:
A.
 ;1
B.
1;
C. D. Không có.
Câu 11. Hàm số
32
3 9 2y x x x
đồng biến trên khoảng nào?
A.
3;1
B.
1;3
C.
 ;1
và
3;
D.
 ;3
và
1;
Câu 12. Các khoảng nghịch biến của hàm số
32
31y x x
là:
A.
;1 , 2;
B.
0;2
C.
2;
D.
Câu 13. Cho hàm số
32
3
33
2
y x x x
. Khẳng định đúng là
A. Phương trình
'0y
vô nghiệm. B. Hàm số đồng biến trên
1
;
3
.
C. Hàm số trên đồng biến trên
1
;
3
. D. Hàm số trên nghịch biến trên .
Câu 14. Các khoảng đồng biến của hàm số
3
26y x x
là:
A.
; 1 , 1; 
B.
1;1
C.
1;1
D.
0;1
Câu 15. Các khoảng nghịch biến của hàm số
3
2 6 20y x x
là:
A.
; 1 , 1; 
B.
1;1
C.
1;1
D.
0;1
Tìm điều kiện để hàm số đơn điệu trên
Câu 16. Hàm số
32
31y x x mx
luôn đồng biến trên khi
A.
3m
B.
3m
C.
3m
D.
3m
Câu 17. Hàm số
3
1
17
3
y x m x
nghịch biến trên thì điều kiện của m là:
A.
1m
B.
2m
C.
1m
D.
2m
Câu 18. Cho hàm số
3
2
1
32
xm
y x mx
, hàm số đồng biến trên tập xác định của nó khi
A.
0;4m
B.
 ;0 4;m
C.
 ;0 4;m
D.
0;4m
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1A. Sự đồng biến, nghịch biến của hàm số
3
Câu 19. Cho hàm số:
2
3
1
2 2016
32
mx
y x x
. Với giá trị nào của
m
, hàm số luôn đồng
biến trên tập xác định.
A.
22m
B.
22m
C.
2 2 2 2mm
D. Một kết quả khác
Câu 20. Cho hàm số
32
2 1 2y x m x m x
, với giá trị nào m thì hàm số đồng biến
trên tập xac định:
A.
7 45 7 45
22
m

B.
7 45 7 45
22
m

C.
7 45 7 45
22
m

D.
7 45 7 45
22
m

Câu 21. Định m để hàm số
32
1
2(2 ) 2(2 ) 5
3
m
y x m x m x
luôn nghịch biến khi:
A.
25m
B.
2m 
C.
1m
D.
23m
Câu 22. Với điều kiện nào của m thì hàm số
2)2()12(
23
xmxmmxy
luôn đồng biến
trên tập xác định của nó?
A.
0m
B.
m0
C.
m0
D.
m0
Câu 23. Cho hàm số
32
y mx (2m 1)x mx 7
. Có bao nhiêu giá trị nguyên của tham số m
để hàm số nghịch biến trên ?
A. Không có giá trị B. 2
C. 0 D. Vô số giá trị
Tìm điều kiện để hàm số đơn điệu trên khoảng K cho trước
Câu 24. Hàm số
3
35y x mx
nghịch biến trong khoảng
1;1
thì m bằng:
A.
1
B.
2
C.
3
D.
1
Câu 25. Với giá trị nào của m hàm số
32
3 ( 1) 4y x x m x m
nghịch biến trên (-1;1)
A.
10m
B.
10m
C.
10m
D.
5m
Câu 26. Tìm m để hàm số
32
1
1 3 10
3
y x m x m x
đồng biến trên
0;3
A.
12
7
m
B.
12
7
m
C.
mR
D.
7
12
m
Câu 27. Hàm số
32
31y x x mx
đồng biến trên khoảng
0;
khi
A.
0m
B.
3m
C.
3m
D.
0m
Câu 28. Hàm số
32
2 3(2 1) 6 ( 1) 1y x m x m m x
đồng biến trên khoảng
(2; )
khi:
A.
1m
B.
1m
C.
2m
D.
1m
1A. Sự đồng biến, nghịch biến của hàm số
4
Câu 29. Cho hàm số
32
3 4(1)y x x mx
. Tìm tất cả các giá trị của tham số m để hàm số (1)
đồng biến trên khoảng (

; 0)?
A.
1.m
B.
3.m
C.
3.m
D.
3.m
Câu 30. Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
2y x mx m
đồng biến trên
khoảng
;0
.
A.
0m
B.
0m
C. Không có
m
D. Mọi
m
HÀM BẬC BỐN TRÙNG PHƯƠNG
Tìm các khoảng đơn điệu của hàm số
Câu 31. Hàm số
42
21y x x
đồng biến trên các khoảng nào?
A.
1;0
B.
1;0
và
1;
C.
1;
D.
x
Câu 32. Khoảng đồng biến của
42
24y x x
là:
A. (-∞; -1) B. (3;4) C. (0;1) D. (-∞; -1) , (0; 1).
Câu 33. Khoảng nghịch biến của hàm số
42
13
3
22
y x x
là
A.
 ;3
và
0; 3
B.




3
0;
2
và





3
;
2
C.
3;
D.
3;0
và
3;
Câu 34. Hàm số
43
85y x x
nghịch biến trên khoảng:
A.
( 6;0)
B.
(0; )
C.
( ; 6)
D.
( ; )
Câu 35. Hàm số
4 3 2
4 4 2y x x x
nghịch biến trên các khoảng
A.
( 1;0).
B.
 ( ; 2).
C. D.
 ; 2 ; 1;0
Câu 36. Bảng biến thiên sau đây là của hàm số nào.
x

3
0
3

'y
0
0
0
y

5
2

2
2
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1A. Sự đồng biến, nghịch biến của hàm số
5
A.
42
15
3
22
y x x
B.
42
1
2
4
y x x
C.
42
15
2
22
y x x
D.
42
13
3
42
y x x
Câu 37. Cho hàm số
42
2 3 1y x mx m
(1) (m là tham số). Tìm m để hàm số (1) đồng biến
trên khoảng (1; 2).
A.
1m
B.
01m
C.
0m
D.
0m
Câu 38. Cho hàm số
4
2
1
2
x
yx
, hàm số đồng biến trên khoảng nào?
A.
,0 ; 1, 
B.
, 1 ; 0,1
C.
1,0 ; 1, 
D.
, 
Câu 39. Hàm số
42
1
23
4
y x x
nghịch biến trong khoảng nào sau đây:
A.
;0
B. (0; 2) C.
2;
D.
0;
Câu 40. Các khoảng đồng biến của hàm số
42
13
1
42
y x x
là:
A.
( ; 3)
và
(0; 3)
. B.
( 3;0)
và
( 3; )
C.
3
;
2



D. Trên .
Câu 41. Hàm số
4
1
2
x
y
đồng biến trên khoảng nào?
A.
( ;0)
B.
(1; )
C.
( 3;4)
D.
( ;1)
HÀM PHÂN THỨC
Tìm các khoảng đơn điệu của hàm số
Câu 42. Các khoảng nghịch biến của hàm số
21
1
x
y
x
là:
A.
;1
B.
1;
C.
 ;
D.
;1
và
1;
Câu 43. Cho hàm số

2
.yx
x
Khoảng nghịch biến của hàm số là:
A.
;0
và
0;
B.
1;0
C. D. Không có.
Câu 44. Cho hàm số
2
23
.
1
xx
y
x
Khoảng nghịch biến của hàm số là:
A.
 ;1
và
1;
B.
1;
C. D. Không có.
Câu 45. Cho hàm số

1
.yx
x
Khoảng nghịch biến của hàm số là:
A.
 ;1
và
1;
B.
1;0
và
0;1
C. D. Không có
1A. Sự đồng biến, nghịch biến của hàm số
6
Câu 46. Cho hàm số

2
89
.
5
xx
y
x
Khoảng nghịch biến của hàm số là:
A.
;5
và
5;
B.
5;
C. D. Không có.
Câu 47. Hàm số
2x 3
y f(x)
x1

nghịch biến trên:
A.
1; 
B.
 ;1 ; 1;
C.
1; 
D.
;2
Câu 48. Hàm số
2
1
x
y
x
nghịch biến trên các khoảng:
A.
;1
và
1;
B.
1; 
C.
1; 
D.
0;
Câu 49. Cho hàm số
2
.
2
x
y
x
Khoảng đồng biến của hàm số là:
A.
 ;2
và
2;
B.
1;0
C. D. Không có.
Câu 50. Cho hàm số

1
2.
1
yx
x
Khoảng đồng biến của hàm số là:
A.
 ;1
B.
1;
C. D. Không có.
Câu 51. Cho hàm số
2
.
1
x
y
x
Khoảng đồng biến của hàm số là:
A.
 ;1
B.
1;
C. D.
1;1
Câu 52. Hàm số có bảng biến thiên như hình bên là
A.
25
2
x
y
x
B.
23
2
x
y
x
C.
3
2
x
y
x
D.
21
2
x
y
x
Nguyễn Văn Lực
www.facebook.com/VanLuc168
'y
x
y

2
2

2


1A. Sự đồng biến, nghịch biến của hàm số
7
Câu 53. Hàm số nào sau đây có bảng biến thiên như hình bên:
x

1

'y
+
+
y

2
2

A.
23
1
x
y
x
B.
23
1
x
y
x
C.
23
1
x
y
x
D.
3
2
x
y
x
Câu 54. Bảng biến thiên sau đây là của hàm số nào?
-
-
2
1
1
+
-
+
-
y
y'
x
A.
2x 1
y
x2
B.
x3
y
x2
C.
x3
y
x2
D.
x3
y
2x 1
Câu 55. Cho hàm số
27
2
x
y
x
có đồ thị (C). Hãy chọn mệnh đề sai :
A. Hàm số có tập xác định là:
D
\2
B. Đồ thị cắt trục hoành tại điểm
7
;0
2
A



C. Hàm số luôn nghịch biến trên
D. Có đạo hàm
2
3
'
( 2)
y
x
Câu 56. Cho hàm số
( ) ( 0, 0)
ax b
y f x ac ad bc
cx d
và
D
là tập xác định của
hàm số. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên từng khoảng xác định, khi
'0y x D
B. Hàm số đồng biến trên từng khoảng xác định, khi
'0y x D
C. Hàm số nghịch biến trên từng khoảng của tập xác định, khi
'0yx
D. Hàm số nghịch biến trên từng khoảng của tập xác định, khi
'0yx
Câu 57. Cho hàm số
1
1
x
y
x
. Chọn khẳng định đúng.
A. Hàm số nghịch biến trên các khoảng
;1
và
1; 
B. Hàm số đồng biến trên các khoảng
;1
và
1; 
C. Hàm số nghịch biến trên các khoảng
;1
và
1; 
D. Hàm số đồng biến trên các khoảng
;1
và
1; 
1A. Sự đồng biến, nghịch biến của hàm số
8
Câu 58. Cho hàm số
4
2
y
x
. Khẳng định đúng là
A. Nghịch biến trên
B. Nghịch biến trên
\ {2}D
C. Nghịch biến trên các khoảng
 ;2 ; 2;
D. Đồng biến trên các
 ;2 ; 2;
Câu 59. Kết luận nào sau đây về tính đơn điệu của hàm số
21
1
x
y
x
là đúng
A. Hàm số đồng biến trên các khoảng (–; –1) và (–1; +).
B. Hàm số luôn luôn đồng biến trên
\1
C. Hàm số nghịch biến trên các khoảng (–; –1) và (–1; +).
D. Hàm số luôn luôn nghịch biến trên
\1
Câu 60. Cho hàm số
21
1
x
y
x
. Khẳng định nào sau đây là khẳng định sai?
A. Đồ thị hàm số có tiệm cận đứng là
1x
.
B. Hàm số không xác định tại điểm
1x
.
C. Hàm số nghịch biến trên .
D. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng
1
2
.
Câu 61. Các khoảng đơn điệu của hàm số

2
1
1
xx
y
x
là:
A. Đồng biến trên các khoảng
và
.
Nghịch biến trên các khoảng
0;1
và
1;2 .
B. Đồng biến trên khoảng
;1 .
Nghịch biến trên khoảng
0;2 .
C. Đồng biến trên khoảng
2; .
Nghịch biến trên khoảng
0;2 .
D. Đồng biến trên khoảng
2; .
Nghịch biến trên khoảng
0;1 .
Câu 62. Cho hàm số
2
23
1
xx
y
x

. Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
( ; 1)
và nghịch biến trên khoảng
( 1; ).
B. Hàm số nghịch biến trên
.
C. Hàm số đồng biến trên khoảng (2;4).
D. Hàm số nghịch biến trên các khoảng
( ; 1)
và
( 1; ).
Tìm điều kiện để hàm số đơn điệu
Câu 63. Giá trị nào của m thì hàm số
2
xm
y
x
nghịch biến trên từng khoảng xác định
A.
2m
B.
2m
C.
2m
D.
2m
Câu 64. Hàm số
78mx m
y
xm

. luôn đồng biến trên từng khoảng xác định với m
A.
81m
B.
81m
C.
41m
D.
41m
1A. Sự đồng biến, nghịch biến của hàm số
9
Câu 65. Tìm các giá trị thực của tham số
m
để hàm số
2
2
1
x mx
y
x

đồng biến trên từng khoảng
xác định của nó.
A.
3m
B.
3m
C.
2 2 2 2m
D.
22m 
hoặc
22m
.
Câu 66. Tìm tất cả các giá trị thực của tham số
m
để hàm số
xm
y
x1
đồng biến trên từng
khoảng xác định của nó.
A.
m1
B.
m1
C.
m1
D.
m1
Câu 67. Hàm số
x
y
xm
đồng biến trên
2;
khi và chỉ khi
A.
0m
B.
0m
C.
2m
D.
2m
Câu 68. Các giá trị của tham số m để hàm số
25mx
y
xm
nghịch biến trên khoảng
( ;1)
là:
A.
55m
B.
51m
C.
55m
D.
1m 
Câu 69. Tìm tất cả các giá trị thực của tham số m để hàm số
2
2
mx
y
xm
nghịch biến trên từng
khoản xác định của nó.
A.
2m 
hoặc
2m
B.
22m
C.
22m
D.
2m
hoặc
2m
HÀM BẬC HAI, HÀM CHỨA CĂN
HÀM LƯỢNG GIÁC, LOGARIT
Câu 70. Tìm khoảng đồng biến của hàm số
2
42y x x
A.
2;
B.
;2
C.
;2
và
2;
D.
Câu 71. Tìm khoảng nghịch biến của hàm số
2
13
22
y x x
A.
1;
B.
 ;1
C.
1;
D.
 ;1
và
1;
Câu 72. Tìm khoảng nghịch biến của hàm số
2
1
: 2 5.
2
P y x x
A.
2;
B.
;2
C.
2;
D.
;2
và
2;
Câu 73. Tìm khoảng đồng biến của hàm số
2
: 2 5.P y x x
A.
1;
B.
 ;1
C.
 ;1
và
1;
D.
Câu 74. Khoảng đồng biến của hàm số

2
2y x x
là
A.
;1
B.
0;1
C.
1;2
D.
1;
Câu 75. Cho hàm số

2
4.yx
Khoảng nghịch biến của hàm số là:
A.
0;2
B.
2;0
C.
2;2
D.
1A. Sự đồng biến, nghịch biến của hàm số
10
Câu 76. Hàm số
2
y 2 x x
nghịch biến trên khoảng
A.



1
;2 .
2
B.



1
1; .
2
C.
1;2 .
D.
2; .
Câu 77. Cho hàm số
2
2 1 .y x x mx
Tìm tất cả các giá trị thực của tham số
m
để hàm số
đồng biến trên .
A.
2m 
B.
0m
C.
1m 
D.
1m
Câu 78. Cho hàm số
ln
x
y
x
,
fx
đồng biến trong các khoảng nào sau đây?
A.
0;1
B.
1;e
C.
0;e
D.
;e
Câu 79. Hàm số
lny x x
luôn đồng biến trên khoảng
A.




1
;
10
B.




1
;
e
C.
;e
D.
1;
Câu 80. Với giá trị nào của
m
thì hàm số
1
x
x
e
y
em
đồng biến trên
2; 1 ?
A.
1
1.m
e

B.
1.m
C.
2
11
hoaëc 1.mm
e
e
D.
2
1
.m
e
Câu 81. Giá trị b để hàm số
siny x bx
nghịch biến là:
A.
;1
B.
1;
C.
1;
D.
;1
Câu 82. Tìm tất cả các giá trị thực của tham số
m
để hàm số
( 3) (2 1)cosy m x m x
nghịch
biến trên
R
.
A.
2
4
3
m
B. Không có
m
. C.
1
3
2
m
. D.
1
2
2
m
Câu 83. Tìm m để hàm số
32
sin 3sin sin 4y x x m x
đồng biến trên khoảng



0;
2
.
A.
0m
B.
0m
C.
0m
D.
0m
Câu 84. Hàm số
2 cosy m x x
đồng biến trên khi
A.
0m
B.
01m
C.
1
0
2
m
D.
11
22
m
Câu 85. Cho hàm số
sin 3 cos .y x x mx
Tìm tất cả các giá trị thực của tham số
m
để hàm
số đồng biến trên
.
A.
2m 
B.
3m 
C.
2m
D.
1m
1A. Sự đồng biến, nghịch biến của hàm số
11
Câu 86. Cho hàm số
2sin tan 3 f x x x x
xác định, liên tục trên nửa khoảng
0;
2


.
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên nửa khoảng
0;
2


.
B. Hàm số có cực trị trên nửa khoảng
0;
2


.
C. Hàm số đồng biến trên nửa khoảng
0;
2


.
D. Hàm số đồng biến trên khoảng
0;
4



và nghịch biến trên khoảng
;
42




.
Câu 87. Cho bất đẳng thức
sinxx
(1). Khẳng định nào sau đây đúng?
A. (1) luôn đúng khi
0;
2
x
B. (1) luôn đúng khi
0;
2
x
C. (1) luôn đúng khi
0;
2
x
D. (1) luôn đúng khi
0;
2
x
Câu 88. Cho hàm số
sinx 3
y
sinx m
. Hàm số đồng biến trên
0;
2



khi:
A.
m 0 1 m 3
B.
3m
C.
0 m 3
D.
m3
Câu 89. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
2
cos
sin
mx
y
x
nghịch biến trên
;
32




.
A.
5
.
4
m
B.
1.m
C.
2.m
D.
0.m
Câu 90. Tìm m để hàm số
2
sin
cos
mx
y
x
nghịch biến trên
0;
6
?
A.
5
4
m
B.
1m
C.
2m
D.
0m
Câu 91. Tìm tất cả các giá trị thực của tham số m để hàm số
sin
sin 1
xm
y
x
nghịch biến trong
khoảng
;.
2



A.
1.m
B.
1.m
C.
1.m
D.
1.m
1A. Sự đồng biến, nghịch biến của hàm số
12
Câu 92. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
tan 2
tan
x
y
xm
đồng biến trên
khoảng



0;
4
A.
0m
B.
12m
C.
0m
hoặc
12m
D.
2m
Câu 93. Tìm tất cả các giá trị thực của m sao cho hàm số
tan 10
tan
x
y
xm
đồng biến trên khoảng
0; .
4



A. m
1 B. m
2
C.
1 10m
D. m
0
hoặc
1 10m
1C 2D 3C 4A 5C 6B 7A 8B 9D 10C
11D 12A 13D 14A 15B 16D 17C 18D 19B 20D
21D 22A 23A 24A 25C 26A 27C 28D 29B 30A
31B 32D 33A 34C 35D 36A 37A 38C 39D 40A
41A 42D 43D 44A 45B 46D 47A 48A 49A 50D
51D 52D 53B 54C 55C 56A 57C 58C 59A 60C
61A 62C 63C 64A 65A 66A 67A 68B 69B 70A
71C 72B 73A 74B 75A 76A 77D 78D 79B 80C
81B 82A 83C 84D 85A 86C 87B 88A 89A 90A
91B 92A 93D
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B. Cực trị của hàm số
13
HÀM BẬC BA
Tìm điểm cực đại, cực tiểu của hàm số
Câu 1. 
3
34y x x
là:
A.
x
1 B.
x
1 C.
x
3 D.
x
3
Câu 2. 

3
34y x x
là:
A.



1
;1
2
B.



1
;1
2
C.




1
;1
2
D.



1
;1
2
Câu 3. 
32
69y x x x
là
A.
1;4
B.
3;0
C.
0;3
D.
4;1
Câu 4. 
32
3 3 2y x x x
A.
3 4 2
B.
3 4 2
C.
3 4 2
D.
3 4 2
Câu 5. 
32
2 3 2y x x
là
A.
0; 2 .
B.
2;2 .
C.
1; 3 .
D.
1; 7 .
Câu 6. 
y
CD

32
1
32
3
y x x x
.
A.
11
y
3
CD
B.
5
y
3
CD
C.
y1
CD
D.
y7
CD
Câu 7. 
3
2
2
23
33
x
y x x
là
A. (-1;2) B.
2
3;
3



C. (1;-2) D. (1;2)
Câu 8. 
3
3y x x

A.  B. 
C. 
1x
D. 
Câu 9. 
32
y x 3x 2
là:
A. 3 B. 2 C. 1 D. 0
Câu 10. 
3
31y x x
. Tích c

tr

A. 0 B. -3 C. -6 D. 3
CỰC TRỊ CỦA HÀM SỐ
1B. Cực trị của hàm số
14
Câu 11. 
32
5 7 3y x x x
là:
A.
1;0
B.
0;1
C.
7 32
;
3 27



D.
7 32
;
3 27



Câu 12. 
32
1
3 9 5
8
y x x x
là
A. -1 B. 3 C. 0 D. 2
Câu 13. 
CT
y

32
2 3 2y x x
?
A.
3
CT
y
B.
2
CT
y
C.
0
CT
y
D.
1
CT
y
Tìm m để hàm số đạt cực đại, cực tiểu
Câu 14. 
2
3
1
4
33
mx
yx
 m 
A.
1m
B.
2m
C.
3m
D.
4m
Câu 15. 
32
( ) . (2 4) 1
32
xx
f x m m x
 
2x
.
A.
4m
B.
m
C.
4m
D.
4m
Câu 16.  
m

32
3 2 1y x mx x

1x

A. 
.m
B. 
.m
C.
6.m
D.
5
.
2
m
Câu 17. 
3 2 2
22y x mx m x

1x
khi
A.
2m
B.
3m
C.
1m
D.
1m 
Câu 18. 
32
3y x x mx
c
A.
0m
B.
0m
C.
0m
D.
0m
Câu 19. 
3 2 2
21y x mx m m x

1x
khi
A.
3m
B.
1m
C.
2m
D.
Câu 20. 
32
2 3 1 6 2y x m x m x

A.
3m
B.
3m
C.
m
D. 
m
Câu 21. Giá 
32
( 2) 3y m x x mx m

A.
3;1m
\{ 2}
B.
3;1m
C.
; 3 1;m  
D.
3m
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B. Cực trị của hàm số
15
Câu 22. a tham 
32
y x (m 1)x 2mx 3

x1
A.
m2
B.
5
m
4
C.
1
m
4
D.
m1
Câu 23. 
m

32
1y x mx x

1x
?
A.
0m
B.
1m
C.
2m
D.
2m
Tìm m để hàm số đạt cực đại, cực tiểu thỏa điều kiện cho trước
Câu 24. T

h
m s
32
1
( 2) (5 4) 3 1
3
y x m x m x m
x
1
, x
2
sao cho
12
2.xx
A.
0m
B.
1m 
C.
0m
D.
1m 
Câu 25.  m 
3
2
( 2) (4 8) 1
3
x
y m x m x m

12
,xx
sao cho
12
2xx
A.
1
2
m
B.
3
2
m
C.
1 m
D.
2m
Câu 26. 
32
32
xx
y mx
có hoành

A.
2m 
B. m > 1. C.
2m
D. m >2.
Câu 27.       
32
31y x x mx
    
12
,xx
 
n
22
12
3xx
là:
A.
2m 
B.
3
2
m
C.
1m
D.
1
2
m
Câu 28. 
3 2 3
34y x mx m


20AB
A.
1m
B.
2m
C.
1; 2mm
D.
1m
Câu 29. 

2
1
x mx m
y
x

A.
25
B.
52
C.
45
D.
5
Câu 30. 
32
32y x x mx
(m 
m


a  th h
m s 
1yx
khi
A.
0m
B.
1m
C.
2m
D.
3m
1B. Cực trị của hàm số
16
Câu 31. 
3 2 2 2
3 3( 1) 3 1y x x m x m
. Tìm
m


A.
0
1
2
m
m
B.
0
1
2
m
m
C.
1
2
m
D.
1
2
m
Câu 32. 
32
3 3 1y x mx m
(m m 

d:
8 74 0xy
A.
1m
B.
1m 
C.
2m
D.
2m 
Câu 33. 
3 2 3
34y x mx m

m
C

()
m
C

 :
yx
A.
1
2
m 
B.
1
2
m 
C.
0m
D.
1
;0
2
mm
Câu 34. 
m

3 2 3
: 3 2
m
C y x mx m
có hai

,AB

AB

:2d y x
.
A.
11
;.
22
m




B.
11
;.
22
m




C.
11
;.
22
m




D.
11
;.
22
m




Câu 35.  
2;2M
  
3 2 3
: 3 3 1 1
m
C y x mx m x m
   
m
C

,AB
và tam giác
ABM

M

m


A.
1m
. B.
1m
.
C. Không có
m
. D. 
m
.
HÀM BẬC BỐN
Tìm điểm cực đại, cực tiểu của hàm số
Câu 36. 
CT
y

42
21y x x
.
A.
2
CT
y
B.
1
CT
y 
C.
1
CT
y
D.
0
CT
y
Câu 37 
4
2
5
3
22
x
yx
có   là
A. 3 B. 0 C. 2 D. 1
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B. Cực trị của hàm số
17
Câu 38. 
43
43
xx
y 
là:
A. 0 B.
3
4
C.
1
12
D.
3
4
Câu 39. 
42
42y x x
A.  B. 
C.  D. 
Tìm m để hàm số đạt cực trị thỏa điều kiện cho trước
Câu 40. 
4
2
4
x
y mx m

A.
0m
B.
0m
C.
0m
D.
0m
Câu 41. 
4 2 2
2y x mx m m
có 3 
A.
0m
B.
0m
C.
0m
D.
0m
Câu 42. 
42
y 2x 4x 1

giác ABC là:
A. 4 B. 3 C. 2 D. 1
Câu 43. Tìm m 
4 2 2
21y x m x m


A. m = 2. B. m > 4. C. m =
2. D.
5m 
Câu 44. 
4 2 2
2 2 4
m
y x mx m C


A.
1m 
B.
1m 
C.
2m 
D.
1m
Câu 45. 
4 2 4
22y x mx m m

m
C
) có

A.
16.m
B.

3
16.m
C.
3
16.m
D.
5
16.m
Câu 46. Các giá 
m

4 2 2
2( 1)y x m x m


A.
0m
B.
0m
C.
0m
D.
m
Câu 47. 
M

42
21y x mx


A.
3
2 5.m 
B.
3
2 6.m
C.
0.m
D.
3
2 2.m
Câu 48. 
42
1
(3 1) 2( 1)
4
y x m x m
m m 

A.
1
3
m
B.
1
3
m
C.
2
3
m
D.
12
;
33
mm
1B. Cực trị của hàm số
18
Câu 49. 
4 2 4
22y x mx m m


A. m = 1 B. m = -1 C.
3
3m 
D.
3
3m
BÀI TẬP TỔNG HỢP
Câu 50. 
A.
2
2
2
x
y
x
B.
2
2
x
y
x

C.
2
2
x
y
x
D.
2
2
x
y
x

Câu 51. 
A.
2
21
x
y
x
B.
42
45y x x
C.
3
23y x x
D.
32
1
25
3
y x x
Câu 52. 
11
4
yx
x

12
,xx

12
xx

A. 4 B. -4 C. 2 D. 0
Câu 53. 
2 3 4
f ' x x x 1 x 2 x 3

là:
A. 4 B. 3 C. 2 D. 1
Câu 54. 
32
(1 )y x x
có
A.  B.  C.  D. 
Câu 55. 
fx
 
x
1 1
y
0
y
2
3
A. 
1x

1x
B. 
3
C. 
2
D. 
Câu 56. 
2
23y x x
A. A(1;0) B. B(3;0)
C.  D. 
Câu 57. 

xxxy )2cos1()sin1(2
3
4
23

A.
2
2
k
B.
k
C.
2
2
k
D.
k
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B. Cực trị của hàm số
19
Câu 58. 
fx

0
.x

fx

0
x
thì
A.
0
'0fx
B.
0
'0fx
C.
0
'0fx
D.
0
'0fx
Câu 59. 
A. 
B. 
43m

ym

C. 
1x 
D. 
0; 3
Câu 60. 
fx
 
0

A. 
0
'0fx

0
x
B. 
0

0
'0fx
C. 
0
thì
0
'0fx
D. 
0
thì
0
'0fx
Câu 61. 
()y f x
 
+
∞
∞
+
+
_
1
0
0
0
-1
y
y'
x

A. 
B. 
1
.
C. 
1x

0x
.
D.  
Câu 62. 
()y f x
 
x 0 2
y’ + - 0 +
y 0
3
34
1B. Cực trị của hàm số
20

A. 
B. 
3
34
C.  
3
34
D. 
0x

2x
1A 2D 3A 4A 5A 6A 7D 8D 9D 10B
11C 12C 13A 14C 15C 16A 17C 18A 19B 20B
21A 22C 23C 24C 25B 26A 27B 28A 29A 30A
31D 32C 33A 34A 35A 36D 37A 38C 39A 40C
41D 42C 43A 44D 45D 46A 47D 48B 49D 50D
51D 52D 53C 54B 55A 56C 57A 58C 59B 60D
61C 62D
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1C. GTLN, GTNN của hàm số
21
HÀM BẬC BA, BẬC BỐN
Câu 1. Giá trị lớn nhất của hàm số
32
33y x x
trên đoạn
0; 3
là
A.
2
B. 2 C. 3 D.
1
Câu 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
32y x x
trên đoạn
1; 3
là:
A.
4; 0
B.
2 0; 4
C.
2 0; 0
D.
20; 4
Câu 3. Giá trị lớn nhất của hàm số
32
3 9 35y x x x
trên đoạn [-4;4] bằng ?
A.
40
B. 8 C. -41 D. 15
Câu 4. Cho hàm số
3
2
2 3 4
3
x
y x x
xác định trên [-4;0]. Gọi M và m lần lượt là GTLN và
GTNN cùa hàm hàm số thì M + m bằng:
A.
28
3
B.
28
3
C.
28
3
D. -35
Câu 5. Giá trị lớn nhất của hàm số y = 2x
3
+ 3x
2
– 12x + 2 trên đoạn [– 1; 2] là
A. 6 B. 10 C. 15 D. 11
Câu 6. Tìm GTLN và GTNN của hàm số
32
35f x x x
trên đoạn
1;1
A.
1;1 1;1
5 0; 1 1Max f x x Min f x x

B.
1;1 1;1
3; 1Max f x Min f x


C.
1;1 1;1
1; 1Max f x Min f x

D.
1;1 1;1
2; 0Max f x Min f x


Câu 7. Kết luận giá trị nhỏ nhất của hàm số
3
31 y x x
trên khoảng (-;1) là
A.
;1
min 3y

B.
;1
min 1y


C.
;1
min 2y

D.
;1
min 3y


Câu 8. Trên khoảng (0; +) thì hàm số
3
31y x x
:
A. Có giá trị nhỏ nhất là min y = 3 B. Có giá trị lớn nhất là max y = –1
C. Có giá trị nhỏ nhất là min y = –1 D. Có giá trị lớn nhất là max y = 3
Câu 9. Cho hàm số
32
32y x x
. Chọn phương án đúng trong các phương án sau
A.
1;1 1;1
max 0,min 2yy

B.
1;1 1;1
max 2,min 0yy


C.
1;1 1;1
max 2,min 2yy

D.
1;1 1;1
max 2,min 1yy

GTLN, GTNN CỦA HÀM SỐ
1C. GTLN, GTNN của hàm số
22
Câu 10. Cho hàm số
3
35y x x
. Chọn phương án đúng trong các phương án sau
A.
0;2
max 5y
B.
0;2
min 3y
C.
1;1
max 3y
D.
1;1
min 7y
Câu 11. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
42
23y x x
trên
0;2
là:
A.
11, 2Mm
B.
3, 2Mm
C.
5, 2Mm
D.
11, 3Mm
Câu 12. Giá trị nhỏ nhất của hàm số
42
21y x x
trên đoạn
1;1
là:
A.
1
B. 1 C. 0 D. 2
HÀM PHÂN THỨC
Câu 13. Tìm giá trị lớn nhất của hàm số
31
3
x
y
x
trên đoạn
[0;2]
.
A.
[0;2]
1
max
3
y
B.
[0;2]
max 5y
C.
[0;2]
max 5y
D.
[0;2]
1
max
3
y
Câu 14. Tìm GTLN và GTNN của hàm số
1
1
x
fx
x
trên nửa khoảng
2;3
A.
1;1 1;1
3; 2Max f x Min f x


B.
2;3
2Min f x
, không tồn tại
2;3
Max f x
C.
1;1
2;Max f x
không tồn tại
1;1
Min f x
D.
1;1 1;1
2; 1Max f x Min f x


Câu 15. Tìm giá trị lớn nhất của hàm số
4
1
2
yx
x
trên đoạn [-1; 5]
A.
1;5
max 3y
B.
1;5
max 4y
C.
1;5
46
max
7
y
D.
1;5
max 5y

Câu 16. Tìm giá trị lớn nhất của hàm số
2
31
1
xx
y
x
trên đoạn
2;5
?
A.
2;5
max 1y
B.
2;5
11
max
4
y
C.
2;5
max 1y
D.
2;5
11
max
4
y
Câu 17. Tìm giá trị nhỏ nhất của hàm số
2
2
x
y
x
trên
1;4
.
A.
1;4
min 1y 
B.
1;4
min 0y
C.
1;4
min 6y
D.
1;4
min 8y
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1C. GTLN, GTNN của hàm số
23
Câu 18. Cho hàm số:

2
4
1
xx
y
x
, chọn phương án đúng trong các phương án sau
A.
4; 2 4; 2
16
max ,min 6
3
yy
B.
4; 2 4; 2
max 6,min 5yy
C.
4; 2 4; 2
max 5,min 6yy
D.
4; 2 4; 2
max 4,min 6yy
Câu 19. Cho hàm số
2
55
1
xx
y
x

xác định, liên tục trên đoạn
1
1;
2



. Khẳng định nào sau
đây đúng?
A. Hàm số có giá trị nhỏ nhất là
1
2
y



, giá trị lớn nhất là
1.y
B. Hàm số có giá trị nhỏ nhất là
1y
, giá trị lớn nhất là
1
.
2
y



C. Hàm số có giá trị nhỏ nhất là
1y
và
1
2
y



, giá trị lớn nhất là
0.y
D. Hàm số có giá trị nhỏ nhất là
0y
, giá trị lớn nhất là
1
.
2
y



Câu 20. Cho
2
2
1x
f x x
x 4x 5 4

. Gọi
0;3
0;3
M maxf x ;m minf x
, khi đó: M – m
bằng
A.
3
5
B. 1 C.
7
5
D.
9
5
Câu 21. Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số
2
1
x m m
y
x
trên
[0;1]
bằng
2
A.
1
2
m
m
B.
1
2
m
m
C.
1
2
m
m
D.
1
2
m
m
CÁC HÀM KHÁC
Câu 22. Giá trị nhỏ nhất của hàm số f(x) =
2
25xx
trên đoạn [-1;3] là:
A.
22
B.
5
2
C. 2 D.
23
Câu 23. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
63yx
trên đoạn [-1;1] lần lượt là :
A.
6
và 0 B. 3 và
6
C. 1 và -1 D. 3 và
3
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1C. GTLN, GTNN của hàm số
24
Câu 24. Giá trị lớn nhất của hàm số
54yx
trên đoạn [-1 ; 1 ] bằng.
A. 9 B. 3 C. 1 D. 0
Câu 25. Giá trị lớn nhất của hàm số
12y x x
trên
1
4;
2
bằng
A. -1 B.
1
2
C. 0 D. 1
Câu 26. Tìm GTLN và GTNN của hàm số
2
4y x x
A.
2;2 2;2
2 2; 2Max f x Min f x

B.
2;2 2;2
2; 2Max f x Min f x

C.
2 2; 2
DD
Max f x Min f x
D.
2;2 2;2
2; 2Max f x Min f x

Câu 27. Tìm giá trị lớn nhất của hàm số
2 1 6y x x
A. 2 B. 5 C. 3 D. 4
Câu 28. Hàm số
2
1y x x
đạt giá trị lớn nhất bằng
A.
1
2
B.
1
2
C.
2
2
D. -1
Câu 29. Tìm giá trị nhỏ nhất của hàm số
4
2 sin cos2 5y x x
A.
11
min
4
y
B.
11
min
2
y
C.
min 2y
D.
min 3y
Câu 30. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
2
2sin cos 1y x x
. Tổng M+m bằng
A. 0 B. 2 C.
8
25
D.
4
25
Câu 31. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
sin2 -2 3cos 2 3y x x
.
Tính
Mm
.
A.
43 Mm
B.
23Mm
C.
4Mm
D.
1 2 3 Mm
Câu 32. Tìm giá trị lớn nhất của hàm số
44
sin cos sin cosy x x x x
.
A.
1
max
2
y
B.
9
max
8
y
C.
1
max
4
y
D.
3
max
4
y
Câu 33. Cho hàm số
sin 2cos 1
sin cos 2
xx
y
xx


. Khẳng định nào sau đây là đúng?
A.
max 2; min 1yy
. B.
max 1; min 2yy
.
C.
max 2;min 1yy
. D.
max 1;min 2yy
.
Câu 34. Giá trị nhỏ nhất của hàm số
2
22
log 4 log 1y x x
trên đoạn
[1; 8]
là
A.
[1;8]
Min 2
x
y
B.
[1;8]
Min 1
x
y
C.
[1;8]
Min 3
x
y
D. Đáp án khác
1C. GTLN, GTNN của hàm số
25
Câu 35. Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số :
( ) 3y f x x
trên đoạn
1:1
là:
A. 0 B. 3 C. 4 D. 7
BÀI TOÁN ỨNG DỤNG
Câu 36. Một tam giác vuông có cạnh huyền bằng
52
thì diện tích của nó lớn nhất là:
A.
25
8
B.
25
4
C.
25
2
D. 25
Câu 37. Chu vi của một tam giác là
16cm
, biết độ dài một cạnh của tam giác là
6a cm
. Tìm
độ dài hai cạnh còn lại
,bc
của tam giác sao cho tam giác đó có diện tích lớn nhất.
A.
4 ; 6b cm c cm
B.
3 ; 7b cm c cm
C.
2 ; 8b cm c cm
D.
5b c cm
Câu 38. Tìm tam giác vuông có diện tích lớn nhất, nếu tổng của cạnh góc vuông và cạnh huyền
bằng hằng số a (a > 0), thì cạnh góc vuông của tam giác đó là:
A. 2a B.
3
a
C.
2
a
D.
2a
Câu 39. Một hình chữ nhật có diện tích là
100
thì chu vi hình chữ nhật nhỏ nhất khi chiều rộng
x
và chiều dài
y
tương ứng là:
A.
25; 4xy
B.
10; 10xy
C.
20; 5xy
D.
50; 2xy
Câu 40. Người ta muốn mạ vàng cho một cái hộp có đáy hình vuông không nắp có thể tích là 4 lít.
Tìm kích thước của hộp đó để lượng vàng dùng mạ là ít nhất. Giả sử độ dày của lớp mạ tại mọi nơi
trên mặt ngoài hộp là như nhau.
A. Cạnh đáy bằng 2, chiều cao bằng 1 B. Cạnh đáy bằng 1, chiều cao bằng 2.
C. Cạnh đáy bằng 3, chiều cao bằng 4 D. Cạnh đáy bằng 4, chiều cao bằng 3.
Câu 41. Người ta cần làm một hộp theo dạng một khối lăng trụ đều không nắp với thể tích lớn
nhất từ một miếng tole hình vuông có cạnh là 1. Thể tích của hộp cần làm là
A.
5
8
V
B.
2
27
V
C.
3
27
V
D.
6
11
V
Câu 42. Một người thợ muốn làm một cái thùng hình hộp chữ nhật không nắp có chiều dài đáy
gấp đôi chiều rộng và có thể tích
3
10 m
. Giá tiền vật liệu làm đáy thùng là
10.000
đồng
2
/m
, vật
liệu làm mặt bên thùng là
5.000
đồng
2
/m
. Hãy xác định kích thước thùng (rộng x dài x cao) để
chi phí làm thùng là nhỏ nhất.
A.
3 3 3
4 4 225
x 2 x 5
15 15 16
m
B.
15 15 16
x 2 x 5
4 4 225
m
C.
5
15 x 2 15 x
15
m
D.
33
3
15 15 16
x 2 x 5
4 4 225
m
Câu 43. Một nhà máy sản suất máy tính vừa làm ra x sản phẩm máy tính và bán với giá p=1000-x
cho một sản phẩm. Biết rằng tổng chi phí để làm ra x sản phẩm là C(x)=3000+20x. Vậy nhà máy
cần sản xuất và bán bao nhiêu sản phẩm để thu được lợi nhuận tốt nhất.
A. 490 B. 480 C. 500 D. 510
1C. GTLN, GTNN của hàm số
26
Câu 44. Một công ty đánh giá rằng sẽ bán được N lô hàng nếu tiêu phí hết số tiền là x vào việc
quảng cáo, N và x liên hệ với nhau bằng biểu thức
2
(x) 30 6, 0 30N x x x
( x tính
theo đơn vị triệu đồng). Số lô hàng lớn nhất mà công ty có thể bán sau đợt quảng cáo và số tiền đã
dành cho việc quảng cáo đó lần lượt là :
A. N(x) = 231; x = 15 B. N(x) = 6; x = 30
C. N(x)= 226; x = 10 D. N(x)= 131; x = 5
Câu 45. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức
2
1
( ) (30 )
40
F x x x
,
trong đó
x
là liều lượng thuốc được tiêm cho bệnh nhân (
x
được tính bằng miligam).
Liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giàm nhiều nhất là:
A. 20 mg B. 30 mg C. 40 mg D. 50 mg
Câu 46. Xét
,xy
là các số thực không âm thỏa mãn điều kiện
2.xy
Tìm giá trị nhỏ nhất của
biểu thức
22
4.S x y xy
A.
min 3.S 
B.
min 4.S 
C.
min 0.S
D.
min 1.S
Câu 47. Xét
,xy
là các số thực dương thỏa mãn điều kiện
2xy
. Đặt
1
.
1
S xy
xy

Khẳng định
nào sau đây đúng ?
A. Biểu thức
S
không có giá trị lớn nhất. B. Biểu thức
S
không có giá trị nhỏ nhất.
C.
3
min .
2
S
D.
max 1.S
Câu 48. Xét x, y là các số thực thuộc đoạn
1;2
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất cùa biểu thức
xy
S
yx
. Tính
mM
A.
5
mM
2
B.
m M 4
C.
9
mM
2
D.
m M 3
Câu 49. Xét
yx,
là các số thực thuộc (0;1] thỏa mãn điều kiện
xyyx 4
. Đặt
.
22
yxS
Khẳng định nào sau đây là đúng ?
A. Biểu thức
S
không có giá trị nhỏ nhất. B. max
9
10
S
C. Biểu thức
S
không có giá trị lớn nhất. D. min
0S
Câu 50. Xét
x
,
y
là các số thực thỏa mãn điều kiện
22
1xy
. Đặt
2
22
26
23
x xy
S
x xy y

. Khẳng
định nào sau đây là đúng?
A. Biểu thức
S
không có giá trị nhỏ nhất. B.
min 6S 
C. Biểu thức
S
không có giá trị lớn nhất. D.
max 2S
1C 2C 3A 4A 5C 6A 7B 8D 9C 10B
11A 12A 13D 14B 15C 16B 17A 18C 19C 20D
21D 22C 23D 24B 25D 26C 27B 28A 29B 30C
31B 32B 33B 34C 35D 36C 37D 38B 39B 40A
41B 42D 43A 44A 45A 46A 47B 48C 49B 50B
1D. Đường tiệm cận
27
Tìm phương trình tiệm cận ngang, tiệm cận đứng
Câu 1. Đồ thị hàm số
21
31
x
y
x
có đường tiệm cận ngang là:
A.
2
3
x
B.
2
3
y
C.
1
3
x 
D.
1
3
y 
Câu 2. Tiệm cận ngang của đồ thị hàm số
2
21
43
x
y
x
là:
A. y = 1 B. y = 2 và y = - 2. C. y = 2 D. y = 1 và y = -1.
Câu 3. Phương trình các đường tiệm cận ngang của đồ thị hàm số
2
2
41
x
y
xx

là:
A.
1
2
y
và
1
2
y 
B.
2y
C.
1
4
y
D.
0y
Câu 4. Đồ thị hàm số
21
2
x
y
x

có tiệm cận đứng và tiệm cận ngang lần lượt là:
A.
2; 2xy
B.
2; 2xy
C.
2; 2xy
D.
2; 2xy
Câu 5. Phương trình các đường tiệm cận của đồ thị hàm số
23
1
x
y
x
là:
A.
1x
và
2y
B.
1x 
và
3y 
C.
3x 
và
1y 
D.
2x
và
1y
Câu 6. Cho đồ thị hàm số
42
21
x
y
x
. Phương trình các đường tiệm cận của đồ thị hàm số là
A.
1
2,
2
yx
B.
1
2,
2
xy
C.
1
,4
2
xy
D.
1
2,
2
yx
Câu 7. Đồ thị hàm số
23
2
x
y
x
có:
A. Có tiệm cận đứng là
2x
và không có tiệm cận ngang
B. Có tiệm cận ngang
2y
và không có tiệm cận đứng
C. Có tiệm cận đứng là
2y
và tiệm cận ngang
2x
D. Có tiệm cận đứng là
2x
và tiệm cận ngang
2y
ĐƯỜNG TIỆM CẬN
1D. Đường tiệm cận
28
Câu 8. Đường tiệm cận ngang của hàm số
3
21
x
y
x
là
A.
1
2
x
B.
1
2
x 
C.
1
2
y 
D.
1
2
y
Câu 9. Đường tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
là:
A.
1y
B.
2x
C.
2y
D.
1x
Câu 10. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào sau đây?
A.

2
2 3 2
.
2
xx
y
x
B.
22
.
2
x
y
x
C.
1
.
1
x
y
x
D.
2
1
.
1
x
y
x
Câu 11. Cho hàm số
31
21
x
y
x
. Khẳng định nào sau đây đúng ?
A. Đồ thị hàm số có tiệm cận ngang là
3
2
y
B. Đồ thị hàm số có tiệm cận đứng là
3
2
y
C. Đồ thị hàm số có tiệm cận đứng là
1
2
x 
D. Đồ thị hàm số không có tiệm cận
Tìm m để đồ thị hàm số có tiệm cận ngang, tiệm cận đứng thỏa điều kiện cho
trước
Câu 12. Đồ thị hàm số
2
m m x 1
y
x2

có đường tiệm cận ngang qua điểm A(–3;2) khi:
A.
m 1 m 2
B.
m 1 m 2
C.
m 1 m 2
D.
m 1 m 2
Câu 13. Cho hàm số
mx
y
xm
1
2
để tiệm cận đứng của đồ thị hàm số đi qua điểm
A 1; 2
thì
A.
m 2
B.
m 2
C.
m
1
2
D.
m
1
2
Câu 14. Cho hàm số
a1x
y
xd
. Nếu đồ thị hàm số có tiệm cận đứng x = 1 và đi qua điểm A(2; 5)
thì phương trình của hàm số là:
A.
2
1
x
y
x
B.
21
1
x
y
x
C.
32
1
x
y
x

D.
1
1
x
y
x
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1D. Đường tiệm cận
29
Câu 15. Tìm tất cả các giá trị của tham số
m
sao cho đồ thị hàm số
2
:
1
m
xm
Cy
mx
có tiệm cận
đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện
tích bằng
8
.
A.
1
4
m 
B.
1
2
m 
C.
1
8
m 
D. Không có
m
thỏa mãn
Câu 16. Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số
2
1
mx
y
xm

tiếp xúc với parabol
2
5yx
.
A. Không có giá trị m B.
5m
C.
6m
D. Với
m
Câu 17. Tìm m để đồ thị hàm số
2
4
2
xm
y
x

có tiệm cận đứng x = 2:
A. m = 1 B. m = -1 C. m = 2 D.
1m 
và
2m
Câu 18. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
:
m
x
Cy
xm
có tiệm cận.
A.
1m
B. Với mọi
m
C.
0m
D. Không có
m
.Câu 19. Với điều kiện nào của tham số m cho dưới đây, đồ thị hàm số
22
2
( ) :
3

m
x
Cy
x x m
chỉ
có một tiệm cận đứng?
A.
.m
B.
2.m
C.
2.m
D. Không có m
Câu 20. Để đường cong
2
2
36
( ):
xx
Cy
x ax a


có đúng 1 đường tiệm cận đứng thì giá trị của
a
là
A.
1.a
B.
2.a
C.
0
.
4
a
a
D.
1
.
2
a
a
Câu 21. Tìm tất cả các giá trị của m để hàm số
2
3
2
x
y
mx
có hai tiệm cận ngang.
A. m = 0 B. m > 0 C. m < 0 D. m =-1
Câu 22. Với giá trị nào của tham số
m
cho dưới đây thì, đồ thị hàm số
1
1
xm
y
x

không có tiệm
cận ngang?
A. Với mọi
m
. B.
0m
C.
1m
D. Không có
m
.
Câu 23. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
2
1
:
m
x
Cy
x x m

có hai
đường tiệm cận đứng.
A. Mọi
m
. B.
1
.
4
2
m
m

C.
1
.
4
2
m
m

D.
2.m
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1D. Đường tiệm cận
30
Tìm số tiệm cận của đồ thị hàm số
Câu 24. Số đường tiệm cận ngang của đồ thị hàm số
2
2x 3
y f(x)
x1

là:
A. 3 B. 2 C. 1 D. 0
Câu 25. Hàm số
2
31
1
x
y
x
có mấy tiệm cận ngang
A. 0 B. 1 C. 2 D. 3
Câu 26. Cho hàm số
1
1
y f x
x

. Số đường tiệm cận của đồ thị hàm số là
A. 0 B. 2 C. 1 D. 3
Câu 27. Cho hàm số
3
2
y
x
.Số tiệm cận của đồ thị hàm số bằng
A. 0 B. 2 C. 3 D. 1
Câu 28. Cho hàm số
31
2
x
y
x
. Số đường tiệm cận của đồ thị hàm số bằng
A. 0 B. 2 C. 3 D. 1
Câu 29. Đồ thị hàm số
2
29
1
x
y
x
có mấy đường tiệm cận ?
A. 1 B. 2 C. 3 D. Không có tiệm cận
Câu 30. Cho hàm số
2
1
2
xx
y
x

. Số đường tiệm cận của đồ thị hàm số bằng:
A.
0
B.
1
C.
2
D.
3
Câu 31. Số đường tiệm cận của đồ thị hàm số
2
1x
y
x
là:
A. 0 B. 1 C. 2 D. 3
Câu 32. Cho hàm số
2
83
6
x
y
xx

. Khẳng định nào sau đây là đúng
A. Đồ thị hàm số có 1 tiệm cận đứng và 1 tiệm cận ngang.
B. Đồ thị hàm số có 2 tiệm cận đứng và 1 tiệm cận ngang.
C. Đồ thị hàm số có 2 tiệm cận ngang và 1 tiệm cận đứng.
D. Đồ thị hàm số không có tiệm cận.
Câu 33. Số đường tiệm cận của đồ thị hàm số
2
2
3
4
xx
y
x
là:
A. 1 B. 2 C. 3 D. 4
1D. Đường tiệm cận
31
Một số bài tập tổng hợp
Câu 34. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số y = x
3
+ 3x – 2 đồng biến trên .
B. Đồ thị hàm số y = 3x
4
+ 5x
2
– 1 cắt trục hoành tại 2 điểm phân biệt.
C. Đồ thị hàm số y =
2
21
1
x
x
có 2 đường tiệm cận.
D. Đồ thị hàm số y =
21
1
x
x
nhận giao điểm hai đường tiệm cận là tâm đối xứng.
Câu 35. Bảng biến thiên sau đây là của hàm số nào?
x

2 +
y
y
1


1
A.
2x 1
.
1
y
x
B.
1
.
1
x
y
x
C.
3
.
2
x
y
x
D.
1
.
2
x
y
x
Câu 36. Cho
C
là đồ thị hàm số
1
2
x
y
x
. Tìm các điểm trên
C
sao cho tổng khoảng cách
từ điểm đó đến 2 tiệm cận là nhỏ nhất
A.
B.
13
1 3;
2



C.
1 3;1 3
D.
2 3;1 3
và
2 3;1 3
Câu 37. Gọi I là giao điểm của tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
(3m 1)x 4
y
xm

. Hỏi I luôn thuộc đường thẳng nào dưới đây?
A.
y 3x 1
B.
y 3x 1
C.
y 3x 1
D.
y 3x 1
Câu 38. Tìm tất cả các điểm M trên đồ thị (C) của hàm số
2
1
x
y
x
sao cho khoảng cách từ M
đến tiệm cận đứng của (C) bằng khoảng cách từ M đến trục Ox.
A.
3 13 1 13 3 13 1 13
( ; ), ( ; )
2 2 2 2
MM
B.
3 13 1 13 3 13 1 13
( ; ), ( ; )
2 2 2 2
MM
C.
3 13 1 13
( ; )
22
M
D.
3 13 1 13
( ; )
22
M
1D. Đường tiệm cận
32
Câu 39. Cho hàm số
2
1
xx
y
x
. Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số đã cho không có tiệm cận đứng.
B. Đồ thị của hàm số đã cho có một tiệm cận ngang.
C. Đồ thị của hàm số đã cho có hai tiệm cận ngang là
1x 
và
1x
D. Đồ thị của hàm số đã cho có hai tiệm cận ngang là
1y 
và
1y
1B 2A 3A 4B 5B 6A 7D 8D 9C 10C
11A 12B 13B 14B 15B 16B 17D 18C 19B 20C
21B 22B 23B 24B 25C 26B 27B 28B 29C 30D
31D 32B 33C 34C 35D 36D 37B 38A 39D
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1E. Đồ thị của hàm số
33
Câu 1. Đồ thị hàm số
1
1
x
y
x
có dạng:
A. B. C. D.
-2 -1 1 2 3
-3
-2
-1
1
2
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 2. Đồ thị nào sau đây là đồ thị của hàm số y = x
3
+ x – 2:
A.
2
2
4
1
B.
4
2
2
1
C.
4
2
2
1
D.
4
2
2
1
Nguyễn Văn Lực
www.facebook.com/VanLuc168
ĐỒ THỊ CỦA HÀM SỐ
1E. Đồ thị của hàm số
34
Câu 3. Đường cong trong hình dưới đây là đồ thị của hàm số
42
4y x x
.
Dựa vào đồ thị, phương trình
42
4 1 0x x m
có 4 nghiệm phân biệt khi
A.
51m
B.
04m
C.
51m
D.
31m
x
y
4
O
1
Câu 4. Đường cong bên là đồ thị của hàm số:
A.
3
y x 3x 2
B.
4
2
x
y 2x 2
4
C.
2x 1
y
x1
D.
1 2x
y
x1
Câu 5. Đồ thị hàm số
42
21y x x
có dạng:
A. B. C. D.
-2 -1 1 2
-2
-1
1
2
x
y
-2 -1 1 2
-2
-1
1
2
x
y
-2 -1 1 2
-2
-1
1
2
x
y
-2 -1 1 2
-2
-1
1
2
x
y
1E. Đồ thị của hàm số
35
Câu 6. Đồ thị sau đây là của hàm số nào?
A.
yx
3
3x 1.
B.
yx
32
3x 1.
C.
yx
3
3x+1.
D.
yx
32
3x 1.
Câu 7. Đồ thị sau đây là của hàm số:
42
4y x x
.Với giá trị nào của m thì phương trình:
42
4 2 0x x m
có bốn nghiệm phân biệt ? Chọn câu đúng.
A.
04m
B.
04m
C.
26m
D.
06m
4
2
-2
-
2
2
-2
2
O
Câu 8. Đồ thị sau đây là của hàm số nào ?
A.
21
1
x
y
x
B.
2
1
x
y
x
C.
1
1
x
y
x
D.
2
1
x
y
x
5
5
4
2
2
4
1
1
-2
x
y
1
3
-1
-2
-1
2
1
O
1E. Đồ thị của hàm số
36
Câu 9. Đồ thị hình bên là của hàm số:
A.
3
2
1
3
x
yx
B.
32
31y x x
C.
32
31y x x
D.
32
31y x x
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 10. Đường cong nào trong hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A,
B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A.
3
3y x x
B.
3
3yx
C.
3
3y x x
D.
3
3y x x
x
y
O
-
-
-
\Câu 11. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hàm số đó là
A.
42
22y x x
B.
3
23 y x x
C.
42
23 y x x
D.
3
23 y x x
.
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1E. Đồ thị của hàm số
37
Câu 12. Đường cong trong hình bên là đồ thị của hàm số nào?
A.
32
2 3 2y x x
B.
32
2 3 2y x x
C.
3
2 6 2y x x
D.
32
2 3 2y x x
Câu 13. Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên
A.
3
31y x x
B.
3
31y x x
C.
3
31y x x
D.
3
31y x x
Câu 14. Đường cong ở hình dưới là đồ thị của hàm số nào sau đây
A.
3
3yx
B.
3
62y x x
C.
3
1yx
D.
3
31y x x
O
y
x
1
1E. Đồ thị của hàm số
38
Câu 15. Đồ thị sau đây là của hàm số nào ?
A.
32
3y x x
B.
32
3y x x
C.
32
3y x x
D.
32
3y x x
Câu 16. Đồ thị dưới đây là đồ thị hàm số
A.
32
34y x x
B.
32
34y x x
C.
42
23y x x
D.
1
1
x
y
x
Câu 17. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
1
1
x
y
x
B.
1
1
x
y
x
C.
1
1
x
y
x
D.
1
1
x
y
x
x
y
3
2
O
4
2
1
1E. Đồ thị của hàm số
39
2
-2
-1
1
O
-1
Câu 18. Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên
A.
3
3y x x
B.
3
3y x x
C.
3
3y x x
D.
3
3y x x
Câu 19. Đường cong cho bởi hình sau là đồ thị của đồ thị hàm số nào ?
A.
42
31y x x
B.
42
1
31
4
y x x
C.
42
21y x x
D.
42
21y x x
Câu 20. Đồ thị sau đây là của hàm số nào? Chọn câu đúng.
A.
21
1
x
y
x
B.
1
1
x
y
x
C.
2
1
x
y
x
D.
3
1
x
y
x
4
2
-1
2
O
1
2
-2
1
1E. Đồ thị của hàm số
40
Câu 21. Cho hàm số
()y f x
xác định và liên tục trên và có bảng biến thiên như sau:
-
∞
-
∞
3
-
0
1
+
+
0
0
+
∞
-
∞
y
y'
x
Khẳng định nào sau đây là đúng?
A. Hàm số không có cực trị.
B. Hàm số có giá trị cực tiểu bằng 3.
C. Hàm số có giá trị lớn nhất bằng 3 và không có giá trị nhỏ nhất.
D. Hàm số đạt cực tiểu tại
0x
và đạt cực đại tại
1x
.
Câu 22. Đồ thị hình bên dưới là đồ thị của hàm số nào sau đây?
A.
42
2 3.y x x
B.
42
2.y x x
C.
42
2.y x x
D.
42
2 3.y x x
y
x
-1
-1
2
1
O
1
1C 2A 3D 4C 5D 6C 7C 8B 9B 10D
11C 12A 13B 14A 15D 16A 17B 18C 19C 20A
21C 22C
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1F. Bài toán tương giao
41
HÀM BẬC BA
Câu 1. Biết rằng đường thẳng
23yx
cắt đồ thị hàm số
32
23y x x x
tại hai điểm
phân biệt A và B, biết điểm B có hoành độ âm. Tìm
B
x
.
A.
0.
B
x
B.
2.
B
x 
C.
1.
B
x 
D.
5.
B
x 
Câu 2. Số giao điểm của đường cong
32
21y x x x
và đường thẳng
12yx
bằng:
A. 0 B. 1 C. 2 D. 3
Câu 3. Biết rằng đồ thị của hàm số
32
32y x x x
cắt đường thẳng
22yx
tại ba điểm
phân biệt. Kí hiệu ba điểm đó là
11
;A x y
,
22
;B x y
và
33
;C x y
. Khi đó tổng
1 2 3
x x x
bằng:
A. 2 B. 3 C. 1 D.
23
Câu 4. Biết rằng đường thẳng
56yx
cắt đồ thị hàm số
3
6y x x
tại điểm duy nhất
00
;xy
. Tìm
0
y
.
A.
0
4y
B.
0
1y 
C.
0
0y
D.
0
6y
Câu 5. Đồ thị hàm số
3
y x 3x 2
cắt trục hoành tại 2 điểm có hoành độ x
1
; x
2
. Khi đó
12
xx
bằng :
A. 2 B. 0 C. – 1 D. – 2
Câu 6. Đường thẳng
ym
cắt đồ thị hàm số
3
y x 3x 2
tại 3 điểm phân biệt khi
A.
0 4.m
B.
4.m
C.
0 4.m
D.
0 4.m
Câu 7. Cho hàm số y = x
3
- 3x
2
+ 1. Đồ thị hàm số cắt đường thẳng y = m tại 3 điểm phân biệt khi
A.
m31
B.
m31
C.
m 1
D.
m 3
Câu 8. Để đường cong
32
( ) : 4C y x mx mx
cắt đường thẳng
( ) : 4d y x
tại 3
điểm phân biệt thì giá trị m bằng:
A.
2m
B.
1m
C.
4m
D.
2m
Câu 9. Cho hàm số
22
13y x x mx m
có đồ thị
m
C
, với giá trị nào của m
thì
m
C
cắt Ox tại 3 điểm phân biệt:
A.
22m
B.
22m
C.
22
1
m
m
D.
22
1
m
m
Câu 10. Đồ thị hàm số
32
63 y x x m x m
cắt trục hoành tại ba điểm phân biệt khi
A.
1m
B.
1m
C.
1
15


m
m
D.
1
15

m
m
BÀI TOÁN TƯƠNG GIAO
1F. Bài toán tương giao
42
Câu 11. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
2
( 1)( )y x x x m
cắt
Ox
tại 3 điểm phân biệt.
A.
1
4
m 
B.
1
à2
4
m v m
C.
1
4
m
D.
1
à2
4
m v m
Câu 12. Sô giao điê
m cu
a đô thi
ha
m sô
2
( 3)( 4)y x x x
vơ
i tru
c hoa
nh la
:
A. 2 B. 3
C. 0 D. 1
Câu 13. Với giá trị nào của m thì phương trình
32
3 1 0
x x m
có hai nghiệm?
A.
1
m
B.
3
m
C.
1
3
m
m
D.
31
m
Câu 14. Phương trình
3
12 2 0x x m
có 3 nghiệm phân biệt với m.
A.
16 16m
B.
18 14m
C.
14 18m
D.
44m
Câu 15. Với các giá trị nào của k thì phương trình
3
3x x k
có ba nghiệm phân biệt?
A.
22k
B.
22k
C.
2k
D.
2k 
Câu 16. Tìm tất cả giá trị thực của tham số
m
để phương trình
32
3x x m
có ba nghiệm phân
biệt.
A.
2.m
B.
0 4.m
C.
0.m
D.
4.m
Câu 17. Phương trình
3
3 2 0x x m
có ba nghiệm phân biệt khi:
A.
04m
B.
04m
C.
4m
D.
0m
Câu 18. Tìm tất cả các giá trị thực của tham số
m
để phương trình
3
32x x m
có ba nghiệm
phân biệt, trong đó có một nghiệm thuộc khoảng
1;0
.
A.
02m
B.
11m
C.
22m
D.
01m
Câu 19. Hình bên là đồ thị hàm số
3
3y x x
. Sử dụng đồ thị đã cho tìm tất cả các giá trị thực
của
m
để phương trình
3 2 2 2
64| | ( 1) (12 | | ( 1))x x x m x
có nghiệm.
A.
22m
B.
m
C.
0m
D.
2m
Câu 20. Tìm các giá trị thực của tham số
m
để đường thẳng
:3d y mx m
cắt đồ thị hàm
số
32
:3C y x x
tại ba điểm phân biệt có hoành độ lần lượt là
1 2 3
,,x x x
thỏa mãn điều
kiện
222
1 2 3
15xxx
.
A.
3
.
2
m
B.
3
.
2
m 
C.
3.m
D.
3.m 
Câu 21. Hình bên dưới là đồ thị của hàm số
.3
3
xxy
Tìm tất cả các giá trị thực của tham số
m
để phương trình
23
3 mxx
có 5 nghiệm phân biệt.
A.
)2;0()0;2( m
B.
)2;0(m
C.
)2;0()0;2( m
D.
)2;0(m
1F. Bài toán tương giao
43
HÀM BẬC BỐN
Câu 22. Số giao điểm của đồ thị hàm số
42
21y x x
với trục Ox là :
A. 1 B. 2 C. 3 D. 0
Câu 23. Tìm m để đồ thị hàm số
42
1y x mx
tiếp xúc với trục hoành tại hai điểm phân biệt.
A.
m2
B.
m2
C.
m1
D.
m1
Câu 24. Giá trị m để đồ thị hàm số
42
21y x mx m
cắt trục tung tại điểm có tung độ
bằng 2 là
A.
3m
B.
3m
C.
2m
D. Không có giá trị m
Câu 25. Tìm m để đường thẳng y = m cắt đồ thị hàm số y = x
4
– 2x
2
+ 3 tại 4 điểm phân biệt.
A. -1 < m < 1 B. 2 < m < 3 C. 0 < m < 1 D. – 1 < m < 0
Câu 26. Đồ thị hàm số
42
23xyx
cắt đường thẳng
ym
tại 4 điểm phân biệt khi
A.
4; 3m
B.
m
4; 3
C.
\m
4; 3
D.
m
Câu 27. Tìm các giá trị thực của tham số
m
để đồ thị hàm số
42
:1
m
C y x mx m
cắt trục
hoành tại bốn điểm phân biệt.
A.
1
.
2
m
m
B. Không có
.m
C.
1.m
D.
2.m
Câu 28. Tất cả các giá trị m để phương trình
42
x 3x 0m
có 4 nghiệm phân biệt là :
A.
13
1
4
m
B.
9
0
4
m
C.
9
0
4
m
D.
13
1
4
m
Câu 29. Phương trình
42
2 1 0x x m
có bốn nghiệm phân biệt khi:
A.
01m
B.
12m
C.
01m
D.
12m
HÀM PHÂN THỨC
Câu 30. Tọa độ giao điểm của
1
( ):
21
x
Cy
x
và
( ): 1d y x
là :
A.
1;1 ,( 1;2)
B.
1;0 ,( 1;2)
C.
1;0 ,(1;2)
D.
1; 2
Câu 31. Đồ thị hàm số
4
21
x
y
x
cắt trục tung tại điểm
M
có tọa độ ?
A.
4; 2 .
B.
4;0 .M
C.
0; 4 .M
D.
0;0 .M
Câu 32. Tọa độ giao điểm của đồ thị hàm số
2
23
2
xx
y
x
và
1yx
là:
A.
(2;2)
B.
(2; 3)
C.
( 1; 0)
D.
(3;1)
1F. Bài toán tương giao
44
Câu 33. Gọi M, N là giao điểm của đường thẳng: y = x +1 và đường cong:
24
1
x
y
x
. Khi đó
hoành độ trung điểm I của đoạn thẳng MN bằng
A.
5
2
B.
1
C.
2
D.
5
2
Câu 34. Hình dưới đây là đồ thị của hàm số
21
.
1
x
y
x
Tìm tất cả các giá trị thực của tham số
m
để phương trình
21
1
x
m
x
có hai nghiệm phân biệt.
A.
2.m
B. Không có giá trị của
.m
C.
2.m 
D. Với mọi
.m
Câu 35. Hình bên là đồ thị của hàm số
21
1
x
y
x
. Tìm tất cả các giá trị thực của tham số
m
để
phương trình
21
31
1
x
m
x

có hai nghiệm phân biệt.
A.
11
33
m
B. Không có
m
. C.
1m
D.
20m
Câu 36. Hình bên là đồ thị của hàm số
21
1
x
y
x
. Tìm tất cả các giá trị thực của tham số
m
để
phương trình
21
2
1
x
m
x
có hai nghiệm phân biệt.
A. Với mọi
m
. B. Không có giá trị của
m
.
C.
0m
D.
0; \ 1m 
Câu 37. Đồ thị
m
C
x1
:
2x
m
y
m
. Với giá trị nào của m thì
m
C
đi qua điểm
1;0M
A. -1 B. 2 C. -2 D. 1
Câu 38. Cho hàm số
21
2
x
y
x
(C). Tìm các giá trị của m để đường thẳng y = x - m cắt đồ thị (C)
tại hai điểm phân biệt .
A.
1m
B.
1m
C.
1m
D.
m
Câu 39. Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
y m 2x
cắt đồ thị hàm số
2x 4
y
x1
tại hai điểm phân biệt.
A.
m4
B.
m4
C.
m4
D.
m4
Câu 40. Cho đồ thị hàm số
2
33
:
1
xx
Cy
x


. Tìm điểm
M
trên đồ thị
C
sao cho
M
cách
đều hai trục tọa độ.
A.
1
;2
2
M



B.
33
;
22
M



C.
33
;
22
M



D.
1
;2
2
M



1F. Bài toán tương giao
45
Câu 41. Cho
C
là đồ thị hàm số
3
1
x
y
x
. Điểm
M
cách đều hai trục tọa độ có tọa độ nào sau
đây?
A.
2;5M
B.
1; 1M
C.
3; 3M
D.
1
2;
3



M
Câu 42. Cho
C
là đồ thị của hàm số
3
1
x
y
x
. Biết rằng, chỉ có hai điểm thuộc đồ thị
C
cách
đều hai điểm
2;0A
và
0; 2B
. Gọi các điểm đó lần lượt là
M
và
N
. Tìm tọa độ trung điểm
I
của đoạn
MN
.
A.
1;1I
B.
3
0;
2
I



C.
3
0;
2
I



D.
2;2I
Câu 43. Cho đồ thị
:
1
x
Cy
x
. Gọi
M
là điểm thuộc
C
sao cho khoảng cách từ
M
đến
đường thẳng
:3 4 0d x y
bằng
1
. Hỏi có tất cả bao nhiêu điểm
M
thỏa mãn điều kiện đề bài?
A. Có
4
điểm. B. Không có điểm nào.
C. Có
2
điểm. D. Có vô số điểm.
Câu 44. Tìm tất cả các giá trị thực của tham số m để phương trình
1
23
1
23
m
m
x
x
chỉ có 1
nghiệm
A. Với mọi m B.
1m
C.
4
1
m
D. Không có giá trị nào của m
Câu 45.
Tìm tất cả các giá trị thực của tham số m để đường thẳng
:d y x m
cắt đồ thị hàm
số (C):
21
2
x
y
x
tại hai điểm phân biệt
A.
14m
B.
1 m
hoặc
4m
C.
4m
D.
m
Câu 46. Gọi M ,N là giao điểm của đường thẳng y = x + 1 và đường cong
24
1
x
y
x
. Khi đó
hoành độ trung điểm I của đoạn thẳng MN bằng
A.
5
2
B. 1 C. 2 D.
5
2
Câu 47. Cho ha
m sô
21
2
x
y
x
(C). Đươ
ng thă
ng
y x m
că t (C) ta
i 2 điê
m A, B sao
cho đô
dài AB nho
nhất khi
A.
1m
B.
2m
C.
3m
D.
1m 
Câu 48. Tổng các giá trị của tham số
m
sao cho đường thẳng
yx
cắt đồ thị hàm số
5x
y
xm
tại hai điểm A và B sao cho
42AB
là
A. 2 B. 5 C. 7 D. Đáp án khác
Câu 49. Cho hai điểm
A
,
B
phân biệt thuộc đồ thị hàm số
()C
:
2
1
x
y
x
sao cho
A
và
B
đối xứng
với nhau qua điểm
(3;3)M
.Tính độ dài
AB
A.
22
B.
52
C.
62
D.
32
1F. Bài toán tương giao
46
Câu 50. Cho đồ thị hàm số
2
:
1
x
Cy
x
. Đường thẳng
:d y x m
cắt đồ thị
C
tại hai điểm
phân biệt
,AB
phân biệt và
22AB
khi
m
nhận giá trị nào trong các giá trị sau đây?
A.
1m
B.
5m
C.
2m 
D.
8m
Câu 51. Đường thẳng
31yx
cắt đồ thị hàm số
2
2 2 3
1
xx
y
x

tại hai điểm phân biệt
A
và
B
. Tính độ dài đoạn thẳng
AB
.
A.
4 10AB
B.
46AB
C.
42AB
D.
4 15AB
Câu 52. Cho đồ thị hàm số
.
1
3
:)(
x
x
yC
Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách
đều hai trục tọa độ. Gọi các điểm đó lần lượt là
NM &
. Tính độ dài đoạn thẳng
.MN
A.
24MN
B.
3MN
C.
22MN
D.
53MN
Câu 53. Đường thẳng
:3d y x
cắt đồ thị
1
( ) :
2
x
Cy
x
tại hai điểm
,AB
phân biệt. Gọi
12
,dd
lần lượt là khoảng cách từ
,AB
đến đường thẳng
:0xy
. Tính
12
d d d
.
A.
32d
B.
32
2
d
C.
6d
D.
22d
Câu 54. Với điều kiện nào của tham số
m
cho dưới đây, đường thẳng
:3d y x m
cắt đồ thị
21
:
1
x
Cy
x
tại hai điểm phân biệt
A
và
B
sao cho trọng tâm của tam giác
OAB
thuộc đồ thị
,C
với
0;0O
là gốc tọa độ.
A.
15 3 13
.
2
m
B.
15 5 13
.
2
m
C.
7 5 5
.
2
m
D. Với mọi
.m
Câu 55. Biết hàm số
3
2
2
x
mmx
y
giảm trên từng khoảng xác định của nó và đồ thị hàm số đi
qua điểm I (4;1). Khi đó giá trị của tham số
m
là
A.
m
B.
1m
C.
3m
D.
1m
và
3m
Câu 56. Cho đồ thị hàm số (C):
2
3
1
xx
y
x
. Hỏi có bao nhiêu điểm thuộc đồ thị hàm số (C) có tọa
độ nguyên (hoành độ và tung độ là những số nguyên)?
A. Có 4 điểm. B. Có vô số điểm.
C. Có 2 điểm. D. Không có điểm nào.
Câu 57. Cho (C ) là đồ thị hàm số
2
1
x
y
x
và đường thẳng
: 1.d y mx
Tìm các giá trị thực
của tham số m để đường thẳng d cắt đồ thị (C ) tại hai điểm A và B phân biệt thuộc hai nhánh khác
nhau của (C ).
A.
0m
B.
0m
C.
0m
D.
0m
1F. Bài toán tương giao
47
Câu 58. Đường thẳng
:3d y x
cắt đồ thị
C
của hàm số
1
2
x
y
x
tại hai điểm
A
và
B
phân
biệt. Khẳng định nào sau đây là đúng?
A. Hai điểm
,AB
nằm về cùng một phía với trục
Ox
.
B. Hai điểm
,AB
nằm về cùng một phía đường thẳng
x+y=0
.
C. Hai điểm
,AB
nằm về cùng một phía với trục
Oy
.
D. Hai điểm
,AB
nằm về cùng một phía với đường thẳng
x-3y=0
.
1C 2B 3B 4D 5C 6A 7A 8C 9D 10D
11D 12D 13C 14C 15A 16B 17A 18D 19A 20C
21A 22D 23B 24A 25B 26B 27A 28B 29B 30B
31C 32C 33B 34A 35A 36D 37A 38D 39A 40B
41B 42A 43A 44B 45D 46B 47B 48C 49A 50C
51A 52A 53A 54B 55A 56A 57B 58C
Nguyễn Văn Lực
www.facebook.com/VanLuc168
1G. Tiếp tuyến của đồ thị hàm số
48
Câu 1. Tiếp tuyến của đồ thị hàm số
32
34y x x
tại điểm có hoành độ
1x
là
A.
9yx
B.
99yx
C.
99yx
D.
9yx
Câu 2. Tiếp tuyến của đường cong
3
2y x x
tại điểm có hoành độ bằng
0
1x
là:
A.
2yx
B.
2yx
C.
2yx
D.
2yx
Câu 3. Tiếp tuyến của đồ thị hàm số
3
yx
tại điểm có hoành độ
0
1x
là:
A.
32yx
B.
32yx
C.
32yx
D.
32yx
Câu 4. Phương trình tiếp tuyến của đồ thị hàm số
21
2
x
y
x

tại điểm có hoành độ
1x
là:
A.
58yx
B.
52yx
C.
52yx
D.
58yx
Câu 5. Tìm phương trình tiếp tuyến của đồ thị hàm số
1
2
x
y
x
tại điểm có hoành độ
3x
.
A.
35yx
B.
3 13yx
C.
3 1 3yx
D.
35yx
Câu 6. Cho hàm số
26
2
x
y
x
(C). Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục
tung là:
A.
26yx
B.
1
3
2
yx
C.
26yx
D.
13
22
yx
Câu 7. Cho
C
là đồ thị của hàm số
32
3 2.y x x
Tìm các tiếp tuyến của
C
đi qua điểm
0;3 .A
A.
3 3.yx
B.
2 3.yx
C.
3 3.yx
D.
4 3.yx
Câu 8. Cho ( C) là đồ thị hàm số
2
1
4
x
yx
.Viết phương trình tiếp tuyến của ( C) đi qua điểm
M(2;-1)
A.
1yx
B.
2 1.yx
C.
3yx
D.
2 3.yx
Câu 9. Có bao nhiêu phương trình tiếp tuyến của đồ thị hàm số (C):
21
1
x
y
x
biết tiếp tuyến
vuông góc với đường thẳng
: 3 2 0d x y
là:
A. 0 B. 1 C. 2 D. 3
Câu 10. Có bao nhiêu tiếp tuyến với đồ thị hàm số
2
1
x
y
x
. Biết tiếp tuyến song song với
đường thẳng
32yx
A. 0 B. 1 C. 2 D. Không có
TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
1G. Tiếp tuyến của đồ thị hàm số
49
Câu 11. Trong tất cả các tiếp tuyến của đồ thị hàm số
3
1
3
y x x
. Tiếp tuyến có hệ số góc nhỏ
nhất bằng :
A. 0 B. 1 C. -1 D. 2
Câu 12. Trong các tiếp tuyến của đồ thị hàm số
3
12 4y x x
có một tiếp tuyến có hệ số góc
k
lớn nhất. Tìm giá trị lớn nhất của
k
.
A.
9k 
B.
0k
C.
12k
D.
12k 
Câu 13. Cho hàm số
32
34y x x
có đồ thị (C). Tìm điểm M thuộc đồ thị (C) sao cho tiếp
tuyến của đồ thị (C) tại điểm đó có hệ số góc lớn nhất?
A.
1; 2
M
B.
1; 0
M
C.
0; 4
M
D.
2;0
M
Câu 14. Cho hàm số (C):
3
62y x x
và đường thẳng
:1d y mx m
. Với giá trị nào của
m thì d cắt (C) tại 3 điểm A, B, C sao cho tổng hệ số góc các tiếp tuyến của đồ thị (C) tại A, B, C
bằng -6?
A.
3m 
B.
1m 
C.
1m
D.
2m
Câu 15. Cho đồ thị hàm số
32
5
(C): y x 2x x
3
. Tiếp tuyến tại gốc tọa độ O của ( C) cắt ( C)
tại điểm thứ hai M. Tìm tọa độ M
A.
10
M 2;
3
B.
10
M 2;
3
C.
10
M 2;
3
D.
10
M 2;
3
Câu 16. Cho đồ thị
32
(C): y x 3x 2
. Tìm một tiếp tuyến của đường cong
(C)
, biết tiếp tuyến
cắt trục
Ox, Oy
lần lượt tại A và B thỏa mãn
OB 9OA
.
A.
y 9x 7
B.
y 9x 25
C.
y 9x 25
D.
y 9x 7
Câu 17. Cho hàm số
32
22y x x x
có đồ thị ( C ) . Gọi
12
,xx
là hoành độ các điểm M, N
trên (C), mà tại đó tiếp tuyến của ( C ) vuông góc với đường thẳng
2017yx
. Khi đó
12
xx
bằng:
A.
4
3
B.
4
3
C.
1
3
D. -1
Câu 18. Gọi
21
( ):
1
x
M C y
x

có tung độ bằng 5 . Tiếp tuyến của (C) tại M cắt các trục tọa độ
Ox, Oy lần lượt tại A và B. Diện tích tam giác OAB bằng:
A.
121
6
y
B.
119
6
C.
123
6
y
D.
125
6
y
1C 2B 3C 4B 5C 6B 7A 8C 9C 10B
11A 12D 13A 14D 15D 16A 17A 18A
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2A. Hàm số lũy thừa – Hàm số mũ
50
Tập xác định của hàm số mũ
Câu 1. Tập xác định của hàm số

2
1yx
là
A.
; 1 1;D
; B.
.D
C.
\1R
D.
1;1D
.
Câu 2. Tập xác định của hàm số
2
4
34y x x
là:
A. [-1;4] B. (-1; 4)
C.
; 1 4; 
D.
; 1 4; 
Câu 3. Hàm số y =
4
2
41x
có tập xác định là:
A. B. (0; +) C.
\
11
;
22



D.
11
;
22



Câu 4. Tập xác định của hàm số
25
(2 6)y x x
là:
A.
3
( ; ) (2; )
2
D  
B.
3
( ;2)
2
D 
C.
\D
3
;2
2



D.
D
Câu 5. Tập xác định của hàm số:

2
2
3
( 4)yx
là
A.
 ( ; 2) (2; )D
B.
\D
{ 2}
C.
( 2;2)D
D.
D
Câu 6. Hàm số
1
2
(1 )yx

có tập xác định là:
A.
D
B.
\ {0}D
C.
D ( ;1) 
D.
Câu 7. Hàm số y =
3
2
1x
có tập xác định là:
A. [-1; 1] B. (-; -1] [1; +)
C. R\{-1; 1} D.
Câu 8. Tập xác định của hàm số

xx
y 9 3
là:
A.
(1;2)
B.
[0; )
C.
[3; )
D.
(0;3)
Câu 9. Hàm số
3
(1 )yx
có tập xác định là:
A.
D
B.
\ {0}D
C.
(0; )
D.
HÀM SỐ LŨY THỪA – HÀM SỐ MŨ
2A. Hàm số lũy thừa – Hàm số mũ
51
Câu 10. Tập xác định của hàm số
2
5
32y x x
là:
A.
;1 2;D  
B.
;1 2;D 
C.
1;2D
D.
D
Đạo hàm của hàm số mũ
Câu 11. Tính đạo hàm của hàm số
12
x
y
A.
1
' .12
x
yx
B.
' 12 ln12
x
y
C.
' 12
x
y
D.
12
'
ln12
x
y
Câu 12. Đạo hàm của hàm số:
1
100
x
y
là
A.
1
' 100 ln10
x
y
B.
' 200.100 ln10
x
y
C.
1
'
1 ln100
y
x
D.
' 1 ln100.yx
Câu 13. Đạo hàm của hàm số
23
2
x
y
là:
A.
23
2.2 . ln 2
x
B.
23
2 .ln 2
x
C.
23
2.2
x
D.
22
(2 x 3)2
x
Câu 14. Cho f(x) =
1
1
2
x
x
. Đạo hàm
'0f
bằng:
A. 2 B. ln2 C. 2ln2 D. Kết quả khác
Câu 15. Đạo hàm của hàm số
1
2
2
( 2 1)y x x
là:
A.
1
2
2
' ( 2 1) (2 2)y x x x
B.
1
2
2
' ( 2 1) (2 2)y x x x
C.
1
2
2
1
' ( 2 1)
2
y x x
D.
1
2
2
' ( 2 1) ( 1)y x x x
Câu 16. Cho f(x) =
22
3
xx
. Giá trị
'(1)f
bằng:
A.
3
8
B.
8
3
C. 2 D. 4
Câu 17. Đạo hàm của hàm số
21
sin2
x
y e x
là:
A.
21
' 2 os2
x
y e c x
B.
21
' 4 os2
x
y e c x
C.
2 1 2 1
' 2 sin2 2 os2
xx
y e x e c x


D.
2 1 2 1
' 2 sin2 2 os2
xx
y e x e c x


Nguyễn Văn Lực
www.facebook.com/VanLuc168
2A. Hàm số lũy thừa – Hàm số mũ
52
Câu 18. Tính đạo hàm của hàm số:
2
51xx
ye

.
A.
2
2 5 1
' 5 1
xx
y x x e

B.
2
51
' 2 5
xx
y x e


C.
2
51
' 2 4
xx
y x e


D.
2
51
' 2 5
xx
y x e


Câu 19. Tính đạo hàm của hàm số:
2x 5x
y e 3.5
A.
2x 5x
y' 2e 5 .ln5
B.
2x 5x
y' 2e 3.5
C.
2x 5x
y' 2e 3.5 .ln5
D.
2x 5x 1
y' 2e 3.5 .ln5

Câu 20. Tính đạo hàm của hàm số
2
( 2 2)
x
y x x e
.
A.
2
'
x
y x e
B.
' (2 2)
x
y x e
C.
'2
x
y xe
D.
'2
x
y xe
Câu 21. Cho hàm số
tan2x
ye
, giá trị của
'
6
f



bằng
A.
3
4.e
B.
3
2.e
C.
4.
D.
3
8.e
Câu 22. Tính đạo hàm của hàm số
x
y 9 1 3x
A.
x
y' 9 (1 3x).ln9 1
B.
x
y' 9 (2 6x)ln9 3
C.
x 2x 1
y' 9 2 6x ln3 3
D.
x
y' 9 (1 3x)ln3 3
Câu 23. Tính đạo hàm của hàm số
1
9
x
x
y
.
A.
2
1 2( 1)ln3
'
3
x
x
y

B.
2
1 ( 1)ln3
'
3
x
x
y

C.
1 2( 1)ln9
'
3
x
x
y

D.
1 2( 1)ln3
'
3
x
x
y

Câu 24. Cho hàm số
3 2.
x
fx
Khẳng định đúng là
A.
' 0 ln3f
B.
' 0 3ln3f
C.
' 1 ln3f
D.
' 2 9f
Câu 25. Cho hàm số
( ) .
x
f x x e
. Giá trị của
''(0)f
là:
A. 1 B. 2e C. 3e D. 2
Câu 26. Đạo hàm bậc hai của hàm số
10
x
y
là:
A.
'' 10
x
y
B.
2
'' 10 .ln10
x
y
C.
2
'' 10 .(ln10)
x
y
D.
'' 10 .ln20
x
y
Câu 27. Đạo hàm của hàm số
1
x
e
y
x
là
A.
2
1
x
e
x
B.
2
( 1) 1
x
ex
x
C.
2
ln 1
xx
xe x e
x
D.
2
( 1) 1
x
ex
x
Câu 28. Đạo hàm của hàm số
21x
ye
là:
A.
21
'2
x
ye
B.
21
1
'
2
x
ye
C.
21
'
x
ye
D.
2
'2
x
ye
2A. Hàm số lũy thừa – Hàm số mũ
53
Câu 29. Đạo hàm của hàm số
2017
x
y
là:
A.
1
' .2017
x
yx
B.
' 2017 .ln 2017
x
y
C.
' 2017
x
y
D.
2017
'
ln 2017
x
y
Rút gọn biểu thức
Câu 30. Biết
4 4 23
xx

. Tính
22
xx
I

.
A.
5I
B.
4I
C.
23I
D.
21I
Câu 31. Cho
9 9 23
xx

. Khi đó biểu thức
5 3 3
1 3 3
xx
xx
P


có giá trị bằng:
A.
5
2
B.
1
2
C.
3
2
D. 2
Câu 32. Gọi
a
và
b
là hai số thực thỏa mãn đồng thời
1ab
và
22
4 4 0,5
ab

. Khi đó tích
ab
bằng:
A.
1
4
B.
1
2
C.
1
2
D.
1
4
Câu 33. Biểu thức
6
3
5
..xxx
(x > 0) viết dưới dạng lũy thừa có số mũ hữu tỉ là
A.
7
3
x
B.
5
2
x
C.
2
3
x
D.
5
3
x
Câu 34. Cho
3
2
6
()
xx
fx
x
. Khi đó
13
10
f



bằng
A.
11
10
B.
4
C.
1
D.
13
10
Câu 35. Cho hàm số
sin x
ye
. Hãy tính giá trị của biểu thức
'cos sin ''M y x y x y
?
A. sinx B. 0 C. 1 D. -1
Câu 36. Rút gọn biểu thức
1
2
4P a b ab




với
a
,
b
là các số dương.
A.
2P a b


B.
P a b


C.
P a b


D.
P a b


Câu 37. Cho a, b là các số dương. Biểu thức
2
11
22
1 2 :
bb
ab
aa






sau khi rút gọn là:
A.
1
a
B.
ab
C.
ab
D.
1
b
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2A. Hàm số lũy thừa – Hàm số mũ
54
Câu 38. Rút gọn biểu thức

52
52
5 3 1 5
.
x
A
xx
(với
0x
) ta được:
A.
Ax
B.
2
Ax
C.
3
Ax
D.
4
Ax
Câu 39. Cho số thực dương a. Giá trị rút gọn của biểu thức
1
21
33
3
8
28
55
5
()
()
a a a
P
a a a
là:
A. P = a + 1 B. P = a – 1 C.
1
1
P
a
D.
1
1
P
a
Câu 40. Cho
2 2 4
xy
. Tìm giá trị lớn nhất của
S x y
.
A.
0s
B.
1S
C.
2S
D.
4S
Câu 41. Cho hàm số
4
()
41
x
x
fx
. Tính tổng:
1 2 2016
( ) ( ) ....... ( )
2017 2017 2017
S f f f
.
A.
2017S
B.
1009S
C.
1008S
D.
1006S
Câu 42. Biểu thức
7
3
3
: ( 0)a a a
viết dưới dạng lũy thừa với số mũ hữu tỉ là:
A.
2
a
B.
2
a
C.
a
D.
1
a
Câu 43. Giá trị biểu thức
11
3 3 9
7 4 4
P


bằng:
A.
1
B.
2
C.
1
D.
2
Câu 44. Giá trị biểu thức
0,75
2
0,5
3
1
27 25
16
Q



bằng:
A. 12 B. 10 C. 8 D. 6
Câu 45. Rút gọn biểu thức
1
4
4
31
42
1
. . 1
1
a a a
Pa
a
aa


ta được kết quả :
A.
Pa
B. P = 1 C. P = a D.
4
Pa
Câu 46. Rút gọn biểu thức
1 9 1 3
4 4 2 2
1 5 1 1
4 4 2 2
( 0, 0)
a a b b
ab
a a b b


, ta được:
A.
ab
B.
ab
C.
.ab
D.
a
b
Câu 47. Rút gọn biểu thức
1
4
4
31
42
1
( 0)
1
a a a
aa
a
aa




, ta được:
A.
a
B.
1a
C.
1a
D.
4
a
Câu 48. Rút gọn biểu thức:
xxxx
:
11
16
x
, ta được:
A.
4
x
B.
6
x
C.
8
x
D.
x
2A. Hàm số lũy thừa – Hàm số mũ
55
Câu 49. Tìm hệ thức liên hệ giữa x và y, biết
1
11
, ( 0, 1).

t
tt
x t y t t t
A.
xy
yx
B.
1
x
y
yx
C.
1
y
y
y x y
D.
yx
yx
Câu 50. Biểu thức K =
3
3
222
333
viết dưới dạng số hữu tỹ:
A.
1
6
2
3



B.
1
12
2
3



C.
1
8
2
3



D.
1
2
2
3



Bài tập tổng hợp
Câu 51. Cho hàm số
2
1
( ) ( ) .5
2
xx
fx
. Khi đó
A.
2
2
( ) 1 .log 5 0f x x x
B.
2
( ) 1 ln2 .ln 5 0f x x x
C.
2
2
( ) 1 .log 5 0f x x x
D.
2
5
( ) 1 .log 2 0f x x x
Câu 52. Cho hàm số
2
4 .9
xx
fx
. Khẳng định nào sau đây là khẳng định sai?
A.
2
4
1 log 9 0.f x x x
B.
2
9
1 log 4 0.f x x x
C.
1 lg4 lg9 0.f x x
D.
1 lg4 lg9 0.
x
f x x
Câu 53. Cho
2
( ) 2 .3
xx
fx
. Khẳng định nào sau đây là khẳng định đúng ?
A.
2
2
( ) 2 log 3 1f x x x
B.
2
( ) 2 2 log 3 1f x x x
C.
2
2
( ) 2 log 3 1f x x x
D.
2
1
( ) 2 log 3 1
2
f x x x
Câu 54. Trong các hàm số sau, hàm số nào nghịch biến trên ?
A.
3
x
y
B.
3
x
y



C.
x
ye
D.
2
5
x
y



Câu 55. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
3
.
1
x
y



B.
.
3
x
y



C.
2
.
x
y
e



D.
.
4
x
y



Câu 56. Cho
>
. Kết luận đúng là
A. < B. > C. + = 0 D. . = 1
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2A. Hàm số lũy thừa – Hàm số mũ
56
Câu 57. Mệnh đề sai là
A. Với a > 0 thì
4
2
3
3
:a a a
B.
3 2 1 2 4 2
4 .2 .2 8
C.
32
33

D.
32
log 2 log 3
Câu 58. Cho số thực a > 1. Khẳng định nào dưới đây là khẳng định sai ?
A.
2
x 1 2x 1
a a x 0 hay x 2

B.
2
x 1 2x 1
a a 0 x 2

C.
2
x 1 2x 1
55
a a 0 x 2

D.
2
3
x 1 2x 1
3
a a x 0 hay x 2

Câu 59. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số
x
ya
với 0 < a < 1 là hàm số đồng biến trên (-: +)
B. Hàm số
x
ya
với a > là hàm số nghịch biến trên (-: +)
C. Hàm số
x
ya
với (0 < a 1) luôn đi qua điểm (a; 1)
D. Hàm số
x
ya
với y =
1
x
a



(0 < a 1) thì đối xứng qua trục tung.
Câu 60. Với a > 0, b> 0, x và y tùy ý. Mệnh đề nào đúng:
A.
.
.
y x y
x
a a a
B.
( ) .
XX
ab a b
C.
x
a
xy
a
y
a
D.
()
y x y
x
aa
1D 2D 3C 4C 5A 6C 7D 8B 9A 10D
11B 12B 13A 14B 15D 16B 17D 18D 19D 20A
21D 22C 23A 24A 25D 26C 27B 28A 29B 30A
31A 32A 33D 34C 35B 36D 37A 38C 39D 40C
41C 42A 43B 44A 45A 46A 47B 48A 49A 50D
51C 52C 53A 54A 55B 56B 57A 58C 59C 60C
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2B. Hàm số lôgarit
57
Tập xác định của hàm số lôgarit
Câu 1. Tập xác định của hàm số
2
log (3 1)
x
y
là
A.
1
( ; )
2
D
B.
(0; )D
C.
[1; )D
D.
1
( ; )
3
D
Câu 2. Tìm tập xác định D của hàm số:
2
3
log 4yx
.
A.
; 2 2;D  
B.
2;2D
C.
; 2 2;D 
D.
2;2D
Câu 3. Tìm tập xác định của hàm số
2
3
log 5 6y x x
là:
A.
( ;2) (3; )D 
B.
(2;3)D
C.
2;3D
D.
( ;2] [3; )D
Câu 4. Tập xác định của D hàm số
2
5
log 2 3y x x
là
A.
; 3 1;D  
B.
; 3 1;D  
C.
; 1 3;D  
D.
1;3D 
Câu 5. Hàm số
2
5
log ( 6 9)y x x
xác định khi
A.
3x
B.
3x
C.
3x
D.
3x
Câu 6. Tìm tập xác định của hàm số:
2
5
log (4 )yx
.
A.
[ 2;2]D 
B.
( ; 2) (2; )D 
C.
( ; 2)D
D.
\{4}DR
Câu 7. Tập xác định D của hàm số y=
32
5
log 2x x x
là
A. (0; 1) B. (1; +) C. (-1; 0) (2; +) D. (0; 2) (4; +).
Câu 8. Biểu thức
2
6
log 2xx
có nghĩa khi
A. 0 < x < 2 B. x > 2 C. -1 < x < 1 D. x < 3
Câu 9. Tìm tập xác định D của hàm số
2
log( 4)yx
.
A.
( ; 2) (2; )D
B.
[ 2;2]D
C.
( 2;2)D
D.
( ; 2] [2; )D
Câu 10. Tìm tập xác định D của hàm số
3
2
2
y log 8 5x 3x
A.
8
D 1;
3



B.
8
D 1;
3




C.
8
D 1;
3




D.
8
D 1;
3



HÀM SỐ LÔGARIT
2B. Hàm số lôgarit
58
Câu 11. Hàm số y =
2
ln 5 6xx
có tập xác định là
A. (0; +). B. (-; 0). C. (2; 3). D. (-; 2) (3; +).
Câu 12. Tập xác định của hàm số
2
9
log (x 1) ln(3 x) 2y
A.
(3; )D
B.
( ; 3)D
C.
( ; 1) ( 1;3)D
D.
( 1; 3)D
Câu 13. Tập xác định của hàm số
4
4
log 3
y
x
là :
A.
0;64 64;
B. C.
\ 64
D.
0;
Câu 14. Tìm tập xác định D của hàm số
3
4
log
4
x
y
x
A.
( ; 4] [4; ) 
B.
[ 4;4]
C.
( ; 4) (4; ) 
D.
(4; )
Câu 15. Hàm số:
162log
3
6,0
x
y
xác định khi:
A.
7x
B.
7x
C.
3x
D.
5x
Câu 16. Tập xác định của hàm số:
1
3
log 3 2yx
là:
A. (3;12] B. (3;12) C. [3;12) D. [3;12]
Câu 17. Tính
36
log 24
theo
12
log 27 a
là
A.
9
62
a
a
B.
9
62
a
a
C.
9
62
a
a
D.
9
62
a
a
Câu 18. Tập xác định của hàm số
3
log ( 1)yx
là:
A.
[1; )
B.
\ {1}D
C.
(1; )
D.
( ;1)
Câu 19. Tập xác định của hàm số
0,3
1
log
5
x
y
x
là :
A.
(1; )
B.
( ;1

C.
( ; 5) (1; ) 
D. Kết quả khác
Câu 20. Tập xác định của hàm số
x2
y log
1x
là:
A.
( ;1) (2; )
B. (1;2)
C.
\ {1}
D.
\ {1;2}
Câu 21. Tập xác định của hàm số

2
y log x 1
là:
A.
(0;1)
B.
(1; )
C.
(0; )
D.
[2; )
Câu 22. Tập xác định của hàm số
3
y 3 log (x 2)
là:
A.
(0;25)
B.
( 2;27)
C.
( 2; )
D.
( 2;25]
2B. Hàm số lôgarit
59
Câu 23. Cho hàm số
1
ln
1
y
x
, ta có:
A.
'1
y
xy e
B.
'1
y
xy e
C.
'1
y
xy e
D.
'1
y
xy e
Câu 24. Tập xác định của hàm số
10
log
3
2
32
x
y
xx

là:
A.
1; 
B.
;1 2;10
C.
;10
D.
2;10
Câu 25. Cho hàm số:
22
ln(2 )y x e
. Tập xác định của hàm số là:
A.
D
B.
1
( ; ).
2
D
e

C.
( ; ).
2
e
D 
D.
1
( ; )
2
D 
Câu 26. Tập xác định của hàm số
2
2
log 2 1y x x
là
A. B.
\ { 1}D
C.
\ {1}D
D.
Câu 27. Tìm tập xác định
D
của hàm số
3
1
log
3
y
x
?
A.
;3
B.
3; 
C.
3; 
D.
;3
Đạo hàm của hàm số lôgarit
Câu 28. Đạo hàm của hàm số
2
2
log 2 1yx
là:
A.
2
2log 2 1
2 1 ln2
x
x
B.
2
4log 2 1
2 1 ln2
x
x
C.
2
4log 2 1
21
x
x
D.
2
2 1 ln2x
Câu 29. Đạo hàm của hàm số
2
3
log 2 1xx
là:
A.
2
22
'
23
x
y
xx

B.
2
'
( 1).ln3
y
x
C.
22
'
ln3
x
y
D.
2
21
'
( 2 1).ln3
x
y
xx

Câu 30. Đạo hàm của hàm số
3
log 0y x x
là
A.
' 3 ln
x
yx
B.
' ln 3yx
C.
1
'
ln 3
y
x
D.
'
ln 3
x
y
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2B. Hàm số lôgarit
60
Câu 31. Đạo hàm của hàm số
2
2017
log (x 1)y
là
A.
2
1
'
1
y
x
B.
2
1
'
(x 1)ln2017
y
C.
2
'
2017
x
y
D.
2
2
'
(x 1)ln2017
x
y
Câu 32. Tính đạo hàm của hàm số
2
ln(2x )yx
với
02x
là:
A.
2
2 2x
'
2x
y
x
B.
2
' (2 2x)(2x )yx
C.
2
1
'
2x
y
x
D.
2
' 2xyx
Câu 33. Tính đạo hàm của hàm số
2
2 lny x x
.
A.
2
' 2ln 4 lny x x x
B.
2
' 2 ln 4 lny x x x x
C.
2
' 2 ln 4lny x x x
D.
2
' 2ln 4lny x x
Câu 34. Cho hàm số:
2
lny x x
. Kết quả của
'y
=?
A.
2
ln 2.x
B.
ln (ln 2).xx
C.
2ln
.
x
x
D.
2 ln .xx
Câu 35. Tính đạo hàm của hàm số
( 1)lny x x
.
A.
' lnyx
B.
1
'
x
y
x
C.
1
' ln
x
yx
x
D.
1
' ln
x
yx
x
Câu 36. Tính đạo hàm số
(1 ln ).lny x x
A.
1 2ln
'
x
y
x
B.
2ln
'
x
y
x
C.
1 2ln
'
x
y
x
D.
2ln
'
x
y
x
Câu 37. Tính đạo hàm của hàm số
ln x
y
x
A.
1
'y
x
B.
1 ln
'
x
y
x
C.
2
1 ln
'
x
y
x
D.
2
1 ln
'
x
y
x
Câu 38. Đạo hàm của hàm số
ln 1x
y
x
là
A.
ln 1x
B.
2
2 ln x
x
C.
1
1
x
D. 1
Câu 39. Hàm số
1 ln
()
x
fx
xx
có đạo hàm là
A.
ln x
x
B.
ln x
x
C.
4
ln x
x
D.
2
ln x
2B. Hàm số lôgarit
61
Câu 40. Hàm số
cos sin
ln
cos sin
xx
y
xx
có đạo hàm bằng
A.
2
.
cos2x
B.
2
.
sin2x
C.
cos2 .x
D.
sin2 .x
Câu 41. Đạo hàm của hàm số
2
ln 1y x x
là:
A.
2
1
1 x
B.
2
1
1xx
C.
2
1xx
D.
2
11
x
x
Câu 42. Hàm số
5
ln
3
x
y



thỏa mãn hệ thức nào sau đây
A.
1
'0
5
y
x

B.
3 ln 5 0yx
C.
5
y
ex
D.
'0yy
Câu 43. Cho hàm số f(x) =
ln 1
x
e
. Tính f
’
(ln2)
A. 2 B. -2 C. 0,3 D.
1
3
Câu 44. Tính đạo hàm của hàm số
1
.ln
1
yx
x
A.
(1 )ln(1 )
'
1
x x x
y
x
B.
(1 )ln(1 )
'
1
x x x
y
x
C.
ln(1 )
'
1
xx
y
x
D.
' ln(1 )y x x
Câu 45. Cho hàm số:
22
ln(2 )y x e
. Đạo hàm cấp 1 của hàm số tại x = e là:
A.
3
4e
B.
4
9e
C.
2
4
9e
D.
2
4
3e
Câu 46. Đạo hàm của hàm số
2
lnyx
là
A.
2
'y
x
B.
2
' lnyx
x
C.
2
2
'y
x
D.
3
2
'y
x
Biểu diễn giá trị lôgarit
Câu 47. Cho
2
log 20 a
. Tính
20
log 5
theo a .
A. a - 2. B. a + 2. C.
2a
a
D.
2a
a
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2B. Hàm số lôgarit
62
Câu 48. Cho
12
log 27 a
.Biểu diễn
6
log 16
theo a
A.
6
4(3 )
log 16
3
a
a
B.
6
3
log 16
3
a
a
C.
6
8
log 16
3
a
a
D.
6
4
log 16
3 a
Câu 49. Đặt
15
log 3 a
. Hãy biểu diễn
25
log 15
theo a.
A.
25
1
log 15
21 a
B.
25
1
log 15
a
a
C.
25
1
log 15
1 a
D.
25
2
log 15
1 a
Câu 50. Cho
7
140
3 7 7
.log 3.log 1
log 63
log 3.log 5.log log 1
x
x
xx
x x x

xác định
.x
A.
2x
B.
4x
C.
3x
D.
5x
Câu 51. Rút gọn biểu thức
19
3
3
1
log 7 2log 49 log
7
A
A. A =
3
3log 7
B. A =
3
log 7
C. A =
3
2log 7
D. A =
3
4log 7
Câu 52. Cho log

23
5 ; log 5ab
. Khi đó
6
log 5
tính theo a và b là:
A.
1
ab
B.
ab
ab
C. a + b D.
22
ab
Câu 53. Cho
33
log 15 , log 10ab
. Giá trị của biểu thức
3
log 50P
theo
a
và
b
bằng:
A.
1P a b
B.
1P a b
C.
21P a b
D.
21P a b
Câu 54. Với
6
log 2m
,
6
log 5n
thì
3
log 5
bằng:
A.
n
m
B.
1
n
m
C.
1
n
m
D.
1
n
m
Câu 55. Nếu
log 6, log 7
12 12
ab
thì
log 7
2
bằng
A.
1
a
b
B.
1 a
b
C.
1
a
b
D.
1
a
a
Câu 56. Cho biết

30 30
log 3 ;log 5ab
. Hãy biểu diễn
30
log 1350
theo a và b:
A. 2a + 2b + 1 B. a + b + 1 C. 2a + b + 1 D. 2a + b
Câu 57. Cho biết
log3 ;log2ab
. Biểu diễn
125
log 30
theo
a
và
b
là
A.
125
12
log 30
a
b
B.
125
2
log 30
1
a
b
C.
125
1
log 30
1
a
b
D.
125
1
log 30
3(1 )
a
b
Câu 58. Biết
log2, log3ab
thì
log0,018
tính theo a và b bằng
A.
2
.
2
ba
B.
2 3.ba
C.
2 2.ba
D.
2 2.ab
2B. Hàm số lôgarit
63
Câu 59. Tìm x thỏa mãn
3 3 3
log 4log 7logx a b
với
0; 0ab
ta được:
A.
47
x a b
B.
47x a b
C.
4 .7x a b
D.
.x a b
Câu 60. Đặt
2
a log 7
;
7
b log 3
. Hãy biểu diễn
42
log 147
theo a và b.
A.
42
a 2 b
log 147
a b 1

B.
42
2b
log 147
1 ab a

C.
42
b 2 a
log 147
1 ab a

D.
42
a 2 b
log 147
1 ab a

Câu 61. Cho
25 2
log 7 ;log 5ab
. Tính
5
log 6,125
?
A.
43ab
B.
3
4a
b
C.
3
4a
b
D.
3
4a
b
Câu 62. Nếu
log2 m
và
ln2 n
thì:
A.
ln20 1
n
m

B.
1
ln20
m
n
C.
ln20
n
n
m

D.
ln20
m
m
n

Câu 63. Cho
2
logam
với
0m
và
1m
và
log (8 )
m
Am
. Khi đó mỗi quan hệ giữa
A
và
a
là:
A.
3 a
A
a
B.
(3 )A a a
C.
3 a
A
a
D.
(3 ).A a a
Câu 64. Cho a, b là hai số dương thỏa mãn a
2
+ b
2
= 7ab thì
7
log ( )
3
ab
bằng giá trị nào sau
đây:
A.
77
1
log log
2
ab
B.
77
1
(log log )
2
ab
C.
77
1
log log
2
ab
D.
77
log log
33
ab
Câu 65. Giả sử ta có hệ thức a
2
+ b
2
= 7ab (a, b > 0). Khi đó
A.
2 2 2
2log log loga b a b
B.
2 2 2
2 log log log
3
ab
ab
C.
2 2 2
log 2 log log
3
ab
ab
D. 4
2 2 2
log log log
6
ab
ab
Câu 66. Giá trị của
log 4
( 0, 1)
a
a a a
bằng:
A. 2 B. 16 C.
1
2
D. 4
Câu 67. Giá trị của
3
log ( 0, 1)
a
a a a
bằng:
A.
1
3
B.
1
3
C.
3
D.
3
Câu 68. Tính
12
77
log .logP x x
, biết
1
x
và
2
x
là hai nghiệm của phương trình
2
77
log 10log 0x x e
.
A.
4e
P
B.
2e
P
C.
e
P
D.
4
e
P
2B. Hàm số lôgarit
64
Câu 69. Nếu
2 2 2
log x 5 log a 4 log b
(a, b > 0) thì x bằng:
A.
54
ab
B.
45
ab
C. 5a + 4b D. 4a + 5b
Câu 70. Biết
12 24
log 18 ,log 54ab
thì
5ab a b
bằng:
A. 0 B. 2 C. 3 D. 1
Bài tập tổng hợp
Câu 71. Nếu
53
53
aa
và
45
log log
56
bb
thì
A.
0 1, 1ab
B.
0 1, 0 1ab
C.
1, 1ab
D.
1, 0 1ab
Câu 72. Cho hàm số
y = log x
a
. Trong các mệnh đề sau mệnh đề nào sai:
A. Hàm số có tập xác định
D
B. Hàm số đồng biến trên
(0;+ )
khi a > 1
C.
x > 0
hàm số có đạo hàm
1
y' =
xlna
D. Đồ thị hàm số luôn nhận trục tung làm tiệm cận đứng
Câu 73. Chọn khẳng định sai trong các khẳng định sau:
A.
ln 0 1xx
B.
2
log 0 0 1xx
C.
11
33
log log 0a b a b
D.
11
22
log log 0a b a b
Câu 74.
Trong các khẳng định sau, khẳng định sai là
A.
3
log 5 0
B.
34
1
log 4 log
3
C.
22
33
log 2007 log 2008
xx
D.
0,3
log 0, 8 0
Câu 75. Cho a, b là các số thực dương ; a,b 1 và a.b 1. Khẳng định sai là
A.
1
log ( ) 1 log
a
a
ab b
B.
1
log ( ) 1 log
a
a
ab b
C.
1
log
1 log
ab
a
a
b
D.
2
1
log
2 log
a
b
b
a
Câu 76. Cho
, , 0a b c
và
1a
. Khẳng định nào sau đây là khẳng định sai?
A.
2log log .
aa
bc bc
B.

1
log log log .
2
a a a
bc b c
C.
1
log .
log
a
bc
bc
a
D.
log log log .
a a a
bc b c
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2B. Hàm số lôgarit
65
Câu 77. Cho các số thực dương a, b, với
a1
. Khẳng định nào sau đây là khẳng định đúng?
A.
23
a a a
log a b 2 log ab log b

B.
23
aa
log a b 2 3log b
C.
23
a a a
log a b 2log b 3log ab
D.
23
aa
log a b 6 1 log b
Câu 78. Cho các số thực dương a, b với a
1. Khẳng định nào sau đây là khẳng định đúng?
A.
2
1
log log
2
a
a
a
b
b
B.
2
log 2 2log
a
a
a
b
b

C.
2
1
log log
4
a
a
a
b
b
D.
2
11
log log
22
a
a
a
b
b

Câu 79. Cho
,ab
dương và
1a
. Các khẳng định nào sau đây đúng:
A.
3
log ( . ) 3 3log
a
a
a b b
B.
3
11
log ( . ) log
33
a
a
a b b
C.
3
1
log ( . ) log
3
a
a
a b b
D.
3
log ( . ) 3log
a
a
a b b
Câu 80. Cho
01a
và

1
. Khẳng định nào sau đây là khẳng định đúng?
A.

1.aa
B.

1.aa
C.

1.aa
D.

1.aa
Câu 81. Nếu
1
1
3
2
( 1) ( 1)aa
và
2 2016
log log
3 2017
bb
thì khẳng định nào sau đây là đúng?
A.
0 1; 1ab
B.
0 1; 1ab
C.
1 2; 1ab
D.
1 2; 1ab
Câu 82. Cho hai số thực a và b, với
54
aa

và
34
log log
45
bb
. Khẳng định nào dưới đây
là khẳng định đúng?
A.
1; 1ab
B.
1; 0 1ab
C.
0 1; 1ab
D.
0 1; 0 1ab
Câu 83. Cho a, b, c >0; a; c; a.b
1. Khẳng định nào dưới đây là khẳng định đúng ?
A.
log
1 log
log
a
a
ab
c
b
c

B.
log
1 log
log
a
a
ab
c
c
c

C.
log
1 log
log
a
a
ab
c
b
c

D.
log
1 log
log
a
a
ab
c
c
c

Câu 84. Tìm mệnh đề đúng trong các mệnh đề sau :
A. Hàm số y =
log
a
x
với 0 < a < 1 là một hàm số đồng biến trên khoảng (0 ; +)
B. Hàm số y =
log
a
x
với a > 1 là một hàm số nghịch biến trên khoảng (0 ; +)
C. Hàm số y =
log
a
x
(0 < a 1) có tập xác định là
D. Đồ thị các hàm số y =
log
a
x
và y =
1
log
a
x
(0 < a 1) đối xứng nhau qua trục hoành.
2B. Hàm số lôgarit
66
Câu 85. Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số
x
ya
và
1
x
y
a



đối xứng nhau qua trục hoành.
B. Đồ thị hàm số
log
a
yx
và
1
log
a
yx
đối xứng nhau qua trục tung.
C. Đồ thị hàm số
log
a
yx
và
x
ya
đối xứng nhau qua đường thẳng
.yx
D. Đồ thị hàm số
x
ya
và
log
a
yx
đối xứng nhau qua đường thẳng
.yx
Câu 86. Trong các mệnh đề sau, mệnh đề nào đúng
A.
22
31
3
log 5 log 7 0,x x x
B.
22
31
3
log 5 log 7 0,x x x
C.
22
33
log 5 log 7 ,x x x
D.
2
3
2
3
log 5
5
,
7
log 7
x
x
x
Câu 87. Cho
,xy
là các số thực dương thỏa mãn
22
9ln 4ln 12ln .ln .x y x y
Đẳng thức nào sau
đây là đúng?
A.
23
xy
B.
32xy
C.
32
xy
D.
xy
Câu 88. Cho các số thực dương
, , ,a b x y
, với
1a
. Khẳng định nào sau đây là khẳng định
đúng?
A.
log
log
log
a
a
a
x
x
yy
B.
11
log
log
a
a
xx
C.
log ( ) log log
a a a
x y x y
D.
log log .log
b b a
x a x
Câu 89. Cho a > 0 và a 1, x và y là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
a
a
a
log x
x
log
y log y
B.
a
a
11
log
x lo g x
C.
a a a
log x y log x log y
D.
b b a
log x log a.log x
Câu 90. Cho các số thực dương a, x, y với
1a
. Khẳng định nào sau đây là khẳng định sai?
A.
log ( ) log log
a a a
xy x y
B.
2
log ( ) 2 log log
a a a
xy x y
C.
1
log log
2
aa
xx
D.
2
log ( ) log 2log
a a a
xy x y
Câu 91. Cho
1a
. Khẳng định sai là
A.
log 0
a
x
khi
1x
B.
log 0
a
x
khi
01x
C. Nếu x
1
< x
2
thì
12
log log
aa
xx
D. Đồ thị hàm số
log
a
yx
có tiệm cận ngang là trục hoành
2B. Hàm số lôgarit
67
Câu 92. Cho a >0, b > 0 thỏa mãn
22
7.a b ab
Chọn mệnh đề đúng trong các mệnh đề sau:
A.
3
log(a b) (loga logb)
2
B.
2(loga logb) log(7ab)
C.
1
3log(a b) (loga logb)
2
D.
1
log (loga logb)
32
ab

Câu 93. Cho
23
1 1 1 1
...
log log log log
k
a
a a a
M
x x x x
( với
1 0, 0ax
). M thỏa mãn
biểu thức nào sau đây:
A.
( 1)
log
a
kk
M
x
B.
( 1)
2log
a
kk
M
x
C.
4 ( 1)
log
a
kk
M
x
D.
( 1)
3log
a
kk
M
x
Câu 94. Chọn khẳng định sai trong các khẳng định sau:
A.
ln 0 1xx
B.
2
log 0 0 1xx
C.
11
33
log log 0a b a b
D.
22
log log 0a b a b
Câu 95. Chọn khẳng định đúng trong các khẳng định sau:
A.
1
5
log 7 0
B.
34
1
log 4 log
3
C.
0,2
log 0,5 0
D.
2
log 5 0
1B 2B 3A 4A 5A 6D 7C 8A 9A 10B
11C 12C 13A 14C 15B 16A 17B 18C 19A 20B
21D 22D 23A 24B 25A 26C 27D 28B 29B 30C
31D 32A 33D 34B 35D 36C 37D 38B 39A 40A
41A 42A 43D 44A 45A 46A 47C 48A 49A 50A
51A 52B 53A 54D 55B 56C 57D 58B 59A 60D
61B 62C 63A 64B 65B 66B 67A 68A 69A 70D
71A 72A 73A 74D 75A 76D 77B 78D 79B 80A
81D 82C 83C 84D 85C 86A 87C 88D 89A 90B
91D 92D 93B 94C 95D
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2C. Phương trình mũ
68
Câu 1. Giải phương trình:
21
28
x
.
A.
1x
B.
5
2
x
C.
2x
D.
4x
Câu 2. Nghiệm phương trình: là
A. x = 1 B. x = 2 C. x = 3 D.
1
3
x
Câu 3. Giải phương trình
2
42
2 .5 1
xx
?
A.
2
2; 2 log 5xx
B.
2;x
C.
2
2 log 5x
D.
2
2 log 5; 1xx
Câu 4. Số nghiệm của phương trình
2
3 .2 1
xx
là:
A. 0 B. 1 C. 2 D. 3
Câu 5. Phương trình
3
3 .2 576
xx
có nghiệm là
A.
4
B.
3
C.
2
D.
1
Câu 6. Cho phương trình
2
56
21
xx
. mệnh đề đúng là :
A. Phương trình có 2 nghiệm dương phân biệt
B. Phương trình có 2 nghiệm trái dấu
C. Phương trình có nghiệm x = 6
D. Tổng các nghiệm của phương trình bằng 4
Câu 7. Nghiệm của phương trình
2 2 2
3 2 6 5 2 3 7
4 4 4 1
x x x x x x
là
A.
1; 2 và 5x x x
B.
1; 2 và 4x x x
C.
0; 2 và 6x x x
D.
1; 2 và 5x x x
Câu 8. Tập nghiệm phương trình
2 2 2
2 2 2 2
4 4 1 4
x x x x x x
là:
A.
0; 1;1;2 .S
B.
0; 2; 1;2 . S
C.
2; 1;1;2 . S
D.
0; 1;1;3 .S
Câu 9. Số nghiệm của phương trình
22
x x 2 x x
2 2 3
A. 2 B. 3 C. 1 D. 4
Câu 10. Tìm số nghiệm của phương trình
33
3 .2 3 .2 2 0

x x x x
.
A. 1. B. 3. C. 2. D. 4.
Câu 11. Phương trình
21
3 4.3 1 0
xx
có 2 nghiệm
12
,xx
trong đó
12
xx
. Khi đó
A.
12
2xx
B.
12
.1xx
C.
12
21xx
D.
12
20xx
Câu 12. Nghiệm của phương trình
9 4.3 45 0
xx
là
A.
2x
B.
3x
C.
1
2
x
D.
1
3
x
PHƯƠNG TRÌNH MŨ
2C. Phương trình mũ
69
Câu 13. Giá trị
x
thỏa mãn phương trình:
1
49 7 8 0
xx
là
A.
0.x
B.
7
log 8.x
C.
x 0
và
x
7
log 8.
D.
x 0
và
x
8
log 7.
Câu 14. Tìm m để phương trình 4
x
- 2
x + 3
+ 3 = m có đúng 2 nghiệm x (1; 3).
A. - 13 < m < - 9 B. 3 < m < 9 C. - 9 < m < 3 D. - 13 < m < 3
Câu 15. Phương trình
4 2 2 0
xx
có nghiệm
x
bằng:
A. 1 B. 1 và -2 C. -2 D. 0
Câu 16. Giải phương trình 4
x
- 6.2
x
+ 8 = 0. Ta có tập nghiệm bằng:
A. {2, 4}. B. {1, 2}. C. {- 1, 2}. D. {1, 4}.
Câu 17. Số nghiệm của phương trình
6.9 13.6 6.4 0
x x x
là:
A. 2 B. 1 C. 0 D. 3
Câu 18. Giải phương trình
2
lg 1 lg lg 2
4 6 2.3 0
x x x
ta được tổng tất cả các nghiệm của
phương trình là:
A.
2
9
B. 0 C.
9
4
D.
1
100
Câu 19. Tìm số nghiệm của phương trình
x 4 2x
4.2 ( 2) 15

A.
2
B.
3
C.
1
D.
0
Câu 20. Cho phương trình
1
3.25 2.5 7 0
xx
và các phát biểu sau:
(1)
0x
là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả hai nghiệm phương trình đều nhỏ hơn 1
(4) Phương trình có tổng hai nghiệm là
5
3
log
7
Số phát biểu đúng là:
A. 1 B. 2 C. 3 D. 4
Câu 21.
2
x log 3
là nghiệm của phương trình nào trong các phương trình sau?
A.
21
22
4
log 3.3 4 log 3 log 9
x
x
B.
3
21
3
8 2 3 2
x
xx

C.
3
21
3
8 2 2
x
xx

D.
21
2
log 2.2 1 4
x

Câu 22.
3x
không là nghiệm của phương trình nào trong các phương trình sau?
A.
2 4 1
3 2.3 27 0.

xx
B.
4
2
log 1 2log ( 2) 2. xx
C.
2 1 1
3 2.3 1 0.

xx
D.
2
4 2 2
log log (2 1) log (4 3). x x x
Câu 23. Tìm nghiệm của phương trình
22
1
3 5 3 5 6.2
xx
x
.
A.
0
1
x
x

B.
0
1
x
x
C.
1
1
x
x

D.
2
2
x
x

2C. Phương trình mũ
70
Câu 24. Giải phương trình:
3 5 10 3 15.3 50 9 1
x x x x
,ta được tổng tất cả
các nghiệm của phương trình là:
A.
2
4 log 6
B.
3
2 log 6
C.
7
1
1 log 5
2
D.
7
1
log 3
3
Câu 25. Giá trị m để phương trình
4 4 2 1 0
xx
m
có nghiệm là
A.
0
1
m
m
B.
01m
C.
1
2
m
D.
1
2
2
m
Câu 26. Phương trình :
4 2 .2 2 0
xx
mm
có hai nghiệm phân biệt khi:
A.
2m
B.
22m
C.
2m
D.
m
Câu 27. Cho phương trình
2
log 100
log 10
1 log
4.3 9.4 13.6 .
x
x
x

Gọi
,ab
lần lượt là hai nghiệm của
phương trình. Tìm tích
.ab
A.
1
.
10
ab
B.
1.ab
C.
100.ab
D.
10.ab
Câu 28. Tính
12
55
xx
S 
, biết
1
x
và
2
x
là hai nghiệm của phương trình
25 6.5 5 0
xx
.
A.
6S
B.
1S
C.
2S
D.
3S
Câu 29. Phương trình
5
2016 2017
xx
có mấy nghiệm?
A.
1
B.
0
C.
2
D.
3
Câu 30. Tìm tất cả các giá trị của tham số m để phương trình
2
2
xx
e e m
có nghiệm.
A.
1m 
B.
10m
C.
10m
D.
1m 
Câu 31. Nghiệm của phương trình
63
3. 2 0
xx
ee
là:
A.
1
0 ln2
3
xx
B.
1
0 ln3
3
xx
C.
1
0 ln2
3
xx
D.
1
0 ln3
2
xx
Câu 32. Phương trình :
1 2 1 2
2 2 2 3 3 3
x x x x x x
có nghiệm:
A. 2 B. 3 C. 4 D. 5
Câu 33. Nghiệm của phương trình
32
(0, 3) 1
x
là:
A.
0x
B.
1x
C.
2
3
x
D.
2
3
x
Câu 34. Phương trình
2 3 4
48
xx
có nghiệm:
A.
6
7
B.
2
3
C.
4
5
D. 2
1C 2D 3A 4C 5C 6A 7A 8B 9A 10A
11C 12A 13B 14A 15D 16B 17A 18D 19C 20A
21B 22C 23C 24B 25A 26C 27B 28A 29A 30A
31C 32A 33C 34A
2D. Phương trình lôgarit
71
Câu 1. Giải phương trình
2
log (3 2) 3x
.
A.
11
3
x
B.
10
3
x
C.
3x
D.
2x
Câu 2. Giải phương trình
3
log ( 1) 3x 
. Ta có nghiệm là:
A.
29x
B.
28x
C.
82x
D.
81x
Câu 3. Phương trình:

4
log (2 8) 2x
có tập nghiệm là
A.
.S
B.
{4}.S
C.
{12}.S
D.
{4;12}.S
Câu 4. Giải phương trình :
2
log 3x 11 4
A. x = 5 B.
13
x
3
C.
17
x
3
D.
20
x
3
Câu 5. Tập nghiệm của phương trình

2
2
log 5 21 4x
là
A.
5; 5
B.
5;5
C.
22
log 5;log 5
D.
Câu 6. Phương trình
3
log 2x
có nghiệm
x
bằng:
A. 1 B. 9 C. 2 D. 3
Câu 7. Nghiệm của phương trình
3
log (2x 1) 2
là:
A. Vô nghiệm B. 1 C. 2 D. 3
Câu 8. Nếu
log 243 5
x
thì x bằng
A. 2 B. 3 C. 4 D. 5
Câu 9.
2log
3
x
là nghiệm của phương trình nào trong các phương trình sau ?
A.
3)93(log)13(log
2
33
xx
B.
0133.3
2
xx
C.
3)93(log).13(log
2
33
xx
D.
3)93(log).33(log
33
xx
Câu 10. Giải phương trình :
2 2 2
log ( 3) log ( 1) log 5xx
:
A. x = - 4 B. x = 2. C. x = 4 D. x = -4; x = 2
Câu 11. Giải phương trình
22
log log ( 1) 1xx
ta được số nghiệm là:
A. 2 B. 0 C. 1 D. 4
Câu 12. Giải phương trình
2 2 2
log log ( 3) log 4xx
A. x = 1 B. x = -4 C. x = 1; x = -4 D. x = 0
Câu 13. Số nghiệm của phương trình
2
33
log 4log 3 7 0xx
là:
A.
1
B.
2
C.
3
D.
0
Câu 14. Nghiệm của phương trình
2
3
3
log ( 1) log (2 1) 2xx
là:
A. Vô nghiệm B. 1 C. 2 D. 3
PHƯƠNG TRÌNH LÔGARIT
2D. Phương trình lôgarit
72
Câu 15. Phương trình
2
log 2 7 1 logx x x
có tập nghiệm là
A.
1;7 .
B.
1;7 .
C.
1.
D.
7.
Câu 16. Tổng các nghiệm của phương trình
2
22
lg lg log 4 2log 0x x x x
là :
A. 101 B. 100 C. 5 D. 0
Câu 17. Tìm nghiệm của phương trình
11
1
4 log 2 log
aa
xx


với
1a
.
A.
2
4
1
1
x
a
x
a
B.
4
1
1
x
a
x
a
C.
2
1
1
x
a
x
a
D.
2
1
1
x
x
a
Câu 18. Phương trình
22
ln 2 2 2 1x x x
có mấy nghiệm?
A.
0
B.
1
C.
2
D.
3
Câu 19. Tìm tất cả các giá trị của tham số m để phương trình
22
33
log log 1 2 1 0x x m
có
nghiệm nằm trong
3
1;3


.
A.
02m
B.
02m
C.
3
1
2
m
D.
3
0
2
m
Câu 20. Nghiệm của phương trình:
33
log 6.2 3 log 4 4 1
xx
là:
A.
2
log 6x
B.
2
log 3x
C.
3
log 2x
D.
2
log 3x 
Câu 21. Phương trình
ln ln 1 0xx
có nghiệm là:
A.
15
2
15
2
x
x
B.
15
2
15
2
x
x
C.
15
4
15
4
x
x
D.
15
4
15
4
x
x
1B 2B 3C 4A 5A 6D 7C 8D 9C 10B
11C 12A 13B 14C 15B 16A 17C 18A 19A 20B
21A
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2E. Bất phương trình mũ
73
Câu 1. Giải bất phương trình:
2
3x
3 81
x
có nghiệm là:
A.
41x
B.
1; 4xx
C.
14x
D.
4; 1xx
Câu 2. Tập nghiệm của bất phương trình



1
3
2
log
51
x
x
là
A.
2;
B.
;0
C.
0;2
D.
0;
Câu 3. Giải bất phương trình
1
23
xx
.
A.
2
log 3x
B.
2
3
log 3x
C.
2
3
log 3x
D.
2
3
log 2x
Câu 4. Giải phương trình
2
1
5 25
x x x
A. [-1;2] B. (-1;2) C. [-1;2) D. (-1;2]
Câu 5. Bất phương trình :
9 3 6 0
xx
có tập nghiệm là:
A.
1; 
B.
;1
C.
1;1
D. Kết quả khác.
Câu 6. Nghiệm của bất phương trình
13
9 36.3 3 0
xx
là:
A.
13x
B.
12x
C.
1 x
D.
3x
Câu 7. Tập nghiệm của bất phương trình
22
3 2.6 7.4 0
x x x
là:
A.
1; +S 
B.
1; 0S 
C.
0; +S 
D.
;1S 
Câu 8. Tìm nghiệm của bất phương trình
1
1
4 2 8
8
2
xx
x
x

.
A.
1x
B.
1
2
x
x

C.
0x
D.
0
2
x
x

Câu 9. Số nghiệm nguyên của bất phương trình
31
13
10 3 10 3
xx
xx


là
A. 0 B. 1 C. 2 D. 3
Câu 10. Bất phương trình
2
x 2x 3
22
có tập nghiệm là:
A.
( ; 1) (3; ) 
B.
1;3
C.
1; 3
D.
( ; 1] [3; ) 
Câu 11. Nghiệm của bất phương trình
2
2
1
8 .2 2
x
xx
là:
A.
1 2.x
B.
1 2.x
C.
1 2 1 2. x
D.
12x
hoặc
1 2.x
BẤT PHƯƠNG TRÌNH MŨ
2E. Bất phương trình mũ
74
Câu 12. Cho hàm số
3
x 2x
f x 3 .4
. Khẳng định nào sau đây là khẳng định sai?
A.
3
3
f x 1 x 4x log 2 0
B.
3
3
f x 1 x x .log 16 0
C.
3
2
f x 1 xlog 3 2x 0
D.
3
2
f x 1 xlog 3 2x 0
Câu 13. Giải bất phương trình
1
25
5
x



.
A.
2x 
B.
2x 
C.
2x
D.
2x
Câu 14. Giải bất phương trình
2
21
39
x x x
.
A.
03x
B.
0x
hoặc
3x
.
C.
10x
D.
01x
Câu 15. Tìm tất cả các giá trị của tham số m để bất phương trình
9 .3 1 0
xx
m
có nghiệm.
A.
2m 
B.
2m
C.
2m 
D.
2m
Câu 16. Giải bất phương trình:
2
55
log log
5 10
xx
x
ta được nghiệm là
A.
1
5
5
x
B.
1
5
5
x
C.
15x
D. Vô nghiệm
Câu 17. Bất phương trình
2 1 2
35
53
xx
có nghiệm là:
A.
3;x 
B.
;1x 
C.
1;x 
D.
;x  
1A 2B 3B 4A 5B 6B 7C 8A 9D 10C
11C 12D 13A 14A 15A 16A 17C
Nguyễn Văn Lực
www.facebook.com/VanLuc168
2F. Bất phương trình lôgarit
75
Câu 1. Giải bất phương trình
2
log ( 2) 3x 
A.
[10; )S 
B.
;10S 
C.
( ;10]S
D.
10;S 
Câu 2. Giải bất phương trình
2
2
log (2 ) 0xx
.
A.
2x
B.
02x
C.
02x
D.
1x
Câu 3. Nghiệm bất phương trình
3
log 2 1 2x 
là
A.
2x
B.
3x
C.
4x
D.
5x
Câu 4.
Nghiệm của bất phương trình
3
log 2 1 3x 
là
A. x > 4. B. x > 14. C. x < 2. D. 2 < x < 14.
Câu 5. Giải bất phương trình:
5
log (2 15) 2x 
.
A.
15
5
2
x
B.
15
2
x 
C.
5x
D.
15
5
2
x

Câu 6. Tập nghiệm của bất phương trình
2
1
2
log 5 7 0xx
là:
A.
;2
B.
2;3
C.
2;
D.
;2 3; 
Câu 7. Nghiệm bất phương trình
2
1
2
log 3 2 1xx
là
A.
( ;1)x
B.
[0;2)x
C.
[0;1) (2; 3]x
D.
[ 0;2) (3;7)x
Câu 8. Giải bất phương trình:
1
3
log 2x 7 3
A.
x 10
B.
x 10
C.
7
x 10
2
D.
7
x 10
2
Câu 9. Tìm m để bất phương trình
2
2
log 4 20x x m
luôn nghiệm đúng với mọi giá trị của
x
:
A.
m4
B.
m4
C.
m 16
D.
m 16
Câu 10. Bất phương trình:
22
log 3 2 log 6 5xx
có tập nghiệm là:
A. (0; +) B.
6
1;
5



C.
1
;3
2



D.
3;1
Câu 11. Tập nghiệm của bất phương trình
2
22
log log 4
4
x
x 
là:
A.
1
; 2; .
2
S

 

B.
1
;4 .
2
S



C.
1
0; 3; .
2
S



D.
1
0; 4; .
2
S



BẤT PHƯƠNG TRÌNH LÔGARIT
2F. Bất phương trình lôgarit
76
Câu 12. Bất phương trình
2
66
log log 6xx
có tập nghiệm là
A.
2;3 .
B.
3;2 \ 0 .
C.
2;3 \ 0 .
D.
; 2 3; . 
Câu 13. Chọn đáp án đúng khi nói về bất phương trình:
22
11
22
log (2 1) log ( 4 5)x x x x
A. Bất phương trình có nghĩa khi:
5x
. B. Tập nghiệm
(1;4]S
.
C. Bất phương trình có nghĩa khi:
1x
. D. Tập nghiệm
;1 (4; )S
.
Câu 14. Tập nghiệm của bất phương trình
2 4 2
log 1 2log 5 1 log 2x x x
là:
A.
3;5S
B.
2;3S
C.
2;5S
D.
4;3S 
Câu 15. Gíá trị của m để bất phương trình
22
22
log (7 7) log ( 4 )x mx x m
có tập nghiệm R
là:
A.
[5; )m
B.
( ;5]m
C.
(2;5]m
D.
( ; 0) (2; )m
Câu 16. Tìm tất cả các giá trị của tham số m để bất phương trình
2
lg lg 3 0x m x m
có
nghiệm nằm trong
1; 
.
A.
3m 
hoặc
6m
. B.
3m 
C.
6m
D.
36m
Câu 17. Nghiệm của bất phương trình
1
3
log (2 ) 1x
là:
A.
5
2
3
x
B.
5
3
x
C.
5
3
x
D.
5
2
3
x
Câu 18. Tập nghiệm của bất phương trình
2
1
2
log ( 2 8) 4xx
là:
A.
6; 4 2;4T
B.
6; 4 2;4T
C.
6;4T 
D.
; 6 4;T  
Câu 19. Bất phương trình
2
log 3 2 0
x

có nghiệm là:
A.
1x
B.
1x
C.
01x
D.
3
log 2 1x
Câu 20. Tập nghiệm của bất phương trình
2
2
3
log 2 1 0xx
là:
A.
3
1;
2



B.
3
0;
2



C.
1
;0 ;
2

 


D.
3
; 1 ;
2

 


Câu 21. Nghiệm của bất phương trình:
2
31
2
1
log log 1
16
x







là:
A.
13
44
x
B.
11
44
x
C.
31
44
x
D.
33
44
x
1D 2D 3C 4B 5D 6B 7C 8C 9A 10B
11D 12C 13B 14B 15C 16A 17A 18A 19B 20C
21B
3A. Nguyên hàm
77
Hàm đa thức, phân thức
Câu 1. 
2
3
2
x
x
là:
A.
2
3
4
x
xC
B.
32
34
xx
C
C.
2
3
2
x
xC
D.
2
3
2
x
xC
Câu 2. Tìm 
5
3
2
1
18
x
f x x




A.
6
3
1
18
x
f x dx C



B.
6
3
61
18
x
f x dx C



C.
6
3
1
1
6 18
x
f x dx C



D.
6
3
1
1
2 18
x
f x dx C



Câu 3. 
'2
( ) 3( 2) , (0) 8f x x f

()y f x
là h
A.
3
2( 2) 8.x 
B.
2
24x 
C.
6 2 4x 
D.
3
2x
Câu 4.       F(x) =mx
3
+(3m+2)x
2
-4x+3       
2
( ) 3 10 4f x x x
là:
A. m = 3 B. m = 0 C. m = 1 D. m = 2
Câu 5. 
3
1
I dx
x
là
A.

2
1
2
C
x
B.
4
1
C
x
C.

2
1
2
xC
D.
3
ln | |xC
Câu 6. 
2
1
()
1
xx
fx
x
.
A.
1
()
1
f x dx x C
x
B.
2
1
( ) 1
( 1)
f x dx C
x
C.
2
( ) ln 1
2
x
f x dx x C
D.
2
( ) ln 1f x dx x x C
Câu 7. 
2
1
()
32
fx
xx

A.
2
( ) ln
1
x
f x dx C
x

B.
2
( ) ln
1
x
f x dx C
x

C.
1
( ) ln
2
x
f x dx C
x

D.
1
( ) ln
2
x
f x dx C
x

NGUYÊN HÀM
3A. Nguyên hàm
78
Câu 8. 
43
2
21
()
xx
fx
x

f(x)
 là
(1) 2F
A.
3
2
15
33
x
x
x
B.
3
2
15
33
x
x
x
C.
3
2
15
33
x
x
x
D.
3
2
1
9
3
x
x
x
Câu 9. 
2
(2 )
( 1)
xx
y
x
A.
2
1
1
xx
y
x
B.
2
1
1
xx
y
x
C.
2
1
x
y
x
D.
2
1
1
xx
y
x
Câu 10. 
'( ) + , '( ) , ( ) , ( )
b
f x ax f f f
x
2
1 0 1 4 1 2
A.
2
51
2
2
x
x
B.
2
15
22
x
x

C.
2
15
22
x
x

D. 
Câu 11. 
2
3
()
2
ax a
Fx
x


2
6
()
2
fx
x
A.
a 1
B.
a 1

a 3
C.
a 3
D.
a 1

a 3
Câu 12. Tìm nguyên hàm
Fx

2
1
()
x
fx
x
A.
1
( ) lnF x x C
x
B.
1
( ) lnF x x C
x
C.
1
( ) lnF x x C
x
D.
1
( ) lnF x x C
x
Câu 13. 
5
( ) 3 1f x x
A.
6
1
( ) 3 1
3
f x dx x C
B.
6
1
( ) 3 1
18
f x dx x C
C.
5
1
( ) 3 1
18
f x dx x C
D.
6
1
( ) 3 1
6
f x dx x C
Nguyễn Văn Lực
www.facebook.com/VanLuc168
3A. Nguyên hàm
79
Hàm căn thức
Câu 14. N
guyên hàm ca hàm s
2
3
2




x x dx
x
là
A.
3
3
4
3ln
33
x
x x C
B.
3
3
4
3ln
33

x
xx
C.
3
3
4
3ln
33
x
x x C
D.
3
3
4
3ln
33
x
x x C
Câu 15. 
2
1f x x x dx
A.
3
2
2
3
1
2
f x dx x C
B.
3
2
2
1
1
3
f x dx x C
C.
3
2
2
2
1
3
f x dx x C
D.
3
2
2
1
1
3
f x dx x C
Câu 16. T
m nguyên h
m c
a h
m s
( ) 3x+2fx
A.
2
( ) x 3x 2 3x+2
9
f x d C
B.
2
( ) x 3x 2 3x+2
3
f x d C
C.
9
( ) x 3x 2 3x+2
2
f x d C
D.
3
( ) x 3x 2 3x+2
2
f x d C
Câu 17. 
2
( ) 1f x x x
là
A.
2
2
1
( ) 1
2
F x x
B.
3
2
1
( ) 1
3
F x x
C.
2
2
2
( ) 1
2
x
F x x
D.
2
2
1
( ) 1
3
F x x
Câu 18. 

3
( ) 3 1f x x
là:
A.
3
( ) (3 1) 3 1f x dx x x C
B.
3
1
( ) 3 1
3
f x dx x C
C.
3
1
( ) (3 1) 3 1
4
f x dx x x C
D.
3
( ) 3 1f x dx x C
Câu 19. 
3
2
14
1
yx
x
là:
A.
3
5
5
14 ln 1
3
x x C
B.
3
5
3
14 ln 1
5
x x C
C.
3
5
3
14 ln 1
5
x x C
D.
3
5
3
14 ln 1
5
x x C
Câu 20. 
1
1
I dx
x

A.
2.I x C
B.
2ln | 1| .I x C
C.
2 2ln | 1| .I x x C
D.
2 2ln | 1 | .I x x C
3A. Nguyên hàm
80
Câu 21. 
x
2x 1 4
d
I

,
 
A.
2x 1 2ln 2x 1 4 .IC
B.
2x 1 ln 2x 1 4 .IC
C.
2x 1 4ln 2x 1 4 .IC
D.
2 2x 1 ln 2x 1 4 .IC
Câu 22. Tìm nguyên hàm
.
dx
I
xx
A.
2ln 1 .I x C
B.
1
2ln .
1
IC
x

C.
1
2ln .I x C
x



D.
2ln .I x x C
Câu 23. Tìm nguyên hàm
2
dx
I
x x x x

.
A.
2
IC
xx
B.
2
1
IC
x
C.
2
1
IC
xx

D.
2
2
IC
xx
Câu 24.  
2
()f x x k

0?k
A.
22
( ) ln
22
xk
f x x k x x k
B.
22
1
( ) ln
22
x
f x x k x x k
C.
2
( ) ln
2
k
f x x x k
D.
2
1
()fx
xk
Câu 25. 
2
( ) ( ) 2 -1f x ax bx c x

2
10 -7 2
()
2 -1
xx
gx
x

1
;
2

A. 3 B. 0 C. 4 D. 2
Câu 26. 
2
( ) ( ) 2 -3g x ax bx c x
 
2
20 -30 7
()
2 -3
xx
fx
x

3
;.
2
A.
,,a b c 4 2 2
B.
,,a b c 1 2 4
C.
,,a b c 2 1 4
D.
,,a b c 4 2 1
Câu 27. 
(I)
2
( ) 1f x x
(II)
2
( ) 1 5f x x
(III)
2
1
()
1
fx
x
(IV)
2
1
( ) -2
1
fx
x

2
( ) ln 1F x x x
A.  B. 
C.  D. 
3A. Nguyên hàm
81
Câu 28. 
2
3
1
()f x x
x

A.
36
25
3 12
( ) ln
55
F x x x x x
B.
3
3
11
()
3
F x x
x
C.
2
3
()F x x x x
D.
35
26
3 12
( ) ln
55
F x x x x x
Câu 29. 
22
()
x
fx
ax
là :
A.
2
1 x
B.
2
ln ax
C.
22
ax
D.
22
ln ax
Hàm lượng giác
Câu 30. 
2
f sinxx
là:
A.
sin2
22
xx
C
B.
sin2
24
xx
C
C.
sin2
24
xx
C
D.
sin2
22
xx
C
Câu 31. T
m nguyên h
m c
a h
m s f(x) = sin(2x + 1)
A.
( ) cos(2 1)f x dx x C
B.
1
( ) cos(2 1)
2
f x dx x C
C.
1
( ) cos(2 1)
2
f x dx x C
D.
( ) cos(2 1)f x dx x C
Câu 32. 
( ) 0
6
F
.
A.
1
( ) cos3
36
F x x x
B.
1
( ) cos3
36
F x x
C.
1
( ) cos3
36
F x x x
D.
1
( ) cos3
36
F x x x
Câu 33. 
32
f x 2x 3x 1 sin2x
khi F(0)=1 là:
A.
43
x x 1 1
F x 2 3 x .cos2x
4 3 2 2
B.
43
x x 1 1
F x 2 3 x .cos2x
4 3 2 2
C.
43
x x 1 1
F x 2 3 x .cos2x
4 3 2 2
D.
43
x x 1 1
F x 2 3 x .cos2x
4 3 2 2
Nguyễn Văn Lực
www.facebook.com/VanLuc168
3A. Nguyên hàm
82
Câu 34. Cho
' ( ) 3 5sinf x x
và
(0) 10f

A.
( ) 3 5cos 2f x x x
B.
3f

C.
3
22
f




D.
( ) 3 5cosf x x x
Câu 35. 
A.
cos sinx dx x C
B.
sin cosx dx x C
C.
xx
e dx e C
D.
2
1
tan
sin
dx x C
x
Câu 36. Kt qu
c
a
2
1 cot x dx
l
A.
tan xC
B.
tan xC
C.
cot xC
D.
cot xC
Câu 37. J =
cosx xdx

A. xsinx cosx + C B. -xsinx cosx + C
C. xsinx + cosx + C D. xsinx - cosx
Câu 38. 
( ) sin3 . os5f x x c x
là
A.
11
( ) os2 os8
4 16
f x dx c x c x C
B.
11
( ) sin2 os8
4 16
f x dx x c x C
C.
11
( ) os2 sin8
4 16
f x dx c x x C
D.
11
( ) os2 os8
4 16
f x dx c x c x C
Câu 39. Tìm nguyên hàm
2
1 1 1
sin cos .I dx
xx
x
A.
12
cos .
4
IC
x

B.
11
sin .
4
IC
x

C.
11
cos .
4
IC
x

D.
12
sin .
4
IC
x

Câu 40. Cho F(x
2
1
os
y
cx
và F(0)=1F(x) là:
A. tanx B. 1-tanx C. 1+tanx D. tanx-1
Câu 41. Tìm nguyên hàm
2
cos
x
I dx
x
.
A.
tanx+ ln cosI x x C
B.
tan x+ ln sinI x x C
C.
tan x-ln sinI x x C
D.
tanx-ln cosI x x C
3A. Nguyên hàm
83
Câu 42. Nguyên hàm F(x) 
3
4
sin
cos
x
fx
x
là:
A.
3
11
3cos cos
C
xx

B.
3
11
3cos cos
C
xx
C.
3
11
3cos cos
C
xx

D.
32
11
3cos cos
C
xx

Câu 43. 
22
1
.
sin cos
fx
xx
A.
cot tan .f x dx x x C
B.
cot tan .f x dx x x C
C.
cot tan .f x dx x x C
D.
cot tan .f x dx x x C
Câu 44. Tìm nguyên hàm
2
.
(cos sin )
dx
I
xx
A.
1
tan .
24



I x C
B.
1
tan .
24



I x C
C.
1
tan .
24



I x C
D.
1
tan .
24



I x C
Câu 45. 





sinx cos sinx
cos sinx cos sinx
x
I dx A B dx
xx

A.

1
.
2
AB
B.
1
.
2
AB
C.
11
,.
22
AB
D.
11
,.
22
AB
Câu 46. 
2
( ) sin 1f x x x
là:
A.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
B.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
C.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
D.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
Câu 47. 
(I)
( ) cosF x x x

2
( ) sin -cos
22
xx
fx
(II)
4
( ) 6
4
x
F x x

3
3
()f x x
x
(III)
( ) tanF x x

( ) -ln cosf x x

A. (I) và (II) B. 
C.  D. 
Câu 48. Tìm nguyên hàm
22
( ) ( tan tan )
x
F x e a x b x c
    
23
( ) tan
x
f x e x

;
22
A.
22
1 2 2
( ) ( tan tan )
2 2 2
x
F x e x x
B.
22
1 2 1
( ) ( tan tan )
2 2 2
x
F x e x x
C.
22
1 2 1
( ) ( tan tan )
2 2 2
x
F x e x x
D.
22
1 2 2
( ) ( tan tan )
2 2 2
x
F x e x x
3A. Nguyên hàm
84
Câu 49. 
2
( ) tanf x x
là :
A.
tan x x C
B.
tan x x C
C.
tan x x C
D.
tan x x C
Câu 50. 
2
( ) os( )f x xc x
là :
A.
1
sinx
2
C
B.
1
sinx
2
C
C.
2
1
sin(x )
2
C
D.
2
1
sin(x )
2
C
Câu 51. Tìm nguyên hàm
Fx

2
sinx xdx
A.
2
11
( ) sin 2 cos2
22
F x x x x x C
B.
2
11
( ) sin 2 cos2
42
F x x x x x C
C.
2
11
cos2
42
F x x x x C



D.
2
11
( ) sin 2 cos2
42
F x x x x x C
Câu 52. Cho
0a
sai :
A.
1
sin cosax b dx ax b C
a
B.
1
cos sinax b dx ax b C
a
C.
1
1
1
ax b dx ax b C

D.
1
ax b ax b
e dx e C
a


Câu 53. F(x) 
( ) sin 2 cosf x x x
là
A.
( ) cos 2 sinF x x x
B.
1
( ) cos2 sin
2
F x x x
C.
( ) cos 2 sinF x x x
D.
2
F(x) sin sinxx
Câu 54. I
2
1
sin2x x dx
x



là :
A.
3
1
ln | | cos2
32
x
x x C
B.
3
1
ln | | cos2
32
x
x x C
C.
3
1
ln | | cos2
32
x
x x C
D.
3
1
ln | | cos2
32
x
xx
Hàm mũ – lôgarit
Câu 55. 
A.

()
xx
y e F x e C
B.
1
()
x
x
y F x e C
e
C.

()
xx
y e F x e C
D.
1
()
x
x
y F x e C
e
3A. Nguyên hàm
85
Câu 56. f(x) = x.e
x
A.
()f x dx
= x.e
x
e
x
+ C B.
()f x dx
= xe
x
+ e
x
+ C
C.
()f x dx
= x.e
x
e
x
D.
()f x dx
= e
x
- x.e
x
+ C
Câu 57. 
2
( ) 2
x
f x xe
.
A.
2
( ) 2
x
f x dx e C
B.
2
2
( ) 2
x
f x dx x e C
C.
2
() 
x
f x dx e C
D.
2
( ) 2
x
f x dx xe C
Câu 58. Tìm nguyên h
1
1
x
fx
e
.
A.
ln 1
x
f x dx x e C
B.
ln 1
x
f x dx x e C
C.
ln 1
x
f x dx x e C
D.
ln 1
x
f x dx x e C
Câu 59. 
x
e
fx
x
.
A.
2
x
f x dx e C
B.
2 x
f x dx e C
C.
2
x
e
f x dx C
D.
x
f x dx e C
Câu 60. 
(I)
2
2
1
ln( 4)
42
xdx
xC
x
(II)
2
1
cot -
sin
xdx C
x
(III)
2cos 2cos
1
sin -
2
xx
e xdx e C
A.  B. I)
C.  D. 
Câu 61. 
ln ln
()
ln
x
fx
xx
là :
A.
2
ln ln 2
2
x
C
B.
2
ln ln
2
x
C
C.
2
ln ln 2
2
x
C
D.
22
ln ln
2
x
C
Câu 62. 
()
x
f x xe

( ) (ax )
x
F x b e

A.
,ab11
B.
,ab 12
C.
,ab21
D.
,ab 11
Câu 63. 
2
1
()
x
f x xe

3
0
2
e
F
là:
A.
2
1
2
x
e
e
B.
2
1
2
x
e
e
C.
2
1
4
x
e
e
D.
2
1
4
x
e
e
3A. Nguyên hàm
86
Câu 64. 
3
( ) (2 )
xx
f x e x e
A.
4
1
( ) 2 2
4
x x x
f x dx xe e e C
B.
4
1
( ) 2 2
4
x x x
f x dx xe e e C
C.
4
1
( ) 2 2
4
x x x
f x dx xe e e C
D.
4
1
( ) 2 2
4
x x x
f x dx xe e e C
Câu 65. Cho
0a
và
1a
.
C
úng ?
A.
.ln
xx
a dx a a C
B.
2
2
2ln
x
x
a
a dx C
a

C.
22xx
a dx a C
D.
22
.ln
xx
a dx a a C
Bài tập tổng hợp
Câu 66. 
A.
2
1
1
xx
dx
x
B.
2
22x x dx
C.
sin 3xdx
D.
3x
e xdx
Câu 67. F(x) f(xG(x 
f(x
A. F(x)
=
G(x
B. G(x)
=
F(x) M trên kh
C. F(x)
=
G(xx 
D. F(x)và G(x
Câu 68. 
A.
2
2
3
xx
fx
x

B.
2
22f x x x
C.
sin3f x x
D.
3x
f x xe
1A 2A 3D 4C 5A 6C 7A 8A 9D 10B
11B 12C 13D 14A 15B 16A 17C 18C 19C 20C
21C 22A 23B 24A 25D 26D 27B 28A 29C 30C
31B 32C 33A 34B 35D 36D 37A 38A 39A 40B
41A 42C 43C 44B 45D 46B 47B 48B 49A 50D
51B 52B 53B 54A 55D 56A 57C 58D 59A 60D
61B 62D 63B 64D 65B 66B 67B 68B
Nguyễn Văn Lực
www.facebook.com/VanLuc168
3B. Tích phân
87
Hàm đa thức, phân thức
Câu 1. 
0
(2 4) 5
b
x dx
là:
A.
5
B.
1;5
C.
1
D.
1;4
Câu 2. Cho tích phân


1
2
0
3 2 ln(2 1)I x x x dx

lnI b a c


A.
a 3
B.
a 3
C.
2
3
a
D.

2
3
a
Câu 3. a
0
23
1
( 1)I x x dx

A.
7
70
I
B.
1
60
I
C.
2
15
I
D.
1
60
I
Câu 4. Tính tích phân I =
1
5
0
(1 )x x dx
A. I = -
1
42
B. I =
1
42
C. I = -
1
6
D. I =
1
6
Câu 5. Tính tích phân:
1
1000
32
0
3 .( 1)I x x x dx
A.
1001
4
3003
B.
1001
3
3000
C.
1000
4
3000
D.
1001
3
3003
Câu 6. Tính tích phân
2
2
1
4xx
I dx
x
A.
29
2
I
B.
11
2
I
C.
11
2
I
D.
29
2
I
Câu 7. 
5
1
ln
21
dx
a
x

A. 2 B. 3 C. 4 D. 5
Câu 8. 
1
2
0
1
F
1x
là:
A.
4
B. -
4
C.
2
D.
6
TÍCH PHÂN
3B. Tích phân
88
Câu 9. 
1
2
0
2 3 6
ln3
21
xx
dx a b
x



A.
21
4
B.
21
4
C.
4
21
D.
4
21
Câu 10. 
1
16
2
0
10
1
x
dx
e
là :
A.
16
1
10 ln
2
e
B.
2
16
2
12
10 ln
2
1
e
e
C.
2
15
2
12
10 ln
2
1
e
e
D.
2
16
2
1
10 ln
2
1
e
e
Câu 11. 
2
2
0
1 15
ln
7
2
dx
x x k


A.
1
B.
4
C.
2
D.
3
4
Câu 12. 
8
1
10
0
3
21
x
dx
x
là :
A.
18 9
9
32
63.3
B.
18 9
9
32
63.3
C.
18 9
9
32
63.3

D.
18 9
9
32
63.3
Câu 13. Tính tích phân:I=
2
1
2 5 7
e
xx
dx
x

A.
4 7 8ee
B.
7 4 8ee
C.
8 7 4ee
D.
4 7 8ee
Câu 14. Tính tích phân
2
5
1
.1I x x dx
:
A.
42
13
B.
13
42
C.
13
42
D.
42
13
Hàm căn thức
Câu 15. Tích phân
1
22
0
1I x x dx

A.
2
B.
8
C.
4
D.
16
Nguyễn Văn Lực
www.facebook.com/VanLuc168
3B. Tích phân
89
Câu 16.  I=
4
2
0
2 4 1
21
xx
dx
x


A.
478
15
I
B.
448
15
I
C.
408
15
I
D.
378
15
I
Câu 17. Tính tích phân
2
2
2
2
0
1
x
I dx
x
A.
1
42
B.
1
84
C.
1
84
D.
1
48
Câu 18.
3
3
2
0
1
x
I dx
x
c
kt qu
l
A.
5
3
B.
5
3
C.
4
3
D.
4
3
Câu 19. Tính tích phân
7
3
2
3
0
1
x dx
I
x
A.
141
10
B.
141
10
C.
141
20
D.
47
10
Câu 20. 
2
3
0
min ; 2I x x dx

A.
4
5
B.
4
5
C.
5
4
D.
5
4
Câu 21. Tính
5
2
0
4I x x dx
A.
3
19
B. 1 C.
3
19
D.
3
28
Câu 22. Tính
2
2
0
4 x dx
A.
2
1
2
B.
2
1
2
C.
2
D.
Câu 23. Tính tích phân
1
2
0
31x x dx
A.
7
3
B.
8
9
C.
7
9
D.
1
Nguyễn Văn Lực
www.facebook.com/VanLuc168
3B. Tích phân
90
Hàm lượng giác
Câu 24. 
6
0
tanI xdx
A.
3
ln
2
B.
3
ln
2
C.
23
ln
3
D.
Câu 25. Tính tích phân:
0
.sinxI x dx
A.
2
I
B.
I 0
C.
I
D.
I 1
Câu 26. T
nh t
ch phân I =
2
3
0
( osx 1) sinx xcd
A.
15
4
I
B.
15
4
I 
C.
15
2
I
D.
15
2
I 
Câu 27. 
4
0
B 2x 3 .sin 4x.dx

là:
A.
3
82
B.
3
28
C.
3
82
D.
3
8
Câu 28. Tính tích phân
2
0
cosI x xdx
A.
1
2
B.
1
2
C.
2
D.
1
2
Câu 29. Tính tích phân
4
s inx
0
cosI e xdx
.
A.
2
2
Ie
B.
2
2
1Ie
C.
2
2
1Ie
D.
2
1
2
Ie
Câu 30. Tính tích phân
2
2
sin 2 cosI x xdx
.
A.
0I
B.
1I
C.
1
3
I
D.
1
6
I
Câu 31. T
ch phân
22
0
sin .cosI x xdx
b ng:
A.
6
B.
3
C.
8
D.
4
3B. Tích phân
91
Câu 32. Tính tích phân
2
23
0
sin cosI x xdx
A.
2
15
B.
3
15
C.
2
13
D.
2
15
Câu 33. Tính tích phân
2
0
( sin )I x x dx

A.
3
32
I


B.
2
32
I


C.
3
5
32
I


D.
2
5
32
I


Câu 34. K
3
0
sinx
A .dx
1 6cosx
là:
A.
1
72
3
B.
1
72
3
C.
1
72
2
D.
72
Câu 35. 
3
22
6
tan cot 2I x x dx


3
2
6
tan cotI x x dx


3
6
tan cotI x x dx

3
6
tan cotI x x dx


3
6
os2x
2
sin2x
c
I dx

3
6
3
ln sin 2 2 ln
2
Ix

A. 2 B. 3 C. 4 D. 5
Câu 36. 
2
x
cos x
dx m
13


2
x
cos x
I dx
13

A.
m
B.
m
4
C.
m
D.
m
4
Câu 37. Tính tích phân:
2
0
2cos
3 2sin
x
I dx
x
A.
5
ln
3
I
B.
3
ln
5
I
C.
5ln3.I
D.
3ln5I
Câu 38. Tích phân
3
4
2
6
1 sin
sin
x
dx
x
là
A.
32
2
B.
3 2 2
2

C.
32
2
D.
3 2 2 2
2

3B. Tích phân
92
Câu 39. Tính tích phân
3
3
0
sinx
cos
I dx
x
A.
3
2
I
B.
3
2
I 
C.
3
2
I 
D.
3
2
I 
Câu 40. Cho 
4
3
0
sin
1
4
.
2
cos
x
dx m
x




1
2
m

A.
1
4
B.
1
4
C.
0
D.
1
Câu 41. 
2
0
max sin ;cosxI x dx

A. 1 B.
2
C.
D. 2
Câu 42. Tính
2
0
2
cos
xdx
A.
2
B.
4
C.
3
2
D.
3
Hàm mũ – lôgarit
Câu 43. 
2
2
0
2
x
e dx
là:
A.
4
e
B.
4
1e
C.
4
4e
D.
4
3e
Câu 44. 
2
1
0
x
I e xdx
,

A.
1
.
2
e
I
B.
21
.
2
e
I
e
C.
1
.
2
e
I

D.
1
.
2
e
I
e
Câu 45. 

0
2
2
x
I x e dx
là
A.
2
31e
B.

2
2(1 )e
C.
2
5
3
e
D.
2
1
1
e
Câu 46. T
ch phân
1
ln
e
I xdx
b ng:
A. 4 B. 3 C. 2 D. 1
Câu 47. T
nh t
ch phân I =
e
1
.lnx. xI x d
A.
2
1
4
e
I
B.
2
1
4
e
I
C.
2
3
4
e
I
D.
2
3
4
e
I
3B. Tích phân
93
Câu 48. Tích phân
1
ln
e
I x xdx

A.
2
2
3
ee
B.
2
2
6
ee
C.
2
2
9
ee
D.
2
2
7
ee
Câu 49. Tính tích phân
2
1
ln
e
I x xdx
.
A.
3
21
9
e
I
B.
3
21
9
e
I
C.
3
2
9
e
I
D.
3
2
9
e
I
Câu 50. Tích phân
1
(x 1)lnxdx
e
I
là
A.
2
3
2
e
B.
2
3
3
e
C.
2
3
4
e
D.
2
3
6
e
Câu 51. 
2
1
.ln( 1)
e
I x x dx
,

A.
52
ln2.
18 3
I
B.
53
ln2.
18 2
I
C.
52
ln2.
18 3
I 
D.
52
ln2.
18 3
I
Câu 52. 
4
3
C 2x.ln 3x 6 .dx
là:
A.
11
12ln6 5ln3
2

B.
11
12ln6 5ln3
2

C.
11
12ln6 5ln3
2

D.
11
12ln6 5ln3
2

Câu 53. 
0
(4 ln 2 ln2)
m
xx
I x dx
. Tìm m khi I=12.
A.
4m
B.
3m
C.
1m
D.
2m
Câu 54. Tính tích phân
1
ln
e
x
I dx
x
A.
2
1
2
e
I
B.
2
1
2
e
I
C.
1
2
I
D.
1
2
I 
Câu 55. Tính tích phân
1
1 ln
e
x
I dx
x
.
A.
2I
B.
1
I
e
C.
Ie
D.
3
2
I
3B. Tích phân
94
Câu 56. Tính tích phân
2
1
ln
e
x
I dx
x
.
A.
2
1I
e

B.
2
1I
e

C.
1
2I
e

D.
1
2I
e

Câu 57. Tính tích phân
2
5
1
ln
I=
x
dx
x
A.
15 4 ln 2
256
B.
14 3 ln 2
256
C.
13 3 ln 2
256
D.
15 4 ln 2
256
Câu 58. Tính tích phân
1
0
1
1
x
x
ex
I dx
xe
A.
2
ln 1 e
B.
2
ln 1e
C.
ln 1 e
D.
ln 1e
Câu 59. 
1
2
0
.
1
x
x
dx a
e

1
2
0
.
1
x
x
I dx
e
A.
1
2
Ia
B.
1Ia
C.
1
3
Ia
D.
1Ia
Câu 60.
1
ln 1
ln 1
e
x
I dx
xx

A.
ln( 1)Ie
B.
ln( 1)Ie
C.
ln( 1)Ie
D.
ln(1 )Ie
Câu 61. Tính tích phân:
1
2 ln
2
e
x
I dx
x
A.
3 2 2 3
3
B.
3 3 2 2
3
C.
3 3 2 2
2
D.
3 3 2 2
3
Câu 62. Tính:
1
22
0
x
K x e dx
A.
2
4
e
K
B.
2
1
4
e
K
C.
2
1
4
e
K
D.
1
4
K
Câu 63. Tính:
3
2
1
3 ln x
I dx
(x 1)
A.
2ln)3ln1(
4
3
I
B.
2ln)3ln1(
4
3
I
C.
2ln)3ln1(
4
3
I
D.
3
I (1 ln3) ln2
4
Câu 64. Tính:
2
sin
0
.cos
x
I e x xdx

.
A.
2
2
e

B.
2
2
e
C.
2
2
e
D.
2
2
e
3B. Tích phân
95
Câu 65. 
ln5
2
ln 2
x
1
x
x
e
d
e
là
A.
22
3
B.
19
3
C.
23
3
D.
20
3
Câu 66. Tính tích phân
1
(2 1)ln
e
x xdx
A.
2
3e
B.
2
1
2
e
C.
2
3
2
e
D.
2
3
2
e
Bất đẳng thức tích phân
Câu 67. 
a

2
0
a
x x dx

A.
1a
B.
1
2
a
C.
2a
D.
3
2
a
Câu 68. 
1m
sao cho
1
ln 1 .x dx m

A.
1.me
B.
2
.me
C.
2.me
D.
.me
Câu 69. Tìm 
1
0
dx
0
2x k
A.
k3
B.
k4
C.
k1
D.
k2
Câu 70. 
S
là 
k

1
ln 2
e
k
dx e
x

. Tìm
S
.
A.
1;2;3S
B.
1;2S
C.
2;3S
D.
S 
Câu 71. Cho
1
0
2
dx
I
xm

0m

m

1I
.
A.
1
0
4
m
B.
1
4
m
C.
11
84
m
D.
0m
Bài tập tổng hợp
Câu 72. Tính tích phân
4
2
1
32I x x dx
A.
19
2
B.
19
2
C.
28
6
D.
19
Câu 73. Tính tích phân
1
xx
1
I 2 2 dx
A.
I 2ln2
B.
2
I
ln2
C.
I ln2
D.
1
I
ln2
3B. Tích phân
96
Câu 74. Tính
2
2
2
1J x dx

A. 3 B. 4 C. 9 D.
2
9
Câu 75. 
10
0
( ) 17f z dz
và
8
0
( ) 12f t dt
thì
10
8
3 ( )f x dx

A. -15 B. 29 C. 15 D. 5
Câu 76.          
10 6
02
( ) 7; ( ) 3f x dx f x dx

  
2 10
06
( ) ( )P f x dx f x dx


A. 3 B. 2 C. 4 D. 1
Câu 77. Tích phân
( ) 0
a
a
f x dx
thì ta có:
A.
()fx
 B.
()fx

C.
()fx

;aa
D. 
1B 2A 3D 4B 5A 6B 7B 8A 9A 10B
11D 12A 13A 14C 15D 16A 17C 18C 19C 20D
21A 22D 23C 24C 25C 26A 27C 28D 29C 30A
31C 32A 33C 34B 35B 36A 37A 38B 39A 40C
41B 42B 43B 44D 45C 46D 47D 48C 49A 50C
51D 52D 53D 54C 55D 56B 57A 58C 59C 60A
61B 62C 63D 64A 65D 66D 67A 68D 69C 70B
71A 72B 73D 74B 75A 76C 77B
Nguyễn Văn Lực
www.facebook.com/VanLuc168
3C. Diện tích hình phẳng
97
Câu 1. 
()y f x

;ab
. 

y f x

,x a x b
là
A.
( ) .
b
a
f x dx
B.
2
( ) .
b
a
f x dx
C.
( ) .
b
a
f x dx
D.
( ) .
a
b
f x dx
Câu 2. Vit công th
c t
nh di
n t
ch S c
a h
nh ph
ng gi
i h
n b
 th
c
a hai h
m s
( ), ( )y f x y g x
v
c

ng th
ng
,x a x b
l
:
A.
[ ( ) ( )]
b
a
S f x g x dx
B.
( ) ( )
b
a
S f x g x dx
C.
( ) ( )
b
a
S f x g x dx
D.
2
[ ( ) ( )]
b
a
S f x g x dx
Câu 3. 
()fx
 
1
1
2
f




 
2
1 2 1 2
( ); ( ) ; 0; 1y f x y f x x x
là:
A.

1
1
2
01
2
( )(1 ( )) ( )( ( ) 1)f x f x dx f x f x dx
B.
1
2
0
( ) ( ( ))f x f x dx
C.
1
2
0
( ( )) ( )f x f x dx
D.

1
1
2
01
2
( ) (1 ( )) ( )( ( ) 1)f x f x dx f x f x dx
Câu 4. 
2
yx
và
2yx
.
A.
3
2
B.
9
2
C. D.
15
2
Câu 5. 
2
yx

2yx
là:
A.
4
3
B.
3
2
C.
5
3
D.
23
15
Câu 6.
Tính di tích hình phng gii hn bi  t hàm s
2
2yx
và
.yx
A.
5
B.
7
C.
9
2
D.
11
2
Câu 7. 

2
2yx
và
24yx
là
A.
3
13
B. 9 C.
13
3
D.
1
9
DIỆN TÍCH HÌNH PHẲNG
3C. Diện tích hình phẳng
98
Câu 8. 
2
( ) : 3P y x

( ) : 2d y x

2x
là:
A. - B.  C.  D. 
Câu 9. 
3
3y x x
và
yx
l
A. 12 B. 4 C. 6 D. 8
Câu 10. 
3
xx
và
2
y x x

A. 12 B. 37
C.
37
12
D.
11
Câu 11. 
3
33y x x
y=5
là:
A.
5
4
B.
45
4
C.
27
4
D.
21
4
Câu 12. 
4
-2x
2

A.
16
15
S
B.
8
15
S
C.
8
15
S
D.
15
8
S
Câu 13. D
i tích hình phng gii hn bi  t hàm s
42
5 3 8,y x x

1;3

A. 100 B. 150 C. 180 D. 200
Câu 14. 
2
4 3 , 3y x x y x
A.
197
6
S
B.
109
6
S
C.
56
3
S
D.
88
3
S
Câu 15. 
;2
x
y e y

1x
b ng
A.
ln2 4Se
B.
2ln2 4Se
C.
2ln2 4Se
D.
2ln2 4Se
Câu 16. 
1
ln , ,y x x x e
e

A.
1
1
e
B.
1
21
e



C.
1
21
e



D.
1
1
e
Câu 17. 
21
1
x
y
x


A. ln2 1. B. ln2. C. ln2 + 1. D. 2ln2 1.
Câu 18. 
1 x
y
x
,
2, 0, 0.y y x


A. ln3 B. ln3 C. 2ln3 D. 2ln3
3C. Diện tích hình phẳng
99
Câu 19. y =
2
2
3
xx
x

,
0,x 2, 2.yx
A. S = 7 4
5
16
ln
B. S = 7 + 4
5
14
ln
C. S =7 + 4
5
16
ln
D. S = 7 - 4
5
14
ln
Câu 20. 
2
11
y ,y
1 x 2
là:
A.
1
2
B.
1
2
C.
5
1
6
D.
5
1
6
Câu 21. 
2
1y x x


A.
2 2 1
3
B.
8
3
C.
2 2 1
D.
2 2 1
3
Câu 22. (H) (P): y = –x
2
+2, y = 0, x = 0, x = 1
M nào trên (P) (H) 
A.
19
;
24
M
B.
17
;
24
M
C.
17
;
24
M
D. M
Câu 23. 
2
4, 0y x y
, x = 3, x 
A. 15 B. 18 C. 20 D. 22
Câu 24. 
2
2x,y x y x

A.
7
2
dvdt
B.
9
2
dvdt
C.
19
2
dvdt
D.
11
2
dvdt
1C 2B 3D 4B 5A 6C 7B 8B 9D 10C
11C 12A 13D 14B 15D 16C 17A 18B 19C 20A
21A 22B 23A 24B
Nguyễn Văn Lực
www.facebook.com/VanLuc168
3D. Thể tích khối tròn xoay
100
Câu 1. 
V


,y f x

Ox

,x a x b a b

Ox
là:
A.
b
a
V f x dx
B.
2
b
a
V f x dx
C.
2
b
a
V f x dx
D.
b
a
V f x dx
Câu 2. (H) 
3 ; ; 0 ; 1y x y x x x

(H) quay quanh Ox.
A.
8
3
B.
2
8
3
C.
2
8
D.
8
Câu 3. 
,1y x x
x. T
y 
A.
3
B.
2
3
C. D.
4
3
Câu 4.               
2
1yx
,
0y
Ox 
a
b
a+b 
A. 11 B. 17 C. 31 D. 25
Câu 5. V 

2
2yx
Ox 
1, 0xx
xung quanh
Ox.
A.
0
22
1
(2 )V x dx
B.
0
22
1
(2 )V x dx
C.
0
2
1
(2 )V x dx
D.
0
2
1
2V x dx
Câu 6. 
22
4 , 2y x y x

Ox
.
A.
14
B.
15
C.
16
D.
17
Câu 7.                 
2
3 ; y x x y x
x là
A.
56
15
B.
6
15
C.
56
15
D.
56
5
THỂ TÍCH KHỐI TRÒN XOAY
3D. Thể tích khối tròn xoay
101
Câu 8. 
2
2y x x


A.
16
15
V
B.
4
3
V
C.
4
3
V
D.
16
15
V
Câu 9.             
2
4 4, 0, 0, 3y x x y x x

Ox
là:
A.
33
.
7
B.
33
.
6
C.
33
.
5
D.
33
.
4
Câu 10. H
2
1yx
và
42yx

HOx là:
A.
4
3
B.
248
3
C.
224
15
D.
1016
15
Câu 11. 
Ox


2
1, 0y x x

2
1yx

1;2
là
A.
15
8
B.
8
15
C.
8
15
D.
15
8
Câu 12.              
1
, 0, ( 1)
2
y y x a a

A.
1
1
a
B.
1
1
a
C.
1
1
a
D.
1
1
a
Câu 13. 
0;xx


(0 )x


2 sinx
.
A.
3
B.
3
C.
23
D.
2
Câu 14. 
0, 2xx


Ox

x
(
02x


2
5x
.
A.
4
B.
C.
3
D.
2
Câu 15.  
0x
và
3x


Ox

x
03x
là

x
và
2
29 x
.
A.
16
B.
17
C.
19
D.
18
Câu 16. 
1yx

4x


A.
7
6
B.
2
7
6
C.
7
6
D.
5
3
3D. Thể tích khối tròn xoay
102
Câu 17.               

2
1 , 0y x y
A.
2
31416
0001
B.
4
3
C.
2
D.
3
2
Câu 18. x 
y =
2
(1 )x ln x
x x = 1.
A.
14
ln2
3 9 6
V



B.
14
ln2
3 9 6
V



C.
14
ln2
3 9 6
V



D.
14
ln2
3 9 6
V



Câu 19. Th
Oy


2
2
, 0, 1.
1
y
x y y
y
A.
3
V
B.
2
V
C.
4
V
D.
3
2
V
Câu 20. 
sin cos , 0, 0,
2
y x x y x x
x 
A.
3
22



B.
3
22



C.
1
22



D.
3
22




Câu 21. 
sin , 0, 0, .y x x y x


A.
2
B.
2
2
C.
2
4
D.
2
Câu 22.                
ln , 1, 2, 0y x x x y

A.
2
2 ln 2 2ln2 1
 B.
2
ln 2 2ln2 1

C.
2
2 ln 2 2ln2 1
 D.
2
ln 2 2ln2 1

Câu 23. 
ln ,y 0, .y x x x e


A.
3
(5e -2)
V=
28
B.
3
(5e -2)
V=
25
C.
3
(5e +2)
V=
27
D.
3
(5e -2)
V=
27
Câu 24. Th
t
ch kh i tr
n xoay sinh b
i h
nh ph
ng gi
i h
n b
i c

ng
x
ye
, tr
c tung v
ye
quay quanh tr
c Ox b ng:
A.
2
( 1)e
B.
2
( 1)
2
e
C.
2
( 2)e
D.
2
( 1)
2
e
Câu 25. 
x
ye


0, 3xx
Ox là:
A.
6
1
2
e
B.
6
1
2
e
C.
6
1
2
e
D.
6
1
2
e
3D. Thể tích khối tròn xoay
103
Câu 26. A 
,
xx
y e y e

và
1.x

A 
A.
22
1
22
ee




B.
22
1
22
ee




C.
22
1
22
ee




D.
22
1
22
ee




Câu 27. Cho hình phng A gii hn b
1
2
.
x
y x e
ng
thng
1, 2xx
và trc hoành . Th tích khi tròn xoay to thành khi quay A quanh trc hoành
bng
A.
42
31
42
ee
B.
42
31
42
ee



C.
42
31
42
ee
D.
42
31
42
ee




Câu 28. H
.
x
y x e


1x
V HOx.
A.
2
( 1)
4
e
B.
2
( 1)
4
e
C.
2
( 1)
2
e
D.
2
( 1)
2
e
Câu 29. 
x
y xe

hoành,
2x

A.
4
1
51
4
e
B.
4
51e
C.
4
51
4
e
D.
4
51e
Câu 30. 
H

2
x
y xe
,
0x
và
1x


H

Ox
.
A.
2e
B.
1e
C.
2e
D.
1e
1C 2A 3B 4C 5A 6C 7A 8D 9C 10C
11B 12C 13C 14A 15D 16A 17B 18A 19B 20A
21B 22C 23D 24D 25A 26D 27B 28A 29C 30C
Nguyễn Văn Lực
www.facebook.com/VanLuc168
4A. Tính toán với số phức
104
Tìm phần thực, phần ảo của số phức
Câu 1. Cho số phức z = 2i-1.Phần thực và phần ảo của số phức z lần lượt là:
A. 2 và -1 B. -2 và 1 C. -1 và 2 D. -2 và -1
Câu 2. Phần thực và phần ảo của số phức
23zi
là
A. Phần thực bằng
2
và phần ảo bằng
3
.
B. Phần thực bằng
2
và phần ảo bằng
3i
.
C. Phần thực bằng
2
và phần ảo bằng
3
.
D. Phần thực bằng
2
và phần ảo bằng
3i
.
Câu 3. Cho số phức:
11 7zi
. Phần thực a và phần ảo b của
z
lần lượt là
A.
11; 7.ab
B.
11; 7.ab
C.
11; 7.ab
D.
11; 7.ab
Câu 4. Phần thực và phần ảo của số phức
4zi
là
A. Phần thực bằng
0
và phần ảo bằng
4
.
B. Phần thực bằng
4
và phần ảo bằng
4i
.
C. Phần thực bằng
0
và phần ảo bằng
4i
.
D. Phần thực bằng
0
và phần ảo bằng
4i
.
Câu 5. Trong các số phức sau, số thực là
A.
3 2 3 2ii
B.
3 2 3 2ii
C.
1 2 1 2ii
D.
5 2 5 2ii
Số phức liên hợp
Câu 6. Cho số phức
13zi
, số phức liên hợp của số phức z là:
A.
13zi
B.
3zi
C.
13zi
D.
3zi
Câu 7. Số phức liên hợp của số phức
12zi
là
A.
12i
B.
12i
C.
2 i
D.
12i
Câu 8. Cho số phức z = -2 – 5i. Tìm phần thực và phần ảo của số phức
z
A. Phần thực bằng 2 và phần ảo bằng -5i
B. Phần thực bằng -2 và phần ảo bằng 5i
C. Phần thực bằng 2 và phần ảo bằng -5
D. Phần thực bằng -2 và phần ảo bằng 5
Nguyễn Văn Lực
www.facebook.com/VanLuc168
TÍNH TOÁN VỚI SỐ PHỨC
4A. Tính toán với số phức
105
Câu 9. Cho số phức
34zi
.Phần thực và phần ảo của số phức
z
là
A. Phần thực bằng
3
và phần ảo bằng
4
.
B. Phần thực bằng
3
và phần ảo bằng
4i
.
C. Phần thực bằng
3
và phần ảo bằng
4i
.
D. Phần thực bằng
3
và phần ảo bằng
4
.
Câu 10. Cho số phức
43zi
. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng – 4 và phần ảo bằng –3i.
B. Phần thực bằng – 4 và phần ảo bằng –3.
C. Phần thực bằng 4 và phần ảo bằng 3i.
D. Phần thực bằng 4 và phần ảo bằng 3.
Câu 11. Cho
z 4 5i.
Tìm phần thực, phần ảo của số phức
z
A. Phần thực bằng 4 và phần ảo bằng 5i.
B. Phần thực bằng 4 và phần ảo bằng 5.
C. Phần thực bằng -4 và phần ảo bằng -5.
D. Phần thực bằng -4 và phần ảo bằng -5i.
Câu 12. Cho số phức z = 6 + 7i. Số phức liên hợp của z có điểm biểu diễn là:
A. (6; 7) B. (6; -7) C. (-6; 7) D. (-6; -7)
Câu 13. Cho số phức z thỏa
(1 ) 4 2i z i
. Tìm phần thực, phần ảo của số phức z.
A. Phần thực bằng 1 và phần ảo bằng 3i
B. Phần thực bằng 1 và phần ảo bằng 3
C. Phần thực bằng -1 và phần ảo bằng -3i
D. Phần thực bằng -1 và phần ảo bằng 3
Câu 14. Cho số phức
zi
.Số phức liên hợp của z là:
A.
zi
B.
z1
C.
z 1 i
D.
z1
Câu 15. Cho số phức z = 2- 3i . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 2 và phần ảo bằng 3
B. Phần thực bằng 2 và phần ảo bằng -3
C. Phần thực bằng 2 và phần ảo bằng 3i
D. Phần thực bằng 2 và phần ảo bằng -3i
Câu 16. Số phức liên hợp của số phức
13zi
là
A.
13zi
B.
13zi
C.
13zi
D.
13zi
Câu 17. Cho số phức z = 1 – 5i. Tìm phần thực, phần ảo của số phức
z
.
A. Phần thực bằng -1 và phần ảo bằng -5i. B. Phần thực bằng -1 và phần ảo bằng -5.
C. Phần thực bằng 1 và phần ảo bằng -5. D. Phần thực bằng 1 và phần ảo bằng -5i.
Phép cộng số phức
Câu 18. Cho hai số phức
12
z 3 2i; z 1 3i
.Tổng của hai số phức
12
z ; z
là :
A.
4i
B.
9i
C.
1 9i
D.
4 5i
Câu 19. Cho số phức z = a + bi. Khi đó số
1
2
zz
là
A. Một số thực B. 2 C. Một số thuần ảo D. i
Câu 20. Cho số phức z = 1 -2i , phần ảo của số phức w = 2z + là:
A. -2 B. 2 C. 4 D. -4
4A. Tính toán với số phức
106
Câu 21. Cho
12
2 3 , 1i z iz
. Tính
12
zzz
A.
33zi
B.
32zi
C.
22zi
D.
32zi
Câu 22. Cho hai số phức z = a + bi và z’ = a’ + b’i. Điều kiện giữa a,b,a’,b’ để z+z’ là một số
thuần ảo là:
A.
a a ' 0
b b' 0


B.

a a ' 0
b, b' bÊt k×
C.
a a' 0
b b'

D.


a a ' 0
b b ' 0
Câu 23. Biết rằng
3 2 3 5 4z i i
. Tìm z
A.
13zi
B.
32zi
C.
1
2
3
zi
D.
1
1
3
zi
Câu 24. Cho số phức
24zi
.Tìm phần thực, phần ảo của số phức
w z i
A. Phần thực bằng -2 và phần ảo bằng -3i B. Phần thực bằng -2 và phần ảo bằng -3
C. Phần thực bằng 2 và phần ảo bằng 3i D. Phần thực bằng 2 và phần ảo bằng 3.
Câu 25. Cho hai số phức
12
z 7 5i; z 3 i
.Số phức
12
z - z
bằng:
A.
4 4i
B.
10 4i
C.
4 4i
D.
4 6i
Câu 26. Cho
12
2 , 5 7i z iz
. Tính
12
zzz
A.
37zi
B.
38zi
C.
76zi
D.
3zi
Câu 27. Cho số phức
z 3 3 4i 4 3i 1
.Số phức liên hợp của z là:
A.
z 24 13i
B.
z 3 3 4i 4 3i 1
C.
z 5 24i
D.
z 13 24i
Câu 28. Cho hai số phức
12
z 1 2i; z 2 3i
.Số phức

12
z - 2z
bằng:
A.
3.i
B.
3 8 .i
C.
5.i
D.
3 8 .i
Câu 29. Cho hai số phức: z
1
= 2 – 3i ; z
2
= -1 + i. Phần ảo của số phức w = 2z
1
– z
2
bằng:
A. -7 B. 5 C. 7 D. -5
Câu 30. Cho
12
2 , 5 7i z iz
. Tính
12
2 zzz
A.
97zi
B.
33zi
C.
93zi
D.
76zi
Câu 31. Cho số phức z
1
= 1 – 3i, z
2
= 2 + i. Tìm số phức w =
12
2zz
A. z = 7i B. 5 i C. – 4 – 7i D. – 7i
Câu 32. Cho
5 2 1 4 3 .z i i i
Khi đó số phức
2zz
bằng:
A.
7 14i
B.
7 42i
C. -7 D.
7 14i
Câu 33. Cho
12
2 3 , 3 4z i z i
. Khi đó
12
53zz
bằng
A.
1 i
B.
3i
C.
12i
D.
13i
Câu 34. Kết quả của phép trừ
(3 4 ) (2 3 )ii
là
A.
3zi
B.
2zi
C.
17zi
D.
57zi
Câu 35. Cho số phức:
35zi
. Tìm phần thực và phần ảo của số phức
zi
A. Phần thực bằng -3 và phần ảo bằng 5 B. Phần thực bằng -3 và phần ảo bằng 4i
C. Phần thực bằng 3 và phần ảo bằng 4 D. Phần thực bằng -3 và phần ảo bằng 4
4A. Tính toán với số phức
107
Phép nhân số phức
Câu 36. Thu gọn
5
zi
ta được:
A.
zi
B.
1z
C.
1z
D.
zi
Câu 37. Số phức
12z i i
có phần thực là:
A. 1 B. 2 C. -1 D. -2
Câu 38. Phần ảo của số phức
11z i i
là:
A. -2 B. 2 C. 0 D. 1
Câu 39. Phần ảo của số phức
22
(1 ) (1 )ii
là:
A. – 4 B. 4 C. 0 D. 1
Câu 40. Số phức
2
(1 i) (4 )i
bằng:
A.
28i
B.
2 8 .i
C.
5 3 .i
D.
3 3 .i
Câu 41. Kết quả của phép tính
2 3 3ii
là:
A.
97i
B.
97i
C.
97i
D.
97i
Câu 42. Thu gọn
2 1 2 ,z i i
khi đó z bằng
A.
43zi
B.
5zi
C.
34zi
D.
22zi
Câu 43. Cho hai số phức
12
z 2i 5; z 1 3i
.Số phức
12
z .z
bằng:
A.
4i
B.
1 17i
C.
11 17i
D.
1 13i
Câu 44. Cho hai số phức
1
25zi
và
2
34zi
. Tìm số phức
12
.z z z
.
A.
6 20zi
B.
26 7zi
C.
6 20zi
D.
26 7zi
Câu 45. Cho số phức
1 2 3
1 3 ; z 2 ; z 3 4z i i i
. Tìm số phức
1 2 2 3
w z z z z
.
A. w= 1+4i B. w=1-4i C. w=-15-4i D. w =15+4i
Câu 46. Cho hai số phức:
12
1 3 ; z 3z i i
. Tính
12
.zz
.
A. i B. 4i C.
2 3 4i
D.
3 1 ( 3 1)i
Câu 47. Tìm phần ảo của số phức
z
, biết
2
2 1 2z i i
.
A.
2
B.
2
C. 5 D.
32
Câu 48. Tìm phần thực của số phức
z
, biết
2 1 2z i i
.
A.
2
B.
1
C.
22
D.
1
Phép chia số phức
Câu 49. Cho số phức z = a + bi 0. Số phức
1
z
có phần thực là:
A. a + b B. a - b C.
22
a
ab
D.
22
b
ab
Câu 50. Phần thực của số phức nghịch đảo của số phức
i
là:
A. 1 B. -1 C. 0 D. –i
Câu 51. Kết quả của phép tính
3
i
là:
A.
3i
B.
i
C. -
i
D.
3i
4A. Tính toán với số phức
108
Câu 52. Số phức z =
34
4
i
i
bằng:
A.
16 13
17 17
i
B.
16 11
15 15
i
C.
94
55
i
D.
9 23
25 25
i
Câu 53. Tìm số phức liên hợp của số phức
1
2
i
i
A.
13
55
i
B.
13
55
i
C.
13
55
i
D.
13
55
i
Câu 54. Giá trị của số phức
3
2 i
là:
A.
63
55
i
B.
36
55
i
C.
63
55
i
D.
36
55
i
Câu 55. Cho hai số phức
12
z 1 2i; z 1 i
.Số phức
1
2
z
z
bằng:
A.
13
22
i
B.
13
22
i
C.
13
22
i
D.
31
22
i
Câu 56. Số phức nghịch đảo của số phức
23i
là:
A.
23
55
i
B.
23
55
i
C.
3
5
i
D.
23i
Câu 57. Viết gọn số phức
3 2 1
1 3 2
ii
z
ii



.
A.
15
13 13
zi
B.
15 55
26 26
zi
C.
15 65
26 26
zi
D.
15 55
26 26
zi
Câu 58. Thu gọn số phức z =


3 2 1
1 3 2
ii
ii
ta được:
A. z =
21 61
26 26
i
B. z =
23 63
26 26
i
C. z =
15 55
26 26
i
D. z =
26
13 13
i
Câu 59. Cho
2 1 2 2 1 2
22
i i i i
z
ii


. Trong các kết luận sau, kết luận nào đúng?
A.
22
.
5
zz
B.
z
là số thuần ảo C.
z
D.
22zz
Câu 60. Cho số phức
54
43
36
i
zi
i
. Khi đó bằng:
A.
20 8i
B.
20 8i
C.
73 17
15 5
i
D.
73 17
15 5
i
Câu 61. Phần thực của số phức
3
1 2 1
i
ii

là:
A.
4
5
B. -
4
5
C.
3
5
D. -
3
5
4A. Tính toán với số phức
109
Môđun của số phức
Câu 62. Cho số phức
23zi
. Modul của số phức z là:
A. 2 B. -3 C.
13
D. 13
Câu 63. Cho số phức z = 5 – 3i. Môđun của số phức z là:
A. 34 B. 2 C.
34
D. 4
Câu 64. Mô đun của số phức
12zi
là
A. 1 B.
5
C. 2 D. 3
Câu 65. Cho số phức
32zi
.Tính môđun của số phức
1zi
A.
14zi
B.
11zi
C.
15zi
D.
1 2 2zi
Câu 66. Cho hai số phức
12
z 3 2i;z 2 i.
Tìm mô đun của số phức :
12
z z .
A.
12
5
zz
B.
12
2
zz
C.
12
13
zz
D.
12
2
zz
Câu 67. Cho hai số phức
1
13zi
và
2
2.zi
Khi đó
12
zz
bằng:
A.
5
B. 5 C.
10
D.
13
Câu 68. Cho 2 số phức
1
3zi
và
2
3 5 .zi
Tính môđun của số phức z
1
– z
2
:
A.
12
| | 73zz
B.
12
| | 13zz
C.
12
| | 3zz
D.
12
| | 5zz
Câu 69. Cho số phức
12
2 6 , 1 2 .z i z i
. Tính modun của số phức
12
zz
A. 5 B. 6 C. 7 D. 8
Câu 70. Cho hai số phức
1
1zi
và
2
45zi
. Môđun của số phức
12
zz
là
A.
25
B.
35
C.
33
D.
53
Câu 71. Cho hai số phức z
1
= 4 + 5i và z
2
= - 1 +2i . Tính môđun của số phức
A.
12
41.zz
B.
12
5.zz
C.
12
3 2.zz
D.
12
34.zz
Câu 72. Cho hai số phức
1
12zi
và
2
3zi
. Tính môđun của số phức
12
2zz
A.
12
2 26zz
B.
12
2 41zz
C.
12
2 29zz
D.
12
2 33zz
Câu 73. Cho hai số phức
1
3zi
,
2
2zi
. Tính giá trị của biểu thức
1 1 2
z z z
.
A.
10
B.
50
C.
5
D.
85
Nguyễn Văn Lực
www.facebook.com/VanLuc168
4A. Tính toán với số phức
110
Câu 74. Cho số phức z thỏa mãn:
3
(1 3 )
1
i
z
i
. Tìm môđun của
z iz
.
A.
82
B.
83
C.
42
D.
43
Câu 75. Cho hai số phức
12
1 3 ,z i z a bi
. Biết
12
34z z i
. Modun của
2
z
là:
A. 3 B.
4
C.
5
D. 5
Câu 76. Cho số phức z = (2 + i)(1 – i) + 1 + 2i. Mô-đun của số phức z là
A.
22
B.
42
C.
17
D.
5
Câu 77. Tính môđun của số phức
3
1 4 1z i i
.
A.
4
B.
29
C.
1
D.
5
Câu 78. Số phức
2
1 2 1z i i
có mô đun là:
A.
52z
B.
50z
C.
22
3
z
D.
10
3
z
Câu 79. Mô đun của số phức
3
5 2 1z i i
là:
A.
7
B.
3
C.
5
D.
2
Câu 80. Cho hai số phức:

1
48zi
và
2
2zi
. Modul của số phức:
12
2.z z z
là
A.
45
B.
5
C. 20 D. 40
Câu 81. Cho hai số phức
1
1zi
và
2
35zi
. Môđun của số phức
1 2 2
.w z z z
A.
130w
B.
130w
C.
112w
D.
112w
Câu 82. Cho số phức z thỏa mãn (1+2i)z+(1-2
z
)i=1+3i . Khi đó mô đun của số phức z là:
A.
11
B.
85
C. 11 D. 85
Câu 83. Môđun của số phức
z
thỏa mãn phương trình
(2 1)(1 ) ( 1)(1 ) 2 2z i z i i
là
A.
2
3
B.
3
2
C.
1
2
D.
1
3
Câu 84. Môđun của số phức
4
3
(1 ) (2 )
(1 2 )
ii
z
i
bằng:
A.
4
5
B.
3
5
C.
6
5
D.
7
5
Câu 85. Cho số phức
z
thỏa mãn
5( )
2
1
zi
i
z
.Môđun của số phức
2
w1zz
là:
A.
4
B.
9
C.
13
D.
13
Câu 86. Tìm môdun của số phức liên hợp của
1 i 2 i
z
1 2i
A.
z2
B.
z 2 2
C.
z1
D.
z 5 2
4A. Tính toán với số phức
111
Câu 87. Tìm môđun của số phức
z
, biết
22
2
(2 3 ) (1 )
(1 2 )
ii
z
i
A.
5
B.
2
5
C.
11
5
D. 5
Câu 88. Số phức z có mô đun nhỏ nhất sao cho :
34z z i
là:
A.
3
2
2
zi
B.
3
2
2
zi
C.
3
2
2
zi
D.
3
2
2
zi
Câu 89. Trong các số phức
z
thỏa mãn
2 4 2z i z i
. Tìm số phức
z
có môđun nhỏ
nhất.
A.
1zi
B.
22zi
C.
22zi
D.
32zi
Câu 90. Trong các số phức z thoả mãn điều kiện
3
23
2
zi
. Số phức z có mođun nhỏ nhất là
A.
26 3 13 78 9 13
13 26
zi
B.
26 2 13 78 3 13
13 26
zi
C.
26 13 78 13
13 26
zi
D.
26 13 78 13
13 26
zi
Câu 91. Cho số phức z thỏa mãn:
12z i z i
. Tìm giá trị nhỏ nhất của
z
?
A.
1
2
B.
2
C.
2
2
D.
1
2
Tìm số phức thỏa điều kiện cho trước
Câu 92. Tính
32
1 2 3z i i
ta được:
A.
38zi
B.
38zi
C.
38zi
D.
38zi
Câu 93. Phần thực của số phức z thỏa mãn:
2
1 2 8 1 2i i z i i z
là
A. 2 B. –3 C. –2 D. 3
Câu 94. Số phức z thoả
2 1 8iz z i
là:
A. z = 7 + 7i B. z = 5 – 2i C. z = 2 + 5i D. z = 1 -2i
Câu 95. Số phức z thỏa
(2 3 ) 1 9z i z i
là:
A. z = -3 -i B. z = -2 -i C. z = 2 -i D. z = 2 + i
Câu 96. Phần ảo của số phức
z
thỏa mãn
2
2 2 1z z i i
là:
A.
13
B.
13
C.
9
D.
9
Nguyễn Văn Lực
www.facebook.com/VanLuc168
4A. Tính toán với số phức
112
Câu 97. Tìm các số phức
z
thỏa mãn
2
2
28z zz z
và
2.zz
A.
12
1 ; 1 .z i z i
B.
12
1 ; 1 .z i z i
C.
12
1 ; 1 .z i z i
D.
12
1 ; 1 .z i z i
Câu 98. Tìm phần thực của số phức z thỏa mãn iz + 4 + 5i = i(6 + 3i)
A. 1 B. 7 C. 11 D. -1
Câu 99. Số phức z thỏa mãn:
(1 i) (2 3 )(1 2 ) 7 3z i i i
. là:
A.
13
22
zi
B.

11
22
zi
C.

3
1
2
zi
D.
13
22
zi
Câu 100. Tìm số phức liên hợp của số phức
1
1 3 2
2
z i i
i
.
A.
17 2
33
i
B.
17 4
55
i
C.
27 4
55
i
D.
17 2
33
i
Câu 101. Cặp số (x;y) thỏa mãn điều kiện
2x 4y 1 x 3y i 4x 2y 3 3x y 5 i
là:
A.



13 3
;
44
B.



53
;
44
C.



11 9
;
44
D.



43 9
;
44
Câu 102. Tìm số phức
z
thỏa mãn:
)1(4)23()2( izizi
.
A.
iz 3
B.
iz 3
C.
iz 3
D.
iz 3
Câu 103. Tìm số phức z, biết
1 2 1 3
1 2 3
ii
z
ii


.
A.
2 36
65 65
zi

B.
2 20
65 65
zi

C.
30 36
65 65
zi

D.
2 36
65 65
zi
Câu 104. Cho số phức
z 2 3i.
Tìm số phức
w iz z.
A.
w 3 5i
B.
z 5 3i
C.
z 5 5i
D.
z 5 5i
Câu 105. Cho số phức z= 1+2i. Số phức
w iz z
là
A. 1+i B. –1+i C. –1–i D. 1–i
Câu 106. Cho số phức
32zi
. Tìm số phức
2.w i z z
A.
1 4 .wi
B.
9 2 .wi
C.
4 7 .wi
D.
4 7 .wi
Câu 107. Cho số phức
52zi
. Tìm số phức
w iz z
A.
33wi
B.
33wi
C.
33wi
D.
33wi
Câu 108. Cho số phức
31
.
22
zi
Tìm số phức
2
1.zz
A.
3 3 1 3
.
22
i

B.
1 3 1 3
.
22
i

C.
13
.
22
i
D.
3 3 1 3
.
22
i

4A. Tính toán với số phức
113
Câu 109. Cho
13
22
zi
. Tính
2
1 zz
A. 2 B. -2 C. 0 D. 3
Câu 110. Phần ảo của số phức
1w zi z
, biết số phức z thỏa mãn:
1 1 3 0i z i
là
A. -1 B. 2 C. 1 D. -2
Câu 111. Số phức
2 3 5 4ix x i
thỏa mãn:
3 1 2 3 4i z i z i
là:
A.
23zi
B.
25zi
C.
15zi
D.
23zi
Câu 112. Cho số phức z, thỏa mãn điều kiện
2
(3 2i)z (2 i) 4 i
. số phức
w (1 z)z
bằng:
A.
3 i
B.
3 11
13 13
i
C.
3 11
13 13
i
D.
3 i
Câu 113. Cho số phức z thỏa mãn điều kiện (1 + i)(z – i) + 2z = 2i. khi đó số phức
2
21
w
zz
z

bằng:
A. -1+3i B.
1 i
C.
i
D. 1+3i
Câu 114. Cho phương trình
1+i
( )
z -(2-i)z = 3
. số phức
w =
i - 2z
1- i
bằng:
A.
93
22
i
B.
32i
C.
11 3
22
i
D.
39
22
i
Câu 115. Cho số phức z thỏa mãn
z
z2
1 2i

. Số phức w = z
2
– z bằng:
A. 3+5i B. 3 +3i C. 1+5i D. 1+3i
Câu 116. Tìm tất cả các số phức
z
thỏa mãn đồng thời hai điều kiện
2z
và
2
z
là số thuần ảo.
A.
1zi
hoặc
1zi
B.
1zi
C.
1zi
D.
1zi
Câu 117. Số phức
z
thỏa mãn
34z z i
A.
7
4
6
zi
B.
74zi
C.
76zi
D.
76zi
Câu 118. Số phức
z
thỏa mãn:
2 10zi
và
. 25zz
là:
A.
34zi
và
5z
B.
34zi
và
5z
C.
43zi
và
5z
D.
43zi
và
5z
Câu 119. Có bao nhiêu số phức z thỏa mãn điều kiện
2
2
z z z
A. 0 B. 1 C. 3 D. 2
Câu 120. Phần thực của số phức
2016
1zi
là:
A.
1008
2
B.
1008
2
C. 0 D. 1
Câu 121. Kết quả của phép tính
2016
.1ii
?
A.
1008
2
B.
1008
2
C.
1008
2
D.
1008
2
4A. Tính toán với số phức
114
Câu 122. Cho số phức
2017
1
1
i
z
i



. Khi đó
7 15
..z z z
có giá trị
A. -i B. i C. 1 D. -1
Câu 123. Tổng
2 3 2009
1 ...i i i i
bằng
A.
1 i
B.
1 i
C. 1 D.
i
Câu 124. Phần thực của số phức
30
(1 )i
bằng
A. 0 B. 1 C.
15
2
D.
15
2
Câu 125. Cho số phức z = a + bi thỏa mãn
2 3 3z iz i
. Tính S = a
2016
+ b
2017
A. S = 0 B. S = 2 C. S
4032 2017
2017
33
5
D. S
4032 2017
2017
33
5




Câu 126. Tìm phần thực của số phức sau:
2 3 20
1 (1 i) (1 i) (1 i) ... (1 i)
A.

10
21
B.
10
2
C.
10
21
D.
10
21
Câu 127. Xét số phức
1
()
1 ( 2 )
m
z m R
m m i


. Tìm m để
1
.
4
zz
.
A.
12m 
B.
1m 
C.
12m
D.
0m
Câu 128. Cho số phức
1.z mi
Xác định m để
3
z
là một số thực.
A.
3
0;
3
mm
B.
0; 3mm
C.
0; 3mm
D.
0; 3mm
Câu 129. Cho (x + 2i)
2
= 3x + yi (x, y R). Giá trị của x và y bằng:
A. x = 1 và y = 2 hoặc x = 2 và y = 4
B. x = -1 và y = -4 hoặc x = 4 và y = 16
C. x = 2 và y = 5 hoặc x = 3 và y = -4
D. x = 6 và y = 1 hoặc x = 0 và y = 4
Câu 130. Cho (x + 2i)
2
= yi (x, y R). Giá trị của x và y bằng
A. x = 1 và y = 4 hoặc x = -1 và y = -4. B. x = 3 và y = 12 hoặc x=-3 và y=-12.
C. x = 2 và y = 8 hoặc x = -2 và y = -8. D. x = 4 và y = 16 hoặc x=-4 và y=-16.
Câu 131. Biết rằng
1 1 2 2
1 , 2z bi z a i
và
12
25z z i
. Tìm
12
,zz
:
A.
12
1 2 , 3 2z i z i
B.
12
1 3 , 1z i z i
C.
12
1 3 , 1 2z i z i
D.
12
2 , 2z i z i
Câu 132. Cho
1 1 1 2 2 2
,z a bi z a b i
và
12
12
14
1
z z i
zz
. Tìm
12
,zz
:
A.
12
2 , 1z i z i
B.
12
3 , 1z i z i
C.
12
2 , 1 2z i z i
D.
12
,2z i z i
Câu 133. Biết rằng
1 1 2 2
2,z a i z a i
và
12
12
13
1
z z i
z z i
. Tìm
12
,zz
:
A.
12
2 , 1z i z i
B.
12
3 , 1z i z i
C.
12
2 , 1 2z i z i
D.
12
,2z i z i
4A. Tính toán với số phức
115
1C 2A 3C 4A 5B 6A 7D 8D 9A 10D
11C 12B 13B 14A 15A 16A 17C 18A 19A 20A
21D 22D 23D 24D 25D 26B 27D 28B 29A 30C
31B 32B 33D 34C 35D 36A 37D 38C 39B 40A
41A 42A 43B 44B 45A 46B 47A 48C 49C 50C
51D 52A 53B 54C 55A 56A 57D 58C 59C 60C
61A 62C 63C 64B 65C 66B 67D 68B 69A 70B
71D 72B 73A 74A 75A 76C 77D 78A 79A 80D
81A 82B 83A 84A 85D 86A 87A 88C 89C 90A
91C 92B 93A 94C 95C 96A 97D 98A 99A 100C
101A 102A 103A 104C 105C 106A
107C 108D 109C 110A 111B 112D
113A 114A 115D 116A 117A 118A
119C 120A 121A 122A 123A 124A
125B 126B 127C 128D 129B 130C
131C 132C 133A
Nguyễn Văn Lực
www.facebook.com/VanLuc168
4B. Tập hợp điểm - biểu diễn số phức
116
Câu 1. Cho số phức
( 1)( 2)z i i i
. Điểm biểu diễn của số phức z là:
A. M(-1;3) B. M(-1;-3) C. M(1;-3) D. M(1;3)
Câu 2. Cho số phức
21zi
. Điểm biểu diễn số phức liên hợp của
z
là:
A.
( 1;2)M
B.
( 1; 2)M
C.
( 2;1)M
D.
(2; 1)M
Câu 3. Cho số phức
3zi
. Điểm biểu diễn số phức
1
z
là:
A.
13
;
44
M
B.
31
;
44
M
C.
13
;
22
M
D.
31
;
22
M
Câu 4. Cho số phức z thoả mãn
1 4 2 0.i z i
Điểm biểu diễn của z có toạ độ là
A. (–3;–1) B. (–3;1) C. (3;–1) D. (3;1)
Câu 5. Cho số phức z thỏa mãn
z 5 i
1i

.Hỏi điểm biểu diễn của z là điểm nào trong các
điểm
M, N, P, Q ở hình bên?
A. Điểm N
B. Điểm M
C. Điểm P
D. Điểm Q
Câu 6. Cho phương trình:
(1 4 ) 5 2i z i z
. Điểm biểu diễn của z trên mặt phẳng tọa độ là
A.



43
;
55
B.



43
;
55
C.



34
;
55
D.



34
;
55
Câu 7. Cho số phức z thỏa mãn
1 2 3i z i
. Hỏi điểm biểu diễn của z là điểm nào trong các
điểm I, J, K, H ở hình bên
A. Điểm K B. Điểm H
C. Điểm I D. Điểm J
TẬP HỢP ĐIỂM – BIỂU DIỄN SỐ PHỨC
x
y
H
K
J
I
-
1
5
-
7
5
7
5
1
5
1
4B. Tập hợp điểm - biểu diễn số phức
117
Câu 8. Cho số phức z thỏa mãn:
(4 ) 3 4i z i
. Điểm biểu diễn của z là:
A.
16 11
;
15 15
M



B.
16 13
;
17 17
M



C.
94
;
55
M



D.
9 23
;
25 25
M



Câu 9. Cho số phức z thỏa mãn
1 2 8 .i z i
Hỏi điểm biểu diễn của z là điểm nào
trong các điểm M, N, P, Q ở hình dưới đây?
A. Điểm P. B. Điểm Q. C. Điểm M. D. Điểm N.
Câu 10. Cho số phức
z
thỏa
1 14 2i z i
. Điểm biểu diễn của số phức
z
trong mặt phẳng
tọa độ Oxy có tọa độ là:
A.
6;8
B.
8;6
C.
8;6
D.
6; 8
Câu 11. Điểm biểu diễn của số phức z thỏa :
2
(1 ) (1 2 )i z i
là:
A.
71
;
22



B.
71
;
22



C.
71
;
22



D.
71
;
22




Câu 12. Gọi A là điểm biểu diễn của số phức
32zi
và B là điểm biểu diễn của số
phức
' 2 3zi
. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai điểm A và B đối xứng nhau qua đường thẳng
yx
.
B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
C. Hai điểm A và B đối xứng nhau qua trục tung.
D. Hai điểm A và B đối xứng nhau qua trục hoành.
Câu 13. Gọi A là điểm biểu diễn của số phức
12zi
và B là điểm biểu diễn của số phức
' 1 2 .zi
Tìm mệnh đề đúng trong các mệnh đề sau :
A. Hai điểm A và B đối xứng nhau qua trục hoành
B. Hai điểm A và B đối xứng nhau qua trục tung
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng nhau qua đường thẳng
yx
Câu 14. Gọi A là điểm biểu diễn của số phức
25zi
và B là điểm biểu diễn của số phức
' 2 5 .zi
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng
yx
Câu 15. Gọi A là điểm biểu diễn số phức
z
, B là điểm biểu diễn số phức
z
. Trong các khẳng
định sau khẳng định nào sai?
A. A và B đối xứng nhau qua trục hoành.
B. A và B trùng gốc tọa độ khi
0z
.
C. A và B đối xứng qua gốc tọa độ.
D. Đường thẳng AB đi qua gốc tọa độ.
4B. Tập hợp điểm - biểu diễn số phức
118
Câu 16. Cho các số phức

1 2 3
4i 2 6i
z ; z 1 i 1 2i ; z
i 1 3 i
. Gọi A, B, C lần lượt là điểm
biểu diễn của các số phức
1 2 3
z , z , z
. Nhận xét nào sau đây là đúng?
A. Ba điểm A,B,C thẳng hàng B. Tam giác ABC là tam giác vuông
C. Tam giác ABC là tam giác cân D. Tam giác ABC là tam giác vuông cân
Câu 17. Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức
1 2 3
1 2 ; 1 3 ; 1 3 .z i i z i z i
Tam giác ABC là:
A. Tam giác cân B. Tam giác đều
C. Tam giác vuông D. Tam giác vuông cân
Câu 18. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức
3 4 ; 'z i M
là điểm
biểu diễn cho số phức
/
1
2
i
zz
. Tính diện tích tam giác OMM’.
A.
'
25
4
OMM
S
B.
'
25
2
OMM
S
C.
'
15
4
OMM
S
D.
'
15
2
OMM
S
Câu 19. Phương trình
2
20x x b
có hai nghiệm phức được biểu diễn trên mặt phẳng phức bởi
hai điểm A, B. Tam giác OAB đều (Với O là gốc tọa độ) thì b bằng
A.
4
3
B.
3
C.
1
3
D.
4
Câu 20. Tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa < 3 là
A. Đường tròn bán kính
3r
B. Hình tròn bán kính
3r
không kể đường tròn bán kính
3r
C. Đường tròn bán kính
9r
D. Hình tròn bán kính
9r
Câu 21. Tìm tập hợp các điểm
M
biểu diễn số phức
z
có phần thực dương thỏa mãn
2z
A. Đường tròn
;2O
.
B. Hình tròn
;2O
.
C. Nửa hình tròn
;2O
nằm bên trái trục tung.
D. Nửa hình tròn
;2O
nằm bên phải trục tung.
Câu 22. Tìm tập hợp các điểm M biểu diễn số phức z, thỏa mãn:
1 z 3
A. Phần hình phẳng nằm hoàn toàn phía ngoài hình tròn
(O;1)
và phía trong
hình tròn
(O;3)
B. Hình tròn
(O;3)
(bỏ gốc tọa độ O)
C. Hình tròn
(O;1)
(bỏ gốc tọa độ O)
D. Đường tròn
(O;1)
Nguyễn Văn Lực
www.facebook.com/VanLuc168
4B. Tập hợp điểm - biểu diễn số phức
119
Câu 23. Cho số phức
;,z a bi a b
.
Để điểm biểu diễn của z trong hình sau, thì điều kiện của
a và b là
A. a + b = 4. B. 2a + 2b > 4.
C. a
2
+ b
2
= 4. D. a
2
+ b
2
< 4.
Câu 24. Cho hai số phức
;,z a bi a b
.
Để điểm biểu diễn của z nằm trong dải (-2; 2) như
hình trên, điều kiện của a và b là:
A.
2
2
a
b
B.
22a
và b R
C.

2
-2
a
b
D. a, b (-2; 2)
Câu 25. Điểm biểu diễn của các số phức
z a ai
với
.a
, nằm trên đường thẳng có phương
trình là:
A. y = 2x B. y = -x C. y = x+ 1 D. y = x
Câu 26. Điểm M trên hình vẽ là điểm biểu diễn của số phức nào sau đây:
x
y
2
M
1
A. (1 + i)z = 3 – i
B. (1 - i)z = 3 – i
C. (1 - i)z = 3 + i
D. (1 + i)z = 3 + i
Câu 27. Cho hai số phức
;,z a bi a b
.
Để điểm biểu diễn của z trong hình sau, thì điều kiện
của a và b là
A.
2
2
a
b
B.
2
-2
a
b
C.
22a
và b R. D. a, b (-2; 2).
y
2
O
x
-2
-2
2
x
y
O
y
2
O
x
-2
4B. Tập hợp điểm - biểu diễn số phức
120
Câu 28. Cho số phức
;,z a bi a b
.
Để điểm biểu diễn của z trong hình sau, thì điều kiện của
a và b là
A.
3
3
a
b
B.
3
-3
a
b
C. a, b (-3; 3). D. a R và -3 < b < 3.
Câu 29. Tập hợp các điểm trong mặt phẳng phức biểu diễn số phức
z
thỏa mãn điều kiện
2
z
là
số ảo là
A. Trục ảo.
B. Trục thực.
C. Hai đường phân giác
yx
và
yx
của các góc tọa độ.
D. Đường phân giác góc phần tư thứ nhất.
Câu 30. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
là một
số thực dương là:
A. Trục hoành (trừ gốc tọa độ O)
B. Truc tung (trừ gốc toạ độ O)
C. Đường thẳng y = x (trừ gốc toạ độ O)
D. Đường thẳng y = -x (trừ gốc toạ độ O)
Câu 31. Cho số phức
12iz
. Điểm biểu diễn của số phức z là
A. Điểm
A
. B. Điểm
B
C. Điểm
C
. D. Điểm
D
.
Câu 32. Cho các số phức z thỏa mãn
12z 
. Biết rằng tập hợp các điểm biểu diễn các số phức
(1 3) 2w i z
là một đường tròn. Bán kính r của đường tròn đó là
A. r = 4. B. r = 8. C. r = 2. D. r = 16.
Câu 33. Tập hợp các điểm biểu diễn số phức z thõa mãn
4 3 2zi
là đường tròn có tâm I,
bán kính R:
A. I(4;3), R =2 B. B.I(4;-3), R =4 C. I(-4;3), R= 4 D. I(4; -3), R= 2
-3
3
y
x
O
4B. Tập hợp điểm - biểu diễn số phức
121
Câu 34. Trên mặt phẳng tọa độ, tìm tập hợp các điểm biểu diễn các số phức
z
thỏa mãn điều kiện
(3 4 ) 2 zi
.
A. Đường tròn tâm
(3;4)I
bán kính
2R
.
B. Đường tròn tâm
(3;4)I
bán kính
2R
.
C. Đường tròn tâm
(3; 4)I
bán kính
2R
.
D. Đường tròn tâm
(3; 4)I
bán kính
2R
.
Câu 35. Cho số phức z thỏa mãn
z 1 2
.Biết rằng tập hợp các điểm biểu diễn các số
phức
w 2z i
là một đường tròn. Tìm bán kính r của đường tròn đó.
A. r = 2 B. r = 1 C. r = -2 D. r = 4
Câu 36. Cho số phức
z
thỏa
12zi
. Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức
z
là một đường thẳng.
B. Tập hợp điểm biểu diễn số phức
z
là một đường Parabol.
C. Tập hợp điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
2
.
D. Tập hợp điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
4
.
Câu 37. Tập hợp các điểm trong mặt phẳng phức biểu diễn cac số phức z thỏa mãn
| 5| 6zz
là đường thẳng có phương trình là:
A.
1
2
x
B.
1
2
x 
C.
1
2
y
D.
1
2
y 
Câu 38. Tập hợp các điểm biểu diễn của số phức z thoả mãn điều kiện
3zi
là đường tròn
có phương trình
A.
22
( 1) 9xy
B.
22
( 1) 9xy
C.
2
( 1) 9xy
D.
22
( 1) 3xy
Câu 39. Tập hợp các điểm trong mặt phẳng biểu diễn số phức z thõa mãn điều kiện
1 2 4zi
là
A. Một đường thẳng B. Một đường tròn
C. Một hình chữ nhật D. Một hình vuông
Câu 40. Tìm tập hợp các điểm M biểu diễn số phức Z, thỏa mãn :
22
( ) 4zz
A. Đường cong
1
y
x
B. Đường cong
1
y
x
C. Đường cong
1
y
x
và đường cong
1
y
x
D. Đường cong
1
y
x
hoặc đường cong
1
y
x
Câu 41. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa
1 2 2i z i
là
A.
22
1 1 1xy
B.
22
1 1 1xy
C.
22
1 1 1xy
D.
22
1 1 1xy
4B. Tập hợp điểm - biểu diễn số phức
122
Câu 43. Cho số phức z thỏa mãn
2 z 2 3i 2i 1 2z
. Tập hợp điểm biểu diễn cho số phức z
là:
A.
12x 32y 47 0
B.
12x 32y 47 0
C.
12x 32y 47 0
D.
12x 32y 47 0
Câu 44. Trên mặt phẳng tọa độ, Tìm tập hợp tất cả các điểm M trong biễu diễn các số phức thỏa
z z 3 4i
A.
2x 3 0
B. Đường thẳng 6x-8y-25=0
C. Đường thẳng 6x+8y-25=0 D. Đường thẳng y-2=0
Câu 45. Trong mp tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa
mãn:
1z i i z
.
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2, –1), bán kính R=
2
.
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, 1), bán kính R=
3
.
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R=
3
.
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R=
2
.
Câu 46. Cho số phức
z
thỏa
21zz
. Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức
z
là một đường thẳng.
B. Tập hợp điểm biểu diễn số phức
z
là một đường Parabol.
C. Tập hợp điểm biểu diễn số phức
z
là một đường tròn.
D. Tập hợp điểm biểu diễn số phức
z
là một đường Elip.
Câu 47. Trên mặt phẳng tọa độ, tìm tập hợp các điểm
M
biểu diễn số phức
z
thỏa mãn
3.
z
zi
A. Đường tròn tâm
9
;0
8
I



bán kính
3
8
R
.
B. Đường tròn tâm
9
0;
8
I



bán kính
9
64
R
.
C. Đường tròn tâm
9
0;
8
I



bán kính
3
8
R
.
D. Đường tròn tâm
9
0;
8
I



bán kính
3
8
R
.
Câu 48. Tìm tập hợp các điểm
M
biểu diễm số phức
z
thỏa mãn:
2
2
zz
.
A. Trục
Ox
và trục
Oy
. B. Trục
Ox
.
C. Trục
Oy
. D. Không có điểm
M
.
Câu 49. Trong mặt phẳng phức
Oxy
, cho số phức
z
thỏa lần lượt một trong bốn điều kiện
:2I z z
;
: . 5II z z
;
: 2 4III z i
,
: 4 3IV i z i
. Hỏi điều kiện nào để số phức
Z có tập hợp biểu diễn là đường thẳng.
A.
I
B.
,I II
C.
,I IV
D.
,,II III IV
4B. Tập hợp điểm - biểu diễn số phức
123
Câu 50. Trên mặt phẳng tọa độ, tìm tập hợp các điểm biểu diễn số phức
z
thỏa mãn
1.
zi
zi
A. Điểm
0;0 .O
B. Đường tròn tâm
0;1 ,I
bán kính
1.R
C. Trục
.Oy
D. Trục
Ox
.
Câu 51. Cho số phức z thỏa mãn
3 4 2zi
và
w 2 1zi
. Trong mặt phẳng phức,
tập hợp điểm biểu diễn số phức w là đường tròn có tâm I, bán kính R. Khi đó
A.
3; 4 , 2IR
B.
4; 5 , 4IR
C.
5; 7 , 4IR
D.
7; 9 , 4IR
Câu 52. Các điểm biểu diễn các số phức
3 ;(z bi b
)
trong mặt phẳng tọa độ, nằm trên
đường thẳng có phương trình là:
A.
3x
B.
3y
C.
xb
D.
yb
Câu 53. Các điểm biểu diễn của số thuần ảo nằm ở đâu trên mặt phẳng tọa độ
A.
Ox
B.
Oy
C.
O
D.
Ox
và
Oy
.
Câu 54. Số phức
23zi
có điểm biểu diễn là
A.
B. C. D.
Câu 55. Gọi M là điểm biểu diễn số phức z trong mặt phẳng phức. Như thế, số
z
được biểu diễn
bởi điểm
A. Đối xứng với M qua O B. Đối xứng với M qua Oy
C. Đối xứng với M qua Ox D. Không xác định được
1B 2A 3A 4A 5B 6A 7D 8B 9B 10D
11D 12A 13B 14B 15A 16B 17D 18B 19A 20B
21D 22A 23D 24B 25D 26C 27C 28D 29C 30A
31A 32A 33A 34D 35D 36C 37B 38B 39B 40C
41C 42B 43C 44D 45A 46C 47A 48A 49D 50D
51A 52B 53C 54A
Nguyễn Văn Lực
www.facebook.com/VanLuc168
4C. Phương trình phức
124
Câu 1. Trong C, phương trình (2 - i)
z
- 4 = 0 có nghiệm là:
A. z =
84
55
i
B. z =
48
55
i
C. z =
23
55
i
D. z =
73
55
i
Câu 2. Trong C, phương trình (i+z)(
z
- 2 + 3i) = 0 có nghiệm là:
A.

23
zi
zi
B.

2
53
zi
zi
C.


23
zi
zi
D.

3
25
zi
zi
Câu 3. Tập nghiệm của phương trình
2
0zz
là
A.
0; 1; i
B.
0; 1;i
C.
0;1; i
D.
0; ;ii
Câu 4. Tìm nghiệm của phương trình
2
0zz
A.
1 2 3 4
1 3 1 3
0; 1; ;
2 2 2 2
z z z i z i
B.
1 2 3 4
1 3 1 3
0; 1; ;
2 2 2 2
z z z i z i
C.
1 2 3 4
1 3 1 3
0; 1; ;
2 2 2 2
z z z i z i
D.
1 2 3 4
1 3 1 3
0; 1; ;
2 2 2 2
z z z i z i
Câu 5. Nghiệm của phương trình
2 5 3 2z i i
là:
A.
z
8 – i B.
z
8 + i C.
z
– 8 – i D.
z
– 8 + i
Câu 6. Tìm các số phức
z
thỏa mãn
2
34zi
.
A.
1
2zi
;
2
2zi
. B.
1
2zi
;
2
2zi
.
C.
1
2zi
;
2
2zi
. D.
1
2zi
;
2
2zi
.
Câu 7. Nghiệm phức của phương trình
2
40z
là:
A.
2zi
hoặc
2zi
B.
2z
C.
2zi
D.
2z
Câu 8. Số nghiệm thực của phương trình
2
3 5 0zz
là
A. B. 1 C. 2 D. 3
Câu 9. Phương trình
2
2 4 0zz
có nghiệm là
A.
13
13
zi
zi
B.
13
13
zi
zi
C.
12
12
zi
zi
D.
23
23
zi
zi
Câu 10. Nghiệm của phương trình
2
2 2 0zz
là:
A.
1
B.
i
C.
1 i
D.
1 i
PHƯƠNG TRÌNH PHỨC
4C. Phương trình phức
125
Câu 11. Giải phương trình
2
2 3 5 0xx
trên tập số phức. Mệnh đề nào sau đây là đúng ?
A. Phương trình có 2 nghiệm phức.
B. Phương trình có 2 nghiệm thực.
C. Phương trình có một nghiệm thực và một nghiệm phức.
D. Phương trình vô nghiệm.
Câu 12. Phương trình
2
5 7 11 0zz
có số nghiệm phức là
A.
2
B.
3
C.
1
D.
4
Câu 13. Trong các phương trình sau, phương trình nào có nghiệm thực
A.
2
3 4 0zz
B.
2
6 10 0zz
C.
2
2 2 3 0zz
D.
2
3zz
Câu 14. Phương trình
4 3 7
2
zi
zi
zi
có nghiệm là
A.
12
3
zi
zi
B.
12
3
zi
zi
C.
12
3
zi
zi
D.
13
32
zi
zi
Câu 15. Tìm các nghiệm phức của phương trình
3
80z
.
A.
1 2 3
2; 1 3 ; 1 3 . z z i z i
B.
1 2 3
2; 1 3 ; 1 3 . z z i z i
C.
1 2 3
2; 1 3 ; 1 3 . z z i z i
D.
1 2 3
2; 1 3 ; 1 3 . z z i z i
Câu 16. Phương trình
32
2 2 0z z z
có bao nhiêu nghiệm phức
A.
3
B.
2
C.
1
D.
4
Câu 17. Tìm tập hợp nghiệm phức của phương trình
32
3 3 63 0.z z z
A.
3;3 2 3 ; 3 2 3 .S i i
B.
3; 3 2 3 ; 3 2 3 .S i i
C.
3; 3 2 3 ;3 2 3 .S i i
D.
3;3 2 3 ; 3 2 3 .S i i
Câu 18. Trong C, phương trình z
4
- 6z
2
+ 25 = 0 có nghiệm là:
A.
zi
B.
;5z i z i
C.
5zi
D. Vô nghiê
m
Câu 19. Phương trình
42
60zz
có nghiệm là
A.
2; 3z z i
B.
2; 3z z i
C.
3; 2z z i
D.
5; 2z z i
Câu 20. Tập nghiệm của phương trình:
42
3 2 0zz
là
A.
{ 1; 2}S
B.
{ ; 2}S i i
C.
{ ; ; 2; 2}S i i i i
D.
S
Câu 21. Nghiệm của phương trình
3 2 3 1 2 5 4x i i i
là
A.
5
1
3
xi
B.
35xi
C.
5
1
3
xi
D.
35xi
Câu 22. Nghiệm của phương trình
2 3 2 3 2 2i x i i
trên tập số phức?
A.
5i
B.
5i
C.
i
D.
i
4C. Phương trình phức
126
Câu 23. Nghiệm của phương trình
2 3 5 4ix x i
trên tập số phức ?
A.
55 14
29 29
i
B.
55 14
19 19
i
C.
55 14
29 29
i
D.
55 14
19 19
i
Câu 24. Cho
12
1 2 ; 1 2z i z i
. Phương trình bậc hai với hệ số thực nhận
12
;zz
làm nghiệm là
A.
2
2 5 0zz
B.
2
2 5 0zz
C.
2
2 5 0zz
D.
2
5 2 0zz
Câu 25. Gọi z
1
, z
2
là hai nghiệm phức của phương trình z
2
– 4z + 9 = 0. Tổng P = |z
1
| + |z
2
| bằng:
A. 3 B. 6 C. 18 D. 4
Câu 26. Gọi
12
,zz
là hai nghiệm phức của phương trình
2
4 7 0zz
. Khi đó
22
12
zz
bằng:
A.
10
B. 7 C.
14
D. 15
Câu 27. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình:
2
z 4z 5 0
. Khi đó,
22
12
zz
bằng:
A. 6 B. 5 C. 4 D. 7
Câu 28. Biết
12
,zz
là các nghiệm của phương trình
2
2 3 3 0 xx
. Tính
22
12
T z z
.
A.
9
4
T
B.
9
4
T
C.
45
16
T
D.
3
4
T
Câu 29. Xác định m để phương trình
2
z mz 3i 0
có 2 nghiệm phức
12
z ,z
thõa mãn
22
12
z z 8
A.
m 3 i
hoặc
m 3 i
B.
m 3 i
hoặc
m 3 i
C.
m 3 i
hoặc
m 3 i
D.
m 3 i
hoặc
m 3 i
Câu 30. Biết
12
,zz
là các nghiệm phức của phương trình
2
2 0.zz
Tính
12
21
.
zz
zz
A.
1
.
2
B.
3
.
2
C.
3
.
2
D.
5
.
2
Câu 31. Biết
1, 2
zz
là các nghiệm của phương trình
2
2 5 0xx
. Tính
12
11
T
zz

.
A.
2
5
T
B.
2
5
T
C.
2
10
T
D.
2
10
T
Câu 32. Cho phương trình
2
2 1 0z m z m
trong đó m là tham số phức; giá trị m để phương
trình có hai nghiệm
12
;zz
thỏa mãn
22
12
10zz
.
A.
2 2 2 ; 2 2 2 .m i m i
B.
4 2 3; 4 2 3mm
C.
1 3 ; 2 3 .m i m i
D.
1 3 ; 1 3 .m i m i
Câu 33. Gọi
12
,zz
là hai nghiệm của phương trình
2
(8 3 )z 13 11 0z i i
. Khi đó, giá trị của
22
12
A z z
bằng
A. 39 B. 29 C. 49 D. 19
Nguyễn Văn Lực
www.facebook.com/VanLuc168
4C. Phương trình phức
127
Câu 34. Gọi
12
, zz
là các nghiệm của phương trình
2
2 5 0zz
. Tính giá trị biểu thức:
22
1 2 1 2
4A z z z z
A. 10 B. 20 C. -10 D. 5
Câu 35. Gọi
12
,zz
là hai nghiệm phức của phương trình:
2
2 3 0zz
. Tìm số phức liên hợp
của số phức
12
w 5 2i z z
?
A.
w 10 4i
B.
w 10 4i
C.
w 10 4i
D.
w 10 4i
Câu 36. Gọi z
1
, z
2
là hai nghiệm phức của phương trình x
3
- 3x
2
+ 4x – 12 = 0. Tính
12
2| | | |P z z
A. P = 0 B. P = 16 C. P = 4 D. P = - 4
Câu 37. Gọi
12
,zz
là hai nghiệm của phương trình
2
2 4 5 0zz
. Khi đó, giá trị của biểu thức
12
4A z z
bằng
A. 6 B. 4 C. 2 D. 5
Câu 38. Phương trình
2
4 14 0zz
có hai nghiệm
12
;zz
. Giá trị của biểu thức
22
12
23A z z
bằng
A.
14
B.
13
C.
14
D.
13
Câu 39. Gọi
12
,zz
là hai nghiệm của phương trình
2
5 10 0zz
, với
1
z
có phần ảo dương.
Phần thực và phần ảo của số phức
12
w 4 2zz
lần lượt là
A.
5; 15
B.
5; 15
C.
5; 15
D.
5; 15
Câu 40. Phương trình
2
5 2 5 1 0z m i z m i
có hai nghiệm
12
;zz
thỏa mãn
22
1 2 1 2
3 . 20 7z z z z i
khi m bằng
A. 2 B. 3 C. -2 D. 1
Câu 41. Kí hiệu
12
,zz
lần lượt là hai nghiệm phức của phương trình
2
2 2 5 0zz
. Giá trị của
biểu thức
22
12
11A z z
bằng:
A.
25
B.
5
C.
5
D.
25
Câu 42. Gọi
1 2 3
, z , zz
là ba nghiệm của phương trình
3
10z
. Khi đó
1 2 3
S | | | | | |z z z
bằng
A. S = 1 B. S = 4 C. S = 2 D. S = 3
Câu 43. Gọi
1 2 3 4
, , ,z z z z
là các nghiệm của phương trình:
42
60zz
. Giá trị của
1 2 3 4
T z z z z
là:
A. 1 B.
2 2 2 3
C.
2 2 2 3
D. 7
Câu 44. Kí hiệu z
1
, z
2
, z
3
và z
4
là bốn nghiệm phức của phương trình
42
2 63 0zz
.
Tính tổng T = | z
1
| + | z
2
| + | z
3
| + | z
4
| .
A.
6.T
B.
2 7.T
C.
3 2 7.T 
D.
6 2 7.T 
4C. Phương trình phức
128
Câu 45. Kí hiệu
1 2 3 4
z ,z ,z ,z
là bốn nghiệm của phương trình
42
z 4z 77 0 .
Tính
tổng
3
1 2 4
S z .
z z z
A.
S 2 7 2 11
B.
S 2 7 2 11
C.
S 2 7
D.
S 2 11
Câu 46. Phương trình z
4
– z
2
– 6 = 0 có 4 nghiệm phức phân biệt. Khi đó tổng môđun của các
nghiệm phức trong phương trình là:
A. 4 B.
2 3 2 2
C.
23
D.
32
Câu 47. Kí hiệu
1 2 3 4
, , ,z z z z
là bốn nghiệm phức của phương trình
42
12 0.zz
Khi đó tổng
1 2 3 4
T z z z z
là :
A. 4 B. 2 C. 4+2 D. 2+ 2
Câu 48. Gọi
12
;zz
là hai nghiệm của phương trình
2
2 3 8 0zz
, với
1
z
có phần ảo < 0. Xác
định phần thực và phần ảo của số phức
12
w 2 3 4z z i
A. Phần thực
3
4
, phần ảo
16 3 55
4
. B. Phần thực
3
4
, phần ảo
16 3 55
4
.
C. Phần thực
3
4
, phần ảo
16 3 55
4
. D. Phần thực
3
4
, phần ảo
16 3 55
4
.
Câu 49. Gọi
12
;zz
là hai nghiệm phức của phương trình:
2
2 10 0zz
. Giá trị của biểu thức
22
12
A z z
là
A.
100
B.
10
C.
20
D.
17
Câu 50. Phương trình
3
8z
có bao nhiêu nghiệm phức với phần ảo âm
A. 1 B. 2 C. 3 D. 4
Câu 51. Giải phương trình
2
2 5 4 0xx
trên tập số phức.
A.

1
57
44
xi
;

2
57
44
xi
. B.

1
57
44
xi
;

2
57
44
xi
C.

1
57
24
xi
;

2
57
24
xi
D.

1
37
44
xi
;

2
37
44
xi
Câu 52. Nghiệm của phương trình:
2
2 3 4 0zz
A.
1,2
3 23
3
i
z

B.
1,2
3 23
4
i
z

C.
1,2
3 23
5
i
z

D.
1,2
3 23
6
i
z

1A 2C 3D 4D 5A 6A 7A 8A 9A 10D
11A 12A 13A 14A 15A 16A 17B 18B 19A 20C
21A 22C 23C 24A 25B 26C 27A 28A 29A 30B
31A 32A 33A 34C 35B 36C 37A 38A 39A 40A
41C 42D 43B 44D 45A 46B 47C 48A 49C 50C
51B 52B
| 1/129
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


ĐỀ CƯƠNG TRẮC NGHIỆM 12 – TẬP 1
1. ỨNG DỤNG ĐẠO HÀM
2. HÀM SỐ LŨY THỪA – MŨ - LÔGARIT
3. NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG 4. SỐ PHỨC Nguyễn Văn Lực
www.facebook.com/VanLuc168 CẦN THƠ – 01/2017
1A. Sự đồng biến, nghịch biến của hàm số
SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ HÀM BẬC BA
Tìm các khoảng đơn điệu của hàm số
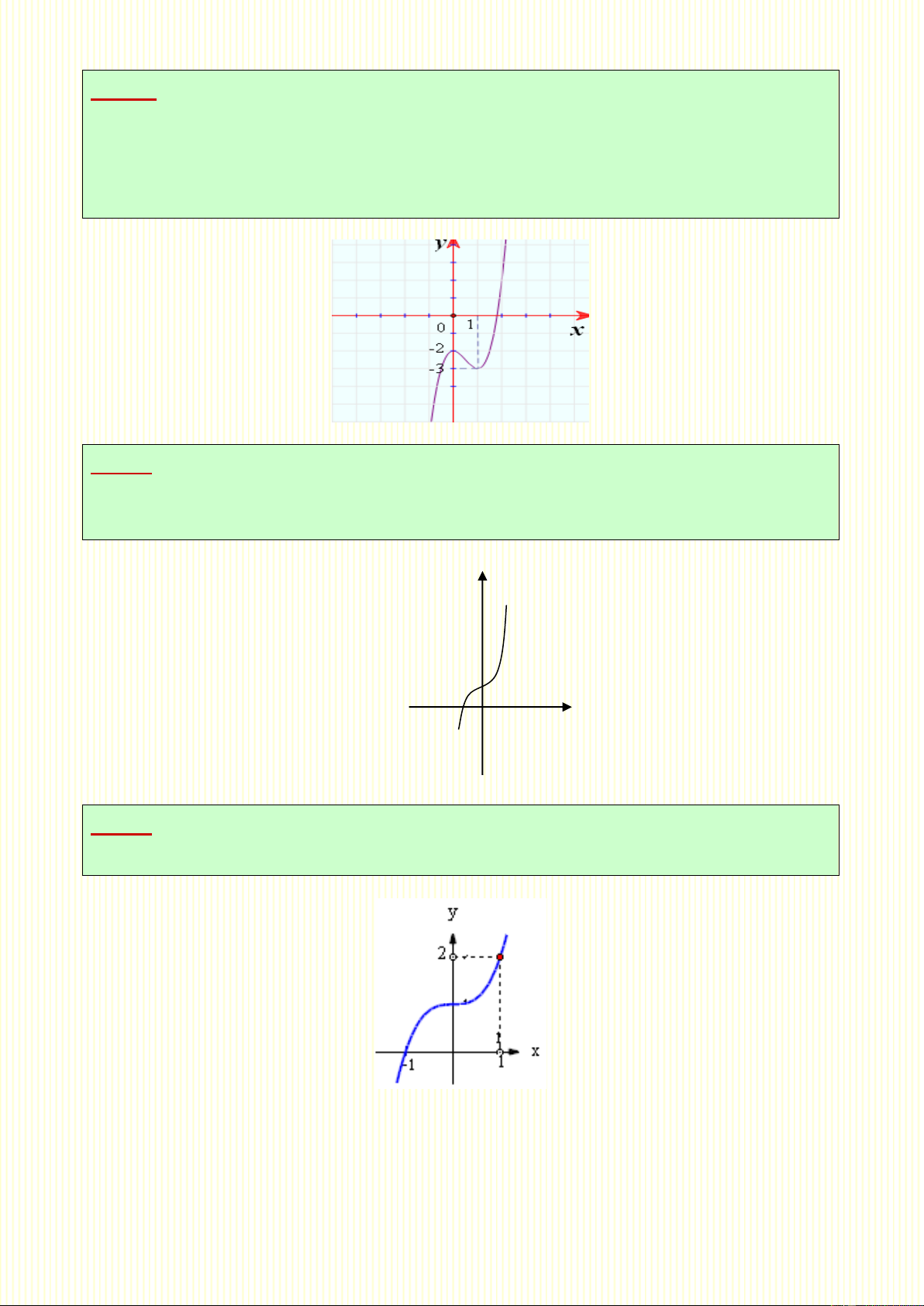
Câu 1. Hàm số y  3 x  2
3x nghịch biến trên khoảng nào? A. ;2 B. 0; C. 2;0 D. 0;4
Câu 2. Cho hàm số y  3 x  2
3x  9x  12, trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số đồng biến trên khoảng ;2
B. Hàm số nghịch biến trên khoảng 1;2
C. Hàm số đồng biến trên khoảng 5;
D. Hàm số nghịch biến trên khoảng 2;5 Câu 3. Hàm số 3 2
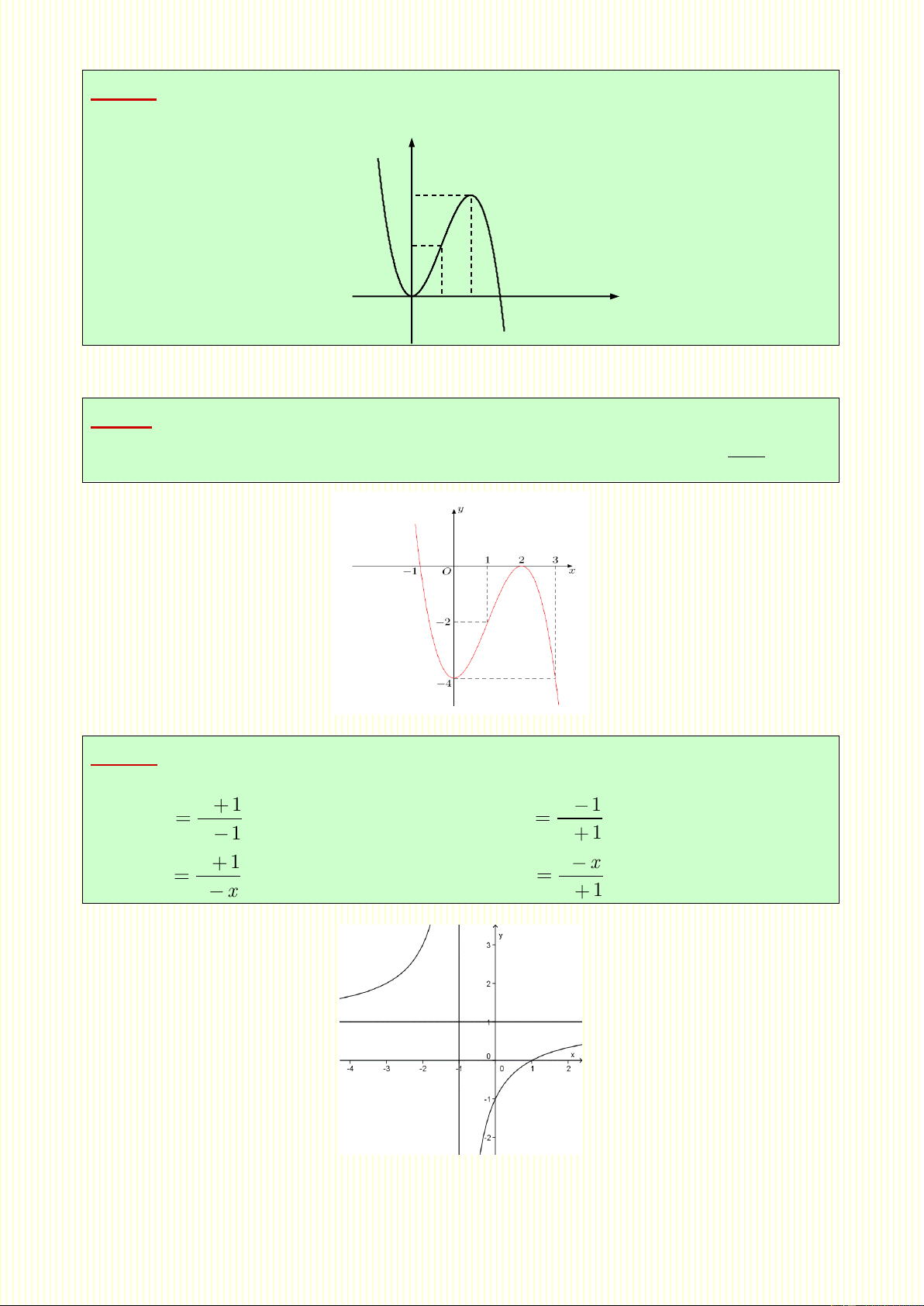
y x  3x  3x  5 đồng biến trên khoảng nào? A. ( ;1  ) B. (1; ) C. ( ;  ) D. ( ;1  ) và (1;)
Câu 4. Các khoảng nghịch biến của hàm số: y x  3 3 4x là  1   1   1 1   1   1  A. ;  ; ;       ;  ;   ;    2   2 B.   2 2 C.   2 D.   2 
Câu 5. Cho hàm số 3 y x  3 2
x  9x  5 . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên ( ) 3 ; 1
B. Hàm số nghịch biến trên khoảng (; ) 1 .
C. Hàm số đồng biến trên mỗi khoảng (; ) 1 , ( ; 3 )
D. Hàm số chỉ đồng biến trên khoảng ( ; 3 ) . Câu 6. Hàm số 3 2
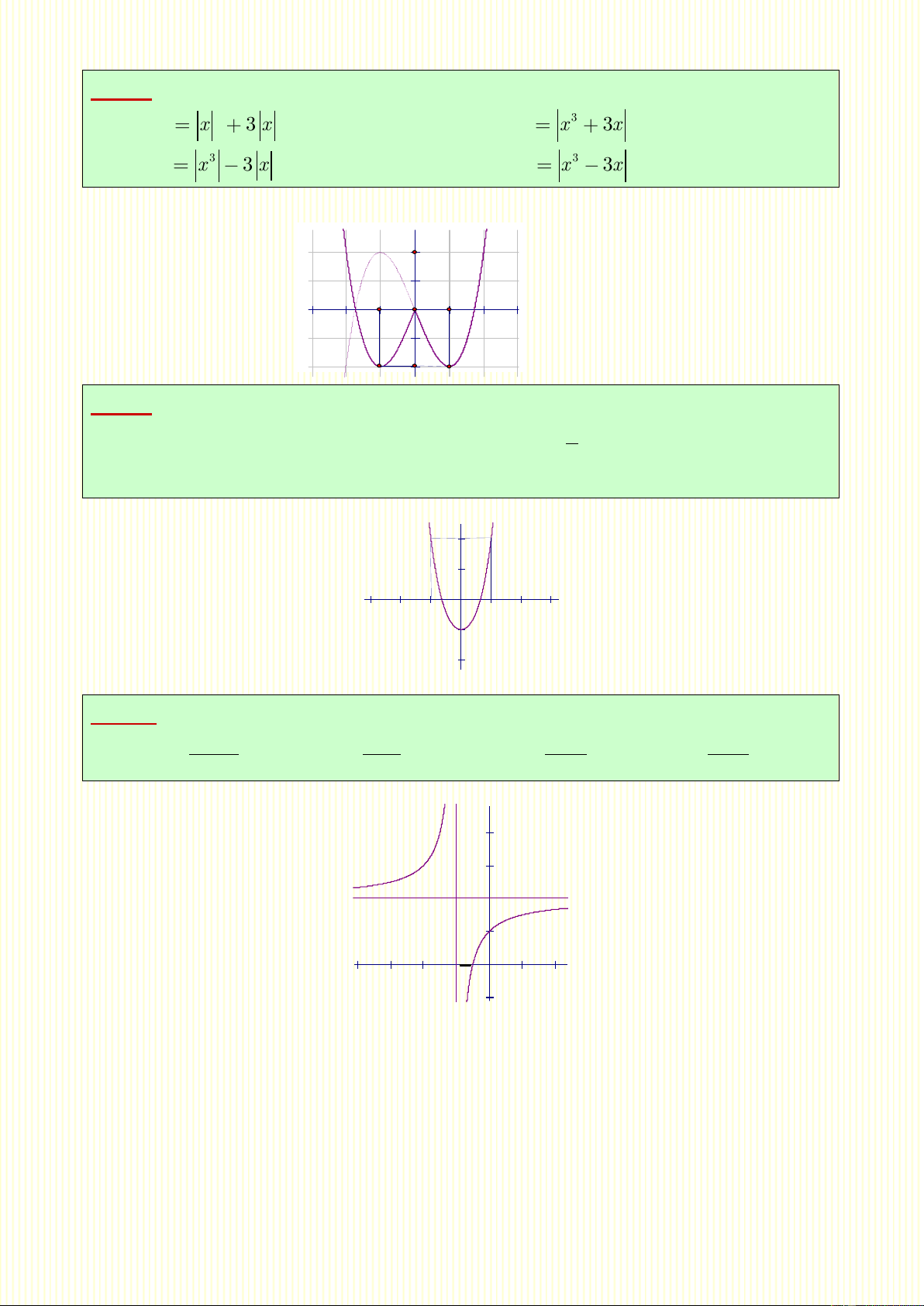
y  x  3x  9x nghịch biến trên khoảng nào sau đây? A. B. ( ; 1);(3; ) C. (3; ) D. ( 1; 3) 3 Câu 7 x . Hàm số 2 y
x x đồng biến trên khoảng nào? 3 A. B.   ;1 C. 1; D.   ;1 và 1; Câu 8. 1 5
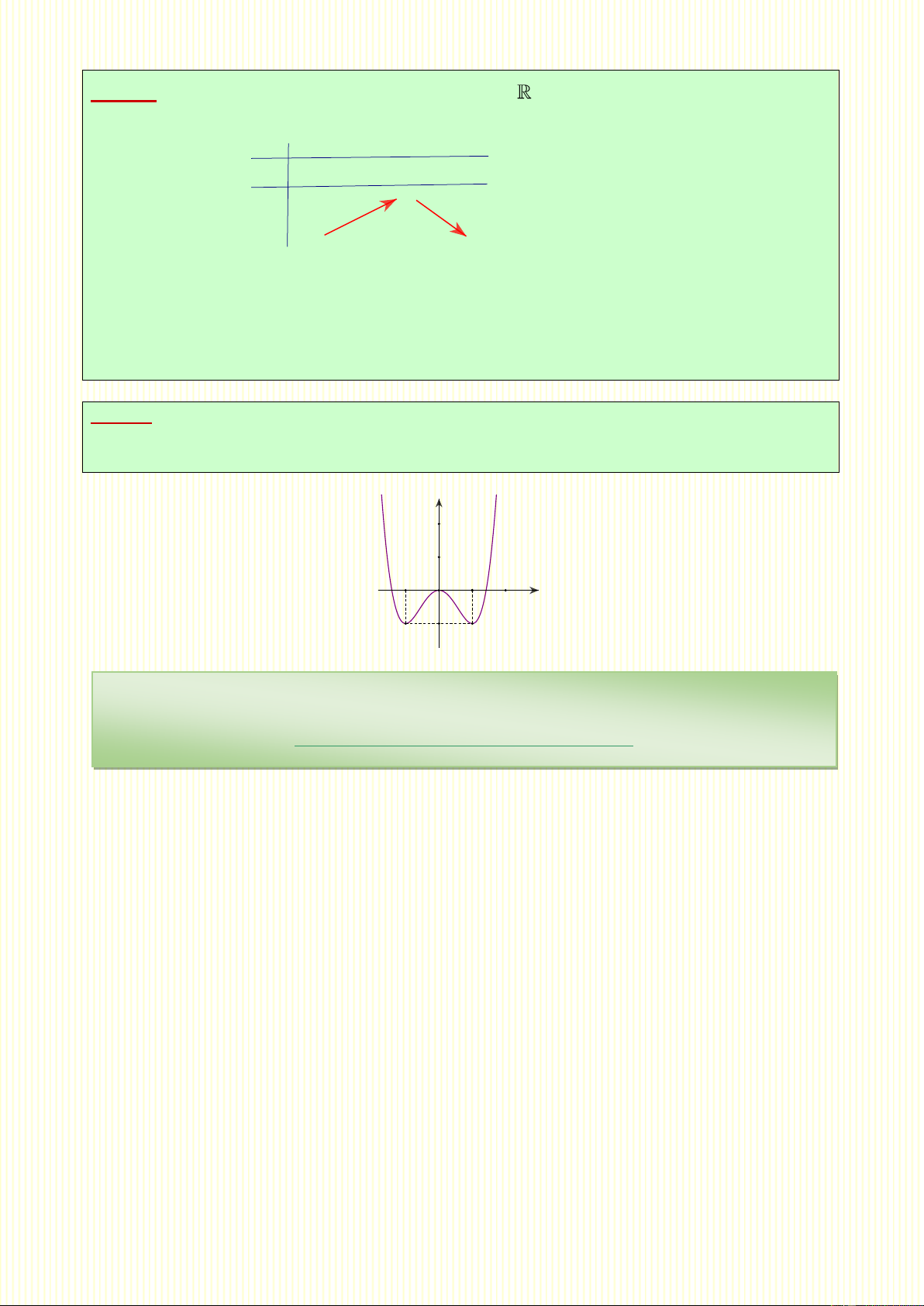
Khoảng nghịch biến của hàm số y  3 x  2 x  3x  là 3 3 A. ;  1 B. 1;3 C. 3; D. ;  1 và 3; Câu 9 4 2
. Cho hàm số y   3 x  2
6x  9x  . Khoảng đồng biến của hàm số là: 3 3 A. ;3 B. 2; C. D. Không có. 1
1A. Sự đồng biến, nghịch biến của hàm số
Câu 10. Cho hàm số y  1 2 x  2
x  2x  10. Khoảng đồng biến của hàm số là: 3 A. ;  1 B. 1; C. D. Không có. Câu 11. Hàm số 3 2 y x 3x 9x
2 đồng biến trên khoảng nào? A. 3;  1 B. 1;3 C. ;  1 và 3;
D. ;3 và 1;
Câu 12. Các khoảng nghịch biến của hàm số 3 2
y  x  3x 1 là: A.  ;  
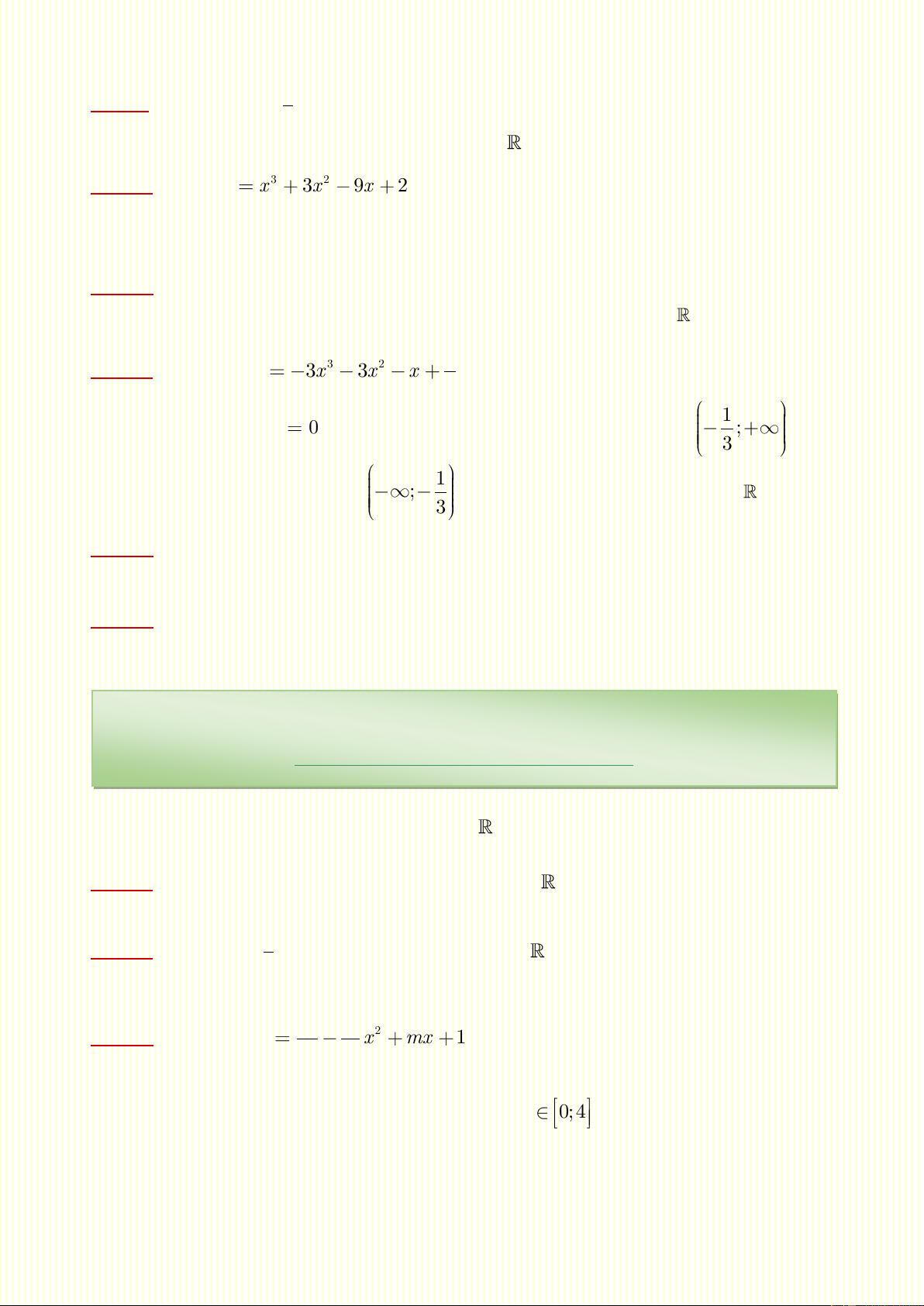
1 , 2; B. 0;2 C. 2;  D. 3 Câu 13. Cho hàm số 3 2 y 3x 3x x
. Khẳng định đúng là 2 1
A. Phương trình y ' 0 vô nghiệm.
B. Hàm số đồng biến trên ; . 3 1
C. Hàm số trên đồng biến trên ; .
D. Hàm số trên nghịch biến trên . 3
Câu 14. Các khoảng đồng biến của hàm số 3
y  2x  6x là: A.  ;   
1 , 1;  B.  1  ;  1 C.  1  ;  1 D. 0;  1
Câu 15. Các khoảng nghịch biến của hàm số 3
y  2x  6x  20 là: A.  ;   
1 , 1;  B.  1  ;  1 C.  1  ;  1 D. 0;  1 Nguyễn Văn Lực
www.facebook.com/VanLuc168
Tìm điều kiện để hàm số đơn điệu trên
Câu 16. Hàm số y  3 x  2
3x mx  1 luôn đồng biến trên khi A. m  3 B. m  3 C. m  3 D. m  3 Câu 17. 1 Hàm số y   3
x  m  
1 x  7 nghịch biến trên
thì điều kiện của m là: 3 A. m  1 B. m  2 C. m  1 D. m  2 3 x m Câu 18 2 . Cho hàm số y x mx
1 , hàm số đồng biến trên tập xác định của nó khi 3 2
A. m  0;4
B. m  ;0  4;
C. m  ;0  4; D. m 0; 4 2
1A. Sự đồng biến, nghịch biến của hàm số 2 1 mx Câu 19. 3 Cho hàm số: y x
 2x  2016 . Với giá trị nào của m , hàm số luôn đồng 3 2
biến trên tập xác định. A. m  2 2 B. m  2 2
C. m  2 2  m  2 2
D. Một kết quả khác Câu 20. Cho hàm số 3
y x  m   2
2 x  m  
1 x  2 , với giá trị nào m thì hàm số đồng biến trên tập xac định: 7   45 7   45 7   45 7  45 A. m B.m  2 2 2 2 7   45 7   45 7   45 7  45 C.m D.m  2 2 2 2  Câu 21 1 m . Định m để hàm số 3 2 y x  2(2  ) m x  2(2  )
m x  5 luôn nghịch biến khi: 3
A. 2  m  5 B. m  2 C. m  1 D.   2 m 3
Câu 22. Với điều kiện nào của m thì hàm số 3
y mx  (2m  ) 1 2 x  (m  )
2 x  2 luôn đồng biến
trên tập xác định của nó? A. m  0 B. m  0 C. m  0 D. m  0 Câu 23. Cho hàm số 3 2 y mx (2m 1)x
mx 7 . Có bao nhiêu giá trị nguyên của tham số m
để hàm số nghịch biến trên ?
A. Không có giá trị B. 2 C. 0 D. Vô số giá trị
Tìm điều kiện để hàm số đơn điệu trên khoảng K cho trước
Câu 24. Hàm số y  3
x  3mx  5 nghịch biến trong khoảng 1;  1 thì m bằng: A. 1 B. 2 C. 3 D. 1
Câu 25. Với giá trị nào của m hàm số 3 2
y x  3x  (m 1)x  4m nghịch biến trên (-1;1) A. m  10 B. m  10 C. m  10 D. m  5 Câu 26. 1
Tìm m để hàm số y   3
x  m   2
1 x  m  3 x 10 đồng biến trên 0;3 3 A. m  12 B. m  12 7 7 C. mR D. m  7 12 Câu 27. Hàm số 3 2 y x 3x mx
1 đồng biến trên khoảng 0; khi A. m 0 B. m 3 C. m 3 D. m 0 Câu 28. Hàm số 3 2 y 2x 3(2m 1)x 6 ( m m 1)x
1 đồng biến trên khoảng (2; ) khi: A. m 1 B. m 1 C. m 2 D. m 1 3
1A. Sự đồng biến, nghịch biến của hàm số Câu 29 3 2
. Cho hàm số y x  3x mx  4(1) . Tìm tất cả các giá trị của tham số m để hàm số (1)
đồng biến trên khoảng (  ; 0)? A. m  1. m m m  3. B.  3. C.  3. D.
Câu 30. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x  2mx m đồng biến trên khoảng ;0. A. m  0 B. m  0
C. Không có m D. Mọi m Nguyễn Văn Lực
www.facebook.com/VanLuc168
HÀM BẬC BỐN TRÙNG PHƯƠNG
Tìm các khoảng đơn điệu của hàm số
Câu 31. Hàm số y  4 x  2
2x  1 đồng biến trên các khoảng nào? A. 1;0
B. 1;0 và 1; C. 1; D.x
Câu 32. Khoảng đồng biến của 4 2 y x 2x 4 là: A. (-∞; -1) B. (3;4) C. (0;1)
D. (-∞; -1) , (0; 1). Câu 33. 1 3
Khoảng nghịch biến của hàm số y  4 x  2 3x  là 2 2  3   3 
A. ; 3 và 0; 3 B. 0;    và  ;     2   2  C.  3;
D.  3;0 và  3; Câu 34. Hàm số 4 3
y x  8x  5 nghịch biến trên khoảng: A. ( 6  ;0)      B. (0; ) C. ( ; 6) D. ( ; ) Câu 35 4 3 2
. Hàm số y x  4x  4x  2 nghịch biến trên các khoảng A. (1; 0). ( ; 2). ;2 ;  B.   C. D.    1;0
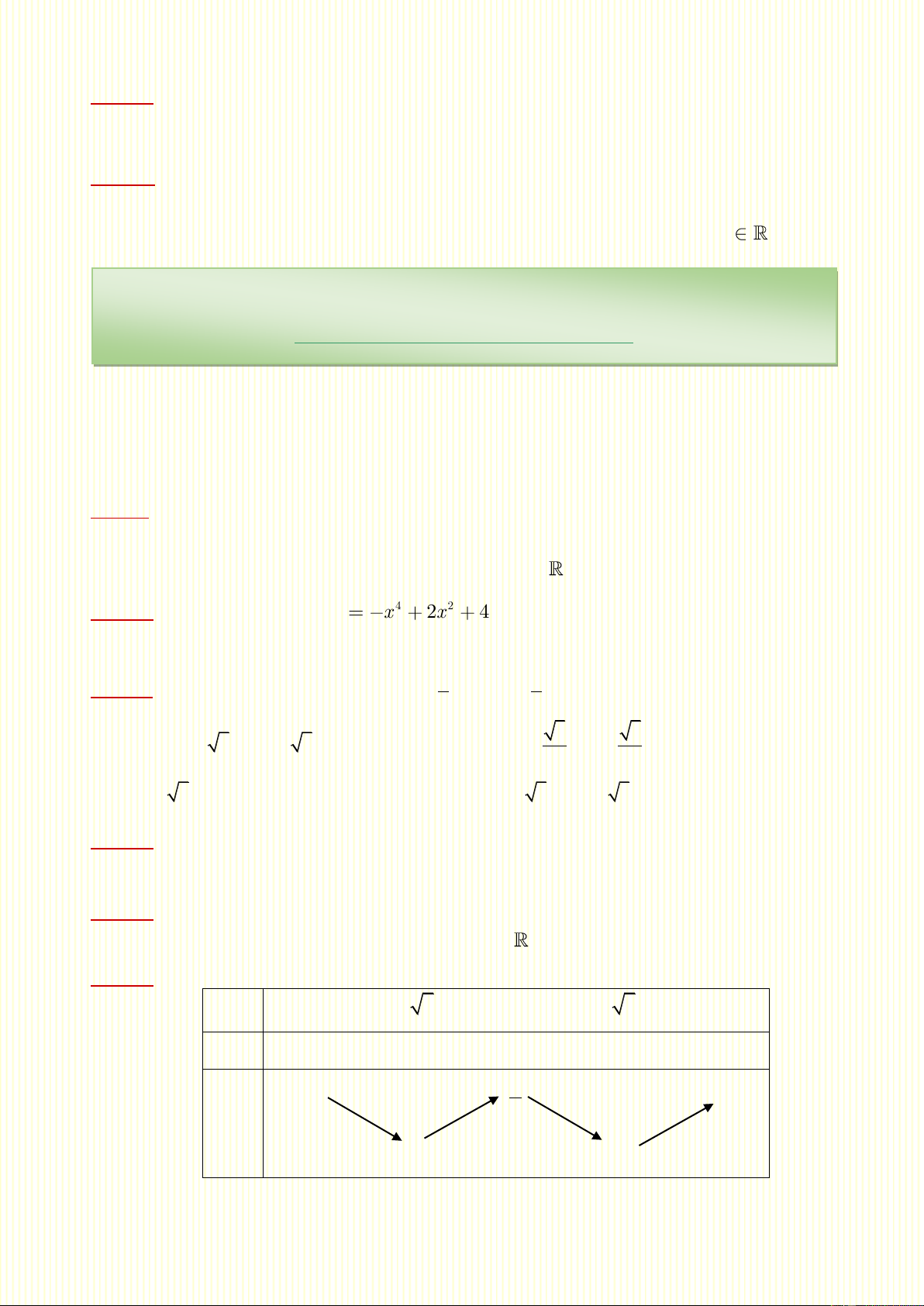
Câu 36. Bảng biến thiên sau đây là của hàm số nào. x   3 0 3  y '  0  0  0   5  y 2 2  2  4
1A. Sự đồng biến, nghịch biến của hàm số 1 5 1 A. 4 2 y x  3x B. 4 2 y   x  2x 2 2 4 1 5 1 3 C. 4 2 y x  2x D. 4 2 y x  3x  2 2 4 2 Câu 37. Cho hàm số 4 2
y x  2mx  3m 1(1) (m là tham số). Tìm m để hàm số (1) đồng biến trên khoảng (1; 2). A. m  1
B. 0  m  1 C. m  0 D. m  0 4 Câu 38 x . Cho hàm số 2 y
x 1, hàm số đồng biến trên khoảng nào? 2
A. ,0;1,  B. ,   1 ;0  ,1
C. 1,0;1,  D. ,  Câu 39 1 . Hàm số 4 2 y  
x  2x  3 nghịch biến trong khoảng nào sau đây: 4 A.  ;  0 B. (0; 2) C. 2;  D. 0;  Câu 40. 1 3
Các khoảng đồng biến của hàm số 4 2 y   x x 1 là: 4 2 A. ( ;   3) và (0; 3) .
B. ( 3;0) và ( 3; )  3 C. ;      D. Trên .  2  4 x
Câu 41. Hàm số y
1 đồng biến trên khoảng nào? 2 A. ( ; 0) B. (1; ) C. ( 3; 4) D. ( ;1) HÀM PHÂN THỨC
Tìm các khoảng đơn điệu của hàm số 2x Câu 42 1
. Các khoảng nghịch biến của hàm số y  là: x 1 A.   ;1 B. 1; C. ; D.   ;1 và 1;
Câu 43. Cho hàm số y x  2 . Khoảng nghịch biến của hàm số là: x
A. ;0 và 0; B. 1;0 C. D. Không có.  2 x  2x Câu 44 3 . Cho hàm số y
. Khoảng nghịch biến của hàm số là: x  1 A. ;  1 và 1; B. 1; C. D. Không có.
Câu 45. Cho hàm số y x  1 . Khoảng nghịch biến của hàm số là: x A. ;  1 và 1;
B. 1;0 và 0;  1 C. D. Không có 5
1A. Sự đồng biến, nghịch biến của hàm số 2 x  8x Câu 46 9 . Cho hàm số y
. Khoảng nghịch biến của hàm số là: x  5
A. ;5 và 5; B. 5; C. D. Không có.  Câu 47 2x 3
. Hàm số y  f (x)  x  nghịch biến trên: 1 A. 1;  B. ;  1 ;1; C.  1  ; D.  ;  2  Câu 48 x 2
. Hàm số y x  nghịch biến trên các khoảng: 1 A.   ;1 và 1; B. 1;  C.  1  ; D. 0;  x Câu 49 2 . Cho hàm số y
. Khoảng đồng biến của hàm số là: x  2
A. ;2 và 2; B. 1;0 C. D. Không có.
Câu 50. Cho hàm số y  1  2x. Khoảng đồng biến của hàm số là: x  1 A. ;  1 B. 1; C. D. Không có. Câu 51 x
. Cho hàm số y
. Khoảng đồng biến của hàm số là: 2 x  1 A. ;  1 B. 1; C. D. 1;  1 Nguyễn Văn Lực
www.facebook.com/VanLuc168
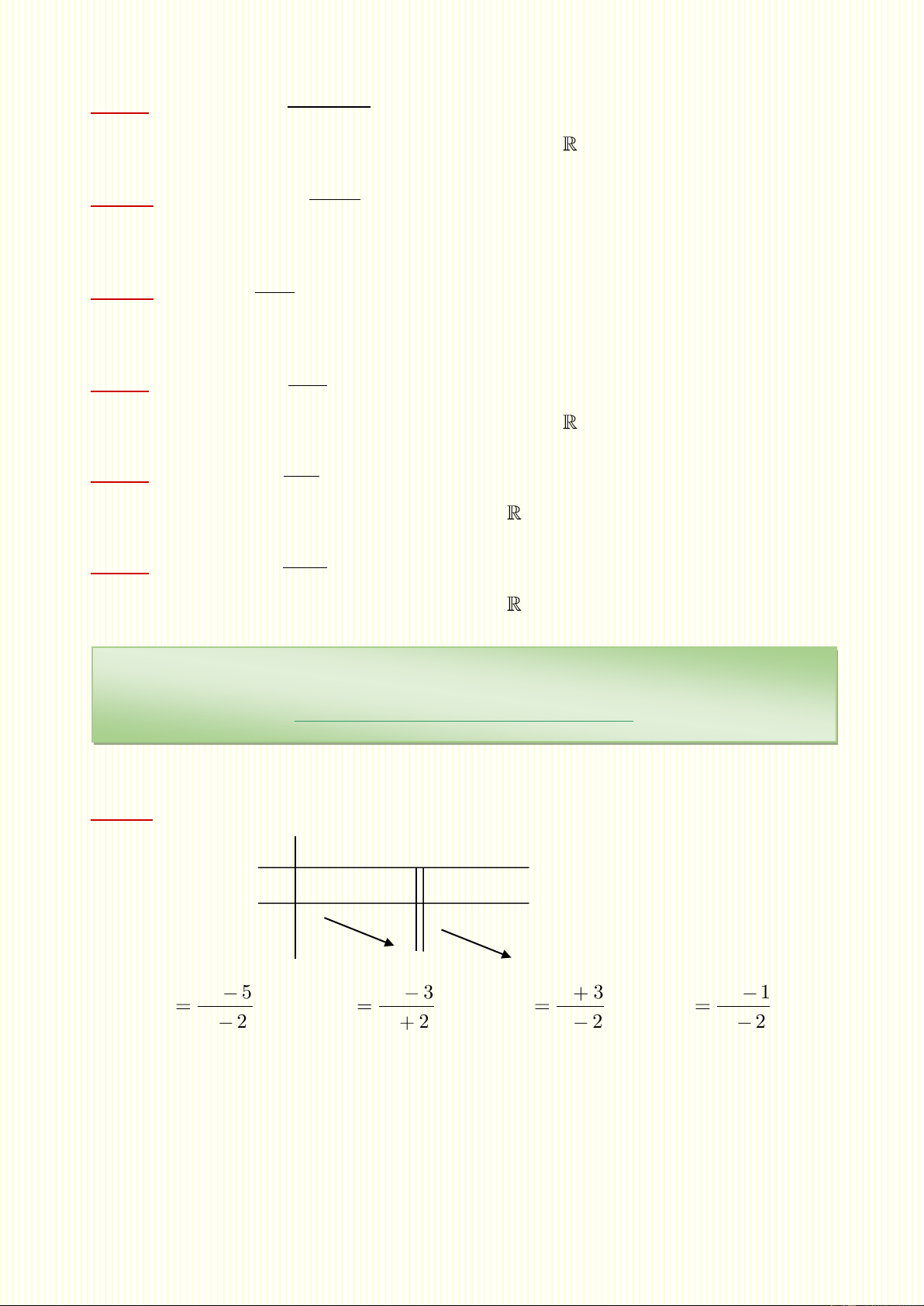
Câu 52. Hàm số có bảng biến thiên như hình bên là  x  2 y '    y 2 2  2x 5 2x 3 x 3 2x 1 A. y B. y C. y D. y x 2 x 2 x 2 x 2 6
1A. Sự đồng biến, nghịch biến của hàm số
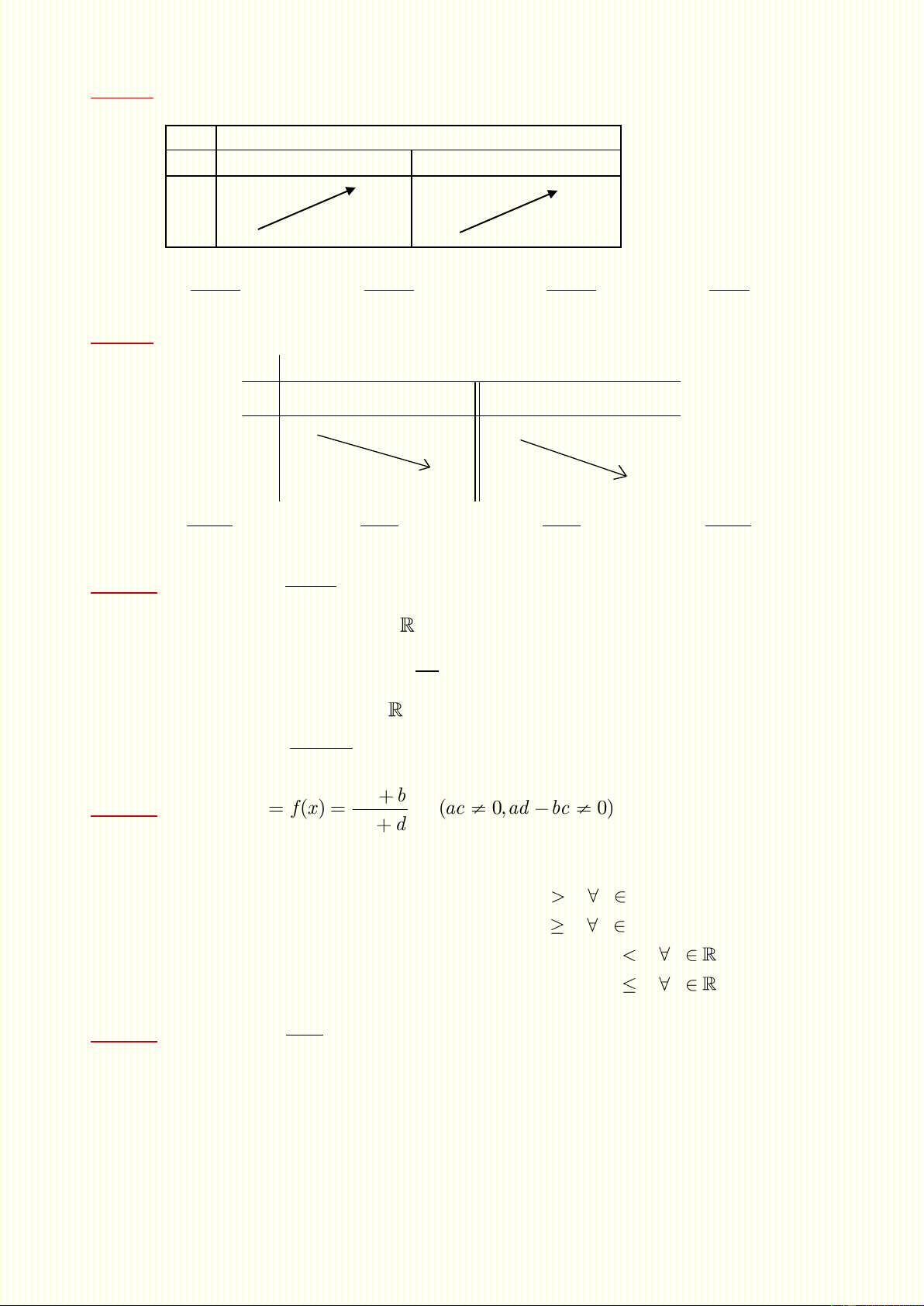
Câu 53. Hàm số nào sau đây có bảng biến thiên như hình bên: x  1  y ' + + y  2 2  2x  3 2x  3 2x  3 x  3 A. y B. y C. y D. y x 1 x 1 1 x x  2
Câu 54. Bảng biến thiên sau đây là của hàm số nào? x 2 -  +  y' - - 1 +  y -  1 2x  1 x  3 x  3 x  3 A. y  B. y  C. y  D. y  x  2 x  2 x  2 2x  1  Câu 55. 2x 7 Cho hàm số y
có đồ thị (C). Hãy chọn mệnh đề sai : x  2
A. Hàm số có tập xác định là: D  \  2  7 
B. Đồ thị cắt trục hoành tại điểm A ; 0    2 
C. Hàm số luôn nghịch biến trên 3 
D. Có đạo hàm y '  2 (x  2) ax b
Câu 56. Cho hàm số y f (x) (ac 0,ad bc
0) và D là tập xác định của cx d
hàm số. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên từng khoảng xác định, khi y ' 0 x D
B. Hàm số đồng biến trên từng khoảng xác định, khi y ' 0 x D
C. Hàm số nghịch biến trên từng khoảng của tập xác định, khi y ' 0 x
D. Hàm số nghịch biến trên từng khoảng của tập xác định, khi y ' 0 x x 1
Câu 57. Cho hàm số y
. Chọn khẳng định đúng. x 1
A. Hàm số nghịch biến trên các khoảng  ;    1 và  1  ;
B. Hàm số đồng biến trên các khoảng  ;    1 và  1  ;
C. Hàm số nghịch biến trên các khoảng   ;1  và 1; 
D. Hàm số đồng biến trên các khoảng   ;1  và 1;  7
1A. Sự đồng biến, nghịch biến của hàm số 4
Câu 58. Cho hàm số y . Khẳng định đúng là x 2
A. Nghịch biến trên
B. Nghịch biến trên D \ {2}
C. Nghịch biến trên các khoảng ;2;2;
D. Đồng biến trên các ;2;2; x Câu 59. 2 1
Kết luận nào sau đây về tính đơn điệu của hàm số y  là đúng x 1
A. Hàm số đồng biến trên các khoảng (–; –1) và (–1; +).
B. Hàm số luôn luôn đồng biến trên \   1
C. Hàm số nghịch biến trên các khoảng (–; –1) và (–1; +).
D. Hàm số luôn luôn nghịch biến trên \   1  Câu 60. Cho hàm số 2x 1 y
. Khẳng định nào sau đây là khẳng định sai? x 1
A. Đồ thị hàm số có tiệm cận đứng là x  1 .
B. Hàm số không xác định tại điểm x  1 .
C. Hàm số nghịch biến trên .
D. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng  1 . 2 2 x x Câu 61 1
. Các khoảng đơn điệu của hàm số y  là: x 1
A. Đồng biến trên các khoảng ;0 và 2; .
Nghịch biến trên các khoảng 0;1 và 1;2.
B. Đồng biến trên khoảng ; 
1 . Nghịch biến trên khoảng 0;2.
C. Đồng biến trên khoảng 2;. Nghịch biến trên khoảng 0;2.
D. Đồng biến trên khoảng 2;. Nghịch biến trên khoảng 0;  1 . 2   Câu 62. x 2x 3 Cho hàm số y x
. Phát biểu nào sau đây là đúng? 1
A. Hàm số đồng biến trên khoảng ( ;  1
 ) và nghịch biến trên khoảng ( 1  ;).
B. Hàm số nghịch biến trên .
C. Hàm số đồng biến trên khoảng (2;4).
D. Hàm số nghịch biến trên các khoảng ( ;  1  ) và ( 1  ;).
Tìm điều kiện để hàm số đơn điệu x Câu 63. m
Giá trị nào của m thì hàm số y
nghịch biến trên từng khoảng xác định x  2 A. m  2 B. m  2 C. m  2 D. m  2   Câu 64 mx 7m 8 . Hàm số y
. luôn đồng biến trên từng khoảng xác định với m x m
A. 8  m  1
B. 8  m  1
C. 4  m  1
D. 4  m  1 8
1A. Sự đồng biến, nghịch biến của hàm số 2   Câu 65. x mx 2
Tìm các giá trị thực của tham số m để hàm số y
đồng biến trên từng khoảng x 1 xác định của nó. A. m  3 B. m  3 C. 2  2  m  2 2 D. m  2
 2 hoặc m  2 2 . 
Câu 66. Tìm tất cả các giá trị thực của tham số mđể hàm số x m y  đồng biến trên từng x 1
khoảng xác định của nó. A. m  1 B. m  1 C. m  1 D. m  1 Câu 67. x Hàm số y
đồng biến trên 2; khi và chỉ khi x m A. m  0 B. m  0 C. m  2 D. m  2  Câu 68 mx 25
. Các giá trị của tham số m để hàm số y   là: x
nghịch biến trên khoảng ( ;1) m A.           5 m 5 B. 5 m 1 C. 5 m 5 D. m  1  Câu 69. mx
Tìm tất cả các giá trị thực của tham số m để hàm số 2 y  nghịch biến trên từng 2x m
khoản xác định của nó.
A. m  2 hoặc m  2
B. 2  m  2
C. 2  m  2
D. m  2 hoặc m  2
HÀM BẬC HAI, HÀM CHỨA CĂN
HÀM LƯỢNG GIÁC, LOGARIT
Câu 70. Tìm khoảng đồng biến của hàm số y  2 x  4x  2 A. 2; B. ;2
C. ;2 và 2; D. Câu 71. 1 3
Tìm khoảng nghịch biến của hàm số y   2 x x  2 2 A. 1; B. ;  1
C. 1; D. ;  1 và 1; Câu 72. 1
Tìm khoảng nghịch biến của hàm số  P : y  2 x  2x  5. 2 A. 2; B. ;2 C. 2;
D. ;2 và 2;
Câu 73. Tìm khoảng đồng biến của hàm số Py  2 : x  2x  5. A. 1; B. ;  1 C. ;  1 và 1; D.
Câu 74. Khoảng đồng biến của hàm số y x  2 2 x là A.   ;1 B. 0;  1 C. 1;2 D. 1;
Câu 75. Cho hàm số y   2 4
x . Khoảng nghịch biến của hàm số là: A. 0;2 B. 2;0 C. 2;2 D. 9
1A. Sự đồng biến, nghịch biến của hàm số Câu 76. Hàm số 2 y 
2  x  x nghịch biến trên khoảng  1   1  A.  ;2.   1; . 1;2 . D. 2;.  2 B.   2 C.    Câu 77. Cho hàm số 2 y
x  2x 1  m .
x Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên . A. m  2 B. m  0 C. m  1 D. m  1 Câu 78. x Cho hàm số y
, f x  đồng biến trong các khoảng nào sau đây? ln x A. 0;  1 B. 1;e C. 0;eD.  ; e 
Câu 79. Hàm số y x ln x luôn đồng biến trên khoảng  1   1  A. ;   B. ;   C.  ; e  D. 1; 10   ex e 1
Câu 80. Với giá trị nào của m thì hàm số y  2  ; 1  ? x đồng biến trên   e m 1 A.m  1. m e B. 1. 1 1 1 C. m  hoaëc  m 1. D. m  . 2 e e 2 e
Câu 81. Giá trị b để hàm số y  sin x bx nghịch biến là: A.   ;1 B. 1; C. 1; D.   ;1
Câu 82. Tìm tất cả các giá trị thực của tham số m để hàm số y  (m  3)x  (2m 1) cos x nghịch biến trên R . 2 1 1
A. 4  m
B. Không có m . C.m  3.
D. 2  m  3 2 2   
Câu 83. Tìm m để hàm số 3 2
y  sin x  3sin x m sin x  4 đồng biến trên khoảng 0;  .  2  A. m  0 B. m  0 C. m  0 D. m  0
Câu 84. Hàm số y 2m cos x
x đồng biến trên khi A. m 0 B. 0 m 1 1 1 1 C. m 0 D. m 2 2 2
Câu 85. Cho hàm số y sinx 3 cosx
mx. Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên .
A. m  2 B. m   3 C. m  2 D. m  1 10
1A. Sự đồng biến, nghịch biến của hàm số   
Câu 86. Cho hàm số f x  2sin x  tan x  3x xác định, liên tục trên nửa khoảng 0;   .  2 
Khẳng định nào sau đây là khẳng định đúng?   
A. Hàm số nghịch biến trên nửa khoảng 0;   .  2    
B. Hàm số có cực trị trên nửa khoảng 0;   .  2    
C. Hàm số đồng biến trên nửa khoảng 0;   .  2        
D. Hàm số đồng biến trên khoảng 0; 
 và nghịch biến trên khoảng ;   .  4   4 2 
Câu 87. Cho bất đẳng thức x
sin x (1). Khẳng định nào sau đây đúng?
A. (1) luôn đúng khi x 0;
B. (1) luôn đúng khi x 0; 2 2
C. (1) luôn đúng khi x 0;
D. (1) luôn đúng khi x 0; 2 2     Câu 88. sin x 3 Cho hàm số y 
. Hàm số đồng biến trên 0;   khi: sin x  m  2 
A. m  0  1  m  3 B. m  3 C. 0  m  3 D. m  3  Câu 89 m cos x
. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  nghịch biến trên 2 sin x     ;   .  3 2  5 A. m  . B. m  1. C. m  2. D. m  0. 4 m sin x
Câu 90. Tìm m để hàm số y nghịch biến trên 0; ? 2 cos x 6 5 A. m B. m 1 C. m 2 D. m 0 4 x Câu 91 m
. Tìm tất cả các giá trị thực của tham số m để hàm số sin y  nghịch biến trong sin x 1    khoảng ;  .    2  A. m  1. B. m  1. C. m  1. D. m  1. 11
1A. Sự đồng biến, nghịch biến của hàm số tan x  2
Câu 92. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  tanx m đồng biến trên    khoảng  0;   4  A. m  0
B. 1  m  2
C. m  0 hoặc 1  m  2 D. m  2  Câu 93. tan x 10
Tìm tất cả các giá trị thực của m sao cho hàm số y  đồng biến trên khoảng tan x m    0; .    4  A. m  1 B. m  2
C. 1  m  10
D. m  0 hoặc 1  m  10 Nguyễn Văn Lực
www.facebook.com/VanLuc168 1C 2D 3C 4A 5C 6B 7A 8B 9D 10C
11D 12A 13D 14A 15B 16D 17C 18D 19B 20D
21D 22A 23A 24A 25C 26A 27C 28D 29B 30A
31B 32D 33A 34C 35D 36A 37A 38C 39D 40A
41A 42D 43D 44A 45B 46D 47A 48A 49A 50D
51D 52D 53B 54C 55C 56A 57C 58C 59A 60C
61A 62C 63C 64A 65A 66A 67A 68B 69B 70A
71C 72B 73A 74B 75A 76A 77D 78D 79B 80C
81B 82A 83C 84D 85A 86C 87B 88A 89A 90A 91B 92A 93D 12
1B. Cực trị của hàm số
CỰC TRỊ CỦA HÀM SỐ HÀM BẬC BA
Tìm điểm cực đại, cực tiểu của hàm số
Câu 1. Điểm cực tiểu của hàm số 3
y  x  3x  4 là: A. x   1 B. x  1 C. x   3 D. x  3
Câu 2. Điểm cực đại của đồ thị hàm số: y x  3 3 4x là:  1   1   1   1  A. ;  1   ;1  ;  1  ;1  2 B.   2 C.   2 D.   2 
Câu 3. Điểm cực đại của đồ thị hàm số 3 2 y x 6x 9x là A. 1;4 B. 3;0 C. 0;3 D. 4;  1
Câu 4. Tìm giá trị cực đại của hàm số 3 2
y x  3x  3x  2 A. 3   4 2 B. 3  4 2 C. 3  4 2 D. 3   4 2
Câu 5. Điểm cực đại của đồ thị hàm số 3 2
y  2x  3x  2 là A. 0; 2  . B. 2; 2. C. 1; 3  . D.  1  ; 7  . 1
Câu 6. Tìm giá trị cực đại y của hàm số 3 2 y x x 3x 2. CD 3 11 5 A. y B. y C. y 1 D. y 7 CD 3 CD 3 CD CD 3 x 2
Câu 7. Điểm cực đại của đồ thị hàm số 2 y
 2x  3x  là 3 3  2  A. (-1;2) B. 3;   C. (1;-2) D. (1;2)  3  Câu 8. Cho hàm số 3
y  x  3x . Hãy chọn khẳng định đúng
A. Hàm số không có cực trị
B. Hàm số có một cực trị
C. Hàm số đạt cực tiểu tại x  1
D. Giá trị cực đại của hàm số là 2
Câu 9. Tổng giá trị cực đại và cực tiểu của hàm số 3 2 y  x  3x  2 là: A. 3 B. 2 C. 1 D. 0 Câu 10. Cho hàm số 3
y x  3x 1. Tích của giá trị cực đại và giá tri ̣ cực tiểu của hàm số bằng: A. 0 B. -3 C. -6 D. 3 13
1B. Cực trị của hàm số
Câu 11. Điểm cực đại của đồ thị hàm số 3 2
y x  5x  7x  3 là:  7 3  2   7 32  A. 1;0 B. 0;  1 C. ;   D. ;    3 27   3 27  1
Câu 12. Giá trị cực đại của hàm số 3 2 y x 3x 9x 5 là 8 A. -1 B. 3 C. 0 D. 2
Câu 13. Tìm giá trị cực tiểu y của hàm số 3 2 y 2x 3x 2 ? CT A. y 3 B. y 2 C. y 0 D. y 1 CT CT CT CT Nguyễn Văn Lực
www.facebook.com/VanLuc168
Tìm m để hàm số đạt cực đại, cực tiểu 2 1 mx
Câu 14. Biết rằng hàm số 3 y   x
 4 đạt cực đại tại
. Khi đó giá trị của m sẽ là: 3 3 A. m  1 B. m  2 C. m  3 D. m  4 3 2 x x
Câu 15. Tìm tất cả giá trị của m để hàm số f (x)   . m
 (2m  4)x 1 , đạt cực đại tại x  2 3 2 . A. m  4 B.m C. m  4 D. m  4
Câu 16. Tìm tất cả giá trị thực của tham số m để hàm số 3 2
y x 3mx  2x 1 nhận điểm x  1 làm điểm cực đại. 5 A. Không tồn tại .
m B. Có vô số . m C. m  6. D. m  . 2 Câu 17. Hàm số 3 2 2
y x  2mx m x  2 đạt cực tiểu tại x  1 khi A. m  2 B. m  3 C. m  1 D. m  1 Câu 18. Hàm số 3 2
y x  3x mx đạt cực tiểu tại x = 2 khi: A. m  0 B. m  0 C. m  0 D. m  0 Câu 19. Hàm số 3 2 2 y x mx m 2m x
1 đạt cực tiểu tại x 1 khi A. m 3 B. m 1 C. m 2 D.
Câu 20. Để hàm số 3
y x  m   2 2 3
1 x  6m  2 x đạt cực đại và cực tiểu thì : A. m  3 B. m  3 C. m
D. Không có giá trị m
Câu 21. Giá trị của m để hàm số 3 2 y (m 2)x 3x mx m
có cực đại và cực tiểu là A. m   3  ;  1 \{ 2} B. m   3  ;  1
C. m   ;  3    1; D. m 3 14
1B. Cực trị của hàm số
Câu 22. Tìm các giá trị thực của tham số m để hàm số 3 2 y x (m 1)x
2mx 3 đạt cực trị tại x 1 5 1 A. m 2 B. m C. m D. m 1 4 4
Câu 23. Với giá trị nào của tham số m thì hàm số 3 2 y x mx x
1 đạt cực tiểu tại điểm x 1 ? A. m 0 B. m 1 C. m 2 D. m 2
Tìm m để hàm số đạt cực đại, cực tiểu thỏa điều kiện cho trước 1
Câu 24. Tìm m để hàm số 3 2 y
x  (m  2)x  (5m  4)x  3m 1, đạt cực trị tại x1, x2 sao cho 3 x  2  x . 1 2 A. m  0
B. m  1 C. m  0 D. m  1
Câu 25. Tìm tất cả các giá trị thực của tham số m để hàm số 3 x 2 y (m 2)x (4m 8)x m
1 đạt cực trị tại các điểm x ,x sao cho x 2 x 3 1 2 1 2 1 3 A. m B. m C. 1 m D. m 2 2 2 3 2 x x
Câu 26. Giá trị của m để hàm số đạt cực đại và cực tiểu của hàm số y    mxcó hoành 3 2 độ lớn hơn m là A. m  2 B. m > 1. C. m  2 D. m >2.
Câu 27. Giá trị của m để hàm số 3 2
y x  3x mx 1 có 2 điểm cực trị x , x thoả mãn 1 2 2 2
x x  3 là: 1 2 3 1
A. m  2 B. m C. m  1 D. m  2 2 Câu 28. Cho hàm số 3 2 3 y x 3mx
4m với tất cả giá trị nào của m để hàm số có 2 điểm cực
trị A và B sao cho AB 20 A. m 1 B. m 2 C. m 1;m 2 D. m 1 2
x mx m
Câu 29. Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số y x 1 bằng : A. 2 5 B. 5 2 C. 4 5 D. 5 Câu 30. Cho hàm số 3 2 y x 3x mx
2 (m là tham số) có đồ thị là (Cm). Các điểm cực đại
và cực tiểu của đồ thị hàm số cách đều đường thẳng y x 1 khi A. m 0 B. m 1 C. m 2 D. m 3 15
1B. Cực trị của hàm số Câu 31. Cho hàm số 3 2 2 2 y x 3x 3(m 1)x 3m
1. Tìm m để đồ thị hàm số có cực
đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O. m 0 m 0 1 1 A. 1 B. 1 C. m D. m m m 2 2 2 2 Câu 32. Cho hàm số 3 2
y  x  3mx  3m 1 (m là tham số). Với giá trị nào của m thì đồ thị
hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường thẳng
d: x  8 y  74  0 A. m  1 B. m  1 C. m  2 D. m  2 Câu 33. Cho hàm số 3 2 3
y x  3mx  4m
có đồ thị ( C ). Xác định m để (C ) có các điểm cực m m
đại, cực tiểu đối đối xứng nhau qua đường thẳng (d) : y x 1 1 1 A. m   B. m   C. m  0 D. m   ; m  0 2 2 2
Câu 34. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C  3 2 3
: y  x  3mx  2m có hai m điểm cực trị ,
A B sao cho đường thẳng AB vuông góc với đường thẳng d : y  2x .  1 1  1 1  1 1  1 1 A. m   ; .   B. m   ; . C. m   ; . D. m   ; .        2 2   2 2  2 2  2 2
Câu 35. Cho điểm M 2; 2 và đồ thị C y x mx m x m . Biết đồ thị m  3     2   3 : 3 3 1  1
C có hai điểm cực trị ,
A B và tam giác ABM vuông tại M . Hỏi giá trị nào của m cho dưới m
đây thỏa mãn bài toán đã cho? A. m  1. B. m  1.
C. Không có m .
D. Có vô số giá trị của m . Nguyễn Văn Lực
www.facebook.com/VanLuc168 HÀM BẬC BỐN
Tìm điểm cực đại, cực tiểu của hàm số
Câu 36. Giá trị cực tiểu y của hàm số 4 2
y x  2x 1. CT A. y  2 B. y  1  C. y  1 D. y  0 CT CT CT CT 4 x 5 Câu 37 Hàm số 2 y
 3x  có số điểm cực trị là 2 2 A. 3 B. 0 C. 2 D. 1 16
1B. Cực trị của hàm số 4 3 x x
Câu 38. Giá trị cực tiểu của hàm số y   là: 4 3 3 1 3 A. 0 B. C.D.  4 12 4 4 2
Câu 39. Khẳng định nào sau đây là đúng về hàm số: y x  4x  2
A. Đạt cực tiểu tại x = 0
B. Có cực đại và cực tiểu
C. Có cực đại, không có cực tiểu
D. Không có cực trị
Tìm m để hàm số đạt cực trị thỏa điều kiện cho trước 4 x
Câu 40. Với giá trị nào của tham số m thì hàm số 2 y
mx m có ba cực trị: 4 A. m  0 B. m  0 C. m  0 D. m  0
Câu 41. Tìm tất cả các giá trị m để đồ thị hàm số 4 2 2
y x  2mx m m có 3 điểm cực trị. A. m  0 B. m  0 C. m  0 D. m  0
Câu 42. Gọi A, B, C là 3 điểm cực trị của đồ thị hàm số 4 2
y  2x  4x 1. Diện tích của tam giác ABC là: A. 4 B. 3 C. 2 D. 1
Câu 43. Tìm m để hàm số 4 2 2
y x  2m x m 1 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 32. A. m = 2. B. m > 4.
C. m = 2. D. m  5 Câu 44. Cho hàm số 4 2 2
y x  2mx  2m  4 C .Tìm m để hàm số có 3 điểm cực trị tạo m
thành một tam giác có diện tích bằng 1. A. m  1 B. m  1 C. m  2 D. m  1 4 2 4
Câu 45. Cho hàm số y x  2mx  2m m . Với những giá trị nào của m thì đồ thị ( Cm ) có
ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có diện tích S=4? A. m  16.
B. m   3 16. C. m  3 16. D. m  5 16.
Câu 46. Các giá trị của tham số m để đồ thị hàm số 4 2 2
y x  2(m 1)x m có ba điểm cực trị
tạo thành 3 đỉnh của một tam giác vuông là A. m  0 B. m  0 C. m  0 D. m
Câu 47. Tìm tất cả các giá trị thực của tham số M để đồ thị hàm số 4 2
y  2x mx 1 có ba điểm
cực trị lập thành một tam giác vuông. A. 3 m  2  5. B. 3 m  2 6. C. m  0. D. 3 m  2 2. 1 Câu 48. Cho hàm số 4 2 y x (3m 1)x 2(m
1)với m là tham số thực. Tìm m để đồ thị 4
hàm số đã cho có 3 điểm cực trị lập thành một tam giác có trọng tâm là gốc tọa độ. 1 1 2 1 2 A. m B. m C. m D. m ; m 3 3 3 3 3 17
1B. Cực trị của hàm số
Câu 49. Tìm m để đồ thị hàm số 4 2 4
y x  2mx m  2m có 3 điểm cực trị tạo thành một tam giác đều. A. m = 1 B. m = -1 C. 3 3 m   3 D. m  3 Nguyễn Văn Lực
www.facebook.com/VanLuc168
BÀI TẬP TỔNG HỢP
Câu 50. Hàm số nào sau đây có cực trị 2  xx  2 x  2 x  2 A. y B. y C. y D. y  2 x  2 x  2 x  2 x  2
Câu 51. Trong các hàm số sau, đồ thị hàm số nào có 2 điểm cực trị. x  2 1 A. y B. 4 2
y x  4x  5 C. 3
y x  2x  3 D. 3 2 y x  2x  5 2x 1 3 1 1
Câu 52. Hàm số y x
đạt cực trị tại điểm x , x . Khi đó tổng x x bằng 4 x 1 2 1 2 A. 4 B. -4 C. 2 D. 0 2 3 4
Câu 53. Một hàm số f(x) có đạo hàm là f 'x  x x  
1 x  2 x  3 . Số cực trị của hàm số là: A. 4 B. 3 C. 2 D. 1 3 2
Câu 54. Hàm số y
x (1 x) có
A. Ba điểm cực trị
B. Hai điểm cực trị
C. Một điểm cực trị
D. Không có cực trị
Câu 55. Cho hàm số f x xác định, liên tục trên
và có bảng biến thiên: x 1 1 y 0 y 2 3
A. Hàm số đạt cực tiểu tại x
1 và đạt cực đại x 1
B. Hàm số đạt giá trị cực đại bằng 3
C. Hàm số đạt giá trị cực tiểu bằng 2
D. Hàm số có đúng một cực trị
Câu 56. Đồ thị hàm số 2 y x  2x  3
A. Có điểm cực đại là A(1;0)
B. Có điểm cực tiểu là B(3;0)
C. Không có cực trị
D. Có 1 điểm cực đại và 1 điểm cực tiểu
Câu 57. Tìm tất cả các giá trị thực của tham số  để hàm số 4 y x3  2 1 (  sin )x2  1
(  cos 2 )x có cực trị. 3   A.    k  2 B.   kC.    k  2 D.   k 2 2 18
1B. Cực trị của hàm số
Câu 58. Giả sử hàm số f x đạt cực trị tại điểm x . Khi đó, nếu f x có đạo hàm tại x thì 0 0
A. f ' x  0
B. f ' x  0
C. f ' x  0
D. f ' x  0 0  0  0  0 
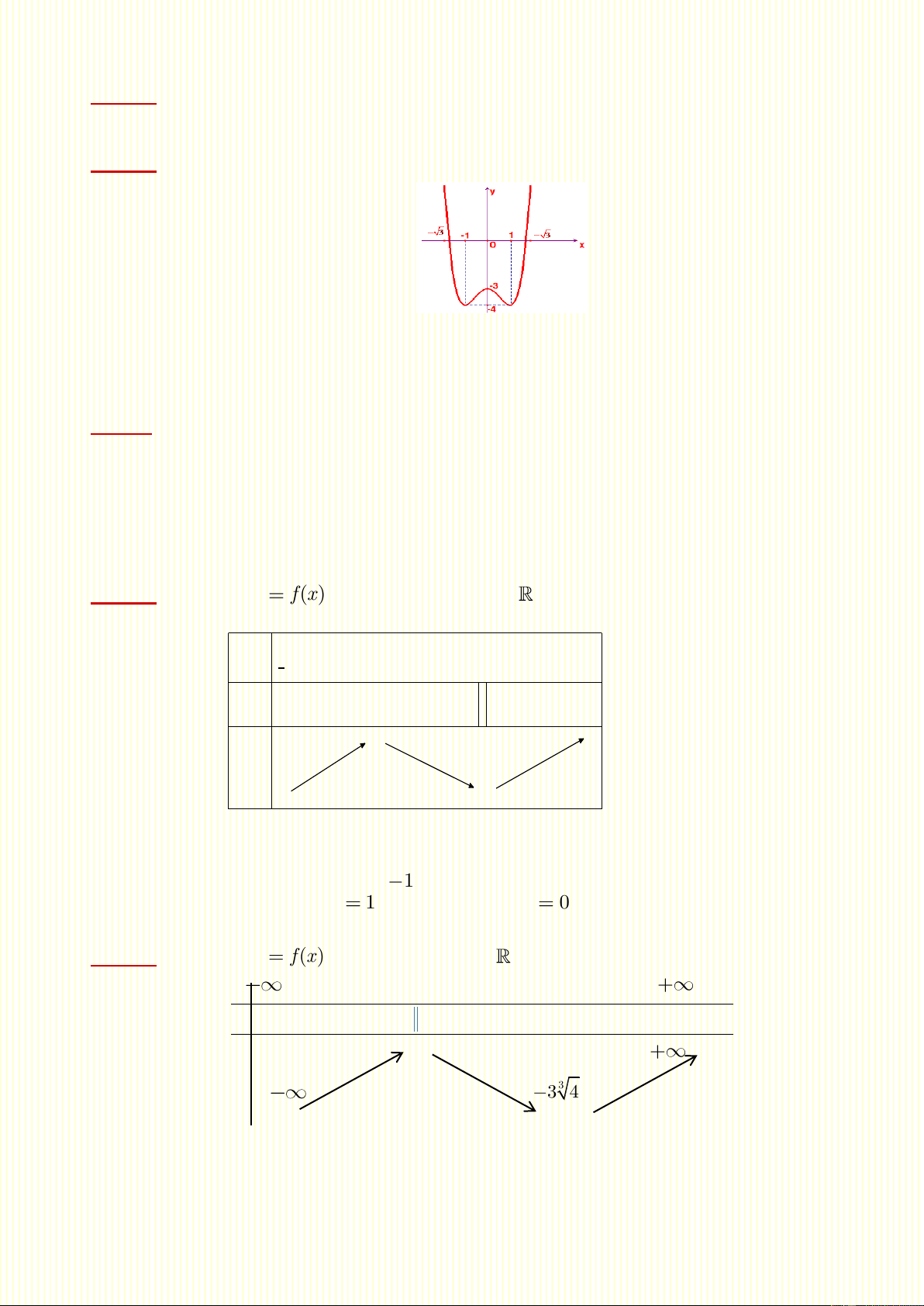
Câu 59. Cho đồ thị hàm số như hình bên.Hãy chọn khẳng định sai.
A. Hàm số có 3 điểm cực trị
B. Với 4  m  3 thì đường thẳng y m cắt đồ thị hàm số tại bốn điểm phân biệt
C. Hàm số đạt cực tiểu tại x  1
D. Đồ thị hàm số có điểm cực đại là 0; 3
Câu 60. Cho hàm số f x có đạo hàm tại x0. Khẳng định nào sau đây là khẳng định đúng:
A. Nếu f ' x  0 thì hàm số đạt cực trị tại x 0  0
B. Hàm số đạt cực trị tại x0 khi và chỉ khi f ' x  0 0 
C. Nếu hàm số đạt cực tiểu tại x0 thì f ' x  0 0 
D. Nếu hàm số đạt cực trị tại x0 thì f ' x  0 0 
Câu 61. Cho hàm số y
f (x) xác định và liên tục trên và có bảng biến thiên: x ∞ -1 0 + ∞ + _ 0 + y' 1 y 0
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực đại bằng 1.
C. Hàm số đạt cực đại tại x
1 và đạt cực tiểu tại x 0 .
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
Câu 62. Cho hàm số y
f (x) xác định, liên tục trên và có bảng biến thiên sau: x 0 2 y’ + - 0 + y 0 3 3 4 19
1B. Cực trị của hàm số
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị
B. Hàm số có giá trị cực tiểu bằng 3 3 4
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 3 3 4
D. Hàm số đạt cực đại tại x
0và đạt cực tiểu tại x 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168
1A 2D 3A 4A 5A 6A 7D 8D 9D 10B
11C 12C 13A 14C 15C 16A 17C 18A 19B 20B
21A 22C 23C 24C 25B 26A 27B 28A 29A 30A
31D 32C 33A 34A 35A 36D 37A 38C 39A 40C
41D 42C 43A 44D 45D 46A 47D 48B 49D 50D
51D 52D 53C 54B 55A 56C 57A 58C 59B 60D 61C 62D 20
1C. GTLN, GTNN của hàm số
GTLN, GTNN CỦA HÀM SỐ
HÀM BẬC BA, BẬC BỐN
Câu 1. Giá trị lớn nhất của hàm số 3 2 y x 3x 3 trên đoạn 0; 3 là A. 2 B. 2 C. 3 D. 1
Câu 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 y x 3x 2trên đoạn 1; 3 là: A. 4; 0 B. 20; 4 C. 20; 0 D. 20; 4
Câu 3. Giá trị lớn nhất của hàm số 3 2
y x  3x  9x  35 trên đoạn [-4;4] bằng ? A. 40 B. 8 C. -41 D. 15 3 Câu 4. x Cho hàm số 2 y
 2x  3x  4 xác định trên [-4;0]. Gọi M và m lần lượt là GTLN và 3
GTNN cùa hàm hàm số thì M + m bằng: 28 28 28 A.B. C.D. -35 3 3 3
Câu 5. Giá trị lớn nhất của hàm số y = 2x3 + 3x2 – 12x + 2 trên đoạn [– 1; 2] là A. 6 B. 10 C. 15 D. 11
Câu 6. Tìm GTLN và GTNN của hàm số f x 3 2
x  3x  5 trên đoạn  1  ;  1
A. Max f x  5  x  0; Min f x  1  x  1   1  ;  1  1  ;  1
B. Max f x  3; Min f x  1  1  ;  1  1  ;  1
C. Max f x  1; Min f x  1   1  ;  1  1  ;  1
D. Max f x  2; Min f x  0  1  ;  1  1  ;  1
Câu 7. Kết luận giá trị nhỏ nhất của hàm số 3
y  x  3x 1 trên khoảng (-;1) là A. min y  3 B. min y  1  C. min y  2 D. min y  3  ;  1 ;  1 ;  1 ;  1
Câu 8. Trên khoảng (0; +) thì hàm số y   3 x  3x 1:
A. Có giá trị nhỏ nhất là min y = 3
B. Có giá trị lớn nhất là max y = –1
C. Có giá trị nhỏ nhất là min y = –1
D. Có giá trị lớn nhất là max y = 3 Câu 9. Cho hàm số 3 2
y x  3x  2 . Chọn phương án đúng trong các phương án sau
A. max y  0, min y  2 
B. max y  2, min y  0  1  ;  1  1  ;  1  1  ;  1  1  ;  1
C. max y  2, min y  2 
D. max y  2, min y  1   1  ;  1  1  ;  1  1  ;  1  1  ;  1 21
1C. GTLN, GTNN của hàm số Câu 10. Cho hàm số 3
y  x  3x  5 . Chọn phương án đúng trong các phương án sau A. max y  5 B. min y  3 C. max y  3 D. min y  7 0;2 0;2  1  ;  1  1  ;  1
Câu 11. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 4 2
y x  2x  3 trên0;2 là:
A. M  11, m  2
B. M  3, m  2
C. M  5, m  2
D. M  11, m  3
Câu 12. Giá trị nhỏ nhất của hàm số 4 2
y x  2x 1 trên đoạn  1  ;  1 là: A. 1  B. 1 C. 0 D. 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168 HÀM PHÂN THỨC 3x 1
Câu 13. Tìm giá trị lớn nhất của hàm số y trên đoạn [0; 2]. x 3 1 1 A. max y B. max y 5 C. max y 5 D. max y [0;2] 3 [0;2] [0;2] [0;2] 3  Câu 14. x
Tìm GTLN và GTNN của hàm số f x 1  2;3
x trên nửa khoảng   1
A. Max f x  3; Min f x  2  1  ;  1  1  ;  1
B. Min f x  2, không tồn tại Max f x 2;  3 2;  3
C. Max f x  2; không tồn tại Min f x  1  ;  1  1  ;  1
D. Max f x  2; Min f x  1  1  ;  1  1  ;  1 4
Câu 15. Tìm giá trị lớn nhất của hàm số y x 1 x  trên đoạn [-1; 5] 2 46 A. max y  3 B. max y  4 C. max y D. max y  5   1  ;  5  1  ;  5  1  ;5 7  1  ;  5 2 x 3x 1
Câu 16. Tìm giá trị lớn nhất của hàm số y trên đoạn 2; 5 ? x 1 11 11 A. max y 1 B. max y C. max y 1 D. max y 2;5 2;5 4 2;5 2;5 4 2 x
Câu 17. Tìm giá trị nhỏ nhất của hàm số y  1; 4 . x  trên   2 A. min y  1  B. min y  0 C. min y  6 D. min y  8 1;4 1;4 1;4 1;  4 22
1C. GTLN, GTNN của hàm số 2 x x  4
Câu 18. Cho hàm số: y
, chọn phương án đúng trong các phương án sau x 1 16 A. max y   ,min y  6
B. max y  6,min y  5 4;2 3 4;2     4;2 4;2    
C. max y  5,min y  6
D. max y  4,min y  6 4;2 4;2     4;2 4;2     2 x  5x  5  1 
Câu 19. Cho hàm số y  1  ; 
 . Khẳng định nào sau x
xác định, liên tục trên đoạn 1  2  đây đúng?  1 
A. Hàm số có giá trị nhỏ nhất là y   , giá trị lớn nhất là y   1 .  2   1 
B. Hàm số có giá trị nhỏ nhất là y  
1 , giá trị lớn nhất là y .    2   1 
C. Hàm số có giá trị nhỏ nhất là y  
1 và y   , giá trị lớn nhất là y 0.  2   1 
D. Hàm số có giá trị nhỏ nhất là y 0 , giá trị lớn nhất là y .    2  1 x Câu 20. Cho f x 2  
 x . Gọi M  max f x;m  minf x , khi đó: M – m 2 x  4x  5 4 0; 3 0; 3 bằng 3 7 9 A. B. 1 C. D. 5 5 5 2 x m m
Câu 21. Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số y trên x 1 [0;1] bằng 2 m 1 m 1 m 1 m 1 A. B. C. D. m 2 m 2 m 2 m 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168 CÁC HÀM KHÁC
Câu 22. Giá trị nhỏ nhất của hàm số f(x) = 2
x  2x  5 trên đoạn [-1;3] là: 5 A. 2 2 B. C. 2 D. 2 3 2
Câu 23. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
6  3x trên đoạn [-1;1] lần lượt là : A. 6 và 0 B. 3 và 6 C. 1 và -1 D. 3 và 3 23
1C. GTLN, GTNN của hàm số
Câu 24. Giá trị lớn nhất của hàm số y 5
4x trên đoạn [-1 ; 1 ] bằng. A. 9 B. 3 C. 1 D. 0 1
Câu 25. Giá trị lớn nhất của hàm số y x 1 2x trên 4; bằng 2 1 A. -1 B. C. 0 D. 1 2
Câu 26. Tìm GTLN và GTNN của hàm số 2
y x  4  x
A. Max f x  2 2; Min f x   2
B. Max f x   2; Min f x  2   2  ;2  2  ;2  2  ;2  2  ;2
C. Max f x  2 2; Min f x  2 
D. Max f x  2; Min f x  2  D D  2  ;2  2  ;2
Câu 27. Tìm giá trị lớn nhất của hàm số y  2 x 1  6  x A. 2 B. 5 C. 3 D. 4 Câu 28. Hàm số 2 y
x 1 x đạt giá trị lớn nhất bằng 1 1 2 A. B. C. D. -1 2 2 2
Câu 29. Tìm giá trị nhỏ nhất của hàm số 4 y 2 sin x cos 2x 5 11 11 A. min y B. min y C. min y 2 D. min y 3 4 2
Câu 30. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số: 2
y  2 sin x  cos x 1. Tổng M+m bằng 25 25 A. 0 B. 2 C. D. 8 4
Câu 31. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  sin 2x - 2 3 cos x  2 3 .
Tính M m .
A. M m  4  3
B. M m  2 3
C. M m  4
D. M m  1 2 3
Câu 32. Tìm giá trị lớn nhất của hàm số 4 4
y  sin x  cos x  sin x cos x . 1 9 1 3 A. max y B. max y C. max y D. max y 2 8 4 4   Câu 33. Cho hàm số sin x 2 cos x 1 y
. Khẳng định nào sau đây là đúng?
sin x  cos x  2 A. max y 2; min y 1 . B. max y 1; min y 2 . C. max y 2; min y 1. D. max y 1; min y 2.
Câu 34. Giá trị nhỏ nhất của hàm số 2 y log x 4 log x 1 trên đoạn [1; 8] là 2 2 A. Min y 2 B. Min y 1 C. Min y 3 D. Đáp án khác x [1;8] x [1;8] x [1;8] 24
1C. GTLN, GTNN của hàm số
Câu 35. Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số : y f (x)  x  3 trên đoạn  1  :  1 là: A. 0 B. 3 C. 4 D. 7
BÀI TOÁN ỨNG DỤNG
Câu 36. Một tam giác vuông có cạnh huyền bằng 5 2 thì diện tích của nó lớn nhất là: 25 25 25 A. B. C. D. 25 8 4 2
Câu 37. Chu vi của một tam giác là 16cm , biết độ dài một cạnh của tam giác là a 6cm . Tìm
độ dài hai cạnh còn lại ,
b c của tam giác sao cho tam giác đó có diện tích lớn nhất. A. b 4cm;c 6cm B. b 3cm;c 7cm C. b 2cm;c 8cm D. b c 5cm
Câu 38. Tìm tam giác vuông có diện tích lớn nhất, nếu tổng của cạnh góc vuông và cạnh huyền
bằng hằng số a (a > 0), thì cạnh góc vuông của tam giác đó là: a a A. 2a B. C. D. a 2 3 2
Câu 39. Một hình chữ nhật có diện tích là 100 thì chu vi hình chữ nhật nhỏ nhất khi chiều rộng x
và chiều dài y tương ứng là:
A. x  25; y  4 x y x y x y B. 10; 10 C. 20; 5 D. 50; 2
Câu 40. Người ta muốn mạ vàng cho một cái hộp có đáy hình vuông không nắp có thể tích là 4 lít.
Tìm kích thước của hộp đó để lượng vàng dùng mạ là ít nhất. Giả sử độ dày của lớp mạ tại mọi nơi
trên mặt ngoài hộp là như nhau.
A. Cạnh đáy bằng 2, chiều cao bằng 1
B. Cạnh đáy bằng 1, chiều cao bằng 2.
C. Cạnh đáy bằng 3, chiều cao bằng 4
D. Cạnh đáy bằng 4, chiều cao bằng 3.
Câu 41. Người ta cần làm một hộp theo dạng một khối lăng trụ đều không nắp với thể tích lớn
nhất từ một miếng tole hình vuông có cạnh là 1. Thể tích của hộp cần làm là 5 2 3 6 A. V B. V C. V D. V 8 27 27 11
Câu 42. Một người thợ muốn làm một cái thùng hình hộp chữ nhật không nắp có chiều dài đáy
gấp đôi chiều rộng và có thể tích 3
10 m . Giá tiền vật liệu làm đáy thùng là 10.000 đồng 2 /m , vật
liệu làm mặt bên thùng là 5.000 đồng 2
/m . Hãy xác định kích thước thùng (rộng x dài x cao) để
chi phí làm thùng là nhỏ nhất. 4 4 225 15 15 16 A. 3 3 3 x 2 x 5 mB. x 2 x 5 m 15 15 16 4 4 225 5 15 15 16 C. 15 x 2 15 x mD. 3 3 3 x 2 x 5 m 15 4 4 225
Câu 43. Một nhà máy sản suất máy tính vừa làm ra x sản phẩm máy tính và bán với giá p=1000-x
cho một sản phẩm. Biết rằng tổng chi phí để làm ra x sản phẩm là C(x)=3000+20x. Vậy nhà máy
cần sản xuất và bán bao nhiêu sản phẩm để thu được lợi nhuận tốt nhất. A. 490 B. 480 C. 500 D. 510 25
1C. GTLN, GTNN của hàm số
Câu 44. Một công ty đánh giá rằng sẽ bán được N lô hàng nếu tiêu phí hết số tiền là x vào việc
quảng cáo, N và x liên hệ với nhau bằng biểu thức 2
N (x)  x  30x  6, 0  x  30 ( x tính
theo đơn vị triệu đồng). Số lô hàng lớn nhất mà công ty có thể bán sau đợt quảng cáo và số tiền đã
dành cho việc quảng cáo đó lần lượt là :
A. N(x) = 231; x = 15
B. N(x) = 6; x = 30
C. N(x)= 226; x = 10
D. N(x)= 131; x = 5
Câu 45. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức 1 2 F (x)  x (30  x) , 40
trong đó x là liều lượng thuốc được tiêm cho bệnh nhân ( x được tính bằng miligam).
Liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giàm nhiều nhất là: A. 20 mg B. 30 mg C. 40 mg D. 50 mg
Câu 46. Xét x, y là các số thực không âm thỏa mãn điều kiện x y  2. Tìm giá trị nhỏ nhất của biểu thức 2 2
S x y  4x . y A. min S  3  . B. min S  4  . C. min S  0. D. min S  1. Câu 47. 1
Xét x, y là các số thực dương thỏa mãn điều kiện x y  2 . Đặt S xy  . xy  Khẳng định 1 nào sau đây đúng ?
A. Biểu thức S không có giá trị lớn nhất.
B. Biểu thức S không có giá trị nhỏ nhất. 3 C. min S  . D. max S  1. 2
Câu 48. Xét x, y là các số thực thuộc đoạn 1;2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị x y
nhỏ nhất cùa biểu thức S y x . Tính m M 5 9 A. m M B. m M 4 C. m M D. m M 3 2 2
Câu 49. Xét x, y là các số thực thuộc (0;1] thỏa mãn điều kiện x y  4xy . Đặt 2 2
S x y .
Khẳng định nào sau đây là đúng ? 10
A. Biểu thức S không có giá trị nhỏ nhất. B. max S  9
C. Biểu thức S không có giá trị lớn nhất. D. min S  0 2 2 x  6xy
Câu 50. Xét x , y là các số thực thỏa mãn điều kiện 2 2
x y  1. Đặt S  . Khẳng 2 2
x  2xy  3y
định nào sau đây là đúng?
A. Biểu thức S không có giá trị nhỏ nhất. B. min S  6 
C. Biểu thức S không có giá trị lớn nhất. D. max S  2 1C 2C 3A 4A 5C 6A 7B 8D 9C 10B
11A 12A 13D 14B 15C 16B 17A 18C 19C 20D
21D 22C 23D 24B 25D 26C 27B 28A 29B 30C
31B 32B 33B 34C 35D 36C 37D 38B 39B 40A
41B 42D 43A 44A 45A 46A 47B 48C 49B 50B 26
1D. Đường tiệm cận ĐƯỜNG TIỆM CẬN
Tìm phương trình tiệm cận ngang, tiệm cận đứng 2x 1
Câu 1. Đồ thị hàm số y
có đường tiệm cận ngang là: 3x 1 2 2 1 1 A. x B. y C. x   D. y   3 3 3 3 2x 1
Câu 2. Tiệm cận ngang của đồ thị hàm số y  là: 2 4x  3 A. y = 1
B. y = 2 và y = - 2. C. y = 2 D. y = 1 và y = -1. x  2
Câu 3. Phương trình các đường tiệm cận ngang của đồ thị hàm số y  là: 2 4x x 1 1 1 A. y  và y   B. y  2 2 2 1 C. y D. y  0 4 2x 1
Câu 4. Đồ thị hàm số y
có tiệm cận đứng và tiệm cận ngang lần lượt là: x  2
A. x  2; y  2
B. x  2; y  2  C. x  2  ; y  2  D. x  2  ; y  2 2  3x
Câu 5. Phương trình các đường tiệm cận của đồ thị hàm số y x  là: 1
A. x  1 và y  2
B. x  1 và y  3
C. x  3 và y  1 
D. x  2 và y  1 4x 2
Câu 6. Cho đồ thị hàm số y
. Phương trình các đường tiệm cận của đồ thị hàm số là 2x 1 1 1 A. y 2,x B. x 2,y 2 2 1 1 C. x ,y 4 D. y 2,x 2 2 2x 3
Câu 7. Đồ thị hàm số y có: x 2
A. Có tiệm cận đứng là x
2 và không có tiệm cận ngang
B. Có tiệm cận ngang y
2 và không có tiệm cận đứng
C. Có tiệm cận đứng là y
2 và tiệm cận ngang x 2
D. Có tiệm cận đứng là x
2 và tiệm cận ngang y 2 27
1D. Đường tiệm cận x  3
Câu 8. Đường tiệm cận ngang của hàm số y  là 2x 1 1 1 1 1 A. x B. x   C. y   D. y 2 2 2 2 2x 1
Câu 9. Đường tiệm cận ngang của đồ thị hàm số y là: x 1 A. y 1 B. x 2 C. y 2 D. x 1
Câu 10. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào sau đây? 2 2x  3x  2 2x  2 1 x  2 1 x A. y  . y  . y  . y  . x 2 C. 1 x D. 2  x B.   1 x 3x 1
Câu 11. Cho hàm số y  2x  . Khẳng định nào sau đây đúng ? 1 3
A. Đồ thị hàm số có tiệm cận ngang là y  2 3
B. Đồ thị hàm số có tiệm cận đứng là y  2 1
C. Đồ thị hàm số có tiệm cận đứng là x   2
D. Đồ thị hàm số không có tiệm cận Nguyễn Văn Lực
www.facebook.com/VanLuc168
Tìm m để đồ thị hàm số có tiệm cận ngang, tiệm cận đứng thỏa điều kiện cho trước  2 m  m x 1
Câu 12. Đồ thị hàm số y  x 
có đường tiệm cận ngang qua điểm A(–3;2) khi: 2 A. m  1   m  2  B. m  1 m  2  C. m  1 m  2 D. m  1   m  2 mx 1
Câu 13. Cho hàm số y A 1; 2
2x m để tiệm cận đứng của đồ thị hàm số đi qua điểm   thì A. m  2 B. m  2 1 1 C. m m 2 D.   2 x Câu 14. Cho hàm số a 1 y
. Nếu đồ thị hàm số có tiệm cận đứng x = 1 và đi qua điểm A(2; 5) x d
thì phương trình của hàm số là: x  2 2x 1 3x  2 x 1 A. y y y y x B. 1 x C. 1 1 D. x x  1 28
1D. Đường tiệm cận x m
Câu 15. Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số C y  có tiệm cận m  2 : mx 1
đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8 . 1 1 1 A. m   B. m   C. m  
D. Không có m thỏa mãn 4 2 8
Câu 16. Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số mx  2 y  tiếp xúc với parabol 2 y x  5 . x m  1
A. Không có giá trị m B. m  5 C. m  6
D. Với m  2 x  4  m
Câu 17. Tìm m để đồ thị hàm số y
có tiệm cận đứng x = 2: x  2 A. m = 1 B. m = -1 C. m = 2
D. m  1 và m  2 x
Câu 18. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C  : y m x  có tiệm cận. m A. m  1
B. Với mọi m C. m  0
D. Không có m x  2
.Câu 19. Với điều kiện nào của tham số m cho dưới đây, đồ thị hàm số (C ) : y  chỉ m 2 2
x  3x m
có một tiệm cận đứng? A.  . m B. m  2. C. m  2. D. Không có m 2 x  3x  6
Câu 20. Để đường cong (C) : y  2 x ax
có đúng 1 đường tiệm cận đứng thì giá trị của a là aa  0 a 1 A. a  1. B. a  2. C. .  D. .  a  4 a  2 x  3
Câu 21. Tìm tất cả các giá trị của m để hàm số y  có hai tiệm cận ngang. 2 mx  2 A. m = 0 B. m > 0 C. m < 0 D. m =-1 x m
Câu 22. Với giá trị nào của tham số m cho dưới đây thì, đồ thị hàm số 1 y  không có tiệm x 1 cận ngang?
A. Với mọi m . B. m  0 C. m  1
D. Không có m . x 1
Câu 23. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C  : y  có hai m 2
x x m
đường tiệm cận đứng.  1   1 m   m   A. Mọi m  . B.  4 . C.  4 . D. m  2. m  2 m  2 Nguyễn Văn Lực
www.facebook.com/VanLuc168 29
1D. Đường tiệm cận
Tìm số tiệm cận của đồ thị hàm số 2x  3
Câu 24. Số đường tiệm cận ngang của đồ thị hàm số y  f (x)  là: 2 x 1 A. 3 B. 2 C. 1 D. 0 3x 1
Câu 25. Hàm số y  có mấy tiệm cận ngang 2 x 1 A. 0 B. 1 C. 2 D. 3 
Câu 26. Cho hàm số y f x 1
x . Số đường tiệm cận của đồ thị hàm số là 1 A. 0 B. 2 C. 1 D. 3 3
Câu 27. Cho hàm số y
.Số tiệm cận của đồ thị hàm số bằng x  2 A. 0 B. 2 C. 3 D. 1 3x 1
Câu 28. Cho hàm số y
. Số đường tiệm cận của đồ thị hàm số bằng x  2 A. 0 B. 2 C. 3 D. 1 2x  9
Câu 29. Đồ thị hàm số y  2
x  có mấy đường tiệm cận ? 1 A. 1 B. 2 C. 3
D. Không có tiệm cận 2 x x 1
Câu 30. Cho hàm số y x
. Số đường tiệm cận của đồ thị hàm số bằng: 2 A. 0 B. 1 C. 2 D. 3 2 x 1
Câu 31. Số đường tiệm cận của đồ thị hàm số y là: x A. 0 B. 1 C. 2 D. 3 8x  3
Câu 32. Cho hàm số y
. Khẳng định nào sau đây là đúng 2 x x  6
A. Đồ thị hàm số có 1 tiệm cận đứng và 1 tiệm cận ngang.
B. Đồ thị hàm số có 2 tiệm cận đứng và 1 tiệm cận ngang.
C. Đồ thị hàm số có 2 tiệm cận ngang và 1 tiệm cận đứng.
D. Đồ thị hàm số không có tiệm cận. 2 x 3x
Câu 33. Số đường tiệm cận của đồ thị hàm số y là: 2 x 4 A. 1 B. 2 C. 3 D. 4 30
1D. Đường tiệm cận
Một số bài tập tổng hợp
Câu 34. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số y = x3 + 3x – 2 đồng biến trên .
B. Đồ thị hàm số y = 3x4 + 5x2 – 1 cắt trục hoành tại 2 điểm phân biệt. 2x 1
C. Đồ thị hàm số y =
có 2 đường tiệm cận. 2 x 1 2x 1
D. Đồ thị hàm số y =
nhận giao điểm hai đường tiệm cận là tâm đối xứng. x 1
Câu 35. Bảng biến thiên sau đây là của hàm số nào? x  2 +  y   y 1   1 2x 1 x 1 x  3 x 1 A. y  . y  . y  . y  . x 1 B. x 1 C. x  2 D. x  2 x  1
Câu 36. Cho C  là đồ thị hàm số y
. Tìm các điểm trên C sao cho tổng khoảng cách x  2
từ điểm đó đến 2 tiệm cận là nhỏ nhất    A. 1; 2   B. 1 3   1 3;  2   C. 1 3;1 3
D. 2  3;1 3 và 2  3;1 3
Câu 37. Gọi I là giao điểm của tiệm cận ngang và tiệm cận đứng của đồ thị hàm số (3m 1)x  4 y 
. Hỏi I luôn thuộc đường thẳng nào dưới đây? x  m A. y  3x 1 B. y  3x 1 C. y  3x 1 D. y  3x 1 x 2
Câu 38. Tìm tất cả các điểm M trên đồ thị (C) của hàm số y
sao cho khoảng cách từ M x 1
đến tiệm cận đứng của (C) bằng khoảng cách từ M đến trục Ox. 3 13 1 13 3 13 1 13 A. M( ; ),M( ; ) 2 2 2 2 3 13 1 13 3 13 1 13 B. M( ; ),M( ; ) 2 2 2 2 3 13 1 13 C. M( ; ) 2 2 3 13 1 13 D. M( ; ) 2 2 31
1D. Đường tiệm cận 2 x x
Câu 39. Cho hàm số y
. Khẳng định nào sau đây là đúng? x 1
A. Đồ thị của hàm số đã cho không có tiệm cận đứng.
B. Đồ thị của hàm số đã cho có một tiệm cận ngang.
C. Đồ thị của hàm số đã cho có hai tiệm cận ngang là x  1 và x  1
D. Đồ thị của hàm số đã cho có hai tiệm cận ngang là y  1  và y  1 Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B 2A 3A 4B 5B 6A 7D 8D 9C 10C
11A 12B 13B 14B 15B 16B 17D 18C 19B 20C
21B 22B 23B 24B 25C 26B 27B 28B 29C 30D
31D 32B 33C 34C 35D 36D 37B 38A 39D 32
1E. Đồ thị của hàm số
ĐỒ THỊ CỦA HÀM SỐ x 1
Câu 1. Đồ thị hàm số y  có dạng: 1 x A. B. C. D. y y y y 2 3 3 3 2 2 2 1 1 x 1 1 x -2 -1 1 2 3 x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3
Câu 2. Đồ thị nào sau đây là đồ thị của hàm số y = x3 + x – 2: B. A. 4 2 2 1 2 1 2 4 C. D. 4 4 2 2 1 1 2 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168 33
1E. Đồ thị của hàm số
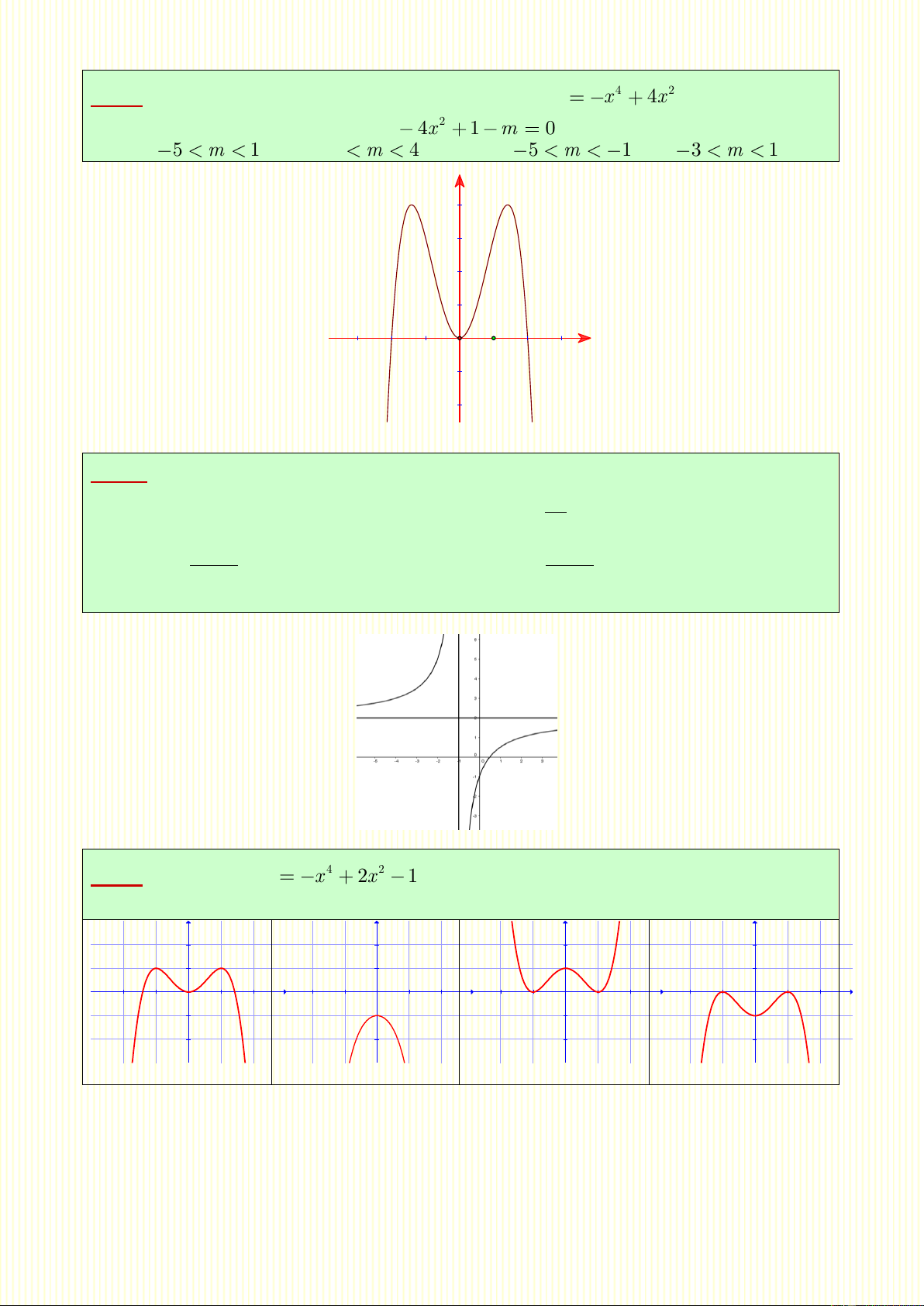
Câu 3. Đường cong trong hình dưới đây là đồ thị của hàm số 4 2 y x 4x .
Dựa vào đồ thị, phương trình 4 2 x 4x 1 m
0 có 4 nghiệm phân biệt khi A. 5 m 1 B. 0 m 4 C. 5 m 1 D. 3 m 1 y 4 1 x O
Câu 4. Đường cong bên là đồ thị của hàm số: 4 x A. 3 y  x  3x  2 B. 2 y   2x  2 4 2x 1 1 2x C. y  y  x  D. 1 x  1
Câu 5. Đồ thị hàm số 4 2 y x 2x 1 có dạng: A. B. C. D. y y y y 2 2 2 2 1 1 1 1 x x x x -2 -1 1 2 -2 -1 1 2 -2 -1 1 2 -2 -1 1 2 -1 -1 -1 -1 -2 -2 -2 -2 34
1E. Đồ thị của hàm số
Câu 6. Đồ thị sau đây là của hàm số nào?
A. y x3  3x 1. 2
B. y  x3  3x  1.
C. y x3  3x+1. 2
D. y  x3  3x  1. y 3 1 -2 1 x -1 O 2 -1 4 2
Câu 7. Đồ thị sau đây là của hàm số: y  x  4x .Với giá trị nào của m thì phương trình: 4 x  2
4x m  2  0 có bốn nghiệm phân biệt ? Chọn câu đúng.
A. 0  m  4
B. 0  m  4
C. 2  m  6
D. 0  m  6 4 2 -2 2 - 2 O 2 -2
Câu 8. Đồ thị sau đây là của hàm số nào ? 2x 1 x 2 x 1 x 2 A. y B. y C. y D. y x 1 x 1 x 1 1 x 4 2 1 -2 5 1 5 2 4 35
1E. Đồ thị của hàm số
Câu 9. Đồ thị hình bên là của hàm số: 3 x A. 2 y    x 1 B. 3 2
y x  3x 1 3 C. 3 2
y  x  3x 1 D. 3 2
y  x  3x 1 y 3 2 1 x -3 -2 -1 1 2 3 -1 -2 -3
Câu 10. Đường cong nào trong hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A,
B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? 3 3 A. y x 3x B. y x 3 3 3 C. y x 3x D. y x 3x y - x - O -
\Câu 11. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hàm số đó là A. 4 2
y  x  2x  2 B. 3
y x  2x  3 C. 4 2
y x  2x  3 D. 3
y  x  2x  3 . Nguyễn Văn Lực
www.facebook.com/VanLuc168 36
1E. Đồ thị của hàm số
Câu 12. Đường cong trong hình bên là đồ thị của hàm số nào? A. 3 2
y  2x  3x  2 B. 3 2 y  2
x  3x  2 C. 3
y  2x  6x  2 D. 3 2 y  2
x  3x  2
Câu 13. Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên A. 3
y x  3x 1 B. 3
y x  3x 1 C. 3
y  x  3x 1 D. 3
y  x  3x 1 y 1 O x
Câu 14. Đường cong ở hình dưới là đồ thị của hàm số nào sau đây A. 3       3       y x 3 B. 3 y x 6x 2 C. y x 1 D. 3 y x 3x 1 37
1E. Đồ thị của hàm số
Câu 15. Đồ thị sau đây là của hàm số nào ? A. 3 2           y x 3x B. 3 2 y x 3x C. 3 2 y x 3x D. 3 2 y x 3x y 4 2 x O 1 2 3
Câu 16. Đồ thị dưới đây là đồ thị hàm số x 1 A. 3 2
y  x  3x  4 B. 3 2
y x  3x  4 C. 4 2
y x  2x  3 D. y x  1
Câu 17. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x 1 x 1 A. y B. y x 1 x 1 x 1 1 x C. y D. y 1 x x 1 38
1E. Đồ thị của hàm số
Câu 18. Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên 3 3 A. y x 3 x B. y x 3x 3 3 C. y x 3 x D. y x 3x 2 1 -2
Câu 19. Đường cong cho bởi hình sau là đồ thị của đồ thị hàm số nào ? 1 A. 4 2
y x  3x 1 B. 4 2 y   x  3x 1 4 C. 4 2
y x  2x 1 D. 4 2
y x  2x 1 2 -1 O 1 -1 -2
Câu 20. Đồ thị sau đây là của hàm số nào? Chọn câu đúng. 2x 1 x 1 x  2 x  3 A. y y y y x 1 B. x 1 C. x 1 D. 1 x 4 2 1 -1 O 2 39
1E. Đồ thị của hàm số
Câu 21. Cho hàm số y f (x) xác định và liên tục trên
và có bảng biến thiên như sau: 0 x -∞ 1 +∞ y' + 0 + 0 - 3 y -∞ -∞
Khẳng định nào sau đây là đúng?
A. Hàm số không có cực trị.
B. Hàm số có giá trị cực tiểu bằng 3.
C. Hàm số có giá trị lớn nhất bằng 3 và không có giá trị nhỏ nhất.
D. Hàm số đạt cực tiểu tại x  0 và đạt cực đại tại x  1 .
Câu 22. Đồ thị hình bên dưới là đồ thị của hàm số nào sau đây? A. 4 2
y  x  2x  3. B. 4 2
y  x  2x . C. 4 2
y x  2x . D. 4 2
y x  2x  3. y 2 1 -1 O 1 x -1 Nguyễn Văn Lực
www.facebook.com/VanLuc168 1C 2A 3D 4C 5D 6C 7C 8B 9B 10D
11C 12A 13B 14A 15D 16A 17B 18C 19C 20A 21C 22C 40
1F. Bài toán tương giao
BÀI TOÁN TƯƠNG GIAO HÀM BẬC BA
Câu 1. Biết rằng đường thẳng y  2x  3 cắt đồ thị hàm số 3 2
y x x  2x  3 tại hai điểm
phân biệt A và B, biết điểm B có hoành độ âm. Tìm x . B A. x  0. B. x  2. C. x  1. D. x  5. B B B B
Câu 2. Số giao điểm của đường cong 3 2 y x 2x x
1 và đường thẳng y 1 2x bằng: A. 0 B. 1 C. 2 D. 3
Câu 3. Biết rằng đồ thị của hàm số 3 2
y x  3x  2x cắt đường thẳng y  2
x  2 tại ba điểm
phân biệt. Kí hiệu ba điểm đó là Ax ; y , Bx ; y và C x ; y . Khi đó tổng x x x 3 3  2 2  1 1  1 2 3 bằng: A. 2 B. 3 C. 1 D. 2 3
Câu 4. Biết rằng đường thẳng y  5
x  6 cắt đồ thị hàm số 3
y x x  6 tại điểm duy nhất
x ; y . Tìm y . 0 0  0 A. y  4 B. y  1 C. y  0 D. y  6 0 0 0 0
Câu 5. Đồ thị hàm số 3
y  x  3x  2 cắt trục hoành tại 2 điểm có hoành độ x1; x2. Khi đó x  x bằng : 1 2 A. 2 B. 0 C. – 1 D. – 2
Câu 6. Đường thẳng y m cắt đồ thị hàm số 3
y  x  3x  2 tại 3 điểm phân biệt khi
A. 0  m  4. B. m  4.
C. 0  m  4.
D. 0  m  4.
Câu 7. Cho hàm số y = x3 - 3x2 + 1. Đồ thị hàm số cắt đường thẳng y = m tại 3 điểm phân biệt khi
A. 3  m  1
B. 3  m  1 C. m  1 D. m  3
Câu 8. Để đường cong 3 2 (C) : y x mx mx
4 cắt đường thẳng (d) : y x 4 tại 3
điểm phân biệt thì giá trị m bằng: A. m 2 B. m 1 C. m 4 D. m 2
Câu 9. Cho hàm số y   x   2 2
1 x mx m   3 có đồ thị C
, với giá trị nào của m m  thì C
cắt Ox tại 3 điểm phân biệt: m
A. 2  m  2
B. 2  m  2  2   m  2  2   m  2 C.D.  m  1 m  1
Câu 10. Đồ thị hàm số 3 2
y x x  m  6 x  3m cắt trục hoành tại ba điểm phân biệt khi m  1 m  1 A. m  1 B. m  1 C.D.  m  15  m  15  41
1F. Bài toán tương giao
Câu 11. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 2
y  (x 1)(x x m) cắt
Ox tại 3 điểm phân biệt. 1 1 1 1 A. m   B. m  à v m  2 C. m D. m  à v m  2 4 4 4 4
Câu 12. Số giao điểm của đồ thi ̣hàm số 2
y  (x  3)(x x  4) với tru ̣c hoành là: A. 2 B. 3 C. 0 D. 1
Câu 13. Với giá trị nào của m thì phương trình 3 2 x 3x m 1 0 có hai nghiệm? m 1 A. m 1 B. m 3 C. D. 3 m 1 m 3
Câu 14. Phương trình 3
x 12x m  2  0 có 3 nghiệm phân biệt với m. A. 1  6  m  16 B. 1  8  m  14 C. 1  4  m  18 D. 4   m  4
Câu 15. Với các giá trị nào của k thì phương trình 3
x  3x k có ba nghiệm phân biệt? A. 2   k  2 B. 2   k  2 C. k  2 D. k  2 
Câu 16. Tìm tất cả giá trị thực của tham số m để phương trình 3 2
x  3x m có ba nghiệm phân biệt. A. m  2.
B. 0  m  4. C. m  0. D. m  4.
Câu 17. Phương trình 3
x  3x  2  m  0 có ba nghiệm phân biệt khi:
A. 0  m  4
B. 0  m  4 C. m  4 D. m  0
Câu 18. Tìm tất cả các giá trị thực của tham số m để phương trình 3
x  3x  2m có ba nghiệm
phân biệt, trong đó có một nghiệm thuộc khoảng  1  ;0 .
A. 0  m  2
B. 1  m  1
C. 2  m  2
D. 0  m  1
Câu 19. Hình bên là đồ thị hàm số 3
y x  3x . Sử dụng đồ thị đã cho tìm tất cả các giá trị thực
của m để phương trình 3 2 2 2
64 | x |  (x 1) (12 | x | m(x 1)) có nghiệm.
A. 2  m  2 B.m C. m  0 D. m  2
Câu 20. Tìm các giá trị thực của tham số m để đường thẳng d : y mx  3m cắt đồ thị hàm số C 3 2
: y x  3x tại ba điểm phân biệt có hoành độ lần lượt là x , x , x thỏa mãn điều 1 2 3 kiện 2 2 2
x x x  15. 1 2 3 3 3 A. m  . B. m   . C. m  3. D. m  3. 2 2
Câu 21. Hình bên dưới là đồ thị của hàm số 3 y x  3 .
x Tìm tất cả các giá trị thực của tham số
m để phương trình 3 2
x  3x m có 5 nghiệm phân biệt.
A. m  ( 2 ) 0 ;  ( ; 0 2) B. m  ( ; 0 2) C. m  ( 0 ; 2 )  ( 2 ; 0 ) D. m  ( 2 ; 0 ) 42
1F. Bài toán tương giao HÀM BẬC BỐN
Câu 22. Số giao điểm của đồ thị hàm số 4 2
y  x  2x 1với trục Ox là : A. 1 B. 2 C. 3 D. 0
Câu 23. Tìm m để đồ thị hàm số 4 2
y x mx  1 tiếp xúc với trục hoành tại hai điểm phân biệt. A. m  2  B. m  2 C. m  1 D. m  1 
Câu 24. Giá trị m để đồ thị hàm số 4 2 y x 2mx m
1 cắt trục tung tại điểm có tung độ bằng 2 là A. m 3 B. m 3 C. m 2
D. Không có giá trị m
Câu 25. Tìm m để đường thẳng y = m cắt đồ thị hàm số y = x4 – 2x2 + 3 tại 4 điểm phân biệt. A. -1 < m < 1
B. 2 < m < 3 C. 0 < m < 1
D. – 1 < m < 0
Câu 26. Đồ thị hàm số 4 2 y x 2x
3 cắt đường thẳng y
m tại 4 điểm phân biệt khi A. m 4; 3 B. m  4  ; 3   C. m \  4  ; 3   D. m
Câu 27. Tìm các giá trị thực của tham số m để đồ thị hàm số C  4 2
: y x mx m 1 cắt trục m
hoành tại bốn điểm phân biệt. m 1 A.  . B. Không có . m C. m  1. D. m  2. m  2
Câu 28. Tất cả các giá trị m để phương trình 4 2
x  3x  m  0 có 4 nghiệm phân biệt là : 13 9 9 13 A. 1  m B. 0  m C.   m  0
D. 1  m  4 4 4 4
Câu 29. Phương trình 4 2 x 2x 1 m
0 có bốn nghiệm phân biệt khi: A. 0 m 1 B. 1 m 2 C. 0 m 1 D. 1 m 2 HÀM PHÂN THỨC x 1
Câu 30. Tọa độ giao điểm của (C) : y d y  x  2x  và ( ) : 1 1 là : A. 1;  1 , ( 1  ;2) B. 1;0,( 1  ;2) C.  1  ;0,(1;2) D. 1; 2 x  4
Câu 31. Đồ thị hàm số y
cắt trục tung tại điểm M có tọa độ ? 2x 1 A. 4; 2  . B. M 4;0.
C. M 0; 4. D. M 0;0. 2 x 2x 3
Câu 32. Tọa độ giao điểm của đồ thị hàm số y và y x 1 là: x 2 A. (2; 2) B. (2; 3) C. ( 1; 0) D. (3;1) 43
1F. Bài toán tương giao x
Câu 33. Gọi M, N là giao điểm của đường thẳng: y = x +1 và đường cong: 2 4 y  . Khi đó x 1
hoành độ trung điểm I của đoạn thẳng MN bằng 5 5 A. B. 1 C. 2 D. 2 2 2x 1
Câu 34. Hình dưới đây là đồ thị của hàm số y
. Tìm tất cả các giá trị thực của tham số m x 1 
để phương trình 2x 1  m có hai nghiệm phân biệt. x 1 A. m  2.
B. Không có giá trị của . m C. m  2. D. Với mọi . m 2x 1
Câu 35. Hình bên là đồ thị của hàm số y
. Tìm tất cả các giá trị thực của tham số m để x 1 2x 1 phương trình
 3m 1 có hai nghiệm phân biệt. x 1 1 1 A.   m
B. Không có m . C. m  1
D. 2  m  0 3 3 2x 1
Câu 36. Hình bên là đồ thị của hàm số y
. Tìm tất cả các giá trị thực của tham số m để x 1 2x 1 phương trình
 2m có hai nghiệm phân biệt. x 1
A. Với mọi m .
B. Không có giá trị của m . C. m  0
D. m  0;  \   1 mx 1
Câu 37. Đồ thị C : y
. Với giá trị nào của m thì C đi qua điểm M  1  ;0 m m  2x m A. -1 B. 2 C. -2 D. 1 x Câu 38. Cho hàm số 2 1 y
(C). Tìm các giá trị của m để đường thẳng y = x - m cắt đồ thị (C) x  2
tại hai điểm phân biệt . A. m  1 B. m  1 C. m  1 D.m
Câu 39. Tìm tất cả các giá trị thực của tham số m để đường thẳng y  m  2x cắt đồ thị hàm số 2x  4
y  x  tại hai điểm phân biệt. 1 A. m  4 B. m  4 C. m  4 D. m  4 x x
Câu 40. Cho đồ thị hàm số C  2 3 3 : y  . Tìm điểm C
M trên đồ thị   sao cho M cách x 1
đều hai trục tọa độ.  1   3 3   3 3   1  A. M ; 2   B. M ;    C. M  ;   D. M  ; 2    2   2 2   2 2   2  44
1F. Bài toán tương giao x
Câu 41. Cho C  là đồ thị hàm số 3 y
. Điểm M cách đều hai trục tọa độ có tọa độ nào sau x  1 đây?  1 
A. M 2;5
B. M 1;   1 C. M 3; 3   D. M 2;     3  x  3
Câu 42. Cho C  là đồ thị của hàm số y
. Biết rằng, chỉ có hai điểm thuộc đồ thị C  cách x 1
đều hai điểm A2;0 và B 0; 2
  . Gọi các điểm đó lần lượt là M và N . Tìm tọa độ trung điểm
I của đoạn MN .  3   3 
A. I 1;  1 B. I 0;    C. I 0;   D. I  2  ;2  2   2  x
Câu 43. Cho đồ thị C  : y
. Gọi M là điểm thuộc C  sao cho khoảng cách từ M đến x 1
đường thẳng d : 3x  4y  0 bằng 1. Hỏi có tất cả bao nhiêu điểm M thỏa mãn điều kiện đề bài? A. Có 4 điểm.
B. Không có điểm nào. C. Có 2 điểm.
D. Có vô số điểm. 3x  2 3m  2
Câu 44. Tìm tất cả các giá trị thực của tham số m để phương trình  chỉ có 1 x  1 m  1 nghiệm A. Với mọi m B. m  1 1 C. m
D. Không có giá trị nào của m 4
Câu 45. Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y  x m cắt đồ thị hàm 2x 1
số (C): y x  tại hai điểm phân biệt 2
A. 1  m  4
B. 1  m hoặc m  4 C. m  4 D. m  2x  4
Câu 46. Gọi M ,N là giao điểm của đường thẳng y = x + 1 và đường cong y  . Khi đó x 1
hoành độ trung điểm I của đoạn thẳng MN bằng 5 5 A. B. 1 C. 2 D. 2 2 2x 1
Câu 47. Cho hàm số y
(C). Đường thẳng y x
m cắt (C) ta ̣i 2 điểm A, B sao x 2
cho đô ̣ dài AB nhỏ nhất khi A. m  1 B. m  2 C. m  3 D. m  1 x  5
Câu 48. Tổng các giá trị của tham số m sao cho đường thẳng y x cắt đồ thị hàm số y x m
tại hai điểm A và B sao cho AB  4 2 là A. 2 B. 5 C. 7 D. Đáp án khác x  2
Câu 49. Cho hai điểm A , B phân biệt thuộc đồ thị hàm số (C) : y x  sao cho A và B đối xứng 1
với nhau qua điểm M (3;3) .Tính độ dài AB A. 2 2 B. 5 2 C. 6 2 D. 3 2 45
1F. Bài toán tương giao x
Câu 50. Cho đồ thị hàm số C  2 : y
. Đường thẳng d : y x m cắt đồ thị C  tại hai điểm x 1 phân biệt ,
A B phân biệt và AB  2 2 khi m nhận giá trị nào trong các giá trị sau đây? A. m  1 B. m  5 C. m  2 D. m  8 2 2x  2x  3
Câu 51. Đường thẳng y  3x  1 cắt đồ thị hàm số y x
tại hai điểm phân biệt A và 1
B . Tính độ dài đoạn thẳng AB . A. AB  4 10 B. AB  4 6 C. AB  4 2 D. AB  4 15 x  3
Câu 52. Cho đồ thị hàm số (C) : y
. Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách x  1
đều hai trục tọa độ. Gọi các điểm đó lần lượt là M & N . Tính độ dài đoạn thẳng MN. A. MN  4 2 B. MN  3 C. MN  2 2 D. MN  3 5 x 1
Câu 53. Đường thẳng d : y x  3 cắt đồ thị (C) : y  tại hai điểm ,
A B phân biệt. Gọi x  2
d , d lần lượt là khoảng cách từ ,
A B đến đường thẳng  : x y  0 . Tính d d d . 1 2 1 2 3 2 A. d  3 2 B. d C. d  6 D. d  2 2 2
Câu 54. Với điều kiện nào của tham số m cho dưới đây, đường thẳng d : y  3x m cắt đồ thị C 2x 1
: y x tại hai điểm phân biệt A và B sao cho trọng tâm của tam giác OAB thuộc đồ thị 1
C, với O0;0 là gốc tọa độ. 15 3 13 15 5 13 7 5 5 A. m   . m   . m   . 2 B. 2 C. 2 D. Với mọi . m 2 mx m  2
Câu 55. Biết hàm số y
giảm trên từng khoảng xác định của nó và đồ thị hàm số đi x  3
qua điểm I (4;1). Khi đó giá trị của tham số m là A. m   B. m 1 C. m 3 D. m 1 và m 3 2 x  3x
Câu 56. Cho đồ thị hàm số (C): y
. Hỏi có bao nhiêu điểm thuộc đồ thị hàm số (C) có tọa x 1
độ nguyên (hoành độ và tung độ là những số nguyên)? A. Có 4 điểm.
B. Có vô số điểm. C. Có 2 điểm.
D. Không có điểm nào. x  2
Câu 57. Cho (C ) là đồ thị hàm số y d y mx  Tìm các giá trị thực
x  và đường thẳng : 1. 1
của tham số m để đường thẳng d cắt đồ thị (C ) tại hai điểm A và B phân biệt thuộc hai nhánh khác nhau của (C ). A. m  0 B. m  0 C. m  0 D. m  0 46
1F. Bài toán tương giao x
Câu 58. Đường thẳng d : y x  3 cắt đồ thị 
C  của hàm số 1 y
tại hai điểm A và B phân x  2
biệt. Khẳng định nào sau đây là đúng? A. Hai điểm ,
A B nằm về cùng một phía với trục Ox . B. Hai điểm ,
A B nằm về cùng một phía đường thẳng x+y=0 . C. Hai điểm ,
A B nằm về cùng một phía với trục Oy . D. Hai điểm ,
A B nằm về cùng một phía với đường thẳng x-3y=0 . Nguyễn Văn Lực
www.facebook.com/VanLuc168
1C 2B 3B 4D 5C 6A 7A 8C 9D 10D
11D 12D 13C 14C 15A 16B 17A 18D 19A 20C
21A 22D 23B 24A 25B 26B 27A 28B 29B 30B
31C 32C 33B 34A 35A 36D 37A 38D 39A 40B
41B 42A 43A 44B 45D 46B 47B 48C 49A 50C
51A 52A 53A 54B 55A 56A 57B 58C 47
1G. Tiếp tuyến của đồ thị hàm số
TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
Câu 1. Tiếp tuyến của đồ thị hàm số 3 2
y x  3x  4 tại điểm có hoành độ x  1 là
A. y  9x
B. y  9x  9
C. y  9x  9
D. y  9x
Câu 2. Tiếp tuyến của đường cong 3
y x  2x tại điểm có hoành độ bằng x 1 là: 0
A. y x  2
B. y x  2
C. y   x  2
D. y   x  2
Câu 3. Tiếp tuyến của đồ thị hàm số 3 y
x tại điểm có hoành độ x 1 là: 0 A. y 3x 2 B. y 3x 2 C. y 3x 2 D. y 3x 2 2x 1
Câu 4. Phương trình tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ x  1 là: x  2
A. y  5x  8
B. y  5x  2
C. y  5x  2
D. y  5x  8 x 1
Câu 5. Tìm phương trình tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ x 3 . x 2 A. y 3x 5 B. y 3x 13 C. y 3x 13 D. y 3x 5 2x  6
Câu 6. Cho hàm số y
(C). Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục x  2 tung là: 1 1 3
A. y  2x  6 B. y x  3
C. y  2x  6 D. y x  2 2 2
Câu 7. Cho C  là đồ thị của hàm số 3 2
y x  3x  2. Tìm các tiếp tuyến của C  đi qua điểm A0;3.
A. y  3x  3.
B. y  2x  3.
C. y  3x  3.
D. y  4x  3. 2 x
Câu 8. Cho ( C) là đồ thị hàm số y
x 1.Viết phương trình tiếp tuyến của ( C) đi qua điểm 4 M(2;-1)
A. y x  1
B. y  2x  1.
C. y x  3
D. y  2x  3. 2x 1
Câu 9. Có bao nhiêu phương trình tiếp tuyến của đồ thị hàm số (C): y biết tiếp tuyến 1 x
vuông góc với đường thẳng d : x 3y 2 0 là: A. 0 B. 1 C. 2 D. 3 x 2
Câu 10. Có bao nhiêu tiếp tuyến với đồ thị hàm số y
. Biết tiếp tuyến song song với x 1 đường thẳng y 3x 2 A. 0 B. 1 C. 2 D. Không có 48
1G. Tiếp tuyến của đồ thị hàm số 1
Câu 11. Trong tất cả các tiếp tuyến của đồ thị hàm số 3 y
x x . Tiếp tuyến có hệ số góc nhỏ 3 nhất bằng : A. 0 B. 1 C. -1 D. 2
Câu 12. Trong các tiếp tuyến của đồ thị hàm số 3
y  x 12x  4 có một tiếp tuyến có hệ số góc
k lớn nhất. Tìm giá trị lớn nhất của k . A. k  9 B. k  0 C. k  12 D. k  12 Câu 13. Cho hàm số 3 2
y  x  3x  4 có đồ thị (C). Tìm điểm M thuộc đồ thị (C) sao cho tiếp
tuyến của đồ thị (C) tại điểm đó có hệ số góc lớn nhất? A. M 1; 2 B. M 1; 0 C. M 0; 4 D. M 2; 0
Câu 14. Cho hàm số (C): 3
y  x  6x  2 và đường thẳng d : y mx m  1 . Với giá trị nào của
m thì d cắt (C) tại 3 điểm A, B, C sao cho tổng hệ số góc các tiếp tuyến của đồ thị (C) tại A, B, C bằng -6? A. m  3 B. m  1 C. m  1 D. m  2
Câu 15. Cho đồ thị hàm số 3 2 5 (C) : y x 2x
x . Tiếp tuyến tại gốc tọa độ O của ( C) cắt ( C) 3
tại điểm thứ hai M. Tìm tọa độ M 10 10 10 10 A. M 2; B. M 2; C. M 2; D. M 2; 3 3 3 3
Câu 16. Cho đồ thị 3 2
(C) : y  x  3x  2 . Tìm một tiếp tuyến của đường cong (C) , biết tiếp tuyến
cắt trục Ox, Oy lần lượt tại A và B thỏa mãn OB  9 OA . A. y  9x  7 B. y  9x  25 C. y  9x  25 D. y  9x  7 Câu 17. Cho hàm số 3 2
y x  2x  2x có đồ thị ( C ) . Gọi x , x là hoành độ các điểm M, N 1 2
trên (C), mà tại đó tiếp tuyến của ( C ) vuông góc với đường thẳng y  x  2017 . Khi đó x x 1 2 bằng: 4 4  1 A. B. C. D. -1 3 3 3 x Câu 18. Gọi 2 1
M  (C) : y
có tung độ bằng 5 . Tiếp tuyến của (C) tại M cắt các trục tọa độ x 1
Ox, Oy lần lượt tại A và B. Diện tích tam giác OAB bằng: 121 119 123 125 A. y B. C. y D. y  6 6 6 6 Nguyễn Văn Lực
www.facebook.com/VanLuc168 1C 2B 3C 4B 5C 6B 7A 8C 9C 10B
11A 12D 13A 14D 15D 16A 17A 18A 49
2A. Hàm số lũy thừa – Hàm số mũ
HÀM SỐ LŨY THỪA – HÀM SỐ MŨ
Tập xác định của hàm số mũ
Câu 1. Tập xác định của hàm số yx    2 1 là
A. D  ;  1 1;; B. D .
C. R \   1
D. D  1;  1 .
Câu 2. Tập xác định của hàm số 4 2 y
x  3x  4 là: A. [-1;4] B. (-1; 4) C.  ;    1  4;  D.  ;    1 4;  
Câu 3. Hàm số y =  x   4 2 4 1 có tập xác định là:  1 1   1 1  A. B. (0; +) C. \  ;  D.  ;    2 2  2 2  
Câu 4. Tập xác định của hàm số 2 5
y  (2x x  6) là: 3 3 A. D  ( ;   )  (2;)
B. D  ( ; 2) 2 2  3  C. D \  ;2 D. D   2 2 2
Câu 5. Tập xác định của hàm số: y x  3 ( 4) là
A. D  (;2) (2;) B. D \ { 2}
C. D  (2;2) D. D 1  Câu 6. Hàm số 2 y  (1  x) có tập xác định là: A. D B. D \ {0} C. D  (;1) D.
Câu 7. Hàm số y = 3  2
1 x có tập xác định là: A. [-1; 1]
B. (-; -1]  [1; +) C. R\{-1; 1} D. x x
Câu 8. Tập xác định của hàm số y  9  3 là: A. (1;2) B. [0;) C. [3;) D. (0;3) Câu 9. Hàm số 3
y  (1  x) có tập xác định là: A. D B. D \ {0} C. (0; ) D. 50
2A. Hàm số lũy thừa – Hàm số mũ
Câu 10. Tập xác định của hàm số 5 2 y x 3x 2 là:
A. D   ;   1  2; 
B. D   ;   1 2;
C. D  1; 2 D. D Nguyễn Văn Lực
www.facebook.com/VanLuc168
Đạo hàm của hàm số mũ
Câu 11. Tính đạo hàm của hàm số 12x y  12x A. 1 ' .12x y x   B. ' 12x y  ln12 C. ' 12x y D. y '  ln12
Câu 12. Đạo hàm của hàm số:   1 100x y là xx A. y  1 ' 100 ln10
B. y '  200.100 ln10 1 C. y '  
y'  x 1 ln100. x D.     1 ln100
Câu 13. Đạo hàm của hàm số 2 3 2 x y là: 2x 3 2x 3 2 3 2 2 A. 2.2 . ln 2 B. 2 . ln 2 C. 2.2 x D. (2 x 3)2 x x1
Câu 14. Cho f(x) = x1
2 . Đạo hàm f '0 bằng: A. 2 B. ln2 C. 2ln2 D. Kết quả khác 1
Câu 15. Đạo hàm của hàm số 2 2
y  (x  2x 1) là: 1 1  A. 2 2
y '  (x  2x 1) (2x  2) B. 2 2
y '  (x  2x 1) (2x  2) 1 1  1  C. 2 2 y '  (x  2x 1) D. 2 2
y '  (x  2x 1) (x 1) 2
Câu 16. Cho f(x) = 2 3 2 x
x . Giá trị f '(1) bằng: 3 8 A. B. C. 2 D. 4 8 3 x
Câu 17. Đạo hàm của hàm số 2 1 y e sin 2x là: 2x 1  2x 1 
A. y '  2e o c s2x
B. y '  4e o c s2x 2x 1  2x 1  2x 1  2x 1 
C. y '  2e sin 2x  2e o c s2x
D. y '  2e sin 2x  2e o c s2x 51
2A. Hàm số lũy thừa – Hàm số mũ 2  
Câu 18. Tính đạo hàm của hàm số: x 5x 1 y e .   2   A.      2 2 5 1 ' 5 1 x x y x x e B. 5 1 '  2  5 x x y x e     C.     2 5 1 ' 2 4 x x y x e D.     2 5 1 ' 2 5 x x y x e
Câu 19. Tính đạo hàm của hàm số: 2x 5x y  e  3.5 A. 2x 5x y'  2e  5 .ln5 B. 2x 5x y'  2e  3.5  C. 2x 5x y'  2e  3.5 .ln5 D. 2x 5x 1 y'  2e  3.5 .ln5
Câu 20. Tính đạo hàm của hàm số 2 ( 2 2) x y x x e . 2 A. ' x y x e B. ' (2 2) x y x e C. ' 2 x y xe D. ' 2 x y xe    Câu 21. Cho hàm số tan 2 x y e
, giá trị của f '  bằng  6  A. 3 4  e . B. 3 2e . C. 4. D. 3 8e .
Câu 22. Tính đạo hàm của hàm số x y  9 1 3x A. x
y'  9 (1 3x).ln9   1 B. x
y'  9 (2  6x)ln9   3 C. x   2x 1 y' 9 2 6x ln 3 3     D. x
y '  9 (1 3x)ln 3   3 x 1
Câu 23. Tính đạo hàm của hàm số y  . 9x 1 2(x 1) ln 3 1 (x 1) ln 3 A. y '  B. y '  2 3 x 2 3 x 1 2(x 1) ln 9 1 2(x 1) ln 3 C. y '  D. y '  3x 3x Câu 24. Cho hàm số   3x f x
 2. Khẳng định đúng là
A. f '0  ln 3
B. f '0  3ln 3 C. f '  1  ln 3
D. f '2  9
Câu 25. Cho hàm số ( )  . x f x
x e . Giá trị của f ' (0) là: A. 1 B. 2e C. 3e D. 2
Câu 26. Đạo hàm bậc hai của hàm số 10x y  là: A. xxx  ' 10x y B. 2 y ' 10 .ln10 C. 2 y '
10 .(ln10) D. y ' 10 .ln 20 x e 1
Câu 27. Đạo hàm của hàm số y là x x e 1 x e (x 1) 1 x ln x xe x e 1 x e (x 1) 1 A. B. C. D. 2 x 2 x 2 x 2 x x
Câu 28. Đạo hàm của hàm số 2 1 y e là: 1 2 1 2x 1 2 1 2 A. ' 2 x y e B. y ' e C. ' x y e D. ' 2 x y e 2 52
2A. Hàm số lũy thừa – Hàm số mũ
Câu 29. Đạo hàm của hàm số 2017x y là: 2017x 1 x A. ' .2017x y x B. y ' 2017 .ln 2017 C. ' 2017x y D. y ' ln 2017 Nguyễn Văn Lực
www.facebook.com/VanLuc168
Rút gọn biểu thức
Câu 30. Biết 4x  4 x  23 . Tính 2x 2 x I    . A. I  5 B. I  4 C. I  23 D. I  21 xx  5  3  3
Câu 31. Cho 9x  9 x  23. Khi đó biểu thức P  13x  có giá trị bằng: 3x 5 1 3 A. B. C. D. 2 2 2 2  
Câu 32. Gọi a và b là hai số thực thỏa mãn đồng thời a b  1 và 2a 2 4
 4 b  0,5 . Khi đó tích ab bằng: 1 1 1 1 A. B. C.D.  4 2 2 4 3 5 Câu 33. Biểu thức 6
x . x . x (x > 0) viết dưới dạng lũy thừa có số mũ hữu tỉ là 7 5 2 5 A. 3 x B. 2 x C. 3 x D. 3 x 3 2 x x  13 
Câu 34. Cho f (x)  . Khi đó f   bằng 6 x 10  11 13 A. B. 4 C. 1 D. 10 10 Câu 35. Cho hàm số sin x y e
. Hãy tính giá trị của biểu thức M y 'cos x ysin x y ' ? A. sinx B. 0 C. 1 D. -1     
Câu 36. Rút gọn biểu thức P  a b  1
2  4 ab với a , b là các số dương.     A.      
P a  2b
B. P a b
C. P a b
D. P a b 2 1 1  b b   
Câu 37. Cho a, b là các số dương. Biểu thức 2 2 1 2
  : a b  sau khi rút gọn là: a a     1 1 A.
B. a b
C. a b D. a b 53
2A. Hàm số lũy thừa – Hàm số mũ  2 x  52 5
Câu 38. Rút gọn biểu thức A
(với x  0 ) ta được: 53  1 5 x .x
A. A x B.  2 A x C.  3 A x D.  4 A x 1 3 2 3 1 3
a ( a a )
Câu 39. Cho số thực dương a. Giá trị rút gọn của biểu thức P  là: 8 5 2 5 8 5
a ( a a ) 1 1 A. P = a + 1
B. P = a – 1 C. P D. P a 1 a 1
Câu 40. Cho 2x  2y  4 . Tìm giá trị lớn nhất của S x y . A. s  0 B. S  1 C. S  2 D. S  4 x Câu 41. Cho hàm số 4 f (x)  . Tính tổng: 4x 1 1 2 2016 S f ( )  f ( )  .......  f ( ) . 2017 2017 2017 A. S  2017 B. S  1009 C. S  1008 D. S  1006 7
Câu 42. Biểu thức 3 3
a : a (a  0) viết dưới dạng lũy thừa với số mũ hữu tỉ là:   A. 2 a B. 2 a C. a D. 1 a 1  1   3  3  9 
Câu 43. Giá trị biểu thức P       bằng:  7  4  4  A. 1 B. 2 C. 1  D. 2  2 0  ,75  1 
Câu 44. Giá trị biểu thức 0,5 3 Q  27   25   bằng: 16  A. 12 B. 10 C. 8 D. 6 4 1  
Câu 45. Rút gọn biểu thức a 1 a a 4 P  .
.a 1 ta được kết quả : 3 1 a 1 4 2 a a A.   P a B. P = 1 C. P = a D. 4 P a 1 9 1 3  4 4 2 2 a a bb
Câu 46. Rút gọn biểu thức 
(a  0, b  0) , ta được: 1 5 1 1  4 4 2 2 a a b b a
A. a b
B. a b C. a.b D. b 1 4
a  1  a a
Câu 47. Rút gọn biểu thức 4 
a (a  0) , ta được: 3 1 a  1   4 2 a a A. a B. a 1 C. a 1 D. 4 a 11
Câu 48. Rút gọn biểu thức: x x x x : 16 x , ta được: A. 4 x B. 6 x C. 8 x D. x 54
2A. Hàm số lũy thừa – Hàm số mũ 1 t
Câu 49. Tìm hệ thức liên hệ giữa x và y, biết t 1  t 1 x t ,   y t
(t  0, t  1). 1 1
A. x y y x
B. x y y x C. y y y x y
D. y x y x 2 2 2
Câu 50. Biểu thức K = 3 3
viết dưới dạng số hữu tỹ: 3 3 3 1 1 1 1 6  2  12  2  8  2  2  2  A.   B.   C.   D.    3   3   3   3  Nguyễn Văn Lực
www.facebook.com/VanLuc168
Bài tập tổng hợp 1 2 x x
Câu 51. Cho hàm số f (x) ( ) .5 . Khi đó 2 2 2 A. f (x) 1 x x.log 5 0 B. f (x) 1 x ln 2 x .ln 5 0 2 2 2 C. f (x) 1 x x .log 5 0 D. f (x) 1 x x.log 2 0 2 5 Câu 52. Cho hàm số   2 4 . x 9x f x
. Khẳng định nào sau đây là khẳng định sai?
A. f x 2
1  x x log 9  0.
B. f x 2
1  x xlog 4  0. 4 9
C. f x  1  lg 4  x lg 9  0. D.
  1 lg4lg9x f x x   0. 2 Câu 53. Cho ( ) 2x .3x f x
. Khẳng định nào sau đây là khẳng định đúng ? A. 2
f (x)  2  x x log 3  1
B. f (x)  2  2x x log 3  1 2 2 1 C. 2
f (x)  2  x x log 3  1
D. f (x)  2 
x x log 3  1 2 2 2
Câu 54. Trong các hàm số sau, hàm số nào nghịch biến trên ? x     x  2  A. 3 x y  
B. y    C. x y e
D. y     3   5 
Câu 55. Trong các hàm số sau, hàm số nào đồng biến trên ? xx x x 1      2     A. y  .   B. y  .   C. y  .   D. y  .    3   3   e   4 
Câu 56. Cho  > . Kết luận đúng là A.  <  B.  >  C.  +  = 0 D. . = 1 55
2A. Hàm số lũy thừa – Hàm số mũ
Câu 57. Mệnh đề sai là 4    
A. Với a > 0 thì 3 3 2
a : a a B. 3 2 1 2 4 2 4 .2 .2  8   C. 3 2 3  3 D. log 2  log 3 3 2
Câu 58. Cho số thực a > 1. Khẳng định nào dưới đây là khẳng định sai ? 2   2   A. x 1 2x 1 a  a  x  0 hay x  2 B. x 1 2x 1 a  a  0  x  2 2 x 1  2x 1  2 3   C.  5    5 a a   0  x  2 D. x 1 3 2x 1 a  a  x  0 hay x  2
Câu 59. Tìm mệnh đề đúng trong các mệnh đề sau: A. Hàm số x
y a với 0 < a < 1 là hàm số đồng biến trên (-: +) B. Hàm số x
y a với a > là hàm số nghịch biến trên (-: +) C. Hàm số x
y a với (0 < a  1) luôn đi qua điểm (a; 1) x  1  D. Hàm số x
y a với y =   (0 < a  1) thì đối xứng qua trục tung.  a
Câu 60. Với a > 0, b> 0, x và y tùy ý. Mệnh đề nào đúng: x x y . x y a xy x y xy A. a .aa B. ( )X  . X ab a b C.ay D. (a ) a a Nguyễn Văn Lực
www.facebook.com/VanLuc168
1D 2D 3C 4C 5A 6C 7D 8B 9A 10D
11B 12B 13A 14B 15D 16B 17D 18D 19D 20A
21D 22C 23A 24A 25D 26C 27B 28A 29B 30A
31A 32A 33D 34C 35B 36D 37A 38C 39D 40C
41C 42A 43B 44A 45A 46A 47B 48A 49A 50D
51C 52C 53A 54A 55B 56B 57A 58C 59C 60C 56 2B. Hàm số lôgarit HÀM SỐ LÔGARIT
Tập xác định của hàm số lôgarit x
Câu 1. Tập xác định của hàm số y log (3 1)là 2 1 1 A. D ( ; ) B. D (0; ) C. D [1; ) D. D ( ; ) 2 3
Câu 2. Tìm tập xác định D của hàm số: y  log  2 4  x 3 .
A. D   ;  2    2; B. D   2  ;2
C. D   ;    2 2;  D. D   2  ;2
Câu 3. Tìm tập xác định của hàm số y  log  2
x  5x  6 là: 3  A.    D  ( ;2) (3; ) B. D  (2;3)
C. D  2;  3 D. D  ( ;  2][3; ) 
Câu 4. Tập xác định của D hàm số 2 y log x 2x 3 là 5
A. D   ;  3    1;
B. D   ;    3  1; 
C. D   ;    1  3;  D. D   1  ;  3 2
Câu 5. Hàm số y  log (x  6x  9) 5 xác định khi A. x  3 B. x  3 C. x  3 D. x  3
Câu 6. Tìm tập xác định của hàm số: 2
y  log (4  x) . 5
A. D  [2; 2] B. D  ( ;  2  ) (2; )  C. D  ( ;  2  )
D. D R \ {4}
Câu 7. Tập xác định D của hàm số y= log  3 2
x x  2x là 5  A. (0; 1) B. (1; +)
C. (-1; 0)  (2; +)
D. (0; 2)  (4; +).
Câu 8. Biểu thức log  2 2x x có nghĩa khi 6 
A. 0 < x < 2 B. x > 2
C. -1 < x < 1 D. x < 3
Câu 9. Tìm tập xác định D của hàm số 2 y log(x 4). A. D ( ; 2) (2; ) B. D [ 2;2] C. D ( 2;2) D. D ( ; 2] [2; )
Câu 10. Tìm tập xác định D của hàm số 2 y  log 8  5x  3x 3 2    8   8   8   8  A. D  1  ;   B. D  1  ;   C. D  1;    D. D  1;    3   3   3   3  57 2B. Hàm số lôgarit Câu 11. Hàm số y =  2
ln x  5x  6 có tập xác định là
A. (0; +). B. (-; 0). C. (2; 3).
D. (-; 2)  (3; +).
Câu 12. Tập xác định của hàm số 2 y log (x 1) ln(3 x) 2 9 A. D (3; ) B. D ( ; 3) C. D ( ; 1) ( 1; 3) D. D ( 1; 3) 4
Câu 13. Tập xác định của hàm số y  log x  là : 3 4
A. 0;64 64;  B. C. \6  4 D. 0;  x  4
Câu 14. Tìm tập xác định D của hàm số y  log 3 x  4 A. ( ;  4  ][4; )  B. [4; 4] C. ( ;  4  ) (4; )  D. (4; ) x
Câu 15. Hàm số: y  log  xác định khi: 0,6 2 3 16 A. x  7 B. x  7 C. x  3 D. x  5
Câu 16. Tập xác định của hàm số: y  log x  3  2 là: 1   3 A. (3;12] B. (3;12) C. [3;12) D. [3;12] Câu 17. Tính log 24 log 27  a 36 theo 12 là 9  a 9  a 9  a 9  a A. 6 B. C. D.  2a 6  2a 6  2a 6  2a
Câu 18. Tập xác định của hàm số y  log ( x  1) là: 3 A. [1; ) B. D \ {1} C. (1; ) D. (;1) x  1
Câu 19. Tập xác định của hàm số y  log0,3 x  là : 5 A. (1; ) B. ( ;1 C. (; 5  )  (1; ) D. Kết quả khác x  2
Câu 20. Tập xác định của hàm số y  log 1 x là: A.  ( ;1)  (2;) B. (1;2) C. \ {1} D. \ {1;2}
Câu 21. Tập xác định của hàm số y  log x 1 2 là: A. (0;1) B. (1;) C. (0;) D. [2;)
Câu 22. Tập xác định của hàm số y  3  log (x  2) 3 là: A. (0;25) B.  ( 2;27) C. (2;) D. (2;25] 58 2B. Hàm số lôgarit 1
Câu 23. Cho hàm số y ln , ta có: x 1 A. ' 1 y xy e B. ' 1 y xy e C. ' 1 y xy e D. ' 1 y xy e 10  x
Câu 24. Tập xác định của hàm số y  log là: 3 2 x  3x  2 A. 1;  B.  ;   1  2;10 C. ;10 D. 2;10
Câu 25. Cho hàm số: 2 2
y  ln(2x e ) . Tập xác định của hàm số là: 1 e 1 A. D B. D  ( ;  ).
C. D  ( ; ). D. D  ( ; ) 2e 2 2
Câu 26. Tập xác định của hàm số y  log  2
x  2x  1 là 2  A. B. D \ { 1} C. D \ {1} D. 1
Câu 27. Tìm tập xác định D của hàm số y log ? 3 3 x A.   ;3  B. 3;  C.3;  D.  ;3   Nguyễn Văn Lực
www.facebook.com/VanLuc168
Đạo hàm của hàm số lôgarit
Câu 28. Đạo hàm của hàm số 2 y  log 2x 1 là: 2   2log 2x 1 4log 2x 1 4log 2x 1 2 2   2   2   A.B. C. 2x   1 ln 2 2x   1 ln 2 2x D. 1 2x  1ln2
Câu 29. Đạo hàm của hàm số log  2
x  2x 1 là: 3  2x  2 2 A. y '  B. y '  2 x  2x  3 (x 1).ln 3 2x  2 2x 1 C. y '  D. y '  ln 3 2
(x  2x 1).ln 3
Câu 30. Đạo hàm của hàm số y  log x x  0 là 3   x A. y ' 3 ln x B. y ' x ln 3 1 x C. y ' D. y ' x ln 3 ln 3 59 2B. Hàm số lôgarit
Câu 31. Đạo hàm của hàm số 2 y log (x 1) là 2017 1 1 A. y ' B. y ' 2 x 1 2 (x 1)ln 2017 2x 2x C. y ' D. y ' 2017 2 (x 1)ln 2017
Câu 32. Tính đạo hàm của hàm số 2
y  ln(2x  x ) với 0  x  2 là: 2  2x A. y '  y    x 2 2x  B. 2 ' (2 2x)(2x ) x 1 C. y '  y   x 2 2x  D. 2 ' 2x x
Câu 33. Tính đạo hàm của hàm số 2
y  2x ln x . A. 2
y '  2 ln x  4x ln x B. 2
y '  2x ln x  4x ln x C. 2
y '  2x ln x  4 ln x D. 2
y '  2 ln x  4 ln x
Câu 34. Cho hàm số: y  2
x ln x . Kết quả của y' =? 2ln x 2 A. ln x  2.
B. ln x (ln x  2). C. . x x x D. 2 ln .
Câu 35. Tính đạo hàm của hàm số y (x 1)ln x . x 1 x 1 x 1 A. y ' ln x B. y ' C. y '
ln x D. y ' ln x x x x
Câu 36. Tính đạo hàm số y  (1 ln x).ln x 1 2ln x 2ln x A. y '  B. y '  x x 1 2ln x 2  ln x C. y '  D. y '  x x ln x
Câu 37. Tính đạo hàm của hàm số y x 1 1 ln x A. y '  B. y '  x x 1 ln x 1 ln x C. y '  D. y '  2 x 2 x ln x 1
Câu 38. Đạo hàm của hàm số y x là 2  ln x 1 A. ln x  1 B. 1 2 x C.x D. 1 1 ln x
Câu 39. Hàm số f (x) có đạo hàm là x x ln x ln x ln x A. B. C. D. 2 ln x x x 4 x 60 2B. Hàm số lôgarit cos x  sin x
Câu 40. Hàm số y  ln cos x  có đạo hàm bằng sin x 2 2 A. . B. . C. cos 2 . x D. sin 2 . x cos 2x sin 2x
Câu 41. Đạo hàm của hàm số y   2
ln x  1  x  là: 1 1 x A. B. C. 2 x  1 x D. 2 1  x 2 x  1  x 2 1  1  xx   Câu 42. Hàm số 5 y  ln 
 thỏa mãn hệ thức nào sau đây  3  1 A. y '  0
B. 3y  ln  x  5  0 x  5 C. y e x  5
D. y ' y  0
Câu 43. Cho hàm số f(x) = ln 1 x e . Tính f’(ln2) 1 A. 2 B. -2 C. 0,3 D. 3 1
Câu 44. Tính đạo hàm của hàm số y x. ln 1 x x (1 x)ln(1 x) x (1 x)ln(1 x) A. y ' B. y ' 1 x 1 x x ln(1 x) C. y ' D. y ' x ln(1 x) 1 x
Câu 45. Cho hàm số: 2 2
y  ln(2x e ) . Đạo hàm cấp 1 của hàm số tại x = e là: 3 4 4 4 A. B. C. D. 4e 9e 2 9e 2 3e
Câu 46. Đạo hàm của hàm số 2 y ln x là 2 2 2 2 A. y ' B. y ' ln x C. y ' D. y ' x x 2 x 3 x Nguyễn Văn Lực
www.facebook.com/VanLuc168
Biểu diễn giá trị lôgarit
Câu 47. Cho log 20  a . Tính log 5 theo a . 2 20 a  2 a  2 A. a - 2. B. a + 2. C. D. a a 61 2B. Hàm số lôgarit
Câu 48. Cho log 27  a .Biểu diễn log 16 theo a 12 6 4(3  a) 3  a 8a 4 A. log 16  B. log 16  C. log 16  D. log 16  6 6 6 6 3  a 3  a 3  a 3  a Câu 49. Đặt log
3  a . Hãy biểu diễn log 15 15 25 theo a. 1 1 a A. log 15  B. log 15  25 25 21 aa 1 2 C. log 15  log 15  25 1 D. 25 a 1 a .
x log 3.log x 1 Câu 50. Cho x 7 log 63  x 140
log 3.log 5.log x x log x  xác định . 1 x 3 7 7 A. x  2 B. x  4 C. x  3 D. x  5 1
Câu 51. Rút gọn biểu thức A  log 7  2 log 49  log 1 9 3 7 3 A. A = 3log 7 B. A = log 7 C. A = 2 log 7 D. A = 4 log 7 3 3 3 3
Câu 52. Cho log 5  ; a log 5  b log 5 2 3 . Khi đó 6 tính theo a và b là: 1 ab 2 2 A. a b a b
B. a b C. a + b D.Câu 53. Cho log 15 , a log 10
b . Giá trị của biểu thức P
log 50 theo a và b bằng: 3 3 3 A. P a b 1 B. P a b 1 C. P 2a b 1 D. P a 2b 1 Câu 54. Với m log 2 , n log 5 thì log 5 bằng: 6 6 3 n n n n A. B. C. D. m m 1 m 1 1 m Câu 55. Nếu a log 6, b log 7 12 12 thì log 7 2 bằng a b a a A. B. C. D. b 1 1 a b 1 a 1
Câu 56. Cho biết log 3  ;
a log 5  b . Hãy biểu diễn log 1350 30 30 30 theo a và b: A. 2a + 2b + 1 B. a + b + 1 C. 2a + b + 1 D. 2a + b
Câu 57. Cho biết log 3  ;
a log 2  b . Biểu diễn log
30 theo a và b là 125 1 2a 2a A. log 30  B. log 30  125 b 125 1 b 1 a 1 a C. log 30  log 30  125 1 D. b 125 3(1 b)
Câu 58. Biết a  log 2, b  log 3 thì log 0,018 tính theo a và b bằng 2b a A. .
B. 2b a  3.
C. 2b a  2.
D. 2a b  2. 2 62 2B. Hàm số lôgarit
Câu 59. Tìm x thỏa mãn log x  4 log a  7 log b với a  0;b  0 ta được: 3 3 3 A. 4 7 x a b
B. x  4a  7b C. x  4 . a 7b D. x  . a b
Câu 60. Đặt a  log 7 ; b  log 3 . Hãy biểu diễn log 147 theo a và b. 2 7 42 a 2  b 2  b A. log 147  B. log 147  42 a  b 1 42 1 ab  a b2  a a 2  b C. log 147  D. log 147  42 1 ab  a 42 1 ab  a
Câu 61. Cho log 7  ;
a log 5  b . Tính log 6,125? 25 2 5 3 3 3
A. 4a  3b B. 4a C.  4a D. 4a b b b
Câu 62. Nếu log 2  m và ln 2  n thì: n m 1 n m A. ln 20  1 B. ln 20  C. ln 20 
n D. ln 20   m m n m n
Câu 63. Cho a  log m với m  0 và m  1 và A  log (8m) . Khi đó mỗi quan hệ giữa A 2 m và a là: 3  a 3  a A. A
B. A  (3  a)a C. A
D. A  (3  a).a a a a b
Câu 64. Cho a, b là hai số dương thỏa mãn a2 + b2 = 7ab thì log ( )bằng giá trị nào sau 7 3 đây: 1 1 A. log a log b B. (log a log b) 7 7 2 7 7 2 1 a b C. log a log b D. log log 7 7 2 7 7 3 3
Câu 65. Giả sử ta có hệ thức a2 + b2 = 7ab (a, b > 0). Khi đó a b A. 2log
a b  log a  log b B. 2 log log a log b 2   2 2 2 2 2 3 a b a b C. log 2 log a log b D. 4 log log a log b 2 2 2 3 2 2 2 6 log 4
Câu 66. Giá trị của a a
(a  0, a  1) bằng: 1 A. 2 B. 16 C. 2 D. 4
Câu 67. Giá trị của log a (a  0, a  1) bằng: 3 a 1 1 A. B.C. 3 D. 3 3 3
Câu 68. Tính P  log x .log
x , biết x và x là hai nghiệm của phương trình 1 2 7 7 1 2 2
 log x 10log x e  0 . 7 7 4e 2e e e A. P      B. PC. PD. P 4 63 2B. Hàm số lôgarit
Câu 69. Nếu log x  5 log a  4 log b (a, b > 0) thì x bằng: 2 2 2 A. 5 4 a b B. 4 5 a b C. 5a + 4b D. 4a + 5b
Câu 70. Biết log 18  a, log 54  b thì ab  5a b bằng: 12 24 A. 0 B. 2 C. 3 D. 1 Nguyễn Văn Lực
www.facebook.com/VanLuc168
Bài tập tổng hợp 5 3 4 5 Câu 71. Nếu 5  3 a a và log  log b 5 b 6 thì
A. 0  a  1, b  1
B. 0  a  1, 0  b  1
C. a  1, b  1
D. a  1, 0  b  1
Câu 72. Cho hàm số y = log x
a . Trong các mệnh đề sau mệnh đề nào sai:
A. Hàm số có tập xác định D
B. Hàm số đồng biến trên (0; + )  khi a > 1 1 C. x
 > 0 hàm số có đạo hàm y' = xlna
D. Đồ thị hàm số luôn nhận trục tung làm tiệm cận đứng
Câu 73. Chọn khẳng định sai trong các khẳng định sau:
A. ln x  0  x  1
B. log x  0  0  x  1 2
C. log a  log b a b  0
log a  log b a b  0 1 1 D. 1 1 3 3 2 2
Câu 74. Trong các khẳng định sau, khẳng định sai là 1 A. log 5 0 B. log 4 log 3 3 4 3 C. log 2007 log 2008 D. log 0, 8 0 2 2 x 3 x 3 0,3
Câu 75. Cho a, b là các số thực dương ; a,b 1 và a.b 1. Khẳng định sai là A. log (ab) 1 log b B. log (ab) 1 log b 1 a 1 a a a 1 1 C. log a D. log b ab 1 log b 2 a 2 log a a b Câu 76. Cho , a ,
b c  0 và a  1. Khẳng định nào sau đây là khẳng định sai? 1 A. 2 log bc  log b . c log bc
log b  log c . a a B. aa a  2 1 C. log bc  .
log bc log b log c. a log a D.   a a a bc 64 2B. Hàm số lôgarit
Câu 77. Cho các số thực dương a, b, với a  1. Khẳng định nào sau đây là khẳng định đúng? A. log  2 3 a b  2log ab  log b 2 3 log a b  2  3log b a   a   a  B. a   a C. log  2 3 a b  2log b  3log ab D. log  2 3 a b  6 1 log b a   a  a  a a  
Câu 78. Cho các số thực dương a, b với a  1. Khẳng định nào sau đây là khẳng định đúng? a 1 a A. log  log b B. log  2  2log b 2 2 b 2 a a a a b a 1 a 1 1 C. log  log b D. log   log b 2 2 b 4 a a b 2 2 a a
Câu 79. Cho a,b dương và a  1 . Các khẳng định nào sau đây đúng: 1 1 A. log ( .
a b)  3  3log b B. log ( . a b)   log b 3 a a 3 3 3 a a 1 C. log ( . a b)  log b D. log ( .
a b)  3log b 3 3 3 a a a a
Câu 80. Cho 0  a  1 và 1     . Khẳng định nào sau đây là khẳng định đúng?        
A. a a  1.
B. a  1  a .
C. 1  a a .
D. a a  1. 1 1   2 2016 Câu 81. Nếu 2 3 (a 1)  (a 1) và log  log
thì khẳng định nào sau đây là đúng? b 3 b 2017 A.             0 a 1;b 1 B. 0 a 1;b 1 C. 1 a 2;b 1 D. 1 a 2;b 1    3   4 
Câu 82. Cho hai số thực a và b, với 5 4 aa và log  log
. Khẳng định nào dưới đây b      4 b   5  là khẳng định đúng?
A. a  1; b  1
B. a  1; 0  b  1
C. 0  a  1; b  1
D. 0  a  1; 0  b  1
Câu 83. Cho a, b, c >0; a; c; a.b  1. Khẳng định nào dưới đây là khẳng định đúng ? log c log c A. a  1 log b B. a  1 log c log a c log a c ab ab log c log c C. a  1 log b D. a  1 log c log a c log a c ab ab
Câu 84. Tìm mệnh đề đúng trong các mệnh đề sau :
A. Hàm số y = log x với 0 < a < 1 là một hàm số đồng biến trên khoảng (0 ; +) a
B. Hàm số y = log x với a > 1 là một hàm số nghịch biến trên khoảng (0 ; +) a
C. Hàm số y = log x (0 < a  1) có tập xác định là a
D. Đồ thị các hàm số y = log x và y = log x (0 < a  1) đối xứng nhau qua trục hoành. a 1 a 65 2B. Hàm số lôgarit
Câu 85. Khẳng định nào sau đây là khẳng định đúng? x  1 
A. Đồ thị hàm số x
y a và y    đối xứng nhau qua trục hoành. a
B. Đồ thị hàm số y  log x và y  log x đối xứng nhau qua trục tung. a 1 a
C. Đồ thị hàm số y  log x và x
y a đối xứng nhau qua đường thẳng y  . x a
D. Đồ thị hàm số x
y a và y  log x đối xứng nhau qua đường thẳng y   . x a
Câu 86. Trong các mệnh đề sau, mệnh đề nào đúng A. log  2
x  5  log  2 x  7  0, x   3 1  3 B. log  2
x  5  log  2 x  7  0, x   3 1  3 C. log  2
x  5  log  2 x  7 , x   3 3  log  2 x  5 3  5 D.x   log  , 2 x  7 7 3 
Câu 87. Cho x, y là các số thực dương thỏa mãn 2 2
9 ln x  4 ln y  12 ln . x ln .
y Đẳng thức nào sau đây là đúng? A. 2 3 x y
B. 3x  2 y C. 3 2 x y
D. x y
Câu 88. Cho các số thực dương a, ,
b x,y , với a
1 . Khẳng định nào sau đây là khẳng định đúng? x log x 1 1 A. log a B. log a y log y a x log x a a C. log (x y) log x log y D. log x log a.log x a a a b b a
Câu 89. Cho a > 0 và a  1, x và y là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau: x log x 1 1 A. a log  B. log  a y log y a x log x a a C. log x  y  log x  log y
D. log x  log a. log x a   a a b b a
Câu 90. Cho các số thực dương a, x, y với a  1. Khẳng định nào sau đây là khẳng định sai?
A. log (xy)  log x  log y B. 2
log (xy )  2log x  log y a a aa a a 1 C. log x  log x D. 2
log (xy )  log x  2 log y a 2 a a a a Câu 91. Cho a 1 . Khẳng định sai là A. log x 0 khi x 1 a B. log x 0 khi 0 x 1 a C. Nếu x x x 1 < x2 thì log log a 1 a 2
D. Đồ thị hàm số y
log x có tiệm cận ngang là trục hoành a 66 2B. Hàm số lôgarit
Câu 92. Cho a >0, b > 0 thỏa mãn 2 2
a b  7a .
b Chọn mệnh đề đúng trong các mệnh đề sau: 3 A. log(a b)  (loga logb)
B. 2(loga logb)  log(7 ab) 2 1 a b 1 C. 3log(a b)  (loga logb) D. log  (loga logb) 2 3 2 1 1 1 1 Câu 93. Cho    ... 
M ( với1  a  0, x  0 ). M thỏa mãn log x log x log x log x 2 3 k a a a a biểu thức nào sau đây: k(k 1) k(k 1) A. M B. M  log x 2log x a a 4k(k 1) k(k 1) C. M D. M  log x 3log x a a
Câu 94. Chọn khẳng định sai trong các khẳng định sau:
A. ln x  0  x  1
B. log x  0  0  x  1 2
C. log a  log b a b  0 1 1 3 3
D. log a  log b a b  0 2 2
Câu 95. Chọn khẳng định đúng trong các khẳng định sau: 1 A. log 7  0 B. log 4  log 1 3 4 3 5 C. log 0,5  0 D. log 5  0 0,2 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B 2B 3A 4A 5A 6D 7C 8A 9A 10B
11C 12C 13A 14C 15B 16A 17B 18C 19A 20B
21D 22D 23A 24B 25A 26C 27D 28B 29B 30C
31D 32A 33D 34B 35D 36C 37D 38B 39A 40A
41A 42A 43D 44A 45A 46A 47C 48A 49A 50A
51A 52B 53A 54D 55B 56C 57D 58B 59A 60D
61B 62C 63A 64B 65B 66B 67A 68A 69A 70D
71A 72A 73A 74D 75A 76D 77B 78D 79B 80A
81D 82C 83C 84D 85C 86A 87C 88D 89A 90B 91D 92D 93B 94C 95D 67
2C. Phương trình mũ PHƯƠNG TRÌNH MŨ
Câu 1. Giải phương trình: 2x 1 2  8 . 5 A. x  1 B. x C. x  2 D. x  4 2
Câu 2. Nghiệm phương trình: là 1 A. x = 1 B. x = 2 C. x = 3 D. x 3  
Câu 3. Giải phương trình 2 x 4 2 2 .5 x  1?
A. x  2; x  2   log 5 B. x  2; 2
C. x  2  log 5 D. x  2   log 5; x  1 2 2
Câu 4. Số nghiệm của phương trình 2 3 . x 2x 1 là: A. 0 B. 1 C. 2 D. 3 x x
Câu 5. Phương trình 3 3 .2 576 có nghiệm là A. 4 B. 3 C. 2 D. 1 2  
Câu 6. Cho phương trình x 5x 6 2
 1. mệnh đề đúng là :
A. Phương trình có 2 nghiệm dương phân biệt
B. Phương trình có 2 nghiệm trái dấu
C. Phương trình có nghiệm x = 6
D. Tổng các nghiệm của phương trình bằng 4      
Câu 7. Nghiệm của phương trình 2 2 2 x 3x 2 x 6 x 5 2 x 3x 7 4  4  4 1 là
A. x  1; x  2 và x  5
B. x  1; x  2 và x  4
C. x  0; x  2 và x  6
D. x  1; x  2 và x  5
Câu 8. Tập nghiệm phương trình 2 2 2 x 2 x x x2 2 x x2 4  4 1 4 là: A. S  0; 1  ;1;  2 . B. S  0; 2  ; 1  ;  2 . C. S   2  ; 1  ;1;  2 . D. S  0; 1  ;1;  3 .
Câu 9. Số nghiệm của phương trình 2 2 x x 2 x x 2 2 3 A. 2 B. 3 C. 1 D. 4
Câu 10. Tìm số nghiệm của phương trình 3  x 3 3 .2 x 3  .2 x x  2  0 . A. 1. B. 3. C. 2. D. 4. x x
Câu 11. Phương trình 2 1 3 4.3 1
0 có 2 nghiệm x ,x trong đó x x . Khi đó 1 2 1 2 A. x x 2 B. x .x 1 C. x 2x 1 D. 2x x 0 1 2 1 2 1 2 1 2 x x
Câu 12. Nghiệm của phương trình 9  4.3  45  0 là 1 1 A. x  2 B. x  3 C. x x 2 D.  3 68
2C. Phương trình mũ x x 1
Câu 13. Giá trị x thỏa mãn phương trình:  49  7  8  0 là A. x  0. B. x  log 8. x 0 x log 8. x 0 x log 7. 7 C.  và  7 D.  và  8
Câu 14. Tìm m để phương trình 4x - 2x + 3 + 3 = m có đúng 2 nghiệm x (1; 3).
A. - 13 < m < - 9 B. 3 < m < 9 C. - 9 < m < 3 D. - 13 < m < 3 x x
Câu 15. Phương trình 4  2  2  0 có nghiệm x bằng: A. 1 B. 1 và -2 C. -2 D. 0
Câu 16. Giải phương trình 4x - 6.2x + 8 = 0. Ta có tập nghiệm bằng: A. {2, 4}. B. {1, 2}. C. {- 1, 2}. D. {1, 4}. x x x
Câu 17. Số nghiệm của phương trình 6.9 13.6 6.4 0 là: A. 2 B. 1 C. 0 D. 3 2 lg x 1 lg x lg x 2
Câu 18. Giải phương trình 4 6 2.3
0 ta được tổng tất cả các nghiệm của phương trình là: 2 9 1 A. B. 0 C. D. 9 4 100
Câu 19. Tìm số nghiệm của phương trình x 42x 4.2  ( 2) 15 A. 2 B. 3 C. 1 D. 0 x x
Câu 20. Cho phương trình 1 3.25 2.5 7 0 và các phát biểu sau: (1) x
0là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả hai nghiệm phương trình đều nhỏ hơn 1 3
(4) Phương trình có tổng hai nghiệm là log 5 7
Số phát biểu đúng là: A. 1 B. 2 C. 3 D. 4 Câu 21. x
log 3 là nghiệm của phương trình nào trong các phương trình sau? 2  x A. log  2 x 1 3.3  4  xlog 3 log 9 B. x x     3 2 1 3 8 2 3 2 2  2 4 xC. x x     3 2 1 3 8 2 2 D. log  2 x 1 2.2 1  4 2 
Câu 22. x  3 không là nghiệm của phương trình nào trong các phương trình sau? xxA. 2 4 1 3  2.3  27  0. B. log
x 1  2 log (x  2)  2. 4 2 xxC. 2 1 1 3  2.3 1  0. D. 2
log x  log (2x 1)  log (4x  3). 4 2 2 2 x 2 x
Câu 23. Tìm nghiệm của phương trình     x 1 3 5 3 5 6.2      . x  0 x  0 x  1 x  2 A. B.C.D.  x  1  x  1 x  1  x  2  69
2C. Phương trình mũ x x x x
Câu 24. Giải phương trình: 3 5 10 3 15.3 50 9
1,ta được tổng tất cả
các nghiệm của phương trình là: A. 4 log 6 B. 2 log 6 2 3 1 1 C. 1 log 5 D. log 3 7 2 7 3
Câu 25. Giá trị m để phương trình 4x  4 2x m   1  0 có nghiệm là m  0 1 1 A.
B. 0  m  1 C. m D.m  2 m  1 2 2
Câu 26. Phương trình : 4x  2 .2x m
m  2  0 có hai nghiệm phân biệt khi: A. m  2
B. 2  m  2 C. m  2 D. m   2 log 100x  log10x 1log x
Câu 27. Cho phương trình 4.3  9.4  13.6 . Gọi ,
a b lần lượt là hai nghiệm của phương trình. Tìm tích . ab 1 A. ab  . ab ab ab  10 B. 1. C. 100. D. 10. Câu 28. Tính x x 1 x 2 5 5x S  
, biết x và x là hai nghiệm của phương trình 25  6.5  5  0 . 1 2 A. S  6 B. S  1 C. S  2 D. S  3 
Câu 29. Phương trình 5
2016x x  2017 có mấy nghiệm? A. 1 B. 0 C. 2 D. 3
Câu 30. Tìm tất cả các giá trị của tham số m để phương trình 2x  2 x e
e m có nghiệm. A. m  1
B. 1  m  0
C. 1  m  0 D. m  1
Câu 31. Nghiệm của phương trình 6x 3 3. x e e  2  0 là: 1 1
A. x  0  x   ln 2
B. x  0  x  ln 3 3 3 1 1
C. x  0  x  ln 2
D. x  0  x  ln 3 3 2    
Câu 32. Phương trình : x x 1 x 2 x x 1 x 2 2  2  2
 3  3  3 có nghiệm: A. 2 B. 3 C. 4 D. 5 x
Câu 33. Nghiệm của phương trình 3 2 (0, 3) 1 là: 2 2 A. x 0 B. x 1 C. x D. x 3 3  
Câu 34. Phương trình 2x 3 4 4  8 x có nghiệm: 6 2 4 A. B. C. D. 2 7 3 5 1C 2D 3A 4C 5C 6A 7A 8B 9A 10A
11C 12A 13B 14A 15D 16B 17A 18D 19C 20A
21B 22C 23C 24B 25A 26C 27B 28A 29A 30A 31C 32A 33C 34A 70
2D. Phương trình lôgarit
PHƯƠNG TRÌNH LÔGARIT
Câu 1. Giải phương trình log (3x 2) 3. 2 11 10 A. x B. x C. x 3 D. x 2 3 3
Câu 2. Giải phương trình log (x 1)  3 . Ta có nghiệm là: 3 A. x  29 B. x  28 C. x  82 D. x  81
Câu 3. Phương trình: log (2x  8)  2 có tập nghiệm là 4 A. S  . B. S  {4}. C. S  {12}.
D. S  {4;12}.
Câu 4. Giải phương trình : log 3x 1  1  4 2 13 17 20 A. x = 5 B. x  C. x  D. x  3 3 3 2
Câu 5. Tập nghiệm của phương trình log 5x 21 4 là 2     A.  5; 5 B. 5;  5 C. log 5;log 5 2 2  D.
Câu 6. Phương trình log
x  2 có nghiệm x bằng: 3 A. 1 B. 9 C. 2 D. 3
Câu 7. Nghiệm của phương trình log (2x 1)  2 là: 3 A. Vô nghiệm B. 1 C. 2 D. 3 Câu 8. Nếu log 243 5 thì x bằng x A. 2 B. 3 C. 4 D. 5
Câu 9. x  log 2 là nghiệm của phương trình nào trong các phương trình sau ? 3 x xxA. log (3  ) 1  log (3 2  ) 9  3
B. 3.3 2  3x  1  0 3 3 x xC. log (3  ). 1 log (3 2  ) 9  3
D. log (3x  ). 3 log (3x  ) 9  3 3 3 3 3
Câu 10. Giải phương trình : log (x  3)  log (x 1)  log 5 : 2 2 2 A. x = - 4 B. x = 2. C. x = 4
D. x = -4; x = 2
Câu 11. Giải phương trình log x log (x 1)
1 ta được số nghiệm là: 2 2 A. 2 B. 0 C. 1 D. 4
Câu 12. Giải phương trình log x  log (x  3)  log 4 2 2 2 A. x = 1 B. x = -4 C. x = 1; x = -4 D. x = 0
Câu 13. Số nghiệm của phương trình 2
log x  4 log 3x  7  0 là: 3 3   A. 1 B. 2 C. 3 D. 0
Câu 14. Nghiệm của phương trình 2
log (x 1)  log (2x 1)  2 là: 3 3 A. Vô nghiệm B. 1 C. 2 D. 3 71
2D. Phương trình lôgarit
Câu 15. Phương trình  2
log x  2x  7  1 log x có tập nghiệm là A.  1  ;  7 . B. 1;  7 . C.   1 . D.   7 .
Câu 16. Tổng các nghiệm của phương trình 2
lg x  lg x log
4x  2log x  0 là : 2   2 A. 101 B. 100 C. 5 D. 0 1 1
Câu 17. Tìm nghiệm của phương trình   1 a  . 4  log x 2  với 1 log x a a  1  1  1 x   x x  x  1 2   a a aA. B. C.D. 1 1  1  1  x x x x  2  4  a a 4  a 2  a
Câu 18. Phương trình
 2x x   2 ln 2 2 
x  2  1 có mấy nghiệm? A. 0 B. 1 C. 2 D. 3
Câu 19. Tìm tất cả các giá trị của tham số m để phương trình 2 2
log x  log x 1  2m 1  0 có 3 3 nghiệm nằm trong 3 1  ;3    . 3 3
A. 0  m  2
B. 0  m  2 C. 1  m D. 0  m  2 2
Câu 20. Nghiệm của phương trình: log 6.2x 3 log 4x    4 1 là: 3   3   A. x  log 6 B. x  log 3 C. x  log 2
D. x   log 3 2 2 3 2
Câu 21. Phương trình ln x  ln  x   1  0 có nghiệm là: 1 5 1 5 x x 2 A. 2 B. 1 5 1 5 x x 2 2 1 5 1 5 x x 4 4 C. D. 1 5 1 5 x x 4 4 Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B 2B 3C 4A 5A 6D 7C 8D 9C 10B
11C 12A 13B 14C 15B 16A 17C 18A 19A 20B 21A 72
2E. Bất phương trình mũ
BẤT PHƯƠNG TRÌNH MŨ
Câu 1. Giải bất phương trình: 2x3x 3  81 có nghiệm là: A.      4   x  1 B. x 1; x 4
C. 1  x  4 D. x 4; x 1  x2  log1   x Câu 2  
. Tập nghiệm của bất phương trình 3 5  1 là A. 2; B. ;0 C. 0;2 D. 0; Câu 3. x x Giải bất phương trình 1 2 3 . A. x log 3 B. x log 3 2 2 3 C. x log 3 D. x log 2 2 2 3 3 Câu 4   . Giải phương trình 2 x x x 1 5  25 A. [-1;2] B. (-1;2) C. [-1;2) D. (-1;2]
Câu 5. Bất phương trình : 9x 3x
  6  0 có tập nghiệm là: A. 1; B.   ;1  C.  1  ;  1 D. Kết quả khác. Câu 6 x x
. Nghiệm của bất phương trình 1 3 9 36.3 3 0 là: A. 1 x 3 B. 1 x 2 C. 1 x D. x 3 Câu 7
. Tập nghiệm của bất phương trình 2x 2 3
 2.6x  7.4x  0 là:
A.S   1; +
B.S    1  ; 0
C.S   0; +
D.S    ;    1 x x 1    Câu 8 4 2 8
. Tìm nghiệm của bất phương trình  8x . 1 2 xx  1  x  0 A. x  1 B.C. x  0 D.  x  2  x  2  3x x 1 
Câu 9. Số nghiệm nguyên của bất phương trình   x 1    x3 10 3 10 3 là A. 0 B. 1 C. 2 D. 3 2 x 2x 3
Câu 10. Bất phương trình  2 
  2  có tập nghiệm là: A.           ( ; 1) (3; ) B.  1;3 C.  1;  3 D. ( ; 1] [3; ) x Câu 11. 2 2
Nghiệm của bất phương trình x 1
8 .2 x   2 là:
A. x  1 2.
B. x  1 2.
C. 1 2  x  1 2.
D. x  1 2 hoặc x  1 2. 73
2E. Bất phương trình mũ
Câu 12. Cho hàm số   3 x 2x f x  3 .4
. Khẳng định nào sau đây là khẳng định sai? A. f x 3 1  x  4x log 2  0 B. f x 3
1  x  x .log 16  0 3 3 C. f x 3 1  x log 3  2x  0 D. f x 3 1  xlog 3 2x  0 2 2 x  
Câu 13. Giải bất phương trình 1  25   .  5  A. x  2 B. x  2 C. x  2 D. x  2
Câu 14. Giải bất phương trình 2 x x2 x 1 3 9   .
A. 0  x  3
B. x  0 hoặc x  3 .
C. 1  x  0
D. 0  x  1
Câu 15. Tìm tất cả các giá trị của tham số m để bất phương trình 9x  .3x m
1  0 có nghiệm. A. m  2 B. m  2 C. m  2 D. m  2
Câu 16. Giải bất phương trình: 2 log5 x log5 5 xx
10 ta được nghiệm là 1 1 A.x  5
B. 5  x
C. 1  x  5 D. Vô nghiệm 5 5 2x 1 x 2 3 5
Câu 17. Bất phương trình có nghiệm là: 5 3
A. x 3; 
B. x   ;1
C. x 1;  D. x   ;   Nguyễn Văn Lực
www.facebook.com/VanLuc168 1A 2B 3B 4A 5B 6B 7C 8A 9D 10C
11C 12D 13A 14A 15A 16A 17C 74
2F. Bất phương trình lôgarit
BẤT PHƯƠNG TRÌNH LÔGARIT
Câu 1. Giải bất phương trình log (x  2)  3 2 A.  S   ;  10  S  10;  S  [10; ) B.   C. S  ( ;10] D.  
Câu 2. Giải bất phương trình 2 log (2x x ) 0 . 2 A. x 2 B. 0 x 2 C. 0 x 2 D. x 1
Câu 3. Nghiệm bất phương trình log 2x 1  2 là 3   A. x 2 B. x 3 C. x 4 D. x 5
Câu 4. Nghiệm của bất phương trình log 2x 1  3 là 3   A. x > 4. B. x > 14. C. x < 2. D. 2 < x < 14.
Câu 5. Giải bất phương trình: log (2x  15)  2 5 . 15 15 15  A.   x  5 B. x   C. x  5 D. x  5 2 2 2
Câu 6. Tập nghiệm của bất phương trình log  2
x  5x  7  0 là: 1  2 A. ;2 B. 2;3 C. 2; D.  ;  2  3;
Câu 7. Nghiệm bất phương trình log  2
x  3x  2  1 là 1  2 A. x ( ;1) B. x [0;2) C. x [0;1) (2; 3] D. x [0;2) (3; 7)
Câu 8. Giải bất phương trình: log 2x  7  3  1   3 7 7 A. x  10
B. x  10 C.   x  10 D.   x  10 2 2
Câu 9. Tìm m để bất phương trình log  2
x  4x  20  m luôn nghiệm đúng với mọi giá trị của x : 2  A. m  4 B. m  4 C. m  16 D. m  16
Câu 10. Bất phương trình: log 3x  2  log 6  5x có tập nghiệm là: 2 2  6   1  A. (0; +) B. 1;  C.  ;3 D.  3  ;  1  5   2  x
Câu 11. Tập nghiệm của bất phương trình 2 log x  log  4 2 2 4 là:  1 1  A. S   ;   2;    . B. S  ;4 .    2 2   1  1 C. S  0;  3;    . D. S  0;  4;    .  2  2 75
2F. Bất phương trình lôgarit
Câu 12. Bất phương trình 2 log x  log
x  6 có tập nghiệm là 6 6   A.  2  ;3. B.  3  ;2 \  0 . C.  2  ;3 \  0 . D.  ;  2   3;.
Câu 13. Chọn đáp án đúng khi nói về bất phương trình: 2
log (2x x 1)  2
log (x  4x  5) 1 1 2 2
A. Bất phương trình có nghĩa khi: x  5 .
B. Tập nghiệm S  (1; 4] .
C. Bất phương trình có nghĩa khi: x  1.
D. Tập nghiệm S  ;  1 (4;).
Câu 14. Tập nghiệm của bất phương trình log x  1  2log 5  x  1  log x  2 là: 2   4   2  
A. S  3;5
B. S  2;3
C. S  2;5 D. S   4  ;3
Câu 15. Gíá trị của m để bất phương trình 2 2 log (7x 7) log (mx 4x )
m có tập nghiệm R 2 2 là: A. m [5; ) B. m ( ; 5] C. m (2;5] D. m ( ; 0) (2; )
Câu 16. Tìm tất cả các giá trị của tham số m để bất phương trình 2
lg x m lg x m  3  0 có
nghiệm nằm trong 1; .
A. m  3 hoặc m  6 . B. m  3 C. m  6
D. 3  m  6
Câu 17. Nghiệm của bất phương trình log (2 x) 1 là: 1 3 5 5 5 5 A. x 2 B. x C. x D. x 2 3 3 3 3
Câu 18. Tập nghiệm của bất phương trình 2 log (x 2x 8) 4 là: 1 2 A. T   6  ; 4    2;4 B. T   6  ; 4    2;4 C. T   6  ;4
D. T   ;  6   4;
Câu 19. Bất phương trình log 3x  2  0 có nghiệm là: 2   A. x 1 B. x 1 C. 0 x 1 D. log 2 x 1 3
Câu 20. Tập nghiệm của bất phương trình log  2
2x x 1  0 là: 2  3  3   3      A. 1  ;   B. 0;   C.   1 ;0  ;    D.    3 ; 1  ;            2 2 2 2   1 
Câu 21. Nghiệm của bất phương trình: 2 log log x     1 là: 3 1   16  2  1 3 1 1 3 1 3 3 A.   x B.   x C.   x D.   x  4 4 4 4 4 4 4 4 1D 2D 3C 4B 5D 6B 7C 8C 9A 10B
11D 12C 13B 14B 15C 16A 17A 18A 19B 20C 21B 76 3A. Nguyên hàm NGUYÊN HÀM
Hàm đa thức, phân thức x
Câu 1. Nguyên hàm của hàm số f(x) 2  3x  là: 2 2 x 3 2 x x 2 x 2 x A. 3 x   C B.   C C. 3 x   C D. 3 x   C 4 3 4 2 2 5 3  x
Câu 2. Tìm nguyên hàm của hàm số f x 2  x  1 18  6 6 3  x  3  xA. f
 xdx   1 C B. f
 xdx  6 1 C 18  18  6 6 3 1  x  3 1  xC. f
 xdx   1 C D. f
 xdx   1 C 6 18  2 18  Câu 3. Nếu ' 2
f (x)  3(x  2) , f (0)  8 thì hàm số y f (x) là hàm số nào sau đây? A. 3 2(x  2)  8.
B.x  2 2  4
C. 6  x  2  4
D.x  3 2
Câu 4. Giá trị m để hàm số F(x) =mx3 +(3m+2)x2-4x+3 là một nguyên hàm của hàm số f x  2
( ) 3x 10x  4 là: A. m = 3 B. m = 0 C. m = 1 D. m = 2 1
Câu 5. Nguyên hàm của I   dx 3 x là 1 1 1 2 3 A.   C C x C ln | x | C 2 2x B.  4 x C.   2 D.  2 x x 1
Câu 6. Tìm nguyên hàm của hàm số f (x) . x 1 1 1 A. f (x)dx x C B. f (x)dx 1 C x 1 2 (x 1) 2 x 2 C. f (x)dx ln x 1 C D. f (x)dx x ln x 1 C 2 1
Câu 7. Tìm nguyên hàm của hàm số f (x)  2 x  3x  2 x  2 x  2 A.
f (x)dx  ln  CB.
f (x)dx  ln  Cx 1 x 1 x 1 x 1 C.
f (x)dx  ln  CD.
f (x)dx  ln  Cx  2 x  2 77 3A. Nguyên hàm 4 3 x 2x 1
Câu 8. Cho hàm số f (x)
. Nguyên hàm F(x) của f(x) biết làF(1) 2 2 x 3 x 3 2 1 5 x 2 1 5 A. x B. x 3 x 3 3 x 3 3 x 3 2 1 5 x 2 1 C. x D. x 9 3 x 3 3 x x(2 x)
Câu 9. Hàm số nào sau đây không là một nguyên hàm của hàm số y 2 (x 1) 2 x x 1 2 x x 1 A. y B. y x 1 x 1 2 x 2 x x 1 C. y D. y x 1 x 1 b
Câu 10. Tìm hàm số f(x) biết rằng f '(x)  ax+ , f '( ) 1  , 0 f ( ) 1  , 4 f ( ) 1  2 2 x 2 2 x 1 5 x 1 5 A.   B.   2 x 2 2 x 2 2 x 1 5 C.   D. Kết quả khác 2 x 2 2 ax a  3 6 
Câu 11. Tìm a để hàm số F (x) 
là một nguyên hàm của hàm số f (x)  x  2 x 22 A. a  1
B. a  1 hoặc a  3 C. a  3
D. a  1 hoặc a  3 x 1
Câu 12. Tìm nguyên hàm F x của hàm số f (x)  2 x 1 1
A. F(x)   ln x   C F(x) ln x C x B.    x 1 1
C. F(x)  ln x   C F(x) ln x C x D.     x
Câu 13. Tìm nguyên hàm của hàm số f x   x  5 ( ) 3 1 1 1 A.
f (x)dx   3x  6 1  C B.
f (x)dx   3x  6 1  C 3 18 1 1 C.
f (x)dx   3x  5 1  C D.
f (x)dx   3x  6 1  C 18 6 Nguyễn Văn Lực
www.facebook.com/VanLuc168 78 3A. Nguyên hàm Hàm căn thức  3 
Câu 14. Nguyên hàm của hàm số 2 x   2  x dx là  x  3 x 4 3 x 4 A. 3  3ln x x C B. 3  3ln x x 3 3 3 3 3 x 4 3 x 4 C. 3  3ln x x C D. 3  3ln x x C 3 3 3 3
Câu 15. Nguyên hàm của hàm số f x 2  x 1 x dx  3 1 A. f
 xdx  1 x 3 2 2  C B. f
 xdx  1 x 3 2 2  C 2 3 2 1 C. f
 xdx  1 x 3 2 2  C D. f
 xdx  1 x 3 2 2  C 3 3
Câu 16. Tìm nguyên hàm của hàm số f (x)  3x+2 2 2 A. f (x) x d  
3x  2 3x+2 C B. f (x) x d  
3x  2 3x+2 C 9 3 9 3 C. f (x) x d  
3x  2 3x+2 C D. f (x) x d  
3x  2 3x+2 C 2 2
Câu 17. Một nguyên hàm của hàm số: 2 f (x) x 1 x là 2 1 3 1 2 2 A. F(x) 1 x B. F(x) 1 x 2 3 2 2 x 2 1 2 2 C. F(x) 1 x D. F(x) 1 x 2 3 3
Câu 18. Nguyên hàm của hàm số f (x)  3x 1 là: 1 A. f x dx x x    3 ( ) (3 1) 3 1 C B.
f (x)dx  3x 1   3 C 3 1 C.
f (x)dx  (3x 1) 3x 1   3 C f x dx x C 4 D.     3 ( ) 3 1 14
Câu 19. Họ các nguyên hàm của hàm số 3 2 y x là: 1 x 5 3 3 5 3 5 A. x 14 ln 1 x C B. x 14 ln 1 x C 3 5 3 3 3 5 3 5 C. x 14 ln 1 x C D. x 14 ln 1 x C 5 5 1
Câu 20. Nếu gọi I dx
, thì khẳng định nào sau đây là đúng? 1 x
A. I  2 x C. B. I  2 ln | x 1| C.
C. I  2 x  2 ln | x 1| C.
D. I  2 x  2 ln | x 1 | C. 79 3A. Nguyên hàm x d
Câu 21. Nếu gọi I  
, thì khẳng định nào sau đây là đúng? 2x 1  4 A. I
2x 1  2ln  2x 1  4  C. B. I
2x 1  ln  2x 1  4  C. C. I
2x 1  4ln  2x 1  4  C.
D. I  2 2x 1  ln  2x 1  4  C. dx
Câu 22. Tìm nguyên hàm I  .  x x 1
A. I  2 ln  x   1  C. B. I  2 ln  C. x 1  1  C. I  2 ln x   C.  
D. I  2 ln x x C.  x dx
Câu 23. Tìm nguyên hàm I   . 2x x x x 2 2 A. I    C B. I    C x x x 1 2 2 C. I    C D. I    C x x 1 2 x x
Câu 24. Hàm số nào sau đây là một nguyên hàm của hàm số 2 f (x) x k với k 0 ? x k 1 x A. 2 2 f (x) x k ln x x k B. 2 2 f (x) x k ln x x k 2 2 2 2 k 1 C. 2 f (x) ln x x k D. f (x) 2 2 x k 2 10x - 7x 2 Câu 25. Nếu 2 f (x) (ax bx
c) 2x -1 là một nguyên hàm của hàm số g(x) 2x -1 trên khoảng 1 ;
thì a+b+c có giá trị là 2 A. 3 B. 0 C. 4 D. 2
Câu 26. Xác định a, b, c sao cho 2 g(x) (ax bx
c) 2x - 3 là một nguyên hàm của hàm số 2 20x - 30x 7 f (x) trong khoảng 3 ; . 2x - 3 2 A. a  , 4 b  , 2 c  2 B. a  , 1 b   , 2 c  4 C. a   , 2 b  , 1 c  4 D. a  , 4 b   , 2 c  1
Câu 27. Trong các hàm số sau: (I) 2 f (x) x 1 (II) 2 f (x) x 1 5 1 1 (III) f (x) (IV) f (x) - 2 2 x 1 2 x 1
Hàm số nào có một nguyên hàm là hàm số 2 F (x) ln x x 1 A. Chỉ (I) B. Chỉ (III) C. Chỉ (II)
D. Chỉ (III) và (IV) 80 3A. Nguyên hàm 2 1
Câu 28. Một nguyên hàm của hàm số 3 f (x) x
là hàm số nào sau đây: x 3 3 12 1 1 A. 3 2 6 5 F (x) x x x ln x B. 3 F (x) x 5 5 3 x 2 3 12 C. 3 F(x) x x x D. 3 2 5 6 F (x) x x ln x x 5 5 x
Câu 29. Một nguyên hàm của hàm số f (x)  là : 2 2 a x A. 2 1 x B. 2 ln a x C. 2 2 a x D. 2 2 ln a x Nguyễn Văn Lực
www.facebook.com/VanLuc168 Hàm lượng giác
Câu 30. Nguyên hàm của hàm số  x 2 f  sin x là: x sin 2x x sin 2x x sin 2x x sin 2x A.   C B.   C C.   C D.   C 2 2 2 4 2 4 2 2
Câu 31. Tìm nguyên hàm của hàm số f(x) = sin(2x + 1) 1  A.
f (x)dx  cos(2x 1)  CB.
f (x)dx
cos(2x 1)  C  2 1 C.
f (x)dx
cos(2x 1)  CD.
f (x)dx   cos(2x 1)  C  2 
Câu 32. Tìm nguyên hàm F(x) của hàm số f(x)=1+ sin3x bieát F ( )  0 . 6 1  1 
A. F (x)  x  cos3x
B. F (x)   cos 3x  3 6 3 6 1  1 
C. F (x)  x  cos3x
D. F (x)  x  cos3x  3 6 3 6
Câu 33. Một nguyên hàm F(x) của hàm số   3 2
f x  2x  3x 1 sin 2x khi F(0)=1 là: A.   4 3 x x 1 1 F x  2  3  x  .cos 2x  B.   4 3 x x 1 1 F x  2  3  x  .cos 2x  4 3 2 2 4 3 2 2 C.   4 3 x x 1 1 F x  2  3  x  .cos 2x  D.   4 3 x x 1 1 F x  2  3  x  .cos 2x  4 3 2 2 4 3 2 2 81 3A. Nguyên hàm
Câu 34. Cho f ' (x)  3  5sin x và f (0)  10 . Trong các khẳng định sau, khẳng định nào đúng:
A. f (x)  3x  5cos x  2
B. f    3    3 C. f   
D. f (x)  3x  5cos x  2  2
Câu 35. Chọn công thức sai trong những công thức sau đây: A. cos x dx sin x C B. sin x dx cos x C 1 x x C. e dx e C D. dx tan x C 2 sin x
Câu 36. Kết quả của  2
1  cot xdx là
A. tan x C
B.  tan x C
C. cot x C
D.  cot x C
Câu 37. J = x cos xdx có kết quả là
A. xsinx – cosx + C
B. -xsinx – cosx + C
C. xsinx + cosx + C
D. xsinx - cosx
Câu 38. Nguyên hàm của hàm số f (x)  sin 3 . x o c s5x là 1 1 A.
f (x)dx  os c 2x  os
c 8x C  4 16 1 1 B.
f (x)dx  sin 2x  os
c 8x C  4 16 1 1 C.
f (x)dx  os c 2x  sin 8x C  4 16 1 1 D.
f (x)dx   os c 2x  os
c 8x C  4 16 1 1 1
Câu 39. Tìm nguyên hàm I  sin cos dx.  2 x x x 1 2 1 1 1 1 1 2 A. I  cos  C. I  sin  C. I  cos  C. I  sin  C. 4 x B. 4 x C. 4 x D. 4 x 1
Câu 40. Cho F(x) là một nguyên hàm của hàm số y
và F(0)=1. Khi đó F(x) là: 2 os c x A. –tanx B. 1-tanx C. 1+tanx D. tanx-1 x
Câu 41. Tìm nguyên hàm I   dx . 2 cos x
A. I x tan x+ ln cosx C
B. I x tan x+ ln sin x C
C. I x tan x-ln sin x C
D. I x tan x-ln cosx C 82 3A. Nguyên hàm sin x
Câu 42. Nguyên hàm F(x) của hàm số f x 3  là: 4 cos x 1 1 1 1 A.   C B.    C 3 3cos x cos x 3 3cos x cos x 1 1 1 1 C.   C D.   C 3 3cos x cos x 3 2 3cos x cos x 1
Câu 43. Tìm nguyên hàm của hàm số f x  . 2 2 sin x cos x A. f
 xdx  cot x tan xC. B. f
 xdx  cot x tan xC. C. f
 xdx  cot x tan xC. D. f
 xdx  cot x tan xC.
Câu 44. Tìm nguyên hàm  .  dx I 2
(cos x  sin x) 1    1    A. I   tan x   C.   B. I  tan x   C.   2  4  2  4  1    1    C. I   tan x   C.   D. I  tan x   C.   2  4  2  4  sinx  cos x  sinx 
Câu 45. Biết I dx A    B dx cos x  sinx  cos x
. Kết quả của A, B lần lượt là  sinx  1 1 1 1 1 1
A. A B  . A B . A ,B . A ,B . 2 B.    2 C.    2 2 D.    2 2
Câu 46. Một nguyên hàm của hàm số: 2
f (x)  x sin 1  x là: A. 2 2 2
F (x)   1  x cos 1  x  sin 1  x B. 2 2 2
F (x)   1  x cos 1  x  sin 1  x C. 2 2 2
F (x)  1  x cos 1  x  sin 1  x D. 2 2 2
F (x)  1  x cos 1  x  sin 1  x
Câu 47. Xét các mệnh đề 2 x x (I) F (x) x
cos x là một nguyên hàm của f (x) sin - cos 2 2 4 x 3 (II) F (x)
6 x là một nguyên hàm của 3 f (x) x 4 x (III) F (x)
tan x là một nguyên hàm của f (x) - ln cos x Mệnh đề nào sai ? A. (I) và (II) B. Chỉ (III) C. Chỉ (II) D. Chỉ (I) và (III)
Câu 48. Tìm nguyên hàm x 2 2 F (x) e (a tan x b tan x
c) là một nguyên hàm của x 2 3 f (x) e tan x trên khoản ; 2 2 x 1 2 1 x 1 2 2 A. 2 2 F (x) e ( tan x tan x ) B. 2 2 F (x) e ( tan x tan x ) 2 2 2 2 2 2 x 1 2 2 x 1 2 1 C. 2 2 F (x) e ( tan x tan x ) D. 2 2 F (x) e ( tan x tan x ) 2 2 2 2 2 2 83 3A. Nguyên hàm
Câu 49. Họ nguyên hàm của hàm số 2
f (x)  tan x là :
A. tan x x C
B. tan x x C
C.  tan x x C
D.  tan x x C
Câu 50. Họ nguyên hàm của hàm số 2
f (x)  x o
c s(x ) là : 1 1 A. s inx  C B.  s inx  C 2 2 1 1 C. 2  sin(x )  C D. 2 s in(x )  C 2 2
Câu 51. Tìm nguyên hàm F x của hàm số f(x)= 2 x sin xdx  1 1 1 1 A. 2 F (x) 
x x sin 2x  cos 2x C B. 2 F (x) 
x x sin 2x  cos 2x C 2 2 4 2 1  1  1 1
C. F x 2  x x  cos 2x C    D. 2 F (x) 
x x sin 2x  cos 2x C 4  2  4 2 Câu 52. Cho a
0 , C là hằng số, kết quả nào sau đây sai : 1 A. sin
 ax bdx   cosax b  C a 1 B. cos
 ax bdx   sinax b  C a  1  
C. ax bdx   
  ax b 1  C 1 ax b 1  D. ax b e dx eCa
Câu 53. Một nguyên hàm F(x) của hàm số f (x) sin 2x cos x là 1 A. F(x) cos 2x sin x B. F(x) cos 2x sin x 2 2 C. F(x ) cos 2x sin x D. F(x) sin x sin x  1 
Câu 54. Kết quả của I 2  x   sin 2x dx   là :  x  3 x 1 3 x 1 A.
 ln | x |  cos 2x C B.
 ln | x |  cos 2x C 3 2 3 2 3 x 1 3 x 1 C.
 ln | x |  cos 2x C D.
 ln | x |  cos 2x 3 2 3 2  Hàm mũ – lôgarit
Câu 55. Trong các phát biểu sau, phát biểu nào là sai: 1  xxx
A. y e
F(x)  e C B. y
F(x)  e C x e 1  xxx
C. y  e
F(x)  e C D. y  
F(x)  e C x e 84 3A. Nguyên hàm
Câu 56. Tìm nguyên hàm của hàm số f(x) = x.ex A. f (x)dx
= x.ex – ex + C B. f (x)dx
= xex + ex + C C. f (x)dx
= x.ex – ex D. f (x)dx
= ex - x.ex + C
Câu 57. Tìm nguyên hàm của hàm số 2 ( )  2 x f x xe . 2 2 A. ( ) 2   x f x dx e C B. 2 ( ) 2   x f x dx x e C 2 2 C. ( )    x f x dx e C D. ( ) 2   x f x dx xe C
Câu 58. Tìm nguyên hàm của hàm số f x 1  . x e 1
A.      ln  x f x dx x e   1  C
B.       ln  x f x dx x e   1  C
C.       ln  x f x dx x e   1  C
D.      ln  x f x dx x e   1  C
Câu 59. Tìm nguyên hàm của hàm số   x e f x  . x
A.     2 x f x dx eC B.    2 x f x dx eC x e C. f
 xdx   C D.    x f x dx eC 2
Câu 60. Trong các mệnh đề sau đây mệnh đề nào đúng ? xdx 1 (I) 2 ln(x 4) C 2 x 4 2 1 (II) cot xdx - C 2 sin x x 1 (III) 2cos 2cos sin - x e xdx e C 2 A. Chỉ (I) B. Chỉ (III) C. Chỉ (I) và (II) D. Chỉ (I) và (III) ln ln x
Câu 61. Họ nguyên hàm của hàm số f (x)  là : x ln x 2 ln ln 2x 2 ln ln xA.C B.C 2 2 2 2  2 ln ln x ln ln 2xC.   C D.C 2 2
Câu 62. Cho hàm số ( ) x
f x  xe . Định a, b để ( )  (ax  ) x F x
b e là một nguyên hàm của f(x) A. a  , 1 b  1 B. a   , 1 b  2 C. a  , 2 b  1 D. a   , 1 b  1 2  e
Câu 63. Một nguyên hàm F(x) của hàm số 1 ( ) x f x xe thỏa F   3 0  là: 2 2 x 1  2  e x 1 e A.e B.e 2 2 2 x 1  2  e x 1 e C.e D.e 4 4 85 3A. Nguyên hàm x x
Câu 64. Tìm nguyên hàm của hàm số 3 f (x) e (2x e ) x x 1 4x x x 1 4x A. f (x)dx 2xe 2e e C B. f (x)dx 2xe 2e e C 4 4 x x 1 4x x x 1 4x C. f (x)dx 2xe 2e e C D. f (x)dx 2xe 2e e C 4 4
Câu 65. Cho a  0 và a  1. C là hằng số. Phát biểu nào sau đây đúng ? 2 x a A. x x
a dx a .ln a CB. 2 x a dx   C  2ln a C. 2 x 2 x a dx aCD. 2 x 2 x
a dx a .ln a C
Bài tập tổng hợp
Câu 66. Không tồn tại nguyên hàm: 2 x x 1 2 A. dx B. x 2x 2dx x 1 3x C. sin 3xdx D. e xdx
Câu 67. Giả sử F(x) là một nguyên hàm của hàm số f(x) trên khoảng (a;b). Giả sử G(x) cũng là một
nguyên hàm của f(x) trên khoảng (a;b). Khi đó:
A. F(x)= G(x) trên khoảng (a;b).
B. G(x) = F(x) – M trên khoảng (a;b) với M là một hằng số nào đó.
C. F(x) = G(x) + C với mọi x thuộc giao của hai miền xác định.
D. F(x)và G(x)là hai hàm số không có sự liên quan.
Câu 68. Không tồn tại nguyên hàm của hàm số nào dưới đây x x
A. f x 2 2  f x  x x x B.   2 2 2 3
C. f x  sin3x D.   3x f x xe Nguyễn Văn Lực
www.facebook.com/VanLuc168 1A 2A 3D 4C 5A 6C 7A 8A 9D 10B
11B 12C 13D 14A 15B 16A 17C 18C 19C 20C
21C 22A 23B 24A 25D 26D 27B 28A 29C 30C
31B 32C 33A 34B 35D 36D 37A 38A 39A 40B
41A 42C 43C 44B 45D 46B 47B 48B 49A 50D
51B 52B 53B 54A 55D 56A 57C 58D 59A 60D
61B 62D 63B 64D 65B 66B 67B 68B 86 3B. Tích phân TÍCH PHÂN
Hàm đa thức, phân thức b
Câu 1. Tập hợp các giá trị của b sao cho (2x  4)dx  5  là: 0 A.   5 B.  1  ;  5 C.   1 D. 1;  4 1 2
Câu 2. Cho tích phân I  3x  2x  ln(2x  1) 
dx . Xác định a biết I b ln a c với a,b,c là 0 các số hữu tỉ 2 2 A. a  3 B. a  3 C. a a 3 D.   3 0 2 3
Câu 3. Kết quả của I x (x 1) dx bằng 1 7 1 2 1 A. I B. I C. I D. I 70 60 15 60 1
Câu 4. Tính tích phân I = 5
x(1 x) dx  0 1 1 1 1 A. I = - B. I = C. I = - D. I = 42 42 6 6 1 1000 3 2
Câu 5. Tính tích phân: I   x  3x .(x   1)dx 0 1001 4 1001 3 1000 4 1001 3 A. 3003 B. 3000 C. 3000 D. 3003 2 2 x  4x
Câu 6. Tính tích phân I dxx 1 29 11 11 29  A. I B. I C. I D. I  2 2 2 2 5 dx Câu 7. Giả sử  ln a  . Giá trị của a là 2x 1 1 A. 2 B. 3 C. 4 D. 5 1 1
Câu 8. Kết quả của F   là: 2 0 1 x     A. B. - C. D. 4 4 2 6 87 3B. Tích phân 1 2 2x  3x  6 Câu 9. Cho biết
dx a b ln 3  . Khi đó a.b bằng : 2x 1 0 21 21 4 4 A. B. C. D. 4 4 21 21 1 16 10
Câu 10. Kết quả của dx  là : 2  0 1 x e 1 2 1 2e A. 16 10 ln e B. 16 10 ln 2 2 2 e 1 2 1 2e 2 1 e C. 15 10 ln D. 16 10 ln 2 2 e 1 2 2 e 1 2 1 15 Câu 11. Cho biết dx  ln  , giá trị của k là : 2
x  2x k 7 0 3 A.1 B. 4 C. 2 D. 4 x 38 1
Câu 12. Kết quả của   dx là : 2x  10 0 1 18 9 3  2 18 9 3  2 A. B. 9 63.3 9 63.3 18 9 3   2 18 9 3  2 C. D.  9 63.3 9 63.3 2
e 2 x  5  7x
Câu 13. Tính tích phân:I= dxx 1
A. 4 e  7e  8
B. 7 e  4e  8
C. 8 e  7e  4
D. 4 e  7e  8 2 5
Câu 14. Tính tích phân I  . x
 1 xdx: 1 42 13 13 42 A.B. C.D. 13 42 42 13 Nguyễn Văn Lực
www.facebook.com/VanLuc168 Hàm căn thức 1 Câu 15. Tích phân 2 2 I x 1 x dx  bằng 0     A. B. C. D. 2 8 4 16 88 3B. Tích phân 4 2 2x  4x 1
Câu 16. Kết quả của I= dx  bằng 2x 1 0 478 448 408 378 A. I B. I C. I D. I  15 15 15 15 2 2 2 x
Câu 17. Tính tích phân I dx  2  0 1 x  1  1  1 1  A.B.C.D. 4 2 8 4 8 4 4 8 3 3 x Câu 18. I
dx có kết quả là 2 0 x 1 5 5 4 4 A. B. C. D. 3 3 3 3 7 3 x dx
Câu 19. Tính tích phân I   3 2  0 1 x 141 141 141 47 A. B. C. D. 10 10 20 10 2
Câu 20. Kết quả của I  min   3; x
2  xdx bằng : 0 4 4 5 5 A. B. C. D. 5 5 4 4 5 Câu 21. Tính 2 I x x  4dx  0 19 19 28 A. B. 1 C.D.  3 3 3 2 Câu 22. Tính 2 4  x dx  0 2  1 2  1  A. B. C. D.  2 2 2 1
Câu 23. Tính tích phân 2
x 3x 1dx  0 7 8 7 A. B. C. D. 1 3 9 9 Nguyễn Văn Lực
www.facebook.com/VanLuc168 89 3B. Tích phân
Hàm lượng giác 6
Câu 24. Kết quả của I tanxdx 0 3 3 2 3 A. ln B. ln C. ln D. 2 2 3 
Câu 25. Tính tích phân: I   x.sinxdx 0  A. I I 0 I I 1 2 B.C.D.   2
Câu 26. Tính tích phân I = 3 ( osx c 1) sinx x d  0 15 15 15 15 A. I B. I   C. I D. I   4 4 2 2 
Câu 27. Kết quả của 4
B   2x  3.sin 4x.dx là: 0  3  3  3  A.B.C.D.  3 8 2 2 8 8 2 8  2
Câu 28. Tính tích phân I x cos xdx  0     A. 1 B. 1  C. D. 1 2 2 2 2 4 s inx
Câu 29. Tính tích phân I e cos xdx . 0 2 2 2 2 1 A. 2 I e B. 2 I e 1 C. 2 I e 1 D. 2 I e 2
Câu 30. Tính tích phân I
sin 2x cos xdx . 2 1 1 A. I 0 B. I 1 C. I D. I 3 6  Câu 31. Tích phân 2 2 I  sin . x cos xdx  bằ ng: 0     A. B. C. D. 6 3 8 4 90 3B. Tích phân 2 2 3
Câu 32. Tính tích phân I sin x cos xdx 0 2 3 2 2 A. B. C. D. 15 15 13 15 
Câu 33. Tính tích phân 2 I
(x  sin x) dx  0 3   2   3  5 2  5 A. I   B. I   C. I   D. I   3 2 3 2 3 2 3 2  sin x
Câu 34. Kết quả của 3 A  .dx  là: 0 1 6 cos x 1 1 1 A.  7  2 B.  7  2 C.  7 2 D.  7  2 3 3 2 3 2 2
Câu 35. Để tính I tan x cot x
2dx . Một bạn giải như sau: 6  3 3 2
Bước 1: I   tan x  cot xdx Bước 2: I tan x cotx dx  6 6  3 3 os c 2x
Bước 3: I  tan x  cot xdx Bước 4: I 2 dx  sin2x 6 6 3 Bước 5: 3 I ln sin 2x 2 ln
. Bạn này làm sai từ bước nào? 2 6 A. 2 B. 3 C. 4 D. 5  2  cos x 2 cos x Câu 36. Biết dx  m  . Tính giá trị của   I dx  x 1 3 x   1 3    A.   m B.  m C.  m D.  m 4 4  2cos x
Câu 37. Tính tích phân: I   2 dx 0 3  2sin x 5 3 A. I  ln I ln I I 3 B.  5 C.  5ln3. D.  3ln 5  4 3 1  sin
Câu 38. Tích phân  x dx là 2  sin x 6 3  2 3  2  2 3  2 3  2 2  2 A. B. C. D. 2 2 2 2 91 3B. Tích phân  3 s inx
Câu 39. Tính tích phân I dx  3 cos x 0 3 3 3 3 A. I B. I   C. I   D. I   2 2 2 2     sin x  4    4  1 1
Câu 40. Cho biết dx  . m  . Khi đó m  bằng : 3 cos x 2 2 0 1 1 A. B. C. 0 D. 1 4 4  2
Câu 41. Kết quả của I  max 
sin ;xcosxdx bằng : 0 A. 1 B. 2 C.D. 2  2 Câu 42. Tính  2 cos xdx 0   2   A. B. C. D. 2 4 3 3
Hàm mũ – lôgarit 2
Câu 43. Giá trị của 2 2 x e dx  là: 0 A. 4 e B. 4 e 1 C. 4 4e D. 4 3e 1  Câu 44. Nếu gọi 2 x I e xdx
, thì khẳng định nào sau đây là đúng? 0 e 1 2e 1 e 1 e 1 A. I  . B. I  . C. I   . D. I  . 2 2e 2 2e x
Câu 45. Kết quả của tích phân: I  x  0 2e dx là 2 5 1 2  A. 3e 1 B.   2 2(1 e ) C.  3 1 2 e D.  2 e e
Câu 46. Tích phân I  ln xdx  bằ ng: 1 A. 4 B. 3 C. 2 D. 1 e
Câu 47. Tính tích phân I = I  . x ln x. x d  1 2 1  e 2 e 1 2 e  3 2 3  e A. I B. I C. I D. I  4 4 4 4 92 3B. Tích phân e
Câu 48. Tích phân I x ln xdx  bằng 1 2 2 2 2 A.e e 2 B.e e 2 C.
e e 2 D.e e 2 3 6 9 7 e 2
Câu 49. Tính tích phân I x ln xdx . 1 3 2e 1 3 2e 1 3 e 2 3 e 2 A. I B. I C. I D. I 9 9 9 9 e
Câu 50. Tích phân I  (x1) lnxdx  là 1 2 e  3 2 e  3 2 e  3 2 e  3 A. B. C. D. 2 3 4 6 e Câu 51. Nếu gọi 2
I x .ln(x 1)dx
, thì khẳng định nào sau đây là đúng? 1 5 2 5 3 A. I    ln 2. B. I    ln 2. 18 3 18 2 5 2 5 2 C. I   ln 2. D. I    ln 2. 18 3 18 3 4
Câu 52. Kết quả của C  2x.ln  3x 6.dx là: 3 11 11 A. 12ln 6  5ln 3  B. 12ln 6  5ln 3  2 2 11 11 C. 12ln 6  5ln 3  D. 12ln 6  5ln 3  2 2 m
Câu 53. Cho m là một số dương và
 (4x ln  2x I x ln 2)dx  . Tìm m khi I=12. 0 A. m  4 B. m  3 C. m  1 D. m  2 e ln x
Câu 54. Tính tích phân I dxx 1 2 e 1 2 e  1 1 1 A. I B. I C. I D. I   2 2 2 2 e 1 ln x
Câu 55. Tính tích phân I dx . x 1 1 3 A. I 2 B. I C. I e D. I e 2 93 3B. Tích phân e ln x
Câu 56. Tính tích phân I dx  . 2 x 1 2 2 1 1 A. I  1  B. I  1  C. I  2  D. I  2  e e e e 2 ln x
Câu 57. Tính tích phân I= dx 5 x 1 15 4 ln 2 14 3 ln 2 13 3 ln 2 15 4 ln 2 A. B. C. D. 256 256 256 256 1 x e 1 x
Câu 58. Tính tích phân I dx  1 xxe 0 A.  2 ln 1 e B.  2 ln e   1
C. ln 1 e
D. ln e   1 1 2 x 1 2 x Câu 59. Biết dx  . a
Tính giá trị của tích phân I  . dx  1 xe 1 xe 0 0 1 1 A. I   a
B. I  1  a C. I   a
D. I  1  a 2 3 e ln x 1 Câu 60. I dx  có kết quả là x ln x 1 1
A. I  ln(e 1)
B. I  ln(e 1)
C. I   ln(e 1)
D. I  ln(1 ) e e 2  ln x
Câu 61. Tính tích phân: I dx  2x 1 3 2  2 3 3 3  2 2 A. B. 3 3 3 3  2 2 3 3  2 2 C. D. 2 3 1 Câu 62. Tính: 2 2 x K x e dx  0 2 e 2 e 1 2 e  1 1 A. K B. K C. K D. K  4 4 4 4 3 3  ln x Câu 63. Tính: I  dx  2 (x 1) 1 3 3 A. I  1 (  ln ) 3  ln 2 B. I  1 (  ln ) 3  ln 2 4 4 3 3 C. I  1 (  ln ) 3  ln 2 D. I  (1  ln 3)  ln 2 4 4  2
Câu 64. Tính:    sinx I e
x.cos xdx . 0     A. e   2 B. e   2 C. e   2 D. e   2 2 2 2 2 94 3B. Tích phân ln 5 2 x e
Câu 65. Giá trị của dx  là x ln 2 e 1 22 19 23 20 A. B. C. D. 3 3 3 3 e
Câu 66. Tính tích phân (2x 1) ln xdx  1 2 e 1 2 e  3 A. 2 e  3 B. C. 2 3 e D. 2 2 2
Bất đẳng thức tích phân a
Câu 67. Xác định số a dương để  2
x x dx đạt giá trị lớn nhất. 0 1 3 A. a  1 B. a C. a  2 D. a  2 2 
Câu 68. Tìm các số thực m  1 sao cho ln x   1 dx  . m 1
A. m e 1. B. 2 m e . C. m  2 . e D. m  . e 1 dx
Câu 69. Tìm số dương k nhỏ nhất, thỏa mãn  0  2x  k 0 A. k  3 B. k  4 C. k  1 D. k  2 e k
Câu 70. Gọi S là tập hợp các số nguyên dương k thỏa mãn điều kiện ln dx e  2  . Tìm S . x 1
A. S  1; 2;  3
B. S  1;  2
C. S  2;  3 D. S   1 dx
Câu 71. Cho I  
, với m  0 . Tìm các giá trị của tham số m để I  1. 2x m 0 1 1 1 1 A. 0  m B. m C.m D. m  0 4 4 8 4
Bài tập tổng hợp 4
Câu 72. Tính tích phân 2 I
x  3x  2 dx  1  19 19 28 A. B. C. D. 19 2 2 6 1
Câu 73. Tính tích phân x x I 2 2 dx 1 2 A. I 2ln 2 B. I ln 2 1 C. I ln 2 D. I ln 2 95 3B. Tích phân 2 Câu 74. Tính 2 J x 1 dx  2  9 A. 3 B. 4 C. 9 D. 2 10 8 10 Câu 75. Nếu f (z)dz 17 và f (t)dt 12 thì
3f (x)dx bằng: 0 0 8 A. -15 B. 29 C. 15 D. 5 10 6
Câu 76. Cho hàm số f(x) liên tục trên (0;10) thỏa mãn
f (x)dx  7; f (x)dx  3   . Khi đó 0 2 2 10 P
f (x)dx f (x)dx   có giá trị là 0 6 A. 3 B. 2 C. 4 D. 1 a Câu 77. Tích phân f (x)dx 0 thì ta có: a
A. f (x ) là hàm số chẵn
B. f (x ) là hàm số lẻ
C. f (x ) không liên tục trên đoạn a;a D. Các đáp án đều sai Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B 2A 3D 4B 5A 6B 7B 8A 9A 10B
11D 12A 13A 14C 15D 16A 17C 18C 19C 20D
21A 22D 23C 24C 25C 26A 27C 28D 29C 30A
31C 32A 33C 34B 35B 36A 37A 38B 39A 40C
41B 42B 43B 44D 45C 46D 47D 48C 49A 50C
51D 52D 53D 54C 55D 56B 57A 58C 59C 60A
61B 62C 63D 64A 65D 66D 67A 68D 69C 70B
71A 72B 73D 74B 75A 76C 77B 96
3C. Diện tích hình phẳng
DIỆN TÍCH HÌNH PHẲNG
Câu 1. Cho hàm số y f (x) liên tục trên đoạn  ;
a b. Công thức tính diện tích hình phẳng giới
hạn bởi hàm số y f x trục hoành và hai đường thẳng x a, x b là b b b a A. f (x)d . xB.f x 2 ( ) d . xC. f (x) d . xD. f (x)d . xa a a b
Câu 2. Viết công thức tính diê ̣n tích S của hình phẳng giới ha ̣n bởi đồ thi ̣ của hai hàm số
y f (x), y g(x) và các đường thẳng x a, x b là: b b
A. S  [ f (x)  g(x)]dxB. S
f (x)  g(x) dxa a b b C. S
f (x)  g(x) dxD. 2
S  [ f (x)  g(x)] dxa a  1 
Câu 3. Cho hàm số f (x) xác định và đồng biến trên [0;1] và có f  1   , công thức tính diện  2  2
tích hình phẳng được giới hạn bởi các đồ thị hàm số y f (x); y f (x) ; x 0; x 1 1 2     1 2 là: 1 2 1 1 2 A.
f (x)(1 f (x))dx f (x)( f (x)   
1)dx B.f (x)  
( f (x)) dx 0 1 0 2 1 1 2 1 2
C. ( f (x))  
f (x )dx D.
f (x) (1 f (x))dx f (x)( f (x)    1)dx 0 0 1 2
Câu 4. Tính diện tích hình phẳng giới hạn bởi các đường 2 y x và y x 2 . 3 9 15 A. B. C. D. 2 2 2
Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y
x và đường thẳng y 2x là: 4 3 5 23 A. B. C. D. 3 2 3 15
Câu 6. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y 2 x và y x. 9 11 A. 5 B. 7 C. 2 D. 2
Câu 7. Diện tích miền D được giới hạn bởi hai đường: y   2
2x và y  2x  4 là 3 13 1 A. 13 B. 9 C. 3 D. 9 97
3C. Diện tích hình phẳng 2
Câu 8. Diện tích hình phẳng giới hạn bởi Parabol (P) : y
3 x , đường thẳng (d) : y 2x trục tung và x 2là: A. -4 (đvdt) B. 4 (đvdt) C. 2 (đvdt) D. 6 (đvdt)
Câu 9. Tính diện tích hình phẳng giới hạn bởi: 3
y x  3x và y x là A. 12 B. 4 C. 6 D. 8
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 3 x x và 2
y x x có kết quả là A. 12 B. 37 37 C. D. 11 12
Câu 11. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 y x 3x
3 và đường thẳng y=5 là: 5 45 27 21 A. B. C. D. 4 4 4 4
Câu 12. Tính diện tích hình phẳng giới hạn bởi (C): y =x4 -2x2 +1 và trục hoành 16 8 8 15 A. S B. S C. S D. S  15 15 15 8
Câu 13. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 2
y  5x  3x  8, trục Ox trên đoạn 1; 3bằng A. 100 B. 150 C. 180 D. 200
Câu 14. Tính diện tích hình phẳng giới hạn bới các đồ thị các hàm số: 2 y x 4x 3 ,y x 3 197 109 56 88 A. S B. S C. S D. S 6 6 3 3 x
Câu 15. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số: y e ; y  2
và đường thẳng x  1 bằng
A. S e  ln 2  4
B. S e  2ln 2  4
C. S e  2ln 2  4
D. S e  2ln 2  4
Câu 16. Diện tích hình phẳng được giới hạn bởi các đường 1
y  ln x, x
, x e và trục hoành là: e 1  1   1  1 A. 1  B. 2 1   C. 2 1   D. 1  ee   e e 2x 1
Câu 17. Diện tích hình phẳng giới bởi đồ thị (C) hàm số y  và hai trục toạ độ là  x 1 A. ln2 – 1. B. ln2. C. ln2 + 1. D. 2ln2 – 1. 1 x
Câu 18. Cho hình phẳng A giới hạn bởi các đường sau: y
, y  2, y  0, x  0. Khi đó x
diện tích hình phẳng là A. –ln3 B. ln3 C. 2ln3 D. –2ln3 98
3C. Diện tích hình phẳng 2 x x  2
Câu 19. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = y    x x  , 0, x 2, 2. 3 5 5 5 5
A. S = 7 – 4 ln
B. S = 7 + 4 ln
C. S =7 + 4 ln
D. S = 7 - 4 ln 16 14 16 14 1 1
Câu 20. Diện tích hình phẳng được giới hạn bời các đường y , y là: 2 1 x 2 A. 1 B. 1 2 2 5 5 C. 1 D. 1 6 6
Câu 21. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x 1 x , trục Ox và đường thẳng x=1. 2 2 1 8 2 2 1 A. B. C. 2 2 1 D. 3 3 3
Câu 22. Gọi (H) là hình phẳng giới hạn bởi các đường (P): y = –x2 +2, y = 0, x = 0, x = 1. Tại
điểm M nào trên (P) mà tiếp tuyến tại đó tạo với (H) một hình thang có diện tích nhỏ nhất 1 9 1 7 1 7 A. M ; B. M ; C. M ;
D. Không tồn tại điểm M 2 4 2 4 2 4
Câu 23. Diện tích của hình phẳng giới hạn bởi các đường: 2
y x  4, y  0 , x = 3, x = 0 bằng: A. 15 B. 18 C. 20 D. 22
Câu 24. Diện tích hình phẳng giới hạn bởi đường cong 2
y x  2 x, y x bằng: 7 9 19 11 A.dvdtB.dvdtC.dvdtD.dvdt 2 2 2 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168
1C 2B 3D 4B 5A 6C 7B 8B 9D 10C
11C 12A 13D 14B 15D 16C 17A 18B 19C 20A 21A 22B 23A 24B 99
3D. Thể tích khối tròn xoay
THỂ TÍCH KHỐI TRÒN XOAY
Câu 1. Công thức thể tích V của khối tròn xoay được tạo khi quay hình cong, giới hạn bởi đồ thị
hàm số y f x, trục Ox và hai đường thẳng x a, x b a b quay xung quanh trục Ox là: b b
A. V   f  xdx B. 2 V f  xdx a a b b C. 2 V   f  xdx D. V f  xdx a a
Câu 2. Cho hình phẳng (H) giới hạn bởi các đường y  3x ; y x ; x  0 ; x  1. Tính thể tích
vật thể tròn xoay khi (H) quay quanh Ox. 8 2 8 A. B. C. 2 8 D. 8 3 3
Câu 3. Cho tam giác giới hạn bởi ba đường y x, x
1, trục Ox. Tính thể tích khối tròn xoay
được tạo bởi phép quay quanh trục Oy của tam giác đó 2 4 A. B. C. D. 3 3 3
Câu 4. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 2 y 1 x , a y
0 quanh trục Ox có kết quả dạng
. Khi đó a+b có kết quả là: b A. 11 B. 17 C. 31 D. 25
Câu 5. Viết công thức tính thể tích V của khối tròn xoay được tạo thành khi quay hình thang cong
giới hạn bởi đồ thị hàm số 2 y 2
x , trục Ox và hai đường thẳng x 1,x 0 xung quanh trục Ox. 0 0 2 2 2 2 A. V (2 x ) dx B. V (2 x ) dx 1 1 0 0 2 2 C. V (2 x )dx D. V 2 x dx 1 1
Câu 6. Tính thể tích hình khối do hình phẳng giới hạn bởi các đường 2 2 y 4 x , y x 2 quay quanh trục Ox . A. 14 B. 15 C. 16 D. 17
Câu 7. Thể tích của vật thể tròn xoay, sinh ra bởi hình phẳng giới hạn bởi các đường 2
y  x  3 ;
x y  x khi quay quanh trục Ox là 56 6 56 56 A. B. C.D. 15 15 15 5 100
3D. Thể tích khối tròn xoay
Câu 8. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số 2
y  2x x , trục hoành. Tính thể tích
V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox. 16 4 4 16 A. V B. V C. V D. V 15 3 3 15
Câu 9. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường 2
y x  4x  4,y  0, x  0, x  3 quay quanh trục Ox là: 33 33 33 33 A. . . . . 7 B. 6 C. 5 D. 4
Câu 10. Gọi (H) là hình phẳng giới hạn bởi các đường 2
y x 1 và y  4x  2 . Khi đó thể tích
khối tròn xoay được sinh ra khi quay hình phẳng (H) quanh trục Ox là: 4 248 224 1016 A. B. C.D. 3 3 15 15
Câu 11. Thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường 2
y x 1, x  0 và các tiếp tuyến với đồ thị hàm số 2
y x 1 tại điểm 1; 2 là 15 8 8 15 A. 8 B.  15 C. 15 D.  8
Câu 12. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng 1 y ,y 0,x a(a
1) quay quanh trục Ox là gì? 2 1 1 A. 1 B. 1 a a 1 1 C. 1 D. 1 a a
Câu 13. Tính thể tích vật thể nằm giữa hai mặt phẳng x 0;x
biết rằng thiết diện của vật thể
với mặt phẳng vuông góc với trục ox tại điểm có hoành độ x (0  x   ) là một tam giác đều có cạnh là 2 sinx .  A. 3 B. C. 2 3 D.  2 3
Câu 14. Tính thể tích của vật thể nằm giữa hai mặt phẳng x  0, x  2 , biết rằng thiết diện của vật
thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0  x  2 ) là một nửa hình tròn đường kính 2 5x . A. 4 B.C. 3 D. 2
Câu 15. Tính thể tích của một vật thể giới hạn bởi hai mặt phẳng x  0 và x  3 , biết rằng thiết
diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x  3 là
một hình chử nhật có kích thước là x và 2 2 9  x . A. 16 B. 17 C. 19 D. 18
Câu 16. Cho hình phẳng H giới hạn bởi các đường y
x 1, trục hoành và x  4 . Thể tích của
khối tròn xoay tạo thành khi quay hình phẳng H quanh trục Ox là: 7 2 7 7 5 A. B. C. D. 6 6 6 3 101
3D. Thể tích khối tròn xoay
Câu 17. Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau quanh trục hoành 2
y  1 x , y  0 31416 4  3 A. B. C. D. 20001 3 2 2
Câu 18. Tính thể tích của khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi các đường y = 2
x ln(1 x ) , trục Ox và đường thẳng x = 1. 1 4  1 4  A. V     ln 2     B. V     ln 2      3 9 6   3 9 6  1 4  1 4  C. V      ln 2     D. V     ln 2      3 9 6   3 9 6 
Câu 19. Thể tích V của khối tròn xoay được tạo bởi phép quay quanh trục Oy hình phẳng giới hạn 2 y
bởi các đường x
, y  0, y  1. 2 y 1    3 A. V B. V C. V D. V  3 2 4 2
Câu 20. Thể tích của vật thể tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường 
y  sin x  cos x, y  0, x  0, x
khi quay quanh trục Ox bằng: 2  3  3  1  3 A.       B.       C.       D.         2 2   2 2   2 2   2 2 
Câu 21. Cho hình phẳng (H) giới hạn bởi các đường y  sin x, x  0, y  0, x   . Thể tích vật thể
tròn xoay sinh bởi hình (H) quay quanh Ox bằng 2  2   A. 2 B. C. D. 2 4 2
Câu 22. Thể tích của vật thể tròn xoay sinh bởi hình phẳng giới hạn bởi các đường
y  ln x, x  1, x  2, y  0 khi nó quay xung quanh trục Ox là: A.  2 2 ln 2  2ln 2   1 (đvtt) B.  2 ln 2  2ln 2   1 (đvtt) C.  2 2 ln 2  2 ln 2   1 (đvtt) D. 2 ln 2  2 ln 2  1 (đvtt)
Câu 23. Cho hình phẳng (H) giới hạn bởi các đường: y x ln x, y  0, x  .
e Tính thể tích của khối
tròn xoay tạo thành khi quay hình (H) quanh trục Ox bằng 3 (5e -2) 3 (5e -2) 3 (5e +2) 3 (5e -2) A. V= B. V= C. V= D. V= 28 25 27 27
Câu 24. Thể tích khối tròn xoay sinh bởi hình phẳng giới ha ̣n bởi các đường x
y e , tru ̣c tung và
y e quay quanh tru ̣c Ox bằng: 2  (e 1) 2  (e 1) A. 2 (e 1) B. C. 2  (e  2) D. 2 2
Câu 25. Thể tích khối tròn xoay do hình phẳng giới hạn bởi đồ thị hàm số  x y e , trục hoành và
hai đường thẳng x  0, x  3 quay quanh trục Ox là:  6e  1  6e  1  6e  1  6e  1 A. B. C. D. 2 2 2 2 102
3D. Thể tích khối tròn xoay
Câu 26. Cho hình phẳng A giới hạn bởi các đường x , x y e y e  
và x  1. Thể tích của khối
tròn xoay tạo thành khi quay hình A quanh trục hoành là 2 2 e e   2 2 e e   A.    1 B.    1  2 2   2 2  2 2 e e   2 2 e e   C.    1 D.    1  2 2   2 2  1
Câu 27. Cho hình phẳng A giới hạn bởi đường cong có phương trình 2 . x y
x e và các đường
thẳng x  1, x  2 và trục hoành . Thể tích khối tròn xoay tạo thành khi quay A quanh trục hoành bằng 3 1 3 1 4 2 3 1 4 2 3 1 A. e e B. 4 2    e e C. e e D. 4 2     e e 4 2      4 2  4 2  4 2 
Câu 28. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số . x y
x e , trục hoành và đường thẳng x
1. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox. 2 2 2 2 A. (e 1) B. (e 1) C. (e 1) D. (e 1) 4 4 2 2
Câu 29. Tính thể tích hình khối do hình phẳng giới hạn bởi đồ thị hàm số x
y xe , trục tung, trục
hoành, x  2 khi quay quanh trục Ox 1  A.  4 5e   1 B.   4 5e   1 C.  4 5e   1 D. 4 5e 1 4 4 x
Câu 30. Kí hiệu H là hình phẳng giới hạn bởi 2 y xe , x 0 và x 1.Tính thể tích vật
thể tròn xoay thu được khi quay hình H quanh trục Ox .
A.  e  2
B. e   1
C. e  2
D.  e   1 Nguyễn Văn Lực
www.facebook.com/VanLuc168
1C 2A 3B 4C 5A 6C 7A 8D 9C 10C
11B 12C 13C 14A 15D 16A 17B 18A 19B 20A
21B 22C 23D 24D 25A 26D 27B 28A 29C 30C 103
4A. Tính toán với số phức
TÍNH TOÁN VỚI SỐ PHỨC
Tìm phần thực, phần ảo của số phức
Câu 1. Cho số phức z = 2i-1.Phần thực và phần ảo của số phức z lần lượt là: A. 2 và -1 B. -2 và 1 C. -1 và 2 D. -2 và -1
Câu 2. Phần thực và phần ảo của số phức z 2 3i là
A. Phần thực bằng 2 và phần ảo bằng 3 .
B. Phần thực bằng 2 và phần ảo bằng 3i .
C. Phần thực bằng 2 và phần ảo bằng 3 .
D. Phần thực bằng 2 và phần ảo bằng 3i .
Câu 3. Cho số phức: z  11 7i . Phần thực a và phần ảo b của z lần lượt là
A. a  11; b  7.
B. a  11; b  7.
C. a  11; b  7.
D. a  11; b  7.
Câu 4. Phần thực và phần ảo của số phức z 4i là
A. Phần thực bằng 0 và phần ảo bằng 4 .
B. Phần thực bằng 4 và phần ảo bằng 4i .
C. Phần thực bằng 0 và phần ảo bằng 4i .
D. Phần thực bằng 0 và phần ảo bằng 4i .
Câu 5. Trong các số phức sau, số thực là
A.  3  2i   3  2i
B. 3  2i  3  2i
C. 1  2i   1   2i
D. 5  2i   5  2i Nguyễn Văn Lực
www.facebook.com/VanLuc168
Số phức liên hợp
Câu 6. Cho số phức z  1 i 3 , số phức liên hợp của số phức z là:
A. z  1 i 3
B. z   3  i C. z  1   i 3 D. z  3  i
Câu 7. Số phức liên hợp của số phức z  1 2i là A. 1  2i B. 1  2i C. 2  i D. 1  2i
Câu 8. Cho số phức z = -2 – 5i. Tìm phần thực và phần ảo của số phức z
A. Phần thực bằng 2 và phần ảo bằng -5i
B. Phần thực bằng -2 và phần ảo bằng 5i
C. Phần thực bằng 2 và phần ảo bằng -5
D. Phần thực bằng -2 và phần ảo bằng 5 104
4A. Tính toán với số phức
Câu 9. Cho số phức z 3 4i .Phần thực và phần ảo của số phức z là
A. Phần thực bằng 3 và phần ảo bằng 4 .
B. Phần thực bằng 3 và phần ảo bằng 4i .
C. Phần thực bằng 3 và phần ảo bằng 4i .
D. Phần thực bằng 3 và phần ảo bằng 4 .
Câu 10. Cho số phức z  4  3i . Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng – 4 và phần ảo bằng –3i.
B. Phần thực bằng – 4 và phần ảo bằng –3.
C. Phần thực bằng 4 và phần ảo bằng 3i.
D. Phần thực bằng 4 và phần ảo bằng 3. Câu 11. Cho z  4
  5i. Tìm phần thực, phần ảo của số phức z
A. Phần thực bằng 4 và phần ảo bằng 5i.
B. Phần thực bằng 4 và phần ảo bằng 5.
C. Phần thực bằng -4 và phần ảo bằng -5.
D. Phần thực bằng -4 và phần ảo bằng -5i.
Câu 12. Cho số phức z = 6 + 7i. Số phức liên hợp của z có điểm biểu diễn là: A. (6; 7) B. (6; -7) C. (-6; 7) D. (-6; -7)
Câu 13. Cho số phức z thỏa (1 i)z  4  2i . Tìm phần thực, phần ảo của số phức z.
A. Phần thực bằng 1 và phần ảo bằng 3i
B. Phần thực bằng 1 và phần ảo bằng 3
C. Phần thực bằng -1 và phần ảo bằng -3i
D. Phần thực bằng -1 và phần ảo bằng 3
Câu 14. Cho số phức z  i .Số phức liên hợp của z là: A. z  i B. z  1 C. z  1  i D. z  1
Câu 15. Cho số phức z = 2- 3i . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 2 và phần ảo bằng 3
B. Phần thực bằng 2 và phần ảo bằng -3
C. Phần thực bằng 2 và phần ảo bằng 3i
D. Phần thực bằng 2 và phần ảo bằng -3i
Câu 16. Số phức liên hợp của số phức z 1 3i là A. z 1 3i B. z 1 3i C. z 1 3i D. z 1 3i
Câu 17. Cho số phức z = 1 – 5i. Tìm phần thực, phần ảo của số phức z .
A. Phần thực bằng -1 và phần ảo bằng -5i.
B. Phần thực bằng -1 và phần ảo bằng -5.
C. Phần thực bằng 1 và phần ảo bằng -5.
D. Phần thực bằng 1 và phần ảo bằng -5i.
Phép cộng số phức
Câu 18. Cho hai số phức z  3  2i; z  1 3i .Tổng của hai số phức z ; z là : 1 2 1 2 A. 4  i B. 9  i C. 1  9i D. 4  5i 1
Câu 19. Cho số phức z = a + bi. Khi đó số z z là 2 A. Một số thực B. 2
C. Một số thuần ảo D. i
Câu 20. Cho số phức z = 1 -2i , phần ảo của số phức w = 2z + là: A. -2 B. 2 C. 4 D. -4 105
4A. Tính toán với số phức Câu 21. Cho z 2 3i, z 1 i . Tính z z z 1 2 1 2 A. z 3 3i B. z 3 2i C. z 2 2i D. z 3 2i
Câu 22. Cho hai số phức z = a + bi và z’ = a’ + b’i. Điều kiện giữa a,b,a’,b’ để z+z’ là một số thuần ảo là: a  a'  0 a  a '  0 a   a'  0 a  a '  0 A.B.C.D.  b  b'  0 b, b' bÊt k× b  b' b  b'  0
Câu 23. Biết rằng 3z 2 3i 5 4i . Tìm z 1 1 A. z 1 3i B. z 3 2i C. z 2 i D. z 1 i 3 3
Câu 24. Cho số phức z 2
4i .Tìm phần thực, phần ảo của số phức w z i
A. Phần thực bằng -2 và phần ảo bằng -3i
B. Phần thực bằng -2 và phần ảo bằng -3
C. Phần thực bằng 2 và phần ảo bằng 3i
D. Phần thực bằng 2 và phần ảo bằng 3.
Câu 25. Cho hai số phức z  7  5i; z  3  i .Số phức z - z bằng: 1 2 1 2 A. 4  4i B. 10  4i C. 4  4i D. 4  6i Câu 26. Cho z 2 i, z 5 7i . Tính z z z 1 2 1 2 A. z 3 7i B. z 3 8i C. z 7 6i D. z 3 i
Câu 27. Cho số phức z  33  4i  43i 1 .Số phức liên hợp của z là: A. z  24 13i
B. z  33  4i  4 3i 1 C. z  5  24i D. z  13  24i
Câu 28. Cho hai số phức z  1 2i; z  2  3i .Số phức   z - 2z bằng: 1 2 1 2 A.   3  . i B.   3  8 . i C.   5  . i D.   3  8 . i
Câu 29. Cho hai số phức: z1= 2 – 3i ; z2 = -1 + i. Phần ảo của số phức w = 2z1 – z2 bằng: A. -7 B. 5 C. 7 D. -5 Câu 30. Cho z 2 i, z 5 7i . Tính z 2z z 1 2 1 2 A. z 9 7i B. z 3 3i C. z 9 3i D. z 7 6i
Câu 31. Cho số phức z 
1 = 1 – 3i, z2 = 2 + i. Tìm số phức w = 2 z z 1 2 A. z = 7i B. 5 i C. – 4 – 7i D. – 7i
Câu 32. Cho z  5  i2i   1  4  3 .
i Khi đó số phức z 2z bằng: A. 7 14i B. 7 42i C. -7 D. 7 14i Câu 33. Cho z 2 3i, z
3 4i . Khi đó 5z 3z bằng 1 2 1 2 A. 1 i B. 3i C. 1 2i D. 1 3i
Câu 34. Kết quả của phép trừ (3 4i) (2 3i) là A. z 3 i B. z 2 i C. z 1 7i D. z 5 7i
Câu 35. Cho số phức: z  3  5i . Tìm phần thực và phần ảo của số phức z i
A. Phần thực bằng -3 và phần ảo bằng 5
B. Phần thực bằng -3 và phần ảo bằng 4i
C. Phần thực bằng 3 và phần ảo bằng 4
D. Phần thực bằng -3 và phần ảo bằng 4 106
4A. Tính toán với số phức
Phép nhân số phức Câu 36. Thu gọn 5 z i ta được: A. z i B. z 1 C. z 1 D. z i
Câu 37. Số phức z i1 2i có phần thực là: A. 1 B. 2 C. -1 D. -2
Câu 38. Phần ảo của số phức z  1 i1 i là: A. -2 B. 2 C. 0 D. 1
Câu 39. Phần ảo của số phức 2 2 (1 i) (1 i) là: A. – 4 B. 4 C. 0 D. 1 Câu 40. Số phức 2
(1 i) (4  i) bằng: A. 2  8i B. 2  8 . i C. 5  3 . i D.   3  3 . i
Câu 41. Kết quả của phép tính 2  3i3  i là: A. 9 7i B. 9 7i C. 9 7i D. 9 7i
Câu 42. Thu gọn z  2  i1 2i, khi đó z bằng
A. z 4 3i B. z 5i C. z 3 4i D. z 2 2i
Câu 43. Cho hai số phức z  2i  5; z  1 3i .Số phức z .z bằng: 1 2 1 2 A. 4  i B. 1  17i C. 11 17i D. 113i
Câu 44. Cho hai số phức z 2 5i và z
3 4i . Tìm số phức z z .z . 1 2 1 2 A. z 6 20i B. z 26 7i C. z 6 20i D. z 26 7i
Câu 45. Cho số phức z  1 3i ; z  2  i ; z  3  4i . Tìm số phức w z z z z . 1 2 3 1 2 2 3 A. w= 1+4i B. w=1-4i C. w=-15-4i D. w =15+4i
Câu 46. Cho hai số phức: z 1 3i ; z  3  i . Tính z .z . 1 2 1 2 A. i B. 4i C. 2 3  4i
D. 3  1  i( 3 1) 2
Câu 47. Tìm phần ảo của số phức z , biết z   2 i 1 2i. A.  2 B. 2 C. 5 D. 3 2
Câu 48. Tìm phần thực của số phức z , biết z   2  i1 2i. A. 2 B. 1  C. 2 2 D. 1
Phép chia số phức
Câu 49. Cho số phức z = a + bi  0. Số phức 1 z có phần thực là: a b A. a + b B. a - b C. D. 2 2 a  b 2 2 a  b
Câu 50. Phần thực của số phức nghịch đảo của số phức i là: A. 1 B. -1 C. 0 D. –i
Câu 51. Kết quả của phép tính 3 là: i A. 3i B. i C. - i D. 3i 107
4A. Tính toán với số phức 3  4i
Câu 52. Số phức z = 4 bằng: i 16 13 16 11 9 4 9 23 A.i B.i C.i D.i 17 17 15 15 5 5 25 25
Câu 53. Tìm số phức liên hợp của số phức 1 i 2 i 1 3 1 3 1 3 1 3 A. i B. i C. i D. i 5 5 5 5 5 5 5 5
Câu 54. Giá trị của số phức 3 là: 2 i 6 3 3 6 6 3 3 6 A. i B. i C. i D. i 5 5 5 5 5 5 5 5
Câu 55. Cho hai số phức z
z  1  2i; z  1  i .Số phức 1 bằng: 1 2 z2 1 3 1 3 1 3 3 1 A.i B.i C.i D.   i 2 2 2 2 2 2 2 2
Câu 56. Số phức nghịch đảo của số phức 2 3i là: 2 3 2 3 3 A. i B. i C. i D. 2 3i 5 5 5 5 5  
Câu 57. Viết gọn số phức 3 2i 1 i z   . 1 i 3  2i 1 5 15 55 15 65 15 55 A. z   i B. z   i C. z   i D. z   i 13 13 26 26 26 26 26 26 3  2i 1 i
Câu 58. Thu gọn số phức z =  1 i 3  2i ta được: 21 61 23 63 15 55 2 6 A. z =  i i i i 26 26 B. z =  26 26 C. z =  26 26 D. z =  13 13
2  i1 2i 2  i1 2i
Câu 59. Cho z  
. Trong các kết luận sau, kết luận nào đúng? 2  i 2  i 22 A. z.z
B. z là số thuần ảo C. z D. z z 22 5 5 4i
Câu 60. Cho số phức z 4 3i . Khi đó bằng: 3 6i 73 17 73 17 A. 20 8i B. 20 8i C. i D. i 15 5 15 5 
Câu 61. Phần thực của số phức 3 i  là:
1  2i1  i 4 4 3 3 A. B. - C. D. - 5 5 5 5 108
4A. Tính toán với số phức Nguyễn Văn Lực
www.facebook.com/VanLuc168
Môđun của số phức
Câu 62. Cho số phức z  2  3i . Modul của số phức z là: A. 2 B. -3 C. 13 D. 13
Câu 63. Cho số phức z = 5 – 3i. Môđun của số phức z là: A. 34 B. 2 C. 34 D. 4
Câu 64. Mô đun của số phức z 1 2i là A. 1 B. 5 C. 2 D. 3
Câu 65. Cho số phức z 3
2i .Tính môđun của số phức z 1 i A. z 1 i 4 B. z 1 i 1 C. z 1 i 5 D. z 1 i 2 2
Câu 66. Cho hai số phức z  3  2i;z  2
  i. Tìm mô đun của số phức : z  z . 1 2 1 2 A. z  z  5 B. z  z  2 C. z  z  13 D. z  z  2 1 2 1 2 1 2 1 2
Câu 67. Cho hai số phức z 1 3i và z 2 . i Khi đó z z bằng: 1 2 1 2 A. 5 B. 5 C. 10 D. 13
Câu 68. Cho 2 số phức z 3i và z 3 5 .
i Tính môđun của số phức z 1 2 1 – z2:
A. | z z | 73
B. | z z | 13
C. | z z | 3
D. | z z | 5 1 2 1 2 1 2 1 2
Câu 69. Cho số phức z 2 6 , i z 1 2 .
i . Tính modun của số phức z z 1 2 1 2 A. 5 B. 6 C. 7 D. 8
Câu 70. Cho hai số phức z 1 i và z 4
5i . Môđun của số phức z z là 1 2 1 2 A. 2 5 B. 3 5 C. 3 3 D. 5 3
Câu 71. Cho hai số phức z1 = 4 + 5i và z2 = - 1 +2i . Tính môđun của số phức
A. z z  41.
B. z z  5.
C. z z  3 2.
D. z z  34. 1 2 1 2 1 2 1 2
Câu 72. Cho hai số phức z  1 2i
z  3  i . Tính môđun của số phức z  2z 1 và 2 1 2
A. z  2z  26 z  2z  41 1 2 B. 1 2
C. z  2z  29 z  2z  33 1 2 D. 1 2
Câu 73. Cho hai số phức z  3  i , z  2  i . Tính giá trị của biểu thức z z z . 1 2 1 1 2 A. 10 B. 50 C. 5 D. 85 109
4A. Tính toán với số phức  3 (1 3i)
Câu 74. Cho số phức z thỏa mãn: z
. Tìm môđun của z iz 1 .i A. 8 2 B. 8 3 C. 4 2 D. 4 3
Câu 75. Cho hai số phức z 1 3i, z a bi . Biết z z
3 4i . Modun của z là: 1 2 1 2 2 A. 3 B. 4 C. 5 D. 5
Câu 76. Cho số phức z = (2 + i)(1 – i) + 1 + 2i. Mô-đun của số phức z là A. 2 2 B. 4 2 C. 17 D. 5
Câu 77. Tính môđun của số phức z   i    i3 1 4 1 . A. 4 B. 29 C. 1 D. 5 Câu 78. Số phức 2
z  1  2i 1  i có mô đun là: 2 2 10 A. z 5 2 B. z 50 C. z D. z 3 3
Câu 79. Mô đun của số phức z   i    i3 5 2 1 là: A. 7 B. 3 C. 5 D. 2
Câu 80. Cho hai số phức: z  4  8i z 2 i z 2z .z 1 và    2 . Modul của số phức:  1 2 là A. 4 5 B. 5 C. 20 D. 40
Câu 81. Cho hai số phức z  1 i và z  3
  5i . Môđun của số phức w z .z z 1 2 1 2 2 A. w  130 B. w  130 C. w  112 D. w  112
Câu 82. Cho số phức z thỏa mãn (1+2i)z+(1-2 z )i=1+3i . Khi đó mô đun của số phức z là: A. 11 B. 85 C. 11 D. 85
Câu 83. Môđun của số phức z thỏa mãn phương trình (2z 1)(1 i) (z 1)(1 i) 2 2i là 2 3 1 1 A. B. C. D. 3 2 2 3 4 Câu 84. (1 i) (2 i)
Môđun của số phức z bằng: 3 (1 2i) 4 3 6 7 A. B. C. D. 5 5 5 5
Câu 85. Cho số phức 5(z i) z thỏa mãn
2 i .Môđun của số phức 2 w 1 z z là: z 1 A. 4 B. 9 C. 13 D. 13 1 i 2 i
Câu 86. Tìm môdun của số phức liên hợp của z 1 2i A. z 2 B. z 2 2 C. z 1 D. z 5 2 110
4A. Tính toán với số phức 2 2   
Câu 87. Tìm môđun của số phức (2 3i) (1 i) z , biết z  2 (1 2i) 2 11 A. 5 B. C. D. 5 5 5
Câu 88. Số phức z có mô đun nhỏ nhất sao cho : z z  3  4i là: 3 3 3 3 A. z    2i B. z    2i C. z   2i D. z   2i 2 2 2 2
Câu 89. Trong các số phức z thỏa mãn z 2 4i z
2i . Tìm số phức z có môđun nhỏ nhất. A. z 1 i B. z 2 2i C. z 2 2i D. z 3 2i
Câu 90. Trong các số phức z thoả mãn điều kiện 3 z 2 3i
. Số phức z có mođun nhỏ nhất là 2 26 3 13 78 9 13 26 2 13 78 3 13 A. z i B. z i 13 26 13 26 26 13 78 13 26 13 78 13 C. z i D. z i 13 26 13 26
Câu 91. Cho số phức z thỏa mãn: z i 1  z  2i . Tìm giá trị nhỏ nhất của z ? 1 2 1 A.  2 B. 2 C. 2 D. 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168
Tìm số phức thỏa điều kiện cho trước Câu 92 3 2
. Tính z  1 2i  3  i ta được: A.           z 3 8i B. z 3 8i C. z 3 8i D. z 3 8i
Câu 93. Phần thực của số phức 2
z thỏa mãn: 1 i 2  iz  8  i  1 2iz là A. 2 B. –3 C. –2 D. 3
Câu 94. Số phức z thoả iz  2z  1   8i là: A. z = 7 + 7i B. z = 5 – 2i C. z = 2 + 5i D. z = 1 -2i
Câu 95. Số phức z thỏa z  (2  3i)z 19i là: A. z = -3 -i B. z = -2 -i C. z = 2 -i D. z = 2 + i
Câu 96. Phần ảo của số phức 2
z thỏa mãn z  2z  2  i 1  i là: A. 13 B. 13 C. 9 D. 9 111
4A. Tính toán với số phức 2 2
Câu 97. Tìm các số phức z thỏa mãn z  2zz z  8 và z z  2. A. z  1
  ;iz 1 .i
z 1 ;iz  1   .i 1 2 B. 1 2 C. z  1   ;iz  1   .i
z 1 ;iz 1 .i 1 2 D. 1 2
Câu 98. Tìm phần thực của số phức z thỏa mãn iz + 4 + 5i = i(6 + 3i) A. 1 B. 7 C. 11 D. -1
Câu 99. Số phức z thỏa mãn: (1 i)z  (2  3i)(1 2i)  7  3i . là: 1 3 1 1 3 1 3 A. z   i B. z   i C. z  1 i D. z    i 2 2 2 2 2 2 2
Câu 100. Tìm số phức liên hợp của số phức z    i  i 1 1 3 2  . 2  i 17 2 17 4 27 4 17 2 A.i B.i C.i D.i 3 3 5 5 5 5 3 3
Câu 101. Cặp số (x;y) thỏa mãn điều kiện
2x  4y 1  x  3y i  4x  2y  3  3x  y  5 i là:  13 3   5 3   11 9   43 9  A.  ;  B. ;    C.  ;  D.  ;   4 4   4 4   4 4   4 4 
Câu 102. Tìm số phức z thỏa mãn: (2  i)z  (3  2i)z  1 ( 4  i) .
A. z  3  i
B. z  3  i
C. z  3  i
D. z  3  i  
Câu 103. Tìm số phức z, biết 1 2i 1 3i z  . 1 i 2  3i 2  36 2  20 30  36 2 36 A. z   i B. z   i C. z   i D. z   i 65 65 65 65 65 65 65 65
Câu 104. Cho số phức z  2  3i. Tìm số phức w  iz  z. A. w  3   5i B. z  5  3i C. z  5   5i D. z  5  5i
Câu 105. Cho số phức z= 1+2i. Số phức w iz z là A. 1+i B. –1+i C. –1–i D. 1–i
Câu 106. Cho số phức z  3  2i . Tìm số phức w  2i z  . z
A. w  1 4 . i
B. w 9  2 . i
C. w  4  7 . i
D. w  4  7 . i
Câu 107. Cho số phức z  5  2i . Tìm số phức w iz z
A. w  3  3i
B. w  3  3i
C. w  3  3i
D. w  3  3i
Câu 108. Cho số phức 3 1 z
 .i Tìm số phức 2 1 z z . 2 2 3  3 1 3 1 3 1 3 A.  . i B.  . i 2 2 2 2 1 3 3  3 1 3 C.  . i D.  . i 2 2 2 2 112
4A. Tính toán với số phức Câu 109. 1 3 Cho z i . Tính 2 1 z z 2 2 A. 2 B. -2 C. 0 D. 3
Câu 110. Phần ảo của số phức w 1 zi z , biết số phức z thỏa mãn: 1 iz 1 3i  0 là A. -1 B. 2 C. 1 D. -2
Câu 111. Số phức 2ix 3 5x 4i thỏa mãn: 3  iz  1 2iz  3  4i là: A. z 2 3i B. z 2 5i C. z 1 5i D. z 2 3i
Câu 112. Cho số phức z, thỏa mãn điều kiện 2
(3  2i)z  (2  i)  4  i . số phức w  (1 z)z bằng: 3 11 3 11 A. 3 i B. i C. i D. 3 i 13 13 13 13  
Câu 113. Cho số phức z thỏa mãn điều kiện (1 + i)(z – z 2z 1
i) + 2z = 2i. khi đó số phức w  2 z bằng: A. -1+3i B. 1 i C. i D. 1+3i
Câu 114. Cho phương trình 1
( +i)z-(2-i)z = 3. số phức w = i - 2z bằng: 1- i 9 3 11 3 3 9 A.i B. 3  2i C.i D.i 2 2 2 2 2 2
Câu 115. Cho số phức z thỏa mãn z  z  2 . Số phức w = z2 – z bằng: 1 2i A. 3+5i B. 3 +3i C. 1+5i D. 1+3i
Câu 116. Tìm tất cả các số phức z thỏa mãn đồng thời hai điều kiện z  2 và 2
z là số thuần ảo.
A. z  1 i hoặc z  1 i
B. z  1 i
C. z  1 i
D. z  1 i
Câu 117. Số phức z thỏa mãn z z 3 4i 7 A. z 4i B. z 7 4i C. z 7 6i D. z 7 6i 6
Câu 118. Số phức z thỏa mãn: z  2  i  10 và .zz 25 là: A. z 3 4i và z 5 B. z 3 4i và z 5 C. z 4 3i và z 5 D. z 4 3i và z 5
Câu 119. Có bao nhiêu số phức z thỏa mãn điều kiện 2 2
z z z A. 0 B. 1 C. 3 D. 2
Câu 120. Phần thực của số phức z    i2016 1 là: A. 1008 2 B. 1008 2 C. 0 D. 1
Câu 121. Kết quả của phép tính i   i2016 . 1 ? A. 1008 2 B. 1008 2 C. 1008 2 D. 1008 2 113
4A. Tính toán với số phức 2017    Câu 122. 1 i
Cho số phức z    . Khi đó 7 15 . z z .z có giá trị 1 i A. -i B. i C. 1 D. -1 Câu 123. Tổng 2 3 2009 1 i i i ... i bằng A. 1 i B. 1 i C. 1 D. i
Câu 124. Phần thực của số phức 30 (1 i) bằng A. 0 B. 1 C. 15 2 D. 15 2
Câu 125. Cho số phức z = a + bi thỏa mãn z  2iz  3  3i . Tính S = a2016 + b2017 4032 2017 3  3 4032 2017  3  3  A. S = 0 B. S = 2 C. S D. S    2017 5 2017  5 
Câu 126. Tìm phần thực của số phức sau:     2   3    20 1 (1 i) (1 i) (1 i) ... (1 i) A.  10 2 1 B.  10 2 C. 10 2 1 D. 10 2 1 
Câu 127. Xét số phức 1 m z
(m R) . Tìm m để 1 z.z
1 m(m  2i) 4 . A. m  1 2 B. m  1 C. m  1   2 D. m  0
Câu 128. Cho số phức z  1 .
mi Xác định m để 3
z là một số thực. 3
A. m  0; m  
B. m  0; m  3
C. m  0; m   3 D. m  0; m   3 3
Câu 129. Cho (x + 2i)2 = 3x + yi (x, y  R). Giá trị của x và y bằng:
A. x = 1 và y = 2 hoặc x = 2 và y = 4
B. x = -1 và y = -4 hoặc x = 4 và y = 16
C. x = 2 và y = 5 hoặc x = 3 và y = -4
D. x = 6 và y = 1 hoặc x = 0 và y = 4
Câu 130. Cho (x + 2i)2 = yi (x, y  R). Giá trị của x và y bằng
A. x = 1 và y = 4 hoặc x = -1 và y = -4.
B. x = 3 và y = 12 hoặc x=-3 và y=-12.
C. x = 2 và y = 8 hoặc x = -2 và y = -8.
D. x = 4 và y = 16 hoặc x=-4 và y=-16.
Câu 131. Biết rằng z 1 b i, z a 2i và z z
2 5i . Tìm z , z : 1 1 2 2 1 2 1 2 A. z 1 2i, z 3 2i B. z 1 3i, z 1 i 1 2 1 2 C. z 1 3i, z 1 2i D. z 2i, z 2 i 1 2 1 2 z z 1 4i Câu 132. Cho z a b i, z a b i và 1 2 . Tìm z , z : 1 1 1 2 2 2 z z 1 1 2 1 2 A. z 2i, z 1 i B. z 3i, z 1 i 1 2 1 2 C. z 2i, z 1 2i D. z i, z 2 i 1 2 1 2 z z 1 3i
Câu 133. Biết rằng z a 2i, z a i và 1 2 . Tìm z , z : 1 1 2 2 z z 1 i 1 2 1 2 A. z 2i, z 1 i B. z 3i, z 1 i 1 2 1 2 C. z 2i, z 1 2i D. z i, z 2 i 1 2 1 2 114
4A. Tính toán với số phức Nguyễn Văn Lực
www.facebook.com/VanLuc168
1C 2A 3C 4A 5B 6A 7D 8D 9A 10D
11C 12B 13B 14A 15A 16A 17C 18A 19A 20A
21D 22D 23D 24D 25D 26B 27D 28B 29A 30C
31B 32B 33D 34C 35D 36A 37D 38C 39B 40A
41A 42A 43B 44B 45A 46B 47A 48C 49C 50C
51D 52A 53B 54C 55A 56A 57D 58C 59C 60C
61A 62C 63C 64B 65C 66B 67D 68B 69A 70B
71D 72B 73A 74A 75A 76C 77D 78A 79A 80D
81A 82B 83A 84A 85D 86A 87A 88C 89C 90A
91C 92B 93A 94C 95C 96A 97D 98A 99A 100C 101A 102A 103A 104C 105C 106A 107C 108D 109C 110A 111B 112D 113A 114A 115D 116A 117A 118A 119C 120A 121A 122A 123A 124A 125B 126B 127C 128D 129B 130C 131C 132C 133A 115
4B. Tập hợp điểm - biểu diễn số phức
TẬP HỢP ĐIỂM – BIỂU DIỄN SỐ PHỨC
Câu 1. Cho số phức z i(i 1)(i  2) . Điểm biểu diễn của số phức z là: A. M(-1;3) B. M(-1;-3) C. M(1;-3) D. M(1;3)
Câu 2. Cho số phức z
2i 1 . Điểm biểu diễn số phức liên hợp của z là: A. M ( 1; 2) B. M ( 1; 2) C. M ( 2;1) D. M (2; 1)
Câu 3. Cho số phức z
3 i . Điểm biểu diễn số phức 1 là: z 1 3 3 1 A. M ; B. M ; 4 4 4 4 1 3 3 1 C. M ; D. M ; 2 2 2 2
Câu 4. Cho số phức z thoả mãn 1  iz  4  2i  0. Điểm biểu diễn của z có toạ độ là A. (–3;–1) B. (–3;1) C. (3;–1) D. (3;1)
Câu 5. Cho số phức z thỏa mãn 1 i z  5  i .Hỏi điểm biểu diễn của z là điểm nào trong các
điểm M, N, P, Q ở hình bên? A. Điểm N B. Điểm M C. Điểm P D. Điểm Q
Câu 6. Cho phương trình: (1  4i)z  5i  2z . Điểm biểu diễn của z trên mặt phẳng tọa độ là  4 3   4 3   3 4   3 4  A.  ;   ;   ;   ;   5 5 B.   5 5 C.   5 5 D.   5 5 
Câu 7. Cho số phức z thỏa mãn 1 2iz  3  i . Hỏi điểm biểu diễn của z là điểm nào trong các
điểm I, J, K, H ở hình bên y A. Điểm K 7 B. Điểm H 5 C. Điểm I I J D. Điểm J 1 1 - 5 5 x 1 H 7 K - 5 116
4B. Tập hợp điểm - biểu diễn số phức
Câu 8. Cho số phức z thỏa mãn: (4  i)z  3  4i . Điểm biểu diễn của z là: 16 11  16 13   9 4   9 23  A. M ;    B. M ;    C. M ;    D. M ;    15 15  17 17   5 5   25 25 
Câu 9. Cho số phức z thỏa mãn 1 2iz  8  .
i Hỏi điểm biểu diễn của z là điểm nào
trong các điểm M, N, P, Q ở hình dưới đây? A. Điểm P. B. Điểm Q. C. Điểm M. D. Điểm N.
Câu 10. Cho số phức z thỏa 1 iz  14  2i . Điểm biểu diễn của số phức z trong mặt phẳng
tọa độ Oxy có tọa độ là: A. 6;8 B. 8;6 C. 8;6 D. 6; 8
Câu 11. Điểm biểu diễn của số phức z thỏa : 2
(1 i)z  (1 2i) là:  7 1   7 1   7 1   7 1  A.  ;   B. ;    C. ;   D.  ;    2 2   2 2   2 2   2 2 
Câu 12. Gọi A là điểm biểu diễn của số phức z
3 2i và B là điểm biểu diễn của số
phức z ' 2 3i . Trong các khẳng định sau, khẳng định nào đúng?
A. Hai điểm A và B đối xứng nhau qua đường thẳng y x .
B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
C. Hai điểm A và B đối xứng nhau qua trục tung.
D. Hai điểm A và B đối xứng nhau qua trục hoành.
Câu 13. Gọi A là điểm biểu diễn của số phức z  1  2i và B là điểm biểu diễn của số phức z '  1  2 .
i Tìm mệnh đề đúng trong các mệnh đề sau :
A. Hai điểm A và B đối xứng nhau qua trục hoành
B. Hai điểm A và B đối xứng nhau qua trục tung
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng nhau qua đường thẳng y x
Câu 14. Gọi A là điểm biểu diễn của số phức z  2  5i và B là điểm biểu diễn của số phức z '  2  5 .
i Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y x
Câu 15. Gọi A là điểm biểu diễn số phức z , B là điểm biểu diễn số phức z . Trong các khẳng
định sau khẳng định nào sai?
A. A và B đối xứng nhau qua trục hoành.
B. A và B trùng gốc tọa độ khi z 0 .
C. A và B đối xứng qua gốc tọa độ.
D. Đường thẳng AB đi qua gốc tọa độ. 117
4B. Tập hợp điểm - biểu diễn số phức 4i 2 6i
Câu 16. Cho các số phức z ; z 1 i 1 2i ; z
. Gọi A, B, C lần lượt là điểm 1 2          i  3 1 3  i
biểu diễn của các số phức z , z , z . Nhận xét nào sau đây là đúng? 1 2 3
A. Ba điểm A,B,C thẳng hàng
B. Tam giác ABC là tam giác vuông
C. Tam giác ABC là tam giác cân
D. Tam giác ABC là tam giác vuông cân
Câu 17. Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức z  1  i
2  i ; z  1  3 ; i z  1
  3 .i Tam giác ABC là: 1    2 3 A. Tam giác cân B. Tam giác đều C. Tam giác vuông
D. Tam giác vuông cân
Câu 18. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức z  3  4i; M ' là điểm 1
biểu diễn cho số phức /  i z
z . Tính diện tích tam giác OMM’. 2 25 25 15 15 A. SSSS   B. C. D. OMM '    4 OMM ' 2 OMM ' 4 OMM ' 2
Câu 19. Phương trình 2 x 2x b
0 có hai nghiệm phức được biểu diễn trên mặt phẳng phức bởi
hai điểm A, B. Tam giác OAB đều (Với O là gốc tọa độ) thì b bằng 4 1 A. B. 3 C. D. 4 3 3
Câu 20. Tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa < 3 là
A. Đường tròn bán kính r  3
B. Hình tròn bán kính r  3 không kể đường tròn bán kính r  3
C. Đường tròn bán kính r  9
D. Hình tròn bán kính r  9
Câu 21. Tìm tập hợp các điểm M biểu diễn số phức z có phần thực dương thỏa mãn z  2
A. Đường tròn O; 2 .
B. Hình tròn O; 2 .
C. Nửa hình tròn O; 2 nằm bên trái trục tung.
D. Nửa hình tròn O; 2 nằm bên phải trục tung.
Câu 22. Tìm tập hợp các điểm M biểu diễn số phức z, thỏa mãn: 1  z  3
A. Phần hình phẳng nằm hoàn toàn phía ngoài hình tròn (O;1) và phía trong hình tròn (O;3)
B. Hình tròn (O;3) (bỏ gốc tọa độ O)
C. Hình tròn (O;1) (bỏ gốc tọa độ O)
D. Đường tròn (O;1) Nguyễn Văn Lực
www.facebook.com/VanLuc168 118
4B. Tập hợp điểm - biểu diễn số phức
Câu 23. Cho số phức z a bi;a,b
. Để điểm biểu diễn của z trong hình sau, thì điều kiện của a và b là y A. a + b = 4. B. 2a + 2b > 4. C. a2 + b2 = 4. D. a2 + b2 < 4. x -2 O 2
Câu 24. Cho hai số phức z a bi;a,b
. Để điểm biểu diễn của z nằm trong dải (-2; 2) như
hình trên, điều kiện của a và b là: y a  2 A.  2 a 2 và b  R b B.     2 x a  2 -2 O 2 C. b D. a, b  (-2; 2)  -2
Câu 25. Điểm biểu diễn của các số phức z a ai với a
. , nằm trên đường thẳng có phương trình là:
A. y = 2x
B. y = -x
C. y = x+ 1 D. y = x
Câu 26. Điểm M trên hình vẽ là điểm biểu diễn của số phức nào sau đây: y M 2 x 1
A. (1 + i)z = 3 – i
B. (1 - i)z = 3 – i
C. (1 - i)z = 3 + i
D. (1 + i)z = 3 + i
Câu 27. Cho hai số phức z a bi;a,b
. Để điểm biểu diễn của z trong hình sau, thì điều kiện của a và b là y x -2 O 2 a 2 a 2 A. B. b 2 b -2 C. 2 a 2 và b  R. D. a, b  (-2; 2). 119
4B. Tập hợp điểm - biểu diễn số phức
Câu 28. Cho số phức z a bi;a,b
. Để điểm biểu diễn của z trong hình sau, thì điều kiện của a và b là y 3 x O a 3 a 3 A. -3 B. b 3 b -3 C. a, b  (-3; 3).
D. a  R và -3 < b < 3.
Câu 29. Tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z thỏa mãn điều kiện 2 z là số ảo là A. Trục ảo. B. Trục thực.
C. Hai đường phân giác y x và y
x của các góc tọa độ.
D. Đường phân giác góc phần tư thứ nhất.
Câu 30. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z2 là một số thực dương là:
A. Trục hoành (trừ gốc tọa độ O)
B. Truc tung (trừ gốc toạ độ O)
C. Đường thẳng y = x (trừ gốc toạ độ O)
D. Đường thẳng y = -x (trừ gốc toạ độ O)
Câu 31. Cho số phức z
1 2i . Điểm biểu diễn của số phức z là A. Điểm A . B. Điểm B C. Điểm C . D. Điểm D .
Câu 32. Cho các số phức z thỏa mãn z 1  2 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  (1 i 3)z  2 là một đường tròn. Bán kính r của đường tròn đó là A. r = 4. B. r = 8. C. r = 2. D. r = 16.
Câu 33. Tập hợp các điểm biểu diễn số phức z thõa mãn z  4  3i  2 là đường tròn có tâm I, bán kính R: A. I(4;3), R =2 B. B.I(4;-3), R =4 C. I(-4;3), R= 4 D. I(4; -3), R= 2 120
4B. Tập hợp điểm - biểu diễn số phức
Câu 34. Trên mặt phẳng tọa độ, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện
z  (3  4i)  2 .
A. Đường tròn tâm I (3; 4) bán kính R  2 .
B. Đường tròn tâm I (3; 4) bán kính R  2 .
C. Đường tròn tâm I (3; 4) bán kính R  2 .
D. Đường tròn tâm I (3; 4) bán kính R  2 .
Câu 35. Cho số phức z thỏa mãn z 1  2 .Biết rằng tập hợp các điểm biểu diễn các số
phức w  2z  i là một đường tròn. Tìm bán kính r của đường tròn đó. A. r = 2 B. r = 1 C. r = -2 D. r = 4
Câu 36. Cho số phức z thỏa z 1 i
2 . Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức z là một đường thẳng.
B. Tập hợp điểm biểu diễn số phức z là một đường Parabol.
C. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 2 .
D. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 4 .
Câu 37. Tập hợp các điểm trong mặt phẳng phức biểu diễn cac số phức z thỏa mãn
| z z  5 | 6 là đường thẳng có phương trình là: 1 1 1 1 A. x B. x   C. y D. y   2 2 2 2
Câu 38. Tập hợp các điểm biểu diễn của số phức z thoả mãn điều kiện z i 3 là đường tròn có phương trình 2 2 2 2 A. x (y 1) 9 B. x (y 1) 9 2 2 2 C. (x 1) y 9 D. x (y 1) 3
Câu 39. Tập hợp các điểm trong mặt phẳng biểu diễn số phức z thõa mãn điều kiện z 1  2i  4 là
A. Một đường thẳng
B. Một đường tròn
C. Một hình chữ nhật D. Một hình vuông
Câu 40. Tìm tập hợp các điểm M biểu diễn số phức Z, thỏa mãn : 2 2 z  (z)  4  A. Đường cong 1 y x B. Đường cong 1 y xC. Đường cong 1 y  và đường cong 1 y x x D. Đường cong 1 y  hoặc đường cong 1 y x x
Câu 41. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa
1iz 2i  2 là 2 2 2 2 A.x   1   y   1 1 B.x   1   y   1 1 2 2 2 2 C.x   1   y   1 1 D.x   1   y   1 1 121
4B. Tập hợp điểm - biểu diễn số phức
Câu 43. Cho số phức z thỏa mãn 2 z  2  3i  2i  1  2z . Tập hợp điểm biểu diễn cho số phức z là:
A. 12x  32y  47  0
B. 12x  32y  47  0
C. 12x  32y  47  0
D. 12x  32y  47  0
Câu 44. Trên mặt phẳng tọa độ, Tìm tập hợp tất cả các điểm M trong biễu diễn các số phức thỏa z z 3 4i A. 2x 3 0
B. Đường thẳng 6x-8y-25=0
C. Đường thẳng 6x+8y-25=0
D. Đường thẳng y-2=0
Câu 45. Trong mp tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa
mãn: z i  1 iz .
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2, –1), bán kính R= 2 .
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, 1), bán kính R= 3 .
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R= 3 .
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R= 2 .
Câu 46. Cho số phức z thỏa 2 z
1 z . Chọn phát biểu đúng:
A. Tập hợp điểm biểu diễn số phức z là một đường thẳng.
B. Tập hợp điểm biểu diễn số phức z là một đường Parabol.
C. Tập hợp điểm biểu diễn số phức z là một đường tròn.
D. Tập hợp điểm biểu diễn số phức z là một đường Elip. z
Câu 47. Trên mặt phẳng tọa độ, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn  3. z i   3
A. Đường tròn tâm 9 I ; 0 
 bán kính R  .  8  8   9
B. Đường tròn tâm 9 I 0;   bán kính R  .  8  64   3
C. Đường tròn tâm 9 I 0; 
 bán kính R  .  8  8   3
D. Đường tròn tâm 9 I 0;    bán kính R  .  8  8
Câu 48. Tìm tập hợp các điểm M biểu diễm số phức z thỏa mãn:   2 2 z z .
A. Trục Ox và trục Oy .
B. Trục Ox . C. Trục Oy .
D. Không có điểm M .
Câu 49. Trong mặt phẳng phức Oxy , cho số phức z thỏa lần lượt một trong bốn điều kiện I : z z 2 ; II : . z z
5; III : z 2i
4 , IV : i z 4i
3 . Hỏi điều kiện nào để số phức
Z có tập hợp biểu diễn là đường thẳng. A. I
B. I , II
C. I , IV
D. II , III , IV 122
4B. Tập hợp điểm - biểu diễn số phức z i
Câu 50. Trên mặt phẳng tọa độ, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn 1. zi
A. Điểm O 0;0.
B. Đường tròn tâm I 0; 
1 , bán kính R  1. C. Trục . Oy D. Trục Ox .
Câu 51. Cho số phức z thỏa mãn z 3 4i 2 và w 2z
1 i . Trong mặt phẳng phức,
tập hợp điểm biểu diễn số phức w là đường tròn có tâm I, bán kính R. Khi đó A. I 3; 4  , R  2
B. I 4;5, R  4
C. I 5;7, R  4
D. I 7;9, R  4
Câu 52. Các điểm biểu diễn các số phức z  3  bi;(b
) trong mặt phẳng tọa độ, nằm trên
đường thẳng có phương trình là: A. x 3 B. y 3 C. x b D. y b
Câu 53. Các điểm biểu diễn của số thuần ảo nằm ở đâu trên mặt phẳng tọa độ A. Ox B. Oy C. O
D. Ox và Oy .
Câu 54. Số phức z  2  3i có điểm biểu diễn là A. B. C. D.
Câu 55. Gọi M là điểm biểu diễn số phức z trong mặt phẳng phức. Như thế, số z được biểu diễn bởi điểm
A. Đối xứng với M qua O
B. Đối xứng với M qua Oy
C. Đối xứng với M qua Ox
D. Không xác định được Nguyễn Văn Lực
www.facebook.com/VanLuc168
1B 2A 3A 4A 5B 6A 7D 8B 9B 10D
11D 12A 13B 14B 15A 16B 17D 18B 19A 20B
21D 22A 23D 24B 25D 26C 27C 28D 29C 30A
31A 32A 33A 34D 35D 36C 37B 38B 39B 40C
41C 42B 43C 44D 45A 46C 47A 48A 49D 50D 51A 52B 53C 54A 123
4C. Phương trình phức PHƯƠNG TRÌNH PHỨC
Câu 1. Trong C, phương trình (2 - i) z - 4 = 0 có nghiệm là: 8 4 4 8 2 3 7 3 A. z =  i B. z =  i C. z =  i D. z =  i 5 5 5 5 5 5 5 5
Câu 2. Trong C, phương trình (i+z)( z - 2 + 3i) = 0 có nghiệm là: z iz  2iz  iz  3i A.B.C.D.
z  2  3i
z  5  3i
z  2  3i
z  2  5i
Câu 3. Tập nghiệm của phương trình 2
z z  0 là A. 0; 1  ;  i B. 0; 1  ;  i C. 0;1;   i D. 0;i;  i
Câu 4. Tìm nghiệm của phương trình 2 z z  0 1 3 1 3
A. z  0; z  1  ; z   ; i z    i 1 2 3 4 2 2 2 2 1 3 1 3
B. z  0; z  1; z   i; z   i 1 2 3 4 2 2 2 2 1 3 1 3
C. z  0; z  1  ; z    i; z   i 1 2 3 4 2 2 2 2 1 3 1 3
D. z  0; z  1  ; z   ; i z   i 1 2 3 4 2 2 2 2
Câu 5. Nghiệm của phương trình z 2  i  53  2i là:
A. z  8 – i B. z  8 + i
C. z  – 8 – i
D. z  – 8 + i
Câu 6. Tìm các số phức z thỏa mãn 2
z  3  4i .
A. z  2  i ; z  2   i .
B. z  2  i ; z  2  i . 1 2 1 2
C. z  2  i ; z  2   i .
D. z  2  i ; z  2  i . 1 2 1 2
Câu 7. Nghiệm phức của phương trình 2 z 4 0 là: A. z 2i hoặc z 2i B. z 2 C. z 2i D. z 2
Câu 8. Số nghiệm thực của phương trình 2 z 3z 5 0 là A. B. 1 C. 2 D. 3
Câu 9. Phương trình 2 z 2z 4 0 có nghiệm là z 1 i 3 z 1 i 3 z 1 i 2 z 2 i 3 A. B. C. D. z 1 i 3 z 1 i 3 z 1 i 2 z 2 i 3
Câu 10. Nghiệm của phương trình 2
z  2z  2  0 là: A. 1  B.i C. 1  i D. 1 i 124
4C. Phương trình phức
Câu 11. Giải phương trình 2 2x 3x 5
0 trên tập số phức. Mệnh đề nào sau đây là đúng ?
A. Phương trình có 2 nghiệm phức.
B. Phương trình có 2 nghiệm thực.
C. Phương trình có một nghiệm thực và một nghiệm phức.
D. Phương trình vô nghiệm.
Câu 12. Phương trình 2 5z
7z 11 0 có số nghiệm phức là A. 2 B. 3 C. 1 D. 4
Câu 13. Trong các phương trình sau, phương trình nào có nghiệm thực A. 2 z 3z 4 0 B. 2 z 6z 10 0 C. 2 2z 2z 3 0 D. 2 z z 3 z i
Câu 14. Phương trình 4 3 7 z 2i có nghiệm là z i z 1 2i z 1 2i A. B. z 3 i z 3 i z 1 2i z 1 3i C. D. z 3 i z 3 2i
Câu 15. Tìm các nghiệm phức của phương trình 3 z  8  0 . A. z  2
 ; z 1 3 ;i z 1 3 .i B. z  2  ; z  1
  3i; z 1 3 .i 1 2 3 1 2 3 C. z  2
 ; z 1 3i; z  1   3 .i D. z  2  ; z  1
  3 ;i z  1   3 .i 1 2 3 1 2 3
Câu 16. Phương trình 3 2 z 2z z 2
0 có bao nhiêu nghiệm phức A. 3 B. 2 C. 1 D. 4
Câu 17. Tìm tập hợp nghiệm phức của phương trình 3 2
z  3z  3z  63  0.
A. S  3;3 2 3 ;i 3   2 3 i. B. S  3; 3   2 3 ;i 3   2 3 i. C. S  3; 3
  2 3 ;i3  2 3 i.
D. S  3;3 2 3 ;i 3   2 3 i.
Câu 18. Trong C, phương trình z4 - 6z2 + 25 = 0 có nghiệm là:
A. z i
B. z  i; z  i 5
C. z i  5 D. Vô nghiê ̣m
Câu 19. Phương trình 4 2 z z 6 0 có nghiệm là A. z 2; z i 3 B. z 2; z i 3 C. z 3; z i 2 D. z 5; z 2i 4 2
Câu 20. Tập nghiệm của phương trình: z  3z  2  0 là
A. S  { 1; 2} B. S  { ; i i 2} C. S  { ;
i  ;ii 2;i 2} D. S  
Câu 21. Nghiệm của phương trình 3x  2  3i1  2i  5  4i là 5 5 A. x 1 i B. x 3 5i C. x 1 i D. x 3 5i 3 3
Câu 22. Nghiệm của phương trình  2  i 3 x i 2  3  2 2i trên tập số phức? A. 5i B. 5i C. i D. i 125
4C. Phương trình phức
Câu 23. Nghiệm của phương trình 2ix 3
5x 4i trên tập số phức ? 55 14 55 14 55 14 55 14 A. i B. i C. i D. i 29 29 19 19 29 29 19 19 Câu 24. Cho z 1 2i; z
1 2i . Phương trình bậc hai với hệ số thực nhận z ; z làm nghiệm là 1 2 1 2 A. 2 z 2z 5 0 B. 2 z 2z 5 0 C. 2 z 2z 5 0 D. 2 z 5z 2 0
Câu 25. Gọi z1, z2 là hai nghiệm phức của phương trình z2 – 4z + 9 = 0. Tổng P = |z1| + |z2| bằng: A. 3 B. 6 C. 18 D. 4
Câu 26. Gọi z , z là hai nghiệm phức của phương trình 2 z 4z 7 0 . Khi đó 2 2 z z bằng: 1 2 1 2 A. 10 B. 7 C. 14 D. 15
Câu 27. Gọi z , z là hai nghiệm phức của phương trình: 2
z  4z  5  0 . Khi đó, 2 2 z  z bằng: 1 2 1 2 A. 6 B. 5 C. 4 D. 7
Câu 28. Biết z , z là các nghiệm của phương trình 2
2x  3x  3  0 . Tính 2 2
T z z . 1 2 1 2 9 9 45 3 A. T   B. T C. T   D. T   4 4 16 4
Câu 29. Xác định m để phương trình 2 z mz 3i
0 có 2 nghiệm phức z , z thõa mãn 1 2 2 2 z z 8 1 2 A. m 3 i hoặc m 3 i B. m 3 i hoặc m 3 i C. m 3 i hoặc m 3 i D. m 3 i hoặc m 3 i z z
Câu 30. Biết z , z z z    . 1
2 là các nghiệm phức của phương trình 2 2 0. Tính 1 2 z z 2 1 1 3 3 5 A. .  . . . 2 B. 2 C. 2 D. 2 Nguyễn Văn Lực
www.facebook.com/VanLuc168 1 1
Câu 31. Biết z z là các nghiệm của phương trình 2
x  2x  5  0 . Tính T   . 1, 2 z z 1 2  2 2  2 2 A. T B. T C. T D. T  5 5 10 10
Câu 32. Cho phương trình 2
z m z  2m 1  0 trong đó m là tham số phức; giá trị m để phương
trình có hai nghiệm z ; z thỏa mãn 2 2 z z  10  . 1 2 1 2 A. m 2 2 2 ; i m 2 2 2 . i B. m 4 2 3;m 4 2 3 C. m 1 3i;m 2 3 . i D. m 1 3i;m 1 3 . i
Câu 33. Gọi z , z là hai nghiệm của phương trình 2 z (8 3i) z 13 11i
0 . Khi đó, giá trị của 1 2 2 2 A z z bằng 1 2 A. 39 B. 29 C. 49 D. 19 126
4C. Phương trình phức
Câu 34. Gọi z , z là các nghiệm của phương trình 2
z  2z  5  0 . Tính giá trị biểu thức: 1 2 2 2 A z
z  4 z z 1 2 1 2 A. 10 B. 20 C. -10 D. 5 2
Câu 35. Gọi z , z z 2z 3 0 1
2 là hai nghiệm phức của phương trình: 
  . Tìm số phức liên hợp
của số phức w  5 2iz z 1 2  ?
A. w  10  4i
B. w  10  4i
C. w  10  4i
D. w  10  4i
Câu 36. Gọi z1, z2 là hai nghiệm phức của phương trình x3 - 3x2 + 4x – 12 = 0. Tính
P  2 | z |  | z | 1 2 A. P = 0 B. P = 16 C. P = 4 D. P = - 4
Câu 37. Gọi z , z là hai nghiệm của phương trình 2 2z 4z 5
0 . Khi đó, giá trị của biểu thức 1 2 A z z 4 bằng 1 2 A. 6 B. 4 C. 2 D. 5
Câu 38. Phương trình 2 z 4z 14
0 có hai nghiệm z ; z . Giá trị của biểu thức 1 2 2 2 A 2 z 3 z bằng 1 2 A. 14 B. 13 C. 14 D. 13
Câu 39. Gọi z , z là hai nghiệm của phương trình 2 z 5z 10
0 , với z có phần ảo dương. 1 2 1
Phần thực và phần ảo của số phức w 4z 2z lần lượt là 1 2 A. 5; 15 B. 5; 15 C. 5; 15 D. 5; 15
Câu 40. Phương trình 2
z  5  m  2iz  5  m  
1 i  0 có hai nghiệm z ; z thỏa mãn 1 2 2 2 z z 3z .z 20 7i khi m bằng 1 2 1 2 A. 2 B. 3 C. -2 D. 1
Câu 41. Kí hiệu z , z lần lượt là hai nghiệm phức của phương trình 2
2z  2z  5  0 . Giá trị của 1 2 biểu thức 2 2
A z 1  z 1 bằng: 1 2 A. 25 B. 5 C. 5 D. 2 5
Câu 42. Gọi z , z , z là ba nghiệm của phương trình 3 z 1 0. Khi đó 1 2 3 S | z | | z | | z | bằng 1 2 3 A. S = 1 B. S = 4 C. S = 2 D. S = 3
Câu 43. Gọi z , z , z , z 4 2
z z  6  0 1 2 3
4 là các nghiệm của phương trình: . Giá trị của
T z z z z 1 2 3 4 là: A. 1 B. 2 2  2 3 C. 2 2  2 3 D. 7
Câu 44. Kí hiệu z   
1 , z2 , z3 và z4 là bốn nghiệm phức của phương trình 4 2 z 2z 63 0 .
Tính tổng T = | z1 | + | z2 | + | z3 | + | z4 | . A. T  6. B. T  2 7.
C. T  3  2 7.
D. T  6  2 7. 127
4C. Phương trình phức
Câu 45. Kí hiệu z , z , z , z là bốn nghiệm của phương trình 4 2 z  4z  77  0 .Tính 1 2 3 4
tổngS  z  z  z  z . 1 2 3 4 A. S  2 7  2 11 B. S  2 7  2 11 C. S  2 7 D. S  2 11
Câu 46. Phương trình z4 – z2 – 6 = 0 có 4 nghiệm phức phân biệt. Khi đó tổng môđun của các
nghiệm phức trong phương trình là: A. 4 B. 2 3  2 2 C. 2 3 D. 3  2
Câu 47. Kí hiệu z , z , z , z là bốn nghiệm phức của phương trình 4 2
z z 12  0. Khi đó tổng 1 2 3 4
T z z z z là : 1 2 3 4 A. 4 B. 2 C. 4+2 D. 2+ 2
Câu 48. Gọi z ; z là hai nghiệm của phương trình 2 2z 3z 8
0 , với z có phần ảo < 0. Xác 1 2 1
định phần thực và phần ảo của số phức w z 2z 3 4i 1 2
A. Phần thực 3 , phần ảo 16 3 55 .
B. Phần thực 3 , phần ảo 16 3 55 . 4 4 4 4 C. Phần thực 3 , phần ảo 16 3 55 .
D. Phần thực 3 , phần ảo 16 3 55 . 4 4 4 4
Câu 49. Gọi z ; z là hai nghiệm phức của phương trình: 2 z 2z 10
0 . Giá trị của biểu thức 1 2 2 2 A z z là 1 2 A.100 B. 10 C. 20 D. 17
Câu 50. Phương trình 3
z  8 có bao nhiêu nghiệm phức với phần ảo âm A. 1 B. 2 C. 3 D. 4 2
Câu 51. Giải phương trình 2x  5x  4  0 trên tập số phức. 5 7 5 7 5 7 5 7 A. x   i x   i x i x i 1 4 4 ; 2 4 4 . B.   1 4 4 ;   2 4 4 5 7 5 7 3 7 3 7 C. x   i x i x i x i 1 2 4 ;   2 2 4 D.   1 4 4 ;   2 4 4
Câu 52. Nghiệm của phương trình: 2
2z  3z  4  0 3   i 23 3   i 23 A. zB. z  1,2 3 1,2 4 3   i 23 3   i 23 C. zD. z  1,2 5 1,2 6 1A 2C
3D 4D 5A 6A 7A 8A 9A 10D
11A 12A 13A 14A 15A 16A 17B 18B 19A 20C
21A 22C 23C 24A 25B 26C 27A 28A 29A 30B
31A 32A 33A 34C 35B 36C 37A 38A 39A 40A
41C 42D 43B 44D 45A 46B 47C 48A 49C 50C 51B 52B 128