Bài tập vật lý điện từ - Vật lý kỹ thuật | Trường Đại học Sư phạm Kỹ thuật Hưng Yên

Bài tập vật lý điện từ - Vật lý kỹ thuật | Trường Đại học Sư phạm Kỹ thuật Hưng Yên được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Thông tin:
17 trang 5 tháng trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bài tập vật lý điện từ - Vật lý kỹ thuật | Trường Đại học Sư phạm Kỹ thuật Hưng Yên

Bài tập vật lý điện từ - Vật lý kỹ thuật | Trường Đại học Sư phạm Kỹ thuật Hưng Yên được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

62 31 lượt tải Tải xuống

Môn: Tiếng Anh Chuyên Ngành (EA1) 11 tài liệu

Trường: Đại Học Sư phạm Kỹ thuật Hưng yên 74 tài liệu

Thông tin:

17 trang 5 tháng trước

Tác giả:

Profile Mai Nguyệt
28
PHẦN III: ĐIỆN - TỪ TRƯỜNG
CHÖÔNG MOÄT
TRÖÔØNG TÓNH ÑIEÄN
3.1-1. Moät thanh coù chieàu daøi
l
ñaët theo truïc Ox nhö hình veõ,
coù maät ñoä thay ñoåi theo x vôùiλ
2
2
o
x
l
λ=λ
, trong ñoù λ
o
laø moät
haèng soá döông. Tính ñieän tröôøng
E
r
taïi ñieåm M coù toïa ñoä x = a.
Ñaùp soá:
( )
+−
+
+
λ
==
a2
1na2
a22
a
kEE
2
o
x
l
l
l
l
l
l
3.1-2. Hai thanh daãn ñieän AB vaø CD
baèng nhau, daøi
m2,0L
=
, coù tieát
dieän nhoû so vôùi chieàu daøi ñöôïc ñaët
vuoâng goùc nhö hình veõ. Cho bieát
m1,0aOCOA
=
=
=
, maät ñoä ñieän
daøi treân thanh AB laø
m/C10
9−
=λ
vaø treân CD laø
λ
−
. Tính ñieän tröôøng
taïi O.
Ñaùp soá:
r
E
naèm treân phaân giaùc cuûa goùc phaàn tö thöù hai vaø
y
O
x
(
)
l+− a
a
a
M
A
C
D
O
B
29
( )
E
a a L
V m
o
= −
+
=
λ
π ε
2
4
1 1
84 /
3.1-3. Cho nöûa ñöôøng troøn (O, a)
mang ñieän tích phaân boá vôùi maät
ñoä ñieän daøi = λ λ
o.
sinθ (λ
o
> 0)
ñöôïc ñaët trong khoâng khí nhö hình
veõ.
Xaùc ñònh vectô cöôøng ñoä ñieän
tröôøng taïi taâm O.
Ñaùp soá:
x
o
o
e
a8
E
r
r
ε
λ
−=
3.1-4. a. Moät daây daãn ñöôïc ñaët trong
khoâng khí vaø ñöôïc uoán thaønh moät cung
troøn baùn kính R, goùc ôû taâm laø , mang α
ñieän tích phaân boá ñeàu vôùi maät ñoä . λ
Tính vectô cöôøng ñoä ñieän tröôøng
r
E
taïi ñieåm O.
b. Moät voøng daây troøn (O, a) ñöôïc
ñaët trong khoâng khí, mang ñieän tích
phaân boá ñeàu vôùi maät ñoä ñieän daøi . Choïn truïc Ox vuoâng goùc λ
vôùi maët phaúng cuûa voøng troøn qua taâm O. Xaùc ñònh vectô cöôøng
ñoä ñieän tröôøng taïi moät ñieåm treân truïc Ox coù toïa ñoä x.
Ñaùp soá: a.
y
e
2
sin
R
k2
E
r
r
α
λ
−=
b.
( )
x
e
ax
xQk
E
r
r
2/3
22
+
=
y
x
O
r
e
x
y
e
r
x
y
θ
x’
r
e
y
O
r
e
x
30
3.1-5. Moät maët baùn caàu baùn kính R ñöôïc ñaët trong khoâng khí,
tích ñieän ñeàu vôùi maät ñoä ñieän maët . Xaùc ñònh vectô cöôøng ñoä σ
ñieän tröôøng taïi taâm O cuûa baùn caàu.
Ñaùp soá :
r
E
ôû treân truïc ñoái xöùng cuûa baùn caàu,
o
4
E
ε
σ
=
3.1-6. Moät ñóa troøn baùn kính R ñöôïc tích ñieän ñeàu vôùi maät ñoä
ñieän maët > 0 vaø ñöôïc ñaët trong chaân khoâng. xaùc ñònh vectô σ
cöôøng ñoä ñieän tröôøng taïi moät ñieåm naèm treân truïc cuûa ñóa vaø
caùch taâm ñóa moät khoaûng x.
Xeùt caùc tröôøng hôïp x >> R vaø x << R .
Ñaùp soá :
r
E
naèm treân truïc cuûa ñóa
( )
E
x
x R
V m
o
= −
+
σ
ε
2
1
2 2
/
Khi x >> R :
( )
m/V
x4
q
E
2
o
επ
=
Khi x << R :
( )
E V m
o
=
σ
ε
2
/
3.1-7. Cho moät daây daøi voâ haïn, mang ñieän tích phaân boá ñeàu
vôùi maät ñoä . Tính thoâng löôïng ñieän tröôøng qua maët truï kín baùn λ
kính R, chieàu cao h, coù truïc truøng vôùi daây.
Ñaùp soá :
o
h
ε
λ
=Φ
3.1-8. Moät khoái truï roãng raát daøi, baùn kính trong
cm5,2r
1
=
vaø
baùn kính ngoaøi
cm5,3r
2
=
, mang ñieän tích phaân boá ñeàu vôùi
maät ñoä ñieän tích khoái , ñöôïc ñaët trong khoâng khí. Moät sôïi daây ρ
maõnh raát daøi, mang ñieän tích phaân boá ñeàu vôùi maät ñoä ñieän daøi
31
m/C8,6
µ
−
=
λ
, ñöôïc ñaët truøng vôùi truïc khoái truï. Tính maät ñoä
ñieän tích khoái ρ cuûa khoái truï ñeå ñieän tröôøng taïi caùc ñieåm beân
ngoaøi khoái truï baèng khoâng.
Ñaùp soá :
( )
33
2
1
2
2
m/C10.61,3
rr
−
=
−π
λ
−=ρ
3.1-9. Moät khoái truï caùch ñieän, daøi voâ haïn, baùn kính
cm5,4R
=
, ñöôïc ñaët trong khoâng khí, mang ñieän tích phaân boá
ñeàu vôùi maät ñoä ñieän tích khoái . Tính bieát raèng ñieän tröôøng ρ ρ
taïi moät ñieåm beân ngoaøi khoái truï, saùt beà maët khoái truï vaø gaàn
taâm khoái truï baèng
C/kN16E
=
.
Ñaùp soá:
3
o
m/C29,6
R
E2
µ=
ε
=ρ
3.1-10. Cho nöûa ñöôøng troøn (O, a)
mang ñieän tích phaân boá vôùi maät ñoä
ñieän daøi
θλ=λ cos
o
(λ
o
laø haèng
soá) ñöôïc ñaët trong khoâng khí nhö
hình veõ. Tính ñieän theá taïi taâm O.
Ñaùp soá:
o
o
2πε
λ
=ϕ
3.1-11. Moät voøng daây troøn baùn kính R ñöôïc ñaët trong khoâng
khí, mang ñieän tích 3Q phaân boá ñeàu treân ba phaàn tö voøng daây
vaø
-Q treân moät phaàn tö voøng daây coøn laïi. Tính ñieän theá taïi:
a. Taâm voøng daây.
b. Moät ñieåm treân truïc cuûa voøng daây caùch taâm moät khoaûng
h.
x
y
θ
x’
O
32
Ñaùp soá:
22
hR
2kQ
b.,
R
2kQ
a.
+
==
ϕϕ
3.1-12. Moät vaønh taâm O baùn kính trong a, baùn kính ngoaøi b,
ñöôïc ñaët trong khoâng khí, mang ñieän tích phaân boá ñeàu vôùi maät
ñoä ñieän maët . Tính ñieän theá taïi moät ñieåm treân truïc vaønh troøn σ
vaø caùch taâm O moät khoaûng x.
Ñaùp soá:
(
)
2222
o
xaxb
2
+−+
ε
σ
=ϕ
3.1-13. Nöûa maët caàu taâm O baùn kính R ñöôïc ñaët trong khoâng
khí, mang ñieän tích phaân boá ñeàu vôùi maät ñoä ñieän maët . Tính σ
ñieän theá taïi taâm O.
Ñaùp soá:
ϕ
σ
ε
=
R
o
2
3.1-14. Moät maët caàu (O, R) ñöôïc ñaët trong khoâng khí, mang
ñieän tích q phaân boá ñeàu. Tính ñieän theá taïi moät ñieåm caùch taâm
O moät khoaûng r trong hai tröôøng hôïp r > R vaø r < R, choïn goác
ñieän theá ôû voâ cöïc.
Ñaùp soá:
)Rr(
R
kq
),Rr(
r
kq
<=ϕ>=ϕ
3.1-15. Moät daây daøi voâ haïn ñöôïc ñaët trong khoâng khí, mang
ñieän tích phaân boá ñeàu vôùi maät ñoä ñieän daøi . Tính ñieän theá taïi λ
moät ñieåm caùch daây moät khoaûng r. Choïn goác ñieän theá taïi ñieåm
caùch daây moät khoaûng d.
Ñaùp soá:
ϕ
λ
πε
=
2
0
ln
d
r
33
3.1-16. Hai maët truï daøi voâ haïn, ñoàng truïc, ñöôïc ñaët trong
khoâng khí, tích ñieän ñeàu vôùi maät ñoä ñieän maët , maët trong σ
mang ñieän döông coù baùn kính R
1
, maët ngoaøi mang ñieän aâm coù
baùn kính R
2
. Tính hieäu theá giöõa hai maët truï.
Ñaùp soá:
1
2
0
1
21
R
R
n
R
l
ε
σ
=ϕ−ϕ
3.1-17. Cho hai maët caàu ñoàng taâm ñöôïc ñaët trong khoâng khí,
tích ñieän ñeàu, ñieän tích maët trong laø q vaø maët ngoaøi laø Q. Tính
hieäu theá giöõa hai maët caàu. Bieát caùc baùn kính maët caàu laø R
1
vaø
R
2
(R
1
< R
2
)
Ñaùp soá:
−
πε
=ϕ−ϕ
210
21
R
1
R
1
4
q
3.1-18. a. Ñieän theá cuûa moät quaû caàu caùch ñieän baùn kính R, tích
ñieän ñeàu vôùi ñieän tích toång coäng Q, ñöôïc cho bôûi:
−=ϕ
2
2
R
r
3
R2
Qk
khi r < R
r
Qk
=ϕ
khi r > R
Tìm ñieän tröôøng taïi moät ñieåm ôû trong (r < R) vaø ôû ngoaøi
(r > R) quaû caàu.
b. Ñieän theá cuûa moät phaân boá ñieän tích ñöôïc xaùc ñònh bôûi:
( )
( )
ϕ
x y z
kQ
x a y z
, , =
− + +
2
2 2
Tìm caùc thaønh phaàn E
x
, E
y
, vaø E
z
cuûa vectô
r
E
gaây bôûi phaân
boá ñieän tích ñoù.
Ñaùp soá: a.
3
R
rQk
E=
(r < R) ;
2
r
Qk
E=
( r > R)
34
b.
(
)
( )
[ ]
E
x
kQ x a
x a y z
x
= − =
−
− + +
∂ϕ
∂
2
2 2
3 2/
( )
[ ]
E
y
kQ y
x a y z
y
= − =
− + +
∂
ϕ
∂
2
2 2
3 2/
( )
[ ]
E
z
kQ z
x a y z
z
= − =
− + +
∂
ϕ
∂
2
2 2
3 2/
3.1-19. Ñieän theá cuûa moät phaân boá ñieän tích trong moät mieàn
khoâng gian ñöôïc cho bôûi (x) = 3x - 2xϕ
2
- x
3
vôùi tính baèng V ϕ
vaø caùc toïa ñoä x, y, z tính baèng m.
a. Tìm caùc ñieåm coù ñieän theá baèng khoâng treân truïc Ox.
b. Tìm bieåu thöùc cuûa vectô cöôøng ñoä ñieän tröôøng.
c. Tìm caùc ñieåm coù ñieän tröôøng baèng khoâng treân truïc Ox.
Ñaùp soá: a. (x) = 0 taïi x = 0, 1m, -3m ϕ
b.
(
)
x
2
e3x4x3E
r
r
−+=
c.
0E =
r
taïi x = 0,535m vaø x = -1,87m
3.1-20. Cho moät thanh daøi 2a ñöôïc ñaët trong khoâng khí, tích
ñieän ñeàu vôùi maät ñoä ñieän daøi λ
a. Tính ñieän theá roài suy ra ñieän tröôøng taïi moät ñieåm M
naèm treân ñöôøng keùo daøi cuûa thanh vaø caùch trung ñieåm
thanh moät khoaûng r.
b. Xeùt tröôøng hôïp r >> a.
Ñaùp soá: a.
ar
ar
lnk
−
+
λ=ϕ
;
22
ar
a2
kE
−
λ
=
;
E
r
höôùng doïc theo thanh
b.
r
a2
k
λ
=ϕ
;
2
r
a2
kE
λ
=
;
35
E
r
höôùng doïc theo thanh
3.1-21. Moät vaønh troøn taâm O, baùn kính R, ñöôïc ñaët trong khoâng
khí, mang ñieän tích q phaân boá ñeàu.
a. Tính ñieän theá roài suy ra ñieän tröôøngϕ
E
r
taïi moät ñieåm
treân truïc vaønh troøn caùch taâm O moät khoaûng x.
b. Xeùt tröôøng hôïp x >> R
Ñaùp soá: a.
22
Rx
q
k
+
=ϕ
;
( )
23
22
Rx
qx
kE
+
=
;
E
r
naèm treân truïc vaønh troøn
b.
x
q
k
=ϕ
;
2
x
q
kE
=
;
E
r
naèm treân truïc vaønh troøn
3.1-22. Moät daây daãn maõnh coù daïng nöûa ñöôøng troøn taâm O, baùn
kính R, ñöôïc ñaët trong khoâng khí, tích ñieän ñeàu vôùi maät ñoä ñieän
daøi . Tính theá naêng cuûa ñieän tích ñieåm q ñaët taïi moät ñieåm treân λ
ñöôøng thaúng qua taâm O, vuoâng goùc vôùi dieän tích cuûa nöûa ñöôøng
troøn vaø caùch taâm O moät khoaûng a.
Ñaùp soá:
22
0
aR4
qR
W
+ε
λ
=
3.1-23. Moät quaû caàu ñaëc taâm O, baùn kính R, ñöôïc ñaët trong
khoâng khí, mang ñieän tích Q. Tính theá naêng cuûa ñieän tích ñieåm
q ñaët caùch taâm O cuûa quaû caàu moät khoaûng r > R.
Ñaùp soá:
r
Qq
kW
=
36
CHÖÔNG HAI
VAÄT DAÃN
3.2-1. Moät quaû caàu kim loaïi, baùn kính R
1
, mang ñieän tích Q
1
.
Ñaët quaû caàu naøy vaøo trong moät voû caàu kim loaïi ñoàng taâm, baùn
kính R
2
> R
1
, mang ñieän tích Q
2
.
a. Tính ñieän tröôøng taïi moät ñieåm caùch taâm quaû caàu moät
khoaûng r. Xeùt 3 tröôøng hôïp: r < R
1
, R
1
< r < R
2
, vaø
r > R
2
.
b. Tính ñieän theá cuûa quaû caàu vaø voû caàu khi:
* Quaû caàu khoâng ñöôïc noái vôùi voû caàu
* Quaû caàu ñöôïc noái vôùi voû caàu
Ñaùp soá: a.
2
2
21
21
2
1
1
Rrkhi
r
)QQ(k
E
,RrRkhi
r
kQ
E,Rrkhi0E
>
+
=
<<=<=
b.
2
21
vcqc
2
21
vc
2
2
1
1
qc
R
)QQ(k
R
)QQ(k
,
R
Q
R
Q
k
+
=ϕ=ϕ
+
=ϕ
+=ϕ
3.2-2. Moät quaû caàu kim loaïi, baùn kính R
1
, ñöôïc tích ñieän ñeán
ñieän theá
ϕ
o
. Ñaët quaû caàu naøy vaøo trong moät voû caàu kim loaïi,
trung hoaø, ñoàng taâm, baùn kính R
2
> R
1
.
a. Tính ñieän tröôøng taïi moät ñieåm caùch taâm quaû caàu moät
khoaûng r. Xeùt 3 tröôøng hôïp: r < R
1
, R
1
< r < R
2
, vaø
r > R
2
.
b. Tính ñieän theá cuûa quaû caàu vaø voû caàu khi:
* Quaû caàu khoâng ñöôïc noái vôùi voû caàu
37
* Quaû caàu ñöôïc noái vôùi voû caàu
Ñaùp soá: a.
221
2
o1
1
Rrkhiva,RrRkhi
r
R
E
,Rrkhi0E
><<
ϕ
=
<
=
b.
o
2
1
vcqc
o
2
1
vcoqc
R
R
;
R
R
,
ϕ=ϕ=ϕ
ϕ=ϕϕ=ϕ
3.2-3. Moät voû caàu kim loaïi, baùn kính R
1
, mang ñieän tích Q
1
. Ñaët
moät quaû caàu kim loaïi baùn kính R
2
< R
1
trung hoaø vaøo trong voû
caàu sao cho chuùng ñoàng taâm vôùi nhau. Noái quaû caàu vôùi ñaát.
Tính ñieän theá cuûa quaû caàu vaø voû caàu.
Ñaùp soá:
2
1
211
)(
,0
R
RRkQ
vcqc
−
==
ϕϕ
3.2-4. Moät quaû caàu kim loaïi, baùn kính R
1
, mang ñieän tích Q
1
.
Ñaët moät quaû caàu naøy vaøo trong moät voû caàu kim loaïi, trung hoaø,
ñoàng taâm, baùn kính R
2
> R
1
. Noái voû caàu vôùi ñaát. Tính ñieän theá
cuûa quaû caàu vaø voû caàu.
Ñaùp soá:
21
121
)(
,0
RR
RRkQ
qcvc
−
==
ϕϕ
3.2-5. Hai vaät daãn ñieän hình caàu, baùn kính
m3,0R
1
=
vaø
m15,0R
2
=
, ñöôïc ñaët raát xa nhau ñeå khoâng coù hieän töôïng ñieän
höôûng vaø ñöôïc noái vôùi nhau baèng daây daãn. Truyeàn cho hai quaû
caàu ñieän tích
C10.6Q
9−
=
. Tính ñieän tích vaø ñieän theá moãi quaû
caàu.
38
Ñaùp soá:
,nC4
RR
QR
Q
21
1
1
=
+
= ,nC2
RR
QR
Q
21
2
2
=
+
=
V120
RR
kQ
21
=
+
=ϕ
3.2-6. Hai vaät daãn ñieän hình caàu taâm O, baùn kính a vaø b, ñöôïc
ñaët raát xa nhau ñeå khoâng coù hieän töôïng ñieän höôûng vaø ñöôïc noái
vôùi nhau baèng daây daãn. Sau khi tích ñieän cho hai quaû caàu, ñieän
tích cuûa quaû caàu (O, a) nhoû hôn ñieän tích cuûa quaû caàu (O, b) n
laàn.
a. Tính tyû soá baùn kính hai quaû caàu.
b. Ñieän tröôøng taïi moät ñieåm treân quaû caàu (O, a) lôùn hôn
hay nhoû hôn bao nhieâu laàn so vôùi ñieän tröôøng taïi moät
ñieåm treân quaû caàu (O, b).
Ñaùp soá: a.
n
a
b
=
b.
n
E
E
)b,O(
)a,O(
=
3.2-7. Hai quaû caàu kim loaïi, baùn kính R
1
vaø R
2
, mang ñieän tích
Q
1
vaø Q
2
, ñöôïc ñaët raát xa nhau ñeå khoâng coù hieän töôïng ñieän
höôûng.
a. Tính ñieän theá moãi quaû caàu.
b. Noái hai quaû caàu baèng moät daây daãn. Tính ñieän theá môùi
cuûa hai quaû caàu, ñieän tích treân moãi quaû caàu vaø löôïng
ñieän tích dòch chuyeån.
Ñaùp soá:
2
2
2
1
1
1
,.
R
kQ
R
kQ
a
==
ϕϕ
,
)(
.
21
21
RR
QQk
b
+
+
=
ϕ
39
,
)(
21
211
1
RR
QQR
Q
+
+
=
′
,
)(
21
212
2
RR
QQR
Q
+
+
=
′
21
1221
RR
RQRQ
Q
+
−
=∆
3.2-8. Hai quaû caàu kim loaïi A vaø B, baùn kính
m1,0a
=
vaø
m2,0b
=
, coù ñieän theá laàn löôït laø
V000.45
A
=ϕ
vaø
V000.45
B
−=ϕ
, ñöôïc ñaët raát xa nhau ñeå khoâng coù hieän töôïng
ñieän höôûng.
a. Tính ñieän tích moãi quaû caàu.
b. Noái hai quaû caàu baèng moät daây daãn. Tính ñieän theá môùi
cuûa hai quaû caàu vaø löôïng ñieän tích dòch chuyeån.
Ñaùp soá: a. Q
A
= 0,5
µ
C, Q
B
= - 1
µ
C
b.
ϕ
= - 15.000 V,
∆
Q = 0,68
µ
C
3.2-9. Tính naêng löôïng ñieän tröôøng cuûa moät quaû caàu baùn kính
R, mang ñieän tích Q phaân boá ñeàu trong theå tích quaû caàu.
Ñaùp soá:
R
5
Q3
kW
2
e
=
3.2-10. Moät quaû caàu kim loaïi coâ laäp, baùn kính r = 20cm, coù ñieän
theá 3.000V. Tính ñieän tích treân quaû caàu vaø toång naêng löôïng ñieän
tröôøng gaây bôûi quaû caàu.
Ñaùp soá: Q = 6,67.10
– 8
C, W
e
= 10
– 4
J
3.2-11. Cöôøng ñoä ñieän tröôøng trong moät mieàn khoâng gian phuï
thuoäc vaøo toïa ñoä x bôûi heä thöùc
x
x
E
E
o
o
=
trong ñoù
m/kV24E
o
=
vaø
m6x
o
=
. Tính toång naêng löôïng ñieän
40
tröôøng döï tröõ trong theå tích hình laäp phöông coù caïnh
m1a
=
,
bieát raèng hai maët hình laäp phöông song song vôùi maët phaúng yOz
coù toïa ñoä laàn löôït laø
0x
=
vaø
m
1
x
=
Ñaùp soá: J6,23
x6
aE
W
2
o
52
oo
e
µ=
ε
=
3.2-12. Moät tuï ñieän phaúng coù khoaûng caùch giöõa hai baûn tuï ñieän
laø
mm1d
=
. Ñieän tröôøng giöõa hai baûn tuï ñieän coù cöôøng ñoä
m/kV3E
o
=
. Naêng löôïng ñieän tröôøng döï tröõ trong tuï ñieän
laø
J10.4W
11
e
−
=
. Tính ñieän dung cuûa tuï ñieän vaø ñieän tích treân
moãi baûn tuï ñieän.
Ñaùp soá: pF9,8
d
E
W2
C
22
e
== ,
pC67,26CW2Q
e
==
41
CHÖÔNG BA
TÖØ TRÖÔØNG CUÛA
DOØNG ÑIEÄN KHOÂNG ÑOÅI
3.3-1.
Hai doøng ñieän thaúng daøi voâ haïn cuøng chieàu, coù
cöôøng ñoä doøng ñieän baèng nhau I = 15A, ñöôïc ñaët song
song nhau trong khoâng khí nhö hình veõ. Xaùc ñònh vectô
caûm öùng töø
B
r
gaây bôûi hai doøng ñieän taïi caùc ñieåm O, M, N,
P, Q coù toïa ñoä laàn löôït laø: y
o
= 0, y
1
= -3cm, y
2
= 3cm, y
3
=
9cm, cm8z
=
.
Ñaùp soá:
0B
o
=
r
,
z
4
M
e)T10
2
(B
r
r
−
−= ,
z
4
N
e)T10
3
2
(B
r
r
−
= ,
z
5
P
e)T10.12(B
r
r
−
−= ,
y
5
Q
e)T10.8,4(B
r
r
−
=
3.3-2.
Hai doøng ñieän thaúng daøi voâ haïn ngöôïc chieàu, coù
cöôøng ñoä doøng ñieän baèng nhau I = 15A, ñöôïc ñaët song
song nhau trong khoâng khí nhö hình veõ.
x
I
-
6cm
6cm
8cm
I
y
O
Q
P
N
M
z
42
Xaùc ñònh vectô caûm öùng töø
B
r
gaây bôûi hai doøng ñieän taïi
caùc ñieåm O, M, N, P, Q coù toïa ñoä laàn löôït laø: 0y
o
= ,
cm3y
1
−=
,
cm3y
2
=
,
cm9y
3
=
y
3
= 9cm, cm8z
=
.
Ñaùp soá:
z
4
o
e)T10(B
r
r
−
−= ,
z
4
NM
e)T10
3
4
(BB
r
r
r
−
−== ,
z
5
P
e)T10.8(B
r
r
−
= ,
z
5
Q
e)T10.6,3(B
r
r
−
−=
3.3-3.
Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng
ñoä A10I
=
, ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
khoâng khí. Ñoaïn AB laø moät phaàn tö cung troøn taâm O, baùn
kính R = 5cm. Ñoaïn BC = CD = R. Caùc ñoaïn Ax vaø Dy laø
hai nöûa doøng ñieän thaúng raát daøi coù ñöôøng keùo daøi qua
taâm O. Tính caûm öùng töø
B
r
taïi ñieåm O.
I
- 6cm
6cm
8cm
I
y
x
O
Q
P
N
M
z
C
R
B
I
y
x
D O A
43
Ñaùp soá:
r
B
vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo
vaø T10.968,52
2R4
I
B
5
o
−
=
+
π
π
µ
=
3.3-4.
Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng
ñoä
A30I
=
, ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
khoâng khí. Ñoaïn BC laø moät phaàn tö cung troøn taâm O, baùn
kính R = 15cm. Cho bieát OA = OB = R. Caùc ñoaïn Ax vaø
Cy laø hai nöûa doøng ñieän thaúng raát daøi coù ñöôøng keùo daøi
qua O. Tính caûm öùng töø
B
r
taïi ñieåm O.
Ñaùp soá:
r
B
vuoâng goùc maët phaúng doøng ñieän, höôùng ra vaø
T10.14,71
4R2
I
B
5
o
−
=
+
π
π
µ
=
3.3-5.
Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng
ñoä
A20I
=
, ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
khoâng khí. Ñoaïn CD laø moät cung troøn taâm O, baùn kính
cm10R
=
vaø chaén goùc ôû taâm laø = 120α
o
. Xaùc ñònh vectô
caûm öùng töø
B
r
taïi ñieåm O.
C
B
R
I
y
x
O
A
44
Ñaùp soá:
r
B
vuoâng goùc maët phaúng doøng ñieän, höôùng ra vaø
T10.65,1333
3
2
R4
I
B
5
o
−
=
++
π
π
µ
=
3.3-6.
Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng
ñoä A25I
=
, ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
khoâng khí. Ñoaïn CD laø moät phaàn tö cung troøn taâm O, baùn
kính R = 20cm, goùc = 30β
o
. Xaùc ñònh vectô caûm öùng töø
B
r
taïi ñieåm O.
Ñaùp soá:
r
B
vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo
vaø T10.87,733
2R4
I
B
5
o
−
=
++
π
π
µ
=
C
α
D
I
y
O
R
x
D
C
β
I
y
O
R
x
45
3.3-7.
Hai ñieåm AB cuûa moät voøng daây daãn kín hình troøn
ñöôïc noái vôùi hai cöïc cuûa nguoàn ñieän khoâng ñoåi. Phöông
daây noái qua taâm O voøng daây. Chieàu daøi caùc daây noái voâ
cuøng lôùn vaø taát caû ñöôïc ñaët trong khoâng khí. Chöùng minh
raèng neáu caùc voøng daây daãn AMB vaø ANB ñoàng chaát vaø
coù tieát dieän ñeàu thì caûm öùng töø B taïi taâm voøng daây baèng
khoâng.
3.3-8.
Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng
ñoä A8I
=
, ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
_
+
M
B
N
A
I
I
R
C
α
D
I
I
y
O
x
46
khoâng khí. Ñoaïn CD laø moät cung troøn taâm O, baùn kính
cm5R
=
. Bieát goùc laø = 120α
o
. Xaùc ñònh vectô caûm öùng
töø
B
r
taïi ñieåm O.
Ñaùp soá:
r
B
vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo
vaø T10.27,623
3
4
R4
I
B
5
o
−
=
−+
π
π
µ
=
3.3-9. Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng
ñoä A16I
=
, ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
khoâng khí. Ñoaïn CD laø moät cung troøn taâm O, baùn kính
cm6R
=
. Bieát goùc laø = 120α
o
. Xaùc ñònh vectô caûm öùng
töø
B
r
taïi ñieåm O.
Ñaùp soá:
r
B
vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo
vaø T10.1,11
3R2
I
B
4
o
−
=
+
π
π
µ
=
3.3-10. Moät daây daãn coù doøng ñieän, cöôøng ñoä I, ñöôïc uoán
thaønh moät ña giaùc ñeàu n caïnh noäi tieáp trong voøng troøn
C
D
I
y
x
R
α
O
I
47
baùn kính R vaø ñöôïc ñaët trong khoâng khí. Xaùc ñònh vectô
caûm öùng töø
r
B
taïi taâm hình ña giaùc. Tính
r
B
khi n . → ∞
Ñaùp soá:
r
B
vuoâng goùc vôùi ña giaùc, coù chieàu thuaän chieàu
doøng ñieän theo qui taéc tay phaûi vaø
B
n I
R
tg
n
o
=
µ
π
π
2
Khi n → ∞ thì B =
R
2
I
o
µ
3.3-11. Moät doøng ñieän, cöôøng ñoä I chaïy trong moät daây
daãn ñöôïc uoán thaønh moät luïc giaùc ñeàu caïnh a R vaø ñöôïc ñaët
trong khoâng khí. Tính caûm öùng töø
r
B
taïi taâm luïc giaùc ñeàu.
Ñaùp soá :
r
B
vuoâng goùc vôùi luïc giaùc ñeàu, coù chieàu thuaän
chieàu doøng ñieän theo qui taéc tay phaûi vaø
B
I
a
o
=
µ
π
3
3.3-12. Moät doøng ñieän, cöôøng ñoä I chaïy trong moät daây
daãn ñöôïc uoán cong nhö hình veõ: (C) laø ñöôøng troøn taâm O,
baùn kính R. Tính r ñeå caûm öùng töø
B
r
taïi ñieåm O baèng
khoâng.
I
I
I
R
r
O
(C)
48
3.3-13. Hai daây daãn daøi voâ haïn coù caùc doøng ñieän cuøng
chieàu vôùi cöôøng ñoä
1
I
vaø
2
I
chaïy qua. Moãi daây ñeàu coù moät
ñoaïn uoán theo moät cung troøn 90
o
treân cuøng ñöôøng troøn taâm O, baùn
kính
a
nhö hình veõ. Tính
2
I
theo
1
I
ñeå caûm öùng töø
B
r
gaây bôûi
caû hai doøng ñieän taïi O baèng
khoâng.
Ñaùp soá:
12
I27,2I =
3.3-14. Moät dieän tích S hình troøn taâm O, baùn kính
cm20R
=
ñöôïc ñaët trong moät töø tröôøng
r
B
coù ñöôøng
caûm öùng töø
r
B
hôïp vôùi dieän tích S moät goùc
o
30=α
vaø coù
ñoä lôùn
t314
o
eBB
−
= vôùi B
o
= 0,25(T). Tính töø thoâng qua
dieän tích S.
Ñaùp soá:
(
)
Wbe10.7,15sineBR
t3143t314
o
2 −−−
=απ=Φ
3.3-15. Cho moät töø tröôøng
r
B
coù ñöôøng caûm öùng töø
naèm ngang, coù ñoä lôùn:
(
)
Tt100sinBB
o
π= vôùi
T10.5B
3
o
−
= . Moät dieän
α
R
O
B
r
n
r
α
b
a
B
r
a
O
I
2
I
1
49
tích S phaúng hình chöõ nhaät coù hai caïnh a = 10cm,
cm15b
=
coù vectô phaùp tuyeán
r
n
hôïp vôùi phöông
r
B
moät
goùc = 45α
o
. Tính töø thoâng qua ñieän tích S.
Ñaùp soá: Wb)t100(sin10.53cos.ab)t100(sinB
6
o
π=απ=Φ
−
3.3-16. Cho moät töø tröôøng coù vectô caûm öùng töø ñöôïc xaùc
ñònh bôûi
z
2
2
o
o
ex
x
B
B
r
r
= vôùi
o
B vaø
o
x laø caùc haèng soá
döông,
z
e
r
laø vectô ñôn vò treân
truïc z. Tính töø thoâng qua dieän
tích hình vuoâng caïnh
o
x2 naèm
trong maët phaúng xOy coù moät
ñænh truøng vôùi goác toïa ñoä O vaø
hai caïnh truøng vôùi hai truïc Ox
vaø Oy nhö hình veõ.
Ñaùp soá:
2
oo
xB
3
16
=Φ
3.3-17. Cho moät töø tröôøng coù
vectô caûm öùng töø ñöôïc xaùc ñònh
bôûi
z
2
eyAtB
r
r
−=
vôùi A laø haèng
soá döông, B tính baèng Tesla, t
baèng giaây vaø y baèng meùt,
z
e
r
laø
vectô ñôn vò treân truïc z.
a. Ñôn vò cuûa A laø gì?
b. Tính töø thoâng qua dieän
y
e
r
z
e
r
l
l
x
e
r
x
y
O
y
e
r
z
e
r
o
x2
o
x2
x
e
r
x
y
O
50
tích hình vuoâng caïnh naèm trong maët phaúng xOy l
coù moät ñænh truøng vôùi goác toïa ñoä O vaø hai caïnh
truøng vôùi hai truïc Ox vaø Oy nhö hình veõ.
Ñaùp soá:
32
At
2
1
l−=Φ
3.3-18. Cho moät doøng ñieän thaúng daøi voâ haïn coù doøng ñieän
cöôøng ñoä I = 18A chaïy qua.
a. Tính töø thoâng qua dieän tích ñaùy SΦ
1
, dieän tích
xung quanh S
2
, vaø dieän tích toaøn phaàn S cuûa moät
maët truï coù baùn kính R = 12cm, chieàu cao h = 20cm,
coù truïc truøng vôùi phöông cuûa doøng ñieän I.
b. Tính töø thoâng qua dieän tích hình chöõ nhaät SΦ
3
(hình veõ). Bieát a = 10cm.
Ñaùp soá: a. 0
SSS
21
=Φ=Φ=Φ
b.
( )
Wb10.32,4
R
aR
n
2
hI
7
o
S
3
−
=
+
π
µ
=Φ l
I
I
a
h
R
S
2
S
1
S
3
51
3.3-19. Cho khung daây hình chöõ nhaät ABCD coù caùc caïnh
a = 3cm, b = 4cm ñöôïc ñaët caïnh moät doøng ñieän thaúng daøi
voâ haïn coù cöôøng ñoä I = 30A. Khung daây vaø doøng ñieän
cuøng naèm trong moät maët phaúng. Caïnh AB song song vôùi
doøng ñieän vaø caùch doøng ñieän moät ñoaïn c = 1,5cm. Tính töø
thoâng qua dieän tích phaúng giôùi haïn bôûi khung daây.
Ñaùp soá:
( )
Wb10.64,2
c
ac
n
2
bI
7o
−
=
+
π
µ
=Φ l
3.3-20. Saùu daây daãn coù doøng ñieän vôùi cöôøng ñoä
1
I
,
2
I
,
3
I
,
4
I
,
5
I
,
6
I
coù chieàu höôùng ra hoaëc höôùng vaøo maët
phaúng hình veõ. Tính löu soá cuûa vectô caûm öùng töø doïc
theo caùc ñöôøng cong kín (C
1
): ñöôøng lieàn neùt, vaø (C
2
):
ñöôøng chaám chaám nhö hình veõ.
c
I
C
D
a
b
A
B
52
Ñaùp soá:
(
)
564o
C
IIId.B
1
−+µ=
∫
l
r
(
)
432o
C
IIId.B
2
−−µ=
∫
l
r
3.3-21. Cho moät oáng daây (solenoid) daøi a = 30cm, ñöôøng
kính
mm10d
=
, goàm n = 500 voøng daây daãn ñöôïc quaán saùt
nhau, coù doøng ñieän A5I
=
chaïy qua. Tính töø thoâng gôûi
qua moät voøng daây phaúng hình troøn ñöôøng kính cm4D
=
ñaët vuoâng goùc vôùi truïc, coù taâm truøng vôùi taâm oáng daây.
Ñaùp soá:
a
4
dnI
2
0
πµ
=Φ
3.3-22. Cho moät oáng daây (solenoid) daøi a, ñöôøng kính
mm32D
=
, coù
100n
o
=
voøng/cm ñöôïc quaán saùt nhau, coù
doøng ñieän A5,2I
=
chaïy qua. Tính töø thoâng gôûi qua ñieän
tích phaúng hình troøn ñöôøng kính mm16d
=
ñaët vuoâng goùc
vôùi truïc, coù taâm truøng vôùi taâm oáng daây.
Ñaùp soá:
4
dIn
2
o0
πµ
=Φ
×
×
×
I
1
I
5
I
4
I
6
I
2
I
3
d
C
D
a
b
A
I
2
I
1
B
53
3.3-22. Cho khung daây hình chöõ nhaät coù caïnh a vaø b ñöôïc
ñaët gaàn moät doøng ñieän thaúng daøi voâ haïn coù cöôøng ñoä I
1
.
Khung daây vaø doøng ñieän cuøng naèm trong cuøng maët phaúng.
Caïnh AB song song vôùi I
1
vaø caùch I
1
moät ñoaïn d.
Xaùc ñònh phöông chieàu vaø ñoä lôùn cuûa löïc taùc duïng leân
khung daây neáu trong khung daây coù doøng ñieän I
2
chaïy qua.
Ñaùp soá :
r
F
naèm trong maët phaúng khung daây, vuoâng goùc I
1
,
höôùng xa doøng I
1
Ñaùp soá :
+
−
π
µ
=
bd
1
d
1
2
aII
F
21o
3.3-23. Moät electron, sau khi ñöôïc gia toác baèng moät hieäu
ñieän theá U, chuyeån ñoäng song song vôùi moät daây daãn thaúng
daøi vaø caùch daây daãn moät khoaûng r. Tìm löïc taùc duïng leân
electron neáu coù doøng ñieän vôùi cöôøng ñoä I chaïy qua daây
daãn .
Ñaùp soá :
m
Ue2
r2
eI
F
o
π
µ
=
3.3-23. Moät electron chuyeån ñoäng vôùi vaän toác
s/m10.1,2v
7
=
trong moät töø tröôøng ñeàu
B
r
.
a. Caûm öùng töø B coù giaù trò nhoû nhaát baèng bao nhieâu
neáu löïc töø taùc duïng leân electron laø
N10.4,5F
15−
=
.
b. Caûm öùng töø B coù giaù trò baèng bao nhieâu neáu vaän
toác
v
r
cuûa electron hôïp vôùi töø tröôøng moät goùc
o
45=α .
Ñaùp soá : a. T10.61,1B
3
min
−
=
54
b. T10.27,2B
3−
=
3.3-24. Moät electron coù naêng löôïng W bay vaøo moät ñieän
tröôøng ñeàu coù cöôøng ñoä ñieän tröôøng E theo phöông vuoâng
goùc vôùi ñöôøng söùc ñieän tröôøng. Hoûi phaûi ñaët moät töø tröôøng
coù phöông chieàu vaø caûm öùng töø nhö theá naøo ñeå chuyeån
ñoäng cuûa electron khoâng bò leäch phöông.
Ñaùp soá:
W2
m
EB =
3.3-25. Moät thanh kim loaïi AB, coù
chieàu daøi , ñöôïc ñaët song song vôùi l
moät daây daãn thaúng raát daøi coù doøng
ñieän I chaïy qua vaø caùch daây daãn moät
khoaûng r. Haõy tính suaát ñieän ñoäng
caûm öùng xuaát hieän trong thanh khi
thanh kim loaïi di chuyeån vôùi vaän toác
khoâng ñoåi
v
r
theo phöông vuoâng goùc
vôùi daây daãn.
Ñaùp soá: ξ
C
r2
vI
0
π
µ
=
l
3.3-26. Moät thanh kim loaïi
AB, coù chieàu daøi , ñöôïc ñaët l
vuoâng goùc vôùi moät daây daãn
thaúng raát daøi coù doøng ñieän I
chaïy qua vaø ñaàu A gaàn daây
daãn nhaát caùch daây daãn moät
I
v
r
l
r
A
B
I
v
r
B
A
r
l
55
khoaûng r. Haõy tính hieäu ñieän theá xuaát hieän giöõa 2 ñaàu
thanh khi thanh kim loaïi di chuyeån vôùi vaän toác khoâng ñoåi
v
r
theo phöông song song vôùi daây daãn. Ñieän theá ôû A hay ôû
B cao hôn?
Ñaùp soá:
+
π
µ
=
r
1n
2
vI
U
0
AB
l
l , Ñieän theá ôû A cao hôn.
3.3-27. Moät thanh kim loaïi CD daøi
cm80L
=
quay quanh moät truïc
vuoâng goùc vôùi thanh vaø ñi qua ñaàu C
vôùi vaän toác 5voøng/s trong moät töø
tröôøng ñeàu T3,0B
=
coù ñöôøng caûm
öùng töø song song vôùi truïc quay nhö
hình veõ. Tính hieäu ñieän theá giöõa hai
ñaàu thanh. Ñieän theá ôû C hay ôû D cao hôn?
Ñaùp soá:
V3U
CD
−=
. Ñieän theá ôû D cao hôn.
3.3-28. Moät daây daãn thaúng
coù ñieän trôû
0
R öùng vôùi moät
ñôn vò chieàu daøi. Daây ñöôïc
gaáp thaønh 2 caïnh cuûa moät
goùc 2 . Moät thanh chaén CD α
cuõng laøm baèng daây daãn aáy,
ñöôïc ñaët vuoâng goùc vôùi
ñöôøng phaân giaùc cuûa goùc
2α ñeå taïo vôùi daây daãn treân
moät maïch kín. Maïch kín naøy ñaët trong töø tröôøng ñeàu
B
r
vuoâng goùc vôùi dieän tích phaúng cuûa maïch. Khi thanh CD
D
C
B
r
⊗
C
D
B
r
⊗
v
r
α
O
56
chuyeån ñoäng vôùi vaän toác v
r
khoâng ñoåi theo phöông song
song vôùi ñöôøng phaân giaùc, haõy xaùc ñònh chieàu vaø cöôøng ñoä
doøng ñieän caûm öùng trong maïch kín.
Ñaùp soá:
( )
α+
α
=
sin1R
sin.v.B
I
0
c
, I
c
ngöôïc chieàu kim ñoàng hoà
3.3-29. Moät daây daãn coù ñieän trôû R
0
öùng vôùi moät ñôn vò
chieàu daøi, ñöôïc uoán thaønh ba phaàn tö voøng troøn baùn kính
r. Moät thanh chaén MN cuõng baèng daây daãn aáy tröôït treân ba
phaàn tö voøng troøn vôùi vaän toác v
r
. Daây daãn vaø thanh chaén
taïo thaønh moät chu vi kín. Caû heä
thoáng ñöôïc ñaët trong töø tröôøng
ñeàu
B
r
vuoâng goùc vôùi maët phaúng
cuûa chu vi. Xaùc ñònh chieàu vaø
cöôøng ñoä cuûa doøng ñieän caûm öùng
chaïy trong chu vi theo goùc . Boû α
qua ñieän trôû caùc choã tieáp xuùc.
Ñaùp soá:
( )
α+α
α
=
sinR
sin.v.B
I
0
c
, I
c
cuøng chieàu kim ñoàng hoà
3.3-30. Moät thanh kim loaïi AB coù chieàu daøi a ñöôïc ñaët
tieáp xuùc vaø vuoâng goùc vôùi hai thanh kim loaïi naèm ngang
song song caùch nhau moät khoaûng cm25a
=
.
N
M
v
r
α
O
B
r
57
Hai ñaàu thanh ngang ñöôïc noái vôùi moät ñoaïn maïch goàm
moät pin 6V noái tieáp vôùi moät ñieän trôû
Ω
=
1
R
ñeå taïo thaønh
maïch kín. Caû heä ñöôïc ñaët trong moät töø tröôøng ñeàu
T5,0B
=
coù ñöôøng caûm öùng töø vuoâng goùc vôùi ñieän tích
cuûa maïch kín nhö hình veõ. Ñeå thanh AB chuyeån ñoäng vôùi
vaän toác khoâng ñoåi, ngöôøi ta taùc duïng leân thanh moät löïc
N25,0F
=
.
a. Xaùc ñònh phöông chieàu cuûa löïc
F
r
vaø cöôøng ñoä
doøng ñieän trong maïch.
b. Tính hieäu ñieän theá giöõa hai ñaàu thanh AB.
Ñaùp soá: a. Löïc
F
r
vuoâng goùc vôùi thanh AB vaø höôùng veà
phiaù traùi,
A
2
I
=
b. V4U
AB
=
3.3-31. Moät thanh kim loaïi AB coù chieàu daøi a ñöôïc ñaët
tieáp xuùc vaø vuoâng goùc vôùi hai thanh kim loaïi naèm ngang
song song caùch nhau moät khoaûng cm50a
=
. Hai ñaàu
thanh ngang ñöôïc noái vôùi ñieän trôû
Ω
=
3R ñeå taïo thaønh
maïch kín. Caû heä ñöôïc ñaët trong moät töø tröôøng ñeàu
T15,0B
=
coù ñöôøng caûm öùng töø vuoâng goùc vôùi ñieän tích
cuûa maïch kín. Xaùc ñònh löïc caàn thieát taùc duïng leân thanh
R
A
a
B
×
B
r
58
ñeå laøm thanh chuyeån ñoäng vôùi vaän toác khoâng ñoåi
s/m2v
=
theo phöông vuoâng goùc vôùi thanh nhö hình veõ.
Ñaùp
s
o
á: N10.75,3
R
vaB
F
3
22
−
==
3.3-32. Moät töø tröôøng ñeàu toàn taïi trong moät mieàn khoâng
gian coù phöông vuoâng goùc vôùi maët phaúng xOz trong ñoù
bieân traùi vaø bieân phaûi cuûa töø tröôøng ñeàu song song vôùi maët
phaúng yOz vaø ñeàu caùch noù moät khoaûng L. Vectô caûm öùng
töø
B
r
höôùng theo chieàu döông cuûa truïc Oy khi
0x
<
vaø
höôùng theo chieàu aâm cuûa truïc Oy khi
0x
>
nhö moâ taû ôû
hình veõ beân. Moät khung daây daãn hình vuoâng ABCD, caïnh
L, naèm trong maët phaúng xOz, chuyeån ñoäng theo chieàu
döông truïc Ox vôùi vaän toác khoâng ñoåi v. Caùc caïnh AB vaø
CD song song vôùi maët phaúng yOz vaø luùc 0t
=
caïnh AB ôû
taïi bieân traùi cuûa töø tröôøng. Xaùc ñònh suaát ñieän ñoäng caûm
öùng trong khung daây khi khung daây chuyeån ñoäng qua mieàn
coù töø tröôøng treân.
R
A
a
B
v
r
×
B
r
59
Ñaùp soá:
BLv
C
−=ξ
khi
vLt0 <<
BLv2
C
=ξ khi
vL2tvL <<
BLv
C
−=ξ khi
vL3tvL2 <<
(neáu choïn vectô ñôn vò phaùp tuyeán
n
r
cuûa dieän tích ABCD
höôùng theo chieàu döông cuûa truïc Oy)
3.3-33. Moät khung daây daãn hình chöõ nhaät caïnh a vaø b, coù
ñieän trôû toång coäng laø R, ñöôïc ñaët trong töø tröôøng ñeàu
B
r
bieán thieân theo thôøi gian theo qui luaät
tcosBB
o
ω=
r
r
vôùi
o
B
r
khoâng ñoåi vaø hôïp vôùi maët phaúng khung daây moät goùc . α
Xaùc ñònh cöôøng ñoä doøng ñieän caûm öùng trong khung daây.
Ñaùp soá: tsin.sin
R
baB
I
o
C
ωα
ω
=
3.3-34. Moät daây daãn thaúng raát
daøi coù doøng ñieän vôùi cöôøng ñoä
τ
−
=
t
0
eII chaïy qua, ñöôïc ñaët
B
A
C
D
L
O
y
x
z
L
L
B
r
B
r
a
I
d
b
60
song song vôùi caïnh b cuûa moät khung daây hình chöõ nhaät, coù
2 caïnh a vaø b, ôû trong cuøng maët phaúng vôùi khung daây.
Caïnh khung daây gaàn daây daãn nhaát caùch daây daãn moät
khoaûng d. Xaùc ñònh suaát ñieän ñoäng caûm öùng vaø chieàu doøng
ñieän caûm öùng trong khung daây.
Ñaùp soá:
+
πτ
µ
=ξ
τ
−
d
a
1ne
2
bI
t
00
C
l ,
I
c
cuøng chieàu kim ñoàng hoà
3.3-35. Moät daây daãn thaúng raát
daøi coù doøng ñieän vôùi cöôøng ñoä I
khoâng ñoåi chaïy qua, ñöôïc ñaët
song song vôùi caïnh b cuûa moät
khung daây hình chöõ nhaät, coù 2
caïnh a vaø b, ôû trong cuøng maët
phaúng vôùi khung daây. Khung
daây di chuyeån vôùi vaän toác khoâng
ñoåi v
r
theo phöông vuoâng goùc
vôùi doøng ñieän I vaø ra xa doøng
ñieän. Ñieän trôû toång coäng cuûa khung daây laø R. Xaùc ñònh vaø
chieàu vaø cöôøng ñoä doøng ñieän caûm öùng trong khung daây
vaøo thôøi ñieåm maø caïnh khung daây gaàn daây daãn nhaát caùch
daây daãn moät khoaûng r.
Ñaùp soá:
( )
arrR2
vabI
I
0
C
+π
µ
= ,
I
c
ngöôïc chieàu kim ñoàng hoà.
a
I
r
R
b
| 1/17

Tài liệu khác của Đại Học Sư phạm Kỹ thuật Hưng yên

Preview text:

λ = 2  1 − 1  ( ) E   = 84 V m /
PHẦN III: ĐIỆN - TỪ TRƯỜNG π ε 4  a a + L o CHÖÔNG MOÄT
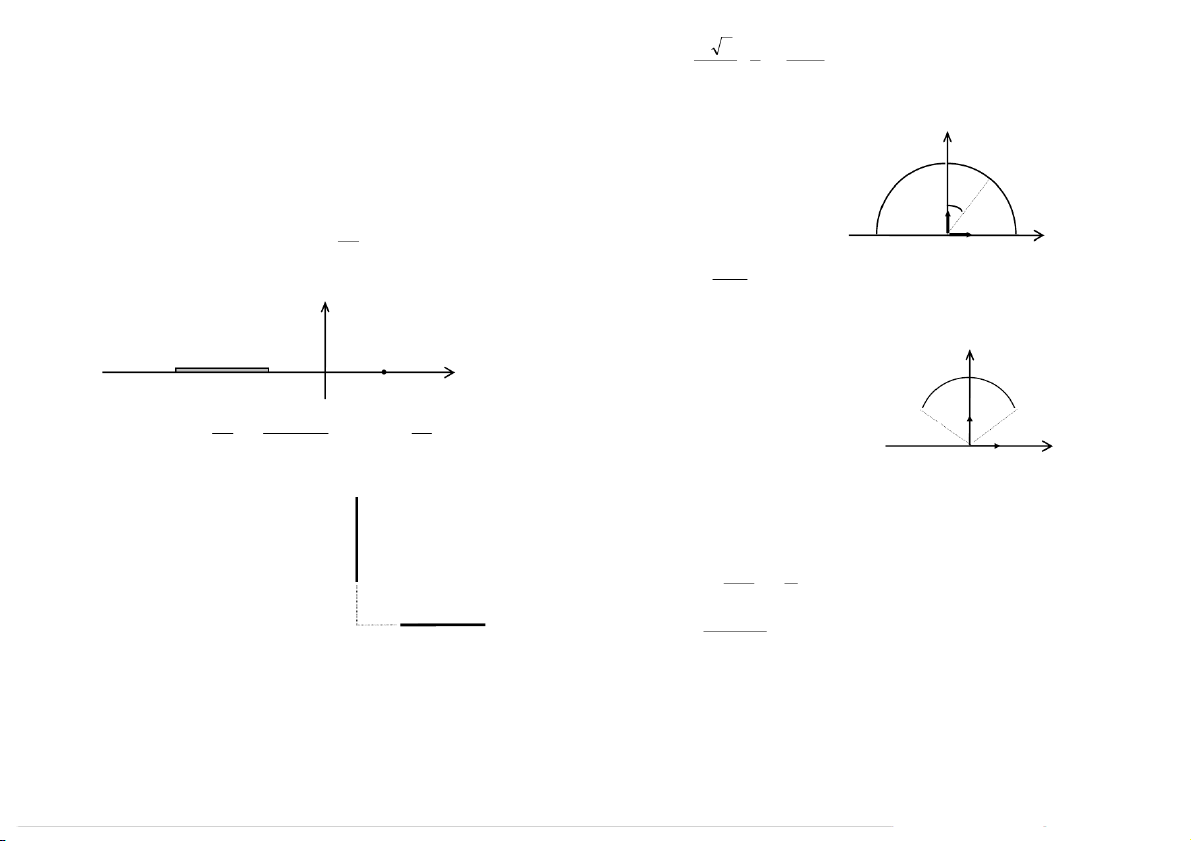
3.1-3. Cho nöûa ñöôøng troøn (O, a)
TRÖÔØNG TÓNH ÑIEÄN
mang ñieän tích phaân boá vôùi maät y
ñoä ñieän daøi λ = λo.sinθ (λo > 0)
ñöôïc ñaët trong khoâng khí nhö hình θ
3.1-1. Moät thanh coù chieàu daøi l ñaët theo truïc Ox nhö hình veõ, veõ. r e y 2 x
Xaùc ñònh vectô cöôøng ñoä ñieän
coù maät ñoä λ thay ñoåi theo x vôùi λ = λ , trong ñoù λ o 2 o laø moät tröôøng taïi taâm O. l x’ O re x r r λ r x
haèng soá döông. Tính ñieän tröôøng E taïi ñieåm M coù toïa ñoä x = a. Ñaùp soá: = − o E e ε x 8 a y o
3.1-4. a. Moät daây daãn ñöôïc ñaët trong M y
khoâng khí vaø ñöôïc uoán thaønh moät cung ( ) − + a l
troøn baùn kính R, goùc ôû taâm laø α, mang a O a x
ñieän tích phaân boá ñeàu vôùi maät ñoä λ. r λ r e  a y l  l  Ñaùp soá: = = o + E E k
Tính vectô cöôøng ñoä ñieän tröôøng E l l x 2   ( + )− a 2  n 1+  a 2  l  2 a 2 l   taïi ñieåm O.
b. Moät voøng daây troøn (O, a) ñöôïc O r e x x
3.1-2. Hai thanh daãn ñieän AB vaø CD D
ñaët trong khoâng khí, mang ñieän tích baèng nhau, daøi L= m 2 , 0 , coù tieát
phaân boá ñeàu vôùi maät ñoä ñieän daøi λ. Choïn truïc Ox vuoâng goùc
dieän nhoû so vôùi chieàu daøi ñöôïc ñaët
vôùi maët phaúng cuûa voøng troøn qua taâm O. Xaùc ñònh vectô cöôøng
ñoä ñieän tröôøng taïi moät ñieåm treân truïc Ox coù toïa ñoä x.
vuoâng goùc nhö hình veõ. Cho bieát λ OA= OC= a= m 1 , 0 r k 2  α , maät ñoä ñieän =−  r C Ñaùp soá: a. E  sin  e y R  2
daøi treân thanh AB laø λ = 10−9 C/m  r x Q k
vaø treân CD laø −λ . Tính ñieän tröôøng r = O b. E ( ) e 3/ 2 x + taïi O. A B x2 a2 r
Ñaùp soá: E naèm treân phaân giaùc cuûa goùc phaàn tö thöù hai vaø 28 29 λ = −
3.1-5. Moät maët baùn caàu baùn kính R ñöôïc ñaët trong khoâng khí, 8 ,
6 µ C/ m, ñöôïc ñaët truøng vôùi truïc khoái truï. Tính maät ñoä
tích ñieän ñeàu vôùi maät ñoä ñieän maët σ. Xaùc ñònh vectô cöôøng ñoä
ñieän tích khoái ρ cuûa khoái truï ñeå ñieän tröôøng taïi caùc ñieåm beân
ñieän tröôøng taïi taâm O cuûa baùn caàu.
ngoaøi khoái truï baèng khoâng. r σ λ
Ñaùp soá : E ôû treân truïc ñoái xöùng cuûa baùn caàu, E = ρ = − = − 3 10 . 61 , 3 C/ m 4 ε Ñaùp soá : ( ) 3 π 2 − 2 o r r 2 1
3.1-6. Moät ñóa troøn baùn kính R ñöôïc tích ñieän ñeàu vôùi maät ñoä
3.1-9. Moät khoái truï caùch ñieän, daøi voâ haïn, baùn kính
ñieän maët σ > 0 vaø ñöôïc ñaët trong chaân khoâng. xaùc ñònh vectô R= cm 5 , 4
, ñöôïc ñaët trong khoâng khí, mang ñieän tích phaân boá
cöôøng ñoä ñieän tröôøng taïi moät ñieåm naèm treân truïc cuûa ñóa vaø
ñeàu vôùi maät ñoä ñieän tích khoái ρ. Tính ρ bieát raèng ñieän tröôøng
caùch taâm ñóa moät khoaûng x.
taïi moät ñieåm beân ngoaøi khoái truï, saùt beà maët khoái truï vaø gaàn
Xeùt caùc tröôøng hôïp x >> R vaø x << R . r
taâm khoái truï baèng E= 1 kN 6 /C .
Ñaùp soá : E naèm treân truïc cuûa ñóa 2ε E σ ρ =  x Ñaùp soá: o 3 = 2 , 6 9 C µ / m =   − ( ) E 1  V / m R 2ε  2 +  2 o x R q = ( )
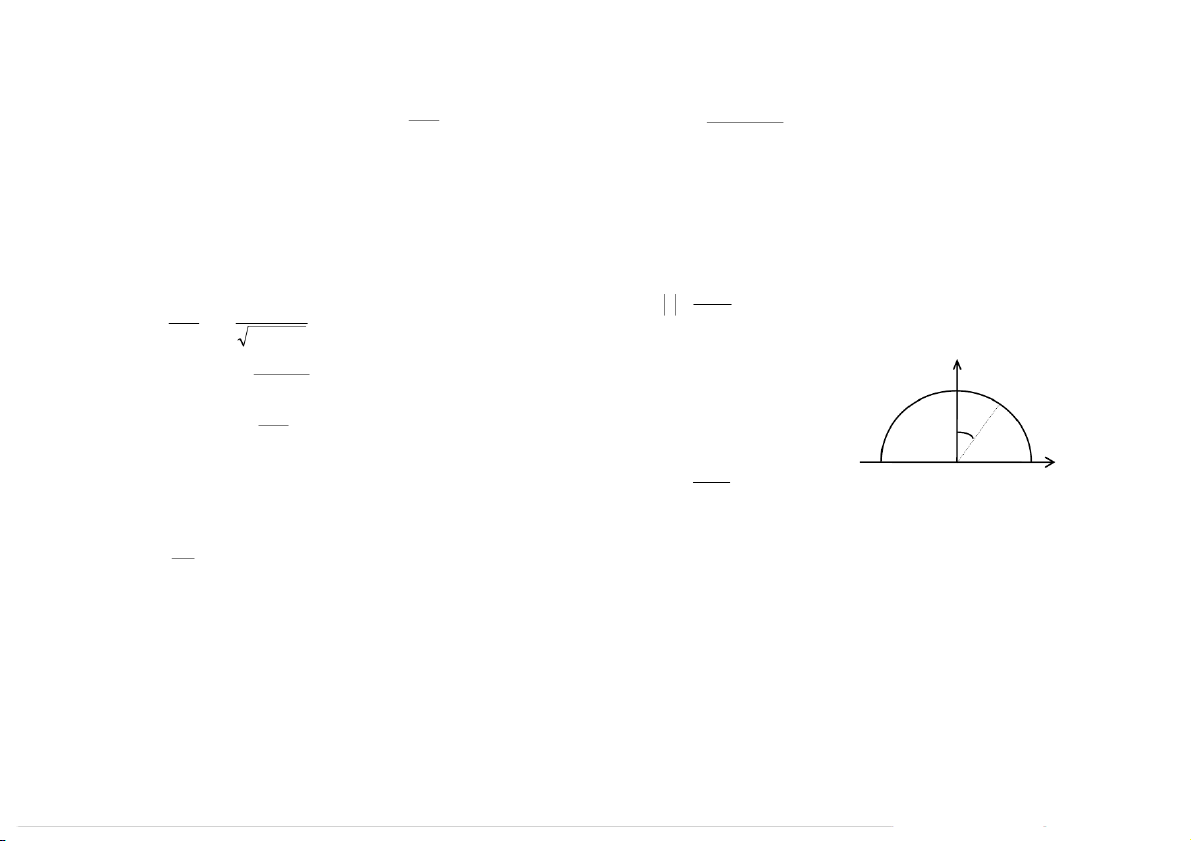
3.1-10. Cho nöûa ñöôøng troøn (O, a) y Khi x >> R : E V / m 4 ε π x 2
mang ñieän tích phaân boá vôùi maät ñoä o λ = λ cos σ ñieän daøi θ (λ o o laø haèng θ Khi x << R : = ( ) E V / m 2ε
soá) ñöôïc ñaët trong khoâng khí nhö o
hình veõ. Tính ñieän theá taïi taâm O. λ ϕ = o x’ O x
3.1-7. Cho moät daây daøi voâ haïn, mang ñieän tích phaân boá ñeàu Ñaùp soá: 2πε
vôùi maät ñoä λ. Tính thoâng löôïng ñieän tröôøng qua maët truï kín baùn o
kính R, chieàu cao h, coù truïc truøng vôùi daây. λh
3.1-11. Moät voøng daây troøn baùn kính R ñöôïc ñaët trong khoâng Ñaùp soá : Φ = ε
khí, mang ñieän tích 3Q phaân boá ñeàu treân ba phaàn tö voøng daây o vaø =
-Q treân moät phaàn tö voøng daây coøn laïi. Tính ñieän theá taïi:
3.1-8. Moät khoái truï roãng raát daøi, baùn kính trong r c 5 , 2 m vaø 1 a. Taâm voøng daây. baùn kính ngoaøi r = cm 5 , 3
, mang ñieän tích phaân boá ñeàu vôùi 2
b. Moät ñieåm treân truïc cuûa voøng daây caùch taâm moät khoaûng
maät ñoä ñieän tích khoái ρ, ñöôïc ñaët trong khoâng khí. Moät sôïi daây h.
maõnh raát daøi, mang ñieän tích phaân boá ñeàu vôùi maät ñoä ñieän daøi 30 31 2kQ 2kQ Ñaùp soá: a. ϕ = , b. ϕ =
3.1-16. Hai maët truï daøi voâ haïn, ñoàng truïc, ñöôïc ñaët trong 2 2 R R h +
khoâng khí, tích ñieän ñeàu vôùi maät ñoä ñieän maët σ, maët trong
mang ñieän döông coù baùn kính R1, maët ngoaøi mang ñieän aâm coù
3.1-12. Moät vaønh taâm O baùn kính trong a, baùn kính ngoaøi b,
baùn kính R2. Tính hieäu theá giöõa hai maët truï. σ
ñöôïc ñaët trong khoâng khí, mang ñieän tích phaân boá ñeàu vôùi maät R R Ñaùp soá: ϕ − ϕ = 1 2 n l
ñoä ñieän maët σ. Tính ñieän theá taïi moät ñieåm treân truïc vaønh troøn 1 2 ε R 0 1
vaø caùch taâm O moät khoaûng x. σ ( ) Ñaùp soá: ϕ = 2 + 2 − 2 + 2 b x a x 2
3.1-17. Cho hai maët caàu ñoàng taâm ñöôïc ñaët trong khoâng khí, ε o
tích ñieän ñeàu, ñieän tích maët trong laø q vaø maët ngoaøi laø Q. Tính
hieäu theá giöõa hai maët caàu. Bieát caùc baùn kính maët caàu laø R1 vaø
3.1-13. Nöûa maët caàu taâm O baùn kính R ñöôïc ñaët trong khoâng R2 (R1 < R2)
khí, mang ñieän tích phaân boá ñeàu vôùi maät ñoä ñieän maët σ. Tính q  1 1  ϕ − ϕ = ñieän theá taïi taâm O. Ñaùp soá: 1 2  − πε  σ 4 R R R 0  1 2  Ñaùp soá: ϕ = ε 2 o
3.1-18. a. Ñieän theá cuûa moät quaû caàu caùch ñieän baùn kính R, tích
ñieän ñeàu vôùi ñieän tích toång coäng Q, ñöôïc cho bôûi:
3.1-14. Moät maët caàu (O, R) ñöôïc ñaët trong khoâng khí, mang Q k  2 r 
ñieän tích q phaân boá ñeàu. Tính ñieän theá taïi moät ñieåm caùch taâm ϕ =  3− khi r < R 2   R 2 R
O moät khoaûng r trong hai tröôøng hôïp r > R vaø r < R, choïn goác  
ñieän theá ôû voâ cöïc. Q k ϕ = khi r > R kq kq r Ñaùp soá: ϕ = (r > ) R , ϕ = (r R < ) r R
Tìm ñieän tröôøng taïi moät ñieåm ôû trong (r < R) vaø ôû ngoaøi (r > R) quaû caàu.
3.1-15. Moät daây daøi voâ haïn ñöôïc ñaët trong khoâng khí, mang
b. Ñieän theá cuûa moät phaân boá ñieän tích ñöôïc xaùc ñònh bôûi:
ñieän tích phaân boá ñeàu vôùi maät ñoä ñieän daøi ( ) λ. Tính ñieän theá taïi kQ ϕ x y , z, =
moät ñieåm caùch daây moät khoaûng r. Choïn goác ñieän theá taïi ñieåm ( − ) x a2 +y2 z + 2
caùch daây moät khoaûng d. r λ d
Tìm caùc thaønh phaàn Ex, Ey, vaø Ez cuûa vectô E gaây bôûi phaân Ñaùp soá: ϕ = πε ln boá ñieän tích ñoù. 2 r 0 Q k r E= Q k E= Ñaùp soá: a. (r < R) ; ( r > R) 3 R 2 r 32 33 ∂ ϕ ( − ) r kQ x a b. E = − = Ehöôùng doïc theo thanh x ∂ x ([ − )2 + 2 + 2 ] x a y z 3 /2 ∂ϕ
3.1-21. Moät vaønh troøn taâm O, baùn kính R, ñöôïc ñaët trong khoâng kQ y E = − =
khí, mang ñieän tích q phaân boá ñeàu. y ∂ y [( − )2 + 2 +2 ] x a y z 3 /2 r
a. Tính ñieän theá ϕ roài suy ra ñieän tröôøng Etaïi moät ñieåm ∂ϕ kQ z
treân truïc vaønh troøn caùch taâm O moät khoaûng x. E = − = z ∂ [ z ( − ) b. 2 ] x a + y
Xeùt tröôøng hôïp x >> R 2 z +2 3 /2 q ϕ = qx = Ñaùp soá: a. k ; E k ( ) ; 2 + 2 x R 3 2 2 + 2 x R
3.1-19. Ñieän theá cuûa moät phaân boá ñieän tích trong moät mieàn r
khoâng gian ñöôïc cho bôûi ϕ (x) = 3x - 2x2 - x3 vôùi ϕ tính baèng V
E naèm treân truïc vaønh troøn
vaø caùc toïa ñoä x, y, z tính baèng m. q q b. ϕ = k ; E = k ;
a. Tìm caùc ñieåm coù ñieän theá baèng khoâng treân truïc Ox. x 2 x r
b. Tìm bieåu thöùc cuûa vectô cöôøng ñoä ñieän tröôøng.
E naèm treân truïc vaønh troøn
c. Tìm caùc ñieåm coù ñieän tröôøng baèng khoâng treân truïc Ox.
Ñaùp soá: a. ϕ (x) = 0 taïi x = 0, 1m, -3m
3.1-22. Moät daây daãn maõnh coù daïng nöûa ñöôøng troøn taâm O, baùn r ( ) b. = 2 E x 3 + x 4 − 3 er
kính R, ñöôïc ñaët trong khoâng khí, tích ñieän ñeàu vôùi maät ñoä ñieän x r c. E 0
= taïi x = 0,535m vaø x = -1,87m
daøi λ. Tính theá naêng cuûa ñieän tích ñieåm q ñaët taïi moät ñieåm treân
ñöôøng thaúng qua taâm O, vuoâng goùc vôùi dieän tích cuûa nöûa ñöôøng
troøn vaø caùch taâm O moät khoaûng a.
3.1-20. Cho moät thanh daøi 2a ñöôïc ñaët trong khoâng khí, tích qRλ
ñieän ñeàu vôùi maät ñoä ñieän daøi λ Ñaùp soá: W = a. ε +
Tính ñieän theá roài suy ra ñieän tröôøng taïi moät ñieåm M 2 2 4 R a 0
naèm treân ñöôøng keùo daøi cuûa thanh vaø caùch trung ñieåm thanh moät khoaûng r.
3.1-23. Moät quaû caàu ñaëc taâm O, baùn kính R, ñöôïc ñaët trong
b. Xeùt tröôøng hôïp r >> a.
khoâng khí, mang ñieän tích Q. Tính theá naêng cuûa ñieän tích ñieåm r a + a 2 λ Ñaùp soá: a. ϕ= kλ ln ; E k = ;
q ñaët caùch taâm O cuûa quaû caàu moät khoaûng r > R. r a − 2− 2 r a qQ r Ñaùp soá: W =k E höôùng doïc theo thanh r a 2 λ a 2 λ b. ϕ=k ; E k = ; r 2 r 34 35 CHÖÔNG HAI
* Quaû caàu ñöôïc noái vôùi voû caàu = < VAÄT DAÃN E 0 khi r R , 1 ϕ Ñaùp soá: a. R = 1 o E khi R < r< R v , a khi r > R 2 1 2 2
3.2-1. Moät quaû caàu kim loaïi, baùn kính R r 1, mang ñieän tích Q1.
Ñaët quaû caàu naøy vaøo trong moät voû caàu kim loaïi ñoàng taâm, baùn R ϕ = ϕ ϕ = 1 , ϕ ; kính R qc o vc o
2 > R1, mang ñieän tích Q2. R 2
a. Tính ñieän tröôøng taïi moät ñieåm caùch taâm quaû caàu moät b. R
khoaûng r. Xeùt 3 tröôøng hôïp: r < R ϕ = ϕ = 1 ϕ 1, R1 < r < R2, vaø qc vc o R r > R 2 2 .
b. Tính ñieän theá cuûa quaû caàu vaø voû caàu khi:
* Quaû caàu khoâng ñöôïc noái vôùi voû caàu
3.2-3. Moät voû caàu kim loaïi, baùn kính R 1, mang ñieän tích Q1. Ñaët
* Quaû caàu ñöôïc noái vôùi voû caàu
moät quaû caàu kim loaïi baùn kính R2 < R1 trung hoaø vaøo trong voû kQ = < =
caàu sao cho chuùng ñoàng taâm vôùi nhau. Noái quaû caàu vôùi ñaát. 1 E 0 khi r R , E khi R < r < R , 1 1 2 2
Tính ñieän theá cuûa quaû caàu vaø voû caàu. Ñaùp soá: a. r kQ(R − R ) k Q ( + Q ) ϕ = ϕ = = 1 1 2 , 0 1 2 E khi r > R Ñaùp soá: qc vc 2 2 2 R r 1  Q Q  k Q ( + Q ) 1 2 ϕ = 1 2 ϕ = k + ,
3.2-4. Moät quaû caàu kim loaïi, baùn kính R qc   vc R R R 1, mang ñieän tích Q1. b.  1 2  2
Ñaët moät quaû caàu naøy vaøo trong moät voû caàu kim loaïi, trung hoaø, k Q ( + Q ) ϕ = ϕ = ñoàng taâm, baùn kính R 1 2
2 > R1 . Noái voû caàu vôùi ñaát. Tính ñieän theá qc vc R
cuûa quaû caàu vaø voû caàu. 2 kQ( R − R ) Ñaùp soá: ϕ = ϕ = 1 2 1 , 0 vc qc
3.2-2. Moät quaû caàu kim loaïi, baùn kính R RR
1, ñöôïc tích ñieän ñeán 1 2
ñieän theá ϕ o. Ñaët quaû caàu naøy vaøo trong moät voû caàu kim loaïi,
trung hoaø, ñoàng taâm, baùn kính R = 2 > R1 .
3.2-5. Hai vaät daãn ñieän hình caàu, baùn kính R m 3 , 0 vaø 1
a. Tính ñieän tröôøng taïi moät ñieåm caùch taâm quaû caàu moät R = 1 , 0 m
5 , ñöôïc ñaët raát xa nhau ñeå khoâng coù hieän töôïng ñieän
khoaûng r. Xeùt 3 tröôøng hôïp: r < R 2 1, R1 < r < R2, vaø
höôûng vaø ñöôïc noái vôùi nhau baèng daây daãn. Truyeàn cho hai quaû r > R2. caàu ñieän tích Q= 1 .
6 0−9C . Tính ñieän tích vaø ñieän theá moãi quaû
b. Tính ñieän theá cuûa quaû caàu vaø voû caàu khi:
* Quaû caàu khoâng ñöôïc noái vôùi voû caàu caàu. 36 37 R Q R Q ′ R(Q + Q ) ′ R (Q +Q ) Ñaùp soá: Q = 1 = n 4 C, = 2 = n 2 C, Q = 1 1 2 Q , = 2 1 2 , Q 1 R + R 2 R + R 1 R + R 2 R + R 1 2 1 2 1 2 1 2 kQ − ϕ = =12 V 0 Q R Q R ∆ = + 1 2 2 1 Q R R R + R 1 2 1 2
3.2-6. Hai vaät daãn ñieän hình caàu taâm O, baùn kính a vaø b, ñöôïc
3.2-8. Hai quaû caàu kim loaïi A vaø B, baùn kính a= m 1 , 0 vaø
ñaët raát xa nhau ñeå khoâng coù hieän töôïng ñieän höôûng vaø ñöôïc noái b= m 2 , 0
, coù ñieän theá laàn löôït laø ϕ = 4 0 . 5 0 V 0 vaø
vôùi nhau baèng daây daãn. Sau khi tích ñieän cho hai quaû caàu, ñieän A ϕ = − 4 0. 5 0 V 0
tích cuûa quaû caàu (O, a) nhoû hôn ñieän tích cuûa quaû caàu (O, b) n
, ñöôïc ñaët raát xa nhau ñeå khoâng coù hieän töôïng B laàn. ñieän höôûng.
a. Tính tyû soá baùn kính hai quaû caàu.
a. Tính ñieän tích moãi quaû caàu.
b. Ñieän tröôøng taïi moät ñieåm treân quaû caàu (O, a) lôùn hôn
b. Noái hai quaû caàu baèng moät daây daãn. Tính ñieän theá môùi
hay nhoû hôn bao nhieâu laàn so vôùi ñieän tröôøng taïi moät
cuûa hai quaû caàu vaø löôïng ñieän tích dòch chuyeån.
ñieåm treân quaû caàu (O, b).
Ñaùp soá: a. QA = 0,5µC, QB = - 1µC b E
b. ϕ = - 15.000 V, ∆Q = 0,68µC Ñaùp soá: a. = n b. ( a, O ) = n a E ( ,Ob)
3.2-9. Tính naêng löôïng ñieän tröôøng cuûa moät quaû caàu baùn kính
R, mang ñieän tích Q phaân boá ñeàu trong theå tích quaû caàu.
3.2-7. Hai quaû caàu kim loaïi, baùn kính R1 vaø R2, mang ñieän tích Q 3 2 Q Ñaùp soá: W = k
1 vaø Q2, ñöôïc ñaët raát xa nhau ñeå khoâng coù hieän töôïng ñieän e R 5 höôûng.
a. Tính ñieän theá moãi quaû caàu. b.
3.2-10. Moät quaû caàu kim loaïi coâ laäp, baùn kính r = 20cm, coù ñieän
Noái hai quaû caàu baèng moät daây daãn. Tính ñieän theá môùi
theá 3.000V. Tính ñieän tích treân quaû caàu vaø toång naêng löôïng ñieän
cuûa hai quaû caàu, ñieän tích treân moãi quaû caàu vaø löôïng
tröôøng gaây bôûi quaû caàu. ñieän tích dòch chuyeån. kQ kQ
Ñaùp soá: Q = 6,67.10 – 8 C, We = 10 – 4 J Ñaùp soá: ϕ = ϕ = 1 2 a. , 1 2 R R 1 2
3.2-11. Cöôøng ñoä ñieän tröôøng trong moät mieàn khoâng gian phuï k(Q +Q ) b. ϕ = 1 2 , E = R+ R
thuoäc vaøo toïa ñoä x bôûi heä thöùc E o x trong ñoù 1 2 xo E = 2 k 4 V / m vaø x = m
6 . Tính toång naêng löôïng ñieän o o 38 39
tröôøng döï tröõ trong theå tích hình laäp phöông coù caïnh a= m 1 , CHÖÔNG BA
bieát raèng hai maët hình laäp phöông song song vôùi maët phaúng yOz TÖØ TRÖÔØNG CUÛA
coù toïa ñoä laàn löôït laø x = 0 vaø x = m 1 ε E 2a5
DOØNG ÑIEÄN KHOÂNG ÑOÅI Ñaùp soá: W o o = = 6 , 23 µJ e 6x 2 o
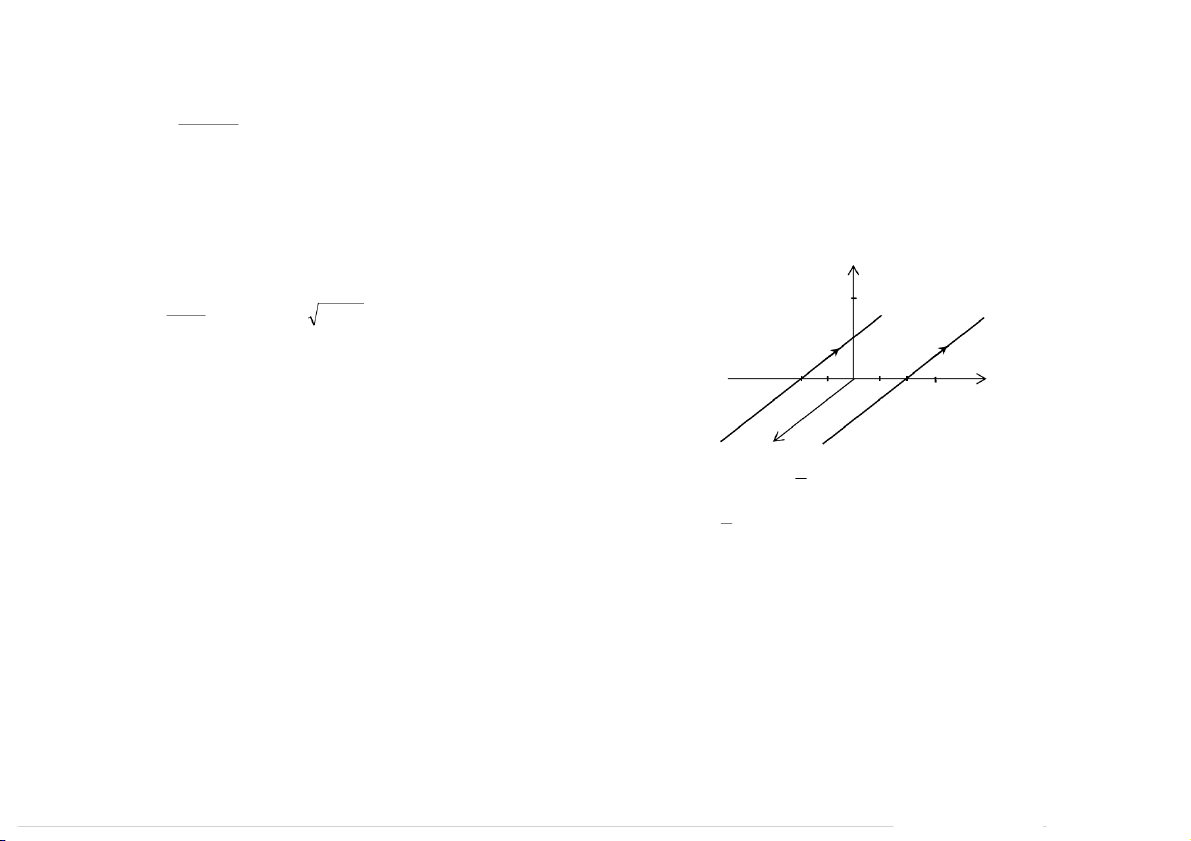
3.3-1. Hai doøng ñieän thaúng daøi voâ haïn cuøng chieàu, coù
cöôøng ñoä doøng ñieän baèng nhau I = 15A, ñöôïc ñaët song
3.2-12. Moät tuï ñieän phaúng coù khoaûng caùch giöõa hai baûn tuï ñieän
song nhau trong khoâng khí nhö hình veõ. Xaùc ñònh vectô laø d= m
1 m. Ñieän tröôøng giöõa hai baûn tuï ñieän coù cöôøng ñoä r
caûm öùng töø B gaây bôûi hai doøng ñieän taïi caùc ñieåm O, M, N, E = k
3 V / m. Naêng löôïng ñieän tröôøng döï tröõ trong tuï ñieän o
P, Q coù toïa ñoä laàn löôït laø: yo = 0, y1 = -3cm, y2 = 3cm, y3 = laø W = 1 .
4 0−11J. Tính ñieän dung cuûa tuï ñieän vaø ñieän tích treân e 9cm, z= c 8 m. z moãi baûn tuï ñieän. W 2 Q 8cm Ñaùp soá: C e = = pF 9 , 8 , Q= C 2 W = 2 6 , 6 p 7 C E d 2 2 e I I - 6cm N P M O 6cm y x r r 2 Ñaùp soá: B = 0 , −4 B = − ( 10 T) er , o M z r 2 r −4 r − r B =( 10 T) e , 5 B = − 1 ( 21 . 0 T) e , N z 3 P z r 5 B 1 . 8 , 4 ( 0− = T) er Q y
3.3-2. Hai doøng ñieän thaúng daøi voâ haïn ngöôïc chieàu, coù
cöôøng ñoä doøng ñieän baèng nhau I = 15A, ñöôïc ñaët song
song nhau trong khoâng khí nhö hình veõ. 40 41 r z
Ñaùp soá: B vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo µ π Q I 8cm vaø B o   − =  + 2 =  9 , 5 6 1 . 8 0 5T 4πR 2  I I - 6cm N P
3.3-4. Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng M O I = 30 6cm y ñoä
A , ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
khoâng khí. Ñoaïn BC laø moät phaàn tö cung troøn taâm O, baùn
kính R = 15cm. Cho bieát OA = OB = R. Caùc ñoaïn Ax vaø x
Cy laø hai nöûa doøng ñieän thaúng raát daøi coù ñöôøng keùo daøi r
Xaùc ñònh vectô caûm öùng töø r
B gaây bôûi hai doøng ñieän taïi
qua O. Tính caûm öùng töø B taïi ñieåm O.
caùc ñieåm O, M, N, P, Q coù toïa ñoä laàn löôït laø: y = 0, o y = − c 3 m, y = c 3 m, y = c 9 my z= 8 . B 1 2 3 3 = 9cm, cm r r r 4 Ñaùp soá: 4 B − r = 1 ( 0− − T) er , 4 B = B = − ( 10 T) e , o z M N z I 3 r r R 5 − r − r B = 1 . 8 ( 0 T) e , 5 B = − 1 . 6 , 3 ( 0 T) e x y P z Q z A O C
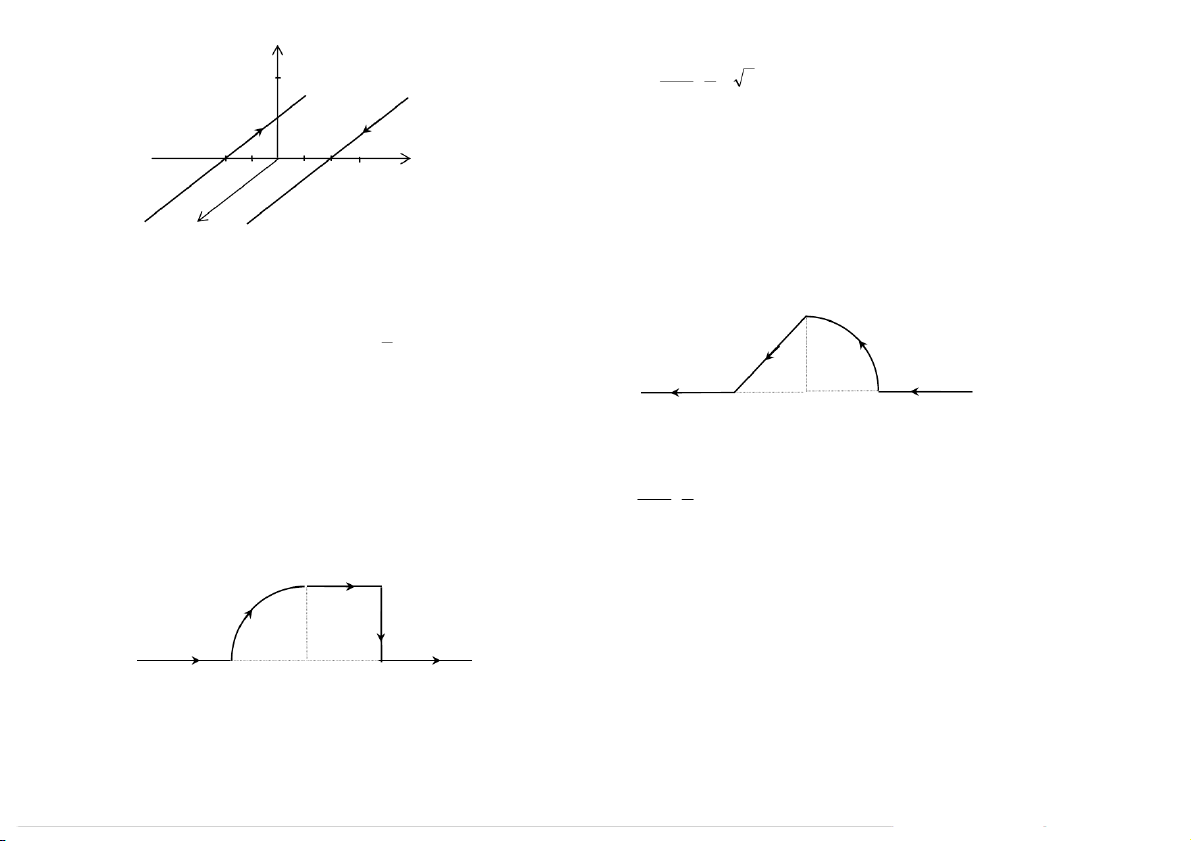
3.3-3. Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng ñoä I =1 A
0 , ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong r
khoâng khí. Ñoaïn AB laø moät phaàn tö cung troøn taâm O, baùn
Ñaùp soá: B vuoâng goùc maët phaúng doøng ñieän, höôùng ra vaø µ π oI
kính R = 5cm. Ñoaïn BC = CD = R. Caùc ñoaïn Ax vaø Dy laø B  = + 1  1 , 7 1 . 4 0− =  T 5 π
hai nöûa doøng ñieän thaúng raát daøi coù ñöôøng keùo daøi qua 2 R  4  r
taâm O. Tính caûm öùng töø B taïi ñieåm O.
3.3-5. Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng B C ñoä I = 2 A
0 , ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong I
khoâng khí. Ñoaïn CD laø moät cung troøn taâm O, baùn kính o R R = 1 c
0 m vaø chaén goùc ôû taâm laø α = 120 . Xaùc ñònh vectô x y r
caûm öùng töø B taïi ñieåm O. A O D 42 43 y D
3.3-7. Hai ñieåm AB cuûa moät voøng daây daãn kín hình troøn
ñöôïc noái vôùi hai cöïc cuûa nguoàn ñieän khoâng ñoåi. Phöông R I
daây noái qua taâm O voøng daây. Chieàu daøi caùc daây noái voâ α
cuøng lôùn vaø taát caû ñöôïc ñaët trong khoâng khí. Chöùng minh O
raèng neáu caùc voøng daây daãn AMB vaø ANB ñoàng chaát vaø
coù tieát dieän ñeàu thì caûm öùng töø B taïi taâm voøng daây baèng x C khoâng. r M
Ñaùp soá: B vuoâng goùc maët phaúng doøng ñieän, höôùng ra vaø µ π oI  2 B = + 3+ 3   1 6 , 3 1 . 5 0− = 5T 4 R π  3  A B
3.3-6. Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng N ñoä I = 2 A
5 , ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong I I
khoâng khí. Ñoaïn CD laø moät phaàn tö cung troøn taâm O, baùn
kính R = 20cm, goùc β = 30o. Xaùc ñònh vectô caûm öùng töø _ + r B taïi ñieåm O. x C
3.3-8. Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng I ñoä I = A
8 , ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong R I O β D O y R r α
Ñaùp soá: B vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo µ I C y I π D vaø B   o =  + 3+ 3 =  8 , 7 71 . 0 5 − T 4 R π 2 x   44 45
khoâng khí. Ñoaïn CD laø moät cung troøn taâm O, baùn kính
baùn kính R vaø ñöôïc ñaët trong khoâng khí. Xaùc ñònh vectô r r R= c
5 m. Bieát goùc laø α = 120o. Xaùc ñònh vectô caûm öùng
caûm öùng töø B taïi taâm hình ña giaùc. Tính B khi n → ∞. r r töø B taïi ñieåm O.
Ñaùp soá: B vuoâng goùc vôùi ña giaùc, coù chieàu thuaän chieàu r µ Ñaùp soá: π
B vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo = n o I µ π
doøng ñieän theo qui taéc tay phaûi vaø B tg π oI  4 2 R n vaø B  − =  + 3− 2 =  2 , 6 71 . 0 5 T 4 R π µ  3  I Khi n → ∞ thì B = o R 2
3.3-9. Moät daây daãn thaúng daøi voâ haïn coù doøng ñieän cöôøng ñoä I =1 A
6 , ñöôïc uoán cong nhö hình veõ vaø ñöôïc ñaët trong
3.3-11. Moät doøng ñieän, cöôøng ñoä I chaïy trong moät daây
khoâng khí. Ñoaïn CD laø moät cung troøn taâm O, baùn kính
daãn ñöôïc uoán thaønh moät luïc giaùc ñeàu caïnh a R vaø ñöôïc ñaët r R= c
6 m. Bieát goùc laø α = 120o. Xaùc ñònh vectô caûm öùng
trong khoâng khí. Tính caûm öùng töø B taïi taâm luïc giaùc ñeàu. r r töø B taïi ñieåm O.
Ñaùp soá : B vuoâng goùc vôùi luïc giaùc ñeàu, coù chieàu thuaän I µ = 3 o I
chieàu doøng ñieän theo qui taéc tay phaûi vaø B π y a C D α R
3.3-12. Moät doøng ñieän, cöôøng ñoä I chaïy trong moät daây O
daãn ñöôïc uoán cong nhö hình veõ: (C) laø ñöôøng troøn taâm O, I r
baùn kính R. Tính r ñeå caûm öùng töø B taïi ñieåm O baèng khoâng. x I r
Ñaùp soá: B vuoâng goùc maët phaúng doøng ñieän, höôùng vaøo µ π oI vaø B  = + 1   1 . 1 , 1 0− = 4 T I r 2 R π I  3  R O (C)
3.3-10. Moät daây daãn coù doøng ñieän, cöôøng ñoä I, ñöôïc uoán
thaønh moät ña giaùc ñeàu n caïnh noäi tieáp trong voøng troøn 46 47
3.3-13. Hai daây daãn daøi voâ haïn coù caùc doøng ñieän cuøng
tích S phaúng hình chöõ nhaät coù hai caïnh a = 10cm, r
chieàu vôùi cöôøng ñoä I vaø I chaïy qua. Moãi daây ñeàu coù moät b= 1 c
5 m coù vectô phaùp tuyeán rn hôïp vôùi phöông B moät 1 2
ñoaïn uoán theo moät cung troøn 90o
goùc α = 45o . Tính töø thoâng qua ñieän tích S.
treân cuøng ñöôøng troøn taâm O, baùn Ñaùp soá: Φ = B (s 1 in 00 π t)a c. b osα = 531 . 0−6 (s 1 in 00 t π ) Wb O o
kính a nhö hình veõ. Tính I a 2 r
theo I ñeå caûm öùng töø B gaây bôûi
3.3-16. Cho moät töø tröôøng coù vectô caûm öùng töø ñöôïc xaùc 1
caû hai doøng ñieän taïi O baèng r B I r o 2 1 I2 ñònh bôûi B =
x e vôùi B vaø x laø caùc haèng soá khoâng. 2 z x o o o Ñaùp soá: I = 2 , 2 7I
döông, er laø vectô ñôn vò treân 2 1 z
truïc z. Tính töø thoâng qua dieän y
3.3-14. Moät dieän tích S hình troøn taâm O, baùn kính tích hình vuoâng caïnh x 2 naèm r o x 2 R= 2 c
0 m ñöôïc ñaët trong moät töø tröôøng B coù ñöôøng
trong maët phaúng xOy coù moät o r
caûm öùng töø B hôïp vôùi dieän tích S moät goùc α =30o vaø coù
ñænh truøng vôùi goác toïa ñoä O vaø ñoä lôùn − 31 t 4 B= B e vôùi B
hai caïnh truøng vôùi hai truïc Ox o
o = 0,25(T). Tính töø thoâng qua dieän tích S. vaø Oy nhö hình veõ. er y r B 16 Ñaùp soá: 2 Φ = B x er O er x 2 o o x 3 z x o α O
3.3-17. Cho moät töø tröôøng coù y R
vectô caûm öùng töø ñöôïc xaùc ñònh r r 2 − = − l 31 t 4 −3 3 − 1 t 4 ( ) Ñaùp soá: Φ =π R B e sinα = 15 1 . 7 , 0 e Wb bôûi 2 B At ye vôùi A laø haèng o z
soá döông, B tính baèng Tesla, t
baèng giaây vaø y baèng meùt, er laø
3.3-15. Cho moät töø tröôøng z r nr er
B coù ñöôøng caûm öùng töø
vectô ñôn vò treân truïc z. y
naèm ngang, coù ñoä lôùn:
a. Ñôn vò cuûa A laø gì? ( ) α er r z O er l x B= B s 1 in 00 t T vôùi B
b. Tính töø thoâng qua dieän x o π B = 1 . 5 0− 3T . Moät dieän b o a 48 49
tích hình vuoâng caïnh l naèm trong maët phaúng xOy
3.3-19. Cho khung daây hình chöõ nhaät ABCD coù caùc caïnh
coù moät ñænh truøng vôùi goác toïa ñoä O vaø hai caïnh
a = 3cm, b = 4cm ñöôïc ñaët caïnh moät doøng ñieän thaúng daøi
truøng vôùi hai truïc Ox vaø Oy nhö hình veõ.
voâ haïn coù cöôøng ñoä I = 30A. Khung daây vaø doøng ñieän 1 Ñaùp soá: 2 3 Φ = − At
cuøng naèm trong moät maët phaúng. Caïnh AB song song vôùi l 2
doøng ñieän vaø caùch doøng ñieän moät ñoaïn c = 1,5cm. Tính töø
thoâng qua dieän tích phaúng giôùi haïn bôûi khung daây.
3.3-18. Cho moät doøng ñieän thaúng daøi voâ haïn coù doøng ñieän
cöôøng ñoä I = 18A chaïy qua.
a. Tính töø thoâng Φ qua dieän tích ñaùy S a 1, dieän tích A D
xung quanh S2, vaø dieän tích toaøn phaàn S cuûa moät I
maët truï coù baùn kính R = 12cm, chieàu cao h = 20cm, c
coù truïc truøng vôùi phöông cuûa doøng ñieän I. b
b. Tính töø thoâng Φ qua dieän tích hình chöõ nhaät S3
(hình veõ). Bieát a = 10cm. B C I a R µ Ib c+a o − = 7 ( ) Ñaùp soá: Φ = n l 6 , 2 1 . 4 0 Wb 2π c h S S 2 3
3.3-20. Saùu daây daãn coù doøng ñieän vôùi cöôøng ñoä I , I , 1 2
I , I , I , I coù chieàu höôùng ra hoaëc höôùng vaøo maët S 3 4 5 6 1
phaúng hình veõ. Tính löu soá cuûa vectô caûm öùng töø doïc I
theo caùc ñöôøng cong kín (C1): ñöôøng lieàn neùt, vaø (C2):
ñöôøng chaám chaám nhö hình veõ. Ñaùp soá: a. S Φ = S Φ = S Φ = 0 1 2 µ I h R+a o − = 7 ( ) b. Φ = n l 3 , 4 1 . 2 0 Wb S π 3 2 R 50 51
3.3-22. Cho khung daây hình chöõ nhaät coù caïnh a vaø b ñöôïc
ñaët gaàn moät doøng ñieän thaúng daøi voâ haïn coù cöôøng ñoä I1. × ×
Khung daây vaø doøng ñieän cuøng naèm trong cuøng maët phaúng. I1 I5 I4
Caïnh AB song song vôùi I1 vaø caùch I1 moät ñoaïn d. I6 I
Xaùc ñònh phöông chieàu vaø ñoä lôùn cuûa löïc taùc duïng leân 2
khung daây neáu trong khung daây coù doøng ñieän I × 2 chaïy qua. r r = µ ( + − )
Ñaùp soá : F naèm trong maët phaúng khung daây, vuoâng goùc I Ñaùp soá: d . B I I I ∫ 1, l I o 4 6 5 3 höôùng xa doøng I1 C1r µ = µ ( − − ) I I a  1 1  d . B I I I ∫ = o 1 − l Ñaùp soá : F 2 o 2 3 4 π  + d b 2  d  C 2
3.3-21. Cho moät oáng daây (solenoid) daøi a = 30cm, ñöôøng
3.3-23. Moät electron, sau khi ñöôïc gia toác baèng moät hieäu kính d= 1 m
0 m, goàm n = 500 voøng daây daãn ñöôïc quaán saùt
ñieän theá U, chuyeån ñoäng song song vôùi moät daây daãn thaúng
nhau, coù doøng ñieän I = 5A chaïy qua. Tính töø thoâng gôûi
daøi vaø caùch daây daãn moät khoaûng r. Tìm löïc taùc duïng leân
qua moät voøng daây phaúng hình troøn ñöôøng kính D= c 4 m
electron neáu coù doøng ñieän vôùi cöôøng ñoä I chaïy qua daây
ñaët vuoâng goùc vôùi truïc, coù taâm truøng vôùi taâm oáng daây. daãn . µ nI d π 2 µ I e 2 e U Ñaùp soá: 0 Φ = Ñaùp soá : F o = a 4 2 r π m
3.3-22. Cho moät oáng daây (solenoid) daøi a, ñöôøng kính
3.3-23. Moät electron chuyeån ñoäng vôùi vaän toác D= 3 m
2 m, coù n =100voøng/cm ñöôïc quaán saùt nhau, coù = r 7 o v 1 . 1 , 2 0 s /
m trong moät töø tröôøng ñeàu B . doøng ñieän I= 5 ,
2 A chaïy qua. Tính töø thoâng gôûi qua ñieän
a. Caûm öùng töø B coù giaù trò nhoû nhaát baèng bao nhieâu
tích phaúng hình troøn ñöôøng kính d= 1 m 6 m ñaët vuoâng goùc
neáu löïc töø taùc duïng leân electron laø F= 1 . 4 , 5 0 1 − 5 N .
vôùi truïc, coù taâm truøng vôùi taâm oáng daây.
b. Caûm öùng töø B coù giaù trò baèng bao nhieâu neáu vaän µ n I d π 2 Ñaùp soá: 0 o Φ = A b D
toác vr cuûa electron hôïp vôùi töø tröôøng moät goùc 4 o α = 45 . I1 − I Ñaùp soá : a. 3 2 B = 10 . 61 , 1 T min d a 52 53 B C b. B= 10 . 27 , 2 −3 T
khoaûng r. Haõy tính hieäu ñieän theá xuaát hieän giöõa 2 ñaàu
thanh khi thanh kim loaïi di chuyeån vôùi vaän toác khoâng ñoåi
3.3-24. Moät electron coù naêng löôïng W bay vaøo moät ñieän
vr theo phöông song song vôùi daây daãn. Ñieän theá ôû A hay ôû
tröôøng ñeàu coù cöôøng ñoä ñieän tröôøng E theo phöông vuoâng B cao hôn?
goùc vôùi ñöôøng söùc ñieän tröôøng. Hoûi phaûi ñaët moät töø tröôøng µ I v Ñaùp soá: =  l  U 0 l 
n 1+  , Ñieän theá ôû A cao hôn.
coù phöông chieàu vaø caûm öùng töø nhö theá naøo ñeå chuyeån AB π r 2  
ñoäng cuûa electron khoâng bò leäch phöông. m
3.3-27. Moät thanh kim loaïi CD daøi Ñaùp soá: B E = D W 2 L= c 80 m quay quanh moät truïc
vuoâng goùc vôùi thanh vaø ñi qua ñaàu C
vôùi vaän toác 5voøng/s trong moät töø
3.3-25. Moät thanh kim loaïi AB, coù C chieàu daøi tröôøng ñeàu B = 3 , 0 T coù ñöôøng caûm
l , ñöôïc ñaët song song vôùi A r
moät daây daãn thaúng raát daøi coù doøng
öùng töø song song vôùi truïc quay nhö ⊗ B
ñieän I chaïy qua vaø caùch daây daãn moät vr
hình veõ. Tính hieäu ñieän theá giöõa hai I
khoaûng r. Haõy tính suaát ñieän ñoäng l
ñaàu thanh. Ñieän theá ôû C hay ôû D cao hôn? = −
caûm öùng xuaát hieän trong thanh khi Ñaùp soá: U V
3 . Ñieän theá ôû D cao hôn. B CD
thanh kim loaïi di chuyeån vôùi vaän toác
khoâng ñoåi vr theo phöông vuoâng goùc r
3.3-28. Moät daây daãn thaúng vôùi daây daãn. coù ñieän trôû C R öùng vôùi moät µ 0 I lv Ñaùp soá: ξ 0
ñôn vò chieàu daøi. Daây ñöôïc C = 2 r π
gaáp thaønh 2 caïnh cuûa moät α ⊗ vr
goùc 2α. Moät thanh chaén CD O r B
3.3-26. Moät thanh kim loaïi
cuõng laøm baèng daây daãn aáy,
AB, coù chieàu daøi l , ñöôïc ñaët
ñöôïc ñaët vuoâng goùc vôùi
vuoâng goùc vôùi moät daây daãn
ñöôøng phaân giaùc cuûa goùc D
thaúng raát daøi coù doøng ñieän I vr
2α ñeå taïo vôùi daây daãn treân r
chaïy qua vaø ñaàu A gaàn daây I A B
moät maïch kín. Maïch kín naøy ñaët trong töø tröôøng ñeàu B
daãn nhaát caùch daây daãn moät
vuoâng goùc vôùi dieän tích phaúng cuûa maïch. Khi thanh CD l 54 r 55
chuyeån ñoäng vôùi vaän toác rv khoâng ñoåi theo phöông song A
song vôùi ñöôøng phaân giaùc, haõy xaùc ñònh chieàu vaø cöôøng ñoä
doøng ñieän caûm öùng trong maïch kín. r α R × s . v . B in a B Ñaùp soá: = I , I c R ( +
1 sinα ) c ngöôïc chieàu kim ñoàng hoà 0 B
3.3-29. Moät daây daãn coù ñieän trôû R0 öùng vôùi moät ñôn vò
Hai ñaàu thanh ngang ñöôïc noái vôùi moät ñoaïn maïch goàm
chieàu daøi, ñöôïc uoán thaønh ba phaàn tö voøng troøn baùn kính
moät pin 6V noái tieáp vôùi moät ñieän trôû = Ω R 1 ñeå taïo thaønh
r. Moät thanh chaén MN cuõng baèng daây daãn aáy tröôït treân ba
maïch kín. Caû heä ñöôïc ñaët trong moät töø tröôøng ñeàu
phaàn tö voøng troøn vôùi vaän toác rv. Daây daãn vaø thanh chaén B = 5 ,
0 T coù ñöôøng caûm öùng töø vuoâng goùc vôùi ñieän tích
taïo thaønh moät chu vi kín. Caû heä
cuûa maïch kín nhö hình veõ. Ñeå thanh AB chuyeån ñoäng vôùi
thoáng ñöôïc ñaët trong töø tröôøng M N
vaän toác khoâng ñoåi, ngöôøi ta taùc duïng leân thanh moät löïc r α
ñeàu B vuoâng goùc vôùi maët phaúng F= 25 , 0 N .
cuûa chu vi. Xaùc ñònh chieàu vaø O r
a. Xaùc ñònh phöông chieàu cuûa löïc F vaø cöôøng ñoä
cöôøng ñoä cuûa doøng ñieän caûm öùng vr r doøng ñieän trong maïch.
chaïy trong chu vi theo goùc α. Boû B
b. Tính hieäu ñieän theá giöõa hai ñaàu thanh AB.
qua ñieän trôû caùc choã tieáp xuùc. r α
Ñaùp soá: a. Löïc F vuoâng goùc vôùi thanh AB vaø höôùng veà s . v . B in Ñaùp soá: = I , I phiaù traùi, I = A 2 c R (α + si α
n ) c cuøng chieàu kim ñoàng hoà 0 b. U = 4V AB
3.3-30. Moät thanh kim loaïi AB coù chieàu daøi a ñöôïc ñaët
3.3-31. Moät thanh kim loaïi AB coù chieàu daøi a ñöôïc ñaët
tieáp xuùc vaø vuoâng goùc vôùi hai thanh kim loaïi naèm ngang
tieáp xuùc vaø vuoâng goùc vôùi hai thanh kim loaïi naèm ngang
song song caùch nhau moät khoaûng a= c 25 m.
song song caùch nhau moät khoaûng a= c 50 m. Hai ñaàu
thanh ngang ñöôïc noái vôùi ñieän trôû = Ω R 3 ñeå taïo thaønh
maïch kín. Caû heä ñöôïc ñaët trong moät töø tröôøng ñeàu B= T 15 , 0
coù ñöôøng caûm öùng töø vuoâng goùc vôùi ñieän tích
cuûa maïch kín. Xaùc ñònh löïc caàn thieát taùc duïng leân thanh 56 57
ñeå laøm thanh chuyeån ñoäng vôùi vaän toác khoâng ñoåi y v = m
2 /s theo phöông vuoâng goùc vôùi thanh nhö hình veõ. A L L r B C B × r R a B vr O Ñaùp L x s B r o D A B B a z 2 v 2 á: F = = 10 . 75 , 3 − 3 N ξ = − 0 t < L < R Ñaùp soá: BLv khi v C ξ = 2BLv khi L v t < 2 < L v C
3.3-32. Moät töø tröôøng ñeàu toàn taïi trong moät mieàn khoâng ξ = B − Lv khi 2L v t < < L 3 v
gian coù phöông vuoâng goùc vôùi maët phaúng xOz trong ñoù C
(neáu choïn vectô ñôn vò phaùp tuyeán nr cuûa dieän tích ABCD
bieân traùi vaø bieân phaûi cuûa töø tröôøng ñeàu song song vôùi maët
höôùng theo chieàu döông cuûa truïc Oy)
phaúng yOz vaø ñeàu caùch noù moät khoaûng L. Vectô caûm öùng r
töø B höôùng theo chieàu döông cuûa truïc Oy khi x < 0 vaø
3.3-33. Moät khung daây daãn hình chöõ nhaät caïnh a vaø b, coù
höôùng theo chieàu aâm cuûa truïc Oy khi x > 0 nhö moâ taû ôû
ñieän trôû toång coäng laø R, ñöôïc ñaët trong töø tröôøng ñeàu
hình veõ beân. Moät khung daây daãn hình vuoâng ABCD, caïnh r r
Bbieán thieân theo thôøi gian theo qui luaät B= rB cos t ω vôùi
L, naèm trong maët phaúng xOz, chuyeån ñoäng theo chieàu o r
döông truïc Ox vôùi vaän toác khoâng ñoåi v. Caùc caïnh AB vaø
B khoâng ñoåi vaø hôïp vôùi maët phaúng khung daây moät goùc α. o
CD song song vôùi maët phaúng yOz vaø luùc t = 0 caïnh AB ôû
Xaùc ñònh cöôøng ñoä doøng ñieän caûm öùng trong khung daây.
taïi bieân traùi cuûa töø tröôøng. Xaùc ñònh suaát ñieän ñoäng caûm B abω Ñaùp soá: I o = sinα s . in t ω
öùng trong khung daây khi khung daây chuyeån ñoäng qua mieàn C R coù töø tröôøng treân. a
3.3-34. Moät daây daãn thaúng raát
daøi coù doøng ñieän vôùi cöôøng ñoä I − = t τ I I e chaïy qua, ñöôïc ñaët 0 b 58 d 59
song song vôùi caïnh b cuûa moät khung daây hình chöõ nhaät, coù
2 caïnh a vaø b, ôû trong cuøng maët phaúng vôùi khung daây.
Caïnh khung daây gaàn daây daãn nhaát caùch daây daãn moät
khoaûng d. Xaùc ñònh suaát ñieän ñoäng caûm öùng vaø chieàu doøng
ñieän caûm öùng trong khung daây. µ − I b t a Ñaùp soá: ξ = 0 0 τ   e ln 1+ , C πτ 2  d 
Ic cuøng chieàu kim ñoàng hoà
3.3-35. Moät daây daãn thaúng raát
daøi coù doøng ñieän vôùi cöôøng ñoä I a
khoâng ñoåi chaïy qua, ñöôïc ñaët
song song vôùi caïnh b cuûa moät
khung daây hình chöõ nhaät, coù 2 I
caïnh a vaø b, ôû trong cuøng maët b
phaúng vôùi khung daây. Khung r
daây di chuyeån vôùi vaän toác khoâng
ñoåi vr theo phöông vuoâng goùc R
vôùi doøng ñieän I vaø ra xa doøng
ñieän. Ñieän trôû toång coäng cuûa khung daây laø R. Xaùc ñònh vaø
chieàu vaø cöôøng ñoä doøng ñieän caûm öùng trong khung daây
vaøo thôøi ñieåm maø caïnh khung daây gaàn daây daãn nhaát caùch daây daãn moät khoaûng r. µ I v ab Ñaùp soá: I 0 = , C π ( + ) 2 R r r a
Ic ngöôïc chieàu kim ñoàng hoà. 60